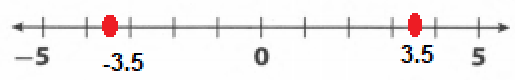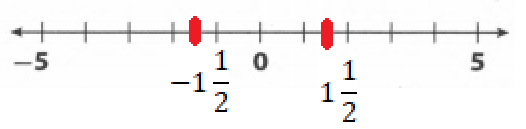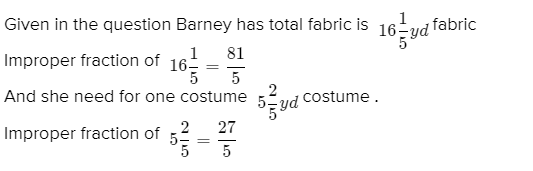Go Math Answer Key - Math Book Answers

Go Math! Grade 6 Chapter 1 Integers Exercise 1.3 Answers

November 18, 2024August 8, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers

Page 5 Problem 1, Answer

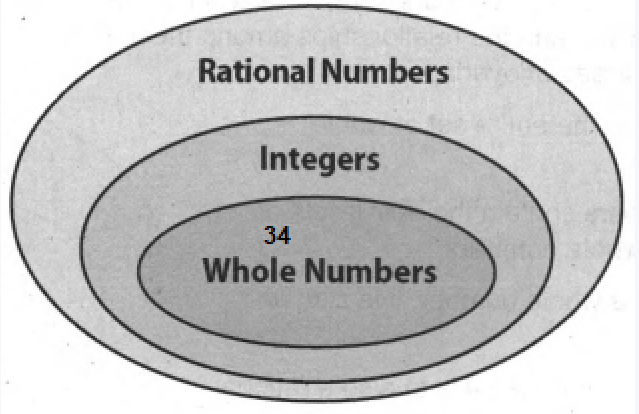
Given the number 6.

We need to graph the number on the number line

The number6 on the number line is shown below: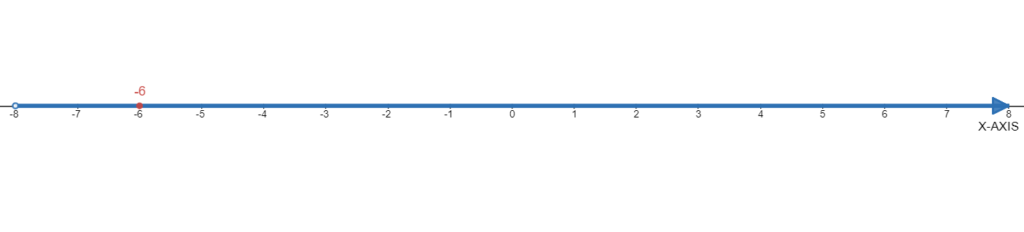 $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 1 page 5$

Page 5 Problem 2, Answer

Given the number 3.

We need to graph the number on the number line.

The number 3 on the number line is shown below: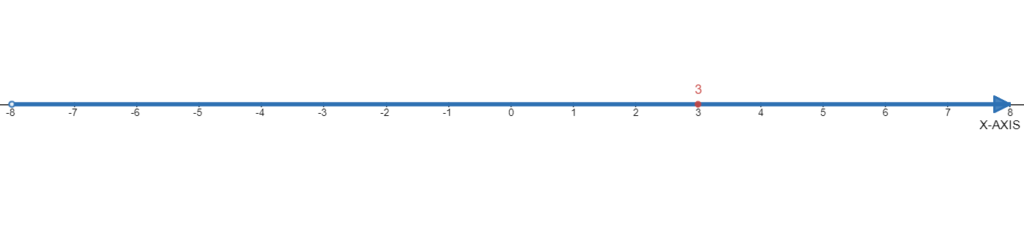 $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 2$

Page 5 Problem 3, Answer

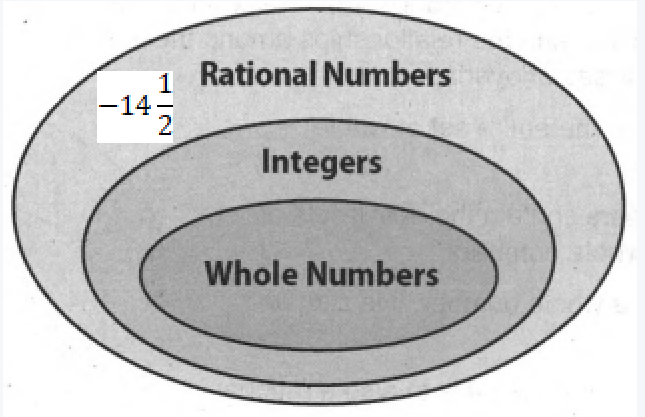
Given the number−3.

We need to graph the number on the number line.

The number−3 on the number line is shown below:

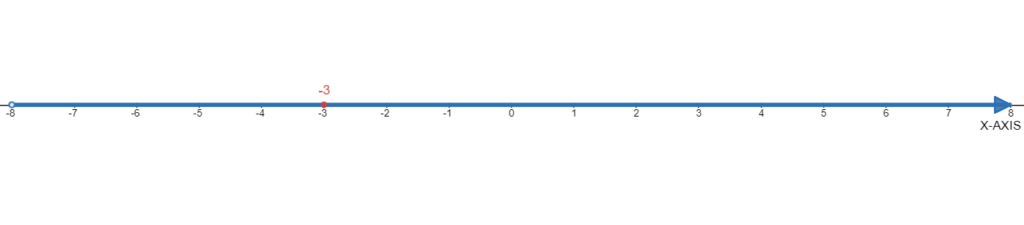
$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 3$

Go Math Grade 6 Chapter 1 Integers Exercise 1.3 Answers

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 5 Problem 4, Answer

$Go Math! Practice Fluency Workbook Grade 6 Chapter 1 Integers Exercise 1.3 Answer Key$

Given the number 5.

We need to graph the number on the number line.

The number on the number line is shown below:

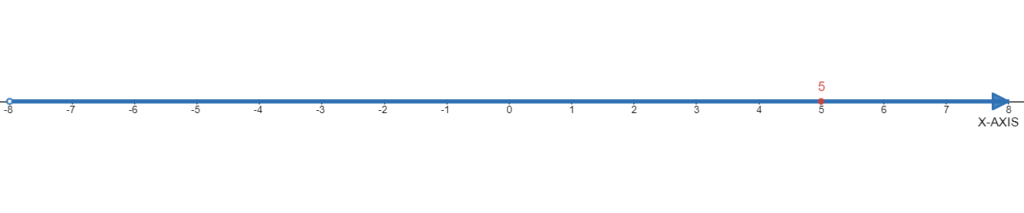
$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 4$
Page 5 Problem 5, Answer

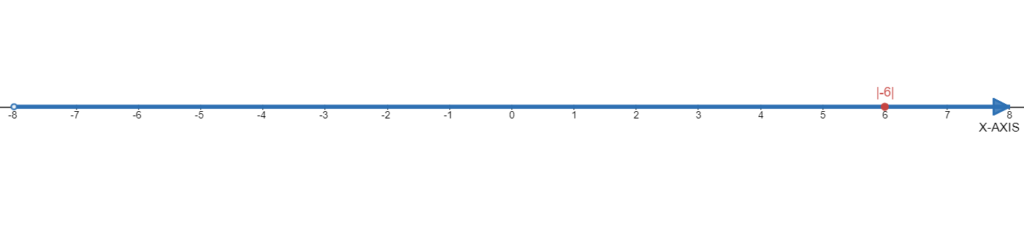
Given the number∣−6∣ .

We need to use the number line to find each absolute value.

The absolute value of∣−6∣ is 6 as shown below:

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 5$

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 5 Problem 6, Answer

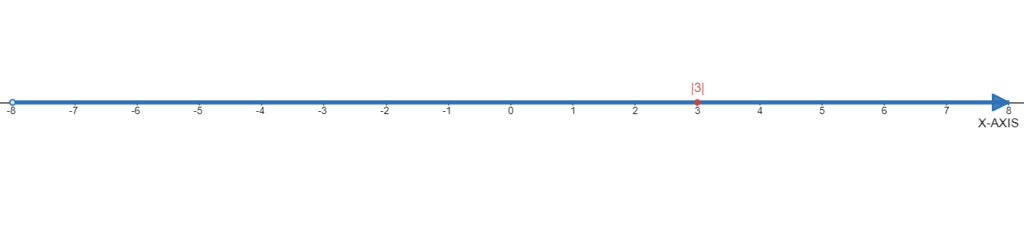
Given the number|3|.

We need to use the number line to find each absolute value.

The absolute value of|3|is 3 as shown below:

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 6$ Page 5 Problem 7, Answer

Given the number|8| .

We need to use the number line to find each absolute value.

The absolute value of|8| is 8 as shown below: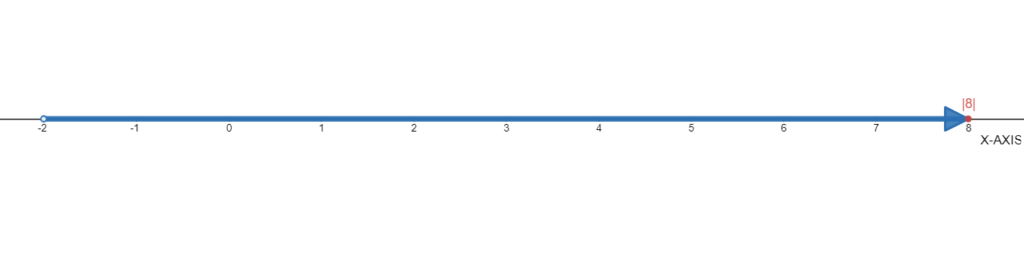 $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 7$

Page 5 Problem 8, Answer

Given the number|6|.

We need to use the number line to find each absolute value.

The absolute value of |6| is 6 as shown below: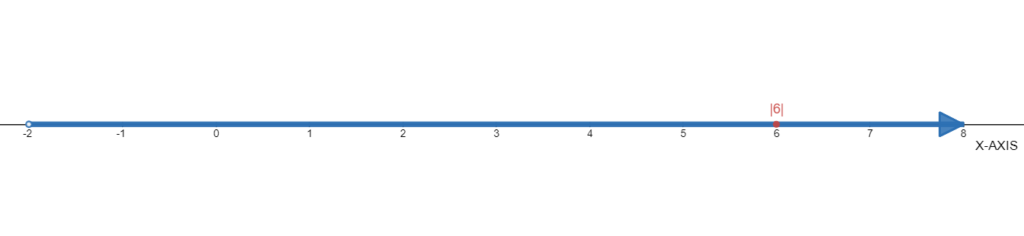 $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 8$

Page 5 Problem 9, Answer

Given the number∣−3∣.

We need to use the number line to find each absolute value.

The absolute value of∣−3∣ is 3 as shown below: $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 9$

Go Math Grade 6 Exercise 1.3 Integers Solutions

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 5 Problem 10, Answer

Given the number|5|.

We need to use the number line to find each absolute value.

The absolute value of|5| is5 as shown below: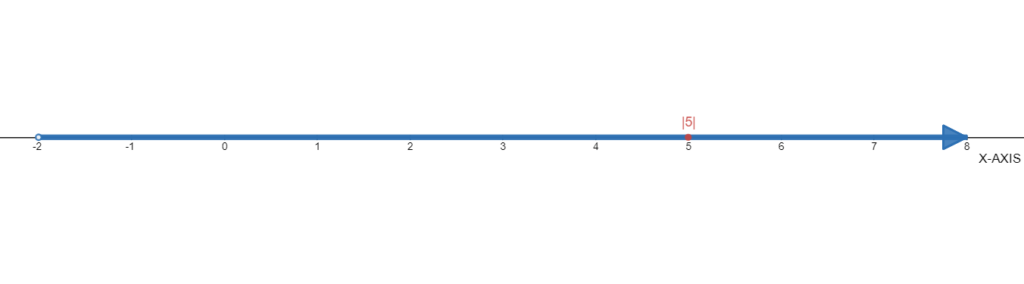 $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 10$

Page 5 Problem 11, Answer

Given the numbers6 and −6.

We need to find each absolute value and tell what do we notice.

The absolute values of 6 and −6 is shown below: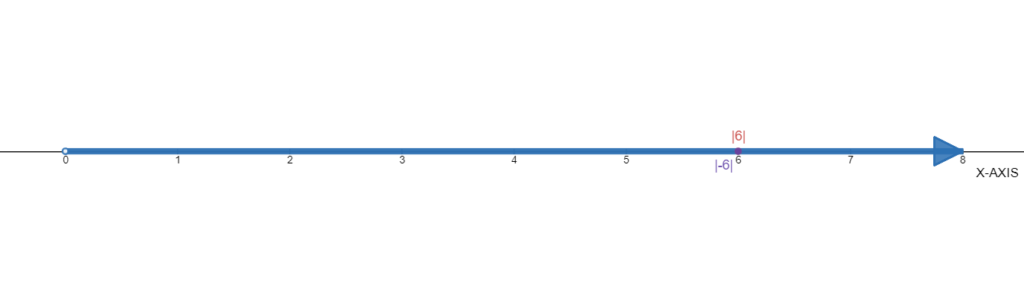 $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 11$

Page 5 Problem 12, Answer

Given the numbers 6 and −6 or 3 and −3.

We need to find each absolute value and tell what do we notice.

The absolute values are: We call∣−3∣ and ∣3∣ ∣−6∣ and ∣6∣ as equal numbers.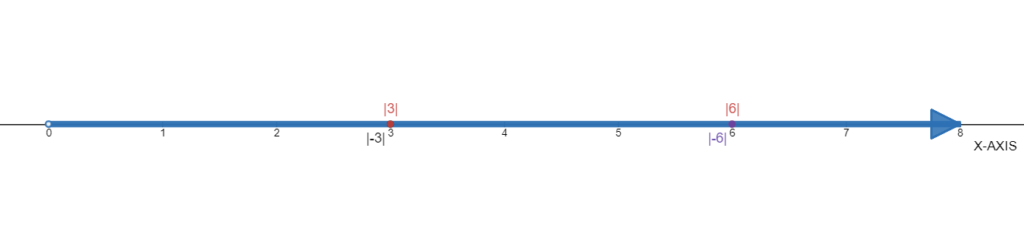 $Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1$

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 5 Problem 13, Answer

Given the table:

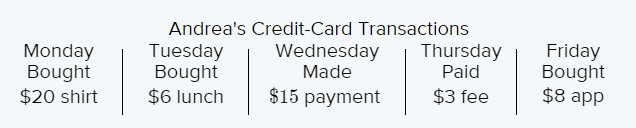
$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers table 1$

Write a negative integer to show the amount spent on each purchase on monday.

Hence the negative integer to show the amount spent on each purchase on Monday is−20.

Page 5 Problem 14, Answer

Given the table:

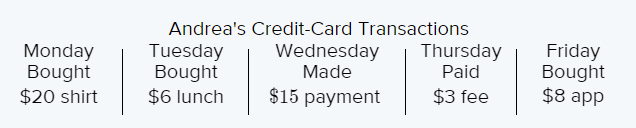
$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 14$

Write a negative integer to show the amount spent on each purchase on Tuesday.

Hence the negative integer to show the amount spent on each purchase on Tuesday is−6.

Page 5 Problem 15, Answer

Given the table:

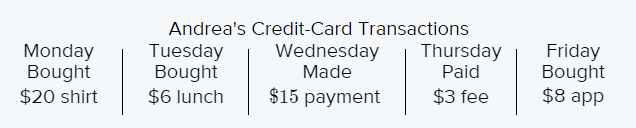
$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 15$

Write a negative integer to show the amount spent on each purchase on Friday.

Hence the negative integer to show the amount spent on each purchase on Friday is−8.

Solutions For Go Math Grade 6 Chapter 1 Exercise 1.3 Integers

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 5 Problem 16, Answer

Given the table:

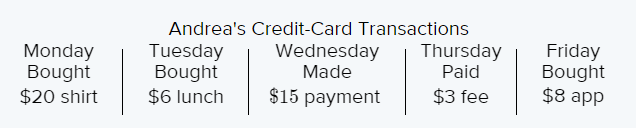
$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 16$

Find the absolute value of each transaction on Monday.

The absolute value of the transaction on Monday is20.

Page 5 Problem 17, Answer

The given table is,

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 17$

We have to find the absolute value of each transaction on Tuesday.

We will take the modulus of the transaction.

The absolute value of the transaction on Tuesday is 6

Page 5 Problem 18, Answer

The given table is,

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers problem 18$

We have to find the absolute value of each transaction on Wedneday.

We will take the modulus of the transaction.

The absolute value of a payment of Wednesday is15

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 5 Problem 19, Answer

The given table is,

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 19$

We have to tell on which day did Andrea spend the most on her card.

We will observe the table.

On observing the table carefully we observed that Andrea spent most on her card on Monday

Page 5 Problem 20, Answer

We have to show that, |3+10|=|3|+|10|.

We will find the value of L.H.S. and R.H.S.

We will check the values are the same or not.

Hence we showed |3+10|=|3|+|10|

Page 5 Problem 21, Answer

The given statement is How many different integers can have the same absolute value? ________ Give an example.

We have to fill in the blanks.

We will see the cases of the modulus.

The revised statement is, How many different integers can have the same absolute value? 2

Give an example. −3 and 3

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 6 Exercise 1, Answer

We have to match the absolute value of 15

The absolute value of 15 is ⇒∣15∣ ⇒15

The row C is the correct match.

Page 6 Exercise 2,Answer

We have to match the negative integer.

The negative integer is −15

The correct match is d

Page 6 Exercise 3, Answer

We have to match opposite of −7

The opposite of −7 is 7

The correct match is b

Go Math Grade 6 Integers Exercise 1.3 Key

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 6 Exercise 4,Answer

We have to match opposite of 7

The opposite of 7 is −7

The correct match is a

Page 6 Exercise5,Answer

We have to match ∣−15∣ The value of ∣−15∣ is 15

The correct match is c

Page 6 Exercise6,Answer

We have to find the value of ∣−3∣

We will use the concept of modulus.

The value of ∣−3∣ is 3

Page 6 Exercise7,Answer

We have to find the value of |5|

We will use the concept of modulus.

The value of |5| is 5

Page 6 Exercise 8, Answer

We have to find the value of ∣−7∣

We will use the concept of modulus.

The value of ∣−7∣ is 7

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 6 Exercise 9, Answer

We have to find the value of |6|

We will use the concept of modulus.

The value of |6| is 6

Page 6 Exercise 10,Answer

We have to find the value of |0|

We will use the concept of modulus.

The value of |0| is 0

Page 6 Exercise 11,Answer

We have to find the value of ∣−2∣

We will use the concept of modulus.

The value of ∣−2∣ is 2

Page 6 Exercise 12,Answer

We have to find the value of∣−10∣

We will use the concept of modulus.

The value of ∣−10∣ is 10

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 1 Integers Page 6 Exercise 13,Answer

We have to find the value of |−3/4|

We will use the concept of modulus.

The value of |−3/4| is 3/4

Page 6 Exercise 14,Answer

We have to find the value of|0.8|

We will use the concept of modulus.

The value of |0.8| is 0.8

Page 6 Exercise15, Answer

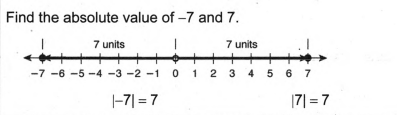
The given conditions are, Abby has been absent from class. How would I explain to her what absolute value is? Use the number line and an example in our explanation.

The absolute value of any number is its distance from 0 on the number line . Since the distance is always positive or 0 ,absolute value is positive or 0.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 1 Integers exercise 15$

Detailed Answers For Go Math Grade 6 Chapter 1 Exercise 1.3

Go Math Answer Key

Go Math! Grade 6 Chapter 2 Factors and Multiples Exercise 2.1 Answers

November 18, 2024August 7, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples

Page 7 Problem 1 Answer

A number is given to us 5.

We have to find all the factors of the given number.

The factors of the given number are: => 5, 1

Page 7 Problem 2 Answer

A number is given to us 15.

We have to find all the factors of the given number.

The factors of the given number are: 15,5,3,1

Page 7 Problem 3 Answer

A number is given to us 60.

We have to find all the factors of the given number.

The factors of the given number are: 60,30,20,15,12,10,6,5,4,3,2,1

$Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.1 Answer Key$

Page 7 Problem 4 Answer

A number is given to us 6.

We have to find all the factors of the given number.

The factors of the given number are: 6,3,2,1

Go Math Grade 6 Chapter 2 Factors And Multiples Exercise 2.1 Answers

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 7 Problem 5 Answer

A number is given to us 12.

We have to find all the factors of the given number.

The factors of the given number are: 12,6,4,3,2,1

Page 7 Problem 6 Answer

A number is given to us 36.

We have to find all the factors of the given number.

The factors of the given number are: 36,18,12,9,6,4,3,2,1

Page 7 Problem 7 Answer

Numbers are given to us 6,9.

We have to find the GCD of the given numbers.

The GCD of the given numbers is:3

Page 7 Problem 8 Answer

Numbers are given to us 4,8.

We have to find the GCF of the given numbers.

The factors of the given numbers are: 4=2×2×1, 8=2×2×2×1

So the GCF of the given numbers is: 2×2×1=4

The GCF of the given numbers is: 4

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 7 Problem 9 Answer

Numbers are given to us 8,12.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

8=2×2×2×1
12=3×2×2×1

So the GCF of the given numbers is:

2×2×1 ⇒4

The GCF of the given numbers is: 4

Page 7 Problem 10 Answer

Numbers are given to us 6,15.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

6=3×2×1
15=5×3×1

So the GCF of the given numbers is: 3

The GCF of the given numbers is: 3

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 7 Problem 11 Answer

Numbers are given to us10,15.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

10=5×2×1
15=5×3×1

So the GCF of the given numbers is: 5×1=5

The GCF of the given numbers is: 5

Page 7 Problem 12 Answer

Numbers are given to us 9,12.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

9=3×3×1
12=3×2×2×1

So the GCF of the given numbers is 3×1=3

The GCF of the given numbers is: 3

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 7 Problem 13 Answer

Sum of numbers if given to us44+40.

We have to rewrite the sum as the product of GCF and a new sum.

The factors of the numbers are:

44=11×2×2×1
40=5×2×2×2×1

So the GCF is: 2×2×1=4

Now rewriting the sum: 44+40=4×(11+10)

The given sum can also be written as: 44+40=4×(11+10)

Page 7 Problem 14 Answer

Sum of numbers if given to us15+81 .

We have to rewrite the sum as the product of GCF and a new sum.

The factors of the numbers are:

15=5×3×1
81=3×3×3×3×1

So the GCF is: 3×1=3

Now rewriting the sum: 15+81=3×(5+27)

The given sum can also be written as: 15+81=3×(5+27)

Go Math Grade 6 Exercise 2.1 Factors And Multiples Solutions

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 7 Problem 15 Answer

Sum of numbers if given to us13,52.

We have to rewrite the sum as the product of GCF and a new sum.

The factors of the numbers are:

13=13×1
52=13×2×2×1

So the GCF is:
13×1=13

Now rewriting the sum: 13+52=13×(1+4)

The given sum can also be written as: 13+52=13×(1+4)

Page 7 Problem 16 Answer

Sum of numbers if given to us is 64,28.

We have to rewrite the sum as the product of GCF and a new sum.

The factors of the numbers are:

64=2×2×2×2×2×2×1
28=7×2×2×1

So the GCF is: 2×2×1=4

Now rewriting the sum: 64+28=4×(16+7)

The given sum can also be written as: 64+28=4×(16+7)

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 7 Problem 17 Answer

The data about beads in necklaces are given to us. We have to find now many necklaces that can be made from the given number of beads and how many beads are there in every necklace.

The GCF of the number of beads is:

24=3×2×2×2×1
30=5×3×2×1
⇒3×2×1=6

So the number of necklaces is six.

Now the number of individual beads are:

24/6 =4 Jade beads
30/6 =5 Teak beads

The total number of necklaces that can be made from the beads is 6.

There will be4 Jade beads and 5 teak beads in each of the necklace.

Page 7 Problem 18 Answer

The data about a marine-life store is given to us.We have to find the greatest number of tanks that can be set up, that contain equal number of fishes.

The GCF of the number of fishes is:

12=3×2×2×1
24=3×2×2×2×1
30=5×3×2×1
⇒3×2×1=6

A total of6 tanks can be set up in the marine-life store.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 8 Exercise 1 Answer

Numbers are given to us 32,48.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

32=2×2×2×2×2×1
48=3×2×2×2×2×1

So the GCF of the given numbers is:

2×2×2×2×1=16

The GCF of the given numbers is: 16

Page 8 Exercise 2 Answer

Numbers are given to us 18,36.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

18=3×3×2×1
36=3×3×2×2×1

So the GCF of the given numbers is:

3×3×2×1=18

The GCF of the given numbers is:18

Solutions For Go Math Grade 6 Chapter 2 Exercise 2.1 Factors And Multiples

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 8 Exercise 3 Answer

Numbers are given to us 28,56,84.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

28=7×2×2×1
56=7×2×2×2×1
84=7×3×2×2×1

So the GCF of the given numbers is: 7×2×2×1=28

The GCF of the given numbers is: 28

Page 8 Exercise 4 Answer

Numbers are given to us 30,45,75.

We have to find the GCF of the given numbers.

The factors of the given numbers are:

30=5×3×2×1
45=5×3×3×1
75=5×5×3×1

So the GCF of the given numbers is: 5×3×1=15

The GCF of the given numbers is: 15

Page 8 Exercise 5 Answer
Sum of numbers if given to us is 9,15.

We have to rewrite the sum as the product of GCF and a new sum.

The factors of the numbers are:

9=3×3×1
15=5×3×1

So the GCF is 3×1=3

Now rewriting the sum: 9+15=3×(3+5)

The given sum can also be written as: 9+15=3×(3+5)

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors And Multiples Page 8 Exercise 6 Answer

Sum of numbers if given to us100+350.

We have to rewrite the sum as the product of GCF and a new sum.

The factors of the numbers are:

100=5×5×2×2×1
350=7×5×5×2×1

So the GCF is: 5×5×2×1=50

Now rewriting the sum: 100+350=50×(2+7)

The given sum can also be written as: 100+350=50×(2+7)

Page 8 Exercise 7 Answer

Sum of numbers if given to us12+18+21.

We have to rewrite the sum as the product of GCF and a new sum.

The factors of the numbers are:

12=3×2×2×1
18=3×3×2×1
21=7×3×1

So the GCF is 3×1=3

Now rewriting the sum: 12+18+21=3×(4+6+7)

The given sum can also be written as: 12+18+21=3×(4+6+7)

Go Math Grade 6 Factors And Multiples Exercise 2.1 Key

Go Math Answer Key

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Answer Key

November 18, 2024August 6, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 2 Factors and Multiples

Page 9 Problem 1 Answer

Given :- number 3

Find to the question first three multiple of 3

Multiples of 3 are the product obtained when an integer is multiplied by 3

First three multiples are:- 3,6,9

First three multiples of 3 are 3,6,9.

Page 9 Problem 2 Answer

Given:- number is 7

Find to the question first three multiples of 7

Multiples of 7 are the products obtained when an integer is multiplied by 7

First three multiples are:- 7,14,21

First three multiple of 7 are 7,14,21

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Page 9 Problem 3 Answer

Given:- number is 12

Find to the question first three multiples of 12

Multiples of 12 are the products obtained when an integer is multiplied by 12

We need to multiply 12 by 1,2,3

First three multiples are:- 12,24,36

First three multiples of 12 are 12,24,and 36.

$Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Answer Key$

Go Math Practice Fluency Workbook Grade 6 Chapter 2 Factors And Multiples Exercise 2.2 Answer Key

Page 9 Problem 4 Answer

Given:- number is 200

Find to the question first three multiples of 200

Multiples of 200 are the products of obtained when an integer is multiplied by 200

We nee to multiply 200 by 1,2,3

First three multiples are :- 200,400,600

First three multiples of 200 are 200,400,600.

Page 9 Problem 5 Answer

Given :- number is 2 & 3

Find to the question least common multiple of 2 & 3

Multiples of 2 are 2,4,6,8,… etc.

Multiples of 3 are 3,6,9,12… etc.

Here we can see the least multiple of 2 is 2 and 3 is 3

Least common multiple of 2 & 3 is 6

LCM of 2 &3 is =6

Least Common multiple of 2 & 3 is 6 and the LCM of 2 & 3 = 6

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Page 9 Problem 6 Answer

Given :- number is 4 & 5

Find to the question least common multiple of 4 & 5

Multiples of 4 is 4,8,12,16,20….etc.

Multiples of 5 are 5,10,15,20… etc.

Here we can see the least common multiple of 4 & 5 is 20

LCM of 4 & 5= 20

Least common multiple of 4 & 5 is 20 LCM of 4 & 5=20

Page 9 Problem 7 Answer

Given :- number is 6 & 7

Find to the question Least common multiple of 6 & 7

Multiples of 6 are 6,12,18,24,30,36,42…etc.

Multiples of 7 are 7,14,21,28,35,42…etc.

Here we can see Least common multiple of 6 & 7 is 42.

Least common multiple of 6 & 7 = 42

Page 9 Problem 8 Answer

Given :- number is 2,3 & 4

Find to the question least common multiple of 2,3 & 4

Multiple of 2 are 2,4,6,8,10,12,14,…etc.

Multiple of 3 are 3,6,9,12,15,…etc.

Multiples of 4 are 4,8,12,16…etc.

Here we can see Least common factor of 2,3 & 4 is 12

Least common factor of 2,3 & 4 is 12 .

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Page 9 Problem 9 Answer

Given :- number is 5,6 & 7

Find to the question the least common factor of 5,6 & 7

Multiples of 5 are 5,10,15,20,25,30,35…etc.

Multiples of 6 are 6,12,18,24,30,…etc

Multiples of 7 are 7,14,21,28,…etc.

Here we can see the least common factor of 5,6,&7 is 210

The least common factor of 5,6 & 7 is 210 .

Page 9 Problem 10 Answer

Given :- number is 8,9 & 10

Find to the question the least common factor of 8,9& 10

Multiples of 8 are 8,16,24,32…etc.

Multiples of 9 are 9,18,27,36…etc.

Multiples of 10 are 10,20,30,40…etc.

Here we can see the least common multiple of 8,9 & 10 is 360

The lease common multiple of 8,9 & 10 is 360 .

Page 9 Problem 11 Answer

Given :- 60 peoples are invited to a party .there are 24 cups in a package and 18 napkins in a package.

Find :- least number of packages of cups and napkins that can be bought if each party guest gets one cup and one napkin . Using multiple and factor concept and proceed .

Given,
Number of cups in a package=24

Number of napkins in a package =18

Let total number of package of cups and napkins respectively x & y

Equation of total cups bought =24×x

Equation of total napkin bought =18×y

Total people invited to the party =60

as party guest gets one cup and one napkin total cups and napkins required :- Total number of cups bought

24×x≥60

x≥60

24 x≥2.5

Number of package should be an integer therefor x=3

Total number of napkins bought

18×y≥60

y≥10

3 y≥3.3

Number of package should be an integer therefor y=3

Least number of packages of cups bought are 3 and napkins is 4

Go Math Grade 6 Practice Fluency Workbook Exercise 2.2 Factors And Multiples Solutions

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Page 9 Problem 12 Answer

Given :- Given 45 members in science club .caps come in package of 3 and the shirts come in package of 5

Find :- what is the least number of packages of caps and shirts . Using multiple and factor concept and proceed .

Given , Caps come in package of 3 and the shirts come in package of 5

Total number of member in science club =45

Let total number of packages of caps and shirts x & y respectively .

Equation of caps ordering =3×x

Equation of shirts ordering =y×5

If club members get one cap and one shirts then required caps and shirts package :- Total number of caps ordered

3×x≥45

x=15

Total number of shirts ordered

5×y≥45

y=9

The least number of caps and shirts 15 & 9 respectively.

We need 15 packages of caps and 9 packages of shirts and that is least number of caps and shirts packages.

Page 9 Problem 13 Answer

Given :- Some hot dogs come in packages of 8 and hot dog buns packages of 7

Find :- why would a backer of hot dog buns package 7 hot dog buns to a package? We use here least common multiple concept .

Given , Hot dogs come in packages of 8 and hot dog buns packages of 7

So we need to find here the LCM of 8 & 7 LCM of 8,7 =56

We need 7 packages of hot dogs and 8 packages of buns.

Page 9 Problem 14 Answer

Find to the question how are the GCF and the LCM alike and different .

GCF is the greatest common factor is the greatest real number shared between two integers .what makes this number a factor is that it is a whole,real number that two integers share- that is , when broken down to their lowest multiples,the largest integer that is shared between the two numbers is their greatest common factor.

And the other hand,the lowest common multiple is the integer shared by two numbers that can be divided by both number.

The biggest difference between the GCF and LCM is that one is based upon what can divide evenly into two numbers,while the other depends on what number shared between two integers can be divided by the two integers (LCM).

Page 10 Exercise 1 Answer

Given:- number is 2,9

Find to the question the least common multiple of 2,9

Multiples of 2 are 2,4,6,8…etc

Multiples of 9 are 9,18,27…etc

Here we can see The least common multiple of 2 & 9 is 18

Least common multiple of 2 & 9 is 18.

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Page 10 Exercise 2 Answer

Given :- number is 4 & 6

Find to the question least common multiple of 4 & 6

Multiples of 4 are 4,8,12…etc

Multiples of 6 are 6,12,18…etc

Here we can see the least common factor of 4 & 6 is 12.

The least common factor of 4 & 6 is 12.

Solutions For Go Math Grade 6 Chapter 2 Exercise 2.2 Factors And Multiples

Page 10 Exercise 3 Answer

Given :- number is 4 & 10

Find to the question the least common multiple of 4 & 10

Multiples of 4 are 4,8,12,16,20…etc.

Multiples of 10 are 10,20,30…etc

Here we can see the least common multiple of 4 & 10 is 20

The least common factor of 4 & 10 is 20.

Page 10 Exercise 4 Answer

Given :- number is 2,5 & 6

Find to the question the least common multiple of 2,5 & 6

Multiples of 2 are 2,4,6,8,10,12,14…etc.

Multiples of 5 are 5,10,15,20,25…etc

Multiples of 6 are 6,12,18,24…etc.

Here we can see the least common multiple of 2,5 & 6 is 30.

The least common multiple of 2,5,& 6 is 30.

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Page 10 Exercise 5 Answer

Given :- number is 3,4 & 9

Find to the question the least common factor of 3,4 & 9

Multiples of 3 are 3,6,9,12…etc

Multiples of 4 are 4,8,12,16…etc.

Multiples of 9 are 9,18,27,36…etc.

Here we can see the least common multiple of 3,4 & 9 is 36.

The least common multiple of 3,4 & 9 is 36.

Page 10 Exercise 6 Answer

Given :- number is 6,8,10 & 12

Find to the question the least common multiple of 6,8,10 &12

Multiples of 6 are 6,12,18,24,30,36…etc

Multiples of 8 are 8,16,24,32,40…etc.

Multiples of 10 are 10,20,30,40,50…etc.

Multiples of 12 are 12,24,36,48,60…etc.

Here we can see the least common factor of 6,8,10,12 is 120

The least common factor of 6,8,10 & 12 is 120.

Go Math! Practice Fluency Workbook Grade 6 Chapter 2 Factors and Multiples Exercise 2.2 Page 10 Exercise 7 Answer

Given:- pads of paper 4 to a box, pencils come 27 to a box, and erasers come 12 to a box.

Find:- What is the least number of kits that can be made with paper, pencils, and erasers Using least common multiple concepts?

Given,
Pads of paper 4 to a box, pencils come 27 to a box and erasers come 12 to a box.

We want to make kits that can be made with paper,pencils, and erasers so Least common multiple of 4,27 & 12 is 108

So we can make 108 kits with paper pencils and eraser.

We can make 108 kits with pencil, eraser, and paper.

Go Math Grade 6 Factors And Multiples Exercise 2.2 Key From Practice Fluency Workbook

Go Math Answer Key

Grade 6 Chapter 3 Rational Numbers Exercise 3.1 Solutions

November 18, 2024August 5, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers

Page 11 Problem 1 Answer

We have given the number as 0.3 Asked to write each rational number in the form a/b

To get the required answer we just need to change the given number in the fractional form.To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as 0.3

So here we get the fractional form as 0.3/1=3/10

For the given number 0.3 we get the fractional form as3/10

Page 11 Problem 2 Answer

We have given the number as 2 x 7/8

Asked to write each rational number in the form a/b

To get the required answer we just need to change the given number in the fractional form.To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as

⇒ $2 \frac{7}{8}$

So here we get the fractional form as

⇒ $2 \frac{7}{8}$

⇒ $=\frac{23}{8}$

For the given number 2×7/8

we get the fractional form as23/8

Page 11 Problem 3 Answer

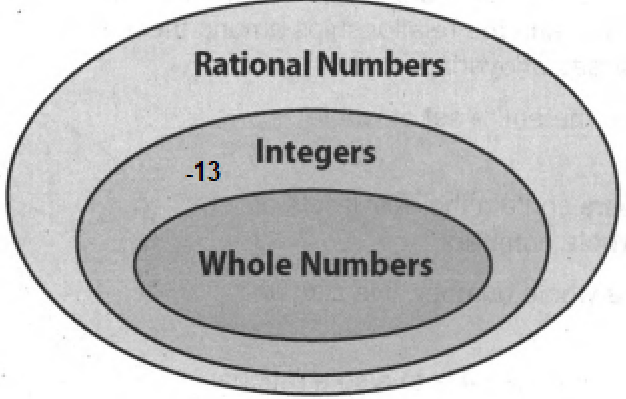
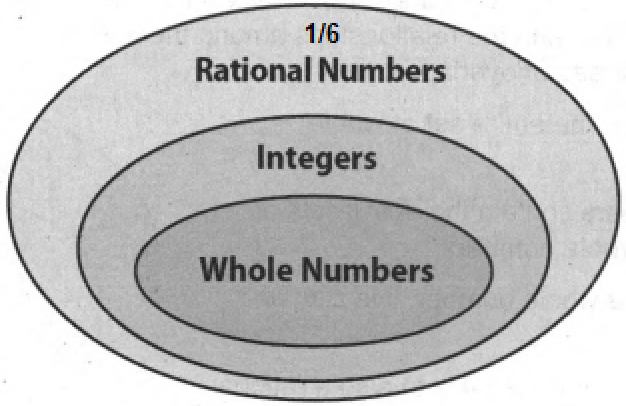
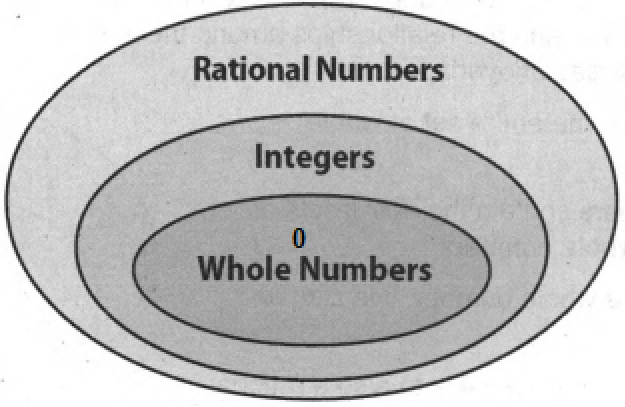
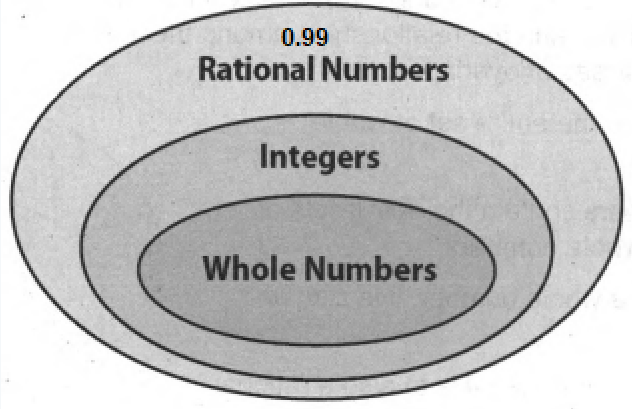
$Go Math! Practice Fluency Workbook Grade 6 Chapter 3 Rational Numbers Exercise 3.1 Answer Key$

We have given the number as −5 and Asked you to write each rational number in the form

To get the required answer we just need to change the given number in the fractional form. To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as −5

So here we get the fractional form as −5/1

For the given number −5

we get the fractional form as−5/1

Page 11 Problem 4 Answer

We have given the number as 16 and Asked to write each rational number in the forma/b

To get the required answer we just need to change the given number in the fractional form. To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as 16

So here we get the fractional form as 16/1

For the given number 16

we get the fractional form as16/1

Grade 6 Chapter 3 Rational Numbers Exercise 3.1 Solutions

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers Page 11 Problem 5 Answer

We have given the number as −1×3/4

Asked to write each rational number in the forma/b

To get the required answer we just need to change the given number in the fractional form.To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as

⇒ $-1 \frac{3}{4}$

So here we get the fractional form as

⇒ $ -1 \frac{3}{4}$

⇒ $\frac{-7}{4}$

For the given number −1×3/4

we get the fractional form as−7/4

Page 11 Problem 6 Answer

We have given the number as −4.5
Asked to write each rational number in the form a/b

To get the required answer we just need to change the given number in the fractional form. To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as

-4.5

So here we get the fractional form as

⇒ $\frac{-4.5}{1}$

⇒ $ \frac{-45}{10}$

⇒ $ \frac{-9}{2}$

For the given number −4.5

we get the fractional form as−9/2

Page 11 Problem 7 Answer

We have given the number as 3
Asked to write each rational number in the form a/b

To get the required answer we just need to change the given number in the fractional form.To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as 3

So here we get the fractional form as 3/1

For the given number 3

we get the fractional form as 3/1

Page 11 Problem 8 Answer

We have given the number as 0.11

Asked to write each rational number in the form a/b

To get the required answer we just need to change the given number in the fractional form.To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number a

0.11

So here we get the fractional form as

⇒ $\frac{0.11}{1} $

⇒ $\frac{11}{100}$

For the given number 0.11

we get the fractional form as11/100

Grade 6 Exercise 3.1 Rational Numbers Answers

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers Page 11 Problem 9 Answer

We have given the number as −13
Asked to place each number in the correct place on the Venn diagram.To get the right place for the number in the diagram we have to analyze the number first. To place the number in the diagram we have to write that number within the circle of that category only.

We have given the number as −13

The nature of the given number is an integer

The given number −13 is an integer and placed in the diagram is given as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 9$

Page 11 Problem 10 Answer

We have given the number as 1/6

Asked to place each number in the correct place on the Venn diagram. To get the right place for the number in the diagram we have to analyze the number first.

To place the number in the diagram we have to write that number within the circle of that category only. We have given the number as 1/6

The nature of the given number is a rational number

The given number1/6 is a rational number and placed in the diagram is given

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 10$

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers Page 11 Problem 11 Answer

We have given the number as 0. Asked to place each number in the correct place on the Venn diagram.

To get the right place for the number in the diagram we have to analyze the number first.

To place the number in the diagram we have to write that number within the circle of that category only.

We have given the number as 0

The nature of the given number is a whole number The given number 0 is a whole number and the place in the diagram is given as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 11$

Page 11 Problem 12 Answer

We have given the number as 0.99 Asked to place each number in the correct place on the Venn diagram.

To get the right place for the number in the diagram we have to analyze the number first.

To place the number in the diagram we have to write that number within the circle of that category only.

We have given the number as 0.99

The nature of the given number is rational number The given number 0.99 is a rational number and the place in the diagram is given as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 12$

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers Page 11 Problem 13 Answer

We have given the number as −6.7
Asked to place each number in the correct place on the Venn diagram. To get the right place for the number in the diagram we have to analyze the number first.

To place the number in the diagram we have to write that number within the circle of that category only. We have given the number as −6.7

The nature of the given number is a rational number

The given number 6.7 is a rational number and its place in the diagram is given as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 13$

Page 11 Problem 14 Answer

We have given the number as 34 Asked to place each number in the correct place on the Venn diagram. To get the right place for the number in the diagram we have to analyze the number first.

To place the number in the diagram we have to write that number within the circle of that category only. We have given the number as 34

The nature of the given number is a whole number

The given number 34 is a whole number and the place in the diagram is given as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 14$

Page 11 Problem 15 Answer

We have given the number as −14x/2 and Asked to place each number in the correct place on the Venn diagram.

To get the right place for the number in the diagram we have to analyze the number first.

To place the number in the diagram we have to write that number within the circle of that category only.

We have given the number as −14×1/2

The nature of the given number is a rational number

The given number −14×1/2 is a rational number and placed in the diagram is given

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 15$

Solutions For Grade 6 Chapter 3 Exercise 3.1 Rational Numbers

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers Page 12 Exercise 1 Answer

We have given the number as−12

So here we get the fractional form as−12/1

For the given number −12

we get the fractional form as −12/1 and the nature of the number as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers exerciose 1$

Page 12 Exercise 2 Answer

We have given the number as 7.3 Asked to write each rational number in the form a/b, then circle the name of each set to which the number belongs.

o, get the required answer we just need to change the given number in the fractional form.

To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as

7.3

So here we get the fractional form as

⇒ $\frac{7.3}{1}$

⇒ $\frac{73}{10}$

For the given number 7.3 we get the fractional form as73/10 and the nature of the n

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers exerciose 2$

Page 12 Exercise 3 Answer

We have given the number as 0.41 Asked to write each rational number in the form a/b, then circle the name of each set to which the number belongs.

To get the required answer we just need to change the given number in the fractional form.

To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as

0.41

So here we get the fractional form as

⇒ $\frac{0.41}{1}$

⇒ $\frac{41}{100}$

For the given number 0.41

we get the fractional form as 41/100 and the nature of the number as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers exerciose 3$

Page 12 Exercise 4 Answer

We have given the number 6 Asked to write each rational number in the form a/b, then circle the name of each set to which the number belongs.

To get the required answer we just need to change the given number in the fractional form.

To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as 6

So here we get the fractional form as 6/1

For the given number 6

we get the fractional form as 6/1 and the nature of the number

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers exerciose 4$

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers Page 12 Exercise 5 Answer

We have given the number as 3×1/2

Asked to write each rational number in the form a/b, then circle the name of each set to which the number belongs.

To get the required answer we just need to change the given number in the fractional form.

To write in the fractional form we must know that the by default denominator of the number is always one.

We have given the number as

⇒ $3 \frac{1}{2}$

So here we get the fractional form as

⇒ $3 \frac{1}{2}$

⇒ $\frac{7}{2}$

For the given number 3×1/2

we get the fractional form as 7/2 and the nature of the number as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers exerciose 5$

Grade 6 Rational Numbers Exercise 3.1 Key

Go Math Answer Key

Go Math! Grade 6 Exercise 3.2: Rational Numbers Answers

November 18, 2024August 3, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 3 Rational Numbers

Page 13 Problem 1 Answer

We have given the number as 3.5 Asked to graph each number and its opposite on a number line.

To get the required number we first find the opposite of the given number by multiplying the negative sign with it.

Then mark the numbers that are opposite of each other on the given graph.

We have given the number as 3.5

We get the opposite of the given number as −3.5

For the given number 3.5

we get the opposite of it −3.5 and numbers on the line as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 1$

Page 13 Problem 2 Answer

We have given the number as −2.5 and Asked to graph each number and its opposite on a number line.

To get the required number we first find the opposite of the given number by multiplying the negative sign with it.

$Go Math! Practice Fluency Workbook Grade 6 Chapter 3 Rational Numbers Exercise 3.2 Answer Key$

Then mark the numbers that are opposite of each other on the given graph.

We have given the number as 2.5

We get the opposite of the given number as
−(−2.5)
=2.5

For the given number −2.5

we get the opposite number as 2.5 and on the num

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 2$

Go Math Grade 6 Exercise 3.2 Rational Numbers Answers

Page 13 Problem 3 Answer

We have given the number as 2×1/2 Asked to graph each number and its opposite on a number line.

To get the required number we first find the opposite of the given number by multiplying the negative sign with it.

Then mark the numbers that are opposite of each other on the given graph.

For the given number 2×1/2

we get the opposite number as −2×1/2 and on the number line as

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 3$

Page 13 Problem 4 Answer

We have given the number as −1×1/2 Asked to graph each number and its opposite on a number line.

To get the required number we first find the opposite of the given number by multiplying the negative sign with it.

Then mark the numbers that are opposite of each other on the given graph.

For the given number −1×1/2, we get the opposite number as 1×1/2 and on the number line a

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 3 Rational Numbers 4$

Page 13 Problem 5 Answer

We have given the number as 4.25 and Asked to name the opposite of the given number.

To get the required number we first find the opposite of the given number by multiplying the negative sign with it.

Then on solving the sign convention, we will get the required opposite number. We have given the number as 4.25

We get the opposite of the number as −4.25

For the given number 4.25

we get the opposite of it as −4.25

Page 13 Problem 6 Answer

We have given the number as −5×1/4 and Asked to name the opposite of the given number.

To get the required number we first find the opposite of the given number by multiplying the negative sign with it.

Then on solving the sign convention, we will get the required opposite number.

We have given the number as

⇒ $-5 \frac{1}{4}$

We get the opposite of the number as

⇒ $-\left(-5 \frac{1}{4}\right)$

⇒ $5 \frac{1}{4}$

For the given number −5×1/4

we get the opposite of it as 5×1/4

Go Math Grade 6 Exercise 3.2 Rational Numbers Solutions

Page 13 Problem 7 Answer

We have given the number as 1/2 and Asked to name the opposite of the given number.

To get the required number we first find the opposite of the given number by multiplying the negative sign with it.

Then on solving the sign convention, we will get the required opposite number.

For the given number 1/2

we get the opposite of it as −1/2

Page 13 Problem 8 Answer

We have given the number as 2×1/3 Asked to Name the absolute value of the given number.

Here to get the absolute value of the given number we just have to write the numerical part of the number.

We have given the number as

⇒ $2 \frac{1}{3}$

We get the absolute of the number as

⇒ $\left|2 \frac{1}{3}\right|$

⇒ $2 \frac{1}{3}$

For the given number 2×1/3

we get the absolute of it as 2×1/3

Page 13 Problem 9 Answer

We have given the number −3.85 and Asked to Name the absolute value of the given number.

Here to get the absolute value of the given number we just have to write the numerical part of the number.

We have given the number as −3.85

We get the absolute of the number as ∣−3.85∣ =3.85

For the given number −3.85

we get the absolute of it as 3.85

Page 13 Problem 10 Answer

We have given the number as −6.1 and Asked to Name the absolute value of the given number.

Here to get the absolute value of the given number we just have to write the numerical part of the number.

We have given the number as−6.1

We get the absolute of the number as ∣−6.1∣ =6.1

For the given number −6.1

we get the absolute of it as 6.1

Page 13 Problem 11 Answer

Given:- The elevations of checkpoints along a marathon route in a table

To Find:- To determine the opposite values of each checkpoint elevation

The elevation of checkpoints A, B, C.D, and E are 15.6,17.1,5.2,−6.5,−18.5 feet respectively.

The opposite values of the checkpoints A, B, C, D, and E would be −15.6,−17.1,−5.2,6.5,18.5 feet respectively.

The opposite values of the checkpoints A, B, C, D, and E would be 15.6,−17.1,−5.2,6.5,18.5 feet respectively.

Solutions For Go Math Grade 6 Exercise 3.2 Rational Numbers

Page 13 Problem 12 Answer

Given:- The elevations of checkpoints along a marathon route in a table

To Find:- To determine the checkpoint which is closest to the sea level

The elevation of any point is considered from the sea level which would be at 0 feet.

So, the checkpoint that would be closest to the sea level would be the smallest value or the smallest absolute value of the data given in the table.

From the data given in the table, we can notice that the smallest value and the checkpoint that would be closest to the sea level would be 5.2 feet at checkpoint C.

The checkpoint that would be closest to the sea level would be at checkpoint C at 5.2 feet.

Page 13 Problem 13 Answer

Given:- The elevations of checkpoints along a marathon route in a table

To Find:- To determine the checkpoint which is furthest from the sea level

The elevation of any point is considered from the sea level which would be at 0 feet.

So, the checkpoint that would be furthest from the sea level would be the largest value or the largest absolute value of the data given in the table.

From the data given, the absolute values of the checkpoints A, B, C, D, and E are 15.6,17.1,5.2,6.5,18.5.

Therefore, we can conclude from the absolute values of the data given that Checkpoint E at 18.5 feet would be the furthest from the sea level.

The checkpoint that would be furthest from the sea level would be at checkpoint E at 18.5 feet.

Page 14 Exercise 1 Answer

Given:- Are the opposite of −6.5 and the absolute value of −6.5 the same?

To Find:- To determine whether the opposite and the absolute value of the given number −6.5 are the same or not

We know that the opposite value of a negative number would always be positive of the same number. So, the opposite of −6.5 would be 6.5.

We also know that the absolute value of a number is always positive. So, the absolute value of −6.5 would be 6.5.

Therefore, the opposite and the absolute value of the given number−6.5 are the same.

The opposite and the absolute value of the given number−6.5 are the same.

Page 14 Exercise 2 Answer

Given:- Are the opposite of 3×2/5 and the absolute value of 3×2/5 the same?

To Find:- To determine whether the opposite and the absolute value of the given fraction or mixed number are the same We know that the opposite value of a positive number would always be negative of the same number. So, the opposite of 3×2/5 would be−3×2/5.

We also know that the absolute value of a number is always positive. So, the absolute value of 3×2/5 would be 3×2/5.

Therefore, we can clearly say that the opposite and the absolute value of the mixed fraction 3×2/5 are not the same.

The opposite and the absolute value of the mixed fraction 3×2/5 are not the same.

Go Math Grade 6 Rational Numbers Exercise 3.2 Key

Page 14 Exercise 3 Answer

Given:- Write a rational number whose opposite and absolute value are the same

To Find:- To write the example of a rational number whose opposite and absolute value are the same and to given the appropriate explanation We know that the opposite value of a positive number would always be negative of the same number and the opposite value of a negative number would be positive of the same number.

Also, the absolute value of a number is always positive. So, we can say that the opposite value and the absolute value of any number would be positive and the same.

For example, the absolute value and the opposite of the number 5.5 would be 5.5.

The rational number whose opposite and absolute values are the same are−5.5 which would be 5.5

Page 14 Exercise 4 Answer

Given:- Write a rational number whose opposite and absolute values are opposite

To Find:- To write the example of a rational number whose opposite and absolute value are opposite and to give the appropriate explanation

We know that the opposite value of a positive number would always be negative of the same number and the opposite value of a negative number would be positive of the same number.

Also, the absolute value of a number is always positive. So, we can say that a rational number whose opposite and absolute values are opposite would be any positive number.

For example, the opposite value of the rational number 5.5 would be − 5.5. At the same time, the absolute value of the same rational number 5.5 is 5.5.

The rational number whose opposite and absolute values are not the same or opposite is 5.5

Detailed Answers For Go Math Grade 6 Exercise 3.2 Rational Number

Go Math Answer Key

Go Math! Grade 6 Exercise 4.1: Operations with Fractions Answers

November 18, 2024July 18, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions

Page 17 Problem 1 Answer

we have to use the greatest common factor to write each answer in the simplest form. To multiply two fractions, multiply the numerators and then multiply the denominators

⇒ $\frac{2}{3} \cdot \frac{6}{7}=\frac{2 \cdot 6}{3 \cdot 7}=\frac{12}{21}$

Since 12 and 21 have a GCF of 3, We can reduce the fraction by dividing the numerator and denominator by 3 :

⇒ $\frac{12}{21}=\frac{12 \div 3}{21 \div 3}=\frac{4}{7}$

From the above step, we will get the answer 4/7

Page 17 Problem 2 Answer

we have to use the greatest common factor to write each answer in the simplest form. To multiply two fractions, multiply the numerators and then multiply the denominators.

⇒ $\frac{3}{4} \cdot \frac{2}{3}=\frac{3 \cdot 2}{4 \cdot 3}=\frac{6}{12}$

Since 6 and 12 have a GCF of 6, We can reduce the fraction by dividing the numerator and denominator by 3 :

⇒ $\frac{6}{12}=\frac{6 \div 6}{12 \div 6}=\frac{1}{2}$

From the above step, we will get the answer1/2.

$Go Math! Practice Fluency Workbook Grade 6 Chapter 4 Operations with Fractions Exercise 4.1 Answer Key$

Go Math Grade 6 Exercise 4.1 Operations With Fractions Answers

Page 17 Problem 3 Answer

we have to use the greatest common factor to write each answer in the simplest form. To multiply two fractions, multiply the numerators and then multiply the denominators

⇒ $\frac{8}{21} \cdot \frac{7}{10}=\frac{8 \cdot 7}{21 \cdot 10}=\frac{56}{210}$

Since 56 and 210 have a GCF of 14, We can reduce the fraction by dividing the numerator and denominator by 3 :

⇒ $\frac{56}{210}=\frac{56 \div 14}{210 \div 14}=\frac{4}{15}$

From the above step, we will get the answer on 4/15

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 17 Problem 4 Answer

we have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators

When multiplying a whole number and a fraction, if the denominator of the fraction divides evenly into the whole number, you can complete this division and then multiply the quotient by the numerator of the original fraction:

⇒ $24 \cdot \frac{5}{6}=\frac{24}{6} \cdot 5=4 \cdot 5=20$

From the above step, we will get the answer20

Page 17 Problem 5 Answer

We have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators

⇒ $32 \cdot \frac{3}{8}=\frac{32}{8} \cdot 3=4 \cdot 3=12$

From the above step, we will get the answer 12.

Page 17 Problem 6 Answer

we have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators

⇒ $21 \cdot \frac{3}{7}=\frac{21}{7} \cdot 3=3 \cdot 3=9$

From the above step, we will get the answer 9

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 17 Problem 7 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator.

The LCM of 15 and 6 is 30 s0 rewrite the fractions to have a denominator of 30:

⇒ $\frac{4}{15}+\frac{5}{6}=\frac{4 \cdot 2}{15 \cdot 2}+\frac{5 \cdot 5}{6 \cdot 5}=\frac{8}{30}+\frac{25}{30}$

Now that the fractions have a common denominator, you can add the numerators to add the fractions:

⇒ $\frac{8}{30}+\frac{25}{30}=\frac{8+25}{30}=\frac{33}{30}$

Reducing the fraction by dividing the numerator and denominator by the GCF of 3 gives:

⇒ $\frac{33}{30}=\frac{33 \div 3}{30 \div 3}=\frac{11}{10}$

Converting the improper fraction to a mixed number then gives:

⇒ $\frac{11}{10}=1 \frac{1}{10}$

From the above step, we will get the answer 11/10.

Go Math Grade 6 Exercise 4.1 Operations With Fractions Solutions

Page 17 Problem 8 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator

The LCM of 12 and 20 is 60 so rewrite the fractions to have a denominator of 30:

⇒$\frac{5}{12}-\frac{3}{20}=\frac{5 \cdot 5}{12 \cdot 5}-\frac{3 \cdot 3}{20 \cdot 3}=\frac{25}{60}-\frac{9}{60}$

Now that the fractions have a common denominator, you can add the numerators to add the fractions:

⇒$\frac{25}{60}-\frac{9}{60}=\frac{25-9}{60}=\frac{16}{60}$

Reducing the fraction by dividing the numerator and denominator by

⇒$\frac{16}{60}=\frac{16 \div 4}{60 \div 4}=\frac{4}{15}$

From the above step, we will get the answer 4/15.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 17 Problem 9 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator.

The LCM of 12 and 20 is 60 so rewrite the fractions to have a denominator of 30:

⇒ $\frac{3}{5}+\frac{3}{20}=\frac{3 \cdot 4}{5 \cdot 4}+\frac{3}{20}=\frac{12}{20}+\frac{3}{20}$

Now that the fractions have a common denominator, you can add the numerators to add the fractions:

⇒ $\frac{12}{20}+\frac{3}{20}=\frac{12+3}{20}=\frac{15}{20}$

Reducing the fraction by dividing the numerator and denominator by

⇒ $\frac{15}{20}=\frac{15 \div 5}{20 \div 5}=\frac{3}{4}$

From the above step, we will get the answer 3/4.

Page 17 Problem 10 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator

The LCM of 8 and 24 is 24 so rewrite the fractions to have a denominator of 24:

⇒$\frac{5}{8}-\frac{5}{24}=\frac{5 \cdot 3}{8 \cdot 3}-\frac{5}{24}=\frac{15}{24}-\frac{5}{24}$

Now that the fractions have a common denominator, you can add the numerators to add the fractions:

⇒$\frac{15}{24}-\frac{5}{24}=\frac{15-5}{24}=\frac{10}{24}$

Reducing the fraction by dividing the numerator and denominator by then the GCF of 2 gives.

⇒$\frac{10}{24}=\frac{10 \div 2}{24 \div 2}=\frac{5}{12}$

From the above step, we will get the answer 5/12.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 17 Problem 11 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator

The LCM of 12 and 8 is 24 so rewrite the fractions to have a denominator of 24:

⇒ $3 \frac{5}{12}+1 \frac{3}{8}=3 \frac{5 \cdot 2}{12 \cdot 2}+1 \frac{3 \cdot 3}{8 \cdot 3}=3 \frac{10}{24}+1 \frac{9}{24}$

Now the fraction has a common denominator, you can add the mixed numbers by adding the whole numbers and adding the numerators.

⇒ $3 \frac{10}{24}+1 \frac{9}{24}=4 \frac{10+9}{24}=4 \frac{19}{24}$

From the above step, we will get the answer 4×19/24.

Page 17 Problem 12 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator.

The LCM of 10 and 18 is 90 so rewrite the fractions to have a denominator of 90:

⇒$2 \frac{9}{10}-1 \frac{7}{18}=2 \frac{9 \cdot 9}{10 \cdot 9}-1 \frac{7 \cdot 5}{18 \cdot 5}=2 \frac{81}{90}-1 \frac{35}{90}$

Now the fraction has a common denominator, you can add the mixed numbers by adding the whole numbers and adding the numerators.

⇒$2 \frac{81}{90}-1 \frac{35}{90}=1 \frac{81-35}{90}=1 \frac{46}{90}$

Reducing the fraction by dividing the numerator and denominator by then the GCF of 2 gives.

⇒$1 \frac{46}{90}=1 \frac{46 \div 2}{90 \div 2}=1 \frac{23}{45}$

From the above step, we will get the answer 1×23/45.

Page 17 Problem 13 Answer

We have to solve the given question: Louis spent 12 hours last week practicing guitar. If 1/4

of the time was spent practicing chords, To find: how much time did Louis spend practicing chords?

It is given that Loius spent 12 hours last week practicing guitar and that 1/4

of that time was spent practicing chords. To find the number of hours he spent practicing chords, we must find:12×1/4

⇒ $12 \cdot \frac{1}{4}=\frac{12}{4} \cdot 1=3 \cdot 1=3$hours

From the above step, we will get the answer 3 hours

Solutions For Go Math Grade 6 Exercise 4.1 Operations With Fractions

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 17 Problem 14 Answer

It is given that Angie and her friends ate 3/4

of the pizza and her brother ate 2/3 of what was left. To find how much of the original pizza that her brother ate, we must first find how much was left after Angie and her friends ate pizza.

They started with a whole pizza so we can subtract $\frac{3}{4}$from a whole to find how much is left. Remember that you need to get a common denominator before you can subtract:

⇒ $1-\frac{3}{4}=\frac{4}{4}-\frac{3}{4}=\frac{4-3}{4}=\frac{1}{4}$

Her brother then at $\frac{2}{3}$ of the remaining $\frac{1}{4}$ of the pizza. To find what fraction of the original pizza he ate, we can then find:

⇒ $\frac{1}{4}.\frac{2}{3}$

To multiply two fractions multiply the numerators and then multiply the denominators:

⇒ $\frac{1}{4} \cdot \frac{2}{3}=\frac{1 \cdot 2}{4 \cdot 3}=\frac{2}{12}$

Since 2 and 12 have a GCF of 2, we can reduce the fraction by dividing the numerators and denominators by 2:

⇒ $\frac{2}{12}=\frac{2 \div 2}{12 \div 2}=\frac{1}{6}$ of the pizza.

From the above step, we will get the answer 1/6 of the pizza.

Page 18 Exercise 1 Answer

we have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators.

⇒$\frac{3}{4} \cdot \frac{7}{9}=\frac{3 \cdot 7}{4 \cdot 9}=\frac{21}{36}$

Since 21 and 36 have a GCF of 3, we can reduce the fraction by dividing the numerators and denominators by 3:

⇒$\frac{21}{36}=\frac{21 \div 3}{36 \div 3}=\frac{7}{12}$

From the above step, we will get the answer/12

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 18 Exercise 2 Answer

we have to use the greatest common factor to write each answer in simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators.

⇒ $\frac{2}{7} \cdot \frac{7}{9}=\frac{2 \cdot 7}{7 \cdot 9}=\frac{14}{63}$

Since 14 and 63 have a GCF of 7, we can reduce the fraction by dividing the numerators and denominators by 7:

⇒ $\frac{14}{63}=\frac{14 \div 7}{63 \div 7}=\frac{2}{9}$

From the above step, we will get the answer 2/9

Page 18 Exercise 3 Answer

we have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators.

⇒ $\frac{7}{11} \cdot \frac{22}{28}=\frac{7 \cdot 22}{11 \cdot 28}=\frac{154}{308}$

Since 154 and 308 have a GCF of 154, we can reduce the fraction by dividing the numerators and denominators by 154:

⇒ $\frac{154}{308}=\frac{154 \div 154}{308 \div 154}=\frac{1}{2}$

From the above step, we will get the answer1/2

Page 18 Exercise 4 Answer

we have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators.

Remember that a whole number can be written as a fraction with 1 as the denominator:

⇒ $8 \cdot \frac{3}{10}=\frac{8}{1} \cdot \frac{3}{10}=\frac{8 \cdot 3}{1 \cdot 10}=\frac{24}{10}$

Since 24 and 10 have a GCF of 2, we can reduce the fraction by dividing the numerators and denominators by 2:

⇒ $\frac{24}{10}=\frac{24 \div 2}{10 \div 2}=\frac{12}{5}$

Rewriting the improper fraction as a mixed number then gives:

⇒ $\frac{12}{5}=2 \frac{2}{5}$

From the above step, we will get the answer 2×2/5.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 18 Exercise 5 Answer

we have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators.

⇒ $\frac{4}{9} \cdot \frac{3}{4}=\frac{4 \cdot 3}{9 \cdot 4}=\frac{12}{36}$

Since 12 and 36 have a GCF of 12, we can reduce the fraction by dividing the numerators and denominators by 12:

⇒ $\frac{12}{36}=\frac{12 \div 12}{36 \div 12}=\frac{1}{3}$

From the above step, we will get the answer 1/3.

Page 18 Exercise 6 Answer

we have to use the greatest common factor to write each answer in the simplest form.

To multiply two fractions, multiply the numerators and then multiply the denominators

⇒ $\frac{3}{7} \cdot \frac{2}{3}=\frac{3 \cdot 2}{7 \cdot 3}=\frac{6}{21}$

Since 6 and 21 have a GCF of 3, we can reduce the fraction by dividing the numerators and denominators by 3:

⇒ $\frac{6}{21}=\frac{6 \div 3}{21 \div 3}=\frac{2}{7}$

From the above step, we will get the answer2/7

Go Math Grade 6 Operations With Fractions Exercise 4.1 Key

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 18 Exercise7 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator.

The LCM of 9 and 12 is 36 so rewrite the fractions to have a denominator of 36:

⇒$\frac{7}{9}+\frac{5}{12}=\frac{7 \cdot 4}{9 \cdot 4}+\frac{5 \cdot 3}{12 \cdot 3}=\frac{28}{36}+\frac{15}{36}$

Now the fraction has a common denominator, you can add the mixed numbers by adding the whole numbers and adding the numerators.

⇒$\frac{28}{36}+\frac{15}{36}=\frac{28+15}{36}=\frac{43}{36}$

Converting the improper fraction to a mixed number then gives:

⇒$\frac{43}{36}=1 \frac{7}{36}$

From the above step, we will get the answer1x7/36

Page 18 Exercise 8 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator.

The LCM of 24 and 8 is 24 so rewrite the fractions to have a denominator of 24:

⇒$\frac{21}{24}-\frac{3}{8}=\frac{21}{24}-\frac{3 \cdot 3}{8 \cdot 3}=\frac{21}{24}-\frac{9}{24}$

Now the fraction has a common denominator, you can add the mixed numbers by adding the whole numbers and adding the numerators.

⇒$\frac{21}{24}-\frac{9}{24}=\frac{21-9}{24}=\frac{12}{24}$

Reducing the fraction by dividing the numerator and denominator by then the GCF of 2 gives.

⇒$\frac{12}{24}=\frac{12 \div 12}{24 \div 12}=\frac{1}{2}$

From the above step, we will get the answer 1/2.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 18 Exercise 9 Answer

We have to add and subtract the given equation using the least common multiple as the denominator.

To add fractions with unlike denominators, you must first rewrite the fractions to have a common denominator.

The LCM of 15 and 12 is 60 so rewrite the fractions to have a denominator of 60:

⇒ $\frac{11}{15}+\frac{7}{12}=\frac{11 \cdot 4}{15 \cdot 4}+\frac{7 \cdot 5}{12 \cdot 5}=\frac{44}{60}+\frac{35}{60}$

Now the fraction has a common denominator, you can add the mixed numbers by adding the whole numbers and adding the numerators.

⇒ $\frac{44}{60}+\frac{35}{60}=\frac{44+35}{60}=\frac{79}{60}$

Converting the improper fraction to a mixed number then gives:

⇒ $\frac{79}{60}=1 \frac{19}{60}$

From the above step, we will get the answer 1×19/60.

Detailed Answers For Go Math Grade 6 Exercise 4.1 Operations With Fractions

Go Math Answer Key

Go Math! Grade 6 Exercise 4.2: Operations with Fractions Solutions

November 18, 2024July 17, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions

Page 19 Problem 1 Answer

we have to find the reciprocal of 5/7

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

The reciprocal of 5/7 is then 7/5.

From the above step, we get the reciprocal 7/5.

Page 19 Problem 2 Answer

we have to find the reciprocal of 3/4

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

The reciprocal of 3/4 is then 4/3.

From the above step we get the reciprocal of 3/4 is then 4/3.

Page 19 Problem 3 Answer

we have to find the reciprocal of 3/5

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

The reciprocal of 3/5 is then 5/3.

From the above step we get the reciprocal of 3/5 is then 5/3.

$Go Math! Practice Fluency Workbook Grade 6 Chapter 4 Operations with Fractions Exercise 4.2 Answer Key$

Page 19 Problem 4 Answer

we have to find the reciprocal of 1/10

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

The reciprocal of 1/10 is then 10/1, which can be simplified to 10.

From the above step we get the reciprocal of 1/10 is then 10/1, which can be simplified to 10.

Go Math Grade 6 Exercise 4.2 Operations With Fractions Solutions

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 5 Answer

we have to find the reciprocal of 4/9

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

The reciprocal of 4/9 is then 9/4.

From the above step we get the reciprocal of 4/9 is then 9/4

Page 19 Problem 6 Answer

we have to find the reciprocal of 13/14

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

The reciprocal of 13/14 is then 14/13.

From the above step we get the reciprocal of 13/14 is then 14/13.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 7 Answer

we have to find the reciprocal of 7/12

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

The reciprocal of 7/12 is then 12/7.

From the above step we get the reciprocal of 7/12 is then 12/7.

Page 19 Problem 8 Answer

We need to find the reciprocal of 3/10.

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

Flipping the numerator and denominator, of $\frac{3}{10} \text { we get: } \frac{10}{3} \text {. }$

Also $\frac{3}{10} \times \frac{10}{3}=1$ holds.

10/3 is the reciprocal of 3/10.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 9 Answer

We need to find the reciprocal of 5/8.

To find the reciprocal of a fraction, you can then flip the fraction so the numerator and denominator switch places.

Flipping the numerator and denominator, $\frac{5}{8} \text { we get: } \frac{8}{5} \text {. }$

Also, $\frac{5}{8} \times \frac{8}{5}=1$ holds.

8/5 is the reciprocal of 5/8.

Page 19 Problem 10 Answer

We need to divide 5/6 and 1/2 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{5}{6} \div \frac{1}{2}=\frac{5}{6} \cdot \frac{2}{1}$

⇒ $\frac{10}{6}$

Reduce the fraction by dividing the numerator and denominator by their GCF of 2;

⇒ $\frac{10 \div 2}{6 \div 2}=\frac{5}{3}$

⇒ $1 \frac{2}{3} .$

The quotient of 5/6 and 1/2 equals 1×2/3.

Go Math Grade 6 Exercise 4.2 Operations With Fractions Answers

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 11 Answer

We need to divide 7/8 and 2/3 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{7}{8} \div \frac{2}{3}=\frac{7}{8} \cdot \frac{3}{2}$

⇒ $\frac{21}{16}$

Converting the improper fraction to a mixed number then gives $\frac{21}{16}=1 \frac{5}{16}$

The quotient of 7/8 and 2/3 is 1×5/16.

Page 19 Problem 12 Answer

We need to divide 9/10 and 3/4 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{9}{10} \div \frac{3}{4} =\frac{9}{10} \cdot \frac{4}{3}$

⇒ $\frac{36}{30}$

Reduce the fraction by dividing the numerator and denominator by their GCF of 6 :

⇒ $\frac{36 \div 6}{30 \div 6}=\frac{6}{5}$

⇒ $1 \frac{1}{5} .$

The quotient of 9/10 and 3/4 equals 1×1/5.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 13 Answer

We need to divide 3/4 and 9 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{3}{4} \div 9 =\frac{3}{4} \cdot \frac{1}{9} $

⇒ $\frac{3}{36}$

Reduce the fraction by dividing the numerator and denominator by their GCF of 3:

⇒ $\frac{3 \div 3}{36 \div 3}=\frac{1}{12} \text {. }$

The quotient of 3/4 and 9 is 1/12.

Page 19 Problem 14 Answer

We need to divide 6/9 and 6/7 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{6}{9} \div \frac{6}{7} =\frac{6}{9} \cdot \frac{7}{6}$

⇒ $\frac{42}{54}$

Reduce the fraction by dividing the numerator and denominator by their GCF of 6:

⇒ $\frac{42 \div 6}{54 \div 6}=\frac{7}{9}$

The quotient of 6/9 and 6/7 is 7/9.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 15 Answer

We need to divide 5/6 and 3/10 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{5}{6} \div \frac{3}{10}=\frac{5}{6} \cdot \frac{10}{3}$

⇒ $\frac{50}{18}$

Reduce the fraction by dividing the numerator and denominator by their GCF of 2:

⇒ $\frac{50 \div 2}{18 \div 2}=\frac{25}{9}$

⇒ $=2 \frac{7}{9} .$

The quotient of 5/6 and 3/10 is 2×7/9.

Page 19 Problem 16 Answer

We need to divide 5/6 and 3/4 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

when dividing by a fraction we must first rewrite it as multiplying by its

⇒ $\Rightarrow \frac{5}{6} \div \frac{3}{4} =\frac{5}{6} \cdot \frac{4}{3}$

⇒ $\frac{20}{18}$

Reduce the fraction by dividing the numerator and denominator by their

⇒ $\frac{20 \div 2}{18 \div 2}=\frac{10}{9} $

⇒ $\quad=1 \frac{1}{9} .$

The quotient of 5/6 and 3/4 is 1×1/9.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 17 Answer

We need to divide 5/8 and 3/5 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

when dividing by a fraction we must first rewrite it as multiplying by its

⇒ $\frac{5}{8} \div \frac{3}{5} =\frac{5}{8} \cdot \frac{5}{3}$

⇒ $\frac{25}{24} .$

Reduce the fraction by dividing the numerator and denominator by their

⇒ $\frac{25}{24}=1 \frac{1}{24}$

The quotient of 5/8 and 3/5 is 1×1/24.

Page 19 Problem 18 Answer

We need to divide 21/32 and 7/8 and express it in a simpler form.

Dividing by a number is the same as multiplying by its reciprocal.

when dividing by a fraction we must first rewrite it as multiplying by its

⇒ $\frac{21}{32} \div \frac{7}{8} =\frac{21}{32} \cdot \frac{8}{7}$

⇒ $ \frac{168}{224}$

Reduce the fraction by dividing the numerator and denominator by their

⇒ $\frac{168 \div 56}{224 \div 56}=\frac{3}{4} \text {. }$

The quotient of 21/32 and 7/8 is 3/4.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 19 Answer

Given: Mrs. Marks has 3/4 pound of cheese to make sandwiches. She needs1/32 pounds of cheese for each sandwich.

We need to find the number of sandwiches she can make.

We will use the division of fractions to solve this.

We need to divide the total amount of cheese by the amount of cheese on each sandwich

⇒ $\frac{3}{4} \div \frac{1}{32}$

when dividing by a fraction we must first rewrite it as multiplying by its reciprocal

⇒ $\frac{3}{4} \div \frac{1}{32}=\frac{3}{4} \cdot 32$

Multiplying then gives:

⇒ $\frac{3}{4} \cdot 32=3 \cdot \frac{32}{4}$

= 3 . 8

= 24 Sandwiches

Mrs. Marks can make a total of 24 sandwiches with the cheese she has.

Page 19 Problem 20 Answer

Given: In England, mass is measured in units called stones.

One pound equals 1/14th of a stone and a cat weighs 3/4 stone.

We need to find the weight of the cat in pounds.

We will use the division of fractions to solve this.

The cat weighs about 10×1/2 pounds.

Solutions For Go Math Grade 6 Exercise 4.2 Operations With Fractions

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 19 Problem 21 Answer

Given: One point is equal to 1/72 inch. Esmeralda wants the text on the title page to be 1/2 inch tall.

We need to find what font size should she use.

We will use the division of fractions to solve this.

Esmeralda should use 36 points for her research paper.

Page 20 Exercise 1 Answer

We need to divide 1/4 and 1/3 and express it in a multiplication expression.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{1}{4} \div \frac{1}{3}=\frac{1}{4} \cdot \frac{3}{1}$

⇒ $ \frac{1}{4} \cdot \frac{3}{1}=\frac{1 \cdot 3}{4 \cdot 1}$

⇒ $\frac{3}{4} .$

1/4÷1/3 can be expressed as 1/4.3/1= 3/4.

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 20 Exercise 2 Answer

We need to divide 1/2 and 1/4 and express it in a multiplication expression.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{1}{2} \div \frac{1}{4}=\frac{1}{2} \cdot \frac{4}{1}$

⇒ $ \frac{1}{2} \cdot \frac{4}{1}=\frac{1 \cdot 4}{2 \cdot 1}$

⇒ $\frac{4}{2} .$

= 2

1/2÷ 1/4 can be expressed as 1/2.4/1 = 2.

Page 20 Exercise 3 Answer

We need to divide 3/8 and 1/2 and express it in a multiplication expression.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{3}{8} \div \frac{1}{2} \text { can be expressed as } \frac{3}{8} \cdot \frac{2}{1}=\frac{3}{4} \text {. }$

Page 20 Exercise 4 Answer

We need to divide 1/3 and 3/4 and express it in a multiplication expression.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{1}{3} \div \frac{3}{4} \text { can be expressed as } \frac{1}{3} \cdot \frac{4}{3}=\frac{4}{9} \text {. }$

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 20 Exercise 5 Answer

We need to divide 1/5 and 1/2 and express it in a multiplication expression.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ 

Page 20 Exercise 6 Answer

We need to divide 1/6 and 2/3 and express it in a multiplication expression.

Dividing by a number is the same as multiplying by its reciprocal.

When dividing by a fraction, we must first rewrite it as multiplying by its reciprocal:

⇒ $\frac{1}{6} \div \frac{2}{3} \text { can be expressed as } \frac{1}{6} \cdot \frac{3}{2}=\frac{1}{4} \text {. }$

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations With Fractions Page 20 Exercise 7 Answer

Given :- a dividing fraction 1/8 ÷ 2/5

Find:- the simplest form of expression. First, write the expression as a multiplication expression and then get the answer in fraction form.

Multiplying the first fraction by the second fraction reciprocal 1/8×5/2 = 5/18

Simplest form of $\frac{1}{8} \div \frac{2}{5} \text { is } \frac{5}{18} \text {. }$

Page 20 Exercise 8 Answer

Given :- a expression 1/8 ÷ 1/2

Find:- the simplest form of expression. First, write the expression as a multiplication expression and then get the answer in fraction form.

The simplest form of $\frac{1}{8} \div \frac{1}{2} \text { is } \frac{1}{4} \text {. }$

Multiply the first fraction by the reciprocal of the second fraction
1/8×2/1

=2/8

=1/4

Go Math Grade 6 Operations With Fractions Exercise 4.2 Key

Go Math Answer Key

Go Math! Grade 6 Exercise 4.3: Operations with Fractions Solutions

November 18, 2024July 7, 2023 by Alekhya

Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 4 Operations with Fractions

Page 21 Problem 1 Answer

Given :- a mixed number 10×1/2

Find:- The reciprocal of the given number and confirm number and reciprocal multiplication is one. First, convert the mixed number in improper fraction and take reciprocal of the fraction.

Given in the question a expression in form of mixed number.

First, convert mixed fraction in improper fraction and then take the reciprocal of the term .

expression in form of improper fraction is 10×1/2 = 21/2

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 1$

Reciprocal of the 10×1/2 is 2/21 And we proved multiplication of both terms is one.

$Go Math! Practice Fluency Workbook Grade 6 Chapter 4 Operations with Fractions Exercise 4.3 Answer Key$

Page 21 Problem 2 Answer

Given :- a mixed number 6×3/7

Find:- The reciprocal of the given number and confirm number and reciprocal multiplication is one .First convert the mixed number in improper fraction and take reciprocal of the fraction.

Given in the question a expression in form of mixed number .

First, convert mixed fraction in improper fraction and then take the reciprocal of the term .

expression in form of improper fraction is 6×3/7 = 45/7

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 2$

Reciprocal of the 6×3/7 is 7/45 And we proved the multiplication of both term is one.

Page 21 Problem 3 Answer

Given :- a mixed number 2×8/9

Find:- The reciprocal of the given number and confirm number and reciprocal multiplication is one. First convert the mixed number in improper fraction and take reciprocal of the fraction.

Given in the question a expression in form of mixed number.

First, convert mixed fraction in improper fraction and then take the reciprocal of the term.

expression in form of improper fraction is 2×8/9=26/9

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 3$

Reciprocal of the expression 2×8/9 is 6/29 And we proved multiplication of both term is one.

Go Math Grade 6 Exercise 4.3 Operations With Fractions Solutions

Page 21 Problem 4 Answer

Given :- a mixed number 15×1/4

Find:- The reciprocal of the given number and confirm number and reciprocal multiplication is one .First convert the mixed number in improper fraction and take reciprocal of the fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 4$

Reciprocal of the term 61/4 is 4/61 And we proved multiplication of both term is one.

Page 21 Problem 5 Answer

Given :- a mixed number 9×2/3

Find:- The reciprocal of the given number and confirm number and reciprocal multiplication is one .First convert the mixed number in improper fraction and take reciprocal of the fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 5$

Reciprocal of the expression 9×2/3 = 2/29 And we proved multiplication of both terms is one .

Page 21 Problem 6 Answer

Given :- a expression 7×5/8

Find:- The reciprocal of the given number and confirm number and reciprocal multiplication is one .First convert the mixed number in improper fraction and take reciprocal of the fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 6$

Reciprocal of the expression 7×5/8 is 8/61 And we proved the multiplication of both terms is one .

Page 21 Problem 7 Answer

Given :- a expression 8/10÷1×5/6

Find:- The simplest form of the given expression .First convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 7$

Simplest form of the expression 8/10÷1×5/6 is 24/55.

Page 21 Problem 8 Answer

Given :- a expression 2÷1×6/7

Find:- The simplest form of the given expression .First convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 8$

Simplest form of the expression is 2÷1×6/7=1×1/13.

Page 21 Problem 9 Answer

Given :- a expression 3×3/5÷2×1/4

Find:- The simplest form of the given expression First convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 9 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 9 2$

Simplest form of the expression 3×3/5÷2×1/4 is 1×11/25.

Page 21 Problem 10 Answer

Given :- a expression 4×1/2÷2×3/8

Find:- The simplest form of the given expression .First convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 10 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 10 2$

Simplest form of the expression 4×1/2÷2×3/8 is 1×17/19.

Page 21 Problem 11 Answer

Given :- a expression 5×5/6÷3×1/6

Find:- The simplest form of the given expression.First, convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 11 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 11 2$

Simplest form of the 5×5/6÷3×1/6 =1×16/19.

Page 21 Problem 12 Answer

Given :- a expression 11/12÷2×5/8

Find :- The simplest form of the given expression .First convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 12 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 12 2$

Simplest form of the expression 11/12÷2×5/8 is 22/63

Go Math Grade 6 Exercise 4.3 Operations With Fractions Answers

Page 21 Problem 13 Answer

Given :- a expression 1×9/13÷3/8

Find:- The simplest form of the given expression .First convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 13 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 13 2$

Simplest form of the expression 1×9/13÷3/8 is 4×20/39

Page 21 Problem 14 Answer

Given :- a expression 6×4/5÷3×2/9

Find :- The simplest form of the given expression.First, convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 14 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 14 2$

Simplest form of the expression 6×4/5÷3×2/9 is 68/145.

Page 21 Problem 15 Answer

Given :- a expression 9×2/3÷6×8/9

Find :- The simplest form of the given expression. First, convert the mixed fraction in improper fraction then multiply the first fraction by reciprocal of the second fraction.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 15 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 15 2$

Simplest for of the expression 9×2/3÷6×8/9 is 1 25/62.

Page 21 Problem 16 Answer

Given:- Area of the concrete is 36×5/6 and the width of the concrete is 5×2/3

Find :- picnic table is 7foot, table would fit along the diagonal.

We need to find the length of the concrete by formula area=length ×width.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 16 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 16 2$

Length of the concrete is 6.5ft and length of the table is 7ft so we can table would fit along the diagonal.

Page 21 Problem 17 Answer

Given:- Width of the mirror is 13×3/4 inches and area of the mirror is 225 square inches.

Find:- we can feet mirror in place of 15 inches by16 inches.

We need to find the length of the mirror by Area=length ×width.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 17 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 17 2$

Length of the mirror is 16.36 inches and the mirror space is 15 by 16 inches So we can’t feet mirror in given space.

Page 21 Problem 18 Answer

Given :- Barney has 16×1/5 yd fabric and for one costume she need 5×2/5

Find:- how many costumes she makes by the 16×1/5 yd fabric.

We need to divide the total fabric by the fabric used in one costume and get the answer.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 18 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions 18 2$

She makes 3 costumes in 16×1/5 yd fabric.

Page 22 Exercise 1 Answer

Given :- a term is 9/14

Find- reciprocal of the given term .

We know the reciprocal of the x is 1/x

Given in the question a term 9/14

Reciprocal of the 9/14=14/9

By the definition of reciprocal.

Multiplication of both terms is 9/14×14/9 is 1

Reciprocal of the 9/14 is 14/9

Page 22 Exercise 2 Answer

Given :- a term 3×1/2

Find:- the reciprocal of the term .

First, we need to convert the mixed in improper fraction .and then take reciprocal.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e2$

Multiplication of both terms is 7/2×2/7=1

Reciprocal of the term 3×1/2=2/7.

Page 22 Exercise 3 Answer

Given reciprocal is 10×2/3

To do: Find the given reciprocal

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e3$

The reciprocal of 10×2/3 is 3/32.

Page 22 Exercise 4 Answer

Given a division

To do: Complete the given division in the simplest form

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e4 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e4 2$

Page 22 Exercise 5 Answer

Given a division

To do: Complete the given division in the simplest form.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e5 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e5 2$

Solutions For Go Math Grade 6 Exercise 4.3 Operations With Fractions

Page 22 Exercise 6 Answer

Given a division

To do: Complete the given division in the simplest form

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e6 1$

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e6 2$

Page 22 Exercise 7 Answer

Given a division

To do: Complete the given division in the simplest form

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e7$

The result of the given division is 6×1/4

Page 22 Exercise 8 Answer

Given a division

To do: Complete the given division in the simplest form.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e 8$

The result of the given division is 7/16.

Go Math Grade 6 Operations With Fractions Exercise 4.3 Key

Page 22 Exercise 9 Answer

Given a division

To do: Complete the given division in the simplest form.

$Go Math! Practice Fluency Workbook Grade 6, California 1st Edition, Chapter 4 Operations with Fractions e 9$

The result of the given division is 1×2/3.

Go Math Answer Key