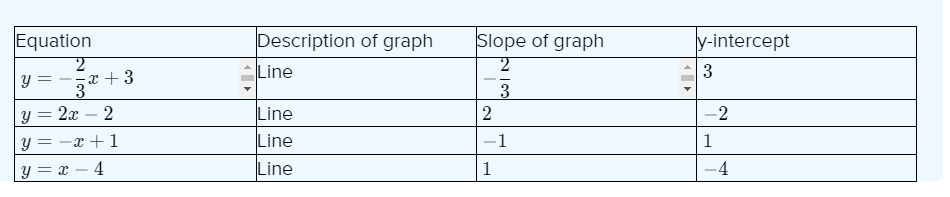
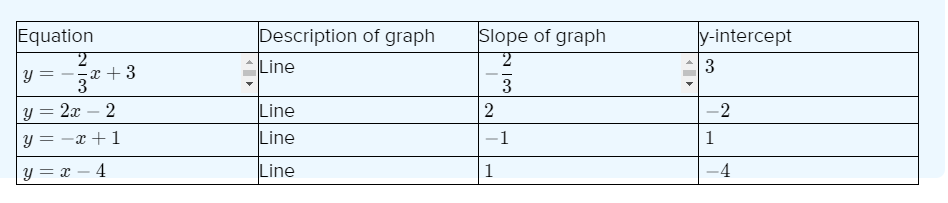
Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.4

Page 112 Exercise 2 Answer

Given: The scatter plot shows the median ages of American women at their first marriage for selected years from 1960 through 2010.

Hence, We have to draw a line that approximates the data. and write an equation of the line.
Firstly, We will observe the given graph carefully, then we draw line approximates from the given data.
After that, locate the points in the graph so that to find the equation of the line,
Using two-point slope formula that is \(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\).

From the given graph. The line approximates the data is

From the above step graph points are(1960,20),(2010,26)

By using the two-point slope formula \(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

Where,x₁ =1960, x₂=2010, y₁ =20, y₂=26.

On putting the values we get

3x−25y=5380

An equation of the line is And, the graph is

Given: The scatter plot shows the median ages of American women at their first marriage for selected years from 1960 through 2010.

Big Ideas Math Algebra 1 Chapter 4 Writing Linear Functions Answer Key

Hence, We have to write a conclusion from the equation we wrote   From  the above solution  we get  3x−25y=5380

This equation tells that on increasing the x,y is also increasing. But the rate differs. that is, 3x=25y+5380

This means that as the years increase the ages is also increase.

The conclusion is on increasing the years, the age of American women at first marriage is also increasing.

Given: The scatter plot shows the median ages of American women at their first marriage for selected years from 1960
through 2010.

Hence, We have to predict the median age of American women at their first marriage in the year 2020.

We will take the help from the above solution, Then put the value of x which is equal to 2020 and we will get the age that is y.

The median age of American women at their first marriage in the year 2020 is 27 years.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.4 Page 114 Exercise 1 Answer

Given:

Hence, We have to find the weight of the baby when the baby is four months old.

Firstly, We will observe the given graph carefully

Then, from the given graph

x−axis denotes the age of the baby and y-axis denotes the weight of the baby.

Therefore, for a 4-month-old baby’s weight according to the graph is 14 pounds.

The weight of the baby when the baby is four months old is 14
pound.

Given:

Hence, We have to find the age of the baby when the baby weighs 17.2 pounds.

Firstly, We will observe the given graph carefully, Then, from the given graph

x-axis denotes the age of the baby, and y−axis denotes the weight of the baby.

Therefore, if the baby’s weight is 17.2 pounds then the baby’s age from the graph is 8 months.

The age of the baby when the baby weighs 17.2 pounds is 8 months.

Big Ideas Math Student Journal Exercise 4.4 Solutions

Given:

Hence, We have to find What tends to happen to the weight of the baby as the age increases.

Firstly, We will observe the given graph carefully, Then, from the given graph.

As we know x-axis denotes the age of the baby and y−axis denotes the weight of the baby.

So, as the age of the baby increases then the weight of the baby also increases but not linearly, as we see in the graph that in some points the flow or linear increment is not followed.

The age of the baby increases similarly the weight of the baby is also increases but not linearly, as we see in the graph that in some points the flow or linear increment is not followed.

Page 115 Exercise 2 Answer
Given:
A graph with many coordinates

To find, the correlation of the coordinates.
We label the coordinates according to their quadrant positions

Mark the signs of different coordinates in different quadrants

Since the y values increase as the x values increase, there is a positive correlation.

For the given graph,x and y show a positive correlation.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.4 Page 115 Exercise 3 Answer

Given:
A graph with points in three quadrants

To find If x and y show a positive, a negative, or no correlation
We arrange them with respect to the position of their coordinates

From the graph
There are 2 points in the first quadrant, so the points are of the form (x,y)

There are 4 points in the second quadrant, so the points are of the form (−x,y)

There are no points in the third quadrant

There are 2 points in the fourth quadrant, so the points are of the form (x,−y)

In the first quadrant, there are 2 points on the horizontal axis, so the coordinates are of the form (x,0)

In the second quadrant, there is 1 point on the vertical axis, so the coordinates are of the form (0,y)

Since the y values decrease as the x values increase, there is a negative correlation.

For the given graph,x and y show a negative correlation.

Writing Linear Functions Practice Problems Chapter 4

Page 115 Exercise 4 Answer

Given:

To find  Tell whether x and y show a positive, a negative, or no correlation.

We can see from the above graph that there is no pattern between the x -values and the y -values.

Also, the points are scattered all over the coordinate plane.

Since the points represent the ordered pairs (x,y), thus, we can see that there is no correlation between x-values and y-values.

We can see clearly that if x increases, then, we cannot see any pattern in the y-values. Similarly, if y increases, then, we cannot see any pattern in the x-values.

The values of x and y show no correlation.

Big Ideas Math Algebra 1 Exercise 4.4 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.4 Page 115 Exercise 5 Answer

Given:

To find Tell whether x and y show a positive, a negative, or no correlation. We can see from the above graph that as x increases, the value of y also increases.

Also, the points are moving from left to right in the coordinate plane. Since the points represent the ordered pairs (x,y), thus, we can see that there is a positive correlation between x -values and y-values.

The values of x and y show a positive correlation.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2

Page 101  Essential  Question  Answer

We have to explain how we use a slope and the point to write an equation.

We can use the point-slope form and represent an equation. The point-slope form is y=mx+b,

We put the value of x, and y from the given point and put the value of the given slope to find the value of constant′ b′.

Then put these values in the point-slope form of the equation, Then er get the required equation.

To write an equation of a line when you are given the slope and a point on the line by using the point-slope form of the line.

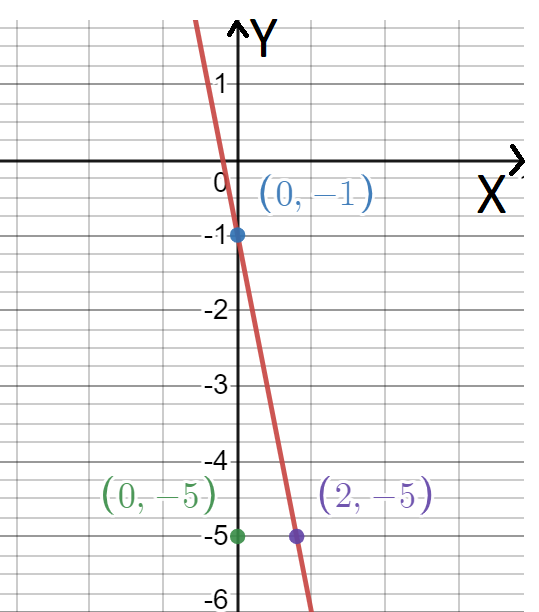
Page 101  Exercise 1  Answer

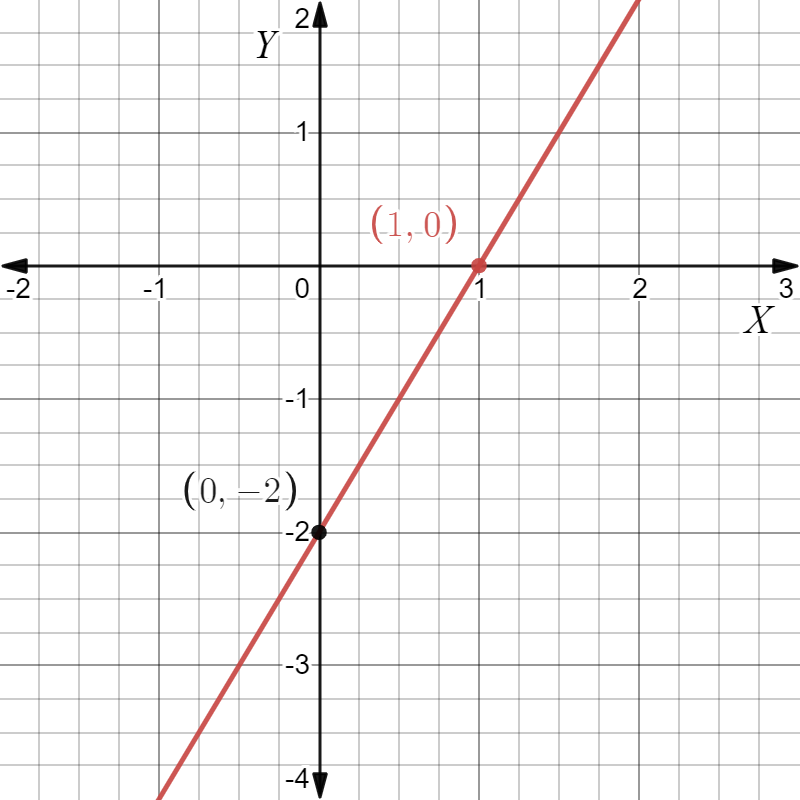
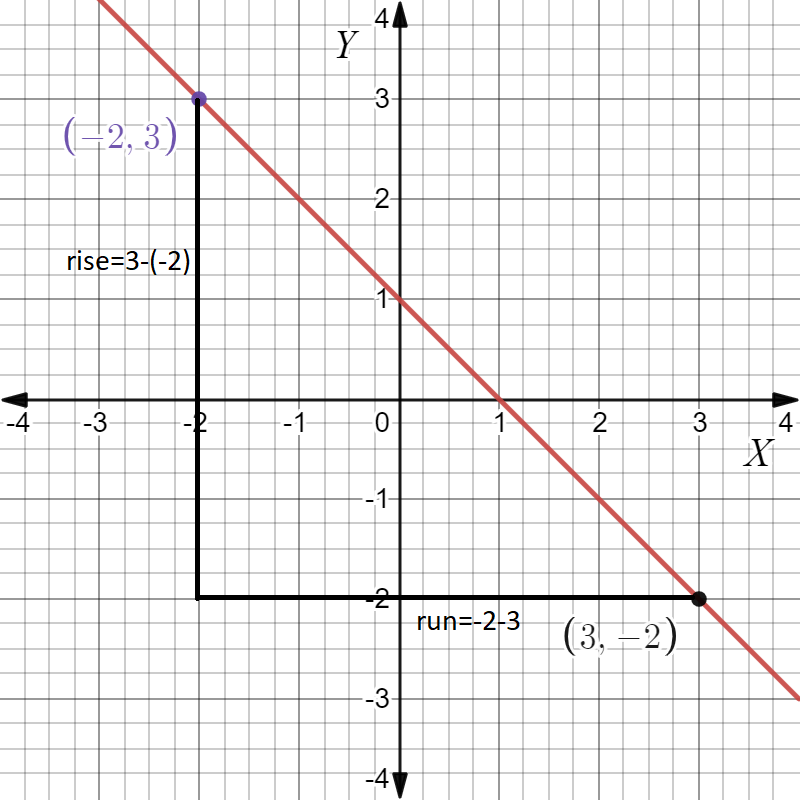
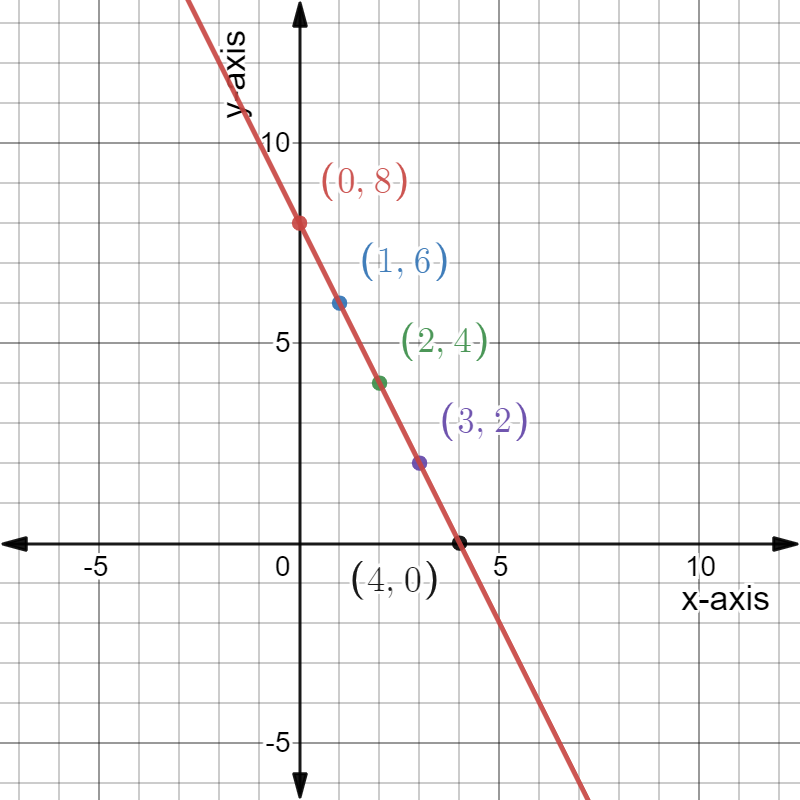
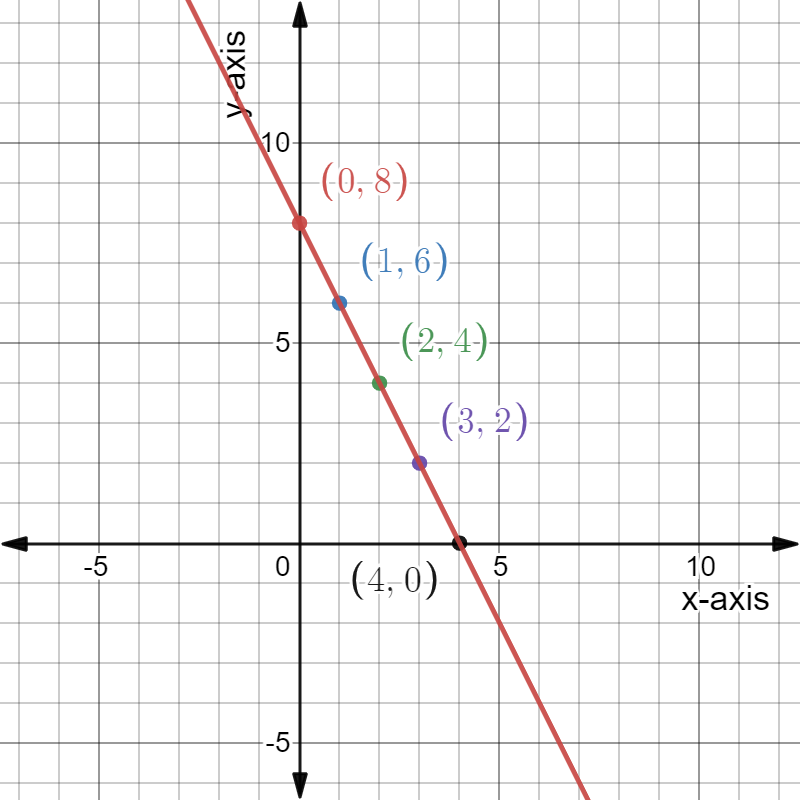
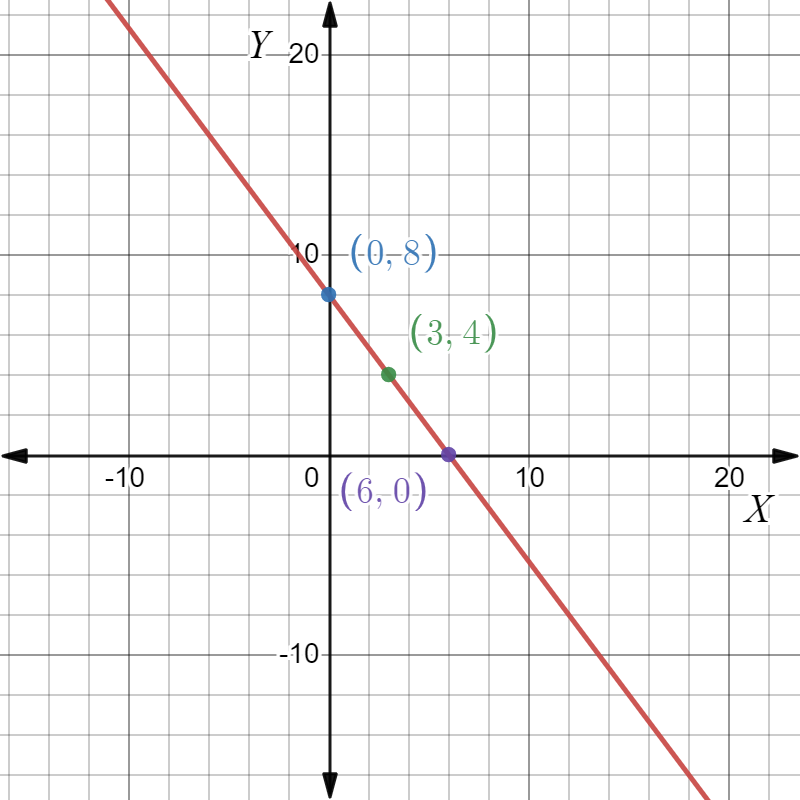
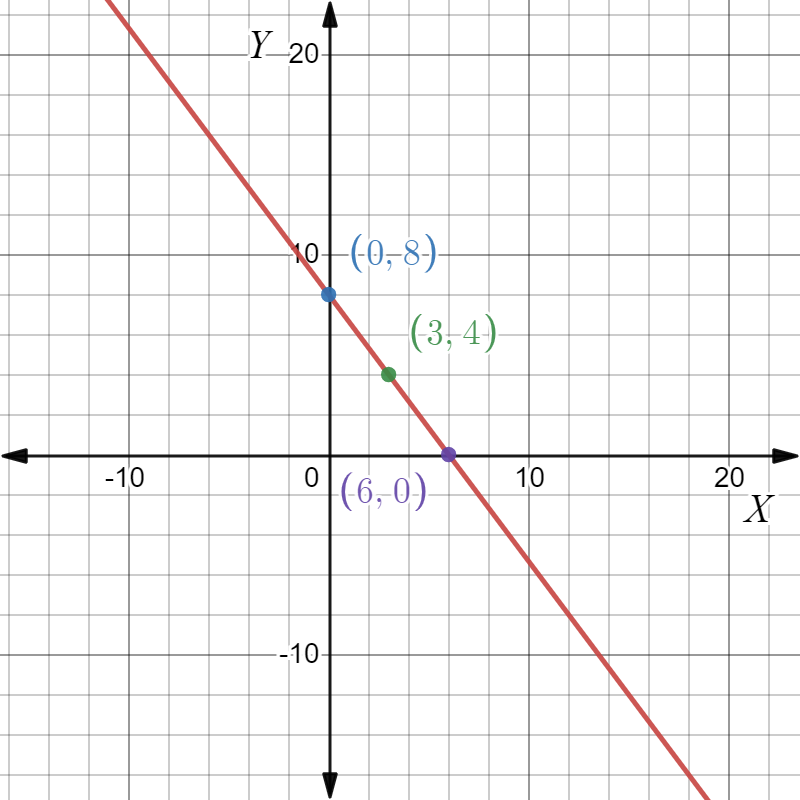
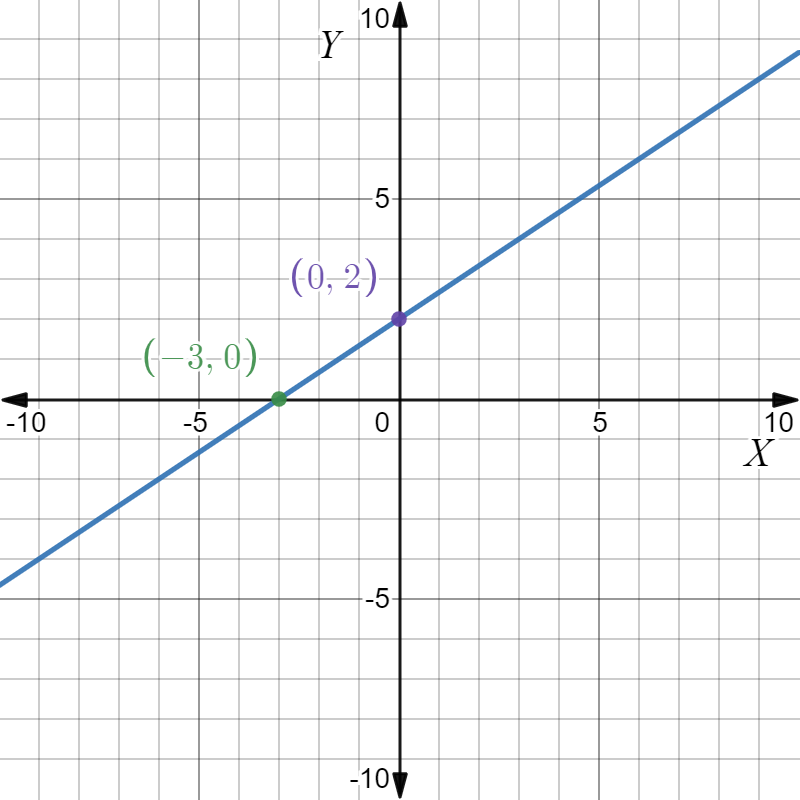
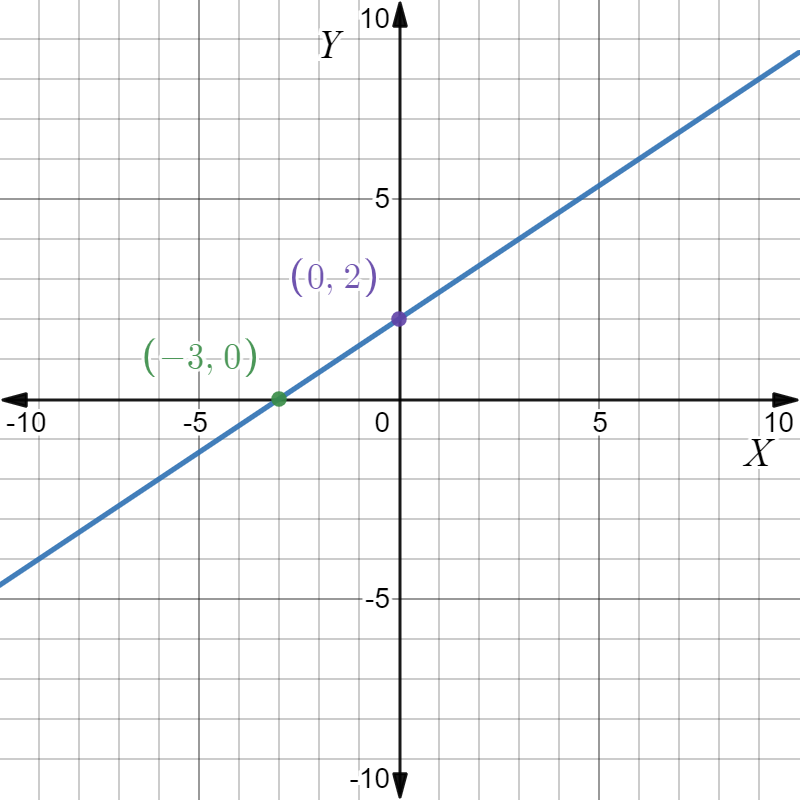
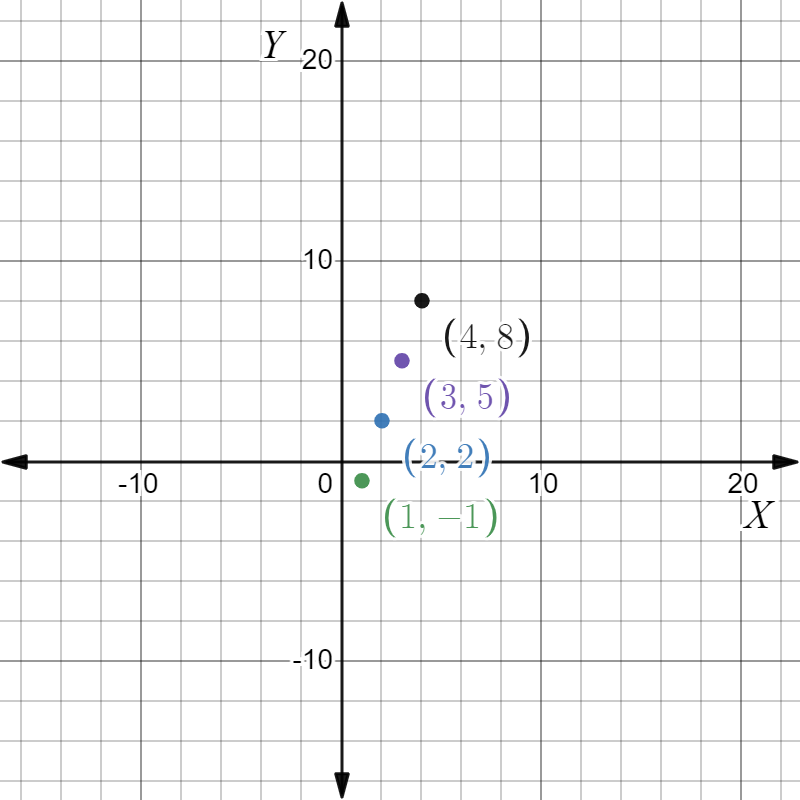
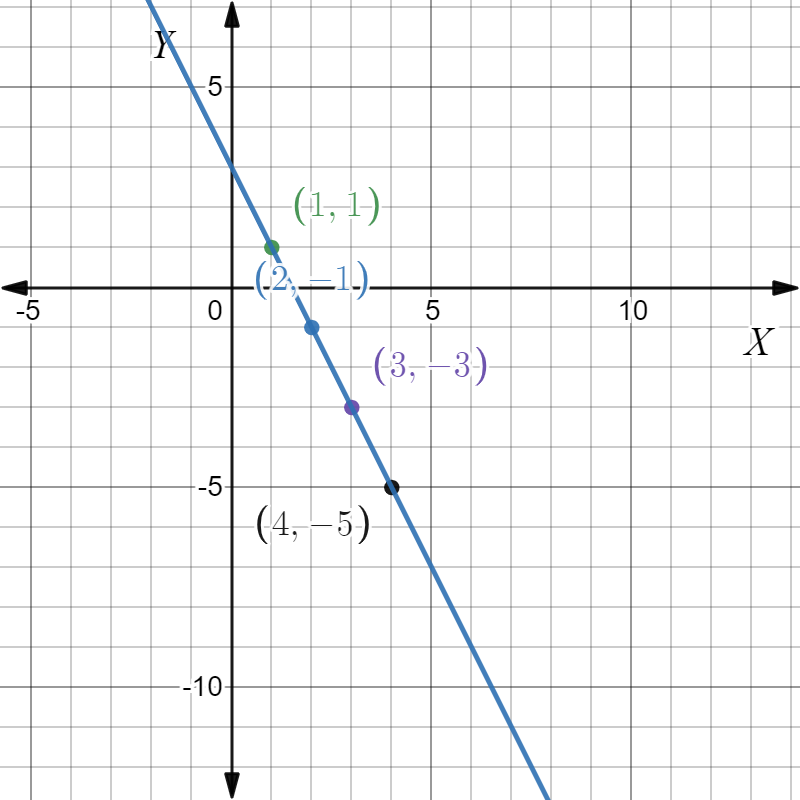
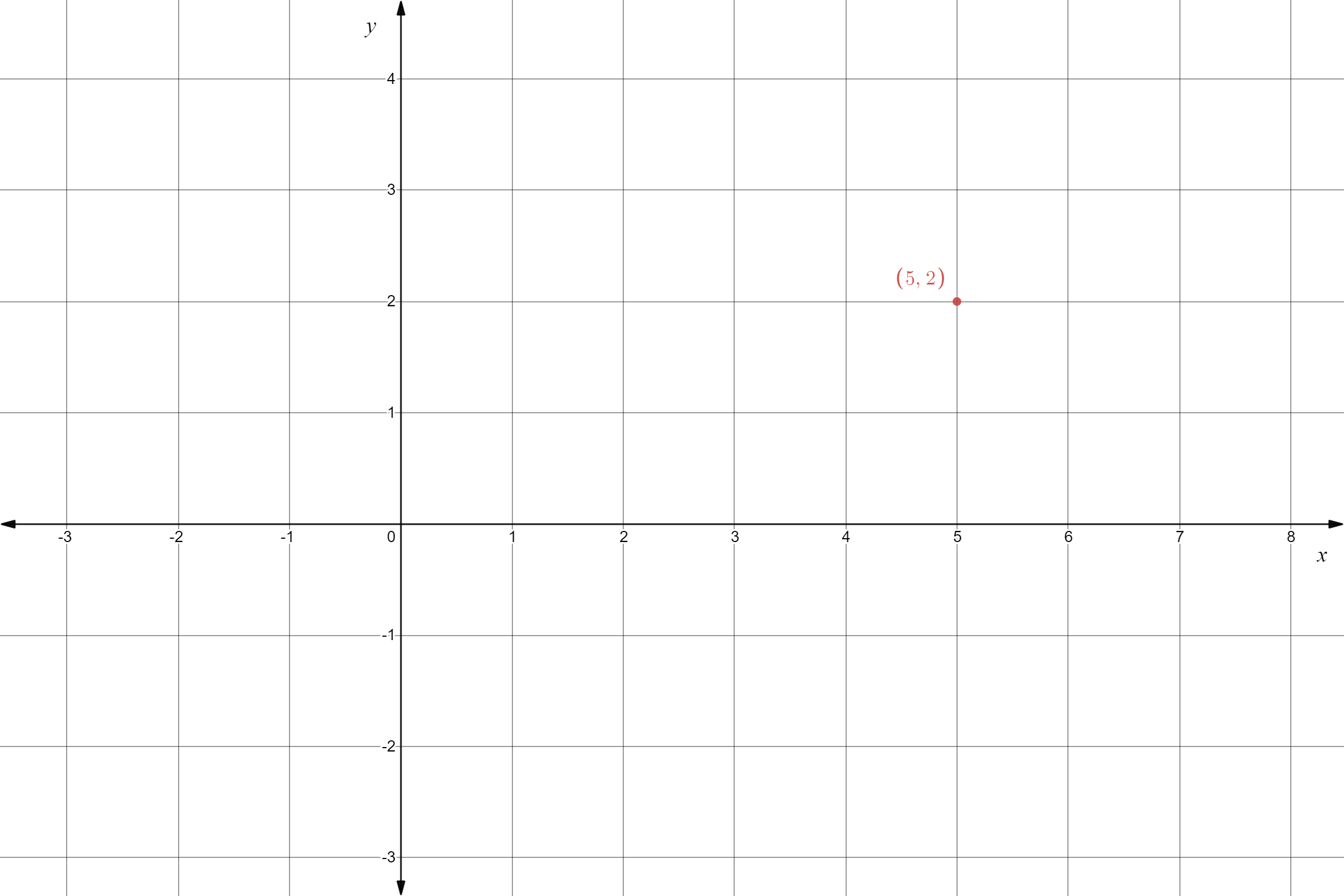
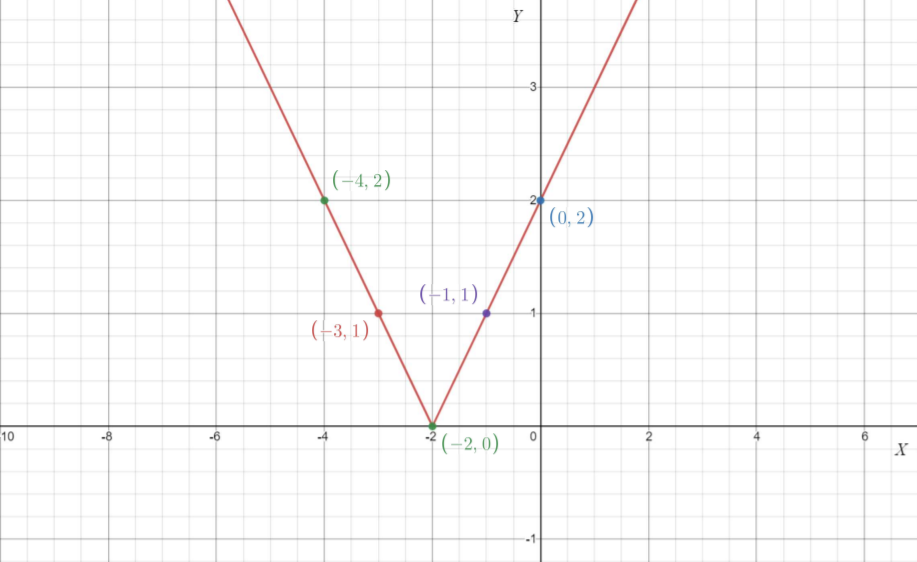
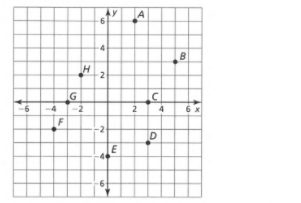
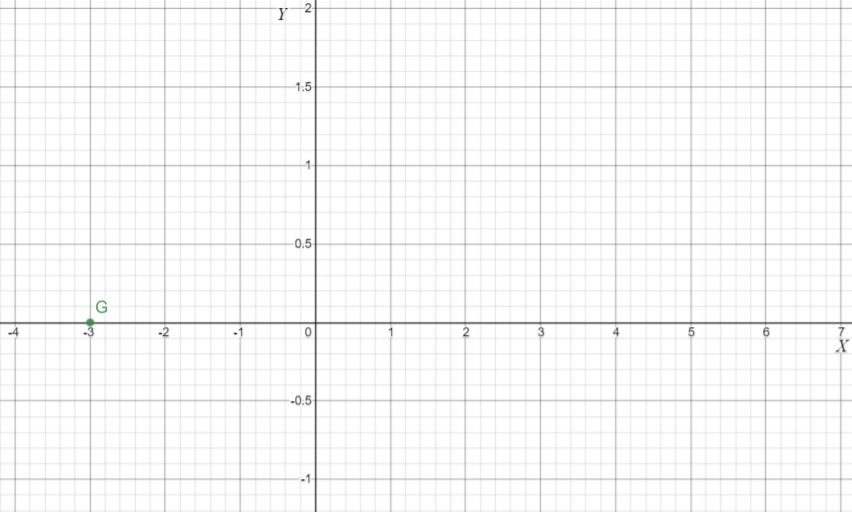
Given: The slope is \(m=\frac{1}{2}\) and the point is given below

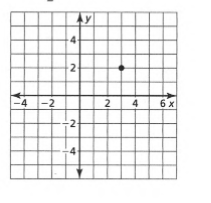
To find  Sketch the line that has the given slope and passes through the given point. Find the y-intercept of the line. Write an equation of the line.

Summary: Identify the point and substitute it and the slope in the point-slope equation. Find the y-intercept by putting x=0 in the equation and solving for y. Plot the point and the intercept and join to get the graph.

From the graph

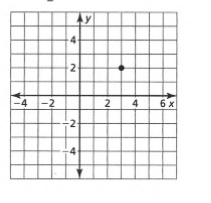
The point is (x₁,y₁)=(3,2). Given the slope is \(m=\frac{1}{2}\). Substituting the values in the point-slope equation,
​y−y₁=m(x−x₁)

y−2=\(\frac{1}{2}\)(x−3)

y-2\(=\frac{x}{2}-\frac{3}{2}\)

y\(=\frac{x}{2}-\frac{3}{2}\)+2

y\(=\frac{x}{2}+\frac{1}{2}\)

Put x=0 in y\(=\frac{x}{2}+\frac{1}{2}\).

​y=0+\(-\frac{1}{2}\)

y=\(-\frac{1}{2}\) which is the y -intercept.

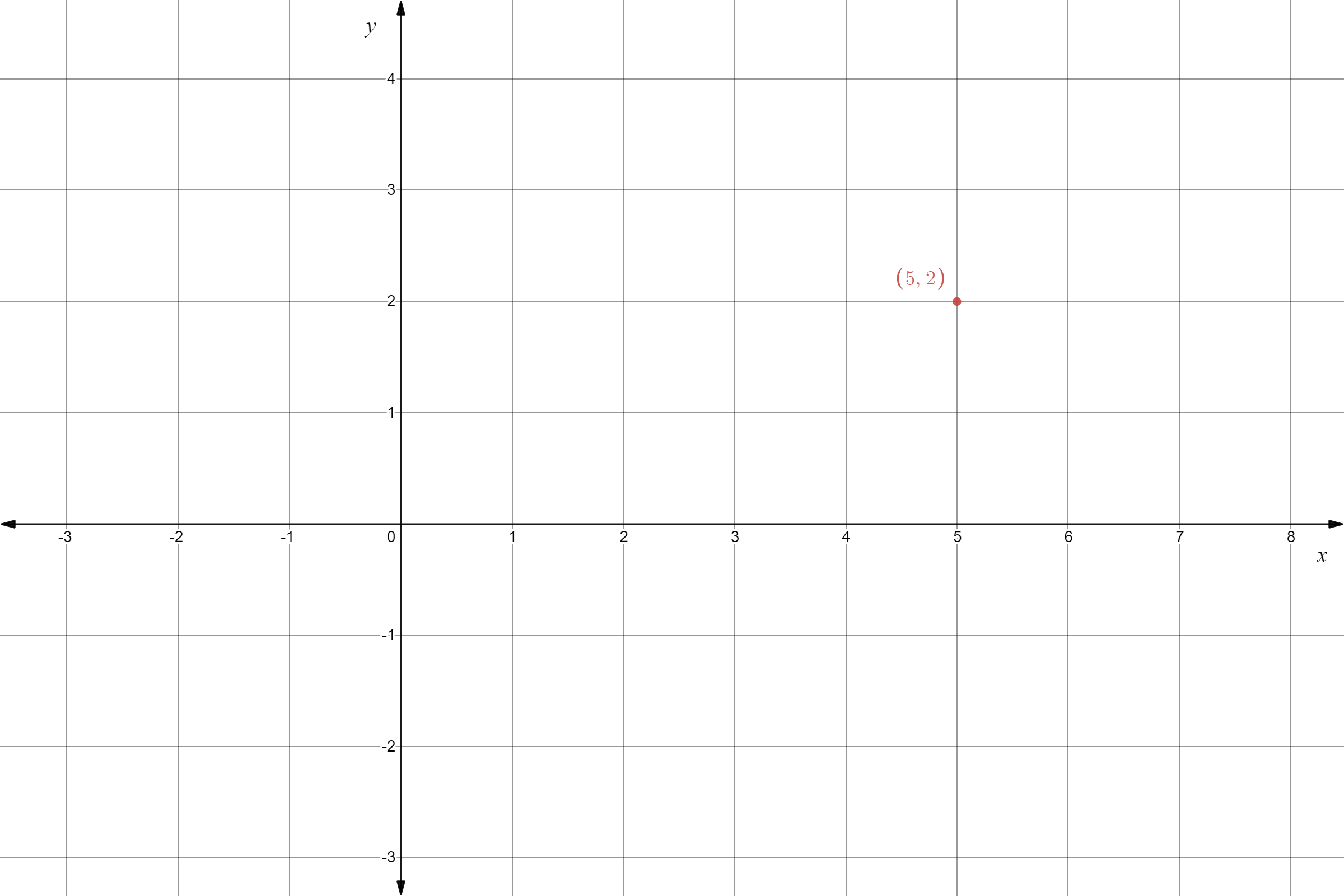
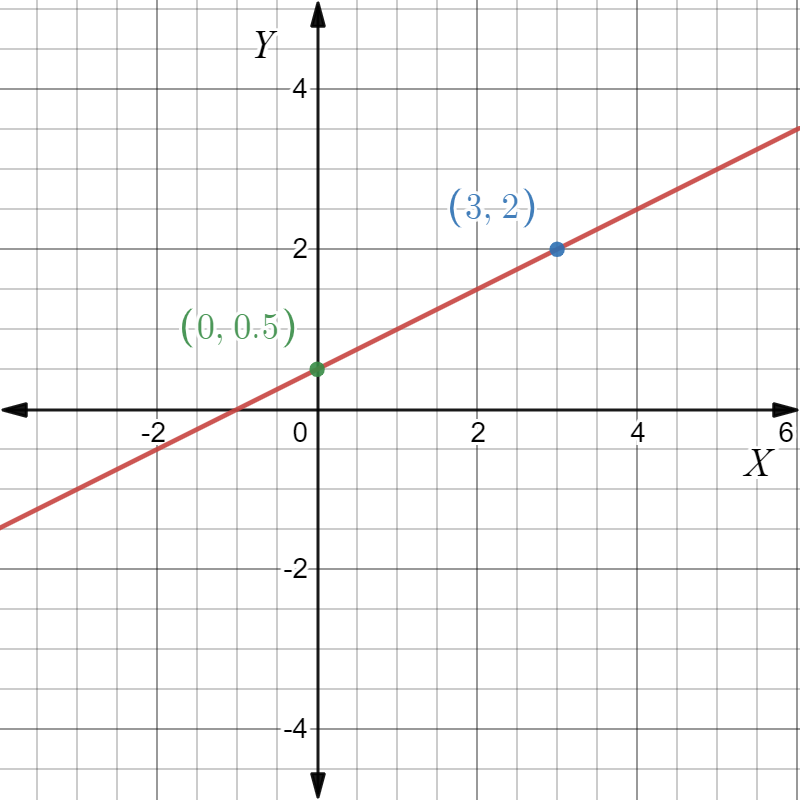
Plot the points (0,\(-\frac{1}{2}\)),(3,2) and join to get the graph.

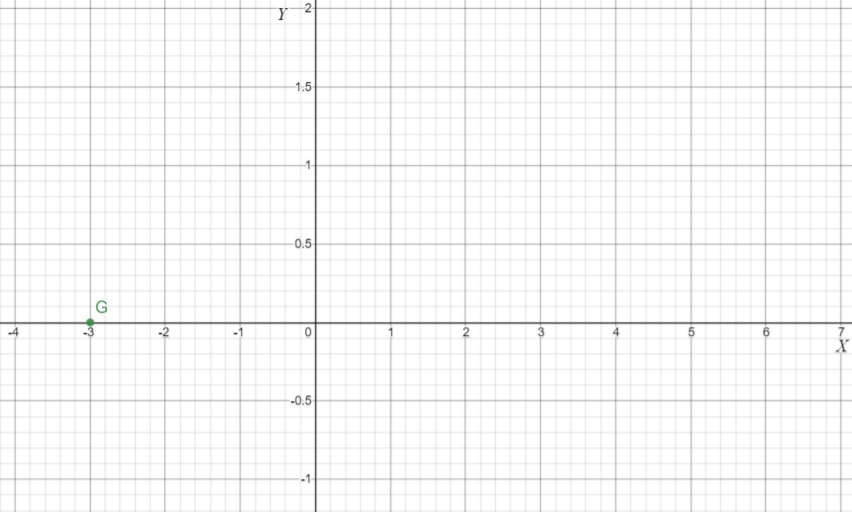
Given the point as

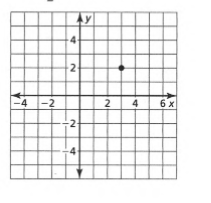
And the slope m=\(-\frac{1}{2}\)

The equation of the line is y\(=\frac{x}{2}+\frac{1}{2}\) and the y intercept is \(-\frac{1}{2}\). The graph is as follows.

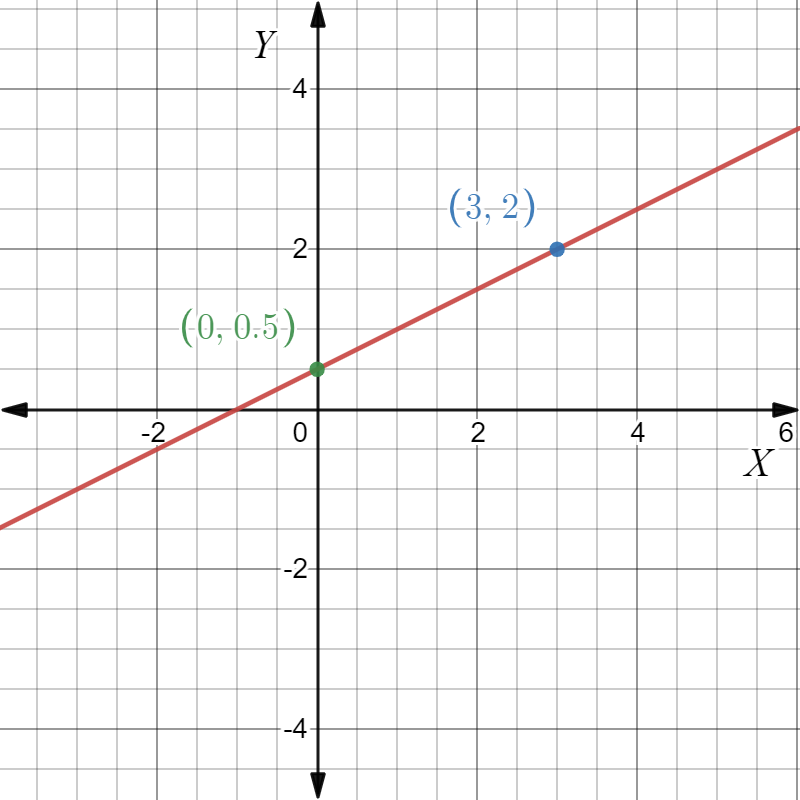
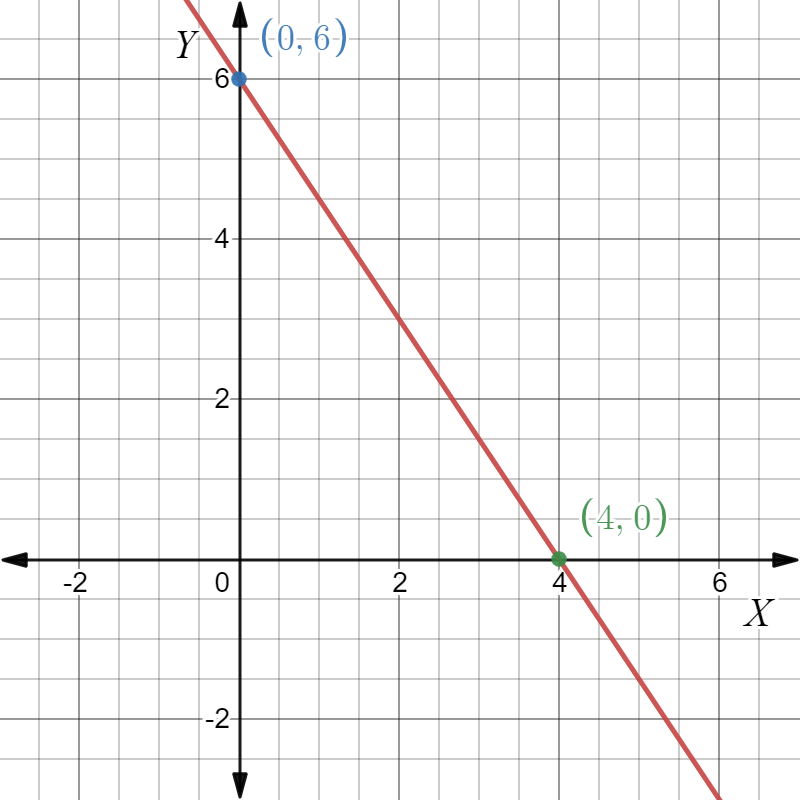
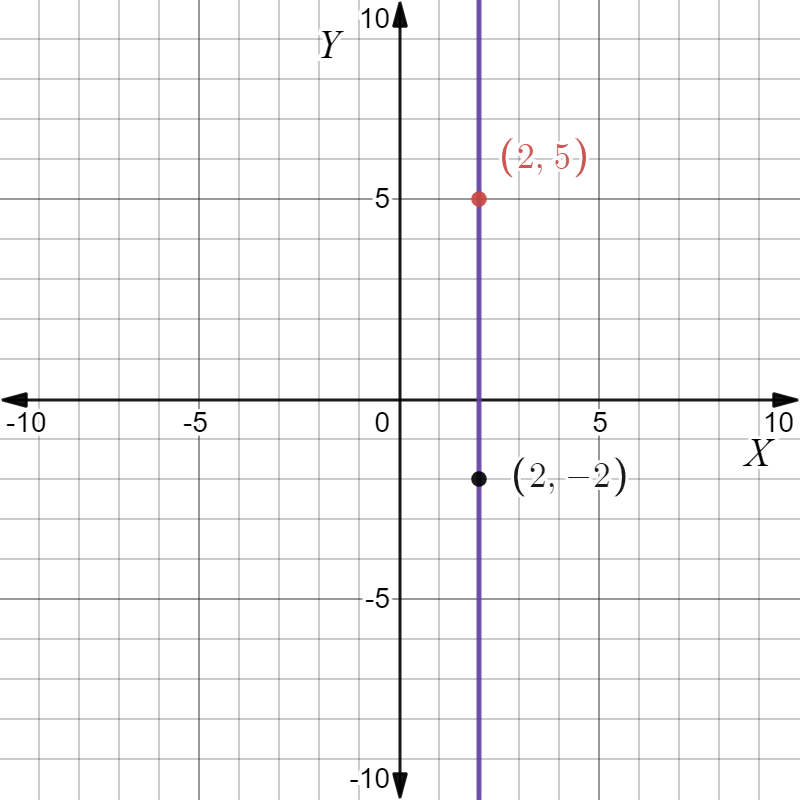
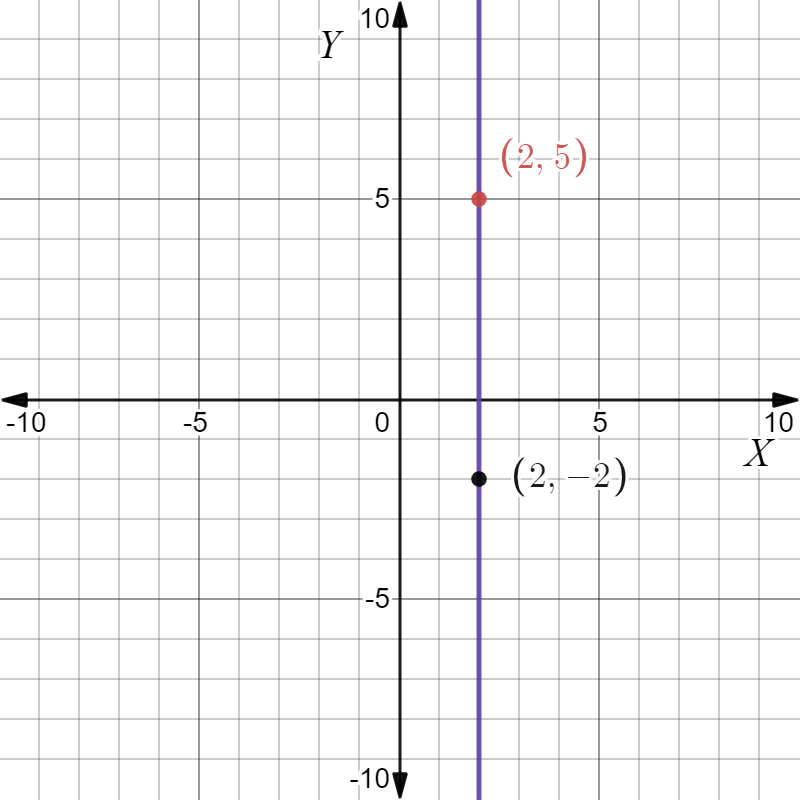
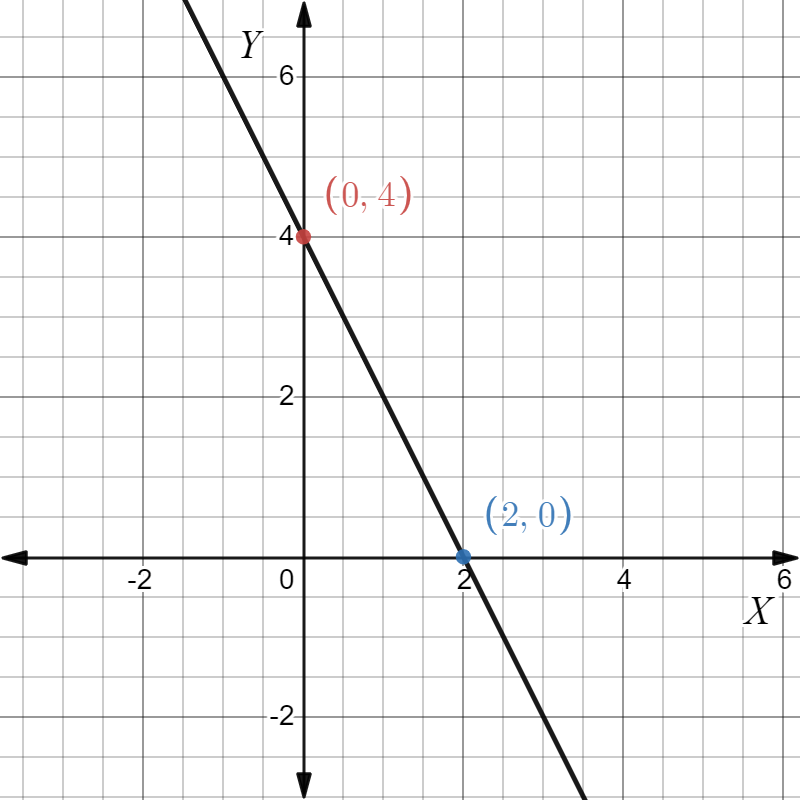
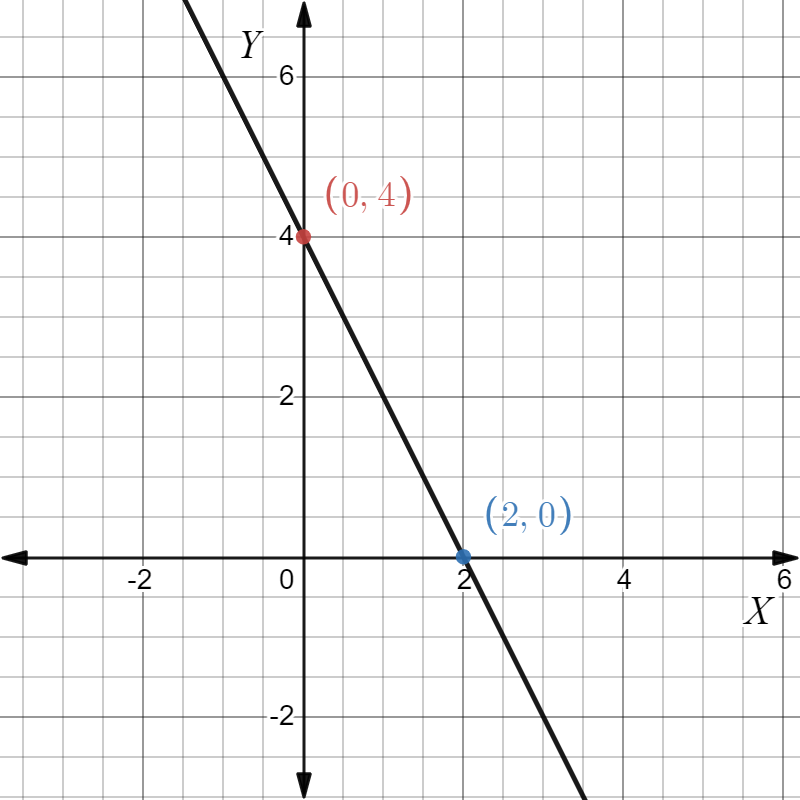
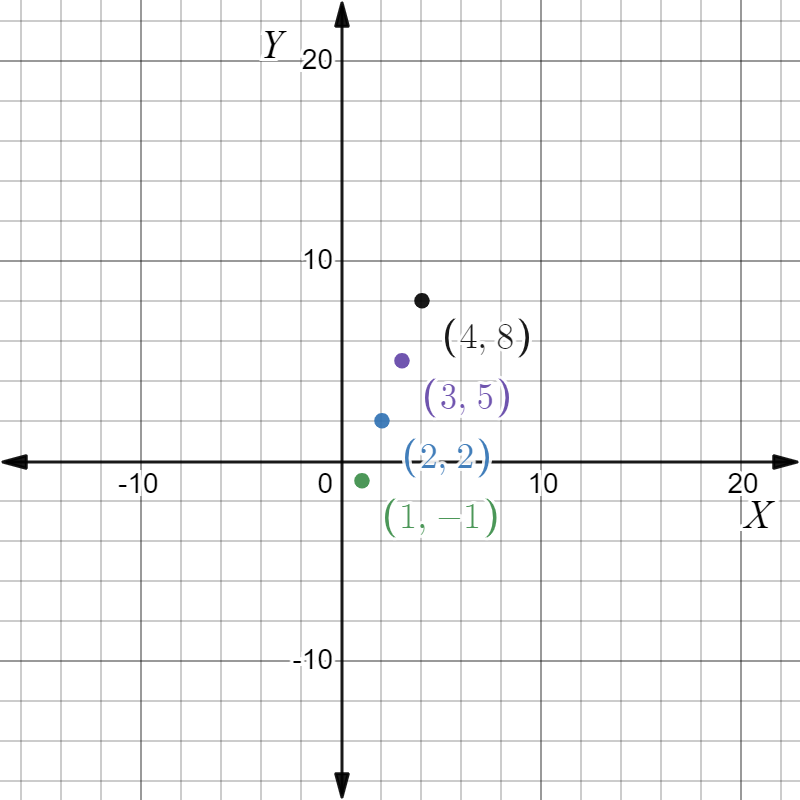
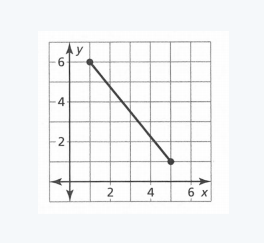
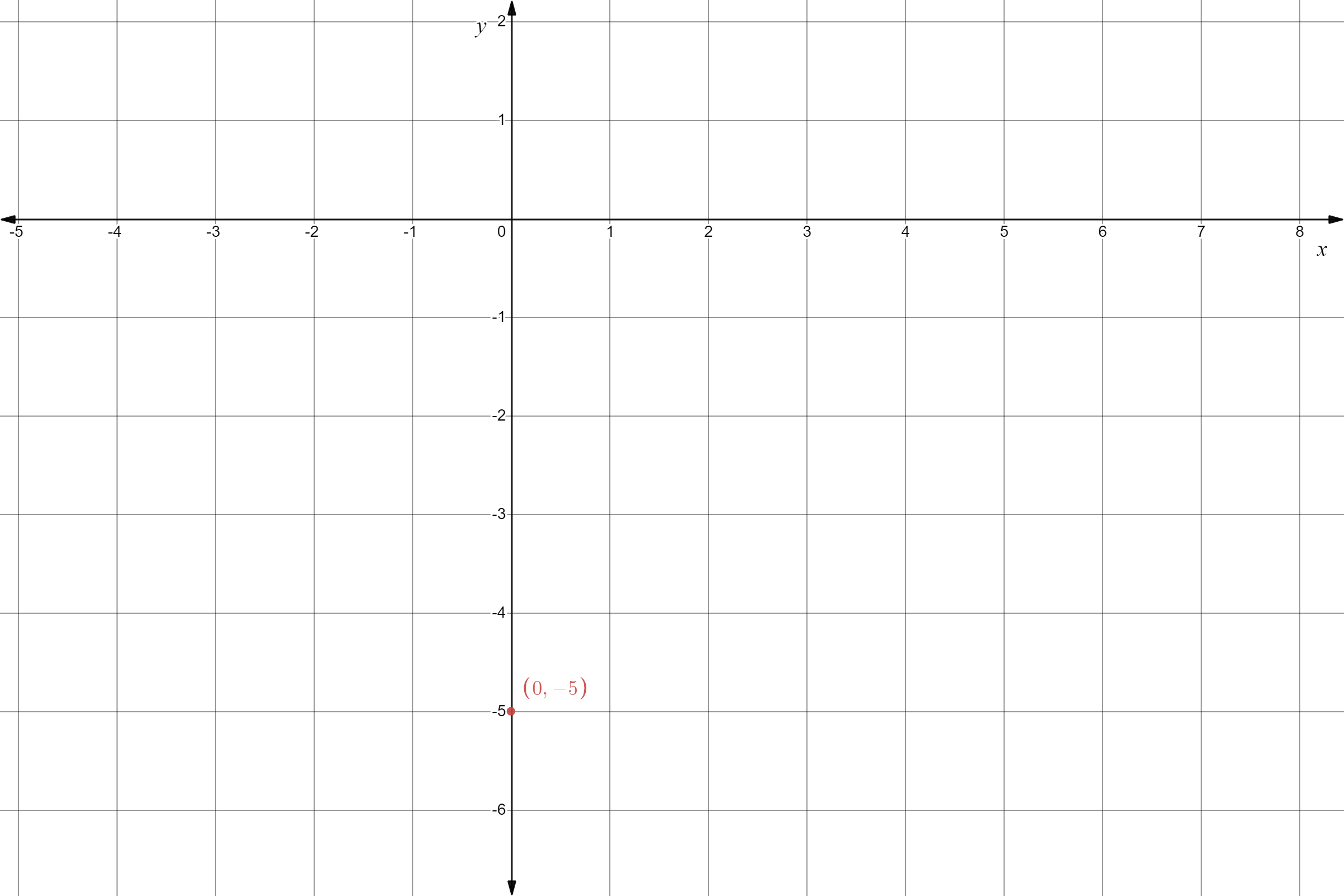
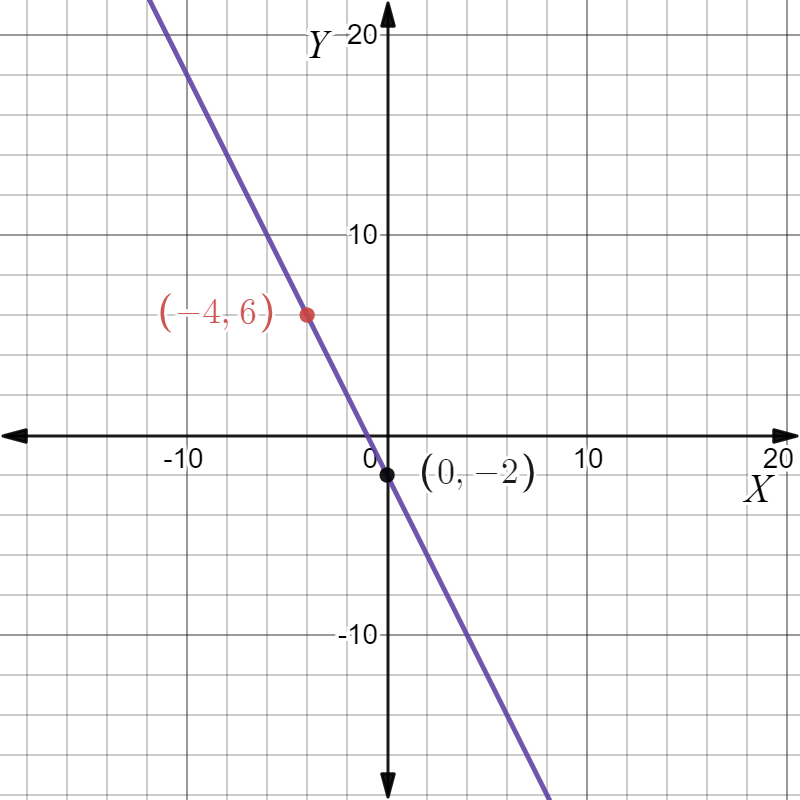
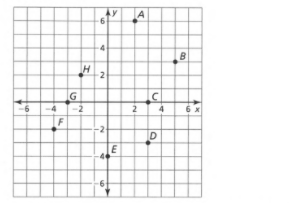
Given: The point as in the graph, and the slope as m=−2.

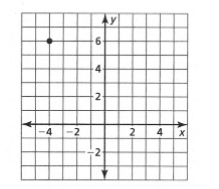
To find Sketch the line that has the given slope and passes through the given point. Find the y-intercept of the line. Write an equation of the line.

Summary: Identify the point and substitute it and the slope in the point-slope equation. Find the y-intercept by putting x=0 in the equation and solve for y. Plot the point and the intercept and join to get the graph.

From the graph

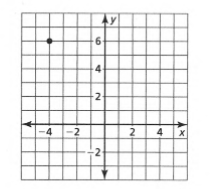
The point is (x₁,y₁)=(−4,6). Given the slope is m=−2. Substitute in the point-slope equation
​y−y₁=m(x−x₁)
y−6=−2(x−−4)
y−6=−2x−8
y=−2x−8+6
y=−2x−2
​
Put x=0 in this,
​y=−2(0)−2
y=−2
​ which is the y-intercept.

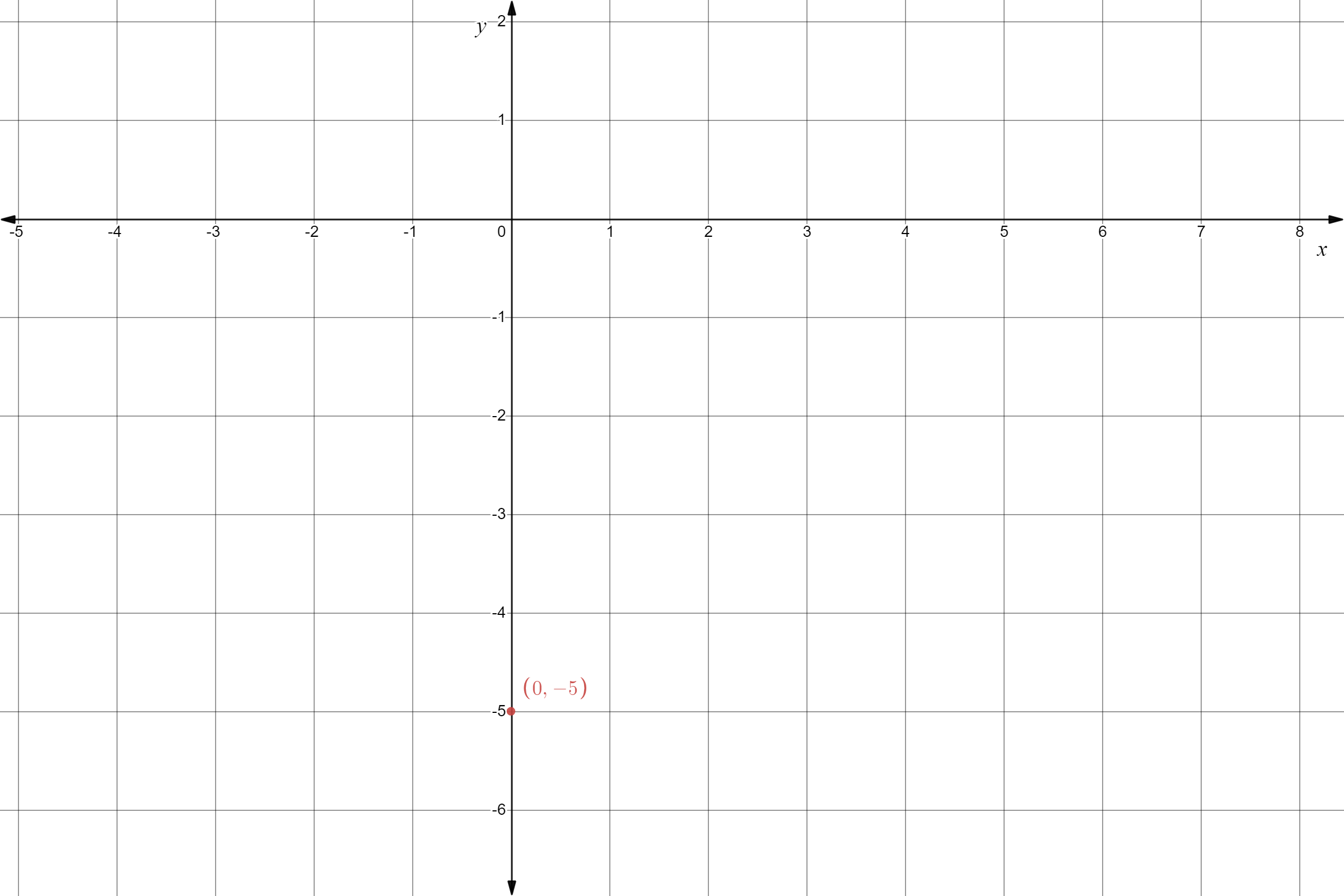
The points are (−4,6),(0,−2). Plot and join them.

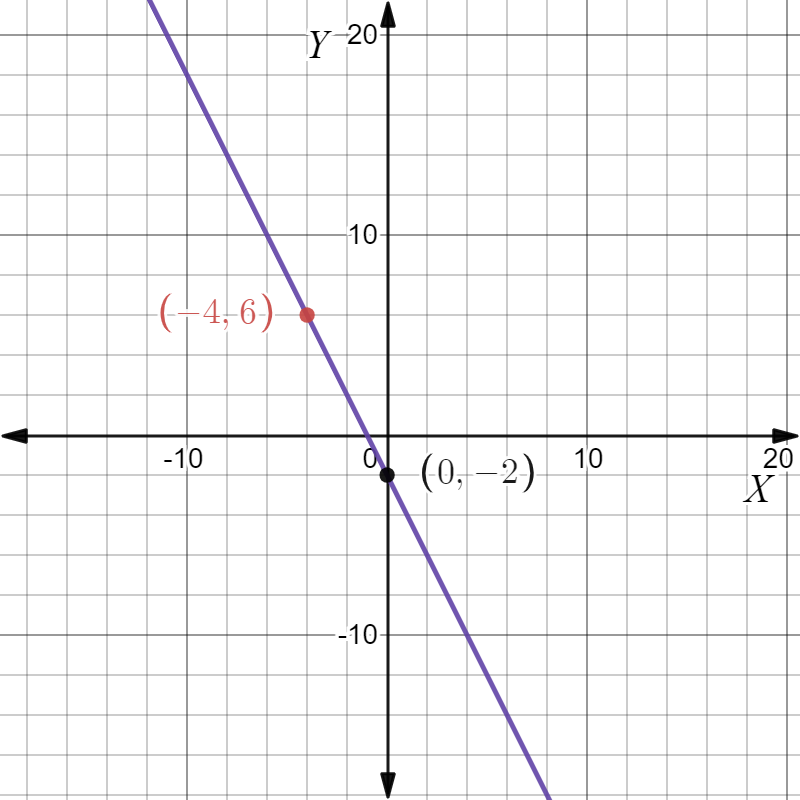
Given the point as in the Graph and the slope as m=−2.

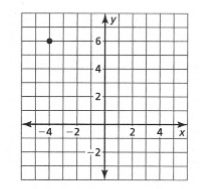
The equation of the line is y=−2x−2 and the y-intercept is −2. The graph is given below.

Big Ideas Math Algebra 1 Chapter 4 Exercise 4.2 Solution

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 101  Exercise 2  Answer

Given the graph

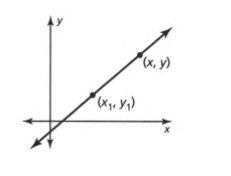
The slope is given by, m\(=\frac{y-y_1}{x-x_1}\)

Cross multiplying we get the point-slope equation of a line. y−y₁ =m(x−x₁).

Given a non vertical line and a point on it as below

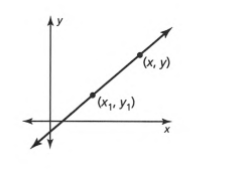
The slope is given by m\(=\frac{y-y_1}{x-x_1}\) and the point-slope equation of the line is y−y₁=m(x−x₁).

Page 102   Exercise 3  Answer

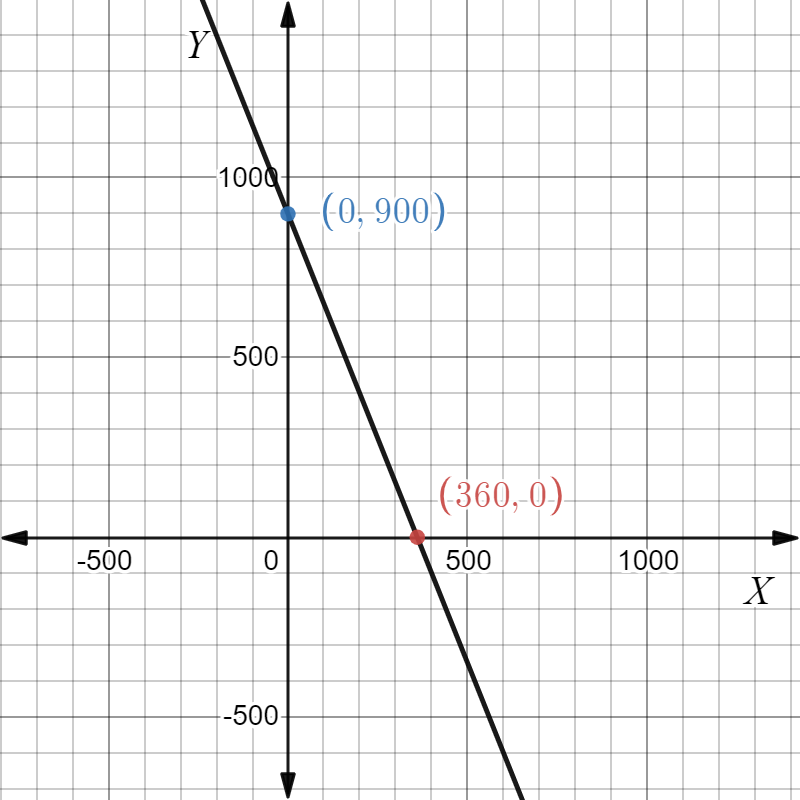
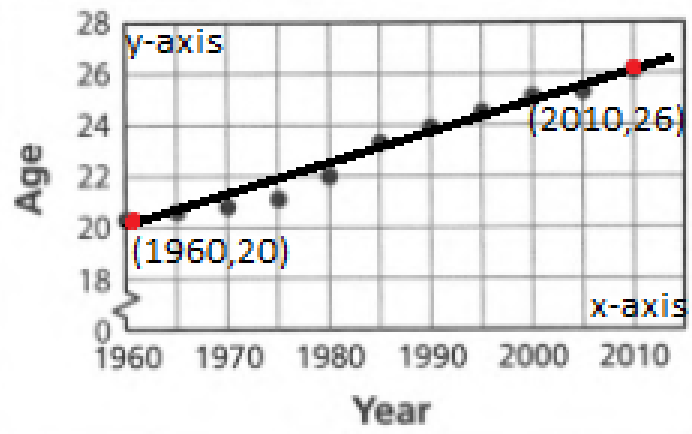
Given, we have saved $25 per month. And now we have $175 in our savings account.

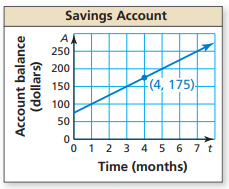
It is required to write an equation that represents the balance A after t months. To do this, use the result from Exploration 2:
y−y₁=m(x−x₁), where m is slope and line passes through the point (x₁,y₁).

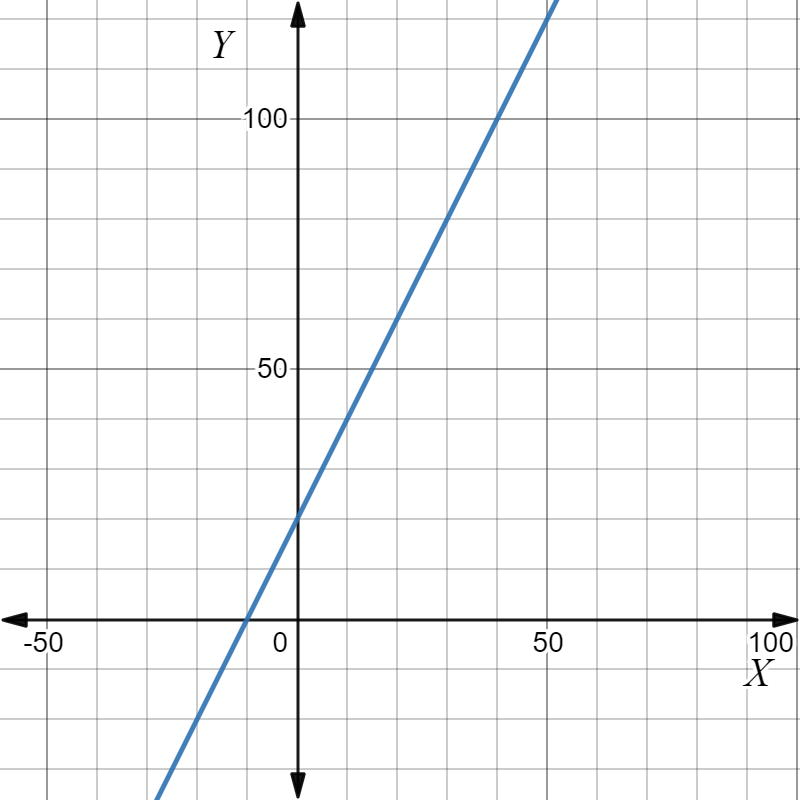
Consider the graph Savings Account.

Let (x₁,y₁)=(4,175).
Since we have saved $25
per month. Thus, let it be m=25.

Now, consider the result from Exercise  2: y−y₁=m(x−x₁), Where m is slope and line passes through the point (x₁,y₁).
Substitute (x₁,y₁)=(4,175)and m=25. Replace x with t and replace y with A.

We have y−y₁=m(x−x₁)

⇒A−175=25(t−4)
​
⇒A=25t−100+175

∴A=25t+75
​
The equation is A=25t+75.

An equation that represents the balance A after t months is A=25t+75.

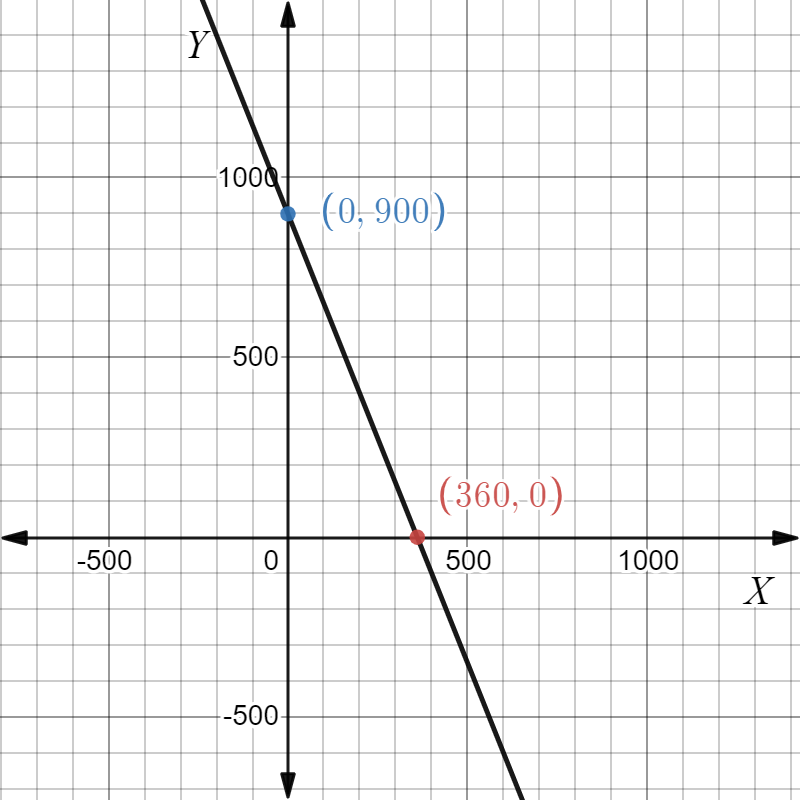
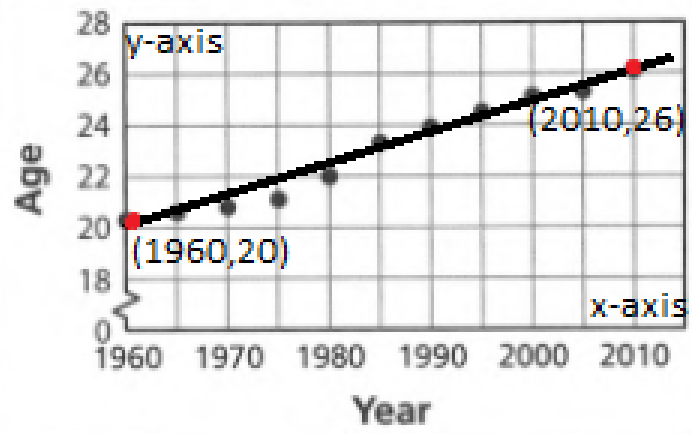
Given, An equation that represents the balance A after t months is A=25t+75.

It is required to verify the above equation by using the graphing calculator.

To do this, use the graphing calculator TI−84 Plus to plot the graph of the equation. And then verify with the given graph in Exercise 3.

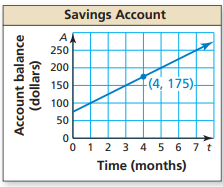
Consider the equation that represents the balance A after t months is A=25t+75.

Let’s graph it by using the graphing calculator Tl−84 Plus.

On the calculator press Y=, and then enter the expression 25x+75 in Y₁=.

Now, to see its graph press GRAPH key on the calculator.

Let’s adjust the window view.

Press the window key and change it to a graph in Exercise 3.

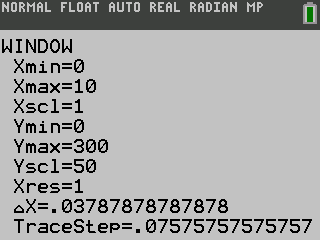
Now, press GRAPH key on the calculator.

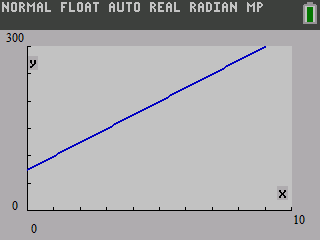
Therefore, the graph of y=25x+75 using a graphing calculator is similar to the given graph in  Exercise 3.

A graph of the equation A=25t+75 that represents the balance A after t months by using a graphing calculator is given below.

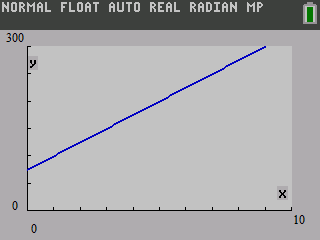
And it is similar to the given graph in Exercise 3.

Writing Linear Functions Exercise 4.2 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 102  Exercise 4  Answer

We know that the slope of a line is the ratio of the difference in the coordinates to the difference in the coordinates of any two points on it. Let be a point on the line whose slope is. Let be an arbitrary point on the line.

Then the slope is given by, m\(=\frac{y-y_1}{x-x_1}\)

Cross multiplying we get the point-slope equation for the line.

y-y₁=m(x-x₁).

Given a point (x₁,y₁)on the line whose slope is m, the point-slope equation of the line is y−y₁=m(x−x₁).

Page 102  Exercise 5  Answer

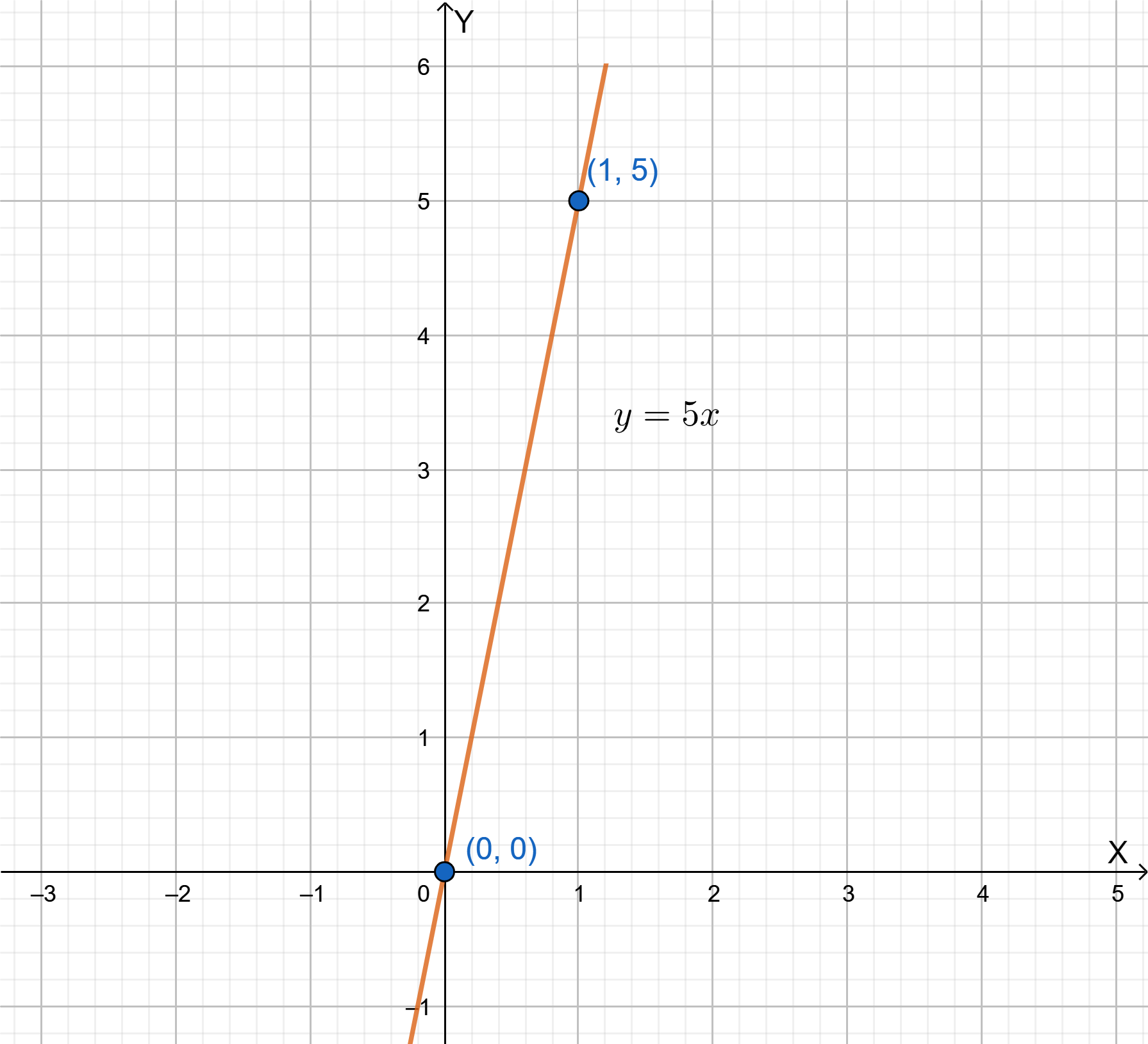
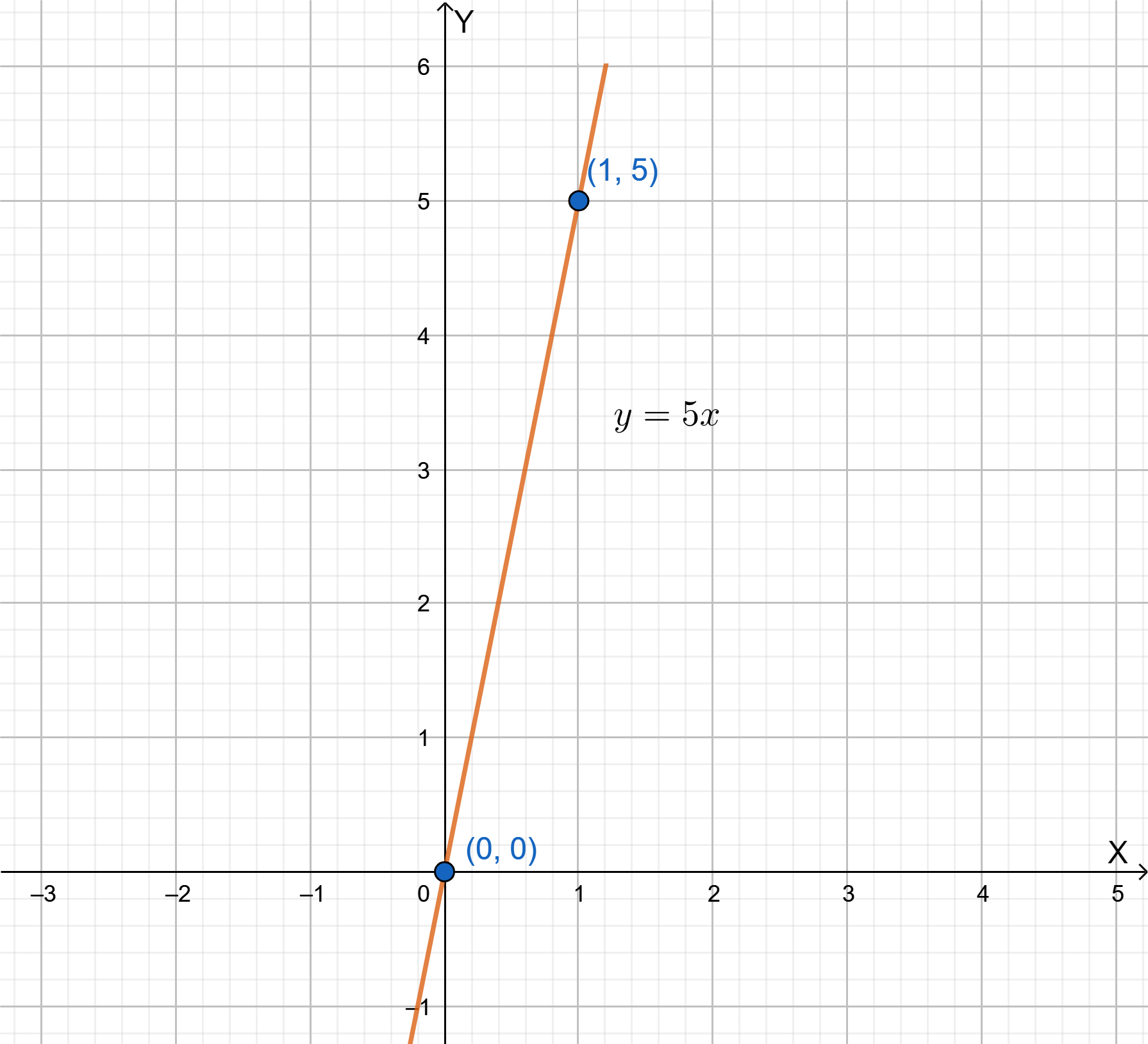
To find an example, let us choose a point and a slope.
Let ​m=5(x₁,y₁)=(0,4)
​

To find the equation of the line with the given slope and pass through the given point, substitute the values in the point-slope equation of the line.
​y−y₁=m(x−x₁)
y−4=5(x−0)
y−4=5x
y=5x+4
​
This is the equation of the required line.

The example of how to write an equation of a line when you are given the slope and a point on the line is given below.

Let the point be (0.4)and the slope of the line be m=5, then the equation of the line obtained using the point-slope form is

y=5x+4.

Page 104 Exercise 1 Answer

Given: The point (−2,1), the slope is ​m=−3.
​
To find The equation of the line.

Summary: Use the point-slope form of a line. Substitute the values in it and simplify.

The point and the slope given are, (−2,1)=(x1,y1)
m=−3
​y−y₁=m(x−x₁)
y−1=−3(x−(−2))
​
Simplifying we get
​y−1=−3x−6
y=−3x−6+1
y=−3x−5
​The equation of the line with slope m=−3 and passing through the point (−2,1) is y=−3x−5.

Algebra 1 Student Journal Chapter 4 Exercise 4.2 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 104  Exercise 2  Answer

Given: We have a slope, m=2 and the point x₁ =3, y₁=5

To find The point-slope form of the straight line formed.

Summary: We have the specific point as (3,5) and slope as 2.
We know that the point-slope form is given as, y−y₁ =m(x−x₁), we will so get the required equation by substituting the values in the equation.

We have, slope m=2 And specific points, x₁=3,y₁=5

On substituting the values in the general equation of point-slope, y−y₁ =m(x−x₁)
We get, y−5=2(x−3)
Which is equal to,y=2x−1

The point-slope form of the straight line is, y=2x−1

Page 104  Exercise 3  Answer

Given: We have a slope, m=−1 and the point as(−1,−2)

To find The point-slope form of the straight line formed.

Summary: We have the specific point of the straight line x₁ =−1,y₁ =−2 and slope value equal to −1.

Now we know that the point-slope form is given as, y−y₁ =m(x−x₁) where x₁,y₁ denotes the specific point and m denotes slope of the straight line, we will so get the required equation by substituting the values in the equation.

We have the slope, m=−1

And the specific point as, (x₁,y₁)=(−1,−2)

If we substitute the values in general form of a point-slope equation we will get, y−(−2)=(−1)[x−(−1)]

We can also write, y+2=−x−1

Which gives, y+x=−3

The point-intercept form of the given straight line gives y+x=−3

Big Ideas Math Writing Linear Functions Exercise 4.2 Help

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 104  Exercise 4  Answer

Given: We have a slope, m=\(\frac{4}{3}\) and the coordinates of a point as,(5,0)

To find The point-slope form of the straight line formed.

Summary: We have the specific point x₁ =5,y₁ =0 and slope as \(\frac{4}{3}\).

Now the point-slope form is generally given as y−y₁ =m(x−x₁) now on substituting the given values in the general equation we will find the equation in point-slope form for the given straight line.

We have slope,m=\(\frac{4}{3}\) And the coordinates of point, x₁=5,y₁=0

Now substituting the values in y−y₁ =m(x−x₁)

We get,y−0=\(\frac{4}{3}\) (x−5)

Which gives,3y=4x−20

The equation in point-slope form is given as 3y=4x−20

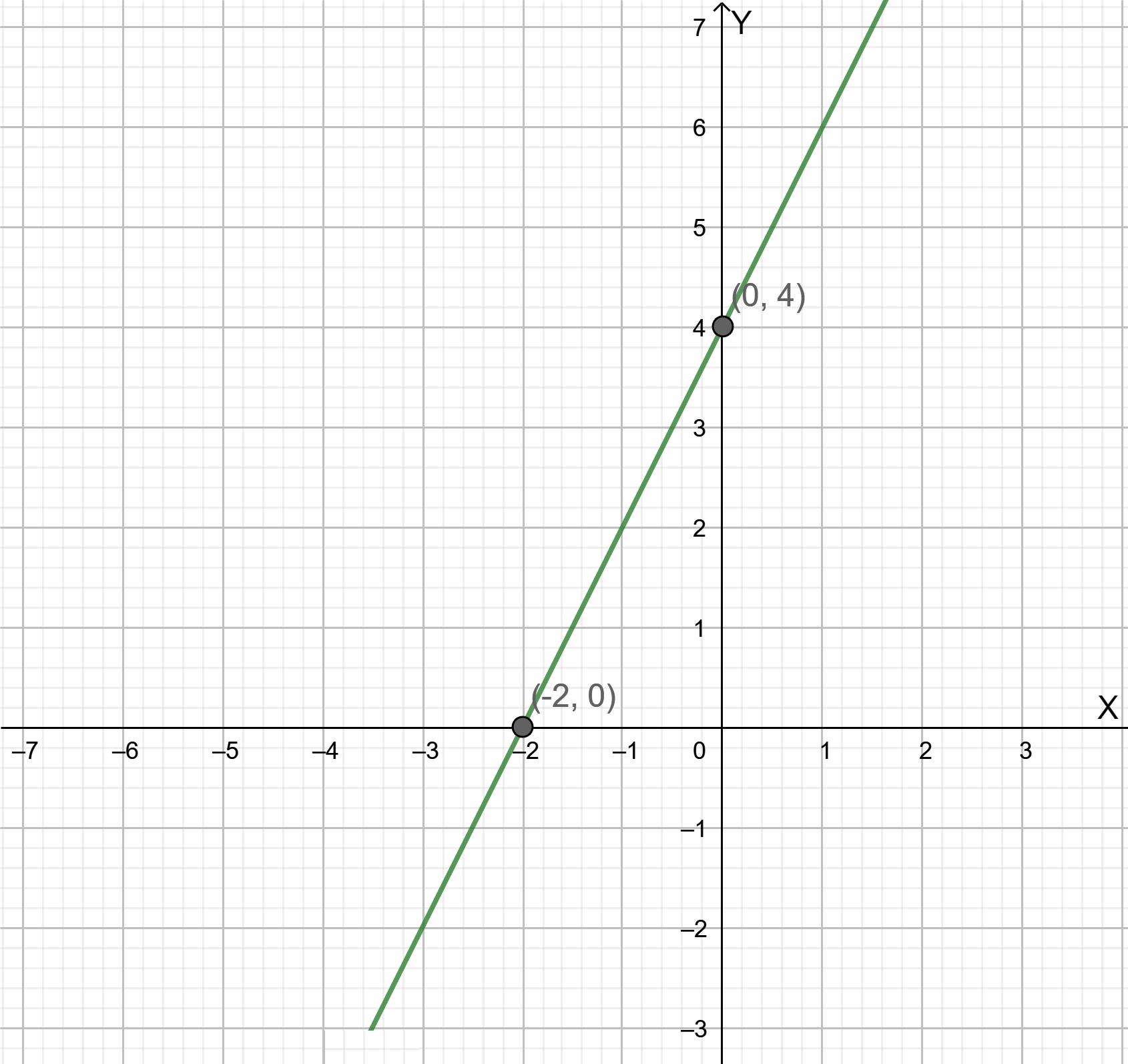
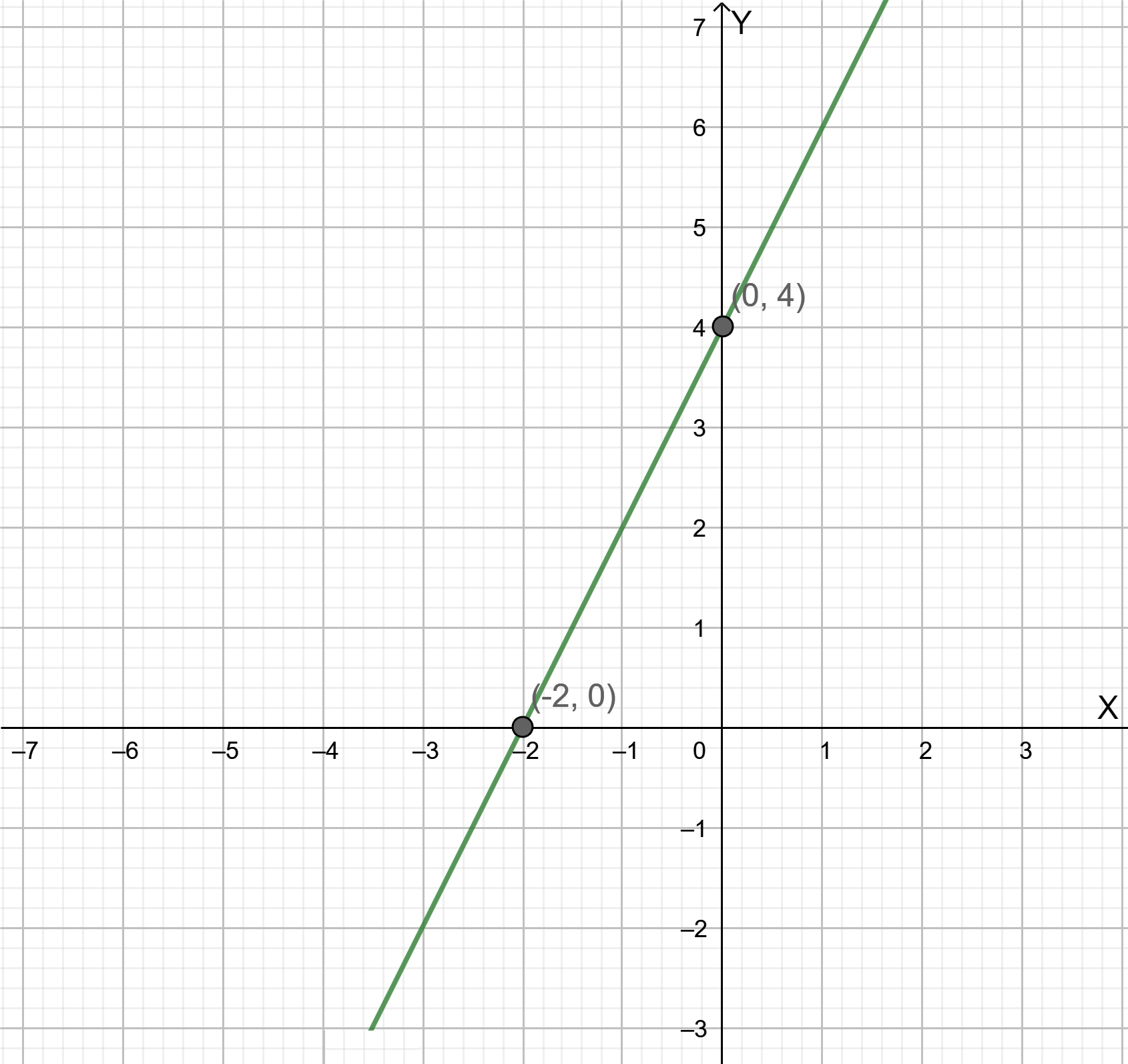
Page 104  Exercise 5  Answer

Given: We have a slope, m=7 and the point as (0,4)

To find The point-slope form of the straight line formed.

Summary: We have the specific point (0,4) and slope as 7 in the question itself.

And we know that the point-slope form is given as, y−y₁ =m(x−x₁)

Where m, is the slope and x₁,y₁ denotes the coordinates of a specific given point, we will so get the required equation by substituting the values in the general equation.

We are given, slope, m=7, And coordinates of a specific point as,(x₁,y₁)=(0,4)

Now substituting the values in y−y₁=m(x−x₁)

We get,y−4=7(x−0) Which gives, y=7x+4

The equation of a straight line in point-slope form is given as y=7x+4

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 104  Exercise 6  Answer

Given: We have the specific coordinates of points as, x₁=1,y₁=2 and the slope m=\(\frac{-1}{2}\)

To find The equation of straight line in point-slope form.

Summary: We have the specific point as x₁=1,y₁=2 and slope as m=\(\frac{-1}{2}\) Now, We know that the point-slope form is given as, y−y₁ =m(x−x₁), we will so get the required equation by substituting the values in the general equation in point-slope form.

We have, slope m=\(\frac{-1}{2}\) And the coordinates of specific point, (x₁,y₁)=(1,2)

Now substituting the values in y−y₁=m(x−x₁)
We get , y−2=\(\frac{-1}{2}\)(x−1)
Which is equal to,2y+x=3

The straight line equation in point-slope form is given as 2y+x=3

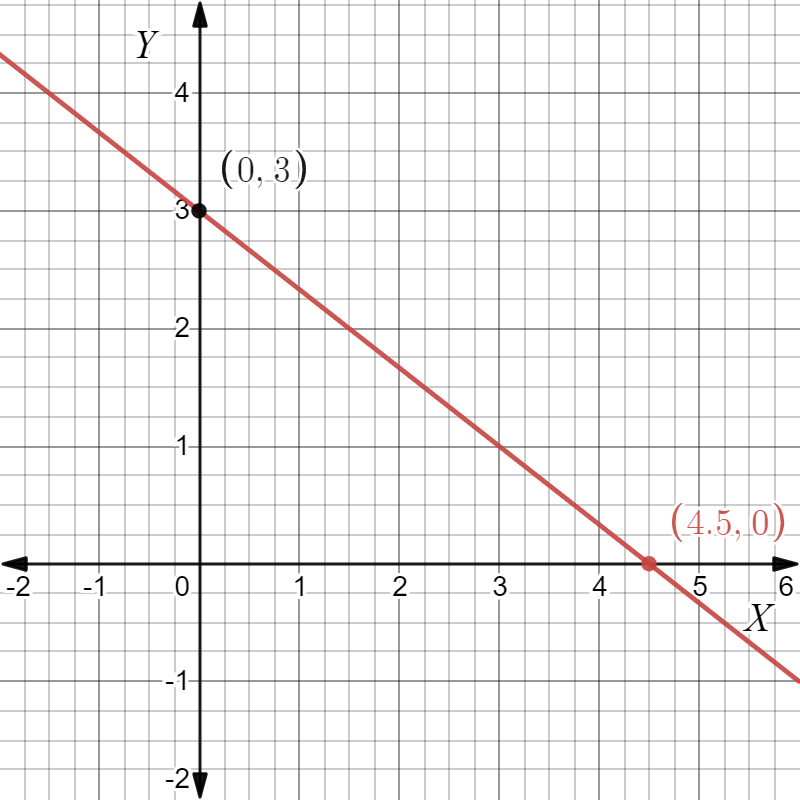
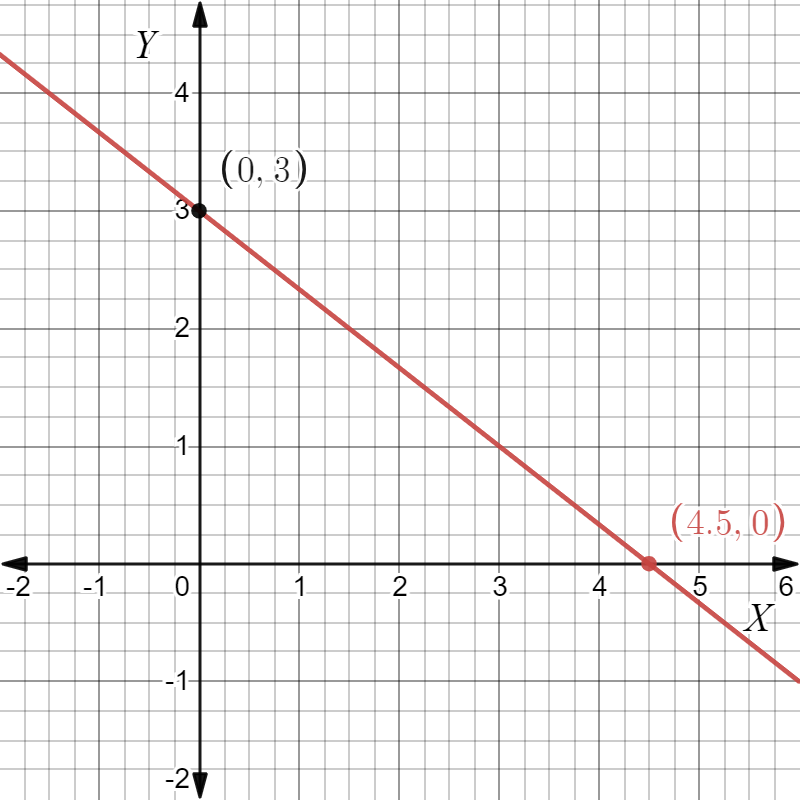
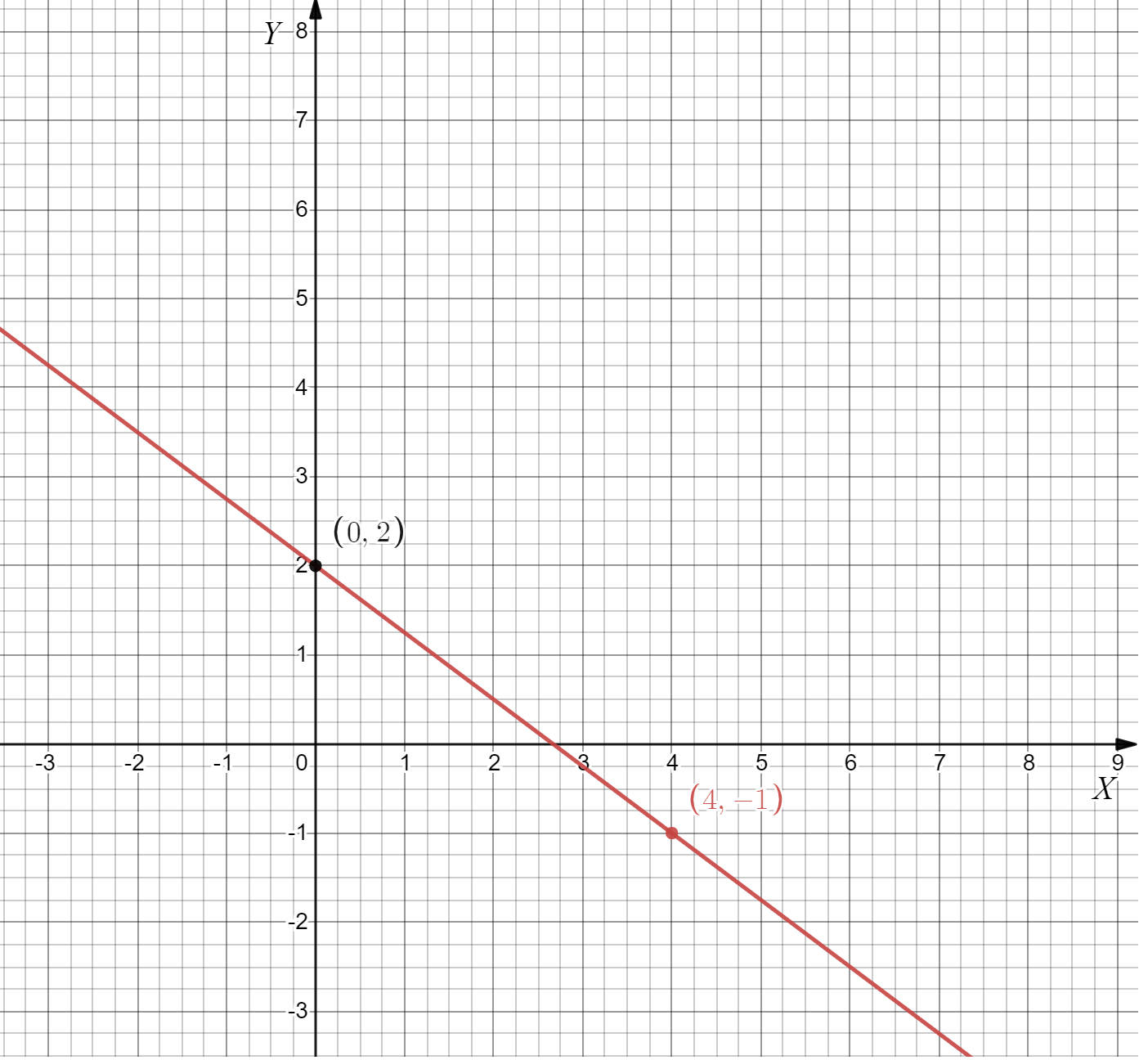
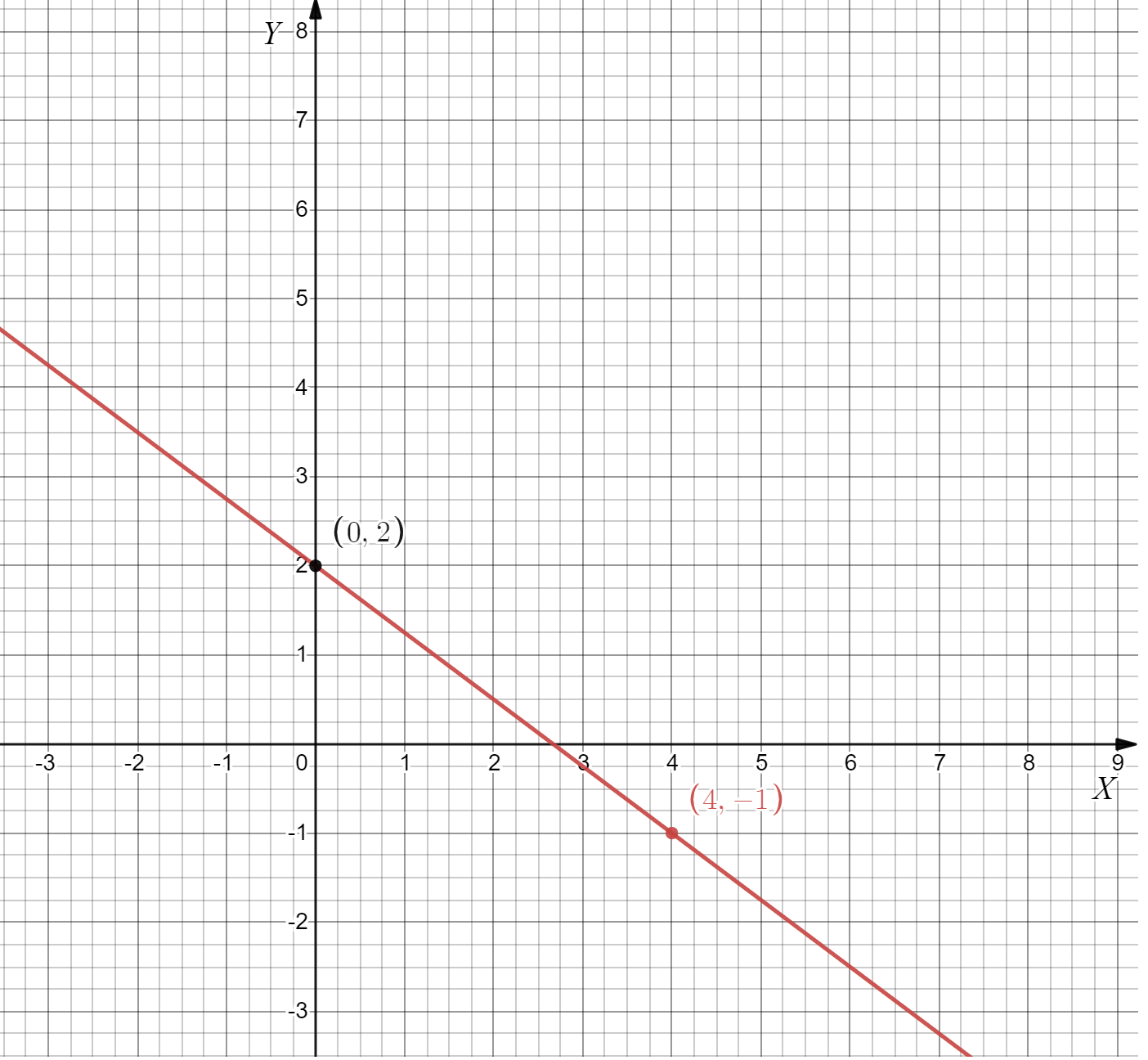
Page 104  Exercise 8  Answer

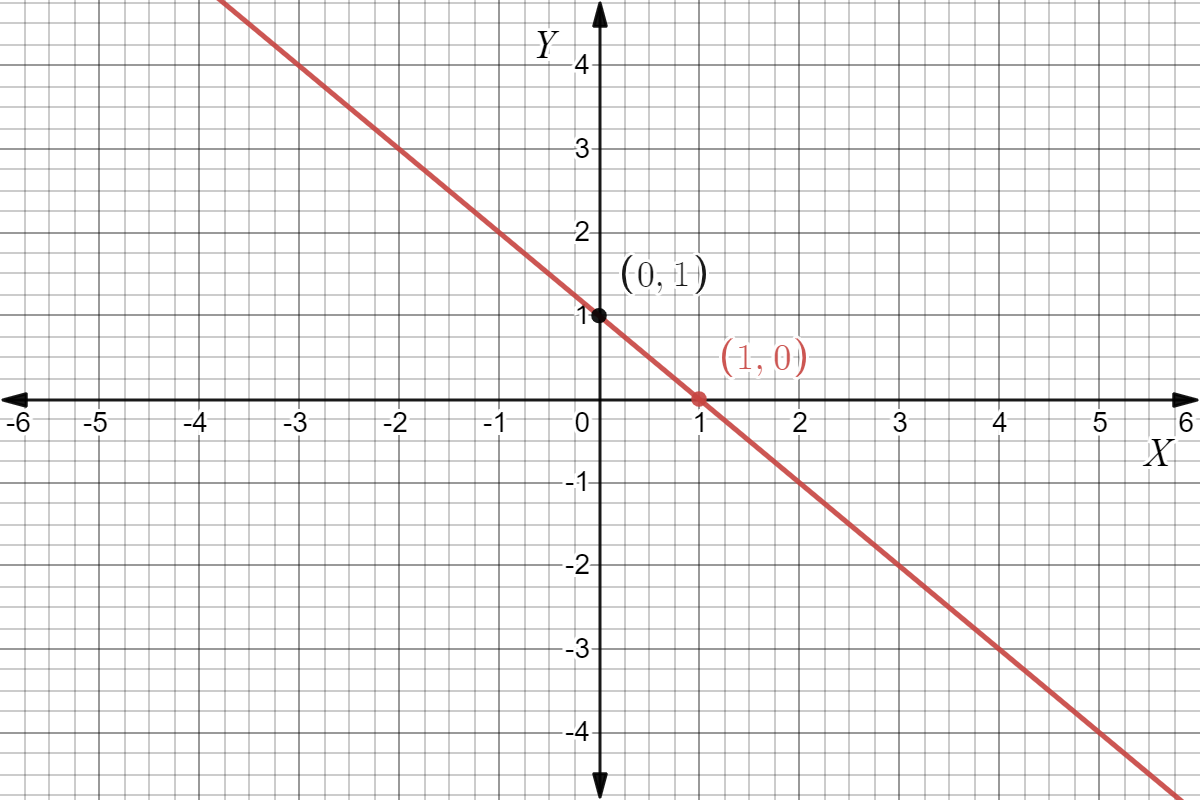
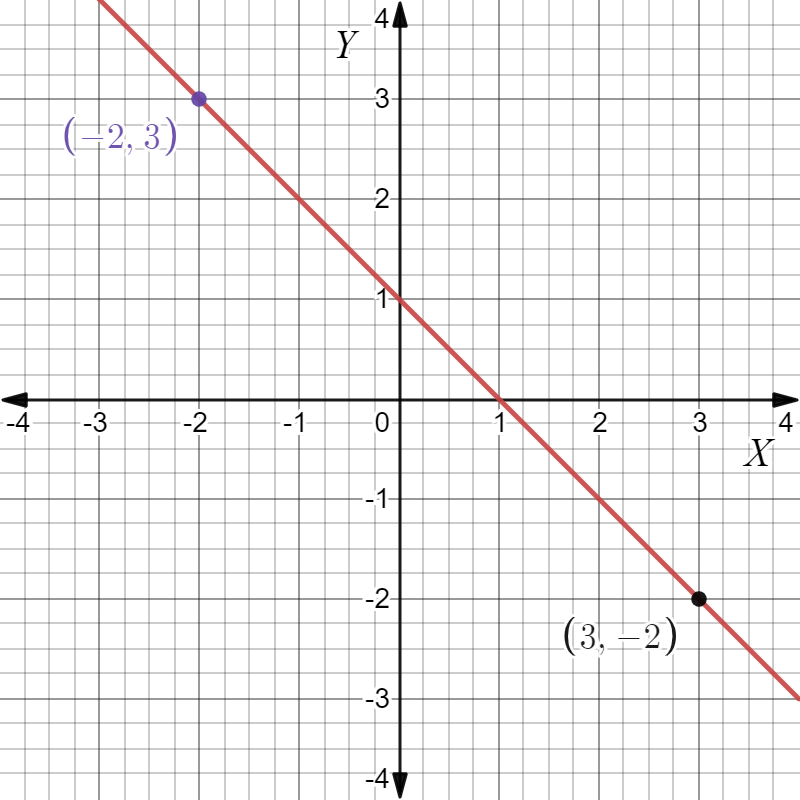
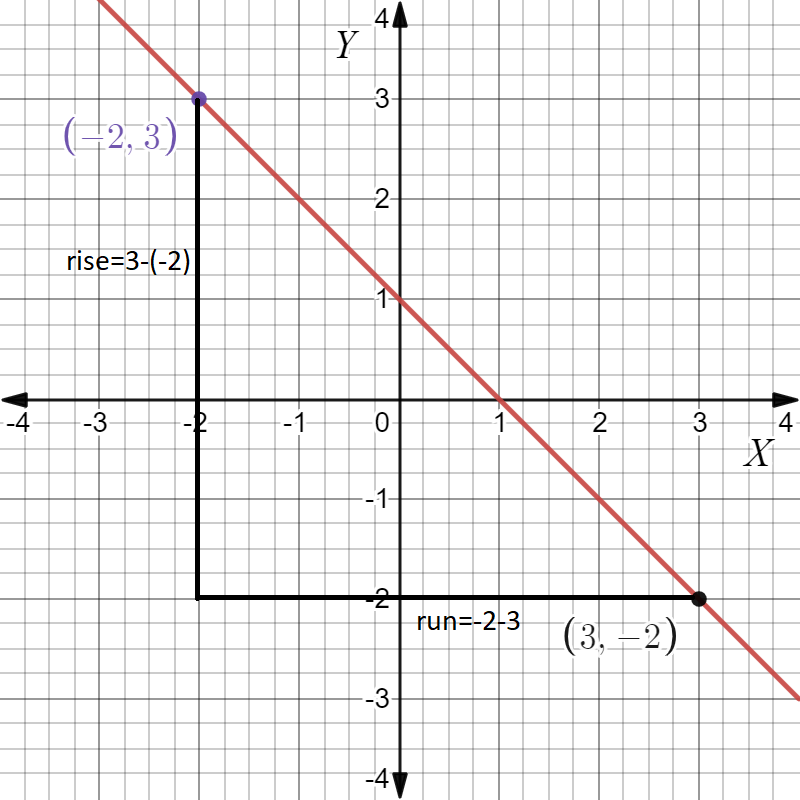
Given: We have the graph of a straight line as

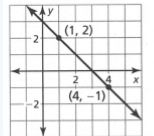
To find The equation in slope-intercept form.

Summary: We have the graph of a straight line which when observed shows the intercept is equal to3, and the two points are given as(1,2),(4,−1) which will give us the value of slope which is found using,m\(=\frac{y_2-y_1}{x_2-x_1}\).

And the values of slope and intercept when substituted in the general slope-intercept form of straight line, we will get the equation of this given line.

The graph of a straight line as

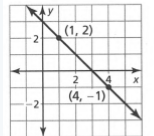
From the graph we can see The intercept c=3

And ​(x₁,y₁)=4,−1, (x₂,y₂)=1,2
​
Then slope,m\(=\frac{2-(-1)}{1-4}\)

Which gives,m=−1

On substituting the values of slope and intercept in y=mx+c, We get,y=−1x+3

The given straight line gives y=−x+3 in slope-intercept form.

Chapter 4 Exercise 4.2 Step-By-Step Solutions Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 104  Exercise 9  Answer

Given: We have the graph of a straight line as

To find The equation in slope-intercept form.

Summary: The graph shows the value of intercept as 4, and the coordinate of two points as, (−2,−3),(2,−1) which will give us the value of the slope, as the slope is the ratio of difference of two of the coordinates, and the intercept and slope values will give us the ultimate equation of the straight line in slope-intercept form.

The graph of a straight line as

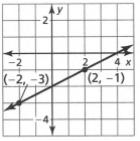
The intercept c=4

And coordinates, (x₁,y₁)=−2,−3 ( x₂, y₂ )=2,−1
​
Which gives the slope,​m=−\(\frac{-1-(-3)}{2-(-2)}\)

⇒m=\(\frac{1}{2}\)

​On substituting the value of intercept and slope in the general equation, we get,​y=\(\frac{1}{2}\)+x+4

⇒2y=x+8
​
The straight line in slope-intercept form gives,2y=x+8

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 104  Exercise 11  Answer

Given: We have the graph of a straight line as

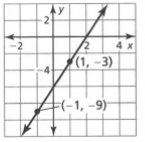
To find The equation in slope-intercept form.

Summary: If we observe the graph we can see the intercept is 2, and the slope is calculated using the formula,m\(=\frac{y_2-y_1}{x_2-x_1}\) where the x,y

Represents the coordinates of two points on the graph. On substituting the values of x,y we will find the slope. Then we can substitute the values we get in the slope-intercept form to find the equation of the straight line.

The graph of a straight line is give as

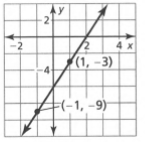
We can see that the intercept,c=2 and​ x₁=1,x₂ =−1 y₁ =−3 y₂ =−9
​
Which when substituted gives, a slope

m=−\(\frac{-9-(-3)}{-1-1}\)

⇒m=3

On substituting the values of intercept and slope in general equation, We get,y=3x+2

The straight line in slope intercept form gives y=3x+2

Page 104  Exercise 12  Answer

Given: We have the graph of a straight line as

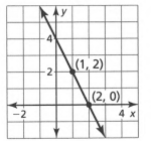
To find The equation in slope-intercept form.

Summary: If we observe the graph we can see the intercept is 2 and the slope is calculated by m\(=\frac{y_2-y_1}{x_2-x_1}\) where the x,y represents the coordinates of two given points on the graph.

On substituting the values of x,y we will find the slope. Then we can substitute the values we get in the slope-intercept form to find the equation of the straight line.

The graph of a straight line is given as

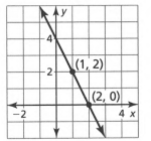
The graph gives, intercept c=2
Coordinate of points as,​ x₁ =1 x₂=2 y₁=2 y₂=0
​
Which gives, slope m−\(=\frac{-2}{2-1}\)

⇒m=−2

Now if we substitute the values of slope and intercept in general form, We get,y=−2x+2

The straight line gives y=−2x+2 in slope intercept form.

Exercise 4.2 Big Ideas Math Algebra 1 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 105  Exercise 13  Answer

Given: We have the function,f(−3)=−1,f(−2)=4

To find The linear equation satisfying the function.

Summary: We can interpret the slope as the difference of ratio of coordinates of by y,x.

This will give us the value of the slope, and substituting values from any of the functions in the general form will give us the equation to find the value of the intercept.

This when substituted in the general equation of straight line we will find the linear function.

We have,​f(−3)=−1

f(−2)=4
​
Then slope,​m=\(\frac{4+1}{-2+3}\)

⇒m=5
​

On substituting any function and slope in general form,
We get,​−1=−15+c
c=14
​

On substituting the values, We get the equation in linear form as
y=5x+14

The linear expression gives,y=5x+14

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 105  Exercise  14 Answer

Given: We have,f(−2)=1,f(1)=7

To find The linear equation satisfying the function.

Summary: We can interpret the slope as the difference of ratio of coordinates of y,x

This will give us the value of the slope, and substituting values from any of the functions in the general form will give us the equation to find the value of the intercept.

This when substituted in the general equation of straight line we will find the linear function.

We have,​f(−2)=1 f(1)=7
​
Then slope,​m\(=\frac{7-1}{1+2}\)
​
m=2

On substituting any function and slope in general form
We get,​1=−4+c
c=5
​
On substituting the values, We get the equation in linear form as,y=2x+5

The linear expression gives,y=2x+5

Page 105  Exercise 15  Answer

Given: We have,f(−1)=2,f(3)=3

To find The linear equation satisfying the function.

Summary: We can interpret the slope as the difference of ratio of coordinates of y,x.

This will give us the value of the slope, and substituting values from any of the functions in the general form will give us the equation to find the value of the intercept.

This when substituted in the general equation of straight line we will find the linear function.

We have,​f(−1)=2 f(3)=3
​
Then slope,​m\(=\frac{3-2}{3+1}\)

⇒m\(=\frac{1}{4}\)
​
On substituting any function and slope in general form

We get, ​2=\(\frac{1}{4}\)(−1)+c

⇒c=2+\(\frac{1}{4}\)

⇒c=\(\frac{9}{4}\)

​On substituting the values, We get the equation in linear form as

​y=\(\frac{1}{4}\)+\(\frac{9}{4}\)

⇒4y=x+9
​
The linear expression gives,4y=x+9

How To Solve Exercise 4.2 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 105  Exercise 16  Answer

Given: We have f(0)=−2,f(4)=−1

To find The linear equation satisfying the function.

Summary: We can interpret the slope as the difference of ratio of coordinates of x,y.

This will give us the value of the slope, and substituting values from any of the functions in the general form will give us the equation to find the value of the intercept.

This when substituted in the general equation of straight line we will find the linear function.

We have,​f(0)=−2
f(4)=−1
​
Then slope,​m\(\frac{-2+1}{-4}\)

⇒m\(=\frac{1}{4}\)

On substituting any function and slope in general form

We get,​(−2)\(=\frac{1}{4}\)(0)+c

−2=c
​
On substituting the values, We get the equation in linear form as

y\(=\frac{1}{4}\)x−2

The linear expression gives,4y=x−8

Page 105  Exercise 17  Answer

Given: We havef(1)=0,f(0)=8

To find The linear equation satisfying the function.

Summary: We can interpret the slope as the difference of ratio of coordinates of x,y.

This will give us the value of the slope, and by substituting values from any of the function in the general form will give us the equation to find the value of intercept.

This when substituted in the general equation of straight line we will find the linear function.

We have,​f(1)=0

f(0)=8
​
Then slope,​m\(=\frac{8}{-1}\)

⇒m=−8
​
On substituting any function and slope in general form, we get, 8=c

On substituting the values, We get the equation in linear form as,
y=−8x+8

The linear expression gives,y=−8x+8

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 105  Exercise 18  Answer

Given: We have, f(3)=5,f(2)=6

To find  The linear equation satisfying the function.

Summary: We can interpret the slope as the difference of ratio of coordinates of y by x.

This will give us the value of the slope, and by substituting values from any of the function in the general form will give us the equation to find the value of intercept.

This when substituted in the general equation of straight line we will find the linear function.

We have,( ​x₁,y₁) =(3,5) , (x₂,y₂)=(6,2)
​
Which will give, ​m\(=\frac{2-5}{6-3}\)

m=1
​

On substituting the value of slope and either of the function will give us, ​5=3+c
⇒c=2
​
If we substitute the values of slope and intercept in the general equation

we will get, y=x+2

The linear expression of the function gives y=x+2

Page 105  Exercise 19  Answer

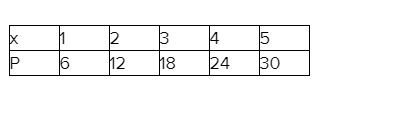
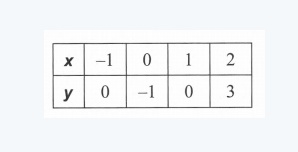
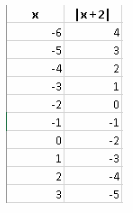
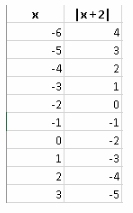
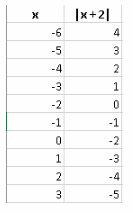
Given: We have the data as

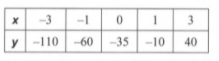
To find Whether linear equation expression for the given data is possible or not.

Summary: We have the data of x, and y.

If we find the slopes of the points we will find the value is the same, now it implies that linear equation form is possible which is determined by substituting the value of slope and intercept in the equation of straight line as y=mx+c.

where m and c denotes slope and intercept respectively.

We have the data of

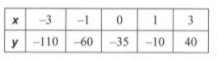
Now let us consider, ​(x₁ ,y₁) =(−3,−110), (x₂ ,y₂) =(−1,−60)
​
Then the slope for this point can be given as, ​m\(=\frac{-60-(-110)}{-1-(-3)}\)

⇒m=25
​

Now, let us consider two other points from the data as, ​(x₁′,y₁′)=(3,40), (x₂ ′,y₂ ′)=(1,−10)
​
Then the slope for these point will be, ​m=\(\frac{-10-40}{1-3}\)

⇒m=25
​
We can see slopes are equal for all the points, then linear equation is possible.

On substituting the values in y=mx+c
We get the linear equation,y=25x−35

The given data can be represented in linear equation form as,y=25x−35

Page 105  Exercise 20  Answer

Given: We have the data as

To find Whether the given data be represented in linear equation form.

Summary: We have the data of x,y and we can approach the question by finding the value of slope between two different points, in this one we can see pair of two points representing the same line gives a different slope which implies that the linear equation form for this data is not applicable.

We have the data as

We can consider two points,​(x₁,y₁)=(−1,18) (x₂ ,y₂ )=(−3,−98)
​
Then the slope,​m\(=\frac{-98-18}{-3+1}\)

⇒m=58
​

Now let us consider two more points as,​(x₁′,y₁′)=(1,62)
(x₂′,y₂′)=(3,142)
​
Then the slope,​m\(=\frac{142-62}{3-1}\)

⇒ m=40
​
We can see that the two slopes representing one line are not equal, which implies we cannot represent the data in linear equation form.

We cannot express the data in linear equation form.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.2 Page 105  Exercise 21  Answer

Given: We have, speed=60 miles per hour distance travelled in 3hrs=265 miles

To find A linear function D, that drives in h, hours and distance travelled in7hrs.

Summary: We have the distance covered in 3hrs=265 miles, then in one hour \(\frac{265}{3}\) miles are covered. Also, we are already given that the distance covered in one hour is 60 miles. Then if we multiply 7 we will find the distance travelled in that period of time, and we will find a linear equation for the function.

The distance covered in one hour=60miles

We can represent the time as x, and distance as y

And the distance covered in 3hrs=265 miles.

Then distance covered in ​7hrs=7×60 miles =420miles
​

Linear function to represent the given condition can be like, y=mx+c where m,c are constants

We can replace the values of y,x, and m by 60,1,6

y=60, x=1, m=6

We get, y=mx+c

​60=6(1)+c

60=6+c

c=60-6

⇒c=54
​
Then the equation can be given as, D=6h+54 The linear expression for covering D, distance in h hour is given as, D=6h+54 where the distance covered in 7 hrs=420miles

Big Ideas Math Student Journal Exercise 4.2 Examples

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.7

Page 90 Essential Question Answer

We know the graph of the absolute value function |x| is a V-shaped graph pointed at the origin.

The graph is shifted to the right by h units if h is positive in the function |x−h| and the original graph is shifted to the left by h units if it is negative. That is the graph of |x−h| will be pointed at h.

Multiplying a number a>0 opens up the graph whereas if a<0 then the graph opens down. Adding k>0 to this function translates the graph k units up whereas if k<0 the graph is translated k units down.

The values a,h,k in the absolute value function g(x)=a|x−h|+k decide the transformations of the graph ∣ |x|. The graph of g(x) will be V-shaped pointed at h, the graph opens up if a>0 and opens down if a<0. The translates k units up if k>0 and translated down by k units if it is negative.

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.7 Page 94 Exercise 4 Answer

Given: r(x)=|x+2| and graph f(x)=|x| and a table with different values of x

To find  the domain and range of the given equation

Solution: plotting r(x)=|x+2| with the points from the values in the table

We have to calculate the values of r(x) with x in the table:
When ​x=−4
r(x)=∣x+2∣=∣−4+2∣
⇒ r(x)=∣−2∣=2
​

When, ​x=−3
r(x)=∣−3+2∣=∣−1∣
⇒ r(x)=1
​

When ​x=−2
r(x)=∣−2+2∣=∣0∣
⇒ r(x)=0
​

When ​x=−1
r(x)=∣−1+2∣=∣1∣
⇒r(x)=1
​

When ​x=0
r(x)=|0+2|=|2|
⇒r(x)=2
​
This will be tabulated as:

And then plot these points in the graph

Now we have the given points and the graph as r(x)=|x+2| is.

And We have the given graph of f(x)=|x|

Now, plotting the graph of f(x)=|x| and r(x)=|x+2|
Together for comparison from the graph, it is clearly visible that the graph of r(x)=|x+2| is a horizontal stretch by 2 of the graph
f(x)=|x|

And the domain is all real numbers and the range is y≥0

The Domain of the function r(x) are all Real Numbers
The Range of the function r(x) is y≥0
And the compared graph is

The graph touches different values on horizontal axes with a stretch of 2

Big Ideas Math Student Journal Exercise 3.7 Examples

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise

Page 95 Exercise 1 Answer

Given: The graph with points plotted in it

To find the Ordered pair of A

Solution: From the graph, we can see the cartesian coordinator

Firstly we have to check where A lies in the graph and then draw a horizontal perpendicular line and vertical perpendicular lines to the y-axis and x-axis respectively.

From the graph, we can clearly see the location of point A, the x-axis to the origin is, 2, and the y-axis to the origin is 6. The ordered pair is written as which is (2,6)

The ordered pair of A is (2,6)

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise Page 95 Exercise 3 Answer

Given: Graph with different points on it

To find the ordered pair of E

Solution: The cartesian plotting from the graph is the representation on axes

From the graph, draw a horizontal perpendicular line and vertical perpendicular lines to the y-axis and x-axis respectively from point A which looks like

On calculating we find that the value of the x-axis is 0 as the point E lies on the y-axis so only the y-axis value is −4 as the value is down the origin. So the x-axis becomes 0 and the y-axis becomes −4

The ordered pair of E is (0,−4)

Big Ideas Math Algebra 1 Chapter 4 Writing Linear Functions Exercise Solutions

Page 95 Exercise 5 Answer

Given: The graph on the points already plotted on that

To find the point lies in Quadrant IV

Solution: the plotted points on the graph is from the cartesian plane

From the given graph, we can clearly see that the points in which values of the x-axis are positive and the y-axis are negative are highlighted in the below graph

From the above graph, we can see that the only point where the x-axis is positive and the y-axis is negative is D. The value of D is(2,−3) which is in quadrant IV

From the graph, the point that lies in Quadrant IV is D.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise Page 95 Exercise 6 Answer

Given: A well-plotted graph with different points

To find points located on the negative x-axis

Solution: From the graph, the label of the axes on the negative side

We have the graph where we have to check the left side of origin which shows the negative value of x-axis as

From the above graph, we can clearly see that only one point G is on the left side of the origin and the value of that point is −3 on the x-axis and 0 on the y-axis. So the value of the axis is(−3,0)

The point located on the negative axis is G as shown in the graph

Writing Linear Functions Exercises Big Ideas Math Chapter 4

Page 95 Exercise 7Answer

Given: The equation x−y=−12

To find the solution for y

Solution: Using the given equation, we have to solve it by having y on the left and the remaining values on the right side of the equal sign.

We have the given equation
​x−y=−12
Now taking x on the right side, the equation becomes
−y=−12−x

Now taking negative signs from both sides to make them positive, so
​−1(y)=−1(12+x)
y=12+x
​

The solved equation x−y=−12 for y is
y=12+x

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise Page 95 Exercise 8 Answer

Given: The given equation is 8x+4y=16

To find the solution for y

Solution: From the given equation, we have to solve them by taking y on left and others on the right

Now from the given equation
​8x+4y=16
4(2x+y=4)
Taking 4 commons from the whole equation to eliminate

Now we have
​2x+y=4
⇒ y=4−2x
​

Solving 8x+4y=16 for y we get
y=4−2x

Page 95  Exercise 9  Answer

Given: Equation with variables 3x−5y+15=0

To find the solution of y

Solution: we have to use the given equation to solve it for y

We have the equation
​3x−5y+15=0
Taking 5y on another side, we get,
3x+15=5y or 5y=3x+15

Now, divide the whole equation with 5 we get

\(\frac{1}{5}\) (5y=3x+15)

⇒y\(=\frac{3}{5} x+3\)

The equation 3x−5y+15=0 solved for y is

y\(=\frac{3}{5} x+3\)

Algebra 1 Student Journal Chapter 4 Writing Linear Functions Exercises

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise Page 95 Exercise 10 Answer

Given: 0=3y−6x+12

To find, Solve the given equation.
Here we evaluate the equation for y.

By evaluating

​3y−6x+12=0

3y=6x−12

3y=3(2x−4)

y\(=\frac{3}{3}(2 x-4)\)

y=2x−4
​

The value of the given equation is y=2x−4

Chapter 4 Writing Linear Functions Practice Problems Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise Page 95 Exercise 11 Answer

Given: y−2=3x+4y

To find, Solve the given equation.
Here we evaluate the equation for y.

By solving
​y−2=3x+4y

4y−y=−2−3x

3y=−2−3x

y\(=\frac{-2}{3}-\frac{3 x}{3}\)

y\(=\frac{-2}{3}-x\)

The value of the given equation is y\(=\frac{-2}{3}-x\)

Big Ideas Math Chapter 4 Writing Linear Functions Practice Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.5

Page 79  Essential Question  Answer

The graph of the line y=mx+b is a straight line with slope m passing through the point (0,b) as b is the y-intercept.

For example:  y=x+2 has a slope and passes through the point (0,2).
​x=2⇒
y=2+2
=4
​
(2,4) is another point on the line.

The graph of the linear equation y=mx+b is a straight line with slope ​m and the y-intercept as b. The line passes through the point (0,b).

Page 79  Exercise 1  Answer

The given graph is

The equation of the graph is \(y=\frac{2}{3} x+2\), which is of the slope-intercept form. The coefficient of x is the slope of the line and the constant term is the y-intercept. Therefore,

The slope of the line is \(\frac{2}{3}\) The intercept is 2.

Also from the graph, it can verify that the y-coordinate of the point that intersects the y-axis is 2, which is the y-intercept.

The graph of the line is as follows

The slope of the line,\(y=\frac{2}{3} x+2\) is \(\frac{2}{3}\)and the y intercept is 2.

In the question, the straight line is given as y=−2x−1, and the graph of the straight line is also given. We have to find the slope and y-intercept of the straight line. We are going to use the formula for slope to verify the result.

The given equation of the straight line is y=−2x−1.
By comparing with the equation of the straight line y=mx+c, we see that
The slope of the straight line is−2 and the y-intercept is−1.

Now, from the graph, we can see that the y-intercept of the straight line is−1.
Again, in the graph, the rise and the run of the straight line is shown in the given graph as follows

|

Therefore, considering the points(0,−1) and(2,−5), the slope of the straight line is calculated as follows
​Slope\(=\frac{\text { rise }}{\text { run }}\)

​
=-2

The slope and y-intercept of the line y=−2x−1 are−2 and−1, respectively, these are also verified from the following graph

Big Ideas Math Algebra 1 Chapter 3 Exercise 3.5 Solution

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.5 Page 79  Exercise  2  Answer

In the question, the given equation is \(y=-\frac{2}{3} x+3\)
We have to determine the slope and y-intercept of the line.
We are going to use the formula for the slope.

The graph of the line is as follows

From the graph, we see that the line crosses the y-axis at point(0,3), whose y-coordinate is 3.
Therefore, the y-intercept of the line is 3.

In the graph, by considering two points(0,3) and(4.5,0), the slope of the line is calculated as follows

Slope\(\frac{\text { rise }}{\text { run }}\)

\(=-\frac{2}{3}\).

The slope and y-intercept of the line \(y=\frac{2}{3} x+2\) are \(\frac{2}{3}\) and 3, respectively, which are obtained from the following graph

Putting the values in the table, we get

In the question, the given equation is y=2x−2.
We have to determine the slope and y-intercept of the line.
We are going to use the formula for the slope.

The graph of the line is as follows

From the graph, we see that the line crosses the y-axis at point(0,−2), whose y-coordinate is−2.
Therefore, the y-intercept of the line is−2.

In the graph, by considering two points(1,0) and(0,−2) the slope of the line is calculated as follows

slope=\(\frac{\text { rise }}{\text { run }}\)

=2.
​

The slope and y-intercept of the line y=2x−2 are 2 and−2, respectively, which are obtained from the following graph

Putting the values in the table, we get

In the question, the given equation is y=−x+1.
We have to determine the slope and y-intercept of the line.
We are going to use the formula for the slope.

​
The graph of the line is as follows

From the graph, we see that the line crosses the y-axis at point(0,1), whose y-coordinate is 1.
Therefore, the y-intercept of the line is 1.

In the graph, by considering two points(0,1) and(1,0), the slope of the line is calculated as follows

Slope\(=\quad \frac{\text { rise }}{\text { run }}\)

=−1.
​

The slope and y-intercept of the liney=−x+1 are−1 and 1, respectively, which are obtained from the following graph

Putting the values in the table, we get

In the question, the given equation is y=x−4.
We have to determine the slope and y-intercept of the line.
We are going to use the formula for the slope.

The graph of the line is as follows

From the graph, we see that the line crosses the y- axis at point(0,−4), whose y-coordinate is−4.
Therefore, the y-intercept of the line is−4.

In the graph, by considering two points(4,0)
and(0,−4),
the slope of the line is calculated as follows

slope\(=\quad \frac{\text { rise }}{\text { run }}\)

=1.
​
​
The slope and y-intercept of the line y=x−4 are 1 and−4, respectively, which are obtained from the following graph

Putting the values in the table, we get

Graphing Linear Functions Exercise 3.5 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.5 Page 80 Exercise 3 Answer

In the question, the equation of the straight line is given as y=mx+b.
We have to determine how the value of m
Effect the graph of the equation.
Since slope measures the rate of change in the dependent variable, i.e.,y as the independent variable, i.e.,x changes.
Mathematically the slope of a line is defined as

slope\(=\frac{\text { rise }}{\text { run }}\)

\(=\frac{\text { change in } y}{\text { change in } x}\).

Thus, the greater the slope the steeper the line.
The slope shows both steepness and direction.
With a positive slope, the line moves upward when going from left to right.
With a negative slope, the line moves down when going from left to right.
If two linear functions have the same slope they are parallel.
The effect of the slope is clearly shown in the following graph.

In the equation,y=mx+b,m represents the slope of the line and the effect of the value of m can be understood from the following the given in below

In the question, the equation of the straight line is given as y=mx+b.
We have to determine how the value of b
Effect the graph of the equation.
Since b represents the y-intercept of the line, this means, the distance of the point, at which the line crosses the y-axis, from the origin.
Therefore, we get the two points

1. Increasing the y-intercept moves the graph up.
2. Decreasing the y-intercept moves the graph down.

In the equation,y=mx+b,b represents the y-intercept of the line and by changing it, we can move the graph of the line upwards or downwards.

In the question, the equation of the straight line is given as y=mx+b.
We have to verify the effect of the slope and y-intercept of the line by considering an equation of a line.

Let us choose the equation of line as y=−x+1.
The slope of the line is−1.
Varying the slope of the line, we get the following graph

From the given graph, the following points are verified:

The greater the slope the steeper the line.

The slope shows both steepness and direction.

With a positive slope, the line moves upward when going from left to right.

With a negative slope, the line moves down when going from left to right.

Again, the y-intercept of the line is 1.
Now, varying the y-intercept, we get the following graph

From the given graph, the following points are verified:

1. Increasing the y-intercept moves the graph up.
2. Decreasing the y-intercept moves the graph down.

The effects of the slope and y-intercept on the equation y=mx+b are verified from the following graphs considering the equation y=−x+1

(1) varying only m:

(2) varying only b:

Big Ideas Math Linear Functions Exercise 3.5 Help

Page 83 Exercise 3 Answer

In the question, a straight line is given in the graph.
We have to find the slope of the line by describing it.
We are going to use the formula for the slope.

The given graph is

Now, considering the points(−2,3) and(3,−2) on the line, the rise and the run are indicated in the following graph

Therefore, from the graph, the rise of the line is calculated as:
​3−(−2)=3+2
=5
​
And the run is calculated as −2−3=−5.
Thus, the slope of the given line is calculated as follows

slope \(=\frac{\text { rise }}{\text { run }}\)

​
\(=\frac{5}{-5}\)

=−1.
​

From the given graph, the slope of the given line is calculated as−1.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.5 Page 83 Exercise 5 Answer

In the question, the points which lie on a line are presented in a table.
We have to determine the slope of the line.
We are going to use the formula for slope.

The points which lie on the line are given as:
(−3,11),(−1,3),(1,−5),(3,−13).

Considering any two points we can calculate the slope of the line.
Without loss of generality, let us consider the points(−3,11) and(1,−5).

Now, using the formula for the slope of a straight line, we get the slope of the required line as

​Slope=\(=\frac{1-(-3)}{-5-11}\)

This result can be verified by taking any other two points.
If the points represented by the table lie on a line, the slope of the line is
\(-\frac{1}{4}\)

Chapter 3 Exercise 3.5 Step-By-Step Solutions Big Ideas Math

Page 83 Exercise 6 Answer

In the question, the given straight is 6x+4y=24.
We have to find the y-intercept and slope of the line.
We are going to draw a graph and use the formula for the slope.

The given straight line is 6x+4y=24.
The graph of the straight line is given below

From the graph, we see that the graph of the given straight line crosses the y-axis at point(0,6), whose y-coordinate is 6.

Therefore, the y-intercept of the straight line is 6.

Again in the graph, considering the points(0,6) and(4,0) on the line, we can calculate the slope of the line as follows

​Slope\(=\frac{\text { change in } y}{\text { change in } x}\)

\(=-\frac{2}{3}\).

​
The slope and the y-intercept of the linear equation 6x+4y=24, which are obtained from the given graph are\(-\frac{2}{3}\) and 6, respectively.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.5 Page 83 Exercise 7 Answer

In the question, the given straight is y\(=-\frac{3}{4} x+2\)
We have to find the y-intercept and slope of the line.
We are going to draw a graph and use the formula for the slope.

The given straight line is y=\(-\frac{3}{4} x+2\)
The graph of the straight line is given below

From the graph, we see that the graph of the given straight line crosses the y-axis at point(0,2), whose y-coordinate is 2.
Therefore, the y-intercept of the straight line is 2.

Again in the graph, considering the points(0,2) and(4,−1), we can calculate the slope of the line as follows
slope\(=\frac{\text { change in } y}{\text { change in } x}\)

The slope and the y-intercept of the linear equation\(y=-\frac{3}{4} x+2\)which are obtained from the given graph are 2 and \(-\frac{3}{4}\) respectively.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.5 Page 83 Exercise 8 Answer

Given: The equation is y=5x.
To find They− intercept and the slope of the line. Let us draw a graph and use the formula for the slope.

The given straight line is y=5x
The graph of the straight line is given below

The equation passes through the origin. So the y−intercept will be 0.

Again in the graph, considering the points(1,5) and(0,0), we can calculate the slope of the line as follows

​Slope\(=\frac{y_2-y_1}{x_2-x_1}\)

Slope \(=\frac{0-5}{0-1}\)

Slope \(\frac{-5}{-1}\)

Slope=5
​

The slope and the y-intercept of the linear equation y=5x which are obtained from the given graph are 5 and 0 respectively.

Exercise 3.5 Big Ideas Math Algebra 1 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.5 Page 83 Exercise 9 Answer

Given: A linear function f models a relationship in which the dependent variable decreases 6 units for every 3 units the independent variable decreases and the value of the function at 0 is 4.

To find The graphical representation, Slope, x−intercept andy−intercept.We will sketch the graph of the function and use it to calculate the result.

Since the dependent variable decreases 6 units for every 3 units the independent variable increases

​Slope=\(\frac{-6}{-3}\)

Slope=2
​

The equation for the function isf(x)=0.
we write it as y=mx+c
Here the slope is m=2
The value of the function at 0 is 4
So the intercept is b=4

Substituting the above values, we get
y=2x+4
But given that they coordinate,y=0
​0=2x+4
2x=−4
x=−2
​

The graphical representation of the equation y=2x+4 is

The slope, x−intercept, andy−intercept are 2,−2, and 4. The graph will be

Algebra 1 Exercise 3.5 Explanation Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.4

Page 74 Exercise 1 Answer

Given: It is given that we sold total $16 tickets. Each adult ticket cost $4 and each child ticket cost $2.

To find We have to find the equation that relates x and y, where x represents the number of adult tickets. Let y represent the number of child tickets.

We will multiply the variable to the corresponding price of tickets and put that equal to the total price of tickets.

Let x represent the number of adult tickets. Let y represent the number of child tickets.

Each adult ticket cost $4 and each child ticket cost $2.

The equation representing the given scenario is

The equation that relates “x” and “y’ is 4x+2y=16.

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Given: The total cost of tickets and the cost of each adult and child ticket is given to us.

To find  We have to fill up the given table.

We will put the value of “x” and get different values of “y”.

Let us put different values of “x” in the equation 4x+2y=16 and get different values of “y”. We get

⇒ ​x=0
4×0+2y=16
y=8

⇒x=1
4×1+2y=16
2y=12
y=6

⇒x=2
4×2+2y=16
y=4

⇒x=3
4×3+2y=16
2y=4
y=2

⇒x=4
y=16−16
y=0
​

The different combinations are shown in the table below

The table of combinations is shown below

Given: We have a table that shows the different combinations of tickets we might have sold.

To find We have to plot the points from the table and have to describe the pattern formed by the points.

We will first plot the points after that we will join them and observe the type of plot to tell the pattern formed by these points.

The points from the table are plotted below

The pattern formed by these points is a straight line.

The graph is shown below

The pattern formed by these points is a straight line.

The total amount is $16
The cost of each adult ticket is $4
The cost of each child ticket is $2
The equation representing this case is,
4x+2y=16

where x is the number of adult tickets sold and y is the number of child tickets sold. having the value of x, we can substitute it in the linear equation and only one unknown is present, which we can solve by suitable arithmetic operations.

That is, 2y=16−4x

Thus we can find the number of child tickets sold.

Given you sold a total of $16 worth of tickets to a fundraiser. The tickets are of two types, adult tickets are $4 each and child tickets are $2 each. If we have the number of adult tickets, x sold we can find the number of child tickets sold, y by substituting the value in the equation,

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.4 Page 75 Exercise 2 Answer

Given that you sold a total of $48 worth of cheese.
The cost of one swiss cheese per pound is $8
The cost of cheddar cheese per pound is $6
Let the number of pounds of Swiss cheese be x
Let the number of pounds of cheddar cheese be y.
Then we can say that the total cost of sold cheese is the sum of the costs of totals of both the swiss cheese and the cheddar cheese.

Therefore the equation becomes 8x+6y=48.

Given that you sold a total of $48 worth of cheese, where the cost of swiss cheese per pound is $8 and the cost of cheddar cheese per pound is $6. Let x and y represent the number of pounds of Swiss cheese and cheddar cheese.

Then the equation relating x and y is 8x+6y=48.

Given: The equation representing the situation is 8x+6y=48, where x and y
represents the number of pound of swiss cheese and cheddar cheese sold so that the total cost is $48. The coefficients of the variables represent the cost of each of the item.

To find the domain and range of the equation, its graph and also solve for y.

Summary: To solve for isolate the variable in the LHS using suitable arithmetic operations that preserve the equality sign. Choose some values for any of the variables and solve for the unknown. This way find two points plot them on the graph and join them to get the straight line. The domain is the set of all values the variable can take and the range is the set of all output values.

The equation we got is
8x+6y=48

Subtract 8xon both sides
​6y=−8x+48

\(y=\frac{-4 x}{3}+8\)
To find two points, choose some values. Put x=0 in the above equation implies y=8.

Put ​x=3

y=−4+8

y=4
​

We have got two points as (0,8)(3,4). Plot the points and join them to obtain the graph.

​The domain is the set of all input values of the variables.

The range is the set of all output values.

8x+6y=48

Since x and y are numbers of pounds of swiss and cheddar cheese, the domain is the set of all solutions of the linear equation such that both are whole numbers. The range is only one value, that is {48}.

​
Given that you sold a total of $48 worth of cheese. Swiss cheese costs $8 per pound.

Cheddar cheese costs $6 per pound.

The equation we get is 8x+6y=48 where x and y represent the number of pounds of swiss cheese and cheddar cheese sold respectively.

Solving for y we get\(y=\frac{-4}{3} x+8\).

The domain of the equation is {(x,y);8x+6y=48,x,y ∈W}, where W is the set of all whole numbers.

The range of the equation is {48}.

The graph of the equation is

In the earlier part of the problem we got the graph of the equation representing this case, that is 8x+6y=48 as

We observe that the point that crosses the x-axis is (6,0) and its x-coordinate is 6, which is the x-intercept. And the point that crosses the y-axis is (0,8)​ and its y-coordinate is 8, which is the y-intercept.

Given you sold a total of $48 worth of cheese. Swiss cheese costs $8 per pound. Cheddar cheese costs $6 per pound.

The equation we got is 8x+6y=48, where x and y represent the number of pounds of swiss cheese and cheddar cheese sold.

From the graph of the equation, we found that the x-intercept is 6 and the y-intercept is 8. The graph is as follows

The equation we got, in this case, is 8x+6y=48 where x and y represent the number of pounds of swiss cheese and cheddar cheese respectively. Their coefficients represent the cost of each of the corresponding items in dollars.

To find the x-intercept we substitute y=0 in the linear equation, 8x+6y=48, and solve for x.

That is,8x=48

\(x=\frac{48}{8}\)
​
x=6

To find the y-intercept we substitute x=0 in the equation, 8x+6y=48, and solve for y.

​6y=48

​\(y=\frac{48}{6}\)

y=8

This is because a point on the x-axis is of the form (x,0), and a point on the y
axis is of the form (0,y).

Given you sold a total of $48worth of cheese, whereas swiss cheese costs $8
per pound and cheddar, cheese costs $6 per pound. This equation representing the case is 8x+6y=48, where x and y represents the number of pounds of swiss cheese and cheddar cheese respectively. The x-intercept is 6 and the y-intercept is 8.

Given that you sold a total of $48 worth of cheese, whereas swiss cheese costs $8
per pound and cheddar, cheese costs $6 per pound.

The equation is 8x+6y=48, where x and y represent the number of pounds of swiss and cheddar cheese respectively.

We found in the earlier part that the x-intercept is 6. This means that if no cheddar cheese was sold then the number of pounds of swiss cheese to be sold so as the total price is $48 is 6.

Similarly, the y-intercept is 8. This says that if no amount of swiss cheese was sold then 8 pounds of cheddar cheese has to be sold so that the total cost is $48.

Given you sold a total of $48 worth of cheese, whereas swiss cheese costs $8
per pound and cheddar, cheese costs $6 per pound. The equation representing the case is 8x+6y=48, where x and y represent the number of pounds of swiss cheese and cheddar cheese sold respectively. The x and y intercepts are 6 and 8 respectively. This means if no amount of cheddar cheese was sold then 6 pounds of swiss cheese has to be sold and if no amount of swiss cheese was sold then 8 pounds of cheddar cheese has to be sold so that the total cost is $48.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.4 Page 75 Exercise 3 Answer

The equation Ax+By=C represents a straight line, provided A, B are not both zero.

If B=0 and A≠0 then the equation is of the form x=\(\frac{C}{A}\)
; constant which represents a vertical line that is a line parallel to the y-axis.

If A=0 and B≠0 then the equation is of the form y=\(\frac{C}{B}\)
; constant which represents a horizontal line, that is a line parallel to the x-axis.

If both ​A≠0 B≠0, then the equation can be written as
​By=−Ax+C

y=−\(\frac{A}{B}\)x+\(\frac{C}{B}\)

​
This is the slope-intercept form of the linear equation. The graph is a straight line with slope as the coefficient of x and the y-intercept is the constant.

The equation, Ax+By=C is the standard form a linear equation. The graph of the equation is a straight line. It can be a horizontal line or a vertical line or a line with a particular slope which intersects the axes at some points.

Page 77 Exercise 2 Answer

To draw the line x=2, we choose two points of the form (2,y), say, (2,−2),(2,5). Plot these points on the graph and join them.

The graph of the linear equation, x=2, is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.4 Page 78 Exercise 5 Answer

Given: The linear equation is 5x−2y=−30.

To find The x and y intercepts of the graph of the linear equation.

Summary: For a point on the x-axis, the y coordinate is 0 and for a point on the y-axis, the x coordinate is 0. To find the x-intercept put y=0 and solve for x.

Similarly to find the y-intercept put x=0 in the linear equation and solve for y.

Put y=0
In 5x−2y=−30

​5x=−30

x=−30

x=−6
​
The x-intercept.

Put x=0
In 5x−2y=−30

​−2y=−30

y=15

The y-intercept is 15.

The x and y intercepts of the linear equation, 5x−2y=−30 is −6, and 15 respectively.

Page 78 Exercise 6 Answer

Given: The linear equation is −8x+12y=24.

To find the x and y intercepts and thus draw the graph.

Summary: To find the x-intercept put y=0 and solve for x. Similarly to find the y-intercept put x=0 in the linear equation and solve for y.

Plot the points on the axes and join them to obtain the graph.

To find the intercepts
Put y=0

In −8x+12y=24.

​−8x=24

x=−3
​
The point at which the line crosses the x-axis is (−3,0).
Put x=0

In −8x+12y=24.

​12y=24

y=2
​
The point at which the line intersects the y-axis is (0,2).

Having got both the intercepts, plot the points, (−3,0,)(0,2) on the graph and join them.

The x and y intercepts of the linear equation, −8x+12y=24 is −3 and 2 respectively. And its graph is as follows

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.4 Page 78 Exercise 7 Answer

Given: The linear equation is 2x+y=4.

To find the x and y intercepts of the line and thus draw the graph of the equation.

Summary: First find the intercepts. Put y=0 in the linear equation and solve for x to obtain the x-intercept.

Similarly, put x=0 in the equation and solve for y to obtain the y-intercept. Plot the point on their respective axes. Join them to get the graph.

Let us find the intercepts.
Put y=0

In 2x+y=4.

​2x=4

x=2
​
The point that intersects the x-axis is (2,0).

Put x=0 in 2x+y=4.

​2×0+y=4

y=4
​
The point that intersects the y-axis is (0,4).

Plot the points, (2,0), and (0,4) on the axis and join them to obtain the graph.

The x and y intercepts of the linear equation, 2x+y=4 are 2 and 4 respectively. And the graph of the equation is as follows.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.4 Page 78 Exercise 8 Answer

Given: The equation, 25x+10y=9000, where x is the number of sweatshirts sold and y is the number of baseball caps sold. And the coefficients are the cost of each item corresponding to the variable in dollars.

To find the intercepts of the linear equation and interpret them.

Summary: Putting y=0 in the equation and solving for x gives us the x-intercept and Putting x=0 in the equation and solving for y gives us the y-intercept. We can interpret the result in terms of the items and the cost that the variables represent.

Put y=0
In 25x+10y =9000.

​25x=9000

x=360
​
The point that crosses the x-axis is(360,0).

Put x=0

In 25x+10y=9000.

​10y=9000

=900
​
The point that intersects the y-axis is(0,900).

The variables represent the following
x=The number of sweatshirts sold.

25=The cost of one sweatshirt in dollars.

y=The number of baseball caps sold.

10=The cost of one baseball cap.

9000=Total amount to be collected to attend the band competition.

The point (360,0) tells us that the number of sweatshirts sold if no baseball caps were sold is 360.

The point (0,900) tells us that the number of baseball caps to be sold if no sweatshirts were sold is 900.

The equation is 25x+10y=9000, where x and y represent the number of sweatshirts and baseballs to be sold so as to get the amount of 9000 dollars to attend a band competition. Also, the coefficients 25 and 10 represent the amount of each sweatshirt and baseball cap in dollars.

The x and y intercepts are 360 and 900 respectively. This says that the number of sweatshirts sold when no baseball caps were sold is 360 and the number of baseball caps to be sold when no sweatshirts were sold is 900, so as to achieve the target amount.

Given: the equation 25x+10y=9000, are the number of sweatshirts and baseballs sold and their coefficients represent the cost of respective item in dollars.

To find the number of baseball caps sold if the number of sweatshirts sold is 258.

Summary: Substitute x=258 in the given linear equation and solve for y.

Put x=258
In 25x+10y=9000.

​25×258+10y=9000

6450+10y=9000
​

Subtract 6450 on both sides of the equation.
​10y=9000−6450

10y=2550

y=225

which is the number of baseball caps sold.

Given: The equation 25x+10y=9000 models the given situation, where x and y represent the number of sweatshirts and baseball caps sold so that the total amount collected is $9000.

To find the graph of the solution and two more possible solutions in this context.

Summary: Choose some values for the variables and solve for the other. Thus obtain two points. Plot and join them to get the graph.

To find the solutions in this context find out solutions of the equation so that they are whole numbers since the variables represent a number.

In part (a) of the problem we found that the x and y intercepts of the equation, 25x+10y=9000 are 360,900 respectively.

So two points on the line are (360,0), and (0,900). Plot the points and join them.

Since the variables represent a number of items sold, the domain of the equation, 25x+10y=9000 is {(x,y);25x+10y=9000,x,y ∈W}, where W is the set of all whole numbers.

The equation can be written as
​10y=9000−25x

Let ​x=2⇒

=895
​

Let ​x=4⇒

=890
​

If the number of sweatshirts sold is 2 then the number of baseball caps sold is 895. If the number of sweatshirts sold is 4 then the number of baseball caps sold is 890.

The equation 25x+10y=9000 represents the situation, where x and y represent the number of sweatshirts and baseball caps sold so that the total amount collected is $9000. Two possible solutions are (2,895), and (4,890). The graph of the equation is.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.2

Page 64  Essential Question  Answer

Given:- A  function.

We have to check its linearity.

Simplify the equation as closely as possible to the form of y=mx+b.

Check to see if your equation has exponents. If it has exponents, it is nonlinear.

If your equation has no exponents, it is linear.

To check the linearity:- Simplify the equation as closely as possible to the form of y=mx+b Check to see if your equation has exponents. If it has exponents, it is nonlinear. If your equation has no exponents, it is linear.

Big Ideas Math Algebra 1 Chapter 3 Exercise 3.2 Solution

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.2 Page 64 Exercise 1 Answer

Given:-  ​l=x
b=2x
​
We have to complete the table.

We will first find the perimeter for each value.

And we also have to tell about the linearity of the function.

The perimeter is given by:
​2(l+b)
=2(x+2x)
=2(3x)
=6x
​
The table becomes

The graph for the given data is

As the function becomes
f(x)=6x

Therefore, the function is linear.

The graph for the perimeter of length x and breadth 2x is and the function is linear.

We are given a table:

We are asked to fill the sequence of the given table, graph the values and check if they are linear or non-linear.

In order to do that we have to take the values of x and find the area of the rectangle.

The length and breadth values can be obtained using the given in below.

The area is then filled in the table.

A graph is to be plotted using data from the table.

Using the graph, determine whether it is linear or non-linear.

1. Value of x=1

Value of length:
​2×x=2×1
=2

​Value of breadth: ​x=1

Area: ​l×b=2×1
=2

​
2. Value of x=2

Value of length:
​2×x=2×2
=4
​
Value of breadth: x=2

Area: ​l×b=4×2
=8
​

3. Value of x=3

Value of length:
​2×x=2×3
=6
​
Value of breadth: x=3

Area: l×b=6×3
=18
​

4. Value of x=4

Value of length:
​2×x=2×4
=8
​
Value of breadth: x=4

Area: l×b=8×4
=32
​

5. Value of x=5

Value of length:
​2×x=2×5
=10
​
Value of breadth: x=5

Area:
​l×b=10×5
=50
​

Plotting values in the table:

Graph for the given table:

Determine whether linear or non-linear
The graph does not give a straight line, therefore it is non-linear.

The values of the given table are:

The graph obtained is:

The function is linear as the graphs give a straight line.

We are given a table:

We are asked to fill the sequence of the given table, graph the values and check if they are linear or non-linear.

In order to do that we have to take the values of x and find the circumference of the circle.

The values represent the radius.

The circumference is then filled in the table.

A graph is to be plotted using data from the table.

Using the graph, determine whether it is linear or non-linear.

1. Value of radius:
radius r=1

Circumference: ​2×π×r
=2×3.14×1
=6.28
​

2. Value of radius:
radius r=2

Circumference: ​2×π×r
=2×3.14×2
=12.56
​

3. Value of radius:
radius r=3

Circumference: ​2×π×3
=2×3.14×3
=18.84
​

4. Value of radius:
radius r=4

Circumference: ​2×π×r
=2×3.14×4
=25.12
​

5. Value of radius:
radius r=5

Circumference: ​2×π×5
=2×3.14×5
=31.4
​

Plotting values in the table:

Graph for the given table:

Determine whether linear or non-linear
The graph gives a straight line, therefore it is linear.

The values of the given table are:

The graph obtained is:

The function is linear as the graphs give a straight line.

We are given a table:

We are asked to fill the sequence of the given table, graph the values and check if they are linear or non-linear.

In order to do that we have to take the values of r and find the area of the circle.

The values represent the radius.

The area is then filled in the table.

A graph is to be plotted using data from the table.

Using the graph, determine whether it is linear or non-linear.

1. Value of radius:
radius r=1

Area: ​π×r²
=3.14×12
=3.14
​

2. Value of radius: 
radius r=2

Area: ​π×r²
=3.14×22
=12.56
​

3. Value of radius: 
radius r=3

Area: ​π×r²
=3.14×32
=28.26
​

4. Value of radius: 
radius r=4

Area: ​π×r²
=3.14×42
=50.24
​

5. Value of radius:
radius r=5

Area: ​π×r²
=3.14×52
=78.5
​

Plotting values in the table:

Graph for the given table:

Determine whether linear or non-linear

The graph does not give a straight line, therefore it is non-linear.

The values of the given table are

Table :

The graph obtained is:

The function is non-linear as the graphs do not give a straight line.

Graphing Linear Functions Exercise 3.2 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.2 Page 65 Exercise 2 Answer

We are asked to refer to Exercise 1.

We are asked to give a reason for the patterns in Exercise 1 to be functions.

The patterns/sequences from Exercise 1 are

The perimeter of a rectangle:
​2l+2b
f(x)=2×(2x+x)
f(x)=2×(3x)
f(x)=6x
​where l is length and b is a breadth

Area of a rectangle:
​l×b
f(x)=2×x×x
f(x)=2×x²

​Circumference of a circle:
​2×π×r
f(r)=2×3.14×r
f(r)=6.28×r
​
Area of circle:
​π×r²
f(r)=3.14×r²

They all represent a function as they all accept input in the form of or and give a proper output.

Page 65  Exercise 3  Answer

We are asked ways to determine whether a given function is linear or non-linear.

First, take out points from the function by calculating random values.

Plot the points so obtained in a graph.

If the graph gives a straight line then the function is linear.

If it does not give a straight line then the given function is non-linear.

Example:
Linear function:
f(x)=2+3x

Graph:

Non-linear function:
f(x)=3+x2

Graph:

A given function is said to be linear if the graph of the function gives a straight line. A function is called non-linear if its graph does not give a straight line.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.2 Page 65 Exercise 4 Answer

We are asked to describe two real-life patterns: one linear and one non-linear.
In order to do that we have to get any real-life incident and plot a graph to show whether it is linear or non-linear.

Linear pattern:
Suppose a kid on his birthday received a piggy bank from his grandmother.

The grandmother added 20 $ to the piggy bank before giving it as a gift.

Now the kid is collecting coins in a piggy bank.

He adds 12 $ every day.

Then the total amount inside the piggy bank gives a linear function.

Then the function can be written as
f(x)=20+2×x

where x represents the number of days.

Graph:

Non-linear function:
The values of weather conditions of a given place when calculated on a daily basis.

The weather of any place fluctuates every day and doesn’t remain constant.

Suppose in the Thar desert of India, the heat level in summer increases exponentially during the day and drops during the night.

Then the function can be written as
f(x)=x²

Graph:

Two real-life examples of linear and non-linear are:

Linear: A kid added 2 $ every day in his piggy bank that already contains 20 $.
Function: f(x)=20+2x.

Non-linear: The weather condition of the Thar desert in summer (rising exponentially )in terms of heat received during the day and night.
Function: f(x)=x².

Page 68  Exercise 1  Answer

We are given a graph

We are asked to check whether the given graph is linear or non-linear.

A linear pattern when traced in a graph provides a straight line.

A non-linear pattern when traced in a graph provides curves or any other pattern that is not straight.

The graph here does not display a proper straight line.

It is non-linear.

The given graph is non-linear as it does not represent a straight line.

Algebra 1 Student Journal Chapter 3 Exercise 3.2 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.2 Page 68 Exercise 3 Answer

We are given a table

We are asked to check whether the table represents a linear function or a non-linear function.

A linear function when traced in a graph gives a straight line.

A non-linear function when traced in a graph gives a curve or any other figure that is not straight.

In order to do that we have to plot a graph with the given values.

And then check for linear or non-linear.

Graph:

The points are linearly placed.

Hence, it is linear in nature.

The points from the table can be traced to get a straight line, displaying its linear characteristic.

Page 68  Exercise 4  Answer

We are given a table

We are asked to check whether the table represents a linear function or a non-linear function.

A linear function when traced in a graph gives a straight line.

A non-linear function when traced in a graph gives a curve or any other figure that is not straight.

In order to do that we have to plot a graph with the given values.

And then check for linear or non-linear.

Graph:

The points are not in a straight line.

Hence the function is non-linear.

The points from the table do not produce a straight line, representing a non-linear characteristic.

Big Ideas Math Linear Functions Exercise 3.2 Help

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.2 Page 68 Exercise 5 Answer

We are given a function y=3−2x.

We are asked to check whether it is linear or non-linear.

In order to do that we have to obtain points from the given equation.

Using these points we have to plot a graph.

If the points are in a straight line then the given function is linear.

If not, then the function is non-linear.

1. Value of x=1

Value of :
​y=3−2x
=3−2×1
y=1
​

2. Value of x=2

Value of :
​y=3−2x
=3−2×2
y=−1
​

3. Value of x=3

Value of :
​y=3−2x
=3−2×3
y=−3
​

4. Value of x=4

Value of :
​y=3−2x
=3−2×4
y=−5
​

Graph:

The given graph represents a straight line.

It is a linear function.

The graph for the function y=3−2x represents a straight line making the function a linear function.

Page 68  Exercise  6  Answer

We are given a function y=−\(y=-\frac{3}{4} x^3\).

We are asked to check whether it is linear or non-linear.

In order to do that we have to obtain points from the given equation.

Using these points we have to plot a graph.

If the points are in a straight line then the given function is linear.

If not, then the function is non-linear.

1. Value of x=1

Value of :
​y=\(\frac{-3}{4} x^3\)

=\(\frac{-3}{4} 1^3\)

=−0.75
​

2. Value of x=2

Value of :
​y=\(\frac{-3}{4} x^3\)

=\(\frac{-3}{4} 2^3\)

=−6

​
3. Value of x=3

Value of :
​y=\(\frac{-3}{4} x^3\)

=\(\frac{-3}{4} 3^3\)

=−20.25
​

4. Value of x=4

Value of :
​y=\(\frac{-3}{4} x^3\)

=−48
​

Graph:

The graph does not represent a straight line.

It is non-linear.

The graph of the given function y= \(\frac{-3}{4} x^3\) does not represent a straight line, making the function a non-linear function.

Graph:

Page 68  Exercise 7  Answer

We are given a graph

We are asked to find the domain of the function and also to determine whether the domain is discrete or continuous.

In order to do that we have to get the domain values from the graph.

Then analyze the values to check for discrete or continuous.

Domain:
The domain of a function is all the input values.
Here we have to get the values of the x-axis from the graph.
They are: (1,6)
The domain of the given graph is (1,6).

Check for discrete and continuous:
A domain is said to be discrete if the values are just points while it is called continuous if the values are continuously obtained in a range.

Domain: (1,6)
From the graph, we can trace a straight line with the following domain. They are continuous in nature as they display a range.

The given graph has a domain as (1,6).

The domain is continuous in nature.

Chapter 3 Exercise 3.2 Step-By-Step Solutions Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.2 Page 68 Exercise 8 Answer

We are given a graph

We are asked to find the domain of the function and also to determine whether the domain is discrete or continuous.

In order to do that we have to get the domain values from the graph.

Then analyze the values to check for discrete or continuous.

Domain:
The domain of a function is all the input values.
Here we have to get the values of the x-axis from the graph.
They are:(1,2,3)
It has multiple points as a domain. It does not display a range.

Check for discrete and continuous:
A domain is said to be discrete if the values are just points while it is called continuous if the values are continuously obtained in a range.

Domain: 1,2,3
The domain of the given function is in points and is not continuous. It is discrete.

The given graph has a domain of 1,2,3 points. It has a discrete domain as it does not display a range

Exercise 3.2 Big Ideas Math Algebra 1 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.1

Page 59 Exercise 2 Answer

Given:- {(0,8),(1,8),(2,8),(3,8)}

We have to determine whether each relation represents a function.

We can see that every element of the domain is connected with exactly one element of the codomain.

Therefore, the given relation is a function.

The relation {(0,8),(1,8),(2,8),(3,8)} is a function.

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Given:- {(8,0),(8,1),(8,2),(8,3)}

We have to determine whether each relation represents a function.

We can see that one element of the domain is connected with more than one element of the codomain which contradicts the definition of the function.

Therefore, the given relation is not a function.

The relation {(8,0),(8,1),(8,2),(8,3)} is not a function.

Given:- {(1,8),(2,9),(3,10),(3,11)}

We have to determine whether each relation represents a function.

We can see that one element {3} of the domain is connected with more than one element of the codomain which contradicts the definition of the function.

Therefore, the given relation is not a function.

The relation {(1,8),(2,9),(3,10),(3,11)} is not a function.

Given:- {(1,6),(2,4),(5,4),(5,5),(7,5),(7,8)}

We have to determine whether each relation represents a function.

We can see that one or more elements ({5,7}) of the domain are connected with more than one element of the codomain which contradicts the definition of the function.

Therefore, the given relation is not a function.

The relation {(1,6),(2,4),(5,4),(5,5),(7,5),(7,8)} is not a function.

Given:- {(−2,5),(−1,8),(0,6),(1,6),(2,7)}

We have to determine whether each relation represents a function.

We can see that every element of the domain is connected with exactly one element of the codomain.

Here, the range is the same for the two elements of the domain, which is not a problem.

Therefore, the given relation is a function.

The relation {(−2,5),(−1,8),(0,6),(1,6),(2,7)} is a function.

Big Ideas Math Algebra 1 Chapter 3 Exercise 3.1 Solution

Given:- {(−2,0),(−1,0),(−1,1),(0,1),(1,2),(2,2)}

We have to determine whether each relation represents a function.

We can see that one or more elements ({−1}) of the domain are connected with more than one element of the codomain which contradicts the definition of the function.

Therefore, the given relation is not a function.

The relation {(−2,0),(−1,0),(−1,1),(0,1),(1,2),(2,2)} is not a function.

Given:- Each radio frequency x in a listening area has exactly one radio station y.

We have to determine whether each relation represents a function.

We can see that every element of the domain is connected with exactly one element of the codomain.

Therefore, the given relation is a function.

The relation “Each radio frequency x in a listening area has exactly one radio station y.” is a function.

Given:- The same television station can be found on more than one channel.

We have to determine whether each relation represents a function.

We can see that one or more elements of the domain are connected with more than one element of the codomain which contradicts the definition of the function.

Here, domain means television and range is for channels.

Therefore, the given relation is not a function.

The relation “The same television station can be found on more than one channel.” is not a function.

Given:- x=2

We have to determine whether each relation represents a function.

We can see that one or more elements of the domain are connected with more than one element of the codomain which contradicts the definition of the function.

Here, an element {2} of the domain is connected with every element of the range.

Therefore, the given relation is not a function.

The relation x=2 is not a function.

Given:- y=2x+3

We have to determine whether each relation represents a function.

We can see that every element of the domain is connected with exactly one element of the codomain.

Moreover, a linear equation is always a function.

Therefore, the given relation is a function.

The relation y=2x+3 is a function.

Graphing Linear Functions Exercise 3.1 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.1 Page 60 Exercise 3 Answer

Given:- A function.

We have to write some examples of relations which are functions.

In the functions, each element of the domain must be connected with exactly one element of the range.

Some examples of functions are
​y=x
y=mx+c
{(1,1),(1.4,1),(2,2),(2.4,2)}
y=4
​

The examples of relations which are functions are
y=x
y=mx+c
{(1,1),(1.4,1),(2,2),(2.4,2)}
y=4
​

Given:- A function.

We have to write some examples of relations that are not functions.

In the functions, each element of the domain must be connected with exactly one element of the range.

Some examples of relations that are not functions
​x=9
{(1,1),(1,1.4),(2,2),(2,2.4)}
{(1,1),(2,1),(3,1),(5,1)}
​

The examples of relations that are not functions are.
x=9
{(1,1),(1,1.4),(2,2),(2,2.4)}
{(1,1),(2,1),(3,1),(5,1)}

Page 63  Exercise 1  Answer

Given:- {(−2,4),(0,4),(1,5),(−2,5)

We have to determine whether each relation represents a function.

We can see that one or more elements of the domain are connected with more than one element of the codomain which contradicts the definition of the function.

Here, an element {−2} of the domain is connected with more than one element of the range.
Therefore, the given relation is not a function.

The relation {(−2,4),(0,4),(1,5),(−2,5)} is not a function.

Algebra 1 Student Journal Chapter 3 Exercise 3.1 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.1 Page 63  Exercise 2 Answer

Given:- {(0,3),(1,1),(2,1),(3,0)}

We have to determine whether each relation represents a function.

We can see that every element of the domain is connected with exactly one element of the codomain.

Therefore, the given relation is a function.

Page 63  Exercise 4   Answer

Given:- graph of y=x²

We have to determine whether each relation represents a function.

We can see that every element of the domain is connected with exactly one element of the codomain.

Moreover, a quadratic equation in two variables is always a function.

Therefore, the given relation is a function.

The relation y=x²  is a function.

Page 63  Exercise 5  Answer

Given:- A graph whose ordered pairs are {(1,4),(2,4),(0,4),(3,3),(4,3),(5,3)}
We have to find its domain and range.

The domain is the set of elements on the left side of the ordered pairs, i.e.,
{0,1,2,3,4,5}

The range is the set of elements on the right side of the ordered pairs, i.e.,
{3,4}

The domain and the range of {(1,4),(2,4),(0,4),(3,3),(4,3),(5,3)} are {0,1,2,3,4,5} and {3,4} respectively.

Big Ideas Math Linear Functions Exercise 3.1 Help

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.1 Page 63 Exercise 6 Answer

Given:- A graph whose equation is given by y=|x|

We have to find its domain and range.

From the graph, we can see that
The domain is [−3,3]
And the range is [0,3].

The domain and the range are [−3,3] and [0,3] respectively.

Page 63  Exercise 7  Answer

Given:- y=12x

We have to tell the independent and dependent variables.

Here, y represents the number of pages of text a computer printer can print and x represents time.

The function is y=12x

Here, x i.e., time is an independent variable

And y, i.e., the number of pages that can print is a dependent variable.

The number of pages that can print is a dependent variable that depends upon an independent variable time.

Chapter 3 Exercise 3.1 Step-By-Step Solutions Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise

Page 58 Exercise 2 Answer

Given:- (2,2)

We have to plot the point on the graph.
We also have to describe the location of the point.

(2,2)on the graph is

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Location:

The required point is two units right from the origin and two units above the x−axis.

The required point on the graph is

Big Ideas Math Algebra 1 Chapter 3 Graphing Linear Functions Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise Page 58 Exercise 4 Answer

Given:- (5,2)

We have to plot the point on the graph.
We also have to describe the location of the point.

(5,2) on the graph is

Location:
The required point is five units right from the origin and two units above the x−axis.

The required point on the graph is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise Page 58 Exercise 5 Answer

Given:- 5 units down and on the y−axis.

We have to plot the point on the graph.
We also have to describe the location of the point.

The graph for the point that is on the y-axis and 5 units down from the origin is

The required point on the graph is (0,−5)

Graphing Linear Functions Chapter 3 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise Page 58 Exercise 6 Answer

Given:- 2x+1 , x=3

We have to find the value of the expression for the given value of x.
We just have to substitute the given value of the variable in the expression.

Substituting the value of x in the expression
​2x+1
x=3
=2(3)+1
=6+1
=7
​
The value of 2x+1 at x=3 is 7.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise Page 58 Exercise 7 Answer

Given:- 16−4x , x=−4

We have to find the value of the expression for the given value of x.
We just have to substitute the given value of the variable in the expression.

Substituting the value of x in the expression
​16−4x
x=−4
=16−4(−4)
=16+16
=32
​
The value of 16−4x at x=−4 is 32.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise Page 58 Exercise 9 Answer

Given:- −9−3x ,x=5

We have to find the value of the expression for the given value of x.
We just have to substitute the given value of the variable in the expression.

Substituting the value of x in the expression
​−9−3x
x=5
=−9−3(5)
=−9−15
=−24
​
The value of −9−3x at x=5 is −24.

Algebra 1 Student Journal Chapter 3 Graphing Linear Functions Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise Page 58 Exercise 10 Answer

Given:- Length =24−3x

We have to find the value of the expression for the given value of x.
We just have to substitute the given value of the variable in the expression.

The length of a side of a square =24−3x
Length at x=6
​=24−3(6)
=24−18
=6ft
​
The length of the side of the square when x=6 is 6 ft.

Chapter 3 Graphing Linear Functions Step-By-Step Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.6

Page 53 Exercise  2  Answer

The given graph is

We plot x+2=0 in the number line asx=−2

The required graph is

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Given: The given equation is |x+2|≤3.

To find The points that are within 3 units from the point you found in Page 53 Exercise  2 .
Observe the equation then make a graph for it.

Consider the given equation
We find the point 3 units (from left to right) away from a point in Page 53 Exercise  2

The inequality of given data is, we plot x=−5 and x=1

Big Ideas Math Algebra 1 Chapter 2 Exercise 2.6 Solution

Given: The given equation is ∣x+2∣≤3.

To find The number line to solve an absolute value inequality.
Observe the equation then make a graph for it.

Consider the given equation

We solve the inequality as follows
​∣x+2∣≤3​
x+2≤3
​x+2​

Now subtract 2 from both sides
x+2−2≤3−2​
x≤1
x+2≤−3x+2−2≤−3−2​

Again subtract 2 from both sides
x≤−5​x≤x≤1

We draw −5≤x≤1 as follows

The inequality of given data is, we plot −5≤x≤1.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.6 Page 54 Exercise 3 Answer

Given: The absolute value inequality |x+2|≤3.

To find The absolute value inequality.
Observe the spreadsheet then fill data in it.

According to the question,
Make a spreadsheet it.

We use a spreadsheet to solve the absolute value inequality

Given: The absolute value inequality |x+2|≤3.

To find The solution using the spreadsheet.
Observe the spreadsheet then fill data in it.

According to the given data
Make spreadsheet.

Using the spreadsheet, we can see that the values for x in Exercises 1 and 2 can be found in the spreadsheet’s values.

We notice that the values for x are found in the values in the spreadsheet.

Solving Linear Inequalities Exercise 2.6 Big Ideas Math

Given: The absolute value inequality |x+2|≤3.

To find The solutions using the spreadsheet
Observe the spreadsheet then fill data in it.

According to the given data
Make spreadsheet.
We can use a spreadsheet to solve an absolute value inequality by plugging in the values of x to the formula.

We use a spreadsheet to solve an absolute value inequality by plugging in the values of x to the formula.

Page 54 Exercise 4  Answer

There are three approaches for solving an absolute value inequality.

These methods include algebraic (using linear inequalities), visual (using a number line), and numerical (using a calculator) ( using spreadsheets).

If the absolute value expression equals a negative number, the equation has no solution because an absolute value can never be negative.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.6 Page 54 Exercise 5 Answer

There are three approaches for solving an absolute value inequality.

These methods include algebraic (using linear inequalities), visual (using a number line), and numerical (using a calculator) (using spreadsheets ).

All three strategies are effective and simple to master. Personally, I favour the graphical way because it is the most transparent of the three; nevertheless, this does not preclude you from utilising the other two.

If the absolute value expression equals a negative number, the equation has no solution because an absolute value can never be negative.

Page 56 Exercise 3  Answer

Given: The given equation is 3|2a+5|+10≤37
To find The inequality.
Observe the question and make a graph for it.

Consider the given equation

First, solve for a
3|2a+5|+10≤37

We separate this inequality into two
​3(2a+5)+10≤37

Now distribute
3.2a+3.5+10≤37

Then simplify
6a+15+10≤37
6a+25≤37
6a+25−25≤37−25

Now subtract 25 from both sides
6a≤12

Then divide both sides by 6
a≤2

Divide both sides by
6a+15−15≥−27−15

Now subtract by 15 from both sides
​6a≥−42

a≥−7
​

Now we plot the data to graph a≤2 and a≥−7

The inequality of given data is, we plot a≤2 and a≥−7

Algebra 1 Student Journal Chapter 2 Exercise 2.6 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.6 Page 56 Exercise 4 Answer

Given: The given equation is∣y−3∣≤4.
To find The inequality.
Observe the question and make a graph for it.

Consider the given equation

First, we solve for y
|y−3|≤4

Separate this inequality into two.
y−3≤4​

Now add 3 to both sides
y−3+3≤4+3

y≤7

y−3≥−4

y−3+3≥−4+3​

Again add 3 to both sides
y≥−1

Now we plot the data to graph,y≤7 and y≥−1

The inequality of given data is, we plot y≤7 and y≥−1

Page 56 Exercise 5  Answer

Given: The given equation is |3+r|−4<0
To find The inequality.
Observe the question and make a graph for it.

Consider the given equation.

First, we solve for r
|3+r|−4<0

Separate this inequality into two
​3+r−4<0
r−1<0

Now add 1 to both sides
r−1+1<0+1
​r<1
3+r<0+4
3+r>−4​
3+r−3>−4−3

Subtract 3 from both sides,
r>−7

Now we plot the graph r<1 and r>−7 as follows

The inequality of given data is, we plot r<1 and r>−7.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.6 Page 57 Exercise 7 Answer

Given:The given equation is​\(\left|\frac{x}{4}-7\right|<-2\)
To find The inequality.
Observe the question and make graph for it.

Consider the given equation

First, we solve for x

\(\frac{x}{4}\)−7+7<−2+7​

Now add 7 to both sides

Now multiply both sides by 4

x<-20

Again add 7 to both sides.

\(\frac{x}{4}\)−7+7>2+7​

\(\frac{x}{4}\)>9

Now multiply both sides by 4

\(\frac{x}{4}\).4>9⋅4​

x>36

For equation make graph x<−20 and x>36

The inequality of given data is, we plot x<−20 and x>36.

Big Ideas Math Linear Inequalities Exercise 2.6 Help

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.6 Page 57 Exercise 8 Answer

Given: The given equation is |4x−7|+8≥17
To find The inequality.
Observe the question and make graph for it.

Consider the given equation

First, we solve for x
|4x−7|+8≥17

We separate the inequality into two
​4x−7+8≥17
​4x+1≥17
4x+1−1≥17−1
4x≥16
​
Now divide by 4 both sides
​
\(\frac{4 x}{4} \geq \frac{16}{4}\)

x≥4

4x−7+8≥−17
​
Subtract 8 from both sides.
​4x−7+8−8≥17−8
4x−7≤−9
​
Add 7 to both sides.
4x−7+7≤−9+7

​\(x \leq-\frac{1}{2}\)

​For equation make graph,x≥4 and \(x \leq-\frac{1}{2}\)

The inequality of given data is, we plot,x≥4 and \(x \leq-\frac{1}{2}\)

Page 57 Exercise 9  Answer

Given: The given equation is 6|2−k|+14>14
To find The inequality.
Observe the question and make a graph for it.

Consider the given equation

First, we solve for k
6|2−k|+14>14

Separate this inequality into two
​6|3−k|+14>14

Subtract 14 on both sides.
​6(3−k)+14−14>14−14

​6(3−k)>0

3−k>0

Now subtract 3 from both sides
3−k−3>0−3

​−k>−3

​Simplify

​6(3−k)+14−14>14−14

6(3−k)>0
​
\(\frac{-k}{-1}>\frac{-3}{-1}\)

Divide both sides by -1
k<3

For equation make graph,k<3

The inequality of given data is, we plot k<3

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.6 Page 57 Exercise 10 Answer

Given:The given is, the average starting salary for a new worker is 25000.
To find The range of the starting salaries.
Observe the given data the solve for the answer.

According to the given data.
Solve for the salary, s as follows
​−1800≤∣s−25000∣≤1800

−1800+25000≤s≤1800+25000

23200≤s≤26800
​
The salary is from 23200 to 26800.

Chapter 2 Exercise 2.6 Step-By-Step Solutions Big Ideas Math