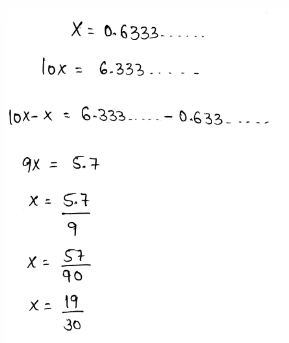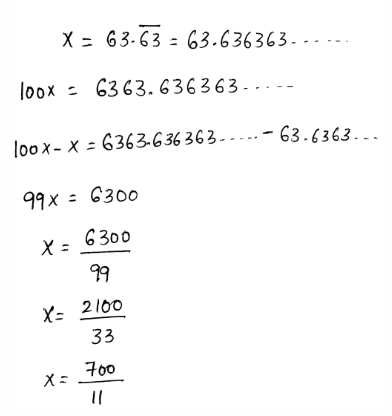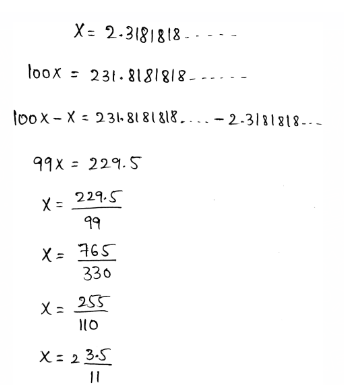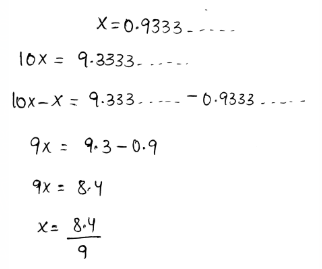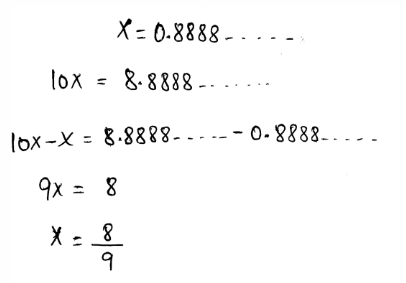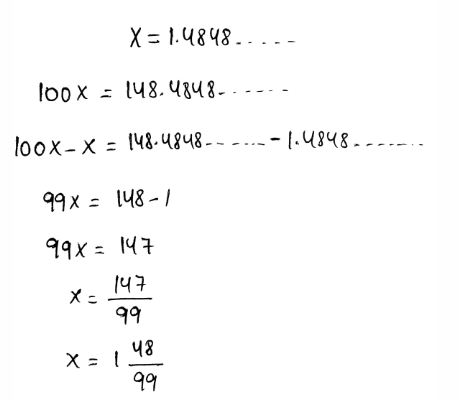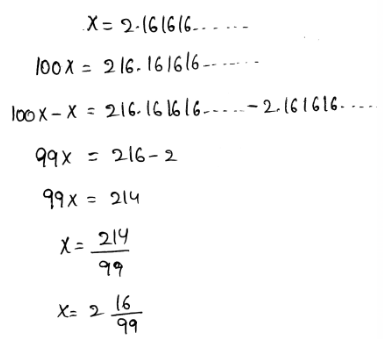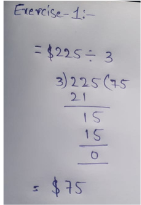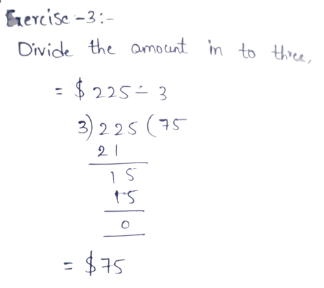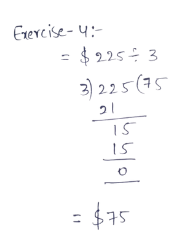Schindler

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.2 Real Number Solutions

Page 13 Exercise 1 Answer

Given that, Sofia wrote a decimal as a fraction. Her classmate Nora says that her method and answer are not correct. Sofia disagrees and says that this is the method she learned.

We need to construct Arguments whether Nora or Sofia is correct or not.

The given decimal is 0.12112111211112…

Here, Sofia wrote this decimal as a fraction.

But it cannot be represented as a fraction since the given number is an irrational number.

Only terminating and repeating decimals can be represented as a fraction.

Here, the decimal is not terminating and it is not repeating. Thus, it cannot be represented as a fraction.

Nora’s Argument is correct. The given number cannot be represented as a fraction since it is an irrational number.

Page 13 Exercise 2 Answer

We need to write another nonterminating decimal number that can not be written as a fraction.

Only terminating and repeating decimals can be represented as a fraction.

If the decimal is not terminating and it is not repeating, it cannot be represented as a fraction.

Some of the examples of nonterminating decimal numbers that can not be written as fractions are,
​
0.15267389…

0.3512649…

0.125112511125…
​
Another nonterminating decimal number that can not be written as a fraction is 0.125112511125…

Page 13 Exercise 1 Answer

We need to find whether 0.12112111211112… is a rational number or not.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Here, the given number 0.12112111211112… is non-terminating and non-repeating in nature.

Hence, it is an irrational number.

The given decimal 0.12112111211112… is an irrational number.

Envision Math Grade 8 Student Edition Exercise 1.2 Real Numbers Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 14 Question 1 Answer

We need to explain how an irrational number is different from a rational number.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Terminating and repeating decimals are known as rational numbers while non-terminating and non-repeating decimals are known as irrational numbers.

Page 14 Exercise 1 Answer

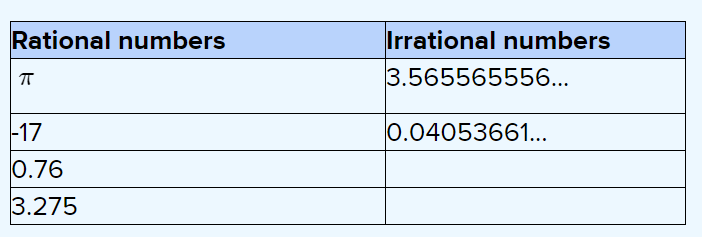
We need to classify the below numbers as rational or irrational.

The numbers are

π

3.565565556…

0.04053661…

-17

0.76

3.275

Irrational numbers cannot be represented as a fraction. Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature. Only rational numbers can be represented as a fraction while irrational numbers cannot.

Rational numbers are:
​
π=3.14159

−17

0.76

3.275
​
Irrational numbers are:

3.565565556…

0.04053661…

Page 15 Exercise 2 Answer

We need to classify the below numbers as rational or irrational.
\(\frac{2}{3}\),√25,−0.75,√2,7,548,123

Irrational numbers cannot be represented as a fraction. Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature. Only rational numbers can be represented as a fraction while irrational numbers cannot.

Rational numbers are:

\(\frac{2}{3}\),√25,−0.75,7,548,123

Irrational number is: √2

Rational numbers: \(\frac{2}{3}\),√25,−0.75,7,548,123

Irrational numbers: √2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 14 Exercise 1 Answer

Given that, Jen classifies the number 4.567 as irrational because it does not repeat. We need to construct arguments whether Jen is correct or not.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The number 4.567 is terminating in nature.

Hence, the given number is a rational number.

Jen’s argument is incorrect.

Page 16 Exercise 1 Answer

We need to describe the difference between the irrational number and a rational number.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Terminating and repeating decimals are known as rational numbers while non-terminating and non-repeating decimals are known as irrational numbers.

Page 16 Exercise 3 Answer

We need to explain whether a number could ever be both rational and irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

A number could never be both rational and irrational. It has to be one or the other.

Real Number Solutions Grade 8 Exercise 1.2 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 16 Exercise 4 Answer

We need to explain whether the number 65.4349224… is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number 65.4349224… is non-terminating and non-repeating in nature.

Hence, it is an irrational number.

The given number 65.4349224… is an irrational number.

Page 16 Exercise 5 Answer

We need to explain whether the number√2500 is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number √2500 = 50 is a perfect square number.

Hence, it is an rational number.

The given number √2500 is an rational number.

Envision Math Grade 8 Chapter 1 Exercise 1.2 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 16 Exercise 6 Answer

We need to classify each number as rational or irrational.
The numbers given are,
​
\(4.2 \overline{7}\)

0.375

0.232342345…

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Rational numbers are:

0.375

Irrational numbers are:

0.232342345…

Rational numbers: \(4.2 \overline{7}, 0.375, \frac{-13}{1}\)

Irrational numbers: 0.232342345…, \(\sqrt{62}\)

Page 17 Exercise 7 Answer

We need to explain whether the number5.787787778… is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number 5.787787778… is non-terminating and non-repeating in nature.

Hence, it is an irrational number.

The given number 5.787787778… is an irrational number.

Envision Math 8th Grade Exercise 1.2 Step-By-Step Real Number Solution

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 17 Exercise 8 Answer

We need to explain whether the number √42 is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number √42 is not the square root of a perfect square number.

Hence, it is an irrational number.

The given number √42 is an irrational number.

Page 17 Exercise 10 Answer

We need to circle the irrational number in the given list:

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.
​
\(7.2 \overline{7}=7.27777 \ldots\)

These are rational numbers since it is repeating and terminating in nature.

The number √15 is irrational since 15 is not a perfect square number.

The irrational number is circled below,

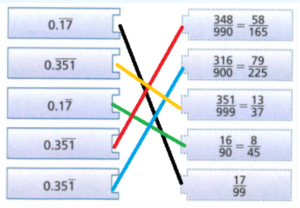
Page 17 Exercise 11 Part (a) Answer

The given numbers are 5.737737773…,26,√45 \(\frac{-3}{2}\),0,9

We need to find the rational numbers in it.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The rational numbers are 26,\(\frac{-3}{2}\),0,9

The rational numbers in the list will be 26,\(\frac{-3}{2}\),0,9

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 18 Exercise 14 Answer

We need to check whether the decimal form of \(\frac{13}{3}\) is a rational number or not.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The decimal form of the given number is,

The given number is non-terminating and repeating in nature.

Thus, the given number is rational.

The decimal form of \(\frac{13}{3}\) is rational.

How To Solve Exercise 1.2 Real Numbers In Envision Math Grade 8

Page 18 Exercise 18 Answer

We need to find the rational numbers among the following:

1. 1.111111…

2. 1.567…

3. 1.101101110…

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

1. 1.111111…

This number is rational since it is repeating in nature.

2. 1.567…

This number is irrational since it is non-repeating and non-terminating in nature.

3. 1.101101110…

This number is irrational since it is non-repeating and non-terminating in nature.

The correct option is (E) I only.

Only 1. 1.111111… is rational others are irrational.

Envision Math Grade 8 Exercise 1.2 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 18 Exercise 19 Answer

We need to classify the given numbers as rational or irrational.

The numbers are

The given numbers are \(\frac{8}{5}, \pi, 0, \sqrt{1}, 4.46466 \ldots,-6, \sqrt{2}\)

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represendted as a fraction while irrational numbers cannot.

\(\frac{8}{5}, \pi=\frac{22}{7}, 0, \sqrt{1},-6\) are rationa since it is terminating in nature.

4.46466…., √2 are irrational since it is nonterminating and the roots are not of the perfect squares.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1

Page 2 Question 1 Answer

A real number would be any number which can be discovered in the actual world. Numbers can be found all around us.

Natural numbers are being used to count objects.

Rational numbers are being used to portray fractions.

Irrational numbers are being used to calculate the square root of an amount.

Integers are used to measure temperature, among other things.

These various types of numbers combine form a gathering of real numbers.

Except complex numbers, everything come under real numbers.

It is denoted by R and it is the union of both rational and irrational numbers and it is represented by \(R=Q \cup \bar{Q}\)

Page 2 Question 2 Answer

A real number would be any number which can be discovered in the actual world. Numbers can be found all around us.

Natural numbers are being used to count objects.

Rational numbers are being used to portray fractions.

Irrational numbers are being used to calculate the square root of an amount.

Integers are used to measure temperature, among other things.

These various types of numbers combine to form a gathering of real numbers.

Real numbers are used in many places to solve problems. For example, it is used to portray fractions, determine square roots, measure temperature, and for counting things, etc.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 1 Answer

We know that the addition of zeroes at the end of a decimal number doesn’t change its value.

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite.

The given number terminates at this point. Thus, it is a terminating decimal.

A finite number of decimals can also be represented in the form of repeating zeroes at the end.
For example,
​
12.2750000 or 12.275

15.840000 or 15.84
​
These are some of the examples of terminating decimal which has repeating zeros in it.

A terminating decimal is a decimal that ends in repeating zeros.

Page 5 Exercise 2 Answer

We know that the addition of zeroes at the end of a decimal number doesn’t change its value.

But if the decimal gets repeated again and again, the loop goes endlessly and the digits repeat forever.

A number that has an infinite number of decimals in it is termed to be the repeating decimals.

A repeating decimal doesn’t terminate at any point. The decimal will be infinite.

For example,

15.57 or 15.575757….

These are some of the examples of repeating decimal which has repeating digits in it.

A repeating decimal is a decimal in which a digit or digits repeat endlessly.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 4 Answer

We can write any number as a fraction.

A fraction can be used to describe the part of the things.

It is described as a part of a whole or a part of a set.

The division of any number is said to be the fraction.

For example, if we are going to eat half of the eight eggs we have, it is represented as,

A fraction is a number that can be describe a part of a whole, a part of a set, a location on a number line, or a division of whole numbers.

Page 5 Exercise 7 Answer

Given decimal is 7.0001

We need to determine whether the given decimal is terminating or repeating.

The given number is 7.0001

It can also be written as 7.00010000000000000000…

Since they both represent the same.

This is because the addition of zeroes at the end of a decimal number doesn’t change its value.

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite. i.e., .0001.

The given number terminates at this point. Thus, it is a terminating decimal.

The given number 7.0001 is a terminating decimal.

Page 5 Exercise 9 Answer

Given decimal is \(1.1 \overline{7} 8\)

We need to determine whether the given decimal is terminating or repeating.

The given number is \(1.1 \overline{7} 8\)

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite.

If the number of decimals is infinite and the number gets repeated again and again, it is referred as repeating decimal.

The given number doesn’t terminate at any point as it has an infinite number of decimals.

The number 178 gets repeated again and again.

The given number can also be represented as 1.178178178…

Thus, it is a repeating decimal.

The given number \(1.1 \overline{7} 8\) is a repeating decimal.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 10 Answer

Given decimal is −4.03479

We need to determine whether the given decimal is terminating or repeating.

The given number is −4.03479

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite.

The given number terminates at this point as it has a finite number of decimals. Thus, it is a terminating decimal.

The given number -4.03479 is a terminating decimal.

Page 5 Exercise 11 Answer

We need to find the product of 2.2

Performing multiplication on the given numbers, we get,

2.2 = 2 x 2
= 4

Thus, the product will be 4.

The product of 2.2 = 4

Page 5 Exercise 12 Answer

We need to find the product of -5 . -5

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​
(−5)⋅(−5)=5×5

=25
​
Thus, the product will be 25.

The product of −5 ⋅ −5 = 25

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 13 Answer

We need to find the product of 7⋅7

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​
7 ⋅ 7 = 7 × 7

= 49
​
Thus, the product will be 49

The product of 7⋅7 = 49

Page 5 Exercise 14 Answer

We need to find the product of −6⋅(−6)⋅(−6)

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​

​
Thus, the product will be −216

The product of −6⋅(−6)⋅(−6) = −216

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 16 Answer

We need to find the product of −9⋅(−9)⋅(−9)

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​
​
The product of −9⋅(−9)⋅(−9) = −729​

Page 5 Exercise 17 Answer

We need to simplify the given expression (4⋅10)+(5⋅100)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (4.10) + (5.100) = 540

Page 5 Exercise 19 Answer

We need to simplify the given expression (2.100)+(7.10)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (2.100)+(7.10) = 270

Page 5 Exercise 20 Answer

We need to simplify the given expression (9⋅1000)+(4⋅10)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (9⋅1000)+(4⋅10)=9040

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 21 Answer

We need to simplify the given expression (3⋅1000)−(2⋅100)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is being simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and subtracting the result, we get,
​

​
The simplification of the given number results (3.1000) – (2.100) = 2800

Page 5 Exercise 22 Answer

We need to simplify the given expression (2⋅10)+(7⋅100)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is being simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (2.10) + (7.100) = 720

Page 6 Exercise 1 Answer

We need to use the Graphic organizer to help you understand new vocabulary terms such as cube root, irrational number, a perfect cube, perfect square, scientific notation, and square root.

Cube root can be found by finding a number that when multiplied three times by itself gives the original number.

A square root can be found by finding a number that when multiplied two times by itself gives the original number.

If we multiply an integer three times by itself, it will result in a perfect cube.

If we multiply an integer two times by itself, it will result in a perfect square.

Expressing the biggest or the smallest number in decimal form is referred to the scientific notation.

A number that cannot be expressed as a fraction is said to be an irrational number.

Cube Root:

Definition – A number which when multiplied 3 times by itself gives the original number.

Example – \(\sqrt[3]{64}=4\)

Irrational number:

Definition – A number that cannot be expressed as a fraction but in decimal form.

Example – 0.24556766666…

Perfect cube:

Definition – The number obtained If we multiply an integer 3 times by itself.

Example – 3×3×3=27

Perfect square:

Definition – The number obtained If we multiply an integer 2 times by itself.

Example – 3×3=9

Scientific notation:

Definition – Expressing the biggest or the smallest number in decimal form.

Example – 1.543543543… = \(1.5 \overline{4} 3\)

Square Root:

Definition – A number which when multiplied 2 times by itself gives the original number.

Example – \(\sqrt[2]{16}=4\)

Page 7 Exercise 1 Answer

Given that, Jaylon has a wrench labeled 0.1875 inch and bolts labeled in fractions of an inch. We need to find which size bolt will fit best with the wrench.

The given bolt sizes are \(\frac{3}{8}, \frac{1}{8}, \frac{3}{16}, \frac{1}{4}\)inches.

Solving each fraction to find the equivalent size as that of the wrench given,
​
\(\frac{3}{8}=0.375\)

The bolt size which best fit the wrench is \(\frac{3}{16}\) inch bolt.

\(\frac{3}{16}\) inch size bolt will fit best with the wrench.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 7 Exercise 1 Answer

We need to explain how we can write these numbers in the same form.

The given wrench size is 0.1875 inch

This is of in decimal form.

Meanwhile, the given bolt \(\frac{3}{8}, \frac{1}{8}, \frac{3}{16}, \frac{1}{4}\)inches.

This is of fractional form.

We can easily convert the given fractions to decimals by dividing the fractions given.

It can be done as follows,

We can write the given numbers in the same form by converting the fractions into decimals.

Page 7 Exercise 1 Answer

We need to explain why is it useful to write a rational number as a fraction or as a decimal.

A unique feature of a rational number is that it can be written in the form of a fraction.

Not every decimal is denoted to be the rational number.

Only repeating and the terminating decimal can come under the category of rational number.

It is useful to write it as a fraction or a decimal to make the computations easier.

It is useful to write a rational number as a fraction or as a decimal to help make the calculations easier.

Page 8 Exercise 1 Answer

Given that, in another baseball division, one team had a winning percentage of 0.444…..We need to determine the fraction of their games the team won.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The winning percentage is converted to fractions as,
​

Page 9 Exercise 2 Answer

We need to write the repeating decimal 0.63333… as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The repeating decimal 0.6333… is converted to fraction as \(\frac{19}{30}\)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 9 Exercise 3 Answer

We need to write the repeating decimal 4.1363636… as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The repeating decimal 4.1363636… is converted to fraction as \(\frac{455}{110}\)

Page 10 Exercise 2 Answer

We need to explain why we multiply by a power of 10 when writing a repeating decimal as a rational number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
We can determine the power of ten to multiply by in the second step at the right is by calculating how many places after the decimal does the given numbers gets repeated.

Here, the given number gets repeated after one decimal place. Thus, the power of ten is one.

This step is done to convert the given repeating number to a fraction.

We can multiply a repeating decimal by a power of 10 when writing a repeating decimal as a rational number to convert it to a fractional number.

Page 10 Exercise 3 Answer

We need to explain how we could decide which power of 10 to multiply an equation when writing a decimal with repeating digits as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10.

Subtract both the expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
We can determine the power of ten to multiply by in the second step at the right is by calculating how many places after the decimal does the given numbers gets repeated.

Here, the given number gets repeated after one decimal place. Thus, the power of ten is one.

We can determine the power of ten to multiply an equation when writing a decimal with repeating digits as a fraction by determining the number of places after the decimal does the given number gets repeated.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 10 Exercise 4 Answer

Given that, a survey reported that \(63 . \overline{63}\)% of moviegoers prefer action films. This percent represents a repeating decimal. We need to write it as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given percent is written as a fraction as \(\frac{700}{11}\)

Page 10 Exercise  5 Answer

We need to write the given decimal 2.3181818… as a mixed number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The mixed fraction of the given repeating decimal is \(x=2 \frac{3.5}{11}\)

Page 11 Exercise 10 Answer

Given that, Tomas asked 15 students whether summer break should be longer. He used his calculator to divide the number of students who said yes by the total number of students. His calculator showed the result as 0.9333….. . We need to write this number as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given decimal 0.9333… is equal to \(x=\frac{8.4}{9}\)

Page 11 Exercise 12 Answer

We need to write the given decimal \(0 . \overline{8}\) as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

The given decimal is converted into a fraction as \(x=\frac{8}{9}\)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 12 Exercise 13 Answer

We need to write the given decimal \(1 . \overline{48}\) as a mixed number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given decimal is converted into a mixed number as \(x=1 \frac{48}{99}\)

Page 12 Exercise 14 Answer

We need to write the given decimal \(0 . \overline{6}\)

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,
​

The given decimal is converted into a fraction as \(\frac{6}{9}\)

Page 12 Exercise 15 Answer

Given that a manufacturer determines that the cost of making a computer component is $2.161616. We need to write the cost as a fraction and as a mixed number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given decimal is converted into a fraction as \(\frac{214}{99}\) and as a mixed number as \(2 \frac{16}{99}\)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 12 Exercise 16 Answer

We need to explain the need for the number of repeating digits we use while writing a repeating decimal as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

The power of the number ten which we can use to convert the decimal to fraction can be obtained by looking into the number of repeating digits in a decimal.

If the number of repeating digits is two, then the power of ten multiplied with the decimal will also be two.

When writing a repeating decimal as a fraction, the number of repeating digits we use matters the most since it determines the power of ten which we multiply it with the decimal to make it as a fraction.

Page 12 Exercise 17 Answer

When writing a repeating decimal as a fraction, we need to explain why does the fraction always have only 9s or 9s and Os as digits in the denominator.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

The power of the number ten which we can use to convert the decimal to fraction can be obtained by looking into the number of repeating digits in a decimal.

If the number of repeating digits is two, then the power of ten multiplied with the decimal will also be two.

The subtraction of any number of the power of ten by one will result in a number 9 or the multiples of it.

This is why the denominator is always 9 or 9 and 0.

The number divided by 9s or 9s and 0s will result in repeating decimals. That is why when we convert that to a fraction, the denominator is always 9s or 9s and 0s.

Page 12 Exercise 18 Answer

We need to find the decimal which is equivalent to \(\frac{188}{11}\)

The given fraction is \(\frac{188}{11}\)

Converting the given fraction to a decimal by dividing the fraction, thus we get,

= \(17 . \overline{09}\)

The decimal which is equivalent to \(\frac{188}{11} \text { is (A) } 17 . \overline{09}\)

Page 12 Exercise 19 Answer

We need to draw lines to connect each repeating decimal on the left with an equivalent fraction on the right.

Solving each fraction one by one, we get,

\(\frac{13}{37}=0.351351 \ldots=0.3 \overline{5}\) 1

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1

Page 16 Exercise 1 Answer

Given Nori, her friend, and her mother bought a baseball game ticket package. The package includes good seats, lunch, and a chance to get autographs from players. The total cost for the three of them is $375.

The objective is to find an equation of that shows how much each of them still owes and the other question to consider is have the problem been solved before.

The amount that each still owes can be found by defining a variable to unknown and use the known quantities.

Find the equation of that each owes.

Nori, her friend, and her mother bought a baseball game ticket package.

The package includes good seats, lunch, and a chance to get autographs from players.

The total cost for the three of them is $375.

They each paid a $50 deposit.

Total cost is$375

Each paid $50 deposit.

Define a variable.
​x  =  $50
y  =  $50
z  =  $50
​

Total amount paid as deposit is,

x + y + z = $50 + $50 + $50

= $150

Find the total amount that has to be pay.

Total cost of the ticket is$375

= $375 − $150

=$225

Find the amount that each still owes.

Total amount they owe divided by 3.

= $225 ÷ 3

= $75
​
The amount that each still owes is $75.

I have solved similar problems before.

The final answer is that each still owes $75 and the similar problem has been solved before.

Envision Math Grade 8 Standards For Mathematical Practice Exercise 1 Solutions

Page 16 Exercise 2 Answer

Given Nori, her friend, and her mother bought a baseball game ticket package. The package includes good seats, lunch, and a chance to get autographs from players. The total cost for the three of them is $375.

The objective is to find that what information are necessary and what are not necessary.

The necessary and unnecessary information can be found by observing the problem.

Find what information are necessary and what are not necessary.

Nori, her friend, and her mother bought a baseball game ticket package.

The package includes good seats, lunch, and a chance to get autographs from players.

The total cost for the three of them is $375.

They each paid a $50 deposit.

Necessary information:

The total cost for the three of them is $375.

They each paid a $50 deposit.

Unnecessary information:

The package includes good seats, lunch, and a chance to get autographs from players

The necessary information is that the total cost for the three of them is$375 and they each paid a $50 deposit.

The unnecessary information is the package includes good seats, lunch, and a chance to get autographs from players.

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 16 Exercise 3 Answer

Given Nori, her friend, and her mother bought a baseball game ticket package. The package includes good seats, lunch, and a chance to get autographs from players. The total cost for the three of them is $375.

The objective is to check whether the answer make sense.

The answer whether it makes sense or not can be found using the results we obtained.

Check whether the answer make sense.

Nori, her friend, and her mother bought a baseball game ticket package. The package includes good seats, lunch, and a chance to get autographs from players. The total cost for the three of them is $375.

The answer found is that the amount that each still owes is $75.

Yes, it makes send because total amount paid is $375.

For each of them the price of the ticket will be $150

Subtract total amount paid minus total deposit amount.

= $375 − $150

= $225

Divide the amount into three,

= $ 225÷3

= $ 75

Yes, the answer makes sense.

Envision Math Grade 8 Volume 1 Standards For Mathematical Practice Answers

Page 16 Exercise 4 Answer

Given Nori, her friend, and her mother bought a baseball game ticket package. The package includes good seats, lunch, and a chance to get autographs from players. The total cost for the three of them is $375.

The objective is to find whether the solution pathway is same as the classmate.

The amount that each still owes can be found by defining a variable to unknown and use the known quantities.

Find whether the solution pathway is same as the classmate.
Nori, her friend, and her mother bought a baseball game ticket package. The package includes good seats, lunch, and a chance to get autographs from players. The total cost for the three of them is $375.

The solution pathway is,

Total cost is $375

Each paid $50 deposit.

Define a variable.
​x = $50
y = $50
z = $50
​
Total amount paid as deposit is,
x + y + z = $50 + $50 + $50

= $150

Find the total amount that has to be pay.

Total cost of the ticket is $375

= $375 − $150

= $225

Find the amount that each still owes.

Total amount they owe divided by3.

​= $225 ÷ 3

= $75
​
The amount that each still owes is $75.

The solution pathway is same for me as well as for my classmate.

Envision Math Grade 8 Student Edition Solutions For Standards For Mathematical Practice Exercise 1

Page 18 Exercise 2 Answer

Given Michael’s class is conducting an experiment by tossing a coin. Tails has come up 5 times in a row. That means the next toss will land heads up.

The objective is to find what arguments can be present to defend the conjecture.

The conjecture can be found using the information provided.

Find what arguments can be present to defend the conjecture.

Michael’s class is conducting an experiment by tossing a coin.

The table below shows the results of the last tosses.

The two outcomes of the toss of a coin are heads or tails. For any individual toss of the coin, the outcome will be either heads o. tails. The two outcomes (heads or tails) are therefore mutually exclusive; if the coin comes up heads on a single toss, it cannot come up tails on the same toss.

The arguments that can be present to defend the conjecture is,

A coin can land on heads or tails, so there are two equally likely outcomes.

Because there may be either head or tail.

The arguments that can be present to defend the conjecture is,

A coin can land on heads or tails, so there are two equally likely outcomes.

Solutions For Envision Math Grade 8 Exercise 1 Standards For Mathematical Practice

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 18 Exercise 3 Answer

Given Michael’s class is conducting an experiment by tossing a coin. The table below shows the results of the last 9 tosses.

The objective is to find what conjecture can be made about the solution to the problem.

The conjecture can be found using the information provided.

Find what conjecture can be made about the solution to the problem.

Michael’s class is conducting an experiment by tossing a coin.

The table below shows the results of the last 9 tosses.

The conjecture that can be made about the solution to the problem is,

Total observations=25

Required outcome Tails {T,T,T,T,T}

This can occur only ONCE!

The conjecture made is as there are continuous five tails, this may end up with head at next toss.

Envision Math Exercise 1 Solutions For Grade 8 Standards Practice

Page 19 Exercise 1 Answer

Given the class decided to toss two coins at the same time. They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

The objective is to find the representation that is used to show the relationship among quantities or variables.

The representation can be found using the modelling capability.

Find the representation that is used to show the relationship among quantities or variables.

The class decided to toss two coins at the same time.

They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

The possible outcomes are, HH, TT, TH, & HT

Representation of the outcomes is,

The representation of the relationship among the quantities is,

Page 19 Exercise 2 Answer

Given the class decided to toss two coins at the same time. They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

The objective is to find the way to make our model to work better.

The representation can be found using the modelling capability.

Find the way to make our model to work better.

The class decided to toss two coins at the same time.

They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more

likely that the coins will show one heads and one tails.

To make the model better if it doesn’t work, use table representation.

If the model doesn’t work, the choose better model like table representation

Page 19 Exercise 3 Answer

Given the class decided to toss two coins at the same time. They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

The objective is to find the assumption that can be made to simplify the problem.

The simplified problem can be found using the better assumption.

Determine the assumption that can be made to simplify the problem.

The class decided to toss two coins at the same time.

They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

When we toss two coins simultaneously then the possible of outcomes are:

(Two heads) or (one head and one tail) or (two tails) i.e., in short (H,H)(H,T)(T,T) respectively;

Where H is denoted for head and T is denoted for tail.

The assumption made to simplify the problem is when two coins is tossed simultaneously the possible of outcomes are: (Two heads) or (one head and one tail) or (two tails)

Standards For Mathematical Practice Envision Math Grade 8 Solutions Exercise 1

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 19 Exercise 4 Answer

Given the class decided to toss two coins at the same time. They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

The objective is to check whether the solution make sense.

The simplified problem can be found using the better assumption.

Check whether the solution make sense.

The class decided to toss two coins at the same time. They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

The solution obtained is,

The possible outcomes are,

HH, TT, TH, & HT

The solution makes sense.

Yes. The solution or prediction we had makes sense. Because on flipping two coins the outcomes should be both heads or both tails or one head and one tail.

Practice Problems For Envision Math Grade 8 Standards Exercise 1

Page 19 Exercise 5 Answer

Given the class decided to toss two coins at the same time. They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

The objective is to find is there something that is forgotten or not considered.

The representation can be found using the modelling capability.

Find is there something that is forgotten or not considered.

The class decided to toss two coins at the same time. They wanted to decide whether it is more likely that both coins will show the same side, heads-heads or tails-tails, or more likely that the coins will show one heads and one tails.

There is nothing that is forgotten or not considered while predicting the solution.

Nothing is forgotten or not considered while predicting the solution.

Envision Math Grade 8 Chapter Standards Practice Exercise 1 Worksheet Answers

Page 20 Exercise 1 Answer

Given The Golden Company uses signs in the shape of golden rectangles to advertise its products. In a golden rectangle the length of the longer side is about 1.618 times longer than the shorter side. Draw rectangles to scale to create templates of possible small, medium, and large advertising signs.

The objective is to find whether different tools can be used.

The tools that are to be used can be found by strategical thinking.

Find whether different tools can be used.
The Golden Company uses signs in the shape of golden rectangles to advertise its products. In a golden rectangle the length of the longer side is about times longer than the shorter side.

Draw rectangles to scale to create templates of possible small, medium, and large advertising signs.
Large advertising signs.

Medium advertising signs.

Small advertising signs.

Different tools can be used to make design and technology software’s for drawing.

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 20 Exercise 2 Answer

Given The Golden Company uses signs in the shape of golden rectangles to advertise its products. In a golden rectangle the length of the longer side is about times longer than the shorter side. Draw rectangles to scale to create templates of possible small, medium, and large advertising signs.

The objective is to find what other resources can uses to reach the solution

The tools that are to be used can be found by strategical thinking.

Find what other resources can uses to reach the solution.
The Golden Company uses signs in the shape of golden rectangles to advertise its products. In a golden rectangle the length of the longer side is about times longer than the shorter side.

The other resources that can be used to help reach the solution is technical drawing software where the measurements will be given and content to be advertise will also be given.

The technical drawing software is the resource that is used to reach the solution.

Page 21 Exercise 1 Answer

Given the explanation about golden rectangle advertisement and their dimensions.

The objective is to state the meaning of variables and symbols used.

The variables and symbols used can be found using the information provided

State the meaning of variables and symbols used.

The work is precise enough and appropriate.

Draw the shorter side and then multiply that dimension by 1.618 to determine the length of the longer side.

Length L = Shorter side x1.618
Width W =1.618 cm

The variables used are,

L for length of the rectangle.

W for width of the rectangle.

Symbols that are used is,

Equal to =

Multiplication x

The symbols used are equal to and multiplication.

The variables used are L and W.

Page 21 Exercise 2 Answer

Given the explanation about golden rectangle advertisement and their dimensions.

The objective is to specify the units of measure using.

The variables and symbols used can be found using the information provided.

State the meaning of variables and symbols used.

The work is precise enough and appropriate.

Draw the shorter side and then multiply that dimension by 1.618 to determine the length of the longer side.

Length L = Shorter side x1.618

Width W =1.618cm

The variables used are,
L for length of the rectangle.
W for width of the rectangle.
Symbols that are used is,
Equal to =

Multiplication x

The units of measure that is specified is centimetre or cm.

The units of measure that is specified is centimetre or cm.

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 21 Exercise 3 Answer

Given the explanation about golden rectangle advertisement and their dimensions.

The objective is to find whether the work is precise or exact enough.

The precision used can be found using the result got.

Find whether the work is precise or exact enough.

I am using the appropriate tools to make sure that the dimensions of the templates are precise.

The work is precise and exact because the appropriate tools are used.

Page 21 Exercise 4 Answer

Given the explanation about golden rectangle advertisement and their dimensions.

The objective is to find whether the explanation carefully formulated.

The variables and symbols used can be found using the information provided.

Find whether the explanation carefully formulated.

Length L = Shorter side x1.618
Width W = 1.618cm

The variables used are,

L for length of the rectangle.

W for width of the rectangle.

Symbols that are used is,

Equal to =

Multiplication x1

The units of measure that is specified are centimetre or cm.

Yes, the information provided are carefully formulated.

Yes, the explanations provided are carefully formulated.

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 22 Exercise 1 Answer

Given that Stuart is studying cell division. The table below shows the number of cells after a certain number of divisions.

The objective is to make a chart that shows drawings of the cell divisions through 10 divisions.

The chart can be found using the table and the explanation provided.

Make a chart that shows drawings of the cell divisions through 10 divisions.

The table below shows the number of cells after a certain number of divisions.

The structure for the problem is,
1 cell becomes 2 cells and 2 cells become 4 cells, and so on.

The attributes that are used in the drawing is a tree chart to describe the cells and their division.

Page 22 Exercise 2 Answer

Given that Stuart is studying cell division. The table below shows the number of cells after a certain number of divisions.

The objective is to find the patterns in numbers that are described.

The patterns in number can be found using observation.

Find the patterns in numbers that are described.

Stuart is studying cell division. The table shows the number of cells after a certain number of divisions.

Initial cell is one and on further cell division, it becomes 2.

2 cells become 4

4 cells become 8 and so on….

1, 2, 4, 8, 16, 32, 64, 128, 256,….

This sequence has a factor of 2 between each number.

Each term (except this first term) is found by multiplying the previous term by 2.

The pattern obtained in a geometric sequence.

The pattern in numbers can be described as GEOMETRIC SEQUENCE.

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 22 Exercise 3 Answer

Given that Stuart is studying cell division. The table below shows the number of cells after a certain number of divisions.

The objective is to find th expressions or equations in different ways.

The patterns in number can be found using observation.

Find the expressions or equations in different ways.

Stuart is studying cell division. The table below shows the number of cells after a certain number of divisions.

1, 2, 4, 8, 16, 32, 64, 128, 256,…..

This sequence has a factor of 2 between each number.

Each term (except the first term) is found by multiplying the previous term by 2.

The pattern obtained in geometric sequence.

The equation of expression that can is noticed is 2n.

Example:

Initial cell is one and on further cell division, it becomes 2.

On second division is should become 4.

For that multiply the cells obtained in initial division by 2.

The expression or equation can be viewed in different ways. The expression we obtained is 2n.

How To Solve Envision Math Grade 8 Standards For Mathematical Practice Exercise 1

Page 23 Exercise 1 Answer

Given the explanation about cell division.

The objective is to find the general method or shortcut to solve the problem.

The general methods can be found using simple formulas and observing.

Find the general method or shortcut to solve the problem.

From the figure, it is observed that the cells are divided from one cell.

The general method that can be used to solve the problem is,

Number of cells multiplied by 2 is the result.

It is noticed that when calculations are repeated.

Then we can find more general methods and shortcuts.

The final answer is that it can be generalized and the shortcut used is power tables as the cells divided is multiplied by two will give the result.

Page 23 Exercise 2 Answer

Given the explanation about cell division.

The objective is to find that an expression or equation can be derived.

The general methods can be found using the simple formulas and observation.

Find an expression or equation that can be derived from the examples.

The example obtained is,

The expression or equation that can be derived is,

N = n x 2

Equation:

4 * 2 = 8

Where N = total number of cells.

n = number of cells divided.

The final answer is that an expression that can be derived is n N = n x 2

Envision Math Grade 8 Standards For Mathematical Practice Exercise 1 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1 Page 23 Exercise 3 Answer

Given the explanation about cell division.

The objective is to find that how reasonable are the results.

The general methods can be found using the simple formula and observation.

Find that how reasonable are the results.

The expression or equation that can be derived is,

Where N = total number of cells.
n = number of cells divided.

The result obtained is so reasonable that, using expression we obtained, number of cells that are divided can be found out easily without drawing 1024 cells in a chat that takes time hardly.

The final answer is that, the result we are getting is so reasonable that using the formula we obtained, it can be used to solve the cell divide.

Envision Math Grade 8 Volume Student Edition Solutions Chapter 1 Real Numbers Topic 1

Page 37 Exercise 1 Answer

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Terminating and repeating decimals are known as rational numbers while non-repeating decimals are known as irrational numbers.

Envision Math Grade 8 Chapter 1 Topic 1 Solution Guide

Envision Math Grade 8 Volume Student Edition Solutions Chapter 1 Real Numbers Topic 1 Page 37 Exercise 3 Answer

We need to find whether the number √8 is greater than, less than or equal to 4.

Finding where the given square root number lie in the number line, thus,
​
√4 < √8 < √9

2 < √8 < 3
​
Thus, the value of √8 is less than the number 3.

Therefore, the number √8 is less than the number 4.

The number √8 is less than the number 4.

Page 37 Exercise 4 Answer

We need to solve m² = 14

Solving the given expression, we get,
​
m² = 14

m = √14

m = ±√14

The solutions are m = +√14 and m = −√14

Envision Math Grade 8 Chapter 1 Topic 1 Real Numbers Solutions

Envision Math Grade 8 Volume Student Edition Solutions Chapter 1 Real Numbers Topic 1 Page 37 Exercise 6 Answer

We need to write \(1 . \overline{12}\) as a mixed number.

Writing the given numbers as a mixed fraction, we get,

x = 1.121212…

100x = 112.121212…

100x – x = 112.121212… – 1.121212…

99x = 112 – 1

99x = 111

The number is represented as mixed fraction as \(x=1 \frac{12}{99}\)

Real Numbers Topic Solutions Grade 8 Envision Math

Envision Math Grade 8 Volume Student Edition Solutions Chapter 1 Real Numbers Topic 1 Page 38 Exercise 1 Answer

Given that the table shows the results of the draw. The students who drew rational numbers will form the team called the Tigers. The students who drew irrational numbers will form the team called the Lions. We need to list the members of each team.

The students who drew rational numbers will form the team called the Tigers.

The students who drew irrational numbers will form the team called the Lions.

Lydia drawn √38

The number 38 is not a perfect square. Hence, it is an irrational number.

Marcy drawn \(6.3 \overline{4}\)

The number is repeating in nature. Hence, it is a rational number.

Caleb drawn √36

The number 36 is a perfect square. Hence, it is a rational number.

Ryan drawn 6.343443444…

The number is non terminating and non-repeating. Hence, it is an irrational number.

Anya drawn \(6 . \overline{34}\)

The number is repeating in nature. Hence, it is a rational number.

Chan drawn √34

The number 34 is not a perfect square. Hence, it is an irrational number.

Lydia – Irrational number

Marcy – Rational number

Caleb – Rational number

Ryan – Irrational number

Anya – Rational number

Chan – Irrational number

Team Tigers:

Marcy, Caleb, Anya

Team Lions:

Lydia, Ryan, Chan

Team Tigers:

Marcy, Caleb, Anya

Team Lions:

Lydia, Ryan, Chan

Envision Math Grade 8 Chapter 1 Topic 1 Answers

Envision Math Grade 8 Volume Student Edition Solutions Chapter 1 Real Numbers Topic 1 Page 38 Exercise 2 Answer

Given that the student on each team who drew the greatest number will be the captain of that team. We need to find who will be the captain of the Tigers.

The numbers drawn by the members of the team Tigers will be,

Marcy – \(6.3 \overline{4}\)

Cleb – √36

Anya – \(6 . \overline{34}\)

Thus, the numbers are,

\(6.3 \overline{4}\) = 6.344444…

√36 = 6

\(6 . \overline{34}\) = 6.343434…

The greatest number among them will be \(6.3 \overline{4}\)

Therefore, Marcy will be the captain of the Tigers.

Marcy will be the captain of the Tigers.

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5

Envision Math Grade 8, Volume 1, Chapter 1: Real Number

Page 31 Exercise 1 Answer

Given that, Janine can use up to 150 one-inch blocks to build a solid, cube-shaped model. We need to find the dimensions of the possible models that she can build. Also, find how many blocks would Janine use for each model.

Find the perfect cubes from 0 to 150

​1 × 1 × 1 = 1

2 × 2 × 2 = 8

3 × 3 × 3 = 27

4 × 4 × 4 = 64

5 × 5 × 5 = 125

6 × 6 × 6 = 216
​
The total number of blocks given is 150. Thus, all possible dimensions less than 150 are our solutions.

The dimensions of the possible models that she can build will be,
​
2 × 2 × 2

3 × 3 × 3

4 × 4 × 4

5 × 5 × 5

​

Multiplying Rational Numbers: Solutions for Envision Math Grade 8 Exercise 1.5 Page 31 Exercise 2 Answer

We need to explain how the dimensions of a solid related to its volume.

The dimensions of the possible models that Janine can build will be,
​2 × 2 × 2

3 × 3 × 3

4 × 4 × 4

5 × 5 × 5
​
The dimensions of a solid are related to its volume since they are building a solid, cube-shaped model.

The volume of the cube will be V = s3 where s is the length of the edge of the cube.

The dimensions of a solid are related to its volume since the dimensions consist of nothing but the length of the edge of the cube.

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 31 Exercise 1 Answer

Given that, Janine wants to build a model using \(\frac{1}{2}\)-icnh cubes. We need to find how many \(\frac{1}{2}\)-icnh cubes would she use to build a solid, cube-shaped model with side lengths of 4 inches.

Let x be the number of \(\frac{1}{2}\) inch cube with the side length of 4 inches.

The equation formed from the given information will be,

x = 4 x 2

x = 8

Therefore, she needs 8 blocks per side.

Thus, the number of little cubes she needs will be,

V = 8 × 8 × 8 = 512

Therefore, she needs to use 512, \(\frac{1}{2} x=4\) inch cubes to build a cube-shaped model with a side length of 4 inches.

She needs to use 512, \(\frac{1}{2} x=4\) inch cubes to build a cube-shaped model with a side length of 4 inches.

Page 32 Question 1 Answer

We need to explain how we can solve equations with squares and cubes.

In order to solve equations with squares, find the number obtained by multiplying the given number two times itself.

For example, if the number is 4

The square of the given number is,

4 × 4 = 16

The square of 4 is 16

In order to solve equations with cubes, find the number obtained by multiplying the given number three times itself.

For example, if the number is 2

The cube of the given number is

2 × 2 × 2 = 8

The cube of 2 is 8

Solve equations with squares by finding the number obtained by multiplying the given number two times itself. Similarly, solve equations with cubes by finding the number obtained by multiplying the given number three times itself.

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 32 Exercise 1 Answer

We need to find the side length, s, of the square below.

The area of the square is A=100m²

The side of the square will be 10m.

Page 32 Exercise 2 Answer

We need to solve x³ = 64

​
The value of x = 4

Page 33 Exercise 3 Answer

We need to solve a³ = 11

The solutions are c=√27 and c=−√27

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 32 Exercise 1 Answer

We need to explain why are there two possible solutions to the equation s² = 100 And also, we have to explain why only one of the solutions is valid in this situation.

​
Here, we have taken the value of s as +10 since we know that the value of the length cannot be a negative one.

The value of the length cannot be negative. This is why we have taken only the positive value of s

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 34 Exercise 2 Answer

Suri solved the equation x² = 49 and found that x=7

We need to find the error Suri made.

The value of x = +7 and x = −7. The values are both positive and negative. This is the error Suri made.

We need to explain why are the solutions to x² = 17 is irrational.

The solutions are irrational since the square root of 17 is not a perfect square number.

The solutions are irrational since the square root of 17 is not a perfect square.

Page 34 Exercise 5 Answer

Given that, If a cube has a volume of 27 cubic centimeters, We need to find the length of each edge by using the volume formula V = s³

​
The length of each edge will be 3cm.

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 34 Exercise 7 Answer

We need to solve x³ = −215

​
The solution is x = \(-\sqrt[3]{215}\)

Multiplying Rational Numbers: Solutions for Envision Math Grade 8 Exercise 1.5 Page 35 Exercise 9 Answer

We need to solve a³ = 216

The solution is a = 6

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 35 Exercise 12 Answer

We need to solve y² = 81

The solutions are y = +9 and y = −9

Page 35 Exercise 13 Answer

We need to solve w³ = 1000

The solution is w = 10

Page 35 Exercise 14 Answer

The area of a square garden is given as A=121ft². We need to find how long is each side of the garden.

The length of the side of the garden is 111ft

Page 35 Exercise 15 Answer

We need to solve b² = 77

The solutions are b = +√77 and b = −√77

Page 36 Exercise 19 Answer

Given that, Manolo says that the solution of the equation g² = 36 is g = 6 because 6 × 6 = 36

Check whether Manolo’s reasoning is complete or not

Therefore, Manolo’s reasoning is wrong.

Page 36 Exercise 20  Answer

We need to solve \(\sqrt[3]{-512}\)

The solution is \(\sqrt[9]{-512}=-8\)

We need to explain how we can check that our result \(\sqrt[3]{(-8)^3}\).

To verify the result, find the cube of the obtained result,

Thus, we get,

−8 × −8 × −8 = −512

Thus, our obtained result is correct.

The cube of -8 is -512. Hence, it is verified.

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 36 Exercise 21 Answer

Given that, Yael has a square-shaped garage with 228 square feet of floor space. She plans to build an addition that will increase the floor space by 50%. We need to find the length, to the nearest tenth, of one side of the new garage.

The length, to the nearest tenth, of one side of the new garage is 18.5ft

Page 36 Exercise 22 Answer

Given that the Traverses are adding a new room to their house. The room will be a cube with a volume of 6,859 cubic feet. They are going to put in hardwood floors, which costs $10 per square foot. We need to find how much will the hardwood floors cost.

The given volume is 6859ft³

The hardwood floor costs 3610 dollars.

Multiplying Rational Numbers: Solutions For Envision Math Grade 8 Exercise 1.5 Page 36 Exercise 23 Answer

Given that, while packing for their cross-country move, the Chen family uses a crate that has the shape of a cube.

If the crate has the volume V=64 cubic feet, we need to find the length of one edge.

The length of one edge will be 4ft

Given that, While packing for their cross-country move, the Chen family uses a crate that has the shape of a cube.

The Chens want to pack a large, framed painting. If the framed painting has the shape of a square with an area of 12 square feet, we need to find the painting will fit flat againsts a side of the crate.

Thus, the area of the cube is more than that of the given square. Thus, it can fit flat on the floor.

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions

Page 19 Exercise 1 Answer

Given that, Courtney and Malik are buying a rug to fit in a 50-square-foot space. We need to determine which rug should they purchase.

We need to buy a rug to fit in a 50-square-foot space. Therefore, we need to buy a rug which is smaller than this.

The first rug will be,

7ft × 7ft = 49ft²

The second rug is of circle-shaped, thus, its area will be,
​
A = πr²

A = \(\frac{22}{7} \times 4^2\)

A = 50.2857
​
The third rug area will be,
​
⇒ \(6 \mathrm{ft} \times 8 \frac{1}{2} \mathrm{ft}=6 \mathrm{ft} \times \frac{17}{2} \mathrm{ft}\)

=3 × 17ft²

= 51ft²

​Only the first rug is smaller than the 50 square foot space. Therefore, it is

Courtney and Malik should purchase the first rug whose dimensions are 7ft x 7ft

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 19 Exercise 1 Answer

We need to explain how we have decided which rug Courtney and Malik should purchase.

As we need to find a rug which has to be fit in the space of 50 square foot.

We need to buy a rug which is smaller than the space.

Thus, we need to find the areas of all three rugs and then decide which one’s area is less than 50 square foot.

The area of the first rug is, A=49ft2

The area of the second rug is, A=50.2857ft2

The area of the third rug is, A = 51ft2

We have decided which rug to buy by finding the areas of all three rugs and determining which one’s area is smaller than 50 square foot.

Page 20 Question 1 Answer

We need to explain how we can compare and order rational and irrational numbers.

We can compare and order rational and irrational numbers by the following ways:

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Rational numbers are terminating and repeating while irrational numbers are non-terminating and non-repeating in nature.

Envision Math Grade 8 Exercise 1.3 Real Numbers Answers

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 20 Exercise 1 Answer

We need to determine which decimals we can use to find a better approximation.

Find the two closest consecutive perfect squares of the given number √74

The perfect squares which is closest to them is √64 and √81

Thus, the given number √74 is between the numbers 8 and 9

As we can see that the number √74 is closest to 9 more than the number 8.

Thus, ​8 < √74 < 9

8.5 < √74

Thus, squaring the decimals above 8.5 and below 9 we get,
​
8.6 × 8.6 = 73.96

8.7 × 8.7 = 75.69

8.8 × 8.8 = 77.44

8.9 × 8.9 = 79.21
​
Therefore, the number √74 is about 8.6ft

For finding the better approximation, square decimals between 8.5 and 8.9 since √74 > 8.5

Page 20 Exercise 1 Answer

We need to find between which two whole numbers is √12

The two closest perfect square roots of the given number √12 is,√9 and √16

Thus,
​
√9 < √12 < √16

3 < √12 < 4
​
Thus, the given number is between 3 and 4

The number √12 lies between the whole numbers 3 and 4

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 21 Exercise 2 Answer

We need to compare and order the following numbers:

√11, \(2 \frac{1}{4}\), −2.5, 3.6, −3.97621…

Finding where the given square roots numbers lie in the number line, thus,
​
√9 < √11 < √16

3 < √11 < 4

3 < √11 < 3.5
​
Since it is closer to the number 9 than 16.

\(2 \frac{1}{4}\) = 2.250

Thus, ordering the given numbers, we get,

Comparing and ordering the given numbers, we get,

Page 22 Exercise 1 Answer

We need to explain how we can compare and order rational and irrational numbers.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Find some rational number closer to the irrational number. Then compare the other one with the obtained estimate for the irrational number to order them.

Find some rational number closer to the irrational number. Then compare the other one with the obtained estimate for the irrational number to order them.

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 22 Exercise 3 Answer

We need to find which one is a better approximation of √20. The given approximated values are 4.5 or 4.47

Finding where the given square root number lie in the number line, thus,
​
√16 < √20 < √25

4 < √20 < 5
​
The number 20 is closer to 4 than 5.

Thus, 4 < √20 < 4.5

Thus, squaring the decimal values to find a better estimate, we get,
​
4.47 × 4.47 = 19.9809

4.5 × 4.5 = 20.25
​
Thus, 4.47 is a better estimate.

4.47 is a better estimate of √20

Real Number Solutions Grade 8 Exercise 1.3 Envision Math

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 22 Exercise 5 Answer

We need to approximate √18 to the nearest tenth and plot the number on a number line.

Finding where the given square root number lie in the number line, thus,
​
√16 < √18 < √25

4 < √18 < 5

4 < √18 < 4.5
​
since √18 is closer to 4 than 5.

Thus, squaring the decimal values to find a better estimate, we get,
​
4.1 × 4.1 = 16.81

4.2 × 4.2 = 17.64

4.3 × 4.3 = 18.49

4.4 × 4.4 = 19.36
​
Thus, the number 4.2 is the better estimate.

The number 4.2 is the better estimate.

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 22 Exercise 6 Answer

We need to compare 5.7145… and √29 and find which one is greater than the other.

Finding where the given square root number lie in the number line, thus,
​
√25 < √29 < √36

5 < √29 < 6

5 < √29 < 5.5
​
The number √29 is closer to 5 than 6

Thus, squaring the decimal values to find a better estimate, we get,
​
5.2 × 5.2 = 27.04

5.3 × 5.3 = 28.09

5.4 × 5.4 = 29.16
​
Thus, 5.3 is a better estimate of √29

Therefore, √29 < 5.7145…

Comparing the numbers, we get, √29 < 5.7145…

Page 23 Exercise 9 Answer

We need to compare -1.9612… and -√5 and find which one is greater than the other.

Finding where the given square root number lie in the number line, thus,
​
−√4 < −√5 < −√9#

−2 < −√5 < −3

Therefore, ordering the given numbers we get,

−√5 < -1.96312…

Ordering the numbers, we get,

−√5 < -1.96312…

Envision Math Grade 8 Chapter 1 Exercise 1.3 Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 24 Exercise 13  Answer

Given that, Rosie is comparing √7 and 3.4444….. She says that

√7 > 3.4444… because √7 = 3.5.

We need to check whether the comparison is correct or not.

Finding where the given square root number lie in the number line, thus,
​
√4 < √7 < √9

2 < √7 < 3

2.5 < √7 < 3
​
Thus, √7 < 3.4444…

The comparison made by Rosie is incorrect.

Given that, Rosie is comparing √7 and 3.4444….. She says that

√7 > 3.4444… because √7 = 3.5.

We need to find the mistake Rosie likely made.

Finding where the given square root number lie in the number line, thus,
​
√4 < √7 < √9

2 < √7 < 3

2.5 < √7 < 3
​
Thus,
​
√7 < 3.444…

√7 = 2.646
​
The comparison made by Rosie is incorrect since the value of √7 = 2.646

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 24 Exercise 14 Answer

We need to approximate −√23 to the nearest tenth. Also, draw the point on the number line.

Finding where the given square root number lie in the number line, thus,
​
−√16 > −√23 > −√25

−4 > −√23 > −5

−4.5 > −√23 > −5
​
Thus, squaring the decimal values to find a better estimate, we get,
​
4.6 × 4.6 = 21.16

4.7 × 4.7 = 22.09

4.8 × 4.8 = 23.04

4.9 × 4.9 = 24.01
​
So, a better approximate is -4.7

The better approximate is -4.7

Envision Math 8th Grade Exercise 1.3 Step-By-Step Real Number Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 24 Exercise 15  Answer

Given that, the length of a rectangle is twice the width. The area of the rectangle is 90 square units. Note that you can divide the rectangle into two squares.

We need to find an irrational number represents the length of each side of the squares.

The given area of the rectangle is 90
square units.
Dividing the given area of the rectangle into two equal squares, we get,

The area of the square is 45 square units.

The length of each side of the square is,

Area = side²

45 = s²

s = √45

An irrational number represents the length of each side of the squares is √45

Given that the length of a rectangle is twice the width. The area of the rectangle is 90 square units. Note that you can divide the rectangle into two squares.

We need to estimate the length and width of the rectangle.

From part (a), we have divided the rectangle into two equal squares of length of each side is a = √45

The width of the rectangle will be a

Thus,
​
a = √45

√36 < √45 < √49

6 < √45 < 7

6.5 < √45 < 7
​
Thus, squaring the decimal values to find a better estimate, we get,
​
6.6 × 6.6 = 43.56

6.7 × 6.7 = 44.89

6.8 × 6.8 = 46.24
​
Thus, a = 6.7

The length of the rectangle will be,
​
l = 2a

l = 2 × 6.7

l = 13.4
​
The width is l = a = 6.7

The length and width of the rectangle is 6.7,13.4 respectively.

How To Solve Real Numbers Exercise 1.3 In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.3 Real Number Solutions Page 24 Exercise 17  Answer

The area of a square poster is 31 square inches. We need to find the length of one side of the poster to the nearest whole inch.

The given area of the square poster is 31 square inches.

The length of one side of the poster is,
​
A = s²

31 = s²

s = √31

Finding where the given square root number lie in the number line, thus,
​
√25 < √31 < √36

5 < √31 < 6
​
The number √31 is closer to 6 than 5.

The length of one side of the poster to the nearest whole inch is 6.

The area of a square poster is 31 square inches. We need to find the length of one side of the poster to the nearest tenth of an inch.

The given area of the square poster is 31 square inches.

The length of one side of the poster is s=√31

Finding where the given square root number lie in the number line, thus,
​
√25 < √31 < √36

5 < √31 < 6

5.5 < √31 < 6
​
Thus, squaring the decimal values to find a better estimate, we get,

5.5 × 5.5 = 30.25

5.6 × 5.6 = 31.36

5.7 × 5.7 = 32.49

5.8 × 5.8 = 33.64
​
Therefore, the length of one side of the poster to the nearest tenth of an inch is 5.6

The length of one side of the poster to the nearest tenth of an inch is 5.6