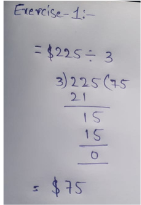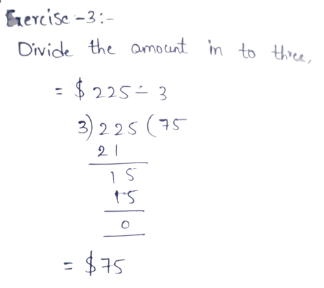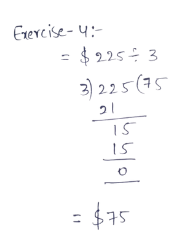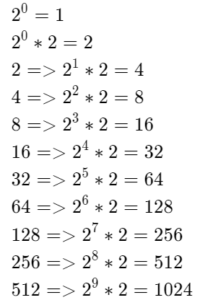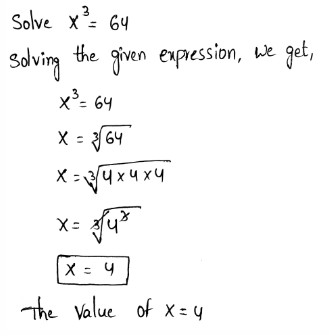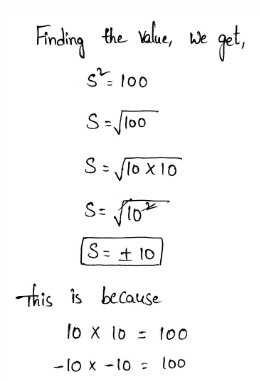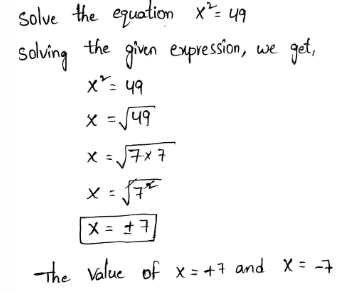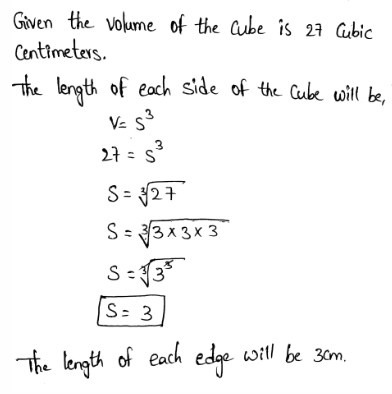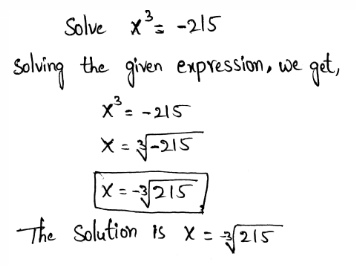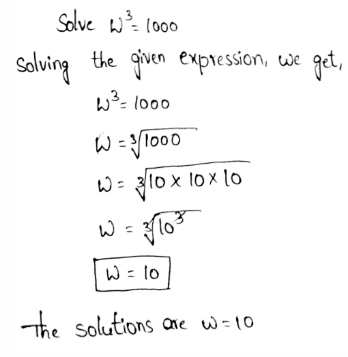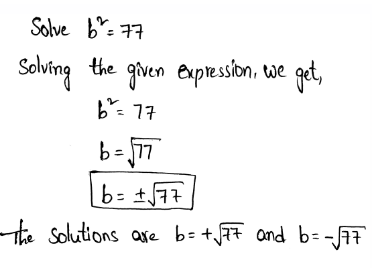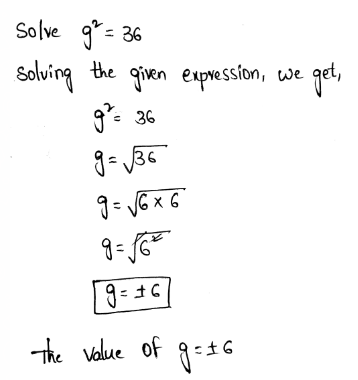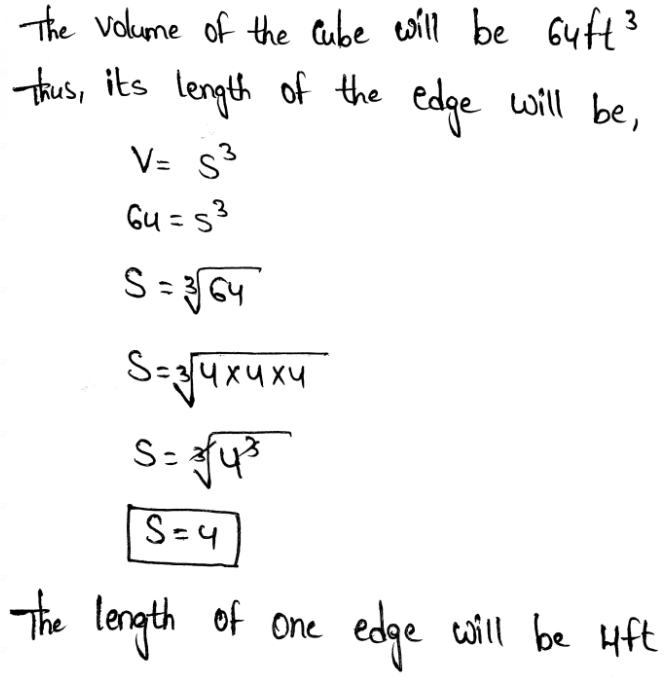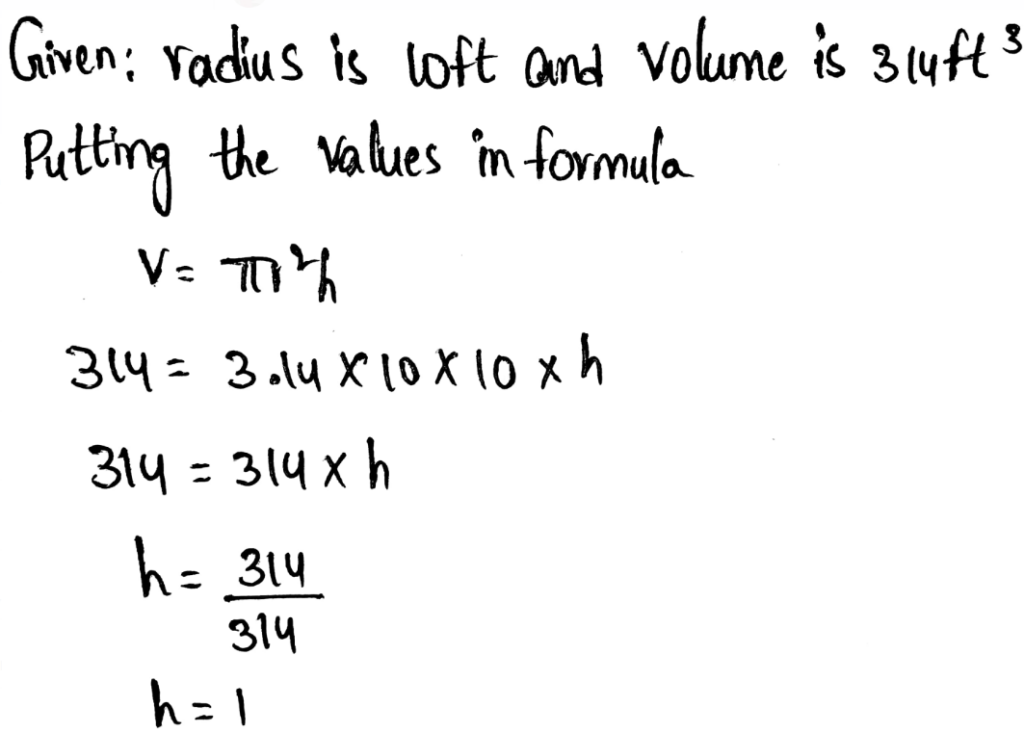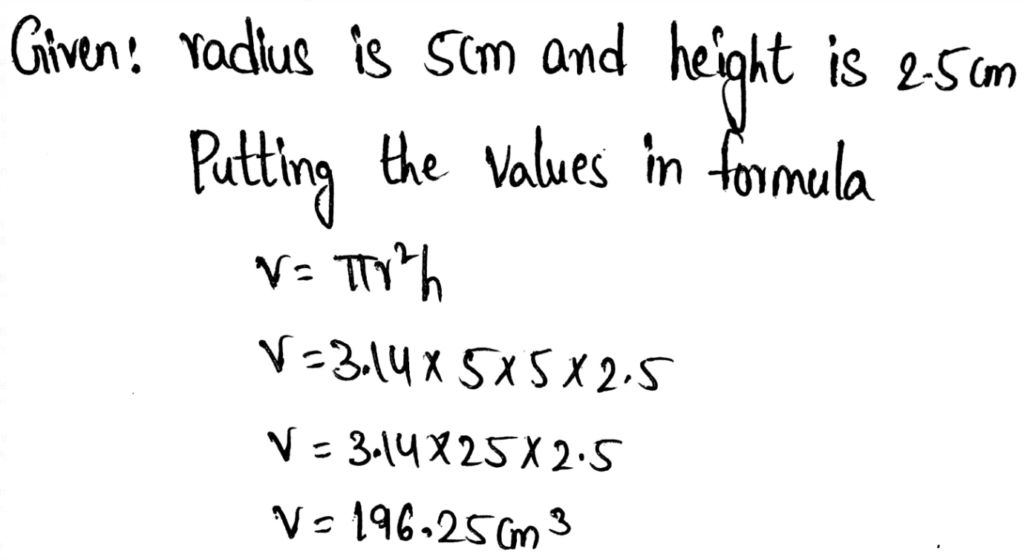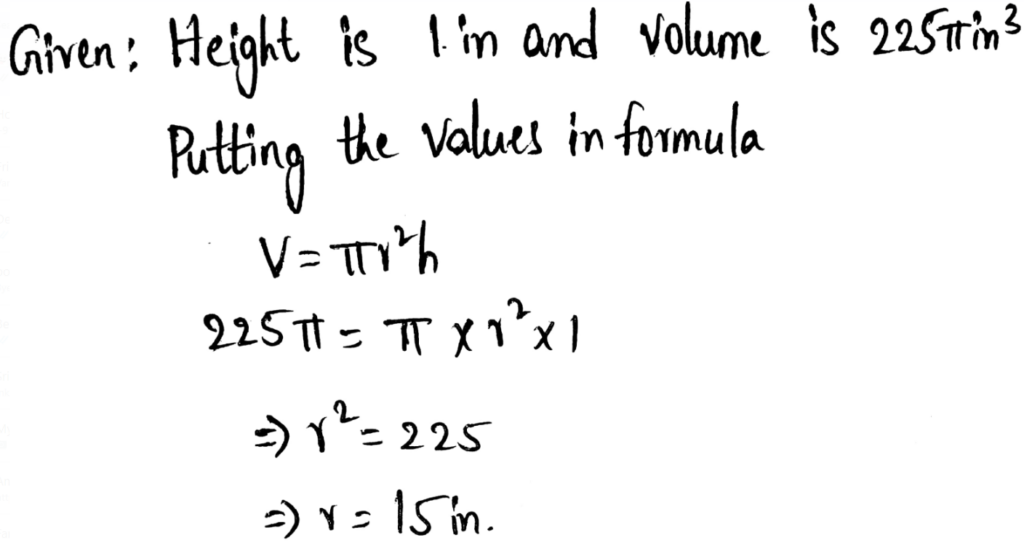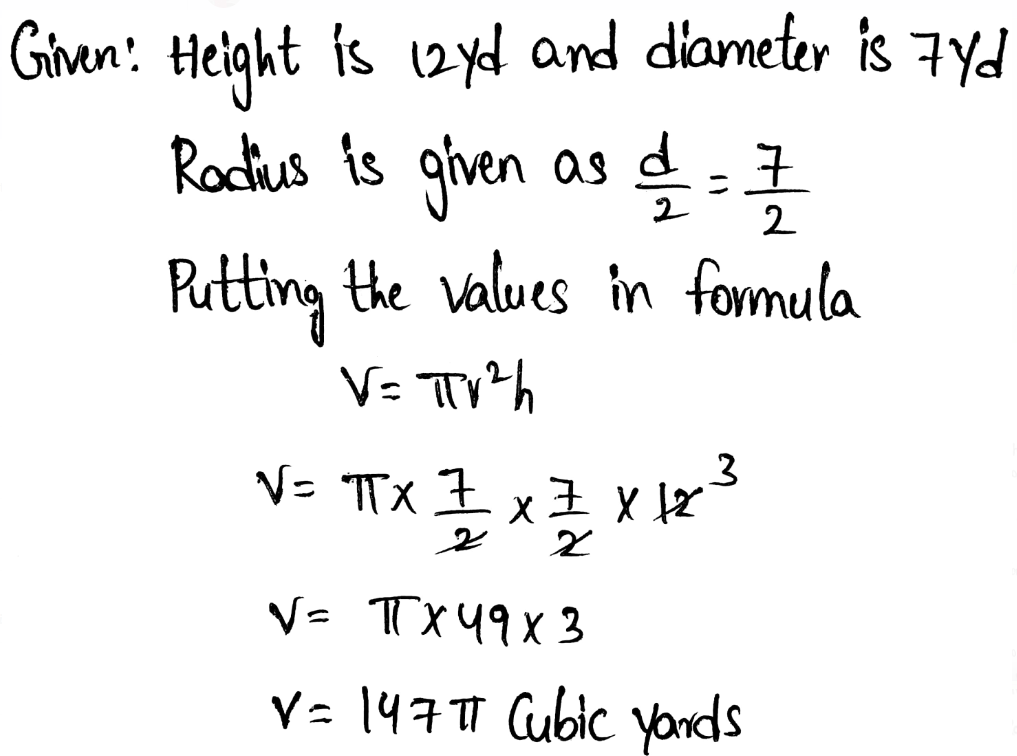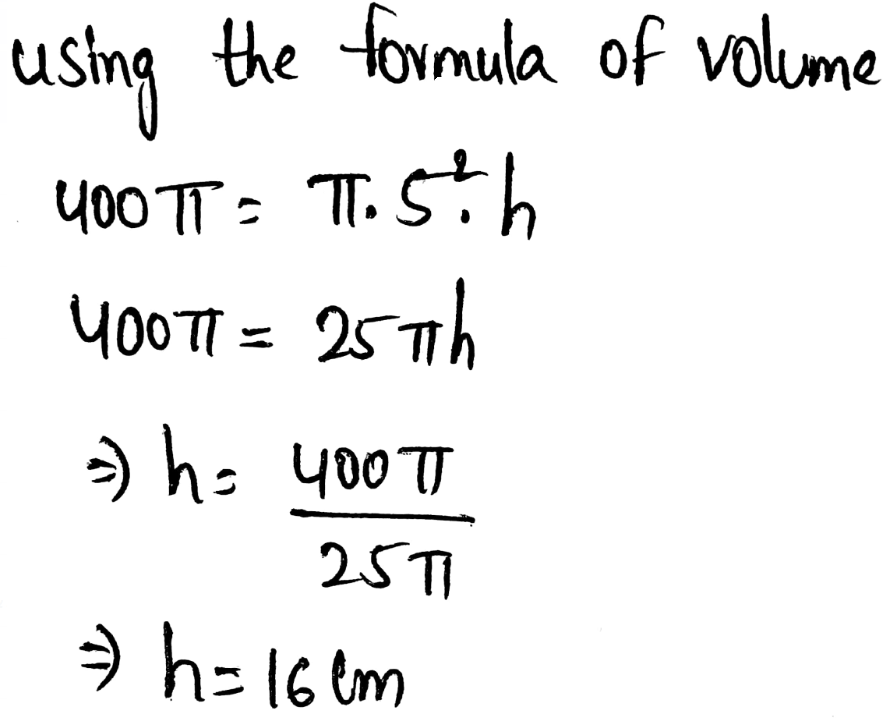Envision Algebra 1 Assessment Readiness Workbook Chapter 1 Standards Practice
Page 8 Exercise 2 Answer
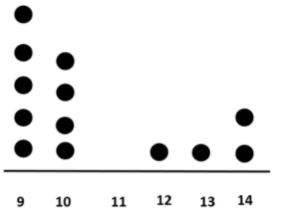
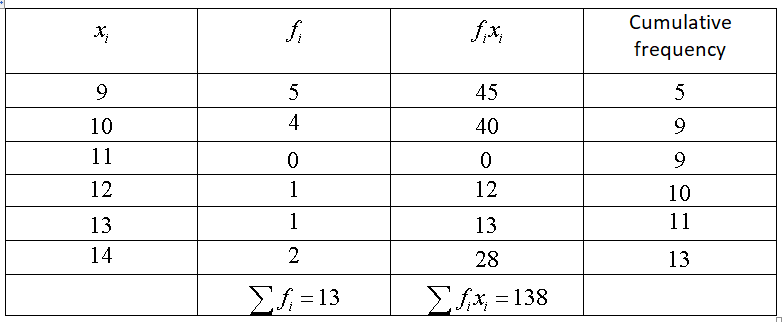
The given expression is 4(xy)2− 2x + 5y.
It is required to find the value of the given expression when the value of x is 6 and y is 2.
To find the value of the given expression, rewrite the given expression. Substitute the given values for x and y. Then solve further to get the result.
The given expression is 4(xy)² – 2x+5y
Substitute 6 for x and 2 for y in the given expression.
4(xy)²-2x+5y = 4(6×2)²-2(6)+5(2)
4(xy)²-2x+5y=4(12)² -2(6)+5(2)
4(xy)²-2x+5y= 4(144)-12+10
4(xy)²-2x+5y=576-2
4(xy)²-2x+5y=574
The value of the expression 4(xy)2 − 2x + 5y is 574.
Page 8 Exercise 3 Answer
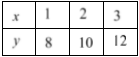
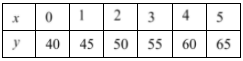
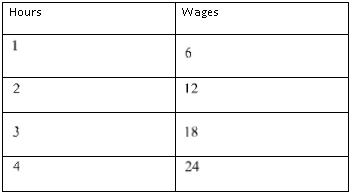
It is given that Camilla and Nadia start a business tutoring students in maths. They rent an office for $250 per month and charge $20 per hour per student.
It is required to calculate the profit they make each month if they have 10 students. It is also required to write a linear equation to solve this.

To find the profit, subtract the rent amount from the total amount they get from students. Then solve the linear equation and get the result.
Let x be the profit they make each month. Also, there are 4 weeks in a month.
The profit can be calculated by subtracting the rent amount from the total amount they get from students.
So the linear equation is
x=4(10×20)-250
x=4(200)-250
x=800-250
x=550
Therefore, Camilla and Nadia make a profit of $550 per month.
Camilla and Nadia make a profit of $550 per month. Also the linear equation is x = 4(10×20) − 250.
It is given that Camilla and Nadia start a business tutoring students in maths. They rent an office for $250 per month and charge $20 per hour per student.
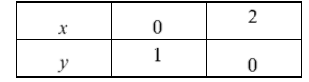
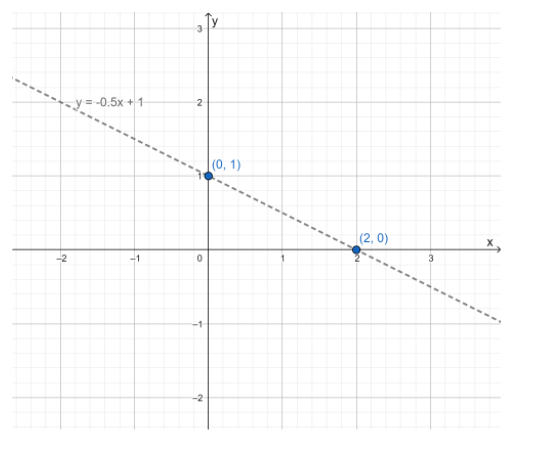
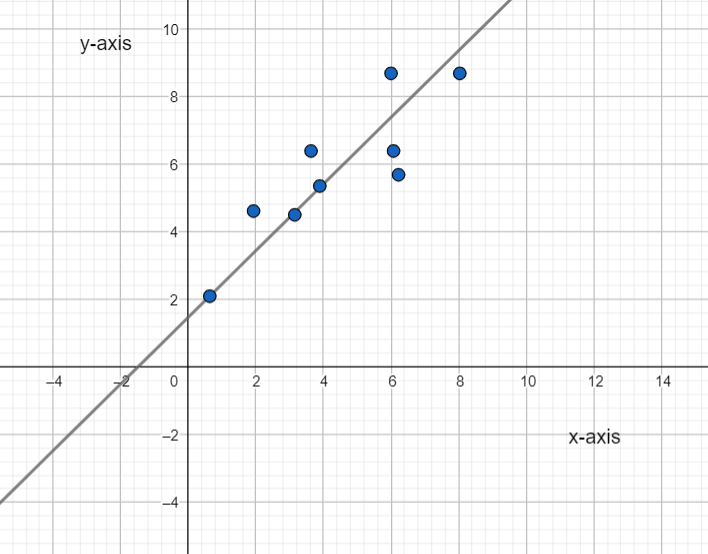
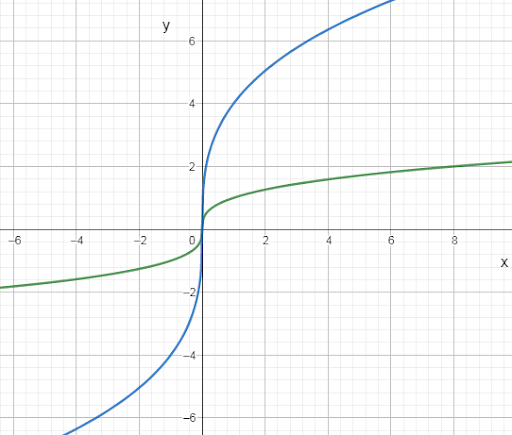
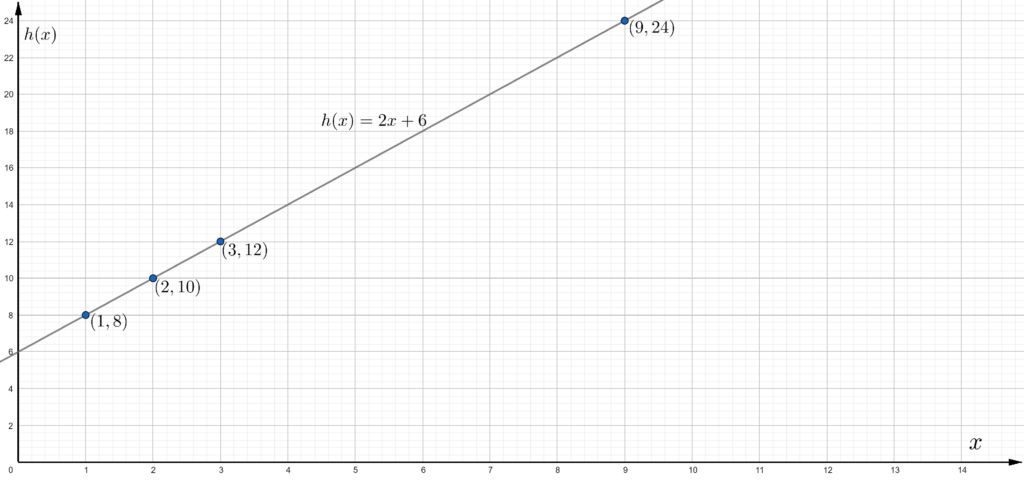
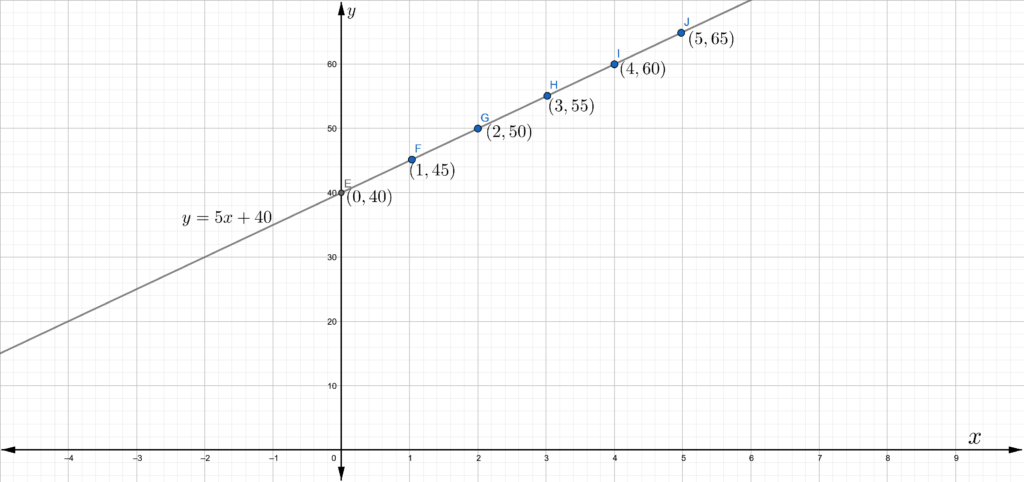
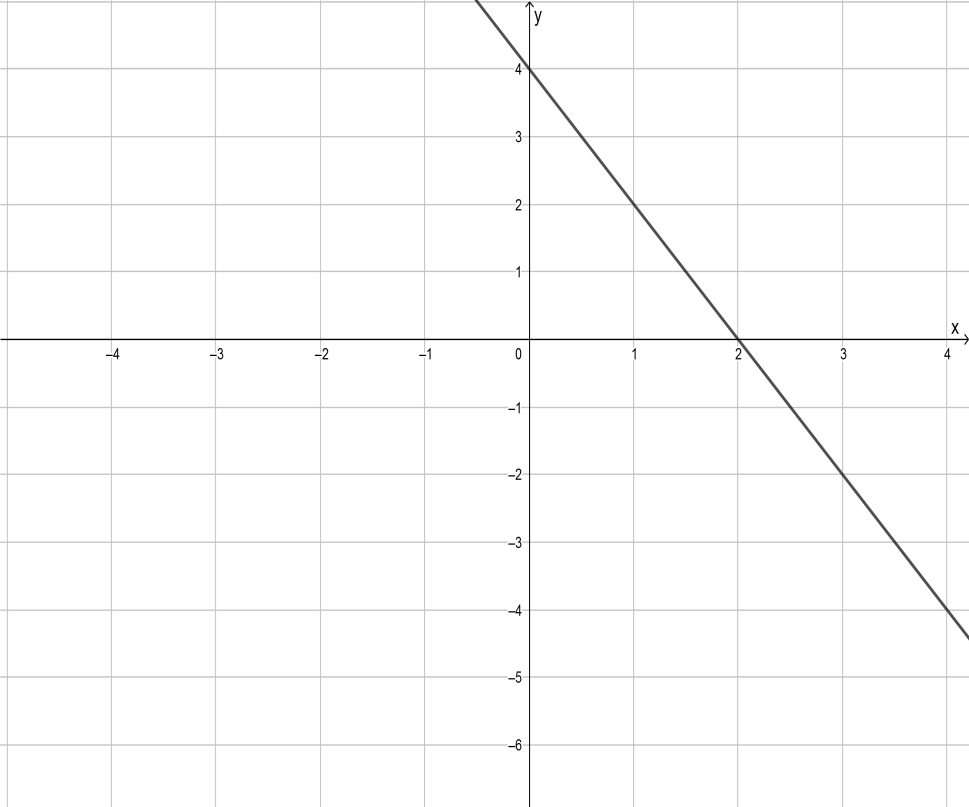
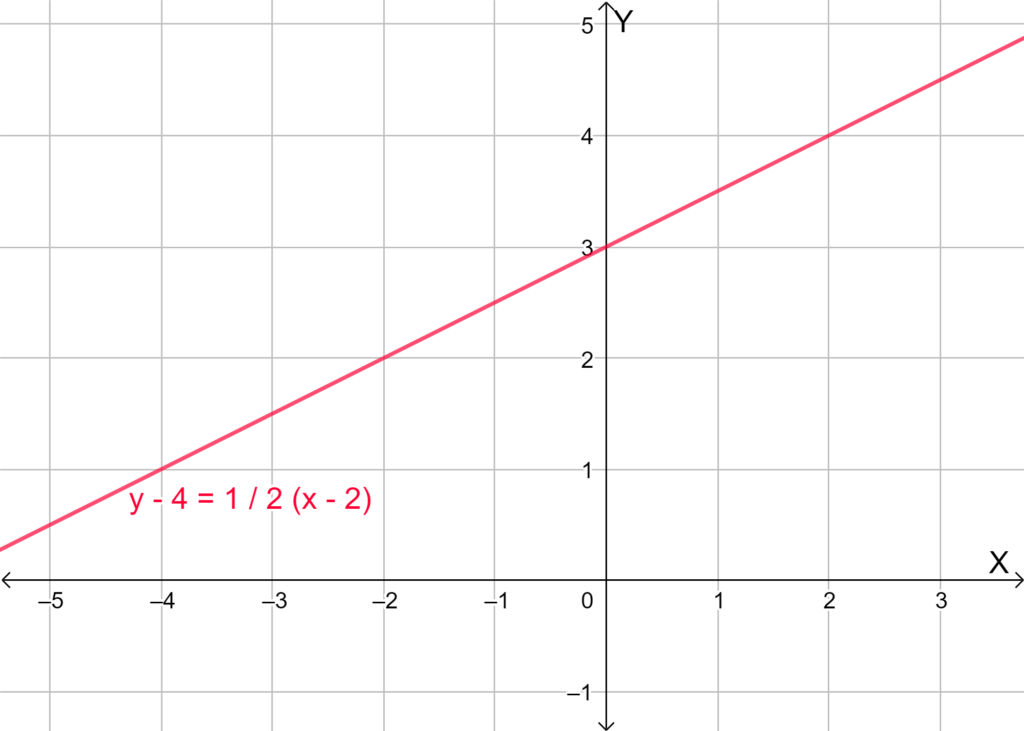
If they have 10 students it is required to sketch the graph for the resulting linear equation.
To sketch the graph, use dynamic geometry software.
Let x be the profit they make each month. Also, there are 4 weeks in a month.
The profit can be calculated by subtracting the rent amount from the total amount they get from students.
So the linear equation is x = 4(10×20) − 250.
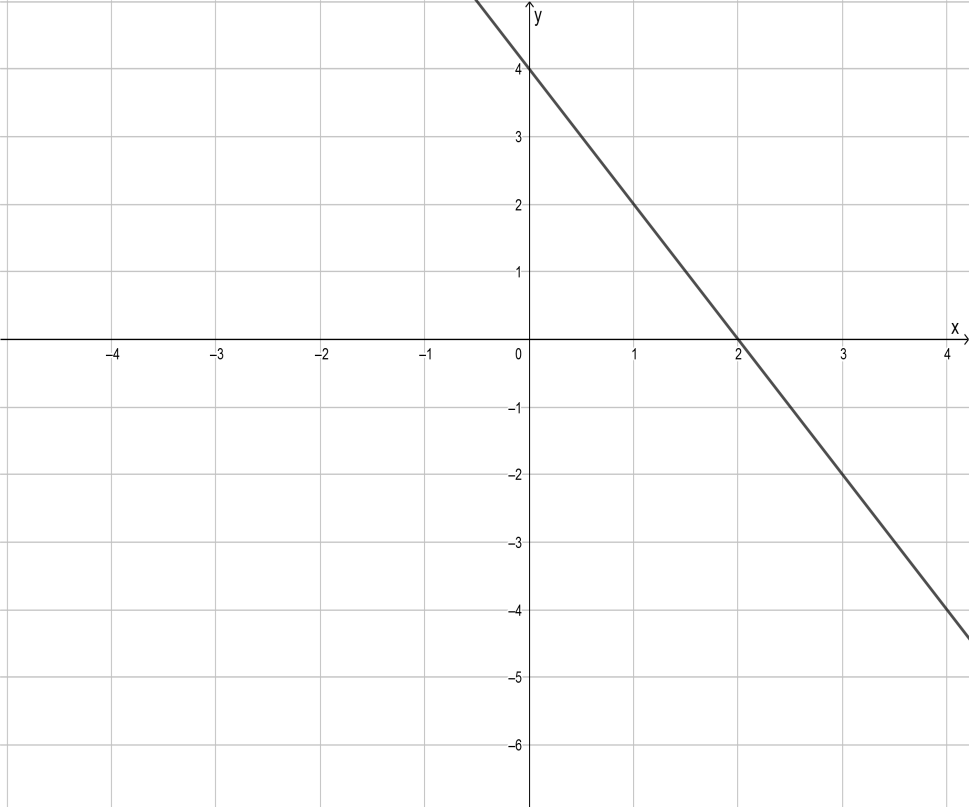
The graph of the equation is given below.
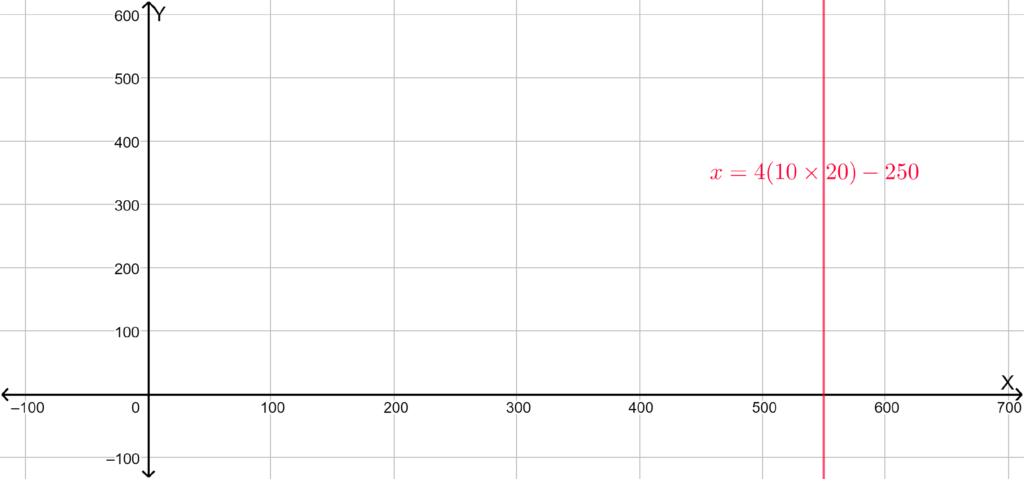
Hence the graph of the equation x = 4(10×20) − 250 is,

Envision Algebra 1 Chapter 1 Standards Practice 2 Answer Key
Page 9 Exercise 1 Answer
The given sequence is 2,24,46,68,90,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common difference is a constant and equals the difference between any two consecutive terms.
Subtract the first two terms
a2 – a1 =24-2
a2 – a1 =22
Subtract the third term from the second term.
a3 – a2 =24-2
a3 – a2 =22
Subtract the Fourth term from the Third term.
a4 – a3 =68-46
a4 – a3 =22
Hence the common difference id d=22
The formula for expressing arithmetic sequences in their recursive form is an = an-1 + d, where d is the common difference of the given sequence, an is the nth element and an-1 is the (n−1)th element.
Substitute 22 for d in the recursive form.
an = an-1 + 22
Hence the correct answer is option A
Option B
The given sequence is 2,24,46,68,90,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common difference is a constant and equals the difference between any two consecutive terms.
Subtract the first two terms
a2 – a1 =24-2
a2 – a1 =22
Subtract the third term from the second term.
a3 – a2 =46-24
a3 – a2 =22
Subtract the Fourth term from the Third term.
a4 – a3 =68-46
a4 – a3 =22
Hence the common difference is d=22
The formula for expressing arithmetic sequences in their recursive form is an = an-1 + d, where d is the common difference of the given sequence, an is the nth element and an-1 is the (n−1)th element.
Substitute 22 for d in the recursive form.
an = an-1 + 22
Here a1 is 2 and an is an-1 + 22 which is not equal to an = an-1 − 22, so option B is incorrect.
Option C
The given sequence is 2,24,46,68,90,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common difference is a constant and equals the difference between any two consecutive terms.
Subtract the first two terms
a2 – a1 =24-2
a2 – a1 =22
Subtract the third term from the second term.
a3 – a2 =46-24
a3 – a2 =22
Subtract the Fourth term from the Third term.
a4 – a3 =68-46
a4 – a3 =22
Hence the common difference is d=22.
The formula for expressing arithmetic sequences in their recursive form is an = an-1 + d, where d is the common difference of the given sequence, an is the nth element and an-1 is the (n−1)th element.
Substitute 22 for d in the recursive form.
an = an-1 + 22
Here a1 is 2 and an is an-1 + 22 which is not equal to an = an+1 + 22, so option C is incorrect.
Option D
The given sequence is 2,24,46,68,90,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common difference is a constant and equals the difference between any two consecutive terms.
Subtract the first two terms
a2 – a1 =24-2
a2 – a1 =22
Subtract the third term from the second term.
a3 – a2 =46-24
a3 – a2 =22
Subtract the Fourth term from the Third term.
a4 – a3 =68-46
a4 – a3 =22
Hence the common difference is d=22
The formula for expressing arithmetic sequences in their recursive form is an = an-1 + d, where d is the common difference of the given sequence, an is the nth element and an-1 is the (n−1)th element.
Substitute 22 for d in the recursive form.
an = an-1 + 22
Here a1 is 2 and an is an-1 + 22 which is not equal to an = an+1 − 22, so option D is incorrect.
The recursive form of the given arithmetic sequence is an = an-1 + 22, so the correct option is A.
Envision Algebra 1 Assessment Readiness Workbook Chapter 1 Practice 2 Solutions
Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 10 Exercise 1 Answer
Given the formula pV = nRT.
It is asked to solve the given formula for T.
To solve the problem, simplify the given formula pV = nRT, and solve it for T.
P.V=n.R.T
Divide both sides by n.R.
⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)
The formula for T is T = \(\frac{p V}{n R}\).
So option C is correct.
Option A
Given the formula pV = nRT.
It is asked to solve the given formula for T.
To solve the problem, simplify the given formula pV = nRT, and solve it for T.
P.V=n.R.T
Divide both sides by n.R.
⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)
The formula for is T = \(\frac{p V}{n R}\) which is not equal to,
T = pV – nR
Option B
Given the formula pV = nRT.
It is asked to solve the given formula for T.
To solve the problem, simplify the given formula pV = nRT, and solve it for T.
P.V=n.R.T
Divide both sides by n.R.
⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)
The formula for T is T = \(\frac{p V}{n R}\) which is not equal to,
T = pVnR
Option D
Given the formula pV = nRT.
It is asked to solve the given formula for T.
To solve the problem, simplify the given formula pV = nRT, and solve it for.
P.V=n.R.T
Divide both sides by n.R.
⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)
The formula for T is T = \(\frac{p V}{n R}\) which is not equal to,
T = pV
The formula for T is T = \(\frac{p \cdot V}{n \cdot R}\), so option C is the correct option.
Page 11 Exercise 1 Answer
Given a system of equations,
4y − 3x = 14
y + 3x = 10
It is asked to solve the given equations.
To solve the problem make any one coefficient of the equation the same and then take a difference of both the equations. It will eliminate one variable, and then solve for x or y. Then put the value of x or y in any of the given equations to get both x and y.
Multiply the second equation by 5.
5(y+3x)=5(10)
5y+15x=50
Subtract the equation (of step 1) from the first given equation.
5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2
so the value of x is 2
Now put the value of x in the second equation and simplify
y=3×2=10
y+6=10
y=4
So the solved ordered pair is (2,4) so the correct option is A.
Option B
Subtract the equation (of step 1) from the first given equation.
5(y+3x)=5(10)
5y+15x=50
Subtract the equation (of step 1) from the first given equation.
5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2
so the value of x is 2
Now put the value of x in the second equation and simplify
y=3×2=10
y+6=10
y=4
So the solved ordered pair is (2,4) which is not equal to (4,2) so option B is not correct.
Option C
Subtract the equation (of step 1) from the first given equation.
5(y+3x)=5(10)
5y+15x=50
Subtract the equation (of step 1) from the first given equation.
5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2
so the value of x is 2
Now put the value of x in the second equation and simplify
y=3×2=10
y+6=10
y=4
So the solved ordered pair is (2,4) which is not equal to (−2,−4) so option C is not correct.
Option D
Subtract the equation (of step 1) from the first given equation.
5(y+3x)=5(10)
5y+15x=50
Subtract the equation (of step 1) from the first given equation.
5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2
so the value of x is 2
Now put the value of x in the second equation and simplify
y=3×2=10
y+6=10
y=4
So the solved ordered pair is (2,4) which is not equal to (2,−4) so option D is not correct.
Option A is the correct option that is (2,4).
Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 11 Exercise 2 Answer
Given a system of equations,
x + 4y = 6
3x − 4y = 14
It is asked to solve the given equations.
To solve the problem add or take the difference of both the equations to eliminate any one variable from the equation, then solve for x or y. Then put the value of x or y in any of the given equations to get both x and y.
Add both of the equations and then simplify.
Given the System of equations,
x+4y=6
3x-4y=14
Add both of the equations and then simplify.
x+4y+(3x-4y) =6+(14)
x+4y+3x-4y=6+14
4x=20
x=5
So the value of x is 5
Now up the value of x in the first equation and simplify
5+4y=6
4y=6-5
4y=1
\(y=\frac{1}{4}\)
So the solved ordered pair is \(\left(5, \frac{1}{4}\right)\).
The ordered pair of the given system of equation is \(\left(5, \frac{1}{4}\right)\).
Page 11 Exercise 3 Answer
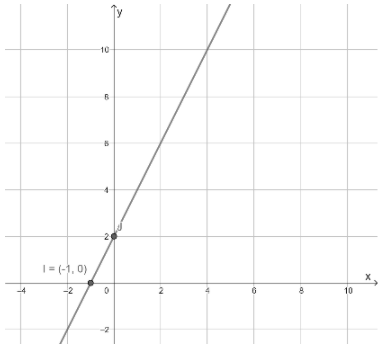
Given that the total money spent is $52, the total number of movies watched is 6, the matinee cost is $7 and the evening show costs $12.
It is asked how many of each movie type he attends and to solve it by graphing.
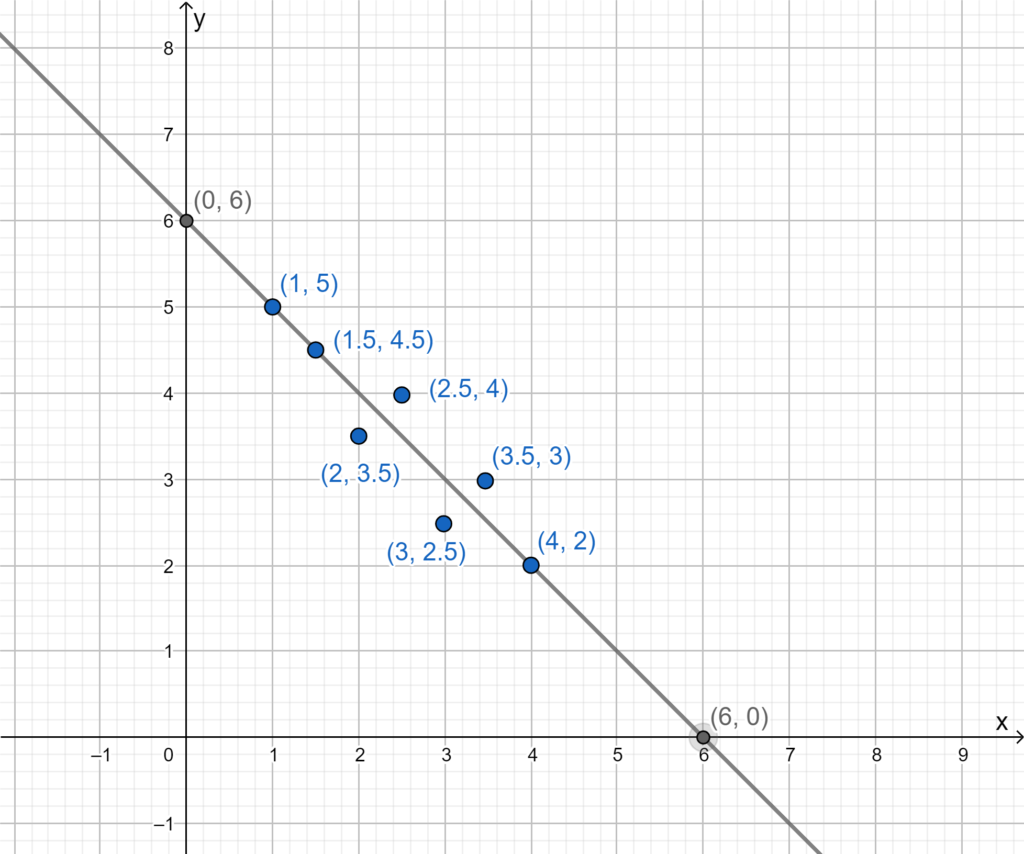
To solve the problem first form the pair of equations according to the given information that is total movie watched and total money spent and then plot the graph using the equation in slope-intercept form that is \(\frac{x}{h}+\frac{y}{k}=1\), where h and k are the intercepts on the axes. The intersection in the graph is the solution of the equations.
Let x be the number of times Alejandro has gone to a matinee and y be the number of times he has attended the evening show. Then, the equation formed by the given data is,
x + y = 6
7x + 12y = 52
Solve this equation and write them in slope-intercept form.
\(\frac{x}{6}+\frac{y}{6}\) = 1
\(\frac{x}{\frac{52}{7}}+\frac{y}{\frac{13}{3}}\) = 1
Plot the lines using intercept on the graph.
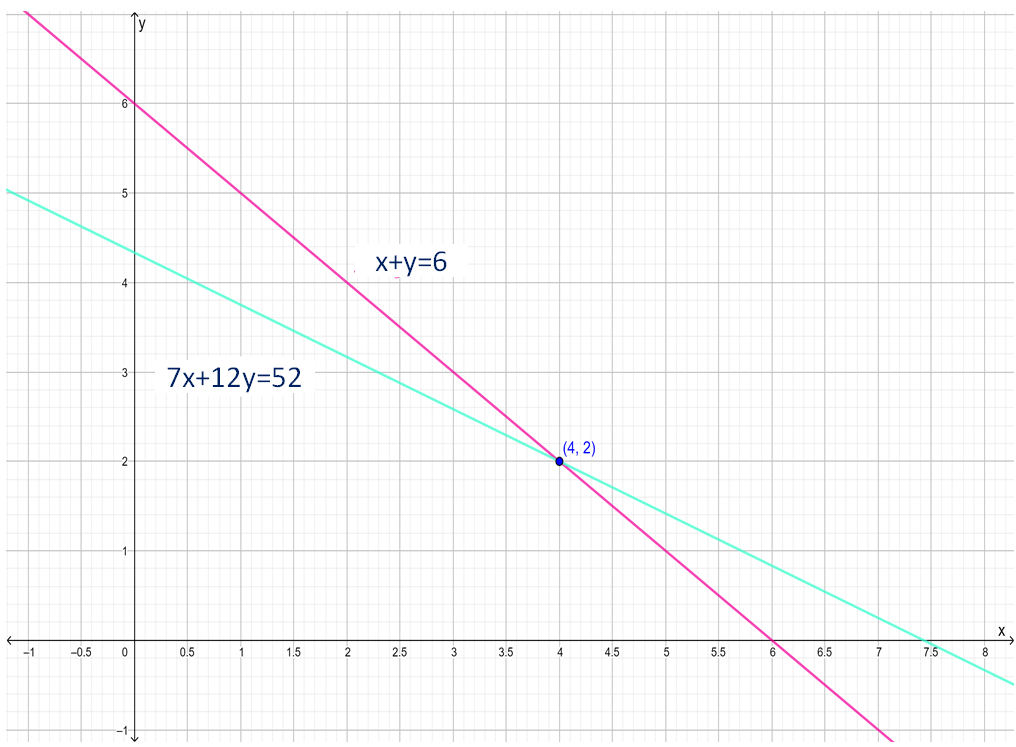
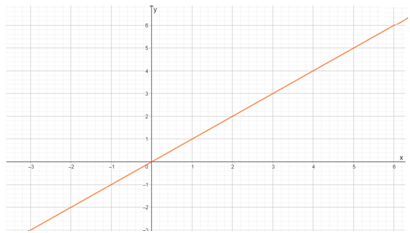
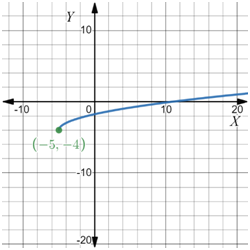
Here the intersection point is (4,2).
So x = 4 and y = 2
So he attended 4 matinees and 2 evening shows.
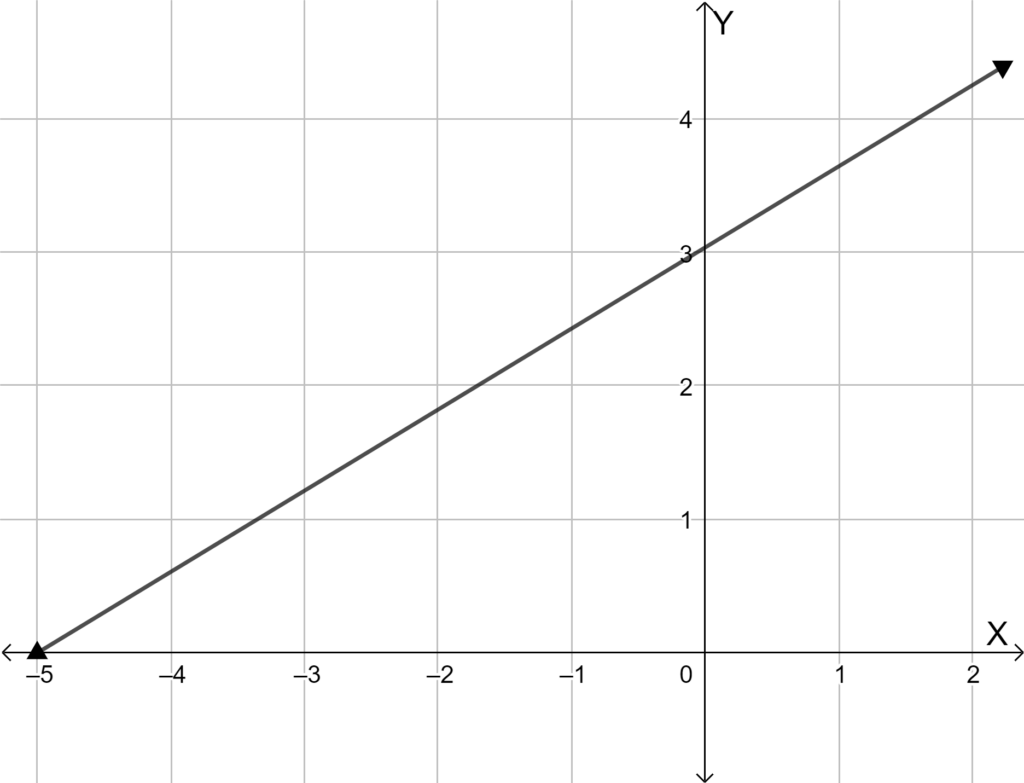
The graphical plot of the equations formed is,

Alejandro attended 4 matinee movies and 2 evening show movies.
It is asked why the intersection of the graphs is the solution.
The intersection of the graph is the solution because it is the only point that satisfies both equations.
The equations are,
The Equations are, x+y=6
7x+12y=52
Multiply the first equation by 7 and subtract the second equation
(7x+7y)-(7x+12y)=42-52
7x+7y-7x-12y=-10
-5y=-10
\(y=\frac{10}{5}\)
y=2
put the value of y in the first equation
x+y=6
x+2=6
x=6-2
x=4
So the solution is (2,4) which is the same as the intersection point. Also, these are the only points that satisfy both the equations.
The intersection of the graph is the solution because it is the only point that satisfies both equations.
Page 13 Exercise 1 Answer
A system of inequalities is given.
y > −x + 2
y < x + 4
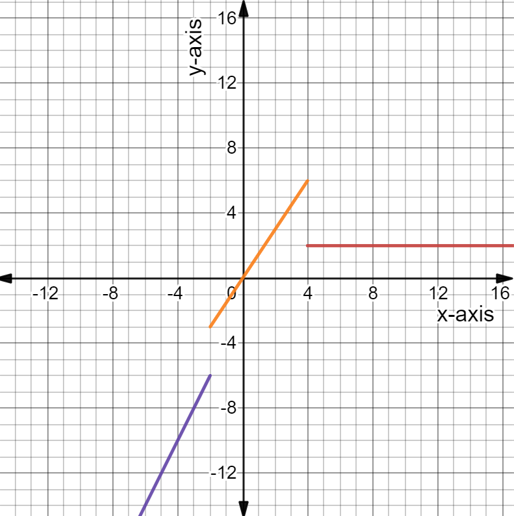
It is asked to identify the graph of the solution of the given system from the options given below.
A
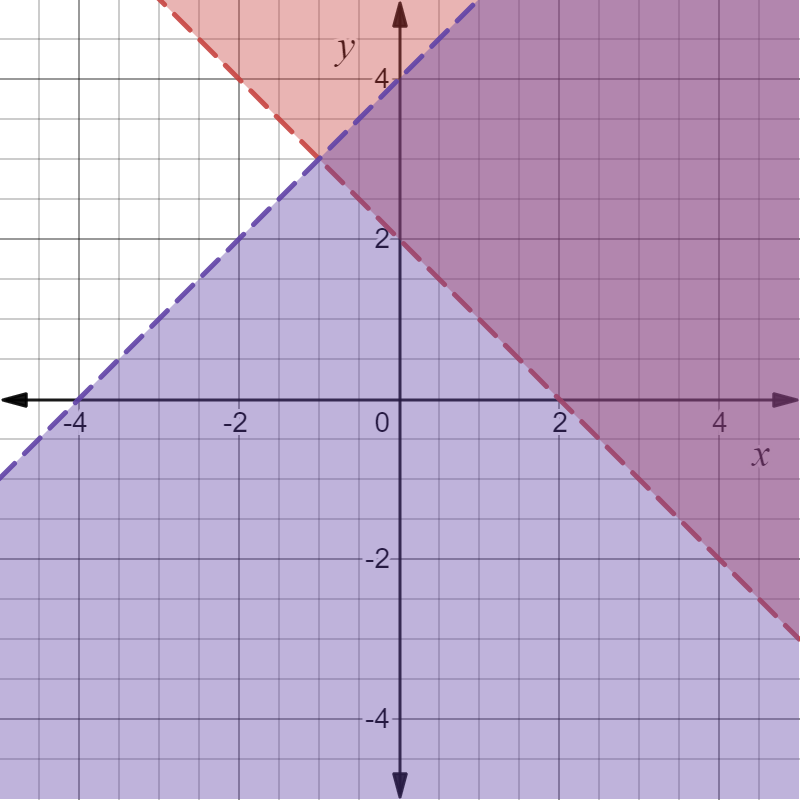
B
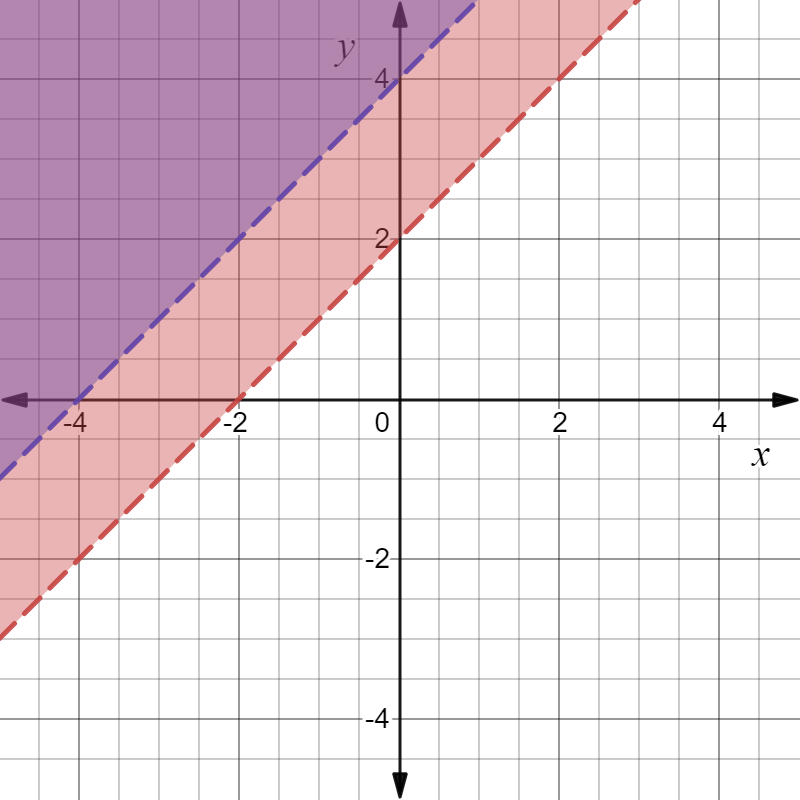
C
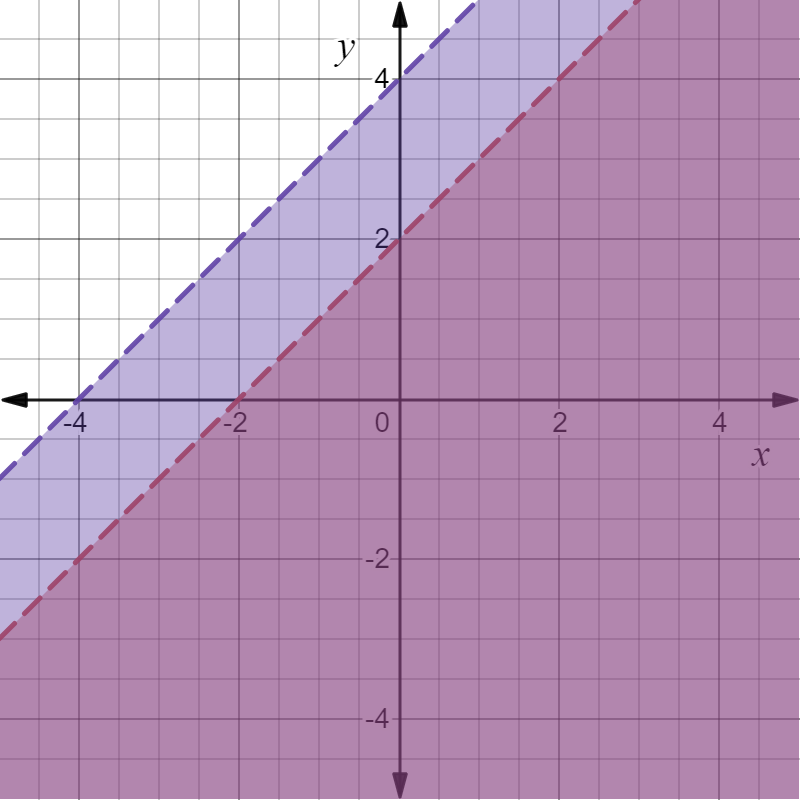
D

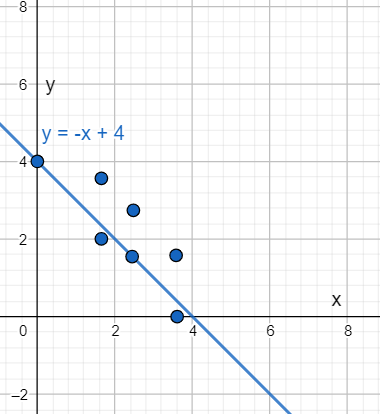
To solve this question, first consider the given inequalities as simple lines y = −x + 2 and,
y = x + 4. Determine its x and y intercepts for both and draw corresponding lines passing through these points. As the inequality y > −x + 2 is greater than the inequality, shade the area above the line, and for less than inequality y < x + 4, shade the area below the line. The common shaded area will be the solution for the given system.
Substitute 0 for y and determine the x-intercept of the line y = −x + 2.
0 = −x + 2
−x = −2
x = 2
Thus the x-intercept of the line y = −x + 2 is (2,0).
Substitute 0 for x and determine the y intercept of the line y = −x + 2.
y = 0 + 2
y = 2
Thus the y-intercept of the line y = −x + 2 is (0,2).
Substitute 0 for y and determine the x intercept of the line y = x + 4.
0 = x + 4
x = −4
Thus the x-intercept of the line y = x + 4 is (−4,0).
Substitute 0 for x and determine the y intercept of the line y = x + 4.
y = 0 + 4
y = 4
Thus the y-intercept of the line y = x + 4 is (0,4).
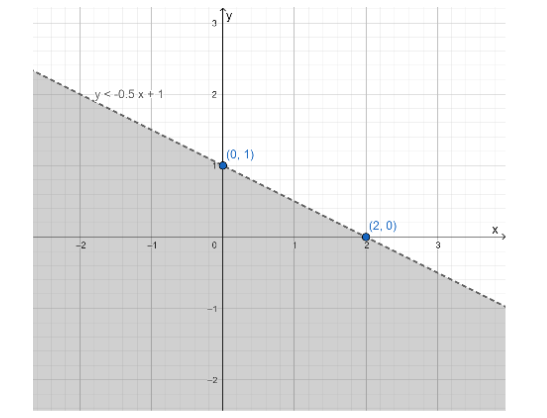
Plot the points (2,0) and (0,2), draw a line passing through them, and shade the area above the line to show the inequality y > −x + 2. Similarly, Plot the points (−4,0) and (0,4), draw a line passing through them, and shade the area below the line to show the inequality y < x + 4.
The common shaded area is the solution of the system.
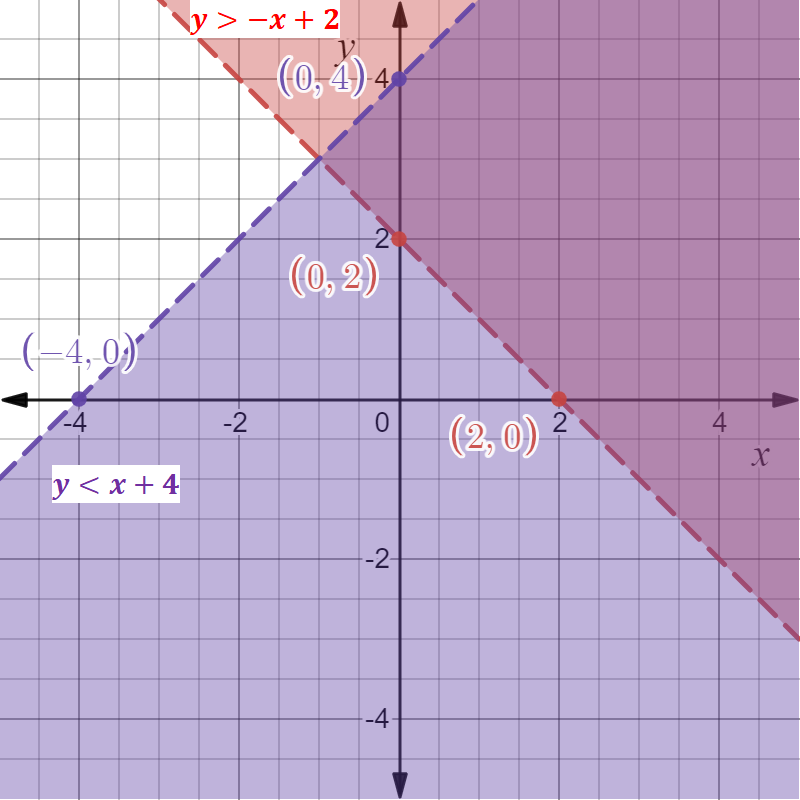
Compare the graphs given in the options and determine the correct answer.
The graph given in option A is exactly similar to the obtained graph which represents the solution of the system of inequalities,
y > −x + 2
y < x + 4
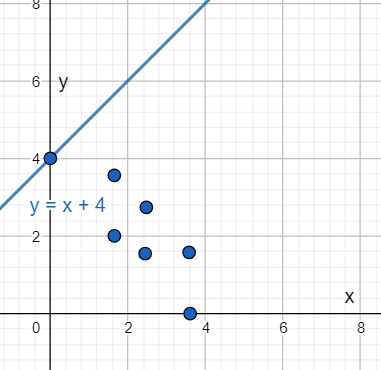
The graph given in option B represents the system of inequality,
y > x + 2
y > x + 4
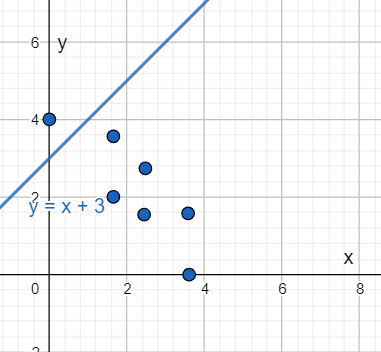
The graph given in option C represents the system of inequality,
y < x + 2
y < x + 4
The graph given in option D represents the system of inequality,
y < −x + 2
y < x + 4
Thus, option A is the correct answer.
The graph of the solution of the given system is obtained and therefore, option A is the correct answer.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 13 Exercise 2 Answer
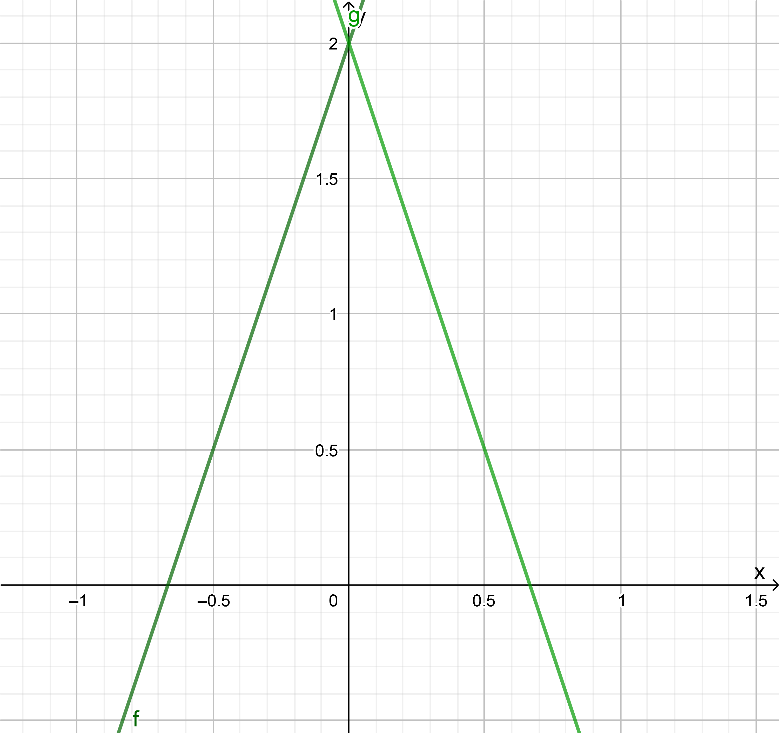
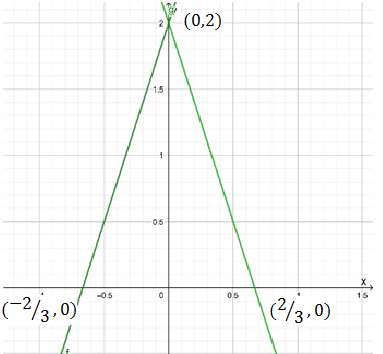
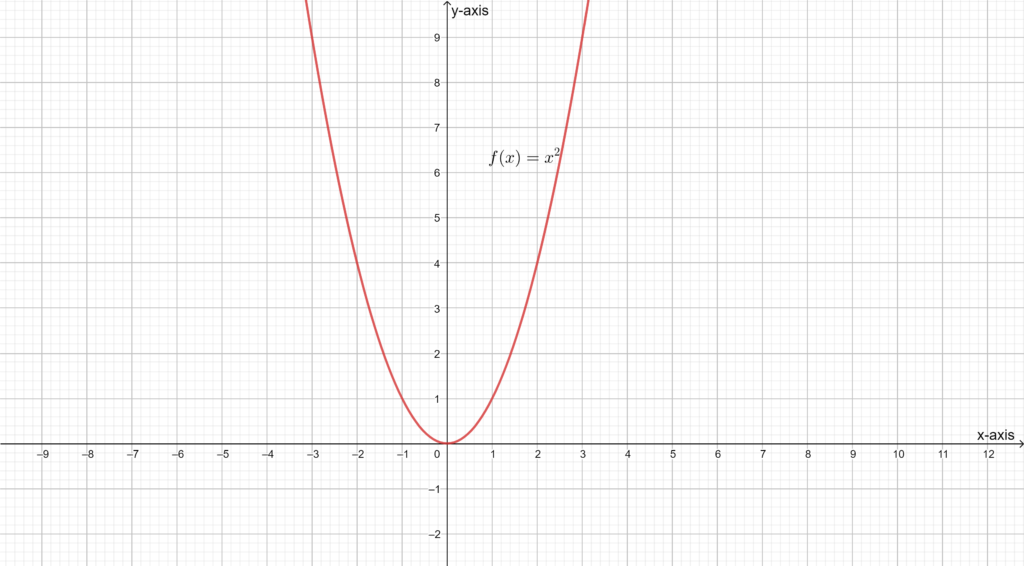
The function g(x) = \(\frac{1}{3}|x-2|+10\) is given.
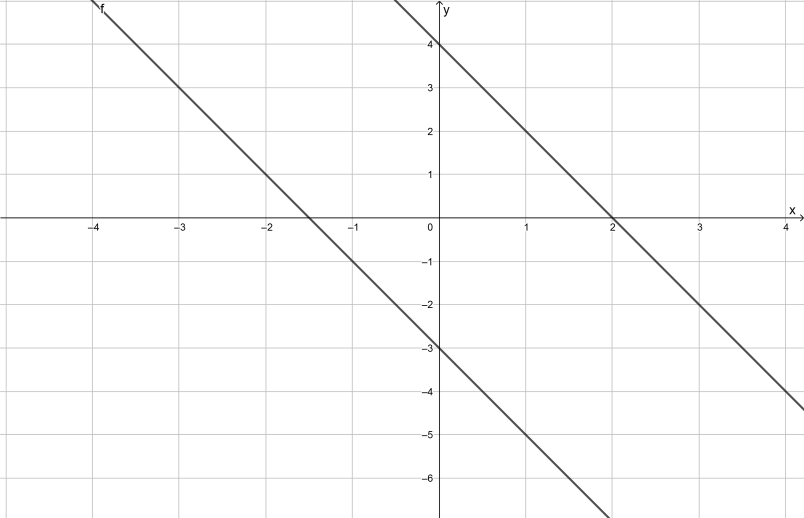
It is asked to compare the given graph with the parent graph f(x) = ∣x∣.
To solve this question, first plot the graphs of f(x) = ∣x∣ and,
g(x) = \(\frac{1}{3}|x-2|+10\). Then observe the second graph and how it changes concerning the first graph.
Ploth the graphs of f(x) = ∣x∣ and,g(x) = \(\frac{1}{3}|x-2|+10\) in a single screen and compare them.
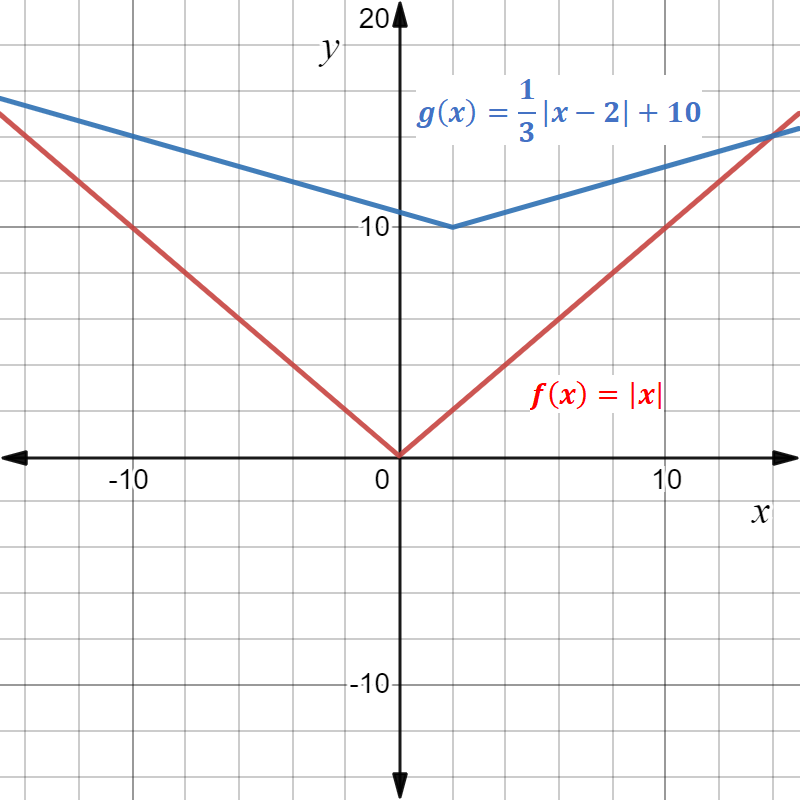
In the function, the value in the mode is x−2 which means that it is shifted 2 units to the right side of the parent graph which can be seen from the graph.
Thus, \(\frac{1}{3}\) is multiplied with |x – 2|, which is greater than zero and less than one, which indicates that the graph is vertically stretched by \(\frac{1}{3}\) units from the parent graph.
Finally, 10 is added to \(\frac{1}{3}\)|x-2|, which indicates that the graph is shifted 10 units vertically upward which also can be seen from the graph.
The graph of g(x) = \(\frac{1}{3}|x-2|+10\) is compared with its parent graph,
f(x) = |x| and three important results are obtained.
First, horizontal shift of 2 units to the right side.
Second, vertical stretch of \(\frac{1}{3}\)|x-2| units.
Third, a Vertical shift of 10 units in the upward direction.
Envision Algebra 1 Student Edition Standards Practice 2 Guide
Page 13 Exercise 3 Answer
It is given that Manuel wants to raise between $250 and $350 for charity. His parents donated $70 and he plans to ask others to contribute $10.
It is asked to write an inequality to determine the number of people who will be needed to contribute for Manuel to reach his goal.
To obtain the inequality, let the number of contributors be x. Each contributor will need to donate $10.Therefore, the total amount to be collected is $10x.
But it is given that Manuel already has $70 donated by his parents. Let y be the total amount of charity he would collect, then y = 70 + 10x.
This amount will be between $250 and $350. Therefore, the inequality to solve the problem will be,
Given, 250<y<350
250<70+10x<35
Simplify Further,
250-70<10x<350-70
180<10x<280
18<x<28
The inequality to solve the problem is 18 < x < 28.
It is given that Manuel wants to raise between $250 and $350 for charity. His parents donated $70 and he plans to ask others to contribute $10.
It is asked to show the solution on the graph to determine the number of people who will be needed to contribute for Manuel to reach his goal and explain the same in words.
To solve this question, use the inequality obtained in the previous part of this exercise which is,
250 < 70 + 10x < 350. First, solve this inequality for x and then graph the solution.
Solve the inequality 250 < 70 + 10x < 350 for x.
Subtract 70 forms from all parts of inequality,
250 − 70 < 70 + 10x − 70 < 350 − 70
180 < 10x < 280
Divide by 10 in all parts of inequality,
⇒\(\frac{180}{10}<\frac{10 x}{10}<\frac{280}{10}\)
18 < x < 28
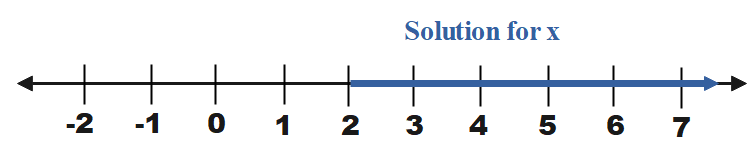
Thus, the number of people who will be needed to contribute for Manuel to reach his goal is between 18 and 28.
To graph this solution, first plot the line y = 70 + 10x.
After that show the range of the money collection which is 250 < y < 350. For this, draw two lines, y = 250 and, y = 350, and shade the area between them.
After that from the intersection points of this region and the line y = 70 + 10x, draw two vertical lines that will give the solution of the system which is the range 18 < x < 28.
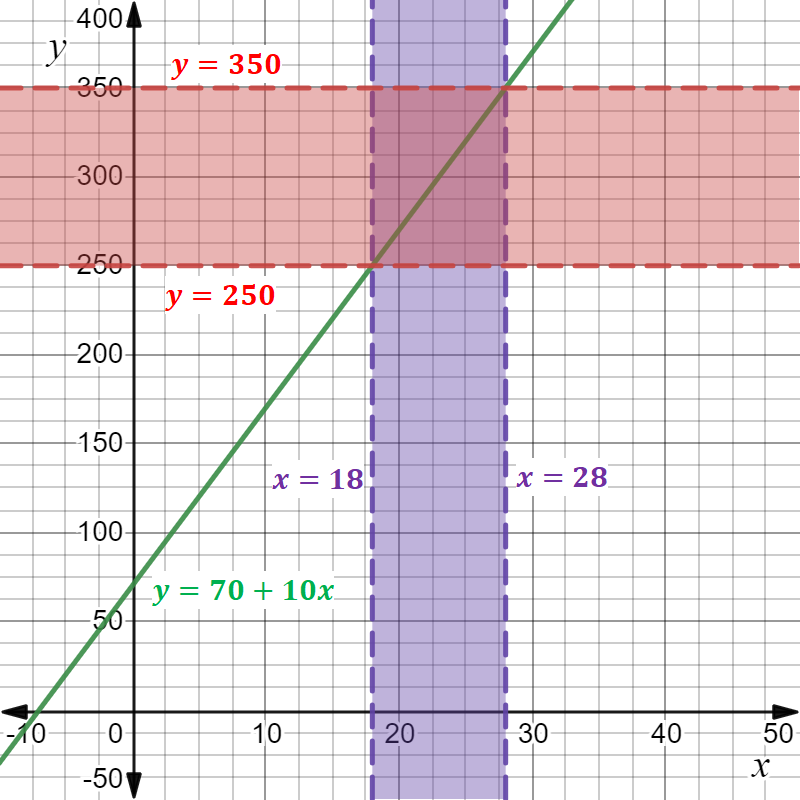
The number of people who will be needed to contribute for Manuel to reach his goal is between 18 and 28. The graph of the solution is obtained.

Page 14 Exercise 1 Answer
An equation is given as \(\frac{x}{3}=\frac{10}{15}\).
It is required to solve the given equation for x.
Given equation \(\frac{x}{3}=\frac{10}{15}\)
Multiply both sides of the equation \(\frac{x}{3}=\frac{10}{15} \text { by } 3 .\)
Hence, option A is correct.
Option B
Multiply both sides of the equation,
Given equation \(\frac{x}{3}=\frac{10}{15} .\)
Multiply both sides of the equation \(\frac{x}{3}=\frac{10}{15}\) by 3
\(\begin{aligned}
& \frac{x}{3} \times 3=\frac{10}{15} \times 3 \\
& x=\frac{30}{15} \\
& x=2
\end{aligned}\)
In Option B, the value of x is given as 3.
Hence, option B is incorrect.
Option C
Multiply both sides of the equation,
Given equation \(\frac{x}{3}=\frac{10}{15}\)
Multiple both sides of the equation \(\frac{x}{3}=\frac{10}{15} \text { by } 3 \text {. }\)
\(\begin{aligned}
& \frac{x}{3} \times 3=\frac{10}{15} \times 3 \\
& x=\frac{30}{15} \\
& x=2
\end{aligned}\)
In option C, the value of x is given as 12. Hence, option C is incorrect.
Option D
Multiply both sides of the equation,
Given equation \(\frac{x}{3}=\frac{10}{15}\)
Multiple both sides of the equation \(\frac{x}{3}=\frac{10}{15} \text { by } 3 \text {. }\)
\(\begin{aligned}
& \frac{x}{3} \times 3=\frac{10}{15} \times 3 \\
& x=\frac{30}{15} \\
& x=2
\end{aligned}\)
In option D, the value of x is given as 15. Hence, option D is incorrect.
The correct answer is option A, the value of x is 2.
Page 14 Exercise 2 Answer
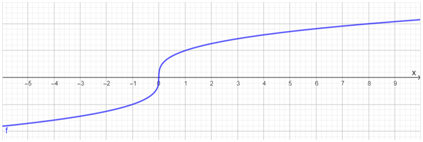
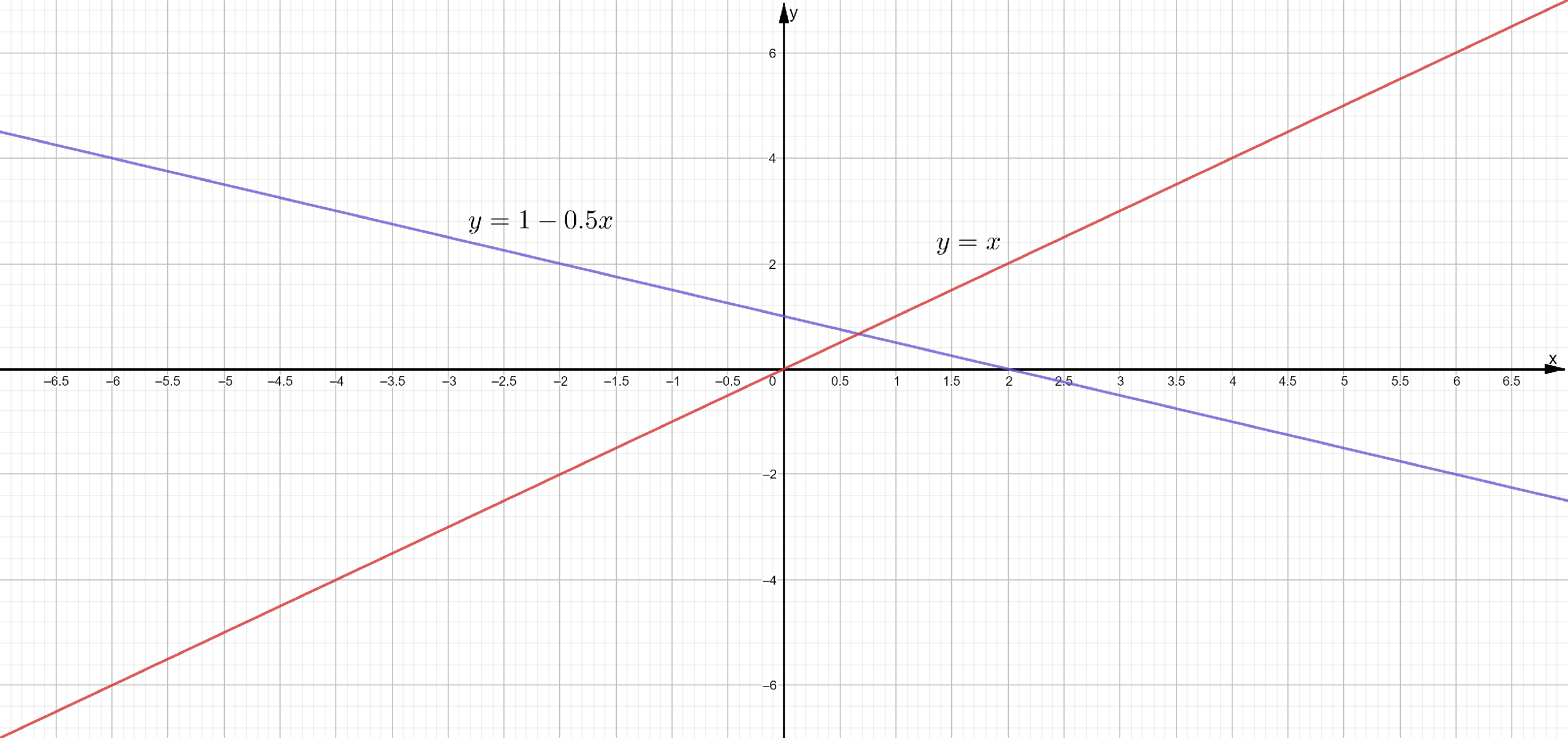
A function is given as,
⇒\(f(x)=\left\{\begin{array}{l}
1-0.5 x, x<1 \\
x, x \geq 1
\end{array}\right.\)
It is required to graph the given function.
To do so, draw the given lines, and then for the line y = 1 − 0.5x, limit the line for the values where x is greater than 1. For the line y = x, limit the line for values where x is smaller than or equal to 1.
Draw the lines on the graph,
y = 1 − 0.5x
y = x
Limit the line for the values where x is greater than 1. For the line y = x, limit the line for values where x is smaller than or equal to 1.
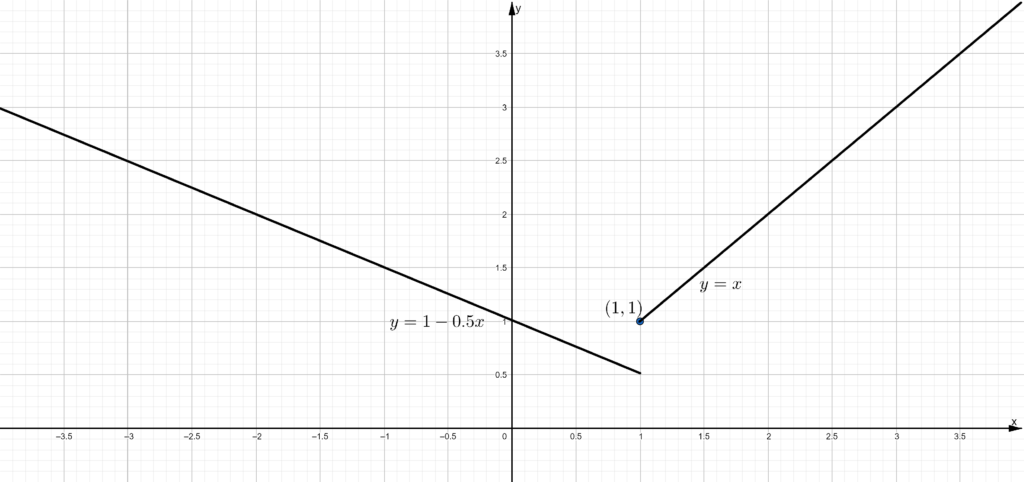
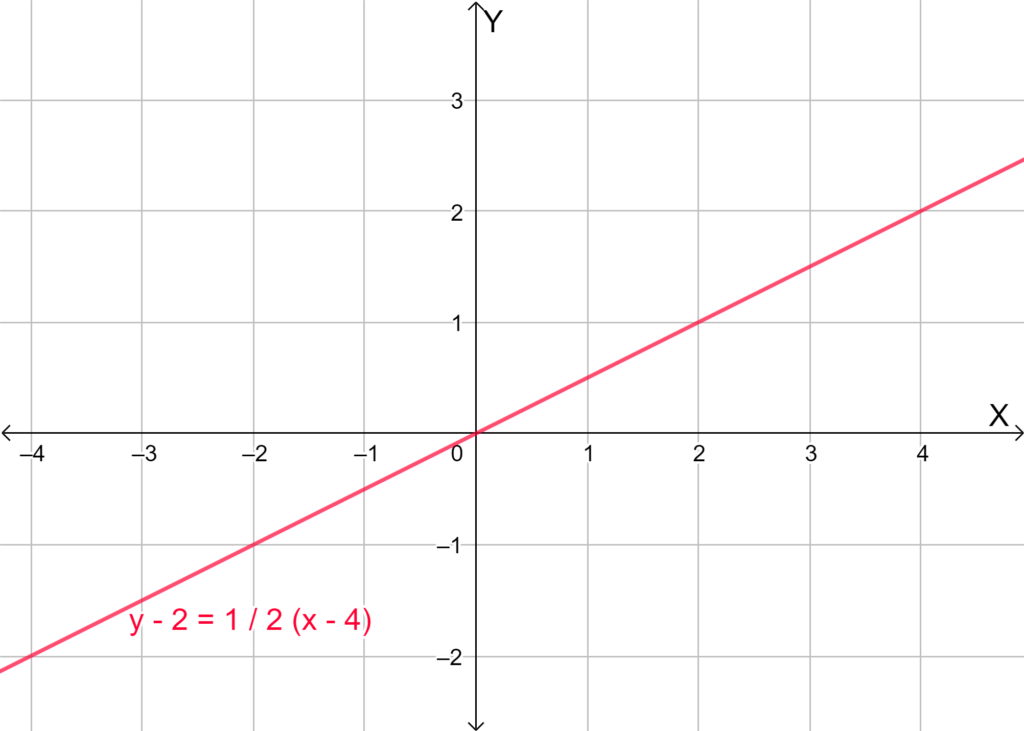
The graph of the given function is drawn as,

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 14 Exercise 3 Answer
It is given that the length of a rectangle is 4 more than twice its width and the perimeter can be no more than 92 ft.
It is required to write an inequality to find all the possible values of the width of the rectangle.
To do so, let the width be x. Form the expression for the length and perimeter of a rectangle. Apply the given condition that the perimeter can be no more than 92 ft.
Let the width be x.
Given that the length of the rectangle is 4 more than twice its width. Hence, the length will be 2x+4.
The Perimeter of the rectangle, with x width and 2x+4 length, is
p=2((x)+(2x+4))
p=2(3x+4)
It is given that the perimeter can be no more than 92ft. Hence,
2(3x+4)≤92
3x+4≤46
3x≤42
x≤14
The width cannot be negative and 0. Hence, the inequality for width x is, 0 < x ≤ 14.
The inequality to solve the problem is 0 < x ≤ 14.
It is given that the length of a rectangle is 4 more than twice its width and the perimeter can be no more than 92 ft.
It is required to graph the inequality and describe the solution in words.
To do so, draw a graph only with the x-axis and represent the inequality on the graph. Also, describe the solution in words.
The inequality for width x is, 0 < x ≤ 14.
Represent the inequality on the graph.
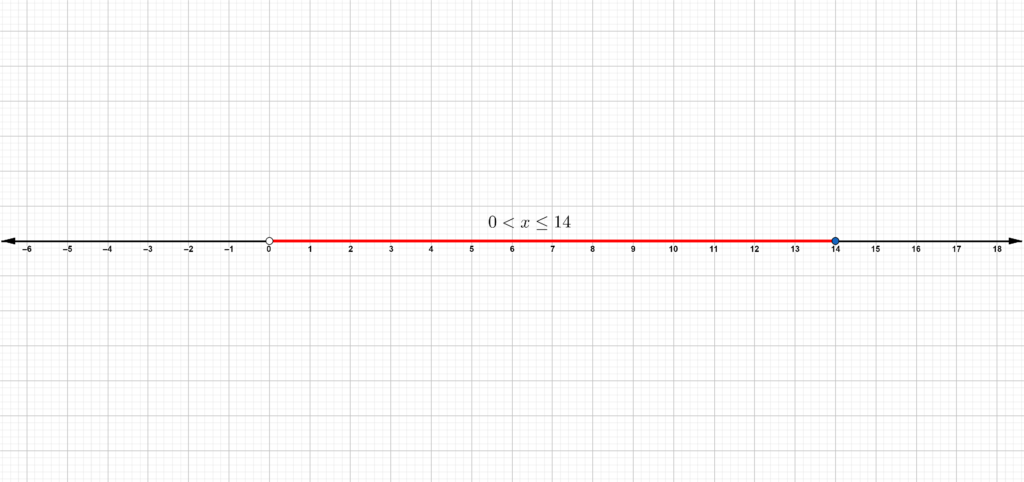
The possible values of width are greater than 0 and less than or equal to 14 ft.
The representation of inequality as a graph is,

The solution in words is written as the possible value of width is greater than 0 and less than or equal to 14 ft.
Page 15 Exercise 1 Answer
The given expression is 6−2x3y−5.
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
Given Expression 6-3 x3 y-5
⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{6^2 y^5}\)
⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{36 y^5}\)
So the correct option is C.
Option A
The given expression is 6−2x3y−5.
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
Given Expression 6-3 x3 y-5
⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{6^2 y^5}\)
⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{36 y^5}\)
The simplified form is \(\frac{x^3}{36 y^5}\) which is not equal to -12x35y so option A is incorrect.
Option B
The given expression is 6−2x3y−5.
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
Given Expression 6-3 x3 y-5
⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{6^2 y^5}\)
⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{36 y^5}\)
The simplified form is \(\frac{x^3}{36 y^5}\) which is not equal to -36x3y so option B is incorrect.
Option D
The given expression is 6−2x3y−5.
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
6−2x3y−5 = \(\frac{x^3}{6^2 y^5}\)
6−2x3y−5The simplified form is \(\frac{x^3}{36 y^5}\) which is not equal to \(\frac{x^3}{12 y^5}\) so the option D is incorrect.
The simplified form of 6−2x3y−5 is \(\frac{x^3}{36 y^5}\), so the correct option is C.
Page 15 Exercise 2 Answer
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)
⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)
So the correct option is C.
Option A
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)
⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)
The simplifed form is \(5 a t^{\frac{4}{3}}\) which is not equal to \(5^{\frac{1}{3}} a t^2\) so the option A is incorrect.
Option B
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)
⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)
The simplifed form is \(5 a t^{\frac{4}{3}}\) which is not equal to \(5^{\frac{2}{3}} a^{\frac{1}{3}} t^{\frac{4}{3}}\) so the option B is incorrect.
Option D
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).
It is required to simplify the given expression.
To simplify the given expression use the algebraic identity.
The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)
⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)
⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)
The simplified form is \(5 a t^{\frac{4}{3}}\) which is not equal to 125a3t4 so option D is incorrect.
The simplified form of \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\) is \(5 a t^{\frac{4}{3}}\), so the correct option is C.
How To Solve Envision Algebra 1 Standards Practice 2 Problems
Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 15 Exercise 3 Answer
The given expression is \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{5}}\right)\).
It is required to simplify the given expression.
To simplify the given expression, use the algebraic identity.
Rewrite the given expression; use the algebraic identity aman = am+n to simplify the expression.
The Given expression is \(\left(4g \frac{1}{3} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{5}}\right)\)
⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=(4 \cdot 2 \cdot 3)\left(g^{\frac{1}{3}} \cdot g^{\frac{2}{3}}\right)\left(h^{\frac{3}{5}} \cdot h^{\frac{1}{5}}\right)\)
⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=(24)\left(9 \frac{1}{3}+\frac{2}{3}\right)\left(h^{\frac{3}{5}+\frac{1}{5}}\right)\)
⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=(24)\left(g^{\frac{3}{3}}\right)\left(h^{\frac{4}{5}}\right)\)
⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=24 g h^{\frac{4}{5}}\)
The simplified form of the given expression \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{5}}\right)\) is \(24 g h^{\frac{4}{5}}\).
Page 15 Exercise 4 Answer
It is given that b−(xy) can be written as \(\frac{1}{\left(b^x\right)^y}\) for all real numbers x and y.
It is required to find whether the given statement is correct and show examples to justify your explanation.
To simplify the given expression, use the algebraic identity.
Use the algebraic identity to simplify the given expression.
b-(xy) = \(\frac{1}{b^{(x y)}}\)
b-(xy) = \(\frac{1}{\left(b^x\right)^y}\)
Hence the given statement is correct.
The given statement b-(xy) = \(\frac{1}{\left(b^x\right)^y}\) is correct.
Page 16 Exercise 1 Answer
The given sequence is 4,16,64,256,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common ratio is a constant and equals the ratio between any two consecutive terms.
Divide the first two terms
⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)
Divide the third term and the second term
⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)
Hence the common ratio is r=4
The formula for expressing geometric sequences in their recursive form is an = an−1⋅r, where r is the common ratio of the given sequence, an is the nth element and an−1 is the (n−1)th element.
Substitute 4 for r in the recursive form.
an = an−1 ⋅ 4
an = 4an−1
Hence the correct answer is option B.
Option A
The given sequence is 4,16,64,256,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common ratio is a constant and equals the ratio between any two consecutive terms.
Divide the first two terms
⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)
Divide the third term and the second term
⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)
Hence the common ratio is r=4
The formula for expressing geometric sequences in their recursive form is an = an−1⋅r, where r is the common ratio of the given sequence, an is the nth element and an−1 is the (n−1)th element.
Substitute 4 for r in the recursive form.
an = an−1 ⋅ 4
an = 4an−1
Here a1 is 4 and an is 4an−1 which is not equal to a1 = 0, so option A is incorrect.
Option C
The given sequence is 4,16,64,256,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common ratio is a constant and equals the ratio between any two consecutive terms.
Divide the first two terms
⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)
Divide the third term and the second term
⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)
Hence the common ratio is r=4
The formula for expressing geometric sequences in their recursive form is an = an−1⋅r, where r is the common ratio of the given sequence, an is the nth element and an−1 is the (n−1)th element.
Substitute 4 for r in the recursive form.
an = an−1 ⋅ 4
an = 4an−1
Here a1 is 4 and an is 4an−1 which is not equal to an = 4 + 4an−1, so option C is incorrect.
Option D
The given sequence is 4,16,64,256,…
It is required to find the recursive formula for the given sequence.
To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.
The common ratio is a constant and equals the ratio between any two consecutive terms.
Divide the first two terms
⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)
Divide the third term and the second term
⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)
Hence the common ratio is r=4
The formula for expressing geometric sequences in their recursive form is an = an−1⋅r, where r is the common ratio of the given sequence, an is the nth element and an−1 is the (n−1)th element.
Substitute 4 for r in the recursive form.
an = an−1 ⋅ 4
an = 4an−1
Here a1 is 4 an is 4an−1 which is not equal to a1 = 0 and an is 4 + an−1, so option D is incorrect.
Hence the correct answer is option B.
Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 17 Exercise 1 Answer
Given the expression 5n6 − n4 − 3n2 − 2n + 4.
It is required to find the number of terms in the expression.
The number of terms is usually the number of terms in the fully expanded form of the polynomial.
In the given expression there are 5 terms and the degree of every term is different, so the expression cannot be simplified further.
Hence the number of terms in the given expression is 5.
The correct option is C.
The given expression is 5n6 − n4 − 3n2 − 2n + 4.
Since the degrees in the expression are different and the expression is in fully expanded form. So, the number of terms in the expression is exactly 5, not more or less. So, the options A, B, and D are not correct.
The correct answer is Option (C), the number of terms in the given expression is 5.
Page 17 Exercise 2 Answer
Given the monomial 4a5bc.
It is required to find the number of terms in the monomial. The degree of a monomial is the sum of the exponents of the variable.
The sum of the exponents of the variable is 5 + 1 + 1 = 7.
Hence the degree of the monomial is 7.
The correct option is D.
Given the monomial 4a5bc.
The degree of a monomial is the sum of the exponents of the variable.
The sum of the exponents of the variable is 7.
Hence options A, B, and C are incorrect.
The correct answer is Option (D), the degree of the monomial is 7.
Page 17 Exercise 4 Answer
A new house worth $250,000 depreciates at a rate of 16% a year. It is required to explain the situation in terms of growth or decay. If the value increases with time, then the given situation is of growth and if the value decreases with time, then the given situation is of decay. In the given situation, the value of the house decreases by 16% every year. Therefore the given situation is of decay.
The given situation is of decay because the value of the house reduces every year by 16%.
A new house worth $250,000 depreciates at a rate of 16% a year.
It is required to write a function to model the situation.
To do so, find the worth of the house after one year and after two years. Observe the sequence of the initial worth of the house, worth after one year, worth after two years, and as a result, a function can be written to model the situation.
Find the worth of the house after one year.
The initial worth of the house is $250,000.
The worth of the house after one year will be,
Worth after one year = 250,000 − 0.16 × 250,000
Worth after one year = 250,000 × 0.84
Find the worth of the house after two years.
The worth of the house after two years will be,
Worth after two year = 250,000 − 0.16 × (250,000×0.84)
Worth after two year = 250,000 × 0.84 × 0.84
Model the function of the situation.
Let W be the worth of the house after n years.
The function of this situation can be modeled as,
W = $250,000 × (0.84)n
The function to model the situation can be represented as W = $250,000 × (0.84)n, where W is the worth of the house and n is the number of years.
A new house worth $250,000 depreciates at a rate of 16% a year.
It is required to write a function to model the situation.
To do so, find the worth of the house after one year and after two years. Observe the sequence of the initial worth of the house, worth after one year, worth after two years, and as a result, a function can be written to model the situation. As a result, the value of the house after 5 years can be determined.
Find the worth of the house after one year.
The initial worth of the house is $250,000.
The worth of the house after one year will be,
Worth after one year = 250,000 − 0.16 × 250,000
Worth after one year = 250,000 × 0.84
Find the worth of the house after two years.
The worth of the house after two years will be,
Worth after two year = 250,000 − 0.16 × (250,000×0.84)
Worth after two year = 250,000 × 0.84 × 0.84
Find the function for the situation.
Let W be the worth of the house after n years.
The function of this situation can be modeled as
w=$250000x(0.84)n
Find the value of the house after 5 years
substitute 5 for n in the function
w=$ 250,000 x(0.84)n
w=$ 250,000 x(0.84)5
w=$ 250,000 x(0.4182
w=$104,550
The worth of the house after 5 years is $104,550.
Envision Algebra 1 Standards Practice 2 Step-By-Step Explanation
Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 18 Exercise 1 Answer
The given expression is (x−3)2.
It is required to solve the given expression.
Use the algebraic identity (a−b)2 = a2 − 2ab + b2 to simplify the given expression. Choose x for a and 3 for b.
Given Expression, (x-3)²
(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9
So the correct option is C.
Option A
The given expression is (x−3)2.
It is required to solve the given expression.
Use the algebraic identity (a−b)2 = a2 − 2ab + b2 to simplify the given expression. Choose x for a and 3 for b.
Given Expression, (x-3)²
(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9
The simplified form of the given expression is x2 – 6x + 9 which is not equal to 2x – 6 so option A is incorrect.
Option B
The given expression is (x−3)2.
It is required to solve the given expression.
Use the algebraic identity (a−b)2 = a2 − 2ab + b2 to simplify the given expression. Choose x for a and 3 for b.
Given Expression, (x-3)²
(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9
The simplified form of the given expression is x2 – 6x + 9 which is not equal to x2 + 9 so option B is incorrect.
Option D
The given expression is (x−3)2.
It is required to solve the given expression.
Use the algebraic identity (a−b)2 = a2 − 2ab + b2 to simplify the given expression. Choose x for a and 3 for b.
Given Expression, (x-3)²
(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9
The simplified form of the given expression is x2 – 6x + 9 which is not equal to x2 – 9x – 6 so option D is incorrect.
The simplified form of x2 − 6x + 9 is x2 − 6x + 9, so the correct option is C.
Page 18 Exercise 2 Answer
The given expressions are,
(5x2 + 10x + 6) − (2x2 − 4x + 6)
x(3x + 14)
6x2 − (9x2 + 12x) − 2x
(x2 + 6x2) + (−4x2 + 2x − 4x + 16x)
It is required to classify the given equations as those equivalent to 3x2 + 14x and not equivalent to 3x2 + 14x.
To do so, simplify each given expression and check whether it is equivalent to 3x2 + 14x or not.
Simplify the first given expression (5x2 + 10x + 6) − (2x2 − 4x + 6).
Given expression (5x²+10x+6)-(2x²-4x+6)
(5x²+10x+6)-(2x²-4x+6)= 5x²+10x+6-2x²+4x-6
(5x²+10x+6)-(2x²-4x+6)= (5-2)x² +(10+4)x+6-6
(5x²+10x+6)-2x²-4c+6)=3x²+14
Therefore, (5x2 + 10x + 6) − (2x2 − 4x + 6) is equivalent to 3x2 + 14x.
Simplify the second given expression x (3x + 14).
x(3x + 14) = 3x2 + 14x
Therefore, x(3x+14) is equivalent to 3x2 + 14x.
Simplify the third given expression 6x2 − (9x2 + 12x) − 2x.
Given expression 6x²-(9x² +12x)-2x
6x²-(9x²+12x)-2x=6x²-9x²-12x-2x
6x²-(9x²+12x)-2x=(6-9)x²-(12-2)x
6x²-(9x²+12x)-2x=-3x²-14x
Therefore, 6x2 − (9x2 + 12x) − 2x is not equivalent to 3x2 + 14x.
Simplify the fourth given expression (x2 + 6x2) + (−4x2 + 2x − 4x + 16x).
Given Expression (x²+6x²)+(-4x²+2x-4x+16x)
(x²+6x²)+(-4x²+2x-4x+16x)=x²+6x²-4x²+2x-4x+16)x
(x²+6x²)+(-4x²+2x-4x+16x)=(1+6-4)x²+(2-4+16)x
(x²+6x²)+ (-4x²+2x-4x+16x)=3x²+14x
Therefore, (x2 + 6x2) + (−4x2 + 2x −4x + 16x) is equivalent to 3x2 + 14x.

Page 18 Exercise 3 Answer
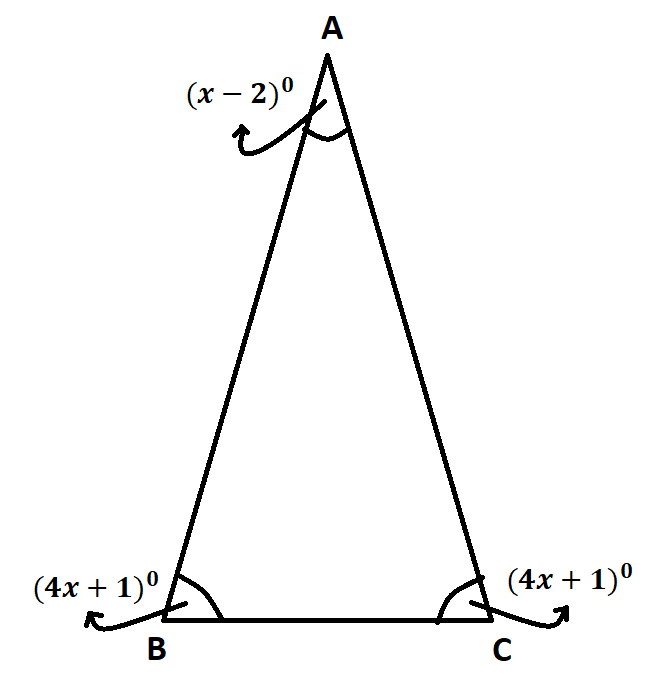
It is given that the length of a rectangular sandbox is 4x + 1 and the width of the sandbox is x − 2.
It is required to find a polynomial in standard form which represents the area of the sandbox.
To do so, use the area of the rectangle formula. Substitute the given values of length and breadth. Solve further to find the polynomial.
The area of a rectangle is A=lw.
Substitute 4x+1 for 1 and x-2 for w
Solve further to find the formula
A=(4x+1)(x-2)
A=(4x)(x)-2(4x)+1(x)+1(-2)
A=4x²-8x+x-2
A=4x²-7x-2
Hence the polynomial in standard form which represents the area of the sandbox is 4x2 − 7x − 2.
It is given that the length of a rectangular sandbox is 4x+1 and the width of the sandbox is x−2.
It is required to find a polynomial in standard form which represents the area of the sandbox. And name the polynomial based on its degree and number of terms.
To do so, use the area of the rectangle formula. Substitute the given values of length and breadth. Solve further to find the polynomial. Then name the polynomial based on its degree and number of terms.
The area of a rectangle is A=lw.
Substitute 4x+1 for 1 and x-2 for w
Solve further to find the formula
A=(4x+1)(x-2)
A=(4x)(x)-2(4x)+1(x)+1(-2)
A=4x²-8x+x-2
A=4x²-7x-2
The polynomial is 4x2 − 7x − 2.
The name of the polynomial 4x2 − 7x − 2 based on the degree is a quadratic polynomial because this polynomial has degree 2.
The name of the polynomial 4x2 − 7x − 2 based on the number of terms is trinomial because this polynomial has three terms.
The name of the polynomial 4x2 − 7x − 2 based on the number of terms is trinomial and its name based on the degree is quadratic polynomial.
Page 19 Exercise 1 Answer
The given polynomial is 5x2 + 27x − 18.
It is required to factorize the given polynomial.
The Given polynomial is 5x²+27x-18
5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)
So the correct answer is option C.
Option A
Factorize the given polynomial 5x2 + 27x − 18.
The Given polynomial is 5x²+27x-18
5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)
Which is not equivalent to (5x+3)(x+6)
so option A is incorrect.
Option B
Factorize the given polynomial 5x2 + 27x − 18.
The Given polynomial is 5x²+27x-18
5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)
Which is not equivalent to (5x−2)(x−9)
so option B is incorrect.
Option D
Factorize the given polynomial 5x2 + 27x − 18.
The Given polynomial is 5x²+27x-18
5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)
Which is not equivalent to (5x+2)(x−9)
so option D is incorrect.
The factor of the polynomial 5x2 + 27x − 18 is (5x−3)(x+6), so the correct option is C.
Page 19 Exercise 2 Answer
The given expression is (x−3)2.
It is required to simplify the given expression.
To solve the given expression, use the algebraic identity.
Use the algebraic identity (a−b)3 = a3 − 3a2b + 3ab2 − b3. Choose x for a and 3 for b and solve further.
The given expression, (x-3)³
(a-b)³=a³-3a²b+3ab²-b³
(x-3)³=x³-9x²+3x(3)²-(3)³
The simplified form of (x−3)3 is x3 − 9x2 + 27x − 27.
The given expression is (x−3)2.
It is required to simplify the given expression and name it based on the degree.
To solve the given expression, use the algebraic identity. Name the simplified form based on degree.
Use the algebraic identity (a−b)3 = a3 − 3a2b + 3ab2 − b3. Choose x for a and 3 for b and solve further.
The given expression,(x-3)²
(a-b)³=a³-3a²b+3ab²-b³
(x-3)³=x³-9x²+3x(3)²-(3)³
(x-3)³=x³-9x²+27x-27
This is a cubic polynomial because it has degree 3.
The name of the polynomial x3 − 9x2 + 27x − 27 based on degree is a cubic polynomial.
Page 19 Exercise 3 Answer
A figure is given in the question.
It is required to find the area of the rectangle given in the figure.
To do so, use the area of the rectangle formula. Substitute the given values of length and breadth. Solve further to find the polynomial.
The given figure is,
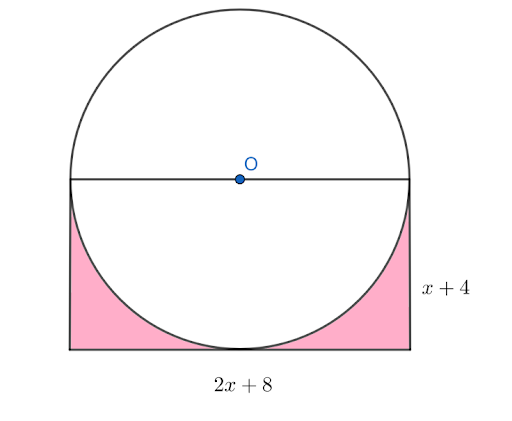
From the figure, the length of the rectangle is 2x + 8 and its width is x + 4.
The area Of a rectangle is A=lw
Substitute 2x+8 for 1 and x+4 for w
solve further to find the polynomial
A=(2x+8)(x+4)
A=(2x)(x)+2x)(4)+8(x)+8(4)
A=2x²+8x+8x+32
A=2x²+16x+32
The area of the rectangle in the given figure is 2x2 + 16x + 32.
A figure is given in the question. It is also given that the value of π is 3.14.
It is required to find the area of the circle given in the figure.
To do so, use the area of the circle formula. Substitute the given values of radius. Solve further to find the polynomial.
The given figure is,

From the figure, the radius of the circle is x+4.
The area of a circle is A= πr²
Substitute x+4 for r and 3.14 for π
Solve further to find the polynomial
A=(3.14)(x+4)²
A=(3.14)(x²+8x+16
A=(3.14)(x²)+(3.14)(8x)+(3.14)(16)
A=3.14×2+25.12x+50.24
The area of the circle in the given figure is 3.14x2 + 25.12x + 50.24.
A figure is given in the question. It is also given that the value of π is 3.14.
It is required to find the area of the shaded region given in the figure.
To do so, find the area of the circle and the area of the rectangle. Then subtract the area of the circle from the area of the rectangle.
The given figure is,
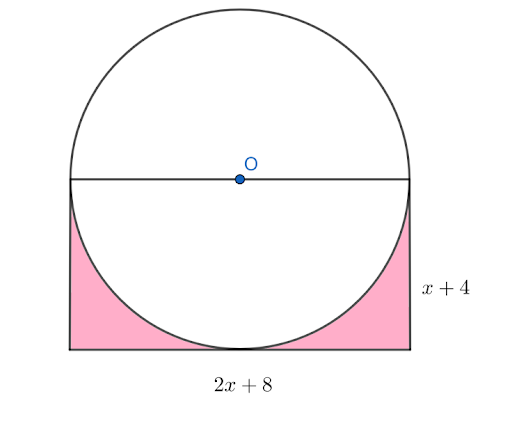
From the figure, the radius of the circle is x+4.
The area of a circle is A= πr²
Substitute x+4 for r and 3.14 for π
Solve further to find the polynomial
A1=(3.14)(x+4)²
A1=(3.14)(x²+8x+16)
A1=(3.14)x²+(3.14)(8x)+(3.14)(16)
A1=3.14x²+25.12x+50.24
From the figure, the length of the rectangle is 2x+8 and its width is x+4.
The area of a rectangle is A=lw
Substitute 2x+8 for 1 and x+4=w
Solve further to find the polynomial.
A2=(2x+8)(x+4)
A2=(2x)(x)+(2x)(4)+8(x)+8(4)
A2=2x²+8x+8x+32
A2=2x²+16x+32
To find The area of the shaded region,
subtract the area of the circle from the area of the rectangle
A=(2x²+16x+32)-)(3.14x²+25.12x+50.24
A=(2-3.14)x²+(16-25.12)x+32-50.24
A=-1.14×2-9.12x-18.24
The area of the shaded region is 3.14x2 + 25.12x + 50.24.
Page 20 Exercise 2 Answer
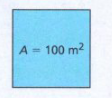
Given is the polynomial representing the area of a square.
64x2 + 96x + 36
It is asked to find the expression for the length of the sides.
To solve the problem use the formula for the area of the square that is side2 and equate it to the given polynomial and then simplify and solve for the side.
Equate the given polynomial with the area of the square that is side 2.
Given Expression 64x² +96x+36
Side² =4((4x)²+2.4x.3+3²)
Side²=(2(4x+3))²
Side2=8x+6
So the expression for the side of the square is (8x+6).
The expression for the side length is (8x+6) units.
Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 20 Exercise 3 Answer
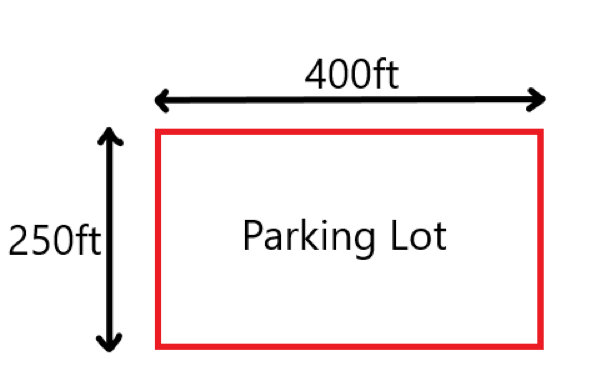
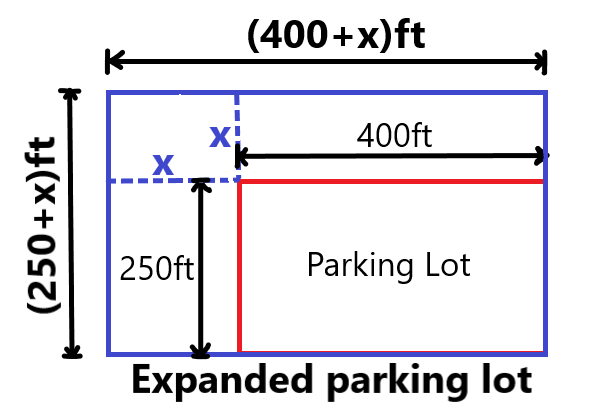
Given, the dimension of the garden is 12m × 8m. A pathway of xm is to be made around the perimeter of the garden having the same area as the garden.
It is asked to sketch the situation and to find a polynomial representing the total area of the garden and pathway.
To solve the problem first sketch the situation and then find the area of the garden using the formula for the area of the rectangle substituting the values of length and breadth
Then find the area of the pathway assuming it to be made up of four different rectangles.
Then add the area of the garden and the area of the pathway to get the polynomial representing the total area of the garden and the pathway.
Sketch of the given situation.
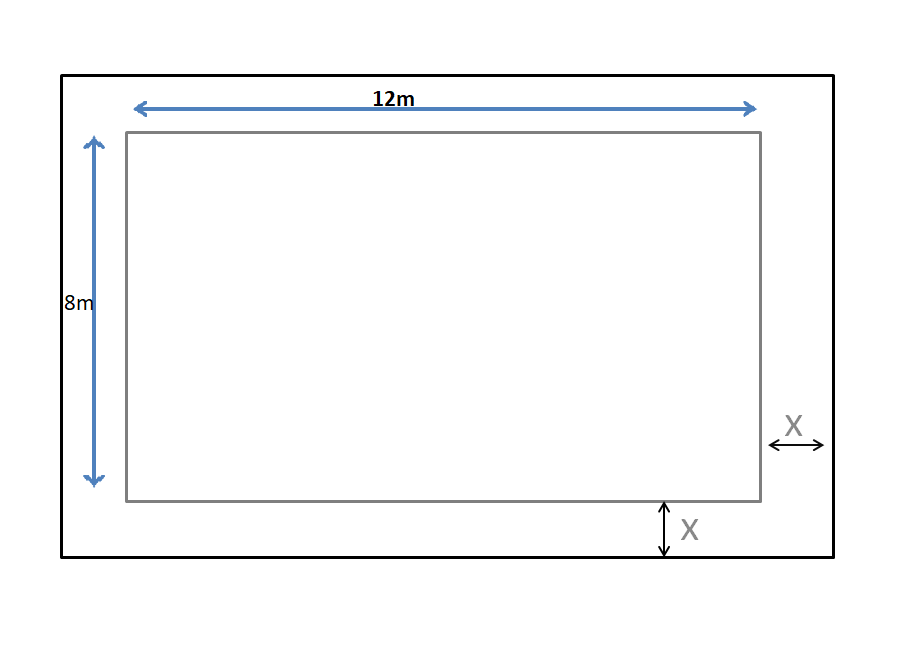
The length of the garden is l = 12m.
Breadth of the garden is b=8m
The area of the garden is,
A=lxb
A=12×8
A=96
So the area of the garden is 96m2.
Assume that the pathway is formed of 4 rectangles. Two rectangles having the length of 12m and breadth of xm, and other two rectangles having the length of 8m + 2xm and breadth of xm, then the total area of the pathway is given by,
A=lxb+lxb+lxb+lxb
⇒ \(\begin{aligned}
& A=(12 \times x)+(12 \times x)+((8+2 x) \times x)+((8+2 x) \times x) \\
& A=2 \cdot(12 \times x)+2 \cdot((8+2 x) \times x) \\
& A=24 x+16 x+4 x^2 \\
& A=4 x^2+40 x
\end{aligned}\)
So the area of the pathway is A = 4x2 + 40x.
The total area will be the sum of the area of the pathway and the area of the garden.
Total Area= Area of the garden+Area of the pathway
2A=96+4x²+40x
A=48+2x²+20x
A=2x²+20x+48
The polynomial for the total area of the garden and the pathway is 2x2 + 20x + 48.
Given, the dimension of the garden is 12m × 8m. A pathway of xm is to be made around the perimeter of the garden having the same area as the garden.
It is asked to find the width of the pathway.
To solve the problem, first equate the area of the pathway from the previous problem with the area of the garden to get a polynomial. Then factorise the polynomial and simplify and solve for x.
The area of the garden is 96m2 and the area of the pathway from the previous part of the question is A = 4×2 + 40x.
Equate the area of the pathway with the area of the garden.
\(\begin{aligned}
& 4 x^2+40 x=96 \\
& x^2+10 x=24 \\
& x^2+10 x-24=0
\end{aligned}\)
So the polynomial is x2+10x-24=0
Now factorize the polynomial to get the value of x.
\(\begin{aligned}
& x^2+10 x-24=0 \\
& x^2+12 x-2 x-24=0 \\
& x(x+12)-2(x+12)=0 \\
& (x-2) \cdot(x+12)=0
\end{aligned}\)
So x = 2 or −12 but as length cannot be negative,
x = 2m
As x is the width of the pathway so width of the pathway is 2m.
The width of the pathway is 2 meters.