Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities
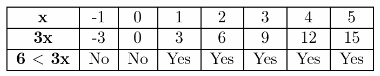
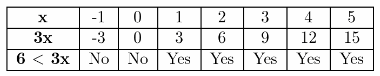
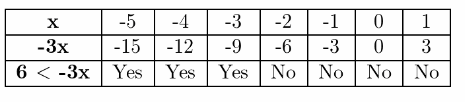
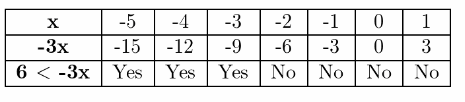
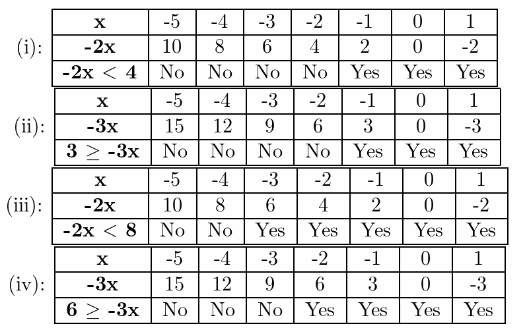
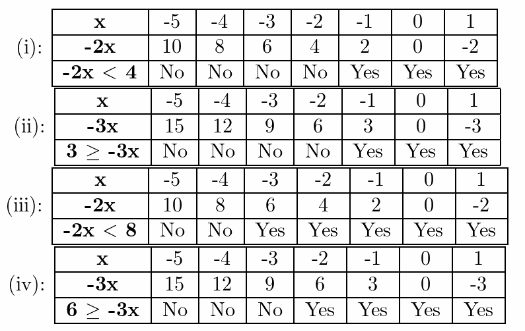
Page 48 Essential Question Answer
An inequality with a closed dot on the number line and a boundary point represented by the “or equal” component of the symbols ≤≤ and≥≥. The sign (∞) denotes an unlimited interval to the right. Use the symbols< for “less than” and > for “greater than” to express ordering relationships.
We can use inequalities to describe intervals on the real number line as a closed dot on the number line and a square bracket in interval notation imply inclusive inequalities with the “or equal to” component.
Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions
Page 49 Exercise 2 Answer
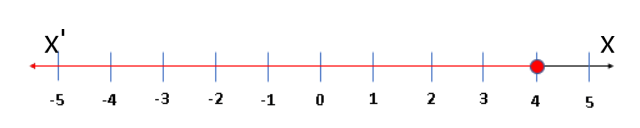
The given graph is
![]()
We represent this inequality using
x≤−6 or x>3
The required solution is x≤−6 or x>3 and graph is
![]()
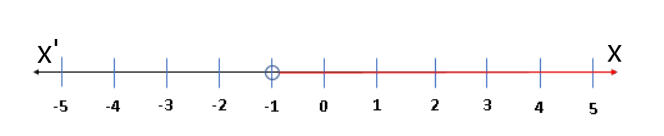
The given graph is
![]()
We represent this inequality using
x<−5 or x≥4
The required solution is x<−5 or x≥4 and graph is
![]()

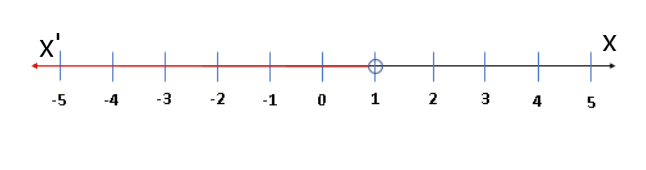
The given graph is
![]()
We represent this inequality using
x≤−4 or x≥5
The required solution isx≤−4 or x≥5 and graph is
![]()
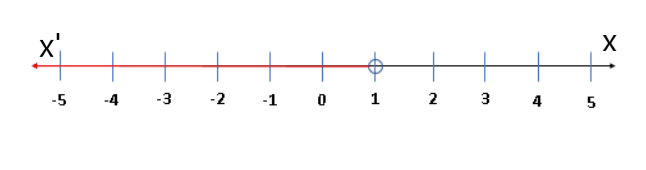
The given graph is
![]()
We represent this inequality using
x<−3 or x>6
The required solution is x<−3 or x>6 and graph is
![]()
We use “or” in these inequalities to represent the union of the graph.
We use “or” in these inequalities to represent the union of the graph.
Big Ideas Math Algebra 1 Chapter 2 Exercise 2.5 Solution
Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.5 page 49 Exercise 3 Answer
We use combinations of inequalities to represent these graphs on the number line.
In addition, we use “and” to get the intersection of the two inequalities, and “or” to get the union of the two inequalities.
We use combinations of inequalities using “and” and “or” statements to represent these graphs on the number line.
Page 51 Exercise 2 Answer
Given: A number less than−2 and greater than or equal to 2.
To find Respective inequality.
Evaluate to get the answer.

We represent this inequality as follows
u<−2
u≥2
u<−2 or u≥2
The plot can be plotted as

The obtained inequality is −2<u≤2 and the plot is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.5 Page 51 Exercise 4 Answer
Given: A number is more than −4 and at most \(-6 \frac{1}{2}\).
To find Respective inequality.
Evaluate to get the answer.

We represent this inequality using the following
c>−4 or c≤\(-6 \frac{1}{2}\)
The plot can be

The obtained inequality is c>−4 or c≤−\(-6 \frac{1}{2}\) and the plot is

Solving Linear Inequalities Exercise 2.5 Big Ideas Math
Page 51 Exercise 5 Answer
Given: A number is no less than −1.5 and less than 5.3.
To find Respective inequality.
Evaluate to get the answer.

We represent this graph using the following inequalities:
c≥−1.5 and c<5.3
The plot obtained is

The obtained inequality is c≥−1.5 and c<5.3 and the plot is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.5 Page 52 Exercise 6 Answer
Given: An inequality 6.4<x−3≤7.
To find The plot of the inequality.
Evaluate to get the answer.

We solve for the inequality as follows
4<x−3≤7 (Given )
4+3<x−3+3≤7+ ( Add 3 to both sides of the inequality )
7<x≤10
The plot is

The obtained inequality is 7<x≤10 and the inequality obtained is

Page 52 Exercise 7 Answer
Given: An inequality 15≥−5g≥−10.
To find The plot of the inequality.
Evaluate to get the answer.

We solve for the inequality as follows
15≥−5g≥−10 (Given)
\(\frac{15}{-5} \geq \frac{-5 g}{-5} \geq \frac{-10}{-5}\) (Divide both sides by −5)
-3≥g≥2 ( Inequality symbol reverse)
−3≤g≤2
The plot obtained is

The obtained inequality is −3≤g≤2 and the plot is

Big Ideas Math Linear Inequalities Exercise 2.5 Help
Page 52 Exercise 8 Answer
Given: An inequality z+4<2 or −3z<−27.
To find The plot of the inequality.
Evaluate to get the answer.

We solve for the inequality as follows
z+4<2 or −3z<−27 (Given)
We separate this inequality to solve for z
1.z+4<2z+4−4<2−4 (Subtract 4 on both sides)
z<−2\-3z<−27 (Divide both sides by −3)
2.\(\frac{-3 z}{-3}<\frac{-27}{-3}\)
z<9 (Inequality reverses)
z<−2 or z>9.
The plot is

The obtained inequality is −2>z>9. and the plot is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.5 Page 52 Exercise 9 Answer
Given: An inequality 2t+6<10 or−t+7≤2.
To find The plot of the inequality.
Evaluate to get the answer.

We solve for the inequality as follows
2t+6<10 or −t+7≤2 (Given)
we separate this inequality to solve for t
1. 2t+6<10 (Subtract6 on both sides )
2t+6−6<10−6
2t<4
t<2
2.−t+7≤2
−t+7−7≤2−7 (Subtract both sides by 7)
−t≤−5
t≥5t<2 or t≥5.
The plot is

The obtained inequality is t≥5t<2 or t≥5. and the plot is

How To Solve Exercise 2.5 Big Ideas Math
Page 52 Exercise 10 Answer
Given: An inequality \(-8 \leq \frac{1}{3}(6 x+24) \leq 12\).
To find The plot of the inequality.
Evaluate to get the answer.

Solve for the inequality as follows
\(-8 \leq \frac{1}{3}(6 x+24) \leq 12\) (Given)
\(-8 \leq \frac{1}{3}(6 x)+\frac{1}{3}(24) \leq 12 \) (Distribute and simplify)
-8≤2x+8≤24
−8−8≤2x+8−8≤24−8 & ( Subtract 8 to both sides )
−16≤2x≤16
\(\frac{-16}{2} \leq \frac{2 x}{2} \leq \frac{16}{2}\) (Divide both sides by 2)
-8≤x≤2
The plot is

The obtained inequality is −8≤x≤2. The plot obtained is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.5 Page 52 Exercise 11 Answer
Given: An inequality−60≤(h−50)≤60.
To find The range of values in which the machine operates.
Evaluate to get the answer.
Let us consider and solve for h
−60≤2(h−50)≤60 (Given)
−60≤2(h)+2(−50)≤60 (Distribute )
−60≤2h−100≤60
−60+100≤2h−100+100≤60+100 (Add 100 to both sides of the inequality )
40≤2h≤160
\(\frac{40}{2} \leq \frac{2 h}{2} \leq \frac{160}{2}\) (Divide both sides by 2)
20≤h≤80.
The obtained inequality after the evaluation is 20≤h≤80.
Big Ideas Math Student Journal Exercise 2.5 Examples