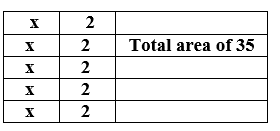
Go Math! Practice Fluency Workbook Grade 6, California 1st Edition Chapter 7 Representing Ratios and Rates
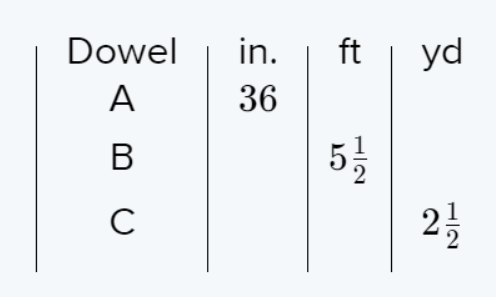
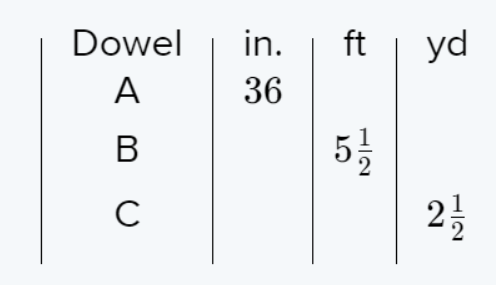
Question. Find the unknown value in the proportion 4/5 = ?/20 and to round to the nearest tenth value.
Given a proportion 4/5 =?/20
To find the unknown value in the proportion and to round to the nearest tenth if needed.
Since proportions are comparisons between two equal ratios their fractions in the lowest term must be equal and by finding the
relationship between the two given ratios we can calculate the unknown value.
The given proportion is 4/5 =?/20
The denominators of both ratios are given so compare them to find the relationship between the two numbers.
Then by calculating what number the numerator is to be multiplied we can find the unknown value.
From the given proportion we see that5.4=20
So, we need to multiply by 4
4/5 =4.4/5.4
Multiply, 4/5 =?/20
So, the unknown value is 16
The unknown value in the proportion 4/5 =?/20 is 16
Go Math Grade 6 Exercise 7.2 Applying Ratios And Rates Solutions
Question. Find the unknown value in the proportion 3/7 = ?/35 and to round to the nearest tenth.
Given a proportion 3/7 =?/35
To find the unknown value in the proportion and to round to the nearest tenth if needed.
Since proportions are comparisons between two equal ratios their fractions in the lowest term must be equal and by finding the relationship between the two given ratios we can calculate the unknown value.
From the given proportion we see that7.5=35
So, we need to multiply by 5

3/7 =3.5/7.5
Multiply, 3/7 =15/35
So, the unknown value is 15
The unknown value in the proportion 3/7 =?/35 is15
Question. Find the unknown value in the proportion 4/3 = 12/? and to round to the nearest tenth value.
Given a proportion 4/3 =12/?
To find the unknown value in the proportion and to round to the nearest tenth if needed.
Since proportions are comparisons between two equal ratios their fractions in the lowest term must be equal and by finding the
relationship between the two given ratios we can calculate the unknown value.
The given proportion is 4/3 =12/?
The numerators of both ratios are given so compare them to find the relationship between the two numbers.
Then by calculating what number the denominator is to be multiplied we can find the unknown value.
From the given proportion we see that 4.3=12
So, we need to multiply by 3
4/3 =4.3/3.3
Multiply, 4/3 =12/9
So, the unknown value is 9
The unknown value in the proportion 4/3 =12/? is 9
Go Math Grade 6 Exercise 7.2 Applying Ratios And Rates Answers
Question. Find the unknown value in the proportion 13/15 = 52/? and to round to the nearest tenth value.
Given a proportion 13/15 =52/?
To find the unknown value in the proportion and to round to the nearest tenth if needed.
Since proportions are comparisons between two equal ratios their fractions in the lowest term must be equal and by finding the between the two given ratios, we can calculate the unknown value.
The given proportion is 13/15 =52/?
The numerators of both ratios are given so compare them to find the relationship between the two numbers.
Then by calculating what number the denominator is to be multiplied we can find the unknown value.
From the given proportion we see that 13.4=52
So, we need to multiply by 4
13/15 =13.4/15.4
Multiply, 13/15 =52/60
So, the unknown value is 60
The unknown value in the proportion 13/15 =52/? is 60
Question. Wayne has a recipe on a three-inch-by-five-inch index card that he wants to enlarge to 15 inches long. Find out how wide the enlargement.
Given that Wayne has a recipe on a three-inch-by-five-inch index card that he wants to enlarge to 15 inches long.
To find out how wide the enlargement will be.
The given dimensions are written in the form of a ratio and we know that comparisons between two equal ratios will have the same fractions in the lowest term so by finding the relationship between the two given values we can calculate the width of the index card.
It is given that Wayne has a recipe on a 3-inch-by-5-inch index card.
So, the length of the card is 5 inches and the width of the card is 3 inches.
The ratio of the index card is width/length =3/5
Wayne wants to enlarge it to 15 inches long so to get a length of 15 we have to multiply the denominator by 3
Then multiply the numerator and denominator by 3 to get the new dimensions since they are equivalent ratios.
3/5 =3.3/5.3
Multiply, 3/5 =9/15
So, the width of the card will be 9 inches.
Wayne has a recipe on a 3-inch-by-5-inch index card that he wants to enlarge to 15 inches long then the enlargement will be 9 inches wide.
Solutions For Go Math Grade 6 Exercise 7.2 Applying Ratios And Rates
Question. Sharon is decreasing the size of a diagram of a leaf that is 30 centimeters long by 10 centimeters wide. Find out how long centimeters.
Given that Sharon is decreasing the size of a diagram of a leaf that is 30 centimeters long by 10 centimeters wide.
If the reduced diagram is 4 centimeters wide then, to find out how long will the diagram be.
The given dimensions are written in the form of a ratio and we know that comparisons between two equal ratios will have the
same fractions in the lowest term so by finding the relationship between the two given values we can calculate the length of the diagram of a leaf.
It is given that Sharon is decreasing the size of a diagram of a leaf that is 30 centimeters long by 10 centimeters wide.
So, the length of the diagram is 30cm and the width is10cm
The ratio of the diagram is length/width =30/10
Reduce the ratio to its simplest form,
length/width =3⋅10/1⋅10
length/width =3/1
If the reduced diagram is four centimeters wide, then to get a width of4 to multiply the denominator by 4
Then multiply the numerator and denominator by 4 to get the new dimensions since they are equivalent ratios.
3/1 =3.4/1.4
Multiply, 3/1 =12/4
So, the length of the diagram will be 12cm
Sharon is decreasing the size of a diagram of a leaf that is 30 centimeters long by 10 centimeters wide to 4 centimeters wide, then the diagram will be 12 centimeters long.
Question. A wood stove burns four same-sized logs in two hours. Find out the number of logs the stove can burn in eight hours.
Given that a wood stove burns four same-sized logs in two hours.
To find out the number of logs the stove can burn in eight hours.
The given information is written in the form of a ratio and we know that comparisons between two equal ratios will have the
same fractions in the lowest term so by finding the unit rate we can calculate the number of logs the stove can burn in eight hours.
It is given that a wood stove burns 4 same-sized logs in 2 hours.
The number of logs is 4 and the number of hours it takes is 2
So, the ratio is logs/hours =4/2
To calculate the unit rate, reduce the ratio.
logs/hours =2.2/2.1
Cancel common factors, logs/hours =2/1
In one hour, the woodstove burns 2 logs.
So, the number of logs the stove burns is 2 times the number of hours it takes.
So, in8 hours, the stove will burn twice the number of hours it takes
⇒2⋅8=16
So, in 8 hours the stove burns 16 logs.
A wood stove burns 4 same-sized logs in 2 hours, then the stove can burn 16 logs in 8 hours.
Question. The number of stamps is in 2012 five U.S. postal stamps cost $2.20. Find out how much seven stamps cost.
Given that in 2012 five U.S. postal stamps cost $2.20.
To find out how much seven stamps cost.
The given information is written in the form of a ratio and we know that comparisons between two equal ratios will have the same fractions in the lowest term so by finding the unit rate we can calculate the cost of seven stamps.
It is given that in 2012, five U.S. postal stamps cost $2.20
The number of stamps is five and their cost is $2.20
So, the ratio is
cost/stamps =2.20/5
To calculate the unit rate, reduce the ratio.
cost/stamps =0.44×5/5.1
Cancel common factors,
cost/stamp =0.44/1
For one stamp, the cost is $0.44
So, the cost of the stamps is 0.44 times the number of stamps.
The cost of seven stamps is0.44 times7
That is,0.44×7=3.08
So, the cost of seven stamps is $3.08
In 2012, five U.S. postal stamps cost $2.20 then seven stamps cost $3.08
Question. The distance between Saugerties and Kingston in inches. Find the actual distance between Saugerties and Kingston.
Given the distance between Saugerties and Kingston in inches.
To find the actual distance between Saugerties and Kingston.
The distance between Saugerties and Kingston in inches is given and the scale of the map is given so using the scale calculates
the actual distance between Saugerties and Kingston in miles.
It is given that the distance between Saugerties and Kingston is 4 inches.
It is also given that scale in the map is 1in =2.5mi.
So, on the map, the number of miles is equal to 2.5 times the number of inches.
If the distance is 4 inches then the number of miles is 2.5 times 4
That is, the actual distance between Saugerties and Kingston is = 2.5×4
Multiply,
The actual distance between Saugerties and Kingston is 10 miles.
The actual distance between Saugerties and Kingston is10mi.
Question. The scale of a map is 1in = 250mi and City A is 378mi miles from City B. Find how far is its distance on the map and round to the nearest tenth if needed.
Given that the scale of a map is 1in=250mi and City A is 378mi miles from City B.
To find how far is its distance on the map and round to the nearest tenth if needed.
Using the scale of the map, calculate the relationship between inches and miles to find the distance between City A and City B in inches on the map.
It is given that the scale of a map is 1in =250mi
So, the number of miles is equal to 250 times the number of inches on the map.
That is, the number of inches on the map is equal to the number of miles divided by250
If the actual distance between City A and City B is 378mi then the distance on the map is 378 divided by 250 =378/250
Dividing,=1.512
Rounding to the nearest tenth,≈1.5in
The scale of a map is 1in=250 mi. and City A is378 miles from City B then its distance on the map is rounded to the nearest tenth is 1.5 in
Question. The Twelve eggs cost $2.04. Find the cost of eighteen eggs.
Given twelve eggs cost $2.04
To find the cost of eighteen eggs.
The given proportion is reduced to its simplest form so that the denominator is one then the cost of eighteen eggs is calculated.
It is given that the cost of twelve eggs is $2.04
Then the proportion is cost/eggs =2.04/12
To calculate the unit rate, reduce the ratio.
cost/eggs =0.17×12/12×1
Cancel common factors,
cost/eggs =0.17/1
The cost of one egg is $0.17
So, the cost of eggs is 0.17 times the number of eggs.
The cost of 18 eggs is 0.17 times 18
0.17×18=3.06
Then the cost of 18 eggs is $3.06
If twelve eggs cost $2.04 then eighteen eggs cost $3.06
Question. Seven pounds of grapes cost $10.43. Find how much three pounds cost.
Given seven pounds of grapes cost $10.43
To find how much three pounds would cost.
The given proportion is reduced to its simplest form so that the denominator is one then the cost of three pounds of grapes is calculated.
It is given that seven pounds of grapes cost $10.43
Then the proportion is
cost/pound =10.43/7
To calculate the unit rate, reduce the ratio.
cost/pound =1.49×7/7×1
Cancel common factors,
cost/pound =1.49/1
For one pound of grapes, the cost is $1.49
So, the cost of the grapes is 1.49 times the number of pounds.
The cost of three pounds is1.49 times3
1.49×3=4.47
Then the cost of three pounds of grapes is $4.47
If seven pounds of grapes cost $10.43 then three pounds of grapes cost $4.47
Go Math Grade 6 Applying Ratios And Rates Exercise 7.2 Key
Question. Roberto wants to reduce a drawing that is 12 inches long by 9 inches wide. Find the width of the new drawing.
Given that Roberto wants to reduce a drawing that is 12 inches long by 9 inches wide.
If his new drawing is 8 inches long then, we have to find the width of the new drawing.
The given proportion is reduced to its simplest form so that the number needed to be multiplied is found and the width of the new drawing is calculated.
It is given that Roberto wants to reduce a drawing that is 12 inches long by 9 inches wide.
The length of the drawing is 12 inches and the width of the drawing is 9 inches.
Then the proportion is
length/width =12/9
Reducing to its simplest form.
length/width =4.3/3.3
length/width =4/3
If his new drawing is 8 inches long, then we can multiply the numerator by 2
So, multiply the numerator and denominator by 2 since they are equivalent ratios.
length/width =4.2/3.2
Multiply,
length/width =8/6
The width of the new drawing is 6 inches.
Roberto wants to reduce a drawing that is 12 inches long by 9 inches wide to 8 inches long, then the new drawing will be 6 inches wide.