Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 5 Operations with Decimals
Page 25 Problem 1 Answer
The given expression is 585÷13.
We are asked to estimate the quotient by rounding off the dividend and the divisor to the largest possible value.
The answer can be found by rounding off the dividend and the divisor to the nearest value.
Here, 13 is the divisor and 585 dividend.
That would be 10&600 respectively. Now, find the value of 600/10
This will give you the required answer.
The expression is 585÷13. Here 585 is closer to 600
Rounding off the value 585, we get 600.
The value 13 is closer to ten. Rounding of 13, we have:10.
Thus, we have the quotient of 600÷10 as 60
The estimated quotient value of 585÷13 by rounding the dividend and the divisor to the largest place value is 60
Page 25 Problem 2 Answer
The given expression is 2,756÷53.
We are asked to find the quotient. The answer can be found by rounding off the dividend and the divisor to the nearest value.
Here, is the divisor and dividend are 53&2756 respectively.
When rounding off, we have 50&3000 Now, find the value of the quotient. This will give you the required answer.
The given expression is: 2,756÷53. The value 2756 is closer to 3000
Rounding the value 2756 to the largest place value, we have: 3000.
Similarly, 53 is closest to 50. Thus, the quotient value is 3000/50=60.
The estimated value of the quotient of 2,756÷53 by rounding the dividend and the divisor to the largest place value is 60

Go Math Grade 6 Exercise 5.1 Operations With Decimals Solutions
Go Math! Grade 6 Exercise 5.1: Operations with Decimals Solutions Page 25 Problem 3 Answer
The given expression is 22,528÷98.
We are asked to find the value of the quotient when the dividend and the divisor is rounded to the largest value.
The answer can be found by rounding off the dividend and the divisor to the nearest value.
Here, is the divisor and dividend are98&22528 respectively.
When rounding off, we have 100&20,000 Now, find the value of the quotient. This will give you the required answer.
The expression 22,528÷98. The value 22528 is closest to 20,000.
Similarly, the value 98 is closest to 100. Thus, the quotient value is 20,000/100 = 200.
The estimated value of the quotient of the expression 22,528÷98 by rounding the dividend and the divisor to the largest place value is 200.
Page 25 Problem 4 Answer
The given expression is 7,790÷210.
We are asked to find the value of the quotient when the dividend and the divisor is rounded to the largest value.
The answer can be found by rounding off the dividend and the divisor to the nearest value.
Here, is the divisor and dividend are 210&7790 respectively.
When rounding off, we have 200&8000.
Now, find the value of the quotient. This will give you the required answer.
The given expression is 7,790÷210
The value 7790 is closest to 8000.
Similarly, the value 210 is closest to 200. So, the quotient value of 8000/200 =40.
The estimated quotient of the expression 7,790÷210 by rounding the dividend and the divisor to the largest place value is 40.
Go Math! Grade 6 Exercise 5.1: Operations with Decimals Solutions Page 25 Problem 5 Answer
The given expression is 17,658÷360.
We are asked to find the value of the quotient when the dividend and the divisor is rounded to the largest value.
The answer can be found by rounding off the dividend and the divisor to the nearest value. Here, is the divisor and dividend are 360&17658respectively.
When rounding off, we have 400&20,000 Now, find the value of the quotient.
This will give you the required answer.
The expression is 17,658÷360. The value 17658 is closer to 20,000 than 10,000.
Similarly, the value 360 is closest to 400. Thus, the quotient value is: 20,000/400=50.
The estimated quotient value of 17,658÷360 by rounding the dividend and the divisor to the largest place value is 50.
Page 25 Problem 6 Answer
The given expression is 916÷320.
We are asked to find the value of the quotient when the dividend and the divisor is rounded to the largest value.
The answer can be found by rounding off the dividend and the divisor to the nearest value.Here, is the divisor and dividend are320&916 respectively.
When rounding off, we have 300&900 Now, find the value of the quotient.This will give you the required answer.
The expression is 916÷320.
The value 916 is closer to 900 than 1000. Similarly, the value 320 is closer to 300 than 400. Thus, the quotient value of 900/300 =3.
The estimated quotient value of the expression is916÷320 by rounding the dividend and the divisor to the largest place value is 3
Go Math Grade 6 Exercise 5.1 Operations With Decimals Answers
Go Math! Grade 6 Exercise 5.1: Operations with Decimals Solutions Page 25 Problem 7 Answer
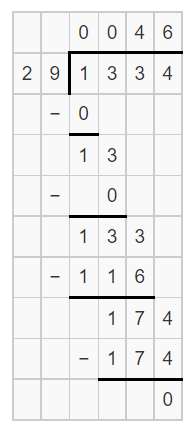
The given expression is 1334÷29. We are asked to find the quotient of 1334÷29 by long division method.The answer can be found by writing the number as dq+r.
Then find the quotient for the value 1334 when divided by 29. Perform the operation by long division.
The expression is 1334÷29. 1334 can be written as 29×46+0.
That is, 1334 is divisible by 29. The quotient obtained is: 46
The quotient of 1334÷29 using long division method is 46:
Page 25 Problem 8 Answer
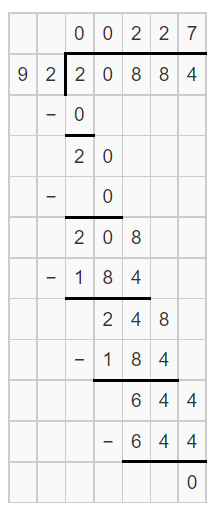
The given expression is 20884÷92.
We are asked to find the quotient of the expression by long division method. The answer can be found by writing the number as dq+r.
Then find the quotient for the value 20884 when divided by 92. Perform the operation by long division.
The expression is 20884÷92. Write the expression 20884 in the form dq+r.
Thus, we have: 227×92+0. That is the quotient value is q=227.
The quotient value of 20884÷92 using long division method is:
Page 25 Problem 9 Answer
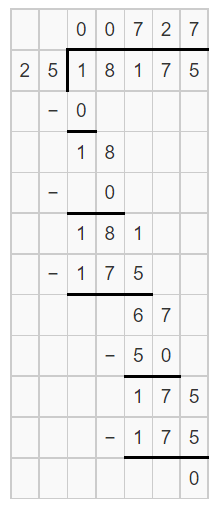
The given expression is 18175÷25. We are asked to find the value of the quotient 18175÷25 using the long division method.
The answer can be found by found by writing the expression in the form dq+r.
Find the value of q when 18175 is divided by 25. Represent this by the long division method.
The expression is 18175÷25. It can be written as 727×25+0.
Hence, the remainder is 0 .So, the quotient value of 18175÷25 is 727.
The value of the quotient for the expression 18175÷25 using the long division method is 727.
Go Math! Grade 6 Exercise 5.1: Operations with Decimals Solutions Page 25 Problem 10 Answer
The given expression is 2902÷18. We are asked to find the quotient and the remainder value by the method of long division.
The answer can be found by writing the number as dq+r, where q,r are the quotient and remainder.
Find the quotient value of 2902 when divided by 18. Write the answer in the long division form.
The expression is 2902÷18. It can be written as 18×161+4. Here, the remainder is 4.
That is, the number is not perfectly divisible by 18. The quotient is: 161
The quotient and the remainder value of 2902÷18by long division method is 161 and 4 respectively.:

Page 25 Problem 11 Answer
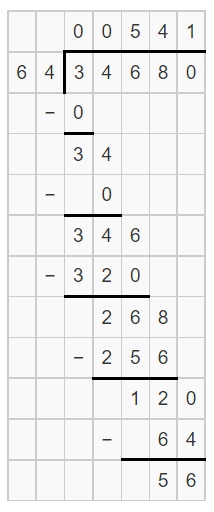
The given expression is 34680÷64.We are asked to find the remainder and the quotient of the expression.
The answer can be found by writing the number in dq+r form, where r,q are the remainder and the quotient respectively.
Find the quotient value of 34680 when divided by 64. Similarly, find the remainder. This will give you the required answer.
The expression is 34680÷64. The value 34680 can be written as 34680=64×541+56.
From the above expansion, we have: q=541 and The remainder is r=56.
The remainder and the quotient of the expression 34680÷64 are 56 and 541.
Solutions For Go Math Grade 6 Exercise 5.1 Operations With Decimals
Go Math! Grade 6 Exercise 5.1: Operations with Decimals Solutions Page 25 Problem 12 Answer
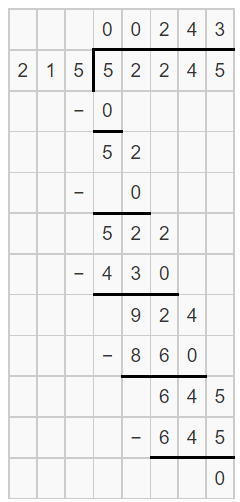
The given expression is 52245÷215. We are asked to find the remainder and the quotient of the expression.
The answer can be found by writing the value as dq+r, where r,q are the remainder and the quotient respectively.
From the expansion, write down the remainder and the quotient value.Reflect the value in the long division form.
The expression is: 52245÷215. Writing the expression 52245 as dq+r, we have:243×215+0.
Here, r=0 and The value of quotient is q=243. The remainder and the quotient of the expression 52245÷215 using the long division method are 0&243respectively.
Page 25 Problem 13 Answer
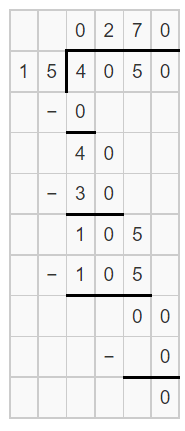
Given that there were 4050 students from 15 different school district. We are asked to find the average number of students in the museum.
The answer can be found by using the definition of average.Find the quotient of 4050/15.
This will give you the required answer. The number of students are 4050. Number of school district are: 15.
Thus, the average number of students from each school is: 4050/15
15•270=4050
∴4050/15=270.
Hence, there were an average of 270 students from each school district.
The average number of students from each school district are 270.
Page 25 Problem 14 Answer
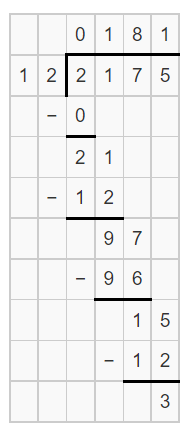
Given that, The Appalachian Trail is 2175 miles long and a hiker averages twelve miles each day.
We are asked to find how long will it take her to hike the length of the trail.
The answer can be found using the definition of average.Find the quotient value of 2175/12.
This would give the number of days. The total distance is 2175 miles.
Each day the hiker completes a distance of 12 miles.
Thus, the number of days taken for him to complete the journey is: 2175/12 = 181.25
That is, it would take 181 days and six hours. It would take 181.25 days for the hiker to hike the length of the trail.
Go Math Grade 6 Operations With Decimals Exercise 5.1 Key
Go Math! Grade 6 Exercise 5.1: Operations with Decimals Solutions Page 26 Exercise 1 Answer

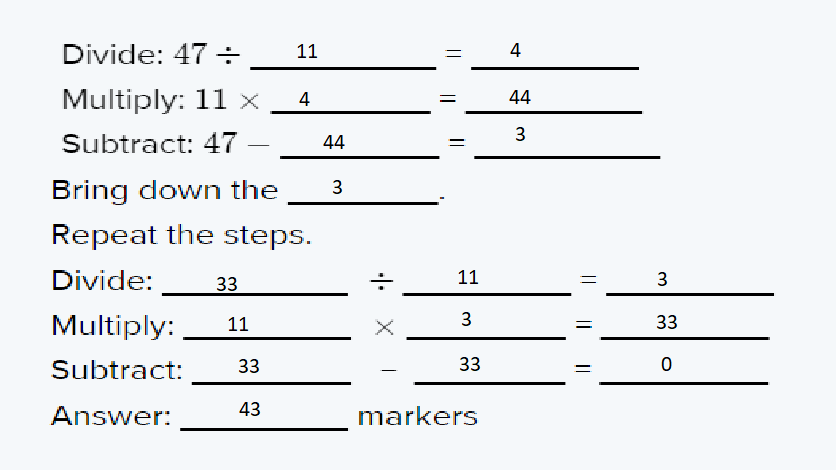
We are asked to fill these up and hence find the number of markers available for each table.The answer can be found by the process of division.
Divide the number 47/11 and find the quotient and the remainder, Bring down the remainder and the other remaining number.
Find the quotient when divided by eleven. Find the quotient. This will give you the required answer.


She will put on 43 markers on each table:
Go Math Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 1: Integers Exercise 1.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 1: Integers Exercise 1.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 1: Integers Exercise 1.3 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 2: Factors and Multiples Exercise 2.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 2: Factors and Multiples Exercise 2.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 3: Rational Numbers Exercise 3.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 3: Rational Numbers Exercise 3.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 3: Rational Numbers Exercise 3.3 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 4: Operations with Fractions Exercise 4.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 4: Operations with Fractions Exercise 4.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 4: Operations with Fractions Exercise 4.3 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 4: Operations with Fractions Exercise 4.4 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 5: Operations with Decimals Exercise 5.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 5: Operations with Decimals Exercise 5.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 5: Operations with Decimals Exercise 5.3 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 5: Operations with Decimals Exercise 5.4 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 5: Operations with Decimals Exercise 5.5 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 8: Percents Exercise 8.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 8: Percents Exercise 8.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6 Chapter 8: Percents Exercise 8.3 Answer Key
- Go Math! Practice Fluency Workbook Grade 6, Chapter 6: Representing Ratios and Rates Exercise 6.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6, Chapter 6: Representing Ratios and Rates Exercise 6.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6, Chapter 6: Representing Ratios and Rates Exercise 6.3 Answer Key
- Go Math! Practice Fluency Workbook Grade 6, Chapter 7: Applying Ratios and Rates Exercise 7.1 Answer Key
- Go Math! Practice Fluency Workbook Grade 6, Chapter 7: Applying Ratios and Rates Exercise 7.2 Answer Key
- Go Math! Practice Fluency Workbook Grade 6, Chapter 7: Applying Ratios and Rates Exercise 7.3 Answer Key
- Go Math! Practice Fluency Workbook Grade 6, Chapter 7: Applying Ratios and Rates Exercise 7.4 Answer Key




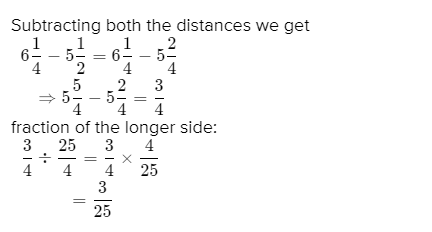


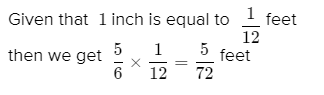












 Page 5 Problem 7, Answer
Page 5 Problem 7, Answer