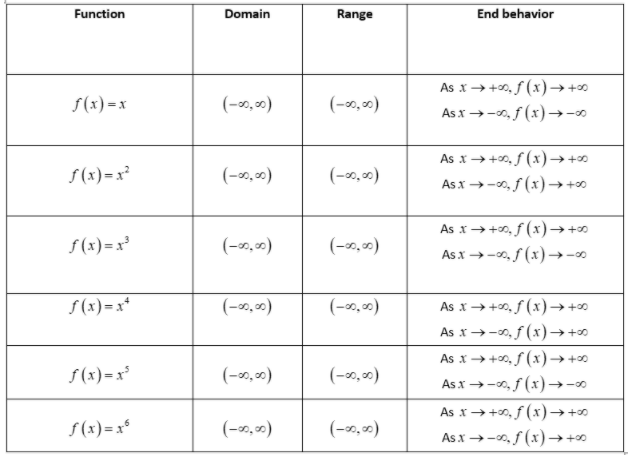
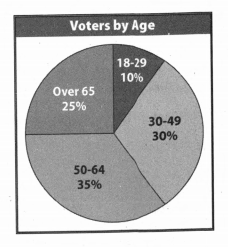
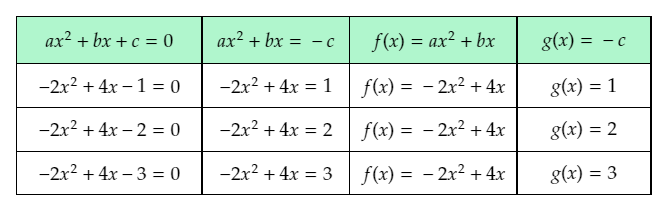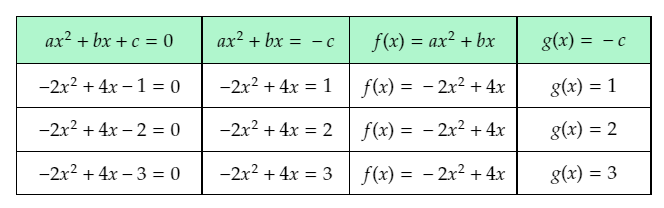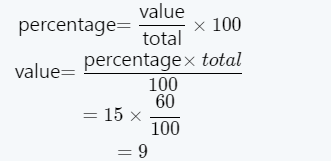Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3)
Page 139 Problem 1 Answer
- The complex solutions of a quadratic equation can be calculated either by completing the square, or by using the quadratic formula.
- To complete the square and calculate the complex solutions of a quadratic equation, first the equation is rewritten in the form x2+bx=c. Next, the value of b is identified, and (b/2)2 is calculated.
- The value of (b/2)2 is added on both sides of the rewritten equation, and the left-side of the equation is factorised.
Finally, the definition of square root is used, and the equation is solved for the required values of x.
To use the quadratic formula and calculate the complex solutions of a quadratic equation, the equation is rewritten in the form ax2+bx+c=0
and the values of a,b,c are written. Then, the values of a,b,c are substituted in the quadratic formula and the expression is simplified to determine the required values of x.
To calculate the complex solutions of a quadratic equation, the completing the square method or the quadratic formula are used.
To calculate the complex solutions of a quadratic equation by completing the square, rewrite the quadratic equation in the form x2+bx=c, calculate the value of (b/2)2, add (b/2)2 on both sides of the rewritten equation, factor the left-side of the equation, use the definition of square root, and finally, solve the resulting equation for x.

Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 139 Problem 2 Answer
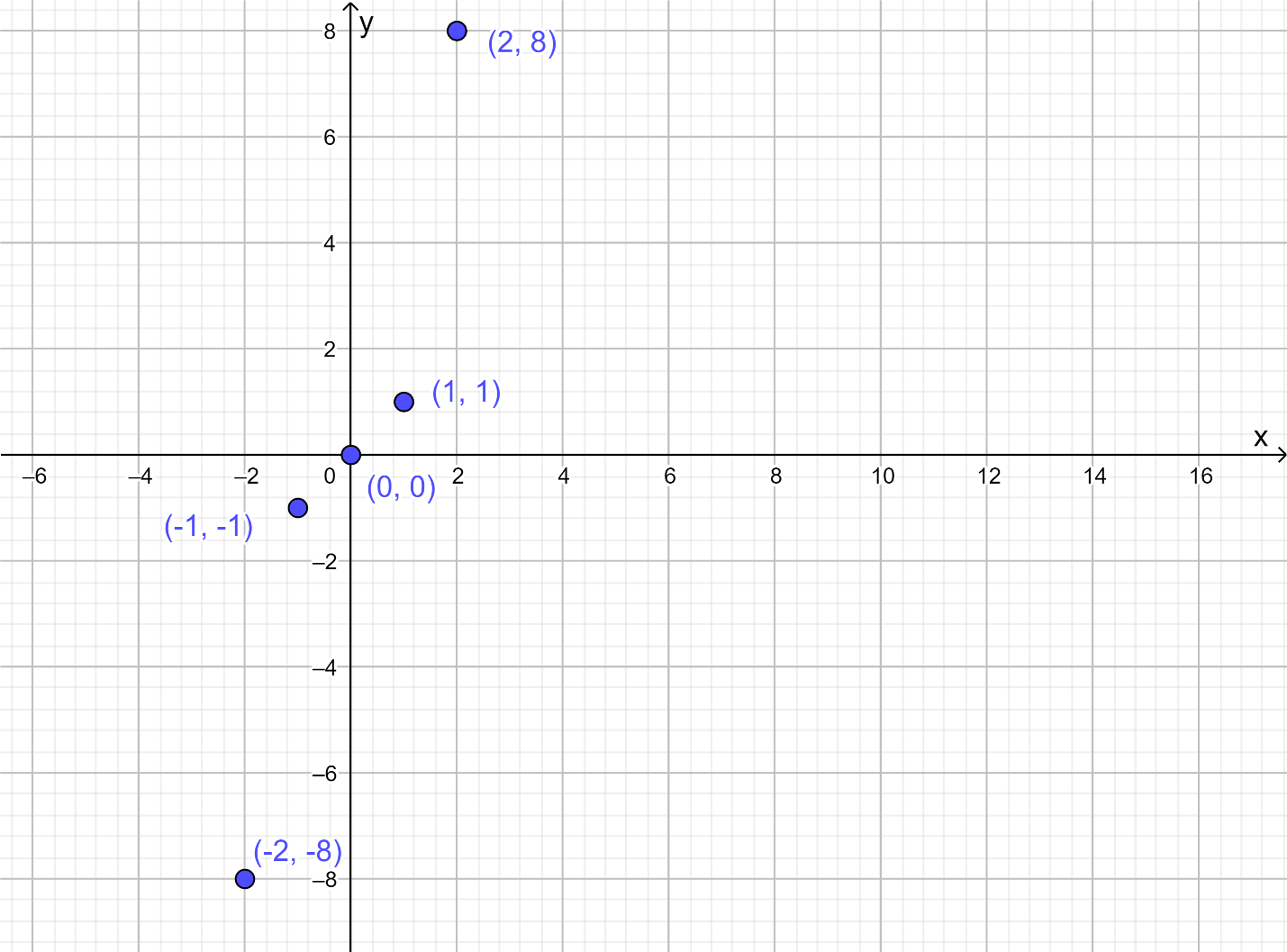
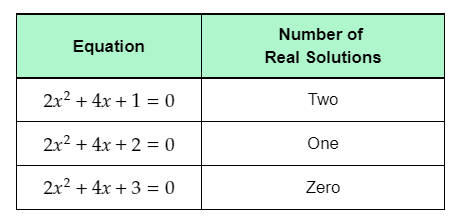
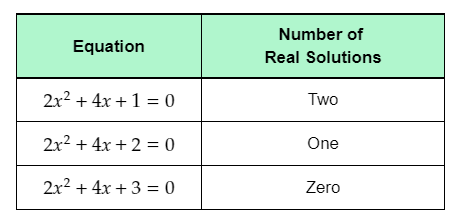
- The given table shows three quadratic equations of the form ax2+bx+c=0.
- The question requires to complete the given table.
- To complete the given table, rewrite the equations using subtraction to fill the second column.
- Then, use the left and right sides of the rewritten equations to determine the expressions for f(x) and g(x), and use them to fill the third and fourth columns of the table.
- The first given quadratic equation is 2x2+4x+1=0.
- Subtract 1 from both sides of the equation to rewrite it in the form ax2+bx=−c.
2x2+4x+1−1=0−12x2+4x=−1
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x), the obtained function is f(x)=2x2+4x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=−1.
The second given quadratic equation is 2x2+4x+2=0
Subtract 2 from both sides of the equation to rewrite it in the form ax2+bx=−c.
2x2+4x+2−2=0−2
2x2+4x=−2
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x), the obtained function is f(x)=2x2+4x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=−2.
The third given quadratic equation is 2x2+4x+3=0.
Subtract 3 from both sides of the equation to rewrite it in the form ax2+bx=−c.
2x2+4x+3−3=0−3
2x2+4x=−3
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x), the obtained function is f(x)=2x2+4x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=−3.
Complete the table using the rewritten equations, and the obtained expressions for f(x) and g(x).

The completed table is:

HMH Algebra 2 Volume 1 Module 3 Chapter 3 Exercise 3.3 solutions
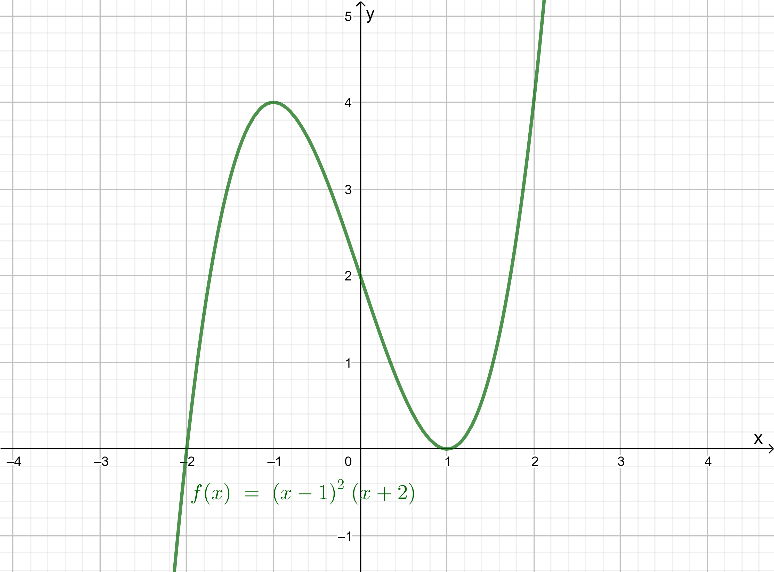
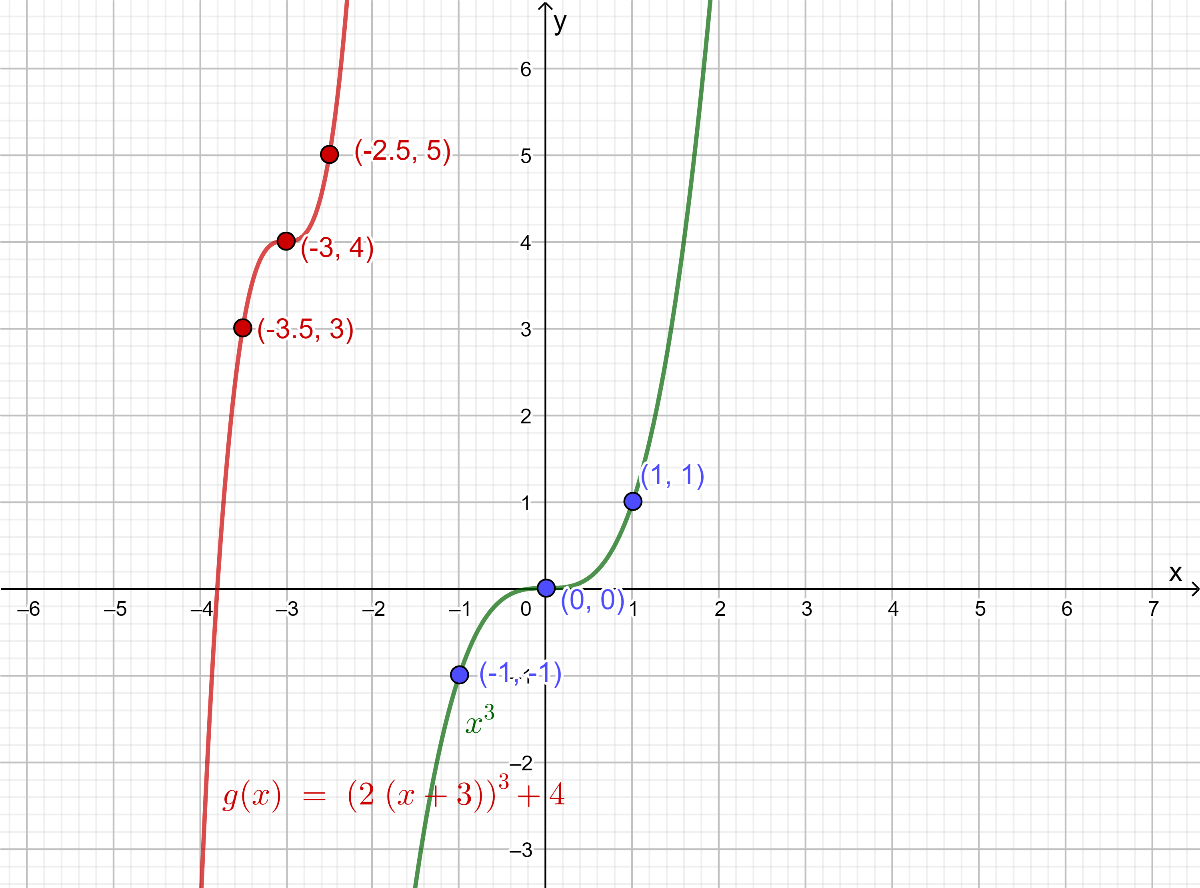
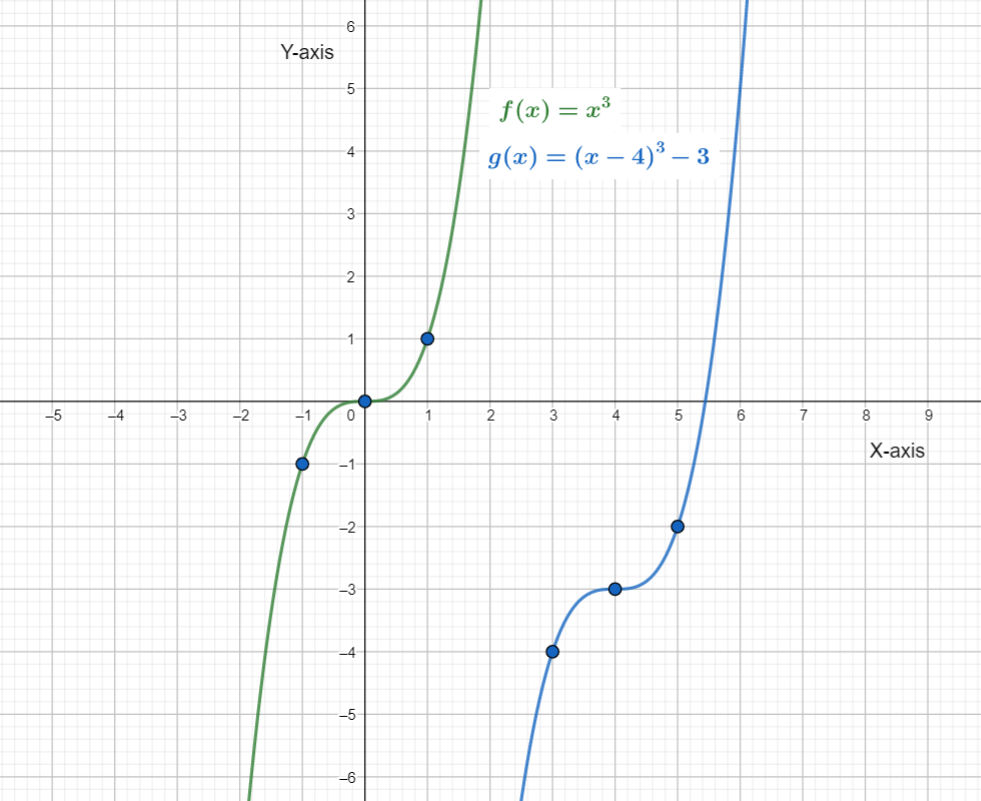
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 139 Problem 3 Answer
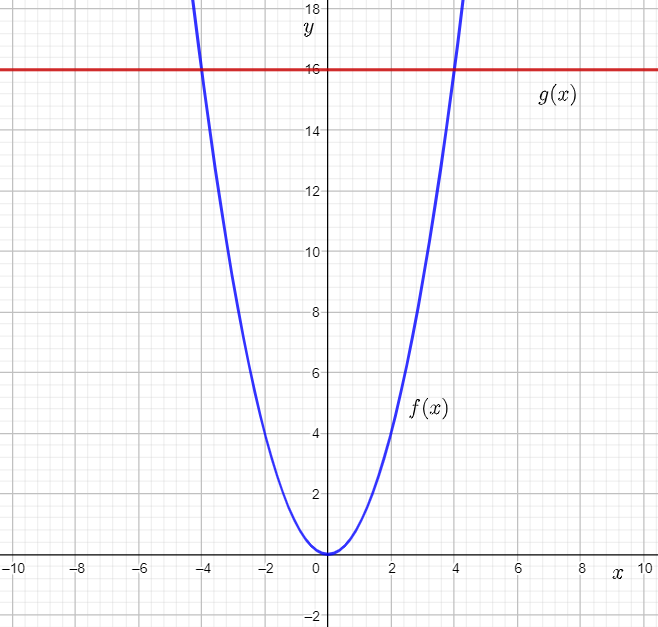
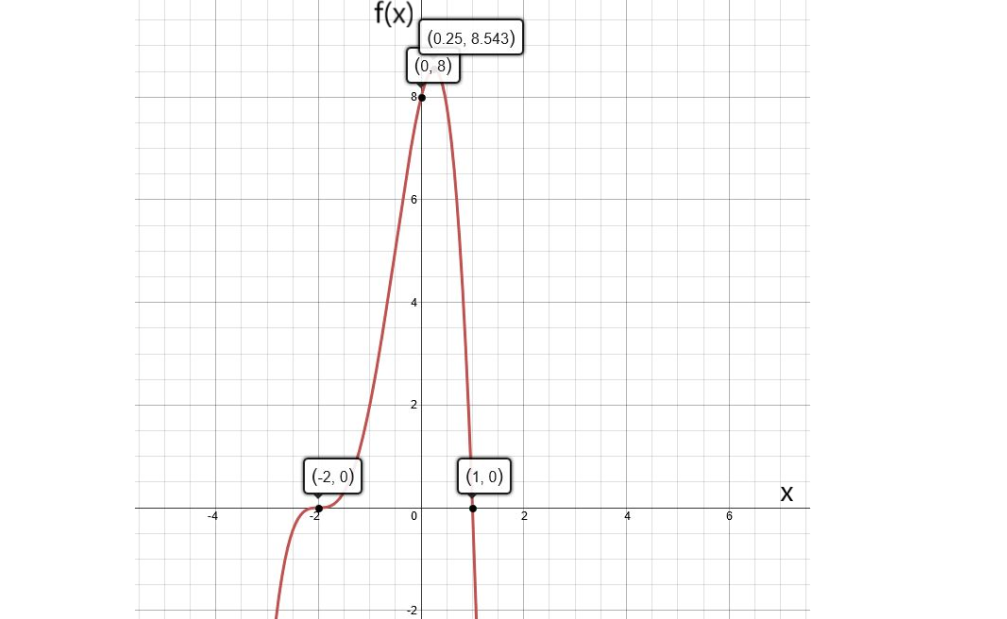
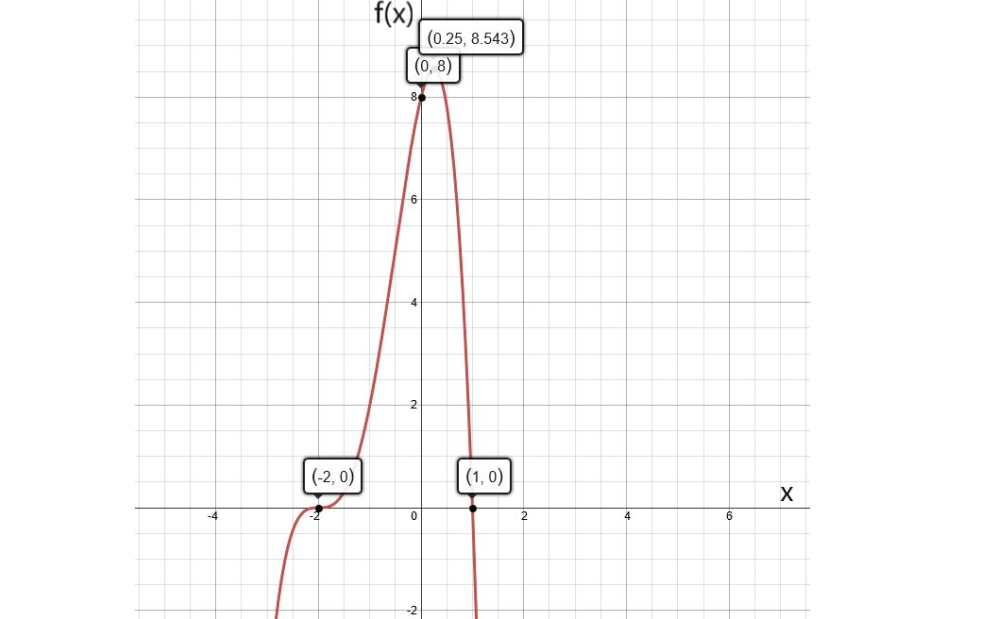
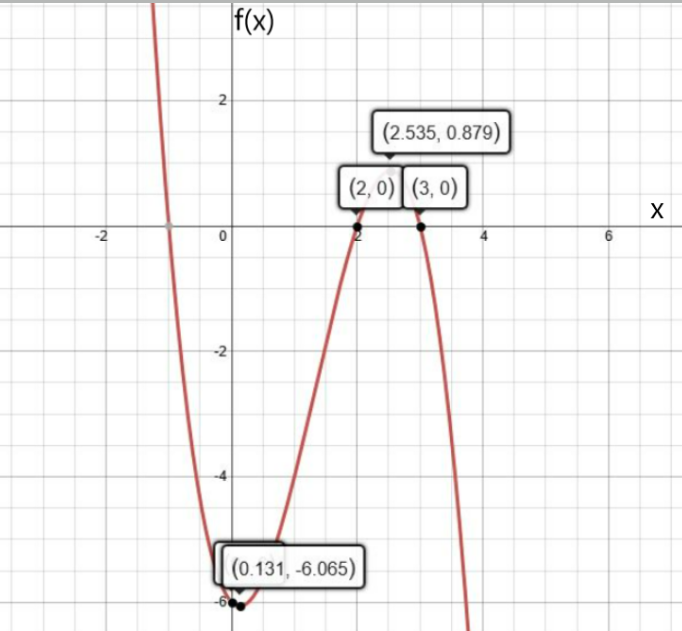
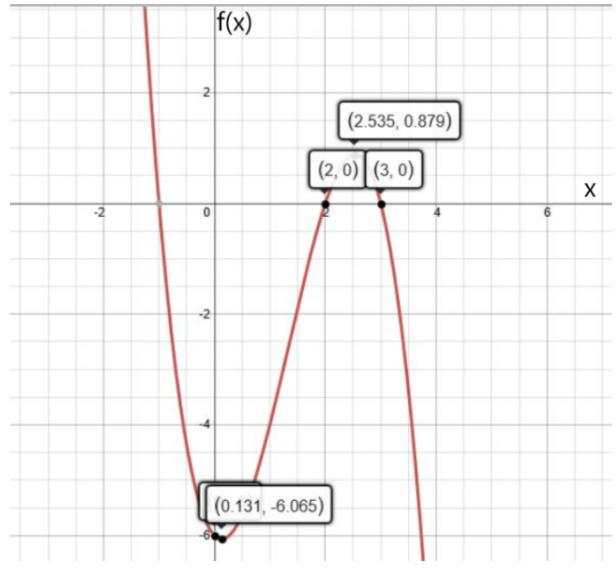
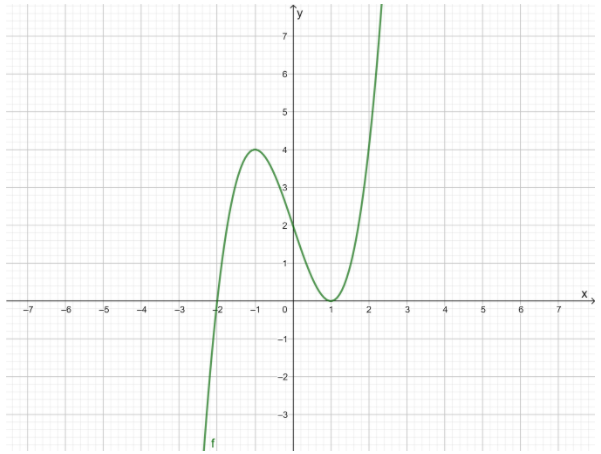
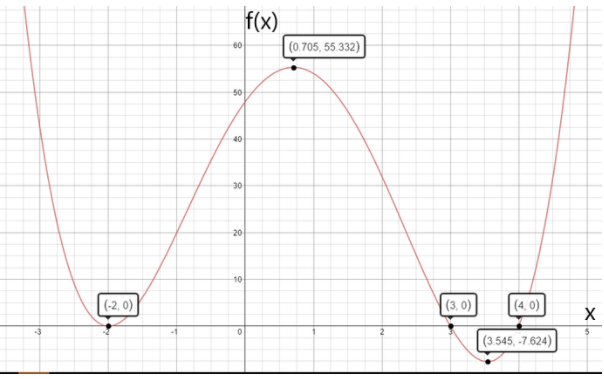
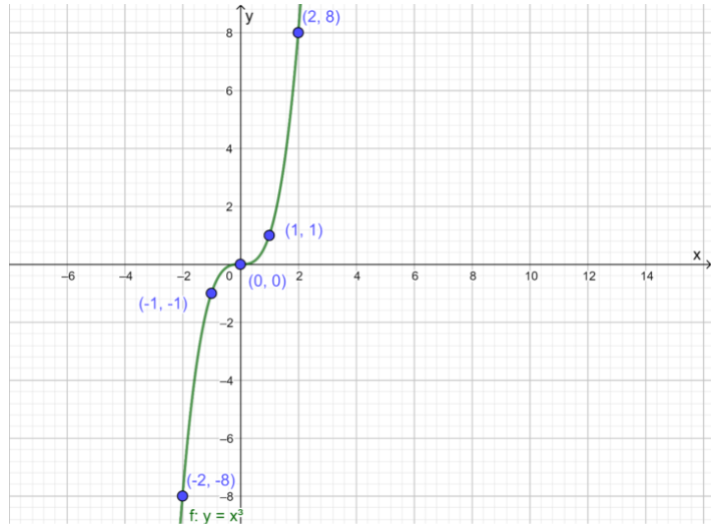
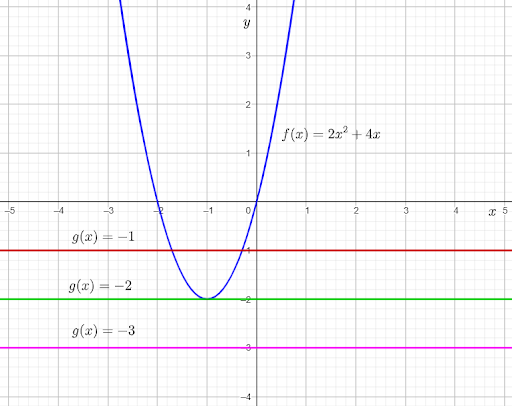
The given graph shows the graph of the function f(x)=2x2+4x.
The question requires to graph each g(x) and then complete the given table.
Given the following table, as completed in the previous part of this exercise

To draw the graph and complete the given table, write the functions g(x)
to be graphed, and then graph them on the given graph using horizontal lines.
Then, use the points of intersection of f(x) and g(x)=−1 to determine the number of points where they are equal.
Then, use the expressions for the two functions, and rewrite the equation with 0 on one side.
Next, use the number of points of intersection to write the number of real solutions of the obtained equation.
Similarly, find the points of intersection, and thus the number of real solutions of the remaining two equations, and complete the table.
The graph of a constant function g(x)=a is a horizontal line having the y-intercept a.
From the completed table from previous part of the exercise, it can be determined that functions to be graphed are:
g(x)=−1
g(x)=−2
g(x)=−3
Graph the functions on the given graph by drawing horizontal lines having the y-intercept equal to the right-hand side of the equation.
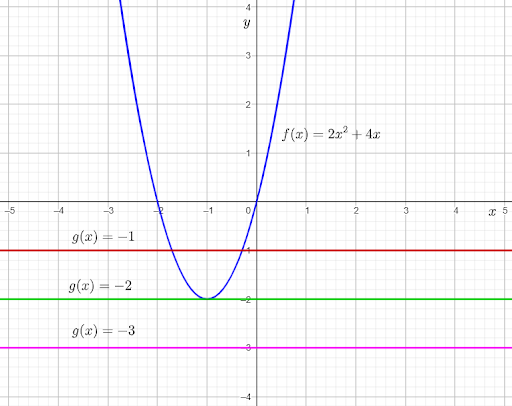
From the graph, it can be observed that the graph of f(x) and g(x)=−1intersect each other at two points.
This means that 2x2+4x=−1 for two real values of x.
Adding 1 on both sides, the equation becomes 2x2+4x+1=0.
Therefore, the equation 2x2+4x+1=0 has two real solutions.
From the graph, it can be observed that the graph of f(x) and g(x)=−2 touch each other at one point.
This means that 2x2+4x=−2 for one real value of x.
Adding 2 on both sides, the equation becomes 2x2+4x+2=0.
Therefore, the equation 2x2+4x+2=0 has one real solution.
From the graph, it can be observed that the graph of f(x) and g(x)=−3
do not touch or intersect each other at any point.This means that 2x2+4x=−3 for no real value of x.
Adding 3 on both sides, the equation becomes 2x2+4x+3=0.
Therefore, the equation 2x2+4x+3=0 has no real solutions.
Complete the table using the determined number of real solutions of each equation.
The required graph of each g(x) on the given graph is:
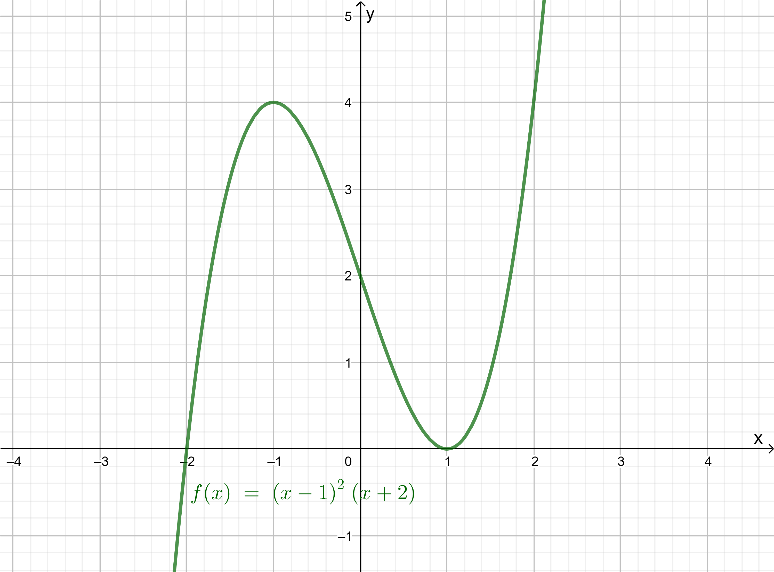
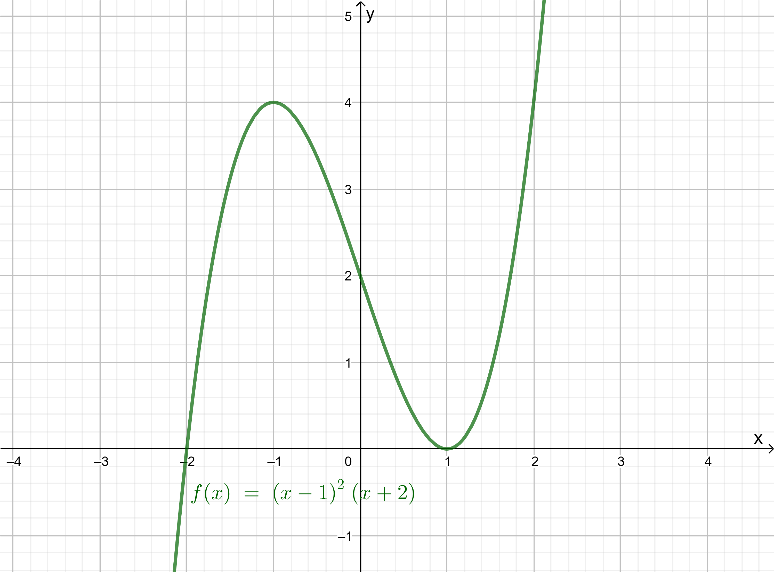
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 139 Problem 4 Answer
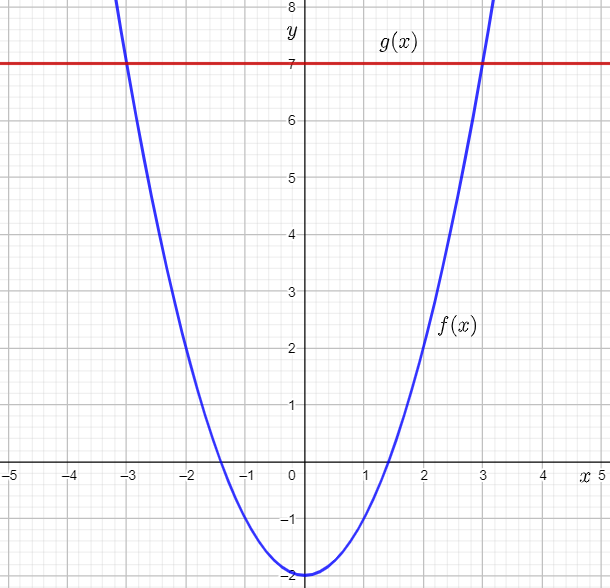
The given tables show three quadratic equations of the form ax2+bx+c=0. The given graph shows the graph of the function f(x) equal to −2x2+4x.
The question requires to complete the two given tables and graph the functions g(x).
To complete the first given table, rewrite the equations using subtraction to fill the second column.
Then, use the left and right sides of the rewritten equations to determine the expressions for f(x)
and g(x), and use them to fill the third and fourth columns of the table.
To draw the graph and complete the second given table, write the functions g(x) to be graphed, and then graph them on the given graph using horizontal lines.
Then, use the points of intersection of f(x)and g(x)=1 to determine the number of points where they are equal.
Then, use the expressions for the two functions, and rewrite the equation with 0 on one side.
Next, use the number of points of intersection to write the number of real solutions of the obtained equation.
Similarly, find the points of intersection, and thus the number of real solutions of the remaining two equations, and complete the second table.
The first given quadratic equation is −2x2+4x−1=0.
Add 1 on both sides of the equation to rewrite it in the form ax2+bx=−c.
−2x2+4x−1+1=0+1
−2x2+4x=1
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x), the obtained function is f(x)=−2x2+4x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=1.
The second given quadratic equation is −2x2+4x−2=0.
Add 2 on both sides of the equation to rewrite it in the form ax2+bx=−c.
−2x2+4x−2+2=0+2
−2x2+4x=2
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x), the obtained function is f(x)=−2x2+4x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=2.
The third given quadratic equation is −2x2+4x−3=0.
Add 3 on both sides of the equation to rewrite it in the form ax2+bx=−c.
−2x2+4x−3+3=0+3
−2x2+4x=3
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x), the obtained function is f(x)=−2x2+4x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=3.
Complete the first table using the rewritten equations, and the obtained expressions for f(x) and g(x).
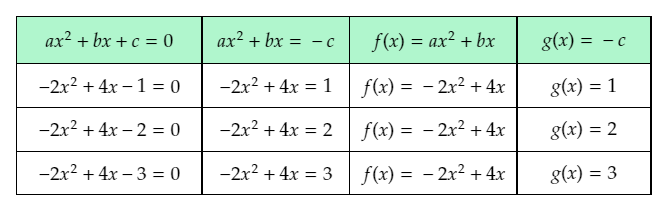
The graph of a constant function g(x)=a is a horizontal line having the y-intercept a.
From the completed table from previous part of the exercise, it can be determined that functions to be graphed are:
g(x)=1
g(x)=2
g(x)=3
Graph the functions on the given graph by drawing horizontal lines having the y-intercept equal to the right-hand side of the equations.
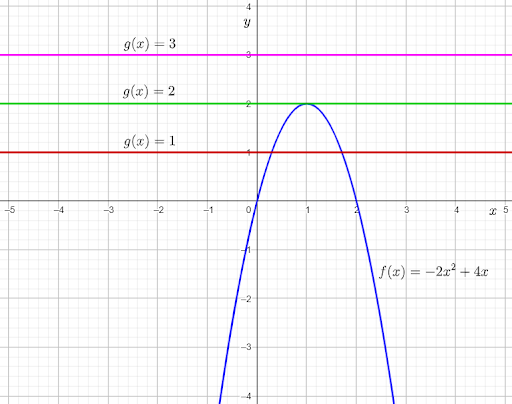
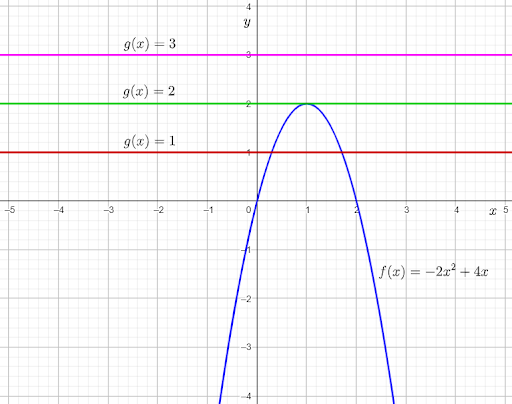
From the graph, it can be observed that the graph of f(x) and g(x)=1intersect each other at two points.
This means that −2x2+4x=1 for two real values of x.
Subtracting 1 from both sides, the equation becomes −2x2+4x−1=0.
Therefore, the equation −2x2+4x−1=0 has two real solutions.
From the graph, it can be observed that the graph of f(x) and g(x)=2 touch each other at one point.
This means that −2×2+4x=2 for one real value of x.
Subtracting 2 from both sides, the equation becomes −2x2+4x−2=0.
Therefore, the equation −2x2+4x−2=0 has one real solution.
From the graph, it can be observed that the graph of f(x) and g(x)=3 do not touch or intersect each other at any point.This means that −2x2+4x=3 for no real value of x.
Subtracting 3 from both sides, the equation becomes −2x2+4x−3=0.
Therefore, the equation −2x2+4x−3=0 has no real solutions.
Complete the table using the determined number of real solutions of each equation.
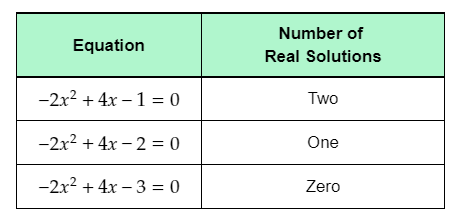
The completed first table is:
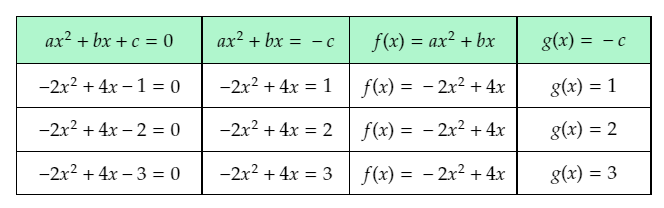
The required graph of each g(x) on the given graph is:
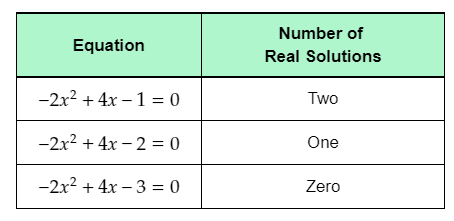
HMH Algebra 2 Module 3 Chapter 3 Quadratic Equations Exercise 3.3 answers
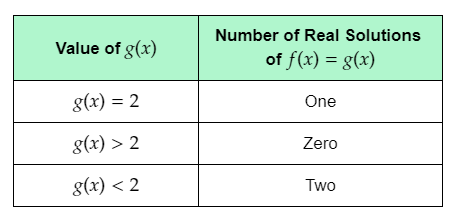
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 140 Problem 5 Answer
It is given that the minimum value of f(x) noticed from steps A and B of Explore 1 is −2.
The given table shows the values of g(x), and the corresponding number of real solutions of f(x)=g(x).
The question requires to complete the given table.
Given the following graph, as drawn in step B of Explore 1:
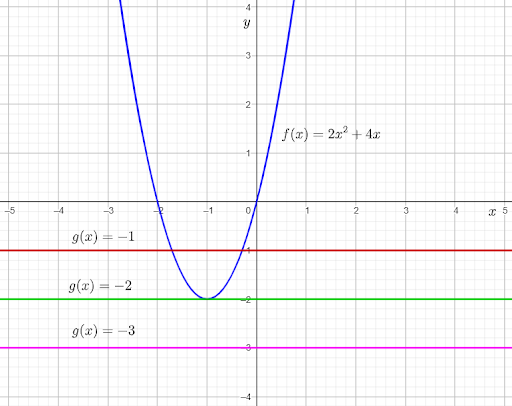
To complete the given table, use the graph to determine the number of points of intersection of f(x) and g(x)=−2, and write the number of real solutions of the given equation.
Next, use the graph to determine the number of points of intersection of f(x) and the horizontal lines represented by g(x)>−2, and write the number of real solutions of the given equation.
Similarly, find the number of real solutions of the given equation when g(x)<−2.
Finally, use the obtained number of real solutions to complete the given table.
From the graph, it can be observed that the graph of f(x) and g(x)=−2 touch each other at one point.
This means that when g(x) is equal to the minimum value of f(x), that is −2, f(x)=g(x) for one real value of x.
Thus, the number of real solutions of f(x)=g(x) is one when g(x) is equal to −2.
The graph of g(x)>a for each value of a represents a horizontal line above the line g(x)=a.
From the graph, it can be observed that each horizontal line passing through the graph of f(x) above the line g(x)=−2 intersects the parabola at two points.
This means that when g(x) has a value greater than −2, the graph of f(x) and g(x) intersect each other at two points.
Therefore, when g(x) has a value greater than the minimum value of f(x), that is −2, f(x)=g(x) for two real values of x.
Thus, the number of real solutions of f(x)=g(x) is two when g(x)>−2.
The graph of g(x)<a for each value of a represents a horizontal line below the line g(x)=a.
From the graph, it can be observed that each horizontal line below the line g(x)=−2
does not intersect the parabola at any point.
This means that when g(x) has a value less than −2, the graph of f(x) and g(x) do not intersect each other.
Therefore, when g(x) has a value less than the minimum value of f(x), that is −2, f(x) is not equal to g(x) for any real value of x.
Thus, the number of real solutions of f(x)=g(x) is zero when g(x)<−2.
Complete the table using the determined number of real solutions of f(x)=g(x) for each g(x).
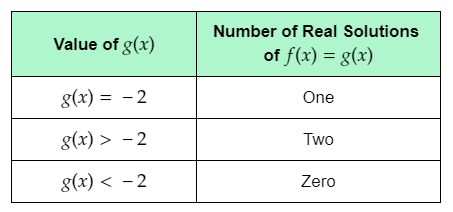
The completed table is:
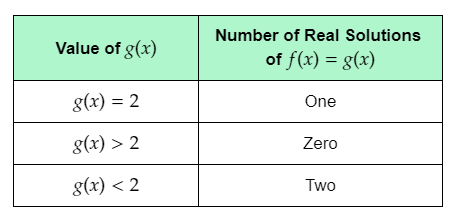
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 140 Problem 6 Answer
It is given that the maximum value of f(x) noticed from step C of Explore 1 is 2.
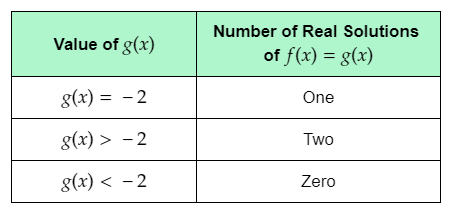
The given table shows the values of g(x), and the corresponding number of real solutions of f(x)=g(x).
The question requires to complete the given table.
Given the following graph, as drawn in step C of Explore 1:
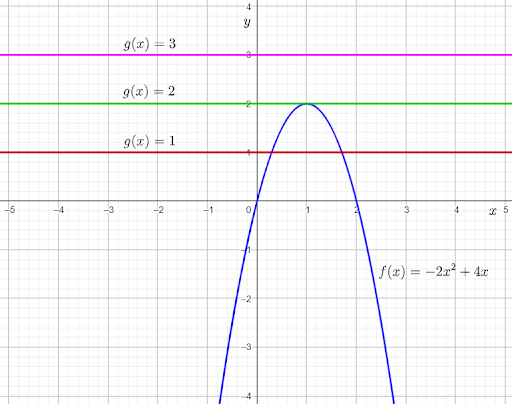
To complete the given table, use the graph to determine the number of points of intersection of f(x)
and g(x)=2, and write the number of real solutions of the given equation.
Next, use the graph to determine the number of points of intersection of f(x) and the horizontal lines represented by g(x)>2, and write the number of real solutions of the given equation.
Similarly, find the number of real solutions of the given equation when g(x)<2.
Finally, use the obtained number of real solutions to complete the given table.
From the graph, it can be observed that the graph of f(x) and g(x)=2 touch each other at one point.
This means that when g(x) is equal to the maximum value of f(x), that is 2, f(x)=g(x) for one real value of x.
Thus, the number of real solutions of f(x)=g(x) is one when g(x) is equal to 2.
The graph of g(x)<a for each value of a represents a horizontal line below the line g(x)=a.
From the graph, it can be observed that each horizontal line passing through the graph of f(x) below the line g(x)=2 intersects the parabola at two points.
This means that when g(x) has a value less than 2, the graph of f(x) and g(x) intersect each other at two points.
Therefore, when g(x) has a value less than the maximum value of f(x), that is 2, f(x)=g(x) for two real values of x.
Thus, the number of real solutions of f(x)=g(x) is two when g(x)<2.
The graph of g(x)>a for each value of a represents a horizontal line above the line g(x)=a.
From the graph, it can be observed that each horizontal line above the line g(x)=2 does not intersect the parabola at any point.
This means that when g(x) has a value greater than 2, the graph of f(x) and g(x) do not intersect each other.
Therefore, when g(x) has a value greater than the maximum value of f(x), that is 2, f(x) is not equal to g(x) for any real value of x.
Thus, the number of real solutions of f(x)=g(x) is zero when g(x)>2
Complete the table using the determined number of real solutions of f(x)=g(x) for each g(x).
The completed table is:
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 140 Problem 7 Answer
It is given that the maximum value of f(x) given in Reflect 2 is 2. Also, it is given that equation ax2+bx+c=0
where a>0 has real solutions when b2−4ac≥0. The steps used to generalize the results of Reflect 1 are given.
The question requires to generalize the results of Reflect 2, and write what is noticed.
Given the following table, as completed in Reflect 2:
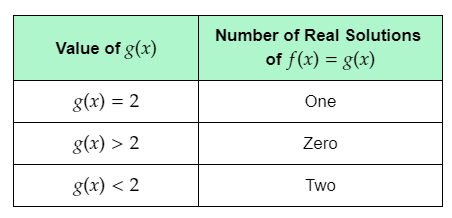
To answer the question, use the table to write the range of values of g(x) for which f(x)=g(x) has real solutions.
Then, determine the maximum value of f(x) by substituting −b/2a for x in the function, and simplifying it.
Next, use the obtained maximum value of f(x) to form an inequality in terms of g(x).
Finally, rewrite the inequality to form a general expression, generalize the result by writing the relation for which ax2+bx+c=0
has real solutions, and write what is observed using the given information.
The quadratic equation ax2+bx+c=0, where a<0, can be written as:ax2+bx=−c
The function f(x) used in Reflect 2 is of the form ax2+bx, where a<0.
The function g(x) is of the form −c.
From the table, it can be observed that the equation f(x)=g(x), where g(x) is equal to −c, has real solutions when g(x) is less than or equal to the maximum value of f(x), that is 2.
The maximum value of f(x) occurs at x=−b/2a.
Calculate the maximum value of f(x) by substituting x=−b/2a in the function, and simplifying the expression.
f(−b/2a)=a(−b/2a)2+b(−b/2a)
f(−b/2a)=a(b2/4a2)−b2/2a
f(−b/2a)=b2/4a−b2/2a
f(−b/2a)=−b2/4a
Therefore, the equation f(x)=g(x) has real solutions when g(x)≤−b2/4a.
Substitute −c for g(x) in the inequality g(x)≤−b2/4a, add b2/4a on both sides, and multiply both sides by the negative number 4a.
−c≤−b2/4a
b2/4a−c≤0
4a(b2/4a−c)≥4a(0)
b2−4ac≥0
Therefore, the equation ax2+bx+c=0
where a<0 has real solutions when b2−4ac≥0.
It is given that equation ax2+bx+c=0 where a>0 has real solutions when b2−4ac≥0.
Thus, it can be concluded that the equation ax2+bx+c=0 has real solutions when b2−4ac≥0 for all real values of a.
The equation ax2+bx+c=0 where a<0 has real solutions when b2−4ac≥0.
It is observed that equation ax2+bx+c=0 has real solutions when b2−4ac≥0 for all real values of a.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 141 Problem 8 Answer
The given equation is x2−2x+7=0.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c.
Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Subtract 7 from both sides of x2−2x+7=0.
x2−2x+7−7=0−7
x2−2x=−7……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is −2.
Therefore, the value of (b/2)2 is (−2/2)2=4/4, that is 1.
Add the value of (b/2)2, that is 1, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2−2ab+b2=(a−b)2, and simplify the right-hand side expression.
x2−2x+1=−7+1
(x−1)2=−7+1
(x−1)2=−6
Use the definition of square root to simplify (x−1)2=−6, and then add 1 on both sides.
(x−1)2=−6
x−1=±√−6
x=1±√−6
Therefore, the required solutions are x=1+√−6 and x=1−√−6.
It can be observed that the solutions x=1±√−6 contain the square root of a negative number.
Therefore, the solutions are non-real.
Thus, there are two non-real solutions: x=1+√−6 and x=1−√−6.
The required solutions are x=1+√−6 and x=1−√−6.The solutions are non-real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 142 Problem 9 Answer
From part A of the example, it can be observed that the equation 3x2+9x−6=0 has two real solutions: −3+√17/2 and −3−√17/2.
Every real number a can be written as the complex number a+0i, having the imaginary part equal to 0.
This means that every real number is a complex number.
The real solutions −3+√17/2 and −3−√17/2 can be written as the complex solutions −3+√17/2+0i and −3−√17/2+0i respectively.
This means that both the real solutions of the equation in part A are complex.
Therefore, the equation in part A has two complex solutions, having the imaginary part equal to 0.
From part B of the example, it can be observed that the equation x2−2x+7=0 has two non-real solutions: 1+√−6 and 1−i√6.
The non-real solutions 1+√−6 and 1−√−6 can be written as the complex solutions 1+i√6and 1−i√6 respectively, having non-zero real and imaginary parts.
This means that both the non-real solutions of the equation in part B are complex.
Therefore, the equation in part B has two complex solutions, having non-zero real and imaginary parts.
The equations in part A and part B both have two complex solutions because every real and non-real number is a complex number.
This means that the solutions of the equation in part A are real and complex, and the solutions of the equation in part B are non-real and complex.
HMH Algebra 2 Chapter 3 Exercise 3.3 Quadratic Equations key
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 142 Problem 10 Answer
The given equation is x2+8x+17=0.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c. Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Subtract 17 from both sides of x2+8x+17=0.
x2+8x+17−17=0−17
x2+8x=−17……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is 8.
Therefore, the value of (b/2)2 is (8/2)2
=(4)2, that is 16.
Add the value of (b/2)2, that is 16, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2+2ab+b2=(a+b)2, and simplify the right-hand side expression.
x2+8x+16=−17+16
(x+4)2=−17+16
(x+4)2=−1
Use the definition of square root to simplify (x+4)2=−1.
Then, subtract 4 from both sides, and rewrite the expression using the imaginary unit i.
(x+4)2=−1
x+4=±√−1
x=−4±√−1
x=−4±i
Therefore, the required solutions are x=−4+i and x=−4−i.
It can be observed that the solutions x=−4±i contain the imaginary unit i, which is equal to the square root of the negative number −1.
Therefore, the solutions are non-real. Thus, there are two non-real solutions: x=−4+i and x=−4−i.
The required solutions are x=−4+i and x=−4−i. The solutions are non-real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 142 Problem 11 Answer
The given equation is x2+10x−7=0.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c.
Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Add 7 on both sides of x2+10x−7=0.
x2+10x−7+7=0+7
x2+10x=7……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is 10.
Therefore, the value of (b/2)2 is (10/2)2=(5)2, that is 25.
Add the value of (b/2)2, that is 25, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2+2ab+b2=(a+b)2, and simplify the right-hand side expression.
x2+10x+25=7+25
(x+5)2=7+25
(x+5)2=32
Use the definition of square root to simplify (x+5)2=32, and then subtract 5 from both sides.
(x+5)2=32
x+5=±√32
x=−5±√32
Rewrite the expression √32, use the product property of square roots, and simplify the square root.
x=−5±√16⋅2
x=−5±√16⋅√2
x=−5±4√2
Therefore, the required solutions are x=−5+4√2 and x=−5−4√2.
It can be observed that the solutions x=−5±4√2 do not contain the square root of a negative number or the imaginary unit i.Therefore, the solutions are real.
The required solutions are x=−5+4√2 and x=−5−4√2.
The solutions are real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 142 Problem 12 Answer
It is given that the function A(w)=w(50−w) gives the area of the given garden in square feet, where w
is the width of the garden in feet.
The question requires to determine whether the garden can have an area equal to 700 square feet.
It is required to answer this by writing an equation for the given situation, and then determining whether the solutions are real or non-real.
To answer the question, let the area A(w) be equal to 700 square feet.
Then, use the given function to form a quadratic equation in terms of w. Next, compare the equation to aw2+bw+c=0 and identify the values of a,b,c.
Finally, determine the discriminant of the equation to determine whether the solutions are real or non-real, and thus, determine whether the area can be equal to 700 square feet or not.
Let the area of the garden be equal to 700 square feet. Therefore, A(w)=700.
Substitute w(50−w) for A(w) in A(w)=700. Then, multiply the terms, and subtract 700 from both sides.
w(50−w)=700
50w−w2=700−w2+50w−700=0……………(1)
Comparing the equation (1) to the equation aw2+bw+c=0, it can be determined that the values of a,b,c are −1,50,−700 respectively.
Substitute −1 for a, 50 for b, and −700 for c in the formula for discriminant b2−4ac. Then, multiply the terms, and subtract the terms.
b2−4ac=(50)2−4(−1)(−700)
=2500−2800
=−300
The discriminant is equal to −300, which is less than 0.
This means that the equation A(w)=700 has two non-real solutions.
Therefore, there is no real value of w for which the area of the garden is equal to 700 square feet.
Thus, the garden cannot have an area equal to 700 square feet.
No, the garden cannot have an area equal to 700 square feet.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 143 Problem 13 Answer
It is given that the height h of a triangular sail is twice the length of its base b, where the height and base are given in inches.
The question requires to determine whether the area of a triangular sail can be equal to 10 square inches.
It is required to answer this by writing an equation for the given situation, and then determining whether the solutions are real or non-real.
To answer the question, use the given information and the formula for area of a triangle to write an equation for the given situation.
Next, let the area A(b) of the sail be equal to 10 square inches. Then, use the obtained function for area to form a quadratic equation in terms of b.
Next, compare the equation to pb2+qb+r=0 and identify the values of p,q, and r.
Finally, determine the discriminant of the equation to determine whether the solutions are real or non-real, and thus, determine whether the area can be equal to 10 square inches or not.
From the given information, it can be determined that h=2b.
Substitute 2b for h in the formula A=1/2bh for area of a triangle, and multiply the terms.
A=1/2b(2b)
A=b2
A(b)=b2
Let the area of the triangular sail be equal to 10
square inches. Therefore, A(b)=10.
Substitute b2 for A(b) in A(b)=10, and subtract 10 from both sides.
b2=10
b2−10=0……………(1)
Comparing the equation (1) to the equation pb2+qb+r=0, it can be determined that the values of p,q,r are 1,0,−10 respectively.
If a quadratic equation is in the form pb2+qb+r=0, then its determinant is equal to q2−4pr.
Substitute 1 for p, 0 for q, and −10 for r in the formula for discriminant q2−4pr. Then, multiply the terms, and add the terms.
q2−4pr=(0)2
−4(1)(−10)
=0+40
=40
The discriminant is equal to 40, which is greater than 0.
This means that the equation A(b)=10 has two real solutions.
Therefore, there is some real value of b for which the area of the triangular sail is equal to 10
square inches.
Thus, the triangular sail can have an area equal to 10 square inches.
Yes, the area of the triangular sail can be equal to 10 square inches.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 143 Problem 14 Answer
The given equation is 7x2+2x+3=−1.
The question requires to solve the given equation using the quadratic formula, and then check one of the solutions using substitution.
To solve the equation, rewrite the equation in the form ax2+bx+c=0. Then, identify the values of a,b,c
, and substitute the values in the quadratic formula. Next, simplify the expression on the right side to obtain the required solutions.
Finally, substitute one of the solutions in the given equation, and simplify using the distributive property of multiplication and the value of i2 to prove that both sides of the equation are equal.
Add 1 on both sides of 7x2+2x+3=−1.
7x2+2x+3+1=−1+1
7x2+2x+4=0……………(1)
Comparing the equation (1) to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 7,2,4 respectively.
Substitute 7 for a, 2 for b, and 4 for c in the quadratic formula x=−b±√b2−4ac/2a. Then, multiply the terms and combine the terms in the square root.
x=−2±√(2)2−4(7)(4)/2(7)
x=−2±√4−112/14
x=−2±√−108/14
Rewrite the square root using the imaginary unit i. Then, simplify the square root, and simplify the expression.
x=−2±i√108/14
x=−2±i√36⋅3/14
x=−2±6i√3/14
x=−1±3i√3/7
Thus, the required solutions are:
x=−1/7−3i√3/7
x=−1/7+3i√3/7Consider the solution x=−1/7−3i√3/7.
Substitute −1/7−3i√3/7 for x in the given equation 7x2+2x+3=−1.
Then, square the term −1−3i√3/7 in the equation, substitute −1 for i2, and simplify the expression in the parentheses.
7(−1/7−3i√3/7)2
+2(−1/7−3i√3/7)+3=?
−1/7(1/49+6i√3/49+27i2/49)+2(−1/7−3i√3/7)+3=?
−1/7(1/49+6i√3/49+27(−1)/49)+2(−1/7−3i√3/7)+3=?
−1/7(1/49+6i√3/49−27/49)+2(−1/7−3i√3/7)+3=?
−1Apply the distributive property of multiplication, combine the terms, and simplify the expression on the left side.
1/7+6i√3/7−27/7−2/7−6i√3/7+3=?
−1/−28/7+3=?
−1/−4+3=?
−1/−1=−1
Thus, the solution x=−1/7−3i√3/7 is checked.
The required solutions are:x=−1/7−3i√3/7
x=−1/7+3i√3/7
The solution x=−1/7−3i√3/7 is checked.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 145 Problem 15 Answer
The given equation is x2+8x+12=2x.
The question requires to solve the given equation using the quadratic formula, and then check one of the solutions using substitution.
To solve the equation, rewrite the equation in the form ax2+bx+c=0. Then, identify the values of a,b,c, and substitute the values in the quadratic formula.
Next, simplify the expression on the right side to obtain the required solutions.
Finally, substitute one of the solutions in the given equation, and simplify using the distributive property of multiplication and the value of i2 to prove that both sides of the equation are equal.
Subtract 2x from both sides of x2+8x+12=2x.
x2+8x+12−2x=2x−2x
x2+6x+12=0……………(1)
Comparing the equation (1) to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,6,12 respectively.
Substitute 1 for a, 6 for b, and 12 for c in the quadratic formula x=−b±√b2−4ac/2a. Then, multiply the terms and combine the terms in the square root.
x=−6±√(6)2−4(1)(12)/2(1)
x=−6±√36−48/2
x=−6±√−12/2
Rewrite the square root using the imaginary unit i. Then, simplify the square root, and simplify the expression.
x=−6±i√12/2
x=−6±i√4⋅3/2
x=−6±2i√3/2
x=−3±i√3
Thus, the required solutions are:
x=−3−i√3
x=−3+i√3
Consider the solution x=−3−i√3.
Substitute −3−i√3 for x in the given equation x2+8x+12=2x. Then, square the term −3−i√3 in the equation, substitute −1 for i2, and simplify the expression in the parentheses.
(−3−i√3)2+8(−3−i√3)+12=?
2(−3−i√3)(9+6i√3+3i2)+8(−3−i√3)+12=?
2(−3−i√3)(9+6i√3+3(−1))+8(−3−i√3)+12=?
2(−3−i√3)(9+6i√3−3)+8(−3−i√3)+12=?
2(−3−i√3)
Apply the distributive property of multiplication, combine the terms, and simplify the expression on the left side.
9+6i√3−3−24−8i√3+12=?
−6−2i√3
18−24−2i√3=?
−6−2i√3−6−2i√3
=−6−2i√3
Thus, the solution x=−3−i√3 is checked.
The required solutions are:
x=−3−i√3
x=−3+i√3
The solution x=−3−i√3 is checked.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 145 Problem 16 Answer
The given equation is ax2+bx+c=0. The given solution is p+qi.
The question requires to what should be the other solution of the equation, and explain how it is determined.
Let the other solution of the given equation be the complex number f+gi.
To answer the question, use the property for sum of roots of a quadratic equation, and the assumed solution and the given solution to write an equation for the sum of the solutions.
Then, observe both sides to determine the value of the imaginary part of the sum, and solve the resulting equation to determine one of the constants in the assumed solution.
Next, use the property for product of roots of a quadratic equation, and the assumed solution and the given solution to write an equation for the product of the solutions.
Then, observe both sides to determine the value of the imaginary part of the product, and solve the resulting equation to determine the other constant in the assumed solution.
Finally, use the constants to determine the other solution, and explain why is it the solution.
The sum of the two solutions of the quadratic equation ax2+bx+c=0 is the quotient −b/a.
Therefore, the sum of f+gi and p+qi is −b/a.
Form an equation for the sum of the solutions, and group the real and imaginary parts.
(f+gi)+(p+qi)=−b/a
(f+p)+(gi+qi)=−b/a
(f+p)+(g+q)i=−b/a
The right-hand side expression −b/a is a real number.
Therefore, (f+p)+(g+q)i must also be a real number. This means that the imaginary part (g+q) is equal to 0.
Equate g+q and 0, and subtract q from both sides.
g+q=0
g=−q
The product of the two solutions of the quadratic equation ax2+bx+c=0 is the quotient c/a.
Therefore, the product of f+gi and p+qi is c/a.
Form an equation for the product of the solutions.
Then, multiply the terms, substitute −1 for i2, and group the real and imaginary parts.
(f+gi)(p+qi)=c/a
fp+fqi+gpi+gqi2=c/a
fp+fqi+gpi+gq(−1)=c/a
fp+fqi+gpi−gq=c/a
(fp−gq)+(fq+gp)i=c/a
The right-hand side expression c/a is a real number.
Therefore, (fp−gq)+(fq+gp)i must also be a real number.
This means that the imaginary part fq+gp is equal to 0.
Equate fq+gp and 0, substitute −q for g, divide both sides by q, and add p on both sides.
fq+gp=0
fq+(−q)p=0
fq−pq=0
q(f−p)=0
f−p=0
f=p
Substitute −q for g and p for f in the solution f+gi.
f+gi=p+(−q)i
f+gi=p−qi
Therefore, the other solution of the given equation is p−qi.
Thus, it can be observed that the other solution must be p−qi
such that the sum and product of the solutions are equal to −b/a and c/a respectively.
The other solution of the equation must be p−qi because the sum and product of the solutions of the given equation are equal to −b/a and c/a respectively only if the two solutions are complex conjugates of each other.
Step-by-step solutions for HMH Algebra 2 Module 3 Exercise 3.3
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 145 Problem 17 Answer
To complete the square, first the equation is rewritten in the form x2+bx=c. Next, the value of b is identified, and (b/2)2 is calculated.
The value of (b/2)2 is added on both sides of the rewritten equation, and the left-side of the equation is factorized.
Finally, the definition of square root is used, and the equation is solved for the required values of x.
To use the quadratic formula, the equation is rewritten in the form ax2+bx+c=0 and the values of a,b,c are written. Then, the values of a,b,c
are substituted in the quadratic formula and the expression is simplified to determine the required values of x.
It can be observed that using the quadratic formula to solve a quadratic equation is much simpler and faster as compared to solving a quadratic equation by completing the square.
Thus, using the quadratic formula to solve a quadratic equation is much easier than completing the square.
Using the quadratic formula to solve a quadratic equation is much easier than completing the square because quadratic formula only requires to rewrite the equation in the form ax2+bx+c=0, identify the values of a,b,c, and substitute them into the quadratic formula to obtain the values of x.
The completing the square method takes much longer to solve and is more complex because it involves rewriting the equation in the form x2+bx=c, calculating (b/2)2, adding (b/2)2 on both sides, factoring the left-side, using the definition of square root, and finally, solving the resulting equation.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3)Page 146 Problem 18 Answer
The given graph shows the graph of the function f(x) equal to x2+6x. The given equations are:
x2+6x+6=0
x2+6x+9=0
x2+6x+12=0
The question requires to use the given graph to determine the number of real solutions of the given equations.
To determine the number of real solutions, rewrite the equations using subtraction in the form ax2+bx=−c, and equate the left and right sides of the rewritten equations to f(x) and g(x).
Then, draw the graph of each g(x) on the given graph using horizontal lines. Next, use the points of intersection of f(x)
and g(x) to determine the number of points where they intersect.
Finally, use the points to determine the number of real solutions for each g(x), and thus the number of real solutions for each equation.
The first given quadratic equation is x2+6x+6=0.
Subtract 6 from both sides of the equation to rewrite it in the form ax2+bx=−c.
x2+6x=−6
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x) gives the function f(x)=x2+6x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=−6.
The second given quadratic equation is x2+6x+9=0.
Subtract 9 from both sides of the equation to rewrite it in the form ax2+bx=−c.
x2+6x=−9
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x) gives the function f(x)=x2+6x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=−9.
The third given quadratic equation is x2+6x+12=0.
Subtract 12 from both sides of the equation to rewrite it in the form ax2+bx=−c.
x2+6x=−12
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x) gives the function f(x)=x2+6x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=−12.
Construct a table having columns for the given equations, the rewritten equations, and the obtained expressions for f(x) and g(x).

From the completed table from previous part of the exercise, it can be determined that functions to be graphed are:
g(x)=−6
g(x)=−9
g(x)=−12
Graph the functions on the given graph by drawing horizontal lines having the y-intercept equal to the right-hand side of the equations.
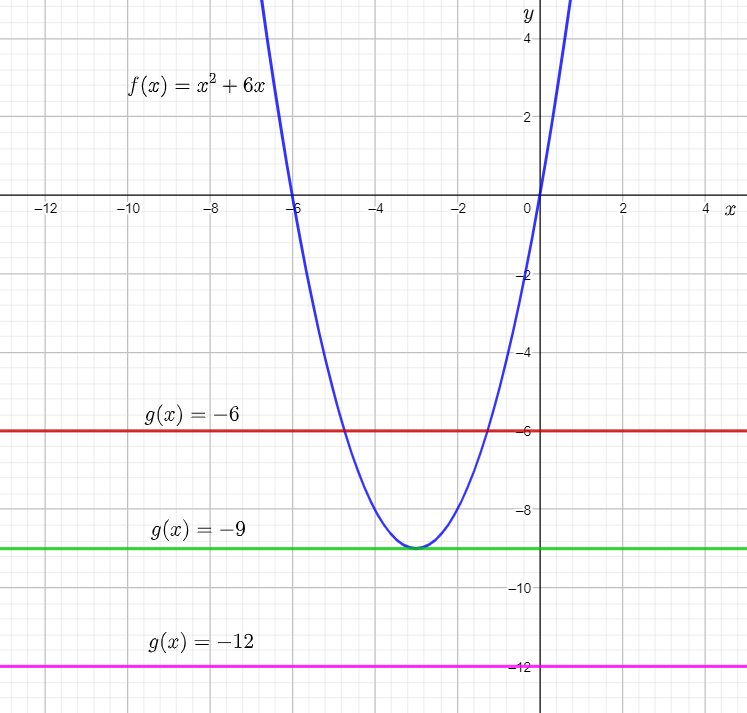
From the graph, it can be observed that the graph of f(x) and g(x)=−6
intersect each other at two points.
This means that x2+6x=−6 for two real values of x.
Adding 6 on both sides, the equation becomes x2+6x+6=0.
Therefore, the equation x2+6x+6=0 has two real solutions. This is because the value of g(x)
is greater than the minimum value of f(x), that is −9.
From the graph, it can be observed that the graph of f(x) and g(x)=−9 touch each other at one point.
This means that x2+6x=−9 for one real value of x.
Adding 9 on both sides, the equation becomes x2+6x+9=0.
Therefore, the equation x2+6x+9=0 has one real solution. This is because the value of g(x)
is equal to the minimum value of f(x), that is −9.
From the graph, it can be observed that the graph of f(x) and g(x)=−12 do not touch or intersect each other at any point.
This means that x2+6x=−12 for no real value of x.
Adding 12 on both sides, the equation becomes x2+6x+12=0.
Therefore, the equation x2+6x+12=0 has no real solution.
This is because the value of g(x) is less than the minimum value of f(x), that is −9.
The equation x2+6x+6=0 has two real solutions.
This is because the equation can be written as x2+6x equal to −6, where the left-hand side represents the given function f(x), and the right-hand side represents the function g(x).
The equation has two real solutions because the graphs of f(x) and g(x) intersect at two points.
The equation x2+6x+9=0 has one real solution.
This is because the equation can be written as x2+6x equal to −9, where the left-hand side represents the given function f(x), and the right-hand side represents the function g(x).
The equation has one real solution because the graphs of f(x) and g(x) intersect at one point.
The equation x2+6x+12=0 has no real solution.
This is because the equation can be written as x2+6x equal to −12, where the left-hand side represents the given function f(x), and the right-hand side represents the function g(x).
The equation has no real solution because the graphs of f(x) and g(x) intersect at no points.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 146 Problem 19 Answer
The given graph shows the graph of the function f(x) equal to −1/2x2+3x. The given equations are:
−1/2x2+3x−3=0
−1/2x2+3x−9/2=0
−1/2x2+3x−6=0
The question requires to use the given graph to determine the number of real solutions of the given equations.
To determine the number of real solutions, rewrite the equations using subtraction in the form ax2+bx=−c, and equate the left and right sides of the rewritten equations to f(x) and g(x).
Then, draw the graph of each g(x) on the given graph using horizontal lines.
Next, use the points of intersection of f(x) and g(x) to determine the number of points where they intersect.
Finally, use the points to determine the number of real solutions for each g(x), and thus the number of real solutions for each equation.
The first given quadratic equation is −1/2x2+3x−3=0.
Add 3 on both sides of the equation to rewrite it in the form ax2+bx=−c.
−1/2x2+3x=3
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x) gives the function f(x)=−1/2x2+3x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=3.
The second given quadratic equation is −1/2x2+3x−9/2=0.
Add 9/2 on both sides of the equation to rewrite it in the form ax2+bx=−c.
−1/2x2+3x=9/2
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x) gives the function f(x)=−1/2x2+3x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=9/2.
The third given quadratic equation is −1/2x2+3x−6=0.
Add 6 on both sides of the equation to rewrite it in the form ax2+bx=−c.
−1/2x2+3x=6
The left-hand side of the equation is of the form ax2+bx. Equating the left-hand side of the rewritten equation to f(x) gives the function f(x)=−1/2x2+3x.
The right-hand side of the equation is of the form −c. Equating the right-hand side of the rewritten equation to g(x), the obtained function is g(x)=6.
Construct a table having columns for the given equations, the rewritten equations, and the obtained expressions for f(x) and g(x).

From the completed table from previous part of the exercise, it can be determined that functions to be graphed are:
g(x)=3
g(x)=9/2
g(x)=6
Graph the functions on the given graph by drawing horizontal lines having the y-intercept equal to the right-hand side of the equations.
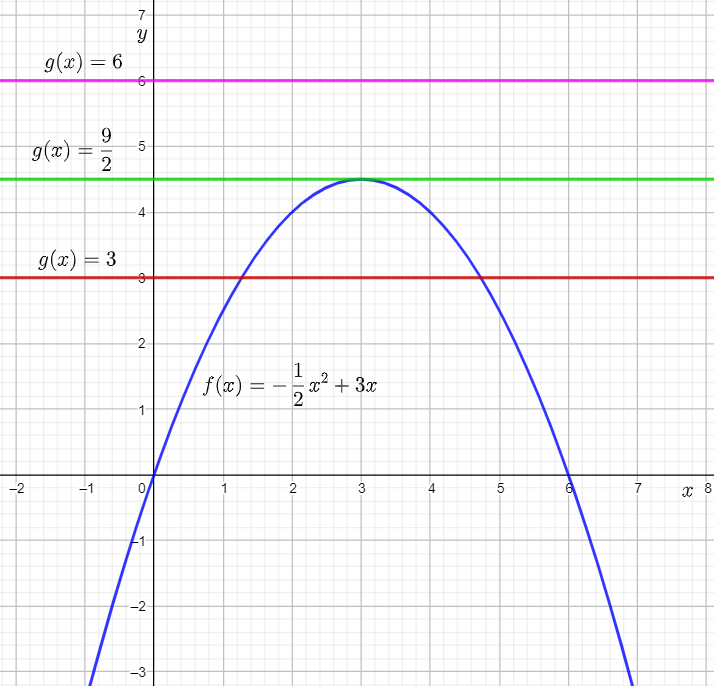
From the graph, it can be observed that the graph of f(x) and g(x)=3 intersect each other at two points.
This means that −1/2x2+3x=3 for two real values of x.
Subtracting 3 from both sides, the equation becomes −1/2x2+3x−3=0.
Therefore, the equation −1/2x2+3x−3=0 has two real solutions.
From the graph, it can be observed that the graph of f(x) and g(x)=9/2 touch each other at one point.
This means that −1/2x2+3x=9/2 for one real value of x.
Subtracting 9/2 from both sides, the equation becomes −1/2x2+3x−9/2=0.
Therefore, the equation −1/2x2+3x−9/2=0 has one real solution.
From the graph, it can be observed that the graph of f(x) and g(x)=6 do not touch or intersect each other at any point.
This means that −1/2x2+3x=6 for no real value of x.
Subtracting 6 from both sides, the equation becomes −1/2x2+3x−6=0.
Therefore, the equation −1/2x2+3x−6=0 has no real solution.
The equation −1/2x2+3x−3=0 has two real solutions.
This is because the equation can be written as −1/2x2+3x equal to 3, where the left-hand side represents the given function f(x), and the right-hand side represents the function g(x).
The equation has two real solutions because the graphs of f(x) and g(x) intersect at two points.
The equation −1/2x2+3x−9/2=0 has one real solution.
This is because the equation can be written as −1/2x2+3x equal to 9/2, where the left-hand side represents the given function f(x), and the right-hand side represents the function g(x).
The equation has one real solution because the graphs of f(x) and g(x) intersect at one point.
The equation −1/2x2+3x−6=0 has no real solution.
This is because the equation can be written as −1/2x2+3x equal to 6, where the left-hand side represents the given function f(x), and the right-hand side represents the function g(x).
The equation has no real solution because the graphs of f(x) and g(x) intersect at no points.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 146 Problem 20 Answer
The given equation is x2+2x+8=0.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c. Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Subtract 8 from both sides of x2+2x+8=0.
x2+2x+8−8=0−8
x2+2x=−8……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is 2.
Therefore, the value of (b/2)2 is (2/2)2
=(1)2, that is 1.
Add the value of (b/2)2, that is 1, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2+2ab+b2=(a+b)2, and simplify the right-hand side expression.
x2+2x+1=−8+1
(x+1)2=−8+1
(x+1)2=−7
Use the definition of square root to simplify (x+1)2=−7. Then, subtract 1 from both sides, and rewrite the expression using the imaginary unit i.
(x+1)2=−7
x+1=±√−7
x=−1±√−7
x=−1±i√7
Therefore, the required solutions are x=−1+i√7 and x=−1−i√7.
It can be observed that the solutions x=−1±i√7 contain the imaginary unit i, which is equal to the square root of the negative number −1.
Therefore, the solutions are non-real.
The required solutions are x=−1+i√7 and x=−1−i√7.
The solutions are non-real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 147 Problem 21 Answer
The given equation is x2−5x=−20.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, compare the equation to x2+bx=c.
Then, identify the value of b, and calculate (b/2)2. Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Let the equation x2−5x=−20 be equation (1).
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is −5.
Therefore, the value of (b/2)2 is (−5/2)2=25/4.
Add the value of (b/2)2, that is 25/4, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2−2ab+b2=(a−b)2, and simplify the right-hand side expression.
x2−5x+25/4
=−20+25/4
(x−5/2)2=−20+25/4
(x−5/2)2=−55/4
Use the definition of square root to simplify (x−5/2)2=−55/4. Then, add 5/2 on both sides, and rewrite the expression using the imaginary unit i.
(x−5/2)2=−55/4
x−5/2=±√−55/4
x=5/2±√−55/4
x=5/2±i√55/4
Apply the quotient property of square roots, and then simplify the square root in the denominator.
x=5/2±i√55/√4
x=5/2±i√55/2
x=5±i√55/2
Therefore, the required solutions are x=5+i√55/2 and x=5−i√55/2.
It can be observed that the solutions x=5±i√55/2 contain the imaginary unit i, which is equal to the square root of the negative number −1.
Therefore, the solutions are non-real.
The required solutions are x=5+i√55/2 and x=5−i√55/2.
The solutions are non-real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 147 Problem 22 Answer
The given equation is 5x2−6x=8.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c. Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Divide both sides of 5x2−6x=8 by 5.
5x2−6x/5=8/5
x2−6/5
x=8/5……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is −6/5.
Therefore, the value of (b/2)2 is (−6/5)(2/2)=(−3/5)2, that is 9/25.
Add the value of (b/2)2, that is 9/25, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2−2ab+b2=(a−b)2, and simplify the right-hand side expression.
x2−6/5
x+9/25=8/5+925
(x−3/5)2=8/5+9/25
(x−3/5)2=49/25
Use the definition of square root to simplify (x−3/5)2=49/25, and then add 3/5 on both sides.
(x−3/5)2=49/25
x−3/5=±√49/25
x=3/5±√49/25
Apply the quotient property of square roots, and then simplify the square roots.
x=3/5±√49/√25
x=3/5±7/5
When x is equal to 3/5−7/5, the simplified value of x is 3−7/5, that is −4/5.
When x is equal to 3/5+7/5, the simplified value of x is 3+7/5=10/5, that is 2.
Therefore, the required solutions are x=−4/5 and x=2.
It can be observed that the solutions do not contain the square root of a negative number, or the imaginary unit i.
Therefore, the solutions are real.
The required solutions are x=−4/5 and x=2.
The solutions are real.
HMH Algebra 2 Chapter 3 Quadratic Equations detailed solutions
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 147 Problem 23 Answer
The given equation is 7x2+13x=5.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c.
Then, identify the value of b, and calculate (b/2)2. Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Divide both sides of 7x2+13x=5 by 7.
7x2+13x/7=5/7
x2+13/7
x=5/7……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is 13/7.
Therefore, the value of (b/2)2 is (13/7)22=(13/14)2, that is 169/196.
Add the value of (b/2)2, that is 169/196, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2+2ab+b2=(a+b)2, and simplify the right-hand side expression.
x2+13/7
x+169/196
=5/7+169/196
(x+13/14)2=5/7+169/196
(x+13/14)2=309/196
Use the definition of square root to simplify (x+13/14)2=309/196, and then subtract 13/14 from both sides.
(x+13/14)2=309/196
x+13/14=±√309/196
x=−13/14±√309/196
Apply the quotient property of square roots, and then simplify the square roots.
x=−13/14±√309/√196
x=−13/14±√309/14
x=−13±√309/14
Therefore, the required solutions are x=−13+√309/14 and x=−13−√309/14.
It can be observed that the solutions x=−13±√309/14 do not contain the square root of a negative number, or the imaginary unit i.
Therefore, the solutions are real.
The required solutions are x=−13+√309/14 and x=−13−√309/14.
The solutions are real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 147 Problem 24 Answer
The given equation is −x2−6x−11=0.
The question requires to solve the given equation by completing the square, and then state whether the obtained solutions are real or non-real.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c. Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions, and observe them to state whether they are real or non-real.
Multiply both sides of −x2−6x−11=0 by −1, and then subtract 11 from both sides.
−1(−x2−6x−11)=−1(0)
x2+6x+11=0
x2+6x=−11……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is 6.
Therefore, the value of (b/2)2 is (6/2)2
=(3)2, that is 9.
Add the value of (b/2)2, that is 9, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2+2ab+b2=(a+b)2, and simplify the right-hand side expression.
x2+6x+9=−11+9
(x+3)2=−11+9
(x+3)2=−2
Use the definition of square root to simplify (x+3)2=−2.
Then, subtract 3 from both sides, and rewrite the expression using the imaginary unit i.
(x+3)2=−2
x+3=±√−2
x=−3±√−2
x=−3±i√2
Therefore, the required solutions are x=−3+i√2 and x=−3−i√2.
It can be observed that the solutions x=−3±i√2. contain the imaginary unit i, which is equal to the square root of the negative number −1.
Therefore, the solutions are non-real.The required solutions are x=−3+i√2 and x=−3−i√2.
The solutions are non-real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 147 Problem 25 Answer
The given equation is 7x2−11x+10=0.
The question requires to state the number of solutions without solving the equation, and determine whether the solutions are real or non-real.
To answer the question, compare the equation to ax2+bx+c=0 and identify the values of a,b,c.
Then, calculate the discriminant of the equation, and observe its value to determine the number and type of solutions of the given equation.
It can be observed that the given equation is a quadratic equation of the form ax2+bx+c=0.
Comparing the given equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 7,−11,10 respectively.
Substitute 7 for a, −11 for b, and 10 for c in the formula for discriminant b2−4ac. Then, multiply the terms, and subtract the terms.
b2−4ac=(−11)2
−4(7)(10)
=121−280
=−159
The discriminant is equal to −159, which is less than 0.
This means that the equation 7x2−11x+10=0 has two non-real solutions.
Thus, the number of solutions of the given equation is two, and the two solutions are non-real.
The given equation has two solutions.
The two solutions of the given equation are non-real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 147 Problem 26 Answer
The given equation is −x2−2/5
x=1.
The question requires to state the number of solutions without solving the equation, and determine whether the solutions are real or non-real.
To answer the question, rewrite the equation in the form ax2+bx+c=0 and identify the values of a,b,c.
Then, calculate the discriminant of the equation, and observe its value to determine the number and type of solutions of the given equation.
Subtract 1 from both sides of −x2−2/5
x=1.
−x2−2/5
x−1=1−1
−x2−2/5
x−1=0…………(1)
Comparing the equation (1) to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are −1,−2/5,−1 respectively.
Substitute −1 for a, −2/5 for b, and −1 for c in the formula for discriminant b2−4ac. Then, multiply the terms, and subtract the terms.
b2−4ac=(−2/5)2
−4(−1)(−1)
=4/25−4
=4−100/25
=−96/25
The discriminant is equal to −96/25, which is less than 0.
This means that the equation −x2−2/5 x=1 has two non-real solutions.
Thus, the number of solutions of the given equation is two, and the two solutions are non-real.
The given equation has two solutions.
The two solutions of the given equation are non-real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 147 Problem 27 Answer
The given equation is 4x2+9=12x.
The question requires to state the number of solutions without solving the equation, and determine whether the solutions are real or non-real.
To answer the question, rewrite the equation in the form ax2+bx+c=0 and identify the values of a,b,c.
Then, calculate the discriminant of the equation, and observe its value to determine the number and type of solutions of the given equation.
Subtract 12x from both sides of 4x2+9=12x.
4×2+9−12x=12x−12x
4x2−12x+9=0…………(1)
Comparing the equation (1) to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 4,−12,9 respectively.
Substitute 4 for a, −12 for b, and 9 for c in the formula for discriminant b2−4ac. Then, multiply the terms, and subtract the terms.
b2−4ac=(−12)2
−4(4)(9)
=144−144
=0
The discriminant is equal to 0.
This means that the equation 4x2+9=12x has one real solution.
Thus, the number of solutions of the given equation is one, and the solution is real.
The given equation has one solution.
The one solution of the given equation is real.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 150 Problem 28 Answer
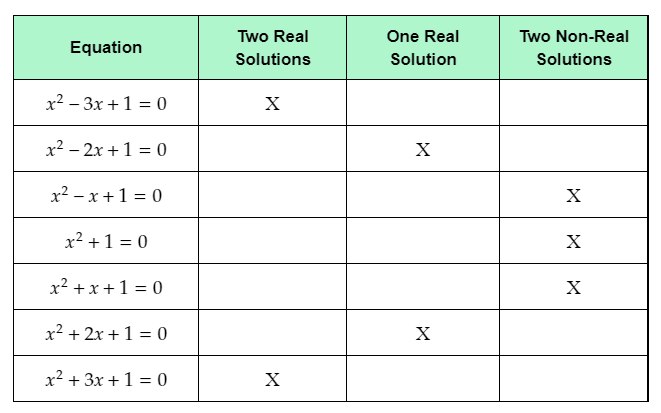
The given table shows seven quadratic functions.
The question requires to complete the given table by placing X marks in the column which corresponds to the number and type of solutions of the given equations.
To complete the table, compare each equation to ax2+bx+c=0 and identify the values of a,b,c.
Then, calculate the discriminant of each equation, and observe its value to determine the number and type of solutions of each given equation.
Finally, use the determined number and type of solutions and place the X mark in the corresponding column for each equation to complete the table.
The first given equation is x2−3x+1=0.
Comparing the equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,−3,1 respectively.
Calculate the discriminant of the equation using the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(−3)2
−4(1)(1)
=9−4
=5
The discriminant is equal to 5, which is greater than 0.
This means that the equation x2−3x+1=0 has two real solutions.
The second given equation is x2−2x+1=0.
Comparing the equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,−2,1 respectively.
Calculate the discriminant of the equation using the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(−2)2
−4(1)(1)
=4−4
=0
The discriminant is equal to 0.
This means that the equation x2−2x+1=0 has one real solution.
The third given equation is x2−x+1=0.
Comparing the equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,care 1,−1,1 respectively.
Calculate the discriminant of the equation using the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(−1)2
−4(1)(1)
=1−4
=−3
The discriminant is equal to −3, which is less than 0.
This means that the equation x2−x+1=0 has two non-real solutions.
The fourth given equation is x2+1=0.
Comparing the equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,0,1 respectively.
Calculate the discriminant of the equation using the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(0)2
−4(1)(1)
=0−4
=−4
The discriminant is equal to −4, which is less than 0.
This means that the equation x2+1=0 has two non-real solutions.
The fifth given equation is x2+x+1=0.
Comparing the equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,1,1 respectively.
Calculate the discriminant of the equation using the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(1)2
−4(1)(1)
=1−4
=−3
The discriminant is equal to −3, which is less than 0.
This means that the equation x2+x+1=0 has two non-real solutions.
The sixth given equation is x2+2x+1=0.
Comparing the equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,2,1 respectively.
Calculate the discriminant of the equation using the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(2)2
−4(1)(1)
=4−4
=0
The discriminant is equal to 0.
This means that the equation x2+2x+1=0 has one real solution.
The seventh given equation is x2+3x+1=0.
Comparing the equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,3,1 respectively.
Calculate the discriminant of the equation using the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(3)2−4(1)(1)
=9−4
=5
The discriminant is equal to 5, which is greater than 0.
This means that the equation x2+3x+1=0 has two real solutions.
Complete the given table by placing X mark in the column which represents the number and type of solutions for each equation.
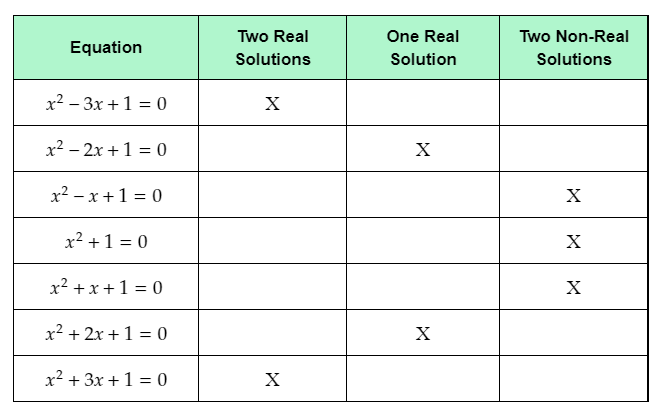
The completed table with the X marks placed in the appropriate columns is:
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 151 Problem 29 Answer
The given equation is −x2+2x−3=0. Also, a student’s attempt at solving the equation by completing the square is given.
The question requires to determine the error in the student’s solution, and correct it.
To find and correct the error, observe the solution and determine whether the student has correctly written the equation in the form x2+bx=c before factoring the left side of the equation, and observe whether the factoring is correct.
Then, rewrite the equation in the form x2+bx=c. Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the correct solutions of the given equation.
When solving a quadratic equation by completing the square, the quadratic equation is written in the form x2+bx=c before factoring the left side of the equation.
It can be observed that in the student’s solution, the quadratic equation is written as −x2+2x=3 before factoring the left side of the equation.
The coefficient of x2 in the rewritten equation is −1, instead of 1.
Therefore, the error in the solution is that the student has not written the quadratic equation in the form x2+bx=c before factoring the left side of the equation.
Multiply both sides of −x2+2x−3=0 by −1, and then subtract 3 from both sides.
−1(−x2+2x−3)=−1(0)
x2−2x+3=0
x2−2x=−3……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is −2.
Therefore, the value of (b/2)2 is (−2/2)2
=(−1)2, that is 1.
Add the value of (b/2)2, that is 1, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2−2ab+b2=(a−b)2, and simplify the right-hand side expression.
x2−2x+1=−3+1
(x−1)2=−3+1
(x−1)2=−2
Use the definition of square root to simplify (x−1)2=−2.
Then, add 1 on both sides, and rewrite the expression using the imaginary unit i.
(x−1)2=−2
x−1=±√−2
x=1±√−2
x=1±i√2
Therefore, the correct solutions are x=1+i√2 and x=1−i√2.
The error in the solution is that the student has not written the quadratic equation in the form x2+bx=c before factoring the left side of the equation.
This is because the student has written the quadratic equation in the form −x2+bx=c, where the coefficient of x2 is −1, instead of 1.
The correct solutions are x=1+i√2 and x=1−i√2.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 151 Problem 30 Answer
The given equation is x2+8x+c0.
The question requires to determine the values of c for which the given equation has one real solution, two real solutions, and two non-real solutions.
To determine the values, compare the equation to ax2+bx+c=0 and identify the values of a,b,c. Then, calculate the discriminant of the equation.
Next, take the case where the equation has one real solution, equate the determinant to 0, and solve the equation to determine the value of c.
Similarly, take the cases where the equation has two real or two non-real solutions, form inequalities using the determinant and the number 0, and solve them to determine the values of c for which the equation has two real or two non-real solutions.
It can be observed that the given equation is a quadratic equation of the form ax2+bx+c=0.
Comparing the given equation to the equation ax2+bx+c=0, it can be determined that the values of a,b,c are 1,8,c respectively.
Substitute 1 for a and 8 for b in the formula for discriminant b2−4ac, and multiply the terms.
b2−4ac=(8)2
−4(1)(c)
=64−4c
The discriminant is equal to 64−4c.
First case: The given equation has one real solution.
If the quadratic equation has one real solution, then the discriminant 64−4c is equal to 0.
Add 4c on both sides of 64−4c=0, and then divide both sides by 4.
64−4c=0
64=4c
16=c
Therefore, the given equation has one real solution if c=16.
Second case: The given equation has two real solutions.
If the quadratic equation has two real solutions, then the discriminant 64−4c is greater than 0.
Add 4c on both sides of 64−4c>0, and then divide both sides by 4.
64−4c>0
64>4c
16>c
Therefore, the given equation has two real solutions if c<16.
Third case: The given equation has two non-real solutions. If the quadratic equation has two non-real solutions, then the discriminant 64−4cis less than 0.
Add 4c on both sides of 64−4c<0, and then divide both sides by 4.
64−4c<0
64<4c
16<c
Therefore, the given equation has two non-real solutions if c>16.
The given equation has one real solution if c=16. two real solutions if c<16, and two non-real solutions if c>16.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 152 Exercise 1 Answer
It is given that the projectile motion model h(t)=−16t2+v0t+h0 models the ball’s height in t seconds, where v0 is the initial vertical velocity in feet per second, and h0 is the initial height in feet.
Also, it is given that the ball is hit when it is 4 feet above the ground, and it travelled vertically after being hit at the speed 80 feet per second.
Matt’s claim is that the ball must have reached the height 110 feet.
The question requires to model the ball’s height using the given information, and then use the model to determine whether Matt’s claim is correct or not.
To answer the question, use the initial vertical velocity and initial height of the ball in the projectile equation to determine the model for the ball’s height.
Next, let the height h(t) be equal to 110 feet.
Then, use the model and the height to form a quadratic equation in terms of t.
Next, compare the equation to at2+bt+c=0 and identify the values of a,b, and c.
Finally, determine the discriminant of the equation to determine whether the solutions are real or non-real, and thus, determine whether it is possible for the ball to reach a height of 110 feet.
The initial vertical velocity of the ball is the speed at which it travelled vertically after being hit, that is 80 feet per second.
The initial height of the ball is the height at which it is hit, that is 4 feet.
Substitute 80 for v0 and 4 for h0 in the projectile motion model h(t)=−16t2+v0t+h0.
h(t)=−16t2+80t+4
Thus, the model for the height of the ball in t seconds is h(t)=−16t2+80t+4.
Let the height of the ball be 110 feet. Therefore, h(t)=110.
Substitute −16t2+80t+4 for h(t) in h(t)=110, and subtract 110 from both sides.
−16t2+80t+4=110
−16t2+80t−106=0……………(1)
The equation based on Matt’s claim is −16t2+80t−106=0.
Comparing the equation (1) to the equation at2+bt+c=0, it can be determined that the values of a,b,c are −16,80,−106 respectively.
Substitute −16 for a, 80 for b, and −106 for c in the formula for discriminant b2−4ac. Then, multiply the terms, and subtract the terms.
b2−4ac=(80)2−4(−16)(−106)
=6400−6784
=−384
The discriminant is equal to −384, which is less than 0.
This means that the equation −16t2+80t−106=0 has two non-real solutions.
Therefore, there is no real value of t for which the height of the ball is equal to 110 feet.
Thus, the ball cannot reach the height equal to 110 feet, and Matt’s claim is not correct.
The model for the height of the ball in t seconds is h(t)=−16t2+80t+4.
The equation based on Matt’s claim is −16t2+80t−106=0.
Matt’s claim is not correct. The ball cannot reach the height equal to 110 feet.
Solutions for Quadratic Equations HMH Algebra 2 Module 3 Exercise 3.3
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 152 Exercise 2 Answer
It is given that the projectile motion model h(t)=−16t2+v0t+h0 models the ball’s height in t seconds, where v0 is the initial vertical velocity in feet per second, and h0 is the initial height in feet.
Also, it is given that the ball is hit when it is 4 feet above the ground, and it travelled vertically after being hit at the speed 80 feet per second.
The question requires to determine whether the ball reaches a height of 100 feet or not, and explain the reasoning.
Given that the model for the height of the ball in t seconds is h(t)=−16t2+80t+4, as determined in the previous part of this exercise.
To answer the question, let the height h(t) be equal to 100 feet. Then, use the model and the height to form a quadratic equation in terms of t.
Next, compare the equation to at2+bt+c=0 and identify the values of a,b, and c.
Finally, determine the discriminant of the equation to determine whether the solutions are real or non-real, and thus, determine whether it is possible for the ball to reach a height of 100 feet.
Let the height of the ball be 100 feet. Therefore, h(t)=100.
Substitute −16t2+80t+4 for h(t) in h(t)=100, and subtract 100 from both sides.
−16t2+80t+4=100
−16t2+80t−96=0……………(1)
Comparing the equation (1) to the equation at2+bt+c=0, it can be determined that the values of a,b,c are −16,80,−96 respectively.
Substitute −16 for a, 80 for b, and −96 for c in the formula for discriminant b2−4ac. Then, multiply the terms, and subtract the terms.
b2−4ac=(80)2
−4(−16)(−96)
=6400−6144
=256
The discriminant is equal to 256, which is greater than 0.
This means that the equation h(t)=100 has two real solutions.
Therefore, there is some real value of t for which the height of the ball is equal to 100 feet.
Thus, the ball does reach a height of 100 feet.
The ball does reach a height of 100 feet. This is because the quadratic equation −16t2+80t−96=0
representing the height of the ball as 100
feet has two real solutions. There exists some real value of t for which the height of the ball is equal to 100 feet.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 152 Exercise 3 Answer
It is given that the projectile motion model h(t)=−16t2+v0t+h0 models the ball’s height in t seconds, where v0 is the initial vertical velocity in feet per second, and h0
is the initial height in feet. Also, it is given that the ball is hit when it is 4 feet above the ground, and it travelled vertically after being hit at the speed 80 feet per second.
Also, hmax represents the maximum height of the ball.
The question requires to show how the value of hmax can be found using the discriminant of the quadratic formula.
Given that the model for the height of the ball in t seconds is h(t)=−16t2+80t+4, as determined in part (a) of this exercise.
To determine the maximum height, let the height h(t) be equal to hmax.
Then, use the model and the height to form a quadratic equation in terms of t.
Next, compare the equation to at2+bt+c=0 and identify the values of a,b, and c.
Then, determine the discriminant of the equation and equate it to 0 to form a linear equation in terms of hmax.
Finally, solve the equation for hmax to determine the maximum height, and explain how it is calculated.
Let the height of the ball be maximum. Therefore, h(t)=hmax.
Substitute −16t2+80t+4 for h(t) in h(t)=hmax, and subtract hmax from both sides.
−16t2+80t+4=hmax
−16t2+80t+(4−hmax)=0……………(1)
Comparing the equation (1) to the equation at2+bt+c=0, it can be determined that the values of a,b,c are −16,80,4−hmax respectively.
Substitute −16 for a, 80 for b, and 4−hmax for c in the formula for discriminant b2−4ac. Then, multiply the terms, and combine the terms.
b2−4ac=(80)2−4(−16)(4−hmax)
=6400+256−64hmax
=6656−64hmax
The discriminant is equal to 6656−64hmax.
The solutions of the equation −16t2+80t+(4−hmax)=0 represent the time at which the ball reaches the maximum height.
The ball reaches the maximum height only once. This is because after reaching the maximum height, it starts falling down.
Therefore, the equation −16t2+80t+(4−hmax)=0 has only one real solution.
Thus, the discriminant of the equation should be equal to 0.
Equate the discriminant 6656−64hmax to 0, add 64hmax on both sides, and divide both sides by 64.
6656−64hmax=0
6656=64hmax
6656/64=hmax
104=hmax
Therefore, the maximum height of the ball is 104 feet.
Thus, the maximum height is calculated by using the model and the maximum height to form the equation −16t2+80t+(4−hmax)=0, calculating the discriminant and equating it to 0, and finally solving the resulting linear equation for hmax.
The ball does reach a maximum height of 104 feet.
This is calculated by writing the equation −16t2 +80t+(4−hmax)=0 using the given model, calculating the discriminant of the equation, equating the discriminant to 0, and solving the resulting equation for hmax.
The discriminant of the equation is equated to 0 because the ball reaches the maximum height only once.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 152 Exercise 4 Answer
It is given that the projectile motion model h(t)=−16t2+v0t+h0 models the ball’s height in t seconds, where v0 is the initial vertical velocity in feet per second, and h0
is the initial height in feet. Also, it is given that the ball is hit when it is 4 feet above the ground, and it travelled vertically after being hit at the speed 80 feet per second.
The question requires to determine the time when the ball reaches its maximum height.
Given that the model for the height of the ball in t seconds is h(t)=−16t2+80t+4, as determined in part (a) of this exercise.
Given that the maximum height of the ball is 104 feet, as determined in the previous part of this exercise.
To answer the question, let the height h(t) be equal to the maximum height of 104 feet.
Then, use the model and the height to form a quadratic equation in terms of t, and compare the equation to at2+bt+c=0 to identify the values of a,b,c.
Finally, use the quadratic formula, and simplify the expression to determine the time when the ball reaches its maximum height.
Let the height of the ball be the maximum height of 104 feet. Therefore, h(t)=104.
Substitute −16t2+80t+4 for h(t) in h(t)=104, and subtract 104 from both sides.
−16t2+80t+4=104
−16t2+80t−100=0……………(1)
Comparing the equation (1) to the equation at2+bt+c=0, it can be determined that the values of a,b,c are −16,80,−100 respectively.
Substitute −16 for a, 80 for b, and −100 for c
in the quadratic formula t=−b±√b2−4ac/2a.
Then, multiply the terms, combine the terms in the square root, and simplify the expression.
t=−(80)±√(80)2−4(−16)(−100)/2(−16)
t=−80±√6400−6400/−32
t=−80±√0/−32
t=−80/−32
t=2.5
Therefore, the time in which the ball reaches its maximum height is 2.5 seconds.
The ball reaches the maximum height in 2.5 seconds.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 153 Exercise 5 Answer
A quadratic equation can be used to model a real-world problem.
Then, the equation can be solved for one variable by using completing the square method, factoring, or the quadratic formula, and thus, obtain the required solutions.
For example: There is a rectangular field which has an area equal to 875
square feet, and the ratio of its length and width is 7:5. It is required to determine the dimensions of the field.
The length and width of the field can be written as 7m and 5m respectively.
Since the area is given as 875 square feet, the area can be modelled using the quadratic equation 7m⋅5m=875.
This equation can be solved to obtain the values of m, and thus, obtain the dimensions of the rectangular field.
Thus, the real-world problems can be modelled using quadratic equations, and then solved to determine the required solutions.
Quadratic equations can be used to model real-world problems such as the area of a rectangular field when the ratio of the dimensions is given.
Then, the given area can be substituted in the equation, and the quadratic equation can be solved using completing the square method, factoring, or the quadratic formula to obtain the solutions.
The accepted solution can then be used to determine the dimensions of the rectangular field. Similarly, other real-world problems can be solved using quadratic equations.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 154 Exercise 6 Answer
The given equation is x2−16=0.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using addition, and use the definition of square root to simplify the expression.
Add 16 on both sides of x2−16=0, use the definition of square root, and simplify the square root to solve the equation.
x2−16+16=0+16
x2=16
x=±√16
x=±4
Thus, the required solutions are x=±4.
The required solutions are x=±4.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 154 Exercise 7 Answer
The given equation is 2x2−10=0.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using addition and division, and use the definition of square root to simplify the expression.
Add 10 on both sides of 2x −10=0, and then divide both sides by 2.
2x2−10+10=0+10
2x2=10
2x2/2=10/2
x2=5
Use the definition of square root to solve the equation x2=5.
x2=5
x=±√5
Thus, the required solutions are x=±√5.
The required solutions are x=±√5.
HMH Algebra 2 Volume 1 Exercise 3.3 Quadratic Equations guide
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 154 Exercise 8 Answer
The given equation is x2+6x+10=0.
The question requires to solve the given equation by completing the square.
To solve the equation by completing the square, rewrite the equation in the form x2+bx=c. Then, identify the value of b, and calculate (b/2)2.
Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation to determine the required solutions.
Subtract 10 from both sides of x2+6x+10=0.
x2+6x+10−10=0−10
x2+6x=−10……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is 6.
Therefore, the value of (b/2)2 is (6/2)2=(3)2, that is 9.
Add the value of (b/2)2, that is 9, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2+2ab+b2=(a+b)2, and simplify the right-hand side expression.
x2+6x+9=−10+9
(x+3)2=−10+9
(x+3)2=−1
Use the definition of square root to simplify (x+3)2=−1. Then, subtract 3 from both sides, and rewrite the expression using the imaginary unit i.
(x+3)2=−1
x+3=±√−1
x=−3±√−1
x=−3±i
Therefore, the required solutions are x=−3+i and x=−3−i.
The required solutions are x=−3+i and x=−3−i.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 154 Exercise 9 Answer
The given equation is x2−4x+4=0.
The question requires to solve the given equation by factoring it.
To solve the equation, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the given quadratic equation, solve it to obtain the values of x, and thus, obtain the required solution.
The constant in the given quadratic equation is 4.
Write the pair of factors of the constant 4.
1 and 4
2 and 2
−1 and −4
−2 and −2
It can be observed that the sum of the pair of factors −2 and −2 is equal to the coefficient of the middle term in the given quadratic equation, that is −4.
Therefore, the left-hand side of the given quadratic equation can be factorised as (x−2)(x−2).
Thus, the equation becomes (x−2)(x−2)=0.
The equation (x−2)(x−2)=0 is true only when x−2 is equal to 0.
When x−2 is equal to 0, the value of x is equal to 2.
Thus, the required solution is x=2.
The required solution is x=2.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 154 Exercise 10 Answer
The given equation is x2−x−30=0.
The question requires to solve the given equation by factoring it.
To solve the equation, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the given quadratic equation, solve it to obtain the values of x, and thus, obtain the required solutions.
The constant in the given quadratic equation is −30.
Write the pair of factors of the constant −30.
1 and −30
2 and −15
3 and −10
5 and −6
6 and −5
10 and −3
15 and −2
30 and −1
It can be observed that the sum of the pair of factors 5 and −6 is equal to the coefficient of the middle term in the given quadratic equation, that is −1.
Therefore, the left-hand side of the given quadratic equation can be factorised as (x+5)(x−6).
Thus, the equation becomes (x+5)(x−6)=0.
The equation (x+5)(x−6)=0 is true only when either x+5 is equal to 0, or x−6 is equal to 0.
When x+5 is equal to 0, the value of x is equal to −5.
When x−6 is equal to 0, the value of x is equal to 6.
Thus, the required solutions are x=−5 and x=6.
The required solutions are x=−5 and x=6.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 154 Exercise 11 Answer
Assume the quadratic equation ax2+bx+c=0. First, the quadratic equation is rewritten in the form x2+b/a
x+c/a=0 by division, such that the coefficient of x2 is 1.Then, the constant in the quadratic equation is identified, that is the value of c/a.
Then, the pair of factors of the constant c/a are written. Next, the pair of factors whose sum is equal to coefficient of the middle term is chosen.
In the rewritten quadratic equation, the coefficient of the middle term is b/a.
Therefore, if there is a pair of factors p and q of the constant c/a, that is pq=c/a, then the sum of the factors p and q is b/a.
This means that if there is no pair of factors of the constant c/a whose sum is not equal to the coefficient of the middle term is b/a, then the quadratic equation cannot be solved by factoring.
Thus, a quadratic equation of the form x2+bx+c=0 can be solved by factoring only if there exists a pair of factors of the constant whose sum is equal to the coefficient of the middle term.
It is possible to solve a quadratic equation by factoring if there exists a pair of factors of the constant whose sum is equal to the coefficient of the middle term.
The constant and coefficient of middle term are taken only after writing the equation such that the coefficient of x2 is 1.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 154 Exercise 12 Answer
The complex solutions of a quadratic equation can be calculated either by completing the square, or by using the quadratic formula.
To complete the square and calculate the complex solutions of a quadratic equation, first the equation is rewritten in the form x2+bx=c. Next, the value of b is identified, and (b/2)2 is calculated.
The value of (b/2)2 is added on both sides of the rewritten equation, and the left-side of the equation is factorised.
Finally, the definition of square root is used, and the equation is solved for the required values of x.
Each quadratic equation is in the form ax2+bx+c=0.This equation can be written in the form x2+b/a
x=−c/a using subtraction and division.
Therefore, it is possible to solve the equation by completing the square. Thus, every quadratic equation can be solved by completing the square.
Every quadratic equation can be solved by completing the square because each quadratic equation can be written in the form x2+bx=c using operations of addition, subtraction, multiplication, and/or division.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 13 Answer
The given equation is 2x2−16=0.
The question requires to solve the given equation.
To solve the equation, isolate the square x2 on one side of the equation using addition and division.
Then, use the definition of square root and the product property of square roots to simplify the expression.
Add 16 on both sides of 2x2−16=0, and then divide both sides by 2.
2x2−16+16=0+16
2x2=16
2x2/2
=16/2
x2=8
Use the definition of square root to solve the equation x2=8, use the product property of square roots, and simplify the expression.
x2=8
x=±√8
x=±√4⋅2
x=±√4⋅√2
x=±2√2
Thus, the required solutions are x=±2√2.
The required solutions are x=±2√2.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 14 Answer
The given equation is 2x2−6x−20=0.
The question requires to solve the given equation.
To solve the equation, first remove the common factor from the equation.
Then, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the quadratic equation, solve it to obtain the values of x, and thus, obtain the required solutions.
Divide both sides of 2x2−6x−20=0 by 2.
2x2−6x−20/2=0/2
x2−3x−10=0
Thus, the given quadratic equation becomes x2−3x−10=0.
The constant in the quadratic equation x2−3x−10=0 is −10.
Write the pair of factors of the constant −10.
1 and −10
2 and −5
5 and −2
10 and −1
It can be observed that the sum of the pair of factors 2 and −5 is equal to the coefficient of the middle term in the rewritten quadratic equation x2−3x−10=0, that is −3.
Therefore, the left-hand side of the rewritten quadratic equation can be factorised as (x+2)(x−5).
Thus, the equation becomes (x+2)(x−5)=0.
The equation (x+2)(x−5)=0 is true only when either x+2 is equal to 0, or x−5 is equal to 0.
When x+2 is equal to 0, the value of x is equal to −2.
When x−5 is equal to 0, the value of x is equal to 5.
Thus, the required solutions are x=−2 and x=5.
The required solutions are x=−2 and x=5.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 15 Answer
The given equation is 2x2+2x−2=0.
The question requires to solve the given equation.
To solve the equation, rewrite the equation in the form x2+bx=c.
Then, identify the value of b, and calculate (b/2)2. Then, add (b/2)2 on both sides of the rewritten equation, factor the left-side expression using algebraic identities, and use the definition of square root.
Finally, solve the obtained equation and use the quotient property of square roots to determine the required solutions.
Add 2 on both sides of 2x2+2x−2=0, and then divide both sides by 2.
2x2+2x−2+2=0+2
2x2+2x=2
2x2+2x/2=2/2
x2+x=1……………(1)
Comparing the equation (1) to the equation x2+bx=c, it can be determined that the value of b is 1.
Therefore, the value of (b/2)2 is (1/2)2=1/4.
Add the value of (b/2)2, that is 1/4, on both sides of equation (1).
Then, factorise the left-hand side expression using the algebraic identity a2+2ab+b2=(a+b)2, and simplify the right-hand side expression.
x2+x+1/4=1+1/4
(x+1/2)2=1+1/4
(x+1/2)2=5/4
Use the definition of square root to simplify (x+1/2)2=5/4, and then subtract 1/2 from both sides.
(x+1/2)2=5/4
x+1/2=±√5/4
x=−1/2±√5/4
Apply the quotient property of square roots, and simplify the square root in the denominator.
x=−1/2±√5/√4
x=−1/2±√5/2
x=−1±√5/2
Therefore, the required solutions are x=−1+√5/2 and x=−1−√5/2.
The required solutions are x=−1+√5/2 and x=−1−√5/2.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 16 Answer
The given equation is x2+x=30.
The question requires to solve the given equation by factoring it.
To solve the equation, first rewrite the given equation in standard form using subtraction.
Then, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the quadratic equation, solve it to obtain the values of x, and thus, obtain the required solutions.
Subtract 30 from both sides of x2+x=30.
x2+x−30=30−30
x2+x−30=0
Thus, the given quadratic equation becomes x2+x−30=0.
The constant in the quadratic equation x2+x−30=0 is −30.
Write the pair of factors of the constant −30.
1 and −30
2 and −15
3 and −10
5 and −6
6 and −5
10 and −3
15 and −2
30 and −1
It can be observed that the sum of the pair of factors 6 and −5 is equal to the coefficient of the middle term in the rewritten quadratic equation x2+x−30=0, that is 1.
Therefore, the left-hand side of the rewritten quadratic equation can be factorised as (x+6)(x−5).
Thus, the equation becomes (x+6)(x−5)=0.
The equation (x+6)(x−5)=0 is true only when either x+6 is equal to 0, or x−5 is equal to 0.
When x+6 is equal to 0, the value of x is equal to −6.
When x−5 is equal to 0, the value of x is equal to 5.
Thus, the required solutions are x=−6 and x=5.
The required solutions are x=−6 and x=5.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 17 Answer
The given equation is x2−5x=24.
The question requires to solve the given equation by factoring it.
To solve the equation, first rewrite the given equation in standard form using subtraction.
Then, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the quadratic equation, solve it to obtain the values of x, and thus, obtain the required solutions.
Subtract 24 from both sides of x2−5x=24.
x2−5x−24=24−24
x2−5x−24=0
Thus, the given quadratic equation becomes x2−5x−24=0
The constant in the quadratic equation x2−5x−24=0 is −24.
Write the pair of factors of the constant −24.
1 and −24
2 and −12
3 and −8
4 and −6
6 and −4
8 and −3
12 and −2
24 and −1
It can be observed that the sum of the pair of factors 3 and −8 is equal to the coefficient of the middle term in the rewritten quadratic equation x2−5x−24=0, that is −5.
Therefore, the left-hand side of the rewritten quadratic equation can be factorised as (x+3)(x−8).
Thus, the equation becomes (x+3)(x−8)=0.
The equation (x+3)(x−8)=0 is true only when either x+3 is equal to 0, or x−8 is equal to 0.
When x+3 is equal to 0, the value of x is equal to −3.
When x−8 is equal to 0, the value of x is equal to 8.
Thus, the required solutions are x=−3 and x=8.
The required solutions are x=−3 and x=8.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 18 Answer
The given equation is −4x2+8=24.
The question requires to solve the given equation.To solve the equation, isolate the square x2 on one side of the equation using subtraction and division.
Then, use the definition of square root, the product property of square roots, and the imaginary unit i to simplify and rewrite the expression.
Subtract 8 from both sides of −4x2+8=24, and then divide both sides by −4.
−4x2+8−8=24−8
−4x2=16
−4x2−4=16−4
x2=−4
Use the definition of square root to solve the equation x2=−4, use the product property of square roots, and rewrite the expression using the imaginary unit i.
x2=−4
x=±√−4
x=±√(4)(−1)
x=±√4⋅√−1
x=±2i
Thus, the required solutions are x=±2i.
The required solutions are x=±2i.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 19 Answer
The given equation is x2+30=24.
The question requires to solve the given equation.
To solve the equation, isolate the square x2 on one side of the equation using subtraction.
Then, use the definition of square root, the product property of square roots, and the imaginary unit i
to simplify and rewrite the expression.
Subtract 30 from both sides of x2+30=24 and then use the definition of square root to solve the equation.
x2+30−30=24−30
x2=−6
x=±√−6
Use the product property of square roots to rewrite the square root in x=±√−6, and rewrite the expression using the imaginary unit i.
x=±√−6
x=±√(−1)(6)
x=±√−1⋅√6
x=±i√6
Thus, the required solutions are x=±i√6.
The required solutions are x=±i√6.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 20 Answer
The given equation is x2+4x+3=0.
The question requires to solve the given equation.
To solve the equation, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the given quadratic equation, solve it to obtain the values of x, and thus, obtain the required solutions.
The constant in the given quadratic equation is 3.
Write the pair of factors of the constant 3.
1 and 3
−1 and −3
It can be observed that the sum of the pair of factors 1 and 3 is equal to the coefficient of the middle term in the given quadratic equation, that is 4.
- Therefore, the left-hand side of the given quadratic equation can be factorised as (x+1)(x+3).
- Thus, the equation becomes (x+1)(x+3)=0.
- The equation (x+1)(x+3)=0 is true only when either x+1 is equal to 0, or x+3 is equal to 0.
- When x+1 is equal to 0, the value of x is equal to −1.
- When x+3 is equal to 0, the value of x is equal to −3.
- Thus, the required solutions are x=−3 and x=−1.
- The required solutions are x=−3 and x=−1.
HMH Algebra 2 Quadratic Equations Module 3 Exercise 3.3 answer key
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 155 Exercise 21 Answer
- The given equation is 7m⋅5m=875.Assume that there is a rectangular field which has an area equal to 875 square feet, and the ratio of its length and width is 7:5.
- The length and width of the field can be written as 7m and 5m respectively.
- Therefore, the area 875 square feet of the rectangular field would be the product of 7m and 5m, that is 7m⋅5m=875.
- Thus, the given equation can be used to model the situation where the area of a rectangular field is 875 square feet, and the ratio of its length and width is 7:5.
- The equation 7m⋅5m=875 can be used to model the situation where the ratio of the length and width of a rectangular field is 7:5, and its area is 875 square feet.
Quadratic Equations in HMH Algebra 2 (1st Edition, Module 3, Chapter 3, Exercise 3.3) Page 156 Exercise 22 Answer
The given quadratic function is f(x)=ax2+bx+c. Assume that a>0.
- When the value of x moves away from the x-coordinate of the vertex of the graph of the function f(x), the value of f(x) increases.
- This means that the graph of the function f(x)=ax2+bx+c forms a parabola opening upward when the leading coefficient a>0, and forms a U-shaped graph.
- Assume that a<0. When the value of x
- moves away from the x-coordinate of the vertex of the graph of the function f(x), the value of f(x) decreases.
- This means that the graph of the function f(x)=ax2+bx+c forms a parabola opening downward when the leading coefficient a<0, and forms an inverted U-shaped graph.
- Assume that a=0. When a is equal to 0, the given function becomes f(x)=bx+c.
- This means that when a=0, the function is linear and not quadratic.
- Therefore, the graph of the function is a straight line when a=0.
The graph of the quadratic function opens upward when a>0 because if the leading coefficient a is positive, then the value of f(x) increases as the value of x moves away from the x-coordinate of the vertex of f(x), and forms a U-shaped graph.
The graph of the quadratic function opens downward when a<0 because if the leading coefficient a is negative, then the value of f(x) decreases as the value of x moves away from the x
-coordinate of the vertex of f(x), and forms an inverted U-shaped graph.
When a=0, the given function is a linear function, and not a quadratic function. The graph of the function would be a straight line.