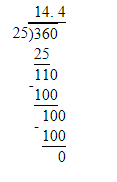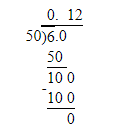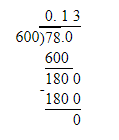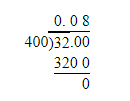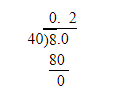Alekhya

HMH Algebra 2, Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.3 Absolute Value, Functions, Equations And Inequalities

Page 87 Problem 1 Answer

The absolute value expression in an absolute value inequality is generally of the form ∣ax+b∣.

An absolute value inequality can be solved either graphically or algebraically.

To solve an absolute value inequality graphically, the left and right sides of the inequality are assumed to be the functions f(x) and g(x) respectively.

Then, the two functions are graphed on the same coordinate grid. Finally, the intervals on the x-axis which satisfy the given inequality are observed to find the required solution.

To solve an absolute value inequality algebraically, first the operations of multiplication, division, addition, and subtraction are used to isolate the absolute value expression of the form ∣ax+b∣ on one side of the inequality.

Then, the constant on the other side of the inequality and the sign of inequality are used to rewrite the inequality as one or two linear inequalities.

Finally, the obtained inequalities are solved for x to find the required solution.

The solutions of an absolute value inequality can be obtained either graphically or algebraically.

The graphic method of solving an absolute value inequality involves assuming the left and right sides of the inequality to be the functions f(x) and g(x) respectively, graphing the two functions on the same coordinate grid, and finally, observing the intervals on the x-axis which satisfy the given inequality to find the required solution.

The algebraic method of solving an absolute value inequality involves isolating the absolute value expression on one side of the inequality, then using the constant on the other side of the inequality and the sign of inequality to rewrite the inequality as one or two linear inequalities, and finally, solving the obtained inequalities for x to find the required solution.

Page 87 Problem 2 Answer

The given table contains the possible solutions of the given absolute value inequality ∣x∣+2<5.

The question requires to determine which of the integers between −5 and 5 are solutions of the given inequality, and complete the given table by writing ‘yes’ or ‘no’ if the number is a solution of the given inequality.

Then, it is required to plot the solutions on the number line.

To complete the table and plot the solutions, use the given integers, substitute them in the given absolute value inequality, and checking whether the number satisfies the inequality or not.

Then, write ‘yes’ against the numbers that satisfy the inequality and are a solution, or write ‘no’ otherwise. Finally, plot the solutions on the given number line.

Substitute −5 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​∣−5∣+2<5

5+2<5

7<5

This inequality is not true. Therefore, x=−5 is not a solution of the given absolute value inequality.

Substitute −4 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​​∣−4∣+2<5

4+2<5

6<5

This inequality is not true. Therefore, x=−4 is not a solution of the given absolute value inequality.

Substitute −3 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​​∣−3∣+2<5

3+2<5

5<5

This inequality is not true. Therefore, x=−3 is not a solution of the given absolute value inequality.

Substitute −2 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​​∣−2∣+2<5

2+2<5

4<5

This inequality is true. Therefore, x=−2 is a solution of the given absolute value inequality.

Substitute −1 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​​∣−1∣+2<5

1+2<5

3<5

​This inequality is true. Therefore, x=−1 is a solution of the given absolute value inequality.

Substitute 0 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​​∣0∣+2<5

0+2<5

2<5

​This inequality is true. Therefore, x=0 is a solution of the given absolute value inequality.

Substitute 1 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​∣1∣+2<5

1+2<5

3<5

This inequality is true. Therefore, x=1 is a solution of the given absolute value inequality.

Substitute 2 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​​∣2∣+2<5

2+2<5

4<5

​This inequality is true. Therefore, x=2 is a solution of the given absolute value inequality.

Substitute 3 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​∣3∣+2<5

3+2<5

5<5

This inequality is not true. Therefore, x=3 is not a solution of the given absolute value inequality.

Substitute 4 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​∣4∣+2<5

4+2<5

6<5

​This inequality is not true. Therefore, x=4 is not a solution of the given absolute value inequality.

Substitute 5 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.

​∣5∣+2<5

5+2<5

7<5

This inequality is not true. Therefore, x=5 is not a solution of the given absolute value inequality.

Complete the given table by writing ‘yes’ against the numbers that are solutions of the given absolute value inequality, and ‘no’ against the numbers that are not solutions of the given absolute value inequality.

Plot the obtained solutions on the given number line.

The required solutions are the integers −2,−1,0,1,2.

The completed table is:

The required plot of the solutions on the number line is:

HMH Algebra 2 Volume 1 Module 2 Chapter 2 Exercise 2.3 Solutions

HMH Algebra 2, Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.3 Absolute Value, Functions, Equations And Inequalities Page 87 Problem 3 Answer

The given table contains the possible solutions of the given absolute value inequality ∣x∣+2>5.

The question requires to determine which of the integers between −5 and 5

are solutions of the given inequality, and complete the given table by writing ‘yes’ or ‘no’ if the number is a solution of the given inequality.

Then, it is required to plot the solutions on the number line.

To complete the table and plot the solutions, use the given integers, substitute them in the given absolute value inequality, and checking whether the number satisfies the inequality or not.

Then, write ‘yes’ against the numbers that satisfy the inequality and are a solution, or write ‘no’ otherwise.

Finally, plot the solutions on the given number line.

Substitute −5 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣−5∣+2>5

5+2>5

7>5

​This inequality is true. Therefore, x=−5 is a solution of the given absolute value inequality.

Substitute −4 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣−4∣+2>5

4+2>5

6>5

​This inequality is true. Therefore, x=−4 is a solution of the given absolute value inequality.

Substitute −3 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​∣−3∣+2>5

3+2>5

5>5

​This inequality is not true. Therefore, x=−3 is not a solution of the given absolute value inequality.

Substitute −2 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣−2∣+2>5

2+2>5

4>5

​This inequality is not true. Therefore, x=−2 is not a solution of the given absolute value inequality.

Substitute −1 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣−1∣+2>5

1+2>5

3>5

​This inequality is not true. Therefore, x=−1 is not a solution of the given absolute value inequality.

Substitute 0 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣0∣+2>5

0+2>5

2>5

​This inequality is not true. Therefore, x=0 is not a solution of the given absolute value inequality.

Substitute 1 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣1∣+2>5

1+2>5

3>5

​This inequality is not true. Therefore, x=1 is not a solution of the given absolute value inequality.

Substitute 2 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣2∣+2>5

2+2>5

4>5

​This inequality is not true. Therefore, x=2 is not a solution of the given absolute value inequality.

Substitute 3 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​∣3∣+2>5

3+2>5

5>5

​This inequality is not true. Therefore, x=3 is not a solution of the given absolute value inequality.

Substitute 4 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣4∣+2>5

4+2>5

6>5

​This inequality is true. Therefore, x=4 is a solution of the given absolute value inequality.

Substitute 5 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.

​​∣5∣+2>5

5+2>5

7>5

​This inequality is true. Therefore, x=5 is a solution of the given absolute value inequality.

Complete the given table by writing ‘yes’ against the numbers that are solutions of the given absolute value inequality, and ‘no’ against the numbers that are not solutions of the given absolute value inequality.

Plot the obtained solutions on the given number line.

The required solutions are the integers −5,−4,4,5.

The completed table is:

The required plot of the solutions on the number line is:

HMH Algebra 2 Module 2 Chapter 2 Exercise 2.3 Absolute Value Functions Answers

Page 87 Problem 4 Answer

The given equation is ∣x∣+2=5.

The question requires to write the solutions of the given equation, and then relate them to the solutions obtained in the previous two parts of this exercise.

Given that the integers between −5 and 5 that are the solutions of the absolute value inequality ∣x∣+2<5 are −2,−1,0,1,2, as calculated in part (a) of this exercise.

Given that the integers between −5 and 5 that are the solutions of the absolute value inequality ∣x∣+2>5 are −5,−4,4,5, as calculated in the previous part of this exercise.

To solve the equation, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, observe the solutions obtained in the previous two parts of this exercise, and relate the solutions of the given absolute value equation.

Subtract 2 from both sides of ∣x∣+2=5.

∣x∣=3

Rewriting the equation, the two equations obtained are x=−3 or x=3.

Thus, the two solutions of the given absolute value equation are x=−3 or x=3.

The integers solutions between −5 and 5 of the absolute value inequality ∣x∣+2<5 are −2,−1,0,1,2.

The integers solutions between −5 and 5 of the absolute value inequality ∣x∣+2>5 are −5,−4,4,5.

It can be observed that solutions contain all the integers between −5 and 5, except −3 and 3.

These remaining integers are the solutions of the absolute value equation ∣x∣+2=5.

Thus, the solutions of ∣x∣+2<5, ∣x∣+2>5, and ∣x∣+2=5 are distinct and not repeated, and each integer between −5 and 5 is the solution of either one of the two inequalities, or the equation.

The required solutions are x=−3 or x=3.

The solutions of ∣x∣+2<5 and ∣x∣+2>5 contain all the integers between −5 and 5, except −3 and 3, which are the solutions of the absolute value equation ∣x∣+2=5.

The solutions of ∣x∣+2<5, ∣x∣+2>5, and ∣x∣+2=5 are different and not repeated. Also, each integer between −5 and 5 is the solution of either one of the two inequalities, or the equation.

HMH Algebra 2, Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.3 Absolute Value, Functions, Equations And Inequalities Page 87 Problem 5 Answer

It is given that x is a real number.

The given absolute value inequalities are ∣x∣+2<5 and ∣x∣+2>5.

The question requires to graph all real solutions of the two absolute value inequalities on the given number lines.

Given that the solutions of the absolute value equation ∣x∣+2=5 are −3,3, as calculated in the previous part of this exercise.

To graph the solutions, observe the given solutions of the absolute value equation ∣x∣+2=5, form intervals using the two solutions, and check the value of the left-hand side of the inequalities for all real values.

Then, graph the solutions on the given number lines for both the inequalities.

The solutions of the absolute value equation ∣x∣+2=5 are −3,3.

When x<−3, the value of ∣x∣+2 is greater than 5, which does not satisfy the inequality ∣x∣+2<5.

When x=−3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2<5.

When x is between −3 and 3, both not included, the value of ∣x∣+2 is less than 5, which satisfies the inequality ∣x∣+2<5.

When x=3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2<5.

When x>3, the value of ∣x∣+2 is greater than 5, which does not satisfy the inequality ∣x∣+2<5.

Thus, the solution of the absolute value inequality ∣x∣+2<5 is −3<x<3.

Graph the obtained solutions of ∣x∣+2<5 on the given number line.

Consider the absolute value inequality ∣x∣+2>5.

When x<−3, the value of ∣x∣+2 is greater than 5, which satisfies the inequality ∣x∣+2>5.

When x=−3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2>5.

When x is between −3 and 3, both not included, the value of ∣x∣+2 is less than 5, which does not satisfy the inequality ∣x∣+2<5.

When x=3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2>5.

When x>3, the value of ∣x∣+2 is greater than 5, which satisfies the inequality ∣x∣+2>5.

Thus, the solution of the absolute value inequality ∣x∣+2>5 is x<−3 or x>3.

Graph the obtained solutions of ∣x∣+2>5 on the given number line.

The graph of all real solutions of ∣x∣+2<5 is:

The graph of all real solutions of ∣x∣+2>5 is:

HMH Algebra 2 Exercise 2.3 Absolute Value Equations And Inequalities Key

Page 88 Problem 6 Answer

The absolute value inequality ∣x∣+2>5 can be simplified as ∣x∣>3.

This equation is true for all values of x greater than 3, that is x>3, and for all values of x less than −3, that is x<−3.

There is no value of x that is within both the intervals x<−3 and x>3.

Therefore, the solution for the given inequality will be written as a disjunction, that is using the word “or”.

Thus, the solution for the inequality ∣x∣+2>5 is the disjunction x<−3 or x>3.

The solution for the given inequality will be written as a disjunction using the word “or” because there is no value of x lying within both the intervals x<−3 and x>3.

Therefore, the required solution for the inequality ∣x∣+2>5 is the disjunction x<−3 or x>3.

Page 88 Problem 7 Answer

The given absolute value inequalities are ∣x∣+2≤5 and ∣x∣+2≥5.

The question requires to describe the solutions of the given absolute value inequalities using inequalities that do not include an absolute value.

Given that the solutions of the absolute value equation ∣x∣+2=5 are −3,3, as calculated in the previous part of this exercise.

To graph the solutions, simplify the given absolute value inequalities, and check the value of the left-hand side of the inequalities for all real values using intervals.

Then, write the solutions for which the inequalities are satisfied as intervals which do not contain any absolute values.

The first given absolute value inequality ∣x∣+2≤5 can be simplified as ∣x∣≤3.

When x<−3, the value of ∣x∣ is greater than 3, which does not satisfy the inequality ∣x∣≤3.

When x=−3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≤3.

When x is between −3 and 3, both not included, the value of ∣x∣ is less than 3, which satisfies the inequality ∣x∣≤3.

When x=3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≤3.

When x>3, the value of ∣x∣ is greater than 3, which does not satisfy the inequality ∣x∣≤3.

Therefore, the solutions of the absolute value inequality ∣x∣+2≤5 are all the values between the integers −3 and 3, both included.

Thus, the solution of the absolute value inequality ∣x∣+2≤5 is the interval −3≤x≤3.

The second given absolute value inequality ∣x∣+2≥5 can be simplified as ∣x∣≥3.

When x<−3, the value of ∣x∣ is greater than 3, which satisfies the inequality ∣x∣≥3.

When x=−3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≥3.

When x is between −3 and 3, both not included, the value of ∣x∣ is less than 3, which does not satisfy the inequality ∣x∣≥3.

When x=3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≥3.

When x>3, the value of ∣x∣ is greater than 3, which satisfies the inequality ∣x∣≥3.

Therefore, the solutions of the absolute value inequality ∣x∣+2≥5 are all the values lesser than or equal to −3, or greater than and equal to 3.

Thus, the solution of the absolute value inequality ∣x∣+2≥5 is the disjunction x≤−3 or x≥3

HMH Algebra 2, Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.3 Absolute Value, Functions, Equations And Inequalities Page 88 Problem 8 Answer

The given absolute value inequality is ∣x−2∣−3<1.

The question requires to solve the given inequality graphically.

To solve the given inequality, let f(x) and g(x) be functions equal to left and right side of the given inequality respectively.

Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).

Next, write the transformations used to form f(x) from the parent absolute value function, take two points lying on the parent absolute value function, and use them to determine two points lying on f(x).

Next, plot the points and vertex, and use them to graph the function f(x) along with the constant function g(x).

Finally, write the intervals of x where the graph of f(x) is below the graph of g(x).

The given inequality is of the form f(x)<g(x).

Let f(x)=∣x−2∣−3 and g(x)=1.

The required solutions are the intervals on the x-axis where the graph of f(x) lies below the graph of g(x).

The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).

The vertex of f(x) is the point where (0,0) will be mapped using translations.

It can be observed that f(x) involves translations of h(x) by 2 units to the right and 3 units down.

Therefore, the vertex of f(x) is the point (0+2,0−3)=(2,−3).

The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.

The transformations used to form f(x)=∣x−2∣−3 from the parent absolute value function can be used to determine the two points lying on f(x).

The x-coordinate of the points lying on h(x) will be shifted 2 units to the right when mapped to f(x).

The y-coordinate of the points lying on h(x) will be moved down 3 units.

Therefore, the point (2,2) moves to (2+2,∣2∣−3)=(4,−1).

The point (−2,2) moves to (−2+2,∣2∣−3)=(0,−1).

Plot the vertex (2,−3) and the points (0,−1) and (4,−1), and then draw straight lines to plot the graph of f(x)=∣x−2∣−3.

Plot the function g(x)=1 as a horizontal line on the grid where f(x) is plotted.

The graph of f(x) lies below the graph of g(x) between x=−2 and x=6.

Thus, the solution of the inequality ∣x−2∣−3<1 is x>−2 and x<6.

The solution of the inequality ∣x−2∣−3<1 is x>−2 and x<6.

The solution is obtained using the graph:

Page 89 Problem 9 Answer

The inequality in part (A) changes from ∣x+3∣+1>4 to ∣x+3∣+1≥4.

Let f(x) be equal to ∣x+3∣+1, and g(x) be equal to 4.

The given inequality is of the form f(x)≥g(x).

The required solutions are the intervals on the x-axis where the graph of f(x) lies above the graph of g(x), or intersects it.From the graph, it can be observed that the graph of f(x)

lies above the graph of g(x) when x<−6 and x>0.

Also, the graph of f(x) intersects the graph of g(x) when x is equal to −6 or 0.

Thus, the solution of the inequality ∣x+3∣+1≥4 is x≤−6 or x≥0.

It can be observed that the solution x<−6 or x>0 of ∣x+3∣+1>4 changes to x≤−6 or x≥0 when the inequality changes to ∣x+3∣+1≥4.

The signs of inequality of the solution changed to include equal to.

The solution of the inequality ∣x+3∣+1≥4 is x≤−6 or x≥0.

The solution x<−6 or x>0 of ∣x+3∣+1>4 changes to x≤−6 or x≥0 when the inequality changes to ∣x+3∣+1≥4.

The signs of inequality of the solution are changed to include equal to in the solution of the new inequality.

HMH Algebra 2 Chapter 2 Exercise 2.3 Solutions For Absolute Value Functions

HMH Algebra 2, Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.3 Absolute Value, Functions, Equations And Inequalities Page 89 Problem 10 Answer

The graph of f(x) lies entirely above the graph of g(x).

This means that the graph of f(x) lies above the graph of g(x) for all values of x.

The solution of the inequality f(x)>g(x) is the interval where the graph of f(x) lies above the graph of g(x).

Therefore, the inequality f(x)>g(x) has infinitely many solutions lying in the interval (−∞,∞).

The solution of the inequality f(x)<g(x) is the interval where the graph of f(x) lies below the graph of g(x).

Since the graph of f(x) lies above the graph of g(x) for all values of x, the inequality f(x)<g(x) has no solution.

The inequality f(x)>g(x) has infinitely many solutions lying in the interval (−∞,∞).

The inequality f(x)<g(x) has no solution.

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities

Page 77 Problem 1 Answer

The absolute value expression in an absolute value equation is generally of the form ∣ax+b∣.

To solve an absolute value equation, first, the operations of multiplication, division, addition, and subtraction are used to isolate the absolute value expression ∣ax+b∣  on one side of the equation.

If the absolute value expression ∣ax+b∣  is equal to a negative number, then the equation cannot be solved and there is no solution.

If the absolute value expression ∣ax+b∣ is equal to 0, then the equation can be written as the linear equation ax+b=0, which can then be solved to obtain the only solution of the absolute value equation.

If the absolute value expression ∣ax+b∣ is equal to a positive number, then the equation can be written as a disjunction of two linear equations, which can then be solved to obtain the two solutions of the absolute value equation.

An absolute value equation can be solved by isolating the absolute value expression in the equation on one side of the equation, and determining whether the equation can be solved.

Then, the equation can be written as either one linear equation or a disjunction of two linear equations, which can be solved to obtain the required solutions.

Page 77 Problem 2 Answer

The given absolute value equation is 2∣x−5∣−4=2. The steps to solve the equation graphically are given.

The question requires to solve the given equation.

To solve the given equation, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.

Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them on the vertex to determine the vertex of f(x).

Next, write the coefficient of the expression with the independent variable in the given function to write the stretch or compress required.

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on f(x) using the transformations used to form f(x) from h(x).

Next, plot the points and vertex, and use them to graph the function f(x)  along with the constant function g(x), and mark the points of intersection.

Finally, write the x-coordinates of those points to obtain the required solutions.

Let f(x)=2∣x−5∣−4 and g(x)=2.

The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).

The vertex of f(x) is the point where (0,0) will be mapped using translations.

It can be observed that f(x) involves translations of h(x) by 5 units to the right and 4 units down.

Therefore, the vertex of f(x) is the point (0+5,0−4)=(5,−4).

The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.

Compare the function f(x) to f(x)=a∣x−h∣−k, and write the value of the constant a.

a=2

Since ∣a∣=2, that is ∣a∣>1, the graph of f(x) will involve a vertical stretch of the parent absolute value function by a factor 2.

The transformations used to form f(x)=2∣x−5∣−4 from the parent absolute value function can be used to determine the two points lying on f(x).

The x-coordinate of the points lying on h(x) will be shifted 5 units to the right when mapped to f(x).

The y-coordinate of the points lying on h(x) will be vertically stretched by a factor of 2, and then moved down 4 units.

Therefore, the point (2,2) moves to (2+5,2⋅∣2∣−4)=(7,0).

The point (−2,2) moves to (−2+5,2⋅∣2∣−4)=(3,0).

Plot the vertex (5,−4) and the points (7,0) and (3,0), and then draw straight lines to plot the graph of f(x)=2∣x−5∣−4.

Plot the function g(x)=2 as a horizontal line on the grid where f(x) is plotted and mark the points of intersection of f(x) and g(x).

It can be observed that the points of intersection are (2,2) and (8,2).

Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is 2 and 8.

The solutions of the given equation are the x-coordinates of the points of intersection, that is 2 and 8.

Page 77 Problem 3 Answer

The given function is 2∣x−5∣−4=2. Let f(x) be equal to 2∣x−5∣−4, and g(x) be equal to 2.

The points of intersection of the graphs of the two functions are (2,2) and (8,2), as calculated in the previous part of this exercise.

Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is 2 and 8.

This can be written as the disjunction x equal to 2 or x equal to 8.

The required solution of the given equation is the disjunction x=2 or x=8.

HMH Algebra 2 Module 2 Chapter 2 Exercise 2.2 Solutions

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 77 Problem 4 Answer

Assume an absolute value equation ∣ax+b∣=c.The two equations formed by rewriting the equation are ax+b equal to −c or ax+b equal to c.

The two equations formed have one solution each because they are linear equations.

Therefore, the absolute value equation has two solutions.

The absolute value equation ∣ax+b∣=c cannot have three or four solutions because the expression inside the absolute value parentheses is a linear expression, that is an expression with degree 1.

Therefore, the two equations formed are linear equations which one possible solution each.

Since most absolute value equations have a linear expression of the form ax+b inside the absolute value parentheses, most absolute value equations are expected to have two solutions.

Most absolute value equations are expected to have two solutions because most absolute value equations have a linear expression of the form ax+b inside the absolute value parentheses.

Most absolute value equations generally do not have three or four solutions because the two equations formed by rewriting the common absolute value equation ∣ax+b∣=c are linear equations with only one solution each.

Page 77 Problem 5 Answer

Assume an absolute value equation ∣ax+b∣=c.If c is equal to a negative number, then the equation cannot be solved because the absolute value expression ∣ax+b∣ cannot be equal to the negative number c.

Therefore, an absolute value equation will have no solution if the equation is of the form ∣ax+b∣=c, where c<0.

The graph of an absolute value equation with no solution does not contain any points because there is no point which satisfies the equation.

If c is equal to 0, then the equation can be written as the linear equation ax+b=c, which has only one solution.

Therefore, an absolute value equation will have only one solution if the equation is of the form ∣ax+b∣=0.

The graph of an absolute value equation with one solution is a straight line because it can be written as a linear equation.

An absolute value equation will have no solution if the equation is of the form ∣ax+b∣=c, where c<0.

The graph of such an absolute value equation does not contain any points.

An absolute value equation will have only one solution if the equation is of the form ∣ax+b∣=0.

The graph of such an absolute value equation is a straight line.

Page 78 Problem 6 Answer

The given equation is 1/2∣x+2∣=10.

The question requires to solve the given equation algebraically, and then graph its solutions on the number line.

To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Multiply both sides of 1/2∣x+2∣=10 by 2.

∣x+2∣=20

Rewriting the equation, the two equations obtained are x+2=20 or x+2=−20.

Subtract 2 from both sides of x+2=20.

x=18 Subtract 2 from both sides of x+2=−20.

x=−22

Thus, the two solutions are x=−22 or x=18.

Graph the obtained solutions on the given number line.

The required solutions are x=−22 or x=18.

The required graph of the solutions on the number line is:

Page 77 Problem 7 Answer

The given equation is −2∣3x−6∣+5=1.

The question requires to solve the given equation algebraically, and then graph its solutions on the number line.

To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Subtract 5 from both sides of the equation, and divide both sides by −2.​

−2∣3x−6∣=−4

∣3x−6∣=−4/−2

∣3x−6∣=2​

Rewriting the equation, the two equations obtained are 3x−6=2 or 3x−6=−2.

Add 6 on both sides of 3x−6=2 and divide both sides by 3.​

3x=8

x=8/3

Add 6 on both sides of 3x−6=−2 and divide both sides by 3.​

3x=4

x=4/3

Thus, the two solutions are x=4/3 or x=8/3.

Graph the obtained solutions on the given number line.

The required solutions are x=4/3 or x=8/3.

The required graph of the solutions on the number line is:

Absolute Value Functions And Inequalities Exercise 2.2 Answers HMH Algebra 2

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 78 Problem 8 Answer

The given equation is 3∣4x−5∣−2=19.

The question requires to solve the given equation algebraically, and then graph its solutions on the number line.

To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Add 2 on both sides of the equation, and divide both sides by 3.

​3∣4x−5∣=21

∣4x−5∣=7

Rewriting the equation, the two equations obtained are 4x−5=7 or 4x−5=−7.

Add 5 on both sides of 4x−5=7 and divide both sides by 4.

​4x=12

x=3

​Add 5 on both sides of 4x−5=−7 and divide both sides by 4.

​4x=−2

x=−2/4

x=−1/2

Thus, the two solutions are x=−1/2 or x=3.

Graph the obtained solutions on the given number line.

The required solutions are x=−1/2 or x=3.

The required graph of the solutions on the number line is:

Page 79 Problem 9 Answer

The given equation is 9∣4/3 x−2∣+7=7.

The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.

Then, it is required to write “no solution” if there is no solution, or solve the equation if it has a solution.

To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not.

Then, rewrite the equation, and solve the equation for x to find the solution.

Subtract 7 from both sides of the equation, and divide both sides by 9.​

9∣4/3x−2∣=0

∣4/3x−2∣=0​

The absolute value expression ∣4/3x−2∣ is equal to the non-negative number 0.

Thus, the equation can be solved.

Rewriting the equation, the equation obtained is 4/3

x−2=0.

Add 2 on both sides of 4/3x−2=0 and multiply both sides by 3/4.​

4/3

x=2

x=6/4

x=3/2

Thus, the solution is x=3/2.

Yes, the given equation can be solved. The required solution is x=3/2.

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 79 Problem 10 Answer

The given equation is 3/5∣2x−4∣−3=−3.

The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.

Then, it is required to write “no solution” if there is no solution, or solve the equation if it has a solution.

To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not.

Then, rewrite the equation, and solve the equation for x to find the solution.

Add 3 on both sides of the equation, and multiply both sides by 5/3.​

3/5

∣2x−4∣=0

∣2x−4∣=0

The absolute value expression ∣2x−4∣ is equal to the non-negative number 0.

Thus, the equation can be solved.

Rewriting the equation, the equation obtained is 2x−4=0.

Add 4 on both sides of 2x−4=0 and divide both sides by 2.

2x=4

x=2​

Thus, the solution is x=2.

Yes, the given equation can be solved. The required solution is x=2.

Page 81 Exercise 1 Answer

The given absolute value equation is 2∣x+1∣+5=9.

The question requires to solve the given absolute value equation graphically.

To solve the given equation graphically, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.

Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).

Next, write the transformations used to form the points on the function f(x) from the points on the parent absolute value function, and use two points lying on the parent absolute value function to determine two points on f(x).

Next, plot the points and vertex, and use them to graph the function f(x)  along with the constant function g(x), and mark the points of intersection.

Finally, write the x-coordinates of those points as a disjunction to obtain the required solution.

Let f(x)=2∣x+1∣+5 and g(x)=9.

The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).

The vertex of f(x) is the point where (0,0) will be mapped using translations.

It can be observed that f(x) involves translations of h(x) by 1 unit to the left and 5 units up.

Therefore, the vertex of f(x) is the point (0−1,0+5)=(−1,5).

The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣. Compare the function f(x) to f(x)=a∣x+h∣+k, and write the value of the constant a.

a=2

Since ∣a∣=2, that is ∣a∣>1, the graph of f(x) will involve a vertical stretch of the parent absolute value function by a factor 2.

The transformations used to form f(x)=2∣x+1∣+5 from the parent absolute value function can be used to determine the two points lying on f(x).

The x-coordinate of the points lying on h(x) will be shifted 1 unit to the left when mapped to f(x).

The y-coordinate of the points lying on h(x) will be vertically stretched by a factor of 2, and then moved up 5 units.

Therefore, the point (2,2) moves to (2−1,2⋅∣2∣+5)=(1,9).

The point (−2,2) moves to (−2−1,2⋅∣2∣+5)=(−3,9).

Plot the vertex (−1,5) and the points (−3,9) and (1,9), and then draw straight lines to plot the graph of f(x)=2∣x+1∣+5.

Plot the function g(x)=9 as a horizontal line on the grid where f(x) is plotted and mark the points of intersection of f(x) and g(x).

It can be observed that the points of intersection are (−3,9) and (1,9).

Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is −3 and 1. This can be written as the disjunction x=−3 or x=1.

The required solution of the given equation is the disjunction x=−3 or x=1.

HMH Algebra 2 Chapter 2 Exercise 2.2 Solutions Guide

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 81 Exercise 2 Answer

The given absolute value equation is −2∣x+5∣+4=2.

The question requires to solve the given absolute value equation graphically.

To solve the given equation graphically, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.

Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).

Next, write the transformations used to form the points on the function f(x) from the points on the parent absolute value function, and use two points lying on the parent absolute value function to determine two points on f(x).

Next, plot the points and vertex, and use them to graph the function f(x) along with the constant function g(x), and mark the points of intersection.

Finally, write the x-coordinates of those points as a disjunction to obtain the required solution.

Let f(x)=−2∣x+5∣+4 and g(x)=2.

The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).

The vertex of f(x) is the point where (0,0) will be mapped using translations.

It can be observed that f(x) involves translations of h(x) by 5 units to the left and 4 units up.

Therefore, the vertex of f(x) is the point (0−5,0+4)=(−5,4).

The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.

Compare the function f(x) to f(x)=a∣x+h∣+k, and write the value of the constant a.

a=−2

Since ∣a∣=2, that is ∣a∣>1, the graph of f(x) will involve a vertical stretch of the parent absolute value function by a factor 2.

Since a=−2, that is a<0, the graph of f(x) will involve a reflection of the parent absolute value function about the x-axis.

The transformations used to form f(x)=−2∣x+5∣+4 from the parent absolute value function can be used to determine the two points lying on f(x).

The x-coordinate of the points lying on h(x) will be shifted 5 units to the left when mapped to f(x).

The y-coordinate of the points lying on h(x) will be reflected about the x-axis, vertically stretched by a factor of 2, and then moved up 4 units.

Therefore, the point (2,2) moves to (2−5,−2⋅∣2∣+4)=(−3,0).

The point (−2,2) moves to (−2−5,−2⋅∣2∣+4)=(−7,0).

Plot the vertex (−5,4) and the points (−3,0) and (−7,0), and then draw straight lines to plot the graph of f(x)=−2∣x+5∣+4.

Plot the function g(x)=2 as a horizontal line on the grid where f(x) is plotted and mark the points of intersection of f(x) and g(x).

It can be observed that the points of intersection are (−6,2) and (−4,2).

Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is −6 and −4. This can be written as the disjunction x=−6 or x=−4.

The required solution of the given equation is the disjunction x=−6 or x=−4.

Page 81 Exercise 3 Answer

The given absolute value equation is ∣3/2(x−2)∣+3=2.

The question requires to solve the given absolute value equation graphically.

To solve the given equation graphically, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.

Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).

Next, write the transformations used to form the points on the function f(x) from the points on the parent absolute value function, and use two points lying on the parent absolute value function to determine two points on f(x).

Finally, plot the points and vertex, use them to graph the function f(x) along with the constant function g(x), and check the points of intersection to determine the solution if any.

Let f(x)=∣3/2(x−2)∣+3 and g(x)=2.

The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).

The vertex of f(x) is the point where (0,0) will be mapped using translations.

It can be observed that f(x) involves translations of h(x) by 2 units to the right and 3 units up.

Therefore, the vertex of f(x) is the point (0+2,0+3)=(2,3).

The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.

Compare the function f(x) to f(x)=∣1/b(x−h)∣+k, and write the value of the constant b.

​1/b=3/2

b=2/3

Since ∣b∣=2/3, that is 0<∣b∣<1, the graph of f(x) will involve a horizontal stretch of the parent absolute value function by a factor 2/3.

The transformations used to form f(x)=∣3/2(x−2)∣+3 from the parent absolute value function can be used to determine the two points lying on f(x).

The x-coordinate of the points lying on h(x) will be horizontally stretched by a factor of 2/3, and then shifted 2 units to the right when mapped to f(x).

The y-coordinate of the points lying on h(x) will be moved up 3 units.

Therefore, the point (2,2) moves to (2/3⋅2+2,∣2∣+3)=(10/3,5).

The point (−2,2) moves to (2/3⋅(−2)+2,∣2∣+3)=(2/3,5).

Plot the vertex (2,3) and the points (2/3,5) and (10/3,5), and then draw straight lines to plot the graph of f(x)=∣3/2(x−2)∣+3.

Plot the function g(x)=2 as a horizontal line on the grid where f(x) is plotted.

It can be observed that the graphs do not intersect at any point.

Therefore, there is no value of x for which f(x) is equal to g(x), that is for which ∣3/2(x−2)∣+3=2.

Thus, the given equation has no solution.

The given absolute value equation has no solution.

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 81 Exercise 4 Answer

The given equation is ∣2x∣=3.

The question requires to solve the given equation algebraically, and then graph its solutions on the number line.

To solve the equation and graph the solutions, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Rewriting the given equation, the two equations obtained are 2x=3 or 2x=−3.

Divide both sides of 2x=3 by 2.

​2x/2=3/2

x=1.5

​Divide both sides of 2x=−3 by 2.

​2x/2=−3/2

x=−1.5

Thus, the two solutions are x=−1.5 or x=1.5.

Graph the obtained solutions on the given number line.

The required solutions are x=−1.5 or x=1.5.

The required graph of the solutions on the number line is:

Page 81 Exercise 5 Answer

The given equation is ∣1/3x+4∣=3.

The question requires to solve the given equation algebraically, and then graph its solutions on the number line.

To solve the equation and graph the solutions, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Rewriting the given equation, the two equations obtained are 1/3x+4=3 or 1/3x+4=−3.

Subtract 4 from both sides of 1/3x+4=3, and multiply both sides by 3.​

1/3

x=−1

x=−3​

Subtract 4 from both sides of 1/3x+4=−3, and multiply both sides by 3.

1/3

x=−7

x=−21

Thus, the two solutions are x=−21 or x=−3.

Graph the obtained solutions on the given number line.

The required solutions are x=−21 or x=−3.

The required graph of the solutions on the number line is:

Page 82 Exercise 6 Answer

The given equation is 3∣2x−3∣+2=3.

The question requires to solve the given equation algebraically, and then graph its solutions on the number line.

To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Subtract 2 from both sides of the equation, and divide both sides by 3.

​3∣2x−3∣=1

∣2x−3∣=1/3

Rewriting the equation, the two equations obtained are 2x−3=1/3 or 2x−3=−1/3.

Add 3 on both sides of 2x−3=1/3 and divide both sides by 2.

​2x=1/3+3

2x=10/3

x=5/3

Add 3 on both sides of 2x−3=−1/3 and divide both sides by 2.

​2x=−1/3+3

2x=8/3

x=4/3

Thus, the two solutions are x=4/3 or x=5/3.

Graph the obtained solutions on the given number line.

The required solutions are x=4/3 or x=5/3.

The required graph of the solutions on the number line is:

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 82 Exercise 7 Answer

The given equation is −8∣−x−6∣+10=2.

The question requires to solve the given equation algebraically, and then graph its solutions on the number line.

To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Subtract 10 from both sides of the equation, and divide both sides by −8.

​−8∣−x−6∣=−8

∣−x−6∣=−8/−8

∣−x−6∣=1​

Rewriting the equation, the two equations obtained are −x−6=1 or −x−6=−1.

Add 6 on both sides of −x−6=1, and multiply both sides by −1.

−x=7

−x(−1)=7(−1)

x=−7

​Add 6 on both sides of −x−6=−1, and multiply both sides by −1.

​−x=5

−x(−1)=5(−1)

x=−5

Thus, the two solutions are x=−5 or x=−7.

Graph the obtained solutions on the given number line.

The required solutions are x=−5 or x=−7.

The required graph of the solutions on the number line is:

Page 82 Exercise 8 Answer

The given equation is −3∣x−3∣+3=6.

The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.

Then, it is required to write “no solution” if it cannot be solved, or solve the equation and graph the solution(s) if it can be solved.

To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not to determine if the equation can be solved.

Subtract 3 from both sides of the equation, and divide both sides by −3.

​−3∣x−3∣=3

∣x−3∣=3/−3

∣x−3∣=−1

The absolute value expression ∣x−3∣ cannot be equal to the negative number −1.

Thus, the equation cannot be solved, and has no solution.

No, the equation cannot be solved, and has no solution.

Module 2 Chapter 2 Absolute Value And Equations Problems HMH

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 82 Exercise 9 Answer

The given equation is 2(∣x+4∣+3)=6.

The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.

Then, it is required to write “no solution” if it cannot be solved, or solve the equation and graph the solution(s) if it can be solved.

To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not.

Then, rewrite the equation, and solve the equation for x to find the solution. Finally, graph the solution on the given number line.

Divide both sides of the equation 2(∣x+4∣+3)=6 by 2, and then subtract 3 from both sides.

​∣x+4∣+3=3

∣x+4∣=0

The absolute value expression ∣x+4∣ is equal to the non-negative number 0.

Thus, the equation can be solved.

Rewriting the equation, the equation obtained is x+4=0.

Subtract 4 from both sides of x+4=0.

x=−4

Thus, the solution is x=−4.

Graph the obtained solution on the given number line.

Yes, the given equation can be solved. The required solution is x=−4.

The required graph of the solution on the number line is:

Page 82 Exercise 10 Answer

The given equation is 7∣1/2x+31/2∣−2=5.

The question requires to solve the given absolute value equation.

To solve the equation, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.

Next, mark the solutions on the given number line.

Add 2 on both sides of the equation 7∣1/2x+31/2∣−2=5, rewrite the mixed fraction as an improper fraction, and divide both sides by 7.

​7∣1/2x+31/2∣=7

7∣1/2x+7/2∣=7

∣1/2x+7/2∣=1

​Rewriting the equation, the two equations obtained are 1/2x+7/2=1 or 1/2x+7/2=−1.

Subtract 7/2 from both sides of 1/2x+7/2=1 and multiply both sides by 2.

​1/2x=1−7/2

1/2x=−5/2

x=−5​

Subtract 7/2 from both sides of 1/2x+7/2=−1 and multiply both sides by 2.

​1/2x=−1−7/2

1/2x=−9/2

x=−9

Thus, the two solutions are x=−9 or x=−5.

Graph the obtained solutions on the given number line.

The required solutions are x=−9 or x=−5.

The required graph of the solutions on the number line is:

Page 83 Exercise 11 Answer

The given equation is −5∣−3x+2∣−2=−2.

The question requires to solve the given absolute value equation.

To solve the equation, isolate the absolute value on one side of the equation, rewrite the equation, and solve the equation for x to find the solution.

Next, mark the solution on the given number line.

Add 2 on both sides of the equation −5∣−3x+2∣−2=−2, and then divide both sides by −5.

​−5∣−3x+2∣=0

∣−3x+2∣=0

Rewriting the equation, the equation obtained is −3x+2=0.

Add 3x on both sides of −3x+2=0, and divide both sides by 3.

2=3x

2/3=x

Thus, the solution is x=2/3.

Graph the obtained solution on the given number

The required solution is x=2/3.

The solution can be represented on the given number line as:

Page 81 Exercise 12 Answer

It is given that the depth of the river bottom in feet is given by the absolute value function d(h)=1/5

∣h−240∣−48, where h is the horizontal distance from the left-hand shore in feet. Also, it is given that buoys are to be placed where the river bottom is 30 ft below the surface.

The question requires to determine the horizontal distance from the left-hand shore where the buoys should be placed.

To determine the horizontal distances, substitute the depth of the river bottom as −30

ft in the given absolute value function, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x

to find the solutions, and thus, the horizontal distances from the left-hand shore where the buoys should be placed.

The depth of the river bottom is 30 ft when d(h)=−30.

Substitute −30 for d(h) in d(h)=1/5∣h−240∣−48, add 48 on both sides, and multiply both sides by 5.

​−30=1/5∣h−240∣−48

18=1/5∣h−240∣

90=∣h−240∣

Rewriting the equation, the two equations obtained are h−240=90 or h−240=−90.

Add 240 on both sides of h−240=90.

h=330 Add 240 on both sides of h−240=−90.

h=150

Thus, the buoys should be placed 150 feet and 330 feet away from the left-hand shore.

The buoys should be placed 150 feet and 330 feet away from the left-hand shore.

Page 84 Exercise 13 Answer

Subtract 2 from both sides of the equation −1/2∣3x−3∣+2=1, and multiply both sides by −2.

−1/2

∣3x−3∣=−1

∣3x−3∣=2

​Rewriting the equation, the two equations obtained are 3x−3=−2 or 3x−3=2.

Add 3 on both sides of 3x−3=−2 and divide both sides by 3.

​3x=1

x=1/3

Add 3 on both sides of 3x−3=2 and divide both sides by 3.

​3x=5

x=5/3

Therefore, the two solutions are x=1/3 or x=5/3.Thus, the values of x satisfying the given equation are option (A) x=5/3and option (C) x=1/3.

The given equation is written as ∣3x−3∣=2 where the absolute value expression is isolated.

When x is equal to −5/3, the value of ∣3(−5/3)−3∣ is ∣−5−3∣=8 and not 2. Thus, option (B) is incorrect.

When x is equal to −1/3, the value of ∣3(−1/3)−3∣ is ∣−1−3∣=4 and not 2. Thus, option (D) is incorrect.

When x is equal to 3, the value of ∣3(3)−3∣ is ∣9−3∣=6 and not 2. Thus, option (E) is incorrect.

When x is equal to −3, the value of ∣3(−3)−3∣ is ∣−9−3∣=12 and not 2. Thus, option (F) is incorrect.

When x is equal to 1, the value of ∣3(1)−3∣ is ∣3−3∣=0 and not 2. Thus, option (G) is incorrect.

When x is equal to −1, the value of ∣3(−1)−3∣ is ∣−3−3∣=6 and not 2. Thus, option (H) is incorrect.

The values of x satisfying the given equation are option (A) x=5/3 and option (C) x=1/3.

HMH Algebra 2 Chapter 2 Absolute Value And Inequalities Solutions

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.2 Absolute Value, Functions, Equations And Inequalities Page 84 Exercise 14 Answer

The given equation is −3∣x−4∣−4=3. The incorrect solution for solving the given equation is given.The given solution involves the equation ∣x−4∣=−7/3.

The absolute value ∣x−4∣ cannot be equal to the negative number −7/3.

Therefore, the equation cannot be solved and has no solution.

Thus, the error in the solution is that the equation ∣x−4∣=−7/3 cannot be rewritten as the given disjunction of the two linear equations.

The correct answer is that the given equation cannot be solved and has no solution.

The error in the solution is that the equation ∣x−4∣=−7/3  is never true, and cannot be rewritten as the given disjunction of the two linear equations.

There is no correct solution because the given equation cannot be solved, and thus, has no solution.

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities

Page 64 Problem 1 Answer

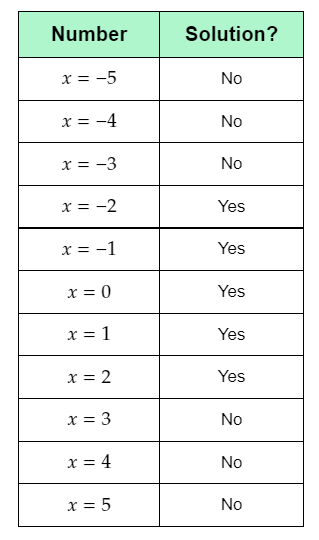
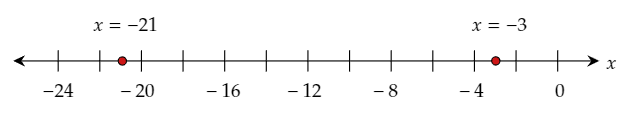
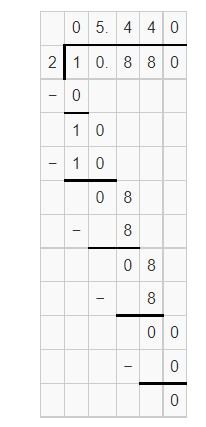
The given equation is r+9=7.

The question requires to solve the given equation.

To find the required value, use subtraction in the given equation to isolate the variable r on one side of the equation.

Subtract 9 from both sides of the given equation, and combine the terms.

​r+9−9=7−9

r=−2

Thus, the solution is r=−2.

The required solution is r=−2.

Page 64 Problem 2 Answer

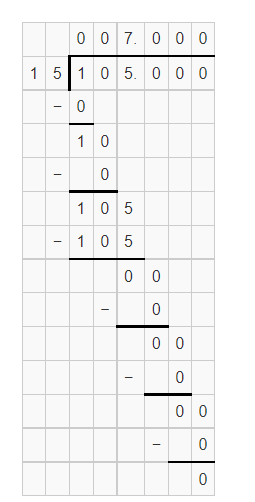
The given equation is w/4=−3.

The question requires to solve the given equation.

To find the required value, use multiplication in the given equation to isolate the variable w on one side of the equation.

Multiply both sides of w/4=−3 by 4.

​W/4(4)=−3(4)

w=−12

Thus, the solution is w=−12.

The required solution is w=−12.

Page 64 Problem 3 Answer

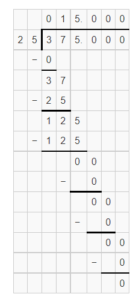
The given equation is 10b=14.

The question requires to solve the given equation.

To find the required value, use division in the given equation to isolate the variable b on one side of the equation.

Divide both sides of 10b=14 by 10.

​10b/10=14/10

b=1.4

Thus, the solution is b=1.4.

The required solution is b=1.4.

HMH Algebra 2 Module 2 Chapter 2 Exercise 2.1 Solutions

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 64 Problem 4 Answer

The given equation is 3y=2(x−3).

The question requires to determine the slope and y-intercept.

To determine the required slope and y-intercept, isolate the variable y on one side of the equation using division to rewrite it in slope-intercept form.

Then, compare the obtained equation with the slope-intercept form y=mx+b to find the values of m and b, and thus, the required slope and y-intercept.

Multiply the terms in the equation 3y=2(x−3), and then divide both sides by 3.

​3y=2x−6

3y/3=2x−6/3

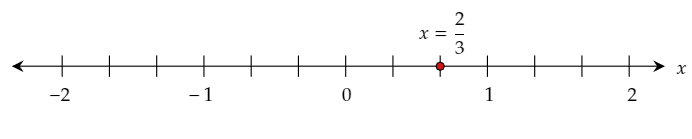
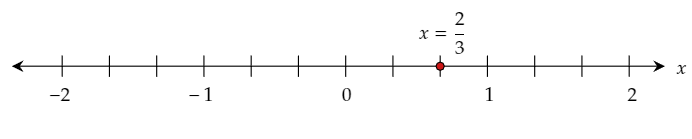
y=2/3

x−2…………(1)

​Compare equation (1) with the slope-intercept form y=mx+b, and write the values of m and b.​

m=2/3

b=−2

Thus, the slope and y-intercept of the given equation are 2/3 and −2respectively.

The required slope and y-intercept are 2/3 and −2 respectively.

Page 64 Problem 5 Answer

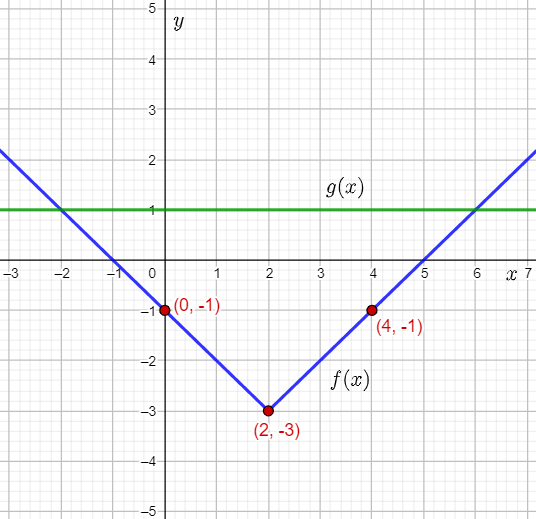
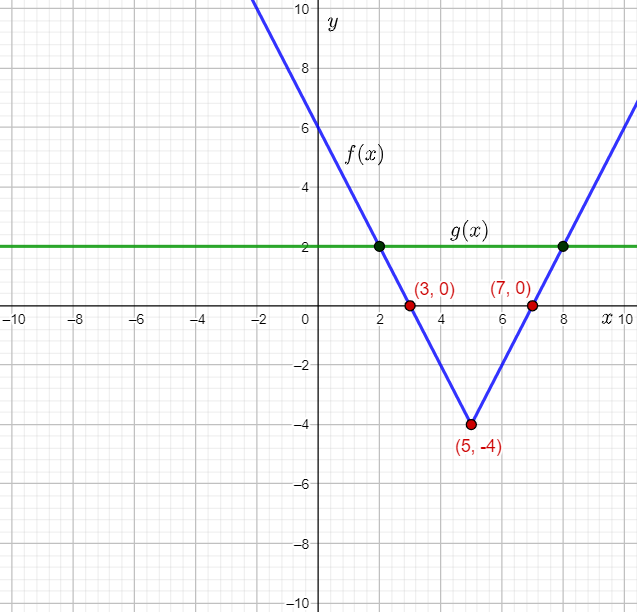
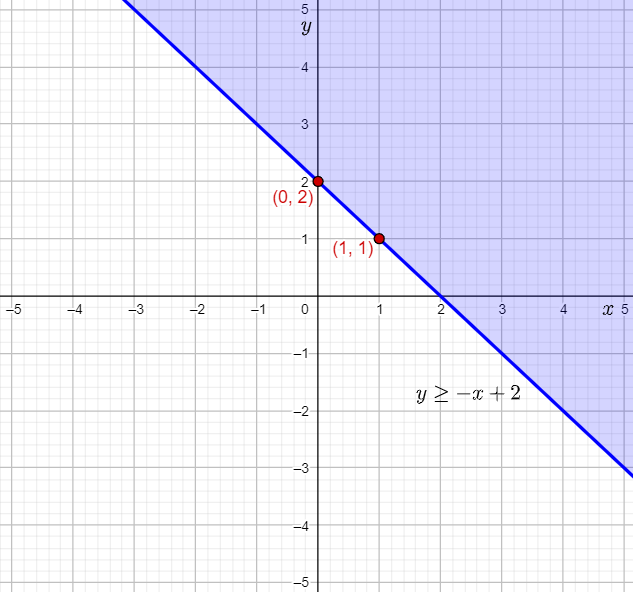
The given inequality is y≥−x+2.

The question requires to graph and label the given inequality on the coordinate plane.

To graph, the inequality, write the equation for the boundary line of the given inequality, and compare it to the slope-intercept form y=mx+b to find the values of m and b, and thus, find the slope and y-intercept of the boundary line.

Then, use the slope and y-intercept to find two points lying on the boundary line.

Next, use an arbitrary point to determine the direction in which the graph of the inequality will be shaded.

Finally, use the obtained points to graph and label the given inequality on the coordinate plane.

The equation of the boundary line for the inequality y≥−x+2 is: y=−x+2

Compare the equation of the boundary line with the slope-intercept form y=mx+b, and write the values of m and b.​

m=−1

b=2

Therefore, the slope and y-intercept are −1 and 2 respectively.

Thus, the boundary line passes through (0,2).

The slope of the boundary line is −1, that is −1/1.

The point (0,2) lies on the boundary line.

Therefore, a second point lying on the boundary line is 0+1,2−1)=(1,1).

Assume the arbitrary point (0,0).

Substitute 0 for x and 0 for y in the inequality y≥−x+2.

0≥−0+2

0≥2

Therefore, the point (0,0) does not satisfy the inequality y≥−x+2.

Thus, the inequality y≥−x+2 will be shaded away from the  the origin (0,0).

Graph the y-intercept of (0,2), plot the second point (1,1), draw a solid line through the points, and shade the region above the line, that is away from the origin (0,0).

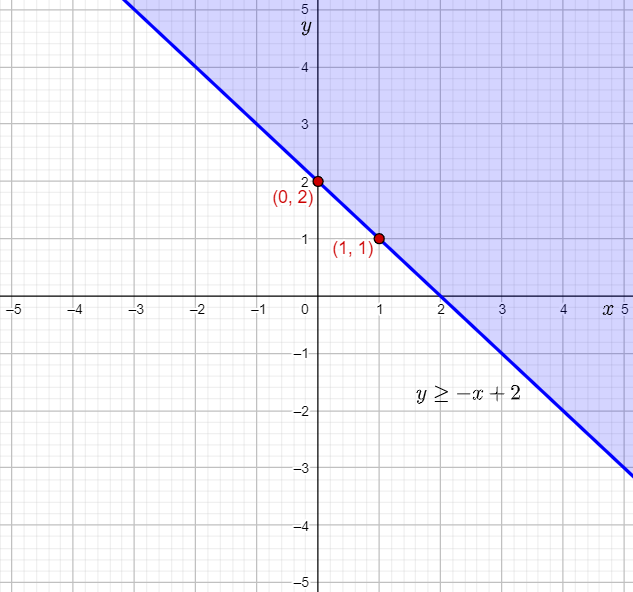
Then, label the inequality graphed.

The required labelled graph is

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 64 Problem 6 Answer

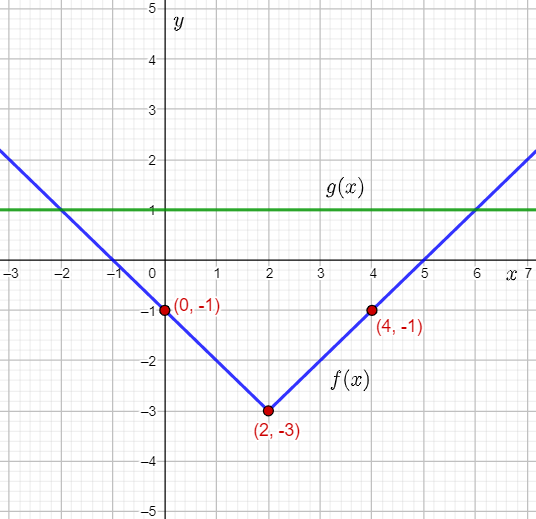
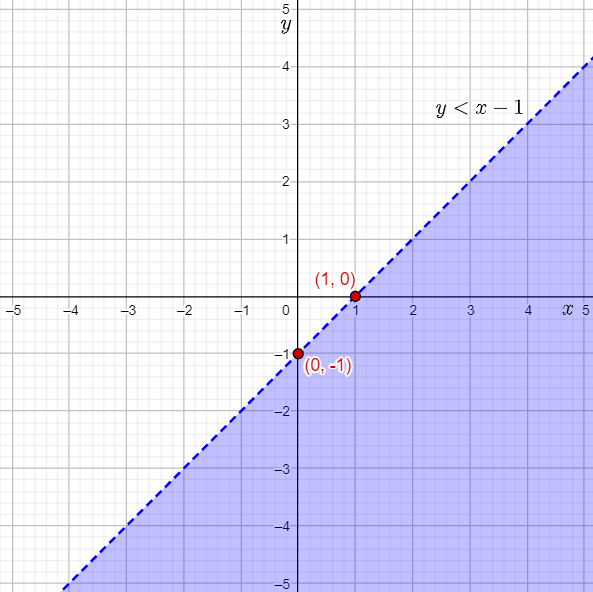
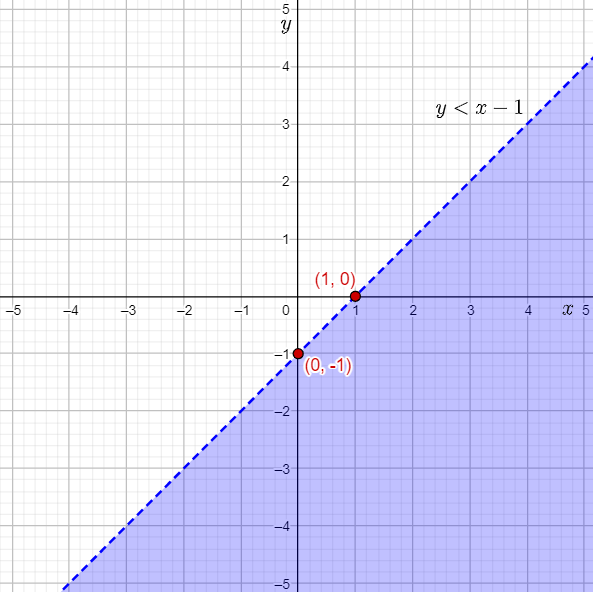
The given inequality is y<x−1.

The question requires to graph and label the given inequality on the coordinate plane.

To graph the inequality, write the equation for the boundary line of the given inequality, and compare it to the slope-intercept form y=mx+b to find the values of m and b, and thus, find the slope and y-intercept of the boundary line.

Then, use the slope and y-intercept to find two points lying on the boundary line.

Next, use an arbitrary point to determine the direction in which the graph of the inequality will be shaded.

Finally, use the obtained points to graph and label the given inequality on the coordinate plane.

The equation of the boundary line for the inequality y<x−1 is: y=x−1

Compare the equation of the boundary line with the slope-intercept form y=mx+b, and write the values of m and b.

​m=1

b=−1

Therefore, the slope and y-intercept are 1 and −1 respectively.

Thus, the boundary line passes through (0,−1).

The slope of the boundary line is 1, that is 1/1.

The point (0,−1) lies on the boundary line.

Therefore, a second point lying on the boundary line is 0+1,−1+1)=(1,0).

Assume the arbitrary point (0,0).

Substitute 0 for x and 0 for y in the inequality y<x−1.

​0<0−1

0<−1

Therefore, the point (0,0) does not satisfy the inequality y<x−1.

Thus, the inequality y<x−1 will be shaded away from the origin (0,0).

Graph the y-intercept of (0,−1), plot the second point (1,0), draw a dashed line through the points, and shade the region below the line, that is away from the origin (0,0).

Then, label the inequality graphed.

The required labelled graph is:

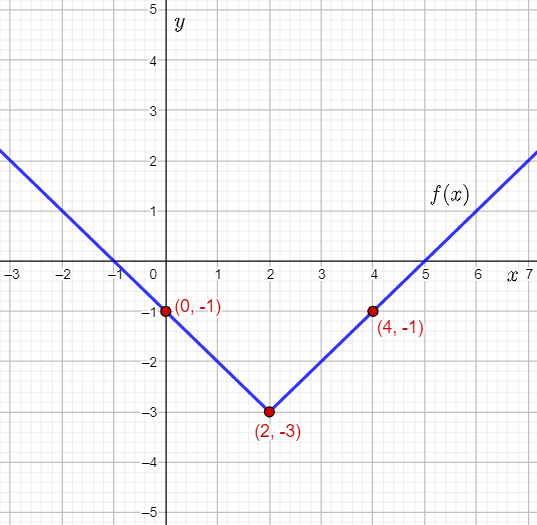
The features of the graph of an absolute value function can be identified by sketching its graph and observing the features.

First, the input-output table for the absolute value function has to be constructed.

Next, the coordinates of a few points lying on the graph are written and plotted.

Then, the graph of the absolute value function is graphed using the points.

The drawn graph can be observed to find the features of the absolute value function such as its shape, symmetry, domain, and range.

The features of the graph of an absolute value function can be identified by sketching its graph and observing the features such as its shape, symmetry, domain, and range.

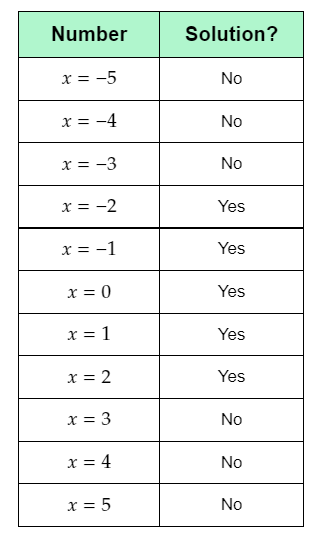
Page 65 Problem 7 Answer

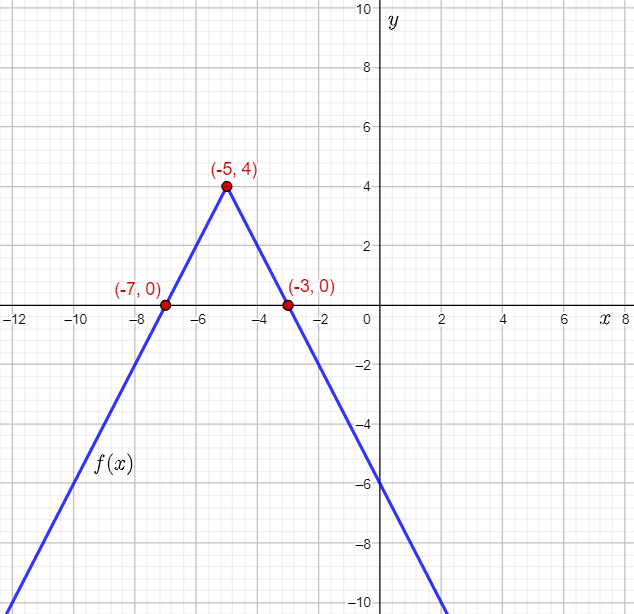
The given table shows the values of some inputs of the absolute value function f(x)=∣x∣, which can be written as the piecewise function:

f(x)={x x≥0−x x<0

The question requires to complete the given input-output table.

To complete the table, use the given piecewise function to determine the value of output for each input, and then use the outputs to complete the input-output table.

Substitute −8 for x in the absolute value function f(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

f(−8)=∣−8∣

=−(−8)

=8

​Therefore, when the input is −8, the output is 8.

Substitute −4 for x in the absolute value function f(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

​f(−4)=∣−4∣

=−(−4)

=4

Therefore, when the input is −4, the output is 4.

Substitute 0 for x in the absolute value function f(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

​f(0)=∣0∣

=0

Therefore, when the input is 0, the output is 0.

Substitute 4 for x in the absolute value function f(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

​f(4)=∣4∣

=4

​Therefore, when the input is 4, the output is 4.

Substitute 8 for x in the absolute value function f(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

​f(8)=∣8∣

=8

Therefore, when the input is 8, the output is 8.

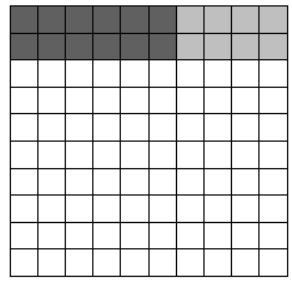
Complete the given input-output table using the calculated outputs.

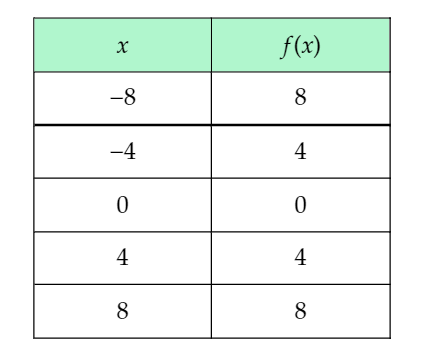
The completed input-output table is:

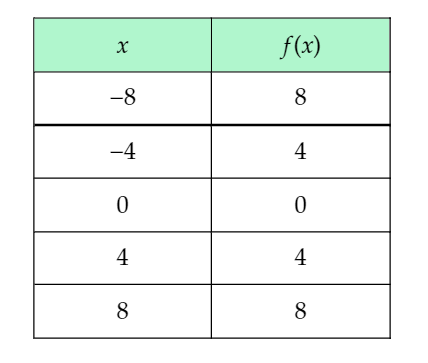
Page 65 Problem 8 Answer

It is given that the absolute value function f(x)=∣x∣  can be written as the piecewise function:

f(x)={ x x≥0−x x<0​

The question requires to plot the points obtained from the previous part of this exercise on the coordinate grid, and use the points to complete the graph of the absolute value function.

Given the input-output table completed in the previous part of this exercise:

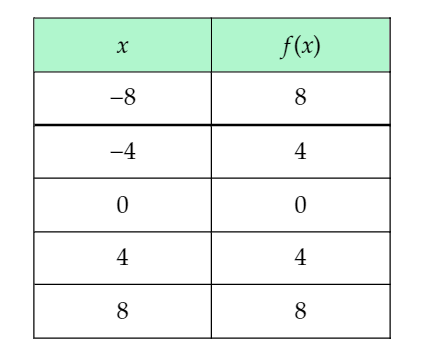
To plot the points and graph the function, use the input-output table to write the coordinates of points lying on the graph of f(x)=∣x∣, and connect the points to sketch the graph of the function.

The points lying on the graph of f(x)=∣x∣ are of the form (x,f(x)).

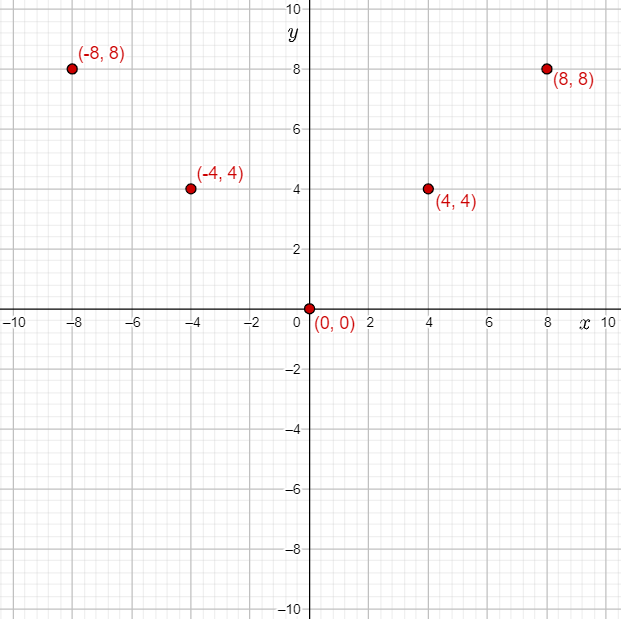
From the input-output table, it can be determined that the points (−8,8),(−4,4),(0,0),(4,4),(8,8) lie on the graph of f(x)=∣x∣.

Plot the points on the coordinate grid.

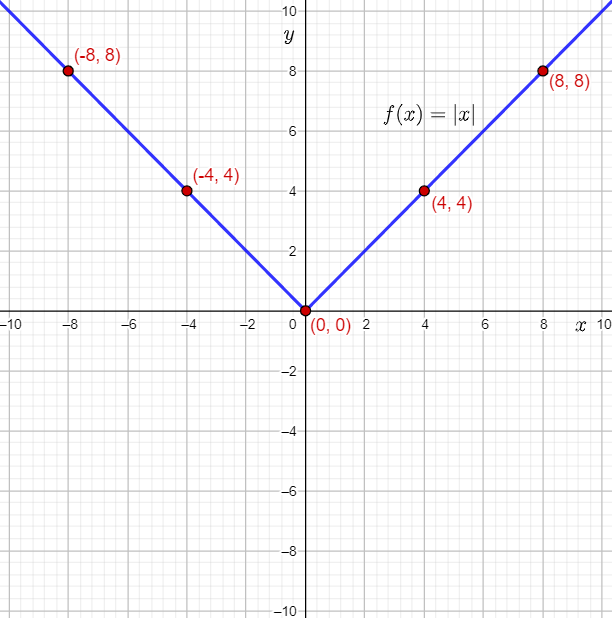
Join the points and draw straight lines to form the graph of the function f(x)=∣x∣.

The required plot of the points, and the graph of the function f(x)=∣x∣ is:

Absolute Value Functions And Inequalities Exercise 2.1 Answers HMH Algebra 2

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 65 Problem 9 Answer

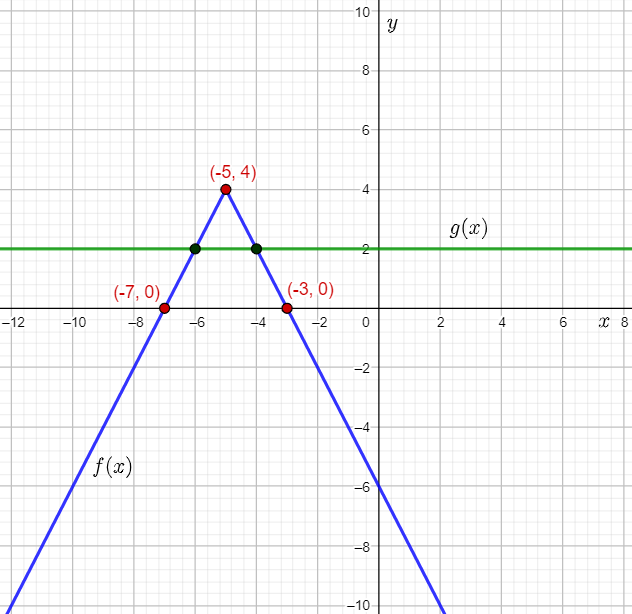
The given incomplete statements state the features of the graph of the absolute value function f(x)=∣x∣.

The question requires to complete the given statements about the features of the absolute value function, using the graph sketched in the previous part of this exercise.

Given the graph of the absolute value function f(x)=∣x∣ sketched in the previous part of this exercise:

To complete the statements, observe the graph of the function and use it to determine the line about which the function is symmetric, its domain, and its range.

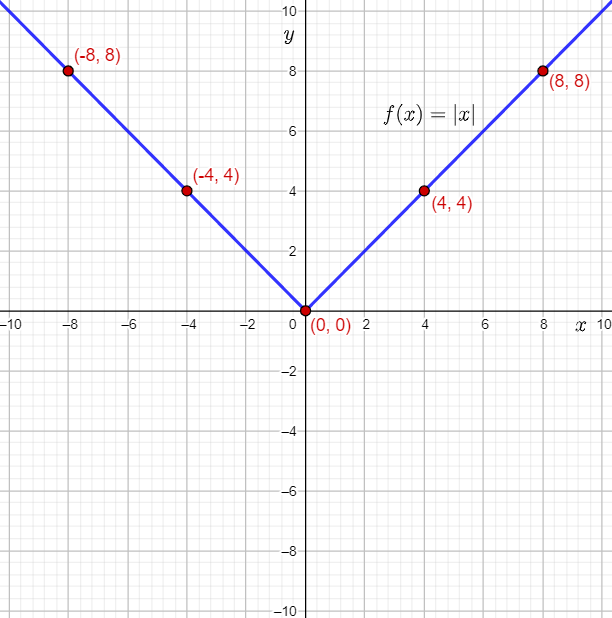
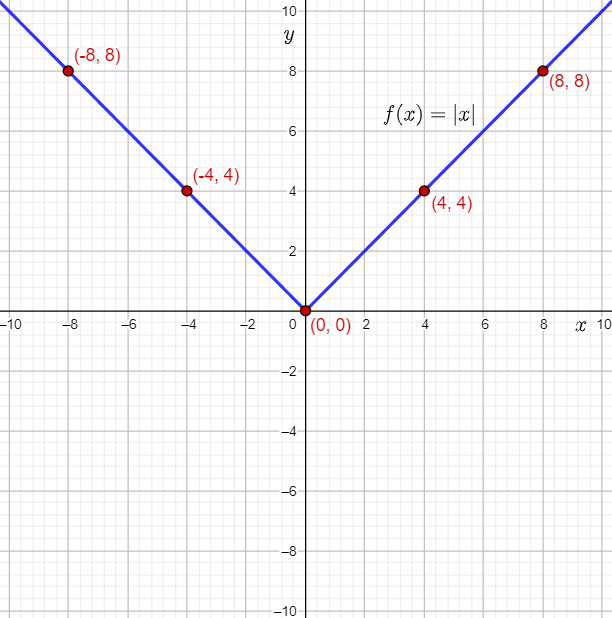
From the graph of the absolute value function, it can be observed that f(x)=∣x∣ is symmetric about the y-axis.

This means that the absolute value function f(x)=∣x∣ is an even function.

It can be observed that the graph of the function f(x)=∣x∣ stretches infinitely towards the left and right. Therefore, the absolute value function is defined for all values of x.

Hence, the domain of f(x)=∣x∣ is all real numbers.

It can be observed that the points lying on the graph of the function f(x)=∣x∣lie either on, or above the x-axis. Therefore, the values of the outputs f(x) can be either 0, or greater than 0.

Thus, the range of f(x)=∣x∣ is all non-negative real numbers.

The function f(x)=∣x∣ is symmetric about the y-axis, and therefore is an even function.

The domain of f(x)=∣x∣ is all real numbers.

The range of f(x)=∣x∣ is all non-negative real numbers.

Page 66 Problem 10 Answer

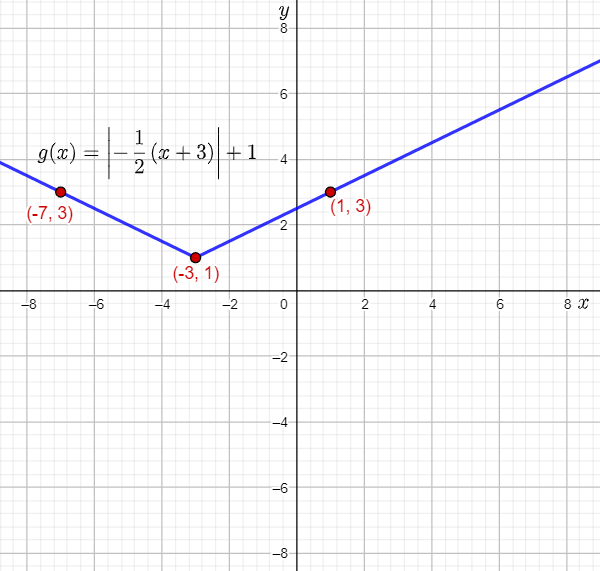
The given function is g(x)= −1/2(x+3)+1 . The incomplete solution to graph the function is given.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To sketch the graph, write the translations used to form the given function from the parent absolute value function f(x)=∣x∣, and use them on the vertex to determine the vertex of g(x).

Next, write the coefficient of the expression with the independent variable in the given function to write the stretch or compress required.

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x) from f(x).

Finally, plot the points and vertex and graph the given function.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

It can be observed that g(x) involves translations of f(x) by 3 units to the left and 1 unit up.

Therefore, the vertex of g(x) is the point (0−3,0+1)=(−3,1).

The points (2,2) and (−2,2) lie on the parent absolute value function f(x)=∣x∣.

Compare the function g(x) to g(x)=∣−1/b(x+h)+k|, and write the value of the constant b.b=2

Since ∣b∣=2, that is ∣b∣>1, the graph of g(x) will involve a horizontal stretch of the parent absolute value function by a factor 2.

Since b is negative, the graph of g(x) will involve a reflection of the parent absolute value function about the y-axis.

The transformations used to form g(x)=∣−1/2(x+3)+1∣ from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be reflected in the y-axis, horizontally stretched by a factor of 2, and shifted 3 units to the left when mapped to g(x).

The y-coordinate of the points lying on f(x) will be moved up 1 unit.

Therefore, the point (2,2) moves to (−2⋅2−3,∣2∣+1)=(−7,3).

The point (−2,2) moves to (−2⋅(−2)−3,∣2∣+1)=(1,3).

Plot the vertex (−3,1) and the points (−7,3) and (1,3), and then draw straight lines to sketch the graph of g(x)=∣−1/2(x+3)+1∣.

The vertex of g(x) is (−3,1).

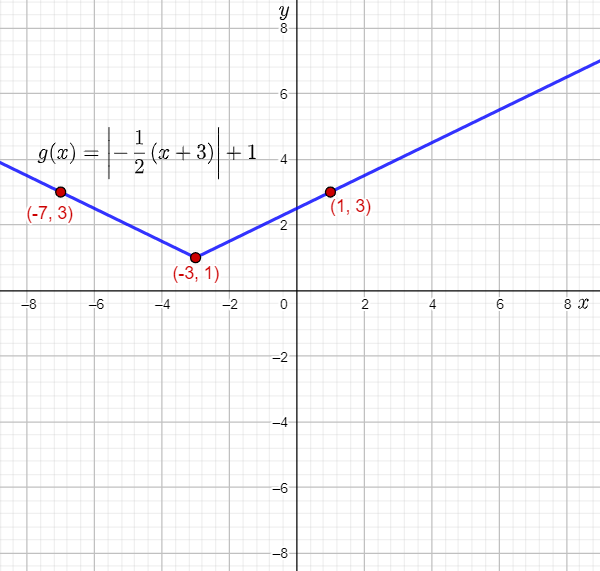
Two points lying on g(x) are (−7,3) and (1,3).

The required grap

Page 67 Problem 11 Answer

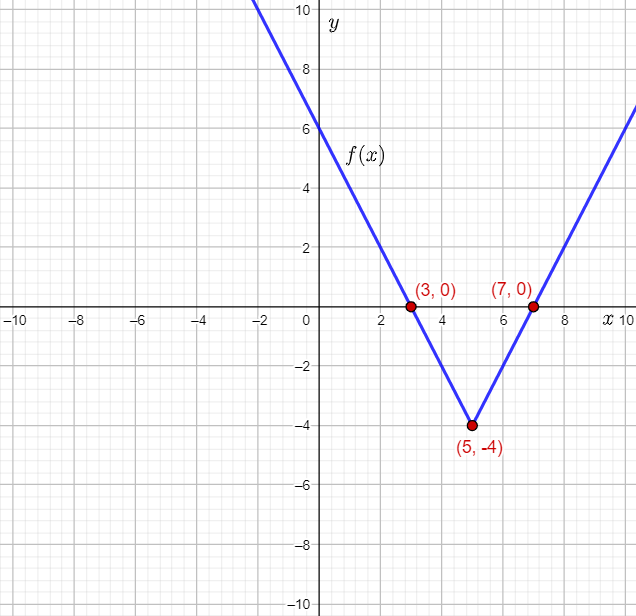
The given graph shows the graph of an absolute value function. The incomplete steps used to find the function are given.

The question requires to write the function in the form g(x)=a∣1/b(x−h)+k| for the given graph, when b=1.

To determine the function, let the given function be g(x)=a∣1/b(x−h)+k|, use the graph to find the vertex, and thus, the values of h,k.

Then, rewrite the function using the obtained values.

Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of a. Finally, use the value of a in the function to obtain the function in the required form.

Let the given function be g(x)=a∣1/b(x−h)+k|.

From the graph, it can be observed that the vertex of g(x) is at (1,6).

This means that the values of h and k are 1 and 6 respectively.

Substitute 1 for b, 1 for h, and 6 for k in g(x)=a∣1/b(x−h)+k|.

​g(x)=a∣1/1(x−1)+6|

g(x)=a∣x−1∣+6………………(1)

​From the graph, it can be observed that the point with the integer coordinates (0,3) lies on the graph.

Substitute 0 for x, and 3 for g(x) in equation (1), subtract 6 from both sides, and solve for a.

​g(x)=a∣x−1∣+6

3=a∣0−1∣+6

3=a∣−1∣+6

−3=a(1)

−3=a​

Substitute −3 for a in g(x)=a∣x−1∣+6.

g(x)=−3∣x−1∣+6

Thus, the required form of the absolute value function is g(x)=−3∣x−1∣+6.

The required form of the graphed function is g(x)=−3∣x−1∣+6.

Page 67 Problem 12 Answer

The given function is g(x)=−1/5∣(x+6)∣+4.

The question requires to find the vertex and two points of the given function, and use them to graph g(x).

To graph the function, compare the given function to the parent absolute value function, and use the translations on its vertex to determine the vertex of g(x).

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x)

from f(x).

Finally, plot the points and vertex and graph the given function.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

It can be observed that g(x) involves a translation of f(x) by 6 units to the left and 4 units up.

Therefore, the vertex of g(x) is the point (0−6,0+4)=(−6,4).

The points (8,8) and (−8,8) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=−1/5∣(x+6)∣+4 from the parent absolute value function can be used to determine the two points lying on g(x).

The coefficient of the absolute value in the given function g(x)=−1/5∣(x+6)∣+4 is −1/5, which is less than 1.

The x-coordinate of the points lying on f(x) will be shifted 6 units to the left when mapped to g(x).

The y-coordinate of the points lying on f(x) will be reflected about the x-axis by multiplying by −1, vertically compressed by the factor 1/5, and then shifted 4 units up when mapped to g(x).

Calculate the location where the point (8,8) will be mapped.​

(8−6,−1/5⋅∣8∣+4)=(2,−1/5⋅8+4)

=(2,−8/5+4)

=(2,12/5)

​Thus, (2,12/5) lies on the graph of g(x).

Calculate the location where the point (−8,8) will be mapped.

(−8−6,−1/5⋅∣8∣+4)=(−14,−1/5⋅8+4)

=(−14,−8/5+4)

=(−14,12/5)

Thus, (−14,12/5) lies on the graph of g(x).

Plot the vertex (−6,4) and the points (2,12/5) and (−14,12/5), and then draw straight lines to sketch the graph of g(x)=−1/5∣(x+6)∣+4.

The vertex of g(x) is (−6,4).

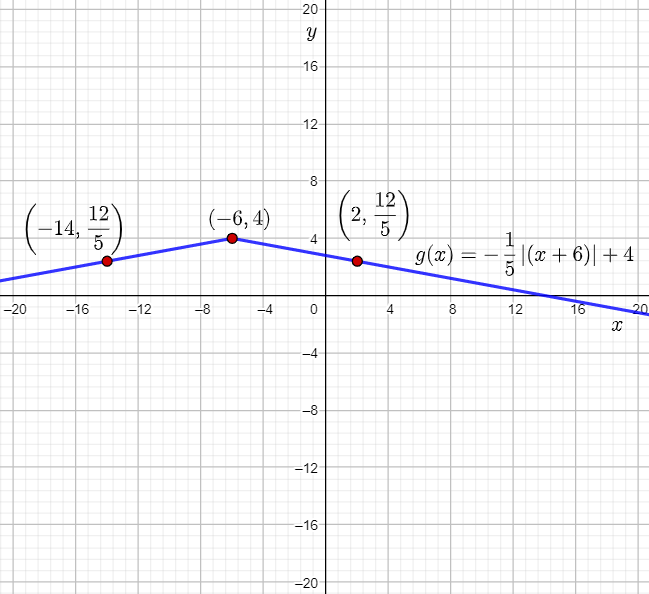
Two points lying on g(x) are (−14,12/5) and (2,12/5).

The required graph of g(x) is:

HMH Algebra 2 Chapter 2 Exercise 2.1 Solutions Guide

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 68 Problem 13 Answer

The given graph shows the graph of an absolute value function.

The question requires to write the function graphed in the form g(x)=a∣1/b(x−h)+k|.

To determine the function, assume b=1, use the graph to find the vertex, and thus, the values of h,k. Then, rewrite the function using the obtained values.

Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of a.

Finally, use the value of a in the function to obtain the function in the required form.

Let b=1.

From the graph, it can be observed that the vertex of the graphed absolute value function is (−5,−1).

This means that the values of h and k are −5 and −1 respectively.

Substitute 1 for b, −5 for h, and −1 for k in the equation g(x)=a∣1/b(x−h)+k|.​

g(x)=a∣1/1(x−(−5))+(−1)|

g(x)=a∣x+5∣−1………………(1)​

From the graph, it can be observed that the point (−8,5) lies on the graph.

Substitute −8 for x, and then 5 for g(−8) in equation (1), add 1

on both sides, and then divide both sides by 2.​

g(−8)=a∣−8+5∣−1

5=a∣−3∣−1

6=a(3)

2=a

Substitute 2 for a in g(x)=a∣x+5∣−1.

g(x)=2∣x+5∣−1

Thus, the required form is g(x)=2∣x+5∣−1.

The required form of the graphed function is g(x)=2∣x+5∣−1.

Page 69 Problem 14 Answer

It is given that a beam of light that originates from a point 10 ft above the floor, reflects off a mirror 15 ft away from the wall containing the source of the light.

Also, it is given that after reflecting, it hits the opposite wall which is 8.5 ft away from the mirror.

The question requires to determine the height from the floor where the light hits the other wall after reflecting off the mirror.

To determine the height, draw the diagram representing the given situation, label the diagram, and let the base of the first wall be the origin.

Then, observe that the path of the ball is the graph of an absolute value function, and write a general function for the path.

Assume b=1, use the graph to find the vertex, and thus, the values of h,k.

Then, rewrite the function using the obtained values. Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of a.

Then, use the value of a in the function to obtain the function representing the path of the light.

Finally, use the distance of the second wall from the origin in the function, simplify to find the required height, and justify the answer.

Label the diagram representing the given sit

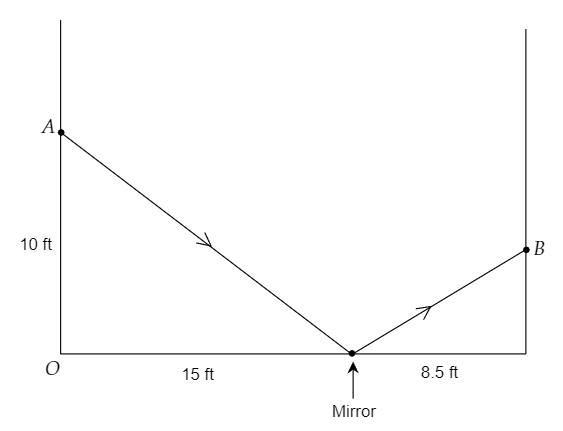
Here, A and B represent the points at which the light originates from and hits the other wall respectively.

The model of the path of the light will be of the form g(x)=a∣1/b(x−h)+k|.

Let the base of the first wall be the origin (0,0).

Therefore, the vertex of g(x) is the point at which the mirror is placed, that is (15,0).

Assume that b=1.

The vertex of the path of the ball is (15,0).

This means that the values of h and k are 15 and 0 respectively.

Substitute 1 for b, 15 for h, and 0 for k in the equation g(x)=a∣1/b(x−h)+k|.

g(x)=a∣/1/1(x−15)+0|

g(x)=a∣x−15∣………………(1)​

Another point on g(x) is the point from which the light originates from, that is (0,10).

Substitute 0 for x, and then 10 for g(0) in equation (1), and then divide both sides by 15.

​g(0)=a∣0−15∣

10=a∣−15∣

10=a(15)2/3=a

​Substitute 2/3 for a in g(x)=a∣x−15∣.

g(x)=2/3∣x−15∣

Thus, the function representing the path of the light is g(x)=2/3∣x−15∣.

The value of g(x) at x=15+8.5, that is 23.5 ft will give the height of the light beam on the opposite wall.

Substitute 23.5 for x in g(x)=2/3∣x−15∣, and simplify the expression.

​g(23.5)=2/3∣23.5−15∣

=2/3∣8.5∣

=2/3(8.5)

=17/3

≈5.67

​Therefore, the value of g(23.5) is about 5.67.

Thus, the beam hits the opposite wall at a height of about 5.67 ft.

The answer of 5.67 ft makes sense because the function is symmetric with respect to the vertical line passing through the vertex (15,0), that is x=15.

The distance from this vertical line to the second wall is a little more than half the distance from the line to the first wall from where the beam originates.

Since the beam originates at a height of 10 off the floor, the beam, after reflection, should hit the second wall at a height of a little over 1/2(10)=5 ft.

Thus, the answer 5.67 ft is justified.

The light beam hits the other wall at a height of about 5.67 ft.

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 70 Problem 15 Answer

It is given that a student bounces a ball 3 m away from himself from a height of 1.4 m, to pass it to the other student standing.

The question requires to determine the position where the second student must stand to catch the ball at the height 1.2 m.

To determine the position, draw the diagram representing the given situation, label the diagram, and assume the point at which the first student stands as the origin.

Then, observe that the path of the ball is the graph of an absolute value function, and write a general function for the path.

Assume b=1, use the graph to find the vertex, and thus, the values of h,k. Then, rewrite the function using the obtained values.

Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of a.

Then, use the value of a in the function to obtain the function representing the path of the ball.

Finally, use the height at which the second student has to catch the ball in the function, and solve for x to find the required position.

Draw the diagram representing the given situation.

Here, A and B represent the points at which first and second student catch the ball respectively.

Point C represents the point where the ball bounces.

The graph of the path of the ball can be represented by the function g(x)=a∣1/b(x−h)+k|.

Let the point O where the first student stands be the origin (0,0).

Therefore, the vertex of the graph of the function is (3,0).

Assume that b=1.

The vertex of the path of the ball is (3,0).

This means that the values of h and k are 3 and 0 respectively.

Substitute 1 for b, 3 for h, and 0 for k in the equation g(x)=a∣1/b(x−h)+k|.

​g(x)=a∣1/1(x−3)+0|

g(x)=a∣x−3∣………………(1)

​

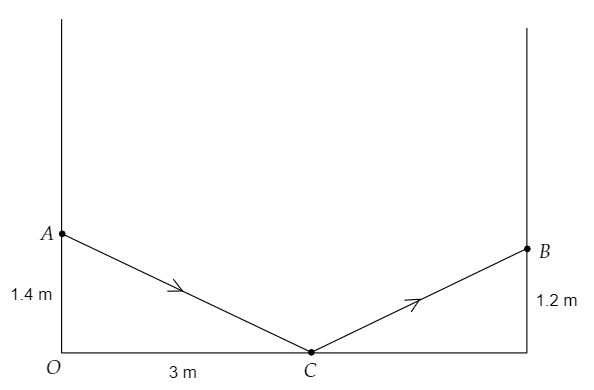
From the graph, it can be observed that the point (0,1.4) represents the point where the first student catches the ball.

Substitute 0 for x, and then 1.4 for g(0) in equation (1), and then divide both sides by 3.

​g(0)=a∣0−3∣

1.4=a∣−3∣

1.4=a(3)

1.4/3=a

​Substitute 1.4/3 for a in g(x)=a∣x−3∣.

g(x)=1.4/3∣x−3∣

Thus, the function representing the path of the ball is g(x)=1.4/3∣x−3∣.

The second student catches the ball at a height of 1.2 m.

Substitute 1.2 for g(x) in g(x)=1.4/3∣x−3∣, and multiply both sides by 3/1.4.

​1.2=1.4/3∣x−3∣1.2(3/1.4)=1.4/3(3/1.4)∣x−3∣

6(3/7)=∣x−3∣18/7=∣x−3∣………………(2)

​Form two equations by rewriting the absolute value in equation (2).

​18/7=x−3

18/7=−(x−3)

Simplify the right-hand side of 18/7=−(x−3), and solve for x.

​18/7=−x+3

x=3−18/7

x=3/7

x≈0.43

This value of x implies that the student must stand 0.43 m to the right of the origin.

However, the ball bounces 3 m away from the origin, and between the two students.

Thus, the value of x cannot be 0.43.

Add 3 on both sides of the other equation 18/7=x−3.

​18/7+3=x−3+3

39/7=x

5.57≈x

This value of x implies that the student must stand 5.57 m to the right of the origin.

Thus, the second student must stand about 5.57 m away from the first student to catch the ball at a height of 1.2 m.

The answer of 5.57 m makes sense because the function is symmetric with respect to the vertical line passing through the vertex (3,0), that is x=3.

The height at which the second student catches the ball is about 1.2

1.4≈0.857 times the height at which the first student catches the ball.

Therefore, the beam bounces at a distance of 3 m away from the first wall, it should hit the second wall when the distance of the vertical line from the second wall is about 0.857(3)=2.57 m.

This means that the second student should stand at about 3+2.57=5.57 m from the first student.

Thus, the answer 5.57 m is justified.

The second student must stand about 5.57 m away from the first student to catch the ball at a height of 1.2 m.

Page 70 Problem 16 Answer

The parameters in the general form g(x)=a∣1/b(x−h)+k| of the absolute value function are a,b,h,k.

The parameters h and k represent the x-coordinate and y-coordinate of the vertex of the function.

Parameter b determines the factor by which the x-coordinates of points lying on the parent absolute value function are stretched, compressed, and/or reflected to form the x-coordinates of the points lying on g(x).

The parameter a determines the factor by which the y-coordinates of points lying on the parent absolute value function are stretched, compressed, and/or reflected to form the y-coordinates of the points lying on g(x).

In the general form g(x)=a∣1/b(x−h)+k| of the absolute value function, the parameters h and k represent the x-coordinate and y-coordinate of the vertex of the function, the parameter b determines the factor by which the x-coordinates of points lying on the parent absolute value function are stretched, compressed, and/or reflected to form the x-coordinates of the points lying on g(x), and finally, the parameter a determines the factor by which the y-coordinates of points lying on the parent absolute value function are stretched, compressed, and/or reflected to form the y-coordinates of the points lying on g(x).

How To Solve Absolute Value Functions Exercise 2.1 HMH Algebra 2

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 70 Problem 17 Answer

The vertex of f(x)=∣x∣ is the origin (0,0).When the function f(x)=∣x∣ is vertically stretched or compressed, the y-coordinates of the points lying on it are multiplied by a factor.

When the function is horizontally stretched or compressed, the x-coordinates of the points lying on it are multiplied by a factor.

Since the product of 0 and the factor is always 0, the coordinates of the vertex remain (0,0) after multiplication by the factor.

Therefore, the vertex remains same when the function is stretched or compressed.

When the function f(x)=∣x∣ is vertically translated up or down, a constant is added or subtracted from the y-coordinates of the points lying on it.

When the function is horizontally translated to the left or right, a constant is added or subtracted from the x-coordinates of the points lying on it.

When a constant is added or subtracted from the coordinates of the vertex (0,0), the resulting vertex is a point other than (0,0).

Therefore, the vertex does not remain the same when the function is translated.

The vertex remains same when the function is stretched or compressed because the coordinates of the vertex remain (0,0) after multiplication by any factor.

The vertex does not remain the same when the function is translated because the vertex is not (0,0) after a constant is added to or subtracted from either of the coordinates.

Page 70 Problem 18 Answer

Every absolute value function is of the form g(x)=a∣1/b(x−h)+k|.

The graph of an absolute value function is formed using two inclined straight lines with the vertex as the common initial point.

The graph of an absolute value function is symmetric about the vertical line passing through the vertex.The domain of graph of an absolute value function is all real numbers.

The shape of the graph of an absolute value function is similar to the letter V or an inverted V, formed using two inclined straight lines with the vertex as the common initial point.

The graph of an absolute value function is symmetric about the straight vertical line that passes through its vertex.

The domain of the graph of every absolute value function is all real numbers.

Page 71 Exercise 1 Answer

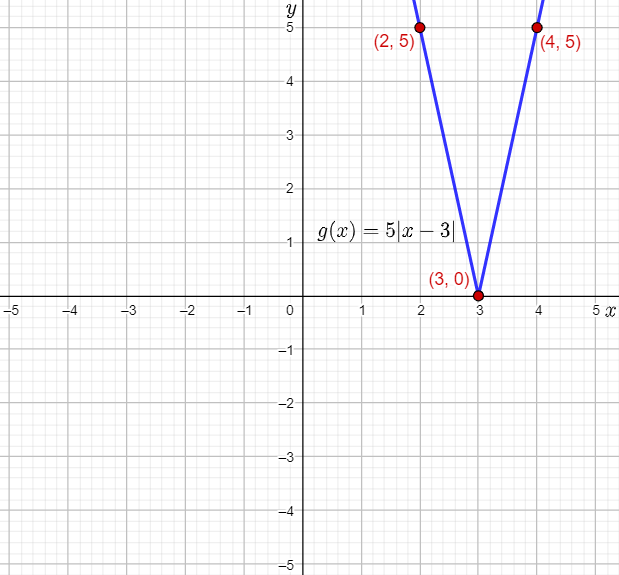
The given function is g(x)=5∣x−3∣.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To answer the question, compare the function to g(x)=a∣1/b(x−h)+k|to find the values of the constants, and then predict the shape and position of the graph in comparison to the graph of the parent absolute value function.

Next, graph the function on a graphing calculator and verify the prediction.

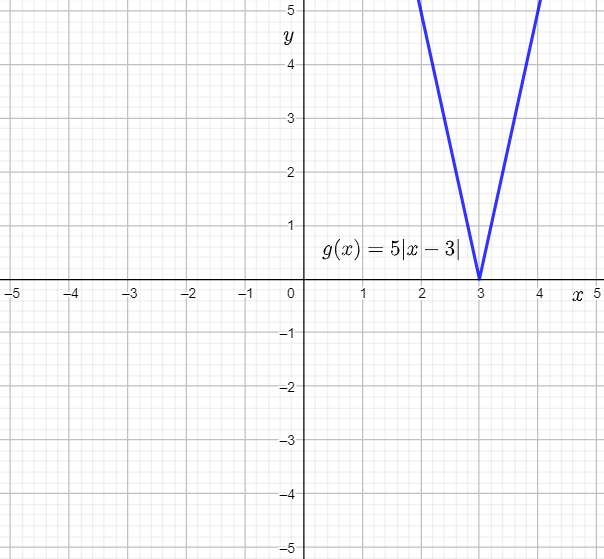
To sketch the graph, compare the given function to the parent absolute value function, and use the translations on its vertex to determine the vertex of g(x).

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x) from f(x).

Finally, plot the points and vertex and graph the given function.

Rewrite the given function in the form g(x)=a∣1/b(x−h)+k|.

g(x)=5∣1/1(x−3)+0|

Compare the function g(x) to g(x)=a∣1/b(x−h)+k|, and write the values of the constants.

​a=5

b=1

h=3

k=0

The value of a is positive. Therefore, the graph of g(x) will open upwards.

Since a=5, the graph of g(x) will be a vertically stretch of the parent absolute value function by a factor 5.

Since h=3, the graph of g(x) will be a horizontal translation of the parent absolute value function by 3 units to the right.

Since k=0, the graph of g(x) will not be involve a vertical translation of the parent absolute value function.

Therefore, it is predicted that the graph of g(x) will open upwards.

It will be a vertically stretch of the parent absolute value function by a factor 5, will involve a horizontal translation of the parent absolute value function by 3 units to the right, and will not be involve a vertical translation of the parent absolute value function.

On the graphing calculator, press the Y= key, and assign 5∣x−3∣ to Y₁.

Next, set the viewing rectangle to [−5,5] by [−5,5], and press the GRAPH key to obtain the required graph of the function.

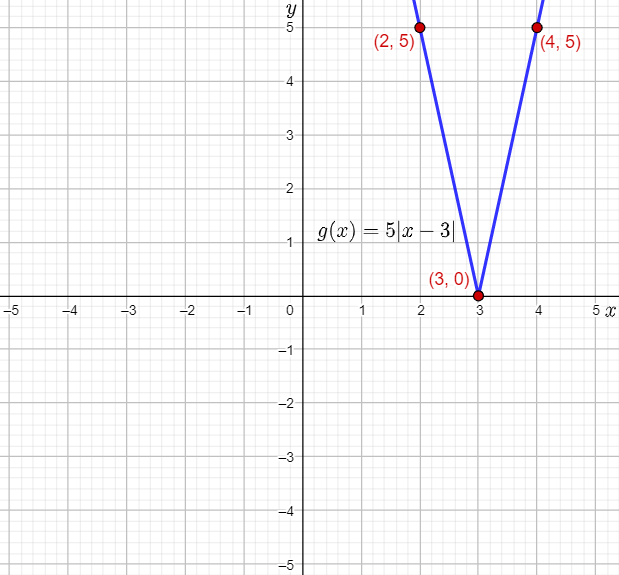
From the graph, it can be observed that the prediction is verified.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

Therefore, the vertex of g(x) is the point (0+3,0)=(3,0).

The points (1,1) and (−1,1) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=5∣x−3∣ from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be shifted 3 units to the right when mapped to g(x).

The y-coordinate of the points lying on f(x) will be vertically stretched by the factor 5 when mapped to g(x).

Calculate the location where the point (1,1) will be mapped.

​(1+3,5⋅∣1∣)=(1+3,5⋅1)

=(4,5)

Thus, (4,5) lies on the graph of g(x).

Calculate the location where the point (−1,1) will be mapped.

​(−1+3,5⋅∣1∣)=(−1+3,5⋅1)

=(2,5)

Thus, (2,5) lies on the graph of g(x).

Plot the vertex (3,0) and the points (4,5) and (2,5), and then draw straight lines to sketch the graph of g(x)=5∣x−3∣.

It is predicted that the graph of g(x) will open upwards, will be a vertically stretch of the parent absolute value function by a factor of 5, will involve a horizontal translation of the parent absolute value function by 3 units to the right, and will not be involve a vertical translation of the parent absolute value function.

The prediction is verified using the following graph made using a graphing calculator:

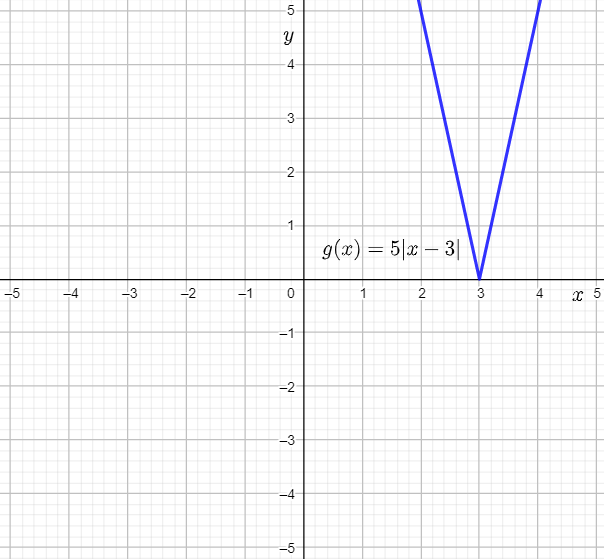
The required sketched graph of g(x) is:

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 71 Exercise 2 Answer

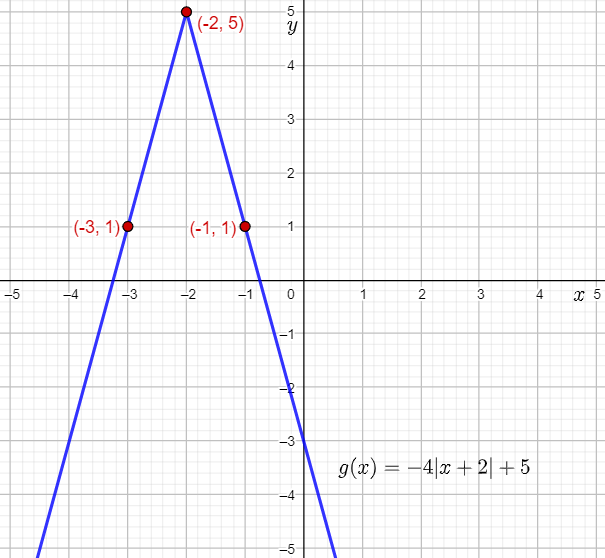
The given function is g(x)=−4∣x+2∣+5.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To answer the question, compare the function to g(x)=a∣1/b(x−h)+k| to find the values of the constants, and then predict the shape and position of the graph in comparison to the graph of the parent absolute value function.

Next, graph the function on a graphing calculator and verify the prediction.

To sketch the graph, compare the given function to the parent absolute value function, and use the translations on its vertex to determine the vertex of g(x).

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x)

from f(x).

Finally, plot the points and vertex and graph the given function.

Rewrite the given function in the form g(x)=a∣1/b(x−h)+k|.

g(x)=−4∣1/1(x+2)+5|

Compare the function g(x) to g(x)=a∣1/b(x−h)+k|, and write the values of the constants.

​a=−4

b=1

h=−2

k=5

​The value of a is negative. Therefore, the graph of g(x) will open downwards.

Since a=−4, the graph of g(x) will be a vertically stretch of the parent absolute value function by a factor 4, and a reflection about the x-axis.

Since h=−2, the graph of g(x) will be a horizontal translation of the parent absolute value function by 2 units to the left.

Since k=5, the graph of g(x) will involve a vertical translation of the parent absolute value function by 5 units up.

Therefore, it is predicted that the graph of g(x) will open downwards.

It will be a reflection of the parent absolute value function about the x-axis, a vertically stretch by a factor 4, a horizontal translation by 2 units to the left, and finally, a vertical translation by 5 units up.

On the graphing calculator, press the Y= key, and assign −4∣x+2∣+5 to Y₁.

Next, set the viewing rectangle to [−5,5] by [−5,5], and press the GRAPH key to obtain the required graph of the function.

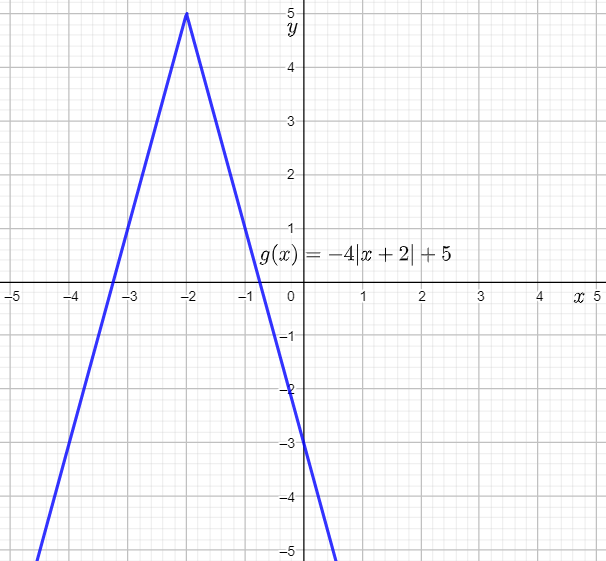
From the graph, it can be observed that the prediction is verified.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

Therefore, the vertex of g(x) is the point (0−2,0+5)=(−2,5).

The points (1,1) and (−1,1) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=−4∣x+2∣+5 from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be shifted 2 units to the left when mapped to g(x).

The y-coordinate of the points lying on f(x) will be reflected about the x-axis by multiplying by −1, vertically stretched by the factor 4, and translated 5 units up when mapped to g(x).

Calculate the location where the point (1,1) will be mapped.

(1−2,−4⋅∣1∣+5)=(1−2,−4⋅1+5)

=(−1,−4+5)

=(−1,1)

Thus, (−1,1) lies on the graph of g(x).

Calculate the location where the point (−1,1) will be mapped.

​(−1−2,−4⋅∣1∣+5)=(−1−2,−4⋅1+5)

=(−3,−4+5)

=(−3,1)

​Thus, (−3,1) lies on the graph of g(x).

Plot the vertex (−2,5) and the points (−1,1) and (−3,1), and then draw straight lines to sketch the graph of g(x)=−4∣x+2∣+5.

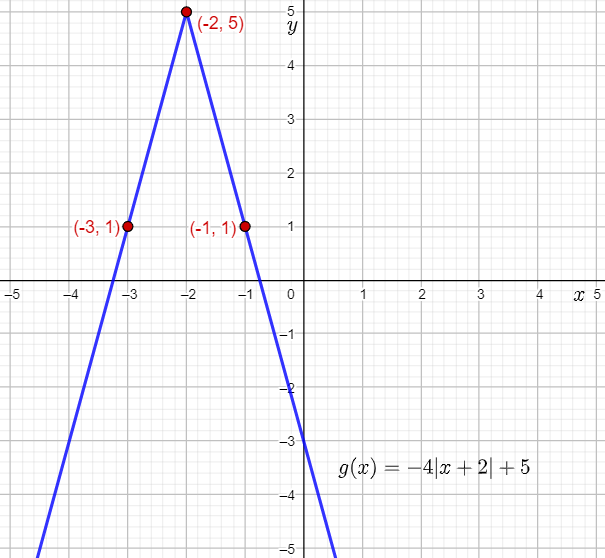
It is predicted that the graph of g(x) will open downwards, will be a reflection of the parent absolute value function about the x-axis, a vertical stretch by a factor 4, a horizontal translation by 2 units to the left, and finally, a vertical translation by 5 units up.

The prediction is verified using the following graph made using a graphing calculator:

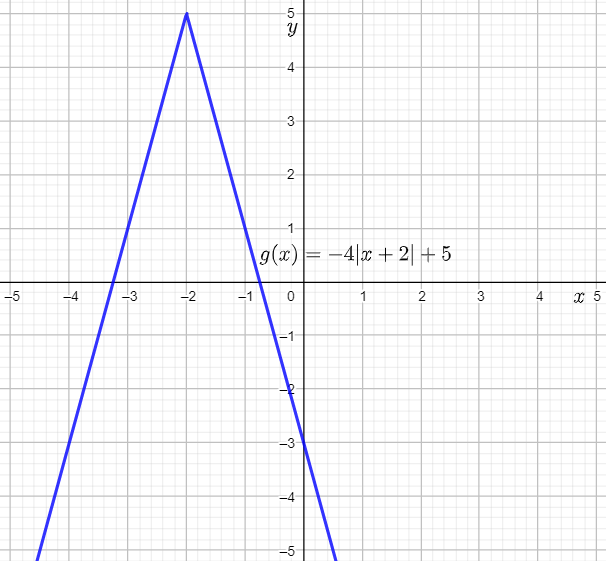
The required sketched graph of g(x) is:

Page 71 Exercise 3 Answer

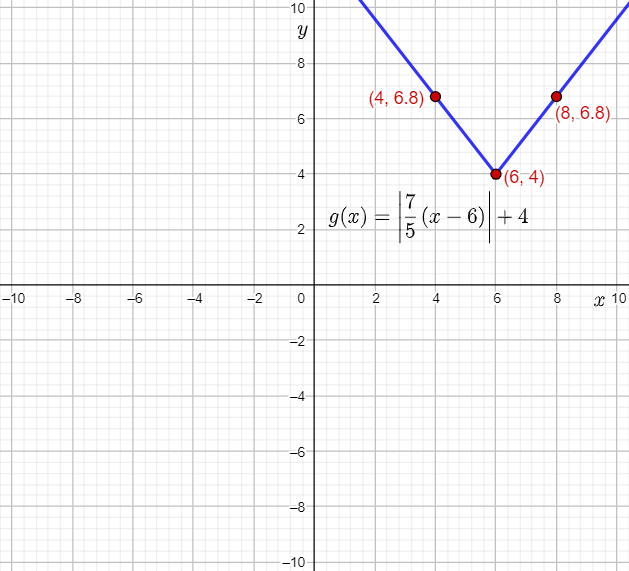
The given function is g(x)=∣7/5(x−6)+4|.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To answer the question, rewrite and compare the function to g(x)=a∣(x−h)∣+k to find the values of the constants, and then predict the shape and position of the graph in comparison to the graph of the parent absolute value function.

Next, graph the function on a graphing calculator and verify the prediction.

To sketch the graph, compare the given function to the parent absolute value function, and use the translations on its vertex to determine the vertex of g(x).

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x)

from f(x).

Finally, plot the points and vertex and graph the given function.

Rewrite the given function in the form g(x)=a∣(x−h)∣+k.

g(x)=7/5∣x−6∣+4

Compare the function g(x) to g(x)=a∣(x−h)∣+k, and write the values of the constants.

​a=7/5

h=6

k=4

​The value of a is positive. Therefore, the graph of g(x) will open upwards.

Since a=7/5, the graph of g(x) will be a vertically stretch of the parent absolute value function by a factor 7/5.

Since h=6, the graph of g(x) will be a horizontal translation of the parent absolute value function by 6 units to the right.

Since k=4, the graph of g(x) will involve a vertical translation of the parent absolute value function by 4 units up.

Therefore, it is predicted that the graph of g(x) will open upwards. It will be a vertically stretch of the parent absolute value function by a factor 7/5, a horizontal translation by 6 units to the right, and finally, a vertical translation by 4 units up.

On the graphing calculator, press the Y= key, and assign |7/5(x−6)+4| to Y₁.

Next, set the viewing rectangle to [−10,10] by [−10,10], and press the GRAPH key to obtain the required graph of the function.

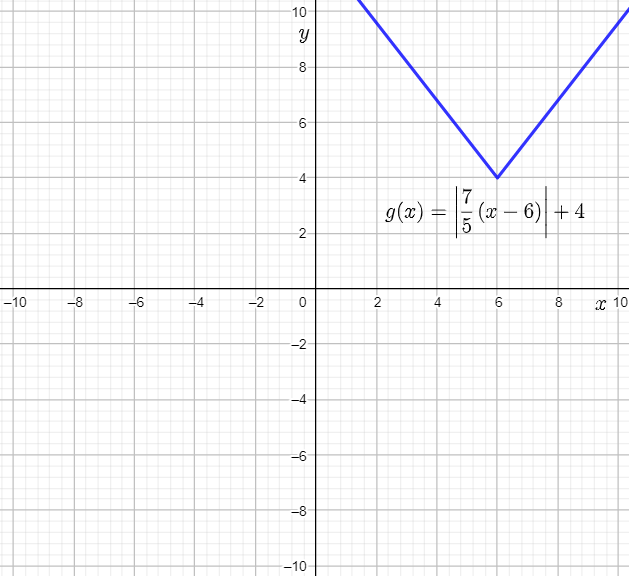
From the graph, it can be observed that the prediction is verified.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

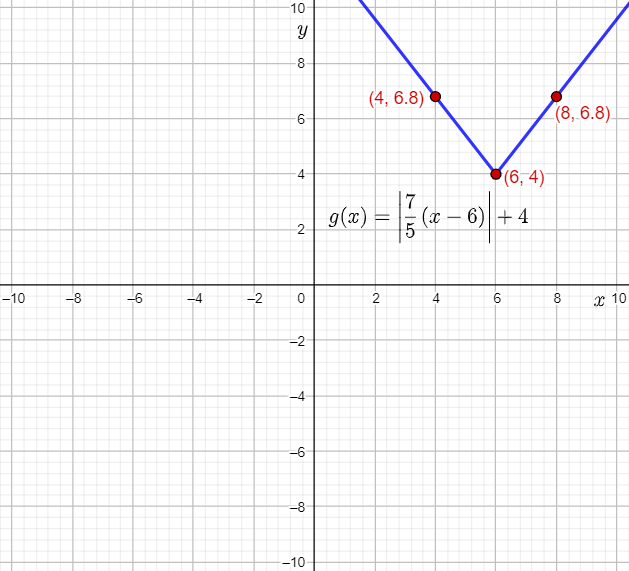
Therefore, the vertex of g(x) is the point (0+6,0+4)=(6,4).

The points (2,2) and (−2,2) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=7/5∣x−6∣+4 from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be shifted 6 units to the right when mapped to g(x).

The y-coordinate of the points lying on f(x) will be vertically stretched by the factor 7/5, and translated 4 units up when mapped to g(x).

Calculate the location where the point (2,2) will be mapped.

(2+6,7/5⋅∣2∣+4)=(2+6,7/5⋅2+4)

=(8,14/5+4)

=(8,34/5)

=(8,6.8)

Thus, (8,6.8) lies on the graph of g(x).

Calculate the location where the point (−2,2) will be mapped.

​(−2+6,7/5⋅∣2∣+4)=(−2+6,7/5⋅2+4)

=(4,14/5+4)

=(4,34/5)

=(4,6.8)

Thus, (4,6.8) lies on the graph of g(x).

Plot the vertex (6,4) and the points (4,6.8) and (8,6.8), and then draw straight lines to sketch the graph of g(x)=∣7/5(x−6)+4|.

It is predicted that the graph of g(x) will open upwards, will be vertically stretch of the parent absolute value function by a factor 7/5, a horizontal translation by 6 units to the right, and finally, a vertical translation by 4 units up.

The prediction is verified using the following graph made using a graphing calculator:

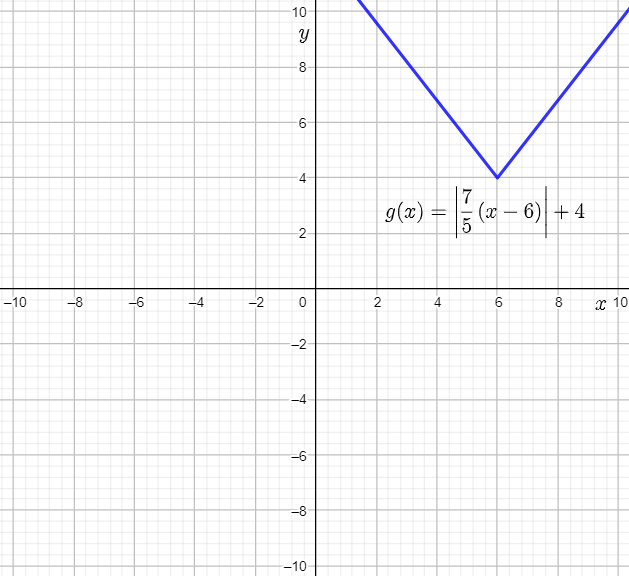
The required sketched graph of g(x) is:

Solutions For Chapter 2 Exercise 2.1 Absolute Value And Inequalities HMH

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 71 Exercise 4 Answer

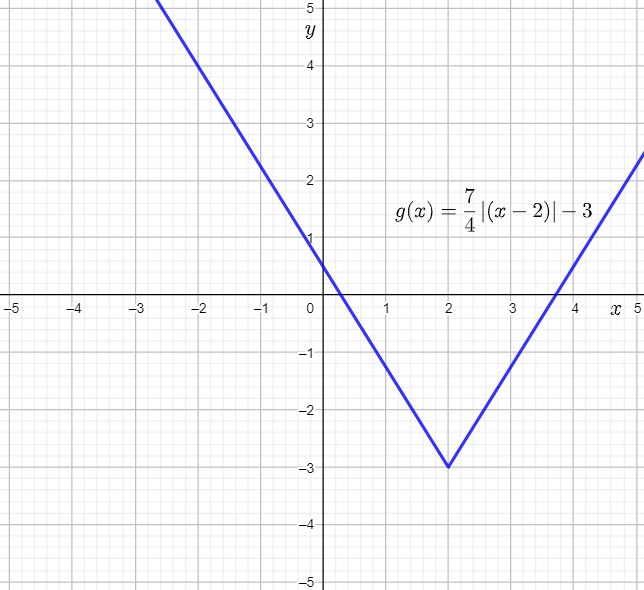
The given function is g(x)=7/4∣(x−2)∣−3.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To answer the question, compare the function to g(x)=a∣(x−h)∣−k to find the values of the constants, and then predict the shape and position of the graph in comparison to the graph of the parent absolute value function.

Next, graph the function on a graphing calculator and verify the prediction.

To sketch the graph, compare the given function to the parent absolute value function, and use the translations on its vertex to determine the vertex of g(x).

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x)

from f(x).

Finally, plot the points and vertex and graph the given function.

Compare the function g(x) to g(x)=a∣(x−h)∣−k, and write the values of the constants.

​a=7/4

h=2

k=3

The value of a is positive. Therefore, the graph of g(x) will open upwards.

Since a=7/4, the graph of g(x) will be a vertically stretch of the parent absolute value function by a factor 7/4.

Since h=2, the graph of g(x) will be a horizontal translation of the parent absolute value function by 2 units to the right.

Since k=3, the graph of g(x) will involve a vertical translation of the parent absolute value function by 3 units down.

Therefore, it is predicted that the graph of g(x) will open upwards. It will be a vertical stretch of the parent absolute value function by a factor 7/4, a horizontal translation by 2 units to the right, and finally, a vertical translation by 3 units down.

On the graphing calculator, press the Y= key, and assign 7/4∣(x−2)∣−3 to Y₁.

Next, set the viewing rectangle to [−5,5] by [−5,5], and press the GRAPH key to obtain the required graph of the function.

From the graph, it can be observed that the prediction is verified.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

Therefore, the vertex of g(x) is the point (0+2,0−3)=(2,−3).

The points (2,2) and (−2,2) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=7/4∣(x−2)∣−3 from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be shifted 2 units to the right when mapped to g(x).

The y-coordinate of the points lying on f(x) will be vertically stretched by the factor 7/4, and translated 3 units down when mapped to g(x).

Calculate the location where the point (2,2) will be mapped.

​(2+2,7/4⋅∣2∣−3)=(2+2,7/4⋅2−3)

=(4,7/2−3)

=(4,1/2)

=(4,0.5)

Thus, (4,0.5) lies on the graph of g(x).

Calculate the location where the point (−2,2) will be mapped.

​(−2+2,7/4⋅∣2∣−3)=(−2+2,7/4⋅2−3)

=(0,7/2−3)

=(0,1/2)

=(0,0.5)

Thus, (0,0.5) lies on the graph of g(x).

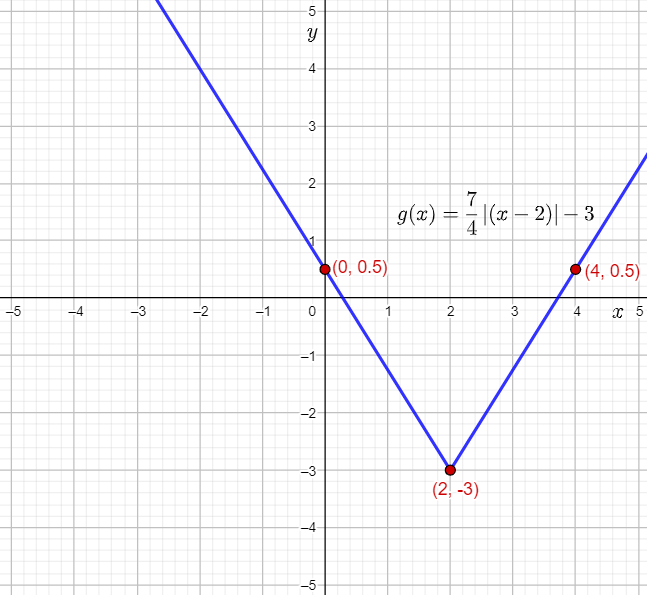
Plot the vertex (2,−3) and the points (4,0.5) and (0,0.5), and then draw straight lines to sketch the graph of g(x)=7/4∣(x−2)∣−3.

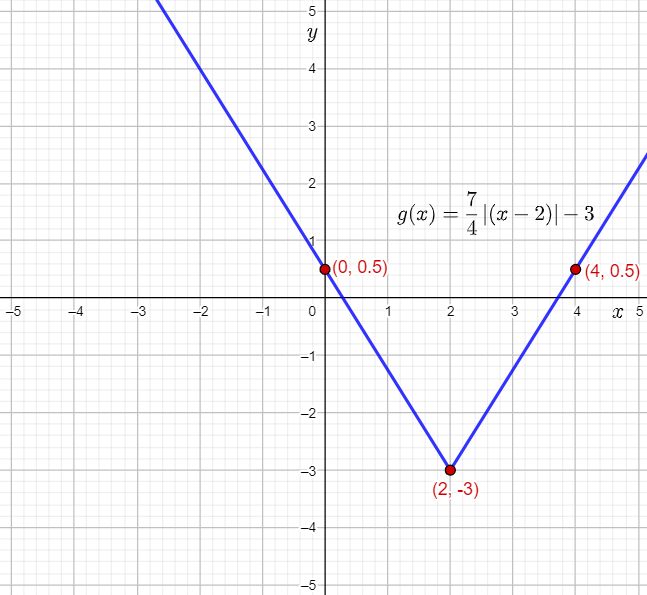
It is predicted that the graph of g(x) will open upwards, will be vertical stretch of the parent absolute value function by a factor 7/4, a horizontal translation by 2 units to the right, and finally, a vertical translation by 3 units down.

The prediction is verified using the following graph made using a graphing calculator:

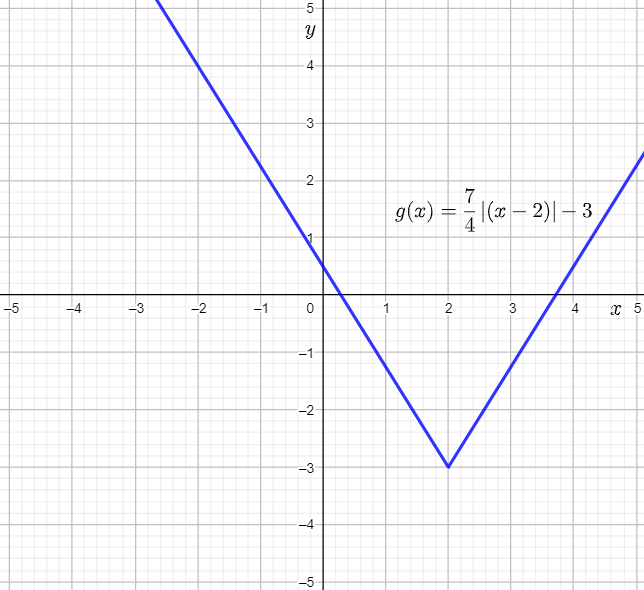
The required sketched graph of g(x) is:

Page 72 Exercise 5 Answer

The given function is g(x)=∣x∣.

The question requires to graph the given function, and determine its domain and range.

To graph the function, use the piecewise definition of the absolute value function g(x)=∣x∣ to form an input-output table.

Then, use the input-output table to write the coordinates of points lying on the graph of g(x)=∣x∣, and connect the points to sketch the graph of the function.

Finally, use the graph to determine the domain and range of the function.

The absolute value function g(x)=∣x∣ can be defined as the piecewise function:g(x)={x x≥0−x x<0

Substitute −8 for x in the absolute value function g(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

g(−8)=∣−8∣

=−(−8)

=8

Therefore, when the input is −8, the output is 8.

Substitute −4 for x in the absolute value function g(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

​g(−4)=∣−4∣

=−(−4)

=4

​Therefore, when the input is −4, the output is 4.

Substitute 0 for x in the absolute value function g(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.​

g(0)=∣0∣

=0​

Therefore, when the input is 0, the output is 0.

Substitute 4 for x in the absolute value function g(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

​g(4)=∣4∣

=4

​Therefore, when the input is 4, the output is 4.

Substitute 8 for x in the absolute value function g(x)=∣x∣, and simplify using the piecewise definition of the absolute value function.

g(8)=∣8∣

=8

Therefore, when the input is 8, the output is 8.

Construct an input-output table using the calculated inputs and outputs.

The points lying on the graph of g(x)=∣x∣ are of the form (x,g(x)).

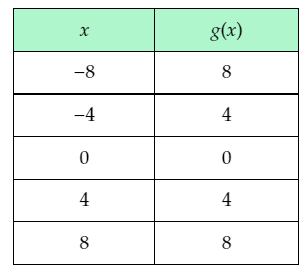
From the input-output table, it can be determined that the points (−8,8),(−4,4),(0,0),(4,4),(8,8) lie on the graph of g(x)=∣x∣.

Plot the points, join them, and draw straight lines to form the graph of the function g(x)=∣x∣.

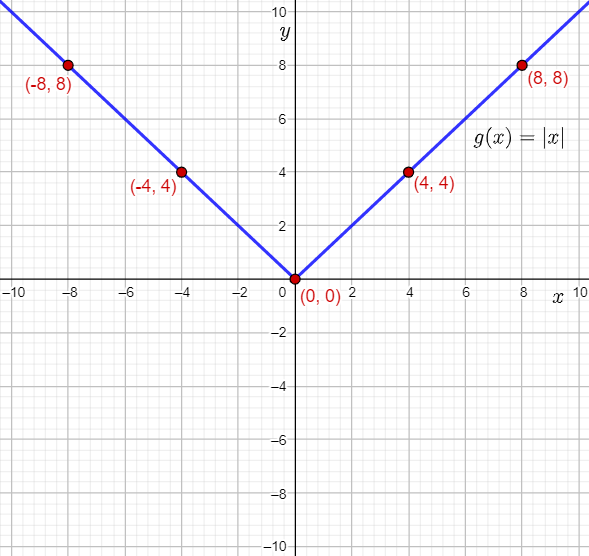
From the graph, it can be observed that the graph of the function g(x)=∣x∣ stretches infinitely towards the left and right.

Therefore, the given absolute value function is defined for all values of x.

Hence, the domain of g(x)=∣x∣ is (−∞,∞).

Also, it can be observed that the points lying on the graph of the function g(x)=∣x∣ lie either on, or above the x-axis.

Therefore, the values of the outputs g(x) can be either 0, or greater than 0.

Thus, the range of g(x)=∣x∣ is [0,∞).

The required graph is:

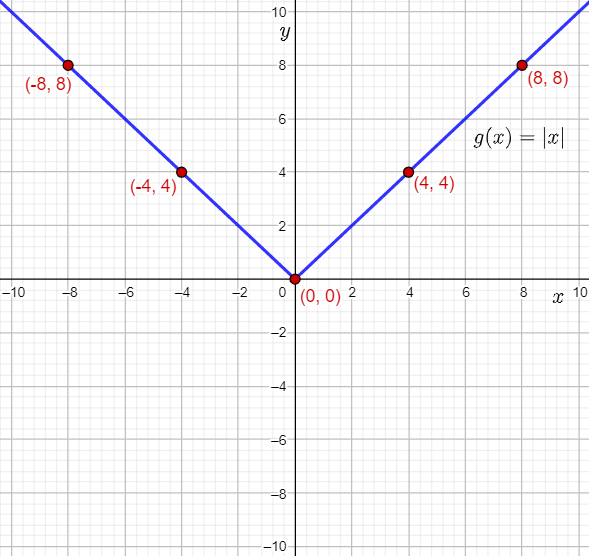
The domain of g(x)=∣x∣ is (−∞,∞).

The range of g(x)=∣x∣ is [0,∞).

Page 72 Exercise 6 Answer

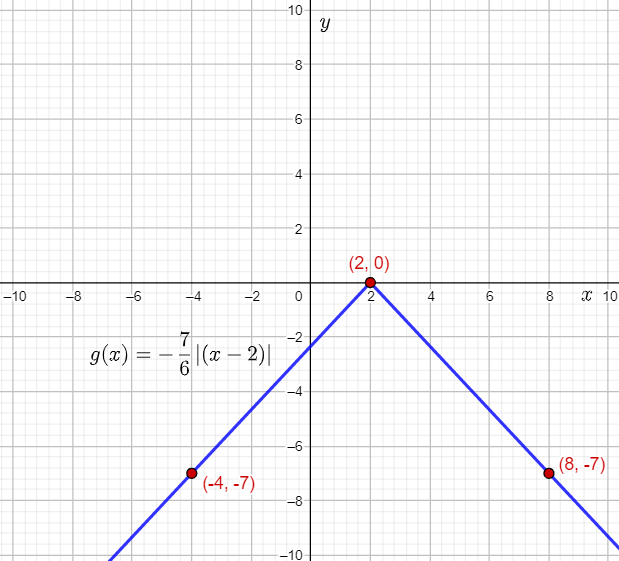
The given function is g(x)=−7/6∣(x−2)∣.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To sketch the graph, write the translations used to form the given function from the parent absolute value function f(x)=∣x∣, and use them on the vertex to determine the vertex of g(x).

Next, write the coefficient of the absolute value in the given function to find the factor by which the parent absolute function will be vertically stretched.

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x)

using the transformations used to form g(x) from f(x). Next, plot the points and vertex and graph the given function.

Finally, use the drawn graph to find and write the domain and range of the function.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

It can be observed that g(x) involves a translation of f(x) by 2 units to the right.

Therefore, the vertex of g(x) is the point (0+2,0)=(2,0).

Compare the function g(x) to g(x)=−a∣(x−h)∣, and write the value of the constant a.a=7/6

Since a=7/6, that is ∣a∣>1, the graph of g(x) will involve a vertical stretch of the parent absolute value function by a factor 7/6.

Since the coefficient of the absolute value ∣(x−2)∣ in the given function is −7/6, that is negative, the graph of g(x) will involve reflection of the parent absolute value function about the x-axis.

The points (6,6) and (−6,6) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=−7/6∣(x−2)∣ from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be shifted 2 units to the right when mapped to g(x).

The y-coordinate of the points lying on f(x) will be reflected about the x-axis, and then vertically stretched by the factor 7/6.

Calculate the location where the point (6,6) will be mapped.

​(6+2,−7/6⋅∣6∣)=(6+2,−7/6⋅6)=(8,−7)

Calculate the location where the point (−6,6) will be mapped.​

(−6+2,−7/6⋅∣6∣)=(−6+2,−7/6⋅6)

=(−4,−7)

​Therefore, the two points (−4,−7) and (8,−7) lie on the graph of g(x).

Plot the vertex (2,0) and the points (−4,−7) and (8,−7), and then draw straight lines to sketch the graph of g(x)=−7/6∣(x−2)∣.

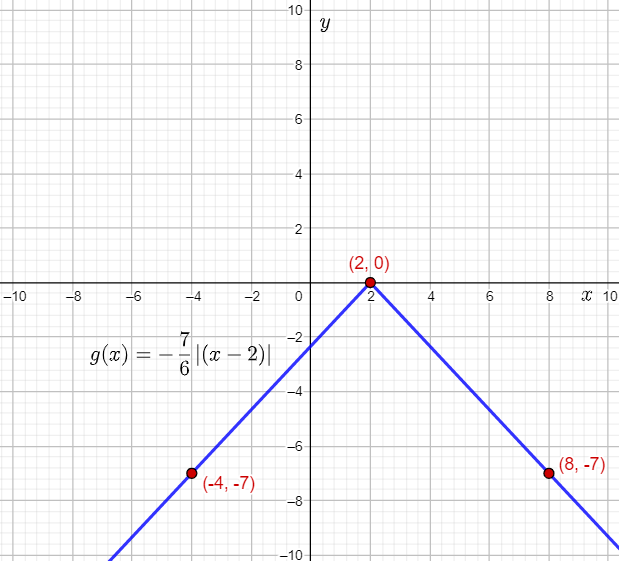
From the graph, it can be observed that the graph of the function g(x)=−7/6∣(x−2)∣ stretches infinitely towards the left and right. Therefore, the given absolute value function is defined for all values of x.

Hence, the domain of g(x)=−7/6∣(x−2)∣ is (−∞,∞).

Also, it can be observed that the y-coordinates of the points lying on the graph of the function g(x)=−7/6∣(x−2)∣ are either 0, or less than 0.

Thus, the range of g(x)=−7/6∣(x−2)∣ is (−∞,0].

The required graph is:

The domain of g(x) is (−∞,∞).

The range of g(x) is (−∞,0].

HMH Algebra 2 Volume 1 Exercise 2.1 Walkthrough

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 71 Exercise 7 Answer

The given function is g(x)=∣5/7(x−4)|.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To sketch the graph, write the translations used to form the given function from the parent absolute value function f(x)=∣x∣, and use them on the vertex to determine the vertex of g(x).

Next, write the coefficient of the absolute value in the given function to find the factor by which the parent absolute function will be vertically stretched.

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x) from f(x).

Next, plot the points and vertex and graph the given function.

Finally, use the drawn graph to find and write the domain and range of the function.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

It can be observed that g(x) involves a translation of f(x) by 4 units to the right.

Therefore, the vertex of g(x) is the point (0+4,0)=(4,0).

Rewrite the given function.

g(x)=5/7∣(x−4)∣

Compare the function g(x) to g(x)=a∣(x−h)∣−k, and write the value of the constant a.

a=5/7

Since a=5/7, that is 0<a<1, the graph of g(x) will involve a vertical compression of the parent absolute value function by a factor 5/7.

The points (4,4) and (−4,4) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=5/7∣(x−4)∣ from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be shifted 4 units to the right when mapped to g(x).

The y-coordinate of the points lying on f(x) will be vertically compressed by the factor 5/7 when mapped to g(x).

Calculate the location where the point (4,4) will be mapped.

(4+4,5/7⋅∣4∣)=(4+4,5/7⋅4)

=(8,20/7)

Calculate the location where the point (−4,4) will be mapped.

​(−4+4,5/7⋅∣4∣)=(−4+4,5/7⋅4)

=(0,20/7)

Therefore, the two points (0,20/7) and (8,20/7) lie on the graph of g(x).

Plot the vertex (4,0) and the points (0,20/7) and (8,20/7), and then draw straight lines to sketch the graph of g(x)=∣5/7(x−4)∣.

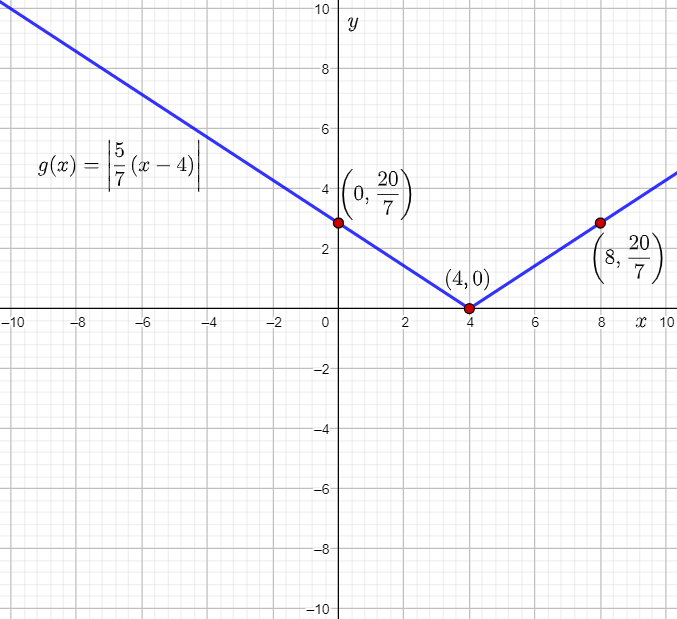
From the graph, it can be observed that the graph of the function g(x)=∣5/7(x−4)∣ stretches infinitely towards the left and right.

Therefore, the given absolute value function is defined for all values of x.

Hence, the domain of g(x)=∣5/7(x−4)∣ is (−∞,∞).

Also, it can be observed that the y-coordinates of the points lying on the graph of the function g(x)=∣5/7(x−4)∣ are either 0 or greater than 0.

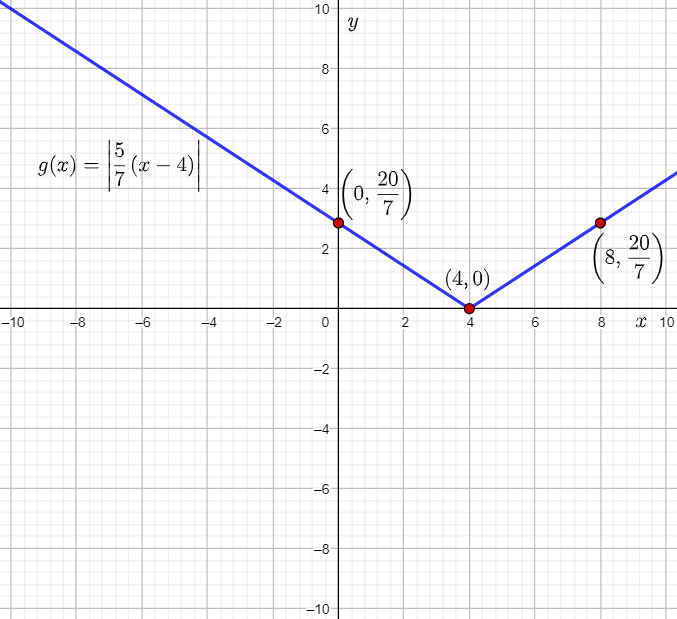
Thus, the range of g(x)=∣5/7(x−4)∣is [0,∞).

The required The domain of g(x) is (−∞,∞).

The range of g(x) is [0,∞).

Page 72 Exercise 8 Answer

The given function is g(x)=∣−7/3(x+5)−4|.

The question requires to predict how the graph of the given function will look, and verify this using a graphing calculator.

Then, it is required to sketch the graph of the given function.

To sketch the graph, write the translations used to form the given function from the parent absolute value function f(x)=∣x∣, and use them on the vertex to determine the vertex of g(x).

Next, write the coefficient of the absolute value in the given function to find the factor by which the parent absolute function will be vertically stretched.

Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on g(x) using the transformations used to form g(x) from f(x).

Next, plot the points and vertex and graph the given function. Finally, use the drawn graph to find and write the domain and range of the function.

The vertex of the parent absolute value function f(x)=∣x∣ is (0,0).

The vertex of g(x) is the point where (0,0) will be mapped using translations.

It can be observed that g(x) involves translations of f(x) by 5 units to the left and 4 units down.

Therefore, the vertex of g(x) is the point (0−5,0−4)=(−5,−4).

Rewrite the given function.​

g(x)=7/3∣−(x+5)∣−4

g(x)=7/3∣(x+5)∣−4

Compare the function g(x) to g(x)=a∣(x+h)∣−k, and write the value of the constant a.

a=7/3

Since a=7/3, that is a>1, the graph of g(x) will involve a vertical stretch of the parent absolute value function by a factor 7/3.

The points (3,3) and (−3,3) lie on the parent absolute value function f(x)=∣x∣.

The transformations used to form g(x)=7/3∣(x+5)∣−4 from the parent absolute value function can be used to determine the two points lying on g(x).

The x-coordinate of the points lying on f(x) will be shifted 5 units to the left when mapped to g(x).

The y-coordinate of the points lying on f(x) will be vertically stretched by the factor 7/3, and shifted down by 4 units.

Calculate the location where the point (3,3) will be mapped.

(3−5,7/3⋅∣3∣−4)=(3−5,7/3⋅3−4)

=(−2,7−4)

=(−2,3)

​Calculate the location where the point (−3,3) will be mapped.

​(−3−5,7/3⋅∣3∣−4)=(−3−5,7/3⋅3−4)

=(−8,7−4)

=(−8,3)

​Therefore, the two points (−8,3) and (−2,3) lie on the graph of g(x).

Plot the vertex (−5,−4) and the points (−8,3) and (−2,3), and then draw straight lines to sketch the graph of g(x)=∣−7/3(x+5)−4|.

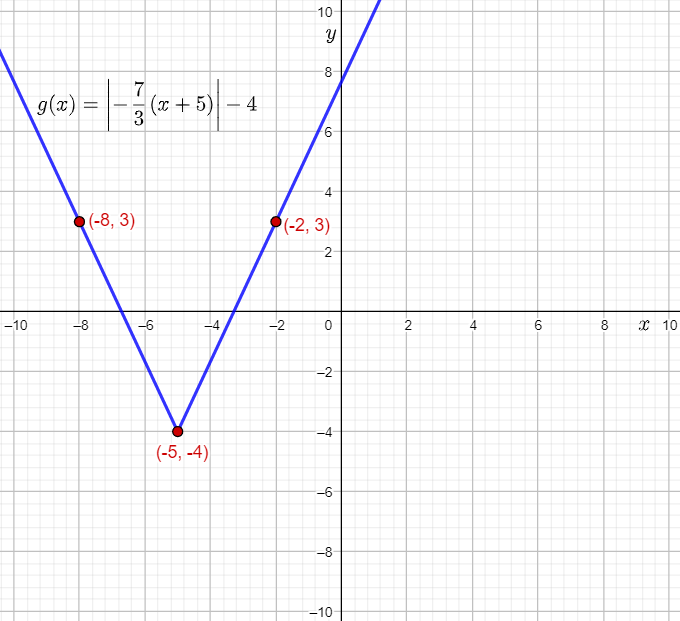
From the graph, it can be observed that the graph of the function g(x)=∣−7/3(x+5)−4| stretches infinitely towards the left and right.

Therefore, the given absolute value function is defined for all values of x.

Hence, the domain of g(x)=∣−7/3(x+5)−4| is (−∞,∞).

Also, it can be observed that the y-coordinates of the points lying on the graph of the function g(x)=∣−7/3(x+5)−4| are either −4, or greater than −4.

Thus, the range of g(x)=∣−7/3(x+5)−4| is [−4,∞).

The required graph is:

The domain of g(x) is (−∞,∞).

The range of g(x) is [−4,∞).

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 72 Exercise 9 Answer

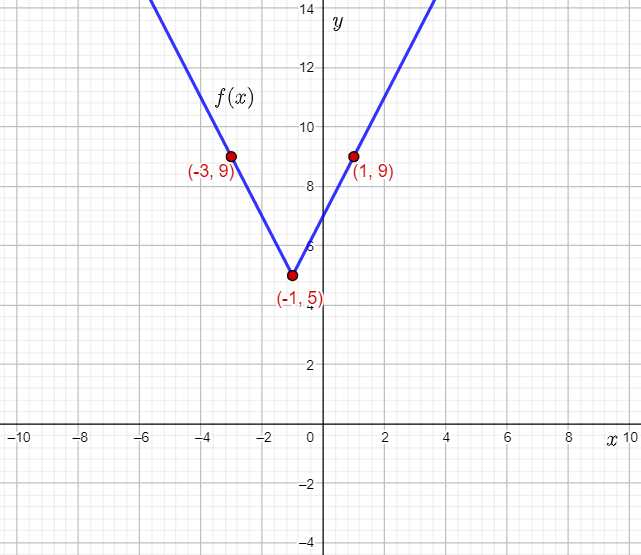
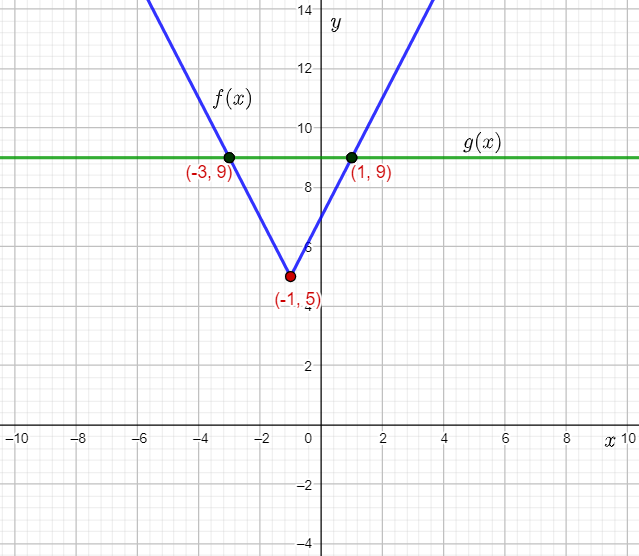
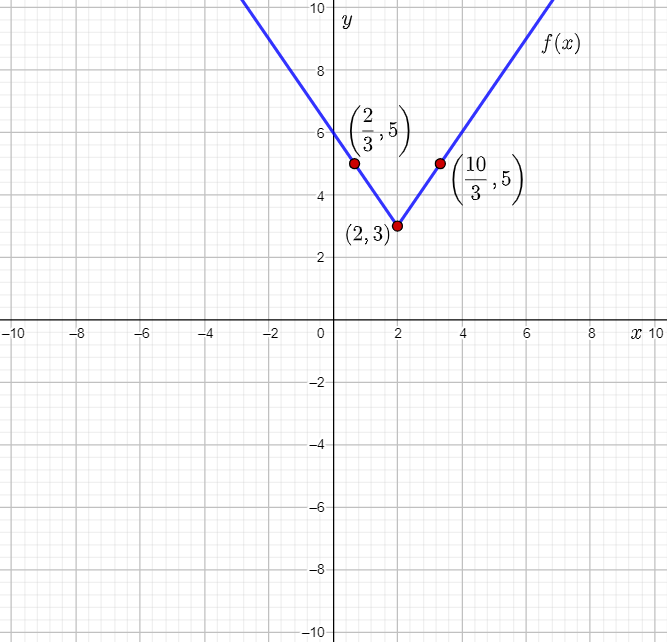
The given graph shows the graph of an absolute value function.

The question requires to write the function in standard form for the given graph, when a=1.

To determine the function, let the given function be g(x)=a∣1/b(x−h)+k|, use the graph to find the vertex, and thus, the values of h,k.

Then, rewrite the function using the obtained values.

Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of b.

Finally, use the value of b in the function to obtain the function in the required form.

Let the given function be g(x)=a∣1/b(x−h)+k|, that is an absolute value function in standard form.

From the graph, it can be observed that the vertex of the graphed absolute value function is (−7,4).

This means that the values of h and k are −7 and 4 respectively.

Substitute 1 for a, −7 for h, and 4 for k in g(x)=a∣1/b(x−h)+k|.

g(x)=1∣1/b(x−(−7))+4|

g(x)=∣1/b(x+7)+4|………………(1)

From the graph, it can be observed that the point (−6,6) lies on the graph.

Substitute −6 for x, and then 6 for g(−6) in equation (1), and subtract 4 from both sides.

​g(−6)=∣1/b(−6+7)+4|

6=∣1/b(1)+4|

2=∣1/b|……………(2)

​Form two equations by rewriting the absolute value in equation (2).

​2=1/b

2=−1/b

If 2 is equal to 1/b, then b=1/2.

If 2 is equal to −1/b, then b=−1/2.

Since the absolute value in g(x)=∣1/b(x+7)+4| remains the same for both values of b, consider the value b=1/2.

Substitute 1/2 for b in g(x)=∣1/b(x+7)+4|, and simplify the equation.

​g(x)=∣1/12(x+7)+4|

g(x)=∣2(x+7)∣+4

g(x)=2∣(x+7)∣+4

Thus, the graphed absolute value function is g(x)=2∣(x+7)∣+4.

The required absolute value function is g(x)=2∣(x+7)∣+4.

Page 72 Exercise 10 Answer

The given graph shows the graph of an absolute value function.

The question requires to write the function in standard form for the given graph, when b=1.

To determine the function, let the given function be g(x)=a∣1/b(x−h)+k|, use the graph to find the vertex, and thus, the values of h,k.

Then, rewrite the function using the obtained values

. Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of a.

Finally, use the value of a in the function to obtain the function in the required form.

Let the given function be g(x)=a∣1/b(x−h)+k|, that is an absolute value function in standard form.

From the graph, it can be observed that the vertex of the graphed absolute value function is (4,3).

This means that the values of h and k are 4 and 3 respectively.

Substitute 1 for b, 4 for h, and 3 for k in g(x)=a∣1/b(x−h)+k|.​

g(x)=a∣1/1(x−4)+3|

g(x)=a∣x−4∣+3………………(1)​

From the graph, it can be observed that the point (0,2) lies on the graph.

Substitute 0 for x, and then 2 for g(0) in equation (1), subtract 3 from both sides, and then divide both sides by 4.

​g(0)=a∣0−4∣+3

2=a∣−4∣+3

−1=a(4)

−1/4=a​

Substitute −1/4 for a in g(x)=a∣x−4∣+3.

g(x)=−1/4∣x−4∣+3

Thus, the graphed absolute value function is g(x)=−1/4∣x−4∣+3.

The required absolute value function is g(x)=−1/4∣x−4∣+3.

Page 74 Exercise 11 Answer

The vertex of f(x)=∣x∣, that is the parent absolute value function, is (0,0).

The vertex of y=∣x+6∣−4 is the point where (0,0) will be mapped using translations.

It can be observed that y=∣x+6∣−4 involves translations of f(x) by 6 units to the left and 4 units down.

Therefore, the vertex of the function y=∣x+6∣−4 is the point:

(0−6,0−4)=(−6,−4)

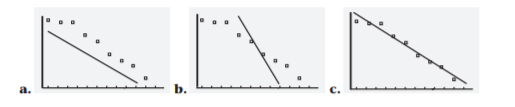
From the given graphs, only the graph in option (C) has the vertex at (−6,−4).

Thus, the graph of the function y=∣x+6∣−4 is the graph in option (C).

The graph in option (A) has the vertex at (6,−4), and not at (−6,−4).

Thus, the graph in option (A) is not the graph of the function y=∣x+6∣−4.

The graph in option (B) has the vertex at (6,4), and not at (−6,−4).

Thus, the graph in option (B) is not the graph of the function =∣x+6∣−4.

The graph of the function y=∣x+6∣−4 is the graph in option (C).

Exercise 2.1 Absolute Value Worked Examples HMH Algebra 2

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 74 Exercise 12 Answer

The vertex of f(x)=∣x∣, that is the parent absolute value function, is (0,0).

The vertex of y=∣x−6∣−4 is the point where (0,0) will be mapped using translations.

It can be observed that y=∣x−6∣−4 involves translations of f(x) by 6 units to the right and 4 units down.

Therefore, the vertex of the function y=∣x−6∣−4 is the point:

(0+6,0−4)=(6,−4)

From the given graphs, only the graph in option (A) has the vertex at (6,−4).

Thus, the graph of the function y=∣x−6∣−4 is the graph in option (A).

The graph in option (B) has the vertex at (6,4), and not at (6,−4).

Thus, the graph in option (B) is not the graph of the function y=∣x−6∣−4.

The graph in option (C) has the vertex at (−6,−4), and not at (6,−4).

Thus, the graph in option (C) is not the graph of the function y=∣x−6∣−4.

The graph of the function y=∣x−6∣−4 is the graph in option (A).

Page 74 Exercise 13 Answer

The vertex of f(x)=∣x∣, that is the parent absolute value function, is (0,0).

The vertex of y=∣x−6∣+4 is the point where (0,0) will be mapped using translations.

It can be observed that y=∣x−6∣+4 involves translations of f(x)

by 6 units to the right and 4 units up.

Therefore, the vertex of the function y=∣x−6∣+4 is the point: (0+6,0+4)=(6,4)

From the given graphs, only the graph in option (B) has the vertex at (6,4).

Thus, the graph of the function y=∣x−6∣+4 is the graph in option (B).

The graph in option (A) has the vertex at (6,−4), and not at (6,4).

Thus, the graph in option (A) is not the graph of the function y=∣x−6∣+4.

The graph in option (C) has the vertex at (−6,−4), and not at (6,4).

Thus, the graph in option (C) is not the graph of the function y=∣x−6∣+4.

The graph of the function y=∣x−6∣+4 is the graph in option (B).

Page 75 Exercise 14 Answer

The vertex of f(x)=∣x∣, that is the parent absolute value function, is (0,0).

The vertex of y=∣x+3∣+2 is the point where (0,0) will be mapped using translations.

It can be observed that y=∣x+3∣+2 involves translations of f(x) by 3 units to the left and 2 units up.

Therefore, the vertex of the given function is the point (0−3,0+2)=(−3,2).

The given graph is not the graph of the function y=∣x+3∣+2  because the vertex of the function in the graph is (3,2) and not (−3,2).

The function in the graph involves translations of the parent absolute value function f(x)=∣x∣ by 3 units to the right and 2 units up.

Thus, the correct equation shown in the graph is y=∣x−3∣+2.

The graphed function is not the graph of y=∣x+3∣+2 because the vertex of the function in the graph is (3,2), and the vertex of the given function is (−3,2).

The correct equation shown in the graph is y=∣x−3∣+2.

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 71 Exercise 15 Answer

It is given that the golf ball is at the point (2.5,2), the hole where the golf ball is to be shot is at (9.5,2), and the point where the golf ball banks off the side wall is (6,8).

The question requires to equation of the path of the ball.

To determine the equation, draw the graph representing the given situation.

Then, observe that the path of the ball is the graph of an absolute value function, and write a general function for the path.

Assume b=1, use the graph to find the vertex, and thus, the values of h,k. Then, rewrite the function using the obtained values.

Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of a.

Finally, use the value of a in the function to obtain the function representing the path of the ball.

Draw the graph representing the given points, and join them to show the path of the ball.

It can be observed that the path of the ball is the graph of an absolute value function.

Let the equation for the path of the ball be represented by the function g(x)=a∣1/b(x−h)+k|.

Assume that b=1.

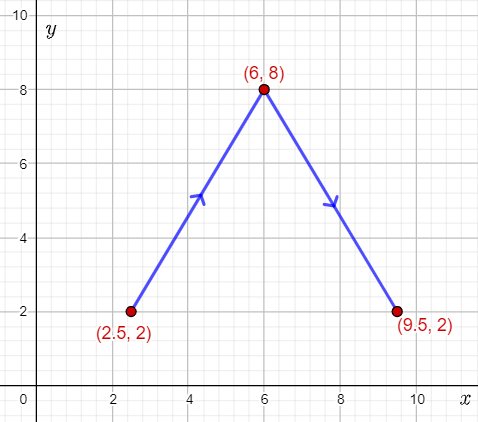
From the graph, it can be determined that the vertex of the graph of the function is (6,8).

This means that the values of h and k are 6 and 8 respectively.

Substitute 1 for b, 6 for h, and 8 for k in the equation g(x)=a∣1/b(x−h)+k|.

​g(x)=a∣1/1(x−6)+8|

g(x)=a∣x−6∣+8………………(1)​

The path of the ball starts from the point (2.5,2).

Substitute 2.5 for x, and then 2 for g(2.5) in equation (1). Then, subtract 8 from both sides, and divide both sides by 3.5.

​g(2.5)=a∣2.5−6∣+8

2=a∣−3.5∣+8

−6=a(3.5)

−6/3.5=a

−12/7=a

​Substitute −12/7 for a in g(x)=a∣x−6∣+8.

g(x)=−12/7∣x−6∣+8

Thus, the equation representing the path of the ball is g(x)=−12/7∣x−6∣+8.

The required equation is g(x)=−12/7∣x−6∣+8.

Page 75 Exercise 16 Answer

It is given that the golf ball is at the point (2.5,2), the hole where the golf ball is to be shot is at (9.5,2), and the point where the golf ball banks off the side wall is (6,8).

The question requires to determine if the player makes the shot.

Given the equation g(x)=−12/7∣x−6∣+8 representing the path of the ball as calculated in the previous part of this exercise.

To answer the question, substitute the point (9.5,2) on the equation for path of the ball, and check whether the point lies on the path.

Substitute 9.5 for x and 2 for g(9.5) in equation g(x)=−12/7∣x−6∣+8, and simplify both sides of the equation.​

g(9.5)=−12/7∣9.5−6∣+8

2=−12/7∣3.5∣+8

2=−12/7(3.5)+8

2=−6+8

2=2

The point (9.5,2) satisfies the equation for the path of the ball because the equation 2=2 is always true.

Therefore, the point (9.5,2)representing the hole where the golf ball is aimed at lies on the path of the ball.

Thus, the player makes the shot.

Yes, the player makes the shot because the point (9.5,2) representing the hole, where the golf ball is to be shot, lies on the path of the ball.

Page 76 Exercise 17 Answer

It is given that the orchestra starts at fortissimo, changes to pianissimo after four measures, and again increases to fortissimo after four more measures.

Also, it is given that a fortissimo and pianissimo are at sound levels 90 and 50 decibels respectively.

The question requires to determine the function representing the sound level s as a function of the number of measures m.

To determine the function, use the points of the form (m,s) and the given information to find three points lying on the graph of the required function.

Plot the points, join them, observe the graph formed, and write the required function as a general absolute value function.

Assume b=1, use the graph to find the vertex, and thus, the values of h,k.

Then, rewrite the function using the obtained values.

Next, find a point other than vertex lying on the graph, and substitute its coordinates in the function to find the value of a.

Then, use the value of a in the function to obtain the function representing the sound level.

The points (m,s) can be used to represent the sound level at a particular number of measures.

The initial sound level at zero number of measures is s=90 decibels.

The sound level after four number of measures is s=50 decibels.

The sound level after eight number of measures is s=90 decibels.

Therefore, the points (0,90),(4,50),(8,90) lie on the graph of the function representing the sound level.

Plot the points, and join them to show the graph of the function representing the sound level.

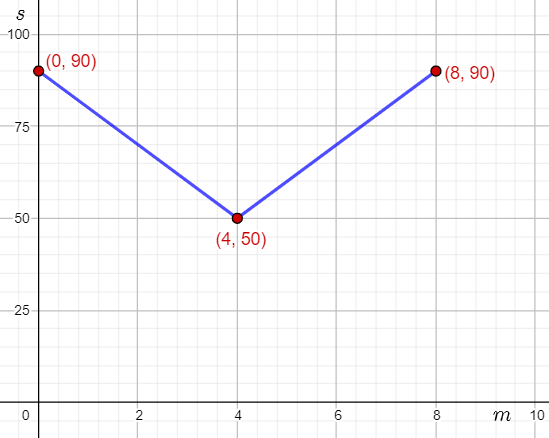
The graph of the function representing the sound level s as a function of the number of measures m can be represented by the function s=a∣1/b(m−h)+k|.

Assume that b=1.

The vertex of the function is the point is the relative extrema (4,50).

This means that the values of h and k are 4 and 50 respectively.

Substitute 1 for b, 4 for h, and 50 for k in the equation s=a∣1/b(m−h)+k|.

​s=a∣1/1(m−4)+50|

s=a∣m−4∣+50………………(1)

​The point representing the initial sound level at zero numbers of measures is the point (0,90).

Substitute 0 for x and 90 for s in equation (1). Then, subtract 50 from both sides, and then divide both sides by 4.

​90=a∣0−4∣+50

90=a∣−4∣+50

40=a(4)

10=a

​Substitute 10 for a in s=a∣m−4∣+50.

s=10∣m−4∣+50

Thus, the function representing the sound level s as a function of the number of measures m is s=10∣m−4∣+50.

The required function is s=10∣m−4∣+50.

HMH Algebra 2 Volume 1 1st Edition Module 2 Chapter 2 Exercise 2.1 Absolute Value, Functions, Equations And Inequalities Page 76 Exercise 18 Answer

It is given that the orchestra starts at fortissimo, changes to pianissimo after four measures, and again increases to fortissimo after four more measures.

Also, it is given that a fortissimo and pianissimo are at sound levels 90 and 50 decibels respectively.

The question requires to determine the number of measures at which the orchestra is at the loudness of mezzo forte, that is 70 decibels.

Given the equation s=10∣m−4∣+50 representing the sound level s as a function of the number of measures m, as calculated in the previous part of this exercise.

To determine the number of measures, substitute the sound level as 70 in the function for the sound level, and solve the equation for m by rewriting the absolute value.

Substitute 70 for s in equation s=10∣m−4∣+50, subtract 50 from both sides, and divide both sides by 10.

​70=10∣m−4∣+50

20=10∣m−4∣

2=∣m−4∣………………(1)

​Form two equations by rewriting the absolute value in equation (1).

​2=m−4

2=−(m−4)

Add 4 on both sides of 2=m−4 to solve for m.

​2+4=m−4+4

6=m

​Simplify the right-hand side of 2=−(m−4), and solve for m.

​2=−m+4

m=4−2

m=2

​The two values of m are 2 and 6.

Thus, the orchestra is at the loudness of mezzo forte in 2 measures and in 6 measures.

The required number of measures at which orchestra is at the loudness of mezzo forte are 2 measures and 6 measures.

Page 76 Exercise 19 Answer

It is given that the orchestra starts at fortissimo, changes to pianissimo after four measures, and again increases to fortissimo after four more measures.

Also, it is given that a fortissimo and pianissimo are at sound levels 90 and 50 decibels respectively.

The question requires to describe how the graph of the given function will look.

Given the equation s=10∣m−4∣+50 representing the sound level s as a function of the number of measures m, as calculated in part (a) of this exercise.

To answer the question, compare the given function to the general form s=a∣(m−h)∣+k to find the values of the constants, and then describe the graph using the transformations that are required to form the function from the parent absolute value function.

Compare the function for sound level to the general form s=a∣(m−h)∣+k, and write the values of the constants.

​a=10

h=4

k=50​

The value of a is positive. Therefore, the graph of s=10∣m−4∣+50 will open upwards.

Since ∣a∣=10, that is greater than 1, the graph will be a vertical stretch of the parent absolute value function by a factor 10.

Since h=4, the graph will be a horizontal translation of the parent absolute value function by 4 units to the right.

Since k=50, the graph will involve a vertical translation of the parent absolute value function by 50 units up.

Therefore, the graph of s=10∣m−4∣+50 will open upwards.

It will be a vertical stretch of the parent absolute value function by a factor 10, a horizontal translation by 4 units to the right, and finally, a vertical translation 50 units up.

The graph of s=10∣m−4∣+50 will open upwards and will be a vertical stretch of the parent absolute value function by a factor 10, a horizontal translation by 4 units to the right, and finally, a verical translation 50 units up.

Algebra 2 Volume 1 1st Edition Unit 1 Functions

Page 2 Problem 1 Answer

In the question, the following words are given:
Coefficient
Domain
Function
Inequality
Interval
Quadratic function
Range
Transformation

The diagram of an information wheel is given as shown below:

It is required to complete the information wheel using correct words from the given list.

To solve this, use the appropriate words from the list to replace the terms in the diagram, using the definitions of those words.

From the diagram, f(x)=3x²

is a function of x and hence, it can be termed as a function.

3 is the coefficient of x².

From the definition of domain, the domain of the function f(x)=3x²is the set of all real numbers.

The range of the function is all the outputs and is given as y=3x².

Finally, since x² is always positive, the interval will contain only non-negative real numbers.

Draw the diagram of the information wheel with the correct words:

The complete information wheel using correct words from the given list is shown below:

HMH Algebra 2 Volume 1 Unit 1 Functions overview

HMH Algebra 2 Volume 1 1st Edition Unit 1 Functions Page 2 Problem 2 Answer

In the question, the given incomplete sentence is: A ________ is a constant in the equation of a curve that yields a family of similar curves as it changes.

It is required to complete the sentence. To solve this, use the given sentence and the definition of parameter to find an appropriate word to complete the sentence.

A Parameter is a constant in the equation of a curve that yields a family of similar curves as it changes.

A Parameter is a constant in the equation of a curve that yields a family of similar curves as it changes.

HMH Algebra 2 Unit 1 Functions Key Concepts

HMH Algebra 2 Volume 1 1st Edition Unit 1 Functions Page 2 Problem 3 Answer

In the question, the given incomplete sentence is: A function f(x) such that f(x)=f(−x) is an ________.

It is required to complete the sentence. To solve this, use the given sentence and the definition of an even function to find an appropriate word to complete the sentence.

A function f(x) such that f(x)=f(−x) is an Even Function.

Solutions For HMH Algebra 2 Unit 1 Functions

HMH Algebra 2 Volume 1 1st Edition Unit 1 Functions Page 2 Problem 4 Answer

In the question, the given incomplete sentence is: A compound statement that uses the word or is a _________.

It is required to complete the sentence. To solve this, use the given sentence and the definition of disjunction to find an appropriate word to complete the sentence.

A disjunction uses the word or in a compound statement.