Algebra 2, Volume 1 1st Edition Module 2 Absolute Value, Functions, Equations And Inequalities
Page 87 Problem 1 Answer
The absolute value expression in an absolute value inequality is generally of the form ∣ax+b∣.
An absolute value inequality can be solved either graphically or algebraically.
To solve an absolute value inequality graphically, the left and right sides of the inequality are assumed to be the functions f(x) and g(x) respectively.
Then, the two functions are graphed on the same coordinate grid. Finally, the intervals on the x-axis which satisfy the given inequality are observed to find the required solution.
To solve an absolute value inequality algebraically, first the operations of multiplication, division, addition, and subtraction are used to isolate the absolute value expression of the form ∣ax+b∣ on one side of the inequality.
Then, the constant on the other side of the inequality and the sign of inequality are used to rewrite the inequality as one or two linear inequalities.
Finally, the obtained inequalities are solved for x to find the required solution.
The solutions of an absolute value inequality can be obtained either graphically or algebraically.
The graphic method of solving an absolute value inequality involves assuming the left and right sides of the inequality to be the functions f(x) and g(x) respectively, graphing the two functions on the same coordinate grid, and finally, observing the intervals on the x-axis which satisfy the given inequality to find the required solution.
The algebraic method of solving an absolute value inequality involves isolating the absolute value expression on one side of the inequality, then using the constant on the other side of the inequality and the sign of inequality to rewrite the inequality as one or two linear inequalities, and finally, solving the obtained inequalities for x to find the required solution.
Page 87 Problem 2 Answer
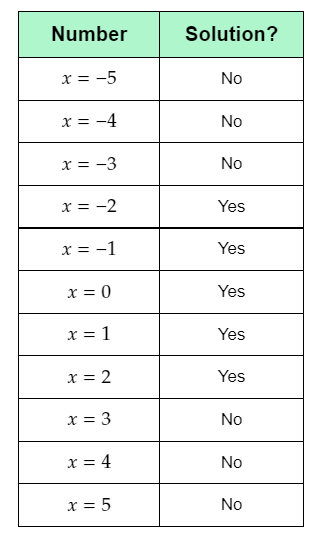
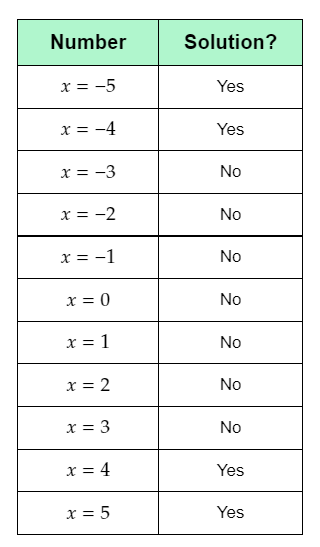
The given table contains the possible solutions of the given absolute value inequality ∣x∣+2<5.
The question requires to determine which of the integers between −5 and 5 are solutions of the given inequality, and complete the given table by writing ‘yes’ or ‘no’ if the number is a solution of the given inequality.
Then, it is required to plot the solutions on the number line.
To complete the table and plot the solutions, use the given integers, substitute them in the given absolute value inequality, and checking whether the number satisfies the inequality or not.
Then, write ‘yes’ against the numbers that satisfy the inequality and are a solution, or write ‘no’ otherwise. Finally, plot the solutions on the given number line.
Substitute −5 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣−5∣+2<5
5+2<5
7<5
This inequality is not true. Therefore, x=−5 is not a solution of the given absolute value inequality.
Substitute −4 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣−4∣+2<5
4+2<5
6<5
This inequality is not true. Therefore, x=−4 is not a solution of the given absolute value inequality.
Substitute −3 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣−3∣+2<5
3+2<5
5<5
This inequality is not true. Therefore, x=−3 is not a solution of the given absolute value inequality.
Substitute −2 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣−2∣+2<5
2+2<5
4<5
This inequality is true. Therefore, x=−2 is a solution of the given absolute value inequality.
Substitute −1 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣−1∣+2<5
1+2<5
3<5
This inequality is true. Therefore, x=−1 is a solution of the given absolute value inequality.
Substitute 0 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣0∣+2<5
0+2<5
2<5
This inequality is true. Therefore, x=0 is a solution of the given absolute value inequality.
Substitute 1 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣1∣+2<5
1+2<5
3<5
This inequality is true. Therefore, x=1 is a solution of the given absolute value inequality.
Substitute 2 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣2∣+2<5
2+2<5
4<5
This inequality is true. Therefore, x=2 is a solution of the given absolute value inequality.
Substitute 3 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣3∣+2<5
3+2<5
5<5
This inequality is not true. Therefore, x=3 is not a solution of the given absolute value inequality.
Substitute 4 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣4∣+2<5
4+2<5
6<5
This inequality is not true. Therefore, x=4 is not a solution of the given absolute value inequality.
Substitute 5 for x in the absolute value inequality ∣x∣+2<5, and simplify the left-hand side.
∣5∣+2<5
5+2<5
7<5
This inequality is not true. Therefore, x=5 is not a solution of the given absolute value inequality.
Complete the given table by writing ‘yes’ against the numbers that are solutions of the given absolute value inequality, and ‘no’ against the numbers that are not solutions of the given absolute value inequality.
Plot the obtained solutions on the given number line.
The required solutions are the integers −2,−1,0,1,2.
The completed table is:
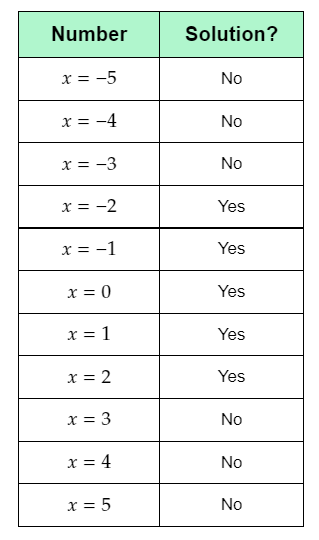
The required plot of the solutions on the number line is:
Page 87 Problem 3 Answer
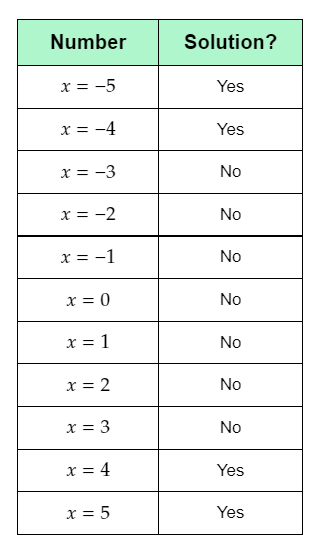
The given table contains the possible solutions of the given absolute value inequality ∣x∣+2>5.
The question requires to determine which of the integers between −5 and 5
are solutions of the given inequality, and complete the given table by writing ‘yes’ or ‘no’ if the number is a solution of the given inequality.
Then, it is required to plot the solutions on the number line.
To complete the table and plot the solutions, use the given integers, substitute them in the given absolute value inequality, and checking whether the number satisfies the inequality or not.
Then, write ‘yes’ against the numbers that satisfy the inequality and are a solution, or write ‘no’ otherwise.
Finally, plot the solutions on the given number line.
Substitute −5 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣−5∣+2>5
5+2>5
7>5
This inequality is true. Therefore, x=−5 is a solution of the given absolute value inequality.
Substitute −4 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣−4∣+2>5
4+2>5
6>5
This inequality is true. Therefore, x=−4 is a solution of the given absolute value inequality.
Substitute −3 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣−3∣+2>5
3+2>5
5>5
This inequality is not true. Therefore, x=−3 is not a solution of the given absolute value inequality.
Substitute −2 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣−2∣+2>5
2+2>5
4>5
This inequality is not true. Therefore, x=−2 is not a solution of the given absolute value inequality.
Substitute −1 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣−1∣+2>5
1+2>5
3>5
This inequality is not true. Therefore, x=−1 is not a solution of the given absolute value inequality.
Substitute 0 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣0∣+2>5
0+2>5
2>5
This inequality is not true. Therefore, x=0 is not a solution of the given absolute value inequality.
Substitute 1 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣1∣+2>5
1+2>5
3>5
This inequality is not true. Therefore, x=1 is not a solution of the given absolute value inequality.
Substitute 2 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣2∣+2>5
2+2>5
4>5
This inequality is not true. Therefore, x=2 is not a solution of the given absolute value inequality.
Substitute 3 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣3∣+2>5
3+2>5
5>5
This inequality is not true. Therefore, x=3 is not a solution of the given absolute value inequality.
Substitute 4 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣4∣+2>5
4+2>5
6>5
This inequality is true. Therefore, x=4 is a solution of the given absolute value inequality.
Substitute 5 for x in the absolute value inequality ∣x∣+2>5, and simplify the left-hand side.
∣5∣+2>5
5+2>5
7>5
This inequality is true. Therefore, x=5 is a solution of the given absolute value inequality.
Complete the given table by writing ‘yes’ against the numbers that are solutions of the given absolute value inequality, and ‘no’ against the numbers that are not solutions of the given absolute value inequality.
Plot the obtained solutions on the given number line.
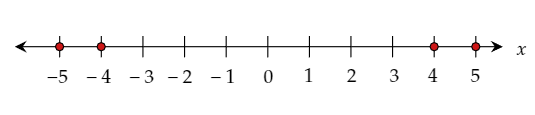
The required solutions are the integers −5,−4,4,5.
The completed table is:
The required plot of the solutions on the number line is:
Page 87 Problem 4 Answer
The given equation is ∣x∣+2=5.
The question requires to write the solutions of the given equation, and then relate them to the solutions obtained in the previous two parts of this exercise.
Given that the integers between −5 and 5 that are the solutions of the absolute value inequality ∣x∣+2<5 are −2,−1,0,1,2, as calculated in part (a) of this exercise.
Given that the integers between −5 and 5 that are the solutions of the absolute value inequality ∣x∣+2>5 are −5,−4,4,5, as calculated in the previous part of this exercise.
To solve the equation, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, observe the solutions obtained in the previous two parts of this exercise, and relate the solutions of the given absolute value equation.
Subtract 2 from both sides of ∣x∣+2=5.
∣x∣=3
Rewriting the equation, the two equations obtained are x=−3 or x=3.
Thus, the two solutions of the given absolute value equation are x=−3 or x=3.
The integers solutions between −5 and 5 of the absolute value inequality ∣x∣+2<5 are −2,−1,0,1,2.
The integers solutions between −5 and 5 of the absolute value inequality ∣x∣+2>5 are −5,−4,4,5.
It can be observed that solutions contain all the integers between −5 and 5, except −3 and 3.
These remaining integers are the solutions of the absolute value equation ∣x∣+2=5.
Thus, the solutions of ∣x∣+2<5, ∣x∣+2>5, and ∣x∣+2=5 are distinct and not repeated, and each integer between −5 and 5 is the solution of either one of the two inequalities, or the equation.
The required solutions are x=−3 or x=3.
The solutions of ∣x∣+2<5 and ∣x∣+2>5 contain all the integers between −5 and 5, except −3 and 3, which are the solutions of the absolute value equation ∣x∣+2=5.
The solutions of ∣x∣+2<5, ∣x∣+2>5, and ∣x∣+2=5 are different and not repeated. Also, each integer between −5 and 5 is the solution of either one of the two inequalities, or the equation.
Page 87 Problem 5 Answer
It is given that x is a real number.
The given absolute value inequalities are ∣x∣+2<5 and ∣x∣+2>5.
The question requires to graph all real solutions of the two absolute value inequalities on the given number lines.
Given that the solutions of the absolute value equation ∣x∣+2=5 are −3,3, as calculated in the previous part of this exercise.
To graph the solutions, observe the given solutions of the absolute value equation ∣x∣+2=5, form intervals using the two solutions, and check the value of the left-hand side of the inequalities for all real values.
Then, graph the solutions on the given number lines for both the inequalities.
The solutions of the absolute value equation ∣x∣+2=5 are −3,3.
When x<−3, the value of ∣x∣+2 is greater than 5, which does not satisfy the inequality ∣x∣+2<5.
When x=−3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2<5.
When x is between −3 and 3, both not included, the value of ∣x∣+2 is less than 5, which satisfies the inequality ∣x∣+2<5.
When x=3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2<5.
When x>3, the value of ∣x∣+2 is greater than 5, which does not satisfy the inequality ∣x∣+2<5.
Thus, the solution of the absolute value inequality ∣x∣+2<5 is −3<x<3.
Graph the obtained solutions of ∣x∣+2<5 on the given number line.
Consider the absolute value inequality ∣x∣+2>5.
When x<−3, the value of ∣x∣+2 is greater than 5, which satisfies the inequality ∣x∣+2>5.
When x=−3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2>5.
When x is between −3 and 3, both not included, the value of ∣x∣+2 is less than 5, which does not satisfy the inequality ∣x∣+2<5.
When x=3, the value of ∣x∣+2 is equal to 5, which does not satisfy the inequality ∣x∣+2>5.
When x>3, the value of ∣x∣+2 is greater than 5, which satisfies the inequality ∣x∣+2>5.
Thus, the solution of the absolute value inequality ∣x∣+2>5 is x<−3 or x>3.
Graph the obtained solutions of ∣x∣+2>5 on the given number line.
The graph of all real solutions of ∣x∣+2<5 is:
The graph of all real solutions of ∣x∣+2>5 is:
Page 88 Problem 6 Answer
The absolute value inequality ∣x∣+2>5 can be simplified as ∣x∣>3.
This equation is true for all values of x greater than 3, that is x>3, and for all values of x less than −3, that is x<−3.
There is no value of x that is within both the intervals x<−3 and x>3.
Therefore, the solution for the given inequality will be written as a disjunction, that is using the word “or”.
Thus, the solution for the inequality ∣x∣+2>5 is the disjunction x<−3 or x>3.
The solution for the given inequality will be written as a disjunction using the word “or” because there is no value of x lying within both the intervals x<−3 and x>3.
Therefore, the required solution for the inequality ∣x∣+2>5 is the disjunction x<−3 or x>3.
Page 88 Problem 7 Answer
The given absolute value inequalities are ∣x∣+2≤5 and ∣x∣+2≥5.
The question requires to describe the solutions of the given absolute value inequalities using inequalities that do not include an absolute value.
Given that the solutions of the absolute value equation ∣x∣+2=5 are −3,3, as calculated in the previous part of this exercise.
To graph the solutions, simplify the given absolute value inequalities, and check the value of the left-hand side of the inequalities for all real values using intervals.
Then, write the solutions for which the inequalities are satisfied as intervals which do not contain any absolute values.
The first given absolute value inequality ∣x∣+2≤5 can be simplified as ∣x∣≤3.
When x<−3, the value of ∣x∣ is greater than 3, which does not satisfy the inequality ∣x∣≤3.
When x=−3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≤3.
When x is between −3 and 3, both not included, the value of ∣x∣ is less than 3, which satisfies the inequality ∣x∣≤3.
When x=3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≤3.
When x>3, the value of ∣x∣ is greater than 3, which does not satisfy the inequality ∣x∣≤3.
Therefore, the solutions of the absolute value inequality ∣x∣+2≤5 are all the values between the integers −3 and 3, both included.
Thus, the solution of the absolute value inequality ∣x∣+2≤5 is the interval −3≤x≤3.
The second given absolute value inequality ∣x∣+2≥5 can be simplified as ∣x∣≥3.
When x<−3, the value of ∣x∣ is greater than 3, which satisfies the inequality ∣x∣≥3.
When x=−3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≥3.
When x is between −3 and 3, both not included, the value of ∣x∣ is less than 3, which does not satisfy the inequality ∣x∣≥3.
When x=3, the value of ∣x∣ is equal to 3, which satisfies the inequality ∣x∣≥3.
When x>3, the value of ∣x∣ is greater than 3, which satisfies the inequality ∣x∣≥3.
Therefore, the solutions of the absolute value inequality ∣x∣+2≥5 are all the values lesser than or equal to −3, or greater than and equal to 3.
Thus, the solution of the absolute value inequality ∣x∣+2≥5 is the disjunction x≤−3 or x≥3
Page 88 Problem 8 Answer
The given absolute value inequality is ∣x−2∣−3<1.
The question requires to solve the given inequality graphically.
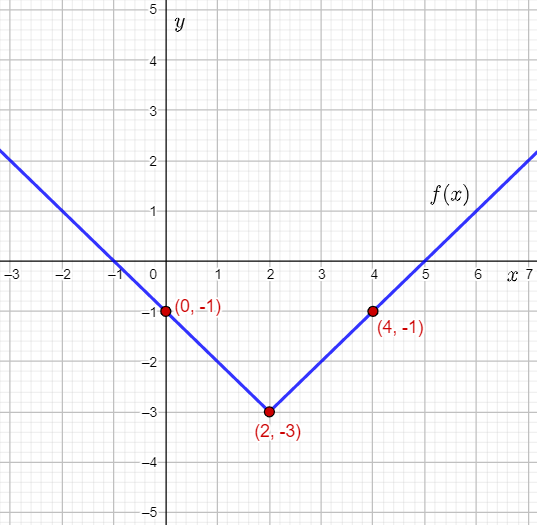
To solve the given inequality, let f(x) and g(x) be functions equal to left and right side of the given inequality respectively.
Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).
Next, write the transformations used to form f(x) from the parent absolute value function, take two points lying on the parent absolute value function, and use them to determine two points lying on f(x).
Next, plot the points and vertex, and use them to graph the function f(x) along with the constant function g(x).
Finally, write the intervals of x where the graph of f(x) is below the graph of g(x).
The given inequality is of the form f(x)<g(x).
Let f(x)=∣x−2∣−3 and g(x)=1.
The required solutions are the intervals on the x-axis where the graph of f(x) lies below the graph of g(x).
The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).
The vertex of f(x) is the point where (0,0) will be mapped using translations.
It can be observed that f(x) involves translations of h(x) by 2 units to the right and 3 units down.
Therefore, the vertex of f(x) is the point (0+2,0−3)=(2,−3).
The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.
The transformations used to form f(x)=∣x−2∣−3 from the parent absolute value function can be used to determine the two points lying on f(x).
The x-coordinate of the points lying on h(x) will be shifted 2 units to the right when mapped to f(x).
The y-coordinate of the points lying on h(x) will be moved down 3 units.
Therefore, the point (2,2) moves to (2+2,∣2∣−3)=(4,−1).
The point (−2,2) moves to (−2+2,∣2∣−3)=(0,−1).
Plot the vertex (2,−3) and the points (0,−1) and (4,−1), and then draw straight lines to plot the graph of f(x)=∣x−2∣−3.
Plot the function g(x)=1 as a horizontal line on the grid where f(x) is plotted.
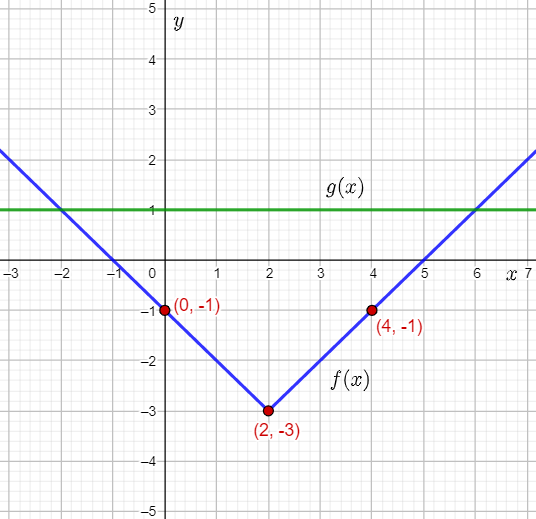
The graph of f(x) lies below the graph of g(x) between x=−2 and x=6.
Thus, the solution of the inequality ∣x−2∣−3<1 is x>−2 and x<6.
The solution of the inequality ∣x−2∣−3<1 is x>−2 and x<6.
The solution is obtained using the graph:
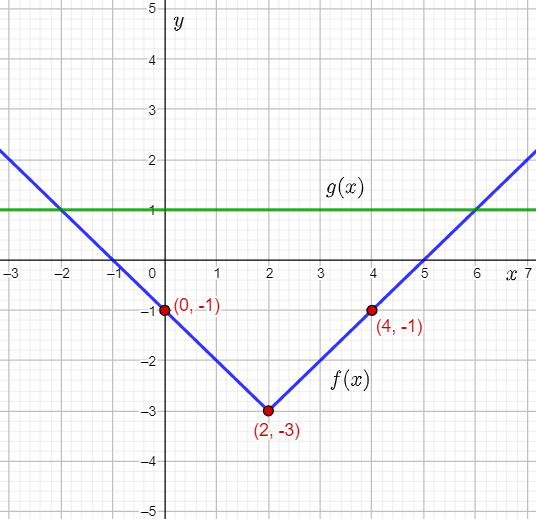
Page 89 Problem 9 Answer
The inequality in part (A) changes from ∣x+3∣+1>4 to ∣x+3∣+1≥4.
Let f(x) be equal to ∣x+3∣+1, and g(x) be equal to 4.
The given inequality is of the form f(x)≥g(x).
The required solutions are the intervals on the x-axis where the graph of f(x) lies above the graph of g(x), or intersects it.From the graph, it can be observed that the graph of f(x)
lies above the graph of g(x) when x<−6 and x>0.
Also, the graph of f(x) intersects the graph of g(x) when x is equal to −6 or 0.
Thus, the solution of the inequality ∣x+3∣+1≥4 is x≤−6 or x≥0.
It can be observed that the solution x<−6 or x>0 of ∣x+3∣+1>4 changes to x≤−6 or x≥0 when the inequality changes to ∣x+3∣+1≥4.
The signs of inequality of the solution changed to include equal to.
The solution of the inequality ∣x+3∣+1≥4 is x≤−6 or x≥0.
The solution x<−6 or x>0 of ∣x+3∣+1>4 changes to x≤−6 or x≥0 when the inequality changes to ∣x+3∣+1≥4.
The signs of inequality of the solution are changed to include equal to in the solution of the new inequality.
Page 89 Problem 10 Answer
The graph of f(x) lies entirely above the graph of g(x).
This means that the graph of f(x) lies above the graph of g(x) for all values of x.
The solution of the inequality f(x)>g(x) is the interval where the graph of f(x) lies above the graph of g(x).
Therefore, the inequality f(x)>g(x) has infinitely many solutions lying in the interval (−∞,∞).
The solution of the inequality f(x)<g(x) is the interval where the graph of f(x) lies below the graph of g(x).
Since the graph of f(x) lies above the graph of g(x) for all values of x, the inequality f(x)<g(x) has no solution.
The inequality f(x)>g(x) has infinitely many solutions lying in the interval (−∞,∞).
The inequality f(x)<g(x) has no solution.