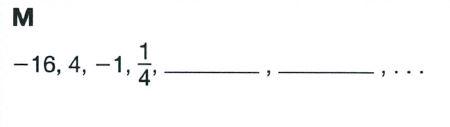
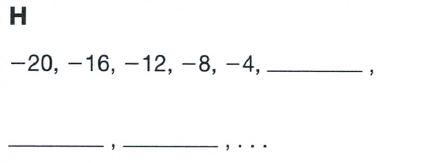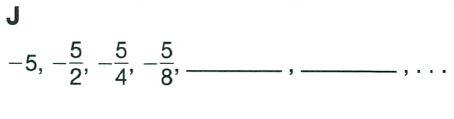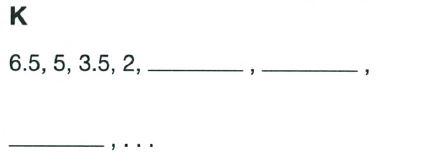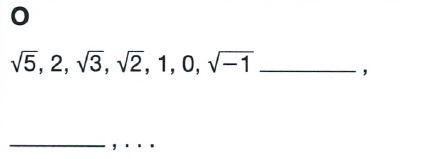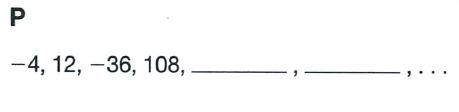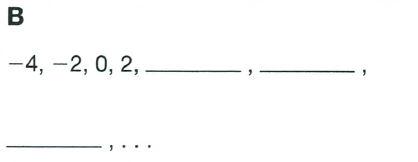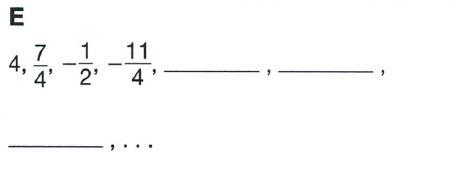Chapter 3 Numeric And Algebraic Expressions
Section 3.5: Evaluate Algebraic Expressions
Page 145 Exercise 1 Answer
Multiply the number of hours, which is h, by the rental price of a bike. Add to that the cost of a lock and a basket.
h x 12.50 + 1.75 + 2.25
To find the cost of renting this equipment for 4 hours, replace the variable h in the previous expression with 4.
4 x 12.50 + 1.75 + 2.25 (Find the product)
= 50 + 1.75 + 2.25 (find the sum)
= 51.75 + 2.25 (Find the sum)
= 54
Result
h x 12.50 + 1.75 + 2.25
To cost of renting a bike, a lock, and a basket for 4 hours is $54.
Page 145 Exercise 1 Answer
For each hour that a helmet is rented one pays $12.50, so we multiply the number of hours h by the price. To the result, we add the price of a helmet. Since the helmet is rented for a flat fee, we don’t multiply it by h.
The expression which represents how much it costs to rent a bike and helmet for h hours is:
h × 12.50 + 5.25.
If a bike and helmet are rented for 3 hours, simply replace h with 3 in the expression above.
3 × 12.50 + 5.25 (Find the product.)
= 37.50 + 5.25 (Find the sum.)
= 42.75
Result
h × 12.50 + 5.25
It would cost $42.75 to rent a bike and a helmet for 3 hours.
Page 146 Exercise 1 Answer
If t equals 10, then the value of the expression can be found as follows.
50 − t (Replace the variable t with 10.)
= 50 − 10 (Find the difference.)
= 40
The value of the expression 50 − t, when t is 10, is 40.
If t equals 20, then the value of the expression can be found as follows.
50 − t (Replace the variable t with 20.)
= 50 − 20 (Find the difference.)
= 30
The value of the expression 50 − t, when t is 20, is 30.
If t equals 25, then the value of the expression can be found as follows.
50 – t (Replace the variable t with 25)
= 50 – 25 (Find the difference)
= 25
The value of the expression 50 – t, when t is 25, is 25.
An algebraic expression can be evaluated using substitution, which is replacing the variable in the expression with a number and then calculating the value of the whole expression.
Result

An algebraic expression can be evaluated using substitution, which is replacing the variable in the expression with a number and then calculating the value of the whole expression.
Page 147 Exercise 2 Answer
Evaluating the given expression for a = 10 gives:
3.4 + 12a ÷ 4 = 3.4 + 12(10) ÷ 4 Substitute a = 10.
= 3.4 + 120 ÷ 4 Multiply.
= 3.4 + 30 Divide.
= 33.4 Add.
Result
33.4
Page 147 Exercise 3 Answer
We know that the number of tiles he needs to buy is represented by the expression 27 ÷ s2 where s is the side length in feet of a square tile.
If the tiles have side lengths of \(\frac{3}{4}\) foot, then s = \(\frac{3}{4}\).
Evaluating the expression for s = \(\frac{3}{4}\) gives:
\(27 \div s^2=27 \div\left(\frac{3}{4}\right)^2\) Substitute s = \(\frac{3}{4}\).
= \(27 \div\left(\frac{3}{4} \cdot \frac{3}{4}\right)\) Rewrite the power as multiplication.
= \(27 \div \frac{9}{16}\) Multiply.
= 27 . \(\frac{16}{9}\) Rewrite as multiplying by the reciprocal.
= \(\frac{432}{9}\) Multiply.
= 48 Reduce the fraction by dividing.
He must then buy 48 tiles.
Result
48 tiles
Page 148 Exercise 1 Answer
To evaluate an algebraic expression use substitution, which is replacing a variable with a specific number. Then calculate to find the value of the whole expression.
For example, an algebraic expression is
8 ÷ 2 + b − 4,
and the value of b is 4.
8 ÷ 2 + b − 4 (Substitute the variable b with its value.)
= 8 ÷ 2 + 4 − 4 (Find the quotient.)
= 4 + 4 – 4 (Find the sum.)
= 8 – 4 (Find the difference.)
= 4
Result
To evaluate an algebraic expression use substitution, which is replacing a variable with a specific number. Then calculate to find the value of the whole expression.
Page 148 Exercise 2 Answer
When evaluating expressions, it is important to use the order of operations because evaluating the operations in a different order will give an incorrect value.
For example, evaluating 4 + 2 × 3 using the order of operations gives the correct value of 4 + 2 × 3 = 4 + 6 = 10. Evaluating the expression by adding and then multiplying gives an incorrect value of 4 + 2 × 3 = 6 × 3 = 18.
Result
When evaluating expressions, it is important to use the order of operations because evaluating the operations in a different order will give an incorrect value.
Page 148 Exercise 3 Answer
Evaluating expression with fractions is like evaluating an expression with whole numbers because we still use the same operations to evaluate the expression. The difference is that when dividing by a fraction, we must rewrite it as multiplication, which is something we don’t do when dividing by a whole number.
Page 148 Exercise 4 Answer
We are given the expression 4h, where h is the number of hours and the expression represents the amount she earns.
The number of hours she works can’t be negative so we know that only nonnegative numbers can be substituted for h. For example, we cannot substitute −5 for h but we can substitute 0, 0.5, 2, \(\frac{8}{3}\), etc.
Result
No, only nonnegative numbers can be substituted for h since the number of hours she works can’t be negative.
Page 148 Exercise 5 Answer
To evaluate the expression 3t − 8, when t = 8, use substitution.
3t – 8 (Substitute t with 8.)
= 3 x 8 – 8 (Find the product.)
= 24 – 8 (Find the difference.)
= 16
Result
16
Page 148 Exercise 6 Answer
To evaluate the expression 6w ÷ x + 9, when w = \(\frac{1}{2}\) and x = 3, use substitution.
6w ÷ x + 9 (Substitute w with \(\frac{1}{2}\) and x with 3.)
= 6 x \(\frac{1}{2}\) (Find the product.)
= 3 ÷ 3 + 9 (Find the quotient.)
= 1 + 9 (Find the sum.)
= 10
Result
10
Page 148 Exercise 7 Answer
To evaluate the expression t2 − 12w ÷ x, when t = 8, w = \(\frac{1}{2}\) and x = 3, use substitution.
t2 – 12w ÷ x (Substitute t, with 8, w with \(\frac{1}{2}\) and x with 3.)
= 82 – 12 x \(\frac{1}{2}\) ÷ 3 (Evaluate the power.)
= 64 – 12 x \(\frac{1}{2}\) ÷ 3 (Find the product.)
= 64 – 6 ÷ 3 (Find the quotient.)
= 64 – 2(Find the difference.)
= 62
Result
62
Page 148 Exercise 8 Answer
To evaluate the expression 5x − 2w + t, when t = 8, w = \(\frac{1}{2}\) and x = 3, use substitution.
5x – 2w + t (Substitute w with \(\frac{1}{2}\) and x with 3.)
= 5 x 3 – 2 x \(\frac{1}{2}\) + 8 (Find the product.)
= 15 – 2 x \(\frac{1}{2}\) + 8 (Find the product.)
= 15 – 1 + 8 (Find the difference.)
= 14 + 8 (Find the sum.)
= 22
Result
22
Page 148 Exercise 9 Answer
To evaluate the expression z ÷ 4, when z = 824, use substitution.
z ÷ 4 (Substitute z with 824.)
= 824 ÷ 4 (Find the quotient.)
= 206
Result
206
Page 148 Exercise 10 Answer
To evaluate the expression 6t ÷ 9 − 22, when t = 60, use substitution.
6t ÷ 9 − 22 (Substitute t with 60.)
= 6 × 60 ÷ 9 − 22 (Find the product.)
= 360 ÷ 9 − 22 (Find the quotient.)
= 40 − 22 (Find the difference.)
= 18
Result
18
Page 148 Exercise 11 Answer
To evaluate the expression r ÷ 2.4, when r = 16.8, use substitution.
r ÷ 2.4 (Substitute r with 16.8.)
= 16.8 ÷ 2.4 (Find the quotient.)
= 7
Result
7
Page 148 Exercise 12 Answer
To evaluate the expression 9.85 × s, when s = 4, use substitution.
9.85 × s (Substitute s with 4.)
= 9.85 × 4 (Find the product.)
= 39.4
Result
39.4
Page 148 Exercise 13 Answer
To evaluate the expression x ÷ 12, when x = \(\frac{2}{3}\), use substitution.
x ÷ 12 (Substitute x with \(\frac{2}{3}\))
= \(\frac{2}{3}\) ÷ 12 (Rewrite the whole number as a fraction)
= \(\frac{2}{3}\) ÷ \(\frac{12}{1}\) (Rewrite the expression as a multiplication problem)
= \(\frac{2}{3}\) x \({1}{12}\) (Find the product)
= \(\frac{2}{36}\)
= \(\frac{1}{18}\)
Result
\(\frac{1}{18}\)Page 148 Exercise 14 Answer
To evaluate the expression \(\frac{3}{4}+4 y \div 3\), when y = \(1 \frac{1}{2}\), use substitution
\(\frac{3}{4}+4 y \div 3\) (Substitute y with \(1 \frac{1}{2}\))
= \(\frac{3}{4}\) + 4 x \(1 \frac{1}{2}\) ÷ 3 (Rewrite the mixed number as a fraction)
= \(\frac{3}{4}+4 \times \frac{3}{2} \div 3\) (Find the product)
= \(\frac{3}{4}+\frac{12}{2} \div 3\)
= \(\frac{3}{4}+6 \div 3\) (Find the quotient)
= \(\frac{3}{4}\) + 2
= \(2 \frac{3}{4}\)
Result
\(2 \frac{3}{4}\)Page 149 Exercise 15 Answer
To evaluate the expression 9x, when x = 3, use substitution.
9x (Substitute x with 3.)
9(3) (Find the product.)
= 27
Result
27
Page 149 Exercise 16 Answer
To evaluate the expression \(3 y+\frac{6}{2 x}\), when x = 3 and y = 4, use substitution.
\(3 y+\frac{6}{2 x}\) (Substitute x with 3 and y with 4.)
= \(3(4)+\frac{6}{2(3)}\) (Find the product.)
= \(12+\frac{6}{2(3)}\) (Find the product.)
= 12 + \(\frac{6}{6}\) (Find the quotient.)
= 12 + 1 (Find the sum.)
= 13
Result
13
Page 149 Exercise 17 Answer
To evaluate the expression \(w^2+2+\frac{48}{2 z}\), when w = 5 and z = 8, use subsitution.
\(w^2+2+\frac{48}{2 z}\) (Substitute w with 5 and z with 8)
= \(5^2+2+\frac{48}{2(8)}\) (Evaluate the power)
= \(25+2+\frac{48}{2(8)}\) (Find the product)
= 25 + 2 + \(\frac{48}{16}\) (Find the quotient)
= 25 + 2 + 3 (Fidn the sum)
= 27 + 3 (Find the sum)
= 30
Result
30
Page 149 Exercise 18 Answer
To evaluate the expression x ÷ 4, when x = 1.8, use substitution.
x ÷ 4 (Substitute x with 1.8.)
= 1.8 ÷ 4 (Multiply both numbers by 10.)
= 18 ÷ 40 (Divide.)
= 0.45
Result
0.45
Page 149 Exercise 19 Answer
To evaluate the expression x(3.35), when x = 5, use substitution.
x(3.35) (Substitute x with 5.)
= 5(3.35) (Find the product.)
= 16.75
Result
16.75
Page 149 Exercise 20 Answer
To evaluate the expression 2x + 3.1, when x = 6.4, use substitution.
2x + 3.1 (Substitute x with 6.4.)
= 2(6.4) + 3.1 (Find the product.)
= 12.8 + 3.1 (Find the sum.)
= 15.9
Result
15.9
Exercise 149 Exercise 21 Answer
To evaluate the expression j + \(\frac{3}{8}\), when j = \(\frac{3}{4}\), use substitution.
j + \(\frac{3}{8}\) (Substitute j with \(\frac{3}{4}\))
\(\frac{3}{4}\) + \(\frac{3}{8}\) (Rewrite the fractions with the same denominator)
= \(\frac{6}{8}\) + \(\frac{3}{8}\) (Find the sum)
= \(\frac{6+3}{8}\)
= \(\frac{9}{8}\)
= \(\frac{8}{8}\) + \(\frac{1}{8}\)
= 1 + \(\frac{1}{8}\)
= \(1 \frac{1}{8}\)
Result
\(1 \frac{1}{8}\)Page 149 Exercise 22 Answer
To evaluate the expression 8 − g ÷ \(\frac{7}{8}\), when g = \(\frac{5}{6}\), use substitution.
8 – g ÷ \(\frac{7}{8}\) (Substitute g with \(\frac{5}{6}\).)
= 8 – \(\frac{5}{6}\) ÷ \(\frac{7}{8}\) (Rewrite the division problem as a multiplication problem.)
= 8 – \(\frac{5}{6}\) x \(\frac{8}{7}\) (Find the product of fractions.)
= \(8-\frac{5 \times 8}{6 \times 7}\)
= 8 – \(\frac{40}{42}\)
= 8 – \(\frac{20}{21}\) (Rewrite the whole number as a fractions.)
= \(\frac{8}{1}-\frac{20}{21}\)
= \(\frac{168-20}{21}\)
= \(\frac{148}{21}\)
= \(\frac{147}{21}+\frac{1}{21}\)
= 7 + \(\frac{1}{21}\)
= \(7 \frac{1}{21}\)
Result
\(7 \frac{1}{21}\)Page 149 Exercise 23 Answer
To evaluate the expression 3m ÷ \(\frac{2}{5}\) , when m = \(\frac{2}{3}\) , use substitution.
\(3 m \div \frac{2}{5}\)= 3(\(\frac{2}{3}\)) ÷ \(\frac{2}{5}\) (Substitute m with its value.)
= 2 x \(\frac{5}{2}\) (Rewrite the divison problem as a multiplication problem.)
= 5 (Find the product.)
Result
5
Page 149 Exercise 24 Answer
To evaluate the expression b(3) + 20.4, when b = 8.9, use substitution.
b(3) + 20.4
= 8.9(3) + 20.4 (Substitute b with 8.9.)
= 26.7 + 20.4 (Find the product.)
= 47.1 (Find the sum.)
To evaluate the expression b(3) + 20.4, when b = 5.1, use substitution.
b(3) + 20.4
= 5.1(3) + 20.4 (Substitute b with 5.1.)
= 15.3 + 20.4 (Find the product.)
= 35.7 (Find the sum.)
To evaluate the expression b(3) + 20.4, when b = 0.2, use subsitution.
b(3) + 20.4
= 0.2(3) + 20.4 (Substitute b with 0.2)
= 0.6 + 20.4 (Find the product)
= 21 (Find the sum)
Result

Page 149 Exercise 25 Answer
To evaluate the expression 2j + \(\frac{3}{5}\), when j = \(\frac{1}{2}\), use substitution.
2j + \(\frac{3}{5}\)
= 2(\(\frac{1}{2}\)) + \(\frac{3}{5}\) (Substitute j wiht \(\frac{1}{2}\))
= 1 + \(\frac{3}{5}\) (find the product)
= \(1 \frac{3}{5}\) (Find the sum).
To evalue the expression 2j + \(\frac{3}{5}\), when j = \(\frac{4}{5}\), use substitution.
2j + \(\frac{3}{5}\)
= 2(\(\frac{4}{5}\)) + \(\frac{3}{5}\) (Substitute j wiht \(\frac{4}{5}\))
= \(\frac{8}{5}\) + \(\frac{3}{5}\) (find the product)
= \(\frac{11}{5}\) (Find the sum).
= \(2 \frac{1}{5}\) (Rewrite as a mixed number)
To evalue the expression 2j + \(\frac{3}{5}\), when j = \(1 \frac{3}{4}\), use substitution.
2j + \(\frac{3}{5}\)
= \(2\left(1 \frac{3}{4}\right)+\frac{3}{5}\) (substitute j with \(1 \frac{3}{4}\))
= \(2\left(\frac{7}{4}\right)+\frac{3}{5}\) (Rewrite the mixed number as a fraction)
= \(\frac{14}{4}+\frac{3}{5}\) (Find the product)
= \(\frac{7}{2}+\frac{3}{5}\) (Find the sum)
= \(\frac{35}{10}+\frac{6}{10}\)
= \(\frac{41}{10}\)
= \(\frac{40}{10}+\frac{1}{10}\)
= 4 + \(\frac{1}{10}\)
= \(4 \frac{1}{10}\) (Rewrite as mixed number)
Result

Page 149 Exercise 26a Answer
If Ms. White wants to rent a small car she must pay the weekly fee which is $250. For each mile she drives she must pay additional $0.30. If she drives m miles during the week, she must pay additional 0.30(m)
The expression which shows the amount she will pay for the car is:
250 + 0.30(m).
Result
250 + 0.30(m)
Page 149 Exercise 26b Answer
The expression which shows the amount she will pay for the car is:
250 + 0.30(m).
If Ms. White drove 100 miles, then m = 100, since m represents the number of miles driven during the week.
250 + 0.30(m)
= 250 + 0.30(100) (Substitute m with 100.)
= 250 + 30 (Find the product.)
= 280 (Find the sum.)
If she drove 100 miles, Ms. White must pay $280 in total for renting a small car.
Result
$280
Page 149 Exercise 27 Answer
The expression which show how much Mr. Black needs to pay for renting a luxury car for one week and d days is:
325 + 120d.
Since Mr. Black rented the car for 11 days, which is 1 week and 4 days, we will substitute d = 4 and evalute the expression.
325 + 120d
= 325 + 120(4)
= 325 + 480 (Find the product.)
= 805 (Find the sum.)
Mr. Black needs to pay $805 for an 11-day rental of a luxury car.
Result
$805
Page 149 Exercise 28 Answer
First, write the expression which represents how much it costs to rent a vehicle, for example, let’s take a small van, for d days.
150(d)
When is the value of this product greater than the cost of renting a small van for a week which is $350?
Let’s try with two days – so d = 2.
150(d)
= 150(2) (Substitute d with 2.)
= 300 (Find the product.)
Since 300 is less than 350, it less expensive to rent the small van for 2 days than 1 week. Let’s try with three days – so d = 3.
150(d)
= 150(3) (Substitute d with 3.)
= 450 (Find the product.)
Since 450 is greater than 350, three days is more expensive.
You can then rent a small van for two days before it would be less expensive to rent for the week.
Result
Possible answer: For a small van, you can rent it for two days before it would be less expensive to rent for the week.
Page 150 Exercise 29 Answer
Tamara is making a medium-length necklace so a chain will cost $1.80 and a pendant $3.72, so to find the total cost we need to add those numbers. To this sum, we need to add the cost of b beads that cost $0.25 each. The cost of b beads is the product b(0.25).
The expression which shows how much it will cost Tamara to make the necklace is:
1.80 + 3.72 + b(0.25).
To find the total cost of the necklace if Tamara uses 30 beads, in which case b = 30, use substitution.
1.80 + 3.72 + b(0.25)
= 1.80 + 3.72 + 30(0.25) (Substitute b with 30.)
= 1.80 + 3.72 + 7.5 (Find the product.)
= 5.52 + 7.5 (Find the sum.)
= 13.02 (Find the sum.)
The expression which shows how much it will cost Tamara to make the necklace is 1.80 + 3.72 + b(0.25), and if she uses 30 beads it will cost her $13.02.
Page 150 Exercise 30 Answer
To make a short necklace with one chain and one pendant the cost is the sum of the price of a chain, which is $1.15, and a pendant, which is $2.39.1.15 + 2.39.
To make a long neckle with one chain and one pendant the cost is the sum of the price of a chain, which is $2.25, and a pendant, which is $4.50. 2.25 + 4.50.
To find the cost of s short necklaces and n long necklaces, multiply the cost of one short necklace by s and multiply the cost of one long necklace by n. Add those products and that is the cost.
The expression which shows how much it will cost Ronnie to make s short necklace and n long necklaces is:
s(1.15+2.39) + n(2.25+4.50).
To find the cost for 3 short necklaces and 2 long necklaces use subsitution.
s(1.15+2.39) + n(2.25+4.50)
= 3(1.15+2.39) + 2(2.25+4.50) (Substitute s with 3 and n with 2.)
= 3(3.54) + 2(6.75) (Find the sums in the parentheses.)
= 10.62 + 13.50 (Find the products.)
= 24.12 (Find the sum.)
The expression which shows how much it will cost Ronnie to make s short necklace and n long necklaces is: s(1.15 + 2.39) + n(2.25 + 4.50), and the cost of 3 short necklaces and 2 long necklaces is $24.12.
Page 150 Exercise 31 Answer
The expression
5,432 + 4,564 + 13,908 ÷ 61n
can’t be evaluated as Katrina says since there are no parentheses and finding the quotient has a higher priority than addition. 61n divides only 13,908, not the entire sum.
For example, let’s evaluate the expression if n = 1 the way Katrina would have.
5,432 + 4,564 + 13,908 ÷ 61n
= 5,432 + 4,564 + 13,908 ÷ 61(1) (Substitute n with 1.)
= 5,432 + 4,564 + 13,908 ÷ 61 (Find the product.)
= 23904 ÷ 61 (Find the sum.)
≈ 391.868 (Find the quotient.)
Evaluate the expression if n = 1 the correct way – following the proper order of operations.
5,432 + 4,564 + 13,908 ÷ 61n
= 5,432 + 4,564 + 13,908 ÷ 61(1) (Substitute n with 1.)
= 5,432 + 4,564 + 13,908 ÷ 61 (Find the product.)
= 5,432 + 4,564 + 228 (Find the quotient.)
= 10224 (Find the sum.)
Result
No, the quotient has a higher priority than the addition. 61n divides only 13,908, not the entire sum.
Page 150 Exercise 32 Answer
If an object has a mass of 73,430 kilograms and a volume of 7m3, its density d can be calculated using the formula d = \(\frac{m}{v}\), where m is the mass and v is the volume of the object. To find the density of this particular object use substitution – substitute m with 73, 430 and v with 7.
d = \(\frac{m}{v}\)
d = \(\frac{73430}{7}\) (substitute the variables with their values)
d = 73430 : 7 (Rewrite the fraction as a devision problem).
\(d=10490 \frac{\mathrm{~kg}}{\mathrm{~m}^3}\) (Find the quotient)
Result
The density of the object is \(10490 \frac{\mathrm{~kg}}{\mathrm{~m}^3}\)
Page 150 Exercise 33 Answer
The volume of a cube-shaped bin with side length s of \(\frac{2}{3}\) yard can be found using substitution – substitute the variable s in the formula for the volume of a cube, V = s3, with the value of s = \(\frac{2}{3}\).
V = s3
V = \(\left(\frac{2}{3}\right)^3\) (Substitute s with \(\frac{2}{3}\))
\(V=\frac{2}{3} \times \frac{2}{3} \times \frac{2}{3}\) (Rewrite as repeated multiplication)
V = \(\frac{8}{27}\) (Multiply)
Result
The volume of the cube-shaped bin is \(\frac{8}{27}\) yd3.
Page 150 Exercise 34 Answer
Katie should use substitution to evaluate the expression 15.75 ÷ p + 3p when p = 3.15.
15.75 ÷ p + 3p
= 15.75 ÷ 3.15 + 3(3.15) (Substitute p with 3.15.)
= 5 + 3(3.15) (Find the quotient.)
= 5 + 9.45 (Find the product.)
= 14.45 (Find the sum.)
Result
Katie should use substitution to get 15.75 ÷ 3.15 + 3(3.15), then find the quotient to get 5 + 3(3.15), then the product to get 5 + 9.45, and then find the sum to get a final answer of 14.45.
Page 150 Exercise 35 Answer
To evaluate the expression 5x + (x ÷ 3), when x = 0.09, use substitution.
5x + (x ÷ 3)
= 5(0.09) + (0.09 ÷ 3) (Substitute x with 0.09.)
= 0.45 + (0.09 ÷ 3) (Find the product.)
= 0.45 + 0.03 (Find the quotient.)
= 0.48 (Find the sum.)
To evaluate the expression 5x + (x ÷ 3), when x = 5.1, use substitution.
5x + (x ÷ 3)
= 5(5.1) + (5.1 ÷ 3) (Substitute x with 5.1.)
= 25.5 + (5.1 ÷ 3) (Find the product.)
= 25.5 + 1.7 (Find the quotient.)
= 27.2 (Find the sum.)
To evaluate the expression 5x + (x ÷ 3), when x = 7.2, use substitution.
5x + (x ÷ 3)
= 5(7.2) + (7.2 ÷ 3) (Substitute x with 7.2)
= 36 + (7.2 ÷ 3) (Find the product).
= 36 + 2.4 (Find the quotient).
= 38.4
Result