Houghton Mifflin Harcourt

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions

Page 234 Problem 1 Answer

It is given an expression 3×3. It is required to classify the polynomial by its degree and number of terms.

The degree of the polynomial is 3. The polynomial has only one term so, it is a monomial.

Thus, 3×3 is a cubic polynomial with one term.

The given expression, 3×3 is a cubic monomial.

Page 234 Problem 2 Answer

It is given an expression 9x−3y+7. It is required to classify the polynomial by its degree and number of terms.

The degree of the polynomial is 1. The polynomial has three terms so, it is a trinomial.

Thus, 9x−3y+7 is a linear trinomial.

The given expression, 9x−3y+7 is a linear trinomial.

Page 234 Problem 3 Answer

It is given an expression x²−4. It is required to classify the polynomial by its degree and number of terms.

The degree of the polynomial is 2. The polynomial has two terms so, it is a binomial.

Thus, x²−4  is a quadratic binomial.

The given expression, x²−4 is a quadratic binomial.

Page 234 Problem 4 Answer

It is given an expression x⁵+x⁴. It is required to classify the polynomial by its degree and number of terms.

The degree of the polynomial is 5. Thus, it is a quintic polynomial. The polynomial has two terms so, it is a binomial.

Thus, x²−4  is a quintic binomial.

The given expression, x⁵+x⁴  is a quintic binomial.

HMH Algebra 2 Module 5 Chapter 5 Exercise 5.1 Solutions

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 234 Problem 5 Answer

It is given an expression 5x³−7y²+2. It is required to classify the polynomial by its degree and number of terms.

The degree of the polynomial is 3. Thus, it is a cubic polynomial The polynomial has three terms so, it is a trinomial.

Thus, 5x³−7y²+2  is a cubic trinomial.

The given expression, 5x³−7y²+2 is a cubic trinomial.

Page 234 Problem 6 Answer

It is given an expression x. It is required to classify the polynomial by its degree and number of terms.

The degree of the polynomial is 1. The polynomial has one terms so, it is a monomial.

Thus, x is a linear monomial.

The given expression x is a linear monomial.

Page 234 Problem 7 Answer

It is given a functionh(x)=0.25(x−6)³−1 .

It is required to find the new function after the transformation of 10 units left, 7 units down.

To find the required transformation identify the inflection point then transform it as per given instruction, for x a xis the right direction is positive and left direction is negative, for y

axis up direction is positive and down direction is negative.

The inflection points on h(x)=0.25(x−6)³−1 is (6,−1).

Now, the transformation of 10 units left is (6−10)=−4.

The transformation of 7 units down is (−1−7)=−8  as the downward sides of y axis negative.

Now, the transformed inflection point is (−4,−8).

The new function after transformation ish(x)=0.25(x+4)³−8.

The new function after transformation is h(x)=0.25(x+4)³−8.

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 234 Problem 8 Answer

It is given a function h(x)=(x+9)³−5.

It is required to find the new function after the transformation of 6 units right, 4 units up.

To find the required transformation identify the inflection point then transform it as per given instruction, for x axis the right direction is positive and left direction is negative, for y

axis up direction is positive and down direction is negative.

The inflection points on h(x)=(x+9)³−5 is (−9,−5).

Now, the transformation of 6 units right is (−9+6)=−3  as the right direction of x  axis is positive.

The transformation of 4  units up is (−5+4)=−1  as the up sides of y axis is positive.

Now, the transformed inflection point is (−3,−1).

The new function after transformation is h′(x)=(x+3)³−1.

The new function after transformation is h′(x)=(x+3)³−1 of the transformation of 6 units right, 4

units up of the given function h(x)=(x+9)³−5.

Page 234 Problem 9 Answer

It is given a function f(x)=x³.

It is required to find the new function after the transformation of 3 units right,  2 units up.

To find the required transformation identify the inflection point then transform it as per given instruction, for x axis the right direction is positive and left direction is negative, for y

axis up direction is positive and down direction is negative.

The inflection points on f(x)=x³ is  (0,0).

Now, the transformation of 3  units right is (0+3)=3  as the right direction of x axis is positive.

The transformation of 2 units up is(0+2)=2  as the up sides of y axis is positive.

Now, the transformed inflection point is (3,2)

The new function after transformation is f′(x)=(x−3)³+2.

The new function after transformation is f′(x)=(x−3)³+2.

Polynomial Functions Exercise 5.1 Answers HMH Algebra 2

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 234 Problem 10 Answer

It is given a function g(x)=5(x+1)³−4.

It is required to find the new function after the transformation of 1  units right,4 units up.

To find the required transformation identify the inflection point then transform it as per given instruction, for x axis the right direction is positive and left direction is negative, for y axis up direction is positive and down direction is negative.

The inflection points on g(x)=5(x+1)³−4  is (−1,−4).

Now, the transformation of 1 units right is(−1+1)=0 as the right direction of x axis is positive.

The transformation of 4 units up is (−4+4)=0  as the up sides of y axis is positive.

Now, the transformed inflection point is (0,0).

The new function after transformation is given by,​g′(x)=5(x−0)³+0=5×3

​The new function after transformation is g′(x)=5×3.

Page 235 Problem 11 Answer

It is required to explain that how the given two functions  f(x)=a(x−h)³+k and f(x)=(1/b(x−h))³+k is related to f(x)=x³.

Three of the given function has the highest power of variables 3, it means their degree is 3 so they are all cubic function.

The cubic function f(x)=x³ has three factors, all of which happen to be x . one or more of the xs can be replaced with other linear factors in  x

like this given two functions f(x)=a(x−h)³+k and  f(x)=(1/b(x−h))³+k  without changing the fact that the function is cubic.

Thus, the cubic function f(x)=x³ is the parent function of the given two other function.

The cubic function f(x)=x³  is the parent function of the given two other function

f(x)=a(x−h)³+k and  f(x)=(1/b(x−h))³+k

because the other two are the cubic polynomial.

Every cubic polynomial has the parent function asf(x)=x³.

HMH Algebra 2 Chapter 5 Exercise 5.1 Solutions Guide

Page 236 Problem 12 Answer

It is given the cubic function f(x)=x³.

It is required to find that how can one characterize the rate of change of the function on the intervals [−1,0]  and [0,1] compared with the rate change on the intervals [−2,−1] and [1,2].

To find the required answer obtain the rate change for each interval by f(b)−f(a)/b−a.

As the given function have only x variables so, find the changing rate for the x component on the given intervals [−1,0],[0,1] and [−2,−1] ,[1,2] and compare both obtained values.

The x component  of the intervals[−1,0],[0,1] are−1  and 0.

Thus, the interval is[−1,0].

Now, the rate change for [−1,0] is

​f(0)−f(−1) /0−1

=0−(−1)3/−1

=1/−1

=−1

​Similarly, the x component  of the intervals[−2,−1],[1,2] are−2 and 1 .

Thus,  the interval is [−2,1]. the rate change for[−2,1] is

​f(1)−f(−2)/1−(−2)

=13/−(−2)3/1+3

=1−(−8)/4

=9/4

Thus, the rate change for the interval [−1,0]  is −1

and the rate change for the interval [−2,1] is 9/4 or 2.2.

So, the value of  rate change for the interval [−1,0]

is less than the rate change for the interval [−2,1].

Therefore,  the rate of change of the function on the intervals [−1,0] and [0,1]

is less than the rate change on the intervals [−2,−1] and [1,2].

The rate of change of the function on the intervals [−1,0] and [0,1]  is less than the rate change on the intervals[−2,−1] and [1,2].

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 236 Problem 13 Answer

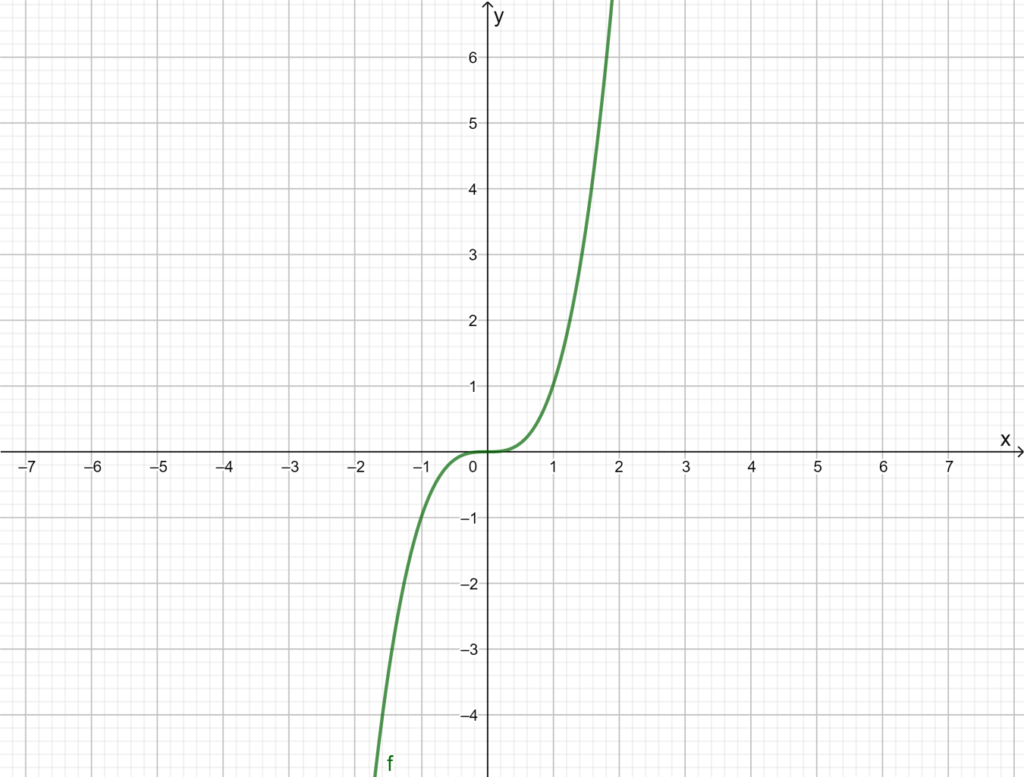
It is given a cubic function f(x)=x³.

It is required to explain the given function symmetric about the origin or not.

To find the required answer, first draw the graph off(x)=x³ then find it whether it symmetric about where or not.

Make the graph of f(x)=x³.

For a function to be symmetrical about the origin ,replace y with −y and x with −x and the resulting function must be equal to the original function.

There is no variable y in the given function, so substitute x as −x and check.

​f(−x)=(−x)³

f(−x)=−x³

​Now, make the graph off(−x)=−x³.

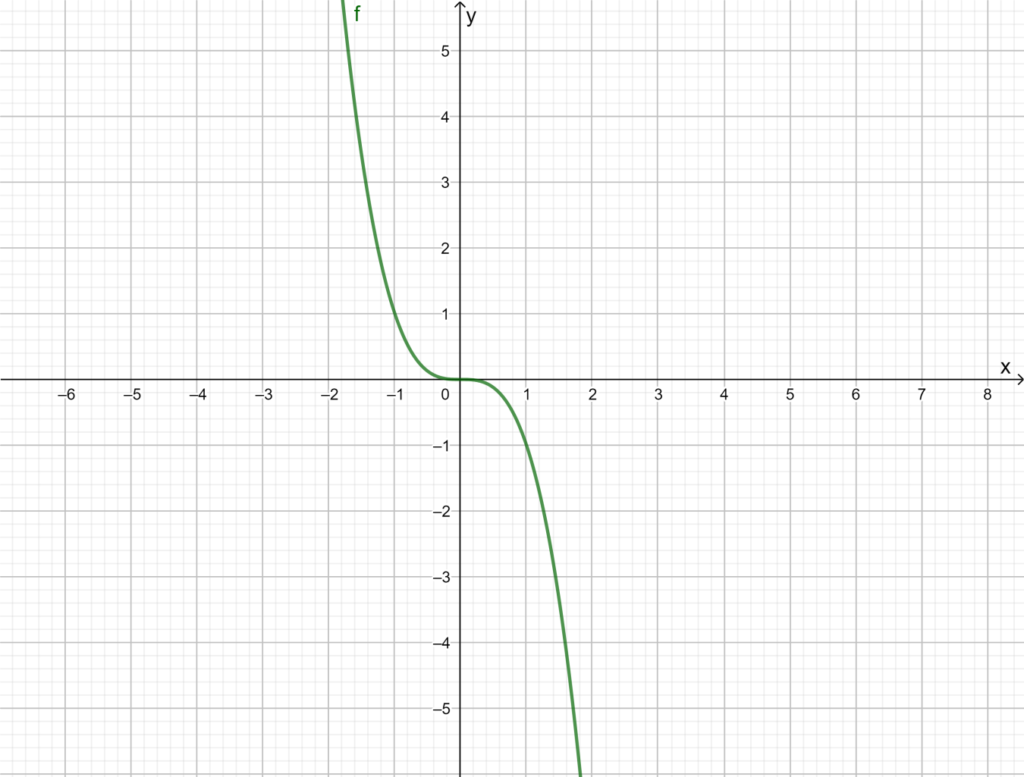
From the two graph it is clearly shows that the graph is symmetric about the origin as every point (x,y) on the graph, the point (−x,−y) is also on the graph.

Thus, the function f(x)=x³ is symmetry about the origin.

The function f(x)=x³ is symmetric about the origin as every point (x,y) on the graph, the point (−x,−y) is also on the graph.

Page 236 Problem 14 Answer

It is given that the graph of the function, $g(x)=(−x)³ is a reflection of the graph of f(x)=x³across the y-axis while the graph of h(x)=−x³ is the reflection of f(x) across the x-axis.

It is required to explain the similarity or differences between the graph of  h(x) and g(x) when graphed using a graphing calculator.

First, plot f(x), g(x), and h(x) using the graphing calculator. Further, notice any similarities or differences in the graph of the function.

Plot the function,f(x),g(x), and h(x).

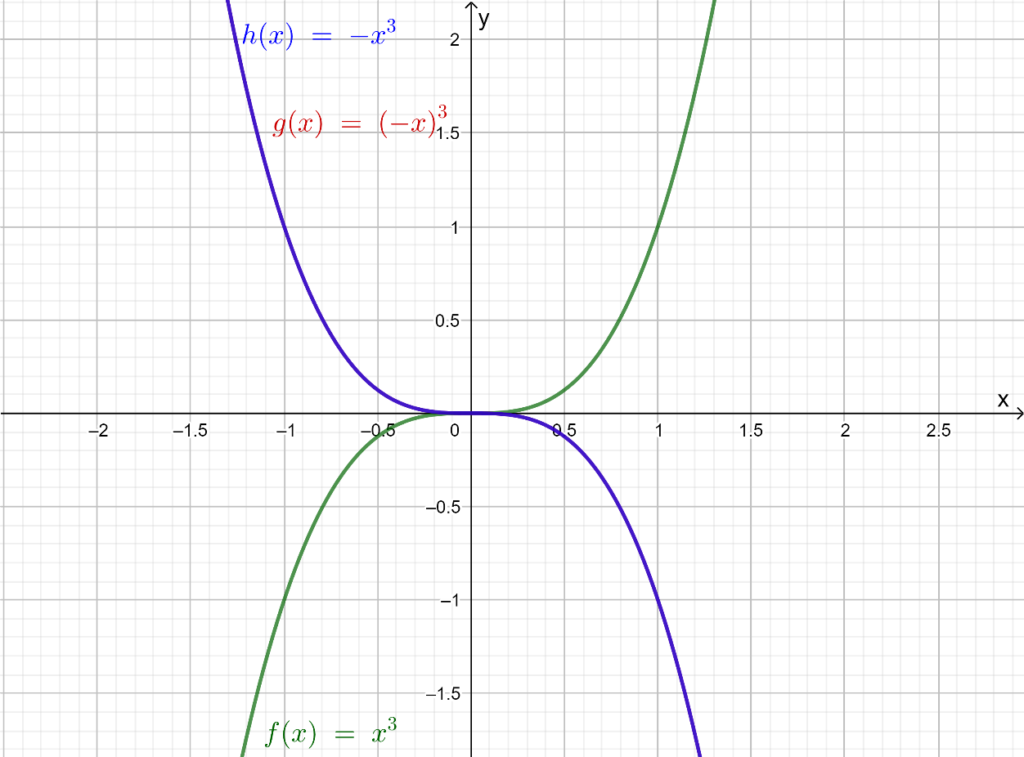
From the graph it is observed that g(x), and h(x) are equivalent function. Therefore, both have the same graph.

The graph of the function g(x)=(−x)³and h(x)=−x³ is equivalent.

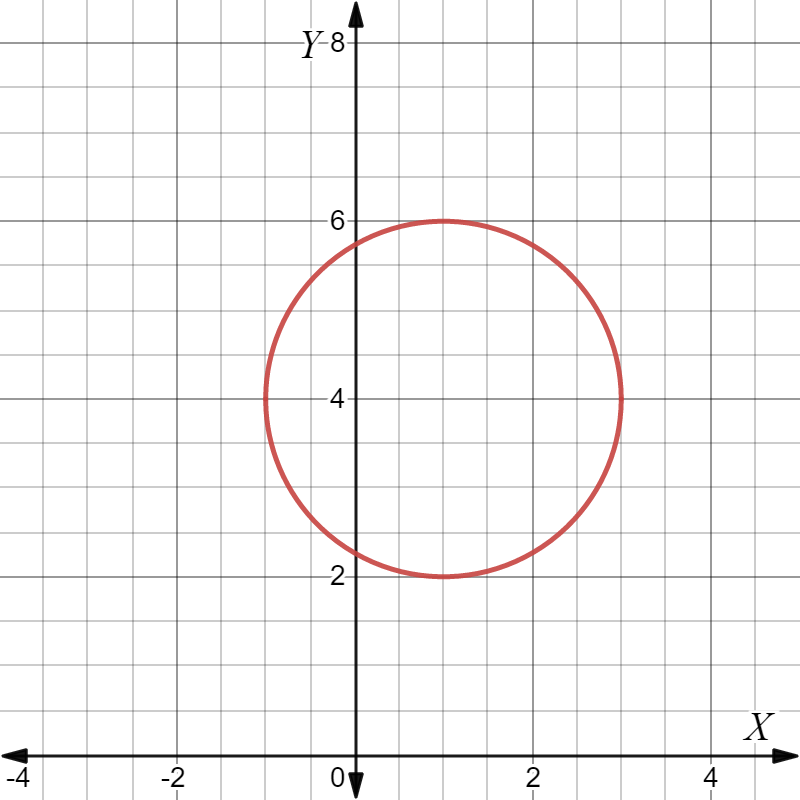
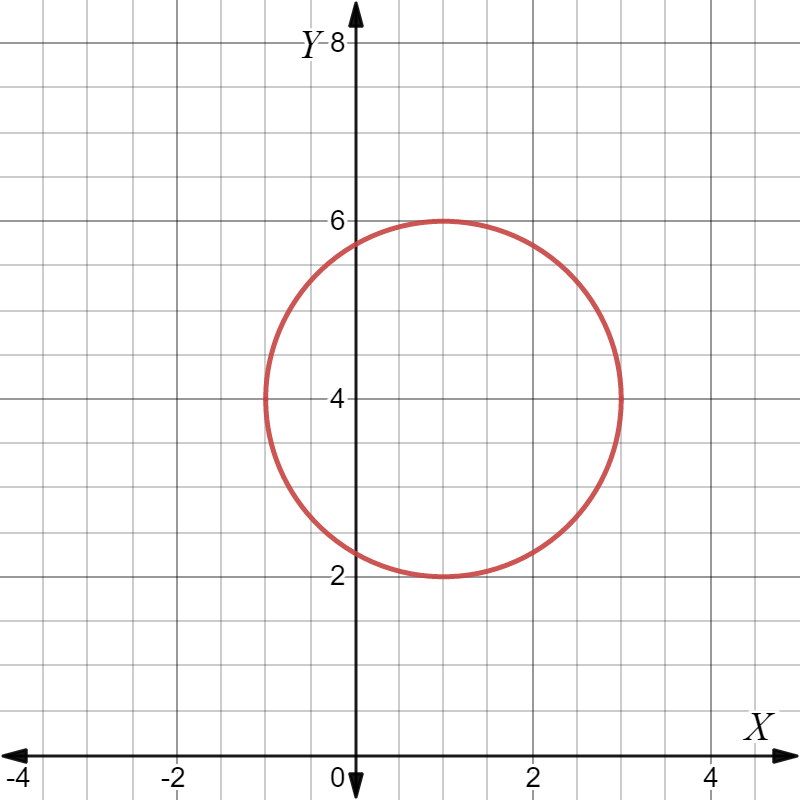
Page 238 Problem 15 Answer

It is given a function, g(x)=−1²(x−3)³. the graph of g(x) is produced by transforming the graph of g(x).

It is required to identify the transformation used and graph the function on the same coordinate plane of f(x) using the reference points, (−1,−1), (0,0), and(1,1)

Take a reflection of given graph f(x)=x³ further compress graph by factor 0.5 vertically and translate by factor 3 to the right.

Now, make a table with x and y coordinates of function g(x)=−1²(x−3)³, and plot the graph with help of coordinates accordingly.

The transformation used to get the graph of g(x) from f(x)  is the reflection of f(x) along y-axis followed by a dilation of scale factor 1², further followed by a translation of 3 units to the right.

The final coordinates will be as follows.

The ordered pairs are (2,0.5),(3,0), and (4,−0.5).

Plot the ordered pairs obtained and get the graph of g(x).

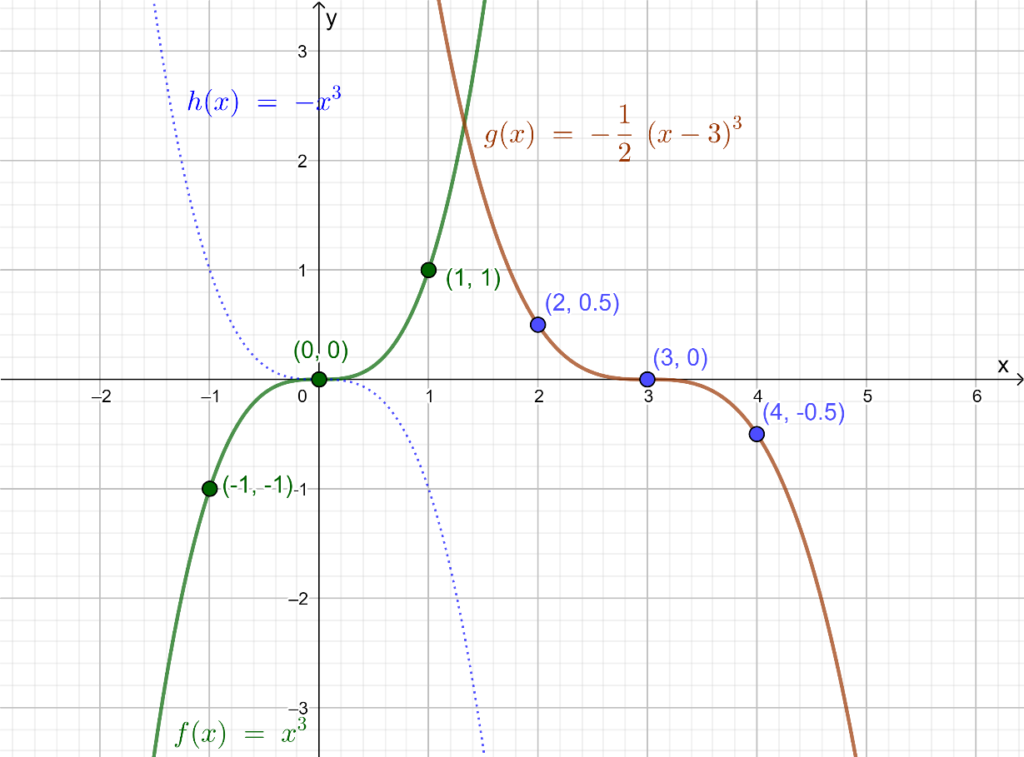
The graph of the function g(x) is as follows:

How To Solve Polynomial Functions Exercise 5.1 HMH Algebra 2

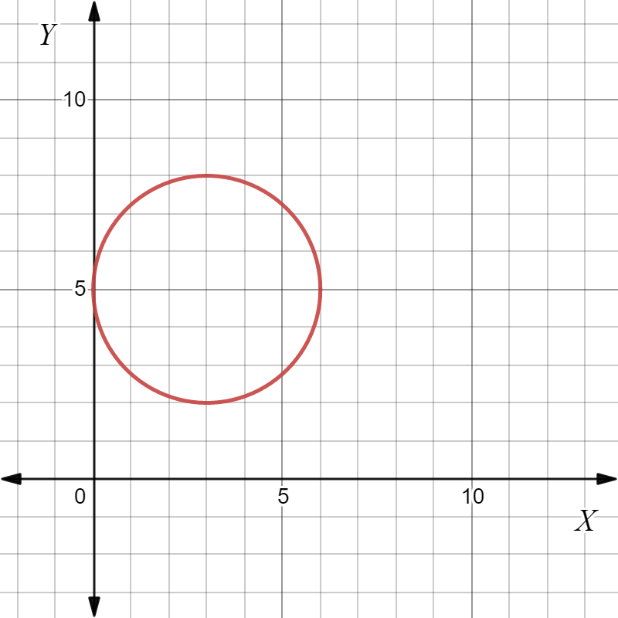
HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 239 Problem 16 Answer

The general equation for cubic function, g(x)=(1b(x−h))³+k is given along with the function’s graph.

It is to write a specific equation by identifying the values of the parameters from the reference point as shown in the graph.

Identify the values of h and k using the graph. Then, find the value of the constant a.

Thus, substitute the value in the equation and get the required answer.

Identify the values of h and k from the point of symmetry. Here, (h,k)=(1,−1).

Therefore, h=1, and k=−1. Identify the values of a. The right most point has general coordinates  (h+b,1+k).

Substituting 1 for h, and -1 for k.

​​(h+b,1+k)=(1+b,0)

(1+b,0)=(5,0)

​Equate 1+b with 5. Subtract 1 from both sides to solve for b.

​​1+b=5

b=5−1

b=4

​Therefore, b=4.

Find the equation of the function.

Substitute b as 4, h as 1, and k as −1 in the equation g(x)=a(x−h)³+k.g(x)=(1/4(x−1))³−1

Therefore, the required function is g(x)=(1/4(x−1))³−1.

The required function is g(x)=(1/4(x−1))³−1.

Page 234 Problem 17 Answer

It is required to discuss why it is important to plot multiple points on the graph of the volume function.Mass and volume are related through density.

Volume function graphs can be expressed as graph changing mass and dimension of object keeping density constant.Hence, volume function graphs can be represented by cubic function.

The value of function keeps on changing at every dimension.Now, as the graph keeps on changing at all dimensions, multiple points are plotted to ensure accuracy of the graph.

The volume function is a cubic function. Multiple points are plotted to ensure the accuracy of the graph.

Page 242 Problem 18 Answer

It is given a function, f(x)=x³. It is to identify which transformation (stretch or compressions, reflection, and translation) change the attributes of the function.

The end behaviour of a graph is defined as what is going on at the ends of each graph, as the function approaches positive or negative infinitely, the leading term determines what the graph looks like as it moves towards infinity.

Therefore, all the transformation changes the attributes of the function.Transformation that changes end behavior are reflection, translation and stretch or compressions.

Transformation that changes end behavior are reflection, translation and stretch or compressions

Module 5 Chapter 5 Polynomial Functions Problems HMH.

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 242 Problem 19 Answer

It is given a function, f(x)=x³. It is to identify which transformation (stretch or compressions, reflection, and translation) change the attributes of the function.

The location of the point of symmetry define position of point of symmetry. Transformation that changes location of the point of symmetry is translation.

The location of point of symmetry are transformed by translation.

Page 242 Problem 20 Answer

It is given a graph of f(x)=x³.

It is to identify which transformation (stretch or compressions, reflection, and translation) changes the attributes of the function.

Symmetry about a point defines the point at the same distance from the central point.

The transformations often preserve the original shape of the function.

Common types of transformations include rotations, translations, reflections, and scaling.

Assume two functions, f(x)=x³and   g(x)=x³+5 which is the translation of the graph of f by 5 units upwards.

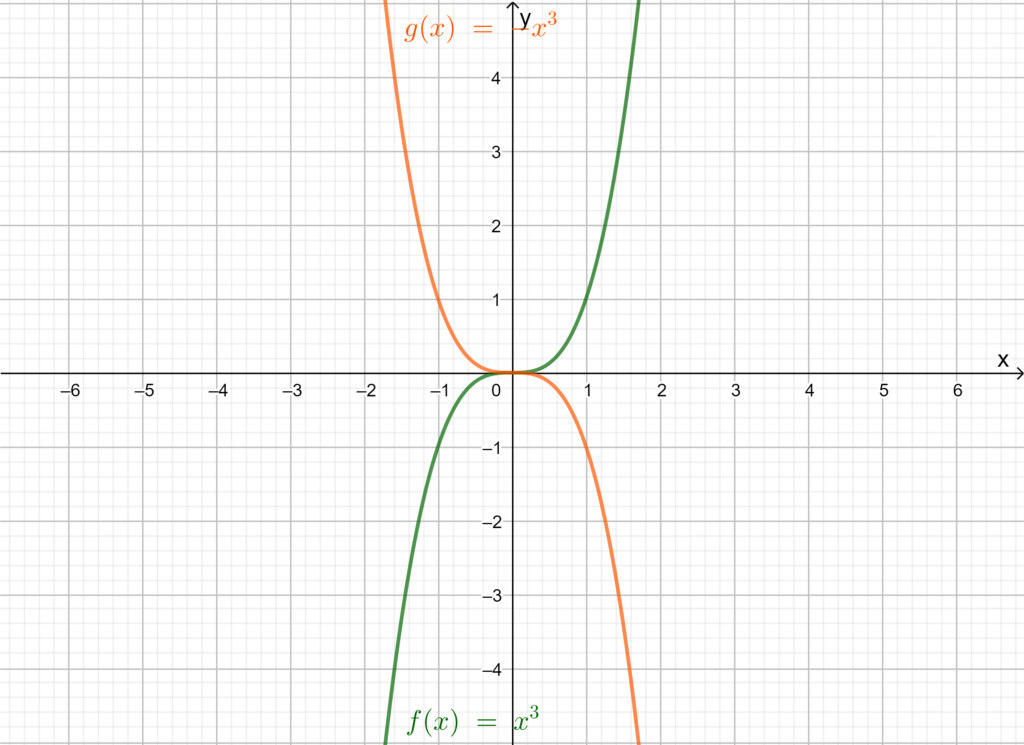
Now, it is evident from the graph that both graphs do not have symmetry. Therefore, this implies that when translation is done the function changes its symmetry.Similarly, consider two functions, f(x)=x³ and  h(x)=−x³.

Observe the graph of these functions.

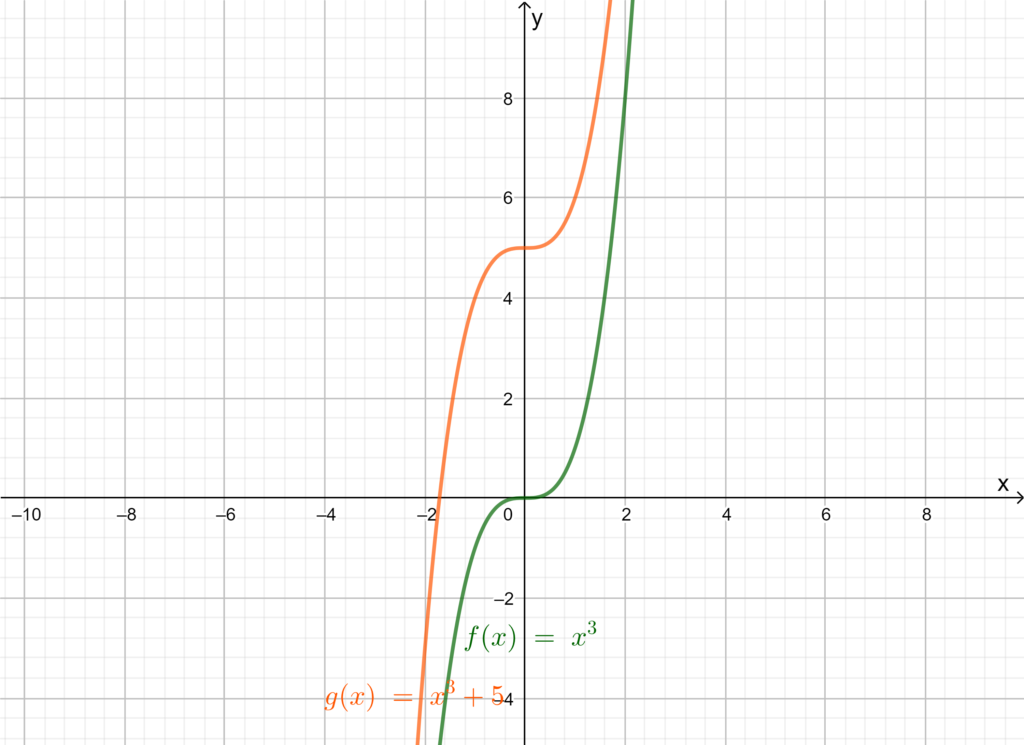
This is a special case where reflection is over the y axis, preserves the symmetry.Hence, the transformations that contribute in changing the symmetry about a point are reflection and translation.

The transformation that changes symmetry about a point is reflection and stretch or compressions.

Page 242 Problem 21 Answer

It is given graph f(x)=x³and g(x)=a(x−h)³+k.

It is to describe transformation on f(x) to obtain g(x).

Following transformation are made on f(x) that gives graph g(x).

First, a vertical stretch by a factor a unit, then translation of h unit to right and k unit to down.

Note that the translation of h unit to right affect only x coordinate whereas, vertical stretch by the factor a unit and translation of k unit to down affect only y coordinate of the point on the graph.

Therefore, the transformation is vertical stretch of the graph of f(x) by a units, followed by a translation of h units right, and k units down.

The transformation to transform f(x) to get the graph of g(x)=a (x−h)³+k is a vertical stretch of the graph of f(x) by a units, followed by a translation of h units right, and k units downwards.

Explain

Page 236 Exercise 1 Answer

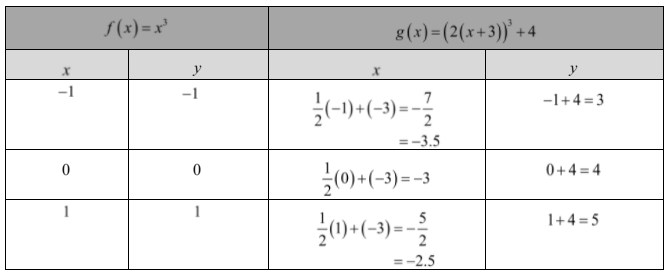
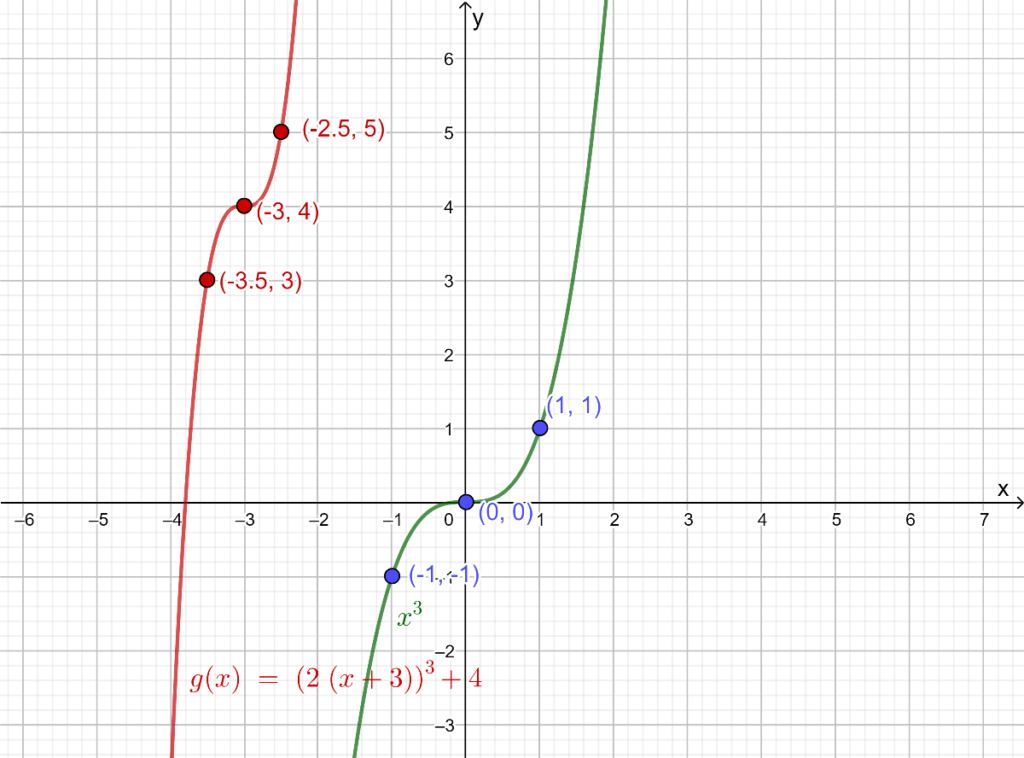
It is given that g(x)=(2(x+3))³+4 and f(x)=x³.

It is required to identify the transformation of the graph f(x)=x³ by applying the transformation using the reference points and draw the graph of given g(x) on the same coordinate plane. It is also required to complete the table.

First, identify the transformation of the graphf(x)=x³. that produce the graph of the given function g(x) , then the graph g(x)on the same coordinate plane as the graph of f(x) by applying the transformation to the reference points (−1,−1),(0,0)and (1,1).

The graph of the transformation of f(x)=x³ , helps to consider the effect of the transformation on the three reference points on the graph of  f(x):(−1,−1),(0,0)  and (1,1) .

The table lists the three points and the corresponding points on the graph of g(x)=a(1/b(x−h))+k.

Notice that the point (0,0), which is the point of symmetry for the graph of f(x), is affected only by the parameters h and k .

The other two reference points are affected by all four parameters.

Compare the given functiong(x)=(2(x+3))³+4 with the equation, g(x)=a(1/b(x−h))³+k.

Therefore, the value of k is 4, a is 1, b is 1/2, and his−3 .

now, fill the table according to these values.

The graph of the given function g(x)=(2(x+3))³+4 on the same coordinate plane of f(x)=x³ by applying the transformation to the reference points (−1,−1),(0,0)and (1,1) is given below.

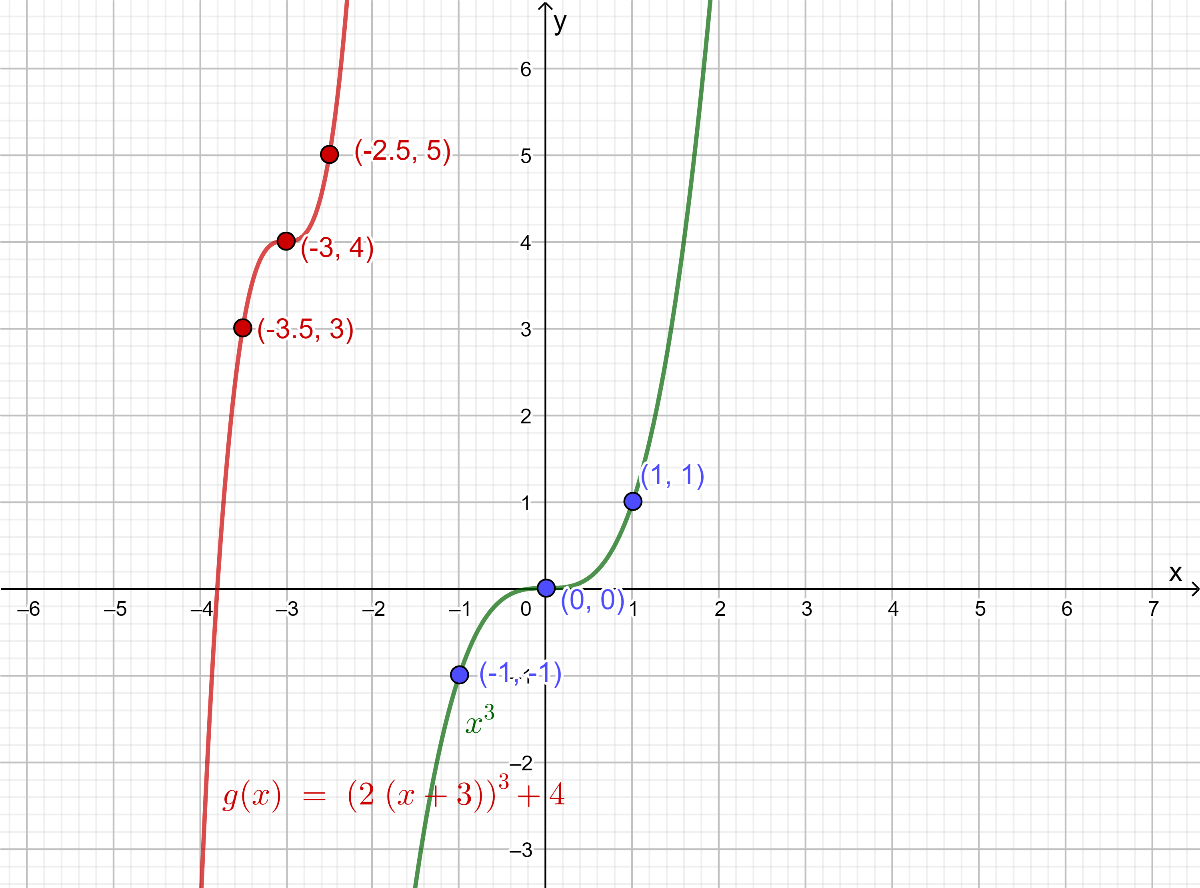
The graph of the given function g(x)=(2(x+3))³+4 on the same coordinate plane as the graph off(x)=x³is shown below.

The complete table is given below.

Page 240 Exercise 2 Answer

It is given a steel ball bearing with a mass of 75  grams and a density of 7.82g/cm³.

It is required to estimate the radius of the steel ball.

To find the required answer graph the function using the calculated values then use the graph to obtain the indicated estimate.

Let r represent the radius of the ball bearing.

The volume V of the bell bearing is V(r)=mr³.

The mass in the ball bearing is m(r)=7.82.

Then ,V(r)=7.82r³.

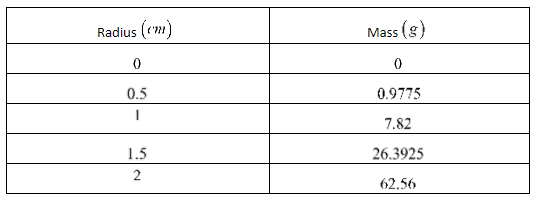
Draw the Graph of the function, V(r)=mr³.

Recognize that the graph is vertical compression of the graph of the parent cubic function by a factor of 7.82.

Then draw the horizontal  linem=75 and estimate the value of r where the graph intersect.

The graph intersect where r≈2.1, so the radius of the steel ball bearing is about 2.1cm.

The estimated radius of the steel ball bearing is about 2.1cm with a mass of 75 grams and a density of 7.82g/cm³.

HMH Algebra 2 Chapter 5 Polynomial Functions Step-By-Step Solutions

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 243 Exercise 3, Answer

It is given a cubic function of f(x)=x³

It is required  to graph the function and state the function’s domain and range

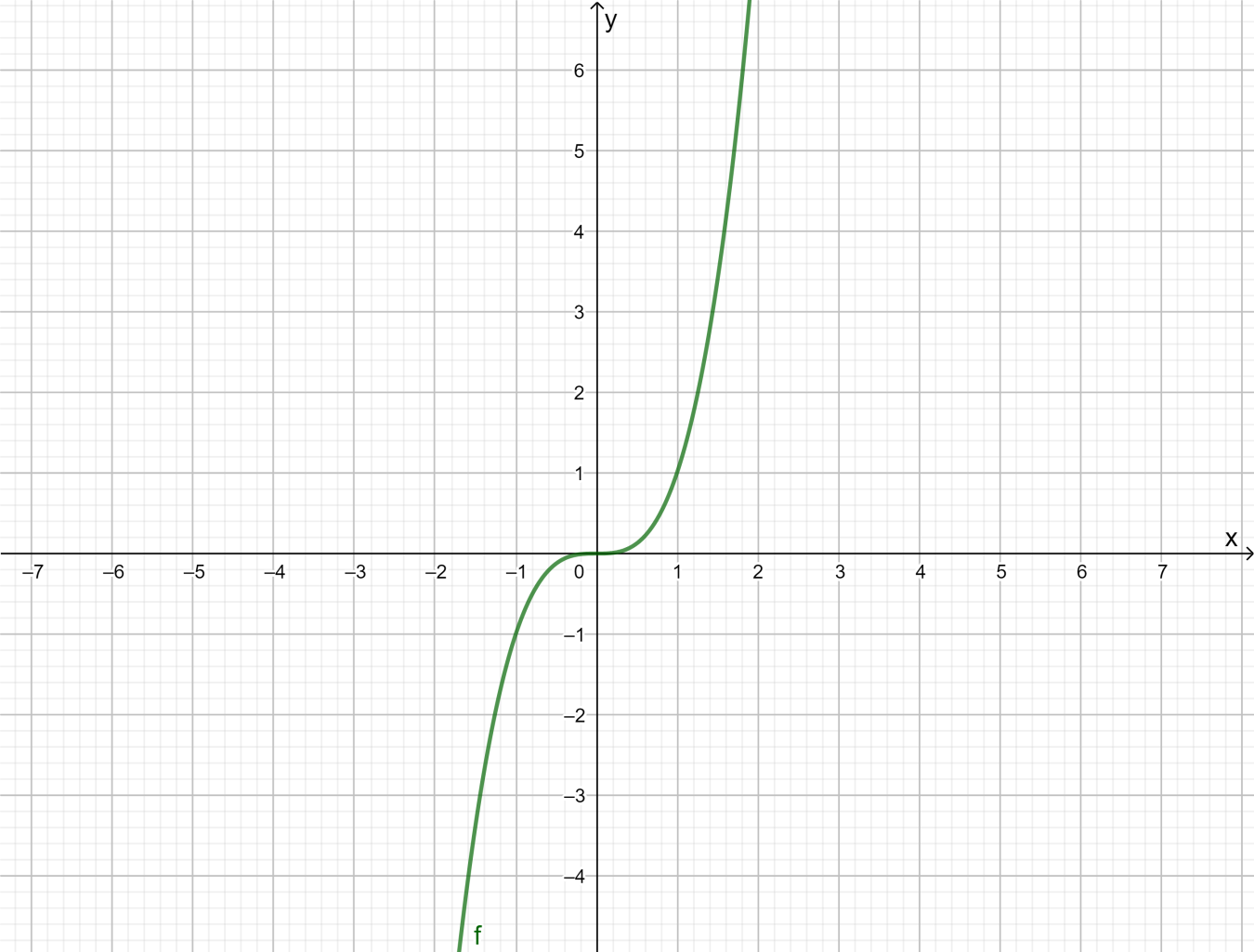
Observe that f(x)=x³ is can take all values lying between −∞ to ∞ Thus, the domain will be (−∞,∞)

When the function takes all values of its domain it gives values lying between −∞ to ∞

Thus, the range will be (−∞,∞)

Therefore, the domain and range of the function is (−∞,∞)

The domain and range of f(x)=x3 is(−∞,∞)

Page 243 Exercise 4, Answer

It is given a function f(x)=x³

It is required  to draw the graph of the function and identify the functions end behaviour

First graph the function by finding the ordered pairs by substituting the values of xas −2, −1, 0, 1, 2.

Then, plot the ordered pairs and join them through a curve to get a graph Then, observe the end behaviour of the function

Find the ordered pairs to plot the graphSubstitute the value of x as −2, −1, 0, 1, 2 simultaneously in y=x³

The ordered pairs will be points (−2,−8),(−1,−1),(0,0) (1,1) and (2,8)

Plot the order pairs

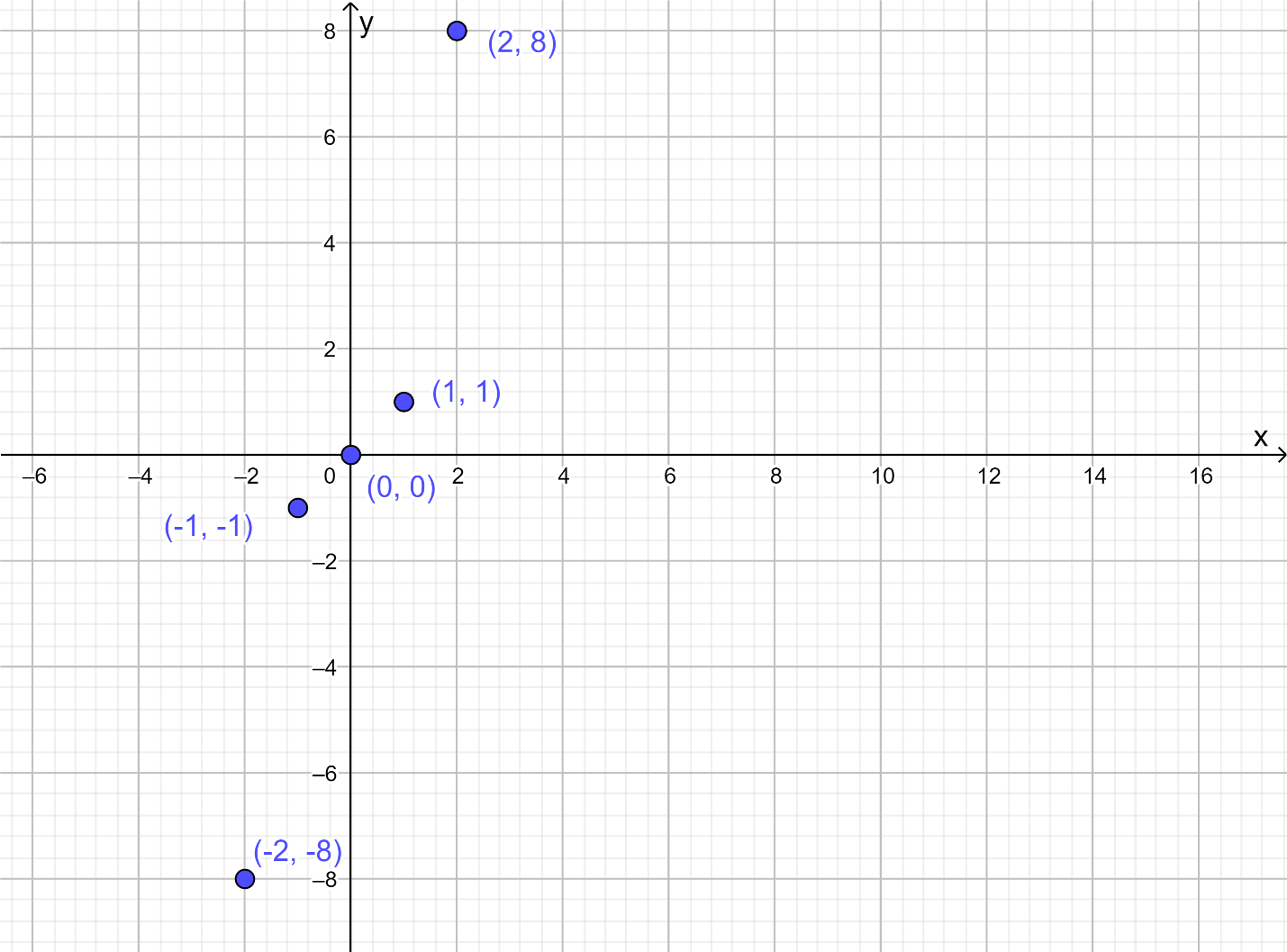
Draw a smooth curve on the obtained pair through the plotted points to obtain the graph f(x)=x³

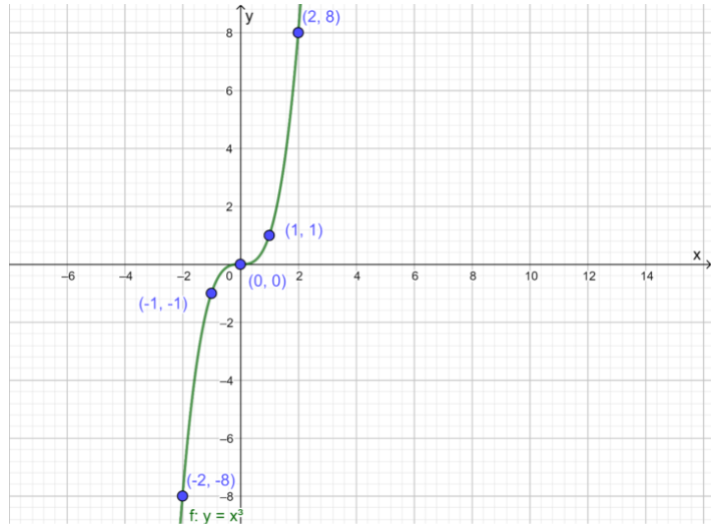
From the graph it is clear that whenx→+∞, the function approaches its positive values Therefore, whenx→+∞, f(x)→+∞ Also, when x>0then, f(x)>0

Similarly, when x→−∞, the function approaches its negative values Therefore,  when x→−∞then, f(x)→−∞

The end behaviour of the function is  when x→+∞, f(x)→+∞and  x→−∞,f(x)→−∞

Page 243 Exercise 5, Answer

It is given the cubic function f(x)=x³

It is required to identify the graph’s x-intercept and y-interceptThe graph of f(x)=x³ inferred from part (b) is as follows

From the graph it is observed that the graph intersects at x-axis is (0,0) and the point where a line crosses the y-axis is also (0,0)

Therefore, x-intercept and the y-intercept is 0

The x-intercept and the y-intercept of the function f(x)=x³ is zero

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 243 Exercise 6, Answer

It is given a cubic function f(x)=x³

It is required to graph the functionf(x)=x³ and identify the intervals where the functions has positive values and where it has negative values

The graph of f(x)=x3 inferred from part (b) is as follow

From the graph, it is observed that for the values of x greater than zero, the function has positive values and for the values of x less than zero, the function has negative values

Thus, the function has the positive values at the interval of (0,+∞) and the negative values at the interval of (−∞,0)

The function f(x)=x³ has the positive values at the interval of (0,+∞) and negative values at the interval of (−∞,0)

Page 243 Exercise 7, Answer

It is given a cubic function f(x)=x³

It is required to identify the intervals where the function is increasing and where it decreasing by using the drawn graph of f(x)=x3

The graph of f(x)=x³ inferred from part (b) is as follows

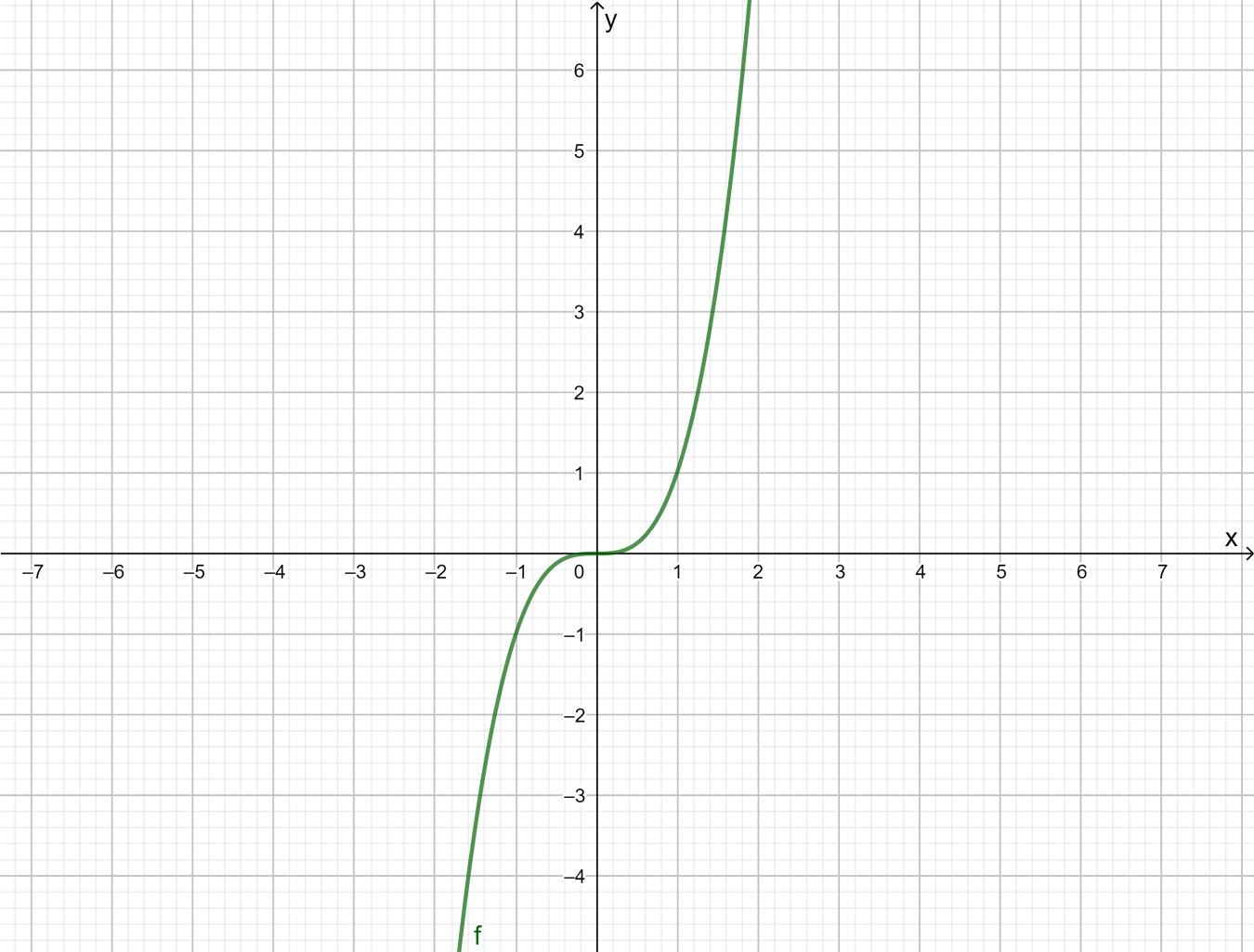
From the graph it is observed  that y=f(x)is increasing when value of x increasing but the value is never decreasing irrespective of x

Thus, the function f(x)=x³ is increasing when x>0 but it never decreasing

The function f(x)=x³ is increasing when x>0and decreasing at ϕ

Page 243 Exercise 8, Answer

It is given a cubic function f(x)=x³

It is required to explain whether the function is even ,odd or neither The graph of f(x)=x3 inferred from part (b) is as follows

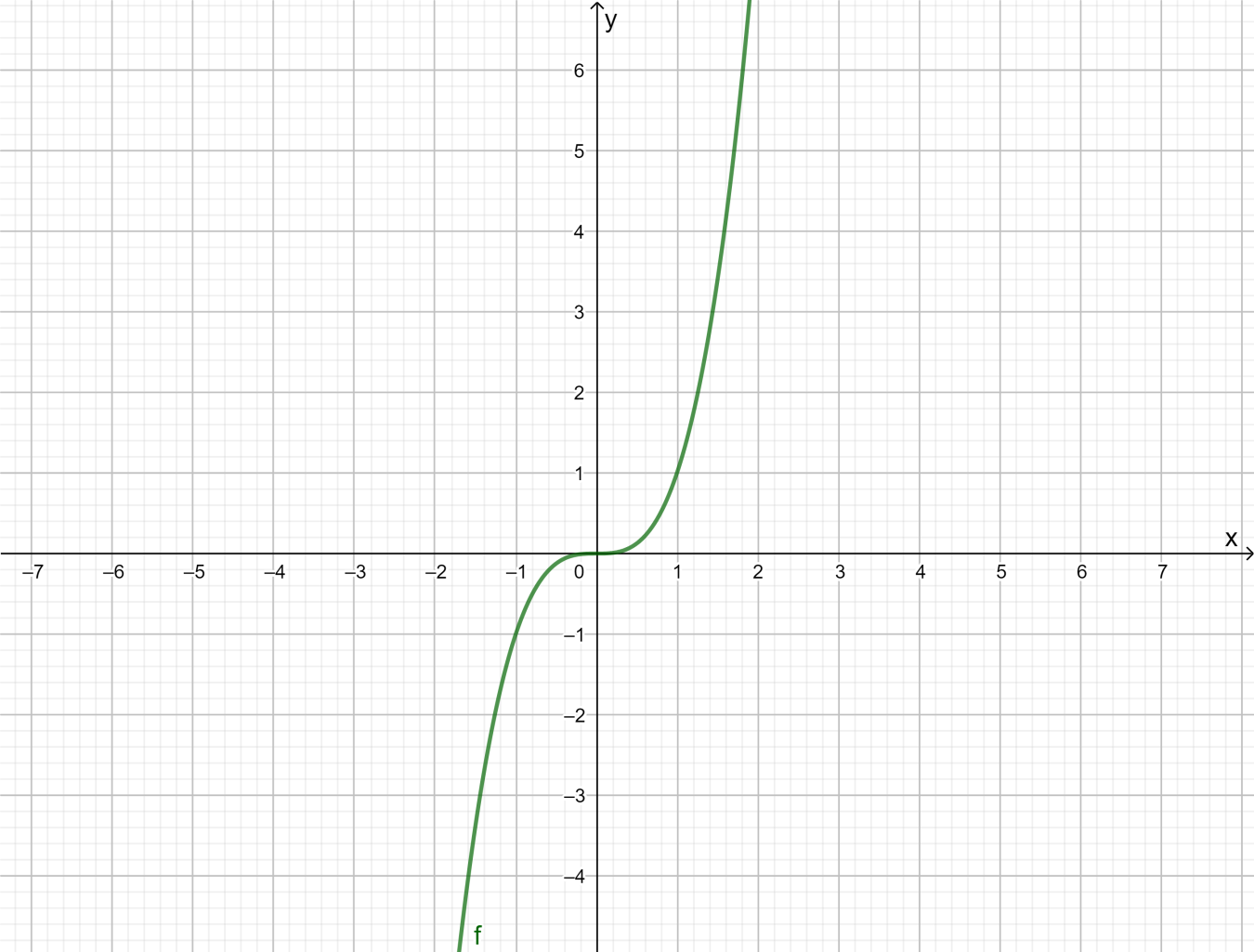
The function is symmetric about the line y=x,so the function is an odd functionTherefore,  the function f(x)=x³ is an odd function

The function f(x)=x³ is an odd function as it is symmetric about the line y=x

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 243 Exercise 9, Answer

It is given a cubic function f(x)=x³

It is required to explain about symmetry of the given functionIt is inferred from the part (f) that the function is oddThe graph off(x)=x³ inferred from part (b) is as follows

From the graph it is clearly shows that the graph is symmetric about the origin as it is an odd function and an odd function is always symmetric about origin

Thus, the function f(x)=x³ is symmetric about origin

The function f(x)=x³ is symmetric about the origin as it is an odd function

Page 243 Exercise 10, Answer

It is given graph that g(x)=(x−4)³

It is to describe how the graph of g(x) is related to the graph of f(x)=x³

Draw graphs for each of the functions separately using a graphing calculator

Then, do the appropriate transformation to make both functions equal graphically which proves given functions are related

The parent function is f(x)=x³ Using graphing calculator, draw the graph of the function f(x)=x³

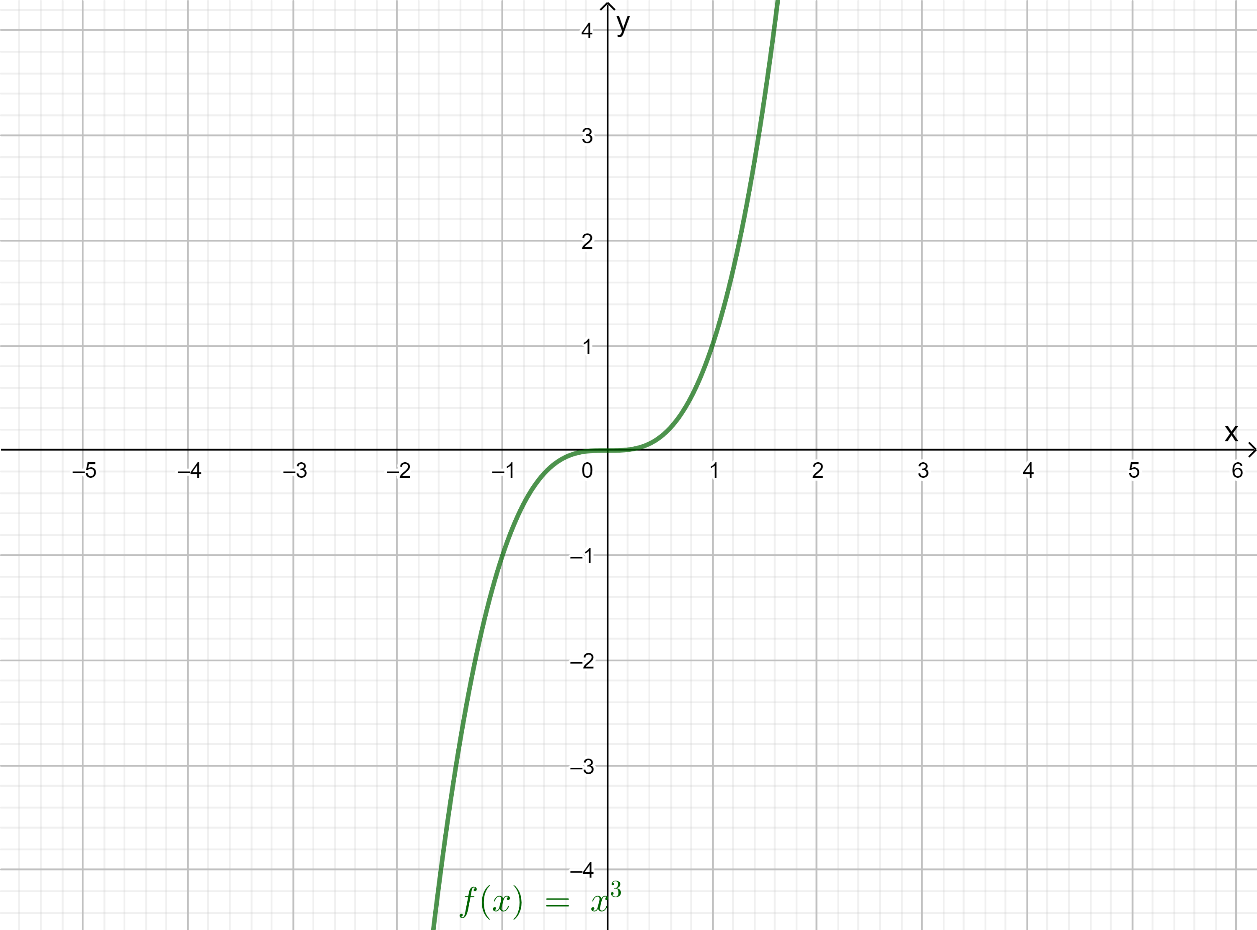
The function, g(x)=(x−4)³ is of the form g(x)=(x−a)

Then, consider the fact that if a is a positive number then, the graph of g(x)=(x−a) occurs from the horizontal translation of the graph of f, a units to the right Here, the value of a is 4

So, translate the graph of f(x)=x³four units to the right

The graph of g(x)=(x−4)³ will be as follows:

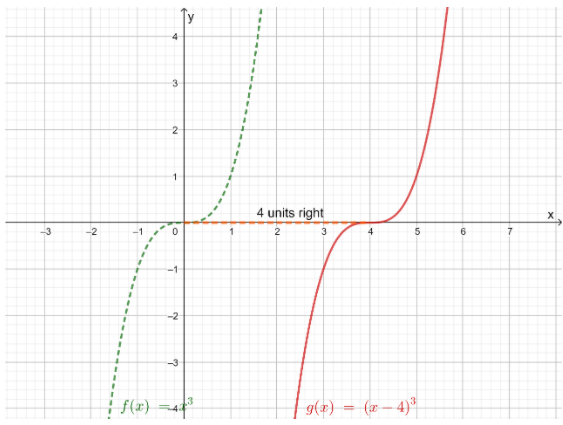
The graph of g(x)=(x−4)³ is the translation of the graph of f(x)=x3 to 4 units to the right

Solutions For Chapter 5 Exercise 5.1 Polynomial Functions HMH

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 243 Exercise 11, Answer

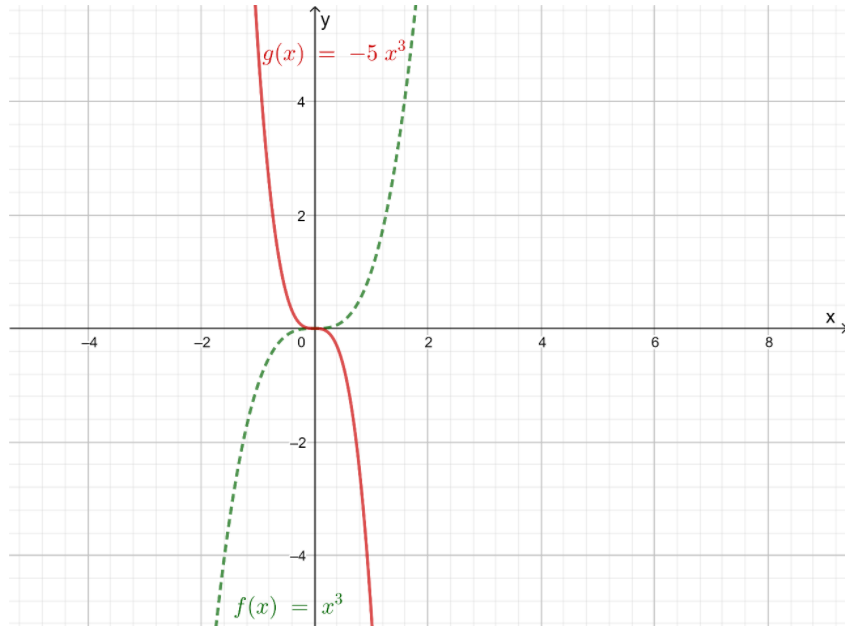
It is given graph that g(x)=−5x³

It is to describe how the graph of g(x) is related to the graph of f(x)=x³

Draw graphs for each of the functions separately using a graphing calculator

Then, do the appropriate transformation using the rules to plot the graph of h(x)=a(1b(x−h))³+kand plot the required graph

The parent function is f(x)=x³Using a graphing calculator, draw the graph of the function f(x)=x³

The given cubic function is of the form h(x)=a(1b(x−h))³+k

For g(x), h=0,k=0, b=−1, and a=5

Thus, according to the rule of the cubic function h(x),the graph of g(x)=−5x³ is  the reflection of f(x) in the y-axis followed by a vertical stretch of a factor of 5

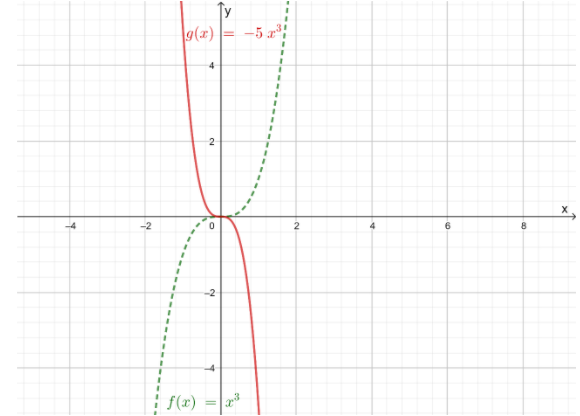
The graph of g(x)=−5x³ is  the reflection off(x) in they-axis followed by a vertical stretch of a factor of 5

Page 243 Exercise 12, Answer

It is given that g(x)=x³+2

It is to describe how the graph of g(x)is related to the graph of f(x)=x³ Draw graphs for each of the functions separately using a graphing calculator

Then, do the appropriate transformation to make both functions equal graphically which proves given functions are related

The parent function is f(x)=x³

Using a graphing calculator, draw the graph of the function f(x)=x³

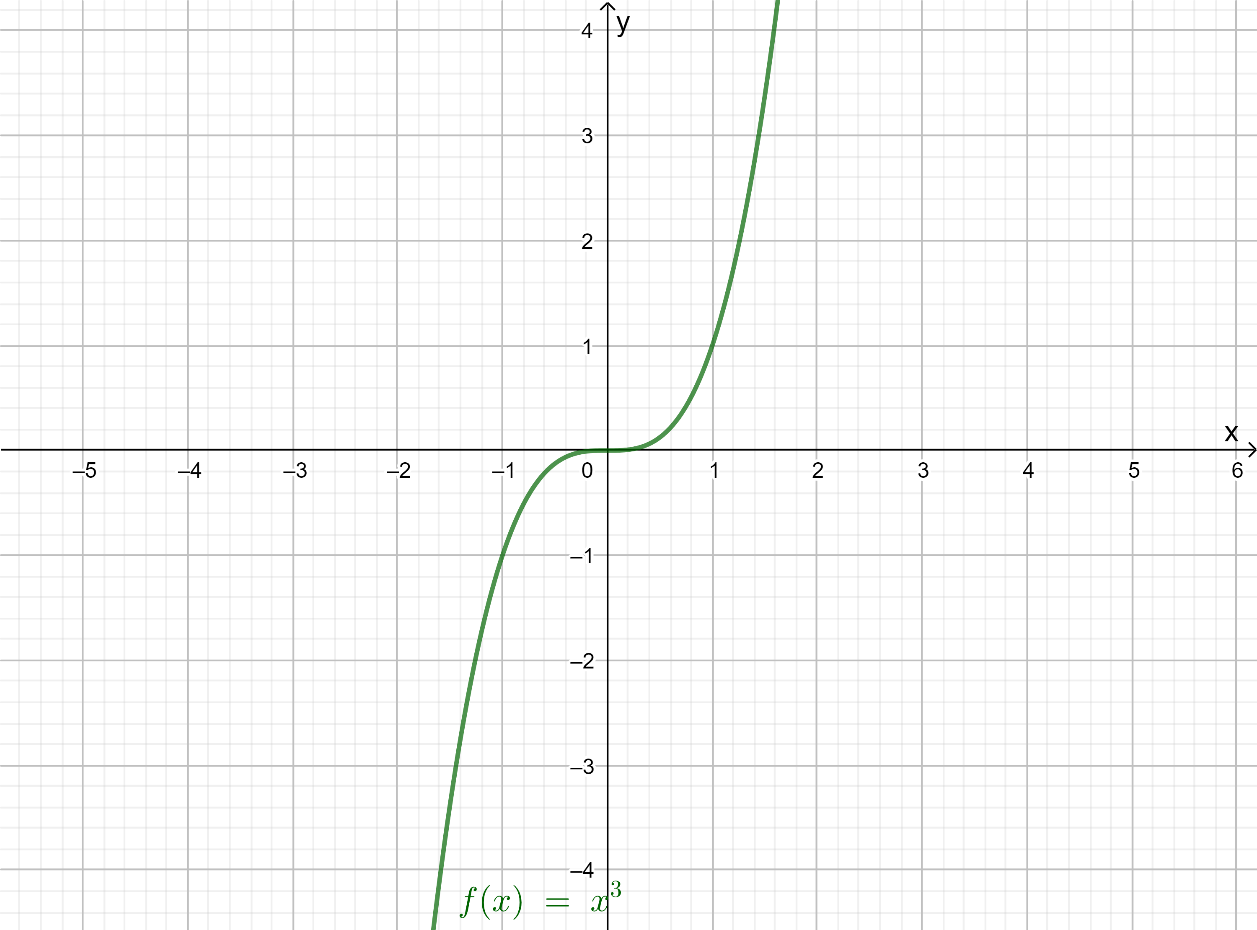
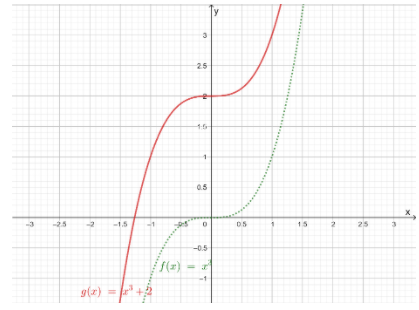
The function, g(x)=x³+2is of the form g(x)=f(x)+k

Then, consider the fact that if a is a positive number then, the graph of g(x)=f(x)+k occurs from the vertical translation of the graph of f, k units to the up Here, the value of k is 2

So, translate the graph of f(x)=x³ two units upwards

The graph of g(x)=(x−4)³ will be as follows:

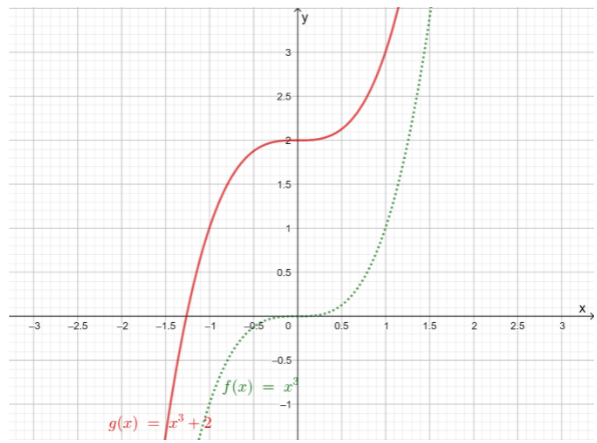
The graph of g(x)=x³ +2 is the translation of the graph of  f(x)=x³ to 2 units upwards

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 243 Exercise 13, Answer

It is given graph that g(x)=(3x)³

It is to describe how the graph of g(x) is related to the graph of f(x)=x³

Draw graphs for each of the functions separately using a graphing calculator

Then, do the appropriate transformation using the rules to plot the graph of h(x)=a(1b(x−h))³+k and plot the required graph

The parent function is f(x)=x³

Using a graphing calculator, draw the graph of the function f(x)=x³

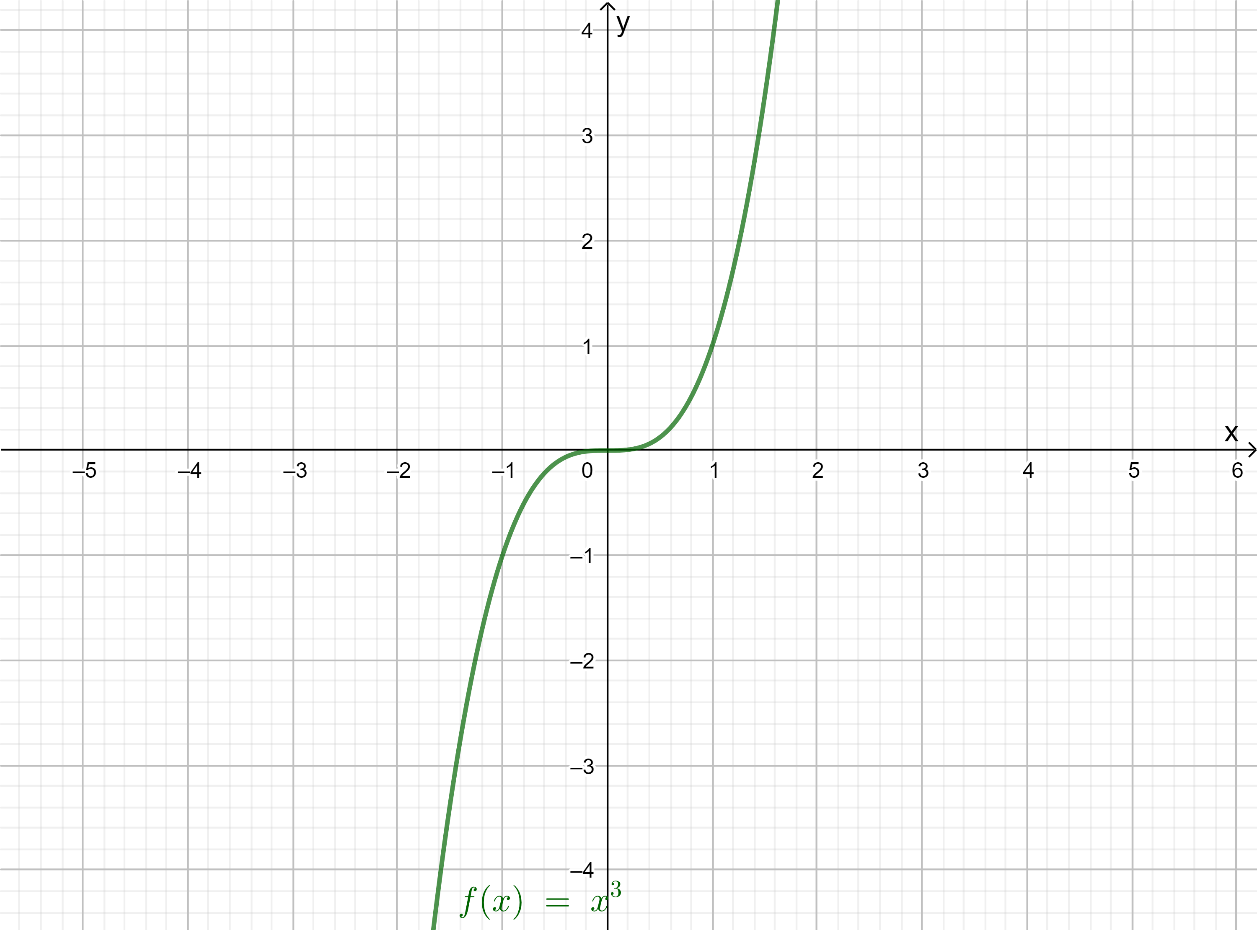
The given cubic function is of the form h(x)=a(1b(x−h))³+k

For g(x), h=0,k=0, b=13, and a=1

Thus, according to the rule of the cubic function h(x),the graph of g(x)=(3x)3is formed by compressing f(x)horizontally by a factor of 3

The graph will be as follows:

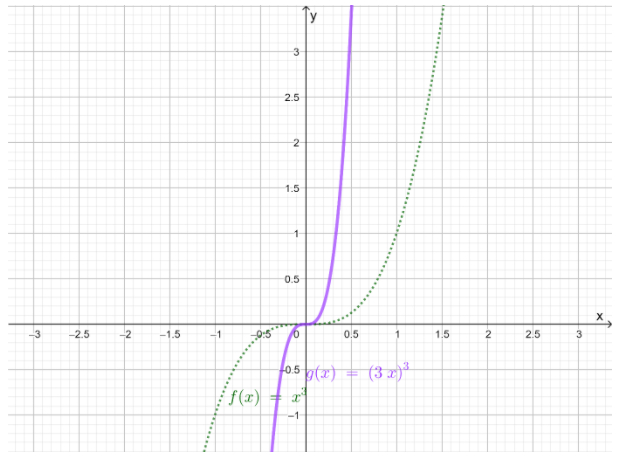
The graph of g(x)=(3x)³ is obtained by compressing f(x) horizontally by a factor of 3

Page 244 Exercise 14, Answer

It is given graph that g(x)=(x+1)³

It is to describe how the graph of g(x) is related to the graph of f(x)=x³

Draw graphs for each of the functions separately using a graphing calculator

Then, do the appropriate transformation to make both functions equal graphically which proves given functions are related

The parent function is f(x)=x³

Using graphing calculator, draw the graph of the function (x)=x³

The function g f(x)=(x+1)³ is of the form g(x)=f(x+a)

Then, consider the fact that ifa is a positive number then, the graph of g(x)=f(x+a) from the horizontal translation of the graph off, a units to the left Here, the value of a is 1

So, translate the graph of f(x)=x³ one unit to the left

The graph of g(x)=(x+1)³ will be as follows:

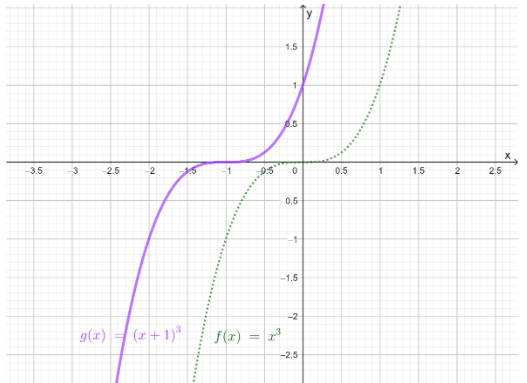
The graph of g(x)=(x+1)³ is the translation of the graph of f(x)=x³ to 1 unit to the left

Page 244 Exercise 15, Answer

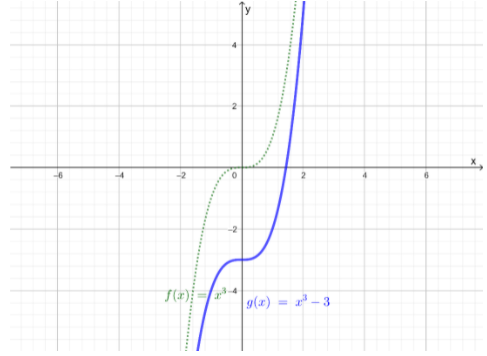
It is given that g(x)=x³−3

It is to describe how the graph of g(x) is related to the graph of f(x)=x³

Draw graphs for each of the functions separately using a graphing calculator

Then, do the appropriate transformation to make both functions equal graphically which proves given functions are related

The parent function is f(x)=x³ Using graphing calculator, draw the graph of the function f(x)=x³

The function, g(x)=x³ −3 is of the form g(x)=f(x)−k

Then, consider the fact that if a is a positive number then, the graph of g(x)=f(x)−k from the vertical translation of the graph of f, k units down Here, the value of k is 3So, translate the graph of f(x)=x³ three units down

The graph of g(x)=x³−3will be as follows:

The graph of g(x)=x³ −3 is the translation of the graph of  f(x)=x³ to 3 units down

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 244 Exercise 16, Answer

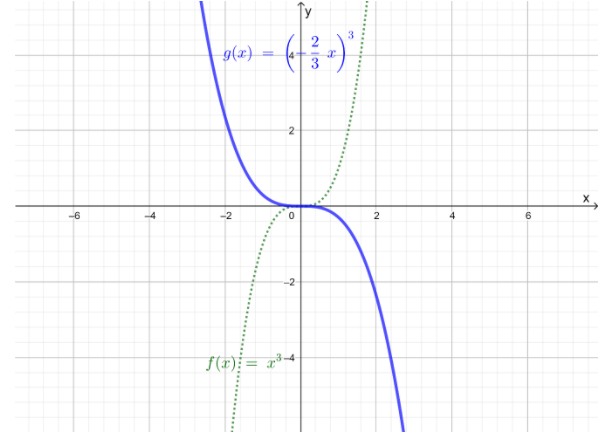
It is given graph that g(x)=(−23x)³

It is to describe how the graph of g(x)is related to the graph of f(x)=x³

Draw graphs for each of the functions separately using a graphing calculator

Then, do the appropriate transformation using the rules to plot the graph of h(x)=a(1b(x−h))³+kand plot the required graph

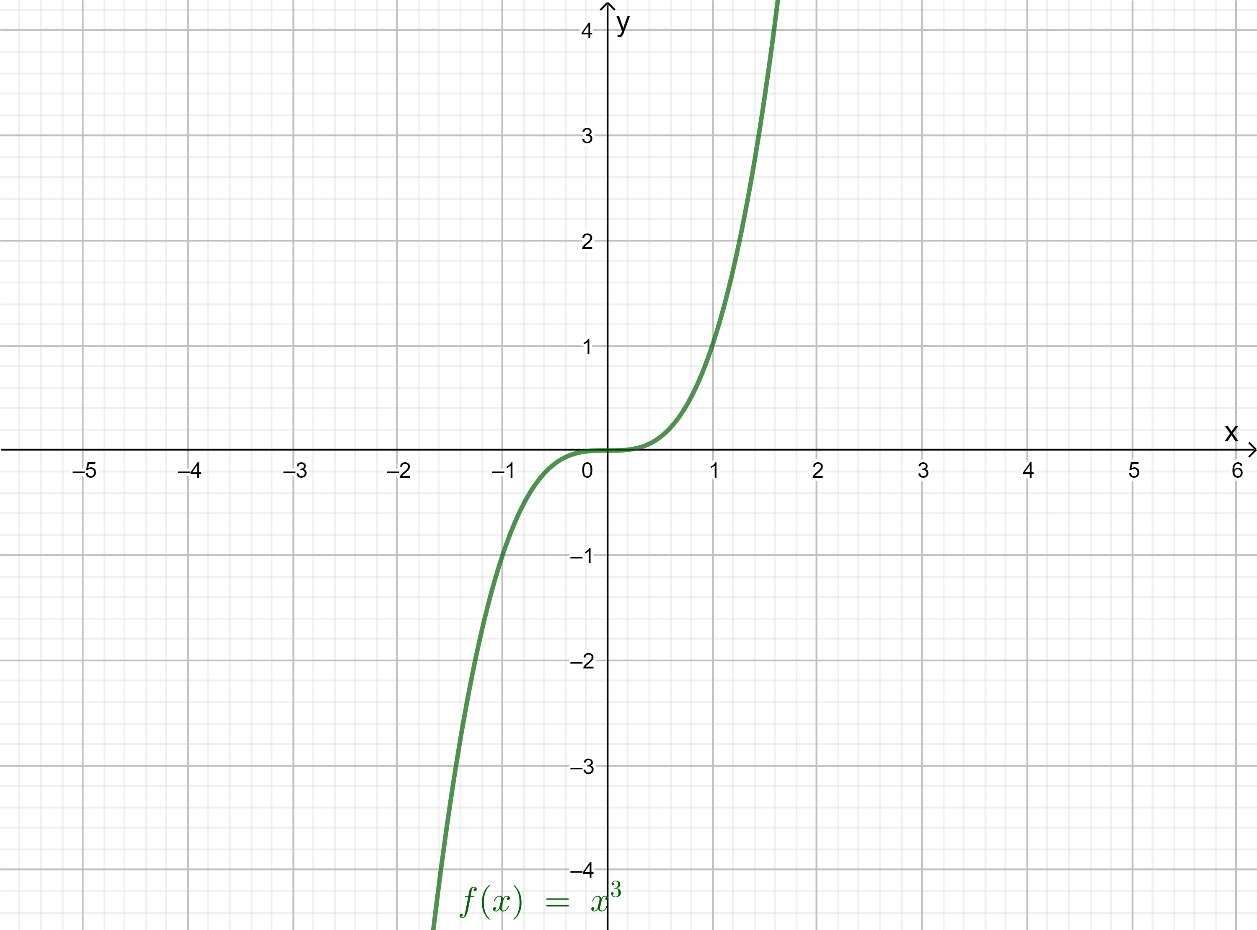
The parent function isf(x)=x³ Using a graphing calculator, draw the graph of the function f(x)=x³

The given cubic function is of the form h(x)=a(1b(x−h))³+k

For g(x), h=0,k=0, b=32, and a=1

Thus, according to the rules of the cubic functionh(x),the graph of g(x)=(−23x)³is obtained by stretching f(x)horizontally by a factor of32, that is, 1.5

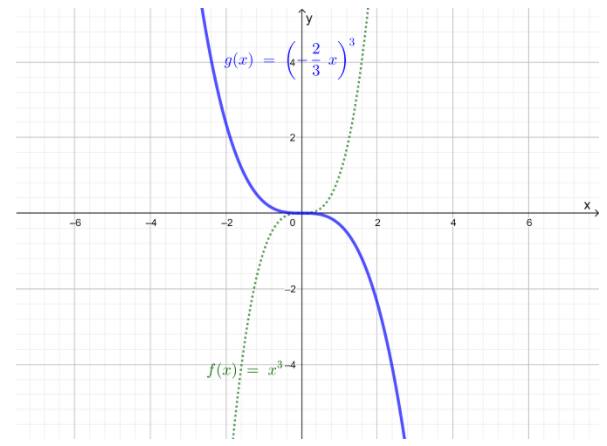
The horizontal stretching  of f(x)by 15units gives the graph of g(x)=(−23x)³

Page 244 Exercise 17, Answer

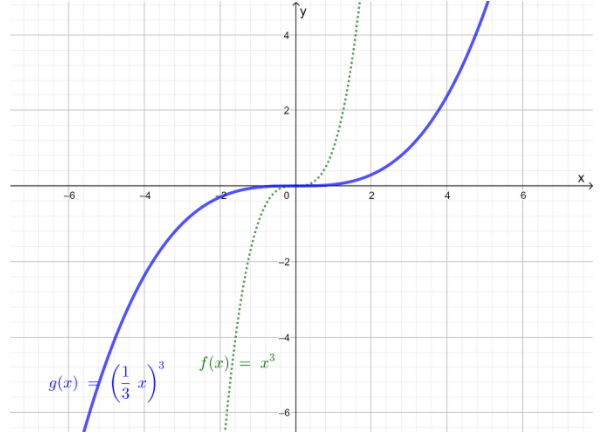
It is given that g(x)=(13x)³

It is required to identify the transformation that produces the graph of g(x)

when the parent function is f(x)=x3and then graph the function,g(x)using the reference points (−1,−1),(0,0), and(1,1)

Observe the type of g(x)then, Identify the transformation Now, make a table x and  y coordinates of function g(x), and plot the graph with the help of coordinates obtained

The given cubic function is of the form h(x)=a(1b(x−h))³+k

For g(x), h=0,k=0, b=3, and a=1

Thus, according to the rules to make the graph of the cubic function h(x), transform the graph of f(x) by horizontally stretching it by a factor of 3

Now, find the coordinates to plot g(x)=(13x)³

Graph both the function on the same plane

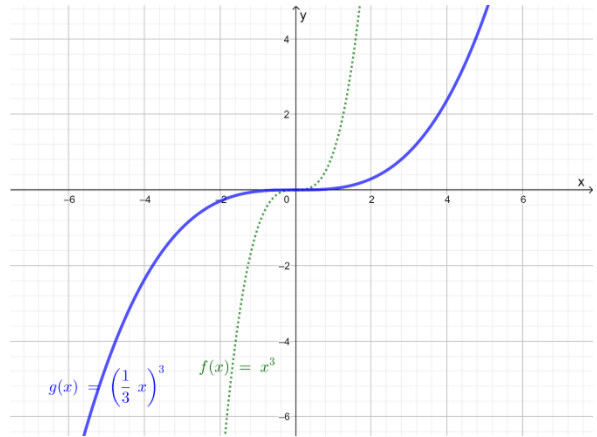
The transformation to graphg(x)=(13x)³using f(x)is horizontally stretchingf(x)by a factor of 3

Exercise 5.1 Polynomial Functions Worked Examples HMH Algebra 2

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 244 Exercise 18, Answer

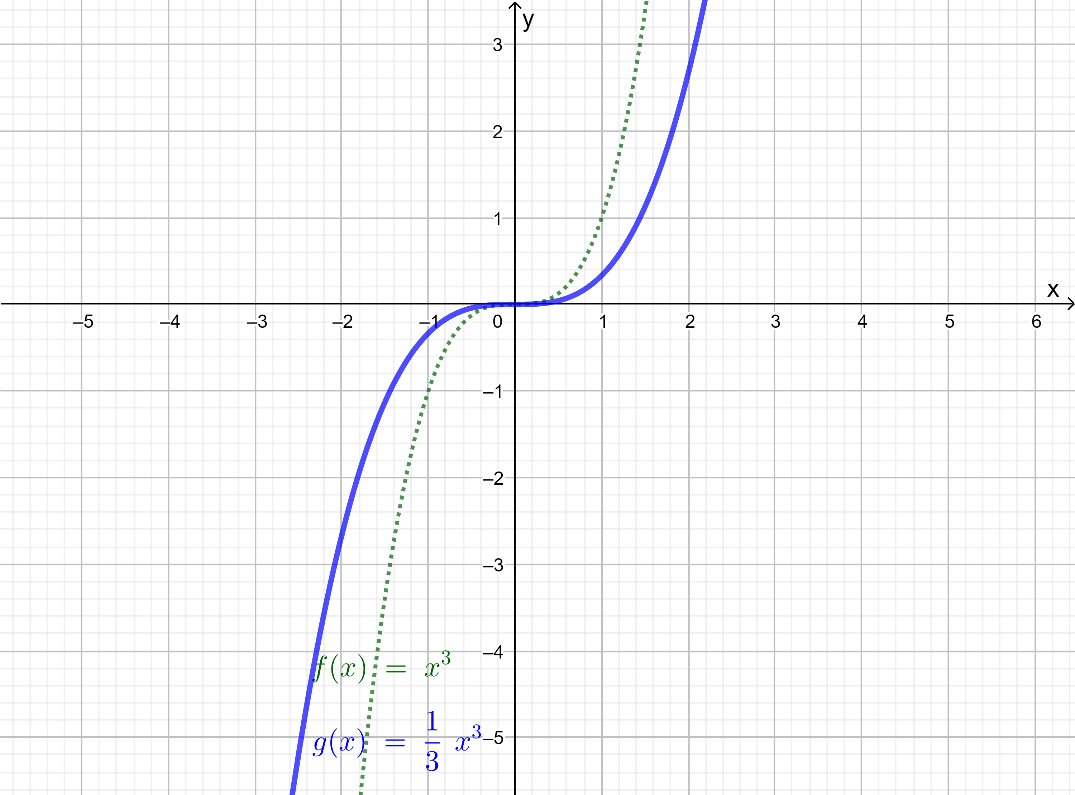
It is given graph that g(x)=1/3×3.

It is required to identify the transformation that produces the graph of g(x) when the parent function is f(x)=x³ and then graph the function, g(x) using the reference points (−1,−1) ,(0,0), and (1,1).

Observe the type of g(x) then, Identify the transformation. Now, make a table x and y coordinates of function g(x), and plot the graph with the help of coordinates obtained.

The parent function is f(x)=x³.

Using a graphing calculator, draw the graph of the function f(x)=x³.

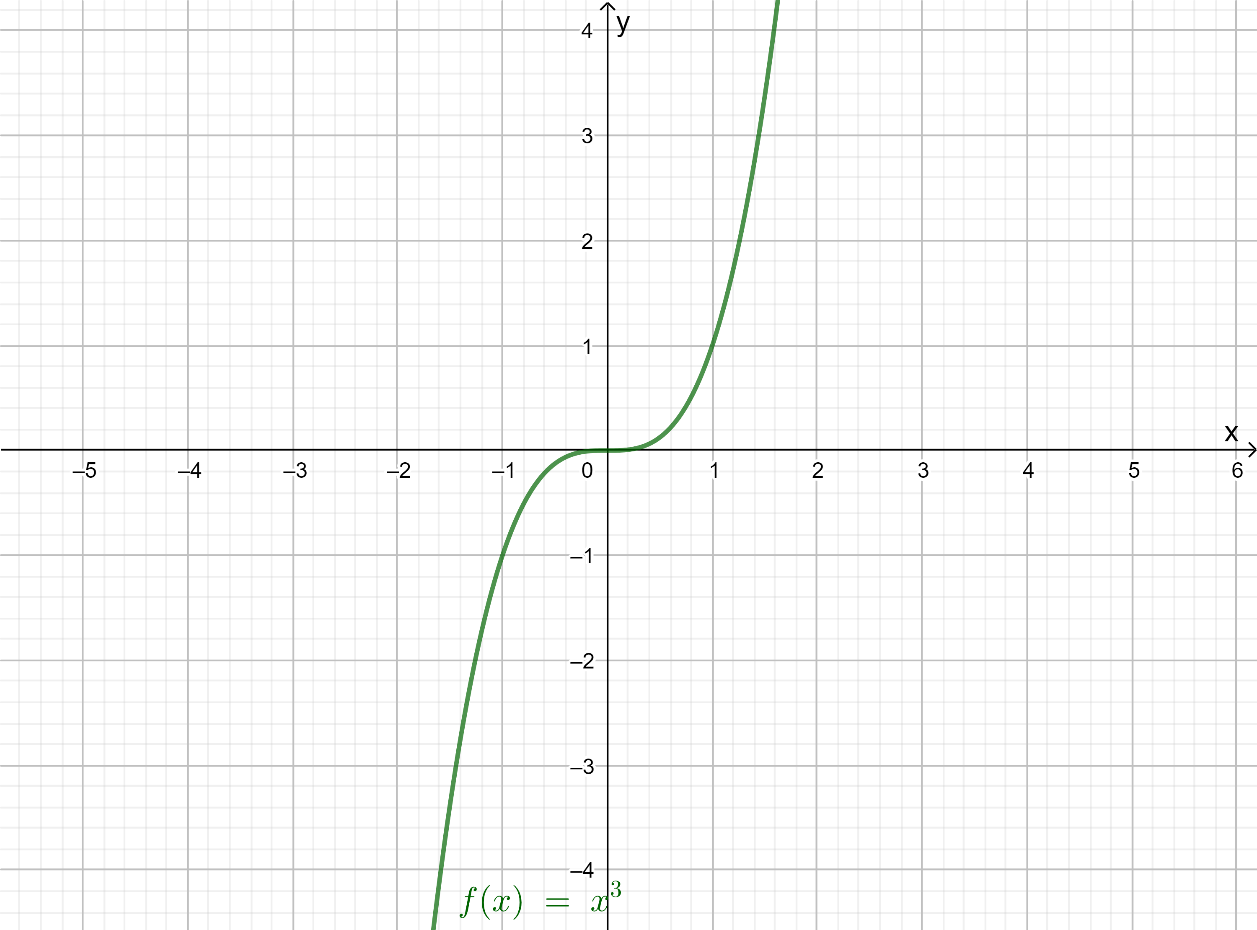
The given cubic function is of the form h(x)=a(1/b(x−h))³+k.

For g(x), h=0,k=0,b=1, and a=1/3.

Therefore, a<1. So, the graph will be compressed.

Thus, according to the rules of the cubic function h(x), the graph of g(x)=1/3x³ is the obtained by compressing f(x) vertically by a factor of 3.

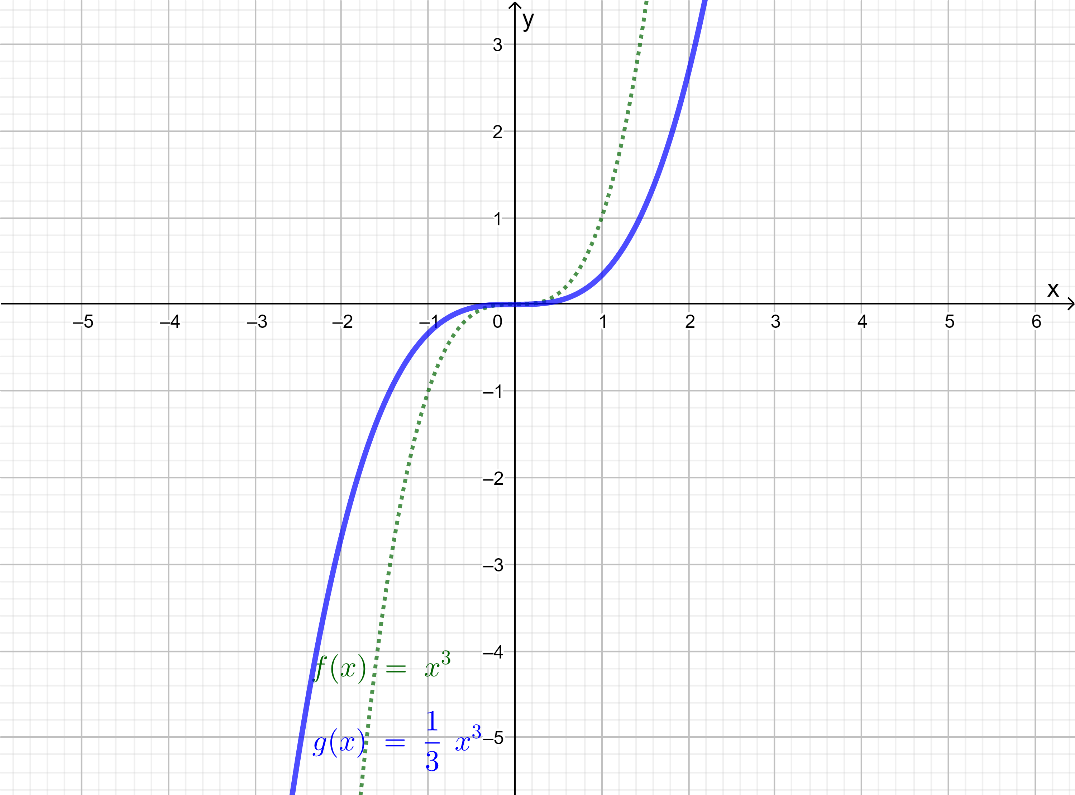
The vertical compression of f(x) by 3 units gives the graph of g(x)=1/4x³.

Page 244 Exercise 19, Answer

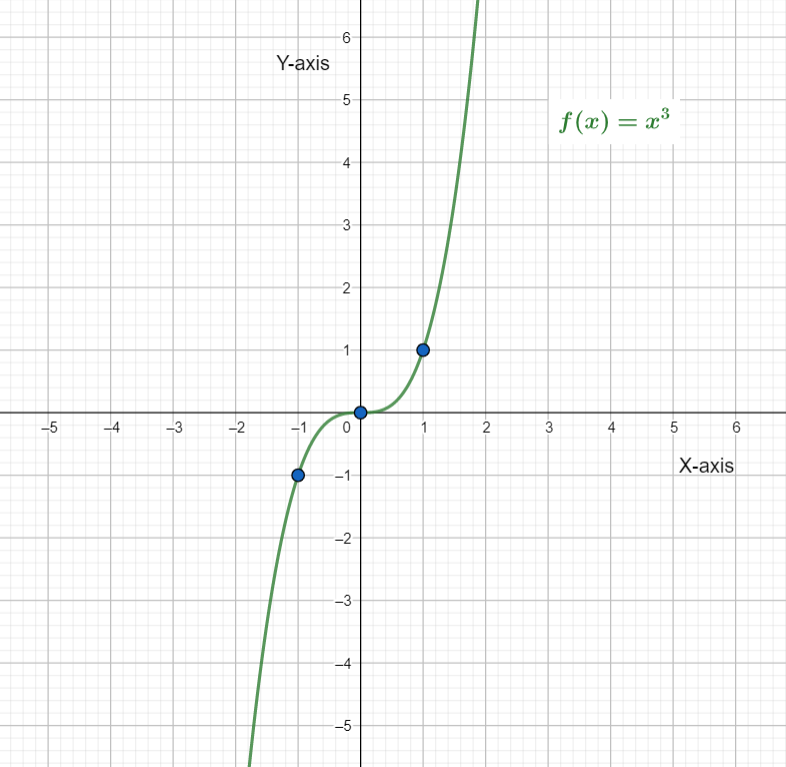
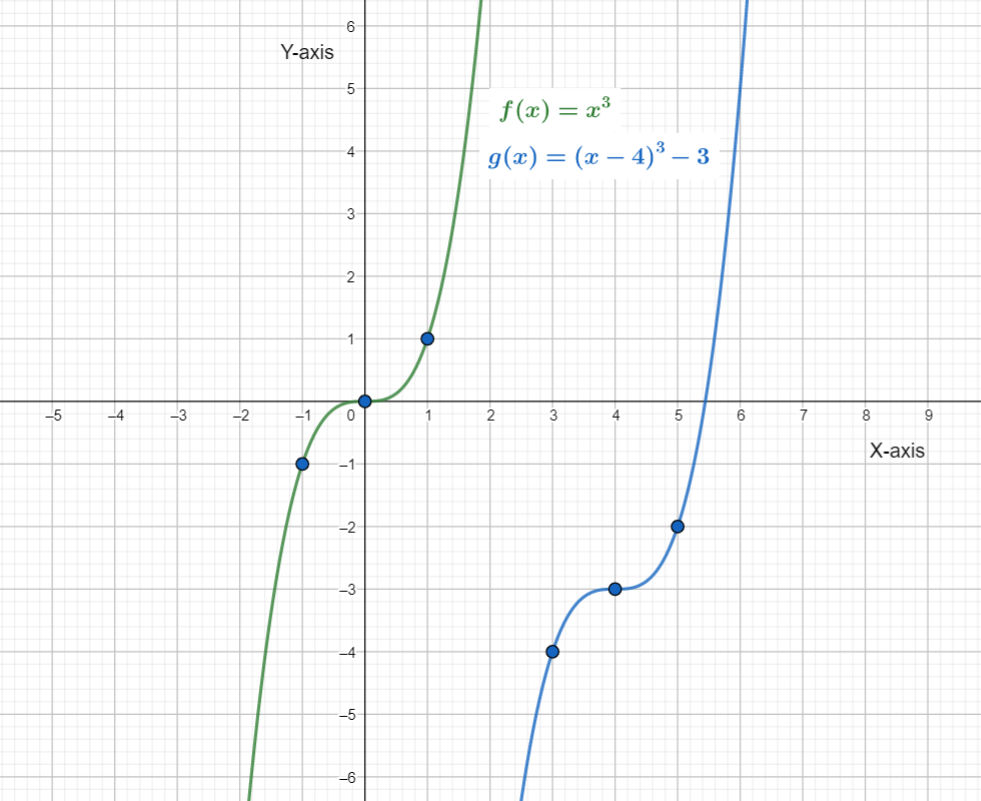
It is given that the function f(x)=x³ is getting transformed to the function  g(x)=(x−4)³−3.

It is asked to identify the transformations then to draw the graph of the function by applying the transformations on the reference points (−1,−1), (0,0)and (1,1).

First, identify the transformations of the graph of f(x)=x³ that produces the graph of the function g(x), then draw the graph for function f(x).

Then apply those transformations in the reference points (−1,−1), (0,0)and (1,1), it will give the reference points for the new function g(x).

Plot those reference points and draw the smooth curve crossing over those points, the graph obtained will be the graph of the given function g(x).

The function f(x)=x³ is getting transformed to the function  g(x)=(x−4)³−3.

The given function is of the form, h(x)=a(1/b(x−h))³+k.

For g(x), h=0,k=0, b=1, and a=1.

The transformations of the graph of f(x) that produces the graph of g(x) are Horizontal translation to the right by 4 units.

Vertical shift to the down by 3 units.

Note that, the Horizontal translation to the right by 4 units will only affect the x-coordinate and the Vertical shift to the down by 3 units will only affect the y-coordinate.

Now, plot the graph of the function f(x).

Then, shift the function f(x) to the right by 4 units and then to the down by 3 units to obtain the function g(x)

The transformations of the graph of f(x) that produces the graph of g(x) are:

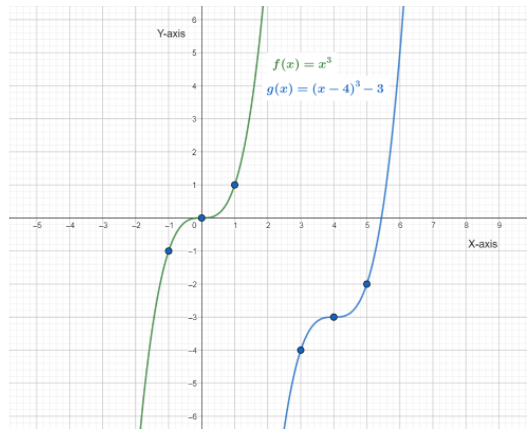
Horizontal translation to the right by 4 units.

Vertical translation to the down by 3 units.

The graph of g(x) on the same coordinate plane as the graph of f(x) by applying the transformations to the reference points (−1,−1), (0,0) and(1,1) is given by,

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 244 Exercise 20, Answer

It is given that the function f(x)=x³ is getting transformed to the function g(x)=(x+1)³+2.

It is asked to identify the transformations then to draw the graph of the function by applying the transformations on the reference points (−1,−1)2,(0,0), and (1,1).

First, identify the transformations of the graph of f(x)=x³ that produces the graph of the function g(x), then draw the graph for function f(x).

Then apply those transformations in the reference points (−1,−1), (0,0), and (1,1), it will give the reference points for the new function g(x).

Plot those reference points and draw the smooth curve crossing over those points, the graph obtained will be the graph of the given function g(x).

The given function is of the form,h(x)=a(1/b(x−h))³+k.

For g(x), h=−1,k=2, b=1, and a=1.

The transformations of the graph of f(x) that produces the graph of g(x) are: Horizontal shifts to the left by 1 units.

Vertical shift to the upward by 2 units.

Note that, the Horizontal shifts to the left by 1 units will only affect the x-coordinate and the Vertical shift to the upward by 2 units will only affect the y-coordinate.

Now, plot the graph of the function f(x).

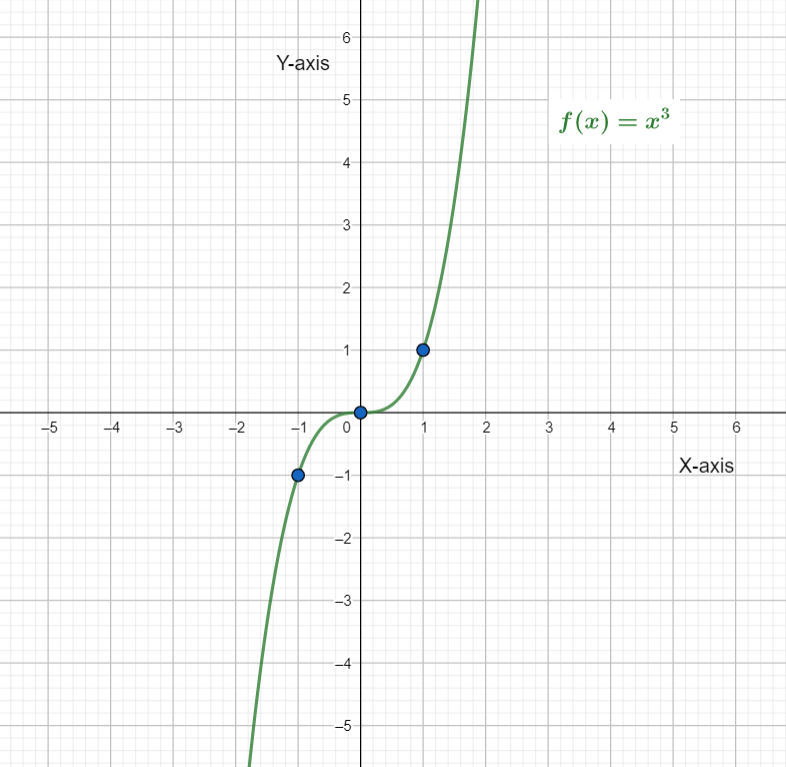
Then, shift the function f(x) to the left by 1 units and then to the upward by 2 units to obtain the function g(x).

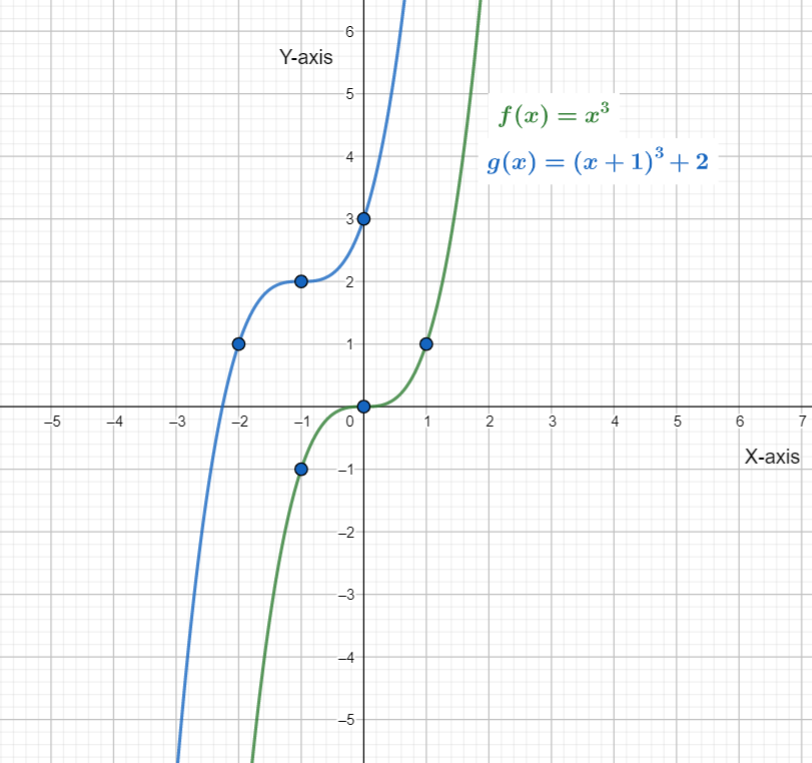
The transformations of the graph of f(x) that produces the graph of g(x) are: Horizontal shifts to the left by 1 units followed by vertical shift to the upward by 2 units.

The graph of g(x) on the same coordinate plane as the graph of f(x) by applying the transformations to the reference points (−1,−1), (0,0) and(1,1) is given by,

Page 244 Exercise 21, Answer

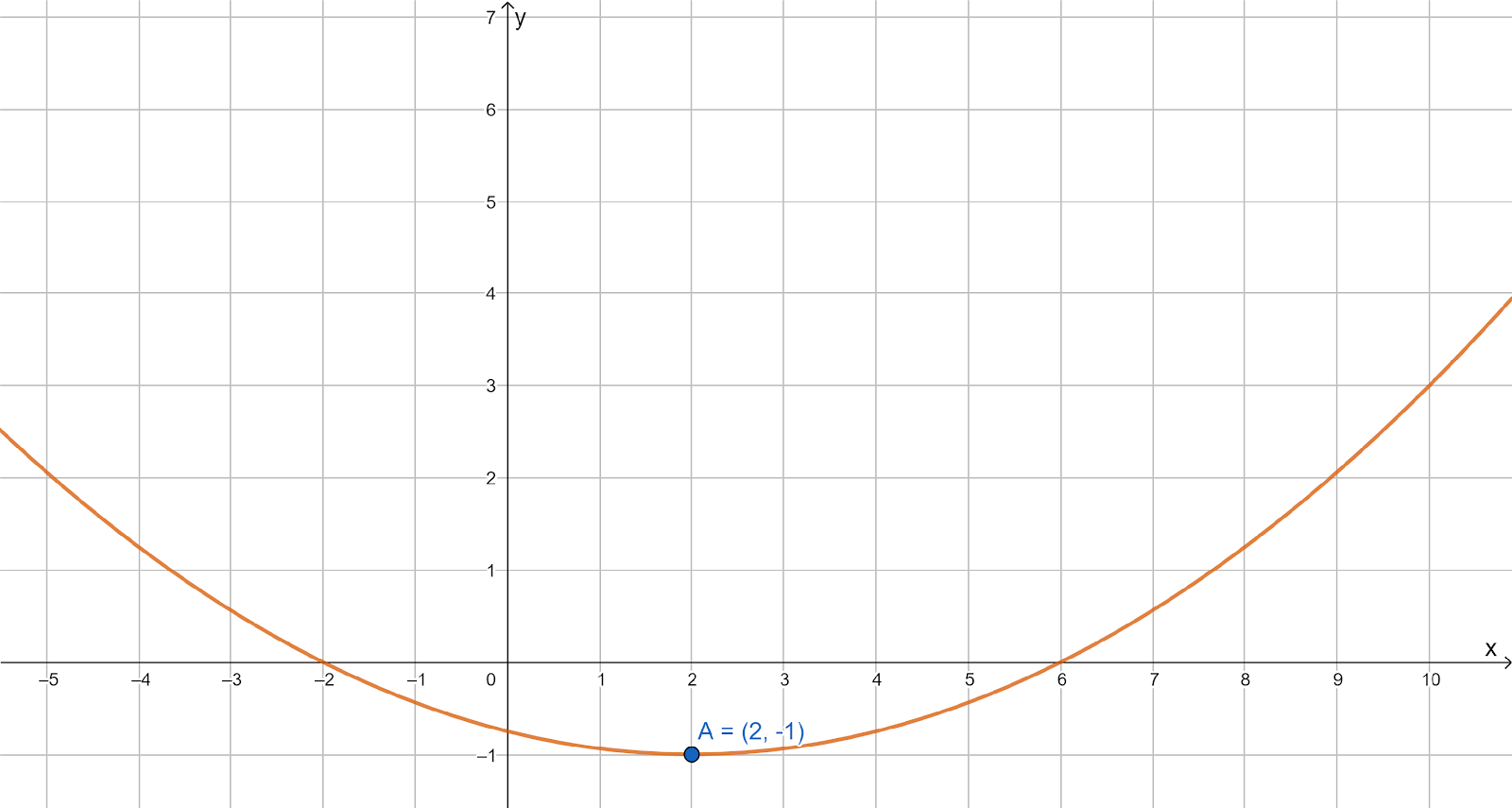
It is given that g(x)=a(x−h)³+k is a general equation for a cubic function and a graph of a function is given with its reference points.

It is asked to write a specific equation by identifying the values of the parameters from the reference points shown in the graph.

First of all, find the point of symmetry, in that, the abscissa is the value of h and the value of ordinate is the value of k.

Then to find the value of a, plug the values of h and k in the parent function and use another reference point to solve the equation.

Finally, substitute all the obtained values in the general equation for the cubic function, that will be the required function for the given graph.

First, identify the point of symmetry from the graph.

(h,k)=(1,4)

Thus, h is equal to 1 and k is equal to 4.

Now, identify the value of a by substituting the values of h, k and using any of the reference point in the general equation.

Therefore, g(x)=a(x−h)³+k

Substituting 1 for h and 4 for k.

g(x)=a(x−1)³+4

Consider the references points (0,7) and substitute 0 for x and 7 for g(x).

​7=a(0−1)³ +4

7=a(−1)+4

7=−a+4

Subtract 4 from both the sides.

​7−4=−a+4−4

3=−a​

Multiply both sides by −1 and rewrite the equation for a.​​

3(−1)=−a(−1)

a=−3​

Thus, a is equal to −3.

Now, substitute all these values in the given general equation of the cubic functiong(x)=a(x−h)³+k.

Thus, g(x)=−3(x−3)³+4

Hence, the required equation for the given function is g(x)=−3(x−3)³+4.

The specific equation by identifying the values of the parameters from the reference points shown in the graph is given by g(x)=−3(x−3)³+4.

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 244 Exercise 22, Answer

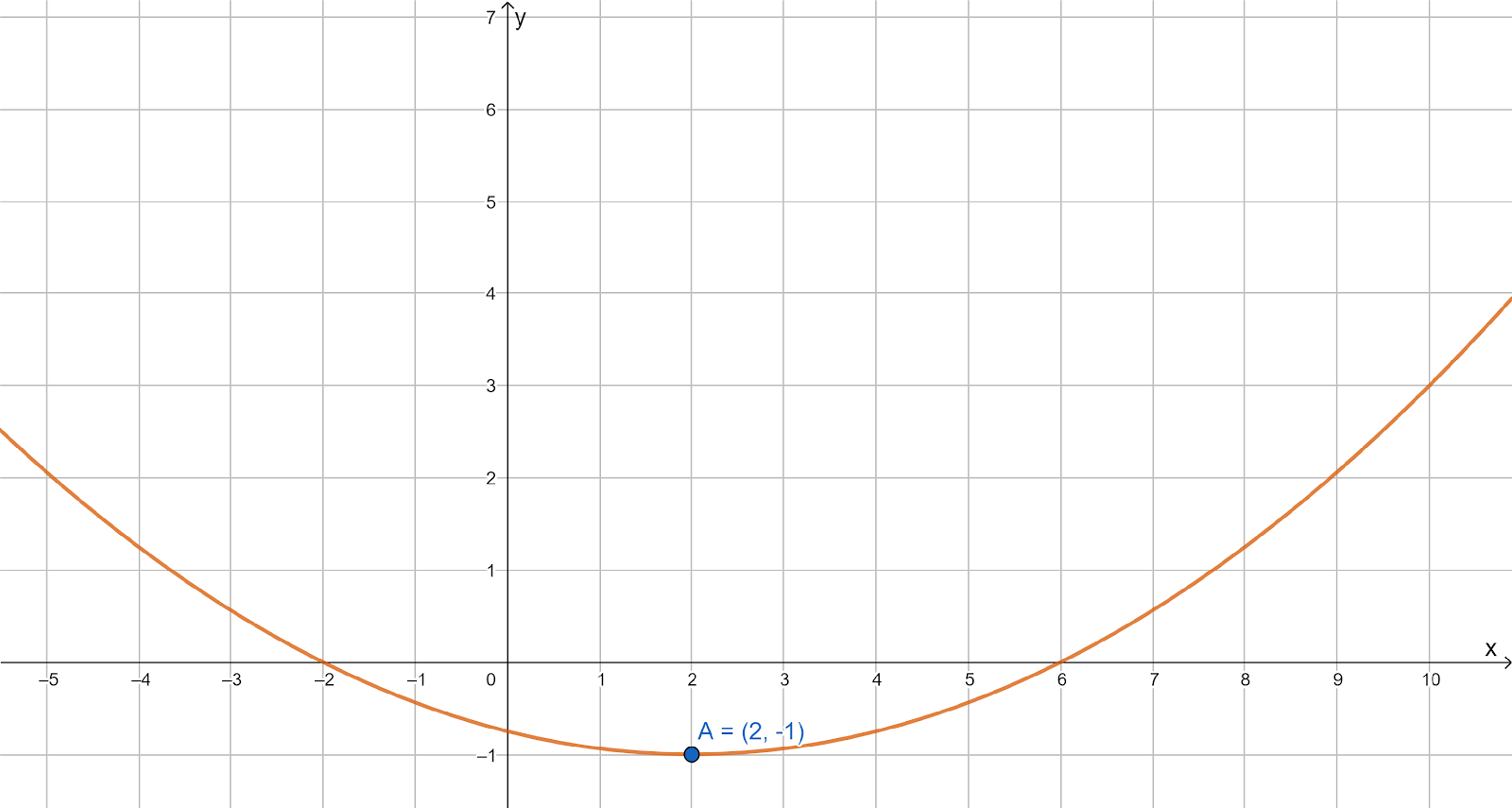
It is given that g(x)=(1/b(x−h))³+k is a general equation for a cubic function and a graph of a function is given with its reference points.

It is asked to write a specific equation by identifying the values of the parameters from the reference points shown in the graph.

First of all, find the point of symmetry, in that, the abscissa is the value of h and the value of ordinate is the value of k.

Then to find the value of b, plug the values of hand k in the parent function and use another reference point to solve the equation.

Finally, substitute all the obtained values in the general equation for the cubic function, that will be the required function for the given graph.

First identify the point of symmetry from the graph.

(h,k)=(2,−1)

Thus, h is equal to 2 and k is equal to −1.

Now, identify the value of b by substituting the values of h, k and using any of the reference point in the general equation.

Therefore, g(x)=(1/b(x−h))³+k

Substituting 2 for h and −1 for k.

g(x)=(1/b(x−2))³+(−1)

Consider the references points (1.5,0) and substitute 1.5 for x and 0 for g(x).​

​0=(1/b(1.5−2))³ +(−1)

0=(1/b(0.5))³−1

0=1/b³(0.5)³−1

0=0.125/b³−1

​Add 1 to both the sides.​

​0+1=0.125/b³

−1+1 /1=0.125/b³

Multiply both sides by b³.

​​1=0.125/b³

1⋅b³=0.125

b³⋅b³ b³=0.125

Take cube root of both the sides.

3√b3=3/√0.125

b=0.5​

Thus, b is equal to 0.5.

​Now, substitute all these values in the given general equation of the cubic function g(x)=(1

b (x−h))³+k.

Thus, ​g(x)=(1/0.5(x−2))³+(−1)

g(x)=(1/0.5(x−2))³−1​

Hence, the required equation for the given function is g(x)=(1/0.5(x−2))³−1.

The specific equation by identifying the values of the parameters from the reference points shown in the graph is given by g(x)=(1/0.5(x−2))³−1.

Page 244 Exercise 23, Answer

It is given that the density of gold is 0.019kg/cm³.

It is asked to estimate the edge length of a cube of gold with a mass of 1 kg by modeling a cubic function and graphing the function using calculated values of the function.

Consider the length as l, then find volume, mass of the gold. Then draw a graph using the mass function with plots mass vs. length.

From the graph, find the value in the X−axis which is the length of the cube of the gold, for mass equal to 1, that will be the required value.

Given that the density of gold is 0.019 kg/cm³.

Assume the length of the edge of the cube be l (in cm). Then, volume of the cube is given by,

V=l³cm³

Since density of the gold is given as 0.019kg/cm³

Therefore, mass of the cube is, ​

​m=Vd

m=0.019l3 kg
​
Now, make a table using the above function.

Draw the graph of the mass function by plotting above points, and recognizing that the graph is a vertical compression of the graph of the parent cubic function by a factor of 0.019.

Then draw the horizontal line m=1 and estimate the value of l where the graph intersects.

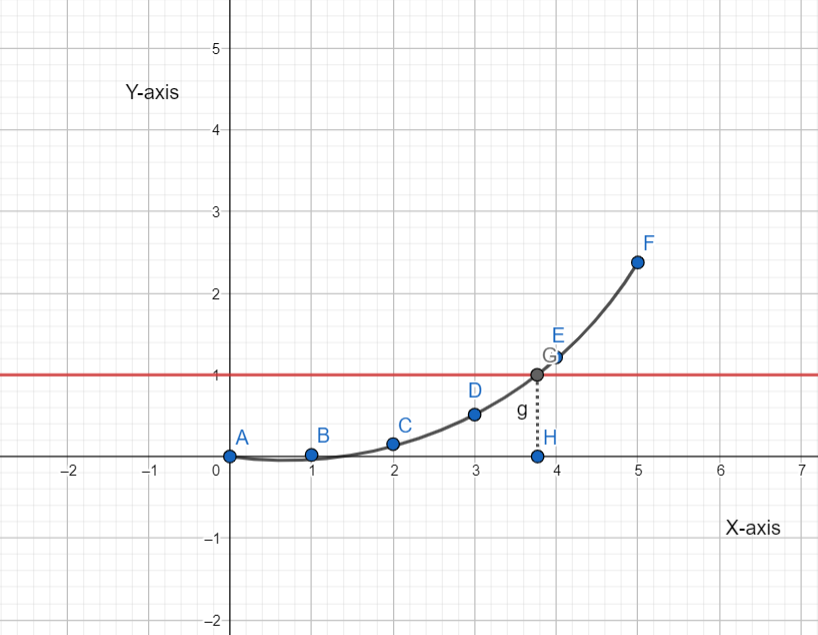
This is given to be 1kg. Thus, 0.019x³=1

Divide both sides by 0.019.​

​0.019x^3/0.019=1

0.019 x³ =1

0.019x³ =52.63

Take cube root of both the sides.​

​3 √x3 =3

√52.63

x=3.74 cm​

Hence, edge length of a cube of gold is 3.74 cm.

The edge length of a cube of gold is 3.74 cm.

HMH Algebra 2 Volume 1 Exercise 5.1 Walkthrough

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 244 Exercise 24, Answer

It is given that a proposed design for a habitable Mars colony is a hemispherical biodome used to maintain a breathable atmosphere for the colonists.

It is asked to estimate the radius of the biodome if it is required to contain 5.5 billion cubic feet of air, by modeling a cubic function and graphing the function using calculated values of the function.

Consider the length as l, then find volume, mass of the gold. Then draw a graph using the mass function with plots mass vs. length.

From the graph, find the value in the X−axis which is the length of the cube of the gold, for mass equal to 1, that will be the required value.

Assume the radius of the hemispherical biodome ber (in foot).

Then, volume of the hemispherical biodome is given by,

V=2/3πr³ feet³

This is given to be 5.5 billion cubic feet.

Thus, 5.5=2/3πr³

Multiply both sides by 3/2π and simplify the equation.​

​5.5⋅3/2π=2

3/πr3⋅(3/2π) 2.62=r³

r³=2.62​

Take cube root on both the sides and simplify the equation.​

​3√r3=3√2.62

r=1.37

​Hence, radius of the biodome is 1.37 thousands of feet.

The radius of the hemispherical biodome is 1.37 thousands of feet.

HMH Algebra 2 Volume 1 1st Edition Module 5 Chapter 5 Exercise 5.1 Polynomial Functions Page 244 Exercise 25, Answer

It is given that the graph of the function f(x)=x³ is been stretched.

It is asked to explain that how horizontally stretching the graph of the function by a factor b can be equivalent to vertically compressing the graph of the same function by a factor a.

Since, a horizontal stretching by a factor can be accomplished by the graph of,​

​f(x)=(1/bx)³

f(x)=1/b³x³

​Thus, horizontal stretching by a factor of b is equivalent to the vertical compression by a factor of b^3.

Page 248 Exercise 26 Answer

It is given that Julio wants to purchase a spherical aquarium and fill it with salt water, which has an average density of 1027g/cm³

Also, he has found a company that sells four sizes of spherical aquariums whose size and diameter is represented by the table

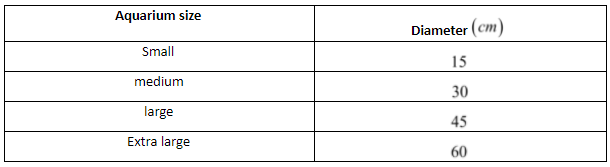
It is required to find that if the stand for Julio’s aquarium will support a maximum of 50kg , what is the largest size tank that he should buy

To find the required answer find the volume with the density of 1027g/cm³ and mass of 50kg by the equation d=m/v

Then, equate the obtained volume with 43πr³and find the radius Double the radius to get the diameter then choose the appropriate size according as the obtain diameter

The density of the salt water is 1.027g/cm³

The aquarium will support a maximum of 50kg or

50×1000=50000g

The formula of volume in terms of density is v=m/d

v=500001027=48685

Thus, the volume is 486855cm³

Equate the obtained volume with the formula of volume of a sphere4

3πr³ to find the radius

4/3πr³

=486855

Multiply both side with 3/4

​πr³

=486855×3/4

​​​​​​​​=36514125
​
Since π=22/7

so multiply both side with722

227×722×r³

=36514125×722r3

=1161813r³
=(2264)³

​Thus, the value of ris 2264

Find the diameter

Multiply the radius obtained by 2
​
​Diameter=2254×2

=4528 cm

≈45 cm

Now, on comparing the obtained diameter with the given diameter according as the size of aquarium, the largest size tank is the large size of 45 cm diameter that should be buy​

The largest size tank that he should buy should have 45 cm diameter

Page 248 Exercise 27, Answer

It is given that Julio wants to purchase a spherical aquarium and fill it with salt water, which has an average density of 1027g/cm³
​
Also, he has found a company that sells four sizes of spherical aquariums whose size and diameter is represented by the table is inferred from part (a) that he should buy is the large size of 45 cm diameter if the stand for Julio’s aquarium will support a maximum of 50kg with the density of 1027g/cm³

It is required to find whether the suggestion of friend is correct or not Julio’s friend suggests that he can buy a larger tank if he uses fresh water, which has a density of 10 g/cm³

It To find the required answer find the volume with the density of 10 g/cm³ and mass of 50kg by the equation d=mv

Then equal the obtain volume with 4/3πr³and find the radius Twice the obtain radius to get the diameter then choose the appropriate size according as the obtain diameter

Then compare the obtain diameter for both the density 1027g/cm3 and 10 g/cm3to fin the suggestion of Julio’s friend is logical or not

The density of the water is 10 g/cm³

Aquarium will support a maximum of 50kg or50×1000=50000 g

The formula of volume in terms of density is v=md

Substitute m as 50000 g and d as 10 g/cm³
​
v=5000010=50000 cm³

Thus, the volume is 50000 cm³

Equate the obtained volume with the formula of volume of a sphere 43πr3to find the radius

43πr³=50000

Multiply both side with 3/4 and substitute π=22/7​πr³

=50000×3/4

=37500

​Multiply both sides by 7/22​

227×7

22×r³

=37500×7

22r³=1193181r=(2285)³

Find the diameter

Multiply the radius obtained by 2​

​Diameter=2285×2

=457 cm

The diameter of the tank is 457 cm when fresh water is used

Observe that the diameter of the largest tank Julio could buy is 45 cm

Thus, when freshwater has used the diameter of the Tank is slightly greater Therefore, the suggestion of the friend is correct

The suggestion made by the friend that Julio could buy a larger tank if he uses freshwater of density 10 g/cm3is correct because the diameter of the tank when freshwater is used is 457 whereas the tank he bought earlier was of 45 cm diameter

Algebra 2 Volume 1 1st Edition Unit 2 Quadratic Functions, Equations, And Relations Page 110 Problem 1 Answer

A figure containing five sections is given, where the middle section includes the graph of a quadratic function, and the remaining four sections contain some information.

Also, a few ✓ words are given in the question.

The question requires to complete the graphic by placing one suitable ✓ word in each of the four sections of the frame surrounding the graph.

To complete the graphic, observe the expressions and words written in each of the surrounding four sections, use the given graph of a quadratic function, and the formulas for discriminant and quadratic formula to choose a suitable word to be placed in each of the four sections.

Then, write the suitable words in the sections and thus, complete the graphic.

The top section of the frame includes the expression √0²−4(1)(−1).

This expression is in the form √b²−4ac, that is the root of the discriminant.

Thus, the suitable word to be written in the top section of the frame is ‘discriminant’.

The bottom section of the frame includes the expression −0±√0²−4(1)(−1)/2(1).

This expression is in the form −b±√b²−4ac/2a, that is the right-hand side of the quadratic formula x=−b±√b²/−4ac/2a.

Thus, the suitable word to be written in the bottom section of the frame is ‘quadratic formula’.

The left section of the frame includes the point (0,−1).

From the graph, it can be observed that the point (0,−1)is the vertex of the graph of the function.

Thus, the suitable word to be written in the left section of the frame is ‘vertex’.

The right section of the frame includes the term y-axis.

From the graph, it can be observed that the graph of the function is symmetrical about the y-axis.

Thus, the suitable word to be written in the right section of the frame is ‘axis of symmetry’.

Write the suitable words in the respective sections in the given frame to complete the graphic.

The required completed graphic is:

HMH Algebra 2 Volume 1 Unit 2 Quadratic Functions Overview

HMH Algebra 2 Volume 1 1st Edition Unit 2 Quadratic Functions, Equations, And Relations Page 110 Problem 2 Answer

A parabola is a curve where every point lying on the parabola is equidistant from a fixed line and a fixed point.

The fixed line and the fixed point are respectively called the directrix of the parabola, and the focus of the parabola.

Therefore, every point on a parabola is equidistant from a fixed line, called the directrix, and a fixed point, called the focus.

Every point on a parabola is equidistant from a fixed line, called the directrix, and a fixed point, called the focus.

HMH Algebra 2 Unit 2 Quadratic Equations Solutions

HMH Algebra 2 Volume 1 1st Edition Unit 2 Quadratic Functions, Equations, And Relations Page 110 Problem 3 Answer

A number which is not real is called a complex number.Every complex number is in the form a+bi, where i=√−1.

Here, a and bare called the real and imaginary part of the complex number.

Therefore, a complex number is any number that can be written as a+bi, where a and b are real numbers and i=√−1.

A complex number is any number that can be written as a+bi, where a and bare real numbers and i=√−1.

HMH Algebra 2 Unit 2 Quadratic Functions And Relations Key

HMH Algebra 2 Volume 1 1st Edition Unit 2 Quadratic Functions, Equations, And Relations Page 110 Problem 4 Answer

A matrix is a set of numbers that are arranged in rows and columns.

The arrangement of the numbers in the rows and columns forms a rectangle.

This rectangle formed by the arrangement is a rectangular array.

Therefore, a matrix is a rectangular array of numbers.

The vocabulary term required to complete the statement is ‘matrix’ because a matrix is a rectangular array of numbers.

So the final answer is: A matrix is a rectangular array of numbers.

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations

Page 203 Problem 1 Answer

It is given three equations having three variables.

It is required to show that how to find the solutions to the given equation.

To find the solution of the equation find the value of one of the variables in form of the other two.

Then substitute it on the other two-equation to get the equation in two variables. After that use linear algebra to solve the equation in two variables.

Substitute the obtained values in the previous equation to get the value of substituted variables.

The value of all variables is obtained.

Page 203 Problem 2 Answer

Three figures are given in the question.

It is required to determine how many points lie on all three given planes.

For figure one all the plans are parallel to each other hence there is no such points which is common between three planes.

For figure two here two planes are parallel which and one plan intersect other at different line hence plane hence no such points are there.

For figure three plans are not parallel but all each plan intersects at different lines, hence no such point exists in this case.

None of the given has set of points which lies in all the three plans.

HMH Algebra 2 Volume 1 Module 4 Chapter 4 Exercise 4.4 Solutions

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 203 Problem 3 Answer

A figure is given in the question.

It is required to determine how many points lie on all three given planes.

All the plans are perpendicular to each other and intersect at only one point. Hence there is only one point common in all three plans.

There is only one point common in all three plans.

Page 203 Problem 4 Answer

A figure is given in the question.

It is required to determine how many points lie on all three given planes.

In the given figure arrange in such a manner that they intersect at a common line,

Hence all the points which satisfy the equation of line of intersection will lies in all three planes.

Three plans intersect along a common line of intersection.

All the points which satisfy the line of interaction will be lies on all the three planes.

Page 204 Problem 5 Answer

It is given that the vertical parabola equation is given by y=ax²+bx+c.

It is required to find the parabola that passes through the points (2,1),(−1,4) and (−2,3).

Substitute the coordinates of point into the general equation y=ax²+bx+c to get three equations. Solve the equations for three variables x,y and z.

Put the obtained values back in the general equation to get the required parabola equation.

Substitute (2,1),(−1,4) and (−2,3) in the equation y=ax²+bx+c to obtain three equations.

1=a(2)²+b(2)+c

4=a(−1)²+b(−1)+c

3=a(−2)²+b(−2)+c

Simplify the equations.

1=4a+2b+c

4=a−b+c

3=4a−2b+c​

From third equation, c=4−a+b. Put the obtained value in other equations.

3a+3b=−3

3a−b=−1​

Solve the two equations by substituting b=3a+1 in 3a+3b=−3.​

3a+3(3a+1)=−3

3a+9a+3=−3

12a=−6

a=−1/2

So, the value of b is −3/2+1=−1/2.

The value of c is,​

c=4−(−1/2)+(−1/2)

=4+1/2−1/2

=4​

Therefore, the equation of parabola is,

y=(−1/2)x²+(−1/2)x+4−2y=x²+x−8

x²+x+2y−8=0​

The equation of the vertical parabola passing through the points (2,1),(−1,4) and (−2,3)

is x²+x+2y−8=0.

Page 204 Problem 6 Answer

t is required to give an example of three planes that intersect at exactly one point.

One such combination of the plane is xy−plane,yz−plane and zx−plane which intersect at only one point that is (0,0,0).

So, xy−plane,yz−plane and zx−plane which intersect at only one point that is (0,0,0).

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 206 Problem 6 Answer

It is given three equations, x+2y+z=8 ……eq(1)

2x+y−z=4 ……eq(2)

x+y+3z=7 ……eq(3)

It is required to find the value of x,y and z for the given equations.

To solve this, substitute the value of y from eq (2) on eq(1) and eq(3) to get the equations in two variables.

Then solve the equations of two variables by using linear algebra.

After that, find the value y with the help of x and z obtained previously.

It is given three equations,

x+2y+z=8 ……eq(1)

2x+y−z=4 ……eq(2)

x+y+3z=7 ……eq(3)

From eq(2),

2x+y−z=4

y=4−2x+z

Substituting the value of y on eq(1) equation become,

x+2y+z=8

x+2(4−2x+z)+z=8

x+8−4x+2z+z=8

−3x+3z=0

−x+z=0

Therefore, x=z ……eq (4)

Substituting the value of y on eq (3) equation become,​

x+y+3z=7

x+(4−2x+z)+3z=7

−x+4z=3

From, eq(4)

−z+4z=3

3z=3

z=1​

So, x=1

Now substituting the value of x and z on the equation of y,​

y=4−2x+z

y=4−2+1

y=3

So, the values are

x=1

y=3

z=1​

Therefore, the value of x,y and z for the given equations are,​

x=1

y=3

z=1​

Page 206 Problem 7 Answer

It is given three equations, 2x−y−3z=1 ……eq(1)

4x+3y+2z=−4 ……eq(2)

−3x+2y+5z=−3 ……eq(3)

It is required to find the value of x,y and z

for the given equations.

To solve this, substitute the value of y from eq(1) on eq(2) and eq(3) to get the equations in two variables.

Then, solve the equations of two variables by using linear algebra.

After that, find the value y with the help of x and z obtained previously.

It is given three equations,

2x−y−3z=1 ……eq(1)

4x+3y+2z=−4 ……eq(2)

−3x+2y+5z=−3 ……eq(3)

From eq(1),​

2x−y−3z=1

y=2x−3z−1

Substituting the value of y on eq(2) equation become,​

4x+3y+2z=−4

4x+3(2x−3z−1)+2z=−4

4x+6x−9z−3+2z=−4

10x−7z=−4

Thus, 7z−10x=4 ……eq(4)

Substituting the value of y on eq(3) equation become,​

−3x+2y+5z=−3

−3x+2(2x−3z−1)+5z=−3

x−z=−1

Thus, x−z=1 ……eq(5)

Adding ten times eq (5) to eq (4)

−3z=14

z=−14/3

From, eq(5)​

x=1+z

x=1−14/3

x=−11/3

Now, for y

y=2x−3z−1

y=2⋅(−11/3)−3⋅(−14/3)−1​

Simplify it to get the result,​

y=−22/3+42/3−1

y=−22+42−3/3

y=17/3

The values of x,y, and z for the given equations are,​

x=−11/3

y=17/3

z=−14/3​

Page 207 Problem 8 Answer

It is given that the system of equations is

{  x+2y+3z ​=9   ​(1)

{   x+3y+2z =5        (2)

{    x+4y−z =−5       (3).

It is required to solve the system for three variables x,y, and z.

Subtract the second equation from the first equation to eliminate x.

Now subtract the third equation from the first equation to eliminate x.

Solve these two equations for y and z.

Now find the value of x by putting the values of y and z.

Start by subtracting equation 2 from equation 1 to eliminate x​

x+3y+2z−(x+2y+3z)=5−9

3y+2z−2y−3z=−4

y−z=−4

Subtract equation 3 from 1 to eliminate x.​

x+4y−z−(x+2y+3z)=−5−9

4y−z−2y−3z=−14

y−2z=−7​

This results in a system of two linear equations.​

y−z=−4

y−2z=−7

Solve the two equations for y and z.​

y−z−y+2z=−4+7

z=3​

Find the value of y.

y=z−4

=3−4

=−1

Find the value of x.​

x+2(−1)+3(3)=9

x−2+9=9

x=2​

The solution of the system

{   x+2y+3z=9 ​(1)

{   x+3y+2z =5     (2)

{    x+4y−z =−5    (3)

is the ordered triple (2,−1,3).

HMH Algebra 2 Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And Systems Of Equations Answers

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 209 Problem 9 Answer

It is given three equations,​

x+2y+z=8…..eq(1)

2x+y−z=4…..eq(2)

x+y+3z=7…..eq(3)

It is required to solve the equation by the elimination method.

To solve this, add eq(1) with eq(2) then a relation between x and y are obtained. Then substitute the obtained value on eq(3) to get the value of z.

Given equations are,​

x+2y+z=8…..eq(1)

2x+y−z=4…..eq(2)

x+y+3z=7…..eq(3)​

Add eq(1) with eq(2).​

3x+3y=12

3(x+y)=12

x+y=4…..eq(5)​

Now, substituting the obtained value in eq(3)

x+y+3z=7

4+3z=7

3z=3

Divide both sides by 3.

z=1

Substituting the value of z on eq(1)

x+2y+1=8

x+2y=7…..eq(6)​

Subtracting eq(5) with eq(6)

y=3

Substituting the value of y on eq(5)

x+y=4

x+3=4

Subtract 3 from both sides.​

x+3−3=4−3

x=1

Values of the variable after elimination method are,  ​

x=1

y=3

z=1​

Page 209 Problem 10 Answer

It is given three equations,​

2x−y−3z=1…..eq(1)

4x+3y+2z=−4…..eq(2)

−3x+2y+5z=−3…..eq(3)​

It is required to solve the equation by the elimination method.

To solve this, add three times eq(1) with eq(2) then a relation between x and z are obtained.

Again, add two times eq(1) with eq(3) then another relation between x and z are obtained. Now solve the obtained equation to get the value of x and z.

Then substitute the obtained values on eq(3) to get the value of y.

Given equations are,

2x−y−3z=1…..eq(1)

4x+3y+2z=−4…..eq(2)

−3x+2y+5z=−3…..eq(3)

Adding three times eq(1) with eq(2)

10x−7z=−1…..eq(4)

Adding two times eq(1) with eq(3)

x−z=−1…..eq(5)

For, solving subtract 7 times eq(5) from eq(4)​

3x=6

x=2

Substituting the value of x on eq(5)​

x−z=−1

2−z=−1

z=3

Substituting the obtained values on eq(3) to get the value of y,

−3x+2y+5z=−3

−6+2y+15=−3

2y=−12

y=−6​

Values are,​

x=2

y=−6

z=3​

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 209 Problem 11 Answer

It is given that the system of equations is

{​     x+2y+3z=9

{     x+3y+2z=5

{     x+4y−z=−5.

It is required to solve the system with the matrix method.

Write the system of equations as a matrix. Perform row operations on the matrix till it gets converted into an identity matrix. Find the corresponding triples to the identity matrix.

The system \(\{\begin{array}{c}x+2 y+3 z=9 \\ x+3 y+2 z=5 \\ x+4 y-z=-5\end{array}\) can be written as a matrix as,

Apply \(R 2 \rightarrow-R 1+R 2\) on the matrix.

Apply \(R 3 \rightarrow-R 1+R 3\) on the matrix.

Apply \(R 3 \rightarrow-2 R 2+R 3\) on the matrix.

Apply \(R 3 \rightarrow 0.5 R 3\) on the matrix.

Apply \(R 2 \rightarrow R 3+R 2\) on the matrix.

Apply \(R 1 \rightarrow-3 R 3+R 1\) on the matrix.

Apply \(R 1 \rightarrow-2 R 2+R 1\) on the matrix.

The solution of the system

{   x+2y+3z=9

{   x+3y+2z=5

{   x+4y−z=−5   is the ordered triple (2,−1,3).

Page 212 Problem 12 Answer

It is given three equations,

x+2y+z=8 ……eq(1)

2x+y−z=4 ……eq(2)

x+y+3z=7 ……eq(3)

It is required to find the value of x,y and z for the given equations.

To solve this use gaussian elimination method then use row elimination method, after that simplify to get the solution.

It is given three equations,

x+2y+z=8 ……eq(1)

2x+y−z=4 ……eq(2)

x+y+3z=7 ……eq(3)

Then use gaussian elimination use to convert linear equation into matrix form

Now use certain operation, first \(R 2 \rightarrow R 2-2 R 1\)

Then \(R 3 \rightarrow R 3-R 1\)

Then \(R 3 \rightarrow R 3-\frac{1}{3} R 2\)

Again \(R 1 \rightarrow R 1+\frac{2}{3} R 2\)

Now, \(R 1 \rightarrow R +R 3\); \(R 2 \rightarrow R 2-3 R 3\)

Then, \(\left[\begin{array}{cccc}
1 & 0 & 0 & 3 \\
0 & -3 & 0 & -12 \\
0 & 0 & -1 & 3
\end{array}\right]\)

Then divide \(R 1 \rightarrow \frac{-1}{3} R 1\) and \(R 1 \rightarrow(-1) R 1\)

Hence the solution will be,

x=3

y=4

z=-3

The solution of the system of equations will be,​

x=3

y=4

z=−3​

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 213 Problem 13 Answer

It is given that the number of shirts is equal to the number of ties and four times the number of pairs of pants. The cost of shirts is 35, ties are 25, pants are 40 and the total cost is 560.

It is required to tell the number of shirts, pants, and ties.

Form a system of equations from the given data. Solve the equations to get the values of shirts, pants, and ties.

Let the number of shirts, ties, and pants be s,t, and p respectively.

The system of equations from the given data is,

s=t                ​(1)

s=4p             (2)

35s+25t+40p=560         (3)

Substitute s/ 4 for p and s for t in equation (3).​

35s+25(s)+40(1/4s)=560

35s+25s+10s=560

70s=560

s=8​

Find the value of t.​

t=s

=8

Find the value of p.​

p=s/4

=8/4

=2​

The student bought 8 shirts, 8 ties and 2 pairs of pants.

Page 215 Problem 14 Answer

It is required to tell why a system has to have at least as many equations as unknown variables to have a unique solution.

A system must have at least as many numbers of equations as the number of variables.

For instance, if one tries to solve the system of three variables but only two equations are given, then the value of only two variables can be obtained and that too in the terms of the third variable.

This doesn’t solve the system and the system remains unsolved.

That’s why a minimum of three equations are required to solve a system of three variables.

Thus, a system needs to have at least as many equations as unknowns.

It is necessary for a system to have at least as many equations as variables as only then the equations can be solved to find the unknown values.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 215 Problem 15 Answer

It is required to find how a system of three linear equations can be solved.

Find the value of one variable from the first equation in the terms of other two variables.

Substitute the obtained value into the other two equations.

Now solve those obtained equation for these two variables.

Then put the values of these two variables in the value of third variable to get its value.

Put all three variable values in any of the equations to verify the answer.

A system of three linear equations can be solved by the method of substitution.

Page 216 Problem 16 Answer

It is given that the system is

{​4x+y−2z=−6          ​(1)

{    2x−3y+3z=9       (2)

{   x−2y=0                (3).

It is required to solve the system by substitution.

Find the value of x from x−2y=0. Substitute the value in other two equations. Solve for y and z.

Find x from its obtained value.

The value of x is 2y.

Substitute 2y for x in 4x+y−2z=−6 and 2x−3y+3z=9.

4(2y)+y−2z=−6

8y+y−2z=−6

9y−2z=−6

2(2y)−3y+3z=9

y+3z=9

Solve the equations.​

9y−2z=−6

y+3z=9

Put z=9−y/3 in  9y−2z=−6.

9y−2(9−y/3)=−6

27y−18+2y=−18

29y=0

y=0

So, the value of x is also 0 as x=2y.

The value of z is,

y+3z=9

3z=9

z=3

The solution of the system

{​4x+y−2z=−6           (1)

{    2x−3y+3z=9         (2)

{     x−2y=0                (3)  is, (0,0,3).

Page 216 Problem 17 Answer

Three linear equations in three variables are given.​

4x+y−2z=−6 (1)

2x−3y+3z=9 (2)

x−2y=0 (3)

It is required to find the solution to the given system by elimination.

To find the solution to the given system by elimination, select any two equations and eliminate anyone of the variable by multiplying and addition certain factors.

Then, eliminate one more variable with the resultant equation and the third equation.

Thus, find the value of the remaining variable.

Then, by substitution find the values of other two variables.

Eliminate the variable z.

Multiply equation (1) by 3 and multiply equation (2) by 2.​

12x+3y−6z=−18 (4)

4x−6y+6z=18 (5)​

Add equation (1) and equation (2).​

12x+3y−6z=−18

4x−6y+6z=18

16x−3y+0=0  (6)

Find the value of y.

Multiply equation (3) by 16 and subtract it from equation (6).​

16x−32y=0

(−)16x−3y=0

0−29y=0

y=0

Therefore, x=0.

Use the value of x and y to find z.

Substitute zero for x,y in the equation 4x+y−2z=−6.​

4(0)+(0)−2z=−6

z=3​

The solution to the given system of equations is (0,0,3).HMH Algebra 2 Chapter 4 Exercise 4.4 Quadratic Equations Key

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 217 Problem 18 Answer

Three linear equations in three variables are given.​

x+5y+3z=4 (1)

4y−z=3 (2)

6x−2y+4z=0 (3)

It is required to find the solution to the given system by elimination.

To find the solution to the given system by elimination, select any two equations and eliminate anyone of the variable by multiplying and addition certain factors.

Then, eliminate one more variable with the resultant equation and the third equation.

Thus, find the value of  the remaining variable. Then, by substitution find the values of other two variables.

Make an equation in terms of y and z.

Multiply equation (1) by −6 and add it to equation (3).​

−6x−30y−18z=−24

6x−2y+4z=0

0−32y−14z=−24

16y+7z=12 (4)​

Find the value of z.Multiply equation (2) by −4 and add it to equation (4).​

−16y+4z=−12

16y+7z=12

11z=0

z=0​

Find the value of y.

Substitute zero for z in the equation 4y−z=3.

​4y−0=3

y=3/4​

Find the value of x.

Substitute zero for z, 3/4 for y in the equation x+5y+3z=4.​

x+5(3/4)+3(0)=4

x=4−15/4

x=1/4​

The solution to the given system of equations is (1/4,3/4,0).

Page 28 Problem 19 Answer

Three linear equations in three variables are given.​

x+5y+3z=4 (1)

4y−z=3 (2)

6x−2y+4z=0 (3)

It is required to find the solution to the given system by elimination.

To find the solution to the given system by matrices, write down the corresponding augmented matrix for the given system.

Then, try to get an identity matrix by performing certain row transformations.

The augmented matrix for the given system is \(\left[\begin{array}{ccc|c}1 & 5 & 3 & 4 \\ 0 & 4 & -1 & 3 \\ 6 & -2 & 4 & 0\end{array}\right]\).

Add \(-6 R_1\) to \(R_3\).

Add \(8 R_2\) to \(R_3\) and then divide the row by -22.

Add \(R_3\) to \(R_2\) and then divide the row by 4.

Add \(-5 R_2\) to \(R_1\).

Add \(-3 R_3\) to \(R_1\).

This means that,

The solution to the given system of equations is (1/4,3/4,0).

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 219 Problem 20 Answer

Three linear equations in three variables are given.

2x−y+3z=5 (1)

−6x+3y−9z=−15 (2)

4x−2y+6z=10 (3)

It is required to find the solution to the given system by elimination.

To find the solution to the given system by matrices, write down the corresponding augmented matrix for the given system.

Then, try to get an identity matrix by performing certain row transformations.

The augmented matrix for the given system is \(\left[\begin{array}{ccc|c}2 & -1 & 3 & 5 \\ -6 & 3 & -9 & -15 \\ 4 & -2 & 6 & 10\end{array}\right]\).

Divide \(R_2\) by 3 and \(R_3\) by 2 .

Since all given three equations are same, the solution to the given system cannot be determined.

Hence, the given system is inconsistent.

The given system of equation is inconsistent and there is no solution to the system.

Page 219 Problem 21 Answer

It is given that the vertical parabola equation is given by y=ax²+bx+c.

It is required to find the parabola that passes through the points (3,7),(30,−11) and (0,−1).

Substitute the coordinates of point into the general equation y=ax²+bx+c to get three equations.

Solve the equations for three variables x,y and z.

Put the obtained values back in the general equation to get the required parabola equation.

Substitute (3,7),(30,−11) and (0,−1) in the equation y=ax²+bx+c to obtain three equations.

7=a(3)²+b(3)+c

−11=a(30)²+b(30)+c

−1=a(0)²+b(0)+c

Simplify the equations.​

7=9a+3b+c

−11=900a+30b+c

−1=c​

Substitute −1 for c in the other two equations.​

9a+3b−1=7

900a+30b−1=−11

On simplifying the equations,​

9a+3b=8

90a+3b=−1​

Solve the two equations by substituting 8−9a for 3b in 90a+3b=−1.​

90a+8−9a=−1

81a=−9

a=−9

Therefore, ​b=8−9(−9)/3

b=89/3 Therefore, the equation of parabola is,​

y=(−9)x²+(89/2)x−1−2y=19x²−89x+2

19x²−89x+2y+2=0​

The equation of the vertical parabola passing through the points (3,7),(30,−11) and (0,−1) is 19x²−89x+2y+2=0.

Page 220 Problem 22 Answer

It is given that in triangle XYZ, the measure of angle X is equal to eight times the sum of the measures of other two angles and the measure of angle Y is equal to three times the measure of angle Z.

It is required to find the measures of all the angles.

The given problem involves, three linear equations in three variables.

Form three different equations by using the given data and the fact that the sum of all three angles of a triangle is 180

degrees. Then, solve the system by substitution method.

Let the measures of the three angles of the triangle be (x,y,z).

Here, x+y+z=180.

Substitute 3z for y,8(y+z) for x in the equation x+y+z=180. Simplify the equation and solve for z.​

8(y+z)+3z+z=180

8(3z+z)+3z+z=180

32z+3z+z=180

z=180/36

z=5​

Substitute five for z in the equation y=3z.​

y=3(5)

y=15​

Substitute 5 for z,15 for y in the equation x=8(y+z).

x=8(15+5)

x=8(20)

x=160

​The measure of angle X is 160∘.

The measure of angle Y is 15∘.

The measure of angle Z is 5∘.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 220 Problem 23 Answer

It is given that the sum of the ages of James, Dan, Paul is 120 years.

James is three times the age of Dan and Paul is two times the sum of the ages of James and Dan.

It is required to find the ages of the three persons.

The given problem involves three linear equations in three variables. Form three different equations by using the given data.

Then, solve the system by substitution method.

Let the age of James be x.

Let the age of Dan be y.

Let the age of Paul be z.

Here, x+y+z=120.​

x=3y

z=2(x+y)​

Substitute 3y for x,2(x+y) for z in the equation x+y+z=120. Simplify the equation and solve for y.

3y+y+2(x+y)=120

4y+(3y+y)=120

8y=120

y=120/8

y=15​

Substitute 15 for y in the equation x=3y.​

x=3(15)

x=45​

Substitute 15 for y,45 for x in the equation z=2(x+y).​

z=2(45+15)

z=2(60)

z=120​

The age of James is 45 years.

The age of Dan is 15 years.

The age of Paul is 120 years.

Page 220 Problem 24 Answer

It is given that the total number of shares are 10000 where stock A is four times stock B

and stock C is equal to the sum of A and B.

It is required to find the value of each stock.

Make three equations for the three variables A,B and C

from the given data. Find the value of any two variables in terms of the remaining one variable.

Substitute the values in any equation to get the value of that remaining variable. Now use this value to get the values of the other two variables.

Make three equations for the given data.

A+B+C=10000

A=4B

C=5B

Substitute 4B for A and 5B for C in the equation A+B+C=10000.

4B+B+5B=10000 Solve the equation for B.​

10B=10000

B=1000

Find A and C by putting B=1000.​

A=4(1000)=4000

C=5(1000)=5000​

The shares of each stock A,B and C are 4000,1000 and 5000 respectively.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 221 Problem 25 Answer

It is required to find when a system has an infinite number of solutions and when it has zero solutions.

A system has an infinite number of solutions when its equations are parallel to each other or when their graphs are the same.

A system has no solutions when its equations do not intersect at a point.

The system has an infinite number of solutions when its equations are equal algebraically and graphically.

The system has zero solutions when its equations do not have an intersection point.

Page 221 Problem 26 Answer

It is given that the student tried to solve the system \(\left\{\begin{array}{l}5 x+7 y+9 x=0 \\ x-y+z=-3 \\ 8 x+y=12\end{array}\right.\) and wrote the determinant as \(\left[\begin{array}{lll}5 & 7 & 9 \\ 1 & -1 & 1 \\ 8 & 1 & 0\end{array}\right]\)

It is required to find and then correct the error done by the student.

The first equation of the system 5x+7y+9 x=0 can be further simplified as,

(5 x+9 x)+7 y=0

14 x+7 y=0

2 x+y=0

The student misread 9x as 9z and wrote the determinant as \(\left[\begin{array}{ccc}5 & 7 & 9 \\ 1 & -1 & 1 \\ 8 & 1 & 0\end{array}\right]\) which is incorrect.

However, the correct determinant should be \(\left[\begin{array}{ccc}2 & 1 & 0 \\ 1 & -1 & 1 \\ 8 & 1 & 0\end{array}\right]\) as the coefficient of z in the first equation is 0 .

So, the correct determinant is \(\left[\begin{array}{ccc}2 & 1 & 0 \\ 1 & -1 & 1 \\ 8 & 1 & 0\end{array}\right]\).

The student committed an error as he took \(9 \mathrm{x}\) as \(9 \mathrm{z}\) and the correct determinant is \(\left[\begin{array}{ccc}
2 & 1 & 0 \\
1 & -1 & 1 \\
8 & 1 & 0
\end{array}\right]\)

Page 221 Problem 27 Answer

It is given that the system of equations is

{​7x+y+6z=1

{   −x−4y+8z=9.

It is required to find why the given system of equations cannot be solved.

The given system consists of three variables x,y and z   .

To solve the values of three variables, at least three equations are required.

But the given system has only two equations.

Therefore, the given system cannot be solved.

The system of equations

{​    7x+y+6z=1

{   −x−4y+8z=9​

cannot be solved as its equations have three variables but it has only two equations.

HMH Algebra 2 Exercise 4.4 Systems Of Equations Answer Guide

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 222 Exercise 1 Answer

It is given that the part B is four times that of C, the part A is one-fifth of B+C and the number of parts is 6000.

The previous and new costs are 0.25,0.50,0.75 and 0.60,0.40,0.60 for parts A,B and C respectively.

It is required to find if the company would be able to buy the same quantity of parts at the price of 3000 or not.

Find the value of A,B and C from the given data. Find the cost for the values 0.60,0.40,0.60 by substituting for A,B and C. Check if it is equal to 3000 or not.

Make three equations for the given data.​

0.25A+0.50B+0.75C=3000

B=4C

A=1/5(B+C)​

Solve for the value of C.

Substitute 4C for B and 1/5(B+C) for A in the equation 0.25A+0.50B+0.75C=3000.

0.25(1/5(B+C))+0.50(4C)+0.75C=3000

0.25(1/5(4C+C))+0.50(4C)+0.75C=3000

3C=3000

C=1000​

Find the value of B and A.

Substitute 1000 for C in B=4C to find B.​

B=4(1000)

=4000

Substitute 4C for B and 1000 for C in A=1/5(B+C) to find B.

A=1/5(4C+C)

=1/5(5C)

=C

=1000​

Find the new cost for the parts.

0.60A+0.40B+0.60C=0.60(1000)+0.40(4000)+0.60(1000)

=600+1600+600

=2800

The new price is $200 less than the previous cost of $3000.

The company will not be able to buy the same quantity of parts at the previous price as the new price is less than the previous price of $3000.

Page 223 Exercise 2 Answer

It is required to find how the systems of equations can be used to solve real-world problems.

Take the important data from the problem that may help in writing some equations.

Define variables for the unknown quantities.

Write the equations by using the defined variables.

Use substitution or graphing to solve the system of equations.

Verify the evaluated values of variables by putting the ordered pair in the original equations.

Now answer the questions according to the real-world problems.

A real world problem can be solved easily by taking some variables, making equations from the data and then solving them to get the answer.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 224 Exercise 3 Answer

It is given that the center of the circle is at (−7.5,15) and its radius is 1.5.

It is required to find the equation of a circle.

Substitute (−7.5,15) for (h,k) and 1.5 for r in the general equation (x−h)²+(y−k)²=r² and simplify it to get the equation for the given circle.

Put (−7.5,15) for (h,k) and 1.5 for r in (x−h)²+(y−k)²=r².​

(x−(−7.5))²+(y−15)²=(1.5)²

(x+7.5)²+(y−15)²=(1.5)²

Simplify the expression.​

(x+7.5)²+(y−15)²=(1.5)²

x²+56.25+15x+y²+225−30y=2.25

x²+y²+15x−30y+279=0​

The equation of the circle with center at (−7.5,15) and radius 1.5 is x²+y²+15x−30y+279=0.

Page 224 Exercise 4 Answer

It is given that the equation of the circle is (x−5)²+(y−8)²=144.

It is required to find the center and the radius of the circle.

Compare the given equation of circle with the general equation to get the coordinates of the center and length of its radius.

The centre of the circle is, (5,8).

The radius of the circle is given by,​

r²=144

r=√144

r=±12

Ignore the value −12 as the length of radius cannot be negative.

Hence, the length of the radius is 12.

The center and radius of the circle with the equation (x−5)²+(y−8)²=144 are (5,8) and 12 respectively.

Page 224 Exercise 5 Answer

It is given that the equation of the circle is x²+(y+6)²=50.

It is required to find the center and the radius of the circle.

Compare the given equation of circle with the general equation to get the coordinates of the center and length of its radius.

The centre of the circle is, (0,−6).

The radius of the circle is given by,

r²=50

r=√50

r=±5√2

Ignore the value −5√2 as the length of radius cannot be negative.

Hence, the length of the radius is 5√2.

The center and radius of the circle with the equation x²+(y+6)²=50 are (0,−6) and 5√2 respectively.

Page 224 Exercise 6 Answer

It is given that the system of equations is,

{​    x−3y=2

{   y=x²+2x−34.

It is required to find the solutions of the given system.

Plot the given system of equations. Check if the given curve and the line meet at any point or not.

Find the coordinates of such points. These intersection points are the solutions of the system.

Draw the graph of the system

{​   4x+3y=1

{    y=x2

{   −x−1 on an online geometry calculator.

The curve y=x²−x−1 and the line 4x+3y=1 meet at two points on the graph.

The intersection points of the system are (−6.7,−2.9) and (5,1).

The solution of the given system of equations

{​      4x+3y=1

{     y=x²−x−1    are (−6.7,−2.9) and (5,1).

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 224 Exercise 7 Answer

It is given that the system of equations is,

{​   3x+5y−2z=−7

{  −2x+7y+6z=−3

{   8x+3y−10z=−11.

It is required to find the solutions of the given system.

Find the value of z from any one of the equations. Substitute its value in the other two equations to get them in terms of x and y.

Solve for the two variables and find the value of z from these.

The value of z from the first equation is given by,​

3x+5y−2z=−7

2z=3x+5y+7

z=3x+5y+7/2​

Put this value of z in the equation −2x+7y+6z=−3.​

−2x+7y+6(3x+5y+7/2)=−3

−2x+7y+9x+15y+21=−3

7x+22y=−24

Put this value of z in the equation 8x+3y−10z=−11.​

8x+3y−10(3x+5y+7/2)=−11

8x+3y−15x−25y−35=−11

7x+22y=−24

As both the equations obtained are equal, the number of solutions is infinite.

There are infinite solutions of the given system of equations

​{    3x+5y−2z=−7

{    −2x+7y+6z=−3

{      8x+3y−10z=−11. 

Page 225 Exercise 8 Answer

It is given a circle with center C(0,−2) and radius r=1.

It is required to find the equation of a given circle.

To solve this, substitute the point of centre in place of (h,k) and value of radius in place of r in the standard equation of circle.

Given circle have center C(0,−2) and radius r=1.

Substitute the value of center C(0,−2) and radius r=1 on equation,

(x−h)²+(y−k)²=r²

(x−0)²+(y−(−2))²=12

x²+(y+2)²=1​

So, the equation of circle is,x²+(y+2)²=1

The equation of the circle is,x²+(y+2)²=1

Page 225 Exercise 9 Answer

It is given equation of a circle,x²+y²=25

It is required to find the center and radius of the given circle.

To solve this, compare the given equation to the standard equation to get center and radius.

Given equation of circle is,x²+y²=25

Now, standard equation of circle having centre C(h,k) and radius r is (x−h)²+(y−k)²=r².

Then by comparing, center is C(0,0) and radius is r=5.

For the given circle center is C(0,0) and radius is r=5.

Page 225 Exercise 10 Answer

It is given equation of a circle,(x−18)²+(y+18)²=70

It is required to find the center and radius of the given circle.

To solve this, compare the given equation to the standard equation to get center and radius.

Given equation of circle is,(x−18)²+(y+18)²=70

Now, standard equation of circle having centre C(h,k) and radius r is (x−h)²+(y−k)²=r².

Then by comparing, center is C(18,−18) and radius is r=√70.

For the given circle center is C(18,−18) and radius is r=√70. 

Page 225 Exercise 11 Answer

It is given two equations

y+12=4x

y−20=x²−8x

It is required to find the value of x and y for given equations.

To solve this put the value of y from first equation in second equation.

Then solve the obtained equations by using basic calculations to get the value of x and y.

It is given two equations

y+12=4x…..eq(1)

y−20=x²−8x…..eq(2)

Substituting the value of y from eq(1) on eq(2),​

y−20=x²−8x

4x−12−20=x²−8x

4x−32=x²−8x

So, the equation becomes x²−12x+32=0

Solving the equation,

x²−12x+32=0

x²−8x−4x+32=0

x(x−8)−4(x−8)=0

(x−4)(x−8)=0

So, values of x=4,8

For these values of x the values of y=4,20 respectively.

Solution of the given equations are (4,4) and (8,20).

Page 225 Exercise 12 Answer

It is given two equations​

y=x+2

2y−12=2x²−8x

It is required to find the value of x and y for given equations.

To solve this put the value of y from first equation in second equation.

Then solve the obtained equations by using basic calculations to get the value of x and y.

It is given two equations​

y=x+2…..eq(1)

2y−12=2x²−8x…..eq(2)

Substituting the value of y from eq(1) on eq(2),

2y−12=2x²−8x

2(x+2)−12=2x²−8x

2x+4−12=2x²−8x

2x−8=2x²−8x

So, the equation becomes​

2x²−10x+8=0

x²−5x+4=0

Solving the equation,

​x²−5x+4=0

x²−x−4x+4=0

x(x−1)−4(x−1)=0

(x−4)(x−1)=0

So, values of x=4,1

For these values of x the values of y=6,3 respectively.

Solution of the given equations are (4,6) and (1,3).

Page 225 Exercise 13 Answer

It is given three equations, −3x−12y−3z=0 ……eq(1)

x+4y+z=10 ……eq(2)

−2x−8y−2z=−34 ……eq(3)

It is required to find the value of x,y and z for the given equations.

To solve this use a gaussian elimination method then use row elimination method, after that simplify to get the solution.

It is given three equations, −3x−12y−3z=0 ……eq(1)

x+4y+z=10 ……eq(2)

−2x−8y−2z=−34 ……eq(3)

Now use certain operations, first \(R 2 \rightarrow R 2+\frac{1}{3} R 1\);  \(R 3 \rightarrow R 3-\frac{2}{3} R 1\)

Here all the coefficient terms of R 2, R 3 is zero hence the system of equation has no solution.

Then use gaussian elimination use to convert linear equation into matrix form

The given system of equations has no solution.

Step-By-Step Solutions For HMH Algebra 2 Module 4 Exercise 4.4

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 225 Exercise 14 Answer

It is required to discuss real life world situation that might involve three linear equation variables.

To solve this let consider a student shopping for clothes. He needs to buy four times of shirts of pants.

And he also needs to buy five times as many shirts as ties.

Here shirts costs $80, tie cost $50 and cost of pant is $70 how many shirts and pants and tiles did he got if he will spend only a sum of $1000.

In this problem there are three variables that are number of pants number of ties and number of shirts.

And equation will be,  ​

4s=p

s=4t

80s+50t+70p=1000

This can be solved by the method of gaussian elimination method.

The real-life problem could be to solve this let consider a student shopping for clothes.

He needs to buy four times of shirts of pants. And he also needs to buy five times as many shirts as ties.

Here shirts costs $80, tie cost $50 and cost of pant is $700 how many shirts and pants and tiles did he got if he will spend only a sum of $1000. 

Page 226 Exercise 15 Answer

It is given the focus and the directrix for three cases.

It is required to determine whether the parabola is horizontal or not in each case.

This can be done by using the equation of directrix, if the directrix is vertical then the parabola must be horizontal.

For part A, the focus is located at (−5,0) and the equation of its directrix is x=5.

So, in this case the directrix is vertical. Thus, the parabola in this case is horizontal.

For part B, the focus is located at (4,0) and the equation of its directrix is x=−4.

So, in this case the directrix is vertical. Thus, the parabola in this case is horizontal.

For part C, the focus is located at (0,−3) and the equation of its directrix is y=3.

So, in this case the directrix is horizontal. Thus, the parabola in this case is vertical.

The parabola is horizontal for part A and B but the parabola in part C is not horizontal.

Page 226 Exercise 16 Answer

It is given a system of equations y=x²+6x+10 and y+6=2x.

It is required to determine whether the following statements are correct or not.

This can be done by rewriting the equation then try to solve this system graphically by making a graph of the equations.

For part A: Yes, it is possible to rearranged the given system of equations to write the linear equation in terms of x making y the subject of the formula.

Thus, the equation y+6=2x can also be written asy=2x−6.

For part B: No, the given system of equations can be solved by both graphically as well as algebraically, by substituting the value of y from the linear equation into the quadratic equation.

For part C: No, the given system of equations has no solutions as shown by its graphical solution below.

Statement in part A is correct while the statements in other two parts are wrong. This can be shown with the help of the diagram drawn below.

Page 226 Exercise 17 Answer

It is given a system of three equations.

It is required to explain how a system of three equations does in three variables can have infinitely many solutions.

An infinite number of solutions can result from several situations.

The three planes could be same, so that a solution will be the solution to the other two equations.

All three equations could be different, but they intersect on a line, which has infinite solutions.

A system of three equations in three variables have infinitely many solutions.

Page 226 Exercise 18 Answer

It is given that Robin solved a quadratic equation.

It is required to describe and correct her mistake.

This can be done by finding the mistake and then write the correct solution.

The mistake is in the third step where she has incorrectly written −4 on simplifying (−2)².

This should be equal to .4 Therefore, the correct solution is as follows:

x=−(−2)±√(−2)²−4(1/4)(7)/2(1/4)

x=2±√4−7/1/2

x=4±2√−3

x=4±2i√3​

The mistake is in the third step, (−2)²≠−4 and the correct solution is x=4±2i√3.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 227 Exercise 19 Answer

It is given a function f(x)=3(x−7)²+2.

It is required to determine whether the following statements are true or false.

This can be done by plotting the graph of the function then checking every part separately.

Draw the graph of the function.

Clearly, the axis of symmetry for f(x) is x=7 as shown in the diagram above.

As the minimum value of f(x) is 2 and maximum value is infinity then the range of f(x) is {2,∞}.

The vertex of the function f(x)=3(x−7)²+2 is (7,2) as shown in the diagram.

The statement in part A is true as the axis of symmetry is x=7 but the statements in part B

and C are false as the range of f(x) is {2,∞} and its vertex is (7,2).

Page 227 Exercise 20 Answer

It is given the following equations.It is required to determine whether the equations have real roots or not.

This can be done by checking the signs of the numbers on both side of the equality.

For part A: In equation x²−25=0.

This can also be written as x²=25. Thus, both sides have positive numbers therefore, this equation has real roots.

For part B: In equation −1/2x²−3=0.

This can also be written as x²=−6.

Thus, left hand side contains a negative number and the right-hand side contain a negative number which cannot be possible therefore, this equation does not have real roots.

For part C: In equation 3x²−4=2.

This can also be written as x²=2.

Thus, both sides have positive numbers therefore, this equation has real roots.

The equations x²−25=0 and 3x²−4=2

have real roots while the equation −1/2x²−3=0 does not have real roots.

HMH Algebra 2 Chapter 4 Quadratic And Systems Of Equations Exercise 4.4 Solutions

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 227 Exercise 21 Answer

It is given an equation 3x²−12x+15=0.

It is required to determine whether the following statements are true or false.

This can be done by solving this equation to calculate its roots and then solve it by completing the square method.

Divide the equation by 3.

x²−4x+5=0

Now this quadratic equation cannot be split so that it can make two factors.

So, the equation x²−4x+5=0 cannot be equal to (x−5)(x+1)=0.

Now find its discriminant.

D=(−4)²−4⋅1⋅5

D=16−20

D=−4​

Thus,x=−b±√D/2a

x=4±2i/2

x=2±i

Now for solving the equation x²−4x+5=0

by completing the square method, add (−4/2)2

=4 on both side of the equality. Therefore,

x²−4x+4=−5+4

(x−2)²=−1

x=2±i

The statements in part A and B are false while the statement in part C is true.

Page 227 Exercise 22 Answer

It is given a system of equations y=2x²−3x+5 and y−3=x.

It is required to determine whether the following statements are correct or not.

This can be done by rewriting the equation then try to solve this system graphically by making a graph of the equations.

For part A: No, the given system of equations can be solved by both graphically as well as algebraically.

For part B: Yes, it is possible to rearrange the given system of equations to write the linear equation in terms of x making y the subject of the formula.

Thus, the equation y−3=x can also be written as y=x+3.

For part C: No, the given system of equations has only one solution as shown by its graphical solution below.

Statement in part B is correct while the statements in other two parts are wrong. This can be shown with the help of the diagram drawn below.

Page 228 Exercise 23 Answer

A quadratic equation is given as −4x²+x=3.

It is required to explain which method can be used to solve the equation and then solve it using that method.

The methods of factoring and completing squares cannot be used to solve the given equation as the discriminant is negative.

Therefore, only the quadratic formula can be used to solve the equation.

The given equation can be written as 4x²−x+3=0.

Substitute 4 for a, −1 for b, 3 for c in the formula x=−b±√b²−4ac/2a.​

x=−(−1)±√(−1)²−4(4)(3)/2(4)

x=1±√1−48/8

x=1±i√47/8

To solve the given equation, only the quadratic formula can be used as the roots are complex.

The solution to the given equation is 1±i√47/8.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 228 Exercise 24 Answer

It is given that Ronald says that f(x)=0.5x+1.5 is an inverse of g(x)=−1.5x+4

It is required to check whether Ronald is correct with explanation.

Writing the inverse of g(x) means writing x as a function of g(x).

Then, replacing x by f(x) and g(x) by x.

Find the inverse and check whether it is the same as Ronald’s answer.

Write x as a function of g(x) from equation g(x)=−1.5x+4.

g(x)=−1.5x+4

1.5x=4−g(x)

x=4−g(x)/1.5

x=2.66−0.66g(x)

​Replace x by f(x) and g(x) by x in equation x=2.66−0.66g(x).

f(x)=2.66−0.66x.Therefore, the statement of Ronald is incorrect.

The inverse of the given equation is f(x)=2.66−0.66x.

Page 228 Exercise 25 Answer

It is given that Keille wants to build a wire fence. A 80 feet roll provides an area of 100 feet squares and a 40 feet roll provides an area of 400 feet squares.

It is required to write a relation between the areas provided by the two rolls.

With the 80 ft. roll, Keille can build a fence of 100 feet squares.

With the 40ft. roll, Keille can build a fence of 400 feet squares.

This means that the area with 80ft. roll is four times larger than the area with 40 ft. roll.

If the area with 80 ft. roll is y and the area with 40ft. roll is x, then the relation between the two rolls can be written as y=4x.

Page 228 Exercise 26 Answer

It is given that Keille wants to build a wire fence. A 80 feet roll provides an area of 100 feet squares and a 40 feet roll provides an area of 400 feet squares.

It is required to show that the largest pen built from a 80 feet roll is two times the largest pen built from a 40 feet roll.

From the given figure, the largest pen built from 80 feet roll is of width 40 feet and the largest pen built from 40 feet of roll is 20 feet.

Therefore, the largest pen built from 80 feet roll is two times the largest pen built from 40 feet roll.

The largest pen built from a 80 feet roll is two times the largest pen built from a 40 feet roll.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.4 Quadratic Equations And System Of Equations Page 229 Exercise 27 Answer

The table for the light produced by high-pressure sodium vapour streetlamps for different energy usage is given below.

It is required to find a quadratic model for the light output with respect to energy use.

To find a quadratic model for the light output with respect to energy usage, use Microsoft Excel and the plot the point by considering the energy usage values as x-coordinates and the light output values as y-coordinates. Select the trend-line to be quadratic and paste the equation.

Consider the energy usage values as x-coordinates and the light output values as y-coordinates.

Plot the given points in Microsoft Excel and choose the trend-line as polynomial of order two.

From the graph, the equation of the quadratic model of the given data is y=0.1875x²+84.339x−863.55.

The equation of the quadratic model of the given data is y=0.1875x²+84.339x−863.55.

Page 229 Exercise 28 Answer

The table for the light produced by high-pressure sodium vapour streetlamps for different energy usage is given below.

It is required to find a linear model for the light output with respect to energy use.

To find a linear model for the light output with respect to energy usage, use Microsoft Excel and the plot the point by considering the energy usage values as x-coordinates and the light output values as y-coordinates. Select the trend-line to be linear and paste the equation.

Consider the energy usage values as x-coordinates and the light output values as y-coordinates.

Plot the given points in Microsoft Excel and choose the linear trend-line.

From the graph, the equation of the linear model of the given data is y=119.38x−2159.4.

The equation of the linear model of the given data is y=119.38x−2159.4.

Page 229 Exercise 29 Answer

The table for the light produced by high-pressure sodium vapour street lamps for different energy usage is given below.

It is required to estimate the light output for a 200-watt bulb in both the model, linear as well as quadratic.

To estimate light output for a 200-watt bulb, from the quadratic model, substitute 200

for x in the equation y=0.1875x²+84.339x−863.55 and simplify.

To estimate light output for a 200-watt bulb, from the linear model, substitute 200

for x in the equation y=119.38x−2159.4 and simplify.

Substitute 200 for x in the equation y=0.1875x²+84.339x−863.55 and simplify.

y=0.1875(200)²+84.339(200)−863.55

y=23504.25

Therefore, the estimated value of the light output for a 200-watt bulb, from the quadratic model is 23504.25 lumens.

Substitute 200 for x in the equation y=119.38x−2159.4 and simplify.

y=119.38(200)−2159.4

y=21716.6

Therefore, the estimated value of the light output for a 200 watt bulb from the linear model, is 1716.6 lumens.

The estimated value of the light output for a 200-watt bulb, from the quadratic model is 23504.25 lumens.

The estimated value of the light output for a 200-watt bulb, from the linear model, is 21716.6 lumens.

Page 229 Exercise 30 Answer

The table for the light produced by high-pressure sodium vapor streetlamps for different energy usage is given below.

It is required to determine which model of the two- linear and quadratic gives a better estimate.

The quadratic model gives a better estimate as all the points on the graph almost lie on the curve.

The quadratic model gives a better estimate as all the points on the graph almost lie on the curve.

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations

Page 189 Problem 1 Answer

It is given a system composed of a linear equation in two variables and a quadratic equation in two variables.

It is required to determine how to solve this system.

Solve one of the two equations for one of the variables in terms of the other.

Substitute the expression for this variable into the second equation, then solve for the remaining variable.

Substitute that solution into either of the original equations to find the value of the first variable. If possible, right the solution as an ordered pair.

Check the solution in both equations

Solve the system of two equations in two variables by using substitution method.

Page 189 Problem 2 Answer

It is given two graphs.

It is required to examine a way by which the line could intersect the parabola.

This can be done by reflecting the line with respect to x-axis.

Reflect the line shown in the graph with respect to x-axis.

Line can intersect the parabola by reflecting it with respect to x-axis.

Step-by-step solutions for HMH Algebra 2 Module 4 Exercise 4.1

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 189 Problem 3 Answer

It is given a line and a parabola.

It is required to sketch three graphs showing intersection at one point, at two point and no intersection.

This can be done by taking an equation of a line and a parabola then graph these equations.

Let a parabola (x+2)²=4(y−1) and a line y=1.

Let a parabola (x+2)²=4(y−1) and a line y=3.

Let a parabola (x+2)²=4(y−1) and a line y=−3.

The required graphs are,For intersecting at one point

Page 189 Problem 4 Answer

It is given a linear and a quadratic function.

It is required to determine that at how many points does a constant linear function can intersect a quadratic function.

A constant horizontal line can intersect a quadratic function at 2 points.

For example: Let a parabola (x+2)²=4(y−1) and a line

A constant horizontal line can intersect a quadratic function at 2 points. It can be shown as,

Page 190 Problem 5 Answer

It is given a parabola and a line.

It is required to discuss whether a line has to be horizontal to intersect a parabola at exactly one point.

Let a horizontal parabola be y²=4ax.

Now there may be a vertical line that intersects the horizontal parabola at a point.

Yes, there should be a vertical line that intersects the parabola at a point.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 190 Problem 6 Answer

A linear-quadratic system is given as y=1/2(x−3)²

3x+y=4.5

It is required to solve the given system graphically.

To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.

Plot the graph of y=1/2

(x−3)².

Plot the graph of y=4.5−3x.

From the graph, it is understood that there is a unique solution for the two given equations at (0,4.5).

Therefore, the solution to given linear-quadratic system is (0,4.5).

The solution to given linear-quadratic system is (0,4.5).

Page 191 Problem 7 Answer

It is given a linear-quadratic system y+3x=0 and y−6=−3x².

It is required to solve this linear-quadratic system graphically.

This can be done by plotting the graph of these two equations then check the intersecting points.

Plot the graph of the equation y+3x=0 and y−6=−3x².

The graph of the two equations intersects each other at two points (−1,3) and (2,−6).

This implies that these are the solutions of this system of equations.

The solutions of this system are (−1,3) and (2,−6) which can be shown by the graph:

Page 191 Problem 8 Answer

It is given that the linear-quadratic system is

{       y=1/4(x−3)²

{       3x−2y=13.

It is required to solve the given system.

Solve the system by substitution. The first equation is solved for y.

Substitute the expression 1/4(x−3)²

for y in the equation 3x−2y=13 to solve for x.

Put 1/4(x−3)²

for y in the equation 3x−2y=13.

13=3x−2(1/4(x−3)²)

13=3x−1/2(x−3)²

13=−1/2x²+6x−9/2

26=−x²+12x−9

0=x²−12x+35​

Solve the equation for x.

x²−12x+35=0

x²−7x−5x+35=0

x(x−7)−5(x−7)=0

(x−5)(x−7)=0

x=5,7​

Put the value of x as 5 in the equation 3x−2y=13.

3(5)−2y=13

2y=2

y=1

Put the value of x as 7 in the equation 3x−2y=13.​

3(7)−2y=13

2y=8

y=4

The solutions of the given system

{     ​y=1/4(x−3)²

{      3x−2y=13    are (5,1) and (7,4).

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 192 Problem 9 Answer

A statement is given.

It is required to determine the way to check algebraic solutions for reasonableness.

One can check algebraic solutions for reasonableness by substituting the solution in the given equations and check whether the solution satisfies all the given equations.

Algebraic solutions can be checked for reasonableness by substituting the solution in the given equations and checking whether the solution satisfies all the given equations.

Page 193 Problem 10 Answer

A linear-quadratic system is given as x−6=−1/6y²

2x+y=6

It is required to solve the given system algebraically.

To solve the given system algebraically, substitute the expression for one the variable from one equation into the second equation and then solve for that variable.

Then, with this value find the value of the second variable.

Substitute 6−y²

for x in the equation x−6=−1/6y².

Simplify the equation.

(6−y²)−6=−1/6y²

3−y²−6=−1/6y² 

−y²−3=−1/6y²

Multiply both sides of the equation −y²−3=−1/6y² by −6 and simplify.

−6(−y²−3)=−6(−1/6y²)2y+18=y²

y²−2y−18=0​

Substitute −2 for b, 1 for a, −18 for c in the formula y=−b±√b²−4ac/2a.

y=−(−2)±√(−2)²−4(1)(−18)/2(1)

y=2±√4+72/2

y=2±√76/2

y=1±4.35​

Therefore, y=5.35,−3.35.

Therefore, x=6−5.35/2

x=−0.65/2

x=−0.325​ Or​

x=6−(−3.35)/2

x=9.35/2

x=4.675​

Therefore, the solutions to the given system are (4.675,−3.35),(−0.325,5.35).

The solutions to the given system are (4.675,−3.35),(−0.325,5.35).

Page 193 Problem 11 Answer

A linear-quadratic system is given as: x−y=7

x²−y=7

It is required to solve the given system algebraically.

To solve the given system algebraically, substitute the expression for one the variable from one equation into the second equation and then solve for that variable.

Then, with this value find the value of the second variable.

Solve for the value of x by the method of substitution.

Substitute x−7 for y in the equation x²−y=7. Simplify the equation.

x²−(x−7)=7

x²−x+7=7

x(x−1)=0

Therefore, x=0,1.

Use the values of x to find the values of y.

Therefore, ​y=0−7

y=−7​ Or​

y=1−7

y=−6

Therefore, the solutions to the given system are (0,−7),(1,−6).

The solutions to the given system are (0,−7),(1,−6)

HMH Algebra 2 Module 4 Chapter 4 Exercise 4.3 Quadratic Equations and Systems of Equations answers

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 193 Problem 12 Answer

It is given that the range of radio station is a circle given by, x²+y²=2025.

The highway is expressed by the equation, y−15=1/20x.

It is required to tell the points where car enters the highway and then exits the range of station.

Solve the system by substitution. The first equation is solved for y. Substitute the expression 1/20

x+15 for y in the equation x²+y²=2025 to solve for x.

Make a quadratic equation in terms of x.

Put 1/20

x+15 for y in the equation x²+y²=2025.​

x²+(1/20x+15)²=2025

x²+1/400

x²+225+3/2

x=2025/401

400x²+3/2

x−1800=0

401x²+600x−720000=0​

Solve the equation for x.​

x=−600±√600²−4(401)(−720000)

2(401)=600±√1,155,240,000

80²≈43.17,41.63​

Use the value of x to get the value of y.

Put the value of x as 43.17 in the equation y=1/20

x+15.

y=1/20

(43.17)+15

y=17.15

Put the value of x as 41.63 in the equation y=1/20

x+15.

y=1/20(41.63)+15

y=17.08​

The car will be within the radio station’s broadcast area between the points (43.17,17.15) and (41.63,17.08).

Page 196 Problem 13 Answer

The equation of the orbit of earth’s satellite is given as x²/49+y²/51=1.

The equation of the path of an asteroid is given as y=1/28     x−7.

It is required to find the points where the asteroid may collide with the satellite.

To find the points of collision, draw the graph of the line and the ellipse on a graphing calculator. Then, find the points of intersection.

Draw the graph of y=1/28 x−7 on a graphing calculator.

Draw the graph of x²/49+y²/51=1 on a graphing calculator.

From the graph, the point of intersect of the orbit and the path of the asteroid is (−1.166,−7.042),(1.646,−6.941).

Therefore, the asteroid may collide with the satellite at two points, (−1.166,−7.042),(1.646,−6.941).

The asteroid may collide with the satellite at two points, (−1.166,−7.042),(1.646,−6.941).

Page 196 Problem 14 Answer

It is given that the path of the trapeze is modelled by y=1/4x²+16.

The path of the zip-line is modelled by y=2x+12.

It is required to find the point where the trapeze artist can grab the second acrobat.

To find the required point, the given system algebraically. Substitute the expression for one the variable from one equation into the second equation and then solve for that variable.

Then, with this value find the value of the second variable.

Make a quadratic equation in terms of x.

Substitute 2x+12 for y in the equation y=1/4x²+16. Simplify the equation.​

2x+12=1/4x²+16

1/4x²−2x+16−12=0

1/4x²−2x+4=0​

Solve the equation for x.

Multiply both sides of the equation 1/4x²−2x+4=0 by 4 and simplify.​

4(1/4x²−2x+4)=4(0)

x²−8x+16=0

(x−4)²

=0

Therefore, x=4.

Find the value of y using x.

Therefore, y=2(4)+12

y=8+12

y=20

Therefore, the point where the trapeze artist can grab the second acrobat is (4,20).

The point where the trapeze artist can grab the second acrobat is (4,20).

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 196 Problem 15 Answer

It is given that a parabola opens to the left.

It is required to identify an infinite set of parallel lines that intersect the parabola only once.

Since the parabola opens to the left, a horizontal line, say y=a;a∈R, will intersect the parabola only once.

Similarly, there will be infinite number of such horizontal lines that intersect the parabola at only point.

Therefore, the set of parallel lines that intersect the parabola only once is y=a;a∈R.

If a parabola opens to the left, the set of parallel lines that intersect the parabola only once is y=a;a∈R.

Page 196 Problem 16 Answer

A statement is given.

It is required to mention how to solve a system consisting of a linear equation in two variables and a quadratic equation in two variables.

To solve the system algebraically, substitute the expression for one the variable from the linear equation into the second equation and then solve for that variable by using identity

(a+b)²=a²+2ab+b² and the quadratic formula.

Then, with this value find the value of the second variable by substituting it in the linear equation.

To solve the system algebraically, substitute the expression for one the variable from the linear equation into the second equation and then solve for that variable by using identity (a+b)²

=a²+2ab+b² and the quadratic formula.

Then, with this value find the value of the second variable by substituting it in the linear equation.

Page 197 Exercise 1 Answer

It is required to tell the number of intersection points on the graph.

The curve on the graph meets at x−axis, then at y−axis and again at x−axis. So, the total number of intersection points of the curve is 3.

The straight line intersects the x−axis and then has an intercept at y−axis. So, total number of intersections for the line is 2.

Also, the curve and the line intersect at one point.

So, the total number of intersections are, 3+2+1=6 points.

There are 6 points of intersection are on the graph.

Page 197 Exercise 2 Answer

It is given that the system of equations is,

{   ​y=x²+3x−2

{    y−x=4.

It is required to tell the number of intersection points on the graph of given system.

Plot the given system of equations. Check if the given curve and the line meet at any point or not. Count the number of such points.

Draw the graph of the system

{​     y=x²+3x−2

{     y−x=4    on an online geometry calculator.

The curve y=x²+3x−2 and the line y−x=4 meet at two points on the graph.

The curve y=x²+3x−2 meets twice at x−axis and once at y−axis.

The curve y−x=4 meets once at both x−axis and y−axis.

Therefore, the number of intersection points is 2+2+1+1+1=7.

There are 7 points of intersection on the graph of the system

{      ​y=x²+3x−2

{     y−x=4. 

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 197 Exercise 3 Answer

It is given that the system of equations is,

{   ​y=−(x−2)²+4

{     y=−5.

It is required to solve the system graphically.

Plot the given system of equations. Check if the given curve and the line meet at any point or not.

Find the coordinates of such points.

These intersection points are the solutions of the system.

Draw the graph of the system

{​y=−(x−2)²+4

{   y=−5 on an online geometry calculator.

The curve y=−(x−2)²+4 and the line y=−5 meet at two points on the graph.

The two points are (−1,−5) and (5,−5).

The solutions of the system

{​y=−(x−2)²+4

{    y=−5 are (−1,−5) and (5,−5). 

Page 197 Exercise 4 Answer

A linear-quadratic system is given as: y−3=(x−1)²

2x+y=5

It is required to solve the given system graphically.

To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.

Plot the graph of y−3=(x−1)².

Plot the graph of 2x+y=5.

From the graph, the line intersects the parabola at two points (−1,7),(1,3).

Therefore, the solution to the given linear-quadratic system is (−1,7),(1,3).

The solution to the given linear-quadratic system is (−1,7),(1,3).

Page 197 Exercise 5 Answer

A linear-quadratic system is given as: x=y²−5−x+2y=12

It is required to solve the given system graphically.

To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.

Plot the graph of x=y²−5.

Plot the graph of −x+2y=12.

From the graph, it is understood that there is no unique solution for the two given equations.

Therefore, the given linear-quadratic system has no solution.

The given linear-quadratic system has no solution as there is no point of intersection between the two graphs.

Page 197 Exercise 6 Answer

A linear-quadratic system is given as:

x−4=(y+1)²

3x−y=17

It is required to solve the given system graphically.

To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.

Plot the graph of x−4=(y+1)².

Plot the graph of 3x−y=17.

From the graph, the line intersects the parabola at two points (5.77,0.33),(5,−2).

Therefore, the solution to the given linear-quadratic system is (5.77,0.33),(5,−2).

The solution to the given linear-quadratic system is (5.77,0.33),(5,−2).

Page 198 Exercise 7 Answer

A linear-quadratic system is given as: (y−4)²+x²

=−12x−20

x=y

It is required to solve the given system graphically.

To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.

Plot the graph of (y−4)²+x²

=−12x−20.

Plot the graph of x=y.

From the graph, it is understood that there is no unique solution for the two given equations.

Therefore, the given linear-quadratic system has no solution.

The given linear-quadratic system has no solution as there is no point of intersection between the two graphs.

Page 198 Exercise 8 Answer

It is given that the linear-quadratic system is

{   ​6x+y=−16

{      y+7=x².

It is required to solve the given system.

Substitute the value of y from y+7=x² in the equation

6x+y=−16. Find the value of x from the obtained equation. Put the obtained value of x in the equation

y+7=x² to get the value of y.

Put the value of y as x²−7 in 6x+y=−16.

6x+x²−7=−16

x²+6x−7+16=0

x²+6x+9=0​

Solve the equation for x.

x=−6±√6²−4(1)(9)/2(1)

x=−6±√36−36/2

x=−6/2

x=−3​

Put the value of x as −3 in the equation 6x+y=−16.

6(−3)+y=−16−18+y=−16

y=−16+18

y=2

Hence, the value of x is −3 and y is 2.

The solution of the given system

{​    6x+y=−16

{    y+7=x² is (−3,2).

Page 197 Exercise 9 Answer

It is given that the linear-quadratic system is

{   ​y−5=(x−2)²

{   x+2y=6.

It is required to solve the given system.

Substitute the value of y from y−5=(x−2)² in the equation

x+2y=6. Find the value of x from the obtained equation. Put the obtained value of x in the equation x+2y=6 to get the value of y.

Put the value of y as (x−2)²+5 in x+2y=6.

x+2((x−2)²+5)=6

x+2(x²+4−4x+5)=6

x+2(x²−4x+9)=6

2x²−7x+18=6

2x²−7x+12=0​

Solve the equation for x.​

x=−(−7)±√(−7)²−4(2)(12)/2(2)

x=7±√49−96/4

x=7±√−47/2

As x has an imaginary value, y also does not have a real value.

So, there is no solution for the given system.

The solution for the given system {​y−5=(x−2)²

x+2y=6​ does not exist as x and y both have imaginary values.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 198 Exercise 10 Answer

It is given that the linear-quadratic system is

{  ​y²−26=−x²

{      x−y=6.

It is required to solve the given system.

Substitute the value of y from x−y=6 in the equation y²−26=−x².

Find the value of x from the obtained equation. Put the obtained values of x in the equation x−y=6 to get the value of y.

Put the value of y as x−6 in y²−26=−x².​

(x−6)²−26=−x²

x²+36−12x−26=−x²

2x²−12x+10=0

x²−6x+5=0​

Solve the equation for x.​

x=−(−6)±√(−6)²−4(1)(5)/2(1)

x=6±√16/2

x=6+4/2,6−4/2

x=5,1​

Put the value of x as 5 in the equation x−y=6 to find the corresponding value of y.​

5−y=6

y=−1

Put the value of x as 1 in the equation x−y=6 to find the corresponding value of y.​

1−y=6

y=−5​

The solutions for the given system

{  ​y²−26=−x²

{  x−y=6   are (5,−1) and (1,−5).

Page 198 Exercise 11 Answer

It is given that the linear-quadratic system is

{  ​y−3=x²−2x

{     2x+y=1.

It is required to solve the given system.

Substitute the value of y from y−3=x²−2x in the equation 2x+y=1.

Find the value of x from the obtained equation. Put the obtained values of x in the equation 2x+y=1 to get the value of y.

Put the value of y as x²−2x+3 in 2x+y=1.​

2x+x²−2x+3=1

x²+3=1

x²=−2

x=√−2

As x has an imaginary value, y also does not have a real value.

So, there is no solution for the given system.

The solution for the given system {​y−3=x²−2x

{    2x+y=1 does not exist as x and y both have imaginary values.

Page 198 Exercise 12 Answer

It is given that the linear-quadratic system is

{     ​y=x²+1

{     y−1=x.

It is required to solve the given system.

Substitute the value of y from y=x²+1 in the equation y−1=x.

Find the value of x from the obtained equation. Put the obtained values of x in the equation

y−1=x to get the value of y.

Put the value of y as x²+1 in y−1=x.

x²+1−1=x

x²=x

x²−x=0

x(x−1)=0

x=0,1​

Put the value of x as 0 in the equation y−1=x to find the corresponding value of y.

y−1=0

y=1

Put the value of x as 1 in the equation y−1=x to find the corresponding value of y.​

y−1=1

y=2​

The solutions for the given system

{​       y=x²+1

{     y−1=x           are (0,1) and (1,2). 

HMH Algebra 2 Chapter 4 Exercise 4.3 Quadratic Equations key

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 198 Exercise 13 Answer

It is given that the linear-quadratic system is

{   y=x²+2x+7

{    y−7=x.

It is required to solve the given system.

Substitute the value of y from y=x+7 in the equation y=x²+2x+7.

Find the value of x from the obtained equation.

Put the obtained values of x in the equation y=x+7 to get the value of y.

Put the value of y as x+7 in y=x²+2x+7.

x+7=x²+2x+7

x²+x=0

x(x+1)=0

x=0,−1​

Put the value of x as 0 in the equation y=x+7 to find the corresponding value of y.

y=0+7

y=7

Put the value of x as −1 in the equation y=x+7 to find the corresponding value of y.​

y=−1+7

y=6​

The solutions for the given system

{  ​y=x²+2x+7

{  y−7=x    are (0,7) and (−1,6).

Page 199 Exercise 14 Answer

It is given that Jason is driving his car at a constant velocity of 60 miles per hour. The distance that Alan travelled is given by, d=3600t².

It is required to find the time taken by Alan to catch up with Jason.

Substitute v for d/t in the equation. Put the given value of v to find t.

The equation d=3600t² can be written as,​d/t

=3600t

v=3600t

Put v=60 in the equation.

60=3600t

t=60/3600

t=1/60

The time taken by Alan to catch up with Jason is 1/60 hours.

Page 199 Exercise 15 Answer

It is given that the equation of the cannonball’s flight is given by y=2+0.12x−0.002x².

The hill slope has an equation,

y=0.15x.

It is required to find where the cannonball lands on the hill.

Substitute the value of y from y=0.15x in the equation

y=2+0.12x−0.002x².

Find the value of x from the obtained equation. Put the obtained value of x in the equation

y=0.15x to get the value of y.

Put the value of y as 0.15x in y=2+0.12x−0.002x².​

2+0.12x−0.002x²=0.15x

0.002x²+0.03x−2=0

2x²−30x−2000=0

x²−15x−1000=0​

Solve the equation for x.

x=−(−15)±√(−15)²−4(1)(−1000)/2(1)

x=15±√4225/2

x=15+65/2,15−65/2

x=40,−25​

Ignore the negative value x=−25 as distance cannot be negative.

Put the value of x as 40 in the equation y=0.15x.​

y=0.15(40)

y=6​

The cannonball lands on the hill at 6 units.

Page 199 Exercise 16 Answer

It is given that the equation of the quarter is given by y=64−2x². The balloon has an equation, y=6x+8.

It is required to find when the balloon and quarter pass each other.

Substitute the value of y from y=6x+8 in the equation y=64−2x².

Find the value of x from the obtained equation.

Put the value of y as 6x+8 in y=64−2x².​

6x+8=64−2x²

2x²+6x−56=0

x²+3x−28=0​

Solve the equation for x.​

x=−3±√(3)²−4(1)(−28) /2(1)

x=−3±√121/2

x=−3+11/2,−3−11/2

x=4,−7

Ignore the negative value x=−7 as the time cannot be negative.

The quarter and the balloon pass each other after 4 seconds.

Page 200 Exercise 17 Answer

It is given that the circular region is x²+y²=400 and service area is a straight line given by,

y=3x+20.

It is required to find the length of the service road.

Substitute the value of y from y=3x+20 in the equation

x²+y²=400. Find the value of x from the obtained equation.

Put the obtained value of x in the equation y=3x+20 to get the value of y.

Find the distance between the intersection points.

Put the value of y as 3x+20 in x²+y²=400.

x²+(3x+20)²=400

x²+9x²+400+120x=400

10x²+120x=0

x²+12x=0

x=0,−12​

Put the value of x as 0 in the equation y=3x+20.

y=3(0)+20

y=20

Put the value of x as −12 in the equation y=3x+20.​

y=3(−12)+20

y=−36+20

y=−16​

Find the distance between the points (0,20) and (−12,−16).​

D=√(−12−0)²+(−16−20)²

=√144+1296

≈37.95

The length of the service road is 37.95 units.

HMH Algebra 2 Exercise 4.3 Systems of Equations answer guide

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.3 Quadratic Equations And System Of Equations Page 200 Exercise 18 Answer

It is given that the system of equations is,

{​     y−7=x²−5x

{    y−2x=1   and the student gave (1,3) as the solution.

It is required to verify that student is correct or not.

Plot the given system of equations. Check if the given curve and the line meet at any point or not.

Find the coordinates of such points. These intersection points are the solutions of the system.

Verify if the intersection points match with the answer of the student.

Draw the graph of the system

{​ y−7=x²−5x

{    y−2x=1 on an online geometry calculator.

The curve y−7=x²−5x and the line y−2x=1 meet at one point on the graph.

The intersection point is (1,3).

The student gave a reasonable answer as (1,3) because it is the only intersection point of the given system { ​y−7=x²−5x

{   y−2x=1.

Page 201 Exercise 19 Answer

It is given that the student gave

{​  y²=−(x+1)²+9

{    y=x²−4x+3  as a linear-quadratic system.

It is required to verify tell if the student is correct or not.

A linear-quadratic system requires at least one linear equation and one quadratic equation.

The student is incorrect as both y²=−(x+1)²+9 and

y=x²−4x+3 are quadratic equations.

One of them should have been a linear equation to make the system correct.

The student’s answer { ​y²=−(x+1)²+9

{   y=x²−4x+3   is wrong as both are quadratic equations.

Page 201 Exercise 20 Answer

It is given that the system of quadratic functions are y=100x² and y=0.001x².

It is required to find whether there is a line possible that is not horizontal as well as vertical but passes through the vertex of both.

The lines y=100x² and y=0.001x²

cannot be solved as they have no common intersection point.

Therefore, the number of solutions of the system is zero.

Hence, there is no line possible that can pass through both of the vertices.

There is no line possible that passes through the vertex of both curves but is not horizontal as well as vertical.

Page 201 Exercise 21 Answer

It is given that that there is a system of linear and quadratic equation.

It is required to find why a system of a linear equation and a quadratic equation cannot have an infinite number of solutions.

A quadratic equation always forms a parabola.

A linear equation forms a line.

Two equations have an infinite number of solutions when they have the same graph

But a parabola and a straight line can’t be the same.

That’s why a system of a linear equation and a quadratic equation cannot have an infinite number of solutions.

A system of a linear equation and a quadratic equation cannot have an infinite number of solutions because they don’t have the same graph.

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations

Page 158 Problem 1 Answer

It is given an equation y=3x−2.

It is required to graph the equation in x−y plane.

To solve this minimum two points are required which satisfy the given equation y=3x−2.

Then plot the obtained points on the graph then join them to draw the graph of the equation.

It is given an equation y=3x−2.

To solve this minimum two points are required which satisfy the given equation y=−x+5.

Then plot the obtained points on the graph then join them to draw the graph of the equation.

To find the points on the line let’s consider y=0. For this value of y the value of x will be

y=3x−2

0=3x−5

x=5/3

So, one point satisfying the equation y=3x−2 is (5/3,0).

For second point let’s consider x=0. For this value of x the value of y will be y=3x−2

y=0−2

y=2

So, other point satisfying the equation y=3x−2 is (0,2).

Now forming the graph of equation y=3x−2 by using the points solved above that are (5/3,0) and (0,2).

The graph is,

The graph of the equation y=3x−2 is,

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 158 Problem 2 Answer

It is given an equation 5−3x=7(x−1)

It is required to solve the equation to find the value of x.

To solve the given equation, perform the basic calculation to get the value of x.

It is given an equation 5−3x=7(x−1)

To get the value of x from equation 5−3x=7(x−1).

Firstly, use distributive property​5−3x=7(x−1)

5−3x=7x−7

Now, adding 7  on both sides,

5−3x+7=7x−7+7

12−3x=7x

Adding 3x  on both sides

12−3x+3x=7x+3x

12=10x

Dividing both sides by 10

12/10=10x/10

6/5=x

So, x=6/5

For the equation 5−3x=7(x−1)

x=6/5.

Page 158 Problem 3 Answer

It is given an equation 3x+2(x−1)=28

It is required to solve the equation to find the value of x.

To solve the given equation, perform the basic calculation to get the value of x.

It is given an equation 3x+2(x−1)=28

To get the value of x from equation 3x+2(x−1)=28.

Firstly, use distributive property 3x+2(x−1)=28

3x+2x−2=28

On further calculations equation becomes,

5x−2=28

Adding 2 to both sides,

​5x−2+2=28+2

5x=30

Dividing both side by 5,

​5x/5=30/5

x=6​

For the equation 3x+2(x−1)=28,

x=6.

Page 158 Problem 4 Answer

It is given two equations

​5x−2y=4

3x+2y=−12

It is required to find the value of x and y for given equations.

To solve this, find the value of y from first equation then put this value of y in second equation.

Then, solve the obtained equations by using basic calculations to get the value of x and y.

It is given two equations

5x−2y=4…….eq(1)

3x+2y=−12…….eq(2)

From eq(1)

y=5x−4/2

Substituting the value of y from eq(1)  on eq(2),

3x+2(5x−4/2)=−12

3x+5x−4=−12

8x−4=−12

Adding 4 on both sides,

8x−4+4=−12+4

8x=−8

Dividing both side by 8,

​8x/8=−8/8

x=−1

Substituting the obtained value of x in y=5x−4/2

y=5⋅(−1)−4/2

y=−5−4/2

y=−9/2

For the given equations the value of x and y are x=−1

y=−9/2

So, the solution of equation is (−1,−9/2).

Page 159 Problem 5 Answer

It is required to find the standard equation of circle.

The standard equation of circle is (x−h)²+(y−k)²=r².

Standard equation of circle gives the idea of the centre and radius of the circle.

In the above equation (h,k) is the centre of circle and r is the radius of the circle.

The standard equation of circle is (x−h)²+(y−k)²=r².

Standard equation of circle gives the idea of the centre and radius of the circle.

In the above equation (h,k) is the centre of circle and r is the radius of the circle.

HMH Algebra 2 Volume 1 Module 4 Chapter 4 Exercise 4.1 solutions

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 159 Problem 6 Answer

It is given a circle with centre C(h,k) and radius r.

It is given P(x,y) an arbitrary point on the given circle and another point A(x,k)  which have same x−coordinate with P and same y−coordinate as C.

It is required to show that Δ CAP is right angle triangle.

Given circle have centre C(h,k) and radius r.

Given P(x,y) an arbitrary point on the given circle and another point A(x,k) which have same x−coordinate with P and same y−coordinate as C.

Taking the slope of CA,

​m1=k−k/h−x

m1=0/h−x

m1=0

So, CA is parallel to x−axis.

Taking the slope of PA,

​m2=y−k/x−x

m2=y−k/0

m2=∞

So, PA is parallel to y−axis.

Also x−axis and y−axis are perpendicular to each other. So, ΔCAP is right angle triangle having right angle at A.

ΔCAP is right angle triangle having right angle at A.

Page 159 Problem 7 Answer

It is given a circle with centre C(h,k) and radius r.

It is given P(x,y) an arbitrary point on the given circle and another point A(x,k) which have same x−coordinate with P and same y−coordinate as C.

It is required to find the length of sides AC, AP, and CP.

To solve this use distance formula to find the length of sides AC,AP and CP.

Given circle have centre C(h,k) and radius r.

Given P(x,y) an arbitrary point on the given circle and another point A(x,k) which have same x−coordinate with P and same y−coordinate as C.

Now, length of AC is ​AC=√(h−x)²+(k−k)²

AC=√(h−x)²

AC=(h−x)​

Now, length of AP is ​AP=√(x−x)²+(y−k)²

AP=√(y−k)²

AP=(y−k)

Now, length of CP

​CP=√(x−h)²+(y−k)²

CP=√r²

CP=r​

Length of AC is, AC=(h−x)

Length of AP is, AP=(y−k)

Length of CP is,

CP=r.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 159 Problem 8 Answer

It is given a circle with centre C(h,k) and radius r.

It is given P(x,y) an arbitrary point on the given circle and another point A(x,k) which have same x−coordinate with P and same y−coordinate as C.

It is required to find the equation of circle by using Pythagoras theorem on Δ CAP.

To solve this use distance formula to find the length of sides AC,AP and CP.

Then use Pythagoras theorem on Δ CAP

Given circle have centre C(h,k) and radius r.

Given P(x,y) an arbitrary point on the given circle and another point A(x,k) which have same x−coordinate with P and same y−coordinate as C.

Now, length of AC is​ AC=√(h−x)²+(k−k)²

AC=√(h−x)²

AC=(h−x)​

Now, length of AP is ​AP=√(x−x)²+(y−k)²

AP=√(y−k)²

AP=(y−k)

Now, length of CP is ​CP=√(x−h)²+(y−k)²

CP=√r²

CP=r​

Applying Pythagoras theorem on Δ CAP.

AC²+AP²=CP²

Substituting the value of length of sides,

(h−x)²+(y−k)²=r²

Equation of circle will be,(h−x)²+(y−k)²=r².

Page 160 Problem 9 Answer

It is required to prove that why isn’t absolute value used in the equation of the circle.

The general equation of a circle is (x−h)²+(y−k)²=r², here all the terms are squared, and squared number is always a positive number.

Therefore, the absolute value function is not needed here because the terms here are already positive.

The absolute value function is not needed here because the terms here are already positive.

Page 160 Problem 10 Answer

It is required to show that why does the equation of the circle also apply to the cases in which P  has the same x− coordinate as C or same y− coordinate as C so that Δ CAP doesn’t exist.

To equation of the circle will apply independent of ΔCAP as when the x− coordinate of P is that of C.

Then the point P will be directly above C such that Δy that is the difference in their y− coordinate of P is that of C.

After that the point P will be on the right of C

such that Δx that is difference in their x− coordinate will be equal to the radius of the circle.

The equation of the circle will apply independent of ΔCAP because in both cases the points cases the point P will be r unit away from C.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 161 Problem 11 Answer

It is given a circle with center C(1,−4)

and radius r=2.

It is required to find the equation of given circle.

To solve this substitute the point of centre in place of (h,k) and value of radius in place of r in standard equation of circle.

Substitute the value of center C(1,−4) and radius r=2 on equation,(x−h)²+(y−k)²=r²

​(x−1)²+(y−(−4))²=2²

(x−1)²+(y+4)²=4

So, the equation of circle is,(x−1)²+(y+4)²=4

The equation of the circle is,(x−1)²+(y+4)²=4.

Page 161 Problem 12 Answer

It is given a circle with center C(−2,5) and passes through point P(−2,−1).

It is required to find the equation of given circle.

To solve this, firstly find the value of radius which is equal to the distance between center C(−2,5) and point P(−2,−1).

Then substitute the point of centre in place of (h,k) and value of radius In place of r in standard equation of circle.

Given circle has center C(−2,5) and passes through point P(−2,−1).

Distance between C(−2,5) and P(−2,−1) is ​CP=√(−2−5)²+(−1+2)²

CP=√72+12

CP=√49+1

CP=√50

Also, CP=r

So, r=√50

Substituting the value of center C(−2,5) and radius r=√50 on equation,

(x−h)²+(y−k)²=r²

​(x−(−2))²+(y−5)²=(√50)²

(x+2)²+(y−5)²=50​

Equation of circle is,(x+2)²+(y−5)²=50.

Page 162 Problem 13 Answer

It is given equation of a circle x²+y²+4x+6y+4=0.

It is required to graph the circle after writing the equation in standard form.

To solve this, convert the given equation to the standard form. Then plot the circle on the graph.

The given circle has equation x²+y²+4x+6y+4=0.

To convert the equation to standard form complete square method is used

​(x²+2⋅2⋅x+2²)+(y²+2⋅3⋅x+3²)+4−4−9=0

(x²+4x+4)+(y²+6x+9)+(−9)=0

(x²+4x+4)+(y²+6x+9)=9

(x+2)²+(y+3)²

=32

So, the equation of circle is,

(x+2)²

+(y+3)²

=3²

This circle has centre (−2,−3) and radius r=3.

Now plotting the circle on graph,

He equation of circle is,

(x+2)²

+(y+3)²

=3²

Graph of the circle is,

Page 162 Problem 14 Answer

It is given equation of a circle 9x²+9y²−54x−72y+209=0.

It is required to graph the circle after writing the equation in standard form.

To solve this, write the equation of circle in general form then convert the given equation to the standard form. Then plot the circle on the graph.

The given circle has equation 9x²+9y²−54x−72y+209=0.

Divide the equation by 9,

​9/9x²+9/9y²−54/9x−72/9y+209/9=0

x²+y²−6x−8y+209/9=0​

To convert the equation to standard form complete square method is used

​(x²−2⋅3⋅x+32)+(y²−2⋅4⋅x+42)+209/9−9−16=0

(x²−6x+9)+(y²−8x+16)−16/9=0

(x−3)²+(y−4)²=16/9

(x−3)²+(y−4)²=(4/3)²

So, the equation of circle is,

(x−3)²+(y−4)²=(4/3)²

Now plotting the circle on graph,

The equation of circle is,(x−3)²+(y−4)²=(4/3)²

Graph of the circle is,

Page 164 Problem 15 Answer

It is given that Sasha delivers newspapers that live within a 4- block radius of her house. Her house is located at point (0,−1) as shown in the graph below.

It is required to determine which houses does Sasha deliver newspapers.

This can be done by finding the inequality by using the equation of circle then make a graph of the required area.

Find the equation of circle by substituting the values in the general equation.

Substitute ​h=0,k=−1 andr=4 in the equation of circle

(x−h)²+(y−k)²=r².

(x−0)²+(y−(−1))²=4²

Now simplify.

(x)²+(y+1)²=16

Since she delivers newspapers to subscribers within a 4-mile radius; the required inequality becomes:

(x)²+(y+1)²<16

Graph the inequality and the points.

It can be seen that Sasha can only deliver newspaper to subscriber at points B,D and E.

The inequality will be x²+(y+1)²<16.

Sasha can only deliver newspaper to subscriber at points B,D and E.

HMH Algebra 2 Module 4 Chapter 4 Exercise 4.1 Quadratic Equations and Systems of Equations answers

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 164 Problem 16 Answer

It is given an equation ax²+ay²+cx+dy+e=0.

It is required to do something in order to graph it.

This can be done by forming the equation of a circle by using the completing the square method.

The general equation of the circle shows that both the x² and y² terms have a coefficient of 1.

⇒ \(\left(x^2+2 x\left(\frac{c}{2 a}\right)\right)+\left(y^2+2 y\left(\frac{d}{2 a}\right)\right)=-e\)

⇒ \(\left(x^2+2 x\left(\frac{c}{2 a}\right)+\left(\frac{c}{2 a}\right)^2\right)+\left(y^2+2 y\left(\frac{d}{2 a}\right)+\left(\frac{d}{2 a}\right)^2\right)=-e+\left(\frac{c}{2 a}\right)^2+\left(\frac{d}{2 a}\right)^2\)

⇒ \(\left(x+\frac{c}{2 a}\right)^2+\left(y+\frac{d}{2 a}\right)^2=-e+\frac{c^2}{4 a^2}+\frac{d^2}{4 a^2}\)

⇒ \(\left(x+\frac{c}{2 a}\right)^2+\left(y+\frac{d}{2 a}\right)^2=\frac{c^2+d^2-4 a^2 e}{4 a^2}\)

Therefore, the equation of the circle will be: x²+c/ax+y²+d/a y=−e

Now apply completing the square method to write it in a form comparable with the general equation.

The center of this circle lies on (h,k)=(−c²a,−d²a) and the radius r of the circle is equal to √c²+d²−4a²e/4a².

Page 165 Problem 17 Answer

It is given the center (−4,−3) of the circle containing the point P(2,5).

It is required to write the equation of the circle.

This can be done by finding the radius the circle by using the distance formula then use general form of the circle to write the equation.

Calculate the radius by using the distance formula.

​r=CP

​​​=√(2−(−4))²+(5−(−3))²

=√(6)²+(8)²

​​​=√36+64

​​​=√100

​​​=10

Write the equation of the circle by using the general form of the circle.

Substitute h=−4,k=−3, and r=10 in the equation (x−h)²+(y−k)²=r².

​(x−(−4))²+(y−(−3))²=(10)²

(x+4)²+(y+3)²=(10)².

The required of the circle is (x+4)²+(y+3)²=(10)².

Page 164 Problem 18 Answer

It is given an equation 4x²+4y²+8x−16y+11=0.

It is required to write the general equation of the circle and then graph the circle.

This can be done by converting the given equation into the general form of the circle then graph the circle by determining the centre and radius of circle.

Convert the equation 4x²+4y²+8x−16y+11=0 into the general form of the circle.

​4x²+4y²+8x−16y+11=0

4(x²+2x)+4(y²−4y)+11=0

4(x²+2x+12)+4(y²−4y+(2)²)=−11+4(12)+4(22)4(x+1)²+4(y−2)²=9

(x+1)²+(y−2)²=9/4

(x+1)²+(y−2)²=(3/2)²

Thus, the general equation of the circle is (x+1)²+(y−2)²=(3/2)².

The centre of the circle is C=(−1,2) and the radius of the circle is equal to r=3/2.

Now graph the circle.

The general equation of the circle is (x+1)²+(y−2)²=(3/2)² and it can be shown as:

Page 164 Problem 19 Answer

It is given the locations of the homes of five friends, a pizza restaurant, and the school they attend. It is also given that in order to ride the bus to school, the student must live more than 2

miles from the school.

It is required to write an inequality representing the given situation and draw a circle to solve the problem.

This can be done by writing the genera; form of the circle then according to the given condition set the inequality then plot the circle with the given locations.

Write the equation of the circle with center (1,−2) and radius r=2.

Substitute h=1,k=−2 and r=2 in the equation (x−h)²+(y−k)²=r².

​(x−1)²+(y−(−2))²=2²

(x−1)²+(y+2)²=4.

Now write the inequality which represents the given situation.

As the locations must be greater than 2 miles in order to ride a bus to school. So, the inequality will be:

(x−1)²+(y+2)²>4

The required graph will be drawn like:

In the graph shown above, the shaded region represents the required area.

The points A,B,C are outside the circle satisfy the inequality.

Alonzo, Barbara, and Constance are eligible to ride the bus.

Page 165 Exercise 1 Answer

It is given the center (−7,−1) of a circle and its radius is equal to 13.

It is required to write the equation of the circle.

This can be done by using the standard equation of the circle.

We have to substitute ​r=13,h=−7 and k=−1 in the equation

(x−h)²+(y−k)²=r².

​(x+7)²+(y+1)²=13²

(x+7)²+(y+1)²=169​

The equation of the circle is (x+7)²+(y+1)²=169.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 165 Exercise 2 Answer

It is given that a circle is centred at (−8,2) and contains the point (−1,6).

It is required to find the equation of the circle.

To find the equation of the circle, substitute the given values in the formula (x−h)²+(y−k)²=(x1−h)²+(y1−k)².

Simplify the equations by using the identity (a+b)²=a²+2ab+b².

Substitute (−8,2) for (h,k), (−1,6) for (x1,y1) in the inequality (x−h)²+(y−k)²=(x1−h)²+(y1−k)².

Simplify the equations by using the identity (a+b)²=a²+2ab+b².

​(x−(−8))²+(y−2)²=(−1−(−8))²+(6−2)²

(x+8)²+(y−2)²=(7)²+(4)²

x²+16x+64+y²−4y+4=49+16x²+16x+y²−4y+3=0​

The equation of the circle centred at (−8,2) and containing the point (−1,6) is x²+16x+y²−4y+3=0.

Page 165 Exercise 3 Answer

It is given that a circle is centred at (5,9) and contains the point (4,8).

It is required to find the equation of the circle.

To find the equation of the circle, substitute the given values in the formula (x−h)²+(y−k)²=(x1−h)²+(y1−k)².

Simplify the equations by using the identity (a+b)²=a²+2ab+b².

We have to substitute (5,9) for (h,k), (4,8) for (x1,y1) in the inequality (x−h)²+(y−k)²=(x1−h)²+(y1−k)².

Simplify the equations by using the identity (a+b)²=a²+2ab+b².

​(x−5)²+(y−9)²=(4−5)²+(8−9)²

x²−10x+25+y²−18y+81=(−1)²+(−1)²

x²−10x+y²−18y+(81+25)=1+1x²−10x+y²−18y+104=0​

The equation of the circle centred at (5,9) and containing the point (4,8) is x²−10x+y²−18y+104=0.

Page 165 Exercise 4 Answer

The equation of a circle is given as x²+y²−2x−8y+13=0.

It is required to write the given equation in the standard form and then plot the graph of the circle.

To write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius, obtain perfect squares for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Then, plot the graph of the circle on a graphing calculator by using the standard form.

Write the given equation of the circle in the form (x−h)²+(y−k)²=r².

The given equation of the circle can be written as x²−2x+1+y²−8y+16+13=1+16.

On simplifying the equation and making perfect squares for the x,y,terms,

​(x²−2x+1)+(y²−8y+16)+13=1+16

(x−1)²+(y−4)²+13=17

(x−1)²+(y−4)²=4

(x−1)²+(y−4)²=2²

This means that the radius of the circle r is 2 and the centre C is (1,4).

Plot the graph of the circle with equation (x−1)²+(y−4)²=2² by using a graphical calculator.

The equation of the given circle in the standard form is (x−1)²+(y−4)²=2².

The graph of the circle is shown below.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 166 Exercise 5 Answer

The equation of a circle is given as x²+y²+6x−10y+25=0.

It is required to write the given equation in the standard form and then plot the graph of the circle.

To write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius, obtain perfect squares for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Then, plot the graph of the circle on a graphing calculator by using the standard form.

Write the given equation of the circle in the form (x−h)²+(y−k)²=r².

The given equation of the circle can be written as x²+6x+9+y²−10y+25+25=9+25.

On simplifying the equation and making perfect squares for the x,y terms,

​(x²+6x+9)+(y²−10y+25)+25=9+25(x−3)²+(y−5)²+25=34

(x−3)²+(y−5)²=9

(x−3)²+(y−5)²=3²

This means that the radius of the circle r is 3 and the centre C is (3,5).

Plot the graph of the circle with equation (x−3)²+(y−5)²=3² by using a graphical calculator.

The equation of the given circle in the standard form is (x−3)²+(y−5)²=3².

The graph of the circle is shown below.

Page 166 Exercise 6 Answer

The equation of a circle is given as x²+y²+4x+12y+39=0.

It is required to write the given equation in the standard form and then plot the graph of the circle.

To write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius, obtain perfect squares for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Then, plot the graph of the circle on a graphing calculator by using the standard form.

Write the given equation of the circle in the form (x−h)²+(y−k)²=r².

The given equation of the circle can be written as x²+4x+4+y²+12y+36+39=4+36.

On simplifying the equation and making perfect squares for the x,y terms,

​(x²+4x+4)+(y²+12y+36)+39=4+36

(x+2)²+(y+6)²=40−39(x+2)²+(y+6)²=1

(x+2)²+(y+6)²=12

This means that the radius of the circle r is 1 and the centre C is (−2,−6).

Plot the graph of the circle with equation (x+2)²+(y+6)²=12 by using a graphical calculator.

The equation of the given circle in the standard form is (x+2)²+(y+6)²=12.

The graph of the circle is shown below.

Page 166 Exercise 7 Answer

The equation of a circle is given as 8x²+8y²−16x+32y−88=0.

It is required to write the given equation in the standard form and then plot the graph of the circle.

Write the given equation of the circle in the form \((x-h)^2+(y-k)^2=r^2\).

Divide both sides of the equation \(8 x^2+8 y^2-16 x+32 y-88=0$ by eight.

⇒ [latex]\frac{8 x^2+8 y^2-16 x+32 y-88}{8}\)

⇒ \(x^2+y^2-2 x+4 y-11=0\)

The given equation of the circle can be written as \(x^2-2 x+1+y^2+4 y+4-11=1+4 \text {. }\)

On simplifying the equation and making perfect squares for the x, and y terms, \(\left(x^2-2 x+1\right)+\left(y^2+4 y+4\right)-11=5\)

⇒ \((x-1)^2+(y+2)^2=5+11\)

⇒ \((x-1)^2+(y+2)^2=16\)

⇒ \((x-1)^2+(y+2)^2=4^2\)

This means that the radius of the circle r is 4 and the centre C is (1,-2).

To write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where ( h,k ) is the centre and r is the radius, obtain perfect squares for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Then, plot the graph of the circle on a graphing calculator by using the standard form.

Plot the graph of the circle with equation (x−1)²+(y+2)²=4² by using a graphical calculator.

The equation of the given circle in the standard form is (x−1)²+(y+2)²=4².

The graph of the circle is shown below.

HMH Algebra 2 Chapter 4 Exercise 4.1 Quadratic Equations key

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 167 Exercise 8 Answer

The equation of a circle is given as 2x²+2y²+20x+12y+50=0.

It is required to write the given equation in the standard form and then plot the graph of the circle.

The given equation of the circle can be written as \(x^2+10 x+25+y^2+6 y+9+25=25+9 \text {. }\)

On simplifying the equation and making perfect squares for the x, and y terms,

⇒ \(\left(x^2+10 x+25\right)+\left(y^2+6 y+9\right)+25=34\)

⇒ \((x+5)^2+(y+3)^2=34-25\)

⇒ \((x+5)^2+(y+3)^2=9\)

⇒ \((x+5)^2+(y+3)^2=3^2\)

This means that the radius of the circle r is 3 and the centre C is (-5,-3).

Write the given equation of the circle in the form \((x-h)^2+(y-k)^2=r^2\).

Divide both sides of the equation \(2 x^2+2 y^2+20 x+12 y+50=0\) by two.

⇒ \(\frac{2 x^2+2 y^2+20 x+12 y+50}{2}=\frac{0}{2}\)

⇒ \(x^2+y^2+10 x+6 y+25=0\)

To write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius, obtain perfect squares for the x,y terms by adding necessary numbers on both sides of the equation and simplify to the standard form.

Then, plot the graph of the circle on a graphing calculator by using the standard form.

Plot the graph of the circle with equation (x+5)²+(y+3)²=3² by using a graphical calculator.

The equation of the given circle in the standard form is (x+5)²+(y+3)²=3².

The graph of the circle is shown below,

Page 167 Exercise 9 Answer

The equation of a circle is given as 12x²+12y²−96x−24y+201=0.

It is required to write the given equation in the standard form and then plot the graph of the circle.

The given equation of the circle can be written as \(x^2-8 x+16+y^2-2 y+1+\frac{201}{12}=16+1 \text {. }\)

On simplifying the equation and making perfect squares for the x, and y terms,

⇒ \(\left(x^2-8 x+16\right)+\left(y^2-2 y+1\right)+\frac{201}{12}=17\)

⇒ \((x-4)^2+(y-1)^2=17-\frac{201}{12}\)

⇒ \((x-4)^2+(y-1)^2=\frac{204-201}{12}\)

⇒ \((x-4)^2+(y-1)^2=\left(\frac{1}{2}\right)^2\)

This means that the radius of the circle r is \(\frac{1}{2}\) and the centre C is (4,1).

Write the given equation of the circle in the form \((x-h)^2+(y-k)^2=r^2\). Divide both sides of the equation \(12 x^2+12 y^2-96 x-24 y+201=0\) by twelve.

⇒ \(\frac{12 x^2+12 y^2-96 x-24 y+201}{12}=\frac{0}{12}\)

⇒ \(x^2+y^2-8 x-2 y+\frac{201}{12}=0\)

To write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius, obtain perfect squares for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Then, plot the graph of the circle on a graphing calculator by using the standard form.

Plot the graph of the circle with equation (x−4)²+(y−1)²=(1/2)² by using a graphical calculator.

The equation of the given circle in the standard form is (x−4)²+(y−1)²=(1/2)².

The graph of the circle is shown below.

Page 167 Exercise 10 Answer

The equation of a circle is given as 16x²+16y²+64x−96y+199=0.

It is required to write the given equation in the standard form and then plot the graph of the circle.

The given equation of the circle can be written as \(x^2+4 x+4+y^2-6 y+9+\frac{199}{16}=4+9 \text {. }\)

On simplifying the equation and making perfect squares for the x,y terms, \(\left(x^2+4 x+4\right)+\left(y^2-6 y+9\right)+\frac{199}{16}=13\)

⇒ \((x+2)^2+(y-3)^2=13-\frac{199}{16}\)

⇒ \((x+2)^2+(y-3)^2=\frac{9}{16}\)

⇒ \((x+2)^2+(y-3)^2=\left(\frac{3}{4}\right)^2\)

This means that the radius of the circle r is \(\frac{3}{4}\) and the centre C is (-2,3)

Write the given equation of the circle in the form \((x-h)^2+(y-k)^2=r^2\).

Divide both sides of the equation \(16 x^2+16 y^2+64 x-96 y+199=0\) by 16.

⇒ \(\frac{16 x^2+16 y^2+64 x-96 y+199=0}{16}=\frac{0}{16}\)

⇒ \(x^2+y^2+4 x-6 y+\frac{199}{16}=0\)

To write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius, obtain perfect squares for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Then, plot the graph of the circle on a graphing calculator by using the standard form.

Plot the graph of the circle with equation (x+2)²+(y−3)²=(3/4)² by using a graphical calculator.

The equation of the given circle in the standard form is (x+2)²+(y−3)²=(3/4)².

The graph of the circle is shown below.

Page 170 Exercise 11 Answer

The equation of a circle is given as x²+18x+y²+22y−23=0.

It is required to find the radius and the coordinates of the centre.

To find the radius and the centre of the circle, write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius.

Obtaining perfect square for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Write the given equation of the circle in the form (x−h)²+(y−k)²=r².

The given equation of the circle can be written as x²+18x+81+y²+22y+121−23=81+121.

On simplifying the equation and making perfect squares for the x,y terms,​(x²+18x+81)+(y²+22y+121)−23=81+121

(x+9)²+(y+11)²−23=20²

(x+9)²+(y+11)²=225

(x−(−9))²+(y−(−11))²=15²

This means that the radius of the circle r is 15 and the centre C is (−9,−11).

The radius of the circle r is 15 and the centre C is (−9,−11).

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 170 Exercise 12 Answer

The equation of a circle is given as x²+y²−18x+22y+33=0.

It is required to find the radius and the coordinates of the centre.

To find the radius and the centre of the circle, write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius.

Obtaining perfect square for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

Write the given equation of the circle in the form (x−h)²+(y−k)²=r².

The given equation of the circle can be written as x²−18x+81+y²+22y+121+33=81+121.

On simplifying the equation and making perfect squares for the x,y terms, ​(x²−18x+81)+(y²+22y+121)+33=81+121

(x−9)²+(y+11)²+33=202

(x−9)²+(y+11)²=169

(x−9)²+(y−(−11))²=13²

This means that the radius of the circle r is 13 and the centre C is (9,−11).

The radius of the circle r is 13 and the centre C is (9,−11).

Page 170 Exercise 13 Answer

The equation of a circle is given as 25x²+25y²−450x−550y−575=0.

It is required to find the radius and the coordinates of the centre.

The given equation of the circle can be written as \(x^2-18 x+81+y^2-22 y+121-23=81+121 \text {. }\)

On simplifying the equation and making perfect squares for the x, y terms, \(\left(x^2-18 x+81\right)+\left(y^2-22 y+121\right)-23=81+121[latex]

⇒ [latex](x-9)^2+(y-11)^2=202+23\)

⇒ \((x-9)^2+(y-11)^2=225\)

⇒ \((x-9)^2+(y-11)^2=15^2\)

This means that the radius of the circle r is 15 and the centre C is (9,11)

Write the given equation of the circle in the form \((x-h)^2+(y-k)^2=r^2\). Divide both sides of the equation \(25 x^2+25 y^2-450 x-550 y-575=0\) by 25 .

⇒ \(\frac{25 x^2+25 y^2-450 x-550 y-575}{25}=\frac{0}{25}\)

⇒ \(x^2+y^2-18 x-22 y-23=0\)

To find the radius and the centre of the circle, write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius.

Obtaining perfect square for the x, and y terms by adding necessary numbers on both sides of the equation and simplifying to the standard form.

The radius of the circle r is 15 and the centre C is (9,11).

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 170 Exercise 14 Answer

The equation of a circle is given as 25x²+25y²+450x−550y+825=0.

It is required to find the radius and the coordinates of the centre.

The given equation of the circle can be written as \(x^2+18 x+81+y^2-22 y+121+33=81+121 \text {. }\)

On simplifying the equation and making perfect squares for the x, y terms,

⇒ \(\left(x^2+18 x+81\right)+\left(y^2-22 y+121\right)+33=81+121\)

⇒ \((x+9)^2+(y-11)^2=202-33\)

⇒ \((x+9)^2+(y-11)^2=169\)

⇒ \((x+9)^2+(y-11)^2=13^2\)

This means that the radius of the circle r is 13 and the centre C is (-9,11).

Write the given equation of the circle in the form \((x-h)^2+(y-k)^2=r^2\). Divide both sides of the equation \(25 x^2+25 y^2+450 x-550 y+825=0\) by 25 .

⇒ \(\frac{25 x^2+25 y^2+450 x-550 y+825}{25}=\frac{0}{25}\)

To find the radius and the centre of the circle, write the given equation in the standard form, i.e. (x−h)²+(y−k)²=r², where (h,k) is the centre and r is the radius.

Obtaining perfect square for the x,y terms by addition necessary numbers on both sides of the equation and simplify to the standard form.

The radius of the circle r is 13 and the centre C is (−9,11).

Page 171 Exercise 15 Answer

It is given that the sprinkler is located at the point (5,−10) and its range is 12 feet.

The other points are the coordinates of plants.

It is required to determine the plants which do not get water by writing an inequality and draw a circle.

The range is a circle with radius 12, centred at (5,−10).

Since the plant must be out of the circle for, use the inequality (x−h)²+(y−k)²>r².

Then, draw the graph of the circle on a graphing calculator by substituting the coordinates in the equation of a circle. Note down the points that lie outside the circle.

Substitute (5,−10) for (h,k),12 for r in the inequality (x−h)²+(y−k)²>r².

​(x−5)²+(y−(−10))²>12²

(x−5)²+(y+10)²>12²

​Plot the graph of the circle with equation (x−5)²+(y+10)²=12² by using a graphical calculator.

From the graph, the points strictly outside the circle are A,B,C,E,G.

Therefore, the plant that do not get water are A,B,C,E,G.

The plant that do not get water are A,B,C,E,G.

Page 171 Exercise 16 Answer

It is given that two sprinklers are located at the points (5,−10),(10,10) and their range is 12 feet.

The other points are the coordinates of plants.

It is required to determine the plants, which do not get water by writing an inequality and drawing the circles.

Since the plant must be out of the two circles for, use the inequality (x−h)²+(y−k)²>r².

Then, draw the graph of the circles on a graphing calculator by substituting the coordinates in the equation of a circle. Note down the points that lie outside the circles.

From part (a) of the exercise, the inequality for the sprinkler at (5,−10) is (x−5)²+(y+10)²>12².

For the second inequality, substitute (10,10) for (h,k),12 for r in the inequality (x−h)²+(y−k)2>r².

(x−10)²+(y−10)²>12².

Plot the graph of the circle with equation (x−5)²+(y+10)²=12² by using a graphical calculator.

Plot the graph of the circle with equation (x−10)²+(y−10)²=12² by using a graphical calculator

From the graph, the points strictly outside both the circle are A,B,C.

Therefore, the plants that do not get water are A,B,C.

The plants that do not get water are A,B,C.

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 171 Exercise 17 Answer

It is given that two sprinklers are located at the points (5,−10),(10,10) and their range is 12 feet.

The other points are the coordinates of plants.

It is required to determine the position of the third sprinkler such that all the plants get water and draw the circle for all the three sprinklers.

For third sprinkler choose the point (−15,0).

Substitute the values in the standard form and the plot the graph of  the circle. Note that all points should be inside any of the circles.

From part (b) of the exercise, the graph for the two sprinklers is as follows:

For the third circle, substitute (−15,0) for (h,k),12 for r in the equation (x−h)²+(y−k)²=r².

​(x−(−15))²+(y−0)²=12²

(x+15)²+y²=12²

​Plot the graph of the circle with equation (x+15)²+y²=12² in the graph of part (b), by using a graphical calculator.

From the graph, it is clear that if the third sprinkler is at the point (−15,0) then all the remaining points are covered.

Therefore, for all the plants to get water the third sprinkler can be placed at (−15,0).

The position of the third sprinkler such that all the remaining plants are watered is (−15,0).

Page 172 Exercise 18 Answer

It is given that the Sun is placed at S(0,0) and the Venus rotates around the Sun in a circular orbit, which passing  through V(41,53).

It is required to write the equation for the orbit of Venus and determine the distance between Venus and Sun if each unit in the coordinate plane represents  one million miles.

Here, the centre of the circle is S(0,0) and it passes through V(41,53), To find the equation of the orbit, substitute the given values in the formula

(x−h)²+(y−k)²=(x1−h)²+(y1−k)².

Simplify the equations by using the identity (a+b)²=a²+2ab+b².

The distance between the Sun and Venus is equal to the radius of the orbit multiplied by the length of each unit in the coordinate plane.

We have to substitute (0,0) for (h,k),(41,53) for (x1,y1) in the inequality (x−h)²+(y−k)²=(x1−h)²+(y1−k)².

Simplify the equations by using the identity (a+b)²=a²+2ab+b².

​(x−0)²+(y−0)²=(41−0)²+(53−0)²

x²+y²=1681+2809

x²+y²=4490

x²+y²≈672

This means that the radius of the orbit is 67 units.

Therefore, the distance between the Sun and Venus is 67 million miles.

The equation of the orbit of Venus is x²+16x+y²−4y+3=0 and the distance between the Sun and Venus is 67 million miles.

HMH Algebra 2 Exercise 4.1 Systems of Equations answer guide

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 173 Exercise 19 Answer

It is given that a unit circle is a circle with radius one units and centred at the origin.

It is required to write the equation of a unit circle.

To find the equation of a unit circle, substitute (0,0)

for (h,k),1 for r in the equation (x−h)²+(y−k)²=r².

Substitute (0,0) for (h,k),1 for r in the equation (x−h)²+(y−k)²=r² and simplify.

​(x−0)²+(y−0)²=1²

x²+y²=1​

The equation of a unit circle is x²+y²=1.

Page 173 Exercise 20 Answer

It is given that a Pythagorean triple is an ordered triple of three positive integers (a,b,c)

such that a²+b²=c².

It is required to find two points on the circle in the first quadrant, by using the Pythagorean triple (3,4,5).

Consider the Pythagorean triple (3,4,5) such that c=5.

Here, the radius of the unit circle is c=1.

Therefore, dividing the triples by five, (3/5,4/5,5/5)=(3/5,4/5,1).

This means that the coordinates of a point on the circle in the first quadrant are (3/5,4/5).

Similarly, the triple can be (4/5,3/5,1).

Therefore, the second point on the circle in the first quadrant, with respect to the triple (3,4,5) is (4/5,3/5).

The coordinates of two points on the circle in the first quadrant are (3/5,4/5), and (4/5,3/5).

Page 173 Exercise 21 Answer

It is given that a Pythagorean triple is an ordered triple of three positive integers (a,b,c) such that a²+b²=c².

It is required to find six other points on the circle in the other three quadrants, by using the result of part (b) of the exercise and symmetry of a circle.

In part (b) of the exercise, the points on the circle in first quadrant are (3/5,4/5),(4/5,3/5).

The relation between the points in second quadrant with respect to points in first quadrant is (x,y)≡(−x,y).

Therefore, two points on the circle, in the second quadrant are (−3/5,4/5), and (−4/5,3/5).

The relation between the points in third quadrant with respect to points in first quadrant is (x,y)≡(−x,−y).

Therefore, two points on the circle, in the third quadrant are (−3/5,−4/5),(−4/5,−3/5).

The relation between the points in fourth quadrant with respect to points in first quadrant is (x,y)≡(x,−y).

Therefore, two points on the circle, in the fourth quadrant are (3/5,−4/5),(4/5,−3/5).

The coordinates of six other points on the circle are (−3/5,4/5),(−4/5,3/5),(−3/5,−4/5),(−4/5,−3/5),(3/5,−4/5),(4/5,−3/5).

Step-by-step solutions for HMH Algebra 2 Module 4 Exercise 4.1

HMH Algebra 2 Volume 1 1st Edition Module 4 Chapter 4 Exercise 4.1 Quadratic Equations And System Of Equations Page 173 Exercise 22 Answer

It is given that a Pythagorean triple is an ordered triple of three positive integers (a,b,c)

such that a²+b²+c².

It is required to find eight points on the circle by using a Pythagorean triple other then (3,4,5).

(7,24,25) is a Pythagorean triple.

Therefore, the two points on the unit circle in the first quadrant are (7/25,24/25),(24/25,7/25).

Similarly, two points on the unit circle in the second quadrant are (−7/25,24/25),(−24/25,7/25).

Two points on the unit circle in the third quadrant are (−7/25,−24/25),(−24/25,−7/25).

Two points on the unit circle in the fourth quadrant are (7/25,−24/25),(24/25,−7/25).

Eight point on a unit circle with respect to the Pythagorean triple (7,24,25) are (7/25,24/25),(24/25,7/25),(−24/25,7/25)(−7/25,24/25),(−7/25,−24/25),(−24/25,−7/25),(7/25,−24/25),(24/25,−7/25)

Page 174 Exercise 23 Answer

It is given that a highway runs straight east-west and is at a distance of 6 miles from a radio tower, whose broadcast range is 10 miles.

It is required to find the length of the highway for which the car will be in the range of the broadcast.

To find the length of the highway for the mentioned case, use the Pythagoras theorem.

Substitute 6 for a, 10 for c in the formula c²=a²+b².

Simplify and solve for b. Here, b is the half of the required length of the highway.

Then, multiply the value of b by two.

We have to substitute 6 for a, 10 for c in the formula a²+b²=c².

Simplify and solve for b.

​6²+b²=10²

36+b²=100

b²=100−36

b²=64

b=8

Multiply 8 by 2.

2×8=16

Therefore, the length of the highway for which the car will get the signal of the tower is 16 miles.

The length of the highway for which the car will get the signal of the tower is 16 miles.

Page 17 Exercise 24 Answer

It is given that a highway runs straight east-west and is at a distance of 6 miles from a radio tower, whose broadcast range is 10 miles.

The car is travelling at a constant speed of 60 miles per hour.

It is required to find the amount of time the car is within the range of the signal.

From part (a) of the exercise, the distance for which the car is within the range of the signal is 16 miles.

Then, use the formula for calculating time when the constant speed and distance covered are known.

We have to substitute 60 for v, 16 for d in the formula t=d/v.

Simplify the expression by using division.

​t=60/16

t=3.75​

The amount of time the car is within the range of the signal is 3.75 hours.

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations

Page 175 Problem 1 Answer

A statement is given.

It is required to explain how distance formula is connected with deriving the equations for horizontal and vertical parabolas.

A parabola is a locus of a point which is equidistant from a fixed line and a fixed point.

To find the equation of a parabola, the distance between a point and the fixed point is equated to the distance between the point and the fixed line.

Therefore, the distance formula is needed in deriving the equation of a parabola.

The distance formula is connected with deriving the equations for horizontal and vertical parabolas as the distance between a point and the fixed point is equated to the distance between the point and the fixed line.

Page 175 Problem 2 Answer

An incomplete statement is given as the coordinates of the focus of the parabola are given by ____.

It is required to complete the statement.

The coordinates of the focus of the parabola are given by (p,0).

The complete statement is the coordinates of the focus of the parabola are given by (p,0).

HMH Algebra 2 Volume 1 Module 4 Chapter 4 Exercise 4.2 Solutions

Page 175 Problem 3 Answer

A statement is given.

It is required to write the expression for the distance from a point (x,y) on the parabola to the focus of the parabola.

The coordinates of the focus of a parabola is given as (p,0).

The distance formula between two points (x₁,y₁),(x₂,y₂) is given as d=√(x₁−x₂)²+(y₁−y₂)².

Therefore, the distance from a point (x,y) on the parabola to the focus of the parabola is d=√(x−p)²+y².

The distance from a point (x,y) on the parabola to the focus of the parabola is d=√(x−p)²+y².

Page 175 Problem 4 Answer

It is given that the equation of the directrix of a parabola is given as x=−p.

It is required to find the point of intersection of a horizontal line from a point (x,y) on the parabola and the directrix of the parabola.

The x−coordinate of every point on the directrix is −p.

Therefore, the point of intersection of a horizontal line and the directrix is (−p,y).

The point of intersection of a horizontal line from a point (x,y)

on the parabola and the directrix of the parabola is (−p,y).

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations  Page 175 Problem 5 Answer

It is given that a horizontal line from a point (x,y) on the parabola intersects the directrix of the parabola.

It is required to write the expression for the distance between the point on the parabola and the point of intersection between the horizontal line and the directrix.

From part (c) of the exercise, the point of intersection between the horizontal line and the directrix is (−p,y).

The distance formula between two points (x₁,y₁),(x₂,y₂) is given as d=√(x¹−x²)²+(y₁−y₂)².

Therefore, the distance from a point (x,y) on the parabola to the mentioned point of intersection is d=√(x−(−p))²+(y−y)².

On simplifying, d=x+p.

The distance between the point on the parabola and the point of intersection between the horizontal line and the directrix is d=x+p.

Page 175 Problem 6 Answer

A statement is given.

It is required to equate the distance between a point on the parabola and the focus to the distance between the point and the directrix and simplify the equation.

From part (b) of the exercise, the distance from a point (x,y) on the parabola to the focus of the parabola is d=√(x−p)²+y².

From part (d) of the exercise, the distance between the point on the parabola and the point of intersection between the horizontal line and the directrix is d=x+p.

Equate both the distances and square on both sides of the equation. Expand the expression by using the formula (a+b)²=a²+2ab+b².

Equate both the distances and square on both sides of the equation. Expand the expression by using the formula (a+b)2=a²+2ab+b².

(√(x−p)²+y2)²=(x+p)²

(x−p)²+y²=x²+2px+p²

x²−2px+p²+y²=x²+2px+p²

The equation on equating the distance between a point on the parabola and the focus to the distance between the point and the directrix is x²−2px+p²+y²=x²+2px+p².

HMH Algebra 2 Module 4 Chapter 4 Exercise 4.2 Quadratic Equations And Systems Of Equations Answers

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 175 Problem 7 Answer

A statement is given.

It is required to collect the terms in the equation obtain in part (e) of the exercise.

From part (e) of the exercise, the equation obtained is x²−2px+p²+y²=x²+2px+p².

On collecting the like terms, the equation simplifies to (x²−x²)+(−2p−2p)x+(p²−p²)+y²=0.

On simplifying further, 0.x²−4px+0.p²+y²=0.

The simplified equation of a parabola is 0.x²−4px+0.p²+y²=0.

Page 175 Problem 8 Answer

It is given that 0⋅x²−4px+0⋅p²+y²=0.

It is required to convert this in the horizontal form of parabola.

The given equation is 0⋅x²−4px+0⋅p²+y²=0

Which can also be written as −4px+y²=0

Now add 4px on both sides then the equation will become y²=4px.

The standard form for a horizontal parabola is y²=4px.

Page 176 Problem 9 Answer

It is required to explain why directrix places on the line x=−p.

Loci of all the points that are equidistant from a point called focus and a line called the directrix.

since the vertex of this parabola lines on the origin with its focus on (p,0); the directrix must be p units on the other sides of the origin and other side of the original and it is perpendicular to the axis of symmetry therefore x=−p is a directrix.

The directrix must be p units on the other sides of the origin and other side of the original and it is perpendicular to the axis of symmetry therefore x=−p is a directrix.

Page 176 Problem 10 Answer

It is required to explain why directrix places on the line x=−p.

The general equation of a parabola with its vertex on the origin is y²=4px. This is when the vertex is (0,0).

If the vertex lies on the point (h,k) which implies that (0,0) is shifted to (h,k).

Hence y is replaced by y−k and x with x−h.

Then the new equation will become (y−k)²=4p(x−h).

If the vertex lies on the point (h,k) which implies that (0,0) is shifted to (h,k).

Hence y is replaced by y−k and x with x−h.

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 176 Problem 11 Answer

It is given the focus of parabola is located at (0,−2) and the equation of its directrix is y=2.

It is required to determine the equation of the parabola with vertex (0,0) and plot the parabola, the focus and the directrix.

This can be done by finding the general equation of the parabola then plot the graph accordingly.

We have to substitute values of h=0,k=0 and p=−2 in the equation (x−h)²=4p(y−k).

(x−0)²=4(−2)(y−0)

x²=−8y

Now plot a graph of the parabola, the focus and the directrix.

The equation of the parabola is x²=−8y.

It can be shown by a graph drawn below:

Page 177 Problem 12 Answer

It is given a parabola with focus(2,0) and directrix x=−2.

It is required to find the equation of parabola and plot it on graph.

To solve this check that the parabola is vertical or horizontal with the help of directrix.

After that use the suitable standard equation of parabola and place the value of a in standard equation to get the equation of parabola.

Given parabola have focus(2,0) and directrix x=−2. Since the directrix is parallel to y−axis so the parabola is horizontal parabola.

Now, standard equation of horizontal parabola is y²=4ax where (a,0) is the focus of parabola. Substituting the value of a in the equation,

y²=4⋅2⋅x

y²=8x​

Thus, equation of the parabola is,y²=8x

Plotting the parabola,

Therefore, equation of the parabola is,y²=8x

Graph of the parabola,

HMH Algebra 2 Chapter 4 Exercise 4.2 Quadratic Equations Key

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 177 Problem 13 Answer

It is given a parabola with focus(0,−1/2) and directrix y=1/2.

It is required to find the equation of parabola and plot it on graph.

To solve this check that the parabola is vertical or horizontal with the help of directrix.

After that use the suitable standard equation of parabola and place the value of a in standard equation to get the equation of parabola.

Given parabola have focus(0,−1/2) and directrix y=1/2.

Since the directrix is parallel to x−axis so, the parabola is vertical parabola.

Now, standard equation of horizontal parabola is x²=4ay where (0,a) is the focus of parabola.

Substituting the value of a in the equation,​x²=4⋅(−1/2)⋅y

x²=−2y​

Thus, equation of the parabola is,x²=−2y

Plotting the parabola,

Therefore, equation of the parabola is,x²=−2y Plotting the parabola,

Page 178 Problem 14 Answer

It is given the focus of parabola is located at (−1,−1) and the equation of its directrix is x=5.

It is required to determine the equation of the parabola with vertex (0,0)

and plot the parabola, the focus and the directrix.

This can be done by finding the general equation of the parabola then plot the graph accordingly.

It is known that, p=(x​value​of​focus)−(x​value​of​directrix)/2

p=−1−(5)/2

p=−3

Here, k= the y-coordinate of the focus   =−1.

The x−​value of the focus is h+p, so h+p=−1

h=−1+3

h=2

Substitute values of h=2,k=−1 and p=−3 in the equation(y−k)²=4p(x−h).

(y+1)²=4(−3)(x−2)(y+1)²

=−12(x−2)

Now plot a graph of the parabola, the focus and the directrix.

The equation of the parabola is (y+1)²=−12(x−2) and it can be drawn as:

Page 179 Problem 15 Answer

It is given a parabola with focus(5,−1) and directrix x=−3.

It is required to find the equation of parabola and plot it on graph.

To solve this check that the parabola is vertical or horizontal with the help of directrix.

After that use the suitable standard equation of parabola and place the value of a in standard equation to get the equation of parabola.

Given parabola have focus (5,−1) and directrix x=−3.

Since the directrix is parallel to y−axis so the parabola is horizontal parabola.

So, the standard equation of parabola is (y−k)²=4a(x−h).

For, value of a

a=5−(−3)/2

a=5+3/2

a=4

Now, for finding the value of (h,k)

k will be same as that of value of y−coordinate as focus have,k=−1

For the value of h

h+4=5

h=1

Now, substituting the value of (h,k) in equation.

Thus, equation of parabola is (y−(−1))²

=4⋅4⋅(x−1)(y+1)²

=16(x−1)​

Thus, equation of the parabola is,(y+1⁾²

=16(x−1)

Plotting the parabola,

Equation of the parabola is,(y+1)²=16(x−1)

Graph of the parabola is,

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations  Page 179 Problem 16 Answer

It is given a parabola with focus(5,−1) and directrix x=−3.

It is required to find the equation of parabola and plot it on graph.

To solve this check that the parabola is vertical or horizontal with the help of directrix.

After that use the suitable standard equation of parabola and place the value of a in standard equation to get the equation of parabola.

Given parabola have focus(−2,0) and directrix y=4.

Since the directrix is parallel to x−axis so the parabola is vertical parabola.

So, the standard equation of parabola is (x−h)²

=4a(y−k)

So, focus will be (h,k+p)=(−2,0)

Thus, ​h=−2

k+a=0

Also, directrix

​y=k−a

4=k−a

So, the values

​k=2

a=−2

Now, the equation of parabola is,

(x−(−2))²

=4⋅(−2)(y−2)(x+2)²

=(−8)(y−2)​

Equation of the parabola is,(x+2)²

=(−8)(y−2)

Plotting the equation,

Therefore, equation of the parabola is,(x+2)²=(−8)(y−2)

Graph of the equation,

Page 179 Problem 17 Answer

It is given an equation y²+2x+8y+18=0.

It is required to convert the given equation into the standard form of a parabola and graph the parabola, the focus and the directrix.

This can be done by converting the given equation into its standard form then find the focus and equation of the directrix then plot the graph of required parabola.

Isolate the y terms.y²+8y=−2x−18

Add 4²  on both sides.

y²+8y+4²=−2x−18+16

Now convert the above equation into its standard form.​

(y+4)²=−2x−2(y+4)²=−2(x+1)​

Now on comparing the above equation with the standard equation (y−k)²=4p(x−h).

4p=−2

⇒p=−1/2

h=−1,

k=−4

Focus =(h+p,k)

=(−3/2,−4).

Directrix: x=h−p

=−1/2.

Based on the data above the graph must be drawn like:

The equation of the parabola is (y+4)²=−2(x+1) and this can be drawn as:

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 191 Problem 18 Answer

It is given equation of parabola y²−12x−4y+64=0

It is required to convert the given equation in standard form of the parabola and graph the parabola.

To solve this, use complete square method then by further solving convert it in standard form.

Given equation of parabola is y²−12x−4y+64=0

y²−4y=12x−64

y²−2⋅2⋅y+4=12x−64+4

(y−2)²=12(x−5)

(y−2)²=4⋅3⋅(x−5)​

Equation of parabola is(y−2)²=12(x−5)

Graph of the parabola is,

Equation of parabola is (y−2)²=12(x−5)

Graph of the parabola is,

Page 181 Problem 19 Answer

It is given equation of parabola x²+8x−16y−48=0

It is required to convert the given equation in standard form of the parabola and graph the parabola.

To solve this, use complete square method then by further solving convert it in standard form.

Given equation of parabola is, x²+8x−16y−48=0

To solve this rearrange it the use complete square method the convert

x²+8x=16y−48

x²+2⋅4⋅x+16=16y−48+16

(x+4)²=16(x−2)(x+4)²

=4⋅4⋅(x−2)​

Equation of parabola is (x+4)²

=16(x−2)

Graph of the parabola is,

Equation of parabola is(x+4)²=16(x−2)

Graph of the parabola is,

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 181 Problem 20 Answer

It is given that the focal length of a telescope is 140 mm and the mirror has a 70 mm diameter.

It is required to determine the depth of the bowl of the mirror.

This can be done by finding the equation of the parabola then substituting the value of y

with the point that lies on the telescope.

The distance from the bottom of the mirror’s bowl to the focus is p.

The vertex location is not specified, so use (0,0) for simplicity.

The equation for the mirror is a horizontal parabola (with x the distance along the telescope and y the position out from the centre).

(y−0)²=4p(x−0)

Now p is equal to 140 mm as it is the focal length.

y²=540x

Since the diameter of the bowl of the mirror is 70 mm, the points at the rim of the mirror have why values of 35 mm and −35 mm.

The x- value of either point will be the same as the x-value of the point directly above the bottom of the bowl, which equals the depth of the bowl.

Since the points on the rim lie on the parabola use the equation of the parabola to solve for the x-value of either edge of the mirror.

352

=560x

⇒x=2.1875mm​

The bowl is approximately 2.19 mm deep.

Page 182 Problem 21 Answer

A football team needs one more field goal to win the game. The goalpost that the ball must clear is 10

feet off the ground. The path of the football after kicked for a 35−yard goal is given by the equation (y−11)=−0.0125(x−20)²

It is given equation and the point (35,10/3).

The horizontal distance to covered by the ball is 35 yard and the vertical distance must be at least 10 feet or 10/3 yard to pass the goal post therefore

It is required to find the equation of parabola and plot it on graph.

The trajectory of the ball is such that is passes above the goalpost which means that the team scored the field goal and therefore won the game.

Page 183 Problem 22 Answer

It is given the focus and the vertex of the parabola.

It is required to determine a relationship between the separation of the focus, vertex, and the shape of the parabola.

If the focus is located at the y-axis, then the parabola must be vertical and vice versa.

If the focus is located at the x-axis, then the parabola must be horizontal and vice versa.

In the equation x²=4py, y=ax²

is only possible if a=1/4p.

There must be a vertical parabola when the focus is located at the y-axis while the parabola must be horizontal when it’s focus is located at the x-axis.

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations  Page 183 Problem 23 Answer

It is given two variables x and y.

It is required to derive an equation relating x and y from the definition of a parabola based on focus and directrix by using the distance formula.

This can be done by finding the distance between the point on the parabola and the focus.

Then calculate the distance between the point on the parabola and the directrix then equating both distances to derive the equation of the parabola.

Let a parabola that open upwards or downwards, then the directrix will be a horizontal line of the form y=c.

Let (a,b) be the focus and let y=c be the directrix.

Let (x₀,y₀) be any point on the parabola.

Now calculate the distance between the point (x₀,y₀) and (a,b).

√(x₀−a)²+(y₀−b)²

Now calculate the distance between the point (x₀,y₀) and the line y=c.

∣y₀−c∣

Here, the distance between the point and the line is the difference between their y-coordinates.

Now equate the above two equations.

√(x₀−a)²+(y₀−b)²

=∣y₀−c∣

Square both sides.

(x₀−a)²+(y₀−b)²=(y₀−c)²

Now simplify the equation.

(x₀−a)²+b²−c²=2(b−c)y₀

The equation in (x₀,y₀) is true for all other values on the parabola and hence on the parabola And hence rewrite the equation with (x,y).

Therefore, the equation will be: (x−a)²+b²−c²=2(b−c)y

The equation of the parabola is (x−a)²+b²−c²=2(b−c)y.

Page 183 Exercise 1 Answer

It is given the focus of parabola is located at (3,0) and the equation of its directrix is x=−3.

It is required to determine the equation of the parabola with vertex (0,0) and plot the parabola, the focus and the directrix.

This can be done by finding the general equation of the parabola then plot the graph accordingly.

Substitute values of ​h=0,k=0 and p=3 in the equation

(y−k)²=4p(x−h).

(y−0)²=4(3)(x−0)

y²⁼12x

Now plot a graph of the parabola, the focus and the directrix.

The equation of the parabola is y²=12x.

Page 183 Exercise 2 Answer

It is given the focus of parabola is located at (0,2) and the equation of its directrix is y=−2.

It is required to determine the equation of the parabola with vertex (0,0) and plot the parabola, the focus and the directrix.

This can be done by finding the general equation of the parabola then plot the graph accordingly.

We have to substitute values of h=0,k=0 and p=2 in the equation

(x−h)²=4p(y−k).

(x−0)²=4(2)(y−0)x²=8y​

Now plot a graph of the parabola, the focus and the directrix.

The equation of the parabola is x²=8y.

Page 184 Exercise 3 Answer

It is given that the vertex of a parabola is at (−3,6) and directrix is x=−1.75.

It is required to find the equation of the parabola.

The equation of the directrix of a parabola is given as x=−p.

To find the equation of the parabola, substitute (−3,6) for (h,k), 1.75

for p in the equation (y−k)²=4p(x−h).

We have to substitute (−3,6) for (h,k), 1.75

for p in the equation (y−k)²=4p(x−h).

Simplify the equation by using the identity (a+b)²=a²+2ab+b².

​​(y−6)²=4(1.75)(x−(−3))

y²−12y+36=(7)(x+3)

y²−12y+36=7x+21

y²−12y−7x+15=0

​The equation of the parabola with vertex (−3,6) and the given directrix is y²−12y−7x+15=0.

HMH Algebra 2 Exercise 4.2 Systems Of Equations Answer Guide

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 184 Exercise 4 Answer

It is given that the vertex of a parabola is at (6,20) and focus at (6,11).

It is required to find the equation of the parabola.

To find the equation of the parabola, substitute (6,20)

for (h,k), (6,11)

for (h,p) in the equation (x−h)²

=4(p−k)(y−k).

We have to substitute (6,20)

for (h,k), (6,11)

for (h,p) in the equation (x−h)²

=4(p−k)(y−k).

Simplify the equation by using the identity (a+b)²=a²+2ab+b².

(x−6)²=4(11−20)(y−20)

x²−12x+36=4(−9)(y−20)

x²−12x+36=−36y+720

x²−12x+36y−684=0​

The equation of the parabola with vertex (6,20) and focus at (6,11) is x²−12x+36y−684=0.

Page 184 Exercise 5 Answer

It is given that the focus of a parabola is at (5,3) and directrix is x=7.

It is required to find the equation of the parabola.

To find the equation of the parabola, substitute (5,3)

for (x₁,y₁), (x,y)

for (x₂,y₂) in the formula d=√(x₂−x₁)2+(y₂−y₁)².

Then, substitute (x,7)

for (x1,y1), (x,y)

for (x2,y2) in the formula d=√(x₂−x₁)²+(y²−y₁)².

Equate the two distances and simplify the equation further.

We have to substitute (5,3)

for (x₁,y₁), (x,y)

for (x₂,y₂) in the formula d=√(x₂−x₁)²+(y₂−y₁)².

d=√(x−5)²+(y−3)²

d=√x²−10x+25+y²−6y+9

We have to substitute (x,7)

for (x₁,y₁), (x,y)

for (x₂,y₂) in the formula d=√(x₂−x₁)²

+(y₂−y₁)².​

d=√(x−x)²+(y−7)²

d=√0+y²−14y+49

Equate the two distance. Simplify the equation by squaring on both sides. ​

√x²−10x+25+y²−6y+9

=√0+y²−14y+49

x²−10x+25+y²−6y+9=y²−14y+49x²−10x−8y−15=0​

We have to plot the equation x²−10x−8y−15=0 by using a graphing tool.

The equation of the parabola with focus (5,3) and the given directrix is x²−10x−8y−15=0.

The graph of the parabola is as follows:

Page 184 Exercise 6 Answer

It is given that the focus of a parabola is at (−3,3) and directrix is x=3.

It is required to find the equation of the parabola.

To find the equation of the parabola, substitute (−3,3)

for (x₁,y₁), (x,y)

for (x₂,y₂) in the formula d=√(x₂−x₁)²+(y₂−y₁)².

Then, substitute (x,7)

for (x₁,y₁), (x,y)

for (x₂,y₂) in the formula d=√(x₂−x₁)²+(y₂−y₁)².

Equate the two distances and simplify the equation further.

We have to substitute (−3,3)

for (x₁,y₁), (x,y)

for (x₂,y₂) in the formula d=√(x₂−x₁)²+(y₂−y₁)².​

d=√(x−(−3))²+(y−3)²

d=√x²+6x+9+y²−6y+9

We have to substitute (3,y)

for (x₁,y₁), (x,y)

for (x₂,y₂) in the formula d=√(x₂−x₁)²+(y₂−y₁)².​

d=√(x−3)²+(y−y)²

d=√x²−6x+9

Equate the two distance. Simplify the equation by squaring on both sides.​

√x²+6x+9+y²−6y+9

=√x²−6x+9

x²+6x+9+y²−6y+9=x²−6x+9y²−6x+12x+9=0

Plot the equation y²−6x+12x+9=0 by using a graphing tool.

The equation of the parabola with focus (5,3) and the given directrix is y²−6x+12x+9=0

The graph of the parabola is as follows:

Page 184 Exercise 7 Answer

The equation of a parabola is given as y²−20x−6y−51=0.

It is required to write the equation in standard form and the plot the parabola along with its focus and directrix.

Write the given equation in the form (y−k)²=4p(x−h).

Then, the vertex of the parabola is (h,k), its focus is (h+p,k) and the equation of the directrix isx=h−p.

The equation can be written as (y²−6y+9)−20(x+51/20)=9.

On simplifying the equation,

(y²−6y+9)=20(x+51/20+9/20)

(y−3)²=4(5)(x−(−3))

This means that the vertex of the parabola is at (−3,3), the focus is at (2,3) and the equation of the directrix is x=−8.

We have to plot the equation (y−3)²=4(5)(x−(−3)) by using a graphing tool.

The standard form of the given equation (y−3)²=4(5)(x−(−3)).

The plot of the parabola is:

Page 184 Exercise 8 Answer

The equation of a parabola is given as x²−14x−12y+73=0.

It is required to write the equation in standard form and the plot the parabola along with its focus and directrix.

Write the given equation in the form (x−h)²=4p(y−k).

Then, the vertex of the parabola is (h,k), its focus is (h,k+p) and the equation of the directrix is y=k−p.

The equation can be written as (x²−14x+49)−12(y−73/12)=49.

On simplifying the equation,

(x²−14x+49)=12(y−73/12+49/12)

(x−7)²=12(y−24/12)

(x−7)²=4(3)(y−2)​

This means that the vertex of the parabola is at (7,2), the focus is at (7,5) and the equation of the directrix is y=−1.

We have to plot the equation (x−7)²=4(3)(y−2) by using a graphing tool.

The standard form of the given equation (x−7)²=4(3)(y−2).

The plot of the parabola is:

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 184 Exercise 9 Answer

It is given that the equation of the cross-section of a parabolic satellite dish is y=1/50x².

It is required to find the distance between the focus and the vertex of the cross-section.

If the equation of the parabola is of the form x²=4py, then the distance between the focus and the vertex is p.

Here, the given equation is x²=4(12.5)y.

Therefore, the distance between the focus and the vertex is 12.5 inches.

The focus of the satellite dish is 12.5 inches far from the vertex of the cross-section.

Page 185 Exercise 10 Answer

It is a given equation of parabola y+1=1/16(x−2)².

It is required to convert the given equation in standard form of the parabola and graph the parabola.

To solve this, convert it in standard form. Then plot the correct graph for the given equation.

It is a given equation of parabola y+1=1/16(x−2)².

Now to convert equation in standard form multiply 16,

Then, y+1=1/16(x−2)²

16(y+1)=(x−2)²

4⋅4(y+1)=(x−2)²

So, the equation is,(x−2)²=16(y+1)

By comparing the obtained equation with standard equation,​

h=2 k=−1​

Now plotting the parabola on graph,

The equation will be (x−2)²=16(y+1).

Graph of the parabola is,

Page 185 Exercise 11 Answer

It is given equation of parabola y−1=1/16(x+2)²

It is required to convert the given equation in standard form of the parabola and graph the parabola.

To solve this, convert it in standard form. Then plot the correct graph for the given equation.

It is given equation of parabola y−1=1/16(x+2)²

Converting equation in standard form,

y−1=1/16(x+2)²

16(y−1)=(x+2)²

4⋅4(y−1)=(x+2)²

So, the equation is, (x+2)²=4⋅4⋅(y−1)

By comparing the obtained equation with standard equation,​

h=−2 k=1​

Now plotting the parabola on graph,

The equation is, (x+2)²=4⋅4⋅(y−1)

Graph of the parabola is,

Step-By-Step Solutions For HMH Algebra 2 Module 4 Exercise 4.2

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 185 Exercise 12 Answer

It is a given equation of parabola x+1=−1/16(y−2)².

It is required to convert the given equation in standard form of the parabola and graph the parabola.

To solve this, convert it in standard form. Then plot the correct graph for the given equation.

The given equation of parabola is x+1=−1/16(y−2)².

Converting equation in standard form,​

x+1=−1/16(y−2)² 

−16(x+1)=(y−2)²

−4⋅4(x+1)=(y−2)²

So, the equation is,(y−2)²=−16(x+1)

By comparing the obtained equation with standard equation,​

h=−1 k=2​

Now plotting the parabola on graph,

The equation is,(y−2)²=−16(x+1)

Graph of the parabola is,

Page 186 Exercise 13 Answer

It is given an upward- opening parabola with focus(−p,0) and directrix x=p.

It is required to find the equation of the parabola.

To solve this, find the vertex of parabola then substitute it on the standard equation of parabola to get the equation of parabola.

Given parabola has focus(−p,0) and directrix x=p.

From this vertex will be,(h,k)=(0,0)

So, h=0 k=0

Now, substituting the values on standard equation,

(y−0)²=4⋅p⋅(x−0)

y²=4px​

Equation of the parabola is, y²=4px.

Page 186 Exercise 14 Answer

It is given that a ball is projected in a parabolic path y−4=−4/1521(x−39)².

The tennis net is $3feet$ high and the total length of the court is 78 feet.

The position of player is x=0

It is required to find out how far the net is located from the player.

To solve this, find the distance between the player and net which will be equal to half of the total length of the court.

The tennis net is 3 feet high and the total length of the court is 78 feet.

The position of player is x=0

Now, the distance between the players and net is,1/2×78=39 feet

So, distance between the player and net =39 feet.

Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations Page 186 Exercise 15 Answer

It is given that a ball is projected in a parabolic path y−4=−4/1521(x−39)².

The tennis net is 3 feet high and the total length of the court is 78 feet.

The position of player is x=0

It is required to show why the ball will go over the net.

To solve this, write the equation in standard form then find the value of vertical distance y by substituting the value of x=39.

Since, the net is at x=39.

Given equation is,​ y−4=−4/1521(x−39)²

(x−39)²=−1521/4(y−4)

Substituting the value x=39 to get the value of y,

(39−39)²=−1521/4

(y−4)0=−1521/4(y−4)

y−4=0

y=4

Now the height of the net is 3 feet but the ball goes to a height of 4 feet.

Ball does not touch the net because the height of the net is 3 feet but the ball goes to a height of 4 feet.

Page 186 Exercise 16 Answer

It is given that a ball is projected in a parabolic path y−4=−4/1521(x−39)².

The tennis net is 3 feet high and the total length of the court is 78 feet.

The position of player is x=0

It is required to show that the ball lands either inside the court or on the opposite end line.

To solve this, find the range of the trajectory of the ball.

Given equation is, y−4=−4/1521(x−39)²

(x−39)²=−1521/4(y−4)

Total range of the ball is, 2⋅39=78 feet

So, the ball will land on the opposite end line on the other side of the court.

The ball will land on the opposite end line on the other side of the court.

Page 187 Exercise 17 Answer

It is required to find the length of the latus rectum of the parabola.

To solve this let’s consider a parabola y²=4ax which has vertex (0,0) and focus (a,0).

Now find the endpoints of the latus rectum which will lie vertically above and below the focus.

So, there x− coordinate will be a.

Then substitute a in place of x to get the value of y for the points. Then find the distance between the points.

Let’s consider a parabola y²=4ax which has vertex (0,0) and focus (a,0).

Then x− coordinate of the latus rectum is a. Now solving for y− coordinate​

y²=4ax

y²=4⋅a⋅a

y²=(2a)²

y=±2a

So, the endpoints of latus rectum are (a,2a),(a,−2a)

Since x− coordinate of the points are the same, taking the distance between the endpoints of the latus rectum is 4a by laterally solving.

So, length of latus rectum =4a

Length of latus rectum =4a