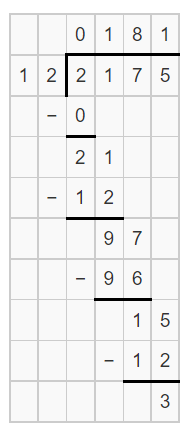
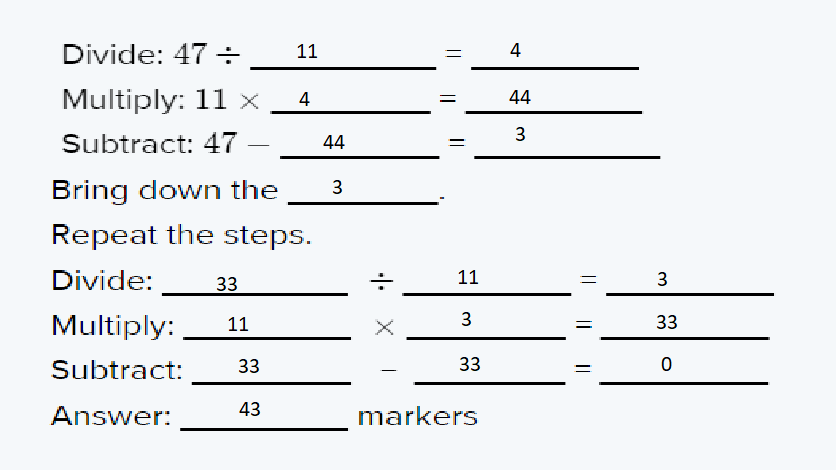
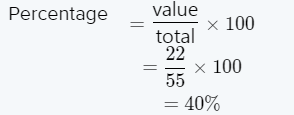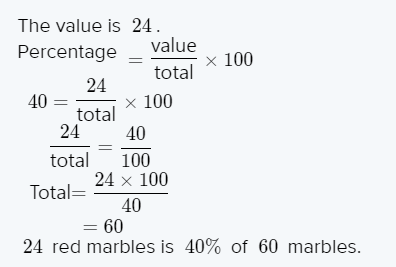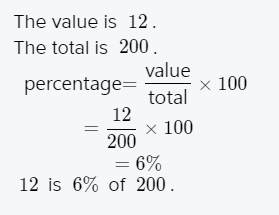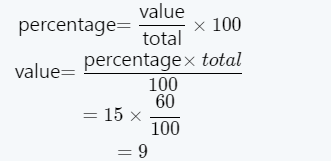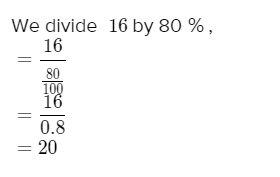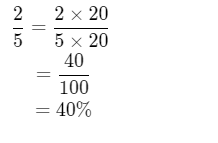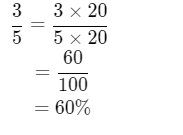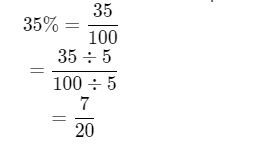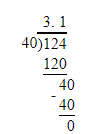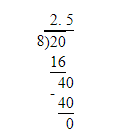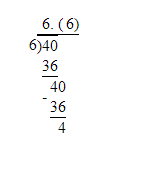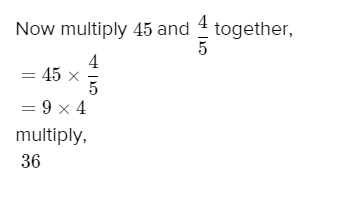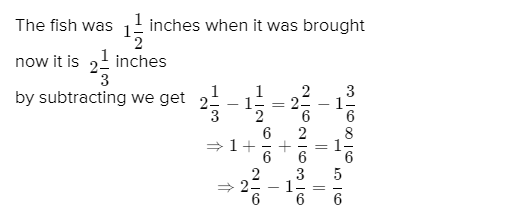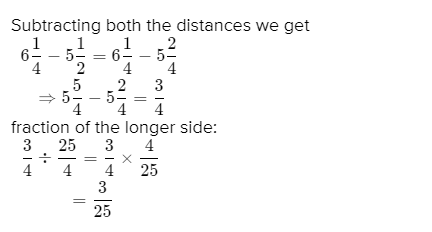Go Math! Practice Fluency Workbook Grade 6 California 1st Edition Chapter 8 Percents
Page 51 Problem 1 Answer
Given: The percent was given as 0.17
Find: Here, Write each decimal as a percent.
Solution: To convert a decimal to a percent, move the decimal point two places to the right and then write the % symbol after the number.
Therefore: 0.17=17%
The result of converting a decimal to a percent,17%
Page 51 Problem 2 Answer
The given decimal number is 0.56 .We have to write the given decimal number in percentage form.
Multiply by 100 to convert a number from decimal to percent then add a percent sign %.
We have to multiply the given decimal number by 100 to convert it into percent and then add the percent sign.
⇒0.56×100=56/100×100=56%
0.56 is written as 56%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 3 Answer
The given decimal number is 0.04. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a number from decimal to percent then add a percent sign %.
We have to multiply the given decimal number by 100 to convert it into percent and then add the percent sign.
⇒0.04×100=4/100×100=4%
0.04 is written as 4%.

Go Math Grade 6 Exercise 8.2 Understanding Percents Answers
Page 51 Problem 4 Answer
The given decimal number is 0.7.We have to write the given decimal number in percentage form.
Multiply by 100 to convert a number from decimal to percent then add a percent sign %.
We have to multiply the given decimal number by 100 to convert it into percent and then add the percent sign.
⇒0.7×100=7/10×100 = 70%.
0.7 is written as 70%.
Page 51 Problem 5 Answer
The given decimal number is 0.025. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a number from decimal to percent then add a percent sign %.
We have to multiply the given decimal number by 100 to convert it into percent and then add the percent sign.
⇒0.025×100=25/1000×100
=25/10
=2.5%
0.025 is written as 2.5%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 6 Answer
The given decimal number is 0.803. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a number from decimal to percent then add a percent sign %.
We have to multiply the given decimal number by 100 to convert it into percent and then add the percent sign.
⇒0.803×100=803/1000×100=803/10=80.3%
0.803 is written as 80.3%.
Page 51 Problem 7 Answer
The given decimal number is 1.3. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a number from decimal to percent then add a percent sign %.
We have to multiply the given decimal number by 100 to convert it into percent and then add the percent sign.
⇒1.3×100 = 13/10×100.
=13×10
=130%
1.3 is written as 130%.
Page 51 Problem 8 Answer
The given decimal number is 2.10. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a number from decimal to percent then add a percent sign %.
We have to multiply the given decimal number by 100 to convert it into percent and then add the percent sign.
⇒2.1×100=21/10×100
=21×10
=210%
2.1 is written as 210%.
Solutions For Go Math Grade 6 Exercise 8.2 Understanding Percents
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 9 Answer
The given fraction is 13/50. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒13/50×100=13×2
=26%
13/50 is written as 26%.
Page 51 Problem 10 Answer
The given fraction is 3/5. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒3/5×100=3×20
=60%
3/5 is written as 60%.
Page 51 Problem 11 Answer
The given fraction is 3/20. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒3/20×100=3×5
=15%
3/20 is written as 15%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 12 Answer
The given fraction is 127/100.We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒127/100×100=127%.
127/100 is written as 127%.
Page 51 Problem 13 Answer
The given fraction is 5/8. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒5/8×100
=0.625×100
=62.5%
5/8 is written as 62.5%.
Page 51 Problem 14 Answer
The given fraction is 45/90. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒45/90×100
=45/9×10
=5×10
=50%
45/90 is written as 50%.
Go Math Grade 6 Understanding Percents Exercise 8.2 Key
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 15 Answer
The given fraction is 7/5. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒7/5×100
=7×20
=140%
7/5 is written as 140%.
Page 51 Problem 16 Answer
The given fraction is 19/25. We have to write the given decimal number in percentage form.
Multiply by 100 to convert a fraction to percent then add a percent sign %.
We have to multiply the given fraction by 100 to convert it into percent and then add the percent sign.
⇒19/25×100
=19×4
=76%
19/25 is written as 76%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 17 Answer
Three numbers are given: 0.3,19/50,22%. We have to arrange the given numbers in increasing order.
We can convert all the given numbers either as fractions or decimal numbers or as a percent.
The given first number is 0.3. To convert the decimal number in percent, we have to multiply it by 100 and then add percent sign, “%”.
⇒0.3×100
=3/10×100
=3×10
=30%
So, 0.3 is 30%.
The second given number is 19/50.
To convert the fraction in percent, we have to multiply it by 100 and then add percent sign, “%”.
⇒19/50×100
=19×2
=38%.
So, 19/50 is 38%.
The given third number is 22% which is already a percent. Now, on comparing all the three percents, we get
∴38%>30%>22%.
⇒19/50>0.3>22%.
The final order of the numbers from the least to greatest is 22%<0.3<19/50.
Page 51 Problem 18 Answer
Three numbers are given: 11%,1/8,2/25. We have to arrange the given numbers in increasing order.
We can convert all the given numbers either as fractions or decimal numbers or as a percent.
The given first number 11% is already a percent. So, we have to convert the remaining two fractions, 1/8&2/25 to percent now.
∴To convert the fraction in percent, we have to multiply it by 100 and then add percent sign, “%”.
⇒1/8×100
=25/2%
=12.5%
and 2/25×100
=2×4
=8%.
Now, on comparing all the three percents, we get
∴8%<11%<12.5%,
⇒2/25<11%<1/8.
Page 51 Problem 19 Answer
Three numbers are given: 5/8,0.675,5%.
We have to arrange the given numbers in increasing order.We can convert all the given numbers either as fractions or decimal numbers or as a percent.
The first given number is 5/8. To convert the fraction in percent, we have to multiply it by 100 and then add the percent sign, “%”.
⇒5/8×100
=5×12.5
=62.5%.
So, 5/8 is 62.5%.
The given second number is 0.675. To convert the decimal number in percent, we have to multiply it by 100 and then add the percent sign, “%”.
⇒0.675×100
=675/1000×100
=675/10%
=67.5%.
So, 0.675 is 67.5%.
The given third number is 5% which is already a percent. Now, on comparing all the three percents, we get
∴5%<62.5%<67.5%,
⇒5%<5/8<0.675.
The final order of the numbers from the least to greatest is 5%<5/8<0.675.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 20 Answer
Three numbers are given: 1.25,0.51,250% . We have to arrange the given numbers in increasing order.
We can convert all the given numbers either as fractions or decimal numbers or as a percent.
The first two given numbers are 1.25&0.51 which are decimal numbers.
To convert the decimal number into percent, we have to multiply it by 100 and then add the percent sign, “%”.
⇒1.25×100
=125/100×100
=125%
and
⇒0.51×100
=51/100×100
=51%.
The given third number is 250% which is already a percent. Now, on comparing all the three percents, we get
∴51%<125%<250%,
⇒0.51<1.25<250%.
The final order of the numbers from the least to greatest is 0.51<1.25<250%.
Page 51 Problem 21 Answer
Three numbers are given: 350/100,0.351,27%. We have to arrange the given numbers in increasing order.
We can convert all the given numbers either as fractions or decimal numbers or as percent.
The first given number is 350/100.
To convert the fraction in percent, we have to multiply it by 100 and then add the percent sign, “%”.
⇒350/100×100=350%
So, 350/100 is 350%.
The given second number is 0.351.
To convert the decimal number into percent, we have to multiply it by 100 and then add the percent sign, “%”.
⇒0.351×100
=351/1000×100
=351/10%
=35.1%.
So, 0.351/ is 35.1%.
The given third number is 27% which is already a percent. Now, on comparing all the three percents, we get
∴27%<35.1%<350%,
⇒27%<0.351<350/100.
The final order of the numbers from the least to greatest is 27%<0.351<350/100.
Page 51 Problem 22 Answer
Given: – There are three given numbers 4/8,0.05,51%. We have to order these number from the least to greatest.
We can order the numbers by simplifying the fractions and percentages until it becomes a number with a decimal point which makes comparison easier.
Simplifying the first fraction 4/8
=2⋅2/2⋅2⋅2
=1/2
=0.5
The second number is already in its decimal representation. There is no further simplification possible.
The third number is in its percentage form. Using the definition of percentage, we can express the number as 51%=51/100
=0.51
Now, comparing the three numbers, we have 0.51>0.5>0.05
This implies 51%>4/8>0.05
The final order of the numbers from the least to greatest is 0.05<4/8<51%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 51 Problem 23 Answer
Given: – During one hour, 6 out of 25 cars were travelling above the speed limit.
We have to find what percent of the cars were traveling above the speed limit.
Multiplying the numerator and denominator with a number that can make the denominator equal to 100.
The corresponding numerator is the required percentage.
The fraction form for the cars travelling above the speed limit is 6/25.
Multiplying the numerator and denominator with 4, we get
=6⋅4/25⋅4
=24/100
The numerator of the fraction with denominator 100 is the required percentage. 6/25=24%
The percentage of the cars that were travelling above the speed limit is 24%.
Page 51 Problem 24 Answer
Given: – At Oaknoll School, 90 out of 270 students own computers.
We have to find the percentage of students who do not own computers.
Multiplying the numerator and denominator with a number that can make the denominator equal to 100.
The corresponding numerator is the required percentage.
The number of students who do not use computers is 270−90=180.
The fraction form for the number of students who don’t use the computers is 180/270.
Simplifying the fraction, we get 90⋅2/90⋅3=2/3
The numerator of the fraction with denominator 100 is the required percentage. After rounding off to the nearest tenth, the percentage will be 2/3=66.7%

The percent of students at Oaknoll School that do not own computers (rounded to the nearest tenth) is 66.7%.
Page 52 Exercise 1 Answer
Given: – The given number in decimal form is 0.34.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 3.
After shifting the decimal point two places to the right, the number becomes 034.0
Now adding the percentage symbol, the final value in percentage form is 34%.
Writing the decimal as a percent, we get 34%.
Page 52 Exercise 2 Answer
Given: – The given number in decimal form is 0.06.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 0.
After shifting the decimal point two places to the right, the number becomes 006.0 (or) 6.
Now adding the percentage symbol, the final value in percentage form is 6%.
Writing the decimal as a percent, we get 6%.
Detailed Solutions For Go Math Grade 6 Exercise 8.2 Understanding Percents
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 3 Answer
Given: – The given number in decimal form is 0.93.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 9.
After shifting the decimal point two places to the right, the number becomes 093.0 (or) 93.
Now adding the percentage symbol, the final value in percentage form is 93%.
Writing the decimal as a percent, we get 93%.
Page 52 Exercise 4 Answer
Given: – The given number in decimal form is 0.57.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 5.
After shifting the decimal point two places to the right, the number becomes 057.0 (or) 57.
Now adding the percentage symbol, the final value in percentage form is 57 %.
Writing the decimal as a percent, we get 57%.
Page 52 Exercise 5 Answer
Given: – The given number in decimal form is 0.8.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 8.
After shifting the decimal point two places to the right, the number becomes 080.0 (or) 80.
Now adding the percentage symbol, the final value in percentage form is 80%.
Writing the decimal as a percent, we get 80%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 6 Answer
Given: – The given number in decimal form is 0.734.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 7.
After shifting the decimal point two places to the right, the number becomes 073.4 (or) 73.4.
Now adding the percentage symbol, the final value in percentage form is 73.4 %.
Writing the decimal as a percent, we get 73.4%.
Page 52 Exercise 7 Answer
Given: – The given number in decimal form is 0.082.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 0.
After shifting the decimal point two places to the right, the number becomes 008.2 (or) 8.2.
Now adding the percentage symbol, the final value in percentage form is 8.2%
Writing the decimal as a percent, we get 8.2%.
Page 52 Exercise 8 Answer
Given: – The given number in decimal form is 0.225.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 2.
After shifting the decimal point two places to the right, the number becomes 022.5 (or) 22.5.
Now adding the percentage symbol, the final value in percentage form is 22.5%
Writing the decimal as a percent, we get 22.5%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 9 Answer
Given: – The given number in decimal form is 0.604.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 6.
After shifting the decimal point two places to the right, the number becomes 060.4 (or) 60.4.
Now adding the percentage symbol, the final value in percentage form is 60.4%.
Writing the decimal as a percent, we get 60.4%.
Page 52 Exercise 10 Answer
Given: – The given number in decimal form is 0.09.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 0.
After shifting the decimal point two places to the right, the number becomes 009.0 (or) 9.
Now adding the percentage symbol, the final value in percentage form is 9%.
Writing the decimal as a percent, we get 9%.
Page 52 Exercise 11 Answer
Given: – The given number in decimal form is 0.518.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 0 and 5.
After shifting the decimal point two places to the right, the number becomes 051.8 (or) 51.8.
Now adding the percentage symbol, the final value in percentage form is 51.8 %.
Writing the decimal as a percent, we get 51.8%.
Page 52 Exercise 12 Answer
Given: – The given number in decimal form is 1.03.
We have to find the percentage form of this decimal.
By appropriately shifting the decimal point, we can express a decimal in its percentage form.
The given number has its decimal point in between 1 and 0.
After shifting the decimal point two places to the right, the number becomes 103.0 (or) 103.
Now adding the percentage symbol, the final value in percentage form is 103%.
Writing the decimal as a percent, we get 103%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 13 Answer
Given: – The given fraction is 3/10.
We have to express the fraction as a percentage.
Multiplying the numerator and denominator with a number that can make the denominator equal to 100.
The corresponding numerator is the required percentage.
Multiply the numerator and the denominator with 10.
3⋅10/10⋅10=30/100
The numerator of the fraction with denominator 100 is the required percentage.
3/10=30%
Writing the fraction as a percent, we get 30%.
Page 52 Exercise 14 Answer
Given: – The given fraction is 2/50.
We have to express the fraction as a percentage.
Multiplying the numerator and denominator with a number that can make the denominator equal to 100.
The corresponding numerator is the required percentage.
Multiply the numerator and denominator with 2.
2⋅2/50⋅2=4/100
The numerator of the fraction with denominator 100 is the required percentage.
4/100=4%
Writing the fraction as a percentage, we get 4%.
Page 52 Exercise 15 Answer
Given: – The given fraction is 7/20.
We have to express the fraction as a percentage.
Multiplying the numerator and denominator with a number that can make the denominator equal to 100.
The corresponding numerator is the required percentage.
Multiply the numerator and denominator by 5.
7⋅5/20⋅5=35100
The numerator of the fraction with denominator 100 is the required percentage.
7/20=35%
Writing the fraction as a percentage, we get 35%.
Practice Problems For Go Math Grade 6 Exercise 8.2 Understanding Percents
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 16 Answer
Given: – The given fraction is 1/5.
We have to express the fraction as a percentage.
Multiplying the numerator and denominator with a number that can make the denominator equal to 100.
The corresponding numerator is the required percentage.
Multiply the numerator and denominator with 20.
1⋅20/5⋅20=20/100
The numerator of the fraction with denominator 100 is the required percentage.
1/5=20%
Writing the fraction as a percentage, we get 20%.
Page 52 Exercise 17 Answer
Given: – The given fraction is 1/8.
We have to express the fraction as a percentage.
Multiplying the numerator and denominator with a number that can make the denominator equal to 100.
The corresponding numerator is the required percentage.

The numerator of the fraction with denominator 100 is the required percentage.
1/8=12.5%
Writing the fraction as a percentage, we get 12.5%.
Page 52 Exercise 18 Answer
Given: The fraction is 3/25
To find: Express the fraction as a percent.Summary: To convert a fraction into a percent, we divide the numerator by the denominator.
Multiply the decimal with 100. Another way is to multiply the numerator and the denominator with some number so that the denominator becomes 100.
The corresponding numerator is the required percentage.
Multiply the numerator and the denominator with 4.
3×4/25×4=12/100
The numerator of the fraction with denominator 100 is the required percentage.
3/25=12%
We can write the fraction 3/25 as 12%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 19 Answer
Given: The fraction is 3/4
To find: Express the fraction as a percent.Summary: To convert a fraction into a percent, we divide the numerator by the denominator.
Multiply the decimal thus obtained with 100.
Divide the numerator by the denominator.
3/4=0.75
Multiply the decimal with 100.
0.75×100=75
3/4=75%
We can write the fraction 3/4 as 75%.
Page 52 Exercise 20 Answer
Given: The fraction is 23/50.
To find: Express the fraction as a percent.
Summary: We can convert a fraction into a percent, by first dividing the numerator by the denominator and then multiplying the decimal with 100.
Another way is to multiply the numerator and the denominator with some number so that the denominator becomes 100, and the numerator is the percentage.
Multiply the numerator and the denominator with 2.
23×2/50×2=46/100
The numerator of the fraction with denominator 100 is the required percentage.
23/50=46%
Converting the fraction into percentage we get, 23/50
=46%.
Page 52 Exercise 21 Answer
Given: The fraction is 11/20.
To find: Express the fraction as a percent.
Summary: To convert a fraction into a percent, we divide the numerator by the denominator.
Multiply 100 to the decimal. Or else, multiply the numerator and the denominator with some number so that the denominator becomes 100.
And the corresponding numerator is the required percentage.
Multiply the numerator and the denominator with 5.
11×5/20×5=55/100.
The numerator of the fraction with denominator as 100 is the percentage.
11/20=55%.
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 22 Answer
Given: The fraction is 43/50
To find: Express the fraction as a percent.
Summary: First we divide the numerator by the denominator. Multiply the decimal with 100.
Another way is to multiply the numerator and the denominator with some number so that the denominator becomes 100.
Then the corresponding numerator becomes the required percentage.
Multiply the numerator and the denominator with 2.
43×2/50×2=86/100.
The numerator of the fraction with denominator as 100 is the required percentage.
43/50=86%.
Converting the fraction into percentage, we get, 43/50=86%.
Page 52 Exercise 23 Answer
Given: The fraction is 24/25
To find: Express the fraction as a percent.Summary: In order to convert a fraction into a percent, divide the numerator by the denominator.
Multiply the decimal with 100. Alternate way is to multiply the numerator and the denominator with some number so that the denominator becomes 100, so that the corresponding numerator is the required percentage.
Multiply both numerator and the denominator with 4.
24×4/25×4=96/100.
The required percentage is the numerator of the fraction with denominator as 100.
24/25=96%.
Converting the fraction to the percentage we get,
24/25=96%.
Step-By-Step Solutions For Go Math Grade 6 Understanding Percents Exercise 8.2
Go Math Grade 6 Exercise 8.2: Understanding Percents Solutions Page 52 Exercise 24 Answer
Given: The fraction is 7/8.
To find: Express the fraction as a percent.
Summary: To convert a fraction into a percent, first we divide the numerator by the denominator.
Then multiply the decimal with 100. Another way is to multiply the numerator and the denominator with some number so that the denominator becomes 100.
The corresponding numerator is the required percentage.
Divide the numerator by the denominator.
7/8=0.875
Multiply the decimal with 100.
0.875×100=87.5
7/8=87.5%.
We can write the given fraction 7/8 as 87.5%
Go Math Answer Key