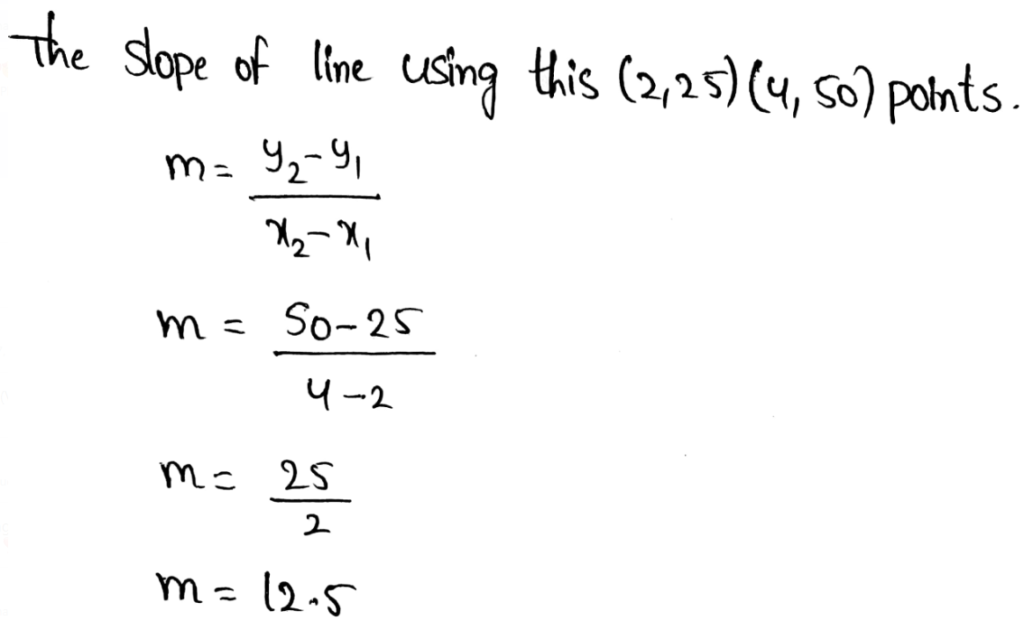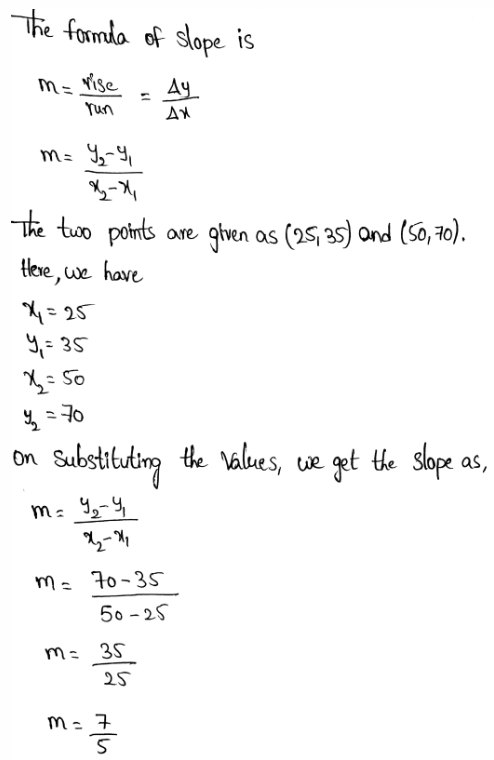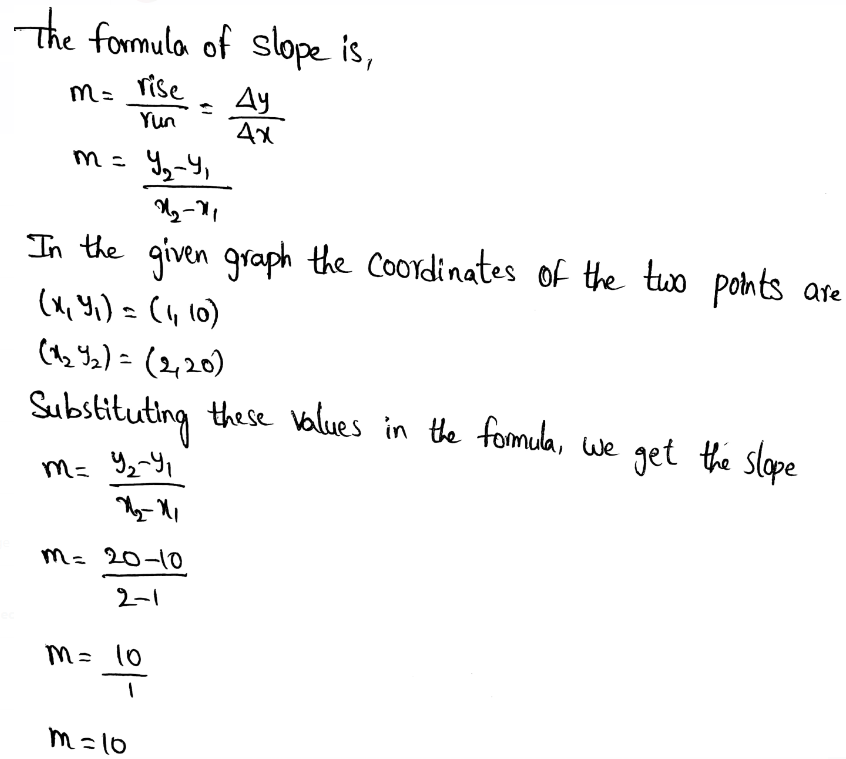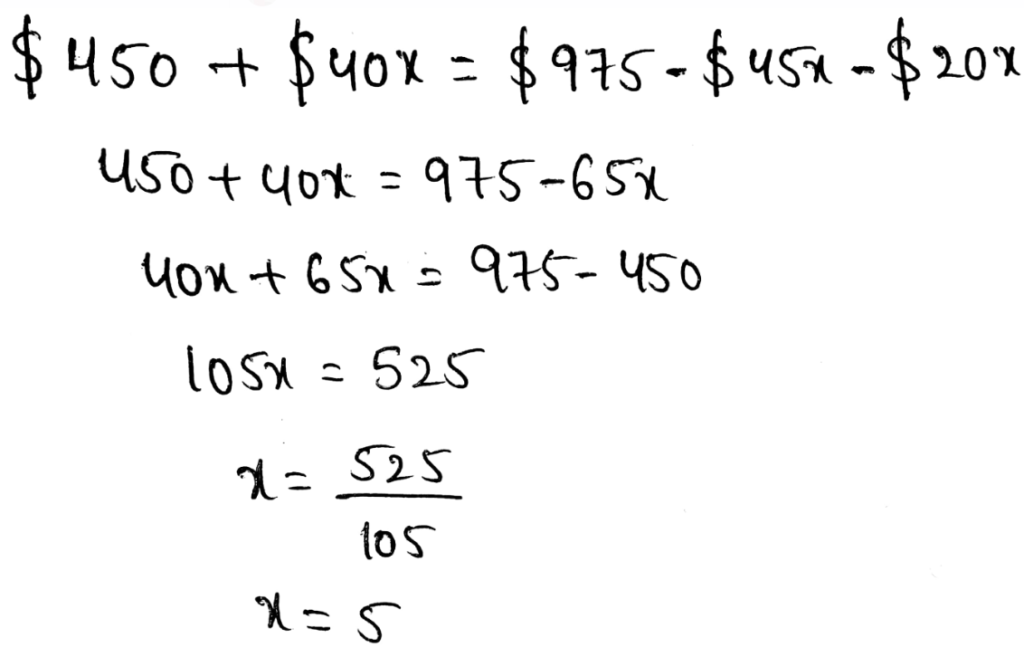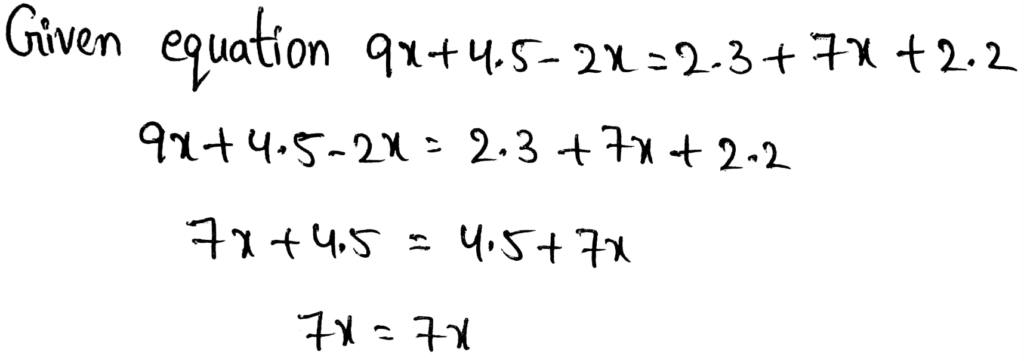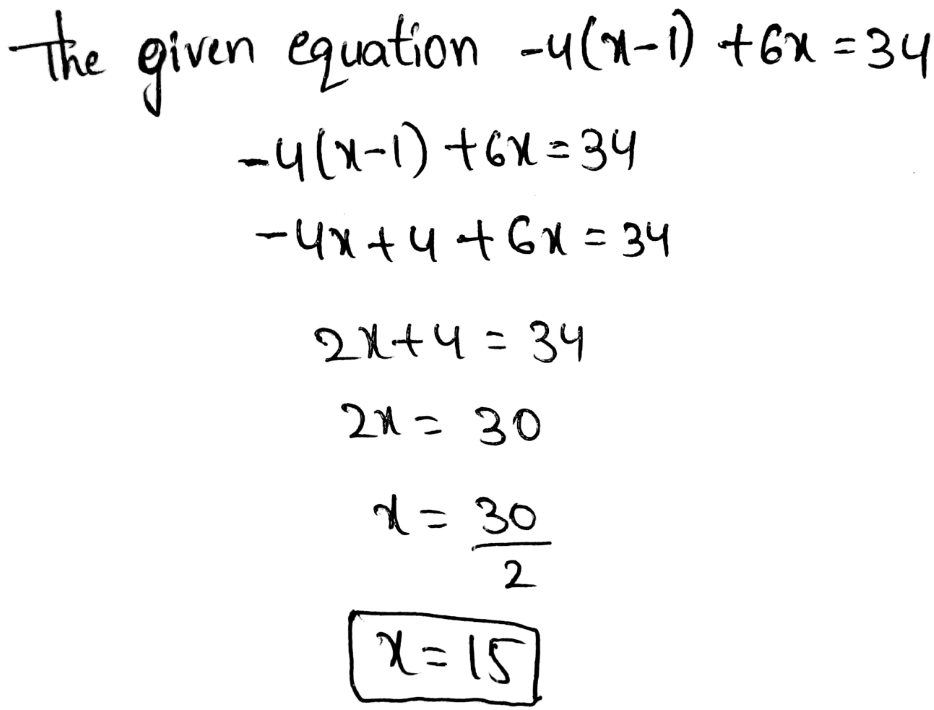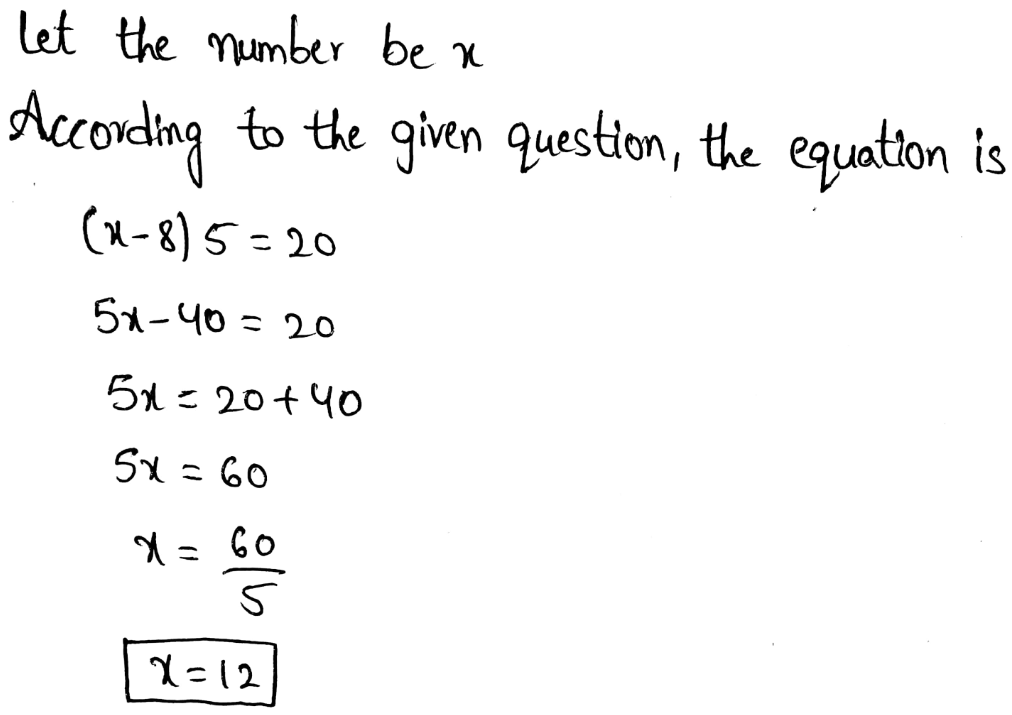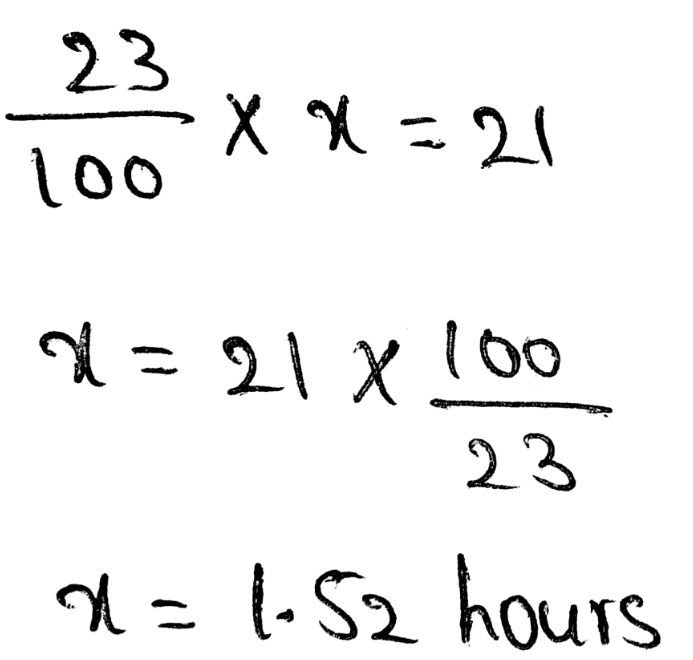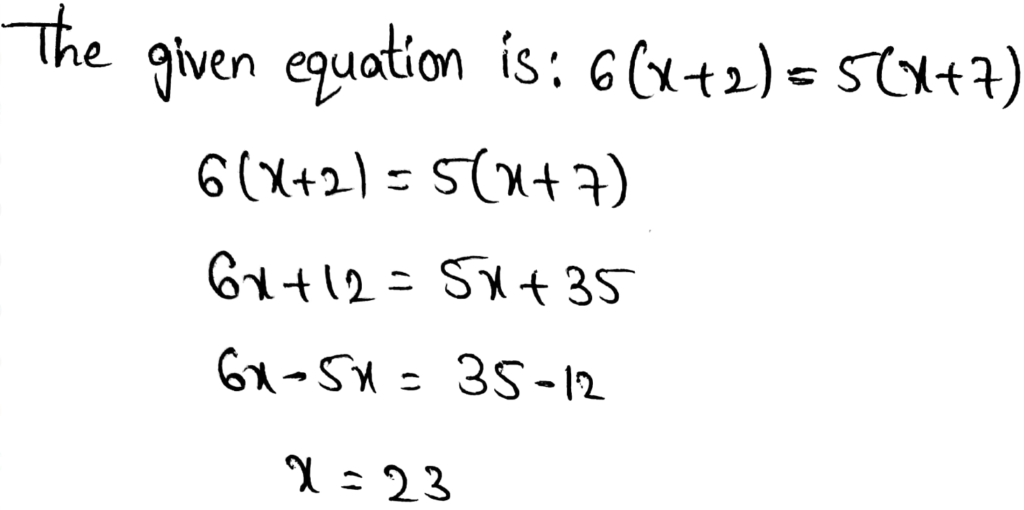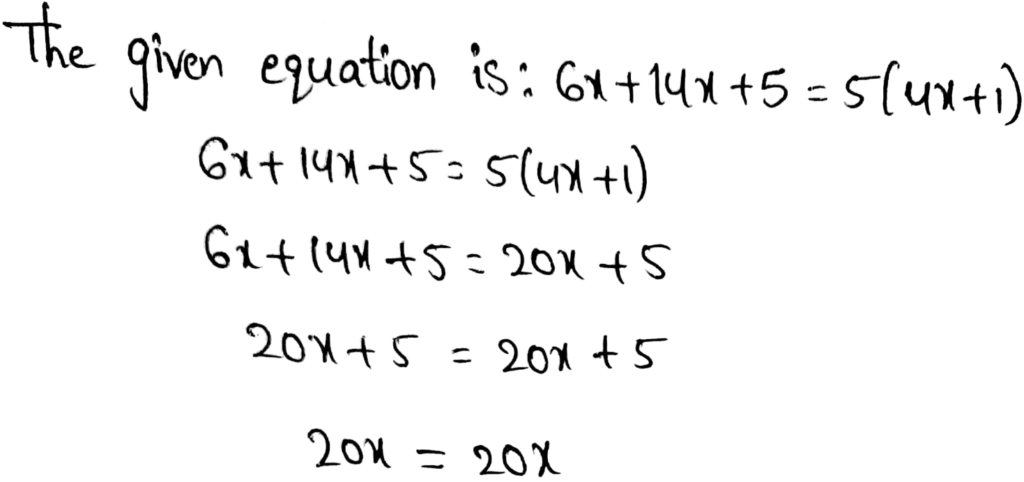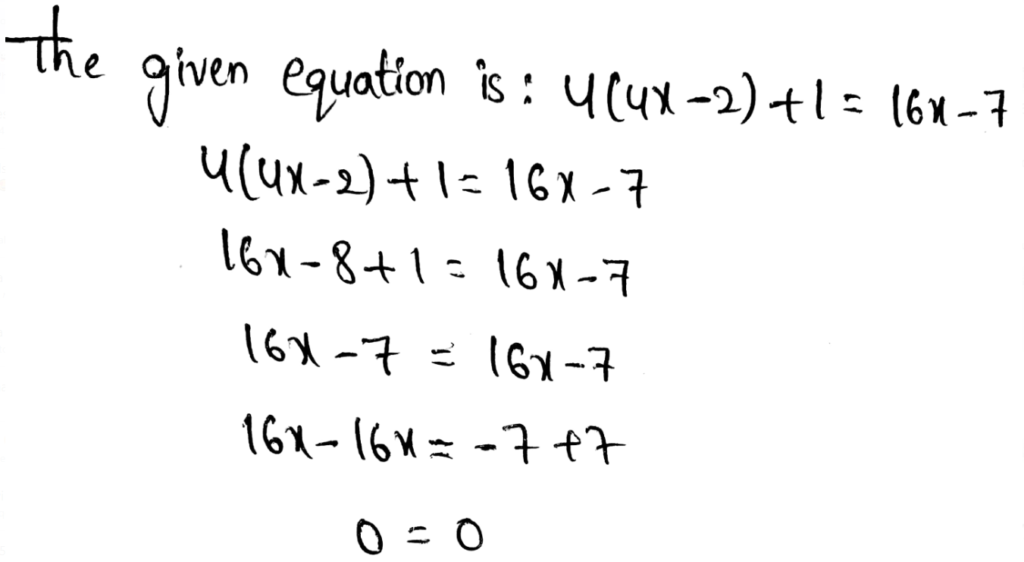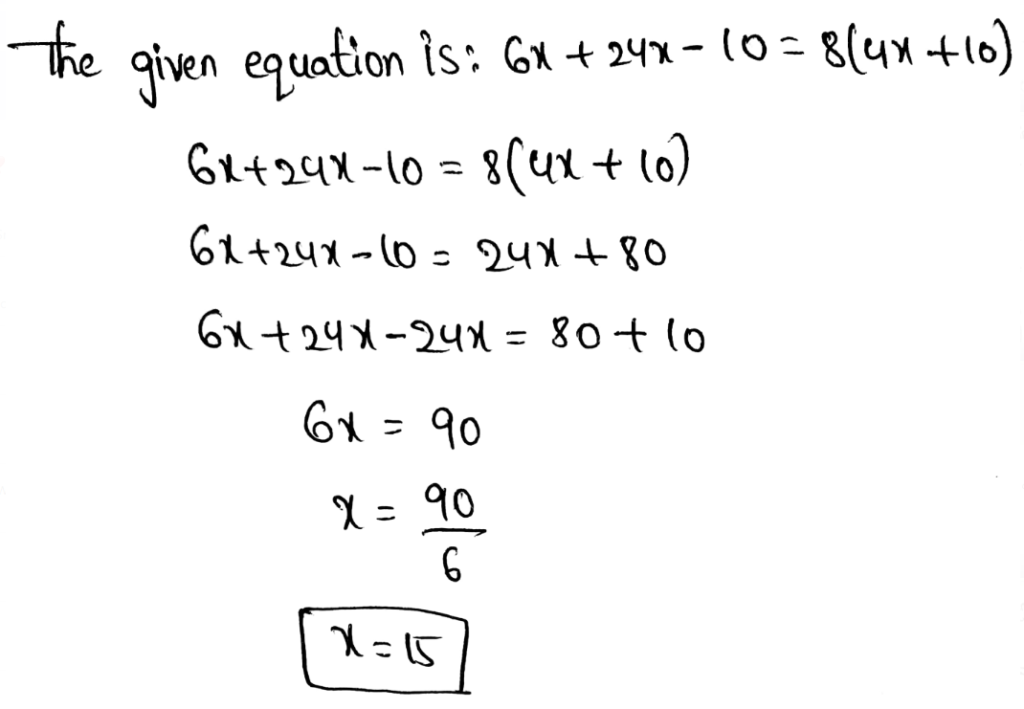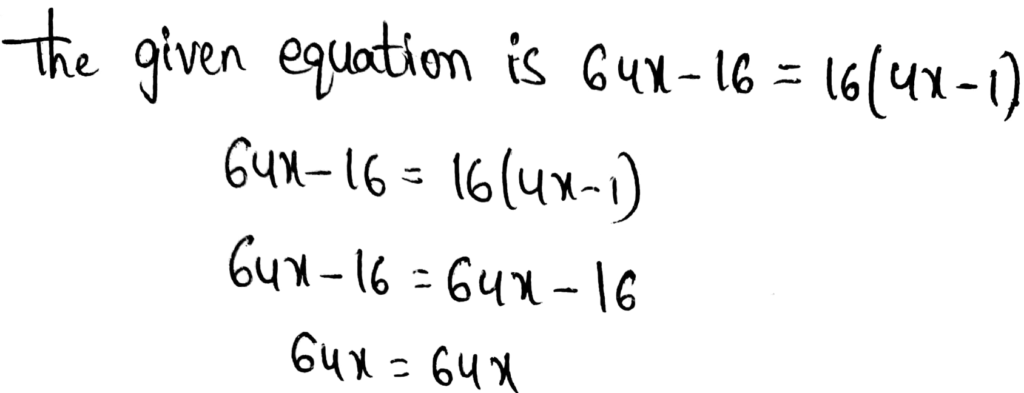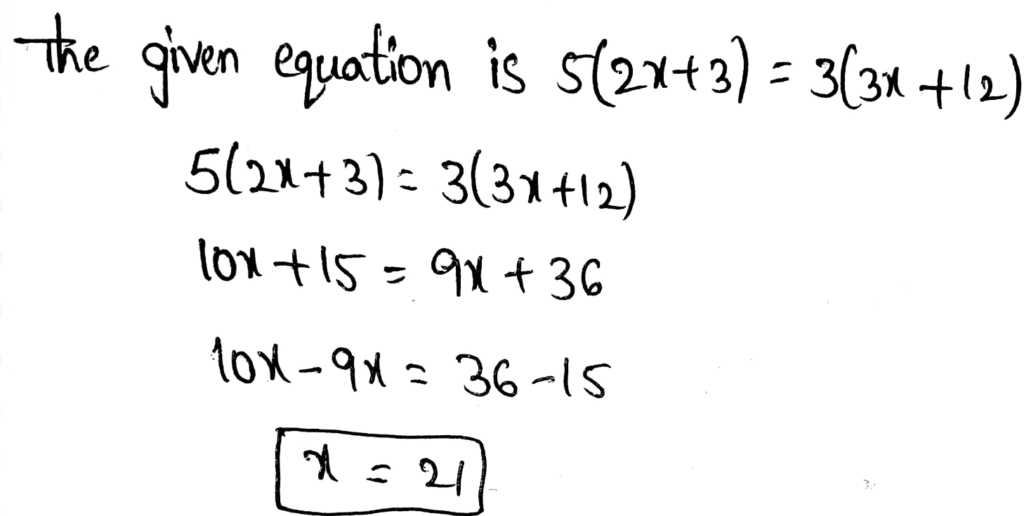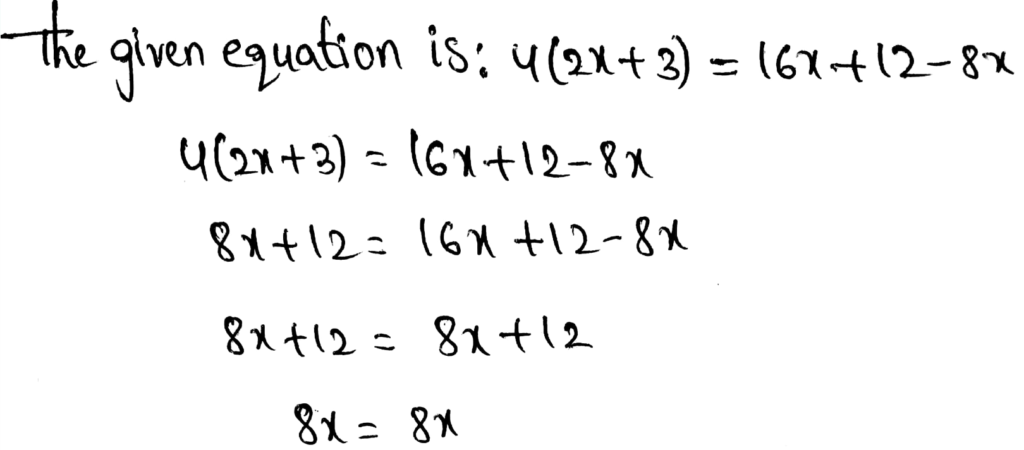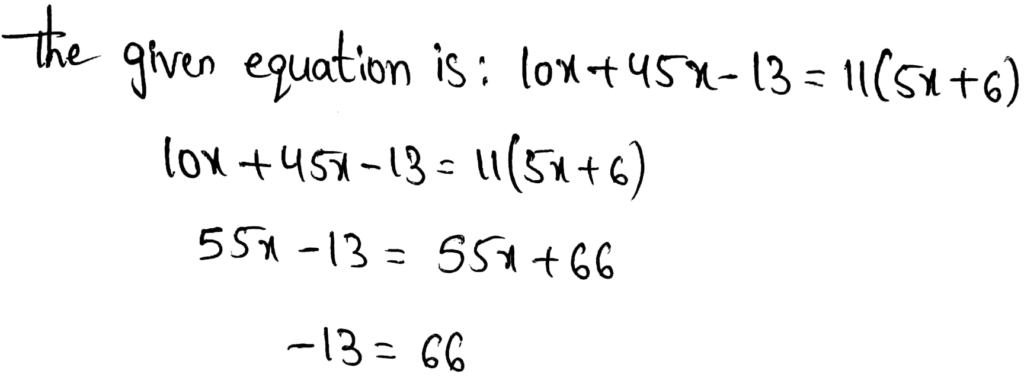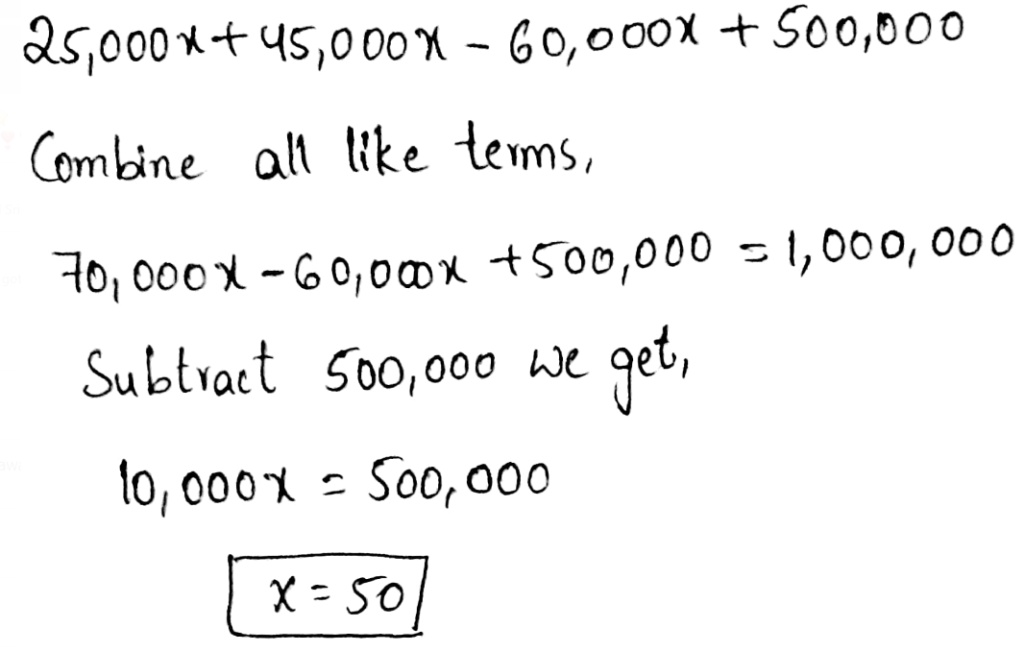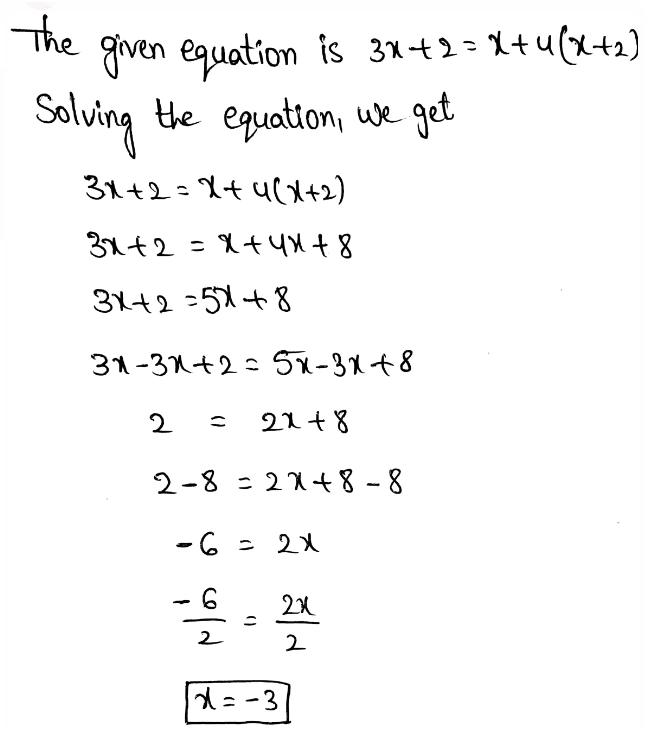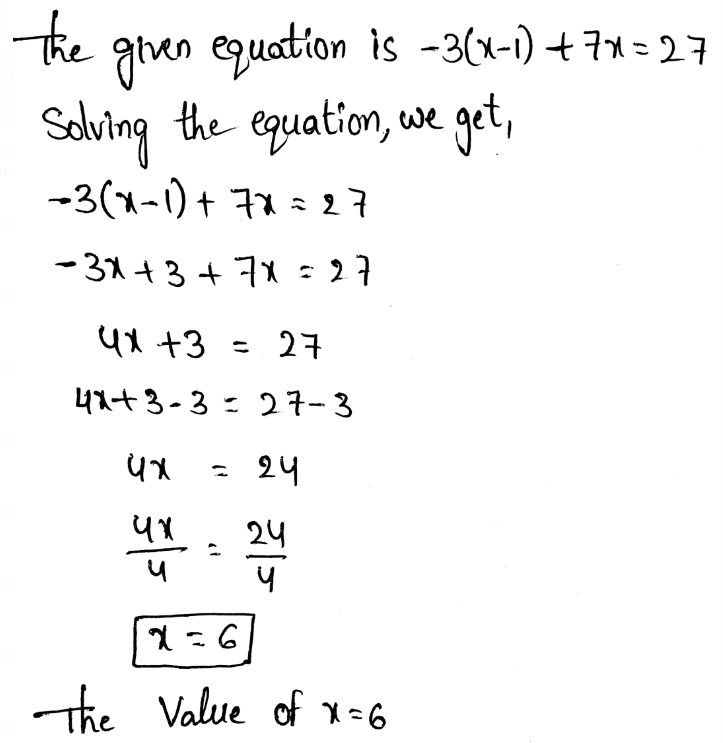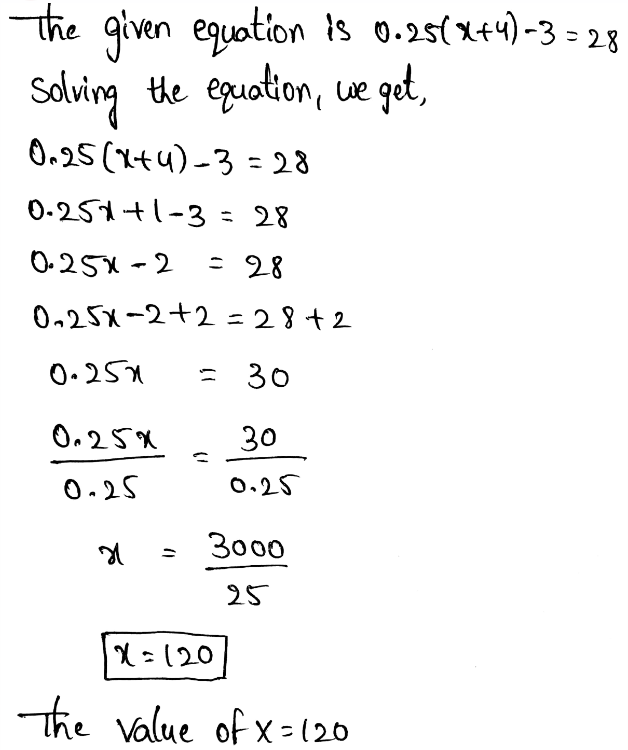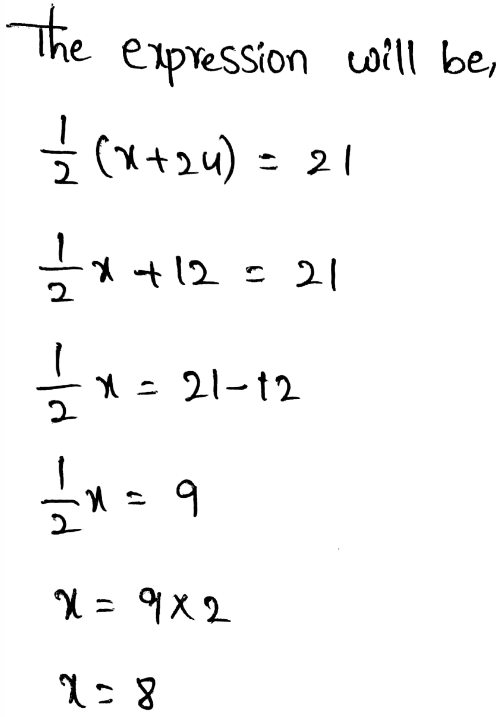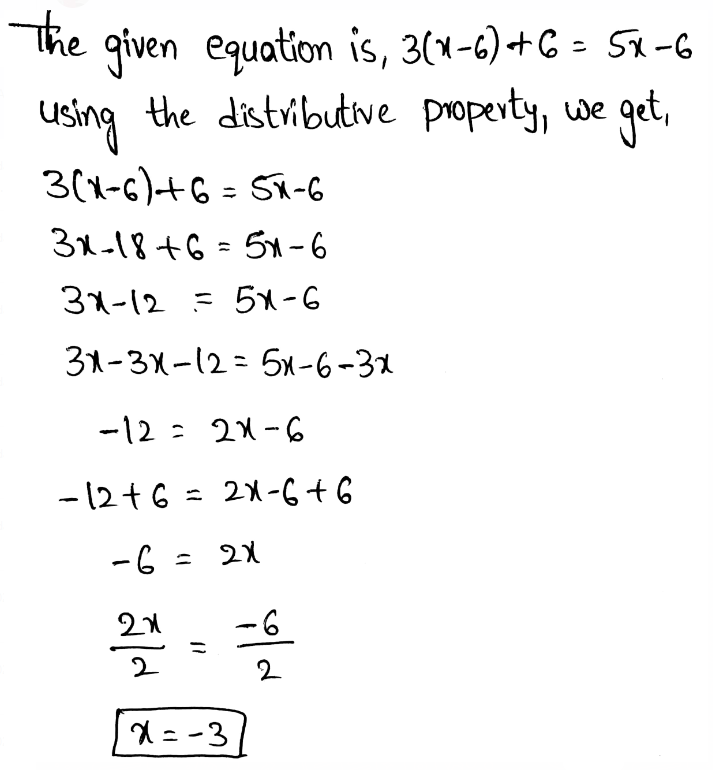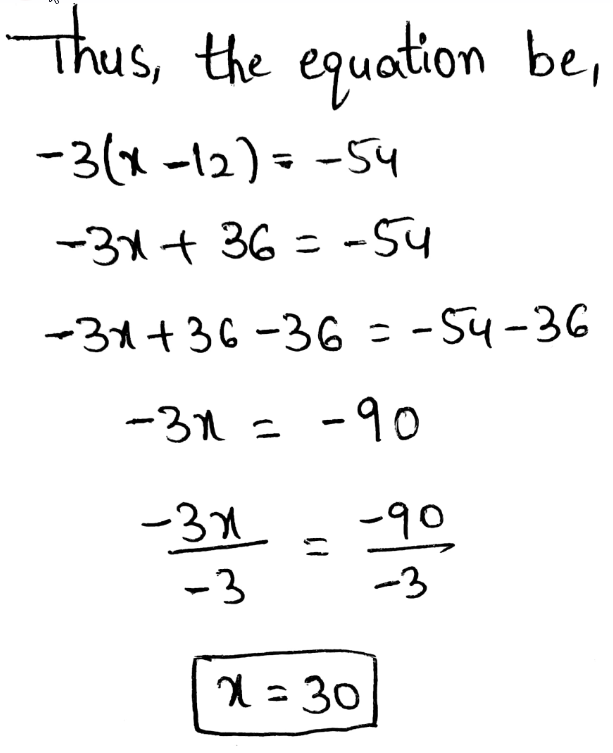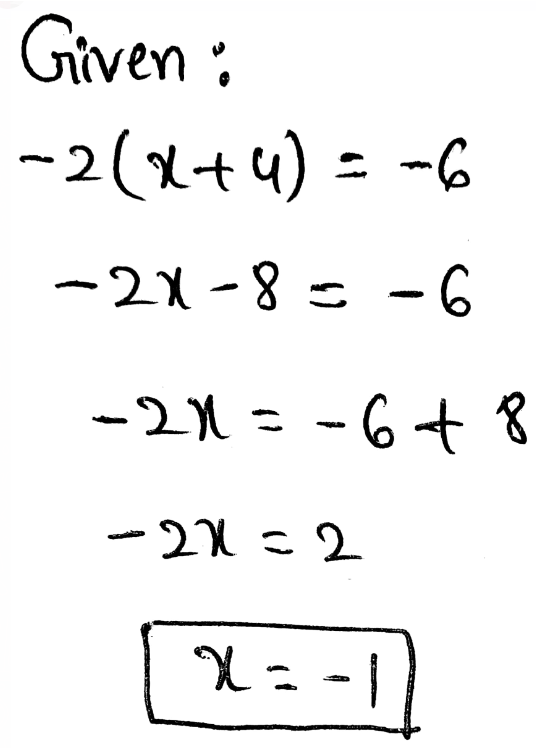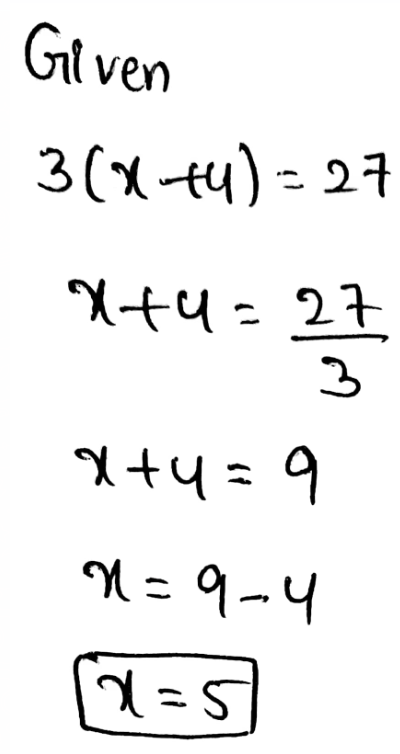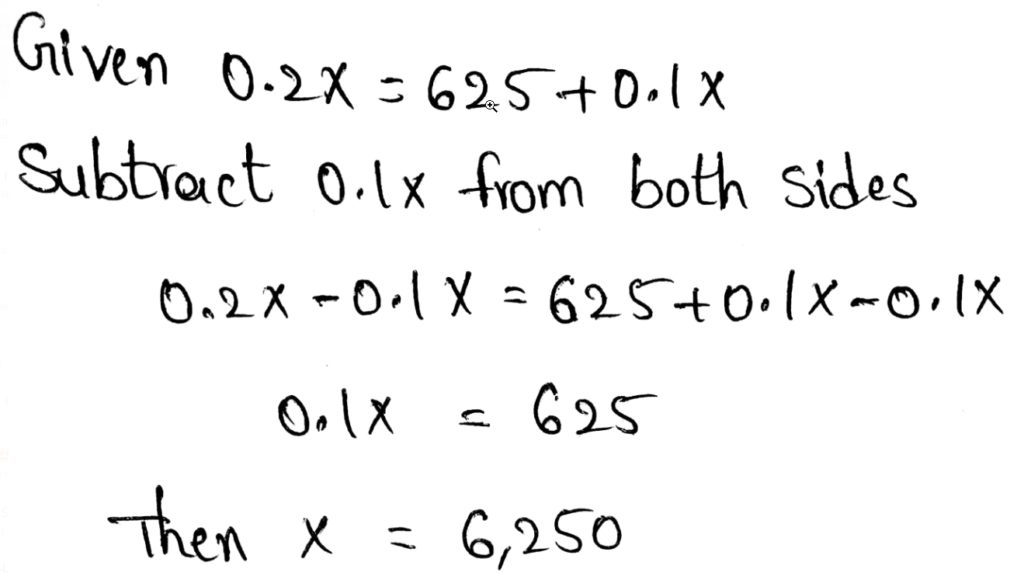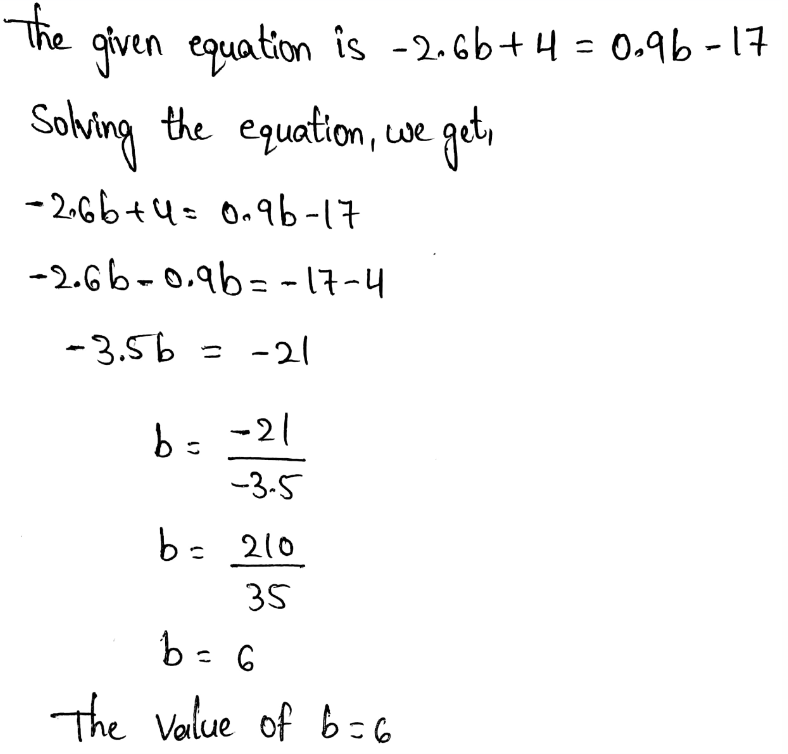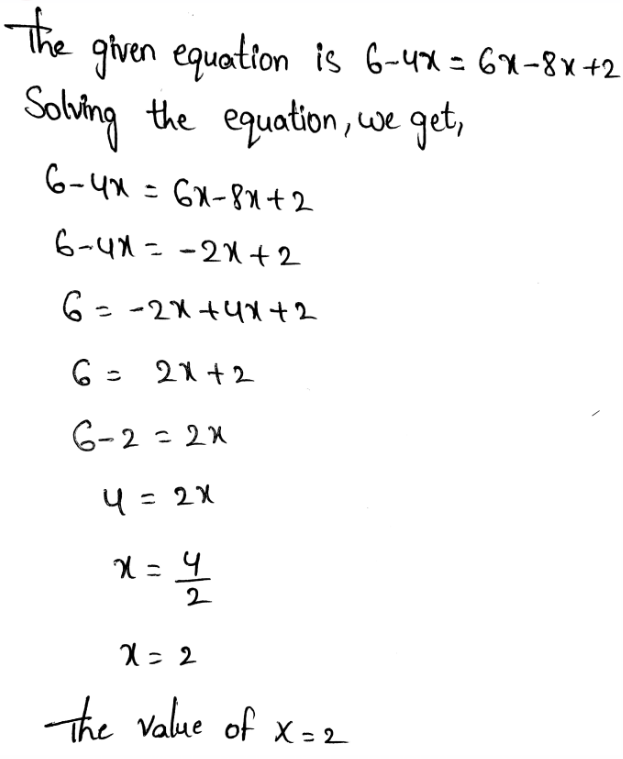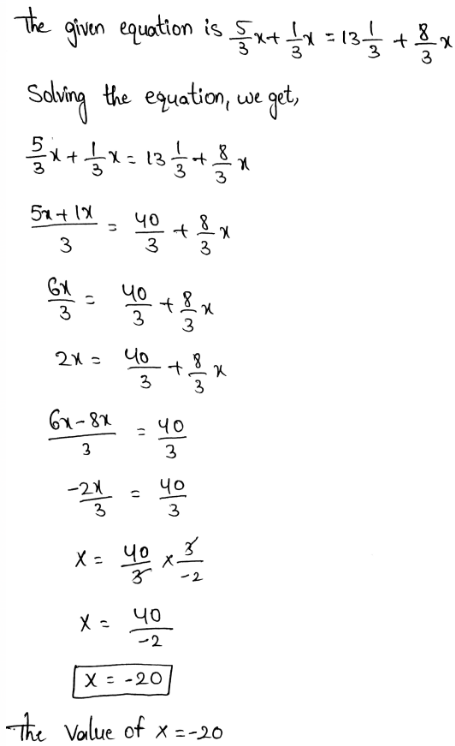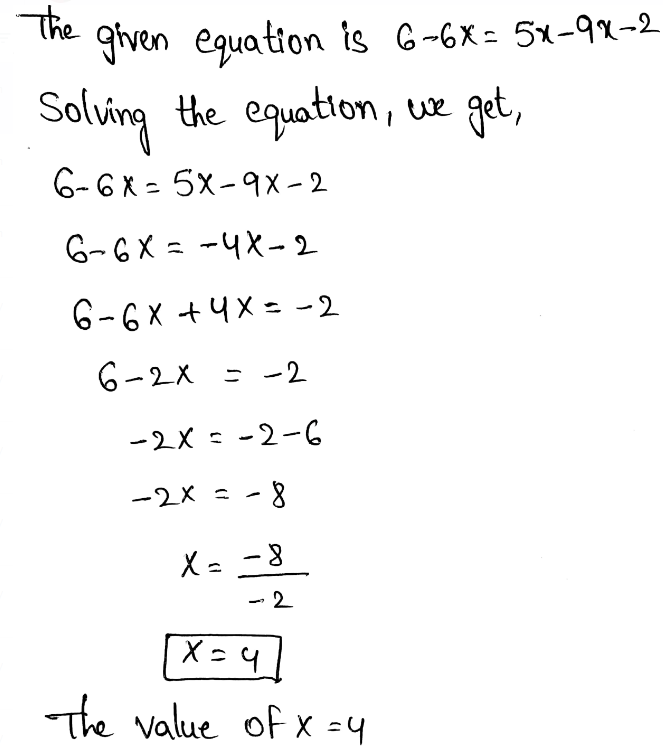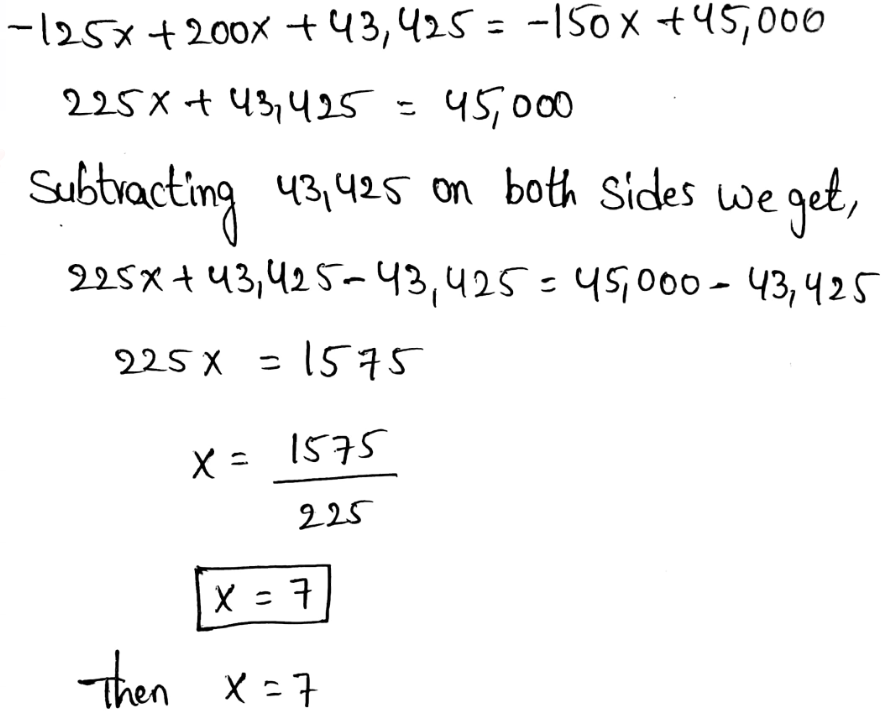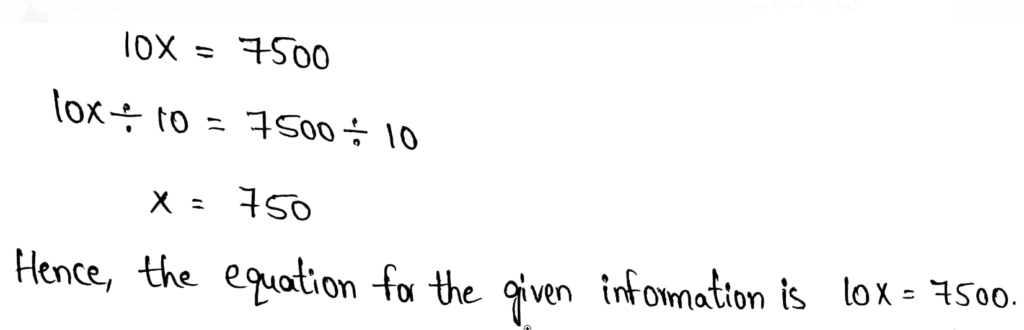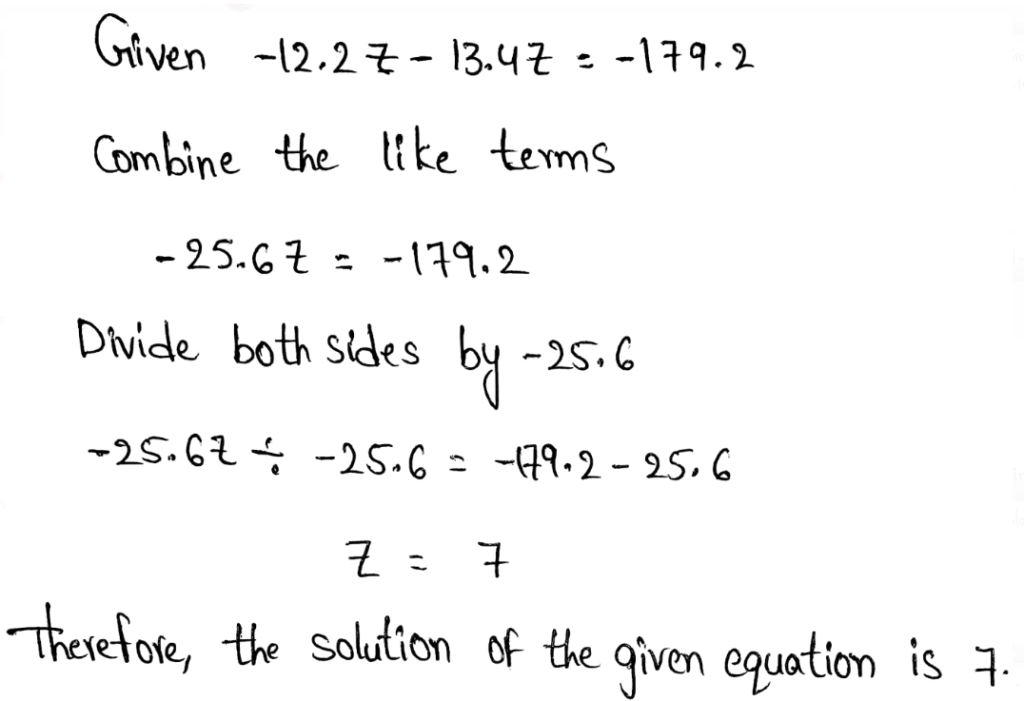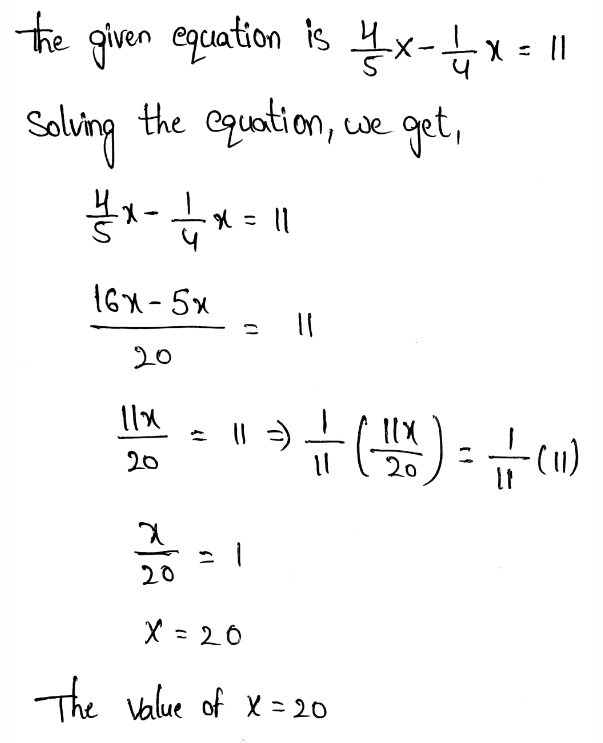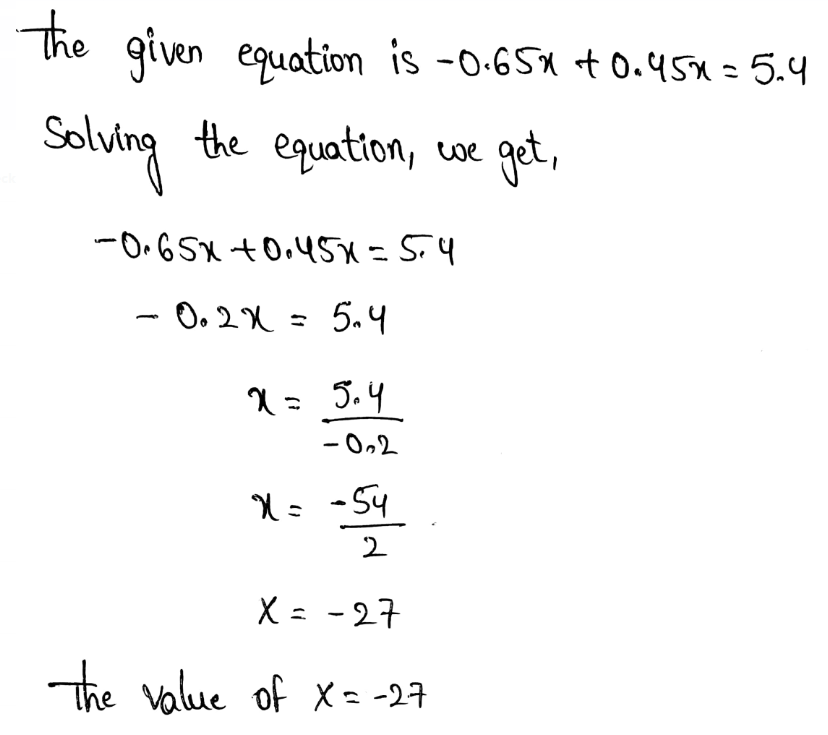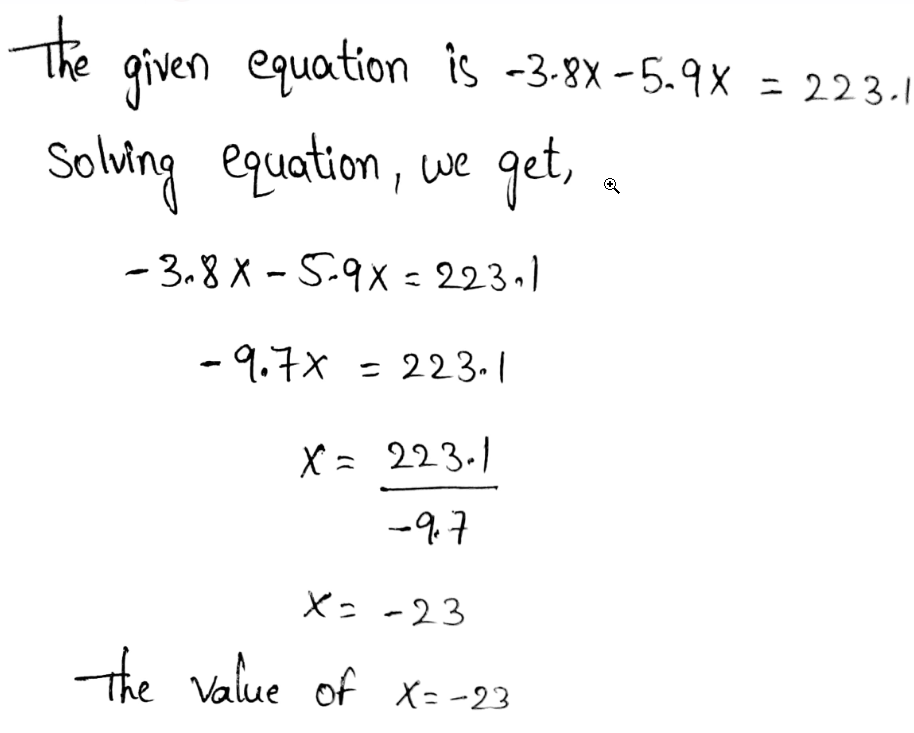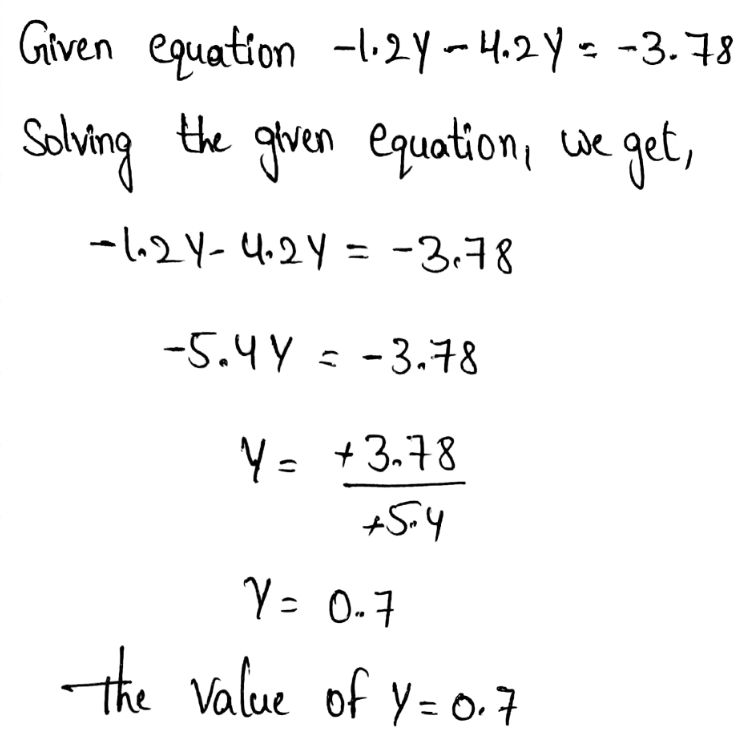Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8

Page 135 Exercise 1 Answer

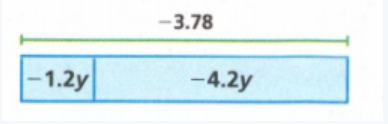
To find the age of horse in human years.

We find that by first dividing the horse age with 5 and after that multiplying the result by 2

10 * 2 = 20

The horse is 20 years old in human years.

So now we have to subtract 8 years from the years of the horse and we will get,

20 − 8 = 12

Hence, the horse was 12 human years old when Alex was born.

Page 135 Exercise 1 Answer

To find the age of cat in human years.

To find out how old is the cat in human years.

We have to divide the cat years with 8 and after that multiply the result with 2.

8 * 2 = 16

Hence, the cat is 16 human years old.

Page 136 Question 1 Answer

The y−intercept is the value of y−coordinate in point at which the line crosses the y−axis.

When the line crosses through the origin, the y−intercept is 0.

When the line crosses above the origin, the y−intercept is positive.

When the line crosses below the origin, the y−intercept is negative.

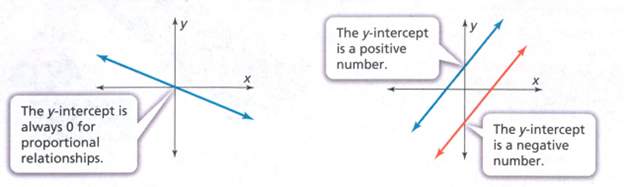
The y−intercept is the value of y−coordinate in point at which the line crosses the y−axis.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.8 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 136 Exercise 1 Answer

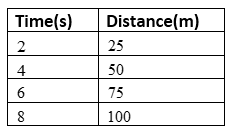
The given table is,

We need to find the pattern that we can see in the costs of different numbers of games given.

From the given table, the cost of one game is $4

The cost of three games is $8.

The difference between the cost and the number of games will be,
​
(3−1)games = (8−4)dollars

2games = 4dollars

1game = 2dollars
​
Thus, for the increase in one game, the cost increases by $2.

This can be represented by the equation,

(1+n)games = (4+2(n))dollars

Thus for 10 games, the cost will be,
​
(1+n)games = (4+2(n))dollars

(1+9)games = (4+2(9))dollars

10games = (4+18)dollars

10games = 22dollars
​
Thus, a certain pattern is observed.

The pattern which we observe in the costs of different numbers of games is that after every one game, there is $2 increase in the price.

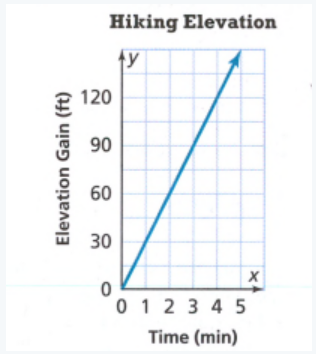
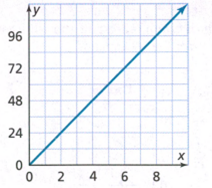
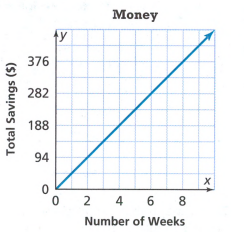
Page 136 Exercise 1 Answer

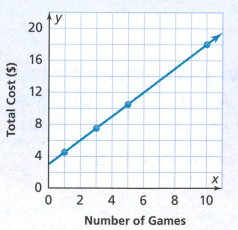
We have to find the slope of the given line.

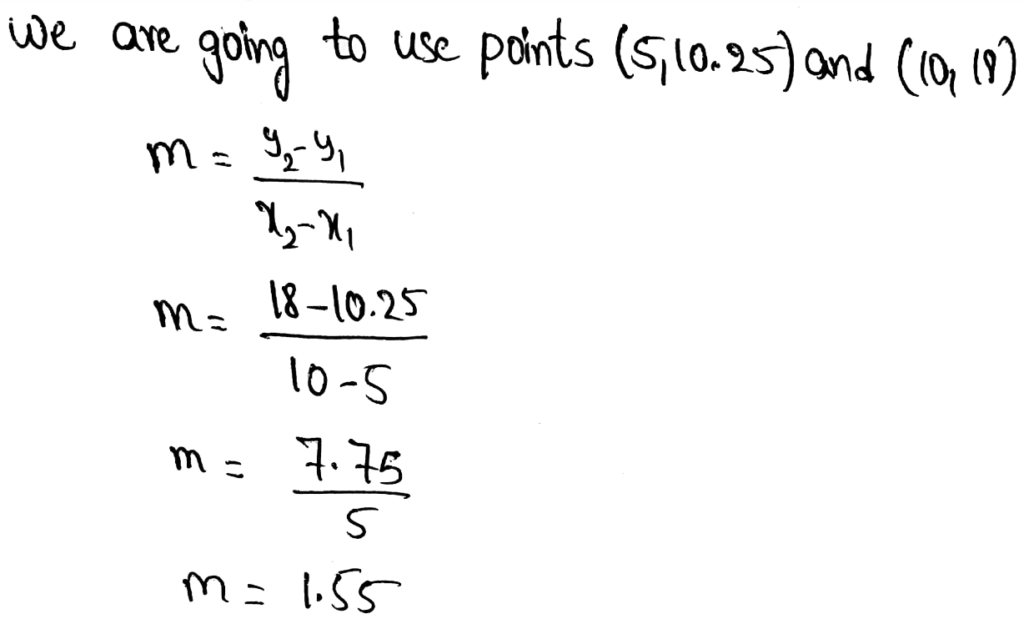
The cost of each game is 1.55

The y−intercept has to be read from the graph but it is not clear.

We are going to say that the y−intercept is 3.5.

Hence, the y−intercept is 3.5.

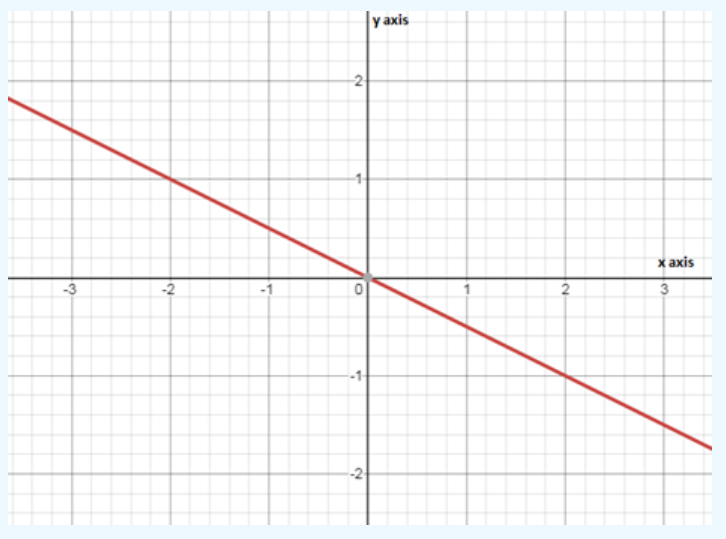
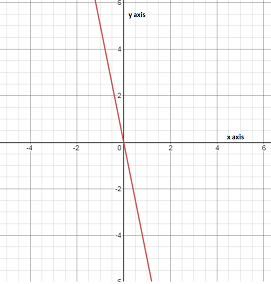
Page 137 Exercise 2 Answer

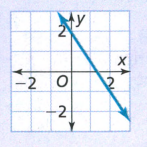
We can see that the y-intercept is 2 because the value of y-coordinate is 2 When the line crosses the y-axis.

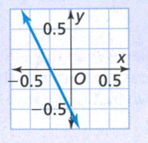
We can see that the y-intercept is -0.5

y-intercept for the first graph is 2 and for the second graph is -0.5.

Envision Math Grade 8 Exercise 2.8 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 136 Exercise 1 Answer

We need to explain why does the y-intercept represent the cost to rent bowling shoes in these examples.

The y−intercept can be found when the value of x = 0

This means that the y−intercept is the value when there are no games.

That is, the number of games played is zero.

The y−intercept of the line is obtained to be $2.

This means that the cost to rent bowling shoes is $2.

At the y−intercept, the number of games played is zero. This is why the y−intercept represents the cost to rent bowling shoes.

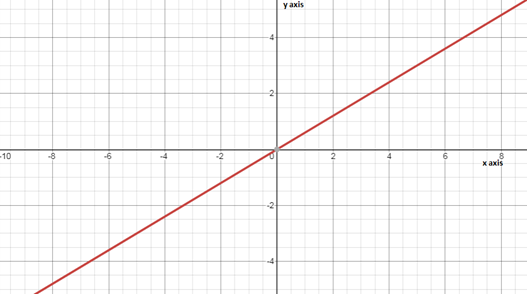
Page 138 Exercise 1 Answer

The y−intercept is the value of y−coordinate in point at which the line crosses they−axis.

When the line crosses through the origin, the y−intercept is0

When the line crosses above the origin, the y−intercept is positive.

When the line crosses below the origin, the y−intercept is negative.

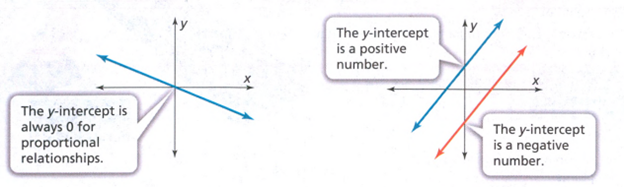
The y-intercept is the value of y-coordinate in point at which the line crosses the y−axis.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 138 Exercise 2 Answer

Since we know that the y−intercept is always 0 for the proportional relationships and the Bradyn’s graph passes through the origin which is point(0,0), that means that the both lines has y−intercept 0.

Hence, the both y−intercepts are 0.

Page 138 Exercise 3 Answer

When the line crosses above the origin, the y−intercept is positive.

When the line crosses below the origin, the y−intercept is negative.

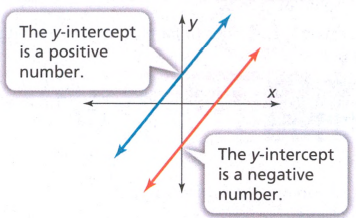
When the line crosses above the origin, the y-intercept is positive.

When the line crosses below the origin, the y-intercept is negative.

Analyze And Solve Linear Equations Grade 8 Exercise 2.8 Envision Math

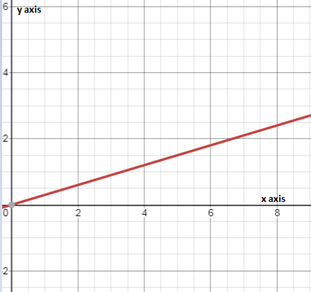
Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 138 Exercise 5 Answer

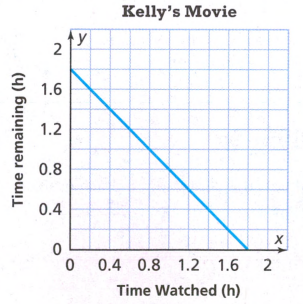
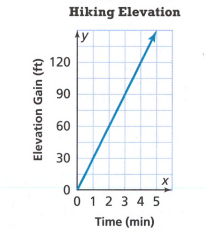
The y−intercept on the given graph is 1.8

This means that the movie is 1.8 hours long.

Hence, the y−intercept on the given graph is 1.8.

Page 139 Exercise 6 Answer

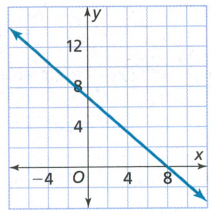
The y−intercept is the point where the graph crosses the y−axis.

This means that we need to find the point which has x−coordinate is 0

The line crosses the y−axis at the point(0,7).

So, the y−intercept is 7.

Hence, the line crosses the y−axis at the point(0,7). So, the y−intercept is 7.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 139 Exercise 7 Answer

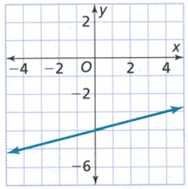
The y−intercept is the point where the graph crosses the y−axis.

This means that we need to find the point which has x−coordinate is 0

The line crosses the y−axis at the point (0,−4).

So, the y−intercept is −4.

Hence, the y−intercept is −4.

Page 139 Exercise 8 Answer

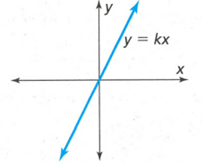
We can see from the graph the line passes through the origin.

This means that the graph passes through the point (0,0) and that means that the y-intercept is 0.

Hence, the y-intercept is 0.

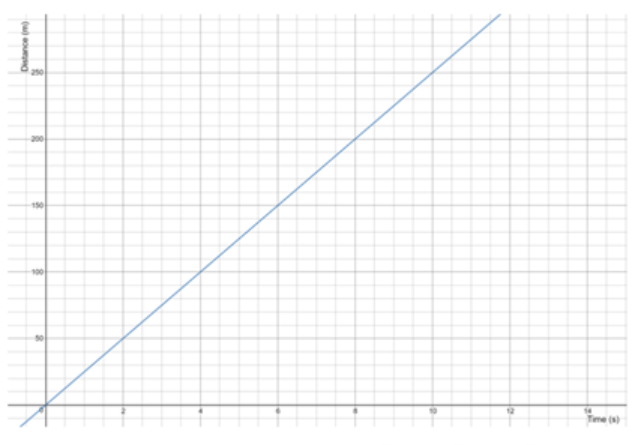
Page 139 Exercise 9 Answer

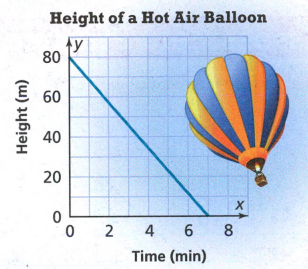
We have to find the value of y−coordinate in the point at which the line crosses the y−axis.

We can see from the graph this point is(0,80). So,the y−intercept is 80

The height of the air balloon when it began to descent was 80 meters.

Hence, the height of the air balloon was 80 meters.

Envision Math Grade 8 Chapter 2 Exercise 2.8 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 139 Exercise 10 Answer

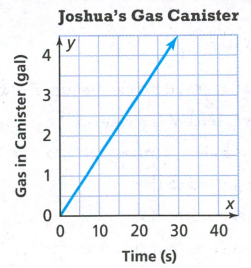
We can see from the graph the line crosses through the origin. So the y−intercept is 0.

When the y-intercept is for the given function it means that there was no gas in the canister.

Hence, the y−intercept is 0.

Page 140 Exercise 11 Answer

The y−intercept is the point where the graph crosses the y−axis.

This means that we need to find the point which has x−coordinate is 0

The line crosses the y−axis at the point(0,4).

So, the y−intercept is 4.

Hence, the y−intercept is 4.

The y−intercept tells us what the temperature was when it was sunrise.

The y−intercept tells us the temperature at sunrise.

Envision Math 8th Grade Exercise 2.8 Step-By-Step Linear Equation Solutions

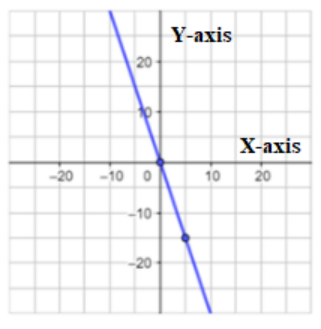
Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 140 Exercise 12 Answer

Given

To find/solve

a. Explain your friend’s possible error.

A y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. These points satisfy x = 0.

On the given graph we can see that the y-intercept is -4. The student had switched the x-intercept and y-intercept.

The student has switched x and y intercepts.

The student has switched x and y intercepts.

To find/solve

Draw a line on the graph that does represent a y-intercept of 3.

On the given graph we can see the line that has y-intercept is 3.

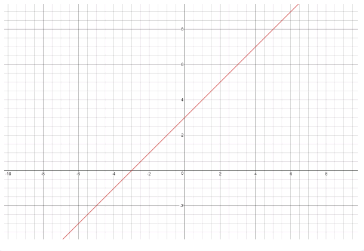
Draw a line that crosses the y-axis at y = 3.

Draw a line that crosses the y-axis at y = 3.

How To Solve Exercise 2.8 Linear Equations In Envision Math Grade 8

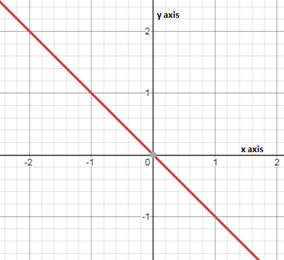
Page 140 Exercise 13 Answer

Given

Graph

To find/solve

What is the y-intercept.

We simply have to look closely at each graph and find the point at which the line passes through the y-axis.

As we can see from the first graph the y-intercept is at point (0,-3) which means that the y-intercept of given graph is -3.

As for the second graph we can see that the point at which he line crosses the y-axis is (0,3). This means that the y-intercept for the second graph is 3.

The y-intercept of first graph is -3 and of the second graph is 3.

The y-intercept of first graph is -3 and of the second graph is 3.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7

Page 129 Exercise 1 Answer

It is given that A group of college students developed a solar-powered car and entered it in a race.

The car travels at a constant speed of 100 meters per 4 seconds.

We have to graphically represent the distance over time.

We know that the students have developed a solar powered car.

The speed of the car is constant which is 100 meters in 4 seconds.

We can graphically represent the same as below:

On x-axis we will mark the time, while distance on y-axis.

The given graph is the representation of distance over time.

It is given that A group of college students developed a solar-powered car and entered it in a race.

The car travels at a constant speed of 100 meters per 4 seconds.

We have to find the expression which can show the distance the car will travel over time.

We know that the students have developed a solar powered car.

The speed of the car is constant which is 100 meters in 4 seconds.

The expression for the same can be evaluated, but for which first we need to find the unit rate.

Thus, we divide the distance with time and get unit rate as

Therefore, the expression will be y = 25x.

The expression which can show the distance the car will travel over time will be y = 25x

It is given that A group of college students developed a solar-powered car and entered it in a race.

The car travels at a constant speed of 100 meters per 4 seconds.

We have to compare the representation and the expression of distance over time, and tell which shows clearly.

We know that the students have developed a solar powered car.

The speed of the car is constant which is 100 meters in 4 seconds.

The representation of the distance over time is

The expression for the same can be evaluated, but for which first we need to find the unit rate.

Thus, we divide the distance with time and get unit rate as

Therefore, the expression will be 25x.

On comparing the both, we can observe that the expression will provide much clear results ad compared to representation.

This is because representation would not be able to give clear result when the time period is longer.

On comparing the both, we can observe that the expression y = 25x will provide much clear results ad compared to representation.

This is because representation would not be able to give clear result when the time period is longer.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.7 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 130 Question 1 Answer

The table given shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.

We have to find the quantities to find the unit rate in order to compare the proportional relationship.

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as proportional relationship.

We are given the data regarding the relationship between the number of miles Manuel walks and the amount of money he will raise.

If we have to compare the proportional relationships, we will use the quantities Money Raised and the Miles Walked.

On doing so, we can find the amount of money earned for each mile which is unit rate.

The quantities that we should use to find the unit rate are Money Raised and the Miles Walked so that the proportional relationships can be compared.

Page 130 Exercise 1 Answer

We have to build a fence for which the length and cost is given.

We have to find the relation between the length of the fence and the cost.

We know that the students in Meg’s class are building a fence around the class garden.

For fencing and costing, the length of fence and the cost for each feet is to be known.

The length of fencing and cost both factors are related to each other.

This is because, to calculate the complete costing of the fencing work, we will have to multiply the total length of the fence suppose in feets and the cost required to build fence of 1 feet, which is its rate.

The length of fencing and cost both factors are related to each other as both are needed to find total costing.

Envision Math Grade 8 Exercise 2.7 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 130 Exercise 1 Answer

The graph of distance per gallon is given.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The equation for line involving slope is, y = mx.

Thus, the equation for the given line will be y = 20x.

The relationship given will tell us the amount of gasoline used for a certain distance.

The slope of the line is obtained as 20 and the equation for line is y = 20x.

Page 131 Exercise 2 Answer

The graph of a line is given.

We have to find the equation of the line.

The general equation of a line is y = mx, where m is the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

On substituting the value of slope in equation of line we get,

y = 0.4x

The equation of the line is obtained as y = 0.4x.

The graph of a line is given.

We have to find the equation of the line.

The general equation of a line is y = mx, where m is the slope of the line.

Here the equation given is y=−3x, so the slope is −3.

We consider the first point as (0,0).

For the second point, we take as x = 5 and then y = −3x = −3(5) = −15

So, the second point will be (5,−15)

Using, these two points we will draw the graph as below:

The graph of the line is obtained as

Analyze And Solve Linear Equations Grade 8 Exercise 2.7 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 130 Exercise 1 Answer

We need to explain how to do the equations y = mx and y = kx can be compared.

The equation y = mx represents that the relationship is proportional to each other.

That is the equation represents a linear equation.

Here, m is the slope of the line.

The equation y = kx is compared with y = mx

Thus, it denotes that,

k = m

This means that the slope of the line is k

This refers that the rate of change is k

When we compare both equations, the slope or the rate of change of the equation is m = k

Page 131 Exercise 1 Answer

We need to generalize the concept that the lines that slant upward from left to right have positive slopes. Lines that slant downward from left to right have negative slopes.

We know that when we plot linear equations, the graph will be of a straight line.

The straight line may go upwards or downwards depends upon the slope or its rate of change.

If the slope or the rate of change of the equation is negative, then the lines will slant downwards from left to right.

This will result in a negative slope.

If the slope or the rate of change of the equation is positive, then the lines will slant upwards from left to right.

This will result in a positive slope.

If the slope or the rate of change of the equation is negative, then the lines will slant downwards from left to right.

If the slope or the rate of change of the equation is positive, then the lines will slant upwards from left to right.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 132 Exercise 1 Answer

Any equation of proportional relationship looks like y = mx where “m” is the slope.

This means that the slope will show us how fast will the line increase or decrease and tells us the unit rate.

Any equation of proportional relationship looks like y = mx where “m” is the slope.

This means that the slope will show us how fast will the line increase or decrease and tells us the unit rate.

Page 132 Exercise 2 Answer

The graphs of lines that are in the form like y = mx always pass through the origin.

The graphs of lines that are in the form like y = mx always pass through the origin. They will only differ in the rate of increasing or decreasing of the line.

Page 132 Exercise 3 Answer

Given

To find the slope of the line using this (2,25)(4,50) points.

Hence, the equation is y = 12.5x

Page 132 Exercise 4 Answer

Given:

To find the slope and the constant of the proportionality we simply have to use two points that we can read from the graph.

The slope and the constant of proportionality are both 30.

Given:

To find the slope and the constant of the proportionality we simply have to use two points that we can read from the graph.

The graphs of the straight lines have equation that is equivalent to So, the equation is y = 30x

Therefore, the equation of the line is y = 30x

Envision Math Grade 8 Chapter 2 Exercise 2.7 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 132 Exercise 5 Answer

Given:

\(y=-\frac{1}{2} x\) To solve the graph equation

We are going to use two points that we can get from equation and through those two points we simply have to draw a straight line.

We are going to find the y when x = 0 and x = −2

y=\(-\frac{1}{2} * 0\)

y = 0

y=\(-\frac{1}{2} *-2\)

y = 1

The two points are (0,0) and (-2,1)

The graph of the line is

Page 133 Exercise 6 Answer

To find the equation of the line

We are going to use two points which are (4, 280) and (2, 140)

=\(\frac{140}{2}\)

= 70

The slope of the line is 70.

The equation of the line is y = 70x.

The heart’s resting heart rate is 70 beats each minute.

The heart’s resting heart rate is 70 beats each minute.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 133 Exercise 7 Answer

We can use two points from the graph which are (3, 0.75) and (4, 1)

=\(\frac{0.25}{1}\)

=\(\frac{1}{4}\)

The slope of the line is \(\frac{1}{4}\)

The equation of the given line is equivalent to y = mx

Hence, the equation of the line is y = \(\frac{1}{4}\)x.

Page 133 Exercise 8 Answer

Given

y = −x

Since we have minus sign before the x−that means that our line will be decreasing and the line that he drew is increasing.

He forgot to reflect given line across x−axis

The right graph is

No, the graph is wrong.

The correct graph is

Envision Math 8th Grade Exercise 2.7 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 133 Exercise 9 Answer

Given

We can use two points from the graph which are (2,24) and (4,48)

​
\(m=\frac{y_2-y_1}{x_2-x_1}\)

=\(\frac{24}{2}\)

= 12

The slope of the line is 12.

Given

If an equation is equivalent to y = mx then the equation represents a proportional relationship.

The graph of a proportional relationship always goes through the point(0,0) and it will always be a straight line

The graph of a proportional relationship always goes through the point(0,0) and it will always be a straight line.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 134 Exercise 10 Answer

Given

y = −5x

We are going to use the points which are x = 0 and x = −1

​y = −5x

y = −5(0) = 0

y = −5(−1) = 5
​
The two points are(0,0) and (−1,5).

To graph the line is

Page 134 Exercise 11 Answer

Given

We are going to use the points which are x = 0 and x = -5

= 0

= -3

The two points are (0,0) and (-5, -3).

To graph the line is

How To Solve Exercise 2.7 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 134 Exercise 12 Answer

If they are giving out a 70% off the price of the ticket that simply means that we pay 30%of the original amount.

So the equation is y = 0.3x.

Hence, the equation of the given situation is y = 0.3x

Given

y = 0.3x From the part (a)

We are going to find will have x = 0 and x = 5.
​
y = 0.3x

y = 0.3(0)

= 0

y = 0.3(5)

= 1.5
​
The two points are (0,0) and (5,1.5).

Now as we know the line can only be in the quadrant I because the price of the ticket cannot be negative.

The price of the ticket cannot be negative

Envision Math Grade 8 Exercise 2.7 Practice Problems

Page 134 Exercise 13 Answer

Given

We can use two points from the graph which are (2,94) and (4,188)

The equation of the given line is equivalent to y = mx

The equation of the line is y = 47x.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6

Page 123 Exercise 1 Answer

We are given that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

We have to find that how much Rashida will earn refereeing soccer games in this fall.

We know that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

In order to calculate the money earned by Rashida by refereeing soccer games in this fall, we will first find the money she gets for 1 game, which will be evaluated when we divide the money earned by her by the number of games.

When she is the referee for 5 games,

Thus, Rashida earns $19.7 for refereeing one game.

In this fall she was the referee for 14 games, so she earns

14 × 19.7 = 275.8

Therefore, she earns $275.8 for 14 games.

Rashida will earn $275.8 for refereeing 14 soccer games this fall.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.6 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 123 Exercise 1 Answer

We are given that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

We have to find the relation between the number of games and her earnings.

We know that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

In order to calculate the money earned by Rashida by refereeing soccer games in this fall, we will first find the money she gets for 1 game, which will be evaluated when we divide the money earned by her by the number of games.

As Rashida gets her earnings from the game in which she is a referee, there is a relation between the number of games for which she works to her earnings.

Earning and number of games are related, as the earning can be calculated based on the rate and number of game in which she is a referee.

Envision Math Grade 8 Exercise 2.6 Analyze And Solve Linear Equations

Page 123 Exercise 1 Answer

We are given that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

We have to find the change in her earnings if she was paid on basis of per hour.

We know that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

She is paid on the basis of the number of games in which she is a referee.

In case, she is paid on the basis of hours she work, it is necessary to know that for how many hours does she work as a referee.

Also, the amount to be paid to be working for one hour is to be known.

Thus, on basis of hours, her earnings will be calculated where number of hours and pay per hour will be multiplied.

Rashida’s earnings will change if she was paid by hour and not by game, which completely depends on the number of hours she has worked.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 124 Question 1 Answer

We have to define the term slope.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Slope is the change in y divided by the change in x.

Page 124 Exercise 1 Answer

It is given that Jack graphs how far he plans to bike over a 3-day charity ride.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the line is obtained as 30.

Analyze And Solve Linear Equations Grade 8 Exercise 2.6 Envision Math

Page 125 Exercise 2 Answer

It is given that The graph shows the proportions of red and blue food coloring that Taylor mixes to make purple frosting.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope implies that to get the purple food colour, for every 5 blue drops we need to add 7 red drops.

The slope of the line is obtained as \(\frac{7}{5}\) which means that for every 5 blue drops we need to add 7 red drops.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 124 Exercise 1 Answer

It is given that Jack graphs how far he plans to bike over a 3-day charity ride.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

The constant of proportionality is the ratio of vertical distance to the horizontal distance.

The slope of a line is the same as the constant of proportionality.

There is no difference in them at all.

Unit Rate is the rate in which the second quantity is compared to the first quantity.

Whereas, the slope is the unit rate because in it, the second quantity or changes in y is compared to the first quantity which is change in x.

The slope of a line, unit rate and constant of proportionality all are the same.

Page 125 Exercise 1 Answer

We have to tell the relation among coordinates when the slope is negative.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Therefore, Slope is the change in y divided by the change in x.

When the slope is obtained as a negative value, there is decreasing or descending nature of quantities observed.

Negative slope simply means that the two variables are related negatively.

This means that when x increases, the value of y decreases and similarly, when x decreases, value of y increases.

Negative slope implies that the two variable or coordinates are negatively related to each other.

This means that when x increases, the value of y decreases and similarly, when x decreases, value of y increases.

Envision Math Grade 8 Chapter 2 Exercise 2.6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 126 Exercise 1 Answer

We have to define the term slope.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Slope is the change in y divided by the change in x.

Page 126 Exercise 2 Answer

We have to define slope and unit rate and find their relation.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Unit Rate is the rate in which the second quantity is compared to the first quantity.

Whereas, the slope is the unit rate because in it, the second quantity or change in y is compared to the first quantity which is change in x.

The slope of a line and unit rate both are the same.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 126 Exercise 3 Answer

We have to define the term slope.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

The ratio of any two points located along a straight line is always constant.

As we know slope is nothing but the ratio.

Thus, the slope of a straight line among any two points is always constant or the same.

The slope of a straight line among any two points is always constant or the same, because the the ratio of any two points located along a straight line is always constant.

Page 126 Exercise 4 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the given line is obtained as 3.

Envision Math 8th Grade Exercise 2.6 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 126 Exercise 5 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

In the given problem situation, the dimensions of the model airplane as the ratio of centimetres to feet is given.

As the slope obtained is 5/3, it denotes that 5cm of dimension, will be equivalent to 3 feet of the dimension.

The slope obtained is 5/3, it denotes that 5 cm of dimension, will be equivalent to 3 feet of the dimension.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 127 Exercise 7 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the given line is obtained as 5.

Page 127 Exercise 8 Answer

We have to find the slope of the line passing through the given points (0,0) and (2,4).

The given graph tells us about the number of soda bottles which a machine makes over the given time.

In order to find, the number of bottles made in one minute, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The slope of the line that passes through the points (0,0) and (2,4) is obtained as 2.

How To Solve Exercise 2.6 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 127 Exercise 9 Answer

We have to find the slope of the line passing through the given points (2.1,-4.2) and (2.5,-5).

The given graph tells us about the number of soda bottles which a machine makes over the given time.

In order to find, the number of bottles made in one minute, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The slope of the line that passes through the points (2.1,-4.2) and (2.5,-5) is obtained as -2.

Page 128 Exercise 11 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the given line is obtained as 10.

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

In this problem situation, the slope obtained tells us that how many calories Natalia can burn in one minute.

The slope of the given line is obtained as 10, which tells us the amount of calories burned in one minute.

Envision Math Grade 8 Exercise 2.6 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 128 Exercise 12 Answer

We have to find the speed of the car from the graph given.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

We have to evaluate the speed of the car, for which we will consider the point (1,64) which is on the line.

As we know that if we divide the y-coordinate with the x-coordinate, we get the unit rate.

The speed of the car is obtained from the point as

The speed of the car is obtained as 64miles/hr

We have to identify the error that Anna made.

The given graph tells us about the speed of the car which is the ratio of distance given in miles to the time which is in hours.

Anna took Time on the x-axis and Distance over the y-axis, which is not appropriate and hence the error he made.

He must take Distance on the x-axis while Time on the y-axis.

Anna took Time on the x-axis and Distance over the y-axis, which is the error he made.

Page 128 Exercise 13 Answer

We have to find the slope of the line passing through the given points (0,0) and (2,4).

The given data tells us that the water level rises 11 centimetres every 5 minutes, which means the slope is 11/5.

In order to find the slope, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The value of y is obtained as 22.

Envision Math Exercise 2.6 Linear Equations Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 128 Exercise 14 Answer

We have to find the slope of the line passing through the given points (15,21) and (25,35).

In order to find the slope, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The slope of the line that passes through the points (15,21) and (25,35) is obtained as 1.4.

We have to find the slope of the line passing through the given points (15,21) and (25,35).

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as proportional relationship.

We know that the line would definitely pass through the origin.

As the line in graph A does contradicts the statement, hence it is wrong.

The points we have are (15,21) and (25,35).

From the x and y coordinates of both the points, we can observe that the y-coordinate is greater than the x-coordinate.

This is seen in the graph B and not in graph C.

Thus, graph B is correct.

The graph B represents the given relationship between the two points.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5

Page 117 Exercise 1 Answer

Given

Meili going to pick the apple and between the apples.

Which orchard should mei li choose?

We simply going to solve each of given equation and find value for each.

20x =7.25

Divide both side of the equation by 20.

x ≈ 0.36

Price per lb for annie’s apple orchard is about $0.36

12x = 5

Divide both sides of the equation by 12

x ≈ 0.42

Now we can see that price per lb for franklin’s fruit orchard is about x ≈ 0.42

We simply compare values for first and second apple orchard to see which is cheaper.

0.36 < 0.42

Annie’s apple orchard is cheaper than franklin’s fruit orchard and that is why mei li should choose annie’s apple orchard.

She should pick annie’s apple orchard.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.5 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 117 Exercise 1 Answer

We need to explain what information provided can be used to support the answer.

In Annie’s Apple Orchard, 20 lb costs $7.25

In Franklin’s fruit Orchard, 12 lb costs $5.00

The unit rate of each will be,

For Annie’s,

For Franklin’s,

Thus, Meili choose Franklin’s fruit Orchard since it costs less than Annie’s.

The information provided regarding the weight of the apple and its costs can be used to support my answer.

Page 117 Exercise 1 Answer

Given

Meili going to pick the apple and between the apples.

Which orchard should mei li choose?

We simply found out what is the price per one lb of apples. After we found that, we simply had to compare the results, the one that is cheaper is obviously the one she should pick.

We simply found out what is the price per one lb of apples. After we found that, we simply had to compare the results, the one that is cheaper is obviously the one she should pick.

Envision Math Grade 8 Exercise 2.5 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 118 Question 1 Answer

Given

How can compare relationship proportional in different ways?

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.

For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.

For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Page 118 Exercise 1 Answer

Given

The equation is y = 2.5x

Who makes birds at a faster rate?

As we can see from the graph, Marlo makes 2 origami birds in 10 minutes, and we simply have to make an equation from this and calculate how much he needs to make 1 bird.

2y = 10x

Divide both side of the equation by 2.

y = 5x

This means that josh makes twice as many origami birds as Marlo makes.

Josh makes them faster.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 118 Exercise 1 Answer

Given

The equation is y = 2.5x

How do you lines compare.?

As we can see from the graph, marlo makes 2 origami birds in 10 minutes, and we simply have to make an equation from this and calculate how much he needs to make 1 bird.

This means that josh makes twice as many origami birds as marlo makes.

Josh makes them faster.

Analyze And Solve Linear Equations Grade 8 Exercise 2.5 Envision Math

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5

Page 120 Exercise 1 Answer

Given

How can compare relationship proportional in different ways?

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.

For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.
For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Envision Math Grade 8 Chapter 2 Exercise 2.5 Practice Problems

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 120 Exercise 2 Answer

Given

Find the unit of rate or constant ?

We simply have to read from the graph for which ever of the values on the axis we need.

For example if the unit of hours is on the x-axis than we simply have to put that into the relation with the value that is on the y-axis.

We can find the unit rate or constant of proportionality for a relationship represented in a graph by:

Simply reading from the graph for which ever of the values on the axis we need.

For example if the unit of hours is on the x-axis than we simply have to put that into the relation with the value that is on the y-axis

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5

Page 120 Exercise 3 Answer

Given

Why can you use the constant of proportionality with any representation ?

We can use constant of proportionality with any representation because we can find the unit rate or the constant from the any data that we are given.

We can use constant of proportionality with any representation because we can find the unit rate or the constant from the any data that we are given.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 120 Exercise 4 Answer

Given

The points are (0,0) and (4,24)

Who earn more per hour ?

We can simply graph both functions and see which of them makes more money

On the graph we can see function for Amanda and function for petra.

From the graph we can see that Amanda earns more money per hour

Amanda earns more money per hour.

How To Solve Exercise 2.5 Linear Equations In Envision Math Grade 8

Page 121 Exercise 6 Answer

Given

Find the unit of rate for Sam and bobby?

Who cycled faster?

First we have to find the unit rate for Sam.

Since we can see from the table that he can cycle at 20 miles in 2 hours we simply have to divided the number of miles with hours to find out how much he cycles in one hour.

20 ÷ 2 = 10

He can cycle at speed of 10mi/h

Now to find out the unit rate for bobby we are going to use points (2,18) and (4,36)

Again we simply have to divide miles with the hours to find out the unit rate for bobby.
​
18 ÷ 2 = 9

36 ÷ 4 = 9
​
We can see that bobby can cycle at speed of 9mi/h.

Sam can cycle faster.

Envision Math Grade 8 Chapter 2 Exercise 2.5 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 121 Exercise 7 Answer

Given

y = 5x the equation y is amount of money and x is the selling pizza. Which pizzeria makes more money per pizza?

We are simply going to divide the number of pizzas sold for Leo’s pizza so we can simply compare the results.

The first point that we can see on the graph is (2,24) and we are going to use that point to find the unit rate for him.

24 ÷ 2 = 12

This means that Leo’s pizza makes money by the equation y = 12x

We can simply compare this result to the unit rate of Pauli’s pizzeria with the rate of Leo’s pizza.

15x > 12x

This means that Pauli’s pizzeria takes in more money per pizza.

Pauli’s pizzeria takes in more money per pizza.

Envision Math 8th Grade Exercise 2.5 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 122 Exercise 9 Answer

The table given shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.

We have to find the quantities to find the unit rate in order to compare the proportional relationship.

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as proportional relationship.

We are given the data regarding the relationship between the number of miles Manuel walks and the amount of money he will raise

If we have to compare the proportional relationships, we will use the quantities Money Raised and the Miles Walked.

On doing so, we can find the amount of money earned for each mile which is unit rate.

The quantities that we should use to find the unit rate are Money Raised and the Miles Walked so that the proportional relationships can be compared.

The table given shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.

We have to compare the amount of money raised per mile by the three people.

In order to calculate the money raised per mile, we will have to divide the money raised by the miles walked by considering the values given from the table.

We will first calculate for Manuel as below:

Thus, Manuel gets the amount $15 for each mile walked.

It is already given that Petra earns $15 for every mile, which is the same as Manuel.

So, we can express amount earned by Petra and Manuel by y = 15x

The equation for the money raised by Beth is given as y = 20x

Now we compare the two equations,

15x < 20x

This concludes that Beth earns the maximum amount of money for per mile walked.

On comparing the money raised by the three people for every mile, Beth earns the most.

Envision Math Grade 8 Student Edition Solutions Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1

Page 111 Exercise 3 Answer

It is given that Edy has $450 in her saving account.

After how many months will Edy and Juan have the same amount of money in their accounts

Let the time at which Edy and Juan will have same amount of money be x. So, according to given question:

After 5 months, Edy and Juan will have same amount of money in their accounts.

Envision Math Grade 8 Volume 1 Chapter 2 Topic 2.1 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 111 Exercise 4 Answer

Infinite many solution means that every value is the solution of the given equation.

The equation that has infinite many solution is:

Option c is correct.

Page 111 Exercise 5 Answer

The given equation is −4(x − 1) + 6x = 34

To find: solve the given equation

The value of x is 15.

Envision Math Grade 8 Topic 2.1 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 111 Exercise 6 Answer

Hakeem subtracted 8 from a number, then multiplied the difference by 5. So, the result was 20.

​
The value of x is 12.

Page 112 Exercise 1 Answer

It is given that the race is of 42 miles and hector is completed 18 miles at a speed of 12 miles per hour.

Let x be the hours needed for Wanda to catch up with Hector.

Hector has already completed 18 miles at a speed of 12 miles per hour.

So, after x more hours, Hector will travel 18 + 12x miles.

Wanda travels at 16 miles per hour. In x hours, she travel 16x miles.

If Wanda catches up to Hector, then
​
16x = 18 + 12x

4x = 18
​
x = 4.5 hours.

Wanda will catch up to Hector in 4 hours and 30 minutes.

It is given that the race is of 42 miles and hector is completed 18 miles at a speed of 12 miles per hour.

Wanda will catch up to Hector at 16x miles, i.e. 72 miles.

But the race is of 42 miles. So, Wanda will catch up to Hector after the race.

Wanda will not catch up to Hector before the race is completed.

It is given that the race is of 42 miles and hector is completed 18 miles at a speed of 12 miles per hour.

Distance till finish line is 42 miles.

The speed at which Wanda is travelling is 16 miles per hour.

The speed Wanda should travel = \(\frac{42}{16}=2.625\) miles per hour.

Wanda could travel at a constant speed of 2.625 miles per hour to catch up Hector at the finish line.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 113 Exercise 1 Answer

The video mentioned above shown some images that predict the charge left in the laptop before it completely drained off.

The device runs out of power and the battery percentage is dropping.

The charger was left at home so the laptop runs only for certain hours.

The reason is for knowing the amount of time left for a certain percentage of charge left in the laptop.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “How much time is left before the laptop charge completely drained off?”.

“How much time is left before the laptop charge completely drained off?”.

This is the question that made up my mind after watching this video.

Page 113 Exercise 2 Answer

The video mentioned above shown some images that predict the charge left in the laptop before it completely drained off.

The device runs out of power and the battery percentage is dropping.

The charger was left at home so the laptop runs only for certain hours.

The reason is for knowing the amount of time left for a certain percentage of charge left in the laptop.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “How much time is left before the laptop charge completely drained off?”.

The main question that I will answer that I saw in the video is “How much time is left before the laptop charge completely drained off?”.

Analyze And Solve Linear Equations Grade 8 Topic 2.1 Envision Math

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 113 Exercise 3 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

The reason is for knowing the amount of time left for a certain percentage of charge left in the laptop.

The first question that comes to my mind after watching this video is “How much time is left before the laptop charge completely drained off?”.

The laptop will run 8 hours when it is fully charged. The charge left now is 25%.

Hence, it can run another two hours before it completely drained off.

An answer that I was predicted to this main question is two hours.

An answer that I was predicted to this main question is two hours. I found my answer by evaluating the 25% of 8 hours.
​

= 2 hours

Page 113 Exercise 5 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too early to be the answer is 0 hours since the charge is still remaining hence we cannot say it is completely drained.

A number that is too late to be the answer is 8 hours since it can only happen when the charge is full. We know that the charge has already drained up to a certain percent.

My prediction is two hours.

Plotting my prediction on the same number line, I get,

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 114 Exercise 6 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

In this situation, information regarding the number of hours it took for the laptop to completely charge is more helpful to know.

This is because I can use that information to charge my laptop completely using another charger and I can continue with my work.

In this situation, information regarding the number of hours it took for the laptop to completely charge is more helpful to know. I can use that information to charge my laptop completely.

Page 114 Exercise 7 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

To get the information I need regarding the number of hours it took to charge, I can use a similar charger to charge it and calculate the number of percentages charged for every 5 mins to calculate how long it will take to charge completely.

A charger can be used to get the information I need. The laptop took 1.5 hours to charge completely.

Envision Math Grade 8 Chapter 2 Topic 2.1 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 114 Exercise 8 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure the number of hours left before it completely drained off.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

From this way, I have found out that the charge left can make the laptop run for two more hours.

Page 114 Exercise 9 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is 2 hours.

This is the same as my prediction.

The answer to the Main Question is two hours. It is equal to my prediction.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 115 Exercise 10 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is 2 hours.

This is the same as my prediction.

The answer that I saw in the video is also the same.

The answer that I saw in the video is two hours.

Page 115 Exercise 11 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is two hours.

This is the same as my prediction.

My answer matches the answer in the video. This is because the number of hours can be easily determined by the battery percentage.

My answer matches the answer in the video. This is because the number of hours can be easily determined by the battery percentage.

Envision Math 8th Grade Topic 2.1 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 115 Exercise 12 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is two hours.

This is the same as my prediction.

My answer matches the answer in the video. This is because the number of hours can be easily determined by the battery percentage.

I’m not going to change my model.

No, I would not change my model now that I know the answer.

Page 116 Exercise 13 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure the number of hours left before it completely drained off.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

The model helps me answer the Main Question by making an accurate calculation of battery percentage and the number of hours the battery remains when it is fully charged and to know the number of hours left before it completely drained off.

How To Solve Topic 2.1 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 116 Exercise 15 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

After 35 minutes, he started charging his phone. 21 minutes later, the battery is at 23%.

Envision Math Grade 8 Volume 1 Student Edition Solutions  Chapter 2 Analyze And Solve Linear Equations

Page 103 Exercise 1 Answer

Given:

Jasmine’s expression: 2(3x + 6)

James’s expression: 3(2x + 4)

We consider the table with four more values and draw conclusion:

We observe that whichever number we take, the result is same for both the expressions. This proves that Jasmine and James are of the same age. Since Jasmine and James are twins, this table yields the same result. This is true for every whole number.

We observe that whichever number we take, the result is same for both the expressions. This proves that Jasmine and James are of the same age.

Since Jasmine and James are twins, this table yields the same result. This is true for every whole number.

Envision Math Grade 8 Volume 1 Exercise 2.4 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 104 Question 1 Answer

A one-variable equation is the equation which only has one variable.

If the equation two or more variables then it becomes a linear equation in two variables or so on.

The solution of an equation is based on the number of variable present in the equation.

Therefore, one-variable equations will always have on unique solution.

Yes, a one variable equation always have one and unique solution.

Page 104 Exercise 1 Answer

There are two ways to solve this problem.

The first way is to draw a bar diagram to represent the perimeters. Then we have to decompose and reorder the bar diagram to solve for x.

The other way is to write an equation to represent equal perimeters. Then use inverse operations and properties of equality to solve.

Then draw the bar diagram.

Choose whichever way is easier.

We can use bar diagram to represent the equal perimeters by first drawing a bar diagram to represent the perimeters.

Then we have to decompose and reorder the bar diagram to solve for x.

The other way is to write an equation to represent equal perimeters. Then use inverse operations and properties of equality to solve for x.

Then draw the bar diagram.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 105 Exercise 2 Answer

Given:

The equation is:

​
Because 8≠3 there is no solution for the given expression.

Envision Math Grade 8 Exercise 2.4 Linear Equations Answers

Page 106 Exercise 3 Answer

The equation is:

3x + 1.5 = 2.5x + 4.7

When we mentally solve this equation we get x = 6.4

Therefore the given equation 3x + 1.5 = 2.5x + 4.7 has only one solution.

Therefore the equation 3x + 1.5 = 2.5x + 4.7 has one solution.

Given:

The equation is:

3(x + 2) = 3x − 6

When we mentally solve this equation we get 6 ≠ −6

Therefore the given equation 3(x + 2) = 3x − 6 has no solution.

Therefore the equation 3(x + 2) = 3x − 6 has no solution.

Given:

The equation is:

9x − 4 = 5x − 4 + 4x

When we mentally solve this equation we get 9x − 4 = 9x − 4

Therefore the given equation 9x − 4 = 5x − 4 + 4x has infinitely many solutions.

Therefore the equation 9x − 4 = 5x − 4 + 4x has infinitely many solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 104 Exercise 1 Answer

When we solve an equation, we generally obtain a value of x.

The value of x obtained by solving the equation is the solution of the equation.

There is a possibility that the solution obtained is a whole number, rational number, a fraction or an integer. Nonetheless, it is the solution of the equation.

So yes, if the value of x is negative, the equation will still be true.

Yes, if the value of x is negative, the equation will still be true because, the value of x negative or positive is still the solution of the equation.

Page 107 Exercise 1 Answer

A one-variable equation is an equation that only has one variable.

If the equation two or more variables then it becomes a linear equation in two variables or so on.

The solution of an equation is based on the number of variables presents in the equation.

Therefore, one-variable equations will always have on a unique solution.

Yes, a one-variable equation always have one and unique solution.

Linear Equations Solutions Grade 8 Exercise 2.4 Envision Math

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 107 Exercise 2 Answer

Given:

The equation is:

6x + 12 = 2(3x + 6)

When we mentally solve this equation we get 6x + 12 = 6x + 12

Therefore the given equation 6x + 12 = 2(3x + 6) has infinitely many solutions.

Therefore Kaylee’s equation 6x + 12 = 2(3x + 6) has infinitely many solutions.

Page 107 Exercise 3 Answer

Given:

Height of the first plant is represented by the expression: 3(4x + 2)

Height of the second plant is represented by expression: 6(2x + 2)

We consider the two expressions and put them into a table to see if for the same whole, they yield the same result.

We observe that even after days the plants do not grow of the same height.

No, it is not possible for the plants to be of the same height.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 107 Exercise 4 Answer

Given:

The equation is: 3(2.4x + 4) = 4.1x + 7 + 3.1x

To find : solve the given equation

We consider:
​

Because 12 ≠ 7 the equation has no solution.

The equation 3(2.4x + 4) = 4.1x + 7 + 3.1x has no solution.

Page 107 Exercise 5 Answer

Given:

The equation is:

7x + 3x − 8 = 2(5x − 4)

We consider:
​
7x + 3x − 8 = 2(5x − 4)

10x − 8 = 10x − 8
​
Because 10x − 8 = 10x − 8 the equation has infinitely many solutions.

The equation 7x + 3x − 8 = 2(5x − 4) has infinitely many solutions.

Envision Math Grade 8 Chapter 2 Exercise 2.4 Solutions

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 107 Exercise 6 Answer

Given:

Todd buys peaches and a carton of vanilla yogurt. Agnes buys apples and a jar of honey

They bought the same number of pieces of fruit.

Peaches = $1.25 each

Vanilla Yogurt = $4

Apples = $1 each

Honey = $6

Let x be the number of fruits bought by Todd and Agnes.
Forming the two equations

Todd:

1.25x + 4

Agnes:

1x + 6

We equate the two equations:
​
1.25x + 4 = 1x + 6

0.25x = 2
​
x = 8

If both Agnes and Todd buy 8 fruits, then it is possible that they both pay the same amount.

The situation in which Agnes and Todd pay the same amount for their purchases is if they buy 8 fruits each.

Envision Math 8th Grade Exercise 2.4 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 108 Exercise 8 Answer

Given:

The given equation is 4(4x + 3) = 19x + 9 − 3x + 3

To find : solve the given equation

We consider:|

​
Since 12 is equal to 12, the equation has infinite solutions.

Since, the equation 4(4x + 3) = 19x + 9 − 3x + 3 has infinite solutions.

Page 108 Exercise 11 Answer

Given:

Store A’s prices are represented by the expression 15x − 2

Store B’s prices are represented by the expression 3(5x + 7)

Let x be the rates.

Equating the two equations

We consider:
​
15x − 2 = 3(5x + 7)

15x − 2 = 15x + 21
​
−2 ≠ 21

Since −2 ≠ 21 the store never charges the same rate.

We observe that −2 ≠ 21, therefore, the store never charges the same rate.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 109 Exercise 12 Answer

When the equation is equivalent to 0 = 0 the given equation will have infinitely many solutions.

When the equation is equivalent to a ≠ b, a and b being the two solutions, the given equation will not have any solution.

The equations having infinite solutions or no solutions will keep on going no matter how many times we get no solution and no matter how many times we get an infinite number.

Solving equations with no solution are similar to solving equations with infinite solutions because both will keep on going no matter how many times

we get no solution and no matter how many times we get an infinite number.

Page 109 Exercise 13 Answer

Given:

The given equation is: 0.9x + 5.1x − 7 = 2(2.5x − 3)

To find: solve the given equation

We consider:
​
0.9x + 5.1x − 7 = 2(2.5x − 3)

6x − 7 = 5x − 6
​
x = 1

The equation has only one solution.

The equation 0.9x + 5.1x − 7 = 2(2.5x − 3) has only one solution.

How To Solve Exercise 2.4 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 109 Exercise 15 Answer

Given:

The given equation is: 49x + 9 = 49x + 83

We consider:
​
49x + 9 = 49x + 83

49x − 49x + 9 = 49x − 49x + 83
​
9 ≠ 83

The equation does not have any solution.

The equation 49x + 9 = 49x + 83 has no solution.

The given equation is: 49x + 9 = 49x + 83

To find: solve the given equation

Solution:

49x + 9 = 49x + 83

+9 = 83 which is false. So, the equation has no solution.

Examples of equations having no solution is:

−9(x + 6) = −9x + 108 and 7(y − 8) = 7y + 42

−9(x + 6) = −9x + 108 and 7(y − 8) = 7y + 42 are the equations in one variable that have no solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 109 Exercise 16 Answer

The given equation is: 6(x + 2) = 5(x + 7)

The given equation 6(x + 2) = 5(x + 7) has only one solution.

Page 109 Exercise 17 Answer

The given equation is: 6x + 14x + 5 = 5(4x + 1)

To find: Write a word problem or any expression that this expression represents

The equivalent form of 6x + 14x + 5 = 5(4x + 1) is 100x + 25 = 100x + 25

The given equation 6x + 14x + 5 = 5(4x + 1) has infinite many solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 19 Answer

The equations should have one equation, no solution and infinite many solutions.

The equation that have one solution:

2x + 1 = 9

The equation that has no solution:

5x − 3x + 6 = 2x + 7 − 2

The equation that have infinitely many solutions:

7(8x + 5) − 35 = 4(14x)

2x + 1 = 9 have only one solution

5x − 3x + 6 = 2x + 7 − 2 has no solution

7(8x + 5) − 35 = 4(14x) has infinite many solution.

Page 110 Exercise 20 Answer

The given equation is: 4(4x − 2) + 1 = 16x − 7

The given equation has no solution.

Equation 4(4x – 2) + 1 = 16x – 7 has no solution.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 21 Answer

The given equation is : 6x + 26x − 10 = 8(4x + 10)

To find: solve the given equation

The value of x is 15.

Page 110 Exercise 22 Answer

The given equation is 64x − 16 = 16(4x − 1)

The given equation 64x – 16 = 16(4x – 1) has infinite many solutions.

Envision Math Grade 8 Exercise 2.4 Practice Problems

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 23 Answer

The given equation is 5(2x + 3) = 3(3x + 12)

To find: solve the given equation

The given solution 5(2x + 3) = 3(3x + 12) has only one solution.

Page 110 Exercise 24 Answer

The given equation is: 4(2x + 3) = 16x + 12 − 8x

To find: Which of the following best describes the solution to the equation

The given equation 4(2x + 3) = 16x + 12 − 8x has infinite many solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 25 Answer

The given equation is: 10x + 45x − 13 = 11(5x + 6)

To find: solve the given equation

Which is false, so the equation has no solution.

The statement which is true is: the equation has no solution.

Envision Math Grade 8 Student Solutions Volume 1 Chapter 2 Analyze And Solve Linear Equations

Page 97 Exercise 1 Answer

Given

Water flows through one pipe at a rate of 25,000 gallons an hour and through the other pipe at 45,000 gallons an hour.

To find/solve

Water leaves the system at a rate of 60,000 gallons an hour.

We have to write an equation where the variable will be the gallons that are leaving and entering the system per hour. The right side of the equation will have the maximum amount of gallons the tank can holes.

If we are asked to find the time needed for 3 tanks we simply multiply 50.3 = 150 hours

150 hours.is required to fill 3 tanks

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.3 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 97 Exercise 1 Answer

Given

Statement

To find/solve.

The bar model is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities.

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

Yes, it is basically a graphical representation of data using bars of different heights. In real life, bar graphs are commonly used to represent business data.

Yes, it is basically a graphical representation of data using bars of different heights. In real life, bar graphs are commonly used to represent business data.

Page 97 Exercise 1 Answer

Given

Expression 4(3x + 7x − 5)

To find/solve

Equals 40x − 20.

In the task it should say to simplify given expression so that it would be equal to

40x + 20, not 4x − 20

First way to simplify the expression:

4(3x + 7x + 5)

We get 4(10x + 5)

Then 40x + 20

Next to multiply 4 by the terms inside the parentheses

4(3x + 7x + 5)

12x + 28x + 20

First way is to combine like terms and then multiply 4 with the terms inside the parentheses. The second way is to multiply 4 with the terms inside the parentheses and then combine like terms.

First way is to combine like terms and then multiply 4 with the terms inside the parentheses. The second way is to multiply 4 with the terms inside the parentheses and then combine like terms.

Envision Math Grade 8 Exercise 2.3 Student Edition Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 98 Question 1 Answer

To find/solve: How can you use the Distributive Property to solve multistep equations?

When we are solving multistep equations, distributive property helps us with solving parentheses

Example

2(3x + 3) = 7

In the given equation, we use the distributive property so we can solve the parentheses.

2.3x + 2.3 = 7

When we are solving multistep equations, distributive property helps us with solving parentheses.

Page 98 Exercise 1 Answer

To find/solve: How can you find the solution of the equation using the bar diagram?

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

The bar model is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities.

Bar models are most often used to solve number problems with the four operations- addition and subtraction, multiplication and division.

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

The bar model is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities.

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 99 Exercise 2 Answer

Given

To find/solve

In the first step, we have to solve brackets on both sides

Here x = -8

x = -8 is the required answer

Page 98 Exercise 1 Answer

Given: can u add x to -5x on the left side of the equation as the first step

To find/solve: explain the given statement

First, we have to multiply the value in front of the parentheses with values in brackets

No we can’t add x to −5x on the left side of the equation as the first step because parentheses have higher priority than subtracting. First we need to solve the parentheses. Subtracting and adding our last operations to priority list.

No we can’t add x to −5x on the left side of the equation as the first step because parentheses have higher priority than subtracting. First we need to solve the parentheses. Subtracting and adding are the last operations on priority list.

Linear Equations Grade 8 Exercise 2.3 Envision Math Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 100 Exercise 2 Answer

Given

3(3x – 5x) + 2 = −8

To find: first step when solving the equation

The first step is to combine like terms in the parenthesis
​
3(3x − 5x) + 2 = −8

3.(−2x) + 2 = −8
​
The first step is to combine like terms in the parenthesis.

Page 100 Exercise 4 Answer

The given equation is 3x + 2 = x + 4(x + 2)

We need to solve the given equation.

​
The value of x = −3

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 100 Exercise 5 Answer

The given equation is −3(x − 1) + 7x = 27

We need to solve the given equation.

​
The value of x = 6

Page 100 Exercise 7 Answer

The given equation is 0.25(x + 4) − 3 = 28

We need to solve the given equation.

​
The value of x = 120

Envision Math Grade 8 Chapter 2 Exercise 2.3 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 101 Exercise 8 Answer

Given that, Lori bought a shirt and a hat at a half-off sale. If she spent a total of $21 on the two items, we need to find the original price of the hat.

The original price of the shirt is $24

The original price of the hat is x

Given that these are sold at a half rate and the total money spent is $21

The original price of the hat is $18

Page 101 Exercise 9 Answer

We need to use the Distributive Property to solve the given equation 28 − (3x + 4) = 2(x + 6) + x

The given is, 28−(3x+4)=2(x+6)+x

​
The value of x = 2

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 101 Exercise 10 Answer

We need to use the Distributive Property to solve the given equation 3(x − 6) + 6 = 5x − 6

The given equation is, 3(x − 6) + 6 = 5x − 6

​
The value of x = −3

Page 102 Exercise 15 Answer

We need to use the Distributive Property to solve the given equation 4x − 2(x − 2) = −9 + 5x − 8

The given equation is, 4x − 2(x − 2) = −9 + 5x − 8

Solving the given using the distributive property, we get,
​
​
The value of x = 7

Envision Math 8th Grade Exercise 2.3 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 102 Exercise 16 Answer

We need to use the Distributive Property to solve the equation 2(m + 2) = 22

We need to describe what it means to distribute the 2 to each term inside the parentheses.

The given equation is, 2(m + 2) = 22

Solving the given using the distributive property, we get,
​
​
The value of m = 9

We need to multiply two to each one of the terms inside the parentheses to distribute the 2 to each term.

How To Solve Exercise 3.1 Functions In Envision Math Grade 8

Page 102 Exercise 17 Answer

We need to find Peter’s number.

Let the unknown number be x

Subtract 12 from x and multiply the difference by −3

The result is −54

Thus, the equation be,
​
​
Peter’s number is 30

Envision Math Grade 8 Chapter 2 Exercise 2.3 Practice Problems

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 102 Exercise 19 Answer

Given:

−2(x + 4) = −6

We consider:

​
The required solution is x = −1

How To Solve Exercise 2.3 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 102 Exercise 20 Answer

Given:

3(x + 4) = 27

We consider:

​
The required solution is x = 5

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 91 Exercise 1 Answer

We need to explain how can we use an equation to show that expressions are equal.

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

Combine any like terms on each side of the equation: x-terms with x-terms and constant with constant.

Arrange the terms in the same are identical, then the two expressions are equivalent.

Combine any like terms on each side of the equation: x-terms with x-terms and constant with constant.

Arrange the terms in the same are identical, then the two expressions are equivalent.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.2 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 91 Exercise 1 Answer

We need to explain what expressions can we write to represent the amount of money collected by each boy.

Also, we need to explain how we can use these expressions to write an equation.

It seems form the picture that Jaxson has 14 checks and 15 dollars, and Bryon has 50 dollars and 7checks. It is given that each check is x dollars.

The dollar value of the checks is the number of checks times the value of each check.

Jaxson then got 14x + 15 dollars and Bryon got 50 + 7x dollars. They collected the same amount so we can set them equal to write the equation.

The equation is 14x + 15 = 50 + 7x.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 92 Question 1 Answer

Given

statement

To find/solve

Inverse operations.

We use inverse operations for getting all variables on one side and values on the other.

Example :

5x + 9 = 3x − 8

We subtract 3x from both sides of the equation, since 3x is on the right side of the equation.

We use inverse operations for getting all variables on one side and values on the other.

We use inverse operations for getting all variables on one side and values on the other.

Analyzing Linear Equations Grade 8 Exercise 2.2 Envision Math

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 92 Exercise 1 Answer

Given

Class A was given a sunflower with a height of 8 centimeters that grows at a rate of \(3 \frac{1}{2}\) centimeters per week. Class B was given a sunflower with a height of 10 centimeters that grows at a rate of \(3 \frac{1}{2}\) centimeters per week.

To find/solve

After how many weeks are the sunflowers the same height?

We put the sunflower of class A on one side of the equation and the sunflower of class B on the other side of the equation. We must add variables to the rate of growth of each sunflower.

After 8 weeks the sunflowers will be the same height.

Envision Math Grade 8 Chapter 2 Exercise 2.2 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 93 Exercise 2 Answer

Given

96 − 4.5y − 3.2y = 5.6y + 42.80

To find/solve

We have to apply a mathematical operation to the equation until we have only variables on one side and only values on another side of the equation.

y = 4 is the required answer

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 94 Exercise 2 Answer

Given

Statement

To find/solve

Inverse operations and properties of equality are important when solving equations.

Inverse operations help us get all variables on the same side of the equation.

Properties of equality are important because they give us a new equation that is equivalent to the original.

Properties of equality are important because they give us a new equation that is equivalent to the original.

Properties of equality are important because they give us a new equation that is equivalent to the original.

Envision Math 8th Grade Exercise 2.2 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 94 Exercise 4 Answer

Given

Maria and Liam work in a banquet hall. Maria earns a 20% commission on her food sales. Liam earns a weekly salary of $625 plus a 10% commission on his food sales.

To find/solve

What amount of food sales will result in Maria and Liam earning the same amount for the week?

First, we have to make an equation with commissions as a variable. On one side of the equation will be Maria and on the other Liam.

6,250 dollars of food sales will result in Maria and Liam earning the same amount for the week.

6,250 dollars of food sales will result in Maria and Liam earning the same amount for the week.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 94 Exercise 7 Answer

The given equation is −2.6b + 4 = 0.9b − 17

We need to solve the given equation and find the value of b

Solving the equation, we get,

The value of b = 6

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 8 Answer

The given equation is 6 − 4x = 6x − 8x + 2

We need to solve the given equation and find the value of x

The value of x = 2

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 9 Answer

The given equation is \(\frac{5}{3} x+\frac{1}{3} x=13 \frac{1}{3}+\frac{8}{3} x\)

We need to solve the given equation and find the value of x

The value of x = -20

How To Solve Exercise 2.2 Linear Equations In Envision Math Grade 8 

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 10 Answer

Given

Town 1 snow depth: \(3 \frac{1}{2}\) inches every hour

Town 2 snow depth: \(2 \frac{1}{4}\) inches every hour

Towns will be equal in snow depth is \(\frac{4}{5}\) of hour or 48 minutes.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 12 Answer

The given equation is 6 − 6x = 5x − 9x − 2

We need to solve the given equation and find the value of x

​
The value of x = 4

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 13 Answer

Given

Each month, 200 people on average move into town. A nearby town has a population of 45,000.

To find/solve

Write an equation that represents this situation and solve.

We have to write an equation with one town on one side and the other town on another side of the equation.

In about 7 months the population of towns will be the same.

Envision Math Grade 8 Chapter 2 Exercise 2.2 Practice Problems

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 96 Exercise 14 Answer

Given

statement

To find/solve

After how many months will the total cost for each health club be the same?

We have to make an equation with one health club on one side and second health club on other side of the equation.

Monthly fee will be our variable.

After 4 months.

After 4 months will the total cost for each health club be the same.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 96 Exercise 15 Answer

Given

The price of Stock A at 9 am. Was $12.73. since then, the price has been increasing at the rate of $0.06 per hour. At noon, the price of Stock B was $13.48. It begins to decrease at the rate of $0.14 per hour

To find/solve

How many hours will the prices of the stocks be the same?

We have to make an equation with Stock A on one side of the equation and Stock B on the other side of the equation.

We have to increase Stock A for 3 hours so that it will be growing before stock B starts falling.

After 2.85 hours Stock A and Stock B will have the same prices.

After 2.85 hours Stock A and Stock B will have the same prices.

Envision Math Exercise 2.2 Linear Equations Detailed Answers

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 96 Exercise 16 Answer

Given

In an academic contest, correct answers earn 12 points and incorrect answers lose 5 points. In the final round, school A starts with 165 points and gives the same number of correct and incorrect answers.

To find/solve

A. Which equation models the scoring in the final round and the outcome of the contest?

On the left side of the equation will be school A. School A has 165 points from before and score 12 per correct answer and lose 5 per incorrect answer. The answers will be our variable.

165 + 12x − 5x

The second part of the equation will be school B which came into finals with 65 points, and gave only correct answer for 12 points.

12x + 65

Now we put those two expressions into same equation.

165 + 12x − 5x = 65 + 12x

165 + 12x – 5x = 65 + 12x is the required answer

Given

In an academic contest, correct answers earn 12 points and incorrect answers lose 5 points. In the final round, school A starts with 165 points and gives the same number of correct and incorrect answers.

To find/solve

How many answers did each school get correct in the final round?

On the left side of the equation will be school A. School A has 165 points from before and score 12 per correct answer and lose 5 per incorrect answer. The answers will be our variable.

165 + 12x − 5x

The second part of the equation will be school B which came into finals with 65 points, and gave only correct answer for 12 points.

12x + 65

Now we put those two expressions into same equation.

165 + 12x − 5x = 65 + 12x

First we have to write combined like terms

165 + 7x = 65 + 12x

Subtract 12x from both sides.

165 − 5x = 65

Now subtract 165 from both sides of the equation, we get

−5x = −100

x = 20

Both schools gave 20 correct answers.

Both schools gave 20 correct answers.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 85 Exercise 1 Answer

To represent the relationship between the number of laptops and the total cost, we can draw a bar diagram

The bar diagram will be divided into 10 parts, one part for each computer, and the total length will represent the total cost of $7500.

Since each laptop has the same cost, each part of the bar diagram can be labeled as x, where x represents the cost of 1 laptop.

The diagram for the representation of relationship between the number of laptops and the total cost

The bar diagram will be divided into10
parts, one part for each computer, and the total length will represent the total cost of $7500.

Read and Learn More Envision Maths Grade 8 Volume 1

Since each laptop has the same cost, each part of the bar diagram can be labeled as x, where x represents the cost of 1 laptop.

Hence, the equation for the given information is 10x = 7500.

Envision Math Grade 8 Volume 1 Exercise 2.1 Answer Key

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 85 Exercise 1 Answer

It is important because we can use one variable for one value.

If each laptop would cost a different than we would have different variables.

It is important because we can use one variable for one value.

If each laptop would cost a different than we would have different variables.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 86 Exercise 1 Answer

We need to explain why we can use the same variable to represent the number of placements and to represent the number of napkins.

We have to combine the coefficients easily. So, the number of placements and the number of napkins use the same variable.

We have to ease to combine the coefficients. So the number of placements and the number of napkins uses the same variable.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 87 Exercise 2 Answer

We need to explain how does the original price and the sale price relate.

The sale price of the computer screen is $130

The price of the computer before the sale is $200

The computer was sold for 35% off the original price.

The sale price is 100 − 35 = 65% of the given original price.

Analyzing Linear Equations Grade 8 Exercise 2.1 Envision Math Solutions

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 86 Exercise 1 Answer

Given:

Each necklace costs $9.99

Each bracelet costs $7.99

Total costs $53.94

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 87 Exercise 2 Answer

Given:

Grocery bill $150

Discount 5%

If something has a discount of 5% that means that they pay 95% of the original price.

Now we can write an equation with 0.95 of the bill and on the right side the price Nat paid.

0.95x = 150

Divide both sides by 0.95
​
0.95x ÷ 0.95 = 150 ÷ 0.95

x ≈ 157.89
​
Hence, the grocery bill before the discount was ≈ 157.89

Envision Math Grade 8 Exercise 2.1 Solutions

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 87 Exercise 3 Answer

Given:

Solve for d

Hence, the value of d is -60.

Given:

−9.7d − (−12.81d) = 8.54

Hence, the value of d is ≈ 2.746.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 86 Exercise 1 Answer

Given:

9.99s + 7.99s + 4.6 = 53.94

To find: Can you combine the s terms and 4.6? Explain.

We cannot combine the s terms and 4.6 because there can only be either variables on one side or normal values.

​
So, we cannot combine terms and 4.6.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 2 Answer

The like terms are recognized in the equation by having the same variable and exponents

Example:

12d + 3d = 24

12d And 3d are like terms.

The like terms are recognized in the equation by having the same variable and exponents.

Envision Math 8th Grade Analyzing Linear Equations Exercise 2.1

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 3 Answer

Given

In the given equation first, we rewrite our like terms in fraction form or decimal form.

Both of them need to be written in some form

First we rewrite our like terms in fraction form or decimal form. both of them need to be written in same form and then combined by subtracting the coefficients.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 5 Answer

Given

Total population: 350,000

Decreased population 3%

If we know that the population of a city decreased by 30% and now is 350,000 this means that 350,000 is 0.7 of the population that was 10 years ago.

​
Therefore, 10 years ago the population of the same city was 500,000.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 6 Answer

Given

−12.2z − 13.4z = −179.2

​
Therefore, the solution of the given equation is 7.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 7 Answer

The given equation is \(\frac{4}{5} x-\frac{1}{4} x=11\)

We need to solve the given equation and find the value of x

Solving the equation, we get,

The value of x = 20

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 8 Answer

The given equation is −0.65x + 0.45x = 5.4

We need to solve the given equation and find the value of x

​
The value of x = -27

How To Solve Exercise 2.1 In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 10 Answer

The given equation is −3.8x − 5.9x = 223.1

We need to solve the given equation and find the value of x

​
The value of x = -23

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 12 Answer

The given equation is \(-\frac{3}{5} x-\frac{7}{10} x+\frac{1}{2} x=-56\)

Solving the equation, we get,

The value of x = 70

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 16 Answer

We need to write an equation that can be represented by the bar diagram, then we need to solve the unknown value.

The equation that can be represented by the bar diagram is,

−1.2y − 4.2y = −3.78

​
The equation that can be represented by the bar diagram is,

−1.2y − 4.2y = −3.78

The value of y = 0.7

Envision Math Grade 8 Chapter 2 Linear Equations Exercise 2.1 Answers

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 17 Answer

The given equation is \(\frac{2}{3} h-156=3 \frac{13}{24}\)

We need to solve the given equation and find the value of h

Solving the given equation, we get,

The value of h = 239.25

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 18 Answer

Given

The total cost of the notebooks and binders was $27.08.

To find/solve

Draw a bar diagram to represent the situations.

Nathan had bought one notebook and one binder in value 0.95 + 5.82 for each class. If we want to find how many classes does Nathan have, we just make an equation with value for each class on one side as variable and the money that he spent on the other side.

0.95x + 5.82x = 27.08

6.77x = 27.08

Now we divide both sides of the equations with the factor next to x.

6.77x/6.77 = 27.08

x = 4

Nathan is taking 4 classes.

Nathan is taking 4 classes.

Envision Math Grade 8 Volume 1 Linear Equations Practice Exercise 2.1

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 20 Answer

Given

A 132 inch board is cut into two pieces. One piece is three time the length of the other.

To find/solve

Draw a bar diagram to represent the situation.

We simply have to divide the bar diagram on two pieces where one piece is exactly 3 times larger than the other piece.

The total length of whole diagram is 132 in

Simply divide the diagram that is total of 132 in, on 2 pieces where one piece is 3 times larger than the other.

Simply divide the diagram that is total of 132 in, on 2 pieces where one piece is 3 times larger than the other.

Given

A 132 inch board is cut into two pieces. One piece is three time the length of the other.

To find/solve

write and solve an equation to find the length of the shorter piece.

If we cut a board in two pieces where one piece is three times the length of the other this means that if we split one whole into four parts with one being three times the other part, this simply means;

So if we know that whole board is 132 inch we can simply multiply this number with value of shorter part which is \(\frac{1}{4}\)

Shorter part is 33 inches long.

Shorter part is 33 inches long.

Overview of Envision Math Grade 8 Volume Student Edition Solutions

Envision Math is a comprehensive mathematics curriculum designed for students from kindergarten through eighth grade, aligning with the Common Core standards. The Grade 8 Volume Student Edition is particularly focused on enhancing students’ understanding of critical mathematical concepts and problem-solving skills. This article provides an in-depth look at the solutions available for the Envision Math Grade 8 curriculum, highlighting key topics, resources, and strategies for effective learning.

Envision Math Grade 8 Volume Student Edition Solutions Key Topics Covered

The Envision Math Grade 8 curriculum is divided into several essential topics, each aimed at building a strong mathematical foundation. The primary topics include:

• Real Numbers: Understanding rational and irrational numbers, operations with real numbers, and properties of exponents.
• Linear Equations: Analyzing and solving linear equations, including multi-step equations and systems of equations.
• Functions: Using functions to model relationships and understanding the differences between linear and nonlinear functions.
• Bivariate Data: Investigating data sets involving two variables, constructing scatter plots, and interpreting linear associations.
• Systems of Linear Equations: Solving systems using various methods such as graphing, substitution, and elimination.
• Congruence and Similarity: Exploring transformations, congruent figures, and similarity in geometric figures.
• Pythagorean Theorem: Applying the Pythagorean theorem to solve problems involving right triangles.
• Surface Area and Volume: Calculating surface area and volume for various three-dimensional shapes.

These topics not only prepare students for high school mathematics but also foster critical thinking and analytical skills essential for real-world applications.

• Chapter 1: Real Numbers
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.3
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.4
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.5
  • Envision Math Grade 8 Volume 1 Student Edition Solutions chapter 1 Real Number Exercise 1.6 Real Number
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Topic 1 Review Essential Questions
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Topic 13 Act Mathematical Modeling
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.8
  • Envision Math Grade 8 Volume 1 Student Edition Solutions chapter Standards for Mathematical Practice Exercise 1
  • Envision Math Grade 8 Volume Student Edition Solutions Chapter 1 Real Numbers Topic 1
• Chapter 2: Analyze and Solve Linear Equations
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.1
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.2
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.3
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.4
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.5
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9
• Chapter 3: Use Functions to Model Relationships
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.1
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.2
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.6
• Chapter 4 : Investigate Bivariate Data
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.4
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5
• Chapter 5 Analyze And Solve System Of Linear Equations
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.1
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3
  • Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4