Envision Math

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 257 Exercise 1 Answer

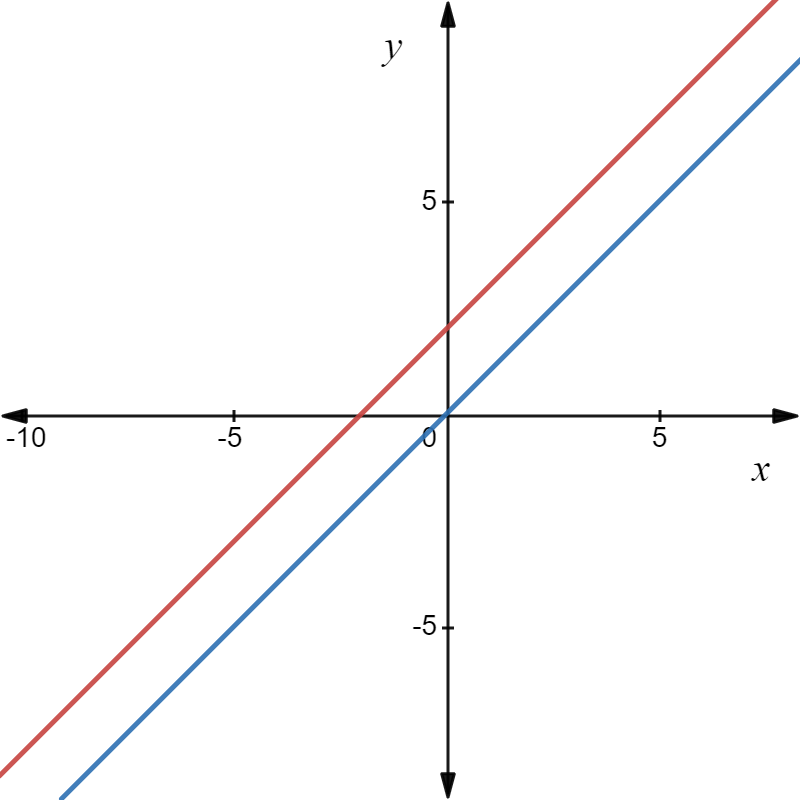
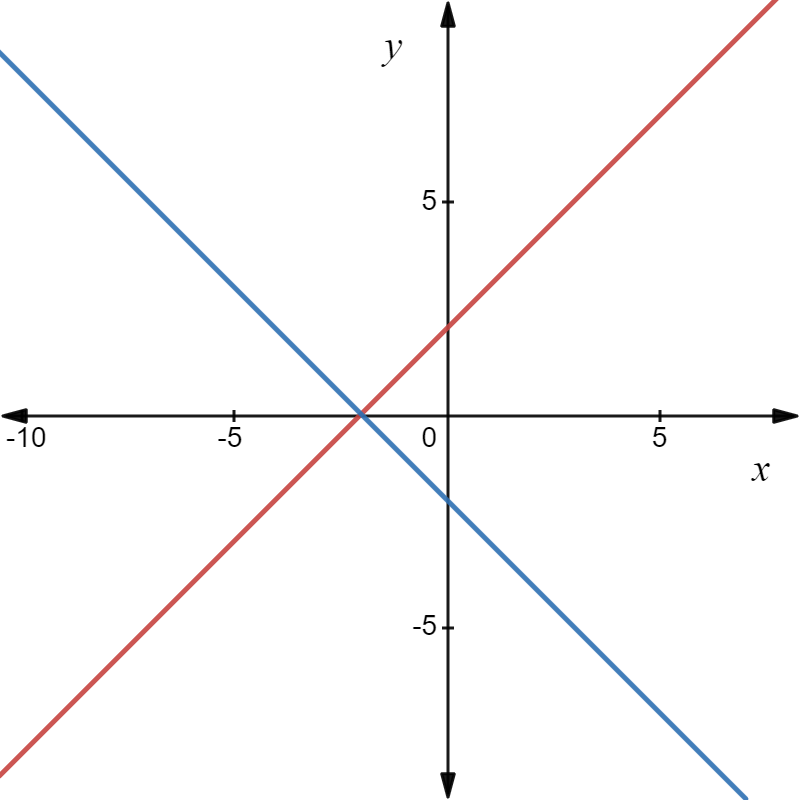
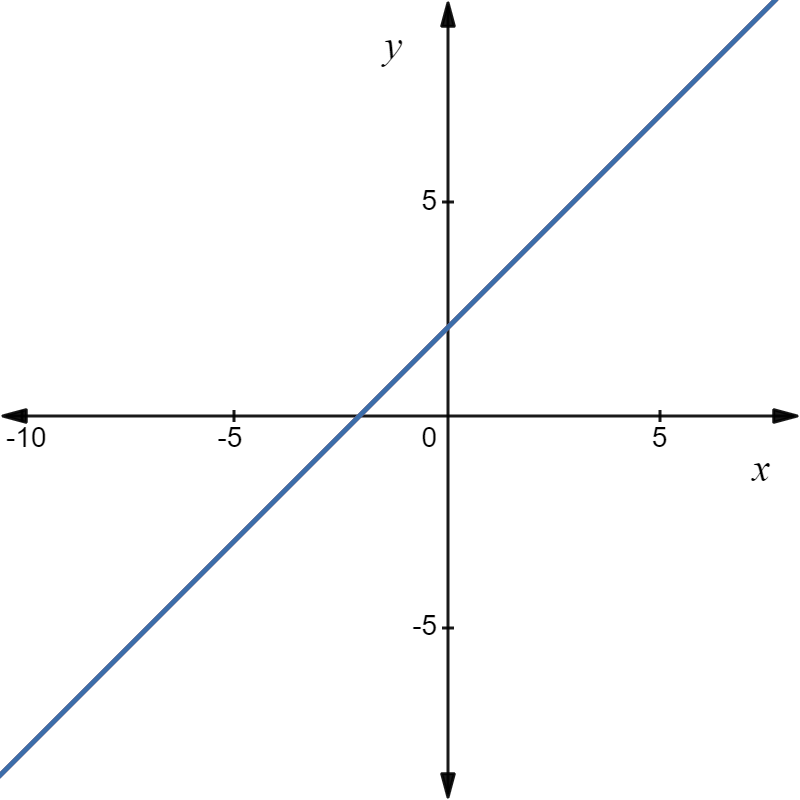
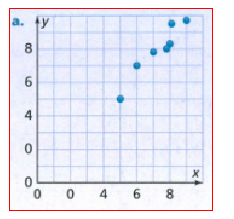
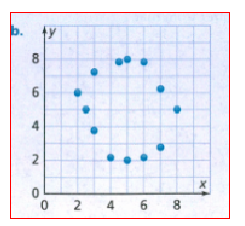
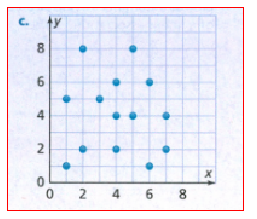
Given: Draw three pairs of lines, each showing a different way that two lines can intersect or not intersect.

How are these pairs of lines related?

There are n ways 2 lines can relate to each other.

The first way is that they are parallel, meaning they do not have any intersections.

The second way is if they are not parallel, but are not the same line. in this case, they have exactly 1 intersection.

The third and last way is, if the lines are the same, in this case, all of their points are the same.

That means they intersect at infinitely many points.

2 lines cannot have 2 points in common because 2 points clearly define a line.

That means if there is a line passing through both points, there cannot be another that does the same.

2 lines cannot have 2 points in common because 2 points clearly define a line.

If they have more than 1 point in common, it means they are the same line and have infinitely many common points.

Envision Math Grade 8 Volume 1 Chapter 5.2 Solutions

Page 263 Focus On Math Practice Answer

To find: What does the point of intersection of the lines represent in the situation?

Point of intersection means the point at which two lines intersect.

The coordinates of the point of intersection represent the solution to both linear equations simultaneously.

The coordinates of the point of intersection represent the values of x and y that satisfy both equations at the same time.

Page 264 Essential Question Answer

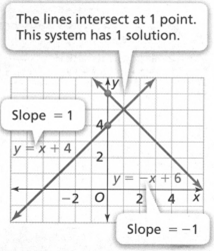
To Find: How does the graph of a system of linear equations represent its solution?

Each pair of lines represents a system of linear equations. A system of linear equations is formed by two or more linear equations that use the same variables.

you can use the graphs to determine the number of solutions for each system.

The equations of the linear system
​
y = x + 4

y = −x + 6
​
have different slopes.

The system has 1 solution (1,5).

A solution of a system of linear equations is an ordered pair that makes all equations in the system true.

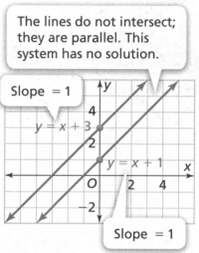
The equations of the linear system
​
y = x + 3

y = x + 1
​
have the same slopes and different y−intercepts.

The system has no solution.

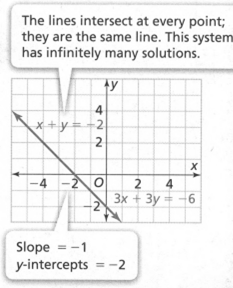
The equations of the linear system
​
x + y = −2

3x + 3y = −6
​
have the same slopes and the samey−intercepts. They represent the same line.

The system has infinitely many

Systems of equations can be solved by looking at their graphs.

A system with one solution has one point of intersection.

A system with no solution has no points of intersection.

A system with infinitely many solutions has infinite points of intersection.

Analyze And Solve Systems Of Linear Equations Envision Math Exercise 5.2 Answers

Page 264 Try It Answer

Given: ​

​y = 3x + 5

y = 2x + 4
​
To find: The solution is the point of intersection.

y = 3x + 5

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = 3x + 5,x = 0

Substitute x = 0

y = 3 × 0 + 5

Calculate the product

y = 0 + 5

Remove 0

y = 5

Using the same method, calculate the values of y for a few other values of x

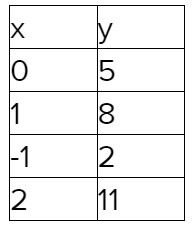
Plot the points on the graph.

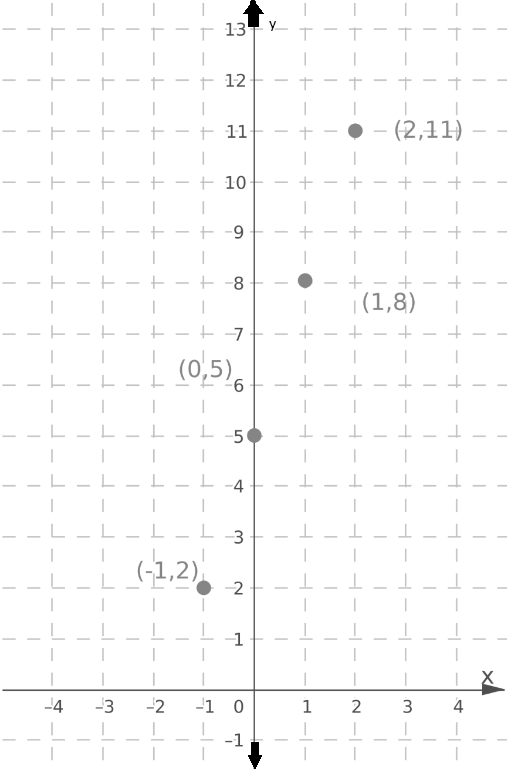
Draw a line through the plotted points.

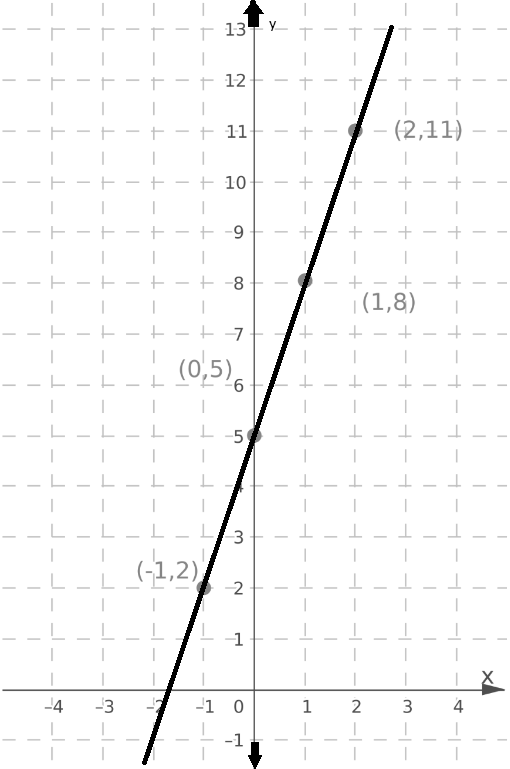
Using the same method, graph the line y = 2x + 4.

The lines intersect at the point (−1,2).

The point of intersection (−1,2) is the solution of the system.

Page 264 Convince Me Answer

Given:
​
y = 3x + 5

y = 2x + 4
​
Find: the point of intersection of the graphs represent the solution of a system of linear equations.

Find the points and then plot the points and second equation to find the point of intersection.

Given: y = 3x + 5

The first equation is written in the slope-intercept form.
Calculate the value of y for x = 0,
​
y = 3x + 5

y = 3(0) + 5

y = 0 + 5

y = 5
​
Using the same method, calculate the values of y for a few other values of x,

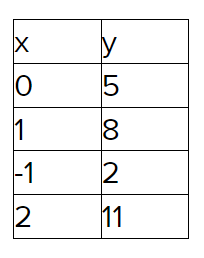
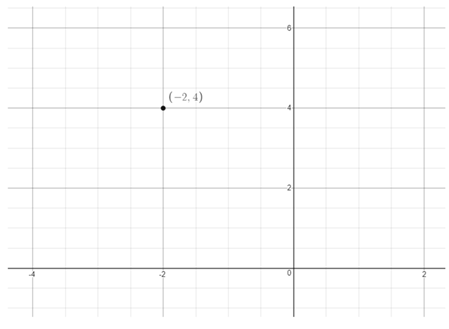
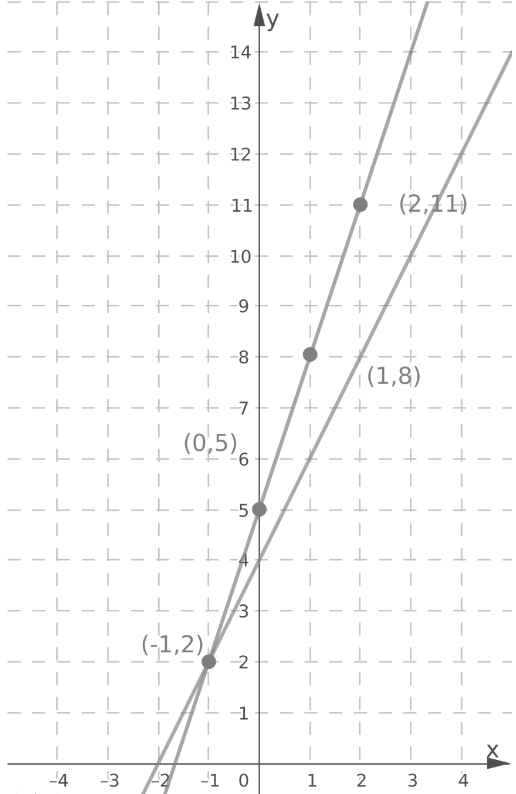
Plot the points on the graph (0,5),(1,8),(−1,2),(2,11) and the equation y = 2x + 4 draw a line as shown below:

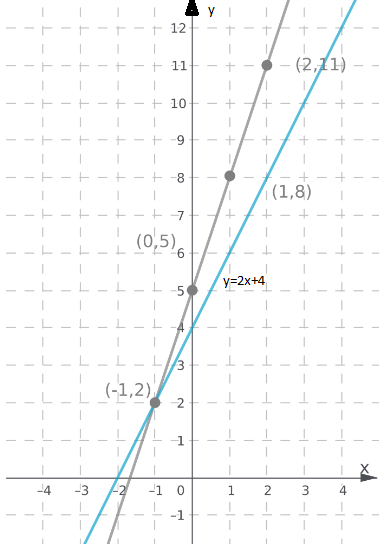
The above graph show that the point of intersection is (−1,2).

The point of intersection of the graphs belongs to the first and the second line at the same time and satisfies the equations of both graphs.

Therefore, the point of intersection (−1,2) is a point that satisfies the system of the equations of the two graphs.

Page 266 Exercise 1 Answer

To find: How does the graph of a system of linear equations represent its solution?

Each pair of lines represents a system of linear equations. A system of linear equations is formed by two or more linear equations that use the same variables.

you can use the graphs to determine the number of solutions for each system.

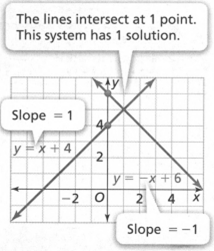
The equations of the linear system
​
y = x + 4

y = −x+ 6
​
have different slopes.

The system has 1 solution(1,5).

A solution of a system of linear equations is an ordered pair that makes all equations in the system true.

The equations of the linear system
​
y = x + 3

y = x + 1
​
have the same slopes and different y−intercepts.

The system has no solution.

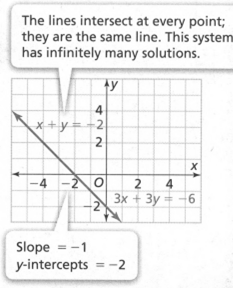
The equations of the linear system
​
x + y = −2

3x + 3y = −6
​
have the same slopes and the same y−intercepts. They represent the same line.

The system has infinitely many solutions.

Systems of equations can be solved by looking at their graphs.

A system with one solution has one point of intersection.

A system with no solution has no points of intersection.

A system with infinitely many solutions has infinite points of intersection.

Envision Math Grade 8 Chapter 5.2 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 266 Exercise 2 Answer

Given: If a system has no solution.

To Find: what do you know about the lines being graphed?

A system has a solution if the lines have a point of intersection.

If a system has no solution, therefore the lines are parallel to each other.

If a system has no solution, the lines being graphed are parallel to each other.

Page 266 Exercise 4 Answer

Given: ​

​y = −3x − 5

y = 9x + 7
​
graph each system of equations and find the solution.

y = -3x – 5

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = −3x −5,x = 0

Substitute x = 0

y = −3 × 0−5

Calculate the product

y = 0 − 5

Remove 0

y = −5

Using the same method, calculate the values of y for a few other values of x.

Plot the points (-2, 1), (-1, -2), (0, -5) and (1, -8).

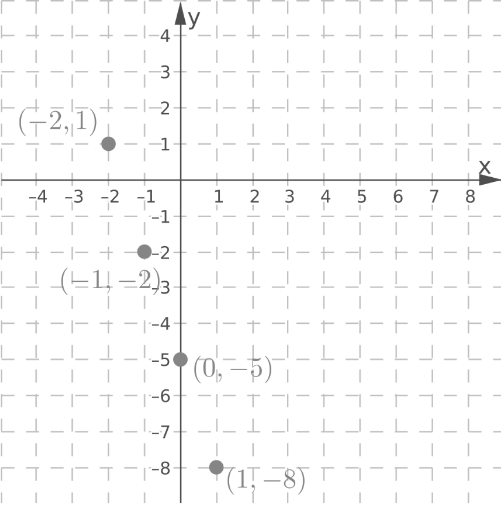
Draw a line through the plotted points.

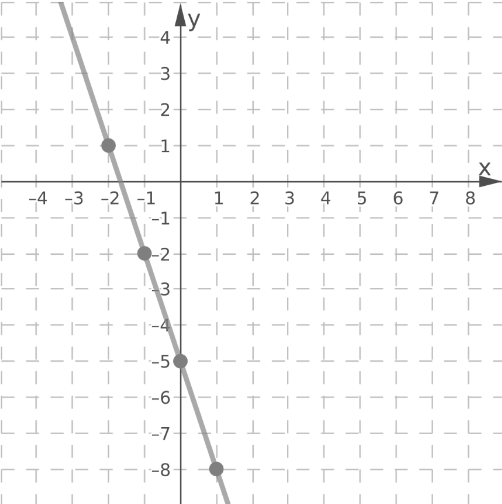
Using the same method, graph the line y = 9x + 7.

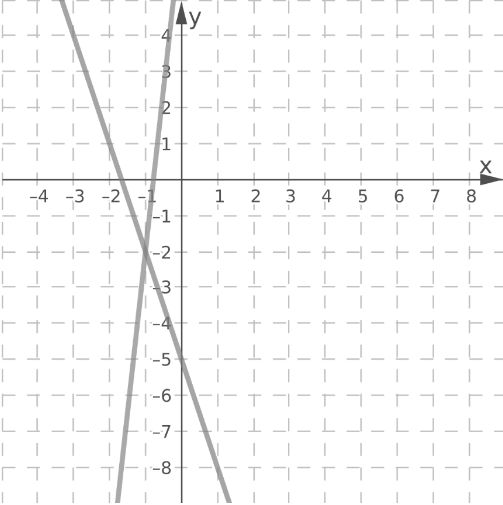
The lines intersect at the point (-1, -2).

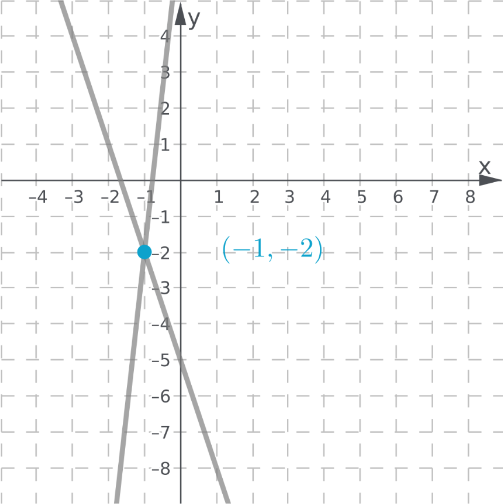
The point of intersection (−1,−2) is the solution of the system.

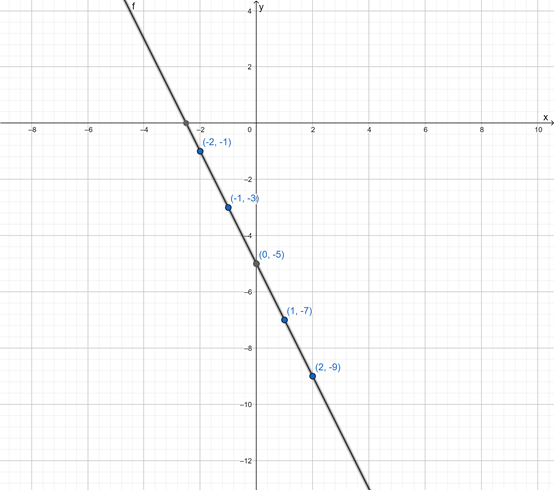
Page 266 Exercise 5 Answer

Given: ​

​y = −2x − 5

6x + 3y = −15
​
graph each system of equations and find the solution.

y = 2x – 5

The first equation is in slope-intercept form.

Write the second equation in slope-intercept form:

6x + 3y = −15

Move the variable to the right

3y = −15 − 6x

Divide both sides

y = −5 − 2x

Reorder the terms

y = −2x − 5

Equations of both lines are equal, so lines are the same.

Calculate the value of y for x = −2:

y = −2x − 5,x = −2

Substitute x = −2

y = −2 × (−2)−5

Multiply

y = 4 − 5

Calculate

y = −1

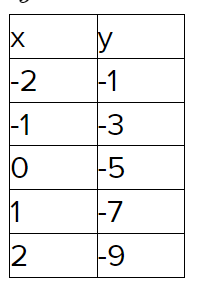
Using the same method, calculate the values of y for a few different values of x

Plot the points on a coordinate plane.

Draw a line through the plotted points.

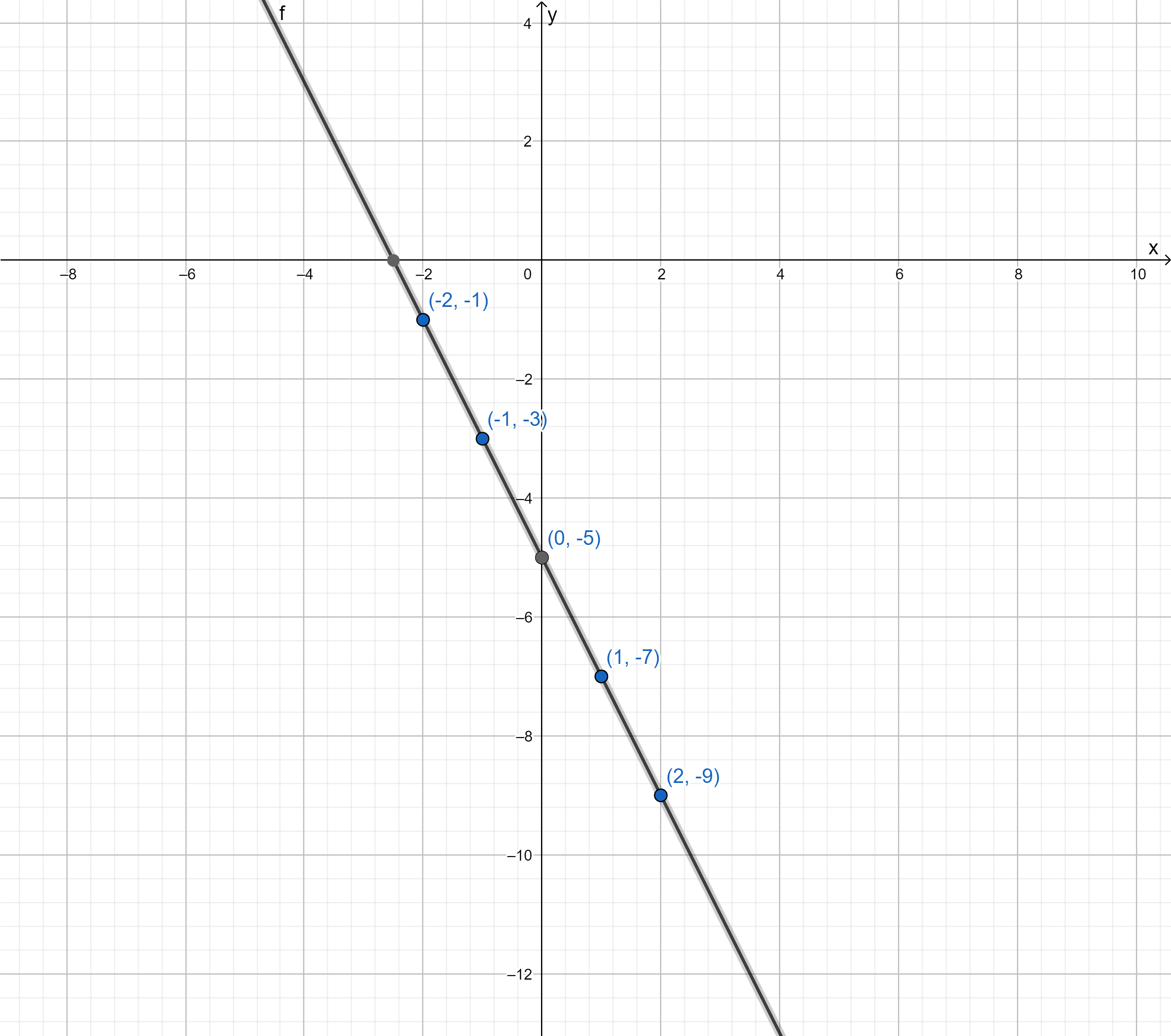
Each point on the line represents a solution.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

Page 266 Exercise 6 Answer

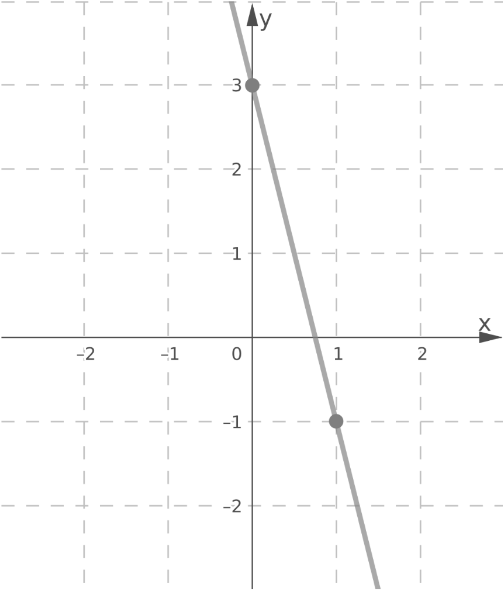
Given: ​

​y = −4x + 3

8x + 2y = 8
​
graph each system of equations and find the solution.

In order to graph y = −4x + 3, calculate two points on the line.

Calculate the value of y for x = 0:

y = −4x + 3,x = 0

Substitute x = 0

y = −4 × 0 + 3

Calculate the product

y = 0 + 3

Remove 0

y = 3

Calculate the value of y for x = 1:

y = −4x + 3,x = 1

Substitute x = 1

y = −4 × 1 + 3

Calculate the product

y = −4 + 3

Calculate

y = −1

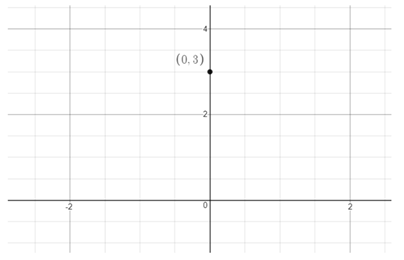
Thus, the points(0,3) and (1,−1) are on the graph of

y = −4x + 3.

Plot the points(0,3) and (1,−1).

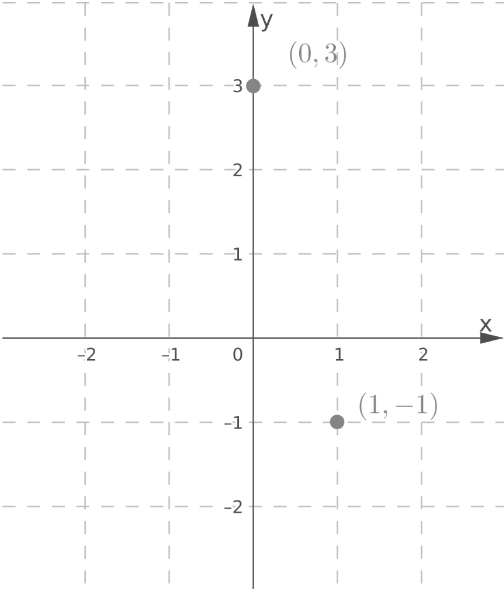
Graph y = −4x + 3 by drawing a line through the points.

Write the second equation in the slope-intercept form:

8x + 2y = 8

Move the variable to the right

Divide both sides

y = 4 − 4x

Reorder the terms

y = −4x + 4

Calculate the value of y for x = 0:

y = −4x + 4,x = 0

Substitute x = 0

y = −4 × 0 + 4

Calculate the product

y = 0 + 4

Remove 0

y = 4

Step 8

Calculate the value of y for x = 1:

y = −4x + 4,x = 1

Substitute x = 1

y = −4 × 1 + 4

Calculate the product

y = −4 + 4

Eliminate the opposites

y = 0

Thus, the points (0,4) and (1,0)are on the graph of 8x + 2y = 8.

Plot the points(0,4) and (1, 0).

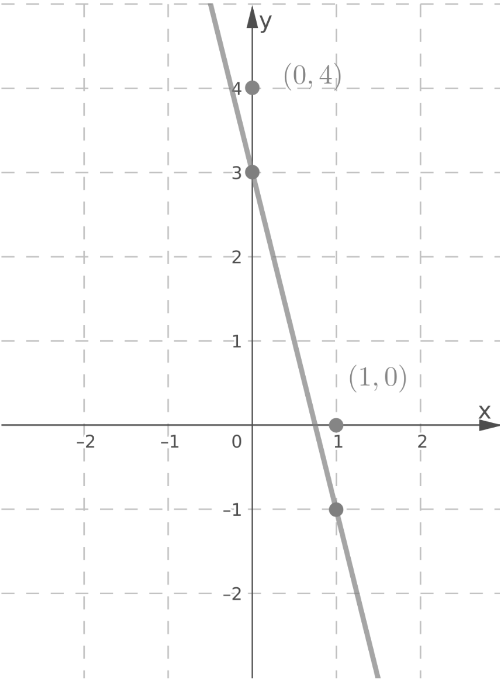
Graph 8x + 2y = 8 by drawing a line through the points.

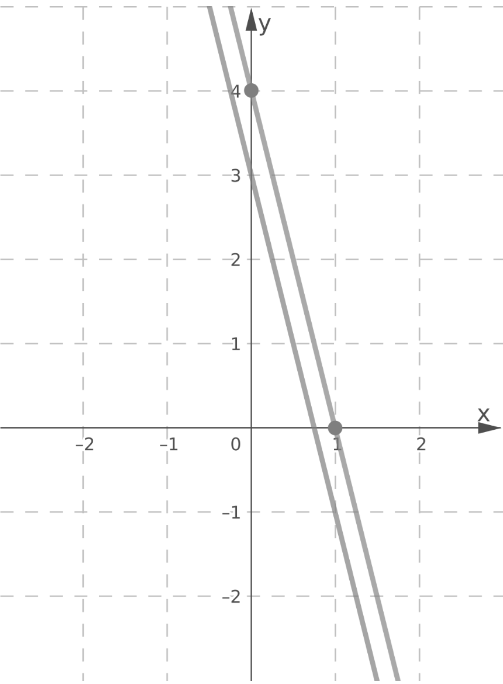
Lines y = −4x + 3 and 8x + 2y = 8 are parallel.

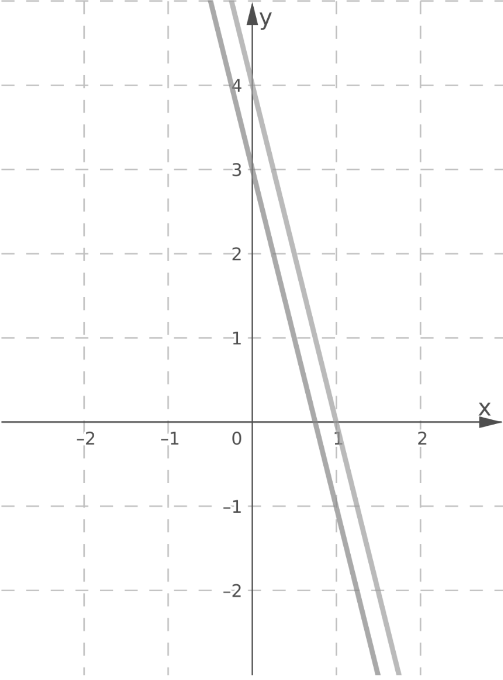
Since the lines are parallel, there is no point of intersection.

Therefore, the system has no solution.

The lines y = −4x + 3 and 8x + 2y = 8 are parallel, so the system has no solution.

Solutions For Envision Math Grade 8 Exercise 5.2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 267 Exercise 7 Answer

Given: ​x + 4y = 8

3x + 4y = 0
​
Graph each system of equations to determine the solution.

Rewrite the first equation in slope-intercept form:

x + 4y = 8

Move the variable to the right

4y = 8 − x

Divide both sides

y = \(2-\frac{1}{4} x\)

Reorder the terms

y = \(-\frac{1}{4} x+2\)

Calculate the value of y for x = 0:

y = \(-\frac{1}{4} x+2, x=0\)

Substitute x = 0

y = \(-\frac{1}{4} \times 0+2\)

Calculate the product

y = 0 + 2

Remove 0

y = 2

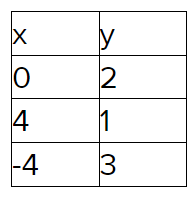
Using the same method, calculate the values of y for a few other values of x.

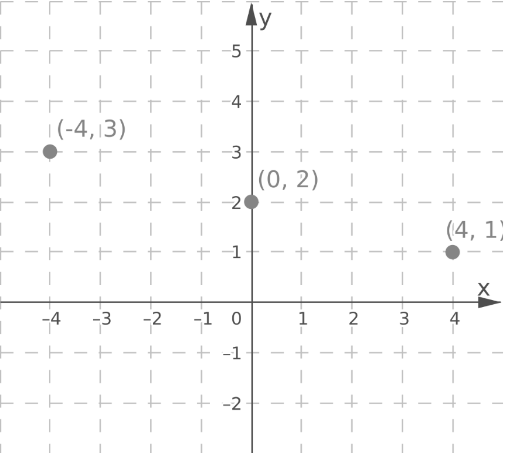
Plot the points (0,2),(4,1),(−4,3)

Draw a line through the plotted points.

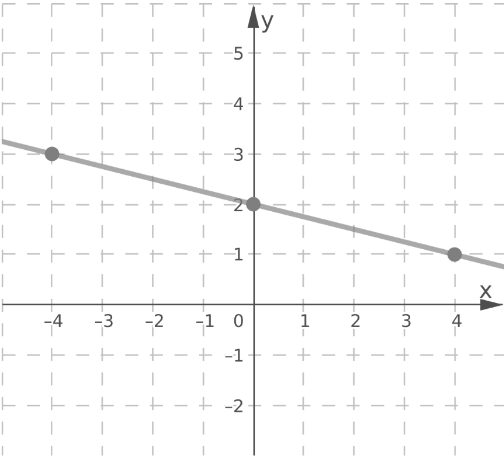
Using the same method, graph the line 3x + 4y = 0.

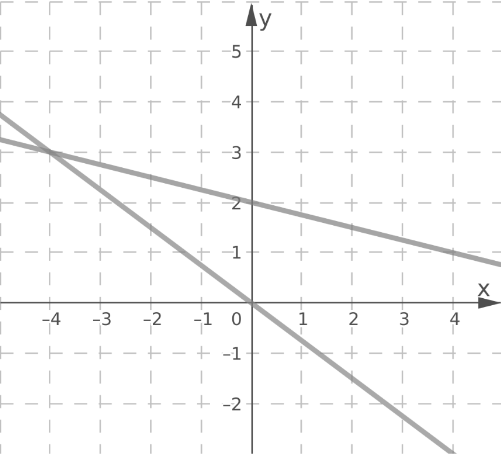
The lines intersect at the point (−4,3).

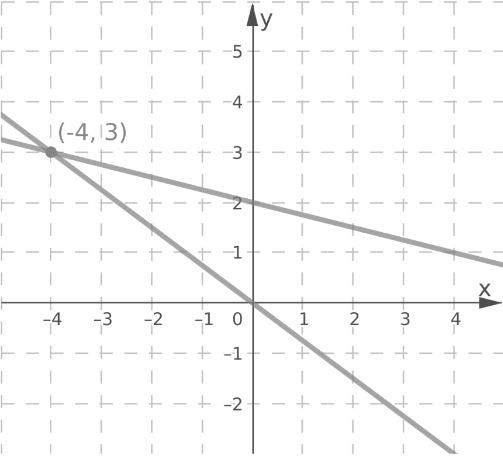
The point of intersection (−4,3) is the solution of the system.

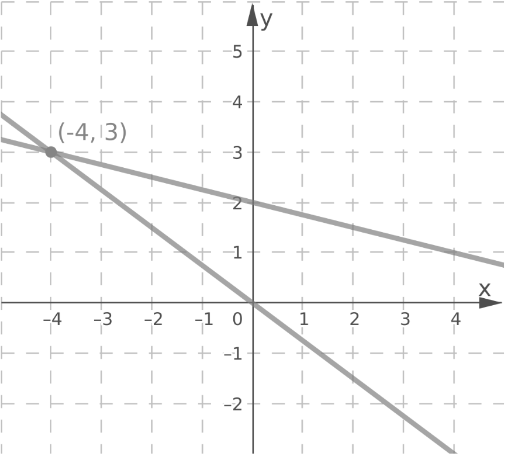
Page 267 Exercise 8 Answer

Given: ​

​2x − 3y = 6

4x − 6y = 12
​
graph each system of equations to determine the solution.

Write the first equation in slope-intercept form:

2x − 3y = 6

Move the variable to the right

−3y = 6 − 2x

Change the signs

3y = −6 + 2x

Divide both sides

y = \(-2+\frac{2}{3} x\)

Reorder the terms

y = \(\frac{2}{3} x-2\)

Write the second equation in slope-intercept form:

4x – 6y = 12

Move the variable to the right

-6y = 12 – 4x

Change the signs

6y = -12 + 4x

Divide both sides

y = \(-2+\frac{2}{3} x\)

Reorder the terms

y = \(\frac{2}{3} x-2\)

Equations of both lines are equal, so lines are the same.

Calculate the value of y for x = -9

y = \(\frac{2}{3} x-2, x=-9\)

Substitute x = -9

y = \(\frac{2}{3} \times(-9)-2\)

Multiply

Reduce

y = -2 x 3 -2

Calculate

y = -8

Using the same method, calculate the values of y for a few different values of x

Plot the points(−9,−8),(−6,−6),(−3,−4),(6,2) and (9,4).

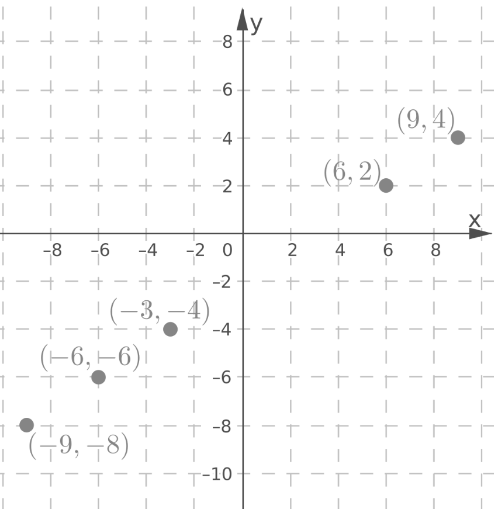
Draw a line through the plotted points.

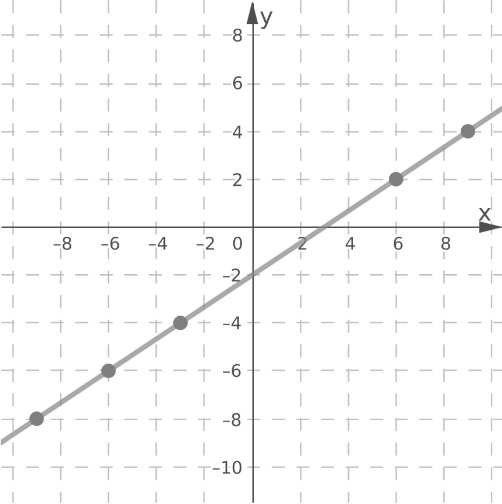
Each point on the line represents a solution.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

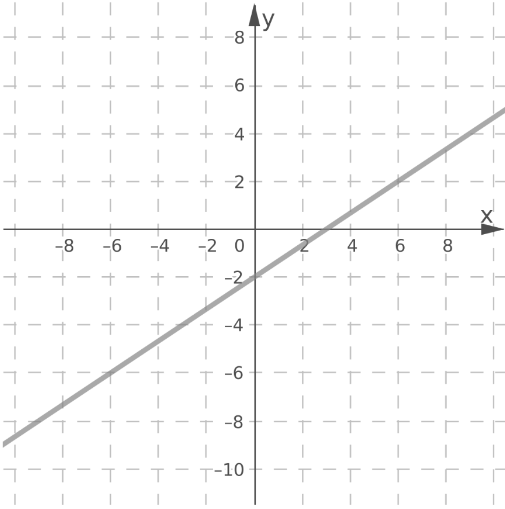
Envision Math Grade 8 Volume 1 Chapter 5.2 Practice Problems

Page 267 Exercise 11 Answer

Given: ​

​y = 1.5x + 1

y = −1.5x + 5.5
​
To Find: Graph the system of equations, then estimate the solution.

We have,

y = 1.5x + 1

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = 1.5x + 1,x = 0

Substitute x = 0

y = 1.5 × 0 + 1

Calculate the product

y = 0 + 1

Remove 0

y = 1

Using the same method, calculate the values of y for a few other values of x.

Plot the points (-2, -2), (0, 1), (2, 4), (4, 7) and (6, 10)

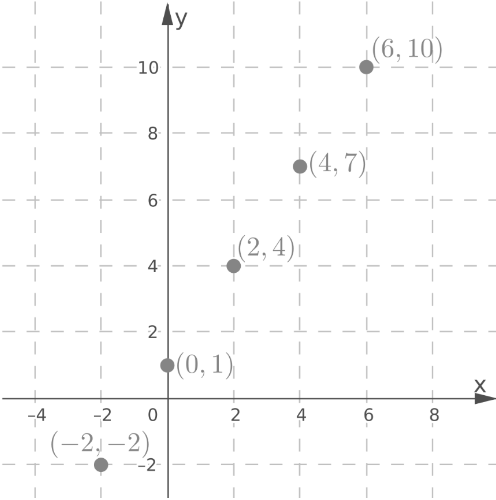
Draw a line through the plotted points.

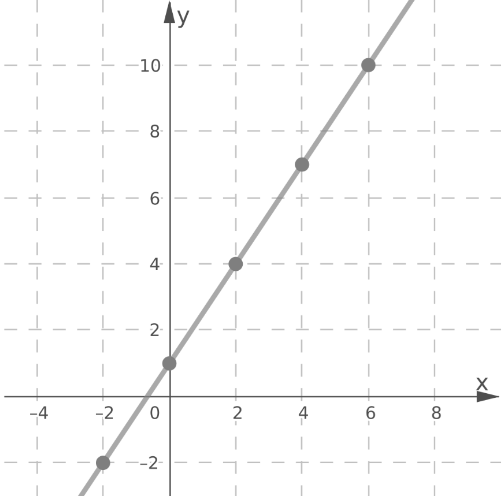
Using the same method, graph the line y = -1.5x + 5.5.

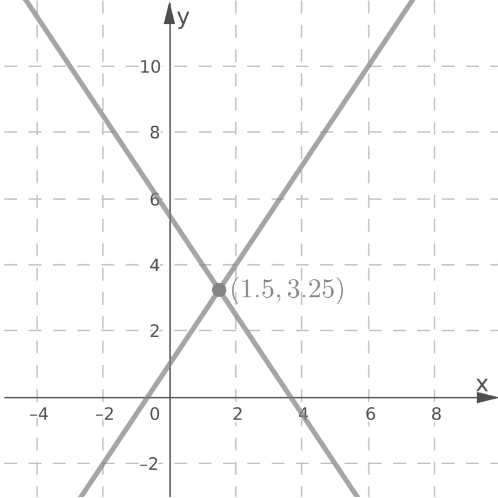
The lines intersect at the point (1.5,3.25).

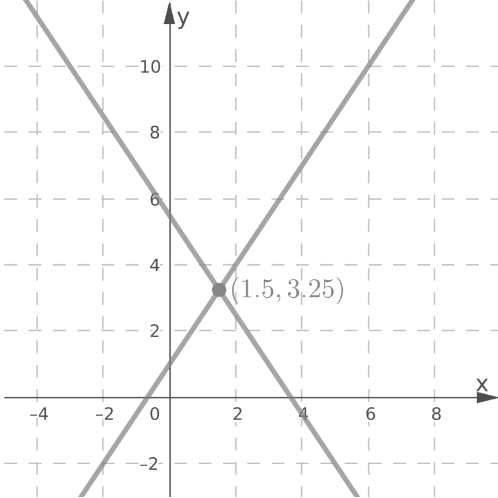
The point of intersection (1.5,3.25) is the solution of the system.

Envision Math 8th Grade Systems Of Equations Topic 5.2 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 268 Exercise 12 Answer

Given:

​−3y = −9x + 3

−6y = −18x − 12
​
To Find: graph and determine the solution of the system of equations.

Write the first equation in the slope-intercept form:

−3y = −9x + 3

Calculate

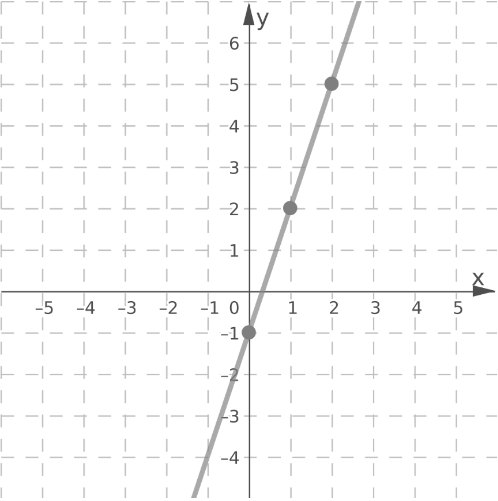
y = 3x − 1

Calculate the value of y for x = 0:

y = 3x−1,x = 0

Substitute x = 0

y = 3 × 0 − 1

Calculate the product

y = 0 − 1

Remove 0

y = −1

Using the same method, calculate the values of y for a few other values of x.

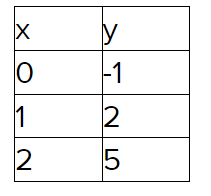
Plot the points (0,−1),(1,2),(2,5)

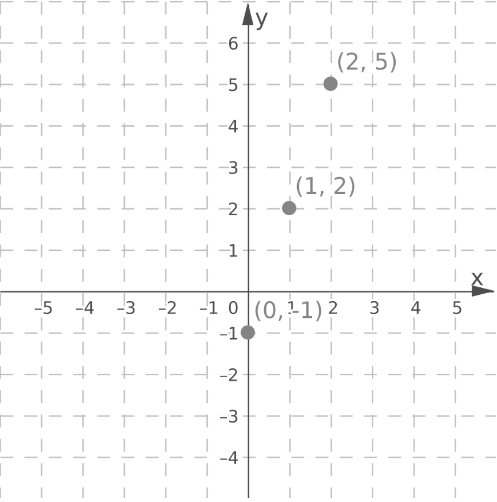
Draw a line through the plotted points.

Write the second equation in slope-intercept form:

−6y = −18x − 12

Change the signs

6y = 18x + 12

Divide both sides

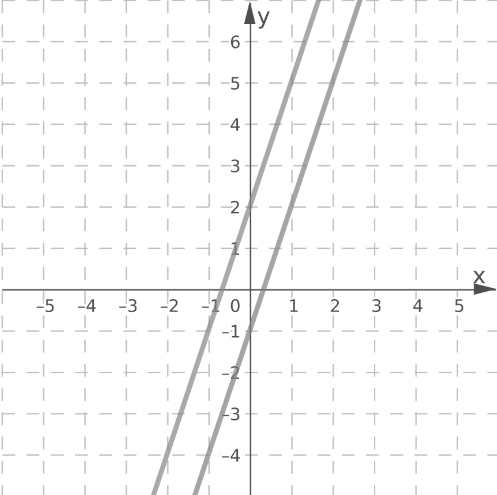
y = 3x + 2

Using the same method, graph the line y = 3x + 2.

Lines y = 3x − 1 and y = 3x + 2 are parallel.

Since the lines are parallel, there is no point of intersection.

Therefore, the system has no solution.

The lines y = 3x − 1 and y = 3x + 2 are parallel, so the system has no solution.

Envision Math Grade 8 Topic 5.2 Graphing Linear Systems Solutions

Page 268 Exercise 13 Answer

Given: ​

​x + 5y = 0

25y = −5x
​
To Find: graph and determine the solution of the system of equations.

Write the first equation in slope-intercept form:

x + 5y = 0

Calculate

y = \(-\frac{1}{5} x\)

Write the second equation in slope-intercept form:

25y = −5x

Divide both sides

25y ÷ 25 = −5x ÷ 25

Divide

Rewrite

y = \(-\frac{5}{25} x\)

Reduce the fraction

y = \(-\frac{1}{5} x\)

Equations of both lines are equal, so lines are the same.

Calculate the value of y for x = -10:

y = \(-\frac{1}{5} x, x=-10\)

Substitute x = -10

y = \(-\frac{1}{5} \times(-10)\)

Multiply

Reduce

y = 2

Using the same method, calculate the values of y for a few different values of x

Plot the points (-10, 2), (-5, 1), (0, 0), (5, -1) and (10, -2).

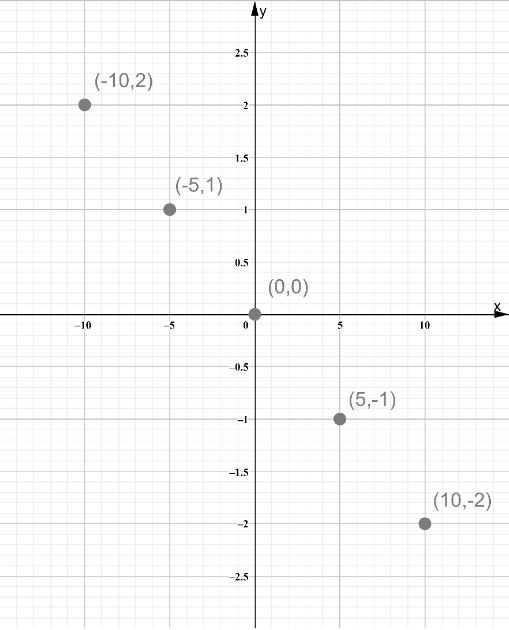
Draw a line through the plotted points.

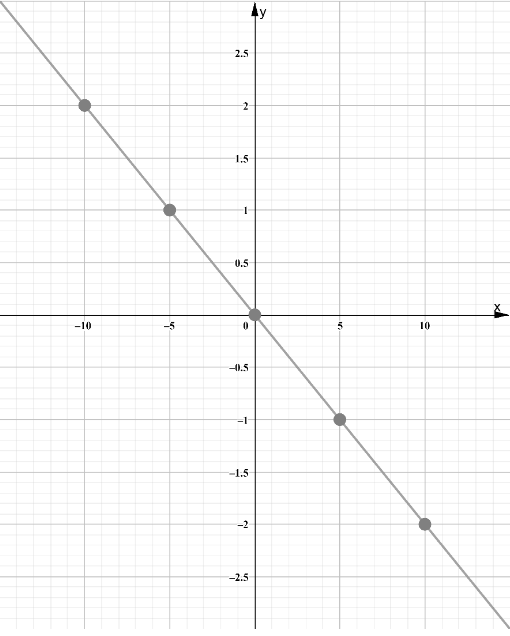
Each point on the line represents a solution.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

Envision Math Grade 8 Chapter 5.2 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 268 Exercise 14 Answer

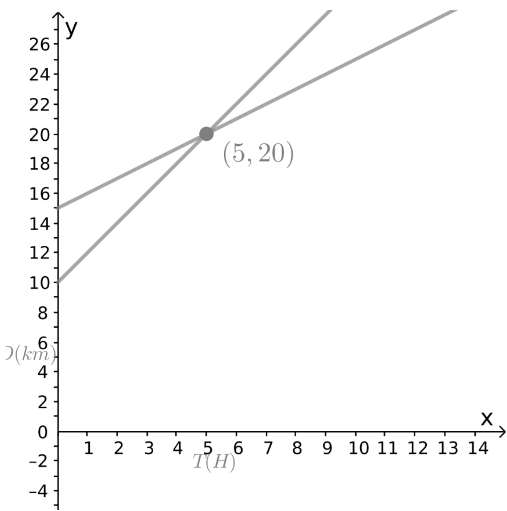
Given: Higher Order Thinking The total cost, c, of making n copies can be represented by a system of equations.

To find: How many copies you need to make for the total cost to be the same at both stores.

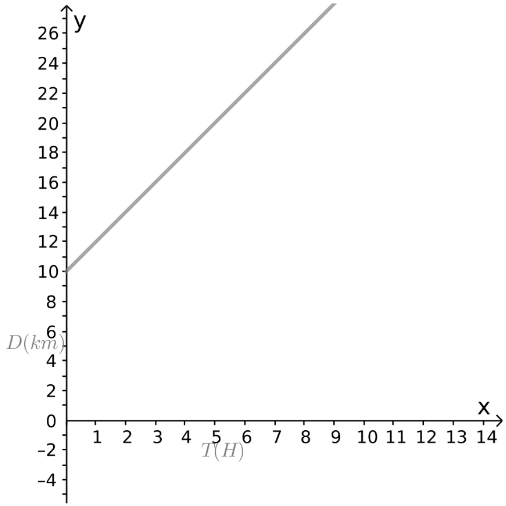
The first shop offers an unlimited number of items n for $5.The equation representing the price c in the first shop is given by:

c = 5

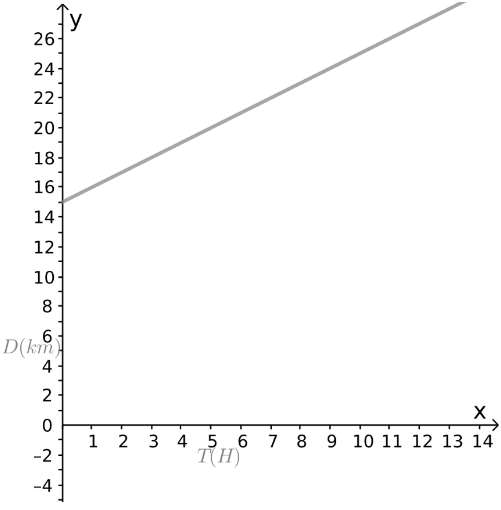
The second shop charges 20ϕ = $0.2 per item and additional $2 for the service.

The equation representing the price c in the second shop is given by:

c = 0.2n + 2

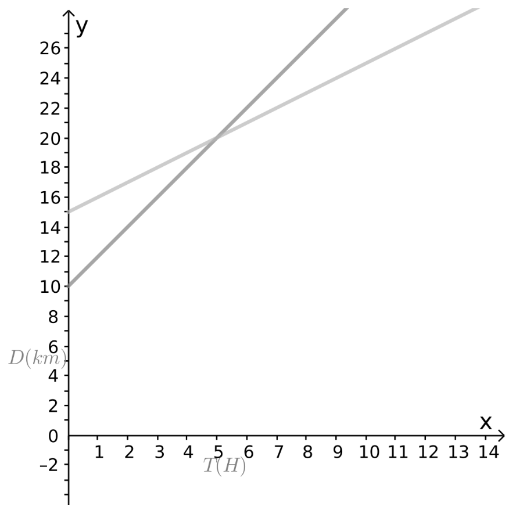
Since the price of the service in the first shop is $5 regardless of the number of items, find the number of items the second shop offers for $5

Find the number of items the second shop offers for $5 by solving the system.

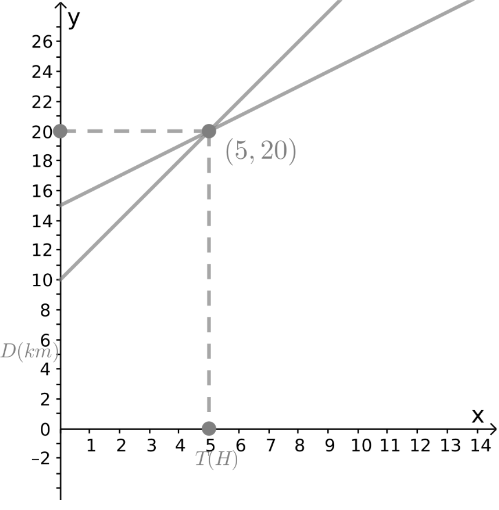
Set the sides equal 5 = 0.2n + 2

Solve the equation n = 15

A possible solution is (c,n) = (5,15)

Check the solution

Simplify

The ordered pair is a solution.

(c,n) = (5,15)

It follows that the second shop offers 15 items for $5.

For the total price to be the same in both shops, the number of items purchased in the second shop must be 15.

Given: Higher Order Thinking The total cost, c, of making n copies can be represented by a system of equations.

To explain, If you have to make a small number of copies, which store should you go to.

The cost in store W is $5 for any number of copies.

The cost in store z is given by the equation:

C = 2 + 0.2n

Where C is the cost and n is the number of copies.

C = 2 + 0.2n

The store z is preferred as far as the number of copies costs less than $5. express this using the inequality:

2 + 0.2n < 5

Solve the inequality for n:

2 + 0.2n < 5

Move the constant to the right

0.2n < 5 − 2

Calculate

0.2n < 3

Divide both sides of the inequality by 0.2

n < 15

Store z is preferred for a small number of copies less than 15.

Store z is preferred for a small number of copies less than 15.

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 257 Exercise 1 Answer

Given: Draw three pairs of lines, each showing a different way that two lines can intersect or not intersect.

How are these pairs of lines related?

There are n ways 2 lines can relate to each other.
The first way is that they are parallel, meaning they do not have any intersections.

The second way is if they are not parallel, but are not the same line. in this case, they have exactly 1 intersection.

The third and last way is, if the lines are the same, in this case, all of their points are the same.

That means they intersect at infinitely many points.

2 lines cannot have 2 points in common because 2 points clearly define a line.

That means if there is a line passing through both points, there cannot be another that does the same.

2 lines cannot have 2 points in common because 2 points clearly define a line.

If they have more than 1 point in common, it means they are the same line and have infinitely many common points.

Envision Math Grade 8 Volume 1 Chapter 5.1 Solutions

Page 257 Focus On Math Practice Answer

To find: Look for Relationships is it possible for any of the pairs of lines drawn to have exactly two points in common?

Here we will see every relation between two lines and try to find the pairs of lines have exactly two points in common.

Here two lines are parallel means they have no common point,

Here two lines intersects at one point means they have one common point,

Here two lines are coincidental means they have infinite common points,

Here we see all possibilities like two lines have maximum infinite common points and minimum zero common points but that is not possible to have two common points.

Two lines can’t have exactly two common points.

Analyze And Solve Systems Of Linear Equations Envision Math Answers

Page 258 Essential Question Answer

If the two lines have different slopes, the system has exactly one solution (whether the lines have the same intercept or different intercepts).

If they have the same slope and the same intercept they are the same line, so there are infinitely many solutions to the system.

If they have the same slope and different intercepts then they are parallel and there is no solution to the system.

The slopes are different. The lines intersect at 1 point.

The slopes are the same, and the y-intercepts are different. The lines are parallel.

The slopes are the same, and the y-intercepts are the same. The lines are the same(coincident)

Page 258 Try It Answer

Given: y = x + 1, y = 2x + 2

To find: To explain how many solutions does this system of equation has.

y = x + 1

The first equation is written in slope-intercept form.

y = 2x + 2

The second equation is written in slope-intercept form.
​
y = 1x + 1

y = 2x + 2
​
Notice that the equations of the linear system have different slopes.

Since the equations have different slopes, the system has one solution.

The system of equations has one solution. The equations have different slopes, so lines intersect at one point.

Page 259 Try It Answer

Given:
​y = −3x + 5
y = −3x − 5
​
To determine how many solutions does each system of equations has.

Here first we try to compare both equation’s slop and intercept.

Two lines equations:
y=−3x+5
…(1)

y=−3x−5
…(2)

Here we can see both lines slops are equal (m1 and m2 = −3) and y−intersects are different(c1 ≠ c2).

So lines are parallel and they have no solution.

The system of equations y = −3x + 5 and y = −3x − 5 have no solution.

Given: y = 3x + 4, 5y − 15x − 20 = 0

To determine how many solutions does each system of equations has.

y = 3x + 4

The first equation is written in slope-intercept form.

Rewrite the second equation in slope-intercept form:

5y − 15x − 20 = 0

5y − 15x − 20 = 0

Move the expression to the right

5y = 15x + 20

Divide both sides by 5

y = 3x + 4

Since both equations have the same slope-intercept form, they represent the same line.

Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Envision Math Grade 8 Chapter 5.1 Explained

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 260 Exercise 1 Answer

To find: How are slopes and y-intercepts related to the number of solutions of a system of linear equations?

Deanna drew the pairs of lines below.

Each pair of lines represents a system of linear equations. A system of linear equations is formed by two or more linear equations that use the same variables.

you can use the graphs to determine the number of solutions for each system.

The equations of the linear system
​
y = x + 4

y = −x + 6
​
have different slopes.

The system has 1 solution(1,5).

A solution of a system of linear equations is an ordered pair that makes all equations in the system true.

The equations of the linear system
​
y = x + 3

y = x + 1
​
have the same slopes and differenty−intercepts.

The system has no solution.

The equations of the linear system
​
x + y = −2

3x + 3y = −6
​
have the same slopes and the samey−intercepts. They represent the same line.

The system has infinitely many solutions.

Systems of equations can be solved by looking at their graphs.

A system with one solution has one point of intersection.

A system with no solution has no points of intersection.

A system with infinitely many solutions has infinite points of intersection.

Page 260 Exercise 2 Answer

Given: ​

​3x + y − 2 = 0
5x + y − 2 = 0
​
To find: Construct Arguments Macy says that any time the equations in a system have the same y-intercept, the system has infinitely many solutions. Is Macy correct? Explain.

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Consider the following system of equations:
​
3x + y − 2 = 0

5x + y − 2 = 0
​
Now,

3x + y − 2 = 0

Write the equation in the slope-intercept form:

3x + y − 2 = 0

y = −3x + 2

Similarly, it follows that the slope-intercept form of 5x + y − 2 = 0 is:

5x + y − 2 = 0

y = -5x + 2

it is clear that the equations have the same y−intercepts viz. 2.

Solve the system of equations:

3x + y − 2 = 5x + y − 2 = 0

Rewrite the expression

{​3x + y − 2 = 0
5x + y − 2 = 0
​
Move constants to the right

{​3x + y = 2
5x + y = 2
​
Multiply both sides

{​3x + y = 2
−5x − y = −2
​
Eliminate one variable by adding the equations

-2x = 0

Divide both sides

x = 0

Substitute the value of x

3 × 0 + y = 2

Solve the equation

y = 2

A possible solution is

(x,y) = (0,2)

Check the solution
​
3 × 0 + 2 − 2 = 5 × 0 + 2 − 2

= 0
​
Simplify
​0 = 0

= 0
​
The ordered pair is a solution

(x,y) = (0,2)

It follows that the system has a unique solution.

Hence, Macy is not correct.

A system of equations has infintie solutions if the y-intercepts are equal and slopes are equal as well. Macy is incorrect.

Solutions For Envision Math Grade 8 Exercise 5.1

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 260 Exercise 5 Answer

a

Substitute \(\frac{1}{2} x=y\) into the equation to find the value of y:

y = y + 3

Subtract y from both sides of the equation:

y – y = y – y + 3

Calculate the differences:

0 = 0 + 3

Add the numbers:

0 = 3

Since the statement 0 = 3 is false, the system of linear equations has no solution.

The solution yields to 0 = 3 which is false, the system of equations has no solution.

Page 261 Exercise 7 Answer

convert the given equations in slope intercept form and then derive their sloped and y-intercepts individually. Further, compare them are make a conclusion.

7y = 13.3x – 56

Divide equation of rover B by 7 on both sides.

Simplify the equation.

Divide

Reduce

Convert the expression

Multiply both sides

70y = 133x – 560

Divide both sides

Rover B: \(y=\frac{19}{10} x-8\)

Compare the equation of rover B with the slope-intercept form of the equation.

The slope obtained for the equation of rover B is m_B = \(\frac{19}{10}\).

Convert m_B to the decimal number.

m_B = 1.9

The y-intercept obtained for the equation of rover B is b_B = -8.

Rover A: y = 1.9x − 8

Similarly, compare the equation of rover A with the slope-intercept form of the equation.

The slope obtained for the equation of rover A is m_A = 1.9.

The y−intercept obtained for the equation of rover A
is b_A = −8.

Comparing m_A and m_B shows m_A= m_B

Comparing b_A and b_B shows b_A = b_B.

The system of equations has infinite solutions as slopes and y−intercepts are the same for both equations.

The slope for the rover A equation is equal to the slope for the rover B equation. The y−intercepts of the equations are −8. The system of equations has infinite solutions.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 261 Exercise 8 Answer

Given: ​

y = x − 3

4x − 10y = 6
​
To find: How many solutions does this system have?

Convert the equation in a slope-intercept form then simplify the equation and find the slope and intercept.

y = x – 3

The first equation is written in slope-intercept form.

Rewrite the second equation in slope-intercept form:

4x − 10y = 6

Move the variable to the right

−10y = 6 − 4x

Change the signs

10y = -6 + 4x

Divide both sides

Reorder the terms

y = 1x – 3

The equations of the linear system have different slopes.

The system has one solution.

Envision Math Grade 8 Volume 1 Chapter 5.1 Practice Problems

Page 261 Exercise 10 Answer

Given: ​−64x + 96y = 176

56x − 84y = −147
​
To find: What can you determine about the solution(s) of this system?

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Rewrite the first equation in slope-intercept form:

−64x + 96y = 176

Move the variable to the right

96y = 176 + 64x

Divide both sides

Reorder the terms

Rewrite the second equation in slope-intercept form:

56x − 84y = −147

Move the variable to the right

−84y = −147−56x

Change the signs

84y = 147 + 56x

Divide both sides

Reorder the terms

The equations have equal slopes.

The equations have different y−intercepts.

Therefore, the graphs of the equations are parallel lines, so the system has no solution.

Equations have equal slopes, but different y−intercepts, so the system has no solution.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 261 Exercise 11 Answer

Given: ​

​y = 8x + 2

y = −8x + 2
​
To Find: Determine whether this system of equations has one solution, no solution, or infinitely many solutions.

Solve the system of equations then Eliminate one variable by adding the equations to find the ordered pair is a solution.

Solve the system of equations:

y = 8x + 2

y = −8x + 2
​
Simplify

−8x + y = 2

8x + y = 2
​
Eliminate one variable by adding the equations

2y = 4

Divide both sides

y = 2

Substitute the value of y

8x + 2 = 2

Solve the equation

x = 0

A possible solution is
(x,y)=(0,2)

Check the solution

​2 = 8 × 0 + 2

2 = −8 × 0 + 2
​
Simplify

2 = 2

2 = 2
​
The ordered pair is a solution

One solution

The given system of equations has one solution.

Page 261 Exercise 12 Answer

Given: ​

​2x + y = 14

2y + 4x = 14
​
To Find: Construct Arguments Maia says that the two lines in this system of linear equations are parallel. Is she correct? Explain.

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Rewrite the first equation in slope-intercept form:

2x + y = 14

Move the variable to the right

y = 14 − 2x

Reorder the terms

y = −2x + 14

Rewrite the second equation in slope-intercept form:

2y + 4x = 14

Move the variable to the right

2y = 14 − 4x

Divide both sides

y = 7 − 2x

Reorder the terms

y = −2x + 7

Now,
​
y = −2x + 14

y = −2x + 7
​
The equations have equal slopes.
​
y = −2x + 14

y = −2x + 7
​
The equations have different y−intercepts.

Therefore, the graphs of the equations are parallel lines.

Equations have equal slopes, but different y−intercepts, so the linear equations are parallel.

Maia is correct.

Page 261 Exercise 13 Answer

Given: ​

​y = 2x + 10

y = x + 15
​
To find: Describe a situation that can be represented by using this system of equations. Inspect the system to determine the number of solutions and interpret the solution within the context of your situation.

Compare the equation with a slope-intercept form of the linear equation then According to the slope-intercept form make graphs and solve equations.

Let y and x be the total distance covered by a man in kilometres and the time taken to cover the distance in hours respectively.

Compare the equation y = 2x + 10 with a slope-intercept form of the linear equation:

m = 2,b = 10

According to the slope-intercept form, the y-intercept value is 10 means, at 0 hours the first person covered 10 kilometres.

To draw a line, calculate y for some values of x.

y = 2x + 10

Substitute the value of x = 1 in the equation:

y = 2(1) + 10

Solve for y:

y = 2 × 1 + 10

Calculation

y = 12

In the same manner, complete the table.

Plot the points (1,12),(2,14) and (3,16)

Draw a line through the points.

The line y = 2x + 10 shows the first person’s time-distance relation.

In the same manner, draw the line y = x + 15 that shows the second person’s time-distance relation.

Draw the lines y = 2x + 10 and y = x + 15 in the same plane.

The two lines are meet at a point (5,20).

Since the lines are meet at one point, it has one solution.

The system has one solution that is (5,20)

It represents two persons will meet at 20 kilometres distance after 5 hours.

Envision Math 8th Grade Systems Of Equations Topic 5.1 Key Concepts

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 262 Exercise 14 Answer

Given: ​

12x + 51y = 156

−8x − 34y = −104
​
To find: does this system has one solution, no solutions, or infinitely many solutions? Write another system of equations with the same number of solutions that uses the first equation only.

Simplify each equation in the system, observe both equations. If the equations in the system are multiples of common equations then it has infinitely many solutions.

Simplify each equation in the system.

Simplify the first equation:

12x + 51y = 156

Simplify

4x + 17y − 52 = 0

After simplification, the first equation is:

4x + 17y − 52 = 0

Simplify the second equation:

−8x − 34y = −104

Simplify

4x + 17y − 52 = 0

After simplification, the second equation is:

4x + 17y − 52 = 0

After simplification, both equations are equal.

If the equations in the system are multiples of common equations then it has infinitely many solutions.

Since the system has infinitely many solutions.

The common equation of the system is:

4x + 17y − 52 = 0

To find the second equation in another system, the common equation is multiplied by any number.

The equation 4x + 17y − 52 = 0 is multiplied by 4 on both sides: 4(4x + 17y − 52) = 4(0)

Any expression multiplied by 0 is 0 :

4(4x + 17y − 52) = 0

Multiply each term in the parentheses by 4 :

16x + 68y − 208 = 0

Add 208 on both sides of an expression:

16x + 68y − 208 + 208 = 0 + 208

Cancel the terms:

16x + 68y = 0 + 208

Simplify the right side of the equation:

16x + 68y = 208

Since the equations in the system are multiples of the common equations, the system has infinitely many solutions.

Another system of equations with infinitely many solutions is:
​
12x + 51y = 156

16x + 68y = 208

​Envision Math Grade 8 Topic 5.1 Graphing Linear Systems Solutions

Page 262 Exercise 16 Answer

Given: ​

​4x + 3y = 8

8x + 6y = 2
​
To find: the system has one solution, no solution, or an infinite number of solutions?

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Rewrite the first equation in slope-intercept form:

4x + 3y = 9

Move the variable to the right

3y = 9 – 4x

Divide both sides

Reorder the terms

Rewrite the second equation in slope-intercept form:

8x + 6y = 2

Move the variable to the right

6y = 2 – 8x

Divide both sides

Reorder the terms

The equations have equal slopes.

The equations have different y−intercepts.

Therefore, the graphs of the equations are parallel lines, so the system has no solution.

Equations have equal slopes, but different y−intercepts, so the system has no solution.

Envision Math Grade 8 Chapter 5.1 Lesson Breakdown

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 262 Exercise 17 Answer

Given: Qx + Ry = S and y = Tx + S

what circumstances does the system of equations have infinitely many solutions?

Solve the equations for ythen simplify the equation and find the slope and y−intercept.

Solve the first equation for y:

Qx + Ry = S

Move the expression to the right

Ry = S − Qx

Divide both sides

Separate the fraction

Write as a product

The equation is now written in slope-intercept form.

For the system to have infinitely many solutions, the slopes of the lines and the y-intercepts must be equal.

The Slopes of the lines are \(-\frac{Q}{R} \text { and } T\).

The y-intercepts of the lines are \(\frac{S}{R} \text { and } S\).

The system has infinitely many solutions if:

Page 262 Exercise 19 Answer

Choose the statement that correctly describes how many solutions there are for this system of equations.

Solve the given systems of equations:

Simplify

Multiply both sides

Eliminate one variable by adding the equations

−7y = −21

Divide both sides

y = 3

Substitute the value of $y$

−2x + 3 × 3 = 9

Solve the equation

x = 0

A possible solution is

(x,y) = (0,3)

Check the solution

Simplify

The ordered pair is a solution

One solution

Notice that the slopes of the two equations are different.

Therefore the given system of equations has exactly one solution because the slopes are not equal.

The given system of equations has exactly one solution because the slopes are not equal because that options (A),(B) and (C) statements are incorrect.

Therefore, the correct option is (D) Exactly one solution because the slopes are not equal.

Envision Math Grade 8 Solutions, Systems Of Linear Equations

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 2 Answer

Given: When lines are the same distance apart over their entire lengths, they are _____________________ .

To find: Choose the best term from the box to complete each definition.

Parallel lines are lines in a plane that do not intersect at any point; for example, two straight lines in a plane that do not collide at any point are said to be parallel. Curves that do not touch or intersect and maintain a constant minimum distance are considered to be parallel.

When lines are the same distance apart over their entire lengths, they are parallel.

Envision Math Grade 8 Solutions, Systems of Linear Equations Page 255 Exercise 4 Answer

Given: A _________ is a relationship between two variables that gives a straight line when graphed.

To find: Choose the best term from the box to complete each definition.

Linear equations are nothing but yet another subset of “equations”. Any linear calculations requiring more than one variable can be done with the help of linear equations. The standard form of a linear equation in one variable is of the form ax + b = 0. Here, x is a variable, and a and b are constants. While the standard form of a linear equation in two variables is of the form ax + by = c. Here, x and y are variables, and a, b and c are constants.

A linear equation is a relationship between two variables that gives a straight line when graphed.

Envision Math Grade 8 Volume 1 Chapter 5 Systems Of Linear Equations Solutions

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 5 Answer

Given: y = 2x − 3

To find: Identify the slope and the y − intercept of the equation.

The equation is written in slope-intercept form.

y = 2x + (−3)

On comparing the equation by slope-intercept form we get,

The slope is 2 and the y-intercept is −3.

The slope is 2 and the y-intercept is −3.

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 6 Answer

Given: y = −0.5x + 2.5

To find: Identify the slope and the y−intercept of the equation.

The equation is written in slope-intercept form.

y = −0.5x + 2.5

On comparing the equation by slope-intercept form we get,

The slope is −0.5 and the y-intercept is 2.5.

The slope is −0.5 and the y-intercept is 2.5.

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 7 Answer

Given: y − 1 = −x

To find: Identify the slope and the y−intercept of the equation.

Write the equation in slope-intercept form:

y − 1 = −x

Move the constant to the right

y − 1 + 1 = −x + 1

Remove the opposites

y = −x + 1

On comparing the equation by slope-intercept form we get,

The slope is −1 and the y-intercept is 1.

The slope is −1 and the y−intercept is 1.

Envision Math Grade 8 Chapter 5 Analyze And Solve Systems Of Equations

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 8 Answer

Given: \(y=\frac{2}{3} x-2\)

To find: Graph the equation.

From the slope-intercept form of a line, it follows:

m = \(\frac{2}{3}\), b = -2

Since the y-intercept of the line is −2, it follows that the line passes through the point (0,−2)

Draw the graph of the equation and plot point (0,−2),

The graph of the equation is shown below,

Envision Math Chapter 5 Systems Of Linear Equations Detailed Answers

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 9 Answer

Given: y = −2x + 1

To find: Graph the equation.

From the slope-intercept form of a line, it follows:

m = −2,b = 1

Since the y-intercept of the line is 1, it follows that the line passes through the point (0,1).

Draw the graph of the equation and plot point (0,1),

The graph of the equation is shown below,

Envision Math 8th Grade Chapter 5 Step-By-Step Systems Of Equations Solutions

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 10 Answer

Given: y − x = 5

To find: Solve the equation for y.

y – x = 5

Move the variable to the right-hand side by adding its opposite to both sides,

y − x + x = 5 + x

Since two opposites add up to zero, remove them from the expression,

y = 5 + x

Use the commutative property to reorder the terms,

y = x + 5

Therefore, the value of y is x + 5.

Systems Of Linear Equations Solutions Grade 8 Envision Math Chapter 5

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 11 Answer

Given: y + 0.2x = −4

To find: Solve the equation for y.

y + 0.2x = -4

Move the variable to the right-hand side by adding its opposite to both sides

y + 0.2x − 0.2x = −4−0.2x

Since two opposites add up to zero, remove them from the expression

y = −4−0.2x

Use the commutative property to reorder the terms,

y = −0.2x−4

Therefore, the value of y is −0.2x−4.

Envision Math Grade 8 Chapter 5 Solutions Guide

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 12 Answer

Given: \(-\frac{2}{3} x+y=8\)

To find: Solve the equation for y.

Move the expression to the right-hand side by adding its opposite to both sides,

Since two opposites add up to zero, remove them from the expression,

Use the commutative property to reorder the terms,

The value of y is \(\frac{2}{3} x+8\).

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3

Page 243 Exercise 1 Answer

The video mentioned above shown some images that predict the height and the length of various humans and things.

The reason is for knowing the average height each of them follows and how much it will grow in their lifetime.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”

“What is my height and is that normal for my age?”

This is the question that made up my mind after watching this video.

Page 243 Exercise 2 Answer

The video mentioned above shown some images that predict the height and the length of various humans and things.

The reason is for knowing the average height each of them follows and how much it will grow in their lifetime.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The main question that comes to my mind after watching this video is “Is that height normal for my age?”.

The main question that I will answer that I saw in the video is “Is that height normal for my age?”.

Page 243 Exercise 3 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

An answer that I was predicted to this main question is 158 cm and it is below average for my age.

An answer that I was predicted to this main question is 158 cm and it is below average for my age. I found my answer by measuring myself using a tape and the people of my age are far taller than me this means that I’m shorter than them.

Envision Math Grade 8 Volume 1 Chapter 4.3 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 243 Exercise 4 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too small to be the answer is 50 cm since infants grow 50 cm within the age of three.

A number that is too large to be the answer is 214 cm since the percentage of 7 footers is only 0.000038%.

On the number line below, we have written a number that is too small to be the answer. Also, we have written a number that is too large.

Page 243 Exercise 5 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too small to be the answer is 50 cm since infants grow 50 cm within the age of three.

A number that is too large to be the answer is 214 cm since the percentage of 7 footers is only 0.000038%.

My height is 158 cm.

Plotting my prediction on the same number line, I get,

Page 244 Exercise 6 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

In this situation, information regarding the average height of a normal healthy person of my age would be more helpful to know.

This is because I can use that information to know that my height is normal or not.

In this situation, information regarding the average height of a normal healthy person of my age would be more helpful to know.

I can use that information to know that my height is normal or not.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 244 Exercise 7 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

To get the information I need regarding the height, I have to use a measuring tape.

This will determine the height of every person accurately.

A measuring tape can be used to get the information I need. My height is 158 cm.

Investigate Bivariate Data Envision Math Topic 4.3 Answers

Page 244 Exercise 8 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure your height several times.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

From this way, I have found out that my height is 158 cm and it is below average.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 244 Exercise 9 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

I have found out that my height is 158 cm.

The average height of a person of my age is 175 cm.

This is far greater than my prediction.

The answer to the Main Question is that the average height of a person of my age is 175 cm. It is far greater than my prediction.

Page 245 Exercise 10 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

The answer that I saw in the video is 175 cm as the average height for my age.

Envision Math Grade 8 Chapter 4.3 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 245 Exercise 11 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

My answer doesn’t match the answer in the video. This is because my genetic factors and lack of physical work are some of the reasons for my shorter height.

My answer doesn’t match the answer in the video. This is because genetic factors play a vital role in deciding one’s height.

Page 245 Exercise 12 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

My answer doesn’t match the answer in the video. This is because my genetic factors and lack of physical work are some of the reasons for my shorter height.

I am going to do some physical exercises, stretching, and yoga to increase my height in order to change my model.

Yes, I would change my model now that I know the answer.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 246 Exercise 13 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure your height several times.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

The model helps me answer the Main Question by making accurate measurements of my height and to know whether my height is normal or not for my age.

Page 246 Exercise 14 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

My answer doesn’t match the answer in the video. This is because my genetic factors and lack of physical work are some of the reasons for my shorter height.

The height which I notice in my classmate’s model is that he is 185 cm tall.

This helps me to know under which conditions people’s height is increasing.

The calculations differ based on the genetic factors and physical conditions I am in. This helps me to know under which conditions people’s height is increasing.

Solutions For Envision Math Grade 8 Topic 4.3

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 246 Exercise 15 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The length of my classmate’s wingspan is 185 cm.

I have also calculated his height which is also 185 cm.

This means that both his wingspan or arm span and his height are equal.

My classmate’s wingspan is 185 cm. This is equal to my classmate’s height. My model predicts my classmate’s actual height well.

Page 247 Exercise 1 Answer

The number of visits, age, months, and time are examples of measurement data.

Colors, gender, and nationality are examples of categorical data.

If 7out of 20 people prefer reading a book to watching a movie, then saying that 35 of the people polled prefer reading a book is the relative frequency.

The number of visits, age, months, and time are examples of measurement data.

Colors, gender, and nationality are examples of categorical data.

If 7 out of 20 people prefer reading a book to watching a movie, then saying that 35 of the people polled prefer reading a book is the relative frequency.

Envision Math Grade 8 Topic 4.3 Graphing Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 247 Exercise 1 Answer

This scatter plot shows a positive association between vacation and hours of employees at ABC Corporation.

Some of the points are far from the trend line. This shows a weak association.

This scatter plot shows a weak, positive linear association between experience and vacation of employees at ABC Corporation.

Page 249 Exercise 1 Answer

Since we can see that in the given graph as the x-coordinate increases than the y-coordinate is decreasing

This means there is a negative association.

We can draw a trend line to see whether the association is weak or strong.

Place the pencil in the middle of all points and draw a line.

As we can see the points are not really close to the trend line which means there is a weak negative association.

There is a weak negative association.

Envision Math Grade 8 Chapter 4.3 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 249 Exercise 2 Answer

If we look at the graph we can already see that the data are not linear when the points shape as than the association is no longer linear.

Hence, the data is not linear.

Page 249 Exercise 1 Answer

Given

y = 6x + 120

y = $570

To find – expected number of copiers sold

Therefore, the expected number of copies sold is 75

Envision Math Grade 8 Volume 1 Chapter 4.3 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 249 Exercise 2 Answer

Given

y = 6x + 120

x = 100

Substitute 100 for x and simplify
​

​
Therefore, the expected wage for given employee is 720.

Envision Math 8th Grade Topic 4.3 Key Concepts

Page 251 Exercise 1 Answer

Given:

A)​ (6,−0.5y + 20−0.5y = 13)

−y + 20 = 13

−y = 13 − 20

−y = −7

y = 7

(6,7)
​
B)​ (4−3x + 7x = −8,7)

4 + 4x = −8

4x = −8 −4

4x = −12

x = \(-\frac{12}{4}\)

(−3,7)
​
C)​ (2x + 4 − 6x = 24,5)

4 − 4x = 24

−4x = 24 − 4

−4x = 20

x = −5

(−5,5)
​
D)​ (5x + 6 − 10x = 31,1)

−5x + 6 = 31

−5x = 31 − 6

−5x = 25

x = −5

(−5,1)
​
E)​ (7x − 3 − 3x = 13,−2)

4x − 3 = 13

4x = 13 + 3

x = 4

(4,−2)
​
F)​ (4,− 12y + 8y − 21 = −5)

−4y − 21 = −5

−4y = −5 + 21

−4y = 16

y = −4

(4,−4)
​
G)​ (44 = 6x − 1 + 9x,−5)

44 = 15x − 1

45 = 15x

x = 3

(3,−5)
​
H)​ (−5, 4y + 14 − 2y = 4)

2y + 14 = 4

2y = 4 − 14

2y = −10

y = −5

(−5,−5)
​
I)​ (−5, 15 + y + 6 + 2y = 0)

21 + 3y = 0
​
3y = −21

y = −7

(−5,−7)
​
J)​ (4,3y + 32 − y = 18)

2y + 32 = 18

2y = 18 − 32

2y = −14

y = −7

(4,−7)
​
K)​ (6, 5y + 20 + 3y = −20)

8y + 20 = −20

8y = −20 − 20

8y = −40

y = −5

(6,−5)
​
L)​ (9x − 14 − 8x = −8,−1)

x − 14 = −8

x = −8 + 14

x = 6

(6,−1)
​
M)​ (−3,−5y + 10 − y = −2)

−6y + 10 = −2

−6y = −2 −10

−6y = −12

y = 2

(−3,2)
​
N)​ (−3,− 5y + 10 − y = −2)

−6y + 10 = −2
​
−6y = −2 −10

−6y = −12

y = 2

(−3,2)
​

If we simply look at the graph, than we know that we simply have to remove letter’s’ from the word seven, and we are left with ‘even’.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5

Page 237 Exercise 1 Answer

Given:

The total number of users using a small screen is 66.

The number of students using a small screen is 48.

The number of adults using the small screen is 18.

To find- How can you use the data to compare the percent of students who chose the small screen to the percent of adults who chose the small screen?

The data from the table can be used to analyse the usage of small screen between adults and students.

It can also help to understand the interested crowd and help in future business propositions.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.5 Bivariate Data Solutions

Page 237 Exercise 1 Answer

When categorized data is put into a two-way frequency tables, one category is represented by the rows and other is represented by columns.

Percentage of the given data gives a clear idea of the population surveyed.

Percentage also makes it easier to understand the given data in a two-way relative frequency table.

Percentage changes the way of interpretation of data because it makes it easier to understand the result of the surveyed population.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 238 Question 1 Answer

Two-way frequency tables are used to analyse survey results.

The data in the relative frequency table is always in the form of decimals, percentage or fractions.

Two-way relative frequency tables show percentages rather than counts.

Two-way relative frequencies are good for seeing if there is an association between two variables.

Two-way relative frequency tables show percentages rather than counts. This gives a visual representation of possible relationships between two sets of categorical data. This gives a better advantage for showing relationships between sets of paired data.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.5 Bivariate Data Solutions

Page 238 Exercise 1 Answer

Both the frequency tables are used to represent the categorical data.

On both the tables one category is represented by rows and other category is represented by column.

Both of the two-way tables show the relationship between paired categorical data. Both of the tables help in interpretation of data in the tables to draw conclusions.

Two-way relative frequency table is similar to a two-way frequency tables as both the tables are used to represent the categorical data, they show the relationship between paired categorical data, and they both help in interpretation of data in the tables to draw conclusions.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 238 Exercise 1 Answer

Given that, Asha asked 82 classmates whether they play sports on the weekend. The results are shown in the two-way frequency table below.

We need to use Asha’s two-way frequency table to complete the two-way relative frequency table.

For finding the percentage to complete the two-way relative frequency table, we need to divide each value in the cell by the total number of boys and girls polled together.

Here, the total count is 82

Thus, finding the percentage of each of them, we get,

\(\frac{21}{82} \times 100\) = 25.6

\(\frac{18}{82} \times 100\) = 21.9

\(\frac{39}{82} \times 100\) = 47.5

\(\frac{26}{82} \times 100\) = 31.7

\(\frac{17}{82} \times 100\) = 20.7

\(\frac{43}{82} \times 100\) = 52.4

\(\frac{47}{82} \times 100\) = 57.3

\(\frac{35}{82} \times 100\) = 42.6

Thus, completing the two-way relative frequency table, we get,

Investigating Bivariate Data Grade 8 Exercise 4.5 Envision Math

Page 239 Exercise 2 Answer

The percentage of students who choose e-books is 52%

The percentage of students who choose audiobooks is 48%

We see that the percentage of students using e-books is greater than the percentage of students using audiobooks.

This means that students prefer e-books over audiobooks.

The percentage of students using e-books is greater than the percentage using audiobook. This shows that students prefer using e-books over audiobooks.

The percentage of students in 7th grade who choose e-books is 41.1%

The percentage of students in 7th grade who choose audiobooks is 58.9%

We see that the 7th graders have greater tendency to choose audiobooks over e-books.

From the given data, we observe that the percentage of 7th graders using audiobooks is greater than the percentage of e-book users.

Envision Math Grade 8 Chapter 4 Exercise 4.5 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 238 Exercise 1 Answer

A frequency table is a chart that shows the popularity or mode of a certain type of data.

A relative frequency table is a chart that shows the popularity or mode of a certain type of data based on the population sampled.

The data presented by a relative frequency table is always represented by fractions, decimals or decimals.

The data in the two-way frequency table is in counts as in whole numbers.

The difference between a two-way frequency table and a two-way relative frequency table is that the data in the table is differently represented. The data in the relative table is represented by percentage, fractions and decimals. The data in frequency table is represented by a count that is whole numbers.

Page 240 Exercise 1 Answer

Two-way frequency tables are used to analyse survey results.

The data in the relative frequency table is always in the form of decimals, percentage or fractions.

Two-way relative frequency tables show percentages rather than counts.

Two-way relative frequencies are good for seeing if there is an association between two variables.

Two-way relative frequency tables show percentages rather than counts. This gives a visual representation of possible relationships between two sets of categorical data. This gives a better advantage for showing relationships between sets of paired data.

Page 240 Exercise 2 Answer

Two-way relative frequency table contains the data that is computed into percentage.

Also, this data is a relative data that is this data is not completely accurate.

Relative data doesn’t always add to 100%, proving that accuracy of the relative frequency table being almost correct.

Since the data in the two-way relative frequency table is not completely accurate, the percentage of the rows or columns percentages not total 100%.

Envision Math 8th Grade Exercise 4.5 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 240 Exercise 5 Answer

Given:

The total number of left-handed people that have an artistic ability is 86.

The total numbers of people that have the artistic ability are 101.

We convert the counts into percentage to get the answer.

We consider:

The percentage of left-handed people with artistic ability =

\(\frac{86}{101} \times 100\) = 0.8514 x 100 = 85.14

There are 85.14% of left-handed people surveyed with artistic ability.

Page 241 Exercise 7 Answer

Given

We consider:

This is the required two-way frequency table.

How To Solve Exercise 4.5 Bivariate Data In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 241 Exercise 8 Answer

Given:

We consider:

This is the required two-way frequency table.

Page 241 Exercise 9 Answer

Given:

We observe that the percentage of the 4-door car is 53% that is greater than the percentage of 2-door cars.

Therefore, the 4-door car is more popular.

To Find: Which type of car is more popular

After observing the given data, we conclude that 4-door cars are more popular.

Envision Math Grade 8 Exercise 4.5 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 242 Exercise 10 Answer

Given:

We observe that the percentage of girls who do not like raspberries is 48%.

Therefore, 48% percent of girls do not like raspberries.

After observing the given data, we conclude that 48% of girls do not like raspberries.

Given:

We observe that the gender and the responses are correlated.

The question is asked to both boys and girls.

Therefore, the data in the above table is evidence that gender and the responses are associated.

As the question is asked to both Girls and Boys, the data in the given table explains the association between the gender and the responses. Furthermore, these responses help in bifurcation of the data gender-wise.

Envision Math Exercise 4.5 Bivariate Data Detailed Answers

Page 242 Exercise 11 Answer

Given:

We consider:

This is the required two-way frequency table.

This is the required table.

Given:

We understand that the responses help to categorize the employees into day or night shifts. The given table is evidence to the association of Shifts and the responses.

After observing the table, we realize that this table helps in categorization of employees in Day or night Shifts. Hence, the shifts and the responses are associated.

Envision Math Grade 8 Exercise 4.5 Solution Guide

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 242 Exercise 12 Answer

We simply have to look in the table and compare the percentage for positive improvements from each medicine.

AS we can see the medicine B has 74 of people had the improvement while only 26 of the people that were given medicine 26 showed some improvement.

A greater percent of people given Medicine B saw an improvement.

Yes, we can see in the given table, the percent of the people that took either medicine A or Bare shown in the table which is the evidence that the improvement was related to the type of medicine.

Yes there is evidence that the improvements are related to the type of the medicine.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1

Page 229 Exercise 6 Answer

Given : a scatter plot

We have to check which statement are correct.

Given scatter plot

From the scatter plot it is clear that:

Majority of the elevations are in a cluster between 1,250 meters and 2,250 meters.

There is a gap in the data between 500 meters and 1,250 meters.

As the elevation increases the mean annual temperature decreases.

Therefore, first, second and fourth statements are correct.

First, second and fourth statements are correct

Envision Math Grade 8 Volume 1 Chapter 4 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1Page 230 Exercise 1 Answer

A table is given and we have to construct a scatter plot.

We will take ERA on x−axis and number of wins on y−axis and plot the graph from the data given in the table.

Given table:

Taking ERA on x−axis and number of wins on y−axis and plotting the graph.

We get the following scatter plot:

The scatter plot is :

Given: a table

We have to explain the relationship between ERA and number of wins.

From part 1(a) we have the following scatter plot

From the scatter plot it is clear as the points are closer to the trend line it is strong negative association.

We can conclude that as the ERA increases number of wins decreases.

It is strong negative association.

A table is given.

First, we will draw a trend line then we will find the slope and y-intercept using scatter plot.

Drawing trend line by placing a pencil in middle of the points on the scatter plot obtained in part 1(a).

Taking points (1,14) and (2.5,10)

Slope = m=\(\frac{y_2-y_1}{x_2-x_1}=\frac{10-14}{2.5-1}=-2.6\)

Substituting values of slope and y-intercept in y=mx+c

We get the equation:

y = −2.6x + 16

Given ERA is 6, therefore, x = 6

Substituting x = 6 in y = −2.6x + 16

We get,

y = −2.6(6) + 16 = 0.4

Therefore, the number of wins of a pitcher with an ERA of 6 is 0.4.

Scatter plot with trend line:

The equation is y = −2.6x + 16

The number of wins of a pitcher with an ERA of 6 is 0.4

Investigate Bivariate Data Envision Math Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1Page 231 Exercise 1 Answer

Given: a table of poll results

We have to use the table and describe the poll result.

Given table

From the table it is clear that there are 43 people that are under 35 or are 35 years old and there are 57 people that are older than 35 years old.

Therefore, we can say that majority of the people are over 35 years old.

Majority of the people are over 35 years old.

Given: a table of poll results

We have to determine that what information the owner can get from the table.

Given table

From the table it is clear that:

Most of the people that are 35 or under 35 years old are there for snowboarding.

Most of the people that are older than 35 years are there for skiing

Therefore, we can say that most of the people that are under 35 or are 35 years old, they prefer snowboarding and the people that are older than 35 years, they prefer skiing.

Most of the people that are under 35 or are 35 years old, they prefer snowboarding and the people that are older than 35 years, they prefer skiing.

Given: a table of poll results

The majority of people that come to ski resort are over 35 years old, and they prefer skiing.

The rest of the people are 35 or under 35 years old and they prefer snowboarding over skiing.

Overall snowboarding is preferred over skiing.

The majority of people that come to ski resort are over 35 years old, and they prefer skiing.

The rest of the people are 35 or under 35 years old and they prefer snowboarding over skiing.

Overall snowboarding is preferred over skiing.

Envision Math Grade 8 Chapter 4.1 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 231 Exercise 1 Answer

Given table:

we have to use a different method to show the relationship between people’s age and the activity they prefer.

To display the data to show the relationship between people’s age and the activity they prefer we can use any other kind of diagram other than the table.

We can use any kind of diagram to show the relationship between people’s ages and which activity they prefer.

Page 232 Question 1 Answer

We have to explain how does a two-way frequency table show the relationships between sets of paired data.

Two-way frequency tables are a visual representation of the possible relationships between two sets of categorical data.

The categories are labeled at the top and the left side of the table, with the frequency (count) information appearing in the four (or more) interior cells of the table. The “totals” of each row appear at the right, and the “totals” of each column appear at the bottom.

For example: you conducted a survey at your school asking 100 people, whether they prefer digital or print textbooks.

Out of 100 people 42 students and 6 teachers like digital textbooks and 28 students and 24 teachers prefer print textbooks.

Here, teacher and students are one category (row category) and digital and print textbook are second type of category (column category).

Constructing two-way frequency table for this survey we get:

Explained how does a two-way frequency table show the relationships between sets of paired data.

Page 232 Exercise 1 Answer

Given table:

We have to complete the two-way frequency table by simply calculating the data missing in rows and columns.

Given table is :

The total of a row is represented on the right

Therefore, 32 − 19 = 13

13 is the value which will goes into top left corner.

The total of a column is represented at the bottom

Therefore, total YES votes are 13 + 28 = 41.

Total NO votes are 34

Therefore, 34 − 19 = 15

15 will go into middle of NO column.

Total votes of city B are 28 + 15 = 43

We know that total number of people are 75.

The complete two-way frequency table is:

The complete two-way frequency table is:

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 233 Exercise 2 Answer

Given: in total 100 students were asked.

Out of the 100 students, 19 girls rode in a car, 7 girls rode the bus, and 27 girls took the train.

Out of the boys, 12 took the train, 25 rode in a car and 10 rode the bus.

We have to construct a two-way frequency table.

We will simply write the given data in the table and we have to tell which mode of transportation is more preferred.

Given: out of the 100 students, 19 girls rode in a car, 7 girls rode the bus, and 27 girls took the train.

Out of the boys, 12 took the train, 25 rode in a car and 10 rode the bus.

Total students asked = 100

Constructing the two-way frequency table by writing the given data into the table.

From the table it is clear that most preferred transport (used) is car, out of 100 students that were asked 44 students go by car.

Two-way frequency table:

Most used mode of transportation is the car.

Page 232 Exercise 1 Answer

Given: two-way frequency table

We have to tell what pattern do we see from the table.

Given table:

From the table it is clear that most of the people have rain boots, out of 75 people 41 people have rain boots.

Most of the people own rain boots.

Solutions For Envision Math Grade 8 Bivariate Data

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Practice Page 234 Exercise 1 Answer

we have to explain how does a two-way frequency table show the relationship between sets of paired categorical data.

Two-way frequency tables are a visual representation of the possible relationships between two sets of categorical data.

The categories are labeled at the top and the left side of the table, with the frequency (count) information appearing in the four (or more) interior cells of the table. The “totals” of each row appear at the right, and the “totals” of each column appear at the bottom.

The two-way frequency table show the relationship between paired categorical data in the columns and rows.

The total the bottom right corner displays the total number of each cell in the table.

A two-way frequency table show the relationship between sets of paired categorical data.

In the columns and rows and the table makes easy to draw a conclusion and makes interpretation easy.

Page 234 Exercise 3 Answer

We have to explain how we can use the structure of a two-way frequency table to complete it.

First, we look for the column or row which have two values in it and to find the last value we use simple addition and subtraction to complete the table.

Let’s suppose we have a two-way frequency table with some data already in it.

We know that, the total of a row is displayed on the right and the total of a column is displayed on the bottom.

When we have two values in the row or column, we can find the last value by simple addition or subtraction, the total count is always equal to the sum of values in row or column.

The total count is always equal to the sum of values in row or column.

we can use addition or subtraction to find the last value when two values are already given in a row or column.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 234 Exercise 4 Answer

Given:

Total players are 60

We have to complete the table.

We can us addition or subtraction to complete the table, first we will look for that row or column which have two values in it.

Total number of players are 60.

Given table:

First, we will look for that row or column which have two values in it.

The total number of underclassmen students are 28

Therefore, 28 − 18 = 10

10 is the value that will come in the middle of first row.

The total number of the free throws are 31

Therefore, 31 − 18 = 13

13 is the value that will come in the middle of first column.

The total number of upperclassmen will be 13 + 19 = 32

Total number of 3-point shots are = 10 + 19 = 29

We know total players are 60.

Putting the calculated values in the table we get,

The complete two-way frequency table is:

Envision Math Grade 8 Chapter 4 Homework Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 234 Exercise 5 Answer

Given a table:

We have to explain whether the given statement is correct or not.

Given statement is false.

Given table is:

From the table it is clear that there are more high school students that wear contacts than middle school students that wear glasses

20 > 13

The given statement is incorrect.

Page 235 Exercise 8 Answer

Given:

We are given the frequency table. We have to solve this frequency table to conclude the survey.

We consider the blank as x

Now,

The second column,
​
25 + 2 + 24 = x

∴ x = 51
​
The third column,
​
14 + x + 21 = 47

∴ x = 47 − 35

x = 12
​
Now, we consider the Total row,

We have:
​
44 + 51 + 47 + 42 + x = 203

∴ x = 203 − 184

x = 19
​
Now, we consider the fifth column:

We have:
​
4 + 8 + x = 19

∴ x = 19 − 12

x = 7
​
Now, we consider the third row:

We have:
​
x + 24 + 21 + 3 + 7 = 73

∴ x = 73 − 55

x = 18
​
Now, we consider the first column:

We have:
​
x + 1 + 18 = 44

∴ x = 44 − 19

x = 25
​
Now, we consider the first row:

We have:
​
25 + 25 + 14 + x + 4 = 72

∴ x = 72 − 68

x = 4
​
Now we consider the total column:

We have:
​
72 + x + 73 = 203

∴ x = 203 − 145

x = 58
​
Now, we consider the second row:

We have:
​
1 + 2 + 12 + x + 8 = 58

∴ x = 58 − 23

x = 35
​

Envision Math Grade 8 Chapter 4.1 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 235 Exercise 9 Answer

We are given the frequency table. Observe the given table to solve this question.

We observe the table.

The students studying for 1 to 2 hours are 147 in number.

The number of studying for 5 to 6 hours are 104

The statement states that more students study for 5 to 6 hours than for 1 to 2 hours.

This statement is False as the number of students studying for 5 to 6 hours is less than 1 to 2 hours.

The statement is false because the number of students studying for 1 to 2 hours is more than 5 to 6 hours.

Page 236 Exercise 10 Answer

Given:

Construct a single, two-way frequency table to show the results.

We observe rain in NYC on Friday is 4, Saturday is 5, and Sunday is 6.

We observe that no rain in NYC on Friday is 6, Saturday is 5 and Sunday is 4.

We observe that rain in LA on Friday is 2, Saturday is 0 and Sunday is 1.

We observe that no rain in LA on Friday is 8, Saturday is 10, Sunday is 9.

Given:

Through A.

We observe the frequency table from a.

We understand that the day that received the least rain in both LA and NYC is Saturday.

Saturday only has rain as 5.

Saturday saw the least rain in both NYC and LA with frequency as 5.

How To Solve Envision Math Grade 8 Topic 4.1

Page 236 Exercise 11 Answer

Given:

The total number of animals was 74.

There were 39 cats out of which 25 were male and 14 were female.

There were 35 dogs out of which 23 were male and 12 were female.

This is the required table.

Given:

Through A.

We observe the frequency table from a.

We understand that the total number of males at the adoption centre is 48.

We also observe that the total number of females at the adoption centre is 26.

We observe that for males there a greater need for adoption at the centre.

Males have a greater need to be adopted at the adoption center because the number of males at the adoption center is greater than the females.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3

Page 223 Exercise 1 Answer

Given

Trend line passing through (25,100) and (80, 550).

To find/solve

Would this indicate that more or fewer calories were burned per minute? Explain.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

First we have to plot the second trend line. After we have plotted the new trend line, we can see that new trend line is below the current trend line which means that fewer calories were burned per minute. Also the new trend line is ascending slower.

This would indicate that fewer calories were burned per minute.

This would indicate that fewer calories were burned per minute.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.3 Bivariate Data Solutions

Page 224 Question 1 Answer

Given

Statement

To find/solve

Linear models help you to make a prediction.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 224 Exercise 1 Answer

Given

To find/solve

In 2025, the average fuel consumption is predicted to be about

First we are going to find the y-intercept. On the given graph the y-intercept is 15

Now we have to find the slope.

To find the slope we are going to use two points which are (10,18),(20,21)

Now that we know the equation of the trend line which is y = 0.3x − 15, we can simply find out the average fuel consumption in 2025.

The average fuel consumption in 2025 is predicted to be about 28.5 mpg.

The average fuel consumption in 2025 is predicted to be about 28.5 mpg.

Envision Math Grade 8 Exercise 4.3 Investigate Bivariate Data

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 225 Exercise 2 Answer

Given

ingredients needed to make 50,000 smoothies on a day when the high temperature is expected to reach 90∘F

To find/solve

Employees expect to have enough ingredients for the day’s smoothie sales.

To find out whether the Smoothie cafe is going to have enough ingredients we are simply going to use the equation from the last task.

The x that we are going to use is 90 because that is the temperature.
​

y = \(\frac{3}{5} .90+8\)

y = 54 + 8

y = 62
​
The expected number of smoothies to be sold on that day is about 62 thousands which mean that the cafe is not going to have enough ingredients.

The cafe is not going to have enough ingredients.

The cafe is not going to have enough ingredients.

Page 224 Exercise 1 Answer

Given- linear model

To find- Why can you use a linear model to predict the y value for a given x value.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

On linear model we can draw a trend line, which will show us how the result will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

On linear model we can draw a trend line, which will show us how the result will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

Investigating Bivariate Data Grade 8 Exercise 4.3 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 226 Exercise 1 Answer

Given- linear model

To find/solve- Linear models help you to make a prediction.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

Page 226 Exercise 3 Answer

Given- linear model

To find- Prediction about any x-value.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

If we know the equation then we can find the prediction about any x-value.

If we do not know the equation for the given linear model that we simply first have to find that.

Yes, we can find the prediction about any x- value.

If we know the equation then we can find the prediction about any x-value.

If we do not know the equation for the given linear model that we simply first have to find that.

Yes, we can find the prediction about any x value.

Envision Math Grade 8 Chapter 4 Exercise 4.3 Solutions

Page 226 Exercise 4 Answer

Given

To find/solve

a. Using the slope, predict the difference in the amount spent on groceries between a family with five children and a family with two children.

We simply have to use two different x values which are 2 and 5. After that we simply have to subtract the value so we know the difference.
​
​
The difference is about $63,24.

The difference in amount spent on groceries between a family with five children and a family with two children is $63,24.

The difference is about $63,24.

The difference in amount spent on groceries between a family with five children and a family with two children is $63,24.

Given

To find/solve

b. How many children can you predict a family has if the amount spent on groceries per week in $169.47?

We are simply going to substitute the y, with 169.46 and calculate for x after that.

First we have to subtract 85.15 from both sides of the equation.
​
169.47 − 85.15 = 21.08x

84.32 = 21.08x
​
No we can simply divide both sides of the equation with 21.08

X = 4.

The family has 4 children.

The family has 4 children.

Envision Math 8th Grade Exercise 4.3 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 227 Exercise 6 Answer

Given

To find/solve

what the difference between the gas prices in 2013 and 2001 is

To find out what is the difference we simply have to find the equation for given graph.

First, we are going to find the slope.

To do so we are going to use two points from the trend line (3,18) and (6,25)

Secondly, we have to draw the line to the y-axis so we can find the y-intercept.

Now we can simply subtract the values

4.19 – 1.43 = 2.76

The difference between the gas prices in 2013 and 2001 is 2.76

The difference between the gas prices in 2013 and 2001 is 2.76.

How To Solve Exercise 4.3 Bivariate Data In Envision Math Grade 8

Page 228 Exercise 8 Answer

Given

To find/solve

what the hiker’s elevation will be after 145 minutes.

Finally we only have to round up the result to the nearest whole number.

y ≈ 1958

The biker’s elevation will be 1958ft after 145 minutes.

The biker’s elevation will be 1958ft after 145 minutes.

Page 228 Exercise 9 Answer

Given

To find/solve

How long it will take to fill the tank with 375 gallons of water.

If we look closely at the graph we can see that one point is (9,190) which the about the half way to the point at which we have 375 gallons.

Since we have a straight line, we can simply multiply give x-coordinate with 2 to get the time needed to fill the tank with 375 gallons of water.

9.2 = 18

18 hours is going to be needed for 375 gallons to be in the tank.

18 hours is going to be needed for 375 gallons to be in the tank.

Envision Math Grade 8 Exercise 4.3 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 228 Exercise 11 Answer

Given: two points (0,453) and (10,359)

First, we will find the slope from the given points and find out the y-intercept.

Points from which trend line passes: (0,453) and (10,359)

From (0,453)it is clear that y-intercept is +453

Therefore, c = +453

Now, slope = \(\frac{y_2-y_1}{x_2-x_1}=\frac{359-453}{10-0}=-9.4\)

Therefore, m = -9.4

Now, substituting values of m and c in y = mx + c

We get, y = −9.4x + 453

Therefore, the trend line equation is y = −9.4x + 453

Option (D) is correct option.

The trend line equation is y = −9.4x + 453

Option (D) is correct option.

Envision Math Exercise 4.3 Bivariate Data Detailed Answers

Page 228 Exercise 12 Answer

Given: altitude = 415.4 feet

We will substitute the value y = 415.4 in y = -9.4x + 453 and solve it.

Given: altitude (y) = 415.4

Substituting value of y = 415.4 in y = −9.4x + 453

We get,
​
415.4 = −9.4x + 453

x = \(\frac{-37.6}{-9.4}=4\)

It will take 4 minutes to be at an altitude of 415.4 feet.

It will take 4 minutes.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2

Page 217 Exercise 1 Answer

It is given that Angus has a big test coming up.

We have to make a general statement about which option leads to a better result.

The data regarding Angus is given, where it is given that in different test at what time he sleeps and when he gets up.

On observing the given data, we can observe that in the test 6, Angus goes to bed at 9pm which is early and, in that test, he scores the highest marks and the best result.

Therefore, the better option which will lead to a better result is that he should go to bed early for the best results in the test.

The better option which will lead to a better result is that he should go to bed early for the best results in the test.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.2 Bivariate Data Solutions

Page 217 Exercise 1 Answer

We need to find the other factors should Angus take into consideration to make a decision.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

If we look closely at the test and their result, we can see that when he goes to bed early then Angus has the best results. The results differ by only a little but still the results are better when he goes to bed early.

The results are better when he goes to bed early.

The results are better when he goes to bed early.

Page 218 Question 1 Answer

We need to explain how we can describe the association of two data sets.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

We describe the relationship between the two sets of data with associations.

We can use the scatter plot for given relationship to determine whether there is strong, weak or no association.

We describe it with association.

We describe the relationship between the two sets of data with associations.

We can use the scatter plot for given relationship to determine whether there is strong, weak or no association.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2 Page 218 Exercise 1 Answer

To find – The relationship might there be between the two measurements

Correlation coefficient values can range between +1.00 to -1.00.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

The value of the correlation coefficient tells us about the strength and the nature of the relationship.

Correlation coefficient values can range between +1.00 to -1.00.

Statistical measures which show a relationship between two or more variable or two or more sets of data. For example, generally there is a high relationship or correlation between parent’s education and academic achievement.

Statistical measures which show a relationship between two or more variable or two or more sets of data. For example, generally there is a high relationship or correlation between parent’s education and academic achievement.

Envision Math Grade 8 Exercise 4.2 Investigate Bivariate Data

Page 218 Exercise 1 Answer

Given that, Georgia and her classmates also measure their foot length. Use a pencil to find the trend line. We need to sketch the trend line for the scatter plot.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Simply place the pencil on the scatter plot so it goes right through the middle of all point and then sketch line.

Place the pencil on the scatter plot so it goes right through the middle of all points and then sketch that line.

Place the pencil on the scatter plot so it goes right through the middle of all points and then sketch that line.

Page 219 Exercise 2 Answer

To find the association between the data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association.

Given graph has strong association.

To find the association between the data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association.

Given graph has weak association.

To find the association between the data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association.

Given graph has no association.

Investigating Bivariate Data Grade 8 Exercise 4.2 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2 Page 220 Exercise 1 Answer

We need to explain how we can describe the relationship between the two sets of data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

The value of the correlation coefficient tells us about the strength and the nature of the relationship.

Correlation coefficient values can range between +1.00 to -1.00.

The relationship between the two sets of data is described using associations.

We can determine whether the two sets of data are having strong, weak, or have no associations between them.

Associations describe the relationship between the two sets of data.

Using a scatter plot, we can determine whether the given two sets of data is having strong, weak, or no association.

Page 220 Exercise 2 Answer

Given- a trend line

To find- How does a trend line describe the strength of the association?

If the points are close to the trend line then the association is strong

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association

We use the pencil to find the trend line. If the points are close to the trend line then the association is strong, if they are scattered around but not so close to the pencil, then the association is weak and if the points are scattered all around the graph, then there is no association.

We use the pencil to find the trend line. If the points are close to the trend line then the association is strong, if they are scattered around but not so close to the pencil, then the association is weak and if the points are scattered all around the graph, then there is no association.

Envision Math Grade 8 Chapter 4 Exercise 4.2 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2 Page 220 Exercise 5 Answer

To find- The association between the data.

The value of the correlation coefficient tells us about the strength and the nature of the relationship.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil then the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil and do not have any pattern then there is no association.

Given graph has no association.

Page 221 Exercise 6 Answer

Given

To find/solve
Best model of the data

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

If we look closely at the lines on the graph, then we can see that the line that we need is m.

All of the points are more close to line m than any other line.

Hence the best model is the line m.

All of the points are more close to line m than any other line.

Hence the best model is the line m.

Page 221 Exercise 8 Answer

To find- Positive or negative linear association.

A positive correlation is a relationship between two variables that move in tandem—that is, in the same direction.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Since we have the time working and the amount of money earned, then we know that the graph is going to be positive meaning that the more time working we have, the more money we are going to earn.

This is going to be a positive association.

This is going to be a positive association.

Envision Math 8th Grade Exercise 4.2 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2Page 221 Exercise 9 Answer

Given

To find/solve

Relationship between the data .

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

As we can see on the graph the trend line is going to be descending which means that the association is going to be negative.

If we draw the trend line with pencil, then we can see the association is strong negative.

On the given graph we can see strong negative association.

If we draw the trend line with pencil, then we can see the association is strong negative.

On the given graph we can see strong negative association.

How To Solve Exercise 4.2 Bivariate Data In Envision Math Grade 8

Page 222 Exercise 13 Answer

Given- scatter plot showing a linear relationship.

To find- if a scatter plot shows a linear relationship

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

The y-values change with respect to the x-values at a constant rate. This means that the points are going to be forming a line.

The y-values change with respect to the x-values at a constant rate.

The y-vales change with respect to thex-values at a constant rate. This means that the points are going to be forming a line.

The y-values change with respect to the x-values at a constant rate.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1

Page 211 Exercise 1 Answer

Based on the given data, we have to predict Luciana’s strategy.

The data regarding Luciana’s campaign is given.

From the data is observed that the maximum number of subscribers are gained when Luciana does around five to six social media posts in a day.

Thus, her strategy should simply be that she must do 5-6 social media posts every day. She should be careful and not do less than 5 social media posts on any day of the campaign in order to get the most number of subscribers.

Luciana’s strategy must be to do 5-6 social media posts each day in order to get most subscribers.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.1 Bivariate Data Solutions

Page 212 Exercise 2 Answer

Based on the given data, we have to tell the pattern between the time after posting and the number of new views.

The data regarding number of views on homepage is given.

From the data given, we can observe that when the time after posting the blog is more than 4 hours then the number of new views is decreased to two-digit numbers.

While when the time after posting is just 1-4 hours, then the new views are high and in three-digit numbers.

The pattern between the time after posting and the number of new views is than when time increases new views are decreased and when time is less, the number of new views is more.

Page 211 Exercise 1 Answer

Based on the given data, we have to tell the pattern between the time after posting and the number of new views.

The data regarding Luciana’s last social media campaign.

From the data given, we can observe that when she does around 1-4 social media posts in a day then she gets less number of new subscribers.

When she does 5-6 posts in a day, the highest numbers of subscribers are obtained.

But, when her posts are more than 6 in a day, again the number of subscribers decreases. This is the pattern observed from the data.

The pattern observed is that if there are 5-6 posts in a day new subscribers are increased, while if posts are less than 5 or more than 6 the number of subscribers are decreased.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 212 Exercise 1 Answer

We are required to find the coordinates of the point that represents the data in the fourth column.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

In the given data, age is in the x-coordinate while the number of entries is the y-coordinate.

In the fourth column, age is given as 13 years and the number of entries is 9.

Thus, the coordinate of that point will be (13,9).

The coordinates of the given point are (13,9).

Envision Math Exercise 4.1 Bivariate Data Detailed Answers

Page 213 Exercise 2 Answer

We have to describe the association between the two data sets.

Also we need to tell what the association suggests.

A scatter plot is a mathematical diagram which tells the relationship between paired data.

The scatter plot shows the relationship or association between the two sets of data.

There are three different types of association-

Positive association: The y-values increase as the x-values increase.

Negative association: The y-values decrease as the x-values increase.

No association: There is no consistent pattern between the x and y values.

From the graph given, we can observe that the association among the points scored and the minutes played is the positive associations.

This means that the y- values tend to increase when the x- values increase.

The association observed from the graph is positive association.

Envision Math Grade 8 Exercise 4.1 Investigate Bivariate Data

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 212 Exercise 1 Answer

We have to tell how the scale for both x and y axis will be chosen.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

In the given data, age is given as 10,11,12,13,14,15 years.

There is just a single value increment among the two values.

Age is marked on x-axis, so the scale on x-axis will be starting from 0 and will be increased by 1 unit only up to 15.

The number of entries is given as 8,8,9,9,10,10.

There is just a single value increment among the two values.

The number of entries is marked on y-axis, so the scale on x-axis will be starting from 0 and will be increased by 1 unit only up to 10.

The scale on x-axis is from 0 to 15 with increment of one unit only.

The scale on y-axis is from 0 to 10 with increment of one unit only.

Page 214 Exercise 1 Answer

We have to tell that how scatter plot shows the relationship between paired data.

Two sets of data are said to be paired if there exists a one-to-one relationship among them.

The relationship among the paired data is represented by a method of drawing scatter plot.

Scatter plot is a mathematical diagram on which points or coordinated of the data are plotted.

The scatter plot is used to tell the relationship among paired data by identifying the association among them.

The scatter plot shows the relationship or association between the two sets of data.

There are three different types of association-

Positive association: The y-values increase as the x-values increase.

Negative association: The y-values decrease as the x-values increase.

No association: There is no consistent pattern between the x and y values.

The relationship between paired data is observed based on the type of association which exists.

Investigating Bivariate Data Grade 8 Exercise 4.1 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 214 Exercise 2 Answer

We have to tell what scale must be used to construct the given scatter plot.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

On the x-axis, the hours of sleep will be marked. The scale will range from 0 to 9. This is because Marcy does not sleep more than 9 hours.

On the y-axis the points in the game will be marked. The scale for the same will be from 0 to 27 as the maximum points in a game is 27 only.

The scale on x-axis, will be from 0 to 9, on which the hours of sleep will be marked.

The scale on y-axis, will be from 0 to 27, on which the points in the game will be marked.

Envision Math Grade 8 Exercise 4.1 Solution Guide

Page 214 Exercise 3 Answer

We have to tell whether the statement given by Kylie is correct or not.

Kylie says that every scatter plot will have a cluster, gap and outlier.

We know that a scatter plot is a mathematical diagram.

The points on a scatter plot can be grouped or ungrouped. So, every scatter plot may not always be a cluster.

A gap on scatter plat is defined as the area where there are no data points.

This can only happen when the points are ungrouped and not always.

There may be an outlier in each scatter plot, but we can have a scatter plot which does not have a point away from rest all other points.

Thus, from all the above definitions, the statement made by Kylie is not correct.

Kylie says that every scatter plot will have a cluster, gap and outlier. This statement is wrong.

Envision Math Grade 8 Exercise 4.1 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 214 Exercise 5 Answer

We have to tell why clusters and outliers must be present in the scatter plot.

Germaine constructs a scatter plot to show how many people visit different theme parks in a month.

A group of points which are located closely around each other is called a cluster.

An outlier in each scatter plot, is the point which lies away from rest all other points.

In the given scatter plot, a cluster will obviously be present because we are aware that the people who tend to visit different theme parks for few months.

It is also possible that for some months, people do not want to visit a different theme park, so this will be an outlier in the graph.

In the given graph of scatter plot, clusters will be present because people may wish to visit different theme parks every month and outlier will be there are there are may be situation when they are not willing to visit a different theme park.

Envision Math Grade 8 Chapter 4 Exercise 4.1 Solutions

Page 215 Exercise 6 Answer

We have to complete the given scatter plot.

A scatter plot consists a coordinate plane which consists of two axis, one horizontal and the other vertical intersecting each other.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

In order to complete the scatter, we have to tell what points will be marked on the x and y-axis.

On the x-axis, the racing time in minutes will be marked.

On the y-axis, the laps will be marked.

The completed scatter plot will be

The scatter plot is completed as

Envision Math 8th Grade Exercise 4.1 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 215 Exercise 8 Answer

We have to complete the scatter plot.

A Scatter plot is a mathematical diagram that represents the data.

We are given the data which shows the monthly attendance in thousands at museums in one country over a 12-month period.

The scatter plot will be completed on marking the data points as below:

The completed scatter plot is

The table shows the monthly attendance in thousands at museums in one country over a 12-month period.

We have to identify outliers in the scatter plot given

We are given the data which shows the monthly attendance in thousands at museums in one country over a 12-month period.

An outlier is a point, which is a single point away from all the other points plotted on the scatter plot.

On observing the scatter plot, the two outliers observed are the points (6,36) and (12,3).

The outliers identified are the points (6,36) and (12,3).

The table shows the monthly attendance in thousands at museums in one country over a 12-month period.

We have to identify the reason for existence of outlier.

We are given the data which shows the monthly attendance in thousands at museums in one country over a 12-month period.

An outlier is a point, which is a single point away from all the other points plotted on the scatter plot.

On observing the scatter plot, the two outliers observed are the points (6,36) and (12,3).

There was some discount on price of ticket to museum, which caused the first outlier which is (6,36).

In the month of December, some people do not visit museum because of holidays, so there is the second outlier (12,3).

The outliers are there because of discount on price and holidays in December.

How To Solve Exercise 4.1 Bivariate Data In Envision Math Grade 8

Page 216 Exercise 10 Answer

We have to check whether the given statements are true or not.

A scatter plot consists a coordinate plane which consists of two axis, one horizontal and the other vertical intersecting each other.

Ten athletes ran two races of the same length. The scatter plot shows their times.

The scatter plot is

On observing the scatter plot graph, the true statements which are:

Eight of the times for the second race were less than 17 seconds.

There were three athletes who had the same time in both races.

Thus, the false statements are

Nine of the times for the first race were at least 16 seconds.

There were seven athletes who were faster in the second race than in the first.

There were three athletes whose times in the two races differed by exactly 1 second.

The true statements are

Eight of the times for the second race were less than 17 seconds.

There were three athletes who had the same time in both races.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4

Page 206 Question 1 Answer

We have to tell the method to represent the relationship between paired data.

Using the same representation, predictions are to be made.

Two sets of data are said to be paired if there exists a one-to-one relationship among them.

The relationship among the paired data is represented by a method of drawing scatter plot.

Scatter plot is a mathematical diagram on which points or coordinated of the data are plotted.

The scatter plot has various uses, one of which is to make predictions regarding the data.

For which a best fit line is drawn and based on the location of points around the best fit, predictions are drawn whether the data is strong or not.

Scatter plot is used to represent the relationship between paired data and best fit line helps to make predictions in this method.

Envision Math Grade 8 Volume 1 Chapter 4 Topic 4 Bivariate Data Solutions

Page 209 Exercise 1 Answer

We are required to complete the given definition with appropriate word.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is
​

​m = \(\frac{\Delta y}{\Delta x}\)

​
m = \(\frac{y_2-y_1}{x_2-x_1}\)

Therefore,

Slope is the change in y divided by the change in x.

Slope is the change in y divided by the change in x.

Envision Math Grade 8 Topic 4 Investigate Bivariate Data

Page 209 Exercise 2 Answer

We are required to complete the given definition with appropriate word.

In simple words, ratio is defined as the comparison of two quantities by dividing them.

A ratio of two quantities suppose p and q is represented p:q

Ratio is equivalent to fractions.

Therefore,

A relationship where for every x unit of one quantity there are y units of another quantity is a ratio.

A relationship where for every x unit of one quantity there are y units of another quantity is a ratio.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 3 Answer

We are required to complete the given definition with appropriate word.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

Therefore,

The x-axis is the horizontal line in a coordinate plane.

The x-axis is the horizontal line in a coordinate plane.

Page 209 Exercise 4 Answer

We are required to complete the given definition with appropriate word.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

Therefore,

The y-axis is the vertical line in a coordinate plane.

The y-axis is the vertical line in a coordinate plane.

Page 209 Exercise 5 Answer

We have to mark the given point (-2,4) on coordinate plane.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is y-coordinate.

In the given point (-2,4) the x-coordinate is -2 and the y-coordinate is 4.

We mark the point as below:

The point (-2,4) is labelled on coordinate plane as below:

Investigating Bivariate Data Grade 8 Topic 4 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 6 Answer

We have to mark the given point (0,3) on coordinate plane.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is y-coordinate.

In the given point (0,3) the x-coordinate is 0 and the y-coordinate is 3.

We mark the point as below:

The point (0,3) is labelled on coordinate plane as below:

Envision Math Grade 8 Chapter 4 Topic 4 Solutions

Page 209 Exercise 7 Answer

We have to mark the given point (3,-1) on coordinate plane.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is y-coordinate.

In the given point (3,-1) the x-coordinate is 3 and the y-coordinate is -1.

We mark the point as below:

The point (3,-1) is labelled on coordinate plane as below:

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 8 Answer

We have to mark the given point (−4,−3) on the coordinate plane.

A two-dimensional plane that consists of two axes, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is the y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is the y-coordinate.

In the given point (−4,−3) the x-coordinate is −4 and the y-coordinate is −3.

We mark the point as below:

The point −4,−3 is labeled on the coordinate plane as below:

Page 209 Exercise 9 Answer

We have to find slope among the given points (4,6) and (-2,8).

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

m = \(\frac{\Delta y}{\Delta x}\)

​
m = \(\frac{y_2-y_1}{x_2-x_1}\)

Slope is the change in y divided by the change in x.

Here we have the two points as (4,6) and (-2,8).

Slope between the pair of points (4,6) and (-2,8) is obtained as m = \(-\frac{1}{3}\)

Envision Math 8th Grade Topic 4 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 11 Answer

We have to find slope among the given points (5,-1) and (-3,-7).

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

m = \(\frac{\Delta y}{\Delta x}\)

​
m = \(\frac{y_2-y_1}{x_2-x_1}\)

Slope is the change in y divided by the change in x.

Here we have the two points as (5,-1) and (-3,-7).

Slope between the pair of points (5,-1) and (-3,-7) is obtained as m = 3/4.

Page 209 Exercise 12 Answer

We have to express the fraction \(\frac{36}{60}\) as percent.

A per cent is a one part among 100 quantities.

In order to express the fraction as percent, first we divide and get the fraction as decimal.

Now, the percent is obtained by multiplying the decimal obtained with 100.

0.6 × 100 = 60

Thus, the fraction is expressed as 60%.

The fraction \(\frac{36}{60}\) is obtained as 60%.

How To Solve Bivariate Data In Topic 4 Envision Math Grade 8

Page 210 Exercise 1 Answer

The given vocabulary terms are,

Measurement data

Scatter plot

Cluster

Gap

Outlier

Trend line

Categorical data

Relative frequency table

We need to state their definitions and examples.

Measurement data

Definition – the type of data provided by figures

Examples – Length, Speed, height, distance.

Scatter plot

Definition – A mathematical diagram that displays values for correlated variables into a set of information using Cartesian coordinates.

Examples –

Cluster

Definition – A group of data that are very close to each other.

Examples –

Gap

Definition – The missed out points or information in a datasheet.

Examples –

Outlier

Definition -A value that seems to be separate or lies outside the given range.

Examples –

Trend line

Definition – A line drawn to show the direction in which the data prevails.

Example

Categorical data

Definition – A data that can be split down into groups.

Examples – Age, sex, etc.

Relative frequency table

Definition – The popularity or mode of data based on the samples obtained.

Examples – I ate 10 donuts out of 15: the frequency of eating is 10. the relative frequency of winning is \(\frac{10}{15}=\frac{2}{3} \times 100=66.6^{\%}\).

Measurement data – the type of data provided by figures.

Scatter plot – A mathematical diagram that displays values for correlated variables into a set of information using Cartesian coordinates.

Cluster – A group of data that are very close to each other.

Gap – The missed out points or information in a datasheet.

Outlier -A value that seems to be separate or lies outside the given range.

Trend line – A line drawn to show the direction in which the data prevails.

Categorical data – Data that can be split down into groups.

Relative frequency table – The popularity or mode of data based on the samples obtained.