Business Mathematics - Math Book Answers

CA Foundation Maths Solutions

November 9, 2024July 5, 2024 by Sainavle

CA Foundation Maths Solutions For Chapter 7 Sets, Function & Relations

November 15, 2024July 5, 2024 by Alekhya

CA Foundation Maths Solutions For Chapter 7 Sets, Function & Relations

Sets Introduction:

A set is a group of elements or objects that share at least one characteristic or property.
The objects within one set are similar in some respect.
Mathematically, a set can be defined as a group of well-defined objects that are similar in some respect. These objects are called the elements of the set.
For example, consider the set of vowels in the English alphabet. Let this set is represented by the letter V. This set contains 5 elements- a, e, i, o, u. this can also be written as:
V ≡ {a, e, i, o, u}
The following two conventions should be adhered to while denoting a set
1. A set must be denoted by a capital letter.
2. The elements of the set must be denoted in small letters.
A few examples of sets are given below:
A ≡ {1,2,3,4,5}
B≡ {a,b,c,d,e}
In the above examples, A and B are the names of the sets while 1,2,3,4,5, and a,b,c,d,e are the elements belonging to these sets respectively.
The symbol ∈ is used to denote that an element belongs to a particular set. Hence, to denote that 1 belongs to set A, write it as: 1 ε A
ε Is a Greek letter called epsilon.
In number systems, numbers can be classified in various ways as per their characteristics. The standard notations used to denote the commonly used sets of numbers are as shown below:

Read and Learn More CA Foundation Maths Solutions

N ≡ set of all natural numbers = {1,2,3,4,5 … )
W ≡ set ofall whole numbers= {0,1,2,3,4, … }
I ≡ set ofall Integers = {…..-3, -2, -1,0,1,2,3,…}
Q ≡ set ofall rational numbers
R ≡ set of all real numbers
P ≡ set ofall prime numbers
C ≡ set ofall complex numbers

Cardinality of Sets

Cardinality of a set refers to the total number of elements that are present in the set. For example, V= {a, e, i, o, u}
The cardinality of this set of vowels V is 5 as the total number of elements in the set is 5, This can be represented as: |V| = 5 or n(V) = 5

CA Foundation Maths Chapter 7 Sets, Functions, And Relations Solutions

CA Foundation Maths Solutions For Chapter 7 Classification Of Sets based On Cardinality

Based on the concept of cardinality, sets can be classified into the following types:

Null Set/ Void Set/ Empty Set

Consider the set B≡ { )

This set has no elements. Hence, the cardinality of this set is zero.

This can be represented as:

|B| =0 or n (B) =0

Such a set is called a null set or a void set or an empty set. A null set can be represented as:

B≡ ∅

Infinite Set

Consider the set of natural numbers.

N= set of all natural numbers= {1, 2, 3, 4….}

This set does not have a final element. The number of elements n this set cannot be counted and is hence, infinite.

Such sets, where the cardinality of the set cannot be exactly determined, are called infinite sets. All the standard sets mentioned above are infinite sets.

Finite Set

Consider the set of the factors of a number, say 12. The factors of 12 are 1, 2, 3, 4, 6, and 12.

If this set is denoted by S, then S = {1,2,3,4,6,12}.

The cardinality of this set is 6. Since this set has a finite number of elements, it is known as a finite set. Hence, sets which have a finite number of elements are called finite sets.

Singleton Set /Singlet

A set which has one and only one element in it is called a singleton set or a singlet.

For example,

A≡ {a}
B≡ {0}

In the above cases, A and B are both singleton sets.

Note:

In the second example, B is not an empty set. It contains the element 0.

B would have been an empty set ifit did not contain any elements, i.e., B ≡ { }

CA Foundation Maths Solutions For Chapter 7 Equivalent And Equal Sets

Equivalent sets

Two finite sets are said to be equivalent if their cardinality is the same, i.e., n(A) = n (B)

For example, if A ≡ {1,2,3,} and B ≡ {4,5,6}

Then, n {A} = n (B} = 3

Hence, A and B are equivalent sets.

Equal sets

Two sets are said to be equal if and only if they contain the same elements.

This implies that every elements of set B is present in set A and every element of set A is present in set B

For example, if A ≡ {a, b, c} and B ≡{c, b, a} then A and B are said to be equal sets.

Equality of sets is denoted as A = B. Note that the order in which the elements of the two equal sets are written is not important.

Two equal sets are always equivalent, but two equivalent sets may or may not be equivalent.

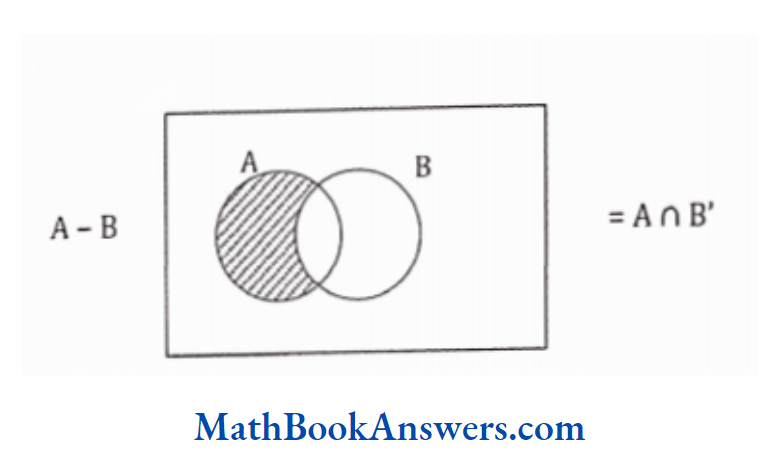
Representation of a Set

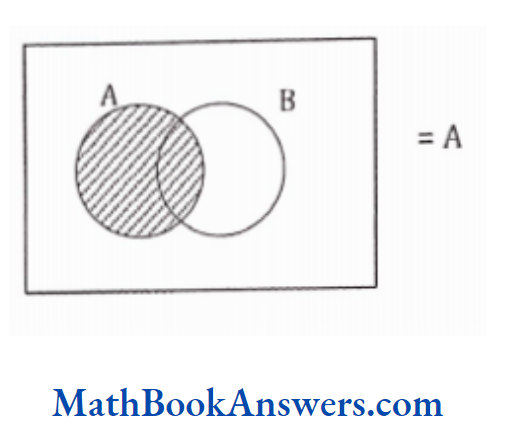
There are two ways of representing a set. They are,

Roster notation
Set Builder notation (or Rule Method)

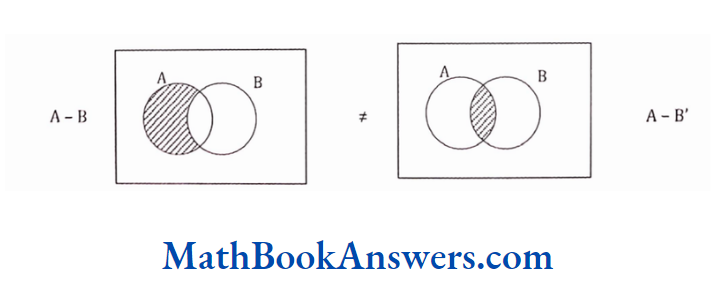
Roster Notation

Consider the set of vowels:

V ≡ (a, e, i, o, u}

Here, each vowel is individually listed down in the set V.

This method in which each element of a set is specified within the set is called the Roster method.

Note:

To denote an infinite set (such as the set of natural numbers) using the Roster method, write the first few elements followed by ‘…’ to indicate continuation up to infinity.

N ≡ (1, 2,3 }

Set Builder Notation

In the set Builder notation, instead of writing down every single element of a set, the common property of the elements of the set is described.

For example, in the Roster notation the set of the first five natural numbers is written as follows:

D≡ {1,2,3,4,5}

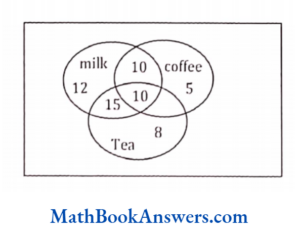
Now, if one were to describe this set in words, the description would say, “set D is a set of all elements x such that x is a natural number and x lies between 1 and 5 (both inclusive)”.

This is written in set Builder notation as follows:

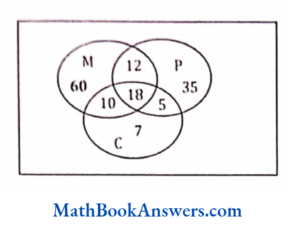
D≡ {x|x ∈ N and 1 ≤ x ≤ 5}

Note:

The symbol | is read as “such that”.

Consider another example,

V≡{a, e, i, o, u)

This can be written as “the set V is a set of elements x, such that x is a vowel from the English alphabet.”

This can be written in set Builder notation as: V≡ {x|x is a vowel from the English alphabet)

Hence, in general, if all the elements of a set A have a common property B, then the set can be expressed in the set builder form in the following way:

A≡{x|x has property B}

Examples:

1. Convert the following sets from the set Builder notation to the Roster notation: P= {y|y ∈ w and y < 3)

Solution:

Here, P is a set of all numbers y, such that y is a whole number less than 3. The whole numbers less than 3 are 0,1 and 2. Hence, set P can be written in Roster notation as: P ={0,1,2}

2. Convert the following sets from the set Builder notation to the Roster notation: M ={x|x²- 5x + 6 = 0}

Solution:

Here, M is a set of all such numbers x that satisfy x² -5x + 6 = 0. To find the values of x, solve this quadratic equation.

x² – 5x + 6 = 0

x²- 3x- 2x + 6 = 0

x(x- 3)- 2(x- 3) = 0

(x – 3)(x- 2) = 0

X=3 or x=2

Hence, the set M can be written in the Roster form as: M ≡ {2,3}

CA Foundation Maths Chapter 7 Detailed Solutions

CA Foundation Maths Solutions For Chapter 7 Subsets And Supersets

Consider the set ofall students in a particular college. Now, the set of first year students studying in the same college is a part of this bigger set of all students.

Such a set, which is entirely present in a bigger set, is called a subset of the bigger set.

The bigger set is called the superset of the smaller set. Each element of the subset is definitely an element of the superset as well.

However, every element of the superset need not be part of the subset.

A is said to be the superset of B.

Consider the following example:

A≡ {1,2,3,4,5,6} and B≡ {1,2,3,}

Note that every element of the set B is also an element of the set A.

Hence, B is a subset of A or B is contained in A. A is said to be the superset of B.

Note:

A Null set is a subset of every set. Eveiy set is a subset of itself.

Mathematically, a subset is defined as: A is a subset of B if and only if every element of A is an element of B.

This is denoted as follows:

A⊆ B

For example,

A ≡ {1,2}, B ≡ { 1,2}
A ≡ {1,2,3}, B ≡ {1,2,3,4} in both cases, A £ B

In the first example,

B is also a subset of A. Hence, A ⊆ B and B ⊆ A.

∴ Set B = set A

Hence, both the sets are equal. Hence, two equal sets are subsets of each other.

Such a subset is called an Improper subset. Subset A is an improper subset of B if A = B.

In the second example,

B is not a subset of A, which can be denoted by B ⊄ A.

Such a subset, where the superset also contains other elements, is called a proper subset.

Set A is said to be a proper subset of B if A ⊆ B but B ⊆ A.

A proper subset is denoted by the symbol ⊂. Thus, in the second example A⊂B.

Power Set

A Power set is the set of all subsets of a set. Consider a set A≡ {1,2,3}

Now, consider a set {1}. This set is a subset of A. similarly, {1, 2} is also a subset of A similarly, list down all the subsets of A. they would be:

{1}
{2}
{3}
{1,2}
{1,3}
{2,3}
{1,2,3} …(Every set is a subset of itself)
{ } …. (Null set is a subset of every set)

Total number of subsets = 8

Hence, a set of these subsets is called the power set of A.

P≡{{ 1 },{2},{3},{1,2},(1,3),(2,3),{1,2,3},{ } } If is the number of elements (cardinality) in a set is n, then the cardinality of the power set is given by 2ⁿ.

CA Foundation Maths Solutions For Chapter 7 Universal Set

Consider a college, consisting of students from three streams- Arts (set A), Commerce (set C) and Science (set S). All these students together form the set of all the students in the entire
college. Such a set is called a Universal set (set U).

A universal set is a set containing all the elements under consideration. It is represented by the capital letter U.

3. The universal set for the set of all numbers is as follows:

U≡ {-∞…….. ∞}. It includes all natural numbers, integers, rational numbers, irrational numbers, and so on.

CA Foundation Maths Solutions For Chapter 7 Complement of A Set

The concept of complement of a set logically flows from the concept of a universal set.

The complement of a set A, which is a subset of a universal set IJ, includes all the elements present in U which are not present in A. it is denoted by A’.

Suppose,

U ≡ (a,b,c,d,e,f,g,h,i) and

A ≡ {a,b,c,d,e},

Then A’, or complement of the set A ≡ {f,g,h,i}

CA Foundation Maths Solutions For Chapter 7 Union And Intersection Of Sets

Consider the following example.

In a room, there are 5 people a, b, c, d, e. Out of them, a, b and c are men while d and e are women. Also, a and e study science while b, c and d study commerce.

∴ The set of males is: M ≡ (a,b, c)

The set of females is: F≡ {d, e)

The set of science students is S ≡ (a, e)

The set of commerce students is C≡(b,c,d}

If the number of female students who have taken science is to be found, find the elements common to the set of females (F) and the set of Science students (S).

This is called an intersection of set F and set S and is denoted by F ∩ S.

Hence, in the above case, F ∩ S ≡ (e)

Thus, an intersection of two sets is formed by the elements that are common to both the sets.

Similarly, consider sets M and F. There is no common element between them,

Hence, M ∩ F =ø

Such sets which have no element in common are called disjoint sets.

Now, consider the females who have not taken science. Here, check the set F and remove all elements ofset S present In this set. This is called the difference between two sets.

F – S ≡ {d}

Thus, difference of set A and set 13 is defined as the elements present in A blit not present in B.

A – B ≡ { x| x ∈ A and x ∉ B}

Now, suppose one wants to represent a set containing “either males or commerce students or both”. This would imply taking all the elements from set M and set C together into one set. This is called the union of set M and set C and is denoted by M∪C.

Thus, M∪C ≡{a,b,c,d}

Thus, the elements common to both M and C are not counted twice. Thus, the elements belonging to the intersection set are subtracted from the union set.

Hence, M∪C = M+C – M ∩ C

Note:

Though b and c exist in both sets, they are written only once while writing the union. This is because no element is ever written twice while writing a set.

CA Foundation Maths Solutions For Chapter 7 Venn Diagrams

Sets can also be represented using diagrams known as Venn diagrams.
This method of representing sets is especially useful when multiple sets are given.
The closed figure corresponding to a set is used to denote that only the elements within this
closed figure belong to this set.
Any element lying outside this figure does not belong to this set. Though sets can be represented in the form of circles, triangles, rectangles and so on, the most commonly used figure in Venn Diagrams is a circle.
Consider the following example.
Let U be the universal set containing all the whole numbers between (and not including) 0 and 11.

Hence, U ≡ (1,2,3,4,5,6,7,8,9,10}

Let P be the set containing all the prime numbers between 0 and 11 (not including the two).

Thus. P ≡ (2,3,5,7)

Let E be the set containing all the even numbers between 0 and 11.

Hence, E = (2,4,6,8,10)

Hence P U E ={2,3,4,5,6,7,8,10}

Also, P ∩ E = {2}

This can be represented using a Venn diagram in the following manner.

This can be represented using a Venn diagram in the following manner

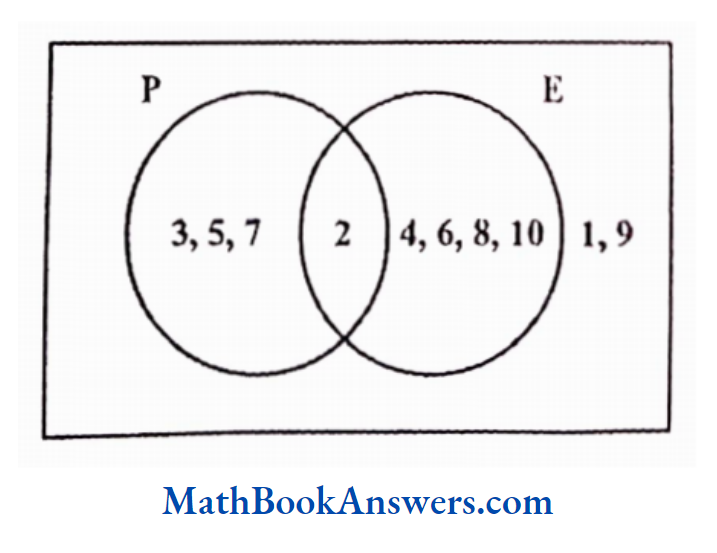
In the above diagram, the universal set is represented by the rectangle while all the other sets are represented by circles.

The common portion between the two sets P and E is the intersection of these two sets.

The universal set contains two numbers, 1 and 9, which do not belong to the set of prime or even numbers. Hence, they are written outside both the circles but within the universal set.

Now, consider the cardinality of these sets.

N(P) = 4, n(E) = 5 and n (PUE) = 8

Thus if we observe, n (PUE)≠ n(P)+n(E)

As explained earlier, the union set is obtained by adding the individual sets and subtracting the intersection set from the sum of individual sets.

Hence, n (P U E) = n (P) +n (E) – n [P ∩ E)

i.e., n (P U E) = 4 +5 -1 = 8

To generalize this, for any two sets A and B,

n (A U B) =n (A) +n(B) -n (A∩B)

Solved Examples

3. In a class of 100 students, 60 play foot balls, 40 play hockey while 10 do not play any sport. Find the number of students who play both hockey and football.

Solution:

N (U) = 100

Since 10 students do not play any game. Let F and H be the set of students playing football and hockey respectively,

n(FUH) = 100-10 =90

∴ n (F) =60

∴ n (H) = 40

The set of students who play both the games is n (F ∩ H)

∴ n(FUH) = n(F)+n(H)-n(F∩H)

∴ 90= 60+40-n (F ∩ H)

Hence, n (F ∩ H) = 100-90 = 10

∴10 students play both football and hockey.

Similarly, consider a universal set as shown below:

U≡ {1, 2, 3,4, 5, 6, 7,8, 9,15)

Let A be the set of all even numbers. Hence, A≡ {2,4,6,8}

Let B be the set ofal perfect squares. Hence, B ≡ {1,4,9}

Let C be the set ofall composite numbers. Hence, C ≡{4, 6, 8, 9, 15}

This can be represented using a Venn diagram as follows:

This can be represented using a Venn diagram as follows

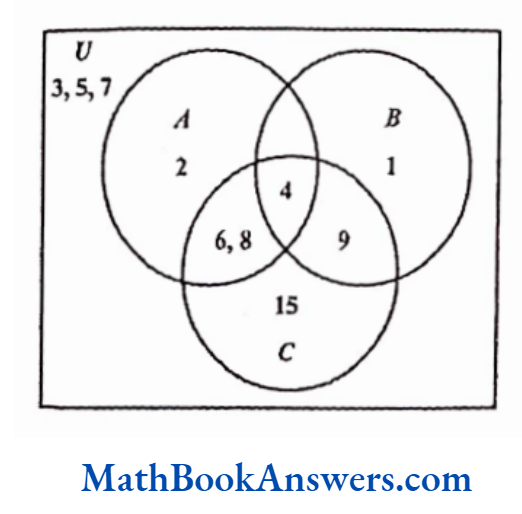
Such a Venn diagram is also known as a three-level diagram.

For a three-level diagram, the formula is

n (A U B U C) =n (A)+ n(B) +n(c)- n(A ∩ B) -n(A ∩ C) – n(B ∩ C)+ n (A ∩ B ∩ C)

So in this case,

n(AUBUC) = 4 + 3 + 5-1- 3- 2 +1 = 7

4. Mow many numbers lying in the range 5000 to 10000 are divisible by 7,11 or 137

Solution:

Let A, B and C be the set of numbers divisible by 7,1 1 and 1 3 respectively.

Lowest number in set A = 5005 and the highest number in A = 9996

∴ Number of Elements in A = $\frac{9996-5005}{7}+1=714$

Lowest number in set B = 5005 and the highest number in B = 9999

∴ Number of elements in B= 455

Lowest number in C= 5005 and the highest number in C= 9997

∴ Number of Elements in C = 385

Similarly,

Number of elements divisible by both 7 and 11=Number of elements in the set A ∩ B =65

Number of elements in the set A ∩ B =65

Number of elements in the set A ∩ C =55

Number of elements in the set B ∩ C =35

Number of elements in the set A ∩ B ∩ C = 5

∴Number of elements in the set A U B U C

n(A U B U C) = n(A) + n(B) + n(C)- n(A ∩ B)- n(A ∩ C)- n(B ∩ C) + n(A ∩ B ∩ C)

n(A U B U C) = 714+ 455+ 385 – 65 – 55- 35 +5 = 1404

5. Draw Venn diagrams for:

A – B – C
A ∩ B ∩ C’
A U B U C’

Solution:

1) A – B – C

A - B - C

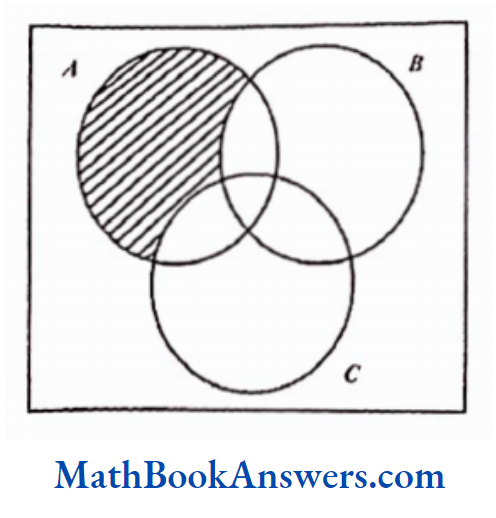
The shaded part comprises all the elements belonging to the set A – B – C

2) A ∩ B∩ C’

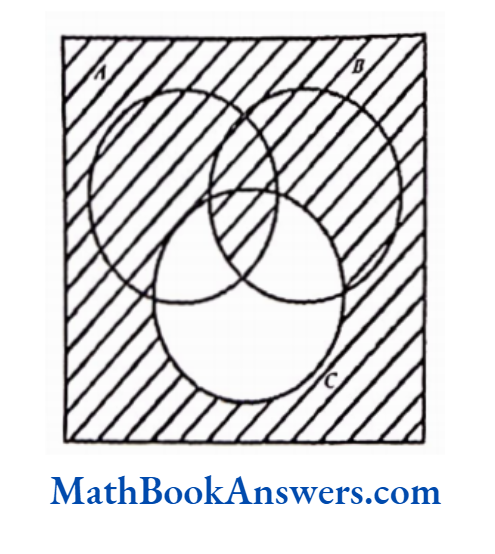
A n B n c'

3) A ∪ B ∪ C’

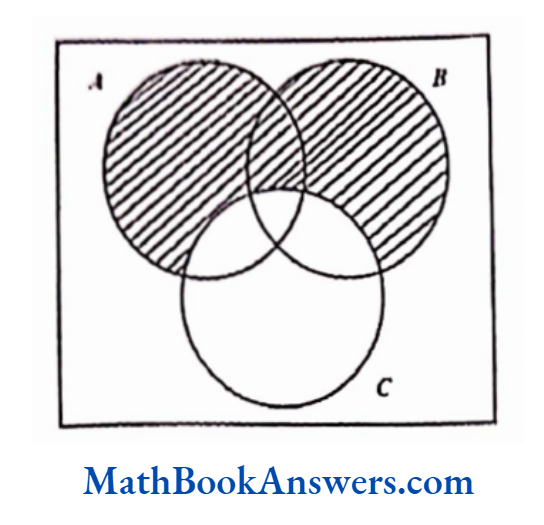
A u B u C

6. Express the following as Venn diagrams:

Every bull is an animal
Some bulls are in the stock market
No animal is a bull

Solution:

Let A = set of Animals, B = set ofbulls, C= set of things in the stock market

Every bull is an animal

Everybull is an animal

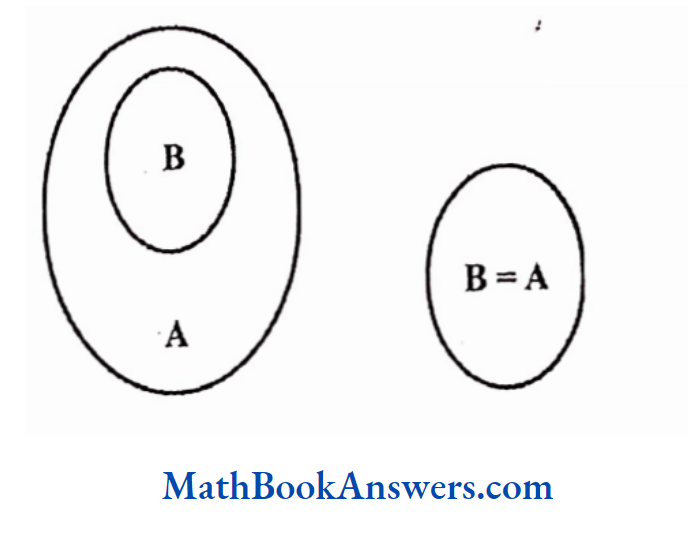
The first figure above is the general form of representing “Every bull is an animal”.

The second figure is true if and only if set B = set A i.e., every bull is an animal and vice versa. In the first figure, some animals may not be bulls.

Some bulls are in the stock market.

This can be represented in 3 different ways as shown

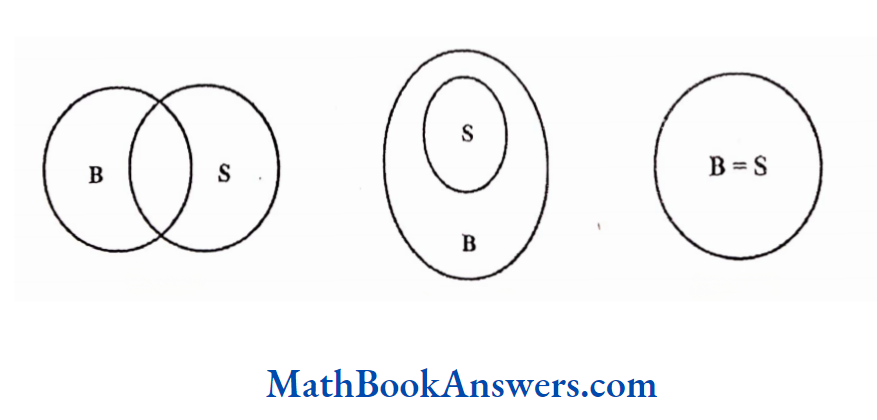
Some bulls are in the stock market

1: only some elements are common to set B and set S.

2: set S is a subset of set B i.e., all the things in the stock market are bulls. Hence, only some bulls will be things in the stock market.

3: set S = set B

No animal is a bull

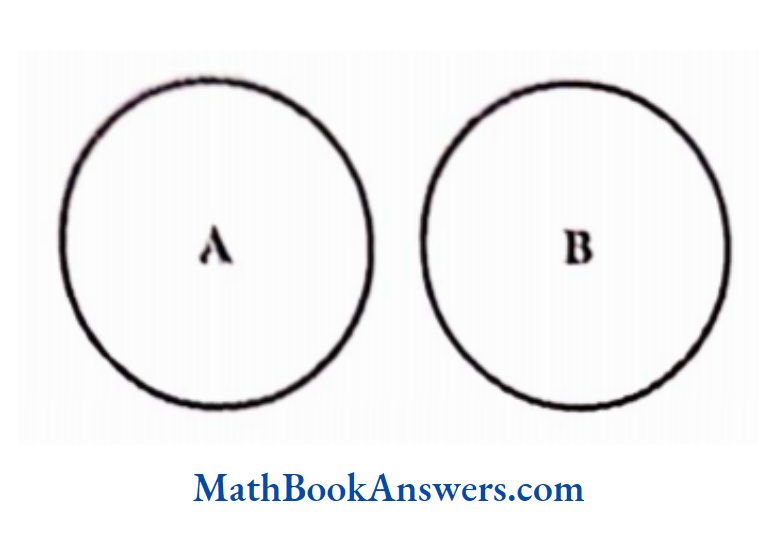
No animal is a bull

Here, A and B are disjoint sets.

7. Three of a popular actor’s films, A, B and C, were nominated for the best film award. 60 persons were asked which film deserved the award the most. 16 people thought only C deserved it. The number of people who thought that all the three films equally deserved the award was twice the number of people who thought that B and C deserved the award but A did not. The number of people who thought that B deserved the award was equal to twice the number ofpeople who thought all the three equally deserved it. The number of people who thought that A and B, but not C deserved the award was equal to the number ofpeople who thought that only A or A and C but not B deserved it. Find the maximum number ofpeople who thought that all the three films deserved the award?

Solution:

From the given data, we can draw the following Venn diagram.

From the given data, we can draw the following Venn diagram

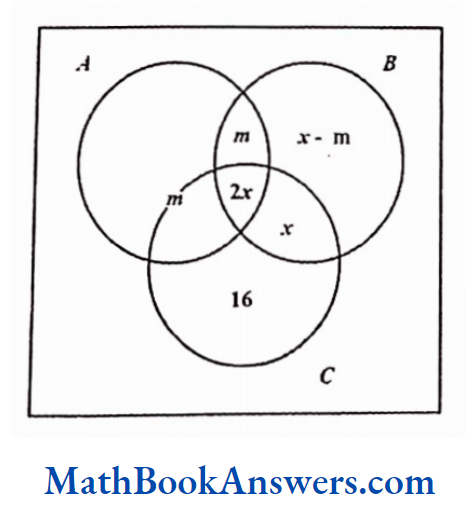
Here, x denotes the number of people who thought that all the three films deserved the award and m denotes the number of people who thought that oniy A or both A and C but not B deserved the award.

Hence, in the figure, m indicates the sum of the number of people who think that oniy A should get the award and the number of people who think that both A and but not B should get the award.

Thus,

2m+x -m +2x+x+16=60

∴ m+4x=44

∴ x is maximum when m = 0

∴ x = 11

∴2x = 22

The maximum no. of people who thought that all the three films deserved the award =22

CA Foundation Maths Solutions For Chapter 7 Properties of Sots

Union of any sot with a null set is equal to the original set. A ∪ ø = A
Intersection ofany set with a null set is equal to a null set. A∩ ø = 0
The intersection of any set with its complement is a null set. A ∩A’ = 0
The union ofany set with its complement is the universal set. A U A = U
(A ∩ B)’ = A‘ U B’
(A ∪ B)’ = A’ ∩ B’
The last two properties are called De Morgan’s laws.
Associative Property
(A U B) U C = A U (B U C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Distributive Property
A U (B ∩ C) = (A U B) ∩ (A U C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Note:

For any two sets A and B,

n(A ∪ B) = n(A) +n(B)- n (A ∩ B)

For any three sets A, B and C, n(A U B U C) = n(A) + n{B) + n(C)- n(A ∩ B)- n(A ∩ C)-n(B ∩ c) + n(A ∩ B ∩ C)

How To Solve Sets, Functions, And Relations In CA Foundation

CA Foundation Maths Solutions For Chapter 7 Exercise – 1: Sets

Choose the most appropriate option or options (1) (2) (3) or (4).

1. The number of subsets of the set {2, 3, 5} is

3
8
6
none of these

Answer: (2)

No of subsets of a set with n elements = 2ⁿ

2. The number of subsets of a set containing n elements is

2ⁿ
2^-n
n
none of these

Answer: (1) 2ⁿ

No of subsets of a set with n elements = 2ⁿ

3. The null set is represented by

$\{\Phi\}$
{0}
ø
none of these

Answer: (3) ø

Null set = ∅

4. A = (2, 3, 5, 7), B { 4, 6, 8, 10} then A ∩ B can be written as

{ }
$\{\Phi\}$
(AUB)’
None of these

Answer: (1) { }

There is no element common to A & B

A ∩ B = { }

5. The set {x|0<x<5} represents the set when x may take integral values only

{0, 1, 2, 3, 4, 5}
{1,2, 3, 4}
{1, 2, 3, 4, 5}
none of these

Answer: (2){1, 2,3,4}

{x|0 < x < 5}

X can take 1, 2, 3, 4 but not 0, 5

6. The set {0, 2, 4, 6, 8, 10} can be written as

{2x | 0<x <5}
(x : 0<x<5}
{2x : 0≤x≤5}
none of these

Answer: (3} {2x : 0 ≤ x ≤ 5}

{0,2(1}, 2(2), 2(3), 2(4), 2(5)}

(2x : 0 ≤ x ≤ 5}

Using Q.7 to Q.10 If P = (1, 2, 3, 5, 7}, Q = (1, 3, 6, 10, 15},
Universal Set S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

7. The cardinal number of P ∩ Q is

3
2
0
none of these

Answer: (2)2

P ∩ Q = (1, 3} -> 2 elements

8. The cardinal number of P U Q is

10
9
8
none of these

Answer: (3) 8

Cardinal no ->n(P U Q}

n(PUQ} = n(P) + n (Q) – n (P ∩ Q}

=5+5-2=8

9. n (P’) is

10
5
6
none of these

Answer: (1) 10

n (P’}) = n (Universal set} – n (P)

= 15-5 = 10

10. n(Q’) is

4
10
4
none of these

Answer: (2)10

n (Q’) = n (Universal set} – n (P)

= 15-5 = 10

11. The set of cubes of the natural number is

a finite set
an infinite set
a null set
none of these

Answer: (2) an infinite set

-> required set = {1, 8, 27,…}

12.The set {2*|x is any positive rational number} is

an infinite set
a null set
a finite set
none of these

Answer: (1) an infinite set

-> required set = {2, 4, 8,…… }

13. {1- (-1)^x} for all integral x is the set

{0} 00
{2}
(0, 2}
none of these

Answer:(3) {0, 2}

-> {1 – (-1)^x} = 0 when x is even

{1 – (-1)^x}= 2 when x is odd

For x ∈ integral -> set is {0, 2}

14. E is a set of positive even number and 0 is a set of positive odd numbers, then E ∪ O is a

set of whole numbers
a set of rational number
N
none of these

Answer: (2) N

E U 0 = all natural no. -> N

15. If R is the set of positive rational number and E is the set of real numbers then

R⊆E
R⊂E
E⊂R
none of these

Answer: (2)R⊂ E

as all rational no belong to real no.

16. If N is the set ofnatural numbers and I is the set ofpositive integers, then

N=1
N⊂1
N⊆ 1
none of these

Answer: (1) N = 1

->N = {1,2, 3,…….}

I = {1, 2,3…… }

N = 1

17. If I is the set of isosceles triangles and E is the set of equilateral triangles, then

I⊂E
E⊂l
E =I
none of these

Answer: (2) E ⊂ 1

-> as all equilateral triangles are isosceles

But all isosceles are not equilateral

18. If R is the set of isosceles right angled triangles and I is set of isosceles triangles, then

R=1
R⊃I
R⊂l
none of these

Answer: (3)R⊂1

-> all right angle isosceles triangle are isosceles but all isosceles are not right-angled.

19. {n(n+1)/2: n is a positive integer} is

a finite set
an infinite set
is an empty set
none of these

Answer: (2) infinite set

{1,3,6……………….}

20. If A = {1, 2, 3, 5, 7}, and B = {x² : x∈A}

n(b) = n(A)
n(B) > n(A)
n(A)= n(B)
n(A)<n(B)

Answer: (3) n (A) = n (B)

A = {1,2, 3, 5, 7} n (A) = 5

B = (1,4, 9, 25, 49) n(B) = 5

N (A) = n (B)

21. AUA is equal to

A
E
ø
none of these

Answer: (1) A

A U A = A

22. A ∩ A is equal to

ø
A
E
none of these

Answer: (2)A

->A ∩ A = A

23. (AUB)’ is equal to

(A’nB)’
A’UB’
A’nB’
none of these

Answer: (3) A’ n B’

(A U B)’ = 1 – (A U B)

= 1 – (A U B)

(A U B)’ = 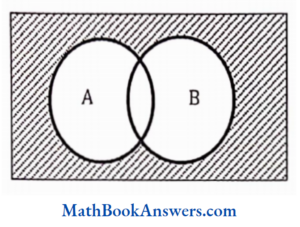. A’, n B’

24. (A∩B)’ is equal to

(A’ u B)’
A’ U B’
A’ ∩ B’
none of these

Answer: (2) A’ U B’

(A ∩ B)’ 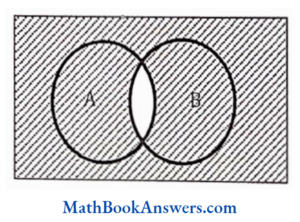= A’ U B’

25. A∪ E is equal to (E is a superset of A)

A
E
ø
none of these

Answer: (2) E

26. A∩E is equal to (E is a superset of A)

A
E
ø
none of these

Answer: (1) A

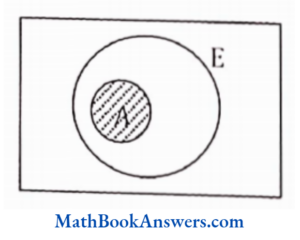
27. E∪E is equal to (E is a superset of A)

E
ø
2E
none of these

Answer: (1) E

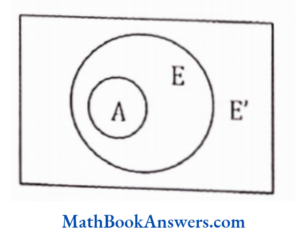
28. A∩ E’ is equal to (E is a superset of A)

E
ø
A
none of these

Answer: (2) ø

29. A ∩ ø is equal to (E is a superset of A)

A
E
ø
none of these

Answer: (3) ø

30. AUA’ is equal to (E is a superset of A)

E
ø
A
none of these

Answer: (3) E

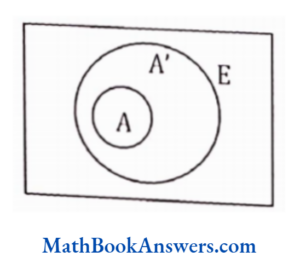30 th answer E = E

31. If K = { 1, 2, 3. 4, 5, 6, 7, 8, 9}, the subset of E satisfying 5 + x > 10 is

{5, 6, 7, 8, 9}
{6, 7,8, 9}
{7, 8, 9}
none of these

Answer: (2) {6, 7, 8, 9}

->E = 1 to 9

5 + x > 10

X > 5

x = 6, 7, 8, 9

32. If A Δ n = (A-B) U (B-A} and A = { 1. 2, 3, 4). B = {3,5,7} than A ΔB is

{1,2, 4, 5, 7}
{3}
{1,2, 3, 4, 5, 7}
none of these

Answer: (c) A Δ B = (A – B) U (B – A)

A = {1,2, 3, 4}

B = {3, 5,7}

A- B = {1, 2, 4}

B – A = (5, 7}

(A – B) U (B – A) = {1, 2, 4, 5, 7}

33. If A has 32 elements, B has 42 elements and A U B has 62 elements, the number of elements in A ∩ B is

12
74
io
none of these

Answer: (1) 12

n (A ∩ B) = n (A) + n (B) -n (A∩B)

62 = 32 + 42 – n (A ∩ B)

n (A ∩ B) = 74- 62 -> 12

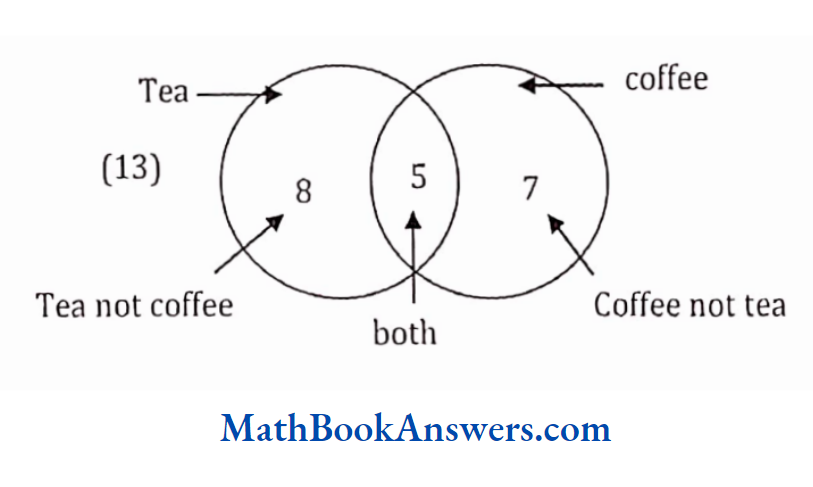
34. In a group of 20 children, 8 drink tea but not coffee and 13 like tea. The number of children drinking coffee but not tea is

6
7
1
none of these

Answer: (2) 7

35. The number of subsets of the sets {6, 8, 11} is

9
6
8
none of these

Answer: (3) 8 No. of subsects = 2ⁿ= 2³ = 8

36. The sets V = {x / x+2=0), R={x / x²+2x=0} and S = {x : x² + x- 2 = 0} are equal to one another if x is equal to

-2
2
1/2
none of these

Answer: (1) -2

If we go by choices

V = 0 = -2 + 2

R = 4 – 4 = 0

S=4-2-2=0

V = R = S for- 2

37. If the universal set E = {x |x is a positive integer <25}, A = {2, 6, 8, 14, 22}, B = {4, 8, 10, 14} then

(A n B}’=A’ U B’
(A n B]’= A’ n B’
(A’ n B)’= 0
none of these

Answer:(1) (A ∩ B)’ = A’ U B’

-> (A ∩ B) = {8, 14}

(A ∩ B)’ = {1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15 ………}

A’ = {1, 3,4,……24}

B’ = {1, 2, 3 ……….24} A’ U B’ = {1, 2, 3, 4, 5, 6, 7………. }

(A ∩ By = A’ U B’

38. If the set P has 3 elements, Q four and R two then the set P x Q x R contains

9 elements
20 elements
24 elements
none of these

Answer: P = 3 elements, Q = 4 elements R = 2 elements

n (P x Q x R) = 3 x 4 x 2 = 24 -> (3) 24

39. Given A = {2, 3}, B = {4, 5}, C = {5, 6} then A x (B∩C) is

{(2, 5), (3,5)}
{(5,2),(5,3)}
{(2, 3), (5, 5)}
none of these

Answer: A = {2,3} B = {4, 5}, C = {5, 6} A x (B ∩ C) B ∩ C = {5}

A x (B ∩ C) = {(2, 5), (3,5)}

(1) {(2,5), (3,5)}

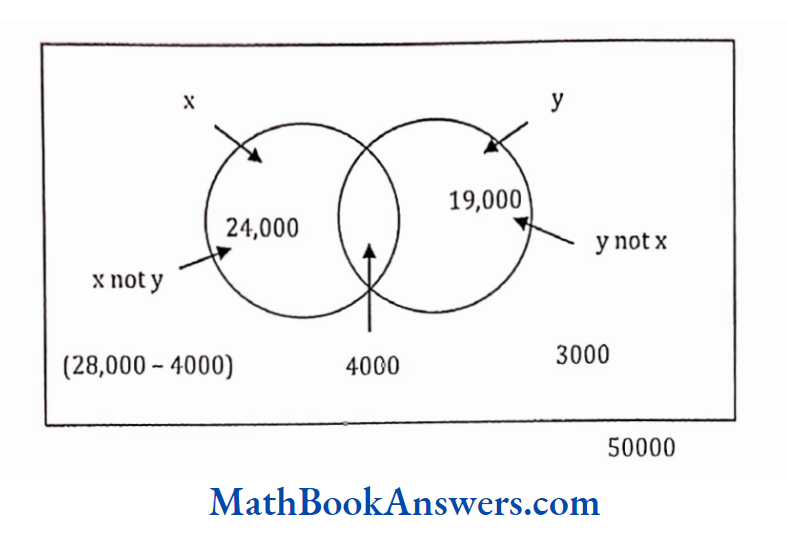
40. A town has a total population of 50,000. Out of it 28,000 read the newspaper X and 23,000 read Y while 4,000 read both the papers. The number of persons not reading X and Y both is

2,000
3,000
2,500
none of these

Answer: (2) 3000

Total Population 50000

41. If A = {1, 2, 3, 5, 7} and B = {1, 3, 6, 10, 15}. Cardinal number of A-B is

3
4
6
none of these

Answer: (1) 3

A – B = {2, 5, 7} ->3

42. At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. The number of women doctors attending the conference is

2
4
1
none of these

Answer: (3) 1

Total Indian attendees -> 29 + 23 = 52

Let M = 23 men w = 29 women D represent doctors

We are given

n (M U D) = 24

n (M) + n (D)- n (M ∩ D) = 24

23 + 4 – n (M ∩ D) = 24

n (M ∩ D) = 3

no. of male doctors = 3

Total doctors 4 & all Indian

no. of female doctors = 4-3 = 1

43. Let A = {a, b}. Set of subsets of A is called power set of A denoted by P(A}. Now n(P(A)) is

2
4
3
none of these

Answer: (2) 4

A = {a, b)

P (A) power set

n (P(a))

No. of subsets = 2² = n (Power set) = 4

44. Out or 2000 employees In an office 40% preferred Coffee (c), 54% liked (T), 64% used to smoke (S). Out of the total 28% used C and T, 32% used T and S and 30% preferred C and S, only 6% did none of these. The number having all the three Is

360
300
380
none of these

Answer: (1) 360

Coffee -> 48% = n (c) = 960

Tea -> 54% = n (T) = 1080

Smoke -> 64% = n(s) = 1280

n (c ∩ T) = 560 b (T ∩ S) = 640 n (C ∩ S) = 600

120 ->none

n(CUSUT) = 2000 -120 = 1880

1880 = n (c) + n (T) + n (s) – n(C∩T) – n (T∩S) – n (C ∩ S) + n (C ∩ S ∩ T)

1880 = 960 + 1080 + 1280 – 560 – 640 – 600 + n (C∩S∩T)

1880- 1520 = n (C∩S∩T) = 360

45. Following set notations represent: A⊂B; x ∉ A; A⊃B; {0}; A⊄ B

A is a proper subset of B; x is not an element of A; A contains B; singleton with an only element zero; A is not contained in B.
A is a proper subset of B; x is an element of A; A contains B; singleton with an only element zero; A is contained in B.
A is a proper subset of B; x is not an element of A; A does not contain B; contains elements other than zero; A is not contained in B.
None

Answer: (1)

A ⊂ B = A is proper subset of B
X ∉ A = x does not belong to A
A ⊃ B = A contains B
{0} = singleton with element 0
A ⊄ B = A is not contained in B

46. Represent the following sets in set notation: – Set of all alphabets in English language, set of all odd integers less than 25, set of all odd integers, set of positive integers x satisfying the equation x²+5x+7=0 :

A = {x:x is an alphabet in English}, 1 = (x:x is an odd integer>25},I = {2, 4, 6, 8 ….} I = {x: x²+5x+7=0}
A= {x:x is an alphabet in English},I = {x:x is an odd integer<25}, 1 = {1, 3, 5, 7 ….} I = {x: x²+5x+7=0}
A = {x:x is an alphabet in English},I = {x:x is an odd integer £ 25},I = (1, 3, 5, 7 ….} I = {x: x²+5x+7=0}
None

Answer: (2)

—> A = (x : x alphabet in english}

—>I = (x: x is odd integer < 25}

—>I = (x: x is set ofall odd int) = {1, 3.5,….. }

->I = {x: x² + 5x + 7 = 0}

47. Rewrite the following sets in a set builder form: – A = {a, e, i, o, u} B = {1, 2, 3, 4 ….} C is a set of integers between -15 and 15.

A = {x:x is a consonant}, B= {x:x is an irrational number}, C = {x:-15<x<15^ x is a fraction}
A = (x:x is a vowel}, B= {x:x is a natural number}, C = {x: -15³X³15^ x is a whole number}
A = {x:x is a vowel}, B = {x:x is a natural number}, C = {x: -15 <x<15^ X is a whole number}
None

Answer: (1)

A = {x: x is a vowel}

B = {1, 2, 3, 4,…..}->B={x| x is a natural no.}

C = {x: – 15 < x < 15 A x is a whole no}

48. If V = (0, 1, 2, …9}, X = {0, 2, 4, 6, 8}, Y = {3, 5, 7} and Z = {3 7} then YUZ, (VUY) ∩ X, (XUZ)UV are respectively: –

{3,5, 7},{0, 2,4,6, 8}, {0, 1, 2, …9}
{2,4, 6},{0, 2,4, 6, 8}, {0,1, 2, …9}
{2, 4, 6}, {0,1, 2, …9},{0, 2, 4, 6, 8}
None

Answer: (1) Go by choices

49. In question No. (48) (X U Y) ∩ Z and (ø ∪ V) nø are respectively: –

{0, 2, 4, 6, 8},ø
{3, 7}, ø
{3, 5, 7}, ø
None

Answer: (b) (3, 7},ø

-> (ø u V) ∩ ø -> ø

-> (x U y) n z -> x U y = (0, 2, 3,4,5, 6, 7, 8}

Z = (3, 7}

X U y ∩ Z = (3, 7}

50. What is the relationship between the following sets? A = {x:x is a letter in the word flower} B = {x:x is a letter in the word flow} C = {x:x is a letter in the word wolf} D = {x:x is a letter in the word follow}

B=C=D and all these are subsets of the set A
B=C≠D
B≠C≠D
None

Answer:(1) B = C = D ⊂ A

51. Comment on the correctness or otherwise or the following statements: –
(1) {a, b, c) = (c, b, a}
(2) {a,b,c,d)) ⊂ (a.c.d)
(3) {b} ∈ {{b}}
(4) {b} ⊂ ((b)) and
(5)ø ⊂{{b}}.

Only (4) is incorrect
(2) (3) are incorrect
(1) (2) are incorrect
All are incorrect

Answer: (1) only (4) is incorrect

->(b) ⊄ {{b}} as b is not an element of({b}}

-> ø ⊂ {{b}} as ø is not an element of {b}}

52. If A=(a, b, c). B=(a, b). C = (a, b, d}, D=(c, d) and E=(d) state which of the following statements are correct: –

(1)B⊂A
(2) D ≠ C
(3) C⊃E
(4) D ⊂ E
(5) D ⊂ B
(6) D = A
(7) B ⊄ C
(8) E⊂A
(9) E ⊄B
(10) a∈ A
(11) a⊂A
(12) (a) ∈ A
(13) (a) ⊂ A

(1) (2) (3) (9) (10) (13) only are correct
(2) (3) (4) (10) (12) (13) only are correct
(1) (2) (4) (9) (11) (13) only are correct
None

Answer: (1) is correct

53. Let A = (0), B = (0 1), C =ø, D = (0), E = (x|x is a human being 300 years old), F = (x|x ∈ A and x e B} state which of the following statements are true: –

(1) A ⊂ B
(2) B = F
(3) C ⊂D
(4) C= E
(5) A = F
(6) F = 1 and
(7) E = C = D

(1) (3) (4) and (5) only are true
(1) (2) (3) and (6) only are true
(1) (2) (3) and (4) are true
None

Answer: (1) is correct

54. If A = (0, 1} state which of the following statements are true: –

(1) (1) ⊂ A
(2) {1} ∈ A
(3) ø ∈ A
(4) 0 ∈ A
(5) 1 ⊂ A
(6) {0} ∈ A
(7) ø ⊂ A

(1) (4) and (7) only are true
(2) (3) and (6) only are true
(1) (4) and (6) only are true
None

Answer: (1) is correct

55. State whether the following sets are finite, infinite or empty: –

(1) X = (1, 2, 3,…..500)
(2) Y ={y: y=a²; a is an integer)
(3) A = (x:x is a positive integer multiple of 2)
(4) B = (x:x is an integer which is a perfect root of 26<x<35)

finite infinite infinite empty
infinite finite infinite empty
infinite infinite finite empty
None

Answer: (1) is correct

56. If A = {1, 2, 3, 4} B = {2, 3, 7, 9) and C = (1, 4, 7, 9} then

A ∩ B ≠ ø B ∩ C≠ ø A ∩ C≠ ø but A ∩ B ∩ C = ø
A ∩ B = ø B ∩ C = ø A ∩ C =ø A ∩B ∩C=ø
A ∩ B ≠ ø B ∩ C ≠ ø A ∩ C≠ ø A ∩ B ∩ C ≠ ø
None

Answer: (1) A ∩ B = (2, 3} B∩C = (7,9) A ∩ C = {1,4}

A∩B∩C=ø

57. If the universal set isX = (x:x ∈ N, 1≤ x ≤ 12} and A = (1, 9, 10), B = (3, 4, 6, 11, 12} and C = (2, 5, 6} are subsets of X then set A U (B ∩ C) is_.

{3, 4, 6, 12}
{1, 6, 9, 10}
{2, 5, 6,11}
None

Answer: (2) {1,6, 9, 10}

-> B ∩ C = {6}

A U (B ∩ C) = {1, 6, 9,10}

58. Identify the elements of P if set Q = (1, 2, 3} and P x Q = {(4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5,3), (6,1), (6,2), (6,3)}

{3, 4, 5}
{4, 5, 6}
{5, 6, 7}
None

Answer: (2) (4,5.6}

Set P will have the preimages of ordered

pairs of p x Q P= {4,5.6}

59. If A = (2, 3}, B = {4, 5), C = (5, 6} then A x (B U C) is

{(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
{(2,5), (3,5)}
{(2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (4, 6), (5, 5), (5, 6)}
None

Answer: (1)

B U C -> {4, 5, 6}

A x {B U C} = {(2, 4}, (2, 5), (2, 6), (3, 4), (3,5), (3,6)}

60. Complaints about works of canteen had been about Mess (M) Food (F) and Service (S). Total complaints 173 were received as follows :-n(M)=110,n(F)=55,n(S)=67,n(M∩F∩S’)=20,n(M∩S∩F’)=11 and n(F∩S∩M’)=16.Determine the complaints about all the three

6
53
35
None

Answer: (1) 6

n (M∩F∩S’) = 20

n (M∩S∩F’) = 11

n (F(∩S∩M’) = 16

-> n (M U FUS) = 173

173 = n (M) + n (F) + n(S) – n (M∩F) – n

(F∩S) – n (S∩M) + n (M∩S∩F)

173 = 110 + 55 + 67 – (20 + x) – (11 + x) – (16 +x) + x

59 = 20 + x+11+ x+16 + x-x

2x = 12 -> x = 6

61.Out of total 150 students 45 passed in Accounts 50 in Maths. 30 in Costing 30 in both Accounts and Maths. 32 in both Maths and Costing 35 in both Accounts and Costing. 25 students passed in all the three subjects. Find the number who passed at least in any one of the subjects.

63
53
73
None

Answer: (2) 53

n (A∩M) = 30

n (M∩C) = 32

n (A∩C) = 35

n (A∩M∩C) = 25

n (A∪M∪C) = 45 + 50 + 30-32-35 + 25

62. After qualifying out of 400 professionals, 112 joined industry, 120 started practice and 160 joined as paid assistants. There were 32, who were in both practice and service 40 in both practice and assistantship and 20 in both industry and assistantship. There were 12 who did all the three. Find how many could not get any of these.

88
244
122
None

Answer: (1) 88

n (Industry) 112 n (I n paid) = 20

n (practice) 120 n (Paid n practice) = 40

n (paid) 160

n (I U P U S)

= 112+ 120 + 160-20-40-32 + 12

= 32

no who are unemployed

= 400-312 = 88

63. On a survey of 100 boys it was found that 50 used white shirt 40 red and 30 blue. 20 were habituated in using both white and red shirts 15 both red and blue shirts and 10 blue and white shirts. Find the number ofboys using all the colours.

20
25
30
None

Answer: (2) 25

n (w) = 50 n (R) = 40 n (B) = 30

n (W ∩ R) = 20 n (R ∩ B) = 15

n (B ∩ w) = 10.

n (W ∪ R ∪ B) =n (w) + n (R) + n (B) – n (w ∩ R) – n (R ∩ B)- n (B ∩ w) + n (B ∩ R ∩ w)

100 = 50 + 40 + 30 – 20 – 15 – 10 + n (B ∩ R ∩ w)

n (B ∩ R ∩ w) = 25

64. Out of 60 students 25 failed in paper (1), 24 in paper (2), 32 in paper (3), 9 in paper (1) alone, 6 in paper (2) alone, 5 in papers (2) and (3) and 3 in papers (1) and (2). Find how many failed in all the three papers.

10
60
50
None

Answer: (1) 10

n (P1 ∩ P2’∩ P3’) = 9

n (P1∩P2∩P3’) = 6

n (P2∩P3∩P1′) = 5 n (P1∩ P2 ∩P3’) = 3

n (P2) = n (P2 alone) + n (P2 ∩ P3 ∩ P1’) + n (P1 ∩ P2 ∩ P2’) + n (P1 ∩ P2 ∩ P3)

24 = 6 + 5 + 3 + n (P1 ∩ P2 ∩ P3)-> 10

65. Out of 1000 students 658 failed in the aggregate, 166 in the aggregate and in group-] 434 in aggregate and in group-II, 372 in group-1, 590 in group-11 and 126 in both the groups. Find out how many failed in all the three.

Answer: (1) 106

1000 students,

658 failed in aggregate,

166 aggregate & G1,

434 in aggregate & G2,

372 in G1,

590 in G2,

126 in both G1 & G2

1000 = n (A) + n (G1) + n (G2) – n (G1 ∩ A) – n (G2 ∩A)- n (G1 ∩ G2) + n (G1 ∩ G2 ∩ A)

1000 = 658 + 372 + 590 – 166- 434 – 126 + n (G1 ∩ G2 ∩ A)

n (G1 ∩ G2 ∩ A) = 106

66. For any set A, (A’)’ is equal to

A’
A
none of these

Answer: (2) A

67. Let A and B be two sets in the same universal set. Then, A – B =

A ∩ B
A’∩ B
A ∩ B’
none of these

Answer: (3) A ∩ B’

68. For any two sets A and B, A ∩ (A U B) =

A
B
D
none of these

Answer: (1) A

69. If A = {1, 3, 5, B} and B = {2, 4), then

4 6 A
{4} c A
B⊂A
none of these

Answer: (4) none of these

70. For any two sets A and B, (A – B) u (B – A) =

(A – B) ∪ A
(B – A) U B
(AUB)-(A∩ B)
(A U B) n (A ∩ B)

Answer: (3) (AUB)-(A∩ B)

71. Which of the following statement is false:

A – B = A ∩ B’
A – B = A – (A ∩ B)
A – B = A – B’
A – B = (A U B) – B

Answer: (3) A – B = A – B’

72. For any three sets A, B and C

A ∩ (B – C) = (A ∩ B)- (A ∩ C)
A ∩ (B – C) = (A ∩ B) – C
A U (B – C) = (A U B) ∩ (A U C’)
All of these

Answer: (4) All of these

73. Let A = {x: x ∈R, x > 4} and B = {x ∈ R: x < 5}. Then, A n B =

[4, 5]
[4,5]
[4,5]
[4,5]

Answer: (2) (4.5)

i.e. all real no. between 4 & 5 excluding 4 &5

74. Let u be the universal set containing 700 elements. If A, B are sub-sets ofu such that n (A)- 200, n (B) = 300 and n (A ∩ B) = 100. Then, n (A’ ∩ B’) =

400
600
300
none of these

Answer: (3)

= universal – b (A U B)

= 700 – (n (A +n(B)-n(A ∩ B))

= 700 -(200 + 300 -100)

= 300

75. Let A and B be two sets such that n [A] = 16, n [B] = 14, n [A U B] = 25. Then, n [A ∩ B) is equal to

30
50
5
none of these

Answer: (3)

= n (A) + n (B) – n (A U B)

= 30-25

= 5

76. If A = {1, 2, 3, 4, 5}, then the number of proper subsets of A is

Answer: (3) no. of proper subsets

= 2ⁿ-1

= 32-1

= 31

77. In set-builder method the null set is represented by

{}
ø
{x:x≠x}
{x:x=x}

Answer: (3) (x:x≠x)

In set builder form

78. If A and B are two disjoint sets, then n (A U B) is equal to

n (A) + n (B)
n (A) + n (B)- n (A ∩ B)
n (A) + n (B) + n [A ∩ B]
n (A)∩ (B)

Answer: (a) n (A) + n (B)

We know n (A U B) = n (A) + n (B)

– n (A ∩ B)

n (A U B) = n (A) + n (B)

n (A ∩ B)00000 = 0 disjoint sets.

79. For two sets A U B = A iff

B⊆A
A⊆B
A ≠B
A = B

Answer: (1) B ⊆ A

A U B = A

Means A is superset of B

80. If A and B are two sets such that n (A) = 70, n (B) = 60, n (A U B) = 110, then n [A ∩ B) is equal to

Answer: (4) 20

n (A ∩) = n (A) + n (B) – n (A U B)

= 70 + 60-110

= 20

81. In a city 20% of the population travels by car, 50% travels by bus and 10% travels by both and bus. Then, persons travelling by car or bus is

Answer: (3) 60%

n (C U B) = n (C) + n (B) – n (C∩B)

= 20 + 50-10

= 60%

82. lf A∩B = B, then

A⊆ B
B⊆A
A = ø
B = ø

Answer: (2) B ⊆ A

83. An investigator interviewed 100 students to determine their preference of three drinks: milk, coffee and tea. The investigator reported that 10 students take all three drinks milk, coffee and tea; 20 students take milk and coffee; 25 students take milk and tea; 20 students take coffee and tea; 12 students take milk only; 5 students take coffee only and 8 students take tea only. Then the number of students who did not take any of three drinks is

Answer: (4) 30

n (M∩C∩T) = 10

n (MUCUT)

= 12+5+10+10

= 70

do not drink

= 100-70 = 30

84. Two finite sets have m and n elements. The number of elements In the power set of first set Is 48 more than the total number of elements in power set of the second set. Then, the values, of m and n are:

Answer: (3) 6, 4

Let x be no of elements in second set’s power set n (P(S₂)) = x

N (P (S1)) = 48 + x

X = 2ⁿ

48+x=2^m

48 = 2^m – 2ⁿ

2ⁿ (2^m-n– 1) = 48

2ⁿ (2^m-n – 1) = 16 x 3

2ⁿ= 16

2^m-n-1= 3

2ⁿ = 16

2^m-n = 4

n=4

2^m/2ⁿ=4

2^m=64

m = 6

85. In a class of 175 students the following data shows the number of students opting one or more subjects. Mathematics 100; Physics 70; Chemistry 40; Mathematics and Physics 30; Mathematics and Chemistry 28; Physics and Chemistry 23; Mathematics, Physics and Chemistry 18. How many students have offered Mathematics alone?

Answer: (3)

86. For any two sets A and B, A ∩ (A U B)’ is equal to

A
B
ø
A ∩ B

Answer: (3) ø

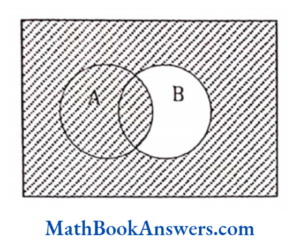
-> no interaction

87. Let F1 be the set of all parallelograms, F2 the set of all rectangles, F3 the set of all rhombuses, F4 the set ofall squares and F5 the set oftrapeziums in a plane. Then F1 may be equal to

F₂ ∩ F₃
F₃ ∩ F₄
F₂ U F₃
F₂ U F₃ U F₄U F₁

Answer: (4) F₂∪F₃∪F₄∪F₁

As all rectangle, square, rhombus are parallelograms only.

88. Out of 20 members in a family, 11 like to take tea and 14 like coffee. Assume that each one likes atleast one of the two drinks. Find how many like both coffee and tea:

Answer: (4)

Given that

n[T] = 11; n(C) = 14

and n(TUC) = 20

n(TUC) = n(T) + n(c) – n[T∪C]

= 11+14-20 = 5

(4) is correct

89. In a group of 70 people, 45 speak hindi, 33 speak English and 10 speak neither Hindi nor English. Find how many can speak both English as well as Hindi:

Answer: (3) n(H} = 45; n(E} = 33

n(H ∪ E}’ = 10 => n(H ∪ E) = 70-10 = 60

∴ (H∪E} = n(H) + n(E} – n(H ∪ E)

= 45 + 33-60 = 18

(3} is correct

90. In a survey of 300 companies, the number of companies using different media – newspapers (N), Radio (R) and Television (T) are as follows: n(N) = 200, n(R) = 100, n(T) = 40, n(N∩R] = 50, n(R∩T) = 20, n(N∩T) = 25 and n(N∩R∩T) = 5. Find the number of companies using none of these media:

20 companies
250 companies
30 companies
50 Companies

Answer: (2) n(N∪R∪T} = n(N} + n(R) + n(T) – n(N∩R] – n(N∩T} – n(R∩T} + n(N∩R∩T}

= 200 + 100 + 40-50-20-25 + 5

= 250

No. of companies using no media

= 300 – n(NURUT)

= 300-250 = 50

(4) is correct

91. In a town of 20,000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers, then the number of families which buy A only is

6600
6300
5600
600.

Answer: (1) Given

n(A) = 40% ; n(B) = 20% ; n(C) = 10%

n(A∩B) = 5%; n(B∩C) = 4%

n(C∩A) = 4%; n(A∩B∩C) = 2%

No. of families which buy only A

= n(A) – n(A∩B) – n(A∩C) + n(A∩B∩C) = 40-5-4+2 = 33%

= 20,000 x 33% = 6600

(1) is correct

92. Out of total 150 students, 45 passed in accounts, 30 in economics and 50 in maths, 30 in both accounts and maths, 32 in both maths and economics, 35 in both accounts and economics, 25 students passed in all the three subjects. Find the numbers who passed atleast in anyone of the subjects:

63
53
73
None.

Answer: (2) Total students = 150

n(A) = 45 ; n(E) = 30; n(M) = 50;

n(A∩M) = 30; n(M∩E) = 32

n(A∩M) = 35; n(M∩E∩M) = 25

∴ n (A∪E∪M) = 45 + 30 + 50 – 30 – 35 + 25 = 53

(2) is correct.

93. If A = {p,q,r,s}, B = {q,s,t), C = {m,q,n} find C – (A∩B)

{m,n}
{P<q}
{r,s}
{p,r}

Answer: (1)

⊂-(A ∩ B) ={m,q,n} – {p,q,r,s} ∩ {q,s,t}

= {m,q,n} – {q,s}

= { m;n }

(1) is correct.

94. If A = {X : X² – 3X + 2 = 0} B = {X:X²-4x + 12 = 0}, B-A =

{-6}
{1}
{1,2}
{2,-6}

Answer: x²- 3x + 2 = 0

Or x(x-2)-1(x-2)=0

Or (x-2) (x-1) = 0

x = 1;2

A = {1,2}

And x² + 4x – 12 = 0

Or x² + 6x – 2x – 12 = 0

Or x(x+6)-2(x+6)=0

Or (x+6) (x-2) = 0

x = -6 ; 2

B -A = {-6;2} -{1;2} ={-6}

A (1) is correct

95. For any two sets A and B, A∩(A’UB)=___________ where A’ represent the compliment of the set

A∩B
AUB
AUB
None of these

Answer: Tricks: Take an example and then decide the answer

Let U = {0,1,2,3,4,5}

A = {0,1,2,3}

B = {2,3,4,5}

A¹ = U – A = {4;5}

A¹ U B = {4,5} U{2,3,4,5}

= {2,3,4,5}

∴ A ∩ (A¹ U B}

= {0,1,2,3} ∩ {2,3,4,5}

∴ (1) is correct

2nd method = (A∩A’) U (A∩B} = { } U (A∩B} = A ∩ B

96. If A c B, then following is true

A ∩ B = B
A U B = B
A ∩ B = A
A ∩ B

Answer: (2)

97. There are 40 students, 30 of them passed in English, 25 of them passed in maths and 15 of them passed in both. Assuming that every student has passed atleast in one subject. How many students passed in English only but not in math’s.

Answer: (1) total students = 40

n(E) = 30; n(M) = 25

(E∩M)= 15

No. of stds. Passed in English only

n(E) – n(E∩M)

= 30-15 = 15

(1) is correct

98. If A = (1,2,3,4,5), B = (2,4) and C = (1,3,5) then (A -C) x B is

{(2,2),(2,4),(4,2),(4,4),(5,2),(5,4)}
{(1,2),(1,4),(3,2),(3,4),(5,2),(5,4)}
{(2,2),(4,2),(4,4),(4,5)}
{(2,2(,(2,4),(4,2),(4,4)}

Answer: (4) is correct

(A-C)xB = {2,4}x{2,4}=

{(2,2),(2,4),(4,2),(4,4)}

99. For any two sets A and B the set (AUB’)’ is equal to (where denotes compliment of the set)

B-A
A-B
A’-B’
B’-A’

Answer: (1) is correct

Tricks: Let U = {1,2,3,4,5}

A = {0,1,2,3}; B = {1,2,3}

B’ = U – B = {0,4,5}

A∪B’ = {0,1,2,4,5}

(AUB’)’ = U- (A U B’)= {3}

Then go by choices

For (1) B – A = {1,2,3} – {0,1,2} ={3}

(A∪B’)’ =U -(AUB’) = {3}

2 nd Method

(A∪B’)’

= A’D(B’)’

= A’ ∩ B

= B – A ∩ B

= B- A

100. The number of proper sub-set of the set {3,4,5,6,7} is

Answer: (2) No. of proper sub -sets = 2ⁿ– 1

= 2⁵-1 = 31

101. For a group of 200 person, 100 are interested in music, 70 in photography and 40 in swimming, furthermore 40 are interested in both music and photography, 30 in both music and swimming, 20 in photography and swimming and 10 in all the three. How many interested in photography but not in music and swimming?

Answer: (4) is correct

Let A = No. of persons interested in Music

B = No. of persons interested in photography

C = No. of persons interested in swimming

n(A) = 100; n(B) = 70; n(C) = 40;

n(A∩B) = 40; n(A∩C) = 30;

n(B∩C) = 20; n(A∩B∩C)= 10.

n(B∩A¹ ∩ C¹) = n(B) – n(B∩A) – n(B∩C)+n(A∩BnC)

= 70-40-20+10

= 20

102. Of the 200 candidates who were interviewed for a position at call center, 100 had a two wheeler, 70 had a credit card and 140 had a mobile phone 40 of them had both a two-wheeler and a credit card, 30 had both a credit card and mobile phone, 60 had both a two-wheeler and a mobile and 10 had all the three. How many candidates had none of them?

Answer: (3) is correct

Let n(A) = No. of candidates having two wheeler

n(B) = No. of candidates having credit cards

n(C) = No. of candidates having mobile phone.

Given

n(A) = 100; n(B) = 70; n(c) = 140

n(A∩B) = 40; n(B∩C)= 30; n(C∩A) = 60

n(A ∩ B ∩ C) = 10

n(A U B U C) = 100 + 70 + 140- 40-30-60 + 10 = 190

No. of candidates having none = 200 – 190= 10

103. In a class of 50 students 35 opted for Maths, 37 opted for commerce. The number of such student who opted for both maths and commerce is

Answer: (3) is correct

n(M) = No. of students opted for Maths = 35

n(C) = No. of students opted for commerce = 37

So; (MUC) = 50

n(M∩C) = 35 + 37- 50 = 22

104. A = (2,3), B=(4,5), C=(5,6) then Ax(B∩C)

[(5,2),(5,3)]
[(2.4),(5,3)]
[(2,5),(3,5)]
[(3,5),(2,6)]

Answer: (2)

B ∩ C = {4,5} ∩ {5,6} = {5}

= {(2,5);(3,5)}

105. In a class of 80 students, 35% play only cricket, 45% only tennis, how many play cricket?

Answer: Given n(C – T) = n(C) – n(C ∩ T) = 35%

n(T- C) = n(T) – n(C∩T) = 100

or; 35 + n(C∩T) + 45 + n(C∩T) – n(C∩T) = 100

or 80 + n(C∩T) = 100

n(C∩T) = 20%

n(C) = 35 + n(C∩T) = 35 + 20 = 55%

= 80 x 55% = 44

106. If set A = (x:x/2 ∈ z,0 ≤ 12}

B = {x: x is one digit prime number} and

C = {x:x/3 ∈ N, x ≤ 12} then A ∩ (B ∩ C) =

0
Set A
Set B
Set C

Answer: (1)

A = {2,4,6,8,10}

B = {2,3,5,7}

C = {3,6,9,12}

A ∩ (B ∩ C) = ø

No common element in all 3 sets.

107. Let A be the set of the squares ofnatural numbers and x ∈ A, y ∈ A. Then__________

x + y ∈ A
x- y ∈ A
x/y∈ A
xy ∈ A

Answer: (4) is correct

A = {x/x is the squares of natural Nos.} = {1,4,9,16,25……….. }

Tricks: then go by choices

Let x = 1: y = 4 ∈ A

x+y = 1 + 4 = 5 ∉ A.

x – y = 1 -4 = 3 ∉ A.

x/y=1/4 ∉ A.

But xy = 1 x 4 = 4 ∈ A.

(4) is correct.

108. The number of sub-sets formed from the letters of the word “ALLAHABAD”

128
16
32
None

Answer: (3) is correct

Let X = {Letters of word ALLHABAD)

= {A, L, H, B, D}

No. ofsub-sets = 2⁵ = 32

109. If f(x) =$ \frac{x-1}{x} \text { and } g(x)=\frac{1}{1-x} $then fog(x) =

x-1
x
1-x
-x

Answer: $\mathrm{fog}(\mathrm{x})=\mathrm{f}\{\mathrm{g}(\mathrm{x})\}=\frac{g(x)-1}{g(x)}$

$=\frac{\frac{1}{1-x}-1}{\frac{1}{1-x}}=\left(\frac{1-1+x}{1-x}\right) \times \frac{(1-x)}{1}$

= x
Option (2) is correct

110. In a class of 35 students, 16 students play football and 24 students play cricket. Assume that each one play atleast one game, then number of students who play both the games is_______________

Answer: N (F ∩ C) =n (F) + n(C)- n(F U C)

= 16 + 24-35 = 5

Option (1) is correct.

111. If A = {ø,{ø}} then the Power Set of A is

{ø}, {0}
{ø,{ø},{ø}},A}
A
{A}, {ø}

Answer: (2)

A = {ø;{ø; }}

P(A) = {{}};{ø};{{ø}};{ø;{∅}}

= {ø;{ø};{{ø};A}}

112. If A = {x:x = 3ⁿ-2n – 1, where n∈ N}, B = {x:x = 4(n – 1}, where n∈N}. Then

A ⊂B
B⊂A
A = B
None

Answer: (1)

Putting n= 1,2,3……….; we Ret

A = {x/x = 3ⁿ – 2n – 1}

= {0 ; 4 ; 20 ; }

B = {x/x = 4(n – 1)}

= {0;4;8; 12; 16; 20;………}

Clearly ; A ⊂ B

113. The numbers of proper sub-sets of the set {3, 4, 5, 6, 7} is :

Answer: (2)

Formula

No. of proper sub-sets = 2ⁿ -1

= 2⁵-1 = 31

CA Foundation Maths Sets, Functions, And Relations Practice Problems

114. If A = {1, 2, 3, 4, 5, 6, 7} and B = {2, 4, 6, 8}. Cardinal number of A – B is:

Answer: A ∩ B = {1, 2, 3, 4, 5, 6, 7} n {2, 4,6,8}

= {2, 4, 6} => n (A ∩ B) = 3

n (A – B) = n(A) -n(A ∩ B)

=7-3=4

115. If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}; B = {1, 3, 4, 5, 7, 8}; C = {2, 6, 8} Then find (A – B) U C

{2, 6}
{2,6,8}
{2, 6, 8, 9}
None

Answer: (3)

A-B = A-(A ∩ B)

= {1,2, 3,4, 5, 6, 7, 8,9}

{1,3, 4, 5, 7, 8}

= {2,6,9}

(A – B) U C = {2 ; 6 ; 9} U {2 ; 6 ; 8}

{2 ; 6 ; 8 ; 9}

(3) is correct.

116. The no. of sub-set of the set (3, 4, 5} is:

Answer: (2)

No. of sub-sets = 2ⁿ = 2³ = 8

CA Foundation Maths Solutions For Chapter 7 Function And Relation

Introduction

A Function is a rule that describes the dependence between two quantities and is generally denoted by f(x).

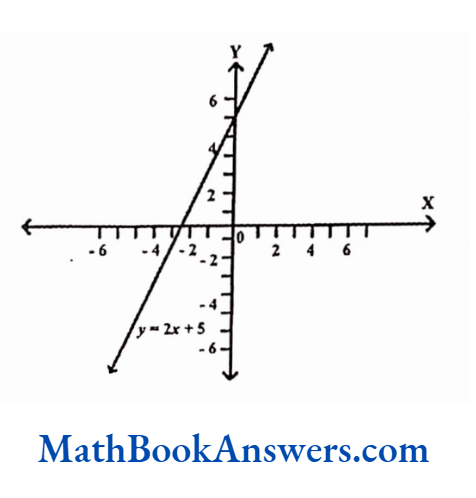
Take for e.g., f (x) = 2x+5

Let y= f(x)

In the above case, x is the input, y is the output and f(x) is the function that processes the input according to a certain rule to give the output.

The function f here multiplies the input value x by 2 and then adds 5 to it to give the corresponding value of the output y.

For this function, different values of x give different values of y. By plotting these points and joining them the following figure is obtained.

Function and Relation

Any function in general can be reprinted through the diagram given below.

Any function in general can be reprinted through the diagram given below

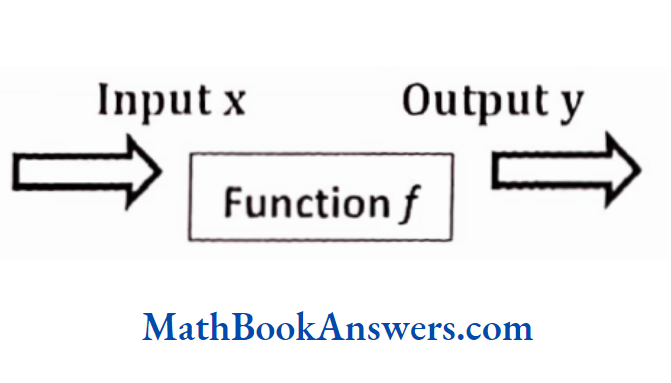
If x be the input and y the output fora function/, then the function is denoted as y = f(x).

This indicates that when input x is processed by a function /, the output obtained is y.

Thus, x is also called the independent variable, while y is called the dependent variable.

Therefore, a function can be considered to be a machine that transforms a given input into the corresponding output according to a certain rule defined by that function.

Some other examples of functions are

f(x) = x² + 3x-7

f(x) = cosx

f(x) = log ( |x| + 5)

A function can be represented using formulae, tables, graphs, algorithm, arrows etc.

The concepts of an ordered pair, Cartesian product and relation need to be understood to understand functions.

Cartesian Product

Consider two sets A and B

A ≡ {1,2,3}

B≡ {1.2,3.4}

The set of all ordered pairs of elements from A and elements from B, known as the Cartesian product, gives all the ways to possibly relate the elements of set A with those of set B.

The Cartesian product A x B is given by

Ax B ≡ {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4)(3,1), (3,2), (3,3), (3,4)}

Ax B ≡ {(a,b)| a ∈ A, b ∈ B}

Also,BxA = {(b, a) b∈ B, a ∈ A)

In a Cartesian product, the order in which a and b are written is important.

∴Ax B ≠ B x A

It is evident that the number of elements in the Cartesian product is the product of the number of elements in the two sets A and B.

Consider the following example.

Let set S= {I,II,III} represent three students and set M≡ {56,29,45}represent their scores out of 100 in maths in some order.

Then the different ways in which the students and marks can be related is represented by the Cartesian product Ax B.

∴ S x M≡ {(I,56), (I,29), (I,45), (II, 56), (II,29), (II, 45), (III, 56), (III, 29), (III, 45)}

Relations

Understand the concept of relation before moving on to functions.

Consider two sets P and Q.

P ≡ {1,2,3,4}

Q≡ {1,2,3,4,5,6,7,8,9,10}

Let R ≡ {(1,1), (2,4), (3,9)}

Observe that R ⊆ PxQ.

But elements of R have been chosen in a specific way i.e. (p, q) ∈ R only if q = p²

Thus R = {{p,q)| q = p², p ∈ P, q ∈ Q}

R is called a relation from P to Q and this is denoted by p R q or p~q

In general, any relation is a set of ordered pairs (p , q) ∈ PxQ Such that there exists some definite relationship R between p and q.

Note:

If R ≡ {{p,q)\q = p²,p∈P,q∈Q],it is not necessary that all elements of P and Q are a part of the relation.

Domain, Co- Domain and Range

The above relation R from p to Q can be expressed in the form of a diagram as follows:

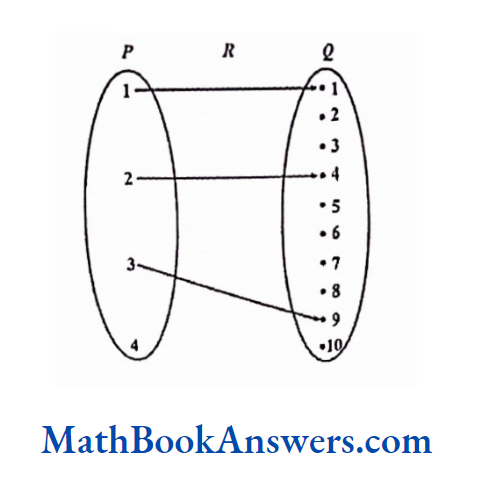
Domain, Co- Domain and Range

The direction of the arrow indicates the direction of the relation.

In the above figure the relation exists from set P to set Q and not vice versa.

The set of all first elements in the ordered pairs that belong to R is called the domain of R.

In this example, Domain ≡ {1,2,3}

Hence Domain ⊆ p.

The set of all second elements in the ordered pairs that belong to R is called the range of R.

In this example, Range = {1,4,9}.

Hence, Range ⊆ Q.

Q is called the co-domain of R. Thus, range ⊆ co-domain.

In other words, A function can be denoted as y= f{x}, where x is the independent variable and y is the dependent variable as discussed above.

Domain: The domain of a function is set of all the values that an independent variable can take i.e. values of “x” in this case.

Range: The range of a function is set of all the values which a dependent variable will take corresponding to the values taken by independent variables i.e. Values of “y” obtained corresponding to the value of x.

Types of Relations

Many-Many Relation

Consider the following relation.

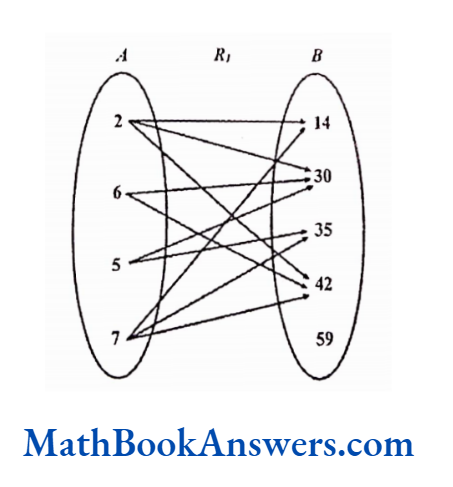
Many-Many Relation

A ≡ {2,6,5,7},B ≡ {14,30,35,42,59}

Relation R₁has ordered pairs (a,b)such that be is multiple of a

R₁ = {(2,14), (2,30), (2,42), (6,30), (6,42), (5,30), (5,35), (7,14), (7,35), (7,42)}

In this relation, more than one element in the domain has the relation with the same element in the range. Also, one element in the domain has the relation with more than one element in the range. Such a relation is called a many-many correspondence.

One-Many Relation

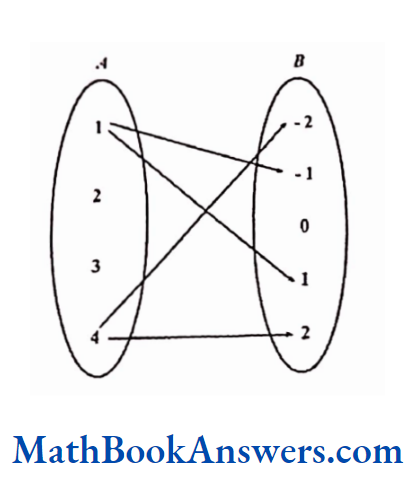
One-Many Relation

If A ≡ {1,2,3,4}, B ≡ {-2, -1,0,1,2}

Relation R₂has ordered pairss (a, b)such that b is the square root of a.

R₂ ≡ {(1,-1), (1,1), (4, -2), (4,2)}

In this relation, one element in the domain has the relation with more than one element in the range. Such a relation is called a one-many correspondence.

One-One Relation

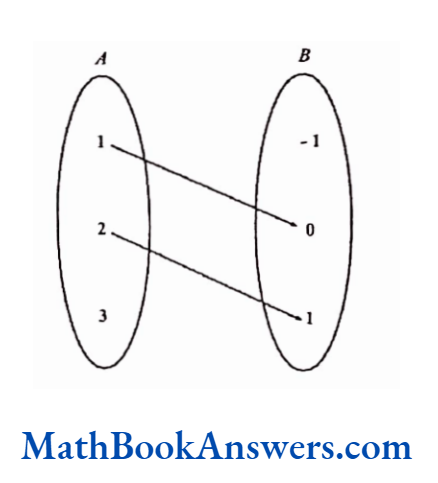
One-One Relation

If A≡ {1,2,3}, B ≡{-1,0,1}

If A ≡ {1,2,3), B ≡ {-1,0,1}

Relation R₃ has ordered pairs (a, b) such that b = (a- 1)

R₃ ≡ {(2,1), (2,1)}

In this relation, one element in the domain has the relation with exactly one element in the range. Such a relation is called a one – one correspondence.

Many-One Relation

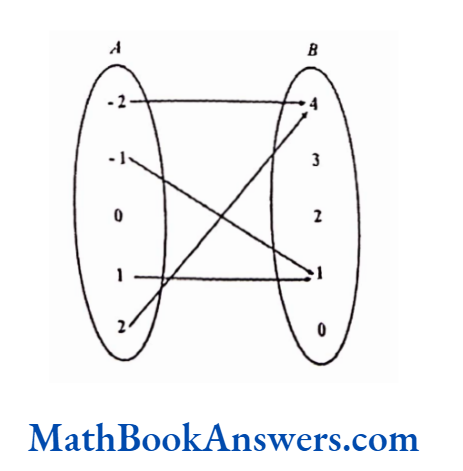
Many-One Relation

A≡ {-2,-1,0,1,2), B ≡ {0,1,2,3,4)

Relation R₄ has ordered pairs [a,b] such that b is the square of a

R₄ = {(-2,4), (-1,1), (1,1), (2.4)}

In this relation, more than one element in the domain has the relation with the same element in the range. Such a relation is called a many-one correspondence.

Equivalence Relation

Equivalence Relation

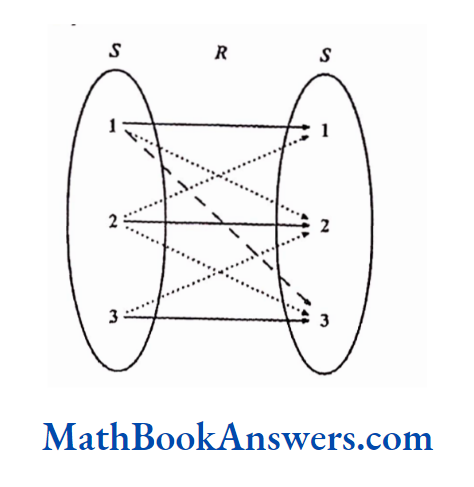
Let S be a set and R be a relation between S and itself.

R is called an equivalence relation on S if the relation R has the following three properties:

Reflexivity: Every element of S is related to itself

Symmetry: If an element s is related to t then t is related to s

Transitivity: If an element s is related to t and t is related to u, then s is related to u.

Consider the set S ≡ {1,2,3}

Now a relation R from S ~S is said to be an equivalence relation if:

S~S = {(1,1), (2,2), (3,3), (1,3), (3,1), (1,2), (2,1), (2,3), (3,2)}

Here the reflexivity relation exists as every element i.e., 1, 2, 3 is related to itself.

In addition, the symmetry relationship exists as every element is related to all other elements and vice versa i.e.,1 is related to 2 and 2 is related to 1.

Also, transitive relationship is satisfied since reflexive and symmetry relationships are satisfied i.e.,1 is related to 2,2 is related to 3 and simultaneously 1 is related to 3.

Congruence and equality are two common equivalence relations.

Functions

Any relation between sets A and B, is a function ifit satisfies the following conditions.

It should be a one- one or many -one relation.
Every element in A should be a part of the domain.

Thus, every function is a relation. However, not every relation need be a function.

Functions

Thus, if A and B are two sets and if there exists a relation so that each element of A is related with one and only one element of B, then a function from A to B exists.

Example 1:

Is the following relation a function?

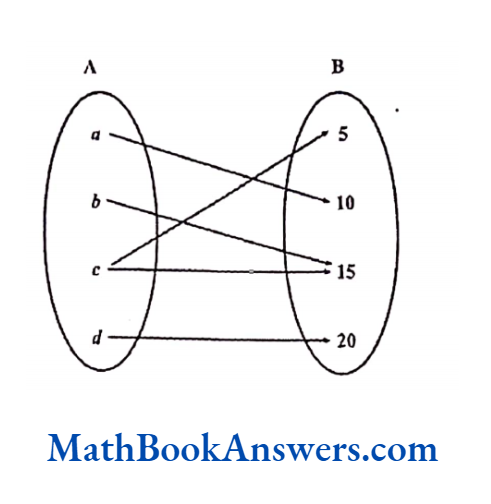
Example 1

Solution:

This relation is a many – many relations because c has a relation with 5 as well as 15. Also, b and c both have a relation with 15. Therefore, this is not a function.

Example 2:

Example 2

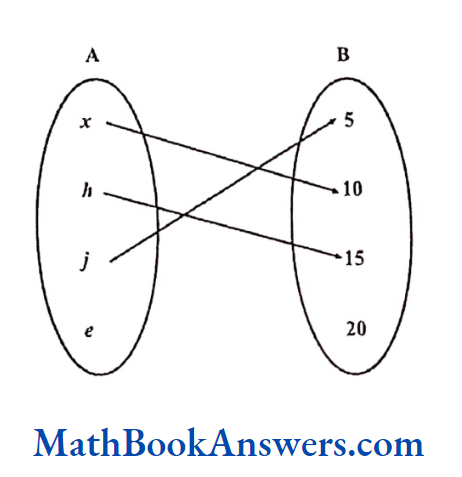
Find whether the relation shown above represents a function or not.

Solution:

This is a one- one relation. However, every element of A is not in the domain.

Hence, this is not a function.

Example 3:

Find the value of f(x) = $\frac{x^6}{2 x-3}+\mathrm{x} \text { at } \mathrm{x}=\frac{3}{2} \text { and at } \mathrm{x}=1$

Solution:

To find the value of a function at some value of the independent variable, substitute this value of the variable in the function.

$\text { Put } \mathrm{x}=\frac{3}{2} \text { in } f(x)=\frac{x^6}{2 x-3}+x$

Thus, $f\left(\frac{3}{2}\right)=\left(\frac{1.5^6}{0}\right) \frac{3}{2}=\infty$ ,which is not defined.

Hence the function f(x)is not defined at x= 3/2

At x =1, $f(1)=\frac{1^6}{2-3}+1=0$

Types of Function

Into and on to Functions

A Function f : A → B is called a function from A onto B if the range of f = co-domain.

Thus, if every element of B has a pre-image in A, then f: A→B is a function from A onto B.

If there is at least one element of B that has no pre-image in A, then f : A → B is a function from A into B.

Thus functions can be of four kinds – one-one into, one-one onto, many-one into and manyone onto.

Example 4:

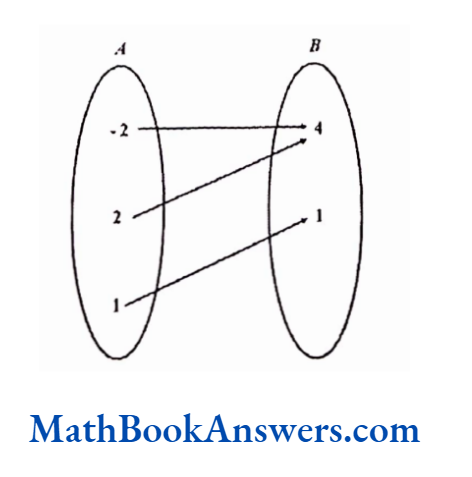
Is the given relation an onto function?

Find the co-domain and range for the function.

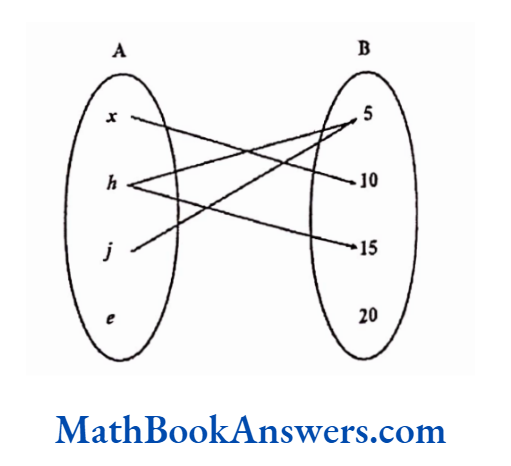
Example 4

Solution:

In this function,

Co-domain ≡ {5,10,15,20}

Range≡ {5,10,15}

This is not an onto function because the element 20 in B does not have a pre-image in A.

Injective, Surjective and Bijective Functions

An injective function, also called an injection is a one- one function.

Thus, a function f is an injective if and only if whenever f (x) = f (y),x = y

A many-one function is not an injection.

A subjective function, also called a surjection, is an onto function.

Thus a function f: X → Y is a surjective if and only if its range f{x} is equal to its co-domain Y.

A function f: X → Y is a bijective function or a bijection if for every y in Y, there is exactly one x in X such that f (x)=y.

Alternatively, f is bijective ifit is both one- one {injective} and onto {surjective}.

Even and Odd Functions

Even Functions

Let y=f (x) be a function such that x, y ∈ R.

If the values of f (x) and f(- x) are the same for all values of x in the domain, then the function is said to be an even function. For example, consider f(x) = x²

Here, f(1) = 1. also/(-1) = 1.

Similarly,f(-1) = -1² =1² = f (x)

Thus, f (x) is an even function. Other examples of even functions are cos x,|x|, x²ⁿ; n ∈ N

An even function of the form y=f(x) is symmetrical about they-axis. Similarly, an even function ofthe form x=f (y) is symmetrical about the x-axis.

The following graph shows the even function f (x) = x²- 3x² + 2

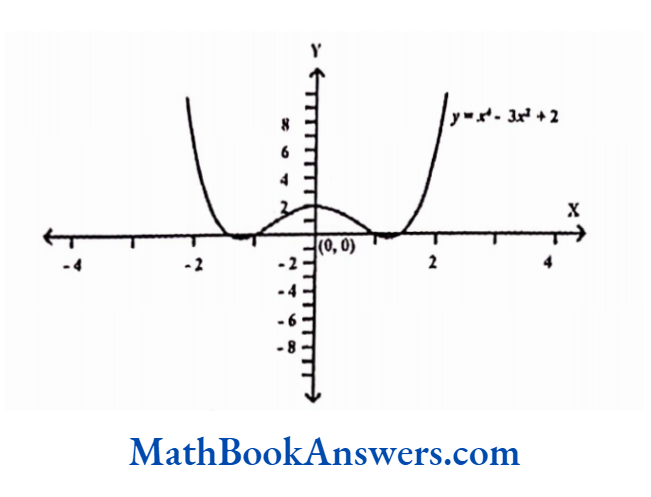
Even Functions

Thus, the graph of an even function appears the same on both sides of the y- axis. The left half of the plane appears as the mirror image of the right half of the plane.

Properties of Even Functions:

The sum, difference, product, or division of any two even functions is also an even function.

CA Foundation Maths Solutions For Chapter 7 Odd Functions

Let y = f (x)be a function such that x, y ∈ R.

If f (x) = -f(-x) for all values of x in the domain, then the function is said to be an odd function.

Consider the function f(x) = x³

Here,f(1) = 1 while f(-1) = -1

Similarly, for any x, f(-x) = (-x)³ = -x³ = -f(x)

Thus f (-x) = -f (x) and f (x) = -f (-x)

Hence, this is an odd function.

Other examples of odd functions are sin x, tan x, x ²ⁿ⁺¹; n ∈ N

For odd functions the inverted left half of the graph looks like the mirror image of the right half of the graph.

In other words, an odd function is symmetrical about the origin.

The following graph shows the odd function f(x) = x³ + sin x

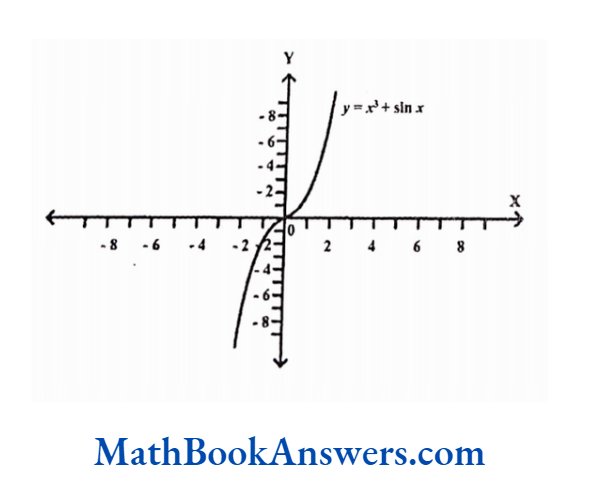
Odd Functions

Properties of Odd Functions:

The sum or difference of any two odd functions is an odd function.

Division or product of an even number of odd functions is an even function whereas that of an odd number of odd functions is an odd function. i.e„ odd function raised to
an even power is an even function whereas and odd function raised to an odd power is an odd function.

CA Foundation Maths Solutions For Chapter 7 Neither Even nor Odd Functions

There are functions that satisfy the conditions neither of an even nor of an odd function. Such functions are said to be neither even nor odd functions.

For example: f (x) = x³ + 1

f(-x) = (-x)³ + 1 = -x³ + 1

∴ f (x) ≠ ± f(-x).

Thus, it is neither an even nor an odd function.

Note:

The only function that is both even and odd is the function defined by f (x) = 0 for all real x.

Every function can be expressed as a sum of an odd and an even function.

Even function x Odd function ≡ Odd function

Even function/odd function ≡ Odd function

Even function ± Odd function ≡ Neither even nor odd function

Composite Functions

Let two functions f and g be defined as f : A → B and g: B → C, such that f(x) = 2x + 1 and g (y) = y + 5

Then a function from A to C, g°f: A A → C, can be defined as

g° f (x) = g [ f (x)]

= f(x) + 5

= 2x + 1 + 5 = 2x + 6

If A = {1,3,5 }, then the function g° f (x)can be shown as follows:

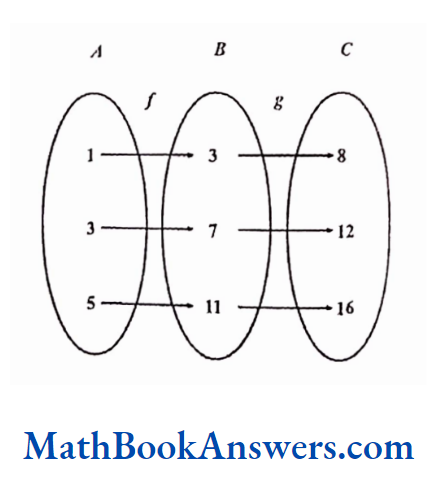
Composite function

Such a function is called a Composite function.

Example 5:

f(x) = x⁴

g(x) =√x,x > 0

Find g°f (2).

Solution:

g°f(x) = g(f(x))

f(2) = 2⁴ = 16

g(f(2)) = g(16)

g(f(2)) = g(16) = √16 = 4

Note that g°f(x) = g[f(x)] = f[x⁴]

= √x⁴

= x²

Example 6:

f(x) = 2x² – 5x + 9

g(x) = 3x + 7

Find f°g(x)and g°f(x). is fºg(x) = g°f(x)?

Solution:

f°g(x) = f[g(x)] = f(33x + 7)

Substitute g(x)for x in f (x).

f[g(x)] = 2(3x + 7)²- 5(3x + 7) + 9

= 2(9x² + 42x + 49)- 15x- 35 + 9

= 18x² + 69x + 72

g°f(x) = g[f(x)] = g(2x²- 5x + 9)

= 3(2x² – 5x + 9) + 7

= 6x² – 15x + 34

Thus ,f° g (x) ≠ g° f (x)

Chapter 7 CA Foundation Maths Answer Key

CA Foundation Maths Solutions For Chapter 7 Piecewise Functions

A function, which has different definitions depending on the value of the independent variable, is a piecewise Function. Thus, the definition of function changes according to the domain.

For example:

y = x/2 for x ≤ 0,

= x for 0 < x < 2 and

= 2 for x ≥ 2

The modulus function is a piecewise function.

Example 7:

Find the value of f(2), f(-2)and f(0) for the function

f(x) = 2x + 3 for- ∞ ≤ x ≤ 0

= 2x- 3 for 0 < x ≤ ∞

Solution:

Here, two functions are defined for two different domains.

So, to find f(-2), use f(x) = 2x + 3

Thus, f(-2) =-1

However, for f(2) use the function f(x) = 2x- 3

Thus, f (2) = 2(2) -3 = 1

At x=0,we use f(x) = 2x + 3

∴ f(0) = 3

Inverse Functions

If f: A -> B Is a one one onto function, then for each x ∈ B, there exists one and only one y ∈ B such that f(x) = y

If one defines a relation from B to A such that for each £ B, there exists one and only one x ∈ A such that f(x) = y, then the relation is a function from B to A denoted by

f¹:B → A, and defined as f¹ (y) = x.

such a function is called an inverse function.

Consider the two functions given below:

f(x) = 2x + 3, where x ∈ I

g(x) =x-3/2 where x∈ I

For x = 3,

f(3) = 2(3) + 3 = 9

g(9) = (9-3)/2,= 3 = x

We can see that g(f(x)) = x for all x∈ l.

In such a case,g(x) is called the inverse of f(x). This is denoted by g (x) = f¹(x)

Note:

g(x) = f¹ {x) does not necessarily mean that f(x)) = g¹(x)

In the above example,

f(x) = 2x + 3 where x∈ I

g(x) = x-3/2, where x∈ I

Algebraically,f(g(x)) = 2(x- 3/2 + 3 = x)

But if x is even, say x=4, g(4) = 0.5 ∉ I

f(g(4)) is not defined as g(4) does not belong to the domain of f.

f(x) ≠ g^-1(x)

However, if the domains of f(x)and g(x)were x ∈ R, then the two functions would be inverses of each other.

Note that not all functions have an inverse.

Consider the function y = x², x ∈ I

The range of this function is y ∈ I, y≥ 0

For y = 1,x can be -1 or 1.

Thus, each value of y does not give a unique value of x.

If the inverse of the function y=x² was g(x), then g (1) would be both 1 and -1 which would make g(x) a one-many relation, which cannot be a function.

CA Foundation Maths Solutions For Chapter 7 Condition for A Function to Have an Inverse:

The function should be a one-one relation. This ensures that the inverse relation is also one-one. If the function is many-one, the inverse relation is one- many and hence is not a function.

The co-domain of the original function becomes the domain of its inverse and vice-versa. Thus, the inverse relation will be a function if and only if the co-domain = range; of the function is a one-one onto function.

In other words, for a function to have an inverse it must be a bijection. Graphically a function y= f(x) has an inverse if no two points on the graph have the same y coordinate

Example 8:

Find out if the inverse of the following functions exists.
1. f(x) = x², where the domain and the co- domain are the set of integers;
2. f(x) = x- 3, where the domain and the co- domain are the set of integers.
3.f(x) = x², where the domain is {x|x ∈ R,x ≥ 0 }

Solution:

f(x) = X²

1. Here, we have f(-1) = f(1) = 1. Hence, this is a many-one relationship. Therefore, the inverse of this function does not exist.

2. f (x) = x- 3

Here, for each value of x, we have only one value of x-3.

Hence,it is a one- one relationship.

Also, f(x) = x- 3, so x = f(x) + 3

Thus, every value of f (x) corresponds to a unique integer value of x. So the function f(x) is an onto function.

Hence, this function is both one-one and onto. Hence, it has an inverse function.

f(x) =x²,{x|x∈R,x ≥ 0}

In this function, the domain is restricted to the set of positive real numbers and so is the co-domain.

The function is a one-one onto function.

∴ f(x)has an inverse.

CA Foundation Maths Solutions For Chapter 7 Steps to Find the Inverse of a Function

The inverse of a function can be found easily using three algebraic steps. However, this method should be used only after verifying that the inverse exists.

The steps are:

Write down the function in the form y = f(x).
Solve for x, Replace x with f^-1 (y)
Replace y with x to get the inverse function.

For example, consider/(x) = x- 3

Step 1: write down y = f(x).

Hence y = x- 3

Step 2: solve for x.

Thus, x- y + 3

Since y = /(x),x = f^-1{y)

Thus f^-1 (y) = y + 3

Step 3: Replace y by x in the above equation to get f^-1 (x) = x + 3

Thus, if we follow the four steps given above, we can find the inverse of any function.

Example 9:

Find the inverse function of:

1. $f(x)=\frac{2 x+3}{7 x+5}$

2. f(x)=e^x

Solution:

$\text { 1) } f(x)=\frac{2 x+3}{7 x+5}$

Step 1:

$\mathrm{Y}=f(x)=\frac{2 x+3}{7 x+5}$

Step 2:

y(7x + 5) = 2x + 3

7xy + 5y = 2x + 3

7xy- 2x = 3- 5y

x{7y- 2) = 3- 5y

$x=\frac{3-5 y}{(7 y-2)}$

Step 3:

Writing x as f^-1(y),

$x=f^{-1}(y)=\frac{3-5 x}{(7 y-2)}$

Step 4: Replacing y in the above equation by x,

$f^{-1}(x)=\frac{3-5 x}{(7 x-2)}$

2) f(x) = e^x

Step 1: y = f(x) = e^x

Step 2: y = e^x

Take log on both sides

log y = log e^x

log y = x log e [ log a^b = b log (a)]

∴ log y = x [log e = 1]

∴ x = log y

Step 3: x = f¹ (y) = log y

Step 4: Replacing y in the above equation by x,

f¹ (x) = log x

Some Standard Functions

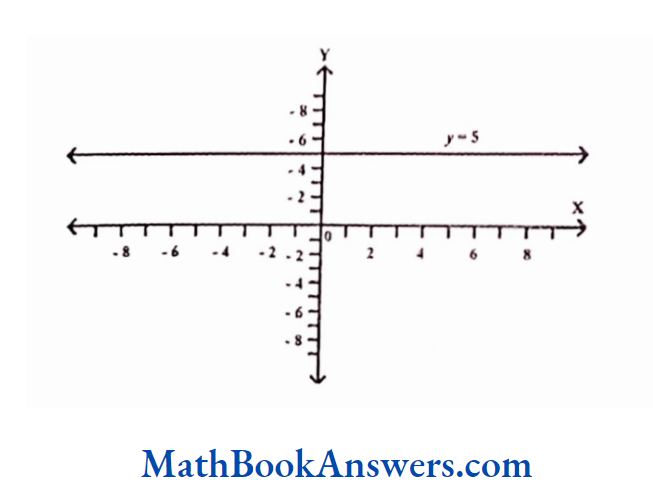
Constant Function

A Constant function is f(x) = c, where c ∈ R. The range of the function is {c} The graph of a constant function is as shown.

Constant Function

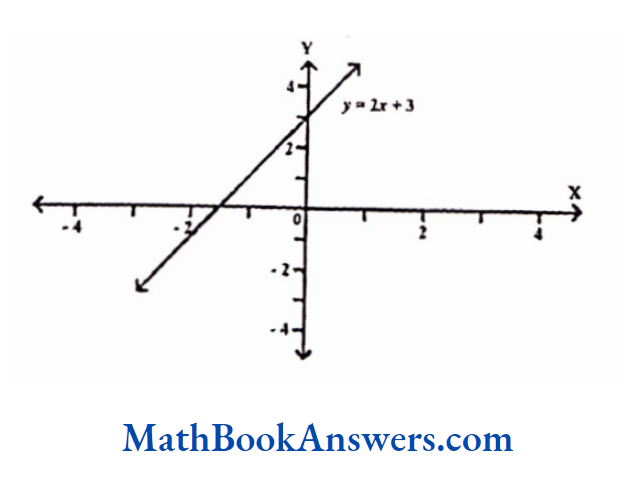
Linear Function

A linear function is of the form y = ax + b, where, a and b are real numbers. The graph of a linear function is a straight line. It intersects the x- axis at-b/a and it intersects the y-axis at be. The function y = x, passes through the origin.

Linear Function

Modulus Function

The modulus runction is used to find the positive value of an expression. It is also called the absolute value function. The function is denoted by

f(x) = |x|.

Thus.

f(x) = x if x ≥ 0

= -x if x < 0

The modulus function is an even function. Graphically it can be shown as,

The modulus function is an even function. Graphically it can be shown as

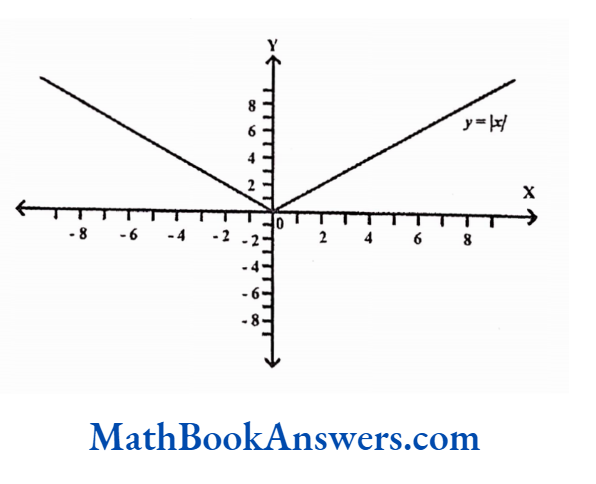
CA Foundation Maths Solutions For Chapter 7 Exercise – 2: Relation

Choose the most appropriate option/options (1) (2) (3) or (4).

1. “Is smaller than” over the set of eggs in a box is

Transitive (T)
Symmetric (S)
Reflexive (R)
Equivalence (E)

Answer: (1) Transitive (T)

Let a be S₁ & b be in S₂: a < b

∴ (a, b) are a part of relation

Let c be in S₃: b < c

∴ a < b < c

-> a < c

(a, c) are part of relation not reflexive because it is smaller than not equal to & not symmetric as a < b but b < a then.

2. “Is equal to” over the set of all rational numbers is

[By using R = Reflexive; T = Transitive, S = Symmetric and E = Equivalence from Q. No. 2 to 8]

Answer: (4) Equivalence

a, a∈R->a = a

-> (a, a) ∈ R reflexive

a,b∈R->a=b

-> b = a -> (b, a) ∈ R symmetric

a,b∈R->a = b

b, c∈R->b = c

∴ a = c

∴ (a, c)∈ R

∴ transitive

∴ equivalence

3. “has the same father as”……over the set of children

R
S
T
All of these

Answer: (4) All of these

-> a has same father as himself reflexive

-> a & b have same father as b & a symmetric

-> a & b have same father & b & c have same father

Implies a & c have same father -> transitive

4. “is perpendicular to” over the set ofstraight lines in a given plane is

Answer: (2) S

a line cannot be perpendicular to itself

∴ not reflexive

a line perpendicular to another line

L₁ ⊥ L₂ -> L₂ ⊥ L_{1 ∴} symmetric

A line perpendicular to L₂ & L₂ ⊥ L₃

Implies L₁ || L₃

∴ not transitive

5. “is the reciprocal of’…… over the set of non-zero real numbers is

S
R
T
none of these

Answer: (1)S

a number is not a reciprocal of itself

∴ not reflexive

a number is reciprocal ofanother say

a =1/b -> b =1/a ∴ symmetric

let a, b e R & let b, c ∈ R

a=1/b b=1/c → 1/a=1/c->a=c

a,c ∉ R not transitive

6. {(x, y)/x ∈ x, y ∈ y, y = x } is

R
S
T
All of these

Answer: (4) All of these

7. {(x,y) / x + y = 2x where x and y are positive integers}, is

Answer: (4)E

{(x,y):y=2x-x}

->{(x,y):x = y}

It is reflexive, Transitive, symmetric

∴ equivalence

8. “Is the square of over n set of real numbers is

R
S
T
none of these

Answer: (4) none of these

[a, a] ∉ R as a² ∴ not reflexive

(a, b) ∈ R ≠>(b, a) ∈ R as a² = b ≠>b² = a

∴ not symmetric

(a, b) ∈ R ⇔ (b, c) ∈ R a² = b, b² = c => a⁴ =c not transitive

9. If A = {1,2,4}, B = {2,4,5} C = {2,5}, then (A-B) x (B – C) is

{(1,2),(1,5),(2,5}}
{(1,4}}
(1,4)
none of these

Answer: (2) {[1,4)}

A = {1, 2, 4}

B = {2, 4, 5}

C = {2, 5}

A- B = {1}

B – C = {4}

A – B x B – C

=>{(1,4)}

10. If R is a relation on the set A = { 1,2,3,4,5,6,7,8,9} given by x R y ⇔ y = 3x, then R =

{(3,1), (6,2), (8,2), (9,3)
{(3,1),(6,2),(9,3)
{(3,1), (2,6), (3,9)}
None of these.

Answer: (4) none of these

R – {(1, 3], (2,6),………….. (9,27)}

11. Let A = {1,2,3} B = {1,3,5}. If relation R from A to B is given by R = {(1,3),(2,5),(3,3) then R^-1 is

{(3,3),(3,1),(5,2)}
{(1,3),(2,5),(3,3)}
{ (1,3),(5,2)}
none of these

Answer: (1) {(3,3), (3, 1), (5,2)}

R = ((a,b) (a, c)}

R^-1 = {(b, a), (b, c)}

12. If A = {1,2,3}, B = {1,4,6,9} and R is relation from A to B defined by ‘x is greater than y. The range of R is

{1,4,6,9}
{4,6,9}
{ 1 }
none of these

Answer: (3) 1

R : {(x, y) : x > y, x ∈ A, y ∈ B)

Range => 1

As x ∈ A will be greater than only 1 from

y ∈ B

13. If R = {(x,y) : x,y ∈ Z, x² + y² ≤ 4} is a relation on Z, then domain of R is

{0,1,2}
{0.-1.-2}
{-2,-1,0,1,2}
none of these

Answer:(3) domain (-2,-1,0,1,2}

14. A relation R Is defined from (2,3,4,5) to {3,6,7,10} by: x R y ⇔ x is relatively prime to y. then, domain of R is

{2,3,5}
{3,5}
{2,3,4}
{2,3,4,5}.

Answer: (4) (2,3,4,5)

Domain of R : A→ B = A

15. Let R be a relation on N defined by x + 2y = 8. The domain of R is

{2,4,8}
{2,4,6,8}
{2,4,6}
{1,2,3,4}.

Answer: (3) {2.4,6)

For y to be a N no

X should be even < 8 & > 0

{2,4,6}

16. If the set A has p elements, B has q elements, then the number of elements in A x B is

p + q
p + q +1
pq
P2

Answer: (3)

n (A) = P n(B) = q (3) pq

n (AxB) = pq

17. Let R be a relation from a set A to a set B, then

R = A U B
R = A ∩ B
R⊆ AxB
R ⊆ B x A.

Answer: (3)R⊆AxB

All relations are a subset of the Cartesian product

18. R is a relation from a finite set A having m elements to a finite set B having n elements then the number of relations from A to B is

2^mn
2^mn-1
2mn
mⁿ

Answer: (1) 2^mn

If a relations is from A→ B

A has in elements B has n elements

Then no. of relations is 2^mn

19. If R is a relation on a finite set having n elements, then the number of relations on A is

2ⁿ
2^n²
n²
nⁿ.

Answer: (2) 2^n²

Relation → A → A

A has n elements no. of relations is

2^mn = 2^n²

20. $\text { If } f(x)=\frac{2+x}{2-x} \text {, then } f^{-1}(x) \text { : }$

$\frac{2(x-1)}{x+1}$
$\frac{2(x+1)}{x-1}$
$\frac{x+1}{x-1}$
$\frac{x-1}{x+1}$

Answer: (1)$ \mathrm{f}(\mathrm{x})=\frac{2+x}{2-x}=y(\text { let })$

2 + x = 2y- xy
Or x + xy = 2y-2
Or x(1 + y) = 2 (y-1)

$\text { Or } \mathrm{x}=\frac{2(y-1)}{1+y}$ $f-1(x)=\frac{2(x+1)}{x-1}$

(1) is correct

CA Foundation Sets, Functions, And Relations Solved Examples

21. In the set N of all natural numbers the relation R defined by a R b “if and only if a divide b’, then the relation R is:

Partial order relation
Equivalence relation
Symmetric relation
None of these.

Answer: (1) it is transitive relation, i.e. partial order relation

22. On the set of lines, being perpendicular is a__________

Reflexive
Symmetric
Transitive
None of these

Answer: (2) is correct

It is symmetric relation because it x is perpendicular to y

Then y is also perpendicular to x

23. If A = {1,2,3} then the relation R = {{1,1},(2,3),(2,2),{3,3),(1,2)} on A is:

Reflexive
Symmetric
Transitive
Equivalence

Answer: (1) is correct

Reflexive relation.

x R x; (x;x)∈R

here, (1,1),(2,2),(3,3)∈ R

So; it is Reflexiv

24. The range of the reltation {(1,0)(2,0),(3,0)(4,0)(0,0) is

{1,2,3,4,0}
{0}
{1,2,3,4}
None

Answer: (2) is correct

Range = {0}

CA Foundation Maths Solutions For Chapter 7

25. If a relation S = {1,2,3} then {(1,1),(2,2),(1,2),(2,1)} is symmetric and

Reflexive but not transitive
Reflexive as well as transitive
Transitive but not reflexive
Neither transitive nor reflexive

Answer: If S = {1,2,3} then

Then relation {{1,1); (1,2); (2,1)} is symmetric and transitive but not reflexive.

(3) is correct

26. If A = {1, 2} and B = {3,4}. Determine the number of relations from A and B:

Answer: (2)

No. of Relations = 2^n(AxB)

=2^(2×2) = 16.

27. A = {1,2, 3, 4 .. 10} a relation on A, R = {x,y):x + y = 10, x ∈ A, Y ∈ A, x ≥ Y} then domain of R^-1 is

{1,2, 3,4,5}
{0, 3, 5, 7, 9}
{1,2, 4, 5, 6, 7}
None

Answer: (1)

Given ; A = {1, 2, 3,…….; 10}

R = {x;y) / x + y= 10;X ∈A;Y ∈A;x≥y}

=> R = (5 ; 5) ; (6 ; 4) ; (7 ; 3) ; (8 : 2) ; (9 :1)

=> R^-1 = (5 ; 5) ; (4; 6) ; (3 ; 7) ; (2 ; 8) ; (1 ;9)

Domain of R^-1 = (5 ; 4; 3 ; 2 ;1)

CA Foundation Maths Solutions For Chapter 7 Exercise – 3: Function

Choose the most appropriate option/options (1) (2) (3) or (4}.

1. If A = {x,y,z}, B = {p, q, r, s) which of the relation on A to B are function.

{n, p),(x,q), (y, r), (z, s}},
{(x, s}, (y, s), (z, s)}
{(y, p), (y, q), (y, r), (z, s),
{(x, p), (y, r), (z, s}}

Answer:(2) in a function, element from domain can have only one range in range and every element has a image

2. {(x, y)|x+y = 5} where x, y ∈ R is

not a function
a composite function
one-one mapping
none of these

Answer: (3) one-one mapping

3. {(x, y) | x = 4} where x, y ∈ R is a

not a function
function
one-one mapping
none of these

Answer: (1) not a function

as only one element has an image in the rang

4. {(x, y}, y=x²} where x, y ∈ R is

not a function
a function
inverse mapping
none of these

Answer: (2) a function

As every element in domain has only one image

5. {(x, y}|x<y} where x, y ∈ R is

not a function
one-one mapping
a function
none of these

Answer: (1) not a function

6. The domain of {(1, 7), (2, 6)} is

{1, 6}
{7, 6}
{1, 2}
{6,7}

Answer: {(1,7), (2, 6)}

Domain (3) {1, 2}

Set of first elements of a pair of a function

7. The range of {(3, 0), (2, 0), (1, 0), (0, 0}} is

{0,0}
{0}
{0, 0, 0, 0}
none of these

Answer: (2) {0}

Set of second elements of a pair of function

8. The domain and range of {{x,y} : y = x²} where x, y ∈ R is

(reals, natural numbers)
(reals, positive reals)
(reals, reals)
none of these

Answer: (2) (reals, positive reals)

Domain can take any real value & y = x² -> y will only take positive real no.

9. Let the domain of x be the set {1}. Which of the following functions are equal to 1

f(x) = x², g(x) = x
f(a) = x, g(x) = 1-x
f(x) = x² + x + 2, g(x) = (x+ l)²
none of these

Answer: (1) f(x) = x², g (x) = x

f1) = 1² = 1 & g(1) =1

∴ 1

10. If f(x) = 1/1-x, f(-1} is

0
1/2
0
none of these

Answer: (2) 1/2

$f(x)=\frac{1}{1-x}$ $f(-1)=\frac{1}{1-(-1)}=\frac{1}{2}$

-> (2) 1/2

11. If g(x} = (x-1)/x, g(-1/2) is

Answer: (4) 3

$g(x)=\frac{x-1}{x}$ $g(-1 / 2)=\frac{-3 / 2}{-1 / 2} \rightarrow 3$

12. If f(x} = 1/1-x and g(x) = (x-1}/x, than fog(x} is

x
1/x
-x
none of these

Answer: (1) x

$f(x)=\frac{1}{1-x} g(x)=\frac{x-1}{x}$ $f o g(x)=f(g(x))=\frac{1}{1-g(x)}$ $=\frac{1}{1-\frac{(x-1)}{x}}$ $=\frac{1(x)}{x-x+1} \rightarrow \frac{x}{1} \rightarrow \mathrm{X}$

13. If f(x) = 1/1-x and g(x) = (x-1)/x, then gof(x) is

x-1
x
1/x
none of these

Answer: (2) x

$f(x)=\frac{1}{1-x}$

$g(x)=\frac{(x-1)}{x}$ gof(x)

$g(\mathrm{f}(\mathrm{x}))=\frac{f(x)-1}{f(x)}$ $=\frac{\frac{1}{1-x}-1}{\frac{1}{1-x}}$ $\rightarrow \frac{\frac{1-1+x}{1-x}}{\frac{1}{1-x}} \rightarrow \frac{x}{1} \rightarrow \mathrm{x}$

14. The function f(x) = 2^x is

one-one mapping
one-many
many-one
none of these

Answer:(1) one-one mapping

15. The range of the function f(x) = log₁₀(1 + x) for the domain of real values of x when is 0≤ x ≤ 9 is

[0,1]
[0,1,2]
[0, -1]
none of these

Answer: (1) [0, 1]

16. The Inverse function f^-1 of f(x) = 2x is

1/2x
x/2
1/x
none of these

Answer: (2) x/2

f(x) = 2x

y = 2x->x =y/2

∴ Inverse -> f^-1 =x/2

17. If f(x)= x+3, g(x) = x², then fog(x) is

x² + 3
x² + x + 3
(x + 3)²
none of these

Answer: (1) x² + 3

Fog x = f(g(x)) = g(x) + 3 = x² + 3

18. If f(x) = x+3, g[x] = x², then f(x).g(x] is

(x + 3)²
x² + 3
x³ + 3x²
none of these

Answer:(3) x³ + 3x²

f(x).y(x) = (x + 3) (x²) = x³ + 3x²

19. The Inverse h^-1 when h(x) = log₁₀x is

log₁₀x
10x
log₁₀(1/x)
none of these

Answer: (2) 10x

h(x) = log₁₀ x

y = log₁₀x -> 10y = x

h^-1 = 10x

20. For the function h(x) = 10^1+x the domain of real values of x where 0 ≤ x ≤ 9, the range is

10 ≤ h(x) ≤ 10¹⁰
0 ≤ h(x) ≤ 10¹⁰
0<h(x)<10
none of these

Answer:(1) 10 ≤ h(x) ≤10¹⁰

h(x).10x+1, 0 ≤ x ≤ 9

at 0 smallest→ 10¹

At 9 biggest value→ 10¹⁰

10 ≤ h(x) ≤ 10¹⁰

21. Let A = (1,2,3), B = (2,3,4), then which of the following is a function from A to B?

{(1,2),(1,3),(2,3),(3,3)}
{(1,3), (2,4)}
{(1,3),(2,2), (3,3)}
{(1,2),(2,3),(3,2),(3,4)}.

Answer: (3) {(1,3), (2,2), (3,3)}

for a function every element in domain should have an image & not more than one

22. If f: Q —» Q is defined as f (x) = x², then f^-1 (9) is equal to

3
-3
{-3,3}
0

Answer:(3) {-3.3}

y = x²

x=y

f^-1(x)=y

f^-1=9

or -3->{-3,3}

23. Let f(x) = | x-1|. Then,

f(x²) = [f(x)]²
f(x+y) = f (x) f(y)
f(|x|) = |f(x)|
none of these

Answer: (4) none of these

24. If A = {1,2,3}, B = {x, y}, then the number of functions that can be defined from A into B is

12
8
3f(x)
-f(x)

Answer: (2) 8

25. Let A = {x ∈ R : x ≠ 0, – 4 ≤ x ≤ 4} and f: A —> R be defined by f(x) = |x|/x for x ∈ A. Then A is

{1,-1,}
{x:0≤x≤4}
{1}
{x:-4≤ x ≤ 0}

Answer: (1) {1,-1}

$\frac{|x|}{x}=\left\{\begin{array}{cc}
1 & 4 \geq x>0 \\
-1 & -4 \leq x<0
\end{array}\right.$

26. If f:R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x² + 7, then the values of x such that g (f(x)) = 8 are

1,2
-1,2
-1,-2
1,-2

Answer: (3) -1, -2

g(f(x)) = 8

f(x)² + 7 = 8

(2x + 3)² =1

2x + 3 = 1 or 2x + 3 = 1

2x = -2 X = -1

x = -2

27. Let R is the set of real numbers, such that the function f: R→ R and g : R → R are define by f(x) = x² + 3x + 1 and g(x) = 2x- 3. Find (fog):

4x² + 6x + 1
x² + 6x +1
4x²- 6x + 1
x² – 6x + 1.

Answer: (3) f(x) = x² + 3x + 1

g(x) = 2x – 3

fog = f{g(x)}

= f (2x – 3)

= (2x- 3)² + 3(2x – 3) +1

4x²- 2.2X.3 + 9 + 6x – 9 + 1

= 4x² – 6x + 1

(3) is correct

28. If R is the set ofreal numbers such that the function f: R →R is defined by f(x) = (x+1)², then find (fof)

(x+1)²+ 1
x²+1
{(x+1)²+1}²
None

Answer:(3) f(x) = (x + 1)²

fof=f{f(x)} = f{(x+1)²)

= { (X + 1)² + 1)²

(3) is correct

29. If f: R → R. f(x) = 2x + 7, then the inverse of f is:

f^-1 (x) = (x-7)/2
f^-1 (x) = (x + 7)/2
f^-1(x) = (x – 3)/2
None.

Answer: (1) Let y = f(x) = 2x+ 7

Or 2x = y-7

Or$x=\frac{y-7}{2}$

$f^{-1}(x)=\frac{x-7}{2}$

30. Let f: R → R be such that f(x) = 2^x, then f(x+y) equals:

f(x) + f(y)
f(x). f(y)
f(x) ÷ f(y)
None of these

Answer: (2) f(x) = 2X

f(x+y) = 2x+y = 2x2y = f(x).f(y)

(2) is correct

31. If A = {1,2,3,4,}; B = {2,4,6,8,} f(1) = 2, f(2) = 4, f{3) = 6 and f(4) = 8, and f: A->B then f^-1f: A->B then f-1 is:

{(2,1),(4.2),(6,3),(8,4)}
{(1,2),(2,4),(3,6),(4,8)}
{(1.4),(2,2),(3,6),(4,8)}
None of these

Answer:(1) f^-1 = {(2,1),(4,2),(6,3)1(8,4)}

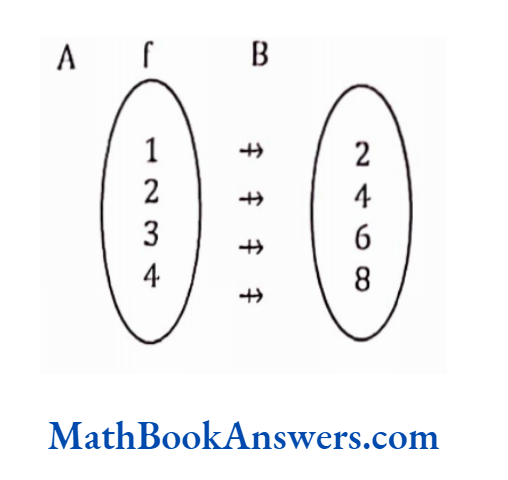
(1) is correct

32. If f(x) = x² + x -1 and 4f(x) = f(2x) then find ‘x’

4/3
3/2
-3/4
None of these

Answer:(2) f(x) = x² + x-1

And 4f(x) = f(2x)

Or 4(x² + x- 1) = (2x)²+ 2x-1

Or 4x² + 4x – 4 = 4x² + 2x-1

Or4x-2x = 4-1

Or 2x = 3 x = 3/2

(2) is correct

33. X = {x,y,w,z} y ={1,2,3,4); H={(x,1);(y,2);(y,3);(z,4);(x,4)}

H is a function from x to y
H is not a function from x to y
H is a relation from y to x
None of these

Answer:(2) H is not a function from x to y because x has 2 images 1 & 4

(2) is correct

34. Given the function f(x) = (2x+3), then the value of f(2x) – 2f(x) + 3 will be:

Answer: (4) f(x) = 2x + 3

f(2x) – 2 f(x) + 3

= 2(2x) + 3 – 2(2x+3)+3

= 4x + 3 – 4x – 6 + 3 =0

(4) is correct

35. If f(x) = 2x + h then find f(x+h)-2f(x)

h-2x
2x-h
2x+h
None of these

Answer:(1) f(x) = 2x + h

f(x + h) – 2f(x)

= 2x + 2h + h – 4x – 2h

= h – 2x

(1) is correct

36. If F: A→ R a real valued function defined by f(x) =1/x then

R
R -{1}
R-{0}
R-N

Answer: (2)

f(x) =1/x is defined at all x ∈ R except x = 0

A = R – {0}

(3) is correct

37. If f: R — R, f(x) = x + 1, g: R → R g[x) = x² +1 then fog(-2) equals to

6
5
-2
None

Answer: (1) f(x) = x + 1

g(x) = x² + 1. => g(-2) = (-2)² +1 = 5

fog (-2) = f{g(-2)) = f(5)

=5+1=6

(1) is correct

38. If f(x-1) = x²- 4x + 8, then f(x+1) =

x² + 8
x² + 7
x² + 4
x² – 4x

Answer: (3) f(x-1)=x²-4x + 8

=(x-1-1)2-4 (x-1+1) + 8

f(x+1) = (x+ 1 + 1)² – 4(x+ 1 + 1)+8

= (x+2)²- 4(x+2) + 8

= x² + 4x + 4-4x-8 + 8

= x² + 4

(3) is correct

39. If A – {±2, +3}B = {1,4,9)ANS F = {(2,4),(-2,4),(3,9){-3,4)} Then F is defined as:

One to one function from A into B
One to one function from A onto B
Many to one function from A onto B
Many to one function from A into B.

Answer:(3)

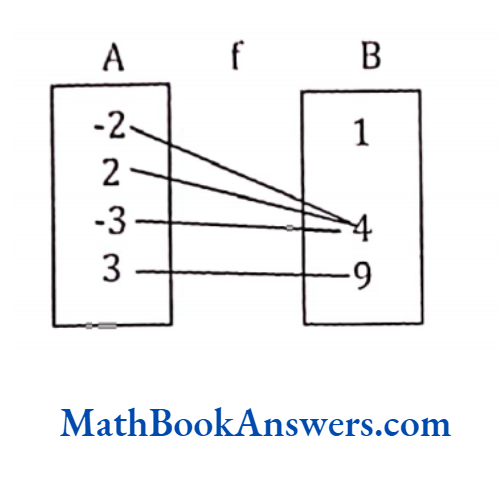
(3) is correct

40. $\text { If } f(x)=\frac{x}{\sqrt{1+x^2}} \text { and } g(x)=\frac{x}{\sqrt{1-x^2}} \text { find fog? }$

x
1/x
$\frac{x}{\sqrt{1+x^2}}$
$x \sqrt{1+x^2}$

Answer:

(1) fog = f{g(x)}$=f\left(\frac{x}{\sqrt{1-x^2}}\right)$

$=\frac{\frac{x}{\sqrt{1-x^2}}}{\sqrt{1+\frac{x^2}{1-x^2}}}$ $=\frac{\frac{x}{\sqrt{1-x^2}}}{\sqrt{\frac{1-x^2+x^2}{1-x^2}}}$ $=\frac{x}{\sqrt{1-x^2}} \times \frac{\sqrt{1-x^2}}{\sqrt{1}}=x$

(1) is correct

41. E(x) = 3 +x, for -3 < x < 0 and 3 – 2x for 0<x<3, then value of f(2) will be

-1
1
3
5

Answer: (1) is correct

f(x) = 3 + 2x; when -3 < x < 0

= 3- 2x ; when 0 < x < 3

f(x=2) = 3- 2x² = -1

2 lies in 2nd condition

42. The range of the function f: N —> N; = (-1)^x-1 , is

{0,-1}
{1,-1}
{1,0}
{1,0,-1}

Answer: (2) is correct

f(x)-(-1)x-1

If x= odd no.

f(x) = odd no.

f(x) = 0; even N.

Range = {1 ; -1)

Domain = {Any real No.}

43. If f: R —> R is a function, defined by f(x) = 10x – 7, if g(x) = f^-1 {x), then the value of g(x) is
equal to

$\frac{1}{10 x-7}$
$\frac{1}{10 x+7}$
$\frac{x+7}{10}$
$\frac{x-7}{10}$

Answer: (3) is correct

Let y= f(x) = 10x-7

Or 10x = y + 7

$x=\frac{y+7}{10}$ $f-1(x)=\frac{x+7}{10}$ $g(x)=\frac{x+7}{10}$

44. If f(x) = x+2, g(x} = 7^x then go f(x} =

7^x.x+2.7^x
7^x+2
(7^x)+2
None

Answer: f(x) = x+2 ; g(x) = 7x

g,pf(x) = g{f(x)} = g(x+2) = 7^x+2

(2) is correct

45. If f(x)=$\log \left(\frac{1+x}{1-x}\right) \text { then } f\left(\frac{2 x}{1+x^2}\right)$

f(x)
2f(x)
3 f(x}
-f(x)

Answer: (2)

$f\left(\frac{2 x}{1+x^2}\right)=\log \left(\frac{1+\frac{2 x}{1+2 x^2}}{1-\frac{2 x}{1+x^2}}\right)$ $=\log \left(\frac{1+x^2+2 x}{1+x^2-2 x}\right)$ $=\log \frac{(1+x)^2}{(1-x)^2}=\log \left(\frac{1+x}{1-x}\right)^2$ $=2 \log \left(\frac{1+x}{1-x}\right)=2 f(x)$

(2) is correct

46.$\text { If } f(x)=\frac{x^2-25}{x-5} \text { then } f(5) $

0
1
10
Undefined

Answer: (4) is correct

$f(5)=\frac{x^2-25}{x-5}=\frac{5^2-25}{5-5}=\frac{0}{0}$

Undefined

47. $\mathrm{f}(\mathrm{x})=\left(a-x^n\right)^{\frac{1}{n}}$,a > 0 and n is positive integer then f [f(x)] =

x
a
x¹^/n
a ¹^/n

Answer: (1) is correct

$\mathrm{f}\{\mathrm{f}(\mathrm{x})\}=\mathrm{f}\left\{\left(\mathrm{a}-\mathrm{x}^{\mathrm{n}}\right)^{1 / n}\right\}$ $=\left[a-\left\{\left(a-x^n\right)^{\frac{1}{n}}\right\}^n\right]^{\frac{1}{n}}$ $=\left[a-\left(a-x^n\right)\right]^{\frac{1}{n}}=\left[x^n\right]^{\frac{1}{n}}=x$

48. If A = {1,2,3} and B = {4,6,7} then the relation R = {(2,4)(3,6)} is

A function
A function from A to B
Both {a} and (b}
Not a function

Answer: (4) is correct.

Note: -1 has no image

49. $\text { If } f(x)=\frac{x}{x-1} \text {, then } \frac{f(x / y)}{f(y / x)}=$ ___________

x/y
y/x
-x/y
-y/x

Answer:

$f(x)=\frac{x}{x-1}$ $f(x / y)=\frac{x / y}{x / y-1}=\frac{x / y}{\frac{x-y}{y}}=\frac{x}{x-y}$ $f(y / x)=\frac{y / x}{y / x-1}=\frac{y / x}{\frac{y-x}{x}}=\frac{y}{-(x-y)}$ $\frac{f(x / y)}{f(y / x)}=\frac{\frac{x}{x-y}}{y}=-\frac{x}{y}$

50. Let N be the set of all natural number; E be the set of all even natural numbers then the function f:N→ E defined as f{x) = 2x; V x ∈ N is:

One-one into
One-one onto
Many-one into
Many-one onto

Answer:(2) is correct

N = {1,2, 3,…;n}

E = {2,4, 6……;2n}

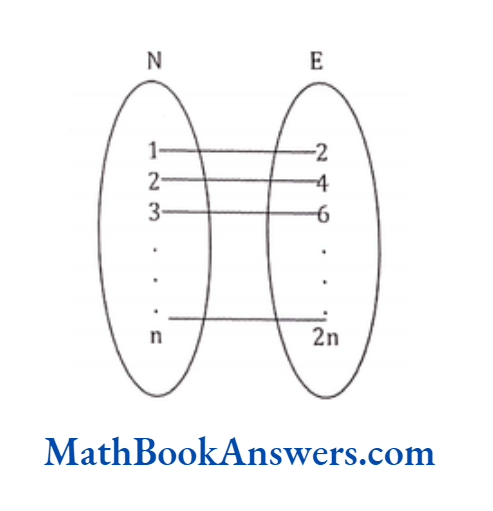
Clearly it is one-one onto mapping

51. Which of these is a function from A →B; A = {x,y,z}; B {a,b,c,d}

{(x,a)(x,b)(y,c)}
{(x,a}(x,b)(y,c)(z,d)}
{9x,a} (y,b) (z.d)}
{(a,x)(b,z)(c,y)}

Answer: (3)

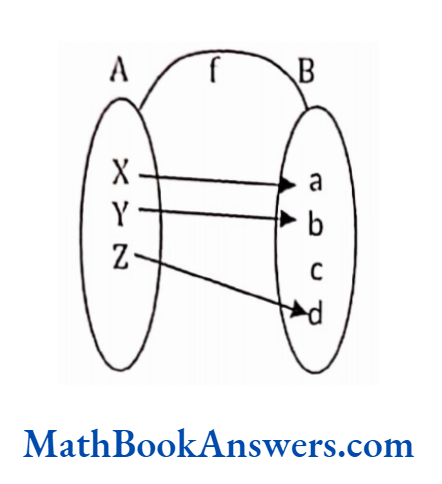
52. If (x) = 2x + 2, g(x) = x², fog(4) = ?

Answer: Fog (x) = f{g(x)}

= f(x²) = 2.x² + 2

Fog (4) = 2 x 4² + 2 = 34

(3) is correct

53. The domain (D) and range (R) of the function f(x) = 2-|x+1|is

D = Real numbers, R = (2,∞)
D= Integers, R= (0,2)
D = Integers, R = (-∞, ∞)
D = Real numbers, R = (-∞,2]

Answer: (4)

Lety = f(x) = 2-|x+1|

For any real values of x: f(x) is defined

Domain = D Real number

Minimum value of |x+1| is zero

Maximum value of range

=2-0=2

Range = – ∞ < y ≤ 2

= (-∞; 2]

54. If f (x) = 100 x then f^-1 (x) =

x/100
1/100x
1/100
None of these

Answer: (1) is correct

Let y = f (x) = 100x

$X=\frac{y}{100} ; \text { So, } f^{-1}(x)=\frac{x}{100}$

Chapter 7 Sets, Functions, And Relations Step-By-Step Solutions

55. f: R —> R is defined by f (x) = 2^x then f is

One- one and onto
Many to one
One-one and into
One to many

Answer: (2) is correct

56.$\text { If } f(x)=\frac{x-1}{x} \text { and } g(x)=\frac{1}{1-x} \text { then fog }(x)=$

x-1
x
1-x
-x

Answer: fog(x) = f{g(x)}$=\frac{g(x)-1}{g(x)}$

$=\frac{\frac{1}{1-x}-1}{\frac{1}{1-x}}=\left(\frac{1-1+x}{1-x}\right) \times \frac{(1-x)}{1}$

= X

Option (2) is correct

57. $\text { If } \mathrm{f}(\mathrm{x})=\frac{x+1}{x+2}=\text { then } \mathrm{f}\left[\mathrm{f}\left(\frac{1}{x}\right)\right]=$____________

$\frac{2 x+3}{3 x+5}$
$\frac{2 x+5}{3 x+2}$
$\frac{3 x+2}{5 x+3}$
$\frac{5 x+2}{2 x+3}$

Answer: (1)

$f\left(\frac{1}{x}\right)=\frac{1 / x+1}{1 / x+2}=\frac{1+x}{x} \times \frac{x}{1+2 x}$ $=\frac{1+x}{1+2 x}$

Now, $\mathrm{f}\left[f\left(\frac{1}{x}\right)\right]=\mathrm{f}\left(\frac{1+x}{1+2 x}\right)$

$=\frac{\frac{1+x}{1+2 x}+1}{\frac{(1+x)}{1+2 x}+2}=\frac{\frac{3 x+2}{1+2 x}}{\frac{5 x+3}{1+2 x}}$ $=\frac{3 x+2}{5 x+3} .$

58. If f(x) = x² and g(x) = √x then

go f(3) = 3
go f(-3) = 9
go f(9) = 3
go f(-9) = 3

Answer:(1)

f(x) = x² ; g(x) = √x

go f(x) = g {f(x)}

√f(x) = √x²

= X

gof(3) = 3

(1) is correct.

CA Foundation Maths Solutions For Chapter 6 Sequence & Series

November 15, 2024July 5, 2024 by Alekhya

CA Foundation Maths Solutions For Chapter 6 Sequence And Series Introduction

Terms arranged in n definite order from ;i sequence. The terms in a sequence may lie numbers, letters, symbols or even words.

Here, we consider general sequences, before moving on to three specific mathematical sequences known as progressions i.e., arithmetic, geometric and harmonic before considering
number series.

CA Foundation Maths Solutions For Chapter 6 Sequences

A Sequence is a logically ordered list of elements related to each other by some relationship.

Identify the pattern followed by the terms in a sequence and use the pattern to find the terms of the sequence, sum of the terms in the sequence or to identify properties of the sequence.

Terms of a sequence are generally denoted by T₁,T₂, T₃,……. T_n

A lot of sequences either display a difference-based or a multiplicative pattern.

However, there are infinite ways in which sequences can be formed. Only a couple of patterns are discussed below to show how to analyze a sequence and mathematically represent it.

Read and Learn More CA Foundation Maths Solutions

Difference

In these sequences, consecutive terms are related to each other in terms of the difference between the two.

This difference can be constant or may follow a logical pattern itself.

For example, consider the sequence 1, 3,7,13, 21, 31

Observe that the difference between successive terms is 2,4,6,8, and 10.

Hence, the pattern followed by the difference is that they are all multiples of 2. Hence, the term after 31 should be 31+12=43. Mathematically, each term of the sequence can be expressed as:

T₁ =1+2×0=1
T₂=1+2×1=3
T₃ =3+2X2=7
T₄ =7+2X3=13
T₅ =13+2×4=21
T₆ =21+2X5=31

Thus, the n,h term of the sequence can be written as T_n = T_n 4+ 2(n — 1)

We can see that the nth term depends on the previous term as well as its position in the sequence.

Hence, T₇= 31+2×6=43

The advantage of representing a sequence mathematically is that later terms of the sequence can be found easily without the need to write the entire sequence.

For instance, in the above case, if T₃₈ is known and the value of T₄₀ is to be found, there is no need to write the entire sequence up to 40 terms. Instead, using the value of T₃₈, the value of T₃₉ and consequently, that of T₄₀ can be found in just 2 steps.

CA Foundation Maths Chapter 6 Sequence And Series Solutions

Solved Examples

Find the 7th term of the sequence 1,2,4,7,11, 16

Solution:

T₁ =1
T2=1+1=2
T3=2+2=4
T4=4+3=7
T5=7+4=11
T₆ =11+5=16

The nth term or this sequence can he expressed as

T_n =T_n-1+(n- 1)
T₇ =T₆ + (7- 1)
= 16+6
=22

Here the 7th term of this sequence would be 16+6=22

Cumulative Sequence

Consider the sequence 1,1,2,3,5,8,13, 21…. From the sequence observes that after the second term, the next term is the sum of the previous two terms. Hence the sequence mathematically represented in the following manner

T₁= 1
T₂=1
T₃ = 1+1=2
T₄ =2+1=3
T₅ =3+2=5
T₆ =5+3= 8
T₇ = 8+5=13
T₈ =13+8=21
and so on.

As can be seen, the next term is the sum of its previous two terms, hence

T_n = T_n-1 + T_n-2

∴T₉= T₈+ T₇

∴ T₉ =21+13=34

In these types of sequences, the pattern is formed with the help of its previous terms.

Solved Examples:

Find the next term of the series 3,4,11,24, 43

Solution:

Difference between the 1st and 2nd term=l

Difference between the 2ml and 3rd term=7=l+6

Difference between the 3rd and 4lh term=13=7+6

Difference between the 4th and 5lh term =19=13+6

Thus, the difference between the 5th and 6th terms=19+6=25.

Hence the next term is 43+25=68.

CA Foundation Maths Solutions For Chapter 6 Progressions

There are 3 specific types of sequences which show a specific mathematical relationship among their terms. These 3 types, also known as progressions, are named Arithmetic
Progression, Geometric Progression and Harmonic Progression

Arithmetic Progression

The terms of a sequence are said to be in Arithmetic Progression (A.P.) when they differ by a constant value known as their Common difference, dented by d. In other words, the
difference between any two consecutive terms in an A.P. is constant. The first term of an A.P. is generally denoted by a.

If d > 0, the A.P. is said to be an increasing A.P.

If d < 0, the A.P. is said to be a decreasing A.P.

If d = 0, each term of the sequence is equal.

Some A.P.s are given below.

1)1,2,3,4……where a= 1 and d= 1
2) 3.7, 11. 15…where a= 1 and d= 1
3) 8,2,-4,-10 … where a = 8 and d =-6

THE nth TERM OF AN A.P.

The first, second, third…nth terms of an A.P. are denoted by T₁, T₂ T₃,….T_n

For any arithmetic progression having the first term a and common difference d,

T₁ = a = a + [1-1) d
T₂ = a + d = a + (2-1) d
T₃ = a + 2d = a + (3-1) d and so on.

Continuing thus, the n,h term of an A.P. is, Tn=a+(n-1) d

Solved Examples

1. Find the fifteenth term of term A.P. -3,-9,-15,…….

Solution:

T_n=a+(n-1) d

Here, a = -3, d= -9-(-3) = -6 and n =15

T₁₅= -3 + (14)(-6)

T₁₅ = -87

2. The ninth term exceeds the fifth term of an A.P. by 32. The sum of the ninth and fifth terms is 114. Find the eighth term of the A.P.

Solution:

T₉ = a + (9 – 1)d = a + 8d

T₅ = a + (5- 1)d = a + 4d

T₉ + T₅ = 32

∴ (a+8d) – (a+4d)=32

∴ 4d=32

∴ d=8

T₉ + T₅ =(a +8d) + (a+4d) =2a+12d

T₉ + T₅ =114

114 = 2(a+6d)

a + 6d = 57

T8= a + 7d = a + 6d + d = 57 + 8 = 65

3. The 54th and the 4th terms of an A.P. are – 61 and 64 respectively. Find the 23rd term.

Solution:

The 54th and 4th term of the given A.P. can be represented as shown below.

a +53d= – 61 ……………………(i)

a + 3d = 64 ……………..(ii)

Subtracting we get

50d = -125

d= -5/2,

a= 64-3d=143/2

Hence the 23rd term = a+22d= 143/2+22(-5/2)=33/2

Sum of N Terms of An A.P.

Let the first term and common difference of an A.P. containing n terms he a and d respectively. Let Tn be the last term of the A.P. Then, the sum of n terms of the A.P. is
S_n= n/2[2a+ (n- 1)d] =n/2[a + T_n]

Solved Examples

1. The sixth and eighth terms of an A.P. are 38 and 52 respectively. Find the sum of the first twelve terms of the A.P.

Solution:

T₆ = a + 5d = 38

T₈ = a + 7d = 52

Solving the two equations, d= 7 and a=3

The sum of12 terms of the A.P. is

S₁₂=12/2[2×3 + (11)7] = 498

2. How many terms of the series -12, -9, -6, … must be taken so that the sum may be become 78?

Solution:

The given sequence is an A.P. with a = -12 and d =3

For an A.P. the sum of the first n terms is

s_n =n/2[2a + (n-l)d]

The sum ofn terms of this sequence is 78

n/2 x [2a + (n- 1)d] = 78

n/2 x [—24 + (n- 1)3] = 78

nx (n- 9) = 52

n=13

Average of the Terms of an A.P.

The average or the arithmetic mean ofn terms of an A.P

$=\frac{S_n}{n}=\frac{n}{2} \times \frac{\left|a+T_n\right|}{n}$

The average of n terms of an A.P

$=\frac{a+T_n}{2}$

The average of n terms of an A.P.

$=\frac{(a+d)+\left(T_n-d\right)}{2}$

The average of n terms of an A.P.

$=\frac{(a+2 d)+\left(T_n-2 d\right)}{2}$

Continuing thus, we see that the average of the terms of an A.P. is equal to the average of its first and nth terms, second and f(n-l),th terms, third and (n-2),th terms and so on.

In general, the average of the terms of the A.P. is equal to the average of the kth term from the beginning and the kth term from the end, or it is equal to average of any two terms
of the A.P. that are equidistant from the beginning and the end.

Also, if n is even the average of the A.P.is equal to the average of its

(n/2) th and (1+n/2)th terms.

if n is odd, the average of the terms of the A.P. is equal to the (n+1/2) th term of the A.P.

Solved Examples

1. The sum of the first nine terms of an A.P. is 387. Pind the fifth term,

Solution:

Since n is odd, the average of the first n terms of the A.P, is equal to the (n = 1)/2th

term = 5″‘ term.

Hence, the average of the first 9 terms of the A.P. = the (9 + 1)/2th term = 5,th term.

∴the 5′” term of the A.P. = 387/9= 43

If any two consecutive terms of an arithmetic progression are known, the series can be completely determined.

2. The fourteenth and fifteenth terms of an A.P. are 25 and 32 respectively. Find the 30th term, sum of the first 30 terms and the first term of the A.P.

Solution:

T₁₄ = a + 13d = 25

T₁₅ = a + 14d = 32

d = 7 and a = -s66

T30-66+29X 7 = 137

The sum of the first n terms = n/2 (a+T_n)

The sum of the first 30 terms

=30/2(-66+137)=1065

3. A teacher observes that the marks that the students in her class have scored are all different. She arranges her students in a line in increasing order of their marks such
that difference in marks scored by any two students next to each other is 4. The lowest marks that any student has scored are 11. The sum of the marks that all her students
have scored is 585. Find the marks scored by the student standing in the middle of the line.

Solution:

Since the difference in the marks of any two adjacent students is 4, the marks of the students standing in the line form an A.P. with a = 11 and d=4

Let there be n students in the class.

s_n = n/2 [2a + (n- l)d]

∴585 = n/2[22 + (n- 1)4]

∴(n) (2n+9) = 585

On solving this equation,

∴n = 15

The 8th student stands in the middle of the line. Since n = 15, the average of the first 15 terms is equal to the value of the (15+1)/2,h term = 8th term.

Hence, the value of the 8lh term of this A.P.

= 585/15 = 39

Hence, the marks of the 8lh student are 39.

Note:

When three terms are in Arithmetic progression, the middle term is the arithmetic mean of the other two. It is always convenient to take three terms in an A.P. as (a-d), a and (a + d).
Similarly, four terms in an A.P. could be taken as a-3d, a-d, a + d and a + 3d; five terms could be taken as a -2d, a – d, a, a+ d, a + 2d.

The advantage of representing terms in tin’s way is that the sum of terms is then obtained in only one unknown, i. e. when the sum of these terms is written mathematically, d cancels out and the sum is expressed only in terms of a.

Sequence And Series Chapter 6 Ca Foundation Answers

Some Properties of an A.P.

If each term of an A.P. is increased, decreased, multiplied or divided by the same non -zero number, then the resulting sequence is also an A.P. In case the terms are increased or decreased by some quantity, the common difference of the new A.P. remains equal to that of the original A.P.

In case the terms are multiplied or divided by a constant c (c≠0), the common difference d accordingly changes to d x c or d/c.

The number of elements in an arithmetic series from n₁ to n₂ with a step size (or common difference) ofm is1 = (n₁-n₂)/m

Solved Examples

1. How many multiples of 13 lie between 1000 and 5000? What is the sum of all these multiples?

Solution:

The lowest multiple of 13 that is greater than 1000 is 1001. The greatest multiple of 13 that is lesser than 5000 is 4992.

Here, m=13, n₁=1001 and n₂=4992

$\text { There are } \frac{4992-1001}{13}+1$

=308 multiples of 13 between 1000 and 5000. The sum ofall these multiples is

S=n/2(a+T_n)

S=308/2(1001+4992)

∴ S=9,22,922

If the sum of the first p terms of an A.P. is equal to the sum of the first q terms of the A.P. such that p and q are different, then the sum of (p + q) terms of the A.P. is zero.

2. The sum of the first 16 terms of an A.P. is equal to the sum of the first 24 terms of the A.P. Find the sum of the first 40 terms of the A.P.
Solution:

∴S₁₆=S24

∴S₍₁₆₊₂₄₎=0

∴S₄₀=0

CA Foundation Maths Solutions For Chapter 6 Geometric Progression

The terms of a sequence are said to be in Geometric progression (G.P.) when they increase or decrease by a constant factor. This constant factor is called the common ratio, denoted by r, and can be found by dividing any term of the sequence by the preceding term.

If the first term is positive and common ratio is greater than 1 (or if the first term is negative and the common ratio is less than1 and positive), the G.P. is an increasing G.P.

If the first term is positive and the common ratio is less than 1 and positive (or if the first term is negative and the common ratio is greater than 1), the G.P. is and decreasing G.P.

In other words, if all terms are greater than the preceding terms, the G.P. is an increasing G.P. else it is a decreasing G.P.

If the common ratio is equal to 1, all terms of the G.P. are equal.

A sequence with all terms equal is both, an A.P. and a G.P.

If the first term is a, the terms of the progression are a, ar, ar², ar³……………

THE nth TERM OF A.G.P

If T₁, T₂, T₃ ….Tn denote consecutive terms of a G.P. then

T₁= a= ar^1-1

T₂ – ar= ar^2-1

T₁= ar2= ar^3-1

Continuing thus, the n,h term of the geometric progression is given by T_n= ar^n-1

Solved Examples

1. Find the fifth tern if the G.P. whose first terms is 3 and the common ratio is 1/3.

Solution:

a=3 and r= (1/3)

The 5th term =ar^5-1= ar⁴=3(1/3)^5-1

=3/81

=1/27

2. The product of the first five terms of an A.P. is 28. Find the third term.

Solution:

ax arx ar²xar³xar⁴=28

a⁵r¹⁰ =28

(ar²)⁵= 28

ar² =⁵√28

∴the third term = ⁵√28

Alternatively, In such a case, assume the central term to be a and find the other terms from this point onwards, In this case, there are 5 terms in all. Hence, let the third term of this G.P. be a.

Hence, the 1st, 2nd 4th, and 5″‘ terms will be a/r², a/r, ar, and ar².

a/r²xa/rxaxarxar²=28

a⁵=28

The third term =a= ⁵√28

In case the G.P. has an even number of terms, one can take the two central terms to be a/r and ar and proceed from there.

Sum of N Terms of a G.P.

The sum of n terms or a G.P. with

r< 1 is a(1-rⁿ)/1-r The sum of n terms of a G.P. with

r <1 is a(rⁿ-1)/r-1 The sum of an infinite number of terms of a decreasing G.P.

=a/1-r

Geometric Mean

If terms

a₁,a₂,a_n are in G.P. then the Geometric mean G of these n terms is given by

G=ⁿ√a₁xa₂xa₃x…………..xa_n

If three terms are in G.P. then the middle term is the Geometric mean of the other two terms. If a, b and c are in G.P. (a, c > 0 or a, c < 0), then b is the geometric mean of a and c, and is given by b = ac or b² = ac

If n is even, the geometric mean of the terms of the G.P. is equal to the geometric mean of its (n/2) th and 1+(n/2)th terms.

If n is odd, the geometric mean of the terms of the G.P. is equal to the

(n+1/2)th term of the A.P.

Note:

While solving problems, three terms in G.P. can be assumed to be a/r, a and ar. Similarly, four terms in G.P. can be assumed to be a/r³, a/r, ar and ar³.

The advantage of representing terms in this way is that the product of terms is then obtained in only one unknown, i.e. in the product, r cancels out and the product is then expressed only in terms of a.

Some Properties of a G.P.

If each term of a G.P.is multiplied or divided by the some non-zero quantity, then the resulting sequence is also a G.P. with the common ratio remaining the

The reciprocals of the terms of a given G.P. also form a G.P. where the ratio is the reciprocal of that of the earlier G.P.

In a finite G.P. the product of two terms equidistant from the first and the last terms is same as the product of the first and the last term.

Exercise – 1: Arithmetic Progression (AP)

Choose the most appropriate option ( 1 ), ( 2 ), ( 3) or (4).

1. The nth element of the squence 1,3,5,7………………is

n
2n – 1
2n +1
none of these

Answer: (2) 2n – 1

Seq =1,3,5,7…

a = 1 d = 2

a_n = 1 + (n-l)d= 1 + [n-1)2

= 1 + 2n – 2 = 2n – 1

2. The nth element of the sequence -1, 2, -4, 8 is

(-1 )ⁿ2^n-1
2^n-1
2ⁿ
none of these

Answer: (1)(-1)ⁿ2^n-1

Seq = -1,2, -4, 8

a = 1

n = 1 (-1)1 21-1 =-l

n = 2 (-1)2 22-1 = 2

n = 3 (-1)3 23-1 = -4

a_n= (-1)ⁿ 2^n-1

3. $\sum_{i=4}^7 \sqrt{2 i-1}$

$\sqrt{7}+\sqrt{9}+\sqrt{11}+\sqrt{13}$
$\sqrt[2]{7}+2 \sqrt{9}+2 \sqrt{11}+2 \sqrt{13}$
$\sqrt[2]{7}+2 \sqrt{9}+2 \sqrt{11}+2 \sqrt{13}$
None of these

Answer: (1) $\sqrt{7}+\sqrt{9}+\sqrt{11}+\sqrt{13}$

$=\mathrm{i}=4 \sum_{i=4}^7 \sqrt{8-1}=\sqrt{7}$ $\sqrt{7}+\sqrt{9}+\sqrt{11}+\sqrt{13}$ $=\mathrm{i}=5 \sqrt{2 i-1}=\sqrt{9}$

4. The sum to 00 of the series -5,25,-125,625…..can be written are

$\sum_{k=1}^{\infty}(-5)^k$
$\sum_{k=1}^{\infty} 5^k$
$\sum_{k=1}^{\infty}-5^k$
none of these

Answer: (1)

$\sum_{k=1}^{\infty}(-5)^k$

= -5,25,-125,625

= (-5)¹, (-5)²,( 5)³

= (-5)^k

5. The first three terms of sequence when nth term tn is n2- 2n are

-1,0,3
1, 0, 2
-1,0,-3
none of these

Answer: (1) -1,0,3

= nth terms = tn = n² – 2n

=1st term = t₁ = 1 – 2 = -1

= 2nd term = t₂ = 4 – 4 = 0

= 3rd term = t₃ = 9 – 6 = 3

6. Which term of the progression -1,-3,-5,………Is -39

21st
20 th
19th
none of these

Answer:(2) 20 th

= a = -1 d = -2

a_n= -39

-1 + (n-1) (-2) = -39

(n-1) (-2) = -38

n – 1 = 19. Therefore, n = 20

7. The value of x such that 8x + 4, 6x- 2, 2x + 7 will form an AP is

15
2
15/2
none of the these

Answer: (3) 15/2

= d will be same if in AP

= d = a_n+1+an

= 6x – 2 – 8x- 4 = 2x + 7 – 6x + 2

-2x – 6 = -4x + 9

2x=15 Therefore, x =15/2

8. The mth term of an A. P. is n and nth term is m. The rth term ofit is

m + n +r
n + m- 2r
m + n + r/2
m + n – r

Answer: (4) m + n – r

1) = a_m = a+(m-1)d

a + dm- d = n

2) = a_n= a + (n-1)d

a + dn – d = m

Substracting 2) from 1]

d + dn – d = m

a + dm – d = n
– – +

a (n-m) = m-n

d = -1

a = m + n – 1

a_r = m + n -1 (r-1) (-1)

=m+n-1-r+1

= m + n – r

9. The number of the terms of the series………….will amount to 155 is

30
31
32
none of these

Answer: (1) 30 and (2) 31

$=10+9 \frac{2}{3}+9 \frac{1}{3}+9 \ldots \ldots$ $=10+\frac{29}{3}+\frac{28}{3}+9+\ldots \ldots$

= a= 10 d= -1/3

S_n = n/2 (2a + (n- l)d)

155 =n/2(20 + (n-1)-1/3

310 = 20n -1/3n(n-1

310 = 20n-1/3(n2-n)

930 = 60n – n² + n

n² – 61n + 930 =

n(n-30) -31(n-30) = 0

n = 31 n = 30

10. The nth term of the series whose sum to n terms is 5n² + 2n is

3n – 10
10n – 2
10n – 3
none of these

Answer: (3)

= S_n = 5n² + 2n

S₁ = a₁ = 5+2 = 7

S₁ = a₁ + a₂ = 5(2)² + 2(2) = 24

S₂-S₁ = a₂

24-7 = a₂

a₂= 17

d = a₂-a₂= 10

a_n = 7 + (n-1) 10

= 7 + 10n – 10

= 10n – 3

11. The 20th term of the progression 1, 4, 7, 10,……is

58
52
50
none of these

Answer: (1) 58

= 1,4,7,10

a = 1, d = 3

a_n = 1 + (n-1)3

= 1 + 3n – 3

= 3n – 2

a₂₀ = 3(20)-2 = 58

12. The last term of the series 5, 7, 9,…..to 21 terms is

44
43
45
none of these

Answer: (3) 45.

= a₂₁ = 5 + (n-1)2

= 5 + (20)2

= 45

13. The last term of the A.P. 0.6, 1.2, 1.8,… to 13 terms is

8.7
7.8
7.7
none of these

Answer: (2) 7.8

= a₁₃ = 0.6 + (12) 0.6

= 0.6 (1+12)

= 0.6 x 13 = 7.8

14. The sum of the series 9, 5, 1,…. to 100 terms is

-18,900
18,900
19,900
none of these

Answer: (1) -18,900

S₁₀₀ = n/2 (2a + (n – 1)d) = 50(18 + 99(-4))

= 18-396

= -18,900.

15. The two arithmetic means between -6 ami 1 4 is

2/3,1/2
$2 / 3,7 \frac{1}{3}$
$-2 / 3,-7 \frac{1}{3}$
none of these

Answer: (2) 2/3, 7 1/3

Two A-M between – 6 & 14

a=-6 a4=14

a₄=-6+3d=14

3d=20 d=20/3

$\mathrm{a}_2=-6+\frac{20}{3}=\frac{2}{3} \mathrm{a}_3=-6+\frac{40}{3}=+7 \frac{1}{3}$

16. The sum of three integers in AP is 15 and their product is 80. The integers are

2, 8, 5
8, 2, 5
2, 5, 8
8, 5, 2

Answer: (3) & (4)

= let 3 integers be a – d, a, a + d

Sum = a-d + a + a + d = 3a=15->a = 5.

(a – d) (a + d) a = 80

(a² – d²)a = 80

a² – d² = 16

a² – 16 = d²

25 – 16 = d² = 9 -7 d =±3.

AP when a = 5, d = 3

2,5,8

AP when a = 5, d = -3

8,5,2.

17. The sum of n terms of an AP is 3n² + 5n. The series is

8,14,20,26
8, 22, 42, 68
22, 68, 114,
none of these

Answer: (1)

S₁ = 3 + 5 = 8 = a,

S₂ = 12 + 10 = 22

a₂ = S2 – S1 = 14, d = 6

Series -> 8, 14, 20,……..

18. The number of numbers between 74 and 25,556 divisible by 5 is

5,090
5,097
5,095
none of these

Answer: (2) 5097

-7 75.80,……….25,555

It forms an AP with a = 75 d = 5

25,555 = Last term = a_n

A_n = 75 + (n-1)5

25,555 = 75 +(n-1)5

25480 = (n-1)5

5096 = n-1

5097 = n.

19. The pth term of an AP is (3p- 1)/6. The sum of the first n terms of the AP is

n(3n + 1)
n/12 (3n + 1)
n/12 (3n – 1)
none of these

Answer: (2) n/2(3n + l)

$\rightarrow \mathrm{a}_1=\frac{3(2)-1}{6}=\frac{2}{6}=\frac{1}{3}$ $a_2=\frac{3(2)-1}{6}=\frac{5}{6}$ $d=\frac{5}{6} \frac{-2}{6}=\frac{3}{6}=\frac{1}{2}$ $3_n=\frac{n}{2}(2 a+(n-1) d)=\frac{n}{2}\left(\frac{2}{3}+\right.$ $\left.(n-1) \frac{1}{2}\right) \text {. }$ $\frac{n}{2}\left(\frac{2}{3}+\frac{1}{2} n-\frac{1}{2}\right)=\frac{n}{2}\left(\frac{1}{6}+\frac{1}{2} n\right)$ $=\frac{n}{12}(1+3 n)$

20. The arithmetic mean between 33 and 77 is

50
45
55
none of these

Answer: (3) 55.

AM = a + C

$A M=\frac{a+c}{2}=\frac{33+77}{22}=\frac{110}{2}=55$

21. The 4 arithmetic means between -2 and 23 are

3, 13, 8, 18
18, 3, 8, 13
3, 8, 13, 18
none of these

Answer: (3) 3,8,13,18

->-2,_,_,_,_,_,23

a = 2

a₆= 23 = a + 5d = 23

-2 + 5d = 23

d = 5.

a₂=-2+5=3

a₃=3+5=8

a₄=8+5=13,

a₅=13+5=18.

Given = -2,3,8,13,18,23.

22. The first term of an A.P is 14 and the sums of the first five terms and the first ten terms are equal is magnitude but opposite in sign. The 3rd term of the AP is

6×4/11
6
4/11
none of these

Answer: $6 \frac{4}{11}.$

-> S₅ = -S₁₀

$\frac{5}{2}(28+4 d)=-\left(\frac{10}{2}\right)(28+9 d)$

28 + 4d = -56 -18d

22d = -84

d=-84/22=42/11

a₃=14+2(-42/11)

=70/11

= 6×4/11

23. The sum of a certain number of terms of an AP series -8, -6, -4,……is 52. The number of terms is

12
13
11
none of these

Answer: (2) 13.

S_n = 52

a = -8, d==2

S_n =n/2 (-16 + (n-1)2)

52 x 2 = n(-16+2n-2) = 104

= -18n + 2n²

2n²- 18n-104 = 0

n²- 9n – 52 = 0

n²- 13n + 4n – 52 = 0

n(n-13)+4(n-13)=0

n = 13

24. The first and the last term of an AP are -4 and 146. The sum of the terms is 7171. The number of terms is

101
100
99
none of these

Answer: (1) 101

S_n = n/2(a + 1)

7171=n/2(-4 + 146)

14342 = n(142)

n = 101

25. The sum of the series 3 x1/2 + 7 + 10 x1/2 + 14 + …. to 17 terms is

530
535
535×1/2
none of these

Answer: (3) 535×1/2

a = 3.5 d=3.5

S₁₇ = 17/2(3.5×2 + (17 -1)3.5)

= 17/2(7 + 56) = 535×1/2

26. Three numbers are in AP and their sum is 21. If 1, 5, 15 are added to them respectively, they form a G. P. The numbers are

5, 7,9
9,5,7
7, 5,9
none of these

Answer: (1) 5,7,9

= S = 3a = 24 = a = 7

If 1,5,15 are added terms are

a-d + 1, a + 5, a + d + 15

8 – d, 12, 22+d -> GP

∴12/8-d=22+d/12

144 = (22+d) (8-d)

144=176-22d+8d-d²

d² + 14d – 32 = 0

d² + 16d – 2d – 32 = 0

d(d+16)-2(d+16) =0

d = 2, d = -16

If a = 7, d = 2

= AP = 5,7,9

If a= 7, d= -16

AP = 23,7,-9

27. If p, q and r are in A.P. and x, y, z are in G.P. then xq-r. yr-q. Zp-q is equal to

0
-1
1
none of these

Answer: (3) 1

q-p = r-q

p-q = q-r

2q = p+r

y² = xz

x^q-r.y^r-p.z^p-q

x^p-q.z^p-q.y^r-p

(x·z)^p-q.y^r-p

(y)^2p-2q.y^r-p

y^2p-2Q+r-P

y^p+r-2q→y^p+r-2q →y^2q-2q→y⁰= 1 (p +r = 2q)

28. The sum of 3 numbers in A.P. is 15. If 1, 4 and 19 be added to them respectively, the results are is G. P. The numbers are

-26, 5, -16
2, 5, 8
5,8,2
none of these

Answer: (1),(2)

a-d, a, a+d

be in AP

a-d+a+d+a=15

a=5

if 14,19 added

terms 6-d, 9, 24+d = GP

81 = (6-d)(24+d)

81 = 144 + 6d – 24d – d²

d² + 18d – 63 = 0

d² + 21d -3d – 63 = 0

d(d+21) -3 (d+21) = 0

d=21,d=3, -> d=3, and d=-21

Series = 2,5,8 if a = 5, d=3

Series = -26,5,-16 if a = 5, d = -21

29. If the terms 2x, (x+10) and (3x+2) be in A.P., the value of x is

7
10
6
none of these

Answer: (3) 6.

same common difference = d

x + 10 – 2x = 3x + 2 – x- 10

10-x = 2x-8

18 = 3x

x = 6

30. If A be the A.M. of two positive unequal quantities x and y and G be their G. M, then

A < G
A>G
A ≥ G
A ≤ G

Answer: (b) A > G.

If two unequal quantities present

AM > GM

A > G

CA Foundation Maths Chapter 6 Detailed Solutions

31 The A.M. of two positive numbers is 40 and their G. M. is 24. The numbers are

(72, 8)
(70,10)
(60,20)
none of these

Answer: (1) 72,8

AM=a+c/2 ac=GM²

80 = a + c ac = 576

$80=\frac{576}{c}+c \quad a=\frac{576}{c}$

80c = 576 + c²

C²- 80c + 576 = 0

C²- 72c- 8c + 576 = 0

C(c-72)-8 (c-72) = 0

C = 72, C = 8

If C = 72, a = 8

If C = 8, a= 72,8

= 72,8

32. Three numbers are in A.P. and their sum is 15. If 8, 6, 4 be added to them respectively, the

2, 6, 7
4,6,5
3,5,7
none of these

Answer: (3) 3,5,7

Sum = 15

13a = 15s = a= 5

If 8,6,4 is added respectively

13-d, 11,9 + d -> GP

121 = (13-d) (9+d)

121 = 117 + 13d -9d -d²

d² – 4d + 4 = 0

d²- 2d -2d + 4 = 0

d(d-2)-2(d-2) = 0

d = 2.

Series -> 3,5,7.

33. A sum of is paid off in 30 instalments such that each instalment is *?10 more than the proceeding instalment. The value of the 1st instalment is

36
30
60
none of these

Answer: (4) none of the above

S₃₀ = 6240

6240 =30/2(2a + 290)

416 = 2a + 290

2a =126 a = 63

34. If x, y, z are in A.P. and x, y, (z + 1) are in G.P. then

(x- z)² = 4x
z² = (x- y]
z = x- y
none of these

Answer: (1)

x,y, (z+1) = GP

y² = (z + 1)x

2y = x +z

y = x + z

$y^2=\left(\frac{x+2}{4}\right)^2 \rightarrow 4(z+1) x=(x+z)^2$

4xz + 4x = x² + z²+ 2zx

2xz + 4x = x² + z²

4x = x² + z² – 2xz

(x- z)²= 4x

35. The numbers x, 8, y are in G.P. and the numbers x, y, -8 are in A.P. The value of x and y are

(-8, -8)
(16,4)
(8,8)
none of these

Answer: (1) (2)

X,8,y = GP

X,y,-8 = AP

2y-64/2 = —8 -> 2y²- 64 = -8y

2y² + 8y- 64 = 0

Y² + 4y- 32 = 0

Y² + 8y- 4y- 32 = 0

y(y+8) – 4y- 32 = 0

y(y+8) – 4 (y+8) = 0

y = 4 y=-8

x= 16 x=-8

36. The sum of all odd numbers between 200 and 300 is

11,600
12,490
12,500
24,750

Answer: (4) 12,500

201,203,…….299

AP with a = 201, d = 2

I = 299, a = 201, d = 2

299 = 201 + (n – 1) 2

98= (n- 1)2

49 = n-1= n = 50

S₅₀= n/2 (a + 1) = 25 (201 + 299)

= 12,500

37. The sum of all natural numbers between 500 and 1000 which are divisible by 13, is

28,405
24,805
28,540
none of these

Answer: (1) 28,405

= 507,520,……. 988

AP, a = 507 d = 13 I = 988

988 = 507 + (n – 1) 13

481 = (n – 1) 13

37 = n-1 = n = 38

S₃₈ = 38/2 (507 + 988) = 28,405

38. If unity is added to the sum of any number of terms of the A.P. 3, 5, 7, 9…….the resulting sum is

‘a’ perfect cube
‘a’ perfect square
‘a’ number
none of these

Answer: (2) Perfect square

If 1 is added to any sum

It is same as adding1 as

A term of AP, So AP becomes

AP: 1,3, 5, 7……….

These are n natural odd number

Now sum of first n natural odd no. is n2 i.e. perfect square

39. The sum of all natural numbers from 100 to 300 which are exactly divisible by 4 or 5 is

10,200
15,200
16,200
none of these

Answer: (3) 16,200

Natural no. divisible by 4 or 5

= natural no divisible by 4 + natural no divisible by 5

= natural no divisible by 4 & 5 i.e. 20

100, 104………..300

AP -> a = 100 d = 41 = 300

N = 51 terms

= S₅₁ = 51/2 (100+300)

Sum of natural no divisible by 4 = 10200

For divisible by 5

100,105,…..300

AP, a = 100 I = 300 d = 5 n=41

S₄₁ = 41/2 (100 + 300) = 8200

Sum of natural no divisible by 5 = 8200

For4&5

100,120,…..300

AP a = 100 d = 20, I = 300, n = 11

S₁₁ = 11/2 (100 + 300) = 2200

∴ sum of natural no divisible by 4 or 5

= 10200 + 8200-2200= 16200

40. The sum of all natural numbers from 100 to 300 which exactly divisible by 4 and 5 is

2,200
2,000
2,220
none of these

Answer: (1) 2200

Divisible by 4 & 5

i.e. divisible by 4 x 5 = 20

100,120……300

AP -> a = 100 d = 20 I = 300 n = 11

S₁₁ =11/2 (100 + 300)

= 2200

41. A person pays 975 by monthly instalment each less then the former by 5. the first instalment is 100.The time by which the entire amountwill be paid is

10 months
15 months
14 months
none of these

Answer: (2) 15 months

a = 100

d = -5

100,95,…….

S_n = 975, n =?

975 =n/2 (200 + (n – 1) (-5))

1950 = n (200 – 5n + 5)

1950 = 205 – 5n²

5n²- 205n+ 1950 = 0

n² – 41n + 390 = 0

n²-26n- 15n + 390 = 0

n (n – 26) – 15 (n-26) = 0

n = 15 or n = 26

15 months

42. A person saved 16,500 in ten years. In each year after the first year he saved 100 more than he did in the precedinh year. The amount of money he saved in the 1st year was

1000
1500
1200
none of these

Answer: (3)

d = 100

S₁₀ = 16500

16500 = 10/2 (2a + 9 (100))

33000 = 10 (2a + 900)

3300 -900 = 2a

a = 1200

CA Foundation Maths Solutions For Chapter 6 Exercise – 2: Geometric Mean

Choose the most appropriate option (1), (2), (3) or (4)

1. The 7th term of the series 6, 12, 24,……… is

384
834
438
none of these

Answer: (1) 384

GP: 6, 12, 24,

A = 6 r=12/6=2

a₇ = ar^7-1 = ar⁶

= 6(2)⁶ =384

2. t₈ of the series 6, 12, 24,…is

786
768
867
none of these

Answer: (2) 768

GP: 6, 12, 24….

a = 6, r = 2

a₈= ar^8-1 = ar⁷

= 6 (2)⁷ =768

3. t₁₂ of the series -128, 64, -32, ….is

– 1/16
16
1/16
none of these

Answer: (3) 1/16

t₁₂ = a¹¹ =- 128 (-1/2 )11 =1/16

4. The 4th term of the series 0.04, 0.2, 1, … is

0.5
1/2
5
none of these

Answer: (3) 5

0.04, 0.2, 1,………….

a = 0.04 r= 5

a₄=ar³

=0.04(5)³ = 5

5. The last term of the series 1, 2, 4,…. to 10 terms is

512
256
1024
none of these

Answer: (1) 512

a = 1, r=2

a₁₀ = ar⁹ = 1(2)⁹ = 512

6. The last term of the series 1, -3, 9, -27 up to 7 terms is

297
729
927
none of these

Answer: (1) 729
a = 1, r = -3

a₇ = ar⁶= 1(-3)⁹ =729

7. The last term of the series x2, x, 1, …. to 31 terms is

x²⁸
1/x
1/x²⁸
none of these

Answer: (3) 1/x²⁸

a = x², r = 1/x

a₃₁=ar₃₀=x²(1/x)³⁰

=x²x1/x³⁰=x^-28=1/x²⁸

8. The sum of the series -2, 6, -18, …. to 7 terms is

-1094
1094
– 1049
none of these

Answer: (1) -1094

a = -2, r = -3

a₇= ar⁶ = -2(-3)⁶ = -1458

GP = -2, 6,-18,……-1458

S_n =Ir-1/r-1 =-1094

9. The sum of the series 243, 81, 27, …. to 8 terms is

36
$\left(36 \frac{13}{30}\right)$
$36 \frac{1}{9}$
none of these

Answer: (4) none of these

a = 243 r = -1/3

$S_8=\frac{a\left(1-r^n\right)}{1-r}=\frac{243\left(1-\frac{1}{3}_3^8\right)}{1-\frac{1}{3}}$ $=\frac{243(0.999847) .3}{2}$

= 364.4445 = 364.45

10. The sum of the series $\frac{1}{\sqrt{3}}+1+\frac{3}{\sqrt{3}}+\ldots . . \text { to } 18 \text { terms is }$

$9841 \frac{(1+\sqrt{3})}{\sqrt{3}}$
9841
$\frac{9841}{\sqrt{3}}$
none of these

Answer:

$9841 \frac{(1+\sqrt{3})}{\sqrt{3}}$ $a=\frac{1}{\sqrt{3}}, \quad r=\sqrt{3}$ $S_{18}=\frac{a\left(r^n-1\right)}{r-1}=\frac{1}{\sqrt{3}} \frac{\left(\left(\sqrt{3)}^{18}-1\right)\right.}{\sqrt{3}-1}$ $\frac{1}{\sqrt{3}} \frac{\left(\sqrt{3}^{18}-1\right)(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\frac{1}{\sqrt{3}} \frac{\left(\sqrt{3}^{18}-1\right)(\sqrt{3}+1)}{3-1}$ $=\frac{1}{2 \sqrt{3}}\left(\sqrt{3}^{18}-1\right)(\sqrt{3}+1)$ $=9841 \frac{(1+\sqrt{3})}{\sqrt{3}}$

11. The second term of a G P is 24 and the fifth term is 81. The series is

16,36,24, 54,..
16, 24,36,54,..
24,36, 53,…
none of these

Answer: (3)

16, 24, 36, 54

ar = 24 ar⁴ = 81

$\frac{a r^4}{a r}=\frac{81}{27}=r^3=\frac{81}{27}$ $=r^3=\left(\frac{3}{2}\right)^3 \quad r=\frac{3}{2}$ $\mathrm{ar}=24=\mathrm{a}=\frac{24.2}{3}=16$

12. The sum of 3 numbers of a G P is 39 and their product is 729. The numbers are

3, 27, 9
9,3, 27
3, 9. 27
none of these

Answer: (3)

Sum = 39 product =729

a/r, a, ar

a/r.a.ar=729

a³=729

a/r+a+ar=39

9/r+9+9r=39

9(1/r+1+r)=39

$9\left(\frac{1+r+r^2}{r}\right)=39$

9 (1 + r + r²) = 39x

9 + 9x + 9x² = 39r

9r²-30r + 9 = 0

9r²- 27r- 3r + 9 = 0

9r(r-3)-3 (r-3) = 0

r=3/9 r=3

when, r = 3, GP = 3, 9,27

When r= 1/3 GP = 27, 9,3

13. In a G. P, the product of the first three terms 27/8. The middle term is

3/2
2/3
2/5
none of these

Answer: (1) 3/2

GP= a/r, a, ar

a/r.a.ar=27/8=a³=27/8=a=3/2

14. If you save 1 paise today, 2 paise the next day 4 paise the succeeding day and so on, then your total savings in two weeks will be

163
183
163.83
none of these

Answer:(3) 163.83 Rs

a₁₄ = ar¹³, a = 1, r = 2

= 1(2)¹³ =8192

$S_{14}=\frac{I r-a}{r-1}=\frac{16384-1}{1}=16383 \text { paise }$

= 163.83 Rs.

15. Sum of n terms of the series 4 + 44 + 444 + …………. is

4/9 {10/9 (10ⁿ -1) -n}
10/9 ( 10ⁿ -1 ) -n
4/9(10ⁿ-!) -n
none of these

Answer:(1) 4/9 {10/9 (10ⁿ -1) -n}

4 + 44 + 444 +………

4/9(9 + 99 + 999 +…..)

=4/9[(10-1)+(10²-1)+(10³-1)+…..(10ⁿ-1)]

=4/9(10+10²+10³……10ⁿ-n)

=4/9(10+10²+10³……10ⁿ-1)-n)

$=\frac{4}{9}\left(10\left(\frac{10^n-1}{9}\right)-n\right)$ $=\frac{4}{9}\left(\frac{10}{9}\left(10^n-1\right)-n\right)$

16. Sum of n terms of the series 0.1 + 0.11 + 0.111 + … is

1/9 {n – ( 1-(0.1)ⁿ)}
1/9 {n- (1-(0.1)ⁿ)/9)
n-1 – (0.1)ⁿ/9
none of these

Answer:(2) 1/9 {n- (l-(0.1)ⁿ)/9)

= 0.1 +0.11 + 0.111 +……….

= 1/9(0.9 + 0.99 +……)

= 1/9[(1-1/10)+(1-1/10²+…..)

= 1/9[n-(1/10+1/10²+……)]

= 1/9[n-1/10(1+1/10+1/10²+…….)]

$=\frac{1}{9}\left[n-\frac{1}{10}\left(\frac{1-\frac{1}{10}}{1-\frac{1}{10}}\right)\right]$ $=\frac{1}{9}\left[n-\frac{1}{10}\left(\frac{1-10^{-n}}{9}\right) 10\right]$ $=\frac{1}{9}\left[n-\left(\frac{1-10^{-n}}{9}\right)\right]$

=1/9 {n- (l-(0.1)ⁿ)/9)

17. The sum of the first 20 terms of a G. P is 244 times the sum of its first 10 terms. The common ratio is

±√3
±3
√3
none of these

Answer:(1) ±√3

$\frac{a\left(r^{20}-1\right)}{r-1}=244 \frac{(a)\left(r^{10}-1\right)}{r-1}$

r²⁰ – 1 = 244 (r¹⁰– 1)

y² – 1 = 244 (y- 1)

y² – 1 = 244y – 244

y² – 244y + 243 = 0

y² – 243y – y + 243 = 0

y (y – 243) – 1 (y – 243) = 0

y = 243 y=1

y = r¹⁰

r¹⁰ = 243 r¹⁰ = 1

(±√3)¹⁰=243 r=±1

r= ±√3

18. Sum of the series 1 + 3 + 9 + 27 +….is 364. The number of terms is

5
6
11
none of these

Answer: (2) 6

$S n=\frac{a\left(r^n-1\right)}{r-1}$ $=364=\frac{1\left(3^n-1\right)}{2}$

19. The product of 3 numbers in G P is 729 and the sum of squares is 819. The numbers are

9, 3, 27
27, 3, 9
3, 9, 27
none of these

Answer: (3) 3, 9, 27

Product 729 ; sum of squares = 819

a/r. a . ar = 729

a³ = 729

a = 9

a/r,9,9r = 9²/r² + 81 + 81r² = 819

81(1/r²+1+ r²) = 819

81 (1 + r² + r⁴) = 819r²

81 + 81r- + 81r⁴ = 819r²

81r⁴ – 819r² + 81r² + 81 = 0 = 81 r⁴

738r² + 81 = 0

9r⁴ – 82r²+ 9 = 0

9r⁴ – 81r² — 1 r² + 9 = 0

$9 r^2\left(r^2-9\right)-1\left(r^2-9\right)=r^2 \frac{1}{9}, r^2=9=r \frac{ \pm 1}{3}$

r = ±3

When ± 3, a = 9

GP = 3,9,27 & -3,9,-27

When ± 1/3 a=9

GP= 27,9,3 & -27,9,-3

20. The sum of the series 1 + 2 + 4 + 8 + .. ton term

2ⁿ-1
2n – 1
1/2ⁿ -1
none of these

Answer: 2ⁿ – 1

$S_{11}=\frac{1\left(2^n-1\right)}{2-i}=2^n-1$

21. The sum of the infinite GP 14, – 2, + 2/7,- 2/49, + … is

$4 \frac{1}{12}$
$12 \frac{1}{4}$
12
none of these

Answer: $12 \frac{1}{4}$

$S_n=\frac{a}{1-r}=\frac{14}{1+\frac{1}{7}}=\frac{7 \times 14}{8}=\frac{49}{4}=12 \frac{1}{4}$

22. The sum of the infinite G. P. 1 – 1/3 + 1/9 – 1/27 +… is

0.33
0.57
0.75
none of these

Answer: (3) 0.75

$\mathrm{S}_{\mathrm{n}}=\frac{a}{1-r}=\frac{1}{1+\frac{1}{3}}=\frac{3}{4}=0.75$

23. The number of terms to be taken so that 1 + 2 + 4 + 8 + will be 8191 is

10
13
12
none of these

Answer: (2) 13

s_n= 8191

a = 1 r = 2

$S_n=\frac{1\left(2^n-1\right)}{1}=8191$

2ⁿ = 8192 n=B

24. Four geometric means between 4 and 972 are

12,36, 108,324
10,36, 108,320
12, 24,108,320
none of these

Answer: (1)

a = 4 I = 972

ar^n-1 = 972

ar⁵ = 972

4r⁵ = 972

r⁵ = 243 = r = 3

4,12,36,108,324, 972

25. The sum of 1 + 1/3 + 1/32 + 1/33 + … + 1/3n-1 is

2/3
3/2
4/5
none of these

Answer: (b)3/2

a = 1 x =1/3

$S=\frac{a}{1-x}=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}$

26. The sum of the infinite series 1 + 2/3 + 4/9 + .. is

1/3
3
2/3
none of these

Answer: (2) 3.

a = 1 x = 2/3

$S=\frac{a}{1-x}=\frac{1}{1-\frac{2}{3}}=\frac{3}{1}=3$

27. The sum of the first two terms of a G.P. is 5/3 and the sum to infinity of the series is 3. The common ratio is

1/3
2/3
– 2/3
none of these

Answer: (2) & (3)

$\frac{a}{1-x}=3$

a = 3(l-x) = 3 -3x

a(l+x)=5/3

(3-3X)(1+X)=5/3

3(1-X)(1+x)=5/3==1-X²=5/9

$1-\frac{5}{9}=x^2=\frac{4}{9}=x^2=x=\frac{2}{3}$

How To Solve Sequence And Series In CA Foundation

CA Foundation Maths Solutions For Chapter 6

28. The sum of three numbers in G.P. is 70. If the two extremes by multiplied each by 4 and the mean by 5, the products are in AP. The numbers are

12, 18, 40
10, 20, 40
40, 20, 10
none of these

Answer: (2) & (3)

a + ax + ax² = 70

A.P = 4a, 5ax, 4ax²

10ax = 4a + 4ax²

10ax = 4a(1+x²)

5/2 x=1+x²

2x²- 5x + 2 = 0

2x²- 4a- x + 2 = 0

2x(x- 2) — 1(x — 2) = 0

x= 1/2,X = 2.

29. Given x,y,z. are in G.P. and Xp = Yq = Zσ then 1/p,1/q.1/a are In

A.P
G.P
Both A.P & G.P
None of these

Answer: (1)AP

X^p = Y^q = Z^σ

y² = xz

X^p = Y^q = Z^σ = k

$x=k^{\frac{1}{p}}, y=k^{\frac{1}{q}}, z=k^{\frac{1}{\sigma}}$ $k^{\frac{2}{q}}=k^{\frac{1}{p}} \cdot k^\sigma$ $k^{\frac{2}{q}}=k^{\frac{1}{p}}+\sigma$ $\frac{2}{9}=\frac{1}{p}+\frac{1}{\sigma}=2\left(\frac{1}{q}\right)=\frac{1}{p}+\frac{1}{\sigma}$ $\frac{1}{p}, \frac{1}{q}, \frac{1}{\sigma} \text { are in AP. }$

30. The sum of 1.03 + ( 1.03 )²+ ( 1.03 )³+ …. to n terms is

103 {(1.03)ⁿ– 1}
103/3 {(1.03)ⁿ– 1}
(1.03)n -1
none of these

Answer: (2)

1.03(1 + (1.03) +(1.03)² +……(1.03)ⁿ-1)

$1.03\left(\frac{(1.03)^n-1}{1.03-1}\right)$ $\frac{1.03}{0.03}\left((1.03)^n-1\right)$ $\left.=\frac{103}{3}\right)\left((1.03)^n-1\right)$

31. The nth term of the series 16, 8, 4…..is 1/217. The value of n is

20
21
22
none of these

Answer: (3) 22

a = 16 r = 1/2.GP

ar^n-1=a_n=1/2¹⁷

$\frac{16}{2^{n-1}}=\frac{1}{2^{17}}=\frac{1}{2^{n-1}}=\frac{1}{2^{17} \cdot 2^4}$ $=\frac{1}{2^{n-1}}=\frac{1}{2^{21}}$

n- 1 = 21 -> n = 22

32. The sum of n terms of a G.P. whose first terms 1 and the common ratio is 1/2 , is equal to 1×127/128. The value of n is

7
8
6
none of these

Answer: (2)8

$S_{n}=1 \frac{127}{128}=\frac{255}{128}$ $\frac{\left(1-0.5^n\right)}{1-0.5}=\frac{255}{128}$ $\frac{\left(1-0.5^n\right)}{0.5}=\frac{255}{128}$ $1-0.5^n=\frac{127.5}{128}$

33. t₄ of a G.P. in x, t₁₀ = y and t₁₆ = z. Then

x² = yz
z² = xy
y² = zx
none of these

Answer: (3)

T₄ = X, t₁₀ = y,t₁₆ = z.

ax³ = x ax⁹ = y ax¹⁵ = z

y² = a²x¹⁹

y² = xz

34. 1 f x, y, z are in G.P., then

y²= xz
y (z² + x²) = x(z² + y²)
2y = x+z
none of these

Answer: (1)

x,y,z in GP

y² = xz

35. At 10% C.I. p.a., a sum of money accumulate to 9625 in 5 years. The sum invested initially is

5976.37
5970
5975
5370.96

Answer: (1)

Sum of money at end 9625

Time series

Initial investment =? = a

Amt = a

Amount at end first yr= a + 0.1a = a(1.1)

Amount at end second yr = a(1.1) + a(0.1)(1.1)

= a(1.1+0.11)

= a(1.21) = a(1.1)²

Amount at end of third = a(1.1)³

Amount at end of n = a(1.1)ⁿ

9625 = a(1.1)ⁿ

9625 = a(1.1)⁵

a = 5976.37

36. The population of a country was 55 crores in 2005 and is growing at 2% p.a C.I. the population is the year 2015 is estimated as

5705
6005
6700
none of these

Answer:

(3) 6700

Population initial = 55

Time 10 years

Population at end ofyr= 55 + 55(0.2) = 55(1.02)

At end ofyr 2 = 55(1.02) + 55(1.02)

(0.02) = 55(1.02)²

At end ofyrs = 55(1.02)ⁿ

S₁₀ = a(l + r)ⁿ = 55(1.02)¹⁰

S₁₀ = 6700.

CA Foundation Maths Solutions For Chapter 6 Exercise – 3 (Mix- AP and GP)

1. What is the arithmetic mean of the arithmetic progression 6,8,10,12,14,16?

Answer: Arithmetic mean = sum of the terms/number of terms

$=\frac{6+8+10+12+14+16}{6}$

= 66/6

= 11

Choice (2)

CA Foundation Maths Solutions For Chapter 6

2. What is the geometric mean of the geometric progression 2,4,8,16?

32
√32
64
8

Answer:

Geometric mean= [(2)(4)(8)(16)]^1/4

=[(21)(22)(23)(24)]^1/4=2^10/4 = √32

Alternative solution:

Geometric mean of a geometric progression

$=\sqrt{\text { first term } \times \text { last term }}$ $=\sqrt{(2)(16)}$

=32

Choice (2)

3. What is the fourth term of the arithmetic progression in which the first term is 4 and the seventh term is 28?

Answer: The fourth term is equidistant (3 teams away) from the first and the seventh term in the arithmetic progression.

the fourth term is the arithmetic mean of the first term and the seventh term in an A.P.

fourth term $=\frac{4+28}{2}$

32/2=16

choice (1)

4. What is the sum to 7 terms of the arithmetic progression in which the first term is 2 and the common difference is 4?

Answer: Sum of the first n terms of an A.P

$=s_n=\left(\frac{n}{2}\right)[2 a+(n-1) d]$ $s_n=\left(\frac{7}{2}\right)[2(2)+(7-1) 4]$ $=\left(\frac{7}{2}\right)[4+24]=\frac{7}{2}(28)=98$

choice (2)

5. What is the sum to 8j terms of an arithmetic progression in which the first term is 3 and the last term is 31?

136
58.5
132
Cannot be determined

Answer: Given first term=3 and the last term=31

As we don’t know the total number of terms, we cannot find the common difference.

we cannot find the sum of first 8 terms of the Progression, choice (4)

6. What is the arithmetic mean of an arithmetic progression with 13 terms, in which the 7lh term is 9?

9
91/7
95/7
Cannot be determined

Answer: Given total number of terms is 13, i.e. n=13 in an A.P. if n is odd

then $\frac{(n+1)^{t h}}{2}$ term is the arithmetic mean of that A.P.

as $\frac{(13+1)}{2}=7^{t h}$ ,term is the arithmetic mean

Given 7th term is 9

9 is the arithmetic mean

Choice (1)

7. What is the sum to 15 terms of an arithmetic progression’ whose 8th term is 4?

30
60
40
Cannot be determined

Answer: The 8th term is equidistant from first term and 15 terms

8th term is the arithmetic of first 15 terms sum of first 15 terms = 15x (eight term)=15(4)

=60

Choice (2).

8. What is the sum of all the terms in an arithmetic progression in which the first term is 5, the last term is 15 and the number of terms is 11?

55
110
115
Cannot be determined

Answer: in A.P

S_n=(n/2)[first term+last term]

S_n=(11/2)[5+15]=110

Choice (2)

9. What is the seventh term of an arithmetic progression whose first term is 9 and the common difference is 3?

Answer: in an A.P. n 1,1 term (t_n) = a+ (n-1) d

t₇ = 9 + (7- 1)3 = 9 + 6(3) = 27

choice (1)

10. What is the fourth term so a ‘geometric progression in which the second term is 4 and the sixth term is 64?

Answer: fourth term is equidistant from the second term and the sixth term.

in a G.P. the fourth term is the geometric mean of the second term and the sixth terms

Fourth term = $\sqrt{(\text { second term)(sixth term) }}=\sqrt{(4)(64)}=16$

choice (4).

11. What is the sum to 4 terms of a geometric progression whose first term is 6 and the common ratio is 3?

Answer: In a G.P.

$S_n=\frac{a\left(1-r^n\right)}{1-r}$ where is the common ration, a the first term and sn in the sum to n term.

$S_4=\frac{6\left(1-3^4\right)}{1-3}=\frac{6(1-81)}{2}$

=(3)(80)= 240

Choice (4)

12. In an arithmetic progression having 100 terms, the m th term form the beginning and the mthTerm from the end is 10 and 20 respectively what is the sum of all the terms?

3000
1500
3200
Cannot be determined

Answer:

As the average of the kth term from the beginning and the kth term from the end is equal to the arithmetic mean the average of 10 and 20 is the arithmetic mean i.e. the mean is

$\frac{10+20}{2}=15$

in an A.P. as S_n = n (AM.)

S₁₀₀ = 100(15) = 1500

Choice (2)

13. If m n and p are arithmetic progression then the m th term and pth term of arithmetic progression are in

Arithmetic progression
Geometric progression
Not neccessarly in arithmetic progression or geometric progression

Answer: Given m,n, and pare in A.P.

Let n-m =p- n = k

n = m + k,p = m + 2k

consider an A.P.

CA Foundation Maths Solutions For Chapter 6

a₁,a₂,a₃,a₄,…….whose connon difference is d.

a_m + d = a_m + 1[a_m is mth term]

a_m+ kd = a_m+k = a_n m+k

a_m + kd = a_m+2k = a_p m+2k

a_p – a_n = [a_m + 2kd]- (a_m + kd] = kd

a_n – a_m = a_p – a_n = kd ∴ a_m ,a_n and a_p are in A.P

m term, nth term and pth term are in A. P

Choice (1)

14. If m . n and p are in arithmetic progression then m th term, n th term and pth term of a geometric progression are in

Arithmetic progression
Geometric progression
Not neccessarly in arithmetic progression or geometric progression

Answer: Given m, n and p are in A.P.

Let n-m=p-n=k

n = m + k,p = m + 2k

Consider a G.P

g1,g2,g3——— whose common ratio is r.

gm(r) = gm+1 [gm is mth term]

gm(rk)gm+k = gn [m+k=n]

gm(r2) = gm+2k = gp [m+2k=p]

$\frac{g_p}{g_m}=\frac{g_m r^{2 k}}{g_m r^k}=r^{-k}$ $\frac{g_n}{g_m}=\frac{g_p}{g_{11}}=r^k$

gm,gn and gp are in G. P.

Choice (2)

15. If sum of first 51 terms of an arithmetic progression is zero , then which of the following terms is zero?

13th
26th
17th
Cannot be determined

Answer: In an A.P. if the sum of the first n terms is Zero, and dn is odd, the

$\frac{(n+1)^{t h}}{2}$ term is zero.

$\left(\frac{51+1}{2}\right)^{t h}$

26th term is zero

Choice (2)

16. If the sum of first 20 terms of an arithmetic progression is 30 and the sum of first 50 terms is also 30 then what is the sum of 21st term and the 50th term?

0
30
15
Cannot be determined

Answer: Given S₂₀=30 and S₅₀ = 30

S₅₀ = S₂₀ + t₂₁+——-+t₅₀

30 = 30 + t₂₁ +————-t₅₀

t₂₁+t₂₂——–+t₅₀=0

the mean of t₂₁ and t₅₀ is zero.

choice (1)

17. If the positive numbers m, n and p are in geometric progression then Ion gm, logn and log p are in

Arithmetic progression
Geometric progression
Cannot be determined

Answer: Given m, n and p are in G. P.

$\text { Let } \frac{n}{m}=\frac{p}{n}=r$

n = mr and p = mr²

Let log m=a…..(1)

Log n == log (mr)

= log m + log r[ log(xy) = logx + logy]

Let log r=b logn = a + b…..(2)

Log p = log (mr)²log m+ log r² =log m +2 log r [ log r² = 2logr]

∴ log p = a + 2b…..(3)

From 1,2,3

Log m, log n and log p are in A.P.

Choice (1)

18. If the geometric mean of two distinct positive numbers is 4, then the arithmetic mean of these two numbers is

<4
=4
>4
Cannot be determined

Answer: For any two unequal positive numbers a and b

$\frac{a+b}{2}>\sqrt{a b}$

Given √ab =4

Arithmetic mean, $\frac{a+b}{2}>4$

Choice (3)

19. What is the seventh term of a geometric progression whose first term is 3 and common ratio is 2?

Answer: In a G.P.

T_n = ar^n-1

T₇ = 3(2)^7-1

= 3(64) = 192

Choice (3)

20. What Is the product of first 9 terms of a geometric progression’ having a total of 13 terms given that 51th term is 2?

512
32
16
Cannot be determined

Answer: The 5th term is equidistant from the first term and the 9th term

5th term is the geometric mean of first and ninth term and moreover, it is the geometric mean of first 9 terms the product of the first n terms in a G.P = (Geometric mean of first n
terms)ⁿ

Product = 2⁹ = 512

Choice (1)

21. What is the geometric mean of the geometric progression having a total of 13 terms given the 7lh term is 4?

2
4
16
Cannot be determined

Answer: In G.P. if the number of terms is n which is odd, then the middle term i.e. $\left(\frac{n+1}{2}\right)^{t h}$ term is the geometric mean.

$\left(\frac{13+1}{2}\right)^{\text {th }}$ term i. e. the 7th term is the geometric mean i. e. the geomeric mean is 4.

Choice (2)

22. What is the sum of infinite geometric series 1,1/2,1/4,1/8,1/16,….?

$1 \frac{255}{256}$
2
3
4

Answer: Common ratio = $\frac{1 / 2}{1}=\frac{1}{2}$

$S_a=\frac{a}{1-1}=\frac{1}{1-1 / 2}=2$

Choice (2)

CA Foundation Maths Solutions For Chapter 6

23. Every number of an infinite geometric progression of positive terms is equal to m times the sum of the numbers is equal to m times the sum of the numbers that follow it. What is the common ratio of the progression?

$\frac{m}{m+1}$
$\frac{1}{m+1}$
$\frac{2}{m+1}$
Cannot be determined

Answer:

Let the geometric progression be a, ar, ar², …. given a = m $\left(\mathrm{ar}+\mathrm{ar}^2+\cdots=\frac{\mathrm{ar}}{1-\mathrm{r}}\right.$

=>mr = 1-r ⇒ mr + r = 1

$\mathrm{r}=\frac{1}{m+1}$

Choice (2)

24. What is the sum to 7 terms of a geometric progression whose first term is 1 and the 4th term is 27?

1093
2186
3279
4372

Answer: Given a= 1,t4= 27

t₄ = ar³

27 = (1)r³->r = 3

$S_7=\frac{1\left(1-3^7\right)}{1-3}=\frac{1-2187}{2}=\frac{-2186}{-2}=1093$

Choice (1)

25. What is the sum of the cubes of first (9 natural numbers?

45
2025
91125
Cannot be determined

Answer: Sum of the first 9 natural numbers = $\frac{9(9+1)}{2}=45$

Sum of the cubes of first n natural numbers = (sum of first n natural numbers)²

∴ Sum of the cubes of first 9 natural numbers =45²=2025

=2025

Choice (2)

26. In an arithmetic progression, the first and the last terms are 9 and 96 respectively if the sum of all the terms of the progression is 4200, what is the common difference ?

80
$\frac{76}{79}$
70
$\frac{87}{79}$
$\frac{83}{79}$

Answer:

Let the number of terms in the arithmetic progression be n.

$\frac{n}{2}[9+96]=4200 \Rightarrow n=80 \text {. }$

21th term = a+20d where a=9.

96= 9+(n-1)d = 9 + 79d

$\mathrm{d}=\frac{87}{79}$

Choice (4)

27. The sum of the first 30 terms of an arithmetic progression is 4500 the ratio of the first 20 terms and the last 10 terms in 4:5 find the first term.

Answer: Let the first term and the common difference of the arithmetic progression be a and d respectively.

$\frac{30}{2}[2 a+29 d]=4500$ 2a + 29d = 300

Sum of the first 20 terms= $\frac{4}{9}(4500)=2000$

$\frac{20}{2}[2 a+19 d] 2000$

2a = 19d = 200

Subtraction the second equation from the first 10d = 100=>d = 10

First term = $\frac{300-29 d}{2}=5$

Choice (4)

28. The sum of all the three digit numbers which leave a remainder of 3 when divided by 7 is

64215
70720
64320
70821
64160

Answer: The first three-digit number when divided by 7 leaving a remainder of 3 is 101 and the last three-digit number when divided by 7 leaving a remainder of 3 is 997.

101 = 7 X 14 + 3

997 = 7 X 142 + 3

Number of 3 digit multiples of 7= $\frac{997-101}{7}+1$ = 129 the sum of all these numbers =

$\frac{129}{2}[101+997]=129(549)=70821$

Choice (4)

29. The sum of all the natural numbers from 200 to 600 (both inclusive ) which are neither divisible by 8 nor by 12 is

1,23,968
1,33,068
1,33,268
1,87,332
1,34,168

Answer: Let the sum of all the natural numbers from 200 to 600 which are divisible neither by 8 nor by 12 be P.

P= sum ofall natural numbers from 200 to 600 – (sum ofall natural numbers divisible by either 8 or 12)

=sum of the first 600 natural numbers- sum of the first 200 natural numbers – (sum of all 3 digit natural numbers from 200 to 600 divisible by 8= sum of all 3 digit
natural numbers from 200 to 600 divisible by k12 – sum of all 3 digit numbers from 200 to 600 numbers divisible by both 8 and 12)

$=\frac{(600)(601)}{2}-\frac{(199)(200)}{2}$

– (200+208+…..+600)

+ (204+212+…. +600)

– (216+240+….+600) =(180300-19900)

$-\left[\frac{51}{2}(200+600)+\frac{34}{2}(204+600)-\frac{17}{2}(216+600)\right]=133268$

Choice (3)

30. The sum of four terms in arithmetic progression is 64. The sum of the squares of the first and the last term is 64 more than the sum of the squares of the second and the third terms. Find the first term, if the second term is less than third term.

Answer: Let the four numbers be a-3d, a-d, a + d and a-3d. a -3d+a-d+a+d+a+3d=64

4a = 64

a=16

(a- 3d)² + (a + 3d)² = (a- d)² + (a + d)² + 64

=> 18d² = 2d² + 64

d=√4 = 2 as d > 0

The first term = a- 3d = 10.

Choice (5)

CA Foundation Maths Sequence And Series Practice Problems

31. There are four distinct numbers in a sequence such that the first and the last terms are equal, the first three numbers progression and the last three are in geometric progression, find the common ratio of the last three numbers.

1
-1
-1/2
-2
2

Answer: Let the second, third and fourth numbers which are in geometric progression be a, ar and ar² respectively the first number = the fourth number = ar²

Since the first three are in arithmetic progression, ar², a and ar are in arithmetic progression.

=>2a =ar²+ ar

As the numbers are distinct, a≠0 and r≠1

=> 2=r²+r=>r²+r-2=0=>r=1 or -2 since r≠1,r=-2

Since r≠1,r=-2

Choice (4)

32. Four times the ninety first term of an arithmetic progression is equal to 5 times its eighty first terms. If the thirty first term of the progression is -630, find its fifty first term.

Answer: Let the first term and the common difference of the arithmetic progression be a and d.

4(a+90d) = 5 (a+80d)=>-40d=a

Thirty-first term of the at arithmetic progression =a +30d= -630 d=+63.

Fifty first term of that arithmetic progression =a+50d=-40d+50d=+10d=630

Choice (3)

33. The ratio of the sum of the first n terms of two arithmetic progressions is given by 5n+4:8n-15. Find the ratio of the 12th terms of the two arithmetic progressions.

125:161
119:169
123:166
115:169
119:238

Answer: Let the two arithmetic progressions’ have first terms and common differences as a₁,d₁ and a₂,d₂ respectively. Ratio of the sum of their first n terms

$=\frac{\frac{n}{2}\left[2 a_1+(n-1) d_1\right]}{\frac{n}{2}\left[2 a_2+(n-1) d_2\right]} \quad \frac{a_1+\frac{n-1}{2} d_1}{a_2+\frac{n-1}{2} d_2}=\frac{5 n+4}{8 n-15} \ldots \ldots$

Ratio of their 12th terms = $\frac{a_1+11 d_1}{a_2+11 d_2}$

Substituting $\frac{n-1}{2}=11$ in the L.H.S. we get ratio of their 12th terms.

$=\frac{5(23)+4}{8(23)-15}=\frac{119}{169}$

Choice (2)

CA Foundation Maths Solutions For Chapter 6

34. The number of terms of the series 40,37, 34,… for which the sum is 282 is _________

Answer: The first term of the arithmetic progression series is 40 and the common difference is -3 let the number of terms in the series for which the sum is 282 be n

$\frac{n}{2}[2(40)+(n-1)(-3)]=282$ $\frac{n}{2}[83-3 n]=282$

3n²- 83n + 564 = 0

3n(n-12)-47(n-12)=0

(n-12)(3n-47)=0

n=12 or 47/3 as n is an integer, n = 12.

Choice (5)

35. The sum of the first, sixth, eighth, ninth and thirteenth terms of an arithmetic progression is 243. Find the sum of the first 13 terms of the arithmetic progression.

1134
1296
1458
526.5
1588

Answer: Let the first term and the common difference of the arithmetic progression be a and d respectively.

a + (a + 4d) + (a + 5d) + (a + 7d) + (a + 8d) + a + 12d) = 243

6a = 36d = 243……. (1)

Sum of the first 13 terms = [2a + 12d] = 13[a = 6d] \(=\frac{(13)(243)}{6}(\text { from }(1))=526.5[latex]

Choice (4)

36. If 5x+y,3x+2y and 3x+y are in arithmetic progression and 5x+1, 3(x+1) and 3x are in geometric progression, find (x,y).

(4,3)
(5,2)
(3/2,3/2)
(3,3)
(3/4,3/4)

Answer: 2(3x + 2y)=5x + y + 3x + y

6x + 4y = 8x + 2y=>x = y

[3(x + 1)]² = (5x + 1)3x

9x² + 18x + 9 = 15×2 + 3x

6x²- 15x- 9 = 0

Dividing both sides by 3

2x²- 5x- 3 = 0

(2x =1)(x-3) = 0

X=-1/2 or 3; going by the choices, x=3,

Choice (4)

37. The maximum value of the sum of the series series 50,46,42,…is

Answer: Let the number of terms of the series which give the maximum sum be n

Sum =n/2[2(50)+(n-1)(-4)]

=n/2[104-4n]=n[52-2n]=2n[26-n]

When the sum of two quantities is constant, their product is maximum when the quantities are equal as n and 26-n have a constant sum of 26 their product is maximum when n = 26-n

26/2=13=n

Maximum sum = (2)(13)(13)=338

Choice (5)

38. In a geometric progression the first three terms are 10n +36,6ct + 12 and 4a respectively, find the sixth term of the geometric progression if

a > 0
5
2
3
9
6

Answer: (6n + 12)² =(10a+36) 4a

36a² + 144a + 144 = 40a² + 144a

144 = 4a², a = 6 as a > 0

sixth term of the G. P = [latex](10 a+36)\left(\frac{6 a+12}{10 a+36}\right)^5=96\left(\frac{48}{96}\right)^5=3\)

Choice (3)

39. A ball dropped from 36 m above the ground rebounds to 1/3rd of the height it falls from. If it continues to rebound in this manner, find the total distance the ball can cover.

96m
72m
54m
76m
108m

Answer:

the height to which the ball rebounds after the first fall = 36 (1/3)=12m the 2nd time it falls from 12m height. The distance the ball rebounds after the second time it falls =

36(1/3)(1/3)= 4m, it falls from 4 m height

Likewise the distance rebounded by the ball after every time can be found to be (1/3) of distance rebounded after the previous time it fell

Total distance it covers, 36+12+12+4+4+…a= (36+12+4+…a)+(12+4+…a)

=(36+12+4+…..a)+(12+4+…..a)= $\left(\frac{36}{1-1 / 3}\right)+\left(\frac{12}{1-1 / 3}\right)$

54 + 18=72m.

Choice (2)

40. Three distinct numbers in geometric progression have a product of 1728 the sum of the products taking two numbers at a time is 456. Find the least number.

Answer: Let the numbers in geometric progression be a/r,a and ar(a/r)(a)(ar)=1728

$a=\sqrt[3]{1728}=12$ $\frac{a}{r}(a r)+a(a r)+\frac{a}{r}(a)=456$ $a^2\left(1+r+\frac{1}{r}\right)=456$ $\frac{r+r^2+1}{r}=\frac{456}{12^2}=\frac{19}{6}$

6r+6r² + 6 = 19r

6r² -13r + 6 = 0

3r(2r- 3)- 2(2r- 3) = 0

(3r-2) (2r-3)=0, r= 2/3 or 3/2

The least number = $\frac{12}{3 / 2}$

Choice (1)

41. The value of sum of first 75 terms of the sequence 150 x 2 + 148 x 4 + 6146 x 6 + is

252850
292600
273950
284050
231300

Answer: Given series is 150 x 2 + 148 x 4 + 146 x 6 +….75 terms

The numbers 150, 148, 146 … from an arithmetic progression, with a=150, d=-2.

The numbers 2, 4, 6…… from an arithmetic progression with a=2, d=2

Hence, tn then nth term of the series is:

[150 + (n- 1)(—2)][2 + (n- 1)2] = (152- 2n)2n.

t_n = 304n – 4n²

Hence sum to 75 terms is s75 = 304(1 + 2 + 3 …+ 75)- 4(1² + 2² + 3² + 75²)

$=304 \times \frac{75 \times 76}{2}-4 \times \frac{75 \times 76 \times 151}{6}=292600$

Choice (2)

42. The sum of the first 20 terms of the series $\frac{3}{2}+\frac{15}{4}+\frac{47}{8}+\cdots \text { is }$

$\frac{\left(2^{20}\right)(420)-2^{20}+1}{2^{20}}$
$\frac{\left(2^{20}\right)(210)-2^{20}+1}{2^{20}}$
$\frac{\left(2^{20}\right)(210)+2^{20}+1}{2^{20}}$
$\frac{\left(2^{20}\right)(420)+2^{20}+1}{2^{20}}$
$\frac{\left(2^{20}\right)(420)-2^{20}-1}{2^{20}}$

Answer:

$\frac{3}{2}+\frac{15}{4}+\frac{47}{8}+\cdots \text { for } 20 \text { terms }$ $=2-\frac{1}{2}+4-\frac{1}{4}+6-\frac{1}{8}+\cdots \text { for } 20 \text { terms }$

=2+4+6+…for 20 terms— $\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots\right)$ for 20 terms = 2(1 + 2 + 3+…. +20)

$\frac{\frac{1}{2}\left(1-\left(\frac{1}{2}\right)^{20}\right)}{1-\frac{1}{2}}=\left[\frac{(420)(2)^{20}-2^{20}+1}{2^{20}}\right]$

Choice (1)

43. The maximum number of terms common to the arithmetic progression 3,7, 11, 15, 19,23,…403 and 5,11,17,23,29,35,… 505 is

Answer: The first common term to both arithmetic progressions is 11 and the common differences of the first and second arithmetic progressions are 4 and 6 respectively the next term common to both arithmetic progressions is 23 = 11+ L.C.M, of common differences of the two progressions= 11+12.

It can be confirmed that the term common to both series have a common difference of 12 the last term common to both progressions is less than minimum of last terms of both
progressions i.e. 403. Let n terms be common to both progressions.

The last term common to both arithmetic progressions is 11 + 12(n – 1). This is less than 403.

$n-1<\frac{(403-11)}{12}=32 \frac{2}{3}$

$n<33 \frac{2}{3}$ Hence n must be a maximum of 33.

44. Find the value of $\frac{1}{3^2-2^2}+\frac{1}{7^2-2^2}+\frac{1}{11^2-2^2}+$ $\cdots+\frac{1}{39^2-2^2}$

5/41
31/41
18/37
19/37
10/41

Answer:

$\frac{1}{3^2-2^2}=\frac{1}{(3-2(3+2)}=\frac{1}{4}\left[1-\frac{1}{5}\right]$ $\frac{1}{7^2-2^2}=\frac{1}{(7-2)(7+2)}=\frac{1}{4}\left[\frac{1}{5}-\frac{1}{9}\right]$ $\frac{1}{39^2-2^2}=\frac{1}{(39-2)(39+2)}=\frac{1}{4}\left[\frac{1}{37}-\frac{1}{41}\right]$

the required sum is 1/4[1-1/41}=10/41

Choice (5)

CA Foundation Maths Solutions For Chapter 6

45. If an is defined as follows, find the value of a50

1. a_n = 1,if n = 0

2. a_n = a_n – 1,if n = 3k, k being a positive integer

3. a_n = 3 a_n-1 If n = 3k + 1, where k is a whole number

4. a_n = 2 a_n-1 if n = 3k + 2, where k is a whole number

6¹⁷
3¹²2¹⁷
3¹⁷2¹⁸
6¹⁸
none of these

Answer: Tabulating the values of a, we have a₀ = 1

a₁ = 3

a₂ = 2(3)

a₃ = 2(3)

a₄ = 2(3)²

a₅ = 22(3)²

a₆ = 22(3)²

a₇ = 22(3)³

a₈ = 23(3)³

46. the first 15 terms of the series 32.1 + 42. 2 + 52. 3 + 62. 4 + 72. 5 +…..is _____________

16120
24420
21840
20840
19840

Answer: Each of the terms being added is of the form (a + 2)² a where 1 <a <15

Their sum =$ \sum_{a=1}^{15}(a+2)^2 a=\sum_{n=1}^{15} a^3+4 a^2+4 a$

$=\left(\frac{a(a+1)}{2}\right)^2+4\left(\frac{1}{6}\right) a(a+1)(2 a+1)+\frac{4 a(a+1)}{2}$ $=\left(\frac{15(16)}{2}\right)^2+4\left(\frac{1}{6}\right)(15)(16)(31)+\frac{4(15)(16)}{2}$

=(120)² + (4)(40)(31) + 480 = 19840

Choice (5)

47. 3100 – 2(396 + 397 + 398 + 399) =

3⁹⁶
2(3⁹⁶)
3⁹⁷
4(3⁹⁶)
5(3⁹⁶)

Answer:

3¹⁰⁰ – 2(3⁹⁶+ 3⁹⁷ + 3⁹⁸ + 3⁹⁹)

= 3¹⁰⁰– (2)3⁹⁶(3⁴ – 1)/(2) = 3⁹⁶

Choice (1)

48. A Eugenics research worker is working with two types of bacteria. One type triples in number every ten minutes while the other one becomes 5 times in the same time, if the total number of bacteria after half an hour is 1118, what was the total numberat the beginning?

Answer: Let there be x bacteria of the first kind and y of the second.

27x + 125y = 1118

The remainder of 1118/27 is 11

Taking successive multiplies of 125, the remainders are 17,7,24,14,4,21,11 (Add 17 or subtract 10)

27(9)+125(7)=1118

Hence 27(9+125)+125(7-27) and other such expression are also equal to 1118, but x=9, y=8 is the only solution in positive integers.

At the beginning there were 9+7=16 bacteria.

Choice (3)

49. The sum to infinity of the series a² (a² + b²) + a⁴(a⁴ + b⁴) + a⁶(a⁶ + b⁶) +…. where |a|≤1 and |b| ≤1 is

$\frac{a^2 b^2+a^4+2 a^6 b^2}{\left(1-a^2 b^2\right)\left(1-a^4\right)}$
$\frac{a^2 b^2-a^4-2 a^6 b^2}{\left(1-a^2 b^2\right)\left(1-a^4\right)}$
$\frac{a^2 b^2-a^4+2 a^6 b^2}{\left(1-a^2 b^2\right)\left(1-a^4\right)}$
$\frac{a^2 b^2+a^4+2 a^6 b^2}{\left(1-a^2 b^2\right)\left(1-a^4\right)}$
$\frac{a^2 b^2-a^4-2 a^6 b^2}{\left(1-a^2 b^2\right)\left(1-a^4\right)}$

Answer:

The series when expended becomes

a⁴ + a²b² + a⁸ + a⁴b⁴ + a¹² + a⁶b⁶ + …..∞

= a⁴ + a⁸ + a¹² +……∞

$=\frac{a^4}{1-a^4}+\frac{a^2 b^2}{1-a^2 b^2}=\frac{a^4\left(1-a^2 b^2\right)+a^2 b^2\left(1-a^4\right)}{\left(1-a^4\right)\left(1-a^2 b^2\right)}=\frac{a^4-2 a^6 b^2+a^2 b^2}{\left(1-a^4\right)\left(1-a^2 b^2\right)}$

Choice (1)

50. If S=3+7x+llx2 + 15×3 + …..(3 +4n)xn…and |x| < 1,S =

$\frac{3+x}{(1-x)^2}$
$\frac{3+x}{1+x^2}$
$\frac{3-x}{(1-x)^2}$
$\frac{3-x}{(1+x)^2}$
none of these

Answer:

S=3+7X+11x² + 15x³ +……-> (1)

Sx = 3x + 7x² +11x³+…..-> (2)

(1)- (2)

5(1- x) = 3 + 4x + 4x² + 4x³ + ……..

= -1+4/1-x = x + 3/1-x

S = (x + 3)/(1- x)²

Choice (1)

51. Chidanand and Dharmesh joined a company on 1 jan 1991. Chidanand was offered a starting salary of Rs. 3000 p.m. with an kannual increment of Rs.500 p.m. Dhamesh was put on a starting salary of RS.2000 p.m. with a six monthly increment of Rs. 350 p.m. if they continued working till 31 December 2000, how much more or less did Dharmesh receive compared to chidanand?

Rs.9000 more
Rs.9000 less
Rs.7500 more
Rs.7500 less
Rs. 4500 more

Answer: Chidanand’s first monthly salary is Rs.3000

His last monthly salary is Rs.7500

His average monthly salary is Rs.5250

Dharmesh’s first monthly salary is Rs.2000

His last monthly salary is is Rs 8650

His average monthly salary is Rs 5325

Dharkmesh gets 10(12) (5325-5250) = Rs. 9000 more than chidanand.

choice (1)

Chapter 6 CA Foundation Maths Answer Key

52. The sum of the first n terms of an arithmetic progression is p. the sum of the first 2n terms is Q. if Q= (4/P, find the sum of the first 3n terms of the arithmetic progression

Answer:

The sum of the first n terms is p₁ (say),that of the next n terms is P₂(say) and that of the third set of n terms is P₃ (say)

P₁, P₂, P₃ Have to be in arithmetic progression.

As P₃ are in arithmetic progression.

P₃are in aritmetic progression. P₃ = 2(Q- P)- P = 2Q- 3P …. (1)

The sum of the first 3n terms is P₁ + P₂ + p₃ = Q+P₃ = Q + (2Q- 3P)from (1) = 3Q- 3P.

As Q =4/3p,P₁ + P₂ + P₃ = 4P-3P = P

Choice (4)

53. The ratio of the sum of first 20 terms of an arithmetic progression and the sum of its first 30 terms is 10:31 if the common difference of the arithmetic progression is 2, find the first term.

$-6 \frac{3}{8}$
$-9 \frac{7}{8}$
$-8 \frac{3}{8}$
$-10 \frac{5}{8}$
$-9 \frac{5}{8}$

Answer: Let the first term and the common difference of the terms in arithmetic progression be a and d respectively

$=\frac{\frac{20}{2}[2 a+19 d]}{\frac{30}{2}[2 a+29 d]}=\frac{10}{31} \Rightarrow \frac{2(2 a+19 d}{3(2 a+29 d)}=\frac{10}{31}$

124a + 117d = 60a + 870d

64a = -308d

a=-308/64(2)

$-9 \frac{5}{8}$

Choice (5)

54. Find the sum (1)(3)+ (3)(5)+ (5)(7) + (7)(9) + …………………………………. up to 50 terms.

171700
171850
1717750
1701650
171650

Answer: (1)(3)+(3)(5)+(5)(7)+(7)(9)+……

The first parts of each term 1.3,5,7,9,… are in arithmetic progression and its nth term is (2n-1) the second parts of each term 3,5,7,9,1 1,… are also in arithmetic progression and its nth term is (2n+1)

the n term of the series is (2n-1) (2n+1) =4n² – 1

the sum ofn term of the series is (4n2-1)

= Σ(4n²- 1) =4 ∑ n² – ∑1 =$\frac{4 n(n+1)(2 n+1)}{6}-n$

The sum of the first 50 terms of the series $=\frac{4 \times 50 \times 51 \times 101}{6}-50$

=100 x 17 x 101- 50

= 171700-50=171650

Choice (5)

55. Find the sum $\frac{1}{2}+\frac{2^2}{2^2}+\frac{3^2}{2^3}+\frac{4^2}{2^4}+$

$\frac{5^2}{2^5}+\frac{6^2}{2^6}+\cdots$

Answer:

$\text { let } S=\frac{1^2}{2}+\frac{2^2}{2^2}+\frac{3^2}{2^3}+\frac{4^2}{2^4}+\frac{5^2}{2^5}+\frac{6^2}{2^6}+\cdots$ $\frac{S}{2}=\frac{1}{2^2}+\frac{2^2}{2^3}+\frac{3^2}{2^4}+\frac{4^2}{2^5}+\frac{5^2}{2^6}+\cdots$ $S-\frac{S}{2}=\frac{S}{2}=\frac{1}{2}+\frac{3}{2^2}+\frac{5}{2^3}+\frac{1}{2^4}+\frac{9}{2^5}+\frac{11}{2^6}+\cdots$ $\frac{S}{4}=\frac{1}{2^2}+\frac{3}{2^3}+\frac{5}{2^4}+\frac{7}{2^5}+\frac{9}{2^6}+\cdots$ $=\frac{1}{2}+\left[\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\cdots\right]$ $=\frac{1}{2}+\frac{1 / 2}{1-1 / 2}=\frac{1}{2}+1=\frac{3}{2} \Rightarrow S=\frac{3}{2} \times 4=6$

56. A total of 810 balls are arranged in N layers. The ith layer from the top where 2 < i < N has 4 more balls than the layer immediately above it. Which of the following is not a possible value of N?

Answer: The number of balls in the 1st, 2nd … nth layer from the top be f let the top are in arithmetic progression. Let the number of balls in the 1st layer from the top be f
total number of balls = N/2(2f+ (N – 1)4)

810 = N(f+ (n- 1)2)

To satisfy the above equation, N must be a factor of 810 only choice (5) violates this condition

Choice (5)

57. X is the set of the first 1990 natural numbers. A is an arithmetic progression having at least 3 elements. First element is the least element of x and its last element is the greatest element of x How many possibilities does a have?

Answer: The least element of A is 1 and its greatest element is 1990 suppose A has N elements and a common difference of D. then 1990= 1+(N-1) D (N-1)D=1989 =3²(17) (13)——(1)
N ≥ 3

1989 has (3) (2) (2) or 12 factors or 6 pairs of factors.

(N-1)D=1(1989)= 3(663)=9(221)=13(153)=17(117)=39(51)

As N ≥ 3, ,N-1 ≥ 2

N-1 can be 3,9,13,17,39,51,117,153,221,663 or 1989 i.e. N can have 11 values.

Choice (2)

58. Find the number of common terms to the sequences 7,11.15,19,23…..411 and 8,13,18,23,…..463

Answer: The two equerries are Aps. For any two Aps, their common terms also from on AP.

Moreover, the common difference of that AP is the LCM of the common differences of the Aps the common difference of the first and second Aps are 4 and 5 respectively the AP of common terms has a common difference of 20.

First common term to the two Aps = 23 suppose the AP of common terms has n terms then the nth cannot exceed min (last terms of the Aps) i.e. min (411,463)=411. Also N must be the largest value satisfying this condition.

∴ 23 + 20(N- 1) ≤ 411

20N = 3 ≤ 411

N ≤ 20.4

N = 20

Choice (5)

59. The nth term of the series 6,13,20,Is 636. Find n.

Answer: The nth term of an arithmetic progression with the first term a and common difference d is given by a +(n-1) d. for the given series.

a=6 and d=7 its nth term =>6+(n-1)7=636⇒n=91

Choice (2)

60. The sum of sixty numbers in arithmetic progression is 7,800. The largest of the numbers is 12 times the smallest. Find the smallest number.

Answer: Let the smallest numberbe a and common difference of the arithmetic progression be largest number = 12a

Sum of the 60 numbers =60/2[a+12a]

390a=7800

a=20

Choice (5)

61. The sum of three numbers in arithmetic progression is 36.the sum of the squares of the three numbers is 464. Find the smallest number.

Answer: Let the three numbers be a-d a and a+d

a-d + a + a + d = 36.

3a=36 a=12

(12- d)² + 12² + (12 + d)² = 464

d² = 16

d=√16=±4

If d is either +4 or -4 the numbers are 8, 12,16 the smallest is 8.

Choice (1)

62. Find the sum of all the numbers divisible by 8 and lying between 300 and 950.

90,960
1,00,480
96,480
50,544
52,648

Answer: The first number divisible by 8 above 300 is 304= (8x 38) the last number before 950 divisible by 8 is 944 i.e.8 x 118

Total number ofmultiples between 304 and 944

$=\frac{9 \cdot 4-30 \cdot}{8}+1=81, n=81 .$

Sum of all these numbers 81/2(304- 944) = 50544.

Choice (4)

63. The seventh term of a geometric progression is 3645. If the product of its first 3 terms is 3375, find the first term of the geometric progression.

Answer: Let the first, second and third terms of the geometric progression be a/r, a and ar respectively

a/r a ar = a³ =3375 =>a=√3375 = 15

Seventh term of the geometric progression =$\frac{a}{r} r^6$= ar⁵(since first term is a/r) 15r⁵=3645

r⁵ = 243

r=⁵√243 = 3

a/r=5

Choice (1)

64. A geometric progression has a sum to infinity. The value of the cube of any term is 1 /8th of the cube of the sum of the terms which follow it . find the sixth term of the geometric progression if the first term is 4.

$\frac{2}{3}$
$\frac{64}{81}$
$\frac{128}{243}$
$\frac{256}{729}$
$\frac{512}{2187}$

Answer: Let the series be 4, 4r, 4r², 4r³

Given that,(4)³ = $\frac{1}{8}\left\{\frac{4r}{1-r}\right\}^3$

$\Rightarrow 4=\frac{1}{2}\left(\frac{4 r}{1-r}\right)$

r=2/3

the sixth term = ar⁵ = (4)(2/3)⁵=128/243

Choice (3)

65. There are three numbers in arithmetic progression having a sum of 51. If the first is increased by 2, the second is increased by 1 and the third is increased by 3, the numbers would be in geometric progression. Find the smallest number in the geometric progression.

Answer: Let the first second and third numbers in arithmetic progression be a- d a and a + d.

a-d + a = a = d = 3a = 51=>a = 17

a-d + 2,a + 1 and a + d + 3 i.e. (19- d) (20 + d) = 324

=> d² + d- 56 = 0=>d = -8 or 7

So, the numbers in geometric progression are either 27, 18 and 12 or 12, 18 and 27, so whatever be the case the smallest is 12.

Choice (2)

66. The product of three numbers in geometric progression is 1728. If their sum is 37, find the smallest number.

Answer:

Let (a/r) a and ar be the numbers in geometric progression. Given that (a/r) (a)(ar) = 37

=>12/r+ 12 + 12r=37=>12r² – 25r +12 = 0

=>(3r- 4)(4r- 3) = 0=>r = 3/4 or 4/3

the numbers are 9,12,16 or 16, 12, 9, in either case, the smallest is 9.

Choice (1)

67. A geometric progression has the sum to infinity 4. The sum to infinity of the sum of the squares of the terms of the geometric progression is 6. Find the first term of the geometric progression.

24/11
32/11
96/11
40/11
16/11

Answer:

Let the first term be a and the common ratio be r.

$\frac{a}{1-r}=4 \ldots .$ $\frac{a^2}{1-r^2}=6 \ldots \ldots(2)$ $\Rightarrow \frac{a}{1-r}\left(\frac{a}{1+r}\right)=6$

from (1)and (3), We have,

$a=\frac{6}{4}(a+r)=(1-r) \Rightarrow \frac{11}{2} r=\frac{5}{2}$

r=5/11 first term = 4(1-r)=24/11

Choice (1)

68. An infinite geometric progression having a finite sum has its first term as 12. The difference of the third and the fifth terms of the geometric progression is 9/4 if the common ratio is a rational number; find the sum to infinity of the terms of the geometric progression.

12 or 15
16 or 10
20 or 12
24 or 8
12 or 8

Answer:

Let the common ratio of the geometric progression be r. the third term of the geometric progression =12r²

The fifth term of the geometric progression 12r⁴

As the geometric progression has a sum to infinity, -1 < r < 1

Hence r² < r⁴ = 9/4

Let r = a

12(a- a²) =9/4

48a- 48a² -9 = 0

16a² – 16a + 3 = 0, dividing both sides by 3

16a² – 12a -4a + 3

4a (4a- 3)- 1(4a- 3) = 0

(4a- 3)(4a- 1) = 0

a = 3/4 or 1/4

r=±1/2 as r is rational sum to infnity= $\frac{12}{1 \pm \frac{1}{2}}$

= 24 or 8

Choice (4)

69. Find the sum of the squares of the first 12 terms of the arithmetic progression for which the sum of the first n terms is 3n² + 6n

12450
13170
14100
26316
24216

Answer:

Given s_n = n(3n + 6)

a = T₁ = S₁ = 1(3 + 6) = 9

T₂ = S₂– S₁ = 2(6 + 6)- 9 = 15

d=T₂– T₁ = 15- 9 = 6

the series is 9,15,21,….

Sum of the squares of the first 12 terms of the arithmetic progression

=9² + 15² + 21²+ …….+ 75²

=3²(3²+5²+7²+…..25²)

=3²(1²+ 2²+ 3² +4² +…..+ 25²)+- 3²(1²)

=3²[(1² + 2² + 3² + 4² +….. 26²)- (2² + 4² +……+ 26²)- 1²]

$=9\left[\frac{(26)(27)(53)}{8}-\frac{2^2(13)(14)(27)}{6}-1\right]$

=9[117(53)-4(63)(13)-1]

=9(6201-3276-1]

=9[2924]=26316

Choice (4)

70. The sum of the first 12 terms of log31/2X + log31/4 x log31/6X + … 312 find x.

Answer:

$\log \frac{1}{3^2} x+\log \frac{1}{3^4} x+\log \frac{1}{3^6} x+\cdots$ $\frac{\log _3 x}{\log _3 3^{1 / 2}}+\frac{\log _3 x}{\log _3 3^{1 / 4}}+\frac{\log _3 x}{\log _3 3^{1 / 6}}+\cdots \text { for } 12 \text { terms }$

(Rewriting each term being added which is in the form

$\log _{\frac{1}{b^2}} a a s \frac{\log a}{\log b^{\frac{1}{2}}}$

and taking the base for both numerator and denominator as 3)

$\frac{\log _3 x}{\frac{1}{2} \log _3{ }^3}+\frac{\log _3 x}{\frac{1}{4} \log _3{ }^3}+\frac{\log _3 x}{\frac{1}{6} \log _3 3}+\cdots \text { for } 12 \text { term }$

= 2log₃ x +4log₃ x +6log₃ x +8log₃ x + + 24log₃ x

=(2+4+6+….+24) log₃ x= 156(log₃ x) = 132

=> log₃ x= 2=> x= 3² = 9

Choice (1)

71. If p² = q² -q⁴ + q⁶ – q⁸ +….. ∞, find P given |q| < 1

$\frac{ \pm q}{\sqrt{1-q^2}}$
$\frac{ \pm(q+1)}{\sqrt{q^2+1}}$
$\frac{ \pm q}{\sqrt{q^2-1}}$
$\frac{ \pm q}{\sqrt{q^2+1}}$
$\frac{ \pm(q-1)}{\sqrt{q^2+1}}$

Answer:

Given p² = q²- q⁴ + q⁶– q⁸ +….is an infinite geometric progression with |q| <1 =>|q²| < 1. the common ratio of the geometric progression is -q²

$p^2=\frac{q^2}{1-\left(q^2\right)}=\frac{q^2}{1+q^2} \Rightarrow p=\frac{ \pm q}{\sqrt{1+q^2}}$

Choice (4)

72. There are three numbers in geometric progression. When the middle number is tripled. The numbers will be in arithmetic progression. If the common ratio is greater than 1, find its value.

4+3√2
3+4√2
3√2-4
3+2√2
6+3√2

Answer: Let the three numbers be a, 3ar and ar² therefore a, 3ar and ar2 are in arithmetic progression

2(3ar) = a + ar²

r² – 6r + 1 = 0

$r=\frac{6 \pm \sqrt{32}}{2}$

3±2√2

as r > 1,r = 3 + 2√2 Choice (4)

CA Foundation Sequence And Series Solved Examples

73. The 10th term of an arithmetic progression is 15. II the sum of the squares of the 7th, 10th and the 13th terms is minimum, the common difference is_.

Answer: Let the first term and common difference of the arithmetic progression be a and d respectively given that a+9d=15.

(a+6d)²+(a+9d)²+(a+12d)²

(a+9d-3d)²+(a+9d)²+(a+9d+3d)²

(15-3d)²+15²+(15+3d)²

=3(15)²+18d² this is minimum, when d=0.

Choice (1)

74. The sum to infinity of a geometric progression is 39/2. The sum to infinity of squares of the terms of the geometric progression is 253.5. Find the sum to infinity of cubes of the terms of the geometric progression.

252.5
240.5
253.5
260.5
None of these

Answer:

Let the first term and common ratio of the geometric progression be a and r respectively

$\frac{a}{1-r}=\frac{30}{2} \ldots \ldots$ $\frac{a^2}{1-r^2}=253.5=\frac{507}{2} \ldots . .2$ $\left(\frac{a}{1-r}\right)^2=\left(\frac{39}{2}\right)^2$

Squaring (1 ) on both sides… (3)

Dividing (2)by (3)and simplifying

$\frac{\frac{a^2}{(1-r)(1+r)}}{\frac{a^2}{(1-r)^2}}=\frac{\frac{507}{2}}{\frac{1521}{4}} \Rightarrow \frac{1-r}{1+r}=\frac{2}{3} \Rightarrow r=\frac{1}{5}$ $\text { from }(1), a=\frac{39}{2}(1-r)=\frac{78}{5}$

sum of the cubes of the terms of the GP

$=\frac{a^3}{(1-r)^3}=\frac{\left(\frac{78}{5}\right)^3}{\left(\frac{1}{5}\right)^3}=\frac{(78)(78)(78)}{124}=\frac{78(39)(39)}{31} \text { which is }>1000$

Choice (5)

75. Find the 50th term of the following series. 1 + 3 + 7 + 13 + 21 +….

2451
2561
2781
2341
2671

Answer:

S₅₀ = 1 + 3 + 7 + 13 +…… T₄₉ + T₅₀ … ( 1)

Also s₅₀ = 1 + 3 + 7 + 13 + …..T₄₉ + T₅₀ … (2)

(1)- (2) =>0 = (1 + 2 + 4 + 6 +…..50 terms)- T50

=> T₅₀ = 1 + (2 + 4 + 6 + ……49 term)

=> T₅₀ = 1(49)(50)/2=1 + 2450 = 2451

Choice (1)

76.The terms a₁, a₂……..a₁₇ in arithmetic progression. If a₃ +a₈ + a₁₁ + a₁₄ = 100, then a₁ + a₂+ +a₃……… a₁₇ =__________

Answer:

if1st term T₁ = a, then nth Term T_n = a + (n- 1)d.

Given a₃ + a₈ + a₁₁ + a₁₄= 100

a₁+ 2d + a₁ + 7d + a₁10d + a₁+ 13d = 100

=>4a₁+ 32d = 100=>2a₁+ 16d = 50……(1)

To find: a₁+ a₂ + a₃ +…… a₁₇

= n/2 [first term + last term | =>17/2 |a₁ + a₁₇| = 17/2 |a₁ + a₁₇ + 16d]

=17/2[2a₁ + 16d] = 17(50)/2 = 425

Choice (4)

77. If five distinct numbers a, b, c, d, e are in arithmetic progression with common difference of ‘D’, then a- 3b+5c-5d+2e is equal to D

Answer:

Let x be the common difference

=>b = a + x, c = a + 2x, d = a + 3x and e = a + 4x.

a- 3b + 5c- 5d + 2e

= a- (3a + 3x) + (5a + 10x) – (5a + 15x) + 2a + 8x)

= (a — 3a + 5a- 5a + 2a) + (-3x + 10x- 1 5x + 8x) =0 + 0 = 0

Choice (4)

78. If in a geometric progression the fifth term is 8 times the second term and the sum of the first, third and sixth terms Is 111, what is the 7th term?

Answer: Let the first term of GP= A and common ratio = R

=>AR^N-1 = Nth term =>AR⁴= 8(AR)

=>R³ = 8=>R = 2 ……..(1)

A+AR² + AR⁵ = 111

=>A{1 + R² + R⁵) = 111…..(2)

Put R =2 in (2) => A( 1 + 4 + 32) = 11 1 => A =111/37 = 3

7th Term = AR⁶=3x (2⁶)=192

Choice (5)

79. If the sum of $1+\frac{2}{x}+\frac{4}{x^2}+\frac{8}{x^3}+\cdots \infty$ is finite and x>0, then which of the following is true?

X> 2
X < 2
X > 1/2, x < 2
X < 1/2
1/2 < x < 2

Answer:

Since the sum $1+\frac{2}{x}+\frac{4}{x^2}+\cdots \infty$ is finite, its common ratio should be less than 1.

$S_{\infty}=\frac{a}{1-r}$

common ratio = $\frac{2}{\frac{x}{1}}=\frac{2}{x}$

But r < 1

$\Rightarrow \frac{2}{x}<1 \Rightarrow \frac{x}{2}>1 \Rightarrow x>2$

Choice (1)

80. In an arithmetic progression, the 10th term is 11 and the 11th term is 10, How many consecutive terms (starting from the first term) o f the arithmetic progression should be considered so as to make their sum equal to zero?

Answer:

T_n=a+(n-1)d

(a= first term,d= common difference, Tn = n th term)

T₁₀ = a+9d=11……………(1)

T₁₁= a+10d=10…………….(2)

solving (1) and (2)

d= – 1, a = 20

Say ‘n’ terms are needed so as to make sum =0

=>n/2[2a+(n-1)d]=0

=>n/2[40+(n-1)(-1)]=0

=>40 – n + 1 = 0=>n =41

first 41 terms of the arithmetic progression when added give the sum as zero

Choice (2)

81. The first, second and third terms of a geometric progression with distinct terms, are equal to the first, ninth and thirty-first terms, respectively of an arithmetic progression. If the first term of either progression is 11. Find the common ratio of the geometric progression.

Answer: Let the GP be 11,11r, 11r²,r=1

The 1st 9th and 31st terms or the arithmetic progression are 11, 11+8d,11+30d

11r = 11 + 8d=>11 (r- 1) = 8d …. (1)

11r² =11 + 30d =>11(r²-1 )= 30d….(2)

(2) + (1)=>r+= 1 15/4 =>r =11/4

choice (2)

82. The first term of an arithmetic progression consisting of integers, is the common ratio of a geometric progression. The first term of the geometric progression is the common difference of the arithmetic progression. The sum of the first 11 terms of the arithmetic progression is 341 and the sum of the first three terms of the geometric progression is 18. Find the sum of the common difference and the common ratio.

Answer: If r is the common ratio of the geometric progression and d is the common difference of arithmetic progression first term of arithmetic progression = r and that of geometric
progression =d.

11/2[2r +(11-1)d] = 341

=>r+ 5d = 31…. (1)

=>d+ dr +dr² = 18

As arithmetic progression consists of only integers,both r and d are integers, so, Geometric progression also consists of only integers, By trial and error we get r=1and d=6
r + d = 7

Choice (5)

83. The three terms a + 2b, b+2c are c +2a are in arithmetic progression. The three terms 16a, 2(b + c), and c are in geometric progression. The ratio of the common difference of the arithmetic progression to the common ratio of the geometric progression could be

-2
4
8
-16
0

Answer:

b+2c- (a+2b) =(c+2a)-(b+2c)

=>2b + 4c = c + 3a + 2b => a = c … (1)

(2b + 2c)² = 16ac=>4b² + 8bc + 4c² = 16ac …. (2)

From (1) and d(2) ,we get

4(b + c)² = 16c²=>b² + 2bc- 3c = 0

=>(b + 3c) (b- c) = 0=>b = c or – 3c

When b =c, the common difference

= (b + 2c)- (a + 2b) = 3c- 3c =0

the common ratio = $\frac{2(b+c)}{16 a}=\frac{2(2 c)}{16 c}=\frac{1}{4}$

their ratio = $\frac{0}{1 / 4}=0$

When b =-3c the common difference = (b + 2c)- (a + 2b) = (-3c + 2c)- (c- 6c) = 4c

the common ratio = $\frac{2(b+c)}{16 a}=\frac{2(c-3 c)}{16 c}=\frac{-1}{4}$

their ratio = $\frac{4 c}{1 / 4}=-16 c$

0 is given is the choices

Choice (5)

Chapter 6 Sequence And Series Step-By-Step Solutions

84. A number of saplings were lying at a point P, by the side of a straight road. Raju planted these saplings in a straight line with a distance of 20 meters between consecutive saplings. The first sapling was planted 20 m from P and all the saplings were planted on the same side of P. Raju carried only one sapling at a time and returned to P after planting each sapling, including the last one. If he travelled a total distance of 2.2 km, find the number of saplings that he planted.

Answer: To carry the first sapling to plant it and return, Raju has to travel 40 m. to carry the second one to plant it and return, Raju has to travel 80 m. Hence until he plants the final sapling (nth sapling) he will have to travel

40(1 + 2 + ….n) = 2200(given)

n(n+1)/2 = 55=>n² + n – 110 = 0=>n = 10 or- 11

Hence n = 10, as n > 0 Choice (1)

85. In an arithmetic progression, the sum of the squares of the seventh term and the eleventh term is 482. The product of its second term and the sixteenth term is 29. Find the product of its first and the seventeenth terms.

31
-31
-33
33
None of these

Answer: Let the first term and common difference of the arithmetic progression be a and d respectively.

Given that t_7² + t_11² = 482

=>2a² + 32ad + 136d² = 482 …. (1)

And (a + d) (a + 15d) = 29

=a² + 16ad+15d²=29………..(2)

By (1) – 2 x (2), we get

106d² = 482- 58 = 424

=>d² = 4………(3)

Consider, t₁ x t₁₇ = a(a + 16d) = a² + 16 ad

= (2)- 15 x (3) = 29 -15X4 = -31

Choice (2)

86. The sum of the squares of the first and fifth term of an arithmetic progression is 218. If the third term is less than the first term, and the sum of these two terms is 16, find the first term.

Answer: Let the first term of the arithmetic progression be a and the common difference be d.

Sum of the squares of the first and the fifth term

=a²+(a+4d)²=218

a²+4ad+8d²=109……………. (1)

a+(a+2d)=16

=>a+d=8=>a=8-d……………..(2)

Substituting a=8-d in (1) (8-d)²+4(8-d)d+8d²=104

5d²+16d-45=0 D=-5 or 1.8 As t₃<t₁,d<0,d=5

Substituting=-5 in (2). A=13. Hence, the first term of the arithmetic progression is 13

Choice (4)

87. The sum of the first n terms of an arithmetic progression is given by 3n²+4n. Find the 6th term of the arithmetic progression.

Answer: Let the first term and the common difference of the arithmetic progression be a and d respectively.

n/2(2a+(n-1)d)=3n²+4n=n(3n+4).

Comparing both sides d/2 = 3 (Whatever multiplies of n2)

In L.H.S. equals that in R.H.S.)

d=6. 2a-d/2=4, a=7.

The 6lh term of the arithmetic progression = a+5d=37.

Choice (3)

88. The sum of all the perfect squares from 50 to 2500 is

39825
40975
41895
44785
42785

Answer: The Sum of all the perfect squares from 50 to 2500

=the (sum of all perfect squares from 1 to 2500) – (Sum of all squares from 1 to 50).

Sum of the squares first n natural numbers

$\frac{n(n+1)(2 n+1)}{6}$

We have 50 perfect squares from 1 to 2500 whose sum is 1/6(50)(51)(101)

=25x17x101 =171700/4 = 42925…..(1)

Sum of all perfect squares from 1 to 7

= 1² + 2² + 3² + 4² + 5² + 6² + 7²

= 1/6(7)(8)(15) = 140……(2)

Required sum = 42925- 140 = 42785.

Choice(5)

89. a₁ = 1.5 and for n > l,a_n = 3a_n-1 + 4.Find a₃₀

3³⁰ -1
3²⁹(7/2)-2
3²⁹(7/2) + 2
3³⁰ +1
3³⁰(7/2) + 2

Answer:

a₁ = 1.5

a₂ = 3a₁ + 4

a₃ = 9a₁ + 4(1 + 3)

a₄ = 27a₁ + 4(1 + 3 + 3²) … and

a₃₀ = 3²⁹a₁ + 4 + 4(3) + 4(3²) + (3²⁸)

$=3^{29}(3 / 2)+\frac{4\left(3^{29}-1\right)}{2}=2\left(\frac{7}{2}\right) 3^{29}-2$

Choice (2)

90. How many terms, at the maximum, of the progression 2, 5, 8……can be considered, if the sum of the terms is to be less than 3000?

Answer: Let the maximum number of terms for which the sum of the terms of the A.P is less than 3000 be n.

The A.P has a first term of 2 and a common difference of 3. Sum of first n terms

$\left.=\frac{n}{2}[2(2)+n-1) 3\right]<3000$

n[1+3n] < 6000.

going by the choices only when n = 44,

we have the value ofthe expression n(3n + 1)being less than 6000 .

Hence n = 44.

Choice (2)

CA Foundation Maths Solutions For Chapter 5 Permutations And Combinations

November 15, 2024July 5, 2024 by Alekhya

CA Foundation Maths Solutions For Chapter 5 Permutations And Combinations Introduction

The concept of permutations and combinations is used to select or arrange some items out of a group according to certain predetermined conditions. This concept helps find the number of ways to arrange, select or reject these items.

The concepts of permutations and combinations derive from the principles of Factorials and the Fundamental principle of counting.

Factorial

The factorial of a natural number n, denoted by n! or |n_is the product of all-natural numbers from 1 up to n.

n! = 1 x 2 x 3 x … x (n- 1) x n

The factorials of the first few natural numbers are as given below.

The factorials of the first few natural numbers are as given below

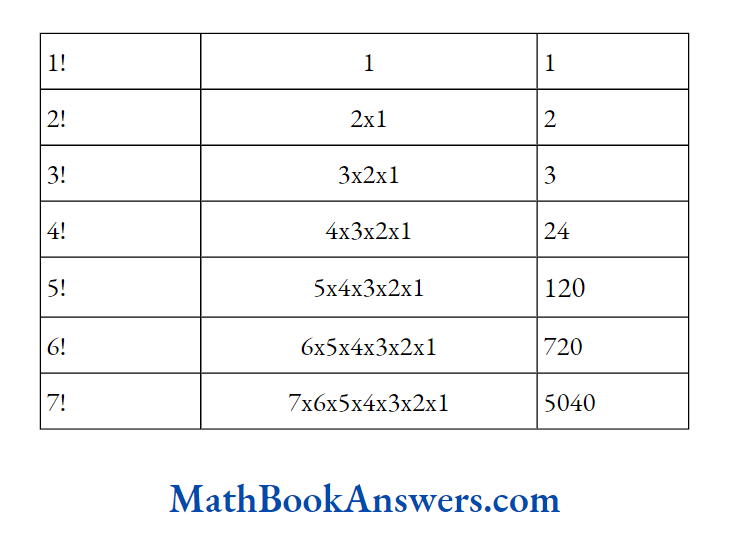
Remember:

n! = nx [(n- 1) x (n- 2) x (n- 3) x … x 1]
n! = n x (n- 1)!
n! = n x (n- 1) x (n- 2)!

Read and Learn More CA Foundation Maths Solutions

The factorial of 0 is defined to be one.

∴ 0! = 1

The factorial of negative numbers is not defined.

Permutations and Combinations

The task of selecting a number of objects from a given set of objects involves a number of choices the number of choices available depends on the purpose of selection.

If the order of selection is unimportant, the selection is called a combination, if the order of selection is important, the selection is called a permutation.

Consider the case ofselecting two out of three students A, B and C.

CA Foundation Maths Chapter 5 Permutations And Combinations Solutions

Case 1:

Suppose the task is to select two students out of A, B and C and rank them according to the marks they have scored. The different possibilities that exist are as follows:

The different possibilities that exist are as follows

Note that the selection (A, is different from the selection (B, A] here.

Total number of selections = 6

Here, the students are first selected and then arranged for a purpose. This kind of selection is called a permutation.

Case II:

Now suppose that the task is just to select two students out of three. In such a case, the order in which the students are selected is not important.

Hence, the possibilities in this case are (A, B), (B, C] and (A, C]

Note that (A, and (B, in the above case mean the same thing as both groups imply that students A and B have been selected.

Here, they do not need to be ranked.

total number of selections = 3

Here, the important thing is to just select the students and not to arrange them.

This kind of selection is called a combination.

Remember:

Permutations involve selection and then, arrangement of objects while combinations involve only selection of objects.

Example:

Suppose 4 people out of 7 are to be arranged for a photograph. This involves first selecting the 4 people and then arranging them. This is a permutation.

On the other hand, if 4 people out of 7 are to be chosen for a team, it just involves selecting the 4 people without any arrangement. This is a combination.

CA Foundation Maths Solutions For Chapter 5 Solved Example:

Find out whether the following tasks involve permutations or combinations.

Arranging five girls on five chairs for a photograph
Forming a committee of five people from then boys and five girls.
Electing a captain and a vice -captain from a team of11.
Selecting a king or a queen from a pack of cards.

Solution:

Here, the girls need to be arranged such that there are five girls on five chairs. Since, it involves arranging the five girls; it is a case of permutations.
Here, just select five people out of ten boys and five girls. There is no arrangement involved. So, it is a case of combinations.
This task involvers selecting two people, and then arranging them in order, the first one being the captain and the second being the vice-captain. Hence, this is a case of permutations.
Here, just select two cards. In the previous task, a player selected was to be ‘made’ the captain or vice -captain. Here, just select a king or a queen out of the kings and queens in the pack of cards. Hence, this is a case of combinations.

To find the number of ways in which the permutations and combinations can be counted, first understand the fundamental principle of counting.

Fundamental Principle of Counting

Fundamental Principle of Counting

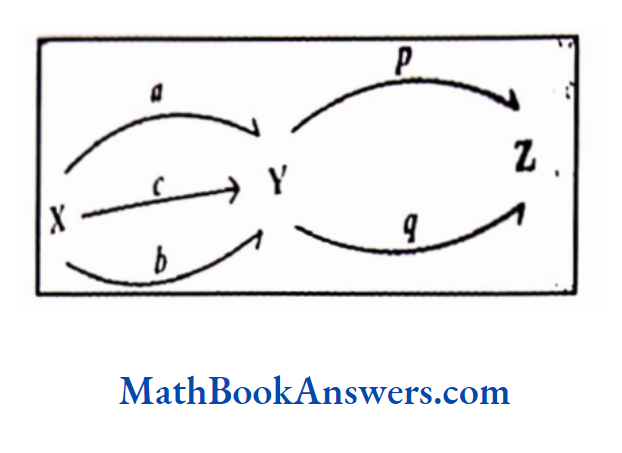
Suppose one needs to travel from X to Z via Y. There are three routes a, b, c, available to go from X to Y and two routes p, q available to go from Y to Z Ifone travels from X to Y taking the route a, then one can travel from Y to Z in two ways.

Thus, for every choice of route that one makes for travelling form X to Y, there are two ways to travel from Y to Z. As there are three routes to travel from X to Y, there are 2+2+2+=3x 2 ways to travel form X to z via Y.

The routes are (a,p),(a,q), b,p), (b,q),(c,p) and (c,q). If one considers travelling from X to Y as task 1, and travelling from Y to Z as another task 2, task 1 can be permed in 3 ways, task 2 can be performed in 2 ways, and task 1 and task 2 together can be performed in 3x 2 = 6 ways.

In general, the fundamental principle of counting says that, if we can accomplish one takes in xx ways, another task in x2 ways, and so on, until the n”‘ task which can be done in x„ ways
then all these tasks can be accomplished in X1×X2×X3× …xn ways.

Remember:

Consider two tasks; task 1 that can be done in m ways & task 2 that can be done in n ways.
Task 1 and task 2 can be done in m x n ways
Task 1 OR task 2 can be done in m + n ways.

Solved Examples:

1. Josephine likes to have passwords that have eight characters, the first four being different vowels and the last four being different numbers. How many different passwords can she have?

Solution:

The first four characters of Josephine’s password are to be chosen form the five vowels the first vowel can be chosen in 5 different ways. As all of them have to be different, the second
can be chosen only in 4 ways, the third in 3 ways and the last in 2 ways.

Similarly, the four numbers have to be different. Hence, the four numbers can be chosen form the 10 digits from 0 to 9 in 10, 9, 8 and 7 ways respectively.

Thus, the number of different passwords that Josephine can have.

= 5x4x3x2x 10 x9x8x7 = 604800

2. How many numbers greater than 5000 can be formed by arranging the digits 4, 5, 7, 9 using each digit only once?

Solution:

Since the number has to be greater than 5000, the first digit can be chosen in 3 ways only, I.e., it can be 5,7 or 9

Once this diÿit is chosen, the next, digit can be chosen in 3 ways, the next in 2 and the next in 1.

Thus, 3x3x2x1 = 18 such numbers can be formed.

Hence, 18 numbers greater than 5000 can be formed by arranging the digits 4,5,7, 9 using each digit only once.

3. How many numbers can be formed using the digits 4, 5, 7,9, if repetition ofdigits is allowed?

Solution:

In this case, there is no repetition of digits, also, there is no condition as to whether should be greater than or less than something, for each place one can choose any of the 4 digits

Thus, 4x4x4x4 = 256 such numbers can be formed.

Hence, 256 numbers can be formed using any of the digits 4, 5, 7, 9 if repetition of digits is allowed.

4. Four medical representatives Rl, R2, R3 and R4 are to visit one doctor each on Thursday. The doctors are Dl, D2, D3, and D4, Rl Will not visit only D1 and R2 will visit only D2 or D3. In how many ways can the visits be done such that no two representatives visit the same doctor?
Solution:

the total number of ways in which the vistis can be done

R2 can visit ldoctor (D2 or D3) in 2 ways. Then Rl is left with 2 choices (D2 /D3 or D4)

After this, R3 and R4 have 2 and 1 choices.

∴ the total number of ways in which the vistis can be done = 2x2x2x1= 8

5. Eight buildings in a residential complex are to be painted on their outsides in any one colour form among cream, blue, green, pink and white. The buildings are in a row. Two buildings can have the same colour but two adjacent buildings cannot. In how many ways can the buildings
be painted?

Solution:

The first building can be painted using any one of the five colours in 5 ways. The second building can be painted using any of the remaining four colours in 4 ways. The third building
can have any colour except the one with which the second building is painted.

Thus it can be painted in 4 ways. Thus, each building can be painted in 4 different ways using a colour except the one used to colour the previous building. Hence, the fourth, fifth, sixth, seventh and eighth buildings can be painted using 4 colours each.

Thus, the total number of ways in which the buildings can be painted = 5 x 4⁷

CA Foundation Maths Solutions For Chapter 5 Permutations

If there are n objects ami one is supposed to arrange r (r < n) objects out of these, then the number of ways in which this can be done is written as nPr and is read as “the number of
permutations of n objects taken rata time”

The number of permutations is given as:

${ }^3 P_2=\frac{n!}{(n-r)!}$

The case where 2 out of 3 students were to be ranked can be written as ${ }^3 \mathrm{P}_2$.

${ }^3 P_2=\frac{n!}{(3-2)!}=6$

Remember:

If r= 0,

${ }^n P_2=\frac{n!}{(n-0)!}=1$

If r= 1,

$n P_1=\frac{n!}{(n-1)!}=n$

if r = n ,

${ }^n \mathrm{P}_{\mathrm{n}}=\frac{n!}{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n!$

if r = n-1,

${ }_n P_{n-1}=\frac{n!}{(n-n+1)!}=\frac{n!}{1!}=\frac{n!}{1}=n!$

Permutations with Repetitions

If one has to form words using the letters A, B and C, one can make 3P.j= 6 words i.e., ABC, ACB, BAC, BCA, CAB AND CBA.

But, if one has to from words using the letters A, B and A, then one can make only 3 different words- AAB, ABA and BAA.

Thus, repetition of letters reduces the number of words that can be formed.

Therefore, in case the n elements that are to be arranged among themselves have some repeated elements among them, the number of permutations is not equal to MP„ or not equal
to n!

If n objects are to be arranged among themselves and these contain p identical objects of one kind q identical objects of another kind, r identical objects of still another kind and so on, the total number of ways in which they can be arranged is given by $\frac{n!}{p!q!r!\ldots}$

Solved Examples:

1. How many words can be formed by arranging the letters of the word WEEDED?

Solution:

Total number of letters in the word WEEDED=6.

D occurs 2 times and E occurs 3 times.

Hence, the total number of words that can be formed by arranging these letters is:

$\frac{6!}{2!\times 3!}=60$

Thus 60 words can be formed by arranging the letters of the word WEEDED.

2. Akash has is DVDs out of which 3 are of a movie A, 5 are of a movie B and the rest are all different in how many ways can he arrange the DVDs on a shell?
Solution:

There are 15 objects out of which 3 are of one kind and 5 are ofanother kind.

The total number ofarrangements possible $=\frac{15!}{3!\times 5!}$

Circular Arrangements

The number of ways in which n objects can be arranged in a circle= (n-l)!

Explanation:

Consider four people A, B, C and D sitting on a circular table.

Consider four people A, B, C and D sitting on a circular table

All the four arrangements shown above are one and the same as the beginning and end of a circle cannot be determined. However, had the four arrangements been linear, had the four arrangements been linear, they would be ABCD, DABC, CDAB and BCDA, which would be four different linear arrangements.

Thus, 4 linear arrangements. Would give rise to 1 circular arrangement.

But 4 people would give 4! Linear arrangements

4 people would give 4!/4 = 3! Circular arrangements.

Similarly, if there were n objects, n linear arrangements would give 1 circular arrangement.

n! Linear arrangements would give n! /n = (n-l)! Circular arrangements.

The number of ways in which n objects can be arranged in a circle = (n-l)!

Solved Examples:

1. In how many ways can 5 people be seated around a circular table?

Solution:

n objects can be arranged in a circle in (n-l)! Ways.

Similarly, 5 people can be seated around a circular table in (5-1)! = 4! =24 ways.

2. Seven girls and five boys are to be seated around a circular table such that two of the girls want to sit next to each other, in how many ways can they be seated?

Solution:

There are 12 people to be seated in a circle, as two girls want to sit next to each other; we consider them to be one entity.

Hence there are 11 people to be arranged in a circle, this can be done in 10! Ways

The two girls can be arranged among themselves in 2! Ways.

Thus the total number of ways in which the seven girls and five boys can be arranged = 10!x 2!

3. Five boys and five girls are to be arranged in a circle such that no two girls are next to each other, in how many ways can they be arranged?

Solution:

Since no two girls are to be next to each other, the boys and girls need to be arranged alternately.

Hence, the five boys can be arranged in a circle in 4! Ways.

There are five places in between the boys, in which the girls can be arranged in 5! Ways.

The total number of ways in which the five boys and five girls can be arranged= 4!x 5!

Note that once the boys are seated, the positions of the girls are relative to the positions of the boys and hence their arrangement is treated as a linear arrangement.

Some circulate arrangements are such that clockwise or anticlockwise arrangements are the same. A necklace is a typical example ofsuch a circular arrangement.

The number of arrangements of n objects in such a fashion is $\frac{(n-1)!}{2}$

4. In how many ways can 6 different beads be arranged to from a necklace?

Solution:

In a necklace, clokwise and anticlockwise arrangements are same.

n objects canbe arranged in a necklace in [ltex]1 / 2 \times(n-1)!\text { ways. }[/latex]

Thus, 6 beabs can form a necklace in $ 1 / 2 \times(6-1)!=\frac{5!}{2}=60 \text { ways. }$

Permutations And Combinations Chapter 5 CA Foundation Answers

CA Foundation Maths Solutions For Chapter 5 Combinations

If there are in objects and out of them (r < n) are to be selected, them the number of ways in which this can be done is ” C r and is read as “the number of combinations of objects taken r at a time”.
The number of combinations is given as:

${ }^n C_r=\frac{n!}{(n-r)!r!}$

If 2 students out of 3 are to be selected, it can be written as ${ }^3 C_2$

${ }^3 C_2=\frac{3!}{(3-2)!2!}=3$

Thus, there, are 3 different ways in which 2 objects out of 3 can be selected. These 3 different possible cases are as given in case II.

Explanation:

Consider n objects out of which r are to be selected. Any combination of r objects out of these n objects can be arranged in $r P_r$ ways, thus one combination of r objects gives r! Permutations.

As the number of combinations of n objects taken r at a time ${ }^n \mathrm{C}_{\mathrm{r}}$ these combinations in all give

${ }^{\mathrm{n}} \mathrm{C}_r \times r \text { ! Permutations. }$

This is nothing but the number of permutations of n objects taken r at a time.

$\begin{aligned}
& { }^n \mathrm{P}_{\mathrm{r}}={ }^n \mathrm{C}_{\mathrm{r}} \times r! \\
& { }^n \mathrm{C}_{\mathrm{r}}=\frac{{ }^n \mathrm{Cr}}{r!}=\frac{n!}{(n-r)!r!}
\end{aligned}$

Remember:

If r=0

${ }^n C_0=\frac{n!}{(n-0)!\times 0!}=1$

If r=1,

${ }^n C_1=\frac{n!}{(n-1)!\times 1!}=n$

If r=n,

${ }^n C_n=\frac{n!}{(n-n)!\times n!}=1$

If r =n-1

${ }^n C_{n-1}=\frac{n!}{(n-n+1)!\times(n-1)!}=\frac{n!}{1!\times(n-1)!}=n$

Some more useful rules involving Combinations

1. The number of ways in n which identical things can be divided in r groups when each person may get any number of things, including zero=$ (n+r-1) C_{(r-1)}$

2. The number of ways in n which identical things can be divided in r groups when each person may get at least one thing = ${ }_{(n+r-1)} C_{(r-1)}$

Solved Examples:

1. In how many ways can 24 chocolates be distributed among 4 children such that each one of them gets some or none?

Solution:

The number of distributions is $(21+1-1) C_{(4-1)}={ }^{27} C_3=2925$

2. How many solution does the equation x + y +z= 10 have, if x, y, and z are natural numbers?

Solution:

Since x, y and z are all natural numbers; they cannot have a value 0. Hence, their value has to beadiest 1. Hence; this is similar to a problem of distributing 10 chocolates (each chocolate
corresponds to the number 1) among 3 people so that each person has at least one chocolate.

Thus, the number of solutions of this equation is given by $ { }^{10 \cdot 1} \mathrm{C}_{3 \cdot 1}={ }^9 \mathrm{C}_2=36$

Remember:
The fundamental principle of counting says that, if we can accomplish one task in xx x x2 x x3 x ,…x„ ways.

If task 1 can be done in m ways and task 2 can be done in n ways then:

1. Task 1 and task 2 can be done in m xn ways.

2. Task 1 or task 2 can be done in m + n ways

The number of permutations of n objects taken rat a time is given by: ${ }^n P_r=\frac{n!}{(n-r)!}$

If n objects are to be arranged among themselves and these contain p identical objects of one kind, q identical objects of another kind, r identical objects of still another kind and
so on, the total number of ways in which they can be arranged is given by $\frac{n!}{p!q!r!_m}$

The number of permutations of n different things taken r at a time when repetition is allowed = n x n x n x…..r times = nr

The number of ways in which n objects can be arranged in a circle when clockwise and anticlockwise arrangements are different = (n-l)l

The number of ways in which n objects can be arranged in a circle when clockwise and anticlockwise arrangements are same = (n-l)l / 2

Number ofselections of k consecutive things out of n things in a row =n-k+l

The number of combinations of n objects taken r at a time is given by

${ }^n C_r=\frac{n!}{(n-r)!r!}$

$\begin{aligned}
& { }^n P_r={ }^n C_r x r! \\
& { }^n C_r={ }^n C_{n-r} \\
& \text { if }{ }^n C_x={ }^n C_y \text { then } x=y \text { or } x+y=n \\
& { }^n C_r={ }^{n \cdot 1} C_r+{ }^{n \cdot 1} C_{r-1}
\end{aligned}$

the number of ways in which none or some elements from a set of n elements is

${ }^n \mathrm{C}_{10}+{ }^n \mathrm{C}_1+$ ${ }^n C_2+\ldots .+{ }^n C_n=2 n$

the number of ways in which n identical things can be divided in r groups when each person may get any number of things, including zero =$n+r-1) C_{(r-1)}$

the number of ways in which n identical things can be divided in r groups when each person may get at least one thing $=11+r-1) C_{(r-1)}$

CA Foundation Maths Solutions For Chapter 5 Exercise – 1 Permutations

Choose the most appropriate option (1) (2) (3) or (4)

l. ${ }^4 P_3$ i is evaluated as

43
34
24
None of these

Answer: (3) 24 $\text { We know } \mathrm{nP}_{\mathrm{r}}=\frac{n!}{(n-r)!}$

${ }^4 P_3=\frac{4!}{(4-3)!}=\frac{4!}{1!}=24 $

2.${ }^4 P_4$ is equal to[/latex]

1
24
0
none of these

Answer: (2) 24 $\text { We know }{ }^n \mathrm{P}_{\mathrm{r}}=\frac{n!}{(n-r)!} \quad{ }^4 \mathrm{P}_4=\frac{4!}{0!}=\frac{4!}{1}=24$

3. 7! is equal to

5040
4050
5050
none of these

Answer: ( 5040 71 = 7x6x5x4x3x2x1 = 5040

4. 0! is a symbol equal to

0
1
Infinity
none of these

Answer: (1 01 = 1

5. In $n P_{r^{\prime}}$ n is always

an integer
a fraction
a positive integer
none of these

Answer: Integer

6. In $n P_{r^{\prime}}$ the restriction is

n > r
n ≥ r
n ≤ r
none of these

Answer: n ≥ r.

7. $\text { In nP } P_r=n(n-1)(n-2) \ldots \ldots \ldots \ldots \ldots \ldots \ldots(n-r+1) \text {, }$ the number of factors is

Answer: r

8. $n P_r$ can also written as

$\frac{n!}{(n-r)!}$
$\frac{n!}{r!(n-r)!}$
$\frac{r!}{(n-r)!}$
None of these

Answer: $\text { ( } \frac{n!}{(n-r)!}$

9.$m+n P_2=56, m-n P_2=30 \text { then }$

m =6, n = 2
m = 7, n= 1
m=4, n=4
none of these

Answer:

$=\frac{(m+n)!}{(m+n-2)!}=56$

= (m+n) (m+n-1) = 56

= m + n = 8

$\frac{(m-n)!}{(m-n-2)!}=30$

(m-n) (m-n-1) = 30

m – n = 6

10.$\text { if } 5 \mathrm{P}_{\mathrm{r}}=60 \text {, }$ then the value of r is

3
2
4
none of these

Answer: (1) 3 $\frac{5!}{(5-r)!}=60$

2 = (5 – r)! r = 3

11. $\text { If } n_1+n_2 \mathbf{P}_2=132, n_1-n_2 \mathbf{P}_2=30$ then,

n 1 =6, n2=6
n1=10,n2=2
n1 = 9, n2 = 3
none of these

Answer: (3)

n₁=9 n₂=3

=(n₁+n₂)(n₁+n₂-1)=132

n₁+n₂=12

n₁=9

(n₁-n₂)(n₁-n₂-1)=30

n₁-n₂=6

n₂=3

12. The number of ways the letters of the word ‘COMPUTER’ can be rearranged is

40,320
40,319
40,318
none of these

Answer:

40319

= Computer can be arranged in 8! Ways 8! = 40320

But we have to rearranged i.e., computer will not be counted 40320- 1 = 40319 ways.

13. The number of arrangements of the letters in the word ‘FAILURE’, so that vowels are always coming together is

576
575
570
none of these

Answer: ( 576

= FAILURE = 7 letters

If vowels are clubbed as x

Total 4 letters FLR x

These can be arranged in 41 ways. Also, the vowels can arrange in 41 ways

No. of arrangement = 41 x 41= 576

14. 1 0 examination papers are arranged in such a way that the best and worst papers never come together. The number ofarrangements is

9(8)!
10!
8(9)!
none of these

Answer: 89!

= Best fit worst paper be clubbed as 1 total papers =10-2 + 1 =9

9 Papers can be arranged in 91 ways

The 2 papers can be internally arranged in 2 ways No of arrangement’s = 2×91

When worst paper & best paper can be arranged

Now total arrangements = 101

Arrangement when both papers do not come together 10×91-2×91 = 9! [10-2)

= 101-2×9! = 9! x 8 = 89!

15. n articles are arranged in such a way that 2 particular articles never come together. The number of such arrangements is

(n-2) (n – 1]!
(n-1) (n-2)l
n!
none of these

Answer: ( (n – 2) (n-1)!

16. If 12 school teams are participating in a quiz contest, then the number of ways the first, second and third positions may be won is

1,230
1,320
3,210
none of these

Answer:

(1320

= 12 school terms, 3 positions

Can be given & arranged in ${ }^{12} \mathrm{P}_3 \quad=\frac{12!}{9!}=12 \times 11 \times 10=1320$

17. The sum of all 4-digit number containing the digits 2, 4, 6, 8, without repetitions is

1,33,330
1,22,220
2,13,330
1,33,320

Answer: 1,33,320.
= 4 digit number from 2,4,6,8

Without repetition can be made in 41 ways = 24 ways

24 numbers will be formed.
6 no. will end with 2
6 no. will end will 4
6 no. will end will 6
6 no. will end will 8

17 th answer

= 1,33,320

18. The number of 4-digit numbers greater than 5,000 can be formed out of the digits 3,4,5,6 and 7(No. digit is repeated]. The number ofsuch is

72
27
70
none of these

Answer: 72

= 4 digit no. > 5000 first digit cannot be 3,4 it will be 5,6,7

4 digit no

3x4x3x2 =72

19. 4-digit numbers to be formed out of the figures 0, 1, 2, 3, 4 [no digit is repeated] then number of such numbers is

120
20
96.
none of these

Answer: 96

= 4 digit number of 0,1,2,3,4 0 cannot occupy first digit’s place

4 digit no

4x4x3x2 = 96

20. The number of ways the letters of the word ‘TRIANGLE’ to be arranged so that the word ‘angle’ will be always present is

Answer: 24
Triangle has 0 letters.
If we chib angle as 1 No. of letters = 8- 5 + 1 = 4
4 letters can be arranged in 41 ways. There is no internal arrangement = 24 ways

21. If the letters word ‘DAUGHTER’ are to be arranged so that vowels occupy the odd places, then number of different words are

2,880
676
625
576

Answer: 2,880

= Daughter’s 5 consonants 3 vowels

Daughters has 4 odd places

3 vowels can occupy in 4P3 ways

First 5 consonants can be arranged in 51 ways

Total = 51 x4p3 = 2880 ways

22. The number of ways in which 7 girls form a ring is

700
710
720
none of these

Answer: 720
= 7 girls form a ring = i.e. circular permutation

$=\frac{1}{0}(n-1)!\quad=\frac{1}{0} \times 6!\quad=6 \times 5 \times 4 \times 3 \times 2=360 \times 2 \quad=720$

23. The number of ways in which 7 boys sit in a round table so that two particular boys may sit together is

240
200
120
none of these

Answer:

240
= Two come togethers <— club = total 7 – 2 + 1 = 6 boys to be arranged
= m 2 (6-1) ! = 240 ways

24. If 50 different jewels can be set to form a necklace then the number of ways is

1/2×50!
1/2×49!
49!
none of these

Answer: $\text { (} 1 / 249 \text { ! }$

= so different vowels form a necklace in $\frac{1}{2}(n-1)!\text { Ways }$

$\text { i.e. } \frac{1}{2}(50-1)!=\frac{1}{2} 49 \text { ! }$

25. 3 ladies and 3 gents can be seated at a round table so that any two and only two of the ladies sit together. The number of ways is

70
27
72
none of these

Answer: (72
= 3 ladies 3 gents
Constraint —> only 2 & only 2 sit together 2 ladies can let selected & arranged in ${ }^3 P_2$ ways

Constraint

The remaining ladies out of 4 cannot Occupy places adjustment to the 2 only in 2 ways

The remaining 3 men can occupy places in 31 ways

$\text { Total } \rightarrow{ }^3 \mathrm{P}_2 \times 31 \times 2=72 \text { ways. }$

26. The number of ways in which the letters of the word ‘DOGMATIC’ can be arranged is

40,319
40,320
40,321
none of these

Answer: 40,320
DOGMATIC 8 letters can be arranged in 8!

27. The number of arrangements of10 different things taken 4 at a time in which one particular thing always occurs is

2015
2016
2014
none of these

Answer: 2016 $=4 \times{ }^9 \mathrm{P}_3 \text { ways to arrange }=2016$

28. The number of permutations of 10 different things taken 4 at a time in which one particular thing never occurs is

3.020
3,025
3,024
none of these

Answer: 3024 $={ }^9 \mathrm{P}_4=3024$

29. Mr. X and Mr. Y enter into a railway compartment having six vacant seats. The number of ways in which they can occupy the seats is

Answer: (30. = Mr x can occupy & vacant seats in 6 ways
Mr Y will occupy remaining 5 seat in 5 ways. Total 30 ways

30. The number of numbers lying between 100 and 1000 can be formed with the digits 1, 2, 3, 4, 5, 6, 7 is

210
200
110
none of these

Answer: 210

= 3 digit numbers > 100
From 1.2,3,4,5,6,7
first digit can be 1,2,3,4,5,6,7
Second digit can be repeated therefore ways
Similarly third digit with remaining 5 no. in 5 ways =7x6x5 = 210 ways

CA Foundation Maths Chapter 5 Detailed Solutions

31. The number of numbers lying between 10 and 1000 can be formed with the digits 2,3,4,0,8,9 is

124
120
125
none of these

Answer: 120

= two digit & three digit between 10 – 1000

0 can occupy first place The no. of ways = 6x5x4 = 120 ways

32. In a group of boys, the number of arrangements of 4 boys is 12 times the number of arrangements of 2 boys. The number of boys in the group is

10
8
6
none of these

Answer: 6 $\frac{(n)(n-1)(n-2)(n-3)}{n(n-1)}=12 \quad n=6 .$

33. The total number of 9-digit numbers of different digits is

10(9)!
8(9)!
9(9)!
none of these

Answer: 99!
= first digit cannot be 0. 9 ways

= total ways = 9x9x8x7x6x5x4x3x2xl = 99!

34. The number of ways in which 6 men can be arranged in a row so that the particular 3 men sit together, is

$(1) ${ }^4 P_4$
(2) ${ }^1 P_4 \times{ }^3 P_3$
(3) $(3)^2$$
(none of these

Answer:$\text { (}{ }^4 \mathrm{P}_4 \times{ }^3 \mathrm{P}_3$ = let 3 particulars men be 1

Total men 6 – 3 +1 = 4. They can sit in 41 ways

Internal arrangement among 3 particular Men can be made in 31 ways.

= Total = 41 x 31 ways

35. There are 5 speakers A, B, C, D and E. The number of ways in which A will speak always before B is

24
4 x 2
5
none of these

Answer: (a] 24.
= S speakers

S speakers

Total = 5 — 2 + 1 = 4 speakers They can speak in 41 ways.

Now there will be no internal arrangement i.e. A is before B-‘- 41 ways

36. There are 10 trains plying between Calcutta and Delhi. The number of ways in which a person can go from Calcutta to Delhi and return by a different train is

99
90
80
none of these

Answer: 90.
= Let us say he takes an one train for going = 10 ways are possible

While coming he can take any train from the removing 9 trains in = 9 ways

Total = 10 x 9 = 90

37. The number of ways in which 8 sweats of different sizes can be distributed among 8 persons of different ages so that the largest sweat always goes to be younger assuming that each one of then gets a sweat is

8
5040
5039
none of these

Answer: (5040
Sweats = 8 person (diffjv younger one gets largest rest 7 will get 7 sweats in 7! Ways

38. The number of arrangements in which the letters of the word ‘MONDAY’ be arranged so that the words thus formed begin with M and do not end with N is

720
120
96
none of these

Answer:96.
= MONDAY 6 letters

Word should begin with M = 1 Way.

It cannot end with N, N can occupy any expect last position = 5 ways

Rest 4 letters can arrange in 4! Ways

4 letters can arrange in 4 ways

1x1x2x3x4x4 =96 ways.

39. The total number of ways in which six V and four ’-’signs can be arranged in a line such that no two ’-’ signs occur together is

(7)!./ (3)!
(6)! x (7)!/(3)!
35
none of these

Answer: 35 = Among 6 + here are 7 intervals

_+_+_+_+_+_+

No. of filling 7 gaps by 4’-‘signs

$={ }^7 \mathrm{C}_4=35$

40. The number of ways in which the letters of the word ‘MOBILE’ lie arranged so that consonants always occupy the odd places is

36
63
30
none of these.

Answer: 36.

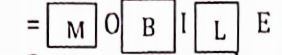
3 consonants 3 vowels

= M O B I L E = 3 consonants 3 vowels

3 consonants can be occupy places in ${ }^4 P_3 \text { ways }=31 \text { ways }$

Vowels can occupy 3 places in ${ }^3 P_3 \text { ways }$

= 3! = 6 total 3! x 3! = 36

41. 5 persons are sitting in a round table in such way that Tallest Person is always on the rightside of the shortest person; the number ofsuch arrangements is

6
8
24
none of these

Answer: 6.

Let tallest, shortest come together

Total persons = 5- 2 + l = 4

4 People can arrange in (n-1] ways = 31 ways = 6 ways there is no internal arrangement 6 ways.

CA Foundation Maths Solutions For Chapter 5 Exercise – 2 – Combinations

Choose the most appropriate option (1, 2, 3 or 4)

1. The value of ${ }^{12} \mathrm{C}_4+1{ }^{12} \mathrm{C}_3 \text { is }$

715
710
716
none of these

Answer:

715

$\begin{aligned}
& \frac{12!}{4!8!}+\frac{12!}{3!9!} \\
& \frac{12 \times 11 \times 10 \times 9}{4 \times 3 \times 2 \times 1}+\frac{12 \times 11 \times 10}{3 \times 2 \times 1}
\end{aligned}$

495+220=715

2. $\text { If }{ }^n p_r=336 \text { and } n C_r=56 \text {, }$ , then n and r will be

(3.2)
(8, 3)
(7,4)
none of these

Answer:

(2) 8, 3)

$\frac{{ }^n P_r}{{ }^n P_r}=\frac{336}{56}=\frac{\frac{n!}{(n-r)!}}{\frac{n!}{r!(n-r)!}}=6$

r ! = 6 r = 3, n = 8

3. $\text { If }{ }^{18} \mathrm{C}_{\mathrm{r}}={ }^{18} \mathrm{C}_{\mathrm{r}+2}$ the value of ${ }^r \mathrm{C}_5$ is

55
50
56
none of these

Answer:

(3) 56

${ }^{18} C_r={ }^{18} C_{r+2}$ $=\frac{\frac{18!}{r!(18-r)!}}{\frac{18!}{(r+2)!(18-r-2)!}}=1$ $=\frac{\frac{18!}{r!(18-r)(17-r)(16-r)!}}{\frac{18!}{(x+2)(r+1) r!(16-r)!}}=1$ $=\frac{(r+2)(r+1)}{(18-r)(17-r)}=1$

r² + 3r + 2 = 306 – 35 r + r2

38r= 304 = r = 8

$8 C 5=\frac{8!}{5!3!}=\frac{8 \times 7 \times 6}{3 \times 2 \times 1}=56$

4. $\text { If }{ }^n C_{r-1}=56,{ }^n C_r=28 \text { and }{ }^n C_{r+1}=8 \text {, }$ then r is equal to

8
6
5
none of these

Answer:

$\frac{{ }^n C_r}{{ }^n C_{r+1}}=\frac{28}{8}=\frac{\frac{n!}{r!(n-r)!}}{\frac{n!}{(r+1)^{!}(n-r-1)!}}=\frac{7}{2}$ $\frac{\frac{n!}{r!(n-r)(n-r-1)!}}{\frac{n!}{(r+1) r!(n-r-1)!}}=\frac{7}{2}$ $\frac{r+1}{n-r}=\frac{7}{2} \quad=2 r+r=7 n-7 r$

9 r- 7n + 2 = 0 (1)

$\frac{{ }^n C_r-1}{{ }^n C_r}=\frac{56}{28}$ $\frac{\frac{n!}{(r-1)!(n-r-1)!}}{\frac{n!}{r!(n-r)!}}=2 \frac{\frac{n!}{(r-1)!(n-r-1)(n-r)!}}{\frac{n!}{r(r-1)!(n-r)!}}=$ $\frac{r}{n-r+1}=2=r=2 n-2 r+2$

3r- 2n = 2 (2)

Multiply (2) by 3 = 9r- 6n = 6
Subtracting (2) from (1)

9r- 7n = -2

9r – 6n = 6

-n = – 8 = n = 8, r = 6

5. A person has 8 friends. The number of ways in which he may invite one or more of them to a dinner is.

250
255
200
none of these

Answer: 255

= 8 friends, lie invites one or more

Total ways

$={ }^8 \mathrm{C}_1+{ }^8 \mathrm{C}_2+{ }^8 \mathrm{C}_3+{ }^8 \mathrm{C}_4+{ }^8 \mathrm{C}_5+{ }^8 \mathrm{C}_6+{ }^8 \mathrm{C}_7+{ }^8 \mathrm{C}_8$

= 8 + 28 + 56 + 70 + 56 + 28 + 8 +1

= 255

6. The number of ways in which a person can chose one or more of the four electrical appliances: T.V, Refrigerator, Washing Machine and a cooler is

15
25
24
none of these

Answer: 15

$={ }^4 \mathrm{C}_1+{ }^4 \mathrm{C}_2+{ }^4 \mathrm{C}_3+{ }^4 \mathrm{C}_4$

He may select 1 or more in above way =4+6+4+1=15

7. $\text { If }{ }^n C_{10}={ }^n C_{14} \text { then }{ }^{25} C_n \text { is }$

24
25
1
none of these

Answer: 25

n = 10 + 14 = 24

25C24 $=\frac{25!}{24!1!}=25$

8. Out of 7 gents and 4 ladies a committee of 5 is to be formed. The number of committees such that each committee includes at least one lady is

400
440
441
none of these

Answer: 441

7 gents 4 ladies committee = 5 members

Committee includes atleast 1 lady

Different cases will be 1 lady, 2 ladies, 3 ladies or 4 ladies

When 1 ladies selected

$\rightarrow{ }^1 \mathrm{C}_1 \times{ }^7 \mathrm{C}_4=4 \times 35=140$

When 2 ladies selected

$\rightarrow{ }^1 \mathrm{C}_2 \times{ }^7 \mathrm{C}_3=6 \times 35=210$

When 3 ladies selected

$\rightarrow{ }^1 \mathrm{C}_3 \times{ }^7 \mathrm{C}_2=4 \times 21=84$

When 4 ladies selected

$\rightarrow{ }^4 \mathrm{C}_4 \times{ }^7 \mathrm{C}_1=1 \times 7=7$

Total when atleast 1 or more ladies
selected = 441

9. $\text { If }{ }^{28} C_{2 r}:{ }^{2 \cdot 1} C_{2 r-1}=225: 11 \text {, }$ then the value of r is

7
5
6
none of these

Answer: (1)7

$\frac{{ }^{28} C_{2 r}}{{ }^{24} C_{2 r-4}}=\frac{\frac{28!}{(2 r)!(28-2 r)!}}{\frac{24!}{(2 r-4)!(28-2 r)!}}=\frac{225}{11}$ $\frac{\frac{28!}{(2 r)!}}{\frac{24!}{(2 r-4)!}}=\frac{225}{11}$ $=\frac{28 \times 27 \times 26 \times 25}{(2 r)(2 r-1)(2 r-2)(2 r-3)}=\frac{225}{11}$

= 24024 = (2r) (2r – l)(2r – 2)(2r – 3)

= 14 x 13 x 12 x ll = 2r (2r – 1) (2r – 2) (2r- 3)

2r = 14 -> r = 7

10. The number of diagonals in a decagon is

30
35
45
none of these

Answer: (b)35

A decagon has 10 points
diagonal will join 2 points
No of ways 2 points can be selected

$={ }^{10 \prime} \mathrm{C}_2=45 \text { lines }$

Total lines joining 2 points = 45 (-) lines making the sides of decagon (10)

Total diagonals 35

11. There are 12 points in a plane of which 5 are collinear. The number of triangles is

200
211
210
none of these

Answer: (210
-» 12 points 5 collinear

For a triangle 3 non collinear points are required

Note: if are selected any 3 points from 5 collinear they will form a line & not a trianle

Total ways = 12C3-5C3

$=\frac{12!}{3!9!}-\frac{5!}{3!2!}$

= 220-10 = 210

12. The number of straight lines obtained by joining 16 points on a plane, no three of them being on the same line is

120
110
210
none of these

Answer: 120

-» 16 points; no collinear points for a straight line 2 points are required Total ways of obtaining a straight line

$={ }^{16} \mathrm{C}_2=\frac{16!}{2!14!}=\frac{16 \times 15}{2}=120$

13. At an election there are 5 candidates and 3 members are to be elected. A voter is entitled to vote for any number of candidates not greater than the number to be elected. The number of ways a voter choose to vote is

20
22
25
none of these

Answer: 25

election 5 candidates, 3 are elected when voter elects 1 candidate

$\rightarrow{ }^5 \mathrm{C}_1=5$

when voter elects 2 candidates

$\rightarrow{ }^5 \mathrm{C}_2=10$

when voter elects 3 candidates

$\rightarrow{ }^5 \mathrm{C}_3=10$

Total ways a voter chooses to votes = 25

14. Every two persons shakes hands with each other in a party anil the total number of handshakes is 66. The number of guests in the party is

Answer: 12
Total hand shake = 66
For a hand shake 2 hands are
selected

$\begin{aligned}
& { }^n C_2=66 \\
& \frac{n!}{2!(n-2)!}=66 \quad \frac{n(n-1)(n-2)!}{(n-2)!}=132
\end{aligned}$

n(n-l)= 132
n (n – 1) = 12 x 11 n = 12

15. The number of parallelograms that can be formed from a set of four parallel lines intersecting anotherset of three parallel lines is

Answer: 18
Set 1 = 4 parallel lines set 2 -* 3 parallel lines are intersecting for a parallelogram 2 lines from set 1 & 2 from set 2 need to be selected

Total ways = $ { }^4 \mathrm{C}_2 \times{ }^3 \mathrm{C}_2=6 \times 3=18$

16. The number of ways in which 1 2 students can be equally divided into three groups is

5775
7575
7755
none of these

Answer: 5775

Total ways of selecting

$={ }^{12} C_4 \times{ }^8 C_4 \times 4 C 4$

= 495 x 70 x 1 = 34650

So 3 groups are formed & order of selection is not important

So Total no. of ways $=\frac{34650}{3!}=5775$

17. 8 points are marked on the circumference of a circle. The number of chords obtained by joining these in pairs is

25
27
28
none of these

Answer: 28

for a cords 2 points are required total ways = ${ }^8 \mathrm{C}_2$ = 28 ways

18. A committee of 3 ladies and 4 gents is to be formed out of 8 ladies and 7 gents. Mrs. X refuses to serve in a committee in which Mr. Y is a member. The number ofsuch committees is

1530
1500
1520
1540

Answer: 1540

Committee of 3L4G out of 8L&7G

Mrs x refuses to serve in which Mr y is member

Total committees that can be formed without taking constraint

$={ }^8 \mathrm{C}_3 \times{ }^7 \mathrm{C}_4=56 \times 35=1960$

Case: When x & y come together, no. of committees

2 ladies out of 7 & 3G out of 6 gents

$={ }^7 \mathrm{C}_2 \times{ }^6 \mathrm{C}_3=21 \times 20=420$

Therefore no. of committees when x y don’t come together

= 1960-420 = 1540

19. $\text { If }{ }^{5000} \mathrm{C}_{92}={ }^{199} \mathrm{C}_{92}+{ }^{1{ }^{99} \mathrm{C}_91}$ then n is

Answer: (499

${ }^{n+1} C_r={ }^n C_r+{ }^n C_{r-1}$
n = 499, r = 92

${ }^{500} \mathrm{C}_{92}={ }^{499} \mathrm{C}_{92}+\mathrm{n}^{\mathrm{n}} \mathrm{C}_{92-1} \quad \mathrm{n}=499$

20. The Supreme Court lias given a 6 to 3 decision upholding a lower court; the number of ways it can give a majority decision reversing the lower court is

Answer: 256
6 to 3 decision -» upholding lower court

No. of judges = 9

To lower a decision, we need 50% T i.e. min 5 judges

No. of ways = ${ }^9 \mathrm{C}_9+{ }^9 \mathrm{C}_8+{ }^9 \mathrm{C}_7+{ }^9 \mathrm{C}_6+{ }^9 \mathrm{C}_5$

= 1 + 9 + 36 + 84 + 126 = 256

21. Five bulbs of which three are defective are to be tried in two bulb points in a dark room. Number of trials the room shall be lighted is

Answer: 7

5 bulbs. 3 defective

Total way of selecting

22. The ways ofselecting 4 letters from the word ‘EXAMINATION’ is

136
130
125
none of these

Answer: 136

All letters distinct EXAMINATION

$={ }^8 C_4 \text { ways }=70 \text { ways }$

2 letters same, 2 distinct
$\rightarrow{ }^3 \mathrm{C}_1 \times{ }^7 \mathrm{C}_2=63 \text { ways }$

2 1etters alike & 2 letters alike
$\rightarrow{ }^3 \mathrm{C}_2=3 \text { ways }$

Total ways = 136 ways

23. ${ }^{51} \mathrm{C}_{31} \text { is equal to }$

⁵¹C₂₀
2.⁵⁰C₂₀
2.⁴⁵C₁₅
none of these

Answer: (1)

⁵¹C₂₀

—>ⁿC_r=ⁿCn-r

⁵¹C₃₁=⁵¹C_51-3

=⁵¹C₂₀

24. A candidate is required to answer 6 out of 12 questions which are divided into two groups containing 6 questions in each group. He is not permitted to attempt not more than four from any group. The number of choices are.

750
850
800
none of these

Answer: (850

Total cases

1) 3 from G1 & 3 from G2

$={ }^6 \mathrm{C}_3 \times{ }^6 \mathrm{C}_3=400$

2) 2 from G1 & 4 from G2

$={ }^6 \mathrm{C}_2 \times{ }^6 \mathrm{C}_4=225$

3) 4 from G1 & 2 from G2

$={ }^6 \mathrm{C}_4 \times{ }^6 \mathrm{C}_2=225$

Total ways of choosing = 850

25. The results of 8 matches (Win, Loss or Draw) are to be predicted. The number of different forecasts containing exactly 6 correct results is

316
214
112
none of these

Answer: 112
6 correct results can be predicted
$\text { in }{ }^8 C_6 \text { ways }=\frac{56}{2} 28 \text { ways }$

The remain 2 matches result are incorrect either it is lose or draw

Ml -> 2 ways M2 -» 2 ways Total 4 ways

Total ways of 6 correct exactly out of 8 matches =28×4=112

26. The number of 4 digit numbers formed with the digits 1, 1, 2, 2, 3, 4 is

100
101
201
none of these

Answer: none of these

4 digit numbers 1,1,2,2,3,4

When nil (Hulls art’ different $4 P_4$ ways – 4 ways = 24

When one digit repeated, remaining 2 different

${ }^2 \mathrm{C}_1 \times{ }^3 \mathrm{C}_2 \times \frac{11}{2!} \text { (arrangement) }$ = 2 x 3 x 12 = 72

When double repetition occurs

${ }^2 C_2 \times \frac{4!}{2!2!}=6 \text { ways }$

Total = 102 ways

27. The number of ways a person can contribute to a fund out of 1 ten-rupee note, 1 five rupee note, 1 two-rupee and 1 one rupee note is

15
25
10
none of these

Answer: 15

He can give any1 note in ${ }^4 \mathrm{C}_1$ ways = 4

He may contribute 2 notes in ${ }^4 \mathrm{C}_2$ = 6

He may contribute 3 noes in ${ }^4 \mathrm{C}_3$ = 4

He may contribute all four notes in ${ }^4 \mathrm{C}_4$ ways =1

Total ways = 15

28. The number of ways in which 9 things can be divided into twice groups containing 2,3, and 4 things respectively is

1250
1260
1200
none of these

Answer: 1260

9 things into twice group of 2,3 & 4

$\text { Total ways }={ }^9 \mathrm{C}_2 \times{ }^7 \mathrm{C}_3 \times{ }^4 \mathrm{C}_4$ = 1260

29. ${ }^n C_1+{ }^n C_2+{ }^n C_3+{ }^n C_1+\ldots . .+{ }^n C_n \text { equals }$

2n -1
2n
2n +1
none of these

Answer:

2n- 1

${ }^n C_1+{ }^n C^2 \ldots \ldots \ldots \ldots \ldots{ }^n C_{n-1}+{ }^n C_n$ $\text { we know }(1+x)^n={ }^n C_0 x^0+{ }^n C_1 x^1 \ldots \ldots \ldots$ ${ }^n C_n x^n$

x = 1

$\begin{aligned}
& (1+1)^n=1+{ }^n C_1+{ }^n C_2 \ldots \ldots \ldots{ }^n C_n \\
& 2^n-1={ }^n C_1+{ }^n C_2 \ldots \ldots{ }^n C_n
\end{aligned}$

How To Solve Permutations And Combinations In CA Foundation

CA Foundation Maths Solutions For Chapter 5 Exercise-3

(Mix Exercise – Perimilnllons & Combinations)

1. In how many ways can the letters of the word ’LEADER’ be arranged?

72
144
360
720
None of those

Answer: The word ‘LEADER’ contains 6 letters, namely 1 L, 2E, 1A, 1D) and IR.

Required number of ways =$\frac{6!}{(1!)(2!)(1!)(1!))}=360$ .

2. In how many different ways ran the loiters of the word ‘RUMOUR’ ho nrmilled?

80
90
30
720
None of these

Answer: The word ‘RUMOUR’ contains 6 letters, namely 2R, 2U, 1M and 1U.

Required number of ways =$\frac{6!}{(2!)(2!)(1!)(1!)}=180$

3. How many words can he formed from the letters of the word ‘SIGNATURE’ so that the vowels always come together?

720
1440
2880
3600
17280

Answer:

The word ‘SIGNATURE’ contains 9 different letters.

When the vowels IAUE are taken together, they can be supposed to form an entity, treated as one letter.

The, the letters to be arranged are SNGTR (IAUE)

These 6 letters can be arranged in ${ }^6 P_6=6!=720 \text { ways. }$

The vowels in the group (IAUE) can be arranged amongst themselves in ${ }^4 P_4=4!=24 \text { ways. }$

Required number of words = (720 * 24) = 17280.

4. In how many different ways can the letters of the word ‘OPTICAL’ he arranged so that the vowels always together?

120
720
4320
2160
None of these

Answer:

The word OPTICAL’ contains 7 different letters.

When the vowels OIA are always together, they can be supposed to form one letter.

Then, we have to arrange the letters PTCL (OIA).

Now, 5 letters can be arranged in 5 ! = 120 ways.

The vowels (OLA) can be arranged among themselves in 3 ! = 6 ways.

Required number of ways = (120 x 6) = 720.

5. In how many different ways can the letters of the word ’SOFTWARE’ he arranged in such a way that the vowels come together?

120
300
1440
13440
720

Answer:

The word ‘SOFTWARE’ contains 8 different letters.

When the vowels OAE are always together, they can be supposed to form one letter.

Thus, we have to arrange the letters SFTWR (OAE).

Now, 5 letters can be arranged in 6 ! = 720 ways

The vowels (OAE) can be arranged among themselves in 3 ! = 6 ways.

Required number of ways = (720 x 6) = 4320.

6. In how many different ways can the letters of the word ‘LEADING’ he arranged in such a way that the vowels always come together?

360
480
720
5040
None of these

Answer: The word LEADING’ has 7 different letters.

When the vowels EAI are always together, they can be supposed to form one letter.

Then, we have to arrange the letters LDNG (EAD.

Now, 5 letters can be arranged in 5 ! = 120 ways.

The vowels (EAI) can be arranged among themselves in 3 ! = 6 ways.

Required number of ways = (120 x 6) = 720.

7. In how many different ways can the letters of the word ‘JUDGE’ be arranged in such a way that the vowels come together?

48
124
160
None of these

Answer:

The word JUDGE’ has 5 different letters.

When the vowels UE are always together, they can be supposed to form one letter.

Then, we have to arrange the letters JDG (UE).

Now, 4 letters can be arranged in 4 ! = 24 ways.

The vowels (UE) can be arranged among themselves in 2 ! = 2 ways.

Required number of ways = (24 x 2) = 48.

8. In how many different ways can the letters of the word ‘AUCTION’ be arranged in such a way that the vowels always come together?

30
240
144
576
None of these

Answer: The word ‘AUCTION’ has 7 different letters.

When the vowels AUIO are always together, they can be supposed to form one letter.

Then, we have to arrange the letters CTN (AUIO).

Now, 4 letters can ho an.ingcd in 4 1 =ÿ 24 ways.

The vowols (AUIO) ran be nrmngi’d among themselves In 4 I = 24 ways,

Required number of ways (24 x 24} – 576.

9. In how many different ways can the letters of the ‘BANKING’ he arranged so that the vowels always come together?

Answer: In The word ’HANKING’, wo Heat the two vowels Al as one letter. Thus, we have UNKNG (Al).

This has 6 letters of which N occurs 2 times and the rest are different.

Number of ways of arranging these letters =$\frac{6!}{(2!)(1!)(1!)(1!)(1!)}=360$

Now, 2 vowels Al can be arranged in 2 ! = 2 ways.

Required number of ways = (360 »2) = 720.

10. In how many different ways can the letters of the word ‘CORPORATION’ be arranged so that the vowels always come together?

810
1440
2880
50400
5760

Answer:

In the word ’CORPORATION’, we treat the vowels OOAIO as one letter. Thus, we have CRPRTN (OOAIO).

This has 7 letters of which R occurs 2 times and the rest are different.

Number of ways of arranging these letters =

$=\frac{7!}{2!}=2520 /$

Now, 5 vowels in which O occurs 3 times and the rest are different, can be arranged in $\frac{5!}{3!}$ = 20 ways.

Required number of ways = (2520 * 20) = 50400.

11. In how many different ways can the letters of the word ‘DETAIL’ be arranged in such a way that the vowels occupy only the odd positions?

Answer: There are 6 letters in the given word, out of which there are 3 vowels and 3 consonants. Let us mark these positions as under: (1) (2) (3) (4) (5) (6)

Now, 3 vowels can be placed at any of the three places out of 4, marked 1, 3, 5.

Number of ways of arranging the vowels =

${ }^3 P_3=3!=6 .$

Also, the 3 consonants can be arranged at the remaining 3 positions.

Number of ways f these arrangements =

${ }^3 P_3=3!=6 .$

Total number of ways = (6 * 6) = 36.

12. In how many ways can a group of 5 men and 2 women be made out of a total of 7 men and 3 women?

Answer:

Required number of ways = $\left({ }^7 C_5 \times{ }^3 C_2\right)=\left({ }^7 C_2 \times{ }^3 C_1\right)=\left(\frac{7 \times 6}{2 \times 1} \times 3\right)=63$

13. In how many ways a committee, consisting of 5 men and 6 women can be formed from 8 men and 10 women?

266
5040
11760
86400
None of these

Answer:

Required number of ways=

(⁸C₅x¹⁰C₆)= (8C₅x¹⁰C₄)= $\left(\frac{8 \times 7 \times 6}{3 \times 2 \times 1} \times \frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1}\right)=11760 .$

14. From a group of 7 men and 6 women, five persons are to be selected to form a committee so that at least 3 men are there on the committee. In how many ways car it do done?

564
645
735
756
None of these

Answer:

We may have (3 men and 2 women) or (4 men and 1 woman) or (5 men only)

Required number of ways = $\left({ }^7 \mathrm{C}_3 \times{ }^6 \mathrm{C}_2\right)+\left({ }^7 \mathrm{C}_4 \times{ }^6 \mathrm{C}_1\right)+\left({ }^7 \mathrm{C}_5\right)$

$=\left(\frac{7 \times 6 \times 5}{3 \times 2 \times 1} \times \frac{6 \times 5}{2 \times 1}\right)+\left({ }^7 C_3 \times{ }^6 C_1\right)+\left({ }^7 C_2\right) \quad=525+\left(\frac{7 \times 6 \times 5}{3 \times 2 \times 1} \times 6\right)+\left(\frac{7 \times 6}{2 \times 1}\right)$

= (525 + 210 + 21) = 756

15. In a group of 6 boys and 4 girls, four children are to be selected. In how many different ways can they be selected such that at least one boy should be there?

159
194
205
209
None of these

Answer: We may have (1 boy and 3 girls) or (2 boys and 2 girls) or (3 boys and 1 girl) or (4 boys).

Required number of ways =$\left({ }^6 \mathrm{C}_1 \times{ }^4 \mathrm{C}_3\right)+\left({ }^6 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2\right)+\left({ }^6 \mathrm{C}_3 \times{ }^4 \mathrm{C}_1\right)+\left({ }^6 \mathrm{C}_4\right)$

$=\left({ }^6 \mathrm{C}_1 \times{ }^1 \mathrm{C}_1\right)+\left({ }^6 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2\right)+\left({ }^6 \mathrm{C}_3 \times{ }^1 \mathrm{C}_1\right)+\left({ }^6 \mathrm{C}_2\right)$ $=(6 \times 4)+\left(\frac{6 \times 5}{2 \times 1} \times \frac{4 \times 3}{2 \times 1}\right)+\left(\frac{6 \times 5 \times 4}{3 \times 2 \times 1} \times 4\right)+\left(\frac{6 \times 5}{2 \times 1}\right)$

= (24 + 90 + 80 + 15) = 209.

16. A box contains 2 white balls, 3 black balls and 4 red balls. In how many ways-can 3 balls be drawn from the box, if at least one black ball is to be included in the draw?

32
48
64
96
None of these

Answer:

We may have (1 black and 2 non-black) or (2 black and 1 non-black) or (3 black).

Required number of ways = $\left({ }^3 \mathrm{C}_2 \times{ }^6 \mathrm{C}_2\right)+\left({ }^3 \mathrm{C}_2 \times{ }^6 \mathrm{C}_1\right)+\left({ }^3 \mathrm{C}_3\right)$

$=\left(3 \times \frac{6 \times 5}{2 \times 1}\right)+\left(\frac{3 \times 2}{2 \times 1} \times 6\right)+1$ =45 + 18 + 1 = 64

17. How many 3-digit numbers can be formed from the digits 2, 3, 5, 6, 7 and 9, which are divisible by 5 and none of the digits is repeated?

Answer:

Since each desired number Is divisible by 5, so we must have 5 at the unit place, So, there is 1 way of doing it.

Tens place can be filled by any of the remaining fi numbers.

So, there are S ways of filling the tens place.

The hundreds place can now be filled by any of the remaining 4 digits. So, there are 4 ways of filling it.

Required number of numbers = (1 × 5 × 4) = 20.

18. Evaluate:$\frac{30!}{28!}$

Answer: $\text { We have, } \frac{30!}{28!}=\frac{30 \times 29 \times(28!)}{28!}=(30 \times 29)=870$

19. Find the value of $\text { (1) }{ }_{60} P_3 \text { (2) }{ }_4 P_4$

Answer:

$\text { (1) }{ }^{60} P_3=\frac{60!}{(60-3)!}=, \frac{60!}{57!}=\frac{60 \times 59 \times 58 \times(57!)}{57!}=(60 \times 59 \times 58)=205320 \text {. }$ $\text { (b) }{ }^4 P_4=4 \text { ! }=(4 \times 3 \times 2 \times 1)=24 \text {. }$

20. Find the value of

$(1) { }^{10} \mathrm{C}_3
(2) { }^{100} \mathrm{C}_{98}
(3) { }^{50} \mathrm{C}_{50}$

Answer:

$\text { (1) }{ }^{10} \mathrm{C}_3=\frac{10 \times 9 \times 8}{31}=\frac{10 \times 9 \times 8}{3 \times 2 \times 1}=120 \text {. }$ $\text { (2) }{ }^{100} \mathrm{C}_{98}={ }^{100} \mathrm{C}_{(100-98)}={ }^{100} \mathrm{C}_2=\frac{100 \times 99}{2 \times 1}=4950 \text {. }$ $\text { (3) }{ }^{50} C_{50}=1 .\left[{ }^n C_n=1\right]$

21. How many words can be formed by using all letters of the word ‘BIHAR?

Answer: The word BIHAR contains 5 different letters.

Required number of words = 5P5 – 5! = (5x4x3x2xl) = 120.

22. How many words can be formed by using all the letters of the word ‘DAUGHTER’ so that the vowels always come together?

Answer:

Given word contains 8 different letters when the vowels AUE are always together, we may suppose them to form an entity, treated as one letter.

Then, the letters to be arranged are DGHTR (AUE).

These 6 letters to be arranged in 6Pfl = 6! = 720 ways.

The vowels in the group (AUE) may be arranged in 3! = 6 ways.

Required number of words = (720 x6) = 4320.

23. How many words can be formed from the letters of the word ‘EXTRA’ so that the vowels are never together?

Answer: The given word contains 5 different letters.

Taking the vowels EA together, we treat them as one letter.

Then, the letters to be arranged are XTR (EA)

These letters can be arranged in 4! = 24 ways.

The vowels EA maybe arranged amongst themselves in 2! =2 ways.

Number ofwords, each having vowels together = (24 x 2) = 48.

Total number ofwords formed by using all the letters of the given words = 5!= (5x4x3x2xl) = 120.

Number of words, each having vowels never together = (120 – 48) =72.

24. How many words can be formed from the letters of the word “DIRECTOR’ so that the vowels are always together?

Answer:

In the given word, we treat the vowels 1E0 as one letter

Thus, we have DRCTR (IEO).

This group has 6 letters of which R dccurs 2 times and others are different.

Number of ways of arranging these letters=$\frac{6!}{2!}$ =360.

Now 3 vowels can be arranged among themselves in 3! = 6 ways.

Required number of ways = (360 x 6) = 2160.

25. In how many ways can a cricket eleven be chosen out of a batch of 15 players?

Answer:

Required number of ways = ${ }^{15} \mathrm{C}_{11}={ }^{15} \mathrm{C}_{(15.11)}={ }^{15} \mathrm{C}_4$

$=\frac{15 \times 14 \times 13 \times 12}{4 \times 3 \times 2 \times 1}=1365 \text {. }$

26. In how many ways. A committee of 5 members can be selected from 6 men and 5 Ladies, consisting of 3 men and 2 ladies?

Answer:

(3 men out 6) and (2 ladies out of 5) are to be chosen.

Required number of ways =

$\left({ }^6 \mathrm{C}_3 \times{ }^5 \mathrm{C}_2\right)=\left(\frac{6 \times 5 \times 4}{3 \times 2 \times 1} \times \frac{5 \times 4}{2 \times 1}\right)=200 .$

27. The number of triangles that can be formed by choosing the vertices from a set of 12 points, seven of which lie on the same straight line, is:

Answer:

(1) No. of triangles =$12 c_3-7 c_3$

$=\frac{12!}{3!9!}-\frac{7!}{314!}=220-35 \quad=185$

28. A code word is to consists of two English alphabets followed by two distinct number from 1 to 9. How many such code words are there?

6,15,800
46,800
7,19,500
4,10,800

Answer:

(2) No. of code words = $26 p_{p_2} \times{ }^9 \mathrm{P}_2$

$=\frac{26.25 \cdot 24!}{24!} \times \frac{9!}{7!}=650 \times 72=46,800$

29. A boy has 3 library tickets and 8 books of his interest in the library. Of these 8, he does not want to borrow mathematics part-II unless mathematics part-I is also borrowed? In how many ways can he choose the three books to be borrowed?

Answer:

29 th answer

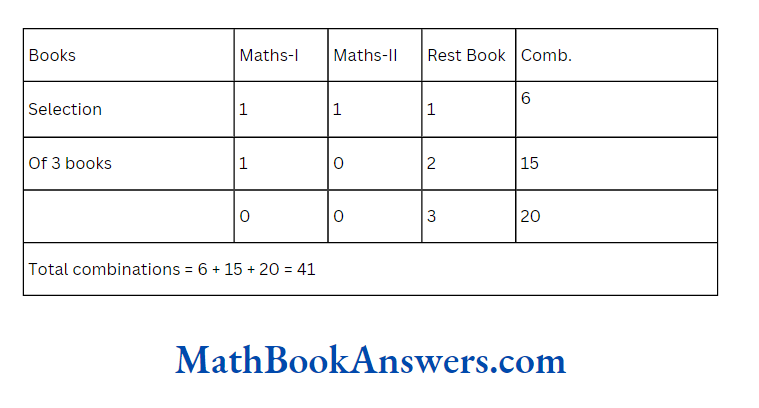
30. A supreme court bench consists of 5 judges. In how many ways, the bench can give a majority division?

Answer:

$\text { (d) } \quad=5 c_3+5 c_4+5 c_5=10+5+1=16$

31. Given: P (7,k) = 60 P (7, k- 3], Then:

Answer: (3]

P(7,K] = 60.p(7,k-3]

$\frac{7!}{(7-k)!}=60 \times \frac{7!}{\mid 7-(k-3)!} \quad \text { or } \frac{1}{(7-k)!}=\frac{60 \times 1}{|7-(k-3)|!}$ $\text { or } \frac{1}{(7-k)!}=\frac{60}{(10-k)(9-k)(8-k)(7-k)!}$

Or(l0-k) (9-k) (8-k] = 60

(Make 3 factors of 60 so that their differences are 1.)

Comparing on both sides: we get

Or(10-k) (0-k) (8-k] = 5.4.3

10-k=5 Or k= 10-5 = 5 k = 5

32. The number of ways in which n books can be arranged on a shelfso that two particular books are not together is:

(n-2) x (n-l)l
(n-1) x (m+1)!
(n-2) x (n-l)l
(n-2) x (n+1)!

Answer:

Total no. of ways to arrange book as Qts. = n! – (n-2+l]!.2!

= n! – (n-2)! 2! n(n-l)! -2(n-l)! = (n-l)!. (n-2)!

33. In how many ways can the letters of the word FAILURE be arranged so that the consonants may occupy only old positions?

Answer: (1)

Consonants = F, L, R

Vowels = A, I, U, E

Total letters = 7

There will be 7 positions of letters

Odd positions are = 1,3,5,7

Even positions are = 2,4,6

From Questions,

No. of words = $4 p_3 \cdot 4!=4!\times 4!$

= 24 x 24 = 576

34. Five bulbs of which three are defective are to be tried in two lights-points in a dark-room. In how many trials the room shall be lighted?

10
7
3
None of these

Answer: (2)

No. of bulbs = 5
Defective bulbs = 3
Non-defective bulbs = 2
No. of point in the room = 2

No. of ways to light the darkroom = $3 c_1 \cdot 2 c_1+3 c_0 \cdot 2 c_2$

= 3 x 2 + 1 x l = 6 + 1 = 7

35. In how many ways can a parly of 4 men and 4 women be seated at a circular table, so that no two women are adjacent?

Answer: (3)

No. of ways to sit 4 women = 4! = 24

Total ways to arrange = 6×24 = 144

36. $\text { If }{ }^6 P_r=24{ }^6 C_r \text {, then find } r \text { : }$

Answer: 1

$6 p_r=24.6 c_r$ $O r \frac{6!}{(6-r)!}=24 \cdot \frac{6!}{r!(6-r)!}$

Or r!=24 or r!=4!

r = 4

37. Find the number of combinations of the letters of the word COLLEGE taken four together:

Answer: (1)

Letters are C, 0, L, L, E, E, G

Case i: 2 same & 2 same letters

= LIFE = Only 1 combination

Case II: LL and 2 out of C, 0, E, G $=1 \times 4 c_2=6$

EE and any 2 out of C, 0, L, G $=1 \times 4 c_2=6$

Case III: All different letters = Any 4 out of C, 0, L, E, G $=5 c_4=5$

Total no. of combinations = l+(6+6) +5 = 18

38. How many words can be formed with the letters of the word ‘ORIENTAL’ so that A and E always occupy odd places:

540
8640
8460
8450

Answer: (2)

As Qts. No. of words = $4 p_2 \times 6!$ [because there are 4 Positions 1,3,5,7 for A & E)

$=\frac{4!}{(4-2)} \times 720=12 \times 720=8640$

39. $\text { If }{ }^{1000} \mathrm{C}_{98}={ }_{999} \mathrm{C}_{97}+\mathrm{x}_{998} \text {, find } \mathrm{x} \text { : }$

999
998
997
1000

Answer: (1) Tricks: go by choices

For (1) RHS = $\left.{ }_{999} C_{97}+999 C_{98} ; \text { if } x=999\right)$

$=999{ }_{C_{97}}+999{ }_{C_{98}}=1000 c_{98}=L H S$

40. How many number greater than a million can be formed with digits 4,5,5,0,4,5,3?

Answer: (2)

No. of Numbers $=\frac{7!}{3!\cdot 2!}-1 \times \frac{6!}{3!.2!}$

[Zero is fixed at 1st position with permutation 1]

=420-60 = 360

41. A building contractor needs three helpers and ten men apply. In how many ways can these selections take place?

Answer: (4)

Selection of 3 helpers out of10

$10_{C_3}=\frac{10!}{3!(10-3)!}=\frac{10.9 .8 .7!}{3.2 \cdot 1.7!}=120$

42. There are three blue balls, four red balls and five green balls. In how many ways can they be arranged in a row?

26,720
27,720
27,820
26,620

Answer: [2] No. ofarrangements = $\frac{12!}{3!.4!5!}=27,720$

43. If C(n,r): C(n, r+1) =1:2 and C(n, r+1) C(n, r + 2) = 2:3, determine the value of n and r:

(14,4)
(12,4)
(14,6)
None

Answer: (1)

Tricks: Go by choices

n = 14; r=4

44. Six seats of articled clerks are vacant in a ‘chartered accountant firm’ how many different batches of candidates can be chosen out of ten candidates?

216
210
220
None

Answer: (2)

No. of selections = ${ }^{10} \mathrm{C}_6=\frac{10!}{6!4!}=210$

45. Six person A, B, C, D, E and F are to be seated at circular table. In how many ways can this be done, if A must always have either B or C on his right and B must always have either C or D on his right?

Answer: (4)

B or C is right side of A

Arrangements are AB, AC,

C or Dis right side of B.

Their arrangement are BC or BD

Arrangement can be made as

Case I ABC, D,E,F can be arranged as [4-1]! = 6

Case II ABD C,E,F can be arranged as = [4-1]! = 6

Case III AC, BD, E,F can be arranged as = (4-1)! = 6

∴ total ways to arranged 6 persons = 6+6+6= 18

46. How many six-digit telephone numbers can be formed by using 10 distinct digits?

106
610
${ }^{10} \mathrm{C}_6$
${ }_{10}^{10} \mathrm{P}_6$

Answer: (4) Is correct

Total no. of (Units = 10 i.c. they are 0,1,2,3…………..;9

NO of six (I if,it distinct telephone no.

Being distinct dibits = ${ }^{10} P_6$

47. In how many ways a committee of 6 members can be formed from a group of 7 boys and 4 girls having at least 2 girls in the committee.

Answer: 3

48. Number of ways of painting a face of a cube by 6 colours is

Answer: (2)

No. of faces of a cube = 6

No. of colours = 6

No, of ways to point 1 face =${ }^6 \mathrm{C}_1=6$

49. $\text { If }{ }^{18} \mathrm{C}_{\mathrm{r}}={ }^{18} \mathrm{C}_{\mathrm{r}+2} \text { find the value of } \mathrm{r}_5 \text {. }$

55
50
56
None of these

Answer:

$\text { (3) If }{ }^{18} \mathrm{C}_{\mathrm{r}}={ }^{18} \mathrm{C}_{\mathrm{r}+2}$

r+r+2 = 18

Or 2r= 16 r= 8

${ }^r C_5={ }^8 C_5=56$

50. 7. Books are to be arranged in such a way so that two particular books are always at first and last place. Final the number of arrangments.

Answer: (3)

Arrangement of 2 particular books = 2! = 2

i.e. either at lsl place or at last place

Arrangement of rest 5 books = 5! = 120

Total arrangements = 2×120 = 240

51. Find the number of arrangements in which the letters of the word ‘MONDAY’ be arranged so that the words thus formed begin with ‘M1 and do not end with ‘N’

720
120
96
None

Answer: (3)

MONDAY

Total no. of words which begins with M = (6-1)! = 120

Total no. of words which begins M and ends With N

Total no. of words which begins with M but do not end with N

=1×4!x1 = 24

= 120-24 = 96

52. In how many ways can 17 billiard balls be arranged if 7 of them are black, 6 red and 4 white?

4084080
1
8048040
None of these

Answer:

(1) Total no. of arrangements

$=\frac{17!}{7!.6!\cdot 4!}=\frac{17.1615 .14 .13 .12 .11 .10 .9 .8 .7!}{7!.6!.4!}=4084080$

=4084080

53. (n+1)! = 20(n-l)!, Find n

Answer: (3)

(n+1) I = 20(n-l)l Or (n+1) n.(n-l)! = 20(n-l)! Or (n+l).n = 5 x 4

n = 4

54. Out of 4 gents and 6 ladies, a committee is to be formed. Find the number of ways the committee can be formed such that it comprises of at least 2 gents and at least the number of ladies should be double of gents.

Answer:

54 th answer

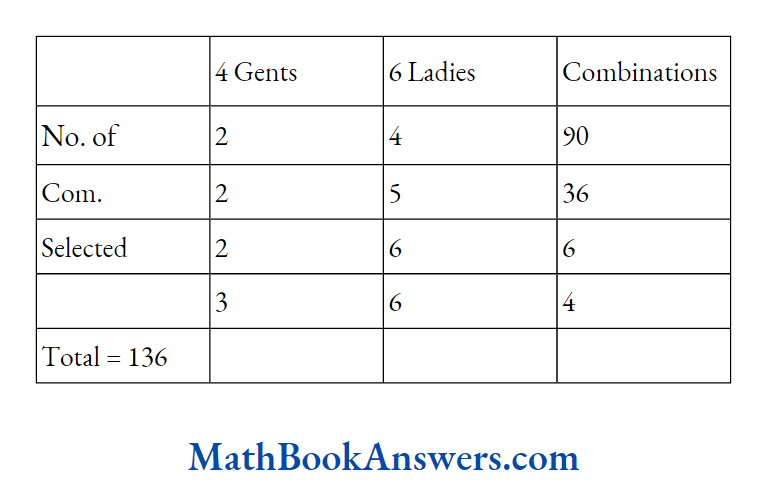
55. In how many ways can the letters of ‘REGULATION’ be arranged so that the vowels come at odd places?

14,400
1,144
1,44,252
None of these

Answer: (1)

REGULATION

Consonants = R,G,L,T,N

Vowels = E,U,A,l,0

Odd places are 1,3,5,7,9

Arrangement of vowels at these Places = ⁵P₅= 5! = 120

Consonants will be arranged at remaining places = 5! = 120

Total No. ofarrangments = 120 x 120 = 14,400

56. Six points are on a circle. The number of quadrilaterals that can be formed are:

30
360
15
None

Answer: (3)

No. of Quadrilaterals

⁶C₄=$\frac{6!}{4!2!}=\frac{6.5 .4!}{4!2!}=15$

CA Foundation Maths Permutations And Combinations Practice Problems

57. The number of ways of arranging 6 boy and 4 girls in a row so that all girls are together is:

61.4!
2(71.4!)
7!.4!
2.(6!.4!)

Answer: (3)

No of arrangement of 6 boys and 4 girls so that all 4 girls are together (6+1)1.41 =71.41 = 120960.

58. How many numbers not exceeding 1000 can be made from the digits 1,2,3,4,5,6,7,8,9 if repetition is not allowed

Answer: (2)

Given digits = 1,2,3,………9

Number less than 1000 will be of1 digit 2 digits and of 3 digits.

Total no. of numbers = ${ }^9 \mathrm{P}_1+{ }^9 \mathrm{P}_2+{ }^9 \mathrm{P}_3$

= 9x9x8+9x8x7 = 585

59. A garden having 6 tall trees in a row. In how many ways 5 children stand, one in a gap between the trees in order to pose for a photograph?

Answer: (2)

1*2*3*4*5*6

Clearly there will be 5 positions for children = ⁵P₅= 120

60. ${ }^{15} \mathrm{C}_3+{ }^{15} \mathrm{C}_3 \text { is equal to: }$

$16_{c_3}$
$30_{c_{16}}$
$15_{c_{16}}$
$15_{c_{15}}$

Answer: (1)

${ }^{15} \mathrm{C}_3+{ }^{15} \mathrm{C}_2={ }^{16} \mathrm{C}_3$

61. How many ways a team of11 players can be made out of15 players if one particular player is not to be selected in the team.

364
728
1,001
1,234

Answer:

(1) No. of ways to make a 11 – member teams

$={ }^{15-1} C_{11}={ }^1 C_{11}=\frac{14!}{11!3!}=364$

62. Find the number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included.

39,000
37,600
39,600
36,000

Answer: (3)

No. of arrangement of 5 things =

${ }^{12-1} C_{5-1} \cdot 5!={ }^{11} C_4 \cdot 5!$ $=\frac{11!}{4!.7!} \times 120=330 \times 120=39600$

63. In how many ways 3 Prizes out of 5 can be distributed amongst 3 brother equally?

Answer: (3)

No. of ways = ${ }^5 \mathrm{C}_1 \cdot{ }^4 \mathrm{C}_1 \cdot{ }^3 \mathrm{C}_1=5.4 .3=60$

64. There are 12 question are to be answered to be Yes or No. how many ways can these be answered?

1024
2048
4096
None

Answer: (3)

No. of ways = 2¹²= 4096

65. The letters the word VIOLENT are arranged so that the vowels occupy even place only. The number of permutations is

Answer: (1) Vowels = I, 0, E Consonants = V, L, N, T

No. of perms of vowels = ³P₃= 3! = 6

Total no. of words = 4! x 3! = 24 x 6 = 144

66. $\text { If } n P_4=20\left(n P_2\right)$ then the value of ‘n’ is___________

-2
7
-2 and 7 both
None of these

Answer: (2) Note: n is always positive GO by choices

67. A man lias 3 sons and 6 schools within his roach, in how many ways, ho can send them to school, if no two of his sons aro to road in the some school?

${ }_6 P_2$
${ }_6 P_3$
6³
3⁶

Answer: (2)

No. of ways = ⁶P₃

68. How many permutations can be formed the letters of the word “DRAUGHT”, if both vowels may not be separated?

720
1,440
140
1,000

Answer: (2)

Total Perms. Of DRAUGHT = 61.2! = 720 x 2 = 1440.

69. $\text { If }{ }^{13} \mathrm{C}_6+2{ }^{13} \mathrm{C}_5+{ }^{13} \mathrm{C}_4={ }^{15} \mathrm{C}_{\text {}} \text { then, } \mathrm{x}=$

Answer:

${ }^{13} \mathrm{C}_6+{ }^{13} \mathrm{C}_5+{ }^{13} \mathrm{C}_5+{ }^{13} \mathrm{C}_4={ }^{15} \mathrm{C}_{\mathrm{x}}$ $\text { Or }{ }^{13} \mathrm{C}_6+{ }^{14} \mathrm{C}_5={ }^{15} \mathrm{C}_{\mathrm{x}}$ $\text { Or }{ }^{15} \mathrm{C}_6+{ }^{14} \mathrm{C}_5={ }^{15} \mathrm{C}_{\mathrm{x}}$ $\text { Or }{ }^{15} \mathrm{C}_6={ }^{15} \mathrm{C}_x$

x=6

70. The total number ofshake hands in a group of10 persons to each other are.

Answer: (1)

Total no. of handshakes = ¹⁰C₂= 45

71. A regular polygon has 44 diagonals then the No. of sides are

Answer: (4)No. of Diagonals in a polygon of “n” sides = ⁿC₂– n = 44

‘Tricks: Go by choices.

$\text { For (a) }{ }^8 C_2-8=28-8 \neq 44$ $\text { For (b) }{ }^9 \mathrm{C}_2-9=36-9 \neq 44$ $\text { For }(\mathrm{c}){ }^{10} \mathrm{C}_2-10=45-10 \neq 44$ $\text { (d) }{ }^{11} \mathrm{C}_2-11=55-11=44$

(4) is correct

72. In how many ways to word “ARTICLE” can be arranged in a row so that vowels occupy even places?

Answer: (2)

In word ARTICLE

Vowels = A,I,E

Positions lor vowels = 2,4,6

Vowels can hr arranged In 3! = 6 ways

Rest letters can lie arranged in 4! = 24 ways

Total No. ofsuch arrangements = 6×24 = 144

73. How many different words can be formed with the letters of the word “LIBERTY”

4050
5040
5400
4500

Answer: (2)

LIBERTY

No. of words = 7! = 5040

74. In how ways can a family consist of 3 children have different birthday in a leap year.

366x365x364
³⁶⁶C₆
³⁶⁵C₃
³⁶⁶C₃-3

Answer:

(1) 1 Leap year = 366

No. of ways = ${ }^{366} \mathrm{C}_1 .{ }^{365} \mathrm{C}_1 .{ }^{36.1} \mathrm{C}_1$

= 366x365x364

75. $\text { If }{ }^{15} \mathrm{C}_{3 \mathrm{r}}={ }^{15} \mathrm{C}_{\mathrm{r}+3} \text { then } \mathrm{r}=$

Answer:

2r =3; so, r = 3/2(In fraction; so invalid)

0r3r+ r+ 3 = 15 0r 4r = 12; so, r=3

76. If 6 times the no. of permutations of n items taken 3 at a times is equal to 7 times the no. of permutations of (n-1) items taken 3 at a time then the value of n will be

Answer:

[latex]6 .{ }^n P_3=7 .(\mathrm{n}-1) \mathrm{P}_3 \text { (given) }\) $\text { Or;6 } \frac{n!}{(n-3)!}=7 \cdot \frac{(n-1)!}{(n-1-3)!}$ $\text { Or; } \frac{6 . n \cdot(n-1)!}{(n-3)(n-4)!}=\frac{7(n-1)!}{(n-4)!}$ $\text { Or } \frac{6 n}{n-3}=7$

Or 6n = 7n – 21 Or n = 21

77. $\text { If }{ }^{1000} \mathrm{C}_{98}={ }^{999} \mathrm{C}_{97}+{ }^x \mathrm{C}_{98}$ then value of x will be

999
998
997
None

Answer:

(1) Tricks: Go by choices

For (1) RHS = ${ }_{1000} \mathrm{C}_{97}+{ }^{999} \mathrm{C}_{901}$

$={ }^{999} \mathrm{C}_{97}+{ }_{999} \mathrm{C}_{98}\left[\mathrm{n}_{\mathrm{r}}={ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}-\mathrm{r}}\right]$ $={ }^{1000} \mathrm{C}_{98} \text { (L.H.S) }$ ${ }^n C_r={ }^n C_{r-1}={ }^{n+1} C_r$

78. ${ }^{{ }^G P_r}=360 \text { then find } r$

4
5
6
None

Answer: (1) Tricks: go by choices:

⁶P_r=360 LHS at r = 4 = ⁶P₄= 6.5.4.3 = 360 R.H.S.

79. If 5 books of English 4 books of Tamil and 3 books of hindi are to be arranged in a single row so that books of same language come together

1,80,630
1,60,830
1,03,680
1,30,680

Answer: (3) Total no. of ways so that same language Books remain together

= 5 !. 4 !. 3 !. 3 !. = 120 x 24 x 6 x 6 = 1,03,680

80. 5 boys and 4 girls are to be seated in row. If the girls occupy even places then the no. of such arrangements

288
2808
2008
2880

Answer: (4)

Total no. ofstudents = 9

For girls’ position may be 2,4,6,8,

Total no. of arrangements of girls ⁴P₄= 4! = 24

For boys = 5! 4! = 120×24 = 2880

81. A Person has 10 friends of which 6 of them are relatives, He wishes to Invite 5 persons so that 3 of them are relatives. In how many ways he can Invites?

Answer:

Friends = 10

Relatives = 6;

so, rest = 4 friends

Selection of 5 in which 3 are relatives = ⁶C₃. 4C₂= 20×6 = 120 (c) is correct

82. A student has 3 books on computer, 3 books on economics, 5 on commerce. If these books are to be arranged subject wise then these can be placed on a sbelf in the_ number, of ways.

25,290
25,920
4,230
4,320

Answer: (1)

Total ways = 3!x3!x5!x3! = 6 x 6 x 120 x 6 = 25920

83. The number of 4-digit members that can be formed from seven digits 1,2,3,5,7,8,9 such that no digit being repeated in any number, which are greater than 3000 are

Answer: For detail see Quicker BMLRS

At 1st place 3,5,7,8,9 these 5 digit are suitable.

So, permutation of 1st place = 5

One of them will be used at that place.

Remaining 6 digits are suitable for next place.

Similarly doing as above, Total ways = 5.6,5.4 = 600

84. A question paper consists 10 questions, 6 in math and 4 in stats. Find out number of ways to solve question paper ifat least one question is to be attempted from each section.

1024
950
945
1022

Answer: (3)

No. of ways to attempt at least one from each (2⁶-1 ) 2⁴-1) = 945.

85. ${ }^{n P_r}=720 \text { and }{ }^n C_r=120 \text { find } r \text { ? }$

Answer: (3)

ⁿP_r=ⁿC_r!=720

120. r! = 720 r!= 6 = 3! r= 3

86. There are 10 students in a class, including 3 girls. The number of ways to arrange them in a row, when any two’ girls out of them never come together

$8_{p_3} \times 7!$
$3_{p_3} \times 7!$
$8_{p_3} \times 10!$
None

Answer: (1)

Rost students = 7

Total no. of permutations of rest 7 stds. = 7!

Total no. of place for girls = 7 + 1 = 8. Total ways to arrange girls = ⁸P₃.(7!)

87. In how many ways can a selection of 6 out of 4 teachers and 8 students be done so as to include at least two teachers?

Answer:

87 answer

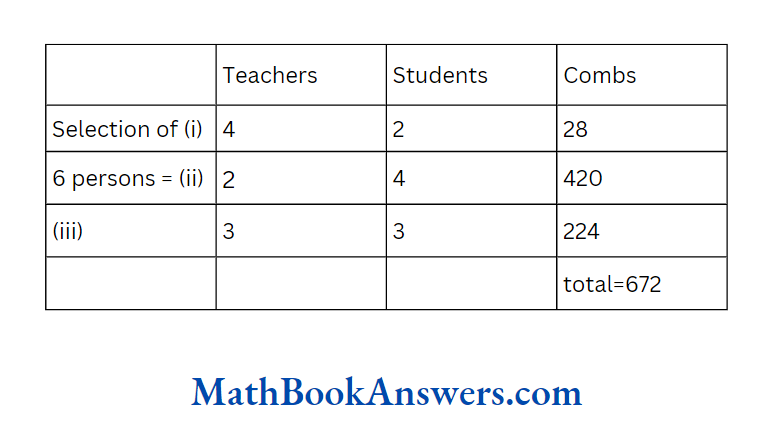
88. The maximum number of points of inter section of10 circles will be

Answer: (3)

To intersect 2 circles out of 10 are required

= ${ }^{10} \mathrm{C}_2$ x 2 = 45 x 2 = 90 Nos. of ways

88 th answer

(Each circle will cut at 2 points)

89. How many numbers between 1,000 and 1 0,000 can be formed with the digits 1, 2, 3, 4, 5, 6

Answer:

(2) is correct.

Total no. of numbers = ${ }^{(} p_4=6.5 .4 .3=360$

90. $\text { If }{ }^{n+1} C_{r+1}:{ }^n C_r:{ }^{n-1} C_{r-1}=8: 3: 1 \text {; }$ then find the value of n.

Answer: (2) is correct

Formula,${ }^n C_r:{ }^{n-1} C_{r-1}=\frac{n}{r}=\frac{3}{1} ; \text { So, } n=3 r$

$\&{ }^{n+1} C_{r+1}:{ }^n C_r=\frac{n+1}{r+1}=\frac{8}{3} ;$

So, 3n + 3 = 8r + 8

Or, 3 x 3r+ 3 = 8r + 8

Or, r= 8- 3 = 5. Hence, n = 3r = 3 x 5 = 15

91. In how many ways 4 members can occupy 9 vacant seats in a row

3204
3024
49
94

Answer: (2) is correct. Total ways = ⁹P₄

= 9.8.7.6 = 3024

92. The number of arrangements that can be formed from the letters of the word ‘ALLAHABAD”

7560
3780
30240
15320

Answer:

$\frac{9!}{(4!) \cdot(2!)}=\frac{9.8 \cdot 7 \cdot 6 \cdot 5(4!)}{(4!) \cdot 2 \cdot 1}=7560$

Option (1) is correct

93. $\text { If }{ }^{10} \mathrm{C}_3+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_5={ }^{11} \mathrm{C}_5$ then the value of n = _______

Answer:

${ }^{10} \mathrm{C}_3+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_5={ }^{11} \mathrm{C}_5$ $\text { Or; }{ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_1+{ }^{10} \mathrm{C}_1+{ }^{10} \mathrm{C}_5={ }^1 \mathrm{C}_5$ $\text { Or; }{ }^{11} C_4+{ }^{11} C_5={ }^1 C_5$ $\mathrm{Or} ;{ }^{12} \mathrm{C}_5={ }^n \mathrm{C}_5 \Rightarrow \mathrm{n}=12$

Option (3) is correct

Chapter 5 CA Foundation Maths Answer Key

94. The number of parallelograms that can be formed by a set of 6 parallel lines intersected by the another set of 4 parallel lines is

Answer:

No. of parallelograms = ${ }^6 \mathrm{C}_2 \cdot{ }^4 \mathrm{C}_2$ =15X6 = 90 Option (2) is correct

95. $^{12} C_3+2,^{12} C_1+{ }^{12} C_5={ }^{14} C_x$ The value of x

3 or 5
5 or 9
7 or 1
9 or 12

Answer:

${ }^{12} \mathrm{C}_3+2{ }^{12} \mathrm{C}_4+{ }^{12} \mathrm{C}_5={ }^{14} \mathrm{C}_x$ $\Rightarrow{ }^{12} C_3+{ }^{12} C_4+{ }^{12} C_4+{ }^{12} C_5={ }^{14} C_x$ $\Rightarrow{ }^{13} \mathrm{C}_4+{ }^{13} \mathrm{C}_5={ }^{11} \mathrm{C}_x$ $\Rightarrow{ }^{14} C_5={ }^{11} C_x \Rightarrow x=5$ $\text { And }{ }^{14} C_5={ }^{14} C_{14 \cdot 5}={ }^{14} C_x \Rightarrow x=14-5=9$

x = 5 or 9

96. The number of ways in which a man can invite one or more of his 7 friends to dinner is

Answer: (3)

No. of ways to invite at least one friend = 2⁷-1 = 128-1 = 127.

97. The number of words from the letters of the letters of the word BHARAT, in which B and H will never come together, is

120
360
240
None

Answer: (3) Use Gap rule.

*A*R*A*T*

Total words = $ \frac{4!}{2!} \times 5 p_2=\frac{24}{2} \times 5 \times 4=240$

98. The value of N in $\frac{1}{7!}+\frac{1}{8!}=\frac{N}{9!} \operatorname{ls}$

Answer: (1)

$\frac{1}{7!}+\frac{1}{8!}=\frac{N}{9!}$ $\mathrm{Or}^{\prime} ; \frac{1}{7!}+\frac{1}{8 \times 7!}=\frac{N}{9 \times 8 \times 7!}$ $\operatorname{Or} ; \frac{1}{7!}\left(1+\frac{1}{8}=\right)=\frac{N}{9 \times 8 \times 7!}$ $\Rightarrow \frac{9}{8}=\frac{N}{9 \times 8}$

99. If ${ }^n P_r$= 270 and ${ }^n C_r$= 120 then r is

Answer: (3)

${ }^n p_r={ }^n C_r, r!$

Or; 720 = 120 (r!)

Or 6 = r! => r! = 3!

r = 3

100. A bag contains 4 red, 3 black and 2 white balls. In how many ways 3 balls can be drawn from this bag so that so that they include at least one black ball?

46
64
86
None

Answer:

100 answer

101. The letters of the words ‘CALCUTTA’ and ‘AMERICA’ are arranged in all possible ways. The ratio of the number of these arrangements is

1:2
2:1
2:2
none of these

Answer: (2) 2:1

Words:

CALCUTTA

N0.of ways= $\frac{8!}{2!2!2!}=5040$

(C, A, T are repeated)

AMERICA

No. of ways = $ \frac{7!}{2!} \text { (A is repeated } \times 2 \text { ) } 2520$

Ratio = 5040 : 2520 = 2:1

102. The number of different words that can be formed with 12 consonants and 5 vowels by taking 4 consonants and 3 vowels in each word is

${ }^{12} \mathrm{C}_4 \times{ }^5 \mathrm{C}_3$
${ }^{17} \mathrm{C}_7$
4950 x 7!
none of these

Answer: (3) 4950x 7!

-» 12 consonants & 5 vowels

Selection of 4 consonants & 3 vowels = ${ }^{12} \mathrm{C}_1 \times{ }^5 \mathrm{C}_3$

Also since words need to be formed arrangement is important

7 letters can arrange themselves in 7 ! ways

Total ways =

${ }^{12} \mathrm{C}_4 \times{ }^5 \mathrm{C}_3 \times 7!=4950 \times 7!\text { ways }$

103. Eight guests have to be seated 4 on each side of a long rectangular table.2 particular guests desire to sit on one side of the table and 3 on the other side. The number of ways in which the sitting arrangements can be made is

1732
1728
1730
1278.

Answer: (2) 1728

Total guests -> 8

If 2 are seated on one side & 3 on other remaining 3 have to be seated

No. of ways = ${ }^3 \mathrm{C}_2 \times{ }^1 \mathrm{C}_1=3 \text { ways }$

Now the four on one side can arrange in 4 ! ways & other side also 4 ! ways

Total = 3×4!x4! = 1728

104. A question paper contains 6 questions, each having an alternative. The number of ways an examine can answer one or more questions is

720
728
729
none of these

Answer: (2) 728

Any question can be solved in 3 ways

(1) 1st alternative (2) 2nd alternative (3) No answer

6 questions will have 36 ways = 729

But there will be one way which will have no answers to all question which is not required

729 – 1 = 728

105. The number of words that can be made by rearranging the letters of the word APURNA so that vowels and consonants appear alternate is

18
35
36
none of these

Answer: (c) 36

A P U R N A 6 letter

3 vowels (A A U)

3 consonants (P R N)

The vowels can arrange in $\frac{3!}{2!}$ ways = 3 ways (A is repeated)

The consonants can arrange in 3! ways = 6 ways

word can be arranged in 18 ways

We will have 2 cases

VCVCVC or CVCVC i.e., 2 ways Total = 36 ways

106. The number of arrangements of the letters of the word ‘COMMERCE’ is

8
8!/2!2!2!
7 !
none of these

Answer: $\text { (2) } \frac{8!}{2!2!2!}$

COMMERCE, 8 letters (M-2, E=2, C=2)

Total arrangements = $\frac{8!}{2!2!2!}$

107. The number of ways in which 8 different beads be strung on a necklace is

2500
2520
2250
none of these

Answer: (2) 2520

8 beads in a necklace

Formula for n beads in necklace is

$\frac{1}{2}(n-1)!=\frac{1}{2}(8-1)!\quad=\frac{7!}{2}=2520$

108. The number of different factors the number 75,600 has Is

120
121
119
none of these

Answer: (1) 120

75600 no. of factors

-» 756 x 100 -» 756 (52) (22)

-»22. 33. 7. 52. 22-24. 33. 52.7

no. of factors (5+1) (4+1) (3+1) (2+1) = 120

109. (n-1) P_r+r ;(n-1) P_{(r-1)} is equal to

${ }^n \mathrm{C}_r$
$ n/(r n-r)$
${ }^n \mathrm{P}_r$
none of these

Answer:

${ }^n P_r$ ${ }^{n-1} P_r+r,(n-1) P_{(r-1)}={ }^n P_r$

110. (2ⁿ)! can be written as

2ⁿ{1.3.5…. (2n-l)}n
2ⁿ n
{1.3.5…..(2n -1)}
none of these

Answer: (1) 2n (1. 3. 5…….(2n – 1) n !

(2n) ! = 2n (2n – 1)……… 3x2x1

= 2” (2n – 2)…….(2n-1)…3×1

= 2″ n ! . (1 . 3 . 5…….(2n – 1))

CA Foundation Permutations And Combinations Solved Examples

CA Foundation Maths Solutions For Chapter 4 Time Value of Money

November 15, 2024July 5, 2024 by Marksparks

CA Foundation Maths Solutions For Chapter 4 Time Value of Money Introduction

People can’t make money or spend it on housing. food, clothing, education, entertainment, etc. Sometimes extra expenditures have also to be met. For example, there might be a marriage in the family; one may want to line house, one may want to set up his or her business, one may want to have a car, and so on.

Some people can manage to put aside some money for such expected and unexpected expenditures. But most people have to borrow money for such contingencies.
From where they can borrow money? Money can be borrowed from friends money lenders or Banks.
If you can arrange a loan from your friend it might be interest-free but if you borrow money from lenders or Banks you will have to pay some charge periodically for using money from money lenders or Banks. This charge is called interest.
Interest can be defined as the price paid by a borrower for the use of a lender’s money.

Why is Interest Paid?

Time value of money: The time value of money means that the value of the unity of money is different in different periods. The sum of money received in the future is less valuable than it is today. In other words, the present worth of money received after some time will be less than the money received today. Since money received today has more value rational investors would prefer current receipts to future receipts. If they postpone their receipts, they will certainly charge some money i.e., interest.
Opportunity Cost: The lender has a choice between using his money in different investments. If he chooses one, he forgoes the return from all others. In other words, lending incurs an opportunity cost due to the possible alternative uses of the lent money.
Inflation: Most economies generally exhibit inflation. Inflation is a fall in the purchasing power of money. Due to inflation a given amount of money buys fewer goods in the future than it will now. The borrower needs to compensate the lender for this.
Liquidity Preference: People prefer to have their resources available in a form that can immediately be converted into cash rather than a form that takes time or money to realize.
Risk Factor: There is always a risk that the borrower will go bankrupt or otherwise default on the loan. Risk is a determinable factor in fixing the rate of interest

Read and Learn More CA Foundation Maths Solutions

CA Foundation Maths Solutions For Chapter 4 Simple Interest

If the interest on a sum borrowed for a certain period is reckoned uniformly, then it is called Simple Interest.
Simple interest is the interest computed on the principal for the entire period of borrowing.
It is calculated on the outstanding principal balance and not on interest previously earned. It means no interest is paid on interest earned during the term of the loan.

Simple Interest – Important Facts and Formulae:

Principal: The money borrowed or lent out for a certain period is called the principal or the sum.

Interest: Extra money paid for using other’s money is called interest.

Simple Interest (S.I.): If the interest on a sum borrowed for a certain period is reckoned uniformly, then it is called simple interest.

Let Principal = P, Rate = R% per annum (p.a.), and Time = T years. Them

⇒ $\text { S.I. }=\left(\frac{P \times R \times T}{100}\right)$

⇒ $\mathrm{P}=\left(\frac{100 \times 5 . I}{R \times T}\right) $

⇒ $\mathrm{R}=\left(\frac{100 \times 5 . I}{P \times T}\right)$

⇒ $\mathrm{T}=\left(\frac{100 \times 5 . I}{P \times R}\right)$

A = Accumulated amount

[Final value of investment]

P = Principal. [Initial value of an investment]

r= Rate of interest

t = time (years.]

I = Amount interest

A = P + I

I = A – P

⇒ $\mathrm{A}=\mathrm{P}\left(1+\frac{1 t}{100}\right)$

CA Foundation Maths Chapter 4 Time Value Of Money Solutions

Solved Sums with Solution:

Question 1. Find the simple interest on Rs. 651000 at $16 \frac{2}{3} \%$per annum for 9 months.
Solution:

⇒ $\mathrm{P}=\mathrm{Rs} 68000, \mathrm{R}=\frac{50}{3} \% \text { p.a and } \mathrm{T}=\frac{9}{12} \text { Years }=\frac{3}{4} \text { years. }$

⇒ $\mathrm{S} .1 .=\left(\frac{P \times R \times S}{100}\right)=R s .\left(68000 \times \frac{50}{3} \times \frac{3}{4} \times \frac{1}{100}\right)=R s .8500 $

Question 2. Find the simple interest on Rs. 3000 at 6ÿ% per annum for the period from 4″’ Fell., 2005 to 18 th April, 2005.
Solution:

⇒ $\text { Time }=(24+31+18) \text { days= } 73 \text { days }=\frac{73}{365} \text { year }=\frac{1}{5} \text { year. }$

⇒ $P=\text { Rs. } 3000 \text { and } R=6 \frac{1}{4} \% \text { p.a. }=\frac{25}{4} \% \text { p.a. }$

⇒ $\text { S.I. }=\text { Rs. Rs. }\left(3000 \times \frac{25}{4} \times \frac{1}{5} \times \frac{1}{100}\right)=\text { Rs. } 37.50 $

Remark: the day on which money is deposited is not counted while the day on which money is withdrawn is counted.

Question 3. A sum at simple interest at 131/2% per annum amounts to Rs. 2502.50 after 4 years, find the sum.
Solution:

Let the sum be Rs. X then, S.l. = Rs$\left(x \times \frac{27}{2} \times 4 \times \frac{1}{100}\right)={Rs} . \frac{27 x}{50}$

⇒ $\frac{77 x}{50}=250250 \Leftrightarrow x=\frac{250250 \times 50}{77}=1625 .$

Question 4. A sum of Rs. 800 amounts to Rs. 920 in 3 years at simple interest. If the interest rate is increased by 3%, it would amount to how much?
Solution:

S.l. =Rs. (920 – 800) = Rs. 120; P=Rs. 800, T= 3 yrs.

⇒ $\mathrm{R}=\left(\frac{100 \times 120}{800 \times 3}\right) \%=5 \% $

⇒ $\text { New rate }=(5+3) \%=8 \%$

⇒ $\text { New S.I. }=\text { Rs. }\left(\frac{800 \times 8 \times 3}{100}\right)=\text { Rs. } 192$

New amount – Rs. (800+192) = Rs. 992.

Question 5. Adam borrowed some money at the rate of 6% p.a. for the first two years, at the rate of 9% p.a. for the next three years, and at the rate of 14% p.a. for the period beyond five years, If he pays a total interest of Rs. 11,400 at the end of nine years, how much money did he borrow?
Solution:

Let the sum borrowed be x. then,

⇒ $\left(\frac{x \times 6 \times 2}{100}\right)+\left(\frac{x \times 9 \times 3}{100}\right)+\left(\frac{x \times 14 \times 4}{100}\right)=11400$

⇒ $\Leftrightarrow\left(\frac{3 x}{25}+\frac{27 x}{100}+\frac{14 x}{25}\right)=11400 \Leftrightarrow \frac{95 x}{100}=11400 \Leftrightarrow\left(\frac{11400 \times 100}{95}\right)=12000$

Hence, sum borrowed = Rs. 12,000

Question 6. A certain sum of money amounts to Rs. 1008 in 2 years and to Rs. 1164 in 31/2 years find the sum and the rate of interest.
Solution:

⇒ $\text { S.I. for } 1 \frac{1}{2} \text { years }=\text { Rs. }(1164-1008)=\text { Rs. } 156 .$

⇒ $\text { S.I. for } 2 \text { years }=\text { Rs. }\left(156 \times \frac{2}{3} \times 2\right)=\text { Rs. } 208 \text {. }$

⇒ $\text { Principal= Rs. }(1008-208)=\text { Rs. } 800 .$

⇒ $\text { Now, } P=800, T=2 \text { and S.I. }=208$

⇒ $\text { Rate }=\left(\frac{100 \times 208}{800 \times 2}\right) \%=13 \% .$

Question 7. At what rate present per annum will a sum of money double in 16 years?
Solution:

Let principals P. then, S.l. = P and T = 16yrs.

⇒ $\text { Rate }=\left(\frac{100 \times P}{P \times 16}\right) \%=6 \frac{1}{4} \% p . a .$

Question 8. The simple interest on a sum of money is $\frac{4}{9}$ of the principal, find the rate present and time, if both are numerically equal.
Solution:

Let sum =Rs. x. then, S.L =Rs.$\frac{4 x}{9}$

Let rate = R % and time = R years.

Then$\left(\frac{x \times R \times R}{100}\right)=\frac{4 x}{9} \text { or } R^2=\frac{400}{9} \text { or } R=\frac{20}{3}=6 \frac{2}{3}$

⇒ $\text { Rate }=6 \frac{2}{3} \% \text { and time }=6 \frac{2}{3} y \text { rs }=6 \text { yrs } 8 \text { Months. }$

Question 9. The simple interest on a certain sum of money for 2ÿ years at 12% per annum is Rs.40 less than the simple interest on the same sum for 3 years at 10% per annum. Find the sum.
Solution:

Let the sum be Rs. X. then,$\left(\frac{x \times 10 \times 7}{100 \times 2}\right)-\left(\frac{x \times 12 \times 5}{100 \times 2}\right)=40$.

⇒ $\frac{7 x}{20}-\frac{3 x}{10}=40 \Leftrightarrow x=(40 \times 20)=800 \text {. }$

Hence, the sum is Rs.800.

Question 10. A sum was put at simple interest at a certain rate for 3 years. Had it been put at 2% higher rate, it would have fetched Rs. 360 more. Find the sum.
Solution:

Let sum= P and original rate= R. then,$\left[\frac{P \times(R+2) \times 3}{100}\right]-\left[\frac{P \times R \times 3}{100}\right]=360$

3PR + 6P – 3PR =36000« 6P =36000o P =6000

Hence, sum =Rs. 6000.

Time Value Of Money Chapter 4 CA Foundation Answers

CA Foundation Maths Solutions For Chapter 4 Exercise – 1

Question 1. A person borrows Rs. 5000 for 2 years at 4% p.a. simple interest; He immediately lends it to another person at $6 \frac{1}{4} \%$ p.a. for 2 years. Find his gain in the transaction per year.

Rs. 112.50
Rs. 125
Rs. 150
Rs. 29

Solution:

⇒ $ \text { Gain in } 2 \text { yrs. }=\text { Rs. }\left[\left(5000 \times \frac{25}{1} \times \frac{2}{100}\right)-\left(\frac{5000 \times 4 \times 2}{100}\right)\right]=\text { Rs. }(625.400)=\text { Rs. } 225$

⇒ $\text { Gain in } 1 \text { year }=\text { Rs. }\left(\frac{225}{2}\right)=\text { Rs. } 112.50 .$

Question 2. How much time will it take for an amount of Rs. 450 to yield Rs.81 as interest at 4.5% per annum of simple interest?

3.5 years
4 years
4.5 years
5 years

Solution:

⇒ $\text { Time }=\left(\frac{100 \times 81}{150 \times 4.5}\right) \text { years }=4 \text { years. }$

Question 3. A sum of Rs. 12,500 amounts to Rs.15, 500 in 4 years at the rate of simple interest what is the rate of interest?

5%
$6 \frac{1}{4} \%$
$6 \frac{1}{4} \%$
$6 \frac{3}{4} \%$

Solution:

S.l.= Rs. (15500-12500] =Rs.3000.

⇒ $\text { Rate }=\left(\frac{100 \times 3000}{12500 \times 4}\right) \%=6 \% \% .$

Question 4. Reena took a loan of Rs. 1200 with simple interest for as many years as the rate of interest. If she paid Rs. 432 as interest at the end of the loan period, what was the rate of interest?

3.6
6
Cannot be determined
None of these

Solution:

Let rate = R% and time = R years. Then,

⇒ $\left(\frac{1200 \times R \times R}{100}\right)=432 \Leftrightarrow \quad 12 R^2=432 \quad \Leftrightarrow \quad R^2=\quad 36 \Leftrightarrow \mathrm{R}=6$

Question 5. A man took a loan from a bank at the rate of 12% p.a. simple interest. After 3 years he had to pay Rs.5400 interest only for the period. The principal amount borrowed by him was:

Rs 2000
Rs 10,000
Rs 15,000
Rs. 20,000

Solution:

⇒ $\text { Principal }=\text { Rs. }\left(\frac{100 \times 5100}{12 \times 3}\right)=\text { Rs. } 15000 .$

Question 6. What is the present worth of Rs.132 due in 2 years at 5% simple interest per annum?

Rs. 112
Rs. 118.80
Rs. 15,000
Rs. 122

Solution:

Let the present worth be Rs. x, then, S.l. =Rs. (132-x).

⇒ $ \left(\frac{x \times 5 \times 2}{100}\right) 132-x \Leftrightarrow 10 x=13200-100 x \Leftrightarrow 110 x=13200 \Leftrightarrow x=120 $

Question 7. A sum fetched a total simple interest of Rs. 4016.25 at the rate of 9 p. c. p.a. in 5 years. What is the sum?

Rs. 4462.50
Rs. 8032.50
Rs. 8900
Rs. 8925
None of these

Solution:

⇒ $\text { principal }=\text { Rs. }\left(\frac{100 \times 4016.25}{9 \times 5}\right)={Rs} .\left(\frac{401625}{45}\right)={Rs} .8925 .$

Question 8. Rs. 800 becomes Rs. 956 in 3 years at a certain rate of simple interest, if the rate ofinterest is increased by 4%, what amount will Rs. 800 become in 3 years?

Rs. 1020.80
Rs 1025
Rs. 1052
Data inadequate
None of these

Solution:

S.l. = Rs. (956-800) = Rs. 1 56.

⇒ $\text { Rate }=\left(\frac{100 \times 156}{800 \times 3}\right) \%=6 \frac{1}{2} \%$

⇒ $\text { New rate }=\left(6 \frac{1}{2}+4\right) \%=10 \frac{1}{2} \%$

⇒ $\text { New S.I. }=\text { Rs. }\left(800 \times \frac{21}{2} \times \frac{3}{100}\right)=\text { Rs. } 252$

New amount =Rs.(800+252)= Rs.1052

Question 9. A certain amount earns a simple interest of Rs.1750 after 7 years. Had the interest been 2% more, how much more interest would it have earned?

Rs. 35
Rs. 245
Rs. 350
Cannot be determined
None of these

Solution:

We need to know the S.I. principal and time to find the rate since the principal is not given, so data is inadequate.

Question 10. In how many years, Rs. 150willproduce the same interest @ 8%as Rs.800 produce in 3 years $\text { @ } 4 \frac{1}{2} \% \text { ? }$

Solution:

P= Rs 800, R=4ÿ% = %, T = 3 years, then,

$\text { S.I. }=\text { Rs. }\left(800 \times \frac{9}{2} \times \frac{3}{100}\right)=R s .108 .$

Now, P =Rs. 150, S.l. = Rs. 108, R= 8%

⇒ $\text { Time }=\left(\frac{100 \times 108}{150 \times 8}\right) \text { years }=9 \text { years. }$

Question 11. A sum invested at 5% simple interest per annum grows to Rs. 504 in 4 years. The same amount at 10% simple interest per annum in 2ÿyears will grow to:

Rs. 420
Rs. 450
Rs. 525
Rs. 550

Solution:

let the sum be Rs. X. then, S.l. = Rs.(504-x).

⇒ $\left(\frac{x \times 5 \times 4}{100}\right)=504 \cdot \mathrm{x} \Leftrightarrow 20 \mathrm{x}=50400-100 \mathrm{x} \Leftrightarrow 120 \mathrm{x}=50400 \Leftrightarrow \mathrm{x}=420$

Now, P= Rs. 420, R= 10%. $\mathrm{T}=\frac{5}{2} \text { years. }$

⇒ ${\text { S.I. }=Rs} .\left(\frac{420 \times 10}{100} \times \frac{5}{2}\right)={Rs} .105$

Amount = Rs, (420+105] = Rs. 525.

Question 12. What will be the ratio of simple interest earned by a certain amount at the same rate of interest for 6 years and that for 9 years?

1 : 3
1: 4
2 : 3
Data inadequate
None Of these

Solution:

Let the principal boI’ ami rale ol interest be R%

Required ratio $=\left\lfloor\frac{\frac{P \times R \times 6}{100}}{\frac{P\times R\times 9}{100}}\right\rfloor=\frac{6 PR}{9 P R}=\frac{6}{9}=2: 3$

Question 13. Nitin borrowed some money at the rate of 6% p.a. for the first three years, 9% p.a. for the next five years, and 13% p.a. for the period beyond eight years, If the total interest paid by him at the end of eleven years is Rs. 8160, how much money did he borrow?

Rs. 8000
Rs. 10,000
12,000
Data inadequate

Solution:

let the sum to Its. X. Then,

⇒ $\left(\frac{x \times 6 \times 3}{100}\right)+\left(\frac{x \times 9 \times 5}{100}\right)+\left(\frac{x \times 13 \times 3}{100}\right)=8160$

18x+45x+39x=(8 1 60 x 100) <=> 102x = 816000 <=> x = 8000.

Question 14. An automobile financier claims to be lending money at simple interest, but he includes the interest every six months for calculating the principal. If he is charging an interest of 10% the effective rate of interest becomes:

10%
10. 25%
10.5%
None of these

Solution:

Let the sum be Rs. 100 then

S.I. for first 6 months Rs.$\text { Rs. }\left(\frac{100 \times 10 \times 1}{100 \times 2}\right)={Rs} .5$

S.l. for last 6 months= Rs.$\left(\frac{105 \times 10 \times 1}{100 \times 2}\right)=Rs .5 .25$

So, the amount at the end of 1 year is Rs. (100+5+5.25)= Rs.110.25.

Effective rate = (110.25-100)= 10.25 %

Question 15. A sum of money at simple interest amounts to Rs. 815 in 3 years and to Rs.854 in 4 years. The sum is:

Rs. 650
Rs. 690
Rs. 698
Rs 700

Solution:

S.l. for 1 year= RS. (854-815)=Rs.39.

S.l. for 3 Years= RS.(39 x 3) = Rs.117.

Principal = Rs.( 815 -117) = Rs. 698.

Question 16. A sum of money lent out at simple interest amounts to Rs. 720 after 2 years and to Rs. 1020 after a further period of 5 years. The sum is:

Rs. 500
Rs. 600
Rs. 700
Rs. 710

Solution:

S.I. for 5 years RS. (1020-720)=Rs.300

S.I. for 2 Years=$\text { RS. }\left(\frac{300}{5} \times 2\right)={Rs} .120$

Principal = Rs.( 720 -120) = Rs. 600.

Question 17. A sum of money amorist to Rs. 9800 after 5 years and Rs. 12005 after 8 years at the same rate of simple interest, the rate of interest per annum is:

Solution:

S.I. for 3 years RS. (12005-9800)=Rs.2205

⇒ $\text { S.I. for } 5 \text { Years }=\text { RS. }\left(\frac{2205}{3} \times 5\right)=\text { Rs. } 3675 \text {. }$

⇒ $\text { Principal }=\text { Rs. }(9800-3675)=\text { Rs. } 6125 \text {. }$

⇒ $\text { Hence, rate }=\left(\frac{100 \times 3675}{6125 \times 5}\right) \%=12 \%$

Question 18. At what rate present of simple interest will a sum of money double itself in 12 years?

$ 8 \frac{1}{4} \%$
$ 8 \frac{1}{3} \%$
$ 8 \frac{1}{2} \%$
$ 9 \frac{1}{2} \%$

Solution:

Letsum=x. then, S.l. = x

⇒ $\text { Rate }=\left(\frac{100 \times S . J}{P \times T}\right)=\left(\frac{100 \times x}{x \times 12}\right) \%=\frac{25}{3} \%=8 \frac{1}{3} \%$

Question 19. At what rate present per annum will the simple interest sum of money be $\frac{2}{5}$ of the amount in 10 years?

4%
$5 \frac{2}{3} \%$
6%
$6 \frac{2}{3} \%$

Solution:

Let sum= x. then, S.I. =$\frac{2 x}{5} \text { Time }=10 \text { Years. }$

⇒ $\text { Rate }=\left(\frac{100 \times 2 x}{x \times 5 \times 10}\right) \%=4 \%$

Question 20. In how much time would the simple interest on a certain sum be 0.125 times the principal at 10% per annum?

$1 \frac{1}{4}years$
$1 \frac{3}{4}years$
$2 \frac{1}{4}years$
$2 \frac{3}{4}years$

Solution:

Let sum= x. then, S.l. = 0.125x=$\frac{1}{8} x, R=10 \%$

⇒ $\text { Time }=\left(\frac{100 \times x}{x \times 8 \times 10}\right) \text { Years }=\frac{5}{4} \text { Years }=1 \frac{1}{4} \text { Years }$

Question 21. A sum of money becomes of itself in 3 years at a certain rate of simple interest the rate annum is:

$5 \frac{5}{9} \%$
$ 6 \frac{5}{9} \%$
18%
25%

Solution:

Let sum= x. then, Amount=$\frac{7 x}{6}, \mathrm{~S} . \mathrm{I}=\left(\frac{7 x}{6}-x\right)=\frac{x}{6} ;$

Time = 3 Years

⇒ $\text { Rate }=\left(\frac{100 \times x}{x \times 6 \times 3}\right) \%=\frac{50}{9} \%=5 \frac{5}{9} \%$

Question 22. Simple Interest on a certain amount is $\frac{9}{16}$of the principal. If the numbers representing principal are lent out, is:

$5 \frac{1}{2}years$
$ 6 \frac{1}{2}years$
7 years
$7 \frac{1}{2}years$

Solution:

let sum = x. tlum, S.l. $=\frac{9}{16} x$

Let rate= R % and Time = R years

⇒ $\left(\frac{x \times R \times R}{100}\right)=\frac{9 x}{16} \Leftrightarrow R^2=\frac{900}{16} \Leftrightarrow R=\frac{30}{4}=7 \frac{1}{2}$

Hence, time = $7 \frac{1}{2} \text { Years. }$

Question 23. A lends Rs. 2500 to B and a certain sum to C at the same time at 7% p.a. simple Interest. If after 4 years, A altogether receives Rs. 1120 as interest from B and C, then the sum lent to C is:

Rs. 700
Rs. 1500
Rs. 4000
Rs. 6500

Solution:

Let the sum lent to C he Rs. X. then,$\left(\frac{2500 \times 7 \times 4}{100}\right)+\left(\frac{x \times 7 \times 4}{100}\right)=1120$

⇒ $ \Leftrightarrow \quad \frac{7}{25} x=(1120-700) \Rightarrow x=\left(\frac{420 \times 25}{7}\right)=1500$

CA Foundation Maths Chapter 4 Detailed Solutions

Question 24. A lent Rs.5000 for 2 years and Rs. 300 for 4 years on simple interest at the same rate of interest and received Rs. 2200 in all from both of them as interest. The rate of interest per annum is:

5%
7%
71 %
10%

Solution:

Let the rate be R% p.a. then,$\left(\frac{5000 \times R \times 2}{100}\right)+\left(\frac{3000 \times R \times 4}{100}\right)=2200$

⇒ $\Leftrightarrow \quad 100 R+120 R=2200 \Leftrightarrow R=\left(\frac{2200}{220}\right)=10 \text { Rate }=10 \%$

Question 25. A sum of Rs 725 is lent at the beginning of a year at a certain rate of interest. After 8 months, a sum of Rs. 362.50 more is lent but at the rate twice the former at the end of the year, Rs.33.50 is earned as interest from both the loans. What was the original rate of interest?

3.6%
4.5%
5%
6%
None

Solution:

Let the original rate be R% then, the new rate = (2R) %.

⇒ $\left(\frac{725 \times R \times 1}{100}\right)+\left(\frac{36250 \times 2 R \times 1}{100 \times 3}\right)=33.50$

(2175+725) R= 33.50x 100 x 3=10050 $\Leftrightarrow \quad R=\frac{10050}{2900}=3.46$

Original rate = 3.46%

Question 26. The difference between the simple interest received from two different sources on Rs. 1500 for 3 years is Rs. 13.50 the difference between their rates of interest is:

0.1%
0.2%
0.3%
0.4%
None

Solution:

⇒ $\left(\frac{1500 \times R_1 \times 3}{100}\right)-\left(\frac{1500 \times R_2 \times 3}{100}\right)=13.50$

4500 (R1 – R2) = 1350o (R1 – R2)=$=\frac{1350}{4500}=0.3 \%$

Question 27. Peter invested an amount of 12000 at the rate of 10 p.c.p.a. simple interest and another amount at the end of 20 p.c.p.a. simple interest. The total interest earned at the end of one year on the total amount invested became 14 p.c.p.a. Find the total amount invested.

Rs. 20,000
Rs. 22,000
Rs 24,000
Rs. 25,000
None

Solution:

Let the second amount be RS. X. Then,

⇒ $\left(\frac{12000 \times 10 \times 1}{100}\right)+\left(\frac{x \times 20 \times 1}{100}\right)=\left[\frac{(12000+x) \times 14 \times 1}{100}\right]$

12000+20x=1 68000+14x ⇔ 6x= 48000 ⇔ x = 8000

Total investment = Rs. (12000+8000) = Rs. 20000

Question 28. If the annual rate of simple interest increases from 10 % to $12 \frac{1}{2}$ % a man’s yearly income increases by Rs. 1250 His principal (in Rs.) is:

45,000
50,000
Rs. 24,600
Rs. 26,000

Solution:

Let the sum be Rs. X, then,$\left(x \times \frac{25}{2} \times \frac{1}{100}\right)-\left(\frac{x \times 10 \times 1}{100}\right)=1250$

⇔ 25x-20x = 250000 ⇔ 5x = 250000 o x = 50000

Question 29. A moneylender finds that due to a fall in the annual rate of interest from 8% to 7- %, his 4 yearly income diminishes by Rs. 61.50 His capital is:

Rs. 22,400
Rs. 23,800
Rs. 24,600
Rs. 26,000

Solution:

Let the capital be Rs. X, then,$\left(\frac{x \times 8 \times 1}{100}\right)-\left(x \times \frac{31}{4} \times \frac{1}{100}\right)=61.50$

32x- 31x = 6150x 4 o x = 24600

Question 30. The price of a T.V. set worth Rs. 20,000 is to be paid in 20 installments of Rs. 1000 each. If the rate of interest is 6 per annum, and the first installment is paid at the time of purchase, then the value of the last instalment covering the interest as well will be:

Rs. 1050
Rs. 2050
Rs. 3000
None of these

Solution:

Money paid in cash = Rs. 1000. Balance payment = Rs. (20000-1000) = Rs. 19000.

Question 31. Mr. Thomas invested an amount of Rs. 13900 divided into two different schemes A and B at the simple interest earned in 2 years Rs. 3508, what was the amount invested in scheme B?

Rs. 6400
Rs. 6500
7200
Rs. 7500
None

Solution:

Let the sum invested in scheme A be Rs. X and that in scheme B be Rs. (13900 – x).

⇒ $\text { Then, }\left(\frac{x \times 14 \times 2}{100}\right)+\left[\frac{13900-x) \times 11 \times 2}{100}\right]=3508$

28x- 22x = 350800 – (13900 x 22) cs 6x = 45000 ⇔ x = 7500.

Question 32. An amount of Rs. 100000 is invested in two types of shares. The first yields an interest of 9% p.a. and the second, 11% p.a. If the total interest at the end of one year is, 9% then the amount invested in each share was:

Rs. 52,500; Rs. 47,500
Rs. 62,500; Rs. 37,500
Rs. 72,500; Rs. 27,500
Rs. 82,500; Rs. 17,500

Solution:

Let the sum invested at 9% be Rs. X and that invested at 11% be Rs. (100000 – x)

Then, $\left(\frac{x \times 9 \times 1}{100}\right)+\left[\frac{(100000-x) \times 11 \times 1}{100}\right]=\left(100000 \times \frac{39}{4} \times \frac{1}{100}\right)$

⇒ $\Leftrightarrow \frac{9 x+1100000-11 x}{100}=\frac{39000}{4}=9750$

2x = (1100000-975000) = 125000 ox = 62500.

The sum invested at 9%= Rs. 62500. The sum invested at 1 1% = Rs. (100000- 62500) = Rs. 37500.

Question 33. David invested a certain amount in three different schemes A, B, and C with the rate of interest of 10 % p.a. 12% p.a., and 15% P.a. Respectively. If the total interest. Accrued in one year was Rs. 3200 and the amount invested in scheme C was 150% of the amount invested in scheme B.

Rs. 5000
Rs. 6500
Rs. 8000
Cannot be determined
None of these

Solution:

let x,y, and z be the amounts invested in schemes A, B, and C respectively. Then,

⇒ $\left(\frac{x \times 10 \times 1}{100}\right)+\left(\frac{y \times 12 \times 1}{100}\right)+\left(\frac{z \times 15 \times 1}{100}\right)=3200$

10x+12y+15z= 320000

Now, z=240% of y$=\frac{12}{5} y$

And,z= 150% of x$x=\frac{3}{2} x \Rightarrow x=\frac{2}{3} z=\left(\frac{2}{3} \times \frac{12}{5}\right) y=\frac{8}{5} y$

From (1), (2) and (3), we have

16y+ 12y + 36y= 320000 o 64y = 320000 ⇔y = 5000

Question 34. A person invested in all Rs. 2600 at 4%, 6%, and 8% per annum simple interest, and at the end of the year, he got the same interest in all three cases, the money invested at 4% is:

Rs. 200
Rs. 600
Rs. 800
Rs. 1200

Solution:

Let the parts be x, y, and [2600-(x + y)]. Then,

⇒ $\frac{x \times 4 \times 1}{100}=\frac{y \times 6 \times 1}{100}=\frac{[2600-(x+y)] \times 8 \times 1}{100}$

⇒ $\frac{y}{x}=\frac{4}{6}=\frac{2}{3} \text { or } y=\frac{2}{3} x$

⇒ $So, \frac{x \times 4 \times 1}{100}=\frac{\left(2600-\frac{5}{3} x\right) \times 8}{100}$

⇒ $\Rightarrow 4 x=\frac{(7800-5 x) \times 8}{3} \Leftrightarrow 52 x=(7800 \times 8) \Leftrightarrow x=\left(\frac{7800 \times 8}{52}\right)=1200 .$

Money invested at4%= Rs.1200

Question 35. Divide Rs. 2379 into 3 parts so that their amounts after 2, 3, and 4 years respectively may be equal, the rate of interest being 5% per annum at simple interest. The first part is:

Rs. 759
Rs. 792
Rs. 818
Rs. 828

Solution:

Let the parts be x, y and [2379 – (x +y)]

⇒ $\mathrm{X}+\left(x \times 2 \times \frac{5}{100}\right)=y+\left(y+3 \times \frac{5}{100}\right)=z+\left(z \times 4 \times \frac{5}{100}\right)$

⇒ $\Rightarrow \frac{11 x}{10}=\frac{23 y}{20}=\frac{6 \mathrm{z}}{5}=\mathrm{k} \quad \Rightarrow \quad \mathrm{x}=\frac{10 \mathrm{k}}{11}, \mathrm{y}=\frac{20 \mathrm{k}}{23}, \mathrm{z}=\frac{5 \mathrm{k}}{6}$

⇒ $ text { But } \mathrm{x}+\mathrm{y}+\mathrm{z}=2379 $

⇒ $ \Rightarrow \frac{10 \mathrm{k}}{11}+\frac{20 \mathrm{k}}{23}+\frac{5 \mathrm{k}}{6}=2379 \quad \Rightarrow \quad 1380 \mathrm{k}+1320 \mathrm{k}+1265 \mathrm{k}=2379 \times 11 \times 23 \times 6 $

⇒ $ \mathrm{k}=\frac{2379 \times 11 \times 23 \times 6}{3965}=\frac{3 \times 11 \times 23 \times 6}{5} $

⇒ $\mathrm{x}=\left(\frac{10}{11} \times \frac{3 \times 11 \times 23 \times 6}{5}\right)=828$

Hence, the first part is Rs. 828

Question 36. Two equal sums of money were lent at simple interest at ll%p.a. for 3 years and 4 years respectively.If the difference in interest for two periods was ₹ 412.50, then each sum is:

₹3,250
₹3,500
₹ 3.750
₹4,350

Solution:

The difference in is due to the time

Rate of interest for the whole

Duration = [11×4.5 – 11×3.5) = 11%

⇒ $P=\frac{\text { Total S.I }}{\text { Interest on ₹1 }}=\frac{412.50}{0.11}=₹ 3750$

Question 37. In how much time would the simple interest on a certain sum be 0.125 times the principal at 10% per annum?

$1 \frac{1}{4}$
$1 \frac{3}{4}$
$2\frac{1}{4}years$
$2 \frac{3}{4}years$

Solution:

⇒ $\mathrm{t}=\frac{1 / P}{r \%}=\frac{0.125}{0.10}=1.25 \mathrm{yrs}$

Details: S . I$ =\frac{p . r. t}{100} $

0r ;$ 0.125 \mathrm{P}=\frac{P, 10 \times t}{100}$

Or t = 0.125×10 = 1.25 yrs

Question 38. Find the number of years in which a sum doubles itself at the rate of 8% per annum.

$11 \frac{1}{2}$
$12 \frac{1}{2}$
$9 \frac{1}{2}$
$13 \frac{1}{2}$

Solution:

⇒ $text { Tricks: } \mathrm{t}=\frac{(x-1) \times 100}{r}$

⇒ $=\frac{(2-1) \times 100}{B}=12.5 \mathrm{yrs} $

Question 39. The time by which a sum of money is 8 times its self if it doubles itself in 15 years.

42 years
43 years
45 years
46 years

Solution:

It is compound interest Qts.

2t2 =815

Or 212 = 815 Or 212 = (23)15 : tz = 45 yrs

Question 40. What is the rate of simple interest if a sum of money amount ₹2,784 in 4 years and ₹2,688 in. 3 years?

l%p.a.
4% p.a.
5% p.a.
8% p.aa

Solution:

⇒ $\text { S.l. pa }=\frac{\text { difference in s.t }}{\text { difference in time }}$

⇒ $\frac{s t_2-s t_1}{t_2-t_1}=\frac{2784-2688}{4-3}=90$

Principal = 1(20(0) – 3 x 00) = 2400

⇒ $\mathrm{r}=\frac{t \times 100}{p \times t}=\frac{96 \times 100}{2400 \times 1}=4 \%$

Question 41. If a simple interest on a sum of money at 6% p.a. for 7 years is equal to twice of simple interest on another sum for 9 years at 5% p.a. the ratio will be:

2:15
7:15
15:7
1:7

Solution:

⇒ $P_1 \frac{6.7}{100}=2 \times \frac{P_{2 .} .9 .5}{100} $

⇒ $\text { Or } \frac{P_1}{P_2}=2 \times \frac{9 \times 5}{6 \times 7}=\frac{15}{7} \Rightarrow \frac{P_1}{P_2}=\frac{15}{7}$

Question 42. By mistake, a clerk, calculated the simple interest on the principal for 5 months at 6.5% p.a. instead of 6 months at 5.5% p.a. if the calculation error was ₹25.40. The original sum of principal was____.

₹60,690
₹60,960
₹90,660
₹90690

Solution:

⇒ $P=\frac{25.40}{\frac{5.5}{100} \times \frac{6}{12}-\frac{6.5}{100} \times \frac{5}{12}}$

⇒ $\frac{25.40 \times 1200}{5.5 \times 6-6.5 \times 5}=₹ 60,960 $

Question 43. If the simple interest on ₹1,400 for 3 years is less than the simple interest on ₹1,800 for the same period by ₹80, then the rate of interest is:

5.67%
6.67%
7.20%
5.00%

Solution:

⇒ $ r=\frac{80 \times 100}{(1800-1400) \times 3}$

= 6.67%

Question 44. The S.l on a sum of money is $ \frac{4}{9}$ of the principal and the No. of years is equal to the rate of interest per annum. Find the rate of interest per annum.

5%
20/3%
22/7%
6%

Solution:

⇒ $\text { S.I. }=\frac{p . r. r}{100} \Rightarrow \frac{1}{9} p .=p \cdot\left(\frac{r}{10}\right)^2 $

⇒ $\frac{r}{10}=\frac{2}{3}r=\frac{20}{3} \%$

Question 45. Simple interest on *2,000 for 5 months at 16% p.a. is_.

₹133.33
₹133.26
₹134.00
₹132.09

Solution:

⇒ $\text { S.I. }=2000 \times \frac{5}{12} \times \frac{16}{100}=₹ 133.33$

Question 46. How much investment is required to yield an Annual income of ₹420 at 7% p.a. simple interest.

₹6,000
₹6,420
₹5,580
₹5,000

Solution:

⇒ $\mathrm{P}=\frac{420 \times 100}{7 \times 1}=₹ 6000$

2 GBC: P= 420+7% button = 16000

Question 47. Mr. X invests ₹90,500 in the post office at 7.5% p.a. simple interest. While calculating the rate was wrongly taken as 5.7% p.a. the difference in amounts at maturity is ₹9,774. Find the period for which the sum was invested.

7 years
5.8years
6 years
8 years

Solution:

⇒ $\mathrm{t}=\frac{9774 \times 100}{90.500 \times(7.5-5.7)}=6 \mathrm{yrs}$

Question 48. If the sum of money when compounded annually becomes ₹1140 in 2 years and ₹1710 in 3 years at rate of interest

Solution:

Interest in 3rd yr= 1710- 1140 = 570

For 3rd yrs.; it will be like S.l

⇒ $\mathrm{r}=\frac{l \times 100}{P . t}=\frac{570 \times 100}{1140 \times 1}=50 \%$

For (c) A = 1140 + 50% (calculator) = 1710

Question 49. In what time will a sum of money double itself at 6.25% p.a at simple interest

5 yrs.
8 years
12 yrs.
16 yrs.

Solution:

⇒ $\mathrm{t}=\frac{(2-1) \times 100}{6.25}=16 \text { years }$

Question 50. What principal will amount to ₹370 in 6 years at 8% p.a. at simple interest

₹210
₹250
₹310
₹350

Solution:

⇒ $ P=\frac{370}{1+6 \times 0.08}=₹ 250$

Question 51. If a sum trip Per in 15 years at the simple rate of interest then the rate of interest per annum will be

13.0%
13.3%
13.5%
18%

Solution:

$\text { Tricks }=\frac{(3-1) \times 100}{1 \times 15}=13.3$

Calculator Tricks: GBC

(2) r = 15 x 13.333%= 200%

A = 1 + 200% (button) = 3

(2) is correct

Question 52. A certain sum of money was invested at a simple rate of interest for three years. If it was invested at 7% higher, the interest have been *882 more, then the sum has been invested at that rate was

₹12,600
₹6,800
₹4,200
₹2,800

Solution:

t=3 years

⇒ $\mathrm{P}=\frac{1 \times 100}{r t}=\frac{882 \times 100}{7 \times 3}=₹ 4200$

Question 53. The sum of money will be doubled in 8 years at S.I. In how many years the sum will be tripled?

20 years
12 years
16 years
None

Solution:

⇒ $ \frac{t_2}{8}=\frac{3-1}{2-1} \quad t_2=16 \text { yrs. }$

Question 54. A sum of 44,000 is divided into 3 parts such that the corresponding interest earned after 2 years, 3 years and 6 years may be equal at the rate of simple interest are 6% p.a. 8% p.a. & 6% p.a., respectively. Then the smallest part of the sum will be.

₹4,000
₹8,000
₹10,000
₹12,000

Solution:

⇒ $ P_1: P_2: P_3=\frac{1}{r_1 t_1}: \frac{1}{r_2 t_2}: \frac{1}{r_3 t_3}$

⇒ $\frac{1}{2 \times 6}: \frac{1}{8 \times 3}: \frac{1}{6 \times 6} $

⇒ $\left[\frac{1}{12}: \frac{1}{24}: \frac{1}{36}\right] \times 72 \text { LCM of denominators }$

=6: 3: 2

So, smallest principal $ =\frac{44000}{6+3+2} \times 2=₹ 8000$

Question 55. No. of years the sum of money becomes 4 times itself at 12% p.a. at simple interest:

Solution:

⇒ $\text { (3) Tricks: } \mathrm{t}=\frac{(4-1) \times 100}{1 \times 12}=25 \mathrm{yrs} \text {. }$

Question 56. No. years of a sum of money becomes 4 times itself at 12% p.a. at simple interest:

Solution:

(3) is correct

⇒ $\text { Tricks: } t=\frac{(4-1) \times 100}{1 \times 12}=25 \mathrm{yrs} \text {. }$

Question 57. If a person lends ₹6,000 for A years and 10,000 for 3 years at S.I. The total interest earned Is ₹2100 then the rate of interest is____.

Solution:

(1) is correct.

For (1): Total SI = 6000 x 4. x 5% + 8000 x 3 x 5% =R2400

So, (1) is correct.

Question 58. In simple interest, a certain sum becomes ₹97,920 in years, and ₹1,15,200 in 5 years, then the rate of interest is:

10%
11.2%
12%
13.6%

Solution:

(3)

⇒ $\text { Tricks: S.I p.a. }=\frac{1,15,200-97,920}{5-3}$=8640

Principal = 97,920 – 3 yrs interest = 97,920 – 3 x 8640 = 72,000

⇒ $r=\frac{8640 \times 100}{72000}=12 \%$

Amounts = 72000 + (12 x 3 = 36) %

Button = (True)

So, option (C) is correct.

Question 59. A person borrows Rs. 5,000 for 2 years at 4% per annual simple interest. He immediately lends to another person at $6 \frac{1}{4} \%$. Per annual for 2 years find his gain in the transaction.

Rs. 112.50
Rs. 225
Rs. 125
Rs. 107.50

Solution:

Interest Gain =$\left(6 \frac{1}{4}-4\right)=2 \frac{1}{4}=2.25 \%$

So, Interest Gain

⇒ $=\frac{5000 \times 2 \times 2.25}{100}=\text { Rs. } 225$

Question 60. A certain money doubles itself in 10 years when deposited on simple interest. It would triple itself in.

30 year
20 years
25 years
15 years

Solution:

⇒ $\frac{t_1}{t_1}=\frac{r_2-1}{r_1-1} \quad \Rightarrow \frac{t_2}{t_0}=\frac{3-1}{2-1} \Rightarrow t_2=20 \mathrm{yrs} .$

Question 61. A certain sum of money Q was deposited for 5 years and 4 months at 4.5% simple interest and amounted to ₹248, then the value of Q is

Solution:

t = 5 yrs 4 months = $5+\frac{1}{12}=\frac{16}{3} \mathrm{yrs}$

⇒ $A=Q\left(1+\frac{1 t}{100}\right)$

⇒ $\text { Or } 248=Q\left[1+\frac{45}{100} \times \frac{16}{3}\right]$

⇒ $ Q=\frac{248 \times 300}{372}={Rs} .200$

Rates for 5 yrs 4 Months = 5 ₹ 4.5% + one-third of 4.5% = 24% Note: 4 months means one-third of one year, so rate for 4 months = one-third of one-year interest rale.

Amounts = 200 + 24% = 248 (True) So, (b) is correct.

Question 62. The certain sum of money became Rs. 692 in 2 yrs. And Rs. 800 in 5 yrs. Then the principle amount is_____.

Rs. 520
Rs. 620
Rs. 720
Rs. 820

Solution:

If a certain sum of money becomes Ai in ti year and A.- in t2 years then

⇒ $\text { S.I. per annum }=\frac{A_2-A_1}{t_2-t_1}$

⇒ $\text { S.I. p. } a=\frac{800-692}{5-2}$

= Rs. 36.

Principal = A – Interest

= 692 – Interest of 2 yrs.

= 692 – 2 x 36 = Rs. 620

(2) is correct

Question 63. A sum of money amount of Rs. 6,200 in 2 years and Rs 7,400 in 3 years as per S.I. then the principal is

Rs. 3,000
Rs. 3,500
Rs. 3,800
None

Solution:

S.I. p.a $=\frac{7400-6200}{3-2}$

= Rs. 1200.

Principal = 6200 – 2 x 1200

= Rs. 3800.

Question 64. P = Rs. 5,000; R = 15% T $=4 \frac{1}{2} \text { using } I=\frac{P T K}{100} \text { then I will be } I=\frac{P r t}{100}$

Rs. 3,375
Rs. 3,300
Rs. 3,735
None

Solution:

⇒ $1=\frac{5000 \times 15 \times 4.5}{1000}=3375$

Question 65. In simple interest if the principal is Rs. 2,000 and the rate and time are the roots of the equation x2-2x- 30 = 0 then simple interest is

Rs. 500
Rs. 600
Rs. 700
Rs. 800

Solution:

x2 – 11 x + 3 0 = 0

Or x2 – 5x – 6x + 30 = 0

0r x(x-5) – 6(x-5) = 0

Or (x-5) (x-6) = 0

= 5 ; 6

If r = 5% then t = 6 yrs.

⇒ $S. I=\frac{{Prt}}{100}=\frac{2000 \times 5 \times 6}{100}$

= Rs. 600.

(2) is correct

Question 66. ₹ 8,000 becomes ₹10,000 in two years at simple interest. The amount that will become ₹6,875 in 3 years at the same rate of interest is:

₹ 4,850
₹ 5,000
₹ 5,500
₹ 5,275

Solution:

⇒ $\text { S.I. } / \text { year }=\frac{10000-8000}{2}=₹ 1000$

⇒ $\mathrm{r}=\frac{1000 \times 100}{8000}=12.5 \% $

⇒ $\mathrm{P}=\frac{A \mathrm{Amt}}{A m \mathrm{at} \ 1}=\frac{6875}{1+0.125 \times 3}$

=5,000

Question 67. The rate of simple: interest on a sum of money is 6% p.a. for the first 3 years, 8% p.a. for the next five years, and 10% years for the period beyond 8 years, if the simple interest accrued by the sum for the period for 10 years is ₹1,560. The sum is:

₹1,500
₹2,000
₹3,000
₹5,000

Solution:

(2) is correct

Single S.l for 1 year = (6×34-8×5+10×2)%

= 78%

⇒ $ \mathrm{P}=\frac{\text { Total } \mathrm{S} .1}{\text { S.I on Rsl }}=\frac{1560}{0.78}=₹ 2000$

Question 68. The rate of simple: interest on a sum of money is 6% p.a. for the first 3 years, 8% p.a. for the next five years, and 10% years for the period beyond 8 years, if the simple interest accrued by the sum for the period for 10 years is ₹ 1,560. The sum is:

₹1,500
₹2,000
₹3,000
₹5,000

Solution:

(2) is correct

Single S.l for 1 year = (6×34-8×5+10×2)%

= 78%

⇒ $\text { Tricks: } \mathrm{P}=\frac{\text { Total } \mathrm{S} .1}{\text { S.I on Rsl }}=\frac{1560}{0.78}=₹ 2000$

How To Calculate Time Value Of Money In CA Foundation

Compound Interest

Compound Interest: Sometimes so happens that the born and the lender agree to fix up a certain unit of time, say yearly half-yearly, or quarterly to settle the previous accounts.

In such cases, the amount after the first unit of tone becomes the principal for the second unit, the amount after the second unit becomes the principal for the third unit, and So on.
After a specified period, the difference between the amount and the money borrowed is called the Compound Interest (abbreviated as C.l.) for that period.

Let Principal = P, Rate = R% per annum, Time = n years.

1. When interest is compound Annually:

Amount =$\mathrm{P}\left(1+\frac{R}{100}\right)^n$

2. When interest is compounded Half-yearly:

Amount = $P\left[1+\frac{(n / 2)}{100}\right]^{2 n}$

3. When interest is compounded Quarterly:

Amount =$\mathrm{P}\left[1+\frac{(R/ 4)}{100}\right]^{4 n}$

4. When interest is compounded Annually but time is in fraction, say $3 \frac{2}{5} \text { years. }$

Amount$=\mathrm{P}\left(1+\frac{R}{100}\right)^3 \times\left(1+\frac{\frac{2}{5} R}{100}\right)$

5. When Rates are different for different years, say R1%, R2%, R3% for 1st, 2nd and 3rd year respectively.

Then, Amount = $\mathrm{P}\left(1+\frac{R_1}{100}\right)\left(1+\frac{R_2}{100}\right)\left(1+\frac{R_3}{100}\right)$

6. Present worth of Rs. X due n years hence is given by:

Present Worth =$=\frac{x}{\left(1+\frac{R}{160}\right)^n} .$

CA Foundation Maths Solutions For Chapter 4 Effective Rate Of Interest

If interest is compounded more than once a year the effective interest rate for a year exceeds the per annum interest rate. Suppose you invest ₹1 0,000 for a year at the rate of 6% per annum compounded semi-annually. The effective interest rate for a year will be more than 6% per annum since interest is being compounded more than once a year. To compute the effective rate of interest first, we have to compute the interest. Let us compute the interest.

Interest for first six months = ₹10,000 ₹ 6/100 ₹ 6/12 = ₹300

Principal for calculation of interest for next six months

= Principal for first period one + Interest for first period

= ₹(10,000 + 300)

= ₹10,300

Interest for next six months = ₹ 10,300 x 6/100 x 6/12 =₹309

Total interest earned during the current year

= Interest for first six months + Interest for next six months

= ₹(300 + 309) = ₹ 609

The interest of ₹ 609 can also be computed directly from the formula or compound Interest, We can compute the effective rate of interest by following the formula

I = PEt

Where I = Amount of interest

E = Effective rate of interest in decimal

t = Period

P = Principal amount

Putting the values we have

609 = 10,000 x E x 1

⇒ $E=\frac{609}{10,000}$

= 0.0609 or

= 6.09%

Thus, if we compound the interest more than once a year effective interest rate for the year will be more than the actual interest rate per annum. But if interest is compounded annually effective interest rate for the year will be equal to the actual interest rate per annum.

So effective interest rate can be defined as the equivalent annual rate of interest compounded annually if interest is compounded more than once a year.

The effective interest rate can be computed directly by following the formula:

E = (1 + i)n – 1

Where E is the effective interest rate

i = actual interest rate in decimal

n = number of conversion period

CA Foundation Maths Solutions For Chapter 4 Effective Interest Rate Solved Examples

Question 1. Find compound interest on Rs. 7500 at 4% per annum for 2 years, compounded annually.
Solution:

⇒ $\text { Amount = Rs. }\left[7500 \times\left(1+\frac{4}{100}\right)^2\right]=\text { Rs. }\left(7500 \times \frac{26}{25} \times \frac{26}{25}\right)=\text { Rs. } 8112$

C.I. = Rs. (8112 – 7500) = Rs. 612.

Question 2. Find compound interest on Rs. 8000 at 15% per annum for 2 years 4 months, compounded annually.
Solution:

time = 2 years 4 months $=2 \frac{4}{12} \text { years }=2 \frac{1}{3} \text { years. }$

⇒ $\text { Amount }=\text { Rs. }\left[8000 \times\left(1+\frac{15}{100}\right)^2 \times\left(1+\frac{\frac{1}{3} \times 15}{100}\right)\right]=\text { Rs. }\left(8000 \times \frac{23}{20} \times \frac{23}{20} \times \frac{21}{20}\right)$

= Rs. 11109.

C.I. = Rs. (11109- 8000) = Rs.3109.

Question 3. Find the compound interest on Rs. 10000 in 2 years at 4% per annum, the interest being compounded half-yearly.
Solution:

Principal = Rs. 10000; Rate= 2% per half- year; time = 2 years = 4 half- years,

Amount=$\text { Rs. }\left[10000 \times\left(1+\frac{2}{100}\right)^4\right]=\text { Rs. }\left(10000 \times \frac{51}{50} \times \frac{51}{50} \times \frac{51}{50} \times \frac{51}{50}\right)$

Rs. 10824.32 C.I. = Rs. (10824-10000) = Rs. 824.32

Question 4. Find the compound Interest on It. 16000; it is 20% per annum for 0 months. Compounded quarterly.
Solution:

principal = Its. 16000; time = 9 months = 3 quarters;

Rate = 20 % per annum = 5% per quarter.

⇒ $\text { Amount = Rs. }\left[16000 \times\left(1+\frac{5}{100}\right)^3\right]=\text { Rs. }\left(16000 \times \frac{21}{20} \times \frac{21}{20} \times \frac{21}{20}\right)=\text { Rs. } 18522 .$

C.I. = Rs. (18522-16000) = Rs. 2522

Question 5. If the simple interest on a sum of money at 5% per annum for 3 years is Rs. 1200, find the compound interest on the same sum for the same period at the same rate.
Solution:

Clearly, Rate = 55 p.a., Time = 3 years, S.I. = Rs. 1200

So, principal = Rs.$\left(\frac{100 \times 1200}{3 \times 5}\right)=\text { Rs. } 8000 \text {. }$

⇒ $\text { Amount }=\text { Rs. }\left[8000\left(1 \times \frac{5}{100}\right)^3\right] \text { Rs. }\left(8000 \times \frac{21}{20} \times \frac{21}{20} \times \frac{21}{20}\right)=\text { Rs. } 9261 .$

C.I. = Rs. (9261-8000) – Rs. 1261

Question 6. At what time will Rs. 1000 become Rs. 1331 at 10% Per annum compounded annually?
Solution:

Principal = Rs. 1000; Amount = Rs.1331;

Rate= 10 %p.a.

Let the time be N years then,

⇒ $\left[1000 \times\left(1+\frac{10}{100}\right)^n\right]=1331 \text { or }\left(\frac{11}{10}\right)^n=\left(\frac{1331}{1000}\right)=\left(\frac{11}{10}\right)^3$

n =3 years.

Question 7. If Rs. 500 amounts to Rs. 583.20 in two years compounded annually find the rate of interest per annum.
Solution:

principal = Rs. 500; Amount =Rs. 583.20; Time = 2 years.;

Let the rate be R% per annum, then

⇒ ${\left[500 \times\left(1+\frac{R}{100}\right)^2\right]=583.20 \text { or }\left(1+\frac{R}{100}\right)^2=\left(\frac{5832}{5000}\right)=\left(\frac{11664}{10000}\right)}$

⇒ $\left(1+\frac{R}{100}\right)^2=\left(\frac{108}{100}\right)^2 \text { or } 1+\frac{R}{100}=\frac{108}{100} \text { or } R=8$

So, rate= 8% p.a.

Question 8. If the compound interest on a certain sum at 16% for 3 years is Rs. 1270 find the simple interest on the same sum at the same rate and for the same period.
Solution:

Let the sum be Rs. X. Then,

⇒ $\text { C.I. }=\left[x \times\left(1+\frac{50}{3 \times 100}\right)^3-x\right]=\left(\frac{343 x}{216}-x\right)=\frac{127 x}{216} $

⇒ $ \frac{127 x}{216}=1270 \text { or } \mathrm{x}=\frac{1270 \times 216}{127}=2160$

Thus, the sum is Rs 2160.

⇒ $\text { S.I. }=\text { Rs. }\left(2160 \times \frac{50}{3} \times 3 \times \frac{1}{100}\right)=\text { Rs. } 1080$

Question 9. The difference between compound interest and simple interest on a certain sum at 10% per annum for 2 years is Rs. 631. Find the sum.
Solution:

Let the sum be Rs. X. Then,

⇒ $\text { C.I. }=x\left(1+\frac{10}{100}\right)^2-x=\frac{21 . x}{100}, S . I .=\left(\frac{x \times 10 \times 2}{100}\right)=\frac{x}{5}$

⇒ $(\text { C. I. })-(\text { S. I. })=\left(\frac{21 \mathrm{x}}{100}-\frac{x}{5}\right)=\frac{\mathrm{x}}{100}$

⇒ $\frac{\mathrm{x}}{100}=631 \Leftrightarrow \mathrm{X}=63100 .$

Hence, the sum is Rs.63,100.

Question 10. Divide Rs. 1301 between A and X, so that the amount of A after 7 years is equal to the amount of B after 9 years, the interest being compounded at 4% per annum.
Solution:

Let the two parts be Rs. X and Rs. (1301- x)

C.I=$x\left(1+\frac{4}{100}\right)^7=(1301-x)\left(1+\frac{4}{100}\right)^9 \Leftrightarrow\left(\frac{26}{25} \times \frac{26}{25}\right)$

⇒ $\Leftrightarrow 625 x=676(1301-x) \Leftrightarrow 1301 x=676 \times 1301 \Leftrightarrow x=676$

So, the two parts are Rs. 676 and Rs. (1301-676) i.e. Rs. 676 and Rs. 625.

Question 11. A certain sum amounts to Rs. 7350 in 2 years and to Rs. 8575 in 3 years. Find the sum and rate present.
Solution:

S.I. on Rs. 7350 for 1 year Rs. (8575- 7350)= Rs. 1225.

⇒ $\text { Rate }=\left(\frac{100 \times 1225}{7350 \times 1}\right) \%=16 \frac{2}{3} \%$

Let the sum be Rs. x then,

⇒ $X\left(1+\frac{50}{3 \times 100}\right)^2=7350 \Leftrightarrow x \times \frac{7}{6} \times \frac{7}{6}=7350 \Leftrightarrow x=\left(7350 \times \frac{36}{49}\right)=5400$

⇒ $\text { sum }=\text { Rs. } 5400$

Question 12. A sum of money amounts to Rs. 6690 after 3 years and to RS. 10035 after 6 years on compound interest find the sum.
Solution:

Let the sum be Rs. P. then,

⇒ $\mathrm{P}\left(1+\frac{R}{100}\right)^3=6690 \quad \ldots \text { (1) } \quad \text { and } \mathrm{P}\left(1+\frac{R}{100}\right)^6=10035$

On dividing, we get$\left(1+\frac{R}{100}\right)^3=\frac{10035}{6690}=\frac{3}{2}$

Substituting this value in (i) we get :

⇒ $P \times \frac{3}{2}=6690 \text { or } P=\left(6690 \times \frac{2}{3}\right)=4460$

Hence, the sum is Rs. 4460

Question 13. A sum of money doubles itself at compound interest in 15 years, in how many years will it become eight times?
Solution:

⇒ $ \mathrm{P}\left(1+\frac{R}{100}\right)^{15}=2 P \quad \Rightarrow\left(1+\frac{R}{100}\right)^{15}=\frac{2 P}{P}=2$

Let$\mathrm{P}\left(1+\frac{R}{100}\right)^n=8 P \Rightarrow\left(1+\frac{R}{100}\right)^n=8=2^3=\left\{\left(1+\frac{R}{100}\right)^{15}\right\}^3[uning (i) ]$

⇒ $\Rightarrow\left(1+\frac{R}{100}\right)^n=\left(1+\frac{n}{100}\right)^{45} \Rightarrow n=45$

Tints, the required time = 45 years.

Question 14. What annual payment will discharge a debt of Rs. 7620 due in 3 years at $16 \frac{2}{3} \%$ per annum compound interest?
Solution:

let each installment be Rs. X then,

(P.W. of Rs. X due 1 year hence) + (P.W. of Rs. X due 2 years hence) + (P.W. of Rs. X due 3 years hence) = 7620.

⇒ $\frac{x}{\left(1+\frac{50}{3 \times 100}\right)}+\frac{x}{\left(1+\frac{50}{3 \times 100}\right)^2}+\frac{x}{\left(1+\frac{50}{3 \times 100}\right)^3}=7620$

⇒ $\Leftrightarrow \frac{6 x}{7}+\frac{36 x}{49}+\frac{216 x}{343}=7620 \Leftrightarrow 294 x+252 x+216 x=7620 \times 343$

⇒ $\Leftrightarrow X=\left(\frac{7620 \times 343}{762}\right)=3430 $

Amount of each instalment= Rs. 3430

Question 15.₹5,000 is invested in a Term Deposit Scheme that fetches interest of 6% per annum compounded quarterly. What will be the interest after one year? What is the effective rate of interest?
Solution:

We know that

I = P [(1 + i)n- 1]

Here P = ₹ 5,000

i = 6% p.a. = 0.06 p.a. or 0.015 per quarter

n = 4

and I = amount of compound interest

putting the values, we have

I = ₹ 5,000 [(1 + 0.015)4 — 1]

= ₹ 5,000 x 0.06136355

= ₹ 306.82

For the effective rate of interest using, I = PEt we find

306.82 = 5,000 x E x 1.

306.82

5000

= 0.0613 or 6.13%

Note: We may arrive at the same result by using

E = (1+i)4 – 1

E = (1 + 0.015)4-1

= 1.0613-1

= 0613 or6.13%

We may also note that the effective rate of interest is not related to the amount of principal. It is related to the interest rate and frequency of compounding the interest.

Question 16. Find the amount of compound interest and effective rate of interest if an amount of ₹20,000 is deposited in a bank for one year at the rate of 8% per annum compounded semi-annually.
Solution:

We know that

1 = P [(1 + i)n- 1]

Here P = ₹20,000

i = 8% p.n. = 8/2 % semi-annually = 0.04

n = 2

I = ₹20,000 IO + 0.04)2- 1 1

= ₹20,000 x 0.08 16

= ₹1,632

The effective rate of interest:

We know that

I = PEt

1,632 = 20,000 x E x 1

⇒ $E=\frac{1632}{20000}$ = =0.0816

= 8.16%

The effective rate of interest can also be computed by following the formula

E = (1 + i)n -1

= (1 + 0.04)2-1

= 0.0816 or 8.16%

Question 17. Which is a better investment 3% per year compounded monthly or 3.2% per year simple interest? Given that (1+0.0025) ‘2 =1.0304.
Solution:

i = 3/12 = 0.25% = 0.0025

= 12

= (1 + i)n -1

= (1 + 0.0025)12 -1

= 1.0304-1 = 0.0304

= 3.04%

With the effective rate of interest (E) being less than 3.2%, the simple interest of 3.2% per year is the better investment.

CA Foundation Maths Time Value Of Money Practice Problems

CA Foundation Maths Solutions For Chapter 4 Exercise – 2

Question 1. Albert invested an amount of Rs. 8000 in a fixed deposit scheme for 2 years at a compound interest rate of 5 p.c.p.a How much amount will Albert get on maturity of the fixed deposit?

Rs. 8600
Rs. 8820
Rs. 8800
Rs. 8840
None of these

Solution:

(2) Amount = $\text { Rs. }\left[8000 \times\left(1+\frac{5}{100}\right)^2\right]=\text { Rs. }\left(8000 \times \frac{21}{20} \times \frac{21}{20}\right)=\text { Rs. } 8820$

Question 2. What will be the compound interest on a sum of Rs. 25000 after 3 years at the rate of 12 p.c.p.a.?

Rs. 9000.30
Rs. 9720
Rs. 10123.20
Rs. 10483.20
None of these

Solution:

(3) Amount = $\text { Rs. }\left[25000 \times\left(1+\frac{12}{100}\right)^3\right]=\text { Rs. }\left(25000 \times \frac{28}{25} \times \frac{28}{25} \times \frac{28}{25}\right)=\text { Rs. } 35123.20 .$

C.I. = Rs. (35123.20-25000) = Rs. 10123.20

Question 3. A man saves Rs. 200 at the end of each year and lends the money at 5% compound interest. How much will it become at the end of 3 years?

Rs. 565.25
635
Rs. 662.02
Rs. 666.50

Solution:

(3) Amount = $\text { Rs. }\left[200 \times\left(1+\frac{5}{100}\right)^3+200\left(1 \times \frac{5}{100}\right)^2+200\left(1+\frac{5}{100}\right)\right]$

⇒ $\text { Rs. }\left[200 \times \frac{21}{20} \times \frac{21}{20} \times \frac{21}{20}+200 \times \frac{21}{20} \times \frac{21}{20}+200 \times \frac{21}{20}\right]$

⇒ $ =R s .\left[200 \times \frac{21}{20}\left(\frac{21}{20} \times \frac{21}{20}+\frac{21}{20}+1\right)\right]=\text { Rs. } 662.02 .$

Question 4. Sam invested Rs. 15000 @10% per annum for one year. If the interest is compounded halfyearly, then the amount received by Sam at the end of the year will be:

Rs. 16,500
Rs.525.50
Rs. 16,537.50
Rs. 18,150
None of these

Solution:

(3) P=15000; R=10%p.a.= 5% per half- year; T=1 year=2 half-years

Amount = ${Rs} .\left[15000 \times\left(1+\frac{5}{100}\right)^2\right]=\text { Rs. }\left(15000 \times \frac{21}{20} \times \frac{21}{20}\right)={Rs} .16537 .50$

Question 5. A bank offers 5% compound interest calculated on half-yearly basis. A customer deposits Rs. 1600 each on 1st of January and 1St July of a year. At the end of the year, the amount he would have gained by way of interest is

Rs. 120
Rs. 121
Rs. 122
Rs. 123

Solution:

⇒ $\text { Amount }=\text { Rs. }\left[1600 \times\left(1+\frac{5}{2 \times 100}\right)^2+1600 .\left(1+\frac{5}{2 \times 100}\right)\right]$

⇒ $\left[1600 \times \frac{41}{40} \times \frac{41}{40}+1600 \times \frac{41}{40}\right]$

⇒ $ \text { = Rs. }\left[1600 \times \frac{41}{40}\left(\frac{41}{40}+1\right)\right]=\text { Rs. }\left(\frac{1600 \times 41 \times 81}{40 \times 40}\right)=\text { Rs. } 3321 .$

C.I. = Rs. (3321-3200) = Rs. 121.

Question 6. What is the difference between the compound interests on RS.5000 for $1 \frac{1}{2}$ years at 4% per annum compounded yearly and half-yearly?

Rs. 2.04
Rs. 3.06
Rs. 4.80
Rs. 8.30

Solution:

(1) C.I. when interest is compounded yearly

⇒ $=\text { Rs. }\left[5000 \times\left(1+\frac{4}{100}\right) \times\left(1+\frac{\frac{1}{2} \times 4}{100}\right)\right]=\text { Rs. }\left(5000 \times \frac{26}{25} \times \frac{51}{50}\right)={Rs} .5304$

C.l. when interest is compounded half-yearly

⇒ $\text { Rs. }\left[5000 \times\left(1+\frac{2}{100}\right)^3\right]={Rs} .\left(5000 \times \frac{51}{50} \times \frac{51}{50} \times \frac{51}{50}\right)={Rs} .5306 .04$

Difference = Rs. (5306.04-5304) = Rs. 2.04.

Question 7. Find the compound interest on Rs. 15625 for 9 months at 16% per annum compounded quarterly.

Rs. 1851
Rs. 1941
Rs. 1951
Rs. 1961

Solution:

(3) P= RS.15625, n=9 months= 3 quarters, R= 1 6% p.a. = 4% per quarter.

Amount =Rs.$\left[15625 \times\left(1+\frac{4}{100}\right)^3\right]=R s .\left(15625 \times \frac{26}{25} \times \frac{26}{25} \times \frac{26}{25}\right)=\text { Rs. } 17576$

C.I. =Rs. (17576 – 15625) =Rs.l951.

Question 8. If the simple interest on a sum of money for 2 years at 5% per annum is Rs. 50, what is the compound interest on the same sum at the same rate and for the same time?

Rs. 51.25
Rs. 52
Rs. 25
Rs. 60

Solution:

(1) Sum Rs.$\left(\frac{50 \times 100}{2 \times 6}\right)=R s .500$

Amount = $\text { Rs. }\left[500 \times\left(1+\frac{5}{100}\right)^2\right]={Rs} .\left(500 \times \frac{21}{20} \times \frac{21}{20}\right)={Rs} .551 .25$

C.l. =Rs. (551.25 -500) =Rs.51.25

Question 9. What will be the difference between simple and compound interest @ 10% per sum of Rs. 1000 after 4 years?

Rs. 31
Rs. 32.10
Rs. 40.40
Rs. 64.10
None of these

Solution:

S.I.= Rs. $\left(\frac{1000 \times 10 \times 4}{100}\right)=\text { Rs. } 400$

⇒ $\text { C.I. }=\text { Rs. }\left[1000 \times\left(1+\frac{10}{100}\right)^4-1000\right]=\text { Rs. } 464.10$

Difference = Rs. (464.10 – 400) = Rs.64.10.

Question 10. The difference between simple interest and compound interest on Rs. 1200 for one year at 10% per annum reckoned half-yearly is:

Rs. 2.50
Rs. 3
Rs. 4.75
Rs. 4
None

Solution:

⇒ $\text { Rs. }\left(\frac{1200-111-1}{100}\right)=Rs. 120$

⇒ $ Rs .\left|1200 \times\left(1+\frac{6}{100}\right)^2-1200\right|=Rs.123$

Difference = Rs. (123-120)= Rs.3

Question 11. The compound interest on Rs. 30000 at 7% per annum Is Rs. 4347. The period (in years) is:

2
$2 \frac{1}{2}$
3
4

Solution:

Amount = Rs. (30000 + 4347) Rs. 34347

let the time be n years then

⇒ $30000\left(1+\frac{7}{100}\right)^{11}=34347 \Leftrightarrow\left(\frac{1117}{1000}\right)^{11}=\frac{34347}{300010}=\frac{11449}{10000}=\left(\frac{107}{100}\right)^2n=2 \text { years. }$

Question 12. The principle that amounts to Rs. 4913 in 3 years at 6% per annum compound interest compounded annually, is:

Rs. 3096
Rs. 4076
Rs. 4085
Rs. 4096

Solution:

(4) $\text { (1) Principal }=\text { Rss. }\left|\frac{4913}{\left(11 \frac{25}{1.1000^3}\right)}\right|=\mathrm{Rs.}\left(4913 \times \frac{16}{17} \times \frac{16}{17} \times \frac{16}{17}\right)=\mathrm{Rs} .4096 \text {. }$

Question 13. In how many years will a sum of Rs. 800 at 10% per annum compounded semi-annually become Rs. 926.10?

$1 \frac{1}{3}$
$1 \frac{1}{2}$
$2 \frac{1}{3}$
$2 \frac{1}{2}$

Solution:

(2) Iet the time and years. Then,

⇒ $ 80\left(0 \times\left(1+\frac{5}{1001}\right)^{2 n}=926.100+\left(1+\frac{5}{100}\right)^{2 n}=\frac{926,1}{10001}\right.$

⇒ $\text { Or }\left(\frac{21}{20}\right)^{2 n}=\left(\frac{21}{20}\right)^3 \text { or } 2 n=3 \text { or } n=\frac{3}{2} n=1 \frac{1}{2} \text { years. }$

Question 14. If the compound interest on a sum for 2 years at $12 \frac{1}{2}$%per annum is Rs.510, the simple interest on the same sum at the same rate for the same period is:

Rs. 400
Rs. 450
Rs. 460
Rs. 480

Solution:

(4) Let the sum he Rs. P, then

⇒ $\left|P\left(\frac{25}{2 \times 100}\right)^2-P\right|=510 \text { or } P\left|\left(\frac{9}{11}\right)^2-1\right|=5100 \text { r } P=\left(\frac{510 \times 64}{17}\right)=1920 $

⇒ $\text { Sum }=\text { Rs. } 1920 .$

⇒ $\text { So, S.I. = Rs. }\left(\frac{1920 \times 25 \times 2}{2 \times 100}\right)=\text { Rs. } 480 .$

Question 15. The compound interest on a certain sum for 2 years at 10% per annum is 525. The simple interest on the same sum for double the time at half the rate present per annum is:

Rs. 400
Rs. 500
Rs. 600
Rs. 800

Solution:

(2) Let the sum be Rs. P, Then,

⇒ $\left|p\left(1+\frac{10}{1001}\right)^2-p\right|=525 \Leftrightarrow p\left|\left(\frac{11}{10}\right)^2-1\right|=525 \Leftrightarrow P=\left(\frac{525 \times 100}{21}\right)=2500$

⇒ $\text { Sum }=\text { Rs. } 25000 . $

⇒ $\text { So, S.I. }=\text { Rs. }\left(\frac{2500 \times 5 \times 1.1}{100}\right)=\text { Rs. } 500$

Question 16. The simple interest on a certain sum of money for 3 years at 8% per annum is half the compound interest on Rs.4000 for 2 years at 10% per annum the sum placed on simple interest is:

Rs. 1550
Rs. 1650
Rs. 1750
Rs. 2000

Solution:

(3) $\text { C.I. }=\text { Rs. }\left|4000 \times\left(1+\frac{10}{100}\right)^2-4000\right|=R s .\left(4000 \times \frac{11}{10} \times \frac{11}{10}-4000\right)=R s .840 . $

⇒ $ S u m=R s .\left(\frac{420 \times 100}{3 \times 8}\right)=\text { Rs. } 1750$

Question 17. There is a 60% increase in an amount in 6 years at simple interest. What will be the compound interest of Rs. 12000 after 3 years at the same rate?

2160
Rs. 3120
Rs. 3972
Rs. 6240
None of these

Solution:

Let P = Rs. 1 00 then, S.l. Rs. 60 anil T= 6 years

⇒ $R=\frac{100 \times 60}{100 \times 6}=10 \% / 0 \mathrm{p.a1} .$

Now, P= Rs. 1 2000, T= 3 years, and R = 1 0% p.a

⇒ $\text { C.I. }=\text { Rs. }\left[12000 \times\left\{\left(1+\frac{10}{100}\right)^3-1\right\}\right]=R s .\left(12000 \times \frac{331}{1000}\right)=R s .3972 .$

Question 18. The difference between compound interest and simple interest on an amount of Rs. 15000 for 2 years is Rs. 96. What is the rate of interest per annum?

8
10
12
8
None of these

Solution:

⇒ $\text { (a) }\left|15000 \times\left(1+\frac{R}{100}\right)^2-15000\right|-\left(\frac{15000 \times R \times 2}{100}\right)=96$

⇒ $\Leftrightarrow 15000\left[\left(1+\frac{R}{100}\right)^2-1-\frac{2 R}{100}\right]=96 \Leftrightarrow 15000\left[\frac{(100+R)^2-10000-200 R}{10000}\right]=96$

⇒ $\Leftrightarrow R^2=\frac{96 \times 2}{3}=64 \Leftrightarrow R=8$

Rate = 8%

Question 19. The difference between simple and compound interests compounded annually on a certain sum of money for 2 years at 4% per annum is Re. 1. The sum (in Rs.) is:

Solution:

(1) Let the sum he Rs. X, Then

⇒ $\text { C.I. }=\left[x\left(1+\frac{4}{100}\right)^2-x\right]=\left(\frac{675}{625} x-x\right)=\frac{51}{625} x .$

⇒ $\text { S.I. }=\left(\frac{x \times 4 \times 2}{100}\right)=\frac{2 x}{25} $

⇒ $ \frac{51 x}{625}-\frac{2 x}{25}=1 \text { or } \mathrm{x}=625 $

Question 20. The difference between the simple interest on a certain sum at the rate of 10% per annum for 2 years and compound interest which is compounded every 6 months is Rs. 124.05. What is the principal sum?

Rs. 6000
Rs. 8000
Rs. 10,000
Rs. 12,000
None of these

Solution:

(2) Let the sum be Rs. P. then

⇒ $\mathrm{P}\left[\left(1+\frac{5}{100}\right)^4-1\right]-\frac{P \times 10 \times 2}{100}=124.05$

⇒ $\Rightarrow \mathrm{P}\left[\left(\frac{21}{20}\right)^4-1-\frac{1}{5}\right]=124.05 \Rightarrow P\left[\frac{194481}{160000}-\frac{6}{5}\right]=\frac{12405}{100} $

⇒ $\Rightarrow \mathrm{P}\left[\frac{194481-192000}{160000}\right]=\frac{12405}{100} \Rightarrow P=\left(\frac{12405}{100} \times \frac{160000}{2481}\right)=8000$

Question 21. On a sum of money, the simple interest for 2 years is Rs.660, while the compound interest is Rs. 696.30 the rate of interest being the same in both cases. The rate of interest is:

10%
10.5%
12%
None of these

Solution:

(4) Difference in C.I. and S.I for 2 years = Rs. (696.30- 660) = Rs. 36.30

S.I. for one year = Rs. 330

S.I. on Rs. 330 for1 year = Rs. 36.30

⇒ $\text { Rate }\left(\frac{100 \times 36.30}{330 \times 1}\right) \%=11 \%$

Question 22. The effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly is:

6.06%
6.07%
6.08%
6.09%

Solution:

(4) Amount of Rs. 100 for a year when compounded half-yearly

⇒ $\text { Rs. }\left[100 \times\left(1+\frac{3}{100}\right)^2\right]={Rs} .106 .09$

Effective rate = (106.09- 100) % = 6.09 %

Question 23. Mr. Dua invested money in two schemes A and B offering compound interest @ 8 P.c.p.a. and 9 p.c.p.a. Respectively. If the total amount of interest accrued through two schemes together in two years was RS. 4818.30 And the total amount invested was Rs. 27000, what was the amount invested in scheme A?

Rs. 12,000
Rs. 13,500
Rs. 15,000
Cannot be determined
None Of these

Solution:

(1) Let the investment in the scheme be Rs. X.

Then, investment in scheme B = Rs. (27000-x)

⇒ $\left[x \times\left\{\left(1+\frac{8}{100}\right)^2-1\right\}+(27000-x)\left\{\left(1+\frac{9}{100}\right)^2-1\right\}\right]=4818.30$

⇒ $\Leftrightarrow\left(x \times \frac{104}{625}\right)+\frac{1881(27000-x)}{10000}=\frac{481830}{100}$

1664x+ 1881 (27000-x) = 48183000

o (1881x- 1664x) = (50787000- 48183000)

⇒ $217 x=2604000 \Leftrightarrow x=\frac{2604000}{217}=12000$

Question 24. A sum of money invested at compound interest amounts to Rs. 800 in 3 years and to Rs.840 in 4 years. The rate of interest per annum is:

$Rs. 2 \frac{1}{2} \%$
4%
5%
$6 \frac{2}{3} \%$

Solution:

(3) S.I. on Rs. 800 for1 year = Rs. (840-800) =Rs.40

⇒ $\text { Rate }=\left(\frac{40 \times 100}{800}\right) \%=5 \%$

Question 25. A sum of money placed at compound interest doubles itself in 5 years. It will amount to eight times itself at the same rate of interest in:

7 years
15 years
24 years
36 years

Solution:

(2) $\mathrm{P}\left(1+\frac{R}{100}\right)^{\mathrm{g}}=2 \mathrm{P} \Rightarrow\left(1+\frac{R}{100}\right)^g=2$

⇒ $Let \mathrm{P}\left(1+\frac{R}{100}\right)^n=8 P \Rightarrow\left(1+\frac{R}{100}\right)^n=8=2^3=\left\{\left(1+\frac{R}{100}\right)^5\right\}^3
[using(i)]$

⇒ $\left(1+\frac{R}{100}\right)^n=\left(1+\frac{R}{100}\right)^{15} \Rightarrow \mathrm{n}=15$

Required time 15 Years.

Question 26. The least number of complete years in which a sum of money put out at 20% compound interest will be more than doubled is:

Solution:

(2)

⇒ $\mathrm{P}\left(1+\frac{20}{100}\right)^{\mathrm{n}}>2 \mathrm{P} \text { or }\left(\frac{6}{5}\right)^{\mathrm{n}}>2 \quad \text { Now, }\left(\frac{6}{5} \times \frac{6}{5} \times \frac{6}{5} \times \frac{6}{5}\right)>2 \text { so, } \mathrm{n}=4 \text { years. }$

Question 27. What annual payment will discharge a debt of Rs. 1025 due in 2 years at the rate of 5% compound interest?

Rs. 550
Rs. 551.25
Rs. 560
Rs. 560.75

Solution:

(2)

bet each installment be Rs. X. Then,

⇒ $\frac{x}{\left(1+\frac{5}{100}\right)}+\frac{x}{\left(1+\frac{5}{100}\right)^2}=1025 \Leftrightarrow \frac{20 x}{21}+\frac{400 x}{441}=1025$

₹820x= 1025×441 ⇔ x = $\left(\frac{1025 \times 441}{120}\right)=551.25 .$. So, the value of each installment = Rs. 551.25

Question 28. A sum of money is borrowed and paid back in two annual installments of Rs. 882 each allowing 5% compound interest. The sum borrowed was:

Rs. 1620
Rs.1640
Rs. 1680
Rs. 1700

Solution:

(2) Principal = (P.W. of Rs. 882 due 1 year hence) + (P.W. of Rs. 882 due 2 years hence

⇒ $=\left[\frac{882}{\left(1+\frac{5}{100}\right)}+\frac{882}{\left(1+\frac{5}{100}\right)^2}\right]=\left(\frac{882 \times 20}{21}+\frac{882 \times 400}{441}\right)={Rs} .1640 .$

Question 29. If the difference between simple interest and compound interest is ₹11 at the rate of 10% for two years, then find the sum:

₹1,200
₹1,100
₹ 1,000
None of these

Solution:

(2) is correct

⇒ $\mathrm{P}=\frac{\text { Difference } \times(100)^2}{(\text { rate })^2} \quad=\frac{11 \times(100)^2}{(10)^2}=₹ 1100$

Question 30. In how many years, a sum will become double at 5% p.a. compound interest?

14.0 years
14.1 years
14.2 years
14.3 Years

Solution:

⇒ $\mathrm{t}=\frac{\log \left(\frac{1}{p}\right)}{m e \log \left(1+\frac{r}{100 m}\right)}=\frac{\log 2}{\log (1.05)}=14.2 \text { yrs. (approx) }$

Chapter 4 CA Foundation Maths Answer Key

Question 31. A sum amount to ₹1331 at a principle of ₹1,000 at 10% compounded annually. Find the time.

3.31 years
4 years
3 years
2 years

Solution:

(3) is correct

For (C); A = 1000$\left(1+\frac{10}{100}\right)^3=₹ 1331$

So; t = 3 yrs

Question 32. The compound interest for a certain sum @ 5% p.a. for the first year is ₹25. The S-I for the same money @ 5% p.a. for 2 years will be.

₹40
₹50
₹60
₹70

Solution:

(2) S.I for 1st yrs. = C.l for 1st years. = 25

S.I. for 2 yrs. For same ‘p’ = 2×25 = 50

Question 33. At what % rate of compound interest corresponding (C.I) will the sum of money become 16 times in four years, if interest is being calculated compounding annually:

r=100%
r=10%
r=200%
r=20%

Solution:

(1) For (a) Let P = 1; A =1$\left(1+\frac{100}{100}\right)^4=(2)^4=16$

(1) is correct

Question 34. If the simple interest on a sum of money at 12% p.a. for two years is 3:3,600. The compound interest on the same sum for two years at the same rate is:

33,816
33,806
33,861
33,860

Solution:

(1) $ P=\frac{3600 \times 100}{12 \times 2}=₹ 15000$

⇒ $\text { C.I. }=15000\left(1+\frac{12}{100}\right)^2-15000=₹ 3816$

Question 35. The effective annual rate of interest corresponding to the nominal rate of 6% p.a. payable half yearly is

6.06%
6.07%
6.08%
6.09%

Solution:

⇒ $r_e=\left[\left(1+\frac{6}{200}\right)^2-1\right] \times 100=6.09 \%$

Question 36. The cost of machinery is 31,25,000/- if its useful life is estimated to be 20 years and the rate of depreciation of its cost is 10% p.a. then the scarp value of the Machinery is [given that (0.9)2=0.1215]

15,187
15,400
15,300
15,250

Solution:

(1) S (Scrap Value) = p$\left(1-\frac{d}{100}\right)^1$

Where P = Principle;

d=rate of depreciation

S = 1,25,000 $\left(1-\frac{10}{100}\right)^{20}=₹ 15,187.50$

Question 37. Mr. X invests the ‘P’ amount at a simple rate of 10% and Mr. Y invests the ‘Q’ amount at a compound interest rate of 5% compounded annually. At the end of two years, both get the same amount of interest, then the relation between two amounts P and Q is given by:

$P=\frac{41 Q}{80}$
$P=\frac{410}{40}$
$P=\frac{41 Q}{100}$
$P=\frac{41 Q}{200}$

Solution:

(1) is correct $\mathrm{S} .\mathrm{I}=\frac{P .10 \times 2}{100}=\frac{P}{5}$

⇒ $C. I=Q\left[\left(1+\frac{5}{100}\right)^2-1\right]=0.1025 . Q$

From Question

S.I = C.I

⇒ $\frac{11 Q}{80}=0.1025 Q$

Or P = 5×0.1025Q = 0.5125Q

⇒ $P=\frac{5125}{10000} Q=\frac{205 Q}{400}=\frac{41 Q}{80}$

⇒ $P=\frac{41 Q}{80}$

Question 38. If the difference between S.I and C. I am 372 at 12% for 2 years. Calculate the amount.

8,000
6,000
5,000
7,750

Solution:

(3)$\mathrm{P}=\frac{(C . I-S . I) \times(100)^2}{12 \times 12}=\frac{72 \times 100 \times 100}{12 \times 12}=₹ 5000$

Question 39. The nominal rate of interest is 9.9% p.a. if interest is compounded monthly. What will be the effective rate of interest?

⇒ $\left({Given}\left(\frac{4033}{4000}\right)^{12}=1.1036\right. \text { (approx)? }$

10.36%
9.36%
11.36%
9.9%

Solution:

(1) $\mathrm{r}_{\mathrm{e}}=\left[\left(1+\frac{9.9}{1200}\right)^{12}-1\right] \times 100 \quad=10.36 \%$

Question 40. The difference between Cl and SI on a certain sum of money for 2 years at 4% per annum is 1. The sum is

Solution:

(1) for 2 yrs Sum of Money =$\frac{\text { Diff.(100) }}{r^2}=\frac{1 \times(100)^2}{4^2}=₹ 625$

Question 41. If the sum of money when compounded annually becomes 1 140 in 2 years and 1710 in 3 years at a rate of interest

Solution:

(3) Interest in 3rd yr. = 511710 – 511140 = 51570

For 3rd yr; it will be like S.l r=$\frac{1 \times 100}{P t}=\frac{570 \times 100}{1140 \times 1}=50 \%$

For (3) A = 1140 + 50% (calculator) = ₹ 1710

Question 42. The difference between and C. I and S.I at 7% p.a. for 2 years is 329.4 then the principal is

35,000
35,5000
36,000
36,500

Solution:

(2) $\mathrm{P}=\frac{\text { Difference } \times(100)^2}{r^2}=\frac{29.4 \times(100)^2}{(7)^2}=₹ 6000 \text {. }$

Question 43. The partners A & B together lent 33903 at 4% p.a. interest compounded annually. After a span of 7 years. A gets the same amount as B gets after 9 years. The share of A in the sum of 33903/- would have been

31875
32280
32028
32820

Solution:

⇒ $A\left(1+\frac{4}{100}\right)^7=B\left(1+\frac{4}{100}\right)^9 \quad \text { Or } \frac{A}{B}=\left(1+\frac{4}{100}\right)^2=\left(\frac{26}{25}\right)^2 =\frac{676}{625}$

⇒ $A: B=676: 625 \quad A=\frac{676}{676+625} \times 3903=₹ 2028$

Question 44. A certain sum of money doubled itself in 4 years at C.I. In how many years it will become 32 times to itself

15 years
24 years
20 years
None

Solution:

2tz = 324

= 2t2 = (25)4 = 220

= t2= 20 yrs.

Question 45. On a certain sum rate of interest @ 10% p.a, S.I = 3 90 Term = 2 year, Find compound interest for the same:

₹544.5
₹94.5
₹ 450
₹ 18

Solution:

⇒ $\text { S.I p.a }=\frac{90}{2}=₹ 45$

Compound interest = 45 + (45+10%) = 94.5

Question 46. If an amount is kept at simple interest, it earns ₹600 in the first 2 years but when kept at compound interest it earns an interest of ₹660 for the same period: then the rate of interest and principal amount respectively are

20%; ₹1200
10%; ₹1200
20%; ₹1500
10%; ₹1500

Solution:

(2)$\text { S.I. }=\frac{1500 \times 2 \times 20}{100}=₹ 600 \text { (true) }$

⇒ $\text { C.I }=1500\left[\left(1+\frac{20}{100}\right)^2-1\right]=₹ 660 \text { (also true) }$

Question 47. Mr. X bought an electronic item for ₹1000. What would be the future value of the same item after two years,if the value is compounded semi-annually at the rate of 22% per annum?

₹1488.40
₹ 1518.07
₹2008.07
₹2200.00

Solution:

(b)

FV = P (1 + i)n

⇒ $1000\left(1+\frac{22}{200}\right)^{2 \times 2}$

= 1518.07 (approx.)

Question 48. The difference between simple interest and compound interest on a certain sum of money invested for 2 years at 5% P.a. is ₹ 30. Then the sum =

10,000
12,000
13,000
None

Solution:

(2)

P=30 + 5% / 5% button = 12,000

Question 49. A sum of money amounts to ₹7803 for one year at the rate of 4% compounded semi-annually then the sum invested is

7,000
7,500
7,750
8,000

Solution:

(2)

P= (4+200+1)+ = button 2 times x 7803 = button

= 7500

Question 50. The difference between simple and compound interest on a sum of ₹10000 for 4 years at the rate of interest 10 % per annum is____

Solution:

C.I-S.I

⇒ $=\left[10,000\left(1+\frac{10}{100}\right)^4-10,000\right]-{\left[\frac{10,000 \times 10 \times 4}{100}\right]}$

(3) is correct

= 4641 – 4000 = 641

Question 51. If the compound interest on a sum for two years at the rate of 5% p.a. is ₹512.50, then the principle is_____.

4,000
3,000
5,000
None of these

Solution:

(3)

Amount = 5000 + 5% + 5% button = 5512.50.

C.I= 5512.50 -5000 = 512.50

Question 52. Find the effective rate of interest corresponding to the nominal rate of interest 7% compounded monthly is_____.

7.68%
7.22%
8.1%
None of these

Solution:

(2)

⇒ $\mathrm{R}_{\mathrm{e}}=\left[\left(1+\frac{7}{1200}\right)^{12}-1\right] \times 100 \%$

= 7.229 % = 7.22%

Question 53. In compound interest, if the amount is 9 times its principles in two years then the rate of interest is?

100%
200%
150%
None of these

Solution:

(2), Given

⇒ $\mathrm{A}=\mathrm{P}\left(1+\frac{r}{100}\right)^1 $

⇒ $\text { Or; } 9 \mathrm{P}=\mathrm{P}\left(1+\frac{r}{100}\right)^2$

⇒ $\text { Or; } 9=\left(1+\frac{r}{100}\right)^2$

⇒ $\text { Or } 3^2=\left(1+\frac{r}{100}\right)^2 \Rightarrow 3=1+\frac{r}{100}$

⇒ $\Rightarrow 2=\frac{r}{100} \Rightarrow r=200 \%$

1 + 200% + 200 % = 9

So, (2) is correct

Question 54. If the difference between compound interest and simple interest for 3 years is ₹ 912 at the rate of 4% p.a. the principle is

₹ 1,87,500
₹ 1,87,000
₹ 1,87,550
₹ 1,85,700

Solution:

(1)

P = 912 + 4% + 4% + (300 + 4)%

= ? 1,87,500

Question 55. If Rs. 1,000 is invested at an interest rate of 5% and the interest is added to the principle every 10 years, then the number of years in which it will amount to Rs. 2,000 is:

$16 \frac{2}{3}$
$6 \frac{1}{4}$
$16 years$
$6 \frac{2}{3}$

Solution:

(1)

Interest is added to the principal every 10 years.

So within 10 years; simple interest will apply.

So, the amount after 10 years

⇒ $=1000+1000 \times \frac{10 \times 5}{100}=R s .1500 \text {. }$

Total amount = Rs. 2000

Extra interest needed = 2000 – 1500 =Rs. 500

⇒ $\text { Time }=\frac{500 \times 100}{1500 \times 5}=\frac{20}{3}=6 \frac{2}{3} \mathrm{yrs} .$

⇒ $\text { So; Total time }=10+6 \frac{2}{3}=16 \frac{2}{3} \mathrm{yrs} .$

Question 56. If an amount is kept at S.I it earns an interest of Rs 600 in the first two years but when kept at the compound interest it earns an interest of Rs. 660 for the same period, then the rate of interest and principal amount respectively are:

20%, Rs. 1,200
20%, Rs. 1,500
10%, Rs. 1,200
10%, Rs. 1.500

Solution:

(2)

⇒ $\text { S.I }=\frac{1200 \times 2 \times 20}{100}=480 \neq 600$

So; (1) is false.

⇒ $S. I=\frac{1500 \times 2 \times 20}{100}=R s .600$

C.I = (-1500+20%+20%) (button)

= 660.

So; (b) is true.

Question 57. If 10,000 is invested at 8% per year compound quarterly, then the value of the investment after 2 years is (given (l+0.2)8= 1.171659)

R 10,716.59
11,716.59
17.1659
None of these

Solution:

(2)

⇒ $F V=100000\left(1+\frac{4}{800}\right)^{2 \times 4}=₹ 11,716.59$

Question 58. A bank pays a 10% rate of interest, interest is calculated half-yearly. A sum of is deposited in the bank. The amount at the end of 1 year will be

Solution:

⇒ $\text { (4) } F V=400\left(1+\frac{10}{200}\right)^2=441$

Question 59. A man deposited 8,000 in the bank for 3 years at 5% per annum compound interest, after 3 years he will get

9,000
8,800
₹9,200
9,261

Solution:

⇒ $\text { (4) } \quad F V=8000\left(1+\frac{5}{100}\right)^3=₹ 9261 \text {. }$

Question 60. If in two years, a principle amounts to when the interest at the rate of r% is compounded annually, then the value of r will be

14
10.5
15
10

Solution:

⇒ $121=100\left(1+\frac{r}{100}\right)^2 \Rightarrow \frac{121}{100}=\left(1+\frac{r}{100}\right)^2$

⇒ ${Or}\left(\frac{11}{10}\right)^2=\left(1+\frac{r}{100}\right)^2 \Rightarrow 1+\frac{r}{100}=\frac{11}{10}$

⇒ ${Or} \frac{r}{100}=\frac{11}{10}-1=\frac{1}{10} $

r = 100%

For $\mathrm{FV}=100\left(1+\frac{10}{100}\right)^2=121 \text { (true) }$

Question 61. The effective rate of interest for one year deposit corresponding to a nominal 7% rate of interest per annum convertible quarterly is

7%
7.4%
7.5%
7.18%

Solution:

(4)

⇒ $r_e=\left[\left(1+\frac{7}{400}\right)^4-1\right] \times 100=7.18 \%$

Question 62. How much will 25,000 amount to in 2 years at compound interest if the rates for the successive years are 4% and 5% per year

27,000
27,300
27,500
27,900

Solution:

(2)

⇒ $F V=25000\left(1+\frac{4}{100}\right) \times\left(1+\frac{5}{100}\right)$

= ₹ 27,3007-

Question 63. at 10% per annum, interest compounded half yearly will become at the end of one year

8800
R 8,900
8820
9,600

Solution:

(3)

⇒ $FV=8000\left(1+\frac{10}{200}\right)^2= 8,820$

Question 64. The value of furniture depreciates by 10% a year, if the present value of the furniture in an office is calculate the value of furniture 3 years ago

30,000
% 40,000
35,000
R 50,000

Solution:

(1) 30000 – 10% – 10% – 10%

button = 2 1870.

Details Method

⇒ $21870 =P\left(1-\frac{10}{100}\right)^3 $

⇒ $P =\frac{21870}{(0.9)^3}=₹ 30,000$

Question 65. If compound interest on a sum for 2 years at 4% per annum is % 102, then the simple interest on the same period at the same rate will be

90
100
4101
93

Solution:

⇒ $\text { (b) } \mathrm{C} . \mathrm{I}=\mathrm{P}\left(1+\frac{4}{100}\right)^2-p=102$

Or P [(1.04)2- 1] = 102

Or Px 0.0816 =102

⇒ $ \text { Or } \mathrm{P}=\frac{102}{0.0816}=1250$

⇒ $\text { S.I }=\frac{p . r. t .}{100}=\frac{1250 \times 4 \times 2}{100}=₹ 100$

Question 66. If the difference between the compound interest compounded annually and simple interest on a certain amount at 10% per annum for two years is 372, then the principal amount is

37,000
37,200
37,500
None of the above

Solution:

(2) P= 372 v 10% + 10% = ₹ 37,200

Question 67. What is the net present value of a piece of property that would be valued at 2 lakh at the end of 2 years? (Annual rate of increase = 5%)

2.00 lakh
1.81 lakh
2.01 lakh
None of the above

Solution:

(2) NPV = $2\left(1+\frac{5}{100}\right)^{-2}=$ 1.81 lakh (approx).

Question 68. The difference between the simple and compound interest on a certain sum for 3 years at 5% p.a. is \228.75. The compound interest on the sum for 2 years at 5% p.a. is:

3,175
3,075
3,275
2,975

Solution:

⇒ $\mathrm{P}=\frac{\text { Difference } \times(100)^3}{r^2(300+r)}[For 3 years only]$

⇒ $=\frac{228.75 \times(100)^3}{5 \times 5(300+5)}=₹ 30,000$

A = 30000 + 5% + 5% buttons = 33075

Or P = = 45,317.33

C.l. = A – P = 33075 – 30000

= 7 3,075 (2) is correct

Question 69. In what time will amount to 8% per annum, when the interest is compounded semi-annually? [Given: (1.04)4 = 1.16986]

2 years
4 years
5 years
7 years

Solution:

⇒ $ A=P\left(1+\frac{r}{100 m}\right)^{m t}$

⇒ $\frac{4,56,976}{3,90,625}=\left(1+\frac{8}{200}\right)^{2 t}$

Or 1.16985856 = (1.04)2t

Or 1.6966 = (1.04)2t

Or (1.04)4 = (1.04)2t

2t = 4 t = 2 years

(1) is correct

Question 70. How long will take to amount to 5% p.a. converted quarterly? [Given: (1.0125)124 = 1.1666]

3 years
3.1 years
13.5 years
12.4 years

Solution:

⇒ $\text { (b) } \frac{A}{p}=\left(1+\frac{5}{400}\right)^{4 t}$

⇒ $ \text { Or } \frac{14000}{12000}=(1.0125)^{4 t}$

Or 1.6666……..(1.0125)4t

Or (1.0125)12.4 = (1.0125)4t

Or 4t = 12,4 t = 3.1 yrs.

(2) is correct

Question 71. If be invested at an interest rate of 5% and the interest is added to the principal every 10 years, then the number of years in which it will amount to is :

$16 \frac{2}{3} years$
$\frac{1}{10} years$
16 years
$6 \frac{2}{3} years$

Solution:

⇒ $Given P=\left\{1000 ; m=\frac{1}{10} ; n=m t=\frac{1}{10} \times t=\right.0.1 \mathrm{t}$

r = 5% p.a

⇒ $\mathrm{A}=\mathrm{P}\left[1+\frac{5}{0.1 \times 100}\right]^{0.1 t}$

⇒ $ \frac{2000}{1000}=(1.50)^{0.1 t}$

⇒ $\text { Or } 0.1 t=\frac{\log 2}{\log (1.5)}$

⇒ $\text { Or } 0.1 \mathrm{t}=1.709 \text { or } \mathrm{t}=\frac{1.709}{0.1}$

= 17.09 = 16$\frac{2}{3}$

(1) is correct

CA Foundation Time Value Of Money Solved Examples

Question 72. A Person deposited ₹5,000 in a bank. The deposit was left to accumulate at 6% compounded quarterly for the first five years and at 8% compounded semiannually for the next eight years. The compound amount at the end of 13 years is:

12621.50
12613.10
13613.10
None.

Solution:

⇒ $A=5000\left(1+\frac{6}{400}\right)^{5 \times 4}\left(1+\frac{8}{200}\right)^{8 \times 2}$

₹12613.17 =₹ 12610.00 (approx.)

(2) is correct

Question 73. Anshul’s father wishes to have 75,000 in a bank account when his first college expenses begin. How much amount does his father deposit now at 6.5% compounded annually if Anshul is to start college 8 years hence from now?

45,320
₹46,360
55,360
1 48,360.

Solution:

(1)

⇒ $ A=P\left(1+\frac{r}{100 m}\right)^{m t}$

⇒ $\text { Or; } 75000=P\left(1+\frac{6.5}{100}\right)^{1 \times B}$

⇒ $\text { Or } P=\frac{75000}{(1.065)^8}=₹ 45,317.33$

(1) is correct

Question 74. The difference between compound interest and simple interest on a certain sum for 2 years @ 10% p.a. is Find the sum:

1,010
1,095
1,000
990

Solution:

(3)

⇒ $\mathrm{P}=\frac{\text { actual }(C . I-S . I)}{(C . I-S t .) a t R e .1 .}$

⇒ $\mathrm{P}=\frac{10}{\left|(1.10)^2-1\right|-0.2}=₹ 1000$

(3) is correct

Question 75. A machine worth Rs 4,90,740 is depreciated at 15% on its opening value each year when its value would reduce to 2,00,000:

5 years 6 months
5 years 7 months
5 years 5 months
None

Solution:

(1) is correct

⇒ $t=\frac{\log (2,00,00 / 4,90,740)}{\log (1-15 / 100)}$

= 5.5 years (approx..)

= 5 yrs. 6 months

Question 76. If the difference between simple interest and compound interest is 11 at the rate of10% for two years, then find the sum:

₹ 1,200
1,100
1,000
None of these

Solution:

(2) is correct

⇒ $\mathrm{P}=\frac{\text { Difference } \times(100)^2}{(\text { rate })^2}$

⇒ $=\frac{11 \times(100)^2}{(10)^2}=₹ 1100$

CA Foundation Maths Solutions For Chapter 4 Annuity

Annuity Definition:

A sequence of payments, generally equal In size, made at equal intervals of time is called an annuity.

Monthly Rent; premiums of LIC; deposit into a recurring account in a bank; equal monthly payments got by a retired government servant as pension and loan installments to houses or automobiles etc.

Some Terms Related With Annuities

Periodic Payment: The size of each payment of an annuity is called the periodic payment of the annuity.
Annual Rent: The sum of all payments of an annuity made in one year is called its annual rent.
Payment Period or Interval: The duration between two successive payments of an annuity is called the payment period (or payment interval) of the annuity
Term: The total duration from the beginning time of the first payment period to the end of the last payment period is called the term of the annuity.
Present value of an Annuity: The sum of the present values of all the payments of an annuity is called the present value or capital value of the annuity.

Annuity regular and Annuity due or immediate

CA Foundation For Maths Chapter 4 Annuity

The annuity may be of two types:

Annuity regular: In an annuity, a regular first payment or receipt takes place at the end of the first period. Consider the following table:

CA Foundation For Maths Chapter 4 Annuity Regular

Annuity Due or Annuity Immediate: When the first receipt or payment is made today (at the beginning of the annuity) it is called annuity due or annuity immediate. Consider the following table:

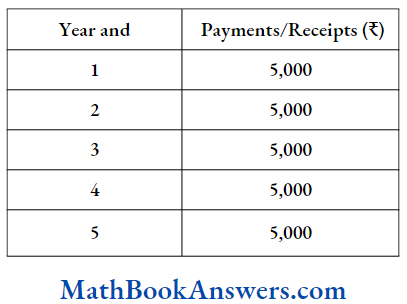
CA Foundation For Maths Chapter 4 Annuity Due or Annuity Immediate

Annuity Regular Or Annuity Ordinary – Formulae

To Find Future Value Amount

⇒ $S=A\left[\frac{(1+i)^n-1}{r}\right] \times 100 \mathrm{~m} .$

Where S = Amount of an Annuity

A = Value of each installment

R = rate of interest

M = No. of conversion periods in a year

N = m.t = No. of in statements made in t yrs.

⇒ $\mathrm{i}=\frac{r}{100 \mathrm{~m}}$ = Rate of interest of one conversion Period

To find the Present Value for an Ordinary Annuity

PV = Present value $=\mathrm{A}\left[\frac{1-(1+i)^{-n}}{i}\right]$

Annuity Immediate Or Due – Formulae

To find the Future Value Amount

FV = Amount s = $\mathrm{A}\left[\left\{\frac{(1+i)^{n+1}-1}{r}\right\} \times 100 m-1\right]$

Present value of annuity due or annuity immediate Present value of annuity due or immediate for n years is the same as an annuity regular for (n – 1] years plus an initial receipt or payment at the beginning of the period.

Calculating the present value of the annuity due involves two steps.

Step 1: Compute the present value of the annuity as if it were an annuity regular for one period short.

Step 2: Add the initial cash payment or receipt to the Step 1 value.

CA Foundation Maths Solutions For Chapter 4 Sinking Fund

It is the fund credited for a specified purpose by way of a sequence of periodic payments over some time at a specified interest rate. Interest is compounded at the end of every period. The size of the sinking fund deposit is computed from A = P.A(n, i) where A is the amount to be saved, P is the periodic payment, and n is the payment period.

Solved Example

Question 1. How much amount is required to be invested every year to accumulate ₹300000 at the end of 10 years if interest is compounded annually at 10%?
Solution:

Here A = 3,00,000

n = 10

i = 0.1

Since A = P.A (n, i)

300000 = P.A.(10, 0.1)

= P x 15.9374248

⇒ $\mathrm{P} \quad=\frac{3,00,000}{15.9374248}=₹ 18,823.62$

This value can also be calculated by the formula of the future value of annuity regular. We know that

⇒ $ A(n \text { i }) =A\left[\frac{(1+i)^n-1}{i}\right]$

⇒ $ 300000 =A\left[\frac{(1+0.1)^{10}-1}{0.1}\right] $

300000= A x 15.9374248

⇒ $\text { A } \quad=\frac{3.00,000}{15.9374248}=₹ 18,823.62$

Chapter 4 Time Value Of Money Step-By-Step Solutions

CA Foundation Maths Solutions For Chapter 4 Leasing

Leasing is a financial arrangement uniter which the owner of the asset (lessor) allows the user of the asset (lessee) to use the asset for a defined period (lease period) for a consideration (lease rental) payable over a given period, This is a kind of taking an asset on rent.

Solved Examples:

Question 1. ABC Ltd. wants to lease out an asset costing ₹3,60,000 for five years. It has fixed a rental of ₹1,05,000 per annum payable annually starting from the end of the first year, Suppose the rate of interest is 14% per annum compounded annually on which money can be invested by the company. Is this agreement favorable to the company?
Solution:

First, we have to compute the present value of the annuity of ₹1,05,000 for five years at the interest rate of 14% p.a. compounded annually.

The present value V of the annuity is given by

V = A.P (n, i)

= 1,05,000 xP(5, 0.14)

= 1,0,5000 x 3.43308 = ₹3,60,473.40

which is greater than the initial cost of the asset and consequently leasing is favourable to the lessor.

Question 2. A company is considering the proposal of purchasing a machine either by making a full payment of ₹4,000 or by leasing it for four years at an annual rate of ₹1,250. Which course of action is preferable if the company can borrow money at 14% compounded annually?
Solution:

The present value V of the annuity is given by

= A.P (n, i)

= 1,250 x p (4, 0.14)

= 1,250 x 2.91 371 = ₹3,642.11

which is less than the purchase price and consequently leasing is preferable

CA Foundation Maths Solutions For Chapter 4 Capital Expenditure (investment decision)

Capital expenditure means purchasing an asset (which results in outflows of money) today in anticipation of benefits (cash inflow) that would flow across the life of the investment. For making investment decisions we compare the present value of cash outflow and the present value of cash inflows. If the present value of cash inflows is greater than the present value of cash outflows decision should be in favor of investment. Let us see how we make capital expenditure (investment) decisions.

Solved Examples:

Question 1. A machine can be purchased for ₹50000. The machine will contribute ₹12000 per year for the next five years. Assume borrowing cost is 10% per annum compounded annually. Determine whether the machine should be purchased or not.
Solution:

The present value of annual contribution

= A.P(n, i)

= 12,000 x P(5, 0.10)

= 12,000 x 3.79079

= ₹45,489.48

which is less than the initial cost of the machine. Therefore machine must not be purchased.

Question 2. A machine with a selling life of seven years costs f1 0,000 while another machine with a useful life of live years costs (111,001). The first machine saves labor expenses of ₹1,900 annually and the second one saves labor expenses of ₹2,200 annually. Determine the preferred course of action. Assume the cost of borrowing as 10% compounded per annum.
Solution:

The present value of annual cost savings for the first machine

= ₹1,900 KP (7, 0.10)

= ₹ 1,900 ⇔ 4.86842

= ₹9,249.99

= ₹9,250

The cost of the machine being ₹10,000 it costs more by ₹750 than it saves in terms of labour cost.

The present value of annual cost savings of the second machine

= ₹2,200 xP(5, 0.10)

= ₹2,200 x 3.79079

= ₹8,339.74

The cost of the second machine is ₹8,000 effective savings in labor cost is ₹339.74. Hence the second machine is preferable.

CA Foundation Maths Solutions For Chapter 4 Valuation Of Bond

A bond is a debt security in which the issuer owes the holder a debt and is obliged to repay the principal and interest. Bonds are generally issued for a fixed term longer than one year.

Solved Example

Question 1. An investor intends to purchase a three-year ₹1,000 par value bond having a nominal interest rate of 10%. At what price the bond may be purchased now if it matures at par and the investor requires a rate of return of 14%?
Solution:

Present value of the bond

⇒ $=\frac{100}{(1+0.14)^1}+\frac{100}{(1+0.14)^2}+\frac{100}{(1+0.14)^3}+\frac{1,000}{(1+0.14)^3}$

= 100 x 0.87719 + 100 x 0.769467 + 100 x 0.674 972 + 1,000 x 0.674972

= 87.719+ 76.947+ 67.497+ 674.972 = ₹907.125

Thus, the purchase value of the bond is ₹907.125

CA Foundation Maths Solutions For Chapter 4 Perpetuity

Perpetuity is an annuity in which the periodic payments or receipts begin on a fixed date and continue indefinitely or perpetually. Fixed coupon payments on permanently invested (irredeemable) sums of money are prime examples of perpetuities.

Solved Example

Question 1. Ramesh wants to retire and receive ₹3,000 a month. He wants to pass this monthly payment to future generations after his death. He can earn an interest of 8% compounded annually. How much will he need to set aside to achieve his perpetuity goal?
Solution:

R = ₹3,000

i = 0.08/12 or 0.00667

Substituting these values in the above formula, we get

⇒ PVA =$\frac{3,000}{0.00667}$

= ₹ 4,49,775

If he wanted the payments to start today, he must Increase the size of the funds to handle the first payment. This is achieved by depositing H52,775 of normal perpetuity received in the beginning = 4,49,775 + 3,000 which provides the immediate payment of ₹3,000 and leaves ₹4,49,775 in the fund to provide the future ₹3,000 payments.

CA Foundation Maths Solutions For Chapter 4 Growing Perpetuity

A stream of cash flows that grow at a constant rate forever is known as growing perpetuity.

The formula for determining the present value of growing perpetuity is as follows:

⇒ $\text { PVA }=\frac{R}{(1+i)^1}+\frac{R(1+g)}{(1+i)^2}+\frac{R(1+g)^2}{(1+i)^3}+\ldots \ldots \ldots . . .+\frac{R(1+g)^{\infty}}{(1+i)^{\infty}}$

⇒ $\sum_{n=1}^{\infty} \frac{R(1+g)^{n-1}}{(1+i)^n}$

⇒ $=\frac{R}{i-g}$

Solved Example:

Question 1. Assuming that the discount rate is 7% per annum, how much would you pay to receive ₹50, growing at 5%, annually, forever?
Solution:

⇒ $\text { PVA }=\frac{R}{i-g}=\frac{50}{0.07-0.05}=2,500$

Net Present Value Technique (NPV):

The net present value technique is a discounted cash flow method that considers the time value of money in evaluating capital investments. An investment has cash flows throughout its life, and it is assumed that a rupee of cash flow in the early years of an investment is worth more than a rupee of cash flow in a later year.

The net present value method uses a specified discount rate to bring all subsequent net cash inflows after the initial investment to their present values (the time of the initial investment is year 0).

CA Foundation Maths Solutions For Chapter 4 Determining Discount Rate

Theoretically, the discount rate or desired rate of return on an investment is the rate of return the firm would have earned by investing the same funds in the best available alternative investment that has the same risk.

Many organizations choose to use the overall cost of capital or Weighted Average Cost of Capital (WACC) that an organization has incurred in raising funds or expects to incur in raising the funds needed for an investment.

The net present value of a project is the amount, in current value of rupees, the investment earns after paying the cost of capital in each period.

Net Present Value

Net present value = Present value of cash inflow – Present value of cash outflow

The steps to calculating net present value are:
Determine the net cash inflow in each year of the investment.
Select the desired rate of return discounting rate or Weighted Average Cost of capital.
Find the discount factor for each year based on the desired rate of return selected.
Determine the present values of the net cash flows by multiplying the cash flows by respective the discount factors of the respective period called the Present Value (PV) of Cash flows
Total the amounts of all PVs of Cash Flows

Decision Rule:

If NPV > 0 Accept the proposal.

lf NPV > 0 Reject the proposal

Solved Example:

Question 1. Compute the net present value for n pro|cct with n not Invoslment of 1,00,000 and cash flows year one Is ₹55,000; for year two Is ₹80,000 and for year three Is 15,000. Further, the company’s cost of capital Is 10%.

|PVIF @ 10% for three years are 0.909, 0.020 and 0.751 |

Solution:

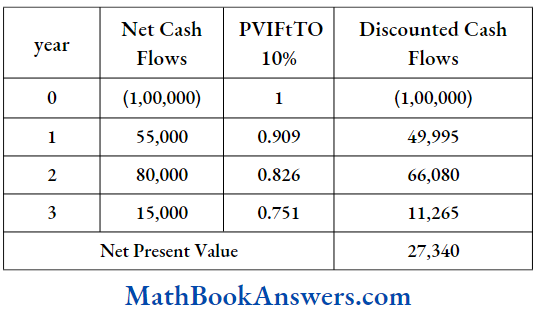
CA Foundation For Maths Chapter 4 Net Present Value

CA Foundation Maths Solutions For Chapter 4 Nominal Rate of Return

The nominal rate is the stated interest rate. If a bank pays 5% annually on a savings account, then 5% is the nominal interest rate. So, if you deposit n00 for 1 year, you will receive in interest.

However, that will probably be worth less at the end of the year than it would have been at the beginning. This is because inflation lowers the value of money.

Nominal Rate of Return – Inflation = Real Rate of Return

Real Rate of Return:

The real interest rate is so named because it states the “real” rate that the lender or investor receives after inflation is factored in; that is, the interest rate that exceeds the inflation rate.

Nominal Interest Rate = Real Interest Rate + Inflation

CA Foundation Maths Solutions For Chapter 4 Effective Rate

It is the actual equivalent annual rate of interest at which an investment grows in value when interest is credited more often than once a year. If interest is paid m times in a year it can be found by calculating:

⇒ $\mathrm{E}_{\mathrm{i}}=\left(1+\frac{i}{m}\right)^m-1$

The chief advantage of knowing the difference between nominal, real, and effective rates is that it allows consumers to make better decisions about their loans and investments. A loan with frequent compounding periods will be more expensive than one that compounds annually.

Effective and nominal interest rates allow banks to use the number that looks most advantageous to the consumer. When banks are charging interest, they advertise the nominal rate, which is lower and does not reflect how much interest the consumer would owe on the balance after a full year of compounding. On the other hand, with deposit accounts where banks are paying interest, they generally advertise the effective rate because it is higher than the nominal rate.

CA Foundation Maths Guide For Time Value Of Money

CA Foundation Maths Solutions For Chapter 4 Compound Annual Growth Rate (CAGR)

Compounded Aiuuml Growth Knlc (CAGR) is an IHISIIIORR mill Inverting specific terms for the smoothed in a mulled gain of mi Investnu it over; I gave time. Is not my accounting I r-rin, 1ml remains widely used, particularly in growth Industries or to compare the growth rates of two investments because CAGR dampens the effect or volatility of periodic returns that can render arithmetic means irrelevant. CAGR is often used to describe the growth over some time of some element of the business, for example, revenue, units delivered, registered users, etc.

⇒ ${CAGR}\left(t_0, t_{11}\right)=\left(\frac{V\left(t_n\right)}{V\left(t_0\right)}\right)^{\frac{1}{t_{01-}-t_0}}-1$

Where V(to) = Beginning Period ; V (tn) = End Period

Solved Example:

Question 1. Suppose the revenues of a company for four years, V(t) in the above formula, have been

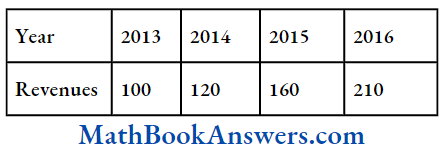
CA Foundation For Maths Chapter 4 Compound Annual Growth Rate

Calculate Compound Annual Growth Rate.
Solution:

tn-to = 2016-2013 =3

The CAGR revenues over the three years from the end of 2013 to the end of 2016 is

CAGR (0, 3) = $\left(\frac{210}{100}\right)^{\frac{1}{3}}-1=1.2774-=27.74 \%$

Applications: These are some of the common CAGR applications:

Calculating average returns of investment funds.
Demonstrating and comparing the performance of investment advisors.
Comparing the historical returns of stocks with bonds or with a savings account.
Forecasting future values based on the CAGR of a data series.
Analyzing and communicating the behavior, over a series of years, of different business measures such as sales, market share, costs, customer satisfaction, and performance.

Solved Examples:

Question 1. Mr. X invests ₹310,000 every year starting today for the next 10 years suppose the interest rate is 8% per annum compounded annually. Calculate the future value of the annuity:

(given that (1+0.08)10 = 2.15892500)

3156454.88
3144865.625
3156554.88
None of these

Solution:

⇒ $A=F V=R\left[\left\{\frac{(1+i)^{n+1}-1}{r}\right\} \times 100 \mathrm{~m}-1\right]$

⇒ $=10,000\left[\frac{(1+0.08)^{10+1}-1}{8} \times 100-1\right]$

Question 2. The present value of an annuity of 33,000 for 15 years at 4.5% p.a. C.l. is: [Given that (1.045)15 = 1.935282]

323,809.67
332,218.67
332,908.67
None of these

Solution:

(2)

⇒ $ P V=R\left|\frac{1-(1+1)^{-11}}{1}\right|$

⇒ $ =3000\left\lceil\frac{1-(1.045)^{-13}}{0.045}\right\rceil$

Question 3. A machine can be purchased for ₹50,000. The machine will contribute Rs. 2,000 per year for five years. Assume the borrowing cost is 10% per annum. Determine whether the machine should be purchased or not:

Should be purchased
Should not be purchased
Can’t say about the purchase
None of the above

Solution:

(2)

⇒ $P V=R\left[\frac{1-(1+i)^{-n}}{i}\right]$

⇒ $P V=12000\left[\frac{1-(1.10)^{-5}}{0.10}\right]$

= ₹45,489.44

It should not be purchased

Question 4. How much amount is required to be invested every year so as to accumulate ₹3,00,000 at the end of 10 years? If interest is compounded annually at 10%? (Given (1.1)⇔=2.5937)

₹18,823.65
₹18,828.65
₹18,832.65
₹18,882.65

Solution:

(1)

⇒ $\mathrm{FV}=\mathrm{R}\left[\frac{(1+i)^n-1}{r} \times 100 \mathrm{~m}\right]$

⇒ $3,00,000=\mathrm{R}\left[\frac{\left(1+\frac{10}{100}\right)^{10}-1}{10} \times 100\right]$

⇒ $\mathrm{R}=\frac{3.00,000}{\left|\frac{(1.1)^{10}-1}{10} \times 100\right|}=₹ 18,823.65$

Question 5. A company is considering the proposal of purchasing a machine either by making a full payment of ₹4,000 or by leasing it for four years at an annual rate of ₹ 1,250. Which course of action is preferable, if the company can borrow money at 14% compounded annually? (Given: (1.14) = 1.68896)

Leasing is preferable
Should be purchased
No difference
None of these

Solution:

(1)

₹4000 = Present value

⇒ $PV=R\left[\frac{1-(1-i)^{-n}}{r} \times 100\right]$

⇒ $=1250\left[\frac{1-\left(1+\frac{14}{100}\right)^{-4}}{14} \times 100\right]=₹ 3642.14$

It is less than the real cost price.

Leasing is better

(1) is correct

Question 6. Vipul purchases a car for ₹5,50,000, nets, I loan of ₹5,00,000 at IS% p.a. from; i hank and balance ISO,000 ho pays as ₹ time of purchase, lie has to pay the whole amount of loan in 12 equal monthly Instalments with Interest starting from the end of the first month, The money he has to pay at the end of every month is:
(Given (1.0125)’₹’= 1.16075452)

₹45,130.43
₹45,230.43
₹45,330.43
None of these

Solution:

Loan value = ₹5,00,000 = PV

R = Instalment value =?

⇒ $P V=R\left[\frac{1-(1+i)^{-11}}{i}\right]$

⇒ $5,00,000=R\left[\frac{1-\left(1+\frac{15}{1200}\right)^{-12}}{i}\right]$

R = ₹45,130.43

Question 7. A company establishes a sinking fund to pay for ₹2,00,000 debt maturing in 20 years. Contributions to the fund are to be made at the end of every year. Find the amount of each annual deposit interest is 5% per annum:

₹6,142
6,049
₹6,052
6,159

Solution:

(2)

₹ 200,000

⇒ $200,000=R\left[\frac{(1+5 / 100)^{-20}-1}{5} \times 100\right] $

⇒ $ R=\frac{2,00,000 \times 5}{\left.\mid(1.05)^{20}-1\right) \mid \times 100}$

⇒ $=₹ 6049 \text { (Approx. })$

Question 8. A company may obtain a machine either by leasing it for 5 years (useful life) at an annual rent of ₹2,000 or by purchasing the machine for ₹8,100. If the company can borrow money at 18% per annum, which alternative is preferable?

Leasing
Purchasing
can’t say
None of these

Solution:

(1) PV = ₹8100

It is an ordinary annuity

= ₹ 6254.34

It is less than ₹8100. (1) Is correct

Question 9. A sinking fund is created for redeeming debentures worth ₹5 lacs at the end of 25 years. How much provision needs to be made out of profits each year provided sinking fund investments can earn interest at 4% p.a.?

12,006
12,040
12,039
12,035

Solution:

⇒ $₹ 5,00,000=R\left\lceil\frac{(1.04)^{25}-1}{0.04}\right]$

R = 12006.00 approx

Question 10. Future value of an ordinary annuity:

$(..) $A(n, 1)=A\left(\frac{(1+1)^n-1}{1}\right)$
$A(n, i)=A\left(\frac{(1+1)^n+1}{i}\right)$
$A(n, i)=A\left(\frac{1-(1+1)^n}{1}\right)$
$ A(n, i)=A\left(\frac{(1+i)^n-1}{\left((1+i)^n\right.}\right)$$

Solution:

(1) It is Formulae.

Question 11. Paul borrows ₹20,000 on condition that repay it with compound interest at 5% p.a. in an annual installment of ₹2,000 each. Find the number of years in which the debt would be paid off.

layers
12years
14years
15years

Solution:

(4)

⇒ $20,000=2000\left[\frac{1-\left(1+\frac{5}{10}\right)^{-1}}{5} \times 100\right]$

⇒ $\text { Or } 10=\left[\frac{1-(1.05)^{-t}}{5}\right] \times 100 $

⇒ $\text { Or } \frac{10 \times 5}{100}=1-(1.05)^{-t}$

Or 0.5-1= (1.05)-t

Or 0.5-1= -(1.05)-t

⇒ ${Or}(1.05)^t=\frac{1}{0.5}=2$

Or $ t =\frac{\log 2}{\log (1.05)}=15$ yrs. approx.$

Question 12. Find the value of an annuity of ₹1,000 payable at the end of each year for 10 years. If the rate of interest is 6% compounding per annum. (given (1.06)-111 = 0.558):

₹7,360
₹8,360
₹12,000
None of these

Solution:

(1) Is correct

⇒ $P V=1000\left[\frac{1-(1.06)^{10}}{0.06}\right] \quad=₹ 7360$

Question 13. The future value of an annuity of ₹ 5,000 is made annually for 8 years at an interest rate of 9% compounded annually (Given that (1.09)8 = 1.99256_____.

₹55,142.22
₹65,142.22
₹65,532.22
₹57,425.22

Solution:

(1)

⇒ $FV=5000\left[\frac{(1.09)^8-1}{0.09}\right]=₹ 55,142.22$

Question 14. How much amount is required to be invested every year to accumulate ₹ 6,00,000 at the end of 10, the year, if interest is compounded annually at a 10% rate of interest?

₹37,467
₹37,476
₹37,647
₹37,674

Solution:

(3)

Let the amount invested annually be = R

⇒ $R=\frac{6,00,000}{\left|\frac{\left(1+\frac{1}{180}\right)^{10}-1}{10} \times 100\right}=₹ 37,647 \text { (approx.) }$

Question 15. The future value of an annuity of ₹1,000 annually for 5 years at the rate of interest of 14% compound annually is

₹5610
₹6610
₹6160
₹5160

Solution:

(2)

⇒ $ \mathrm{FV}=1000\left[\frac{\left(1+\frac{14}{100}\right)^5-1}{14} \times 100\right]$

= ₹6610.104

Question 16. Suppose your mon decides to gift you ₹10,000 every year starting from today for the next sixteen years. You deposit this amount in a bank as and when you receive it and get an 8.5% per annum interest rate compounded annually. What is the present value of this money: (given that P (15,0.085) = 8.304236)

83,042
90,100
93,042
10,100

Solution:

(3)

⇒ $ PV=10,000\left[\frac{1-\left(1+\frac{8.5}{10}\right)^{(-16-1)}}{8.5} \times 100+1\right]$

= 10,000 (8.304236+1) = ₹93,042

Question 17. The future value of an annuity of ₹1500 made annually for 5 years with an interest rate of 10% compounded annually is_

9517.56
9157.65
9715.56
9175.65

Solution:

(2)

⇒ $F V=1500\left[\frac{\left(1+\frac{10}{100}\right)^5-1}{10} \times 100\right]=₹ 9157.65$

CA Foundation Maths Solutions For Chapter 4 Exercise – 3

Question 1. The present value of an annuity of ₹3000 for 15 years at 4.5% p.a Cl is

₹23.809.41
₹32,214.60
₹3 2,908.41
None of these

Solution:

(2) Since no info is given, by default it is annuity regular

Present value =$=A\left[\frac{1-(1+i)^{-n}}{i}\right]$

A = Periodic Payment 1 = interest n = no. of yrs.

⇒ $\text { P.V. }=3000\left[\frac{1-(1.045)^{-15}}{0.045}\right]$ = ₹32,214.60 0.045

Question 2. The amount of an annuity is certain of V150 for 12 years at 3.5% p.a C. I am

₹2.190.28
₹290.28
₹2,180.28
None of these

Solution:

(1) v Amount of annuity certain will be the future value

⇒ $ \text { F.V. }=A\left[\frac{(1+i)^n-1}{i}\right]$

⇒ $150\left[\frac{(1.035)^{12}-1}{0.035}\right]=₹ 2190.28$

Question 3. A loan of ₹ 1 0,000 is to be paid back in 30 equal installments. The amount of each installment to cover the principal and at 4% p.a Cl is

₹587.87
₹587
₹578.30
None of these

Solution:

(3) loan amount is given i.e. P.V of annuity regular is given

⇒ $\text { P. V }=A\left[\frac{1-(1+i)^{-n}}{i}\right]$

⇒ $10,000=A\left[\frac{1-(1.04)^{-30}}{0.04}\right]$

Therefore, A=₹ 578.30

Question 4. A = ₹1,200 n = 12 yearsi = 0.08, V = ?

Using the formula$V=\frac{A}{i}\left[1-\frac{1}{(1+i)^n}\right]$ value of v will be

₹3,039
₹3,990
₹9930
₹9043.30

Solution:

(4)

⇒ $ \mathrm{V} =\frac{A}{i}\left[1 \frac{-1}{(1+i)^n}\right]$

⇒ $\mathrm{V} =\frac{A}{i}\left[1-(1+i)^{-n}\right]$

⇒ $\mathrm{V} =1200\left[\frac{1-(1.08)^{-12}}{0.08}\right]$

V = ₹9043.30

Question 5. a = ₹100 n = 10, /= 5% find the FV of annuity. Using the formula FV = a {(1 + i)” – l)/i, FV is equal to

₹1,258
₹2,581
₹1,528
None of these

Solution:

⇒ $ { (1) } F . V=a =100\left[\frac{(1.05)^{10}-1}{0.05}\right]$

⇒ $ =₹ 1258$

Question 6. If the amount of an annuity after 25 years at 5% p.a C.1 is ₹50,000 the annuity will be

₹1,406.90
₹1,047.62
₹1,146.90
None of these

Solution:

[2] F.V given = 50,000

⇒ $\text { F.V }=\mathrm{A}\left[\frac{(1+i)^n-1}{i}\right]$

⇒ $50,000 =\mathrm{A}\left[\frac{(1.05)^{25}-1}{0.05}\right]$

A = ₹1047.62

Question 7. An annuity of ₹100 amounts to ₹3137.12 at 4.5% p.a C. I. The number of years will be

25 years (appx.)
20 years (appx.)
22 years
None of these

Solution:

(2) F.V = ₹3137.12 A= 100 I = 0.045 n = ?

⇒ $ F \cdot V=A\left[\frac{(1+i)^n-1}{i}\right]$

⇒ $\frac{(F . V)}{A} \mathrm{i}+1=(1+\mathrm{i})^{\prime \prime}$

Question 8. A company borrows ₹10,000 on condition to repay it with compound interest at 5% p.a by annual installments of ₹1000 each. The number of years by which the debt will be clear is

14.2 years
10 years
12 years
None of these

Solution:

(1) P.V or annuity = loan amount = 10,000

⇒ $P \cdot V=A\left[\frac{1-(1+i)^{-n}}{i}\right]$

⇒ $ \frac{10.000}{1000}(0.05)=1-(1+i)^{-n}$

⇒ $(1+i)^n=\frac{1-10.000(0.05)}{1000}$

(1 + i)n =0.5

(l.05)n = 0.5

n = 14.2 yrs

Question 9. Mr. X borrowed ₹5,120 at 12 % % p.a C.I. At the end of 3 years, the money was repaid along with the interest accrued. The amount of interest paid by him is

₹2,100
₹2,170
₹2,000
None of these

Solution:

(2) Principal = 5120 Rate =12.5% Time: 3 yrs

Compound Interest = P [1 + i)”- 1]

= 5120 [(1+0.125)3 – 1]

= 5120 [(1.125P-1]

C.I = 2170

Interest paid by him is 2170

Question 10. Mr. Paul borrows ₹20,000 on condition that repay it with C.I. at 5% p.a in annual installments of ₹2000 each. The number of years for the debt to be paid off is

10 years
12 years
11 years
14.2 years

Solution:

10. (d) P.V of annuity = loan amount = 20,000

⇒ $ \text { P.V }=A\left[\frac{1-(1+i)^{-n}}{i}\right]$

⇒ $20,000=2000\left[\frac{1-(1.05)^{-n}}{0.05}\right]$

0.5=1-(1.05)-n

(1.05)n = 0.5

n = 14.2 yrs

Question 11. A person invests ₹500 at the end of each year with a bank that pays interest at 10% p.a C.I. annually. The amount standing to his credit one year after he has made his yearly investment for the 12th time is.

₹11,761.36
₹10,000
₹12,000
None of these

Solution:

(1) The future value of the annuity after 12 years will be

⇒ $ F .V =A\left[\frac{(1+i)^n-1}{i}\right]$

⇒ $=500\left[\frac{(1.1)^{12}-1}{0.1}\right]$

they are asking for one year after the 12th payment interest will be given at 10% but no 500 is deposited as the year has not ended.

Interest on @ 10% will be added

⇒ $ 10692.14188 \times \frac{10}{100}=1069.2141$

=₹ 11761.36

Question 12. The present value of an annuity of ₹5,000 per annum for 12 years at 4% p.a C.I. annually is

₹46,000
₹46,850
₹15,000
46925.40

Solution:

⇒ $ {P.V }=A\left[\frac{1-(1+i)^{-7}}{i}\right] $

⇒ $5000\left[\frac{1-(1.04)^{-12}}{0.04}\right]$

Question 13. A person desires to create a fund to be invested at 10% Cl per annum to provide for a prize of ₹300 every year. Using V = a/I find V and V will be

₹2,000
₹2,500
₹3,000
None of these

Solution:

(3) V=\frac{a}{1}=\frac{300}{0.1}=₹ 3000

Question 14. What sum should be invested at the end of every year to accumulate an amount of ’796570 at the end of 10 years at the rate of interest 10% compounded annually, (given that A(10;0.1) = 15.9374)

40,000
4,50,000
4,80,000
50,000

Solution:

(4) $R=\frac{796870}{\left|\frac{\left(1+\frac{10}{100}\right)^{10}-1}{10} \times 100\right|}=₹ 50,000$

Question 15. A person invests at the end of each month @ of interest 6% compounding monthly, find the amount of annuity after the 10th payment:

20,456
20,156
20,256
20,356

Solution:

(1) $F V=2000\left[\frac{\left(1+\frac{6}{1200}\right)^{10}-1}{6} \times 1200\right]=₹ 20,456$

Tips For Understanding Time Value Of Money In CA Foundation

CA Foundation Maths Solutions For Chapter 4 Exercise 4- Mix Question And Answers

Question 1. A = ₹5,200. R = 5% p.a., T = 6 years, P will be

₹2,000
₹3.880
₹3,000
None of these

Solution: 1. ₹2,000

Question 2. If P = 1,000, n = 4 years., R = 5% p.a then C. I will be

₹215.50
₹210
₹220
None of these

Solution: 1. ₹215.50

Question 3. The time in which a sum of money will be doubled at 5% p.a C. I am

₹10 years
12 years
14.2 years
None of these

Solution: 3. 14.2 years

Question 4. ‘If A = ₹10,000, n = 18yrs., R = 4% p.a C.I, P will be

₹4,000
₹4,900
₹4,500
4936.30

Solution: 4. 4936.30

Question 5. The time by which a sum of money would treble itself at 8% p.a C. I am

14.28 years
14 years
12 years
None of these

Solution: 1. 14.28 years

Question 6. The present value of an annuity of ₹80 a year for 20 years at 5% p.a is

₹997 (appx.)
₹900
₹1,000
None of these

Solution: 1. ₹ 997 (appx.)

Question 7. A person bought a house paying ₹ 20,000 cash down and ₹4,000 at the end of each year for 25 yrs. at 5% p.a. C.l. The cash-down price is

₹75,000
₹76,000
₹76,375.80
None of these.

Solution: 3. ₹ 76,375.80

Question 8. A man purchased a house valued at ₹3,00,000. He paid ₹2,00,000 at the time of purchase and agreed to pay the balance with interest at 12% per annum compounded half-yearly in 20 equal half-yearly installments. If the first installment is paid after six months from the date of purchase then the amount of each installment is [Given log 10.6 = 1.0253 and log 31.19 = 1.494]

₹8,71 8.45
₹8,769.21
₹7,893.13
None of these.

Solution: 1. ₹8,71 8.45

Question 9. The difference between compound and simple interest at 5% per annum for 4 years on ₹20,000 is _____.

Solution: 4. 310

Question 10. The compound interest on half-yearly rests on ₹10,000 the rate for the first and second years being 6% and for the third year, 9% p.a. is _____.

2,200
2,287
2,285
None

Solution: 4. None

Question 11. The present value of ₹10,000 due in 2 years at 5% p.a. compound interest when the interest is paid every year is ______.

9,070
9,000
9,061
None

Solution: 1. 9,070

Question 12. The present value of ₹10,000 is due in 2 years at 5% p.a. compound interest when the interest is on a half-yearly basis _____.

9,070
9,069
9,061
None

Solution: 3. 9,061

Question 13. lohn son loft 1,00,000 with the direction that it should be divided in such a way that his minor sons Tom, Dick, and Harry aged 9, 12, and 15 years should each receive equally after attaining the age of 25 years. The rate of interest is 3.5%, how much does each son receive after getting 25 years old?

50,000
51,994
52,000
None

Solution: 4. None

Question 14. In how many years will a sum of money double at 5% p.a. compound interest?

15 years 3 months
14 years 2 months
14 years 3 months
15 years 2 months

Solution: 2. 14 years 2 months

Question 15. In how many years does a sum of money treble at 5% p.a. compound interest payable every year?

18 years 7 months
18 years 6 months
18 years 8 months
22 years 3 months

Solution: 15. 22 years 3 months

Question 16. A machine depreciates at 10% of its value at the beginning of a year. The cost and scrap value realized at the time of sale being and respectively. For how many years the machine was put to use?

7 years
8 years
9 years
10 years

Solution: 3. 9 years

Question 17. A machine’s worth is depreciated at 15% on its opening value each year. When its value would reduce to 2,00,000?

4 years 6 months
4 years 7 months
4 years 5 months
5 years 7 months approximately

Solution: 4. 5 years 7 months approximately

Question 18. A machine’s worth is depreciated at 15% of its opening value each year. When its value would reduce by 90%?

11 years 6 months
11 years 8 months
11 years 7 months
14 years 2 months approximately

Solution: 4. 14 years 2 months approximately

Question 19. Alibaba borrows lakhs Housing Loan at 6% repayable in 20 annual installments commencing at the end of the first year. How much annual payment is necessary?

52,420
52,419
52,310
52,320

Solution: 3. 52,310

Question 20. A sinking fund is created for redeeming debentures worth lakhs at the end of 25 years. How much provision needs to be made out of profits each year provided sinking fund investments can earn interest at 4% p.a.?

12,006
12,040
12,039
12,035

Solution: 1. 12,006

Question 21. A machine costs 5,20,000 with an estimated life of 25 years. A sinking fund is created to replace it with a new model at a 25% higher cost after 25 years with a scrap value realization of 25000. what amount should be set aside every year if the sinking fund investments accumulate at 3.5% compound interest p.a.?

16,000
16,500
16,050
16,005

Solution: 3. 16,050

Question 22. Raja aged 40 wishes his wife Rani to have ₹ 40 lakhs at his death. If his expectation of life is another 30 years and he starts making equal annual investments commencing now at 3% compound interest p.a. how much should he invest annually?

84,448
84,450
84,449
84,080

Solution: 4. 84,080

Question 23. Appu retires at 60 years receiving a pension of 14,400 a year paid in half-yearly installments for the rest of his life after reckoning his life expectation to be 13 years and that interest at 4% p.a. is payable half-yearly. What single sum is equivalent to his pension?

1,45,000
1,44,900
1,44,800
1,44,700

Solution: 2. 1,44,900

CA Foundation Maths Solutions For Chapter 1 Ratio And Proportion

November 15, 2024July 5, 2024 by Marksparks

CA Foundation Maths Solutions For Chapter 1 Ratio And Proportion

Ratio Formulas

The ratio of two quantities a and b in the same units, is the fraction £ and we write it as a: b.
In the ratio a: b, we call “an as the first term or antecedent” and “b, the second term or consequent”.
1. Example: The ratio 5: 9 represents with antecedent = 5, consequent = 9.
The multiplication or division of each ratio term by the same non-zero number does not affect the ratio.
1. Example: 4: 5 = 8: 10 = 12: 15 etc. Also, 4: 6 = 2 : 3 i.e. normally a ratio is expressed in simplest form.
The order of the terms in a ratio must be maintained because 3: 5 is not the same as 5 : 3.
Ratio exists only with quantities that have the same unit (kind).
Equality, Greater Equality, and Lesser Equality
- If x > y, then the ratio x: y is called of greater inequality.
- If x < y, then the ratio x: y is called of lesser inequality.
- If x = y, then the ratio a: b is called the ratio of Equal Equality.
Comparison of ratios:
1. We say that (a : b) > (c: d) $\frac{a}{b}>\frac{c}{d^{\prime}}$
2. Compounded Ratio: The compounded ratio of the ratios (a: b), (c : d), (e: f) is ace: pdf.
Duplicate ratio of (a: b)is (a2: b2).
- Sub-duplicate ratio of (a: b) is $(\sqrt{a}: \sqrt{b}).$
- The triplicate ratio of (a: b) is (a3: b3).
- The sub-triplicate ratio of (a: b) is (a1/3: b1/3).
- If $\frac{a}{b}=\frac{c}{d^{\prime}} \text { then } \frac{a+b}{b-b}=\frac{c+d}{c-d^{\prime}}$ (componendo and dividendo)
The inverse ratio of x y is y x.
Commensurable: If the terms of the ratio are integers, the ratio is called commensurable.
Answer: 3: 2
Incommensurable: If the terms of the ratio are not integers, the ratio is called
Incommensurable.
Answer:√3: √2 cannot be expressed in terms of integers. So, it is Incommensurable.

Read and Learn More CA Foundation Maths Solutions

CA Foundation Maths Solutions For Chapter 1 Proportion:

1. The equality of two ratios is called Proportion.

If a: b = c: d, we write, a: b:: c: cl and say that a, b, c, d are in Proportion.

A and d are called extremes, while b and c are called mean terms.

2. Product of means = Product of extremes. This rule is also known as Cross – Product Rule

Thus, a: b: : c: d = (b x c) = (a x d).

3. (1). Fourth Proportional: If a b = c: d, then d is called the fourth proportional to a, b, c.

(2). Third Proportional: If a b = b; c, then c is called the third proportional to a and b.

(3). Mean Proportional: MThe mean proportional between a and b is fab.

4. Properties of Proportion

Cross – Product

If a:b::c:d. $\frac{a}{b}=\frac{c}{d}\mathrm{ad}=\mathrm{bc} .$

Invertendo

If a : b: : c: d.; Then its inverse

b : a: : d: c also becomes in proportion.

If $\frac{a}{b}=\frac{c}{d} \quad \text { Then, } \frac{b}{a}=\frac{a}{c} \text {. }$

Componendo

If a : b: : c: d.

Then a + b:b::c + d:d.

Proof: $\frac{a}{b}+1=\frac{c}{d}+1 \Rightarrow \frac{a+b}{b}=\frac{c+d}{d}$

Dividendo

If a : b = c: d.

Then a-b:b = c-d:d.

Proof:$\frac{a}{b}=\frac{c}{d} \Rightarrow \frac{a}{b}-1=\frac{c}{d}-1$ Or $\frac{a-b}{b}=\frac{c-d}{d }$

Componendo and Dividendo

If a : b : : c : d.; Dividing [3) by (4)

Then $\frac{a+b}{a-b}=\frac{c+d}{c-d}$

Alternendo

Ifa : b: : c : d.

Then a : c:: b : d.

Therefore ratio of alternatives is also in proportion.

Addendum

If a:b = c:d = e:f= $\text { Then each ratio }=\frac{\text { Sum of antecedents of all ratios }}{\text { Sum of consequents of all ratios }}$

⇒ $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\ldots \ldots \ldots \ldots . .=\frac{a+c+e+\cdots \ldots . ..}{b+d+f+\cdots \ldots .}$

Subtrahendo

If $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\ldots \ldots \ldots \ldots \ldots$

Then each ratio

⇒ $=\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\ldots \ldots \ldots \ldots=\frac{a-c-e-\cdots}{b-d-f-…}$

CA Foundation Maths Chapter 1 Ratio And Proportion Solutions

CA Foundation Maths Solutions For Chapter 1 Ratio Exercise – 1

Question 1. The inverse ratio of 11:15 Is

15: 11
$\sqrt{11}: \sqrt{15}$
121: 225
None of these

Answer: 1. 15:11

Ratio → A: B Inverse → B: A ->15:11

Question 2. The ratio of the two quantities is 3 4. If the antecedent is 15, the consequent Is

Answer: 4. 20

Ratio 3:1

3 is antecedent

4 is consequent

15 : x → x = 20

Question 3. The ratio of the quantities is 5: 7. If the consequent of its inverse ratio is 5, the antecedent Is

5
$\sqrt{5}$
7
None of these

Answer: 3. 7

Ratio 5: 7

7 is antecedent

5 consequence

Question 4. The ratio compounded of 2: 3, 9: 4, 5, 6 and 8 10 is

1: 1
1: 5
3 8
None of these

Answer: 1. 1: 1

⇒ $C R \rightarrow \frac{2 \times 4 \times 5 \times 8}{3 \times 4 \times 6 \times 10}=\frac{720}{720}=\frac{1}{1}=1 : 1$

Question 5. The duplicate ratio of 3: 4 is

$\sqrt{3}: 2$
4:3
9: 16
None of these

Answer: 3. 9:16

Duplicate Ratio of 3 : 4 = 32 : 42 = 9 : 16

Question 6. The sub-duplicate ratio of 25: 36 is

6: 5
36 25
50: 72
5: 6

Answer: 5: 6

Sub duplicate $\rightarrow \sqrt{25}: \sqrt{36}=5: 6$

Question 7. The triplicate ratio of 2 : 3 is

8: 27
6: 9
3: 2
None of these

Answer: 1. 8: 27

Triplicate a : b a³: b³ = 2³ : 3³ = 8:27

Question 8. The sub-triplicate ratio of 8: 27 is

27: 8
24: 81
2 : 3
None of these

Answer: 3. 2 : 3

Sub triplicate: $\sqrt[3]{a}: \sqrt[3]{b}=\sqrt[3]{8}: \sqrt[3]{27}=2: 3$

Question 9. The ratio compounded of4: 9 and the duplicate ratio of 3: 4 is

1 4
1 : 3
3 1
None of these

Answer: 1. 1: 4

CR = 4:9 and a duplicate of 34

= 4: 9 and 9 16

⇒ $=\frac{4}{9} \times \frac{9}{16}=\frac{1}{4}=1: 4$

Question 10. The ratio compounded of 4: 9, the duplicate ratio of 3 4, the triplicate ratio of 2: 3 and 9 7 is

2: 7
7 2
2: 21
None of these

Answer: 3. 2: 21

CR = 4: 9 and duplicate of 3: 4 and triplicate of 2 : 3 and 9 7

⇒ $\frac{4}{9} \times \frac{9}{16} \times \frac{8}{21} \times \frac{9}{7}=\frac{2}{21}$

Question 11. The fete compounded of the duplicate ratio of 4 5, triplicate ratio of 1: 3, sub duplicate ratio of81 256, and sub-triplicate ratio of125 512 is

4: 512
3 32
1 12
None of these

Answer: 4. None of these

⇒ $\mathrm{CR}=\frac{16}{25} \times \frac{1}{27} \times \frac{9}{16} \times \frac{5}{8} \rightarrow \frac{1}{120}=1: 120$

Question 12. If a : b = 3 : 4, the value of (2a+3b) : (3a+4b) is

54: 25
8: 25
17: 24
18: 25

Answer: 4. 18: 25

a : b = 3 : 4 → a = 3x, b = 4x

⇒ $\frac{2 a+3 b}{3 a+4 b}=\frac{6 x+12 x}{9 x+16 x}=\frac{18 x}{25 x}=18: 25$

Question 13. Two numbers are in the ratio 2 : 3. If 4 is subtracted from each, they are in the ratio 3:5. The numbers are

(16,24)
(4,6)
(2,30
None of these

Answer: 1. 16, 24

a : b = 2 : 3 → a = 2x, b = 3x

⇒ $\frac{2 x-4}{3 x-4}=\frac{3}{5}$

10x- 20 = 9x- 12

X = 8

a = 16, b = 24

Question 14. The angles of a triangle are in ratio 2:7:11. The angles are

(20°, 70°,90°)
(30°, 70°, 80°)
(18°, 63°, 99°)
None of these

Answer: 3. 18°, 63°, 99°

L in ratios 2:7:11

2x, 7x,1lx

2x + 7x + 11x = 180°

20x = 180 = x = 9

L→ 18, 63,99

Question 15. The division of 324 between X and Y is in the ratio 11: 7. X and Y would get Rupees

(204, 120)
(200, 124)
(180, 144)
None of these

Answer: 4. none of these

$324 x and y in ratio 11: 7

1x + 7x= 324

18x = 324

X= 18

X gets 11 (18) = 198 y gets 7(18) = 126

Question 16. Anand earns t 80 in 7 hours and Pramod in 12 hours. The ratio of their earnings is

32: 21
23: 12
8: 9
None of these

Answer: 1. (a) 32: 21

→ Anand earns in 7 hrs

⇒ $\text {i. e.} ₹ \frac{80}{7}$ in 1 hrs.

Pramodearns in 12 hrs

⇒ $\text {i. e. } ₹ \frac{90}{12}$in 1 hrs.

⇒ $\text { Ratio }=\frac{80}{7} \times \frac{12}{90}=\frac{96}{63}=\frac{32}{21}=32: 21$

Question 17. The ratio of the two numbers is 7: 10 and their difference is 105. The numbers are

(200,305)
(185,290)
(245,350)
None of these

Answer: 3. (245, 350)

Ratio → 7:10 difference = 105

7x – 10 x

10x- 7x = 105

3x = 105 → x= 35 ->245,350

Question 18. P, Q, and R are three cities. The ratio of average temperature between P and Q is 11 12 and that between P and R is 9: 8. The ratio between the average temperature of Q and R is

22: 27
27: 22
32: 33
None of these

Answer: 3. 32: 33

Avg temperature ratio between

P and Q = 11 : 12

P and R = 9 : 8

⇒ $\frac{P}{Q}=\frac{11}{12} \quad \frac{P}{R}=\frac{9}{8}$

⇒ $ \frac{P}{Q}=\frac{11}{12} \quad \frac{P}{R}=\frac{9}{8}$

⇒ $\frac{P}{Q} \times \frac{R}{P}=\frac{11}{12} \times \frac{9}{0}=\frac{R}{Q}=\frac{99}{96}$

Avg temp ratio between Q & R is

⇒ $\frac{Q}{R}=\frac{96}{99}=\frac{32}{33} \quad=32: 33$

Question 19. If x: y = 3 : 4, the value of x² y + xy² : x³ + y³ is

13: 12
12: 13
21: 31
None of these

Answer: 3. 12: 13

X : y = 3 : 4→ x = 3z

X²y + xy²: x³ + y³

= (3z)². 4z + 3z . (4z)² : (3z)³ + (4z)³

= 9z². 4z + 3z. 16z²: 27z³+ 64z³ + 84z³ : 91z³

= 84:91 = 12:13

= 84 : 91 = 12 : 13

Question 20. If p: q is the sub-duplicate ratio of p-x² q-x² then x2 is

$\frac{p}{p+q}$
$\frac{q}{p+q}$
$\frac{pq}{p+q}$
None of these

Answer: 3. $\frac{p q}{p+q}$

→ sub duplicate of = – x² = 9 – x²

⇒ $\frac{\sqrt{p-x^2}}{q-x^2}=\frac{p}{q}$

⇒ $\frac{p-x^2}{q-x^2}=\frac{p^2}{q^2}$

⇒ $q^2\left(p-x^2\right)=p^2\left(q-x^2\right)$

q²p-q² x²= p²q – p²x²

p² x² – q² x² = p²q – q²p

⇒ $x^2=\frac{p^2 q-q^2 p}{p^2-q^2}$

⇒ $=\frac{p q(p-q)}{(p-q)(p+q)}=\frac{p q}{p+q}$

Question 21. If 2s: 3t is the duplicate ratio of 2s – p : 3t – p then

p2 = 6st
p = 6st
2p = 3st
None of these

Answer: 2. p = 6st

⇒ $\frac{(2 s-p)^2}{(3 t-p)^2}=\frac{(2 s)}{(3 t)}$

⇒ $\frac{4 s^2-4 s p+p^2}{9 t^2-6 t p+p^2}=\frac{2 s}{3 t}$

12s² – 12spt + 3p2t = 18st² – 12stp + 2sp²

12s²t – 18st² = p²(2x – 3t) = p² = 6st

Question 22. If p : q = 2 : 3 and x : y = 4 : 5, then the value of 5px + 3qy : lOpx + 4qy is

71: 82
27: 28
17: 28
None of these

Answer: 3. 17: 28

5px + 3qy : 10px + 4qy

40rz + 45rz: 80rz + 60rz

85rz : 140rz

85: 140

17:28 = 17:28

Question 23. The number which when subtracted from each of the terms of the ratio 19:31 reducing it to 1: 4 is

15
5
1
None of these

Answer: 1. 15

Let,x be $\frac{19-x}{31-x}=\frac{1}{4}$

76- 4x. 31 – x

3x = 45

→ x= 15

Question 24. The daily earnings of two persons are in the ratio of 4:5 and their daily expenses are in the ratio of 7 9. If each saves1 50 per day, their daily earnings in 1 are

(40, 50)
(50, 40)
(400, 500)
None of these

Answer: (400.500)

Earning = 4:5

Expenses 7:9

4x, 5x

Savings = 50 each = 1:1

4x – 7y = 50 5x-9y = 50

20x- 35y = 250 (1) 20x – 36y

=200 (2)

Subtracts (2) from (1)

20x – 35y = 250

20x-36y= 200

Y = 50 x= 100

Daily earning = 4x, 5x

= 400,500

Question 25. The ratio between the speeds of two trains is 7: 8. If the second train runs 400 km. in 5 hours, the speed of the first train is

10 Km/hr
50 Km/hr
70 Km/hr
None of these

Answer: 70 km/hr

Ratio between speeds = 7:8

S1 = 7x S2 = 5x

The second train covers 400 km t = 5 hrs

We know

⇒ $\mathrm{S}_2=\frac{d}{t}=\mathrm{S}_2=\frac{400}{5}=80 \mathrm{~km} / \mathrm{hrs}$

S2 = 8x = 80 km/hrs = x = 10

S1 = 7x = 70km/hrs

Ratio And Proportion Chapter 1 CA Foundation Answers

CA Foundation Maths Solutions For Chapter 1 Proportion Exercise – 2

Question 1. The fourth proportional to 4, 6, and 8 is

12
32
48
None of these

Answer: 1. 12

4,6,8.x

4 : 6 = 8: x

x= 12

Question 2. The third proportional to 12, 18 is

24
27
36
None of these

Answer: 2. 27

12,18,x

12 : 18 = 18 : x

X= 27

Question 3. The mean proportion between 25, and 81 is

40
50
45
None of these

Answer: 3. 45

25,x,81

⇒ $\frac{25}{x}=\frac{x}{81}=$ x2 = 2025 ⇒ x=45

Question 4. The number which has the same ratio to 26 that 6 has to 13 is

11
10
21
None of these

Answer: 4. None of these

⇒ $\frac{6}{13}=\frac{x}{26}=x=12 \text {. }$

Question 5. The fourth proportional to 2a, a², c is

ac/2
ac
2/ac
None of these

Answer: 2. ac/2

2a, a²,c, x

⇒ $\frac{2 a}{a^2}=\frac{c}{x}$

⇒ $\frac{2}{a}=\frac{c}{x}=2 x=a c$

⇒ $\mathrm{X}=\frac{ac}{2}$

Question 6.If four numbers 1/2, 1/3, 1 /5, 1/x are proportional then x is

6/5
5/6
15/2
None of these

Answer: 3. 15/2

⇒ $\frac{1}{2}: \frac{1}{3}=\frac{1}{5}: \frac{1}{x}$

3:2 = x:5

⇒ $X=\frac{15}{2}$

Question 7. The mean proportion between 12x² and 27y² is

18xy
81xy
8xy
None of these

Answer: 1. 18xy

12x² a, 27²2

⇒ $\frac{12 x^2}{a}=\frac{a}{27 y^2}$

a²= 324x²y²

a = 18xy

Question 8. If A = B/2 = C/5, then A: B: C is

3: 5: 2
2: 5 : 3
1: 2: 5
None of these

Answer: 3. 1 : 2: 5.

A: B: C

⇒ $\frac{A}{1}=\frac{B}{2}=\frac{C}{5}=1: 2: 5$

⇒ $\text { Tricks: } \frac{x}{a}=\frac{y}{b}=\frac{z}{a} \text { is given }$

x,y,z are in ratio

a: b: c

Question 9. If a/3 = b/4 = c/7, then a + b + c/c is

1
3
2
None of these

Answer: 3. 2

⇒ $\frac{a+b+c}{c}$

⇒ $\frac{a}{c}+\frac{b}{c}+1$

a:b:c = 3:4:7

a = 3x, b = 4x, c = 7x

⇒ $\frac{3 x}{7 x}+\frac{4 x}{7 x}+1=\frac{7 x}{7 x}+1=2$

Question 10. If p/q = r/s = 2.5/1.5, the value of Ps: QR is

3/5
1:1
5/3
None of these

Answer: 2. 1:1

⇒ $\frac{P}{q}=\frac{2.5}{1.5} \rightarrow p=2.5 x, q=1.5 x$

⇒ $\frac{r}{s}=\frac{2.5}{1.5} \rightarrow x=2.5 y, s=1.5 y$

⇒ $\frac{p s}{q r}=\frac{3.75 x y}{3.75 y x}=\frac{1}{1}=1: 1$

Question 11. If x : y = z : w = 2.5 : 1.5, the value of (x + z)/(w+ w) is

1
3/5
5/3
None of these

Answer: 2. 3/5

= x = 2.5x y = 1.5x z = 2.5p, w = 1.5p

⇒ $\frac{x+z}{y+w}=\frac{2.5(r+p)}{1.5(r+p)}=\frac{2.5}{1.5}=\frac{5}{3}$

Question 12. If (5x – 3y)/(5y – 3x) = 3/4, the value of x : y is

2: 9
7: 2
7: 9
None of these

Answer: 4. none of these

4(5x-3y) = 3(5y- 3x)

20x – 12y = 15y- 9x

29x= 27y

⇒ $\frac{x}{y}=\frac{27}{29}$

Question 13. If A : B = 3: 2 and B: C = 3:5 then A:B:c is

9:6:10
6:9:10
10:9:6
None of these

Answer: 9: 6: 10.

A : B: C =?

A:B = 3:2 = 9:6

B:C = B:S=6:10

A : B : C = 9 : 6 : 10

Question 14. If x/2 = y/3 = z/7, then the value of (2x – 5y + 4z)/2y is

6/23
23/6
3/2
17/6

Answer: 4. 17/6

x:y:z= 2:3:7 x = 2x, y=3x, z=7x

⇒ $\frac{2 x-5 y+4 z}{2 y}=\frac{4 x-15 x+28 x}{6 x}$

⇒ $=\frac{17 x}{6 x}=\frac{17}{6}$

Question 15. If x : y = 2 : 3,y: z = 4 : 3 then x:y : z is

2 : 3: 4
4 : 3: 2
3: 2: 4
None of these

Answer: 4. None of these

x:y = 2:3 = 8:12

y:z = 4:3 = 12:9

x:y:z=8: 12:9 =8:12:9

Question 16. Division of into 3 parts in the ratio 4: 5: 6 is

(200,250,300)
(250, 250, 250)
(350, 250,150)
(8 12 9)

Answer: 1. 200, 250, 300.

4x + 5x + 6x= 750

15x = 750

x = 50

→ 750 will be divided as 200,250,300

Question 17. The sum of the ages of 3 persons is 150 years. 10 years ago their ages were in the ratio of 7:8:9. Their present ages are

(45, 50, 55)
(40, 60. 50)
(35,45, 70)
None of these

Answer: 1. 45,50,55

7x, 8x, 9x

Present age

7x + 10, 8x+ 10 + 9x + 10 = 150

24x= 120

x = 5

Present age = 45,50,55

Question 18. The numbers 14, 16, 35, and $2 ‘are not in proportion. The fourth term for which they will be in proportion is

45
40
18
None of these

Answer: 3. 40

14,16,35,x

⇒ $\frac{14}{16}=\frac{35}{x}$

⇒ $\frac{7}{8}=\frac{35}{x} \rightarrow x=40$

Question 19. If x/y = z/w, implies y/x = w/z, then the process is called /

Dividend
Componendo
Alternendo
None of these

Answer: 4. None of these. This is inverted

Question 20. Ifp/q = r/s = p-r/q-s, the process is called

Subtrahendo
Addendum
InVert£hdo
None of these

Answer: 1. subtrabendo

Question 21. If a/b = c/d, implies (a + b)/(a – b) = (c + d)/(c- d), the process is called

Componendo
Dividendo
Componendo and Dividendo
None of these

Answer: 3. Componendo & dividendo

Question 22. Ifu/v = w/p, then (u – v)/(u + v) = (w – p)/(w + p). The process is cached

Invertendo
Alternendo
Addendum
None of these

Answer: 4. None of these

Question 23. 12, 16, * 20 are in proportion. Then * is

25
14
15
None of these

Answer: 3. 15

⇒ $\frac{12}{16}=\frac{x}{20}$

⇒ $\frac{3}{4}=\frac{x}{20} \rightarrow x=15$

Question 24. 4, 9, 13V2 are in proportion. Then is

6
8
9
None of these

Answer: 1. 6

⇒ $\begin{aligned}
& \frac{4}{x}=\frac{9}{13.5}=\frac{36}{9 x}=\frac{9}{13.5} \\
& x \rightarrow 6
\end{aligned}$

Question 25. The mean proportional between 1.4 gms and 5.6 gms is

28 gms
2.8 gms
3.2 gms
None of these

Answer: 2. 2.8gms

x2 =1.4 x 5.6 = 7.84 = x2.8 gms

Question 26. $\frac{a}{4}=\frac{b}{5}=\frac{c}{9} \text { then } \frac{a+b+c}{c} \text { is }$

4
2
7
None of these.

Answer: 2. 2

a : b: c = 4 : 5 : 9

a = 4x

b = 5x

c = 9x

⇒ $\frac{a+b+c}{c}=\frac{18 x}{9 x}=\frac{2}{1}=2 $

Question 27. Two numbers are in the ratio 3: 4; if 6 is added to each term of the ratio, then the new ratio will be 4 5, then the numbers are

14, 20
17, 19
18 and 24
None of these

Answer: 3. 18 and 24

⇒ $\frac{a+6}{b+6}=\frac{4}{5}$

5a + 30 = 4b + 24

5a -4b = -6

15x- 16x = -6

-x = -6

x = 6

a = 18 b=24

Question 28. $\frac{a}{4}=\frac{b}{5} \text { then }$

$\frac{a+4}{a-4}=\frac{b-5}{b+5}$
$\frac{a+4}{a-4}=\frac{b+5}{b-5}$
$\frac{a-4}{a+4}=\frac{b+5}{b-5}$
None of these

Answer: 3. Applying componendo And dividendo

⇒ $\frac{a+4}{a-4}=\frac{b+5}{b-5}$

Question 29. If a : b = 4 : 1 then $\sqrt\frac{a}{b}+\sqrt{\frac{b}{a}} \text { is }$

5/2
4
5
None of these

Answer: 1. 5/2

$\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}=
\sqrt{\frac{4 x}{x}}+\sqrt{\frac{x}{4 x}}
=2+\frac{1}{2}=\frac{5}{2}$

Question 30. If $\frac{x}{b+c-a}=\frac{y}{c+a-b}=\frac{z}{a+b-c} \text { then }$ (b- c)x + (c – a)y + (a – b)z is

1
0
5
None of these

Answer: 2. 0

⇒ $\frac{(b-c) x}{(b-c)(b+c-a)}=\frac{(c-a) y}{(c-a)(c+a-b)}=\frac{(a-b) z}{(a-b)(a+b-c)}$

(b-c)x : (c-a)y: (a-b)z

= (b-c) (b+c-a) : (c-a) (c+a-b) : (a-b)(a+b-c)

= (b-c)x + (c-a)y + (a-b)z

= b² + be- ab -bc – c² + ac- ac + c² + ac – cb – a² + ab + a² + ab – ac- ab – b² + bx

= 0

CA Foundation Maths Chapter 1 Detailed Solutions

CA Foundation Maths Solutions For Chapter 1 Ratio And Proportion Exercise – 3

Question 1. If A : B : C = 2: 3 : 4, then $\frac{A}{B}: \frac{B}{C}: \frac{C}{A}$is equal to :

4: 9: 16
8: 9: 12
8: 9: 16
8: 9: 24

Solution:

Let = 2x, It = 3x and C 4x. Then $\frac{A}{n}=\frac{2 x}{3 x}=\frac{2}{i^{\prime}} \cdot \frac{n}{C}=\frac{3 x}{4 x}=\frac{3}{4} \text { and } \frac{C}{A}=\frac{4}{2 x}=\frac{2}{1}$

⇒ $\Rightarrow \frac{A}{B}: \frac{B}{c}: \frac{c}{A}=\frac{2}{3}: \frac{3}{1}: \frac{2}{1}=8: 9: 24 .$

Question 2. A : B = 2 : 3 , B : C = 4 : 5 and C : D = 6 : 7,then A:B:C:D is

16:22:30:35
16:24:15:35
16:22:30:35
18:24:30:35

Solution:

A: B = 2 : 3. B : C = 4 : 5 =$\left(4 \times \frac{3}{4}\right):\left(5 \times \frac{3}{4}\right)=3: \frac{15}{4}$

And C:D 6:7 =$=\left(6 \times \frac{15}{24}\right):\left(7 \times \frac{15}{24}\right)=\frac{15}{4}: \frac{35}{8}$

A : B : C: D = 2: 3 :$\frac{15}{4}: \frac{35}{8}=16: 24: 30: 35 \text {. }$

Question 3. If 0.75 : x: : 5 : 8, then x is equal of x is :

22: 29
11.20
1.25
1.30

Solution:

(x X 5) = (0.75 x 8)

⇒ $x=\frac{4.8}{4}=1.20$

Question 4. If x: y = 5 : 2, then (8x + 9y) : (8x + 2y) is :

22: 29
6: 61
9: 22
61: 26

Solution:

Let x = 5k and y = 2k. Then $\frac{8 x+9 y}{8 x+2 y}=\frac{(8 \times 5 k)+(9 \times 2 k)}{(8 \times 5 k)+(2 \times 2 k)}=\frac{58 k}{44 k}=\frac{29}{22}$

(8x + 9y) : (8x + 2y) = 29 : 22

Question 5. The salaries of A, B, and C are in the ratio 2 : 3: 5. If the increments of 15%, 10%, and 20% are allowed respectively in their salaries, then what will be the new ratio of their salaries?

3 : 3: 10
10 : 11: 20
23: 33: 60
Cannot be determined

Solution:

Let A = 2k, B = 3k and C = 5k.

A’s new salary =$\left.=\frac{115}{100} \text { of } 2 \mathrm{k}=\left(\frac{115}{100} \times 2 k\right)\right)=\frac{23}{10} \mathrm{k}$

B’s new salary = $\left.=\frac{110}{100} \text { of } 3 k=\left(\frac{110}{100} \times 3 k\right)\right)=\frac{33}{10} k$

Question 6. If Rs. 782 is divided into three parts, proportional to then the first part is:

Rs. 182
Rs. 190
Rs. 196
Rs. 204

Solution:

Given ratio = $\frac{1}{2}: \frac{2}{3}: \frac{3}{4}=6: 8: 9$

⇒ $1^{\text {st }} \text { part }=\operatorname{Rs}\left(782 \times \frac{6}{23}\right)=\operatorname{Rs} .204 .$

Question 7. Two numbers are in the ratio 3: 5. If 9 is subtracted from each, the new number is in the ratio 12: 23. The small number is :

Solution:

Let the number be 3x and 5x. Then $\text { Then, } \frac{3 x-9}{5 x-9}=\frac{12}{23} \Leftrightarrow 23(3 x-9)=12(5 x-9) \Leftrightarrow 9 x=99 x=11 \text {. }$

The smaller number = (3 x 11) = 33

Question 8. Two numbers are in the ratio 1: 2. If 7 is added to both, their ratio changes to 3: 5. The greatest number is :

Solution:

Then $\frac{x+7}{2 x+7}=\frac{3}{5} \rightarrow 5 x+35=6 x+21 \rightarrow x=14$

Greatest number = 2x = 28

Question 9. In a bag, there are coins of 25, p, 10 p, and 5 p in the ratio of 1: 2 : 3. If there are Rs. 30 in all, how many 5 p coins are there?

Solution:

Let the number of 25 p, 10 p, and 5 p coins be x, 2x, and 3x respectively.

Then, sum of their values = $\operatorname{Rs.}\left(\frac{25 x}{100}+\frac{10 \times 2 x}{100}+\frac{5 \times 3 x}{100}\right)=\operatorname{Rs} \cdot \frac{60 x}{100}$

⇒ $\frac{60 . x}{100}=30 \Leftrightarrow \mathrm{x}=\frac{30 \times 100}{60}=50 .$

Hence, the number of 5 p coins = (3 x 50) = 150

Question 10. Salaries the new ratio of Ravibecomesand Sumit40:are57. in What the isratioSumit’s2 : 3. present the salary salary? of each is increased by Rs. 4000,

Rs. 17,000
Rs. 20,000
Rs. 25,500
None of these

Solution:

Let the original salaries of Ravi and Sumit be Rs. 2x and Rs. 3x respectively.

Then $\text { 1. } \frac{2 x+4000}{3 x+4000}=\frac{40}{57} \Leftrightarrow 57(2 x+4000)=40(3 x+4000) \Leftrightarrow 6 x=68000 \Leftrightarrow 3 x=34000$

Sumit’s present salary = (3x + 4000) = Rs. (34000 + 4000) = Rs. 38,000.

Question 11. If Rs. 510 is divided among A, B, and C in such a way that A gets what B gets and B gets what C gets, then their shares are respectively:

Rs. 120, Rs. 240, Rs. 150
Rs. 60, Rs. 90, Rs. 360
Rs. 150, Rs. 300, Rs. 60
None of these

Solution:

⇒ $\left(A=\frac{2}{3} B \text { and } B=\frac{1}{4} C\right) \Leftrightarrow \quad \frac{A}{B}=\frac{2}{3} \text { and } \frac{B}{C}=\frac{1}{4}$

A : B = 2 : 3 and B:C=1:4 = 3:12=>A:B:C = 2:3:12.

⇒ $\text { A’s share }=\text { Rs. }\left(510 \times \frac{2}{17}\right)=\text { Rs. } 60 \text {; B’s share }=\text { Rs. }\left(510 \times \frac{3}{17}\right)=\text { Rs. } 90 \text {; }$

⇒ $\text { C’s share }=\text { Rs. }\left(510 \times \frac{12}{17}\right)=\text { Rs. } 360 \text {. }$

Question 12. The sum of the three numbers is 98. If the ratio of the first to the second is 2 : 3 and that of the second to the third is 5: 8, then the second number is:

Solution:

Let the three parts be A, B, and C Then,

A : B : 2 : 3 and B : C = 5 : 8 $\left(5 \times \frac{1}{5}\right):\left(8 \times \frac{1}{5}\right)=3: \frac{14}{5}$

A : B : C = 2 : 3 :$\frac{24}{5}=10: 15: 24 \Rightarrow B=\left(98 \times \frac{15}{19}\right)=30 .$

Question 13. A fraction which bears the same ratio to $\frac{1}{27} \text { that } \frac{3}{11}$ does to $\frac{5}{9}$ is equal to.

$\frac{1}{55}$
$\frac{1}{11}$
$\frac{3}{11}$
55

Solution:

Let $ x: \frac{1}{27}:: \frac{1}{11}: \frac{5}{9}$

Then $x \times \frac{5}{9}=\frac{1}{27} \times \frac{3}{11} \Leftrightarrow x=\left(\frac{1}{27} \times \frac{3}{11} \times \frac{9}{5}\right)=\frac{1}{55} .$

Question 14. A sum of Rs. 1300 is divided amongst P, Q, R and S such that Then, $\frac{p^{\prime} \text { share }}{Q^{\prime} s \text { share }}=\frac{p^{\prime} \text { share }}{\text { Rsshare }}=\frac{R^{\prime} \text { share }}{S^{\prime} \text { share }}=\frac{2}{3} \text {. }$ P’s share is :

Rs. 140
Rs. 160
Rs. 240
Rs. 320

Solution:

Let P = 2x and Q = 3x. Then $\frac{19}{1}=\frac{2}{3} \Rightarrow R=\frac{3}{2}Q=\left(\frac{3}{2} \times 3 x\right)=\frac{1 x}{2} .$

⇒ $Also, \frac{R}{S}=\frac{2}{3} \Rightarrow S=\frac{3}{2} R=\left(\frac{3}{2} \times \frac{9 x}{2}\right)=\frac{27 x}{1}$

Thus, $\mathrm{P}=2 \mathrm{x}, \mathrm{Q}=3 \mathrm{x}, \mathrm{R}=\frac{9 \mathrm{x}}{2}$ and $\mathrm{S}=\frac{27 \mathrm{x}}{4}$.

⇒ P+(Q+R+S= & 1300 $\Leftrightarrow\left(2 x+3 x+\frac{9 x}{2}+\frac{27 x}{3}\right)=1300 $

⇒ $\Leftrightarrow(8 x+12 x+18 x+27 x)=5200$

⇒ $\Leftrightarrow 65 x=5200 \Leftrightarrow x=\frac{5200}{65}=80 $

P’s share = Rs. (2 * 80) = Rs, 1 60

Question 15. A and B together have Rs. 1210. If $\frac{4}{15}$ of A’s amount is equal to $\frac{2}{5}$ of B’s amount, how much amount does B have?

Rs. 460
484
Rs. 550
664

Solution:

⇒ $\frac{1}{15} A=\frac{2}{5} B=A=\left(\frac{2}{5} \times \frac{15}{4}\right) B \Leftrightarrow A=\frac{3}{2} B \Leftrightarrow \frac{A}{B}=\frac{3}{2} \Leftrightarrow A: B=3: 2$

⇒ $\text { B’s share }=\text { Rs. }\left(1210 \times \frac{2}{4}\right)=\text { Rs. } 484 .$

Question 16. Two numbers are respectively 20% and 50% more than a third number The ratio of the two numbers is:

2: 5

3: 5

4: 5

6: 7

Solution:

Let the third number be x.

Then, first number = 120% of x $=\frac{120 x}{100}=\frac{6 x}{5} ;$

Second number = $150 \% \text { of } \mathrm{x}=\frac{150 x}{100}=\frac{3 x}{2} \text {. }$

Ratio of first two numbers$=\frac{6 x}{5}: \frac{3 x}{2}=12 x: 15 x=4: 5 .$

Question 17. Seats for Mathematics, Physics, and Biology in a school are in the ratio 5:7:8. There is a proposal to increase these seats by 40%, 50%, and 75% respectively. What will be the ratio of increased seats?

2 : 3: 4
6: 7: 8
6: 8: 9
None of these

Solution:

Originally, let the number of seats for Mathematics, Physics, and Biolog}’ be 5x, 7x, and 8x respectively.

Number ofincreased seats are (140% of5x), (50%. of 7x) and (175% of8x) $\left(\frac{140}{100} \times 5 x\right),\left(\frac{150}{100} \times 7 x\right) \text { and }\left(\frac{175}{100} \times 8 x\right) \text { i.e. } 7 \times \text {, } \frac{21 x}{2} \text { and } 14 \times \text {. }$

⇒ Required ratio = $7 \mathrm{x}: \frac{21 x}{2}: 14 \mathrm{x}=21 \mathrm{x}: 21 \mathrm{x}: 28 \mathrm{x}=2: 3: 4$

Question 18. The ratio of the number of boys and girls in a college is 7: 8. If the percentage increase in the number of boys and girls is 20% and 10% respectively, what will be the new ratio?

8: 9
17:18
21: 22
Cannot be determined

Solution:

Originally, numberless the of boys and girls in the college was 7x and 8x respectively. Their increased is number(120%of7x) and (110%8x)

⇒ $\left(\frac{120}{100} \times 7 x\right) \text { and }\left(\frac{110}{100} \times 8 x\right) \text { i.e. } \frac{42 x}{5} \text { and } \frac{44 x}{5} \text {. }$

Required ratio = $=\frac{42 x}{5}: \frac{44 x}{5}=21: 22 .$

Question 19. A sum of money is to be distributed among A, B, C, and D in the proportion of 5: 2: 4 : 3. If C gets Rs. 1000 more than D, what is B’s share?

Rs. 500
Rs. 1500
Rs. 2000
None of these

Solution:

Let the shares of A, B, C and D be Rs. 5x, Rs. 2x, Rs. 4x and Rs. 3x respectively.

Then, 4x – 3x = 1000 ⇔ x = 1000.

B’s share = Rs. 2x = Rs. (2 * 1000] = Rs. 2000

Question 20. If 40% of a number is equal to two-thirds of another number, what is the ratio of the first number to the second number?

2: 5
3: 7
5 : 3
7 : 3

Solution:

Let 40% of A =$\frac{2}{3} B \text {. Then, } \frac{40 A}{100}=\frac{2 B}{3} \Leftrightarrow \frac{2 A}{5}=\frac{2 B}{3} \Leftrightarrow \frac{A}{B}=\left(\frac{2}{3} \times \frac{5}{2}\right)=\frac{5}{3}$

A: B = 5 : 3.

Question 21. The ratio of the earnings of A and B is 4: 7. If the earnings of A increase by 50% and those of B decrease by 25%, the new ratio of their earnings becomes 8: 7. What are A’s earnings?

Rs. 21,000
Rs. 26,000
Rs. 28,000
Data inadequate

Solution:

Let the original earnings of A and B be Rs. 4x and Rs. 7x.

Net earnings of A = 150% or Rs. 4x = Rs$\left(\frac{150}{100} \times 4 x\right)=\mathrm{Rs.} .6 \mathrm{x}$

Net earnings of B = 75% of Rs. 7x = Rs.$\left(\frac{75}{100} \times 7 x\right)=\operatorname{Rs} . \frac{21 x}{4} .$

⇒ $6 x: \frac{21 x}{4}=8: 7 \Leftrightarrow \frac{6 x \times 4}{21 x}=\frac{8}{7} .$

This does not give x. So, the given data is inadequate.

Question 22. The fourth proportional to 5, 8, 15, is:

Solution:

Let the fourth proportional to 5, 8, 15 be x.

Then, 5 : 8 : : 15 : x <=> 5x = (8 x 15) <=> $x=\frac{(8 \times 15)}{5}=24$

Question 23. x varies inversely as the square of y. Given that y = 2 for x = 1. The value of x for y = 6 will be equal to :

3
9
$\frac{1}{3}$
$\frac{1}{9}$

Solution:

Given x = $\frac{k}{y^2}$ . where 1< is a constant.

Now, y = 2 and x = 1 gives 1< = 4, $x \frac{4}{y^2} \Rightarrow x=\frac{4}{6^2} \text {, when } y=6 \Rightarrow x=\frac{4}{36}=\frac{1}{9} \text {. }$

Question 24. If 10% of x = 20% off, then x : y is equal to :

1:2
2: 1
5: 1
10: 1

Solution:

10%ofx = 20% of y a $\Leftrightarrow \frac{10 x}{100}=\frac{20 y}{100} \Leftrightarrow \frac{x}{10}=\frac{y}{5} \Leftrightarrow \frac{x}{y}=\frac{10}{5}=\frac{2}{1} . \mathrm{x} ; \mathrm{y}=2: 1 .$

Question 25. What number should be added to each term in the ratio 19:43, so that it becomes equal to 2:3?

Solution:

Let x be the number to be added.

(19+x) : (43+x)=2:3 57+3x=86+2x x=29

29 must be added to each term in the ratio 19:43 so that it becomes equal to 2:3.

Question 26. A construction company is planning to invest in road and railway line construction in the ratio4:5. If the amount invested in the railway line construction is 6 million, then how much money did the company invest in the road construction?

14 million
10.8 million
4.8 million
2.6 million
7.5 million

Solution:

let the company’s investment in the road construction be x.

4:5=x:6 or4/5=x/6

x=(6x 4)/5 =4.8

The company invested Rs.4.8 million in road construction. Hence, option c

Question 27. If the incomes of A and B are in the ratio 3;4 and their expenditures are in the ratio 2:3, then find the ratio of their savings.

1:1
1:9
1:2
cannot be determined

Solution:

Let the incomes of A and B be 3x and 4x respectively. Let their expenditures be 2y and 3y respectively.

Savings = Income – Expenditure

A’s savings/B’s savings=(3x-2y)/4x-3y) the values of x and y are not known.

Hence, the ratio of savings cannot be determined. Hence, option d

Question 28. The total money collected for New Year celebrations in a certain building was Rs.20,500. The ratio of the amount contributed by the people of the A-wing to that contributed by the people of the B wing was 8:5 also, the ratio of the amount contributed by the people of the B wing to that contributed by the people of the C wing was 2:3 find the amount contributed by the people of the wing.

Rs.5000
Rs.2000
Rs.2500
Rs.3000
Rs.500

Solution:

Since the amount collected by B wing is common to both the ratios; it is to be used to compare the collections of all 3 wings.

Hence, find the LCM of 5 and LCM of 5 and 2=10

The ratio of the amounts contributed by the people of all the three wings- 16:10:15

The amount contributed by each wing is 16x, lOx, and 15x respectively.
16x+10x+15x= 20500 x=500 i.e. 10x= 5000

Hence, the amount collected by B wing is Rs.5000. Hence, Option a

Question 29. 78 is divided into two parts such that the ratio between those two parts in 7:6 finds the product of those two parts.

1215
2808
l512
3276
1014

Solution:

Let one of the parts be x.

The other part is (78-x)

The ratio between the two parts is 7:6

⇒ $\frac{x}{(78-x)}=\frac{7}{6} 6 $

∴ 6x=546-7x

∴ 13x=546

x=42 and (78-x) = 36. Product of 42 and 36 = 1512 Hence, option c.

Question 30. During the elections for the post of building society chairman, the ratio of the number of members with Mr . Shah to that with Mr.Raheja was 6ÿ5 but 24 members from Mr. Shah’s side defected and joined Mr, Raheja. Now the ratio of members with Mr, Shah to that with Mr. Raheja is 2:3 find the number of members siding with Mr. Shah initially.

Solution:

Let the initial number of members with Mr. Shah be 6k and the number of members with Mr.

Raheja be sk. 24 members went over from Mr. Shah’s side to Mr. Itaheja’s side.

Heme, the number of members now supporting Mr. Shah is 6k-24 while the number of members with Mr. Raheja is 5k+24.

This ratio is now 2;3

(6k-24): (5k+24) =2:3

18k-72=10k + 48

8k= 1 20

k= 15

The number of members with Mr. Shah initially =6k=90. Hence, option a

Question 31. Vessel 1 contains 38 litres of milk and vessel 2 contains 24 litres of water. 8 liters of milk is taken from vessel 1 and placed in vessel 2. Then, 201 liters of the mixture is taken from vessel 2 and placed in vessel 1. Find the ratio of milk in vessel 1 to water in vessel 2.

4:9
15:35
15:4
35:9
35:3

Solution:

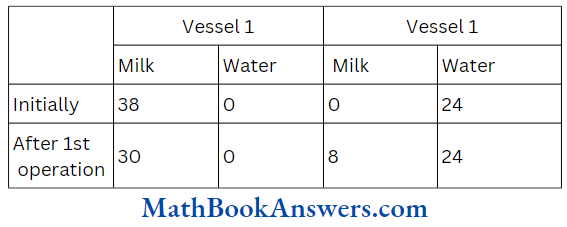
Business Mathematics Ratio And Proportion chapter 1

Now, the ratio of milk to water in vessel 2 is 8:24 = 1:3 and the ratio of milk to the total solution in vessel 2 is 8: 32 = 1:4

Of the 20 liters, 1/4″1 (i.e. 5 liters) is milk, and 3/4″‘ (i.e. 1 5 liters) is water.

After the 2lul iteration, amount of milk in vessel 1=30 +5=35 litres and amount of water in vessel 2= 24- 15 = 9 litres

The ratio of milk in vessel 1 to water in vessel 2 is 35:9. Hence, Option d

Question 32. Does Aakash have coins of 50 paise, 25 paise, and Rs.1.50 in the ratio 1:2:3 (Aakash(e) stays in a country where all are valid currency coins. Also, in his country. 1 rupee equals 100 paise) how many coins of 25 paise does Aakash have if he has got Rs. 6600 in all? 32.

2000
2200
2400
2600
2800

Solution:

The ratio of the number of coins is 1;2:3 for the 50 paise, 25 paise, and Rs. 1.50 coins respectively.

in terms of monetary value, the ratio becomes (1x 0.5):(2x 0.25): (3 x 1.5)which equals o.5:0.5:4.5, i.e., 1:1:9

∴ (1/11)th of the total value comes from 25 paise coins, (1/2)x6600= Rs.600 in the form of 25 paise coins.

The total no. of 25 paise coins is 600/0.25=2400. Hence, option c

Question 33. The annual income of Mr.X and Mr. Y is in the ratio of 9:8 and their expenditures are in the ratio of 5:4 if both individually manage to save Rs. 5000, then B’s expenditure is:

Rs.1,250
Rs.5,000
Rs.6,250
Rs.l1,250
Rs.10,000

Solution:

Let the annual income of Mr. Y be rs9x and 8x respectively.

Also, let their expenditures be Rs. 5y and Rs. 4y respectively.

Both individually save Rs. 5000

Income -Expenditure = savings for Mr. X

9x – 5y = 5000 —-(1)

8x-4y=5000 (2), x=1250

for Y,equations =(1)(2)andy=1250

B’s Mr.expenditure 4y = Rs.5000

Hence, option b

Question 34. If 5x-13y= 3x-8y, find the value of (2×2 + 3y2): [2×2 – 3y2)

50:12
62:39
25:4
31:19

Solution:

5x-13y=3x-8y

2x=5y

X:y=5:2

x²:y² = 25:4

2x²: 3y² =50:12

Using components and Dividendo law, Hence, option d

Question 35. A group of children went to play a game of marbles. Amar had 9 marbles, Akbar had 6 marbles and the youngest Anthony had none. So they decided to share their marbles equally among themselves. In return, Anthony offered to give them his 15 Pokemon cards. He gave the cards in the same proportion in which he received the marbles. How many cards did Akbar get from Anthony?

Solution:

total number of marbles =15

The marbles are distributed in a way that each of them has an equal number of marbles, each of them should have 5 marbles.

Anthony gets 4 marbles from Amar and 1 marble from Akbar, i.e. in the ratio of 4:1

The 15 cards are distributed proportionally

The number of cards Akbar gets = (1/5)x15=3

Hence, option d.

Question 36. Based on their performance in a test, Professor Shetty distributed Rs. 798 among Vinay and Vinit such that 6 times Vinod’s share is equal to 10 times Vinay’s share or 5 times Vinit’s share. How much does Vinod get?

Solution:

Let Vinod’s share be x.

6x= 10X (Vinay’s share)

Vinay’s share=3x/5

Similarly, visit’s share =6x/5

x+ (3x/5) +6x/5) =14x/5 = 798

x= (798/14)x5=57×5=285

Hence, option e,

Question 37. Find the fourth proportional to 3,5 and 27.

45
16.2
135
55

Solution:

Let x be the fourth proportional.

3/5 = 27/x

x = (27×5) /3=45

Hence, option a

Question 38. If $\frac{x-y}{x^2-y^2}=\frac{x^2-y^2}{k}$ , them K =?

(x-y)(x²-y²)
(XY) (x²– y²)
(x+y) (x²– y²)
(x²– y²) (x+y)

Solution:

From the given equation,$\mathrm{k}=\frac{\left(x^2-y^2\right)^2}{x-y} \text { now, }\left(x^2-y^2\right) \text { can be written as }(x+y)(x-y) \text { so we have } \mathrm{k}=\frac{(x+y)^2 \times(x-y)^2}{x-y}$

=(x + y² X (x- y)

= (x+y)(x+y)(x-y)

=[x+y] (x²– y²)

Question 39. The cost of manufacturing a circular cast from the plate is directly proportional to the square root of its diameter. A 24 cm (diameter) plate casts Rs. 346. How much more or less will it cost to many facture 2 plates with diameters 1 8 cm and 8cm?

Rs.143 more
Rs.l53.41 more
Rs.282.31 more
Rs.282.3l less
Rs.l82.3 less

Solution:

Cost is proportional to the square root of the diameter.

Cost=k

xÿ/diameter, Where k is a constant of proportionality

The cost of a plate with 24 cm diameter=k√24 =2k √6

Similarly, the cost of the plate with 18 cm diameter=k√l8 = 3k√2

And the cost of a plate with 8 cm diameter = k V8 = 2k√2

The cost of an 18 cm and 8cm plate = 31<√2 + 2/c√2 =Rs.5k√2

Let the cost of the 18 cm and 8cm plates put together be x.

⇒ $346: \mathrm{x}:: 2 \mathrm{k} \sqrt{6}: 5 \mathrm{k} \sqrt{2}\mathrm{x}=\frac{(346 \times 5 \sqrt{2})}{2 \sqrt{6}}=\frac{346 \times 5}{2 \sqrt{3}}=\frac{173 \times 5}{\sqrt{3}} \approx \frac{173 \times 5}{1.73} \approx 500$

The additional cost of making the plates « 500- 346 = RS. 1 54. Hence, option 2

Question 40. If $\frac{x}{y+z-x}=\frac{y}{z+x-y}=\frac{z}{x+y-z}=r$then r cannot take any value except.

1
$-\frac{1}{2}$
$1 \text { or } \frac{1}{2}$
$1 \text { or } \frac{-1}{2}$

Solution:

⇒ $\text { If } \frac{a}{b}=\frac{c}{d}=\frac{e}{f}=k \text {, }$

⇒ $\text { Then } \frac{a+c+e}{b+d+f}=k$

Using this property, add the numerators and denominators to get,$r=\frac{x+y+z}{x+y+z}=1$

Similarly, if we subtract the denominators and numerators of the first two ratios, you get$r^{\prime}=\frac{x-y}{(y+z-x)-(z+x-y)}=\frac{x-y}{2(y-x)}=\frac{-1}{2}$ r can take the values 1 and -1/2. Hence, option d

Question 41. A precious stone is accidentally broken into 2 pieces whose weights are in the ratio 4;5 the value of the stone is directly proportional to the square of its weight. What is the ratio of the total value of the original (unbroken) stone to the total value of the broken pieces?

41:81
81:41
40:81
81:40
None of these

Solution:

Let the weights of the two pieces be 4x and 5x.

Therefore, the weight of the original stone was 9x.

The value of the stone is directly proportional to the square of its weight.

The values of the original stone and the two pieces. Are proportional to 81×2,16×2 and 25×2.

Hence, the required ratio is 81 : ( 16+25) = 81:41.

Hence, option b

Question 42. Two numbers are in the ratio of 2: 3 and the difference of their squares is 320. The numbers are:

12, 18
16, 24
14,21
None

Solution:

Tricks: (1) ; (2) & (3) all are In ratio

2:3 Rut for option

182 – 122 # 320

242- 162 = (24 + 16) (24 – 16)

= 40 X 8 = 320

Question 43. If p : q is the sub-duplicate ratio ofp – x2: q – x-‘, then x’ is :

$\frac{p}{p+q}$
$\frac{q}{p+q}$
$\frac{q p}{p-q}$
None

Solution:

Detail Method:

⇒ $\frac{\sqrt{p-x^2}}{q-x^2}=\frac{p}{q}$

Squaring on both side; wc get

⇒ $\frac{p-x^2}{q-x^2}=\frac{p^2}{q^2}$

Or pq² – q² x²= p² q – p² x²

Or p2 x²– q² x² = p²q – pq²

Or x² (p² – q²) = Pq (P – q)

Or x2 (p + q) (p-q) = pq (p-q)

⇒ $\text { Or } x^2=\frac{p q}{p+q}$

(4) is correct

Question 44. An alloy is to contain copper and zinc in the ratio 9: 4. The zinc required to melt with 24kg of copper is:

$10 \frac{2}{3} \mathrm{~kg}.$
$10 \frac{1}{3} \mathrm{~kg}$
$9 \frac{2}{3} \mathrm{~kg}$
9 Kg

Solution:

Let Zinc = x kg

⇒ $\frac{9}{4}=\frac{24}{x} \mathrm{x}=\frac{4 \times 24}{9}=\frac{32}{3}$

⇒ $=10 \frac{2}{3} \mathrm{~kg}$

(1) is correct

Question 45. Two numbers are in the ratio 7:8. If 3 is added to each of them, their ratio becomes 8: 9. The numbers are

14, 16
24, 27
21, 24
16, 18

Solution:

Let x be common in the ratio

et x is common in the ratio

Number are 7x and 8x

⇒ $\frac{7 x+3}{8 x+3}=\frac{8}{9}$

Or 64x + 24 = 63x + 27

Or 64x – 63x = 27- 24

Or x = 3

1st number = 7x = 7×3 = 21

2nd number = 8x = 8 x 3 = 24

(3) is correct

Question 46. A box contains ₹56 in the form of coins of one rupee, 50 paise, and 25 pages. The number of 50 paise coins is double the number of 25 paise coins and four times the number of one rupee coins. The numbers of 50paise coins in the box are:

Solution:

Let No. of 50 Paise coins = x

No. of 1 coins =$\frac{x}{4}$

No. of 25 paise coins= $=\frac{x}{2}$

Total value = $\frac{x}{4} \times 1 \times \times 0.50+\frac{x}{2} \times 0.25=56 \quad \text { Or } 0.25 x+0.50 x+0.125 x$

⇒ $\text { Or } 0.875 x=56 \quad \text { Or } x=\frac{56}{0.875}=64$

(1) is correct

Question 47. Eight people are planning to share equally the cost of a rental car. If one person withdraws from the arrangement and the others share equally the entire cost of the car then the share of each of the remaining persons increases to:

$1 / 9$
$1 / 8$
$1 / 7$
$7 / 8$

Solution:

Per Person share increase =$\frac{1}{7}$ of total share

How To Solve Ratio And Proportion CA Foundation

Question 48. A bag contains 187 in the form of 1 rupee, 50 paise, and 10 paise coins in the ratio of 3:4:5. Find the number of each type of coin:

102, 136, 170
136, 102, 170
170, 102, 136
None

Solution:

let x Be common In the 2m ratio

No, of I Kopec; 50 Pulse ;KI 10 Raise

Coins are 3x ; 4x and 5x

3x x I + 4x x 0.50 + 5x x 0.10 = 187

Or 5.50x = 187

⇒ $x=\frac{1117}{5.50}=34$

No.of 1 rupee coins = 3x=3×34=102

No of 50 paise coins = 4x= 4×34=136

No. of 10 Paise coins = 5x = 5 x 34 =170

(1) is correct

Question 49. P, Q, and R are three cities. The ratio of average temperature between P and Q is 11: 12 and that between P and R is 9: 8. The ratio between the average temperature of Q and R is:

22: 27
27: 22
32: 33
None

Solution:

P : Q = 11 : 12 P = 12 : 11

⇒ $\frac{Q}{p} \times \frac{p}{R}=\frac{12}{11} \times \frac{9}{8}$

⇒ $\frac{Q}{R}=\frac{27}{22} \quad Q: R=27: 22$

(2) is Correct

Question 50. ₹407 are to be divided among A, B, and C so that their shares are in the ratio $\frac{1}{4}: \frac{1}{5}: \frac{1}{6}.$ The respective shares of A, B, and C are:

₹165, ₹132,
₹165, ₹110, ₹132
₹132, ₹165
₹110, ₹132, ₹165

Solution:

⇒ $A: B: C=\frac{1}{4}: \frac{1}{5}: \frac{1}{6} \times$ LCM of denominators = 60 = 15:12:10

A’s share =$=\frac{407}{15+12+10} \times 15=\text { Rs. } 165$

B’s share$=\frac{407}{37} \times 12=\text { Rs. } 132$

C’s share$=\frac{407}{37} \times 10=\text { Rs. } 110$

Question 51. The incomes of A and B are in the ratio 3: 2 and their expenditures in the ratio 5 : 3. If each saves ₹1,500, then, B’s income is :

₹6,000
₹4,500
₹3,000
₹7,500

Solution:

Let x be common in the ratio.

A’s income = 3x

B’s income = 2x

⇒ $\frac{3 x-1500}{2 x-1500}=\frac{5}{3}$

Or 10x- 7500 = 9x- 4500

Or 10x-9x = 7500 -4500

Or x = 3000

B’s income = 2x = 2 x 3000

= 6000.

(1) is correct

Question 52. In 40 liter mixture of glycerine and water, the ratio of glycerine and water is 3: 1. The quantity of water added in the mixture to make this ratio 2:1 is:

15 litres
10 litres
8 litres
5 litres

Solution:

Glycerine = $\frac{40}{3+1} \times 3=30 \text { litres. }$

Water =$=\frac{40}{4} \times 1=10 \text { litres }$

Let x liters of water be added to the mixture

⇒ $\text { Then } \frac{30}{10+x}=\frac{2}{1}$

Or, 2x + 20 = 30 or x = 5

(4) is Correct

Question 53. The third proportional to (a² – b²) and (a + b)² is:

$\frac{a+b}{a-b}$
$\frac{a-b}{a+b}$
$\frac{(a-b)^2}{a+b}$
$\frac{(a+b)^3}{a-b}$

Solution:

3rd Proportion$I=\frac{(\text { Mean Prop. })^3}{\text { 1st Proportional }}$

⇒ $=\frac{\left((a+b)^2\right)^2}{a^2-b^2}=\frac{(a+b)^4}{3(a+b)(a+b)}=\frac{(a+b)^3}{a-b}$

(4) is Correct

Question 54. The ages of the two persons are in the ratio of 5:7. Eighteen years ago their ages were in the ratio of 8: 13, and their present ages (in years] are:

50, 70
70, 50
40, 56
None

Solution:

(1) and (3) in the ratio 5: 7 not (2)

For (a) 18 years ago

⇒ $\frac{50-18}{70-18}=\frac{32}{32}=\frac{8}{13} \text { (True) }$

So. (1) is Correct

Question 55. If A, B, and C started a business by investing ₹1,26,000, ₹84,000, and ₹2,10,000. If at the end of the year, profit is ₹2,42,000 then the share of each is:

₹72,600; ₹48,400; ₹1,21,000
₹48,400; ₹1,21,000; ₹72,600
₹72,000; ₹49,000; ₹1,21,000
₹48,000; ₹1,21,400; ₹72,600

Solution:

⇒ $ \text { A’s share }=\frac{\{242,000}{3+2+5} \times 3=₹ 72,600 $

⇒ $\text { B’s share }=\frac{242,000}{20} \times 2=₹ 48,400$

⇒ $\text { C’s share }=\frac{242,000}{10} \times 5=₹ 1,21,000$

Investment ratio is A : B : C = 126,000 : 84,000 : 2,10,000 + 14,000

= 9: 6: 15 + 3

=3:2:5

Question 56. If $\frac{p}{q}=-\frac{2}{3} \text { then the value of } \frac{2 p+q}{2 p-q} \text { is: }$

1
$-\frac{1}{7} $
$ \frac{1}{7}$
7

Solution:

⇒ $\frac{p}{q}=\frac{-2}{3}$

⇒ $\text { Tricks }\frac{2 p+q}{20-q}=\frac{2(-2)+3}{2(-2)-3}=\frac{-4+3}{-4-3}=\frac{-1}{-7}=\frac{1}{7}$

(3) is correct

Question 57. Fourth proportional to x, 2x, (x+1) is:

x+2
x+2
(2x+2)
2x-2

Solution:

Let Fourth Proportional is K

$\frac{x}{2 x}=\frac{x+1}{K}$

Or k.x = 2x (x+1)

Or 1< = 2 (x+1) = 2x+ 2

(3) is correct

Question 58. Wlwt must be added to each term of the ratio 49: 68 so that it becomes 3: 47

Solution:

Let x be added to each term

Then $\frac{49+x}{68+x}=\frac{3}{4}$

Or 196 + 4x = 204 + 3x

Or 4x – 3x = 204 – 196

Or x = 8

(3) is Correct

Question 59. The students of the two classes are in the ratios 5: 7. if 10 students left from each class, the remaining students are in the ratio of 4: 6, then the number of students in each class was.

30, 40
25, 24
40, 60
50, 70

Solution:

(1) : (2) and (3) are not in the ratio 5: 7

(4) is Correct.

Question 60. If A : B = 2:5, then (10A + 3B) is equal to

7:4
7:3
6: 5
7: 9

Solution:

It A : B = 2 : 5 Then

⇒ $\frac{10 A+3 B}{5 A+2 B}=\frac{10 \times 2+3 \times 5}{5 \times 2+2 \times 5}=\frac{35}{20}=\frac{7}{4}$ = 7:4

(1) is Correct

Question 61. In a film shooting, A and B received money in a certain ratio and B and C also received the money in the same ratio. If A gets ₹1,60,000 and C gets ₹2,50,000. Find the amount received by B.

₹2,00,000
₹2,50,000
₹1,00,000
₹1,50,000

Solution:

A: B = B: C

So, B2 = AC;

So, B = AC – y1,60,000 x 2,50,000

= 400 x 500 = 2,00,000

Question 62. The ratio compounded of 4: 5 and sub-duplicate of”a”: 9 is 8: 15. The value of”a” is

Solution:

⇒ $(c) \frac{1}{5} \times \sqrt{\frac{a}{9}}=\frac{8}{15} \quad$ Or \frac{1}{5} \times \sqrt{\frac{a}{3}}=\frac{8}{15}$

⇒ $\sqrt{a}=2 \Rightarrow a=4$

Question 63. Which of the numbers are not in proportion?

6,8,5,7
7,14,6,12
18,27,12,18
8,6,12,9

Solution:

For a $\frac{6}{8}=\frac{3}{4} \neq \frac{5}{7}$

(1) is not in proportion

Question 64. Find two numbers such that the mean proportional between them is 18 and the third proportional to them is 144

9 ; 36
8 ; 32
7 ; 28
6 ; 14

Solution:

(1) is correct

For (a) Mean Proportional of 9 and 36

= √9 x 36 = 18

It satisfies 1st condition.

If144 is its 3rd condition.

362 = 9 x 144

It also satisfies the 2nd Condition.

Question 65. The triplicate ratio of 4: 5 is

125: 64
16: 25
64: 125
120:46

Solution:

(3) Triplicate ratio of 4: 5

= 43 : 5:1= 64 : 125

Question 66. The mean proportion between 24 and 54 is _______.

Solution:

(4) Mean – Proportion = V24 x 54 = 36

Question 67. The ratio of numbers is 1: 2 : 3 and the sum of their squares is 504 then the numbers are

6,12,18
3,6,9
4,8,12
5,10,15

Solution: (1) is correct

Question 68. If P is 25% less than Q and R is 20% higher than Q the Ratio of R and P

5: 8
8: 5
5 : 3
3: 5

Solution:

(2) is correct

Let Q = 100, So, P = 100-025 = 75 and R = 100 + 20 = 120

⇒ $\frac{R}{P}=\frac{120}{75}=\frac{8}{5}$

Question 69. A person has assets worth ₹1, 48, 200. He wishes to divide it among his wife, son, and daughter in the ratio of 3:2:1 respectively. From these assets, the share of his son will be

₹74,100
₹37,050
₹49,400
₹24,700

Solution:

⇒ $=\frac{2}{3+2+1} \times 1,48,200=₹ 49,400$

(3) is correct Share of son

Question 70. If x : y = 2 : 3 then (5x + 2y) : (3x – y) =

19: 3
l6 : 3
7: 2
7 : 3

Solution:

(2) is correct $\frac{5 x+2 y}{3 x-y}=\frac{5 \times 2+2 \times 3}{3 \times 2-3}=\frac{16}{3}$

Question 71. The first, second, and third-month salaries of a person are in the ratio 2:4:5. The difference between the product of the salaries of the first 2 months & last 2 months is ₹4,80,00,000. Find the salary for the second month

₹4,000
₹6,000
₹12,000
₹8,000

Solution:

Let x be common in the ratio.

1st, 2nd and 3rd-month salaries of a person

= 2x; 4x; 5x

From Qts.

4x x 5x – 2x x

4x = 4,80,00,000.

Or, 12x² = 4.80,00,000.

Or, x² = 4,00,000

X = 2000.

2nd month salary = 4x = 4 x 2000

Question 72. 15 (2p2-q2)= 7 pq, where,q are positive then p: q

Solution:

(1) is correct

I5(2p- q ’) = 7

For (a) pul p = 5; q = 6 we get

15|2 X 52- 62| = 3*5*6

Or 15 x 14 = 210

Or 210 = 210

Question 73. Kind the ratio of the third proportional of 1 2; 30 and the mean proportional of 9; 25 :

7: 2
5: 1
9: 4
None of these

Solution:

3″1 proportional $=\frac{30^2}{12}=$ = 75

Mean Proportional = V9 x 25 = 15

Ratio = $=\frac{75}{15}=$ 5 : 1 (b) is correct

Question 74. What must be added to each of the numbers 10, 18, 22, and 38 to make them proportional:

Solution:

(b) is correct

Let x be added.

⇒ $\frac{10+x}{18+x}=\frac{22+x}{38+x}$

x = 2 satisfies it

Question 75. x, y, z together start a business, if x invests 3 times as much as y invests and y investwo-thirdsird of what z invests, then the ratio of capitals of x, y, z is______.

3: 9: 2
6 : 3: 2
3: 6: 2
6: 2 : 3

Solution:

6 = 3×2 and 2 = 3 x $\frac{2}{3}$

Question 76. A bag contains 23 numbers of coins in the form of 1 rupee, 2 rupee, and 5 rupee coins. The total sum of the coins is The ratio between 1 rupee and 2 rupees coins is 3: 2. Then the number of1 rupee coins is

Solution:

Let option (a) be correct.

Let x be common in the ratio.

So, coins = 3x = 12; So, x = 4

No. of ₹ 2 coins=2×4=8

Hence no. of coins of ?5 coins = 23 – 12-8 = 3

Satisfied, So (a) is correct

Question 77. If a : b = 2 : 3, b: c = 4: 5, c: d = 6 : 7 then a : d is

24: 35
8: 15
16: 35
7: 15

Solution:

Option (3) is correct.

Multiply all ratios.

⇒ $=\frac{2}{3} \times \frac{4}{5} \times \frac{6}{7}=\frac{16}{35}$

Question 78. The ratio of the number of five rupee coins to the number of ten rupee coins is 8: 15. If the total value of five rupee coins is 360, then the no. of ten rupee coins is

Solution:

Option (4) is correct.

Total No. of? 5 coins = 360/5 = 72

Let x be common in the ratio.

So, coins = 8x = 72 ; So, x = 9

No. ₹ 10 coins = 15 x 9= 135

Question 79. If $\frac{1}{2}, \frac{1}{3}, \frac{1}{5}, \frac{1}{x}$ are in proportion then x =

$\frac{15}{2}$
$\frac{3}{15}$
$\frac{2}{15}$
$\frac{1}{15}$

Solution:

Option (1) is correct

Product of middle two terms

= Product of extremes $\text { So, } \frac{1}{2 x}=\frac{1}{15} ; x=15 / 2$

Question 80. If (a+b) : (b+c) : (c+a) = 7:8:9 and a + b + c=18 then a : b : c =

5: 4 : 3
3 : 4: 5
4 : 3: 5
4: 5 : 3

Solution:

(3)

Leta : h : c = 4: 3: 5

It is in ratio. So, it should satisfy the given ratio (a+h) : (b+c): (c+a) = 7: H: 9 i.c (4+3): (3+5): (5+4) = 7: 8: 9 (true) Avoid 2ml condition.

In detail, it will take too much time.

Question 81. The mean proportional between 24 and 54

Solution:

Formula Mean Proportion of a and b = √ab

(4) = √24 x 54 = 36

Question 82. $\frac{3 x-2}{5 x+6} $is the duplicate ratio of| then find the value of x:

Solution:

1. Given$\frac{3 x-2}{5 x+6}=\left(\frac{2}{3}\right)^2=\frac{4}{9}$

Tricks: Go by choices

For option (a) putting x = 6 in LHS; we get

⇒ $\frac{3 \times 2-2}{5 \times 2+6}=\frac{4}{9} \text { (R.H.S) }$

Question 83. x:6y : z = 7:4: 110000 then $\frac{x+y+z}{z}$ is:

Solution:

⇒ $\frac{x+y+z}{z}=\frac{7+4+11}{11}=2$

Question 84. If the ratio of two numbers is 7: 11. If 7 is added to each number then the new ratio will be 2 : 3 then the numbers are.

49,77
42,45
43,42
39,40

Solution:

⇒ $\left[\begin{array}{l}49 \div 7=777 \div 11=7\end{array}\right]$ both must be equal. Here it is correct.

now $\frac{49+7}{77+7}=\frac{56}{84}=\frac{2}{3}$

Divide 56 by numerator (2) and 84 by

Denominator (3) we get the same value “28”

CA Foundation Maths Solutions For Chapter 1 Indices

Concepts And Tricks To Remember

1. Laws Of Indices:

a^m x an= a^m+n
$\frac{a^m}{a^n}=a^m-n$
(a^m)ⁿ= a^mn
(ab)ⁿ = aⁿbⁿ
$\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$
a° = 1

2. Surds: Let a be a rational number and n be a positive integer such that $a^{\frac{1}{n}}=\sqrt[n]{a}$ is irrational. Then, $\sqrt[n]{a}$ is called a surd of order n.

3. Laws Of Surds:

$\sqrt[n]{a}=a^{\frac{1}{n}}$
$\sqrt[n]{a b}=\sqrt[n]{a} \times \sqrt[n]{b}$
$\sqrt[n]{\frac{a}{b}+\sqrt[n]{a}} \sqrt[n]{b}$
$(\sqrt[n]{a})^n=a$
$\sqrt[m]{\sqrt[n]{a}}=\sqrt[m n]{a}$
$(\sqrt[n]{a})^m \cdot \sqrt[n]{a^m}.$

Some Related Formulae.

a^m = a x a x a x to m times.
a^e = 1 where a ≠ 0; or ∞
$a^{-1}=\frac{1}{a}$
$a^{-m}=\frac{1}{a^m}$
a^m x aⁿ = a^m+n
- amx a^m x aⁿ x a^r…..=a^m+n+r+
$\frac{a^m}{a^n}=a^{m-n}$
- $\frac{a^m}{a^n}=\frac{1}{a^{n-m}}$
(a^m)ⁿ = a^mn
- a^mn= a^m-n
If a^m = b^m then a=b
- if a^m = aⁿ then m = n
$\sqrt[m]{a^n}=a^{\frac{n}{m}}$
- $\sqrt{a}=a^{\frac{1}{2}}$
- $\sqrt[3]{a}=a^{\frac{1}{3}}$
$\text { if } a^m=k \Rightarrow a=k^{1 / m}$
- $\text { if } a^m=k^n \Rightarrow a=k^{m / m}$
- $\text { If } a^{1 / m}=k \Rightarrow a=k^m $
$\text { if } a^{1 / m}=k^n \Rightarrow a=k^{m / m}$
- $\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}$
$(a b \ldots)^m=a^m \cdot b^m$
- $\sqrt[m]{a b \ldots \ldots \ldots \ldots}=\sqrt[m]{a} \cdot \sqrt[m]{b}\qquad$
$\sqrt{a b}=\sqrt{a} \cdot \sqrt{b}.$
$\left(\frac{a}{b}\right)^m=\left(\frac{b}{a}\right)^{-m}$
If a^b = b² then

Either a = b

Or if a = 2

Then b=4

or if a = 4

Then b = 2

If a > 1 and x < y Then ax < ay

CA Foundation Maths Solutions For Chapter 1 Exercise -1 – Indices

Question 1. $Value of \left(a^{1 / 8}+a^{\cdot 1 / 14}\right)\left(a^{1 / 8}-a^{-1 / 8}\right) \quad\left(a^{1 / 4}+a^{-1 / 4}\right)\left(a^{1 / 2}+a^{-1 / 2}\right) is:$

$a+\frac{1}{a}$
$\mathrm{a} \cdot \frac{1}{a}$
$a^2+\frac{1}{a^2}$
$a^2+\frac{1}{a^2}$

Solution:

⇒ $\left[a^{1 / 8}+a^{\cdot 1 / 8}\right]\left[a^{1 / 8}-a^{1 / 8}\right]\left[a^{1 / 4}+a^{1 / 4}\right]\left[a^{1 / 2}+a^{1 / 2}\right]$

⇒ ${\left[\text { Use formula }(a+b)(a-b)=a^2-b^2\right]}$

⇒ $\left[\left(a^{1 / 8}\right)^2-\left(a^{1 / 8}\right)^2\right]\left[a^{1 / 4}+a^{-1 / 4}\right]\left[a^{1 / 2}+a^{-1 / 2}\right]$

⇒ $\left(a^{1 / 4}-a^{-1 / 4}\right)\left(a^{1 / 4}+a^{-1 / 4}\right)\left(a^{1 / 2}+a^{-1 / 2}\right) $

⇒ $\left[\left(a^{1 / 4}\right)^2-\left(a^{-1 / 4}\right)^2\right]\left[a^{1 / 2}+a^{-1 / 2}\right] $

⇒ $\left(a^{1 / 2}-a^{-1 / 2}\right)\left(a^{1 / 2}+a^{-1 / 2}\right)=\left(a^{1 / 2}\right)^2-\left(a^{-\frac{1}{2}}\right)^2=a-a^{-1}=a-\frac{1}{a}$

(2) is correct

Question 2. Simplification of $\frac{x^{m+3 n} \cdot x^{4 m-9 n}}{x^{6 m-6 n}} \text { is: }$

x^m
x^-m
xⁿ
x^-n

Solution:

⇒ $\frac{x^{m+3 n} \cdot x^{4 m-9 n}}{x^{6 m-6 n}}=x^{m+3 n+4 m-9 n-6 m+6 n}=x^{-m}=x^{-m}$

(2) is correct

Question 3. On simplification$\frac{1}{1+z^{a-b}+z^{a-c}}+\frac{1}{1+z^{b-c}+z^{b-a}}+\frac{1}{1+z^{c-a}+z^{c-b}}$ reduce to:

$\frac{1}{z^{2(a+b+c)}}$
$\frac{1}{z^{2(a+b+c)}}$
1
0

Solution:

⇒ $\frac{1}{1+z^{a-b}+z^{n-c}}+\frac{1}{1+z^{b-c}+z^{b-n}}+\frac{1}{1+z^{c-a}+z^{c-b}}=1 \text { [it is in cyclic order] }$

Question 4. If 4X = 5y = 207- then z is equal to:

xy
$\frac{x+y}{x y}$
$\frac{1}{x y}$
$\frac{x y}{x+y}$

Solution:

(4)

Let$4^x=5^y=20^z \text { then } z \text { is equal to: }$

⇒ $ 4=\mathrm{k}^{1 / x} ; 5=\mathrm{k}^{1 / y} ; 20=\mathrm{k}^{1 / 2}$ 20 = 4×5

⇒ $\mathrm{k}^{1 / 2}=\mathrm{k}^{1 / x} \cdot \mathrm{k}^{\frac{1}{y}} \quad \mathrm{~K}^{1 / 2}=k^{\frac{1}{x}+\frac{1}{y}} \frac{1}{z}=\frac{1}{x}+\frac{1}{y} \Rightarrow \frac{1}{z}=\frac{y+x}{x y}$

⇒ $\mathrm{Z}=\frac{x y}{x+y}$

(4) is correct

Question 5. $\left(\frac{\sqrt{3}}{9}\right)^{5 /2}\left(\frac{9}{3 \sqrt{3}}\right)^{7 / 2} \times 9 \text { is equal to: }$

1
√3
3√3
$\frac{3}{9 \sqrt{3}}$

Solution:

⇒ $\left(\frac{\sqrt{3}}{9}\right)^{5 / 2}\left(\frac{9}{3 \sqrt{3}}\right)^{7 / 2} \times 9 $

⇒ $\left[\left(\frac{3^{1 / 2}}{3^2}\right)^5\left(\frac{3^2}{3 \cdot 3^{1 / 2}}\right)^7\right]^{1 / 2} \times 3^2=\left[3^{\left(\frac{1}{2}-2\right) 5} \times 3^{\left(2-1-\frac{1}{2}\right) 7}\right]^{1 / 2} \cdot 3^2$

⇒ $\left[3^{\frac{-15}{2}} \cdot 3^{\frac{7}{2}}\right]^{\frac{1}{2}} \times 3^2=\left(3^{\frac{-15}{2}+\frac{7}{2}}\right)^{\frac{1}{2}} \cdot 3^2=\left(3^{-4}\right)^{1 / 2} \cdot 3^2=3^{-2} \cdot 3^2=3^{-2+2}=3^0=1$

(1) is correct

Question 6. If 2x – 2x-1,=4, then the value of x x is:

Solution:

2y -2y =4

Or 2x-1(2-1) = 4

Or 2x-1 x 1 = 22 Or 2x-1 = 22

x – 1 = 2

x = 3 xx = 33 = 27

(4) is correct

Question 7. If x = ya, y=zb and z = xc then ABC is:

Solution:

It x = yd; y=zb and z=xc

Then abc=1

it is in cyclic order. :- (2) is correct

Question 8. Ifx = 31/3 + 3 -1/3then find value of 3×3 – 9x

Solution:

Detail Method

It x = 31/3 + 3-1/3______(1)

Cubing on both sides; we get x3:$\left(3^{1 / 3}\right)^3+\left(3^{-1 / 3}\right)^3+3 \cdot 3^{\frac{1}{3}} \cdot 3^{-\frac{1}{3}}\left(3^{\frac{1}{3}}+3^{-1 / 3}\right)$

= 3 + 3-1 + 3xlxx (from (I)

Question 9. Find the value of:$\left[1-\left\{1-\left(1-x^2\right)^{-1}\right\}^{-1}\right]^{-\frac{1}{2}} \text { is }$

1/x
x
1
None of these

Solution:

⇒ $\left[1-\left\{1-\left(1-x^2\right)^{-1}\right]^{-\frac{1}{2}}\left[1-\left\{1-\frac{1}{1-x^2}\right\}^{-1}\right]^{-1 / 2}\right.$

⇒ $
\left[1-\left\{\frac{1-x^2-1}{1-x^2}\right\}^{-1}\right]^{-1 / 2}=\left[1-\left\{\frac{-x^2}{1-x^2}\right\}^{-1}\right]^{-1 / 2}$

⇒ $\left[1-\frac{1-x^2}{-x^2}\right]^{-\frac{1}{2}}=\left[1+\frac{1-x^2}{x^2}\right]^{-\frac{1}{2}}=\left[\frac{x^2+1-x^2}{x^2}\right]^{-1 / 2}$

⇒ $\left(\frac{1}{x^2}\right)^{-1 / 2}=\left(x^{-2}\right)^{-\frac{1}{2}}=x (\mathrm{b})$

(2) is correct

Question 10.$\frac{2^n+2^{n-1}}{2^{n+1}-2^n}$

Solution:

⇒ $\frac{2^n+2^{n-1}}{2^{n+1}-2^n}=\frac{2^n\left(2^0+2^{-1}\right.}{2^n\left(2^1-2^0\right)}=\frac{1+\frac{1}{2}}{2-1}=\frac{3}{2}$

[2] is correct

Put n =1

Question 11. If 2X x3y x 52 = 360. Then what is the value of x,y,z.?

3,2,1
1,2,3
2,3,1
1,3,2

Solution:

If 2x x3y x 5z = 360

x= 3; y = 2; z = 1;

(1) is correct

Question 12. The recurring decimal 2.7777……can be expressed as

24/9
22/9
26/9
25/9

Solution:

⇒ $\frac{24}{9}=2.666 \ldots \ldots \ldots . \neq 2.777 \ldots \ldots$

⇒ $\frac{22}{9}=2.444 \ldots \ldots \ldots . \neq 2.777 \ldots \ldots$

⇒ $\frac{26}{9}=2.888 \ldots \ldots \ldots \neq 2.77 \ldots \ldots$

⇒ $\frac{25}{9}=2.777 \ldots \ldots \ldots . . .2 .777 \ldots \ldots …$

(4) is correct

Question 13. The value of$\frac{\left(3^{n+1}+3^n\right)}{\left(3^{n+3}-3^{n+1}\right)} \text { is equal to }$

Solution:

(2) Put n = 0 $\frac{3+3^0}{3^3-3}=\frac{3+1}{27-3}=\frac{4}{24}=\frac{1}{6}$

Detail Method$\frac{3^{n+1}+3^n}{3^{n+3}-3^{n+1}}=\frac{3^n(3+1)}{3^n\left(3^3-3\right)}=\frac{4}{24}=\frac{1}{6}$

Question 14. Find the value of x, if x.(x)1/3 = (x1/3)x

Solution:

⇒ $(b)x \cdot x^{\frac{1}{3}}=x^{\frac{x}{3}}
or x^{1+\frac{1}{3}}=x^{x / 3}1+\frac{1}{3}=\frac{x}{3}$

⇒ $\frac{4}{3}=\frac{x}{3}\mathrm{x}=4$

Question 15. $If\sqrt{a}+\sqrt[3]{b}+\sqrt[3]{c}=0; then find the value of \left|\frac{a+b+c}{3}\right|^3=$

9abc
$\frac{1}{9 a b c}$
abc
$\frac{1}{a b c}$

Solution:

(3) is correct

Let a = -1; b = -1 and c = 8, because $\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}=\sqrt[3]{-1}+\sqrt[3]{-1}+\sqrt[3]{8}$

$=-1-1+2=0 \text { (R.H.S) } \left[\frac{a+b+c}{3}\right]^3=\left[\frac{-1-1+8}{3}\right]^3=(2)^3=8$

(-l). (-l).(8) = abc

(3) is correct

Question 16. The value of$\left(\frac{y^{\prime}}{y^b}\right)^{a^2+a b+b^2}\left(\frac{y^b}{y^a}\right)^{b^2+b c+c^2}\left(\frac{y^c}{y^a}\right)^{c^2+c a+a^2}$

y
-1
1
6

Solution:

(3) is correct.

Question 17. Ifpx = q,qy = r,rz = p6, then the value of XYZ is…

Solution:

qy = r => (px)y = r => pxy

Now r2 = p6 => (pxy)z =p6=> pxyz = Pb :- xyz = 6

Question 18. The value of $\frac{x^2-(y-z)^2}{(x+z)^2-y^2}+\frac{y^2-(x-z)^2}{(x+y)^2-z^2}+\frac{z^2-(x-y)^2}{(y+z)^2-x^2}=$

0
1
-1
∞

Solution:

(2) is correct

⇒ $\frac{(x+y-z)(x-y+z)}{(x+y+z)(x-y+z)}+\frac{(y+x-z)(y-x+z)}{(x+y+z)(x+y-z)}+\frac{(x-y+z)(z-x+y)}{(x+y+z)(y+z-x)}$

⇒ $=\frac{x+y-z+y-x+z+x-y+z}{x+y+z}=\frac{x+y+z}{x+y+z}=1$

Question 19. If 3X = 5y = (75)z then

$\frac{1}{x}+\frac{2}{y}=\frac{1}{z}$
$\frac{2}{x}+\frac{1}{y}=\frac{1}{z}$
$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$
None

Solution:

⇒ $3^x=5^y=(75)^z \ldots \ldots \text { (1) }$

⇒ $3^1 \times 5^2=75^1 \ldots \ldots .(2)$

Power of(2) + Power of(1)

And put the + sign in the place of”x”.

We get$\frac{1}{x}+\frac{2}{y}=\frac{1}{z}$

So (1) is correct

Question 20. If ABC = 2, then the value of$\frac{1}{1+a+2 b^{-1}}+\frac{1}{1+\frac{b}{2}+c^{-1}}+\frac{1}{1+a^{-1}+c}=$

1
2
$\text { (d) } \frac{1}{2}$
$\text { (d) } \frac{3}{4}$

Solution:

“Puta = 1, b = 2 & c = 1. So abc = 2” in the given question. We get

⇒ $\frac{1}{1+1+\frac{2}{2}}+\frac{1}{1+\frac{2}{2}+1^{-1}}+\frac{1}{1+1^{-1}+1}=1$

Option (1) is correct.

Question 21. If a $=\frac{\sqrt{6}+\sqrt{5}}{\sqrt{6-\sqrt{5}}}, b=\frac{\sqrt{6}-\sqrt{5}}{\sqrt{6+\sqrt{5}}} \text { then the value of } \frac{1}{a^2}+\frac{1}{b^2} \text { is }$

Solution:

⇒ $\frac{1}{a}+\frac{1}{b}= $

⇒ $\frac{\sqrt{6}-\sqrt{5}}{\sqrt{6}+\sqrt{5}}+\frac{\sqrt{6}+\sqrt{5}}{\sqrt{6}-\sqrt{5}}=22$

⇒ $\frac{1}{a^2}+\frac{1}{b^2}=\left(\frac{1}{a}+\frac{1}{b}\right)^2-2\left(\frac{1}{a} \cdot \frac{1}{b}\right)=22^2-2=482
$

(1) is correct.

Question 22. If u5x = v5y = w5z and u2 = vw then xy + 7.x- 2yz =_______.

a
1
2
None of these

Solution:

U5X=VSy=W5z => u2 – vy = wz

see quicker BMLRS chapter: Indices

⇒ $\mathrm{u}^2=\mathrm{VW} ; \frac{2}{x}=\frac{1}{y}+\frac{1}{z}=\frac{y+z}{y z}$

Or; xy + zx = 2yz

Or; xy + zx -2yz = 0

Question 23. $\left(x^{\sum_{n=1}^{\infty} a p^{n-1}}\right)^{1-p}\left(x^{\sum_{n=1}^{\infty} b q^{n-1}}\right)^{1-q}\left(x^{\sum_{n=1}^{\infty} c r^{n-1}}\right)^{1-r}$

$x-(a p+b(c)+c r)$
$x^{a+b+c}$
$x^{(a p+b \varphi+c r)}$
$X^{\text {abe }}$

Solution:

(2)

⇒ $\sum_{n=1}^{\infty} a p^{n-1}=a+a p+a p^2+\cdots=\frac{a}{1-p}$

⇒ $\left(x^{\sum_{n=1}^{\infty} a p^{n-1}}\right)^{1-p}=\left(x^{\frac{a}{1-p}}\right)^{1-p}=x^a $

Similarly doing as above; we get

⇒ $\left(x^{\sum_{n=1}^{\infty} a p^{n-1}}\right)^{1-p}\left(x^{\sum_{n=1}^{\infty} b q^{n-1}}\right)^{1-q}\left(x^{\sum_{n=1}^{\infty} c r^{n-1}}\right)^{1-r}=x^a \cdot \mathrm{x}^b \cdot \mathrm{x}^c \quad=\mathrm{x}^{\cdot+a+b+c}$

(2) is correct

Question 24. $\frac{2^n+2^{n-1}}{2^{n+1}-2^n}$

$\frac{1}{2}$
$\frac{3}{2}$
$\frac{2}{3}$
$\frac{1}{3}$

Solution:

(2)

Put minimum powers-l=0+1 or n=l in the question.

⇒ $ \frac{2^n+2^{n-1}}{2^{n+1}-2^n}=\frac{2^1+2^{1-1}}{2^{1+1}-2^1}=\frac{2+1}{4-2}=\frac{3}{2}$

Question 25. $\frac{2^{m+1} \times 3^{2 m-n+3} \times 5^{n+m+4} \times 6^{2 n+m}}{6^{2 m+n} \times 10^{n+1} \times 15^{m+3}}$

3 2m+2n
3 2n-2m
1
None.

Solution:

Tricks Put m = n = 0 in this equation.$\frac{2^{m+1} \times 3^{2 m-n+3} \times 5^{n+m+4} \times 6^{2 n+m}}{6^{2 m+n} \times 10^{n+1} \times 15^{m+3}}=1$

Question 26. If 2×2 = 2yZ = 12z2 then

$\frac{1}{x^2}+\frac{1}{y^2}=\frac{1}{z^2}$
$\frac{1}{x^2}+\frac{2}{y^2}=\frac{1}{z^2}$
$\frac{2}{x^2}+\frac{2}{y^2}=\frac{1}{z^2}$
None

Solution:

2×2 = 2y2 = 12z2 …(1) (given)

Factorize 12 in terms of 2&3. We get 22 x 31 = 121….(2)

Always write as a power of base of (2) +ÿ Power on the same base of 1; put the “+” sign in the place of the “x” sign.

So $\frac{2}{x^2}+\frac{1}{y^2}=\frac{1}{z^2} \quad \text { So (3) is correct. }$

CA Foundation Maths Ratio And Proportion Practice

Question 27. The value of $\frac{1}{(216)^{-\frac{2}{3}}}+\frac{1}{(256)^{-\frac{3}{4}}}+\frac{1}{(32)^{-\frac{1}{5}}} \text { is }$

Solution:

⇒ $\frac{1}{(216)^{-\frac{2}{3}}}+\frac{1}{(256)^{-\frac{1}{4}}}+\frac{1}{(32)^{-\frac{1}{5}}}=\frac{1}{\left(6^3\right)^{-\frac{2}{3}}}+\frac{1}{\left(4^4\right)^{\left(-\frac{1}{4}\right)}}+\frac{1}{\left(2^5\right)^{-\frac{1}{5}}}$

⇒ $\frac{1}{6^{3 \times \frac{(-2)}{3}}}+\frac{1}{4^{4 \times \frac{(-3)}{4}}}+\frac{1}{2^{5 \times \frac{(-1)}{5}}}=\frac{1}{6^{-2}}+\frac{1}{4^{-3}}+\frac{1}{2^{-1}} $

⇒ $\left(6^2+4^3+2^1\right)=(36+64+2)=102 $

Question 28. The value of[(10)150 + (10) 146] is

1000
10000
100000
106

Solution:

⇒ $(10)^{150} \div(10)^{146}=\frac{(10)^{150}}{(10)^{146}}=(10)^{(150-146)}=10^4=10000$

Question 29. (1000)7+ 1018 = ?

10
100
1000
10000

Solution:

⇒ $(1000)^7 \div 10^{18}=\frac{(1000)^7}{10^{18}}=\frac{\left(10^3\right)^7}{10^{18}}=\frac{10^{(3 \times 7)}}{10^{18}}=\frac{10^{21}}{10^{18}}=(10)^{(21-18)}=10^3=1000$

Question 30.(256)0.16 x (256)0.09 = ?

4
16
64
256.25

Solution:

⇒ $(256)^{0.16} \times(256)^{0.09} =(256)^{(0.16+0.09)}=(256)^{0.25}=(256)^{\left(\frac{25}{100}\right)}$

⇒ $ (256)^{\frac{1}{4}}=\left(4^4\right)^{\frac{1}{4}}=4^{\left(4 \times \frac{1}{4}\right)}=4^1=4$

Question 31. (0.04)-1.5 =?

Solution:

⇒ $(0.04)^{-1.5}=\left(\frac{4}{100}\right)^{-1.5}=\left(\frac{1}{25}\right)^{-\frac{3}{2}}=(25)^{\frac{3}{2}}=\left(5^2\right)^{\frac{3}{2}}=5^{\left(2 \times \frac{3}{2}\right)}=5^3=125$

Question 32. (17)3.5 x (17)? = 178

2.29
2.75
4.25
4.5

Solution:

Let (17)3.5 X (17)x = 178. Then, (17)35+x = (17)8.

3.5 + x = 8 <=> x = (8 – 3.5) » x = 4.5

Question 33. $(64)^{-\frac{1}{2}}-(-32)^{-\frac{4}{5}}=?$

$frac{1}{8}$
$\frac{3}{8}$
$\frac{1}{16}$
$\frac{3}{16}$
None of these

Solution:

⇒ $ (64)^{-\frac{1}{2}}-(-32)^{-\frac{4}{5}}=\left(8^2\right)^{-\frac{1}{2}}-\left\{(-2)^5\right\}^{-\frac{4}{5}}=8^{2 \times \frac{(-1)}{2}}-(-2)^{5 \times \frac{(-4)}{5}}=8^{-1}-(-2)^{-4}$

⇒ $ \frac{1}{8}-\frac{1}{(-2)^4}=\left(\frac{1}{8}-\frac{1}{16}\right)=\frac{1}{16}$

Question 34. (18)3.5 + (27)3.5 x 63.5 = 2? :

3.5
4.5
6
7
None of these

Solution:

⇒ $(18)^{3.5} \div(27)^{3.5} \times 6^{3.5}=2^x $

⇒ $\Leftrightarrow(18)^{3.5} \times \frac{1}{(27)^{3.5}} \times 6^{3.5}=2^x \Leftrightarrow\left(3^2 \times 2\right)^{3.5} \times \frac{1}{\left(3^2\right)^{3.5}} \times(2 \times 3)^{3.5}=2^x$

⇒ $\Leftrightarrow 3^{(2 \times 3.5)} \times 2^{3.5} \times \frac{1}{3^{(3 \times 3.5)}} \times 2^{3.5} \times 3^{3.5}=2^x $

⇒ $3^7 \times 2^{3.5} \times \frac{1}{3^{10.5}} \times 2^{3.5} \times 3^{3.5}=2^x \Leftrightarrow 2^x=2^x \Leftrightarrow \mathrm{x}=7 $

Question 35. (25)7.5 x (5)2.5 + (125)1.5 = 5?

8.5
13
16
17.5
None of these

Solution:

⇒ $\text { Let }(25)^{7.5} \times(5)^{2.5} \div(125)^{1.5}=5^x \text {. Then } \frac{\left(5^2\right)^{7.5} \times(5)^{2.5}}{\left(5^3\right)^{1.5}}=5^x \Leftrightarrow \frac{5^{(2 \times 7.5)} \times 5^{2.5}}{5^{(3 \times 1.5)}}=5^x $

⇒ $\Leftrightarrow \frac{5^{15} \times 5^{2.5}}{5^{4.5}}=5^x \Leftrightarrow 5^x=5^{(15+2.5-4.5)}=5^{13} \Leftrightarrow x=13$

36. The value of$\frac{(243)^{0.13} \times(243)^{0.07}}{(7)^{0.25} \times(49)^{0.075} \times(343)^{0.2}} \text { is : }$

$\frac{3}{7}$
$\frac{7}{3}$
$1 \frac{3}{7}$
$2 \frac{2}{7}$

Solution:

⇒ $ \frac{(243)^{0.13} \times(243)^{0.07}}{7^{0.25} \times(49)^{0.075} \times(343)^{0.2}}=\frac{(243)^{(0.13+0.07)}}{7^{0.25} \times\left(7^2\right)^{0.075} \times\left(7^3\right)^{0.2}}$

⇒ $\frac{(243)^{0.2}}{7^{0.25} \times 7^{(2 \times 0.075)} \times 7^{(3 \times 0.2)}}=\frac{\left(3^5\right)^{0.2}}{7^{0.25} \times 7^{0.15} \times 7^{0.6}}$

⇒ $\frac{3^{(5 \times 0.2)}}{7^{(0.25+0.15+0.6)}}=\frac{3^1}{7^1}=\frac{3}{7^{.}}$

Question 37. $\text { If }\left(\frac{a}{b}\right)^{x-1}=\left(\frac{b}{a}\right)^{x-3} \text {, then the value of } \mathrm{x} \text { is: }$

$\frac{1}{2}$
1
2
$\frac{7}{2}$

Solution:

⇒ $\text { 7. }\left(\frac{a}{b}\right)^{x-1}=\left(\frac{b}{a}\right)^{x-3} \Leftrightarrow\left(\frac{a}{b}\right)^{x-1}=\left(\frac{a}{b}\right)^{-(x-3)}=\left(\frac{a}{b}\right)^{(3-x)}$

⇔ x – 1 = 3 – x 2x = 4 <=> x = 2.

Question 38. If x = 3 + 2V2, then the value of $\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right) \text { is: }$

1
2
2√2
3√2

Solution:

⇒ $\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)^2=x+\frac{1}{x}-2=\left(3+2 \sqrt{2)}+\frac{1}{(3+2 \sqrt{2})}-2\right.$

⇒ $=(3+2 \sqrt{2})+\frac{1}{(3+2 \sqrt{2})} \times \frac{(3-2 \sqrt{2})}{(3-2 \sqrt{2})}-2=(3+2 \sqrt{2})+(3-2 \sqrt{2})-2=4 .$

⇒ $\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)=2$

39. Given that 100 48 = x, IO070 = y and xz = y2, then the value of z is close to :

1.45
1.88
2.9
3.7

Solution:

⇒ $x^z=y^2 \Leftrightarrow\left(10^{0.48}\right)^z=\left(10^{0.70}\right)^2 \Leftrightarrow 10^{(0.48 z)}=10^{(2 \times 0.70)}=10^{1.40}$

⇒ $\Leftrightarrow 0.48 z=1.40 \Leftrightarrow z=\frac{140}{48}=\frac{35}{12}=2.9 \text { (approx). }$

Question 40. If m and n are whole numbers such that”m” = 121, then the value of (m – 1)n+1 is :

1
10
121
1000

Solution:

We know that ll2 = 121. Putting m = 11 and n = 2, we get :

(m- 1)n+1 = (11 – 1)(2+1) = 103 = 1000

Question 41. $\frac{(243)^n \times 3^{2 n+1}}{9^n \times 3^{n-1}}=\text { ? }$

Solution:

Given Expression =$\frac{(243)^{\frac{n}{5}} \times 3^{2 n+1}}{9^n \times 3^{n-1}}=\frac{\left(3^5\right)^{\frac{n}{5}} \times 3^{2 n+1}}{\left(3^2\right)^n \times 3^{n-1}}=\frac{3^{\left(5 \times \frac{n}{5}\right)} \times 3^{2 n+1}}{3^{2 n} \times 3^{n-1}}$

⇒ $\frac{3^n \times 3^{2 n+1}}{3^{2 n} \times 3^{n-1}}=\frac{3^{(n+2 n+1)}}{3^{(2 n+n-1)}}=\frac{3^{3 n+1}}{3^{3 n-1}}=3^{(3 n+1-3 n+1)}=3^2=9 .$

Question 42. $\frac{(24,3)^{\frac{n}{5}} \times 3^{2 n+1}}{9^n \times 3^{n-1}}=?$

0
1/2
1
a m+n

Solution:

⇒ $ \frac{1}{1+a^{(n-m)}}+\frac{1}{1+a^{(m-n)}}=\frac{1}{\left(1+\frac{a^n}{a^m}\right)}+\frac{1}{\left(1+\frac{a^m}{a^n}\right)}$

⇒ $\frac{a^m}{a^m+a^n}+\frac{a^n}{a^m+a^n}=\frac{a^m+a^n}{a^m+a^n}=1 .$

Question 43. $\frac{1}{1+x^{(b-a)}+x^{(c-a)}}+\frac{1}{1+x^{(n-b)}+x^{(c-b)}}+\frac{1}{1+x^{(b-c)}+x^{(a-c)}}=?$

0
1
x a-b-c-a
None of these

Solution:

Given Expression: $ \frac{1}{1+\frac{x^b}{x^a}+\frac{x^c}{x^a}}+\frac{1}{1+\frac{x^a}{x^b}+\frac{x^c}{x^b}}+\frac{1}{1+\frac{x^b}{x^c}+\frac{x^a}{x^c}}$

⇒ $=\frac{x^a}{x^a+x^b+x^c}+\frac{x^b}{x^a+x^b+x^c}+\frac{x^c}{x^a+x^b+x^c}=\frac{x^a+x^b+x^c}{x^a+x^b+x^c}=1 .$

Question 44. $\left(\frac{x^b}{x^c}\right)^{(b+c-a)}\left(\frac{x^c}{x^a}\right)^{(c+a-b)}\left(\frac{x^a}{x^b}\right)^{(a+b-c)}=?$

x abc
1
xab+bc+ca
xa+b+c-a

Solution:

Given Exp. = x(b-c)(b+c-a)x.(c-a)(c+n-b)i x(a-b)(a+b-c)

=x(b~c)(b+c)-a(b-c) x(c-a)(c+a)-b(c-a) x(a-b)(a+b)-c(a-b)

=x(b²-c²+c²-a²+a²-b²) x-a(b-c)-b(c-a)-c(a-b) = (X° x X°) = (1x 1) = 1

Question 45. If 3(x-y) = 27 and 39(x+y) = 243, then x is equal to:

Solution:

3x~y = 27 = 33 ⇔ x-y = x-ÿ=3…..(1)

3X + y = 243 = 35 ⇔ x + y = 5…..(2)

On solving (1) and (2), we get x = 4.

Question 46. 4x-1/4 is expressed as

-4x 1/4
X-1
4/x1/4
none of these

Solution:

(4)

⇒ $4 / x^{1 / 4}$

⇒ $ 4 x^{1 / 4}=\frac{4}{x^{\frac{1}{4}}}$

Question 47. The value of 8 1/3 is

√2
4
2
none of these

Solution:

⇒ $8^{\frac{1}{3}}=\sqrt[3]{8}=\sqrt[3]{2^3}=2$

Question 48. The value of 2 x (32)1/5 is

2
10
4
None of these

Solution:

⇒ $=2 \times(32)^{\frac{1}{5}}=2 \times(32)^{\frac{1}{5}}=2 \times\left(2^5\right)^{\frac{1}{5}}=2 \times 2=4$

Chapter 1 CA Foundation Maths Answer Key

Question 49. The value of 4/(32) 1/5 is

8
2
4
None of these

Solution:

⇒ $(2)=\frac{4}{\left(2^5\right)^{\frac{1}{5}}}=\frac{4}{2}=2$

Question 50. The value of (8/27)1/3 is

2/3
3/2
2/9
none of these

Solution:

⇒ $(1)=\frac{\left(2^3\right)^{\frac{1}{3}}}{\left(3^3\right)^{\frac{2}{3}}}=\frac{2}{3}$

Question 51. The value of 2(256)-1/8 is

1
2
1/2
None of these

Solution:

⇒ $\text { (a) }=\frac{2}{(256)^{\frac{1}{8}}}=\frac{2}{\left(2^8\right)^{\frac{1}{8}}}=\frac{2}{2}=1$

Question 52. 21/2. 43/4 is equal to

a fraction
a positive integer
a negative integer
none of these

Solution:

(2) a positive Integer=$=2^{\frac{1}{2}} \cdot 4^{\frac{3}{4}} \quad=2^{\frac{1}{2}} \cdot\left(2^2\right)^{\frac{3}{4}}=2^{\frac{1}{2}} \cdot 2^{\frac{6}{4}}$

⇒ $=2^{\frac{1}{2}+\frac{6}{4}}=2^{\frac{8}{4}}=2^2=4 .$

Question 53.$\left(\frac{81 x^4}{y^{-8}}\right)^{\frac{1}{4}}$

xy2
x2y
9xy2
None Of these

Solution:

(4) None of these

⇒ $\left(81 x^4 \cdot y^8\right)^{\frac{1}{4}}$

⇒ $ \left(3^4 x^4 y^8\right)^{\frac{1}{4}}=3 \cdot x \cdot y^2 $

Question 54. Xa-b x x b-c is equal to

x
1
0
None of these

Solution:

(4)1

⇒ $=X^{a-b} \times X^{b-c} \times x^{c-a}$

⇒ $^x \cdot a^y=a^{x \cdot y}$

⇒ $ x^{a-b+b-c+c-a}$

⇒ $ =x^0=1$

Question 55. The value of$\left(\frac{2 p^2 q^3}{3 x y}\right)^0 \text { where } p, q, x, y \neq 0 \text { is equal to }$

0
2/3
1
None of these

Solution:

(3)l

= anything raised to 0 is 1.

Question 56. $\text { 56. } \quad\left\{\left(3^3\right)^2 \times\left(4^2\right)^1 \times\left(5^3\right)^2\right\} /\left\{\left(3^2\right)^3 \times\left(4^3\right)^2 \times\left(5^2\right)^3\right\} \text { is }$

Solution:

(4) 0

⇒ $=\frac{\left(3^3\right)^2 \times\left(4^2\right)^3 \times\left(5^3\right)^2}{\left(3^2\right)^3 \times\left(4^3\right)^2 \times\left(5^2\right)^3}=1$

Question 57. Which is true?

$2^{\circ}>(1 / 2)^o$
$2^0<(1 / 2)^0$
$2^0=(1 / 2)^{\circ}$
None of these

Solution:

(3) $20=\left(\frac{1}{2}\right) $

⇒ $2^0=1 \quad\left(\frac{1}{2}\right)^0=1$

⇒ $2^0=\left(\frac{1}{2}\right)^0$

Question 58. If $\text { If } x^{1 / p}=y^{1 / 4}=z^{1 / r} \text { and } x y z=1 \text {, then the value of } p+q+r \text { is }$

1
0
1/2
None of these

Solution:

(2) 0

⇒ $x^{\frac{1}{p}}=y^{\frac{1}{q}}=z^{\frac{1}{r}}=\mathrm{k} $

⇒ $\mathrm{X} k^p \cdot y=k^q \mathrm{z}=k^r$

⇒ $\mathrm{Xyz}=1 $

⇒ $k^p \cdot k^{q} \cdot k^r=1$

⇒ $k^{p+q+r}=k^0=\mathrm{p}+\mathrm{q}+\mathrm{r}=0 .$

Question 59. The value of y a-b x y b-c x ya-b is

y a+b
y
1
1/ya+b-a

Solution:

(4) l/ya+b

⇒ $y^{a-b} \times y^{(1-c} \times y^{(-\cdot a)} \times y^{-a \cdot l)}=y-a-b=y^{-(a+b)}$

⇒ $ \frac{1}{y^{a+b}}$

Question 60. The True option is

$x^{2 / 3}=\sqrt[3]{x^2}$
$^{2 / \beta}=\sqrt{x^3}$
$x^{2 / 3}>\sqrt[3]{x^2}$
$ x^{2 / 3}<\sqrt[3]{x^2}$

Solution:

⇒ $\text { (a) } x^{2 / 3}=\sqrt[3]{x^2}$

⇒ $x^{\frac{m}{n}}=\sqrt[m]{x^m}$

⇒ $x^{\frac{2}{3}}=\sqrt[3]{x^2}$

Question 61. The simplified value of 16x3y2 x 8>x3y-2 is

2xy
xy/2
2
None of these

Solution:

(3) 2

⇒ $=\left(\frac{27}{8}\right)^{\frac{1}{3}} \cdot\left(\frac{213}{32}\right)^{\frac{1}{5}}$

⇒ $=\frac{16 y^2}{x^3} \cdot \frac{x^3}{8 y^2}=2$

Question 62. The value of (8/27)-i/3 x (32/243)-1/5 is

9/4
4/9
2/3
none of these

Solution:

(1) $\frac{9}{4}$

⇒ $=\left(\frac{27}{8}\right)^{\frac{1}{3}} \cdot\left(\frac{213}{32}\right)^{\frac{1}{5}}$

⇒ $\left(\frac{3}{2}\right)^{3 \cdot \frac{1}{3}} \cdot\left(\frac{3}{2}\right)^{5 \cdot \frac{1}{5}}$

⇒ $\left(\frac{3}{2}\right) \cdot\left(\frac{3}{2}\right)=\frac{9}{4}$

Question 63. The value of $\left\{(x+y)^{2 / 3}(x-y)^{3 / 2} / \sqrt{(x+y)} \times \sqrt{(x-y)^3}\right\}^6 \text { is }$

(x+y)2
(x-y)
x + y
None of these

Solution:

c=x+y

⇒ $\left\{\frac{(x+y)^{\frac{2}{3}}(x-y)^{\frac{3}{2}}}{(x+y)^{\frac{1}{2}} \cdot(x-y)^{\frac{3}{2}}}\right\}^6$

⇒ $\left\{(x+y)^{\frac{2}{3}-\frac{1}{2}}\right\}^6 $

⇒ $ (x+y)^{\frac{1}{6}}=x+y$

Question 64. Simplified value of $f(125)^{2 / 3} \times \sqrt{25} \times \sqrt[3]{5^3} \times 5^{1 / 2} \text { is }$

5
1/5
1
none of these

Solution:

(4) none of these

(5)3)2/3 x 5 x 5 x 51/2

= 52 x 5 x 5 x 51/2

5 2+1+1+1/2 = 59/2

Question 65. $\left[\left\{(2)^{1 / 2} \cdot(4)^{3 / 4} \cdot(8)^{5 / 6} \cdot(16)^{7 / 8} \cdot(32)^{9 / 110}\right\}^4\right]^{3 / 25} \text { is }$

A fraction
an integer
l
none of these

Solution:

(2) an integer

⇒ ${\left[\left\{(2)^{1 / 2} \cdot 2^{6 / 4} \cdot 2^{15 / 6} \cdot 2^{28 / 8} \cdot 2^{15 / 10}\right\}^4\right]^{3 / 25}}$

⇒ ${\left[\left\{2^{1 / 2+6 / 4+15 / 6+28 / 8+15 / 10}\right\}^1\right]^{3 / 25}}$

⇒ ${\left[\left\{2^{1 / 2+3 / 2+5 / 2+7 / 2+9 / 2}\right\}^4\right]^{3 / 25}}$

⇒ ${\left[\left\{2^{25 / 2}\right\}^4\right]^{3 / 25}}$

⇒ $=\left[\left\{2^{\frac{25}{2} \times 4}\right\}\right]^{\frac{3}{25}}=\left[2^{\frac{25 \times 2.3}{25}}\right]$

= 26 = 64

Question 66. [1-{1-(1-X2)-1}-1]-1/2 is equal to

x
1/x
1
none of these

Solution:

(1) x

⇒ $\left[1-\left\{1-\left(1-x^2\right)^{-1}\right\}^{-1}\right]^{\frac{-1}{2}}$

⇒ $=\left[1-\left\{1-\left(\frac{1}{1-x^2}\right)\right\}^{-1}\right]^{\frac{-1}{2}}$

⇒ $\left[1-\left\{1-\left(\frac{1-x^2-1}{1-x^2}\right)\right\}^{-1}\right]^{\frac{-1}{2}}$

⇒ $\left[1-\left\{\left(\frac{-x^2}{1-x^2}\right)\right\}^{-1}\right]^{\frac{-1}{2}}$

⇒ $\left[1-\left\{\left(\frac{-x^2}{-x^2}\right)\right\}\right]^{\frac{-1}{2}}=\left[\frac{-x^2-1+x^2}{-x^2}\right]^{\frac{-1}{2}}$

⇒ $ \left[\frac{-1}{-x^2}\right]^{\frac{-1}{2}}=\left[x^2\right]^{\frac{1}{2}}=\mathrm{x}$

Question 67.$\left[\left(x^n\right)^{n-\frac{1}{n}}\right]^{\frac{1}{n+1}}$

xn
xn-1
xn-1
None of these

Solution:

(3) xn-1

⇒ $\left[\left(x^n\right) \frac{n^2-1}{n}\right]^{\frac{1}{n+1}}$

⇒ $ \left[x^{n^2-1}\right]^{\frac{1}{n+1}}$

⇒ $ \left[x^{(n-1)(n+1)}\right]^{\frac{1}{n+1}}=x^{n-1}$

Question 68. If a3- b3 = (a-b) (a2 + ab + b2), then the simplified form of $\left[\frac{x^l}{x^m}\right]^{l^2+l m+m^2} \times\left[\frac{x^m}{x^n}\right]^{m^2+m n+n^2} \times\left[\frac{x^n}{x^l}\right]^{l^2+\ln +n^2}$

0
1
x
None of these

Solution:

(2)

⇒ ${\left[\frac{x^l}{x^m}\right]^{l^2+l m+m^2} \times\left[\frac{x^m}{x^n}\right]^{m^2+m n+n^2} \times\left[\frac{x^n}{x^l}\right]^{l^2+l n+n^2}}$

⇒ ${\left[x^{(l-m)\left(l^2+l m+m^2\right)}\right] \times\left[x^{(m-n)\left(m^2+m n+n^2\right)}\right] \times\left[x^{(n-l)\left(n^2+n l+l^2\right)}\right]}$

⇒ $x^{l^3-m^3} \times x^{m^3-n^3} \times x^{n^3-l^3}$

⇒ $x^{l^3-m^3+m^3-n^3+n^3-l^3}=x^0=1 $

CA Foundation Ratio And Proportion Solved Examples

Question 69. Using (a-b)3 = a3-b3-3ab(a-b) tick the correct of these when x = p 1/3 – p-1/3

$x^3+3 x=p+1 / p$
$x^3+3 x=p-1 / p$
$x^3+3 x=p+1$$
none of these

Solution:

(2)$x^3+3 x=p \frac{-1}{p} $

⇒ $ x=p^{1 / 3}-p^{1 / 3} $

⇒ $x^3=\left(p^{1 / 3}-p^{-1 / 3}\right)^3 =p-\frac{1}{p}-3 p^{1 / 3} \cdot p^{-1 / 3}\left(p^{1 / 3}-p^{-1 / 3}\right)$

⇒ $x^3=p-\frac{1}{p}-3 x x^3+3 x=p \frac{-1}{p}$

Question 70. On simplification, $1 /\left(1+a^{m-n}+a^{m \cdot p}\right)+1 /\left(1+a^{n \cdot m}+a^{n-p}\right)+1 /\left(1+a^{p-m}+a^{p-n}\right)$ is equal to

Solution:

(3)

⇒ $=\frac{1}{1+\frac{a^m}{a^n}+\frac{a^m}{a^p}}+\frac{1}{1+\frac{a^n}{a^m}+\frac{a^n}{a^p}}+\frac{1}{1+\frac{a^p}{a^m}+\frac{a^p}{a^n}}$

⇒ $=\frac{a^{n+p}}{a^{n+p}+a^{m+p}+a^{m+n}}+\frac{a^{m+p}}{a^{m+p}+a^{n+p}+a^{n+m}}+\frac{a^{m+n}}{a^{m+n}+a^{p+n}+a^{p+m}}=\frac{a^{n+P}+a^{m+P}+a^{m+n}+}{a^{n+P}+a^{m+P}+a^{m+n}+}=1$

Question 71. The value of$\left(\frac{x^a}{x^b}\right)^{a+b} \times\left(\frac{x^b}{x^c}\right)^{b+c} \times\left(\frac{x^c}{x^a}\right)^{c+a}$

1
0
2
none of these

Solution:

(1) 1

=x(a-b)(a+b).x(b-c)(b+c).x(c-a)(c+a)

⇒ $x^{a^2-b^2} \cdot x^{b^2-c^2} \cdot x^{c^2-a^2} \Rightarrow x^{a^2-b^2+b^2-c^2+c^2-a^2}=x^0=1$

Question 72. If x =$3^{\frac{1}{3}}+3^{\frac{1}{3}} \text {, then } 3 x^3-9 x \text { is }$

15
10
12
None of these

Solution:

(2) 10

⇒ $x^3=3^{\frac{1}{3}}+3^{-\frac{1}{3}}$

⇒ $ x^3=3+\frac{1}{3}+3.3^{\frac{-1}{3}}\left(3^{\frac{1}{3}}+3^{-\frac{1}{3}}\right) x^3=\frac{10}{3}+\frac{9 x}{3}=3 x^3-9 x=10$

Question 73. If ax = b, by = c, c2 = a, then XYZ is

1
2
3
none of these

Solution:

(1)

⇒ $ a^x=b, b^y=c$

⇒ $\left(a^x\right)^y=c \quad a^{x y^{\prime}}=c, c^z=a \quad\left(c^z\right)^{x y}=c$

⇒ $c^{x y z}=c^1 \quad x y z=1$

Question 74. The value of $\left(\frac{x^a}{x^b}\right)^{\left(a^2+a b+b^2\right)} \times\left(\frac{x^b}{x^c}\right)^{\left(b^2+b c+c^2\right)} \times\left(\frac{x^c}{x^a}\right)^{\left(c^2+c a+a^2\right)}$

1
0
-1
None of these

Solution:

(1) 1

⇒ $x^{(a-b)\left(a^2+a b+b^2\right)} \cdot x^{(b-c)\left(b^2+b c+c^2\right)} \cdot x^{(c-a)\left(c^2+c a+a^2\right)}$

⇒ $x^{a^3-b^3} \cdot x^{b^3-c^3} \cdot x^{c^3-a^3} \cdot=x^{a^3-b^3+b^3-c^3+c^3-a^3} \quad \Rightarrow x^0=1$

Question 75. $\text { If } 2^x=3^y=6 \cdot z, \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \text { is }$

1
0
2
none of these

Solution:

⇒ $2^x=3^y=6^{-z}=k$

⇒ $2=k^{\frac{1}{x}} \cdot 3=k^{\frac{1}{y}} 4=k^{-\frac{1}{z}} $

⇒ $2 \times 3=6 $

⇒ $k^{\frac{1}{x}} \cdot k^{\frac{1}{y}}=k^{-\frac{1}{z}}$

⇒ $ k^{\frac{1}{x}}+k^{\frac{1}{y}}=k^{-\frac{1}{z}}$

⇒ $ \frac{1}{x}+\frac{1}{y}=\frac{-1}{z}=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$

CA Foundation Maths Solutions For Chapter 1 Logarithms

Concepts and Tricks to Remember

1. Logarithm: If a is a positive real number, other than 1 and a'” = x, then we write: m = loga x and say that the value of log x to the base a is m.

Example:

103 = 1000⇔log₁₀ 1000 = 3.

34 = 81 ⇔log₃ 81 = 4

2-3=$\frac{1}{8}$ « log2 =$\frac{1}{8}=-3$

(1)2 = .01 ⇔ log₍₁₀₎0.1 = 2.

2. Properties of Logarithms:

Loga (xy] = log_a X + log_a y

loga$\left(\frac{x}{y}\right)$ = logan-gay

log_a x — 1

Log_a 1 = 0

log_a (xp) = p (log_a x)

log_a X = $\frac{1}{\log _x a}$

log_a X = $\frac{\log _a x}{\log _b a}=\frac{\log _a x}{\log _a a}$

3. Common Logarithms: Logarithms to the base 10 are known as common logarithms. When the base is not mentioned, it is taken as 10.

4. The logarithm of a number contains two parts, namely characteristic and mantissa.

Characteristic: The integral part of the logarithm of a number is called its characteristic.

Case I: When the number is greater than 1.

In this case, the characteristic is one less than the number of digits on the left of the decimal point in the given number.

Case 2: When the number is less than 1.

In this case, the characteristic is one more than the number of zeros between the decimal point and, which is negative.

Instead of -1,-2, etc. We write 1(one bar), 2(two bar)etc.

Example:

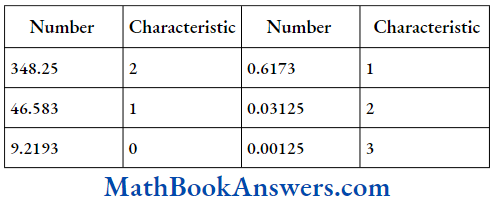
Business Mathematics Ratio And Proportion chapter 2 The First Signification Digit Of The Number

Mantissa: The decimal part of the logarithm of a number is known as its mantissa.

For Mantissa, we look through the log table.

Some more tricks and formulae:

1. If a^b= c = log_a c=b; where a = 1.

2. a^loga^b = b^x

3. log_aⁿ=1

4. log_b _a =log_b x logxa =log_xalog_bx

5. log_ba=log_xa.log_yx.log_zy….log_bk

6. log_ba=log_bx.log_xy.log_yz….log_k

If log_ba=x

Then

⇒ $\log _{\frac{1}{5}} a=-x$

⇒ $\log _b \frac{1}{a}=-x$

⇒ $\log _{\frac{1}{b}} \frac{1}{a}=+x$

⇒ $\log _a b\left(m^n\right)=\frac{n}{b} \log _{a^n}$

⇒ $\log _{a^{\left(m m^n\right)}}=n \log _{a^{m i}}$

⇒ $\log _{\frac{1}{b}} m=\frac{1}{b} \log _{a^m}$

If log_am = log_am ⇒ a = b.

If log_am = log_an ⇒ m = n.

Chapter 1 Ratio And Proportion Step-By-Step Solutions

CA Foundation Maths Solutions For Chapter 1 Logarithms Exercise – 1

Question 1. The value of log2 16is:

$\frac{1}{\mathrm{8}}$
4
8
16

Solution:

Let log1 16 = n. Then, 2″ = 16 = 24 => n = 4

log₂ 16 = n.

Question 2. If log_x4=0.4then the value of x is

Solution:

logs 4 = 0.4

⇒ $\Leftrightarrow \log _{\mathrm{x}} 4=\frac{4}{10}=\frac{2}{5} \Leftrightarrow x^{2 / 5}=4 \Leftrightarrow \mathrm{x}=4^{5 / 2}=\left(2^2\right)^{5 / 2}$

$\Leftrightarrow x=2^{\left(2 \times \frac{5}{2}\right)}=2^5 \Leftrightarrow x=32$

Question 3. If log10 y = 100 log₂X= 10, then the value of:

210
2100
2100
210000

Solution:

log₂ X = 10 ⇒ x = 2¹⁰

log_x y = 100 ⇒ y = x¹⁰⁰ = (2¹⁰)¹⁰⁰ = y= 2¹⁰⁰⁰

Question 4. $\frac{\log \sqrt{8}}{\log 8}$

$\frac{1}{\sqrt{8}}$
$\frac{1}{4}$
$\frac{1}{2}$
$\frac{1}{8}$

Solution:

⇒ $\frac{\log \sqrt{B}}{\log 8}=\frac{\log (B)^{1 / 2}}{\log 8}=\frac{\frac{1}{2} \log 8}{\log 8}=\frac{1}{2} .$

Question 5. Which of the following statements is not correct?

log₁₀ 10=1
log (2 + 3) = log (2 x 3)= log (2×3)
log₁₀ 1 = 0
log (1 + 2 + 3) = log ₁ + log₂+ log₃

Solution:

Since logaa = 1, so log₁₀ 10 = 1.

log (2 + 3)= 5 and log (2 x 3) = log 6 = log 2 + log 3

log (2 + 3) = log (2 + 3).

Since log_a 1 = 0, so log₁₀ 1 = 0.

log (1 + 2 + 3) = log 6 = log (1 x 2 x 3) = log₁ + log ₂ + log ₃.

So, (2) is incorrect.

Question 6. If ax – by, then:

$\log \frac{a}{b}=\frac{x}{y}$
$\frac{\log a}{\log b}=\frac{x}{y}$
$\frac{\log n}{\log b}=\frac{y}{x}$
None

ax = by⇒ log a^x= log b^y⇒ x log a = y log b $\Rightarrow \frac{\log a}{\log b}=\frac{y}{x}$

Question 7. 2 log10 5+ log10 8 – $\frac{1}{2} \log _{10} 4=?$

2
4
2+2log10 2
4-4 log10 2

Solution:

2 log₁₀ 5 + login 8 login 4 = log₁₀ (52) + login 8 – log₁₀$\left(4^{\frac{1}{2}}\right)$

= log₁₀ 25 + log₁₀ 8 – log₁₀ 2 = log₁₀ $\left(\frac{25 \times 8}{2}\right)=\log _{11} 100=2 \text {. }$

Question 8. If loga (ab) = x, then logi, (ab) is:

$\frac{1}{x}$
$\frac{x}{x+1}\$
$\frac{x}{1-x}$
$\frac{x}{x-1}$

Solution:

Loga (ab) = x $\Leftrightarrow \quad \frac{\log a b}{\log a}=\mathrm{x} \quad \Leftrightarrow \quad \frac{\log a+\log b}{\log a}=\mathrm{x}$

⇒ $\Leftrightarrow \quad 1+\frac{\log b}{\log a}=x \quad \Leftrightarrow \quad \frac{\log b}{\log a}=x-1$

⇒ $\Leftrightarrow \quad \frac{\log a}{\log b}=\frac{1}{x-1} \quad \Leftrightarrow \quad 1+\frac{\log a}{\log b}=1+\frac{1}{x-1}$

⇒ $\Leftrightarrow \quad \frac{\log b}{\log a}+\frac{\log a}{\log b}=\frac{x}{x-1} \quad \Leftrightarrow \quad \frac{\log b+\log a}{\log b}=\frac{x}{x-1}$

⇒ $\Leftrightarrow \quad \frac{\log (a b)}{\log b}=\frac{x}{(x-1)} \quad \Leftrightarrow \quad \log _b(a b)=\frac{x}{x-1} .$

Question 9. log2 = x, log₃ = y and log 7 = z, then the value of log (4. √63) is:

$2 x+\frac{2}{3} y=\frac{1}{3} z$
$\text 2 x+\frac{2}{3} y+\frac{1}{3} z$
$2 x-\frac{2}{3} y+\frac{1}{3} z$
$-2 x+\frac{2}{3} y+\frac{1}{3} z$

Solution:

⇒ $\log (4 \cdot \sqrt[3]{63})=\log 4+\log (\sqrt[3]{63})=\log 4+\log (63)^{1 / 3}=\log \left(2^2\right) \log \left(7 \times 3^2\right)^{1 / 3}$

⇒ $=2 \log 2+\frac{1}{3} \log 7+\frac{2}{3} \log 3=2 x+\frac{1}{3} z+\frac{2}{3} y .$

Question 10. If log₁₂27=a,then log₆ 6 is:

$\frac{3-a}{4(3+a)}$
$\frac{3+a}{4(3-a)}$
$\frac{4(3+a)}{(3-a)}$
$\frac{4(3-a)}{(3+a)}$

Solution:

Logi2 27 = a $\frac{\log 27}{\log 12}=a \quad \Rightarrow \quad \frac{\log 3^3}{\log \left(3 \times 2^2\right)}=a$

⇒ $\frac{3 \log 3}{\log 3+2 \log 2}=a \quad \Rightarrow \quad \frac{\log 3+2 \log 2}{3 \log 3}=\frac{1}{a}$

⇒ $\frac{\log 3}{3 \log 3}+\frac{2 \log 2}{3 \log 3}=\frac{1}{a} \quad \Rightarrow \quad \frac{2}{3} \frac{\log 2}{\log 3}=\frac{1}{a}-\frac{1}{3}=\left(\frac{3-a}{3 a}\right)$

⇒ $\frac{\log 2}{\log 3}=\left(\frac{3-a}{2 a}\right) \quad \Rightarrow \quad \log 3=\left(\frac{2 a}{3-a}\right) \log 2$

⇒ $\log _6 16=\frac{\log 16}{\log 6}=\frac{\log 2^4}{\log (2 \times 3)}=\frac{4 \log 2}{\log 2+\log 3}=\frac{4 \log 2}{\log 2\left[1+\left(\frac{2 a}{3-a}\right)\right]}=\frac{4}{\left(\frac{3+\pi}{3-a}\right)}=\frac{4(3-a)}{(3+a)}$

Question 11. If log₁₀5+log₁₀(x+5)+1,then x is equal to:

Solution:

⇒ $\log _{10} 5+\log _{10}(5 x+1)=\log _{10}(x+5)+1$

⇒ $\Rightarrow \log _{10} 5+\log _{10}(5 x+1)=\log _{10}(x+5)+\log _{10} 10$

⇒ $\left.\Rightarrow \log _{10}[5(5 x+1)]=\log _{10} \mid 10(x+5)\right] \Rightarrow 5(5 x+1)=10(x+5)$

⇒ $\Rightarrow 5 x+1=2 x+10 \Rightarrow 3 x=9 \Rightarrow x=3$

Question 12. If log10 7=a then log10$\left(\frac{1}{70}\right)$ is equal to:

-(1+a)
(1+a)-1
$\frac{a}{10}$
$\frac{1}{10 a}$

Solution:

⇒ $\log _{10}\left(\frac{1}{70}\right)=\log _{10} 1-\log _{10} 70=-\log _{10}(7 \times 10)=-\left(\log _{10} 7+\log _{10} 10\right)=-(a+1) .$

Question 13. If log 27 = 1.431, then the value of log 9 is:

0.934
0.945
0.954
0.958

Solution:

log₂₇=1.431=log(3)3=1.431=3log₃=1.431

log₃=0.477 log₉=log(3)2=2log₃=(2×0.477)=0.954

Question 14. If log₁₀2 = 0.3010, then log₂ 10 is equal to:

$\frac{699}{301}$
$\frac{1000}{301}$
0.3010
0.6990

Solution:

⇒ $\log _2 10=\frac{1}{\log _{10} 2}=\frac{1}{0.3010}=\frac{10000}{3010}=\frac{1000}{301} .$

Question 15. If log₁₀2 = 0.3010, then value of log₁₀ 5 is:

0.3241
0.6911
0.6990
0.7525

Solution:

⇒ $\log _{10} 5=\log _{10}\left(\frac{10}{2}\right)=\log _{10} 10-\log _{10} 2=1-\log _{10} 2=(1-0.3010)=0.6990$

Question 16.If log₃=0.477 and (1000)x=3 then x equals

0.0159
0.0477
0.159
10

Solution:

(1000)x = 3⇒ log [(1000)x] = log₃ ⇒ x log 1000 = log₃

⇒ xlog (10) = log 3 ⇒ 3x log₁₀ = log₃

⇒ 3x = log 3 $x=\frac{0.477}{3}=0.159$

Question 17. If log3 = 0.3010 and log 3 = 0.4771, then the value of log 512 is:

2.870
2.967
3.876
3.912

Solution:

⇒ $\log _5 512=\frac{\log 512}{\log 5}=\frac{\log 2^9}{\log \left(\frac{10}{2}\right)}=\frac{9 \log 2}{\log 10-\log 2} \quad=\frac{(9 \times 0.3010)}{1-0.3010}=\frac{2.709}{0.699}=\frac{2709}{699}=3.876 .$

Question 18. If log₁₀ 2 = 0.3010 and log₁₀ 7 = 0.8451, then the value of login 2.8 is:

0.4471
1.4471
2.4471
None of these

Solution:

= login (7 x 22) -1 = logm7 + 2 login2-1

= 0.8451 + 2 x 0.3010 – 1 = 0.8451 + 0.602 -1 = 0.4471

Question 19. If log (0.57) = 1.756, then the value of log 57 + log (0.57)3 + log √0.57 is:

0.902
2.146
1.902
1.146

Solution:

Log (0.57) = 1.756 => log 57 = 1.756 [-. mantissa will remain the same]

log 57 + log (0.57)3 + log V0.57

⇒ $\log 57+3 \log \left(\frac{57}{100}\right)+\log \left(\frac{57}{100}\right)^{1 / 2}$

⇒ $\log 57+3 \log 57-3 \log 100+\frac{1}{2} \log 57-\frac{1}{2} \log 100$

⇒ $\frac{9}{2} \log 57-\frac{7}{2} \log 100=\frac{9}{2} \times 1.756-\frac{7}{2} \times 2=7.902-7=0.902$

Question 20. If log₁₀ 2 = 0.30103, then number of digits in 264 is:

Solution:

Log characteristics(264) = 64 x log₁₀ 19.2 =Hence,(64 x

0.30103)the number 19.26592.of digits in 264 is 20.

Question 21. log₆ + log₅ is expressed as

log 11
log 30
log 5/6
none of these

Solution:

(2) log 30

Log₆ + log₅

We know logab + loga C = log_a b

log₆ + log₅ = log_6×5 = log₃₀

Question 22. log₁₀ 8 is equal to

2
8
3
none of these

Solution:

(3) 3

Log2 8 = log223 = 3 log₂ 2 = 3 x 1 = 3

Question 24. log 32/4 is equal to

log 32/log 4
log 32 – log 4
2
none of these

Solution:

log 32 -log 4

We know log$\frac{b}{c}$ = loga b – loga c

⇒ $\log \frac{32}{4}=\log 32-\log 4$

Question 24. log (1 x 2 x 3) is equal to

log1 + log 2 + log 3
log 3
log 2
none of these

Solution:

(a) log t + log 2 + log 3

We know Ion., be x = Ion,, b + log,, c +

loga x

log (1x2x3) =log₁+ log₂ +log₃

Question 25. The value of log 0.0001to the base 0.1 is

-4
4
1/4
None of these

Solution:

(2) 4

log_0.1 0.0001 = log_0.1 (0.1)⁴ = 4×1 = 4

Question 26. lf 2log_x = 41og₃,thexisequalto

3
9
2
none of these

Solution:

(2)

log x² = log 3⁴ = x² = 3⁴

x²– 81 = x = 9

Question 27. log¹² 64 is equal to

12
6
1
none of these

Solution:

(1) 12

log √2 (√2)12 = 12

Question 28. log² 1728 is equal to

2x/3
2
6
none of these

Solution:

(3)

log2√326.√36

log2√3(2√3)6 =6

Question 29. log (1/81) to the base 9 is equal to

2
1/2
-2
none of these

Solution:

(3) -2

log9 1 – log9 81

0 – 2 =- 2

Question 30. log 0.0625 to the base 2 Is equal to

4
5
l
none of these

Solution:

(4)None of the above

as 0.0625 is divisible only by 2

Question 31. Given log2 = 0.3010 and log3 = 0.4771 the value of log 6 is

0.9030
0.9542
0.778 1
none of these

Solution:

(3) 0.7781

as log 6 = log 2 + log 3

= 0.3010 + 0.4771 =0.7781

Question 32. The value of log2 log2 loga 16

0
2
1
none of these

Solution:

log₂ log₂ log₂ 16 = log₂ log₂ 4

= log₂ 2 =1

Question 33. The value of log $\frac{1}{3}$ to the base 9 is

$\frac{1}{2}$
$\frac{1}{2}$
1
None of these

Solution:

(1)$\frac{-1}{2}$

log₉ $\frac{1}{3}=$ log₉ 1 – log₉ 3

= 0 -log₉ (9)√2 =$\frac{-1}{2}$

Question 34. If log x + log y = log (x+y), y can be expressed as

x-1
x-1
x/x-1
None of these

Solution:

(3) x / x – 1

Log xy = log (x + y)

Xy = x + y

Xy-y = x

Y(x-l) = x

⇒ $Y=\frac{x}{x-1}$

Question 35. The value of log₂[log₂ {logs (log₃₂73)}] is equal to

1
4
0
None of these

Solution:

(2) 0

=log₂[log₂{log₃9}]

=log₂[log₂2]=log₂1=0

Question 36. If log₂ x + log₁₀x + log₁₆ x = 21/4, these x is equal to

8
4
16
None of these

Solution:

⇒ $=\frac{\log _{10} x}{\log _{10} 2}+\frac{\log _{10} x}{\log _{10} 4}+\frac{\log _{10} x}{\log _{10} 16}$

⇒ $ \frac{\log _{10} x}{\log _{10} 2}+\frac{\log _{10} x}{2 \log _{10} 2}+\frac{\log _{10} x}{4 \log _{10} 2}$

⇒ $\frac{4 \log _{10} x+2 \log _{10} x+\log _{10} x}{4 \log _{10} 2} $

⇒ $\frac{\log _{10} x^4+\log _{10} x^2+\log _{10} x}{4 \log _{10} 2}$

⇒ $\frac{\log _{10}\left(x^7\right)}{4 \log _{10}^2}=\frac{21}{4}=\frac{\log _{10} x^7}{\log _{10}{ }^2}=21 $

⇒ $\log _2 X^7=21=\log _2$

Question 37. Given that, log₁₀2 = x and log₃ = y, the value of login 60 is expressed as

x- y + 1
x + y + 1
x — y — 1
None of these

Solution:

(2) x + y+ 1.

Log₁₀ 60 = log₁₀6x 10

= log₁₀ 6 + log₁₀ 10

= log₁₀2 + log₁₀ 3 + 1

= x + y +1

Question 38. Given that log₁₀ 2 = x, log₁₀ 3 = y, then log₁₀ 12 is expressed in terms of x and y as

x + 2y-1
x + y-1
2x +y-l
None of these

Solution:

(3)2x + y-l

= log₁₀ 1-2

= log₁₀6 + log₁₀ 0.2

= log₁₀ (2×3) + log₁₀ $\frac{2}{10}$

= log₁₀ 2 + log₁₀3 + log₁₀ 2 – log₁₀10.

= x + y + x-l=2x + y-l

Question 39. Given that log x = m + n and log y = m -n, the value of log lOx / y2 is expressed in terms of m and n as

1 – m + 3n
m -1 + 3n
m + 3n + 1
None of these

Solution:

(1) 1 – m + 3n.

Log$\frac{10 x}{y^2}$ = log10 + logs- logy2

= log₁₀ + logx- 2logy

=l + m + n- 2 (m-n)

= 1 + 3n – m = 1 – m + 3n

Question 40. The simplified value of 2 log₁₀ 5 + log₁₀ 8 – y2 log₁₀ 4 is

1/2
4
2
None of these

Solution:

(3) 2.

= 21og₁₀ 5 + log₁₀ 8 – log₁₀2

= log₁₀25 + log₁₀8-log₁₀2

= log₁₀25 + log₁₀2 + log₁₀4 – log₁₀2

= log₁₀25 + Iog₁₀4 = log₁₀lOO = 2.

Question 41. log [1 – {1 – (1 – x2)’1}1]1/2 can be written as

log x2
log x
log1/x
None of these

Solution:

(2) log x

⇒ $=\log \left|1-\left(1 \cdot\left(\frac{1}{1-1^{\prime}}\right)\right)+1\right|^{1 / 2} \quad=\log \left|1-\left(\frac{1-x^{-}-1}{1-x^{\prime}}\right)\right|^{1 / / 2}$

⇒ $=\log \left|1-\left(\frac{1-x^1}{-x^2}\right)\right|^{1 / 2}=\log \left|\frac{-x^2-\left(1-x^2\right)}{-x^2}\right|^{-1 / 2}$

Question 42. The simplified value of log $\sqrt[4]{729 \cdot \sqrt[3]{9^{-1} \cdot 27^{-4 / 3}}} \text { is }/$

log 3
log 2
log 1/2
None of these

Solution:

(1) log₃

⇒ $=\log \sqrt[1]{729 \sqrt[2]{9^{-1}\left(3^3\right)^{-4 / 3}}} \quad=\log \sqrt[4]{3^6 \sqrt[3]{3^{-2} \cdot 3^{-4}}}$

⇒ $=\log \sqrt[1]{3^6 \cdot 3^{-6 / 3}} \quad=\log \sqrt[4]{3^4}=\log 3$

Question 43. The value of (log₁₀a x log₁₀b x log₁₀c)3 is equal to

3
0
1
None of these

Solution:

(3) 1

⇒ $\left(\frac{\log _{a^a}}{\log _{a^b}} \times \frac{\log _{a^a}}{\log _{a^c}} \times \log _{a^c}\right)^3=(1)^3=1$

Question 44. The logarithm of 64 to the base 2\2 is

2
√2
1/2
None of these

Solution:

(4) None of these

⇒ $=\log _{\sqrt[2]{2}} 2^6=\log _{\sqrt[2]{2}} 2^4 \sqrt{2}^4=\log _{\sqrt[2]{2}}(\sqrt[2]{2})^4=4$

Question 45. The value of Ingn 25 given log₁₀ 2 = 0.3010 Is

1
2
1.5482
None of these

Solution:

(3) 1.5482

⇒ $ \log _8 5^2=2 \log _8 5=\frac{2 \log _{10} 5}{3 \log _{10^2}} \quad=\frac{2 \log _{10} \frac{1}{2}}{3 \log _{10} 2} \quad=\frac{2}{3} \frac{\left(\log _{10} 10-\log _{10} 2\right)}{\log _{10^2}}$

⇒ $\frac{2}{3} \frac{(1-0.3010)}{0.3010}=1.54817=1.5482 $

Question 46. The value of$\frac{\log _1 8}{\log _3 16 . \log _6 10}$

3log₁₀2
7log₁₀3
3log₆z
None

Solution:

⇒ $\frac{\log _3 B}{\log _7 16 \log _4 10}=\frac{\log _3 2^3}{\log _3 2^4 \times \log _2 210} \quad=\frac{3 \log _3 2}{\frac{4}{2} \log _3 2 \times \frac{1}{2} \log _2 10}=\frac{3}{\log _2 10}=3 \log _{10} 2(\text { a) is correct }$

Question 47. log 144 is equal to:

2log₄+2log₂
4log₂+2log₃
3log₂+4log₃
3log₂-4log₃

Solution:

Log 144 = log (16×9] = log 16 + log 9= log 2⁴ + log 3² = 4 log 2 + 2 log 3

(2) is correct.

Question 48. If log $\left(\frac{a+b}{4}\right)=\frac{1}{2}(\log a+\log b)$ then$: \frac{a}{b}+\frac{b}{a}$.

Solution:

⇒ $\log \left(\frac{a+b}{4}\right)=\frac{1}{2}(\log a+\log \mathrm{b})$

⇒ $\text { Or } \log \left(\frac{a+b}{4}\right)=\log (a b)^{1 / 2} \quad \text { Or } \frac{a+b}{4}=\sqrt{a b} \quad \text { Or } \mathrm{a}+\mathrm{b}=\sqrt[4]{a b}$

Squaring on both sides; we get (a + b)² = 16ab

Or a² + b² + 2ab= 16ab. Or a² + b² = 14ab

⇒ ${Or} \frac{a^2}{a b}+\frac{b^2}{a b}=\frac{14 a b}{a b} [Dividing by ab o both sides]$

⇒ ${Or} \frac{a}{b}+\frac{b}{a}=14$

(2) is correct

Question 49. If log²g x = 3$\frac{1}{3}$ find the value of x

Solution:

(1)

⇒ $\log _{\sqrt{8}^x}=\frac{10}{3} \Leftrightarrow x=(\sqrt{8})^{10 / 3}=\left(2^{2 / 3}\right)^{10 / 3}=2^{\left(\frac{2}{2} \times \frac{10}{3}\right)}=2^5=32 .$

Question 50. Evaluate :

log₅3 x log₂₇ 25
log₉ 27 – log₂₇ 9
1. 2,2
2. $\frac{4}{2}, \frac{1}{6}$
3. $\frac{2}{3}, \frac{5}{6}$
4. None of these

Solution:

(3)

⇒ $(1) \log _5 3 \times \log _{27} 25=\frac{\log 3}{\log 5} \times \frac{\log 25}{\log 27}=\frac{\log 3}{\log 5} \times \frac{\log \left(5^2\right)}{\log \left(3^2\right)}=\frac{\log 3}{\log 5} \times \frac{2 \log 5}{3 \log 3}=\frac{2}{3}$

$Let \log _y 27=n.$

Then 9n = 27 – 32n = 33 ⇔ 2n = 3 »

⇒ $\mathrm{n}=\frac{2}{3}$

Again, let log₂₂ 9 =m.

Then, 27^m= 9 ⇔ 3^3m = 32 ⇔ 3m = 2 ⇔ m = $\mathrm{n}=\frac{2}{3}$

log₉ 27 – log ₂₇ 9=(n-m)=$\left(\frac{3}{2}-\frac{2}{3}\right)=\frac{5}{6}$

Question 51.Simplify:$\left(\log \frac{75}{16}-2 \log \frac{5}{7}+\log \frac{32}{243}\right)$

log 3
log2
2
None of these

Solution:

⇒ $\log \frac{75}{16}-2 \log \frac{5}{9}+\log \frac{32}{243}=\log \frac{75}{16}-\log \left(\frac{5}{9}\right)^2+\log \frac{32}{243}=\log \frac{75}{16}-\log \frac{25}{81}+\log \frac{32}{243}$

⇒ $=\log \left(\frac{75}{16} \times \frac{32}{243} \times \frac{81}{25}\right)=\log 2$

Question 52. If log x = a-b; log y = a + b then log$\left(\frac{10 x}{y^2}\right)$

l-a+3b
a-l+3b
l+3b-l
l-b+3a

Solution:

(1) is correct

log x = a + b; log y = a-b

$\log \left(\frac{10 x}{y^2}\right)=\log _{10}+\log x-\log y^2$ =1 + a + b- 21ogy=l + a + b- 2 (a-b)

=l + a + b-2a + 2b =l- a + 3b

Question 53. If log x = m + n ; logy = m – n then log$\left(\frac{10 x}{y^2}\right)=$

1-m + 3n
m-1+3n
m+3n+1
None

Solution:

(a) If log x = m + n; log y = m-n

Then $\log \left(\frac{10 x}{y^2}\right)$ =log!0 + logx-logy2= 1 + logx- 2 logy = 1 + (m+n) – 2(m-n)

Question 54. The integral part of a logarithm is called______, and the decimal part of a logarithm is called______.

Mantissa, Characteristic
Characteristic, Mantissa
Whole, Decimal
None of these

Solution:

(2) is correct.

Question 55. The value of$\frac{1}{\log _3 60}+\frac{1}{\log _4 60}+\frac{1}{\log _5 60}=$

Solution:

(2) is correct. log₆₀ 30 + log₆₀ 4 + log₆₀ 5 = log₆₀ (3x4x5)+ log₆₀60 =1

Question 56.If log10 (Xÿ + x) – log (x + 1) = 2 then the value of x is

Solution:

(3) is correct.

⇒ $\log _4 \frac{\left(x^2+x\right)}{(x+1)}=2 \quad \text { Or } \log _4\left\{\frac{x(x+1)}{(x+1)}\right\}=2 \quad \text { Or } \log _4 \mathrm{X}=2 \Rightarrow \mathrm{x}=4^2=16$

Question 57. log (l3 + 23 + 3s + + n) = ______.

2 log n + 2 log (n+1) – 2 log 2
log n + 2 log (n + 1) – 2 log
2 log n + log (n + 1) – 2 log 2
None

Solution:

log (l3 + 23 + 33+ + n3)

⇒ $=\log \left(\frac{n(n+1)}{2}\right)^2=2 \log \frac{n(n+1)}{2} \quad=2[\log n+\log (n+1)-\log 2]$

= 2 log n + 2 log(n+l) – 2 log 2 So, (1) is correct.

Question 58. $7 \log \left(\frac{16}{15}\right)+5 \log \left(\frac{25}{24}\right)+31 \log \left(\frac{81}{80}\right)$

0
1
log2
log3

Solution:

Tricks:- $7 \log \left(\frac{16}{15}\right)+5 \log \left(\frac{25}{24}\right)+3 \log \left(\frac{81}{80}\right)$

⇒ $\log \left(\frac{16}{15}\right)^7+\log \left(\frac{25}{24}\right)^5+\log \left(\frac{81}{80}\right)^3=\log \left[\left(\frac{16}{15}\right)^7 \cdot\left(\frac{25}{24}\right)^5 \cdot\left(\frac{81}{80}\right)^3\right]$

We get; it is approx. 2 (3) is correct

Question 59. The value of the expression alog_ab.log_bC.log_cd.log_dt.

t
abcdt
(a+b+c+d+t)
None.

Solution:

alog_ab.log_bc.log_cd.log_dt

=a¹^loga^t=t¹=t

∴ (1) is correct

Question 60. If login on x= then x is given by:

1/100
1/10
1/20
None of these

Solution:

log100000x=$\frac{-1}{4}$

⇒ $ (10000)^{-\frac{1}{4}}=x$

⇒ $ \left(10^4\right)^{-\frac{1}{4}}=x$

⇒ $\mathrm{x}=10^{-1}=\frac{1}{10}$

(2) is correct.

Question 61. Find the value of x which satisfies the relation log10 3 + log10 (4x + 1) = log10 (x + 1) + 1

$\frac{3}{2}$
$\frac{5}{2}$
4
$\frac{7}{2}$

Solution:

log ₁₀ 3=log10(4x+1)=log₁₀(x+1)+1
$\log _{10} 3+\log _{10}(4 x+1)=\log _{10}(x+1)+\log _{10} 10 \Leftrightarrow \log _{10}[3(4 x+1)]=\log _{10}[10(x+1)]$
$\Leftrightarrow 3(4 x+1)=10(x+1) \Leftrightarrow 12 x+3=10 x+10 \Leftrightarrow 2 x=7 \Leftrightarrow x=\frac{7}{2}$

Question 62. Simplify:$\left[\frac{1}{\log _{x y}(x y z)}+\frac{1}{\log _{y z}(x y z)}+\frac{1}{\log _{z x}(x y z)}\right]$

0
1
2
None of these

Solution:

(3)

Given expression = logxyz (xy) + \ogxyz (yz) + logxyz ) (zx)

= logxyz (xy x yz x zx) = logxyz (xyz)2

= 2logxyz(XYZ)=2×1=2

Question 63. If log₁₀ 2 = 0.30103, find the value of log₁₀ 50.
Solution:

log₁₀ 50 = log $\left[\frac{100}{2}\right]$ = log₁₀(, 100- log₁₀ 2 = 2- 0.30103 = 1.69897.

Question 64. Iflog (2a – 3b) = log a – log b, then a = ?

$\frac{3 b^2}{2 b-1}$
$\frac{3 b}{2 b-1}$
$\frac{b^2}{2 b+1}$
$\frac{3 b^2}{2 b+1}$

Solution:

Log(2a-3b)=log$\frac{a}{b}$

Or 2a – 3b =$\frac{a}{b}$

Or 2ab-3b2 Or a(2b- 1) = 3b2

Or $a=\frac{3 b^2}{2 b-1}$

(1) is Correct

Question 65. If log 2 = 0.3010 and log 3 = 0.4771, find the values of:

Log 25
Log 4.5
1. 1.398, 0.6532
2. 1.389, 0.649
3. 1.19, 0.697
4. None of these

Solution:

Log 25 = log$\left[\frac{100}{4}\right]$ = log 100 – log4 = 2-2 log2 = (2 – 2 x 0.3010) = 1.398.

Log 4.5 = log$\left[\frac{9}{2}\right]=$ log 9 – log2 = 21og 3 -log 2 = (2 x 0.4771 – 0.3010) = 0.6532

Question 66. If log 2 = 0.30103, find the number of digits in 256

Solution:

Log (256) = 56 log 2 = (56 x 0.30103) = 16.85768.

Its characteristic is 16 hence, the number of digits in 2s6 is 17.

Question 67. $\frac{1}{\log _{a b}(a b c)}+\frac{1}{\log _{b c}(a b c)}+\frac{1}{\log _{(a b c)}} \text { is equal to: }$

0
1
2
-1

Solution:

⇒ $\frac{1}{\log _{a b}(a b c)}+\frac{1}{\log _{b c}(a b c)}+\frac{1}{\log _{c a}(a b c)}$ = Logabc (ab.bc.ca) = logabc (abc)2

= 2 logabc (abc) = 2×1 = 2

Question 68. Log4 (x2 + x) — log4(x + 1) = 2. Find x

16
0
-1
None of these

Solution:

⇒ $\log _4\left(x^2+x\right)-\log _4(x+1)=2$

Log₁₀(x2 + x)- logA(x + 1) = 2

⇒ $\log _4 \frac{x(x+1)}{x+1}=4^2$

Or x = 14

(1) is correct

Question 69. If logab + loga c = 0 then

b=c
b = -c
b=c=l
b and c are reciprocals.

Solution:

Loga b + Loga c = 0 or Loga (bc) = Loga1 bc =1 b =$\frac{1}{c}$

(4) is correct

Question 70. If log 2 x + log.(X = 6), then the value of x is

Solution:

(1)

Detail method: log₂ x + log , x = 6 (Or )log₂ x + log-22 x = 6 Or log₂ x + log₂x = 6

⇒ $\left(1+\frac{1}{2}\right) \log _2 x=6 \quad \text { Or } \log _2 x=\frac{6 \times 2}{3}=4 x=2^4=16$

Question 71. If log₁₀ Y = 100 and log₂ x = 10, then the value of’Y’is’:

210
2100
21000
210000

Solution:

Log x x = 100

∴ x = 2¹⁰ Now logx y = 100 y = x1000 y = (2¹⁰)¹⁰⁰ = 2¹⁰⁰⁰

Question 72. Which of the following is true?$\text { If } \frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{1}{a b c}$

log (ab+bc+ca) = abc
$\log \left(\frac{1}{b}+\frac{1}{b}+\frac{1}{c}\right)=a b c$
Log (abc) = 0
Log (a+b+c) = 0

Solution:

(4) $\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{1}{a b c}$

Multiplying both sides by a b c $ \frac{a b c}{a b}+\frac{a b c}{b c}+\frac{a b c}{c a}=\frac{a b c}{a b c}$

Or; c + a + b = 1 Or; a + b + c =1

Taking logs on both sides; we get. Log (a+b+c) = log¹⁰ =

Question 73. Find the value of log49.1og32 =

Solution:

(4) log4 9.1og:< 2 = log (22) (32).log3 2 $=\frac{2}{2} \log _2 3 \cdot \log _3 2$=1×1=1

Question 74. If x = log24 12; y=log3G 24; z = log48 36 then xyz +1 =?

Solution:

(c)

XYZ + 1 = log₂₄ 12; y=log36

if 24; z = log₄₈ 36 +1

= log₄₈ 12+log₄₈ 48

= login (12×48) = log₄₈ (12 x 2)2 =2 log₄₈ 24 = 2log3t,24.log₄₈ 36 = 2yz

Question 75. If x2 + y2 = 7xy then log$\frac{1}{3}$(x + y) =

logs + logy
$\frac{1}{2}(\log x+\log y) $
$\frac{1}{3}(\log x+\log y)$
$\frac{1}{3}(\log x \cdot \log y)$

Solution:

(2) is correct $\log _3 \frac{1}{3}(x+y)=\frac{1}{2} 2 \log \left\{\frac{1}{3}(x+y)\right\} $

⇒ $=\frac{1}{2} \log\left\{\frac{1}{3}(x+y)\right\}^2$

⇒ $=\frac{1}{2} \log \left(\frac{x^2+y^2+2 x y}{9}\right)$

⇒ $=\frac{1}{2} \log \left(\frac{7 x y+2 x y}{9}\right)$

⇒ $=\frac{1}{2} \log (x y)=\frac{1}{2}(\log x+\log y)$

CA Foundation Maths Solutions For Chapter 2 Equations

November 15, 2024July 5, 2024 by Marksparks

CA Foundation Maths Solutions For Chapter 4 Equations

Introduction and Meaning:

The equation is defined to be a mathematical statement of equality.

Determination of the value of the variable that satisfies an equation is called a solution of the equation or root of the equation.
An equation in which the highest power of the variable is 1 is called a Linear (or simple) equation.
This is also called the equation of degree 1.
Two or more linear equations involving two or more variables are called Simultaneous Linear Equations.
An equation of degree 2 (Highest Power of the variable is 2) is called Quadratic equation and the equation of degree 3 is called Cubic Equation.

Simple Equation

A simple equation is one unknown x in the form of a x + b = 0.

where a, and b are known constants and a1 0

Note: A simple equation has only one root.

Read and Learn More CA Foundation Maths Solutions

Simultaneous Linear Equations in Two Unknowns

Two such equations a₁x+b₁y +c₁= 0 and a₂ x+b₂y + c₂ = 0 form a pair of simultaneous equations in x and y.
A value for each unknown that satisfies simultaneously both equations will give the roots of the equations.

Method of solution

1. Elimination Method: In this method, two given linear equations are reduced to a linear equation in one unknown by eliminating one of the unknown and then solving for the other unknown

CA Foundation Maths Chapter 2 Equations Solutions

Example 1: Solve, 2x+5y = 9 and 3x- y =5.
Solution:

2x + 5y = 9 …..(1)

3x – y = 5 …..(2)

By making (1) x 1, 2x+5y = 9

And by making (2) x 5, 15x- 5y = 25

Adding 17x- 34 or x- 2. Substituting this values of x in (1) i.e. 5y = 9 – 2x we find;

5y = 9 – 4 =5

y = 1

x = 2,

y =1.

2. Cross Multiplication Method:

Let two equations be:

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

We write the coefficients of x, y, and constant terms and two more columns by repeating the coefficients of x and y as follows:

1 2 3 4

b₁ c₁ a₁ b₁

b₂ c₂ a₂ b₂

⇒ and the result is given by$y: \frac{x}{b 1 c 2-b 2 c 1}=\frac{y}{c 1 a 2-c 2 a 1}=\frac{x}{a 1 b 2-a 2 b 1}$

⇒ so the solution is: x = $=\frac{b 1 c 2-b 2 c 1}{a 1 b 2-a 2 b 1} \quad y=\frac{c 1 a 2-c 2 a 1}{a 1 b 2-a 2 b 1}$

Example 2: Solve 3x+2y+17 =0, 5x-6y-9=0

Solution: 3x +2y 17= 0…..(1)

5x – 6y -9 = 0…..(3)

Method of elimination:

By (1) x 3 we get 9x + 6y + 51 = 0 …

Adding (2) and (3) we get 14x+42=0

Or x=$x=\frac{42}{14}=-3$

Putting x = -3 in (1) we get 3(-3) + 17 = 0

Or, 2y + 8 $=0 \text { or, } y=-\frac{8}{2}-4$

So,x = -3 andy = -4

Method of cross-multiplication:

3x + 2y + 17 = 0

5x – 6y- 9 = 0

⇒ $ \frac{x}{2(-9)-17(-6)}=\frac{y}{17(5)-3(-9)}=\frac{1}{3(-6)-5(2)}$

Or, $ \quad \frac{x}{84}=\frac{y}{112}=\frac{1}{-28}$

Or $\frac{x}{3}=\frac{y}{4}=\frac{1}{-28}$

Or x = -3 , y = -4

Method of Solving Simultaneous Linear Equation with Three Variables

Example 1: Solve for x, y and z:

2x-y + z = 3, x + 3y-2z=ll, 3x-2y + 4z=l

Solution:

(1) Method Of Elimination

2x – y + z = 3…..(1)

x + 3y — 2z =11…..(2)

3x – 2y + 4z = 1…..(3)

By (1) x 2 we get

4x – 2y + 2z = 6…..(4)

By (2) + (4),5x + y= 17…..(5)

By (2) x 2, 2x + 6y- 4z = 22…..(6)

By (3) + (6), 5x + 4y = 23…..(4)

By (5) – (7), – 3y = -6 ory = 2

Putting y = 2 in (5) 5x + 2 = 17, or 5x = 15 or, x=3

Putting = 3andy = 2 in (1)

2×3-2+ z =3

Or 6 – 2 + z = 3

Or 4 + z = 3

Or z=-l

So x- 3, y- 2, Z = -1 is the required solution

(2) Method Of Cross-Multiplication

We write the equations as follows:

2x-y + (z – 3) = 0

x + 3y + (-2z-ll) = 0

By cross multiplication

⇒ $ \frac{x}{-1(-2 z-11)-3(z-3)}=\frac{y}{(z-3)-2(-2 z-11)}=\frac{1}{23-1(-1)}$

⇒ $\frac{x}{20-z}=\frac{y}{5 z+19}=\frac{1}{7}$

⇒ $X=\frac{20-z}{7}, y=\frac{5 z+19}{7}$

Substituting above values for x and y in equation (iii) i.e. 3x- 2y + yz = 1, we have

⇒ $3{20-z}{7}-2{5 z-19}{7}+4 z=1$

Or 60 – 3z = lOz- 38 + 28 z = 7

Or 15z = 7-22 orl5z = -15 or Z=l

⇒ $x=\frac{20-(-1)}{7}=\frac{21}{7}=3, \quad y=\frac{5(-1)+19}{7}=\frac{14)}{7}=2$

Thus x = 3,y= 2, Z= -1.

An equation of the form ax2 + fax + c = 0 where x is a variable and a, b, c are constants with a ≠ 0 is called a quadratic equation or equation of the second degree.

When b = 0 the equation is called a pure quadratic equation; when b * 0 the equation is called an affected quadratic.

Examples:

1. 2x² + 3x + 5 = 0

2. x²-x = 0

3. 5x² – 6x – 3 = 0

The value of the variable say x is called the root of the equation. A quadratic equation has two roots.

How to find out the roots of a Quadratic Equation:

ax² +bx + c = 0 (a ≠ 0)

⇒ $\text { Or } x^2+\frac{b}{a} x+\frac{c}{a}=0$

Or $x^2+2 \frac{b}{2 a} x+\frac{b^2}{4 a^2}=\frac{b^2}{4 a^2}-\frac{c}{a}$

Or$\left(x+\frac{b}{2 a}\right)^2=\frac{b^2}{4 a^2}-\frac{c}{a}$

Or$\mathrm{x}+\frac{b}{2 a}=\frac{ \pm \sqrt{b^2-4 a c}}{2 a}$

Or$\mathrm{x}=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$

Sum and Product of the Roots:

Let one root be a and the other root be p

Now $ \alpha+\beta & =\frac{-b+\sqrt{b^2-4 a c}}{2 a}+\frac{-b-\sqrt{b^2-4 a c}}{2 a}=\frac{-b+\sqrt{b^2-4 a c}-b-\sqrt{b^2-4 a c}}{2 a}$

⇒ $\frac{-2 b}{2 a}=\frac{-b}{a}$

Thus sum of roots = $-\frac{b}{a}=-\frac{\text { coefficient of } x}{\text { coefficient of } x^2}$

⇒ $x \beta=\left(\frac{-b+\sqrt{b^2-4 a c}}{2 a}\right)\left(\frac{-b-\sqrt{b^2-4 a c}}{2 a}\right)=\frac{c}{a}$

So the product of the roots =$\frac{\mathrm{e}}{a}=\frac{\text { Constant term }}{\text { coefficient of } x^2}$

How to Construct a Quadratic Equation

For the equation ax² + bx + c = 0 we have

⇒ $\text { Or } x^2+\frac{b}{a} x+\frac{c}{a}=0$

⇒ $\text { Or } x^2-\left(-\frac{b}{a}\right) x+\frac{c}{a}=0$

Or A-2 – (Sum of the roots) x + Product of the roots = 0

Nature of the Roots

⇒ $X=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$

If b² — 4ac = 0 the roots are real and equal;

If b²– 4ac > 0 then the roots are real and unequal (or distinct);

If b²– 4ac < 0 then the roots are imaginary;

If b²– 4ac is a perfect square (≠0) the roots are real, rational, and unequal (distinct);

If b² – 4ac > 0 but not a perfect square the roots are real, irrational, and unequal.

Since b²– 4ac discriminates the roots b²– 4ac is called the discriminant in the equation ax² + bx + c = 0 as it discriminates between the roots.

Note:

Irrational roots occur in conjugate pairs that is if (m + Vn) is a root then (m – Vn) is the other of the same equation.
If one root is reciprocal to the other root then their product is 1 and so $\frac{c}{a}=1 \text { i.e. } c=\mathrm{a}$
If one root is equal to another root but opposite in sign then.
- Their sum = 0 and so $\frac{b}{a}=1 \text { i.e. } c=\mathrm{a}$

Summary, Tips, Tricks And Formulae

CA Foundation Maths Solutions For Chapter 2 Equations

An equation is defined as a mathematical statement of equality.

Types of equations

Linear equation in one variable.

Linear simultaneous equations in 2 or 3 variables.
Quadratic equations.
Cubic equations.
Bi-quadratic equations.
Exponential equations.

Quadratic Equations

A quadratic equation is defined as the polynomial equation of degree 2.
A quadratic equation can be expressed in the following general form: ax² + ba + x = 0, (a ≠ 0)
A quadratic equation can also be expressed in the factor form as follows: a(x-α){x-β)
1. Here, a and /3 are the roots or solutions of quadratic equations;
2. The general solution of the quadratic equation can be obtained as follows:
$\alpha=\frac{-b+\sqrt{b^2-4}}{2 a} \text { and } \beta=\frac{-b-\sqrt{b^2-4 a c}}{2 a}$
- Sum of roots =$a+\beta=-\frac{b}{a}$
Product of roots =$\alpha\beta=\frac{c}{a}$

Structure of Quadratic Equations

If the sum (S) (α + β) and Product (P) (αβ) of the roots are known, then the quadratic is x² – Sx + P = 0

Sign of Roots of a Quadratic Equation

When c = 0, one root of the equation must be 0,
When h and c are 0, then both the roots must be 0.
If a,b, and c all are 0, both roots are negative.
If a and c are of some sign, opposite to that of, then both the roots will be positive.
If a and c are of opposite signs, one root is positive, and another root is negative.

Nature of Roots

The Expression “b² – 4ac” is called the “Discriminant (D)” of the quadratic equation.

When D> 0, Roots are real and distinct.
When D = 0, Roots are real and equal.
When D < 0, the Roots are imaginary.
When D > 0, Roots are real.
When D is a perfect square, Roots are real, rational, and unequal.
When D is not a perfect square, Roots are real, rational, and unequal.
If roots are equal use b² = 4ac.
If roots are reciprocal of each other, use a = c
If roots are equal but of opposite sign, use b = 0
If roots are reciprocal but opposite in sign, use c = -0

Note

1. Irrational roots will always appear in conjugate pairs.

it = (a- √b) and (1= (a + √b)

2. Imaginary roots will always appear in conjugate pairs.

u = (a- ib) and β = (a + ib)

Cubic Equations

1. A cubic equation is a polynomial equation of degree 3, and the general form is represented as follows:

ax³+ bx² + cx + d = 0; (a ≠ 0)

2. The factor form of the cubic equation is given as follows:

a(x- α)(x- β)(x- γ) = 0

Here, α,β, and γ are the roots or solutions of the cubic equation.

3. Sum of roots = α+β+γ= -b/a

4. Product of the roots = αβγ = -d/a

Bi-Quadratic Equations

A bi-quadratic equation is a polynomial of degree 4, and the general form is represented as follows:

ax⁴+ bx³ + cx² + dx + e = 0; (a * 0)

The factor form of a cubic equation is given as follows:

a(x- α)(x- β)(x-γ)(x-δ) = 0

Here, α, β,andγ are the roots or solutions of the bi-quadratic equation.

The sum of roots = α + β +γ + δ = -b/a

Product of the roots = αβγδ = e/a

Equations Chapter 2 CA Foundation Answers

CA Foundation Maths Solutions For Chapter 2 Exercise – 1

Simple Or Linear Equation in one Variable

Question 1. The equation -7x +1 = 5 – 3 x will be satisfied for x equal to:

2
-1
1
None of these

Solution:

(2)

7x + 1 = 5 – 3x

-4 = 4x

X = -1

Question 2. The root of the equation$1 \frac{x+4}{4}+\frac{x-5}{3}=11$ is

20
10
2
None of these

Solution:

(1)

⇒ $\frac{x+4}{4}+\frac{x-5}{3}=11$

3x+ 12 + 4x – 20 = 132

7x = 140 → x = 20

Question 3. Pick up the correct value of x for$\frac{x}{30}=\frac{2}{45}$

x = 5
x = 7
$x=1 \frac{1}{3}$
None Of these

Solution:

(3)

⇒ $\frac{x}{30}=\frac{2}{45} \rightarrow \frac{x}{2}=\frac{2}{3} \rightarrow \mathrm{x}=\frac{1}{{ }^3} $

Question 4. The solution of the equation $\frac{x+24}{5}=4+\frac{x}{4}$

6
10
16
None of these

Solution:

(3)

⇒ $\frac{x+24}{5}=\frac{4+x}{4}$

⇒ $\frac{4 x+96-5 x}{20}=4$

⇒ $-\mathrm{x}=-16 \rightarrow \mathrm{x}=16$

Question 5. 8 is the solution of the equation

$\frac{x+4}{4}+\frac{x-5}{3}=11$
$\frac{x+4}{2}+\frac{x+10}{9}=8$
$\frac{x+24}{5}=4+\frac{x}{4}$
$\frac{x-15}{10}+\frac{x+5}{5}=4$

Solution:

(2)

⇒ $\frac{x+4}{2}+\frac{x+10}{9}=8 \Rightarrow \frac{8+4}{2} \rightarrow \frac{8+10}{9}=6+2=8$

Question 6. The value of that satisfies the equation$\frac{y+11}{6}-\frac{y+1}{9}=\frac{y+7}{4} \text { is }$

-1
7
1
$-\frac{1}{7}$

Solution:

(3)

⇒ $\frac{3 y+33-2 y+2}{18}=\frac{y+7}{4}$

⇒ $\frac{y+35}{18}=\frac{y+7}{4} \rightarrow \frac{2 y+70}{36}=\frac{9 y+63}{36}$

⇒ 7y = 7 ⇒ y = 1

Question 7. The solution of the equation (p+2) (p-3) + (p+3) (p-4) = p(2p-5) is

6
7
5
None of these

Solution: (1)

Question 8. The equation $\frac{12 x+1}{4}=\frac{15 x-1}{5}+\frac{2 x-5}{3 x-1}$ is true for.

A = 1
x = 2
A = 5
x = 7

Solution:

(4)

⇒ $\frac{12(7)+1}{1}=\frac{85}{4}$

⇒ $\frac{15(7)-1}{1}+\frac{2(7)-5}{3(7)-1}=\frac{425}{20}=\frac{85}{4}$

Question 9. Pick up the correct value x for which$\frac{x}{0.5}-\frac{1}{0.05}+\frac{x}{0.005}-\frac{1}{0.0005}=0$

x = 0
x = 1
x = 10
None of these

Solution:

(3)

⇒ $\frac{10 x}{5}-\frac{100}{5}+\frac{1000 x}{5}-\frac{10000}{5}=0$

⇒ $\frac{1010 x}{5}=\frac{10000+100}{5}$

10l0x = 10100

X = 10

Question 10. The sum of two numbers is 52 and their difference is 2. The numbers are

17 and 15
12 and 10
27 and 25
None of these

Solution:

(3)

Let x lie bigger no, y be a smaller number

27and25

27 + 25 = 52 and 27 – 25 = 2

Question 11. The diagonal of a rectangle is 5 cm and one of at sides is 4 cm. Its area is

20 sq. cm.
l2 sq. cm.
10 sq. cm.
None of these

Solution:

(2)

Diagonal = 5cm

Sides = 4cm x x

42 + x2 = 52 by Pythagoras theorem

x2 = 9

x = 3

Area = 4×3 = I2sq cm

Question 12. Divide 56 into two parts such that three times the first part exceeds.one-third of the second by 48. The parts are.

(20, 36)
(25.31)
(24, 32)
None of these

Solution:

(1)

3x = $\frac{1}{3}$y + 48

⇒ $\frac{1}{3}$

⇒ $\frac{y}{3}$

9x – 144 = y

56 = x + 9x – 144

200 = lOx ⇒ x = 20, y = 36

Question 13. The sum of the digits of a two-digit number is 10. If 18 is subtracted from it the digits in the resulting number will be equal. The number is

37
73
75
None of these

Solution:

(2)

7 + 3 = 10

73-18 = 55

Question 14. The fourth part of a number exceeds the sixth part by 4. The number is

84
44
48
None Of these

Solution:

(3)

⇒ $\frac{x}{4}=\frac{x}{6}+4$

⇒ $\frac{x}{4}-4=\frac{x}{6} \rightarrow 3 x-48=2$

x = 48

Question l5. Ten years ago the age of a father was four times of his son. Ten years hence the age of the father will be twice that of ofIlls son. The present ages of the father and the son are.

(50. 20)
60, 20)
(55,25)
None of these

Solution:

(1)

4 (y – 10] = x – 1o

4y – 40 = x – 10

4y = 3(30)- y = $\frac{x+30}{4}$

(x+ 10] = 2 (y+ 10)

X+ 10 = 2y + 20

⇒ $\frac{x-10}{2}=\frac{x-10}{2}$

X + 30 = 2x – 20 => x = 50, y = 20

Question 16. The product of two numbers is 3200 and the quotient when the larger number is divided by the smaller is 2. The numbers are

(16. 200)
(160, 20)
(60,30)
(80, 40)

Solution:

(4)

xy = 3200 x = 2; y= x= 2y

⇒ $\frac{x}{2}=y$

x2 = 6400 x = 80 y = 40

Question 17. The denominator of a fraction exceeds the numerator by 2. If 5 is added to the numerator the fraction increases by unity. The fraction is.

$\frac{5}{7}$
$\frac{1}{3}$
$\frac{7}{9}$
$\frac{3}{5}$

Solution:

(4)

⇒ $\frac{x}{x+2}$

⇒ $\frac{1+5}{x+2}=\frac{x}{x+2}+1$

x+5=2 x+2

3=x

function $ =\frac{3}{5}$

Question 18. Three persons Mr. Roy, Mr. Paul, and Mr. Singh together have Mr. Paul has less than Mr. Roy and Mr. Singh has got less than Mr. Roy. They have the money.

(₹20,₹16,₹15)
(₹15,₹20,₹16)
(₹25,₹11,₹5)
None of these

Solution:

(1)

20- 16 = 4,

2a- 15 = 5

Question 19. A number consists of two digits. The digits in the ten’s place are 3 times the digits in the unit’s place. If 54 is subtracted from the number the digits are reversed. The number is

Solution:

(3)

9 = 3 (3)

93-54= 39

Question 20. One student is asked to divide half of a number by 6 and the other half by 4 and then to add the two quantities. Instead of doing so, the student divides the given number by 5. If the answer is 4 short of the correct answer then the number was

320
400
480
None of these.

Solution:

(3)

Let number be x $\frac{x}{12}+\frac{x}{8}=4+\frac{x}{5}$

⇒ $\frac{2 x+3 x}{24}=\frac{4+x}{5} \Rightarrow \frac{5 x}{24}-\frac{x}{5}=4$

⇒ $\frac{25 x-24 x}{24 \times 5}=4$

x = 4 x 24 x 5

x = 480

Question 21. If several which the half is greater than $\frac{1}{5}$th of the number by 15 then the number is

50
40
80
None of these

Solution:

(1)

let number be x according to question

⇒ $\frac{x}{2}=\frac{x}{5}+15$

⇒ $\frac{x}{2}-\frac{x}{5}=15$

3x = 150 ⇒ x = 50

Question 22. $\text { If } \frac{x-b c}{b+c}+\frac{x-c a}{c+a}+\frac{x-a b}{a+b}=$ a + b + c the value of x is

a2+b2+c2
a(a+b+c)
(a+b)(b+c)
ab+bc+ca

Solution:

(4)

ab + be + ca

⇒ $\rightarrow \frac{a b+c a}{b+c}+\frac{a b+b c}{a+c}+\frac{b c+c a}{a+b}$

= a+b+c

Question 23. A man rowing at the rate of 5 km in an hour in still water takes thrice as much time going 40 km up the river as in going 40 km down. Find the rate at which the river flows:

4.5km/hr
7.5 km/hr
2.5 km/hr
None

Solution:

Let the speed of the river be x km/hr

Speed of man in still water = 5 km/hr

Speed while upward rowing will be 5 – x

Speed while downward rowing will be 5 + x

We know speed = distance or time

Let the time taken for upward rowing be T1 and the time taken for downward rowing be T2.

According to question TI=3T2

⇒ $\frac{40}{5-x}=3 \frac{40}{5+x}$

5+x = 15 – 3x

x= 2.5 km/hr

(3) is correct

Question 24. If the length of a rectangle is 5 cm more than the breadth and if the perimeter of the rectangle is 40 cm, then the length and breadth of the rectangle will be:

7.5 cm, 2.5 cm
10cm, 5cm
12.5cm, 7.5cm
15.5cm, 10.5cm

Solution:

(3)

1st condition = length is 5cm more than breadth

All options satisfy this condition

II perimeter = 2(l+b) = 40 of rectangle

Only option (c) satisfies it

Detail Method

Let breadth = x; :-length = x + 5

Perimeter = 40

2(x+5+x) = 40

Or 2x + 5 = 20

Or x = $\frac{15}{2}$= 7.5cm

Length = x + 5 = 7.5 + 5 = 12.5

Breadth = x = 7.5cm

(3) is correct

Question 25. For all 2 e R, the line (2+ 2)x + (3- A) y + 5 = 0 Passing through a fixed point, then the fixed point is_____.

(-1,-1)
0,0
2,2
1. 1

Solution:

(2)

For option (b) Point (-1; -1) satisfies the equation

LHS = =(2+ A)x + (3-/1) y + 5

Or (2 + A)(-l]+(3- A) (-l) + 5

-2-A-3+A + 5 = 0 = RHS.

(2) is correct

Question 26. If kx – 4 = (k – l).x which of the following is true

x = -5
x = -4
x = -3
x = 4

Solution:

(4) is correct

Kx- 4 = (k-l)x

Orkx-4 = kx-x

Or -4 = -x

∴ x = 4

CA Foundation Maths Chapter 2 Detailed Solutions

Question 27. The age of a person is 8 years more than thrice the age of the sum of his two grandsons who were twins. After 8 years his age will be 10 years more than twice the sum of the ages of his grandsons. Then the age of the person when the twins were born is_

86 yrs
73 yrs
68 yrs
63 yrs

Solution:

(2) let the age of 1st grandson = x

Person’s age = P = 3(x+x) + 8

P = 6x + 8

After 8 years

P + 8 = 2 [x+8+x+8] + 10

= 2(2x+16) + 10

Or 6x + 8 + 8 = 4x + 32 + 10

Or 2x = 42 -16 = 26

x = 13

Age of person when grandsons

were born

= 6x + 8 – x

= 6 x 13 + 8-13 = 73

(2) is correct

Question 28. In a school number of students in each section is 36. If 12 new students are added, then the number of sections is increased by 4 and the number of students in each section becomes 30. The original number of sections at first is

Solution:

(4) let original No. of sections = x

Total students = 36x

36x+ 12 = (x+4) 30

Or 36x + 12 = 30x + 120

Or 6x = 108 ⇒ x = 18

Question 29. A person on a tour has for his expenses. But the tour was extended for another 16 days, so he must cut his daily expenses by 20. The original duration of the tour had been?

48 days
64 days
80days
96 days

Solution:

Let No. of tour days = x

Expenses per day =$=\frac{9600}{x}$

Now Expense per day =$=\frac{9600}{x+16}$

⇒ $\text { From } \frac{9600}{x}-\frac{9600}{x+16}=20$

From here we get

For (3) LHS

⇒ $\frac{9600}{80}-\frac{9600}{80+16}=20 \text { RHS. }$

(3) is correct

Question 30. The particular company produces some articles in a day. The cost of production per article is more than thrice the number of articles and the total cost of production is on a day then the number of articles is:

Solution:

(1) is correct.

Let (A) be correct.

So cost, per unit = 800/16 =

It is 2 more than 3 times of 16. (as given in Qts.)

Question 31. The sides of an equilateral triangle are shortened by 3 units, 4 units, and 5 units respectively, and then a right-angle triangle is formed. The side of the equilateral triangle was

Solution:

For option [3]

1st side of right-angled A = 8 – 3 = 5

2nd side = 8-4 = 4

And 3rd side = 8-5 = 3

Here; 5; 4 and 3 are making a right-angled

triangle.

So, 52 = 42 + 32

Hence, option (c) is correct

Question 32. A number consists of two digits such that the digit in one’s place is thrice the digit in ten’s place. If 36 is added then the digits are reversed. Find the number

62
26
39
None

Solution:

(2)

[1] 62 → 2 3 x 6 [False]

And 62 + 36 = 98* 26 (false]

(2) 26 clearly 6 = 3×2 (True]

And 26 + 36 = 62 (Orders of digits reversed)

So; (2) is correct.

Exercise – 2

Simultaneous Or Linear Equation In Two Or Three Variable

Question 1. The solution of the set of equations 3x + 4y = 7, 4x-y = 3 is

(1.-1)
(1. 1)
(2.1)
(1.-2)

Solution:

(2)

ax + by = c

px + qy = r

(aq – bp) x = ac

→(-3 -16) x = -7-12

-19 x = – 19

X = 1

3 + 4y = 7 → y = 1

Question 2. The values of X and y satisfying the equations $\frac{x}{2}+\frac{y}{3}=$= 2,x + 2y = 8 are given by the pair.

(3.2)
(-2, -3)
(2.3)
None of these

Solution:

(3)

3x + 2y = 12

x + 2y = 8

2x = 4 ⇒ x = 2

⇒ $y=\frac{8-x}{2} \quad \Rightarrow \frac{8-2}{2}=3$

Question 3.$\frac{x}{p}+\frac{y}{q}=2,$x + y = p + q are satisfied by the values given by the pair.

(x=p,y=q)
(x=q,y=p)
(x=l, y=l)
None of these

Solution:

(1)

GBC

x = p, y = q

Question 4. The solution for the pair of equations$\frac{1}{16 x}+\frac{1}{15 y}=\frac{9}{20}, \frac{1}{20 x}-\frac{1}{27 y}=\frac{4}{45}$ is given by

$\left(\frac{1}{4}, \frac{1}{3}\right)$
$\left(\frac{1}{3}, \frac{1}{4}\right)$
(3,4)
(4,3)

Solution:

(1)

Let 1/x = a, 1/y=b

⇒ $\text { 1) }\frac{a}{16}+\frac{b}{15}=\frac{9}{20}=15 a+16 b$

⇒ $\frac{9}{20} \times 16 \times 15 \Rightarrow 108$

2) $\frac{a}{20}-\frac{b}{27}=\frac{4}{45}$

⇒ $27 a-20 b=\frac{4 \times 20 \times 27}{45}=48$

15a + 16b = 108

27a -20b = 48

By trick refer to question 1

(-300 -432) a = (-2160-768)

a = 4

15 (4) + 16b = 108

16 b = 48

B = 3

⇒ $a=4, b=3 \Rightarrow x=\frac{1}{a}, y=\frac{1}{b} \Rightarrow x=\frac{1}{4} ,y=\frac{1}{3}$

Question 5. Solve for x and y: $\frac{4}{x}-\frac{5}{y}=\frac{x+y}{x y}+\frac{3}{10} \text { and } 3 x y=10(y-x) \text {. }$

(5,2)
(-2,-5)
(2,-5)
(2,5)

Solution:

⇒ $\frac{4}{x}-\frac{5}{y}=\frac{x+y}{x y}+\frac{3}{10}$

⇒ $3 \mathrm{xy}=10(\mathrm{y}-\mathrm{x})$

⇒ $\frac{4}{x}-\frac{5}{y}=\frac{1}{y}+\frac{1}{x}+\frac{3}{10}$

⇒ $3 \mathrm{xy}=10 \mathrm{y}-10 \mathrm{x} \rightarrow 3=\frac{10}{x}-\frac{10}{y}$

⇒ $\frac{3}{x}-\frac{6}{y}=\frac{3}{10} \quad \frac{10}{x}-\frac{10}{y}=3$

⇒ $\text { Let } \frac{1}{y}=a \frac{1}{y}=b$

3a -6b = 3 ….(1)

10a – 10b = 3 → 30a – 30b – 9….. (2)

30a- 60b = 3

⇒ $\frac{30 a-30 b=9}{30 b=6}=\mathrm{b}=\frac{6}{30}$

30a -60b = 3

⇒ $ 30 a-60 \frac{(6)}{30}=3$

⇒ $\rightarrow 30 a-12=3$

⇒ $a=\frac{15}{30}$

⇒ $x=\frac{1}{a}=\frac{30}{15}=2 .$

⇒ $ y=\frac{1}{b}=\frac{30}{6}=5 .$

(4) (2,5)

Question 6. The pair satisfying the equations x + 5y = 36,ÿ = is given by Qpfrbft 1 ” Y>

(l6,4)
(4, 16)
(4, 8)
None of these

Solution:

x + 5y = 36 …….(1)

⇒ $\frac{x+y}{x-y}=\frac{5}{3} \ldots \ldots \ldots \ldots(2)$

3x + 3y = 5x- 5y

2x + lOy = 72….(1)

2x-8y = 0 (2)

2x+10y

Subtract $\frac{2 x-8 y}{18 y}$= 72 —> y = 4.

x + 20 = 36 → x — 16.

(a) (16,4)

Question 7. Solve for x and y : x-3y = 0, x+2y = 20CM 3 Opt >

x = 4, y = 12
x= 12, y = 4
x = 5, y = 4
None of these.

Solution:

x – 3y = 0 x + 2y = 20

x = 3y = 0

x + 2y = 20

by trick (Ql)

(2 + 3)x= (0-(-60))

x = +12

x- 3y = 0 —> 12 -3y = 0 —> 12 = 3y

y = 4

x = 12, y = 4

(2) is correct

Question 8. The simultaneous equations 7x-3y = 31, 9x-5y = 41 have solutions given by

(-4,-1)
(-1.4)
(4,-1)
(3,7)

Solution:

7x-3y = 31, 9x – 5y = 41

By tricks

7x- 3y = 31

9x-5y = 41

(-35 + 27)x = (-155 + 123)

-8x = -32

x = 4

7(4) – 3y = 31

28 – 3y = 31

-3y = 3→ y = -l

(3) (4 .-1)

Question 9. 1.5x + 2.4 y = 1.8, 2.5(x+l) = 7y have solutions as

(0.5, 0.4)
(0.4, 0.5)
$\left(\frac{1}{2}, \frac{2}{5}\right)$
(2,5)

Solution:

1.5x + 2.4y= 1.8 …(1)

2.5x + 2.5 = 7y

15x+ 24y = 18

25x- 70y = -25

15x+ 24y = 18

25x+ 70 = -25

By trick

(-1050 -600)x = (-1260 + 600) – 1650x = -660

x = 0.4

6 + 24y = 18

⇒ $ y=\frac{12}{24}=\frac{1}{2}=0.5$

⇒ $x=0.4, y=0.5$$

Question 10. The values of x and y satisfying the equations$\frac{3}{x+y}+\frac{2}{x-y}=3, \frac{2}{x+y}+\frac{3}{x-y}=3 \frac{2}{3}$ are given by

(1,2)
(-l.-2)
$\left(1, \frac{1}{2}\right)$
(2, 1)

Solution:

(1)

GBC

Question 11. 1.5x + 3.6y = 2.1, 2.5 (x+1) = 6y ‘/’JfY,1

(0-2, 0.5)
(0.5, 0.2)
(2,5)
(-2,-5)

Solution:

By trick

[(-900) -900]x= (-1260 + 900) – 1800x = -360

$x=\frac{360}{1800}=0.2$

3 + 36y = 21

36y= 18 → y = 0.5

Question 12. $\frac{x}{5}+\frac{y}{6}+1=\frac{x}{6}+\frac{y}{5}=28$

(6,9)
(9, 6)
(60,90)
(90, 60)

Solution:

(3)

6x + 5y = 810

5x + 6y = 840

By tricks

6x + 5y = 810

5x + 6y = 840

(36 -25)x = 4860 -4200

llx= 660 x = 60, y = 90.

Question 13. $\frac{x}{4}=\frac{y}{3}=\frac{z}{2} ; 7 x+8 y+5 z=62$

(4,3,2)
(2,3,4)
(3,4,2)
(4,2,3)

Solution:

(1)

7x + 8y + 5z = 62

7(4) + 8(3) + 5(2) = 62

28 + 24 + 10 = 62

⇒ $=\frac{x}{4}=\frac{y}{3}=\frac{z}{2} \rightarrow(4,3,2)$

Question 14. $\frac{x y}{x+y}=20, \frac{y z}{y+z}=40, \frac{z x}{z+x}=24$

(120,60,30)
(60,30, 120)
(30,120,60)
(30,60,120)

Solution:

(4)

⇒ $\frac{x+y}{x y}=\frac{1}{20} \frac{y+z}{y z}=\frac{1}{40} \frac{z+x}{2 x}=\frac{1}{24}$

⇒ $\frac{1}{y}+\frac{1}{x}=\frac{1}{20} \ldots(1) \frac{1}{z}+\frac{1}{y}=\frac{1}{40} \ldots(2) \frac{1}{x}+\frac{1}{z}=\frac{1}{24} \ldots .(3)$

⇒ $\frac{1}{y}=\frac{1}{20}-\frac{1}{x} \frac{1}{24}-\frac{1}{x}+\frac{1}{y}=\frac{1}{40} \frac{1}{z}=\frac{1}{24}-\frac{1}{x}$

⇒ $\frac{1}{24}-\frac{1}{x}+\frac{1}{20}-\frac{1}{x}=\frac{1}{40} $

⇒ $\frac{1}{x}+\frac{1}{x}=\frac{1}{24}+\frac{1}{20}-\frac{1}{40} =\frac{2}{x}=\frac{8}{120} \quad=\frac{x}{2}=\frac{120}{8} \rightarrow x=30 \quad 1 / y=\frac{1}{20}=\frac{1}{3}=10 / 600$

⇒ $=\frac{2}{x}=\frac{5+6-3}{120} x=\frac{1}{z}=\frac{1}{24}-\frac{1}{30}=\frac{6}{720} z=120$

(d) (30, 60, 120)

Question 15. 2x + 3y + 4z = 0,x + 2y – 5z = 0, lOx + 16y- 6z = 0

(0,0,0)
(1,-1, 1)
(3, 2,-1)
(1,0,2)

Solution:

(1)

GBC:(0,0,0)

Question 16. $\frac{1}{3}(x+y)+2z=21,3 x-\frac{1}{2}(y+z)=65, x+\frac{1}{2}(x+y-z)=38$

(4, 9. 5)
(2,9,5)
(24, 9, 5)
(5, 24,9)

Solution:

(3)

⇒ $\frac{1}{3}(24+9)+2(5)=213(24) \cdot \frac{1}{2}(9+5)=65$

⇒ $24+\frac{1}{2}(24+9-5)=38$

Question 17. $\frac{x}{0.01}+\frac{y+0.03}{0.05}=\frac{y}{0.02}+\frac{x+0.03}{0.04}=2$

(1,2)
(0.1, 0.2)
(0.01, 0.02)
(0.02,0.01)

Solution:

⇒ $\frac{x}{0.01}+\frac{y+0.03}{0.05}=\frac{y}{0.02}+\frac{x+0.03}{0.04}=2$

⇒ $100 x+\frac{100 y+3}{5}=2 ; \quad 50 y+\frac{100 x+3}{4}=2$

500x + 100y + 3 = 10; 200y +100x + 3 = 8

500x + lOOy = 7 100x + 200y = 5

Multiply by 2

Subtract

$\begin{gathered}
1000 x+200 y=14 \\
100 x+200 y=5 \\
\hline 900 x=9
\end{gathered}$

x = 0.01 y = 0.02

Question 18. $\frac{x y}{y-x}=110, \frac{y z}{z-y}=132, \frac{z x}{z+x}=\frac{60}{11}$

(12, 11, 10)
(10, 11, 12)
(11,10,12)
(12, 10, 11)

Solution:

(2)

⇒ $ \frac{y-x}{x y}=1 / 110 \frac{z-y}{y z}=1 / 132 \frac{z+x}{z x}=\frac{11}{60}$

⇒ $\frac{1}{x}-\frac{1}{y}=\frac{1}{110} \frac{1}{y}-\frac{1}{z}=\frac{1}{132} \frac{1}{x}+\frac{1}{z}=\frac{11}{60}$

GBC = 10,11,12

(2) is correct

How To Solve Equations In CA Foundation Chapter 2

Question 19. 3x-4y+70z = 0, 2x+3y-10z = 0, x+2y+3z = 13

(1,3, 7)
(1,7, 3)
(2, 4, 3)
(-10, 10, 1)

Solution:

(4)

3x-4y+70z = 0, 2x+3y-10z = 0, x+2y+3z = 1 3

For three variables GBC x = -10,y = 10, z=l

Question 20. The monthly incomes of two persons are in the ratio 4: 5 and their monthly expenses are in the ratio of 7: 9. If each saves 350 per month find their monthly incomes.

(500, 400)
(400, 500)
(300, 600)
(350, 550)

Solution:

(2)

Monthly Income = 4 : 5 i.e., 4x, 5x

Monthly expenses = 7 : 9 i.e. 7y,9y

Saving = Income – Expenses = 50

4x-7y = 50

5x-9y = 50

By trick (-36 + 35)x-450 + 350

-x = -100 = x = 100

Monthly Income = 4x, 5x = (400, 500)

Question 21. Find the fraction which is equal to 1/2 when both its numerator and denominator are increased by 2. It is equal to 3/4 when both are increased by 12.

Solution:

(1)

Let Fraction be$\frac{x}{y}$

⇒ $ \frac{x+2}{y+2}=\frac{1}{2} \quad, \frac{x+12}{y+12}=\frac{3}{4}$

GBC

⇒ $\frac{x}{y}=\frac{3}{8}$

Question 22. The age of a person is twice the sum of the ages of his two sons and five years ago his age was thrice the sum of their ages. Find his present age.

60 years
52 years
51 years
50 years

Solution:

(4)

Let the sum of ages be x, Man’s age = x

Acc. To quest, x = 2(y)…….(1)

x – 5 = 3(y- 10)

x – 5 = 3y- 30

Put (1) in (2) 2y-3y = -25,

y=25

x = 50

Question 23. A number between 10 and 100 is five times the sum of its digits. If 9 is added to it the digits are reversed find the number.

Solution:

(3)

Let the number be (x is one digit, y another)

Number = lOx + y

= 10x + y + 9 = lOy + x = 9x-9y = -9

Also

10x + y = 5(x + y)

10x + y = 5x + 5y

5x = 4y

x = $\frac{4}{5} y \quad=9\left(\frac{4}{5}\right) y-9 y=-9$

= 36y-45y = -45

-9=-45

y=5, x =$\frac{4}{5} \cdot 5$ = 4

Numbers = lOx + y = 45

Question 24. The wages of 8 men and 6 boys amount to 333. If 4 men earn 34.50 more than 5 boys determine the wages of each man and boy.

(31.50,33)
(33,31.50)
(32.50, 32)
(32,32.50)

Solution:

(2)

Let each man’s wage be x & boy’s be y

8x + 6y = 33 …….. (1)

4x- 4.50 = 5y …….(2)

4x = 5y + 4.50

8x= 10y+ 9 ……. (3) (3) Put (3) in (1)

lOy + 9 + 6y = 33

16y = 24 → y = 1.5.v = 3

Question 25. A number consisting of two digits is four times the sum of its digits and if 27 is added to it the digits are reversed. The number is:

Solution:

(3)

Let number be lOx + y

Acc to quest.

lOx + y = 4(x+y)

1 Ox – 4x = 4y- y

6x = 3y

2x = y

Also

10x + y + 27= lOy + x 5y + y + 24= 10y +$\frac{y}{2}$

10y+ 2y + 54 = 20y + y

12y + 54 = 21y

9y = 64-4y = 6 x = 3

Number =36

Question 26. Of two numbers, l/5lh of the greater is equal to 1 /3rd of the smaller, and their sum is 16. The numbers are:

(6,10)
(9,7)
(12,4)
(11,5)

Solution:

(1)

Let two numbers be x,y such that x > y

Acc to question

$ \frac{x}{5}=\frac{y}{3}, \quad x+y=16$ $3 x=5 y \rightarrow x=\frac{5}{3} y$ $\frac{5}{3} y+y=16=5 y+3 y=48 \rightarrow y=6, x=10$

Two numbers are 6, 10

Question 27. y is older than A- by 7 years 15 years back x’s age was 3/4 of/s age. Their present ages are

(x-36,y=43)
(x=50,y=43)
(x=43,y=50)
(x=40,y=47)

Solution:

(1)

$Y=x+7 \text { also, }(y-15) \cdot \frac{3}{4}=x=15$ $y-7=x \quad \frac{3}{4} y-\frac{45}{4}=x-15$

$\frac{3}{4} y-\frac{45}{4}=y-7-15=3 y-45=$4y- 88

= y = 43 y = 43 x = 36

Present ages are 36, 43

Question 28. The sum of the digits in a three-digit number is 12. If the digits are reversed the number is increased by 495 but reversing only of the ten’s and unit digits increases the number by 36. The number is

Solution:

(c)

Three digit no. be lOOx + lOy + z

Reversing all digits

x + y + z = 12,

100z+ lOy + x = lOOx + lOy + z + 495

100z + x = lOOx + z + 495

99z-99x = 495

z-x = 5…(1) z = 5 + x

Reversing ten’s T unit digit no. increases by 36

100x + lOz + y = 100x + lOy + z + 36

9z-9y = 36

z-y = 4

z = 4 + y…..[2]

x + y + z = 12

from (1) and [2]

3z-9 = 12

3z = 21

z-5+z-4+z=12

z = 7

x = 2, y = 3, z = 7

Numbers = 237

Question 29. Two numbers are such that twice the greater number exceeds twice the smaller one by 18 and l/3rd of the smaller and 1/5th of the greater number are together 21. The numbers are:

(36, 45)
(45, 36)
(50, 41)
(55, 46)

Solution:

(2)

Let two numbers be x and y. such that x>y

2x = 2y + 18 And $\frac{1}{3} y+\frac{1}{5} x=21$

2x-2y=18

x-y = 8 5y+3x = 315

x = 9 + y 5y + 27 + 3y = 315

8y = 288 y = 36

x = 45

Question 30. The demand and supply equations for a certain commodity are 4q + 7p = 17 and p = $\frac{q}{3}+\frac{7}{4}$ respectively where p is the market price and q is the quantity than the equilibrium price and quantity are:

$2, \frac{3}{4}$
$3, \frac{1}{2}$
$5, \frac{3}{5}$
None of these

Solution:

⇒ $4 q+7 p=17 \rightarrow p=\frac{17-4 q}{7}$

⇒ $P=\frac{q}{3}+\frac{7}{4}$

For equilibrium

⇒ $\frac{q}{3}+\frac{7}{4}=\frac{17}{7}-\frac{4}{7} q$

⇒ $ \frac{7 q+12 q}{21}=\frac{68-49}{28}=\frac{19 q}{21}=\frac{19}{28}=q=\frac{3}{4}$

⇒ $P=\frac{17-4 q}{7}=\frac{17-3}{7}=2 .$

Question 31. Solving 6x+5y-16=0 and 3x-y-l=0 we get values of andy as

1,1
1,2
-1,2
0,2

Solution:

(2)

6x + 5y= 16

3x-y= 1

By trick

(-6-15)x = -16 -5

-21x = -21 = x = 1

6 + 5y= 16 → y = 2

Question 32. Solving 9x+3y-4z=3 ,x+y-z=0 and 2x-5y-4z=-20 following roots are obtained

2, 3, 4
1,3,4
l, 2,3
None

Solution:

(3)

9x + 3y- 4x = 3, x+y-z=0

2x- 5y- 4x = -2

For three variables

Question 33. A man went to the Reserve Bank of India with 1,000. He asked the cashier to give him 5 and % 10 notes only in return. The man got 175 notes in all. Find how many notes of K 5 and 10 he receives.

(25,150)
(40,110)
(150,25)
None

Solution:

For (1) 25 x 5 + 150 x 10$\neq$ 1000

(2) 40 x 5 + no x 10$\neq$ RS. 1000

(3)150 x5 + 25 x 10 = Rs. 1000

Question 34. The Point of intersection of the lines 2x- 5y = 6 and x+y=3 is

(0,3)
(3,0)
(3,3)
(0,0)

Solution:

(2)

Intersecting Point lies on both straight lines. It will satisfy both ends.

For 00 (0,3) Point 2×0 – 5×3

it is incorrect 6

0Ption (2) (3; 0) satisfies both eqns.

(2) is correct

Question 35. If the equations kx + 2y = 5, 3x + y = 1 has no solution then the value of k is

Solution:

Kx + 2y = 5

3x + y=l

They have no soln. (given)$\frac{k}{3}=\frac{2}{1} \neq \frac{5}{1} ; \Rightarrow$-k = 6

Question 36. The equation x + 5y = 33;$\frac{x+y}{x-y}=\frac{13}{3}$ Has the solution (x,y) as:

(4,8)
(8,5)
(4,16)
(16,4)

Solution:

(2)

For LHS = x + 5y = 8 + 5×5 = 33

⇒ $\frac{x+y}{x-y}+\frac{8+5}{8-5}=\frac{13}{5}$

Clearly (b) satisfies both equations.

Question 37. If 2 x+y = 2 2x-ÿ = v8 then the respective value of and y are_

$1, \frac{1}{2}$
$\frac{1}{2}, 1$
$\frac{1}{2}, \frac{1}{2}$
None of these

Solution:

(a) is correct

+y _ 22x-y = V8 = V21 = 23/2

x+y =$\frac{3}{2}$ (1)

2x-y=$\frac{3}{2}$ (2)

(a)satisfies (1] and (2) both

Question 38. Let Ei,thenE2 are E1, and E2 two E2 are(2,-1)linear_.isequationsa solution in software equation variables E1 only d and y,(-2,-1)(0,1) is a Solution of for equation both the E2.only,equations

x= 0,y = 1;

2x-y = -l, 4x + y = 1

x + y = l,x-y = -1

x + 2y = 2, x + y =1

Solution:

(0; 1) satisfies E1 and E2 both

(2, -l) satisfies 1 Eqn. 2-1 = 1 (true)

But -2; -13 also satisfies E2

i.e -2 –13 = -1 (true)

Question 39. $\text { If } \frac{3}{x+y}+\frac{2}{x-y}=-1 \text { and } \frac{1}{x+y}-\frac{1}{x-y}=\frac{4}{3} \text { then }(x, y) \text { is }$

(2.1)
(1.2)
(-1,2)
(-24)

Solution:

⇒ $\frac{3}{1+2}+\frac{2}{1-2}=1-2=-1 \text { (True) }$

⇒ $\frac{1}{1+2}-\frac{1}{1-2}=\frac{1}{3}+1=\frac{4}{3} \text { (True) }$

So;(2) is correct.

Question 40. The line 3x + 2y = 6 intersects the line 3x – y = 12 in_ quadrant:

Solution:

(4), Eqn. (1) – Eqn. (2); we get

3x + 2y = 6

3x- y = 12

– + –

3y = -6 ⇒ y = -2

From (1); 3x = 6-2y=6-2 (-2) = 10

$ x=\frac{10}{3}$

Coordinate the point of intersection

= (x;y) = $\left(\frac{10}{3} ;-2\right)$

It is in the 4th Quadrant.

CA Foundation Maths Equations Practice

CA Foundation Maths Solutions For Chapter 2 Exercise – 3

Quadratic Equations

Question 1. If the roots of the equation 2×2 + 8x – m’ = 0 are equal then value of m is

-3
– 1
l
-2

Solution:

(4) 2x² 8x- m3 = 0 for equal b2- 4ac = 0

→ 64 + 4.2. m³ = 0

8m³ = – 64

m3 = – 8

m= – 2

Question 2. If 2^x+3 – 32. 2x + 1 = 0 then values of x are

0,1
1,2
0,3
0,-3

Solution:

(4) 2^x+3– 32. 2x + 1 = 0

2^x+3– 9.2x +1 = 0

Question 3. The values of 4+_____1_____

4+_____1_____
4+_____1_____
4+…….CO
1. 1± √2
2. 2+ √5
3. 2± √5
4. None of these

Solution:

4x+1=x²

x² — 4x —1 = 0

x²– 4x- 1

⇒ $X=\frac{4 \pm \sqrt{16+4}}{2}$

⇒ $=2 \pm \sqrt{5}$

Question 4. If be the roots of the equation 2×2 – 4,v -3 = 0 the value of a2 + 32 is

5
7
3
-4

Solution:

(2) 2x²– 4x- 3 = 0

ap is root

→ x² – 2x- $\frac{3}{2}$

α²+ β² = (α + β)² – 2 α β

⇒ $(2)^2+2 \cdot \frac{3}{2}$=7

Question 5. If the sum of the roots of the quadratic equation ax² + bx + c = 0 is equal to the sum of the squares of their reciprocals then$\frac{a^2}{a c}+\frac{b c}{a^2}$ is equal to

2
-2
1
-1

Solution: (1) 2

Question 6. The equation x² -(p+4)x + 2p + 5 = 0 has equal roots the values of p will be.

± 1
2
± 2
-2

Solution:

(3) x² – (p + 4) x + 2p + 5 = 0

For equal roots

b² – 4ac = 0

(p + 4)² – 4 (2p + 5) = 0

p² – 4 = 0

p² = 4

P = ± 2

Question 7. The roots of the equation x2 + (2p-l)x + p2 = 0 are real if.

p>l
p<4
p>1/4
p<1/4

Solution:

(4) x² + (2p-1) x + pz = 0

For real roots

b² – 4ac > 0

(2p-1)²-4(p²)>0

4p² + 1 – 4p – 4p² > 0

1 – 4p > 0

1 > 4p

⇒ $\frac{1}{4} \geq \mathrm{p}$

Question 8. If p and q are the roots of x2 + 2x + 1 = 0 then the values of* + q:i becomes

2
-2
4
-4

Solution:

(2) p and q roots of x² +2x + 1 = 0

p + q = -2

pq = 1

p³+ q³=(p + q) (p²-pq + q²)

= -2 (p² + q²– 1)

= -2 (p+q)²– 2pq – 1)

= -2 (4 – 2 – 1) = -2

Question 9. If L + M + N = 0 and L, M, N are rationales the roots of the equation
(M+N-L)x2+(N+L-M)x+(L+M-N) = 0 are

Real and irrational
Real and rational
Imaginary and equal
Real and equal

Solution:

(2) Real and Rational

Question 10. If one root of 5x² + 13x + p = 0 is reciprocal of the other then the value is

-5
5
1/5
-1/5

Solution:

(2) 5×2 + 13x + p = 0

⇒ $\text { roots } \rightarrow \alpha \cdot \frac{1}{\alpha}$

⇒ ${sum}=\alpha+\frac{1}{\alpha} \quad \text { product }=\frac{p}{5}$

⇒ $\frac{p}{5}=1 \quad \text { p }=5$

Question 11. A solution of the quadratic equation (a+b-2c)x² + (2a-b-c)x + (c+a-2b) = 0 is

x = 1
x = -1
x= 2
x = – 2

Solution:

(2) (a+b-2c)x² + (2a-b-c)x + (c+a-2b) = 0

For x = 1

a + b-2c + 2a-b-c + c + a-2b≠0

for x = -1

a + b -2c -2a + b + c + c + a -2b = 0

∴ x = – 1

Question 12. If the root of the equation x2-8x+m = 0 exceeds the other by 4 then the value of m is

m = 10
m= 11
m = 9
m = 12

Solution:

(4) x² – 8x + m = 0

roots α, α + 4

sum = 8

α+α+4=82 α=4

Product = m

α (α + 4) = m

α² + 4α = m

4 + 8 = m m = 12

Question 13. The values of x in the equation 7(x+2p)² + 5p² = 35xp + 1 17p² are

(4p,-3p)
(4p,3p)
(-4p, 3p)
(-4p,-3p)

Solution:

(1) 7(x + 2p)² + 5p² = 35 xp + 117p²

(4p, -3p)

Question 14. H. The solutions of the equation $\frac{6 x}{x+1}+\frac{6(x+1)}{x}=13 \text { are }$

(2, 3)
(3,-2)
(-2,-3)
(2,-3)

Solution:

⇒ $\frac{6 x}{x+1}+\frac{6(x+1)}{x}=13$

(2,-3)

Question 15. The satisfying values of.v for the equation$\frac{1}{x+p+q}=\frac{1}{x}+\frac{1}{p}+\frac{1}{q} \text { are }$

(p. q)
(-p. -q)
(p, -p)
(-P, q)

Solution:

⇒ $\text { (2) } \frac{1}{x+p+q}=\frac{1}{x}+\frac{1}{p}+\frac{1}{q}$

(-p. -q)

Question 16. The values of for the equation x² + 9x + 18 = 6 – 4x are

(1,12)
(-1,-12)
(1,-12)
(-1,12)

Solution:

(2) x² + 9x + 18 = 6 – 4x

⇒ x² + 13x + 12 = 0

⇒ x² + 12x + x + 12 = 0

⇒ x(x+12) + 1 (x+ 12) = 0

x = -1,-12

Question 17. The values of x satisfying the equation $\sqrt{\left(2 x^2+5 x-2\right)}-\sqrt{\left(2 x^2+5 x-9\right)}=1 \text { are }$

(2, -9/2)
(4,-9)
(2, 9/2)
(-2, 9/2)

Solution:

⇒ $\text { (1) } \sqrt{2 x^2+5 x-2}-\sqrt{2 x^2+5 x-9}=1$

(2. -9/2)

Question 18. The solution of the equation 3x²-17x + 24 = 0 are

(2,3)
$(b) \left(2,3 \frac{2}{3}\right)$
$\left(3,2 \frac{2}{3}\right)$
$\left(3, \frac{2}{3}\right)$

Solution:

(3) 3x² – 17x + 24 = 0

3x² – 8x -9x + 24 = 0

3x (x- 3) – 8 (x- 3) = 0

(3x – 8) (x- 3) = 0

⇒ $x=\frac{8}{3}, x=3$

⇒ $x=3,2 \frac{2}{3}$

Question 19.The equation $\frac{3\left(3 x^2+15\right)}{6}+2 x^2+9=\frac{2 x^2+96}{7}+6$ has got the solution as

(1, 1)
(1/2, -1)
(1. -1)
(2,-1)

Solution:

⇒ $\text { (c) } \frac{3\left(3 x^2+15\right)}{6}+2 x^2+9=\frac{2 x^2+96}{7}+6$

⇒ $\frac{9 x^2+45+12 x^2+54}{6}=\frac{2 x^2+96+42}{7}$

⇒ $\frac{21 x^2+99}{6}=\frac{2 x^2+138}{7}$

Multiply 42

⇒ 147x² + 693 = 12x² + 828

⇒ 135x² = 135

x² =1 → x ±1

Question 20. The sum of two numbers is 8 and the sum of their squares is 34. Taking one number as x form an equation in x and hence find the numbers. The numbers are

(7, 10)
(4,4)
(3, 5)
(2,6)

Solution:

3 + 5 = 8 ⇒ 3² + 5² = 34

(3,5)

Question 21. The difference of two positive integers is 3 and the sum of their squares is 89. Taking the smaller integer as x form a quadratic equation and solve it to find the integers. The integers are

(7,4)
(5, 8)
(3, 6)
(2,5)

Solution:

(2) let two positive integers be a, 3

⇒ α-β = 3

⇒ α² +β² = 89

(5,8)

Question 22. Five times of a positive whole number is 3 less than twice the square of the number. The number is

3
4
-3
2

Solution:

(1) let the number be x

⇒ 5x = 2x² -3

⇒ 2x² – 5x – 3 = 0

⇒ 2x² – 6x + lx – 3 = 0

⇒ 2x(x-3) + 1 (x-3) = 0

⇒ $x=\frac{-1}{2}, x=3$

x is positive

x = 3

Question 23. The area of a rectangular field is 2000 sq.m and its perimeter is 180m. Form a quadratic equation by taking the length of the field as x and solving it to find the length and breadth of the field. The length and breadth are

(205m, 80m)
(50m, 40m)
(60m, 50m)
None

Solution:

(2) Perimeter = 180m

2(1 + b) = 180

L + b = 90

We know I = x

b = 90 – x

Area = 2000 m

∴ x (90 – x) = 2000

⇒ 90x- X² = 2000

⇒ x²-90x + 2000 = 0

⇒ x² – 5Ox – 40x + 2000 = 0

⇒ x (x-50) – 40 (x- 50) = 0

x = 40, 50

Question 24. Two squares have sides p cm and (p + 5) cms. The sum of their squares is 625 sq. cm. The sides of the squares are

(10 cm, 30 cm)
(12 cm, 25 cm)
(15 cm, 20 cm)
None of these

Solution:

(3) Two squares with sides p, p + s cm

⇒ p² + (p+5)² = 625

⇒ p² + p² + 25 + lOp = 625

⇒ 2p²+10p- 600 = 0

⇒ p² + 5p – 300 = 0

⇒ p2 + 20p-15p- 300 = 0

⇒ p (p + 20) – 15 (p+20) = 0

⇒ p = 15,p = -20

⇒ p≠ -20

⇒ p = 15

⇒ p + 5 = 20

Question 25. Divide 50 into two parts such that the sum of their reciprocals is 1/12. The numbers are

(24, 26)
(28, 22)
(27,23)
(20,30)

Solution:

(4) let the first part be x,

second = 50 – x

⇒ $\frac{1}{x}+\frac{1}{50-x}=\frac{1}{2}$

⇒ $\frac{50-x+x}{x(50-x)}=\frac{1}{12}$

⇒ 600 = x (50 – x)

⇒ 600 = 50x – x²

⇒ x²-50x + 600 = 0

⇒ x²– 30x- 20x + 600 = 0

⇒ x (x – 30) – 20 (x- 30) = 0

∴ x = 20, 30

Question 26. There are two consecutive numbers such that the difference of their reciprocals is 1/240. The numbers are

(15, 16)
(17, 18)
(13, 14)
(12, 13)

Solution:

(1) Two numbers be x, x + 1

⇒ $\frac{1}{x}-\frac{1}{x+1}=\frac{1}{240}$

⇒ $\frac{x-x+1}{x(x+1)}=\frac{1}{240} \rightarrow+240=x(x+1)$

⇒ x² + x – 240 = 0

⇒ x² + x- 240 = 0

⇒ x²+ 16x- 15x- 240 = 0

⇒ x (x + 16) – 15 (x +16) = 0

⇒ x = 15, x = -16

∴ x= 15

(15,16)

Question 27. The hypotenuse of a right-angled triangle is 20cm. The difference between its other two sides is 4cm. The sides are

(11cm, 15cm)
(12cm, 16cm)
(20cm, 24cm)
None of these

Solution:

(2) hypotenuse = 20 cm

The difference between the other two sides a and, b is 4

⇒ a – b = 4

⇒ a = 4 + b

⇒ a² + b² = c²

⇒ a² + (a-4)²= c²

⇒ a² + a²+ 16 – 8a = 20²

⇒ 2a² + 8a = 384

⇒ 2a²+ 8a – 384 = 0

⇒ a² – 4a – 192 – 0

⇒ a²– 16a + 12a – 192 = 0

⇒ a (a- 16) + 12 (a—16) = 0

⇒ a = 16

∴ b = a-4 = 12

Question 28. The sum of two numbers is 45 and the mean proportional between them is 18. The numbers are

(15,30)
(32, 13)
(36,9)
(25,20)

Solution:

(3) → 4 (1 = 45)

⇒ $\frac{a}{x}=\frac{x}{\beta} \rightarrow \alpha \beta=x^2$

αβ= 18²

(36.9)

Question 29. The sides of an equilateral triangle are shortened by 12 units 13 units and 14 units respectively and a right-angle triangle is formed. The side of the equilateral triangle is

17 units
16 units
15 units
18 units

Solution:

(1) let the side be x

New sides

x- 12, x- 13, x- 14

new A is night-angled

(x – 14)²+ (x- 13)² = (x – 12)²

Question 30. A distributor of Apple Juice has 5000 bottles in the store that it wishes to distribute in a month. From experience, it is known that demand D (in number of bottles) is given by D = -2000p2 + 2000p + 17000. The price per bottle that will result in zero inventory is

3
5
2
none of these.

Solution:

(1) D = -2000p²+ 2000p + 17000

For zero inventory D = supply

5000 = – 2000p² + 2000p + 17000

2000p² = -2000p – 12000 = 0

p² – p – 6 = 0

p²– 3p + 2p- 6 = 0

P (P – 3) + 2 (p- 3) = 0

P = 3

Question 31. The sum of two irrational numbers multiplied by the larger one is 70 and their difference multiplied by the smaller one is 12; the two numbers are

3√2, 2√3
5√2, 3√5
2√2, 5√2
none of these.

Solution:

⇒ $\alpha(\alpha+\beta)=70$

⇒ $\alpha^2+\alpha \beta=70$

⇒ $\alpha \beta=70-\alpha^2$

⇒ $\beta(\alpha-\beta)=12$

⇒ $\alpha \beta-\beta^2=12$

⇒ $\alpha \beta=12+\beta^2$

⇒ $70-\alpha^2=12+\beta^2$

⇒ $ \alpha^2+\beta^2=58$

⇒ $2 \sqrt{2}, 5 \sqrt{2}$

Question 32. Solving equation x² – (a+b) x + ab = 0 are, value(s) of

a, b
a
b
None

Solution:

(1)

x² – (a + b) x + ab = 0

a, b are values of x

a, b

Question 33. Solving equation x² – 24x + 135 = 0 are, value(s) of x

9, 6
9,15
15,6
None

Solution:

(2) 135-0

x² – 15x -9×4 135 = 0

x- 15,9

Question 34. If $\frac{x}{b}+\frac{b}{x}=\frac{a}{b}+\frac{b}{a}$ the roots of the equation are

a, b² / a
a² , b/a²
a² , b² /a
a, b²

Solution:

⇒ $\text { (a) } \frac{x}{b}+\frac{b}{x}=\frac{a}{b}+\frac{b}{a}$

⇒ $\frac{x^2+b^2}{x b}=\frac{a^2+b^2}{a b}=a x^2+a b^2=a^2 x+b^2 x$

⇒ $a x^2-a^2 x-b^2 x+a b^2=0$

⇒ $a x^2-\left(a^2+b^2\right) x+a b^2=0$

⇒ $x^2-\left(\frac{a^2+b^2}{a}\right) x+b^2=0 $

⇒ $ x^2-\frac{\left(a+b^2\right)}{a} x+b^2=0$

⇒ $\text { Iwo roots } \rightarrow \mathrm{a}, \frac{b^2}{a}$

Question 35. Solving equation $\frac{6 x+2}{4}+\frac{2 x^2-1}{2 x^2+2}=\frac{10 x-1}{4 x}$We get roots as

±l
+l
-1
0

Solution:

⇒ $\frac{6 x+2}{4}+\frac{2 x^2-1}{2 x^2+2}=\frac{10 x-1}{4 x}$

⇒ $x= \pm 1 \rightarrow 2+\frac{1}{4}=\frac{9}{4}$

⇒ $\text { for } x=-1 \rightarrow-1+\frac{1}{4}=\frac{11}{4}$

⇒ $x=1 \rightarrow 2+\frac{1}{4}=\frac{9}{4}$

Question 36. Solving equation 3x² – 14x +16 = 0 we get roots as

±l
2 and$\frac{8}{3}$
0
None

Solution:

(2) 3x² – 8x – 6x 416 = 0

3x² – 6x – 8 x 416 = 0

3x (x – 2) – 8 (x- 2) = 0

⇒ $x=\frac{8}{3},2$

Question 37. Solving equation 3x² – 14x + 8 = 0 we get roots as

±4
+2
$4,\frac{2}{3}$
None

Solution:

(3) 3x² -14x + 8 = 0

3x² – 12x -2x+9 = 0

3x (x – 4) -2 (x – 4) = 0

⇒ $x=\frac{2}{3}, x=4$

Question 38. Solving equation (b-c) x² + (c-a)x + (a-b) = 0 following roots are obtained

$\frac{a-b}{b-c}, 1$
(a-b) (a-c),1
$\frac{b-c}{a-b}, 1$
None

Solution:

(a) (b- c) x2 4 (c – a) x 4 (a – b) = 0

Sum of roots=$\frac{-(c-a)}{(b-c)}=\frac{a-c}{b-c}$

Product =$\frac{a-b}{b-c}$

⇒ $\frac{a-b}{b-c}, 1$

Question 39. Solving equation 7 $\sqrt{\frac{x}{x-1}}+8 \sqrt{\frac{x-1}{x}}=15$ Following roots are obtained.

$\frac{64}{113}, \frac{1}{2}$
$\frac{1}{50}, \frac{1}{65}$
$\frac{49}{101} \frac{1}{65}$
$\frac{1}{50}, \frac{64}{65}$

Solution:

⇒ $\text { (a) } \sqrt[7]{\frac{x}{x-1}}+\sqrt[8]{\frac{x-1}{x}}=15$

Question 40. Solving equalion 6 $\sqrt{\frac{x}{x-1}}+8 \sqrt{\frac{x-1}{x}}=13$ Following roots are obtained.

$\frac{4}{13}, \frac{9}{13}\frac{-4}{13}, \frac{-4}{19}$
$frac{4}{13}, \frac{5}{13}$
$\frac{6}{13},$
$\frac{7}{13}$

Solution:

⇒ $6\left[\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}\right]=13$

⇒ $\frac{4}{13}, \frac{9}{13}$

Chapter 2 CA Foundation Maths Answer Key

Question 41. Solving equation z² -6z + 9 = 4$\sqrt{z^2-6 z+6}$ following roots are obtained.

$\text 3+2 \sqrt{3}, 3-2 \sqrt{3}$
5, 1
all the above
None

Solution:

(3 $z^2-6 z+9=4 \sqrt{z^2-6 z+6}$

All of the above

Question 42. Solving equation$\frac{x 1 \sqrt{12 p-x}}{x-\sqrt{12 p-x}}=\frac{\sqrt{p+1}}{\sqrt{p-1}}$ following roots are obtained.

3p
both 3p and – 4p
Only -4p
-3p4p

Solution:

(1) 3p

Question 43. Solving equation $z+\sqrt{z}=\frac{6}{25}$

$\frac{1}{5}$
$\frac{2}{5}$
$\frac{1}{25}$
$\frac{2}{25}$

Solution:

(3) let √z = a

⇒ $ a 2+a=\frac{6}{25}$

⇒ $25 a 2+25 a-6=0$

⇒ $a=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}$

⇒ $\frac{-25 \pm \sqrt{625-4(25)(-6)}}{50}$

⇒ $\frac{-25 \pm \sqrt{625+600}}{50}$

⇒ $\frac{-25 \pm \sqrt{1225}}{50}$

⇒ $\frac{-25 \pm 35}{50}=\frac{10}{50} \text { or } \frac{-60}{50}=\frac{1}{5} \text { or } \frac{-6}{5}$

⇒ $ a=\sqrt{z} \rightarrow a 2=z $

⇒ $z=\frac{1}{25} \text { or } \frac{36}{25}$

Question 44. Solving equation$z^{10}-33z^5+32=0$the following values of x are obtained

1,2
2,3
2, 1
1,2,3

Solution:

(1) z¹⁰-33z⁵ +32=0

Let z⁵ = a

a² -33a + 32 = 0

a² -32a -1a + 32 = 0

a (a – 32) – 1 (a – 32) = 0

a = 1,32

z⁵= 1,32

= 1,2

Question 45. When $\sqrt{2z+1}+\sqrt{3z+4}=$ 7 the value of z is given by

Solution:

(4) 4

Question 46. Solving equation 6x⁴ + 11x³– 9x²– 11 x + 6 = 0 following roots are obtained

$\frac{1}{2}, -2 \frac{-11 \sqrt{37}}{6}$
$-\frac{1}{2}, 2 \frac{-11 \sqrt{17}}{6}$
$\frac{1}{2}, 2 \frac{5}{6} \frac{-7}{6}$
None

Solution:

(1) 6x⁴ + 11x³– 9x²– llx + 6 = 0

⇒ $\text { For } \frac{1}{2}$

⇒ $6\left(\frac{1}{2}\right)^4+11\left(\frac{1}{2}\right)^3-9\left(\frac{1}{2}\right)^2-11\left(\frac{1}{2}\right)+6$

⇒ $6\left(\frac{1}{16}\right)+11\left(\frac{1}{8}\right)-9\left(\frac{1}{4}\right)-\frac{11}{2}+6$

⇒ $\frac{6}{16}+\frac{22}{16}-\frac{36}{16}-\frac{88}{16}+\frac{96}{16}=0$

For-2

6(—2)⁴+l 1(—2)³ -9 ( —2)2—11 (-2)+6

= 96-88-36 + 22 + 6 = 0

⇒ $\frac{1}{2},-2, \frac{-1 \pm \sqrt{37}}{6}$

Question 47. $\text { If } \frac{x+2}{x-2}-\frac{x-2}{x+2}=\frac{x-1}{x+3}-\frac{x+3}{x-3}$ then the values of x are

$0, \pm \sqrt{6}$
$0, \pm \sqrt{3}$
$0, \pm 2 \sqrt{3}$
None of these

Solution:

$\text { For } 0 \frac{2}{-2}+\frac{2}{2}=\frac{-1}{3}+\frac{3}{-3}$ $-1+1 \neq \frac{-1}{3}-1$

0 is not a solution but all options have 0

None of these

Question 48. If $\frac{x-a}{b}+\frac{x-b}{a}=\frac{b}{x-a}+\frac{a}{x-b}$ then the values of x are

0,(a+b),(a-b)
$0,(a+b), \frac{a^2+b^2}{a+b}$
$0,(a-b) \cdot \frac{a^2+b^2}{a+b}$
$\frac{a^2+b^2}{a+b}$

Solution:

⇒ $0,(a-b) \cdot \frac{a^2+b^2}{a+b}$

Question 49. Solving equation $\left(x-\frac{1}{x}\right)^2-6\left(x+\frac{1}{x}\right)+12=0$ we get roots as follows

0
1
-l
None

Solution:

⇒ $\text { (2) }\left(x-\frac{1}{x}\right)^2-6\left(x+\frac{1}{x}\right)+12=0$

For 1 (O)2 – 6 (2) + 12 = 0

Question 50. Solving equation $\left(x-\frac{1}{x}\right)^2-10\left(x-\frac{1}{x}\right)+24=0$ we get roots as follows

0
1
-l
$(2 \pm \sqrt{5}),(3 \pm \sqrt{10})$

Solution:

⇒ $\text { (4) }\left(x-\frac{1}{x}\right)^2-10\left(x-\frac{1}{x}\right)+24=0$

(2±√5), (3±√I0)

Question 51. Solving equation $ 2\left(x-\frac{1}{x}\right)^2-5\left(x+\frac{1}{x}+2\right)+18=0$ we get roots as under

0
1
-1
-2± √3

Solution:

⇒ $\text { (2) } 2\left(x-\frac{1}{x}\right)^2-5\left(x+\frac{1}{x}+2\right)+18=0$

a, b, c do not satisfy

-2±√3

Question 52. If αβ the roots of equation x² – 5x + 6=0 and α > β then the equation with roots (α + β)and (α – β) is

x² -6x+5=0
2x² -6x+5=0
2x² -5x+6=0
x² -5x+6=0

Solution:

(1) α+ β = 5 αβ=6

x2- 5x + 6

x2 – 3x- 2x + 6

x (x- 3) – 2 (x – 3)

x = 2 or x = 3

α = 3, β = 2 α = 9 β2 = 4

α – β = 1

new equation→

x² – (6) x + 5 = 0

x² – 6x + 5 = 0

Question 53. If αβ are the roots of equation x²-5x+6=0 α > β then the equation with roots(αβ+γ + β) and (α + β²) is

x²-9x+99=0
x²-18x+90=0
x²-18x+77=0
None

Solution:

x²-18x+77=0

Question 54. If alpha beta are the roots of equation x²-5x+6=0 and γ > β then the equation with roots (γβ +γ+β)and )γβ – γ-β)

x²-12x+11=0
2x² -6x+12=0
x²-12x+12=0
None

Solution:

(1) x² -5x+6=0

x²– 3x- 2x + 6 = 0

x = 3, x = 2

α= 3, β = 2

αβ= 6

αβ + α + β= 6 + 3 + 2 =11

αβ – α – β= 6- 3- 2=1

new equation→

x² – (sum) x + product = 0

x²-12x +ll = 0

Question 55. The condition that one or ax2+bx+c=0 the roots of is twice the other is

b²=4ca
2b²=9(c+a)
2b²=9ca
2b²=9(c-a)

Solution:

(3) let two roots be a, 2a

⇒ $3 \alpha=\frac{-b}{a}, 2 \alpha^2=\frac{c}{a}$

⇒ $\alpha=\frac{-b}{3 a} \quad \alpha^2=\frac{c}{2 a}$

⇒ $a^2=\frac{b^2}{9 a^2}\frac{b^2}{9 a^2}=\frac{c}{2 a}$

⇒ $\rightarrow b^2=\frac{c .9 a^2}{2 a}$

⇒ $\rightarrow 2 b^2=c a 9 \quad \rightarrow 2 b^2=9 c a$

Question 56. The condition that one of ax2+bx+c=0 the roots of is thrice the other is

3b²=16ca
b²=9ca
3b²=-16ca
b²=-9ca

Solution:

(1) ax²+bx+c=0

roots → α, 3α

α + 3α =$\frac{-b}{a}$

⇒ $4 \alpha=\frac{-b}{a} \rightarrow \alpha$

⇒ $\frac{-b}{4 a} \rightarrow \alpha^2$

⇒ $\frac{b^2}{16 a^2}$

⇒ $a(3 a)=3 t^2=\frac{c}{a}$

⇒ $a^2=\frac{c}{3 a}=\frac{b^2}{16 a^2}$

⇒ $b^2=\frac{16 a^2 c}{3 a}$

⇒ $3 b^2=16 \mathrm{ac}$

Question 57. If the roots of ax²+bx+c=0 are in the ratic$\frac{p}{q}$ then the value of$\frac{b^2}{(c a)} \text { is }$

$\frac{(p+q)^2}{(p q)}$
$\frac{(p+q)}{(p q)}$
$\frac{(p-q)^2}{(p q)}$
$\frac{(p-q)}{(p q)}$

Solution:

⇒ $\frac{-b}{a}=p y+q y \frac{c}{a}=p q y^2$

⇒ $-b=\mathrm{a}(\mathrm{py}+\mathrm{qy}) \mathrm{c}=a p q y^2$

⇒ $\mathrm{~b}^2=\mathrm{a}^2(\mathrm{py}+\mathrm{qy})^2$

⇒ $\frac{b^2}{c a}=\frac{a^2(p y+q y)^2}{a p q y^2 a}=\frac{(p+q)^2}{p q}$

Question 58. Solving equation$\sqrt{x^2-9 x+18}+\sqrt{x^2+2 x-15}=\sqrt{x^2-4 x+3}$ following roots are obtained

$3, \frac{2 \pm \sqrt{94}}{3}$
$\frac{2 \pm \sqrt{94}}{3}$
$4,-\frac{8}{3}$
$3,4-\frac{8}{3}$

Solution:

⇒ $\sqrt{x^2-9 x+18}+\sqrt{x^2+2 x-15}=\sqrt{x^2-4 x+3}$

⇒ $\sqrt{x^2-6 x-3 x+18}+\sqrt{x^2+5 x-3 x-15}$

⇒ $\sqrt{(x)(x-6)-3}$

⇒ $\sqrt{(x)(x-6)-3(x-6)}+\sqrt{x(x+5)-3(x+5)}$

⇒$\sqrt{x(x-3)-1(x-3)}$

⇒$\sqrt{(x-3)(x-6)}+\sqrt{(x-3)(x+5)}$

⇒ $\sqrt{(x-1)(x-3)}$

⇒ $3, \frac{2 \pm \sqrt{94}}{3}$

Question 59. Solving equation $\sqrt{y^2+4 y-21}+\sqrt{y^2-y-6}=\sqrt{6 y^2-5 y-39}$ following roots are obtained

2, 3, 5/3
2, 3, -5/3
-2, -3, 5/3
-2, -3, -5/3

Solution:

⇒$\sqrt{y^2+4 y-21}+\sqrt{y^2-y-6}=\sqrt{6 y^2-5 y-39}$

⇒$\sqrt{y^2+7 y-3 y-21}+\sqrt{y^2-3 y+2 y-6}$

⇒$\sqrt{6 y^2 18 y+13 y-39}$

⇒$\sqrt{y(y+7)-3(y+7)}+\sqrt{y(y-3)+2(y-3)}$

⇒$\sqrt{6 y(y-3)+13(y-3)}$

⇒$\sqrt{(y-3)(y+7)}+\sqrt{(y+2)(y-3)}$

⇒$\sqrt{(y-3)(6 y+13)}$

⇒$2,3, \frac{-5}{3}$

Question 60. Find the positive value of k for which the equations: x² + kx + 64 = 0 and x² – 8x + k = 0 will have real roots:

Solution:

(2) for real roots

D = b2 – 4ac> 0

For eqn (1]; k² ≥ 4.1.64 ⇒ k > 16……(1)

For eqn (2) (-8)^2≥ 4.1k⇒ k < 16……(2)

∴ (2) is correct.

Question 61. If one root of an equation is 2 + √5. Then the quadric equation is:

x² + 4x -1 = 0
x² – 4x – 1 = 0
x² + 4x +1 = 0
x² – 4x + 1 = 0

Solution:

(2) if one root = 2 + √5 (Irrational conjugate)

Eqn is

X² – (sum of roots) x + product of roots = 0

Or x²– (2 + √5 + 2 -√5)x+ (2 + √5) (2 – √5) = 0

Or x²– 4x + (4- 5) = 0

0r x²-4x-1 = 0

(2) is correct.

Question 62. A man starts his job with a certain monthly salary and earns a fixed increment every year. If his salary was K 1,500 after 4 years of service and 1,800 after 10 years of service, what was his starting salary and what is the annual increment in rupees?

1,300, 50
1,00, 50
1,500, 30
None

Solution:

For (1) salary after 4 years 1300 + 4 x 50 =1500……..(1)

Salary after 10 years = 1300 + 10 x 50 =1800……….(2)

Detail Method

Let fixed salary = a

Increment per yr = b

Salary after t yrs = s

s = a + bt

a + b x 4 = 1500 = a + 4b = 1500…

a + bx 10= 1800 = a + 10b = 1800.

Eqn. (2) – eqn. (1); we get

a + bx 10= 1800

a + 4b =1500

6b = 300 b =$b=\frac{300}{6} ₹ 50$

From (1) a + 4 x 50 = 1500

Or a = 1500 – 200 = 1300

(1) is correct

Question 63. The sides of an equilateral triangle are shortened by 1 2 units, 13 units, and 14 units respectively, and a right-angled triangle is formed. The side of the equilateral triangle is:

17 units
16 units
15 units
18 units

Solution:

For (a] let each side = 17 units.

∴ sides are 17 – 12; 17 – 13 and 17 – 14

= 5; 4 and 3 units respectively

They make a right-angled triangle because the sum of squares of two sides is equal to
square of the largest side.

i.e., 42 + 32 = 52

(1) is correct.

Detail method

Let the length of each side = x

Side of the right angle triangle are x – 12 ; x – 13 and x – 14

by Pythagoras theorem

(x- 12)² = (x- 13)² + (X- 14)²

Or x² – 24x + 144 = x² – 26x + 167 + x² – 28x + 196

Or 0 = x² – 30x + 221

Or x²-17x-13x + 221 = 0

Orx(x-17)-13(x-17) =0

Or (x-17) (x-13) = 0

x = 17; 13

No side = x-13 = 0

x = 17

(a) is correct.

Question 64.The value of $\sqrt{6+\sqrt{6+\sqrt{6+\cdots \ldots to \infty}}} \text { is: }$

Solution:

⇒ $\text { (3) } \sqrt{6+\sqrt{6+\sqrt{6+\cdots \ldots \text { to } \infty}}}=+3$

Find two factors of 6 such that their difference becomes 1.

6 = 3×2

(1) Give + sign for = greater factor

(2) – sign for smaller factor

(3) is correct

Question 65. The area of a rectangular garden is 8000 square meters. The ratio in length and breadth is 5: 4 A path of uniform width, runs all-round the inside of the garden. If the part occupies 3200 m2, what is its width?

Solution:

(3) let x be common in the ratio

length = 5x anil breadth = 4x

Area = 5x x 4x = 8000

Or 20x² = 8000

Or x² = 400 = 20²

∴ x = 20

Length = 5x = 5 x 20 = 100m

Breadth = 4x = 4 x 20 = 80m

Let Width of path = ym

∴ Area of rest part = 8000 – 3200

Or (100 – 2y) (80- 2y) = 4800

Tricks: go by choices.

∴ (3) y = 10 m satisfies it

Width = 10m is correct

Question 66. If (2 +V3) is a root of a quadratic equation x² + px + q = 0 then find the value of p and q.

(4,-1)
(4, 1)
(-4, 1)
(2,3)

Solution:

One root = 2 + V3

Another root = 2- V3

Eqn is

x² — (2 + √3 + 2 – √3)x + √2+√3) (2 – √3) = 0

Or x² – 4x + (4- 3) = 0

Comparing it with x + px + q = 0

p = -4 and q =1

(3) is correct

Question 67. If the area and perimeter of a rectangle are 6000 cm² and 340cm respectively, then the length of a rectangle is:

Solution:

(2)

let length =1

and breadth = b

lb = 6000 _

2(l + b) = 340…….(1)

Or 1 +b = 170…….(2)

Then Go by choices

For (a) if 1 = 140 then b = 170 – 140 = 30

lb = 140 x 30 = 4200* 6000

(a) is not the answer

For (2) if 1 = 120

Then 120 + b = 170

b= 170 -120 = 50

Area = lb = 120 x 50 = 6000

Question 68. A straight line passes through the point (3,2). Find the equations of the straight line.

x + y =1
x + y = 3
x + y = 5
x + y = 2

Solution:

(3) it cannot be solved properly because only one condition is given for the answer

(3) Point (3 ; 2) satisfies x + y = 5

(3) is correct

Question 69. One root of the equation: x² – 2(5+m)x+3(7+m>0 is reciprocal of the other. Find the value of m.

-20/3
7
1/7
117

Solution:

(1)

Let one root = or, then other root =$=\frac{1}{\alpha}$

⇒ $\alpha \times \frac{1}{a}=\frac{3(7+m)}{1}$

1 = 21 + 3m

⇒ $3 m=-2m=\frac{-20}{3}$

(1) is correct

Question 70. Roots of the equation 3x² – 14x – k = 0 will be reciprocal of each other if:

k = -3
k = 0
k = 3
k = 14

Solution:

(3) is correct.

Let one root = a and another root =$=\frac{1}{\alpha}$ (given)

Product of roots = $=\frac{c}{a}$

⇒ $\alpha \times \frac{1}{\alpha}=-\frac{k}{3}$

⇒ $-1=\frac{k}{3} \text { So, K }=-3$

(1) is correct

Question 71. Positive value of for which the roots at equation 12x² + kx + 5 = 0 are in ratio 3 : 2, is

5/12
12/5
$\frac{5 \sqrt{10}}{2}$
5√10

Solution:

(4)

Let a be common in the ratio.

Roots are 3 a and 2 a

Sum of roots =$-\frac{b}{a}$
.
3a + 2a = 5a =$-\frac{k}{12}$

⇒ $\alpha=-\frac{k}{60}$

Product of roots = $3 \alpha+2 \alpha=\frac{c}{a}$

⇒ $6 x^2=\frac{5}{12}$

⇒ $\text { 6. }\left(-\frac{k}{60}\right)^2=\frac{5}{12}, \text { so, } \mathrm{k}^2=250$

k = 5√10

Question 72. If one root of the equation x²– 3x + k = 0 is 2, then value of k will be

Solution:

(3) is correct

2 is a root of given eqn.

2²– 3 x 2 + k = 0

Or-1 + k = 0

∴ k = 2

Question 73. It roots of equation x² + x + r = 0 are ‘a’ and ‘α’ and β = -6. Find the value of V.

$\frac{-5}{3}$
$\frac{7}{3}$
$\frac{-4}{3}$
1

Solution:

(1) is correct

⇒ $\alpha+\beta=\frac{-1}{1}=-1 \ and \alpha \beta=\frac{r}{1}=r$

α³ + β³ = -6

or (α + β)³– 3αβ (α + β) = -6

or (-1)3 — 3r(—1) = -6

Or- 1 + 3r = -6; or 3r = -5

r = -5/3

Question 74. If one root of the equation Px²+ qx + r = 0 is r then the other root of the equation will be

1/q
1/r
1/p
$\frac{1}{p+q}$

Solution:

(3) let a is another root.

⇒ $\mathrm{r} \alpha=\frac{r}{p} \alpha=\frac{1}{p}$

Question 75. If the ratio of the root of the equation 4x² – 6x + p = 0 is 1 : 2 then the value of is

1
2
-2
-l

Solution:

(2) let α be common in the ratio

⇒ $ \alpha+2 \pi=\frac{p}{4}p=8 \alpha^2=8 \cdot \frac{1}{4}=2$

Question 76. If p and q are the root of the equations x² – bx + c = 0, what is the equation whose roots are (pq + p + q) and (pq – p – q)?

x² – 2cx + c² – b² = 0
x² – 2cx + c² + b²= 0
8cx² – 2(a+c)x + c² = 0
cx² + 2bx – (c² – b²) = 0

Solution:

(1)

x² – (p + q)x + pq = 0

b = p + q ; C = pq

New roots are

pq + (p + q) = c + b

pq-(p + q) = c-b

Eqn is

x² – (c + b + c- b)x +(c + b)(c- b) = 0

or x² – 2cx + c² – b² = 0

Question 77. If the arithmetic mean between the roots of a quadratic equation is 8 and the geometric mean between them is 5, the equation is-

x²– 16x-25 = 0
x²– 16x + 25 =
x² – 16x + 5 = 0
None of these

Solution:

(2) let α and β be two roots.

(α+β)/2 = 8 and √αβ = 5

⇒ α+β = 16 and αβ = 25

Eqn. is x²-16x + 25 = 0

Question 78. The minimum value of the function x²– 6x + 10 is-

Solution:

(1) coeff. Of x2 = 1 > 0; function is minimum (formula)

Minimum value =$\frac{4 a c-b^2}{4 a}$

⇒ $=\frac{4.1 .10-(-b)^2}{4 \times 1}=\frac{4}{4}=1$

CA Foundation Equations Solved Examples

Question 79. If one of the roots of the equation x² + px + a is √3 + 2. Then the value of and ‘a’ is

-4,-1
4, -1
4,1
4,1

Solution:

(3) Roots are 2 + √3 and 2 —V3

(conjugate of 2+√3)

Eqn is

x² – (sum of roots) x + product of roots = 0

x²– 4x + (4- 3) = 0

x² + px + a = 0

∴ P = -4; a = 1

Question 80. The roots of equation 2x² + 3x + 7 = 0 are α and β. The value of a αβ^-1+βα^-1

2
3/7
7/2
-19/14

Solution:

⇒ $\text { (d) } \alpha+\beta=-\frac{3}{2} ; \alpha \beta=7 / 2$

⇒ $\frac{\alpha}{\beta}+\frac{\beta}{\alpha}=\frac{\alpha^2+\beta^2}{\alpha \beta}=\frac{(\alpha+\beta)^2-\alpha \beta}{\alpha \beta}$

⇒ $\frac{\frac{9}{4}-2 \cdot \frac{7}{2}}{\frac{7}{2}}=\frac{9-28}{4} \times \frac{2}{7}=\frac{-19}{14}$

Question 81. The quadratic equation x²– 2kx + 1 6 = 0 will have equal roots when the value of is –

Solution:

(4) let roots are or; or

⇒ $\alpha+\alpha=\frac{-(-2 k)}{1} \Rightarrow \alpha=k$

= α.α = k.k => k² = 16 => k = ±4

Question 82. If α, βare roots of x² + 7x+ 11 = 0 then the equation whose roots as (α+β)² And (α – β)²

x²-54x+ 245 = 0
x² — 14x + 49 = 0
x²-24x+ 144 = 0
x² – 50x + 49 = 0

Solution:

(1) is correct

⇒ $\alpha+\beta=-\frac{b}{a}=-\frac{7}{1}=-7$

⇒ $\alpha \beta=\frac{c}{a}=\frac{11}{1}=11$

(α-β)² = (α+β)²– 4ap

= (—7)² -4×11 = 5

Require eqn. is

x² (α+β)² + (α-β)² = 0

or x² – (49+5)x + 49 x 5 = 0

or x²-5x + 245 = 0

(1) is correct

Question 83. If b² – 4ac is a perfect square but not equal to zero then the roots of the equation ax2 + bx + c = 0 are

Real and equal
Real irrational and equal
Real rational and unequal
Imaginary

Solution:

(3) b²– 4ac > 0 and perfect square

Question 84. Divide 80 into two parts so that their products are maximum then the numbers are

15,65
25,55
35,45
40,40

Solution:

(2) is correct

Let 1st part = x

2ml part = 80 – x

Lety = x(80-x) = -x² + 80x

Here co. eff. of x²< 0

Numbers are (40; 40)

Question 85. If a,p is the roots of a quadratic equation if x² + 2x – 3 find the quadratic equation:

x² + 2x – 7 = 0
x² + 2x – 3 = 0
x² – 2x – 3 = 0
x² – 2x +7 = 0

Solution:

(2)

Quadratic eqn is

x2 – (a + p)x + ap = 0

x2 – (-2)x + (-3) = 0

x2 + 2x- 3 = 0

Question 86. Value of k for which roots are equal of given equation 4x² – 12x + k = 0:

144
9
5
None of these

Solution:

(2)

4×2- 12x + k = 0

D = b2 – 4.ac = 0

(-12)2 = 4 x 4.k

Or. 144= 16k

k = 9

Question 87. If difference between the roots of the equation x² – kx + 8 = 0 is 4 then the value of K is

0
±4
±8√3
±4√3

Solution:

(4)

Let a; /? are roots of x² – kx + 8 = 0

⇒ $\alpha+\beta=b / a=-\frac{(-k)}{1}=k \& \alpha \cdot \beta=c / a=8 / 1 $

⇒ $(\alpha-\beta)^2=(\alpha+\beta)^2-4 \alpha \beta=4^2$

⇒ $\Rightarrow k^2-4 \times 8=16$

⇒ $\text { Or } k^2=48 \Rightarrow k= \pm \sqrt{16 \times 6} \Rightarrow k= \pm 4 \sqrt{3}$

Question 88. If a: /? be the roots of x²+x+5 = 0 then$\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}=$

$\frac{16}{5}$
2
3
$\frac{14}{5}$

Solution:

⇒ $\alpha+\beta=-\frac{b}{a}=-\frac{1}{1}=-1$

⇒ $\alpha \beta=\frac{c}{a}=\frac{5}{1}=5$

⇒ $\frac{a}{\beta}+\frac{\beta^2}{u}=\frac{\alpha^3+\beta^3}{\alpha \beta}$

⇒ $\frac{(\alpha+\beta)^3-3 a \beta(\alpha+\beta)}{\alpha \beta}=\frac{(-1)^3-3.5 \cdot(-1)}{5}$

⇒ $\frac{-1+15}{5}=\frac{14}{5}$

Question 89. If the sum of two numbers is 13 and the sum of their squares is 85 then the numbers

6,7
4,9
10,3
5,8

Solution:

(1)

6 + 7= 13 (true)

62+ 72 = 36 + 49 = 85 (True)

Question 90. The difference between the roots of the equation x² – 7x- 9 = 0 is

7
V85
9
2x/85

Solution:

(2)

⇒ $\text { Let } \alpha+\beta=-\frac{b}{a}=-\frac{-7}{1}=7$

⇒ $\propto \beta=\frac{c}{a}=\frac{-9}{1}=-9 $

⇒ $(\alpha-\beta)^2=(\alpha+\beta)^2-4 \propto \beta=7^2-4(-9)=85 $

⇒ $\alpha-\beta=\sqrt{85}$

Question 91. If the roots of the equation kx² — 3x —1 = 0 are the reciprocal of the roots of the equation x² + 3x – 4 = 0 then k=

4
-4
3
-3

Solution:

(1) x² + 3x- 4 = 0

Or x² – 4x + x – 4 =0

Orx(x- 4) +1 (x- 4) = 0

Or; (x- 4) (x + 1) = 0

x = 4; -1

Eqn. having rots $\frac{1}{4} \& \frac{1}{-1}=\frac{1}{4} \&-1 \text { is. }$

⇒ $x^2-\left(\frac{1}{4}-1\right) x+\frac{1}{4}(-1)=0$

⇒ $\text { or } x^2+\frac{-1}{4} x-\frac{1}{4}=0$

Multiplying by 4; we get

4x² + 3c- 1 = 0

Comparing it with le tx² + 3x-1 = 0

We get K = 4

Eqn. having roots the reciprocal of the roots of ax²+ bx + c = 0 is ax² + bx + a = 0 i.e. 1st and last term interchanges

Question 92. If cr + ft = -2 mid aft = -3 where u and \ I are the roots of the equation, which is

x² – 2x -3 = 0
x² + 2x -3 = 0
x² + 2x + 3 = 0
x² – 2x + 3 = 0

Solution:

(2)

Quadratic Eqn. having roots a and |3 is

x² – (a + (3) x + a(3 = 0

or; x² – (-2)x + (-3) = 0

or; x² + 2x- 3 = 0

(2) is correct

Question 93. If a and (1 are the roots of the equation x² + x + 5 = 0 the$\frac{a^2}{\beta}+\frac{\beta^2}{\alpha}$

$\frac{16}{5}$
3
$\frac{14}{5}$
2

Solution:

(3)

Given Eqn. is x² + x + 5 = 0

⇒ $\alpha+\beta=-\frac{b}{a}=-\frac{1}{1}=-1$

⇒ $\alpha \beta=\frac{c}{a}=\frac{5}{1}=5 $

⇒ $\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}=\frac{\alpha^3+\beta^3}{a \beta}$

⇒ $\frac{(\alpha+\beta)^3-3 \alpha \beta(\alpha+\beta)}{\alpha \beta}$

⇒ $\frac{(-1)^3-3 \cdot 5 \cdot(-1)}{5}=\frac{-1+15}{5}=\frac{14}{5}$

Question 94. When two roots of quadratic equation are a,$\alpha, \frac{1}{\alpha}$ then what will be the quadratic equation:

ux² – (cr² + 1)x + cr = 0
ax² – ax² + 1 = 0
ax² – (cr ² + l)x +1=0
None of these

Solution:

(1)

For $\alpha \cdot \frac{1}{a}=1=\frac{c}{a}=\frac{a}{a}=1 \text { (True) }$

Question 95. Let cr and ft be the roots of x2 + 7x + 12 = 0, The the value of$\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha} \text { will be }$

$\frac{19}{141}+\frac{141}{49}$
$\frac{7}{12}+\frac{12}{7}$
$-\frac{91}{12}$
None of these

Solution:

x² + 7x+ 12 = 0

or x²+ 4x + 3x + 12 = 0

or x(x + 4) + 3 (x + 4) = 0

or (x + 4) (x + 3) = 0

x = -3; -4

Letα = —3 ; β = -4

⇒ $\frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}=\frac{9}{-4}+\frac{16}{-3}$

⇒ $-\left[\frac{9}{4}+\frac{16}{3}\right]=-\frac{91}{12}$

2 and Method

⇒ $alpha+\beta=\frac{-7}{1}=-7$

⇒ $\alpha \beta=\frac{c}{a}=\frac{12}{1}=12$

⇒ $ \frac{\alpha^2}{\beta}+\frac{\beta^2}{\alpha}=\frac{\alpha^3+\beta^3}{\alpha \beta}=\frac{(\alpha+\beta)^3-3 \alpha \beta(\alpha+\beta)}{\alpha \beta}$

⇒ $\frac{(-7)^3-3 \times 12(-7)}{12}=-\frac{91}{12}$

Question 96. Find the condition that one root is double the of ax² + bx + c = 0

2b² = 3ac
b²= 3ac
2b² = 9ac
None

Solution:

Let 1st root =1

Then 2nJ root = 2

The Eqn. is

x2-(l + 2)x+lx2 = 0

or x² – 3x + 2 = 0

Comparing it with ax² + bx + c = 0

We get;

a = 1; b = 3; c = 2

Go by choices (GBC)

(1) 2b² = 9ac

2.(-3)2 = 9.1.2

⇒ 18 = 18 (True)

Hence, (3) is (true)

Question 97. Find the quadratic equation in x whose roots are 2 and 3.

x² + 5x + 6 = 0
x² — 5x — 6 = 0
x² – 5x + 6 = 0
x² + 5x- 6 = 0

Solution:

The quadratic equation is (x-2) (x-3) = 0

Or x² — 2x — 3x + 6 = 0 or x²– 5x + 6 = 0

Question 90. If the sum of the roots of a quadratic equation in x is 4 and the constant term of the equation is 15, then find the quadratic equation.

x²– 4x + 1 5 = 0
x² – 4x + 1 5 = 0
x² + 4x+ 15 = 0
x² + 4x+ 15 = 0

Solution:

we know that if s is the sum and p is the product of the roots of a quadratic equation then the equation is x²– 5x + p = 0

Note that the constant term in the equation is nothing but the product of the roots.

Given s=4, p=1 5

The quadratic equation is x² – 4x + 15 = 0

Question 99. Find the roots of the quadratic equation x²– 8Y + 9 = 0

1,9
-1,-9
4+√7, 4-√7
3+√6, 3-√6

Solution:

⇒ $x^2-8 x+9=0 \text { the roots are } \frac{-\Delta \pm \sqrt{D^2-4 a c}}{2 a}$

⇒ $x=\frac{-(-8) \pm \sqrt{(-8)^2-4(1)(0)}}{2(1)}$

⇒ $\frac{8 \pm \sqrt{s t-3 a)}}{2}=\frac{8 \pm \sqrt{2 s}}{2}=\frac{8 \pm 2 \sqrt{7}}{2}=4 \pm \sqrt{7}$

⇒ $\text { roots are } 4+\sqrt{7} \text { and } 4-\sqrt{7}$

Question 100. Find the sum of the roots of the equation, 9x² — 36x + 35 = 0.

36
-36
4
-4

Solution:

he sum of the roots of equation ax² +bx+ c = 0 is -b/a

the sum of the roots of 9x² — 36x+ 35 = 0 is $\frac{-(-36)}{9}=4$

Question 101. If the sum of the roots of a quadratic equation is 11 and the product of the roots is 24, find the roots of the equation.

6,4
12,2
8,3
1,24

Solution:

let a, and p be the roots of the equation. Given, α + β = 11 and αβ = 24

(α- β)² = (α + β)²– 4αβ = ll2- 4(24) = 121- 96 = 25

α- β = 5

(1) ÷ (2)⇒ 22=16⇒α = 8

β= 11-8 = 3

the roots are 8,3.

Question 102. If the sum of the roots of a quadratic equation is 7 and the product of the roots is 12, then find the equation.

x² + 7x + 12 = 0
x² + 7x — 12 = 0
x²– 7x + 12 = 0
x²– 7x — 12 = 0

Solution:

Given the sum of the roots is 7 and the product of the roots is 12.

the equation is

x² -(sum of the roots)x+ (product of the roots) = 0 i. e.x² — 7x + 12 = 0

Question 103. Find the discriminant of the equation 2x² + 3,Y + 4 = 0

Solution:

discriminant of the quadratic equation ax² + bx + c = 0 is b²– 4ac

the discriminant of 2.v2 + 3.v 4-4 = 0 Is

32 — 4(2)(4) = 9 — 32 = —23

Question 104. Construct a quadratic equation whose roots are 4 more than the roots orx2 + lx + 16 = 0

x2 + 15x + 60 = 0
x2 + 7x + 60 = 0
x2- x + 4 = 0
x2 + 15x + 16 = 0

Solution:

to find a new quadratic equation, whose roots are 4 more than the roots of x²+ 7x + 16 = 0

we have to replace x by (x-4)

The equation is (x- 4)² +7(x- 4) + 16 = 0

⇒ x²– 8. Y 4- 16 + 7x – 28 + 16 = 0

⇒ x²– x 4- 4 = 0

Question 105. Construct a quadratic equation whose roots are reciprocals of the roots of the equation 3x² + 5x + 7 = 0

7x² + 5x + 3 = 0
5x² + 7x + 3 = 0
5x² + 3x + 7 = 0
7x² + 3x + 5 = 0

Solution:

to find a new quadratic equation, whose roots are reciprocals of the roots of 3x²+ 5x +7 = 0 we have replaced x by1/x

The equation is$3\left(\frac{1}{x}\right)^2+5\left(\frac{1}{x}\right)+7=0$

7x² + 5A + 3 = 0

Question 106. Construct a quadratic equation whose roots are half roots of the equation x²+5x+9=0

4x² + lOx + 9 = 0
x² + lOx + 36 = 0
4x² + 5x + 36 = 0
4x² + 5x + 9 = 0

Solution:

To find a new quadratic equation, whose roots are half of the roots of the equation,

x² + 5x + 9 = 0 we have dot replace x by 2x the equation is (2,y)2 + 5(2x) + 9=0

⇒ (4×2) + 10.Y + 9 = 0

Question 107. How many distinct roots does the quadratic equation (x- 4)² = 0 have?

Solution:

Here the equation (x- 4)² = 0 is given.

Number of distinct roots = 1

Question 108. Solve for x x⁴– 61x² + 900 = 0

±4. ±5
±5, ±6
±3,±5
±4, ±6

Solution:

x⁴ – 61x² + 900 = 0=>(x²– 36)(x² – 25) = 0

⇒ x=±5,±6

Question 109. Solve for x 3^2x+1 _ 39(3x+2) + 8748 = 0

4
log336
Either (1) or (2)
6

Solution:

3(3^2x)- (39)(9)(3^x) + 8748 = 0

Dividing by 3 and setting y=3^x

y² – 117y + 2916 = 0

⇒ 3^x = 36 or 3X = 81

⇒ x= log336 or x = 4

Question 110. Solve for x$\sqrt{2 x-5}+\sqrt{3 x+4}=8$

8
615
7
Either (2) or [3]

Solution:

⇒ $ \sqrt{2 x-5}+\sqrt{3 x+4}=8 \rightarrow(\mathrm{A})$

By squaring on both sides.

⇒ $5 x-1+2 \sqrt{6 x^2-7 x-20}=64$

⇒ $ 2 \sqrt{6 x^2-7 x-20=-5(x-3)}$

By squaring on both sides

⇒ 4(6x² – 7x- 20) = 25(x² – 26x + 169)

⇒ x²– 622x + 4305 = 0

⇒ (x — 61 5)(x — 7) = 0

Substituting x =7 in (A) we see that V9 + V25 = 8 but for x=615

⇒ $=\sqrt{2(615)-5}+\sqrt{3(615)+4}=\sqrt{1225}+\sqrt{1849}$

35+43=78

To get 8, we have to take the negative root for 1225 The expression V1225 normally stands for the positive square root 35 we would say that x=615 does not satisfy [A)

Hence x =7

Question 111. Which of the following is the root [s] of $\sqrt{3 x+34}+\sqrt{3-2 x}=\sqrt{67+x}$

3
-3
-41/6
1. A or B
2. B or C
3. C or A
4. Only B

Solution:

⇒ $ \sqrt{3 x+34}+\sqrt{3-2 x}=\sqrt{67+x} \rightarrow(A)$

By squaring on both sides,

⇒ $x+37+2 \sqrt{-6 x^2-59 x+102}=67+x $

⇒ $2 \sqrt{-6 x^2-59 x+102}=30$

By squaring on both sides,

⇒ -6x²– 59x + 102=225

⇒ 6x² + 59x+123=0

⇒ (6x+41) (x+3)=0

⇒ x= -41/6 or -3

Substituting -3 in (A) the left-hand side (LIIS)

And if we substitute -41/6 the LHS of (A

⇒ $=\sqrt{3(-3)+34}+\sqrt{3-(-6)}=5+3=8 R H S$

⇒ $\sqrt{-\frac{41}{2}+\frac{68}{2}}+\sqrt{\frac{9}{3}+\frac{41}{3}}=\sqrt{\frac{27}{2}}+\sqrt{\frac{50}{3}}$

⇒ $\frac{9}{\sqrt{6}}+\frac{10}{\sqrt{6}}=\frac{19}{\sqrt{6}} \text { and the RHS }$

⇒ $\sqrt{\frac{402}{6}-\frac{41}{6}}=\sqrt{\frac{361}{6}}=\frac{19}{\sqrt{6}}$

⇒ $\text { Both }-3 \text { and }-41 / 6 \text { satisfy (A) }$

Question 112. Find the value of if one of the roots of x² – 9x + 2p = 0 is 3 more than the other.

Solution:

Let the roots of a and a + 3.

2α + 3 = 9

⇒ α = 3

The other root is 6 and 2p = 18 or p=9

Question 113. Four friends have some coins. Pavan has 2 less than Samir, who has 2 less than Tarun,ifPra has 2 less than Pavan and the product of the number of coins that each of them has is 5760, how many coins in all do they have among themselves?

Solution:

Let the number of coins with Pranav, Pavan, and Samir Tarun be (a-3), (a-1), and (a+1) respectively.

(a² + 3²)(a²– l²)(a + 3)= 5760

Let a2 = k(k- 9)(/c- 1) = 5760

k² – 10k- 5751 = (k- 81)(fc + 71) = 0

⇒k = 81 or- 71

As k is positive, a² = 81⇒a = 9

⇒ (a- 3) + (a- 1) + (a + 1) + (a + 3) = 36

Question 114. If the roots of ax² + bx+c-0 are α and β and the roots of px² + qx + r = 0 are α- k and β-k, then

r= ak² – bk + c
r= ak²– bk- ck²
r= ak + bk + ck²
r= ak² + bk + c

Solution:

(d)

As α— k and β — n are the roots ax² + bx + c = 0

Now, the equation with α — k and β- kas roots are

f(x + k) i.e.a(x-k)² + b(x + k) + c = 0

ax2 + (fa + 2ak)x + (a/c2 + fa/c + c) = 0

By comparing this equation with px² + qx +r = 0, r=ak² + bk + c

Question 115. if the roots of x² + 7x + 10 = 0 are a and /?, find the equation whose roots are $\left(\frac{1-\alpha}{\beta}\right)$ and $\left(\frac{1-\beta}{\alpha}\right)$

x² + 360x + 180 = 0

x²+ 0.36x + 0.18 = 0

x² +36x + 18 = 0

x² + 3.6x + 1.8 = 0

Solution:

(4)

The roots of x² +7x + 10 = 0 area and (3)

α + β = -7 and αβ = 10

⇒ $\text { If } \mathrm{p}=\frac{1-\alpha}{\beta} \text { and } \mathrm{q}=\frac{1-\beta}{\alpha}$

⇒ $P+q=\frac{(\alpha+\beta)-\left(\alpha^2+\beta^2\right)}{\alpha \beta}$

⇒ $=\frac{(\alpha+\beta)-(\alpha+\beta)^2-2 \alpha \beta}{\alpha \beta}$

⇒ $=\frac{(-7)-\left(7^2-2(10)\right)}{10}=-3.6$

⇒ $\text { and } \mathrm{pq}=-\frac{1-\alpha-\beta+\alpha \beta}{\alpha \beta}$

⇒ $=\frac{1-(-7)+10}{10}=1.8$

The equation where roots are p,q is x² + 3.6x + 1.8 = 0

Question 116. A total of Rs.3, 300 is raised by collecting equal amounts from a certain number of people. If there were 22 people more, each person would have to contribute Rs. 200 less to raise the same amount. How many people contributed?

Solution:

Let the number of people and the contribution of each person be n and a respectively,

(n + 22)(a- 200) = na

⇒ 22a – 200n = 4400 → (1)

And na= 3300→ (2)

Substituting the value of from (2) in (1)

22(3300/n)-200n = 4400

⇒ ll(33)/n- n = 22⇒ n² + 22n- 11(33) = 0

⇒ (n + 33)(n- 11) = 0 =>n = 11

Question 117. The sum of two positive numbers is 32. The square of the largest number is 223 more than twice the square of the smaller number. Find the smaller number.

Solution:

(1)

Let the smaller and larger numbers be x and yx + y=32→ (1)

2A2 + 23 = y2 → (2)

⇒ x² + 64x- 1001 = 0⇒(x + 77)(x- 13) = 0

⇒ x = -77 or x = 13

As x cannot be negative x = 13

Question 118. Akash and Badri, together buy 45 notebooks. Each of them buys a different number of books and both of them spend the same amount if Akash had bought his notebooks at the price at which Badri had bought them and Badri had bought his notebooks at the price where Akash had bought them, they would havespentRs. 160 and Rs. 250 respectively. How many notebooks did Badri buy?

Solution:

(1) Akash Badri

No. of notebooks mn

Price a b

We have m + n=45→ (1)

Ma = nb→ (2)

Mb = 160 → (3)

Na = 250 → (4)

From (2) ⇒ m/n = b/a

(3) +(4)⇒ (m/n)2 = (16/25) = (4/5)2

m: n = 4:5

And n=5/9 (45) =25

Question 119. If the roots α and β of x2- 4x- c = 0 satisfy the condition 2α + β = 1, then which of the following is true?

α = -3, β = 7
c=-21
α = -15, β = 3.5
α = 3, β = -7

Solution:

(1)

The α,β are the roots of x²– 4x- c = 0

α+β = 4 and 2a + p = 1 (given)

⇒ a = -3 and P = 7

Question 120. How many of the roots of x² – A + 2 are also the roots of x² + 4x² + 5x + 2 = 0?

Solution:

(2)

The roots of x²– x + 2 are x = 2 and x = -1

of these two roots, only, one of the roots satisfies the cubic equation, i.e. (2)³ + 4(2)² + 5(2) + 2≠0 but (-1)3+ 4(—l)² + 5(-l) + 2 = 0

has real and distinct roots.

Question 121. If one of the roots of x² – ax + b – 0 is 2+√3 and b=a+2+3√3, find the other root.

2-√3
√3- 2
4
-4

Solution:

(4)

the roots of 3x² + 9x + 5 = 0 are p and q p + q=9/3=3 and p q=5/3

⇒ $\frac{1}{p^2}+\frac{1}{q^2}=\frac{p^2+q^2}{p^2 q^2}=\frac{(p+q)^2-2 p q}{p^2 q^2}$

⇒ $\frac{3^2-(10 / 3)}{25 / 9}=\frac{51}{25} \text { and } \sqrt{3 p q}=\sqrt{5}$

⇒ $ p^2+q^2=\sqrt{3 p q}=\frac{51}{25}+\sqrt{5}$

Chapter 2 Equations Step-By-Step Solutions

Question 122. The roots of 35x² + x = 12 are

Rational and equal.
Rational and distinct.
Irrational and equal.
Irrational and unequal

Solution:

(2)

for the equation 35x² + x- 12 = 0 the determinant

s=1² + 4(35)(12) = If,81 = 41² = 18681=41²

the roots are rational (because A is a perfect square)and distinct (because Δ≠0)

Question 123. How many real roots does the equation x⁴ + 2x³ – 10x² – 2x + 1 = 0 have?

Zero
One
Two
Four

Solution:

For equations of the form Ax⁴ + Bx³ + Cx² ± Bx + A = 0, the method illustrated below should be used.

Given the equation, x⁴ + 2x³– 10x²– 2x +1 = 0 …. (1)

Divide (1) by x2 we get $x^2+2 x-10-\frac{2}{x}+\frac{1}{x^2}=0$

⇒ $\Rightarrow\left(x^2+\frac{1}{x^2}\right)+2\left(x-\frac{1}{x}\right)-10=0$

⇒ $\text { Put } \mathrm{x}-\frac{1}{x}=y, \text { then } x^2+\frac{1}{x^2}=y^2+2$

⇒ y² + 2 + 2y- 10 = 0

⇒ (y+4)(y-2) =0

⇒ y= -4 or 2

⇒ $x-\frac{1}{x}=-4 \text { or } x-\frac{1}{x}=2$

⇒ x² + 4x-1 = 0 or x²– 2x-1 = 0 as the discriminant of both the quadratic equations is positive, hence equation (1) has 4 real roots.

Question 124. If the roots of 3 (x² + l)=kx area and 1/α(both real), which of the following could be the value of k?

10
5
-3
3

Solution:

(1)

The roots of 3x² + kx + 3 = 0 are a and 1/α both real quantize.

k²-4(3) (3) ≥ O or k² ≥ 36

only k = 10 satisfies this condition.

Question 125. If the roots of 3x² + (2k + 4)x = -12 are equal, then the value of k is

-5
5
-8
4

Solution:

(4)

As the roots of 3x²+ (2k + 4)x + 12 = 0 are equal A= 0 i.e. (k + 2)² = 3(12) = 36

⇒ k = 4 or- 8 =>k = 4 or- 8

Question 126. For which of the following equations with roots, αβ is α² + β²= 25 And αβ= -12?

x(x – 1) = 12
X(x + 9) = 12
x(x + 1) = 12
Either (1) or (3)

Solution:

(4)

⇒ $a^2+\beta^2=(\alpha+\beta)^2-2 \alpha \beta$

and $ \frac{1}{\alpha^2}-\frac{1}{\beta^2}=\frac{\beta^2-\alpha^2}{\alpha^2 \beta^2}=\frac{(a+\beta)(\beta-\alpha)}{\alpha^2 \beta^2}$

for the required equation with roots a, [3

α² + β² = 25 and a/? = -12

α² + β² + 2αβ = 25 + (2)(—12) = l⇒α + β = 1 or —1

The equation could be x² – x — 12 = 0 or x² + x- 12 = 0

Question 127. If the speed of a vehicle decreases by 10 km, it takes 2 hours more than what it usually takes, to cover a distance of 1 800 km, find the time it usually takes,

24 hours
30 hours
36 hours
18 hours

Solution:

(4)

the data is tabulated below

Speed time Distance

ut 1800⇒ut=1800

u-10 t + 2 1800

ut = (u – 10)(t + 2) = ut + 2u- lOt- 20

⇒ $2 u-10\left(\frac{18 00}{u}\right)=20 \Rightarrow u^2-10 u-9000=0$

(u – 100)(u + 90) = 0 ⇒ u=100

and t = 1800/100=18

Question 128. If one root of x2- 9x + 14 = 0 is the same as one root of x2 – 5x + k = 0, then k =

±6
±14
6,-14
-6,14

Solution:

(3)

the roots of x² – 9x + 14 = 0 are 7 and 2 if 7 is a root of the second equation 7²– 5(7) + k = 0 ⇒ K = 6

Question 129. If the sum of the roots of x²– 5x⁴+ k = 0 and x + k = 0 is 80 then what is/ are the possible real value (s) of k?

±5
±2
±4
±10

Solution:

(2)

the given equation is x²– 5x⁴ + k = 0

the sum of the roots is 80

5k4 = 80⇒k⁴ = 16

±2 are the real values of.

Question 130. How many equations of the form x² + 6x + p = 0 where p is an integer and 0< p < 15, have real roots?

Solution:

(1)

The given equation is x² + 6x + p = 0

This has real roots if and only 6² – 4p≥ 0 i.e., p≤9

10 integral values satisfy this condition.

Question 131. What is the minimum value of the Squares of the roots of the equation x²-(α – 3)x+(α-8)=0 where α is a positive number?

Solution:

(4)

x² – (a- 3) + (a- 8) = 0

The sum of the roots =a-3

The product of the roots= a-8

The sum of the squares of the roots=(a- 3)²– 2(a- 8) = a² — 6a + 9- 2a + 16 = (a² –
8a + 25)

the minimum value of a²– 8a + 25

⇒ $=\frac{4(1)(25)-(-8)^2}{4(1)}=\frac{100-64}{4}=9$

CA Foundation Maths Solutions For Chapter 3 Linear Inequalities

November 15, 2024July 5, 2024 by Schindler

CA Foundation Maths Solutions For Chapter 3 Linear Inequalities Meaning & Introduction

Inequalities are statements where two quantities are unequal but a relationship exists between them.
These types of inequalities occur in business whenever there is a limit on supply, demand, sales, etc.
For example, if a producer requires a certain type of raw material for his factory and there is an upper limit in the availability of that raw material, then any decision he takes about production should involve this constraint also.
The value of the variables that satisfy an inequality is called the solution space and is abbreviated as S.S.
The Objective function attains a maximum or a minimum value at one of the corner points of the feasible solution known as the extreme points of the solution set.

Read and Learn More CA Foundation Maths Solutions

Explanation & Summary of Graphical Method

It involves:

Formulating the linear programming problem, i.e., expressing the objective function and constraints in the standardized format.
Plotting the capacity constraints on the graph paper. For this purpose, normally two terminal points are required. This is done by presuming simultaneously that one of the constraints is zero.
When constraints concern only one factor, then the line will have only one origin point and it will run parallel to the other axis.
Identifying feasible regions and coordinates of corner points. Mostly it is done by breading the graph, but a point can be identified by solving simultaneous equation relating to two lines that intersect to form a point on the graph.
Testing the corner point which gives maximum profit. For this purpose, the coordinates relating to the corner point should put in the objectives function and the optimal point should be ascertained.

For decision-making purposes, sometimes, it is required to know whether the optimal point leaves some resources unutilized. For this purpose, the value of coordinates at the optimal point should be put with constraint to find out which constraints are not fully utilized.

Generally, various type of questions that are asked are on various types:

Identify the Inequality through the shaded region.
Solving Inequalities and getting feasible points.
Find the domain and Range of Inequality.
Inequalities given and to identify the shaded region.

Special Note:

1. IF|m|>n then

m lies between (-∞, -n] U [ n, ∞)

2. IF |m| < n then

m lies between [ -n, n]

CA Foundation Maths Solutions For Chapter 3 Linear Inequalities Exercise 1

Question 1. Graphs of Inclinations arc drawn below

CA Foundation For Maths Chapter 3 Linear Inequalities Graph Of Inequalities

The common region [shaded part) shown in the diagram refers to the inequalities:

5x+ 3y ≤ 30, x + y ≤ 9, y≤ 1/2 x, y<x/2, x ≥ 0, y ≥ 0
5x + 3y. ≥ 30, x + y ≤ 9, y≥ x/3, y≤x/2, x ≥ 0,y ≥ 0.
5x + 3y > 30, x + y > 9, y<x/3, y>x/2, x> 0,y > 0,
5x + 3y > 30, x + y<9, y ≥ 9, y≤x/2, x ≥ 0, y ≥0

Solution: 2. 5x + 3y. ≥ 30, x + y ≤ 9, y≥ x/3, y≤x/2, x ≥ 0,y ≥ 0.

Take a point of the common satisfies all given inequations of option (2). region. Let the testing point be (5 : 3] of the region. This point

Question 2. If $\left|x+\frac{1}{4}\right|>\frac{7}{4}$ then.

$x<\frac{-3}{2} \text { or } x>2$
$x<-2 \text { or } x>\frac{3}{2}$
$-2<x<\frac{3}{2}$
None of these

Solution: 2. $x<-2 \text { or } x>\frac{3}{2}$

CA Foundation For Maths Chapter 3 Linear Inequalities Line

Clearly $\left(-\infty, \frac{-7}{4}\right)$ will lie in 

Or in (7/4) ; ∞)

⇒ $x+\frac{1}{4}<\frac{-7}{4}, \text { or },<\frac{-7}{4}-\frac{1}{4}$

Orx < – 2

Andx $x+\frac{1}{4}>\frac{7}{4} \text { or, } x>\frac{7}{4}-\frac{1}{4} \text { or } x>\frac{3}{2}$

CA Foundation Maths Chapter 3 Linear Inequalities Solutions

Question 3. If $\left|\frac{3 x-4}{4}\right| \leq \frac{5}{12}$, the solutions set is

1. $\left\{x: \frac{19}{18} \leq x \leq \frac{29}{18}\right\}$

2. $\left\{x: \frac{7}{9} \leq x \leq \frac{17}{9}\right\}$

3. $\left\{x: \frac{-29}{18} \leq x \leq \frac{-19}{18}\right\}$

4. None of these

Solution: 2. $\left\{x: \frac{7}{9} \leq x \leq \frac{17}{9}\right\}$

⇒ $\left|\frac{3 x-4}{4}\right| \leq \frac{5}{12}$

⇒ $\frac{-5}{12} \leq \frac{3 x-4}{4} \leq \frac{5}{12}$

Or, $-\frac{5}{3} \leq 3 x-4 \leq \frac{5}{3}$ (Adding 4 to each term)

Or, $\frac{7}{3} \leq 3 x \leq \frac{17}{3} \text {; or } \frac{7}{9} \leq x \leq \frac{17}{9}$

Question 4. On solving the inequalities 6x + y > 18; x +4 y > 12; 2x + y > 10, we get the following situation:

(0,18), (12,0), (4,2) & (2,6)
(3,0), (0,3), (4,2) & (7,6)
(5,0), (0,10), (4,2) & (7,6)
(0,18), (12,0), (4,2), (0,0) & (7,6)

Solution: 1. (0,18), (12,0), (4,2) & (2,6)

1. For 6x + y = 18:

CA Foundation For Maths Chapter 3 Linear Inequalities Equation 1

Point are (3;0);(2;6)

2. For x + 4y= 12:

CA Foundation For Maths Chapter 3 Linear Inequalities xy Equation 2

Point are (3 ; 0] ; [4 ; 2)

3. And 2x = y= 10:

CA Foundation For Maths Chapter 3 Linear Inequalities xy Equation 3

Point are (3 ; 4) & (4 ; 2]

Solving eqn. 6x + y = 18 & 2x + y = 10

Subtracting 4x = 8

∴ x = 2

Putting x = 2 in 2x + y = 10

We get

2 x 2 + y = 10

∴y = 6

Point Is (2 ; ,6)

Point (0; 8) satisfies eqn. 6x + y = 18

Point ( 12 ; 0) satisfies eqn x + 4y = 12 and 2x + y = 10

Point (2 ; 6) satisfies eqn 6x + y = 18 and 2x + y = 10

Question 5. A car manuals luring company manufactures cars of two types A and B. Model A requires 150 man-hours for assembling, 50 man-hours for palnlIni; and 10 man-hours for checking and testing. Model B requires 60 man-hours for assembling ’10 man-hours for painting and 20 man-hours for chocking and testing. There are available 30 thousand man-hours for assembling. 13 thousand man-hours for painting and 5 thousand man-hours for checking and testing. Express the above situation using linear inequalities, bet the company manufactures x units of type A model of car and y units of type II model of car.

Then, the inequalities are:

5x + 2y ≥1000; 5x + 4y ≥ 1300, x + 2y ≤ 500; x £ 0, y ≥ 0.
5x + 2y ≤ 1000; 5x + 4y ≤ 1300, x + 2y ≥ 500; x > 0, y ≥ 0.
5x + 2y ≤ 1000; 5x + 4y ≤ 1300, x + 2y ≤ 500; x > 0, y ≥ 0.
5x + 2y = 1000; 5x + 4y ≥ 1300, x + 2y = 500; x > 0, y ≥ 0.

Solution: 2. 5x + 2y ≤ 1000; 5x + 4y ≤ 1300, x + 2y ≥ 500; x > 0, y ≥ 0.

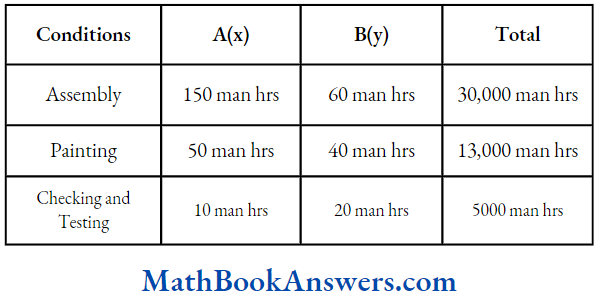
CA Foundation For Maths Chapter 3 Linear Inequalities Conditions

In equation Are

1 50x + 60y ≤ 30,000 ÷ 30 ⇒ 5x +2y ≤ 1,000

50x + 40y ≤ 13000] + 10 ⇒ 5x + 4y ≤ 1300

lO. + 20y ≤ 5000] ÷ 10 ⇒x + 2y ≤ 500

x ≥ 0 & y ≥ 0

Question 6. The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one and this fact is represented by: (taking an experienced person as x and a fresh person as y)

$y \geq \frac{x}{5}$
5y < x
5y > x
None of these

Solution: 1 & 3

1 Fresh with 5 experienced maximum employees.

y Fresh with 5y experienced maximum employees.

From Question

x ≥ 5 y ⇒ 5y ≥ x, OR, y ≥ $x / 5$

Question 7. The shaded region represents

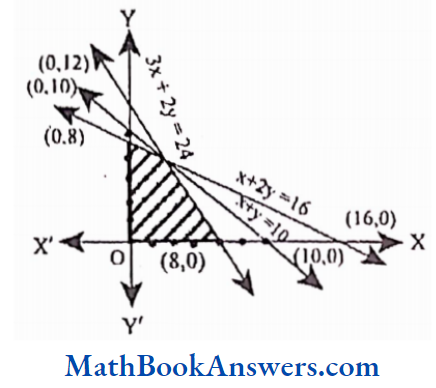
CA Foundation For Maths Chapter 3 Linear Inequalities Shaded Region Represents 1

3x + 2y ≤ 24, x + 2y ≥ 16, x + y ≤ 10x, x ≥ 0,y ≥ 0
3x + 2y ≤24, x + 2y ≤ 16, x + y ≥ 10x, x ≥ 0, y ≥ 0
3x + 2y ≤ 24, x + 2y ≤16, x + y ≤ 10 x, x ≥ 0, y ≥ 0
None of these

Solution: 3. 3x + 2y ≤ 24, x + 2y ≤16, x + y ≤ 10 x, x ≥ 0, y ≥ 0

Question 8. The shaded region represents

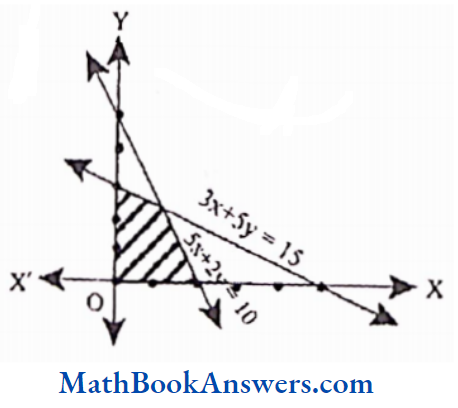
CA Foundation For Maths Chapter 3 Linear Inequalities Shaded Region Represents 2

3x + 5y ≤15, 5x+ 2y ≥10, x,y ≥ 0
3x + 5y≤ 15, 5x + 2y< 10, x,y≥0
3x + 5y ≥ 15, 5x + 2y ≥ 10, x,y≥0
None of these

Solution: 2. 3x + 5y≤ 15, 5x + 2y< 10, x,y≥0

Question 9. The shaded region represents

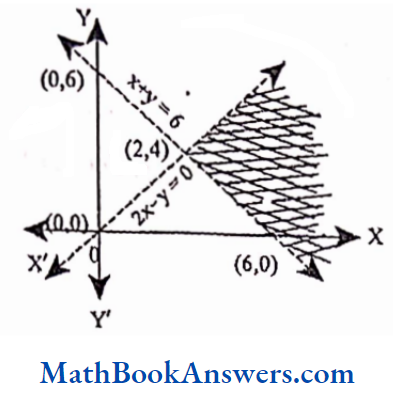
CA Foundation For Maths Chapter 3 Linear Inequalities Shaded Region Represents 3

x + y > 6, 2x- y > 0
x + y < 6, 2x- y > 0
x + y > 6, 2x- y < 0
None of these

Solution: 1. x + y > 6, 2x- y > 0

Question 10. If a > 0 and b < 0, it follows that

$\frac{1}{a}>\frac{1}{b}$
$\frac{1}{a}<\frac{1}{b}$
$\frac{1}{a}=\frac{1}{b}$
None of these

Solution: 1. $\frac{1}{a}>\frac{1}{b}$

⇒ $a>0 \Rightarrow \frac{1}{b}>0$

⇒ $\mathrm{b}<0 \Rightarrow \frac{1}{b}<0$

∴ $\frac{1}{a}>\frac{1}{b}$

Question 11. The linear relationship between two variables in an inequality

ax + by ≤ c
ax. by ≤ c
ax + by ≤ c
ax + bxy ≤ c

Solution: 1. ax + by ≤ c

The linear equation is ax + by = c

Question 12. The solution of the inequality $\frac{(5-2 x)}{3} \leq \frac{x}{6}-5$ is

x ≥ 8
x ≤ 8
x = 8
None of these

Solution: 1. x ≥ 8

⇒ $\frac{5-2 x}{3} \leq \frac{x-5}{6}$

Or $\frac{5-2 x}{3} \leq \frac{x-30}{6}$

Or, $5-2 x \leq \frac{x-30}{7}$

Or, 10 – 4x < x- 30

Or 10 + 30 ≤ N+ 4N

Or 50x ≥ 40

Or x ≥ 40

Question 13. Solution space of inequalities 2x + y < 10 and x-y < 5:

1. Includes the origin.

2. Includes the point (4,3) which one is correct?

only 1
Only 2
Both 1 & 2
None of the above

Solution: 1. only 1

(0,0) satisfies But (4 ; 3) does not satisfy 1

Question 14. On average, an experienced person does 5 units of work while a fresh one 3 units work daily but the employer have to maintain the output of at least 30 units of work per day.

The situation can be expressed as.

5x + 3y ≤ 30
5x + 3y≥30
5x + 3y = 30
None of these

Solution: 2. 5x + 3y≥30

Let no. of experienced persons = x and No. of freshers = y

∴5x +3y > 30

Question 15. Find the range of real of x satisfying the inequalities 3x-2>7and 4x-13>15

x > 3
x > 7
x > 7
x < 3

Solution: 2. x > 7

3x – 2 > 7 ⇒ 3x > 9

∴ x > 3 __________________ (1)

4x > 15 + 23 ⇒ 4x > 28

∴ x > 7 _________________ (2)

Clearly from (1) and (2)

x > 7 satisfies both

Question 16. The shaded region represents

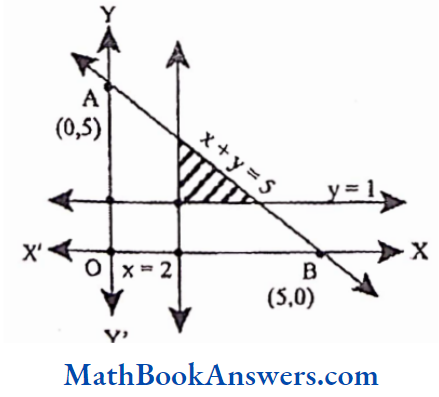
CA Foundation For Maths Chapter 3 Linear Inequalities Shaded Region Represents 4

x + y ≤ 5, x > 2, y ≤ 1
x + y ≤ 5, x > 2, y ≥ 1
x + y ≤ 5, x < 2, y ≥ 1
None of these

Solution: 2. x + y ≤ 5, x > 2, y ≥ 1

Linear Inequalities Chapter 3 CA Foundation Answers

Question 17. The union forbids the employer to employ less than 2 experienced persons (x) for each fresh person (y), this situation can be expressed as

x ≤ y/2
y ≤ x/2
y ≥ x/2
None

Solution: 2. y ≤ x/2

No. of Fresh persons for x Experienced person = x/2

∴ x/2 ≥ y (given)

∴ y ≤ x/2

Question 18. The solution of the inequality 8x + 6 < 12x + 14

(-2.2)
(-2.0)
(2, ∞)
(-2,∞)

Solution: 4. (-2,∞)

8x + 6 < 12x+ 14

Or- 8 < 4x

Or- 2 < x

x > -2

Question 19. The graph of linear inequalities 7x + 9y < 63; x + y > 1; 0 < x s 6 and 0 <, y < 6 has been given below

CA Foundation For Maths Chapter 3 Linear Inequalities The Graph Of Inequalities

BCDB and DEFD
Unbounded
HFGH
ABDFHKA

Solution: 4. ABDFHKA

Common region is ABDFHKA

Question 20. Which of the following graph represents the equality x + y < 6 is

CA Foundation For Maths Chapter 3 Linear Inequalities Following Graph Represents The Equality

Solution: 1.

The graphical representation of x + y

Question 21. The graph of linear inequalities, x + y ≥ 5; x + y ≤ 5; 0 ≤ x ≤ 4 ami 0 ≤ y ≥ 2 is given below:

CA Foundation For Maths Chapter 3 Linear Inequalities The Graph Of Inequalities Given in below

The common region of the inequalities will be:

OABCED
ECDE
Line segment DC
Line Segment BC

Solution: 3. Line segment DC

Question 22. The common region represented by the inequalities 2x + y ≥ 8, x + y ≥ 12, 3x + 2y ≤ 34 is

Unbounded
In feasible
Feasible and bounded
Feasible and Unbounded

Solution: 1. Unbounded

The graphical representation of x + y

2x + y = 8:

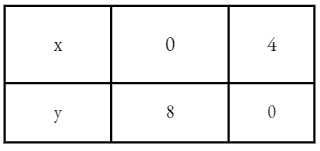
CA Foundation For Maths Chapter 3 Linear Inequalities xy Equations Of The Common Region Inequalities 1

x + y= 12:

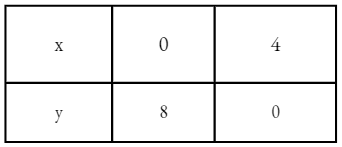
CA Foundation For Maths Chapter 3 Linear Inequalities xy Equations Of The Common Region Inequalities 2

3. 3x+ 2y = 34:

CA Foundation For Maths Chapter 3 Linear Inequalities xy Equations Of The Common Region Inequalities 3

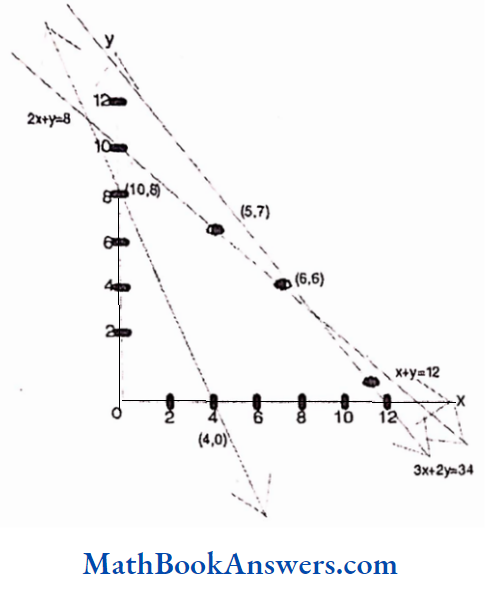
CA Foundation For Maths Chapter 3 Linear Inequalities The Common Region Represented By The Inequalities

Question 23. Bylines x + y = 6, 2x- y = 2, the common region shown is the diagram refers to:

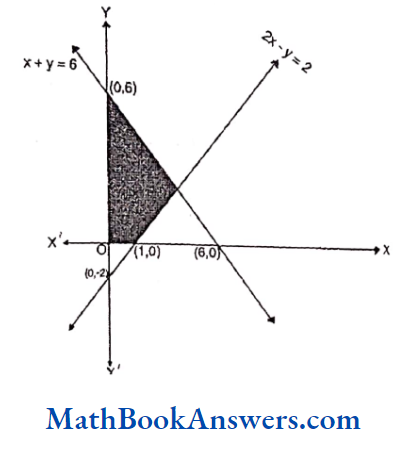
CA Foundation For Maths Chapter 3 Linear Inequalities Common Region Lines

x + y ≥ 6, 2x – y ≤ 2, x ≥ 0, y ≥ 0
x + y ≤ 6, 2x- y ≤ 2, x ≥ 0, y ≥ 0
x + y ≤ 6, 2x- y ≥ 2, x ≥ 0, y ≥ 0
None of these

Solution: x + y ≤ 6, 2x- y ≤ 2, x ≥ 0, y ≥ 0

A point (1,1) (let) satisfies all inequations o

Question 24. The common region of x + y ≤ 6; x + y ≥ 3. Is shown by shaded region

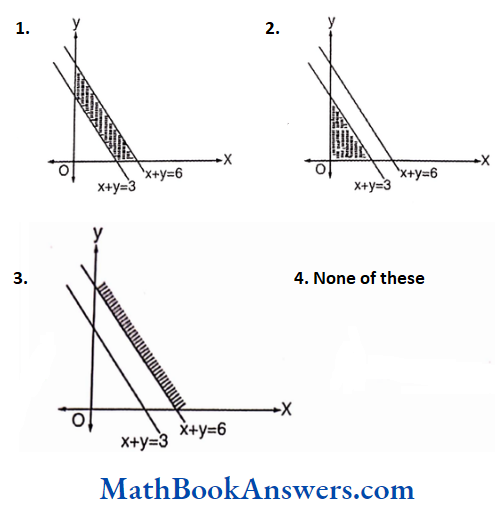
CA Foundation For Maths Chapter 3 Linear Inequalities Common Region Of Lines By Shaded Region

Solution: 1

A Point of the common region of the option (1) satisfies all given constraints x+y≤6 and x+y≥3

Question 25. The inequalities x₁ + 2x₂ ≤ 5; x₁ + x₂≥ 1; x₁ > 0; x₂ ≥ 0 represents the region.

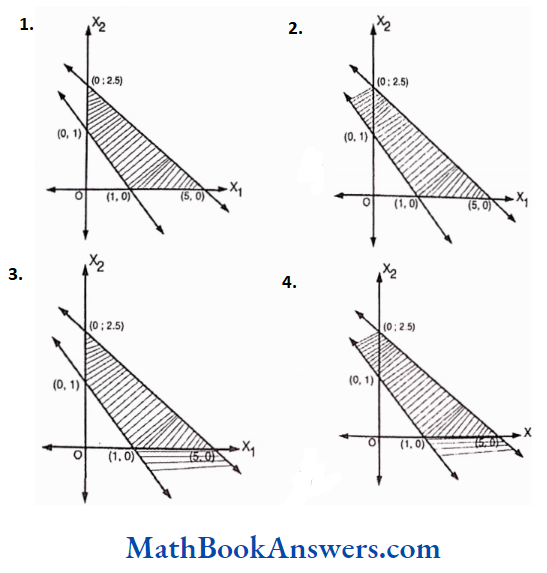
CA Foundation For Maths Chapter 3 Linear Inequalities The Inequalities Represents Region

Solution: 1

Question 26. A dietitian wishes to mix two kinds of food so that the vitamin content of the mixture is at least 9 units of vitamin A, 7 units of vitamin B, 10 units of vitamin C, and 12 units of vitamin D. The vitamin content per kg. ofeach food is shown below.

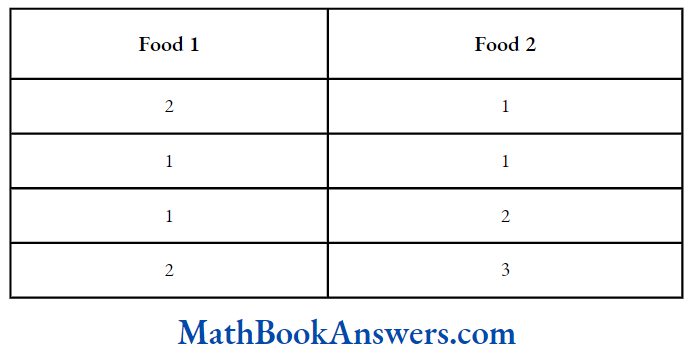
CA Foundation For Maths Chapter 3 Linear Inequalities Food

Assuming x kgs of food I is to be mixed with y kgs of food II the situation can be expressed as

2x + y ≤ 9; x + y ≤ 7; x + 2y ≤ 10; 2x + 3y ≤ 12; x> 0,y > 0
2x + y ≥ 9; x + y ≤ 7; x + 2y ≤ 10; 2x + 3y ≤ 12; x > 0, y > 0
2x + y ≥ 9; x + y ≤ 7; x + y < 10; x + 3y ≤ 12; x > 0, y > 0
2x + y ≥ 9; x + y ≥ 7; x + 2y ≥ 10; 2x + 3y ≥ 12; x > 0, y > 0

Solution: 4. 2x + y ≥ 9; x + y ≥ 7; x + 2y ≥ 10; 2x + 3y ≥ 12; x > 0, y > 0

At least → Minimum 30.

So, use ≥ Sign here.

Constraints are:

2x + y ≥ 9

x + y ≥ 7

x + 2y ≥ 1

2x + 3y ≥ 12

Question 27. The shaped region represented by the Inequalities 4x + 3y ≤ 60, y≥ 2 2x, x ≥ 3, x , 0, y ≥ 0

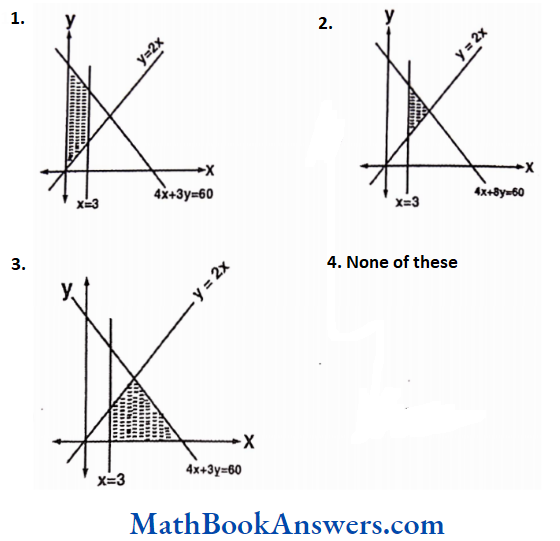
CA Foundation For Maths Chapter 3 Linear Inequalities The Shaped Region Represented By The Inequalities

Solution: 2

Question 28. In the following diagram, the region represented by the inequalities x + 2y ≤ 10, x + y ≤ 6. x ≤ 4 & x ≥ 0, y ≥ 0 is :

CA Foundation For Maths Chapter 3 Linear Inequalities The Region Represented By The Inequalities

OADGO
ADC
ACD
DEG

Solution: 1. OADGO

Question 29. The liner relationship between two variables in an inequality

ax + by ≤ c
ax . by ≤ c
axy + by ≤ c
ax + bxy ≤ c

Solution: 1. ax + by ≤ c

Standard form of Linear Equation

is ax + by = c.

So; ax + by ≤ c is a Linear in equations.

Question 30. On Solving the Inequalities 5x + y ≤ 100, x + y ≤ 60, x ≤ 60, x ≥ 0, y ≥ 0, we get the following situation

(0,0), (20, 0), (10, 50) & (0, 60)
(0, 0), (20, 0), (0„ 100) & (10, 50)
(0, 0), (60, 0), (10, 50) & (0,60)
None of these

Solution: 1. (0,0), (20, 0), (10, 50) & (0, 60)

Question 31. An employer recruits experienced (x) and Ireslt workmen (y) under the condition that he cannot employ more than 11 people. X and Y can be related by Inequality

x=y ≠ 11
x + y ≤ 11, x≥0, y≥0
x + y ≥ 11, x≥0, y≥0
None of these

Solution: 2. x = y ≤ 11, x≥0, y ≥ 0

X + y≤ 11.

And x;y≥ 0

Question 32. The solution set of the inequations x + 2 > 0 and 2x – 6 > 0 is

(-2.∞)
(3, ∞)
(-∞,-2)
(-∞),-3)

Solution: 2. (3, ∞)

x + 2 > 0 ⇒ x > 2

⇒ x = {-l: 0. I, 2, 3, 4,}……………. (1)

And 2x – 6 > 0 ⇒ x > 3

⇒ x = (4 ; 5 ; 6 ; 7 }…………………… (1)

From (1) and (2); we get x = {4, 5, ………} satisfies both conditions.

Solution set = (3,∞ )

Question 33. The common region is represented by the following inequalities

L1 = X₁ + X₂ < 4

L2 = 2X₁ – X₂ > 6; x₁ ≥ 0, X₂≥ 0

CA Foundation For Maths Chapter 3 Linear Inequalities The Common Region Represented By The Following Inequalities

OABC
Outside of OAB
Δ BCE
Δ ABE

Solution: 4. Δ ABE

The common region is ΔABE.

Question 34. An employer recruits experienced (x) and fresh workmen (y) for his firm under the condition that he cannot employ more than 9 people, x and y can be related by inequality

x + y ≠ 9
x + y ≤ 9 x ≥ 0,y ≥ 0
x + y ≥ 9x ≥ 0,y ≥ 0
None of these

Solution: 2. x + y ≤9 x ≥ 0,y ≥ 0

Clearly ⇒ X + y ≤ 9 and x ;y ≤ 0

Question 35. On average, an experienced person does 5 units of work while a fresh one does 3 units of work daily but the employer has to maintain an output of at least 30 units of work per day. This situation can be expressed as

5x + 3y≤30
5x + 3y>30
5x+3y≥30 x ≥ 0, y ≥ 0
None of these

Solution: 3. 5x+3y≥30 x ≥ 0, y ≥ 0

Let no. of experienced person be x.

∴ Work done by x persons = 5x

Let no of fresh ones be y

Work done by y persons = 3y

∴ 5x + 3y ≥30; x ≥0,y ≥0

Question 36. The rules and regulations demand that the employer should employ not more than 5 experienced hands to1 fresh one and this fact can be expressed as

y ≥ x/5
5y ≤ x
5 y ≥ x
Option (1) or (3)

Solution: 3. 5 y ≥ x

Experience person by x/5

Fresh person = y

Since he cannot employ more than

5 experienced hands to fresh one this can be represented as 5y ≥ x.

Question 37. The graph to express the inequality x + y ≤ 9 is

CA Foundation For Maths Chapter 3 Linear Inequalities The Graph To Express The Inequality 1

Answer: 1

Question 38. The graph to express the inequality 5x + 3y ≥ 30 is

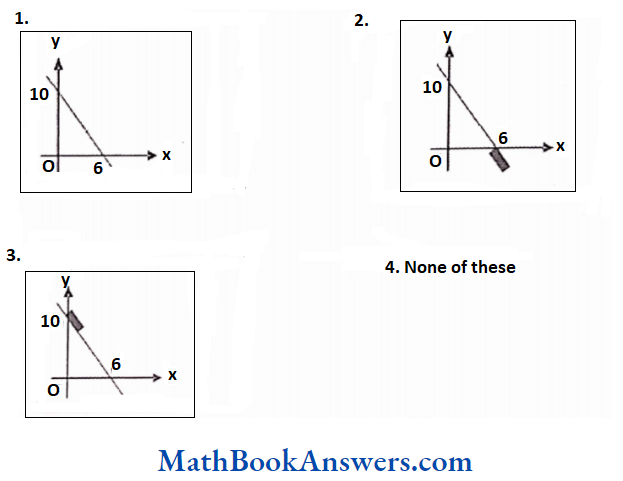
CA Foundation For Maths Chapter 3 Linear Inequalities The Graph To Express The Inequality 2

Solution: 3

Question 39. The graph to express the inequality  is indicated by

CA Foundation For Maths Chapter 3 Linear Inequalities The Graph To Express The Inequality 3

Solution: 4

Question 40. Graphs of the inequalities are drawn below

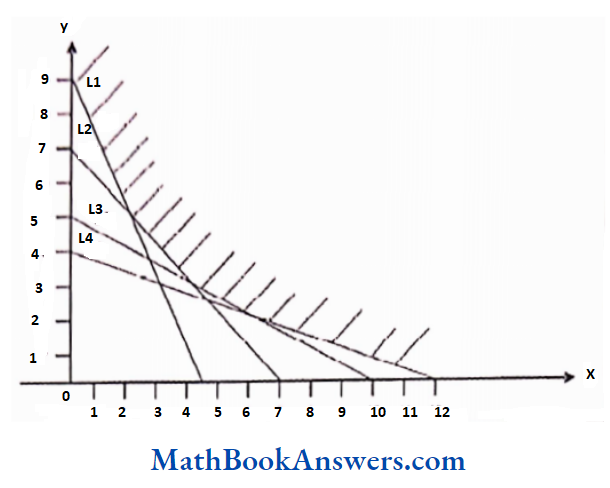
CA Foundation For Maths Chapter 3 Linear Inequalities Graph Of The Inequalities

2x + y≤9, x + y ≥ 7, x + 2y≥ 10, x + 3 y ≥ 12
2x + y ≥ 9, x + y≤ 7, x + 2y ≥ 10, x + 3y≥ 12
2x + y > 9, x + y ≥ 7, x + 2y ≥ 10, x + 3y ≥ 12, x≥ 0,y ≥0
None of these

Solution: 3. 2x + y > 9, x + y ≥ 7, x + 2y ≥ 10, x + 3y ≥ 12, x≥ 0,y ≥0

Take a point for example (8, 5) in a shaded region this satisfies all the equations

CA Foundation Maths Chapter 3 Detailed Solutions

Question 41. The common region satisfied by the inequalities L1: 3x + y > 6, L2: x + y > 4, L3: x + 3y > 6 and L4: x + y < 6 is indicated by

CA Foundation For Maths Chapter 3 Linear Inequalities The Common Region Satisfied By The Inequalities

Solution: 1

Take a point for example (4, 2) in the shaded region this satisfies all the equations of

Question 42. The region indicated by the shading In the graph Is expressed by Inequalities

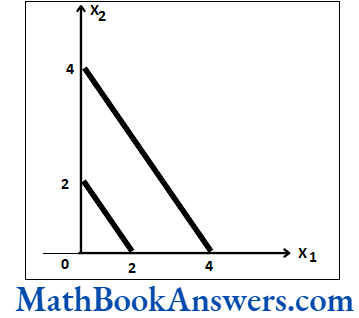
CA Foundation For Maths Chapter 3 Linear Inequalities Shading Graph

x₁+ x₂≤2, 2x₁ + 2x₂ ≥ 8, x₁ ≥ 0, x₂ ≥0,
x₁ + x₂≤ 2, x₁x₂ + x₂ ≤ 4
x₁+x₂≥ 2, 2x₁+ 2x₂≥8
x₁ + 2x₂ ≤2, 2xi + 2x₂ ≥8

Solution: 1. x₁+ x₂≤2, 2x₁ + 2x₂ ≥ 8, x₁ ≥ 0, x₂ ≥0,

Take a point for example (4, 2) which satisfies equation 2 of (a) & (1, 1) which satisfies equation 1

Question 43. The inequalities x₁ ≥ 0, x₂ ≥0, are represented by one of the graphs shown below:

CA Foundation For Maths Chapter 3 Linear Inequalities Inequalities Are Represented By One Of The Graph

Solution: 2

x₁≥ 0, x₂ ≥ 0, the shaded region will be the first quadrant

Question 44.

CA Foundation For Maths Chapter 3 Linear Inequalities Inequality Indicated On The Graph

The region is expressed as

x₁ – x₂> 1
x₁+ x₂ < 1
x₁+ x₂ > 1
None of these

Solution: 3. x₁+ x₂ < 1

Question 45. The inequality x₁ +2x₂≤0 Is Indicated on the graph as

CA Foundation For Maths Chapter 3 Linear Inequalities Inequality Indicated On The Graph

Solution: 1

Question 46.

CA Foundation For Maths Chapter 3 Linear Inequalities The Common Indicated On The Graph

The common region indicated on the graph is expressed by the set of five inequalities

L1: x₁ ≥ 0, L2: x₂ ≥ 0,L3: x₁ + x₂ ≤ 1, L4: x₁ – x₂ ≤ 1. L5: x₁ +2x₂≤0
L1: x₁ ≥ 0, L2: x₂ ≥ 0, L3: x₁ + x₂ ≥ 1, L4: x₁ – x₂ ≥ 1, L5: x₁ +2x₂≤0
L1: x₁≤ 0, L2: x₂ ≤ 0, L3: x₁ + x₂ ≥1, L4: x₁ – x₂ ≥ 1, L5: x₁ +2x₂≤0
None of these

Solution: 2. LI: x₁ ≥ 0, L2: x₂ ≥ 0, L3: x₁ + x₂ ≥ 1, L4: x₁ – x₂ ≥ 1, L5: x₁ +2x₂≤0

Question 47. A firm makes two types of products: Type A and Type B. The profit on product A is Rs. 20 each and that on product B is Rs. 30 each. Both types are processed on three machines Ml, M2, and M3. The time required in hours by each product and the total time available in hours per week on each machine are as follows:

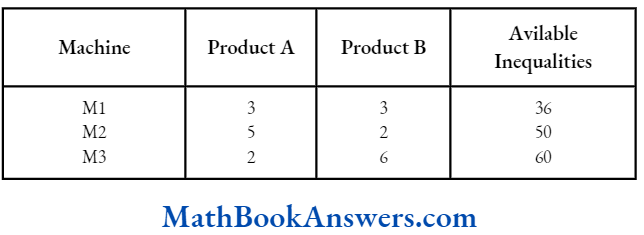
CA Foundation For Maths Chapter 3 Linear Inequalities Machine And Products

The constraints can be formulated taking x₁ = number of units A and x₂ = number of units of B

x₁ + x₂ ≤ 12, 5x₁ + 2x₂ ≤ 50, 2x₁ + 6x₂ ≤ 60
3x₁+ 3x₂ ≥ 36, 5x₁ + 2x₂ ≤ 50, 2x₁+ 6x₂≤60, x₁ ≥ 0, x₂ ≥ 0
3x₁+ 3x₂ ≤ 36, 5x₁ + 2x_2≤ 50, 2x₁ + 6x₁ ≤ 60, x₁ ≥0 ,x₂ ≥ 0
None of these

Solution: 3. 3x₁+ 3x₂ ≤ 36, 5x₁ + 2x₂≤ 50, 2x₁ + 6x₁ 60, x₁ ≥ 0,x₂ ≥ 0

x₁ = number of units A

x₂ = number of units B

For machine 1, man capacity = 36 hrs

3x₂ + 3x₂ ≤ 36

x₁ + x₂≤12

For machine 2, max capacity = 50 hrs

5x₁ + 2x₂ ≤ 50

For machine 3, max capacity = 60 hrs

2x₁+ 6x₂ ≤ 60

x₁≥ 0, x₂ ≥0

Question 48. The set of inequalities L1: x₁ + x₂ ≤ 12, L2: 5x₁ + 2x₂ ≤ 50, L3: x₁+ 3x₂ ≤ 30, x₁ > 0, and x₂ >≥ 0 is represented by

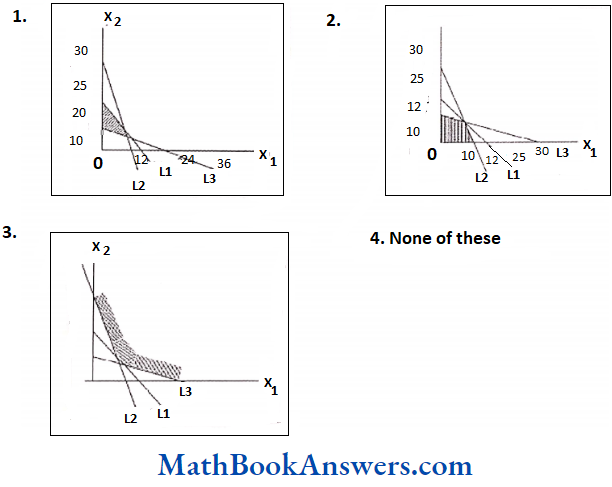
CA Foundation For Maths Chapter 3 Linear Inequalities The Set Of Inequalities

Solution: 2

Question 49. The common region satisfying the set inequalities x ≥ 0, y ≥0, L1: x + y ≤ 5, L2: x+ 2y ≤ 8 and L3: 4x + 3y ≥12 is indicated by

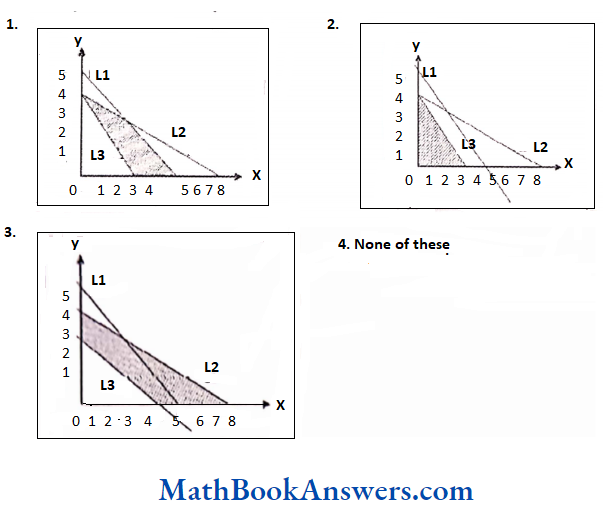
CA Foundation For Maths Chapter 3 Linear Inequalities The Common Region Satisfying

Solution: 1

Question 50. On solving the inequalities 2x+5y ≤ 20, 3x + 2 y ≤12,x≥ 0,y ≥ 0, we get following situation

(0,0), (0,4), (4,0) and (20/11,36/11)
(0,0), (10,0), (0,6) and {20/11,36/11)
(0,0), (0,4), (4,0) and (2,3)
(0,0), (10,0), (0,6) and (2,3)

Solution: 1. (0,0), (0,4), (4,0) and (20/11,36/11)

Question 51. On solving the inequalities 6x + y> 18, x + 4y> 12, 2x + y> 10, we get the following situation

(0,18), (12,0), (4,2) and (2,6)
(3,0), (0,3), (4,2) and (7,6)
(5,0), (0,10), (4,2) and (7,6)
(0,18), (12,0), (4,2), (0,0) and (7,6)

Solution: 3. (5,0), (0,10), (4,2) and (7,6)

Question 52. If x < 7, then

-x < -7
-x ≤ -7
-x > -7
-x ≥ -7

Solution: 3. -x > -7

X < 7 then

– x > -7

Sign change when multiplied by negative

Question 53. If -3x + 17 < -13, then

x ∈ (10, ∞)
x ∈ (10, ∞)
x ∈ (-∞, 10)
x ∈ (-10, 10)

Solution: 1. x ∈ (10, ∞)

-3x + 17 < – 13

-3x < – 30

3x>3y → x>10

→ x ∈ (10, ∞)

Question 54. Given that x, y, and b are real numbers and x < y, b > 0, then

1. $\frac{x}{b}<\frac{y}{b}$

2. $\frac{x}{b} \leq \frac{y}{b}$

3. $\frac{x}{b}>\frac{y}{b}$

4. $\frac{x}{b} \leq \frac{y}{b}$

Solution: 1. x < y , b > 0

⇒ $\frac{1}{b}<\frac{y}{b}$

Since b is positive

Question 55. If x is a real number and |x| < 5, then

x ≥ 5
-5 < x < 5
x ≤-5
-5 ≤ x ≤ 5

Solution: 2. -5 < x < 5

|x|<5

Question 56. If x and a are real numbers such that a > 0 and |x| > a, then

x ∈ (-a, ∞)
x ∈ (∞,-a)
x ∈ (-a, a)
x ∈ (-∞,-a) U (a, ∞)

Solution: 4. x ∈ (-∞,-a) U (a, ∞)

a > 0 |x| > a

Question 57. If |x – 1| > 5, then

x ∈ (-4,6)
x ∈ (- ∞,-4) U (6, ∞)
x ∈ (-4,6)
x ∈ (-∞, 4) U (6, ∞)

Solution: 3. x ∈ (-4,6)

|x-1| > 5 then

X-1 < – 5 or x-1 > 5

X < – 4 or x > 6

How To Solve Linear Inequalities In CA Foundation

Question 58. If |x + 2| < 9, then

x ∈(-7, 11)
x ∈ (-11, 7)
x ∈ (—∞, -7)U (11,∞)
x ∈ (-∞, 7)U (11,∞)

Solution: 2. x ∈ (-11, 7)

|x + 2|<9

-9 < x + 2 < 9

-9-2<x<9-2

-11 < x < 7

x ∈ (-11, 7)

Question 59. The linear inequality representing the solution set given in the following

|x| < 5
|x| > 5
|X| ≥ 5
|x| ≤ 5

Solution: 3. |x| ≥ 5

Question 60. The solution set of the inequation |x +2| ≤ 5 is

(-7.5)
[-7.3]
[-5.5]
(-7,3)

Solution: 2. (-7,3)

Question 61. If$\frac{|x-2|}{x-2} \geq 0$ then

x ∈[2, ∞)
x ∈ (2, ∞)
x ∈ (-∞, 2)
x ∈(-∞, 2]

Solution: 2. x ∈ (2, ∞)

Question 62. If|x + 3| ≥ 10, then

x ∈ (-13, 7]
x ∈(-13, 7]
x ∈ (-∞, – 13)U (7, ∞)
x ∈(-∞, – 13) U (7, ∞)

Solution: 4. x∈ (-∞,-13)U(7,∞)

Question 63. A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B, and the number of man-hours the firm has available per week are as follows:

CA Foundation For Maths Chapter 3 Linear Inequalities Gadget

The profit on sale A is 30 per unit as compared with % 20 per unit of B. This situation can be expressed as

10x + 6y ≤ 1000, 5x + 4y ≤ 600, x,y ≥0
10x + 6y ≤ 1000, 5x + 4y≥600, x,y ≥ 0
10x + 6y ≤ 1000, 5x + 4y ≤ 600, x, y ≤ 0
None of these

Solution: 1. 10x + 6y ≤ 1000, 5x + 4y ≤ 600, x,y ≥0

Question 64. A company is making two products A and B. the cost of producing one unit of products A and B are ?60 and respectively. As per the agreement, the company has to supply at least 200 units of product B to its regular customers. One unit of product A requires one machine hours whereas product B has machine hours available abundantly within the company. Total machine hour available for product A are 400 hours. One unit of each product A and B requires one labour hour each and total of 500 labour hours are available. This situation can be expressed as

x + y≤500, x + 4y ≤ 600, x,y ≥ 0
x + y ≤ 500, x ≤ 200, y ≤ 400, x,y ≥ 0
x + y ≤ 500, x + 2y ≤ 600, x,y ≥ 0
None of the above

Solution: 2. x + y ≤ 500, x ≤ 200, y ≤ 400, x,y ≥ 0

CA Foundation Maths Linear Inequalities Practice

Question 65. A firm manufactures 3 products A, B and C. The profit are K2 and respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product:

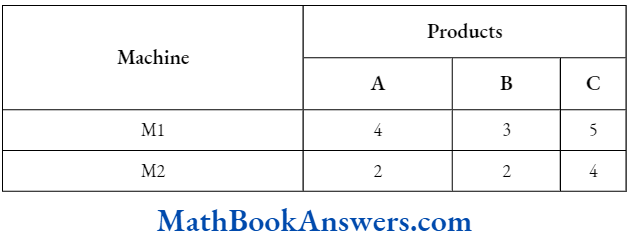
CA Foundation For Maths Chapter 3 Linear Inequalities Machine And Products A Firm Manufacture

Machines M₁ and M₂ have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A’s, 200 B’s and 50 C’ s but not more than 150 A’s. This situation can be expressed as

4x + 3y+ 5z≤ 2000, 2x – 2y + 4z ≤ 2000, 100 ≤ x ≤ 150, y ≥ 200, z ≥ 50, x ≥ 0,y ≥ 0,z ≥ 0.
4x + 3y + 5z ≤ 2000, 2x – 2y + 4z ≤ 2000, 100 ≤ y ≤ 150, x ≥ 200, z ≥ 50, x≥0,y≥0, z≥0.
4x + 3y + 5z ≤ 2000, 2x + 2y + 4z ≤ 2500, 100 ≤ x ≤ 150, y ≥ 200, z ≥ 50 x ≥0, y ≥ 0, z ≥ 0
None of the Above

Solution: 3. 4x + 3y + 5z ≤ 2000, 2x + 2y + 4z ≤ 2500, 100 ≤ x ≤ 150, y ≥ 200, z ≥ 50 x ≥0, y ≥ 0, z ≥ 0

Question 66. A firm manufactures two types of products A and B sells them at a profit of 32 on type A and 33 on type B. Each product is processed on two machines M₁ and M₂. Type A requires one minutes of processing time on Mi and two minutes of M₂ ; type B requires one minute on Mi and one minutes on one M₂. The machine Mi is available for not more than 6 hours 40 minutes while machine M₂ is available for 10 hours during any working day. This situation can be expressed as

x + y≤ 400, 2x + y≤ 600, x ≥0,y≥ 0
x – y ≤ 400, 2x + y ≥ 600, x ≥ 0, y ≥ 0
x + y ≥ 400, 2x + y ≤ 600, x ≥ 0,y≥ 0
None of the above

Solution: 1. x + y≤ 400, 2x + y≤ 600, x ≥0,y≥ 0

Question 67. A rubber company is engaged in producing three types of tyers. A, B and C. each type requires processing in two plant, plant 1 and Plant 2. The capacities of the two plant, in number of tyres per day, are as follows:

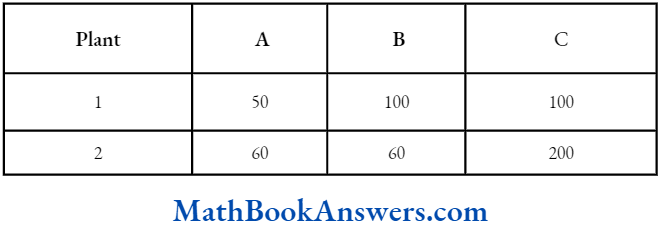
CA Foundation For Maths Chapter 3 Linear Inequalities Plant

The monthly demand for tyres A, B and C is 2500, 3000 and 7000 respectively. If plant 1 cost 3 2500 per day, and plant II cost 33500 per day to operate. This situation can be expressed as

50x + 60y≤ 2500, 100x + 60y ≥ 3000,100x +200y ≤ 7000, x,y≥ 0
50x + 60y ≥ 2500, 100x + 60y ≤ 3000, 100x +200y ≤ 7000, x,y≥ 0
50x + 60y ≥ 2500, 100x + 60y ≥ 3000, 100 x +200y ≥ 7000, x. y ≥ 0
None of these

Solution: 3. 50x + 60y ≥ 2500, 100x + 60y ≥ 3000, 100 x +200y ≥ 7000, x. y ≥ 0

Question 68. A company sells two different products A and B. The two products are produced in the production process and are sold in two 68. different markets. The production process has a total capacity of 45000 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of units of A that can be sold is 7000 and that of B is 10,000. If the profit is 60 per unit for the product A and K 40 per unit for the product B, This situation can be expressed as

5x+ 3y ≤45000, x ≥ 7000, y≤ 10,000, x,y ≥0
5x+3y≤ 45000, x ≤ 7000, y≤ 10,000, x,y ≥0
5x+3y≥ 45000, x ≤ 7000, y≤10,000, x,y ≥ 0
None of these

Solution: 2. 5x+3y≤ 45000, x ≤ 7000, y≤ 10,000, x,y ≥0

Question 69. To maintain his health a person must fulfill certain minimum daily requirements for several kind of nutrients. Assuming that there are only three kinds of nutrients – calcium, protein and calories and the person’s diet consists of only two food items, I and 11, whose price and nutrient context are shown in the table below:

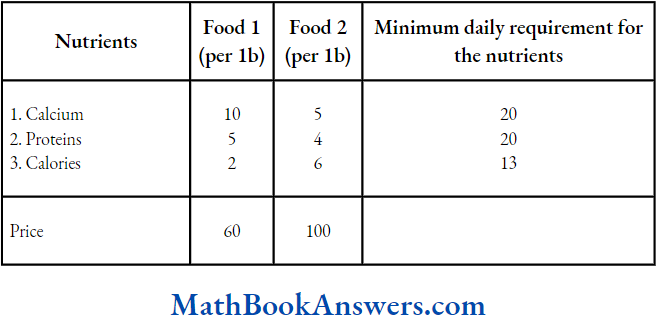
CA Foundation For Maths Chapter 3 Linear Inequalities Nutrients

This situation can be expressed as

10x + 5y ≥ 20, 5x + 4y ≥ 20, 2x + 6y > 13, x, y ≥ 0.
10x + 5y ≤20, 5x + 4y ≥ 20, 2x + 6y > 13, x,y ≥ 0.
10x + 5y ≥ 20, 5x + 4y ≤ 20, 2x + 6y > 13, x, y ≥ 0.
None of these

Solution: 1. 10x + 5y ≥ 20, 5x + 4y ≥ 20, 2x + 6y > 13, x, y ≥ 0.

Question 70. Manufacturers can produce two products, A and B, during a given time period, each of these products requires four different manufacturing operations: grinding, turning, assembling and testing. The manufacturing requirements in hours per unit of products A and B are given below

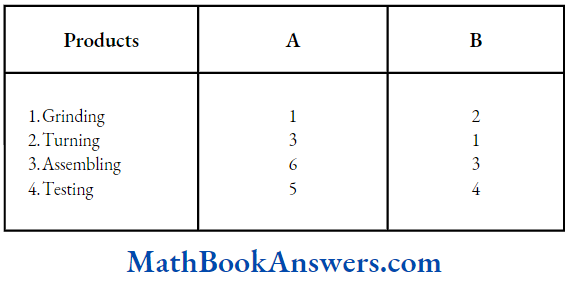
CA Foundation For Maths Chapter 3 Linear Inequalities Products

The available capacities of these operations in hours for the Riven lime period are: grinding 30; turning 60. assembling 200; testing 200. The contribution to profit is V20 for each unit of A and <30 for each unit of B. the firm can sell all that it produces at the prevailing market price. This situation can be expressed as

x + 2y ≥ 30, 3x + y ≤ 60, 2x + 6y ≥ 13, x,y ≥0
x + 2y ≤ 30, 3x + y ≤ 60, 2x + 6y ≤ 13, x,y ≥0
x + 2y ≤ 30, 3x + y ≤ 60, 6x + 3y ≤ 200, 5x + 4y ≤ 200, x,y ≥0
None of these

Solution: 3. x + 2y ≤ 30, 3x + y ≤ 60, 6x + 3y ≤ 200, 5x + 4y ≤ 200, x,y ≥0

Question 71. Vitamins A and B are found in two different foods F₁ and F₂. One unit of food Fi contains 2 units of vitamin A and 3 units of vitamin B. One unit of food F₂ contains 4 units of vitamin A and 2 units of vitamin B. One unit of food F₁and F₂ cost 25 respectively. The minimum daily requirements for a person of vitamin A and B is 40 and 50 units respectively. Assuming that anything over the daily minimum requirement of vitamins A and B is not harmful. This situation can be expressed as’

2x + 4y > 40, 3x + 2y < 50, x > 0, y > 0
2x + 4y > 40, 3x + 2y > 50, x ≥ 0, y ≥ 0
2x + 4y < 40, 3x + 2y> 50, x > 0, y > 0
None of these

Solution: 2. 2x + 4y ≥ 40, 3x + 2y ≥ 50, x ≥ 0, y ≥ 0

Chapter 3 CA Foundation Maths Answer Key

Question 72. An automobile manufacturer makes automobiles and trucks in a factory that is divided into two shops. Shop A, which performs the basic assembly operation, must work 5 man-days on each truck but one 2 man-days on each automobile. Shop B, which performs finishing operations, must work 3 man-days for each automobile or truck that it produces. Because of men and machine limitations, shop A has 180 man-days per week available while shop B has 135 man-days per week. This situation can be expressed as

5x + 2y ≤ 180, 3x + 3y≤ 135, x ≥ 0, y ≥ 0
5x+ 2y ≥ 180, 3x + 3y ≤ 135, x ≥ 0, y ≥ 0
5x + 2y ≤ 180, 3x + 3y ≥135, x ≥ 0, y ≥ 0
None of these

Solution: 1. 5x + 2y ≤ 180, 3x + 3y≤ 135, x ≥ 0, y ≥ 0

Question 73. A firm manufactures two products, each of which must be processed through two departments, 1 and 2. The hourly requirements per unit for each product in each department, the weekly capacities in each department, selling price per unit, labor cost per unit, and raw material cost per unit are summarized as follows

CA Foundation For Maths Chapter 3 Linear Inequalities Departments

This situation can be expressed as

3x+ 2y ≥ 130, 4x + 6y ≤ 260, x ≥0, y ≥ 0
3x + 2y ≤ 130, 4x + 6y ≥ 260, x ≥ 0, y ≥ 0
None of these

Solution: 3. 3x + 2y ≤ 130, 4x + 6y ≤ 260, x ≥ 0, y ≥ 0