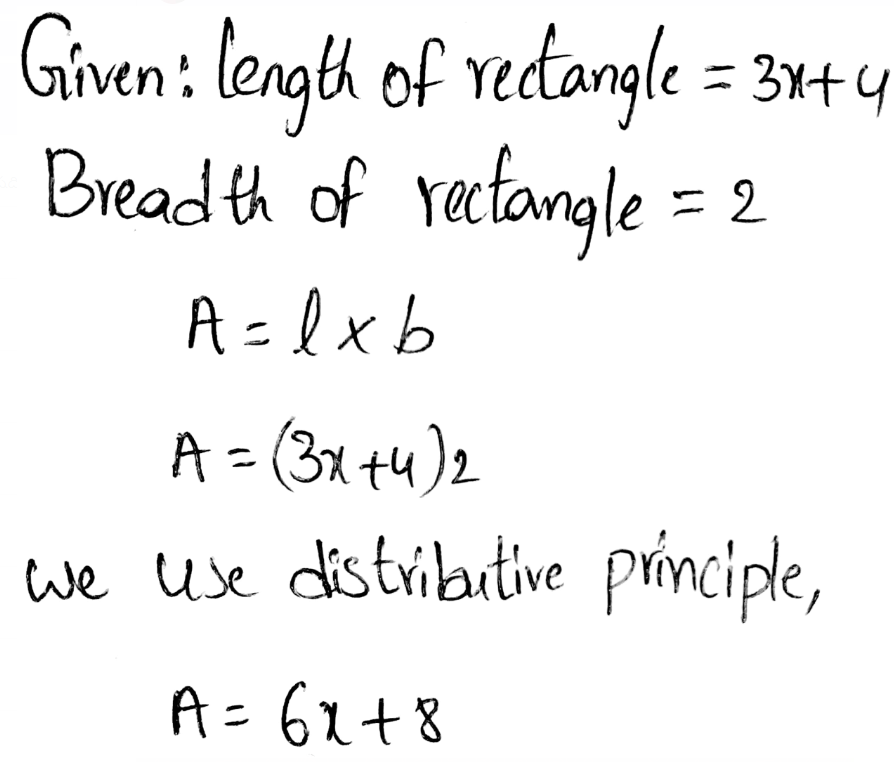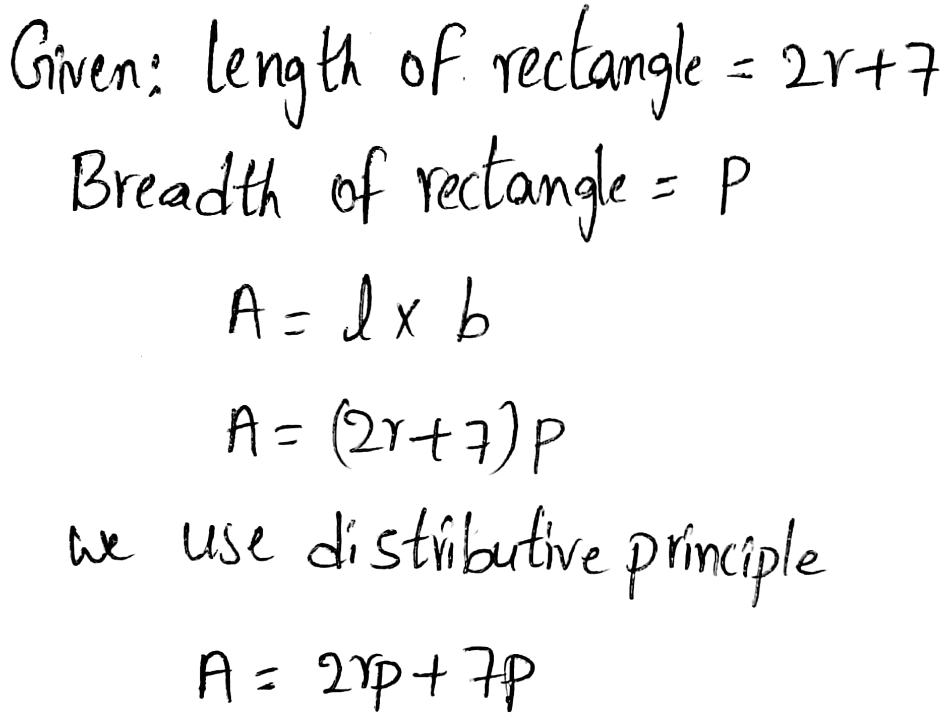Schindler

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials

Page 21 Exercise 3 Answer

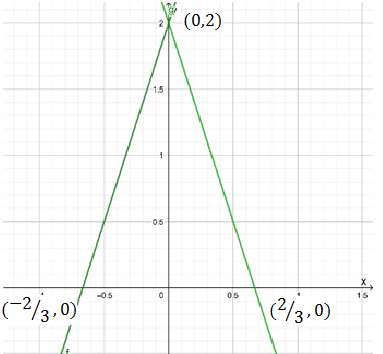
Question: Find the factors of the second-order degree polynomial x² − 17x + 16?

Solution:

Given: x² − 17x + 16

To find: factorize each into a product of two binomials.

Given that x² − 17x + 16

First factorizing as 16 many different ways we can -16x-1,-8x-2,- 4x-4

While testing the combination -16x-1

So,

⇒ \(\begin{aligned}
& x^2-17 x+16 \\
\Rightarrow & x^2-x-16 x+16 \\
\Rightarrow & x(x-1)-16(x-1) \\
\Rightarrow & (x-1)(x-16)
\end{aligned}\)

Finally x2-17x+16=(x-1)(-16)

Thus, the factorization of the second degree polynomial x² − 17x + 16 into a product of two binomials is (x−1)(x−16)

Page 21 Exercise 4 Answer

Question: Find the factors of the second-order degree polynomial x² − 8x + 15?

Solution:

Given: x² − 8x + 15

To find: factorize each into a product of binomials.

Given that x²-18x+15

First factorizing 15 as many different ways

We can -15x-1,-3x-5

While testing the combinations, 3x-5

So, x²-8x+15

⇒ \(\begin{aligned}
& \Rightarrow x^2-5 x-3 x+15 \\
& \Rightarrow x(x-5)-3(x-5) \\
& \Rightarrow(x-3)(x-5)
\end{aligned}\)

Finally, x²-8x+15=(x-3)(x-5)

Thus, the factorization of the second degree polynomial x² − 8x + 15 into a product of two binomials is (x−3)(x−5)

Question: Find the factors of the second-order degree polynomial x² − 16x + 15?

Solution:

Page 21 Exercise 5 Answer

Given: x² − 16x + 15

To find: factorize each into a product of two binomials.

Given that x2-16x+15

First factorizing 15 as many different ways

We can -15x-1,-3x-5

while testing the combinations, -3x-5

So x2-8x+15

⇒ x2-5x-3x+15
⇒ x(x-5)-3(x-5)
⇒ (x-3)(x-5)

Finally, x2-8x+15=(x-3)(x-5)

Thus, the factorization of second degree polynomial x² − 16x + 15 into a product of two binomials is (x−1)(x−5)

Mcgraw Hill Key To Algebra Book 4 Chapter 8 Part 2 Solutions

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 21 Exercise 6 Answer

Question: Find the factors of the second-order degree polynomial x² − 17x + 72?

Solution:

Given: x² − 17x + 72

To find: factorize each into a product of two binomials.

Given that x2-17x+72

First factorizing 72 as many different ways

we can -36x-2,-24x-3,-9x-8

while testing the combinations, -9x-8

so x²-17x+72

⇒ \(\begin{aligned}
& \Rightarrow x^2-9 x-8 x+72 \\
& \Rightarrow x(x-9)-8(x-9) \\
& \Rightarrow(x-8)(x-9)
\end{aligned}\)

Finally, x2-17x+72=(x-9)(x-8)

Thus, the factorization of second degree polynomial x² − 17x + 72 into a product of two binomials is (x−9)(x−8)

Page 21 Exercise 8 Answer

Question: Find the factors of the polynomial x² + 3x − 28?

Solution:

Given: x² + 3x − 28

To find: factorize each into a product of two binomials.

Given that x2+3x-28
First factorising 28 as many different ways

we can 14x-2,7x-4

while testing the combinations, 7x-4

So, x2+3x-28

⇒ \(\begin{aligned}
& \Rightarrow x^2-7 x+4 x-28 \\
& \Rightarrow x(x-7)+4(x-7) \\
& \Rightarrow(x+4)(x-7)
\end{aligned}\)

Finally, x²+3x-28=(x+4)(X-7)

So. the factorization of second-degree polynomial x² + 3x − 28 = (x+7)(x−4) is a product of two binomials.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 21 Exercise 9 Answer

Question: Find the factors of the polynomial x² − 2x − 24?

Solution:

Given: x² − 2x − 24

To find: factorize each into the product of two binomials.

Given that x²-2x-24

first factorizing 24 as many different ways

we can -24×1, -12×2,-6×4

So, x²-2x-24

⇒ \(\begin{aligned}
& \Rightarrow x^2-6 x+4 x-24 \\
& \Rightarrow x(x-6)+4(x-6) \\
& \Rightarrow(x+4)(x-6)
\end{aligned}\)

Finally, x2-2x-24=(x-6)(x+4)

Thus, factorization of second degree polynomial x² − 2x − 24 = (x−6)(x+4) is a product of two binomials.

Page 21 Exercise 10 Answer

Question: Find the factors of the polynomial x² − 2x − 24?

Solution:

We have been given a polynomial x² + 2x − 24 and we have to factorize it.

Given polynomial: x²+2x-24

The factors of the polynomial x² + 2x − 24 are (x−4) and (x+6)

Page 21 Exercise 11 Answer

Question: Find the factors of the polynomial x² + 8x − 20?

Solution:

We have been given a polynomial x² + 8x − 20 and we have to factorize it.

Given polynomial: x²-8x-20

⇒ \(\begin{aligned}
x^2-8 x-20 & =x^2-10 x+2 x-20 \\
& =x(x-10)+2(x-10) \\
& =(x+2)(x-10)
\end{aligned}\)

The polynomial x² + 8x – 20 are (x-2) and (x+10)

Page 21 Exercise 12 Answer

Question: Find the factors of the polynomial x² + 8x − 20?

Solution:

We have been given a polynomial x² − 8x − 20 and we have to factorize it.

Given polynomial: x²+8x-20

⇒ \(\begin{aligned}
x^2+8 x-20 & =x^2+10 x-2 x-20 \\
& =x(x+10)-2(x+10) \\
& =(x-2)(x+10)
\end{aligned}\)

The factors of the polynomial x² − 8x − 20 are (x+2) and (x−10)

Page 21 Exercise 1 Answer

Question: Find the factors of the polynomial x² − 16?

Solution:

We have been given a polynomial x² − 16 and we have to factorize it.

Given polynomial: x²-16

x²-16=x²-4²

=(x+4)(x-4)

[since (a²-b²) = (a+b)(a-b)]

The factors of the polynomial x² – 16 are (x+4) and (x-4).

Key To Algebra Book 4 Multiplying And Factoring Polynomials Part 2 Answers

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 21 Exercise 2 Answer

Question: Find the factors of the polynomial x² − 25?

Solution:

We have been given a polynomial x² − 25 and we have to factorize it.

Given polynomial: x²-25

x²-25=x²-5²

=(x+5)(x-5)

[since (a²-b²) = (a+b)(a-b)]

The factors of the polynomial x² – 25 are (x-5) and (x+5).

Page 21 Exercise 3 Answer

Question: Find the factors of the polynomial x² − 81?

Solution:

We have been given a polynomial x² − 81 and we have to factorize it.

Given polynomial: x²-81

x²-81=x²-9²

=(x+9)(x-9)

[since (a²-b²) = (a+b)(a-b)]

The factors of the polynomial x² – 81 are (x+9) and (x-9).

Page 21 Exercise 4 Answer

Question: Find the factors of the polynomial x² − 4?

Solution:

We have been given a polynomial x² − 4 and we have to factorize it.

Given polynomial: x²-4

x²-4=x²-2²

=(x+2)(x-2)

[since (a²-b²) = (a+b)(a-b)]

The factors of the polynomial x² – 4 are (x+2) and (x-2).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 21 Exercise 5 Answer

Question: Find the factors of the polynomial x² − 1?

Solution:

We have been given a polynomial x² − 1 and we have to factorize it.

Given polynomial: x²-1

x²-1=x²-1²

=(x+1)(x-1)

[since (a²-b²) = (a+b)(a-b)]

The factors of the polynomial x² – 1 are (x+1) and (x-1).

Page 21 Exercise 6 Answer

Question: Find the factors of the polynomial x² − 100?

Solution:

We have been given a polynomial x² − 100 and we have to factorize it.

Consider that:

Given polynomial: x²-100

Consider that:

A²-b²=(a+b)(a-b)
x²-100=x²-10²
=(x+10)(x-10)

[since (a²-b²) = (a+b)(a-b)]

The factors of the polynomial x² − 100 are (x+10) and (x−10).

Page 22 Exercise 2 Answer

Question: Find the factors of the polynomial x² − 4x − 45?

Solution:

The given polynomial is x² − 4x − 45.

The objective is to find the factor of the given polynomial.

The given polynomial is x²-4x-45

⇒ \(\begin{aligned}
x^2-4 x-45 & =x^2-(9-5) x-45 \\
& =x^2-9 x+5 x-45 \\
& =x(x-9)+5(x-9) \\
& =(x+5)(x+9)
\end{aligned}\)

Hence, the factor of the polynomial, x² − 4x − 45 is (x+5)(x−9).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 22 Exercise 3 Answer

Question: Find the factors of the polynomial x² + 18x + 45?

Solution:

The given polynomial is x² + 18x + 45.

The objective is to find the factor of the given polynomial.

The given polynomial x²+18x+45

The polynomial,

x²+18x+45= x²+(15+3)x+45

=x²+15x+3x+45

=x(X+15)+3(x+15)

=(X+3)(x+15)

Now, check the answer

(x+3)(x+15)=x²+15x+3x+45

=x²+18x+45

Hence, the factor of the polynomial, x² + 18x + 45 is (x+3)(x+15).

Page 22 Exercise 4 Answer

Question: Find the factors of the polynomial x² − 12x − 45?

Solution:

The given polynomial is x² − 12x − 45.

The objective is to find the factor of the given polynomial.

The given polynomial is x2-12x-45

The polynomial

x²-12x-45= x2-(15-3)x-45
=x2-15x+3x-45
=x(x-15)+3(x-15)

Now, check the answer

(x+3)(x-15)=x2-15x+3x-45
=x²-12x-45

Hence, the factor of the polynomial, x² – 12x – 45 is (x+3)(x-15).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 22 Exercise 5 Answer

Question: Find the factors of the polynomial x² − 14x + 45?

Solution:

The given polynomial is x² − 14x + 45.

The objective is to find the factor of the given polynomial.

The given polynomial is 2-14x+45

The polynomial,

⇒ \(\begin{aligned}
x^2-14 x+45 & =x^2-(9+5) x+45 \\
& =x^2-9 x-5 x+45 \\
& =x(x-9)-5(x-9) \\
& =(x-5)(x-9)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x-5)(x-9) & =x^2-9 x-5 x+45 \\
& =x^2-14 x+45
\end{aligned}\)

Hence, the factor of the polynomial, x² − 14x + 45 is (x−5)(x−9).

Page 22 Exercise 6 Answer

Question: Find the factors of the polynomial x² + 12x − 45?

Solution:

The given polynomial is x² + 12x − 45.

The objective is to find the factor of the given polynomial.

The given polynomial is  x²+12x-45

The polynomial,

⇒ \(\begin{aligned}
x^2+12 x-45 & =x^2+(15-3) x-45 \\
& =x^2+15 x-3 x-45 \\
& =x(x+15)-3(x+15) \\
& =(x-3)(x+15)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x-3)(x+15) & =x^2+15 x-3 x-45 \\
& =x^2+12 x-45
\end{aligned}\)

Hence, the factor of the polynomial, x² + 12x − 45 is (x−3)(x+15).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 22 Exercise 7 Answer

Question: Find the factors of the polynomial x² + 4x − 45?

Solution:

The given polynomial is x² + 4x − 45.

The objective is to find the factor of the given polynomial.

The given polynomial is x²+4x-45

The polynomial

⇒ \(\begin{aligned}
x^2+4 x-45 & =x^2+(9-5) x-45 \\
& =x^2+9 x-5 x-45 \\
& =x(x+9)-5(x+9) \\
& =(x-5)(x+9)
\end{aligned}\)

Now,  check the answer

⇒ \(\begin{aligned}
(x-5)(x+9) & =x^2+9 x-5 x-45 \\
& =x^2+4 x-45
\end{aligned}\)

Hence, the factor of the polynomial, x² + 4x − 45 is (x−5)(x+9).

Page 22 Exercise 8 Answer

Question: Find the factors of the polynomial x² − 18x + 45?

Solution:

The given polynomial is x² − 18x + 45.

The objective is to find the factor of the given polynomial.

The given polynomial is x²-18x+45

The polynomial,

⇒ \(\begin{aligned}
x^2-18 x+45 & =x^2-(15+3) x+45 \\
& =x^2-15 x-3 x+45 \\
& =x(x-15)-3(x-15) \\
& =(x-3)(x-15)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x-3)(x-15) & =x^2-15 x-3 x+45 \\
& =x^2-18 x+45
\end{aligned}\)

Hence, the factor of the polynomial, x² − 18x + 45 is (x−3)(x−15).

Page 22 Exercise 10 Answer

Question: Find the factors of the polynomial x² − 44x − 45?

Solution:

The given polynomial is x² − 44x − 45.

The objective is to find the factor of the given polynomial.

The given polynomial is x²-44x-45

The polynomial

⇒ \(\begin{aligned}
x^2-44 x-45 & =x^2-(45-1) x-45 \\
& =x^2-45 x+x-45 \\
& =x(x-45)+1(x-45) \\
& =(x+1)(x-45)
\end{aligned}\)

Now, check the answer

(x+1)(x-45)=x²-45x+x-45

=x²-44x-45

Hence, the factor of the polynomial, x² − 44x − 45 is (x+1)(x−45).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 22 Exercise 11 Answer

Question: Find the factors of the polynomial x² + 44x − 45?

Solution:

The given polynomial is x² + 44x − 45.

The objective is to find the factor of the given polynomial.

The given polynomial is x²+44x-45 the polynomial,

⇒ \(\begin{aligned}
x^2+44 x-45 & =x^2+(45-1) x-45 \\
& =x^2+45 x-x-45 \\
& =x(x+45)-(x+45) \\
& =(x-1)(x+45)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x-1)(x+45) & =x^2+45 x-x+45 \\
& =x^2+44 x-45
\end{aligned}\)

Hence, the factor of the polynomial, x² + 44x − 45 is (x−1)(x+45).

Page 22 Exercise 12 Answer

Question: Find the factors of the polynomial x² − 46x + 45?

Solution:

The given polynomial is x² − 46x + 45.

The objective is to find the factor of the given polynomial.

The polynomial

⇒ \(\begin{aligned}
x^2-46 x+45 & =x^2-(45+1) x+45 \\
& =x^2-45 x-x+45 \\
& =x(x-45)-1(x-45) \\
& =(x-1)(x-45)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x-1)(x-45) & =x^2-45 x-x+45 \\
& =x^2-46 x+45
\end{aligned}\)

Hence, the factor of the polynomial, x² − 46x + 45 is (x−1)(x−45).

Page 22 Exercise 13 Answer

Question: Find the factors of the polynomial a² + 17a + 72?

Solution:

The given polynomial is a² + 17a + 72.

The objective is to find the factor of the given polynomial.

The polynomial,

⇒ \(\begin{aligned}
a^2+17 a+72 & =a^2+(8+9) a+72 \\
& =a^2+8 a+9 a+72 \\
& =a(a+8)+9(a+8) \\
& =(a+8)(a+9)
\end{aligned}\)

Now, check the answer

(a+8)(a+9)=a²+9a+8a+72
=a²+17a+72

Hence, the factor of the polynomial, a² + 17a + 72 is (a+8)(a+9).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 22 Exercise 14 Answer

Question: Find the factors of the polynomial a² − a − 72?

Solution:

The given polynomial is a² − a − 72.

The objective is to find the factor of the given polynomial.

⇒ \(\begin{aligned}
a^2-a-72 & =a^2-(9-8) a-+2 \\
& =a^2-9 a+8 a-72 \\
& =a(a-9)+8(a-9) \\
& =(a+8)(a-9)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(a+8)(a-a) & =a^2-9 a+8 a-72 \\
& =a^2-a-72
\end{aligned}\)

Hence, the factor of the polynomial, a² − a − 72 is (a+8)(a−9).

Page 22 Exercise 16 Answer

Question: Find the factors of the polynomial x² − 5x + 4?

Solution:

The given polynomial is x² − 5x + 4.

The objective is to find the factor of the given polynomial.

⇒ \(\begin{aligned}
x^2-5 x+4 & =x^2-(4+1) x+4 \\
& =x^2-4 x-x+4 \\
& =x(x-4)-(x-4) \\
& =(x-1)(x-4)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x-1)(x-4) & =x^2-4 x-x+4 \\
& =x^2-5 x+4
\end{aligned}\)

Hence, the factor of the polynomial, x² − 5x + 4 is (x−1)(x−4).

Page 22 Exercise 17 Answer

Question: Find the factors of the polynomial x² + 3x − 4?

Solution:

The given polynomial is x² + 3x − 4.

The objective is to find the factor of the given polynomial.

⇒ \(\begin{aligned}
x^2-5 x+4 & =x^2-(4+1) x+4 \\
& =x^2-4 x-x+4 \\
& =x(x-4)-(x-4) \\
& =(x-1)(x-4)
\end{aligned}\)

Hence, the factor of the polynomial, x² + 3x − 4 is (x−1)(x+4).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 22 Exercise 18 Answer

Question: Find the factors of the polynomial x² + 4x − 12?

Solution:

The given polynomial is x² + 4x − 12.

The objective is to find the factor of the given polynomial.

The Given polynomial x²+4x-12 the polynomial,

⇒ \(\begin{aligned}
x^2+4 x-12 & =x^2+(6-2) x-12 \\
& =x^2+6 x-2 x-12 \\
& =x(x+6)-2(x+6) \\
& =(x-2)(x+6)
\end{aligned}\)

Now check the answer

⇒ \(\begin{aligned}
(x-2)(x+6) & =x^2+6 x-2 x-12 \\
& =x^2+4 x-12
\end{aligned}\)

Hence, the factor of the polynomial, x² + 4x − 12 is (x−2)(x+6).

Page 22 Exercise 19 Answer

Question: Find the factors of the polynomial x² − 4x + 4?

Solution:

The given polynomial is x² − 4x + 4.

The objective is to find the factor of the given polynomial.

The given polynomial is  x2-4x+4

⇒ \(\begin{aligned}
x^2-4 x+4 & =x^2-(2+2) x+4 \\
& =x^2-2 x-2 x+4 \\
& =x(x-2)-2(x-2) \\
& =(x-2)(x-2) \\
& =(x-2)^2
\end{aligned}\)

Hence, the factor of the polynomial, x² − 4x + 4 is (x−2)².

Page 22 Exercise 20 Answer

Question: Find the factors of the polynomial s² − 10s + 25?

Solution:

The given polynomial is s² − 10s + 25.

The objective is to find the factor of the given polynomial.

The given polynomial is s2-10s+25

The polynomial,

⇒ \(\begin{aligned}
s^2-10 s+25 & =s^2-(5+s) s+25 \\
& =s^2-5 s-5 s+25 \\
& =s(s-5)-5(s-5) \\
& =(s-5)(s-5) \\
& =(s-5)^2
\end{aligned}\)

Now, check the answer

(s-5)²=s³-10s+25

[since (a-b)²=a²-2ab+b²]

Hence, the factor of the polynomial, s² − 10s + 25 is (s−5)².

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 22 Exercise 21 Answer

Question: Find the factors of the polynomial y² − 6y + 9?

Solution:

The given polynomial is y² − 6y + 9.

The objective is to find the factor of the given polynomial.

The given polynomial is y²-6y+9

The poynomial

⇒ \(\begin{aligned}
y^2-6 y+9 & =y^2-(3+3) y+9 \\
& =y^2-3 y-3 y+9 \\
& =y(y-3)-3(y-3) \\
& =(y-3)(y-3) \\
& =(y-3)^2
\end{aligned}\)

Now, check the answer

(y-3)²=y²-6y+9
[since(a-b)²=a²-2ab+b²]

Hence, the factor of the polynomial, y² − 6y + 9 is (y−3)².

Page 22 Exercise 22 Answer

Question: Find the factors of the polynomial a² + 2a + 1?

Solution:

The given polynomial is a² + 2a + 1.

The objective is to find the factor of the given polynomial.

The given polynomial is a²+2a+1

The polynomial,

⇒ \(\begin{aligned}
a^2+2 a+1 & =a^2+(1+1) a+1 \\
& =a^2+a+a+1 \\
& =a(a+1)+(a+1) \\
& =(a+1)(a+1) \\
& =(a+1)^2
\end{aligned}\)

Now, check the answer

(a+1)²=a2+2a+1
(since (a+b)²=a²+2ab+b²]

Hence, the factor of the polynomial, a² + 2a + 1 is (a+1)².

Page 22 Exercise 24 Answer

Question: Find the factors of the polynomial c² − c − 2?

Solution:

The given polynomial is c² − c − 2.

The objective is to find the factor of the given polynomial.

⇒ \(\begin{aligned}
c^2-c-2 & =c^2-(2-1) c-2 \\
& =c^2-2 c+c-2 \\
& =c(c-2)+1(c-2) \\
& =(c+1)(c-2)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(c+1)(c-2) & =c^2-2 c+c-2 \\
& =c^2-c-2
\end{aligned}\)

Hence, the factor of the polynomial, c² − c − 2 is (c+1)(c−2).

Mcgraw Hill Multiplying And Factoring Part 2 Solutions Chapter 8 Key To Algebra

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 1 Answer

Question: Find the factors of the polynomial b² + 4b − 60?

Solution:

Given:

The given equation is b² + 4b − 60.

To find:

The objective is to compute the factor of the given polynomial.

The given eqaution is b2+4b-60

Factorizing the above eqaution

b²+4b-60

⇒ \(\begin{aligned}
& =b^2+(10-6) b-60 \text {; (by middle term factor) } \\
& =b^2+10 b-6 b-60 \\
& =\left(b^2+10 b\right)-(6 b+60) \\
& =b(b+10)-6(b+10) \\
& =(b+10)(b-6)
\end{aligned}\)

The required factorization of the second-degree polynomial is b² + 4b − 60 = (b+10)(b−6).

Page 23 Exercise 2 Answer

Question: Find the factors of the polynomial a² − 3a − 28?

Solution:

Given:

The given equation is a² − 3a − 28

To find:

The objective is to compute the factor of the given polynomial.

The given eqaution is a²-3a-28

Factorizing the abve eqaution

a²-3a-28

⇒ \(\begin{aligned}
& =a^2-(7-4) a-28 ; \text { (by middle term factor) } \\
& =a^2-7 a+4 a-28 \\
& =\left(a^2-3 a\right)+(4 a-28) \\
& =a(a-7)+4(a-7) \\
& =(a-7)(a+4)
\end{aligned}\)

The required factorization of the second-degree polynomial is a² − 3a − 28 = (a−7)(a+4).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 3 Answer

Question: Find the factors of the polynomial m² − 2m − 63?

Solution:

Given:

The given equation is m² − 2m − 63.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is m²-2m-6³
factorizing the above equation
m²-2m-63

⇒ \(\begin{aligned}
& =m^2-(9-7) m-63 \text {; (by middle term factor) } \\
& =m^2-9 m+7 m-63 \\
& =\left(m^2-9 m\right)+(7 m-63) \\
& =m(m-9)+7(m-9) \\
& =(m-9)(m+7)
\end{aligned}\)

The required factorization of the second-degree polynomial is m² − 2m − 63 = (m−9)(m+7).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 4 Answer

Question: Find the factors of the polynomial x² − 7x − 18?

Solution:

Given:

The given equation is x² − 7x − 18.

To find:

The objective is to compute the factor of the given polynomial.

The polynomial

⇒ \(\begin{aligned}
x^2-12 x-45 & =x^2-(15-3) x-45 \\
& =x^2-15 x+3 x-45 \\
& =x(x-15)+3(x-15) \\
& =(x+3)(x-15)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x+3)(x-15) & =x^2-15 x+3 x-45 \\
& =x^2-12 x-45
\end{aligned}\)

The required factorization of the second-degree polynomial is x² − 7x − 18 = (x−9)(x+2).

Page 23 Exercise 6 Answer

Question: Find the factors of the polynomial a² − a − 20?

Solution:

Given:

The given equation is a² − a − 20.

To find:

The objective is to compute the factor of the given polynomial.

The  given equation a²-a-20

Factorizing the above equation

a²-a-20
=a2-(5-4)a-20;(by middle term factor)

⇒ \(\begin{aligned}
& =a^2-5 a+4 a-20 \\
& =\left(a^2-5 a\right)+(4 a-20) \\
& =a(a-5)+4(a-5) \\
& =(a-5)(a+4)
\end{aligned}\)

The required factorization of the second-degree polynomial is a² − a − 20 = (a−5)(a+4).

Page 23 Exercise 8 Answer

Question: Find the factors of the polynomial z² + z − 12?

Solution:

Given:

The given equation is z² + z − 12.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is x2+x-12

Factorizing the above equation,

z²+z-12

⇒ \(\begin{aligned}
& =z^2+(4-3) z-12 ; \text { (by middle term factor) } \\
& =z^2+4 z-3 z-12 \\
& =\left(z^2+4 z\right)-(3 z+12) \\
& =z(z+4)-3(z+4) \\
& =(z-3)(z+4)
\end{aligned}\)

The required factorization of the second-degree polynomial is z² + z − 12 = (z+4)(z−3).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 11 Answer

Question: Find the factors of the polynomial x² − 2x − 3?

Solution:

Given:

The given equation is x² − 2x − 3.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is x²-2x-3

Factorizing the above equation

⇒ \(\begin{aligned}
& x^2-2 x-3 \\
&= x^2-(3-1) x-3 ; \text { (by middle term factor) } \\
&= x^2-3 x+x-3 \\
&=\left(x^2-3 x\right)+(x-3) \\
&= x(x-3)+1(x-3) \\
&=(x+1)(x-3)
\end{aligned}\)

The required factorization of the second-degree polynomial is x² − 2x − 3 = (x−3)(x+1).

Page 23 Exercise 12 Answer

Question: Find the factors of the polynomial x² + 2x − 3?

Solution:

Given:

The given equation is x² + 2x − 3.

To find:

The objective is to compute the factor of the given polynomial.

The given eqaution is x²-2x-3

Factorizing the above eqaution

⇒ \(\begin{aligned}
& x^2+2 x-3 \\
&= x^2+(3-1) x-3 ; \text { (by midd le term factor) } \\
&= x^2+3 x-x-3 \\
&=\left(x^2+3 x\right)-1(x+3) \\
&= x(x+3)-1(x+3) \\
&=(x-1)(x+3)
\end{aligned}\)

The required factorization of the second-degree polynomial is x² + 2x − 3 = (x+3)(x−1).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 14 Answer

Question: Find the factors of the polynomial x² − 8x + 12?

Solution:

Given:

The given equation is x² − 8x + 12.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is x² − 8x + 12.

Factorizing the above eqaution

⇒ \(\begin{aligned}
& x^2-8 x+12 \\
= & x^2-(6+2) x+12 \text {; (by middle term factor) } \\
= & x^2-6 x-2 x+12 \\
= & x(x-6)-2(x-6) \\
= & (x-2)(x-6)
\end{aligned}\)

The required factorization of the second-degree polynomial is x² − 8x + 12 = (x−6)(x−2).

Page 23 Exercise 15 Answer

Question: Find the factors of the polynomial x² − 9x + 8?

Solution:

Given:

The given equation is x² − 9x + 8.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is x² − 9x + 8.

Factorizing the above eqaution,

⇒ \(\begin{aligned}
& x^2-9 x+8 \\
= & x^2-(8+1) x+8 \text {; (by middle term factor) } \\
= & x^2-8 x-x+8 \\
= & \left(x^2-8 x\right)-1(x-8) \\
= & x(x-8)-1(x-8) \\
= & (x-1)(x-8)
\end{aligned}\)

The required factorization of the second-degree polynomial is x² − 9x + 8 = (x−8)(x−1).

Page 23 Exercise 16 Answer

Question: Find the factors of the polynomial s² + 13s + 42?

Solution:

Given:

The given equation is s² + 13s + 42.

To find:

The objective is to compute the factor of the given polynomial.

The given polynomial is s² + 13s + 42.

The polynomial,

⇒ \(\begin{aligned}
x^2-5 x+4 & =x^2-(4+1) x+4 \\
& =x^2-4 x-x+4 \\
& =x(x-4)-(x-4) \\
& =(x-1)(x-4)
\end{aligned}\)

Now, check the answer

⇒ \(\begin{aligned}
(x-1)(x-4) & =x^2-4 x-x+4 \\
& =x^2-5 x+4
\end{aligned}\)

The required factorization of the second degree polynomial is s² + 13s + 42 = (s+7)(s+6)

Chapter 8 Part 2 Multiplying And Factoring Polynomials Mcgraw Hill Key

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 17 Answer

Question: Find the factors of the polynomial x² − 14x + 48?

Solution:

Given:

The given equation is x² − 14x + 48.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is x2-14x+48

Factorizing the above equation,

⇒ \(\begin{aligned}
& x^2-14 x+48 \\
= & x^2-(6+8) x+48 ; \text { (by middle term factor) } \\
= & x^2-6 x-8 x+48 \\
= & \left(x^2-6 x\right)-8(x-6) \\
= & x(x-6)-8(x-6) \\
= & (x-6)(x-8)
\end{aligned}\)

The required factorization of the second-degree polynomial is x² − 14x + 48 = (x−6)(x−8).

Page 23 Exercise 18 Answer

Question: Find the factors of the polynomial x² − 9?

Solution:

Given:

The given equation is x² − 9.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is x²-9

factorizing the above equation,

x²-9

=(x)²-(3)², using the identify

a²-b²=(a+b)(a-b)

=(x+3)(x-3)

The required factorization of the second-degree polynomial is x² − 9 = (x+3)(x−3).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 19 Answer

Question: Find the factors of the polynomial a² − 36?

Solution:

Given:

The given equation is a² − 36

To find:

The objective is to compute the factor of the given polynomial.

The given equation is a²-36

=(a)²-(6)²

=(a+6)(a-6) using the identity

a²-b²=(a+b)(a-b)

The required factorization of the second-degree polynomial is a² − 36 = (a+6)(a−6).

Page 23 Exercise 20 Answer

Question: Find the factors of the polynomial y² − 64?

Solution:

Given:

The given equation is y² − 64.

To find:

The objective is to compute the factor of the given polynomial.

The given eqaution is y²-64

Factorizing the above eqaution

y²-64

=(y)²-(8)²

=(y+8)(y-8) using the identity

a²-b²=(a+b)(a-b)

The required factorization of the second-degree polynomial is y² − 64 = (y+8)(y−8).

Page 23 Exercise 21 Answer

Question: Find the factors of the polynomial x² − 1?

Solution:

Given:

The given equation is x² − 1.

To find:

The objective is to compute the factor of the given polynomial.

The given equation is x² − 1.

Factorizing the above eqaution,

⇒ \(\begin{aligned}
& x^2-1 \\
&=(x)^2-(1)^2 \\
&=(x+1)(x-1) \text { using the identity } \\
& a^2-b^2=(a+b)(a-b)
\end{aligned}\)

The required factorization of the second-degree polynomial is x² − 1 = (x+1)(x−1).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 23 Exercise 22 Answer

Question: Find the factors of the polynomial x² − 49?

Solution:

Given:

The given equation is x² − 49.

To find:

The objective is to compute the factor of the given polynomial.

The given eqaution is x²-49

factorizing the above eqautioon

⇒ \(\begin{aligned}
& x^2-49 \\
&=(x)^2-(7)^2 \\
&=(x+7)(x-7) \text { using the identity } \\
& a^2-b^2=(a+b)(a-b)
\end{aligned}\)

The required factorization of the second-degree polynomial is x² − 49 = (x+7)(x−7).

Page 23 Exercise 23 Answer

Question: Find the factors of the polynomial x² − 16?

Solution:

Given:

The given equation is x² − 16.

To find:

The objective is to compute the factor of the given polynomial.

The gioven eqaution is x²-16

factorizing the above eqaution

⇒ \(\begin{aligned}
& x^2-16 \\
= & x^2-(4)^2 \\
= & (x+4)(x-4) \text { using the identity } \\
\Leftrightarrow & \left.a^2-b^2=(a+b)(a-b)\right]
\end{aligned}\)

The required factorization of the second-degree polynomial x² − 16 = (x+4)(x−4).

Page 24 Exercise 2 Answer

Question: Find the Product Of The Expression 4(x−3)(x+5)?

Solution:

We have been given an expression 4(x−3)(x+5).

We have to multiply the given monomial with the given binomials.

We will find the result by multiplying the binomials first and then multiplying it with the monomial.

The given expression is 4(x-3)(x+5) Multiplying the binomial we get,

⇒ \(\begin{aligned}
4(x-3)(x+5) & =4\left(x^2-3 x+5 x-15\right) \\
& =4\left(x^2+2 x-15\right)
\end{aligned}\)

Multiplying with the monomial we get,

=4x²+8x-60

We have found the result of the expression 4(x−3)(x+5) that is, 4x² + 8x − 60.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 24 Exercise 3 Answer

Question: Find the Product Of The Expression 6(x+5)(x+4)?

Solution:

We have been given an expression 6(x+5)(x+4).

We have to multiply the given monomial with the given binomials.

We will find the result by multiplying the binomials first and then multiplying it with the monomial.

6(x+5)(x+4) multiplying the binomial we get,

⇒ \(\begin{aligned}
6(x+5)(x+4) & =6\left(x^2+5 x+4 x+20\right) \\
& =6\left(x^2+9 x+20\right)
\end{aligned}\)

Multiplying with the monomial we get, =6x²+54x+120

We have found the result of the expression 6(x+5)(x+4)​ that is, 6x² + 54x + 120.

Page 24 Exercise 4 Answer

Question: Find the Product Of The Expression 2(x+3)(x−3)?

Solution:

We have been given an expression 2(x+3)(x−3).

We have to multiply the given monomial with the given binomials.

We will find the result by multiplying the binomials first and then multiplying it with the monomial.

The given expression is 2(x+3)(x-3)

multiplying the binomial we get,

⇒ \(\begin{aligned}
2(x+3)(x-3) & =2\left(x^2-3 x+3 x-9\right) \\
& =2\left(x^2-9\right)
\end{aligned}\)

Multiplying with the monomial we get,

=2x²-18

We have found the result of the expression 2(x+3)(x−3) that is, 2x² − 18.

Page 24 Exercise 6 Answer

Question: Find the Product Of The Expression x(x−5)(x−4)?

Solution:

We have been given an expression x(x−5)(x−4).

We have to multiply the given monomial with the given binomials.

We will find the result by multiplying the binomials first and then multiplying it with the monomial.

The given expression is x(x-5)(x-4) multiplying the binomial we get,

x(x-5)(Xx4)=x(x²-4x-5x+20)

=x(x²-9x+20)

multiplying with the monomial we get,

=x³-9x²+20x

We have found the result of the expression x(x−5)(x−4) that is, x³ − 9x² + 20x.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 24 Exercise 3 Answer

Question: Find the Factors For The Trinomial 5x² + 35x + 60?

Solution:

We have been given a trinomial 5x² + 35x + 60.

We have to first factor out the biggest monomial we can. Then factor the trinomial that’s left into a binomial time a binomial.

We will find the result using the factorization method.

The given expression is, 5×3+35x+60′

Factoring out the monomial, we get

Now, factoring out the binomial we get

⇒ \(\begin{aligned}
5\left(x^2+7 x+12\right) & =5\left(x^2+3 x+4 x+12\right) \\
& =5(x(x+3)+4(x+3)) \\
& =5(x+3)(x+4)
\end{aligned}\)

We have factorized the given trinomial 5x² + 35x + 60 that is,5(x+3)(x+4).

Page 24 Exercise 4 Answer

Question: Find the Factors For The Trinomial x³ + 8x² − 20x?

Solution:

We have been given a trinomial x³ + 8x² − 20x.

We have to first factor out the biggest monomial we can. Then factor the trinomial that’s left into a binomial time a binomial.

We will find the result using the factorization method.

The given trinomial is x³+8x²-20x

Factoring out the monomial, we get

x³+8x²-20x=x(x²+8x-20)

Now, factoring out the binomial we get

⇒ \(\begin{aligned}
x\left(x^2+8 x-20\right) & =x\left(x^2+10 x-2 x-20\right) \\
& =x(x(x+10)-2(x+10)) \\
& =x(x+10)(x-2)
\end{aligned}\)

We have factorized the given trinomial x³ + 8x² − 20x that is, x(x+10)(x−2).

Page 24 Exercise 6 Answer

Question: Find the Factors For The Trinomial a³ − 7a² + 6a?

Solution:

We have been given a trinomial a³ − 7a² + 6a.

We have to first factor out the biggest monomial we can. Then factor the trinomial that’s left into a binomial time a binomial.

We will find the result using the factorization method.

The given trinomial is a³-7a²+6a

Factoring out the monomial, we get

a³-7a²+6a=a(a²-7a+6)

⇒\(\begin{aligned}
a\left(a^2-7 a+6\right) & =a\left(a^2-a-6 a+6\right) \\
& =a(a(a-1)-6(a-1)) \\
& =a(a-1)(a-6)
\end{aligned}\)

We have factorized the given trinomial a³ − 7a² + 6a that is, a(a−1)(a−6).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 25 Exercise 3 Answer

Question: Find the Product of the expression (6x+1)(2x+3)?

Solution:

We have been given an expression (6x+1)(2x+3).

We have to multiply the given pair of binomials.

We will find the result by multiplying each term of the first binomial must be multiplied by each term of the second binomial.

We have multiplied the given pair of binomials (6x+1)(2x+3) that is, 12x² + 20x + 3.

The given pair of binomials is(6x+1)(2x+3) multiplying them we get,

⇒ \(\begin{aligned}
(6 x+1)(2 x+3) & =6 x \cdot 2 x+6 x .3+2 x \cdot 1+1.3 \\
& =12 x^2+18 x+2 x+3 \\
& =12 x^2+20 x+3
\end{aligned}\)

Page 25 Exercise 4 Answer

Question: Find the Product of the expression (5x+3)(3x+4)?

Solution:

We have been given an expression(5x+3)(3x+4).

We have to multiply the given pair of binomials.

We will find the result by multiplying each term of the first binomial must be multiplied by each term of the second binomial.

The given pair of binomials is(5x+3)(3x+4)
multiplying them we get,

⇒ \(\begin{aligned}
(5 x+3)(3 x+4) & =5 x .3 x+5 x .4+3.3 x+3.4 \\
& =15 x^2+20 x+9 x+12 \\
& =15 x^2+29 x+12
\end{aligned}\)

We have multiplied the given pair of binomials (5x+3)(3x+4) that is, 15x² + 29x + 12.

Page 25 Exercise 6 Answer

Question: Find the Product of the expression (4x−1)(3x−1)?

Solution:

We have been given an expression(4x−1)(3x−1).

We have to multiply the given pair of binomials.

We will find the result by multiplying each term of the first binomial must be multiplied by each term of the second binomial.

The given pair of binomials is(4x-1)(3x-1)
multiplying them we get,

⇒ \(\begin{aligned}
(4 x-1)(3 x-1) & =4 x \cdot 3 x-1.4 x-1 \cdot 3 x+(-1) \cdot(-1) \\
& =12 x^2-4 x-3 x+1 \\
& =12 x^2-7 x+1
\end{aligned}\)

We have multiplied the given pair of binomials(4x−1)(3x−1) that is, 12x² − 7x + 1.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 25 Exercise 7 Answer

Question: Find the Product of the expression (3x−5)(2x−5)?

Solution:

We have been given an expression (3x−5)(2x−5).

We have to multiply the given pair of binomials.

We will find the result by multiplying each term of the first binomial must be multiplied by each term of the second binomial.

The given pair of binomials is(3x-5)(2x-5) multiplying them we get,

⇒ \(\begin{aligned}
(3 x-5)(2 x-5) & =3 x \cdot 2 x-5 \cdot 3 x-5 \cdot 2 x+(-5) \cdot(-5) \\
& =6 x^2-15 x-10 x+25 \\
& =6 x^2-25 x+25
\end{aligned}\)

We have multiplied the given pair of binomials (3x−5)(2x−5) that is, 6x² − 25x + 25.

Page 25 Exercise 8 Answer

Question: Find the Product of the expression (4x−3)(x+3)?

Solution:

Given: – (4x−3)×(x+3)

To find – Product

⇒ \(\begin{aligned}
& \text { Given }-(4 x-3) \times(x+3) \\
& \text { we have }=(4 x-3) \times(x+3) \\
& \text { ie., } 4 x(x+3)+(-3) \times(x+3) \\
& \text { or } 4 x^2+12 x+(-3 x)-9 \\
& \text { or } 4 x^2+12 x-3 x-9 \\
& 4 x^2+9 x-9
\end{aligned}\)

Hence the product is 4x² + 9x − 9.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 25 Exercise 9 Answer

Question: Find the Product of the expression (3x+4) (3x−4)?

Solution:

Given – (3x+4) × (3x−4)

To find – Product

⇒ \(\begin{aligned}
& \text { Given }(3 x+4) \times(3 x-4) \\
& \text { we have }=(3 x+4) \times(3 x-4) \\
& =3 x(3 x+4)-4(3 x+4) \\
& =9 x^2+12 x-12 x-16 \\
& =9 x^2-16
\end{aligned}\)

Hence the product is 9x² − 16.

Question: Find the Product of the expression (2x−3)(2x−3)?

Solution:

Page 25 Exercise 12 Answer

Given = (2x−3)×(2x−3)

To find = Product

⇒ \(\begin{aligned}
& \text { Given }=(2 x-3) \times(2 x-3) \\
& \text { we have }=(2 x-3) \times(2 x-3) \\
& =2 x(2 x-3)-3(2 x-3) \\
& =4 x^2-6 x-6 x+9 \\
& =4 x^2-12 x+9
\end{aligned}\)

Hence the product is 4x² − 12x + 9

Question: Find the Product of the expression (4x+1)×(4x+1)?

Solution:

Page 25 Exercise 13 Answer

Given = (4x+1)×(4x+1)

To find =The Product

⇒ \(\begin{aligned}
& \text { Given }=(4 x+1) \times(4 x+1) \\
& \text { we have }=(4 x+1) \times(4 x+1) \\
& =4 x(4 x+1)+1(4 x+1) \\
& =16 x^2+4 x+4 x+1 \\
& =16 x^2+8 x+1
\end{aligned}\)

Hence the product is 16x² + 8x + 1.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 25 Exercise 14 Answer

Question: Expand the Polynomial (3x−7)²

Solution:

Given that (3x−7)².

The aim is to find the expansion.

(3x-7)²

using the binomial theorem

⇒ \(\begin{aligned}
& (x+y)^n={ }^n C_0 x^n+{ }^n C_1 x^{n-1} y+\cdots+{ }^n C_n y^n, \\
& \text { Taking } x=3 x, y=-7, n=2, \\
& (3 x-7)^2={ }^2 C_0(3 x)^2+{ }^2 C_1(3 x)(-7)+{ }^2 C_2(-7)^2 \\
& (3 x-7)^2=9 x^2-42 x+49
\end{aligned}\)

The expansion is (3x−7)² = 9x² − 42x + 49.

Page 27 Exercise 1 Answer

Question: Find the factors of the Polynomial 3x² + 4x + 1

Solution:

Given that 3x² + 4x + 1.

The aim is to find the factor for 3x² + 4x + 1.

Given that 3x² + 4x + 1.

The expression can be written as,

⇒ \(\begin{aligned}
& 3 x^2+4 x+1=3 x^2+3 x+x+1 \\
& 3 x^2+4 x+1=3 x(x+1)+1(x+1) \\
& 3 x^2+4 x+1=(3 x+1)(x+1)
\end{aligned}\)

The factor for the expression is 3x² + 4x + 1 = (3x+1)(x+1).

Page 27 Exercise 2 Answer

Question: Find the factors of the Polynomial 2x² + 3x + 1

Solution:

Given that 2x² + 3x + 1.

The aim is to find the factor for 2x² + 3x + 1.

Given that 2x² + 3x + 1.

the expression can be written as

⇒ \(\begin{aligned}
& 2 x^2+3 x+1=2 x^2+2 x+x+1 \\
& 2 x^2+3 x+1=2 x(x+1)+1(x+1) \\
& 2 x^2+3 x+1=(2 x+1)(x+1)
\end{aligned}\)

The factored expression is, 2x² + 3x + 1 = (2x+1)(x+1).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 27 Exercise 4 Answer

Question: Find the factors of the Polynomial 4x² + 5x + 1

Solution:

Given that 4x² + 5x + 1.

The aim is to find the factor for 4x² + 5x + 1.

Given that 4x²+5x+1 the expression can be written as

⇒ \(\begin{aligned}
& 4 x^2+5 x+1=4 x^2+4 x+x+1 \\
& 4 x^2+5 x+1=4 x(x+1)+1(x+1) \\
& 4 x^2+5 x+1=(4 x+1)(x+1)
\end{aligned}\)

The expression is, 4x² + 5x + 1 = (4x+1)(x+1).

Question: Find the factors of the Polynomial 2x² − 3x + 1

Solution:

Page 27 Exercise 6 Answer

Given that 2x² − 3x + 1.

The aim is to find the factor for 2x² − 3x + 1.

Given that 2x² − 3x + 1. the expression can be written as

⇒ \(\begin{aligned}
& 2 x^2-3 x+1=2 x^2-2 x-x+1 \\
& 2 x^2-3 x+1=2 x(x-1)-1(x-1) \\
& 2 x^2-3 x+1=(2 x-1)(x-1)
\end{aligned}\)

The factor for the expression is (2x−1)(x−1).

Page 27 Exercise 7 Answer

Question: Find the factors of the Polynomial 3x² − 2x − 1

Solution:

Given that 3x² − 2x − 1.

The aim is to find the factors for the 3x² − 2x − 1.

Given that 2x² − 3x + 1. the expression can be written as

⇒ \(\begin{aligned}
& 3 x^2-2 x-1=3 x^2-3 x+x-1 \\
& 3 x^2-2 x-1=3 x(x-1)+(x-1) \\
& 3 x^2-2 x-1=(3 x+1)(x-1)
\end{aligned}\)

The factor for the expression is 3x² − 2x − 1 = (3x+1)(x−1).

Key To Algebra Book 4 Chapter 8 Part 2 Polynomial Problems

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 27 Exercise 8 Answer

Question: Find the factors of the Polynomial 3x² + 2x − 1

Solution:

Given that 3x² + 2x − 1.

The aim is to find the factor for the trinomial.

Given that 3x² + 2x − 1.

The expression can be written as

⇒ \(\begin{aligned}
& 3 x^2+2 x-1=3 x^2+3 x-x-1 \\
& 3 x^2+2 x-1=3 x(x+1)-1(x+1) \\
& 3 x^2+2 x-1=(3 x-1)(x+1)
\end{aligned}\)

The factor for the trinomial is 3x² + 2x − 1 = (3x−1)(x+1).

Page 27 Exercise 12 Answer

Question: Find the factors of the Polynomial 2x² − 7x + 3

Solution:

Given that 2x² − 7x + 3.

The aim is to find the factor for the given expression.

Given that 2x² − 7x + 3.

The expression can be written as

⇒ \(\begin{aligned}
& 2 x^2-7 x+3=2 x^2-6 x-x+3 \\
& 2 x^2-7 x+3=2 x(x-3)-1(x-3) \\
& 2 x^2-7 x+3=(2 x-1)(x-3)
\end{aligned}\)

The factor for the given expression is (2x−1)(x−3).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 27 Exercise 13 Answer

Question: Find the factors of the Polynomial 2x² − 5x − 3

Solution:

Given that 2x² − 5x − 3.

The aim is to find the factor for the given expression.

Given that 2x² − 5x − 3.

The expression can be written as

The factor for the expression is 2x² − 5x − 3 = (2x+1)(x+3).

Page 27 Exercise 14 Answer

Question: Find the factors of the Polynomial 2x² + 5x − 3

Solution:

Given that 2x² + 5x − 3.

The aim is to find the factor for the 2x² + 5x − 3.

Given that 2x² + 5x − 3.

The expression can be written as,

⇒ \(\begin{aligned}
& 2 x^2+5 x-3=2 x^2+6 x-x-3 \\
& 2 x^2+5 x-3=2 x(x+3)-1(x+3) \\
& 2 x^2+5 x-3=(2 x-1)(x+3)
\end{aligned}\)

The factor for the expression is 2x² + 5x − 3 = (2x−1)(x+3).

Page 27 Exercise 15 Answer

Question: Find the factors of the trinomial 2x² − x − 3

Solution:

Given that 2x² − x − 3.

The aim is to find the expression for the 2x² − x − 3.

Given that 2x² − x − 3.
The expression can be written as

⇒ \(\begin{aligned}
& 2 x^2+5 x-3=2 x^2+6 x-x-3 \\
& 2 x^2+5 x-3=2 x(x+3)-1(x+3) \\
& 2 x^2+5 x-3=(2 x-1)(x+3)
\end{aligned}\)

The factor for the trinomial is 2x² − x − 3 = (x+1)(2x−3).

Page 27 Exercise 17 Answer

Question: Find the factors of the trinomial 4a² + 3a − 1

Solution:

To factorize the given trinomials 4a² + 3a − 1

Given trinomials 4a²+3a-1

From this trinomial, we see that a=4,b=3,c=1

Now we have to find two factors whose product is 4x-1=-4 and the sum is 3 we get, 4and-1 as two factors since their product is-4 and the sum is 3 hence

⇒ \(\begin{aligned}
4 a^2+3 a-1 & =4 a^2+4 a-a-1 \\
& =4 a(a+1)-1(a+1) \\
& =(4 a-1)(a+1)
\end{aligned}\)

Therefore the factors of the trinomial of 4a² + 3a − 1 = (4a−1)(a+1).

Page 28 Exercise 4 Answer

Question: Find the factors of the trinomial 4x² − 11x + 6

Solution:

Given trinomial: 4x² − 11x + 6

It is asked to find the factors of the given trinomial.

Given trinomial: 4×2-11x+6

Factoring the given trinomial

4x²-11x+6

⇒ \(\begin{aligned}
& \Rightarrow 4 x^2-(8+3) x+6 \\
& \Rightarrow 4 x^2-8 x-3 x+6 \\
& \Rightarrow 4 x(x-2)-3(x-2) \\
& \Rightarrow(4 x-3)(x-2)
\end{aligned}\)

Checking by multiplying the binomials

(x-2)(4x-3)
⇒ 4x²-3x-8x+6
⇒4x²-11x+6

Therefore, the factors of trinomial 4x² − 11x + 6 = (x−2)(4x−3).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 28 Exercise 5 Answer

Question: Find the factors of the trinomial 16x² − 2x − 5

Solution:

Given trinomial: 16x² − 2x − 5

It is asked to find the factors of the given trinomial.

16x² − 2x − 5

Factoring the given trinomial: 16x² − 2x − 5

⇒ \(\begin{aligned}
& \Rightarrow 16 x^2-(10-8) x-5 \\
& \Rightarrow 16 x^2-10 x+8 x-5 \\
& \Rightarrow 2 x(8 x-5)+1(8 x-5) \\
& \Rightarrow(8 x-5)(2 x+1)
\end{aligned}\)

Checking by multiplying the binomials

⇒ \(\begin{aligned}
& (8 x-5)(2 x+1) \\
& \Rightarrow 16 x^2+8 x-10 x-5 \\
& \Rightarrow 16 x^2-2 x-5
\end{aligned}\)

Therefore, the factors of trinomial 16x² − 2x − 5 = (8x−5)(2x+1).

Page 28 Exercise 6 Answer

Question: Find the factors of the trinomial 6x² + 17x + 5

Solution:

Given trinomial: 6x² + 17x + 5

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² + 17x + 5
Factoring the given trinomial: 6x² + 17x + 5

⇒ \(\begin{aligned}
& \Rightarrow 6 x^2+(15+2) x+5 \\
& \Rightarrow 6 x^2+15 x+2 x+5 \\
& \Rightarrow 3 x(2 x+5)+1(2 x+5) \\
& \Rightarrow(3 x+1)(2 x+5)
\end{aligned}\)

Checking by multiplying the binomials

⇒ \(\begin{aligned}
& (3 x+1)(2 x+5) \\
& \Rightarrow 6 x^2+15 x+2 x+5 \\
& \Rightarrow 6 x^2+17 x+5
\end{aligned}\)

Therefore, the factors of trinomial 6x² + 17x + 5 = (2x+5)(3x+1).

Page 28 Exercise 7 Answer

Question: Find the factors of the trinomial 6x² + 13x + 5

Solution:

Given trinomial: 6x² + 13x + 5

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² + 13x + 5
Factoring the given trinomial: 6x² + 13x + 5

⇒ \(\begin{aligned}
& (2 x+1)(3 x+5) \\
\Rightarrow & 6 x^2+10 x+3 x+5 \\
\Rightarrow & 6 x^2+13 x+5
\end{aligned}\)

Therefore, the factors of trinomial 6x² + 13x + 5 = (3x+5)(2x+1).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 28 Exercise 8 Answer

Question: Find the factors of the trinomial 6x² − 13x − 5

Solution:

Given trinomial: 6x² − 13x − 5

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² − 13x − 5

Factoring the given trinomial: 6x² − 13x − 5

⇒ \(\begin{aligned}
& \Rightarrow 6 x^2-(15-2) x-5 \\
& \Rightarrow 6 x^2-15 x+2 x-5 \\
& \Rightarrow 3 x(2 x-5)+1(2 x-5) \\
& \Rightarrow(3 x+1)(2 x-5)
\end{aligned}\)

Checking by multiplying the binomial:

⇒ \(\begin{aligned}
& (3 x+1)(2 x-5) \\
& \Rightarrow 6 x^2-15 x+2 x-5 \\
& \Rightarrow 6 x^2-13 x-5
\end{aligned}\)

Therefore, the factors of trinomial 6x² − 13x − 5 = (2x−5)(3x+1).

Page 28 Exercise 9 Answer

Question: Find the factors of the trinomial 6x² − 13x + 5

Solution:

Given trinomial: 6x² − 13x + 5

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² − 13x + 5

Factoring the given trinomial: 6x² − 13x + 5

⇒ \(\begin{aligned}
& 6 x^2-13 x+5 \\
\Rightarrow & 6 x^2-(10+3) x+5 \\
\Rightarrow & 6 x^2-10 x-3 x+5 \\
\Rightarrow & 2 x(3 x-5)-(3 x-5) \\
\Rightarrow & (2 x-1)(3 x-5)
\end{aligned}\)

Checking by multiplying the binomial

⇒ \(\begin{aligned}
& (3 x-5)(2 x-1) \\
& \Rightarrow 6 x^2-3 x-10 x+5 \\
& \Rightarrow 6 x^2-13 x+5
\end{aligned}\)

Therefore, the factors of trinomial 6x² − 13x + 5 = (3x−5)(2x−1).

Page 28 Exercise 10 Answer

Question: Find the factors of the trinomial 6x² − 7x − 5

Solution:

Given trinomial: 6x² − 7x − 5

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² − 7x − 5

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2-7 x-5 \\
\Rightarrow & 6 x^2-(10-3) x-5 \\
\Rightarrow & 6 x^2-10 x+3 x-5 \\
\Rightarrow & 6 x^2-10 x+3 x-5 \\
\Rightarrow & 2 x(3 x-5)+(3 x-5) \\
\Rightarrow & (2 x+1)(3 x-5)
\end{aligned}\)

Checking by multiplying the binomials

Therefore, the factors of trinomial 6x² − 7x − 5 = (3x−5)(2x+1).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 28 Exercise 11 Answer

Question: Find the factors of the trinomial 6x² + 7x − 5

Solution:

Given trinomial: 6x² + 7x − 5

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² + 7x − 5

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2+7 x-5 \\
\Rightarrow & 6 x^2+(10-3) x-5 \\
\Rightarrow & 6 x^2+10 x-3 x-5 \\
\Rightarrow & 2 x(3 x+5)-(3 x+5) \\
\Rightarrow & (2 x-1)(3 x+5)
\end{aligned}\)

Checking by multiplying the binomials

⇒ \(\begin{aligned}
& (3 x+5)(2 x-1) \\
\Rightarrow & 6 x^2-3 x+10 x-5 \\
\Rightarrow & 6 x^2+7 x-5
\end{aligned}\)

Therefore, the factors of trinomial 6x² + 7x − 5 = (3x+5)(2x−1).

Page 28 Exercise 12 Answer

Question: Find the factors of the trinomial 8x² + 14x + 3

Solution:

Given trinomial: 8x² + 14x + 3

It is asked to find the factors of the given trinomial.

Given trinomial: 8x² + 14x + 3

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 8 x^2+14 x+3 \\
\Rightarrow & 8 x^2+(12+2) x+3 \\
\Rightarrow & 8 x^2+12 x+2 x+3 \\
\Rightarrow & 4 x(2 x+3)+1(2 x+3) \\
\Rightarrow & (2 x+3)(4 x+1)
\end{aligned}\)

Checking by multiplying the binomial

⇒ \(\begin{aligned}
& (2 x+3)(4 x+1) \\
\Rightarrow & 8 x^2+2 x+12 x+3 \\
\Rightarrow & 8 x^2+14 x+3
\end{aligned}\)

Therefore, the factors of trinomial 8x² + 14x + 3 = (2x+3)(4x+1).

Page 28 Exercise 13 Answer

Question: Find the factors of the trinomial 8x² − 10x + 3

Solution:

Given trinomial: 8x² − 10x + 3

It is asked to find the factors of the given trinomial.

Given trinomial: 8x² − 10x + 3

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 8 x^2-10 x+3 \\
\Rightarrow & 8 x^2-(6+4)+3 \\
\Rightarrow & 8 x^2-6 x-4 x+3 \\
\Rightarrow & 2 x(4 x-3)-1(4 x-3) \\
\Rightarrow & (4 x-3)(2 x-1)
\end{aligned}\)

Checking by multiplying the binomials:

⇒ \(\begin{aligned}
& (4 x-3)(2 x-1) \\
\Rightarrow & 8 x^2-4 x-6 x+3 \\
\Rightarrow & 8 x^2-10 x+3
\end{aligned}\)

Therefore, the factors of trinomial 8x² − 10x + 3 = (4x−3)(2x−1).

Solutions For Multiplying And Factoring Polynomials Part 2 Chapter 8 Key To Algebra Book 4

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 28 Exercise 14 Answer

Question: Find the factors of the trinomial 8x² + 25x + 3

Solution:

Given trinomial: 8x² + 25x + 3

It is asked to find the factors of the given trinomial.

Given trinomial: 8x² + 25x + 3

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 8 x^2+25 x+3 \\
\Rightarrow & 8 x^2+(24+1) x+3 \\
\Rightarrow & 8 x^2+24 x+x+3 \\
\Rightarrow & 8 x^2+24 x+x+3 \\
\Rightarrow & 8 x(x+3)+1(x+3) \\
\Rightarrow & (8 x+1)(x+3)
\end{aligned}\)

Checking By  multiplying the binomials:

⇒ \(\begin{aligned}
& (x+3)(8 x+1) \\
\Rightarrow & 8 x^2+x+24 x+3 \\
\Rightarrow & 8 x^2+25 x+3
\end{aligned}\)

Therefore, the factors of trinomial 8x² + 25x + 3 = (x+3)(8x+1).

Page 28 Exercise 15 Answer

Question: Find the factors of the trinomial 6x² + 14x + 4

Solution:

Given trinomial: 6x² + 14x + 4

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² + 14x + 4

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2+14 x+4 \\
\Rightarrow & 6 x^2+(12+2) x+4 \\
\Rightarrow & 6 x^2+12 x+2 x+4 \\
\Rightarrow & 6 x(x+2)+2(x+2) \\
\Rightarrow & (6 x+2)(x+2)
\end{aligned}\)

Checking By  multiplying the binomials:

⇒ \(\begin{aligned}
& (x+2)(6 x+2) \\
\Rightarrow & 6 x^2+2 x+12 x+4 \\
\Rightarrow & 6 x^2+14 x+4
\end{aligned}\)

Therefore, the factors of trinomial 6x² + 14x + 4 = (2x+4)(3x+1).

Page 28 Exercise 16 Answer

Question: Find the factors of the trinomial 6x² − 10x + 4

Solution:

Given trinomial: 6x² − 10x + 4

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² − 10x + 4
Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2-10 x+4 \\
\Rightarrow & 6 x^2-(6+4) x+4 \\
\Rightarrow & 6 x^2-6 x-4 x+4 \\
\Rightarrow & 6 x(x-1)-4(x-1) \\
\Rightarrow & (x-1)(6 x-4)
\end{aligned}\)

Checking By  multiplying the binomials:

⇒ \(\begin{aligned}
& (x-1)(6 x-4) \\
\Rightarrow & 6 x^2-4 x-6 x+4 \\
\Rightarrow & 6 x^2-10 x+4
\end{aligned}\)

Therefore, the factors of trinomial(x−1)(6x+4) = 6x² − 10x + 4.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 28 Exercise 17 Answer

Question: Find the factors of the trinomial 6x² + 25x + 4

Solution:

Given trinomial: 6x² + 25x + 4

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² + 25x + 4
Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2+25 x+4 \\
\Rightarrow & 6 x^2+(24+1) x+4 \\
\Rightarrow & 6 x^2+24 x+x+4 \\
\Rightarrow & 6 x(x+4)+1(x+4) \\
\Rightarrow & (x+4)(6 x+1)
\end{aligned}\)

Checking By  multiplying the binomials:

⇒ \(\begin{aligned}
& (x+4)(6 x+1) \\
\Rightarrow & 6 x^2+x+24 x+4 \\
\Rightarrow & 6 x^2+25 x+4
\end{aligned}\)

Therefore, the factors of trinomial 6x² + 25x + 4 = (x+4)(6x+1).

Page 28 Exercise 18 Answer

Question: Find the factors of the trinomial 6x² − 23x − 4

Solution:

Given trinomial: 6x² − 23x − 4

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² − 23x − 4

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2-2 x-4 \\
\Rightarrow & 6 x^2-(6-4) x-4 \\
\Rightarrow & 6 x^2-6 x+4 x-4 \\
\Rightarrow & 6 x(x-1)+4(x-1) \\
\Rightarrow & (x-1)(6 x+4)
\end{aligned}\)

Checking by multiplying the binomials:

⇒ \(\begin{aligned}
& (x-1)(6 x+4) \\
\Rightarrow & 6 x^2+4 x-6 x-4 \\
\Rightarrow & 6 x^2-2 x-4
\end{aligned}\)

Therefore, the factors of trinomial 6x² − 23x − 4 = (x−4)(6x+1).

Question: Find the factors of the trinomial 6x² − 2x − 4

Solution:

Page 28 Exercise 19 Answer

Given trinomial: 6x² − 2x − 4

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² − 2x − 4

Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2-2 x-4 \\
\Rightarrow & 6 x^2-(6-4) x-4 \\
\Rightarrow & 6 x^2-6 x+4 x-4 \\
\Rightarrow & 6 x(x-1)+4(x-1) \\
\Rightarrow & (x-1)(6 x+4)
\end{aligned}\)

Checking by multiplying the binomials:

⇒ \(\begin{aligned}
& (x-1)(6 x+4) \\
\Rightarrow & 6 x^2+4 x-6 x-4 \\
\Rightarrow & 6 x^2-2 x-4
\end{aligned}\)

Therefore, the factors of tr

Therefore, the factors of trinomial 6x² − 2x − 4 = (x−1)(6x+4).

Page 28 Exercise 20 Answer

Question: Find the factors of the trinomial 6x² + 10x − 4

Solution:

Given trinomial: 6x² + 10x − 4

It is asked to find the factors of the given trinomial

Given trinomial: 6x² + 10x − 4
Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2+10 x-4 \\
\Rightarrow & 6 x^2+(12-2) x-4 \\
\Rightarrow & 6 x^2+12 x-2 x-4 \\
\Rightarrow & 6 x(x+2)-2(x+2) \\
\Rightarrow & (x+2)(6 x-2)
\end{aligned}\)

Checking by multiplying the binomials:

⇒ \(\begin{aligned}
& (x+2)(6 x-2) \\
\Rightarrow & 6 x^2-2 x+19 x-4 \\
\Rightarrow & 6 x^2+10 x-4
\end{aligned}\)

Therefore, the factors of trinomial 6x² + 10x − 4 = (x+2)(6x−2).

Page 28 Exercise 21 Answer

Question: Find the factors of the trinomial 6x² + 5x − 4

Solution:

Given trinomial: 6x² + 5x − 4

It is asked to find the factors of the given trinomial.

Given trinomial: 6x² + 5x − 4
Factoring the given trinomial:

⇒ \(\begin{aligned}
& 6 x^2+5 x-4 \\
\Rightarrow & 6 x^2+(8-3) x-4 \\
\Rightarrow & 6 x^2+8 x-3 x-4 \\
\Rightarrow & 2 x(3 x+4)-1(3 x+4) \\
\Rightarrow & (3 x+4)(2 x-1)
\end{aligned}\)

Checking by multiplying the binomials:

⇒ \(\begin{aligned}
& (3 x+4)(2 x-1) \\
\Rightarrow & 6 x^2-3 x+8 x-4 \\
\Rightarrow & 6 x^2+5 x-4
\end{aligned}\)

Therefore, the factors of trinomial 6x² + 5x − 4 = (3x+4)(2x−1).

Page 28 Exercise 24 Answer

Question: Find the factors of the trinomial 16x² − 38x − 5

Solution:

Given the trinomial 16x² − 38x − 5

Here it is asked to factor the trinomial.

Given the trinomial: 16x²-38-5

we can break the expression

16x²-38-5=(16x²+2x)+(-40x-5)

here the first term can be written as

16x²+2x=2x(8x+1)

The second term can be written as

-40x-5=-5(8x+1)

so we can write that

⇒ \(\begin{aligned}
16 x^2-38 x-5 & =\left(16 x^2+2 x\right)+(-40 x-5) \\
& =2 x(8 x+1)-5(8 x+1) \\
& =(8 x+1)(2 x-5)
\end{aligned}\)

Therefore, the required answer is (8x+1)(2x−5).

Page 28 Exercise 26 Answer

Question: Find the factors of the Polynomial 16x² + 79x − 5

Solution:

Given the trinomial 16x² + 79x − 5

Here it is asked to factor the trinomial.

Given the trinomial: 16x² + 79x − 5

we can break the expression

16x² + 79x − 5=(16x²+2x)+(80x-5)

here the first term can be written as

16x²+2x=2x(16x+1)

The second term can be written as

80x-5=-5(16x-1)

so we can write that

⇒ \(\begin{aligned}
16 x^2+79 x-5 & =\left(16 x^2-x\right)+(80 x-5) \\
& =x(16 x-1)+5(16 x-1) \\
& =(16 x-1)(x+5)
\end{aligned}\)

Verification \(\begin{aligned}
& (16 x-1)(x+5) \\
= & 16 x^2+80 x-x-5 \\
= & 16 x^2+79 x-5
\end{aligned}\)

Since the product of factors is equal to the factorized trinomial, hence we can say that the obtained factors are correct.

Therefore, the required answer is (16x−1)(x+5). On determining the product of these factors we obtained the trinomial 16x² + 79x − 5. Hence, the answer is verified.

Page 28 Exercise 28 Answer

Question: Find the factors of the Polynomial 16x² + 11x − 5

Solution:

Given the trinomial 16x² + 11x − 5

Here it is asked to factor the trinomial.

Given the trinomial: 16x² + 11x − 5

we can break the expression

16x² + 11x − 5=(16x²+5x)+(16x-5)

here the first term can be written as

16x²-5x=2x(16x+1)

The second term can be written as

16x-5=1(16x-5)

so we can write that

⇒ \(\begin{aligned}
16 x^2+11 x-5 & =\left(16 x^2-5 x\right)+(16 x-5) \\
& =x(16 x-5)+1(16 x-5) \\
& =(16 x-5)(x+1)
\end{aligned}\)

Therefore, the required answer is (16x−5)(x+1).

Page 29 Exercise 1 Answer

Question: Find The Product Of The expression (2s-3)(2s+3)

Solution:

Given the expression

(2s-3)(2s+3)

Here it is asked to multiply the expression.

Given the expression

we know that (a+b)(a-b)=a²-b²

Here we can multiply

(2s-3)(2s+3)=(2s)²-(3)² =4s²-9

Therefore, the answer is 9x² − 4.

Mcgraw Hill Key To Algebra Chapter 8 Part 2 Problem Walkthrough

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 29 Exercise 3 Answer

Question: Find the Product (2s−3)(2s+3)?

Solution:

Given the expression

(2s−3)(2s+3)

Here it is asked to multiply the expression.

Given the expression

(8x-4)(8x+4)

we know that (a+b)(a-b)=a²-b²

Here we can multiply

(8x-4)(8x+4)=(8x)²-4²
=64x²-16

Therefore, the answer is 4s² − 9.

Page 29 Exercise 4 Answer

Question: Find the Product (8x−4)(8x+4)?

Solution:

Given the expression

(8x−4)(8x+4)

Here it is asked to multiply the expression.

Given the expression

(8x-4)(8x+4)

we know that

(a+b)(a-b)=a²-b²

here we can multiply

(8x-4)(8x+4)=(8x)²-4² =64x²-16

Therefore, the answer is 64x² − 16.

Page 29 Exercise 1 Answer

Question: Find the Product (2x+3y)(x−2y)?

Solution:

Given the expression

(2x+3y)(x−2y)

Here it is asked to multiply the expression.

Given the expression

(2x+3y)(x-2y)

we know that

(a+b)(x+d)=ab+ad+bc+bd

here we can multiply

Therefore, the answer is 2x² − xy − 6y².

Page 29 Exercise 2 Answer

Question: Find the Product (5x+y)(3x+2y)?

Solution:

Given:

(5x+y)(3x+2y)

To find:

The multiplication

Apply (a+b)(c+d) = ac + ad + bc + bd

Given:

(5x+y)(3x+y)
we known that

(a+b )(c+d)=ax+ad+bc+bd

here we can apply

⇒ \(\begin{aligned}
(5 x+y)(3 x+2 y) & =5 x \cdot 3 x+5 x \cdot 2 y+y \cdot 3 x+y \cdot 2 y \\
& =15 x^2+10 x y+3 x y+2 y^2 \\
& =15 x^2+13 x y+2 y^2
\end{aligned}\)

The multiplication: (5x+y)(3x+2y) = 15x² + 13xy + 2y²

Page 29 Exercise 4 Answer

Question: Find the Product (2x+5y)(2x−5y)?

Solution:

Given:

(2x+5y)(2x−5y)

To find:

The multiplication

Apply (a+b)(c+d) = ac + ad + bc + bd

Given:

(2x+5y)(2x-5y)

we know that

(a+b)(a-b)=a²-b²

Here we can multiply

(2x+5y)(2x-5y)=(2x)²-(5y)² =4x²-25y²

The multiplication: (2x+5y)(2x−5y) = 4x² − 25y²

Page 29 Exercise 1 Answer

Question: Find the factors of the Equation 16x² − 9?

Solution:

Given:

16x² − 9

To find:

The factors

Apply the difference of squares formula

Given 16x² − 9

To find the factors of the expression:

⇒ \(\begin{aligned}
& 16 x^2-9=4^2 x^2-3^2 \\
& 16 x^2-9=(4 x)^2-3^2 \\
& 16 x^2-9=(4 x+3)(4 x-3)
\end{aligned}\)

∴ x²-y²=(x+y)(x-y)

The factors of the expression: 16x² − 9 = (4x+3)(4x−3)

Page 29 Exercise 3 Answer

Question: Find the factors of the Equation 36x² − 100?

Solution:

Given:

36x² − 100

To find:

The factors

Apply the difference of squares formula

Given expression 36x² − 100

To find the factors of the expression:

∴ x²-y²=(x+y)(x-y)

The factors: 36x² − 100 = 4(3x+5)(3x−5)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 2 Page 29 Exercise 4 Answer

Question: Find the factors of the Equation 81y² − 1?

Solution:

Given:

81y² − 1

To find:

The factors

Apply the difference of squares formula

81y²-1

To find the factors of the expression:

⇒ \(\begin{aligned}
& 81 y^2-1=9^2 y^2-1 \\
& 81 y^2-1=(9 y)^2-1^2 \\
& 81 y^2-1=(9 y+1)(9 y-1)
\end{aligned}\)

∴ x²-y²=(x+y)(x-y)

The factors: 81y² − 1 = (9y+1)(9y−1)

Page 29 Exercise 1 Answer

Question: Find the factors of the Equation 2x² + 5xy + 3y²?

Solution:

Given:

2x² + 5xy + 3y²

To find:

Given: 2x² + 5xy + 3y²

Group into (ax²+4xy)+(vxy+cy²)

To find the factors of the expression:

2x²+5xy+3y²=(2x²+2xy)+(-3xy-3y²)

∴ 4=2,v=3

Factor out common term 3a-2b

2x²+5xy+3y²=2x (x+y)+3y(x+y)

Factor out common term x+y

2x²+5xy+3y²=2x (x+y)+3y(2x+3y)

The factors: 2x² + 5xy + 3y² = (x+y)(2x+3y)

Page 29 Exercise 3 Answer

Question: Find the factors of the Equation 9a² − 3ab − 2b²?

Solution:

Given:

9a² − 3ab − 2b²

To find:

The factors

Group​into​ (ax²+uxy) + (vxy+cy²)

Take common things out

Given: 9a²-3ab-2b²

Group into (ax²+4xy)+(vxy+(y²)

To find the factors of the expression:

9a²-3ab-2b²=(9a²+3ab)+(-6ab-2b²)

∴ 4=3,v=-6

Factor out common term 3a-2b

9a²-3ab -2b²=3a(3a+b)-2b(3a+b)

Factor out common term 3a+b

9a²-3ab -2b²=3a(3a+b)(3a-2b)

The factors: 9a² − 3ab − 2b² = (3a+b)(3a−2b)

Page 29 Exercise 4 Answer

Question: Find the factors of the polynomial 9x² − 16y²?

Solution:

Given:

9x² − 16y²

To find: The factors

Apply the difference of squares formula

9x² − 16y²

To find the factors of the expressions:

⇒ \(\begin{aligned}
& 9 x^2-16 y^2=3^2 x^2-4^2 y^2 \\
& 9 x^2-16 y^2=(3 x)^2-(4 y)^2 \\
& 9 x^2-16 y^2=(3 x+4 y)(3 x-4 y)
\end{aligned}\)

∴ x²-y²=(x+y)(x-y)

The factors: 9x² − 16y² = (3x+4y)(3x−4y)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials

Page 16 Exercise 1 Answer

Question: Find The Product of the Expressions (x+3)(x+2)

Solution:

Given the product expression: (x+3)(x+2)

To multiply out the two binomials x+3 and x+2 and write its product.

Now we multiply out each term of one polynomial to another polynomial:

(x+3)(x+2)

(x+3)(x+2)=x(x+2)+3(x+2)

(using the distributive property)

=x²+5x+3.2

(since x1.x²=x1+1 and combining like terms of the power of x

=x2+5x+6

The product we can write:

3.2=3+3

=6

The final multiplied expression is: (x+3)(x+2) = x² + 5x + 6

Question: Find The Product of the Expressions (y+4)(y+10)

Solution:

Given the product expression: (y+4)(y+10)

Multiply the binomials (y+4) and (y+10) and write its product.

Now we multiply out each term of one polynomial to another polynomial:

(x+3(x+2)

(x+3)(x+2)= x

The final multiplied expression is: (y+4)(y+10) = y² + 14y + 40

Question: Find The Product of the Expressions (x+5)(x+6)

Solution:

Given expression: (x+5)(x+6)

Multiply the binomials (x+5) and (x+6) and write the product.

Now we multiply out each term of one polynomial to another polynomial:

(x+5)(x+6)=x(x+6)+5(x+6)

=x.x+6x+5x+5.6 (using distributive law)

=x2+11x+5.6

(since x1.x1=x1+1 and combining like terms of x

The= x2+11x+30

The product can be viewed as

5.6=6+6+6+6+6
=12+12+6
=30

The final multiplied expression is: (x+5)(x+6) = x² + 11x + 30

Mcgraw Hill Key To Algebra Book 4 Chapter 8 Solutions

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 16 Exercise 6 Answer

Question: Find The Product of the Expressions (x+1)(x+6)

Solution:

Given the product expression: (x+1)(x+6)

To multiply the binomials (x+5) and (x+6) and write its product.

Now we multiply out each term of one polynomial to another polynomial:

Given the product expression: (y+4)(y+10)
(y+4)(y+10)=y(y+10)4(y+10)
=y.y+10y+4y+4.10
(using distributive law)

=y2+14y+4.10

(since x1.x1= x1+1 and combining like terms of power of x

=y2+14y+4.10

(since x1.x1=x1+1 and combining like terms of power of x)

=y2+14y +40

The product can be viewed as:

4.10=10+10+10+10
=20+20
=40

The final multiplied expression is: (x+1)(x+6) = x² + 7x + 6

Page 16 Exercise 7 Answer

Question: Find The Product of the Expressions (a+8)(a+9)

Solution:

Given product expression: (a+8)(a+9)

Multiply the binomials (a+8) and (a+9) and write its product.

Now we multiply out each term of one polynomial to another polynomial:

Given the product expression:(x+5)(x+6)

(x+5)(x+6)=x(x+6)+5(x+6)

=x.x+6x+5x+5.6 (using distributive law)

=x2+11x+5.6

(since x1.x1=x1+1 and combining like terms of x

The= x2+11x+30

The product can be viewed as

5.6=6+6+6+6+6
=12+12+6
=30

The final multiplied expression is: (a+8)(a+9) = a² + 17a + 72

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 16 Exercise 8 Answer

Question: Find The Product of the Expressions (z+3)(z+3)

Solution:

Given product expression: (z+3)(z+3)

To multiply the binomials (z+3) and (z+3) and write its product.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression: (z+3)(z+3)

(z+3)(z+3)=z(z+3)+3(z+3)
=z.z+3z+3z+3.3

(using distributive law)

=za²+6z+9

(since z¹.z¹=z¹+1 combing like terms of z)

=z²+6.z+9

The product can be viewed as

3.3=3+3+3
=6+3
=9

The final multiplied expression is: (z+3)(z+3) = z² + 6z + 9

Page 16 Exercise 1 Answer

Question: Find The Product of the Expressions (x−4)(x−5)

Solution:

Given the product expression: (x−4)(x−5)

Multiply the binomials (x−4) and (x−5) and find the product value.

Now we multiply out each term of one polynomial to another polynomial:

Given that product expression:(x-4)(x-5)
(x-4)(x-5)=x(x-5)-4(x-5)
=x.x-5x-4x+(-4).(-5)

(using  distributive law)

=x2-9x+(-4)++.(-5)(combing like terms)

=x2-9x+20

The product can be viewed as:

(-4).(-5)=4.5

=5+5+5+5
=10+10
=20

The expanded form of the product can be viewed as (x−4)(x−5) = x² − 9x + 20

Key To Algebra Book 4 Multiplying And Factoring Polynomials Answers

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 16 Exercise 2 Answer

Question: Find The Product of the Expressions (x−2)(x−4)

Solution:

Given product expression : (x−2)(x−4)

Multiply the binomials (x−4) and (x−2) and write their product value.

Now we multiply out each term of one polynomial to another polynomial:

Given Product expression: (x-2)(x-4)

(x-2)(x-4)=x(x-4)-2(x-4)
=x.x-4x-2x+(-2).(-4)
(using distributive law)

=x²-6x+(-2).(-4)

(combining like terms)

=x2-6x+8

the product can be viewed as

(-2).(4)=2.4
=4+4
=8

The expanded form of the product is: (x−2)(x−4) = x² − 6x + 8

Page 16 Exercise 3 Answer

Question: Find The Product of the Expressions (x−3)(x−5)

Solution:

Given the product expression: (x−3)(x−5)

Multiply the binomials (x−3) and (x−5) and write the value of the product.

Now we multiply out each term of one polynomial to another polynomial:

Given Product Expession: (x-3)(x-5)
(x-3)(x-5)=x(x-5)-3(x-5)
=x.x-5x-3x+(-3).(-5)

(using distributive law)

= x2-8x+(-3).(-5)

(combining like terms)

=x2-8x+15

the product can be viewed as:

(-3).(-5)=3.5

=5+5+5
=10+5
=15

The expanded form of the product is: (x−3)(x−5) = x² − 8x + 15

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 16 Exercise 4 Answer

Question: Find The Product of the Expressions (x−6)(x−6)

Solution:

Given product expression: (x−6)(x−6)

Multiply the binomials (x−6) and (x−6) and write the product value.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression:(x-6)(x-6)
(x-6)(x-6)=x(x–6)-6(x-6)
=x.x-6x-6x+(-6).(-6)
(using distributive law)
=x2-12x+(-6).(-6)
(combing like terms)
=x2-12x+36
the product can be viewed as:

(-6).(-6)=6.6
=6+6+6+6+6+6
=12+12+12
=24+12
=36

The expanded form of the product is: (x−6)(x−6) = x² − 12x + 36

Page 16 Exercise 5 Answer

Question: Find The Product of the Expressions (x−1)(x−8)

Solution:

Given the product expression: (x−1)(x−8)

Multiply the binomials (x−1) and (x−8) and write the product value.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression: (x-1)(x-8)

(x-1)(x-8)= x(x-8)-1(x-8)
=x.x-8x-x+(-1).(x-8)
(using distributive law)
=x2-9x+8
(combining like terms)
the product can be viewed as:
(-1).(-8)=8.1
=8

= 8 (Since the product of any number with 1 is the number itself)

The expanded form of the product is: (x−1)(x−8) = x² − 9x + 8

Page 16 Exercise 6 Answer

Question: Find The Product of the Expressions (x−7)(x+3)

Solution:

Given the product expression: (x−7)(x+3)

Multiply the binomials (x−7) and (x+3) and write the product value.

Now we multiply out each term of one polynomial to another polynomial:

Given:(x-7)(x+3)
(x-7)(x+3)=x(x+3)-7(x+3)
=x.x+3x-7x+3.(-7)
(using the distributive law)
=x2-4x+3.(-7)
(combining like terms)
=x2-4x-21
The product can be viewed as:

3.(-7)=-7-7-7
=-14-7
=-21

The expanded form of the product is : (x−7)(x+3) = x² − 4x − 21

Chapter 8 Multiplying And Factoring Polynomials Mcgraw Hill Key

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 16 Exercise 7 Answer

Question: Find The Product of the Expressions (x−5)(x+3)

Solution:

Given the product expression: (x−5)(x+3)

Multiply the binomials (x−5) and (x+3) and write its product value.

Now we multiply out each term of one polynomial to another polynomial:

Given: (x-5)(x+3)
(x-5)(x+3)=x(x+3)-5(x+3)
=x.x+3x-5x+(-5).3
(using distributive law)
=x2-2x+(-5).3
(combining like terms)
=x2-2x-15
the product can be viewed as:

3.(-5)=-5-5-5
=-10-5
=-15

The expanded product can be written as: (x−5)(x+3) = x² − 2x − 15

Page 16 Exercise 8 Answer

Question: Find The Product of the Expressions (x+2)(x−6)

Solution:

Given product expression: (x+2)(x−6)

Multiply the binomials (x+2) and (x−6) and write its product value.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression: (x+2)(x-6)
(x+2)(x-6)=x(x-6)+2(x-6)
=x.x-6x+2x+(2).(-6)
(using the distributive property)

= x2-4x+2.(-6)

The product can be viewed as:

2.(-6)=-6-6
=-12

The expanded form of the product: (x+2)(x−6) = x² − 4x − 12

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 16 Exercise 9 Answer

Question: Find The Product of the Expressions (x+8)(x−5)

Solution:

Given product expression: (x+8)(x−5)

Multiply the binomials (x+8) and (x−5) and write its value.

Now we multiply out each term of one polynomial to another polynomial:

Given Product expression:(x+8)(x-5)

(x+8)(x-5)=x(x-5)+8(x-5)
=x.x-5x+8x+8.(-5)
(using the distributive property)
=x2-3+8.(-5)
(combining like terms)

=x2-3x-40

The product can be viewed as:

8.(-5)=-5-5-5-5-5-5-5-5
=-10-10-10-10
=-20-20
=-40

The product in the expanded form is: (x+8)(x−5) = x² + 3x − 40

Page 16 Exercise 10 Answer

Question: Find The Product of the Expressions (x−8)(x+5)

Solution:

Given product expression: (x−8)(x+5)

Multiply the binomials (x−8) and (x+5) and write its value.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression: (x-8)(x+5)

The expanded form of the product is: (x−8)(x+5) = x² − 3x − 40

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1Page 17 Exercise 1 Answer

Question: Find The Product of the Expressions (x+3)(x+2)

Solution:

Given product expression: (x−3)(x−2)

To multiply the binomials (x−2) and (x−3) and write the value.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression: (x-3)(x-2)
(x-3)(X-2)=x(x-2)-3(x-2)
=x.x-2x-3x+(-3).(-2)
=x.x-2x-3x+(-3).(-2)
(using distributive property)
=x2-5x+(-3).(-2)

(combining like terms)

=x2-5x+6

The product can be viewed as
(-3).(-2)=3.2
=3+3
=6

The expanded form of the product is: (x−3)(x−2) = x² − 5x + 6

Page 17 Exercise 2 Answer

Question: Find The Product of the Expressions (x−1)(x−1)

Solution:

Given product expression: (x−1)(x−1)

To multiply the binomials (x−1) and (x−1) and write the value.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression: (x-1)(x-1)

(x-1)(x-1)=x(x-1)-1(x-1)
x.x-x-x+(-1)(-1)
(using the distributive property)

=x2-2x+1

(combining like terms)

The product can be viewed as:

(-1).(-1)=1.1
=1

The expanded form of the product is: (x−1)(x−1) = x² − 2x + 1

Page 17 Exercise 3 Answer

Question: Find The Product of the Expressions (x−7)(x−2)

Solution:

Given the product expression: (x−7)(x−2)

To multiply the binomials (x−7) and (x−2) and write its value.

Now we multiply out each term of one polynomial to another polynomial:

Given the product expression:(x-7)(x-2)
(X-7(x-2)=x(x-2)-7(x-2)
=x.x-2x-7x+(-7)(-2)
(using distributive property)
=x²-9x+(-7)(-2)
(combining like terms)

=x²-9x+14

The product can be viewed as:

(-7).(-2)=7.2
=7+7
=14

The expanded form of the product is: (x−7)(x−2) = x² − 9x + 14

How To Solve Chapter 8 Multiplying And Factoring Polynomials Key To Algebra Book 4

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 17 Exercise 4 Answer

Question: Find The Product of the Expressions (x−3)(x−4)

Solution:

Given the product expression: (x−3)(x−4)

To multiply the binomials (x−3) and (x−4) and write its value.

Now we multiply out each term of one polynomial to another polynomial:

Given the product expression: (x-3)(x-4)

(x-3)(x-4)=x(x-4)-3(x-4)
=x.x-4x-3x+(-3).(-4)

(using distributive law)

=x2-7x+12(combining like terms)

The product can be viewed as:

(-3).(-4)=3.4
=4+4+4
=8+4
=12

The expanded form of the product is: (x−3)(x−4) = x² − 7x + 12

Page 17 Exercise 5 Answer

Question: Find The Product of the Expressions (x+8)(x−3)

Solution:

Given the product expression: (x+8)(x−3)

Multiply the binomials (x+8) and (x−3) and write its value.

Now we multiply out each term of one polynomial to another polynomial:

Given the product expression:(x+8)(x-3)
(x+8)(x-3)=x(x-3)+8(x-3)
=x.x-3x+8x+8(-3)
(using distributive law)

=x²+5x-24(combining like terms)

The product can be viewed as:

8.(-3)=-3-3-3-3-3-3-3-3

=-6-6-6-6
=-12-12
=-24

The expanded form of the product is: (x+8)(x−3) = x² + 5x − 24

Mcgraw Hill Algebra Book 4 Chapter 8 Explanations

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 17 Exercise 6 Answer

Question: Find The Product of the Expressions (x+5)(x−2)

Solution:

Given product expression: (x+5)(x−2)

To multiply the binomials (x+5) and (x−2) and write its value.

Now we multiply out each term of one polynomial to another polynomial:

Given product expression:(x+5)(x-2)
(x+5)(x-2)=x(x-2)+(x-2)
=x.x-2x+5x+5.(-2)
(using distributive law)
=x2+3x-10 (combining like terms)
The product can be viewed as:

5.(-2)=-2-2-2-2-2
-4-4-2

The expanded form of the product is: (x+5)(x−2) = x² + 3x − 10

Page 17 Exercise 7 Answer

Question: Find The Product of the Expressions (a−4)(a−6)

Solution:

We have given:

(a−4)(a−6)

We have to find the above product.

We will multiply the above two expressions to find the resultant polynomial.

Given rectangle length =x+4

Breadth=x-2

A=lxw
we have, l=x+4
w=x-2
The area of a rectangle is A=lxw

This is a quadratic polynomial.

The multiplication (a−4)(a−6) is equal to a² − 10a + 24.

Page 17 Exercise 10 Answer

Question: Find The Product of the Expressions (x+4)(x−4)

Solution:

We have given:

(x+4)(x−4)

We have to find the above product.

We will use the identity

(a+b)(a−b) = a² − b² to find the resultant polynomial.

Given: (a-4)(a-6)

multiply the expressions

(a-4)(a-6)

multiply the expressions

(a-4)(a-6)

=a(a-6)-4(a-6)
=a(a-6)-4(a-6)
=a2-6a-4a+24
=a2-10a+24

This is the required quadratic polynomial.

The product(x+4)(x−4) is equal to x² − 16.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 17 Exercise 12 Answer

Question: Find The Product of the Expressions (x−3)(x+4)

Solution:

We have given:

(x−3)(x+4)

We have to find the above product.

We will multiply the above two expressions to find the resultant polynomial.

Given:(x-3)(x+4)

multiply the expressions

(x-3)(x+4)

=x(x+4)-3(x+4)

=x²+4x-3x-12

=x²+x-12

This is the required polynomial.

The product(x−3)(x+4)​ is equal to x² + x − 12.

Page 17 Exercise 14 Answer

Question: Find The Product of the Expressions (x−6)(x+6)

Solution:

We have given:

(x−6)(x+6)

We have to find the above product.

We will use the identity(a−b)(a+b) = a² − b² here and find the resultant polynomial.

(x-6)(x+6) multiply the expressions:

(x-6)(x+6)

=x²-6²

(since(x-a)(x+a)=x2-a2]

=x²-36

This is the resultant polynomial.

The product(x−6)(x+6) is equal to x² − 36.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 17 Exercise 15 Answer

Question: Find The Product of the Expressions (y+3)(y−3)

Solution:

We have given:

(y+3)(y−3)

We have to find the above product.

We will multiply the above two expressions to find the resultant polynomial.

Given:(y+3)(y-3)

⇒ multiply the expressions

(y+3)(y-3)

=y(y-3)+3(y-3)
=y²-3y+3y-9
=y²-9

This is the resultant quadratic polynomial.

The product (y+3)(y−3) is equal to y² − 9.

Page 17 Exercise 16 Answer

Question: Find The Product of the Expressions (x+9)(x−2)

Solution:

Given:

(x+9)(x−2)

We have to find the above product.

We will multiply the above two expressions to find the resultant polynomial.

Given: (x+9)(X-2)

Multiply the expressions

(x+9)(x-2)
=x(x-2)+9(x-2)
=x²-2x+9x-18
=x²+7x-18

This is the required polynomial.

The product(x+9)(x−2) gives a quadratic polynomial x² + 7x − 18.

Solutions For Multiplying And Factoring Polynomials Chapter 8 Key To Algebra Book 4

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 17 Exercise 1 Answer

Question: Find The Product of the Expressions (x+5)

Solution:

We have given a binomial:

(x+5)

We have to calculate(x+5)².

We will calculate the resultant polynomial by using the identity

(a+b)² = a² + 2ab + b²

Given binomial:(x+5)²

(x+5)²

Here, a=x,b=5

∴(x+5)2=x2+2(x)(5)+4=52
[since(a+b)²=a²+2ab+b²]
=x2²+10x+25

This is the required polynomial.

(x+5)² gives a quadratic polynomial x² + 10x + 25.

Page 17 Exercise 2 Answer

Question: Find The Product of the Expressions (x+4)

Solution:

We have given a binomial:

(x+4)

We have to calculate (x+4)².

We will calculate the resultant polynomial by using the identity:

(a+b)² = a² + 2ab + b²

Given binomial: (x+4)²

(x+4)²

Here a=x, b=4

∴ (x+4)²= x²+2(x)(4)+4²

[Since (a+b)²=a²+2ab+b²]
=x²+8x+16

This is the resultant quadratic polynomial.

(x+4)2 gives a quadratic polynomial x² + 8x + 16.

Page 17 Exercise 3 Answer

Question: Find The Product of the Expressions x + 10

Solution:

We have given a binomial:

x + 10

We have to calculate (x+10)².

We will calculate the resultant polynomial by using the identity:

(a+b)² = a² + 2ab + b²

(x+10)²

here a=x,b=10

∴ (x+10)² =x2+2(x)(10)+100

(since) (a+b)²=a²+2ab+b²]
=x²+20x+100

This is the resultant polynomial.

(x+10)² gives a quadratic polynomial x² + 20x + 100.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 17 Exercise 4 Answer

Question: Find The Product of the Expressions x−5

Solution:

We have given a binomial:

x−5

We have to calculate (x−5)².

We will find the resultant polynomial by using the identity:

(a−b)² = a² − 2ab + b²

Given binomial:(x-5)²

(x-5)²

Here a=x,b=5

using the algebraic identity

This is the required polynomial.

(x−5)² gives a quadratic polynomial x² − 10x + 25.

Page 17 Exercise 6 Answer

Question: Find The Product of the Expressions (x−1)²

Solution:

Given expression is (x−1)²

We have to multiply binomial (x−1) to binomial (x−1)

The result of the multiplication of two binomial is polynomial.

Given binomial:(x-5)²

(x-5)²

Here a=x, b=5

Using the algebraic identity

⇒ \(\begin{aligned}
(a-b)^2 & =a^2-2 a b+b^2 \\
(x-5)^2 & =x^2-2(x)(5)+25 \\
& =x^2-10 x+25
\end{aligned}\)

Page 18 Exercise 1 Answer

Question: Find the area of the rectangle whose length l = x + 4 and width w = x − 2.

Solution:

We have given a rectangle having length l = x + 4 and width w = x − 2.

We have to find the area A of the rectangle.

A = l × w

Here area is a multiplication of two binomial.

Given rectangle length=x+4
breadth=x-2

A=lxw
we have, l=x+4

The area of the rectangle is a =lxw

⇒ \(\begin{aligned}
A & =(x+4)(x-2) \\
& =x^2-2 x+4 x-8 \\
& =x^2+2 x-8
\end{aligned}\)

The area of the rectangle having length (x+4) and width (x-2) is x² + 2x – 8.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 18 Exercise 2 Answer

Question: Find the area of the rectangle whose length l = x + 7 and width w = x − 4.  

Solution:

We have given a rectangle having length l = x + 7 and width w = x − 4.

We have to find the area A of the rectangle.

A = l × w

Here area is the multiplication of two binomials.

Area of rectangle a=lxw

we have, l=x+7

w=x-4

A=(x+7)(x-4)

The area of a rectangle having length x + 7 and width x − 4 is x² + 3x − 28.

Page 18 Exercise 4 Answer

Question: Find the area of the rectangle whose length l = x + 3 and width w = x + 3.

Solution:

We have given a rectangle having length l = x + 3 and width w = x + 3.

We have to find the area A of the rectangle.

A = l × w

Here area is the multiplication of two binomials.

Area of rectangle A= l×w

we have, l=x+3

w=x+3

A=(x+3)(x+3)

=x²+3x+3x+9

=x²+6x+9

The area of rectangle having length (x+3) and width (x+3) is x² + 6x + 9

Page 18 Exercise 5 Answer

Question: Find the area Of the rectangle whose length l = (x+6) and width w = x − 1

Solution:

We have given rectangle having length l = (x+6) and width w = x − 1

We have to find the area A of the rectangle.

A = l × w

To find the area of a rectangle we have to multiply the two binomials.

Area of rectangle A=l×w

we have, l= x+6

w=x-1

A=(x+6)(x-1)

=x²-x+6x-6

=x²+5x-6

The area of a rectangle having length l = x + 6 and width w = (x−1) is x² + 5x − 6.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 19 Exercise 2 Answer

Question: Find the factors of the equation x² + 21x + 20 = (x+…)(x+..).

Solution:

We have been given a trinomial that x² + 21x + 20 = (x+…)(x+..).

We have to fill in each pair of blanks with the right numbers and we have to check our answers.

We will find the result using the factorization method.

The given Trinomial is, x2+21x+20
Factoring out, we get

⇒ \(\begin{aligned}
x^2+21 x+20 & =x^2+x+20 x+20 \\
& =x(x+1)+20(x+1) \\
& =(x+1)(x+20)
\end{aligned}\)

Now let us check answers by multiplying the binomial

(x+1)(x+20)=x.x+20x+x+20

x²+21x+20

We have factorized and filled in the blanks with the right numbers that are, x² + 21x + 20 = (x+1)(x+20), and checked our answers

Page 19 Exercise 3 Answer

Question: Find the factors of the polynomial x² + 12x + 20

Solution:

Given expression is x² + 12x + 20

We have to factorize the polynomial.

We have, x² + 12x + 20

The factor of 20 adds up to 12 is 10 and 2.

Given expression: x²+12x+20

Factoring out, we get

⇒ \(\begin{aligned}
x^2+12 x+20 & =x^2+10 x+2 x+20 \\
& =x(x+10)+2(x+10) \\
& =(x+2)(x+10)
\end{aligned}\)

Re check:

By using multiplying the binomial

Hence it is proved that the factors of polynomials are right.

We have factorized the polynomial as x² + 12x + 20 = (x+10)(x+2)

We have checked the factors of the polynomial.

Page 19 Exercise 4 Answer

Question: Find the factors of the polynomial x² + 14x + 24

Solution:

Given expression x² + 14x + 24

We have to factorize the polynomial.

We have, x² + 14x + 24

The factor of 24 that add up to 14 is 2, 12

Given expression: x²+14×24

Factoring out, we get

⇒ \(\begin{aligned}
x^2+14 x+24 & =x^2+2 x+12 x+24 \\
& =x(x+2)+12(x+2) \\
& =(x+12)(x+2)
\end{aligned}\)

Re-check the answer:

By multiplying the binomial

⇒ \(\begin{aligned}
(x+12)(x+2) & =x^2+2 x+12 x+24 \\
& =x^2+14 x+24
\end{aligned}\)

Hence the factors of polynomials are right.

We have factorized the polynomial as : x² + 14x + 24 = (x+2)(x+12)

Worked Examples For Chapter 8 Multiplying And Factoring Polynomials Mcgraw Hill

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 19 Exercise 5 Answer

Question: Find the factors of the polynomial x² + 9x + 20

Solution:

Given expression x² + 9x + 20

We have to factorize the polynomial.

We have , x² + 9x + 20

The factor of 20 which add up to 9 are 5 and 4.

Given expression: x²+9x+20

Factoring out, we get

Rechexking the answer:

by using multiplying the binomial

(x+4)(x+5)x2+4x+-5x+20
=x2+9x+20

Hence the factors of polynomials are right.

We have factorized the polynomial as : x² + 9x + 20 = (x+4)(x+5)

Page 20 Exercise 4 Answer

Question: Find the factors of the second-order degree polynomial x² + 7x + 10

Solution:

Given that the second-degree polynomial is, x² + 7x + 10

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given expression: x2+7x+10
factoring out, we get

Rechecking the answer:

By multiplying the binomial

(X+2)(x+5)=x²+5x+2x+10

=x²+7x+10

The factorization of the polynomial into a product of two binomials is x² + 7x + 10 = (x+5)(x+2).

Page 20 Exercise 7 Answer

Question: Find the factors of the second-order degree polynomial x² + 5x + 4

Solution:

Given that the second-order degree polynomial is, x² + 5x + 4

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given expression: x2+5x+4

Factoring out, we get

x2+5x+4=x2+x+4x+4
=x(x+1)+4(x+1)
=(x+4)(x+1)

Rechecking the answers:

By multiplying the binomial

(x+4)(x+1)=x2+x+4x+4
=x2+5x+4

The factorization of the polynomial into a product of two binomials is: x² + 5x + 4 = (x+1)(x+4).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 8 Multiplying And Factoring Polynomials 1 Page 20 Exercise 8 Answer

Question: Find the factors of the second-order degree polynomial x² + 2x + 1

Solution:

Given that the second-order degree polynomial is, x² + 2x + 1

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given expression: x2+2x+1
Factoring out, we get

Check:

Now consider the binomial

⇒ \(\begin{aligned}
(x+1)(x+1) & =x^2+x+x+1 \\
& =x^2+2 x+1
\end{aligned}\)

The factorization of the polynomial into a product of two binomials is: x² + 2x + 1 = (x+1)(x+1).

Page 20 Exercise 9 Answer

Question: Find the factors of the second-order degree polynomial x² + 3x + 2

Solution:

Given that the second-order degree polynomial is, x² + 3x + 2

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given Expression: x2+3x+2

factoring out, we get

x2+3x+2=x2+x+2x+2
=x(x+1)+2(x+1)
=(x+2)(x+1)

Check: 

Now consider the binomial

⇒ \(\begin{aligned}
(x+2)(x+1) & =x^2+x+2 x+2 \\
& =x^2+3 x+2
\end{aligned}\)

The factorization of the polynomial into a product of two binomials is: x² + 3x + 2 = (x+1)(x+2).

Page 20 Exercise 10 Answer

Question: Find the factors of the second-order degree polynomial x² + 13x + 36

Solution:

Given that the second-order degree polynomial is x² + 13x + 36

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given expression: x2+13x+36
factoring out, we get

⇒ \(\begin{aligned}
x^2+13 x+3 & =x^2+4 x+9 x+36 \\
& =x(x+4)+9(x+4) \\
& =(x+9)(x+4)
\end{aligned}\)

check:

Now consider the binomial

(x+9)(x+4)=x2+4x+9x+36
=x2+13x+36

The factorization of the polynomial into a product of two binomials is x² + 13x + 36 = (x+4)(x+9).

Question: Find the factors of the second-order degree polynomial x² + 12x + 36

Solution:

Given that the second-order degree polynomial is x² + 12x + 36

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given polynomial: x2+12x+36
factoring out, we get

or

=(x+6)²

Check:

Now consider the binomial

(x+6)(x+6)= x²+6x+6x+36

=x²+12x+36

The factorization of the polynomial into a product of two binomials is x² + 12x + 36 = (x+6)(x+6).

Page 20 Exercise 13 Answer

Question: Find the factors of the second-order degree polynomial x² + 37x + 36

Solution:

Given that the second-order degree polynomial is x² + 37x + 36

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given polynomial: x²+37x+36

Factoring out, we get

x2+37+36= x2+x+36x+36
=x(x+1)+36(X+1)
=(x+36)(X+1)

Check:

Now consider the binomial,

(x+36)(x+1)=x2+x+36x+36
=x2+37x+36

The factorization of the polynomial into a product of two binomials is x² + 37x + 36 = (x+11)(x+36).

Question: Find the factors of the second-order degree polynomial x² + 15x + 36

Solution:

Given that the second-order degree polynomial is x² + 15x + 36

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given polynomial: x²+15x+36

Factoring out, we get

⇒ \(\begin{aligned}
x^2+15 x+36 & =x^2+3 x+12 x+36 \\
& =x(x+3)+12(x+3) \\
& =(x+12)(x+3)
\end{aligned}\)

Check:

Now consider the binomial,

The factorization of the polynomial into a product of two binomials is: x² + 15x + 36 = (x+3)(x+12).

Page 20 Exercise 15 Answer

Question: Find the factors of the second-order degree polynomial x² + 17x + 30

Solution:

Given that the second-order degree polynomial is x² + 17x + 30

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given polynomial: x²+17x+30

Factoring out, we get

Check:

Now consider the binomials

The factorization of the polynomial into a product of two binomials is: x² + 17x + 30 = (x+2)(x+15).

Question: Find the factors of the second-order degree polynomial x² + 11x + 30

Solution:

Given that the second-order degree polynomial is x² + 11x + 30

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule :

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given Polynomial: x²+11x+30

Factoring out, we get

Check:

Now consider the binomial:

(x+6)(x+5)=x²+5x+6x+30

=x²+11x+30

The factorization of the polynomial into a product of two binomials is x² + 11x + 30 = (x+5)(x+6).

Page 20 Exercise 17 Answer

Question: Find the factors of the second-order degree polynomial x² + 13x + 30

Solution:

Given that the second-order degree polynomial is x² + 13x + 30

Here we have to factor the given polynomial into a product of two binomials.

Factorization rule:

Group the first two terms together and then the last two terms together.

Factor out a GCF from each separate binomial.

Factor out the common binomial.

Note that if we multiply our answer out, we do get the original polynomial.

Given polynomial: x2+13x+30
Factoring out, we get

Check:

Now consider the binomial:

(x+10)(x+3)= x²+3x+10x+30

=x²+13x+30

The factorization of the polynomial into a product of two binomials is: x² + 13x + 30 = (x+10)(x+3).

Page 20 Exercise 18 Answer

Question: Find the factors of the second-order degree polynomial x² + 31x + 30

Answer: 

Given: x² + 31x + 30

To find: factorize each into a product of two binomials.

x²+31x+30

First factorizing as 30 many different ways

we can 30×1, 15×2, 10×3

While testing the combinations, 30×1

So,

x²+31x+30

⇒ x²+x+30x+30

⇒x(x+1)+30(x+1)

⇒(x+1)(x+30)

finally, x²+31x+30=(x+1)(x+30)

Thus, the factorization of the second degree polynomial x² + 31x + 30 into a product of two binomials is (x+1)(x+30)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor

Question: Factorize the polynomial 6a−30

Solution:

Given expression is 6a−30

We find factors of the given polynomial

We take out common from the given expression 3 goes into both 6 and 30, so we factor out 3

6a − 30 = 3(2a−10)

The factorization of the given polynomial is 3(2a−10)

Question: Factorize the polynomial 6a−30

Solution:

Given expression is 6a−30

We find factors of a given polynomial

We take out common from the given expression.

6 goes into both 6,30, we take that out as common 6a − 30 = 6(a−5)

The factorization of the given polynomial is 6(a−5)

Question: Factorize the polynomial 6a−30

Solution:

Given expression is 6a−30

We find factors of a given polynomial

We take out common from the given expression.

2 goes into both 6,30, we take that out as common 6a − 30 = 2(3a−15​)

The factorization of the given polynomial is 2(3a−15)

Mcgraw Hill Key To Algebra Book 4 Chapter 6 Solutions

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 11 Exercise 5 Answer

Question: Factorize the polynomial 18x−27

Solution:

Given expression is 18x−27

We find factors of a given polynomial

We take out common from the given expression.

9 goes into both 18,27, we take that out as common 18x − 27 = 9(2x−3)

The factorization of the given polynomial is 9(2x−3)

Question: Factorize the polynomial 4x−32

Solution:

Given expression is 4x−32

We find factors of a given polynomial

We take out common from the given expression.

4 goes into both 4,32, we take that out as common 4x − 32 = 4(x−8)

The factorization of the given polynomial is 4(x−8)

Question: Factorize the polynomial 8y−10

Solution:

Given expression is 8y−10

We find factors of a given polynomial

We take out common from the given expression.

2 goes into both 8,10, we take that out as common 8y − 10 = 2(4y−5)

The factorization of the given polynomial is 2(4y−5)

Question: Factorize the polynomial 5x − 5y + 10z

Solution:

Given expression is 5x − 5y + 10z

We find factors of a given polynomial

We take out common from the given expression.

5 goes into both 5,10, we take that out as common 5x − 5y + 10z = 5(x−y+2z)

The factorization of the given polynomial is 5(x−y+2z)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 11 Exercise 10 Answer

Question: Factorize the polynomial 7x − 7y − 7z

Solution:

Given polynomial is 7x − 7y − 7z

We find factors of a given polynomial

We factorize the given expression.

HCF of 7x,7y,7z is 7,we take that out as common 7x − 7y − 7z = 7(x−y−z)

Factorization of the given polynomial is 7(x−y−z)

Question: Factorize the polynomial 2x² + 18x + 14

Solution:

Given polynomial is 2x² + 18x + 14

We find factors of a given polynomial

We factorize given polynomial

HCF of 2x²,18x,14is 2,we take that out as common 2x² + 18x + 14 = 2(x²+9x+7)

Factorization of the given polynomial is 2(x²+9x+7)

Question: Factorize the polynomial 6a − 18b + 12c

Solution:

Page 11 Exercise 14 Answer

Given polynomial is 6a − 18b + 12c

We find factors of the given polynomial

We factorize the given expression.

HCF of 6a,18b,12cis 6, we take that out as common.

6a − 18b + 12c = 6(a−3b+2c)

The factorization of given polynomial is 6(a−3b+2c)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 11 Exercise 15 Answer

Question: Factorize the polynomial 9x + 12y + 15

Solution:

Given polynomial is 9x + 12y + 15

We find the factors of a given polynomial

We factorize the given expression.

HCF of 9x,12y, and 15 is 3, we take that out as common.

9x + 12y + 15 = 3(3x+4y+5)

The factorization of the given polynomial is 3(3x+4y+5)

Page 11 Exercise 16 Answer

Question: Factorize the polynomial 8a + 12b + 4

Solution:

Given polynomial is 8a + 12b + 4

We find the factors of a given polynomial

We factorize the given expression.

HCF of 8a,12b, and 4 is 4, we take that out as common.

8a + 12b + 4 = 4(2a+3b+1)

The factorization of the given polynomial is 4(2a+3b+1)

Key To Algebra Book 4 Factoring Out A Common Factor Chapter 6 Answers

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 1 Answer

Question: Factorize the biggest term from the polynomial 15y + 5?

Solution:

Given the polynomial to factorize: 15y + 5

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

15y+5=5(3y+1)

Now we see that:

15y+5=5(3y+1)

⇒ \(\frac{15 y}{5}=3 y\)

Here 5 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 15y,5.

The polynomial after factoring out the biggest term is as follows: 15y + 5 = 5(3y+1)

Page 12 Exercise 2 Answer

Question: Factorize the biggest term from the polynomial 7a + 7?

Solution:

Given expression: 7a + 7

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

Given expression: 7a+7
Now we see that:
7a+7=7(a+1)

⇒ \(\begin{aligned}
& \frac{7 a}{7}=a \\
& \frac{7}{7}=1
\end{aligned}\)

Here 7 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 7a,7

The polynomial after factoring out the biggest term is as follows: 7a + 7 = 7(a+1)

Page 12 Exercise 4 Answer

Question: Factorize the biggest term from the polynomial 5 + 20x?

Solution:

Given expression: 5 + 20x

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

5+20x ( factorizing the expression )

5+20x=5(1+4x)
Now we see that:

⇒ \(\begin{aligned}
& \frac{20 x}{5}=4 x \\
& \frac{5}{5}=1
\end{aligned}\)

Here 5 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 5,20x

The polynomial after factoring out the biggest term is as follows: 5 + 20x = 5(1+4x)

Page 12 Exercise 5 Answer

Question: Factorize the biggest term from the polynomial 6x − 2?

Solution:

Given expression: 6x − 2

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

6x-2

Factorizing the expression

6x-2=2(3x-1)

Now we see that:

Here 2 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 6x,2

The polynomial after factoring out the biggest term is as follows: 6x − 2 = 2(3x−1)

Mcgraw Hill Factoring Solutions Chapter 6 Key To Algebra

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 6 Answer

Question: Factorize the biggest term from the polynomial 14n + 21p + 7?

Solution:

Given expression: 14n + 21p + 7

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

14n+21p+7

Factorizing the expression:

14n+21p+7=7(2n+3p+1)

Now we see that:

⇒ \(\begin{aligned}
\frac{14 n}{7} & =2 n \\
\frac{21 p}{7} & =3 p \\
\frac{7}{7} & =1
\end{aligned}\)

Here 7 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 14n,21p,7

The polynomial after factoring out the biggest term is as follows: 14n + 21p + 7 = 7(2n+3p+1)

Page 12 Exercise 7 Answer

Question: Factorize the polynomial 9x − 18y + 3

Solution:

Given expression: 9x − 18y + 3

Factorizing the expression

9x-18y+3=3(3x-6y+1)

Now we see that: 

⇒ \(\begin{aligned}
& \frac{9 x}{3}=3 x \\
& \frac{18 y}{3}=6 y \\
& \frac{3}{3}=1
\end{aligned}\)

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

Here 3 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 9x,18y,3

The polynomial after factoring out the biggest term is as follows: 9x − 18y + 3 = 3(3x−6y+1)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 8 Answer

Question: Factorize the biggest term from the polynomial11 − 22a + 44b?

Solution:

Given expression: 11 − 22a + 44b

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

11-22a+44b

Factorizing the expression:

11-22a+44b=11(1-2a+4b)
Now we see that:

⇒ \(\frac{44 b}{11}=4 b\)

Here 11 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 11, 22a,44b

The polynomial after factoring out the biggest term is as follows: 11 − 22a + 44b = 11(1−2a+4b)

Page 12 Exercise 9 Answer

Question: Factorize the polynomial 5x² + 10x + 5

Solution:

Given expression: 5x² + 10x + 5

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

5x²+10x+5

Factorizing the expression:

⇒ \(\begin{aligned}
5 x^2+10 x+5 & =5\left(x^2+2 x+1\right) \\
& =5\left(x^2+x+x+1\right) \\
& =5(x(x+1)+1(x+1)) \\
& =5(x+1)^2
\end{aligned}\)

we see that:

⇒ \(\begin{aligned}
\frac{5 x^2}{5} & =x^2 \\
\frac{10 x}{5} & =2 x \\
\frac{5}{5} & =1
\end{aligned}\)

Here 5 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 5x²,10x,5

The polynomial after factoring out the biggest term is as follows: 5x² + 10x + 5 = 5(x²+2x+1)

Page 12 Exercise 10 Answer

Question: Factorize the polynomial 28x² + 28x + 7

Solution:

Given expression to factorize: 28x² + 28x + 7

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial as per Sandy’s way.

Given expression: 28×2+28x+7

Factorizing the expression:

28×2+28x+7=7(4×2+4x+1)
=7(4x²+2x+2x+1)
=7(2x(2x+1)+1(2x+1)
=7(2x+1)²

We can see that:

⇒ \(\begin{aligned}
& \frac{28 x^2}{7}=4 x^2 \\
& \frac{28 x}{7}=4 x \\
& \frac{7}{7}=1
\end{aligned}\)

Here 7 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 28x²,28x,7

The polynomial after factoring out the biggest term is as follows: 28x² + 28x + 7 = 7(4x²+4x+1)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 1 Answer

Question: Factorize the polynomial 24x + 28

Solution:

Given expression: 24x + 28

We need to factor out the biggest term from this expression.

Factoring out the biggest term from the expression:

Given expression: 24x+28
factorizing the expression:

24x+28=4(6x+7)
now we see that:

⇒ \(\begin{aligned}
& \frac{24 x}{4}=6 x \\
& \frac{28}{4}=7
\end{aligned}\)

Here 4 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 24x,28

The polynomial after factoring out the biggest term is as follows: 24x + 28 = 4(6x+7)

Page 12 Exercise 3 Answer

Question: Factorize the polynomial 40n − 24

Solution:

Given expression: 40n − 24

We need to factor out the biggest term from this expression.

Factoring out the biggest term from the expression:

Given expression: 4 on -24

Factorizing the expression:

4 on-24= 8(5n-3)

now we see that:

⇒ \(\begin{aligned}
& \frac{40 n}{8}=5 n \\
& \frac{24}{8}=3
\end{aligned}\)

Here 8 is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 40n,24

The polynomial after factoring out the biggest term is as follows: 40n − 24 = 8(5n−3)

Page 12 Exercise 5 Answer

Question: Factorize the polynomial 18x − 30y.

Solution:

Given:

The polynomial is 18x − 30y.

To find:

The objective is to find the greatest factor among the given polynomials.

Consider the given polynomial,

18x − 30y

= 6(3x−5y) Taking GCF

Therefore, the required result is 18x − 30y = 6(3x−5y).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 6 Answer

Question: Factorize the polynomial 100 + 40z.

Solution:

Given:

The polynomial is 100 + 40z.

To find:

The objective is to factor the greatest number among the given polynomials.

Consider the given polynomial,

100 + 40z

= 20(5+2z) Taking GCF

Therefore, the required result is 100 + 40z = 20(5+2z).

Page 12 Exercise 7 Answer

Question: Factorize the polynomial 56x² + 42.

Solution:

Given:

The polynomial is 56x² + 42.

To find:

The objective is to factor the greatest number among the given polynomials.

Consider the given polynomial,

56x² + 42

= 14(4x²+3) Taking GCF

Therefore, the required result is 56x² + 42 = 14(4x²+3).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 8 Answer

Question: Factorize the polynomial 20x + 60y − 100z.

Solution:

Given:

The polynomial is 20x + 60y − 100z.

To find:

The objective is to factor the greatest number among the given polynomials.

Consider the given polynomial,

20x + 60y − 100z

= 20(x+3y−5z) Taking GCF

Therefore, the required result is 20x + 60y − 100z = 20(x+3y−5z).

Page 12 Exercise 9 Answer

Question: Factorize the polynomial 14a − 12b + 6c.

Solution:

Given:

The polynomial is 14a − 12b + 6c.

To find:

The objective is to factor the greatest number among the given polynomials.

Consider the given polynomial,

14a − 12b + 6c

= 2(7a−6b+3c) Taking GCF

Therefore, the required result is 14a − 12b + 6c = 2(7a−6b+3c).

Page 12 Exercise 10 Answer

Question: Factorize the polynomial 24 + 48x + 42x²

Solution:

Given:

The polynomial is 24 + 48x + 42x².

To find:

The objective is to factor the greatest number among the given polynomials.

Consider the given polynomial,

24 + 48x + 42x²

= 6(4+8x+7x²) Taking GCF

Therefore, the required result is 24 + 48x + 42x² = 6(4+8x+7x²).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 11 Answer

Question: Factorize the polynomial 50a − 20b + 30c.

Solution:

Given:

The polynomial is 50a − 20b + 30c.

To find:

The objective is to factor the greatest number among the given polynomials.

Consider the given polynomial,

50a − 20b + 30c

= 10(5a+2b+3c) Taking GCF

Therefore, the required result is 50a − 20b + 30c = 10(5a+2b+3c).

Page 12 Exercise 12 Answer

Question: Factorize the polynomial 6c² + 27c − 15.

Solution:

Given:

The polynomial is 6c² + 27c − 15.

To find:

The objective is to factor the greatest number among the given polynomials.

Consider the given polynomial,

6c² + 27c − 15

= 3(2c²+9c−5) Taking GCF

Therefore, the required result is 6c² + 27c − 15 = 3(2c²+9c−5).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 12 Exercise 13 Answer

Question: Factorize the polynomial 12r + 36s − 60t

Solution:

Given the polynomial

12r + 36s − 60t

Here it is asked to factor out the biggest number.

We know that the factors of 12 are

12 = 1,2,3,4,6,12

and we know that the factors of 36 are

36 = 1,2,3,4,6,9,12,18,36

and we know that the factors of 60 are

60 = 1,​2,​3,​4,​5,​6,​10,​12,​15,​20,​30,​60

So here there are 6

common factors for 12,36,60.

That is

1,2,3,4,6,12

Hence here the greatest common factor is 12

So we can write that

12r + 36s − 60t = 12(r+3s−5t)

Hence the biggest number that can be factored out is 12.

Therefore, the biggest number that can be factored out is 12.

Page 13 Exercise 1 Answer

Question: Find the greatest common factor in the expression 16x − 48?

Solution:

Given the polynomial

16x − 48

Here it is asked to find the greatest common factor.

We know that the factors of 16 are

16 = 1,2,4,8,16

The factors of 48 are

48 = 1,2,3,4,6,8,12,16,24,48

So here there are 5 common factors for 16 and 48.

That is

1,2,4,8,16

Hence the greatest common factor of 16 and 48 is 16.

That is

16x − 48 = 16(x−3)

Therefore, the greatest common factor of 16x − 48 is 16.

How To Solve Chapter 6 Factoring Out A Common Factor Key To Algebra Book 4

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 13 Exercise 2 Answer

Question: Find the greatest common factor in the expression 30x + 45?

Solution:

Given the polynomial

30x + 45

Here it is asked to find the greatest common factor.

We know that the factors of 30 are

30 = 1,​2,​3,​5,​6,​10,​15,​30

And we know that the factors of 45 are

45 = 1,​3,​5,​9,​15,​45

So here there are 4 common factors for 30 and 45.

That is

1,3,5,15

Hence the greatest common factor of 30 and 45 is 15.

That is

30x + 45 = 15(2x+3)

Therefore, the greatest common factor of 30x + 45 is 15.

Page 13 Exercise 4 Answer

Question: Find the greatest common factor in the expression 200x + 80y − 120z?

Solution:

Given the polynomial

200x + 80y − 120z

Here it is asked to find the greatest common factor.

We know that the factors of 200 are

200 = 1,​2,​4,​5,​8,​10,​20,​25,​40,​50,​100,​200

The factors of 80 are

80 = 1,​2,​4,​5,​8,​10,​16,​20,​40,​80

The factors of 120 are

120 = 1,​2,​3,​4,​5,​6,​8,​10,​12,​15,​20,​24,​30,​40,​60,​120

So here there are 8 common factors for 200,80,120.

That is

1,2,4,5,8,10,20,40

Hence the greatest common factor of 200,80 and 120 is 40.

That is

200x + 80y − 120z = 40(5x+2y−3z)

Therefore, the greatest common factor of 200x + 80y − 120z is 40.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 13 Exercise 5 Answer

Question: Find the greatest common factor in the expression 72a − 96b − 48c?

Solution:

Given the polynomial

72a − 96b − 48c

Here it is asked to find the greatest common factor.

We know that the factors of 72 are

72 = 1,​2,​3,​4,​6,​8,​9,​12,​18,​24,​36,​72

The factors of 96 are

96 = 1,​2,​3,​4,​6,​8,​12,​16,​24,​32,​48,​96

The factors of 48 are

48 = 1,​2,​3,​4,​6,​8,​12,​16,​24,​48

So here there are 8 common factors for 72,96,48 are 1,2,3,4,6,8,12,24

Hence the greatest common factor of 72,96,48 is 24.

That is

72a − 96b − 48c = 24(3a−4b−2c)

Therefore, the greatest common factor of 72a − 96b − 48c is 24.

Page 13 Exercise 6 Answer

Question: Find the greatest common factor in the expression 32x² + 40x + 160?

Solution:

Given the polynomial

32x² + 40x + 160

Here it is asked to find the greatest common factor.

We know that the factors of 32 are

32 = 1,​2,​4,​8,​16,​32

The factors of 40 are

40 = 1,​2,​4,​5,​8,​10,​20,​40

The factors of 160 are

160 = 1,​2,​4,​5,​8,​10,​16,​20,​32,​40,​80,​160

So here there are 4 common factors for 32,40,160.

That is

1,2,4,8

Hence the greatest common factor of 32,40,160 is 8.

That is

32x² + 40x + 160 = 8(4x²+5x+20)

Therefore, the greatest common factor of 32x² + 40x + 160 is 8.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 13 Exercise 1 Answer

Question: Find the common factors in the polynomial x² + 3x

Solution:

Given the polynomial

x² + 3x

Here it is asked to find the common factor.

Here we can see that x is common to both terms.

That is

x² + 3x = x(x+3)

Hence the common factor is x.

Therefore, the common factor is x.

Page 13 Exercise 2 Answer

Question: Find the common factors in the polynomial 5a² + 2a

Solution:

Given the polynomial

5a² + 2a

Here it is asked to find the common factor.

Here we can see that a is common to both terms.

That is

5a² + 2a = a(5a+2)

Hence the common factor is a.

Therefore, the common factor is a.

Page 13 Exercise 3 Answer

Question: Find the common factors in the polynomial y² − 7y

Solution:

Given the polynomial

y² − 7y

Here it is asked to find the common factor.

Here we can see that y is common to both terms.

That is

y² − 7y = y(y−7)

Hence the common factor is y.

Therefore, the common factor is y.

Page 13 Exercise 4 Answer

Question: Find the common factors in the polynomial 12x − x²

Solution:

Given the polynomial

12x − x²

Here it is asked to find the common factor.

Here we can see that x is common to both terms.

That is

12x − x² = x(12−x)

Hence the common factor is x.

Therefore, the common factor is x.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 13 Exercise 5 Answer

Question: Find the common factors in the polynomial 3x³ + 2x²

Solution:

Given the polynomial

3x³ + 2x²

Here it is asked to find the common factor.

Here we can see that x² is common to both terms.

That is

3x³ + 2x² = x²(3x+2)

Hence the common factor is x².

Therefore, the common factor is x².

Page 13 Exercise 6 Answer

Question: Find the common factors in the polynomial x⁴ − 5x²

Solution:

Given the polynomial

x⁴ − 5x²

Here it is asked to find the common factor.

Here we can see that x² is common to both terms.

That is

x⁴ − 5x² = x²(x²−5)

Hence the common factor is x².

Therefore, the common factor is x².

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 13 Exercise 7 Answer

Question: Find the common factors in the polynomial a³ + 5a² + 3a

Solution:

Given the polynomial

a³ + 5a² + 3a

Here it is asked to find the common factor.

Here we can see that a is common to both terms.

That is

a³ + 5a² + 3a = a(a²+5a+3)

Hence the common factor is a.

Therefore, the common factor is a.

Page 8 Exercise 13 Answer

Question: Find the common factors in the polynomial 2x³ + x² − 8x

Solution:

Given the polynomial

2x³ + x² − 8x

Here it is asked to find the common factor.

Here we can see that x is common to both terms.

That is

2x³ + x² − 8x = x(2x²+x−8)

Hence the common factor is x.

Therefore, the common factor is x.

Page 13 Exercise 9 Answer

Question: Find the common factors in the polynomial ab + 2b + b²

Solution:

Given the polynomial

ab + 2b + b²

Here it is asked to find the common factor.

Here we can see that b is common to both terms.

That is

ab + 2b + b² = b(a+2+b)

Hence the common factor is b.

Therefore, the common factor is b.

Page 13 Exercise 10 Answer

Question: Find The Common Factor in The Polynomial 5x²y + xy + 7y

Solution:

Given the polynomial

5x²y + xy + 7y

Here it is asked to find the common factor.

Here we can see that y is common to both terms.

That is

5x²y + xy + 7y = y(5x²+x+7)

Hence the common factor is y.

Therefore, the common factor is y.

Mcgraw Hill Key To Algebra Chapter 6 Problem Walkthrough

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common FactorPage 13 Exercise 11 Answer

Question: Find The Common Factor In The Polynomial x³ − 4x² + x

Solution:

Given the polynomial

x³ − 4x² + x

Here it is asked to find the common factor.

Here we can see that x is common to both terms.

That is

x³ − 4x² + x = x(x²−4x+1)

Hence the common factor is x.

Therefore, the common factor is x.

Page 13 Exercise 12 Answer

Question: Find The Common Factor In The Polynomial ab + b² + 2bc

Solution:

Given the polynomial

ab + b² + 2bc

Here it is asked to find the common factor.

Here we can see that b is common to both terms.

That is

ab + b² + 2bc = b(a+b+2c)

Hence the common factor is b.

Therefore, the common factor is b.

Page 14 Exercise 1 Answer

Question: Find The Common Factor In The Polynomial 5x² + 10x

Solution:

Given the polynomial

5x² + 10x

Here it is asked to find the common factor.

Here we can see that 5x is common to both terms.

That is

5x² + 10x = 5x(x+2)

Hence the common factor is 5x.

Therefore, the common factor is 5x and can be written as 5x(x+2).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 14 Exercise 2 Answer

Question: Find The Common Factor In The Polynomial 8a² − 2a

Solution:

Given the polynomial

8a² − 2a

Here it is asked to find the common factor.

Here we can see that 2a is common to both terms.

That is

8a² − 2a = 2a(4a−1)

Hence the common factor is 2a.

Therefore, the common factor is 2a and can be written as 2a(4a−1).

Page 14 Exercise 3 Answer

Question: Find The Common Factor In The Polynomial 4y⁵ + 3y³

Solution:

Given the polynomial

4y⁵ + 3y³

Here it is asked to find the common factor.

Here we can see that y³ is common to both terms.

That is

4y⁵ + 3y³ = y³(4y²+3)

Hence the common factor is y³.

Therefore, the common factor is y³ and can be written as y³(4y²+3).

Page 14 Exercise 4 Answer

Question: Find The Common Factor In The Polynomial x²y² + x³y

Solution:

Given the polynomial

x²y² + x³y

Here it is asked to find the common factor.

Here we can see that x²y is common to both terms.

That is

x²y² + x³y = x²y(y+x)

Hence the common factor is x²y.

Therefore, the common factor is x²y and can be written as x²y(y+x).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 14 Exercise 5 Answer

Question: Find The Common Factor In The Polynomial x²y² + xy

Solution:

Given the polynomial

x²y² + xy

Here it is asked to find the common factor.

Here we can see that xy is common to both terms.

That is

x²y² + xy = xy(xy+1)

Hence the common factor is xy.

Therefore, the common factor is xy and can be written as xy(xy+1).

Page 14 Exercise 6 Answer

Question: Find The Common Factor In The Polynomial 3x + 12x²

Solution:

Given the polynomial

3x + 12x²

Here it is asked to find the common factor.

Here we can see that 3x is common to both terms.

That is

3x + 12x² = 3x(1+4x)

Hence the common factor is 3x.

Therefore, the common factor is 3x and can be written as 3x(1+4x).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 14 Exercise 7 Answer

Question: Find The Common Factor In The Polynomial 6x³ − 9x²

Solution:

Given the polynomial

6x³ − 9x²

Here it is asked to find the common factor.

Here we can see that 3x² is common to both terms.

That is

6x³ − 9x² = 3x²(2x−3)

Hence the common factor is 3x².

Therefore, the common factor is 3x² and can be written as 3x²(2x−3).

Page 14 Exercise 8 Answer

Question: Find The Common Factor In The Polynomial 4x² + 6xy

Solution:

Given the polynomial

4x² + 6xy

Here it is asked to find the common factor.

Here we can see that 2x is common to both terms.

That is

4x² + 6xy = 2x(2x+3y)

Hence the common factor is 2x.

Therefore, the common factor is 2x and can be written as 2x(2x+3y).

Page 14 Exercise 10 Answer

Question: Find The Common Factor In The Polynomial 12a² − 18ab

Solution:

Given the polynomial

12a² − 18ab

Here it is asked to find the common factor.

Here we can see that 3a is common to both terms.

That is

12a² − 18ab = 3a(4a−6b)

Hence the common factor is 3a.

Therefore, the common factor is 3a and can be written as 3a(4a−6b).

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 14 Exercise 11 Answer

Question: Factorize the polynomial -7x³ − 7x²

Solution:

Given: Polynomial -7x³ − 7x²

To find: A factorized form of a given polynomial.

Factorize each of the terms in the given polynomial expression

⇒ 7 × x × x × x − 7 × x × x

As both of the terms have 7 × x × x common. So, from distributive law relation, we can rewrite it as

⇒ 7 × x × x(x−1)

⇒ 7x²(x−1)

Hence, the final factorized form of the given polynomial is 7x²(x−1)

Page 14 Exercise 12 Answer

Question: Factorize the polynomial -25x + 30xy

Solution:

Given: Polynomial -25x + 30xy

To find: A factorized form of a given polynomial.

Factorize each of the terms in the given polynomial expression

⇒ 5 × 5 × x + 2 × 3 × 5 × x × y

As both of the terms have a common 5 × x. So, from distributive law relation, we can rewrite it as

⇒ 5 × x(5+2×3×y)

⇒ 5x(5+6y)

Hence, the final factorized form of the given polynomial is 5x(5+6y)

Worked Examples For Chapter 6 Factoring Out A Common Factor Mcgraw Hill

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 14 Exercise 13 Answer

Question: Factorize the polynomial -x⁶ + x⁵ − x⁴

Solution:

Given: Polynomial -x⁶ + x⁵ − x⁴

To find: A factorized form of a given polynomial.

Factorize each of the terms in the given polynomial expression

⇒ x × x × x × x × x × x + x × x × x × x × x − x × x × x × x

As both of the terms have common x × x × x × x. So, from distributive law relation, we can rewrite it as

⇒ x × x × x × x(x×x+x−1)

⇒ x⁴(x²+x−1)

Hence, the final factorized form of the given polynomial is x⁴(x²+x−1)

Page 14 Exercise 15 Answer

Question: Factorize the polynomial -5a³ + 3a⁴ + 6a³

Solution:

Given: Polynomial -5a³ + 3a⁴ + 6a³

To find: A factorized form of a given polynomial.

Two of the terms have variable with the same power, so the like terms will get added directly,

⇒ 11a³ + 3a⁴

Factorise each of the terms in the given polynomial expression

⇒ 11 × a × a × a + 3 × a × a × a × a

As, both of the terms have common a × a × a. So, from distributive law relation we can rewrite it as

⇒ a × a × a(11+3×a)

⇒ a³(11+3a)

Hence, the final factorized form of the given polynomial is a³(11+3a)

Page 14 Exercise 16 Answer

Question: Factorize the polynomial -6x²y − xy² + 2x²y²

Solution:

Given: Polynomial -6x²y − xy² + 2x²y²

To find: A factorized form of a given polynomial.

Factorise each of the terms in the given polynomial expression

⇒ 2 × 3 × x × x × y − x × y× y + 2 × x × x × y × y

As both of the terms have common x × y. So, from distributive law relation, we can rewrite it as

⇒ x × y(2×3×x−y+2×x×y)

⇒ xy(6x−y+2xy)

Hence, the final factorized form of the given polynomial is xy(6x−y+2xy)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 14 Exercise 17 Answer

Question: Factorize the polynomial -x³y + x²y + x²y²

Given: Polynomial -x³y + x²y + x²y²

To find: A factorized form of a given polynomial.

Factorise each of the terms in the given polynomial expression

⇒ x × x × x × y + x × x × y + x × x × y × y

As both of the terms have common x × x × y. So, from distributive law relation, we can rewrite it as

⇒ x × x × y(x+1+y)

⇒ x²y(x+y+1)

Hence, the final factorized form of the given polynomial is x²y(x+y+1)

Page 14 Exercise 18 Answer

Question: Factorize the polynomial -a³b³ + a²b² + ab

Solution:

Given: Polynomial -a³b³ + a²b² + ab

To find: A factorized form of a given polynomial.

Factorise each of the terms in the given polynomial expression

⇒ a × a × a × b × b × b + a × a × b × b + a × b

As both of the terms have common a × b. So, from distributive law relation, we can rewrite it as

⇒ a × b(a×a×b×b+a×b+1)

⇒ ab(a²b²+ab+1)

Hence, the final factorized form of the given polynomial is ab(a²b²+ab+1)

Page 14 Exercise 19 Answer

Question: Factorize the polynomial -12a³ − 9a² − 6a

Solution:

Given: Polynomial -12a³ − 9a² − 6a

To find: A factorized form of a given polynomial.

Factorise each of the terms in the given polynomial expression

⇒ 2 × 2 × 3 × a × a × a − 3 × 3 × a × a − 2 × 3 × a

As, both of the terms have a common 3 × a. So, from distributive law relation we can rewrite it as

⇒ 3 × a(2×2×a×a−3×a−2)

⇒ 3a(4a²−3a−2)

Hence, the final factorized form of the given polynomial is 3a(4a²−3a−2)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 6 Factoring Out A Common Factor Page 14 Exercise 23 Answer

Question: Factorize the biggest term in the polynomial 63x⁴ + 81x³ − 72x²?

Solution:

Given the polynomial to factorize: 63x⁴ + 81x³ − 72x²

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial.

63x⁴ + 81x³ − 72x²

63x⁴ + 81x³ − 72x²=9x²(7x²+9x-8)

Now see that:

⇒ \(\begin{aligned}
& \frac{63 x^4}{9 x^2}=7 x^2 \\
& \frac{81 x^3}{9 x^2}=9 x \\
& \frac{72 x^2}{9 x^2}=8
\end{aligned}\)

Here 9x² is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 63x⁴,81x³,72x²

The polynomial after factoring out the biggest term is as follows: 63x⁴ + 81x³ − 72x² = 9x²(7x²+9x−8)

Page 14 Exercise 24 Answer

Question: Factorize the biggest term in the polynomial 60a² + 30ab − 90ac?

Solution:

Given the polynomial to factorize: 60a² + 30ab − 90ac

Now:

We have to factorize this polynomial by factoring out the biggest terms out of the polynomial.

60a²+30ab-90ac

60a²+30ab-90ac=30a(2a+b-3c)

Now see that:

⇒ \(\begin{aligned}
\frac{60 a^2}{30 a} & =2 a \\
\frac{30 a b}{30 a} & =b \\
\frac{90 a c}{30 a} & =3 c
\end{aligned}\)

Here 30a is the biggest single term that can be taken out as a factor as it is the greatest term that is a factor of 60a², 30ab,90ac

The polynomial after factoring out the biggest term is as follows: 60a² + 30ab − 90ac = 30a(2a+b−3c)

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle

Page 8 Exercise 1 Answer

Question: Solve The Polynomial 3(2x−5) By Using Distributive Principle?

Solution:

Given Polynomial: 3(2x−5)

Let us solve the equation using the distributive Principle.

⇒ 3(2x-5)

∴  3(2x-5)=3x2x-3×5 ( Using distributive principle )

∴ 3x2x-3×5=6x-15

3(2x−5) ⇒ 6x − 15

Mcgraw Hill Distributive Principle Solutions Chapter 5 Key To Algebra

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 8 Exercise 3 Answer

Question: Solve The Polynomial 2 (3a+4b) By Using Distributive Principle?

Solution:

Given Equation:

⇒ 2 (3a+4b)

To find: Simplify using the distributive principle.

Let us solve the equation using the distributive Principle.

⇒ 2(3a+4b)

∴2 (3a+4b)=2x3a+2x4b

⇒ 6a+8b

2(3a+4b) ⇒ 6a+8b

Page 8 Exercise 5 Answer

Question: Solve The Polynomial 4(3x−y+5) By Using Distributive Principle?

Given:

⇒ 4(3x−y+5)

To find:

Simplify using the distributive principle.

Let us solve the equation using the distributive Principle.

⇒ 4(3x-y+5) (use distributive principle)

∴ (4x3x)-(4xy)+(4×5)

⇒ 12x-4y+20

Using distributive Principle.

4(3x−y+5) ⇒ 12x − 4y + 20

Page 8 Exercise 7 Answer

Question: Solve The Polynomial 6(3x−y+5) By Using Distributive Principle?

Solution:

Given:

⇒ 6(3x−y+5)

To find:

Simplify using the distributive principle

Let us solve the equation using the distributive Principle.

⇒ 6(3x-y+5) use distributive principle

∴ 6x3x-6xy+6×5

⇒ 18x-6y+30 ( Using distributive Principle)

6(3x−y+5) ⇒ 18x − 6y + 30

Chapter 5 The Distributive Principle Mcgraw Hill Algebra Key

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 8 Exercise 1 Answer

Question: Solve The Polynomial −5(2x−4) By Using Distributive Principle?

Solution:

Given:

⇒ −5(2x−4)

To find:

Simplify using the distributive principle

Let us solve the equation using the distributive Principle.

⇒ -5(2x-4) (Use distributive principle)

∴ -5(2x-4) ⇒-5x2x-(-5)x4

⇒ -5(2x-4)⇒-10x+20

−5(2x−4) ⇒ −10x + 20

Page 8 Exercise 2 Answer

Question: Solve The Polynomial −4(3y+5) By Using Distributive Principle?

Solution:

Given:

⇒ −4(3y+5)

To find: Simplify using the distributive principle

Let us solve the equation using the distributive Principle.

⇒ -4(3y+5)

∴ -4(3y+5)⇒-4x3y+(-4)x5

⇒ -4(3y+5)⇒-12y-20

−4(3y+5) ⇒ −12y − 20

Page 8 Exercise 4 Answer

Question: Solve The Polynomial (a+x)−8 By Using Distributive Principle?

Solution:

Given:

⇒ (a+x)−8

To find:

Simplify using the distributive principle

Let us solve the equation using the distributive Principle.

⇒ (a+x)-8 (use distributive principle)

∴ (a+x)-8⇒ 1xa+1×x-8

∴ (a+x)-8⇒a+x-8

(a+x)−8 ⇒ a + x − 8

How To Solve Chapter 5 The Distributive Principle Key To Algebra Book 4

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 8 Exercise 5 Answer

Question: Solve The Polynomial −4(3x²−6x+2) By Using Distributive Principle?

Solution:

Given:

⇒ −4(3x²−6x+2)

To find:

Simplify using the distributive principle

Let us solve the equation using the distributive Principle.

The given equation is:

⇒ -4(3×2-6x+2) (use distributive principle)

∴ -4(3×2-6x+2)

∴ \(-4\left(3 x^2-6 x+2\right)=-4 \times 3 x^2+4 \times 6 x-4 \times 2\)

∴\(-4\left(3 x^2-6 x+2\right)=-12 x^2+24 x-8\)

−4(3x²−6x+2) ⇒ −12x² + 24x − 8

Page 8 Exercise 7 Answer

Question: Solve The Polynomial −1(3x²−6x+2) By Using Distributive Principle?

Solution:

Given: −1(3x²−6x+2)

To find: We have to use the distributive principle to multiply.

We can write

−1(3x²−6x+2) = −(3x²−6x+2)

Further solving using the distributive principle we get

−1(3x²−6x+2) = −3x² + 6x − 2

Hence using the Distributive principle to solve −1(3x²−6x+2) we get −3x² + 6x − 2.

Page 8 Exercise 8 Answer

Question: Solve The Polynomial (3x²+6x−2)(−10) By Using Distributive Principle?

Solution:

Given: (3x²+6x−2)(−10)

To find: We have to use the distributive principle to multiply.

We can write

(3x²−60x+20)(−10) = −(30x²−60x+20)

Further solving using the Distributive principle we get

(3x²−60x+20)(−10) = −30x² + 60x − 20

Hence using Distributive principle to solve (3x²−60x+20)(−10) we get −30x² + 60x − 20

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 8 Exercise 1 Answer

Question: Solve The Polynomial (2x−7)x By Using Distributive Principle?

Solution:

Given: (2x−7)x

To find: We have to use the distributive principle to multiply.

According to the Distributive principle, we just have to multiply the single term times each term in the polynomial

We get

(2x−7)x = 2x² − 7x

Hence using the Distributive principle to solve(2x−7)x we get 2x² − 7x.

Question: Solve The Polynomial (3y+5)y By Using Distributive Principle?

Solution:

Page 8 Exercise 2 Answer

Given: (3y+5)y

To find: We have to use the distributive principle to multiply.

According to Distributive principle, we just have to multiply the single term times each term in the polynomial

We get

(3y+5)y = 3y² + 5y

Hence using Distributive principle to solve (3y+5)y we get 3y² + 5y

Question: Solve The Polynomial 2 (3a+4b) By Using Distributive Principle?

Solution:

Page 8 Exercise 3 Answer

Given: 2 (3a+4b)

To find: We have to use the distributive principle to multiply.

According to the Distributive principle we just have to multiply the single term times each term in the polynomial

We get

x(5−8y) = 5x − 8xy

Hence using the Distributive principle to solve x(5−8y) we get 5x − 8xy.

Question: Solve The Polynomial x(2y²+3x−4) By Using Distributive Principle?

Solution:

Page 8 Exercise 6 Answer

Given: x(2y²+3x−4)

To find: We have to use distributive principle to do the multiplication.

According to Distributive principle, we just have to multiply the single term times each term in the polynomial

We get

x(2y²+3x−4) = 2xy² + 3x² − 4x

Hence using Distributive principle to solve x(2y²+3x−4) we get 2xy² + 3x² − 4x

Mcgraw Hill Algebra Book 4 Chapter 5 Explanations

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 8 Exercise 7 Answer

Question: Solve The Polynomial (2y²+3x−4)xy By Using Distributive Principle?

Solution:

Given:(2y²+3x−4)xy

To find: We have to use distributive principle to do the multiplication.

According to the Distributive principle, we just have to multiply the single term times each term in the polynomial

We get

(2y²+3x−4)xy = 2xy³ + 3x²y − 4xy

Hence using the Distributive principle to solve (2y²+3x−4)xy we get 2xy³ + 3x²y − 4xy.

Page 8 Exercise 1 Answer

Question: Solve The Polynomial 5x(4x−7)By Using Distributive Principle?

Solution:

Given: 5x(4x−7)

To find: We have to use distributive principle to do the multiplication.

According to the Distributive principle, we just have to multiply the single term times each term in the polynomial

We get

5x(4x−7) = 20x² − 35x

Hence using Distributive principle to solve 5x(4x−7) we get 20x² − 35x

Page 8 Exercise 2 Answer

Question: Solve The Polynomial 3a(4a+2) By Using Distributive Principle?

Solution:

Given: 3a(4a+2)

To find: We have to use distributive principle to do the multiplication.

According to the Distributive principle we just have to multiply the single term times each term in the polynomial, We get,

3a(4a+2) = 12a² + 6a

Hence using the Distributive principle to solve 3a(4a+2) we get 12a² + 6a.

Page 8 Exercise 3 Answer

Question: Solve The Polynomial 4x(x²−5)By Using Distributive Principle?

Solution:

Given: 4x(x²−5)

To find: We have to use distributive principle to do the multiplication.

According to the Distributive principle, we just have to multiply the single term times each term in the polynomial

We get

4x(x²−5) = 4x³ − 20x

Hence using Distributive principle to solve 4x(x²−5) we get 4x³ − 20x

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 8 Exercise 4 Answer

Question: Solve The Polynomial (2x+1)2x² By Using Distributive Principle?

Solution:

Given: (2x+1)2x²

To find: We have to use distributive principle to do the multiplication.

According to the Distributive principle we just have to multiply the single term times each term in the polynomial

We get(2x+1)2x² = 4x³ + 2x²

Hence using the Distributive principle to solve (2x+1)2x² we get 4x³ + 2x².

Page 8 Exercise 5 Answer

Question: Solve The Polynomial (3y−6)(−5y) By Using Distributive Principle?

Solution:

Given:(3y−6)(−5y)

To find: We have to use the distributive principle to multiply.

According to the Distributive principle, we just have to multiply the single term times each term in the polynomial

We get (3y−6)(−5y) = −15y² + 30y

Hence using Distributive principle to solve (3y−6)(−5y) we get −15y² + 30y

Page 8 Exercise 6 Answer

Question: Solve The Polynomial 7x(3x+4y) By Using Distributive Principle?

Solution:

We are given the expression 7x(3x+4y).

The objective is to use the Distributive Principle for a multiplication problem.

Given: 7x(3x+4y)
on Applying the distribution Principle, we get

7x(3x+4y)=7x.3x+7x.4y
=21x²+28xy

Hence, using the Distributive principle for the given multiplication problem 7x(3x+4y), we get the result 21x² + 28xy.

Page 8 Exercise 7 Answer

Question: Solve The Polynomial 3a(4a−2b+c) By Using Distributive Principle?

Solution:

We are given the expression 3a(4a−2b+c).

The objective is to use the Distributive Principle for a multiplication problem.

Given: 3a(4a-2b+c)
On applying the distributive principle
3a(4a-2b+c)=3a.4a-3a.2b+3a.c
3a(4a-2b+c)=12a²-6ab+3ac

Hence, using the Distributive principle for the given multiplication problem 3a(4a−2b+c), we get the result 12a² − 6ab + 3ac.

Page 8 Exercise 8 Answer

Question: Solve The Polynomial 5y(3x+4y−8) By Using Distributive Principle?

Solution:

We are given the expression 5y(3x+4y−8).

The objective is to use the Distributive Principle for a multiplication problem.

Given: 5y(3x+4y-8)

On applying the distributive principle, we get

5y(3x+4y-8)=5y.3x+5y.4y-5y.8
=15xy+20y²-40y

Hence, using the Distributive principle for the given multiplication problem 5y(3x+4y−8), we get the result 15xy + 20y² − 40y.

Mcgraw Hill Key To Algebra Chapter 5 Problem Walkthrough

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 8 Exercise 9 Answer

Question: Solve The Polynomial 2xy(3x+4y−8). By Using Distributive Principle?

Solution:

We are given the expression 2xy(3x+4y−8).

The objective is to use the Distributive Principle for a multiplication problem.

Given: 2xy(3x+4y-8)

on applying the distributive principle, we get

2xy(3x+4y-8)=2xy.3x+2xy.4y-32xy.8
=6x2y+8xy2-16xy

Hence, using the Distributive principle for the given multiplication problem 2xy(3x+4y−8), we get the result 6x2y + 8xy² − 16xy.

Page 8 Exercise 10 Answer

Question: Solve The Polynomial 7x²−5x−6)6x² By Using Distributive Principle?

Solution:

We are given the expression 7x²−5x−6)6x².

The objective is to use the Distributive Principle for a multiplication problem.

Hence, using the Distributive principle for the given multiplication problem (7×2−5x−6)6×2, we get the result 42x⁴ − 30x³ − 36x².

Page 8 Exercise 11 Answer

Question: Solve The Polynomial −4b(a−3b+c) By Using Distributive Principle?

Solution:

We are given the expression −4b(a−3b+c).

The objective is to use the Distributive Principle for a multiplication problem.

Given: 2xy(3x+4y-8)
on applying the distributive principle, we get

2xy(3x+4y-8)=2xy.3x+2xy.4y-2xy.8
=6x²y+8xy²-16xy

Hence, using the Distributive principle for the given multiplication problem −4b(a−3b+c), we get the result −4ab + 12b² − 4bc.

Page 8 Exercise 12 Answer

Question: Solve The Polynomial 7x²y(3x²y+2xy²+x³) By Using Distributive Principle?

Solution:

We are given the expression 7x²y(3x²y+2xy²+x³).

The objective is to use the Distributive Principle for a multiplication problem.

Given: 7x²y(3x²y+2xy²+x³)

on applying the distributive principle, we get

7x²y(3x²y+2xy²+x³)=7x²y.3x²y+7x²y.2xy²+7x²y.x³
=21x⁴y²+14x³y³+14x³y³+7x⁵y

Hence, using the Distributive principle for the given multiplication problem 7x²y(3x²y+2xy²+x³), we get the result 21x⁴y² + 14x³y³ + 7x⁵y.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 9 Exercise 1 Answer

Question: Solve The Equation 5(x+3) = 35. And Find The Value of x?

Solution:

We are given the equation 5(x+3) = 35.

The objective is to solve the given equation.

Given: 5(x+3)=35 on applying distributive principle, we get

5x+5.3=35
5x+15=35
5×35-15
5x=20
x= \(\frac{20}{5}\)
x=4

Hence, the solution of the given equation 5(x+3) = 35 is x = 4.

Page 9 Exercise 3 Answer

Question: Solve The Equation 2(3x+15) = 18. And Find The Value of x?

Solution:

We are given the equation 2(3x+15) = 18.

The objective is to solve the given equation.

Given: 2(3x+15)=18
on applying the distributive principle, we get

2.3x+2.15=18
6x+30=18
6x=18-30
6x=-12
\(x=\frac{-12}{6}\)
x-2

Hence, the solution of the given equation 2(3x+15) = 18 is x = −2.

Page 9 Exercise 4 Answer

Question: Find The Value Of x In The Expression 8(x−2) = 32.

Solution:

We are given the equation 8(x−2) = 32.

The objective is to solve the given equation.

Given: 8(x-2)=32
By applying the distributive principle, we get
5x+5.3=35
5x+15=35
5x=35-15
5x=20
x= \(\frac{20}{5}\)
x=4

Hence, the solution of the given equation 8(x−2) = 32 is x = 6.

Page 9 Exercise 5 Answer

Question: Find The Value Of a In The Expression 5(a+3) = 8a.?

Solution:

We are given the equation 5(a+3) = 8a.

The objective is to solve the given equation.

Let Us Assume That a= x

2(3x+15)=18 on applying distributive principle, we get

2.3x+2.15=18

6x+30=18

6x=18-30

6x=-12

x= \(\frac{-12}{6}\)

x=-2

Hence, the solution of the given equation 5(a+3) = 8a is a = 5.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 9 Exercise 6 Answer

Question: Find The Value Of x In The Expression 7x = 4(x+6)?

Solution:

We are given the equation 7x = 4(x+6).

The objective is to solve the given equation.

Given: 7x=4(x+6)

On applying the distributive principle, we get

7x=4.x+4.6

7x=4x+24

7x-4x=24

3x=24

x=8

Hence, the solution of the given equation 7x = 4(x+6) is x = 8.

Page 9 Exercise 7 Answer

Question: Find The Value Of x In The Expression 4(x+5) = 3(x−6)?

Solution:

We are given the equation 4(x+5) = 3(x−6).

The objective is to solve the given equation.

Given: 4(x+5)=3(x-6)

on applying the distributive principle, we get

4x+4.5=3.-3.6

4x+20=3x-18

4x-3x=-18-20

x=-38

Hence, the solution of the given equation 4(x+5) = 3(x−6) is x = −38.

Page 9 Exercise 8 Answer

Question: Find The Value Of x In The Expression 3(2x−5)+4 = 31?

Solution:

We are given the equation 3(2x−5)+4 = 31.

The objective is to solve the given equation.

3(2x-5)+4=31 on applying the distributive principle, we get

3.2x-3.5+4=31

6x-15=31

6x-11=31

6x=31+11

6x=42

x= \(\frac{42}{6}\)

x=7

Hence, the solution of the given equation 3(2x−5) + 4 = 31 is x = 7.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 9 Exercise 9 Answer

Question: Find The Value Of x In The Expression 10 = 18 + 4(3x+7)?

Solution:

We are given the equation 10 = 18 + 4(3x+7).

The objective is to solve the given equation.

10=18+4(3x+7) on applying distributive principle, we get

10=18+4.3x+4.7

10=18+12x+28

10=12x+46

10-46=12x

-36=12x

x= \(\frac{-36}{12}\)

Hence, the solution of the given equation 10 = 18 + 4(3x+7) is x = −3.

Page 9 Exercise 10 Answer

Question: Find The Value Of x In The Expression 3(3x+5) = 2(6x−3)?

Solution:

Given expression is 3(3x+5) = 2(6x−3)

We find the solution for a given expression

We use the distributive principle for a given expression

Given: 3(3x+5)=2(6x-3) ( we use the distributive principle)

3.3x+3.5=2.6x-3.2

9x+15=12x-6

12x-9x=15+6

3x=21

x=\(\frac{21}{3}\)

x=7

The solution for the given polynomial is x = 7.

Page 10 Exercise 1 Answer

Question: Find The Area Of The Rectangle Whose Length  = 3x and Breadth = 2x + 5?

Solution:

Given the length of the rectangle = 3x

Breadth of rectangle = 2x + 5

We find the polynomial for the area of the given rectangle

We write the formula for area of the rectangle,

A=lxb

A=3x(2x+5)

we use distributive principle

A=6x²+15x

The polynomial for the area of a given rectangle is A = 6x² + 15x

Worked Examples For Chapter 5 The Distributive Principle Mcgraw Hill

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 5 The Distributive Principle Page 10 Exercise 2 Answer

Question: Find The Area Of The Rectangle Whose Length  = 3x + 4 and Breadth = 2?

Solution:

Given : Length of rectangle = 3x + 4

Breadth of rectangle = 2

We find a polynomial for the area of the given rectangle

We write the formula for the area of a rectangle,

Polynomial for area of given rectangle is A = 6x + 8

Page 10 Exercise 4 Answer

Question: Find The Area Of The Rectangle Whose Length  = 2r + 7 and Breadth = p?

Solution:

Given: Length of rectangle = 2r + 7

Breadth of rectangle = p

We find the polynomial for area of given rectangle

We write formula for area of rectangle,

The polynomial for area of given rectangle is 2rp + 7p

Page 10 Exercise 6 Answer

Question: Find The Area Of The Rectangle Whose Length  = 7n + 4 and Breadth = 5n?

Solution:

Given: Length of rectangle = 7n + 4

Breadth of rectangle = 5n

We find the polynomial for area of given rectangle

We write the formula for area of rectangle,

A=lxb

a=(7n+4)x(5n)

a= 35n² + 20n (we use distributive principle)

The polynomial for area of a given rectangle is A = 35n² + 20n

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 4 Subtracting Polynomials

Page 4 Exercise 1 Answer

Question: Subtract The Polynomials (3x²+5x−2) and (7x²−5x+4)

Solution: 

Given Polynomials:

(3x²+5x−2) and (7x²−5x+4)

To find: The subtraction of polynomials

3x²-8x+2

(3x²-8x+2)×(-1).3x²-(-1).8x+(-1).2

(3x²-8x+2)×(-1)=-3x²+8x-2-4

(3x²+5x-2)-(7x²-5x+4)= 3x²-7x²+5x-2-4

(3x²+5x-2)-(7x²-5x+4)=-4x²+10x-6

The subtraction of polynomials: (3x²+5x−2) − (7x²−5x+4) = −4x² + 10x − 6

Mcgraw Hill Key To Algebra Book 4 Chapter 4 Solutions

Page 4 Exercise 2 Answer

Question: Subtract The Polynomials (6x²+2x−2) and (x²+4x−1)

Solution: 

Given Polynomials:

(6x²+2x−2) and (x²+4x−1)

To find: The subtraction of polynomials

(6x²+2x-2)-(x²+4x-1)

(6x²+2x-2)-(x²+4x-1)=6x²+2x-2-x²4x+1

(6x²+2x-2)-(x²+4x-1)=6x²-x²+2x-4x-2+1

(6x²+2x-2)-(x²+4x-1)=5x²-2x-1

The subtraction of polynomials: (6x²+2x−2) − (x²+4x−1) = 5x² − 2x − 1

Page 4 Exercise 3 Answer

Question: Subtract The Polynomials (2y²−y+3) and (3y²−y−4)

Solution: 

Given Polynomials:

(2y²−y+3) and (3y²−y−4)

To find: The subtraction of polynomials

(2y²-y+3)-(3y²-y-4)

(2y²-y+3)-(3y²-y-4)=2y²-y+3y²+y+4

(2y²-y+3)-(3y²-y-4)=2y²-3y²-y+y+3+4

(2y²-y+3)-(3y²-y-4)=-y²+7

The subtraction of polynomials: (2y²−y+3) − (3y²−y−4) = −y² + 7

Page 4 Exercise 4 Answer

Question: Subtract The Polynomial (y²+y−6) and (y²+5y−6)

Solution: 

Given Polynomials:

(y²+y−6) and (y²+5y−6)

To find: The subtraction of polynomials

The subtraction of polynomials: (y²+y−6) − (y²+5y−6) = −4y

Key To Algebra Book 4 Subtracting Polynomials Chapter 4 Answers

Page 4 Exercise 5 Answer

Question: Subtract The Polynomials (4x²+3x+5) and (4x²−3x+5)

Solution: 

Given Polynomials:

(4x²+3x+5) − (4x²−3x+5)

To find: The subtraction of polynomials

The subtraction of polynomials: (4x²+3x+5) − (4x²−3x+5) = 6x

Page 4 Exercise 6 Answer

Question: Subtract The Polynomials (3x²+5x−2) and (2x²−3x+7)

Solution: 

Given Polynomials:

(3x²+5x−2) and (2x²−3x+7)

To find: The subtraction of polynomials

The subtraction of polynomials: (3x²+5x−2) − (2x²−3x+7) = x² + 8x − 9

Page 4 Exercise 8 Answer

Question: Subtract The Polynomials (5a²−2a−8) and (a²−6a+3)

Solution: 

Given Polynomials: (5a²−2a−8) and (a²−6a+3)

To find: The subtraction of polynomials

The subtraction of polynomials: (5a²−2a−8) − (a²−6a+3) = 4a² + 4a − 11

Page 4 Exercise 9 Answer

Question: Subtract The Polynomials (8x²−8x−3) and (4x+2)

Solution: 

Given Polynomials:

(8x²−8x−3) and (4x+2)

To find: The subtraction of polynomials

⇒ [latex]\begin{aligned}
& \left(8 x^2-8 x-3\right)-(4 x+2) \\
& \left(8 x^2-8 x-3\right)-(4 x+2)=8 x^2-8 x-3-4 x-2 \\
& \left(8 x^2-8 x-3\right)-(4 x+2)=8 x^2-8 x-4 x-3-2 \\
& \left(8 x^2-8 x-3\right)-(4 x+2)=8 x^2-12 x-5
\end{aligned}\)

The subtraction of polynomials: (8x²−8x−3) − (4x+2) = 8x² − 12x − 5

Mcgraw Hill Subtracting Polynomials Solutions Chapter 4 Key To Algebra

Page 4 Exercise 10 Answer

Question: Subtract The Polynomials (3x²+5x−1) and (4x²−2x+4)

Solution: 

Given Polynomials:

(3x²+5x−1) and (4x²−2x+4)

To find: The Subtraction of polynomials

The subtraction of polynomials: (3x²+5x−1) − (4x²−2x+4) = −x² + 7x − 5

Page 5 Exercise 3 Answer

Question: Subtract The polynomials (3x²+5x−2) and (7x²−5x+4)

Solution: 

Given Polynomials:

(3x+5) , (2x−3) and (4x−6)

To find: The addition of polynomials

The addition of polynomials: (3x+5) + (2x−3) + (4x−6) = 9x − 4

Page 5 Exercise 4 Answer

Question: Find The Addition And Subtract Of The Polynomial (3x²+5x−2) and (7x²−5x+4)

Solution: 

Given Polynomials:

(a+b−c) + (a+b+2c) − (a+b+c)

To find: The addition and subtraction of polynomials

(a+b-c)(a+b+2c)-(a+b+c)

(a+b-c) + (a+b+2c) – (a+b+c) = a + b-c+a+b+2c-a-b-c

(a+b-c)+(a+b+2c)-(a+b+c)=a+a-a+b+b-b-c+2c-c

(a+b-c)+(a+b+2c)-(a+b+c)=a+b

(a+b-c)+(a+b+2c)-(a+b+c)= a+b

Page 5 Exercise 6 Answer

Question: Subtract The Polynomial (3x²+5x−2) and (7x²−5x+4)

Solution: 

Given Polynomials:

(x−y−z) + (x−y−z) − (x−y−z) + (x+y+z)

To find: The addition and subtraction of polynomials

(x-y-z)+(x-y-z)-(x-y-z)+(x+y+z)

(x-y-z+(x-y-z)-(x-y-z)+(x+y+z)=x-y-z-x+y+z+x +y+z

(x-y-z)+(x-y-z)-(x-y-z)+(x+y+z)=x+x-x-y-y+y-7-z+7+7

(x-y-z)+(x-y-z)-(x-y-z)+x+y+z)=2x

(x-y-z) + (x-y-z) – (x – y – z) + (x + y + z) = 2x

Page 5 Exercise 7 Answer

Question: Subtract The Polynomial (3x²+5x−2) and (7x²−5x+4)

Solution: 

Given Polynomials:

(3a²+2b+4) − (a²+b−1) − (a²+2b−1) − (a²+b−2)

To find: The Subtraction of polynomials

(x-y-z)+(x-y-z)-(x-y-z)+(x+y+z)

(x-y-z)+(x-y-z)-(x-y-z)+(x+y+z)=x-y-z+x-y-z-x+y+z+x+y+z

(x-y-z)+(x-y-z)-(x-y-z)+(x+y+z)=x-x-x+x-y-y+y-z-z+z+z

(x-y-z)+(x-y-z)-(x-y-z)+(x+y+z)=2x

(3a²+2b+4) − (a²+b−1) − (a²+2b−1) − (a²+b−2) = -2b + 8

Page 5 Exercise 8 Answer

Question: Subtract The Polynomial (3x²+5x−2) and (7x²−5x+4)

Solution: 

Given Polynomials:

8x − (5x−4) = 25

To find: Value Of x

Given:

3x+4=25

3x=21

x=7

The Value of x is = 7

Page 5 Exercise 9 Answer

Question: Subtract The Polynomial (3x²+5x−2) and (7x²−5x+4)

Solution: 

Given Polynomials:

6x − (4x−5) = 13

To find: The value

To solve the equation:

6x-(4x-5)=13

6x-(4x-5)=6x-4x+5

6x-(4x-5)=2x+5

⇒ 2x+5=13

⇒ 2x=13-5

⇒ 2x=8

⇒ \(x=\frac{8}{2}\)

⇒ x=4

The Value of x = 4

Page 5 Exercise 10 Answer

Question: Solve The Equation 10x − (3x+6) = 8 and find The Value Of X ?

Solution: 

Given Polynomials:

10x − (3x+6) = 8

10x-(3x+6)=8

10x-(3x+6)=10x-3x -6

10x-(3x+6)=7x-6

⇒ 7x-6=8

⇒ 7x=8+6

⇒7x=14

⇒x=\(\frac{14}{7}\)

⇒ x=2

The Value of x = 2

Page 5 Exercise 11 Answer

Question: The Subtraction Of Polynomials (6x+9) − (2x−5) = 38. Then Find The Value Of x?

Solution: 

Given Equation:

(6x+9) − (2x−5) = 38

To find: Value Of x

(6x+9)-(2x-5)=38

(6x+9)-(2x-5)=6x+9-2x+5?

(6x+9)-(2x-5)=4x+14

⇒ 4x+14=38

⇒4x=38-14

⇒4x=24

⇒x=\(\frac{24}{4}\)

⇒ x=6

Solution: x = 6

How To Solve Chapter 4 Subtracting Polynomials Key To Algebra Book 4

Page 5 Exercise 12 Answer

Question: The Subtraction Of Polynomials (9x+10) − (3x+2) = 74, Then Find The Value Of x?

Solution: 

Given Equation:

(9x+10) − (3x+2) = 74

To find: Value Of X

(9x+10)-(3x+2)=74

(9x+10)-3x+2)=9x+10-3x-2

(9x+10)-(3x+2)=6x+8

⇒6x+8=74

⇒6x=74-8

⇒6x=66

⇒ \(x=\frac{66}{6}\)

⇒ x=11

The Value of x = 11

Page 5 Exercise 13 Answer

Question: Find The Perimeter The Sides Are Given Here (3k+4),(2k−1),(3k+4),(2k−1)

Solution: 

Given sides: (3k+4),(2k−1),(3k+4),(2k−1)

To find: The perimeter

To find the perimeter add the following polynomials:

(3k+4),(2k-1),(3k+4),(2k-1)

(3k+4)(2k-1)+(3k+4)+(2k-1)=3k+4+2k-1+3k+4+2k-1

(3k+4)+(2k-1)+(3k+4)+(2k-1)=3k+2k+3k+2k+4-1+4-1

(3k+4)(2k-1)+(3k+4)+(2k-1)=10k+6

The perimeter: 10k + 6

Page 6 Exercise 14 Answer

Question: Find The Perimeter. The Sides Are Given Here (4x−3),(4x−3),(4x−3),(4x−3)?

Solution: 

Given:

The sides: (4m+7),(2m),(5m+7),(2m+1)

To find: The perimeter

(4m+7),(2m),(5m+7),(2m+1)

(4m+7)(2m)+(5m+7)+(2m+1)=4m+7+2m+5m+7+2m+1

(4m+7)+(2m)+(5m+7)+(2m+1)=4m+2m+5m+2m+7+7+1

(4m+7)+(2m)+(5m+7)+(2m+1)=13m+15

The perimeter: 13m + 15

Page 6 Exercise 15 Answer

Question: Find The Perimeter. The Sides Are Given Here (4x−3),(4x−3),(4x−3),(4x−3)?

Solution: 

Given:

The sides: (4x−3),(4x−3),(4x−3),(4x−3)

To find: The perimeter

(4x−3),(4x−3),(4x−3),(4x−3)

(4x-3)+(4x-3)+(4x-3)+(4x-3)=4x-3+4x-3+4x-3+4x-3+4x-3

(4x-3)+(4x-3)+(4x-3)+(4x-3)=4x+4x+4x+4x-3-3-3-3

(4x-3)+(4x-3)+(4x-3)+(4x-3)=16x-12

The perimeter: 16x − 12

Mcgraw Hill Algebra Book 4 Chapter 4 Explanations

Page 6 Exercise 16 Answer

Question: Find The Perimeter. The Sides Are Given Here  (2x+1),(2x+1),(2x+1),(2x+1),(2x+1),(2x+1)?

Solution: 

Given:

The sides: (2x+1),(2x+1),(2x+1),(2x+1),(2x+1),(2x+1)

To find: The perimeter

(2x+1),(2x+1),(2x+1),(2x+1),(2x+1),(2x+1)

(2x+1)+(2x+1)+(2x+1)(2x+1)=2x+x+2x+12x+x+2x+1+2x+1

(2x+1+(2x+1)(2x+1)+(2x+1)=2x+2x+2x+2x+2x+1+1+1+1+1+1+

(2x+1)+(2x+1)+(2x+1)+2x+1)+(2x+1)=12x+6

The perimeter: 12x + 6

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 3 Opposites Of Polynomials

Page 3 Exercise 1 Answer

Question: Find The Opposite Of Polynomial 3x² − 8x + 2

Solution:

Given Polynomial:

3x² − 8x + 2

To find: The opposite polynomial

3x²-8x+2

(3x²-8x+2)×(-1).3x²-(-1).8x+(-1).2

(3x²-8x+2)×(-1)=-3x²+8x-2-4

(3x²+5x-2)-(7x²-5x+4)= 3x²-7x²+5x-2-4

(3x²+5x-2)-(7x²-5x+4)=-4x²+10x-6

The opposite polynomial: −3x² + 8x − 2

Mcgraw Hill Key To Algebra Book 4 Chapter 3 Solutions

Page 3 Exercise 2 Answer

Question: Find The Opposite Of Polynomial 6a + 7b + 4

Solution:

Given Polynomial:

6a + 7b + 4

To find: The opposite polynomial

6a+7b+4

(6a+7b+4)(-1)=(-1).6a+(-1).7b+(-1).4

(6a+7b+4)x(-1)=-6a-7b-4

The opposite polynomial: −6a − 7b − 4

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 3 Opposites Of Polynomials Page 3 Exercise 3 Answer

Question: Find The Opposite Of Polynomial 5x² − 2x − 9

Solution:

Given Polynomial:

5x² − 2x − 9

To find: The opposite polynomial

5x²-2x-9

(5x²-2x-9)(-1)=(-1).5x²– (-1).2x- (-1).9

(5x²-2x-9)(-1)=-5x²+2x+9

The opposite polynomial: −5x² + 2x + 9

Key To Algebra Book 4 Opposites Of Polynomials Chapter 3 Answers

Page 3 Exercise 4 Answer

Question: Find The Opposite Of Polynomial x² − 16

Solution:

Given Polynomial:

x² − 16

To find: The opposite polynomial

x²-16

(x²-16)x(-1)=(-1).x²-(-1).16

(x²-16)x(-1)=-x²+16

The opposite polynomial: −x² + 16

Page 3 Exercise 5 Answer

Question: Find The Opposite Of Polynomial x⁵ + x⁴ + x³ − x² + x − 1

Solution:

Given Polynomial:

x⁵ + x⁴ + x³ − x² + x − 1

To find: The opposite polynomial

⇒ \(\begin{aligned}
& x^5+x^4+x^3-x^2+x-1 \\
& \left(-x^5+x^4+x^3-x^2+x-1\right) x(-1)=(-1) x^5+(-1) \cdot x^4+(-1) \cdot x^3-(-1) \cdot x^2+(-1) \cdot x-(-1) \cdot 1 \\
& \left(x^5+x^4+x^3-x^2+x-1\right) x(-1)=-x^5-x^4-x^3+x^2-x+1
\end{aligned}\)

The opposite polynomial: −x⁵ − x⁴ − x³ + x² − x + 1

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 3 Opposites Of Polynomials Page 3 Exercise 6 Answer

Question: Find The Opposite Of Polynomial −7x − 8

Solution:

Given Polynomial:

−7x − 8

To find: The opposite polynomial

(-7x-8)×(-1)=-(-1).7x-)(-1).8

(-7x-8)x(-1)=7x+8

The opposite polynomial: 7x + 8

Page 3 Exercise 7 Answer

Question: Find The Opposite Of Polynomial x² + 5x − 14

Solution:

Given Polynomial:

x² + 5x − 14

To find: The opposite polynomial

x²+5x-14

⇒ \(\begin{aligned}
& \left(x^2+5 x-14\right)(-1)=(-1) \cdot x^2+(-1) \cdot 5 x-(-1) \cdot 14 \\
& \left(x^2+5 x-14\right)(-1)=-x^2-5 x+14
\end{aligned}\)

The opposite polynomial: −x² − 5x + 14

Chapter 3 Opposites Of Polynomials Mcgraw Hill Algebra Key

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 3 Opposites Of Polynomials Page 3 Exercise 8 Answer

Question: Find The Opposite Of Polynomial −x² − 5x + 14

Solution:

Given Polynomial:

−x² − 5x + 14

To find: The opposite polynomial

-x² -5x+14

The opposite polynomial: x² + 5x − 14

Page 3 Exercise 9 Answer

Question: Find The Opposite Of Polynomial (x²+5x−14) + (−x²−5x+14)

Solution:

Given Polynomial:

(x²+5x−14) + (−x²−5x+14)

To find: Addition of opposite polynomials

(x²+5x−14) + (−x²−5x+14)

(x²+5x−14) + (−x²−5x+14)=(1-1)x²+(5-5)x+(-1+1)14

(x²+5x−14)+(−x²−5x+14)=0.x²+0.x+0.14

(x²+5x-14)+(-x²-5x+14)=0

The addition of opposite polynomial: (x²+5x−14) + (−x²−5x+14) = 0

Key To Algebra Book 4 Chapter 3 Opposites Of Polynomials Problems

Page 3 Exercise 10 Answer

Question: Find The Opposite Of Polynomial (−7x−8) + (7x+8)

Solution:

Given Polynomial:

(−7x−8) + (7x+8)

To find: Addition of opposite polynomials

(-7x-8)+(7x+8)

(-7x-8)+(7x+8)=(-7+7).x+(-1+1).8

(-7x-8)+(7x+8)=0.x+0.8

(-7x-8)+7x+8)=0

The addition of opposite polynomial: (−7x−8) + (7x+8) = 0

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 1 Polynomials Page 1 Exercise 1 Answer

Question 1: Find the Degree Of The Polynomial  x² − 4 ?

Solution:

Given expression is x² − 4.

We Need To find: Degree of x² − 4.

Highest power=2

Therefore, the degree of the polynomial X²-4 of x is 2.

Hence, x² − 4 is a 2-degree polynomial.

Mcgraw Hill Key To Algebra Book 4 Chapter 1 Solutions

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 1 Polynomials Page 1 Exercise 2 Answer

Question 2: Find the Degree Of The Polynomial x² − 5x + 2 ?

Solution:

Given algebraic expression is x² − 5x + 2.

We Need To find: Degree of x² − 5x + 2.

Highest power =2

Therefore, the degree of the given polynomial is 2

Hence, x² − 5x + 2 is a 2-degree polynomial in x.

Key To Algebra Book 4 Polynomials Chapter 1 Answers

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 1 Polynomials Page 1 Exercise 3 Answer

Question 3: Find the Degree Of The Polynomial  6x⁴ ?

Solution:

Given algebraic expression is 6x⁴

We Need To find: Degree of 6x⁴

⇒ \(6 x^4=6 x x^4+0 \times x^3+0 \times x^2+0 \times x^1+0 \times x^0\)

highest power =4

Therefore, the degree of the given polynomial is 4

Hence, 6x⁴ is a 4-degree polynomial in x.

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 1 Polynomials Page 1 Exercise 4 Answer

Question 4: Find the Degree Of The Polynomial  x+5?

Solution:

Given algebraic expression is x+5

We Need To find: Degree of x+5

Highest power =1

Therefore, the degree of the polynomial is 1

Hence, x+5 is a 1-degree polynomial in x.

Chapter 1 Polynomials Mcgraw Hill Algebra Key

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 1 Polynomials Page 1 Exercise 5 Answer

Question 5: Find the Degree Of The monomial  8?

Solution:

Given algebraic expression is 8

We Need To find: Degree of 8

8x=8×x⁰

Highest power =0

Therefore, the degree is 0.

Hence, the 8 is a zero-degree polynomial in x.

How To Solve Chapter 1 Polynomials Key To Algebra Book 4

Mc Graw Hill Key To Algebra Book 4 Polynomials 1st Edition Chapter 1 Polynomials Page 1 Exercise 6 Answer

Question 6: Find the Degree Of The Polynomial  5x³ + 2x² − 4x ?

Solution:

Given algebraic expression is 5x³ + 2x² − 4x

We Need To find: Degree of 5x³ + 2x² − 4x

5x³ + 2x² − 4x =\(5 \times x^3+2 \times x^2-4 \times x^1+0 \times x^0\)

Highest power =3

Therefore, the degree of the given polynomial is 3

Hence, 5x³ + 2x² − 4x is a 3-degree polynomial in x.