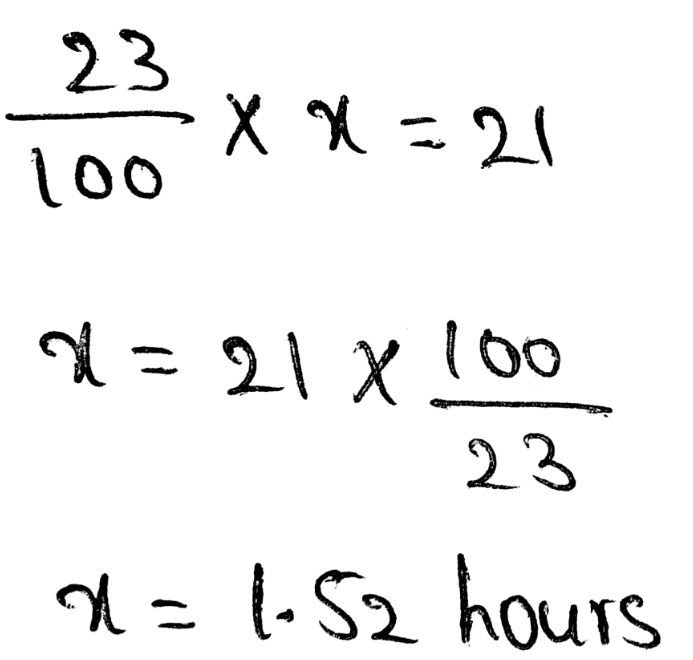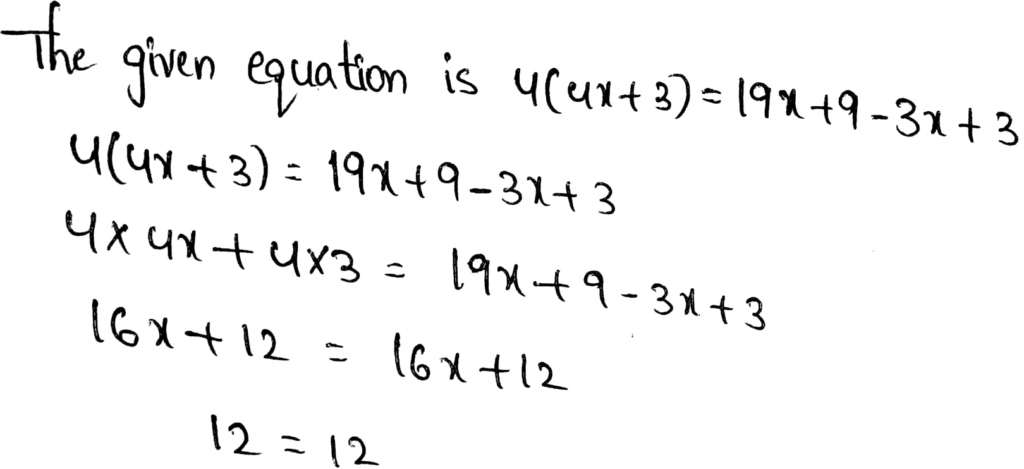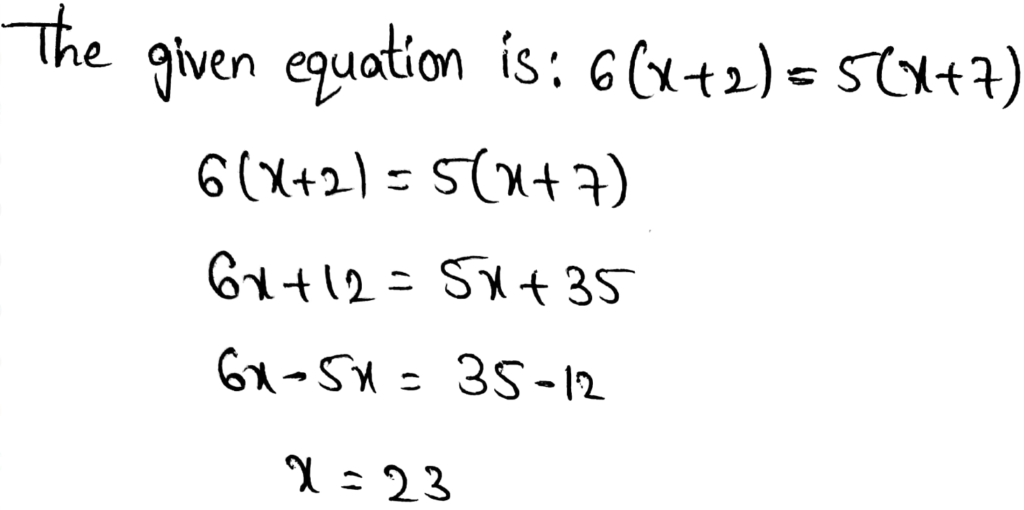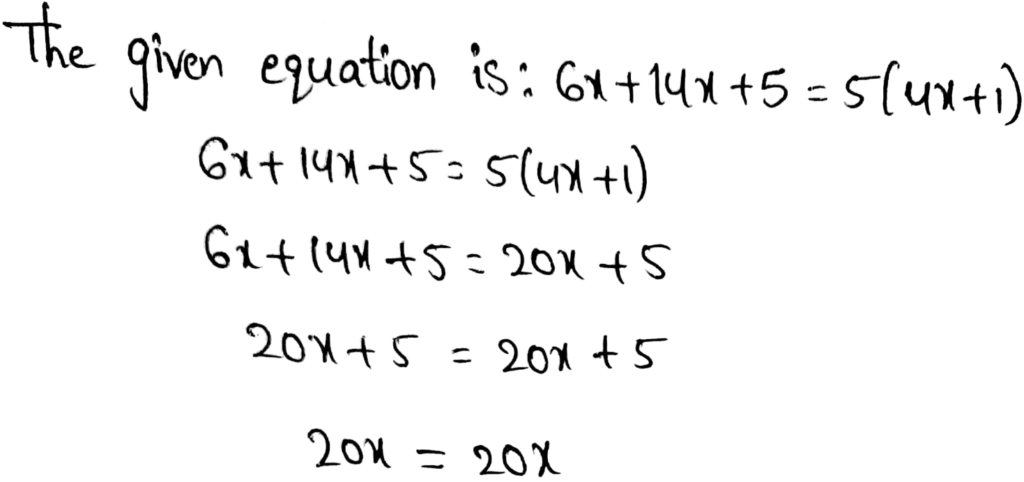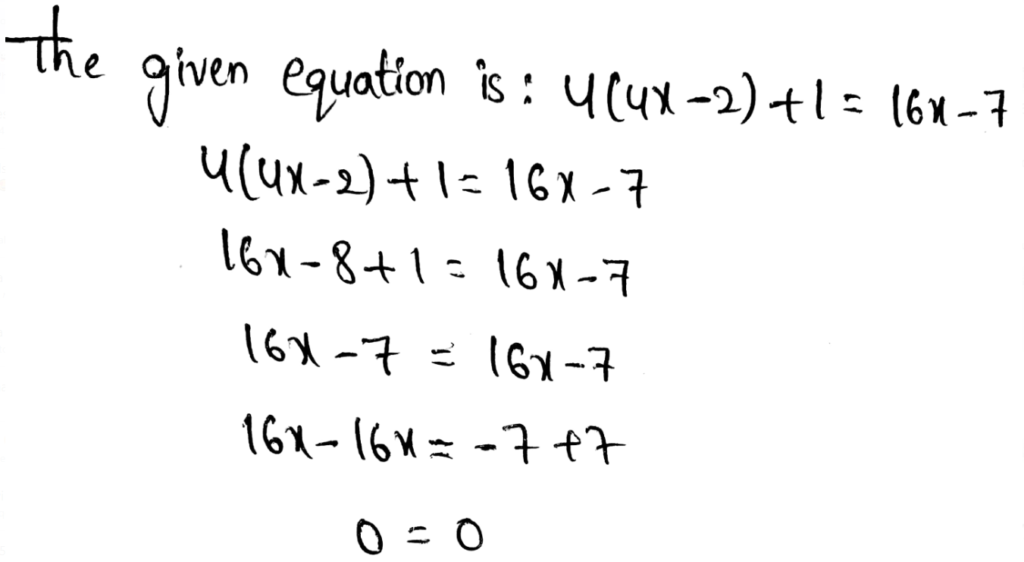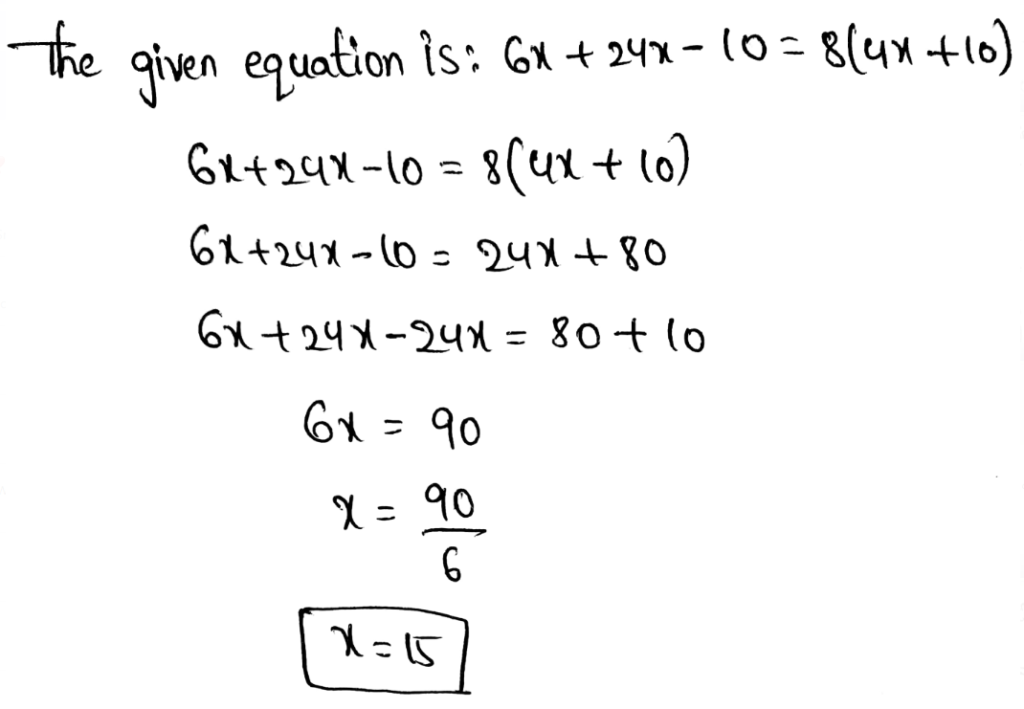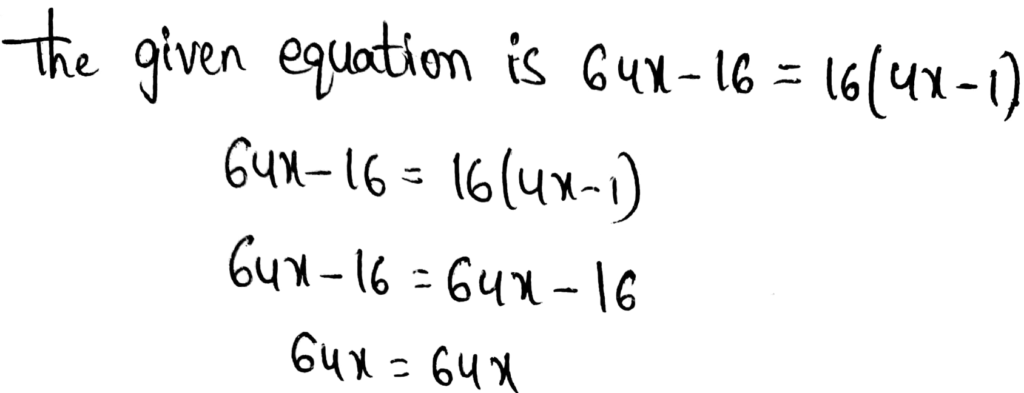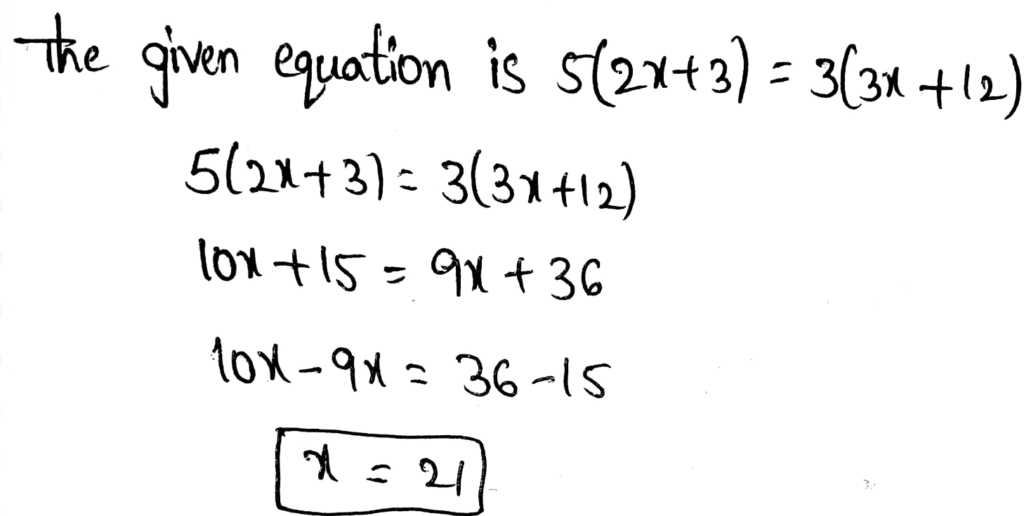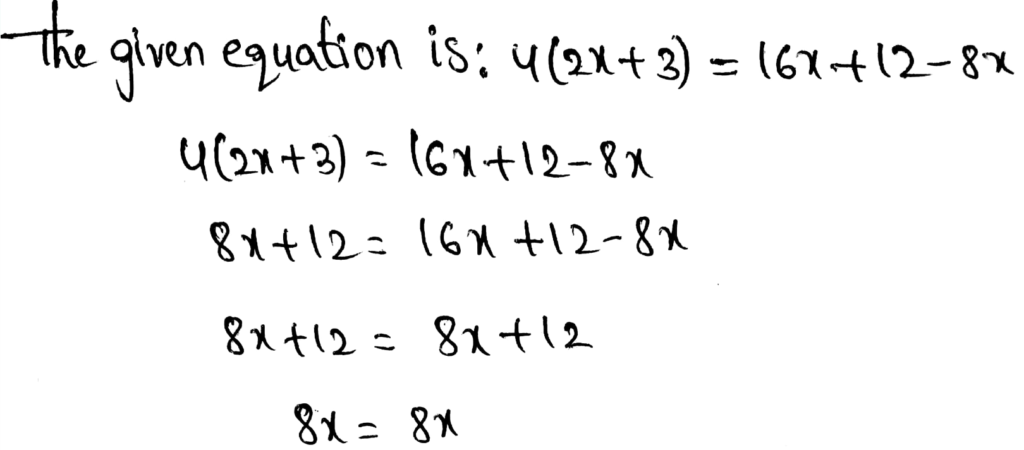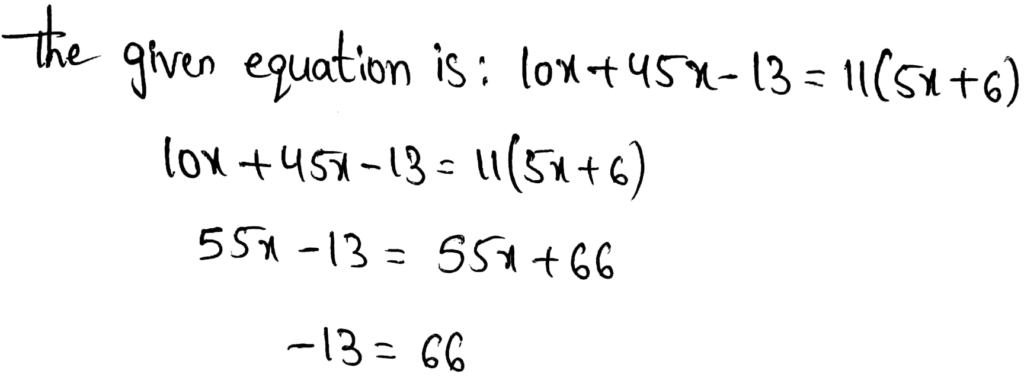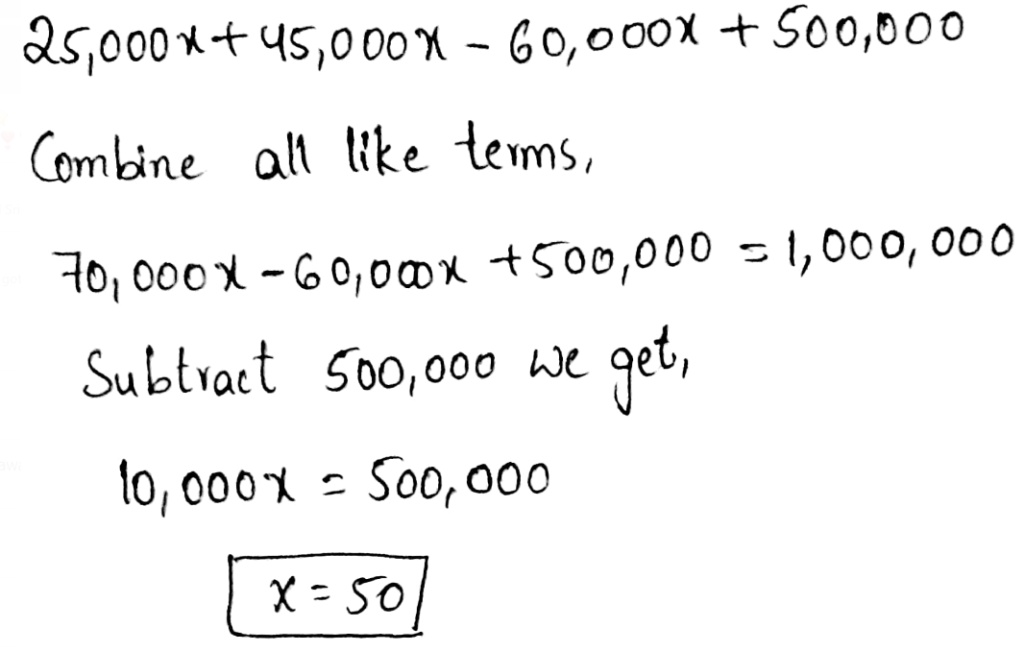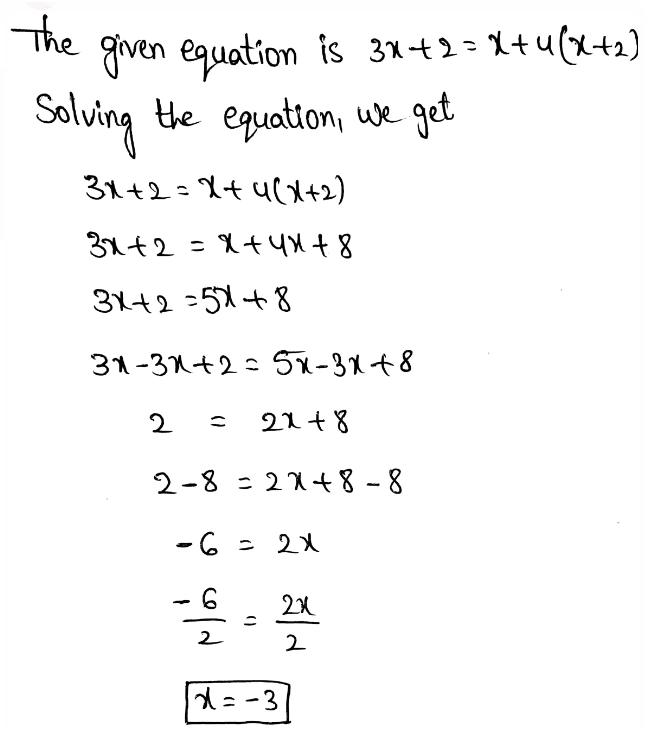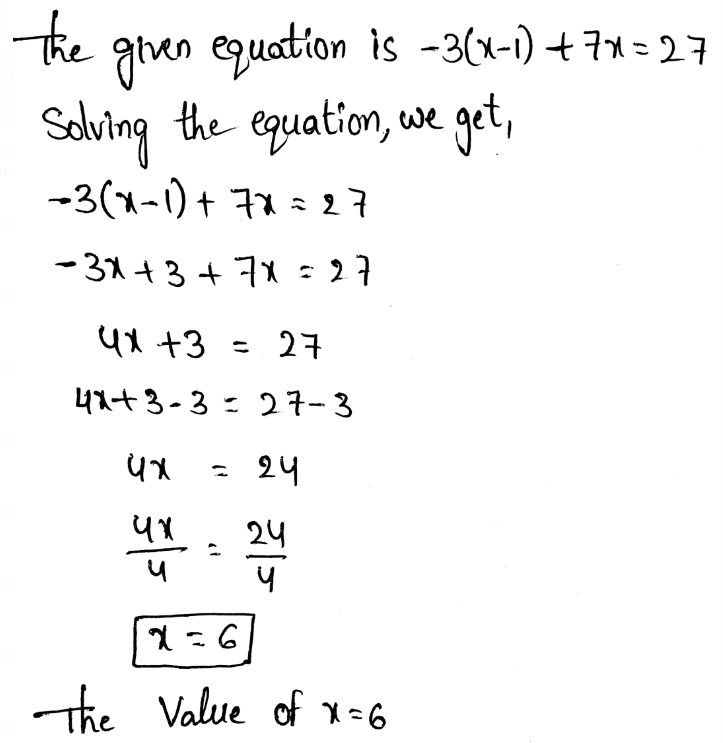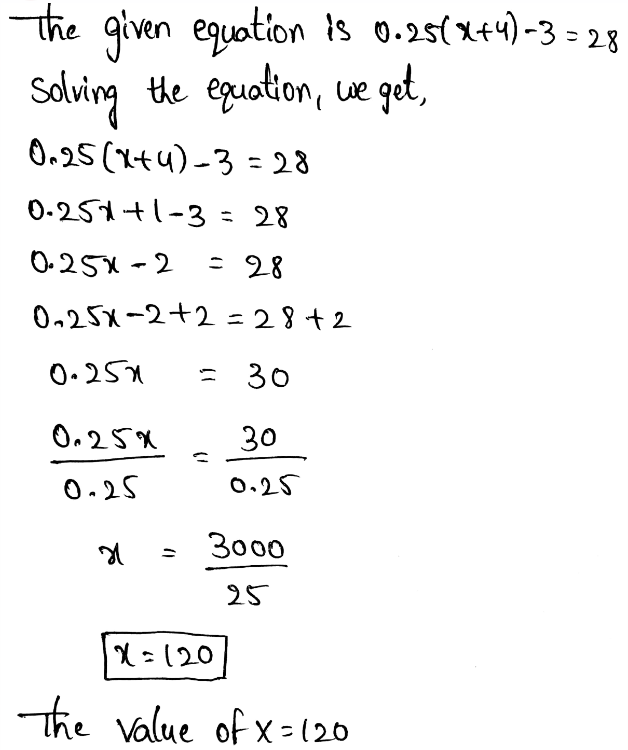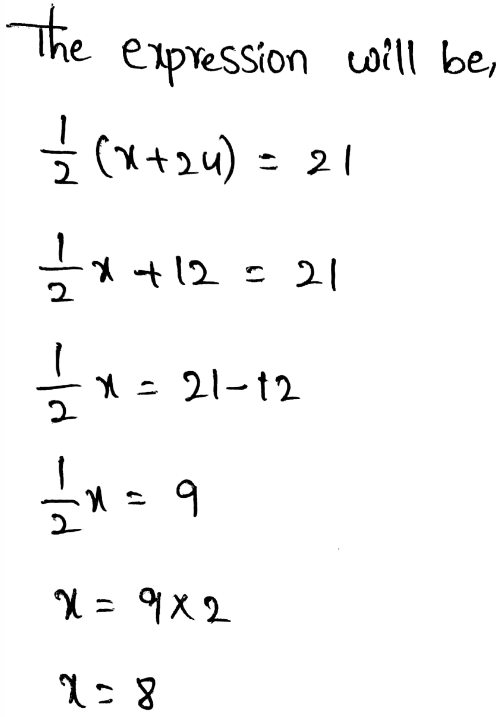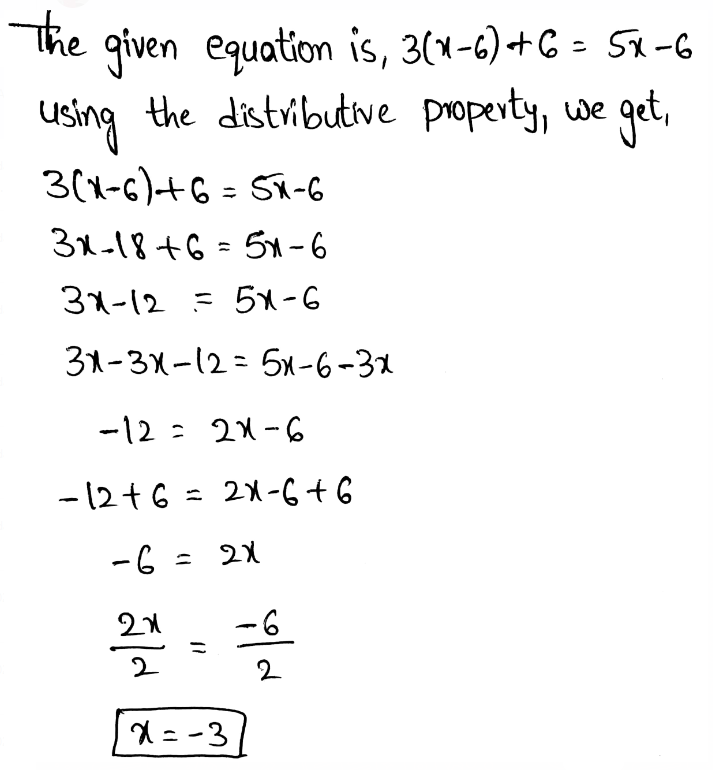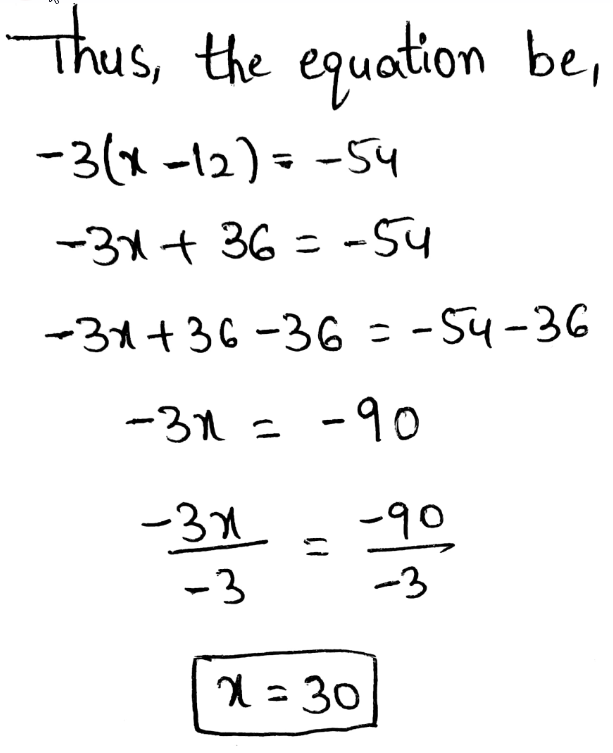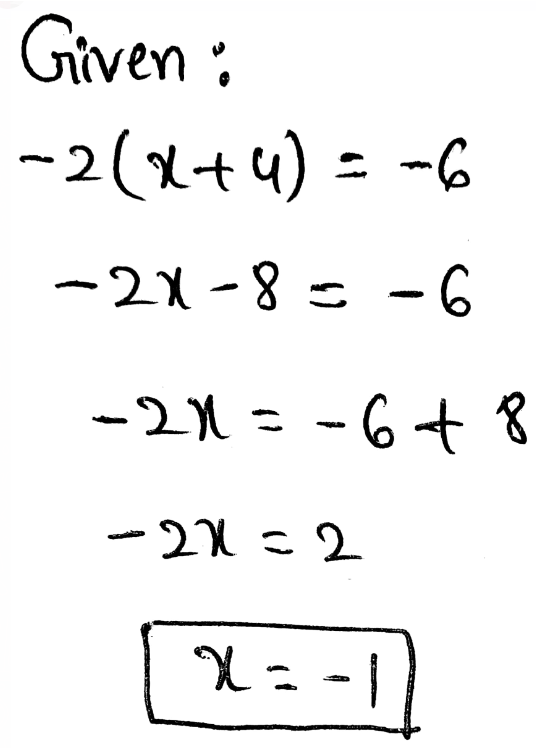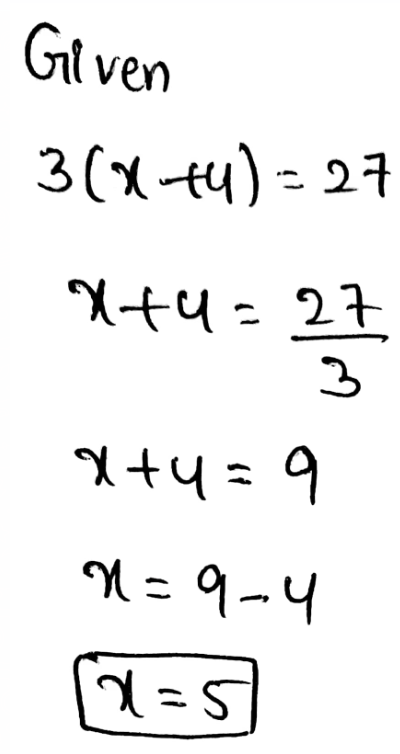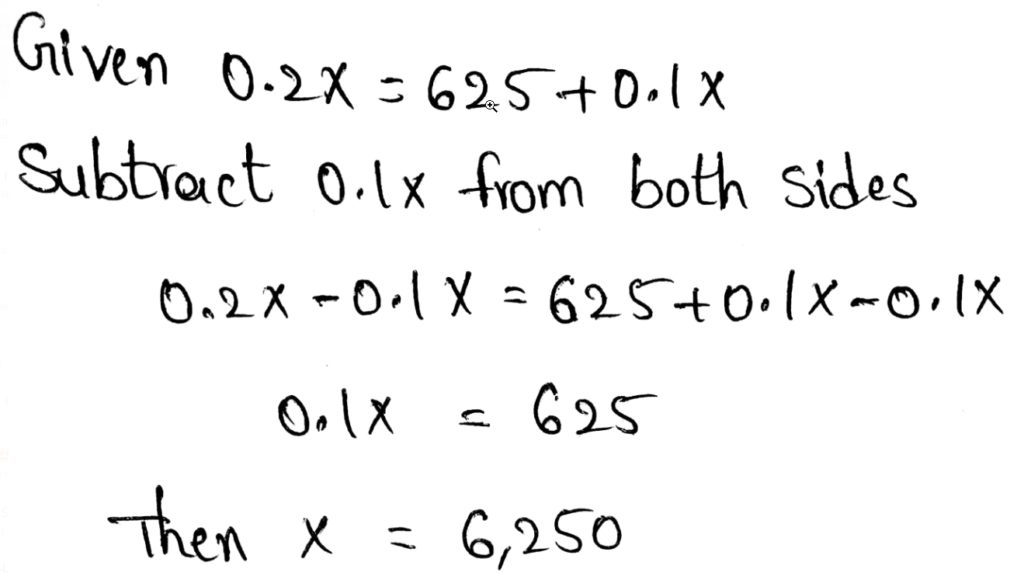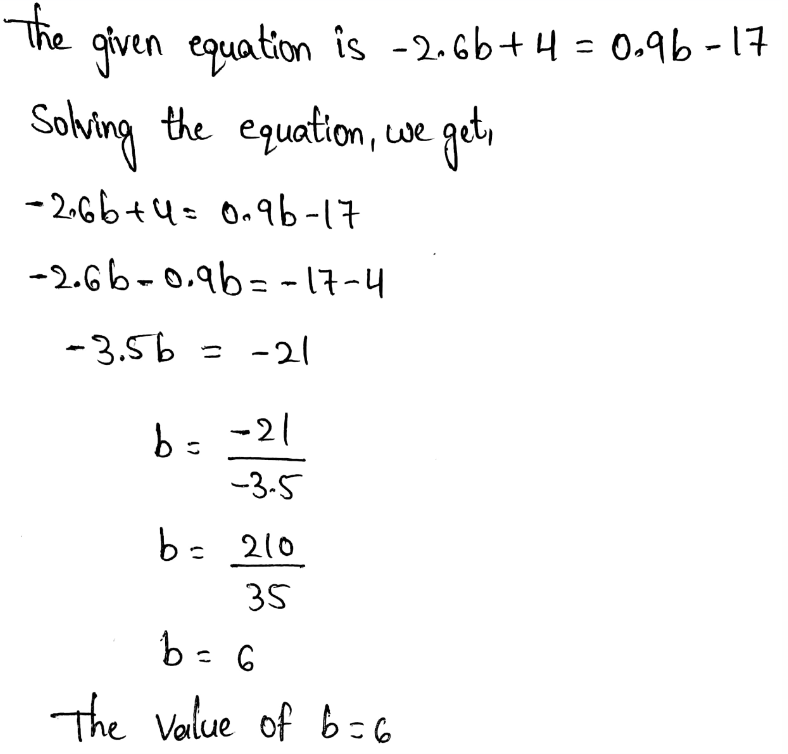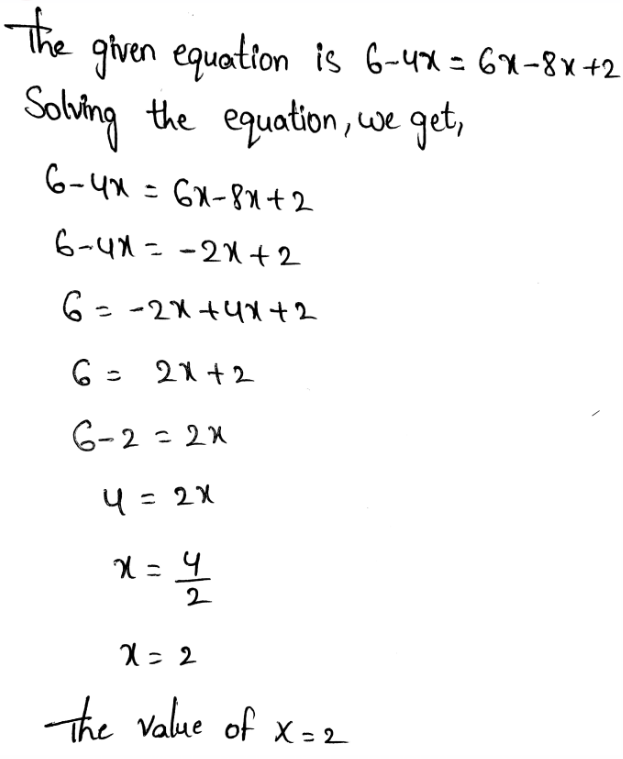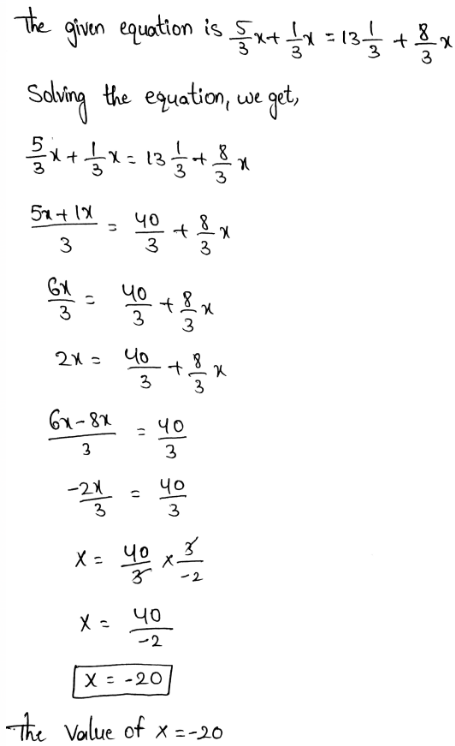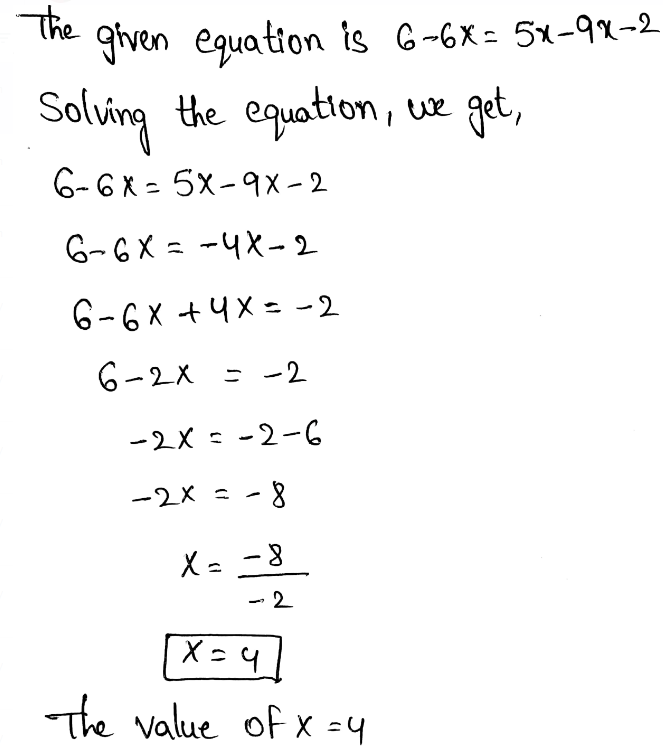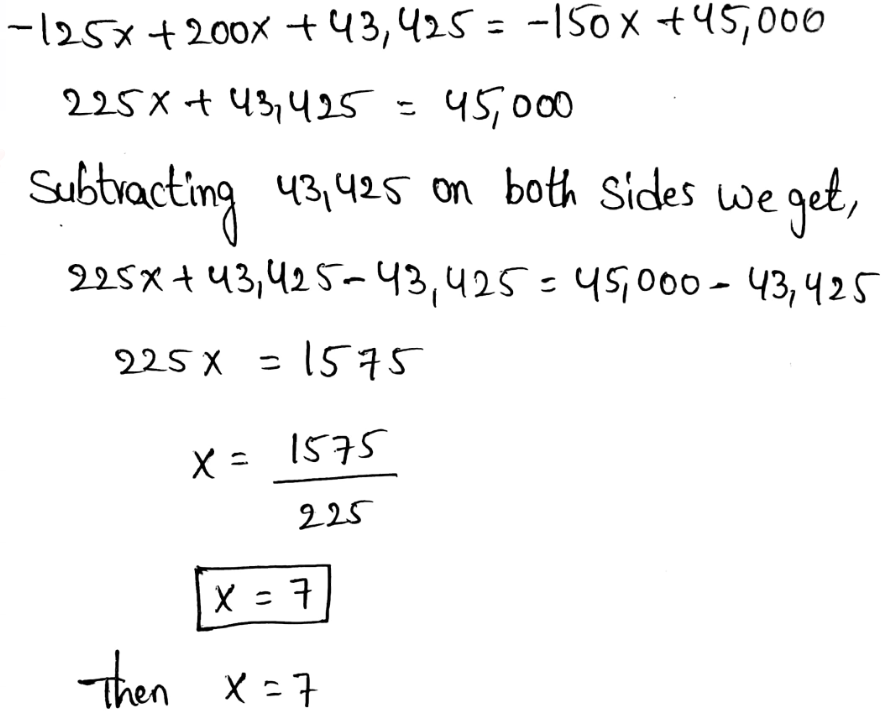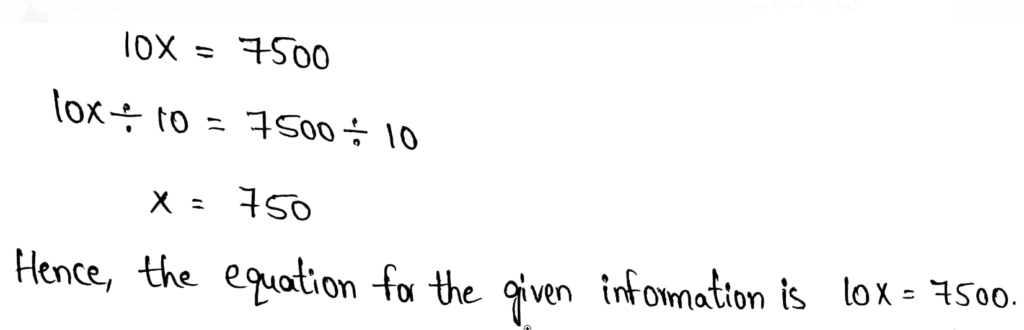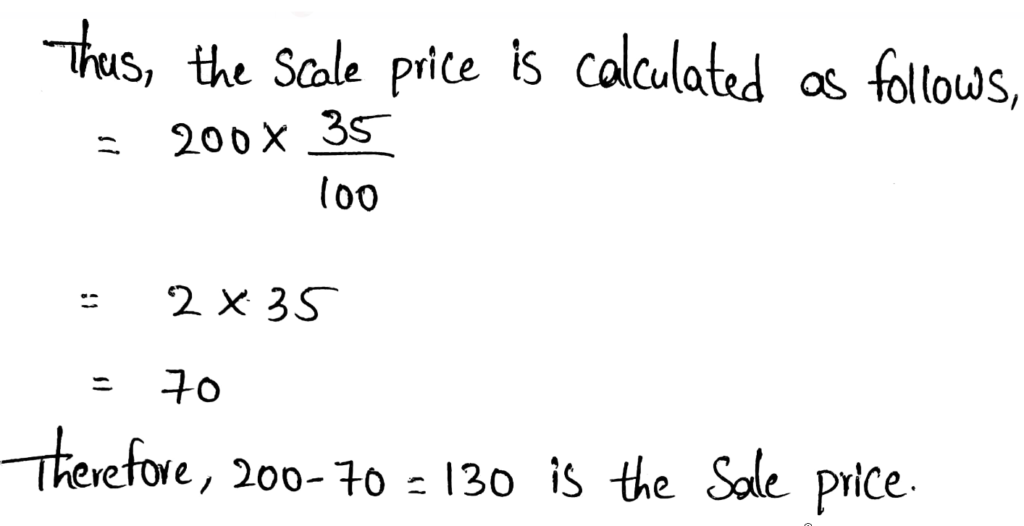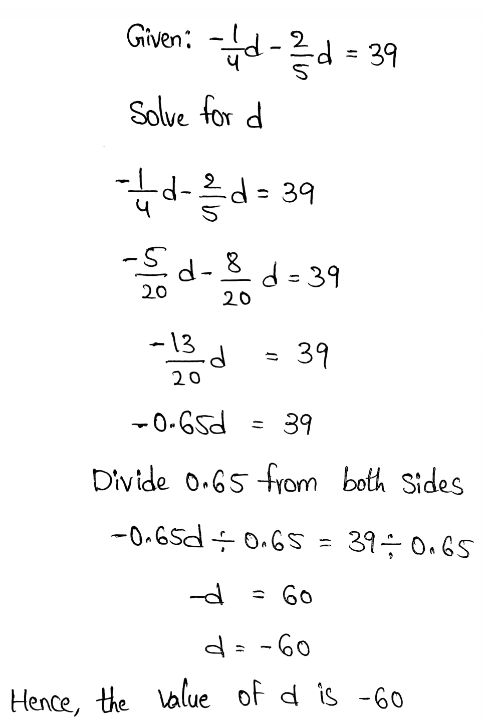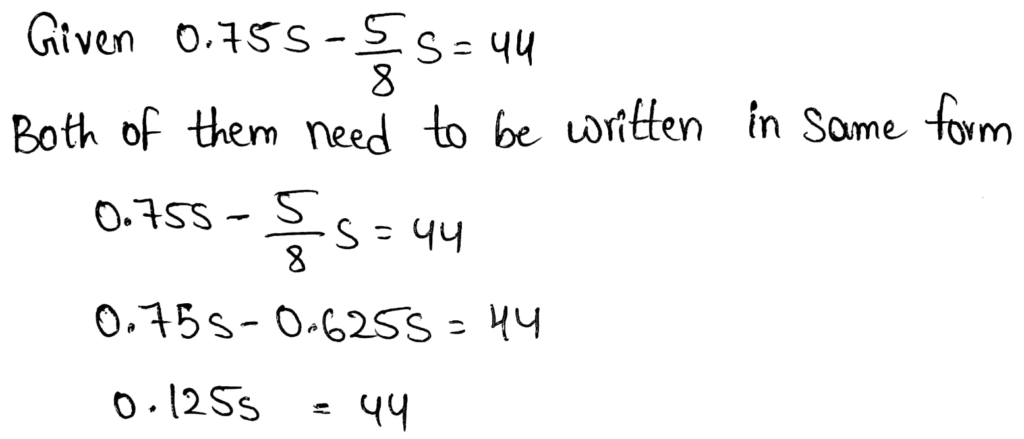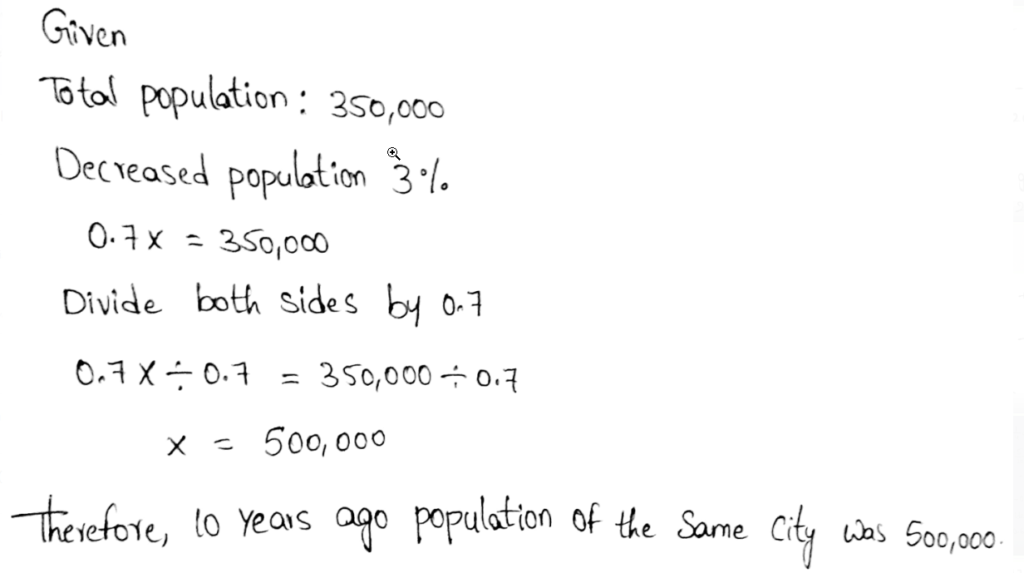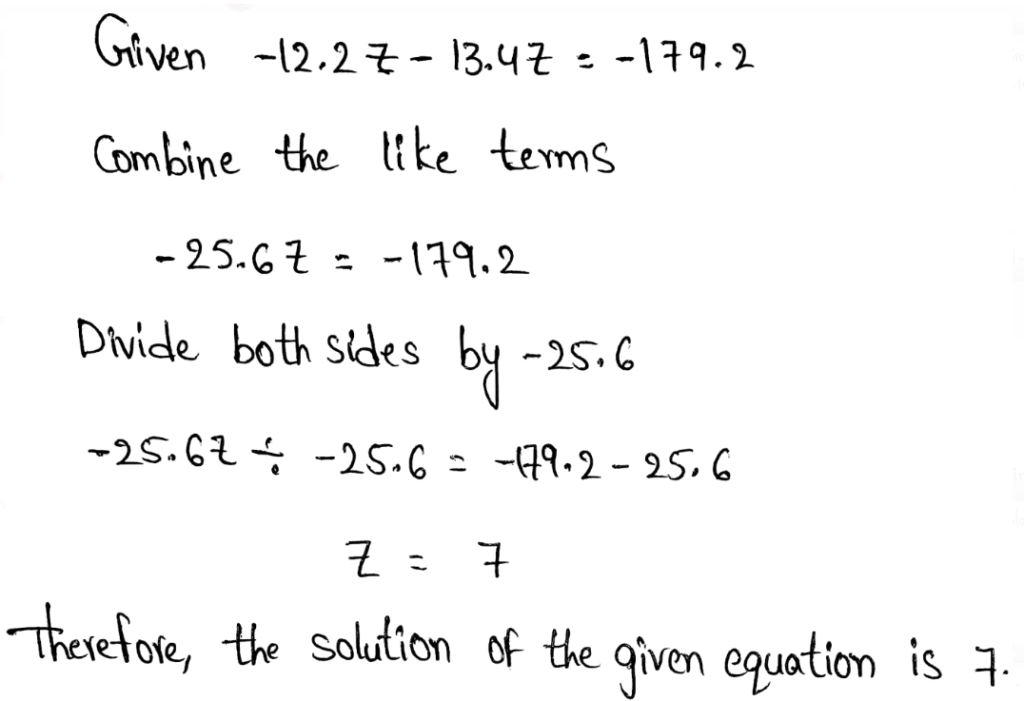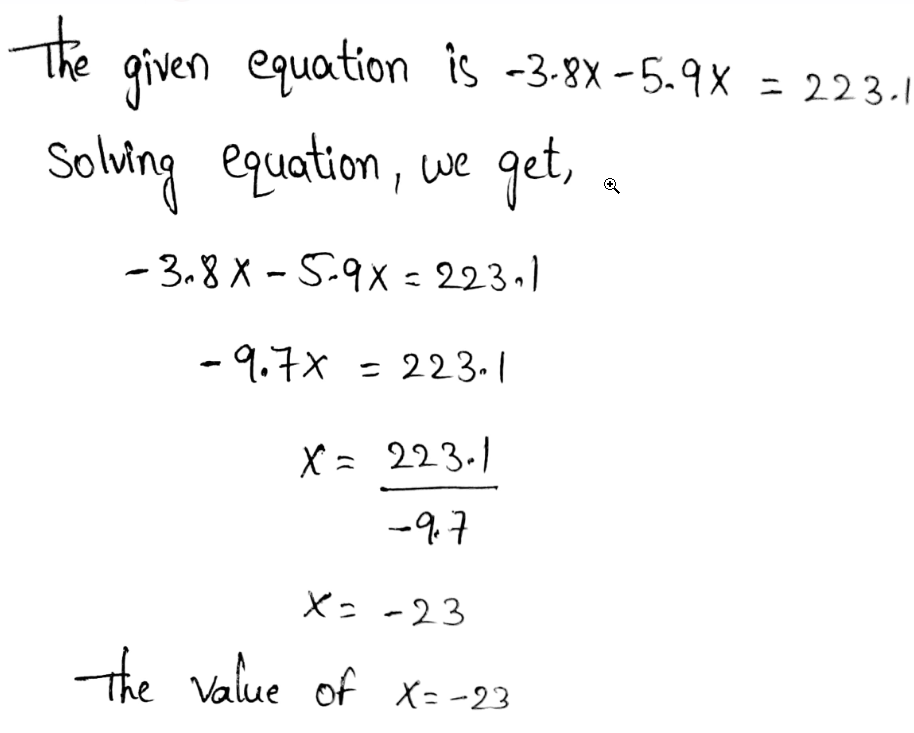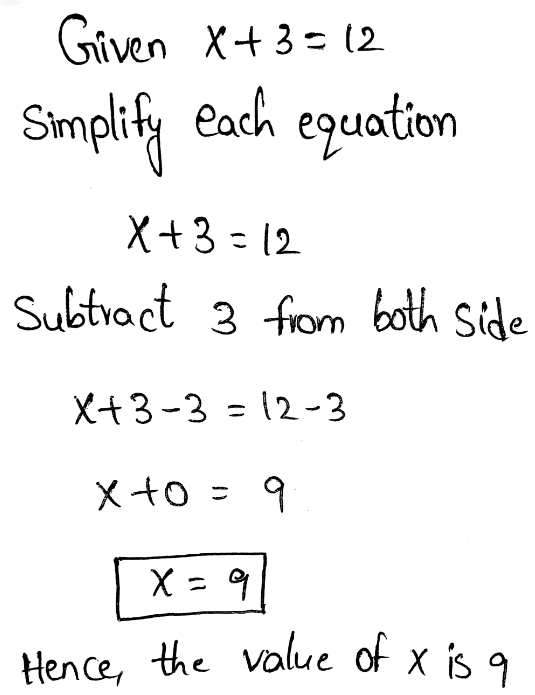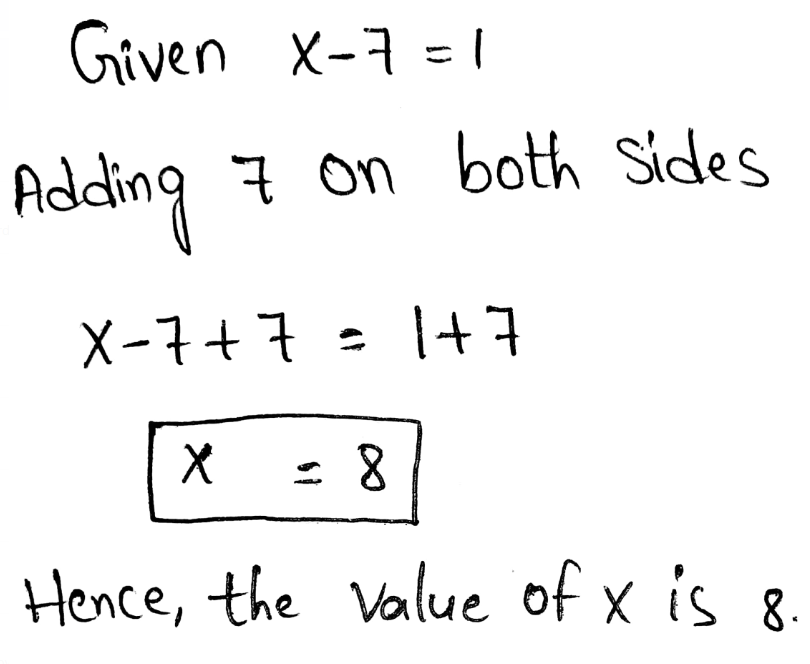Schindler

Envision Math Grade 8 Student Edition Solutions Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1

Page 111 Exercise 3 Answer

It is given that Edy has $450 in her saving account.

After how many months will Edy and Juan have the same amount of money in their accounts

Let the time at which Edy and Juan will have same amount of money be x. So, according to given question:

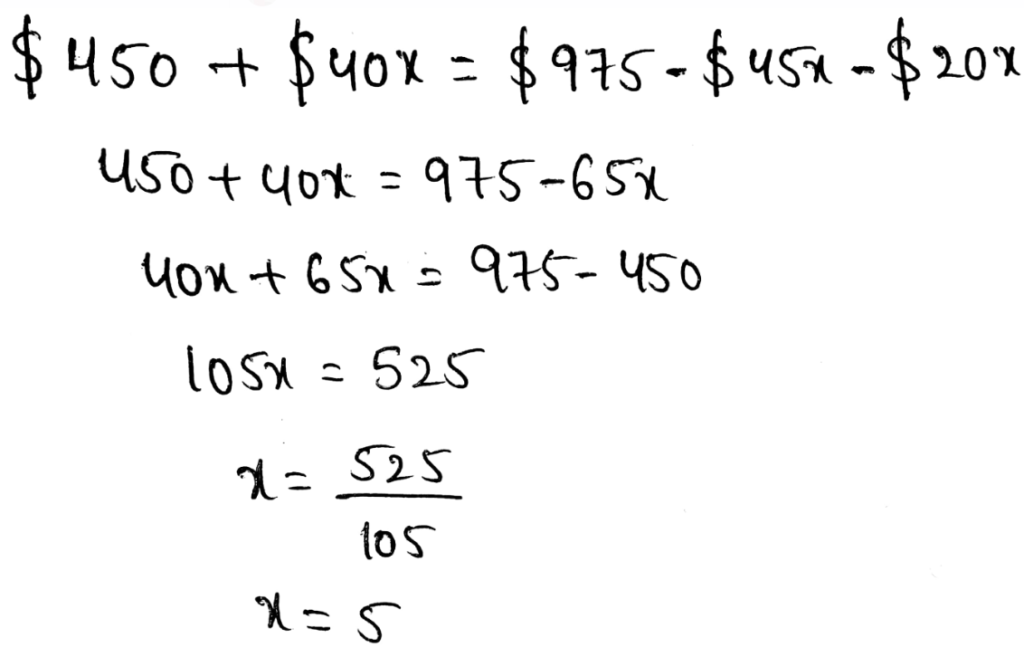
After 5 months, Edy and Juan will have same amount of money in their accounts.

Envision Math Grade 8 Volume 1 Chapter 2 Topic 2.1 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 111 Exercise 4 Answer

Infinite many solution means that every value is the solution of the given equation.

The equation that has infinite many solution is:

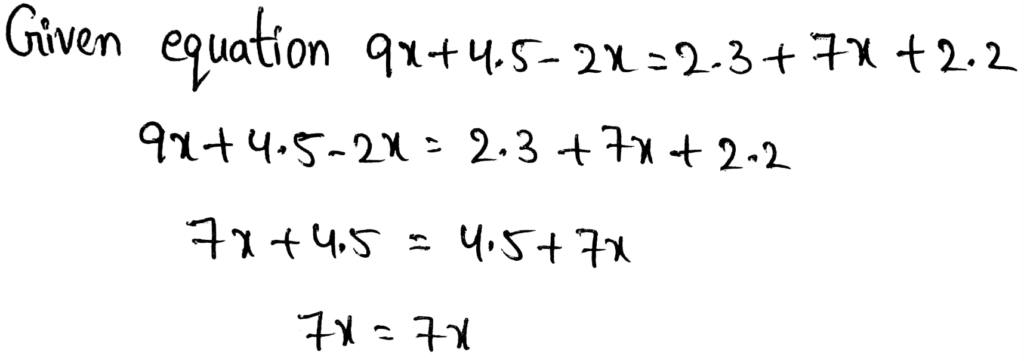
Option c is correct.

Page 111 Exercise 5 Answer

The given equation is −4(x − 1) + 6x = 34

To find: solve the given equation

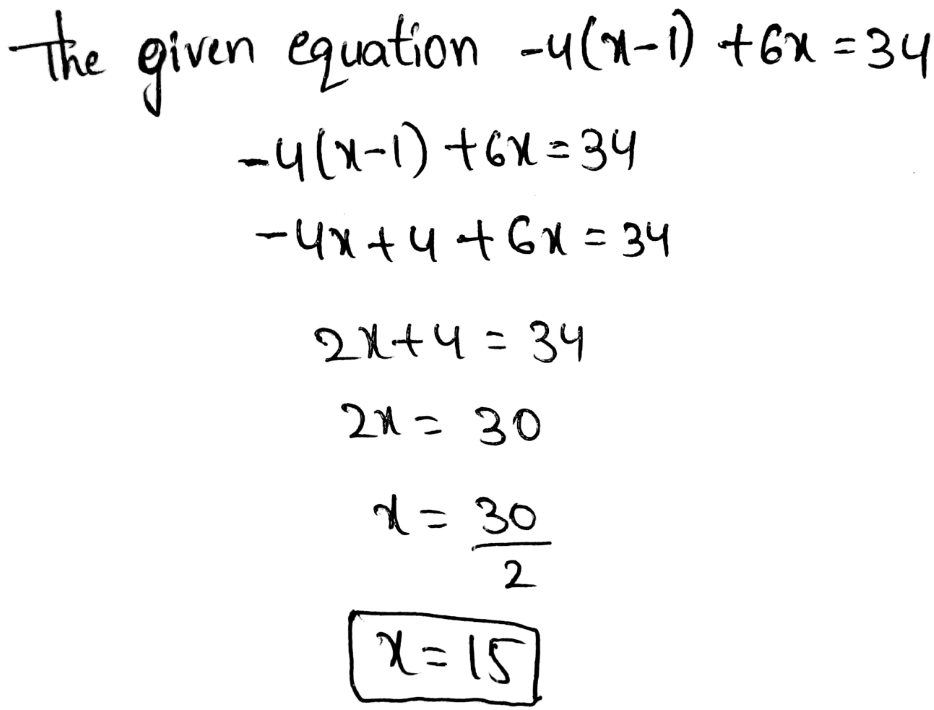
The value of x is 15.

Envision Math Grade 8 Topic 2.1 Analyze And Solve Linear Equations

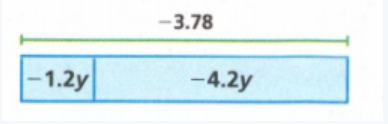
Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 111 Exercise 6 Answer

Hakeem subtracted 8 from a number, then multiplied the difference by 5. So, the result was 20.

​
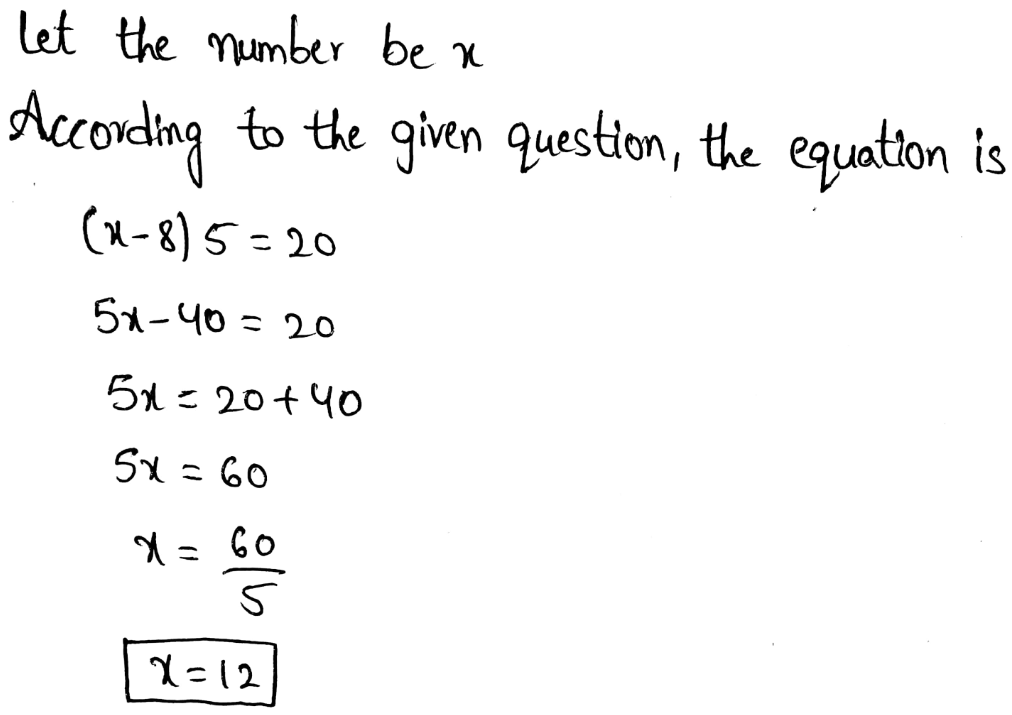
The value of x is 12.

Page 112 Exercise 1 Answer

It is given that the race is of 42 miles and hector is completed 18 miles at a speed of 12 miles per hour.

Let x be the hours needed for Wanda to catch up with Hector.

Hector has already completed 18 miles at a speed of 12 miles per hour.

So, after x more hours, Hector will travel 18 + 12x miles.

Wanda travels at 16 miles per hour. In x hours, she travel 16x miles.

If Wanda catches up to Hector, then
​
16x = 18 + 12x

4x = 18
​
x = 4.5 hours.

Wanda will catch up to Hector in 4 hours and 30 minutes.

It is given that the race is of 42 miles and hector is completed 18 miles at a speed of 12 miles per hour.

Wanda will catch up to Hector at 16x miles, i.e. 72 miles.

But the race is of 42 miles. So, Wanda will catch up to Hector after the race.

Wanda will not catch up to Hector before the race is completed.

It is given that the race is of 42 miles and hector is completed 18 miles at a speed of 12 miles per hour.

Distance till finish line is 42 miles.

The speed at which Wanda is travelling is 16 miles per hour.

The speed Wanda should travel = \(\frac{42}{16}=2.625\) miles per hour.

Wanda could travel at a constant speed of 2.625 miles per hour to catch up Hector at the finish line.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 113 Exercise 1 Answer

The video mentioned above shown some images that predict the charge left in the laptop before it completely drained off.

The device runs out of power and the battery percentage is dropping.

The charger was left at home so the laptop runs only for certain hours.

The reason is for knowing the amount of time left for a certain percentage of charge left in the laptop.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “How much time is left before the laptop charge completely drained off?”.

“How much time is left before the laptop charge completely drained off?”.

This is the question that made up my mind after watching this video.

Page 113 Exercise 2 Answer

The video mentioned above shown some images that predict the charge left in the laptop before it completely drained off.

The device runs out of power and the battery percentage is dropping.

The charger was left at home so the laptop runs only for certain hours.

The reason is for knowing the amount of time left for a certain percentage of charge left in the laptop.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “How much time is left before the laptop charge completely drained off?”.

The main question that I will answer that I saw in the video is “How much time is left before the laptop charge completely drained off?”.

Analyze And Solve Linear Equations Grade 8 Topic 2.1 Envision Math

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 113 Exercise 3 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

The reason is for knowing the amount of time left for a certain percentage of charge left in the laptop.

The first question that comes to my mind after watching this video is “How much time is left before the laptop charge completely drained off?”.

The laptop will run 8 hours when it is fully charged. The charge left now is 25%.

Hence, it can run another two hours before it completely drained off.

An answer that I was predicted to this main question is two hours.

An answer that I was predicted to this main question is two hours. I found my answer by evaluating the 25% of 8 hours.
​

= 2 hours

Page 113 Exercise 5 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too early to be the answer is 0 hours since the charge is still remaining hence we cannot say it is completely drained.

A number that is too late to be the answer is 8 hours since it can only happen when the charge is full. We know that the charge has already drained up to a certain percent.

My prediction is two hours.

Plotting my prediction on the same number line, I get,

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 114 Exercise 6 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

In this situation, information regarding the number of hours it took for the laptop to completely charge is more helpful to know.

This is because I can use that information to charge my laptop completely using another charger and I can continue with my work.

In this situation, information regarding the number of hours it took for the laptop to completely charge is more helpful to know. I can use that information to charge my laptop completely.

Page 114 Exercise 7 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

To get the information I need regarding the number of hours it took to charge, I can use a similar charger to charge it and calculate the number of percentages charged for every 5 mins to calculate how long it will take to charge completely.

A charger can be used to get the information I need. The laptop took 1.5 hours to charge completely.

Envision Math Grade 8 Chapter 2 Topic 2.1 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 114 Exercise 8 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure the number of hours left before it completely drained off.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

From this way, I have found out that the charge left can make the laptop run for two more hours.

Page 114 Exercise 9 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is 2 hours.

This is the same as my prediction.

The answer to the Main Question is two hours. It is equal to my prediction.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 115 Exercise 10 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is 2 hours.

This is the same as my prediction.

The answer that I saw in the video is also the same.

The answer that I saw in the video is two hours.

Page 115 Exercise 11 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is two hours.

This is the same as my prediction.

My answer matches the answer in the video. This is because the number of hours can be easily determined by the battery percentage.

My answer matches the answer in the video. This is because the number of hours can be easily determined by the battery percentage.

Envision Math 8th Grade Topic 2.1 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 115 Exercise 12 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The charger was left at home so the laptop runs only for certain hours.

We need to calculate the number of hours left for the laptop before it gets completely drained off.

An answer that I was predicted is two hours.

This is the same as my prediction.

My answer matches the answer in the video. This is because the number of hours can be easily determined by the battery percentage.

I’m not going to change my model.

No, I would not change my model now that I know the answer.

Page 116 Exercise 13 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure the number of hours left before it completely drained off.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

The model helps me answer the Main Question by making an accurate calculation of battery percentage and the number of hours the battery remains when it is fully charged and to know the number of hours left before it completely drained off.

How To Solve Topic 2.1 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Topic 2.1 Page 116 Exercise 15 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

After 35 minutes, he started charging his phone. 21 minutes later, the battery is at 23%.

Envision Math Grade 8 Volume 1 Student Edition Solutions  Chapter 2 Analyze And Solve Linear Equations

Page 103 Exercise 1 Answer

Given:

Jasmine’s expression: 2(3x + 6)

James’s expression: 3(2x + 4)

We consider the table with four more values and draw conclusion:

We observe that whichever number we take, the result is same for both the expressions. This proves that Jasmine and James are of the same age. Since Jasmine and James are twins, this table yields the same result. This is true for every whole number.

We observe that whichever number we take, the result is same for both the expressions. This proves that Jasmine and James are of the same age.

Since Jasmine and James are twins, this table yields the same result. This is true for every whole number.

Envision Math Grade 8 Volume 1 Exercise 2.4 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 104 Question 1 Answer

A one-variable equation is the equation which only has one variable.

If the equation two or more variables then it becomes a linear equation in two variables or so on.

The solution of an equation is based on the number of variable present in the equation.

Therefore, one-variable equations will always have on unique solution.

Yes, a one variable equation always have one and unique solution.

Page 104 Exercise 1 Answer

There are two ways to solve this problem.

The first way is to draw a bar diagram to represent the perimeters. Then we have to decompose and reorder the bar diagram to solve for x.

The other way is to write an equation to represent equal perimeters. Then use inverse operations and properties of equality to solve.

Then draw the bar diagram.

Choose whichever way is easier.

We can use bar diagram to represent the equal perimeters by first drawing a bar diagram to represent the perimeters.

Then we have to decompose and reorder the bar diagram to solve for x.

The other way is to write an equation to represent equal perimeters. Then use inverse operations and properties of equality to solve for x.

Then draw the bar diagram.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 105 Exercise 2 Answer

Given:

The equation is:

​
Because 8≠3 there is no solution for the given expression.

Envision Math Grade 8 Exercise 2.4 Linear Equations Answers

Page 106 Exercise 3 Answer

The equation is:

3x + 1.5 = 2.5x + 4.7

When we mentally solve this equation we get x = 6.4

Therefore the given equation 3x + 1.5 = 2.5x + 4.7 has only one solution.

Therefore the equation 3x + 1.5 = 2.5x + 4.7 has one solution.

Given:

The equation is:

3(x + 2) = 3x − 6

When we mentally solve this equation we get 6 ≠ −6

Therefore the given equation 3(x + 2) = 3x − 6 has no solution.

Therefore the equation 3(x + 2) = 3x − 6 has no solution.

Given:

The equation is:

9x − 4 = 5x − 4 + 4x

When we mentally solve this equation we get 9x − 4 = 9x − 4

Therefore the given equation 9x − 4 = 5x − 4 + 4x has infinitely many solutions.

Therefore the equation 9x − 4 = 5x − 4 + 4x has infinitely many solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 104 Exercise 1 Answer

When we solve an equation, we generally obtain a value of x.

The value of x obtained by solving the equation is the solution of the equation.

There is a possibility that the solution obtained is a whole number, rational number, a fraction or an integer. Nonetheless, it is the solution of the equation.

So yes, if the value of x is negative, the equation will still be true.

Yes, if the value of x is negative, the equation will still be true because, the value of x negative or positive is still the solution of the equation.

Page 107 Exercise 1 Answer

A one-variable equation is an equation that only has one variable.

If the equation two or more variables then it becomes a linear equation in two variables or so on.

The solution of an equation is based on the number of variables presents in the equation.

Therefore, one-variable equations will always have on a unique solution.

Yes, a one-variable equation always have one and unique solution.

Linear Equations Solutions Grade 8 Exercise 2.4 Envision Math

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 107 Exercise 2 Answer

Given:

The equation is:

6x + 12 = 2(3x + 6)

When we mentally solve this equation we get 6x + 12 = 6x + 12

Therefore the given equation 6x + 12 = 2(3x + 6) has infinitely many solutions.

Therefore Kaylee’s equation 6x + 12 = 2(3x + 6) has infinitely many solutions.

Page 107 Exercise 3 Answer

Given:

Height of the first plant is represented by the expression: 3(4x + 2)

Height of the second plant is represented by expression: 6(2x + 2)

We consider the two expressions and put them into a table to see if for the same whole, they yield the same result.

We observe that even after days the plants do not grow of the same height.

No, it is not possible for the plants to be of the same height.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 107 Exercise 4 Answer

Given:

The equation is: 3(2.4x + 4) = 4.1x + 7 + 3.1x

To find : solve the given equation

We consider:
​

Because 12 ≠ 7 the equation has no solution.

The equation 3(2.4x + 4) = 4.1x + 7 + 3.1x has no solution.

Page 107 Exercise 5 Answer

Given:

The equation is:

7x + 3x − 8 = 2(5x − 4)

We consider:
​
7x + 3x − 8 = 2(5x − 4)

10x − 8 = 10x − 8
​
Because 10x − 8 = 10x − 8 the equation has infinitely many solutions.

The equation 7x + 3x − 8 = 2(5x − 4) has infinitely many solutions.

Envision Math Grade 8 Chapter 2 Exercise 2.4 Solutions

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 107 Exercise 6 Answer

Given:

Todd buys peaches and a carton of vanilla yogurt. Agnes buys apples and a jar of honey

They bought the same number of pieces of fruit.

Peaches = $1.25 each

Vanilla Yogurt = $4

Apples = $1 each

Honey = $6

Let x be the number of fruits bought by Todd and Agnes.
Forming the two equations

Todd:

1.25x + 4

Agnes:

1x + 6

We equate the two equations:
​
1.25x + 4 = 1x + 6

0.25x = 2
​
x = 8

If both Agnes and Todd buy 8 fruits, then it is possible that they both pay the same amount.

The situation in which Agnes and Todd pay the same amount for their purchases is if they buy 8 fruits each.

Envision Math 8th Grade Exercise 2.4 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 108 Exercise 8 Answer

Given:

The given equation is 4(4x + 3) = 19x + 9 − 3x + 3

To find : solve the given equation

We consider:|

​
Since 12 is equal to 12, the equation has infinite solutions.

Since, the equation 4(4x + 3) = 19x + 9 − 3x + 3 has infinite solutions.

Page 108 Exercise 11 Answer

Given:

Store A’s prices are represented by the expression 15x − 2

Store B’s prices are represented by the expression 3(5x + 7)

Let x be the rates.

Equating the two equations

We consider:
​
15x − 2 = 3(5x + 7)

15x − 2 = 15x + 21
​
−2 ≠ 21

Since −2 ≠ 21 the store never charges the same rate.

We observe that −2 ≠ 21, therefore, the store never charges the same rate.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 109 Exercise 12 Answer

When the equation is equivalent to 0 = 0 the given equation will have infinitely many solutions.

When the equation is equivalent to a ≠ b, a and b being the two solutions, the given equation will not have any solution.

The equations having infinite solutions or no solutions will keep on going no matter how many times we get no solution and no matter how many times we get an infinite number.

Solving equations with no solution are similar to solving equations with infinite solutions because both will keep on going no matter how many times

we get no solution and no matter how many times we get an infinite number.

Page 109 Exercise 13 Answer

Given:

The given equation is: 0.9x + 5.1x − 7 = 2(2.5x − 3)

To find: solve the given equation

We consider:
​
0.9x + 5.1x − 7 = 2(2.5x − 3)

6x − 7 = 5x − 6
​
x = 1

The equation has only one solution.

The equation 0.9x + 5.1x − 7 = 2(2.5x − 3) has only one solution.

How To Solve Exercise 2.4 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 109 Exercise 15 Answer

Given:

The given equation is: 49x + 9 = 49x + 83

We consider:
​
49x + 9 = 49x + 83

49x − 49x + 9 = 49x − 49x + 83
​
9 ≠ 83

The equation does not have any solution.

The equation 49x + 9 = 49x + 83 has no solution.

The given equation is: 49x + 9 = 49x + 83

To find: solve the given equation

Solution:

49x + 9 = 49x + 83

+9 = 83 which is false. So, the equation has no solution.

Examples of equations having no solution is:

−9(x + 6) = −9x + 108 and 7(y − 8) = 7y + 42

−9(x + 6) = −9x + 108 and 7(y − 8) = 7y + 42 are the equations in one variable that have no solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 109 Exercise 16 Answer

The given equation is: 6(x + 2) = 5(x + 7)

The given equation 6(x + 2) = 5(x + 7) has only one solution.

Page 109 Exercise 17 Answer

The given equation is: 6x + 14x + 5 = 5(4x + 1)

To find: Write a word problem or any expression that this expression represents

The equivalent form of 6x + 14x + 5 = 5(4x + 1) is 100x + 25 = 100x + 25

The given equation 6x + 14x + 5 = 5(4x + 1) has infinite many solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 19 Answer

The equations should have one equation, no solution and infinite many solutions.

The equation that have one solution:

2x + 1 = 9

The equation that has no solution:

5x − 3x + 6 = 2x + 7 − 2

The equation that have infinitely many solutions:

7(8x + 5) − 35 = 4(14x)

2x + 1 = 9 have only one solution

5x − 3x + 6 = 2x + 7 − 2 has no solution

7(8x + 5) − 35 = 4(14x) has infinite many solution.

Page 110 Exercise 20 Answer

The given equation is: 4(4x − 2) + 1 = 16x − 7

The given equation has no solution.

Equation 4(4x – 2) + 1 = 16x – 7 has no solution.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 21 Answer

The given equation is : 6x + 26x − 10 = 8(4x + 10)

To find: solve the given equation

The value of x is 15.

Page 110 Exercise 22 Answer

The given equation is 64x − 16 = 16(4x − 1)

The given equation 64x – 16 = 16(4x – 1) has infinite many solutions.

Envision Math Grade 8 Exercise 2.4 Practice Problems

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 23 Answer

The given equation is 5(2x + 3) = 3(3x + 12)

To find: solve the given equation

The given solution 5(2x + 3) = 3(3x + 12) has only one solution.

Page 110 Exercise 24 Answer

The given equation is: 4(2x + 3) = 16x + 12 − 8x

To find: Which of the following best describes the solution to the equation

The given equation 4(2x + 3) = 16x + 12 − 8x has infinite many solutions.

Envision Math Grade 8 Volume 1 Linear Equations Exercise 2.4 Solutions Page 110 Exercise 25 Answer

The given equation is: 10x + 45x − 13 = 11(5x + 6)

To find: solve the given equation

Which is false, so the equation has no solution.

The statement which is true is: the equation has no solution.

Envision Math Grade 8 Student Solutions Volume 1 Chapter 2 Analyze And Solve Linear Equations

Page 97 Exercise 1 Answer

Given

Water flows through one pipe at a rate of 25,000 gallons an hour and through the other pipe at 45,000 gallons an hour.

To find/solve

Water leaves the system at a rate of 60,000 gallons an hour.

We have to write an equation where the variable will be the gallons that are leaving and entering the system per hour. The right side of the equation will have the maximum amount of gallons the tank can holes.

If we are asked to find the time needed for 3 tanks we simply multiply 50.3 = 150 hours

150 hours.is required to fill 3 tanks

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.3 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 97 Exercise 1 Answer

Given

Statement

To find/solve.

The bar model is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities.

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

Yes, it is basically a graphical representation of data using bars of different heights. In real life, bar graphs are commonly used to represent business data.

Yes, it is basically a graphical representation of data using bars of different heights. In real life, bar graphs are commonly used to represent business data.

Page 97 Exercise 1 Answer

Given

Expression 4(3x + 7x − 5)

To find/solve

Equals 40x − 20.

In the task it should say to simplify given expression so that it would be equal to

40x + 20, not 4x − 20

First way to simplify the expression:

4(3x + 7x + 5)

We get 4(10x + 5)

Then 40x + 20

Next to multiply 4 by the terms inside the parentheses

4(3x + 7x + 5)

12x + 28x + 20

First way is to combine like terms and then multiply 4 with the terms inside the parentheses. The second way is to multiply 4 with the terms inside the parentheses and then combine like terms.

First way is to combine like terms and then multiply 4 with the terms inside the parentheses. The second way is to multiply 4 with the terms inside the parentheses and then combine like terms.

Envision Math Grade 8 Exercise 2.3 Student Edition Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 98 Question 1 Answer

To find/solve: How can you use the Distributive Property to solve multistep equations?

When we are solving multistep equations, distributive property helps us with solving parentheses

Example

2(3x + 3) = 7

In the given equation, we use the distributive property so we can solve the parentheses.

2.3x + 2.3 = 7

When we are solving multistep equations, distributive property helps us with solving parentheses.

Page 98 Exercise 1 Answer

To find/solve: How can you find the solution of the equation using the bar diagram?

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

The bar model is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities.

Bar models are most often used to solve number problems with the four operations- addition and subtraction, multiplication and division.

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

The bar model is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities.

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 99 Exercise 2 Answer

Given

To find/solve

In the first step, we have to solve brackets on both sides

Here x = -8

x = -8 is the required answer

Page 98 Exercise 1 Answer

Given: can u add x to -5x on the left side of the equation as the first step

To find/solve: explain the given statement

First, we have to multiply the value in front of the parentheses with values in brackets

No we can’t add x to −5x on the left side of the equation as the first step because parentheses have higher priority than subtracting. First we need to solve the parentheses. Subtracting and adding our last operations to priority list.

No we can’t add x to −5x on the left side of the equation as the first step because parentheses have higher priority than subtracting. First we need to solve the parentheses. Subtracting and adding are the last operations on priority list.

Linear Equations Grade 8 Exercise 2.3 Envision Math Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 100 Exercise 2 Answer

Given

3(3x – 5x) + 2 = −8

To find: first step when solving the equation

The first step is to combine like terms in the parenthesis
​
3(3x − 5x) + 2 = −8

3.(−2x) + 2 = −8
​
The first step is to combine like terms in the parenthesis.

Page 100 Exercise 4 Answer

The given equation is 3x + 2 = x + 4(x + 2)

We need to solve the given equation.

​
The value of x = −3

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 100 Exercise 5 Answer

The given equation is −3(x − 1) + 7x = 27

We need to solve the given equation.

​
The value of x = 6

Page 100 Exercise 7 Answer

The given equation is 0.25(x + 4) − 3 = 28

We need to solve the given equation.

​
The value of x = 120

Envision Math Grade 8 Chapter 2 Exercise 2.3 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 101 Exercise 8 Answer

Given that, Lori bought a shirt and a hat at a half-off sale. If she spent a total of $21 on the two items, we need to find the original price of the hat.

The original price of the shirt is $24

The original price of the hat is x

Given that these are sold at a half rate and the total money spent is $21

The original price of the hat is $18

Page 101 Exercise 9 Answer

We need to use the Distributive Property to solve the given equation 28 − (3x + 4) = 2(x + 6) + x

The given is, 28−(3x+4)=2(x+6)+x

​
The value of x = 2

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 101 Exercise 10 Answer

We need to use the Distributive Property to solve the given equation 3(x − 6) + 6 = 5x − 6

The given equation is, 3(x − 6) + 6 = 5x − 6

​
The value of x = −3

Page 102 Exercise 15 Answer

We need to use the Distributive Property to solve the given equation 4x − 2(x − 2) = −9 + 5x − 8

The given equation is, 4x − 2(x − 2) = −9 + 5x − 8

Solving the given using the distributive property, we get,
​
​
The value of x = 7

Envision Math 8th Grade Exercise 2.3 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 102 Exercise 16 Answer

We need to use the Distributive Property to solve the equation 2(m + 2) = 22

We need to describe what it means to distribute the 2 to each term inside the parentheses.

The given equation is, 2(m + 2) = 22

Solving the given using the distributive property, we get,
​
​
The value of m = 9

We need to multiply two to each one of the terms inside the parentheses to distribute the 2 to each term.

How To Solve Exercise 3.1 Functions In Envision Math Grade 8

Page 102 Exercise 17 Answer

We need to find Peter’s number.

Let the unknown number be x

Subtract 12 from x and multiply the difference by −3

The result is −54

Thus, the equation be,
​
​
Peter’s number is 30

Envision Math Grade 8 Chapter 2 Exercise 2.3 Practice Problems

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 102 Exercise 19 Answer

Given:

−2(x + 4) = −6

We consider:

​
The required solution is x = −1

How To Solve Exercise 2.3 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 2 Student Edition Linear Equations Exercise 2.3 Page 102 Exercise 20 Answer

Given:

3(x + 4) = 27

We consider:

​
The required solution is x = 5

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 91 Exercise 1 Answer

We need to explain how can we use an equation to show that expressions are equal.

A bar chart or bar graph or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent.

The bars can be plotted vertically or horizontally. A vertical bar chart is sometimes called a column chart.

Combine any like terms on each side of the equation: x-terms with x-terms and constant with constant.

Arrange the terms in the same are identical, then the two expressions are equivalent.

Combine any like terms on each side of the equation: x-terms with x-terms and constant with constant.

Arrange the terms in the same are identical, then the two expressions are equivalent.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.2 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 91 Exercise 1 Answer

We need to explain what expressions can we write to represent the amount of money collected by each boy.

Also, we need to explain how we can use these expressions to write an equation.

It seems form the picture that Jaxson has 14 checks and 15 dollars, and Bryon has 50 dollars and 7checks. It is given that each check is x dollars.

The dollar value of the checks is the number of checks times the value of each check.

Jaxson then got 14x + 15 dollars and Bryon got 50 + 7x dollars. They collected the same amount so we can set them equal to write the equation.

The equation is 14x + 15 = 50 + 7x.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 92 Question 1 Answer

Given

statement

To find/solve

Inverse operations.

We use inverse operations for getting all variables on one side and values on the other.

Example :

5x + 9 = 3x − 8

We subtract 3x from both sides of the equation, since 3x is on the right side of the equation.

We use inverse operations for getting all variables on one side and values on the other.

We use inverse operations for getting all variables on one side and values on the other.

Analyzing Linear Equations Grade 8 Exercise 2.2 Envision Math

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 92 Exercise 1 Answer

Given

Class A was given a sunflower with a height of 8 centimeters that grows at a rate of \(3 \frac{1}{2}\) centimeters per week. Class B was given a sunflower with a height of 10 centimeters that grows at a rate of \(3 \frac{1}{2}\) centimeters per week.

To find/solve

After how many weeks are the sunflowers the same height?

We put the sunflower of class A on one side of the equation and the sunflower of class B on the other side of the equation. We must add variables to the rate of growth of each sunflower.

After 8 weeks the sunflowers will be the same height.

Envision Math Grade 8 Chapter 2 Exercise 2.2 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 93 Exercise 2 Answer

Given

96 − 4.5y − 3.2y = 5.6y + 42.80

To find/solve

We have to apply a mathematical operation to the equation until we have only variables on one side and only values on another side of the equation.

y = 4 is the required answer

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 94 Exercise 2 Answer

Given

Statement

To find/solve

Inverse operations and properties of equality are important when solving equations.

Inverse operations help us get all variables on the same side of the equation.

Properties of equality are important because they give us a new equation that is equivalent to the original.

Properties of equality are important because they give us a new equation that is equivalent to the original.

Properties of equality are important because they give us a new equation that is equivalent to the original.

Envision Math 8th Grade Exercise 2.2 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 94 Exercise 4 Answer

Given

Maria and Liam work in a banquet hall. Maria earns a 20% commission on her food sales. Liam earns a weekly salary of $625 plus a 10% commission on his food sales.

To find/solve

What amount of food sales will result in Maria and Liam earning the same amount for the week?

First, we have to make an equation with commissions as a variable. On one side of the equation will be Maria and on the other Liam.

6,250 dollars of food sales will result in Maria and Liam earning the same amount for the week.

6,250 dollars of food sales will result in Maria and Liam earning the same amount for the week.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 94 Exercise 7 Answer

The given equation is −2.6b + 4 = 0.9b − 17

We need to solve the given equation and find the value of b

Solving the equation, we get,

The value of b = 6

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 8 Answer

The given equation is 6 − 4x = 6x − 8x + 2

We need to solve the given equation and find the value of x

The value of x = 2

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 9 Answer

The given equation is \(\frac{5}{3} x+\frac{1}{3} x=13 \frac{1}{3}+\frac{8}{3} x\)

We need to solve the given equation and find the value of x

The value of x = -20

How To Solve Exercise 2.2 Linear Equations In Envision Math Grade 8 

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 10 Answer

Given

Town 1 snow depth: \(3 \frac{1}{2}\) inches every hour

Town 2 snow depth: \(2 \frac{1}{4}\) inches every hour

Towns will be equal in snow depth is \(\frac{4}{5}\) of hour or 48 minutes.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 12 Answer

The given equation is 6 − 6x = 5x − 9x − 2

We need to solve the given equation and find the value of x

​
The value of x = 4

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 95 Exercise 13 Answer

Given

Each month, 200 people on average move into town. A nearby town has a population of 45,000.

To find/solve

Write an equation that represents this situation and solve.

We have to write an equation with one town on one side and the other town on another side of the equation.

In about 7 months the population of towns will be the same.

Envision Math Grade 8 Chapter 2 Exercise 2.2 Practice Problems

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 96 Exercise 14 Answer

Given

statement

To find/solve

After how many months will the total cost for each health club be the same?

We have to make an equation with one health club on one side and second health club on other side of the equation.

Monthly fee will be our variable.

After 4 months.

After 4 months will the total cost for each health club be the same.

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 96 Exercise 15 Answer

Given

The price of Stock A at 9 am. Was $12.73. since then, the price has been increasing at the rate of $0.06 per hour. At noon, the price of Stock B was $13.48. It begins to decrease at the rate of $0.14 per hour

To find/solve

How many hours will the prices of the stocks be the same?

We have to make an equation with Stock A on one side of the equation and Stock B on the other side of the equation.

We have to increase Stock A for 3 hours so that it will be growing before stock B starts falling.

After 2.85 hours Stock A and Stock B will have the same prices.

After 2.85 hours Stock A and Stock B will have the same prices.

Envision Math Exercise 2.2 Linear Equations Detailed Answers

Envision Math Grade 8 Volume 1 Chapter 2 Analyzing Linear Equations Exercise 2.2 Page 96 Exercise 16 Answer

Given

In an academic contest, correct answers earn 12 points and incorrect answers lose 5 points. In the final round, school A starts with 165 points and gives the same number of correct and incorrect answers.

To find/solve

A. Which equation models the scoring in the final round and the outcome of the contest?

On the left side of the equation will be school A. School A has 165 points from before and score 12 per correct answer and lose 5 per incorrect answer. The answers will be our variable.

165 + 12x − 5x

The second part of the equation will be school B which came into finals with 65 points, and gave only correct answer for 12 points.

12x + 65

Now we put those two expressions into same equation.

165 + 12x − 5x = 65 + 12x

165 + 12x – 5x = 65 + 12x is the required answer

Given

In an academic contest, correct answers earn 12 points and incorrect answers lose 5 points. In the final round, school A starts with 165 points and gives the same number of correct and incorrect answers.

To find/solve

How many answers did each school get correct in the final round?

On the left side of the equation will be school A. School A has 165 points from before and score 12 per correct answer and lose 5 per incorrect answer. The answers will be our variable.

165 + 12x − 5x

The second part of the equation will be school B which came into finals with 65 points, and gave only correct answer for 12 points.

12x + 65

Now we put those two expressions into same equation.

165 + 12x − 5x = 65 + 12x

First we have to write combined like terms

165 + 7x = 65 + 12x

Subtract 12x from both sides.

165 − 5x = 65

Now subtract 165 from both sides of the equation, we get

−5x = −100

x = 20

Both schools gave 20 correct answers.

Both schools gave 20 correct answers.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 85 Exercise 1 Answer

To represent the relationship between the number of laptops and the total cost, we can draw a bar diagram

The bar diagram will be divided into 10 parts, one part for each computer, and the total length will represent the total cost of $7500.

Since each laptop has the same cost, each part of the bar diagram can be labeled as x, where x represents the cost of 1 laptop.

The diagram for the representation of relationship between the number of laptops and the total cost

The bar diagram will be divided into10
parts, one part for each computer, and the total length will represent the total cost of $7500.

Read and Learn More Envision Maths Grade 8 Volume 1

Since each laptop has the same cost, each part of the bar diagram can be labeled as x, where x represents the cost of 1 laptop.

Hence, the equation for the given information is 10x = 7500.

Envision Math Grade 8 Volume 1 Exercise 2.1 Answer Key

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 85 Exercise 1 Answer

It is important because we can use one variable for one value.

If each laptop would cost a different than we would have different variables.

It is important because we can use one variable for one value.

If each laptop would cost a different than we would have different variables.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 86 Exercise 1 Answer

We need to explain why we can use the same variable to represent the number of placements and to represent the number of napkins.

We have to combine the coefficients easily. So, the number of placements and the number of napkins use the same variable.

We have to ease to combine the coefficients. So the number of placements and the number of napkins uses the same variable.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 87 Exercise 2 Answer

We need to explain how does the original price and the sale price relate.

The sale price of the computer screen is $130

The price of the computer before the sale is $200

The computer was sold for 35% off the original price.

The sale price is 100 − 35 = 65% of the given original price.

Analyzing Linear Equations Grade 8 Exercise 2.1 Envision Math Solutions

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 86 Exercise 1 Answer

Given:

Each necklace costs $9.99

Each bracelet costs $7.99

Total costs $53.94

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 87 Exercise 2 Answer

Given:

Grocery bill $150

Discount 5%

If something has a discount of 5% that means that they pay 95% of the original price.

Now we can write an equation with 0.95 of the bill and on the right side the price Nat paid.

0.95x = 150

Divide both sides by 0.95
​
0.95x ÷ 0.95 = 150 ÷ 0.95

x ≈ 157.89
​
Hence, the grocery bill before the discount was ≈ 157.89

Envision Math Grade 8 Exercise 2.1 Solutions

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 87 Exercise 3 Answer

Given:

Solve for d

Hence, the value of d is -60.

Given:

−9.7d − (−12.81d) = 8.54

Hence, the value of d is ≈ 2.746.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 86 Exercise 1 Answer

Given:

9.99s + 7.99s + 4.6 = 53.94

To find: Can you combine the s terms and 4.6? Explain.

We cannot combine the s terms and 4.6 because there can only be either variables on one side or normal values.

​
So, we cannot combine terms and 4.6.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 2 Answer

The like terms are recognized in the equation by having the same variable and exponents

Example:

12d + 3d = 24

12d And 3d are like terms.

The like terms are recognized in the equation by having the same variable and exponents.

Envision Math 8th Grade Analyzing Linear Equations Exercise 2.1

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 3 Answer

Given

In the given equation first, we rewrite our like terms in fraction form or decimal form.

Both of them need to be written in some form

First we rewrite our like terms in fraction form or decimal form. both of them need to be written in same form and then combined by subtracting the coefficients.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 5 Answer

Given

Total population: 350,000

Decreased population 3%

If we know that the population of a city decreased by 30% and now is 350,000 this means that 350,000 is 0.7 of the population that was 10 years ago.

​
Therefore, 10 years ago the population of the same city was 500,000.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 88 Exercise 6 Answer

Given

−12.2z − 13.4z = −179.2

​
Therefore, the solution of the given equation is 7.

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 7 Answer

The given equation is \(\frac{4}{5} x-\frac{1}{4} x=11\)

We need to solve the given equation and find the value of x

Solving the equation, we get,

The value of x = 20

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 8 Answer

The given equation is −0.65x + 0.45x = 5.4

We need to solve the given equation and find the value of x

​
The value of x = -27

How To Solve Exercise 2.1 In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 10 Answer

The given equation is −3.8x − 5.9x = 223.1

We need to solve the given equation and find the value of x

​
The value of x = -23

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 89 Exercise 12 Answer

The given equation is \(-\frac{3}{5} x-\frac{7}{10} x+\frac{1}{2} x=-56\)

Solving the equation, we get,

The value of x = 70

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 16 Answer

We need to write an equation that can be represented by the bar diagram, then we need to solve the unknown value.

The equation that can be represented by the bar diagram is,

−1.2y − 4.2y = −3.78

​
The equation that can be represented by the bar diagram is,

−1.2y − 4.2y = −3.78

The value of y = 0.7

Envision Math Grade 8 Chapter 2 Linear Equations Exercise 2.1 Answers

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 17 Answer

The given equation is \(\frac{2}{3} h-156=3 \frac{13}{24}\)

We need to solve the given equation and find the value of h

Solving the given equation, we get,

The value of h = 239.25

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 18 Answer

Given

The total cost of the notebooks and binders was $27.08.

To find/solve

Draw a bar diagram to represent the situations.

Nathan had bought one notebook and one binder in value 0.95 + 5.82 for each class. If we want to find how many classes does Nathan have, we just make an equation with value for each class on one side as variable and the money that he spent on the other side.

0.95x + 5.82x = 27.08

6.77x = 27.08

Now we divide both sides of the equations with the factor next to x.

6.77x/6.77 = 27.08

x = 4

Nathan is taking 4 classes.

Nathan is taking 4 classes.

Envision Math Grade 8 Volume 1 Linear Equations Practice Exercise 2.1

Envision Math Grade 8 Volume 1 Analyzing Linear Equations Exercise 2.1 Page 90 Exercise 20 Answer

Given

A 132 inch board is cut into two pieces. One piece is three time the length of the other.

To find/solve

Draw a bar diagram to represent the situation.

We simply have to divide the bar diagram on two pieces where one piece is exactly 3 times larger than the other piece.

The total length of whole diagram is 132 in

Simply divide the diagram that is total of 132 in, on 2 pieces where one piece is 3 times larger than the other.

Simply divide the diagram that is total of 132 in, on 2 pieces where one piece is 3 times larger than the other.

Given

A 132 inch board is cut into two pieces. One piece is three time the length of the other.

To find/solve

write and solve an equation to find the length of the shorter piece.

If we cut a board in two pieces where one piece is three times the length of the other this means that if we split one whole into four parts with one being three times the other part, this simply means;

So if we know that whole board is 132 inch we can simply multiply this number with value of shorter part which is \(\frac{1}{4}\)

Shorter part is 33 inches long.

Shorter part is 33 inches long.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1, Chapter 2 Page 80 Question 1 Answer

We need to explain how we can analyze connections between linear equations and use them to solve problems.

Equations that consist of degree one is said to be the linear equations.

Linear equations will always result in a straight line when plotted on the graph.

The highest degree of the variables present in the linear equations must be one.

A linear equation must have a constant in it.

Linear equations can be solved by doing arithmetical operations on both sides of the equation.

This will not affect the balance of the equation.It can also be solved graphically.

We can analyze connections between linear equations by solving them arithmetically or by graphically, and we can also use them to solve real life problems.

Read and Learn More Envision Math Grade 8 Volume 1 Solutions

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 1 Answer

In an algebraic expression, like terms are terms that have the same variables raised to the same exponent.

Example:

2x²3y

In an algebraic expression, like terms are terms that have the same variables raised to the same exponent.

Envision Math Grade 8 Chapter 2 Solutions For Linear Equations

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 2 Answer

Quantities that represent an unknown value are variables.

Example:

2x³y2

x and y are the variables.

Quantities that represent an unknown value are variables.

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 3 Answer

A proportion is a statement that two ratios are equal.

Examples:

A proportion is a statement that two ratios are equal.

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 4 Answer

Operations that ”undo” each other are inverse operations.

Example:

Square and square root are inverse operations.

3 + 2 = 5

Inverse operation: 3 – 2 = 1

Operations that “undo” each other are inverse operations.

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 5 Answer

Given

4x + 7y − 6z + 6y − 9x

To find: Identify Like terms

In an algebraic expression, like terms are terms that have the same variables raised to the same exponent.

4x + 7y − 6z + 6y − 9x

4x And −9x are like terms

7y And 6y are like terms

Envision Math Grade 8 Analyzing And Solving Linear Equations Answers

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 6 Answer

Given

To find: Identify Like terms

In an algebraic expression, like terms are terms that have the same variables raised to the same exponent.

6u And -9u are like terms

Solutions For Envision Math Grade 8 Volume 1 Chapter 2

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 7 Answer

Given

2x = 10

Hence, the value of X is 5.

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 8 Answer

Given

x + 3 = 12

Hence, the value of X is 9.

Envision Math Grade 8 Chapter 2 Step-By-Step Solutions

Envision Math Grade 8 Volume 1, Chapter 2 Page 83 Exercise 9 Answer

Given

x − 7 = 1

Hence, the value of X is 8.

How To Solve Linear Equations Envision Math Grade 8 Chapter 2

Envision Math Grade 8 Volume 1, Chapter 2 Page 84 Exercise 1 Answer

We need to write what you already know about the lesson in the third column, Also, we need to write a question that you want to be answered about the lesson. After the lesson, we have to complete the fourth column with the answer to your question.

This entire chapter dealt with analyzing and solving the linear equations.