Schindler

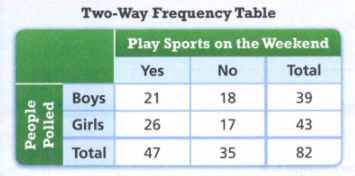
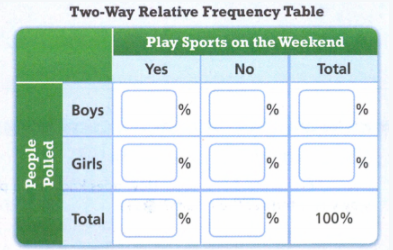
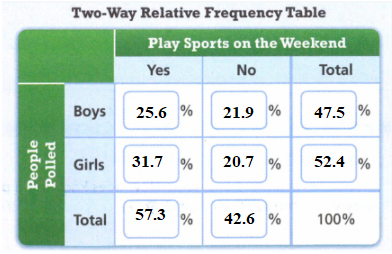
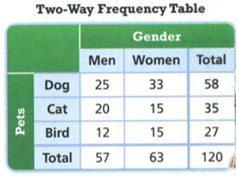
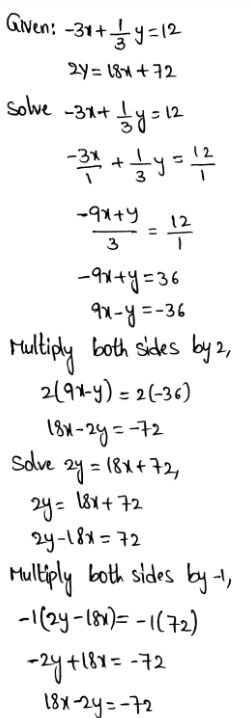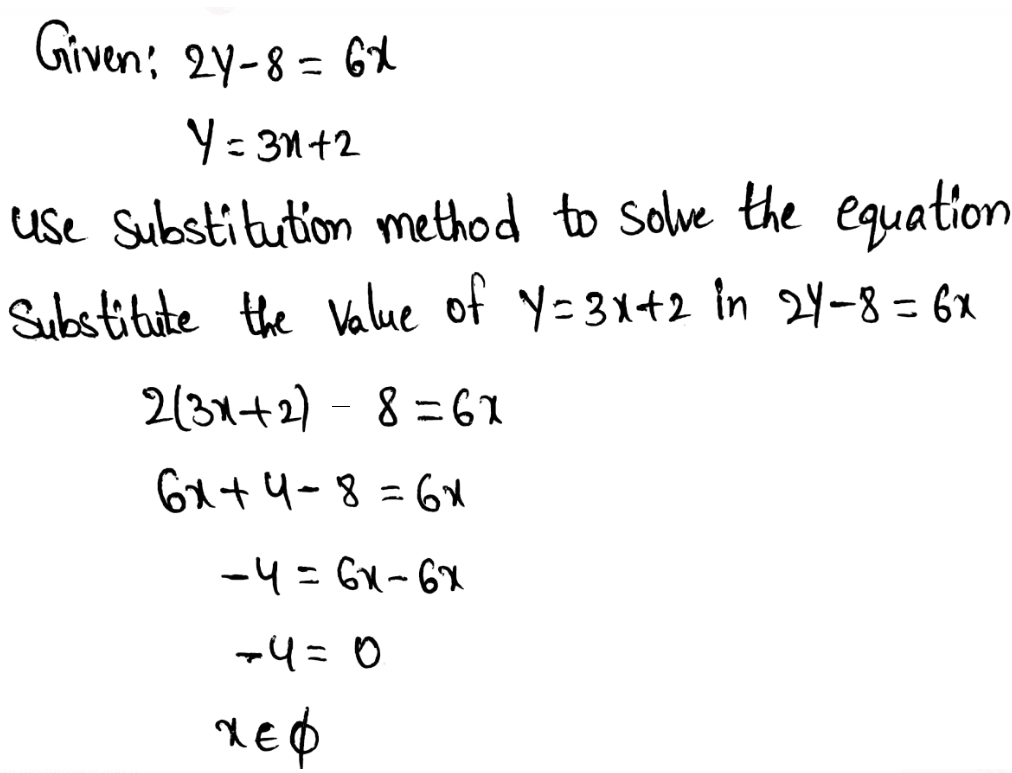Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 297 Exercise 1 Answer

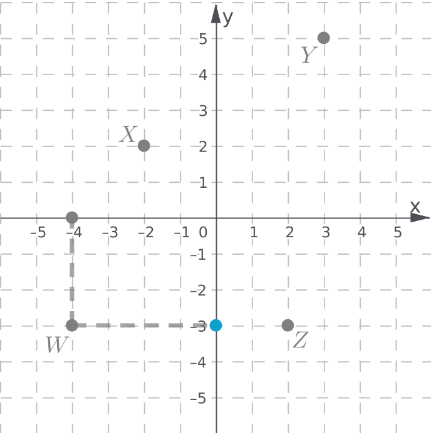
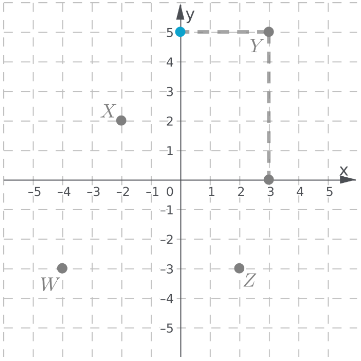
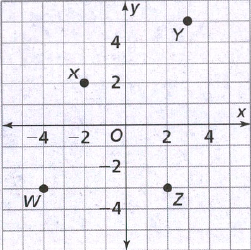
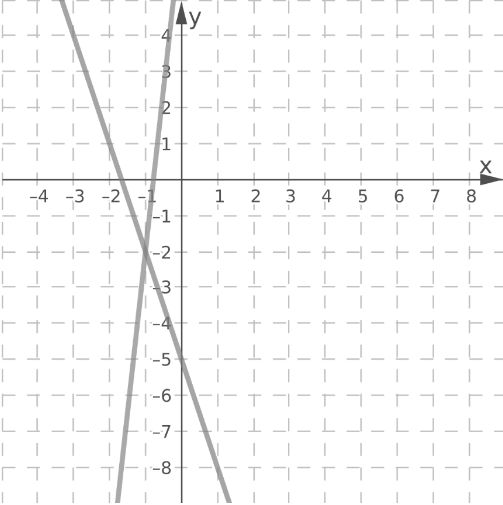
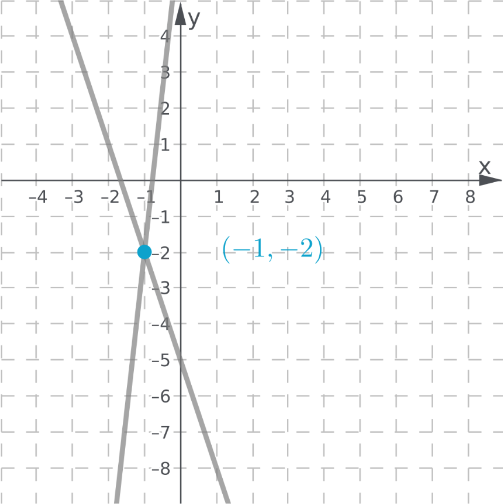
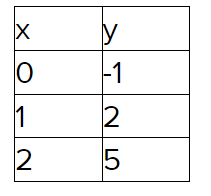
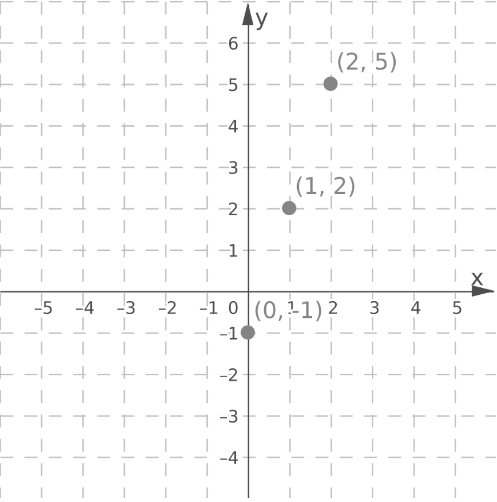
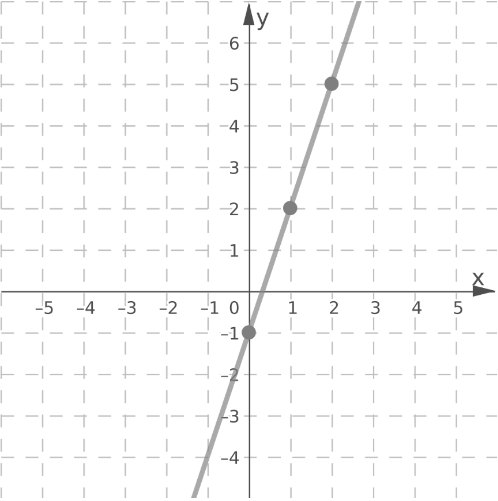
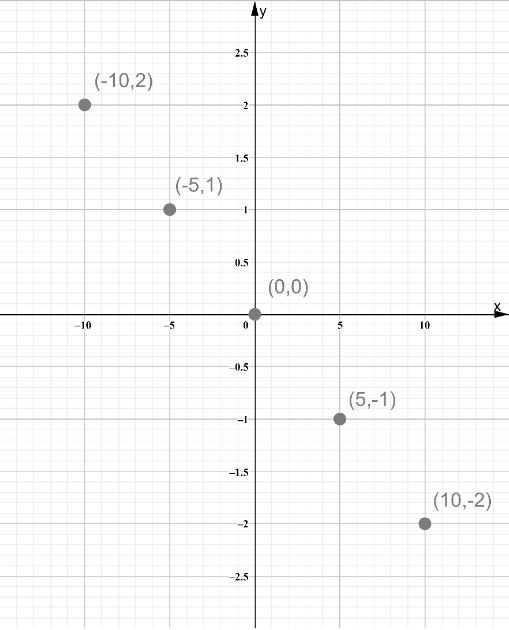
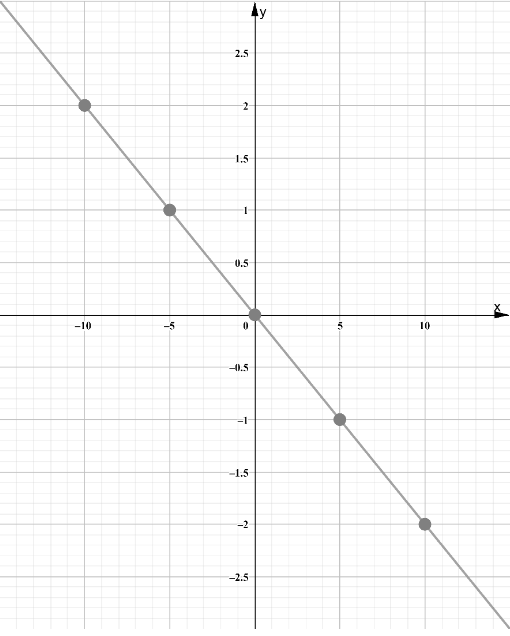
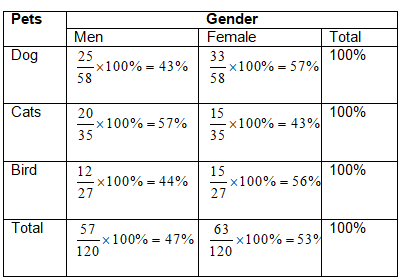
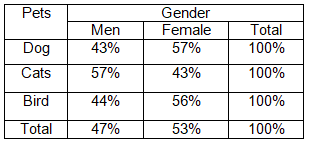
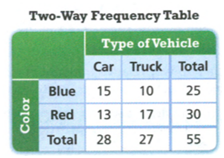
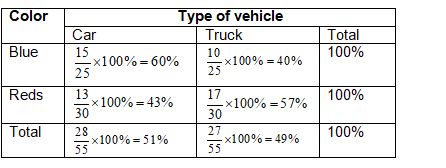
Label the vertices of the figures as ABCD and A′B′C′D′.

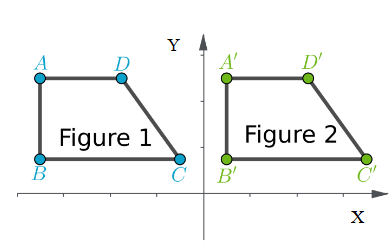
Check for the translation of each vertices.

Notice that there are equal translations and equal inclinations for each vertex.

Therefore, the figures have the same side lengths and same angle measures.

Equal translation and equal inclination of the vertices of the figure will result to the same side lengths and same angle measures of both figures.

Envision Math Grade 8 Volume 1 Chapter 6.1 Solutions

Page 297 Focus On Math Practices Answer

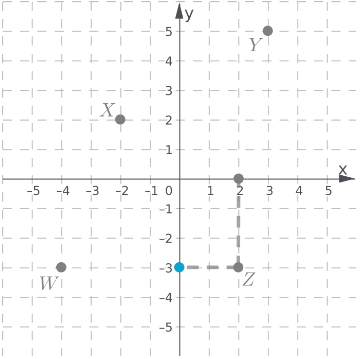
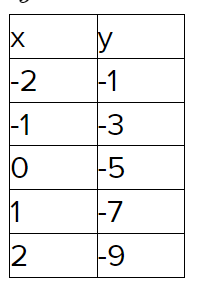
Given:

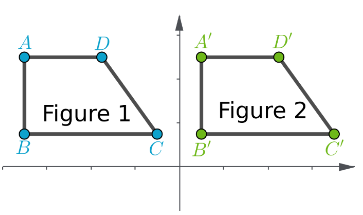
To find:

How to find that the method described shows the side lengths and angle measures equally.

In order to find whether the method described is correct or not we have to refer to the tip mentioned.

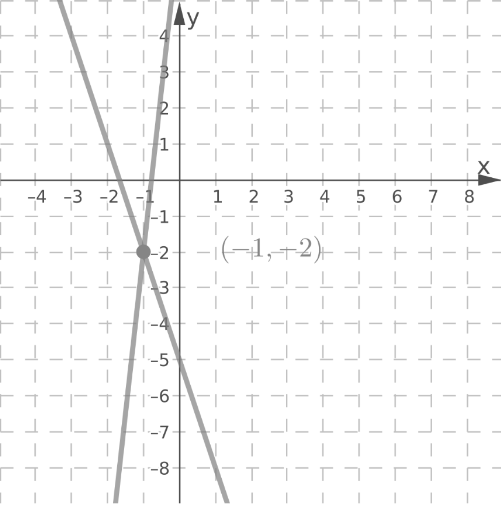
Notice that there are equal translations and equal inclinations for each vertices.

Therefore, the figures have the same lengths and same measures.

Hence, equal translation and inclination of vertices of the figure tell us that the method describes side length and angle measures as equal.

Page 298 Essential Question Answer

To find:

How does translation affect the properties of a two-dimensional figure?

In order to find how translation affects the two-dimensional figure, we have to refer to the tip and make a shape to verify it.

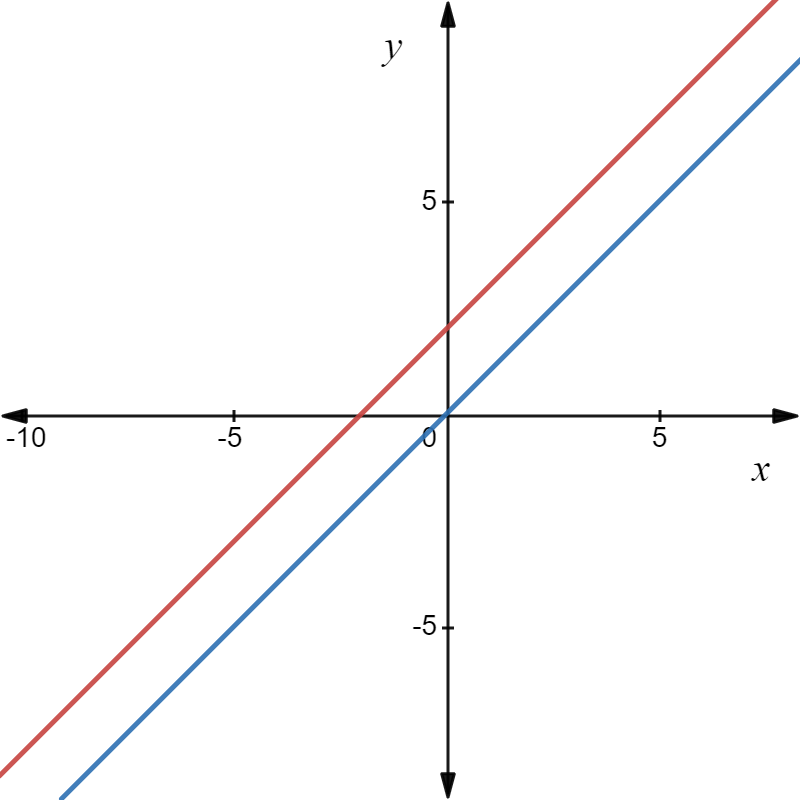
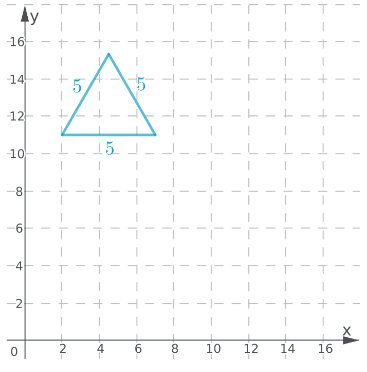
Draw the equilateral triangle;

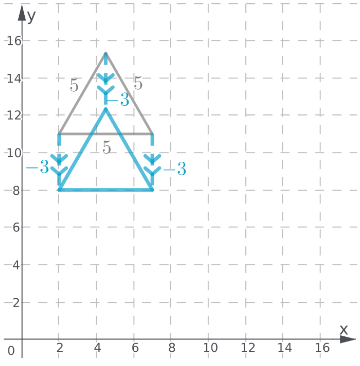
Translate the triangle 3 units downwards from the initial position;

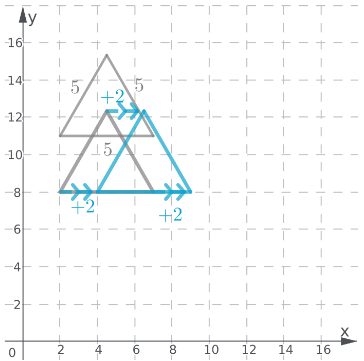
Translate again 2 units to the right from the previous position;

Notice that the shape and the dimensions of the translated triangle are the same as the original triangle;

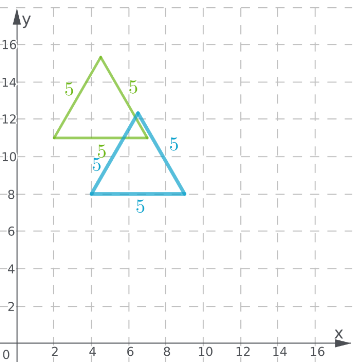
The graph of the triangles is shown. The shape and the dimensions of the translated triangle are the same as the original triangle.

Congruence And Similarity Envision Math Exercise 6.1 Answers

Page 298 Try It Answer

Given:

Use the picture in the example for reference.

To find:

The new location of the table on the plan.

In order to find the new location of the table in the plan refer to the tip mentioned.

Take the arbitrary coordinates for the home such as forming a rectangle.

Using the picture in the example for reference, take arbitrary points forming a square for the fireplace such as

E(0,0),F(0,2),G(2,0) and H(2,2)

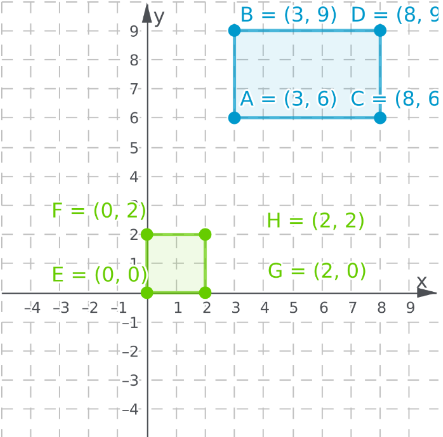
Plot the coordinates for the home and the fireplace.

In order to move the fireplace, translate the coordinates as per instructions.

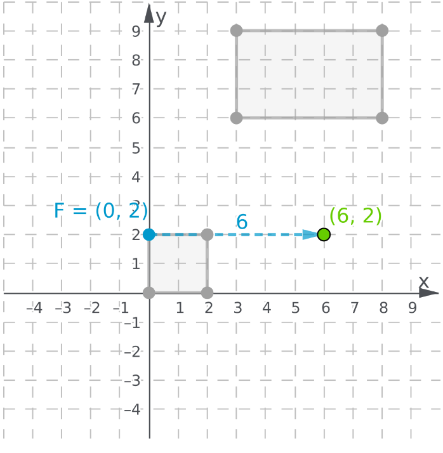
Move the x−coordinate of the point F(0,2) by 6 unitsto the right to get (6,2)

Move the y−coordinate of the new point (6,2) by 3 units towards the downward direction parallel to the negative y−axis to get(6,−1)

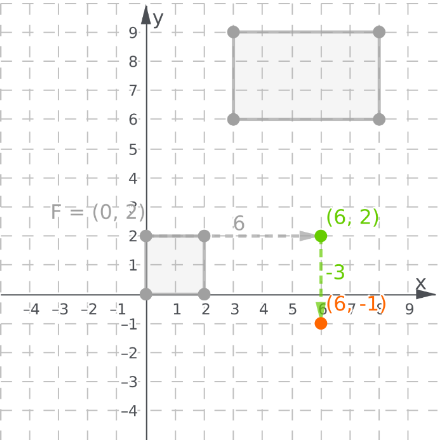
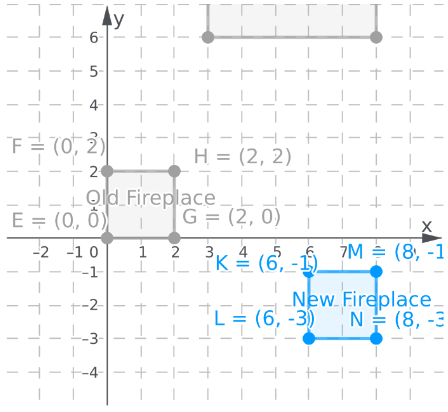
Similarly, translate the other coordinates of the fireplace with the x−coordinate by 6 units to the right and y−coordinate by 3 units to the down.

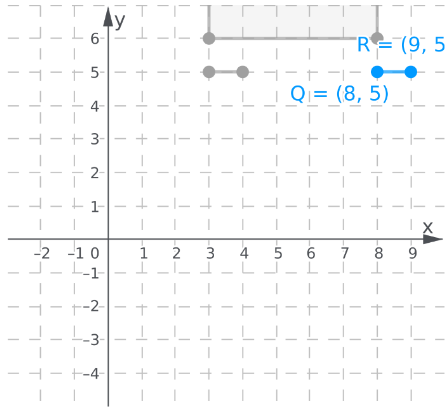
Similarly, plot the coordinates for the original position of the windowO(3,5) and P(4,5) then translate the coordinates pointO(3,5) by 5 units to the right to get Q(8,5)​.

Similarly, translate the other points to get the coordinates of the new window Q(8,5) and (9,5)

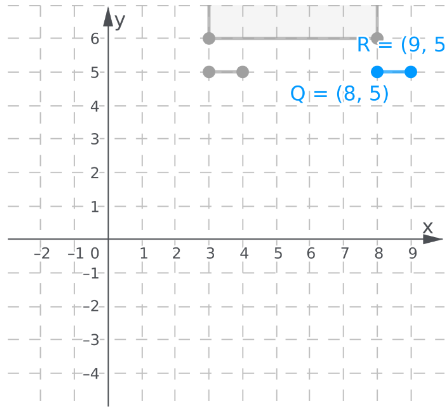
The new location of the window is shown by translating the old coordinates of the position by 5 units to the right.

Page 298 Convince Me Answer

Given:

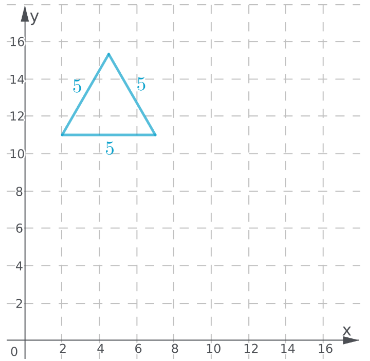
An equilateral triangle with side lengths 5 inches

To find:

The shape and dimensions of the translated figure.

In order to find how translation affects the two-dimensional figure, we have to refer to the tip and make a shape to verify it.

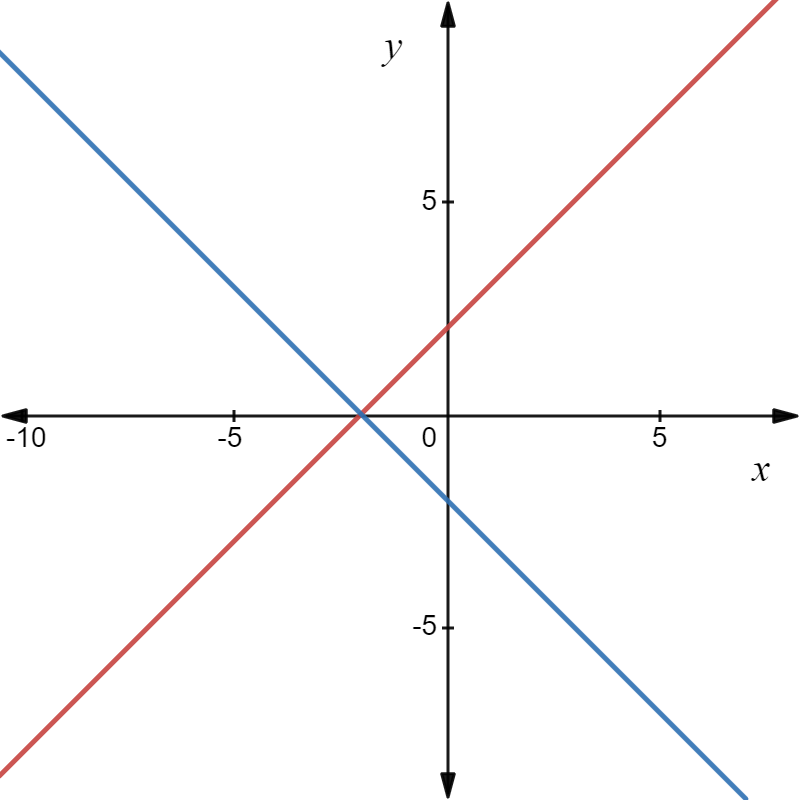
Draw the equilateral triangle;

Translate the triangle 3 units downwards from the initial position;

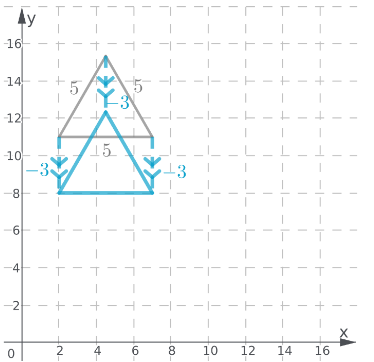
Translate again 2 units to the right from the previous position;

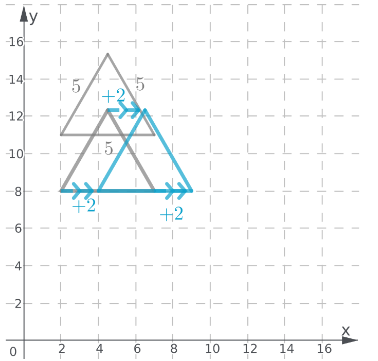
Notice that the shape and the dimensions of the translated triangle are the same as the original triangle;

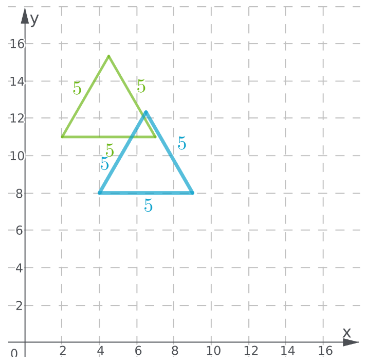
The graph of the triangles is shown. The shape and the dimensions of the translated triangle are the same as the original triangle.

Envision Math Grade 8 Chapter 6.1 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 300 Exercise 2 Answer

Given:

A triangle with its translation.

To find:

How can the side lengths and angle measures for the two triangles be the same?

Recall that translation is a transformation that shifts a figure by space, but does not change the size, shape or orientation of the figure.

Therefore, both shapes are triangles of the same size and with congruent corresponding sides and angles.

Since translation moves the figure by the space and does not change its size, shape or orientation, both the initial triangle and its image are of the same size and with congruent corresponding sides and angles.

Page 300 Exercise 3 Answer

Given:

One vertex of a figure mapped to its image by translating the point 2 units left and 7 units down.

To find:

The rule that maps the other vertices of the figure to their images.

In order to find the rule that maps the vertices of the figure to their image use the tip mentioned.

Let (x, y) be a vertex of the original figure.

(x, y)

Translate the point 2 units left and 7 units down:

(x + (−2),y + (−7))

By using the signs in multiplication, it follows:

(x − 2,y − 7)

The rule that maps the vertices of the figure to their images is:

(x, y) → (x − 2,y − 7)

Page 300 Exercise 4 Answer

Given:

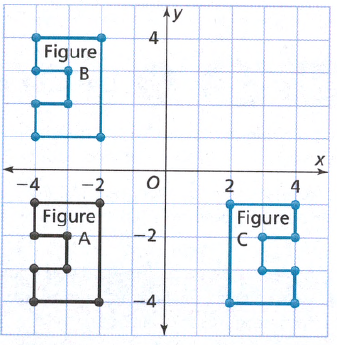
To find:

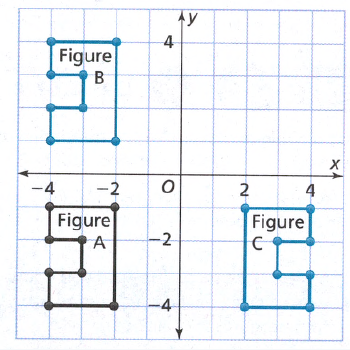
Correct figure which is translation of figure A

In order to find the correct figure which is translation of figure A use the tip mentioned.

The initial and the translated figure have the same size, shape and orientation.

Since figure C have a different orientation from figure A, it is not its image after a translation.

Since figure A and figure B have the same size, shape and orientation, assume that figure B is the image of figure A after a translation.

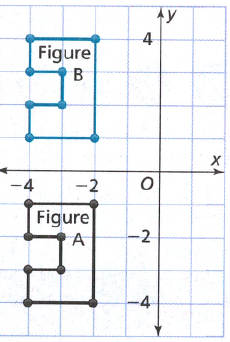
Vertices of figure B are obtained by translating the vertices of figure A 5 units upwards.

The figure B is the image of the figure A after a translation of 5 units upwards.

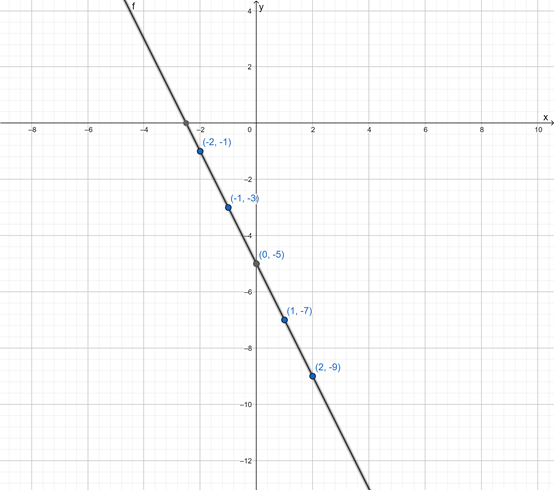
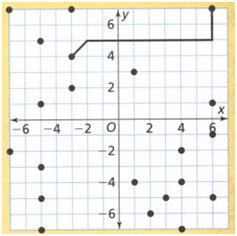
Page 300 Exercise 5 Answer

Given:

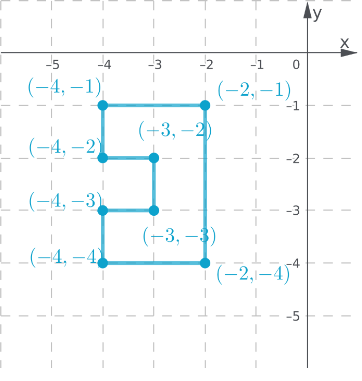
To find:

Graph the translation of Figure A 3 units right and 4 units up.

In order to graph the figure which is translation of figure A use the tip mentioned.

Plot figure A on the coordinate plane,

Translate all the vertices 3 units right

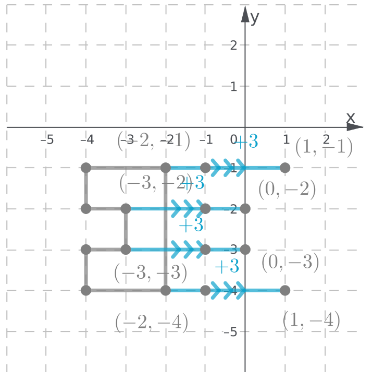
Translate all the vertices from the previous position 4 units up.

Join all the vertices of the figure translated 3 units right and 4 units up.

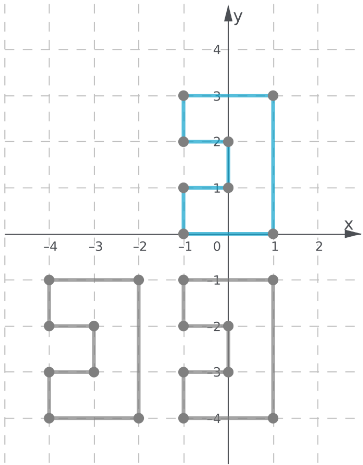
The graph of the translated figure is shown.

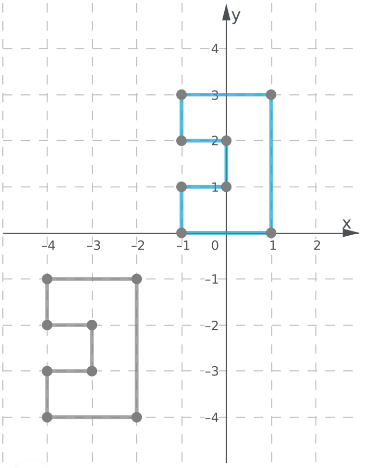
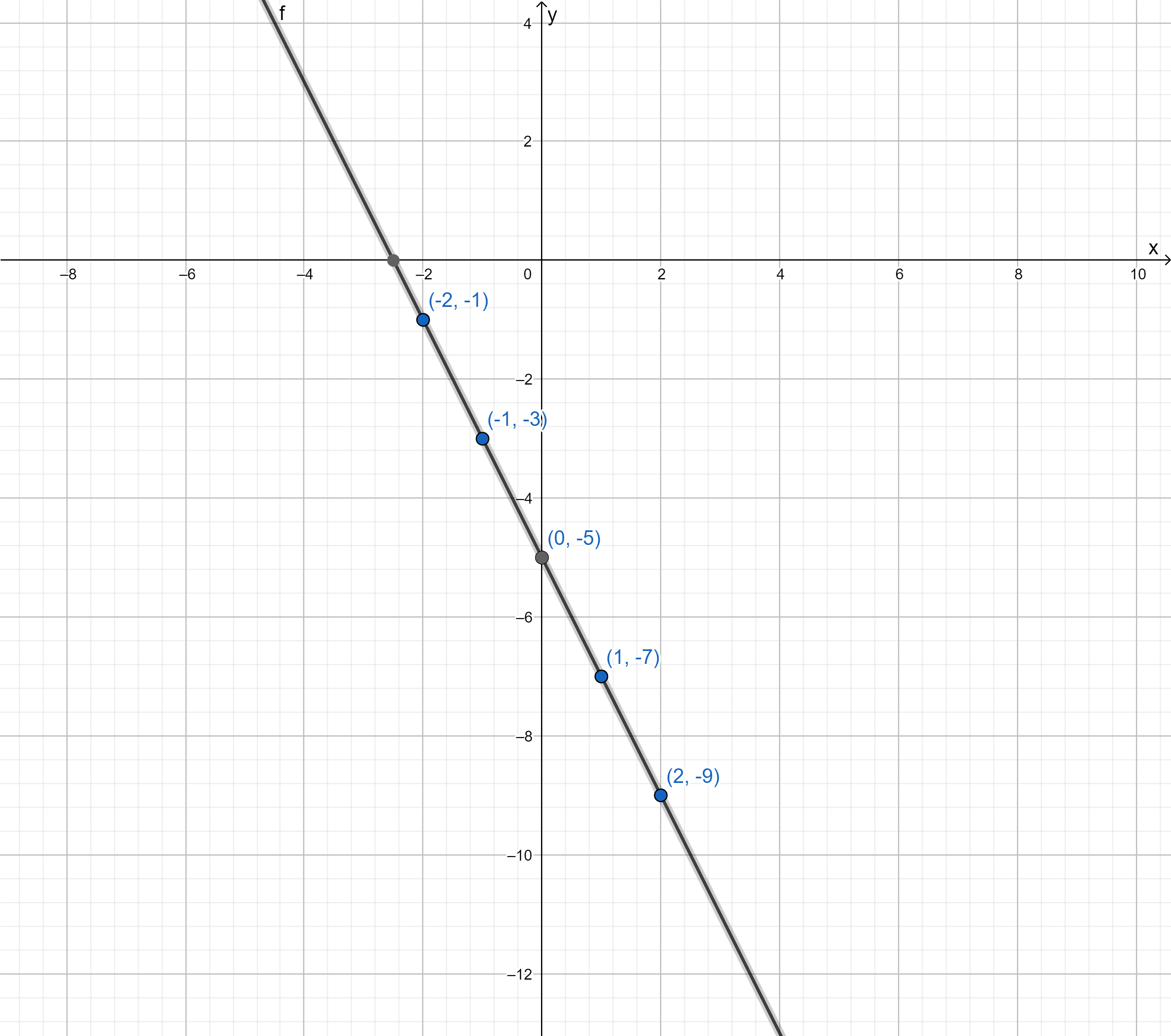
Page 300 Exercise 6 Answer

Given:

To find:

The translation needed to move the figure B to the same position as the image from the item 5.

In order to find the translation needed refer to the tip mentioned and then solve it accordingly.

From B to A the figure was translated 5 units downward.

From A to C the figure was reflected to the other side by multiplying −1 to the x values of figure A.

Figure B was translated 5 units downward then the x values were multiplied by −1 to obtain figure C.

Solutions For Envision Math Grade 8 Exercise 6.1

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 301 Exercise 7 Answer

Given:

The image of GRAM

To find:

Graph of G′R′A′M′ after a translation 11 units right and 2 units up

In order to plot the graph, we have to use the method of translation which is mentioned in the tip.

Translate each vertex 11 units right

Move from the previous position 2 units upward and label the new vertices G′,R′,A′ and M′

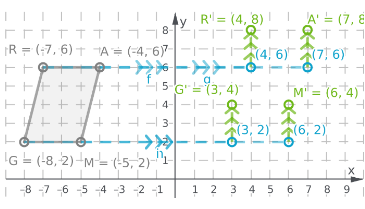
Connect the vertices G′,R′,A′ and M′, to make a G′R′A′M′

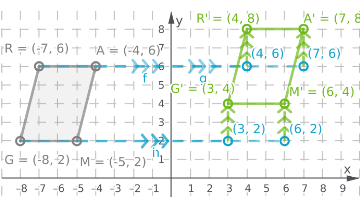
GRAM becomes G′R′A′M′ after translation

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 301 Exercise 9 Answer

Given:

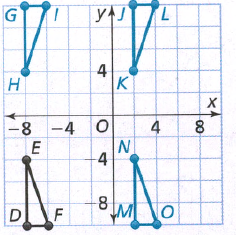
To find:

Triangle whose image is translation of ΔDEF

In order to describe the translation, we need to refer to the tip mentioned.

The initial and the translated figure have the same size, shape, and orientation.

Since triangle △GHI and triangle △JKL have a different orientation from triangle △DEF,they are not its image after a translation.

Since triangle △DEF and triangle △MNO have the same size, shape and orientation, assume that triangle △MNO is the image of triangle △DEF after a translation.

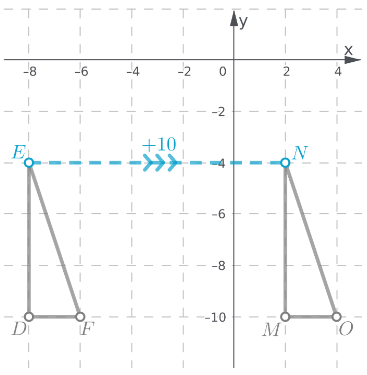
The vertex N is obtained by translating the vertex E 10 units to the right.

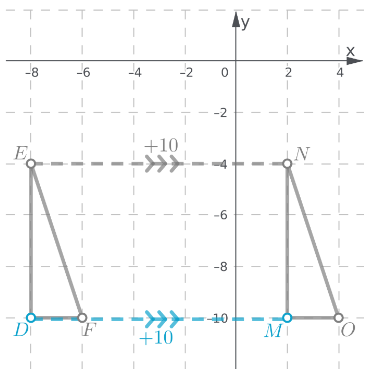
The vertex M is obtained by translating the vertex D10 units to the right.

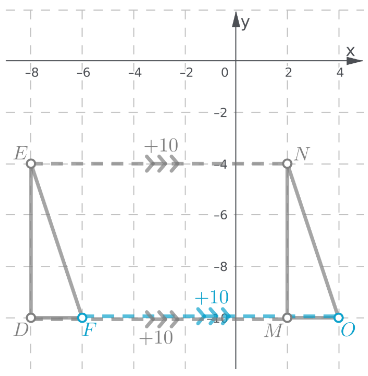
The vertex O is obtained by translating the vertex F 10 units right.

The triangle △MNO is the image of the triangle △DEF after a translation of 10 units right.

Page 301 Exercise 10 Answer

Given: The distance difference of both the figures is 3
unit left and 11 unit down.

To find: The similarities and differences between both the figure.

The similarity between both the figure is both are quadrilateral and on the same plane.

The difference between both the figure is if one lie in X-axis then the second one is in negative Y-axis.

The differences and similarities have been explained.

Envision Math Grade 8 Volume 1 Chapter 6.1 Practice Problems

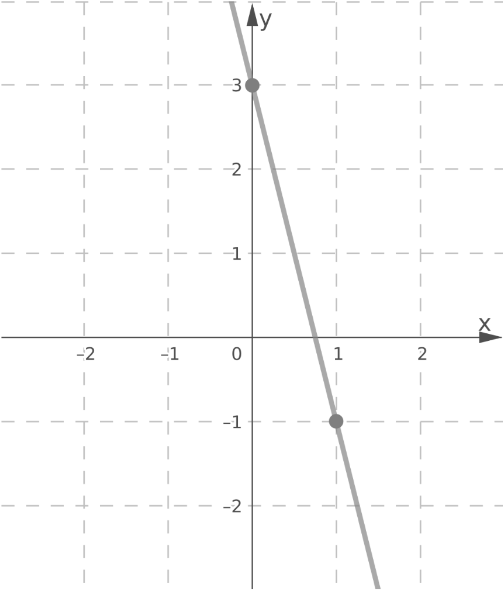
Page 301 Exercise 11 Answer

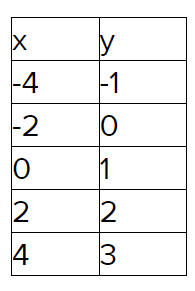
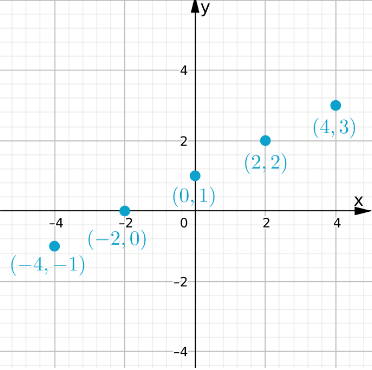
The graph is given.

Have to graph this by shifting some points

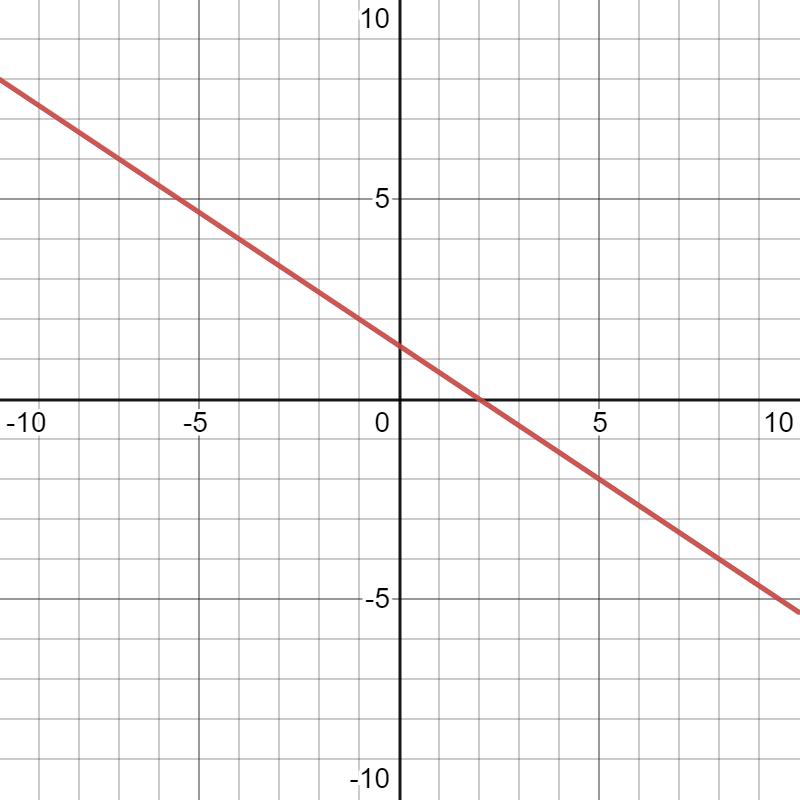
The graph is plotted.

Page 301 Exercise 12 Answer

Given: Length of PQ.

To find: The length of P′Q′.

We will calculate the length by the properties of image formation.

The length of P′Q′ will be negative of the length of PQ.

So, the length of P′Q′ is −2.8

So, the length of P′Q′ is -2.8.

Given: The angle of R.

To find: The angle of R′.

We will calculate the angle by the properties of image formation.

The angle of R′ will be negative of the angle of R.

So, the angle of R′ will be 255 degree.

So, the angle of R′ will be 255 degree.

Envision Math 8th Grade Congruence And Similarity Topic 6.1 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 302 Exercise 13 Answer

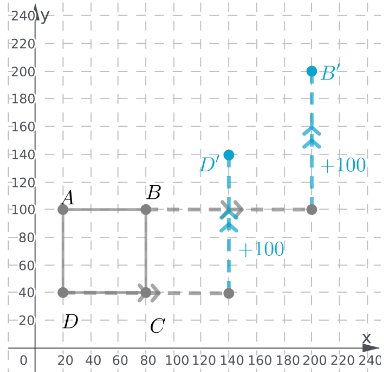
The given figure is shown below:

To draw the image after the given translation

Translate vertex B and D ,120 units to the right.

Move the 2 vertices from the previous position 100 units upward to their final position B′ and D′ respectively.

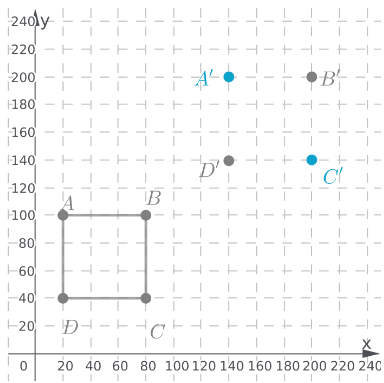
Use a similar pair of translations to plot vertices A′ and C′ respectively.

Join the vertices A′,B′,C′ and D′ to get the translated shape.

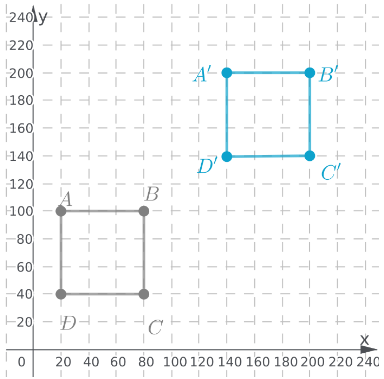
The shape A′B′C′D′ is obtained after translating the given figure ABCD,120 units right and 100 units upwards.

Given:
Length of plot = 240 yards

Length of another plot = 120 yards

Width of plot = 100 yards

To: Find the combined area of the 2 plots in square yards. Step formulation: Find the individual area and then add them.

The combined area of both plots is 69600 yard².

Envision Math Grade 8 Chapter 6.1 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 302 Exercise 14 Answer

Given: Image created by translation.

To: What is true about the preimage of a figure and its image created by a translation?

When the image is translated it moves with the same distance and direction from its preimage. Also the size and shape of the image is same as that of the image.

Correct options are:

1. Each point in the image moves the same distance and direction from the preimage.

3. The preimage and the image are the same size.

4. The preimage and the image are the same shape.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 295 Exercise 1 Answer

Given:

____ have a sum of 90^∘.

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are complementary when they add up to 90^∘.

Hence,

Complementary Angles have a sum of 90^∘.

Page 295 Exercise 2 Answer

Given:.

____ share the same ray.

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are adjacent angles when they share the same ray.

Hence,

Adjacent angles share the same ray.

Envision Math Grade 8 Chapter 6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 3 Answer

Given:.

____ are pairs of opposite angles made by intersecting lines.

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are vertical when they make pairs of opposite angles by intersecting lines.

Hence,

Vertical angles are pairs of opposite angles made by intersecting lines.

Page 295 Exercise 4 Answer

Given:.

____have a sum of 180^∘

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are supplementary when they add up to make an angle of 180^∘.

Hence,

Supplementary angles have a sum of 180^∘.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 6 Answer

Given:

Two integers 6 and \(\frac{1}{2}\)

To find:

The multiplicative sum of the two integers.

In order to find the multiplication of the two integers, we have to multiply the first integer with the second integer.

Hence, 6 x \(\frac{1}{2}\) = 3.

Envision Math Grade 8 Congruence And Similarity Topic 6 Answers

Page 295 Exercise 8 Answer

Given:

To find:

Point W

In order to find the point W

we have to refer to the tip mentioned and follow the following steps.

Move up to the x−axis starting from the point W.

It follows that the x−coordinate of point W is −4

Move right to the y−axis from the point W​

It follows that the y−coordinate of point W is −3

The coordinates of point W are (−4,−3)

Hence, the coordinates of point W are (−4,−3)

Page 295 Exercise 9 Answer

Given:

To find:

Point X

In order to find the point X, we have to refer to the tip mentioned and follow the following steps.

Move downwards towards x−axis starting from the point X. Thus, the value of x−coordinate is −2

Move rightwards towards y−axis from the point X. Thus the value of y− coordinate is 2

Thus the coordinates of the point X(x,y) are (−2,2)

Hence, coordinates of the pointX(x,y) are (−2,2)

Envision Math Grade 8 Volume 1 Student Edition Solutions Guide

Page 295 Exercise 10 Answer

Given:

To find:

Point Y

In order to find the point Y, we have to refer to the tip mentioned and follow the following steps.\

Move downwards towards x−axis starting from the point Y. Thus, the value of x−coordinate is 3

Move leftwards towards y−axis from the point Y. Thus the value of y−coordinate is 5

The coordinates of the point Y are (3,5)

The coordinates of point Y are (3,5).

Solutions For Envision Math Grade 8 Topic 6

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 11 Answer

Given:

To find:

Point Z

In order to find the point Z, we have to refer to the tip mentioned and follow the following steps.

Move upwards towards x−axis starting from the pointZ. Thus, the value of x−coordinate is 2

Move rightwards towards y−axis from the point Z. Thus the value of y−coordinate is −3

Thus, coordinates of point Z are (2,−3)

Hence, the coordinates of point Z are (2,−3)

Grade 8 Envision Math Congruence And Similarity Questions

Page 295 Exercise 12 Answer

Given:

One angle from the pair of supplementary is 130^∘

The missing angle.

In order to find the missing angle we have to refer to the tip and subtract the angle given from 180^∘.

Calculation:

The sum of the supplementary angles = 180^∘

Angle given = 130^∘

If the angles are supplementary then their sum will be equal to 180^∘

Therefore,

Missing angle ​=180 − 130

=180 − 130

= 50^∘

Hence, the missing angle is equal to 50^∘.

Envision Math Topic 6 Congruence And Similarity Step-By-Step Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 13 Answer

Given:.

One angle from the pair of supplementary is 139^∘

To find:

The missing angle.

In order to find the missing angle we have to refer to the tip and subtract the angle given from 180∘.

Calculation:

The sum of the supplementary angles =180^∘

Angle given = 139^∘

If the angles are supplementary then their sum will be equal to 180^∘

Therefore,
​
Missing angle

​= 180 − 139

= 41^∘

Hence, the missing angle is equal to 41^∘.

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 287 Essential Question Answer

Find: to solve a system of linear equation.

A system of linear equations is formed by two or more linear equations that use the same variables.

A linear system solution is the assignment of values to variables in such a way that all the equations are concurrently fulfilled.

Any ordered pair that makes all equations in the system true is a solution of a system of linear equations.

A system of linear equations is formed by two or more linear equations that use the same variable.

Take, for example, a system of linear equations:

The solution of the system is (2,1).

Any ordered pair that makes all equations in the system true simultaneously is a solution of a system of linear equations.

A system of linear equations is formed by two or more linear equations that use the same variables.

Envision Math Grade 8 Volume 1 Chapter 5 Review Exercise Solutions

Page 287 Use Vocabulary In Writing Answer

Find: Use vocabulary terms to find the number of solutions of two or more equations by using the slope and the y-intercept.

The lines will be parallel if the two linear equations have the same slope but distinct y-intercepts.

Because parallel lines never overlap, a system made up of two parallel lines has no solution.

If two linear equations have the same slope and y-intercept, they describe the same line.

There are an unlimited number of solutions since a line crosses itself everywhere.

In any other scenario when the slope varies, the system of equations will have a single solution.

There will be no solution for linear equations with the same slope but a different y-intercept.

There are an unlimited number of solutions to linear equations with the same slope and y-intercept.

In any other scenario, when the slope varies, the system of equations will have a single solution.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 288 Exercise 2 Answer

Given:
​
y = 2x + 10

3y − 6x = 30
​
Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

The equation y = 2x + 10 is written in slope-intercept form.

​
Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Page 288 Exercise 3 Answer

Given

2y = 18x + 72

Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

​
Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Analyze And Solve Systems Of Linear Equations Envision Math Review Exercise Answers

Page 288 Exercise 4 Answer

Given:

y – 2 = 4x

Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

Rewrite the first equation in slope-intercept form,
​

The equations of the linear system have different slopes.

Therefore, the system has no solution.

Since both equations are the not same, they don’t intersect at every point, so the system has no solutions.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 288 Exercise 5 Answer

Given:

Turkey costs $3 per pound at Store A and $4.50 per pound at Store B.

Ham costs $4 per pound at Store B and $6 per pound at Store B.

Michael spends $18 at Store A, and Ashley spends $27 at Store B.

Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-

Let x be the amount of the first kind of meat and y be the second kind of the meat.

Since the boy pays $18 in the first shop, the first equation of the system representing the situation,

3x + 4y = 18

Since the girl pays $27 in the second shop, the second equation of the system representing the situation,

4.5x + 6y = 27

The system of equations,

​
Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Since the system has infinitely many solutions, it follows that there are infinitely many ways for them to buy the same amount of both kinds of meat.

Page 289 Exercise 1 Answer

Given:

y = \(\frac{1}{2} x+1\)

-2x + 4y = 4

Find: graph each system and find the solution.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

Write the second equation in slope-intercept form,

​
Using the same method, calculate the values of y for a few different values of x,

Plot the points (−4,−1),(−2,0),(0,1),(2,2) and (4,3) as shown in the below graph:

Each point on the line represents a solution in the above graph.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

The required graph is:

Envision Math Grade 8 Chapter 5 Review Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 289 Exercise 2 Answer

Given:
​
y = −x − 3

y + x = 2
​
Find: graph each system and find the solution.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

The first equation in the slope-intercept form,

y = −x − 3

Calculate the value of y for x = 0,
​
y = −x − 3

y = −0 − 3

y = −3
​
Using the same method, calculate the values of y for a few other values of x,

Plot the points (0,−3),(1,−4),(2,−5) and (3,−6) and joins the points as shown in the below graph:

The above graph show the slope intercept of y = −x − 3.

Write the second equation in slope-intercept form,
​
y + x = 2

y = 2 − x

y = −x + 2

Graph the line y + x = 2 as shown in the below graph:

The above graph show the slope intercept of y = −x − 3 and y = −x + 2.

Lines y = −x + 2 and y = −x − 3 are parallel, so the system has no solution.

The required graph:

Page 289 Exercise 3 Answer

Given:
​
2y = 6x + 4

y = −2x + 2
​
Find: graph each system and find the solution.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

To graph the first equation 2y = 6x + 4, find the intercepts of the graph of the equation,

2y = 6x + 4

Substitute x = 0 into the equation to find the y-intercept,
​
2y = 6⋅0 + 4

2y = 4

y = 2
​
Since the y-intercept is 2, the first point on the graph of the first equation is (0,2).

Now substitute the value of y = 0 in 2y = 6x + 4,

2(0) = 6x + 4

2(0) – 4 = 6x

-4 = 6x

Since the x-intercept \(-\frac{2}{3}\), the second point on the graph of the first equation is \(\left(-\frac{2}{3}, 0\right)\).

Plot the points (0, 2) and \left(-\frac{2}{3}, 0\right) on the graph as shown below:

To graph the second equation y = −2x + 2, find the intercepts of the graph of the equation,

y = −2x + 2

Substitute x = 0 into the equation to find the y-intercept,
​
y = −2⋅0 + 2

y = −0 + 2

y = 2
​
Since the y-intercept is 2, the first point on the graph of the second equation is (0,2).

Substitute y = 0 in the equation y = −2x + 2,
​
y = −2x + 2

0 = −2x + 2

2x = 2

x = 1
​
Since the x-intercept is 1, the second point on the graph of the second equation is (1,0).

Plot the points(1,0) and (0,2) on the graph as shown below:

The above graph show the slope intercept of y = −2x + 2.

The graph of 2y = 6x + 4 and y = −2x + 2 are shown below:

The above graph shows that the intersection point is (0,2).

Substitute x = 0 and y = 2 into the first equation 2y = 6x + 4,
​
2(2) = 6(0) + 4

4 = 0 + 4

4 = 4
​
It means that the statement is true.

Substitute x = 0 and y = 2 into the first equation y = −2x + 2,
​
y = −2x + 2
​
2 = −2(0) + 2

2 = 0 + 2

2 = 2
​
​It means that the statement is true.

Since both statements are true, the point (0,2) is the solution to the system.

The solution of the given system of equation is (0,2).

The required graph:

Solutions For Envision Math Grade 8 Review Exercise

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 290 Exercise 1 Answer

Given:
​

​−3y = −2x − 1

y = x − 1
​
Find: solve each system.

The solution of the given equation is (x, y) = (4, 3).

Page 290 Exercise 2 Answer

Given:
​
y = 5x + 2

2y − 4 = 10x
​
Find: solve each system.

​
It means the equation has infinite, many solutions.

The solution of the given equation has infinitely many solutions.

Envision Math Grade 8 Volume 1 Chapter 5 Review Practice Problems

Page 290 Exercise 3 Answer

Given:
​
2y − 8 = 6x

y = 3x + 2
​
Find: solve each system.

​
This means the equation has no solution.

There is no solution for the given system of equation. That is x ∈ ∅.

Envision Math 8th Grade Systems Of Equations Review Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 290 Exercise 4 Answer

Given:
​
2y − 2 = 4x

y = −x + 4
​
Find: solve each system.

The solution of the given equation is (x, y)=(1,3).

Page 290 Exercise 1 Answer

Given:
​
−2x + 2y = 2

4x − 4y = 4
​
Find: solve the equation.

There is no solution for the equation.

The statement is false for any value of x and y, so there is no solution. That is (x, y)∈ ∅.

Envision Math Grade 8 Chapter 5 Review Summary

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 290 Exercise 2 Answer

Given:
​
4x + 6y = 40

−2x + y = 4
​
Find: solve the equation.

The solution of the given equation is (x, y) = (1, 6).

Envision Math Grade 8 Topic 5 Review Problems And Solutions

Page 290 Exercise 3 Answer

Given:

A customer at a concession stand bought 2 boxes of popcorn and 3 drinks for $12.

Another customer bought 3 boxes of popcorn and 5 drinks for $19.

Find:

Box of popcorn cost? Drink cost?

Use the elimination method to solve the equation.

Let x be the number of box of popcorn and y the number of drinks.

Since the cost of 2 box of popcorn plus the cost of 3 drinks is $12,

2x + 3y = 12.

And since the cost of 3 box of popcorn plus the cost of 5 drinks is $19,3x + 5y = 19.

A system of equations representing the situation,

​
​The box of popcorn cost $3.

The drink cost $2.

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 277 Exercise 1 Answer

Given: A list of expressions is written on the board.

To Find: How can you make a list of fewer expressions that has the same combined value as those shown on the board? Write the expressions and explain your reasoning.

Like terms are terms whose variables and their exponents are the same.

To combine like terms, add or subtract the coefficients and keep the variables the same.
​
2y  3x  5  -5x

-3y  -2x  -3  5x

Combine the like terms from the given list:
​
2y − 3y ​= −y

3x − 5x − 2x + 5x = x

5 − 3 = 2
​
The new list is obtained by adding and subtracting the coefficients of the like terms, and it looks like: ​−y  x  2

​

Page 277 Focus On Math Practices Answer

Given: Two expressions have a sum of 0.

To find: What must be true of the expressions?

Using the additive inverse property, every two expressions with opposite signs have a sum of 0.

The two expressions must have opposite signs to have a sum of 0.

Envision Math Grade 8 Volume 1 Chapter 5.4 Solutions

Page 278 Essential Question Answer

Find: the properties of equality used to solve systems of linear equations.

We’ve now studied all four equality properties: subtraction, addition, division, and multiplication. For your convenience, we’ve compiled a list of all of them here. You can still have equality if you add, subtract, multiply, or divide the same amount from both sides of an equation.

When there is addition in an equation, the Subtraction Property of Equality is applied. It asserts that the same amount may be subtracted from both sides of the equation without altering the equality.

When there is a subtraction in an equation, the Addition Property of Equality is utilized. It asserts that the same amount may be added to both sides of the equation without affecting the equality.

When you have an equation containing a variable multiplied by a number, you may utilize the Division Property of Equality. It asserts that you can divide both sides of an equation by the same number (as long as that number is not equal to zero) and the equality remains unchanged.

When you have an equation with a variable divided by a number, you may apply the Multiplication Property of Equality. It says that you can multiply both sides of an equation by the same number without affecting the equation’s equality.

By removing a variable, you may use the properties of equality to solve systems of linear equations algebraically.

Elimination is an efficient method when:

Similar variable terms have the same or opposite coefficients, elimination is an effective technique.

One or both equations can be multiplied in such a way that similar variable terms have the same or opposite coefficients.

Page 278 Try It Answer

Given: ​

​2r + 3s = 14

6r − 3s = 6
​
To Find the solutions of r and s.

​
The solution is s = 3.

Page 278 Convince Me Answer

Find a system of equations for a term to be eliminated by adding or subtracting.

To get an equation in one variable, use the elimination approach and either add or subtract the equations. When the coefficients of one variable are opposites, the equations are added to delete a variable; when the coefficients of one variable are equal, the equations are subtracted to eliminate a variable.

For example:
​
​
The solution of the linear system is (0,2).

Which means:

To remove a term by adding, the total of the term’s coefficients must equal zero.

To remove a term by subtracting, the difference between the term’s coefficients must equal zero.

To eliminate a term by adding, the sum of the coefficients of the term must equal 0.

To eliminate a term by subtracting, the difference of the coefficients of the term must equal 0.

Analyze And Solve Systems Of Linear Equations Envision Math Exercise 5.4 Answers

Page 279 Try it Answer

Given: ​

​3x − 5y = −9

x + 2y = 8
​
To find: Use elimination to solve the system of equations.

Solve using the elimination method

(x, y) = (2, 3)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 280 Exercise 1 Answer

Find: the properties of equality used to solve systems of linear equations.

We’ve now studied all four equality properties: subtraction, addition, division, and multiplication. For your convenience, we’ve compiled a list of all of them here. You can still have equality if you add, subtract, multiply, or divide the same amount from both sides of an equation.

When there is addition in an equation, the Subtraction Property of Equality is applied. It asserts that the same amount may be subtracted from both sides of the equation without altering the equality.

When there is a subtraction in an equation, the Addition Property of Equality is utilized. It asserts that the same amount may be added to both sides of the equation without affecting the equality.

When you have an equation containing a variable multiplied by a number, you may utilize the Division Property of Equality. It asserts that you can divide both sides of an equation by the same number (as long as that number is not equal to zero) and the equality remains unchanged.

When you have an equation with a variable divided by a number, you may apply the Multiplication Property of Equality. It says that you can multiply both sides of an equation by the same number without affecting the equation’s equality.

By removing a variable, you may use the properties of equality to solve systems of linear equations algebraically.

Elimination is an efficient method when:

Similar variable terms have the same or opposite coefficients, elimination is an effective technique.

One or both equations can be multiplied in such a way that similar variable terms have the same or opposite coefficients.

Envision Math Grade 8 Chapter 5.4 Explained

Page 280 Exercise 2 Answer

To find: How is solving a system of equations algebraically similar to solving the system by graphing? How is it different?

In both solving a system of equations and solving the system by graphing, the common goal is to find the solution to the system.
Say, for example, that we have a system of equations:

An example of algebraically solving the system follows.

The goal is to find ordered pairs that satisfy both equations.

The ordered pair is a solution

(x, y) = (1,0)

When solving graphically, we graph the first and the second equation and search for points of intersection of the graphs.

The solution – intersection point is represented by the ordered pair of its coordinates.

Both methods produce ordered pairs as solutions if they exist.

If there are no solutions, and impossible equation (such as1 = 0) will emerge in the algebraic method.

In the geometric method, no intersections will be noted when the system has no solutions.

The main difference is in precisely determining the solution.

When graphing, if the coordinates of the intersection are fractions or irrational numbers, the solution is approximated.

The algebraic methods, on the other hand, produce precise values.

In both solving a system of equations algebraically and by graphing, the common goal is to find the solution to the system.

The difference is in the precision of solutions. Algebraic solutions are precise, while the geometric may be approximate.

Solutions For Envision Math Grade 8 Exercise 5.4

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4Page 280 Exercise 3 Answer

Given:

To Find: Construct Arguments Consider the system of equations. Would you solve this system by substitution or by elimination? Explain.

Rewrite the system, using the identity Property of Multiplication:

Notice that the coefficient of y in the first equation, +1, is the inverse of the coefficient of y in the second equation, -1.

Therefore, by adding the 2 equations together, the term y would be cancelled.

The system can be solved through elimination because adding the 2 equations will remove the term y.

Page 280 Exercise 4 Answer

Given: ​

​y − x = 28

y + x = 156
​
To Find: solve each system of equations by using elimination.

The ordered pair is a solution

(x, y) = (64, 92)

Solve using the elimination method

(x, y) = (64, 92)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 280 Exercise 5 Answer

Given: ​

​3c + 6d = 18

6c − 2d = 22
​
To find: solve each system of equations by using elimination.

The ordered pair is a solution

(c, d) = (4, 1)

Solve using the elimination method

(c, d) = (4, 1)

Page 281 Exercise 6 Answer

Given: ​

7x + 14y = 28

5x + 10y = 20
​
To Find: solve each system of equations by using elimination.

The statement is true,

Infinitely many solutions

Solve using the elimination method

Infinitely many solutions

Envision Math Grade 8 Volume 1 Chapter 5.4 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 281 Exercise 7 Answer

Given: ​

​2x − 2y = −4
2x + y = 11
​
To find: Leveled Practice Solve the system of equations using elimination.

The solution to the two equations is:

x = 3,y = 5

Page 281 Exercise 8 Answer

Given: ​

​2y − 5x = −2

3y + 2x = 35
​
To Find: Solve the system of equations using elimination.

Check the solution

Simplify

The ordered pair is a solution

(x, y) = (4, 9)

Solve using the elimination method

(x, y) = (4, 9)

Page 281 Exercise 9 Answer

Given: If you add Natalie’s age and Frankie’s age, the result is 44. If you add Frankie’s age to 3 times Natalie’s age, the result is 70.

To find: Write and solve a system of equations using elimination to find their ages.

Let x be the age of the first person and y the age of the second person.

The sum of ages of the first and the second person is 44, so it follows:

x + y = 44

Since the sum of 3 times the age of the first person and the age of the second person is 70, it follows:

3x + y = 70

A system of equations representing the situation is:
​
x + y = 44

3x + y = 70

Solve the system using elimination:

Check the solution

Simplify

The ordered pair is a solution

(x, y) = (13, 31)

The system of equations is:

The system of equations is:
​
x + y = 44

3x + y = 70
​
The age of the first person is 13 and the age of the second person is 31.

The system of equations is:
​
x + y = 44

3x + y = 70
​
The age of the first person is 13 and the age of the second person is 31.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 281 Exercise 10 Answer

Given: ​

​5x + 10y = 7

4x + 8y = 3
​
To Find: If possible, use elimination to solve the system of equations.

The statement is false

No solution

Solve using the elimination method

No solution

Page 282 Exercise 14 Answer

Given: Consider the system of equations.
​
x − 3.1y = 11.5

−x + 3.5y = −13.5
​
To Find: Solve the system by elimination.

Check the solution

Simplify

The ordered pair is a solution

(x, y) = (-4, -5)

Solve using the elimination method

(x,y) = (−4,−5)

Given: Consider the system of equations.
​
x − 3.1y = 11.5

−x + 3.5y = −13.5
​
To Find: If you solved this equation by substitution instead, what would the solution be? Explain.

The system of equations is given by:

By substitution method, the solution to the system of equations is x = −4 and y = −5.

Envision Math 8th Grade Systems Of Equations Topic 5.4 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 282 Exercise 15 Answer

Given: ​

​3x + 4y = 17

21x + 28y = 109
​
To Find: Higher Order Thinking Determine the number of solutions for this system of equations by inspection only. Explain.

Rewrite the first equation into the slope-intercept form:

Notice, the given equations have the same slope \(-\frac{3}{4}\) but different y intercepts, \(\frac{17}{4} \text { and } \frac{109}{28}\).

Therefore, the system of equations has no solution.

Since the equations, in slope-intercept form, have the same slope but different y-intercepts, the system of equations has no solution.

Envision Math Grade 8 Topic 5.4 Elimination Method Solutions

Page 282 Exercise 16 Answer

Given: Four times a number r plus half a number s equals twelve.

Twice the number r plus a quarter of the number s equals eight.

To Find: What are the two numbers?

Four times a number r plus half a number s equals twelve can be expressed as:

Twice the number r plus a quarter of the numbers equals eight can be expressed as:

Solve the obtained equations:

Multiply both sides

Multiply both sides

Eliminate one variable by adding the equations

0 = -8

The statement is false

No solution

The system of equations has no solution.

The system of equations has no solution.

Envision Math Grade 8 Chapter 5.4 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 282 Exercise 17 Answer

Given: ​

​3m + 3n = 36

8m − 5n = 31
​
To find: Solve the system of equations.

Check the solution

Simplify

The ordered pair is a solution

Solve using the substitution method

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 269 Exercise 1 Answer

To determine the number of solutions of a system by looking at the equations?

The number of solutions of the equation is evident from the slope-intercept form of the equations.

When the equations have different slopes, the system has one solution.

When the equations have the same slopes but different y-intercepts, the system does not have a solution.

When the equations have the same slopes and y-intercepts, the system has infinitely many solutions.

The number of solutions of the system is evident from the slope-intercept form of the equations.

Depending on the slopes and y-intercepts of the equations, the system may have one, infinitely many, or no solutions.

Envision Math Grade 8 Volume 1 Chapter 5.3 Solutions

Page 269 Exercise 2 Answer

Given:
​
2x − 9y = −5

4x − 6y = 2
​
To explain how many solutions does the system of equations has.

Rewrite the first equation in slope-intercept form:

2x − 9y = −5

Move the variable to the right,

−9y = −5 − 2x

Change the signs,

9y = 5 + 2x

Divide both sides by 9,

y = \(\frac{5}{9}+\frac{2}{9} x\)

Use the commutative property to reorder the terms,

y = \(\frac{2}{9} x+\frac{5}{9}\)

Rewrite the second equation in slope-intercept form:

4x − 6y = 2

Move the variable to the right,

−6y = 2 − 4x

Change the signs,

6y = −2 + 4x

Divide both sides by 6 and simplify,

y = \(-\frac{1}{3}+\frac{2}{3} x\)

Use the commutative property to reorder the terms,

y = \(\frac{2}{3} x-\frac{1}{3}\)

Now check the slopes of both the equation,

y = \(\frac{2}{9} x+\frac{5}{9}\)

y = \(\frac{2}{3} x-\frac{1}{3}\)

The equations of the linear system have different slopes this means that the system has one solution.

Therefore, the system has one solution.

Analyze And Solve Systems Of Linear Equations Envision Math Exercise 5.3 Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 269 Exercise 3 Answer

Given:

y + 1 = 2x

y = \(\frac{1}{2} x+2\)

To find: Graph the system of equations and find the solution.

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = −2x + 1,x = 0

Substitute x = 0,

y = −2 × 0 + 1

Calculate the product,

y = 0 + 1

y = 1

Using the same method, calculate the values of y for a few other values of x.

Draw the graph,

Plot the points on the graph.

Draw a line through the plotted points.

Using the same method, graph the line \(y = \frac{1}{2} x+2\).

The lines intersect at the point (−0.4,1.8).

The point of intersection (−0.4,1.8) is the solution of the system and the graph is shown below,

Page 269 Exercise 5 Answer

Given: Finn bought 12 movie tickets. Student tickets cost $4, and adult tickets cost $8.Finn spent a total of $60.

To write and graph a system of equations to find the number of student and adult tickets Finn bought.

Let x be the number of the $4 items and y be the number of the $8 items.

Since the boy bought 12 items in total, the first equation of the system is:

x + y = 12

Solve the equation for y:

x + y = 12

Move the variable to the right,

y = 12 − x

Use the commutative property to reorder the terms,

y = −x + 12

y = -1.x + 12

From the slope-intercept form of a line, it follows:

m = -1, b = 12

Since the boy spent $60 total, the second equation of the system is:

4x + 8y = 60

Move the variable to the right

8y = 60 – 4x

Divide both sides by 8,

y = \(\frac{15}{2}-\frac{1}{2} x\)

Use the commutative property to reorder the terms,

y = \(-\frac{1}{2} x+\frac{15}{2}\)

From the slope-intercept form of a line, it follows:

m = \(-\frac{1}{2}, b=\frac{15}{2}\)

Therefore, the system representing the given situation is:

Draw the line y = -x + 122 using its slope and y-intercept.

y = -x + 12

Since the y-intercept of the line is 12, the line passes through the point (0, 12).

Plot the point (0, 122).

Since the slope of the line is m = \(\frac{-1}{1}\), move 1 unit down and 1 unit right starting from point (0, 12).

It follows that the line passes through point (1, 11) as well.

Draw the line y = \(-\frac{1}{2} x+\frac{15}{2}\) using its slope and y intercept.

y = \(-\frac{1}{2} x+\frac{15}{2}\)

Since the y-intercept of the line is \(\frac{15}{2}\), the line passes through point. \(\left(0, \frac{15}{2}\right)\)

The graph is shown below,

It follows that the lines intersect at point (9,3).

Since the solution to the system is (9,3), it follows that the boy bought 9 items for the price of $4 and 3 items for the price of $8.

The system representing the given situation is:

The boy bought 9 items for the price of $4 and 3 items for the price of $8.

The graph is shown below,

Page 269 Exercise 6 Answer

Given:

−x + 4y = 32

y = mx + 8

The find the value of m.

Rewrite the first equation in slope-intercept form:

−x + 4y = 32

Move the variable to the right,

4y = 32 + x

Divide both sides by 4,

y = \(8+\frac{1}{4} x\)

Notice the value m = \(\frac{1}{4}\) substituted to the second equation will give the system infinitely many solutions since both equations will be equal.

Check the obtained system of equations,

Simplify

Multiply both sides by -1

Eliminate one variable by adding the equations,

0 = 0

The statement is true and has infinitely many solutions.

The value of m is \(\frac{1}{4}\) and it gives infinitely many solutions.

Envision Math Grade 8 Chapter 5.3 Explained

Page 271 Focus On Math Practices Answer

Explain: Can you use the graph to determine the exact number of miles for which the cost of the taxi ride will be the same

There will be a point in the graph where both the lines intersect.

The point of intersection of the lines will give the exact miles for which the cost of both the rides will be the same.

The graph can be used to determine the exact miles for which the cost of both rides will be the same.

Page 272 Essential Question Answer

Systems of linear equations can be solved algebraically. When one of the equations can be easily solved for one of the variables, you can use substitution to solve the system efficiently.

Solve one of the equations for one of the variables. Then substitute the expression into the other equation and solve.

Solve for the other variable using either equation.

Example:

Solve the system −2y − x = −84.91 and 3x + 6y = 254.73 by using substitution.

STEP 1 Solve one of the equations for one variable.
​
−2y − x = −84.91

−x = −84.91 + 2y

= 84.91 − 2y
​
STEP 2 Substitute 84.91 − 2y for x in the other equation.

Then solve.
​
3(84.91−2y) + 6y = 254.73

254.73 − 6y + 6y = 254.73

254.73 = 254.73
​
The result is a true statement. This system has infinitely many solutions.

The substitution method is most useful for systems of 2 equations in 2 unknowns. The main idea here is that we solve one of the equations for one of the unknowns, and then substitute the result into the other equation.

The substitution method can be applied in four steps

Solve one of the equations for either x = or y =.

Substitute the solution from step 1 into the other equation.

Solve this new equation.

Solve for the second variable.

Page 272 Try It Answer

Given:
​
x + y = 50

2x + 5y = 160
​
To find: How many of each type of question was on the exam.

The number of tasks worth two points is represented by x and the number of tasks worth five points is represented by y.

The situation is represented by the following system of equations:

Solve the first equation for y:

x + y = 50

Move the variable to the right,

y = 50 − x

Use the commutative property to reorder the terms,

y = −x + 50

y = -x + 50

Reorder the terms of the equation:

y = 50 – x

Substitute y = 50 − x into the second equation:

2x + 5⋅(50 − x) = 160

Use the Distributive Property to simplify the equation:

2x + 5⋅50 − 5⋅x = 160

Multiply the numbers:

2x + 250 − 5x = 160

Solve the equation for x:

2x + 250 − 5x = 160

Collect like terms

−3x + 250 = 160

Move the constant to the right

−3x = 160 − 250

−3x = −90

Divide both sides by −3

x = 30

There are 30 tasks worth two points.

x + y = 50

Substitute x = 30 into the first equation to obtain y:
​
30 + y = 50

y = 20
​
There are 20 tasks worth five points.

y = 50 – x

2x + 5.(50 – x) = 160

2x + 250 – 5x = 160

There are 30 tasks worth two points.

30 + y = 50

There are 20 tasks worth five points.

Page 272 Convince Me Answer

To find which equation to choose to solve for one of the variables.

When solving the equation for one of the variables, choose the simpler equation in the matter of coefficients of the terms.

Therefore, aim for the equation which has a coefficient of at least one term equal to 1.

Page 273 Try It Answer

Given:

4y + 2x = -6

To find: Solve each system of equations.

Move the expression to the right-hand side by adding its opposite to both sides

Since two opposites add up to zero, remove them from the expression

Substitute the given value of y into the equation, 4y + 2x = -6

Distribute 4 through the parentheses

12 − 2x + 2x = −6

Since two opposites add up to zero, remove them from the expression

12 = −6

The statement is false for any value of x

x ∈ ∅

Since the system has no solution for x, therefore system has no solutions.

Given:

y = \(\frac{1}{4} x-2\)

8y – 2x = -16

To find: Using substitution solve each system of equations.

Substitute the given value of y into the equation 8y – 2x = -16

Distribute 8 through the parentheses

2x − 16 − 2x = −16

Cancel equal terms and eliminate the opposites.

0 = 0

x ∈ R

The statement is true since there are infinitely many solutions for x, the system has infinitely many solutions.

There are infinitely many solutions to the given system of equations.

Solutions For Envision Math Grade 8 Exercise 5.3

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 274 Exercise 1 Answer

Find: substitution, a useful method for solving systems of equations.

The substitution technique is a straightforward approach for solving linear equations algebraically and determining the variables’ solutions. It entails determining the value of the x-variable in terms of the y-variable and then substituting or replacing the value of the x-variable in the second equation, as the name implies.

Substitute to solve a problem of equations:
1. For each variable, solve one of the equations.

2. Step 1’s expression should be substituted into the other equation.

3. Solve the equation that results.

4. To determine the other variable, substitute the result from Step 3 into one of the original equations.

5.Make an ordered pair out of the answer.

Algebraically, systems of linear equations may be solved. When one of the equations is easily solved for one of the variables, substitution can be used to quickly solve the system.

STEP 1: For each variable, solve one of the equations. Then solve the other equation by substituting the expression.

STEP 2: Using either equation, solve for the other variable.

Page 274 Exercise 4 Answer

Given:

y = \(\frac{1}{2} x+4\)

x – y = 8

Find: solve the given equation.

Use substitution method to find the value of x and y.

Substitute the value of y = \(\frac{1}{2} x+4\) in x – y = 8,

Multiply both sides by 2,

2x – x – 8 = 16

x – 8 = 16

x = 16 + 8

x = 24

The value of x = 24.

Now substitute the value of x = 24 in y = \(\frac{1}{2} x+4\),

y = \(\frac{1}{2} \times 24+4\)

y = 12 + 4

y = 16

The value of y = 16

The value of (x, y) = (24,16) by using substitution method.

Envision Math Grade 8 Volume 1 Chapter 5.3 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 274 Exercise 5 Answer

Given:
​
3.25x − 1.5y = 1.25

13x − 6y = 10
​
Find: solve the given equation.

Find the value of x and then use the substitution method to solve the equation.

It means y has no solution. That is y ∈ ∅.

The given equation has no solution.

Page 274 Exercise 6 Answer

Given:
​
y − 0.8x = 0.5

5y − 2.5 = 4x
​
Find: solve the given equation.

Find the value of y and then use the substitution method to solve the equation.

x ∈ R
​
The value of x = x, x ∈ R.

By using the substitution method, the value of

(x, y) = (x,0.5 + 0.8y),x ∈ R.

Page 275 Exercise 7 Answer

Given:
​
p + r = 2,666

p = r + 276
​
Find: Pedro has ______ hits, and Rocky has _____ hits.

Use the substitution method.

Let p be the number of Pedro’s hits and r be the number of Ricky’s hits.

The two teammates have a combined hit total of 2666,

p + r = 2666

Pedro has 276 more hits than Ricky,

p = r + 276

Substitute the value of p = r + 276 in p + r = 2666,
​
(r + 276) + r = 2666

r + 276 + r = 2666

2r + 276 = 2666

2r = 2666 − 276

2r = 2390
​
Divide both sides by 2,

r = 1195

So, Ricky hits r = 1195.

Substitute the value of r = 1195 in p + r = 2666,

p + 1195 = 2666.

Subtract 1195 on both sides,
​
p + 1195 − 1195 = 2666 − 1195

p = 1471
​
The number of Pedro’s hits p = 1471.

Pedro has 1471 hits, and Rocky has 1195 hits.

Page 275 Exercise 8 Answer

Given:
​
2y + 4.4x = −5

y = −2.2x + 4.5
​
Find: solution and ​

2y + 4.4x = −5

y = −2.2x + 4.5

2(−2.2x + ?) + 4.4x = −5

−4.4x + ? + 4.4x = −5

? ≠ −5
​
Use substitution method.

Substitute the value of y = −2.2x + 4.5 in 2y + 4.4x = −5,
​
2(−2.2x + 4.5) + 4.4x = −5

−4.4x + 9 + 4.4x = −5

9 ≠ −5
​
The given equation has no solution.

The statement is not true. There is no solution.

As,
​
2y + 4.4x = −5

y = −2.2x + 4.5

2(−2.2x + 4.5) + 4.4x = −5

−4.4x + 9 + 4.4x = −5

9 ≠ −5

​Envision Math 8th Grade Systems Of Equations Topic 5.3 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 275 Exercise 9 Answer

Given:
​
x + 5y = 0

25y = −5x
​
Find:
​
x + 5y = 0

25y = −5x

x = □y

25y = −5(?)

25y = □y
​
The statement is true. There are     Solutions.

Use substitution method.

Solve for x,
​
x + 5y = 0

x = −5y
​
Substitute the value of x = −5y in 25y = −5x,
​
25y = −5(−5y)

25y = 25y
​
Therefore, the statement is true. There are no solutions.

The statement is true. There are no solutions.

As,
​
x + 5y = 0

25y = −5x

x = −5y

25y = −5(−5y)

25y = 25y

​

Page 275 Exercise 10 Answer

Given:

481 people used the public swimming pool.

The daily prices are $1.25 for children and $2.25 for adults.

The receipts for admission totaled $865.25.

Find: number of children and adults swam at the public pool that day.

Use substitution method.

Let x be the number of children’s and y be the number of adults.

If one day 481 people used to swim, the combined number of children and adults on that day,

x + y = 481.

The ticket for children costs $1.25, and the ticket for adults costs $2.25, so the expression for total earnings on that day,

1.25x + 2.25y

The total earnings for the day were $865.25, so the expression must be equal to this amount,

1.25x + 2.25y = 865.25

Now solve for x,
​
x + y = 481

x = 481 − y

Substitute the value of x = 481 − y in 1.25x + 2.25y = 865.25,
​
1.25(481 − y) + 2.25y = 865.25

601.25 − 1.25y + 2.25y = 865.25

601.25 + 1y = 865.25

y = 865.25 − 601.25

y = 264
​
The number of adults y = 264.

Substitute the value of y = 264 in x = 481 − y,

x = 481 − 264

x = 217
​
The number of children x = 217.

The number of adults y = 264.

The number of children x = 217.

Envision Math Grade 8 Chapter 5.3 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 275 Exercise 11 Answer

Given:
​
6x − 2y = −6

11 = y − 5x
​
And x = −9,y = −4

Find: the correct solution.

Use substitution method.

Solve for y,
​
11 = y − 5x

5x + 11 = y
​
Substitute the value of y = 5x + 11 in 6x − 2y = −6,
​
6x − 2(5x + 11) = −6

6x − 10x − 22 = −6

−4x − 22 = −6

−4x = −6 + 22

−4x = 16
​
Divide both sides by −4,

x = -4

The value of x = -4.

Substitute the value of x = −4 in y = 5x + 11,
​
y = 5(−4) + 11

y = −20 + 11

y = −9
​
The value of y = −9.

The correct solution of the given equation is(x, y) = (−4,−9).

Given:
​
6x − 2y = −6

11 = y − 5x
​
And x = −9,y = −4

Find: error Tim have made.

Use substitution method.

Solve for y in 6x − 2y = −6,
​
6x − 2y = −6

6x + 6 = 2y
​
Divide both sides by 2,

3x + 3 = y-2

The value of y = 3x + 3.

Substitute the value of y = 3x + 3 in 11 = y − 5x,
​
11 = 3x + 3 − 5x

11 − 3 = −2x

8 = −2x
​
Divide both sides by −2,

-4 = x-2

The value of x = -4.

Substitute the value of x = −4 in y = 3x + 3,
​
y = 3(−4) + 3

y = −12 + 3

y = −9
​
The value of y = −9.

The correct solution is (x,y) = (−4,−9).

Tim made an error by substituting the equation into the initial equation rather than into the other one.

The solution to the system is (x,y) = (−4,−9).

The student made an error by substituting the equation into the initial equation rather than into the other one.

Page 276 Exercise 14 Answer

Given:

The perimeter of a photo frame is 36 inches.

The length is 2 inches greater than the width.

Find: the dimensions of the frame.

Use the formula of perimeter and use substitution method.

According to the formula for polygon, the perimeter of the photo frame is the sum of its sides,

P = 2l + 2w

Substitute P = 36 and l = w + 2 in P = 2l + 2w,
​
36 = 2(w + 2) + 2w

36 = 2w + 4 + 2w

36 = 4w + 4

36 − 4 = 4w

32 = 4w
​
Divide both sides by 4,

8 = w

The length of the photo frame 8 inches.

Substitute the value of w = 8 in L = w + 2,
​
L = 8 + 2

L = 10
​
The width of the photo frame is 10 inches.

The dimensions of the frame are:

The length of the photo frame 8 inches.

The width of the photo frame is 10 inches.

Page 276 Exercise 15 Answer

Given:

The capacity of the auditorium is 500 people.

The members would like to false $2,050 every night to cover all expenses, by selling tickets.

Find: each type of ticket must have been sold for the members to raise exactly $2,050.

Use substitution method.

Let d be the number of adult and s be the number of students.

If one day 500 people used the facility, the combined number of adults and student on that day,

d + s = 500.

The ticket for adults costs $6.50, and the ticket for students costs $3.50, so the expression for total earnings on that day,

6.50d + 3.50s.

The total earnings for the day were $2050, so the expression must be equal to this amount,

6.50d + 3.50s = 2050.

Solve for d,
​
d + s = 500

d = 500 − s

Substitute the value of d = 500 − s in 6.5d + 3.5s = 2050,
​
6.5(500 − s) + 3.5s = 2050

3250 − 6.5s + 3.5s = 2050

3250 − 3s = 2050

3250 − 2050 = 3s

1200 = 3s
​
Divide both sides by 3,

s = 400

The number of students s = 400.

Substitute the value of s = 400 in d + s = 500,
​
d + 400 = 500

d = 500 − 400

d = 100
​
The number of adults d = 100.

To raise the fund of $2050, there should be 100 adults and 400 students.

Given:

At one performance, there were three times as many student tickets sold as adult tickets.

There were 480 tickets sold at that performance

Find: ticket sales fall below $2,050.

Use substitution method.

According to question s = 3d.

Since the total number of ticket sold is 480,

d + s = 480

Substitute s = 3d in d + s = 480,
​
d + 3d = 480

4d = 480
​
Divide both sides by 4,

d = 120

So, the number of adults are d = 120.

Substitute the value of d = 120 in s = 3d,
​
s = 3(120)

s = 360
​
So, the number of students are s = 360.

Total earning T from tickets,

T = s × 3.50 + d × 6.50.

Substitute the value of s = 360 and d = 120 in

T = s × 3.50 + d × 6.50,
​
T = s × 3.50 + d × 6.50

T = 360 × 3.50 + 120 × 6.50 = 2040
​
Total earning T from tickets are $2,040.

So, the goal is to fall short,

$2050 − $2040 = $10.

The goal to achieve total payment of $2050 is to fall short by $10.

Envision Math Grade 8 Topic 5.3 Substitution Method Solutions

Page 276 Exercise 16 Answer

Given:

y = 145 – 5x …(1)

0.1y + 0.5x = 14.5 …(2)

Find: the solution of the equation.

Try to compare both equations,

Rearrange the equation(2),

∴ 0.1y = 14.5 − 0.5x

∴y = 145 − 5x (multiply by10)

So here both lines are coincidental and they have infinite solutions.

Option A is correct.

Put x = 20 in eq.(1),

∴ y = 145 − 5(20)

∴ y = 145 − 100

∴ y = 45

means point (20,45) is solution.

Option B is correct.

Put x = 10 in eq.(1),

∴ y = 145 − 50

∴ y = 95

means point (10,95) is solution.

Option C is correct.

Here both lines are coincidental so they have infinite solutions.

So option D is incorrect.

Equations y = 145 − 5x and 0.1y + 0.5x = 14.5 have infinite solutions and (20,45) and (10,95) are also solutions.

Option A,B and C are correct options.

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 257 Exercise 1 Answer

Given: Draw three pairs of lines, each showing a different way that two lines can intersect or not intersect.

How are these pairs of lines related?

There are n ways 2 lines can relate to each other.

The first way is that they are parallel, meaning they do not have any intersections.

The second way is if they are not parallel, but are not the same line. in this case, they have exactly 1 intersection.

The third and last way is, if the lines are the same, in this case, all of their points are the same.

That means they intersect at infinitely many points.

2 lines cannot have 2 points in common because 2 points clearly define a line.

That means if there is a line passing through both points, there cannot be another that does the same.

2 lines cannot have 2 points in common because 2 points clearly define a line.

If they have more than 1 point in common, it means they are the same line and have infinitely many common points.

Envision Math Grade 8 Volume 1 Chapter 5.2 Solutions

Page 263 Focus On Math Practice Answer

To find: What does the point of intersection of the lines represent in the situation?

Point of intersection means the point at which two lines intersect.

The coordinates of the point of intersection represent the solution to both linear equations simultaneously.

The coordinates of the point of intersection represent the values of x and y that satisfy both equations at the same time.

Page 264 Essential Question Answer

To Find: How does the graph of a system of linear equations represent its solution?

Each pair of lines represents a system of linear equations. A system of linear equations is formed by two or more linear equations that use the same variables.

you can use the graphs to determine the number of solutions for each system.

The equations of the linear system
​
y = x + 4

y = −x + 6
​
have different slopes.

The system has 1 solution (1,5).

A solution of a system of linear equations is an ordered pair that makes all equations in the system true.

The equations of the linear system
​
y = x + 3

y = x + 1
​
have the same slopes and different y−intercepts.

The system has no solution.

The equations of the linear system
​
x + y = −2

3x + 3y = −6
​
have the same slopes and the samey−intercepts. They represent the same line.

The system has infinitely many

Systems of equations can be solved by looking at their graphs.

A system with one solution has one point of intersection.

A system with no solution has no points of intersection.

A system with infinitely many solutions has infinite points of intersection.

Analyze And Solve Systems Of Linear Equations Envision Math Exercise 5.2 Answers

Page 264 Try It Answer

Given: ​

​y = 3x + 5

y = 2x + 4
​
To find: The solution is the point of intersection.

y = 3x + 5

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = 3x + 5,x = 0

Substitute x = 0

y = 3 × 0 + 5

Calculate the product

y = 0 + 5

Remove 0

y = 5

Using the same method, calculate the values of y for a few other values of x

Plot the points on the graph.

Draw a line through the plotted points.

Using the same method, graph the line y = 2x + 4.

The lines intersect at the point (−1,2).

The point of intersection (−1,2) is the solution of the system.

Page 264 Convince Me Answer

Given:
​
y = 3x + 5

y = 2x + 4
​
Find: the point of intersection of the graphs represent the solution of a system of linear equations.

Find the points and then plot the points and second equation to find the point of intersection.

Given: y = 3x + 5

The first equation is written in the slope-intercept form.
Calculate the value of y for x = 0,
​
y = 3x + 5

y = 3(0) + 5

y = 0 + 5

y = 5
​
Using the same method, calculate the values of y for a few other values of x,

Plot the points on the graph (0,5),(1,8),(−1,2),(2,11) and the equation y = 2x + 4 draw a line as shown below:

The above graph show that the point of intersection is (−1,2).

The point of intersection of the graphs belongs to the first and the second line at the same time and satisfies the equations of both graphs.

Therefore, the point of intersection (−1,2) is a point that satisfies the system of the equations of the two graphs.

Page 266 Exercise 1 Answer

To find: How does the graph of a system of linear equations represent its solution?

Each pair of lines represents a system of linear equations. A system of linear equations is formed by two or more linear equations that use the same variables.

you can use the graphs to determine the number of solutions for each system.

The equations of the linear system
​
y = x + 4

y = −x+ 6
​
have different slopes.

The system has 1 solution(1,5).

A solution of a system of linear equations is an ordered pair that makes all equations in the system true.

The equations of the linear system
​
y = x + 3

y = x + 1
​
have the same slopes and different y−intercepts.

The system has no solution.

The equations of the linear system
​
x + y = −2

3x + 3y = −6
​
have the same slopes and the same y−intercepts. They represent the same line.

The system has infinitely many solutions.

Systems of equations can be solved by looking at their graphs.

A system with one solution has one point of intersection.

A system with no solution has no points of intersection.

A system with infinitely many solutions has infinite points of intersection.

Envision Math Grade 8 Chapter 5.2 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 266 Exercise 2 Answer

Given: If a system has no solution.

To Find: what do you know about the lines being graphed?

A system has a solution if the lines have a point of intersection.

If a system has no solution, therefore the lines are parallel to each other.

If a system has no solution, the lines being graphed are parallel to each other.

Page 266 Exercise 4 Answer

Given: ​

​y = −3x − 5

y = 9x + 7
​
graph each system of equations and find the solution.

y = -3x – 5

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = −3x −5,x = 0

Substitute x = 0

y = −3 × 0−5

Calculate the product

y = 0 − 5

Remove 0

y = −5

Using the same method, calculate the values of y for a few other values of x.

Plot the points (-2, 1), (-1, -2), (0, -5) and (1, -8).

Draw a line through the plotted points.

Using the same method, graph the line y = 9x + 7.

The lines intersect at the point (-1, -2).

The point of intersection (−1,−2) is the solution of the system.

Page 266 Exercise 5 Answer

Given: ​

​y = −2x − 5

6x + 3y = −15
​
graph each system of equations and find the solution.

y = 2x – 5

The first equation is in slope-intercept form.

Write the second equation in slope-intercept form:

6x + 3y = −15

Move the variable to the right

3y = −15 − 6x

Divide both sides

y = −5 − 2x

Reorder the terms

y = −2x − 5

Equations of both lines are equal, so lines are the same.

Calculate the value of y for x = −2:

y = −2x − 5,x = −2

Substitute x = −2

y = −2 × (−2)−5

Multiply

y = 4 − 5

Calculate

y = −1

Using the same method, calculate the values of y for a few different values of x

Plot the points on a coordinate plane.

Draw a line through the plotted points.

Each point on the line represents a solution.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

Page 266 Exercise 6 Answer

Given: ​

​y = −4x + 3

8x + 2y = 8
​
graph each system of equations and find the solution.

In order to graph y = −4x + 3, calculate two points on the line.

Calculate the value of y for x = 0:

y = −4x + 3,x = 0

Substitute x = 0

y = −4 × 0 + 3

Calculate the product

y = 0 + 3

Remove 0

y = 3

Calculate the value of y for x = 1:

y = −4x + 3,x = 1

Substitute x = 1

y = −4 × 1 + 3

Calculate the product

y = −4 + 3

Calculate

y = −1

Thus, the points(0,3) and (1,−1) are on the graph of

y = −4x + 3.

Plot the points(0,3) and (1,−1).

Graph y = −4x + 3 by drawing a line through the points.

Write the second equation in the slope-intercept form:

8x + 2y = 8

Move the variable to the right

Divide both sides

y = 4 − 4x

Reorder the terms

y = −4x + 4

Calculate the value of y for x = 0:

y = −4x + 4,x = 0

Substitute x = 0

y = −4 × 0 + 4

Calculate the product

y = 0 + 4

Remove 0

y = 4

Step 8

Calculate the value of y for x = 1:

y = −4x + 4,x = 1

Substitute x = 1

y = −4 × 1 + 4

Calculate the product

y = −4 + 4

Eliminate the opposites

y = 0

Thus, the points (0,4) and (1,0)are on the graph of 8x + 2y = 8.

Plot the points(0,4) and (1, 0).

Graph 8x + 2y = 8 by drawing a line through the points.

Lines y = −4x + 3 and 8x + 2y = 8 are parallel.

Since the lines are parallel, there is no point of intersection.

Therefore, the system has no solution.

The lines y = −4x + 3 and 8x + 2y = 8 are parallel, so the system has no solution.

Solutions For Envision Math Grade 8 Exercise 5.2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 267 Exercise 7 Answer

Given: ​x + 4y = 8

3x + 4y = 0
​
Graph each system of equations to determine the solution.

Rewrite the first equation in slope-intercept form:

x + 4y = 8

Move the variable to the right

4y = 8 − x

Divide both sides

y = \(2-\frac{1}{4} x\)

Reorder the terms

y = \(-\frac{1}{4} x+2\)

Calculate the value of y for x = 0:

y = \(-\frac{1}{4} x+2, x=0\)

Substitute x = 0

y = \(-\frac{1}{4} \times 0+2\)

Calculate the product

y = 0 + 2

Remove 0

y = 2

Using the same method, calculate the values of y for a few other values of x.

Plot the points (0,2),(4,1),(−4,3)

Draw a line through the plotted points.

Using the same method, graph the line 3x + 4y = 0.

The lines intersect at the point (−4,3).

The point of intersection (−4,3) is the solution of the system.

Page 267 Exercise 8 Answer

Given: ​

​2x − 3y = 6

4x − 6y = 12
​
graph each system of equations to determine the solution.

Write the first equation in slope-intercept form:

2x − 3y = 6

Move the variable to the right

−3y = 6 − 2x

Change the signs

3y = −6 + 2x

Divide both sides

y = \(-2+\frac{2}{3} x\)

Reorder the terms

y = \(\frac{2}{3} x-2\)

Write the second equation in slope-intercept form:

4x – 6y = 12

Move the variable to the right

-6y = 12 – 4x

Change the signs

6y = -12 + 4x

Divide both sides

y = \(-2+\frac{2}{3} x\)

Reorder the terms

y = \(\frac{2}{3} x-2\)

Equations of both lines are equal, so lines are the same.

Calculate the value of y for x = -9

y = \(\frac{2}{3} x-2, x=-9\)

Substitute x = -9

y = \(\frac{2}{3} \times(-9)-2\)

Multiply

Reduce

y = -2 x 3 -2

Calculate

y = -8

Using the same method, calculate the values of y for a few different values of x

Plot the points(−9,−8),(−6,−6),(−3,−4),(6,2) and (9,4).

Draw a line through the plotted points.

Each point on the line represents a solution.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

Envision Math Grade 8 Volume 1 Chapter 5.2 Practice Problems

Page 267 Exercise 11 Answer

Given: ​

​y = 1.5x + 1

y = −1.5x + 5.5
​
To Find: Graph the system of equations, then estimate the solution.

We have,

y = 1.5x + 1

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = 1.5x + 1,x = 0

Substitute x = 0

y = 1.5 × 0 + 1

Calculate the product

y = 0 + 1

Remove 0

y = 1

Using the same method, calculate the values of y for a few other values of x.

Plot the points (-2, -2), (0, 1), (2, 4), (4, 7) and (6, 10)

Draw a line through the plotted points.

Using the same method, graph the line y = -1.5x + 5.5.

The lines intersect at the point (1.5,3.25).

The point of intersection (1.5,3.25) is the solution of the system.

Envision Math 8th Grade Systems Of Equations Topic 5.2 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 268 Exercise 12 Answer

Given:

​−3y = −9x + 3

−6y = −18x − 12
​
To Find: graph and determine the solution of the system of equations.

Write the first equation in the slope-intercept form:

−3y = −9x + 3

Calculate

y = 3x − 1

Calculate the value of y for x = 0:

y = 3x−1,x = 0

Substitute x = 0

y = 3 × 0 − 1

Calculate the product

y = 0 − 1

Remove 0

y = −1

Using the same method, calculate the values of y for a few other values of x.

Plot the points (0,−1),(1,2),(2,5)

Draw a line through the plotted points.

Write the second equation in slope-intercept form:

−6y = −18x − 12

Change the signs

6y = 18x + 12

Divide both sides

y = 3x + 2

Using the same method, graph the line y = 3x + 2.

Lines y = 3x − 1 and y = 3x + 2 are parallel.

Since the lines are parallel, there is no point of intersection.

Therefore, the system has no solution.

The lines y = 3x − 1 and y = 3x + 2 are parallel, so the system has no solution.

Envision Math Grade 8 Topic 5.2 Graphing Linear Systems Solutions

Page 268 Exercise 13 Answer

Given: ​

​x + 5y = 0

25y = −5x
​
To Find: graph and determine the solution of the system of equations.

Write the first equation in slope-intercept form:

x + 5y = 0

Calculate

y = \(-\frac{1}{5} x\)

Write the second equation in slope-intercept form:

25y = −5x

Divide both sides

25y ÷ 25 = −5x ÷ 25

Divide

Rewrite

y = \(-\frac{5}{25} x\)

Reduce the fraction

y = \(-\frac{1}{5} x\)

Equations of both lines are equal, so lines are the same.

Calculate the value of y for x = -10:

y = \(-\frac{1}{5} x, x=-10\)

Substitute x = -10

y = \(-\frac{1}{5} \times(-10)\)

Multiply

Reduce

y = 2

Using the same method, calculate the values of y for a few different values of x

Plot the points (-10, 2), (-5, 1), (0, 0), (5, -1) and (10, -2).

Draw a line through the plotted points.

Each point on the line represents a solution.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

Envision Math Grade 8 Chapter 5.2 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.2 Page 268 Exercise 14 Answer

Given: Higher Order Thinking The total cost, c, of making n copies can be represented by a system of equations.

To find: How many copies you need to make for the total cost to be the same at both stores.

The first shop offers an unlimited number of items n for $5.The equation representing the price c in the first shop is given by:

c = 5

The second shop charges 20ϕ = $0.2 per item and additional $2 for the service.

The equation representing the price c in the second shop is given by:

c = 0.2n + 2

Since the price of the service in the first shop is $5 regardless of the number of items, find the number of items the second shop offers for $5

Find the number of items the second shop offers for $5 by solving the system.

Set the sides equal 5 = 0.2n + 2

Solve the equation n = 15

A possible solution is (c,n) = (5,15)

Check the solution

Simplify

The ordered pair is a solution.

(c,n) = (5,15)

It follows that the second shop offers 15 items for $5.

For the total price to be the same in both shops, the number of items purchased in the second shop must be 15.

Given: Higher Order Thinking The total cost, c, of making n copies can be represented by a system of equations.

To explain, If you have to make a small number of copies, which store should you go to.

The cost in store W is $5 for any number of copies.

The cost in store z is given by the equation:

C = 2 + 0.2n

Where C is the cost and n is the number of copies.

C = 2 + 0.2n

The store z is preferred as far as the number of copies costs less than $5. express this using the inequality:

2 + 0.2n < 5

Solve the inequality for n:

2 + 0.2n < 5

Move the constant to the right

0.2n < 5 − 2

Calculate

0.2n < 3

Divide both sides of the inequality by 0.2

n < 15

Store z is preferred for a small number of copies less than 15.

Store z is preferred for a small number of copies less than 15.

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 257 Exercise 1 Answer

Given: Draw three pairs of lines, each showing a different way that two lines can intersect or not intersect.

How are these pairs of lines related?

There are n ways 2 lines can relate to each other.
The first way is that they are parallel, meaning they do not have any intersections.

The second way is if they are not parallel, but are not the same line. in this case, they have exactly 1 intersection.

The third and last way is, if the lines are the same, in this case, all of their points are the same.

That means they intersect at infinitely many points.

2 lines cannot have 2 points in common because 2 points clearly define a line.

That means if there is a line passing through both points, there cannot be another that does the same.

2 lines cannot have 2 points in common because 2 points clearly define a line.

If they have more than 1 point in common, it means they are the same line and have infinitely many common points.

Envision Math Grade 8 Volume 1 Chapter 5.1 Solutions

Page 257 Focus On Math Practice Answer

To find: Look for Relationships is it possible for any of the pairs of lines drawn to have exactly two points in common?

Here we will see every relation between two lines and try to find the pairs of lines have exactly two points in common.

Here two lines are parallel means they have no common point,

Here two lines intersects at one point means they have one common point,

Here two lines are coincidental means they have infinite common points,

Here we see all possibilities like two lines have maximum infinite common points and minimum zero common points but that is not possible to have two common points.

Two lines can’t have exactly two common points.

Analyze And Solve Systems Of Linear Equations Envision Math Answers

Page 258 Essential Question Answer

If the two lines have different slopes, the system has exactly one solution (whether the lines have the same intercept or different intercepts).

If they have the same slope and the same intercept they are the same line, so there are infinitely many solutions to the system.

If they have the same slope and different intercepts then they are parallel and there is no solution to the system.

The slopes are different. The lines intersect at 1 point.

The slopes are the same, and the y-intercepts are different. The lines are parallel.

The slopes are the same, and the y-intercepts are the same. The lines are the same(coincident)

Page 258 Try It Answer

Given: y = x + 1, y = 2x + 2

To find: To explain how many solutions does this system of equation has.

y = x + 1

The first equation is written in slope-intercept form.

y = 2x + 2

The second equation is written in slope-intercept form.
​
y = 1x + 1

y = 2x + 2
​
Notice that the equations of the linear system have different slopes.

Since the equations have different slopes, the system has one solution.

The system of equations has one solution. The equations have different slopes, so lines intersect at one point.

Page 259 Try It Answer

Given:
​y = −3x + 5
y = −3x − 5
​
To determine how many solutions does each system of equations has.

Here first we try to compare both equation’s slop and intercept.

Two lines equations:
y=−3x+5
…(1)

y=−3x−5
…(2)

Here we can see both lines slops are equal (m1 and m2 = −3) and y−intersects are different(c1 ≠ c2).

So lines are parallel and they have no solution.

The system of equations y = −3x + 5 and y = −3x − 5 have no solution.

Given: y = 3x + 4, 5y − 15x − 20 = 0

To determine how many solutions does each system of equations has.

y = 3x + 4

The first equation is written in slope-intercept form.

Rewrite the second equation in slope-intercept form:

5y − 15x − 20 = 0

5y − 15x − 20 = 0

Move the expression to the right

5y = 15x + 20

Divide both sides by 5

y = 3x + 4

Since both equations have the same slope-intercept form, they represent the same line.

Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Envision Math Grade 8 Chapter 5.1 Explained

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 260 Exercise 1 Answer

To find: How are slopes and y-intercepts related to the number of solutions of a system of linear equations?

Deanna drew the pairs of lines below.

Each pair of lines represents a system of linear equations. A system of linear equations is formed by two or more linear equations that use the same variables.

you can use the graphs to determine the number of solutions for each system.

The equations of the linear system
​
y = x + 4

y = −x + 6
​
have different slopes.

The system has 1 solution(1,5).

A solution of a system of linear equations is an ordered pair that makes all equations in the system true.

The equations of the linear system
​
y = x + 3

y = x + 1
​
have the same slopes and differenty−intercepts.

The system has no solution.

The equations of the linear system
​
x + y = −2

3x + 3y = −6
​
have the same slopes and the samey−intercepts. They represent the same line.

The system has infinitely many solutions.

Systems of equations can be solved by looking at their graphs.

A system with one solution has one point of intersection.

A system with no solution has no points of intersection.

A system with infinitely many solutions has infinite points of intersection.

Page 260 Exercise 2 Answer

Given: ​

​3x + y − 2 = 0
5x + y − 2 = 0
​
To find: Construct Arguments Macy says that any time the equations in a system have the same y-intercept, the system has infinitely many solutions. Is Macy correct? Explain.

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Consider the following system of equations:
​
3x + y − 2 = 0

5x + y − 2 = 0
​
Now,

3x + y − 2 = 0

Write the equation in the slope-intercept form:

3x + y − 2 = 0

y = −3x + 2

Similarly, it follows that the slope-intercept form of 5x + y − 2 = 0 is:

5x + y − 2 = 0

y = -5x + 2

it is clear that the equations have the same y−intercepts viz. 2.

Solve the system of equations:

3x + y − 2 = 5x + y − 2 = 0

Rewrite the expression

{​3x + y − 2 = 0
5x + y − 2 = 0
​
Move constants to the right

{​3x + y = 2
5x + y = 2
​
Multiply both sides

{​3x + y = 2
−5x − y = −2
​
Eliminate one variable by adding the equations

-2x = 0

Divide both sides

x = 0

Substitute the value of x

3 × 0 + y = 2

Solve the equation

y = 2

A possible solution is

(x,y) = (0,2)

Check the solution
​
3 × 0 + 2 − 2 = 5 × 0 + 2 − 2

= 0
​
Simplify
​0 = 0

= 0
​
The ordered pair is a solution

(x,y) = (0,2)

It follows that the system has a unique solution.

Hence, Macy is not correct.

A system of equations has infintie solutions if the y-intercepts are equal and slopes are equal as well. Macy is incorrect.

Solutions For Envision Math Grade 8 Exercise 5.1

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 260 Exercise 5 Answer

a

Substitute \(\frac{1}{2} x=y\) into the equation to find the value of y:

y = y + 3

Subtract y from both sides of the equation:

y – y = y – y + 3

Calculate the differences:

0 = 0 + 3

Add the numbers:

0 = 3

Since the statement 0 = 3 is false, the system of linear equations has no solution.

The solution yields to 0 = 3 which is false, the system of equations has no solution.

Page 261 Exercise 7 Answer

convert the given equations in slope intercept form and then derive their sloped and y-intercepts individually. Further, compare them are make a conclusion.

7y = 13.3x – 56

Divide equation of rover B by 7 on both sides.

Simplify the equation.

Divide

Reduce

Convert the expression

Multiply both sides

70y = 133x – 560

Divide both sides

Rover B: \(y=\frac{19}{10} x-8\)

Compare the equation of rover B with the slope-intercept form of the equation.

The slope obtained for the equation of rover B is m_B = \(\frac{19}{10}\).

Convert m_B to the decimal number.

m_B = 1.9

The y-intercept obtained for the equation of rover B is b_B = -8.

Rover A: y = 1.9x − 8

Similarly, compare the equation of rover A with the slope-intercept form of the equation.

The slope obtained for the equation of rover A is m_A = 1.9.

The y−intercept obtained for the equation of rover A
is b_A = −8.

Comparing m_A and m_B shows m_A= m_B

Comparing b_A and b_B shows b_A = b_B.

The system of equations has infinite solutions as slopes and y−intercepts are the same for both equations.

The slope for the rover A equation is equal to the slope for the rover B equation. The y−intercepts of the equations are −8. The system of equations has infinite solutions.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 261 Exercise 8 Answer

Given: ​

y = x − 3

4x − 10y = 6
​
To find: How many solutions does this system have?

Convert the equation in a slope-intercept form then simplify the equation and find the slope and intercept.

y = x – 3

The first equation is written in slope-intercept form.

Rewrite the second equation in slope-intercept form:

4x − 10y = 6

Move the variable to the right

−10y = 6 − 4x

Change the signs

10y = -6 + 4x

Divide both sides

Reorder the terms

y = 1x – 3

The equations of the linear system have different slopes.

The system has one solution.

Envision Math Grade 8 Volume 1 Chapter 5.1 Practice Problems

Page 261 Exercise 10 Answer

Given: ​−64x + 96y = 176

56x − 84y = −147
​
To find: What can you determine about the solution(s) of this system?

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Rewrite the first equation in slope-intercept form:

−64x + 96y = 176

Move the variable to the right

96y = 176 + 64x

Divide both sides

Reorder the terms

Rewrite the second equation in slope-intercept form:

56x − 84y = −147

Move the variable to the right

−84y = −147−56x

Change the signs

84y = 147 + 56x

Divide both sides

Reorder the terms

The equations have equal slopes.

The equations have different y−intercepts.

Therefore, the graphs of the equations are parallel lines, so the system has no solution.

Equations have equal slopes, but different y−intercepts, so the system has no solution.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 261 Exercise 11 Answer

Given: ​

​y = 8x + 2

y = −8x + 2
​
To Find: Determine whether this system of equations has one solution, no solution, or infinitely many solutions.

Solve the system of equations then Eliminate one variable by adding the equations to find the ordered pair is a solution.

Solve the system of equations:

y = 8x + 2

y = −8x + 2
​
Simplify

−8x + y = 2

8x + y = 2
​
Eliminate one variable by adding the equations

2y = 4

Divide both sides

y = 2

Substitute the value of y

8x + 2 = 2

Solve the equation

x = 0

A possible solution is
(x,y)=(0,2)

Check the solution

​2 = 8 × 0 + 2

2 = −8 × 0 + 2
​
Simplify

2 = 2

2 = 2
​
The ordered pair is a solution

One solution

The given system of equations has one solution.

Page 261 Exercise 12 Answer

Given: ​

​2x + y = 14

2y + 4x = 14
​
To Find: Construct Arguments Maia says that the two lines in this system of linear equations are parallel. Is she correct? Explain.

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Rewrite the first equation in slope-intercept form:

2x + y = 14

Move the variable to the right

y = 14 − 2x

Reorder the terms

y = −2x + 14

Rewrite the second equation in slope-intercept form:

2y + 4x = 14

Move the variable to the right

2y = 14 − 4x

Divide both sides

y = 7 − 2x

Reorder the terms

y = −2x + 7

Now,
​
y = −2x + 14

y = −2x + 7
​
The equations have equal slopes.
​
y = −2x + 14

y = −2x + 7
​
The equations have different y−intercepts.

Therefore, the graphs of the equations are parallel lines.

Equations have equal slopes, but different y−intercepts, so the linear equations are parallel.

Maia is correct.

Page 261 Exercise 13 Answer

Given: ​

​y = 2x + 10

y = x + 15
​
To find: Describe a situation that can be represented by using this system of equations. Inspect the system to determine the number of solutions and interpret the solution within the context of your situation.

Compare the equation with a slope-intercept form of the linear equation then According to the slope-intercept form make graphs and solve equations.

Let y and x be the total distance covered by a man in kilometres and the time taken to cover the distance in hours respectively.

Compare the equation y = 2x + 10 with a slope-intercept form of the linear equation:

m = 2,b = 10

According to the slope-intercept form, the y-intercept value is 10 means, at 0 hours the first person covered 10 kilometres.

To draw a line, calculate y for some values of x.

y = 2x + 10

Substitute the value of x = 1 in the equation:

y = 2(1) + 10

Solve for y:

y = 2 × 1 + 10

Calculation

y = 12

In the same manner, complete the table.

Plot the points (1,12),(2,14) and (3,16)

Draw a line through the points.

The line y = 2x + 10 shows the first person’s time-distance relation.

In the same manner, draw the line y = x + 15 that shows the second person’s time-distance relation.

Draw the lines y = 2x + 10 and y = x + 15 in the same plane.

The two lines are meet at a point (5,20).

Since the lines are meet at one point, it has one solution.

The system has one solution that is (5,20)

It represents two persons will meet at 20 kilometres distance after 5 hours.

Envision Math 8th Grade Systems Of Equations Topic 5.1 Key Concepts

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 262 Exercise 14 Answer

Given: ​

12x + 51y = 156

−8x − 34y = −104
​
To find: does this system has one solution, no solutions, or infinitely many solutions? Write another system of equations with the same number of solutions that uses the first equation only.

Simplify each equation in the system, observe both equations. If the equations in the system are multiples of common equations then it has infinitely many solutions.

Simplify each equation in the system.

Simplify the first equation:

12x + 51y = 156

Simplify

4x + 17y − 52 = 0

After simplification, the first equation is:

4x + 17y − 52 = 0

Simplify the second equation:

−8x − 34y = −104

Simplify

4x + 17y − 52 = 0

After simplification, the second equation is:

4x + 17y − 52 = 0

After simplification, both equations are equal.

If the equations in the system are multiples of common equations then it has infinitely many solutions.

Since the system has infinitely many solutions.

The common equation of the system is:

4x + 17y − 52 = 0

To find the second equation in another system, the common equation is multiplied by any number.

The equation 4x + 17y − 52 = 0 is multiplied by 4 on both sides: 4(4x + 17y − 52) = 4(0)

Any expression multiplied by 0 is 0 :

4(4x + 17y − 52) = 0

Multiply each term in the parentheses by 4 :

16x + 68y − 208 = 0

Add 208 on both sides of an expression:

16x + 68y − 208 + 208 = 0 + 208

Cancel the terms:

16x + 68y = 0 + 208

Simplify the right side of the equation:

16x + 68y = 208

Since the equations in the system are multiples of the common equations, the system has infinitely many solutions.

Another system of equations with infinitely many solutions is:
​
12x + 51y = 156

16x + 68y = 208

​Envision Math Grade 8 Topic 5.1 Graphing Linear Systems Solutions

Page 262 Exercise 16 Answer

Given: ​

​4x + 3y = 8

8x + 6y = 2
​
To find: the system has one solution, no solution, or an infinite number of solutions?

Convert the equation in a slope-intercept form then simplify the equation and find the slope and y-intercept.

Rewrite the first equation in slope-intercept form:

4x + 3y = 9

Move the variable to the right

3y = 9 – 4x

Divide both sides

Reorder the terms

Rewrite the second equation in slope-intercept form:

8x + 6y = 2

Move the variable to the right

6y = 2 – 8x

Divide both sides

Reorder the terms

The equations have equal slopes.

The equations have different y−intercepts.

Therefore, the graphs of the equations are parallel lines, so the system has no solution.

Equations have equal slopes, but different y−intercepts, so the system has no solution.

Envision Math Grade 8 Chapter 5.1 Lesson Breakdown

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 262 Exercise 17 Answer

Given: Qx + Ry = S and y = Tx + S

what circumstances does the system of equations have infinitely many solutions?

Solve the equations for ythen simplify the equation and find the slope and y−intercept.

Solve the first equation for y:

Qx + Ry = S

Move the expression to the right

Ry = S − Qx

Divide both sides

Separate the fraction

Write as a product

The equation is now written in slope-intercept form.

For the system to have infinitely many solutions, the slopes of the lines and the y-intercepts must be equal.

The Slopes of the lines are \(-\frac{Q}{R} \text { and } T\).

The y-intercepts of the lines are \(\frac{S}{R} \text { and } S\).

The system has infinitely many solutions if:

Page 262 Exercise 19 Answer

Choose the statement that correctly describes how many solutions there are for this system of equations.

Solve the given systems of equations:

Simplify

Multiply both sides

Eliminate one variable by adding the equations

−7y = −21

Divide both sides

y = 3

Substitute the value of $y$

−2x + 3 × 3 = 9

Solve the equation

x = 0

A possible solution is

(x,y) = (0,3)

Check the solution

Simplify

The ordered pair is a solution

One solution

Notice that the slopes of the two equations are different.

Therefore the given system of equations has exactly one solution because the slopes are not equal.

The given system of equations has exactly one solution because the slopes are not equal because that options (A),(B) and (C) statements are incorrect.

Therefore, the correct option is (D) Exactly one solution because the slopes are not equal.

Envision Math Grade 8 Solutions, Systems Of Linear Equations

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 2 Answer

Given: When lines are the same distance apart over their entire lengths, they are _____________________ .

To find: Choose the best term from the box to complete each definition.

Parallel lines are lines in a plane that do not intersect at any point; for example, two straight lines in a plane that do not collide at any point are said to be parallel. Curves that do not touch or intersect and maintain a constant minimum distance are considered to be parallel.

When lines are the same distance apart over their entire lengths, they are parallel.

Envision Math Grade 8 Solutions, Systems of Linear Equations Page 255 Exercise 4 Answer

Given: A _________ is a relationship between two variables that gives a straight line when graphed.

To find: Choose the best term from the box to complete each definition.

Linear equations are nothing but yet another subset of “equations”. Any linear calculations requiring more than one variable can be done with the help of linear equations. The standard form of a linear equation in one variable is of the form ax + b = 0. Here, x is a variable, and a and b are constants. While the standard form of a linear equation in two variables is of the form ax + by = c. Here, x and y are variables, and a, b and c are constants.

A linear equation is a relationship between two variables that gives a straight line when graphed.

Envision Math Grade 8 Volume 1 Chapter 5 Systems Of Linear Equations Solutions

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 5 Answer

Given: y = 2x − 3

To find: Identify the slope and the y − intercept of the equation.

The equation is written in slope-intercept form.

y = 2x + (−3)

On comparing the equation by slope-intercept form we get,

The slope is 2 and the y-intercept is −3.

The slope is 2 and the y-intercept is −3.

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 6 Answer

Given: y = −0.5x + 2.5

To find: Identify the slope and the y−intercept of the equation.

The equation is written in slope-intercept form.

y = −0.5x + 2.5

On comparing the equation by slope-intercept form we get,

The slope is −0.5 and the y-intercept is 2.5.

The slope is −0.5 and the y-intercept is 2.5.

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 7 Answer

Given: y − 1 = −x

To find: Identify the slope and the y−intercept of the equation.

Write the equation in slope-intercept form:

y − 1 = −x

Move the constant to the right

y − 1 + 1 = −x + 1

Remove the opposites

y = −x + 1

On comparing the equation by slope-intercept form we get,

The slope is −1 and the y-intercept is 1.

The slope is −1 and the y−intercept is 1.

Envision Math Grade 8 Chapter 5 Analyze And Solve Systems Of Equations

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 8 Answer

Given: \(y=\frac{2}{3} x-2\)

To find: Graph the equation.

From the slope-intercept form of a line, it follows:

m = \(\frac{2}{3}\), b = -2

Since the y-intercept of the line is −2, it follows that the line passes through the point (0,−2)

Draw the graph of the equation and plot point (0,−2),

The graph of the equation is shown below,

Envision Math Chapter 5 Systems Of Linear Equations Detailed Answers

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 9 Answer

Given: y = −2x + 1

To find: Graph the equation.

From the slope-intercept form of a line, it follows:

m = −2,b = 1

Since the y-intercept of the line is 1, it follows that the line passes through the point (0,1).

Draw the graph of the equation and plot point (0,1),

The graph of the equation is shown below,

Envision Math 8th Grade Chapter 5 Step-By-Step Systems Of Equations Solutions

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 10 Answer

Given: y − x = 5

To find: Solve the equation for y.

y – x = 5

Move the variable to the right-hand side by adding its opposite to both sides,

y − x + x = 5 + x

Since two opposites add up to zero, remove them from the expression,

y = 5 + x

Use the commutative property to reorder the terms,

y = x + 5

Therefore, the value of y is x + 5.

Systems Of Linear Equations Solutions Grade 8 Envision Math Chapter 5

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 11 Answer

Given: y + 0.2x = −4

To find: Solve the equation for y.

y + 0.2x = -4

Move the variable to the right-hand side by adding its opposite to both sides

y + 0.2x − 0.2x = −4−0.2x

Since two opposites add up to zero, remove them from the expression

y = −4−0.2x

Use the commutative property to reorder the terms,

y = −0.2x−4

Therefore, the value of y is −0.2x−4.

Envision Math Grade 8 Chapter 5 Solutions Guide

Envision Math Grade 8 Solutions, Systems Of Linear Equations Page 255 Exercise 12 Answer

Given: \(-\frac{2}{3} x+y=8\)

To find: Solve the equation for y.

Move the expression to the right-hand side by adding its opposite to both sides,

Since two opposites add up to zero, remove them from the expression,

Use the commutative property to reorder the terms,

The value of y is \(\frac{2}{3} x+8\).

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3

Page 243 Exercise 1 Answer

The video mentioned above shown some images that predict the height and the length of various humans and things.

The reason is for knowing the average height each of them follows and how much it will grow in their lifetime.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”

“What is my height and is that normal for my age?”

This is the question that made up my mind after watching this video.

Page 243 Exercise 2 Answer

The video mentioned above shown some images that predict the height and the length of various humans and things.

The reason is for knowing the average height each of them follows and how much it will grow in their lifetime.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The main question that comes to my mind after watching this video is “Is that height normal for my age?”.

The main question that I will answer that I saw in the video is “Is that height normal for my age?”.

Page 243 Exercise 3 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

An answer that I was predicted to this main question is 158 cm and it is below average for my age.

An answer that I was predicted to this main question is 158 cm and it is below average for my age. I found my answer by measuring myself using a tape and the people of my age are far taller than me this means that I’m shorter than them.

Envision Math Grade 8 Volume 1 Chapter 4.3 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 243 Exercise 4 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too small to be the answer is 50 cm since infants grow 50 cm within the age of three.

A number that is too large to be the answer is 214 cm since the percentage of 7 footers is only 0.000038%.

On the number line below, we have written a number that is too small to be the answer. Also, we have written a number that is too large.

Page 243 Exercise 5 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too small to be the answer is 50 cm since infants grow 50 cm within the age of three.

A number that is too large to be the answer is 214 cm since the percentage of 7 footers is only 0.000038%.

My height is 158 cm.

Plotting my prediction on the same number line, I get,

Page 244 Exercise 6 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

In this situation, information regarding the average height of a normal healthy person of my age would be more helpful to know.

This is because I can use that information to know that my height is normal or not.

In this situation, information regarding the average height of a normal healthy person of my age would be more helpful to know.

I can use that information to know that my height is normal or not.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 244 Exercise 7 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

To get the information I need regarding the height, I have to use a measuring tape.

This will determine the height of every person accurately.

A measuring tape can be used to get the information I need. My height is 158 cm.

Investigate Bivariate Data Envision Math Topic 4.3 Answers

Page 244 Exercise 8 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure your height several times.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

From this way, I have found out that my height is 158 cm and it is below average.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 244 Exercise 9 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

I have found out that my height is 158 cm.

The average height of a person of my age is 175 cm.

This is far greater than my prediction.

The answer to the Main Question is that the average height of a person of my age is 175 cm. It is far greater than my prediction.

Page 245 Exercise 10 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

The answer that I saw in the video is 175 cm as the average height for my age.

Envision Math Grade 8 Chapter 4.3 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 245 Exercise 11 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

My answer doesn’t match the answer in the video. This is because my genetic factors and lack of physical work are some of the reasons for my shorter height.

My answer doesn’t match the answer in the video. This is because genetic factors play a vital role in deciding one’s height.

Page 245 Exercise 12 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”.

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

My answer doesn’t match the answer in the video. This is because my genetic factors and lack of physical work are some of the reasons for my shorter height.

I am going to do some physical exercises, stretching, and yoga to increase my height in order to change my model.

Yes, I would change my model now that I know the answer.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 246 Exercise 13 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Measure your height several times.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

The model helps me answer the Main Question by making accurate measurements of my height and to know whether my height is normal or not for my age.

Page 246 Exercise 14 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “What is my height and is that normal for my age?”

The answer that I was predicted to this main question is 158 cm.

The answer that I saw in the video is “175 cm”.

My answer doesn’t match the answer in the video. This is because my genetic factors and lack of physical work are some of the reasons for my shorter height.

The height which I notice in my classmate’s model is that he is 185 cm tall.

This helps me to know under which conditions people’s height is increasing.

The calculations differ based on the genetic factors and physical conditions I am in. This helps me to know under which conditions people’s height is increasing.

Solutions For Envision Math Grade 8 Topic 4.3

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 246 Exercise 15 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The length of my classmate’s wingspan is 185 cm.

I have also calculated his height which is also 185 cm.

This means that both his wingspan or arm span and his height are equal.

My classmate’s wingspan is 185 cm. This is equal to my classmate’s height. My model predicts my classmate’s actual height well.

Page 247 Exercise 1 Answer

The number of visits, age, months, and time are examples of measurement data.

Colors, gender, and nationality are examples of categorical data.

If 7out of 20 people prefer reading a book to watching a movie, then saying that 35 of the people polled prefer reading a book is the relative frequency.

The number of visits, age, months, and time are examples of measurement data.

Colors, gender, and nationality are examples of categorical data.

If 7 out of 20 people prefer reading a book to watching a movie, then saying that 35 of the people polled prefer reading a book is the relative frequency.

Envision Math Grade 8 Topic 4.3 Graphing Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 247 Exercise 1 Answer

This scatter plot shows a positive association between vacation and hours of employees at ABC Corporation.

Some of the points are far from the trend line. This shows a weak association.

This scatter plot shows a weak, positive linear association between experience and vacation of employees at ABC Corporation.

Page 249 Exercise 1 Answer

Since we can see that in the given graph as the x-coordinate increases than the y-coordinate is decreasing

This means there is a negative association.

We can draw a trend line to see whether the association is weak or strong.

Place the pencil in the middle of all points and draw a line.

As we can see the points are not really close to the trend line which means there is a weak negative association.

There is a weak negative association.

Envision Math Grade 8 Chapter 4.3 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 249 Exercise 2 Answer

If we look at the graph we can already see that the data are not linear when the points shape as than the association is no longer linear.

Hence, the data is not linear.

Page 249 Exercise 1 Answer

Given

y = 6x + 120

y = $570

To find – expected number of copiers sold

Therefore, the expected number of copies sold is 75

Envision Math Grade 8 Volume 1 Chapter 4.3 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.3 Page 249 Exercise 2 Answer

Given

y = 6x + 120

x = 100

Substitute 100 for x and simplify
​

​
Therefore, the expected wage for given employee is 720.

Envision Math 8th Grade Topic 4.3 Key Concepts

Page 251 Exercise 1 Answer

Given:

A)​ (6,−0.5y + 20−0.5y = 13)

−y + 20 = 13

−y = 13 − 20

−y = −7

y = 7

(6,7)
​
B)​ (4−3x + 7x = −8,7)

4 + 4x = −8

4x = −8 −4

4x = −12

x = \(-\frac{12}{4}\)

(−3,7)
​
C)​ (2x + 4 − 6x = 24,5)

4 − 4x = 24

−4x = 24 − 4

−4x = 20

x = −5

(−5,5)
​
D)​ (5x + 6 − 10x = 31,1)

−5x + 6 = 31

−5x = 31 − 6

−5x = 25

x = −5

(−5,1)
​
E)​ (7x − 3 − 3x = 13,−2)

4x − 3 = 13

4x = 13 + 3

x = 4

(4,−2)
​
F)​ (4,− 12y + 8y − 21 = −5)

−4y − 21 = −5

−4y = −5 + 21

−4y = 16

y = −4

(4,−4)
​
G)​ (44 = 6x − 1 + 9x,−5)

44 = 15x − 1

45 = 15x

x = 3

(3,−5)
​
H)​ (−5, 4y + 14 − 2y = 4)

2y + 14 = 4

2y = 4 − 14

2y = −10

y = −5

(−5,−5)
​
I)​ (−5, 15 + y + 6 + 2y = 0)

21 + 3y = 0
​
3y = −21

y = −7

(−5,−7)
​
J)​ (4,3y + 32 − y = 18)

2y + 32 = 18

2y = 18 − 32

2y = −14

y = −7

(4,−7)
​
K)​ (6, 5y + 20 + 3y = −20)

8y + 20 = −20

8y = −20 − 20

8y = −40

y = −5

(6,−5)
​
L)​ (9x − 14 − 8x = −8,−1)

x − 14 = −8

x = −8 + 14

x = 6

(6,−1)
​
M)​ (−3,−5y + 10 − y = −2)

−6y + 10 = −2

−6y = −2 −10

−6y = −12

y = 2

(−3,2)
​
N)​ (−3,− 5y + 10 − y = −2)

−6y + 10 = −2
​
−6y = −2 −10

−6y = −12

y = 2

(−3,2)
​

If we simply look at the graph, than we know that we simply have to remove letter’s’ from the word seven, and we are left with ‘even’.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5

Page 237 Exercise 1 Answer

Given:

The total number of users using a small screen is 66.

The number of students using a small screen is 48.

The number of adults using the small screen is 18.

To find- How can you use the data to compare the percent of students who chose the small screen to the percent of adults who chose the small screen?

The data from the table can be used to analyse the usage of small screen between adults and students.

It can also help to understand the interested crowd and help in future business propositions.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.5 Bivariate Data Solutions

Page 237 Exercise 1 Answer

When categorized data is put into a two-way frequency tables, one category is represented by the rows and other is represented by columns.

Percentage of the given data gives a clear idea of the population surveyed.

Percentage also makes it easier to understand the given data in a two-way relative frequency table.

Percentage changes the way of interpretation of data because it makes it easier to understand the result of the surveyed population.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 238 Question 1 Answer

Two-way frequency tables are used to analyse survey results.

The data in the relative frequency table is always in the form of decimals, percentage or fractions.

Two-way relative frequency tables show percentages rather than counts.

Two-way relative frequencies are good for seeing if there is an association between two variables.

Two-way relative frequency tables show percentages rather than counts. This gives a visual representation of possible relationships between two sets of categorical data. This gives a better advantage for showing relationships between sets of paired data.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.5 Bivariate Data Solutions

Page 238 Exercise 1 Answer

Both the frequency tables are used to represent the categorical data.

On both the tables one category is represented by rows and other category is represented by column.

Both of the two-way tables show the relationship between paired categorical data. Both of the tables help in interpretation of data in the tables to draw conclusions.

Two-way relative frequency table is similar to a two-way frequency tables as both the tables are used to represent the categorical data, they show the relationship between paired categorical data, and they both help in interpretation of data in the tables to draw conclusions.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 238 Exercise 1 Answer

Given that, Asha asked 82 classmates whether they play sports on the weekend. The results are shown in the two-way frequency table below.

We need to use Asha’s two-way frequency table to complete the two-way relative frequency table.

For finding the percentage to complete the two-way relative frequency table, we need to divide each value in the cell by the total number of boys and girls polled together.

Here, the total count is 82

Thus, finding the percentage of each of them, we get,

\(\frac{21}{82} \times 100\) = 25.6

\(\frac{18}{82} \times 100\) = 21.9

\(\frac{39}{82} \times 100\) = 47.5

\(\frac{26}{82} \times 100\) = 31.7

\(\frac{17}{82} \times 100\) = 20.7

\(\frac{43}{82} \times 100\) = 52.4

\(\frac{47}{82} \times 100\) = 57.3

\(\frac{35}{82} \times 100\) = 42.6

Thus, completing the two-way relative frequency table, we get,

Investigating Bivariate Data Grade 8 Exercise 4.5 Envision Math

Page 239 Exercise 2 Answer

The percentage of students who choose e-books is 52%

The percentage of students who choose audiobooks is 48%

We see that the percentage of students using e-books is greater than the percentage of students using audiobooks.

This means that students prefer e-books over audiobooks.

The percentage of students using e-books is greater than the percentage using audiobook. This shows that students prefer using e-books over audiobooks.

The percentage of students in 7th grade who choose e-books is 41.1%

The percentage of students in 7th grade who choose audiobooks is 58.9%

We see that the 7th graders have greater tendency to choose audiobooks over e-books.

From the given data, we observe that the percentage of 7th graders using audiobooks is greater than the percentage of e-book users.

Envision Math Grade 8 Chapter 4 Exercise 4.5 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 238 Exercise 1 Answer

A frequency table is a chart that shows the popularity or mode of a certain type of data.

A relative frequency table is a chart that shows the popularity or mode of a certain type of data based on the population sampled.

The data presented by a relative frequency table is always represented by fractions, decimals or decimals.

The data in the two-way frequency table is in counts as in whole numbers.

The difference between a two-way frequency table and a two-way relative frequency table is that the data in the table is differently represented. The data in the relative table is represented by percentage, fractions and decimals. The data in frequency table is represented by a count that is whole numbers.

Page 240 Exercise 1 Answer

Two-way frequency tables are used to analyse survey results.

The data in the relative frequency table is always in the form of decimals, percentage or fractions.

Two-way relative frequency tables show percentages rather than counts.

Two-way relative frequencies are good for seeing if there is an association between two variables.

Two-way relative frequency tables show percentages rather than counts. This gives a visual representation of possible relationships between two sets of categorical data. This gives a better advantage for showing relationships between sets of paired data.

Page 240 Exercise 2 Answer

Two-way relative frequency table contains the data that is computed into percentage.

Also, this data is a relative data that is this data is not completely accurate.

Relative data doesn’t always add to 100%, proving that accuracy of the relative frequency table being almost correct.

Since the data in the two-way relative frequency table is not completely accurate, the percentage of the rows or columns percentages not total 100%.

Envision Math 8th Grade Exercise 4.5 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 240 Exercise 5 Answer

Given:

The total number of left-handed people that have an artistic ability is 86.

The total numbers of people that have the artistic ability are 101.

We convert the counts into percentage to get the answer.

We consider:

The percentage of left-handed people with artistic ability =

\(\frac{86}{101} \times 100\) = 0.8514 x 100 = 85.14

There are 85.14% of left-handed people surveyed with artistic ability.

Page 241 Exercise 7 Answer

Given

We consider:

This is the required two-way frequency table.

How To Solve Exercise 4.5 Bivariate Data In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 241 Exercise 8 Answer

Given:

We consider:

This is the required two-way frequency table.

Page 241 Exercise 9 Answer

Given:

We observe that the percentage of the 4-door car is 53% that is greater than the percentage of 2-door cars.

Therefore, the 4-door car is more popular.

To Find: Which type of car is more popular

After observing the given data, we conclude that 4-door cars are more popular.

Envision Math Grade 8 Exercise 4.5 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 242 Exercise 10 Answer

Given:

We observe that the percentage of girls who do not like raspberries is 48%.

Therefore, 48% percent of girls do not like raspberries.

After observing the given data, we conclude that 48% of girls do not like raspberries.

Given:

We observe that the gender and the responses are correlated.

The question is asked to both boys and girls.

Therefore, the data in the above table is evidence that gender and the responses are associated.

As the question is asked to both Girls and Boys, the data in the given table explains the association between the gender and the responses. Furthermore, these responses help in bifurcation of the data gender-wise.

Envision Math Exercise 4.5 Bivariate Data Detailed Answers

Page 242 Exercise 11 Answer

Given:

We consider:

This is the required two-way frequency table.

This is the required table.

Given:

We understand that the responses help to categorize the employees into day or night shifts. The given table is evidence to the association of Shifts and the responses.

After observing the table, we realize that this table helps in categorization of employees in Day or night Shifts. Hence, the shifts and the responses are associated.

Envision Math Grade 8 Exercise 4.5 Solution Guide

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.5 Page 242 Exercise 12 Answer

We simply have to look in the table and compare the percentage for positive improvements from each medicine.

AS we can see the medicine B has 74 of people had the improvement while only 26 of the people that were given medicine 26 showed some improvement.

A greater percent of people given Medicine B saw an improvement.

Yes, we can see in the given table, the percent of the people that took either medicine A or Bare shown in the table which is the evidence that the improvement was related to the type of medicine.

Yes there is evidence that the improvements are related to the type of the medicine.