Schindler

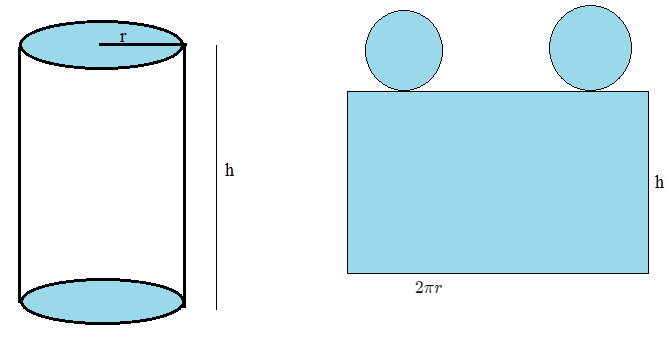
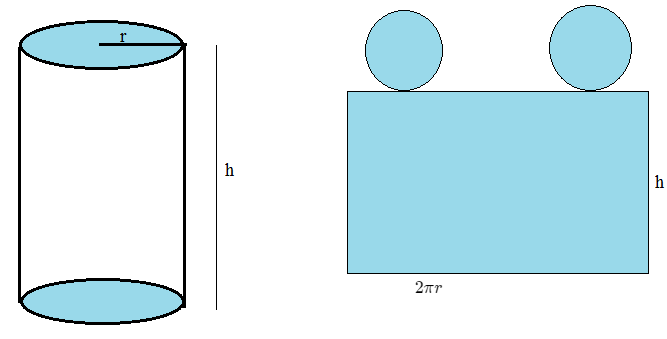
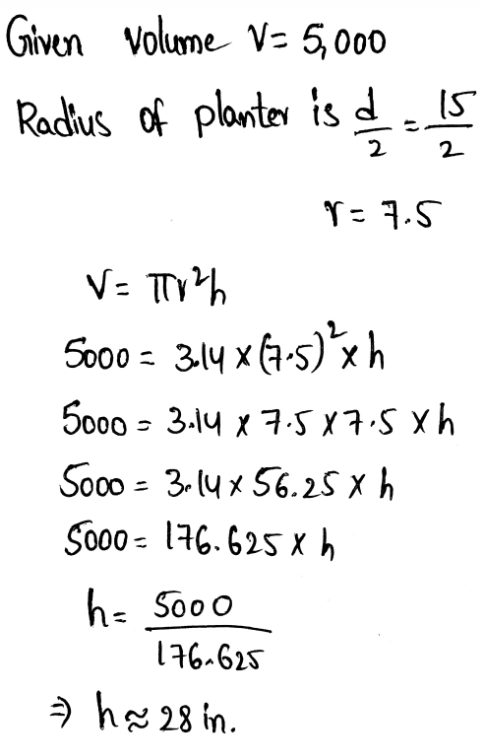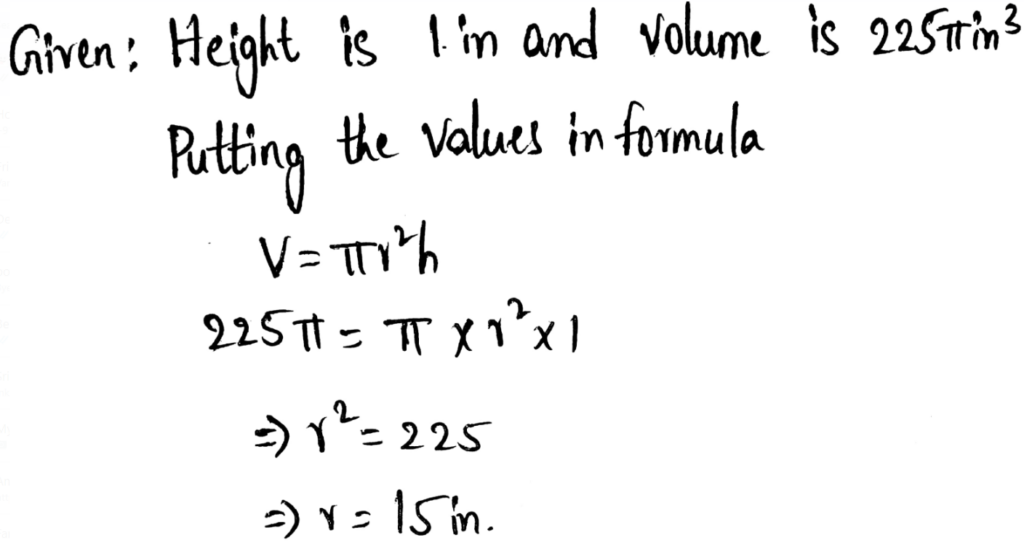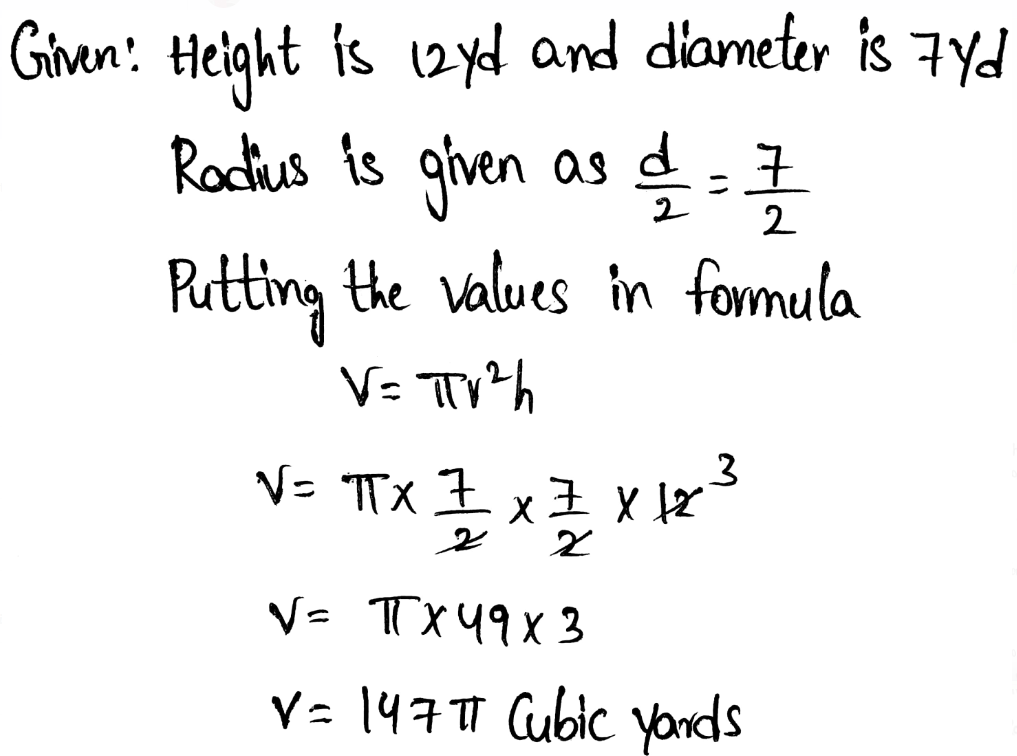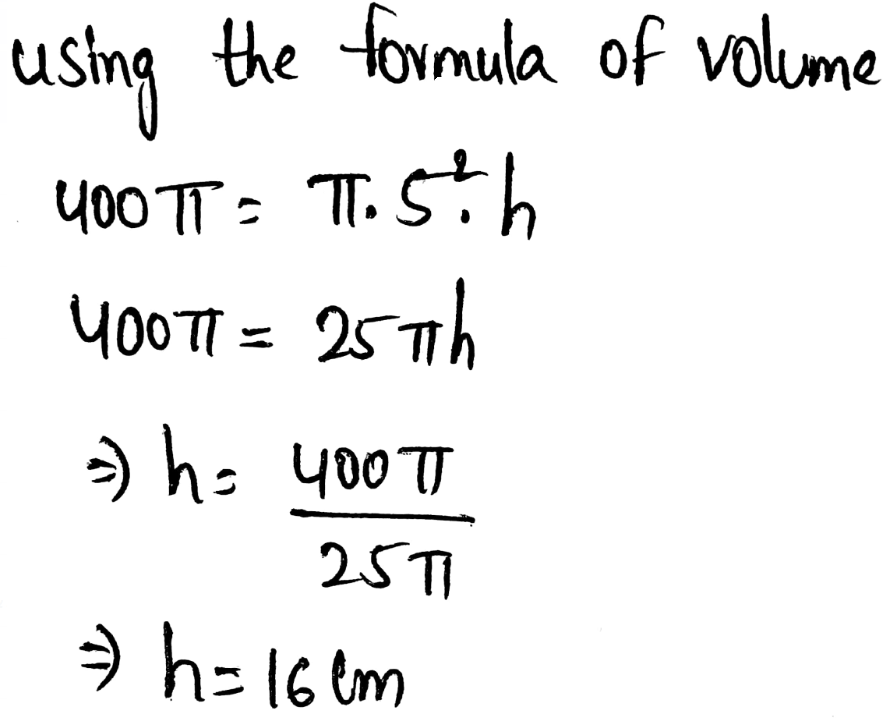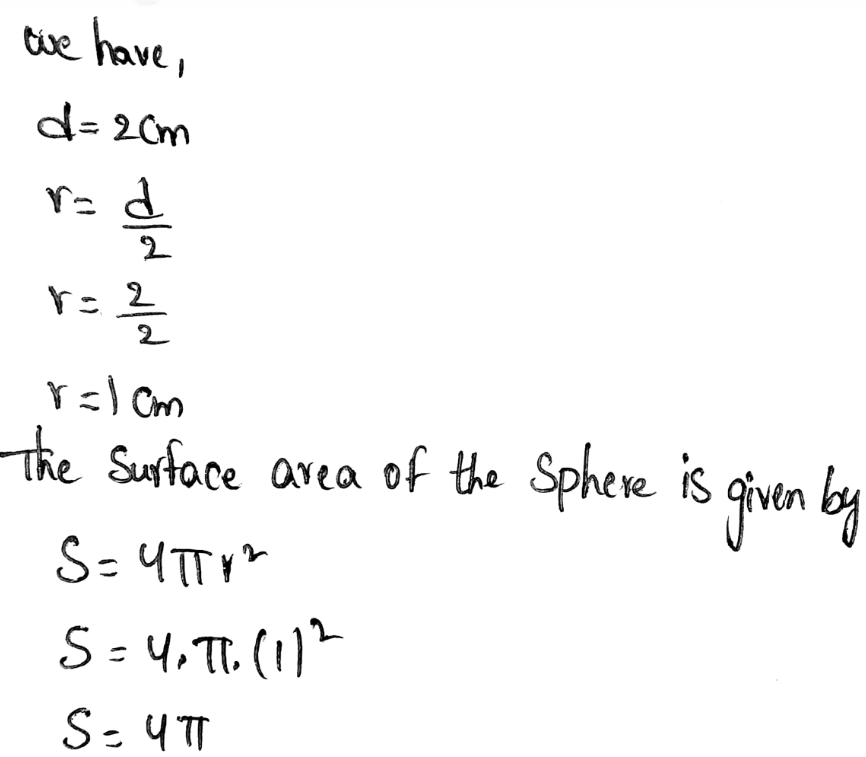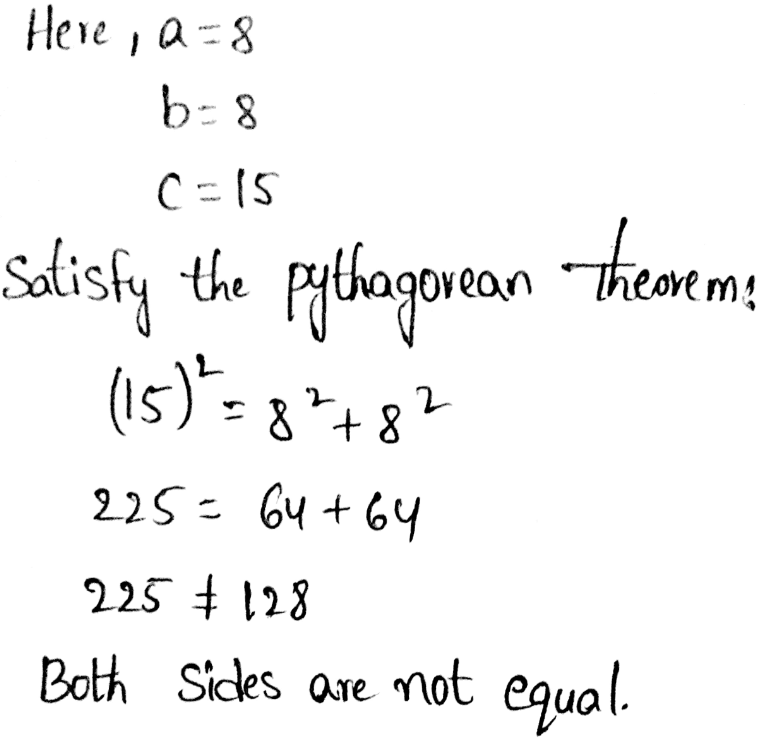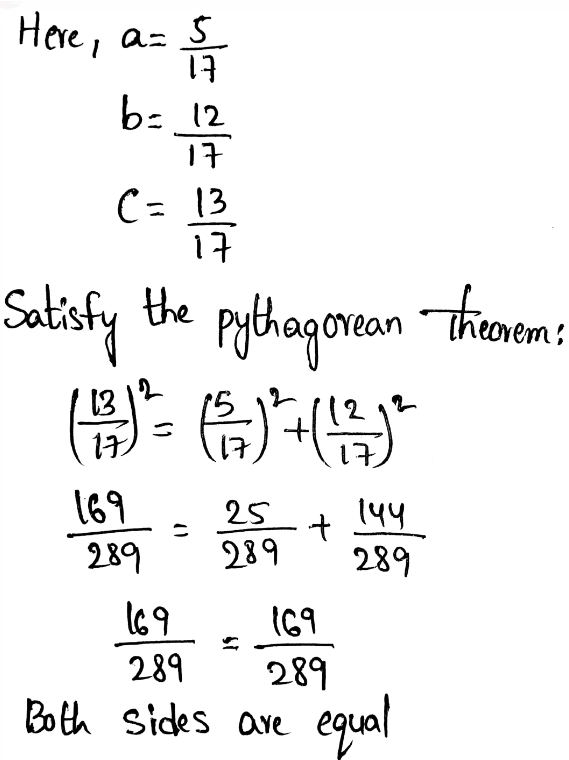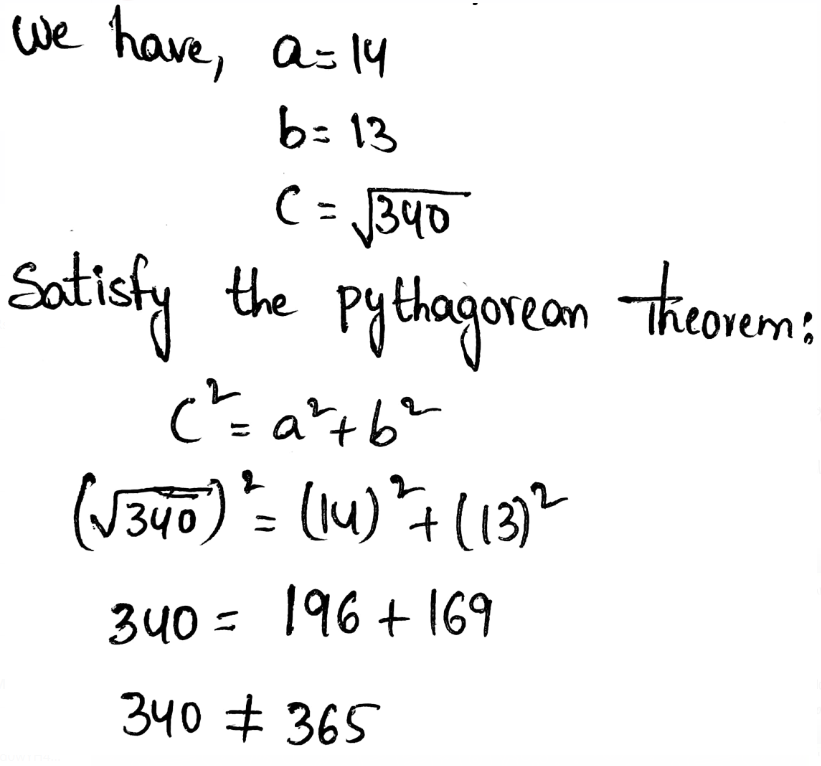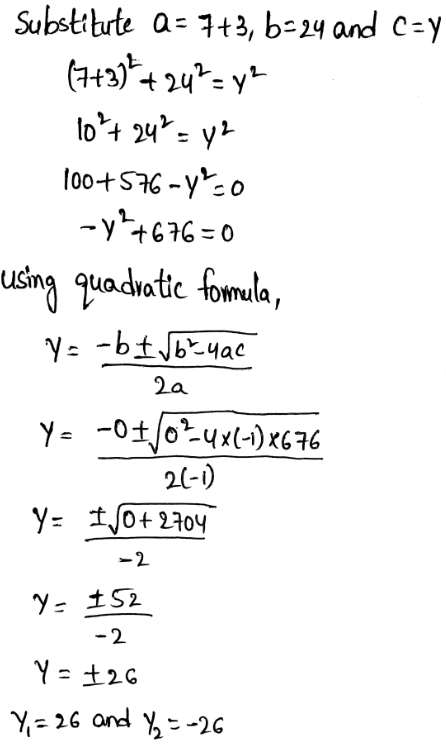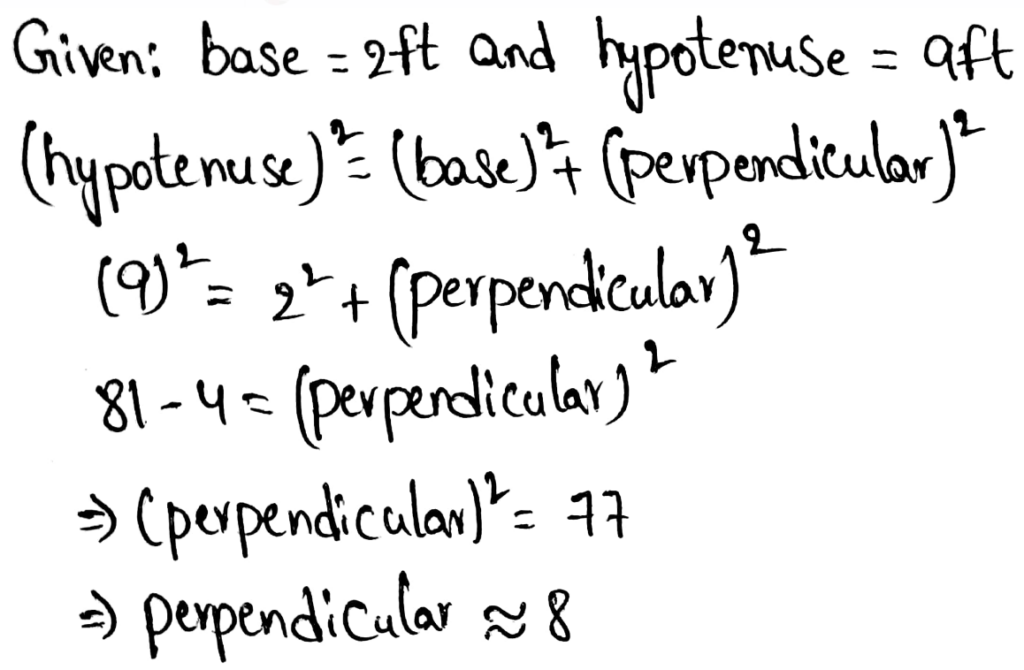Envision Algebra 1 Assessment Readiness Workbook Chapter 3

Page 42 Exercise 2 Answer

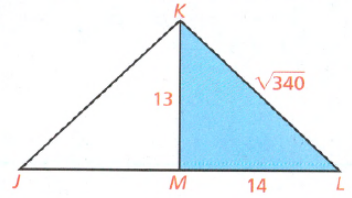
In the question, the given expression is \(\frac{(3)^4(5)^{-3}}{(3)^{-7}(5)^5}\).

It is required to rewrite this expression using positive exponents.

To write the expression using positive exponents, use the definition of negative exponents to convert the numbers with negative powers into positive powers.

Finally, use the concept of multiplication of two same numbers with different exponents.

Rewrite using positive exponents.

Use the definition of negative exponents \(\frac{1}{(3)^{-7}}\) can be rewritten as (3)7 and (5)-3 can be rewritten as \(\frac{1}{(5)^3}\)

Back- substitute these values in the original expression

⇒ \(\frac{(3)^4(5)^{-3}}{(3)^{-7}(5)^5}=\frac{(3)^4(3)^7}{(5)^3(5)^5}\)

Back -substitute these values in the original expression.

⇒ \(\frac{(3)^4(5)^{-3}}{(3)^{-7}(5)^5}=\frac{(3)^4(3)^7}{(5)^3(5)^5}\)

Use the property \(a^m \times a^n=a^{m+n}\)

Add the exponents

⇒ \(\frac{(3)^4(5)^{-3}}{(3)^{-7}(5)^5}=\frac{(3)^{4+7}}{(5)^{3+5}}\)

⇒ \(\frac{(3)^4(5)^{-3}}{(3)^{-7}(5)^5}=\frac{(3)^{11}}{(5)^8}\)

Therefore, the correct option is option \(\text { (A) } \frac{(3)^{11}}{(5)^8}\)

Therefore, the correct option is Option(A) \(\frac{(3)^11}{(5)^8}\).

Option (A) \(\frac{(3)^11}{(5)^8}\) is the positive exponent form of the given expression.

Envision Algebra 1 Chapter 3 Answer Key

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 42 Exercise 3 Answer

In the question, the given equation is ∣3x−3∣ + 3 = 9.

It is required to find the solution to this equation.

To find the solution, isolate the absolute value number on one side of the equation and the rest on the other side. Finally, use the relation ∣a∣ = ±a and solve for x.

Apply the definition of absolute value.

Given equation |3x-3|+3=9

Subtract 3 from both sides

|3x-3|+3-3=9-3
|3x-3|=6

Use the definition of absolute value sign

3x-3=±6

Use   the definition of absolute value sign

3x-3=±6

Find the solution 3x-3=6
add 3 on both sides 3x-3+3=+6+3
3x=9
Divide 3 on both sides
⇒ \(\frac{3 x}{3}=\frac{9}{3}\)

x=3

Find the solution 3x-3=-6

Add 3 on both sides

3x-3+3=-6+3

3x=-3

Divide 3 on both sides

⇒ \(\frac{3 x}{3}=\frac{-3}{3}\)

x=-1

Option (B) -1 and Option (C) 3 are the solutions to the given absolute equation.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 42 Exercise 4 Answer

In the question, it is given that a line is perpendicular to a line that passes through (−2,−2) and(2,4).

It is required to find the equation of a line that is perpendicular to the given line.

To find the equation of that line, first, find the slope of the line passing through the given points. Next, use the relation to find the slope of the perpendicular line. Finally, compare the slope of the perpendicular lines from the set of options given.

Find the slope of the line.

The line passes through (-2,-2) and (2,4) using the formula.

⇒ \(m_1=\left(\frac{4-(-2)}{2-(-2)}\right)\)

Simply the signs

⇒ \(m_1=\left(\frac{4+2}{2+2}\right)\)

Add the terms

⇒ \(m_1=\left(\frac{6}{4}\right)\)

Divide the numerator and denominator by 2

⇒ \(\begin{aligned}
& m_1=\frac{\frac{6}{2}}{\frac{4}{2}} \\
& m_1=\frac{3}{2}
\end{aligned}\)

Find the slope of the perpendicular line using the relation of the slope of two perpendicular lines.

m1xm2=-1

Substitute \(\frac{3}{2}\)  for m1

⇒ \(\frac{3}{2} \times m_2=-1\)

multiply by \(\frac{2}{3}\) on both sides

⇒ \(\frac{3}{2} \times \frac{2}{3} \times m_2=-1 \times \frac{2}{3}\)

Simply the equation \(m_2=\frac{-2}{3}\)

Therefore, the slope of the perpendicular line is \(\frac{-2}{3}\).

Write the equation of the perpendicular line.

Use the general equation of a line.

Slope is \(\frac{-2}{3}\).

Substitute \(\frac{-2}{3}\) form in the general equation of a line.

y = \(\frac{-2}{3}\)x + can

Compare with the given options.

Therefore, option (A) y = \(\frac{-2}{3}\)x – 1 is the equation that represents a line perpendicular to the given line.

Option (A) y = \(\frac{-2}{3}\)x – 1 is the equation that represents a line perpendicular to a line that passes through the points (-2, -2) and (2, 4).

Page 42 Exercise 5 Answer

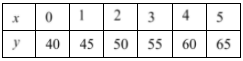
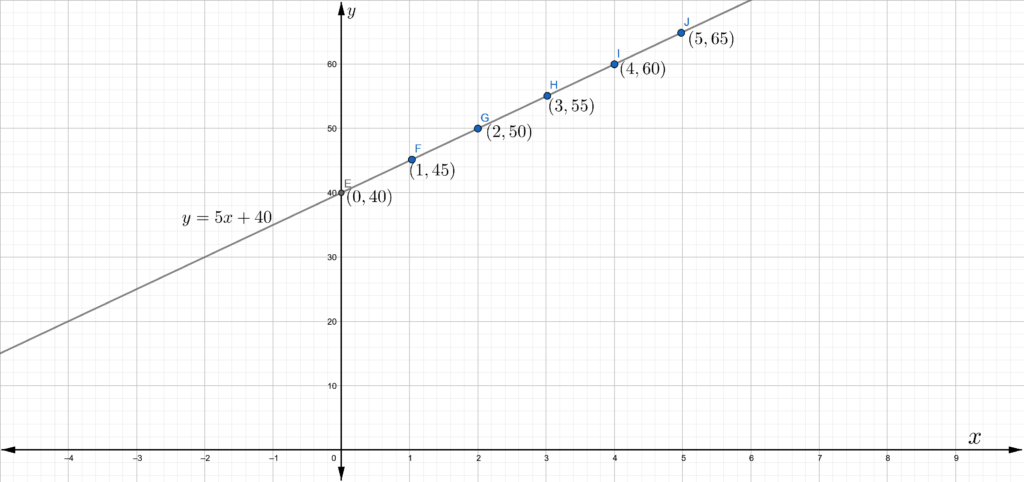
In the question, it is given that the amount Mai saves after working x hours is given by the equation y = 12.5x + 20.

It is required to find the amount that Mai earns per hour.

To find the amount earned per hour, substitute 1 for x in the given equation and solve for y.

Calculate the amount earned per hour.

Given y=12.5x+20​

mai shares ⇒ y=12.5x+20 after working x hours

Substitute 1 for x.

y=12.5(1)+20

Multiply and the terms

y=12.5+20

y=32.5

Therefore, Mai earns 32.5 per hour.

The amount earned by Mai per hour is 32.5.

Envision Algebra 1 Assessment Readiness Workbook Chapter 3 Solutions

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 42 Exercise 6 Answer

In the question, an expression is given as (2x²y²)⁴.

It is required to simplify this expression.

To simplify the expression, use the power of a product rule. Next, use the power of a power rule and simplify the expression.

Simplify the expression.

Given expression (2x²y²)4

⇒ \(\left(2 x^2 y^2\right)^4=2^4\left(x^2\right)^4\left(y^2\right)^4\)

Use the power of a power rule.

⇒ \(\left(2 x^2 y^2\right)^4=2^4 x^{4\times2} y^{4 \times 2}\)

Multiply the powers

⇒ \(\left(2 x^2 y^2\right)^4=2^4 x^8 y^8\)

Simply the terms

⇒ \(\left(2 x^2 y^2\right)^4=16 x^8 y^8\)

Use the power of a product rule

Compare with the given options.

Therefore, Option (C) 16x⁸y⁸ is the simplified form of the given expression.

The simplified form of (2x²y²)⁴ is given by Option (C) 16x⁸y⁸.

Page 43 Exercise 7 Answer

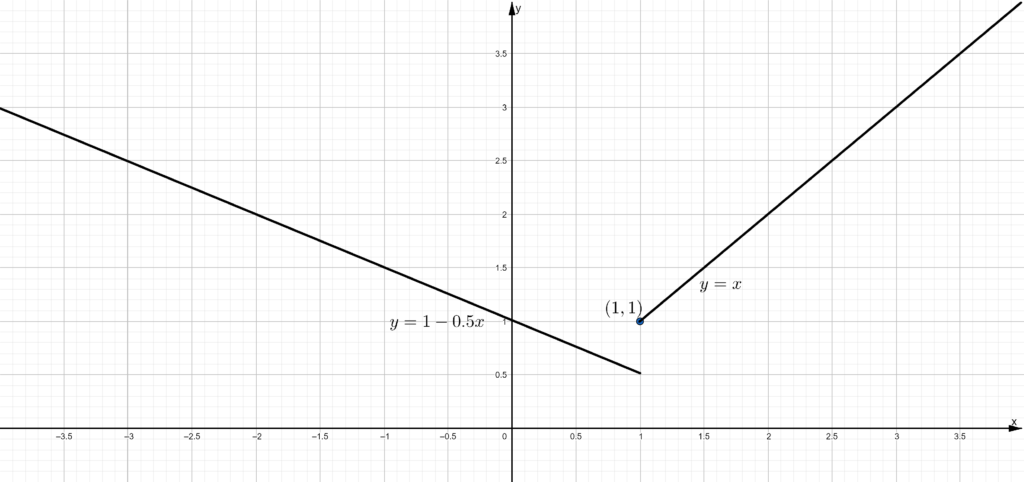
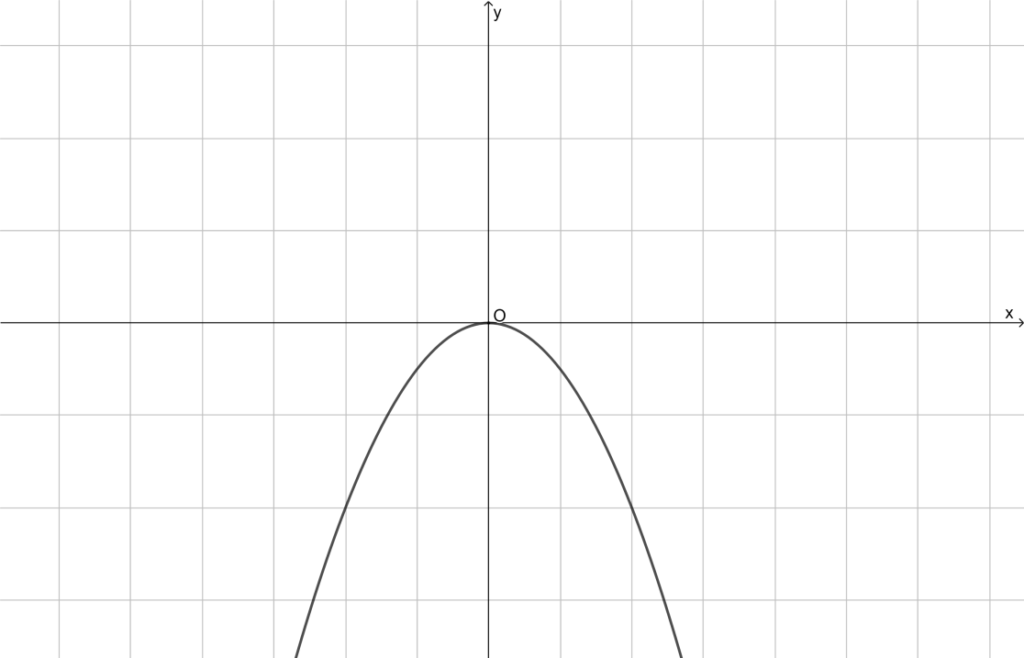
In the question, the given equation of a function is f(x) = ∣3x + 5∣.

It is required to identify the piecewise-defined function that has the same graph as the given function.

The graph of the function

f(x) = |3x + 5| is symmetric about the line x = \(\frac{-5}{3}\).

A piecewise function with the graph same as f(x) = |3x+5| will also change its sign at x = \(\frac{-5}{3}\).

From the given options, the graph of Option (C)

g(x) = \(\left\{\begin{array}{l}
\cdot 3 x+5 ; x \geq \frac{-5}{3} \\
-3 x-5 ; x<\frac{-5}{3}
\end{array}\right.\)

Changes its sign at \(\frac{-5}{3}\).

Therefore,

g(x) = \(\left\{\begin{array}{l}
\cdot 3 x+5 ; x \geq \frac{-5}{3} \\
-3 x-5 ; x<\frac{-5}{3}
\end{array}\right.\) is the correct answer.

The graph of Option (A) g(x) = \(\left\{\begin{array}{l}
3 x+5 ; x \geq 0 \\
-3 x-5 ; x<0
\end{array}\right.\) changes its sign at x = 0 and symmetric about y-axis.

The graph of Option (B) g(x) = \(\left\{\begin{array}{l}
\cdot 3 x+5 ; x \geq \frac{-3}{5} \\
-3 x-5 ; x<\frac{-3}{5}
\end{array}\right.\) changes its sign at x = \(\frac{-3}{5}\).

The graph of Option (D) g(x) = \(\left\{\begin{array}{l}
3 x+5 ; x \geq 0 \\
-3 x-5 ; x<0
\end{array}\right.\) changes its sign at x = 0 and symmetric about y-axis.

Option (C) g(x) = \(\left\{\begin{array}{l}
\cdot 3 x+5 ; x \geq \frac{-5}{3} \\
-3 x-5 ; x<\frac{-5}{3}
\end{array}\right.\) is the piecewise-defined function that has the same graph as the function f(x) = |3x+5|.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 43 Exercise 9 Answer

In the question, it is given that a student scores 87, 78,94, and 84.

It is required to find the score the student must have on the fifth test to get an average score of 87.

To find the fifth score, take the fifth score as some value x. Next, use the formula to find the average of these five scores.

Finally, find the value of x.

Form an equation to calculate the average.

Take the fifth score as x, i.e., P₅ = x.

Consider the formula to find the average of n quantities.

There are five terms and the average is 87.

Substitute 87 for Z and 5 for n.

87 = \(\frac{P_1+P_2+P_3+P_4+P_5}{5}\)

Find the fifth score.

The four scores as 87, 78, 94, and 84respectively.

The four scores as 87,78,94 and 84 respectively.

Substitute p1=87, p2=78, p3=94 and P4=84

Therefore, the fifth score is 92.

The student must earn 92 on the fifth test to get an average score of 87.

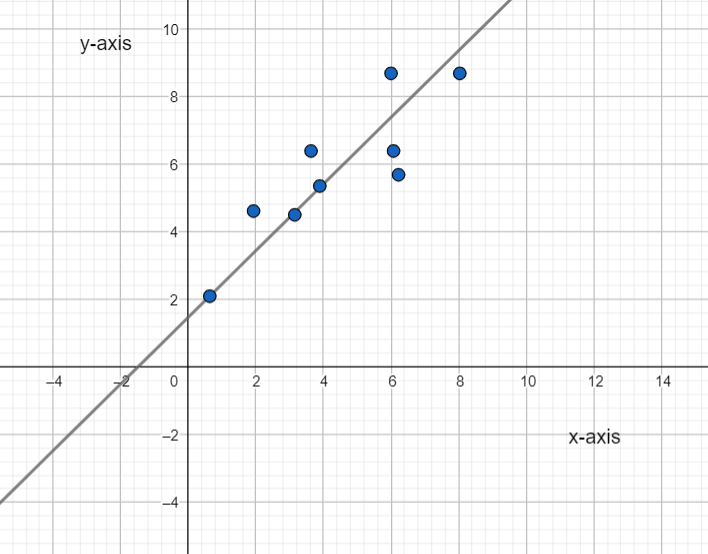
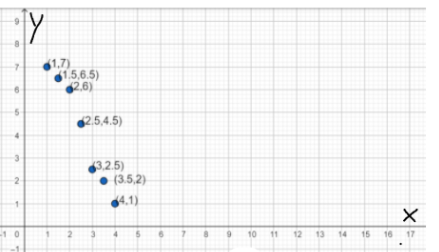
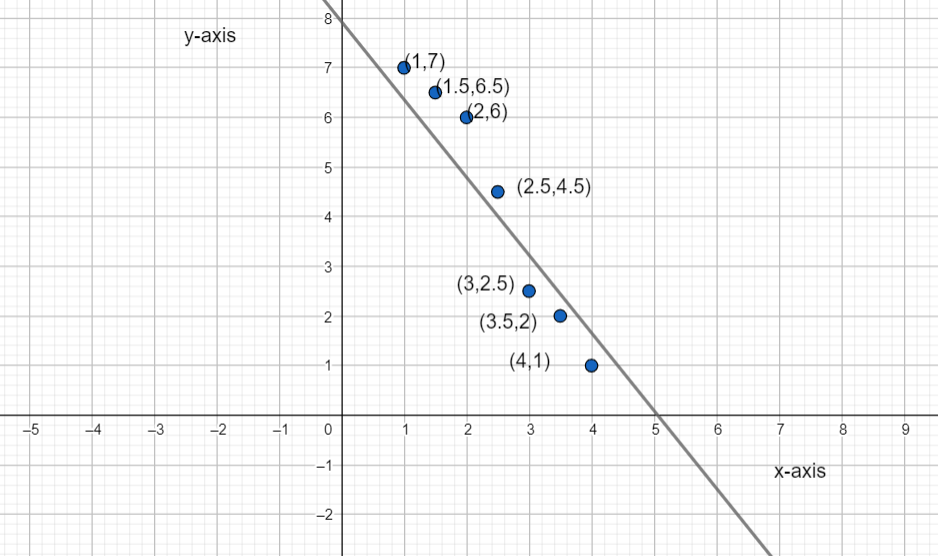
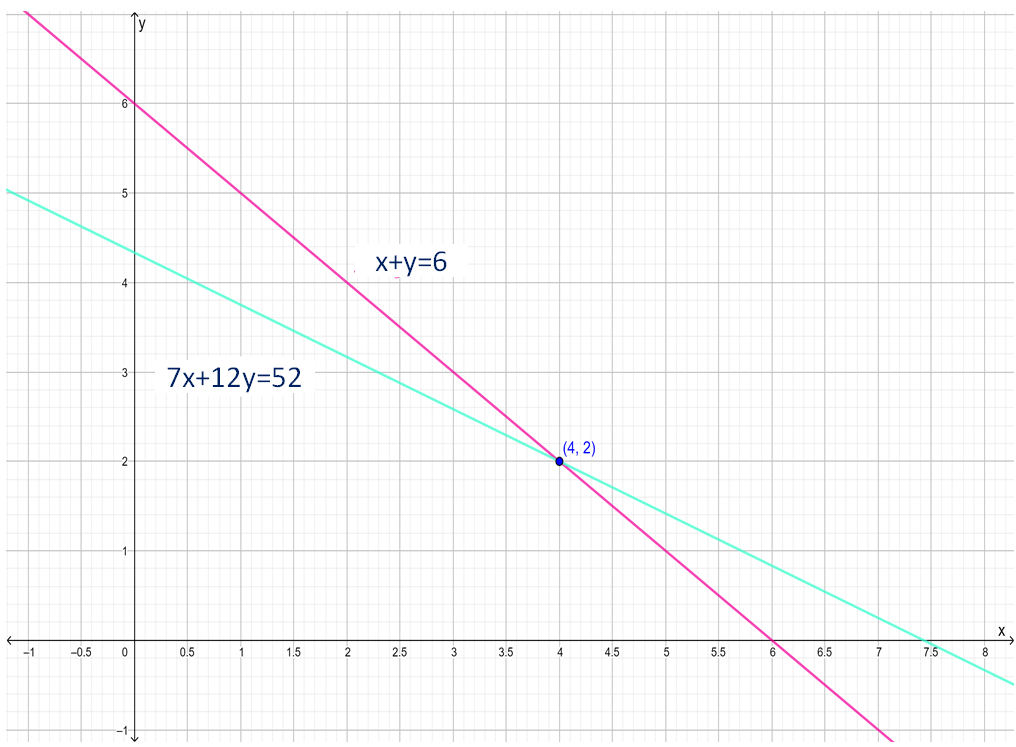
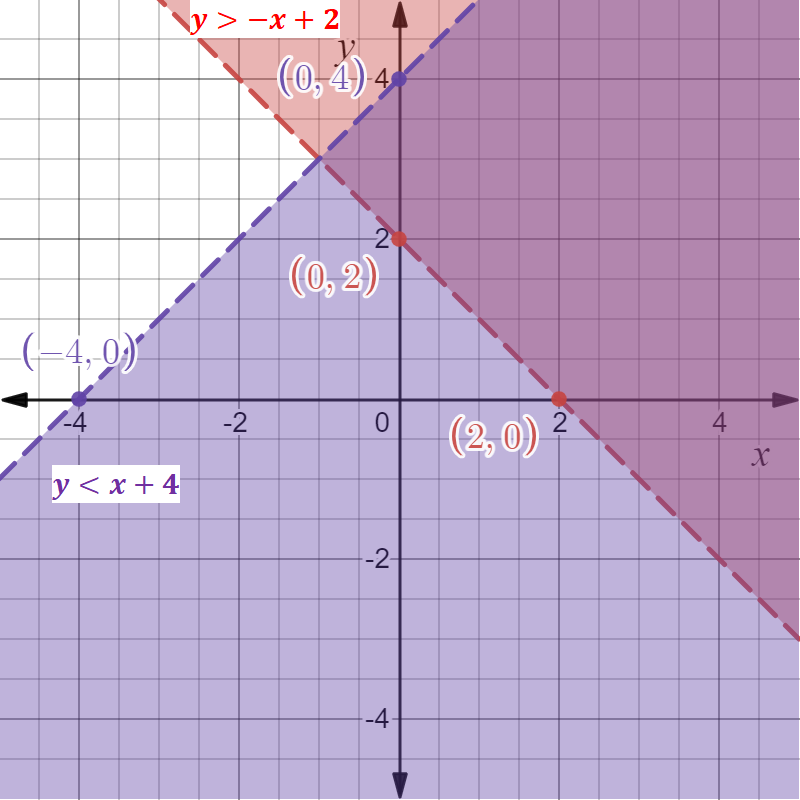
Page 43 Exercise 11 Answer

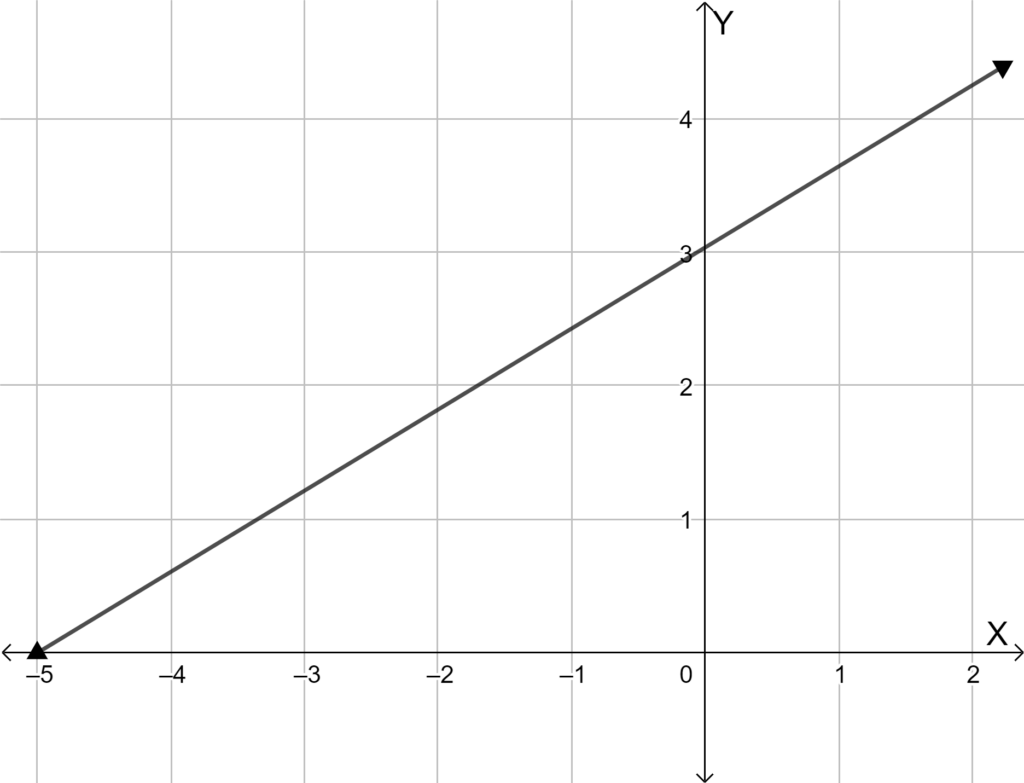
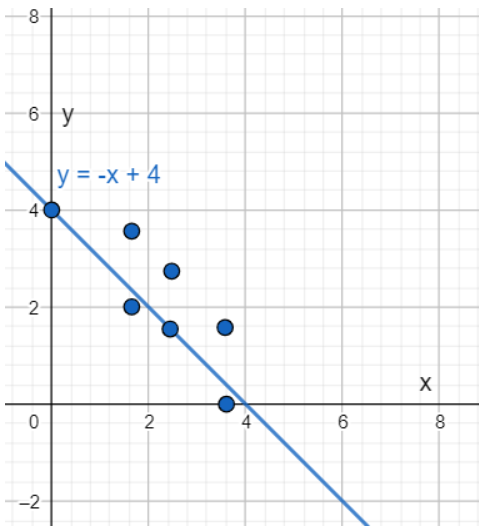
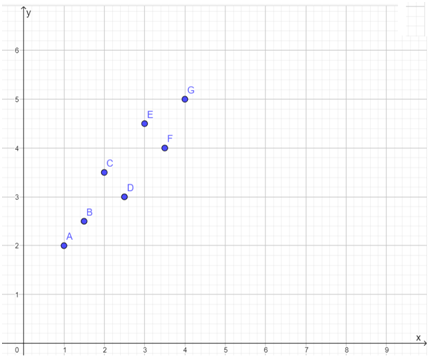
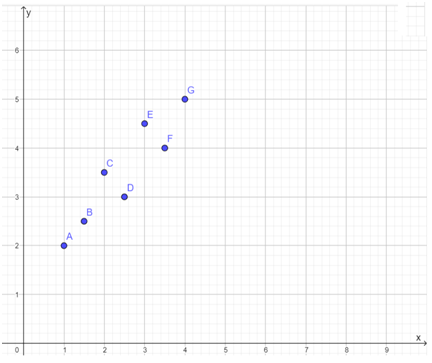
A scatter plot is given in the question.

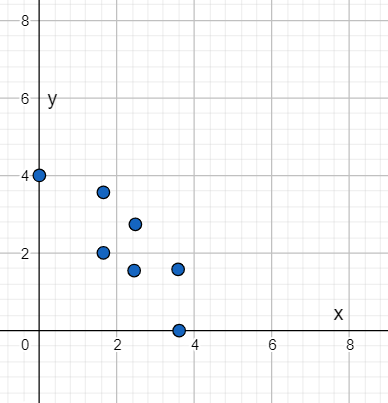
It is required to find the best-fit line for the plot.

Plot the line y = −x + 4 in the given scatter plot.

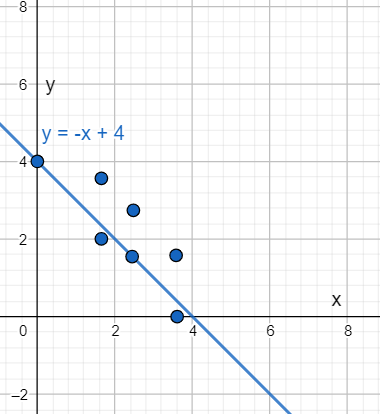
As y = −x + 4 satisfies most points of the plot. So, option (B) is the correct answer.

For option (A),

Plot y = x + 4 in the given scatter plot.

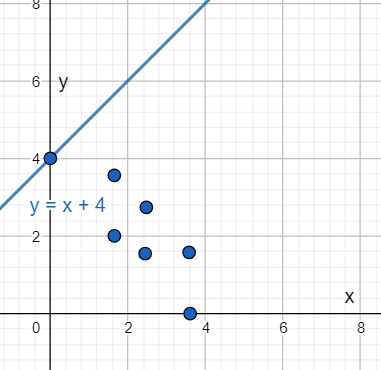
As y = x + 4 does not satisfy most points of the plot. So, option (A) is the incorrect answer.

For option (C)

Plot y = x + 3 in the given scatter plot.

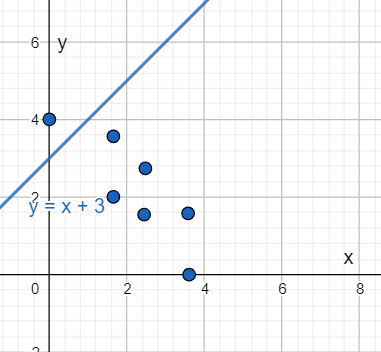
As y = x + 3 does not satisfy most points of the plot. So, option (C) is the incorrect answer.

For option (D).

Plot y = −x + 3 in the given scatter plot.

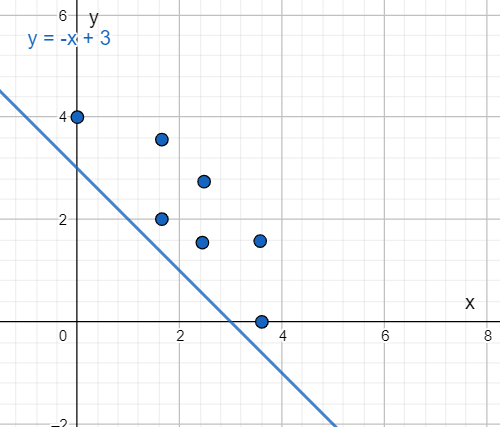
As y = −x + 3 does not satisfy most points of the plot. So, option (D) is the incorrect answer.

x+4 satisfies most points of the scatter plot. So, option (B) is the correct answer.

Page 43 Exercise 12 Answer

⇒ \(\frac{3}{2}\), -√7, -2, -√9, \(\frac{2}{3}\), 1 are given.

It is required to order them from least to greatest.

To find the correct order of increasing numbers, convert the irrational numbers to decimals by approximation, and compare the numbers.

Estimate the value of −√7

Since, 4 < 7 < 9

So,√4 < √7 < √9

2 < √7 < 3

Since 7 is a bit closer to 9 than 4.

So a good approximation, for −√7 is −2.6

Simplify the values of other numbers

⇒ \(\begin{aligned}
& \frac{3}{2}=1.5 \\
& -\sqrt{9}=-3 \\
& \frac{2}{3}=0.667
\end{aligned}\)

Compare the obtained values to get the results

Since, -3<-2.6<-2<0.667<1<1.5

So, the obtained results are as follows

The required order of the numbers from least to greatest is as follows.

-3 < -√7 < -2 < \(\frac{2}{3}\) < 1 < \(\frac{3}{2}\)

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 44 Exercise 13 Answer

A dot plot is given in the question.

It is required to find the mean and median of the given dot plot to near the hundredth.

To find the required value, find the frequency of given data and then calculate the values of mean and median.

Express the frequency of the given data.

As 3 has 1 dot their frequency is 1.

Similarly, frequency distribution will be as follows.

3,4,4,5,5,6,7.7.7.7.8,8,8,8,8.

Calculate The mean of the given data

⇒ \(=\frac{3+4+4+5+5+6+7+7+7+7+8+8+8+8+8}{15}\)

⇒ \(=\frac{95}{15}\)

⇒ \(=\frac{19}{3}\)

= 6.333

Estimate the median of the given data.

Since 7 lies in the middle of the data 3,4,4,5,5,6,7.7.7.7.8,8,8,8,8.

So, 7 is the median of the given data.

The mean and the median of the given dot plot are 6.333 and 7 respectively.

Page 44 Exercise 14 Answer

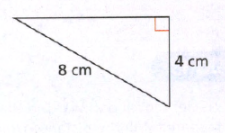
In the question, the area of a rectangle is given by the expression 2x² − 2x − 12, and the width of the rectangle is given by x−3.

It is required to find the length of this rectangle.

To find the length, first, factorize the area expression into a product of simpler expressions. Next, evaluate the terms of the factorized expression other than x−3

Factorize the expression.

Assume A(x) represents the area expression.

Given expression 2x² -2x-12

Take 2 commons from each term

A(x)=2(x²-x-6)

Rewrite -x as 2x-3x

A(x) = 2(x(x+2)-3x-6

Take -3 common from the terms -3x and -6

A(x)=2(x(x+2)-3(x+2))

Take(x+2) common.

A(x)=2 (x+2(x-3)

Observe the factorized expression.

Use the formula for the area of a rectangle.

The width of the rectangle is x−3.

All the terms except x−3 represent the length of this rectangle.

Therefore, length is given by 2(x+2).

The length of the rectangle whose area is given by 2x² − 2x − 12 is 2(x+2).

Page 44 Exercise 15 Answer

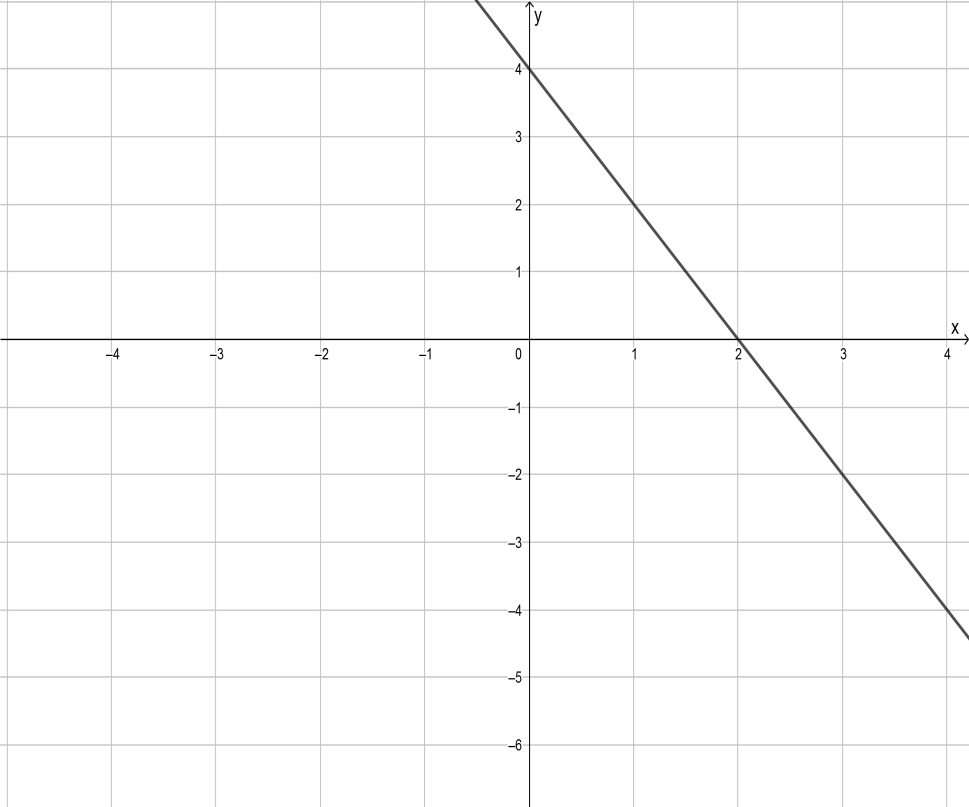
In the question, the given inequality is 3x + 2y < 3.

It is required to graph this inequality.

To create a graphical representation of this inequality, use a graphing utility and draw the graph.

Graph the inequality.

Use a graphing calculator.

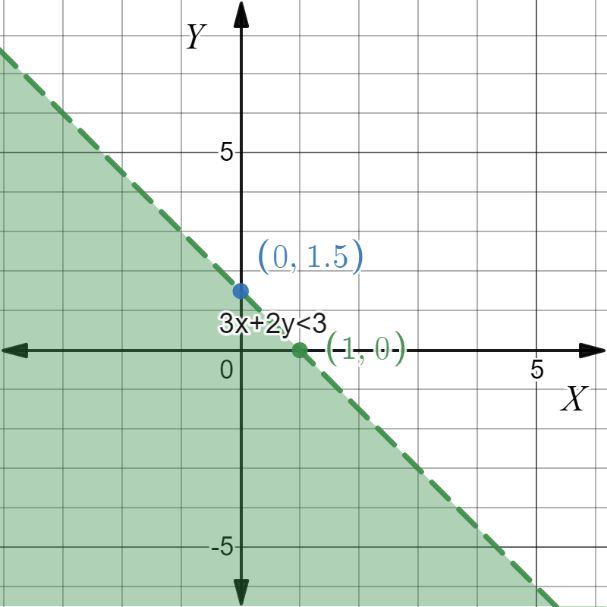
The graph of the inequality 3x + 2y < 3 is –

Page 44 Exercise 16 Answer

In the question, the function is given as f(x) = x² + 4x + 2.

It is required to draw the graph for the given function.

To do so, find the different values and make the table for them. Then draw the graph by plotting the points and making a smooth curve that passes through those points.

Find the values of the function at different points to plot the graph.

Given function f(x)=x²+4x+2

At x=-4 the value of the equation

f(-4)=(-4)²+4(-4)+2
f(-4)=16-16+2
f(-4)=2

The value of the equation is 2

At x=-3 the value of the function

f(-3)=(-3)²+4(-3)+2
f(-3)=9-12+2
f(-3)=-1

The value of the equation is -1

At x=-2 the value of the function

f(-2)=(-2)²+4(-2)+2
f(-2)=4-8+2
f(-2)=-2

The value of the function is -2
At x=-1the value of the function

f(-1)=(-1)²+4(-1)+2
f(-2)=1-4+2
f(-2)=-1

The value of the function is -1
At x=0 the value of the function

f(0)=(0)²+4(0)+2
f(0)=2
The value of the function is 2

The values for the given function are shown in the table.

The graph for the values is shown below.

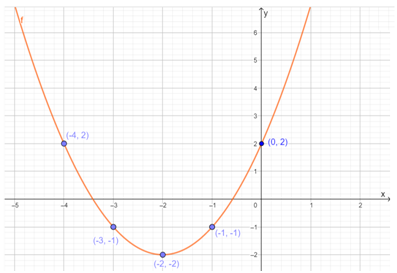
The graph for the given function is shown below.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 45 Exercise 17 Answer

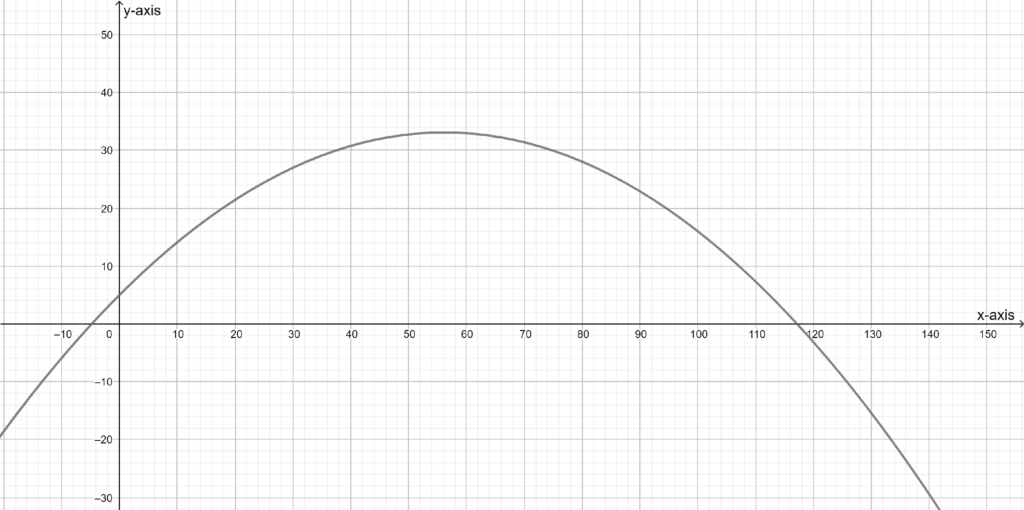
In the question, the statement is given as a ball is thrown directly upward from a height of 25 feet with an initial velocity of 96 feet per second.

Also, the height of the h after t second is given as h = −16t² + 96t + 25.

It is required to find the time taken by the ball to reach the maximum height. Also, it is required to explain it.

Also, it is required to find the maximum height of the ball. And it is needed to explain it.

To do so, find the time that passes from the start of throwing the ball until it comes to maximum height.

Since h describes the ball’s height above the ground, it is the maximum value when instantaneous velocity is equal to zero.

Find the instantaneous velocity by differentiating the equation of height and equate it to zero. Simplify the equation to get time to reach maximum height.

To find the maximum height, substitute the time in h and simplify it.

Find the time to reach maximum height.

Given h=-16t²+96t+25
Differentiate the given equation concerning t.

h'(t)=-16(2)t+96(1)+0

Hence the maximum height is 169 feet.

The ball will reach the maximum height after 3 seconds.

The maximum height is 169 feet.

Page 45 Exercise 18 Answer

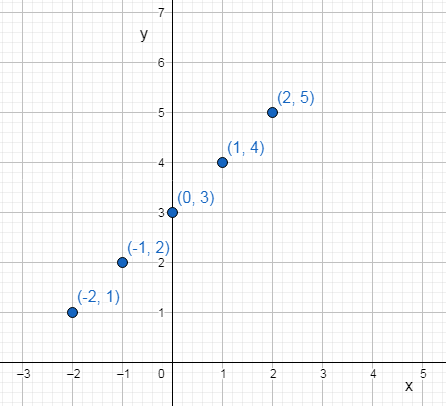
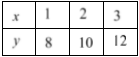
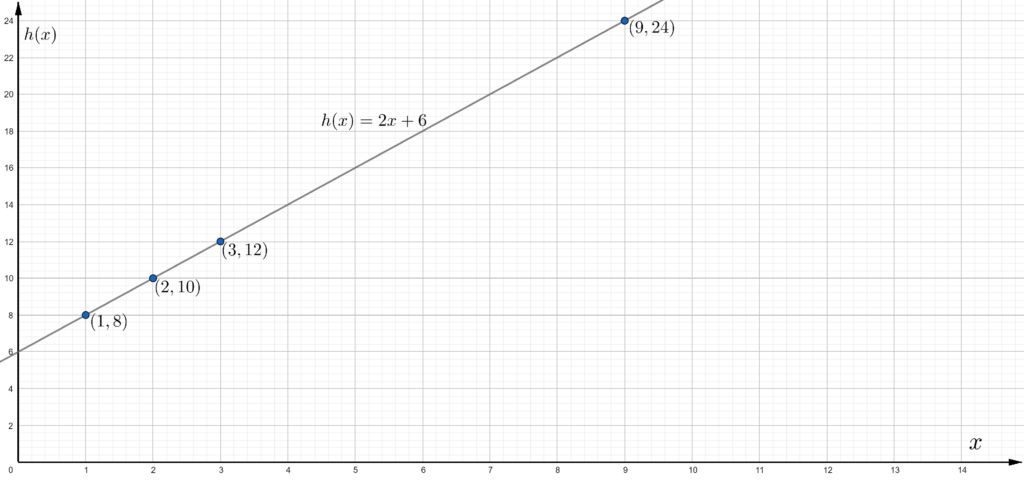
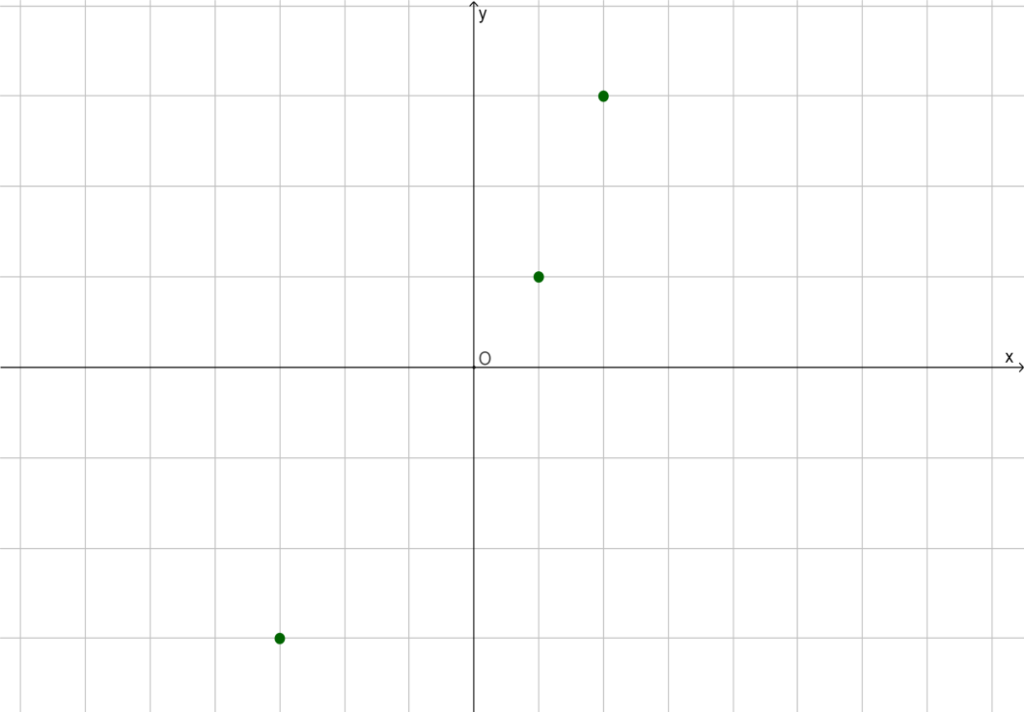
In the question, the values for the function is given as

It is required to make a scatter plot of the data.

And also it is required to find the equation line that best fits.

To do so, use the points to locate them. Then draw the line through the maximum number of points on a scatter plot balancing about an equal number of points above and below the line.

The graph of the given values.

Plot the given points and join them.

The line that fits scatter plots is shown below.

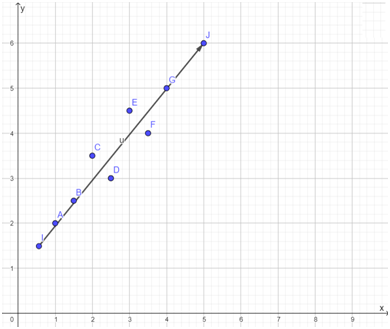
From the graph, the equation of the line is y = 2x.

The scattered plot of the given values is shown below.

The line that fits scatter plots is shown below.

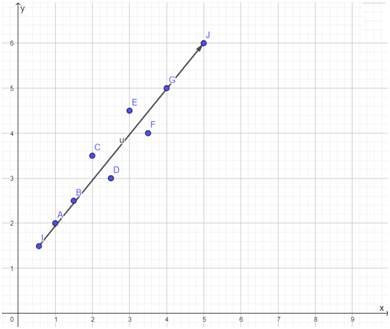
The equation of the line is y = 2x.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 46 Exercise 19 Answer

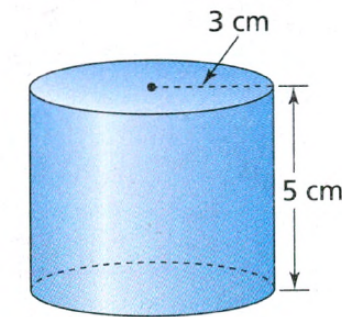
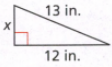
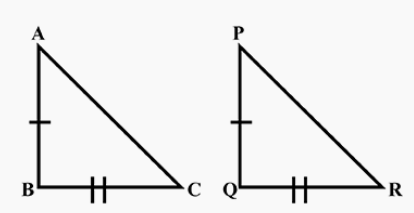
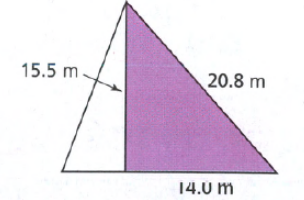
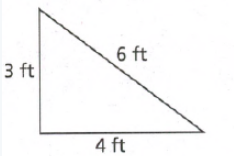
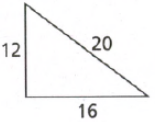
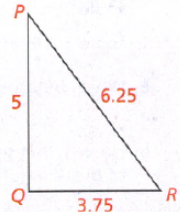
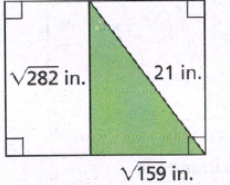
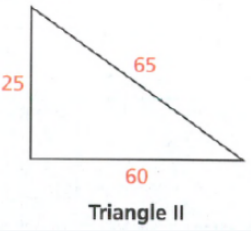
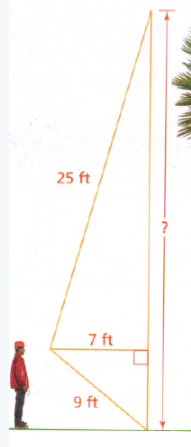
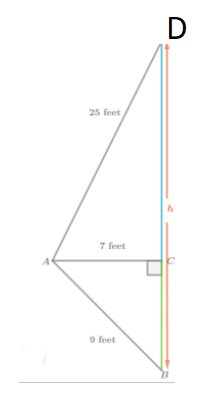
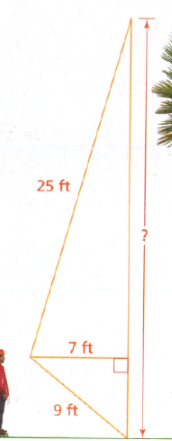
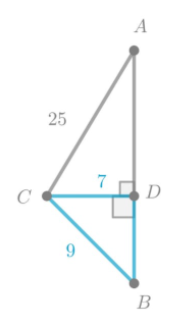
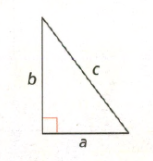
The length of the hypotenuse of a right triangle is given as 40 cm.

Also, the length of the one leg is given as 24 cm.

It is required to find the length of the other leg.

Let x be the length of the leg to be determined.

Substitute the values 24 for a, 40 for c, and x for b in the formula of Pythagoras.

Substitute a=24,b=xc=40

Hence the length of the other leg of the given right triangle is 32 cm.

Thus, the length of the other leg of the given right triangle is 32 cm in option (c).

The length of the other leg of the given right triangle is 20 cm

Thus, the length of the other leg in option (A) is not the correct answer.

The length of the other leg of the given right triangle is 28 cm

Thus, the length of the other leg in option (B) is not the correct answer.

The length of the other leg of the given right triangle is 36 cm

Thus, the length of the other leg in option (D) is not the correct answer.

The length of the other leg of the given right triangle is 32cm in option (c).

Page 46 Exercise 20 Answer

The quadratic equation is given as 3x² + 5x − 5 = −1.

It is required to find the solutions of the given quadratic equation to the nearest hundredth.

To do so, substitute the value 3 for a, 5 for b, and, −4 for c.

Given 3x²+5x-5=1
Add-1 to the equation
3x²+5x-5+1=-1+1
simply above equation
3x²+5x-5+1=0
3x²+5x-4=0

Comparing a given quadratic equation

a=3,b=5,c=-4

substitute the values \(\begin{aligned}
& x=\frac{-5 \pm \sqrt{5^2-4(3)(-4)}}{2(3)} \\
& x=\frac{-5 \pm \sqrt{25+48}}{6} \\
& x=\frac{-5 \pm \sqrt{73}}{6}
\end{aligned}\)

The solutions of the given equation

⇒ \(\begin{aligned}
& x=\frac{-5+\sqrt{73}}{6} \\
& x=0.590 \text { and } \\
& x=\frac{-5-\sqrt{73}}{6} \\
& x=-2.257
\end{aligned}\)

The obtained solutions to the nearest hundredth is x = 0.590 and x = −2.26

Hence options (c) and (d) are correct answers.

From the results of the solution options (a),(b),(e) and (f) are not correct answers

The solutions of the given quadratic equation are options (c) and (d).

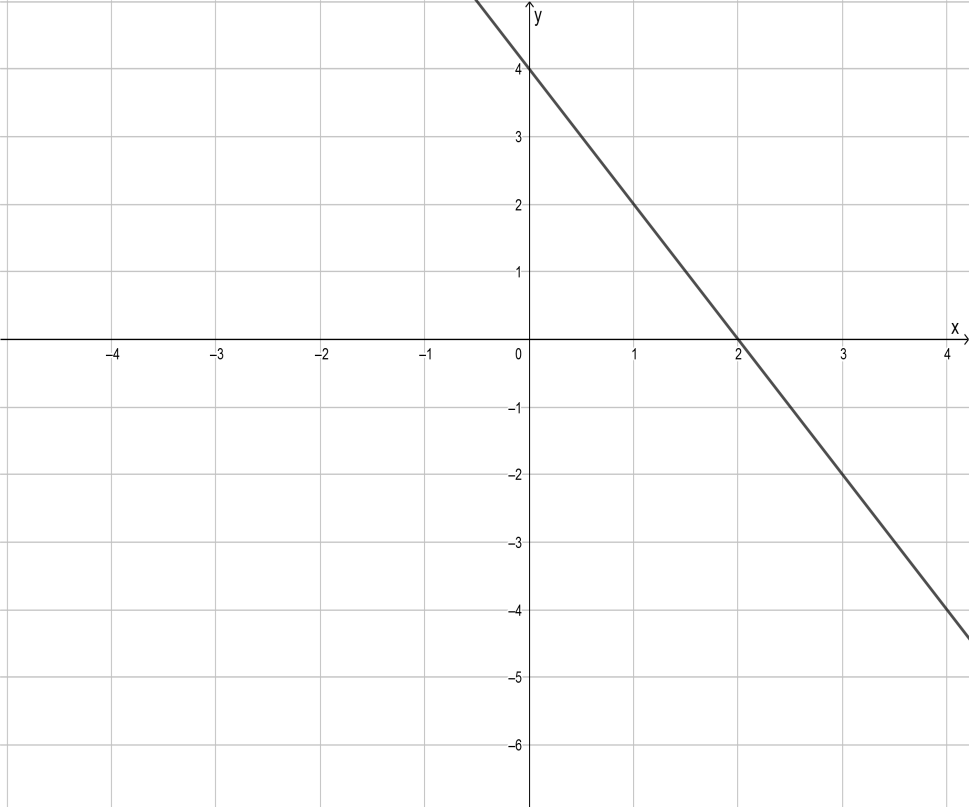
Page 46 Exercise 21 Answer

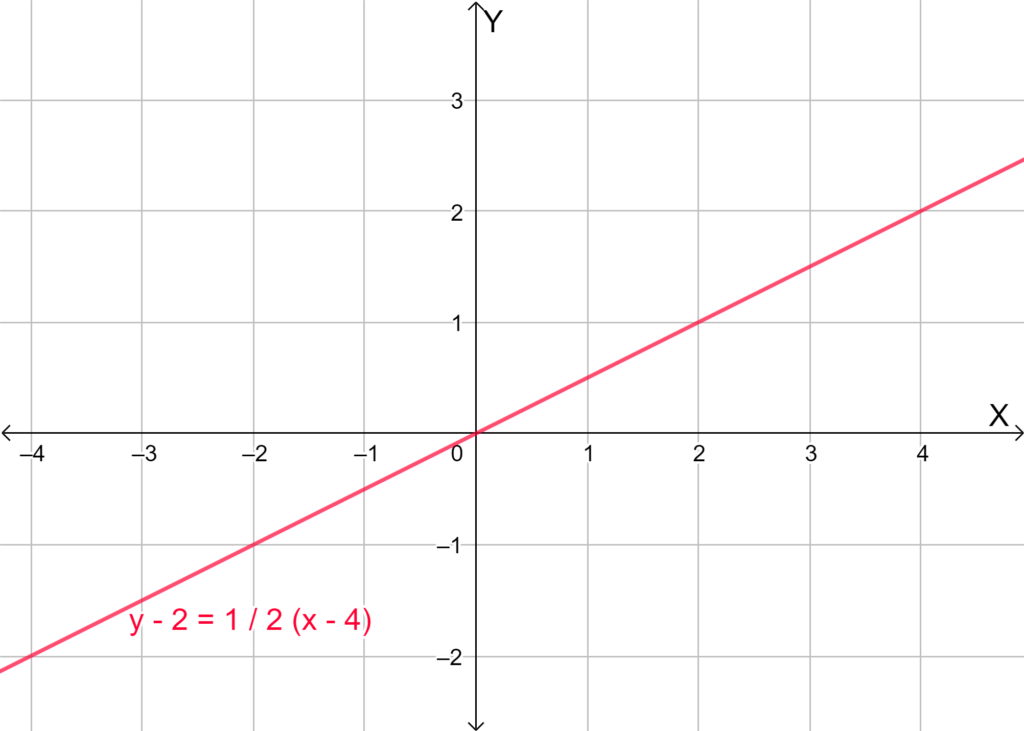
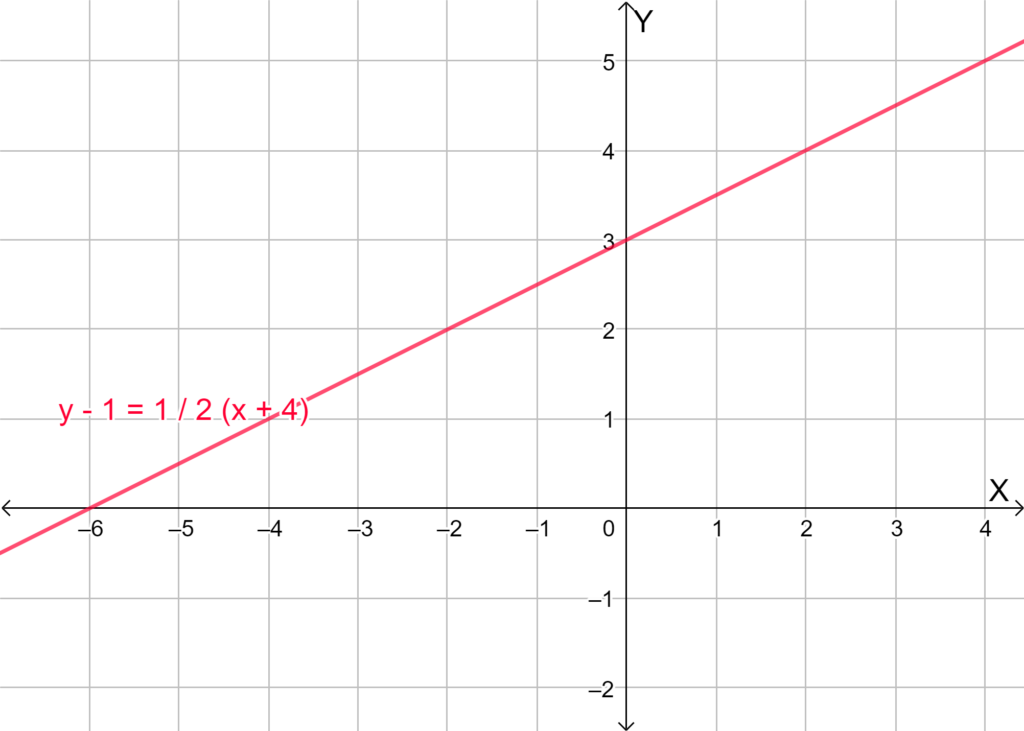
The graph is given as y = 2x − 4.

It is required to describe the given graph as a transformation of the graph y = 2x.

To do so, use the transformation rule. To describe the transformation translate the given graph to a specific unit.

Draw the graph y=x

S substitute x=0 in the equation of the function y=0

The function at x=0 is y=0

Substitute x=-1 in the equation of the function y=-1

The value of the function at c =-1 is y=-1

Substitute x=1 in the equation of the function.

y=1

The value of the function at x=1 is y=1.

From the above different values, the graph is shown below.

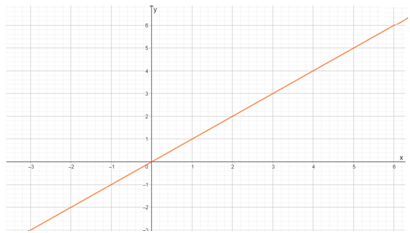
Draw the graph y=2x.

substitute x=o in the equation

From the above different values, the graph is shown below.

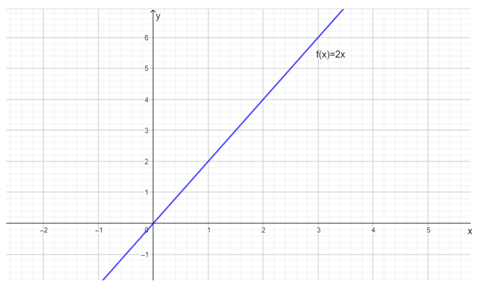
The graph y = 2x stretches the function y = x two times.

Draw the graph y=2x.

Substitute x=0 in the equation of the function y=0

From the above different values, the graph is shown below.

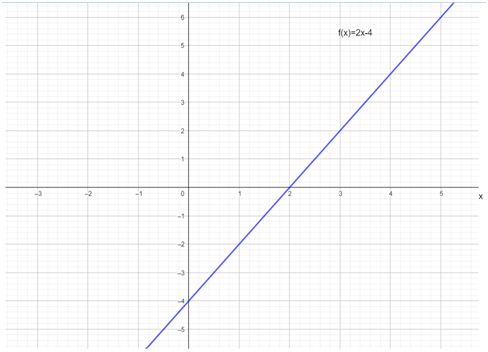
The graph y = 2x − 4 translates vertically the function

y = 2x down 4 units.

Thus, y = 2x − 4 translates vertically the function

y = 2x down 4 units.

The graph y = 2x − 4 translates vertically the function

y = 2x down 4 units.

The correct option is option (A).

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 46 Exercise 22 Answer

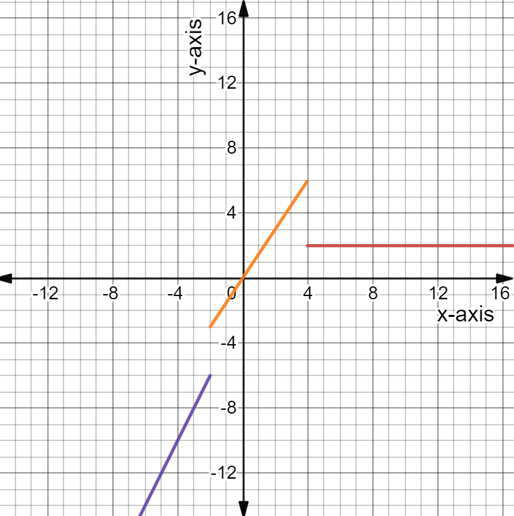
In the question, the inequality is given as −4x−3 < 13.

It is required to draw a graph of the inequality.

To do so, solve the inequality x. Then using that value plot the graph.

Solve for x.

Given -4x-3<13
Add 3 on both sides
-4x-3+3<13+3
Simplify the above inequality.

-4x<16

Divide 4 on both sides

⇒ \(\begin{aligned}
-\frac{4 x}{4} & <\frac{16}{4} \\
x & <-4
\end{aligned}\)

Therefore, the range is given as x∈(−4,∞)

The graph of the given inequality is shown below.

The graph of the given inequality is shown below.

Page 46 Exercise 23 Answer

The values for the function is given as

It is required to find the equation of the function from the given options.

To do so, substitute the values of x in the given options and check the values of y.

Compare the values obtained with the table given.

Consider the equation y=-x+2

substitute the value x=-2 in equation

y=-(-2)+2
y=4

Substitute the value x=-1 in question

The value y obtained is equal to the value in the table.

Therefore option (d) is the answer.

Consider the equation y = 2x.

Substitute the value x = −2 in the equation.

​y = 2(−2)

y = −4

The value y obtained is not equal to the value in the table.

Therefore option (a) is not the answer.

Consider the equation y = −2x.

Substitute the value x = −2 in the equation.

Substitute the value x = −1 in the equation.
​
​y = −2(−1)

y = 2
​
The value y obtained is not equal to the value in the table.

Therefore option (b) is not the answer.

Consider the equation y = x + 2.

Substitute the value x = −2 in the equation.
​
​y = −2 + 2

y = 0
​
The value y obtained is not equal to the value in the table.

Option (d) is the answer.

Page 46 Exercise 24 Answer

In the question, the principal amount is given as $325 and the interest 5 is paid quarterly.

It is required to find the amount to be obtained after 5 years.

To do so, use the amount formula.

Substitute the values $325 for P, 5 for r, 5 for t, and 4 for n in the formula and simplify it.

Find the amount.

⇒ \(A=325\left(1+\frac{5}{100 \times 4}\right)^{4(5)}\)

Simply above equation

⇒ \(A=325\left(1+\frac{5}{400}\right)^{20}\)

Take LCM 400 in the equation

⇒ \(\begin{aligned}
& A=325\left(\frac{400+5}{400}\right)^{20} \\
& A=325\left(\frac{405}{400}\right)^{20}
\end{aligned}\)

Simplify the above equation

A=325(1.0125)20
A=325(1.2820)
A=416.662

Hence the amount obtained after 5 years is $416.662

The amount obtained after 5 years is $416.662.

Envision Algebra 1 Student Edition Chapter 3 Practice Problems

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 47 Exercise 25 Answer

The graph is given as y = \(\sqrt[3]{2 x}\)

It is required to describe the given graph as a transformation of the graph y = \(\sqrt[3]{x}\)

To do so, use the transformation rule. To describe the transformation translate the given graph to a specific unit.

Draw the graph y=\(y=\sqrt[3]{x}\)

When x=-1 the value of the function is

The graph for the different values of the function is given below.

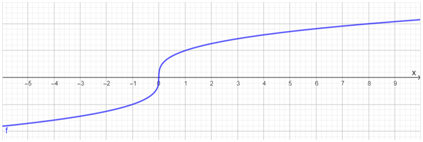
Draw the graph \(y=\sqrt[3]{2 x}\)

When x=-1 the value of the function is \(\begin{aligned}
& y=\sqrt[3]{2(-1)} \\
& y=1.2599
\end{aligned}\)

When x=0 the value of the function is

⇒ \(\begin{aligned}
& y=\sqrt[3]{0} \\
& y=0
\end{aligned}\)

When x=1 the value of the function is

⇒ \(y=\sqrt[3]{2}\)

The graph for the different values of the function is given below.

The graph y = \(\sqrt[3]{2 x}\) translates a horizontal stretch of the function

y = \(\sqrt[3]{x}\) by 2 units.

Thus, the graph of the function y = \(\sqrt[3]{2 x}\) translates a horizontal compress of the function

y = \(\sqrt[3]{x}\) by 2 units.

Therefore option (B) is the correct answer.

The correct option is option (B).

Page 47 Exercise 26 Answer

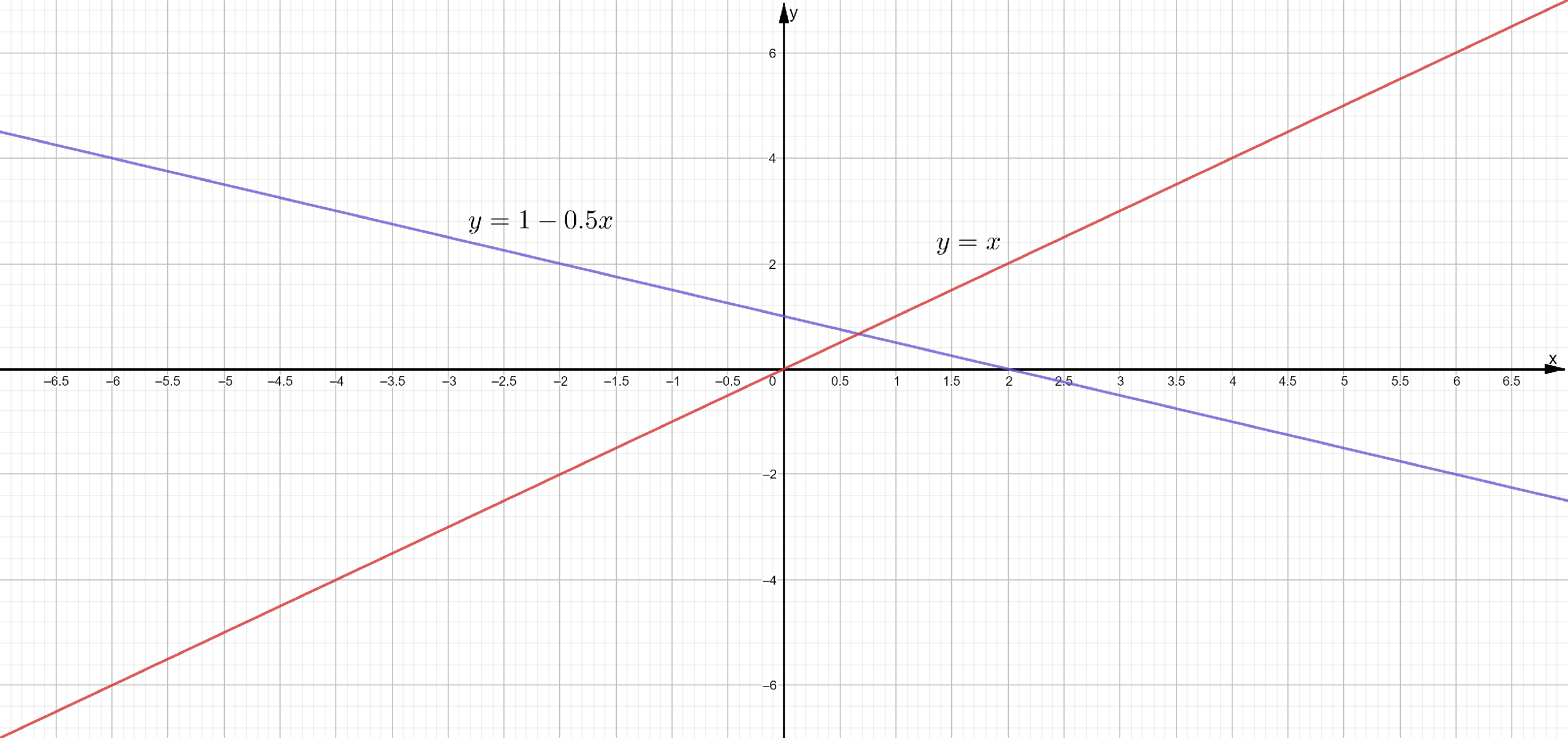
In the question, the given system of equations is y = 2x − 3 and y = x + 4.

It is required to find the solution to this system of equations.

To find the solution to these equations, use the method of substitution i.e., substitute one variable as a function of another variable to one of the equations. Next, solve for one variable and substitute its value in any one equation to find the value of the other variable.

Find the value of x.

Consider the equation y=2x-3

substitute x+4 for y

x+4=2x-3

Subtract 4 on both sides

x+4-4=2x-3-4
x=2x-7

Multiply -1 on both sides

-(-x)=-(-7)
x=7

Find the value of y
Consider the equation y=2x-3
Substitute 7 for x

y=2(7)-3
y=14-3
y-11

Therefore, the solution for this system of equations is x = 7 and y = 11.

The solution to this system of equations is x = 7 and y = 11.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 47 Exercise 27 Answer

In the question, the transformation of a parent function y = √x is shown below –

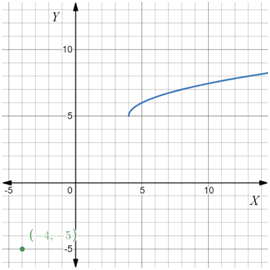
It is required to identify which equation represents this transformation.

y = √x − 4 + 5

Draw the graph of the parent function y = √x using a graphing calculator.

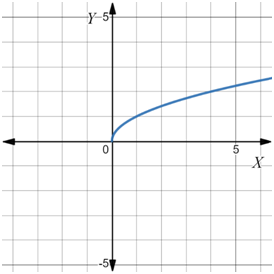
The graph of the parent function starts from the origin.

Transform this as per the given graph.x → x − 4, as the origin shifts 4 along the positive X-axis, and y → y − 5, as the origin shifts 5 along the positive Y-axis.

y= \(y=\sqrt{x-4}+5\)

Substitute x-4 for x and y-5 for y

⇒ \(y-5=\sqrt{x-4}\)

​Add 5 on both sides

y-5+5= \(\sqrt{x-4}+5\)

y= \(\sqrt{x-4}+5\)

Therefore, Option (B) is the correct answer.

y = √x+4 – 5

Draw the graph of y = √x+4 – 5 using a graphing calculator.

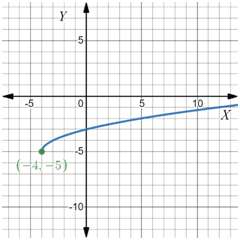
The y = √x+4 − 5 graph does not resemble the transformed graph.

Therefore, Option (A) is not a correct answer.

y = √x-5 + 4

Draw the graph of y = √x-5 + 4 using a graphing calculator.

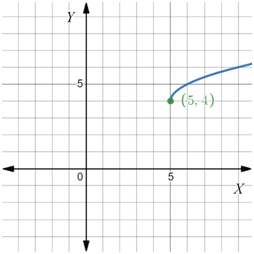
The y = √x−5 + 4 graph does not resemble the transformed graph.

Therefore, Option (C) is not a correct answer.

y = √x−5 + 4

Draw the graph of y = √x−5 + 4 using a graphing calculator.

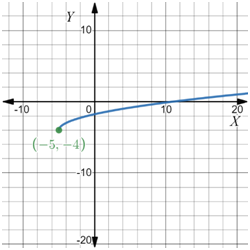
The y = √x+5 − 4 graph does not resemble the transformed graph.

Therefore, Option (D) is not a correct answer.

Option (B) y = √x−4 + 5 is an equation for the given transformation of the graph of the parent function y = √x.

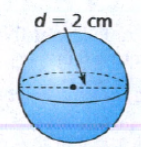
Page 47 Exercise 28 Answer

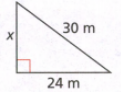
In the question, it is given that a cylinder has a volume of 648πft³ and a height of 18ft.

It is required to find the diameter of this cylinder.

To find the diameter, use the formula for the volume of a cylinder and substitute the values of height and volume.

Find the radius of the base.

Consider the formula for the volume of a cylinder.

Substitute 648π for v and 18 for h

648π= πr² x 18

Divide by 18π on both sides

⇒ \(\begin{aligned}
\frac{648 \pi}{18 \pi} & =\frac{\pi^2 \times 18}{18 \pi} \\
36 & =r^2
\end{aligned}\)

Take square root on both sides

Find the diameter of the cylinder
consider the relation d=2r
Substitute 6 for r
d=2(6)

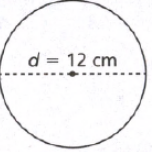
Therefore, the diameter of the given cylinder is 12 feet.

The diameter of a cylinder that has a volume of 648πft³ and a height of 18ft is 12 feet.

Page 48 Exercise 31 Answer

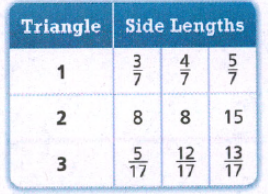
In the question, a set of ages of the members of a sailing club is given as follows –

18,19,24,28,33,37,42, and 46.

It is required to find the change in the mean, median, mode, and range of the ages of the club if a man 42 years old joins the club.

To find the change in the mean, median, mode, and range of the ages of the club, first, find these values for the given dataset.

Next, find these values by adding 42 of them to this dataset. Finally, compare the two values to find the change.

Find the change in the mean.

There are 8 age values at the beginning.

Use the definition of mean.

​Mean1 \(=\frac{18+19+24+28+33+37+42}{8}\)

Add the terms

Mean1= \(\frac{247}{8}\)

Divide the numerator by denominatortor

Mean1 =30.88

Add 42 and recalculate the mean

⇒\(\text { Mean }_2=\frac{18+19+24+28+33+42+46+42}{9}\)

Add the terms

⇒ \(\text { Mean }_2=\frac{289}{9}\)

⇒ \(\text { Mean }_2=\frac{289}{9}\)

Divide the numerator by denominator

Mean2=32.11

The change in  the mean is

Mean2-mean1 = 32.11-30.88

= 1.23

Therefore, in general, the mean of this data set increases by 1.23.

Find the change in the median.

Arrange the terms in increasing order.

18,19,24,28,33,37,42,46

The middle values are 28 and 33.

Use the definition of the median for an even number of terms.

Median₁ = \(\frac{28+33}{2}\)

Add the terms.

Median₁ = \(\frac{61}{2}\)

Divide the numerator by denominator.

Median₁ = 30.5

Add 42 to this set of values and recalculate the median.

Arrange the terms in increasing order.

18,19,24,28,33,37,42,42,46

The middle term is 33.

Use the definition of the median for an odd number of terms.

Median₂ = 33

The change in the median is –

​Median₂ − Median₁ = 33 − 30.5

= 2.5
​
Therefore, in general, the median of this dataset increases by 2.5.

Find the mode change.

Use the definition of mode.

None of the numbers are repeating in the data set.

No mode for the list at the beginning.

Add 42 to this set of values and recalculate the median.

18,19,24,28,33,37,42,42,46

42 is the only repeating value in this data set.

The mode of the new dataset is 42.

Therefore, in general, the data set changes from no mode value to 42 as the new mode value.

Find the change in range.

The maximum and minimum value in the given data set is 46 and 18 respectively.

Use the definition of the range.

Range = 46 − 18

Subtract the terms.

Range₁ = 28

Add 42 to this set of values and recalculate the median.

The maximum and minimum value remains the same.

Therefore, no change in the range of the ages.

The mean of the ages of the members of a sailing club increases by 1.23 when a new member 42 years old join the club.

The median of the ages of the members of a sailing club increases by 2.5 when a new member 42 years old join the club.

The mode of the ages of the members of a sailing club changes from no mode to a value 42 when a new member 42 years old join the club.

The range of the ages of the members of a sailing club remains unchanged when a new member 42 years old join the club..

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 48 Exercise 32 Answer

In the question, an expression is given by 8x⁴ − 4x³ − 24x².

It is required to find the factored form of this expression.

To find the factored form, take common variables and numbers in one parenthesis and the rest in another. Finally, form a product of two simplest forms of expressions.

Write the factored form.

Consider the given expression.

Take a common 4x² from each term of the expression.

Given 8x⁴-4x³-24x²
Take common 4x²
4x²(2x²-x-6)

Rewrite -x as -4x+3x
4x²(2×2-4x+3x-6)
take common 2x and 3

Take (x-2) Common

4x² (x-2)(2x+3)

Therefore, the factored form of the given expression is 4x²(x−2)(2x+3).

The factored form of the expression 8x⁴ − 4x³ − 24x² by taking common terms outside of the parenthesis and rewriting the quadratic equation as a product of two simple expressions is given by 4x²(x−2)(2x+3).

Page 48 Exercise 33 Answer

In the question, it is given that for an obtuse triangle the measure of the angle A is twice the measure of an angle B and the measure of the angle C is 30° greater than the measure of the angle B.

It is required to find the measure of all three angles.

To find the measure of all three angles, use the concept of the sum of measures of the angles inside a triangle. Next, apply the conditions to make the equation with only one unknown value. Finally, find the one unknown value and solve for the rest of the angles.

Find the measure of the angle B.

Use the concept of the sum of the measures of a triangle.

M∠A+M∠B+M∠C=180°

Apply the given conditions

M∠A=2m∠B and
M∠C=m∠B+30°

Substitute 2m∠B for m∠A and m∠B +30° for m∠c.

2m∠B+m∠B+m∠B+30°=180°

Subtract 30° from both sides
2m∠B+m<B+m<B+30°-30°=180°-30°

2m∠B+m∠B+m∠B=150°

4m∠B=150°

Divide by 4 on both sides

∴ The measure of the angle B is 3.75°

Find the measure of the angle A.

The measure of the angle A is two times the measure of the angle B.

Substitute 37.5∘ for m∠B.

m∠A = 2m∠B
m∠A = 2(37.5)

Multiply the terms.

m∠A = 75°

Therefore, the measure of the angle A is 75°.

Find the measure of the angle C.

The measure of the angle C is 30° greater than the measure of the angle B.

Substitute 37.5° for m∠B.
​
​m∠C = m∠B + 30°

m∠C = 37.5° + 30°

Add the terms.

m∠C = 67.5°

Therefore, the measure of the angle C is 67.5°.

The measure of the angle is 75°.

The measure of the angle B is 37.5°.

The measure of the angle C is 67.5°.

Page 48 Exercise 34 Answer

In the question, the given function is f(x) = 4x² − 10x − 6.

It is required to find the zeros of this function.

To find the zeros of the given function, first, equate it zero. Next, find the type of equation and determine the roots.

Find the zeros of the function.

Use the definition of zeros of the function.

Equate the given function to zero.

Given f(x)= 4x²-10x-6

⇒ \(x=\frac{10 \pm \sqrt{(10)^2-4(4)(-6)}}{2(4)}\)

⇒ \(x=\frac{10 \pm \sqrt{(10)^2+4(4)(6)}}{8}\)

⇒ \(x=\frac{10 \pm \sqrt{100+96}}{8}\)

⇒ \(x=\frac{10 \pm \sqrt{196}}{8}\)

⇒ \(x=\frac{10 \pm 14}{8}\)

Therefore, the solutions are

x = \(\frac{10+14}{8}\) and x = \(\frac{10-14}{8}\)

x = \(\frac{24}{8}\) x = \(\frac{-4}{8}\)

x = 3 x = -0.5

Therefore, the zeros of the function are 3 and −0.5.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 3 Page 49 Exercise 35 Answer

In the question, it is given that Dalia has a combination of 24 nickels and quarters for a total of $2.60.

It is required to write a system of equations and determine the number of each type of coin Dalia has.

To write the system of equations, take the number of nickels as x and the number of quarters as $y$ and apply the conditions.

Next, find the number of nickels and quarters by solving this system of equations.

Write the system of equations.

Take the number of nickels as x and the number of quarters as y.

Dalia has a combination of 24 nickels and quarters.

Use this condition and write the first equation.

x + y = 24

1 nickel equals$0.05 and 1 quarter equals $0.25.

Dalia has a total of $2.60.

The sum of x times $0.05 and y times $0.25 will be $2.60.

Use this condition and write the second equation.

0.05x + 0.25y = 2.60

Therefore, the system of equations is x + y = 24 and 0.05x + 0.25y = 2.60.

Find the number of each type of coin.

Use the system of equations from the previous step.

Consider the equation 0.05+0.25y=2.60

Substitute 24-y in x

0.05(24-y)+0.25y=2.60

Simply the parenthesis

1.20-0.05y+0.25y=2.60

Subtract 1.20 from both sides

1.20-0.05y-1.20+0.24y=2.60-1.20-0.05y+0.25y=1.40

The system of equations to determine the type of each coin Dalia has is given by –

x + y = 24 and 0.05x + 0.25y = 2.60

Dalia has 17 nickels and 7 quarters for a total of $2.60.

How To Solve Envision Algebra 1 Chapter 3 Questions

Page 49 Exercise 36 Answer

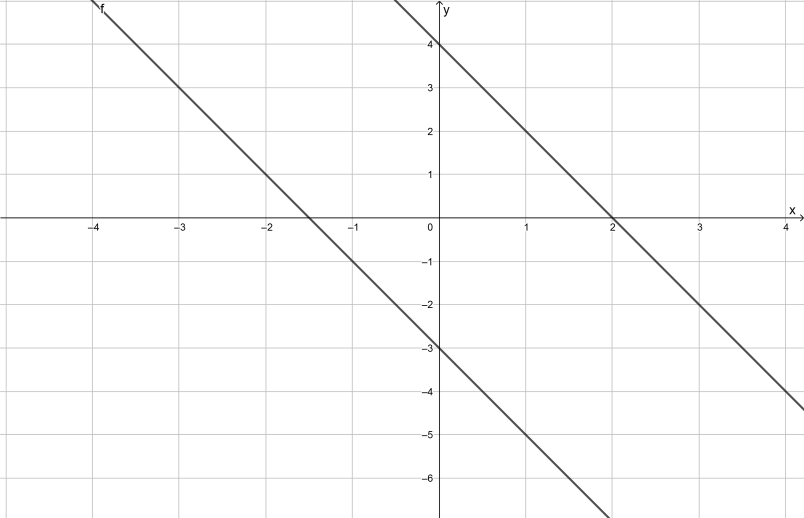
In the question, the given piecewise-defined function is –

f(x) = \(\left\{\begin{array}{l}
\frac{3}{2} x-4 ; x<0 \\
\frac{1}{3} x-4 ; 0 \leq x<6 \\
2 x-10 ; x>6
\end{array}\right.\)

It is required to graph this function.

To create a graphical representation of this piecewise-defined function, use a graphing utility and draw the graph.

Graph the given function.

Use a graphing calculator.

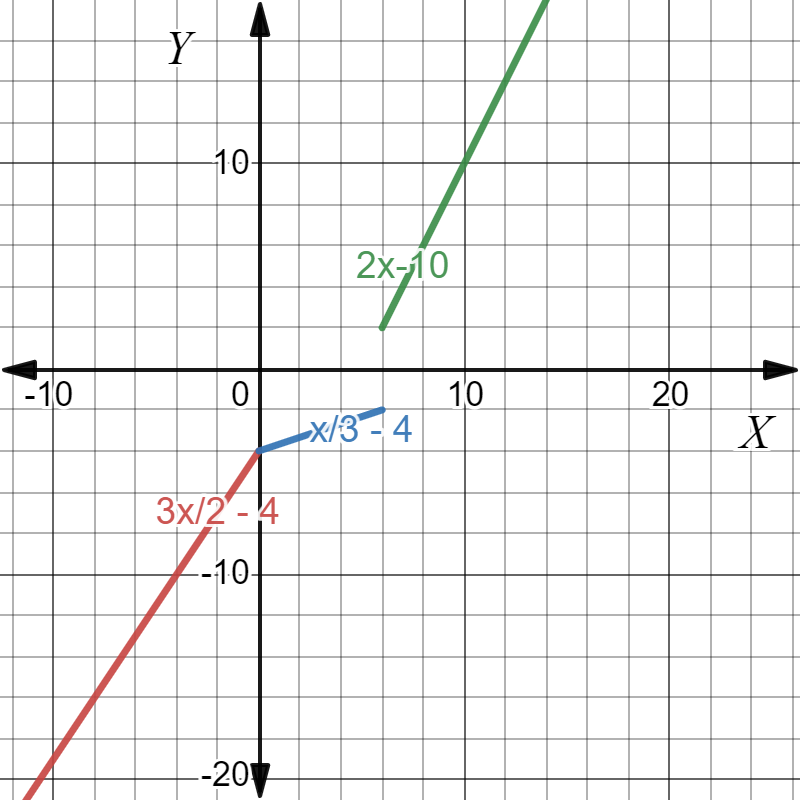
The graph of the given piecewise-defined function is –

In the question, the given piecewise-defined function is –

f(x) = \(\left\{\begin{array}{l}
\frac{3}{2} x-4 ; x<0 \\
\frac{1}{3} x-4 ; 0 \leq x<6 \\
2 x-10 ; x>6
\end{array}\right.\)

It is required to find the domain and range of this function.

To find the domain of this function, observe the graph of the function from the previous part of this problem and write all the possible inputs for x. Next, to find the range of this function, check for all the possible values of f(x).

Find the domain.

Observe the graph from the previous part of this problem.

The function is stretched for all the values of x except 6.

Therefore, the domain of the function is (−∞,6)∪(6,∞).

Find the range.

Observe the graph from the previous part of this problem.

The function is undefined for the interval (−2,2).

Therefore, the range of the function is (−∞,−2)∪(2,∞).

The domain of the given piecewise-defined function is (−∞,6)∪(6,∞).

The range of the given piecewise-defined function is (−∞,−2)∪(2,∞).

In the question, the given piecewise-defined function is –

f(x) = \(\left\{\begin{array}{l}
\frac{3}{2} x-4 ; x<0 \\
\frac{1}{3} x-4 ; 0 \leq x<6 \\
2 x-10 ; x>6
\end{array}\right.\)

It is required to determine the interval for increasing or decreasing of this function.

To find the interval of increasing or decreasing, check for the slope of the line for each interval.

Check the function for x < 0.

The piecewise-defined function for this interval is f(x) = \(\frac{3}{2}\)x – 4.

Compare with the general equation of a line.

m = \(\frac{3}{2}\).

The slope of the line represented by this function is positive.

Therefore, the function is increasing for the interval (−∞,0).

Check the function for 0 ≤ x < 6.

The piecewise-defined function for this interval is f(x) = \(\frac{1}{3}\)x – 4.

Compare with the general equation of a line.

m = f(x) = \(\frac{1}{3}\).

The slope of the line represented by this function is positive.

Therefore, the function is increasing for the interval [0,6).

Check the function for x > 6.

The piecewise-defined function for this interval is f(x) = 2x − 10.

Compare with the general equation of a line.

m = 2.

The slope of the line represented by this function is positive.

Therefore, the function is increasing for the interval (6,∞).

The given piecewise-defined function is increasing for the interval (−∞,6)∪(6,∞).

Envision Algebra 1 Chapter 3 Step-By-Step Solutions

Page 50 Exercise 1 Answer

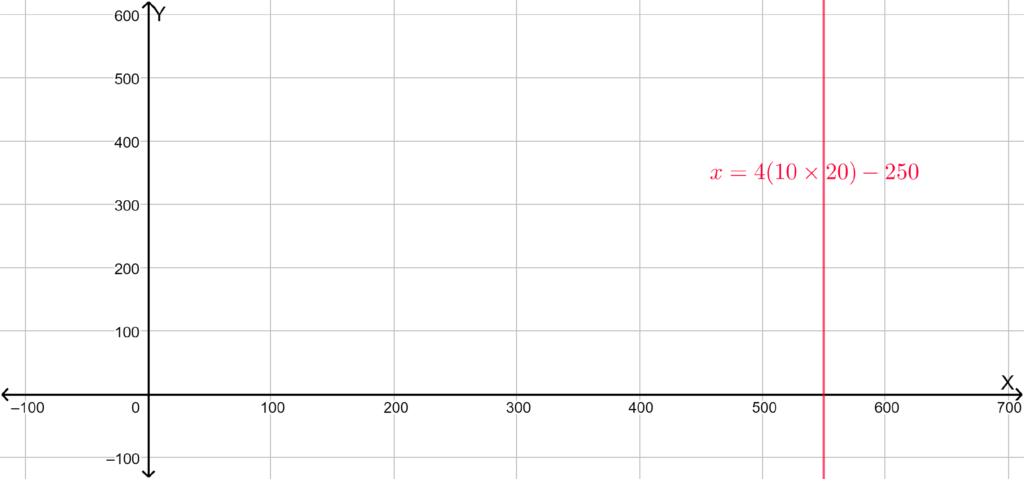
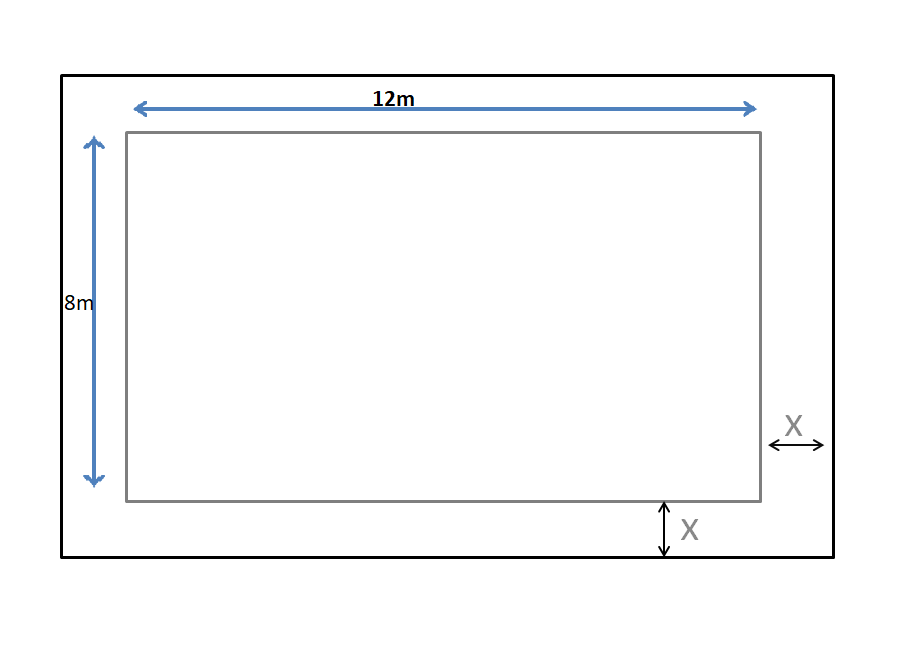
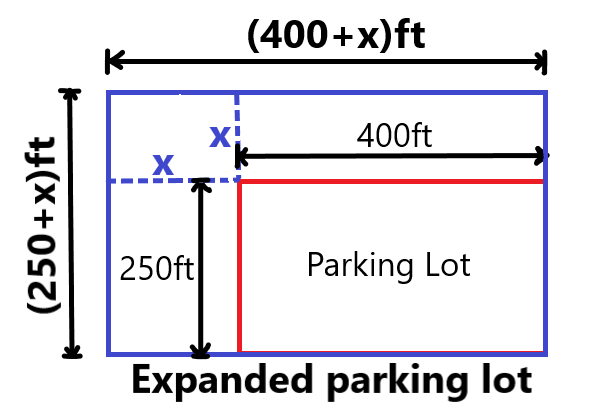
In the question, it is given that a high school rectangular parking lot 400ft long and 250ft wide is expanded to double the area by increasing both its length and width by (x)ft.

It is required to draw a diagram that represents the original rectangular parking lot as well as the expanded parking lot with all the labeling.

To draw a rectangular parking lot, first, draw a rectangle that measures 400ft by 250ft. Next, draw a larger parking lot around the original such that the length and the width of the new rectangle are (x)ft more.

Draw the original parking lot.

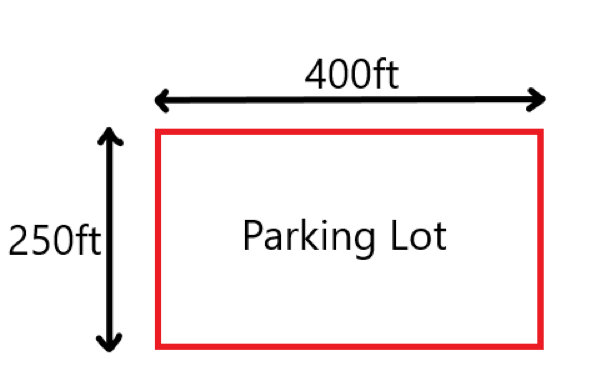
Draw the expanded parking lot.

The diagram of the original parking lot is –

The diagram of the expanded parking lot is –

In the question, it is given that a high school rectangular parking lot 400ft long and 250ft wide is expanded to double the area by increasing both its length and width by (x)ft.

It is required to form an equation that can be used to find x and solve the equation. It is also required to round the answer to the nearest 10ft.

To form an equation, first, find the area of the original parking lot using the formula for the area of a rectangle. Next, increase the length and the width by x and find the area equation for the expanded parking lot.

Finally, double the area substitute this value in the area equation and find the value of x.

Find the area of the original parking lot.

The length is 400ft and the width is 250ft.

Use the formula for the area of a rectangle.

Therefore, the area of the original parking lot is 100000 square feet.

The length and the width are increased by (x)ft.

The new length of the parking lot is (400+x)ft and the width is (250+x)ft.

Use the formula for the area of a rectangle.

Therefore, the area of the original parking lot is given by A = x² + 650x + 100000.

Double the original parking lot area.

The area of the original parking lot is 100000ft².

The area of the expanded parking lot is twice this area.

The area of the expanded parking lot is twice this area

Multiply 100000 by 2

A= 100000×2

A=200000

Substitute A= 20000=x2+650x+100000

Subtract 200000 from both sides

x2+650x+100000-2000000= 100000- 200000

x2+650x+100000=0

Therefore, the equation for the area of the expanded parking lot is given by x² + 650x − 100000 = 0.

Solve the equation.

Compare the equation with the general form of a quadratic equation.

a=1
b=650
c=-100000

Use the formula for the roots of a quadratic equation

⇒ \(x=\frac{-650 \pm \sqrt{(650)^2-4(-100000)}}{2}\)

Multiple The terms -4 and -100000

⇒ \(x=\frac{-650 \pm \sqrt{(650)^2+400000}}{2}\)

Simply the square root

⇒ \(x=\frac{-650 \pm 906.92}{2}\)

Therefore, the roots of this equation are x = 128.46 and x = −778.46.

Round of the x value.

To increase the size of the lot, the only positive value of x is taken.

Round the value 128.46 to the nearest 10.

Therefore, the value of x is 130ft.

The equation that can be used to find the x value is given by x² + 650x − 100000 = 0

The value of x after rounding off to the nearest 10 is 130ft.

In the question, it is given that a high school rectangular parking lot 400ft long and 250ft wide is expanded to double the area by increasing both its length and width by (x)ft.

It is required to find the area of the new portion of the expanded parking lot and find the perimeter of the new parking lot.

To find the area of the new portion, first, calculate the area of the expanded parking lot using the value of x from the previous part of the problem. Next, subtract the area of the original parking lot from this new area value. Finally, to find the perimeter of the new parking lot, calculate the new length and width of the rectangle using the formula for the perimeter of a rectangle.

Calculate the area of the new parking lot.

The value of x from the previous part of the problem is 130ft.

The new length and the new width of the rectangle will be 400 + 130 = 530ft and 250 + 130 = 380ft respectively.

Use the formula for the area of a rectangle.

Substitute 530 for l and 380 for b.

A = 530 × 380

Multiply the terms.

A = 201400ft²

Therefore, the area of the expanded parking lot is 201400ft².

Find the area of the new portion.

The area of the original rectangular parking lot is 100000ft².

Use the formula for the area of an expanded portion.

Substitute 201400 for A_exp and 100000 for A_org.

A_portion = 201400 − 100000

Subtract the terms.

A_portion = 101400ft²

Therefore, the area of the new portion is 101400ft².

Find the perimeter.

The new length and the new width of the rectangle will be 400 + 130 = 530ft and 250 + 130 = 380ft respectively.

Use the formula for the perimeter of a rectangle.

Substitute 530 for l and 380 for b.

P = 2(530+380)

Add the terms inside the parenthesis.

P = 2(910)

Multiply the terms.

P = 1820ft

Therefore, the perimeter is 1820ft.

The area of the new portion of the expanded parking lot is 101400ft².

The perimeter of the new parking lot is 1820ft.

In the question, it is given that a high school rectangular parking lot 400ft long and 250ft wide is expanded to double the area by increasing both its length and width by (x)ft

It is also given that cost of expanding the lot is $1.50 per square foot of new space and the cost of fencing is $20 per foot.

It is required to find the estimated cost of expanding and fencing in the new lot.

To find the estimated cost of expanding, multiply the cost for per square foot to the area of the new portion of the expanded parking lot. Next, to find the cost of fencing in the new lot, multiply the perimeter of the new lot to the fencing cost for per foot distance.

Calculate the cost of expanding.

The area of the new portion of the expanded lot from the previous part of the problem is 101400ft2.

The cost of expanding the parking lot is $1.50 per square foot of new space.

Multiply 101400 by 1.50.

101400 × 1.50 = 152100

Therefore, the cost of expanding the parking lot $152100.

Calculate the cost of fencing.

The perimeter of the new parking lot from the previous part of the problem is 1820ft.

The cost of fencing is $20 per foot.

Multiply 1820 by 20.

1820 20 = 36400

Therefore, the cost of fencing the new parking lot $36400.

The cost of expanding the parking lot is $152100.

The cost of fencing the new parking lot $36400.

In the question, it is given that a high school rectangular parking lot 400ft long and 250ft wide is expanded to double the area by increasing both its length and width by (x)ft. It is also given that the school has only enough money to pay for half the estimated cost, and thus the parking stickers worth $150 to students and $250to faculties are needed to be sold.

It is required to find the number of student and faculty stickers the school must sell.

To find the number of stickers the school must sell, take the number of student stickers as x and take the number of faculty stickers as y. Next, form an equation with the given condition of the price of stickers and the amount needed for expanding and fencing.

Form an equation.

The total cost of expanding and fencing the lost is 152100 + 36400 = $188500.

Half of the total estimated cost is $94250.

Assume the number of student stickers needed to sell is x and the number of faculty stickers needed to sell is y.

Each student sticker is worth $150 and each faculty sticker is worth $250.

Multiply x by 150 and y by 250.

150x + 250y

Equate 150x + 250y to half of the estimated value.

150x + 250y = 94250

Therefore, the amount raised by selling parking stickers is given by 150x + 250y = 94250.

Find the number of each sticker for one value of x.

The equation to find the number of each sticker is 150x + 250y = 94250.

150(300)+250y=94250

Multiply the terms 150 and 300

45000+250y=94250

Subtract 45000 from both sides

45000-45000+250y=94250-45000

250y=49250

Divide by 250 from both sides

⇒ \(\frac{250 y}{250}=\frac{49250}{250}\)

y=197

Find the number of each sticker for another value of x

The equation to find the number of each sticker is 150x+250y=94250

Take 200 as the value of x.

150(200)+250y =94250
30000+250y=94250

Subtract 30000 from both sides

30000-30000+25y=94250-30000

250y=64250

Divide by 250 from both sides

⇒ \(\frac{250 y}{250}=\frac{64250}{250}\)

y=257

Find the nature of the number of each sticker.

When the value of x increases, the value of y decreases.

When the value of x decreases, the value of y increases.

There are no specific values for the number of student stickers and the number of faculty stickers.

There are multiple possible values for each type of sticker.

There is no specific number of student stickers and faculty stickers that the school must sell to raise half of the estimated cost of the expansion and fencing.

There are multiple possible answers to this problem as the number of student stickers and the number of faculty stickers are relative.

Envision Algebra 1 Assessment Readiness Workbook Chapter 2

Page 32 Exercise 1 Answer

It is given that there are five numbers.

a. \(\frac{3}{4}\)

b. √9

c. √12

d. −9

e. √20

It is required to determine all the irrational numbers.

Consider √12. Its value is 2√3 . √3 is an irrational number, hence √12 = 2√3 is an irrational number.

Consider √20. Its value is 2√5 . √5 is an irrational number, hence √20 = 2√5 is an irrational number

Consider \(\frac{3}{4}\). It is a ratio of two integers and hence is a rational number, by definition of rational numbers.

Consider √9. Its value is 3, a rational number.

Consider −9. It is a negative integer and hence a rational number.

Thus option c and option e are irrational numbers.

The correct answer is options c and e, representing irrational numbers √12 and √20.

Page 32 Exercise 2 Answer

It is given that the expression is \(\frac{(7)^{-5}(2)^5}{(7)^4(2)^{-2}}\).

a. \(\frac{7^{11}}{2^7}\)

b. \(\frac{7^{9}}{2^3}\)

c. \(\frac{2^{7}}{7^9}\)

d. \(\frac{2^{3}}{7^1}\)

It is required to determine the option that represents the value of the expression using a positive exponent.

Explanation for the correct option:

Option c represents the correct answer.

Consider the given expression

\(\frac{(7)^{-5}(2)^5}{(7)^4(2)^{-2}}\).

The expression can be written in positive exponent using the law of exponent \(.a^{-n}=\frac{1}{a^n}\).

The exponent obtained after applying the law of exponent is \(\frac{(2)^{2}(2)^5}{(7)^4(7)^{5}}\).

Apply the law of exponent a^p.a^q = a^p+q and simplify, \(\frac{(2)^7}{(7)^9}\).

Explanation for other options:

Options a, b, and d do not represent the correct answer because on simplifying, the result obtained is different.

The correct answer is option c, which represents the expression \(\frac{(7)^{-5}(2)^5}{(7)^4(2)^{-2}}\) in terms of positive exponent \(\frac{(2)^7}{(7)^9}\).

Envision Algebra 1 Chapter 2 Answer Key

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 32 Exercise 3 Answer

It is given that the equation is ∣2x−4∣ + 2 = 16. The set of possible solutions is given.

a. −5

b. −4

c. −2

d. 5

e. 9

It is required to determine all possible solutions of the given equation among the given values.

Consider the given equation ∣2x−4∣ + 2 = 16. Subtract both sides by 2 and the simplified equation obtained is ∣2x−4∣ = 14

The solutions of the absolute value are given by the equations 2x − 4 = 14 and 2x − 4 = −14

The value of x is determined from the first equation 2x − 4 = 14, by adding both sides by 4 and then dividing by 2 is 9, given by option e.

The value of x determined from the second equation 2x − 4 = −14, by adding both sides by 4 and then dividing by 2 is −5, given by option a.

Hence the solution of ∣2x−4∣ + 2 = 16 is −5, 9, given by options a and e.

On simplifying the given equation ∣2x−4∣ + 2 = 16 the possible solution set does not match options b, c, d.

The correct answer is option a and e, which represent the solution of the equation ∣2x−4∣ + 2 = 16.

Page 32 Exercise 4 Answer

It is given that a line is perpendicular to another line. The other line passes through the two points (1,0) and (3,−4). Options are given among which one represents the equation of a line perpendicular to the line passing through two points (1,0) and (3,−4).

a. y = 2x + 2

b. y = \(-\frac{1}{2} x+2\)

c. y = 2x + 2

d. y = \(\frac{1}{2} x+2\)

It is required to determine the equation of the line perpendicular to the line passing through two points (1,0) and (3,−4) among the given options.

Option d represents the equation of the line perpendicular to the line passing through two points (1,0) and (3,−4) among the given options. Consider the slope of the line passing through the points (x1,y1) as (1,0) and (x2,y2) as (3,−4). It is given by the formula m = \(\frac{y_2-y_1}{x_2-x_1}\). On substitution the slope is given by \(\frac{-4-0}{3-1}\)

Hence slope of the line through the points (x1, y1) as (1,0) and (x2, y2) as (3, -4) is \(\frac{-4}{2}\) = -2.

The slope of perpendicular lines is negative reciprocals of each other. Hence, the slope of a line perpendicular to the line passing through the points (1,0) and (3,−4) is the negative reciprocal of the slope of −2, that is \(\frac{1}{2}\).

The equation of a line with slope m is y = mx + c with c as the y-intercept. In the given options equation of the line having slope \(\frac{1}{2}\) is y = \(\frac{1}{2} x+2\), that is option d.

The equation formed by a line passing through points (1,0) and (3,−4) does not match options a, b, and c.

The correct answer is option d. y = \(\frac{1}{2} x+2\) is the equation of the line perpendicular to the line passing through two points (1,0) and (3,-4).

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 32 Exercise 5 Answer

It is given that the amount of saving after working x hours is given by equation y = 9.5x + 25.

It is required to determine earnings per hour.

Consider the equation for the amount of savings after working x hours, y = 9.5x + 25.

In this equation, the constant 25 represents a fixed amount possibly in the form bonus, some initial payment, or initial saving.

Th.5x represents the amount earned when worked for x hours.

Hence the earning per hour, that is for x as 1, is 9.5 × 1 = 9.5.

The earning per hour is 9.5 as determined from the equation y = 9.5x + 25 which represents the amount of savings after working x hours.

Page 32 Exercise 6 Answer

It is given that the expression is (3×4⁴y²)³.

The four options are given.

a. 3x⁷y⁵

b. 3x²y

c. 9x¹²y⁶

d. 27x¹²y⁶

It is required to determine the option that represents the simplified value of the given expression.

Explanation for the correct option:

The correct answer is represented by option d.

Consider the given expression (3x⁴y²)³.

The expression can be simplified using the law of exponent (aⁿ)^m = a^n.m

The exponent obtained after applying the law of exponent is 27x^4.3y^2.3 = 27x¹²y⁶.

Option d is the option that represents the correct answer.

Explanation for other options:

The options a, b, and c do not represent the correct answer because the simplified equation does not match the result.

The correct answer is option d, which represents the expression (3x⁴y²)³ in a simplified manner 27x¹²y⁶.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 33 Exercise 7 Answer

It is given that the function f(x) = |2x – 3|. The options are given a piecewise function out of which one has the same graph as that of f(x).

a. g(x) = \(\left\{\begin{array}{l}
2 x-3, \text { if } x \geq 0 \\
-2 x+3, \text { if } x<0
\end{array}\right.\)

b. g(x) = \(\left\{\begin{array}{l}
-2 x+3, \text { if } x \geq \frac{2}{3} \\
2 x-3, \text { if } x<\frac{2}{3}
\end{array}\right.\)

c. g(x) = \(\left\{\begin{array}{l}
2 x-3, \text { if } x \geq \frac{3}{2} \\
-2 x+3, \text { if } x<\frac{3}{2}
\end{array}\right.\)

d. g(x) = \(\left\{\begin{array}{l}
2 x-3, \text { if } x \geq 0 \\
2 x+3, \text { if } x<0
\end{array}\right.\)

It is required to determine the piecewise function that has the same graph as f(x).

Explanation for the correct option:

Option c represents a piecewise function that has the same graph as f(x).

Consider f(x) = ∣2x−3∣. The function can be given as two piecewise functions

f₁(x) = 2x − 3 and
​
f₂(x) = −(2x−3)

f₂(x) = −2x + 3.

The range of the piecewise function can be given by the value of x as determined when y is 0.

From f₁(x), 2x − 3 = 0, the value of x is obtained by adding 3 on both sides and dividing both sides by 2, the value of x is \(\frac{3}{2}\).

From f₂(x), −2x + 3 = 0, the value of x is obtained by subtracting 3 on both sides and dividing both sides by −2, the value of x is \(\frac{3}{2}\).

The function is 2x−3, with x ≥ \(\frac{3}{2}\).

The function is -2x + 3, with x < \(\frac{3}{2}\).

The function is represented by a piecewise function in option c.

As the functions are the same they have the same graph.

The result obtained when function f(x) = ∣2x−3∣ is simplified does not match options a, b, and d.

The correct option that has the same graph as f(x) = ∣2x−3∣ is given by option c.

Page 33 Exercise 8 Answer

It is given that the function is f(x) = 2x + 5. The given options name different types of equations.

a. exponential

b. linear

c. quadratic

d. none of the above

It is required to determine the equation type of f(x).

The correct answer is option b, linear.

Consider the given equation f(x) = 2x + 5.

The equation is in single independent variable x with power 1.

Hence, the equation f(x) = 2x + 5 represents a linear equation, by definition of linear equation.

An exponential equation is an equation in which the independent variable is an exponent of a constant base.

A quadratic equation is an equation with the highest order of independent variables as 2. In standard form, the quadratic equation is y = ax²+ bx + c.

The correct option is b. The equation f(x) = 2x + 5 is a linear equation.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 33 Exercise 9 Answer

It is given that the scores on the first four tests in one class are 88, 97, 89, 78. The required average score for five tests is 90.

It is required to determine the score to be earned in the fifth test to have an average score of 90.

To determine the score to be earned in the fifth test to have an average score of 90, consider the given scores of four tests and denote the required fifth score as x. Determine the value of x using the formula for average with 5 values,

Average = \(\frac{\text { sum of values }}{\text { number of values }} .\)

Assume the score of the fifth test to be x.

The average of the five test scores is given by the formula Average = \(\frac{\text { sum of values }}{\text { number of values }}.\)

⇒ \(\begin{aligned}
& \text { Average }=\frac{\text { Sum of values }}{\text { number of values }} \\
& 90=\frac{88+97+89+78+x}{5}
\end{aligned}\)

Determine the score of the fifth test x

⇒ \(\begin{aligned}
& 90=\frac{88+97+89+78+x}{5} \\
& 90=\frac{352+x}{5}
\end{aligned}\)

Multiply both sides by 5 and simplify

450=352+x

subtract both sides by 352

450-352=352-352+x

x=98

The score required in the fifth test is 98.

The score to be earned in the fifth test to have an average score of 90 is 98.

Page 33 Exercise 11 Answer

Given: Scatter plot.

It is required to estimate an equation of a line that best fits the given scatter plot.

For this, draw a straight line on the given scatter plot then find the values for m and c from the graph and substitute it in the equation of the straight line.

Draw a straight line that passes through the maximum number of points of a given scatter plot.

All the points in the given plot lie between the positive x-axis and the positive y-axis, so the slope of the line is positive. Also, the angle of inclination of the slope with the positive x-axis is less than 90º and the y-intercept is approx 2.

Therefore,
​
m = 1

c = 2

Substitute 1 for m and 2 for c in the equation y = mx + c.

y = x + 2

Option a represents the line with y-intercept as 3 thus the line moves away from the points.

Option b represents the line with a negative slope so it cannot be the best-fitted line.

Option d represents the line with a negative slope so it cannot be the best-fitted line.

An equation of a line that best fits the given scatter plot is y = x + 2.

Option (C) is correct.

Page 33 Exercise 12 Answer

In the question, the given series is \(\frac{1}{2}\),√7,−√2,−2,\(\frac{3}{4}\),3.

It is required to arrange the given numbers in order from least to greatest.

For this, first, convert the given numbers into integers and then compare them.

Convert numbers other than -2 and 3 into integers

⇒ \(\begin{aligned}
\frac{1}{2} & =0.5 \\
\sqrt{7} & =2.6 \\
-\sqrt{2} & =-1.41 \\
\frac{3}{4} & =0.75
\end{aligned}\)

0.5,2.6-141,0.75

Compare numbers and arrange them in ascending order

-2<-1.41<0.5<0.75<2.6<3
\(-2<-\sqrt{2}<\frac{1}{2}<\frac{3}{4}<\sqrt{7}<3\)

Compare numbers and arrange them in ascending order

The required arrangement of numbers is given as -2 < -√2 < \(\frac{1}{2}\) < \(\frac{3}{4}\) < √7 < 3

Envision Algebra 1 Assessment Readiness Workbook Chapter 2 Solutions

Page 34 Exercise 13 Answer

Given data shown in the dot plot to the nearest hundredth.

It is required to find the mean and median for the given data and tell the reason behind the different values of mean and median.

To find the mean and median it is required to extract data from the given dot plot, then find the mean and the median of the given data using the formula mentioned in the tip section.

Extract and compare information from the given dot plot.

6,6,6,6,7,7,7,7,7,8,8,10,11

Total number of observations is 13.

Substitute required values in the formula,

⇒ \(\begin{aligned}
& \text { Mean }=\frac{\text { Sum of observations }}{\text { total number of observations }} \\
& \text { Mean }=\frac{6+6+6+6+7+7+7+7+7+8+8+10+11}{13}
\end{aligned}\)

Mean =\(\frac{96}{13}\)

Mean =7.38

Here, n is an odd number

Substitute 13 for n in the formula

Median =\(\left(\frac{n+1}{2}\right)^{\text {th }} \text { term }\)

Median = \(\left(\frac{13+1}{2}\right)^{\text {th }} \text { term }\)

Median

Both the values are different because the mean is the average of given numbers and the median is the middle term.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 34 Exercise 14 Answer

Given that the area of the rectangle is 6x² + 8x + 2 and the length of the rectangle is 3x + 1.

It is required to find the width of the rectangle.

To find the width of the rectangle, substitute the given values in the formula given in the tip section. Factorize the numerator part and then solve it.

Substitute 6x² + 8x + 2 for A and 3x + 1 for l in formula A = l × b and simplify.

Given 6x²+8x+2 and the length of the rectangle is 3x+1
A=lxb
Substitute A=6x²+8x+2 and l=3x+1
(3x+1)b=6x²+8x+2

⇒ \(b=\frac{6 x^2+8 x+2}{3 x+1}\)

Factorize the numerator of equation \(b=\frac{6 x^2+8 x+2}{3 x+1}\)

⇒ \(b=\frac{2 x(3 x+1)+2(3 x+1)}{3 x+1}\)

​⇒ \(b=\frac{(2 x+2)(3 x+1)}{(3 x+1)}\)

b=2(x+1)

The required value of the width of the rectangle is 2(x+1).

Page 34 Exercise 15 Answer

In the question, the given inequality is 2x + 3y > 12.

It is required to graph the inequality 2x + 3y > 12.

To graph the inequality 2x + 3y > 12, it is required to plot the graph for 2x + 3y = 12 and then compare the points above and below the line

2x + 3y = 12 and shade the region in which the point satisfies the given inequality.

Plot the graph for 2x + 3y = 12.

Plot points (1,2) and (3,4) in the graph 2x + 3y = 12 and check the given inequality for both points.

For (1,2)

2(1) + 3(2) = 8 < 12

For (3,4)

2(3) + 3(4) = 18 ≥ 12

Shade the region in the graph which satisfies the inequality 2x + 3y > 12.

The required graph for inequality 2x + 3y > 12 is given below.

Page 34 Exercise 16 Answer

Given function: f(x) = x² + 2x + 1

It is required to plot the graph for the given function f(x) = x² + 2x + 1.

For this, it is required to plot a graph for x² and shift this graph to the left 1 unit to get the required graph for f(x) = x² + 2x + 1.

Plot the graph for x².

Compare x² + 2x + 1 with expression (a+b)² = a² + 2ab​ + b².

Thus f(x) = x² + 2x + 1 can be written as (x+1)².

f(x) = x² will shifted to left 1 unit to get f(x) = (x+1)².

Plot graph for f(x) = x² + 2x + 1.

The required graph for f(x) = (x+1)² is given below.

Page 35 Exercise 17 Answer

Given that a ball is thrown directly upward from a height of 10ft and an initial velocity of 32ft/s. The given equation h = −16t² + 32t + 10 gives the height h after t seconds.

It is required to find the maximum height of the ball and the time taken by the ball to reach its maximum height.

For this, use the basic theory of velocity mentioned in the tip section to derive the linear equation and then solve it at the maximum height of the ball to find the time taken by the ball to reach its maximum height. Further, substitute the value of maximum time in the given expression to find the maximum height.

Velocity \(=\frac{d h}{d t}\)

⇒ \(V=\frac{d}{d t}\left(-16 t^2+32 t+10\right)\)

V=-32t+32

At maximum height velocity is zero

0=-32t+32

Solve for t

32t=32

⇒ \(t=\frac{32}{32}\)

t=1 sec

Substitute 1 for t in expression h= -16t²+32t+10

h=-16(1)² +32(1) +10
=-16+32+10
=26ft

The time taken by the ball to reach its maximum height is 1 sec.

The maximum height of the ball is 26ft.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 35 Exercise 18 Answer

Given: A table containing data for 7 points.

It is required to make a scatter plot of the data and estimate an equation of the line of best fit.

To make a scatter plot from the given data, locate the given points in the graph. To estimate the equation of the line, draw a line such that there are equal numbers of points above and below the line at a minimum distance then find x and y intercepts.

Draw a scatter plot.

Draw a line such that there are equal numbers of points above and below the line at minimum distance then find x and y intercepts.

x-intercept is 5.

y-intercept is

Substitute 5 for a and 8 for b in the equation \(\frac{x}{a}+\frac{y}{b}=1\).

⇒ \(\frac{x}{5}+\frac{y}{8}\)=1

An equation of the line of best fit is \(\frac{x}{5}+\frac{y}{8}\)=1.

Page 36 Exercise 20 Answer

Given equation: 2x² + 7x − 2 = 3

It is required to find the solutions of the equation to the nearest hundredth.

To find the solutions of the equation to the nearest hundredth, use the quadratic formula mentioned in the tip section as the given equation is a quadratic equation.

Explanation for the correct option:

Write the given formula 2x² + 7x − 2 = 3 in the general form

Given equation: 2x²+7x-2=3
ax²+bx+c=0
2x²+7x-2=3
2x²+7x-2-3=0
2x²+7x-5=0

Substitute a=2, b=7, c=-5 in formula

Option a and e are the correct answers.

Explanation for other options:

Option b, c, d, and f do not match the values of x obtained while solving the given quadratic expression.

The solutions of the equation to the nearest hundredth are −4⋅11 and 0⋅61.

Options (A) and (E) are correct.

Page 36 Exercise 22 Answer

It is given that the inequality −2x + 2 ≤ 8.

It is required to graph the solution of the given inequality.

To graph the solution of the given inequality, find the solution of the inequality using rules for solving inequality, subtract 2 on both sides of the inequality divide by −2 reverse the sign of inequality, and graph the resulting solution.

Consider the given inequality

-2x+2≤8

Subtract 2 on both sides of the inequality

-2x+2-2≤8-2
-2x≤6

Divide by -2 on both sides and reverse the sign

⇒ \(\frac{-2 x}{-2} \geq \frac{6}{-2}\)

x≥-3

So, the graph of the solution will be,

Hence, the graph of the solution will be,

Page 36 Exercise 23 Answer

It is given that the table of points,

It is required to find which function the table represents.

To plot the points on a graph find the slope of the best-fit line and use the slope-intercept form to find the equation of the line.

Explanation for the correct option:

Plot the points on the graph,

The slope of the best-fit line will be,

The slope of the best-fit line will be,

So the equation of the line in slope-intercept form will be

y=mx+c
y=x+c

Consider the point (o,3) and substitute in the slope-intercept form,

3=0+c
c=3

So, the equation will be,

y=x+3

Explanation for other options:

The equation of the line plotted using the given data does not match the equations of options a, b, and d.

Hence, the correct option will be (c).

Page 36 Exercise 24 Answer

It is given that a $220 deposit in the account that pays 3% interest compounded quarterly.

It is required to find the amount in the account after 5 years.

To find the amount in the account after 5 years, substitute 220 for P, 0.03 for r, 4 for n, and 5 for t in the compound interest formula.

Substitute 220 for P, 0.03 for r, 4 for n, and 5 for t in the formula

Substitute p=220,r=0.03, n=4,t=5

⇒ \(\begin{aligned}
& A=220\left(1+\frac{0.03}{4}\right)^{4 \times 5} \\
& A=220\left(\frac{4.03}{4}\right)^{20} \\
& A=220(1.161) \\
& A=255.42
\end{aligned}\)

Hence, the amount in the account after 5 years will be $255.42.

Page 37 Exercise 25 Answer

It is given that the parent function y = \(\sqrt[3]{x}\).

It is required to describe the graph of y = \(4 \sqrt[3]{x}\) as a transformation of the parent function.

To describe the graph of y = \(4 \sqrt[3]{x}\) as a transformation of the parent function, plot both the curves and observe the transformation.

The graph of the parent function and given function will be,

It can be observed from the graph that the parent function is stretched vertically by a factor of 4 units.

Option a indicates that the function is translated 4 units up but the graph is not shifted thus this option is not applicable.

Option b indicates that the function is compressed vertically by a factor of 4 but from the graph it is seen that there is no vertical compression thus this option is not applied.

Option d indicates the reflection along the line y = 4 but this is also not correct as the graph of the function is not a straight line.

Hence, the correct option is (c), vertical stretch by a factor of 4.

Envision Algebra 1 Student Edition Chapter 2 Practice Problems

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 37 Exercise 26 Answer

It is given that linear equations are

y = 4x + 1 and

y = 3x + 5.

It is required to find the solution of the system of linear equations.

To find the solution of a system of linear equations equate the right side of both the equations as the left sides of the equations are equal. Then solve the equation for x. Substitute the value of x obtained in one of the given equations and find the value of y.

The left-hand side of both the linear equations is equal thus equation is the right-hand side of the equations.

Given Linear Equations are

y=4x+1 and
y=3x+5
4x+1=3x+5

Subtract both sides of the equation by 3x

4x+1-3x=3x+5-3x
x+1=5

Substitute 4 for x in equation y=4x+1

Thus the solution of a system of linear equations is (4,17).

Page 37 Exercise 27 Answer

It is given that the parent function is y = √x.

It is given that the graph of a transformed function is,

It is required to find the equation of transformation of the graph shown in the figure of the parent function y=√x.

To find the equation of transformation of the given graph of the parent function y = √x use the transformation rule :

f(x) + b shifts the function b units upward.

f(x) − b shifts the function b units downward.

f(x+b) shifts the function b units to the left.

f(x−b) shifts the function b units to the right.

Plot the graph of the parent function along with the given graph.

From the graph it is seen that graph of the function is shifted 2 units to the left and 3 units upward.

Thus from transition rule f(x+2)+3.

The equation for the transformation of the graph is given by \(\sqrt{x+2}+3\).

The equation for the transformation of the graph is given by \(\sqrt{x+2}+3\).

The correct answer is option (D).

Page 37 Exercise 28 Answer

It is given that the volume of a cylinder is 320π ft³ and the height is 20 ft.

It is required to find the diameter of the base of the cylinder.

To find the diameter of the base of the cylinder substitute the given values of height and volume in formula V = πr²h and solve r where r is the radius of the base. The diameter is twice the radius thus multiply the value of r by 2 to find the diameter.

Given that the volume of a cylinder is 320πft³​ and height is 20ft

v=πr²h

Substitute 320π =v and h = 20

320π =πr²(20)

Divide both sides of the equation

320π = πr²(20) by 20π

⇒ \(\frac{320 \pi}{20 \pi}=\frac{\pi r^2(20)}{20 \pi}\)

16=r²

Rearrange the equation

r²=16

Square root on both sides

⇒ \(\begin{gathered}
\sqrt{r^2}=\sqrt{16} \\
r=\sqrt{4^2}
\end{gathered}\)

Since r is the length of the radius thus it cannot be negative.

Multiply radius r by 2 to find diameter.
​
D = 2(4)

= 8

The diameter of the cylinder is 8 ft.

Page 37 Exercise 29 Answer

It is given that table shows the preference of students in grades 9th and 10th to listen to music while studying or study in quiet.

It is required to complete the table.

It is required to find the percentage of students in grade 10th who prefer listening to music while studying.

To complete the table given simple addition is required. To find the percentage of students in grade 10th who prefer listening to music while studying divide the number of students who prefer listening to music while studying by the total number of students in grade 10 and multiply by 100.

To complete the table perform addition. Add both rows and columns and write the total result in the last row and last column.

To find the percentage of students in grade 10th who prefer listening to music while studying divide the number of students that prefer listening to music while studying by the total number of students in grade 10 and multiply by 100.

9 students in 10th grade prefer to listen to music while studying out of 40 students in 10th grade.

Thus percentage can be obtained as,

= \(\frac{9}{40} \times 100\)

= 22.5%

The complete table is,

Percent of 10th graders who listen to music while studying is 22.5%.

Page 37 Exercise 30 Answer

It is given that points and slopes are as follows:

(3,18) and (−2,8) \(\frac{1}{2}\)

(2, -5) and (-4, 7)  2

(12, -3) and (-12, 9) \(\frac{-1}{2}\)

(4,-2) and (12, 6)  -2

It is required to match each pair of points to the slope of the line that passes through these points.

To match each pair of points to the slope of the line that passes through these points use formula m = \(\frac{y_2-y_1}{x_2-x_1}\) to find the slope of each line that passes through a given pair of lines and then match them with the correct slope.

Substitute 8 for y2, 18 for y1 -2 for x2 and 3 for x

⇒ \(\begin{aligned}
& m=\frac{y_2-y_1}{x_2-x_1} \\
& m=\frac{8-18}{-2-3} \\
& m=\frac{-10}{-5} \\
& m=2
\end{aligned}\)

The slope of the line that passes through a pair of points (3,18) and (2,8) is 2.

Substitute 7 for y2,-5 for y1-4 for x2 and 2 for x,

⇒ \(\begin{aligned}
& m=\frac{y_2-y_1}{x_2-x_1} \\
& m=\frac{7+5}{-4-2} \\
& m=\frac{12}{-6} \\
& m=-2
\end{aligned}\)

The slope of the line that passes through a pair of points (2,-5) and (-4,7) is -2.

Substitute 6 for y2 x-2 for y1 12 for x2,-4 in formula \(m=\frac{y_2-y_1}{x_2-x_1}\)

⇒ \(\begin{aligned}
m=\frac{y_2-y_1}{x_2-x_1} \Rightarrow m & =\frac{6+2}{12+4} \\
m & =\frac{8}{16} \\
m & =\frac{1}{2}
\end{aligned}\)

Substitute 9 for y2-3 for y1 -12 for x

⇒ \(\begin{aligned}
m=\frac{y_2-y_1}{x_2-x_1} \Rightarrow m & =\frac{9+3}{-12-12} \\
m & =\frac{12}{-24} \\
m & =\frac{-1}{2}
\end{aligned}\)

The slope of the line that passes through a pair of points (12,-3)(-12,9) is \(\frac{-1}{2}\)

The slope of the line that passes through

The slope of the line that passes through a pair of points (3,18) and (−2,8) is 2.

The slope of the line that passes through a pair of points (2,−5) and (−4,7) is −2.

The slope of the line that passes through a pair of points (12,−3) and (−12,9) is \(\frac{1}{-2}\).

The slope of the line that passes through the pair of points (-4, -2) and (12, 6) is \(\frac{1}{2}\).

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 38 Exercise 31 Answer

It is given that the age of members of the chess club is 13,15,22,23,35,38,49,56. A new member whose age is 48 years joins the club.

It is required to describe how the mean, median, mode, and range of the ages of club members are affected after joining of new member.

To describe how the mean, median, mode, and range of the ages of club members are affected after joining of new member first find the mean, median, mode, and range of existing club members then find the mean, median, mode, and range of existing members along with new member and see the changes in the values.

Data for old club members: 13,15,22,23,35,38,49,56

The mean is the sum of all the ages divided by no. of members.

Mean ,= \(\frac{13+15+22+23+35+38+49}{8}\)

Mean = \(\frac{251}{8}\)

Mean = 31.375

Since total number of outcomes are even thus median is given by formula \(\frac{\left(\frac{n}{2}\right)^{t h} \text { term }+\left(\frac{n}{2}+1\right)^{t h} \text { term }}{2}\) where n the total number of outcomes.

Median = \(\frac{\left(\frac{8}{2}\right)^{\text {th }} \operatorname{term}+\left(\frac{8}{2}+1\right)^{\text {th }} \text { term }}{2}\)

Median= \(\frac{4^{\text {th }} \text { term }+5^{\text {th }} \text { term }}{2}\)

From the data, it is seen that the fourth term is 23 and the fifth term is 35 thus simplifying to obtain the median.

median = \(\frac{23+35}{2}\)

= \(\frac{58}{2}\)

= 29

Mode for the given data does not exist because each value occurs only once in the data.

The range of the data is the highest value subtracted by the lowest value of the data set.

From the data, it is seen that the highest value is 56 and the lowest value is 13 thus,

Range = 56 − 13

Data for old club members along with new joining: 13,15,22,23,35,38,48,49,56

The mean is the sum of all the ages divided by no. of members.

mean = \(\frac{13+15+22+23+35+38+48+49+56}{9}\)

= \(\frac{251}{9}\)

= 33.23

since the total number of outcomes is odd the median is given by the formula \(\left(\frac{n+1}{2}\right)^{t h} \text { term }\) where n is the total number of outcomes.

median = \(\left(\frac{9+1}{2}\right)^{t h} \text { term }\)

= 5^th term

From the data it is seen that the fifth term is 35 thus median will be 35.

Mode for the given data does not exist because each value occurs only once in the data.

The range of the data is the highest value subtracted by the lowest value of the data set.

From the data, it is seen that the highest value is 56 and the lowest value is 13 thus,

Range = 56 − 13

From the above data, it is concluded that the mean and median are increased after joining of new member whereas the mode and range of the data remain the same.

It is concluded that the mean and median are increased after joining of new member whereas the mode and range of the data remain the same.

Page 38 Exercise 33 Answer

It is given that the measure of angle A is three times the measure of angle B and the measure of angle C is one-half times the measure of angle B.

It is required to find a measure of all the three angles.

To find a measure of all three angles use the triangle sum property. The sum of all three angles of an obtuse triangle is 180°.

Let the measure of angle B be x.

Use the triangle sum theorem to form an equation as the measure of angle A is three times the measure of angle B and the measure of angle C is one-half times the measure of angle B.

Solve the expression

⇒ \(x^0+3 x^{\circ}+\frac{1}{2} x^0=180^{\circ}\)

Mathematical operations and find the value of x

⇒ \(\begin{aligned}
& x^{\circ}+3 x^{\circ}+\frac{1}{2} x^{\circ}=180^{\circ} \\
& \frac{9}{2} x^{\circ}=180^{\circ}
\end{aligned}\)

Multiply both sides of the expression

⇒ \(\begin{aligned}
& \frac{9}{2} x^{\circ}=180^{\circ} \text { by } \frac{2}{9} \\
& \frac{9}{2} x^{\circ} \times \frac{2}{9}=180^{\circ} \times \frac{2}{9}
\end{aligned}\)

x°=40°

Thus the measure of angle B is 40°.

To find a measure of angle A multiply the measure of B by 3 and simplify.
​
= 3(40°)

= 120°

​To find a measure of angle C divide the measure of B by 2 and simplify.

= \(\frac{40^{\circ}}{2}\)

= 20°

The measure of angle A is 120°, the measure of angle B is 40°, and the measure of angle C is 20°.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 38 Exercise 34 Answer

It is given that the function is f(x) = 2x² − 6x + 4.

It is required to find zeros of the given function.

To find zeros of the function equate the function to 0. Then split the middle term into two terms such that the sum of those two terms is equal to the middle term and the product of those two terms is equal to the first and last term.

Equate the function f(x) = 2x² − 6x + 4 to 0.

Given f(x)= 2x²-6x+4=0

2x²-2x-4x+4=0
2x(x-1)-4(x-1)=0
(2x-4)(x-1)=0

Either (2x-4) is equal to o or (x-1) is equal to 0

Let 2x-4=0

Add 4 on both sides

2x-4+4=0+4
2x=4

Divide both sides into 2

⇒ \(\begin{aligned}
\frac{2 x}{2} & =\frac{4}{2} \\
x & =2
\end{aligned}\)

Let x=1=0

Add 1 on both sides
x-1+1=0+1
x=1

Zeros of the function f(x) = 2x² − 6x + 4 are 2 and 1.

Page 39 Exercise 35 Answer

It is given that total number of coins is 30 and the total cost is $2.10.

It is required to write a system of equations and find the number of each type of coin.

To write a system of equations use the given condition and fact that a nickel worth $0.05 and a dime worth $0.10. Then solve the two equations to find the number of each type of coin.

Let x be the number of nickel coins and y be the number of dime coins.

By the given condition that the total number of coins is 30 the equation formed is x + y = 30.

Then equation is formed by another condition total cost is $2.10 and the fact that a nickel is worth $0.05 and a dime worth $0.10 is 0.05x + 0.10y = 2.10.

Given 0.05+0.10y=2.10-1
rearrange equation x+y=30
y=30-x

Substitute y =30-x in the equation

The system of equations used to determine the number of each type of coin are:

x + y = 30 and

0.05x + 0.10y = 2.10

There are 18 nickel coins and 12 coins of dime.

Envision Algebra 1 Chapter 2 Step-By-Step Solutions

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 2 Page 39 Exercise 36 Answer

It is given that the piecewise function is:

f(x) = \(\left\{\begin{array}{l}
2 x-2 \text { if } x<-2 \\
1.5 x \text { if }-2 \leq x<4 \\
2 \text { if } x>4
\end{array}\right.\)

It is required to plot the given piecewise function.

Graph the piece-wise function

f(x) = \(\left\{\begin{array}{l}
2 x-2 \text { if } x<-2 \\
1.5 x \text { if }-2 \leq x<4 \\
2 \text { if } x>4
\end{array}\right.\) where

the x-axis represents different values of x and the y-axis represents the values of the function obtained while substituting the values of x.

The graph of the piece wise function f(x) = \(\left\{\begin{array}{l}
2 x-2 \text { if } x<-2 \\
1.5 x \text { if }-2 \leq x<4 \\
2 \text { if } x>4
\end{array}\right.\) is as follows,

It is given that the piecewise function is

f(x) = \(\left\{\begin{array}{l}
2 x-2 \text { if } x<-2 \\
1.5 x \text { if }-2 \leq x<4 \\
2 \text { if } x>4
\end{array}\right.\)

It is required to find the domain and range of the function.

To find the domain and range of the function use the definition of range and domain.

The first condition of function shows that it is given that function exists at every point x < −2.

The second condition shows that the function exists at point −2 also.

The third condition shows that the function exists at every point where x>4.

This domain can be written as (−∞,4)∪(4,∞).

The range is a set of all output values. Thus range of functions is the entire real line.

Domain of the function

f(x) = \(\left\{\begin{array}{l}
2 x-2 \text { if } x<-2 \\
1.5 x \text { if }-2 \leq x<4 \\
2 \text { if } x>4
\end{array}\right.\) is

(−∞,4)∪(4,∞) and range is (−∞, ∞).

It is given that the piecewise function is

f(x) = \(\left\{\begin{array}{l}
2 x-2 \text { if } x<-2 \\
1.5 x \text { if }-2 \leq x<4 \\
2 \text { if } x>4
\end{array}\right.\).

It is required to find the interval on which the function is increasing or decreasing.

To find the interval on which function is increasing or decreasing see the graph of the function and use the definition of increasing and decreasing functions to find the interval.

The graph of the function

f(x) = \(\left\{\begin{array}{l}
2 x-2 \text { if } x<-2 \\
1.5 x \text { if }-2 \leq x<4 \\
2 \text { if } x>4
\end{array}\right.\) is,

It is concluded from the graph that the value of the function decreases as the value of x decreases over the interval (−∞,−2).

It is concluded from the graph that the value of the function is increasing as the value of x increases over the interval [−2,4).

It is concluded that over the interval (4,∞) the value of the function remains constant as the value of x increases over the interval (-2, 4).

It is concluded that over the interval (4, ∞) the value of the function remains constant as the value of x increases.

It is concluded from the graph that the value of the function is decreasing as the value of x decreases over the interval (−∞,−2).

It is concluded from the graph that the value of the function is increasing as the value of x increases over the interval [−2,4).

It is concluded that over the interval (4,∞) the value of the function remains constant as the value of x increases over the interval (-2, 4).

It is concluded that over the interval (4, ∞) the value of the function remains constant as the value of x increases.

How To Solve Envision Algebra 1 Chapter 2 Questions

Page 40 Exercise 1 Answer

It is given that the initial height of a baseball is 5ft, and the initial speed is 60ft/s.

It is required to find an equation that represents the ball’s path and graph the equation.

To find an equation that represents the balls path and graph the equation substitute the given values in the formula y = \(-\frac{g}{V^2} x^2+x+y_0\) and simplify to form an equation in x and y. Then use the graphing tool to plot the graph of the function.

Substitute 5 for y0, 60 for V and 32 for g in formula y = \(-\frac{g}{V^2} x^2+x+y_0\) and simplify.

y = \(-\frac{32}{(60)^2} x^2+x+5\)

y = -0.0089x² + x + 5

plot the graph of a function

y = -0.0089x² + x + 5 where the x-axis represents the horizontal distance traveled by the baseball and the y-axis represents the height of the baseball.

The graph of the function along with Felipe’s position is,

From the graph it is seen that ball passed the Felipe’s position thus the ball did not land in Felipe’s gloves.

The equation that represents the ball path is y = −0.0089x² + x + 5.

Graph that represents the equation y = −0.0089x² + x + 5 is as follows,

From the graph it is seen that ball passed the Felipe’s position thus the ball did not land in Felipe’s gloves.

It is given that the initial height of a baseball is 5ft, and the initial speed is 60ft/s.

It is required to find an equation that represents the ball’s path and graph the equation.

To find an equation that represents the ball path and graph the equation substitute the given values in the formula y = \(-\frac{g}{V^2} x^2+x+y_0\) to find the value of x. Thus the point obtained is the point that lies on the ball’s path.

⇒ \(y=\frac{-9}{v^2} x^2+x+y_0\)

Substitute y=5ft,y0=5ft,v=60ftls,g=32ftls²

⇒ \(5=-\frac{32}{(60)^2}\left(x^2\right)+90+5\)

⇒ \(\begin{aligned}
& 0=\frac{-32}{3600} \times x^2+x \\
& 0=-\frac{2 x^2}{225}+x
\end{aligned}\)

Rearrange equation \(\frac{2 x^2}{225}-x=0\)

2x²-225x=0

Take x as a common factor

x(2x-225)=0

Let x = 0.

Thus one point that lies on the ball’s path so that Felipe catches the ball is(0,5) but this is not possible as the ball does not travel any horizontal distance.

Let 2x-225=0

Add 225 on both sides

2x-225+225=0+225

Divide 2 on both sides

⇒ \(\frac{2 x}{2}=\frac{225}{2}\)

x=112.5

Thus the point that lies on the ball’s path so that Felipe catches the ball is (112.5,5).

The points that lie on the ball’s path so that Felipe catches the ball is (112.5,5) because it is given that Felipe is 5ft above the ground so the value of y is substituted as 5ft in the formula y = \(-\frac{g}{V^2} x^2+x+y_0\) with given initial conditions.

It is given that the answer to part b is to be used.

It is required to find an equation that describes the initial height and initial speed for which a friend catches the ball.

To find an equation that describes the initial height and initial speed for which a friend catches the ball substitute the point (112.5,5) for (x,y) in

Substitute (112.5,5) for(x,y)

⇒ \(5=\frac{-9}{v^2}(112.5)^2+(112.5)+y_0\)

⇒ \(\begin{aligned}
& 5-112.5=\frac{-405000}{v^2}+y_0 \\
& -107.5+\frac{405000}{v^2}=y_0
\end{aligned}\)

Thus the equation that describes initial height and initial speed is

⇒ \(y_0=\frac{405000}{V^2}-107.5\).

The equation that describes initial height and initial speed is \(y_0=\frac{405000}{V^2}-107.5\).

There is only one possible equation to describe the initial height and initial speed of the ball.

It is given that a friend catches the ball.

It is required to find the initial height and initial speed for which a friend catches the ball.

To find the initial height and initial speed for which a friend catches the ball, use the hit and trial method and substitute values of V to find values of y₀ in the equation

⇒ \(y_0=\frac{405000}{V^2}-107.5\) and check which value is possible.

Let v=90

Substitute 90 for v in the equation

⇒ \(\begin{aligned}
y_0 & =\frac{405000}{v^2}-107.5 \\
y_0 & =\frac{405000}{(90)^2}-107.5 \\
& =50-107.5 \\
& =-57.5
\end{aligned}\)

But height cannot be negative thus substitution wrong

Let v=60

substitute 60 for v in the equation

⇒ \(\begin{aligned}
y_0 & =\frac{405000}{(60)^2}-107.5 \\
y_0 & =112.5-107.5 \\
& =5
\end{aligned}\)

Thus the initial height and initial speed of the ball are 5 and 60 respectively.

Thus the initial height and initial speed of the ball are 5 and 60 respectively.

Envision Algebra 1 Assessment Readiness Workbook Chapter 1 Standards Practice

Page 8 Exercise 2 Answer

The given expression is 4(xy)²− 2x + 5y.

It is required to find the value of the given expression when the value of x is 6 and y is 2.

To find the value of the given expression, rewrite the given expression. Substitute the given values for x and y. Then solve further to get the result.

The given expression is 4(xy)² – 2x+5y
Substitute 6 for x and 2 for y in the given expression.

4(xy)²-2x+5y = 4(6×2)²-2(6)+5(2)
4(xy)²-2x+5y=4(12)² -2(6)+5(2)
4(xy)²-2x+5y= 4(144)-12+10
4(xy)²-2x+5y=576-2
4(xy)²-2x+5y=574

The value of the expression 4(xy)² − 2x + 5y is 574.

Page 8 Exercise 3 Answer

It is given that Camilla and Nadia start a business tutoring students in maths. They rent an office for $250 per month and charge $20 per hour per student.

It is required to calculate the profit they make each month if they have 10 students. It is also required to write a linear equation to solve this.

To find the profit, subtract the rent amount from the total amount they get from students. Then solve the linear equation and get the result.

Let x be the profit they make each month. Also, there are 4 weeks in a month.

The profit can be calculated by subtracting the rent amount from the total amount they get from students.

So the linear equation is

x=4(10×20)-250​
x=4(200)-250
x=800-250
x=550

Therefore, Camilla and Nadia make a profit of $550 per month.

Camilla and Nadia make a profit of $550 per month. Also the linear equation is x = 4(10×20) − 250.

It is given that Camilla and Nadia start a business tutoring students in maths. They rent an office for $250 per month and charge $20 per hour per student.

If they have 10 students it is required to sketch the graph for the resulting linear equation.

To sketch the graph, use dynamic geometry software.

Let x be the profit they make each month. Also, there are 4 weeks in a month.

The profit can be calculated by subtracting the rent amount from the total amount they get from students.

So the linear equation is x = 4(10×20) − 250.

The graph of the equation is given below.

Hence the graph of the equation x = 4(10×20) − 250 is,

Envision Algebra 1 Chapter 1 Standards Practice 2 Answer Key

Page 9 Exercise 1 Answer

The given sequence is 2,24,46,68,90,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common difference is a constant and equals the difference between any two consecutive terms.

Subtract the first two terms

a₂ – a₁ =24-2
a₂ – a₁ =22

Subtract the third term from the second term.

a₃ – a₂ =24-2
a₃ – a₂ =22

Subtract the Fourth term from the Third term.

a₄ – a₃ =68-46
a₄ – a₃ =22

Hence the common difference id d=22

The formula for expressing arithmetic sequences in their recursive form is a_n = a_n-1 + d, where d is the common difference of the given sequence, an is the nth element and a_n-1 is the (n−1)^th element.

Substitute 22 for d in the recursive form.

a_n = a_n-1 + 22

Hence the correct answer is option A

Option B

The given sequence is 2,24,46,68,90,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common difference is a constant and equals the difference between any two consecutive terms.

Subtract the first two terms

a₂ – a₁ =24-2
a₂ – a₁ =22

Subtract the third term from the second term.

a₃ – a₂ =46-24
a₃ – a₂ =22

Subtract the Fourth term from the Third term.

a₄ – a₃ =68-46
a₄ – a₃ =22

Hence the common difference is d=22

The formula for expressing arithmetic sequences in their recursive form is an = a_n-1 + d, where d is the common difference of the given sequence, a_n is the nth element and a_n-1 is the (n−1)^th element.

Substitute 22 for d in the recursive form.

a_n = a_n-1 + 22

Here a₁ is 2 and an is a_n-1 + 22 which is not equal to an = a_n-1 − 22, so option B is incorrect.

Option C

The given sequence is 2,24,46,68,90,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common difference is a constant and equals the difference between any two consecutive terms.

Subtract the first two terms

a₂ – a₁ =24-2
a₂ – a₁ =22

Subtract the third term from the second term.

a₃ – a₂ =46-24
a₃ – a₂ =22

Subtract the Fourth term from the Third term.

a₄ – a₃ =68-46
a₄ – a₃ =22

Hence the common difference is d=22.

The formula for expressing arithmetic sequences in their recursive form is a_n = a_n-1 + d, where d is the common difference of the given sequence, a_n is the n^th element and a_n-1 is the (n−1)^th element.

Substitute 22 for d in the recursive form.

a_n = a_n-1 + 22

Here a₁ is 2 and an is a_n-1 + 22 which is not equal to a_n = a_n+1 + 22, so option C is incorrect.

Option D

The given sequence is 2,24,46,68,90,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common difference of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common difference is a constant and equals the difference between any two consecutive terms.

Subtract the first two terms

a₂ – a₁ =24-2
a₂ – a₁ =22

Subtract the third term from the second term.

a₃ – a₂ =46-24
a₃ – a₂ =22

Subtract the Fourth term from the Third term.

a₄ – a₃ =68-46
a₄ – a₃ =22

Hence the common difference is d=22

The formula for expressing arithmetic sequences in their recursive form is a_n = a_n-1 + d, where d is the common difference of the given sequence, a_n is the n^th element and a_n-1 is the (n−1)^th element.

Substitute 22 for d in the recursive form.

a_n = a_n-1 + 22

Here a₁ is 2 and an is a_n-1 + 22 which is not equal to a_n = a_n+1 − 22, so option D is incorrect.

The recursive form of the given arithmetic sequence is a_n = a_n-1 + 22, so the correct option is A.

Envision Algebra 1 Assessment Readiness Workbook Chapter 1 Practice 2 Solutions

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 10 Exercise 1 Answer

Given the formula pV = nRT.

It is asked to solve the given formula for T.

To solve the problem, simplify the given formula pV = nRT, and solve it for T.

P.V=n.R.T

Divide both sides by n.R.

⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)

The formula for T is T = \(\frac{p V}{n R}\).

So option C is correct.

Option A

Given the formula pV = nRT.

It is asked to solve the given formula for T.

To solve the problem, simplify the given formula pV = nRT, and solve it for T.

P.V=n.R.T

Divide both sides by n.R.

⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)

The formula for is T = \(\frac{p V}{n R}\) which is not equal to,

T = pV – nR

Option B

Given the formula pV = nRT.

It is asked to solve the given formula for T.

To solve the problem, simplify the given formula pV = nRT, and solve it for T.

P.V=n.R.T

Divide both sides by n.R.

⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)

The formula for T is T = \(\frac{p V}{n R}\) which is not equal to,

T = pVnR

Option D

Given the formula pV = nRT.

It is asked to solve the given formula for T.

To solve the problem, simplify the given formula pV = nRT, and solve it for.

P.V=n.R.T

Divide both sides by n.R.

⇒ \(\begin{aligned}
& \frac{P \cdot V}{n \cdot R}=\frac{n \cdot R \cdot T}{n \cdot R} \\
& \frac{P \cdot v}{n \cdot R}=T
\end{aligned}\)

The formula for T is T = \(\frac{p V}{n R}\) which is not equal to,

T = pV

The formula for T is T = \(\frac{p \cdot V}{n \cdot R}\), so option C is the correct option.

Page 11 Exercise 1 Answer

Given a system of equations,
​
4y − 3x = 14

y + 3x = 10
​
It is asked to solve the given equations.

To solve the problem make any one coefficient of the equation the same and then take a difference of both the equations. It will eliminate one variable, and then solve for x or y. Then put the value of x or y in any of the given equations to get both x and y.

Multiply the second equation by 5.

5(y+3x)=5(10)

5y+15x=50

Subtract the equation (of step 1) from the first given equation.

5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2

so the value of x is 2

Now put the value of x in the second equation and simplify

y=3×2=10
y+6=10
y=4

So the solved ordered pair is (2,4) so the correct option is A.

Option B

Subtract the equation (of step 1) from the first given equation.

5(y+3x)=5(10)

5y+15x=50

Subtract the equation (of step 1) from the first given equation.

5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2

so the value of x is 2

Now put the value of x in the second equation and simplify

y=3×2=10
y+6=10
y=4

​So the solved ordered pair is (2,4) which is not equal to (4,2) so option B is not correct.

Option C

Subtract the equation (of step 1) from the first given equation.​

5(y+3x)=5(10)

5y+15x=50

Subtract the equation (of step 1) from the first given equation.

5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2

so the value of x is 2

Now put the value of x in the second equation and simplify

y=3×2=10
y+6=10
y=4

​So the solved ordered pair is (2,4) which is not equal to (−2,−4) so option C is not correct.

Option D

Subtract the equation (of step 1) from the first given equation.

5(y+3x)=5(10)

5y+15x=50

Subtract the equation (of step 1) from the first given equation.

5y-3x-(5y+15x)=14(50)
5y-3x-5y-15x=-36
-18x=-36
18x=36
x=2

so the value of x is 2

Now put the value of x in the second equation and simplify

y=3×2=10
y+6=10
y=4

​So the solved ordered pair is (2,4) which is not equal to (2,−4) so option D is not correct.

Option A is the correct option that is (2,4).

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 11 Exercise 2 Answer

Given a system of equations,

x + 4y = 6

3x − 4y = 14
​
It is asked to solve the given equations.

To solve the problem add or take the difference of both the equations to eliminate any one variable from the equation, then solve for x or y. Then put the value of x or y in any of the given equations to get both x and y.

Add both of the equations and then simplify.

Given the System of equations,

x+4y=6

3x-4y=14

Add both of the equations and then simplify.

x+4y+(3x-4y) =6+(14)
x+4y+3x-4y=6+14
4x=20
x=5

So the value of x is 5

Now up the value of x in the first equation and simplify

5+4y=6
4y=6-5
4y=1
\(y=\frac{1}{4}\)

So the solved ordered pair is \(\left(5, \frac{1}{4}\right)\).

The ordered pair of the given system of equation is \(\left(5, \frac{1}{4}\right)\).

Page 11 Exercise 3 Answer

Given that the total money spent is $52, the total number of movies watched is 6, the matinee cost is $7 and the evening show costs $12.

It is asked how many of each movie type he attends and to solve it by graphing.

To solve the problem first form the pair of equations according to the given information that is total movie watched and total money spent and then plot the graph using the equation in slope-intercept form that is \(\frac{x}{h}+\frac{y}{k}=1\), where h and k are the intercepts on the axes. The intersection in the graph is the solution of the equations.

Let x be the number of times Alejandro has gone to a matinee and y be the number of times he has attended the evening show. Then, the equation formed by the given data is,
​
x + y = 6

7x + 12y = 52
​
Solve this equation and write them in slope-intercept form.

\(\frac{x}{6}+\frac{y}{6}\) = 1

\(\frac{x}{\frac{52}{7}}+\frac{y}{\frac{13}{3}}\) = 1

Plot the lines using intercept on the graph.

Here the intersection point is (4,2).

So x = 4 and y = 2

So he attended 4 matinees and 2 evening shows.

The graphical plot of the equations formed is,

Alejandro attended 4 matinee movies and 2 evening show movies.

It is asked why the intersection of the graphs is the solution.

The intersection of the graph is the solution because it is the only point that satisfies both equations.

The equations are,
​
The Equations are, x+y=6

7x+12y=52

Multiply the first equation by 7 and subtract the second equation

​(7x+7y)-(7x+12y)=42-52

7x+7y-7x-12y=-10

-5y=-10

y=2

put the value of y in the first equation

x+y=6
x+2=6

x=6-2
x=4

So the solution is (2,4) which is the same as the intersection point. Also, these are the only points that satisfy both the equations.

The intersection of the graph is the solution because it is the only point that satisfies both equations.

Page 13 Exercise 1 Answer

A system of inequalities is given.

y > −x + 2

y < x + 4

It is asked to identify the graph of the solution of the given system from the options given below.

A

B

C

D

To solve this question, first consider the given inequalities as simple lines y = −x + 2 and,

y = x + 4. Determine its x and y intercepts for both and draw corresponding lines passing through these points. As the inequality y > −x + 2 is greater than the inequality, shade the area above the line, and for less than inequality y < x + 4, shade the area below the line. The common shaded area will be the solution for the given system.

Substitute 0 for y and determine the x-intercept of the line y = −x + 2.
​
0 = −x + 2

−x = −2

x = 2
​
Thus the x-intercept of the line y = −x + 2 is (2,0).

Substitute 0 for x and determine the y intercept of the line y = −x + 2.
​
y = 0 + 2

y = 2
​
Thus the y-intercept of the line y = −x + 2 is (0,2).

Substitute 0 for y and determine the x intercept of the line y = x + 4.
​
0 = x + 4

x = −4
​
Thus the x-intercept of the line y = x + 4 is (−4,0).

Substitute 0 for x and determine the y intercept of the line y = x + 4.
​
y = 0 + 4

y = 4
​
Thus the y-intercept of the line y = x + 4 is (0,4).

Plot the points (2,0) and (0,2), draw a line passing through them, and shade the area above the line to show the inequality y > −x + 2. Similarly, Plot the points (−4,0) and (0,4), draw a line passing through them, and shade the area below the line to show the inequality y < x + 4.

The common shaded area is the solution of the system.

Compare the graphs given in the options and determine the correct answer.

The graph given in option A is exactly similar to the obtained graph which represents the solution of the system of inequalities,

y > −x + 2

y < x + 4

The graph given in option B represents the system of inequality,

y > x + 2

y > x + 4

The graph given in option C represents the system of inequality,

y < x + 2

y < x + 4

The graph given in option D represents the system of inequality,

y < −x + 2

y < x + 4

Thus, option A is the correct answer.

The graph of the solution of the given system is obtained and therefore, option A is the correct answer.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 13 Exercise 2 Answer

The function g(x) = \(\frac{1}{3}|x-2|+10\) is given.

It is asked to compare the given graph with the parent graph f(x) = ∣x∣.

To solve this question, first plot the graphs of f(x) = ∣x∣ and,

g(x) = \(\frac{1}{3}|x-2|+10\). Then observe the second graph and how it changes concerning the first graph.

Ploth the graphs of f(x) = ∣x∣ and,g(x) = \(\frac{1}{3}|x-2|+10\) in a single screen and compare them.

In the function, the value in the mode is x−2 which means that it is shifted 2 units to the right side of the parent graph which can be seen from the graph.

Thus, \(\frac{1}{3}\) is multiplied with |x – 2|, which is greater than zero and less than one, which indicates that the graph is vertically stretched by \(\frac{1}{3}\) units from the parent graph.

Finally, 10 is added to \(\frac{1}{3}\)|x-2|, which indicates that the graph is shifted 10 units vertically upward which also can be seen from the graph.

The graph of g(x) = \(\frac{1}{3}|x-2|+10\) is compared with its parent graph,

f(x) = |x| and three important results are obtained.

First, horizontal shift of 2 units to the right side.

Second, vertical stretch of \(\frac{1}{3}\)|x-2| units.

Third, a Vertical shift of 10 units in the upward direction.

Envision Algebra 1 Student Edition Standards Practice 2 Guide

Page 13 Exercise 3 Answer

It is given that Manuel wants to raise between $250 and $350 for charity. His parents donated $70 and he plans to ask others to contribute $10.

It is asked to write an inequality to determine the number of people who will be needed to contribute for Manuel to reach his goal.

To obtain the inequality, let the number of contributors be x. Each contributor will need to donate $10.Therefore, the total amount to be collected is $10x.

But it is given that Manuel already has $70 donated by his parents. Let y be the total amount of charity he would collect, then y = 70 + 10x.

This amount will be between $250 and $350. Therefore, the inequality to solve the problem will be,
Given, 250<y<350

250<70+10x<35

Simplify Further,

250-70<10x<350-70
180<10x<280
18<x<28

The inequality to solve the problem is 18 < x < 28.

It is given that Manuel wants to raise between $250 and $350 for charity. His parents donated $70 and he plans to ask others to contribute $10.

It is asked to show the solution on the graph to determine the number of people who will be needed to contribute for Manuel to reach his goal and explain the same in words.

To solve this question, use the inequality obtained in the previous part of this exercise which is,

250 < 70 + 10x < 350. First, solve this inequality for x and then graph the solution.

Solve the inequality 250 < 70 + 10x < 350 for x.

Subtract 70 forms from all parts of inequality,
​
250 − 70 < 70 + 10x − 70 < 350 − 70

180 < 10x < 280
​
Divide by 10 in all parts of inequality,

⇒\(\frac{180}{10}<\frac{10 x}{10}<\frac{280}{10}\)

18 < x < 28

Thus, the number of people who will be needed to contribute for Manuel to reach his goal is between 18 and 28.

To graph this solution, first plot the line y = 70 + 10x.

After that show the range of the money collection which is 250 < y < 350. For this, draw two lines, y = 250 and, y = 350, and shade the area between them.

After that from the intersection points of this region and the line y = 70 + 10x, draw two vertical lines that will give the solution of the system which is the range 18 < x < 28.

The number of people who will be needed to contribute for Manuel to reach his goal is between 18 and 28. The graph of the solution is obtained.

Page 14 Exercise 1 Answer

An equation is given as \(\frac{x}{3}=\frac{10}{15}\).

It is required to solve the given equation for x.

Given equation \(\frac{x}{3}=\frac{10}{15}\)

Multiply both sides of the equation \(\frac{x}{3}=\frac{10}{15} \text { by } 3 .\)

Hence, option A is correct.

Option B

Multiply both sides of the equation,

Given equation \(\frac{x}{3}=\frac{10}{15} .\)

Multiply both sides of the equation \(\frac{x}{3}=\frac{10}{15}\) by 3

In Option B, the value of x is given as 3.

Hence, option B is incorrect.

Option C

Multiply both sides of the equation,

Given equation \(\frac{x}{3}=\frac{10}{15}\) 

Multiple both sides of the equation \(\frac{x}{3}=\frac{10}{15} \text { by } 3 \text {. }\)

In option C, the value of x is given as 12. Hence, option C is incorrect.

Option D

Multiply both sides of the equation,

Given equation \(\frac{x}{3}=\frac{10}{15}\) 

Multiple both sides of the equation \(\frac{x}{3}=\frac{10}{15} \text { by } 3 \text {. }\)

In option D, the value of x is given as 15. Hence, option D is incorrect.

The correct answer is option A, the value of x is 2.

Page 14 Exercise 2 Answer

A function is given as,

⇒\(f(x)=\left\{\begin{array}{l}
1-0.5 x, x<1 \\
x, x \geq 1
\end{array}\right.\)

It is required to graph the given function.

To do so, draw the given lines, and then for the line y = 1 − 0.5x, limit the line for the values where x is greater than 1. For the line y = x, limit the line for values where x is smaller than or equal to 1.

Draw the lines on the graph,
​
y = 1 − 0.5x

y = x
​

Limit the line for the values where x is greater than 1. For the line y = x, limit the line for values where x is smaller than or equal to 1.

The graph of the given function is drawn as,

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 14 Exercise 3 Answer

It is given that the length of a rectangle is 4 more than twice its width and the perimeter can be no more than 92 ft.

It is required to write an inequality to find all the possible values of the width of the rectangle.

To do so, let the width be x. Form the expression for the length and perimeter of a rectangle. Apply the given condition that the perimeter can be no more than 92 ft.

Let the width be x.

Given that the length of the rectangle is 4 more than twice its width. Hence, the length will be 2x+4.

The ​Perimeter of the rectangle, with x width and 2x+4 length, is

p=2((x)+(2x+4))

p=2(3x+4)

It is given that the perimeter can be no more than 92ft. Hence,

2(3x+4)≤92
3x+4≤46
3x≤42
x≤14

The width cannot be negative and 0. Hence, the inequality for width x is, 0 < x ≤ 14.

The inequality to solve the problem is 0 < x ≤ 14.

It is given that the length of a rectangle is 4 more than twice its width and the perimeter can be no more than 92 ft.

It is required to graph the inequality and describe the solution in words.

To do so, draw a graph only with the x-axis and represent the inequality on the graph. Also, describe the solution in words.

The inequality for width x is, 0 < x ≤ 14.

Represent the inequality on the graph.

The possible values of width are greater than 0 and less than or equal to 14 ft.

The representation of inequality as a graph is,

The solution in words is written as the possible value of width is greater than 0 and less than or equal to 14 ft.

Page 15 Exercise 1 Answer

The given expression is 6⁻²x³y⁻⁵.

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

Given Expression 6^-3 x³ y^-5

⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{6^2 y^5}\)

⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{36 y^5}\)

So the correct option is C.

Option A

The given expression is 6⁻²x³y⁻⁵.

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

Given Expression 6^-3 x³ y^-5

⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{6^2 y^5}\)

⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{36 y^5}\)

The simplified form is \(\frac{x^3}{36 y^5}\) which is not equal to -12x³5y so option A is incorrect.

Option B

The given expression is 6⁻²x³y⁻⁵.

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

Given Expression 6^-3 x³ y^-5

⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{6^2 y^5}\)

⇒ \(6^{-2} x^3 y^{-5}=\frac{x^3}{36 y^5}\)

The simplified form is \(\frac{x^3}{36 y^5}\) which is not equal to -36x³y so option B is incorrect.

Option D

The given expression is 6⁻²x³y⁻⁵.

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

6⁻²x³y⁻⁵ = \(\frac{x^3}{6^2 y^5}\)

6⁻²x³y⁻⁵The simplified form is \(\frac{x^3}{36 y^5}\) which is not equal to \(\frac{x^3}{12 y^5}\) so the option D is incorrect.

The simplified form of 6⁻²x³y⁻⁵ is \(\frac{x^3}{36 y^5}\), so the correct option is C.

Page 15 Exercise 2 Answer

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)

⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)

So the correct option is C.

Option A

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)

⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)

The simplifed form is \(5 a t^{\frac{4}{3}}\) which is not equal to \(5^{\frac{1}{3}} a t^2\) so the option A is incorrect.

Option B

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)

⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)

The simplifed form is \(5 a t^{\frac{4}{3}}\) which is not equal to \(5^{\frac{2}{3}} a^{\frac{1}{3}} t^{\frac{4}{3}}\) so the option B is incorrect.

Option D

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\).

It is required to simplify the given expression.

To simplify the given expression use the algebraic identity.

The given expression is \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5 a t^4 \times 25 a^2}\)

⇒ \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=\sqrt[3]{5^3 a^3 t^4}\)

⇒ \(\begin{aligned}
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5^{\frac{3}{3}} a^{\frac{3}{3}} t^{\frac{4}{3}} \\
& \sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}=5 a t^{4 / 3}
\end{aligned}\)

The simplified form is \(5 a t^{\frac{4}{3}}\) which is not equal to 125a3t4 so option D is incorrect.

The simplified form of \(\sqrt[3]{5 a t^4} \times \sqrt[3]{25 a^2}\) is \(5 a t^{\frac{4}{3}}\), so the correct option is C.

How To Solve Envision Algebra 1 Standards Practice 2 Problems

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 15 Exercise 3 Answer

The given expression is \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{5}}\right)\).

It is required to simplify the given expression.

To simplify the given expression, use the algebraic identity.

Rewrite the given expression; use the algebraic identity a^maⁿ = a^m+n to simplify the expression.

The Given expression is \(\left(4g \frac{1}{3} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{5}}\right)\)

⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=(4 \cdot 2 \cdot 3)\left(g^{\frac{1}{3}} \cdot g^{\frac{2}{3}}\right)\left(h^{\frac{3}{5}} \cdot h^{\frac{1}{5}}\right)\)

⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=(24)\left(9 \frac{1}{3}+\frac{2}{3}\right)\left(h^{\frac{3}{5}+\frac{1}{5}}\right)\)

⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=(24)\left(g^{\frac{3}{3}}\right)\left(h^{\frac{4}{5}}\right)\)

⇒ \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{2}}\right)=24 g h^{\frac{4}{5}}\)

The simplified form of the given expression \(\left(4 g^{\frac{1}{3}} 2 h^{\frac{3}{5}}\right)\left(3 g^{\frac{2}{3}} h^{\frac{1}{5}}\right)\) is \(24 g h^{\frac{4}{5}}\).

Page 15 Exercise 4 Answer

It is given that b−(xy) can be written as \(\frac{1}{\left(b^x\right)^y}\) for all real numbers x and y.

It is required to find whether the given statement is correct and show examples to justify your explanation.

To simplify the given expression, use the algebraic identity.

Use the algebraic identity to simplify the given expression.

b-(xy) = \(\frac{1}{b^{(x y)}}\)

b-(xy) = \(\frac{1}{\left(b^x\right)^y}\)

Hence the given statement is correct.

The given statement b-(xy) = \(\frac{1}{\left(b^x\right)^y}\) is correct.

Page 16 Exercise 1 Answer

The given sequence is 4,16,64,256,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common ratio is a constant and equals the ratio between any two consecutive terms.

Divide the first two terms

⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)

Divide the third term and the second term

⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)

Hence the common ratio is r=4

The formula for expressing geometric sequences in their recursive form is a_n = a_n−1⋅r, where r is the common ratio of the given sequence, an is the n^th element and a_n−1 is the (n−1)^th element.

Substitute 4 for r in the recursive form.
​
a_n = a_n−1 ⋅ 4

a_n = 4a_n−1

​Hence the correct answer is option B.

Option A

The given sequence is 4,16,64,256,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common ratio is a constant and equals the ratio between any two consecutive terms.

Divide the first two terms

⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)

Divide the third term and the second term

⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)

Hence the common ratio is r=4

The formula for expressing geometric sequences in their recursive form is a_n = a_n−1⋅r, where r is the common ratio of the given sequence, a_n is the n^th element and a_n−1 is the (n−1)^th element.

Substitute 4 for r in the recursive form.
​
a_n = a_n−1 ⋅ 4

a_n = 4a_n−1

Here a₁ is 4 and an is 4a_n−1 which is not equal to a₁ = 0, so option A is incorrect.

Option C

The given sequence is 4,16,64,256,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common ratio is a constant and equals the ratio between any two consecutive terms.

Divide the first two terms

⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)

Divide the third term and the second term

⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)

Hence the common ratio is r=4

The formula for expressing geometric sequences in their recursive form is a_n = a_n−1⋅r, where r is the common ratio of the given sequence, a_n is the n^th element and a_n−1 is the (n−1)th element.

Substitute 4 for r in the recursive form.
​
a_n = a_n−1 ⋅ 4

a_n = 4a_n−1

Here a₁ is 4 and an is 4a_n−1  which is not equal to a_n = 4 + 4a_n−1, so option C is incorrect.

Option D

The given sequence is 4,16,64,256,…

It is required to find the recursive formula for the given sequence.

To find the recursive formula, find the common ratio of the given sequence and substitute it in the formula for expressing arithmetic sequences in their recursive form.

The common ratio is a constant and equals the ratio between any two consecutive terms.

Divide the first two terms

⇒ \(\begin{aligned}
& \frac{a_2}{a_1}=\frac{16}{4} \\
& \frac{a_2}{a_1}=4
\end{aligned}\)

Divide the third term and the second term

⇒ \(\begin{aligned}
& \frac{a_3}{a_2}=\frac{64}{16} \\
& \frac{a_3}{a_2}=4
\end{aligned}\)

Hence the common ratio is r=4

The formula for expressing geometric sequences in their recursive form is a_n = a_n−1⋅r, where r is the common ratio of the given sequence, a_n is the n^th element and a_n−1 is the (n−1)^th element.

Substitute 4 for r in the recursive form.
​
a_n = a_n−1 ⋅ 4

a_n = 4a_n−1

Here a₁ is 4 an is 4a_n−1 which is not equal to a₁ = 0 and an is 4 + a_n−1, so option D is incorrect.

Hence the correct answer is option B.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 17 Exercise 1 Answer

Given the expression 5n⁶ − n⁴ − 3n² − 2n + 4.

It is required to find the number of terms in the expression.

The number of terms is usually the number of terms in the fully expanded form of the polynomial.

In the given expression there are 5 terms and the degree of every term is different, so the expression cannot be simplified further.

Hence the number of terms in the given expression is 5.

The correct option is C.

The given expression is 5n⁶ − n⁴ − 3n² − 2n + 4.

Since the degrees in the expression are different and the expression is in fully expanded form. So, the number of terms in the expression is exactly 5, not more or less. So, the options A, B, and D are not correct.

The correct answer is Option (C), the number of terms in the given expression is 5.

Page 17 Exercise 2 Answer

Given the monomial 4a⁵bc.

It is required to find the number of terms in the monomial. The degree of a monomial is the sum of the exponents of the variable.

The sum of the exponents of the variable is 5 + 1 + 1 = 7.

Hence the degree of the monomial is 7.

The correct option is D.

Given the monomial 4a⁵bc.

The degree of a monomial is the sum of the exponents of the variable.

The sum of the exponents of the variable is 7.

Hence options A, B, and C are incorrect.

The correct answer is Option (D), the degree of the monomial is 7.

Page 17 Exercise 4 Answer

A new house worth $250,000 depreciates at a rate of 16% a year. It is required to explain the situation in terms of growth or decay. If the value increases with time, then the given situation is of growth and if the value decreases with time, then the given situation is of decay. In the given situation, the value of the house decreases by 16% every year. Therefore the given situation is of decay.

The given situation is of decay because the value of the house reduces every year by 16%.

A new house worth $250,000 depreciates at a rate of 16% a year.

It is required to write a function to model the situation.

To do so, find the worth of the house after one year and after two years. Observe the sequence of the initial worth of the house, worth after one year, worth after two years, and as a result, a function can be written to model the situation.

Find the worth of the house after one year.

The initial worth of the house is $250,000.

The worth of the house after one year will be,
​
Worth after one year = 250,000 − 0.16 × 250,000

Worth after one year = 250,000 × 0.84

Find the worth of the house after two years.

The worth of the house after two years will be,
​
Worth after two year = 250,000 − 0.16 × (250,000×0.84)

Worth after two year = 250,000 × 0.84 × 0.84

Model the function of the situation.

Let W be the worth of the house after n years.

The function of this situation can be modeled as,

W = $250,000 × (0.84)n

The function to model the situation can be represented as W = $250,000 × (0.84)n, where W is the worth of the house and n is the number of years.

A new house worth $250,000 depreciates at a rate of 16% a year.

It is required to write a function to model the situation.

To do so, find the worth of the house after one year and after two years. Observe the sequence of the initial worth of the house, worth after one year, worth after two years, and as a result, a function can be written to model the situation. As a result, the value of the house after 5 years can be determined.

Find the worth of the house after one year.

The initial worth of the house is $250,000.

The worth of the house after one year will be,
​
Worth after one year = 250,000 − 0.16 × 250,000

Worth after one year = 250,000 × 0.84

Find the worth of the house after two years.

The worth of the house after two years will be,
​
Worth after two year = 250,000 − 0.16 × (250,000×0.84)

Worth after two year = 250,000 × 0.84 × 0.84

Find the function for the situation.

Let W be the worth of the house after n years.

The function of this situation can be modeled as

w=$250000x(0.84)n

Find the value of the house after 5 years

substitute 5 for n in the function

w=$ 250,000 x(0.84)n

w=$ 250,000 x(0.84)5

w=$ 250,000 x(0.4182

w=$104,550

The worth of the house after 5 years is $104,550.

Envision Algebra 1 Standards Practice 2 Step-By-Step Explanation

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 18 Exercise 1 Answer

The given expression is (x−3)².

It is required to solve the given expression.

Use the algebraic identity (a−b)² = a² − 2ab + b² to simplify the given expression. Choose x for a and 3 for b.
​
​Given Expression, (x-3)²

(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9

So the correct option is C.

Option A

The given expression is (x−3)².

It is required to solve the given expression.

Use the algebraic identity (a−b)² = a² − 2ab + b² to simplify the given expression. Choose x for a and 3 for b.

​Given Expression, (x-3)²

(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9

The simplified form of the given expression is x² – 6x + 9 which is not equal to 2x – 6 so option A is incorrect.

Option B

The given expression is (x−3)².

It is required to solve the given expression.

Use the algebraic identity (a−b)² = a² − 2ab + b² to simplify the given expression. Choose x for a and 3 for b.

​Given Expression, (x-3)²

(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9​

The simplified form of the given expression is x² – 6x + 9 which is not equal to x² + 9 so option B is incorrect.

Option D

The given expression is (x−3)².

It is required to solve the given expression.

Use the algebraic identity (a−b)² = a² − 2ab + b² to simplify the given expression. Choose x for a and 3 for b.

​Given Expression, (x-3)²

(a-b)² =a² -2ab+b²
(x-3)²=x²-2(x)(3)+(3)²
(x-3)²=x²-6x+9​

The simplified form of the given expression is x² – 6x + 9 which is not equal to x² – 9x – 6 so option D is incorrect.

The simplified form of x² − 6x + 9 is x² − 6x + 9, so the correct option is C.

Page 18 Exercise 2 Answer

The given expressions are,
​
(5x² + 10x + 6) − (2x² − 4x + 6)

x(3x + 14)

6x² − (9x² + 12x) − 2x

(x² + 6x²) + (−4x² + 2x − 4x + 16x)
​
It is required to classify the given equations as those equivalent to 3x² + 14x and not equivalent to 3x² + 14x.

To do so, simplify each given expression and check whether it is equivalent to 3x² + 14x or not.

Simplify the first given expression (5x² + 10x + 6) − (2x² − 4x + 6).
​
Given expression (5x²+10x+6)-(2x²-4x+6)
(5x²+10x+6)-(2x²-4x+6)= 5x²+10x+6-2x²+4x-6
(5x²+10x+6)-(2x²-4x+6)= (5-2)x² +(10+4)x+6-6
(5x²+10x+6)-2x²-4c+6)=3x²+14
​
Therefore, (5x² + 10x + 6) − (2x² − 4x + 6) is equivalent to 3x² + 14x.

Simplify the second given expression x (3x + 14).

x(3x + 14) = 3x² + 14x

Therefore, x(3x+14) is equivalent to 3x² + 14x.

Simplify the third given expression 6x² − (9x² + 12x) − 2x.
​
Given expression ​6x²-(9x² +12x)-2x

6x²-(9x²+12x)-2x=6x²-9x²-12x-2x
6x²-(9x²+12x)-2x=(6-9)x²-(12-2)x
6x²-(9x²+12x)-2x=-3x²-14x

Therefore, 6x² − (9x² + 12x) − 2x is not equivalent to 3x² + 14x.

Simplify the fourth given expression (x² + 6x²) + (−4x² + 2x − 4x + 16x).
​
Given Expression (x²+6x²)+(-4x²+2x-4x+16x)
(x²+6x²)+(-4x²+2x-4x+16x)=x²+6x²-4x²+2x-4x+16)x
(x²+6x²)+(-4x²+2x-4x+16x)=(1+6-4)x²+(2-4+16)x
(x²+6x²)+ (-4x²+2x-4x+16x)=3x²+14x
​
Therefore, (x² + 6x²) + (−4x² + 2x −4x + 16x) is equivalent to 3x² + 14x.

Page 18 Exercise 3 Answer

It is given that the length of a rectangular sandbox is 4x + 1 and the width of the sandbox is x − 2.

It is required to find a polynomial in standard form which represents the area of the sandbox.

To do so, use the area of the rectangle formula. Substitute the given values of length and breadth. Solve further to find the polynomial.

The area of a rectangle is A=lw.

Substitute 4x+1 for 1 and x-2 for w

Solve further to find the formula

A=(4x+1)(x-2)
A=(4x)(x)-2(4x)+1(x)+1(-2)
A=4x²-8x+x-2
A=4x²-7x-2
​
Hence the polynomial in standard form which represents the area of the sandbox is 4x² − 7x − 2.

It is given that the length of a rectangular sandbox is 4x+1 and the width of the sandbox is x−2.

It is required to find a polynomial in standard form which represents the area of the sandbox. And name the polynomial based on its degree and number of terms.

To do so, use the area of the rectangle formula. Substitute the given values of length and breadth. Solve further to find the polynomial. Then name the polynomial based on its degree and number of terms.

The area of a rectangle is A=lw.

Substitute 4x+1 for 1 and x-2 for w

Solve further to find the formula

A=(4x+1)(x-2)
A=(4x)(x)-2(4x)+1(x)+1(-2)
A=4x²-8x+x-2
A=4x²-7x-2​

The polynomial is 4x² − 7x − 2.

The name of the polynomial 4x² − 7x − 2 based on the degree is a quadratic polynomial because this polynomial has degree 2.

The name of the polynomial 4x² − 7x − 2 based on the number of terms is trinomial because this polynomial has three terms.

The name of the polynomial 4x² − 7x − 2 based on the number of terms is trinomial and its name based on the degree is quadratic polynomial.

Page 19 Exercise 1 Answer

The given polynomial is 5x² + 27x − 18.

It is required to factorize the given polynomial.

The Given polynomial is 5x²+27x-18

5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)

​So the correct answer is option C.

Option A

Factorize the given polynomial 5x² + 27x − 18.

The Given polynomial is 5x²+27x-18

5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)

Which is not equivalent to (5x+3)(x+6)

so option A is incorrect.

Option B

Factorize the given polynomial 5x² + 27x − 18.

The Given polynomial is 5x²+27x-18

5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)

Which is not equivalent to (5x−2)(x−9)

so option B is incorrect.

Option D

Factorize the given polynomial 5x² + 27x − 18.

The Given polynomial is 5x²+27x-18

5x²+27x-18=5x²+30x-3x-18
5x²+27x-18=5x(x+6)-3(x+6)
5x²+27x-18=(x+6)(5x-3)

Which is not equivalent to (5x+2)(x−9)

so option D is incorrect.

The factor of the polynomial 5x² + 27x − 18 is (5x−3)(x+6), so the correct option is C.

Page 19 Exercise 2 Answer

The given expression is (x−3)².

It is required to simplify the given expression.

To solve the given expression, use the algebraic identity.

Use the algebraic identity (a−b)³ = a³ − 3a²b + 3ab² − b³. Choose x for a and 3 for b and solve further.

The given expression, (x-3)³
(a-b)³=a³-3a²b+3ab²-b³
(x-3)³=x³-9x²+3x(3)²-(3)³
​
​The simplified form of (x−3)³ is x³ − 9x² + 27x − 27.

The given expression is (x−3)².

It is required to simplify the given expression and name it based on the degree.

To solve the given expression, use the algebraic identity. Name the simplified form based on degree.

Use the algebraic identity (a−b)³ = a³ − 3a²b + 3ab² − b³. Choose x for a and 3 for b and solve further.

The given expression,(x-3)²

(a-b)³=a³-3a²b+3ab²-b³
(x-3)³=x³-9x²+3x(3)²-(3)³
(x-3)³=x³-9x²+27x-27
​
This is a cubic polynomial because it has degree 3.

The name of the polynomial x³ − 9x² + 27x − 27 based on degree is a cubic polynomial.

Page 19 Exercise 3 Answer

A figure is given in the question.

It is required to find the area of the rectangle given in the figure.

To do so, use the area of the rectangle formula. Substitute the given values of length and breadth. Solve further to find the polynomial.

The given figure is,

From the figure, the length of the rectangle is 2x + 8 and its width is x + 4.

The area Of a rectangle is A=lw

Substitute 2x+8 for 1 and x+4 for w

solve further to find the polynomial

A=(2x+8)(x+4)
A=(2x)(x)+2x)(4)+8(x)+8(4)
A=2x²+8x+8x+32
A=2x²+16x+32

The area of the rectangle in the given figure is 2x² + 16x + 32.

A figure is given in the question. It is also given that the value of π is 3.14.

It is required to find the area of the circle given in the figure.

To do so, use the area of the circle formula. Substitute the given values of radius. Solve further to find the polynomial.

The given figure is,

From the figure, the radius of the circle is x+4.

The area of a circle is A= πr²

Substitute x+4 for r and 3.14 for π

Solve further to find the polynomial

A=(3.14)(x+4)²
A=(3.14)(x²+8x+16
A=(3.14)(x²)+(3.14)(8x)+(3.14)(16)
A=3.14×2+25.12x+50.24

The area of the circle in the given figure is 3.14x² + 25.12x + 50.24.

A figure is given in the question. It is also given that the value of π is 3.14.

It is required to find the area of the shaded region given in the figure.

To do so, find the area of the circle and the area of the rectangle. Then subtract the area of the circle from the area of the rectangle.

The given figure is,

From the figure, the radius of the circle is x+4.

The area of a circle is A= πr²

Substitute x+4 for r and 3.14 for π

Solve further to find the polynomial

A₁=(3.14)(x+4)²
A₁=(3.14)(x²+8x+16)
A₁=(3.14)x²+(3.14)(8x)+(3.14)(16)
A₁=3.14x²+25.12x+50.24

From the figure, the length of the rectangle is 2x+8 and its width is x+4.

The area of a rectangle is A=lw

Substitute 2x+8 for 1 and x+4=w

Solve further to find the polynomial.

A₂=(2x+8)(x+4)
A₂=(2x)(x)+(2x)(4)+8(x)+8(4)
A₂=2x²+8x+8x+32
A₂=2x²+16x+32

To find The area of the shaded region,

subtract the area of the circle from the area of the rectangle

A=(2x²+16x+32)-)(3.14x²+25.12x+50.24
A=(2-3.14)x²+(16-25.12)x+32-50.24
A=-1.14×2-9.12x-18.24

The area of the shaded region is 3.14x² + 25.12x + 50.24.

Page 20 Exercise 2 Answer

Given is the polynomial representing the area of a square.

64x² + 96x + 36

It is asked to find the expression for the length of the sides.

To solve the problem use the formula for the area of the square that is side² and equate it to the given polynomial and then simplify and solve for the side.

Equate the given polynomial with the area of the square that is side 2.
​
Given Expression 64x² +96x+36

Side² =4((4x)²+2.4x.3+3²)
Side²=(2(4x+3))²
Side2=8x+6
​
So the expression for the side of the square is (8x+6).

The expression for the side length is (8x+6) units.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 2 Page 20 Exercise 3 Answer

Given, the dimension of the garden is 12m × 8m. A pathway of xm is to be made around the perimeter of the garden having the same area as the garden.

It is asked to sketch the situation and to find a polynomial representing the total area of the garden and pathway.

To solve the problem first sketch the situation and then find the area of the garden using the formula for the area of the rectangle substituting the values of length and breadth

Then find the area of the pathway assuming it to be made up of four different rectangles.

Then add the area of the garden and the area of the pathway to get the polynomial representing the total area of the garden and the pathway.

Sketch of the given situation.

The length of the garden is l = 12m.
Breadth of the garden is b=8m
The area of the garden is,

A=lxb
A=12×8
A=96

So the area of the garden is 96m².

Assume that the pathway is formed of 4 rectangles. Two rectangles having the length of 12m and breadth of xm, and other two rectangles having the length of 8m + 2xm and breadth of xm, then the total area of the pathway is given by,

A=lxb+lxb+lxb+lxb

⇒ \(\begin{aligned}
& A=(12 \times x)+(12 \times x)+((8+2 x) \times x)+((8+2 x) \times x) \\
& A=2 \cdot(12 \times x)+2 \cdot((8+2 x) \times x) \\
& A=24 x+16 x+4 x^2 \\
& A=4 x^2+40 x
\end{aligned}\)

​So the area of the pathway is A = 4x² + 40x.

The total area will be the sum of the area of the pathway and the area of the garden.

Total Area= Area of the garden+Area of the pathway

2A=96+4x²+40x
A=48+2x²+20x
A=2x²+20x+48
​
The polynomial for the total area of the garden and the pathway is 2x² + 20x + 48.

Given, the dimension of the garden is 12m × 8m. A pathway of xm is to be made around the perimeter of the garden having the same area as the garden.

It is asked to find the width of the pathway.

To solve the problem, first equate the area of the pathway from the previous problem with the area of the garden to get a polynomial. Then factorise the polynomial and simplify and solve for x.

The area of the garden is 96m² and the area of the pathway from the previous part of the question is A = 4×2 + 40x.

Equate the area of the pathway with the area of the garden.

So the polynomial is x2+10x-24=0

Now factorize the polynomial to get the value of x.

\(\begin{aligned}
& x^2+10 x-24=0 \\
& x^2+12 x-2 x-24=0 \\
& x(x+12)-2(x+12)=0 \\
& (x-2) \cdot(x+12)=0
\end{aligned}\)
​
So x = 2 or −12 but as length cannot be negative,

x = 2m

As x is the width of the pathway so width of the pathway is 2m.

The width of the pathway is 2 meters.

Envision Algebra 1 Assessment Readiness Workbook Chapter 1 Standards Practice

Page 2 Exercise 1 Answer

It is given that the expression 0.25b + 6 models the total cost to hit b baseball in the batting cages.

It is asked to determine the cost per baseball from the given options.
​
A. $6.25

B. $6.00

C. $0.25

D. $0.19
​
The cost per baseball means the cost to hit a single baseball. This means the required answer can be obtained by substituting the value 1 for b in the given expression.

Substitute the value 1 for b in the expression 0.25b + 6 to get the cost of hitting 1 baseball. ​

Given 0.25b +6
b=1
Substitute the value of b
0.25b+6
=0.25(1)+6
=0.25(1)+6
=0.25+6
=6.25

Thus, the cost per baseball is $6.25.

The value of the expression 0.25b + 6 can be $6.00 only when no baseball is hit and here it is asked to find the cost to hit a single baseball.

Therefore, option B is the wrong answer.

Also, the minimum value of the expression 0.25b + 6 will be $6.00 even if no baseball is hit, and the values given in options C and D are less than $6.00 which is not possible.

Therefore, options C and D also have wrong answers.

The cost per baseball is $6.25 and therefore, option A is the right answer.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 1 Page 2 Exercise 2 Answer

The following figure is given.

It is asked to find the measure of each angle.

The sum of all the angles of the triangle is 180°. Apply this rule on △ABC, substitute the given values, and then solve the equation to determine the value of the variable x. Then substitute the obtained value in each angle and find their measures.

Apply the rule that the sum of all the angles of the triangle is 180° on △ABC,

Substutitu (x-2) from m<A, (4x+1) for m<B and (4x+1) for m<x.

m<A+m<b+m<c=180
x-2+4x+1+4x+1=180
x+4x+4x-2+1+1=180
9x=180°
Divide both sides by 9

⇒ \(\frac{9 x}{9}=\frac{180}{9}\)

x=20

Substitute the value 20 for x in (x-2) to determine m<A

m<A = x-2

m<A=20-2

m<A=18

Substitute the value 20 for x in (4x+1) to determine m<B.
m<B =4x+1
m<B=4(20=+1
m<B=7=80+1
m<B=81°

As m∠C has the same value, m∠C = 81°.

The measures of the angles of △ABC are,
​
m∠A = 18°
m∠B = 81°
m∠C = 81°

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 1 Page 2 Exercise 3 Answer

A statement of a student is given that the sum of two real numbers is always a rational number.

It is asked to determine if the student is correct and give a reason with an example.

To solve this question, it is important to know that every rational number is a real number. Real numbers also include irrational numbers. The sum of two rational or irrational numbers is always a rational number. Therefore, the given statement is correct.

For example, consider two real numbers \(\frac{1}{2} \text { and } \frac{3}{2}\)

Some of these two real numbers are, ​

​
⇒ \(\frac{1}{2}+\frac{3}{2}\) = \(\frac{4}{2}\)

⇒ \(\frac{1}{2}+\frac{3}{2}\) = 2

Here, 2 is a rational number.

The student is correct because the sum of two real numbers is always a rational number. The sum of two rational or irrational numbers is always a rational number. Therefore, the given statement is correct. For example, consider two real numbers \(\frac{1}{2} \text { and } \frac{3}{2}\)

The sum of these two real numbers is,

⇒ \(\frac{1}{2}+\frac{3}{2}\) = \(\frac{4}{2}\)

\(\frac{1}{2}+\frac{3}{2}\) = 2

Here, 2 is a rational number.

Page 3 Exercise 1 Answer

The statement is given that the sum of a number p and 12 is 34.

It is asked to identify the correct equation which represents this statement from the options given below.​

A. P − 12 = 34

B. 12P = 34

C. P + 12 = 34

D. P + 34 = 12
​
In the given statement the word ‘is’ represents equal to.

On the left side of it there is the phrase the sum of a number p and 12 which is represented as p + 12 and on the right side of it, 34 is given.

Therefore, put equal to sign between these two and obtain the required equation.

p + 12 = 34

Thus, option C is the correct answer.

The equation given in option A, P − 14 = 34 represents that the difference of p and 12 is 34.

The equation given in option B, 12P = 34 represents that the multiplication of p and 12 is 34.

The equation given in option D, P − 14 = 34 represents that the sum of p and 34 is 12.

The given statement is represented by the equation p + 12 = 34 and therefore, option C is the correct answer.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 1 Page 3 Exercise 3 Answer

It is given that the scale model of a skyscraper is 2ft tall and the scale of the model is 1in:7.2m.

It is asked to determine the height of the proposed skyscraper in meters.

To solve this question, first convert the model height from feet into inch as in the scale, inch unit is used. After that assume that the height of the skyscraper in meters is x and then according to the given scale, determine its value,

Covert the given height of the model from feet into inches.
​
1ft = 12in

2ft = 2 × 12

2ft = 24in

Assume the height of the proposed skyscraper as xm and solve for the variable using the given scale.

According to the scale 1in : 7.2m,1in of the model height represents 7.2m tall skyscraper.

The model height is 24in.

Therefore, the actual height of the proposed skyscraper is given by,
​
x = 24 × 7.2

x = 172.8m

The proposed skyscraper is 172.8m tall.

Page 4 Exercise 1 Answer

It is given that Tamika bought 6 apples and 1 juice.

It is required to find the cost of 1 apple if the cost of 1 juice is $1.25 and the total cost is $5.75

Let the cost of an apple be x. The sum of the cost of 6 apples and 1 juice is $5.75.

Therefore, the equation is formed as 6x + 1.25 = 5.75

Subtract 1.25 from both sides of the formed equation.​

Given: 6x+1.25=5.75

Subtract 1.25 from both sides

6x+1.25-1.25= 5.75-1.25

6x=4.50

divide both sides of an equation

⇒ \(\frac{6 x}{6}=\frac{4.50}{6}\)

x=0.75
​
Thus, the cost of 1 apple is $0.75.

Hence, option B is correct.

Let the cost of an apple be x. The sum of the cost of 6 apples and 1 juice is $5.75.

Therefore, the equation is formed as

Given: 6x+1.25=5.75

Subtract 1.25 from both sides

6x+1.25-1.25=5.75-1.25

6x=4.50

divide both sides of an equation

\(\frac{6 x}{6}=\frac{4.50}{6}\) ​

x=0.75

Thus, the cost of 1 apple is $0.75 which is not equal to $0.50.

Hence, option A is incorrect.

Option C

Let the cost of an apple be x. The sum of the cost of 6 apples and 1 juice is $5.75.

Therefore, the equation is formed as

Given: 6x+1.25=5.75

Subtract 1.25 from both sides

6x+1.25-1.25=5.75-1.25

6x=4.50

Divide both sides of an equation

\(\frac{6 x}{6}=\frac{4.50}{6}\) ​

x=0.75

Thus, the cost of 1 apple is $0.75 which is not equal to $1.00.\

Hence, option C is incorrect.

Option D

Let the cost of an apple be x. The sum of the cost of 6 apples and 1 juice is $5.75.

Therefore, the equation is formed as

Given: 6x+1.25=5.75

Subtract 1.25 from both sides

6x+1.25-1.25=5.75-1.25

6x=4.50

Divide both sides of an equation

​\(\frac{6 x}{6}=\frac{4.50}{6}\)

x=0.75

Thus, the cost of 1 apple is $0.75 which is not equal to $0.25.

Hence, option D is incorrect.

The correct answer is option B, the cost of 1 apple is $0.75.

Page 5 Exercise 1 Answer

An inequality is given as −2x ≥ −18.

It is required to solve inequality.

Divide both sides of inequality −2x ≥ −18 by −2. Since −2 is a negative number, therefore, the sign of inequality will get reversed.

⇒ \(\frac{-2 x}{-2} \leq \frac{-18}{-2}\)

x ≤ 9

Therefore, option C is correct.

Option A

An inequality is given as −2x ≥ −18.

It is required to solve the inequality.

Divide both the sides of inequality −2x ≥ −18 by −2. Since −2 is a negative number, therefore, the sign of inequality will get reversed.

⇒ \(\frac{-2 x}{-2} \leq \frac{-18}{-2}\)

Therefore, option A is incorrect.

Option B

An inequality is given as −2x ≥ −18.

It is required to solve the inequality.

Divide both the sides of inequality −2x ≥ −18²  by −2. Since −2 is a negative number, therefore, the sign of inequality will be reversed.

⇒ \(\frac{-2 x}{-2} \leq \frac{-18}{-2}\)

Therefore, option B sin^-1 is incorrect.

Option D

An inequality is given as −2x ≥ −18.

It is required to solve the inequality.

Divide both the sides of inequality −2x ≥ −18 by −2. Since −2 is a negative number, therefore, the sign of inequality will get reversed.

Therefore, option D is incorrect.

The option C is correct, the given inequality is simplified as x ≤ 9.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 1 Page 5 Exercise 2 Answer

An equation y = 3x + 6 and four ordered pairs (3,1), (−3,3), (0,6) and (6,0) are given.

It is required to find which ordered pair is the solution of the given equation.

To do so, substitute the given value of the ordered pair as x and y in the equation. Do this for all four ordered pairs and check which one maintains the equality.

For the order pair (0,6),

Substitute o for x in y=3x+6 and find.

y=3(0)+6

y=0+6

y=6

Hence, (0,6) is a solution. Therefore, option C is correct.

Substitute the given value of the ordered pair as x and y in the equation. Do this for all the other three ordered pairs.

Option A

For the order pair (0,6),

Substitute o for x in y=3x+6 and find y.

y=3(0)+6
y=0+6
y=6

Hence, (3,1) is not a solution. Therefore, option A is incorrect.

Option B

For the order pair(-3,3)
Substitute -3 for x in y=3x+6 and find y.

y=3(-3)+6
y=-9+6
y=-3

Hence, (−3,3) is not a solution. Therefore, option B is incorrect.

Option D

For the ordered pair (6,0)
Substitute 6 for x in y=3x+6 and find y.

​y=3(6)+6
y=18+6
y=24

Hence, (6,0)² is not a solution. Therefore, option D is incorrect.

Option C is correct, the ordered pair which is a solution of the equation y = 3x + 6 is (0,6).

Page 5 Exercise 3 Answer

A function rule is given as h(x) = 2x + 6, where h is the height of the plant in centimeters after x weeks of growth.

It is required to graph the function and find the height of the plant after 9 weeks.

To do so, find the value of y if the value of x is assumed to be 1, 2, and 3.

Represent the ordered pairs obtained as a table and then plot the graph. From the graph, find the height of the plant after 9 weeks.

Given, h(x)=2x+6
letx=1
substitute 1 for x in h(x) = 2x+6 and find value of h

h(1)=2(1)+6
h=2+6
h=8​

Hence, the ordered pair (1,8) is a solution of a given function.

Given, h(x)=2x+6
Letx=2
Substitute 2x for x in h(x) = 2x+6

h=2(2)+6
h=4+6
h=10

​Hence, the ordered pair (2,10) is a solution of a given function.

Given,h(x)=2x+6
Let x=3
substitute 3 for x in h(x)=2x+6

​h=2(3)+6
h=6+6
h=12

Hence, the ordered pair (3,12) is a solution of a given function.

Form a table for the obtained ordered pairs.

Plot the ordered pairs and join them through a line.

The function is plotted as,

Also, after 9 weeks the height of the plant is 24 cm.

Page 5 Exercise 4 Answer

Some ordered pairs are given as (0,40), (1,45), (2,50), (3,55), (4,60) and (5,65).

It is required to represent the ordered pairs as a table.

To do so, form a table with two rows one for x coordinates and the other for y coordinates for the given ordered pairs and then fill the table.

Form a table for the given ordered pairs.

The table for the given ordered pairs is,

Some ordered pairs are given as (0,40), (1,45), (2,50), (3,55), (4,60) and (5,65).

It is required to represent the ordered pairs as an equation.

To do so, assume a general equation of a line and substitute the value of given ordered pairs as x and y in the equation to find the relation between m and c.

Find the value of m and c, then substitute them in the general equation to find the required equation.

Let the equation be y = mx + c.

Then the ordered pair (0,40) will be the solution of the equation.

Let the equation be y=mx+c

for the ordered pair(0,40)

Substitute o for x and 40 for y in y=mx+x

40=m(0)+c
40=o+c
40=c

Then the ordered pair (1,45) will be the solution of the equation.

Substitute 1 for x, 45 for y, and 40 for c in y = mx + c.

Let the equation be y=mx+c
for the ordered pair (1,45)

Substitute 1 for x, 45 for y in y=mx+c

45=m(1)+40
45=m+40
45-40=m+40-40
5=m
​
Substitute 5 for m and 40 for c in y = mx + c.

y = 5x + 40

The given ordered pairs are represented in the equation as y = 5x + 40.

Some ordered pairs are given as (0,40), (1,45), (2,50), (3,55), (4,60) and (5,65).

It is required to represent the ordered pairs and the equation on a graph.

To do so, plot the equation on a graph and the given ordered pairs also.

Plot the equation y = 5x + 40 on a graph and the given ordered pairs also.

The given ordered pairs and the y = 5x + 40 is plotted as,

Given the ordered pairs (0,40), (1,45), (2,50), (3,55), (4,60) and (5,65).

It is required to describe a situation that the ordered pair might represent.

To do so, consider any two ordered pairs and represent them as an equation. Observing the equation, a situation can be determined that the ordered pairs represent.

Form an equation from the ordered pairs (0,40) and (1,45).

The ordered pairs (0,40) and (1,45)
The equation can be written as,

⇒ \(\begin{aligned}
& y=\frac{45-40}{1-0} \cdot x+c \\
& y=5 x+c
\end{aligned}\)

For (0,40)
C=40
The equation becomes y=5x+40

The equation can be written in the form v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration, and t represents the time.

The ordered pairs may represent time and velocity at that time.

Page 6 Exercise 2 Answer

It is given that the slope of the line is 9 and passes through the point (−3,6).

It is required to find the equation of the line.

To do so, substitute the slope of the line and the point in the point-slope form equation. As a result, the equation of the line can be determined.

Substitute the slope of the line and the point in the point-slope form equation.
​
y − 6 = 9(x−(−3))

y − 6 = 9(x+3)
​
The equation of the line is y − 6 = 9(x+3).

So, the correct option is (A)y − 6 = 9(x+3).

It is given that the slope of the line is 9 and passes through the point (−3,6).

Option (B)

The given equation is y − 6 = 9(x−3).

Consider the point (−3,6) and substitute in the equation y − 6 = 9(x−3),
​
Given equation is y+3=9(x-6)
For the ordered pair (-3,6)

y+3=9(x-6)
6+3=9(-3-6)
9=9(-9)
9=-54

The values on both sides of the equation are different, so the option (B) is not correct.

Option (C)

The given equation is y + 3 = 9(x−6).

Consider the point (−3,6) and substitute in the equation y + 3 = 9(x−6),
​
Given equation is y+3=9(x-6)
for the ordered pair(-3,6)

y+3 =9(x-6)
6+3=9(-3-6)
9=9(-9)
9=-54
​
The values on both sides of the equation are different, so option (C) is not correct.

Option (D)

The given equation is y − 6 = −3(x−9).

Consider the point (−3,6) and substitute in the equation y − 6 = −3(x−9),
​
Given equation is y-6 =-3(x-9)
For the ordered pair (-3,6)
y-6=-3(x-9)
6-6=-3(-3-9)
0=-3(-12)
0=36

The values on both sides of the equation are different, so the option (D) is not correct.

The correct answer is Option (A)y − 6 = 9(x+3).

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 1 Page 6 Exercise 3 Answer

It is given that sage earns 6$ per hour.

It is required to make a table and write an equation to show the relationship between the number of hours worked h and the wages earned w.

To do so, take the values of hours and multiply to that of wages earned per hour. If the amount earned per hour is a, then the amount earned for n hours can be calculated by the unitary method shown below,
​
Amount earned per hour = a

Amount earned for n hours = na.

Take the values of hours 1, 2, 3, 4 and multiply with that of wages earned per hour, 6$.

For 1 hour, the wage earned is 6⋅1$ = 6$.

For 2 hours, the wage earned is 6⋅2$ = 12$.

For 3 hours, the wage earned is 6⋅3$ = 18$.

For 4 hours, the wage earned is 6⋅4$ = 24$.

Make a table and write an equation to show the relationship between the number of hours worked h and the wages earned w.

Implement the above values in table. The table can be made as shown below,

The equation to show the relationship between the number of hours worked h and the wages earned w can be written as w = 6⋅h, where w represents the wages earned and h is the number of hours worked.

The table to show the relationship between the number of hours worked h and the wages earned w is shown below,

The equation to show the relationship between the number of hours worked h and the wages earned w is w = 6⋅h.

It is given that sage earns 6$ per hour.

It is required to find how many hours will sage need to work to earn 30$.

To do so, use the unitary method to convert the amount sage earns per hour into the amount sage needs to work to earn 30$. Find the number of hours sage needed to work to earn 1 $​​ and as a result, the number of hours sage need to work to earn 30$ can be determined.

Find the number of hours sage will need to work to earn 30$.

It is given that sage earns 6$ per hour,
​
To earn 6 ​​$​​, number of hour sage will need to work = 1 hour

To earn 1 $​​, number of hour sage will need to work = \(\frac{1}{6} \text { hour }\)

To earn 30 ​​$​​, number of hours sage will need to work = \(\frac{1}{6} \times 30 \text { hours }\)
​
Therefore to earn 30$, sage will need to work 5 hours.

Sage will need to work 5 hours to earn 30$.

Page 6 Exercise 4 Answer

Given the final purchase price of the item is $175.

It is required to find the possible price of the item before each discount.

To do so, add the discount and the purchase price of the item. As a result, the purchase price of the item. As a result, the purchase price of the item before each discount can be determined.

Find the price for a flat discount of $20 off on any purchase.

Price before discount = discount + final purchase price
price before discount = $20+$175
Price before discount = $195

Find the price for a flat discount of 20 off on total purchase
if the price before the discount is p,

⇒ \(\left(P-\frac{20}{100} \cdot P\right)=\$ 175\)

0.8p=$ 175

P=$ 218.75

The possible prices of the item before each discount is $195 and $218.75.

Given the final purchase price of the item is $175.

It is required to find the discount which represents a bigger saving in cost for the customer.

To do so, add the discount and the purchase price of the item. As a result, the purchase price of the item before each discount can be determined. Compare the two prices and the discount which represents a bigger saving in cost can be determined.

Find the price for a flat discount of $20 off on any purchase.

Price before discount = discount + final purchase price
price before discount = $20+$175
Price before discount = $195

Find the price for a flat discount of 20 off on total purchase
if the price before the discount is p,

0.8p=$ 175

P=$ 218.75

A flat discount of 20% represents a bigger saving in cost for the customer.

Page 7 Exercise 1 Answer

Given four graphs as shown below,

(A)

(B)

(c)

(D)

It is required to determine which of the graph is not a function.

In the graph in option(C), the line is parallel to the y-axis.

A function is a relation in which each input has a single output.

In the graph in Option (C), for any value of y, x is the same.

For a single value of input x, the output y could be anything. Therefore the graph is not a function as the output y has more than one value.

The graph in Option(C) is not a function.

A function is a relation in which each input has a single output.

In the graph in option (A), (B) and (D), for every input, there is an output.

The graph in option (A), (B) and (D) are functions.

The correct answer is Option (C).

Page 7 Exercise 2 Answer

Given a graph shown below,

It is required to draw a line on the graph shown above that has the same slope as the line is drawn and passes through (−2,1).

To do so, find the slope of the line given in the graph. Use the slope and the given point to generate an equation and as a result, the required line can be drawn.

Find the equation of the given line.

From the graph x-intercept is 2 and the y-intercept is 4.

The equation can be written as

2x+y=1

From the equation, the slope of the line is -2

find the equation of the line for point (-2,1) and slope -2

The equation of the line can be written as,

y-1=(-2)(x-(-2))
y-1=-2x-4
y=-2x-4+1
y=-2x-3

The y-intercept is −3.

Use the point (−2,1) and y-intercept, -3 to draw the line as shown below,

The line that has the same slope as the line is drawn and passes through (−2,1) is shown below,

Given a graph shown below,

It is required to find the equation of the line that has the same slope as the line is drawn and passes through (−2,1).

To do so, find the slope of the line given in the graph. Use the slope and the given point to generate an equation and as a result, the equation of the line can be determined.

Find the equation of the given line.

From the graph, the x-intercept is 2 and the y-intercept is 4.

The equation can be written as

⇒ \(\frac{x}{2}+\frac{y}{4}=1\)

2x+y=1

From the equation, the slope of the line is -2

Find the equation of the line for point (-2,1) and slope -2

The equation of the line can be written as,

y-1=(-2)(x-(-2))
y-1=-2x-4
y=-2x-4+1
y=-2x-3

The equation of the line is y = −2x − 3.

Envision Algebra 1 Assessment Readiness Workbook Student Edition Chapter 1 Standards Practice 1 Page 7 Exercise 3 Answer

A graph and a set of equations are given in the question. The given equations are,

y – 2 = \(\frac{1}{2}(x-4)\)

y + 4 = 2(x-1)

y – 4 = \(\frac{1}{2}(x-2)\)

y – 1 = 2(x+4) and

y – 1 = \(\frac{1}{2}(x+4)\)

It is required to find which of the given equations matches the given graph.

To draw the graph use dynamic geometry software. Then

The given graph is,

The graph corresponding to the equation y – 2 = \(\frac{1}{2}(x-4)\) is given below.

The graph corresponding to the equation y + 4 = 2(x−1) is given below.

The graph corresponding to the equation y – 4 = \(\frac{1}{2}(x-2)\) is given below.

The graph corresponding to the equation y − 1 = 2(x+4) is given below.

The graph corresponding to the equation y – 1 = \(\frac{1}{2}(x+4)\) is given below.

From the above graphs it can be note that only the graphs in step 4 and 6 matches with the given graph.

Therefore the equations y – 4 = \(\frac{1}{2}(x-2)\), nd y – 1 = \(\frac{1}{2}(x+4)\) are the possible equations of the line drawn.

Envision Math Grade 8 Volume 1 Chapter 8 Solve Problems Involving Surface Area And Volume

Page 423 Exercise 1 Answer

Given:

To find the similarity in the figures:

Apply the formula of the cylinder’s volume and the rectangular’s tank volume.

The similarity found in both shapes is the height of the shapes, which is the same.

They are different because both shapes have different volumes.

Given:

From the part(a), the volume of the rectangular tank is greater than the volume of the circular tank.

Since the volume of the rectangular tank is greater than the volume of the circular tank, the rectangular tank can hold more water.

Hence, Ricardo is correct.

Since the volume of the rectangular tank is greater than the volume of the circular tank, the rectangular tank can hold more water. Hence, Ricardo is correct.

Envision Math Grade 8 Surface Area And Volume Exercise 8.2 Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.2 Page 424 Essential Question Answer

Volume of cylinder is πr²h, where r = radius and h = height

Prisms and cylinders are similar because they both have two bases and a height.

The formula for the volume of a rectangular solid, V = Bh

V = Bh, can also be used to find the volume of a cylinder when area of base is given.

When area of base is given volume for both cylinder and prism is V = Bh

Page 424 Try It Answer

Given: area = 78.5in² and height = 11 in

To find: volume of cylinder

We will use the product of area and height to find the volume.

As we know V = Bh then putting all the values
​
V = 78.5 × 11

= 863.5 in³

Therefore, volume is given as 863.5in³

Page 425 Try It Answer

Given: a cylindrical planter with a base diameter of 15 inches and 5,000 cubic inches is the volume

To find: height of the planter

We will use the formula of volume of cylinder and find the value.

Volume of cylinder is πr²h, where r = radius and h = height

Height of planter is approximately 28 in.

Envision Math Grade 8 Volume 1 Student Edition Chapter 8 Exercise 8.2

Page 426 Exercise 1 Answer

Volume of cylinder is πr²h, where r = radius and h = height

Prisms and cylinders are similar because they both have two bases and a height.

The formula for the volume of a rectangular solid V = Bh

V = Bh can also be used to find the volume of a cylinder when area of base is given.

When area of base is given volume for both cylinder and prism is V = Bh

Page 426 Exercise 2 Answer

As we know the volume is the product of cross sectional area and height.

Cylinder has a circular base so its area is given as πr²

Now for height h, volume is πr² × h

Two measurements you need to know to find the volume of a cylinder is radius and height.

Page 426 Exercise 3 Answer

Given: Cylinder A has a greater radius than Cylinder B.

To find: Cylinder A necessarily have a greater volume than Cylinder B?

Volume of cylinder is πr2h, where r = radius and h = height

Volume depends on radius and height both so it is not necessary.

Cylinder A does not necessarily have a greater volume than Cylinder B.

Solutions For Envision Math Grade 8 Exercise 8.2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.2 Page 426 Exercise 4 Answer

Given: area is 4πmm² and height is 10 mm

To find: Volume of Cylinder

We will use the formula and put the values to find volume

As we know that volume is the product of base area and height.

Volume of the cylinder is 40π mm³

Page 426 Exercise 5 Answer

Given: radius is 10 ft and volume is 314 ft³

To find: height of Cylinder

We will use the formula and put the values to find height.

As we know that volume is the product of base area and height.

Volume of cylinder is one feet.

Page 426 Exercise 6 Answer

Given: radius is 4 cm and circumference is 22.4 cm

To find: Volume of Cylinder

First we will find the radius from circumference.

We will use the formula and put the values to find volume.

Volume of the cylinder is 162.8 cm³

Page 427 Exercise 7 Answer

Given: radius is 5 cm and height is 2.5 cm

To find: Volume of Cylinder

We will use the formula and put the values to find volume

As we know that volume is the product of base area and height.

Volume of cylinder is 196.25 cm³

Page 427 Exercise 9 Answer

Given: height is 1 in and volume is 225π in³

To find: radius of Cylinder

We will use the formula and put the values to find radius.

As we know that volume is the product of base area and height.

Radius is calculated as 15 in.

Envision Math Exercise 8.2 Step-By-Step Solutions Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.2 Page 427 Exercise 10 Answer

Given: height is 8.1 cm and volume is 103 cm³

To find: Radius of Cylinder

We will use the formula and put the values to find radius.

As we know that volume is the product of base area and height.

Radius of the bottle is 2.01 cm.

Page 427 Exercise 11 Answer

Given: height is 3 in and radius is 4 in

To find: Volume of Cylinder

We will use the formula and put the values to find volume.

As we know that volume is the product of base area and height.

Putting the values in formula
​
V = π × 4² × 3

= 48π in³

Volume of the cylinder is 48π in³

Given: height is 3 in and radius is 4 in

To find: is the volume of a cylinder, which has the same radius but twice the height, greater or less than the original cylinder?

We will use the formula and put the values to find radius.

First we will write the original volume and then find the new one.

As we know that volume is the product of base area and height.

The original volume is 48π in³

Now h′ = 2h which will be 6 in

Putting the values in formula
​
V′ = π × 4² × 6

= 96π in³

Clearly 98π in³ > 48π in³ therefore, volume of second cylinder is greater.

Page 428 Exercise 13 Answer

Given: height is 11.7 in and volume is 885 in³

To find: radius of Cylinder

We will use the formula and put the values to find radius.

As we know that volume is the product of base area and height.

Radius of the cylinder is 4.91 in

Given: height is 11.7 in and volume is 885 cubic inches

To find: If the height of the cylinder is changed, but the volume stays the same, then how will the radius change

We will use the formula of volume and find the dependency of volume.

As we know that volume is the product of base area and height.

That means it is dependent on both radius and height.

V α r²h

If the height of the cylinder is changed, but the volume stays the same, then radius will decrease.

Solve Problems Involving Surface Area And Volume Envision Math Solutions Exercise 8.2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.2 Page 428 Exercise 14 Answer

Given: height is 20.7 cm and diameter is 6.9 cm

To find: Volume of Cylinder

First we will find the radius.

We will use the formula and put the values to find volume.

Volume of the cylinder is 773.6 cm³

Page 428 Exercise 15 Answer

Given: height is 21 in, inner radius is 3 in and outer radius is 5 in

To find: Volume of material

We will use the formula and put the values to find radius.

We will find volume with both the radii and the difference will be required volume

As we know that volume is the product of base area and height.

Putting the values in formula to find outer volume
​
V_R = π × 5 × 5 × 21

V_R = 1648.50

As we know that volume is the product of base area and height.

Putting the values in formula for finding volume of inner volume
​
V_r = π × 3 × 3 × 21

V_r = 593.46
​
Difference in volumes is

V_R − V_r = 1648.50 − 593.46

= 1055.04 in³

Volume of the required material is 1055.04in³

Envision Math Grade 8 Chapter 8 Worksheet Solutions Exercise 8.2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.2 Page 428 Exercise 16 Answer

Given: height is 21 cm and volume is 1029πcm³

To find: radius of Cylinder

We will use the formula and put the values to find radius.

As we know that volume is the product of base area and height.

Radius of the Cylinder is 3.9 cm

Page 428 Exercise 17 Answer

Given: height is 12 yd and diameter is 7 yd

To find: Volume of Cylinder

First we will find the radius.

We will use the formula and put the values to find radius.

Radius is given as \(\frac{\mathrm{d}}{2}=\frac{7}{2}\)

As we know that volume is the product of base area and height.

Volume of cylinder is 147π cubic yards

Envision Math Grade 8 Chapter 8 Exercise 8.2 Explained

Page 429 Exercise 1 Answer

A three-dimensional object is in three dimensions having length, width and height.

Example: Cubes, prisms, pyramids, spheres, cones, and cylinders are all examples of three-dimensional objects.

Volume is the product of length, width and height.

Surface areas is the sum of products of length, width and height taken two at a time.

Surface area is a two-dimensional measure.

Volume is a three-dimensional measure.

Page 429 Exercise 3 Answer

Given: A figure of cylinder containing a cone

To find: how much cardboard was used to make the package

First we will find the radius.

Then with the help of tip we will find the surface area.

Radius of the cone is \(\frac{d}{2}\) = 10cm

Putting all the values in the formula

2πrh + 2πr²

S = 2πrh + 2πr²

S = 2π.10.33 + 2π.33.33

= 860π cm²

Surface area for cylinder is 860π cm²

Free Solutions For Envision Math Grade 8 Exercise 8.2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.2 Page 429 Exercise 5 Answer

Given: A figure of sphere with radius as 3 ft

To find: Surface area

Then with the help of tip we will find the surface area.

Putting all the values in the formula of surface area
​

Surface area of the given sphere is 36π ft²

How To Solve Envision Math Grade 8 Surface Area And Volume Problems Exercise 8.2 

Page 429 Exercise 6 Answer

Given: Volume is 400πcm³ and diameter is 10 cm

To find: Which option has the correct height

We will use the formula and put the values to find height.

​

​
So the height does not match with any of the option (A), (C) or (D).

Correct option is (B).

Envision Math Grade 8 Volume 1 Chapter 8 Solve Problems Involving Surface Area And Volume

Page 417 Exercise 1 Answer

Given:

A tube-shaped container is shown below:

To find the figures from the tube:

First, look at the tube from the top and the bottom and then use the definition of circle and rectangle.

The top and the bottom shape of the container are represented by the circle of the radius r as shown

The tube is represented by the rectangle with one side equal to height h of the tube and the other side equal to the circumference of the circle of radius r.

So, the net of the tube-shaped container is shown below:

Hence, the net of a tube container is shown below:

Given:

Since the circular top and bottom fit perfectly on the ends of the container, the circumference of the circles must be equal to the length of the rectangle making up the tubular portion of the container.

Hence, the circumference of the circles must be equal to the length of the rectangle making up the tubular portion of the container.

Envision Math Grade 8 Chapter 8 Exercise 8.1 Solutions

Page 417 Focus On Math Practices Answer

A tube can be draw as

As we can see in the figure, that a tube have 2 circle and 1 rectangle with one side equal to the height h of the tube and the other side equal to the circumference of the circle of radius r.

So, we can conclude that if the circumference of the circles is equal to the length of the rectangle making up the tubular portion of the container then it will definitely represent a tube-shaped container.

Hence, if the circumference of the circles is equal to the length of the rectangle making up the tubular portion of the container then it will definitely represent a tube-shaped container.

Page 418 Try It

Given:

h = 9.5inches

r = 2.5 inches

To find the surface area:

Plug the values in S.A. = 2πr²+ 2πrh.

Hence, the curved surface area is S.A. = 60π square inches.

Envision Math Grade 8 Surface Area And Volume Exercise 8.1 Answers

Page 418 Convince Me Answer

The surface area of the cylinder when we have its height and the circumference of its base.

To find this, let’s take an example:

Find the area of the cylinder if the height of the cylinder is 7 meters and the circumference of its base is 14π.

To find the area of the cylinder:

First, find the radius of the cylinder and plug the values in S.A. = 2πr² + 2πrh.

​
Hence, we can find the area of the cylinder if you only know its height and the circumference of its base.

Page 419 Try It Answer

Given:

r = 7 feet

L = 9 feet

To find the surface area:

First, find the area of the circle and then the curved surface area of the cone and then add them.

Add the areas of the circular base and the curved to calculate the surface area of the cone:
​
A + L = 154 + 198

= 352

Hence, the surface area of the cone is 352 square feet.

Given:

d = 2.7 inches

To find the surface area:

First, find the radius using the formula d = \(\frac{r}{2}\) then plug the value of r in the surface formula.

Hence, the area of the sphere is 22.89 square inches.

Envision Math Grade 8 Volume 1 Student Edition Chapter 8 Exercise 8.1

Page 420 Exercise 3 Answer

Given:

C = 2π

To find the surface area of the cones:

First, find the value of r using the formula of the circumference of the circle.

​
Since 36π ≠ 56π, it follows that not all surface of any cone with base circumference 8π inches are equal.

Hence, the hypothesis of the boy is not correct.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 420 Exercise 4 Answer

Given:

To find the surface area:

First, find the radius of the cylinder using r = \(\frac{d}{2}\) and plug the values in the surface area formula.

Hence, the surface area of the cylinder is 69.1mm².

Page 420 Exercise 6 Answer

Given:

To find the surface area:

First, find the value of r using the diameter than the value in the surface area formula.

Hence, the area of the sphere is 4πcm².

Solutions For Envision Math Grade 8 Exercise 8.1

Page 421 Exercise 7 Answer

Given:

To find the surface area of the cylinder:

Plug the value of r and h in the surface area formula.

Page 421 Exercise 8 Answer

Given:

To find the surface area of the cone:

Plug the value r and l in the surface area formula.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 421 Exercise 9 Answer

Given:

To explain the error and find the correct surface area of the cylinder:

Use the formula S = 2πr² + 2πrh.

​
The surface area of the cylinder is about 498.8 square inches.

The calculated surface area of the girl is 76.9 square inches.

Hence, the girl miscalculates the surface area by using only the first term of the formula for the surface area of a cylinder:

S = 2πr² + 2πrh

S = 2πr²

Plug the values:
​
S = 2(3.14)(3.5)²

S ≈ 76.97

Hence, the correct surface area of the given cylinder is about 494.8 square inches and the girl miscalculates the surface area by using only the first term of the formula for the surface area of a cylinder.

Free Solutions For Envision Math Grade 8 Exercise 8.1

Page 421 Exercise 10 Answer

Given:

To find the correct surface area of the sphere:

Plug the values S = 4πr².

​
So, the surface area of the sphere is 84453.44yd².

Hence, the surface area of the sphere is 84453.44yd².

Envision Math Exercise 8.1 Step-By-Step Solutions Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 422 Exercise 11 Answer

Given:

To explain the error and find the correct surface area of the cylinder:

Use the formula S = 2πr² + 2πrh.

Hence, the surface area of the cylinder is 960.8in.².

Practice Problems For Envision Math Grade 8 Exercise 8.1

Page 422 Exercise 12 Answer

Given:

To find the number of bottles of paint:

Use the formula S = πr² + πrl.

First, draw 2D to understand the problem:

In the cone, the radius of the base is 4.1 and the slant height is l = 8.9.

So, she needs 12 bottles of paint.

Hence, she needs 12 bottles of paint.

Envision Math Grade 8 Chapter 8 Worksheet Solutions Exercise 8.1

Page 422 Exercise 13 Answer

Given:

To find the surface area:

Use the formula S = πr² + πrl.

Hence, the surface area of the cone is 141cm².

Given:

To find affection of the surface area of the cone:

Use the formula S = πr² + πrl.

Based on the part(a), the surface area of the cone (original) is 45π or approximately 141.37 square centimeters.

If the diameter and the slant height is cut in half, that will be

It is seen that the new surface area is \(\frac{1}{4}\)

times the original surface area S = 45π, that is

Hence, the diameter and the slant height of the cone is cut in half, the new surface area will become \(\frac{1}{4}\) times the original surface area.

Solve Problems Involving Surface Area And Volume Envision Math Solutions Exercise 8.1

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 422 Exercise 14 Answer

Given:

To find the surface area of the sphere:

Plug the value in the formula S = 4πr².

Hence, the surface area of the sphere is 1017.4 cm2.

Envision Math Grade 8 Student Edition Solutions Volume 1 Chapter 8 Solve Problems Involving Surface Area And Volume

Page 412 Exercise 1 Answer

A three dimensional object is in three dimensions having length, width and height.

Example: Cubes, prisms, pyramids, spheres, cones, and cylinders are all examples of three-dimensional objects.

Volume is the product of length, width and height.

Surface areas is the sum of products of length, width and height taken two at a time.

Volume of a prism = cross-sectional area × length.

The surface area of a 3D shape is the total area of all its faces.

Envision Math Grade 8 Volume 1 Chapter 8 Topic 8 Surface Area And Volume Solutions

Page 415 Exercise 1 Answer

The figure of circle is shown as

Here r is know as radius from center to circle which is constant throughout.

The radius is the distance from the center to the edge of a circle.

Envision Math Grade 8 Topic 8 Surface Area And Volume Answers

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 415 Exercise 2 Answer

The objects around you are three-dimensional.

A three dimensional object is in three dimensions having length, width and height.

Example: Cubes, prisms, pyramids, spheres, cones, and cylinders are all examples of three-dimensional objects.

Day to day life examples: cup, mobile phone, ball and bottle.

A shape that has length, width, and height is three dimensional.

Page 415 Exercise 3 Answer

A three dimensional object is in three dimensions having length, width and height.

Example: Cubes, prisms, pyramids, spheres, cones, and cylinders are all examples of three-dimensional objects.

Any side of a cube can be considered a base.

Any side of a cube can be considered a base.

Surface Area And Volume Solutions Grade 8 Envision Math Topic 8

Page 415 Exercise 5 Answer

Given:

The ________________ of a circle is a line segment that passes through its center and has endpoints on the circle.

The distance from one point on a circle through the center to another point on the circle.

It is also the longest distance across the circle.

The diameter of a circle is a line segment that passes through its center and has endpoints on the circle.

Hence, the diameter of a circle is a line segment that passes through its centre and has endpoints on the circle.

Envision Math Grade 8 Topic 8 Practice Problems For Surface Area And Volume

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 415 Exercise 7 Answer

Given:

9⋅3.14

To find the product:

Multiply 9 with 3.14.

We have,

9⋅3.14

Multiply the numbers:

= 28.26

It follows that the product is 28.26.

Hence, the product is 28.26.

Page 415 Exercise 8 Answer

Given:

4.2⋅10.5

To find the product:

Multiply 4.2 with 10.5.

We have,

4.2⋅10.5

Multiply the numbers:

= 44.10

It follows that the product is 44.10.

Hence, the product is 44.10.

Surface Area And Volume Solutions Grade 8 Envision Math Topic 8

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 415 Exercise 9 Answer

Given:

Hence, the area of the given circle is 100.48cm².

Envision Math Topic 8 Detailed Answers For Surface Area And Volume

Page 415 Exercise 10 Answer

Given:

To find the area of the circle:

First, find r using the diameter and then plug the value of r,π in the area of the circle formula.

So, the area of the circle is 56.52 cm²

Hence, the area of the given circle is 56.52cm².

How To Solve Surface Area And Volume Problems In Envision Math Grade 8

Page 415 Exercise 11 Answer

Given:

To find the missing value of x:

Use the Pythagorean Theorem and apply it to the given right triangle.

Hence, the missing value is x = 5in.

Envision Math 8th Grade Surface Area And Volume Topic 8 Solutions

Page 415 Exercise 12 Answer

Given:

To find the missing value of x:

Use the Pythagorean Theorem and apply it to the given right triangle.

​
Hence, the missing value is x = 18m.

Envision Math Grade 8 Volume 1 Chapter 7 Understand The Converse Of The Pythagorean Theorem

Page 387 Exercise 2 Answer

The Pythagorean equation states that if the lengths of any two sides are known the length of the third side can be calculated using

(hypotenuse)² = (base)² + (perpendicular)²

It relates the sides of a right triangle in a simple way.

So if the lengths of sides satisfies this, it is a right angled triangle.

If the sides satisfy

(hypotenuse)² = (base)² + (perpendicular)², then it is right angled triangle.

Page 387 Focus On Math Practices Answer

The Pythagorean equation states that if the lengths of any two sides are known the length of the third side can be calculated using

(hypotenuse)² = (base)² + (perpendicular)²

It relates the sides of a right triangle in a simple way.

So if the lengths of sides satisfies this, it is a right angled triangle.

Therefore, Kayla can use the straws that form a right triangle to make a triangle that is not a right triangle.

Kayla can use the straws that form a right triangle to make a triangle that is not a right triangle.

Envision Math Grade 8 Chapter 7 Solutions

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 388 Essential Question Answer

The Pythagorean equation states that if the lengths of any two sides are known the length of the third side can be calculated using

(hypotenuse)² = (base)² + (perpendicular)²

It relates the sides of a right triangle in a simple way.

So if the lengths of sides satisfies this, it is a right angled triangle.

If the sides satisfy (hypotenuse)² = (base)² + (perpendicular)²

then the triangle is right angled.

Page 388 Convince Me Answer

Given: Right angled triangle

To prove :Converse of the Pythagorean Theorem

We will write the converse of Pythagoras theorem and justify it.

The converse of the Pythagorean Theorem:

A triangle in which the sum of the square of the length of two sides is equal to the square of the length of the third side is a right triangle.

That means in a triangle ABC we have AC² = AB² + BC²

To prove: ∠B = 90°

Let us construct another triangle PQR as shown

By SSS congruency we have ΔABC ≅ ΔPQR

Using ‘corresponding sides of congruent parts are similar’ we get ∠B = 90°

Hence converse of Pythagoras theorem is proved.

Page 389 Try It Answer

Given: A triangle with sides 10,√205,√105 feet

To find: whether the triangle is right angled or not.

We will use the Pythagoras formula and verify it.

If the sides satisfy (hypotenuse)² = (base)² + (perpendicular)²

then the triangle is right angled.

By the converse of the Pythagorean Theorem:

​
​The formed triangle is a right angled.

Given lengths form right angled triangle.

Envision Math Grade 8 Converse Of The Pythagorean Theorem Answers

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 390 Exercise 1 Answer

If the triangle is a right triangle, the hypotenuse is its longest side.

Compare side lengths 10,√205,√105

Check if the lengths c = √205,

​
The triangle is a right triangle by the Converse of the Pythagorean Theorem.

Page 390 Exercise 3 Answer

The formula for the Pythagorean Theorem is: a² + b²= c²

The first component that can easily be substituted in the equation is the hypotenuse, which is the longest side of the right triangle. If the hypotenuse is already determined, the remaining values of the side lengths can be substituted in any of the remaining variables in the equation a,b.

Keep in mind that other variables can be used other than a,b, and c.

For example, a right triangle has side lengths of x = 4,

​y = 5

z = 3
​
So, we have

a² + b²= c²

Hence, the longest side of the triangle is to be substituted on the right side of the equation, while the remaining two side lengths are to be substituted on the left side of the equation.

Page 390 Exercise 4 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

​
Both sides are equal

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Page 390 Exercise 5 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is not the right triangle.

Hence, the given triangle is not the right angle triangle.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7

Page 390 Exercise 6 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is not the right triangle.

Hence, the given triangle is not the right-angle triangle.

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 391 Exercise 7 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is not the right triangle.

Hence, the given triangle is not the right angle triangle.

Page 391 Exercise 8 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Envision Math Exercise 7.1 Answers Grade 8

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 391 Exercise 9 Answer

Given:

Length of the triangle 5, 15, and √250.

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have.

​
Hence, the given triangle is the right angle triangle.

Page 391 Exercise 10 Answer

Given:

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Page 391 Exercise 11 Answer

Given:

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Page 391 Exercise 12 Answer

Given:

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

First, check for triangle 1.

So, the triangle is the right triangle.

Now, check for triangle 2.

So, the triangle is not the right triangle.

Now, check for triangle 3

So, the triangle is the right triangle.

Hence, the first and third triangles are right triangles.

Understand The Converse Of The Pythagorean Theorem Envision Math Grade 8 Solutions

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 392 Exercise 14 Answer

Given:

To find whether KM is the height of ΔJKL or not:

Apply the converse of the Pythagorean Theorem and plug the values.

To know if KM is the height of ΔJKL, it must be perpendicular to JL.

KM is perpendicular to JL, ΔKML must be a right triangle.

​
It follows that KM is not perpendicular to JL.

Hence, KM is not the height of ΔJKL using the concept of perpendicular lines and Pythagorean Theorem.

How To Solve Envision Math Grade 8 Converse Of The Pythagorean Theorem Problems

Page 392 Exercise 17 Answer

Given:

To find which of triangle represents right triangle:

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

Here, a = 40

​b = 48

c = 52
​
Satisfy the Pythagorean Theorem:
​
52² = 48² + 40²

2704 ≠ 3904
​
Both sides are not equal.

Hence, it does not represent a right triangle.

We have,

Here, a = 25

​b = 60

c = 65
​
Satisfy the Pythagorean Theorem:
​
65² = 60² + 25²

4225 = 4225
​
Both sides are equal.

Hence, it represents a right triangle.

Hence, option(B) is correct.

Page 393 Exercise 2 Answer

Given:

ΔPQR has side lengths of 12.5 centimeters,30 centimeters, and 32.5 centimeters

To prove ΔPQR is a right triangle:

Hence, it represents a right triangle.

Hence, proved

Hence, we have proved that ΔPQR is a right triangle.

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 393 Exercise 4 Answer

Given:

To find: the unknown side length.

Using the Pythagoras equation:

c² = a² + b²

where c is hypotenuse of the right triangle whereas ‘a’ and ‘b’ are the other two legs.

Let c be the hypotenuse of the triangle and a and b be the length of the legs of the triangle.

Notice that the hypotenuse and one of the side of the right triangle is given:

The length of the second leg is 4√3

Free Envision Math Grade 8 Solutions For Exercise 7.1

Page 393 Exercise 5 Answer

Given: The lengths of the legs of a right triangle are 4.5 inches and 6 inches.

To find: the length of the hypotenuse

Using the Pythagoras equation:

c² = a² + b² where c is hypotenuse of the right triangle whereas ‘a’ and ′b’ are the other two legs.

Let a = 4.5 and b = 6 be the legs of a right triangle.

Substitute a = 4.5 and b = 6 to the

Since the length of the hypotenuse cannot be negative,

therefore, c = 7.5

The length of the hypotenuse is 7.5 inches.

Envision Math Grade 8 Pythagorean Theorem Chapter 7 Worksheet Solutions

Page 393 Exercise 6 Answer

Given: Sides of a triangle

To find: lengths which represent the sides of a right triangle.

Consider 5cm,10cm.15cm

a² + b² = c²

Substitute a = 5,b = 10 and c = 15 if the set of numbers is a pythagorean triple.

5² + 10² = 15²

L.H.S.= 25 + 100 = 125

R.H.S = 225

therefore, 125 ≠ 225

5cm,10cm.15cm does not represent the sides of a right triangle.

Consider 7 in., 14 in., 25 in.

a² + b² = c²

Substitute a = 7,b = 14 and c = 25 if the set of numbers is a pythagorean triple.

7² + 14² = 25²

L.H.S.= 49 + 196

= 245

R.H.S = 625

since 245 ≠ 625

7in.,14in.,25in. does not represent the sides of a right triangle.

Consider 13m,84m,85m

a² + b² = c²

Substitute a = 13,b = 84 and c = 85 if the set of numbers is a pythagorean triple.

13² + 84² = 85²

L.H.S = 169 + 7056

= 7225

R.H.S.= 7225

Since, L.H.S = R.H.S

Therefore, 13m,84m,85m represent the sides of a right triangle.

Consider 5ft,11ft,12ft

a² + b² = c²

Substitute a = 5,b = 11 and c = 12 if the set of numbers is a pythagorean triple.

5² + 11² = 12²

L.H.S = 25 + 121

= 146

R.H.S.= 144

Since, 146 ≠ 144

therefore, 5ft,11ft,12ft does not represent the sides of a right triangle.

Consider 6ft,9ft,√117ft

a² + b² = c²

Substitute a = 6,b = 9 and c = √117 if the set of numbers is a pythagorean triple.

6² + 9² = 117

L.H.S = 36 + 81

= 117

R.H.S = 117

Since, L.H.S = R.H.S

therefore,6ft,9ft,√117ft represent the sides of a right triangle.

Only 13m,84m,85m and 6ft,9ft,√117ft represent the sides of a right triangle.

Solutions For Envision Math Grade 8 Exercise 7.1

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 394 Exercise 1 Answer

Given:

To find: the height of the tree.

Using Pythagoras theorem, we will find the height of the tree.

The height of the tree is the sum of the lengths of the sides BC. and CD, it follows:

h = BC + CD

Notice that the figure is composed of two right triangles △ABC. and △ADC.

Therefore, the length of the sides BC and CD can be determined using the pythagorean Theorem;

a² + b² = c²

In the triangle △ABC, the side AB is the hypotenuse.

a² + b² = c²

Substitute a = BC, b = AC, and c = AB into the equation:

BC² + AC² = AB²

Substitute AC = 7 and AB = 9 into the equation:

Since the length cannot be negative, it follows:

BC ≈ 5.7

Similarly, using the pythagorean theorem, the length of the side CD in the △ADC is 24 .

h = BC + CD

Substitute BC ≈ 5.7 and CD = 24 into the equation:

h ≈ 5.7 + 24

h ≈ 29.7

Therefore, the height of the tree is about 29.7 feet.

Therefore, the height of the tree is about 29.7 feet.

Given:

To find: the height of the tree round to the nearest tenth.

Using pythagoras theorem, we will the height of the tree.

Triangle △BCD is a right triangle.

Substitute BC = 9 and CD = 7 into the Pythagorean Theorem formula, it follows:

Since side length is always positive, it follows:

DB = 4√2

Triangle △ACD is a right triangle.

Substitute AC = 25 and CD = 7 into the Pythagorean Theorem formula, it follows:

Since side length is always positive, it follows:

AD = 24

By using the Segment Addition Postulate, it follows:

AB = AD + DB

Substitute AD = 24 and DB = 4√2 into the equation:

AB = 24 + 4√2

The height of the tree is about 29.7ft.

Given: Javier moves backward so that his horizontal distance from the tree is 3 feet greater.

To find: the distance from his eyes to the top of the tree also be 3 feet greater

Use pythagorean theorem.

In △ABC, substitute a = 7,b = x and c = 25 in the Pythagorean theorem:

The person moves horizontally 3 feet away from tree to the point E

in △EBC. substitute a = 7+3,b = 24 and c = y in the Pythagorean theorem,

The length can not be negative, therefore the value of y is 26

When the person moves 3 feet horizontally, the distance from his eyes to the top of the tree increase by 1 feet.

This can be concluded by using Pythagorean theorem.

Given: the distance from his eyes to the top of the tree is only 20 feet

To find: Could Javier change his horizontal distance from the tree so that the distance from his eyes to the top of the tree is only 20 feet?

cosθ = \(\frac{\text { base }}{\text { hypotenuse }}\)

By the definition of cosine:

cosθ = \(\frac{7}{25}\)

When the person moves away from the tree θ decreases which increases value of cosθ

Increase in the value of cosθ decreases the distance from his eyes to top of tree.

cosθ = \(\frac{7}{25}\)

Notice that cosθ is inversely proportional to the distance from person’s eyes to top of tree.

Increase in the value of cosθ decreases the distance from his eyes to top of tree,

At some goint, the distance from his eyes to top of tree can become 20 feet

Envision Math Grade 8 Volume 1 Chapter 7 Understand The Converse Of The Pythagorean Theorem

Page 381 Focus On Math Practices Answer

We have already proved that the sum of the areas of two squares with sides a and b is the same with the area of a square with side c

We have proved this relationship with all right-angle triangles.

Instead of the actual length of the sides, we have used the symbols a, b, and c

while proving the relationship for Kelly’s triangle.

Hence, this relationship is true for any right-angle triangle. The only mandatory condition is a triangle to be a right angle triangle.

Yes, another right-angle triangle drawn by Kelly will also have the same relationship.

This relationship is true for any right-angle triangle.

Envision Math Grade 8 Chapter 7 Solutions

Page 382 Essential Question Answer

Let the right-angle triangle be ABC

The base of the triangle is a

The height of the triangle is b and hypotenuse side is c

According to the Pythagorean theorem, the sum of the square of the base and height is equal to the square of the hypotenuse side.

So, according to the Pythagorean theorem

a²+ b² = c²

According to the Pythagorean theorem, the sum of the square of two sides of a right-angle triangle is equal to the square of the hypotenuse side.
Hence, the relationship between the side lengths of the right angle triangle is given as a²+ b² = c²

Page 382 Try It Answer

Given: Sides of a right-angle triangle is 15cm, 25cm and 20cm

To find : The equation that describes the relationship between the sides of the right-angle triangle.

We will use the Pythagorean theorem to find the relationship between the length of the sides of the triangle.

Let, the base (a) of the right angle triangle be 15cm

Let the height(b)​ of the right angle triangle be 20cm

Let the hypotenuse side (c) by 25cm

According to the Pythagorean theorem, a²+ b² = c²

Substituting the value, we get,

15² + 20² = 25²

We will solve the equation 15² + 20² = 25², to prove whether the relationship is true.

225 + 400 = 625

Combining common terms, we get,

625 = 625

Hence, the relationship is true.

So, according to the Pythagorean theorem, 15² + 20² = 25²

The equation that describes the relationship between the length of the sides of right triangle is 15² + 20² = 25²

Envision Math Grade 8 Converse Of The Pythagorean Theorem Answers

Page 382 Convince Me Answer

The diagram is

In the above diagram, instead of the actual lengths of the side, symbols like a, b, and c is used.

Since the length of the sides is not given in actual numbers hence, this formula can be applied to any right-angle triangle.

The only mandatory condition is that triangle has to be the right triangle.

Hence, the Pythagorean theorem can be applied to the all right triangle.

The side opposite to the greatest angle is the longest side of the right-angle triangle.

The Pythagorean theorem is applied to all right triangles because the lengths of the sides are given in symbol rather than the actual lengths.

Page 383 Try It Answer

Given:

The hypotenuse = 32 meters.

One leg = 18 meters.

To find : The length of the other leg.

We will use the Pythagorean theorem to find the length of the other leg.

Since we are not given the length of which side is 18meters

We will consider a = 18meters and solve for b

The hypotenuse of the triangle is c = 32 meters

So, the length of the other leg is 10√7

The length of the another leg is 10√7

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 384 Exercise 1 Answer

Let the right-angle triangle be ABC

The base of the triangle is a

The height of the triangle is b and the hypotenuse side of the triangle is c

According to the Pythagorean theorem, the sum of the square of the base and height is equal to the square of the hypotenuse side.

So, according to the Pythagorean theorem a²+ b² = c²

According to the Pythagorean theorem, the sum of the square of two sides of a right-angle triangle is equal to the square of the hypotenuse side.

Hence, the relationship between the side lengths of the right angle triangle is given as a²+ b² = c²

Page 384 Exercise 2 Answer

The given diagram is

The diagram shows that the lengths of the legs are 4unit and 3 unit

While the length of the hypotenuse side is 5unit

we can see that the length of the hypotenuse is longer than other sides.

For any right triangle, the longest side is the hypotenuse side and the Pythagorean theorem is applied to only the right triangle.

Hence, the requested condition is that the square that would form the side of the hypotenuse would have the longest side.

Another condition is that each side of the triangle must be smaller than the sum of the other two sides.

If the side of the triangle are a, b, and c

Then a < b + c, b < a + c and c < a + b

No, any three squares cannot form the right triangle. The square forming the hypotenuse side would have the longest side and another condition is that each side of the triangle should be smaller than the sum of the other sides.

Page 384 Exercise 3 Answer

Given:

To find : Whether Xavier has given the correct length of the hypotenuse side.

In a right-angled triangle, 90-degree angle is the largest angle. The side opposite to the largest angle in a triangle is the longest side.

The triangle is

The length of the two legs are 21 units and 28 units

According to Xavier, the length of the hypotenuse is 18.5 units

But since the length of the other sides are 21 units and 28 units which is longer than Xavier’s hypotenuse side.

But since the length of the hypotenuse cannot be shorter than the other two sides, hence, the length given by Xavier is incorrect.

The length of the hypotenuse side should be longer than the other two sides. But the length of the hypotenuse side given by Xavier is less than the other two sides, hence, the length given by the hypotenuse side is an incorrect length.

Page 384 Exercise 4 Answer

Given: sides of a triangle is 4 and 5

To find: hypotenuse of triangle

We will put the given values in

Hypotenuse = \(\sqrt{\text { base }^2+\text { perpendicular }{ }^2}\)

Hypotenuse of the triangle is ≈6

Page 384 Exercise 5 Answer

Given: perpendicular = 8 and hypotenuse = 14

To find: base of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula

Base of the triangle is approximately 12 ft

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 384 Exercise 6 Answer

Given: perpendicular = 3.7mm and base = 7.5 mm

To find: hypotenuse of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula

Hypotenuse of the given triangle is approximately 8

Page 385 Exercise 9 Answer

Given: perpendicular = 4x + 4 and base = 3x where x = 15

To find: hypotenuse of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Hypotenuse of the given triangle is approximately 78 units.

Page 385 Exercise 10 Answer

Given: perpendicular=12.9cm and hypotenuse = 15.3 cm

To find: base of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Base of the given triangle is approximately a = ≈ 8 cm

Envision Math Exercise 7.1 Answers Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 385 Exercise 11 Answer

Given: perpendicular=10m and base = 24m

To find: hypotenuse of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Hypotenuse of the given triangle is approximately 26 m

Page 385 Exercise 12 Answer

Given: base = 2ft and hypotenuse = 9 ft

To find: perpendicular of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Perpendicular of the given triangle is approximately 8

Envision Math Grade 8 Pythagorean Theorem Chapter 7 Worksheet Solutions

Page 386 Exercise 13 Answer

Given: A triangle where two of the legs are 32 cm and 26 cm

To find: Hypotenuse of triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

Length of hypotenuse of the given triangle is approximately 41 cm

Given: A triangle where two of the legs are 32 cm and 26 cm

To find: What mistake might the student have made?

We will write the dimension of hypotenuse calculated and match it with given one.

As per the calculation using

(hypotenuse)² = base² + perpendicular²

Hypotenuse is approximately 41 cm.

The mistake might be done in taking the values of legs incorrectly or in the formula.

Mistake might be in the formula taken or dimensions taken.

Page 386 Exercise 14 Answer

Given: A figure of triangle where base is 12.75 and hypotenuse is 37.25

To find: unknown side of the triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

Length of perpendicular of the triangle is 35

Understand The Converse Of The Pythagorean Theorem Envision Math Grade 8 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 386 Exercise 16 Answer

Given: A figure of triangle where two sides are 36 and 15 ft

To find: unknown side of the triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

​
Length of hypotenuse of the given triangle is 39 ft.

Solutions For Envision Math Grade 8 Exercise 7.1

Page 386 Exercise 17 Answer

Given: A figure of triangle where base is 11.25 cm and hypotenuse is 35.25 cm

To find: unknown side of the triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

Length of perpendicular of the given triangle is approximately33 cm.

Envision Math Grade 8 Volume 1 Chapter 7 Understand And Apply The Pythagorean

Page 372 Exercise 1 Answer

The Pythagorean Theorem is an equation that relates the side lengths of a right triangle, a²+ b² = c², where a and b are the legs of a right triangle and c is the hypotenuse.

Pythagoras theorem can be used to find any side of a right angled triangle when other two sides are known.

It can be used to know if a triangle is a right angled triangle or not.

Pythagorean Theorem can be used to solve problems

It can be used to find any side of a right angled triangle when other two sides are known.

Using it we can know whether a triangle is a right angled triangle or not.

Envision Math Grade 8 Volume 1 Chapter 7 Pythagorean Theorem Solutions

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 1 Answer

The square root of number y is a number x that satisfies the equation y = x ⋅ x.

The square root of a number is a factor that when multiplied by itself gives the number.

Page 375 Exercise 2 Answer

A line segment that connects two corners but does not form an edge.

We get a diagonal when we join any two corners (called “vertices”) that aren’t already connected by an edge.

A diagonal is a line segment that connects two vertices of a polygon and is not a side.

Envision Math Grade 8 Pythagorean Theorem Chapter 7 Answers

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 3 Answer

The total distance covered by the sides of a polygon is called its perimeter.

We can find the perimeter of any figure by adding all the sides of that figure.

The perimeter of a figure is the distance around it.

How To Solve Pythagorean Theorem Problems In Envision Math Grade 8

Page 375 Exercise 5 Answer

Given: 3² + 4²

To simplify the expression.

Find the squares of both the no. and add them.

On simplifying, we get 25.

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 6 Answer

Given: 2² + 5²

To simplify the expression.

Find the squares of both the no. and add them.

On simplifying, we get 29

Envision Math 8th Grade Chapter 7 Step-By-Step Pythagorean Theorem Solutions

Page 375 Exercise 7 Answer

Given: 10² − 8²

To simplify the expression.

Find the squares of both the no. and add them.

On simplifying, we get 36

Pythagorean Theorem Solutions Grade 8 Envision Math

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 8 Answer

Given: √81

To find: the square root.

Find the factors of the no.

√81 can be written as √9×9

Therefore,

√81 = √9²

Use formula √x² = x

We get

√81 = 9

The square root is 9

Envision Math Grade 8 Chapter 7 Pythagorean Theorem Exercises

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 10 Answer

Given: √225

To find: the square root.

Find the factors of the no.

√225 can be written as √15×15

Therefore,

√225 = √15²

Use formula √x² = x

√225 = 15

The root is 15

Envision Math Grade 8 Chapter 7 Pythagorean Theorem Practice Problems

Page 375 Exercise 11 Answer

Given:

To determine: the distance between the two points.

Use the formula ∣x₂∣−∣x₁∣

The first point is (x₁,y₁)=(2,5)

The second point is (x₂,y₂)=(7,5)

The distance will be ∣x₂∣−∣x₁∣

= ∣7∣ − ∣2∣

= 2 units

The distance between the two points is 2 units.