Marksparks

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions

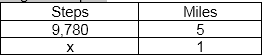
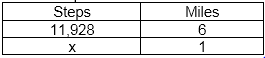
They are different because in the first one, we have 2 diagrams and we have to find the right amount on each one and then add these amounts.

On the other hand in the second representation, we have 2 variables that we change and easily multiply by constants.

They are similar because they have the same end results and the same constants and coefficients.

Question. Use Commutative and distributive property for the equivalent expression 3x – 12

Given:

3x − 12

3x − 12

Use distributive property  a (b + c) = a×b +a×c

3x − 12 = 3(x − 4)

First equivalent expression is 3(x − 4)

Use commutative property a + b = b + a

3x − 12 = −12 + 3x

The second equivalent expression is  −12 + 3x.

Hence, the equivalent expressions are 3(x − 4) and −12 + 3x.

Question. Use commutative and distributive property for the equivalent expression \(-\frac{5}{4}x-\frac{3}{4}\)

Given:

Use commutative property a + b=b + a

\(-\frac{3}{4}-\frac{5}{4}\) x

First equivalent expression is \(-\frac{3}{4}-\frac{5}{4}\) x

Use distributive property a × (b + c) = a × b + a × c

\(\frac{1}{4}\) (−5x−3)

Second equivalent expression is \(\frac{1}{4}\) (−5x−3).

Hence, the equivalent expressions are \(-\frac{3}{4}-\frac{5}{4}\) x and \(\frac{1}{4}\)

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.2 Answer Key

Question. Use the distributive property to -5(x-2) equivalent expression.

Given:

−5(x−2)

− 5 (x − 2)

Use the distributive property to write an equivalent expression.

Distributive property  a × (b+c) = a × b + a × c

​−5(x−2)=−5× x − 5 × (−2)

=−5x + 10
​
Hence, we use the distributive property.

Equivalent expressions are expressions that have the same end value but are written differently.

Commutative property true only for multiplication and addition

Addition: ​ a + b = b + a

Multiplication:  a × b = b × a
​
Subtraction:  4−2 = 2−4

Division:   4 ÷ 2 = 2 ÷ 4

It can’t go with subtraction and division.

The commutative property is true only for multiplication and addition.

Question. Use the associative property when writing equivalent expressions for 2 reasons.

We can use the associative property when writing equivalent expressions for 2 reasons.

We can use it to get 2 values with the same variable in the bracket so we could add/multiply them.

Example:

\(\frac{1}{2} x+\left(\frac{1}{2} x+4\right) \)  Use associative property

x + 4

We can use it to get 2 values with variables in the bracket so we could extract the constant in front of these variables by using the distributive property.

\(\frac{1}{2} x+\left(\frac{1}{2} y+4\right) \)     Use associative property

\(\left(\frac{1}{2} x+\frac{1}{2} y\right)+4\)       Use distributive property

\(\frac{1}{2}\)(x+y)+4

So we can use it to easily add or extract values.

Question. Write an equivalent expression for the -3 + \(\frac{2}{3}\)\frac{1}{3}[/latex]y expression.

Given:

-3 + \(\frac{2}{3}\)y-4-\(\frac{1}{3}\)y

-3 + \(\frac{2}{3}\)y-4-\(\frac{1}{3}\)y

Use commutative property
​
​− 3 − 4 +\(\frac{2}{3}\)y-\(\frac{1}{3}\)y​

− 7 + \(\frac{1}{3}\)y

Hence, the equivalent expression is  −7 + \(\frac{1}{3}\)y

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.2 Answers

Question. Write an expression 3(x – 5) values of the expression for x ’s 1,2 and 3 find out x values.

Given:
​
​3(x − 5)

3x − 15

Put x = 1

​3(x−5) = 3(1 − 5)

= 3(−4)

= −12
​
​3x − 15 = 3(1) − 15

=  3−15

= −12

Put x = 2

​3(x − 5) = 3(2 − 5)

= 3(−3)

= −9

3x−15 = 3(2) − 15

= 6 − 15

= −9

Put x = 3

​3(x−5) = 3(3 − 5)

= 3( − 2)

= −6

3x−15 = 3(3) − 15

= 9 −15

= −6
​Given that we can see that they have the same values for some \(\backslash[x \mid]^{\prime} \)s so they are equivalent.

Property that makes them equivalent is distributive property.

The values of the expression for x ’s 1,2 and 3 are −12,−9, and −6. So they are equivalent.

Question. Write an equivalent expression for the 4x + \(\frac{1}{2}\) + 2x – 3 expression.

Given:

4x + \(\frac{1}{2}\)+2x-3

4x + \(\frac{1}{2}\)  + 2x-3

Use the commutative property

4x + 2x + \(\frac{1}{2}-3\)

6x + \(\frac{5}{2}\)

Hence, the equivalent expression is 6x+\(\frac{5}{2}\)

Envision Math Grade 7 Chapter 5 Equivalent Expressions Exercise 5.2 Solutions

Question. Write an equivalent expression for the -3(7 + 5g) expression.

We need to write an equivalent expression for the given expression

−3 (7 + 5g)

Using the distributive property, the expression becomes

​−3 (7 + 5g) = −3 × 7 + (−3) × 5g

= −21 − 15g

​The equivalent expression is −3(7 + 5g) = − 21 −15g

Question. Write an equivalent expression for the (x + 7) + 3y expression.

We need to write an equivalent expression for the given expression

(x + 7) + 3y

Using the associative property, the expression becomes

(x + 7) + 3y= x + (7 + 3y)

The equivalent expression is (x + 7) + 3y = x + (7 + 3y)

Question. Write an equivalent expression for the \(\frac{2}{9}-\frac{1}{5}\)x expression.

We need to write an equivalent expression for the given expression

\(\frac{2}{9}-\frac{1}{5}\)x

Using the distributive property extracting the common factors out, the expression becomes

\(\frac{2}{9}-\frac{1}{5}\)x  =  \(\frac{1}{5}\)(5×\(\frac{2}{9}\)-x)

=  \(\frac{1}{5}\)(\(\frac{10}{9}\) − x)

​=  \(\frac{1}{5}\) (1.1111……− x)

=  \(\frac{1}{5}\)(\(1 . \overline{1}-x\))

The equivalent expression is \(\frac{2}{9}\) – \(\frac{1}{5}\) x  = \(\frac{1}{5}\)(\(1 . \overline{1}-x\))

Question. Find the which expression is equivalent to t + 4 + 3 – 2t

We need to find which expression is equivalent to  t + 4 + 3 − 2t

The given expression is t + 4 + 3 − 2t

Simplifying it we get

​t + 4 +3−2t = t + 7−2t

=  t − 2t + 7

= −t + 7
​
−t + 7 expression is equivalent to  t + 4 + 3 − 2t

Question. The distance in feet that karina swims in a race is represented by 4d – 4, where d is the distance for each lap. Write an expression equivalent to 4d – 4.

Given that, the distance in feet that Karina swims in a race is represented by 4d − 4, where d is the distance for each lap.

We need to write an expression equivalent to  4d − 4

The given expression is 4d − 4

Using the distributive property, and extracting the common terms, we get

​4d − 4 = 4 × d − 4 × 1

= 4(d − 1)​
​
The equivalent expression is 4(d−1)

Envision Math Grade 7 Exercise 5.2 Solution Guide

Question. Use the associative property to write an expression equivalent to (w + 9) + 3

We need to use the Associative Property to write an expression equivalent to (w + 9) + 3

The given expression is  (w + 9) + 3

Using the associative property, we get

(w + 9) + 3 = w + (9 + 3)

The equivalent expression is (w + 9) + 3 = w + (9 + 3)

Question. Maria said the expression -4n + 3 + 9n – 4 is equivalent to 4n find the error Maria likely made.

Given that, Maria said the expression −4n + 3 + 9n − 4 is equivalent to 4n

We need to find the error Maria likely made.

The given expression is  −4n + 3 + 9n − 4a

Solving the expression, we get

​−4n + 3 + 9n − 4 = −4n + 9n + 3−4

= 5n − 1
​
The equivalent expression is 5n − 1. The possible error maria made is wrong addition and subtraction.

Maria added the wrong numbers which make her to do the error.

Question. Write an expression equivalent to x –  3y + 4.

We need to write an expression equivalent to x − 3y + 4.

Using the distributive property, and extracting the common terms, we get

​x − 3y + 4 = x−3(y−\(\frac{4}{3}\))

= x−3 (y−1.3333…)

= x − 3(\(y−1 . \overline{3}\))
​
The equivalent expression is =x−3(\(y−1 . \overline{3}\))

Question. The group chat shows the amount of money that each puts in to rent a car for a trip, four friends are combining their money. Use the commutative property to write two equivalent expressions.

Given that, To rent a car for a trip, four friends are combining their money.

The group chat shows the amount of money that each puts in.

One expression for their total amount of money is 189 plus p plus 224 plus q.

We need to use the Commutative Property to write two equivalent expressions.

The given expression is 189 + p + 224 + q

Using the commutative property to find the equivalent expression, we get

​189 + p + 224 + q = (189 + 224) + p + q

= 413 + p + q

​Another equivalent expression is

​189 + p + 224 + q = p + q +( 189 + 224)

= p + q + 413
​
The two equivalent expressions are  413 + p + q, p + q + 413

Given that, To rent a car for a trip, four friends are combining their money.

The group chat shows the amount of money that each puts in.

One expression for their total amount of money is 189 plus p plus 224 plus q.

If they need $500 to rent a car, we need to find at least two different pairs of numbers that p and q could be.

The given expression is 189 + p + 224 + q

The amount to rent a car will be $500

Thus, the expression becomes

​189 + p + 224 + q = 500

413 + p + q = 500

p + q = 500 − 413

p + q = 87

​So we need to find two values which added together to get 87 Therefore

​p = 40, q = 47

p = 20, q = 67

The two different pairs of numbers are p = 40, q = 47 and  p = 20, q = 67

Generate Equivalent Expressions Grade 7 Exercise 5.2 Envision Math

Question. Find the expressions is equivalent to \(\frac{3}{5}x + 3\).

We need to find which of the given expressions is equivalent to

Simplifying the given one by one, we get

​\(\frac{2}{5}x \) + 3 \(\frac{1}{5}x \)

= \(\frac{2}{5}x \) + \(\frac{16}{5}x \)

\(\frac{4}{5}x \)− \(\frac{1}{5}x \) + 3 = \(\frac{4x− 1x}{5} \) +3

= \(\frac{3}{5}x \) +3

\(\frac{2}{5}x \) + 3 \(\frac{3}{5}x \) − 1= \(\frac{2}{5}x \) +\(\frac{18}{5}x \) −1

= \(\frac{2x+ 18x}{5} \) −1 = 4x −1

1 + \(\frac{3}{5}\) x + 2  = \(\frac{3}{5}\) x+ 3

1 + \(\frac{x}{5}\)  +  2  = \(\frac{x}{5}\)  + 3

1 + \(\frac{2}{5}\)x  + 3  = \(\frac{2}{5}\)x + 4

The expressions that are equivalent to \(\frac{3}{4}\) x + 3 will be \(\frac{4}{5}\) x- \(\frac{1}{5}\) x + 3 and 1 +  \(\frac{3}{5}\) x + 2

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions

We have to sort the expressions given.

An expression is a mathematical phrase, which consists of variables and constants.

We can sort the given expression into two groups.

One group would contain the expressions which have brackets and the other group will have expressions without brackets.

The first group of expressions will be

​8p + 2p − 8

10p − 8

5p + 8 + 3p

10p + 4 + 2p + 2

3p + 4p + 6 + 5p

The second group of expressions will be
​
​8 (p + 1)

2 (5p − 4)

4 (2p + 2)

3 (4p + 2)

​
The expression are sorted into two groups, one with expressions having brackets and the other without brackets.

We have to sort the expressions given.

An expression is a mathematical phrase, which consists of variables and constants.

We can sort the given expression into two groups.

We can also group the expression with equivalent expressions in them.

In one group, we will put the expressions that can be made one from another by multiplying or extracting a number.

The first group of expressions will be

​10p − 8

2 (5p − 4) = 10

8p + 2p − 8 = 10p − 8

The second group of expressions will be
​
​5p + 8 + 3p = 8p + 8

8 (p + 1) = 8p + 8

4 (2p + 2) = 8p + 8

The third group of expressions will be
​
​3 (4p + 2) = 12p + 6

3p + 4p + 6 + 5p = 12p + 6

10p + 4 + 2p + 2 = 12p + 6
​
The expression can be grouped based on mutually equivalent expressions.

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.1 Answer Key

Question. How can algebraic expressions be used to represent and solve problems.

We have to tell that how can algebraic expressions be used to represent and solve problems.

The combination of variables and constants, in mathematics, is referred to as an expression.

The expression having algebraic terms are called as algebraic expressions.

These expressions are helpful in expressing the problems which consists of variables.

The variables are substituted with values given and then evaluated to obtain the solution or desired result.

The algebraic expressions represent the problems which can be evaluated by substituting values in the expression.

Question. How much it would cost to rent a scooter for 3 1/2 hours and watercraft for 1 ¾ hours.

We have to determine how much it would cost to rent a scooter for 3 1/2 hours and watercraft for 1 ¾ hours.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

The order of operation that will be followed is Brackets, multiplication or division, and addition or subtraction.

The expressions are
​
​s = \(3 \frac{1}{2}\)

= 3.5

w=\(1 \frac{3}{4}\)

= 1.75

We will evaluate as below:

​15.5s + 22.8w = x

15.5cot 3.5 + 22.8.1.75 = x

54.25 + 39.9 = x

x = 94.15
​
The renting of both these amounts of time will cost $94.15.

Question. Misumi used to determine her account balance after “w” week. She gets 3.5 dollars in a day and 8.74 per hour.

We have to give an expression for Misumi used to determine her account balance after “w” week.

She gets 3.5 dollars in a day and 8.74 per hour.

We consider “h” as the number of hours.

h = \(15\frac{1}{2}\)

The order of operation that will be followed is.

Brackets, multiplication or division, addition or subtraction.

We evaluate the expression as below:

​3.5 + 8.74⋅h = x

3.5 + 8.74.5.5 = x

3.5 + 48.07 = x

x = 51.57
​
She will receive the amount of $51.57 in that day.

Question. How should we determine which value to use for the constant and which value to use for the coefficient.

We have to tell that how should we determine which value to use for the constant and which value to use for the coefficient.

An expression is a mathematical phrase, which consists of variables and constants.

We determine the amount after w weeks as the below expression

217 + 25.5.w

In the given expression, w is the coefficient as the number of weeks can be changed.

And the constant amount is 25.5 which she always deposits.

Thus, in a problem, the factor whose value changes in different situations is considered as a variable, as its value varies.

While the value which remains the same is taken as constant.

The values which vary are considered as variables and the ones which are the same are determined as constants.

Envision Math Grade 7 Chapter 5 Equivalent Expressions Exercise 5.1 Solutions

Question. How can algebraic expressions be used to represent and solve problems.

We have to tell that how can algebraic expressions be used to represent and solve problems.

The combination of variables and constants, in mathematics, is referred to as an expression.

The expression having algebraic terms are called as algebraic expressions.

These expressions are helpful in expressing the problems which consist of variables.

The variables are substituted with values given and then evaluated to obtain the solution or desired result.

The algebraic expressions represent the problems which can be evaluated by substituting values in the expression.

Question. Explain how is a constant term different than a variable term for an expression that represents a real-world situation.

We need to explain how is a constant term different than a variable term for an expression that represents a real-world situation.

The constant term is nothing but a term that is constant i.e., the value doesn’t change no matter what.

The variable term is the one which is varying based on different values.

As the name suggests, it is a variable one.

For example, in the expression, 5x + 2 = 0

The term 2 is a constant since it doesn’t change no matter what.

The term x is a variable it changes based on the input.

The value of the constant doesn’t change while that of the variable changes based on its input.

Question. Explain why we can have different values when evaluating an algebraic expression.

We need to explain why we can have different values when evaluating an algebraic expression.

When evaluating an algebraic expression, we may have some different values.

But the end result is always the same. This is because we can choose which operation we can do first.

For example, both addition and subtraction are commutative.

If we do addition first, the values will be different.

Or if we do subtraction first, the values will be different.

But the end result obtained by the expression will be the same.

We can choose which operation we can choose first. This is why we can have different values when evaluating an algebraic expression.

Question. A tank containing 35 gallons of water is leaking at a rate of \(\frac{1}{4}\) gallon per minute. Write an expression to determine the number of gallons left in the tank after m minutes.

Given that, A tank containing 35 gallons of water is leaking at a rate of \(\frac{1}{4}\) gallon per minute.

We need to write an expression to determine the number of gallons left in the tank after m minutes.

Here, the rate is a variable since it varies every minute.

The amount of water is constant.

We need to find the number of gallons left after m minutes.

Thus, the expression becomes

35−\(\frac{1}{4}\) m

The number of gallons left in the tank after m minutes will be 35−\(\frac{1}{4}\) m

Question. Write an algebraic expression that Marshall can use to determine the total cost of buying a watermelon that weighs w pounds and some tomatoes that weigh t pounds. Find how much will it cost to buy a watermelon that weighs \(18\frac{1}{2}\) pounds and 5 pounds of tomatoes.

We need to write an algebraic expression that Marshall can use to determine the total cost of buying a watermelon that weighs w pounds and some tomatoes that weigh t pounds.

We need to find how much will it cost to buy a watermelon that weighs \(18 \frac{1}{2}\) pounds and 5 pounds of tomatoes.

The total of buying will be represented by the expression

0.68w + 3.25t

Given that, t = 5, w = \(18 \frac{1}{2}\)

Substituting this we get

​0.68w + 3.25t = 0.68 × \(18 \frac{1}{2}\)  + 3.25 × 5

=  0.68 × \( \frac{37}{2}\)  + 16.25

= 12.58 + 16.25

=  28.83

He have to pay $28.83 altogether.

Generate Equivalent Expressions Grade 7 Exercise 5.1 Envision Math

Question. Find the value of \(\frac{3}{8}\)x-4.5 when the value of x = 0.4.

The value of \( \frac{3}{8}\)x−4.5 when the value of x = 0.4

Substituting x = 0.4 in the given expression, we get

​\( \frac{3}{8}\)x − 4.5

=  \( \frac{3}{8}\) × 0.4−4.5

=  \( \frac{3}{2}\) × 0.1−4.5

=  0.15 − 4.5

=  −4.35

The value of ​\( \frac{3}{8}\)x − 4.5 = −4.35

Question. Find the value of 8.4n-3.2p when n = 2 and p = 4.

The value of  8.4n−3.2p when n = 2 and p = 4

Substituting the value of n = 2, p = 4 , we get

​8.4n − 3.2p = 8.4(2)−3.2(4)

= 16.8 − 12.8

= 4
​
The value of 8.4n−3.2p = 4

Question. Write an expression that represents the height of a tree that began at 6 feet and increases by 2 feet per year.

We need to write an expression that represents the height of a tree that began at 6 feet and increases by 2 feet per year.

Let y represent the number of years.

Here, the height of the tree initially is 6 feet.

The increase in height will be 2 feet per year.

Here, y represents the number of years.

Thus, the expression will be

6 + 2y

The expression that represents the height of a tree will be 6 + 2y

Question. Evaluate the expression for the value 3d-4 of the variable (s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is 3d−4

The value of d = 1.2

Substituting the value of the variable in the expression, we get

​3d−4 = 3(1.2) − 4

= 3.6 − 4

= −0.4

The value of 3d−4=−0.4

Question. Evaluate the expression for the value 0.5f – 2.3g of the variable(s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is  0.5f−2.3g

The value of f = 12, g = 2

Substituting the value of the variable in the expression, we get

​0.5f − 2.3g = 0.5(12) − 2.3(2)

= 6−4.6

= 1.4

The value of 0.5f − 2.3g = 1.4

Envision Math Grade 7 Exercise 5.1 Solution Guide

Question. Evaluate the given expression for the value \(\frac{2}{3}\) p+3 of the variable (s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is \( \frac{2}{3}\) p+3

The value p= \( \frac{3}{5}\)

Substituting the value of the variable in the expression, we get

= \(\frac{2}{5}+3\)

= \(\frac{2+15}{5}\)

= \(\frac{17}{5}\)

​The value of \( \frac{2}{3}\) p + 3 = \( \frac{17}{5}\) p + 3

Question. Evaluate the expression for the value 34 + \(\frac{4}{9}\)w of the variable(s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is 34 + \( \frac{4}{9}\)w

The value of w = − \( \frac{1}{2}\)

Substituting the value of the variable in the expression, we get

= \(34-\frac{2}{9}\)

= \(\frac{306-2}{9}\)

= \(\frac{304}{9}\)

= 33.78

The value of 34 + \( \frac{4}{9}\)w = 33.78

Question. Find the expression that can be used to determine the total cost of buying g pounds of granola for $3.25 per pound and f pounds of flour for $0.74 per pound.

We need to find the expression that can be used to determine the total cost of buying g pounds of granola for $3.25 per pound and f pounds of flour for $0.74 per pound.

The cost of buying granola is  3.25 × g

The cost of buying flour is  0.74 × f

Therefore, the total cost of buying both will be

3.25 × g + 0.74 × f = 3.25g + 0.74f

The expression that can be used to determine the total cost will be 3.25g + 0.74f

Question. Find the expression that can be used to determine the total weight of a box that by itself weighs 0.2 kilogram and contains p plaques that weigh 1.3 kilograms each.

We need to find the expression that can be used to determine the total weight of a box that by itself weighs 0.2 kilogram and contains p plaques that weigh 1.3 kilograms each.

The weight of the box will be 0.2kg

The number of plaques will be p

The weight of each plaques will be 1.3kg

Thus, the expression will be

Total weight of the box  = 0.2 +1.3p

The expression that can be used to determine the total weight of a box is (A) 1.3p + 0.2

Question. The expression -120 + 13m represents a submarine that began at a depth of 120 feet below sea level and ascended at a rate of 13 feet per minute. Find the depth of the submarine after 6 minutes.

Given that, the expression −120 + 13m represents a submarine that began at a depth of 120 feet below sea level and ascended at a rate of 13 feet per minute.

We need to find the depth of the submarine after 6 minutes.

Here, the given expression is −120 + 13m

Given that, m = 6

Substituting it, we get

​−120 + 13m =−120 + 13(6)

= −120 + 78

= −42
​
The depth of the submarine after 6 minutes will be −42

Question. The capacity is 3000 ft³ The expression to determine the amount of grain left. 

The capacity is  3000 ft³

The rate is \(\frac{3.5 f t^3}{s}\)

The expression to determine the amount of grain left will be

3000 − 3.5s

Here, s is the number of seconds.

The expression to determine the amount of grain left will be 3000 − 3.5s

Question. The expression 5 – 5x to have a negative value, we need to find what must be true about the value of x.

For the expression 5− 5x to have a negative value, we need to find what must be true about the value of x.

The given expression is  5− 5x

The value will be negative when the value of 5x is greater than the number 5.

If x is negative, thus x < 0  the expression becomes positive.

If x = 0 then the expression becomes positive.

If x = 1 then the expression becomes  5−5(1) = 5−5 = 0

If x > 1 then the expression becomes negative.

x >1 must be true about the value of x.

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.1 Answers

Question. The outside temperature was 73°F at 1 P.M and decreases at a rate of 1.5°F each hour. Find the expression that can be used to determine the temperature h hours after 1 P.M.

Given that, the outside temperature was 73 °F at 1 P.M and decreases at a rate of 1.5 °F each hour.

We need to find the expression that can be used to determine the temperature h hours after 1 P.M.

The rate is a variable that varies every hour.

The outside temperature initially was constant.

The temperature decreases thus we need to subtract the temperature from the outside temperature.

The expression that can be used to determine the temperature h hours after 1 P.M will be, 73 − 1.5h

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 5 Generate Equivalent Expressions

Question. How can properties of operations help to generate equivalent expressions that can be used in solving problems.

We have to tell that how can properties of operations help to generate equivalent expressions that can be used in solving problems.

We consider the below example:

On the expression  3 (2 + x), we apply the distributive property to get the equivalent expression as 6 + 3x.

Similarly, we can apply the distributive property on 24+18y to get the equivalent expression as  6 (4x + 3y).

Thus, the properties of operations help to generate equivalent expressions which are of help in solving problems.

The properties of operations help to generate equivalent expressions such as distributive property.

The exploration of activity trackers and the data to develop models based on individual fitness goals is as follows

Fitness tracker

It helps in motivating us.

To maintain a healthy diet.

To set our goals.

Its disadvantages are Lack of accuracy and expensive.

It helps in motivating us, To maintain a healthy diet, To set our goals, Its disadvantages are Lack of accuracy and expensive.

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate an expression it means that we substitute and replace some values.

• We are required to complete the given definition with an appropriate word.
• The combination of variables and constants, in mathematics, is referred to as an expression.
• When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.
• To substitute a value means to replace or exchange variables with the numbers given.
• Therefore, To evaluate a + 3  when a = 7, you can substitute 7 for ‘a’ in the expression.
• To evaluate a + 3 when a = 7, you can substitute 7 for ‘a’ in the expression.
• We are required to complete the given definition with an appropriate word.
• In mathematics, a function or a particular task performed to get some desired result on numbers is called as an operation.
• The digits or terms on which the operation is performed are called as operands.
• There are particular ways and rules to perform an operation.
• The set of rules which conveys that whether which term will go first in the problem is called as the order of operations.
• Therefore, The set of rules used to determine the order in which operations are performed is called the order of operations.
• The set of rules used to determine the order in which operations are performed is called the order of operations.

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate an expression it means that we substitute and replace some values in the place of variables.

We are required to complete the given definition with an appropriate word.

• The combination of variables and constants, in mathematics, is referred to as an expression.
• When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.
• The expression contains two or more terms which may be either variable or constant and are separated by arithmetic signs such as + (or)  −
• Therefore, Each part of an expression that is separated by a plus or minus sign is a term.
• Each part of an expression that is separated by a plus or minus sign is a term.
• We are required to complete the given definition with an appropriate word.
• The combination of variables and constants, in mathematics is referred to as an expression.
• When we multiply two or more terms, the result obtained is called as a product.
• The number of variables which are multiplied are called as factors.
• Therefore, When two numbers are multiplied to get a product, each number is called a factor.
• When two numbers are multiplied to get a product, each number is called a factor.

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate the given expression which is 3(18-7) + 2.

We are required to evaluate the given expression which is  3(18−7) + 2.

The set of rules used to determine the order in which operations are performed is called the order of operations.

In order to evaluate the expression, we will have to follow the below order of operations.

Brackets, multiplication or division, addition or subtraction.

We will evaluate as below:

⇒ ​​3 . (18−7) + 2 = x

⇒ ​​ 3.11 + 2 = x

⇒ ​​ x = 33 + 2

⇒ ​​ x = 35
​
The result of the expression 3(18−7)+2 is obtained as 35.

Question. Evaluate the given expression which is (13 + 2) ÷ (9 – 4).

We are required to evaluate the given expression which is  (13 + 2) ÷ (9 − 4).

The set of rules used to determine the order in which operations are performed is called the order of operations.

In order to evaluate the expression, we will have to follow the below order of operations.

Brackets, multiplication or division, addition or subtraction

We will evaluate as below:

⇒ ​​ ​(13 + 2) ÷ (9 − 4) = x

⇒ ​​ 15 ÷ 5 = x

⇒  ​​ x = 3
​
The result of the expression  (13 + 2) ÷ (9 − 4)  is obtained as 3.

Envision Math Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate the given expression which is 24 ÷ 4.2 – 2.

We are required to evaluate the given expression which is  24 ÷ 4⋅2 − 2.

The set of rules used to determine the order in which operations are performed is called the order of operations.

In order to evaluate the expression, we will have to follow the below order of operations.

Brackets, multiplication or division, addition or subtraction

We will evaluate as below:

⇒ ​​  ​24 ÷ 4.2 − 2 = x

⇒ ​​ 6.2 −2 = x

⇒ ​​ 12 − 2 = x

⇒ ​​ x = 10
​
The result of the expression 24 ÷ 4⋅2 − 2 is obtained as 10.

Question. Evaluate the given expression which is ab by substituting the value of variables as a = -4 and b = 3.

We are required to evaluate the given expression which is ab by substituting the value of variables as a = − 4 and b = 3.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

To substitute a value means to replace or exchange variables with the numbers given.

We have

​a = −4

b = 3

We will evaluate as below:

​⇒   a⋅b

⇒  (−4)⋅(3)

⇒  −12
​
The result of the expression ab is obtained as -12.

Question. Evaluate the given expression which is 2a + 3b by substituting the value of variables as a = -4 and b = 3.

We are required to evaluate the given expression which is  2a+3b by substituting the value of variables as a = -4 and b = 3.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

To substitute a value means to replace or exchange variables with the numbers given.

The order of operation that will be followed is Brackets, multiplication or division, addition or subtraction

We have

​a = −4

b =3

We will evaluate as below:

​⇒  2a + 3b

⇒  2(−4)  + 3(3)

⇒  −8 + 9

⇒  1

The result of the expression 2a + 3b is obtained as 1.

Envision Math Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate the given expression which is 2(a-b) by substituting the value of variables as a = -4 and b = 3.

We are required to evaluate the given expression which is  2(a−b) by substituting the value of variables as a = -4 and b = 3.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

To substitute a value means to replace or exchange variables with the numbers given.

The order of operation that will be followed is. Brackets, multiplication or division, addition or subtraction.

We have

​a = −4

b = 3

We will evaluate as below:

​⇒   2(a−b)

⇒   2(−4−3)

⇒   2(−7)

⇒  −14

The result of  the expression 2(a−b) is obtained as -14.

Envision Math Accelerated Grade 7 Volume 1 Chapter 4 Analyze And Solve Percent Problems

Question. Jaime’s older brother and his three friends want to split the cost of lunch. They also want to leave a 15-20% tip. Determine how much should each person pay.

Given that, Jaime’s older brother and his three friends want to split the cost of lunch. They also want to leave a 15−20 % tip.

We need to determine how much should each person pay.

The total bill amount is $78

Finding the tip amount for each percentage given, we get:

\(\frac{15}{100} \times 78\) = 11.7

\(\frac{20}{100} \times 78\) = 1.56

Thus, the amount including the tip is somewhere between 78 + 11.7  =  89.7 and 78  + 15.6  =  93.6

Splitting the bill amount for each person, thus we get

\(\frac{89.7}{4} \) = 22.425

\(\frac{93.6}{4} \) = 23.4

Each person should pay somewhere in between $22.425 and $23.4

Envision Math Accelerated Grade 7 Chapter 4 Percent Problems Solutions

Question. Find which line on the receipt we have to use to calculate the tip.

We need to find which line on the receipt we have to use to calculate the tip.

The tip is usually calculated after the bill amount.

Here, the total bill amount is necessary to calculate the tip amount.

Therefore, from the given receipt

The last line i.e., the total will be used to calculate the tip.

We have to use the last line on the receipt to calculate the tip.

Conquer Percent Problems: Unleashing the Power of Envision Math Accelerated Grade 7, Chapter 4, Exercise 4.1

Question. Find the 0.08% of 720.

We need to find 0.08% of 720.

Finding the percentage, we get:

= \(\frac{8}{10000} \times 720\)

= \(\frac{8}{1000} \times 72\)

=  \(\frac{576}{1000}\)

=  0.576

The value is 0.576

We need to find 162.5% of 200.

Finding the percentage, we get:

= 162.5×2

= 325
​
The value is 325

We need to find 0.3% of 60.

Finding the percentage, we get:

= \(\frac{3}{1000} \times 60\)

= \(\frac{3}{100} \times 6\)

= \(\frac{18}{100}\)

= 0.18

The value will be 0.18

Analyze And Solve Percent Problems Exercise 4.1 Answers Grade 7

Question. Explain why 51% of a number is more than half of the number.

We need to explain why 51 % of a number is more than half of the number.

We know that half of the number means 50 % of the number.

Here, 51 % of the number means that it will be 1 % more than half.

For example, if the number is 200

Then the half of it will be

\(\frac{200}{2}\)  = 100

Thus, 51 % of the number will be

=  \(\frac{51}{100} \times 200\)

=51 × 2

=102
​
Thus, it will be more than half of the number.

51 % of a number is 1 % more than half of the number.

Question. How do the percents show the relationship between quantities.

We need to how do the percents show the relationship between quantities.

The percentage is also denoted as the ratio.

The ratio is nothing but the comparison between two same or different quantities.

The first term of the percent is often compared to the number 100.

For example, 35 % of shirts are sold denotes that out of 100 shirts, 35 has been sold out.

We can often denote the percent using the sign “%”.

A percent is a ratio in which the first term is compared to 100. It is used for comparing two quantities. Percents are used to calculate the amount of one thing compared to the other. Percents can be used to compare very small or very large quantities as a fraction of 100.

Question. Gene stated that finding 25% of a number is the same as dividing the number by \(\frac{1}{4}\). We need to determine whether Gene is correct or not.

Given that, Gene stated that finding 25 % of a number is the same as dividing the number by \(\frac{1}{4}\).

We need to determine whether Gene is correct or not.

25 % of a number is denoted by

\(\frac{25}{100}\)=\(\frac{1}{4}\)

Thus, when we divide the number by \(\frac{1}{4}\), it is the same as finding 25 % of the number.

For example, if the number is 200.

Thus, \(\frac{25}{100}\) × 200  = 25  ×  2  =  50

Also, \(\frac{200}{4}\) = 50

= 50

The result is the same.

Therefore, Gene is correct.

Envision Math Grade 7 Percent Problems Exercise 4.1 Solution Guide

Question. Find the percent of the 59% number of the 640.

We need to find the percent of the given number.

The given number is 59 % of the 640

Solving the given, we get:

\(\frac{59}{100}\)  ×  640

= \(\frac{59}{10}\)  ×  64

= \(\frac{3776}{10}\)

= 377.6

The answer is  377.6

We need to find the percent of the given number.

The given number is 0.20 % of the  3542

Solving the given, we get:

=  \(\frac{708.4}{100}\)

= 7.084

The answer is 7.084

We need to find the percent of the given number.

The given number is 195 % of the  568

Solving the given, we get:

\(\frac{195}{100}\) × 568

= \(\frac{110760}{100}\)

= 1107.6

The value is 1107.6

We need to find the percent of the given number.

The given number is 74 % of the 920

Solving the given, we get:

\(\frac{74}{100}\) × 920

=\(\frac{68080}{100}\)

= 680.8

The value is 680.8

Grade 7 Envision Math Accelerated Chapter 4 Answers

Question. Water is 2 parts hydrogen and 1 part oxygen  (H₂O). For one molecule of water, each atom has the atomic mass unit. Find what percent of the mass of a water molecule is hydrogen.

Given that, Water is 2 parts hydrogen and 1 part oxygen  (H₂O).

For one molecule of water, each atom has the atomic mass unit, u, shown.

We need to find what percent of the mass of a water molecule is hydrogen.

Finding the total mass, we get

16.00 + 1.01 + 1.01 = 18.02

We need to find what percent of the total mass is hydrogen.

\(\frac{x}{100}\) × 18.02  =  2.02

x  ×  18.02 = 2.02  × 100

x  ×  18.02  =  202

x  =  \(\frac{202}{18.02}\)

x  =  11.2

The percent is 11.2 %

% percent of the mass of a water molecule is hydrogen.

Question. A local little league has a total of 60 players, 80% of whom are right-handed. Find how many right-handed players are there.

Given that, a local Little League has a total of 60 players, 80 % of whom are right-handed.

We need to find how many right-handed players are there.

Let x be the number of right-handed people, thus we get, using equivalent ratios we get
​
\(\frac{x}{60}\)  ×  60

= \(\frac{80}{60}\)  ×  60

x  =  \(\frac{80 \times 60}{100}\)

x  =  \(\frac{4800}{100}\)

x  =  48
​
48 out of 60 players are right-handed.

Question. Sandra’s volleyball team has a total of 20 uniforms. Find how many uniforms are medium-sized.

Given that, Sandra’s volleyball team has a total of 20 uniforms.

20 % are medium-sized uniforms. We need to find how many uniforms are medium-sized.

Let x be the number of medium-sized uniforms, thus we get, using equivalent ratios we get

\(\frac{x}{20}\) × 20

=  \(\frac{20}{100}\) × 20

x  =  \(\frac{400}{100}\)

x  =  4

4 out of 20 uniforms are medium-sized.

Question. Meg is a veterinarian. In a given week, 50% of the 16 dogs she saw were Boxers. Steve is also a veterinarian. In the same week, 7 of the 35 dogs he saw this week were Boxers. Find which part Steve needs to find the part, the whole or the percent.

Given that, Meg is a veterinarian. In a given week, 50 % of the 16 dogs she saw were Boxers.

Steve is also a veterinarian. In the same week, 7 of the 35 dogs he saw this week were Boxers.

Each wants to record the part, the whole, and the percent.

We need to find which part Steve needs to find – the part, the whole, or the percent.

Finding the number of dogs Steve saw:

\(\frac{x}{100}\)  =  7

x  =  7  ×  \(\frac{100}{35}\)

x  =  \(\frac{700}{35}\)

x  =  \(\frac{100}{5}\)

x  =  20

Thus, 20 % of dogs Steve saw. Thus, he needs to find the percent.

Steve needs to find the percent.

Percent Problems Envision Math Chapter 4 Grade 7 Solutions

Question. The registration fee for a used car is 0.8% of the sale price of $5,700. Find the registration fee.

Given that, the registration fee for a used car is 0.8 % of the sale price of $5,700.

We need to determine the fee.

The registration fee is:

\(\frac{0.8}{100}\) × 5700

=  0.8  ×  57

=  45.6

The registration fee is $45.6

Question. The total cost of an item is the price plus the sales tax. Find the sales tax to complete the table.

Given that, the total cost of an item is the price plus the sales tax.

We need to find the sales tax to complete the table.

Then find the total cost of the item.

Finding the sales tax of the item, we get:

\(\frac{4}{100}\) × 40

=  \(\frac{160}{100}\)

=  1.6 dollars

The total price is calculated by adding selling price and sales tax.

Thus, we get

40 + 1.6 = 41.6 dollars

The sales tax is $1.6

The total price is $41.6

Question. Find whether 700% of 5 less than 10, greater than 10 but less than 100 or greater than 100.

We need to find whether 700 % of 5 less than 10, greater than 10 but less than 100 or greater than 100.

Solving the equation, we get:

\(\frac{700}{100}\) × 5

= 7  ×  5

=  35
Thus the value is greater than 10 but less than 100.

The value obtained is 35 which is greater than 10 but less than 100.

Question. A new health drink has 130% of the recommended daily allowance (RDA) for a certain vitamin. The RDA for this vitamin is 45 mg. Find how many milligrams of vitamins are in the drink.

Given that, A new health drink has 130 % of the recommended daily allowance (RDA) for a certain vitamin.

The RDA for this vitamin is 45 mg.

We need to find how many milligrams of vitamins are in the drink.

Finding the vitamin amount of a new health drink, we get:

\(\frac{130}{100}\)  ×  45

= \(\frac{13}{10}\)  ×  45

= \(\frac{13}{2}\)  ×  9

=  58.5

58.5 mg of vitamins are in the drink.

Question. Brad says that if a second number is 125% of the first number, then the first number must be 75% of the second number. Find whether he is correct or not.

Given that, Brad says that if a second number is 125 % of the first number, then the first number must be 75 % of the second number.

We need to find whether he is correct or not.

Finding the percentage of the second number

Here, y be the second number and x be the first number.

Thus, we get:

\(\frac{125}{100}\)  ×  x  =  y

x  =  y  ×  \(\frac{100}{125}\)

x  =  y  ×  \(\frac{4}{5}\)

x  =  y  × 0.8

0.8 is equal to 80 %

Thus, the first number must be 80 % of the second number. Hence, he is incorrect.

Question. Mark and Joe work as jewelers. Mark has an hourly wage of $24 and gets overtime for every hour he works over 40 hours. The overtime pay rate is 150% of the normal rate. Joe makes 5% commission on all jewelry he sells. Find who earns more money in a week if Mark works 60 hours and Joe sells $21,000 worth of jewelry.

Given that, Mark and Joe work as jewelers. Mark has an hourly wage of $24 and gets overtime for every hour he works over 40 hours.

The overtime pay rate is 150 % of the normal rate. Joe makes 5 % commission on all jewelry he sells.

We need to find who earns more money in a week if Mark works 60 hours and Joe sells $21,000 worth of jewelry.

For Mark:

Find his overtime pay rate, thus we get:

​x  =  \(\frac{150}{100}\)  ×  24

x  =  \(\frac{15}{5}\)  × 12

x  =  3 × 12

x  =  36

Finding the total pay rate, we get:

​20  ×  36  =  720

40  ×  24  =  960
​
Thus, the total is, 720  +  960  =  1680

Marks earns more money in a week.

Envision Math 7th Grade Exercise 4.1 Answer Key

Question. A forest covers 43,000 acres. A survey finds that 0.2% of the forest is old-growth trees. Find how many acres of old-growth trees.

Given that, A forest covers 43,000 acres.

A survey finds that 0.2 % of the forest is old-growth trees.

We need to find how many acres of old-growth trees are there.

Finding the acres of the forest which is old-growth trees, we get,

\(\frac{0.2}{100}\)  ×  43000

=  0.2  ×  430

=  2  ×  43

=  86

86 acres of old-growth trees are there.

Question. An Olympic-sized pool, which holds 660,000 gallons of water, is only 63% full. Find how many gallons of water are in the pool.

Given that, an Olympic-sized pool, which holds 660,000 gallons of water, is only 63 % full.

We need to find how many gallons of water are in the pool.

Finding the gallons of water are in the pool, we get

\(\frac{63}{100}\)  ×  660000

=  63  ×  6600

=  415800

415800 gallons of water is in the pool.

Envision Math Accelerated Grade 7 Volume Chapter 1 Integers and Rational Numbers

Question. Find the surfboard width between two surfboard models. Lindy’s board is \(23 \frac{1}{3}\) inches wide. Her board is between the 92 and 102 models.

Given:

To find the surfboard width between two surfboard models.

Lindy’s board is \(23 \frac{1}{3}\) inches wide. Her board is between the 92 and 102 models.

It is like this because

\(23 \frac{1}{3}\) < 24

And

\(23 \frac{1}{4}\) < \(24 \frac{1}{3}\)

The first one is obvious regarding to the second one \(\frac{1}{4}\)=0.25 < \(\frac{1}{3}\)=0.3333.

The first one is obvious regarding to the second one \(\frac{1}{4}\)=0.25 < \(\frac{1}{3}\)=0.3333.

Given:

Lindy’s surfboard wide = \(23 \frac{1}{3}\)

To find:

Between which two surfboards model is her custom surfboard’s width? How do you know?

Lindy’s surfboard wide which is also considered as a width of the surfboard with \(23 \frac{1}{3}\).

Though the thickness is not given we can never bother about it.

\(\frac{70}{3}\) is the width of the surfboard We changed the mixed fraction to a rational number because it is easy to understand.

Model 82 and Model 92 is the two surfboard models of Calvin, compared as wide which is approximately the width of Lindy’s surfboard.

Envision Math Accelerated Grade 7 Chapter 1 Exercise 1.2 solutions

Question. Find how Juanita write the fastball statistic in decimal form \(\frac{240}{384}\)=0.625.

Given:

To find how Juanita write the fastball statistic in decimal form

\(\frac{240}{384}\)=0.625

There were 384 pitches and out of that number 240 were fastballs

This is terminating decimal because after that number five comes infinite number of zeros, none other numbers will appear again.

The answer 0.625 is the decimal form of the fastball statistic

Question. Determine whether it is terminates or non terminates.

Given:

To determine whether it is terminates or non terminates.

1.\(\frac{100}{3}\)

\(\frac{100}{3}\)=\(33 . \overline{3}\)

It is repeating decimal numbers, there is infinite numbers after the decimal point

2. \(\frac{100}{5}\)

\(\frac{100}{5}\)= 20

This is actually an integer, there are only zeros after the decimal point

3.\(\frac{100}{6}\)=

\(\frac{100}{3}\)=\(33 . \overline{3}\)

It is repeating decimal numbers, there is infinite numbers after the decimal point

\(\frac{100}{3}\)=\(33 . \overline{3}\), \(\frac{100}{6}\)\(16 . \overline{6}\) Are repeating decimals. \(\frac{100}{5}\)= 20 Terminating decimals.

Question. Explain the given numbers –\(0.\overline{3}\), 3.1414414441444 are rational numbers or not.

Given:

To explain the given numbers −\(0.\overline{3}\), 3.1414414441444 are rational numbers or not.

First off, we need to know what a rational number is

A rational number is any number that can be made by dividing 2 integers.

For example:

1.5 would be a rational number because 1.5=3/2 (3 and 2 are both integers) With that being said, let’s begin.

First off, let’s start with −0.3, let’s ask ourselves, can we make this number by dividing 2 integers?

The answer is yes, we can, by doing we have the equivalent of −0.3, So now we know it’s a rational number.

As for the second one, it can’t be a rational number because it can’t be made by dividing to integers, so the answer is:

−0.3 Is a rational number, but 3.14144144414444 is not.

-0.3 is a rational number, but 3.14144144414444 is not.

Reasoning:

In mathematics, a rational number is a number that can be expressed as the quotient or fraction p/q of two integers. A numerator p and a non-zero denominator q.

Given:

Total pitches = 384

Fastball used times = 240

To find:

What decimal should Juanita use to update her report?

Times of fastball used divided by the total pitches

Therefore, Juanita should use the decimal 0.6205 to update her report.

Grade 7 Envision Math Exercise 1.2 Integers And Rational Numbers Answers

Question. Write how rational numbers written as decimals.

Given:

To write how rational numbers written as decimals

Rational numbers written as decimals

Any terminating or repeating decimal that can be written as a fraction using algebraic methods

An integer can be written as a fraction simply by giving it a denominator so any integer is a rational number.

Rational numbers become decimals after we divide the numerator with the denominator

Rational numbers become decimals after we divide numerators with denominators.

Question. Write how can you use division to find the decimal equivalent of a rational number.

Given:

To write how can you use division to find the decimal equivalent of a rational number.

How can you use division to find the decimal equivalent of a rational number

The decimal forms of rational numbers either end or repeat a pattern.

To convert fractions to decimals you just divide the top by the bottom divide the numerator by the denominator and if the division doesn’t come out evenly.

You can stop after a certain number of decimal places and round off.

The answer is the numerator divided by the denominator.

Question. Write the difference between a terminating decimal and a repeating decimal number.

Given:

To write the difference between a terminating decimal and a repeating decimal number.

Difference between a terminating decimal and a repeating decimal number.

Terminating decimal ends that means we know how many digits are after the decimal points.

On the other hand, repeating decimals has an infinite number of repeating digits after the decimal points.

The difference only is number of digits.

Question. Write the decimal equivalent of the rational number \(\frac{7}{20}\).

Given:

To write the decimal equivalent of the rational number \(\frac{7}{20}\).

\(\frac{7}{20}\), dividing both the number in two table.

\(\frac{7}{20}\)=\(\frac{3.5}{10}\)

= 0.35

The answer is 0.35.

Given:

To write the decimal equivalent of the rational number

\(\frac{-23}{20}\).

\(\frac{-23}{20}\), dividing both the number in two table.

\(\frac{-23}{20}\)=\(\frac{-1.15}{20}\)

= -1.15

The answer is -1.15.

Given:

To write the decimal equivalent of the rational number \(\frac{1}{18}\)

\(\frac{1}{18}\) dividing both the number in two table.

\(\frac{1}{18}\) =\(\frac{0.5}{9}\)

= 0.0555

\(0.0 \overline{5}\)  (Repeating)

The answer=\(0.0 \overline{5}\) (Repeating).

Given:

To write the decimal equivalent of the rational number\(\backslash\left[\frac{-60}{22} \backslash\right]\)

\(\frac{-60}{22}\), Dividing both the number in two tables

\(\frac{-60}{22}\) =\(\frac{-30}{11}\)

= -2.7272

\(2. \overline{72}\)  (Repeating)

The answer =\(2. \overline{72}\) (Repeating)

Question. A mile has 5280 feet there are 1000 feet left to pass, what part of a mile in decimal forms is left to pass? Find what part of a mile in decimal form, will you drive until you reach the exit?

Given: 

To find what part of a mile in decimal form, will you drive until you reach the exit?

A mile has 5280 feet there are1000 feet left to pass, what part of a mile in decimal form is left to pass?

=\(0. \overline{1893}\)

​The answer =\(0. \overline{1893}\) part of a mile in decimal form is left to pass.

Question. Write the decimal equivalent for each rational number \(\frac{2}{3}\).

Given:

To write the decimal equivalent for each rational number  \(\frac{2}{3}\)

Canceling the number using 3 table

\(\frac{2}{3}\)=\(0. \overline{6}\)

\(0. \overline{6}\) (Repeating)

The answer \( is 0. \overline{6}\) (Repeating )

Question. Write the decimal equivalent for each rational number \(\frac{3}{11}\).

Given:

To write the decimal equivalent for each rational number \(\frac{3}{11}\)

Canceling the number using 11 table

\(\frac{3}{11}\)=\(0. \overline{27}\)

\(0. \overline{27}\) (Repeating)

The answer \( is 0. \overline{27}\) (Repeating )

Question. Write the decimal equivalent for each rational number \(8 \frac{4}{9}\).

Given:

To write the decimal equivalent for each rational number \(8 \frac{4}{9}\)

Converting the mixed fraction into improper fraction

\(8 \frac{4}{9}\)=\(\frac{76}{9}\)

\(\frac{76}{9}\)=\(8. \overline{4}\) (Repeating)

The answer \(8 \frac{4}{9}\)= \(8. \overline{4}\) (Repeating)

Question. Write whether \(1.02 \overline{27}\) a rational number and also explain it.

Given:

To write whether \(1.02 \overline{27}\) a rational number and also explain it.

Yes, it is a rational number.

Explanation:

The given number is a rational number because it can also be written as fraction and it has also repeating digits.

The given number \(1.02 \overline{27}\) is a rational number.

Envision Math Chapter 1 Exercise 1.2 Answer Key

Question. Whether the fraction is terminating or not terminating \(\frac{1}{3}\).

Given:

To tell whether the fraction is terminating or not terminating.

Answer:

The given fraction is nonterminate

\(\frac{1}{3}\)=\(0. \overline{3}\)

Which means the \(\frac{1}{3}\) fraction has the repeating decimal.

The answer is given fraction \(\frac{1}{3}\) is repeating decimal.

Question. Whether the number -34 is a rational number or whole number or integer.

Given:

To tell whether the number −34 is a rational number or whole number or integer.

-34

Answer:

1. The given number −34 is not a whole number because it has a negative sign.

2. The given number can be considered as rational number because it has been written in a fractional form \(\frac{-34}{1}\).

3. The given number−34 is also a integer because the given number is a whole number with a negative sign.

The answer −34 is an integer, a rational number but not a whole number.

Question. Convert decimal to fraction \(2 \frac{5}{8}\).

Given:

To convert \(2 \frac{5}{8}\) into decimal.

To convert decimal to fraction

​\(2 \frac{5}{8}\)=\(\frac{21}{8}\)

2.625

Given:

To tell what was ariel’s likely error.

Ariel takes the value of \(\frac{5}{8}\) =0.58 it is the error of ariel

Explanation :

We are given that Ariel incorrectly the value of

\(2 \frac{5}{8}\)=2.58

We have to convert \(2 \frac{5}{8}\) into a decimal and we have to find the arials error

\(2 \frac{5}{8}\)=2+\(\frac{5}{8}\)

= 2  +  0.625

= 2.625

\(2 \frac{5}{8}\)=2.625 not 2.58

Ariel consider that value \( \frac{5}{8}\)

= 0.58

But actually the value is 0.625

Hence ariel takes value of 0.58 in place of0.625

Solution:

Ariel takes the value of \(\frac{5}{8}\) =0.58 it is the error of ariel.

Question. Find the value of a and b in a√b when you use division to find the decimal form. Find the decimal form we have to divide 3 by 11.

Given:

To find the value of a and b in a√b when you use division to find the decimal form.

To find the decimal form we have to divide 3 by 11

a√b

a=?

b=?

b is numerator = 3

a is denominator = 11

Solution: a = 11,b = 3

Given:

To find decimal form for \(\frac{3}{11}\)

To find the decimal form \(\frac{3}{11}\)

Canceling the terms with 11 table

=\(0. \overline{27}\).

Question. Find the decimal should the digital scale. Daniel wants to find \(3 \frac{1}{5}\) lb of ham.

Given:

To find what decimal should the digital scale.

Daniel wants to find \(3 \frac{1}{5}\) lb of ham

First, we have to change the mixed fraction to a normal fraction.

The scale shoulder read 3.2 lb

The scale should read 3.2 lb

Question. Find number of pounds of port she brought using a decimal \(18 \frac{8}{25}\) is a mixed fraction.

Given:

To find number of pounds of port she brought using a decimal.

\(18 \frac{8}{25}\) is a mixed fraction

In order to convert the mixed fraction to decimal form you need to divide the numerator by the denominator

\(\frac{8}{25}\) = 0.32

Next add the decimal\(\frac{8}{25}\) =0.32 to the whole number from the mixed fraction

18+0.32 = 18.32

This is how many pounds she bought .this decimal terminates.

The 18.32 number of pounds of pork she brought.

Question. Explain the given number 9.373 is a repeating decimal or not.

Given:

To explain the given number 9.373 is a repeating decimal.

9.373

It is not a repeating decimal

Reason:

There are no repeating digits,9.373 the number has only three digit after the decimal point.

It is a rational because rationals are all numbers that can be written as fractions.

The given number 9.373 is not a repeating decimal.

Question. Find how tall will the stack.

Given:

To find how tall will the stack be.

First box=\(3 \frac{3}{11}\)

Second box = 3.27

We have to convert the\(3 \frac{3}{11}\) into the normal form

\(3 \frac{3}{11}\) = 0.27

\(3 \frac{3}{11}\) = 3 + 0.27

3.27

If he stacks both the boxes

3.27 + 3.27 = 6.54

The stack height will be 6.54.

Solutions For Envision Math Accelerated Grade 7 Exercise 1.2

Question. Find the decimal should you watch for on the digital pressure gauge.

Given:

To find what the decimal should you watch for on the digital pressure gauge.

We should watch the dia0.1 on the pressure gauge

The air pressure in the tyre \(32 \frac{27}{200}\)

We need to convert the mixed fraction to decimal number

\(\frac{27}{200}\) = 0.135

\(32 \frac{27}{200}\) = 32 + 0.135

= 32.135

Thus the air pressure in the tyre = 32.135 pounds per square inch

Rounding to the nearest tenths we get 32.1 pounds per square inch

Solution:

The air pressure in the tyre =  32.135 pounds per square inch.

Question. Justify that the pizza should fit to the square box.

Given:

To justify that the pizza should fit to the square box.

Answer: The pizza fit in the box

Explanation:

The diameter of the pizza is D = \(10 \frac{1}{3}\)

The wide of the square box is b = 10.38

Wkt

For the pizza to fit inside the box, it must be fulfilled that

D ≤ b

We need to convert the decimal to a fraction

= \(\frac{519}{50}\)

Convert \(10 \frac{1}{3}\) into improper fraction

Multiply the diameter of the pizza by 50 both numerator and denominator

Multiply the wide of the  box 3 in both numerator and denominator

=\(\frac{1557}{150}\)

Therefore the pizza fit inside the box.

The pizza will fit inside the box.

Question. Convert the fraction to decimal choose the correct answer for \(117 \frac{151}{200}\).

Given:

To choose the correct answer for \(117 \frac{151}{200}\)

Answer:

Convert the fraction to decimal
​
\(\frac{151}{200}\) =0.755

\(117 \frac{151}{200}\) =117+0.755

117.055

117.055 is correct answer.

Envision Math Grade 7 Volume 1 Chapter 1 Exercise 1.2 Guide

Question. Convert the fraction to decimal  find the decimal equivalents for each fraction for \(\frac{-4}{5}, \frac{-5}{6}\).

Given:

To find the decimal equivalents for each fraction for \(\frac{-4}{5}, \frac{-5}{6}\)

To convert the fraction to decimal

\(\frac{-4}{5}\) = -0.8

\(\frac{-5}{6}\) = –\(0.8 \overline{3}\)

The decimal equivalent for \(\frac{-4}{5}\),\(\frac{-5}{6}\)

= −0.8,-\(0.8 \overline{3}\)

Given:

Which is a repeating decimal? which digit is repeating?

To find the repeating decimal.

\(\frac{-4}{5}\) = -0.8

\(\frac{-5}{6}\) = -0.8333……

-0.8333…… is the repeating decimal and the number 3 is repeating.

Envision Math Accelerated Grade 7 Volume 1 Chapter 4 Analyze And Solve Percent Problems

Question. The florist uses purple and white flowers in the ratio of 3 purple flowers to 1 white flower.

Given:

The florist uses purple and white flowers in the ratio of 3 purple flowers to 1 white flower.

The florist uses purple and white flowers in a ratio of 3: 1.

That means there are 4 flowers in 1 arrangement.

He needs to make 30 identical arrangements.
​
​⇒  ​30⋅4 = 120

​⇒  30.3: 30.1
​
​⇒  90: 30

The florist will need 120 flowers for 30 identical arrangements. He will need 90 purple flowers and 30 white flowers.

The florist will need 120 flowers for 30 identical arrangements. He will need 90 purple flowers and 30 white flowers.

It is given that purple and white flowers are in the ratio of 3 purple flowers to 1 white flower.

That means that the purple flower will be related to the white flowers in a ratio of 3:1.

This means if there are 3 white flowers, we will require 9 purple flowers.

Purple will be 3 times the number of white flowers.

Purple flowers are 3 times the number of white flowers.

Envision Math Accelerated Grade 7 Chapter 4 Exercise 4.2 Answer Key

Question. The florist can only buy white flowers that have 3 white flowers and 2 red flowers.

Given:

The florist can only buy white flowers that have 3 white flowers and 2 red flowers.

He needs 90 out of 120 white flowers.

​⇒  90 ÷ 3 = 30

​⇒  30 ÷ 2 = 60
​
He has to buy 30 groups (2 red in every group).

The florist have to buy 60 red flowers, for 30 groups, 2 red flowers for every group.

Percent is the rate, number or amount in each hundred.

A fraction is a ratio or quantity which is not a whole number.

Fractions and percent can represent the same number just differently.

They are equivalent and that is a proportional relationship.

Percent and fractions can represent the same numbers (can be proportional).

Question. Camila makes 2 of her 5 shots attempted. Find the percent for Camila and then compare with Emily’s.

Given:

Camila makes 2 of her 5 shots attempted.

We find the percent for Camila and then compare with Emily’s.
​
\(\frac{2}{5}=\frac{p}{100}\)

0.4 = \(\frac{p}{100}\)

p = 40%

Camila made 40% of her shots. Camila’s percent of the shots made is less than Emily’s.

Camila made 40% of her shots. Camila’s percent of the shots made is less than Emily’s.

Question. Megan’s room is expanded so the width is 150% of 3 meters.

Given:

Megan’s room is expanded so the width is 150% of 3 meters.

We find the width of the room:
​
\( \frac{w}{3}\) = \( \frac{150}{100}\)

w = \(\frac{450}{100}\)

w = 450

The new width of the room is 4.5 meters.

​The new width of Megan’s room is 4.5 meters.

Given:

45% of iron per 8 mg.

We find the amount of iron needed each day:
​
\(\frac{8}{x}=\frac{45}{100}\)

​\(\frac{800}{45} \)

x = 17.8

Therefore, the amount of iron required each day is 17.8mg.

The amount of iron required each day is 17.8 mg.

Percent is the rate, number or amount in each hundred.

A fraction is a ratio or quantity which is not a whole number.

Fractions and percent can represent the same number just differently.

They are equivalent and that is proportional relationship.

Percent and fractions can represent the same numbers (can be proportional).

Given:

We know that  \(\frac{150}{100}\) is 150% and it is greater than 1 whole.

So \(\frac{75}{x}\) must be greater too.

That means that w must be less than 75.

Therefore, w must be less than 75.

Given:

We know that

x = \(\frac{17 \cdot 100}{68}\)

x = 25%

The percent proportion for the given bar diagram is 25%.

Therefore, the percent for the given bar diagram is 25%.

Envision Math Grade 7 Chapter 4 Percent Problems Exercise 4.2 Solutions

Question. Gia researches online that her car is worth $3,000. She hopes to sell it for 85% of that value, but she wants to get at least 70%. Find whether she get what she wanted or not.

Given that, Gia researches online that her car is worth $3,000.

She hopes to sell it for 85% of that value, but she wants to get at least 70%.

She ends up selling it for $1,800.

We need to find whether she get what she wanted or not.

Finding the 85 %, we get
​
\(\frac{85}{100}\)×3000

= 85 × 30

= 2550

Finding the 70 %, we get

\(\frac{70}{100}\)×3000

= 70 × 30

= 2100
​
But she got only $1800

She got less than what she wanted.

Question. The rabbit population in a certain area is 200% of last year’s population. There are 1100 rabbits this year. Find the number of rabbits there would be in the last year.

The rabbit population in a certain area is 200% of last year’s population.

There are 1100 rabbits this year.

We have to find the number of rabbits there would be in the last year.

The population of the rabbit is 200% in the last year.

While the number of rabbits in this year are 1100.

We will equate the number of rabbits to its percentage to calculate the number of rabbits in last year.

The calculation will be

w = 550

Therefore, the number of rabbits last year is 550.

There were 550 rabbits present last year.

Question. There is a company that makes hair-care products had 3000 people try a new shape. It is given that of the 3000 people, 9 had a mild allergic reaction. Find the percent of people who had a mild allergic reaction.

There is a company that makes hair-care products had 3000 people try a new shape.

It is given that of the 3000 people, 9 had a mild allergic reaction.

We have to find the percent of people who had a mild allergic reaction.

There are 3000 people who had hair care products.

Among those 3000 people, 9 of them had allergic reactions.

The ratio of people who had allergic reactions is \(\frac{9}{100}\).

To find the percent from the ratio, we evaluate as below:

p = 0.3

The percent of people who had a mild allergic reaction is 0.3.

Question. There is a survey given about who owned which type of car. Find the percent of people who were completely satisfied with the car.

There is a survey given about who owned which type of car.

We have to find the percent of people who were completely satisfied with the car.

A survey is given regarding people who owned different types of cars.

In the car satisfaction survey, 1100 people were completely satisfied with their car.

740 people were somewhat satisfied while 160 are not at all satisfied.

We have to find the percent of people who were completely satisfied.

The total number of people who were surveyed are

1100 + 740 + 160 = 2000

To find the percent, we evaluate as below:

p = 55

The percent of people who were completely satisfied with their type of car is 55%.

Analyze And Solve Percent Problems Grade 7 Exercise 4.2 Envision Math

Question. The Washington’s buy a studio apartment for $240000. They pay a down payment of $60000. Find that their down payment is what percent of the purchase price.

It is given that the Washington’s buy a studio apartment for $240000. They pay a down payment of $60000.

We have to find that their down payment is what percent of the purchase price.

The Washington’s buy a studio apartment for $240000.

They pay a down payment for the studio apartment is $60000.

We have to find that what percent of purchase price is of their down payment.

To find the percent, we evaluate as below:

p = 25

Their down payment is 25% percent of the purchase price.

It is given that the Washington’s buy a studio apartment for $240000. They pay a down payment of $60000.

We have to find that what percent of purchase price would be of a $12000 down payment.

The Washington’s buy a studio apartment for $240000.

They pay a down payment for the studio apartment is $60000.

We have to find that what percent of purchase price what percent of purchase price would be of a $12000 down payment.

To find the percent, we evaluate as below:

p = 5

The percent of the purchase price would a $12000 down payment be is 5%.

Question. A restaurant customer left $3.50 as a tip. The tax on  the meal was 7% and the tip was 20% of the cost including tax. Find that what information is not necessary to calculate the bill.

It is given that a restaurant customer left $3.50 as a tip.

The tax on the meal was 7% and the tip was 20% of the cost including tax.

The tip left by the customer at a restaurant is $3.50.

They percentage of tax on the meal was 7 % and of the tip it was 20% of the cost including the tax.

We have to find that what information is not necessary to calculate the bill.

For computing the bill, we do not need to include the tax.

The tax is not needed to compute the bill.

It is given that a restaurant customer left $3.50 as a tip.

The tax on the meal was 7% and the tip was 20% of the cost including tax.

The tip left by the customer at a restaurant is $3.50.

They percentage of tax on the meal was 7 % and of the tip it was 20% of the cost including the tax.

We have to find the amount of total bill.

For computing the bill, we will calculate as below:

x = 17.5

To get the total bill, we will also have to add the tip left by the customer.

17.5+3.5=21

The total bill of the customer in the restaurant is $21.

Question. Find the estimate for 380% of 60.

We have to find the estimate for 380% of 60.

The estimate for 380% of 60 will be evaluated as below:

x = 228

Therefore, the estimate is approximately 228.

The estimate for 380% of 60 will be 228.

Question. Marna thinks that about 35% of her mail is junk mail. She gets twice as much regular mail as junk mail. Verify whether the statement is correct or not.

Marna thinks that about 35% of her mail is junk mail.

She gets twice as much regular mail as junk mail.

We have to verify whether the statement is correct or not.

Marna gets twice as much regular mail as junk mail. So, the ratio of regular mail to junk mail is 2 is to 1.

Thus, if we consider the total mail as 100%, the ratio of both will be represented as

2:1=\(66.\overline{6}\) :\(33.\overline{3}\)

But, Marna thinks that she gets 35% mail as junk mail.

Which is not true, because actually, she gets \(33.\overline{3}\) of junk mail.

Therefore, she is not correct.

Marna’s statement is not correct because she gets around \(33.\overline{3}\) of junk mail and not 35%.

Question. Hypatia has read 13 chapters of a book. The book contains total 22 chapters. Find the percent of the chapters she has read.

It is given that Hypatia has read 13 chapters of a book.

The book contains total 22 chapters.

We have to find the percent of the chapters she has read.

The book has 22 chapters and Hypatia has read 13 of them.

The ratio of the chapters she has read will be \(\frac {13}{22}\).

So, the percent of chapters she has read will be

The percentage of the chapters Hypatia has read is\(59 . \overline{09}\)

Envision Math Grade 7 Exercise 4.2 Solution Guide

Question. A survey found that 27% of high school students and 94% of teachers and school employees drive to school. 

A survey found that 27% of high school students and 94% of teachers and school employees drive to school.

The ratio of students to employees is about 10 to 1.

Roger states that the number of students who drive to school is greater than the number of teachers and employees who drive to school.

We have to tell how Roger’s statement could be correct.

The information gained by the survey is that 27% of high school students and 94% of teachers and school employees drive to school.

The ratio of the students to employees is 10:1.

We express the ratio as 10:1 = 1000:100

We evaluate the percentages we get:

\(\frac{27}{100} \cdot 1000\) = 270

\(\frac{94}{100} \cdot 100\) = 94

Thus, if we count the teachers as employees then, Roger’s statement is right.

Roger’s statement is correct if we count the teachers as employees.

Question. Stefan sells Jin a bicycle for $114 and a helmet for $18. The total cost for Jin is 120% of what Stefan spent originally to buy the bike and helmet. How much did Stefan spend originally?

Given:

Stefan sells Jin a bicycle for $114 and a helmet for $18.

The total cost for Jin is 120% of what Stefan spent originally to buy the bike and helmet.

How much did Stefan spend originally?

To find/solve

How much money did he make by selling the bicycle and helmet to Jin?

? = 110

First, multiply both sides by the variable and then by the reciprocal.

110

He make 110 by selling the bicycle and helmet to Jin.

Question. This month you spent 140% of what you spent last month. Last month you spent $30. How much did you spend this month?

Given:

Last month you spent $30.

This month you spent 140% of what you spent last month.

Set up a proportion to model this situation.

To find/solve

How much did you spend this month?

? = 42

First, multiply both sides by the variable and then by the reciprocal.

42

The amount spends this month is 42.

Envision Math Accelerated Grade 7 Chapter 4 Exercise 4.2 Answers

Question. The owner of a small store buys coats for $50.00 each. She sells the coats for $90.00 each find percent of the purchase price is the selling price?

Given:

The owner of a small store buys coats for $50.00 each.

She sells the coats for $90.00 each

To find/solve

What percent of the purchase price is the selling price?

? = 180

First, multiply both sides by the variable and then by the reciprocal.

180

180 percent of the purchase price is the selling price.

Given:

The owner of a small store buys coats for $50.00 each.

The owner increases the sale price the same percent that you found in Part A when she buys jackets for $35 and sells them.

To find/solve

How many jackets must the owner buy for the total jacket sales to be at least $250?

? = 63

250 ÷ 63 = 3.97

3.97 ≈ 4

First, multiply both sides by the variable and then by the reciprocal.

4

4 jackets must the owner buy for the total jacket sales to be at least $250.

Envision Math Accelerated Grade 7 Volume 1 Chapter 4 Analyze And Solve Percent Problems

Question. Show proportional relationships between quantities and be used to solve problems.

We have to tell how can percents show proportional relationships between quantities and be used to solve problems.

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as a proportional relationship.

Percents can be expressed in terms of fraction or ratios.

In order to check whether they show a proportional relationship or not, we can test if their ratios are equivalent or not.

Also, we can graph the quantities and if it comes out as a straight line passing through the origin, then there will be a proportional relationship.

In certain problems when we have the values as same constant multiples, then we can use the concept of proportional relationship to solve the problem.

The knowledge and applications of ratio and proportions can be used to solve problems.

Equivalent ratio or graph of percents can show their proportional relationship.

Equivalent ratio or graph of percents can show their proportional relationship.

Given that, Activity trackers, also called fitness trackers, have become quite popular in recent years.

We need to check whether the data collected is actually helpful to the user.

You and your classmates will explore the types of data that an activity tracker collects, and how that data can help users reach their activity and fitness goals.

Activity trackers are nothing but an app or device which monitors your fitness-related metrics.

Some of the metrics it measures are heartbeats, calories, blood flow, and distance walking or running to enable the user to keep track of their fitness.

This will help people to achieve their fitness goals.

The data collected in those trackers are accurate and is helpful to the user.

The percentage difference will be less than 1% which indicates that the fitness trackers did a great job in tracking data.

Some of the metrics the fitness or activity trackers measure are heartbeats, calories, blood flow, and distance walking, or running to enable the user to keep track of their fitness.

Envision Math Accelerated Grade 7 Chapter 4 Percent Problems Solutions

Question. Comparison between two same or different quantities.

The ratio is nothing but the comparison between two same or different quantities.

A rate usually compares two different quantities.

The units of those quantities must be different.

Rates usually come under ratio. But all ratios cannot be expressed as the rate.

Ratios compare two same or different quantities.

A ratio that relates two quantities with different units of measure is a rate.

The ratio is nothing but the comparison between two same or different quantities.

A rate usually compares two different quantities.

The units of those quantities must be different. Rates usually come under ratio.

But all ratios cannot be expressed as the rate.

Ratios compare two same or different quantities.

When two equal ratios are expressed as a statement, then it is said to be in proportion.

For example:

\(\frac{8}{2}=\frac{36}{9}\)

These two are said to be in proportion since the ratios are equal.

A statement that two ratios are equal is called a proportion.

Question. Comparison between two same or different quantities.

The ratio is nothing but the comparison between two same or different quantities.

A rate usually compares two different quantities.

The units of those quantities must be different.

Rates usually come under ratio. But all ratios cannot be expressed as the rate.

Ratios compare two same or different quantities.

Here, the relationship “3 students out of 5 students” denotes that the units are the same.

This means that the given statement is a ratio, not a rate.

The relationship “3 students out of 5 students” is an example of a ratio.

Grade 7 Envision Math Accelerated Chapter 4 Percent Solutions Guide

Question. Write each number in two equivalent forms as a fraction, decimal, or percent number is 0.29.

We need to write each number in two equivalent forms as a fraction, decimal, or percent.

The given number is 0.29

The given number is 0.29

Writing the given decimal in its equivalent form, we get

​0.29 = \(\frac{29}{100}\)

Writing the given decimal in its equivalent form 0.29 \(=\frac{2.9}{10}\)

Question. Write each number in two equivalent forms as a fraction, decimal, or percent number is 35%.

We need to write each number in two equivalent forms as a fraction, decimal, or percent. The given number is 35 %

The given number is 35 %

Writing the given percent in its equivalent form, we get

​35 = \(\frac{35}{100}\)

=  \(\frac{7}{20}\)

Writing the given percent in its equivalent form, 35% = \(\frac{7}{20}\)

Question. Write each number in two equivalent forms as a fraction, decimal, or percent.

The given number is in the form of a fraction.

We need to write each number in two equivalent forms as a fraction, decimal, or percent.

The given number is \(\frac{2}{5}\)

The given number is \(\frac{2}{5}\)

Writing the given fraction in its equivalent form, we get

\(\frac{2}{5}\)  =  0.4

= \(\frac{40}{100}\)

Writing the given fraction in its equivalent form \(\frac{2}{5}\) = \(\frac{40}{100}\)

Envision Math Accelerated Volume 1 Chapter 4 Percent Problem Answers

Question. Find the unknown number in the given proportion \(\frac{x \text { days }}{4 \text { years }}=\frac{365.25 \text { days }}{1 \text { year }}\)

We need to find the unknown number in the given proportion.

Solving the given proportion, we get

x = 4 × 365.25

x = 1461 days
​
Hence, The required answer is:

Question. find the unknow number in the given proportion \(\frac{33,264 \text { feet }}{x \text { miles }}=\frac{5280 \text { feet }}{1 \text { mile }}\)

We need to find the unknown number in the given proportion.

Solving the given proportion, we get

x \( = \frac{33264}{5280}\)

x =  6.3 miles

Hence the required answer is:

Envision Math 7th Grade Percent Problems Chapter 4 Solutions

Question. A cooking magazine shows a photo of the main dish on the front cover of 5 out of the 12 issues it publishes each year. Write and solve a proportion to determine how many times a photo of the main dish will be on the front cover during the next 5 years.

Given that, A cooking magazine shows a photo of the main dish on the front cover of 5 out of the 12 issues it publishes each year.

We need to write and solve a proportion to determine how many times a photo of the main dish will be on the front cover during the next 5 years.

Given that,\(\frac{5}{12}\)

5 issues per 12 months. i.e., per year.

For five years, it will be

\(\frac{5}{12}\) \(=\frac{x}{12 \times 5}\)

\(\frac{5}{12}\)\(=\frac{x}{60}\)

x = 5 × 5

x = 25
​
Therefore, 25 out of the 60 issues.

25 times a photo of the main dish will be on the front cover during the next 5 years.

How To Solve Percent Problems Envision Math Grade 7 Chapter 4

Question. Complete the first and second columns of this table. While you work through the topic, return to complete the third column as learn the answers to  your questions from the second column.

We need to complete the first and second columns of this table.

While you work through the topic, return to complete the third column as learn the answers to your questions from the second column.

The percentage is also denoted as the ratio.

The ratio is nothing but the comparison between two same or different quantities.

The first term of the percent is often compared to the number 100.

For example, 35 % of shirts are sold denotes that out of 100 shirts, 35 has been sold out.

We can often denote the percent using the sign “%”.

What do I know about percents and how they are used?

A percent is a ratio in which the first term is compared to 100.

It is used for comparing two quantities.

What do I want to learn about how I will use percents in life?

I want to learn about how percents help us in our daily day-to-day life.

What I have learned about how percents are used?

I have learned that the percents are used to calculate the amount of one thing compared to the other.

Percents can be used to compare very small or very large quantities as a fraction of 100.

Envision Math Accelerated Grade 7 Volume 1 Chapter 3 Analyze And Use Proportional Relationships

Question. Allison and her classmates planted bean seeds at the same time as Yuki and her classmates in Tokyo did. Determine who should expect to have the taller plant at the end of the school year.

Given: 

Allison and her classmates planted bean seeds at the same time as Yuki and her classmates in Tokyo did.

Allison is video-chatting with Yuki about their class seedlings Assume that both plants will continue to grow at the same rate.

We need to determine who should expect to have the taller plant at the end of the school year.

The rate of growth of Allison Class’s bean seeds will be

=\(\frac{2.5}{5}\)

= 0.5 inches per day

Converting inches to the centimeter, we know that, 1 inch=2.54 centimeters

Thus, 0.5 inches = \(\frac{2.54}{2}\)

= 1.27 centimeter

The rate of growth of Yuki Class’s bean seeds will be,

=\(\frac{5.5}{4}\)

= 1.375 centimeters per day
​
Therefore, Yuki Class’s bean seeds grow taller per day.

Yuki’s class is expected to have the taller plant at the end of the school year.

Envision Math Accelerated Grade 7 Chapter 3 Exercise 3.2 Answer Key

Question. Explain how we can compare the growth rates of the seedlings.

We need to explain how we can compare the growth rates of the seedlings.

We need to determine the unit rate of each to determine which one will be tallest at the end of the year.

Since both plants will continue to grow at the same rate.

The rate of growth of Allison Class’s bean seeds will be 1.27 centimeters per day.

The rate of growth of Yuki Class’s bean seeds will be 1.375 centimeters per day.

Thus, the rate of growth or the unit rate determines the growth rates of both the seedlings.

This will help us to compare their growth.

The rate of growth or the unit rate helps us compare the growth rates of the seedlings.

Question. Explain what the students must have done before they can compare the heights of the plants.

We need to explain what the students must have done before they can compare the heights of the plants.

We need to determine the unit rate of each to determine which one will be tallest at the end of the year.

Since both plants will continue to grow at the same rate. The rate of growth of Allison Class’s bean seeds will be 1.27 centimeters per day.

The rate of growth of Yuki Class’s bean seeds will be 1.375 centimeters per day.

Thus, the rate of growth or the unit rate determines the growth rates of both the seedlings.

This will help us to compare their growth.

The students must have done finding out the rate of growth of both the seedlings before they can compare the heights of the plants.

Question. Sergio increases his target speed to 30 miles per hour. Determine how many more miles does Sergio need to ride in \(\frac{3}{4}\) hour to achieve this target speed.

Given:

Sergio increases his target speed to 30 miles per hour.

We need to determine how many more miles does Sergio need to ride in

\(\frac{3}{4}\)hour to achieve this target speed.

Forming an equation using the proportional relationship given, we get

\(\frac{30}{4}\)=x

x = 7.5

Therefore, Sergio rode ​7.5 miles in \(\frac{1}{4}\)hour.

Thus, Sergio needs to ride 30−7.5 = 22.5 miles in \(\frac{3}{4}\) hour to achieve this target speed.

Sergio must ride 7.5 miles in \(\frac{1}{4}\)hour to achieve this target speed, so he needs to ride an additional 22.5 miles per \(\frac{3}{4}\) hour.

Question. Bronwyn’s brother Daniel mows the lawn. He can mow 15,000 ft in \(\frac{3}{4}\) hour. Who mows the lawn in less time?

Given:

Every other weekend, Bronwyn’s brother Daniel mows the lawn. He can mow 15,000 ft in \(\frac{3}{4}\) hour.

To find/solve

Who mows the lawn in less time?

He mows more in less time, so he will finish faster than Bronwyn.

Envision Math Grade 7 Chapter 3 Proportional Relationships Exercise 3.2 Solutions

Question. Explain how does the unit rate describe Sergio’s cycling speed and how is the unit rate helpful in determining how much.

We need to explain how does the unit rate describe Sergio’s cycling speed and how is the unit rate helpful in determining how much.

Farther Sergio must cycle in a given amount of time each time he increases his target speed.

The unit rate helps in determining how many miles he travels per hour based on Sergio’s cycling speed.

The unit rate here is the rate of change in the number of miles every hour.

From the given information

\(\frac{30}{4}\)=x

x=7.5 miles

​This is for the target speed of 30 miles he needs to ride 7.5 miles in 15 minutes.

The unit rate describes Sergio’s cycling speed by determining the number of miles he can travel every hour. The unit rate is helpful in determining how much farther Sergio must cycle in a given amount of time each time he increases his target speed.

Question. Jacob mixes \(\frac{1}{3}\) cup of yellow paint for every \(\frac{1}{5}\) cup of blue paint to make green paint. How many cups of yellow paint are needed for 1 cup of  blue paint?

Given:

Jacob mixes \(\frac{1}{3}\) cup of yellow paint for every

\(\frac{1}{5}\) cup of blue paint to make green paint

To find/solve

How many cups of yellow paint are needed for 1 cup of blue paint?

First, we should find unit rate by dividing both by the denominator.

\(\frac{5}{3}\) Cups of yellow paint.

Question. Explain how is making a table of equivalent ratios to find the unit rate similar to finding the unit rate by calculating with fractions.

We need to explain how is making a table of equivalent ratios to find the unit rate similar to finding the unit rate by calculating with fractions.

For example, let the fraction be \(\frac{2}{3}\)

Making the table of equivalent ratios, we get.

Multiply both the numerator and the denominator by the same number, and we get

Therefore, the ratios \(\frac{2}{3}, \frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}\) are equivalent to each other.

The unit rate of the same by using the fractions are given as

​\(\frac{8}{12}\) =\(\frac{4}{6}\)

=\(\frac{2}{3}\)

We can easily see what the terms, with equivalent ratios are.

Both the unit rates and the equivalent ratios are the same.

Equivalent ratios will have the same value when simplified. Equivalent rates can be found similar to the equivalent ratios by performing the same multiplication or the division on both the numerator and the denominator.

Question. Brad buys two packages of mushrooms. Which mushrooms cost less per pound?

Given:

Brad buys two packages of mushrooms.

To find/solve

Which mushrooms cost less per pound?

First, we should find the unit rate by dividing both by the denominator. Cremini:

Chanterelle:

Chanterelle mushrooms cost less per pound.

Analyze And Use Proportional Relationships Grade 7 Exercise 3.2 Envision Math

Question. The recipe calls for \(1 \frac{1}{4}\) cups of flour and \(\frac{1}{2}\). How many cups of flour will Jed need if he uses 3 sticks of butter?

Given:

The recipe calls for \(1 \frac{1}{4}\)cups of flour and

To find/solve

How many cups of flour will Jed need if he uses 3 sticks of butter?

First we should find unit rate by dividing both by denominator.

Now we have to find equivalent ration that shows us how much flour is needed per 3 sticks of butter.

7.5 per 3

7.5 per 3 cups of flour will Jed need if he uses 3 sticks of butter.

Question. Find unit rate by dividing both by denominator Miles \(\frac{3}{5}\) and Hours \(\frac{1}{3}\)

Given:

Miles \(\frac{3}{5}\)

Hours \(\frac{1}{3}\)

To find/solve

First we should find unit rate by dividing both by denominator.

1.8 per 1.

Question. \(\frac{7 \mathrm{mi}}{\frac{1}{3} \mathrm{gal}}\) find unit rate by dividing both by denominator.

Given:

To find/solve.

First we should find unit rate by dividing both by denominator.

\(\frac{7 \mathrm{mi}}{\frac{1}{3} \mathrm{gal}}\)=\(\frac{21}{1}\)

Question. Find unit rate by dividing both by denominator \(\frac{\frac{3}{4}\text{ page }}{2 \text { minutes}}\)

Given:

\(\frac{\frac{3}{4} \text { page }}{2 \text { minutes }}\)

To find/solve

Page in 1 minute.

First we should find unit rate by dividing both by denominator.

\(\frac{3}{8}\) per 1

\(\frac{3}{8}\) per 1

Question. Hadley paddled a Canoe \(\frac{2}{4}\) mile in \(\frac{1}{4}\). How fast did Hadley paddle, in miles per hour?

Given:

Hadley paddled a Canoe\(\frac{2}{4}\) mile in \(\frac{1}{4}\)

To find/solve

How fast did Hadley paddle, in miles per hour?

First we should find unit rate by dividing both by denominator.

\(\frac{2}{4}\) per 1.

Hadley paddle, in miles per hour \(\frac{2}{4}\) per 1.

Question. A box of cereal states that there are 90 calories in a \(\frac{3}{4}\) cup serving. How many Calories are there in 4 cups of cereal?

Given:

A box of cereal states that there are 90 calories in a \(\frac{3}{4}\) cup serving

To find/solve

How many Calories are there in 4 cups of cereal?

First we should find unit rate by dividing both by denominator.

Now we just have to find equivalent ratio that will show the amount per 4.

480 per 4 Calories are there in 4 cups of cereal.

Question. A robot can complete 8 tasks in \(\frac{5}{6}\) hour. How long does it take the robot to complete one task?

Given:

A robot can complete 8 tasks in \(\frac{5}{6}\) hour

To find/solve

How long does it take the robot to complete one task?

We have to find the unit rate that will show us the ratio of fractions.

\(\frac{5}{48}\) per task

\(\frac{5}{48}\) per task take the robot to complete one task.

Given:

A robot can complete 8 tasks in \(\frac{5}{6}\) hour. Each task takes the same amount of time.

To find/solve

How many tasks can the robot complete in one hour?

We have to find unit rate that will show us the ratio of fraction.

\(\frac{48}{5}=9 \frac{3}{5} \text { per } 1\) tasks can the robot complete in one hour.

Envision Math Grade 7 Exercise 3.2 Solution Guide

Question. Find out which car can travel a greater distance on 1 gallon of gas.

Given:

You want to find out which car can travel a greater distance on 1 gallon of gas.

To find/solve

What is the gas mileage, in miles per gallon, for the blue car?

The ratio of miles per gallon

We have to divide both terms by the denominator term.

The gas mileage is \(\frac{71}{3}=23 \frac{2}{3} \text { per } 1\) in miles per gallon, for the blue car.

Given:

You want to find out which car can travel a greater distance on 1 gallon of gas.

To find/solve

What is the gas mileage, in miles per gallon, for the silver car?

The ratio of miles per gallon

We have to divide both terms by the denominator term.

34 per 1.

34 per 1 is the gas mileage, in miles per gallon, for the silver car.

Given:

You are running a fuel economy study. You want to find out which car can travel a greater distance on 1 gallon of gas.

To find/solve

Which car could travel the greater distance on 1 gallon of gas?

Blue car

Silver car

Silver car travel a greater distance on 1 gallon of gas.

Silver car travel a greater distance on 1 gallon of gas.

Question. \(\text { Henry incorrectly said the rate } \frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }}\) can be written as the unit rate \(\) pound per quart. Find the unit rate we have to divide both terms by the denominator.

Given:

\(\text { Henry incorrectly said the rate } \frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }}\) can be written as the unit rate \(\) pound per quart.

To find/solve

What is the correct unit rate?

To find unit rate we have to divide both terms by the denominator.

4 per 1 is the correct unit rate.

Given:

\(\text { Henry incorrectly said the rate } \frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }}\) can be written as the unit rate \(\) pound per quart.

To find/solve

What error did Henry likely make?

Ratios with fractions.

Convert the fractions so they have a common denominator, and multiply both fractions by the common denominator.

Simplify by dividing by the highest common factor.

He probably didn’t divide both terms by denominator.

He didn’t follow rules for finding unit rates.

He didn’t follow rules for finding unit rates.

Envision Math Accelerated Grade 7 Chapter 3 Exercise 3.2 Answers

Question. Ari walked \(2 \frac{3}{4}\) miles at a constant speed of \(2 \frac{1}{2}\)miles per hour. Beth walked \(1 \frac{3}{4}\)miles at a constant speed of \(1 \frac{1}{4}\) miles per hour. Cindy walked for 1 hour and 21 minutes at a constant speed of \(1 \frac{1}{8}\) miles per hour.

Given:

Ari walked \(2 \frac{3}{4}\) miles at a constant speed of \(2 \frac{1}{2}\)miles per hour. Beth walked \(1 \frac{3}{4}\)miles at a constant speed of \(1 \frac{1}{4}\) miles per hour. Cindy walked for 1 hour and 21 minutes at a constant speed of \(1 \frac{1}{8}\) miles per hour.

To find/solve

List the three people in order of the times they spent walking from least time to greatest time.

We should find unit rate of inches per feet.

Ari

Beth

Cindy

From this, we find out that

1.1 < 1.35 < 1.4

The three people in order of the times they spent walking from least time to greatest time is 1.1 < 1.35 < 1.4

Envision Math 7th Grade Exercise 3.2 Step-By-Step Solutions

Question. Fence A is \(1 \frac{4}{5}\) inches long on the blueprint and is to b\(1 \frac{1}{2}\). How long is Fence B on the blueprint/

Given:

Fence A is \(1 \frac{4}{5}\) inches long on the blueprint and is to b\(1 \frac{1}{2}\)

To find/solve

How long is Fence B on the blueprint?

We should find unit rate of inches per feet.

It shows us that there are 6/5 inches per feet. If the fence is long 5 feet we need to multiply

6 inches per 5 feet.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 3 Analyze And Use Proportional Relationships

Question. Basketball contest, Elizabeth made 9 out of 25 free throw attempts. Alex made 8 out of 20 free throw attempts. Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex. Find out whether Janie’s reasoning is correct or not.

Given: In a basketball contest, Elizabeth made 9 out of 25 free throw attempts.

Alex made8 out of 20 free throw attempts. Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.

We need to find out whether Janie’s reasoning is correct or not.

Finding the rates of each of them:

For Elizabeth.

= 0.36

For Alex

= 0.4

The rate Alex is more. Therefore, Alex had a better free-throw record because she made more free throws than Elizabeth.

Janie’s reasoning is wrong.

Given: In a basketball contest, Elizabeth made 9 out of 25 free throw attempts.

Alex made8 out of 20 free throw attempts.

Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.

We need to decide who had the better free-throw record. Justify your reasoning using mathematical arguments.

Finding the rates of each of them:

For Elizabeth:

= 0.36

For Alex:

= 0.4

The rate of Alex is more. Therefore, Alex had a better free-throw record because she made more free throws than Elizabeth.

Alex had a better free-throw record because she made more free throws than Elizabeth.

Envision Math Accelerated Grade 7 Chapter 3 Exercise 3.1 Answer Key

Question. Explain which mathematical model we used to justify our reasoning.

We need to explain which mathematical model we used to justify our reasoning.

Also, explain if there are other models you could use to represent the situation.

Finding the rates of each of them.

The rate for Elizabeth is 0.36

The rate for Elizabeth is 0.4

The rate of Alex is more.

Therefore, Alex had a better free-throw record because she made more free throws than Elizabeth.

The mathematical model which I used here is finding the rates.

We could also use ratios and unit rates to determine the same.

The mathematical model which I used here is finding the rates. We could also use ratios and unit rates to determine the same.

Question. Explain how are ratios, rates, and unit rates used to solve problems.

We need to explain how are ratios, rates, and unit rates used to solve problems.

A rate is nothing but a measurement between two different quantities.

A ratio is a measurement between two same quantities.

A unit rate is a rate at which one quantity differs per unit of another quantity.

Examples are:

Rate –

Distance \(=\frac{\text { Speed }}{\text { Time }}\)

Here, speed and time are of different quantities. Ratio – \(\frac{x}{y}\)

Unit rate –

Distance \(=\frac{50 \text { miles }}{2 \text { hour }}\)

= 25 miles per hour

Here, 25 miles per hour is the unit rate.

The ratios, rates, and unit rates are used to solve problems in order to compare varying quantities by determining the number of units of one quantity per one unit of another quantity.

Question. Jennifer is a lifeguard at the same pool. She earns $137.25 for 15 hours of lifeguarding. Determine how much Jennifer earns per hour.

Given that, Jennifer is a lifeguard at the same pool. She earns $137.25 for 15 hours of lifeguarding.

We need to determine how much Jennifer earns per hour.

Finding the unit rate of Jennifer, we get

= 9.15 dollars per hour

Jennifer earns $9.15 per hour.

Question. A kitchen sink faucet streams 0.5 gallons of water in 10 seconds. A bathroom sink faucet streams 0.75 gallons of water in 18 seconds. Find which faucet will fill a 3-gallon container faster.

Given that, A kitchen sink faucet streams 0.5 gallons of water in 10 seconds.

A bathroom sink faucet streams 0.75 gallons of water in 18 seconds.

We need to find which faucet will fill a 3−gallon container faster.

The rate of kitchen sink faucet is:

​\(\frac{\text { Number of gallons of water }}{\text { Number of seconds }}=\frac{0.5}{10}\)

= 0.05 gallons of water per second.

The rate of bathroom sink faucet is:

​\(\frac{\text { Number of gallons of water }}{\text { Number of seconds }}=\frac{0.75}{18}\)

= 0.042 gallons of water per second
​
The rate of bathroom sink faucet is more. This means that the bathroom sink faucet fills faster.

The bathroom sink faucet will fill a 3−gallon container faster.

Envision Math Grade 7 Chapter 3 Proportional Relationships Worksheet Solutions

Question. Explain how are ratios, rates, and unit rates used to solve problems.

We need to explain how are ratios, rates, and unit rates used to solve problems.

A rate is nothing but a measurement between two different quantities.

A ratio is a measurement between two same quantities.

A unit rate is a rate at which one quantity differs per unit of another quantity.

Examples are:

Rate –

Distance \(=\frac{\text { Speed }}{\text { Time }}\)

Here, speed and time are of different quantities. Ratio – \(\frac{x}{y}\)

Unit rate –

Distance \(=\frac{50 \text { miles }}{2 \text { hour }}\)

=  25 miles per hour

Here, 25 miles per hour is the unit rate.

The ratios, rates, and unit rates are used to solve problems in order to compare varying quantities by determining the number of units of one quantity per one unit of another quantity.

Question. Dorian buys 2 pounds of almonds for $21.98 and 3 pounds of dried apricots for $26.25. Which is less expensive per pound? How much less expensive?

Given:

Dorian buys 2 pounds of almonds for $21.98 and 3 pounds of dried apricots for $26.25.

To find/solve:

Which is less expensive per pound? How much less expensive?

Almonds:

= \(\frac{21.98 \div 2}{2 \div 2}\)

= \(\frac{10.99}{1}\)

Apricots:

= \(\frac{26.25 \div 3}{3 \div 3}\)

= \(\frac{8.75}{1}\)

Now equivalent ratios we get,  10.99 – 8.75  =  2.24, Apricots for 2.24

Apricots for 2.24.

Question. Krystal is comparing two internet service plans. Plan 1 cost $34.99 per month. Plan 2 costs $134.97 every 3 months. Find the krystal plans to stay with one service plan for 1 year, which should she choose? How much will she save?

Given:

Krystal is comparing two internet service plans.

Plan 1 cost $34.99 per month. Plan 2 costs $134.97 every 3 months.

To find/solve:

If Krystal plans to stay with one service plan for 1 year, which should she choose? How much will she save?

Plan 1 :

= \(\frac{34.99 .12}{1.12}\)

= \(\frac{419.88}{12}\)

Plan 2 :

= \(\frac{134.97 \div 3}{3 \div 3}\)

= \(\frac{44.99}{1}\)

Now finding equivalent ratios. Plan 1 is cheaper for 539.88 – 419.88 = 120.

In plan 1 she will save.

Analyze And Use Proportional Relationships Grade 7 Envision Math

Question. Pam read 126 pages of her summer reading book in 3 hours. Zack read 180 pages of his summer reading book in 4 hours. Find they continue to read at the same speeds, will they both finish the 215 page book after 5 total hours of reading?

Given:

Pam read 126 pages of her summer reading book in 3 hours.

Zack read 180 pages of his summer reading book in 4 hours.

To find/solve:

If they continue to read at the same speeds, will they both finish the 215-page book after 5 total hours of reading?

Pam:

=\(\frac{126 \div 3}{3 \div 3}\)

Zack:

=\(\frac{180 \div 4}{4 \div 4}\)

She reads 42 pages per hour and he reads 45 pages per hour. Hence only Zack will finish.

Zack will finish.

Question. Megan walked 5 miles; her activity tracker had counted 9,780 steps. David’s activity tracker had counted 11,928 steps after he walked 6 miles. Find the steps for 1 mile.

Given:

Megan walked 5 miles; her activity tracker had counted 9,780 steps. David’s activity tracker had counted 11,928 steps after he walked 6 miles.

We know that:

Megan’s steps:

We find the steps for 1 mile:

Steps \(=\frac{9780}{5}\)

Steps = 1956

Megan takes 1956 steps per mile.

David’s steps:

We find the steps for 1 mile:

Steps \(=\frac{11928}{6}\)

Steps = 1988

David walks 1988 steps per mile.

Therefore David takes more steps to walk a mile.

1988−1956 = 32 more steps to walk a mile.

David takes more steps to walk 1 mile. David takes 32 more steps.

Question. A package of 5 pairs of insulated gloves costs $29.45. Find the price for 1 glove.

A package of 5 pairs of insulated gloves costs $29.45.

We know that:

We find the price for 1 glove:

Price \(=\frac{29.45}{5}\)

Price = 5.89

A single pair of gloves cost $ 5.89.

Question. Yellow packet white rice costs $6.30 for 18 ounces, Blue packet white rice costs $4.46 for 12 ounces and the green packet of white rice costs $2.59 for 7 ounces. Find the price for 1 ounce of the yellow packet of white rice.

Given:

Yellow packet white rice costs $6.30 for 18 ounces.

Blue packet white rice costs $4.56 for 12 ounces.

The green packet of white rice costs $2.59 for 7 ounces.

We know that:

We find the price for 1 ounce of the yellow packet of white rice:

Price \(=\frac{6.30}{18}\)

Price = 0.35

The price for 1 ounce of Yellow packet rice is $0.35.

We find the price for 1 ounce of the blue packet of white rice:

Price \(=\frac{4.56}{12}\)

Price = 0.38

The price for 1 ounce of Blue packet rice is $0.38.

We find the price for 1 ounce of the green packet of white rice:

Price \(=\frac{2.57}{7}\)

Price = 0.36

The price for 1 ounce of Green packet rice is $0.36.

The yellow package has the lowest cost per ounce of rice.

Question. The 5 panes cost $14.25. She breaks 2 more panes while repairing the damage. Find the cost for 1 pane of glass.

Given:

The 5 panes cost $14.25.

She breaks 2 more panes while repairing the damage.

We find the cost for 1 pane of glass:

Cost \( = \frac{14.25}{5}\)

Cost = 2.85

The cost for 1 pane of glass is $2.85.

We find the cost of 2 panes of glass:

Cost = 2.85 × 2

Cost = 5.7

The cost for 2 panes of glass is $5.70.

Question. The fare for 36 miles is $25.20. Find the cost per mile.

Given:

The fare for 36 miles is $25.20.

We first find the cost per mile:

Cost \(=\frac{25.20}{36}\)

Cost = 0.7

The cost per mile is 25.20.

Therefore, the required fare is

\(=\frac{25.20}{36}\)\(=\frac{x}{47}\)

x = 33.92

The fare for a 47-mile ride is $33.92

Therefore, the cost per mile is $0.7 and the fare for 47 miles is $33.92.

Envision Math Grade 7 Exercise 3.1 Solution Guide

Question. Company A has 12 tigers for $33.24. Company B has 6 tigers for $44.80 and Company C 15 tigers for $41.10. Find the cost per tiger for all the companies.

Given:

Company A: 12 tigers for $33.24.

Company B: 16 tigers for $44.80.

Company C: 15 tigers for $41.10.

We first find the cost per tiger for all the companies:

Company A

Cost = \(\frac{33.24}{12}\)

Cost = 2.77

The cost per tiger for Company A is $2.77.

Company B

Cost = \(\frac{44.80}{16}\)

Cost = 2.8

The cost per tiger for Company B is $2.80.

Company C

Cost = \(\frac{41.10}{15}\)

Cost = 2.74

The cost per tiger for Company C is $2.74.

Company C has the lowest cost per tiger.

Therefore, Company C has the lowest cost per tiger.

Given:

Company C  15 tigers for $41.10.

The cost per tiger for Company C is $2.74.

The students plan to sell the tigers for $5 each.

We know that the lowest cost per tiger is $2.74 for company C.

The students sell the mascots according to $5.

Therefore the profit that the students will make for each tiger they sell is:

profit  =  5−2.74

profit  =  2.26

Therefore, the students will obtain the profit of $2.26 for each tiger they sell.

Question. A contractor purchases 7 dozen pairs of padded work gloves for $103.32. He incorrectly calculates the unit price at $14.76 per pair. Find the cost of 1 unit pair of padded work gloves.

Given:

A contractor purchases 7 dozen pairs of padded work gloves for $103.32.

He incorrectly calculates the unit price at $14.76 per pair.

To find the cost of 1 unit pair of padded work gloves, we divide $103.32 by 84

Cost = \(\frac{103.32}{84}\)

Cost  =  1.23

Therefore, the cost of 1 unit pair of padded work gloves is $1.23.

Therefore, the unit price is $1.23.

Given:

A contractor purchases 7 dozen pairs of padded work gloves for $103.32.

He incorrectly calculates the unit price at $14.76 per pair.

To find the cost of 1 unit pair of padded work gloves, we divide $103.32 by 84

Cost = \(\frac{103.32}{84}\)

Cost = 1.23

Therefore, the cost of 1 unit pair of padded work gloves is $1.23.

He should have divided the total price by 84 since he bought 7 dozen pairs of gloves and 1 dozen equals to 12 units.

Therefore, the error the contractor was likely to make is total number of units. He should remember that there are 84 units and 7 dozen pair of gloves.

Question. A warehouse store sells 5.5-ounce cans of tuna in packages of 6 that cost $9.24. The store also sells 6.5 ounces cans of the same tuna in packages of 3 cans for $4.68. Find the cost of 1 ounce for each package.

Given:

A warehouse store sells 5.5-ounce cans of tuna in packages of 6 that cost $9.24.

The store also sells 6.5 ounces cans of the same tuna in packages of 3 cans for $4.68.

It also sells 3.5-ounce cans in packages of 4 cans for $4.48.

We find the cost of 1 ounce for each package:

Package 1: Cost = 9.24/(5.5 × 5) ​= 9.24/27.5 = 0.33​

Package 2: Cost = 4.68/(6.5 × 3) ​= 4.68/19.5 = 0.24​

Package 3: Cost = 4.48/(3.5 × 4)​ = 4.48/14 = 0.32​

We see that package 3 has the lowest cost per ounce of tuna that is $0.32.

Therefore, package 3 which cost $0.32 per ounce has the lowest cost per ounce of tuna.

Question. Irene’s car had 6 gallons of gas in its 15-gallon tank. Irene wants to fill it at least halfway. The gas costs $3.80 per gallon. Find the total gallon gas has filled.

Given:

Irene’s car had 6 gallons of gas in its 15-gallon tank.

Irene wants to fill it at least halfway. The gas costs $3.80 per gallon.

Irene’s car has a capacity of 15 gallons and it already has 6 gallons of gas filled.

Therefore the remaining capacity of the car’s tank is 9 gallons.

Irene wants to fill the tank at least halfway.

The half of the tank is 7.5 gallons.

We need 1.5 gallons to fill the tank halfway.

If Irene fill her tank it would cost her 9×3.80=34.20$

Therefore, Irene does not need more than 1.5 gallons of gas, and if Irene adds $3.80 and $7.60 worth

Envision Math Accelerated Grade 7 Chapter 3 Practice Answers

Envision Math Accelerated Grade 7 Volume 1  Chapter 3 Analyze And Use Proportional Relationships

Given:

Statement

To find/solve

Proportional relationships can be recognized by using the terms.

Terms are numbers compared in ratios.

Terms can be used to compare and solve the problem using this ratio.

Terms can be used to compare and solve the problem using this ratio.

Given:

Statement

To find/solve

If 2 values have a constant multiple (constant of proportionality ) and can be written as y = kx equation they are proportional (they have a proportional relationship).

Access to safe drinking water is measured by the percentage of the population having access to and using improved drinking water sources.

Improved drinking water sources should, but do not always, provide safe drinking water, and include piped household water connection, and public standpipes.

Question. Solve the given two ratios \(\frac{2 \text { dogs }}{3 \text { cats }}=\frac{2}{3}\) \(\frac{10 \text { dogs }}{15 \text { cats }}=\frac{10}{15}\)

Solve the given two ratios, and we get

=\(\frac{2}{3}\)

Here, we can see that both ratios result in the same answer.

Thus, the given ratios are equivalent to each other.

Thus, they are equivalent ratios.

\(\frac{2 \text { dogs }}{3 \text { cats }}\) and \(\frac{10 \text { dogs }}{15 \text { cats }}\) are an example of equivalent ratios.

The rate comes under the category of ratios.

But all ratios cannot be described as rates.

This is because the ratio deals with the same or different quantities.

While the rate deals with two different quantities.

For example, if we compare speed and distance together, the fraction is said to be the rate. Since the unit of both of them are different.

A rate is a type of ratio that has both terms expressed in different units.

A fraction is said to be the comparison of two quantities.

If we have a fraction in the fraction itself, it is then said to be a complex fraction.

A complex fraction has a fraction in the numerator, denominator, or in both of them.

For example: \(\frac{5}{\frac{12}{7}}\), \(\frac{\frac{8}{7}}{4}\) are some of the examples of the complex fractions.

A complex fraction has a fraction in its numerator, denominator, or both.

Question. Solving the equivalent ratio \(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{? \text { girls }}\)

We need to complete the given equivalent ratio \(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{? \text { girls }}\)

Solving the given equivalent ratio, we get

x = \(8 \times \frac{7}{4}\)

x = 2 × 7

x = 14 girls

Question. Solving the equivalent ratio \(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{? \text { tıres }}{1 \text { car }}\)

We need to complete the given equivalent ratio \(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{? \text { tıres }}{1 \text { car }}\)

Solving the given equivalent ratio, we get

x  =  \(\frac{16}{4}\)

x  =  4 tires

Question. Solving the equivalent ratio \(\frac{8 \text { correct }}{10 \text { total }} = \frac{? \text { correct }}{50 \text { total }}\)

We need to complete the given equivalent ratio \(\frac{8 \text { correct }}{10 \text { total }} = \frac{? \text { correct }}{50 \text { total }}\)

Solving the given equivalent ratio, we get

x  =  \(50 \times \frac{8}{10}\)

x  =  5 × 8

x  =  40 correct

Question. Solving the equivalent ratio \(\frac{16 \text { pearls }}{20 \text { opals }}=\frac{8 \text { pearls }}{? \text { opals }}\)

We need to complete the given equivalent ratio \(\frac{16 \text { pearls }}{20 \text { opals }}=\frac{8 \text { pearls }}{? \text { opals }}\)

Solving the given equivalent ratio, we get

\(\frac{16 \text { pearls }}{20 \text { opals }} = \frac{8 \text { pearls }}{? \text { opals }}\)
​
\(\frac{16}{20}=\frac{8}{x}\)

x  =  \(8 \times \frac{5}{4}\)

x  =  2 × 5

x  = 10 opals

Question. Solving the equivalent ratio \(\frac{7 \text { balls }}{9 \text { bats }}=\frac{? \text { balls }}{27 \text { bats }}\)

We need to complete the given equivalent ratio \(\frac{7 \text { balls }}{9 \text { bats }}=\frac{? \text { balls }}{27 \text { bats }}\)

Solving the given equivalent ratio, we get

x  =  \(27 \times \frac{7}{9}\)

x  =  3 × 7

x  =  21 balls

Question. Write the given situation as a rate. John travels 150 miles in 3 hours. Find the rate at which John travels.

We need to write the given situation as a rate. Here, John travels 150 miles in 3 hours.

Finding the rate at which John travels, we get

= 50 miles per hour

John travels at the rate of 50 miles/hr

Question. Write the given situation as a rate. Here, Cameron ate 5 apples in 2 days. Find the rate at which Cameron eat.

We need to write the given situation as a rate. Here, Cameron ate 5 apples in 2 days.

Finding the rate at which Cameron eats, we get

= 2.5 apples per day

Cameron ate 2.5 apples per day.

Question. Write an equation that represents the pattern in the table. Find the rate of the given data.

We need to write an equation that represents the pattern in the table.

Finding the rate of the given data

\(\frac{y}{x}=\frac{12}{4}\) = 3

\(\frac{y}{x}=\frac{15}{5}\) = 3

\(\frac{y}{x}=\frac{18}{6}\) = 3

\(\frac{y}{x}=\frac{21}{7}\) = 3

\(\frac{y}{x}=\frac{24}{8}\) = 3

Therefore, the ratio is \(\frac{y}{x}=\frac{3}{1}\)

Thus, the equation of the pattern in the table will be

y = 3x

The equation that represents the pattern in the table will be  y = 3x