Alekhya

Financial Algebra 1st Edition Chapter 2 Modeling a Business

Page 108 Problem 1 Answer

Some states about Touchpad         Company: Hewlett Packard

Year released: 2011

Revenue yr. released: $126.0 billion

Touchpad Introduced in July 2011, the TouchPad was Hewlett Packard′s attempt to compete with Apple′s iPad.

With powerful video capability and impressive Processing speeds, the TouchPad was widely anticipated to be among the only products that could give Apple a run for its money.

Despite large-scale press events and promotions, the HP TouchPad was a colossal failure and was discontinued almost immediately.

As a result of the TouchPad′s failure, the company wrote off $885 million in assets and incurred an additional $755 million in costs to wind down its webOS operations, ending all work on the Touchpad’s failed operating system.

Since then, HP has continued to struggle to maintain its edge in the PC market. The once−dominant PC company is in the midst of a multi−year turnaround plan.

While the plan may have recently begun to bear fruit, investors remain cautious.

Name of the product is : Touchpad

The reason behind its rise and fall are mentioned above. The answers of individuals may vary.

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Page 109 Problem 2 Answer

The assessment involves an interview of a local businessperson.

Ask for examples of fixed and variable expenses. Do not ask for amounts as that information is private.

Make a comprehensive list. Also ask about the history of the business and how he or she became involved in it.

The interview of a business person is as follows

The most common fixed expenses are

Rent

Salaries

Electricity bill

Water bill

Natural gas bill

Telephone bill

Transportation

Property expenses

InsuranceInterest expenses etc

Variable Expenses

Raw materials for the production of some product

Credit card fees

Commissions supplies and

production piece rate labor etc

The answer of individuals may vary.

Page 109 Problem 3 Answer

Report is as follows

The top 10  Best Selling Beatles singles are:

She Loves You

Want To Hold Your Hand

Can′t Buy Me Love

I Feel Fine

Day Tripper/We Can Work It Out

Hey Jude

Help!

From Me To You

Hello Goodbye

Get back

According  to some Statistics found online, the Beatles earned approximately 71 million dollars this year and thus it appears that Decca′s decision was a wrong decision as the Beatles were a lot more profitable than expected in 1962.

If a product is released at the wrong time (too early or too late), then the product is more likely to fail.

Decca′s decision was based on the fact that guitar groups were expected to no longer be popular, while this was not the case and thus Decca′s decision was based on the wrong timing.

Answers of individuals may vary.

Page 109 Problem 4 Answer             

Report is as follows

A brand name is a name given to a product or a range of products by the maker of the products.

For this assignment, you will need to get two copies of the same newspaper or magazine.

Then you will need to read through the newspaper/magazine to determine all brand names that are mentioned in the newspaper.

There are many possible brand names that will be mentioned.

For example, some of the most famous brand names are Coca-Cola, Lays, Lego, Burger King, McDonald′s, Google, Yahoo, Amazon, etc.

In general, I suspect that you will find dozens of different brand names in a newspaper or magazine.

Answers of the individuals may vary.

Cengage Financial Algebra 1st Edition Chapter 2 Assessment Modeling A Business Solutions

Page 109 Problem 5 Answer

Assessment is as follows

There are many different breakeven calculators available only. If you search for ”Breakeven calculator” using a search engine, then you will find many possible calculators.

For example, some breakeven calculators are:

https://www.calcxml.com/do/breakeven−analysis

https://goodcalculators.com/break−even−calculator/

https://www.omnicalculator.com/business/break−even

The calculator of calc xml requires the total fixed costs, the variable cost per unit, the sales price per unit and the anticipated unit sales.

The calculator will then return how many units you need to sell to cover your costs and your expected profit/loss and the expected number of sold units.

The calculator of good calculators requires the same input. The calculator will calculate your break even units, total costs, net profit and total revenue.

Moreover, the calculator will also create a table of possible units solds and the corresponds costs/profit.

The calculator of omnicalculators require the per unit costs and the fixed costs, but the calculator also allows us to take into account a markup or sell margin.

The calculator will then return us how many units need to be sold to breakeven and returns the corresponding revenue.

The answers of individuals may vary.

Page 109 Problem 6 Answer

Report is as follows

A profit is a financial benefit which is the result of revenue gained from business activity reduced by costs/expenses/taxes.

Profit is calculated as total revenue decreased by total expenses.

However different companies tend to define a profit in different manners.

The difference often lies in what is included in the total expenses/revenue and what is not included.

For example, some companies will include dividends paid out to shareholders as expenses (while other companies won′t), while other companies will not include the interest and taxes in their profit calculations (as they are interested in the profit when not taking into account the interest and taxes), etc.

Answers of individuals may vary.

Page 109 Problem 7 Answer

The fixed costs are costs that are constant no matter how many units you produce. Some possible fixed costs for a lemonade stand are then:

Setting up the stand (such as a table, chairs, etc.).

Creating a sign (such that people know that they can buy lemonade at the stand and how much it costs) etc

The variable costs are costs that depend on how many units you produce. Some possible variable costs for a lemonade stand are then:

Ingredients for lemonade: lemons, water, sugar

Plastic cups (to serve the lemonade in)

Containers for the lemonade (before being served). etc

The price at which you sell your lemonade should cover your fixed and variables costs.

You should determine the  fixed and variables costs per unit (glass of lemonade) by dividing the total costs by expected the number of sold  units (glasses of lemonade).

The price per glass of lemonade should then exceed the total costs per unit (glass of lemonade)

Answers of individuals may vary.

Page 110 Problem 8 Answer

We have given The following bar graph that gives the values of a 1958 Edsel Villager 9-Passenger Station Wagon during the years 1999-2008.

Because the value depends on the condition of the car, car appraisers rate the condition of a classic car.

On this graph, Condition 2 is the best condition and Condition 6 is the poorest condition.

The bar graph is

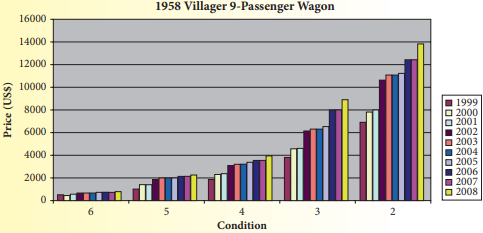
Here we will examine the bar graph and find the approximate value for the 1958 Villager in a condition of 6 in 2008 .

We note that condition 6 is at the very left side of the bar graph.

And the yellow column shows the condition of the car in 2008.

Thus approximate value for the 1958 Villager in a condition of 6 in 2008  = $800

The answer may vary because be take an approximate value.

The approximate value for the 1958 Villager in a condition of 6 in 2008  = $800

Page 110 Problem 9 Answer

We have given The following bar graph that gives the values of a 1958 Edsel Villager 9-Passenger Station Wagon during the years 1999-2008.

Because the value depends on the condition of the car, car appraisers rate the condition of a classic car.

On this graph, Condition 2 is the best condition and Condition 6 is the poorest condition.

The bar graph is

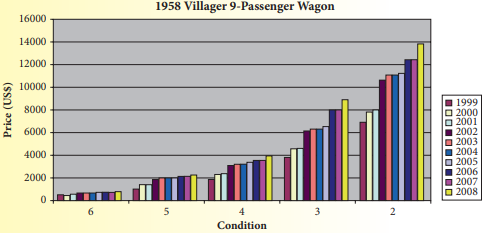
Here we will examine the bar graph and find the approximate value for the 1958 Villager in a condition of 2 in 2008 .

We note that condition 2 is at the very left side of the bar graph.

And the yellow column shows the condition of the car in 2008.

Thus approximate value for the 1958 Villager in a condition of 2 in 2008  = $14,000

The answer may vary because be take an approximate value.

The approximate value for the 1958 Villager in a condition of 6 in 2008  = $14,000

Page 110 Problem 10 Answer

We have given The following bar graph that gives the values of a 1958 Edsel Villager 9-Passenger Station Wagon during the years 1999-2008.

Because the value depends on the condition of the car, car appraisers rate the condition of a classic car.

On this graph, Condition 2 is the best condition and Condition 6 is the poorest condition.

The bar graph is

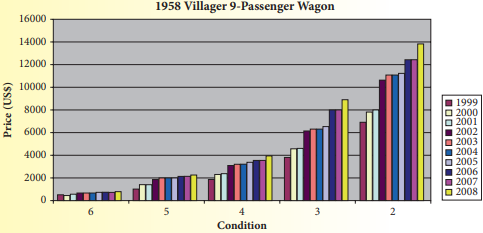
Here we will examine the bar graph and find the approximate difference between a 1958 Villager in a condition of 6 and in a condition of 2 in 2008.

From last two part we have

The approximate value for the 1958 Villager in a condition of 6 in 2008  = $800

The approximate value for the 1958 Villager in a condition of 2 in 2008  = $14,000

Thus the approximate difference between a 1958 Villager in a condition of 6 and in a condition of 2 in 2008 is

$14,000− $800

=      $13,200

The answer may vary because be take an approximate value.

The  approximate difference between a 1958 Villager in a condition of 6 and in a condition of 2 in 2008 is  $13,200

Cengage Financial Algebra Chapter 2 Assessment Modeling A Business Answers

Page 110 Problem 11 Answer

We have given The following bar graph that gives the values of a 1958 Edsel Villager 9-Passenger Station Wagon during the years 1999-2008.

Because the value depends on the condition of the car, car appraisers rate the condition of a classic car.

On this graph, Condition 2 is the best condition and Condition 6 is the poorest condition.

The bar graph is

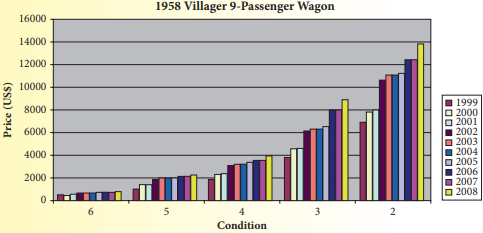
Here we will examine the bar graph and find the approximate difference between a 1958 Villager in a condition of 2  in 1999 and in 2008.

From the bar graph we have

The approximate value for the 1958 Villager in a condition of 2 in 1999 = $7000

The approximate value for the 1958 Villager in a condition of 2 in 2008  = $14,000

Hence difference is = $14,000 −$7000 = $7000

The answer may vary because be take an approximate value.

The  approximate difference between a 1958 Villager in a  condition of 2 in 1999 and in 2008 is  $7000

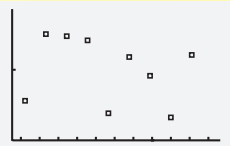
Page 111 Problem 12 Answer

Given scatter plot is

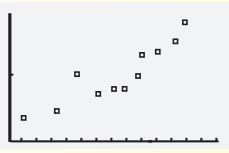
Here for identifying the correlation we will join the given point and check the slope.

If slope is positive then correlation is “positive correlation”.

If slope is negative then correlation is “negative correlation”.

If the line that going through the data points is horizontal then correlation is “no correlation”.

The scatter plot is

If we sketch a line through the given data points, this line will be increasing (positive slope) and thus the data shows a positive correlation.

The given scatter plot shows “positive correlation”.

Page 111 Problem 13 Answer

We have given scatter plot

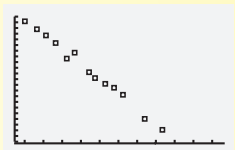
Here for identifying the correlation we will join the given point and check the slope.

If slope is positive then correlation is “positive correlation”.

If slope is negative then correlation is “negative correlation”.

If the line that going through the data points is horizontal then correlation is “no correlation”.

The given scatter plot is

If we sketch a line through the given data points, this line will be increasing (negative slope) and thus the data shows negative correlation.

The given scatter plot shows “negative correlation”.

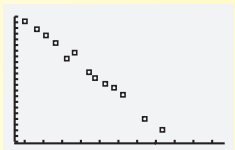
Page 111 Problem 14 Answer

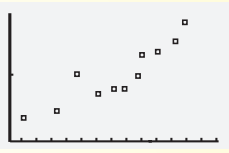
Given scatter plot is

Here for identifying the correlation we will join the given point and check the slope.

If slope is positive then correlation is “positive correlation”.

If slope is negative then correlation is “negative correlation”.

If the line that going through the data points is horizontal then correlation is “no correlation”.

The scatter plot is

If we sketch a line through the given data points, this line will be increasing (positive slope) and thus the data shows a positive correlation.

The given scatter plot shows “no correlation”.

Page 111 Problem 15 Answer

Given scatter plots are:

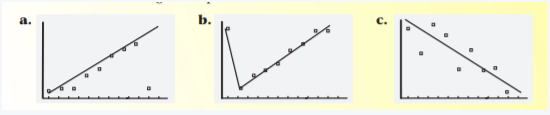
Need to tell which of the following scatter plots does not show a line of best fit.

As a line of best fit is a single line that best fits the scattered points.

The scatter plot(b) consist two lines segments, thus, consists of scattered points that do not lie on the same line.

Whereas in scatter plot(a) and© all the scattered points that lie on the same line.

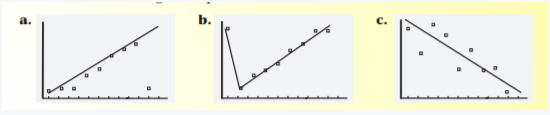
For the scatter plots:

The scatter plot(b)  does not show a line of best fit.

Page 111 Problem 16 Answer

Given correlation coefficient,r=0.17 .

Need to describe the given correlation coefficient using the terms strong, moderate, or weak and positive or negative.

As r=0.17 is positive, thus, the correlation is positive.

The absolute value of the given correlation coefficient,∣r∣=0.17, is less than 0.3, thus, the correlation is weak.

The correlation coefficient, r=0.17, represents a positive and weak correlation.

Page 111 Problem 17 Aswer

Given correlation coefficient,r=−0.62.

Need to describe the given correlation coefficient using the terms strong, moderate, or weak and positive or negative.

As r=−0.62 is negative, thus, the correlation is negative.

The absolute value of the given correlation coefficient is,∣r∣=0.62, and satisfies0.3≤r≤0.75, thus, the correlation is moderate.

The correlation coefficient,r=−0.62, represents a negative and moderate correlation.

Solutions For Cengage Financial Algebra Chapter 2 Assessment Modeling A Business

Page 111 Problem 18 Answer

Given the correlation coefficient,r=−0.88

Need to describe the given correlation coefficient using the terms strong, moderate, or weak and positive or negative.

As r=−0.88 is negative, thus, the correlation is negative.

The absolute value of the given correlation coefficient,∣r∣=0.88 , is more than0.75, thus, the correlation is strong.

The correlation coefficient,r=−0.88 , represents a negative and strong correlation.

Page 111 Problem 19 Answer

Given correlation coefficient,r=0.33

Need to describe the given correlation coefficient using the terms strong, moderate, or weak and positive or negative.

As r=0.33 is positive, thus, the correlation is positive.

The absolute value of the given correlation coefficient is,∣r∣=0.33, and satifies 0.3≤r≤0.75, thus, the correlation is moderate.

The correlation coefficient, r=0.33, represents a positive and moderate correlation.

Page 111 Problem 20 Answer

Given correlation coefficient, r=0.49.

Need to describe the given correlation coefficient using the terms strong, moderate, or weak and positive or negative.

As r=0.49 is positive, thus, the correlation is positive.

The absolute value of the given correlation coefficient is,∣r∣=0.49 , and satisfies 0.3≤r≤0.75, thus, the correlation is moderate.

The correlation coefficient, r=0.49, represents a positive and moderate correlation.

Page 111 Problem 21 Answer

Given correlation coefficient,r=−0.25.

Need to describe the given correlation coefficient using the terms strong, moderate, or weak and positive or negative.

As r=−0.25

is negative, thus, the correlation is negative. The absolute value of the given correlation coefficient,

∣r∣=0.25, is less than 0.3, thus, the correlation is weak.

The correlation coefficient,r=−0.25, represents a negative and weak correlation.

Page 111 Problem 22 Answer

Given correlation coefficient,r=0.91.

Need to describe the given correlation coefficient using the terms strong, moderate, or weak and positive or negative.

As r=0.91 is positive, thus, the correlation is positive.

The absolute value of the given correlation coefficient, ∣r∣=0.91, is more than0.75, thus, the correlation is strong.

The correlation coefficient,r=0.91, represents a positive and strong correlation.

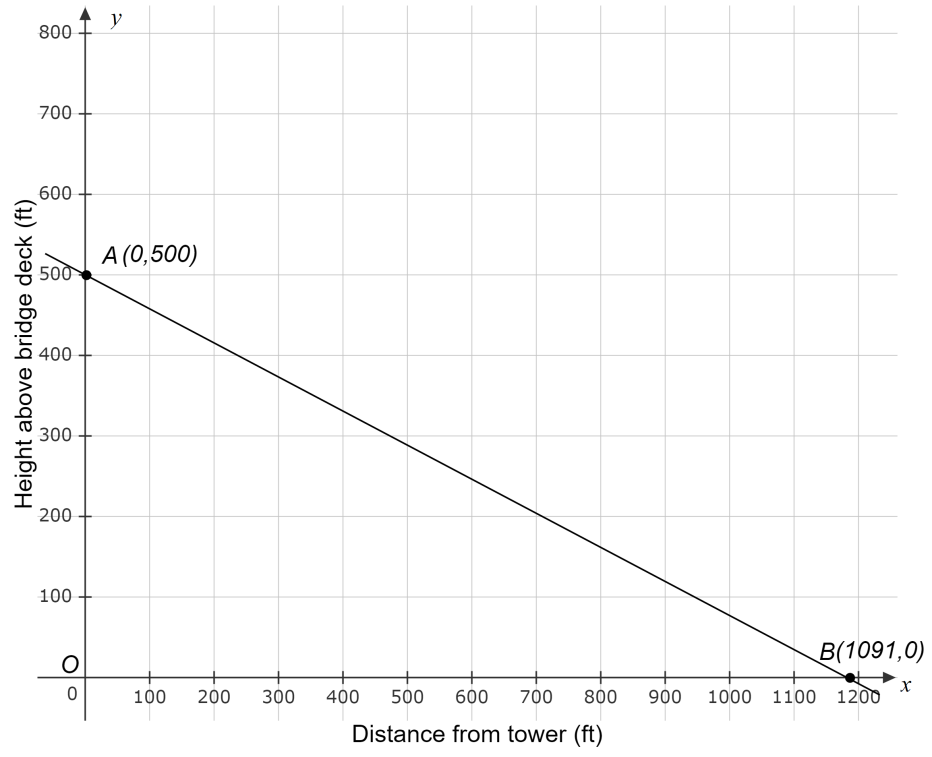
Page 112 Exercise 1 Answer

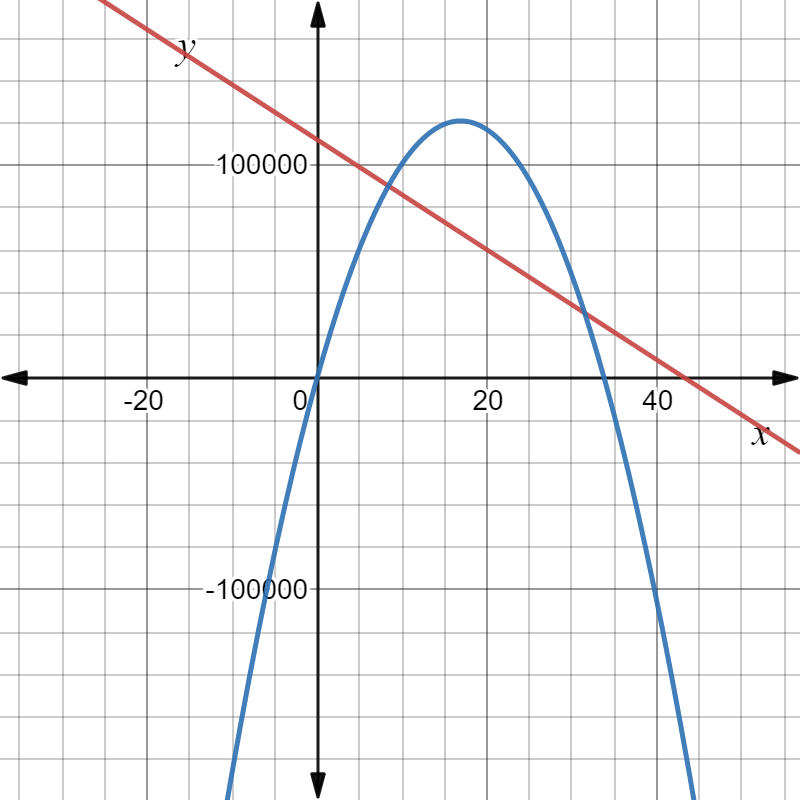
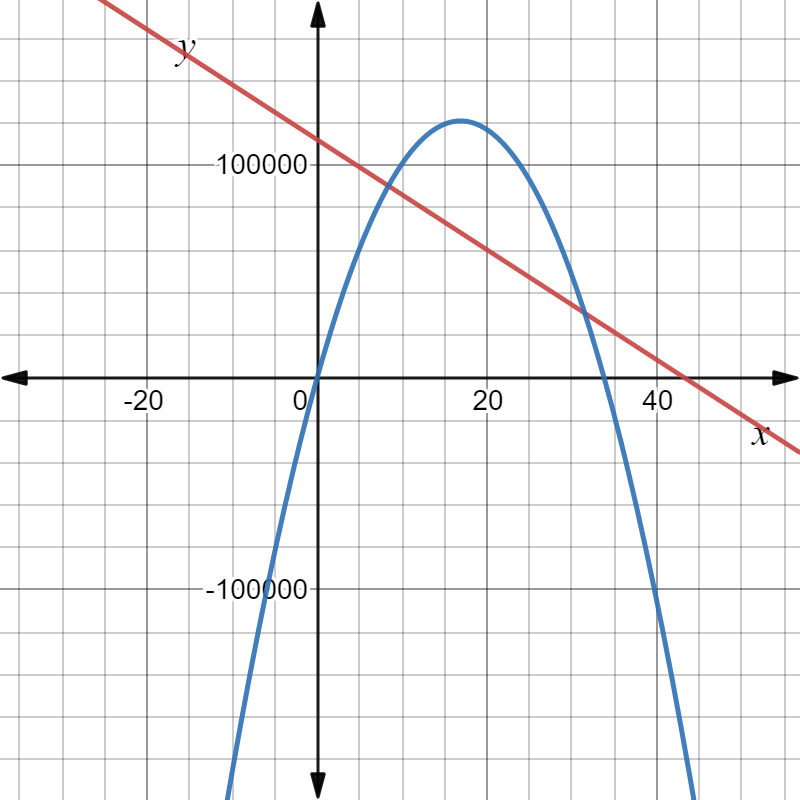
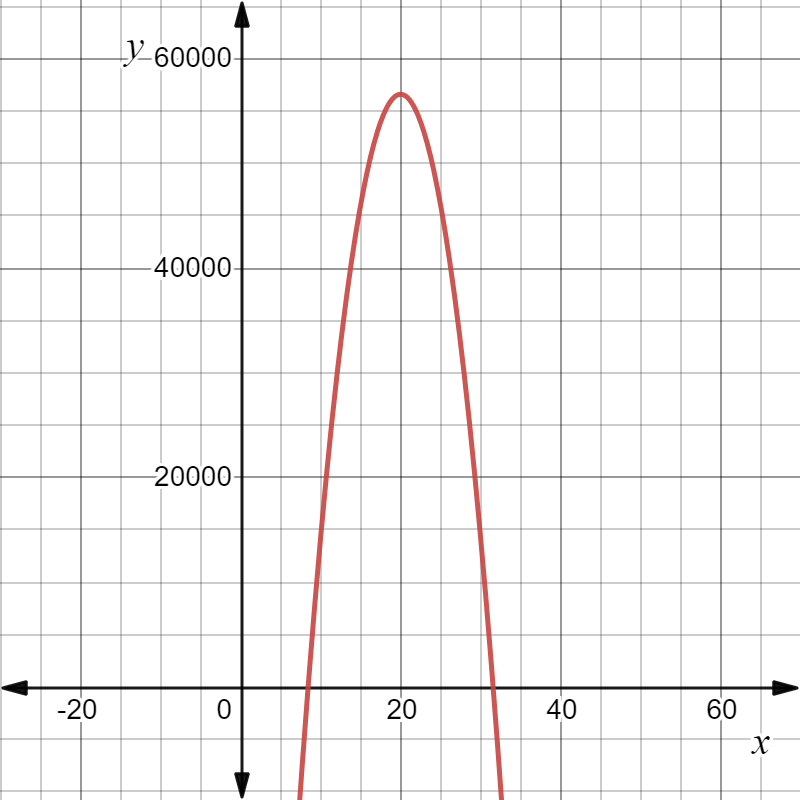
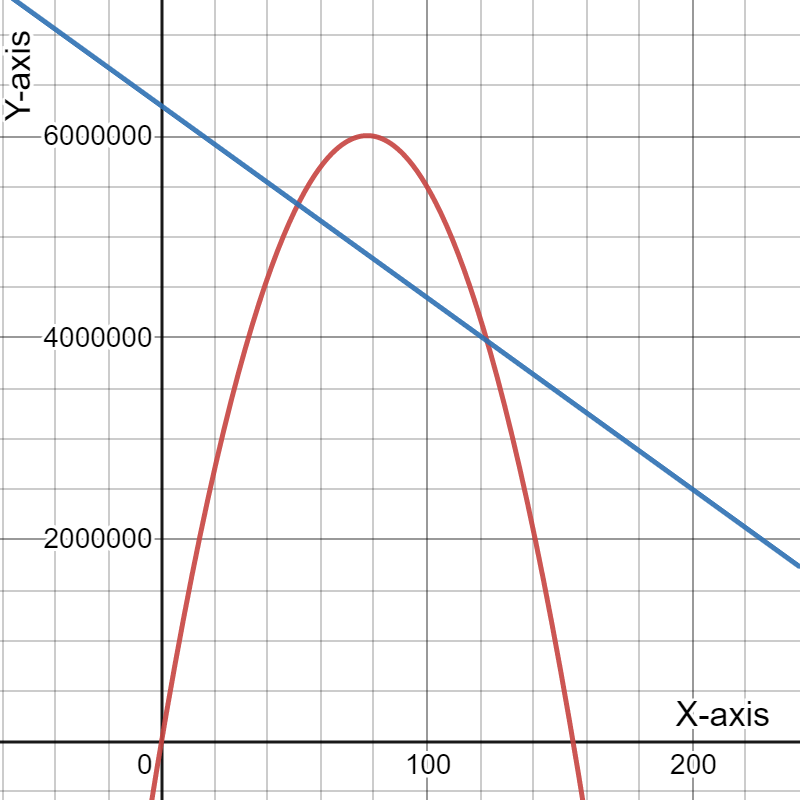
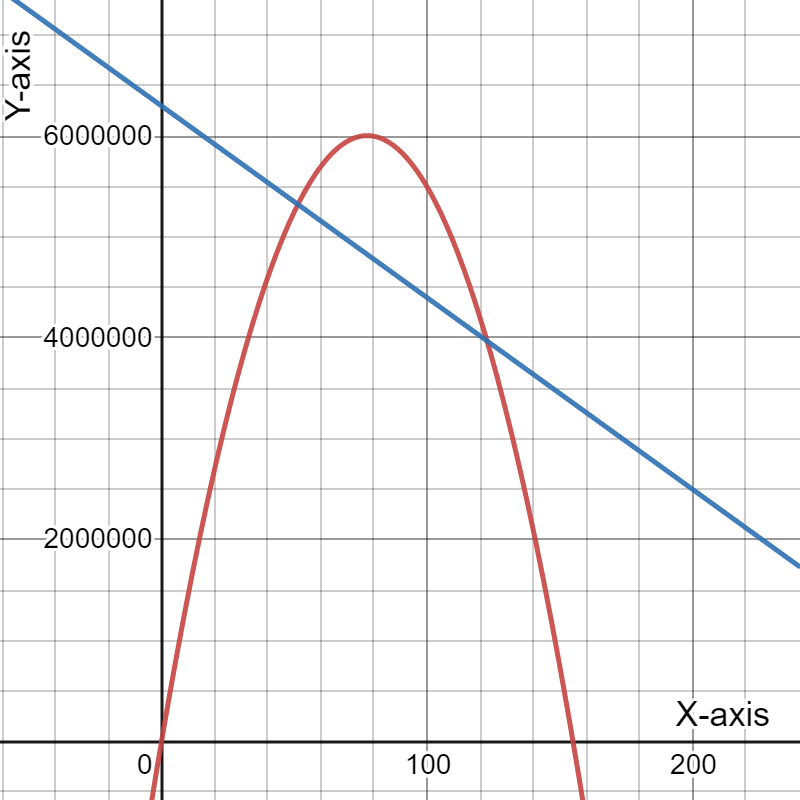
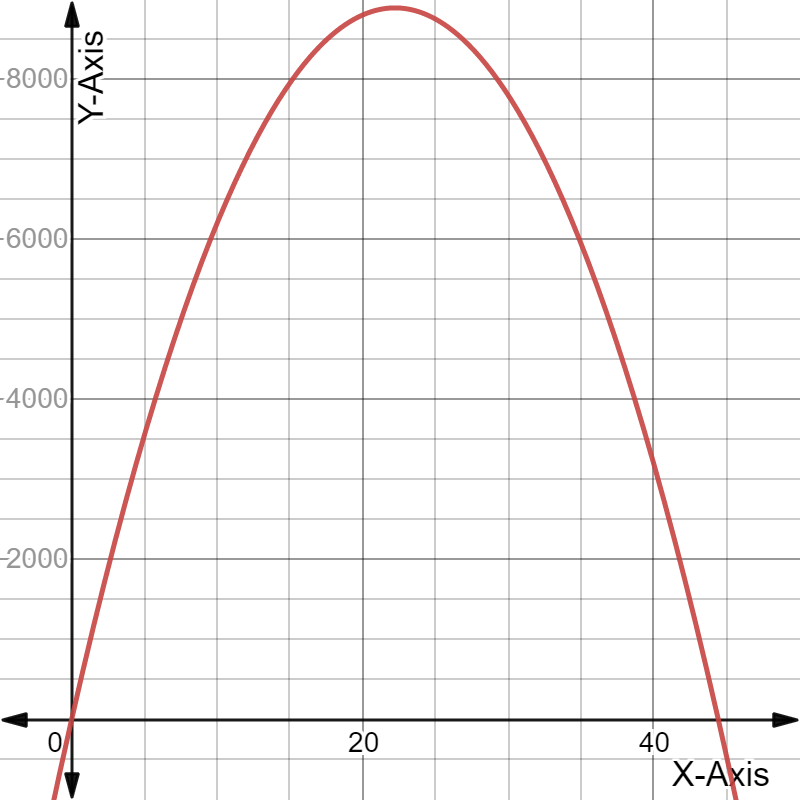
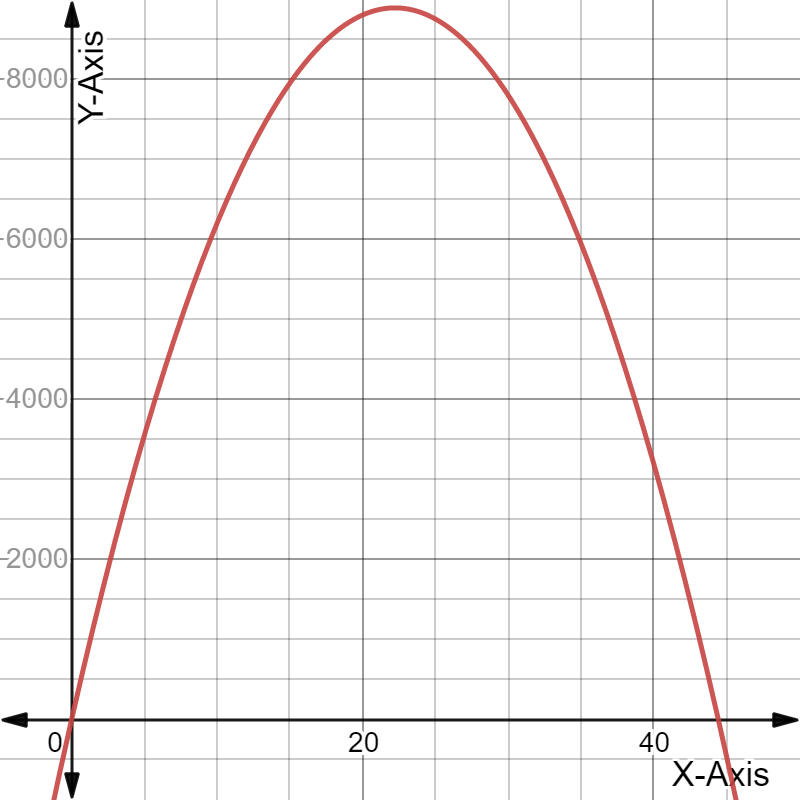
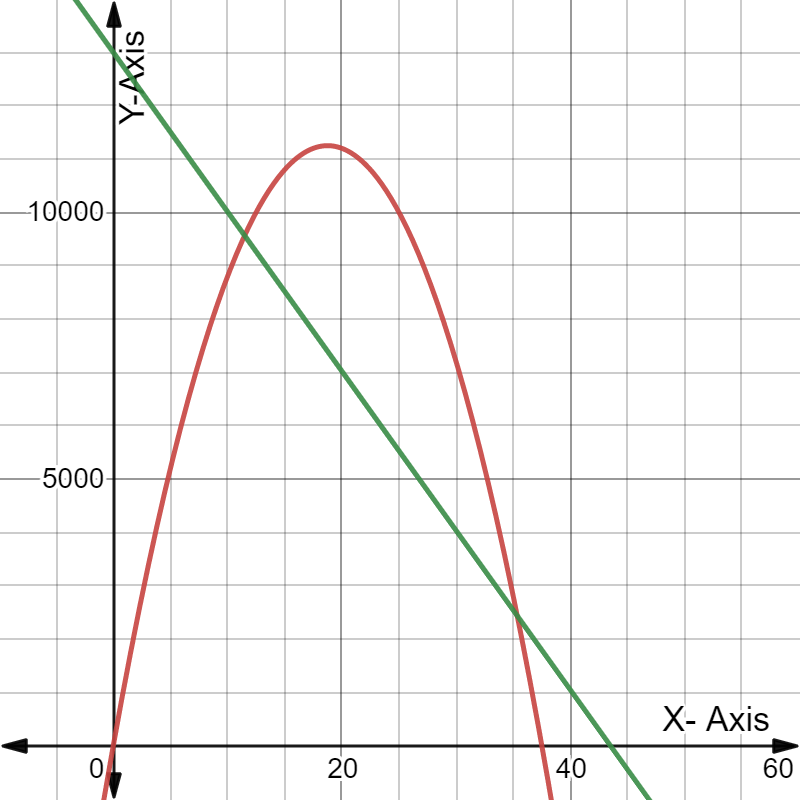
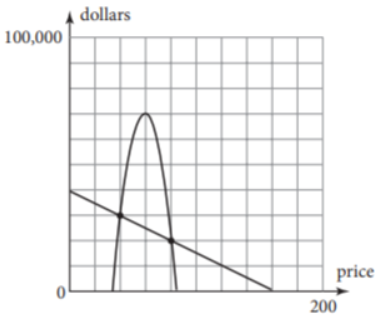
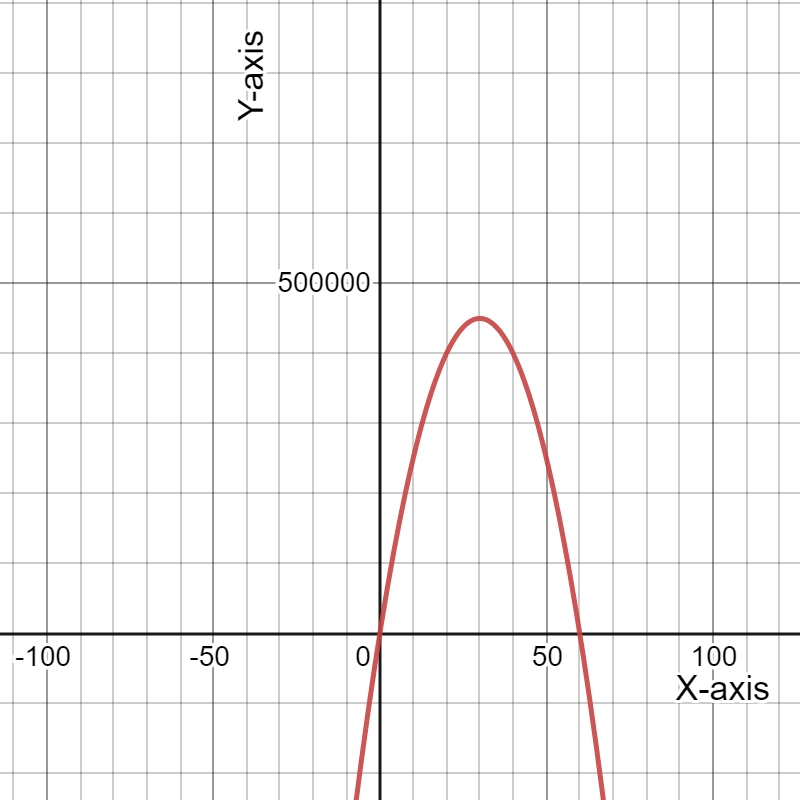
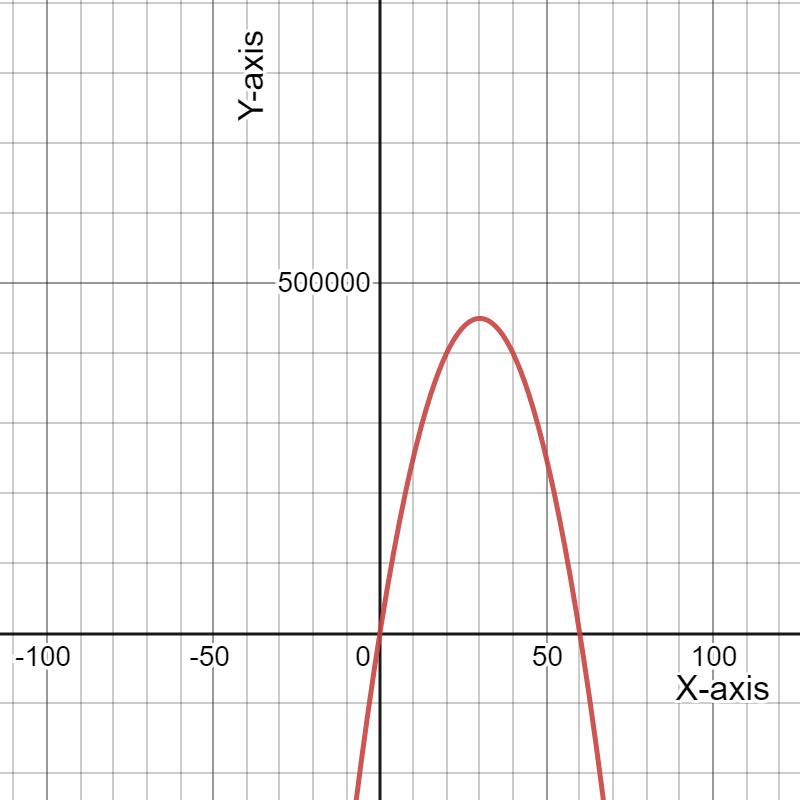
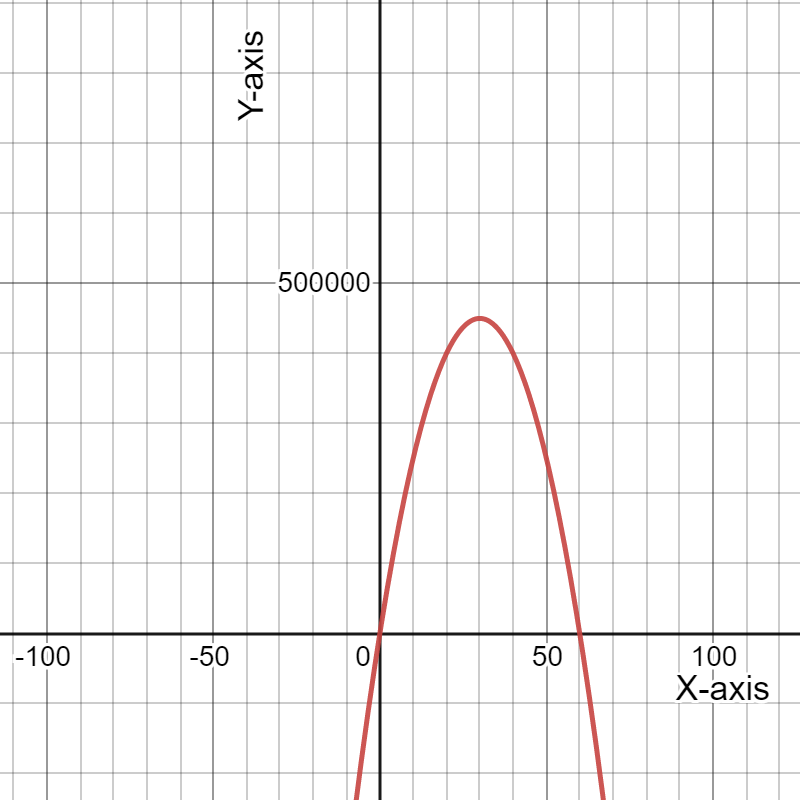
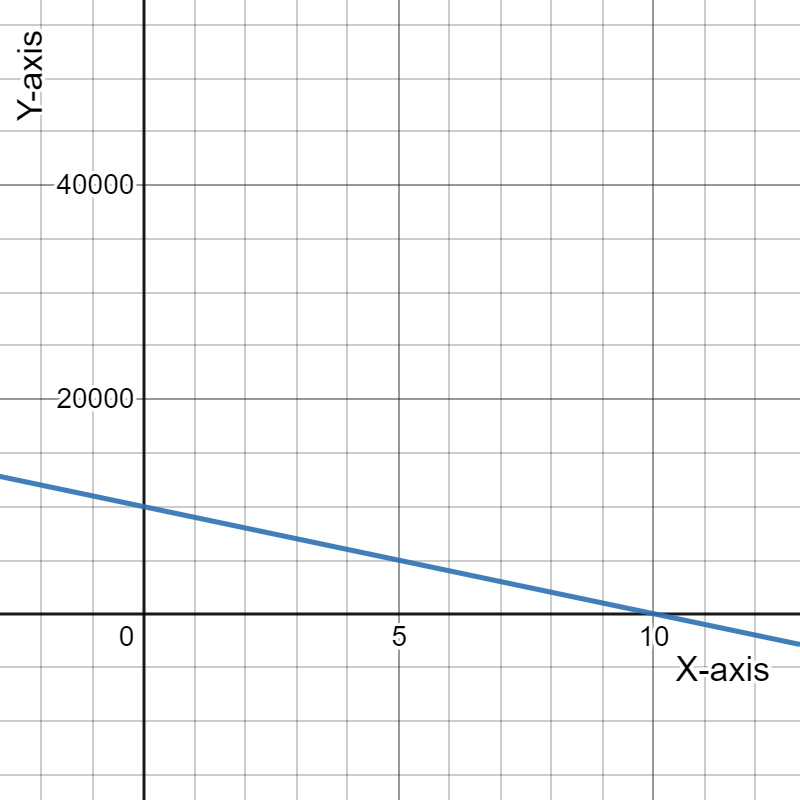
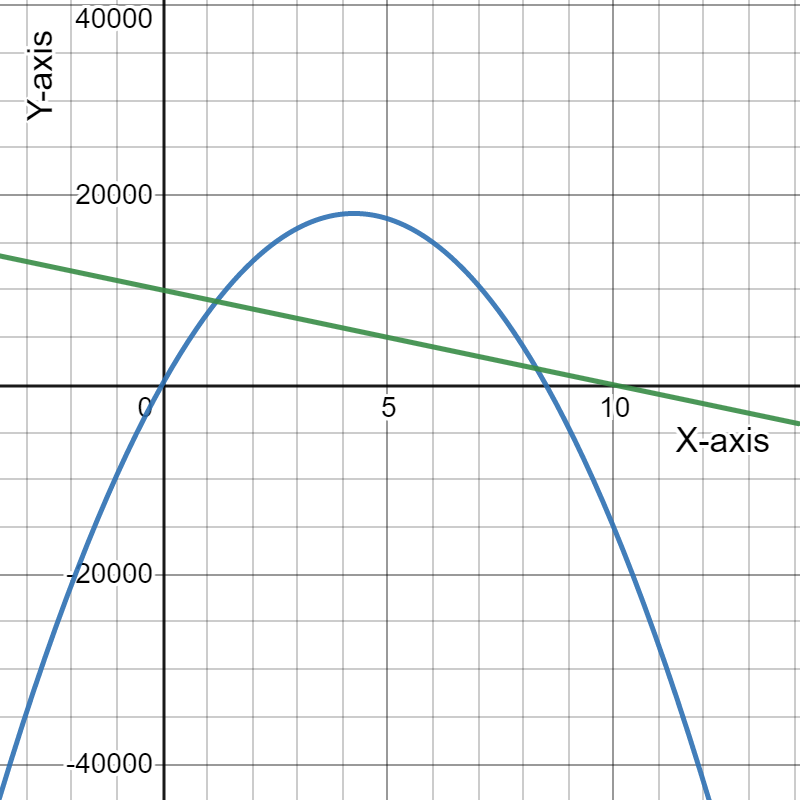
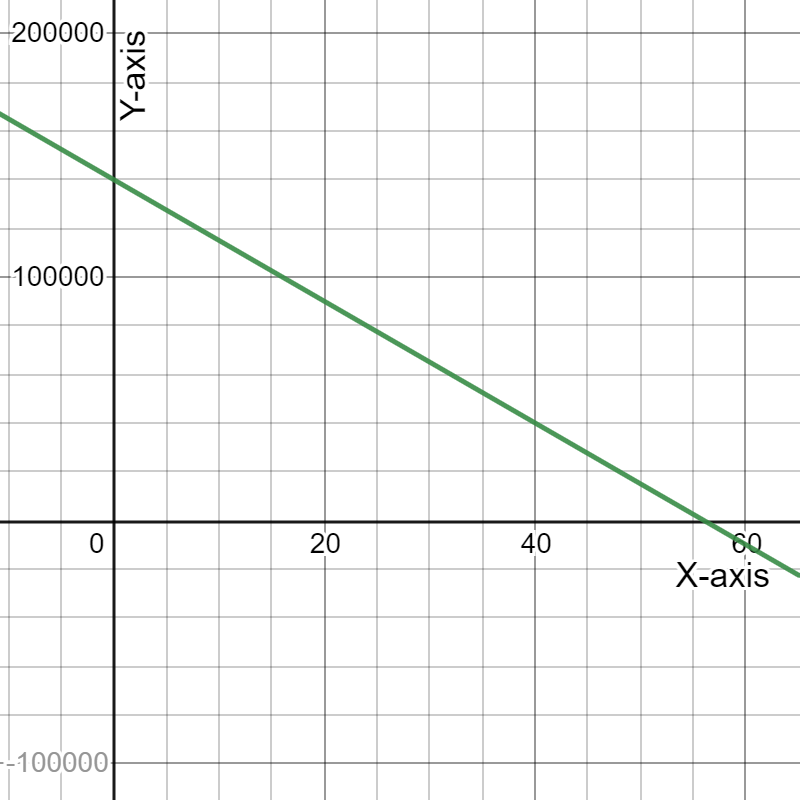
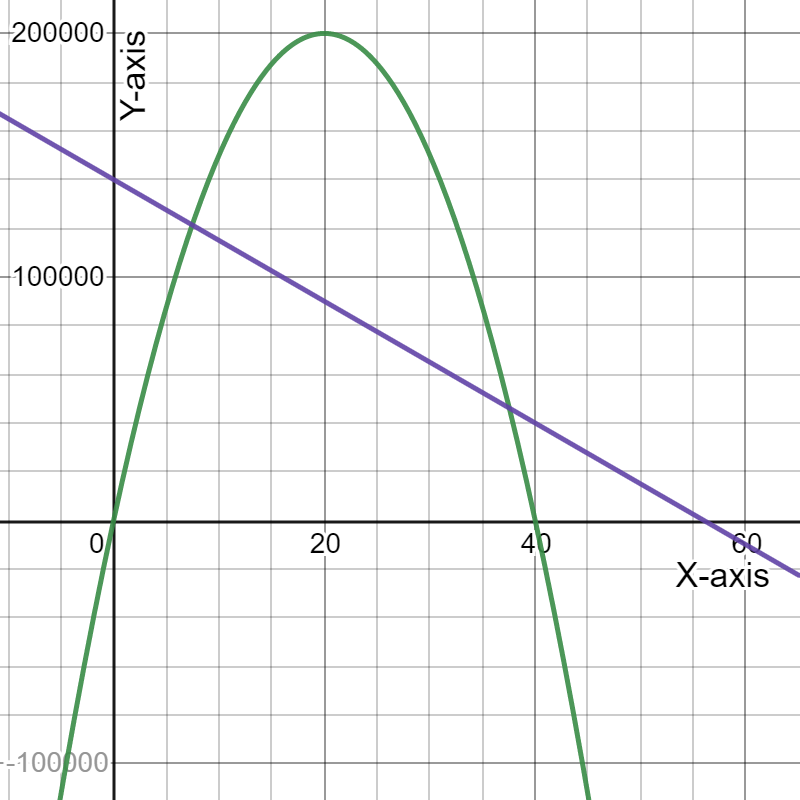
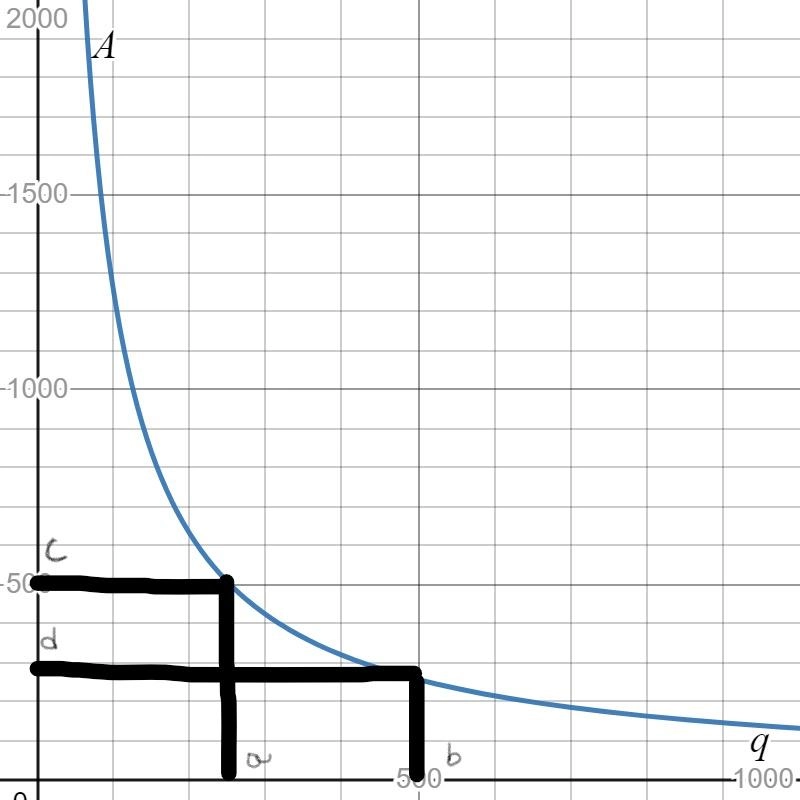
Given the expense function for a particular item be defined as y=−1,950x+53,000

and the revenue function be defined as y=−450x²+10,000x, where x represents price in each equation.

Graph the two functions using the window:

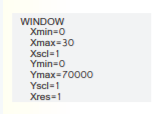
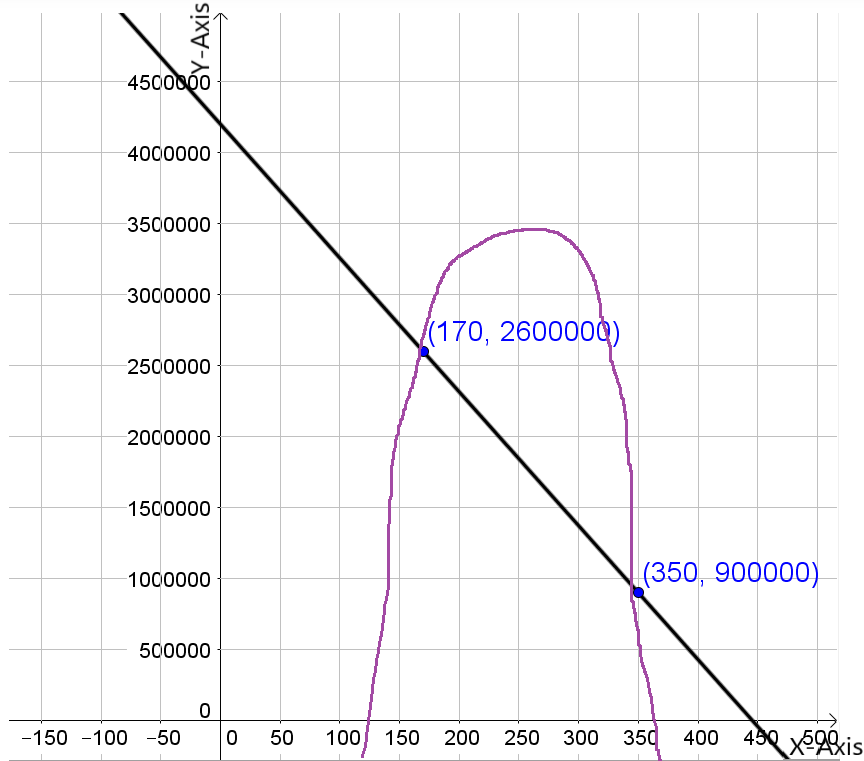
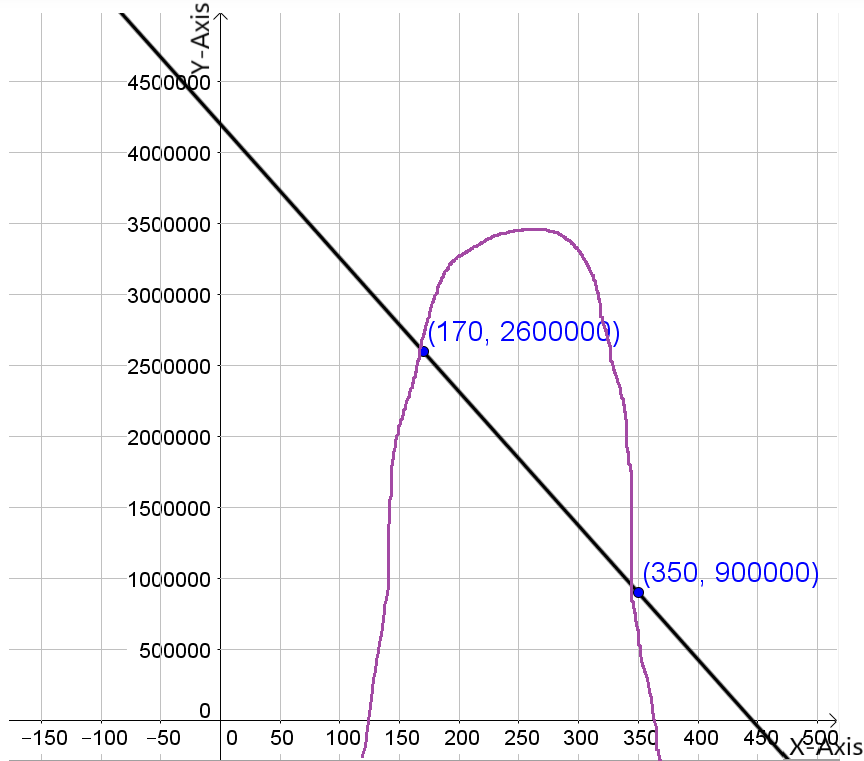
The graph the two functions using the above window is:

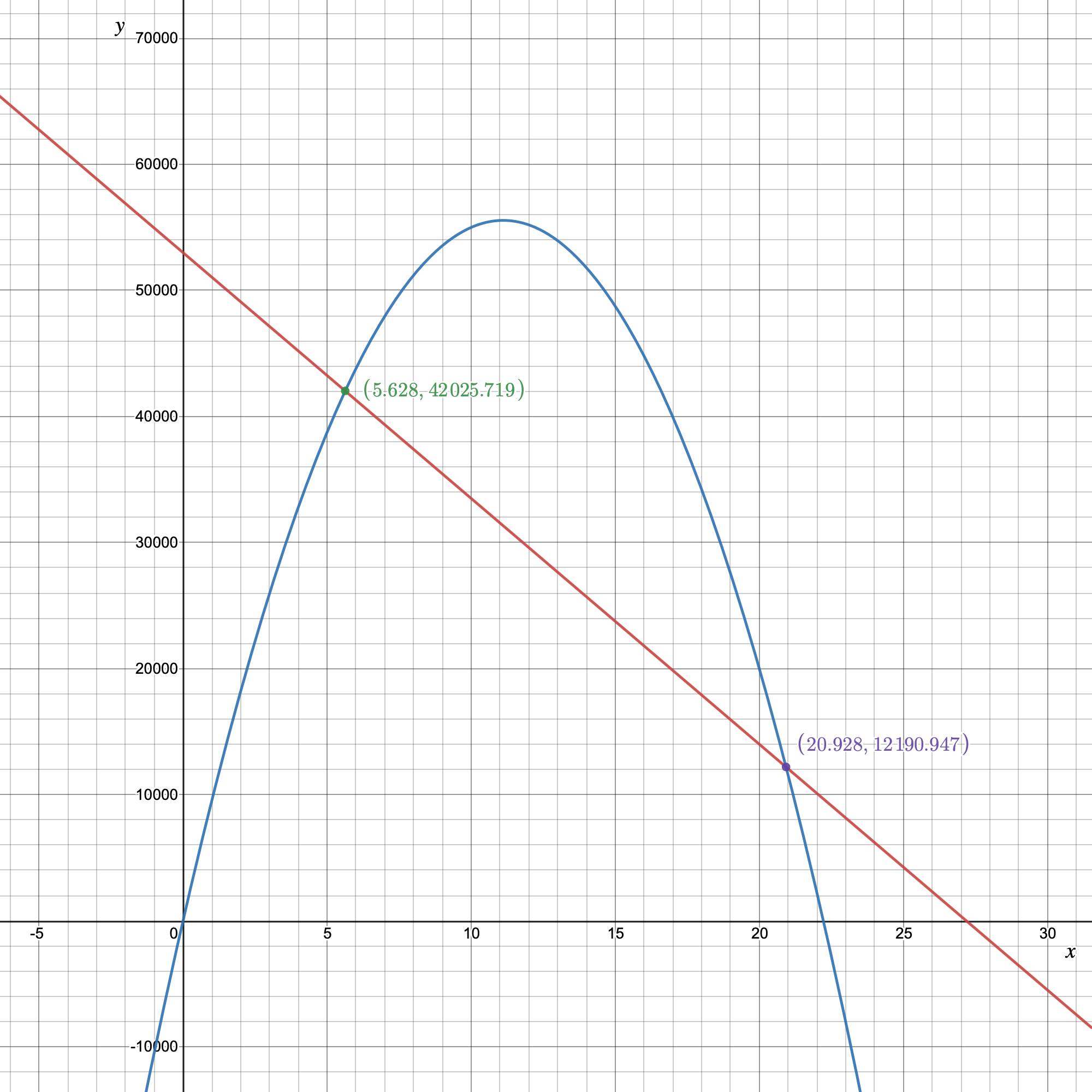
For the expense function for a particular item be defined as y=−1,950x+53,000 and the revenue function be defined as y=−450x²+10,000x.

The graph the two functions using the window:

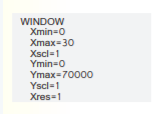
Page 112 Exercise  2 Answer

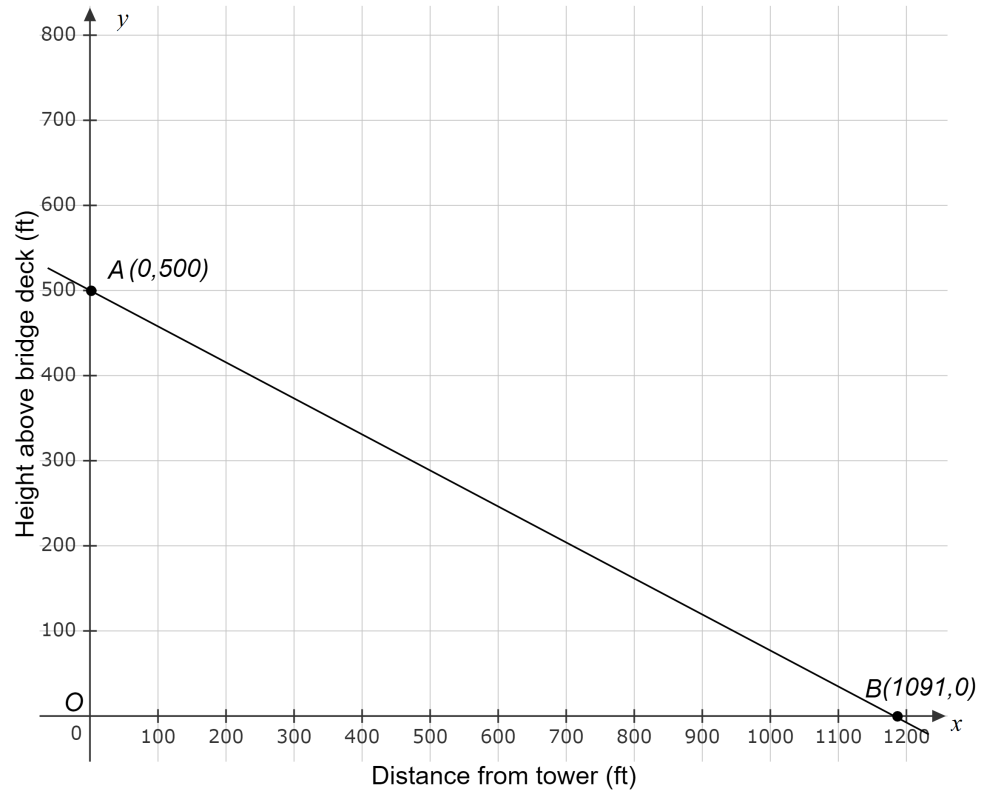
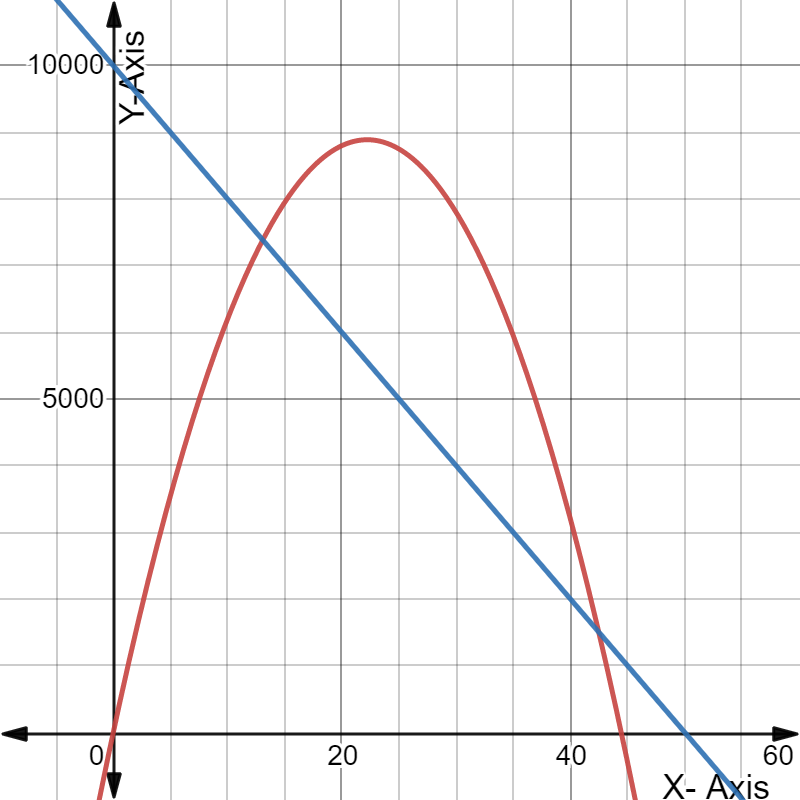
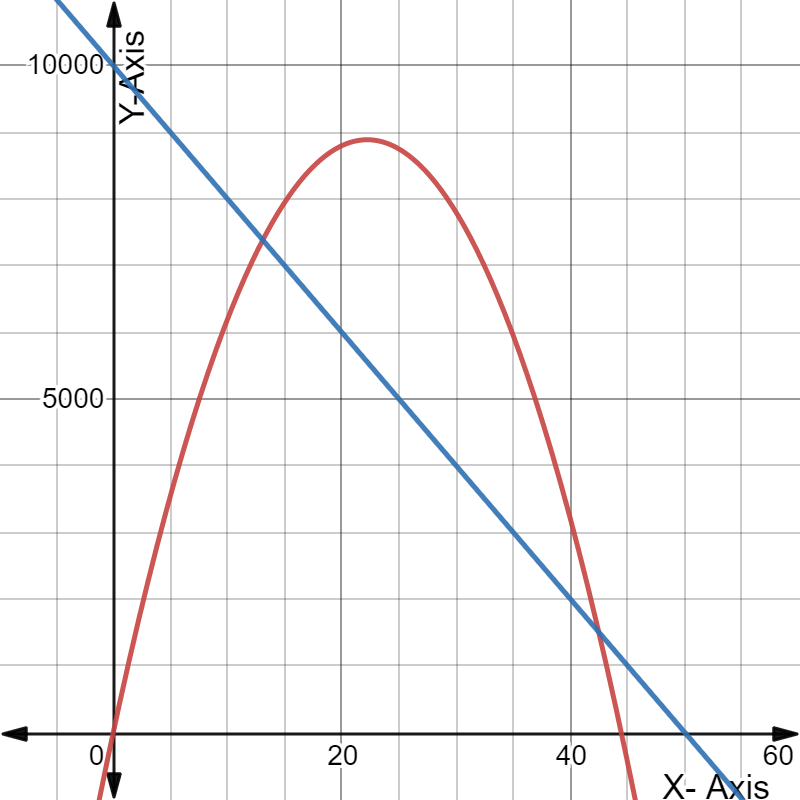
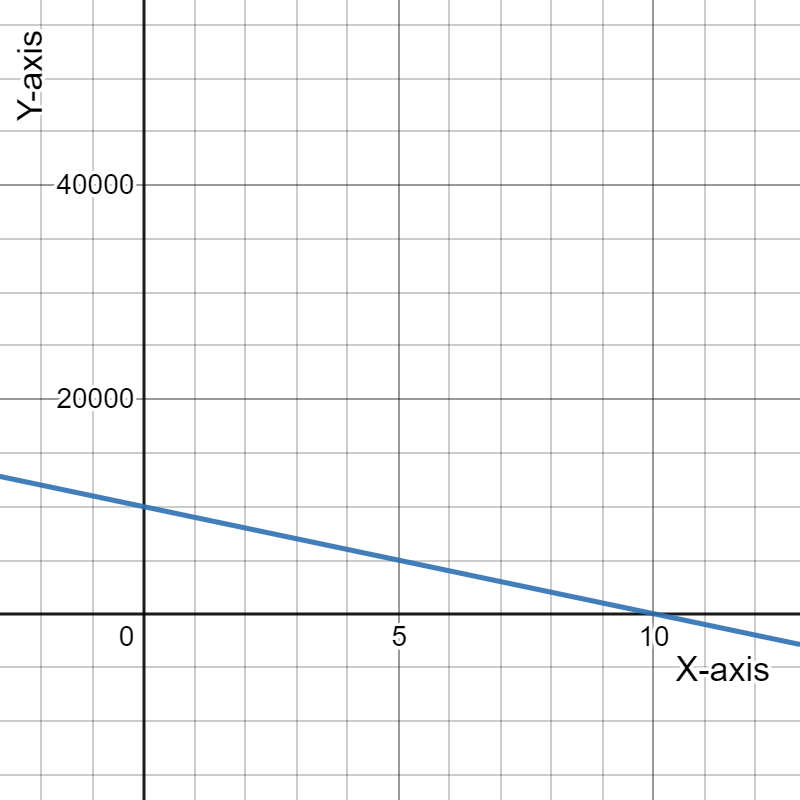
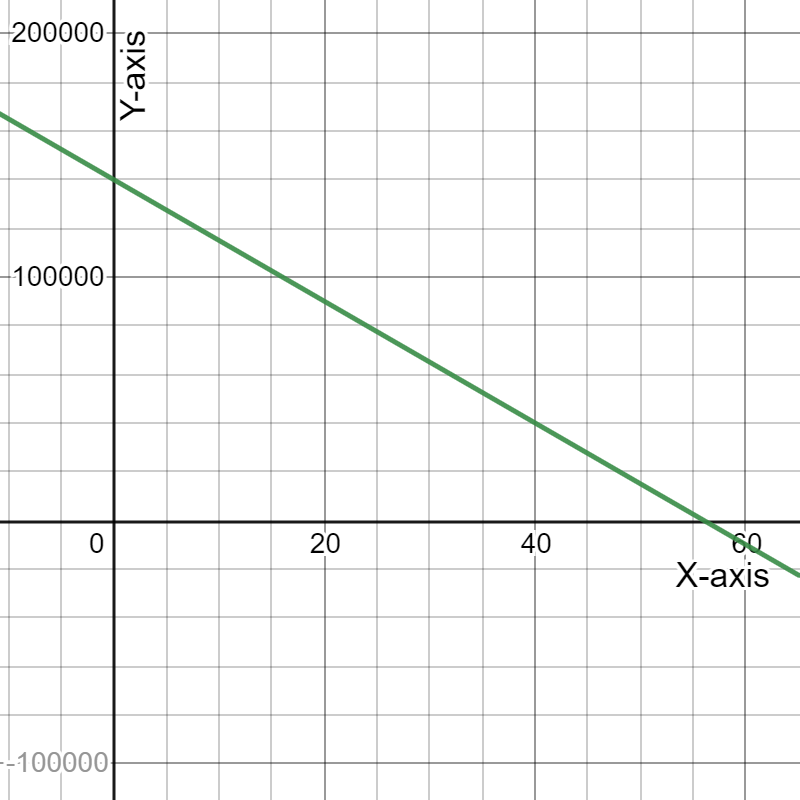
Given the expense function for a particular item be defined asy=−1,950x+53,000 and the revenue function be defined as y=−450x²+10,000x, where x represents price in each equation.

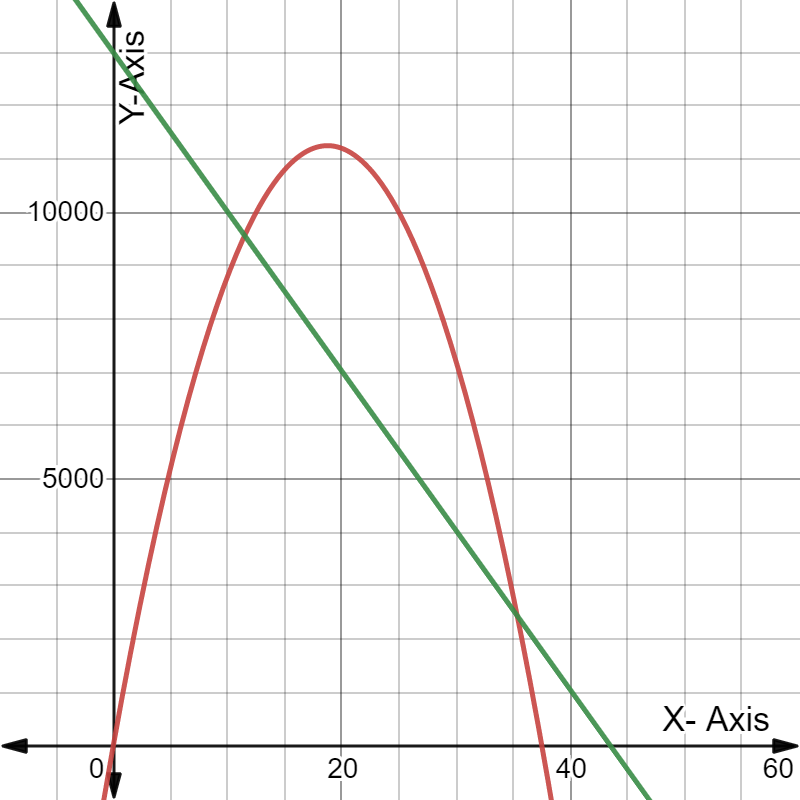
Need to determine the x-coordinate and they-coordinate of the first point where the two graphs intersect and round those values to the nearest whole number.

As the two intersect if they have the same value of(x,y). Using this find the required coordinates.

The graph is:

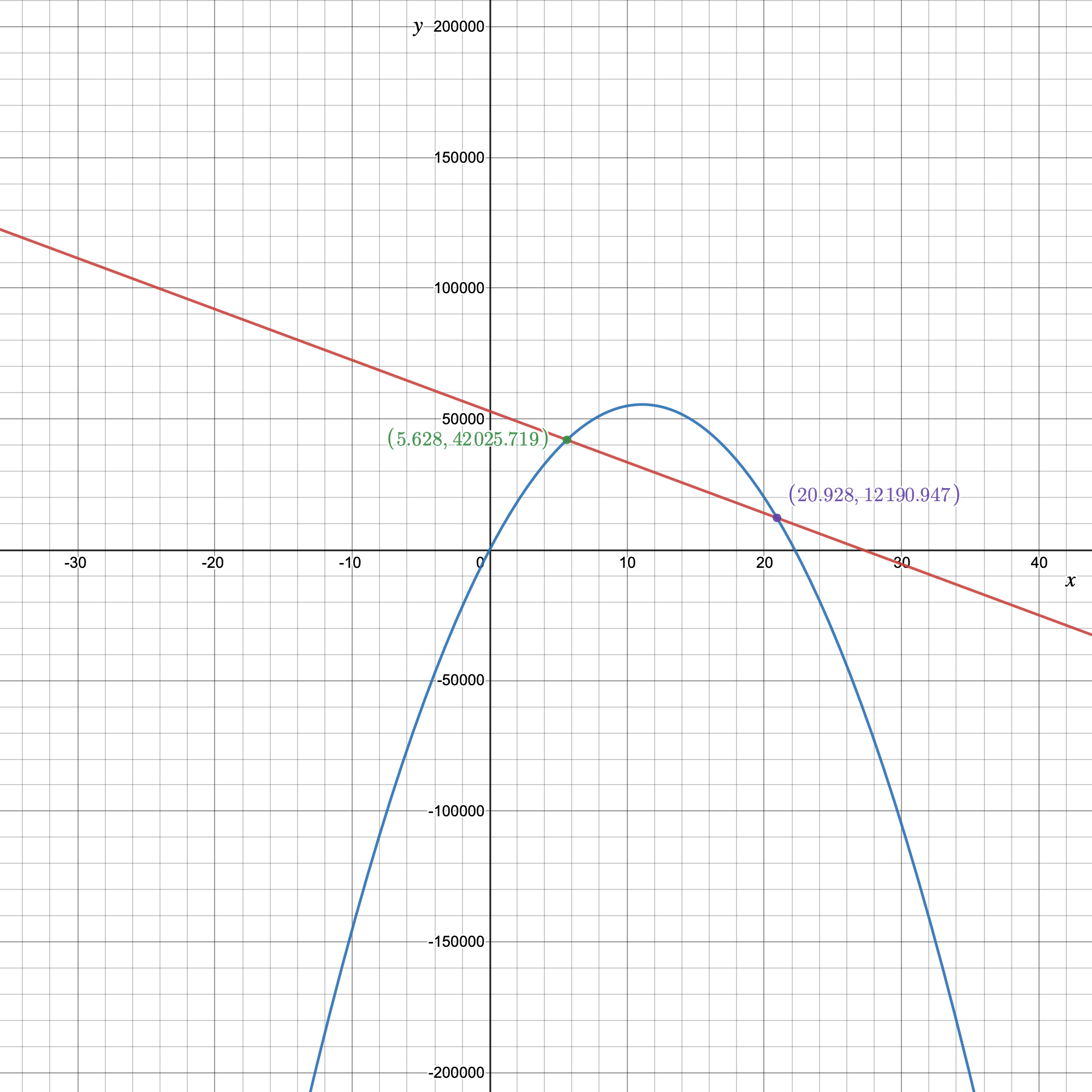
Putting the value of expense finction equals to revenue function gives us:

−1,950x+53,000=−450x²+10,000x

⇒450x²−11,950x+53,000=0​

Using quadratic formula for finding the value of x, gives us:

x=−(−11,950)±√(−11,950)²−4⋅450⋅53,000/2⋅450

=11,950±√142,802,500−95,400,000/900

=11,950±√47,402,500/900

=11,950±6884.94/900

⇒x=11,950+6884.94/900 or

x=11,950−6884.94/900

Solving this further gives us:

x=11,950+6884.94/900

=18,834.64/900

=20.92 and x=11,950−6884.94/900

=5065.06/900

=5.6278≈5.63

The corresponding value of y is y=−1,950x+53,000

=−1,950×(5.6278)+53,000

=42025.79​

The x-coordinate and the y-coordinate of the first point where the two graphs intersect is (5.63,42025.79).

Rounding these values to the nearest whole number gives us(6,42026).

For the expense function for a particular item be defined asy=−1,950x+53,000

and the revenue function be defined asy=−450x²+10,000x, where x

represents price in each equation.

The x-coordinate and the y-coordinate of the first point where the two graphs intersect is (5.63,42025.79).

Rounding these values to the nearest whole number gives us(6,42026)

for the graph:

Cengage Financial Algebra Chapter 2 Modeling A Business Key

Page 112 Exercise  3 Answer

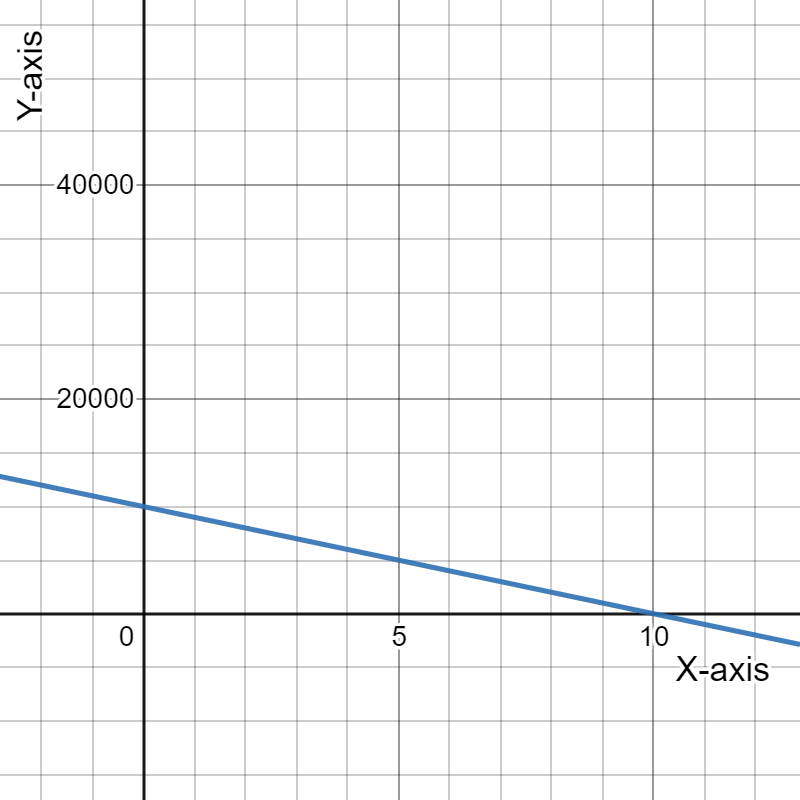
Given the expense function for a particular item be defined as y=−1,950x+53,000

and the revenue function be defined as y=−450x²+10,000x, where xrepresents price in each equation.

Need to tell the significance of the point where the two graphs intersect in the context of expense, revenue, and price.

As at the point of intersection the expense function is equal to the revenue function or the price at which the profit is zero.

Thus, the point is called the break even point for the graph:

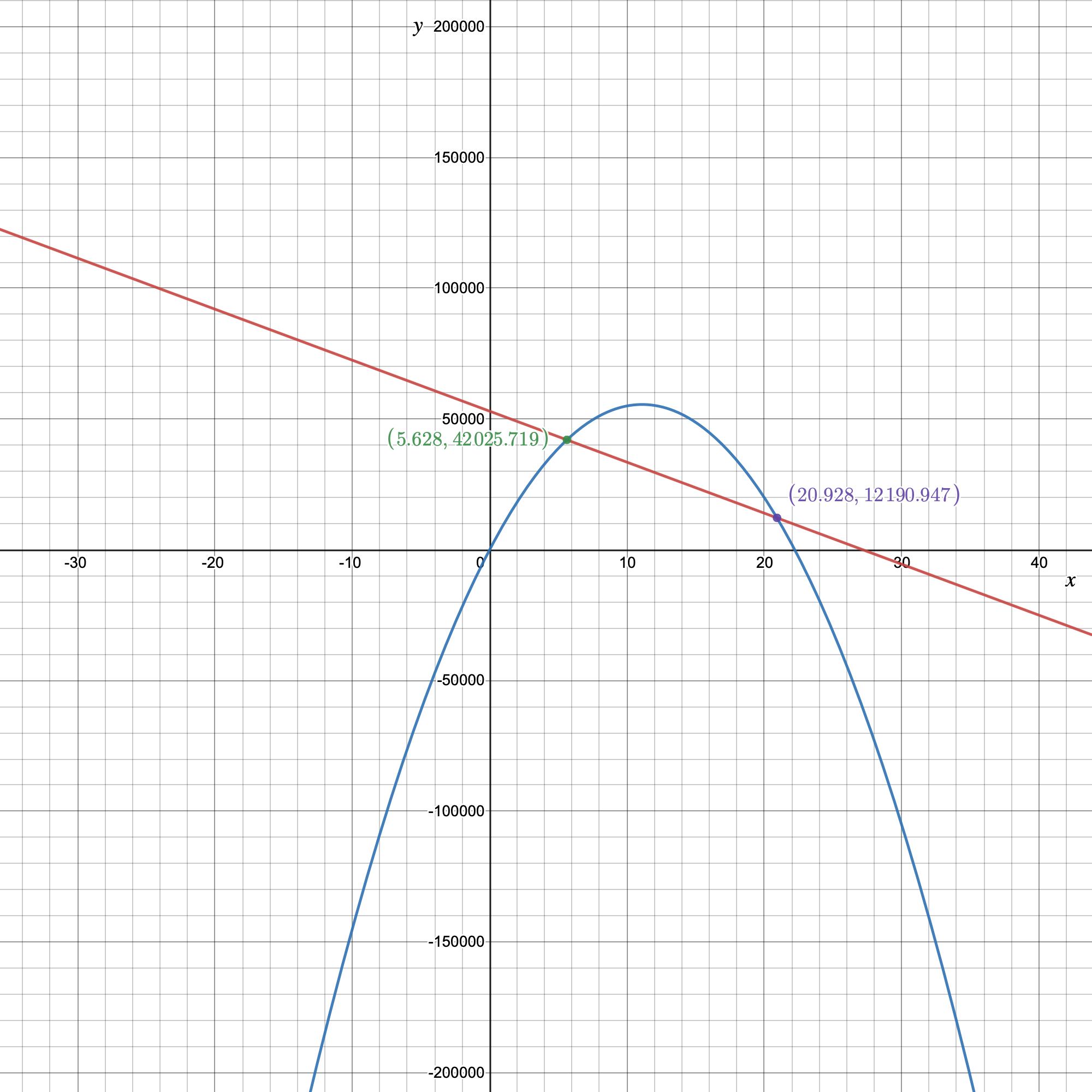
For the expense function for a particular item be defined as y=−1,950x+53,000 and the revenue function be defined as y=−450x²+10,000x, where x represents price in each equation.

The point where the two graphs intersect in the context of expense, revenue, and price is the breakeven point for the graph:

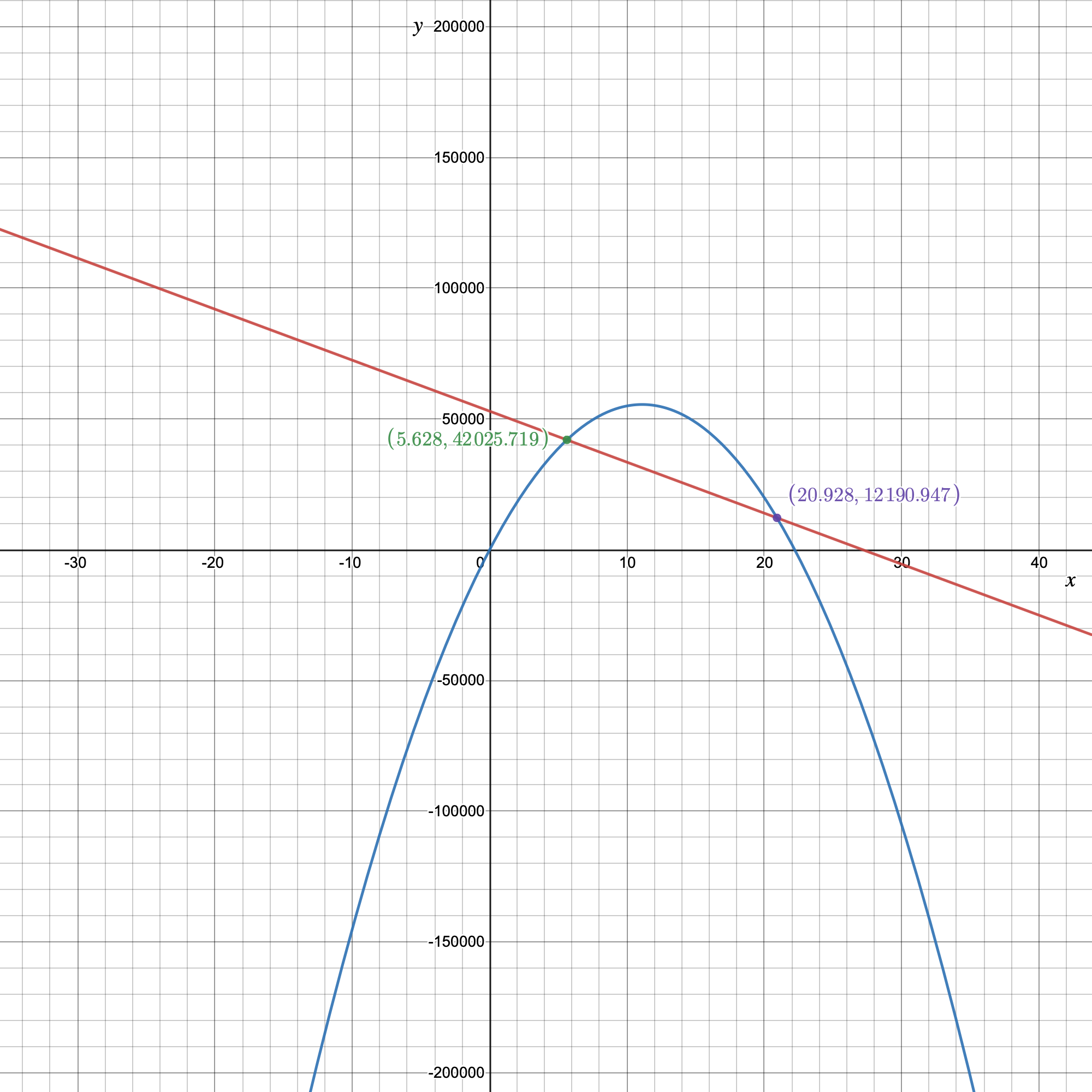
Page 112 Exercise  4 Answer

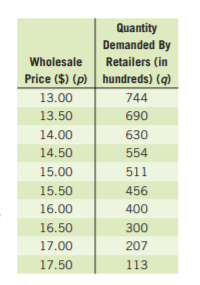
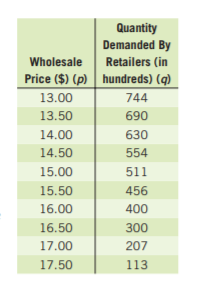
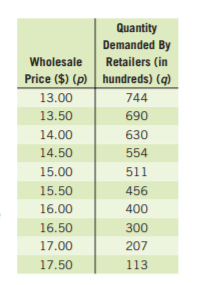
Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To determine what will happen to the quantity demanded as the price of the eyePOD increases.

We need to use the fact that the demand for a product depends on the quality of the product as well as the price of the product.

We know that the demand for a product depends on the quality of the product as well as the price of the product.

Thus, in the case of eyePOD, if the price of the eyePOD increases then certainly the quantity of the product demanded will decrease.

Hence, as the price of the eyePOD increases, the demand for the EyePOD will decrease.

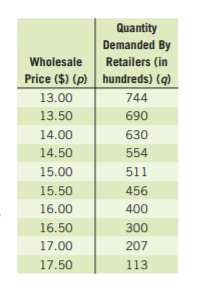
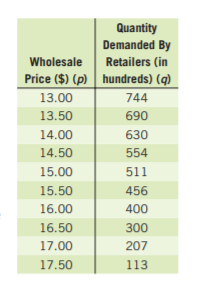
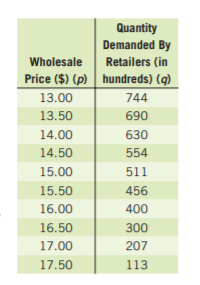
Page 113 Exercise  5 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

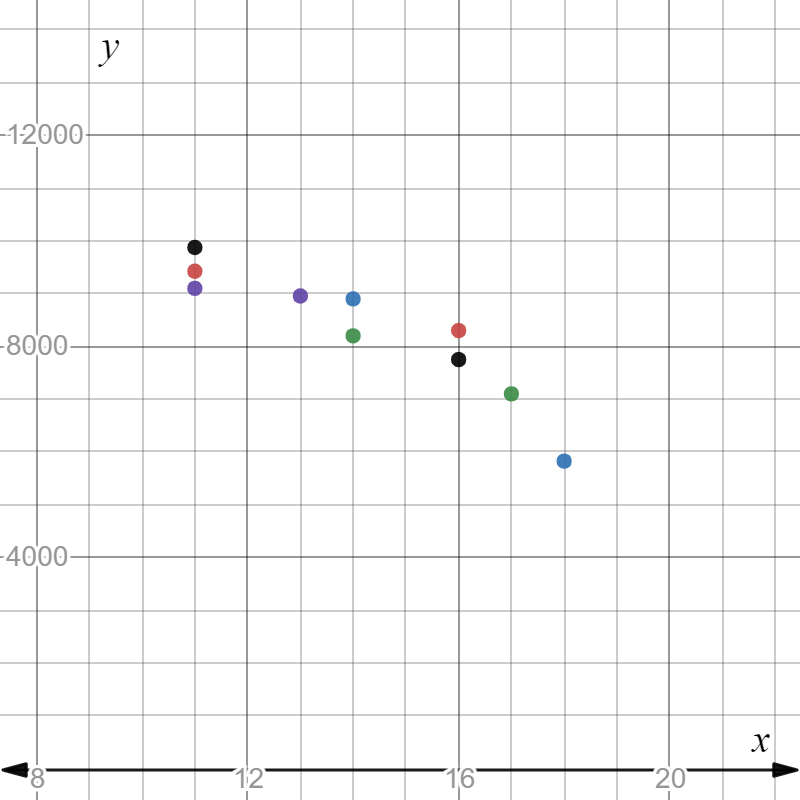
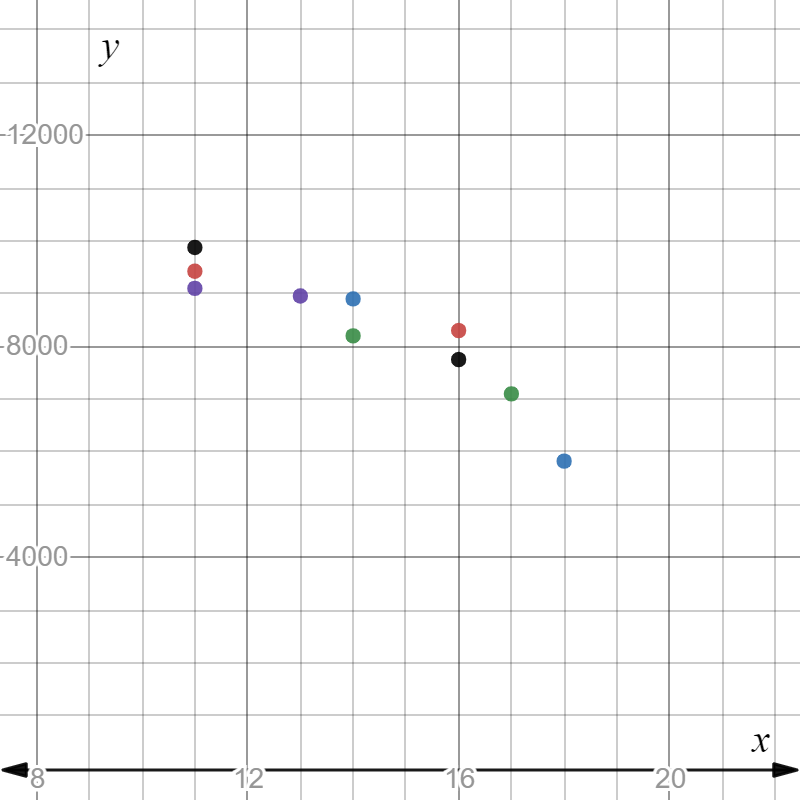
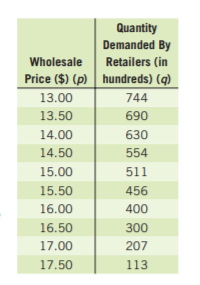
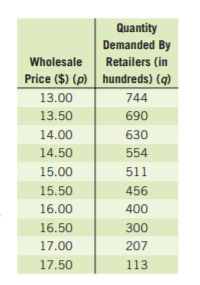
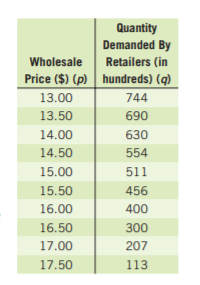
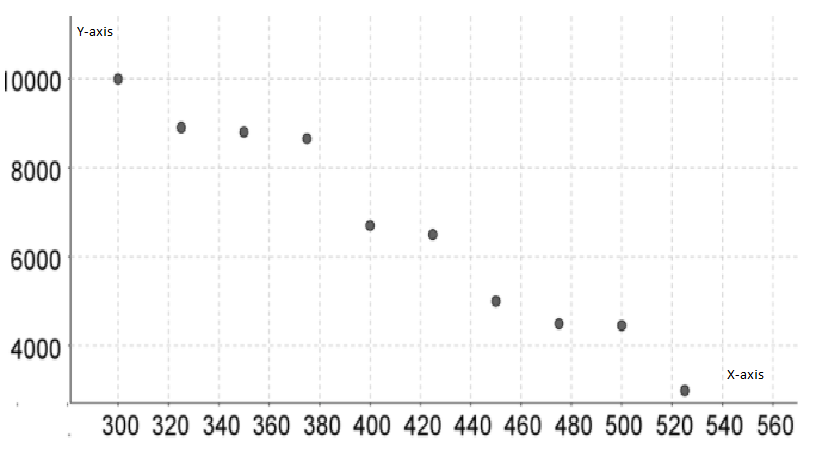
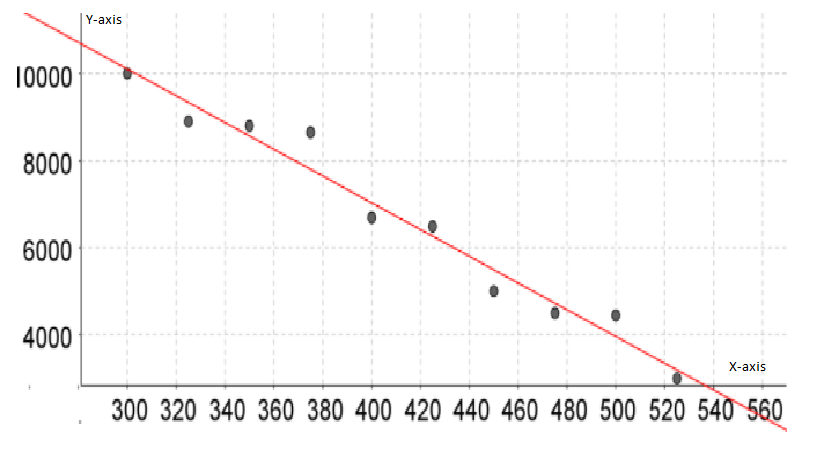
To make a scatterplot of the points represented by(p,q) which are given by​

(300,10,000),(325,8,900),(350,8,800),(375,8,650),(400,6,700)

(425,6,500),(450,5,000),(475,4,500),(500,4,450),(525,3,000)

We need to plot the above-given coordinates on the x,y graph to get the scatterplot.

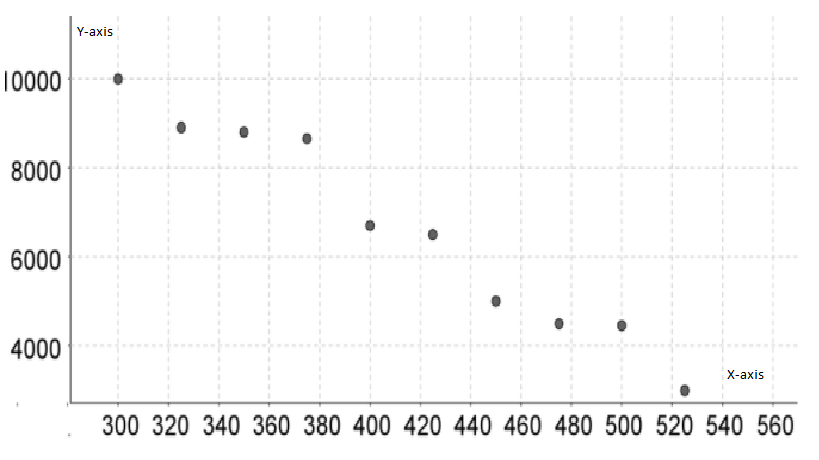
On plotting prices on x−axis  and quantity on y−axis, we get:

Hence, the scatter plot of the data is given by

Page 113 Exercise  6 Answer

Given, a company is interested in producing and selling a new device called an eye POD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To determine the correlation coefficient and to determine whether this line is a good predictor or not.

We need to calculate the correlation coefficient through LinReg(ax+b)L1,L2.

On calculating correlation coefficient through Lin Reg(ax+b)L1,L2, we get:

y=ax+b

a=−30.7393939394

b=19330

r2=0.9659385288

r=−0.9828217177​

Therefore, the correlation coefficient is −0.98 which represents a negative correlation.

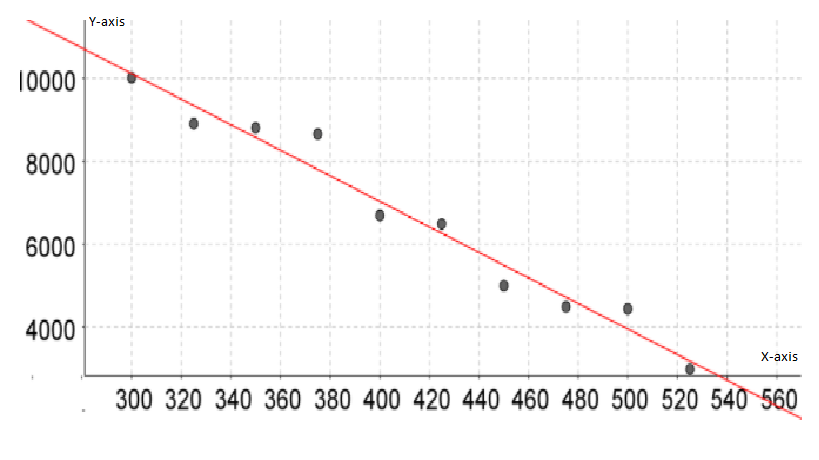
As the correlation is close to ±1, there is a strong correlation.

Thus, we conclude that the line is a good predictor since there is a strong, negative correlation between the price and the demand.

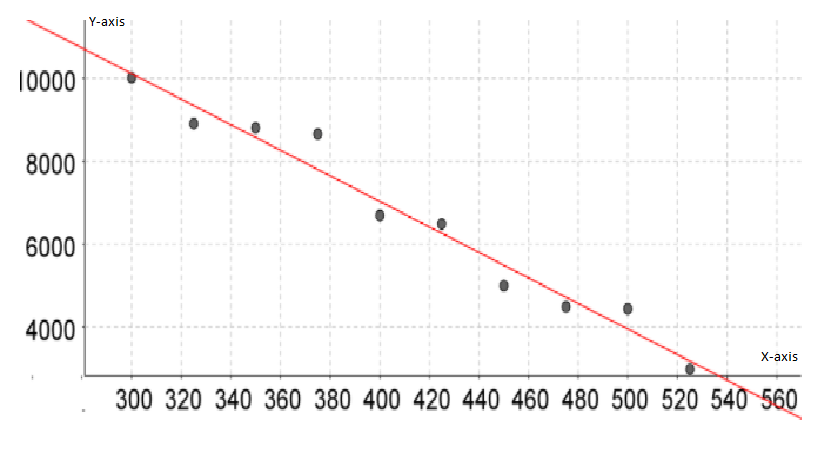
Hence, the correlation coefficient is −0.98 and yes, the regression line is a good .

Page 113 Exercise  7 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To write the regression equation. We need to use Lin Reg(ax+b)L1, L2 to get the equation and then replace x,y with p,q respectively.

Using Lin Reg(ax+b)L1,L2 to get the regression equation,

y​=ax+b

a=−30.7393939394

b=19330

r2=0.9659385288

r=−0.9828217177​

Thus, the regression equation is given by y=ax+b=−30.74x+19330​

On replacing x,y with p,q respectively, we get: q=−30.74p+19330 which is represented by

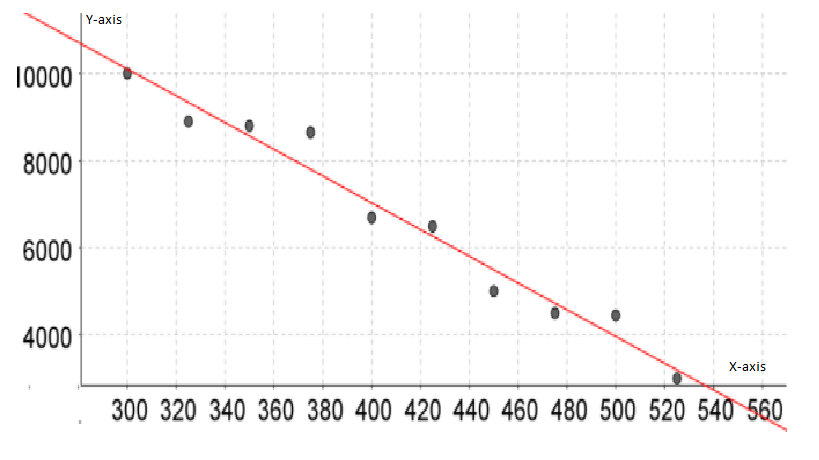
Hence, the regression equation is q=−30.74p+19330 which is represented by

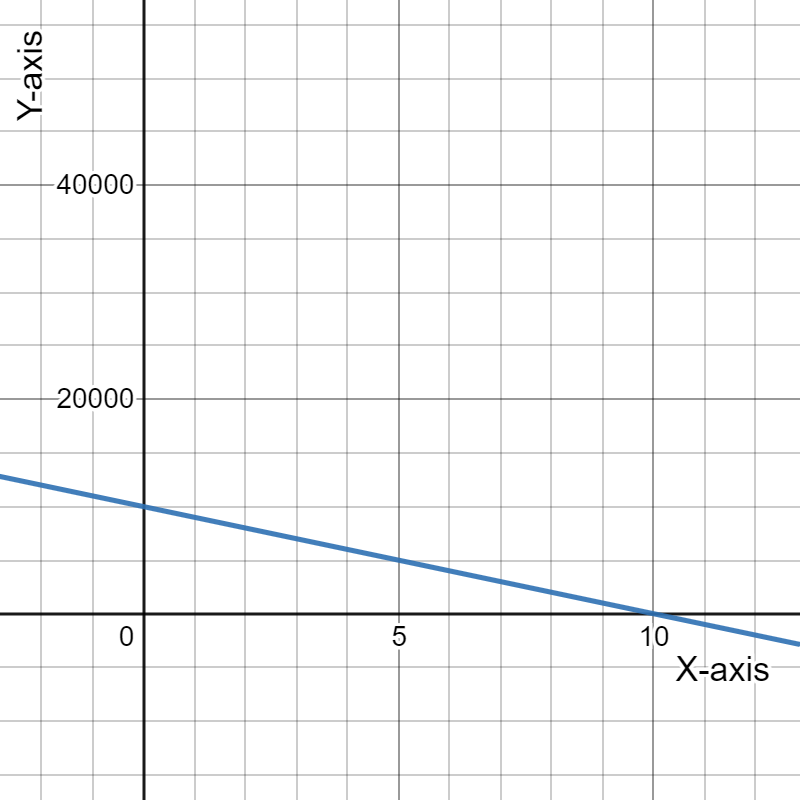
Page 113 Exercise  8 Answer

Given, The accounting department has calculated that this could be the biggest product to hit the market in years.

It anticipates the fixed costs to be $160,000 and the variable cost to be $150 per eye POD.

To  Express expenses E,  as a function of q, the quantity produced.

We need to form an equation with two variables using the given statement.

We have, the fixed cost=$160,000 the variable cost=$150 per eye POD let q represent the number of eye PODs, then the expenses E  can be expressed as

E=150q+160,000

Hence, expenses E,  as a function of q , the quantity produced can be expressed as

E=150q+160,000

Page 113 Exercise  9 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

The horizontal axis represents price, and the vertical axis represents quantity.To express the revenue R, in terms of p and q.

We need to use the fact that the product of the price and the quantity gives the revenue of the product.

We know that the product of the price p and the quantity q gives the revenue R.

Thus, we conclude that the revenue R can be expressed as R=pq

Hence, the revenue R, in terms of p and q can be expressed as R=pq

Page 113 Exercise  10 Answer

Given, A company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To express the revenue R,  in terms of p.

We need to use the fact that the product of the price and the quantity gives the revenue of the product.

We know that the product of the price p and the quantity q gives the revenue R.

Thus, we conclude that the revenue R can be expressed as R=pq

On replacing q with−30.74p+19,330, we get:

R=p(−30.74p+19,330)=−30.74p{2}+19,330p

R=−30.74p{2}+19,330p

​Hence, the revenue R, in terms of p can be expressed as R=−30.74p{2}+19,330p

Page 113 Exercise 11 Answer

Given, A company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eye POD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To express expenses E,  in terms of p.

We need to use the transitive property of dependence and make an equation of two variables.

From the previous exercise15 , the expenses E, in terms of q can be expressed as

E=150q+160,000

Now, on replacing q with −30.74p+19,330, we get:

E=150(−30.74p+19,330)+160,000

=−4,611p+2,899,500+160,000

=−4,611p+3,059,500

​Hence, the expenses E,  in terms of p can be expressed as

E=−4,611p+3,059,500

Page 113 Exercise 12 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eye POD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To determine an appropriate maximum horizontal-axis value.

We need to put zero for the expense function to get the maximum horizontal-axis value.

We have, expense function E=−4,611p+3,059,500 and revenue function R=−30.74p{2}+19,330p from the previous exercise.

On putting expense function as zero, we get:

0=−4,611p+3,059,500

4,611p=3,059,500

p=663.52≈700​

Hence, an appropriate maximum horizontal-axis value is 700.

Page 113 Exercise 13 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eye POD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To determine an appropriate maximum vertical-axis value.

We need to put zero for the price at the expense function to get the maximum vertical-axis value.

We have, expense function E=−4,611p+3,059,500 and

revenue function R=−30.74p{2}+19,330p from the previous exercise.

On putting zero for the price at the expense function, we get:

E=3,059,500≈3,100,000​

Hence, an appropriate maximum vertical-axis value is 3,100,000.

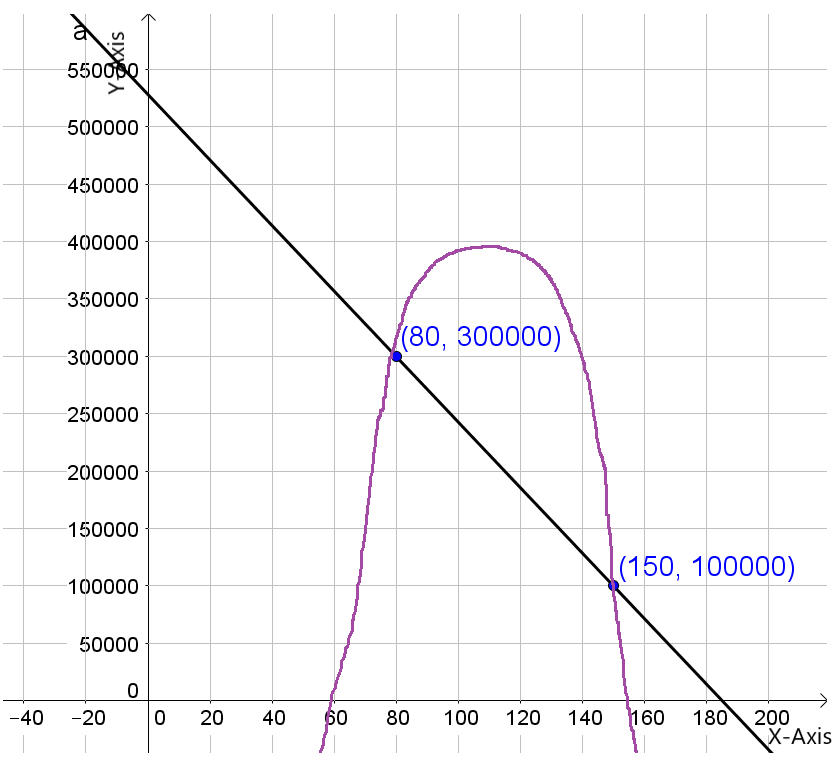
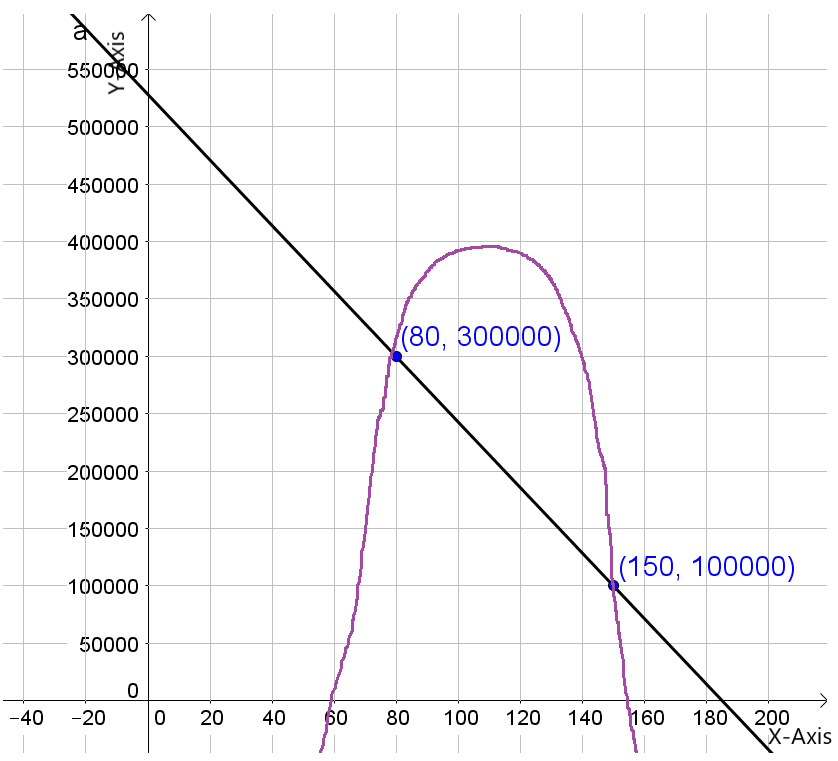
Page 113 Exercise 14 Answer

Given, A company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eye POD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

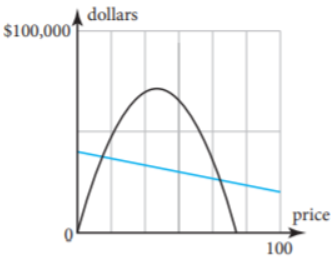
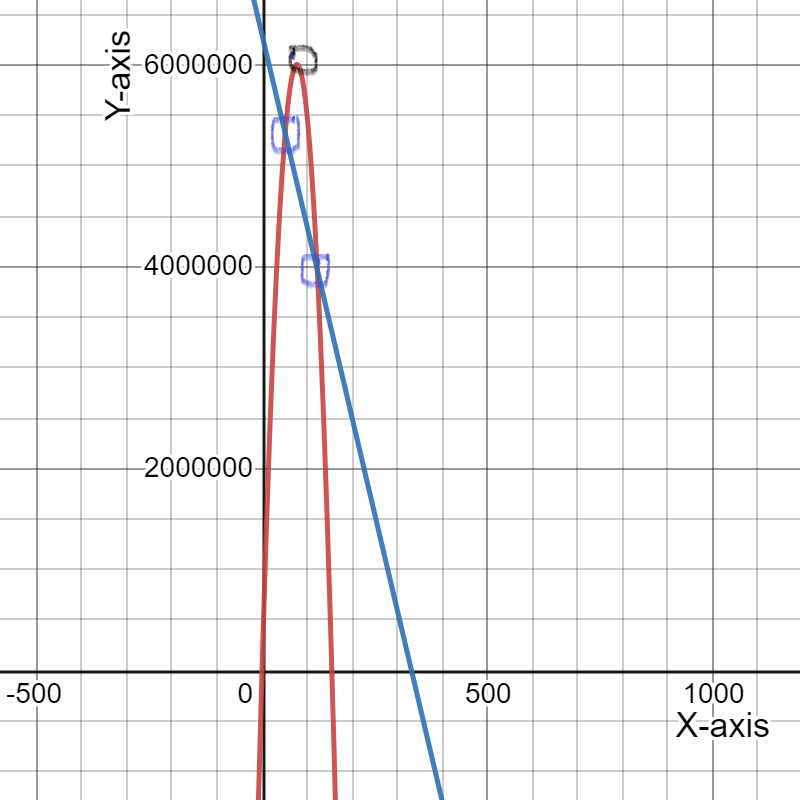
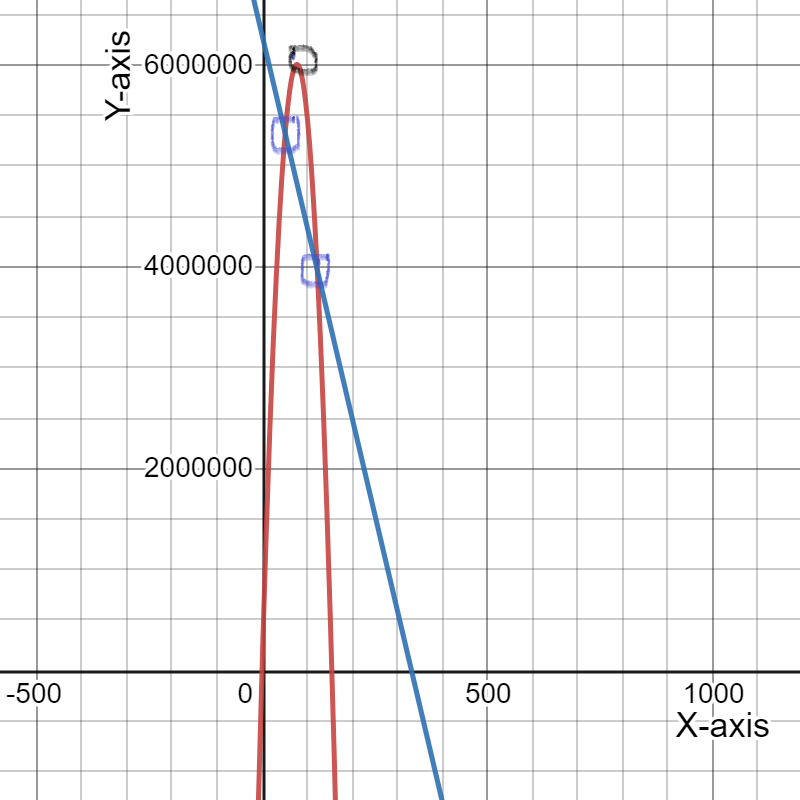
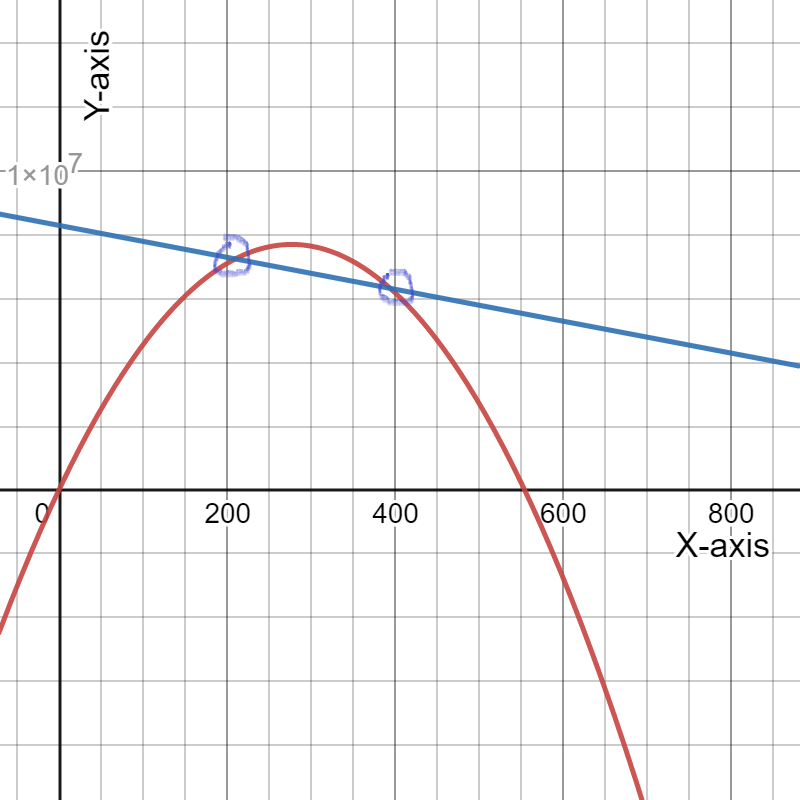
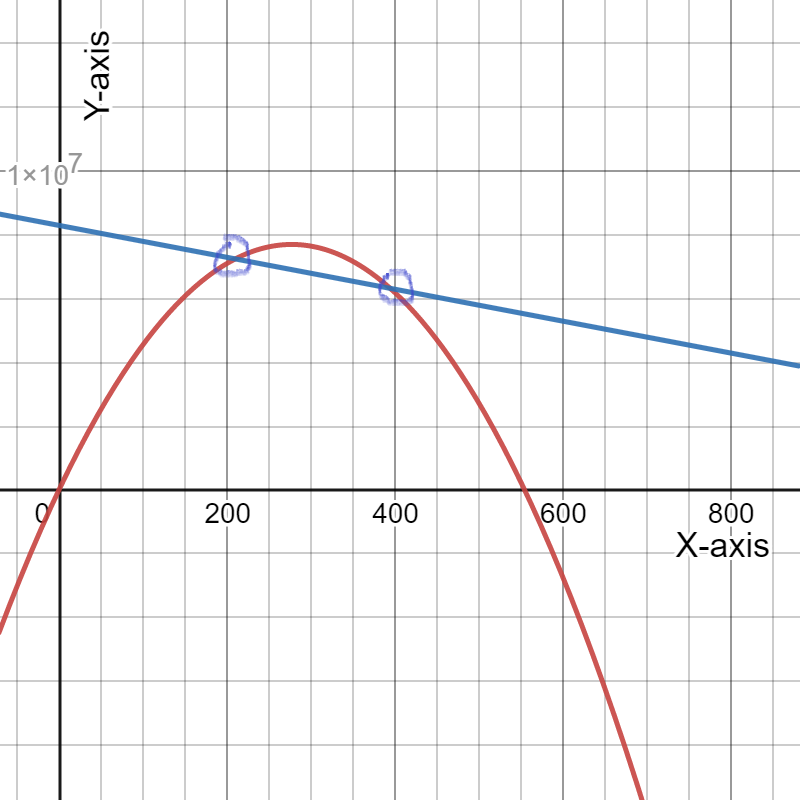
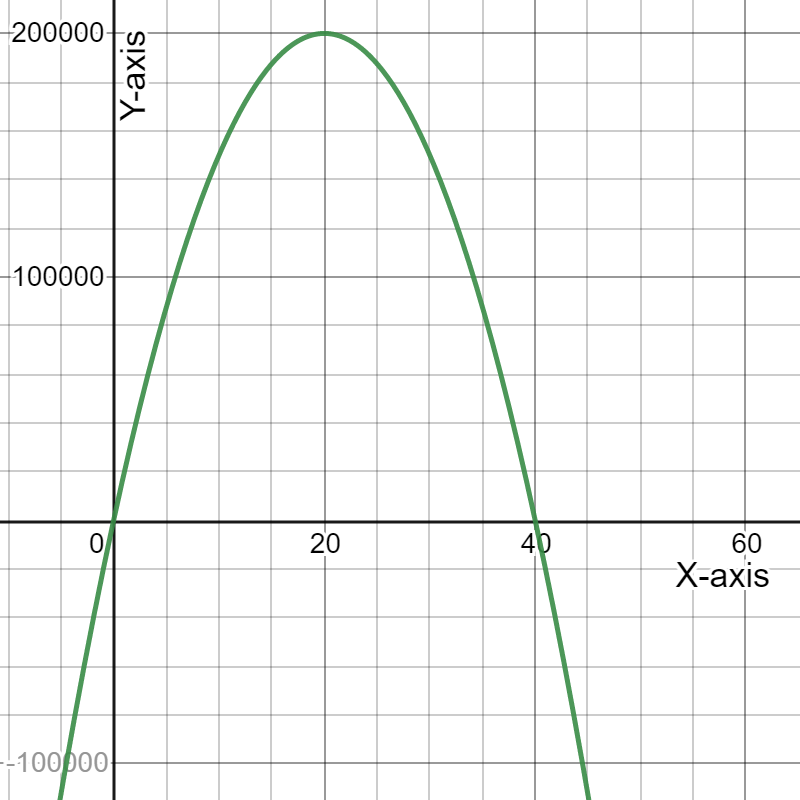
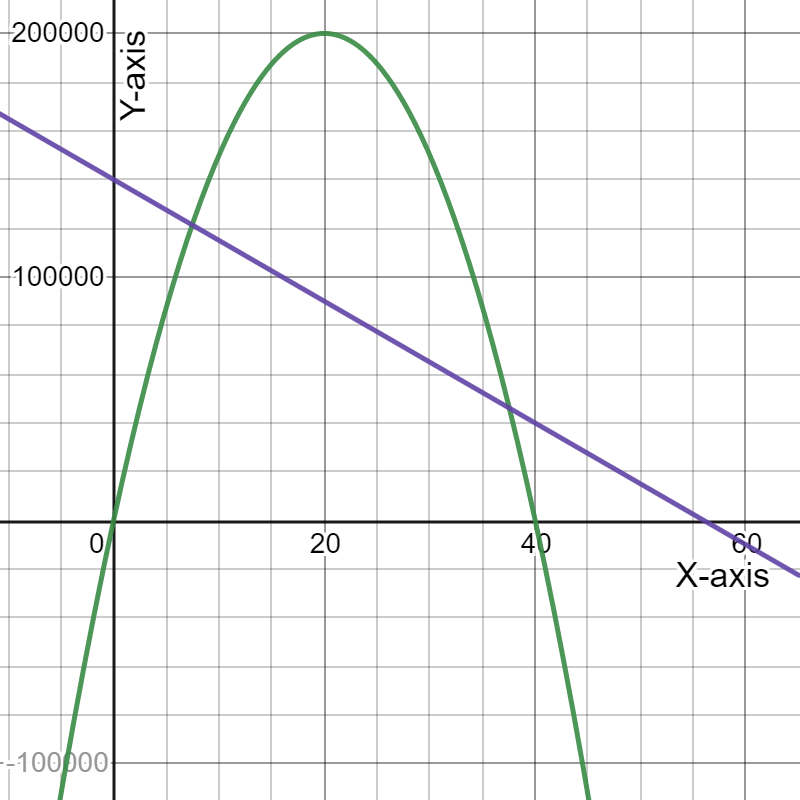
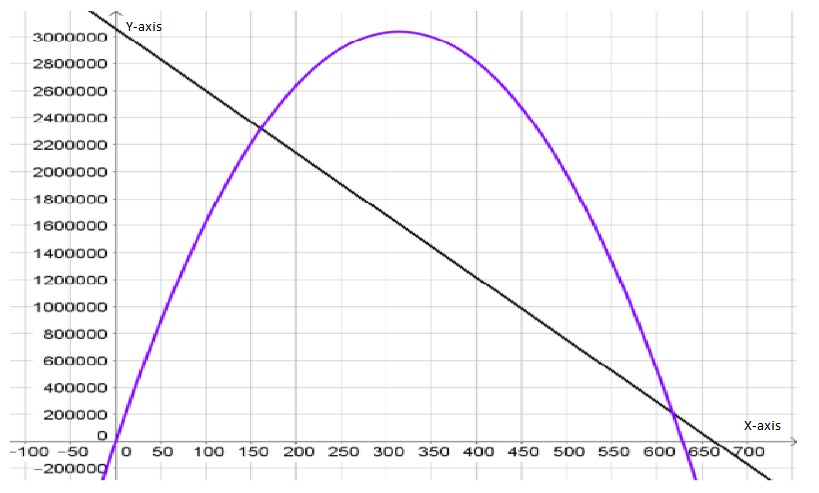
To draw a graph of the expense and revenue functions.

We need to get the (x,y) coordinates of the function to draw the graph.

On drawing expense function, represented by a black line and revenue function, represented by purple parabola, we get:

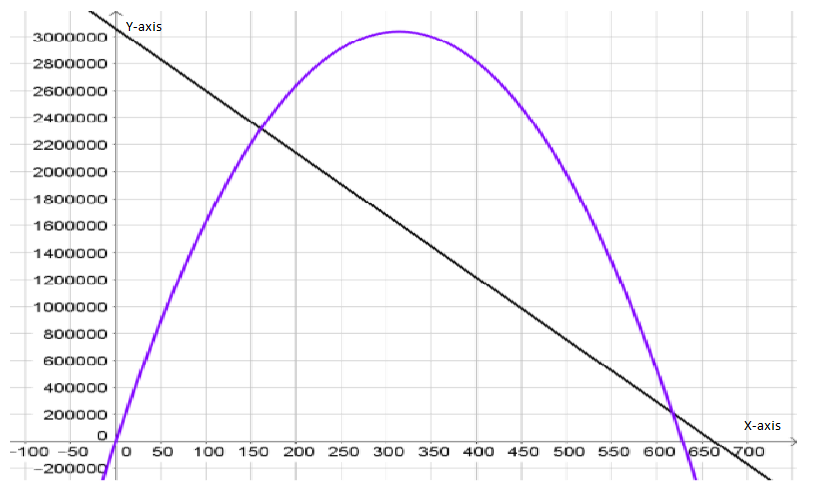
Hence, the graph of the expense and revenue functions is given by

Page 113 Exercise  15 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eye POD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

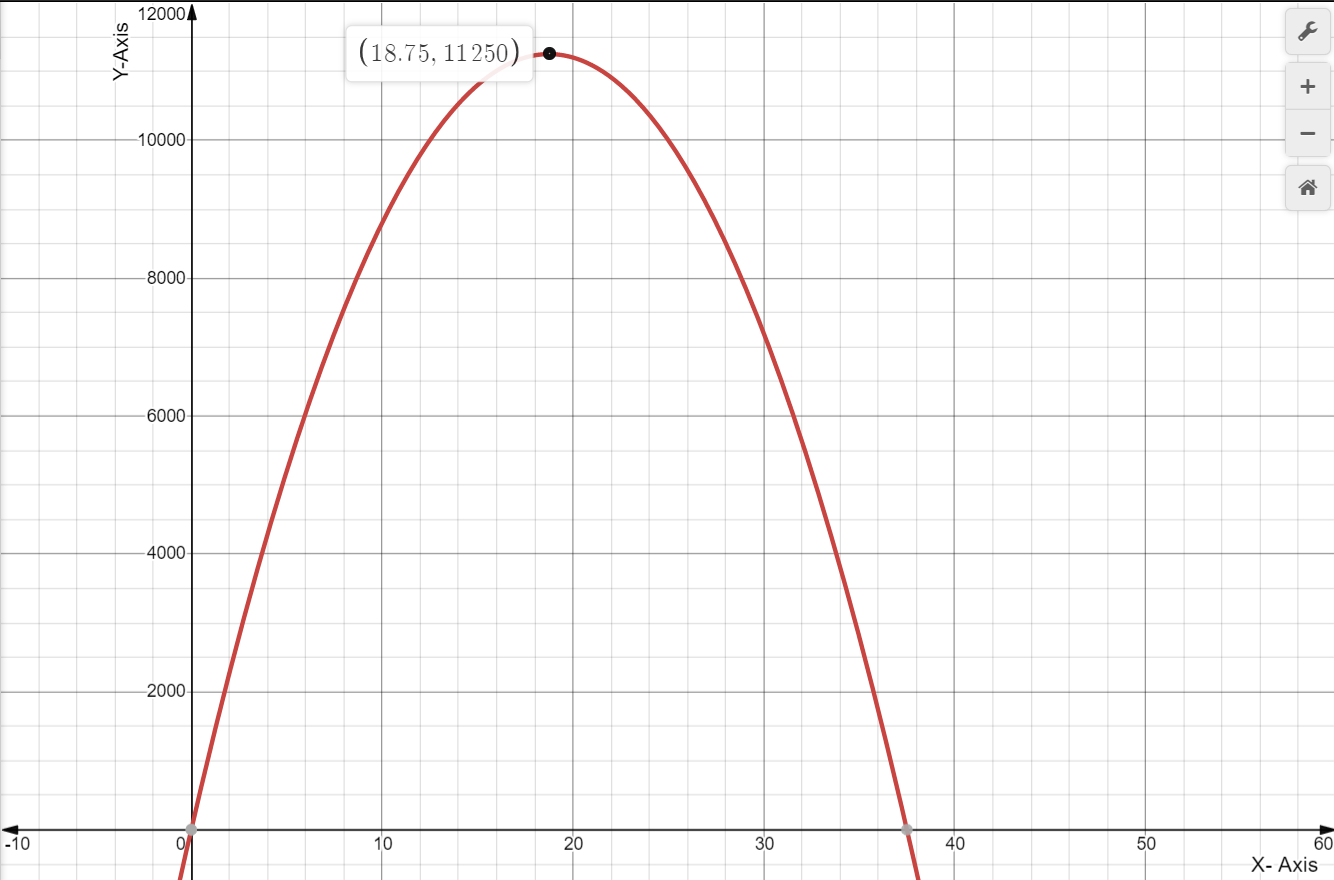
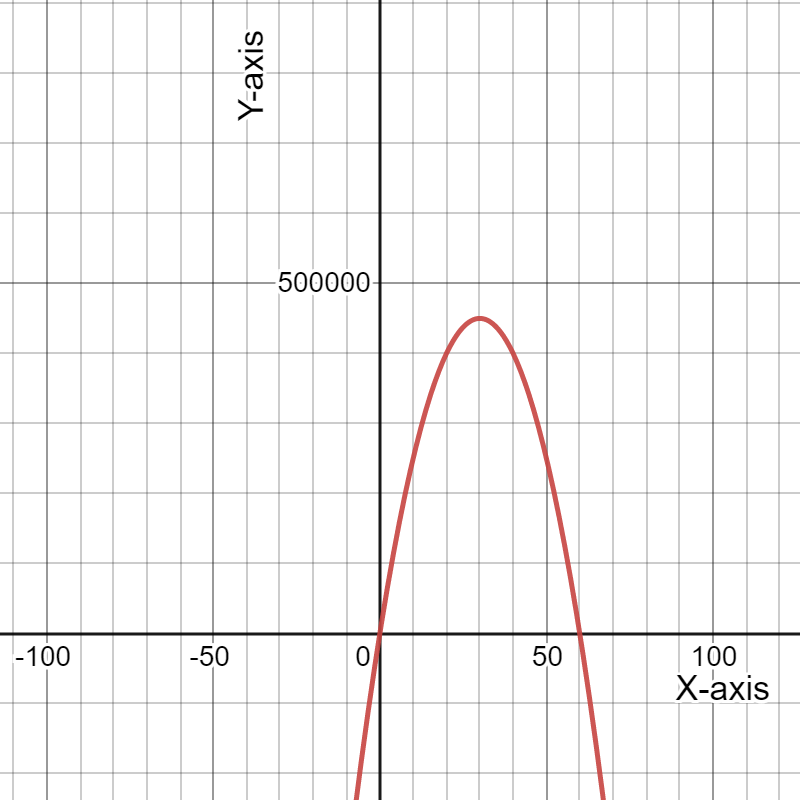
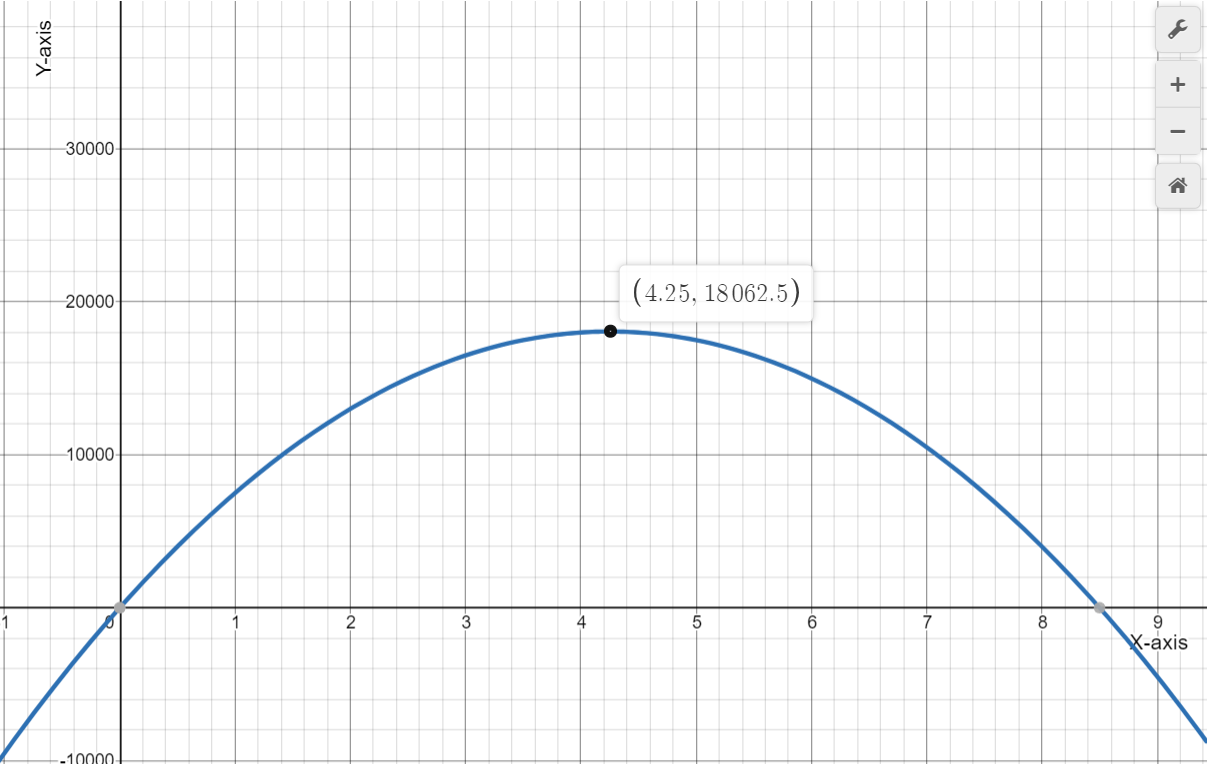
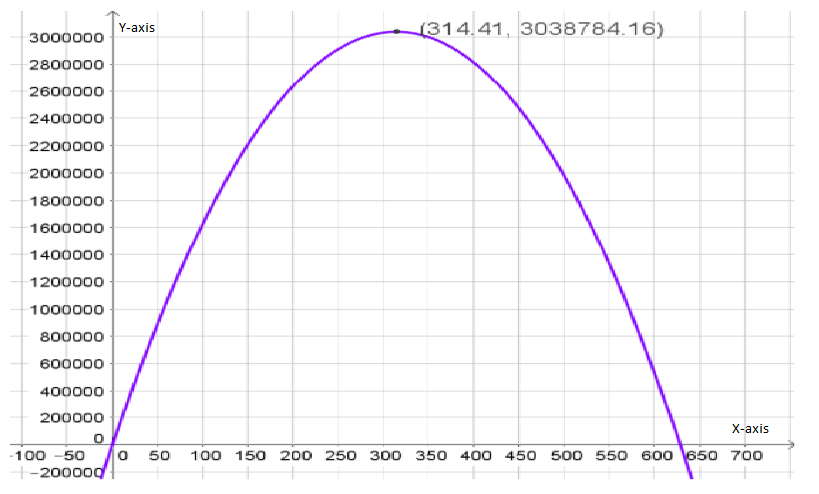
To determine the coordinates of the maximum point on the revenue graph.

We need to use the fact the maximum of a quadratic function y=ax{2}+bx+c  lies at the symmetry x=−b/2a.

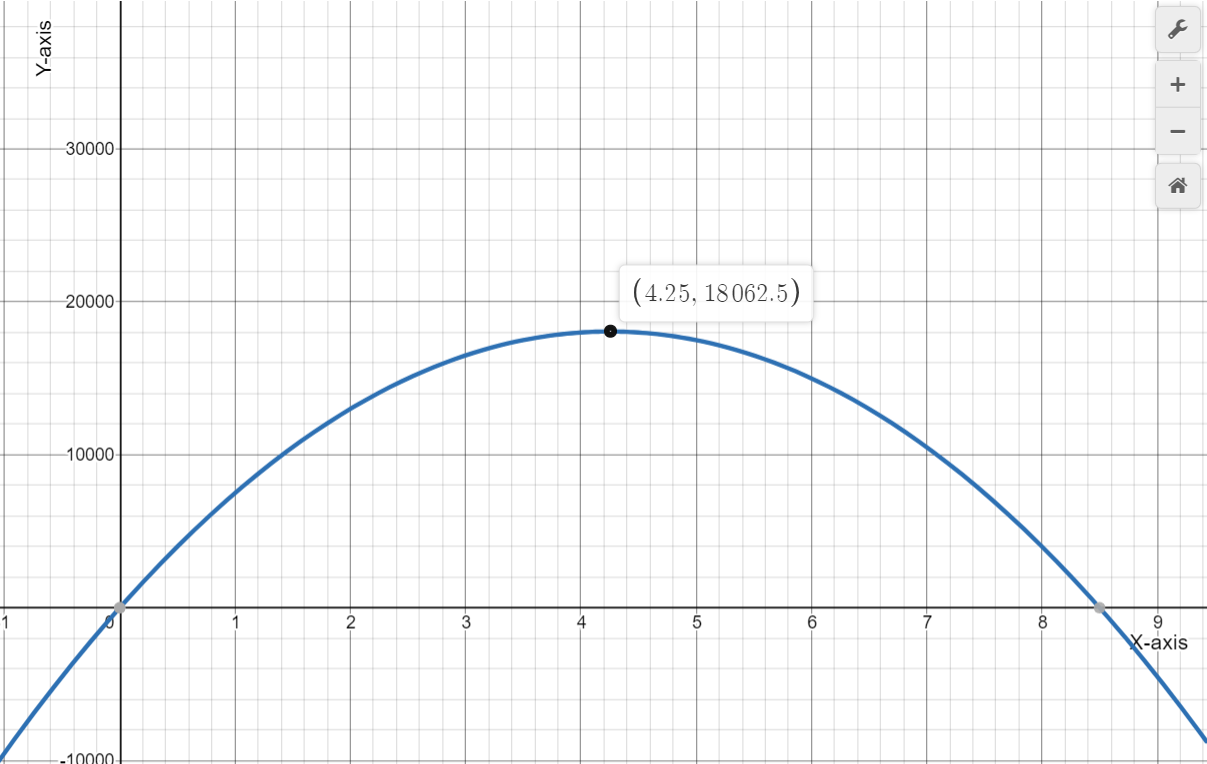
We have the revenue function from the previous exercise R=−30.74p{2}+19,330p.

Since we know that the maximum of a quadratic function y=ax{2}+bx+c lies at symmetry

x=−b/2a.

So, here is a=−30.74

b=19,330 and c=0​

Now, ​p=−b/2a

=−19330/2(−30.74)

≈314.41

​Therefore, the maximum revenue price is $314.41

On putting this value of p in revenue function, we get: R=3,038,784.16 which represents the maximum revenue.

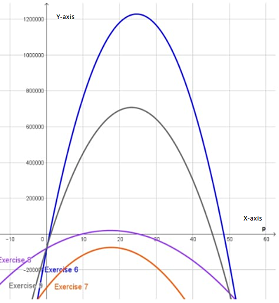
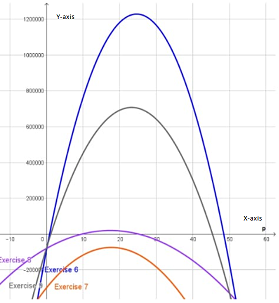
Hence, the coordinates of the maximum point on the revenue graph is

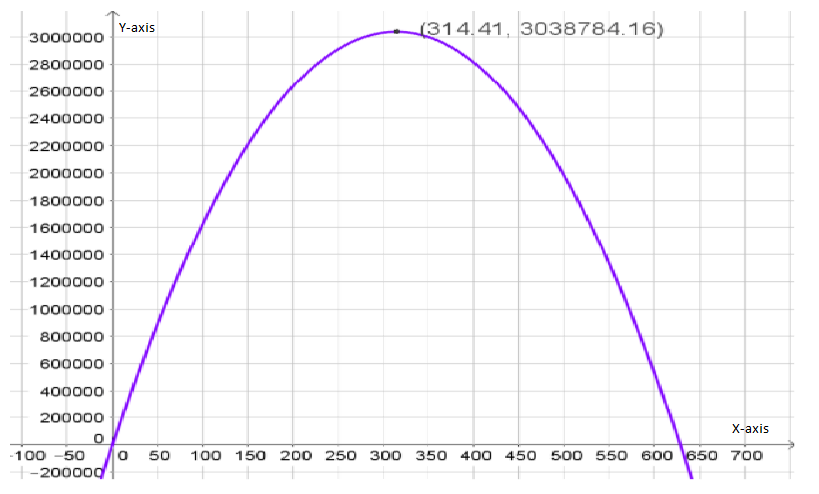
and the graph of the revenue function is given by

Detailed Solutions For Cengage Financial Algebra Chapter 2 Assessment Modeling A Business

Page 113 Exercise  16 Answer

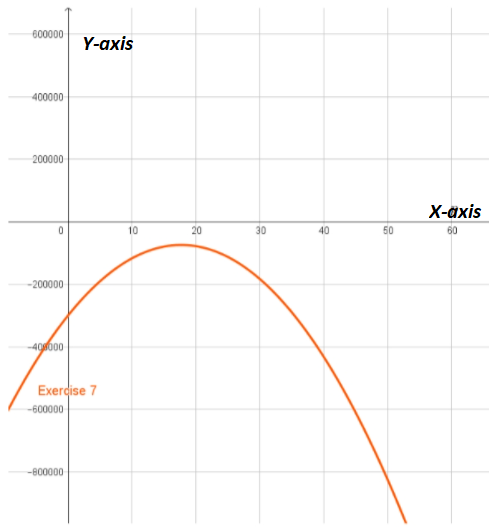
Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To express the profit, P in terms of p.

We need to find the difference between the revenue and the expense function to get the profit function.

We have the revenue and the expense function from the previous exercises as

​E=−4,611p+3,059,500

R=−30.74p²+19,330p

Since the difference between the revenue and the expense function gives the profit function, we get:

P=R−E

=−30.74p{2}+23,941p−3,059,500

​Hence, the profit function P in terms of price p is represented as

=−30.74p{2}+23,941p−3,059,500

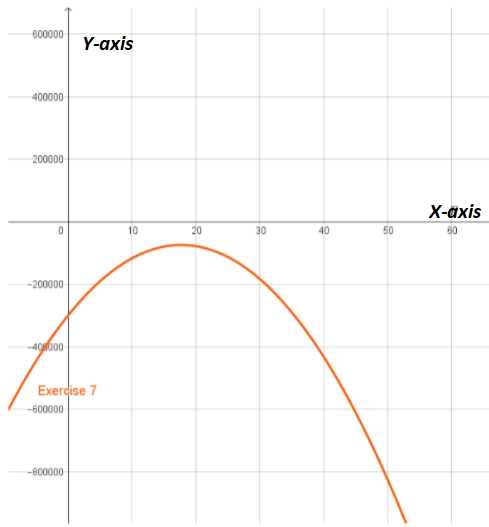
Page 113 Exercise  17 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eye POD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

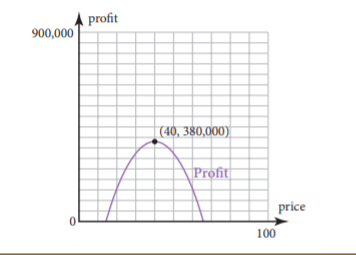
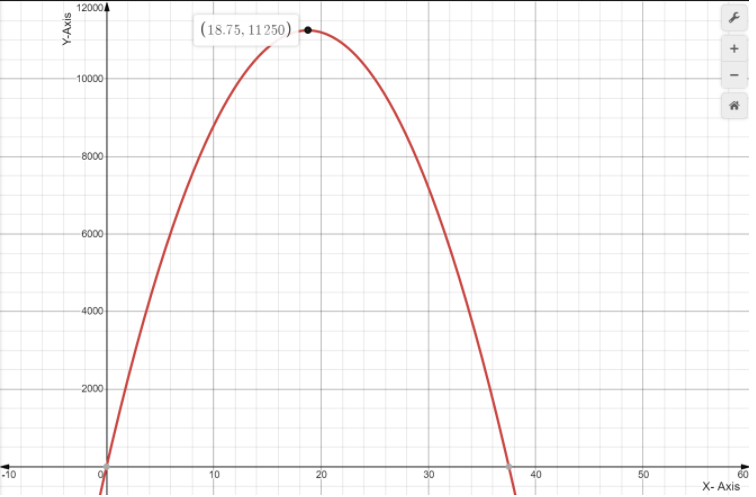
To plot the profit function and to determine the coordinates of the maximum point of the profit graph and determine when the price p is profit maximized.

We need to use the fact the maximum of a quadratic functiony=ax{2}+bx+c lies at the symmetry x=−b/2a.

We have the profit function from the previous exercise P=−30.74p{2}+23,941p−3,059,500

Since we know that the maximum of a quadratic functiony=ax{2}+bx+c lies at symmetry

x=−b/2a

So, here is a=−30.74

b=23,941 and

c=−3,059,500

​Now, ​p=−b/2a

=−23,941/2(−30.74)

≈314.41

​Therefore, the maximum revenue price is$314.41

Now, from the graph, we conclude that maximum profit is made at a price $389.41

Also, the coordinates of the maximum point of the profit graph is

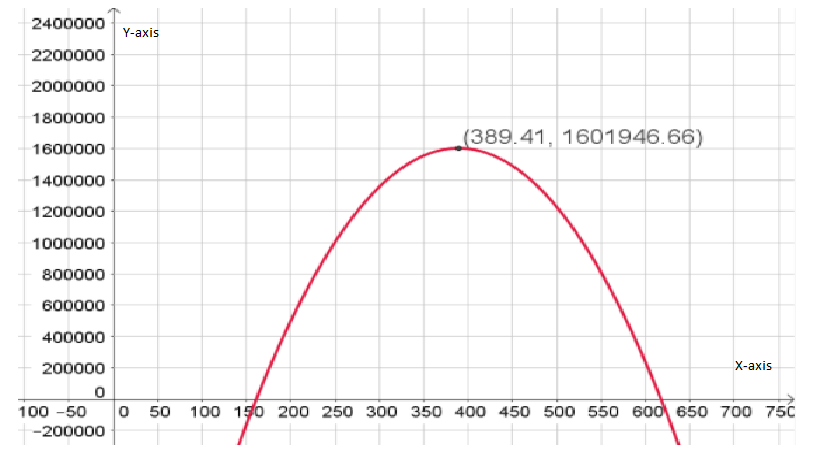
Hence, the coorinates of the maximum point of he profit graph is and the profit is maximized at $389.41.

Page 113 Exercise  18 Answer

Given, a company is interested in producing and selling a new device called an eyePOD (eyewear personal optical device).

The eyePOD is an MP3 and video player built into a pair of sunglasses.

The user can listen to music from the small earphones and watch videos projected on the screen behind the glasses.

To find the shares that must be sold to get enough money to start the business if shares of stock are sold with an initial value of $10.

We need to use the maximum profit price for business profits.

We have the expense function from the previous exerciseE=−4,611p+3,059,500

Also, the maximum profit price is  $389.41

Thus, the expense is given by

​E=−4,611(389.41)+3,059,500

≈$1,263,930.49 which represents the total income of the shares.

Since the cost of each shares is$10. Consider x shares then the total income of the shares is 10x which is given by

10x=1,263,930.49

x=126,393.049

Hence, the number of shares that must be sold to get enough money to start the business is 126,393.049.

Practice Problems For Cengage Financial Algebra Chapter 2 Modeling A Business Assessment

Chapter 2 Solving Linear Inequalities

• • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.1 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.2 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market

Page 31 Problem 1 Answer

Given: Toni purchased 15,000 shares of stock of Target Corporation at $54.88 per share. So, the value of trade was$823,200

Her trade appeared on the stock ticker as [email protected]▼0.17.

To find The difference in the value of trade if the trading was done at the previous day’s closing price.

Solution: We will first find the value of the previous day’s closing price from the ticker.Then we will find the value of trade at that price and check the difference.

We will first find the previous day’s closing price

Previous day’s closing price=54.88+0.17

=$55.05

If Toni had purchased the shares at the previous day’s closing price, then

Value of trade= Number of shares× Price per share

=15,000×55.05

=$825,750

Toni has purchased shares at present for$823,200, so if the purchase was done at the previous day’s closing the difference would be$2550(825,750−823,200)

Toni purchased15,000 shares of stock of Target Corporation at$54.88 per share i.e for$823,200

If she purchased those shares at the previous day’s closing of $55.05, the trading price would be$825,750 and the difference between this trade and the original trade would be$2,550

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Solutions

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 32 Problem 2 Answer

Given: Let,H=day’s High, L=day’s Low, C=day’s close, V=day’s volume

To find A formula that can be used to determine the day’s money flow.

Solution: Day’s money flow=Day′s high+Day′s Low+Day′s Close/3×Day′s Volume

=H+L+C/3×V

Let H represent a day’s High, L represent a day’s Low, C represent a day’s close, and V  represent the day’s volume.

Then, day’s money flow=H+L+C/3×V

Page 33 Problem 3 Answer

Given ;

To find; How might a large trade “move the market”? How might those words apply to what you have learned?

Here the author wants to convey that Large trades involve bigger purchases, usually by institutions.

They have a major effect on the market The number of shares traded in a single day can be greater than the number of a company’s outstanding shares, but this is relatively rareLonger-term traders, on the other hand, are buying or selling off of the news, which also contributes to the increased stock activity.

The day traders or short-term investors provide the liquidity required to trade more shares than the actual shares outstanding.

Hence we conclude that Large trades involve bigger purchases, usually by institutions. They have a major effect on the market

Page 33 Problem 4 Answer

Given: The stock symbol representing Exxon Mobil Corp is XOMThe stock ticker [email protected]▼1.58

To find: The numbers of shares bought by Jessica

Solution: The volume of shares traded by Jessica are0.66K

This can be written as660(0.66×1000) shares

Jessica bought 660 shares of Exxon Mobil Corp

Page 33 Problem 5 Answer

Given: Stock ticker for Exxon Mobil Corp [email protected]▼1.58

To find: Cost of each share

Solution: The amount following the@ symbol in the ticker shows the price of each shareSo, the price of each share of Exxon Mobile Corp is$92.67

Each share of Exxon Mobile Corp cost$92.67

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 33 Problem 6 Answer

Given: The ticker for Exxon Mobile [email protected]▼1.58

To find: Value of trade for Jessica

Solution: From the ticker we get the following information:

Number of shares=0.66K

=660shares

Price of each share=$92.67

So, the Value of trade=660×92.67

=$61,162.2

The value of Jessica’s trade was$61,162.2

Page 33 Problem 7 Answer

Given: Phil sold his shares of Verizon Communications IncThe ticker showing that information is [email protected]▲2.27

To find: Number of shares sold by Phil Solution:

Number of shares sold=3.32K

=3.32×1000

=3320 shares

Phil sold 3320 shares of Verizon Communications Inc

Cengage Financial Algebra Chapter 1 Exercise 1.5 Stock Market Answers

Page 33 Problem 8 Answer

Given: The ticker showing sale of shares of Verizon Communications Inc [email protected]▲2.27

To find: Sale price of each share

Solution: The trade price of each share is shown after the@ symbol in the tickerThus, for this ticker sale price of each share was$38.77

Phil sold shares of Verizon Communications Inc at$38.77 each

Page 33 Problem 9 Answer

Given: The ticker showing sale of shares of Verizon Communications Inc [email protected]▲2.27

To find: The total value of all the shares sold by Phil

Solution: From the ticker, we know that,

Number of shares=3320

Price per share=$38.77

So, value of trade=3320×38.77

=$128,716.4

The total value of all the shares of Verizon Communications Inc sold by Phil is$128,716.40

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 33 Problem 10 Answer

Given: The ticker for Home Depot Inc [email protected]▲1.13

To find: Number of shares of Home Depot that are indicated on the ticker

Solution: Number of shares=32.3M

=32.3×1,000,000

=32,300,000 shares

32,300,000 shares of Home Depot are indicated on the ticker.

Page 33 Problem 11 Answer

Given: The ticker for Sprint Nextel Corporation [email protected]▼0.78

To find: The total value of all of the Sprint Nextel Corporation shares traded.

Solution: From the ticker we get the following information:

Number of shares traded=1.1K

=1.1×1000

=1100 shares

Price per share=$9.14

Value of shares=1100×9.14

=$10,054

The total value of all of the Sprint Nextel Corporation shares traded was$10,054

Solutions For Cengage Financial Algebra Chapter 1 Exercise 1.5 The Stock Market

Page 33 Problem 12 Answer

Given: The ticker for Home Depot Inc [email protected]▲1.13

To find: Interpretation [email protected]

Solution: @29.13 shows that each share of Home Depot Inc was traded at$29.13

@29.13 in the ticker for Home Depot Inc shows that each share of Home Depot Inc was traded at$29.13

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 33 Problem 13 Answer

Given ; [email protected]▲[email protected]▼[email protected]▲[email protected]▼1.58

Given message

To find; How can XOM.66K be interpreted?

We have code given [email protected]▲[email protected]▼[email protected]▲[email protected]▼1.58

Value written just after the company symbol represents the trading volume

XOM 0.66K can be interpreted that 0.66 thousand (or 660 ) shares were traded in a single transaction

Hence the code can interpreted as XOM0.66k can be interpreted that  0.66 thousand or 660 shares were traded in a single transaction

Page 33 Problem 14 Answer

Given: Ticker for Exxon Mobil Corp [email protected]▼1.58

To find: Interpretation of▼1.58

Solution: The downward arrow indicates that the trading price is lower than the closing price of the previous day.

For Exxon Mobil Corp, indicates that the trading price was lower by from the previous day’s closing price.

Page 33 Problem 15 Answer

Given: The ticker for all four stocks are:

[email protected]▲1.13

[email protected]▼0.78

[email protected]▲2.27

[email protected]▼1.58

To find: The previous day’s closing price for each stock

Solution: To find the previous day’s closing price, we will add the value after the downward arrow to the trading price, or we will subtract the value after the upward arrow from the trading price

Previous day’s closing price:

Home Depot Inc=29.13−1.13

=$28

Sprint Nextel Corporation=9.14+0.78

=$9.92

Verizon Communications Inc=38.77−2.27

=$36.5

Exxon Mobil Corp=92.67+1.58

=$94.25

The previous day’s closing price for each stock is:

Home Depot Inc=$28

Sprint Nextel Corporation=$9.92

Verizon Communications Inc=$36.50

Exxon Mobil Corp=$94.25

Page 33 Exercise 1 Answer

Given: The ticker for Procter & Gamble Co: [email protected]▼0.39

To find: Number of shares of PG that were traded

Solution: Number of shares=4.5K

=4.5×1000

=4500 shares

4500 shares of PG were traded as per the information given in the [email protected]▼0.39

Cengage Financial Algebra Exercise 1.5 The Stock Market Key

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 33 Exercise 2 Answer

Given: The ticker for Procter & Gamble Co: [email protected]▼0.39

To find: Cost of each share

Solution: The cost of each share is$66.75

The cost of each share of Procter & Gamble Co was$66.75

Page 33 Exercise 3 Answer

Given: The ticker for Procter & Gamble Co: [email protected]▼0.39

To find: The value of the Procter & Gamble Co trade

Solution: From the ticker, we get the following information:

Number of shares=4.5K

=4.5×1000

=4500 shares

Price per share=$66.75

Value of trade=4500×66.75

=$300,375

The value of the Procter & Gamble Co trade was$300,375

Page 33 Exercise 4 Answer

Given: The ticker information for Procter & Gamble Co

Given code [email protected]▼[email protected]▲[email protected]▼[email protected]▲0.04

To find; Use the following ticker to answer PG [email protected] ∇0.39

Now number of shares =23600=23.6K and price previous day’s closing price=66.75+0.39=67.14

now price increased0.18  from last transaction ie. +0.18−0.39=−0.21

Therefore current price should be 67.14−0.21=66.93

Hence  Michele will see scrolling across her screen for this transaction will be  PG [email protected] ∇0.21

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 34 Exercise 5 Answer

Given ; [email protected]▼[email protected]▲[email protected]▼[email protected]▲0.04

Sarah sold her Disney shares as indicated on the ticker.

To find ; How many shares did she sell?

here we know that Value before @ symbol represents the number of shares traded DIS [email protected]

Number of shares traded 2.55´=2.55∗1000 =2550

​Hence sarah sold 2.55K(2550)  shares of Disney

Page 34 Exercise 6 Answer

Given ; [email protected]▼[email protected]▲[email protected]▼[email protected]▲0.04

Sarah sold her Disney shares as indicated on the ticker.To find ; How much did each share sell for?

Here we know that Value before @ symbol represents the number of shares traded

DIS 2.55K @34.90 1.08

Hence sarah has sold each share at a price of $34.90

Page 34 Exercise 7 Answer

Given; [email protected]▼[email protected]▲[email protected]▼[email protected]▲0.04  Sarah sold her Disney shares as indicated on the ticker.

To find: What was the total value of all the shares Sarah sold?

Here we see that 2.55K are the number of shares $34.90 is the cost of each share DIS 2.55K @34.90 ∇1.08

Value of trade = no. of shares ∗ cost of each share

Hence the value of shares sold =2.55100034.9=88995

Hence we conclude that sarah sold all her share at a price of $88,995

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 34 Exercise 8 Answer

Given ; [email protected]▼[email protected]▲[email protected]▼[email protected]▲0.04

Sarah sold her Disney shares as indicated on the ticker.

To find; What will Sarah see scrolling across her screen for this transaction of DIS?

DIS 2.55K @34.90 1.08 Now number of shares 7600=7.6´ and price previous day’s closing price34.9+1.08=35.98 now price increased 0.98  from last transaction ie. +0.98−1.08=−0.1

Therefore current price should be 35.98−0.1=35.88

Hence Sarah see scrolling across her screen for this transaction of DIS will be  DIS 7.6K @35.88 ∇0.1

Page 34 Exercise 9 Answer

Given: The stock symbols represent the corporations.

To find:  How many shares of Kellogg Co. are indicated on the ticker.

Values before at the rate symbol will give traded shares.

Using the values, we can say that shares of Kellogg Co. are indicated on the ticker will be

0.76k=0.76⋅1000

=760

Thus, we can say that 760 shares of Kellogg Co. are indicated on the ticker where the stock symbols represent the corporations.

Page 34 Exercise 10 Answer

Given: The stock symbols represent the corporations.

To find: How can @36.17  be interpreted.Values before at the rate symbol will give traded shares.

Since, we know that values before @  symbol will give traded shares.

Thus, @36.17 can be interpreted that trading occur at $36.17.

Thus, we can say that @36.17 can be interpreted that trading occur at$36.17.

Page 34 Exercise 11 Answer

Given: The stock symbols represent the corporations.

To find: How can0.76k can be interpreted.Values before at the rate symbol will give traded shares.

Since, we know that values before@ symbol will give traded shares.

Also, we know that k=1000 that can be interpreted which gives us the value of 076k=0.76⋅1000 =760

​Thus, we can say that 0.76K  be interpreted as the trade share will be 760.

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 34 Exercise 12 Answer

Given: The stock symbols represent the corporations.

To find: How can ▲0.04  be interpreted.Direction of arrows tells us about the change in price.

Since we know that direction of arrows tells us about the change in price.

Thus, we can say that ▲0.04 means that price gets increased on comparing with previous days closing price.

Thus, we can say that when the stock symbols represent the corporations then ▲0.04

can be interpreted as price gets increased on comparing with previous days closing price.

Page 34 Exercise 13 Answer

Given: 36,000  shares of ABC at a price of 37.15  which is  $0.72  higher than the previous day’s close.

To find: Write the ticker symbols for each situation. We will try to find the change in the price with the relative days.

Since we know that the price increases with the previous day. So, we can write▲0.72.

Also, the price can be written as

36,000/1000

=36K.

Hence, we can write the ticker symbols as [email protected]▲0.72.

Thus, we can write the ticker symbols as [email protected]▲0.72.

Page 34 Exercise 14 Answer

Given: 1,240 shares of XYZ at a price of $9.17, which is $1.01 lower than the previous day’s close.

To find: Write the ticker symbols for each situation. We will try to find the change in the price with the relative days.

Since we know that the price decreases with the previous day. So, we can write▼1.01. Also, the price can be written as 1240/1000=1.24K.

Hence, we can write the ticker symbols as [email protected]▼1.01.

Thus, we can write the ticker symbols as [email protected]▼1.01.

Page 34 Exercise 15 Answer

Given: Maria is a stock broker and has been following transactions for Ford Motor Co.

To find: Write the stock ticker symbols that would appear on the scroll for the last trade of the day on Wednesday for Ford.

We will try to find the change in the price with the relative days.

Since, the price on previous day can be written as 5600/1000=5.6K.

As, we know that the last trade of the day was $0.56 higher than Tuesday’s close, which gives us the present value as8.11+0.56=$8.67.

Thus, we can write the ticker symbols as [email protected]▲0.56.

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market Page 34 Exercise 16 Answer

Given: Dorothy purchased x thousand shares of Macy’s Inc (M) at y dollars per share.

To find: Express the ticket symbols algebraically.

We will try to find the change in the price with the relative days.

Since the price on current day can be written as$y.Also, we can write the shares price as x⋅1000/1000=x K.

So, the decrease in price will be z.Thus, we can say that the ticket symbols algebraically will be MxK@y▼z.

Page 34 Exercise 17 Answer

Given:

To find: Do numbers reflect a positive or negative money flow?

We will multiply the volume to get the net flow.

On the very first day, we get average as(27.90+26.85+27.75)/3=27.5and

for the second day, we get average as (27.95+27.40+27.66)/3=27.67.

So, for the first day we get the net flow as 79,670,500×27.5=2,190,938,750 and for the second day, we get the net flow as 53,299,800×27.67=1,474,805,466.

Thus, we can say that there will be negative money flow of May−16 for

Page 34 Exercise 18 Answer

Given:

To find: Do numbers reflect a positive or negative money flow.

We will multiply the volume to get the net flow.

On the very first day, we get average as (582.95+575.60+581)/3=579.85

And for the second day, we get average as(584.68+578.32+580)/3=581

So, for the first day we get the net flow as4,342,700×579.85=2,518,114,595

And for the second day, we get the net flow as4,974,100×581=2,889,952,100.

Thus, we can say that there will be positive money flow of June 7 for

Detailed Solutions For Cengage Financial Algebra Chapter 1 Exercise 1.5

Chapter 1 Solving Linear Equations

• • Cengage Financial Algebra 1st Edition Chapter 1 Assessment The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.2 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.3 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.4 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.6 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.7 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.8 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.9 The Stock Market

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business

Page 104 Problem 1 Answer

Given: p=42, E=50q+80,000 and q=80p+100,000

To Determine the expense E

Use the equation for q    q=80p+100,000.

Substitute 42       for q    q=80(42)​+100,000.

Simplify                              q=103,360

Use the equation for E    E=50q+80,000

Substitute q                       E=50(103,360)+80,000

Simplify                               E=5,248,000

Therefore the expense is 5,248,000.

Page 105 Problem 2 Answer

Given:

To show :P=R−E

Graphically, profit is the vertical distance between the revenue and expense functions.

In Figure, the top of the curve(dot)  hits the revenue graph at 40,380,000 when the price is about 25.

The bottom of the vertical line segment hits the expense graph at150,500

at the same price. The vertical length of this segment is 40,380,000−150,500=3887,500 and is the profit the company makes when price is about 25.

P=R−E where P is profit, R is revenue, and E is expenses

The greatest difference between revenue and expense denotes maximum profit.

Hence shown P=R−E

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra Chapter 2.8 Modeling A Business Guide

Page 106 Problem 3 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To find as the price increases, what is expected to happen to the quantity demanded

It is pretty simple, as the price increases, the demand goes down.

As the price increases, the demand goes down.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business Page 106 Problem 4 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

The horizontal axis represents price, and the vertical axis represents quantity

To find if the slope of the demand function is positive or negative with explanation.

From tip, it is clear that, as the price increases, demand goes down.

So, there is inverse relation between price and demand.

Hence, demand will have negative slope.

If the horizontal axis represents price, and the vertical axis represents quantity, demand will have negative slope.

Page 107 Problem 5 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

The company decides to conduct a market research survey to determine the best price for the device.

The variable p represents price, and q represents quantity demanded. The points are listed as(p,q)

(14,8200),(11,9100),(16,7750),(16,8300),(14,8900)

(17.7100).(13.8955),(11.9875),(11.9425).(18.5825)

To make a scatter plot of the data ad to check if the data look like it has a linear form.

The graph is

It almost seem to be a straight line.

The scatter plot of the data is

The data seem linear form.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business Page 107 Problem 6 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To check if  the linear regression line a good predictor and explain.

We will draw graph.

The graph is

It is a good predictor.

The regression line is a good predictor.

Page 107 Problem 7 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To examine the data to see if there is any relationship between the price and the quantity demanded.

To determine the correlation coefficient between price and demand, rounded to nearest hundredth.

To explain the significance of the correlation coefficient.

We will calculate the correlation coefficient using machine.

The correlation coefficient is−0.9156370841≈−0.92

As the coefficient is negative, there is  a negative relation between price and quantity demanded.

Also, since the coefficient is almost one in  magnitude, the relation is strong.

Correlation coefficient between price and demand is≈−0.92

It shows there is a negative relation which is strong too.

Solutions For Exercise 2.8 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business Page 107 Problem 8 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

Fixed cost $24500 variable cost per variable $6.12

To express expense E as a function of q demand.

The variable cost will be6.12q

So, E=6.12q+15400

The expense equation E as a function of demand q is

E=612q+15400.

Page 107 Problem 9 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To express revenue R in terms of p,q

From tip,

R=pq

Revenue R in terms of p,q is R=pq.

Page 107 Problem 10 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To use he transitive property of dependence to express expense, E, in terms of p. Round to the nearest hundredth.

From before,

E=6.12q+24500

q=−423.61p+14315.94

E=−2592.49p+112113.55

Expense E in terms of p is

E=−2592.49p+112113.55.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business Page 107 Exercise 1 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To determine an appropriate maximum horizontal-axis value.

The function E is E=−2592.49p+112113.55

From tip, E=0

p≈44

The maximal horizontal value is 44.

Page 107 Exercise 2 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To determine an appropriate maximum vertical-axis value.

The maximal vertical axis value will be the Expense at price zero

Which is112113.55≈113000

The maximal vertical-axis value is 113000.

Page 107 Exercise 3 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To sketch the graphs of the expense and revenue functions.

The graph is

The graph between revenue function and expense is

Financial Algebra Cengage Modeling A Business Exercise 2.8 Walkthrough

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business Page 107 Exercise 4 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

Determine the coordinates of the maximum point on the revenue graph. Round the coordinates to the nearest hundredth.

The revenue function is

R=−423.61p²+14315.94p

From tip, Maximum occurs at

p≈16.9

R≈120952.14

The coordinates of the maximum point on the revenue graph is(16.9,120952.14).

Page 107 Exercise 5 Answer

A company produces a security device known as Toejack.

Toejack is a computer chip that parents attach between the toes of a child, so parents can track the child’s location at any time using an online system.

The company has entered into an agreement with an Internet service provider, so the price of the chip will be low.

To determine the breakeven points.

The Expense function is

E=−2,592.49p+112,113.55

Revenue function is

R=−423.61p{2}+14,315.94p

−423.61p{2}+14,315.94p=−2,592.49p+112,113.55

p≈31.52,8.40

Points are 31.52,30403.76

8.40,90343.87

​The breakeven points are 31.52,30403.76

8.40,90343.87

​Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business Page 107 Exercise 6 Answer

Here we have

Revenue function found in exercise 12 isR=−423.61p²+14,315.94p

Expense function found in exercise 13 is E=−2,592.49p+112,113.55

By using these functions we will find the profit function.

Profit function is the difference between the revenue function and the expense function

Such thatP=R−E

=−423.61p²+16,908.43p−112,113.55

Thus profit function P, in terms of p. is    −423.61p²+16,908.43p−112,113.55

Page 107 Exercise 7 Answer

We have profit functionP=−423.61p²+16,908.43p−112,113.55

Here first we will value of price at maximum revenue happen and that we will draw the graph.

We have Profit functionP=−423.61p²+16,908.43p−112,113.55

The maximum Profit occurs at the axis of symmetry x=−b/2a for a quadratic function y=ax²+bx+c

Thus p=−16,908.43

2(−423.61)

≈19.96

Thus the maximum profit happens at a price of $19.90.

Graphical representation

The maximum profit happens at a price of $19.90.

Page 107 Exercise 8 Answer

We haveq=−423.61p+14,315.94

R=−423.61p²+14,315.94p

E=−2,592.49p+112,113.55

P=−423.61p²+16,908.43p−112,113.55

​Break-even points are at prices of $8.40 and $31.52 (result exercise 16 ).

The maximum profit price is $19.96

Here by using these results we will answer the given statements.

(1) q Toejacks should be manufactured (produeed) at a price of $19.96 each.

q=−423.61(19.96)+14,315.94=5860.6844≈5861

(2)  Every Toejack will be sold at a price of $19.96 per Toejack, which is the maximum profit price.

(3) & (4)  The breakeven points are reached at a price of $8.40 or 831.52

(5)  The revenue is given by R=−423.61p²+14,315.94p at p=19.96

R=−423.61(19.96)²+14,315.94(19.96)=116979.260624≈8116979.26

(6)  The expenses are given by E=−2,592.49p+112,113.55 at p=19.96

E=−2,592.49(19.96)+112,113.55=60367.4496≈$60367.45

(7)  The profit is given by P=−423.61p²+16,908.43p−112,113.55 at p=19.96

P=−423.61(19.96)² +16,908.43(19.96)−112,113.55=56611.811024≈$56611.81

Answers are  (1)5861(2)$19.96(3)$8.40(4)$31.52(5)$116,979.26(6)$60,367.45(7)$56,611.81

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business Page 107 Exercise 9 Answer

We have E=−2,592.49p+112,113.55

The maximum profit was obtained at a price of $19.90 as derived in a previous exercise.

Assume that the business holders decide to use this price, then we can determine the corresponding

Expenses: E=−2,592.49(19.96)+112,113.55=60367.4496 Thus the total expenses are then $00,367.4490 or approximately $00,307.45

The shares are sold at $5 per share. Let there be x shares, then the total income of the shares is 5x.

The income of the shares should cover the total expenses: 5x=$60,307.45

Thus we obtain x=60,367.45/5

=12,073.49

Thus  12,073.49 shares should be sold.

However, the number of shares should be an integer and thus we should sell at least 12,074 shares to get enough money to start the business.

Number of shares must be sold to get enough money to start the business is 12074.

Chapter 2.8 Cengage Financial Algebra Solutions Explained

Chapter 2 Solving Linear Inequalities

• • Cengage Financial Algebra 1st Edition Chapter 2 Assessment Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.1 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.2 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business

Page 99 Problem 1 Answer

Given: The revenue and expense functions are R=-350p2+18,000p and E=−1,500p+199,000.

To find The profit equation. For doing so, we will use the fact that the difference between the revenue and total cost functions is the profit function.

We know that the difference between the revenue and total cost functions is the profit function.

P=R−E

=(−350p²+18,000p)−(−1,500p+199,000)

=−350p²+19500p−199000​

∴Our required profit equation isP=−350p2+19500p−199000.

Page 100 Problem 2 Answer

Given: Must maximum profit occur at the same price as the maximum revenue?

To find The explanation for the given.

We know that the profit equation is different from the revenue equation.

So, profit and revenue will have different parabolas with different points of maxima.

So, it is not necessary that maximum profit occurs at the same price as the maximum revenue.

No, it is not necessary that maximum profit occurs at the same price as the maximum revenue.

Page 101 Problem 3 Answer

Given: How might the quote apply to what has been outlined in this lesson?

To find: Summarize the lesson’s outline using a quote.

When you create a profit, your revenue exceeds your expenditures.

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

When you lose money, your costs outnumber your earnings.

Because your income exceeds your costs, your expenses are not more than your revenue, implying that you cannot lose money if you earn a profit.

∴ You cannot lose money if you earn a profit.

Cengage Financial Algebra Chapter 2.7 Modeling A Business Guide

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 101 Problem 4 Answer

Given:

To find The range of prices when the profit is made.

For doing so, we will refer to the fact that when the income exceeds the costs, the black curve rises over the blue line, indicating a profit.

When the income exceeds the costs, the black curve rises over the blue line, indicating a profit.

We can see that the horizontal axis is split into six regions between0 and 100, therefore the width between successive tick marks on the horizontal axis is:100/6≈16.67.

The initial crossing of the black curve and the blue line is about two-thirds of the way between the vertical axis and the first tick mark, which corresponds to11.11.

2/3⋅100/6

=100/9

≈11.11

The second crossing of the black curve and blue line occurs about one-third of the way between the fourth and fifth tickmarks, corresponding to72.22.

(4+1/3)⋅100/6

=650/9

≈72.22

When the price is generally between$11.11 and $72.22, we profit.

Page 101 Problem 5 Answer

We have given a graph where the blue graph represents the expense function and the black graph represents the revenue function.

We have to describe the profit situation in terms of the expense and revenue functions.

We will use above information.

Here,We can see that between 0 and 100 on the horizontal axis is divided into 6 areas.

So, the width between the consecutive tick-marks on the horizontal axis is: 100/6

≈16.67

Now, The first intersection between the black curve and blue line is about one third between the vertical axis and the first tick-mark, which corresponds with roughly 11.11.

i.e.1/3⋅100/6

=50/9

≈5.56

The second intersection between the black curve and blue line is about two thirds between the fourth and fifth tick-mark, which corresponds with roughly 72.22

i.e.(4+2/3)⋅100/6

=700/9

≈77.78

Hence,

We make a profit when the price is roughly between $5.56 and $77.78.

Therefore, Price is roughly between $5.56 and $77.78

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 101 Problem 6 Answer

Given : ​

E=−20,000p+90,000

R=−2,170p²+87,000p​

We have to write the profit function for the given expense and revenue functions.

We will use above information.

Here, We have, ​

E=−20,000p+90,000

R=−2,170p²+87,000p

So,P=−2,170p²+87,000p−(−20,000p+90,000)

​=−2,170p²+107,000p−90,000

​Therefore,

P=−2,170p²+107,000p−90,000

Page 101 Problem 7 Answer

Given : ​

E=−6,500p+300,000

R=−720p²+19,000p​

We have to write the profit function for the given expense and revenue functions.

We will use above information.

Here,We have,

E=−6,500p+300,000

R=−720p²+19,000p​

So, ​​P=−720p²+19,000p−(−6,500p+300,000)​

=−720p²+25,500p−300,000​

Therefore,

P=−720p²+25,500p−300,000

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 101 Problem 8 Answer

Given : ​

E=−2,500p+80,000

R=−330p²+9,000p​

We have to write the profit function for the given expense and revenue functions.

We will use above information.

Here, We have, ​

E=−2,500p+80,000

R=−330p²+9,000p​

so,P=−330p²+9,000p−(−2,500p+80,000)​

=−330p²+11,500p−80,000​

Therefore,

P=−330p²+11,500p−80,000

Page 101 Problem 9 Answer

Given : ​

E=−12,500p+78,000

R=−1,450p²+55,000p​

We have to write the profit function for the given expense and revenue functions.

We will use above information.

Here, We have, ​

E=−12,500p+78,000

R=−1,450p²+55,000p

So,P=−1,450p²+55,000p−(−12,500p+78,000)

​=−1,450p²+67,500p−78,000

​Therefore,

P=−1,450p²+67,500p−78,000

Financial Algebra 1st Edition Modeling A Business Exercise Solutions

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 102 Problem 10 Answer

Given: The revenue (black) and expense (blue) functions.

We have to examine the revenue (black) and expense (blue) functions.

And also estimate the price at the maximum profit and explain our reasoning.

We will use above information.

Here, As we know that, A profit is made when the revenue is larger than the expenses.

The maximum profit is then obtained when the difference between the revenue and expenses is largest.

The largest profit then appears to occur slightly to the right of the peak of the black curve.

Hence, The largest profit appears to occur at $25.00.

Therefore, The largest profit appears to occur at $25.00.

Page 102 Problem 11 Answer

Given : Profit functions of Exercises 6−9 models .

We have to determine which profit function models a no profit situation.

We will use above information.

Here, We have, The profit function is the difference between the revenue function and the expense function.

P=−2,170p²+107,000p−90,000

P=−720p²+25,500p−300,000

P=−330p²+11,500p−80,000

P=−1,450p²+67,500p−78,000

Now, the graph of all functions:

As the profit functions models a no profit situation if the profit is always negative (which indicates that we always make a loss and thus never make a profit).

We see that the profit function of exercise 7 models a no profit situation, as the graph lies completely below the horizontal axis, which indicates that the profit is always negative.

Therefore,

Problem 7 model is a no profit situation.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 102 Problem 12 Answer

Given: Profit functions of Exercises 6−9 models.

We have to show that how a profit function look like when no profit can be made.

We will use above information.

Here,The profit functions models a no profit situation if the profit is always negative (which indicates that we always make a loss and thus never make a profit).

As in part (a), we saw that the profit function of problem 7 models a no profit situation, as the graph lies completely below the horizontal axis, which indicates that the profit is always negative.

Thus a profit function lies completely below the horizontal axis when no profit can be made.

Therefore,

Page 102 Problem 13 Answer

Given : P=−400p²+12,400p−50,000

We have to determine the maximum profit and the price that would yield the maximum profit.

We will use above information.

Here,We have, ​​P=−400p²+12,400p−50,000,

a=−400​

b=12,400

c=−50,000​

As we know that the maximum value occurs on the axis of symmetry.

The x-intercept of the axis of symmetry is determined −b/2a=−12,400/2×−400

⇒15.5

So, at p=15.5 the profit will be maximum.

Now, The maximum profit ,​​P=−400(15.5)²+12,400(15.5)−50,000,

P=−96,100+192,200−50,000

​=46,100

​Therefore, The maximum profit is 46,100

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 102 Problem 14 Answer

Given:P=−370p²+8,800p−25,000

We have to determine the maximum profit and the price that would yield the maximum profit.

We will use above information.

Here,

We have, ​​P=−370p²+8,800p−25,000

a=−370​

b=8,800

c=−25,000​

As we know that the maximum value occurs on the axis of symmetry.

The x-intercept of the axis of symmetry is determined −b/2a

=−8,800

2×−370

⇒11.89

So, at p=11.89 the profit will be maximum.

Now,The maximum profit ,​​P=−370(11.89)²+8,800(11.89)−25,000

P=−52,307.68+104,632−25,000

​=27,324.32

​Therefore,

The maximum profit is, P=27,324.32

Chapter 2 Exercise 2.7 Financial Algebra Cengage Walkthrough

Page 102 Problem 15 Answer

Given: P=−170p²+88,800p−55,000

To Determine the maximum profit and the price that would yield the maximum profit for each.

To determine the maximum profit algebraically, recall that the maximum value occurs on the axis of symmetry.

For the profit function given on left side The x – intercept of the axis of symmetry is determined −b/2a

P=−170p²+88,800p−55,000,a=−170,b=88,800, and c=−55,000.

​Calculate −b/2a

=−88,800/2×−170

=261.18

Hence at p=261.18, the profit will be maximum now to find maximum profit substitute this value of p

P=−170(261.18)²+88,800(261.18)−55,000,

P=−11,596,548.71+23,192,784−55,000=11,541,235.29

​At 261.18 the maximum proft would be 11,541,235.29.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 102 Problem 16 Answer

Given: The expense and revenue functions are

E=−1,850p+800,000 and R=−100p²+20,000p.

To Determine the profit function.

Using the formula P=R−E

we get

P=−100p²+20,000p−(−1,850p+800,000)

P=−100p²+21,850p−800,000

​Therefore profit function is  P=−100p²+21,850p−800,000

Page 102 Problem 17 Answer

Given: The expense and revenue functions are

E=−1,850p+800,000 and R=−100p²+20,000p.

To Determine the price, to the nearest cent, that yields the maximum profit.

To determine the maximum profit algebraically, recall that the maximum value occurs on the axis of symmetry. For the profit function given on left side The x – intercept of the axis

of symmetry is determined −b/2a

P=−100p²+21,850p−800,000

a=−100,b=21,850,c=−800,000

​Calculate −b/2a

=−21,850/2×−100

=109.25

Therefore the price, to the nearest cent, that yields the maximum profit at $109.25

Page 102 Problem 18 Answer

Given: The expense and revenue functions are

E=−1,850p+800,000 and R=−100p²+20,000p

Also From previous exercise we know that p=$109.25

To  Determine:  the maximum profit, to the nearest cent.

Hence at  p=109.25

The profit will be maximum now to find maximum profit substitute this value of p

P=−100(109.25)²+21,850(109.25)−800,000,

P=−1,193,556.25+2,387,112.5−800,000=393,556.25

​The maximum profit, to the nearest cent is $393,556.25

How To Solve Cengage Financial Algebra Chapter 2.7

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business Page 102 Problem 19 Answer

Given: The expense and revenue functions are  E=−250p+50,000 and R=−225p²+7,200p

To Determine the profit function.

p=−225p2+7,200p-(250p+50,000)

p=−225p2+7.450p−50.000

Therefore the profit function is P=−225p{2}+7.450p−50.000

Page 102 Problem 20 Answer

Given: expense and revenue functions are E=−250p+50,000 and R=−225p²+7,200p

To Determine: the price, to the nearest cent, that yields the maximum profit.

To determine the maximum profit algebraically, recall that the maximum value occurs on the axis of symmetry.

For the profit function given on left side The x – intercept of the axis of symmetry is determined −b/2a

P=−225p2+7,450p−50,000

a=−225,b=7,450,c=−50,000

Calculate −b/2a

=−7,450/2×−225

=16.56

Therefore the price, to the nearest cent, that yields the maximum profit is at $16.56

Page 102 Problem 21 Answer

Given : The expense and revenue functions are E=−250p+50,000 and R=−225p²+7,200p

Also we know that p=$16.56

To  Determine the maximum profit, to the nearest cent.

Hence at p=25.54 the profit will be maximum now to find maximum profit substitute this value of p

P=−225(16.56)²+7,450(16.56)−50,000

P=−61,702.56+123,372−50,000=11,669.44​

Therefore the maximum profit, to the nearest cent is at $11,669.44

Step-By-Step Guide To Financial Algebra Exercise 2.7

Chapter 2 Solving Linear Inequalities

• • Cengage Financial Algebra 1st Edition Chapter 2 Assessment Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.1 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.2 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business

Page 93 Problem 1 Answer

Given that there is an error when calculating the expense and revenue values

To find how we can improve the error By using basic knowledge

While we are using rounding off values, we can get some minute error in the revenue and expense values.

So, to improve on the error we have to use exact price values instead of the rounding values.

But it is somewhat difficult to calculate with the exact values manually.

Page 94 Problem 2 Answer

Given that ​E=−3500p+238000

R=−500p²+30000p​

To find a,b,c in cellsB11,B12,B13

By using basic calculations

Given that

E=−3500p+238000

R=−500p²+30000p

At breakeven point, The expense equals to revenue

−3500p+238000=−500p²+30000p

−500p²+33500p−238000=0

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

​This equation is similar to the equation in cellB10

The a,b,c values are the values from the equation −500p²+33500p−238000=0

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling A Business Solutions

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business Page 95 Problem 3 Answer

Given that Risk comes from not knowing what you’re doing

To find How might the quote apply to what you have learned

By using the own knowledge

If you don’t know what you are doing, then won’t know if you will make a profit or make a loss.

Moreover, you always won’t realize the extent of the possible loss and this could then provide a very large risk.

In practice, you will need to take into account your total expenses to determine the price of your items such that you won’t make any loss.

However, if you fail to do so, then you have a high risk of making a loss, as you didn’t check which prices will result in a profit for your company.

Page 95 Problem 4 Answer

Given that A supplier of school kits has determined that the combined fixed and variable expenses to market and sell G kits is W

To find breakeven point

By finding the price per item

The breakeven point is the price of one item

So, Breakeven point is W/G

Page 95 Problem 5 Answer

Given that A supplier of school kits has determined that the combined fixed and variable expenses to market and sell G kits is W

To find breakeven point

By finding the price per item

The cost per item is the total cost (which is 80%of W  ) divided by the number of items (2G).

The price per item is 80%×W

2GTo make breakeven the cost per item should equal the price (revenue) per item.

80%×W/2G

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business ​Page 95 Problem 6 Answer

Given that breakeven points are 80,150

To graph using the given data

By using the graph paper

Given that breakeven points are 80,150

At 80 the expense and revenue values are both 300000.

At 150, the expense and revenue values are both 100000.

The graph looks like

The graph is

Page 95 Problem 7 Answer

Given that breakeven points are 170, 350

To graph using the given data

By using the graph paper

Given that breakeven points are 170, 350

At 170 the expense and revenue values are both 2600000.

At 350 the expense and revenue values are both 900000.

The graph looks like

The graph is

Page 95 Problem 8 Answer

Given that expense function is E=−19,000p+6,300,000 and the revenue function is R=−1,000p²+155,000p

To Graph the expense and revenue functions. Label the maximum and minimum values for each axis. Circle the breakeven points.

By using the graphs

Given that

The expense function is E=−19,000p+6,300,000

The revenue function is R=−1,000p²+155,000p

The graph is

The breakeven points are blue circles and black circle is maximum value

The grap is

The breakeven points are blue circles and black circle is maximum value

Cengage Financial Algebra Chapter 2 Exercise 2.6 Modeling A Business Answers

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business Page 95 Problem 9 Answer

Given that: The expense function is E=−19,000p+6,300,000 And The revenue function is R=−1,000p²+155,000p

To find the prices at the breakeven points.

By using basic calculations

Given that

The expense function is E=−19,000p+6,300,000

The revenue function is R=−1,000p²+155,000p

At breakpoints, The revenue is equal to expense

−19,000p+6,300,000=−1,000p²+155,000p

1,000p²−174,000p+6,300,000=0

p=−174,000±√174,0002−4⋅1,000⋅6,300,000/2⋅1,000

=51.38 or 122.62

The graph is

​

The prices at breakeven points are 51.38 or 122.62

The graph is

Page 95 Problem 10 Answer

Given that:

The expense function is

E=−19,000p+6,300,000

The revenue function is

R=−1,000p²+155,000p

To find the revenue and expense amounts for each of the breakeven points.

By using basic calculations

From 7(b)

Breakeven points are 51.38, 122.62

At p=51.38,

The expense is ​​

E=−19,000⋅51.38+6,300,000

​=5,323,780

​So, the revenue=5,323,780

At p=122.62

The expense is

​​E=−19,000⋅122.62+6,300,000

​=3,970,220

​So, the revenue =3,970,220

At p=51.38, The expense and revenue is 5,323,780

At p=122.62, The expense and revenue is 3,970,220

Page 96 Exercise 1 Answer

Given that expense function is E=−5,000p+8,300,000 the revenue function is R=−100p{2}+55,500p

To Graph the expense and revenue functions. Circle the breakeven points.

By using the graphs

Given that expense function is

E=−5,000p+8,300,000 the revenue function is

R=−100p{2}+55,500p

Graph of the expense and revenue functions is

The graph is

Page 96 Exercise 2 Answer

Given that

expense function is

E=−5,000p+8,300,000 the revenue function is R=−100p{2} +55,500p

To find the prices at the breakeven points.

By using basic calculations

Given that expense function is

E=−5,000p+8,300,000 the revenue function is R=−100p{2}+55,500p

At breakeven point, The revenue is equal to expense

−5,000p+8,300,000=−100p²+55,500p

100p²−60,500p+8,300,000=0

p=60,500±√60,5002−4⋅100⋅8,300,000/2⋅100

=210.27 or 394.73​

The breakeven points are 210.3, 394.7

Solutions For Cengage Financial Algebra Chapter 2 Exercise 2.6 Modeling A Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business Page 96 Exercise 3 Answer

Given that expense function is

E=−5,000p+8,300,000 the revenue function is R=−100p{2}+55,500p

To find the revenue and expense amounts for each of the breakeven points

By using the graphs

Given that expense function is

E=−5,000p+8,300,000 the revenue function is R=−100p{2}+55,500p

From 8(b), The breakeven points are 210.27, 394.73

We know that At breakeven point, The revenue is equal to expense

At p=210.27,

The expense is E=−5,000⋅210.27+8,300,000

=7,248,646.67​

The revenue is 7,248,646.67

At p=394.73

The expense is E=−5,000⋅394.73+8,300,000 =6,326,353.33

​The revenue is 6,326,353.33

At p=210.27, The expense and revenue is 7,248,646.27

At p=394.73, The expense and revenue is 6,326,353.33

Page 96 Exercise 4 Answer

Given: The expense function isE=−200p+10,000 and the revenue function isR=−18p{2}+800p.

To find The price at which maximum revenue is reached and the maximum revenue.

For a parabola, the greatest revenue price is found along the axis of symmetry.

For a parabolay=ax{2}+b+c, the greatest revenue price is found along the axis of symmetryx=−b/2a.

We have​a=−32,

b=1200 and

c=0 ​in this situation because ofR=−18p{2}+800p.

p=−b/2a

=−800

2(−18)

=22.22.

As a result, the price at which the greatest revenue is achieved at$22.22.

Calculate the revenue that corresponds to the price of$22.22.

R=−18p²+800p

=−18(22.22)²+800(22.22)

≈$8888.89.

As a result, the maximum revenue is$8888.89.

The graph can be draw

∴ The maximum revenue of $ 8888.89 occurs at a price of $22.22.

Page 96 Exercise 5 Answer

Given: The expense and revenue functions exist.To do: Graph the given.For doing so, we will plot a graph.

The cost function is represented by a straight blue line, whereas the revenue function is represented by a red curve.

The cost function is represented by a straight blue line, whereas the revenue function is represented by a red curve.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business Page 96 Exercise 6 Answer

Given: The expense function is E=−200p+10000 and the revenue function isR=−18p{2}+800p.

To find The prices at the breakeven points.For doing so, we will refer to the fact that at the breakeven point, the revenue and expenditure functions are equal.

At the breakeven point, the revenue and expenditure functions are equal.

−200p+10,000=−18p{2}+800p

⇒18p{2}

−1,000p+10,000=0.

Using the quadratic formula, find the solution.

​p=1,000±√1,000²−4⋅18⋅10,000 /2⋅18

=13.08 or 42.48

​The prices at the breakeven points are$13.08,$42.48.

Page 96 Exercise 7 Answer

Given: Breakeven prices are$13.08,$42.48.

To find The revenue and expense amount for each of the breakeven points.For doing so, we will refer to the fact that at the breakeven point, the revenue equals the expense.

We know that the breakeven prices are$13.08,$42.48.

Expenses corresponding these breakeven prices are​E=−200⋅13.08+10,000=7,384.17

E=−200⋅42.48+10,000

=1,504.72.

At the breakeven point, the revenue equals the expense. So​R=7,384.17,

R=1,504.72.

∴Our required amount of revenue and expenses are$7,384.17,$1,504.72.

Cengage Financial Algebra Exercise 2.6 Modeling A Business Key

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business Page 96 Exercise 8 Answer

Given: The expenses functionE=−300p+13000

and the revenue function isR=−32p{2}+1,200p.

To find: The price at which maximum revenue is reached and the maximum revenue.For a parabola, the greatest revenue price is found along the axis of symmetry.

For a parabolay=ax{2}+b+c, the greatest revenue price is found along the axis of symmetryx=−b/2a.

We have​a=−32,

b=1200 and

c=0 ​in this situation because ofR=−32p{2}+1,200p.

p=−b/2a

=−1200

2(−32)

=18.75.

As a result, the price at which the greatest revenue is achieved at$18.75.

A graph can be plotted as

∴The maximum revenue can be achieved at a price of$18.75.

Page 96 Exercise 9 Answer

Given: The maximum revenue can be achieved at a price of$18.75.

To find The maximum revenue.For doing so we will determine the revenue at a given price using the function provided.

Calculate the revenue that corresponds to the price of$18.75.

R=−18p²+800p

=−18(18.75)²+800(18.75)

≈$11,250.

As a result, the maximum revenue is$11,250.

The maximum revenue is$11,250.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business Page 96 Exercise 10 Answer

Given: The expense and revenue functions exist.To do: Graph the given.For doing so, we will plot a graph.

The cost function is represented by a straight green line, whereas the revenue function is represented by a red curve.

The cost function is represented by a straight green line, whereas the revenue function is represented by a red curve.

Page 96 Exercise 11 Answer

Given: The expense functionE=−300p+13000p, and revenue function isR=−32p{2}+1,200p.

To find The prices at the breakeven points.

For doing so, we will refer to the fact that at the breakeven point, the revenue and expenditure functions are equal.

At the breakeven point, the revenue and expenditure functions are equal.

−300p+13,000=−32p{2}+1,200p

⇒32p{2}

−1,500p+13,000=0.

Using the quadratic formula, find the solution.​

p=1,500±√1,500²−4⋅32⋅13,000 /2⋅32

=11.48 or 35.40

∴The prices at the breakeven points are$11.48,$35.40.

Page 96 Exercise 12 Answer

Given: Breakeven prices are$11.48,$35.40.To find: The revenue and expense amount for each of the breakeven points.

For doing so, we will refer to the fact that at the breakeven point, the revenue equals the expense.

We know that the breakeven prices are$11.48,$35.40.

Expenses corresponding to these breakeven prices are​E=−300⋅11.48+13,000

=9,557.06

E=−300⋅35.40+13,000

=2,308.44.

At the breakeven point, the revenue equals the expense. So​R=9,557.06,

R=2,308.44.

Our required amount of revenue and expenses are$9,557.06,$2,308.44.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business Page 96 Exercise 13 Answer

Given:

To find The price at which the maximum profit is reached.

The highest revenue yields the biggest profit; the revenue is determined by the parabola.

The highest point of the parabola is found on the third vertical line, which occurs at a cost of$60.

∴ The price at which the maximum profit is reached is$60.

Detailed Solutions For Cengage Financial Algebra Chapter 2 Exercise 2.6

Chapter 2 Solving Linear Inequalities

• • Cengage Financial Algebra 1st Edition Chapter 2 Assessment Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.1 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.2 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business

Page 88 Problem 1 Answer

Given ; Fixed costs are$20,000.

cost of ear phone 5 $

The demand function is q=−200p+40,000

To find; Write the expense function in terms of q and determine a suitable viewing window for that function. Graph the expense function.

The expense function is E=5q+20000

Substitute for q to find the expense function in terms of priceq=−200p+40,000

E=5q+20000

E=5(−200p+40,000)+20000

E=−1000P+200000+20000

E=−1000P+220000

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

The horizontal axis represents price, and the vertical axis represents expense.

Both variables must be greater than 0,so the graph is in the first quadrant.

To determine a viewing window

find the points where the expense function intersects the vertical and horizontal axes.

Neither p nor E can be 0 because both a price of 0 and an expense of 0 would be meaningless in this situation.

But, you can use p=0 and E=0 to determine an appropriate viewing window

When p=0

E=−1000P+220000

E=−1000×0+220000

E=220000

​or when E=0

E=−1000P+220000

0=−1000P+220000

1000P=220000

P=220000/1000

P=220

​Hence we have express The expense function asE=5q+20000

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling A Business Solutions

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 88 Problem 2 Answer

Given:

The revenue equation for the Picasso Paints product is:

R= -500p2+30,000p

To find: The revenue if the price per item is set at

Solution: We will substitute the value in the equation

R= -500p²+30,000p

=-500(25)²+30,000(25)

=-312,500+750,000

=437,500

For the Picasso Paints product, if the price is $25 then the revenue will be$437,500

Page 89 Problem 3 Answer

Given that the prices $ 28, $40

To find the revenue

By using the example 3

From example 3 revenue equation is R=−500p²+30000p

for p=28

The revenue is

R=−500⋅(28)²

+30000⋅28

=−392000+840000

=448000

For p=40

The revenue is

R=−500⋅(40)²

+30000⋅40

=−800000+1200000

=400000

So, for p=28

we can get higher revenue

The revenue graph is

For p=28

we get higher revenue

The revenue graph is

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 88 Problem 4 Answer

Given that prices are 7.50,61.00

To find why these prices are not in the best interest of the company

By using the example 3

From example 3 revenue equation is R=−500p²+30000p

The graph is

for p=7.50

The revenue is

R=−500⋅(7.5)²

+30000⋅7.5

=−28125+225000

=196875

For p=61.00

The revenue is

R=−500⋅(61)²

+30000⋅61

=−1860500+1830000

=−30500​

For the prices 7.50,61.00, we get the lowest revenues.

So, these prices are not in the best interest of the company

The revenue graph is

Hence, proves that why those prices are not in the interest of the company

Page 90 Problem 5 Answer

Given that Money often costs too much

To find How might the quote apply to what you have learned

By using my own knowledge

The given quote is similar to another commonly used quote “Time is money”.

Thus if we want to earn money, then we will also have to sacrifice the time to get that money.

However, time is very costly for humans, as we only have a limited time that we get to spend on this planet and we never know when the “end” will be.

Thus money could then often cost too much if we have to sacrifice too much of our time to earn that money.

Cengage Financial Algebra Chapter 2 Exercise 2.5 Modeling A Business Answers

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 90 Problem 6 Answer

Given that the demand function q=−1000p+8500

To find the expense equation

By using the given data

The costs are $1.00  per cup and $1,500.

Let E represent the total cost.

Let q be the demand (number of cups).

Then the total cost is the product of the costs per cup of $1.00 multiplied by the number of cups q, increased by the fixed costs of $1,500.

E=1.00q+1,500

The expense equation is E=1.00q+1,500

Page 90 Problem 7 Answer

Given that the demand function

q=−1000p+8500

To find the expense equation

By using the given data

From 2(a)

Expense equation E=1.00q+1500

given that q=−1000p+8500

By substituting q in E,

​E=1,00(−1,000p+8,500)+1,500

=−1,000p+8,500+1,500

=−1,000p+10,000

​The expense equation is E=−1,000p+10,000

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 90 Problem 8 Answer

Given that the demand function

q=−1000p+8500

To find a viewing window on a graphing calculator for the expense function

By using the given data

From 2(b)

the expense function E=−1000p+10000

The graph for E is

The x-axis should contain values between 0 and 10 for p because the price and the expenses cannot be negative (and when the price is 10

the expenses become zero).

The y-axis should contain values between 0 and 10,000 because the price and the expenses cannot be negative (and the initial expenses are 10,000).

The graph for the expense equation is

The viewing window is

x: o to 10

y: 0 to 10000

Page 90 Problem 9 Answer

Given that the demand function

q=−1000p+8500

To draw the graph

By using the given data

From 2(b)

The expense equation is E=−1000p+10000

The graph is

The graph for the expense equation is

Page 90 Problem 10 Answer

Given that the demand function

q=−1000p+8500

To find the revenue function

By using the given data

The revenue function is the product between the demand function q and the price p.

​​R=pq

​=p(−1,000p+8,500)

=−1,000p²+8,500p

​The revenue function is R=−1,000p²+8,500p

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 90 Problem 11 Answer

Given that the demand function

q=−1000p+8500

To f=draw revenue function

By using the given data

From 2(e)

The revenue function is R=−1,000p²+8,500p

The graph is

Clearly, we can get maximum revenue of 18062.5 for 4.25

The graph for the revenue function is

Maximum revenue: 18062.5 Price: 4.25

Page 90 Problem 12 Answer

Given that the demand function

q=−1000p+8500

To graph the revenue and expense functions on the same coordinate plane.

By using the given data

From 2(b)

Expense function E=−1000p+10000

From 2(e)

Revenue function R=−1,000p²+8,500p

The graph is

The intersection points are 1.2, 8.3

The graph is

The intersection points are 1.2, 8.3

Solutions For Cengage Financial Algebra Chapter 2 Exercise 2.5 Modeling A Business

Page 90 Problem 13 Answer

Given that the demand functionq=−500p+20000

To find the expense equation

By using the given data

The costs are $5.00 per box of 100 and a fixed cost of  40,000. Let q be the demand (number of boxes of 100).

E=5.00q+40,000​

The expense equation is E=5.00q+40,000

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 90 Problem 14 Answer

Given that the demand function

q=−500p+20000

To find the expense equation in terms of p

By using the given data

From 3(a)

The expense equation is E=5.00q+40000

given that q=−500p+20000

By substituting q in E, we get

​E=5.00(−500p+20,000)+40,000

=−2,500p+100,000+40,000

=−2,500p+140,000

​The expense equation is E=−2,500p+140,000

Page 90 Problem 15 Answer

Given that the demand function

q=−500p+20000

To find a viewing window on a graphing calculator for the expense function

By using the given data

From 3(b)

The expense equation is E=−2500p+140000

The graph is

The x-axis should contain values between 0 and 56 for p because the price and the expenses cannot be negative (and when the price is 56  the expenses become zero).

The y-axis should contain values between 0 and 140,000 because the price and the expenses cannot be negative (and the initial expenses are 140,000).

The graph for the expense equation is

The viewing window is:

x-axis: 0 to 56

y-axis: 0 to 140000

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 90 Problem 16 Answer

Given that the demand function

q=−500p+20000

To draw the graph

By using the given data

From 3(b)

The expense equation is E=−2500p+140000

The graph is

The graph for the expense equation is

Page 90 Problem 17 Answer

Given that the demand function

q=−500p+20000

To find the revenue function

By using the given data

Given that q=−500p+20000

The revenue function is

R=pq

​=p(−500p+20,000)

=−500p²+20,000p

​The revenue function is R=−500p²+20,000p

Page 90 Problem 18 Answer

Given that the demand function

q=−500p+20000

To graph the revenue function

By using the given data

From 3(e)

The revenue function is R=−500p²+20,000p

The graph is

We get the maximum revenue of 200000

at p=20

The graph for revenue

The maximum revenue of 200000

at p=20

Cengage Financial Algebra Exercise 2.5 Modeling A Business Key

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business Page 90 Problem 19 Answer

Given that the demand function

q=−500p+20000

To graph the revenue and expense functions on the same coordinate plane

By using the given data

From 3(b)

The expense equation is E=−2500p+140000

From 3(e)

The revenue equation is R=−1000p²+8500p

The graph of expense and revenue equations on the same plane is

The intersection points are 7.5,37.5

The graph of expense and revenue equations on the same plane is

The intersection points are at prices 7.5, 37.5

Chapter 2 Solving Linear Inequalities

• • Cengage Financial Algebra 1st Edition Chapter 2 Assessment Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.1 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.2 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business

Page 81 Problem 1 Answer

Given that expense function for a certain product is E=3.40q+189,000

We have to express the average cost of producing q items algebraically.

Now we have the total cost for the q items as

E=3.40q+189,000

Now we have the average cost of producing as the total cost is divided by the total number of items that is

​3.40q+189,000/q

Average cost=3.40+189,000/q

Hence we have the average cost of producing q items algebraically is 340+189,000/q

Page 83 Problem 2 Answer

We have the  expense function, E=5.00q+60,000

And the revenue function, R=7.00q.

Now we have the breakeven point, set the revenue and expense equations equal to each other.

On equating we have

​E=R

5.00q+60,000=7.00q

2q=60,000

q=30,000

So we have the breakeven point as q=30,000

Hence we have the breakeven point as q=30,000

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Page 84 Problem 3 Answer

Given the statement as

An economist is an expert who will know tomorrow why the things he predicted yesterday didn’t happen today.

We have to interpret the quote.

If we predict about something yesterday then that predictions will be based on many variables and if any one of the variables changes slightly then it leads to different result today.

Therefore If we predict about something yesterday then that predictions will be based on many variables and if any one of the variables changes slightly then it leads to different result today.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling A Business Solutions

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Problem 4 Answer

Given that the Gidget Widget Corporation produces widgets.

The fixed expenses are $65,210 and the variable expenses are $4.22 per widget.

We have to express the expense function algebraically.

Let us assume that E be the total expense And let us assume q as the number of widgets

Now we know that the total expense as sum of expenses is the sum of fixed expenses plus the variable expenses we have

E=65210+4.22q

So we have the expense function algebraically as E=65210+4.22q

We have the expense function algebraically asE=65210+4.22q

Page 84 Problem 5 Answer

Given that A corporation produces mini-widgets.

The fixed expenses are $142,900 and the variable expenses are $1.24 per mini-widget.

We have to find how much does it cost to produce 1 mini-widget

Let us assume that E be the total expense

And Given that the number of widgets be 1

Now we know that the total expense as sum of expenses is the sum of fixed expenses plus the variable expenses we have

E=1.24×1+142,900

=142,901.24

​So we have obtained the cost to produce 1 mini-widget is $142,901.24

Hence the cost to produce 1 mini-widget is $142,901.24

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Problem 6 Answer

Given that A corporation produces mini-widgets.

The fixed expenses are $142,900 and the variable expenses are $1.24 per mini−widget.

We have to find how much does it cost to produce 20,000 mini-widget

Let us assume that E be the total expense

And Given that the number of widgets be 20000

Now we know that the total expense as sum of expenses is the sum of fixed expenses plus the variable expenses we have

E=1.24×20,000+142,900

=24,800+142,900

​=167,700

​So we have obtained the cost to produce 20000 mini-widget is $167,700

Hence the cost to produce 20000 mini-widget is $167,700

Page 84 Problem 7 Answer

Given that A corporation produces mini-widgets.

The fixed expenses are $142,900 and the variable expenses are $1.24 per mini−widget.

We have to express the expense function algebraically.

Let us assume that E be the total expense And let us assume q as the number of widgets

Now we know that the total expense as sum of expenses is the sum of fixed expenses plus the variable expenses we have

E=1.24q+142,900

So we have the expense function algebraically as E=1.24q+142,900

We have the expense function algebraically as E=1.24q+142,900

Cengage Financial Algebra Chapter 2 Exercise 2.4 Modeling A Business Answers

Page 84 Problem 8 Answer

From the above problem we have the expense function algebraically as E=1.24q+142,900

We have to find the slope of the expense function

As we have the expense function algebraically as E=1.24q+142,900

Now on comparing with the general form of the equation y=mx+c

We can say that the slope as 1.24

So we have the slope of the expense function as 1.24

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Problem 9 Answer

Given that A corporation produces mini-widgets.

The fixed expenses are $142,900 and the variable expenses are $1.24 per mini−widget.

We have to give the units that would be used.

As we have the slope as of form dy/dx

That is nothing but the units of y gets divided with the units of x

As we have the y as price so we have the unit as dollars  similarly we have x as number of mini widgets.

So we will have the unit of slope as dollars per mini -widgets.

Hence we have the units of slope as dollars per mini-widgets.

Page 84 Problem 10 Answer

We have the expense function for the Wonder Widget is E=4.14q+55,789

We have to find what is the fixed cost in the expense function

We have the expense function as E=4.14q+55,789

We will get the fixed cost in the expense function by substituing the value of number of mini-widgets as zero that is q=0

So we have the fixed cost as

​ Fixes cost =4.14(0)+55,789

=55,789

​So we have the fixed cost in the expense function as $55,789

Hence we have the fixed cost in the expense function as  $55,789

Page 84 Problem 11 Answer

In the above question they have given expense function of Wonder widgets

E=4.14q+55,789

We need to find the value cost producing for 500 woder widgets

Given

E=4.14q+55,789

The cost of producing q number of widgets is given by the equation replace q with 500 to find the cost of 500 widgets

E=4.14(500)+55,789

=2,070+55,789

=57859

​Hence the total value of cost producing 500 wonder widgets are 57859.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Problem 12 Answer

In the above question they have given expense function of Wonder widgets

E=4.14q+55,789

We need to find the value cost producing for 500 woder widgets

Given

E=4.14q+55,789

We have found the cost of producing 500 widgets in previous part and it is 57859

Average cost for 500 widgets will be cost/500

Average cost =$57,859/500

=$115.718

≈$115.72

​Therefore average cost per producion 500 wonder widgets are 115.72

Page 84 Problem 13 Answer

In the above question they have given expense function of Wonder widgets

E=4.14q+55,789

We need to find the value cost producing for 500 woder widgets

Given

E=4.14q+55,789

The cost of producing q number of widgets is given by the equation  replace q with 600 to find the cost of 600 widgets

E=4.14(600)+55,789

=2,484+55,789

=58,273

​The total cost of producing 600 Wonder Widgets are 58,273.

Page 84 Problem 14 Answer

In the above question they have given expense function of Wonder widgets

E=4.14q+55,789

We need to find the value cost producing for 500 woder widgets

Given

E=4.14q+55,789

We have found the cost of producing 600 widgets in previous part and it is58273

Average cost for 600 widgets will be cost/ 600

Average cost​=$58,273/600

=$97.12166

≈$97.12

​The average cost per600

Wonder widgets is 97.12.

Solutions For Cengage Financial Algebra Chapter 2 Exercise 2.4 Modeling A Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Problem 15 Answer

In the above question they have given expense function of Wonder widgets

E=4.14q+55,789

We need to As the number of widgets increased from 500 to 600 did the average expense per widget increase or decrease

Given

E=4.14q+55,789

$115.72 Average cost per widget in case of 500

$97.12 Average cost per widget in case of 600

As 115.72 is greater than 97.12 it decreased

Therefore As the number of widgets increased from 500 to 600 the average expense per  widget decreased.

Page 84 Problem 16 Answer

In the above question they have given expense function of Wonder widgets

E=4.14q+55,789

We need to find the average cost per widgets of producing 10,000 wonder widgets

Given

E=4.14q+55,789

The cost of producing q number of widgets is given by the equation replace q with 10,000 to find the cost of 10,000 widgets

E=4.14(10,000)+55,789

=41,400+55,789

=97,189

​Average will be cost/10,000

Average cost​=$97,189/10,000

=$9.7189

≈$9.72

​The average cost per producing 10000 wonder widgets are 9.72.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Exercise 1 Answer

Given​

q=−140p+9,000

E=2q+16,000

We need to express expense equation interms of p.

Given

q=−140p+9,000

E=2q+16,000

​Substitute the value of q in terms of p in equation for E

​E=2(−140p+9,000)

=−280p+18,000

​Expense function in term s of p is E=−280p+18,000

Page 84 Exercise 2 Answer

Given​

q=−140p+9,000

E=2q+16,000

​we need to find no. of widgets are demanded at a price of$ 10.00.

The demand function q is given by q= -140p+9,000

p is price

Now to find demand at price =$10 find q at p = 10

q=-140(10)+9,000

=7,600

Therefore 7,600 widgets are needed.

Page 84 Exercise 3 Answer

Given​

q=−140p+9,000

E=2q+16,000

we need to find cost to produce the number of widgetsfrom part b

Cost(Expense) function is given by

E=2q+16,000

q is number of widgets to be produced

Here q=7,600(from part b)

E=2(7,600)+16,000

=31,200

The total cost to produce 7600 widgets is 31200.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Exercise 4 Answer

Given, expense equation as E=11.00q+76,000

Price of $20.00

We need to find items must be sold to reach the breakeven point to fin breakeven point revenue= Expense

Revenue=20q

Equate both and find a

20q=11q+76,000

3.9q=76,000

q=8,444.44 or 8,444

​8,444 items must be sold to reach the breakeven point.

Page 84 Exercise 5 Answer

Given​

Revenue =20q

Expense =11q+76,000

​We need to plot the graph and find the q value.

Ploting the graph of E and R

Hence q value is 8,444

The q value of exersice 9 and graph matches.

Page 84 Exercise 6 Answer

Given

E=4.98q+69,000

E′=4.55q+69,000

The expense equation was recently adjusted from E to E′  in response to the increase in gas prices

​We need find the incerase in the average cost per widget

Given

​E=4.98q+69,000

E′=4.55q+69,000

​Find the difference of new cost and previous cost

E−E′ =4.98q+69,000−(4.55q+69,000)

=0.43q

​So increase in average cost for 1 widget can be found by substituting q=1 in the difference

0.43(1)=0.43

0.43 is the increase in the average cost per widget.

Cengage Financial Algebra Exercise 2.4 Modeling A Business Key

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Exercise 7 Answer

Given

E=4.98q+69,000

E′=4.55q+69,000

The expense equation was recently adjusted from E to E′ in response to the increase in gas prices

Price p=8

We need to find breakeven point prior to the adjustment in the expense function.

To find breakeven point Revenue= expense

Revenue=8q

Expense=4.55q+69,000

equate both and find q

8q=4.55q+69,000

3.3.45q=69,000

q=20,000

E at q =20,000

E= 4.55(20,000)+69,000

=160,000

20,000 items are sold at breakeven point at the cost 160,000

Page 84 Exercise 8 Answer

Given

E=4.98q+69,000

E′=4.55q+69,000

The expense equation was recently adjusted from E to E′  in response to the increase in gas prices

​Price p=8.5

We need to find breakeven point after the adjustment in the expense function

To find breakeven point Revenue= expense

Revenue =8.5q

Expense =4.98q+69,000​

Equate both and find q

8.5q=4.98q+69,000

3.3.52q=69,000

q=19,602.27 or 19,602

​E at q=19,602

E=4.98(19,602)+69,000

=166,617.96 or 166,618​

items are sold at breakeven point at the cost166,618 .

Page 84 Exercise 9 Answer

In the above question they have given a graph We need to observe the graph and answer the question

” What is the breakeven point?”

Answer:-

Breakeven point is the point at which revenue = expense and this can be seen that point of intersection of both  lines is (A,W)

​The break even point is from (A,W).

Page 84 Exercise 10 Answer

In the above question they have given a graph

We need to observe the graph and answer the question

If quantity C is sold and C<A, is there a profit or a loss? Explain.

Answer:-

Drop a vertical line at q<A

then it is visible that revenue is less than expense and hence we can say there will be loss

Hence there will be loss.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 84 Exercise 11 Answer

In the above question they have given a graph

We need to observe the graph and answer the question

If quantity D is sold and D>A, is there a profit or a loss? Explain.

Answer:-

Drop a vertical line at q>A then it is visible that revenue is higher than expense and hence we can say there will be profit.

Hence there will be a profit.

Page 84 Exercise 12 Answer

In the above question they have given a graph

We need to observe the graph and answer the question​

The y−intercept of the expense function is Z.

Interpret what the company is doing if it operates at the point (0,Z).

Answer:-

If company is operating at(0,Z) that means company is not producing any product but still has to pay Z

dollars for the fixed expenses and yes company will be definitely in loss of Z dollars.

Hence the selling no goods but paying Z dollars for fixed expenses.

Page 85 Exercise 13 Answer

Given

E=6.21q+125,000

p=19.95

we need to represent the average expence A for one nokee algebraically.

Given

E for q number of goods is E=6.21q+125,000

Average expense if given by expense for q number of goods divided by q

E=6.21q+125,000/q.

Hence Average expence A for one nokee algebrically is E=6.21q+125,000/q.

Page 85 Exercise 14 Answer

Given

E=6.21q+125,000

p=19.95

we need to represent graph the average expense function.

Plotting the graph​

Set the range of x 0 to 1000

range of y 0 to 2000 and the value of y=6.21+(125,000/x)​

Hence the graph is plotted

Detailed Solutions For Cengage Financial Algebra Chapter 2 Exercise 2.4

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 85 Exercise 15 Answer

Given

E=6.21q+125,000

p=19.95

we need to verify whether the average expense is linear or not.

By observing the graph

As seen in 13 b  the graph of average expense is not linear.

The average expense function is not linear.

Page 85 Exercise 16 Answer

Given

E=6.21q+125,000

p=19.95

we need to find whether the expence function is increasing or decreasing as q increasing.

Hence verage expense function increasing or decreasing as q increases.

Page 85 Exercise 17 Answer

Given

E=6.21q+125,000

p=19.95

if only one Nokee is produced we need to find the average cost per nokee

E for q number of goods is E=6.21q+125,000

Average expense if given by expense for q number of goods divided by q

E=6.21q+125,000/q

For 1 put q=1

6.21+125,000/1

=125,006.21

If only one Nokee is produced, what is the average cost per Nokee125,006.21.

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business Page 85 Exercise 18 Answer

Given

E=6.21q+125,000

p=19.95

if 100,000 Nokee is produced we need to find the average cost per nokee

E for q number of goods is E=6.21q+125,000

Average expense if given by expense for q number of goods divided by q

E=6.21q+125,000/q

For 100,000 put q=100,000

6.21(100,000+125,000

100,000

=7.46

If 100,000 Nokees are produced, then the average cost per Nokee 7.46

Page 85 Exercise 19 Answer

In the above question they have given that Lorne has determined the fixed cost of producing his new invention is N dollars.

Variable cost is $ 10.75

We need to find average cost per item.

Remember ,fixed expenses do not depend on the quality produced.

Thus, regradless of how big ‘W’ is, the fixed cost would still be N.

First find the total cost of producing W items:

=$10.75W+N

Divide by W to find average per item:

=$10.75W+N/W

=$10.75W/W+N/W

=$10.75+n/w

Hence the average cost per producing W item is $10.75+N/W.

Practice Problems For Cengage Financial Algebra Exercise 2.4 Modeling A Business

Chapter 2 Solving Linear Inequalities

• • Cengage Financial Algebra 1st Edition Chapter 2 Assessment Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.1 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.2 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business

Page 76 Problem 1 Answer

Given: Wholesale Price=x dollars

Retail Price=y dollars

To find: The markup amount

Solution:Wholesale price+Markup=Retail Price

x+Markup=y

Markup=y−x

The wholesale price of an item is x dollars and the retail price is y dollars, then the markup is y−x dollars

Page 77 Problem 2 Answer

Given: A banner company sells 5-foot banners to retailers for x dollars. The St. James Sign Shop marks them up90%

To find: Express the retail price at the St. James store

Solution: We will find the value of the markupThen find the retail price

Markup=90%of wholesale price

=90/100×x

=0.9x

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Retail price=Wholesale price+Markup

=x+0.90x

=1.90x

A banner company sells 5 -foot banners to retailers for x dollars and the St. James Sign Shop marks them up90%, then the retail price will be1.90x

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling A Business Solutions

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business Page 77 Problem 3 Answer

If a widget has a low price, many people may want it and will be able to afford it, so a large quantity may be sold.If it has a high price, fewer widgets will be sold.

As the price increases, demand (the quantity consumers want) is likely to decrease, and as price decreases, demand increases.

The graph of the demand function has a negative slope. However, its curvature varies.

The demand function has a negative slope because as the price of a product increases the demand for the product will decrease.

Page 78 Problem 4 Answer

Here, we have to find the store’s markup. It’s given that an automobile GPS system is sold to stores at a wholesale price of $97

A popular store sells them for $179.99

Markup= Retail price−Wholesale price

=   $179.99−$97=$82.99

So, the store’s markup is$82.99

Page 78 Problem 5 Answer

Here, we have to find the retail price of the CD rack. It’s given that a CD storage rack is sold to stores at a wholesale price of $18

Retail price=Markup+Wholesale price

=$13+$18=$82.99

So, the retail price of the CD rack is $82.99

Page 79 Problem 6 Answer

Here, we have to find the equation of the linear regression line.

Enter the ordered pairs(p is wholesale price and y is quantity demanded in hundreds) into your calculator.

Then use the statistics menu to calculate the linear regression equation.

The equation is of the form y=mx+b,where m is the slope and b is the y intercept.

Rounding the slope and y intercept to the nearest hundredth, the equation of the regression line is −136.08p+2,535.79

So, the equation of the linear regression line is q=−136.08p+2,535.79

Page 79 Problem 7 Answer

Here, we have to give the slope of the regression line and interpret the slope as a rate.

As the line is q=−136.08p+2,535.79

Comparing it with y=mx+c,where m is slope,  q=mx+c=−136.08p+2,535.79,gives m=−136.08

The slope is −136.08.As a rate, the slope is expressed as garbage cans per dollar.

For each dollar increase in price, about 136 less garbage cans are demanded.

Page 79 Problem 8 Answer

Here, we have to find the correlation coefficient and interpret it.

Use a graphing calculator to find the correlation coefficient. Round r to the nearest hundredth r=−0.99.

As magnitude of r>0.75 hence strong correlation.

So, the  correlation coefficient is r=−0.99, there is a strong negative correlation.

Page 79 Problem 9 Answer

Here, we have to find how many garbage cans would be demanded at a wholesale price of $18.00.

For demand of garbage bans of downloads put p=18

(do not forget that unit of q was in hundred)

q=−136.08×18+2,535.79

y=−2,449.44+2,535.79

86.35≈86

​So, the garbage cans would be demanded at a wholesale price of $18.00 Is 86 hundred.

Cengage Financial Algebra Chapter 2 Exercise 2.3 Modeling A Business Answers

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business Page 79 Problem 10 Answer

Here, we have to determine whether our answer to part d is an example of extrapolation or interpolation and we have to explain.

In previous question the value of price was $18 which is out of the domain.

So, the answer to part d is an example of extrapolation,$18.00 is not in the domain.

Page 79 Problem 11 Answer

Here, we have to find how much money would the company receive from the garbage can sales. It’s given that

So, the money would the company receive from the garbage can sales is $154,800

Page 79 Exercise 1 Answer

Given that company that produces widgets has found its demand function to be q=−1,500p+90,000

For each dollar increase in the wholesale price we have to find how many fewer widgets are demanded

Now we have given the demand function as q=−1,500p+90,000

Now on  substituing value of p as p+1

q=−1,500(p+1)+90,000

=−1,500p−90,000−1,500

=q−1500​

Therefore we can say that 1500 widgets were demanded for each dollar increase in the wholesale price.

Hence the number of widgets demanded for each dollar increase in the wholesale price is 1500

Page 79 Exercise 2 Answer

Given that company that produces widgets has found its demand function to be q=−1,500p+90,000

For each dollar increase in the wholesale price we have to find how many fewer widgets are demanded

We have to find how  many widgets would be demanded at a price of $20

We have given the demand equation as q=−1,500p+90,000

Now we have

q=−1,500×20+90,000

=−30,000+90,000

=60,000​

Therefore the number of widgets demanded at a price of $20 is 60,000

Hence the number of widgets demanded at a price of $20 is 60,000.

Given that company that produces widgets has found its demand function to be q=−1,500p+90,000

For each dollar increase in the wholesale price we have to find how many fewer widgets are demanded

We have to find how many widgets would be demanded at a price of $21

We have given the demand equation as q=−1,500p+90,000

Now we have

q=−1,500×21+90,000

=−31,500+90,000

=58,500

​Therefore the number of widgets demanded at a price of $21 is 58,500

Hence the number of widgets demanded at a price of $21 is58,500

Solutions For Cengage Financial Algebra Chapter 2 Exercise 2.3 Modeling A Business

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business Page 79 Exercise 4 Answer

Given that company that produces widgets has found its demand function to be q=−1,500p+90,000

For each dollar increase in the wholesale price we have to find how many fewer widgets are demanded

We have to find what is the difference in quantity demanded caused by the $1 increase in wholesale price.

Now we have given the demand function as q=−1,500p+90,000

Now on  substituting value of p as p+1

​q=−1,500(p+1)+90,000

=−1,500p−90,000−1,500

=q−1500

q−q′

=1500​

Therefore the difference in quantity demanded caused by $1 increase in wholesale price is 1500

Hence  the difference in quantity demanded caused by $1 increase in wholesale price is 1500

Page 79 Exercise 5 Answer

Given that company that produces widgets has found its demand function to be q=−1,500p+90,000

For each dollar increase in the wholesale price we have to find how many fewer widgets are demanded

We have to find how many widgets would be demanded at a price of $22.50

We have given the demand equation as q=−1,500p+90,000

Now we have

q=-1,500×22.5+90,000

=-33,750+90,000

=56,250

Therefore the number of widgets demanded at a price of $22.5 is 56,250

Hence the number of widgets demanded at a price of $22.5 is 56,250

Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.3 Modeling a Business Page 79 Exercise 6 Answer

Given that company that produces widgets has found its demand function to be q=−1,500p+90,000

For each dollar increase in the wholesale price we have to find how many fewer widgets are demanded

We have to find how much will all of the widgets cost the store to purchase at a price of $

Now we have the Number of widgets as

q=−1,500×22.5+90,000

=−33,750+90,000

=56,250

​Now we have the cost as  the product of price to the number of widegets that is

cost price=$22.50×56,250

=$1,265,625

​So we have the cost to store all the widgets purchased at a price of $22.5 is $1,265,625

Hence we have the cost to store all the widgets purchased at a price of $22.5 is $1,265,625

Page 79 Exercise 7 Answer

Given that company that produces widgets has found its demand function to be q=−1,500p+90,000

store marks up the widgets that cost $22.50 at a rate of 50%,

We havr to to find the retail price of each widget.

Now we have the markup as the product of the cost with markup rate that is

Markup = $22.5×50%

​=$22.5×0.5

=$11.25

​Now we have the Retail price as the sum of markup to the wholesale price that is

Retail price =$22.5+$11.25

​=$33.75​

So we have the retail price as $33.75

Hence we have the retail price as $33.75

Cengage Financial Algebra Exercise 2.3 Modeling A Business Key

Chapter 2 Solving Linear Inequalities

• • Cengage Financial Algebra 1st Edition Chapter 2 Assessment Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.1 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.2 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.4 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.5 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.6 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.7 Modeling a Business
  • Cengage Financial Algebra 1st Edition Chapter 2 Exercise 2.8 Modeling a Business

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market

Page 6 Problem 1 Answer

Given: Jillian owns60%of the stock in a private catering corporationThere are1,200shares in the entire corporation

To find: The number of shares owned by Jillian

Solution: We will assume that the number of shares owned by Jillian is x

Write the data given as a fraction and solve for x

Let’s assume that the number of shares owned by Jillian is x

60/100=x/1200

[writing the data given as proportion]

72000=100x

[cross multiply]

720=x

[divide both sides by100]

If Jillian owns60% of the stock in a private catering corporation and there are1,200 shares in the entire corporation then he owns 720 shares

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra Chapter 1 Exercise 1.1 Stock Market Answers

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 6 Problem 2 Answer

Given: Two partners are starting a wedding planning business. The total investment is$45,000 in the ratio of 4:5

To find: The contribution of each investor

Solution: We will convert the ratio in the form of x Write an equation for investment by each investor and solve it

The investment is in the ratio of 4:5

So, the investment will be 4x and 5x

The equation showing the investment will be:

4x+5x=45,000

9x=45,000

[combine like terms]

x=5000

[divide each side by 9]

Thus investments will be:

4x=4(5000)=20,000

5x=5(5000)

=25,000

The total investment in the wedding planning business by two investors is of $45,000 in the ratio of4:5

Thus, the investment by the investors is of $20,000 and $25,000 respectively.

Page 7 Problem 3 Answer

The quote by Thomas Edison “Genius is 1% inspiration and 99%  perspiration.

Accordingly, a genius is often merely a talented person who has done all of his or her homework” talks about the importance of hard work.

Here the scientist has emphasized that only having a bright idea and inspiration is not enough to get success, it is more essential to put in the efforts and do hardwork to get success.

In the given quote of Thomas Edison, the words ‘Genius is1% inspiration and99%  perspiration’ shows the importance of efforts in achieving success.

Here, the word perspiration is used to show hardwork.In this lesson, we have learned how investment is made in an organization.

Just like the quote says, only having an idea of good business won’t give results, it requires investments and efforts to get results.

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 7 Problem 4 Answer

Given: Ryan owns three-eighths of a florist shop worth$76,000

To find: The value of Ryan’s share of the business

Solution: Multiply the ownership proportion with the value of the business.

Ryan’s share of business= Ownership proportion× Total value of business

=3/8×76,000

=28,500

Ryan owns three-eighths of a florist shop worth $76,000, which means his share is of$28,500

Page 7 Problem 5 Answer

Given: A corporation issues1,200,000 shares of stock at its beginning to shareholders.

To find: Number of shares a shareholder must own to have a majority of the shares

Solution: To hold the majority of shares, a shareholder must hold at least one share more than 50% shares.

We will multiply the total number of shares by 50% and add 1

To hold the majority share, a shareholder must own at least the following number of shares:

=[50%×total number of shares]+1

=[50%×1,200,000]+1

=600,001

A corporation issues1,200,000 shares of stock at its beginning to shareholders then a shareholder must own atleast 600,001 shares to have a majority of the shares.

Page 7 Problem 6 Answer

Given: A corporation issues1,200,000 shares of stock at its beginning to shareholders.

To find: Number of shares a shareholder must own to have a majority of the shares

Solution: To hold the majority of shares, a shareholder must hold at least one share more than50% shares.

We will multiply the total number of shares by 50% and add 1

To hold the majority share, a shareholder must own at least the following number of shares:

=[50%×total number of shares]+1

=[50%×1,200,000]+1

A corporation issues1,200,000 shares of stock at its beginning to shareholders then a shareholder must own atleast600,001 shares to have a majority of the shares.

Solutions For Cengage Financial Algebra Chapter 1 Exercise 1.1 The Stock Market

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 7 Problem 7 Answer

Given: Julie and Kristen are the partners in a local sporting goods shop They needed $51,000  to start the business so they invested in the ratio 5:12 , respectively.

To find: Money invested by each partner

Solution: Write the ratio in the form of x

Write an equation showing the ownership and solve for x

The investment will be 5x and12x

We will now write the equation for ownership:

5x+12x=51,000

17x=51,000

[combine like terms]

x=3000

[divide each side by 17]

Investments by each partner are:

Investment by Julie=5x=5(3000)

=15,000

Investment by Kristen=12x

=12(3000)

=36,000

Julie and Kristen invest in the ratio of 5:12 for the total investment of $51,000

This means, Julie invests$15,000 and Kristen invests$36,000

Page 7 Problem 8 Answer

Given: Julie and Kristen are the partners in a local sporting goods shop They needed $51,000  to start the business so they invested in the ratio 5:12, respectively.

Thus, Julie invests$15,000 and Kristen invests $36,000

To find: The percent of the business owned by Kristen

Solution: Write Kristen’s investment as a proportion of total investment Multiply the proportion by100 to get the percentage.

We can also first divide the proportion, get the answer in decimals and then multiply by 100 to get the percentage.

Proportion of ownership by Kristen=Kristen′s investment

Total investment    =36,000/51,000

=36/51

=12/17

Percentage ownership=12/17×100

=70.5882%

≈70.6%

[rounded off to the nearest tenth of a percentage]

Julie and Kristen invest in the ratio of 5:12 for the total investment of $51,000

So, Kristen owns 70.6% of the business.

Cengage Financial Algebra Exercise 1.1 The Stock Market Key

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 7 Problem 9 Answer

Given: Julie and Kristen are the partners in a local sporting goods shop and invest in the ratio of 5:12 Investment by Kristen is70.6%

To find: The percent of business that Julie will own if the business grows to $3,000,000

Solution: The amount of total investment does not change the proportion of investment by each partner as the ratio of investment remains the same at 5:12

So, increase in the amount to $3,000,000 from $51,000 has no change in ownership percentage

Percentage of Julie’s ownership=100%−ownership of Kristen

=100%−70.6%

=29.4%

Julie and Kristen invest in the ratio of 5:12 for the total investment of $51,000

Even if the amount increases to$3,000,000 the ratio remains the same as before and so Julie will own29.4%

Page 7 Problem 10 Answer

Given: Joe, Thea, and Taylor invested in a partnership in the ratio1:4:7, respectively.

When the partnership was worth $1.6 million, Thea decides to go to graduate school and sells her part of the partnership to Joe

To find: The amount Joe need to pay Thea to buy her share of the business

Solution: Convert the ratio into an algebraic equation and solve for x Using that find the value of investment of Thea.

Let x represent the amount invested by Joe, 4x represent the amount invested by Thea and7x represent the amount invested by Taylor.

We will use the ratio to write an algebraic equation and solve it for x:

1x+4x+7x=16,00,000

12x=16,00,000

x=16,00,000/12

x=4,00,000/3

x=133,333.33

Value of Thea’s share=4x=4(133,333.33)

=533333.333

≈533,333

[rounded off to nearest dollar]

Joe, Thea, and Taylor invested in a partnership in the ratio 1:4:7, respectively.

Joe needs to pay Thea$533,333 to buy her share of the business when the value of the business is$1.6 million.

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 7 Problem 11 Answer

Given: Joe, Thea, and Taylor invested in a partnership in the ratio 1:4:7 , respectively.

Thea sold her share to Joe when the total value of the investment was$1.6 million

To find: Percent of the business owned by Joe after he buys Thea’s portion

Solution: We will first write the new ownership ratio.Find the value of Joe’s share and then find its percentage

The new ownership ratio between Joe and Taylor will be 5:7

So, we can say Joe’s share is 5x and Taylor’s share is7x.

So, 5x+7x=1,600,000

12x=1600000

[combine like terms]

x=133333.33

[divide each side by12]

Thus Joe’s share will be

5x=5(133333.33)

=666666.67

Percentage of Joe’s ownership: =666666.67

1600000×100

=41.7%

[rounded off to nearest tenth of a percentage]

Joe, Thea, and Taylor invested in a partnership in the ratio1:4:7, respectively If Thea sells her share to Joe, then his new ownership percentage will be41.7%

Page 8 Exercise 1 Answer

Given: Seventy-two percent of the shareholders in a service corporation are women.

The corporation is owned by 45,600 people

To find: The number of shareholders that are women

Solution: Write the percentage as a fractionWrite a proportion for the situation given

Write the percentage as a fraction

72%=72/100

Let x represent women shareholders. So,

72/100=x/45600

[write a proportion]

3283200=100x

[cross multiply]

32832=x

If the corporation is owned by 45,600 people and seventy-two percent of the shareholders in a service corporation are women, then 32,832 shareholders are women.

Page 8 Exercise 2 Answer

The 120 shareholders of a corporation are voting for a new Board of Directors.

Shareholders receive one vote for each share they own.

So if the shareholder will own even one share more than50%  then it will mean that he owns majority of the shares and in that case it will be possible for one shareholder’s votes to choose the new Board of Directors.

The 120 shareholders of a corporation are voting for a new Board of Directors.

Shareholders receive one vote for each share they own.

Thus, it would be possible for one shareholder’s votes to choose the new Board of Directors only if that shareholder owns the majority of shares i.e. more than 50% of shares.

Detailed Solutions For Cengage Financial Algebra Chapter 1 Exercise 1.1

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 8 Exercise 3 Answer

Given: The ownership of the corporation is represented by 2,351,000  shares of stock owned by 111,273  shareholders.

To find: Must all of the shareholders own more than one share of stock?

Solution: The shareholding pattern can be different for each shareholder.

For example, 111272 shareholders can hold 1 share each and the remaining one shareholder can hold all the remaining shares.

There can be many other combinations possible like the one mentioned above.

The ownership of the corporation is represented by 2,351,000  shares of stock owned by 111,273 shareholders.

In this case, it is not essential that all the shareholders should own more than one stock.

For instance, all111,272 can hold one share each and the remaining shareholder can hold the remaining majority of shares.

Page 8 Exercise 4 Answer

Given: The ownership of the corporation is represented by 2,351,000 shares of stock owned by111,273  shareholders.

To find: The percentage of shareholders represented in the meeting if 3,411  shareholders attend the meeting

Solution: We will first write the shareholders attending as a proportion to the total shareholdersThen find its percentage

Let x be the percentage of shareholders present 3411/111273=x/100

341100=111273x

[cross multiply]

3.065=x

[divide each side by111273]

x≈3%

[rounding off to nearest percentage]

If 3411 shareholders attend the meeting from 111273 shareholders, then 3% of shareholders are represented in the meeting.

Page 8 Exercise 5 Answer

Given: The ownership of the corporation is represented by 2,351,000 shares of stock owned by111,273 shareholders.

To find: The percent of the shares that are represented at the meeting if the shareholders who do attend own a combined 1.8 million shares

Solution: We will write the situation as a proportion

Let x be the percentage of shares represented by the shareholders attending the meeting

1,800,000/2,351,000=x/100

180,000,000=2,351,000x

[ cross multiply]

76.56=x

[divide each side by2351000]

x≈77%

[rounded off to nearest percentage]

When the shareholders who attend the meeting own a combined 1.8 million shares of the corporation out of the total 2,351,000  shares,  it represents 77%  of the shares at the meeting.

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 7 Exercise 6 Answer

The top x shareholders in a corporation each own y shares of a certain stock The corporation’s ownership is represented by a total of w shares of stock

To find: The percent of the corporation owned by the top x shareholders

Solution: Find the total number of shares owned by the top x shareholders Find the percentage of that holding

The number of shares held by the top x shareholders= number of top shareholders× shares held by each of those shareholders

=x×y

=xy

Proportion held by the top x shareholders=xy/w

Percentage holding=xy/w×100

=100xy/w%

Where the top x shareholders in a corporation each own y shares of a certain stock and the corporation’s ownership is represented by a total of w  shares of stock then the percent of the corporation owned by the top x shareholders is100 xy/w%

Page 8 Exercise 7 Answer

Given: A sole proprietorship is worth w dollars. The owner loses a lawsuit against him for y dollars where y  is greater than w.

To find: Express algebraically the value of the personal property the owner must forfeit to pay the settlement.

Solution: In a sole proprietorship, the owner is personally liable for losses over and above the value of the business.

So, Value of personal property to be forfeited(P)=Loss−value of business

=y−w

A sole proprietorship is worth w dollars.

The owner loses a lawsuit against him for y  dollars where y  is greater than w

The value of the personal property(P) the owner must forfeit to pay the settlement can be expressed algebraically as: P=y−w

Page 8 Exercise 8 Answer

Given: Six equal partners own a local pizzeria and bought many personal items such as cars, boats, new homes, and so on from the profit.

In order to protect their personal possessions, they decide to incorporate the pizzeria, so that the six partners own shares in the corporation and have limited liability.

The business is worth $675,000.

To find: After an accident, the partners lose a lawsuit and have to pay $1.2 million in damages.

We have to find how much money will each partner personally lose to pay this lawsuit

Solution: In the case of a partnership, the partners are personally liable for losses greater than the capital of the business.

But, in a corporation, the shareholders have limited liability, as in they are only responsible for the amount of each share and nothing more.

Their personal property is not forfeited in case of loss.

Here, the partners converted the pizzeria to a corporation and became shareholders and will have limited liability.

So the loss exceeding the business worth cannot be recovered from those partners.

Six equal partners own a local pizzeria. As the partners made a tremendous profit they bought many personal items such as cars, boats, new homes, and so on.

In order to protect their personal possessions, they decide to incorporate the pizzeria, so that the six partners own shares in the corporation and have limited liability.

The business is worth$675,000.

After an accident, the partners lose a lawsuit and have to pay$1.2 million in damages.

But as the partners are now shareholders, they have limited liability and so they will personally lose othing to pay this lawsuit

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 8 Exercise 9 Answer

Given: Three people invest in a business. The first two invest in the ratio 2:3, and the third person invests twice as much as the other two combined.

The total investment is$30 million.

To find: The value of the investment by the major investor

Solution: We will convert the ratio into an algebraic equation showing total investment and solve it.

Let the three partners be A,B,C

So, investment by A will be 2x and investment by B will be3x

Thus, Investment by C=2(2x+3x)

=2(5x)

=10x

Total investment=A+B+C

30=2x+3x+10x

[substitute values]

30=15x

[combine like terms]

2=x

[divide each side by15]

Investment byC=10x

=10(2)

=20 million dollars

Three people invest in a business The first two invest in the ratio 2:3, and the third person invests twice as much as the other two combined.

The total investment is $30 million.So, the major investor contributed $20 million.

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 8 Exercise 10 Answer

Given: Three people invest in a business. The first two invest in the ratio 2:3, and the third person invests twice as much as the other two combined.

The total investment is $30 million.The major investor has invested$20 million.

To find: If the major investor own more than half the business

Solution: We will find the value of half the business Check if the value of the investment by the major investor is greater than that amount Value of half of the business=30/2

=15 million dollars

The investment by the majority holder is $30 million.

So , we can say that the major investor own more than half the business

Three people invest in a business. The first two invest in the ratio2:3, and the third person invests twice as much as the other two combined.

The total invested is $30 million and from the data we can find that the major investor has invested$20 million Thus, the major investor own more than half the business.

Page 8 Exercise 11 Answer

The major investor has invested $20 million The total investment is$30 million

To find: The fraction of the business the major investor owns

Solution: The fraction of investment by major investor=investment by major investor total investment

=20/30

=2/3

Three people invest in a business. The first two invest in the ratio2:3, and the third person invests twice as much as the other two combined.

The total investment is$30 million and from this data we can find that the major investor has invested $20 million Thus, the major investor owns 2/3 rd  of the business

Practice Problems For Cengage Financial Algebra Exercise 1.1 The Stock Market

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 8 Exercise 12 Answer

Given: Ten years ago, Lisa bought a hair salon for x dollars.

She built up the business and it is now worth nine times what she paid for it

To find: The amount Lisa’s friend must pay Lisa to buy half the business.

Solution: Find the current value of the business Divide that by 2  to find the value of half of the business

Original value of hair saloon=x

dollarsCurrent value of hair saloon=9x

dollarsValue of half the business=9x/2

=4.5x dollars

Ten years ago, Lisa bought a hair salon for x dollars and its current value is 9x dollars.

So, the amount Lisa’s friend must pay Lisa to buy half the business is 4.5x dollars

Page 8 Exercise 13 Answer

Four people invested in a restaurant. One person invested$100,000.

Two others invested in the ratio x:2x, and the fourth person invested an amount equal to the other three investors combined.

So, the expression for the investment by fourth person(D) will be: D=100000+3x

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 8 Exercise 14 Answer

Given: Four people invested in a restaurant. Let the investors be A,B,C,D

Their investments are:

A=$100,000

B=x

C=2x

D=A+B+C   =100000+3x

The total investment was $1,100,000

To find: Equation that allows you to find the amount invested by each person

Solution: Total investment(T)=A+B+C+D

1100000=100000+x+2x+(100000+3x)

[substitute values]

1100000=200000+6x

[Combine like terms]

Four people invested in a restaurant. One person invested$100,000.

Two others invested in the ratiox:2x, and the fourth person invested an amount equal to the other three investors combined.

The equation that allows you to find the amount invested by each person is:

1100000=200000+6x

Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.1 The Stock Market Page 8 Exercise 15 Answer

Given: Four people invested in a restaurant. Let the investors be A,B,C,D

Their investments are:

A=$100,000

B=x

C=2x

D=A+B+C=100000+3x

The total investment(T)  was $1,100,000

To find: Investment by each person

Solution: We will write the given data as an expression for total investment and solve for x

Total Investment=A+B+C+D

1100000=100000+x+2x+(100000+3x)

1100000=200000+6x

900000=6x

150000=x

So value of investment:

A=$100000

B=x   =$150000

C=2x  =2(150000)

=$300000

D=100000+3x

=100000+3(150000)

=100000+450000

=$550000

Four people invested in a restaurant. One person invested $100,000.

Two others invested in the ratiox:2x, and the fourth person invested an amount equal to the other three investors combined.

So, if the investors areA,B,C,Dthen the investments are:

A=$100,000

B=$150,000

C=$300,000

D=$550,000

Step-By-Step Solutions For Cengage Financial Algebra Chapter 1 Exercise 1.1 Cengage

Chapter 1 Solving Linear Equations

• • Cengage Financial Algebra 1st Edition Chapter 1 Assessment The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.2 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.3 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.4 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.5 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.6 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.7 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.8 The Stock Market
  • Cengage Financial Algebra 1st Edition Chapter 1 Exercise 1.9 The Stock Market