Algebra 2 Volume 1 1st Edition Module 4 Quadratic Equations And System Of Equations
Page 189 Problem 1 Answer
It is given a system composed of a linear equation in two variables and a quadratic equation in two variables.
It is required to determine how to solve this system.
Solve one of the two equations for one of the variables in terms of the other.
Substitute the expression for this variable into the second equation, then solve for the remaining variable.
Substitute that solution into either of the original equations to find the value of the first variable. If possible, right the solution as an ordered pair.
Check the solution in both equations
Solve the system of two equations in two variables by using substitution method.
Page 189 Problem 2 Answer
It is given two graphs.
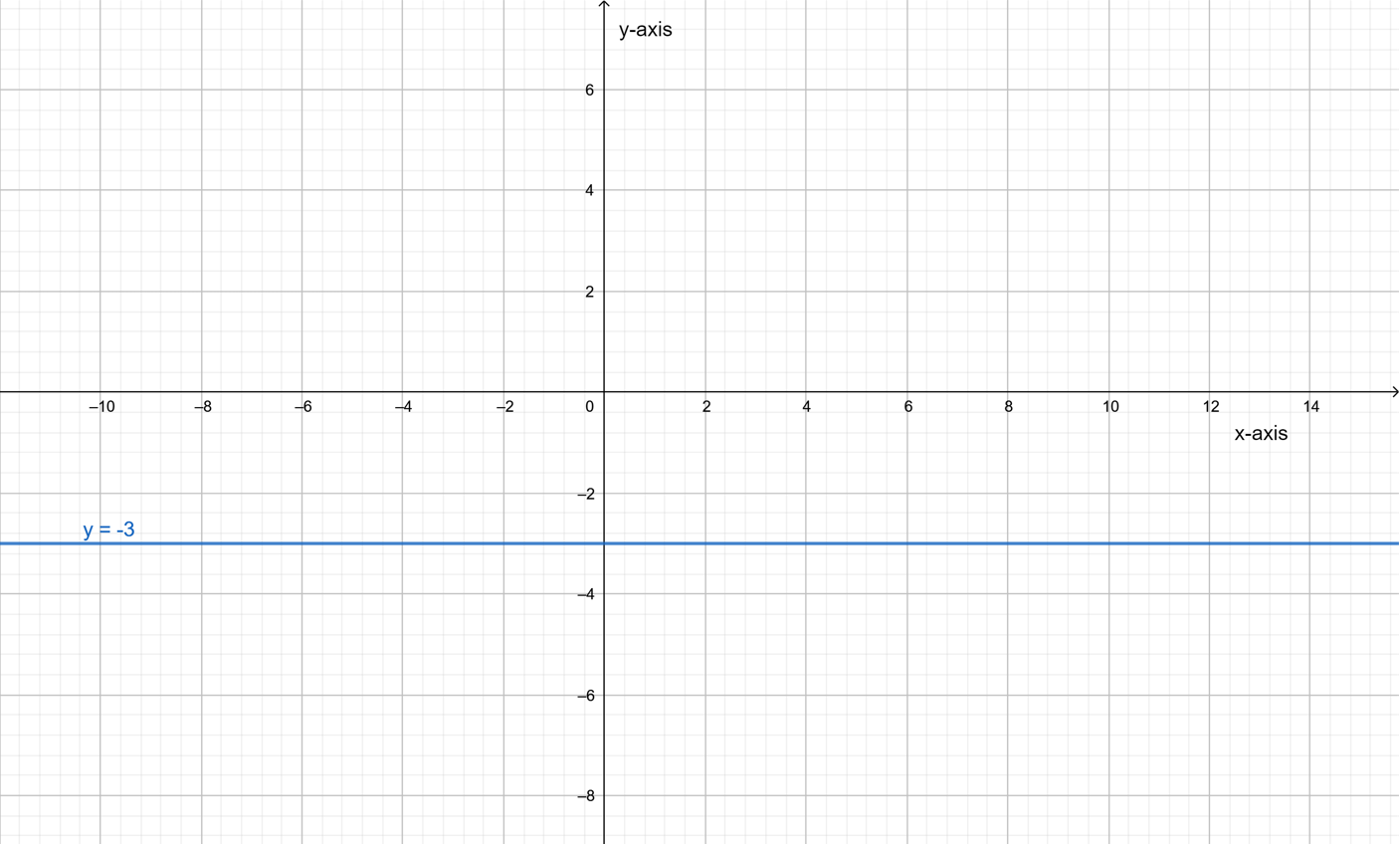
It is required to examine a way by which the line could intersect the parabola.
This can be done by reflecting the line with respect to x-axis.
Reflect the line shown in the graph with respect to x-axis.
Line can intersect the parabola by reflecting it with respect to x-axis.
Page 189 Problem 3 Answer
It is given a line and a parabola.
It is required to sketch three graphs showing intersection at one point, at two point and no intersection.
This can be done by taking an equation of a line and a parabola then graph these equations.
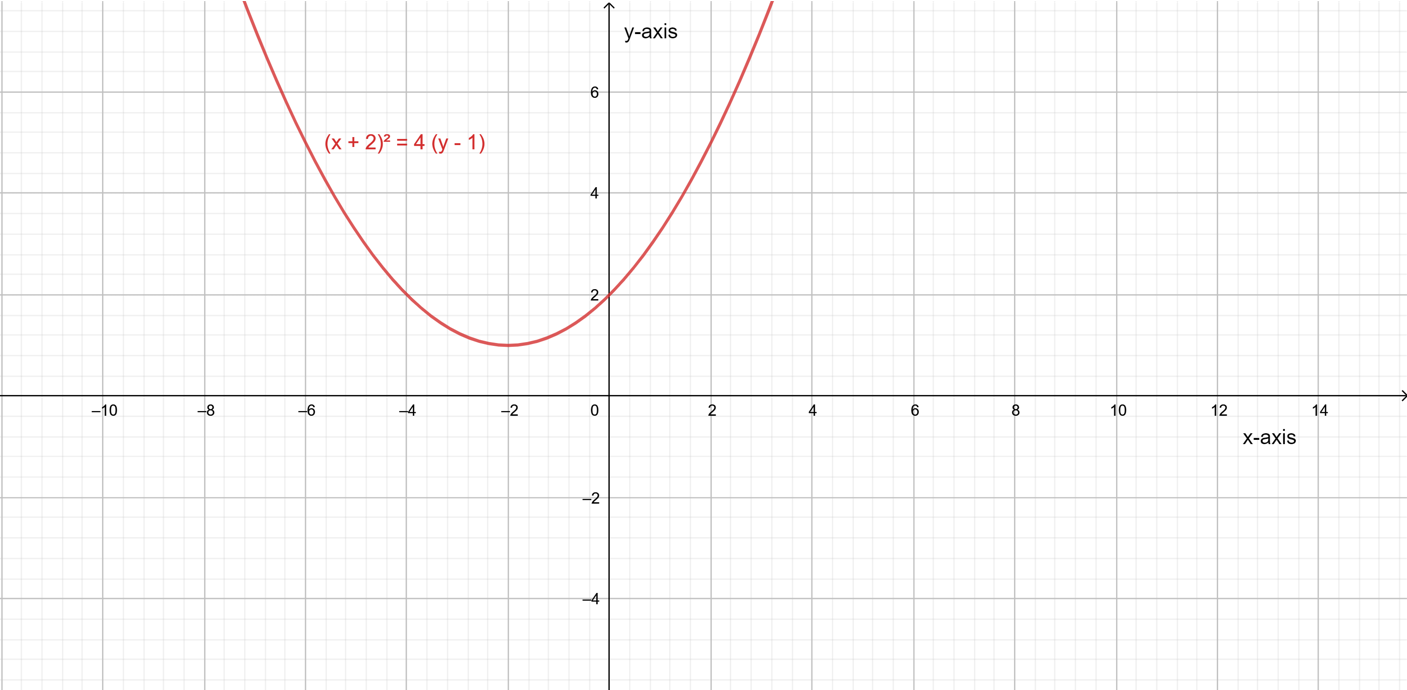
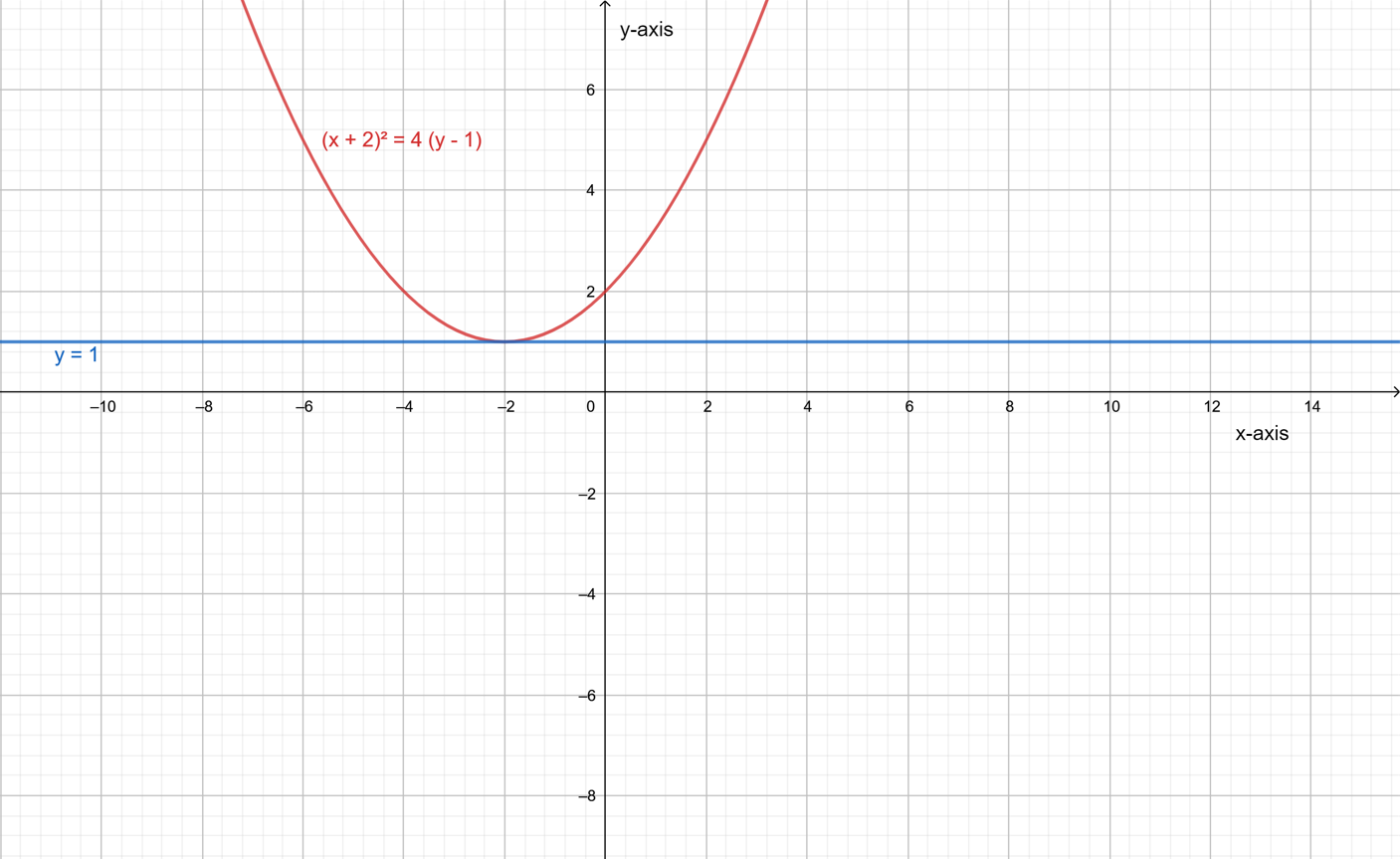
Let a parabola (x+2)2=4(y−1) and a line y=1.
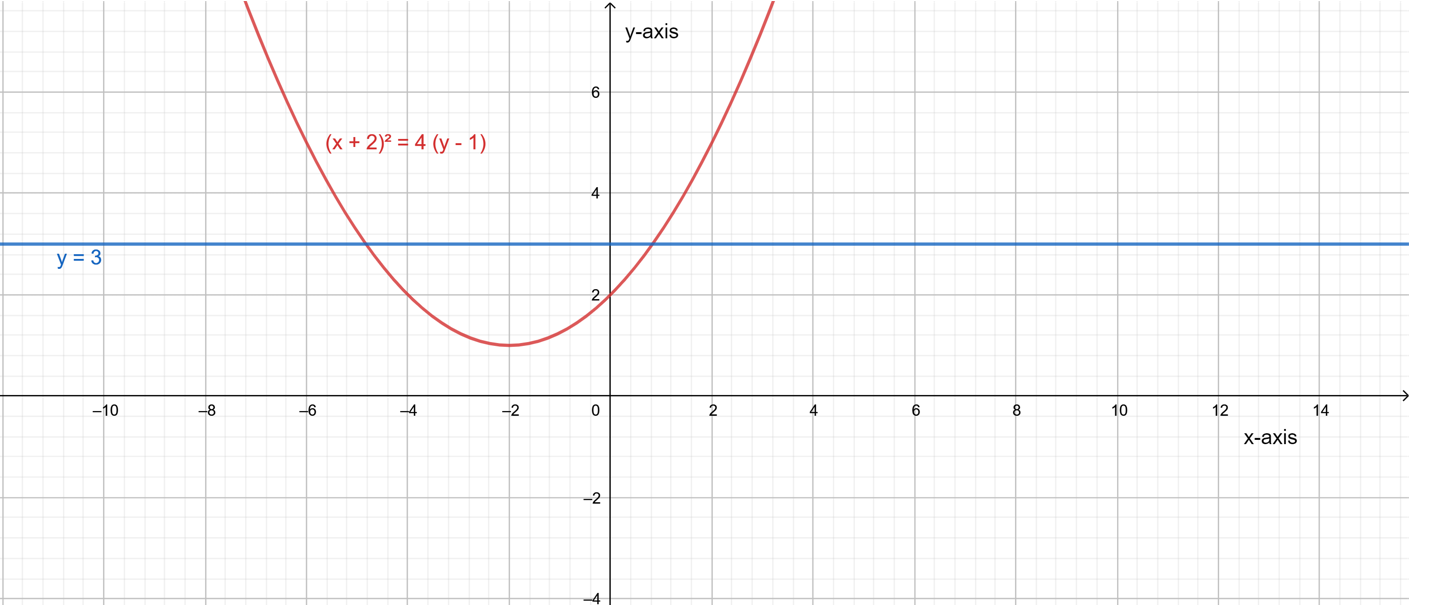
Let a parabola (x+2)2=4(y−1) and a line y=3.
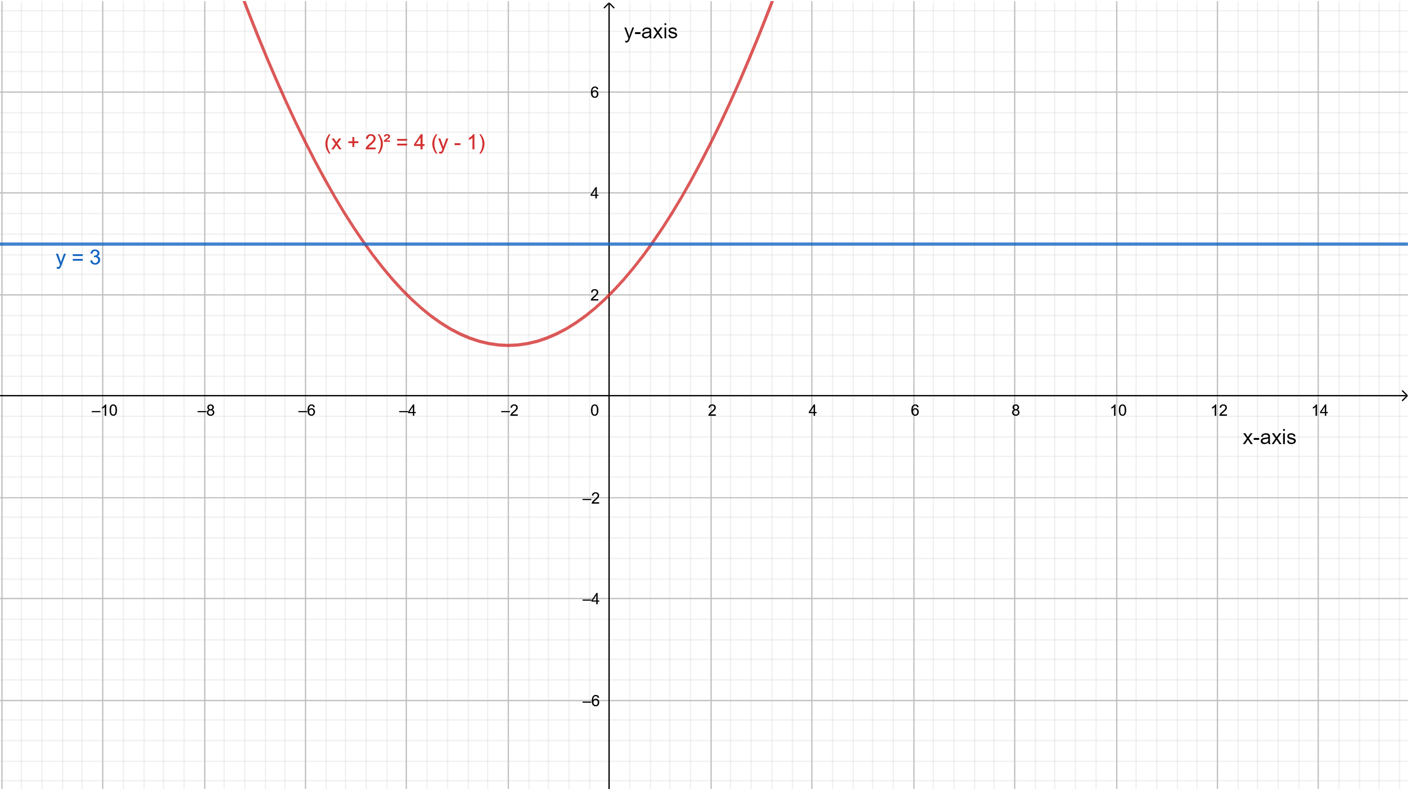
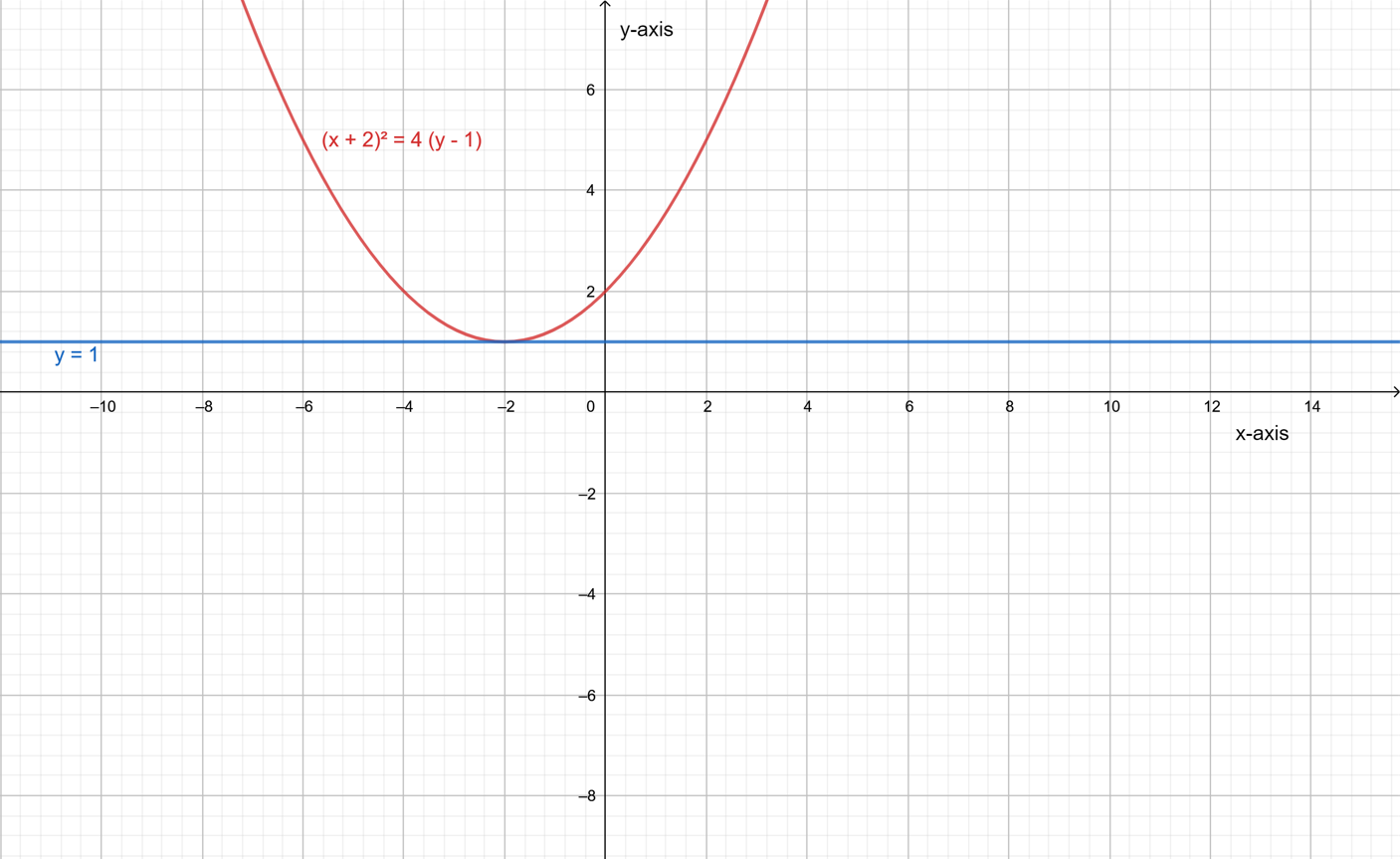
Let a parabola (x+2)2=4(y−1) and a line y=−3.
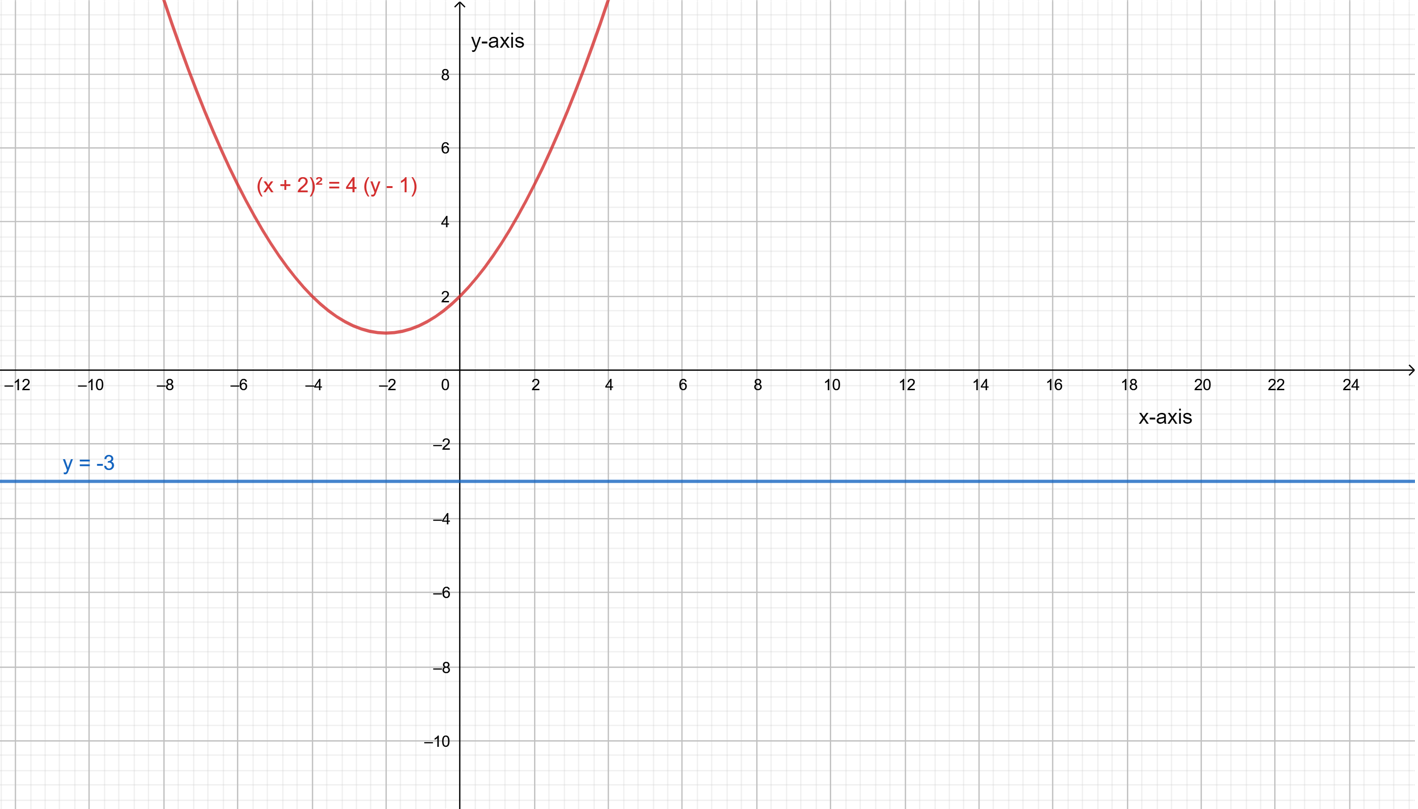
The required graphs are,For intersecting at one point
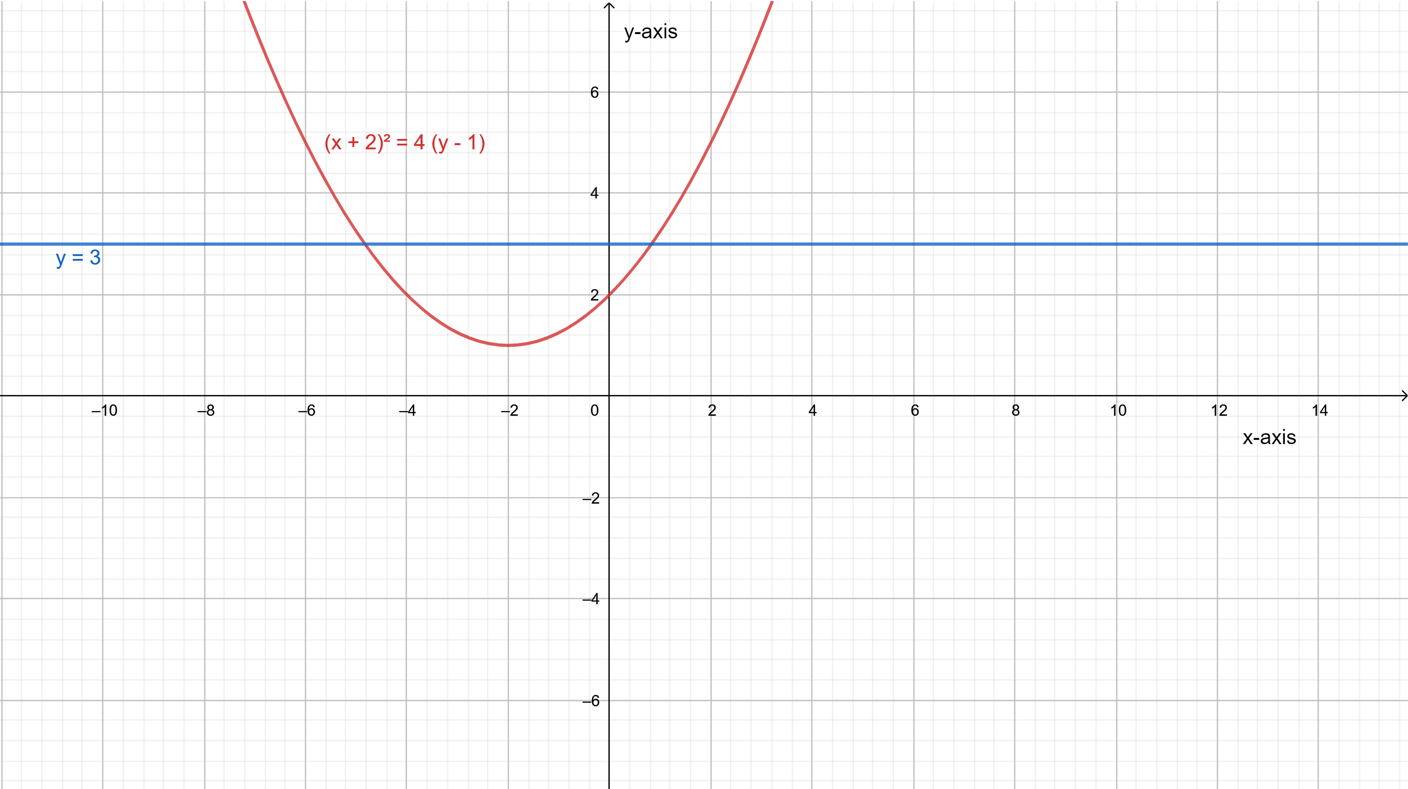
Page 189 Problem 4 Answer
It is given a linear and a quadratic function.
It is required to determine that at how many points does a constant linear function can intersect a quadratic function.
A constant horizontal line can intersect a quadratic function at 2 points.
For example: Let a parabola (x+2)2=4(y−1) and a line
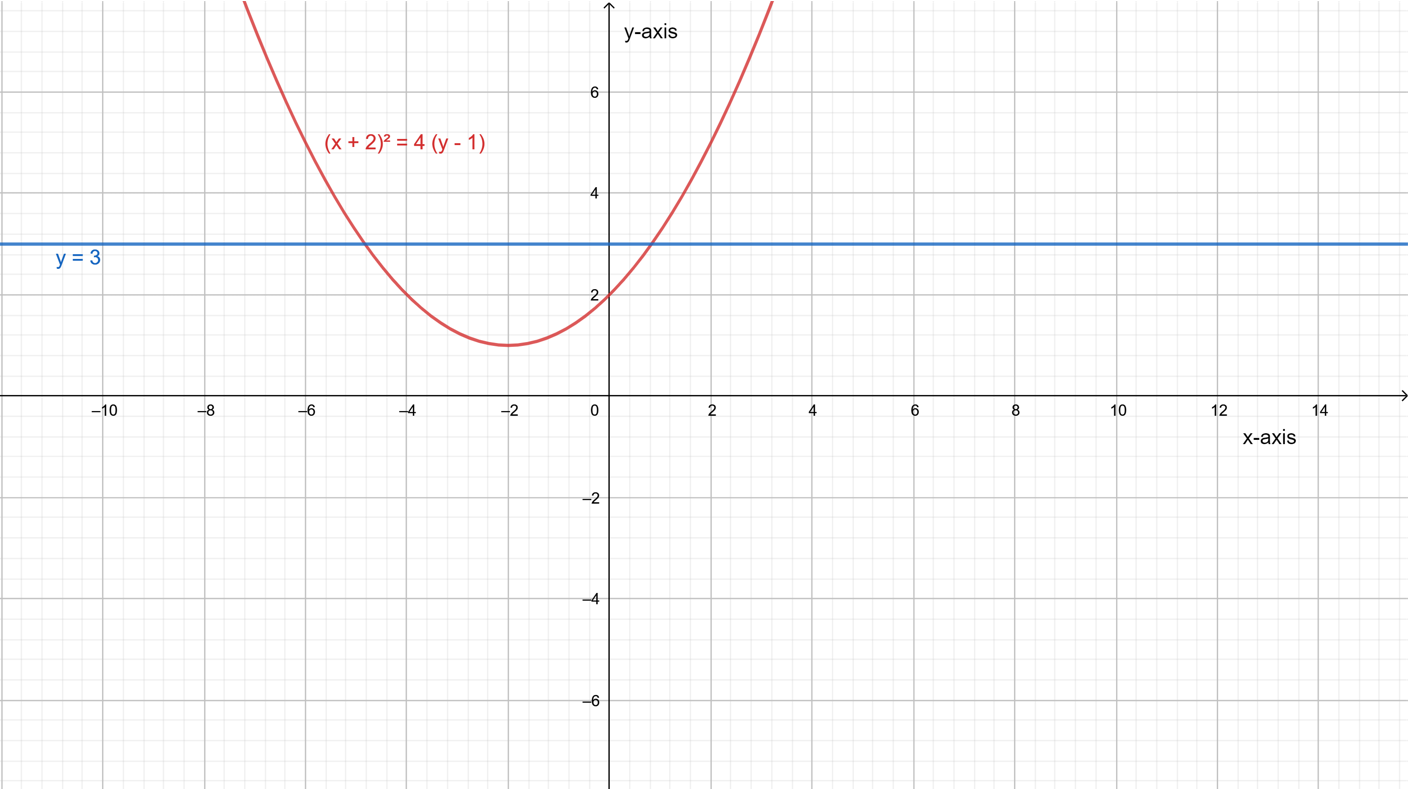
A constant horizontal line can intersect a quadratic function at 2 points. It can be shown as,
Page 190 Problem 5 Answer
It is given a parabola and a line.
It is required to discuss whether a line has to be horizontal to intersect a parabola at exactly one point.
Let a horizontal parabola be y2=4ax.
Now there may be a vertical line that intersects the horizontal parabola at a point.
Yes, there should be a vertical line that intersects the parabola at a point.
Page 190 Problem 6 Answer
A linear-quadratic system is given as y=1/2(x−3)2
3x+y=4.5
It is required to solve the given system graphically.
To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.
Plot the graph of y=1/2
(x−3)2.
Plot the graph of y=4.5−3x.
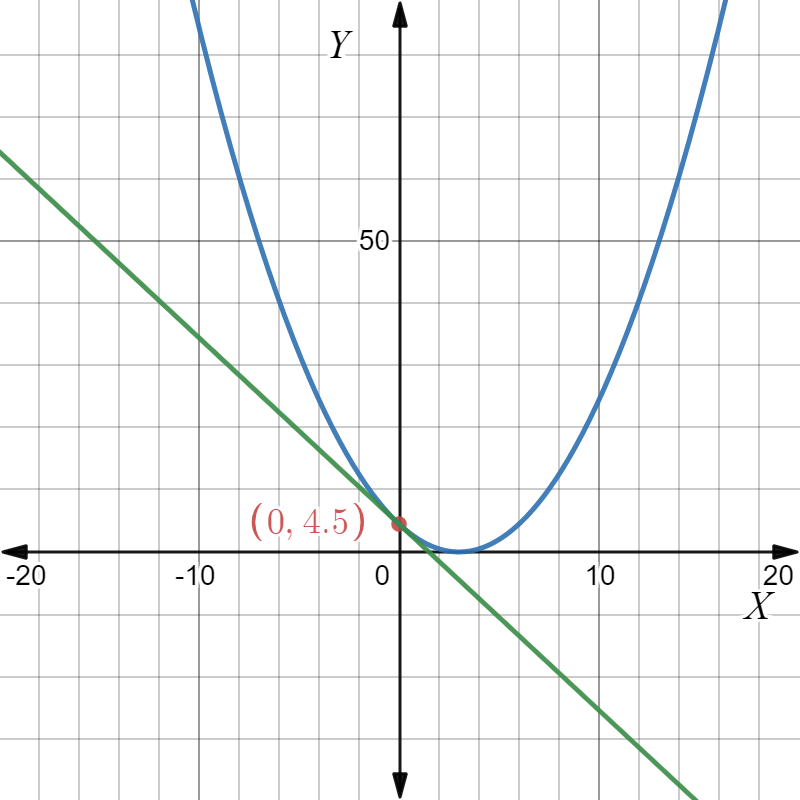
From the graph, it is understood that there is a unique solution for the two given equations at (0,4.5).
Therefore, the solution to given linear-quadratic system is (0,4.5).
The solution to given linear-quadratic system is (0,4.5).
Page 191 Problem 7 Answer
It is given a linear-quadratic system y+3x=0 and y−6=−3x2.
It is required to solve this linear-quadratic system graphically.
This can be done by plotting the graph of these two equations then check the intersecting points.
Plot the graph of the equation y+3x=0 and y−6=−3x2.
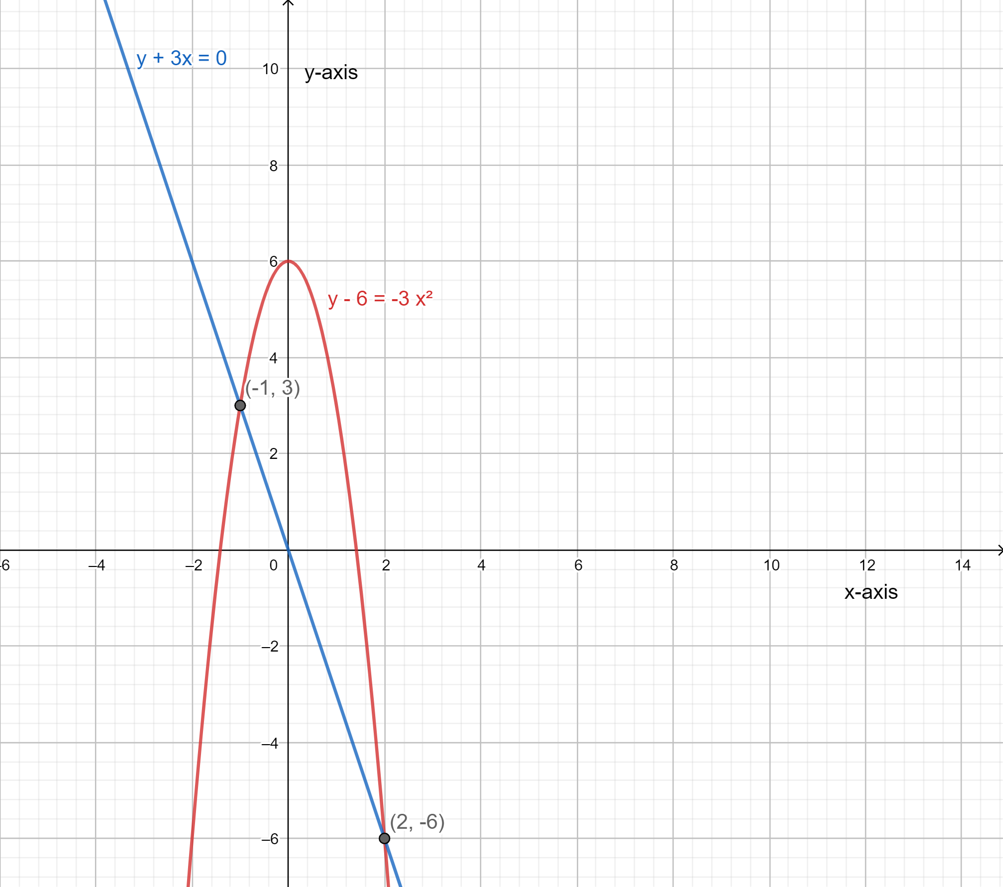
The graph of the two equations intersects each other at two points (−1,3) and (2,−6).
This implies that these are the solutions of this system of equations.
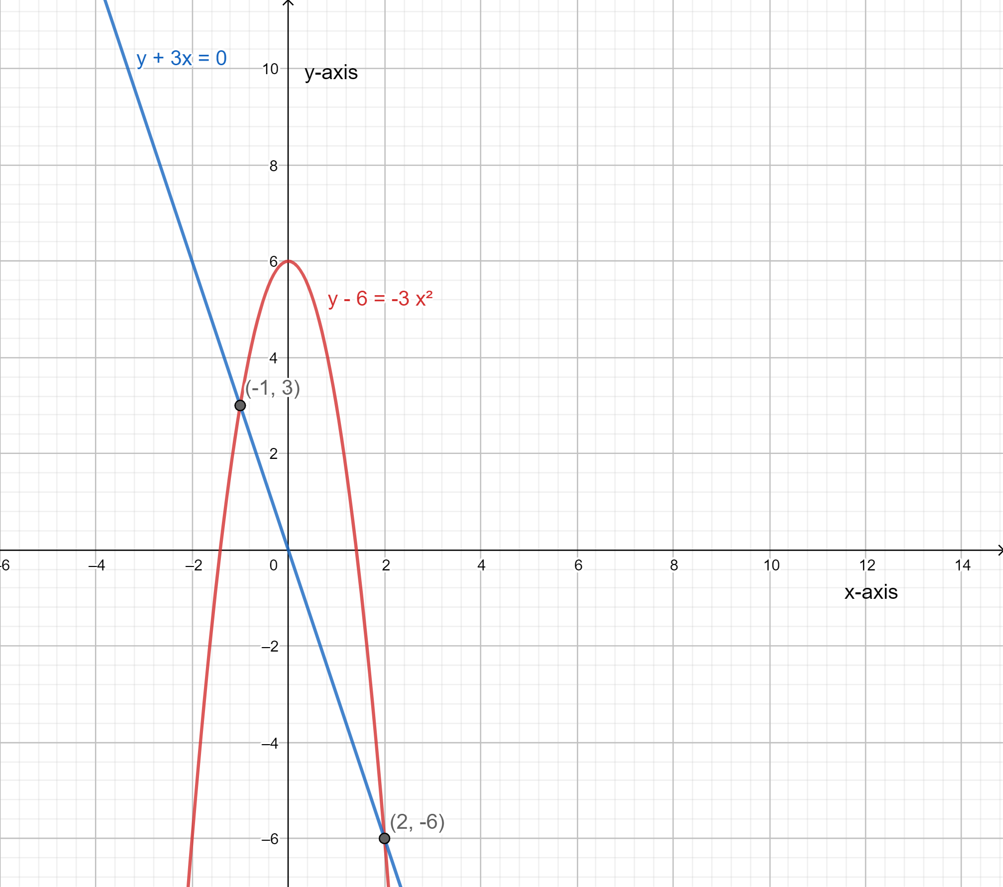
The solutions of this system are (−1,3) and (2,−6) which can be shown by the graph:
Page 191 Problem 8 Answer
It is given that the linear-quadratic system is
{ y=1/4(x−3)2
{ 3x−2y=13.
It is required to solve the given system.
Solve the system by substitution. The first equation is solved for y.
Substitute the expression 1/4(x−3)2
for y in the equation 3x−2y=13 to solve for x.
Put 1/4(x−3)2
for y in the equation 3x−2y=13.
13=3x−2(1/4(x−3)2)
13=3x−1/2(x−3)2
13=−1/2x2+6x−9/2
26=−x2+12x−9
0=x2−12x+35
Solve the equation for x.
x2−12x+35=0
x2−7x−5x+35=0
x(x−7)−5(x−7)=0
(x−5)(x−7)=0
x=5,7
Put the value of x as 5 in the equation 3x−2y=13.
3(5)−2y=13
2y=2
y=1
Put the value of x as 7 in the equation 3x−2y=13.
3(7)−2y=13
2y=8
y=4
The solutions of the given system
{ y=1/4(x−3)2
{ 3x−2y=13 are (5,1) and (7,4).
Page 192 Problem 9 Answer
A statement is given.
It is required to determine the way to check algebraic solutions for reasonableness.
One can check algebraic solutions for reasonableness by substituting the solution in the given equations and check whether the solution satisfies all the given equations.
Algebraic solutions can be checked for reasonableness by substituting the solution in the given equations and checking whether the solution satisfies all the given equations.
Page 193 Problem 10 Answer
A linear-quadratic system is given as x−6=−1/6y2
2x+y=6
It is required to solve the given system algebraically.
To solve the given system algebraically, substitute the expression for one the variable from one equation into the second equation and then solve for that variable.
Then, with this value find the value of the second variable.
Substitute 6−y2
for x in the equation x−6=−1/6y2.
Simplify the equation.
(6−y2)−6=−1/6y2
3−y2−6=−1/6y2
−y2−3=−1/6y2
Multiply both sides of the equation −y2−3=−1/6y2 by −6 and simplify.
−6(−y2−3)=−6(−1/6y2)2y+18=y2
y2−2y−18=0
Substitute −2 for b, 1 for a, −18 for c in the formula y=−b±√b2−4ac/2a.
y=−(−2)±√(−2)2−4(1)(−18)/2(1)
y=2±√4+72/2
y=2±√76/2
y=1±4.35
Therefore, y=5.35,−3.35.
Therefore, x=6−5.35/2
x=−0.65/2
x=−0.325 Or
x=6−(−3.35)/2
x=9.35/2
x=4.675
Therefore, the solutions to the given system are (4.675,−3.35),(−0.325,5.35).
The solutions to the given system are (4.675,−3.35),(−0.325,5.35).
Page 193 Problem 11 Answer
A linear-quadratic system is given as: x−y=7
x2−y=7
It is required to solve the given system algebraically.
To solve the given system algebraically, substitute the expression for one the variable from one equation into the second equation and then solve for that variable.
Then, with this value find the value of the second variable.
Solve for the value of x by the method of substitution.
Substitute x−7 for y in the equation x2−y=7. Simplify the equation.
x2−(x−7)=7
x2−x+7=7
x(x−1)=0
Therefore, x=0,1.
Use the values of x to find the values of y.
Therefore, y=0−7
y=−7 Or
y=1−7
y=−6
Therefore, the solutions to the given system are (0,−7),(1,−6).
The solutions to the given system are (0,−7),(1,−6)
Page 193 Problem 12 Answer
It is given that the range of radio station is a circle given by, x2+y2=2025.
The highway is expressed by the equation, y−15=1/20x.
It is required to tell the points where car enters the highway and then exits the range of station.
Solve the system by substitution. The first equation is solved for y. Substitute the expression 1/20
x+15 for y in the equation x2+y2=2025 to solve for x.
Make a quadratic equation in terms of x.
Put 1/20
x+15 for y in the equation x2+y2=2025.
x2+(1/20x+15)2=2025
x2+1/400
x2+225+3/2
x=2025/401
400x2+3/2
x−1800=0
401x2+600x−720000=0
Solve the equation for x.
x=−600±√6002−4(401)(−720000)
2(401)=600±√1,155,240,000
802≈43.17,41.63
Use the value of x to get the value of y.
Put the value of x as 43.17 in the equation y=1/20
x+15.
y=1/20
(43.17)+15
y=17.15
Put the value of x as 41.63 in the equation y=1/20
x+15.
y=1/20(41.63)+15
y=17.08
The car will be within the radio station’s broadcast area between the points (43.17,17.15) and (41.63,17.08).
Page 196 Problem 13 Answer
The equation of the orbit of earth’s satellite is given as x2/49+y2/51=1.
The equation of the path of an asteroid is given as y=1/28 x−7.
It is required to find the points where the asteroid may collide with the satellite.
To find the points of collision, draw the graph of the line and the ellipse on a graphing calculator. Then, find the points of intersection.
Draw the graph of y=1/28 x−7 on a graphing calculator.
Draw the graph of x2/49+y2/51=1 on a graphing calculator.
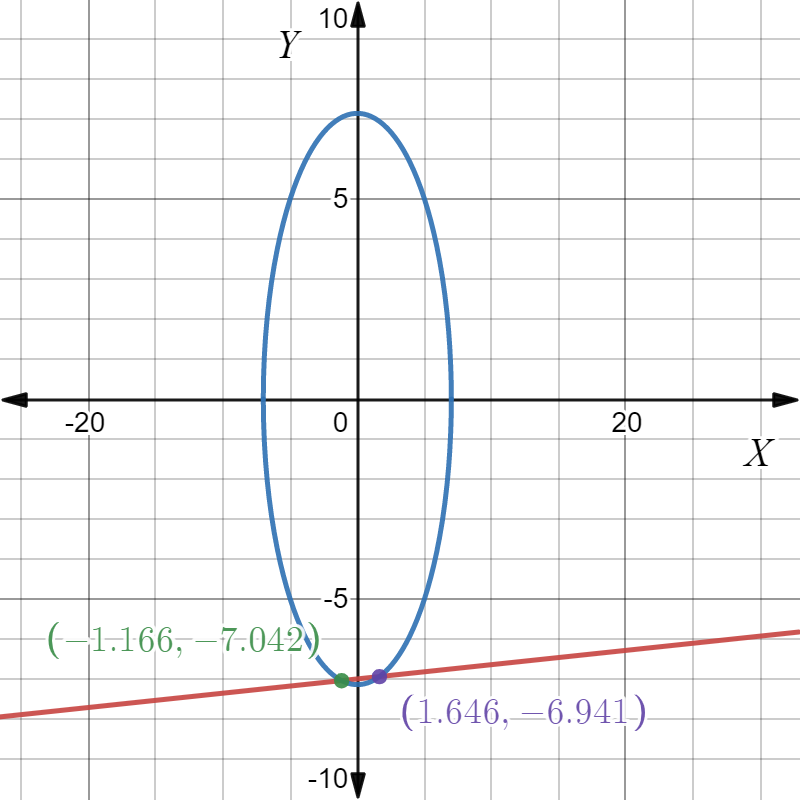
From the graph, the point of intersect of the orbit and the path of the asteroid is (−1.166,−7.042),(1.646,−6.941).
Therefore, the asteroid may collide with the satellite at two points, (−1.166,−7.042),(1.646,−6.941).
The asteroid may collide with the satellite at two points, (−1.166,−7.042),(1.646,−6.941).
Page 196 Problem 14 Answer
It is given that the path of the trapeze is modelled by y=1/4x2+16.
The path of the zip-line is modelled by y=2x+12.
It is required to find the point where the trapeze artist can grab the second acrobat.
To find the required point, the given system algebraically. Substitute the expression for one the variable from one equation into the second equation and then solve for that variable.
Then, with this value find the value of the second variable.
Make a quadratic equation in terms of x.
Substitute 2x+12 for y in the equation y=1/4x2+16. Simplify the equation.
2x+12=1/4x2+16
1/4x2−2x+16−12=0
1/4x2−2x+4=0
Solve the equation for x.
Multiply both sides of the equation 1/4x2−2x+4=0 by 4 and simplify.
4(1/4x2−2x+4)=4(0)
x2−8x+16=0
(x−4)2
=0
Therefore, x=4.
Find the value of y using x.
Therefore, y=2(4)+12
y=8+12
y=20
Therefore, the point where the trapeze artist can grab the second acrobat is (4,20).
The point where the trapeze artist can grab the second acrobat is (4,20).
Page 196 Problem 15 Answer
It is given that a parabola opens to the left.
It is required to identify an infinite set of parallel lines that intersect the parabola only once.
Since the parabola opens to the left, a horizontal line, say y=a;a∈R, will intersect the parabola only once.
Similarly, there will be infinite number of such horizontal lines that intersect the parabola at only point.
Therefore, the set of parallel lines that intersect the parabola only once is y=a;a∈R.
If a parabola opens to the left, the set of parallel lines that intersect the parabola only once is y=a;a∈R.
Page 196 Problem 16 Answer
A statement is given.
It is required to mention how to solve a system consisting of a linear equation in two variables and a quadratic equation in two variables.
To solve the system algebraically, substitute the expression for one the variable from the linear equation into the second equation and then solve for that variable by using identity
(a+b)2=a2+2ab+b2 and the quadratic formula.
Then, with this value find the value of the second variable by substituting it in the linear equation.
To solve the system algebraically, substitute the expression for one the variable from the linear equation into the second equation and then solve for that variable by using identity (a+b)2
=a2+2ab+b2 and the quadratic formula.
Then, with this value find the value of the second variable by substituting it in the linear equation.
Page 197 Exercise 1 Answer
It is required to tell the number of intersection points on the graph.
The curve on the graph meets at x−axis, then at y−axis and again at x−axis. So, the total number of intersection points of the curve is 3.
The straight line intersects the x−axis and then has an intercept at y−axis. So, total number of intersections for the line is 2.
Also, the curve and the line intersect at one point.
So, the total number of intersections are, 3+2+1=6 points.
There are 6 points of intersection are on the graph.
Page 197 Exercise 2 Answer
It is given that the system of equations is,
{ y=x2+3x−2
{ y−x=4.
It is required to tell the number of intersection points on the graph of given system.
Plot the given system of equations. Check if the given curve and the line meet at any point or not. Count the number of such points.
Draw the graph of the system
{ y=x2+3x−2
{ y−x=4 on an online geometry calculator.
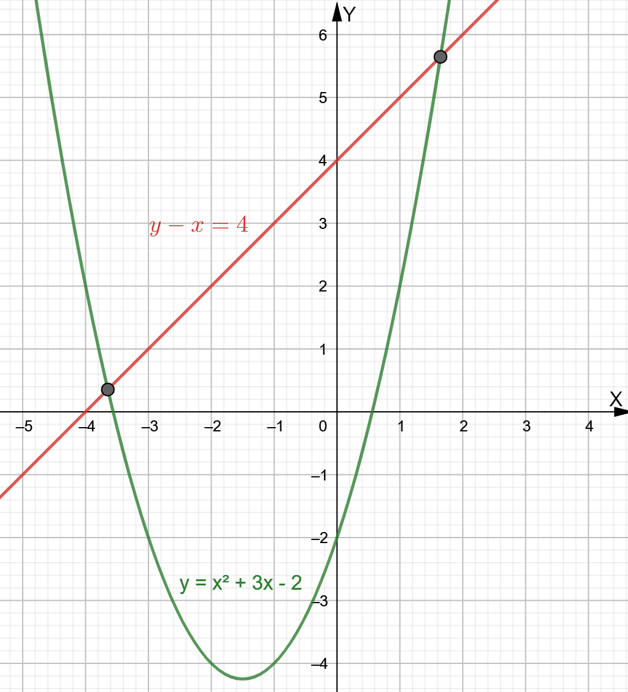
The curve y=x2+3x−2 and the line y−x=4 meet at two points on the graph.
The curve y=x2+3x−2 meets twice at x−axis and once at y−axis.
The curve y−x=4 meets once at both x−axis and y−axis.
Therefore, the number of intersection points is 2+2+1+1+1=7.
There are 7 points of intersection on the graph of the system
{ y=x2+3x−2
{ y−x=4.
Page 197 Exercise 3 Answer
It is given that the system of equations is,
{ y=−(x−2)2+4
{ y=−5.
It is required to solve the system graphically.
Plot the given system of equations. Check if the given curve and the line meet at any point or not.
Find the coordinates of such points.
These intersection points are the solutions of the system.
Draw the graph of the system
{y=−(x−2)2+4
{ y=−5 on an online geometry calculator.
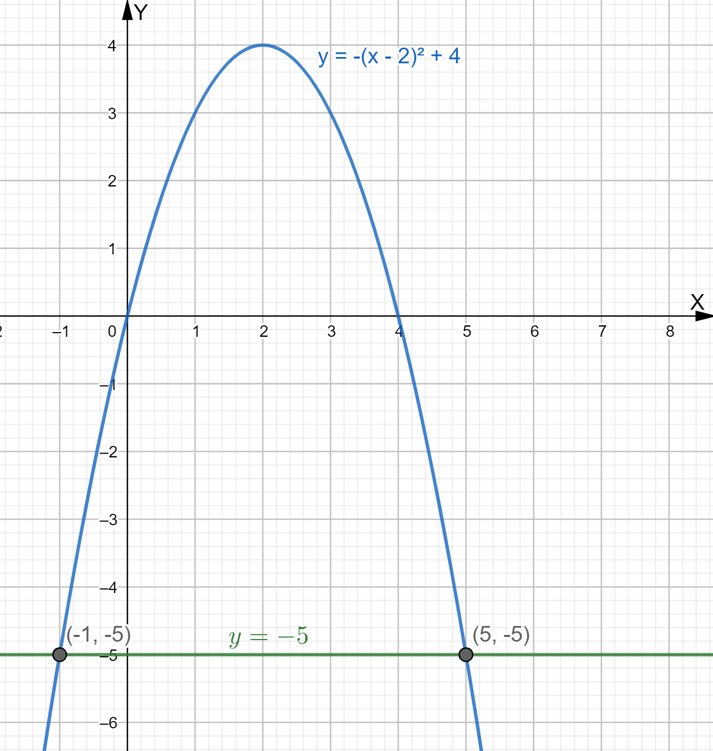
The curve y=−(x−2)2+4 and the line y=−5 meet at two points on the graph.
The two points are (−1,−5) and (5,−5).
The solutions of the system
{y=−(x−2)2+4
{ y=−5 are (−1,−5) and (5,−5).
Page 197 Exercise 4 Answer
A linear-quadratic system is given as: y−3=(x−1)2
2x+y=5
It is required to solve the given system graphically.
To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.
Plot the graph of y−3=(x−1)2.
Plot the graph of 2x+y=5.
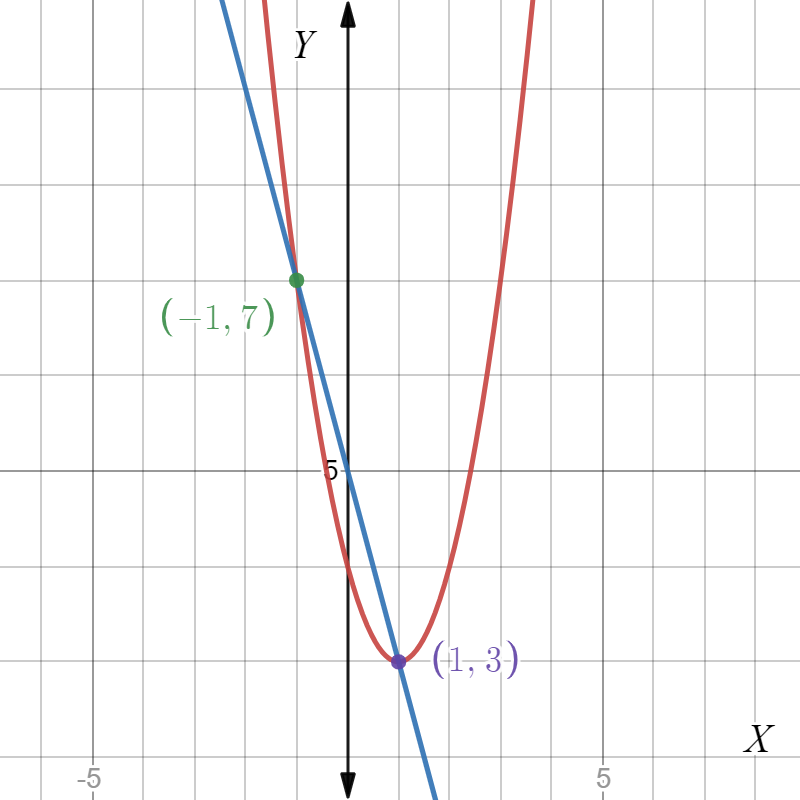
From the graph, the line intersects the parabola at two points (−1,7),(1,3).
Therefore, the solution to the given linear-quadratic system is (−1,7),(1,3).
The solution to the given linear-quadratic system is (−1,7),(1,3).
Page 197 Exercise 5 Answer
A linear-quadratic system is given as: x=y2−5−x+2y=12
It is required to solve the given system graphically.
To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.
Plot the graph of x=y2−5.
Plot the graph of −x+2y=12.
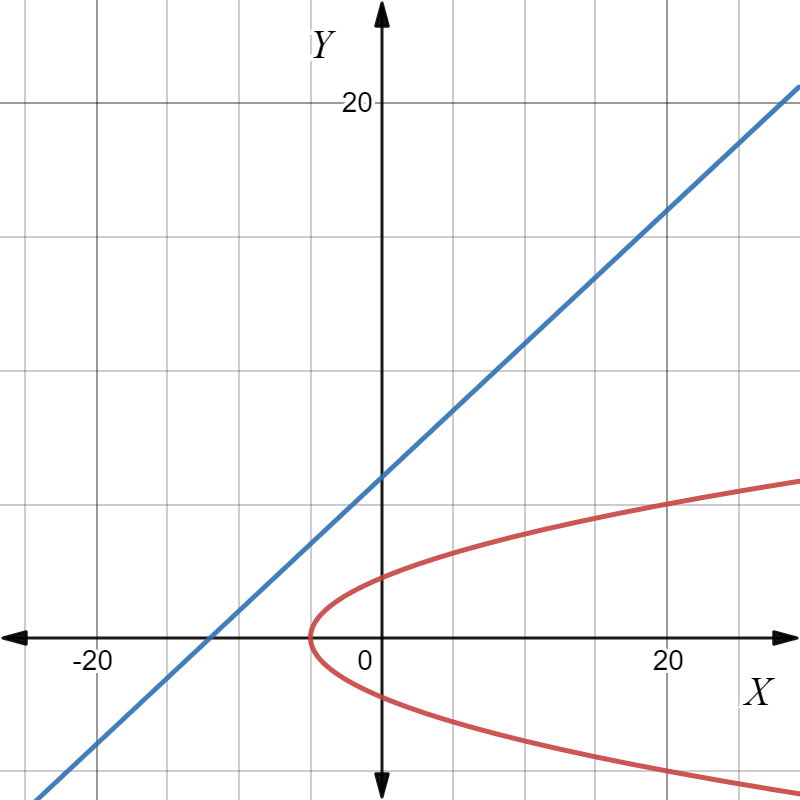
From the graph, it is understood that there is no unique solution for the two given equations.
Therefore, the given linear-quadratic system has no solution.
The given linear-quadratic system has no solution as there is no point of intersection between the two graphs.
Page 197 Exercise 6 Answer
A linear-quadratic system is given as:
x−4=(y+1)2
3x−y=17
It is required to solve the given system graphically.
To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.
Plot the graph of x−4=(y+1)2.
Plot the graph of 3x−y=17.
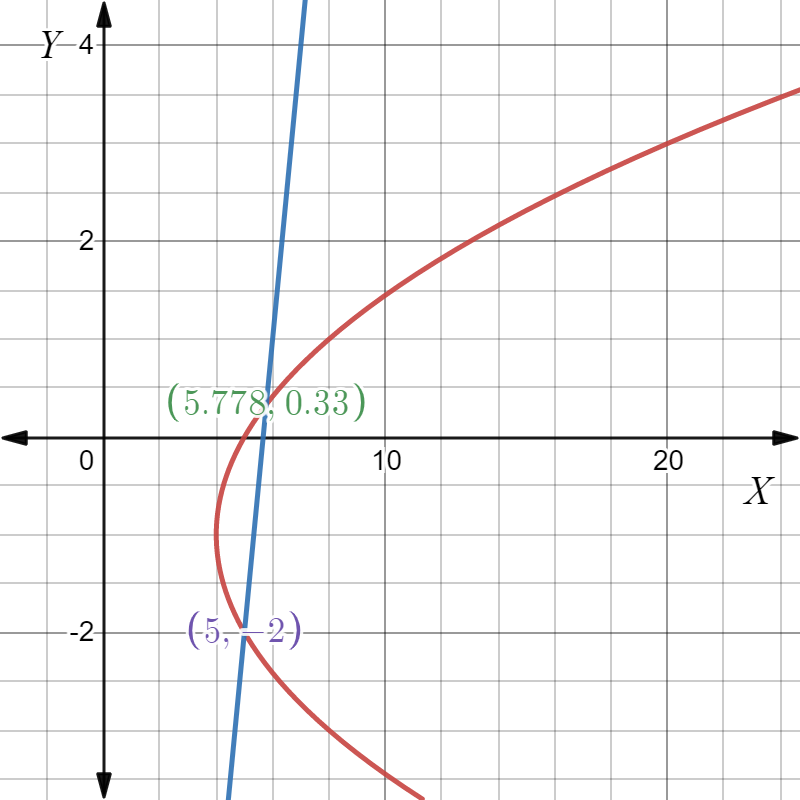
From the graph, the line intersects the parabola at two points (5.77,0.33),(5,−2).
Therefore, the solution to the given linear-quadratic system is (5.77,0.33),(5,−2).
The solution to the given linear-quadratic system is (5.77,0.33),(5,−2).
Page 198 Exercise 7 Answer
A linear-quadratic system is given as: (y−4)2+x2
=−12x−20
x=y
It is required to solve the given system graphically.
To solve the given system graphically, plot the given two equations on a graphing calculator and find whether the two graphs have any point of intersection.
Plot the graph of (y−4)2+x2
=−12x−20.
Plot the graph of x=y.
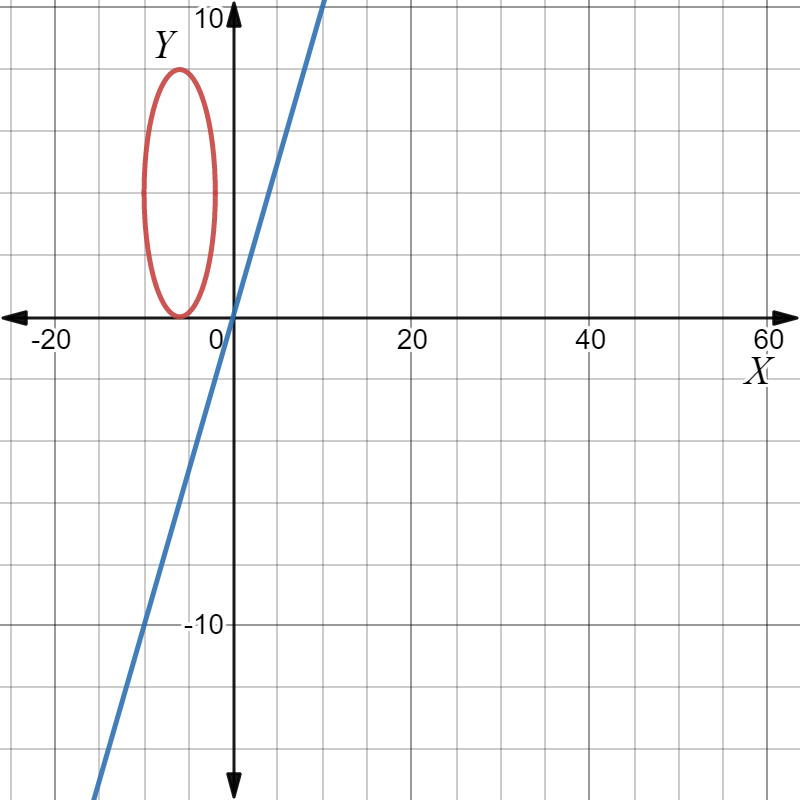
From the graph, it is understood that there is no unique solution for the two given equations.
Therefore, the given linear-quadratic system has no solution.
The given linear-quadratic system has no solution as there is no point of intersection between the two graphs.
Page 198 Exercise 8 Answer
It is given that the linear-quadratic system is
{ 6x+y=−16
{ y+7=x2.
It is required to solve the given system.
Substitute the value of y from y+7=x2 in the equation
6x+y=−16. Find the value of x from the obtained equation. Put the obtained value of x in the equation
y+7=x2 to get the value of y.
Put the value of y as x2−7 in 6x+y=−16.
6x+x2−7=−16
x2+6x−7+16=0
x2+6x+9=0
Solve the equation for x.
x=−6±√62−4(1)(9)/2(1)
x=−6±√36−36/2
x=−6/2
x=−3
Put the value of x as −3 in the equation 6x+y=−16.
6(−3)+y=−16−18+y=−16
y=−16+18
y=2
Hence, the value of x is −3 and y is 2.
The solution of the given system
{ 6x+y=−16
{ y+7=x2 is (−3,2).
Page 197 Exercise 9 Answer
It is given that the linear-quadratic system is
{ y−5=(x−2)2
{ x+2y=6.
It is required to solve the given system.
Substitute the value of y from y−5=(x−2)2 in the equation
x+2y=6. Find the value of x from the obtained equation. Put the obtained value of x in the equation x+2y=6 to get the value of y.
Put the value of y as (x−2)2+5 in x+2y=6.
x+2((x−2)2+5)=6
x+2(x2+4−4x+5)=6
x+2(x2−4x+9)=6
2x2−7x+18=6
2x2−7x+12=0
Solve the equation for x.
x=−(−7)±√(−7)2−4(2)(12)/2(2)
x=7±√49−96/4
x=7±√−47/2
As x has an imaginary value, y also does not have a real value.
So, there is no solution for the given system.
The solution for the given system {y−5=(x−2)2
x+2y=6 does not exist as x and y both have imaginary values.
Page 198 Exercise 10 Answer
It is given that the linear-quadratic system is
{ y2−26=−x2
{ x−y=6.
It is required to solve the given system.
Substitute the value of y from x−y=6 in the equation y2−26=−x2.
Find the value of x from the obtained equation. Put the obtained values of x in the equation x−y=6 to get the value of y.
Put the value of y as x−6 in y2−26=−x2.
(x−6)2−26=−x2
x2+36−12x−26=−x2
2x2−12x+10=0
x2−6x+5=0
Solve the equation for x.
x=−(−6)±√(−6)2−4(1)(5)/2(1)
x=6±√16/2
x=6+4/2,6−4/2
x=5,1
Put the value of x as 5 in the equation x−y=6 to find the corresponding value of y.
5−y=6
y=−1
Put the value of x as 1 in the equation x−y=6 to find the corresponding value of y.
1−y=6
y=−5
The solutions for the given system
{ y2−26=−x2
{ x−y=6 are (5,−1) and (1,−5).
Page 198 Exercise 11 Answer
It is given that the linear-quadratic system is
{ y−3=x2−2x
{ 2x+y=1.
It is required to solve the given system.
Substitute the value of y from y−3=x2−2x in the equation 2x+y=1.
Find the value of x from the obtained equation. Put the obtained values of x in the equation 2x+y=1 to get the value of y.
Put the value of y as x2−2x+3 in 2x+y=1.
2x+x2−2x+3=1
x2+3=1
x2=−2
x=√−2
As x has an imaginary value, y also does not have a real value.
So, there is no solution for the given system.
The solution for the given system {y−3=x2−2x
{ 2x+y=1 does not exist as x and y both have imaginary values.
Page 198 Exercise 12 Answer
It is given that the linear-quadratic system is
{ y=x2+1
{ y−1=x.
It is required to solve the given system.
Substitute the value of y from y=x2+1 in the equation y−1=x.
Find the value of x from the obtained equation. Put the obtained values of x in the equation
y−1=x to get the value of y.
Put the value of y as x2+1 in y−1=x.
x2+1−1=x
x2=x
x2−x=0
x(x−1)=0
x=0,1
Put the value of x as 0 in the equation y−1=x to find the corresponding value of y.
y−1=0
y=1
Put the value of x as 1 in the equation y−1=x to find the corresponding value of y.
y−1=1
y=2
The solutions for the given system
{ y=x2+1
{ y−1=x are (0,1) and (1,2).
Page 198 Exercise 13 Answer
It is given that the linear-quadratic system is
{ y=x2+2x+7
{ y−7=x.
It is required to solve the given system.
Substitute the value of y from y=x+7 in the equation y=x2+2x+7.
Find the value of x from the obtained equation.
Put the obtained values of x in the equation y=x+7 to get the value of y.
Put the value of y as x+7 in y=x2+2x+7.
x+7=x2+2x+7
x2+x=0
x(x+1)=0
x=0,−1
Put the value of x as 0 in the equation y=x+7 to find the corresponding value of y.
y=0+7
y=7
Put the value of x as −1 in the equation y=x+7 to find the corresponding value of y.
y=−1+7
y=6
The solutions for the given system
{ y=x2+2x+7
{ y−7=x are (0,7) and (−1,6).
Page 199 Exercise 14 Answer
It is given that Jason is driving his car at a constant velocity of 60 miles per hour. The distance that Alan travelled is given by, d=3600t2.
It is required to find the time taken by Alan to catch up with Jason.
Substitute v for d/t in the equation. Put the given value of v to find t.
The equation d=3600t2 can be written as,d/t
=3600t
v=3600t
Put v=60 in the equation.
60=3600t
t=60/3600
t=1/60
The time taken by Alan to catch up with Jason is 1/60 hours.
Page 199 Exercise 15 Answer
It is given that the equation of the cannonball’s flight is given by y=2+0.12x−0.002x2.
The hill slope has an equation,
y=0.15x.
It is required to find where the cannonball lands on the hill.
Substitute the value of y from y=0.15x in the equation
y=2+0.12x−0.002x2.
Find the value of x from the obtained equation. Put the obtained value of x in the equation
y=0.15x to get the value of y.
Put the value of y as 0.15x in y=2+0.12x−0.002x2.
2+0.12x−0.002x2=0.15x
0.002x2+0.03x−2=0
2x2−30x−2000=0
x2−15x−1000=0
Solve the equation for x.
x=−(−15)±√(−15)2−4(1)(−1000)/2(1)
x=15±√4225/2
x=15+65/2,15−65/2
x=40,−25
Ignore the negative value x=−25 as distance cannot be negative.
Put the value of x as 40 in the equation y=0.15x.
y=0.15(40)
y=6
The cannonball lands on the hill at 6 units.
Page 199 Exercise 16 Answer
It is given that the equation of the quarter is given by y=64−2x2. The balloon has an equation, y=6x+8.
It is required to find when the balloon and quarter pass each other.
Substitute the value of y from y=6x+8 in the equation y=64−2x2.
Find the value of x from the obtained equation.
Put the value of y as 6x+8 in y=64−2x2.
6x+8=64−2x2
2x2+6x−56=0
x2+3x−28=0
Solve the equation for x.
x=−3±√(3)2−4(1)(−28) /2(1)
x=−3±√121/2
x=−3+11/2,−3−11/2
x=4,−7
Ignore the negative value x=−7 as the time cannot be negative.
The quarter and the balloon pass each other after 4 seconds.
Page 200 Exercise 17 Answer
It is given that the circular region is x2+y2=400 and service area is a straight line given by,
y=3x+20.
It is required to find the length of the service road.
Substitute the value of y from y=3x+20 in the equation
x2+y2=400. Find the value of x from the obtained equation.
Put the obtained value of x in the equation y=3x+20 to get the value of y.
Find the distance between the intersection points.
Put the value of y as 3x+20 in x2+y2=400.
x2+(3x+20)2=400
x2+9x2+400+120x=400
10x2+120x=0
x2+12x=0
x=0,−12
Put the value of x as 0 in the equation y=3x+20.
y=3(0)+20
y=20
Put the value of x as −12 in the equation y=3x+20.
y=3(−12)+20
y=−36+20
y=−16
Find the distance between the points (0,20) and (−12,−16).
D=√(−12−0)2+(−16−20)2
=√144+1296
≈37.95
The length of the service road is 37.95 units.
Page 200 Exercise 18 Answer
It is given that the system of equations is,
{ y−7=x2−5x
{ y−2x=1 and the student gave (1,3) as the solution.
It is required to verify that student is correct or not.
Plot the given system of equations. Check if the given curve and the line meet at any point or not.
Find the coordinates of such points. These intersection points are the solutions of the system.
Verify if the intersection points match with the answer of the student.
Draw the graph of the system
{ y−7=x2−5x
{ y−2x=1 on an online geometry calculator.
The curve y−7=x2−5x and the line y−2x=1 meet at one point on the graph.
The intersection point is (1,3).
The student gave a reasonable answer as (1,3) because it is the only intersection point of the given system { y−7=x2−5x
{ y−2x=1.
Page 201 Exercise 19 Answer
It is given that the student gave
{ y2=−(x+1)2+9
{ y=x2−4x+3 as a linear-quadratic system.
It is required to verify tell if the student is correct or not.
A linear-quadratic system requires at least one linear equation and one quadratic equation.
The student is incorrect as both y2=−(x+1)2+9 and
y=x2−4x+3 are quadratic equations.
One of them should have been a linear equation to make the system correct.
The student’s answer { y2=−(x+1)2+9
{ y=x2−4x+3 is wrong as both are quadratic equations.
Page 201 Exercise 20 Answer
It is given that the system of quadratic functions are y=100x2 and y=0.001x2.
It is required to find whether there is a line possible that is not horizontal as well as vertical but passes through the vertex of both.
The lines y=100x2 and y=0.001x2
cannot be solved as they have no common intersection point.
Therefore, the number of solutions of the system is zero.
Hence, there is no line possible that can pass through both of the vertices.
There is no line possible that passes through the vertex of both curves but is not horizontal as well as vertical.
Page 201 Exercise 21 Answer
It is given that that there is a system of linear and quadratic equation.
It is required to find why a system of a linear equation and a quadratic equation cannot have an infinite number of solutions.
A quadratic equation always forms a parabola.
A linear equation forms a line.
Two equations have an infinite number of solutions when they have the same graph
But a parabola and a straight line can’t be the same.
That’s why a system of a linear equation and a quadratic equation cannot have an infinite number of solutions.
A system of a linear equation and a quadratic equation cannot have an infinite number of solutions because they don’t have the same graph.