Algebra 2 Volume 1 1st Edition Module 3 Quadratic Equations
Page 112 Problem 1 Answer
The given inequality is n−12>9.
The question requires to solve the given inequality.
To solve the inequality, isolate the variable n on one side of the inequality using addition.
Add 12 on both sides of n−12>9.
n−12+12>9+12n>21
Thus, the solution of n−12>9 is n>21.
The required solution is n>21.
Page 112 Problem 2 Answer
The given inequality is −3p<−27.
The question requires to solve the given inequality.
To solve the inequality, isolate the variable p on one side of the inequality using division.
Divide both sides of −3p<−27 by −3.
−3p<−27
−3p/−3>−27
−3p>9
Thus, the solution of −3p<−27 is p>9.
The required solution is p>9.
Page 112 Problem 3 Answer
The given inequality is k/4≥−1.
The question requires to solve the given inequality.
To solve the inequality, isolate the variable k on one side of the inequality using multiplication.
Multiply both sides of k/4 ≥−1 by 4.
4(k/4)≥4(−1)
k≥−4
Thus, the solution of k/4≥−1 is k≥−4.
Page 112 Problem 4 Answer
The given expression is 16p2/2p4.
The question requires to simplified the given expression.
To simplify the expression, rewrite the numbers in the expression as powers of 2, and use the property of exponents am/an=am−n to simplify the expression.
Rewrite 16 and 2 as powers of 2, and use the property am/an = am−n.
16p2/2p4=24p2
21/p4=24−1
p4−2
Subtract the exponents and simplify the expression.
16p2/2p4=23
p2=8
p2 Thus, the required simplified expression is 8p2.
The required simplified form of 16p2
2p4 is 8 p2.
Page 112 Problem 5 Answer
The given expression is 5vw5⋅2v4.
The question requires to simplified the given expression.
To simplify the expression, use the property of exponents am/an=am+n and add the exponents to simplify the expression.
Rewrite the expression, apply the property am/an=am+n, and add the exponents.
5vw5⋅2v4
=5⋅2⋅v1⋅v4⋅w5
=10v1+4/w5
=10v5/w5
Thus, the required simplified expression is 10v5/w5.
The required simplified form of 5vw5⋅2v4 is 10v5/w5.
Page 112 Problem 6 Answer
The given expression is 3x7/y
6x4/y2.
The question requires to simplified the given expression.
To simplify the expression, use the property of exponents am/an=am−n, subtract the exponents, and divide the terms to simplify the expression.
Rewrite the expression, and use the property am/an=am−n.
3x7/y
6x4/y2=3x7/y1
6x4/y2=3x7−4
6y2−1 Subtract the exponents and divide the terms.
3x7/y
6x4/y2=3x3
6y1=x3/2y
Thus, the required simplified expression is x3/2y.
The required simplified form of 3x7/y
6x4/y2 is x3/2y.
Page 112 Problem 7 Answer
The given equation is x2−7x+6=0.
The question requires to solve the given equation by factoring it.
To solve the equation, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the given quadratic equation, and solve it to obtain the values of x, and thus, obtain the required solutions.
The constant in the given quadratic equation is 6.
Write the pair of factors of the constant 6.
1 and 6
2 and 3
−1 and −6
−2 and −3
It can be observed that the sum of the pair of factors −1 and −6 is equal to the coefficient of the middle term in the given quadratic equation, that is −7.
Therefore, the left-hand side of the given quadratic equation can be factorised as (x−1)(x−6).
Thus, the equation becomes (x−1)(x−6)=0.
The equation (x−1)(x−6)=0 is true only when either x−1 is equal to 0, or x−6 is equal to 0.
When x−1 is equal to 0, the value of x is equal to 1.
When x−6 is equal to 0, the value of x is equal to 6.
Thus, the required solutions are 1 and 6.
The required solutions are 1 and 6.
Page 112 Problem 8 Answer
The given equation is x2−18x+81=0.
The question requires to solve the given equation by factoring it.
To solve the equation, write the pair of factors of the constant, and identify the pair of factors whose sum is equal to the coefficient of the middle term.
Then, factorise the left-hand side of the given quadratic equation, and solve it to obtain the values of x, and thus, obtain the required solution.
The constant in the given quadratic equation is 81.
Write the pair of factors of the constant 81.
1 and 81
3 and 27
9 and 9
−1 and −81
−3 and −27
−9 and −9
It can be observed that the sum of the pair of factors −9 and −9
is equal to the coefficient of the middle term in the given quadratic equation, that is −18.
Therefore, the left-hand side of the given quadratic equation can be factorised as (x−9)(x−9).
Thus, the equation becomes (x−9)(x−9)=0.
The equation is true only when is equal to.
When is equal to, the value of is equal to.
Thus, the required solution is.
The required solution is 9.
Page 113 Problem 9 Answer
The square root of any negative number is an imaginary number.
These numbers are not real numbers, and are of the form bi, where b is a real nonzero number, and i is the imaginary unit equal to √−1.
The quadratic equations of the form x2=−a, where a is positive and real, cannot be solved because the square x2 cannot be negative for any real value of x.
Such a quadratic equation can be solved using imaginary numbers by using the definition of square root to rewrite the equation as x=±√−a, and then rewriting ±√−a as the imaginary solutions ±i√a.
If x is negative real number, then the square root √x is called an imaginary number. Imaginary numbers are the non-real numbers of the form bi, where b is a real nonzero number, and i is the imaginary unit equal to √−1.
If a quadratic equation is of the form x2=−a, where a is a real positive number, then imaginary numbers can be used to solve the equation by using the definition of square root to rewrite the equation as x=±√−a, and then rewriting ±√−a using the imaginary unit i to obtain the solutions ±i√a.
Page 113 Problem 10 Answer
The given equation is x2=16.
The question requires to solve the given equation by graphing.
To solve the given equation, let the left-side and right-side of the given equation be the function rules for f(x) and g(x) respectively.
Next, assign both functions to Y1 and Y2 in a graphing calculator, graph the functions, and use the intersect feature of the graphing calculator to find the point of intersection of the two functions.
Finally, use the x-coordinate of the intersection points to find the input values where the graphs intersect, and thus obtain the required solutions.
Write two functions for the expressions on either side of the given equation x2=16.
f(x)=x2
g(x)=16
On a graphing calculator, press the Y= key.
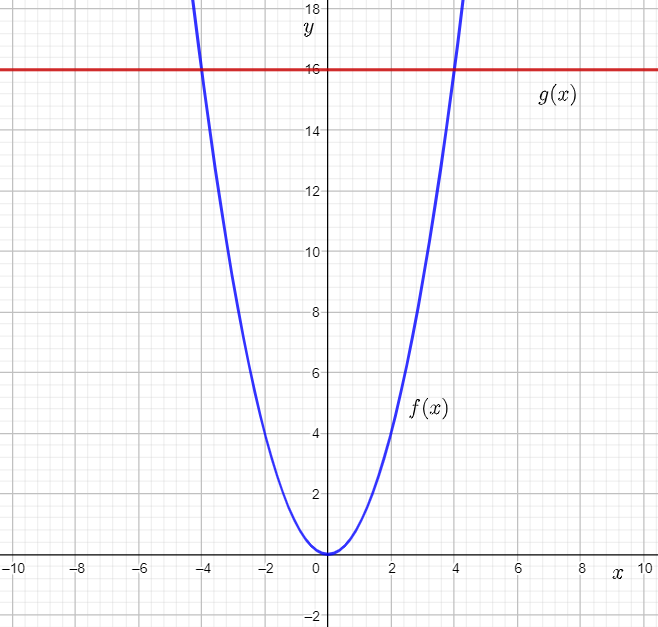
Let Y1=f(x), and assign x2 to Y1.
Let Y2=g(x), and assign 16 to Y2.
Next, set the viewing rectangle to [−10,10] by [−2,18], and press the GRAPH key to obtain the graph of the functions.
From the graph, it can be observed that the graphs of the two functions intersect at the points (−4,16) and (4,16).
The x-coordinates of the points of intersection are −4 and 4.
Therefore, x2=16 when the input value x is equal to either −4 or 4.
Thus, the required solutions are x=4 and x=−4.
The required solutions are x=4 and x=−4.
Page 113 Problem 11 Answer
The given equation is x2=16.
The question requires to solve the given equation by factoring.
To solve the equation, rewrite the equation, and factor it using the algebraic identity x2−y2=(x+y)(x−y).
Then, solve the factored equation using the zero-product property to obtain the values of x, and thus, obtain the required solutions.
Subtract 16 from both sides of x2=16.
x2−16=0
Rewrite the left-hand side expression as a difference of squares, and apply the algebraic identity for the difference of squares x2−y2=(x+y)(x−y).
x2−16=0
x2−42=0
(x+4)(x−4)=0
According to the zero-product property, the equation (x+4)(x−4)=0 is true only when either x+4 is equal to 0, or x−4 is equal to 0.
When x+4 is equal to 0, the value of x is equal to −4.
When x−4 is equal to 0, the value of x is equal to 4.
Thus, the required solutions are x=−4 and x=4.
The required solutions are x=−4 and x=4.
Page 113 Problem 12 Answer
The given equation is x2=16.
The question requires to solve the given equation by taking square roots.
To solve the equation, take the square roots of both sides of the given equation, and simplify the expression.
Take the square roots of both sides of x2=16, and then simplify the square roots.
x2=16
x=±√16
x=±4
Thus, the required solutions are x=±4.
The required solutions are x=±4.
Page 114 Problem 13 Answer
The given equation is x2=5.
The question requires to determine which of the three methods should be used to solve the given equation, and then solve the given equation.
To answer the question, explain whether solving the equation by graphing, solving the equation by factoring, or solving the equation by taking square roots is preferred.
Then, using the preferred method, solve the equation and write its solutions.
The method preferred to solve the equation is taking the square roots.
This is because the given equation is a simple quadratic equation of the form x2=a, and thus, taking the square roots is the easiest and fastest method to obtain the required solutions.
Take the square roots of both sides of x2=5.
x2=5
x=±√5
Thus, the required solutions are x=±√5.
The method preferred to solve the equation is taking the square roots because the given equation is a simple quadratic equation of the form x2=a.
This means that the easiest and fastest method to solve the equation is taking the square roots.
The required solutions are x=±√5.
Page 114 Problem 14 Answer
The given equation is x2=−9.The value of the square root x2
cannot be equal to the negative number −9 for any value of x. This means that the given equation has no solution.
Therefore, the given equation cannot be solved either by graphing, factoring or taking the square roots.
The given equation cannot be solved by any of the three methods because the given equation has no solution.
The left-hand side expression x2 cannot be equal to the right-hand side −9 because the square root cannot be negative.
Page 114 Problem 15 Answer
The given equation is −5x2+9=0.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using subtraction and division.
Then, use the definition of square root, apply the quotient property of square roots, and simplify the expression.
Subtract 9 from both sides of −5x2+9=0, and then divide both sides by −5.
−5x2+9−9=0−9
−5x2=−9
x2=−9/−5
x2=9/5
Use the definition of square root to simplify x2=9/5, apply the quotient property of square roots, and simplify the square root in the numerator.
x=±√9/5
x=±√9/√5
x=±3/√5
Multiply and divide the right-hand side of the equation by √5 to rationalize the denominator.
x=±3/√5⋅√5/√5
x=±3√5/5
Thus, the required solutions are x=±3√5/5.
The required solutions are x=±3√5/5.
Page 115 Problem 16 Answer
The given equation is x2−24=0.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using addition.
Then, use the definition of square root, apply the product property of square roots, and simplify the expression.
Add 24 on both sides of x2−24=0, and then use the definition of square root.
x2−24+24=0+24
x2=24
x=±√24
Rewrite the expression in the square root, apply the product property of square roots, and simplify the square root.
x=±√4⋅6
x=±√4⋅√6
x=±2√6
Thus, the required solutions are x=±2√6.
The required solutions are x=±2√6.
Page 115 Problem 17 Answer
The given equation is −4x2+13=0.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using subtraction and division.
Then, use the definition of square root, apply the quotient property of square roots, and simplify the expression.
Subtract 13 from both sides of −4x2+13=0, and then divide both sides by −4.
−4x2+13−13=0−13
−4x2=−13
x2=−13/−4
x2=13/4
Use the definition of square root to simplify x2=13/4, apply the quotient property of square roots, and simplify the square root in the denominator.
x=±√13/4
x=±√13/√4
x=±√13/2
Thus, the required solutions are x=±√13/2.
The required solutions are x=±√13/2.
Page 115 Problem 18 Answer
It is given that a water balloon is dropped from the rooftop of a five-story building, which is 50
feet above the ground. Also, it is given that the third-story window is at 24 feet above the ground.
The question requires to determine the time taken by the water balloon to pass by the third-story window.
It is required to write the equation, solve it, and write the exact and if the answer is irrational, also write the decimal approximation of the answer to the nearest tenth of a second.
To determine the time, write an equation modelling the height of the water balloon using the initial height and the equation h(t)=h0−16t2.
Then, substitute the required height as 24, and solve the equation for t2.
Finally, use the definition of square root, and apply the quotient property to obtain the value of t, and thus, the required time to the nearest tenth.
The given situation can be modelled using the equation h(t)=h0−16t2, where h(t) is the height of the water balloon after t seconds, and h0 is the initial height of the water balloon.
Since the water balloon is dropped from the rooftop, the initial height of the water balloon is h0=50 ft.
The required height of the water balloon is h(t)=24 feet above the ground.
Substitute h0−16t2 for h(t) and then 50 for h0 in h(t)=24.
h0−16t2=24
50−16t2=24
Subtract 50 from both sides of 50−16t2=24, and then divide both sides by −16.
−16t2=−26
t2=−26/−16
t2=26/16
Use the definition of square root to simplify t2=26/16, apply the quotient property of square roots, and simplify the square root in the denominator.
t=±√26/16
t=±√26/√16
t=±√26/4
The time taken by the water balloon to reach the required height cannot be negative.
Therefore, t=√26/4.
Thus, the water balloon passes by the third-story window after √26/4 ≈ 1.3 seconds.
The equation modelling the given situation is 50−16t2=24.
The required time in which water balloon passes by the third-story window is √26/4≈1.3 seconds.
Page 117 Problem 19 Answer
It is given that a water balloon is dropped from the rooftop of a five-story building, which is 50 feet above the ground.
Also, it is given that the third-story window is at 24 feet above the ground.
The question requires to determine the time taken by the water balloon to hit the ground.
It is required to write the equation, solve it, and write the exact and if the answer is irrational, also write the decimal approximation of the answer to the nearest tenth of a second.
To determine the time, write an equation modelling the height of the water balloon using the initial height and the equation h(t)=h0−16t2.
Then, substitute the required height as 0 ft, and solve the equation for t2.
Finally, use the definition of square root, and apply the product property and quotient property to obtain the value of t, and thus, the required time to the nearest tenth.
The given situation can be modelled using the equation h(t)=h0−16t2, where h(t)
is the height of the water balloon after t seconds, and h0 is the initial height of the water balloon.
Since the water balloon is dropped from the rooftop, the initial height of the water balloon is h0=50 ft.
When the water balloon hits the ground, the height of the balloon is 0 ft.
Therefore, the required height of the water balloon is h(t)=0 feet above the ground.Substitute h0−16t2 for h(t) and then 50 for h0 in h(t)=0.
h0−16t2=0
50−16t2=0
Subtract 50 from both sides of 50−16t2=0, and then divide both sides by −16.
−16t2=−50
t2=−50/−16
t2=50/16
Use the definition of square root to simplify t2=50/16, and apply the quotient property of square roots.
Then, apply the product property of square roots in the numerator and simplify the square root in the denominator.
t=±√50/16
t=±√50/√16
t=±√25⋅√2/4
t=±5√2/4
The time taken by the water balloon to hit the ground cannot be negative.
Therefore, t=5√2/4.
Thus, the water balloon hits the ground in 5√2/4 ≈ 1.8 seconds.
The equation modelling the given situation is 50−16t2=0.
The required time in which water balloon hits the ground is 5√2/4 ≈ 1.8 seconds.
Page 117 Problem 20 Answer
It is given that the function d(t)=8/3t2 models the distance d in feet that an object falls in t seconds on the moon. Also, it is given that a tool is dropped by an astronaut on the moon.
The question requires to determine the time taken by the tool to fall feet.
It is required to write the equation, solve it, and write the exact and if the answer is irrational, also write the decimal approximation of the answer to the nearest tenth of a second.
To determine the time, substitute the distance as 4 ft in the given equation, and solve the equation for t2.
Then, use the definition of square root, and apply the product property and quotient property to obtain the value of t, and thus, the required time to the nearest tenth.
The distance that the tool falls is d(t)=4 feet.Substitute 8/3t2 for d(t) in d(t)=4, and then multiply both sides by 3/8.
8/3t2=43/8⋅8/3
t2=3/8⋅4
t2=3/2
Use the definition of square root to simplify t2=3/2, and apply the quotient property of square roots.
t=±√3/2
t=±√3/√2
Multiply and divide the right-hand side of the equation by √2 to rationalize the denominator.
Then, simplify the square root in the denominator, and use the product property of square roots to simplify the numerator.
t=±√3/√2⋅√2/√2
t=±√3⋅√2/2
t=±√6/2
The time taken by the tool to fall a certain distance cannot be negative.
Therefore, t=√6/2.
Thus, the tool falls 4 feet in √6/2 ≈ 1.2 seconds.
The equation for the given situation is 8/3t2=4.
The required time taken by the tool to fall 4 feet is √6/2 ≈ 1.2 seconds.
Page 117 Problem 21 Answer
The given imaginary number is −i√2.
The question requires to determine the square of the given imaginary number.
To determine the square, square the given imaginary number and use the product property of exponents.
Then, use the value of i2and simplify the expression.
Take the square of −i√2 and use the product property of exponents (ab)m=am⋅bm.
(−i√2)2=(−√2)2⋅i2
Apply the exponent on the base, substitute −1 for i2, and multiply the terms in the expression.
(−i√2)2
=(2)(−1)
=−2
Thus, the square of −i√2 is −2.
The required square of −i√2 is −2.
Page 118 Problem 22
The square of i is given by the equation −1=i2.Rewriting the left-hand side of the equation as a square, the equation becomes (√−1)2=i2.
Using the definition of square root, the equation can be simplified to √−1=±√i2.
Simplifying the right-hand side of this equation, the equation becomes √−1=±i.
Therefore, the positive square root of −1 is i, and the negative square root of −1 is −i.
Thus, the other square root of −1 is −i.
The other square root of −1 is −i because the equation (√−1)2=i2 can be written as √−1=±√i2
using the definition of square root, which implies that the positive square root of −1 is i, and the negative square root of −1 is −i.
Page 118 Problem 23
The given imaginary number is −2i.
The question requires to determine the square of the given imaginary number.
To determine the square, square the given imaginary number and use the product property of exponents.
Then, use the value of i2 and simplify the expression.
Take the square of −2i and use the product property of exponents (ab)m=am⋅bm.(−2i)2=(−2)2⋅i2
Apply the exponent on the base, substitute −1 for i2, and multiply the terms in the expression.
(−2i)2=(4)(−1)
=−4
Thus, the square of −2i is −4.
The required square of −2i is −4.
Page 118 Problem 24
The given equation is 4x2+11=6.
The question requires to solve the given equation by taking square roots and allow for imaginary solutions.
To solve the equation, isolate the square x2 on one side of the equation using subtraction and division.
Then, use the definition of square root, apply the quotient property of square roots, simplify the expression, and rewrite it in the form bi.
Subtract 11 from both sides of 4x2+11=6, and then divide both sides by 4.
4x2+11−11=6−11
4x2=−5
x2=−5/4
Use the definition of square root to simplify x2/=−5/4, apply the quotient property of square roots, rewrite the numerator in the form bi, and simplify the square root in the denominator.
x=±√−5/4
x=±√−5/√4
x=±√(−1)(5)/2
x=±i√5/2
Thus, the required solutions are x=±i√5/2.
The required solutions are x=±i√5/2
Page 119 Problem 25
The given equation is −5x2+3=10.
The question requires to solve the given equation by taking square roots and allow for imaginary solutions.
To solve the equation, isolate the square x2 on one side of the equation using subtraction and division.
Then, use the definition of square root, apply the quotient property of square roots, rewrite the numerator in the form bi, and rationalize the denominator.
Subtract 3 from both sides of −5x2+3=10, and then divide both sides by −5.
−5x2+3−3=10−3
−5x2=7
x2=7/−5
x2=−7/5
Use the definition of square root to simplify x2=−7/5, apply the quotient property of square roots, and rewrite the numerator in the form bi.
x=±√−7/5
x=±√−7/√5
x=±√(−1)(7)/√5
x=±i√7/√5
Multiply and divide the right-hand side of the equation by √5 to rationalize the denominator.
x=±i√7/√5⋅√5/√5
x=±i√35/5
Thus, the required solutions are x=±i√35/5.
The required solutions are x=±i√35/5.
Page 119 Problem 26
The first given equation is 4x2+32=0.The expression x2 is always nonnegative for all real values of x.
This means that 4x2≥0 Therefore, 4x2+32≥32.Therefore, the equation 4x2+32=0 is true only if x2 is negative.
Thus, the solutions of the first given equation 4x2+32=0 are imaginary. The second given equation is 4x2−32=0.
The expression x2 is always nonnegative for all real values of x.
This means that 4x2≥0. Therefore, 4x2−32≥−32. Therefore, the equation 4x2−32=0 is true only if x2 is positive.
Thus, the solutions of the second given equation 4x2−32=0 are real.
It can be observed that the solutions of the first quadratic equation are imaginary, and the solutions of the second quadratic equation are real.
The solutions of the first quadratic equation are imaginary, whereas the solutions of the second quadratic equation are real.
This is because the first equation is true only when x2 is negative, and the second equation is true only when x2 is positive.
Page 119 Problem 27
Assume the imaginary number bi. The square of this number is equal to (bi)2, which can be rewritten as b2/i2 using the product property of exponents.
The expression b2 is always positive because b is a real nonzero number. The expression i2 is the square of √−1.
Therefore, i2 is always equal to the negative number −1.
The product b2/i2 of the positive number b2 and the negative number i2 is always negative.
Thus, the expression (bi)2, that is the square of the imaginary number bi, is always negative.
The square of an imaginary number is always negative.
Page 119 Problem 28
Assume the negative number −b. Here, b is a real nonzero number.The square of the negative number −b is √−b.
The negative number −b can be written as the product of −1 and the real nonzero number b.
Therefore, the square root √−b can be written as √(−1)(b).
Using the product property of square roots, √(−1)(b) can be written as the product of the real number √b, and the imaginary number √−1.
Therefore, √−b =√−1⋅√b.
Rewriting √−1 as the imaginary unit i, the square root of −b becomes √−b=i√b.
Thus, the square root i√b of the negative number −b is obtained by using the definition of square root, rewriting the negative number as the product of −1 and a real number, and then using the product property of square roots.
To find the square roots of a negative number:
First, use the definition of square root, and rewrite the negative number in the square root as the as the product of −1 and a real number.
Next, use the product property of square roots to rewrite the square root as the product of a real square root, and the square root √−1.
Finally, rewrite the square root √−1 as the imaginary unit i to obtain the required square roots.
Page 120 Exercise 1 Answer
The given equation is x2−2=7.
The question requires to solve the given equation by graphing.
To solve the given equation, let the left-side and right-side of the given equation be the function rules for f(x) and g(x) respectively.
Next, assign both functions to Y1 and Y2 in a graphing calculator, graph the functions, and use the intersect feature of the graphing calculator to find the point of intersection of the two functions.
Finally, use the x-coordinate of the intersection points to find the input values where the graphs intersect, and thus obtain the required solutions.
Write two functions for the expressions on either side of the given equation x2−2=7.
f(x)=x2−2
g(x)=7
On a graphing calculator, press the Y= key.
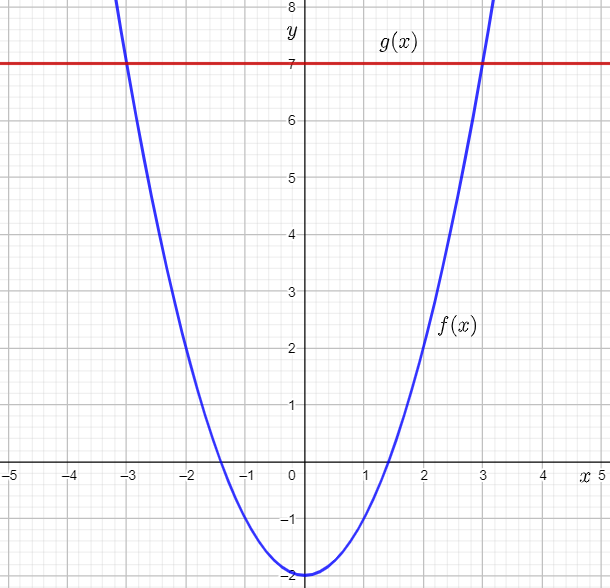
Let Y1=f(x), and assign x2−2 to Y1.
Let Y2=g(x), and assign 7 to Y2.
Next, set the viewing rectangle to [−5,5]
by [−2,8], and press the GRAPH key to obtain the graph of the functions.
From the graph, it can be observed that the graphs of the two functions intersect at the points (−3,7) and (3,7).
The x-coordinates of the two points of intersection of the graphs are −3 and 3.
Therefore, x2−2=7 when the input value x is equal to either −3 or 3.
Thus, the required solutions are x=−3 and x=3.
The required solutions are x=−3 and x=3.
Page 120 Exercise 2 Answer
The given equation is x2−2=7.
The question requires to solve the given equation by factoring.
To solve the equation, rewrite the equation and factor it using the difference of squares x2−y2=(x+y)(x−y).
Then, solve the factored equation using the zero-product property to obtain the values of x, and thus, obtain the required solutions.
Subtract 7 from both sides of x2−2=7.
x2−2−7=7−7
x2−9=0
Rewrite the left-hand side expression as a difference of squares, and apply the algebraic identity for the difference of squares x2−y2=(x+y)(x−y).
x2−9=0
x2−32=0
(x+3)(x−3)=0
According to the zero-product property, the equation (x+3)(x−3)=0 is true only when either x+3 is equal to 0, or x−3 is equal to 0.
When x+3 is equal to 0, the value of x is equal to −3.
When x−3 is equal to 0, the value of x is equal to 3.
Thus, the required solutions are x=−3 and x=3.
The required solutions are x=−3 and x=3.
Page 120 Exercise 3 Answer
The given equation is x2−2=7.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using addition.
Then, take the square roots of both sides of the equation, and simplify the expression.
Add 2 on both sides of x2−2=7.
x2−2+2=7+2
x2=9
Take the square roots of both sides of x2=9, and then simplify the square roots.
x2=9
x=±√9
x=±3
Thus, the required solutions are x=±3.
The required solutions are x=±3.
Page 121 Exercise 4 Answer
The given equation is 4x2=24.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using division, and use the definition of square root to simplify the expression.
Divide both sides of 4x2=24 by 4, and then use the definition of square root.
4x2/4=24/4
x2=6
x=±√6
Thus, the required solutions are x=±√6.
The required solutions are x=±√6.
Page 121 Exercise 5 Answer
The given equation is -x2/5+15.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square on one side of the equation using subtraction and multiplication.
Then, use the definition of square root, apply the product property of square roots, and simplify the expression.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square on one side of the equation using subtraction and multiplication.
Then, use the definition of square root, apply the product property of square roots, and simplify the expression.
Subtract 15 from both sides of −x2/5+15=0, and then multiply both sides by −5.
−x2/5+15−15=0−15
−x2/5=−15
(−5)(−x2/5)=(−5)(−15)
x2=75
Use the definition of square root to simplify the equation x2=75, rewrite the expression in the square root, apply the product property of square roots, and simplify the square root.
x=±√75
x=±√25⋅3
x=±√25⋅√3
x=±5√3
Thus, the required solutions are x=±5√3.
The required solutions are x=±5√3.
Page 121 Exercise 6 Answer
The given equation is 2(5−5x2)=5.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using the distributive property of multiplication, and then subtraction and division.
Then, use the definition of square root, use the quotient property of square roots, and simplify the expression.
Apply the distributive property of multiplication in the left-hand side of 2(5−5x2)=5. Then, subtract 10 from both sides, and divide both sides by −10.
10−10x2=5−10x2
=−5−10x2−10
=−5−10x2
=1/2
Use the definition of square root to simplify x2=1/2, apply the quotient property of square roots, and simplify the square root in the numerator.
x=±√1/2
x=±√1/√2
x=±1/√2
Multiply and divide the right-hand side of the equation by √2 to rationalize the denominator.
x=±1/√2⋅√2/√2
x=±√2/2
Thus, the required solutions are x=±√2/2.
The required solutions are x=±√2/2.
Page 121 Exercise 7 Answer
The given equation is 3x2−8=12.
The question requires to solve the given equation by taking square roots.
To solve the equation, isolate the square x2 on one side of the equation using the addition and division.
Then, use the definition of square root, use the quotient property and product property of square roots, and simplify the expression.
Add 8 on both sides of 3x2−8=12, and divide both sides by 3.
3x2−8+8=12+8
3x2=20
3x2/3=20/3
x2=20/3
Use the definition of square root to simplify x2=20/3, and apply the quotient property of square roots.
x=±√20/3
x=±√20/√3
Rewrite the expression in the numerator, apply the product property of square roots, and simplify the square root.
x=±√4⋅5/√3
x=±√4⋅√5/√3
x=±2√5/√3
Multiply and divide the right-hand side of the equation by √3 to rationalize the denominator.
x=±2√5/√3⋅√3/√3
x=±2√15/3
Thus, the required solutions are x=±2√15/3.
The required solutions are x=±2√15/3.
Page 121 Exercise 8 Answer
It is given that a squirrel drops an acorn from a tree.
The question requires to determine the time taken by the acorn to fall 20 feet.
It is required to write the equation, solve it, and write the exact and if the answer is irrational, also write the decimal approximation of the answer to the nearest tenth of a second.
To determine the time, write an equation modelling the distance that the acorn falls using the equation d(t)=16t2.
Then, substitute the required distance fallen as 20, and solve the equation for t2.
Finally, use the definition of square root, and apply the quotient property to obtain the value of t, and thus, the required time to the nearest tenth.
The given situation can be modelled using the equation d(t)=16t2, where d(t) is the distance that the acorn falls in t seconds.
The distance that the acorn falls is d(t)=20 feet.
Substitute 16t2 for d(t) in d(t)=20.
16t2=20 Divide both sides of 16t2=20 by 16.
16t2/16=20
16t2=20
16t2=5/4
Use the definition of square root to simplify t2=5/4, apply the quotient property of square roots, and simplify the square root in the denominator.
t=±√5/4
t=±√5/√4
t=±√5/2
The time taken by the acorn to fall a certain distance cannot be negative.
Therefore, t=√5/2.
Thus, the acorn falls 20 feet in √5/2 ≈ 1.1 seconds.
The equation modelling the given situation is 16t2=20.
The required time taken by the acorn to fall 20 feet is √5/2 ≈ 1.1 seconds.
Page 121 Exercise 9 Answer
It is given that a window washer drops a squeegee from 60 feet. Also, it is given that another window washer is working squeegee 20 feet above the ground.
The question requires to determine the time taken by the squeegee to pass by the second window washer.
It is required to write the equation, solve it, and write the exact and if the answer is irrational, also write the decimal approximation of the answer to the nearest tenth of a second.
To determine the time, write an equation modelling the height of the squeegee using the initial height and the equation h(t)=h0−16t2.
Then, substitute the required height as 20, and solve the equation for t2.
Finally, use the definition of square root, and apply the quotient property to obtain the value of t, and thus, the required time to the nearest tenth.
The given situation can be modelled using the equation h(t)=h0−16t2, where h(t) is the height of the squeegee after t seconds, and h0 is the initial height of the squee gee.
Since the squeegee is dropped from 60 feet, the initial height of the squeegee is h0=60 ft.
The required height of the squeegee is h(t)=20 feet above the ground.
Substitute h0−16t2 for h(t) and then 60 for h0 in h(t)=20.
h0−16t2=20
60−16t2=20
Subtract 60 from both sides of 60−16t2=20, and then divide both sides by −16.
−16t2=−40
t2=−40
−16t2=10/4
Use the definition of square root to simplify t2=10/4, apply the quotient property of square roots, and simplify the square root in the denominator.
t=±√10/4
t=±√10/√4
t=±√10/2
The time taken by the squeegee to pass by the second window washer cannot be negative.
Therefore, t=√10/2.
Thus, the squeegee passes by the second window washer in √10/2≈1.6 seconds.
The equation modelling the given situation is 60−16t2=20.
The required time taken by the squeegee to pass by the second window washer is √10/2≈1.6 seconds.
Page 122 Exercise 10 Answer
The given figure shows the lengths of the sides of a rectangle, which has an area equal to 45 cm2.
The question requires to determine the lengths of the sides of the rectangle, and write the exact answer and the approximate answer to the nearest tenth.
To determine the lengths, use the formula for area, the given dimensions, and the given area to form an equation modelling the given situation.
Then, solve the equation for x2, and use the definition of square root to obtain the value of x.
Finally, use the obtained value in the expressions for the lengths of the sides of the rectangle to determine the exact answer and approximate answer to the nearest tenth.
From the figure, it can be observed that the length and width of the rectangle are equal to 3x cm and x cm respectively.
The area of the rectangle is equal to the product of its length 3x and width x, that is A=(3x)(x).
The given area of the rectangle is A=45 square cm.
Substitute (3x)(x) for A in A=45, and multiply the terms.
(3x)(x)=45
3x2=45
Divide both sides of 3x2=45 by 3, and use the definition of square root to simplify the equation.
3x2/3=45/3
x2=15
x=±√15
The length of the width, that is x, cannot be negative.
Therefore, x=√15.
Write the length of the shorter side of the given rectangle, and simplify the expression to the nearest tenth.
x=√15≈3.9
Calculate the length of the longer side of the given rectangle, and simplify the expression to the nearest tenth.
3x=3√15 ≈ 11.6
Thus, the lengths of the sides of the rectangle are √15 ≈ 3.9 cm and 3√15 ≈ 11.6 cm.
The length of the shorter side of the given rectangle is √15 ≈ 3.9 cm, and the length of the longer side of the given rectangle is 3√15 ≈ 11.6 cm.
Page 122 Exercise 11 Answer
The given figure shows the lengths of the sides of a rectangle, which has an area equal to 54 cm2.
The question requires to determine the lengths of the sides of the rectangle, and write the exact answer and the approximate answer to the nearest tenth.
To determine the lengths, use the formula for area, the given dimensions, and the given area to form an equation modelling the given situation.
Then, solve the equation for x2, use the definition of square root, and use the product property of square roots to obtain the value of x.
Finally, use the obtained value in the expressions for the lengths of the sides of the rectangle to determine the exact answer and approximate answer to the nearest tenth.
From the figure, it can be observed that the length and width of the rectangle are equal to 3x cm and x cm respectively.
The area of the rectangle is equal to the product of its length 3x and width x, that is A=(3x)(x).
The given area of the rectangle is A=54 square cm.Substitute (3x)(x) for A in A=54, and multiply the terms.
(3x)(x)=54
3x2=54
Divide both sides of 3x2=54 by 3, and use the definition of square root to simplify the equation.
3x2/3=54/3
x2=18
x=±√18
Rewrite the expression in the square root, apply the product property of square roots, and simplify the square root.
x=±√9⋅2
x=±√9⋅√2
x=±3√2
The length of the width, that is x, cannot be negative.
Therefore, x=3√2.
Write the length of the shorter side of the given rectangle, and simplify the expression to the nearest tenth.
x=3√2 ≈ 4.2
Calculate the length of the longer side of the given rectangle, and simplify the expression to the nearest tenth.
3x=3⋅3√2
=9√2 ≈ 12.7
Thus, the lengths of the sides of the rectangle are 3√2 ≈ 4.2 cm and 9√2 ≈ 12.7 cm.
The length of the shorter side of the given rectangle is 3√2 ≈4.2 cm, and the length of the longer side of the given rectangle is 9√2 ≈ 12.7 cm.
Page 122 Exercise 12 Answer
The given imaginary number is 3i.
The question requires to determine the square of the given imaginary number.
To determine the square, square the given imaginary number and use the product property of exponents.
Then, use the value of i2 and simplify the expression.
Take the square of 3i and use the product property of exponents (ab)m=am⋅bm.
(3i)2=(3)2⋅i2
Apply the exponent on the base, substitute −1 for i2, and multiply the terms in the expression.
(3i)2=(9)(−1)
=−9
Thus, the square of 3i is −9.
The required square of 3i is −9.
Page 122 Exercise 13 Answer
The given imaginary number is i√5.
The question requires to determine the square of the given imaginary number.
To determine the square, square the given imaginary number and use the product property of exponents.
Then, use the value of i2 and simplify the expression.
Take the square of i√5 and use the product property of exponents (ab)m=am⋅bm.
(i√5)2=(√5)2⋅i2
Apply the exponent on the base, substitute −1 for i2, and multiply the terms in the expression.
(i√5)2
=(5)(−1)
=−5
Thus, the square of i√5 is −5.
The required square of i√5 is −5.
Page 122 Exercise 14 Answer
The given imaginary number is −i√2/2.
The question requires to determine the square of the given imaginary number.
To determine the square, square the given imaginary number and use the product property of exponents.
Then, use the value of i2 and simplify the expression.
Take the square of −i√2/2 and use the product property of exponents
(ab)m=am⋅bm.(−i√2/2)2=(−√2/2)2⋅i2
Apply the exponent on the base, substitute −1 for i2, and simplify the expression.
(−i√2/2)2=(2/4)(−1)=−2
4=−1/2
Thus, the square of −i√2/2 is −1/2.
The required square of −i√2/2 is −1/2.
Page 122 Exercise 15 Answer
The given equation is 1/2x2+12=4.
The question requires to determine whether the given equation as real solutions or imaginary solutions by solving it.
To answer the question, isolate the square x2 on one side of the equation using subtraction and multiplication.
Then, use the definition of square root, apply the product property of square roots, and rewrite the expression.
Finally, observe the solutions to determine whether they are real or imaginary.
Subtract 12 from both sides of 1/2x2+12=4, and then multiply both sides by 2.
1/2x2+12−12=4−12
1/2x2=−8x2=−16
Use the definition of square root to simplify x2=−16, rewrite the expression, apply the product property of square roots, and simplify the expression.
x=±√−16
x=±√(16)(−1)
x=±√16⋅√−1
x=±4i
Therefore, the solutions are x=±4i.
The solutions include the imaginary unit i.
Thus, the given quadratic equation has imaginary solutions.
The given quadratic equation has imaginary solutions. The solutions are x=±4i.
Page 122 Exercise 16 Answer
The given equation is 5(2x2−3)=4(x2−10).
The question requires to determine whether the given equation as real solutions or imaginary solutions by solving it.
To answer the question, isolate the square x2 on one side of the equation using the distributive property of multiplication, and the operations of addition, subtraction, and division.
Then, use the definition of square root, apply the quotient property of square roots, and rewrite the expression.
Finally, observe the solutions to determine whether they are real or imaginary.
Apply the distributive property of multiplication in 5(2x2−3)=4(x2−10). Then, subtract 4x2 from both sides, add 15 on both sides, and divide both sides by 6.
10x2−15=4x2−40
6x2−15=−40
6x2=−25
x2=−25/6
Use the definition of square root to simplify x2=−25/6, apply the quotient property of square roots, and rewrite the numerator in the form bi.
x=±√−25/6
x=±√−25/√6
x=±√(25)(−1)/√6
x=±5i/√6
Multiply and divide the right-hand side of the equation by √6 to rationalize the denominator.
x=±5i/√6⋅√6/√6
x=±5i√6/6
Therefore, the solutions are x=±5i√6/6.
The solutions include the imaginary unit i.
Thus, the given quadratic equation has imaginary solutions.
The given quadratic equation has imaginary solutions. The solutions are x=±5i√6/6.
Page 123 Exercise 17 Answer
The given equation is x2=−81.
The question requires to solve the given equation by taking square roots and allow for imaginary solutions.
To solve the equation, use the definition of square root, apply the product property of square roots, rewrite the expression in the form bi.
Use the definition of square root to simplify x2=−81, rewrite the expression, apply the product property of square roots, and simplify the expression.
x=±√−81
x=±√(81)(−1)
x=±√81⋅√−1
x=±9i
Thus, the required solutions are x=±9i.
The required solutions are x=±9i.
Page 123 Exercise 18 Answer
The given equation is x2+64=0.
The question requires to solve the given equation by taking square roots and allow for imaginary solutions.
To solve the equation, isolate the square x2 on one side of the equation using subtraction.
Then, use the definition of square root, apply the product property of square roots, rewrite the expression in the form bi.
Subtract 64 from both sides of x2+64=0 , and use the definition of square root to simplify the equation.
x2=−64
x=±√−64
Rewrite the expression in the square root, apply the product property of square roots, and simplify the expression.
x=±√(64)(−1)
x=±√64⋅√−1
x=±8i
Thus, the required solutions are x=±8i.
The required solutions are x=±8i.
Page 123 Exercise 19 Answer
The given equation is 5x2−4=−8.
The question requires to solve the given equation by taking square roots and allow for imaginary solutions.
To solve the equation, isolate the square x2 on one side of the equation using addition and division.
Then, use the definition of square root, apply the quotient property of square roots, simplify the expression, and rewrite it using the imaginary unit i.
Add 4 on both sides of 5x2−4=−8, and then divide both sides by 5.
5x2−4+4=−8+4
5x2=−4
x2=−4/5
Use the definition of square root to simplify x2=−4/5, apply the quotient property of square roots, and rewrite the numerator in the form bi.
x=±√−4/5
x=±√−4/√5
x=±√(4)(−1)/√5
x=±2i/√5
Multiply and divide the right-hand side of the equation by √5 to rationalize the denominator.
x=±2i/√5⋅√5/√5
x=±2i√5/5
Thus, the required solutions are x=±2i√5/5.
The required solutions are x=±2i√5/5.
Page 123 Exercise 20 Answer
The given equation is 7×2+10=0.
The question requires to solve the given equation by taking square roots and allow for imaginary solutions.
To solve the equation, isolate the square x2 on one side of the equation using subtraction and division.
Then, use the definition of square root, apply the quotient property of square roots, simplify the expression, and rewrite it using the imaginary unit i.
Subtract 10 from both sides of 7x2+10=0, and then divide both sides by 7.
7x2+10−10=0−10
7x2=−10
x2=−10/7
Use the definition of square root to simplify x2=−10/7, apply the quotient property of square roots, and rewrite the numerator in the form bi.
x=±√−10/7
x=±√−10/√7
x=±√(10)(−1)/√7
x=±i√10/√7
Multiply and divide the right-hand side of the equation by √7 to rationalize the denominator.
x=±i√10/√7⋅√7/√7
x=±i√70/7
Thus, the required solutions are x=±i√70/7.
The required solutions are x=±i√70/7.
Page 123 Exercise 21 Answer
The given figures show the lengths of the sides of two squares. It is given that the area of the larger square is 42 cm2 greater than the area of the smaller square.
The question requires to determine the lengths of the sides of the squares, and write the exact answer and the approximate answer to the nearest tenth.
To determine the lengths, use the formula for area and the given dimensions to write the areas of the squares.
Then, use the given information and the expression for the areas to form an equation modelling the given situation.
Then, solve the equation for x2, and use the definition of square root to obtain the value of x.
Finally, use the obtained value in the expressions for the lengths of the sides of the two squares to determine the exact answer and approximate answer to the nearest tenth.
From the figure, it can be observed that the length of the side of the larger and smaller square are 2x cm and x cm respectively.
Therefore, the areas of the larger square and smaller square are (2x)2 sq. cm and (x)2 sq. cm respectively.
The area of the larger square, that is (2x)2, is 42 cm2 more than the area of the smaller square, that is (x)2.
Therefore, (2x)2=42+(x)2.
Simplify the equation (2x)2=42+(x)2, and subtract x2 from both sides.
(2x)2=42+(x)2
4x2=42+x2
3x2=42
Divide both sides of 3x2=42 by 3, and use the definition of square root to simplify the equation.
3x2/3=42
3x2=14
x=±√14
The length of the side of the smaller square, that is x, cannot be negative.
Therefore, x=√14.
Write the length of the side of the smaller square, and simplify the expression to the nearest tenth.
x=√14 ≈ 3.7
Calculate the length of the side of the larger square, and simplify the expression to the nearest tenth.
2x=2√14≈7.5
Thus, the lengths of the sides of the smaller square and larger square are √14≈3.7 cm and 2√14≈7.5 cm respectively.
The length of the side of the smaller square is √14≈3.7 cm, and the length of the side of the larger square is 2√14≈7.5 cm.
Page 123 Exercise 22 Answer
The given figures show the lengths of the sides of two squares.
It is given that when the area of the larger square is decreased by 28 cm2, the resulting area is equal to half the area of the smaller square.
The question requires to determine the lengths of the sides of the squares, and write the exact answer and the approximate answer to the nearest tenth.
To determine the lengths, use the formula for area and the given dimensions to write the areas of the squares.
Then, use the given information and the expression for the areas to form an equation modelling the given situation.
Then, solve the equation for x2, use the definition of square root, and then the product property of square roots to obtain the value of x.
Finally, use the obtained value in the expressions for the lengths of the sides of the two squares to determine the exact answer and approximate answer to the nearest tenth.
From the figure, it can be observed that the length of the side of the larger and smaller square are 2x cm and x cm respectively.
Therefore, the areas of the larger square and smaller square are (2x)2 sq. cm and (x)2 sq. cm respectively.
When the area of the larger square is decreased by 28 cm2, the resulting area is (2x)2−28.
The half of the area of the smaller square is 1/2(x)2.
The area (2x)2−28 is equal to half the area of the smaller square, that is 1/2(x)2.
Therefore, (2x)2−28=1/2(x)2.
Simplify the equation (2x)2−28=1/2(x)2, subtract 1/2x2 from both sides, and add 1/2x2 on both sides.
4x2−28=1/2x2
4x2−1/2x2−28=0
7/2x2−28=0
7/2x2=28
Multiply both sides of 7/2x2=28 by 2/7, and use the definition of square root to simplify the equation.
2/7⋅7/2x2=2/7⋅28x2=8
x=±√8
Rewrite the expression in the square root, use the product property of square roots, and simplify the square root.
x=±√4⋅2
x=±√4⋅√2
x=±2√2
The length of the side of the smaller square, that is x, cannot be negative.
Therefore, x=2√2.
Write the length of the side of the smaller square, and simplify the expression to the nearest tenth.
x=2√2≈2.8
Calculate the length of the side of the larger square, and simplify the expression to the nearest tenth.
2x=2⋅2√2
=4√2 ≈ 5.7
Thus, the lengths of the sides of the smaller square and larger square are 2√2 ≈ 2.8 cm and 4√2 ≈ 5.7 cm respectively.
The length of the side of the smaller square is 2√2 ≈ 2.8 cm, and the length of the side of the larger square is 4√2≈5.7 cm.
Page 124 Exercise 23 Answer
It is given that the height of the ball can be modelled using the equation h(t)=h0−16t2, where h is the height of the ball after t seconds as it falls.
Also, it is given that the ball reaches the maximum height 67 feet, and is caught by an outfielder when it is 3 feet above the ground.
The question requires to determine the time in which the outfielder catches the ball after the ball starts descending.
To determine the time, write an equation modelling the height of the ball using the initial height and the equation h(t)=h0−16t2 .
Then, substitute the required height as 3, and solve the equation for t2.
Finally, use the definition of square root to obtain the value of t, and thus, the required time.
The given situation can be modelled using the equation h(t)=h0−16t2, where h(t) is the height of the ball after t seconds, and h0 is the initial height of the ball.
Since the ball reaches the maximum height 67 feet, the initial height of the ball as it falls is h0=67 ft.
The height of the ball when it is caught is h(t)=3 feet above the ground.Substitute h0−16t2 for h(t) and then 67 for h0 in h(t)=3.
h0−16t2=3
67−16t2=3
Subtract 67 from both sides of 67−16t2=3, and then divide both sides by −16.
−16t2=−64
t2=−64
−16t2=4
Use the definition of square root to simplify t2=4, and then simplify the square root.
t=±√4
t=±2
The time in which the outfielder catches the ball after the ball starts descending cannot be negative.
Therefore, t=2.
Thus, the outfielder catches the ball 2 seconds after the ball starts to descend.
The outfielder catches the ball 2 seconds after the ball starts to descend.
Page 124 Exercise 24 Answer
The outfielder catches the ball 2 seconds after the ball starts to descend, as calculated in the previous exercise.
This means that the ball descends from the maximum height 67 feet to 3 feet in 2 seconds.
Therefore, the time taken by the ball to hit the ground, after it starts descending, will also be approximately equal to 2 seconds.
Assume that the time taken by the ball to reach the maximum height is equal to the time taken by the ball to hit the ground from its maximum height.
Therefore, the time taken by the ball to reach the maximum height will be approximately equal to 2 seconds.
The total time for which the ball was in the air is equal to the time taken by it to reach the maximum height, and the time taken by it to descend from the maximum height 67 feet to 3
feet.
Thus, the total time is equal to approximately 2+2, that is about 4 seconds.
The total time is equal to approximately 2+2, that is about 4 seconds.
This is because the total time is equal to the time taken by it to reach the maximum height, and the time taken by it to descend from the maximum height 67 feet to 3 feet.
It is assumed that the time taken by the ball to reach the maximum height is equal to the time taken by the ball to hit the ground from its maximum height, which is approximately 2 seconds.
Page 125 Exercise 25 Answer
It is given that the aspect ratio of the images is the ratio of the image width to its height, and the aspect ratio of the images on the given HDTV screen is 16:9.
Also, it is given that the area of the HDTV screen is equal to 864 square inches.
The question requires to determine the dimensions of the screen.
To determine the dimensions, use the given aspect ratio to form expressions for the image width and image height.
Then, use the formula for area, the expressions for the dimensions, and the given area to form an equation modelling the area.
Then, solve the equation for x2, and use the definition of square root to obtain the value of x.
Finally, use the obtained value in the expressions for the image width and image height to determine the exact and approximate dimensions of the screen.
The given aspect ratio of the images on the given HDTV screen is 16:9.
This means that the ratio of the image width to the image height on the given HDTV screen is 16:9.
Let the image width and image height be equal to 16x and 9x respectively.
The area of the HDTV screen is equal to the product of the image width 16x and the image height 9x, that is A=(16x)(9x).
The given area of the rectangle is A=864 square inches.
Substitute (16x)(9x) for A in A=864, and multiply the terms.
(16x)(9x)=864
144x2=864
Divide both sides of 144x2=864 by 144, and use the definition of square root to simplify the equation.
144x2
144=864
144x2=6
x=±√6
If the variable x is negative, then the image width 16x and the image height 9x are negative, which is not possible.
Therefore, x=√6.
Calculate the image width of the HDTV screen, and simplify the expression to the nearest hundredth.
16x=16√6≈39.19
Calculate the image height of the HDTV screen, and simplify the expression to the nearest hundredth.
9x=9√6≈22.05
Thus, the width and height of the HDTV screen are 16√6≈39.19 inches and 9√6≈22.05 inches respectively.
The width of the HDTV screen is 16√6≈39.19 inches, and the height of the HDTV screen is 9√6 ≈ 22.05 inches.
Page 126 Exercise 26 Answer
It is given that a suspension bridge has two parabolic cables connected between the towers, and vertical cables are suspended from the parabolic cables.
The given table shows the displacements of three vertical cables from the shortest cable, and the height of those cables.
The question requires to determine the quadratic function for the height of the parabolic cable above the road as a function of the displacement from the lowest point of the cable.
Then, it is required to determine the distance between the towers if the maximum height of the parabolic cable is 48 m above the road.
To determine the model, let the equation be h(x)=ax2+bx+c.
Then, use the first row data from the given table to obtain the value of c.
Next, use the data from the second and third rows to form two equations, and solve them to determine the values of the remaining constants.
Finally, use the constants in the assumed equation to determine the required equation.
To determine the distance between the towers, substitute the height as 48
m in the quadratic equation, and use the definition of square root to obtain the value of x.
Then, use the value to find the horizontal displacement of the parabolic cable from the left tower to its lowest position, and the horizontal displacement of the parabolic cable from the right tower to its lowest position.
Finally, a Let the required equation be h(x)=ax2+bx+c, where h(x) is the height of the parabolic cable when the horizontal displacement from the lowest point is x m.
The lowest point of the parabolic cable is the point at which the shortest vertical cable is suspended.
Also, the height of the parabolic cable above the ground is equal to the height of the vertical cable suspended at that point.
When the displacement of a vertical cable from the shortest vertical cable is 0 m, the height of the vertical cable is 3 m.
This means that when the horizontal displacement of the parabolic cable from its lowest point is 0 m, the height of the parabolic cable above the ground is 3 m.
Substitute 0 for x and 3 for h(x) in h(x)=ax2+bx+c, and simplify the expression.
3=a(0)2+b(0)+c
3=a(0)+b(0)+c
3=0+0+c
3=c
When the displacement of a vertical cable from the shortest vertical cable is 1 m, the height of the vertical cable is 3.05 m.
This means that when the horizontal displacement of the parabolic cable from its lowest point is 0 m, the height of the parabolic cable above the ground is 3.05 m.
Substitute 1 for x, 3.05 for h(x), and 3 for c in h(x)=ax2+bx+c, simplify the expression, and subtract 3 from both sides.
3.05=a(1)2+b(1)+3
3.05=a(1)+b(1)+3/0.05=a+b…………………(1)
When the displacement of a vertical cable from the shortest vertical cable is 2 m, the height of the vertical cable is 3.2 m.
This means that when the horizontal displacement of the parabolic cable from its lowest point is 2 m, the height of the parabolic cable above the ground is 3.2 m.
Substitute 2 for x, 3.2 for h(x), and 3 for c in h(x)=ax2+bx+c, simplify the expression, and subtract 3 from both sides.
3.2=a(2)2
+b(2)+3
3.2=a(4)+b(2)+3
0.2=4a+2b…………………(2)
Equation (1) can be rewritten as a=0.05−b.
Substitute 0.05−b for a in equation (2), multiply the terms, and solve the equation for b.
0.2=4(0.05−b)+2b
0.2=0.2−4b+2b
0.2=0.2−2b
0=−2b
0=b
Substitute 0 for b in equation (1).
0.05=a+0
0.05=a
Thus, the equation h(x)=ax2+bx+c becomes:
h(x)=0.05x2+0x+3
h(x)=0.05x2+3
Thus, the equation modelling the height of the parabolic cable is h(x)=0.05×2+3.
Let the height of the parabolic cable be equal to its maximum height 48. Therefore, h(x)=48.
Substitute 0.05x2+3 for h(x) in h(x)=48, subtract 3 from both sides, and divide both sides by 0.05.
Then, use the definition of square root, and simplify the square root.
0.05x2+3=48
0.05x2=45
x2=900
x=±√900
x=±30
The horizontal displacement of the parabolic cable from its lowest point, that is x, cannot be negative.
Therefore, x=30.
The displacement of the parabolic cable from its lowest point is equal to 30 m when the cable is at the maximum height.
This means that at the point where the parabolic cable connects to the left tower, that is at its maximum height on the left side, the horizontal displacement of the parabolic cable from the shortest vertical cable is 30 m.
Similarly, at the point where the parabolic cable connects to the right tower, that is at its maximum height on the right side, the horizontal displacement of the parabolic cable from the shortest vertical cable is 30 m.
The distance between the towers is equal to the sum of the horizontal displacement of the parabolic cable from the left tower to its lowest position, and the horizontal displacement of the parabolic cable from the right tower to its lowest position.
Thus, the distance between the towers is equal to 30+30=60 m.
The quadratic equation modelling the height of the parabolic cable is h(x)=0.05x2+3, where h(x) is the height of the parabolic cable when the horizontal displacement from the lowest point is x m.
The distance between the towers is equal to 30+30=60 m.