Algebra 2 Volume 1 1st Edition Module 2 Absolute Value, Functions, Equations, And Inequalities
Page 77 Problem 1 Answer
The absolute value expression in an absolute value equation is generally of the form ∣ax+b∣.
To solve an absolute value equation, first, the operations of multiplication, division, addition, and subtraction are used to isolate the absolute value expression ∣ax+b∣ on one side of the equation.
If the absolute value expression ∣ax+b∣ is equal to a negative number, then the equation cannot be solved and there is no solution.
If the absolute value expression ∣ax+b∣ is equal to 0, then the equation can be written as the linear equation ax+b=0, which can then be solved to obtain the only solution of the absolute value equation.
If the absolute value expression ∣ax+b∣ is equal to a positive number, then the equation can be written as a disjunction of two linear equations, which can then be solved to obtain the two solutions of the absolute value equation.
An absolute value equation can be solved by isolating the absolute value expression in the equation on one side of the equation, and determining whether the equation can be solved.
Then, the equation can be written as either one linear equation or a disjunction of two linear equations, which can be solved to obtain the required solutions.
Page 77 Problem 2 Answer
The given absolute value equation is 2∣x−5∣−4=2. The steps to solve the equation graphically are given.
The question requires to solve the given equation.
To solve the given equation, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.
Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them on the vertex to determine the vertex of f(x).
Next, write the coefficient of the expression with the independent variable in the given function to write the stretch or compress required.
Then, take two points lying on the parent absolute value function, and determine the location where they will be mapped on f(x) using the transformations used to form f(x) from h(x).
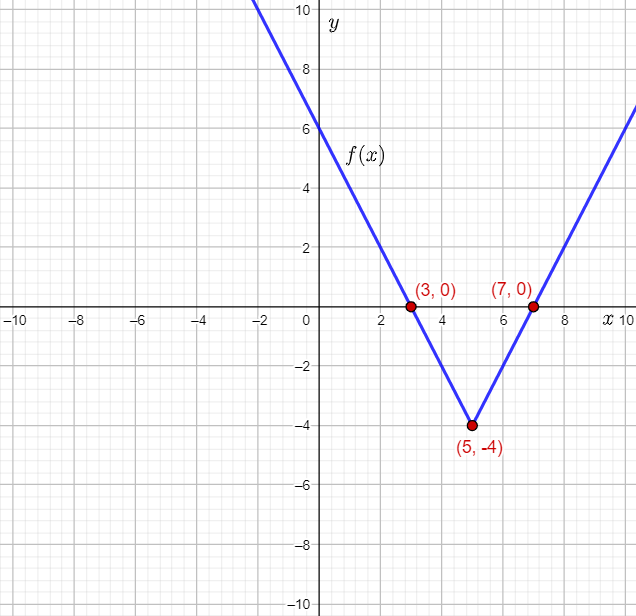
Next, plot the points and vertex, and use them to graph the function f(x) along with the constant function g(x), and mark the points of intersection.
Finally, write the x-coordinates of those points to obtain the required solutions.
Let f(x)=2∣x−5∣−4 and g(x)=2.
The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).
The vertex of f(x) is the point where (0,0) will be mapped using translations.
It can be observed that f(x) involves translations of h(x) by 5 units to the right and 4 units down.
Therefore, the vertex of f(x) is the point (0+5,0−4)=(5,−4).
The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.
Compare the function f(x) to f(x)=a∣x−h∣−k, and write the value of the constant a.
a=2
Since ∣a∣=2, that is ∣a∣>1, the graph of f(x) will involve a vertical stretch of the parent absolute value function by a factor 2.
The transformations used to form f(x)=2∣x−5∣−4 from the parent absolute value function can be used to determine the two points lying on f(x).
The x-coordinate of the points lying on h(x) will be shifted 5 units to the right when mapped to f(x).
The y-coordinate of the points lying on h(x) will be vertically stretched by a factor of 2, and then moved down 4 units.
Therefore, the point (2,2) moves to (2+5,2⋅∣2∣−4)=(7,0).
The point (−2,2) moves to (−2+5,2⋅∣2∣−4)=(3,0).
Plot the vertex (5,−4) and the points (7,0) and (3,0), and then draw straight lines to plot the graph of f(x)=2∣x−5∣−4.
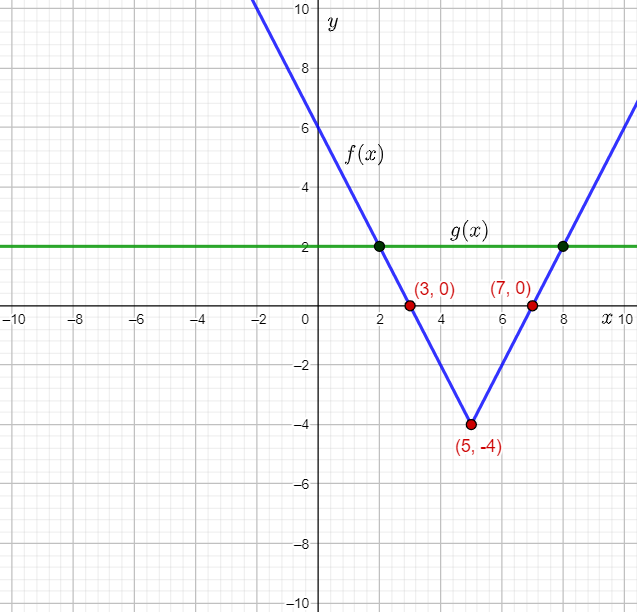
Plot the function g(x)=2 as a horizontal line on the grid where f(x) is plotted and mark the points of intersection of f(x) and g(x).
It can be observed that the points of intersection are (2,2) and (8,2).
Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is 2 and 8.
The solutions of the given equation are the x-coordinates of the points of intersection, that is 2 and 8.
Page 77 Problem 3 Answer
The given function is 2∣x−5∣−4=2. Let f(x) be equal to 2∣x−5∣−4, and g(x) be equal to 2.
The points of intersection of the graphs of the two functions are (2,2) and (8,2), as calculated in the previous part of this exercise.
Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is 2 and 8.
This can be written as the disjunction x equal to 2 or x equal to 8.
The required solution of the given equation is the disjunction x=2 or x=8.
Page 77 Problem 4 Answer
Assume an absolute value equation ∣ax+b∣=c.The two equations formed by rewriting the equation are ax+b equal to −c or ax+b equal to c.
The two equations formed have one solution each because they are linear equations.
Therefore, the absolute value equation has two solutions.
The absolute value equation ∣ax+b∣=c cannot have three or four solutions because the expression inside the absolute value parentheses is a linear expression, that is an expression with degree 1.
Therefore, the two equations formed are linear equations which one possible solution each.
Since most absolute value equations have a linear expression of the form ax+b inside the absolute value parentheses, most absolute value equations are expected to have two solutions.
Most absolute value equations are expected to have two solutions because most absolute value equations have a linear expression of the form ax+b inside the absolute value parentheses.
Most absolute value equations generally do not have three or four solutions because the two equations formed by rewriting the common absolute value equation ∣ax+b∣=c are linear equations with only one solution each.
Page 77 Problem 5 Answer
Assume an absolute value equation ∣ax+b∣=c.If c is equal to a negative number, then the equation cannot be solved because the absolute value expression ∣ax+b∣ cannot be equal to the negative number c.
Therefore, an absolute value equation will have no solution if the equation is of the form ∣ax+b∣=c, where c<0.
The graph of an absolute value equation with no solution does not contain any points because there is no point which satisfies the equation.
If c is equal to 0, then the equation can be written as the linear equation ax+b=c, which has only one solution.
Therefore, an absolute value equation will have only one solution if the equation is of the form ∣ax+b∣=0.
The graph of an absolute value equation with one solution is a straight line because it can be written as a linear equation.
An absolute value equation will have no solution if the equation is of the form ∣ax+b∣=c, where c<0.
The graph of such an absolute value equation does not contain any points.
An absolute value equation will have only one solution if the equation is of the form ∣ax+b∣=0.
The graph of such an absolute value equation is a straight line.
Page 78 Problem 6 Answer
The given equation is 1/2∣x+2∣=10.
The question requires to solve the given equation algebraically, and then graph its solutions on the number line.
To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Multiply both sides of 1/2∣x+2∣=10 by 2.
∣x+2∣=20
Rewriting the equation, the two equations obtained are x+2=20 or x+2=−20.
Subtract 2 from both sides of x+2=20.
x=18 Subtract 2 from both sides of x+2=−20.
x=−22
Thus, the two solutions are x=−22 or x=18.
Graph the obtained solutions on the given number line.
The required solutions are x=−22 or x=18.
The required graph of the solutions on the number line is:
Page 77 Problem 7 Answer
The given equation is −2∣3x−6∣+5=1.
The question requires to solve the given equation algebraically, and then graph its solutions on the number line.
To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Subtract 5 from both sides of the equation, and divide both sides by −2.
−2∣3x−6∣=−4
∣3x−6∣=−4/−2
∣3x−6∣=2
Rewriting the equation, the two equations obtained are 3x−6=2 or 3x−6=−2.
Add 6 on both sides of 3x−6=2 and divide both sides by 3.
3x=8
x=8/3
Add 6 on both sides of 3x−6=−2 and divide both sides by 3.
3x=4
x=4/3
Thus, the two solutions are x=4/3 or x=8/3.
Graph the obtained solutions on the given number line.
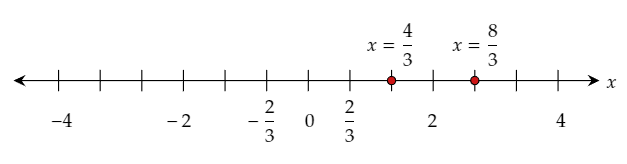
The required solutions are x=4/3 or x=8/3.
The required graph of the solutions on the number line is:
Page 78 Problem 8 Answer
The given equation is 3∣4x−5∣−2=19.
The question requires to solve the given equation algebraically, and then graph its solutions on the number line.
To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Add 2 on both sides of the equation, and divide both sides by 3.
3∣4x−5∣=21
∣4x−5∣=7
Rewriting the equation, the two equations obtained are 4x−5=7 or 4x−5=−7.
Add 5 on both sides of 4x−5=7 and divide both sides by 4.
4x=12
x=3
Add 5 on both sides of 4x−5=−7 and divide both sides by 4.
4x=−2
x=−2/4
x=−1/2
Thus, the two solutions are x=−1/2 or x=3.
Graph the obtained solutions on the given number line.
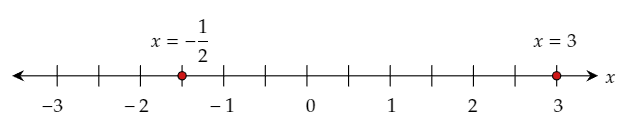
The required solutions are x=−1/2 or x=3.
The required graph of the solutions on the number line is:
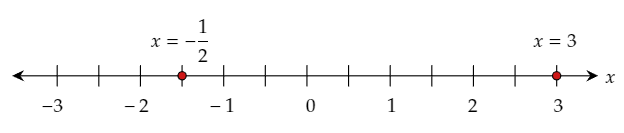
Page 79 Problem 9 Answer
The given equation is 9∣4/3 x−2∣+7=7.
The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.
Then, it is required to write “no solution” if there is no solution, or solve the equation if it has a solution.
To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not.
Then, rewrite the equation, and solve the equation for x to find the solution.
Subtract 7 from both sides of the equation, and divide both sides by 9.
9∣4/3x−2∣=0
∣4/3x−2∣=0
The absolute value expression ∣4/3x−2∣ is equal to the non-negative number 0.
Thus, the equation can be solved.
Rewriting the equation, the equation obtained is 4/3
x−2=0.
Add 2 on both sides of 4/3x−2=0 and multiply both sides by 3/4.
4/3
x=2
x=6/4
x=3/2
Thus, the solution is x=3/2.
Yes, the given equation can be solved. The required solution is x=3/2.
Page 79 Problem 10 Answer
The given equation is 3/5∣2x−4∣−3=−3.
The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.
Then, it is required to write “no solution” if there is no solution, or solve the equation if it has a solution.
To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not.
Then, rewrite the equation, and solve the equation for x to find the solution.
Add 3 on both sides of the equation, and multiply both sides by 5/3.
3/5
∣2x−4∣=0
∣2x−4∣=0
The absolute value expression ∣2x−4∣ is equal to the non-negative number 0.
Thus, the equation can be solved.
Rewriting the equation, the equation obtained is 2x−4=0.
Add 4 on both sides of 2x−4=0 and divide both sides by 2.
2x=4
x=2
Thus, the solution is x=2.
Yes, the given equation can be solved. The required solution is x=2.
Page 81 Exercise 1 Answer
The given absolute value equation is 2∣x+1∣+5=9.
The question requires to solve the given absolute value equation graphically.
To solve the given equation graphically, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.
Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).
Next, write the transformations used to form the points on the function f(x) from the points on the parent absolute value function, and use two points lying on the parent absolute value function to determine two points on f(x).
Next, plot the points and vertex, and use them to graph the function f(x) along with the constant function g(x), and mark the points of intersection.
Finally, write the x-coordinates of those points as a disjunction to obtain the required solution.
Let f(x)=2∣x+1∣+5 and g(x)=9.
The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).
The vertex of f(x) is the point where (0,0) will be mapped using translations.
It can be observed that f(x) involves translations of h(x) by 1 unit to the left and 5 units up.
Therefore, the vertex of f(x) is the point (0−1,0+5)=(−1,5).
The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣. Compare the function f(x) to f(x)=a∣x+h∣+k, and write the value of the constant a.
a=2
Since ∣a∣=2, that is ∣a∣>1, the graph of f(x) will involve a vertical stretch of the parent absolute value function by a factor 2.
The transformations used to form f(x)=2∣x+1∣+5 from the parent absolute value function can be used to determine the two points lying on f(x).
The x-coordinate of the points lying on h(x) will be shifted 1 unit to the left when mapped to f(x).
The y-coordinate of the points lying on h(x) will be vertically stretched by a factor of 2, and then moved up 5 units.
Therefore, the point (2,2) moves to (2−1,2⋅∣2∣+5)=(1,9).
The point (−2,2) moves to (−2−1,2⋅∣2∣+5)=(−3,9).
Plot the vertex (−1,5) and the points (−3,9) and (1,9), and then draw straight lines to plot the graph of f(x)=2∣x+1∣+5.
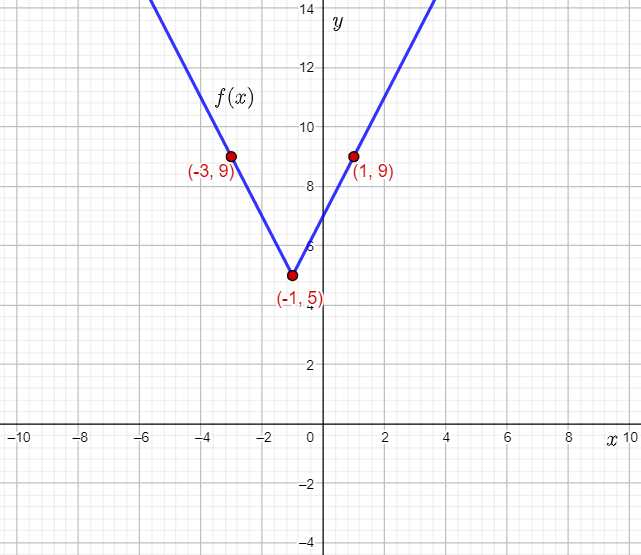
Plot the function g(x)=9 as a horizontal line on the grid where f(x) is plotted and mark the points of intersection of f(x) and g(x).
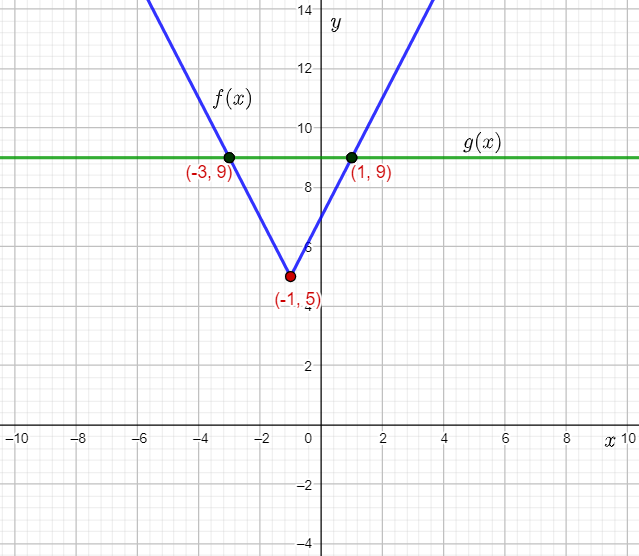
It can be observed that the points of intersection are (−3,9) and (1,9).
Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is −3 and 1. This can be written as the disjunction x=−3 or x=1.
The required solution of the given equation is the disjunction x=−3 or x=1.
Page 81 Exercise 2 Answer
The given absolute value equation is −2∣x+5∣+4=2.
The question requires to solve the given absolute value equation graphically.
To solve the given equation graphically, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.
Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).
Next, write the transformations used to form the points on the function f(x) from the points on the parent absolute value function, and use two points lying on the parent absolute value function to determine two points on f(x).
Next, plot the points and vertex, and use them to graph the function f(x) along with the constant function g(x), and mark the points of intersection.
Finally, write the x-coordinates of those points as a disjunction to obtain the required solution.
Let f(x)=−2∣x+5∣+4 and g(x)=2.
The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).
The vertex of f(x) is the point where (0,0) will be mapped using translations.
It can be observed that f(x) involves translations of h(x) by 5 units to the left and 4 units up.
Therefore, the vertex of f(x) is the point (0−5,0+4)=(−5,4).
The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.
Compare the function f(x) to f(x)=a∣x+h∣+k, and write the value of the constant a.
a=−2
Since ∣a∣=2, that is ∣a∣>1, the graph of f(x) will involve a vertical stretch of the parent absolute value function by a factor 2.
Since a=−2, that is a<0, the graph of f(x) will involve a reflection of the parent absolute value function about the x-axis.
The transformations used to form f(x)=−2∣x+5∣+4 from the parent absolute value function can be used to determine the two points lying on f(x).
The x-coordinate of the points lying on h(x) will be shifted 5 units to the left when mapped to f(x).
The y-coordinate of the points lying on h(x) will be reflected about the x-axis, vertically stretched by a factor of 2, and then moved up 4 units.
Therefore, the point (2,2) moves to (2−5,−2⋅∣2∣+4)=(−3,0).
The point (−2,2) moves to (−2−5,−2⋅∣2∣+4)=(−7,0).
Plot the vertex (−5,4) and the points (−3,0) and (−7,0), and then draw straight lines to plot the graph of f(x)=−2∣x+5∣+4.
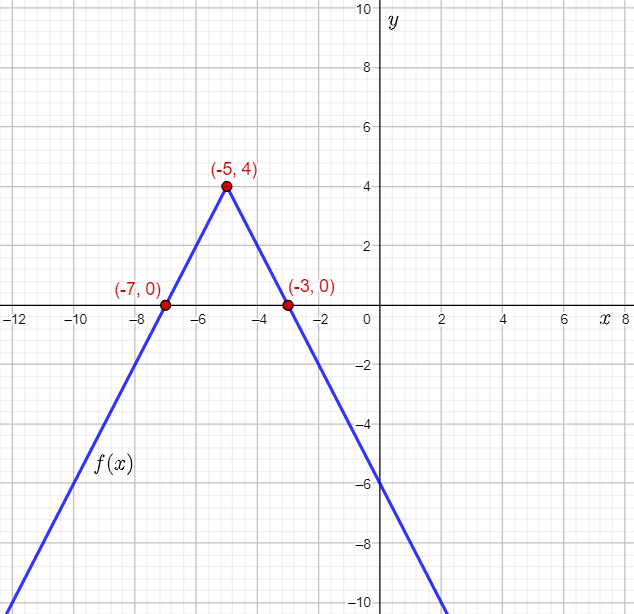
Plot the function g(x)=2 as a horizontal line on the grid where f(x) is plotted and mark the points of intersection of f(x) and g(x).
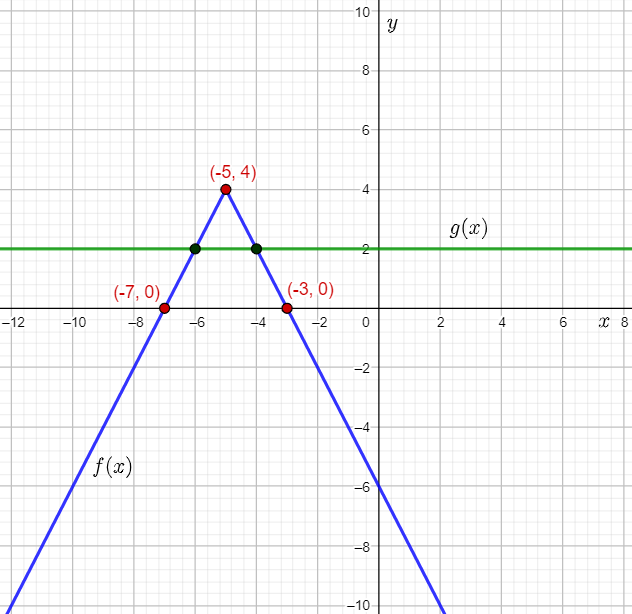
It can be observed that the points of intersection are (−6,2) and (−4,2).
Thus, the solutions of the given equation are the x-coordinates of the points of intersection, that is −6 and −4. This can be written as the disjunction x=−6 or x=−4.
The required solution of the given equation is the disjunction x=−6 or x=−4.
Page 81 Exercise 3 Answer
The given absolute value equation is ∣3/2(x−2)∣+3=2.
The question requires to solve the given absolute value equation graphically.
To solve the given equation graphically, let f(x) and g(x) be functions equal to left and right side of the given equation respectively.
Then, write the translations used to form the function f(x) from the parent absolute value function h(x)=∣x∣, and use them to determine the vertex of f(x).
Next, write the transformations used to form the points on the function f(x) from the points on the parent absolute value function, and use two points lying on the parent absolute value function to determine two points on f(x).
Finally, plot the points and vertex, use them to graph the function f(x) along with the constant function g(x), and check the points of intersection to determine the solution if any.
Let f(x)=∣3/2(x−2)∣+3 and g(x)=2.
The vertex of the parent absolute value function h(x)=∣x∣ is (0,0).
The vertex of f(x) is the point where (0,0) will be mapped using translations.
It can be observed that f(x) involves translations of h(x) by 2 units to the right and 3 units up.
Therefore, the vertex of f(x) is the point (0+2,0+3)=(2,3).
The points (2,2) and (−2,2) lie on the parent absolute value function h(x)=∣x∣.
Compare the function f(x) to f(x)=∣1/b(x−h)∣+k, and write the value of the constant b.
1/b=3/2
b=2/3
Since ∣b∣=2/3, that is 0<∣b∣<1, the graph of f(x) will involve a horizontal stretch of the parent absolute value function by a factor 2/3.
The transformations used to form f(x)=∣3/2(x−2)∣+3 from the parent absolute value function can be used to determine the two points lying on f(x).
The x-coordinate of the points lying on h(x) will be horizontally stretched by a factor of 2/3, and then shifted 2 units to the right when mapped to f(x).
The y-coordinate of the points lying on h(x) will be moved up 3 units.
Therefore, the point (2,2) moves to (2/3⋅2+2,∣2∣+3)=(10/3,5).
The point (−2,2) moves to (2/3⋅(−2)+2,∣2∣+3)=(2/3,5).
Plot the vertex (2,3) and the points (2/3,5) and (10/3,5), and then draw straight lines to plot the graph of f(x)=∣3/2(x−2)∣+3.
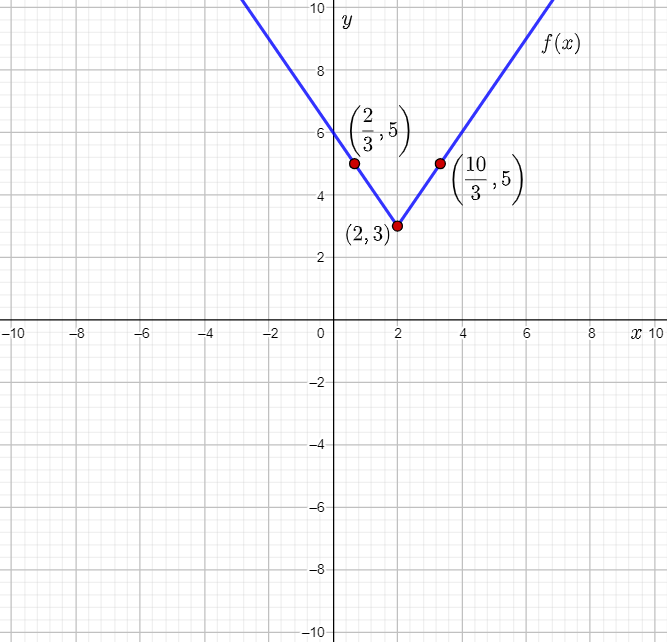
Plot the function g(x)=2 as a horizontal line on the grid where f(x) is plotted.
It can be observed that the graphs do not intersect at any point.
Therefore, there is no value of x for which f(x) is equal to g(x), that is for which ∣3/2(x−2)∣+3=2.
Thus, the given equation has no solution.
The given absolute value equation has no solution.
Page 81 Exercise 4 Answer
The given equation is ∣2x∣=3.
The question requires to solve the given equation algebraically, and then graph its solutions on the number line.
To solve the equation and graph the solutions, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Rewriting the given equation, the two equations obtained are 2x=3 or 2x=−3.
Divide both sides of 2x=3 by 2.
2x/2=3/2
x=1.5
Divide both sides of 2x=−3 by 2.
2x/2=−3/2
x=−1.5
Thus, the two solutions are x=−1.5 or x=1.5.
Graph the obtained solutions on the given number line.
The required solutions are x=−1.5 or x=1.5.
The required graph of the solutions on the number line is:
Page 81 Exercise 5 Answer
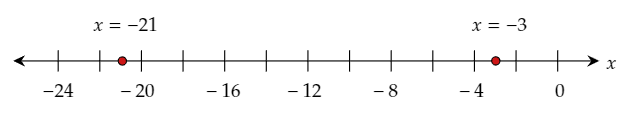
The given equation is ∣1/3x+4∣=3.
The question requires to solve the given equation algebraically, and then graph its solutions on the number line.
To solve the equation and graph the solutions, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Rewriting the given equation, the two equations obtained are 1/3x+4=3 or 1/3x+4=−3.
Subtract 4 from both sides of 1/3x+4=3, and multiply both sides by 3.
1/3
x=−1
x=−3
Subtract 4 from both sides of 1/3x+4=−3, and multiply both sides by 3.
1/3
x=−7
x=−21
Thus, the two solutions are x=−21 or x=−3.
Graph the obtained solutions on the given number line.
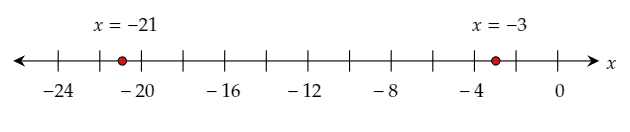
The required solutions are x=−21 or x=−3.
The required graph of the solutions on the number line is:
Page 82 Exercise 6 Answer
The given equation is 3∣2x−3∣+2=3.
The question requires to solve the given equation algebraically, and then graph its solutions on the number line.
To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Subtract 2 from both sides of the equation, and divide both sides by 3.
3∣2x−3∣=1
∣2x−3∣=1/3
Rewriting the equation, the two equations obtained are 2x−3=1/3 or 2x−3=−1/3.
Add 3 on both sides of 2x−3=1/3 and divide both sides by 2.
2x=1/3+3
2x=10/3
x=5/3
Add 3 on both sides of 2x−3=−1/3 and divide both sides by 2.
2x=−1/3+3
2x=8/3
x=4/3
Thus, the two solutions are x=4/3 or x=5/3.
Graph the obtained solutions on the given number line.
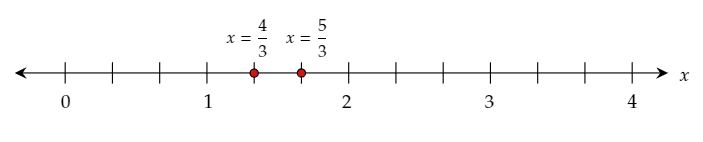
The required solutions are x=4/3 or x=5/3.
The required graph of the solutions on the number line is:
Page 82 Exercise 7 Answer
The given equation is −8∣−x−6∣+10=2.
The question requires to solve the given equation algebraically, and then graph its solutions on the number line.
To solve the equation and graph the solutions, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Subtract 10 from both sides of the equation, and divide both sides by −8.
−8∣−x−6∣=−8
∣−x−6∣=−8/−8
∣−x−6∣=1
Rewriting the equation, the two equations obtained are −x−6=1 or −x−6=−1.
Add 6 on both sides of −x−6=1, and multiply both sides by −1.
−x=7
−x(−1)=7(−1)
x=−7
Add 6 on both sides of −x−6=−1, and multiply both sides by −1.
−x=5
−x(−1)=5(−1)
x=−5
Thus, the two solutions are x=−5 or x=−7.
Graph the obtained solutions on the given number line.
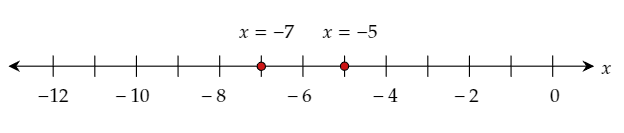
The required solutions are x=−5 or x=−7.
The required graph of the solutions on the number line is:
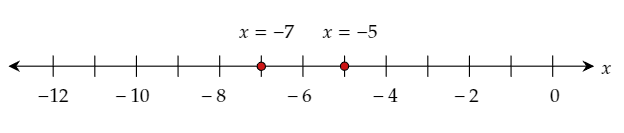
Page 82 Exercise 8 Answer
The given equation is −3∣x−3∣+3=6.
The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.
Then, it is required to write “no solution” if it cannot be solved, or solve the equation and graph the solution(s) if it can be solved.
To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not to determine if the equation can be solved.
Subtract 3 from both sides of the equation, and divide both sides by −3.
−3∣x−3∣=3
∣x−3∣=3/−3
∣x−3∣=−1
The absolute value expression ∣x−3∣ cannot be equal to the negative number −1.
Thus, the equation cannot be solved, and has no solution.
No, the equation cannot be solved, and has no solution.
Page 82 Exercise 9 Answer
The given equation is 2(∣x+4∣+3)=6.
The question requires to isolate the absolute value expression on one side of the equation and determine if the given equation has a solution.
Then, it is required to write “no solution” if it cannot be solved, or solve the equation and graph the solution(s) if it can be solved.
To answer the question, isolate the absolute value expression on one side of the equation, and check whether the right-hand side of the equation is non-negative or not.
Then, rewrite the equation, and solve the equation for x to find the solution. Finally, graph the solution on the given number line.
Divide both sides of the equation 2(∣x+4∣+3)=6 by 2, and then subtract 3 from both sides.
∣x+4∣+3=3
∣x+4∣=0
The absolute value expression ∣x+4∣ is equal to the non-negative number 0.
Thus, the equation can be solved.
Rewriting the equation, the equation obtained is x+4=0.
Subtract 4 from both sides of x+4=0.
x=−4
Thus, the solution is x=−4.
Graph the obtained solution on the given number line.
Yes, the given equation can be solved. The required solution is x=−4.
The required graph of the solution on the number line is:
Page 82 Exercise 10 Answer
The given equation is 7∣1/2x+31/2∣−2=5.
The question requires to solve the given absolute value equation.
To solve the equation, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x to find the solutions.
Next, mark the solutions on the given number line.
Add 2 on both sides of the equation 7∣1/2x+31/2∣−2=5, rewrite the mixed fraction as an improper fraction, and divide both sides by 7.
7∣1/2x+31/2∣=7
7∣1/2x+7/2∣=7
∣1/2x+7/2∣=1
Rewriting the equation, the two equations obtained are 1/2x+7/2=1 or 1/2x+7/2=−1.
Subtract 7/2 from both sides of 1/2x+7/2=1 and multiply both sides by 2.
1/2x=1−7/2
1/2x=−5/2
x=−5
Subtract 7/2 from both sides of 1/2x+7/2=−1 and multiply both sides by 2.
1/2x=−1−7/2
1/2x=−9/2
x=−9
Thus, the two solutions are x=−9 or x=−5.
Graph the obtained solutions on the given number line.
The required solutions are x=−9 or x=−5.
The required graph of the solutions on the number line is:
Page 83 Exercise 11 Answer
The given equation is −5∣−3x+2∣−2=−2.
The question requires to solve the given absolute value equation.
To solve the equation, isolate the absolute value on one side of the equation, rewrite the equation, and solve the equation for x to find the solution.
Next, mark the solution on the given number line.
Add 2 on both sides of the equation −5∣−3x+2∣−2=−2, and then divide both sides by −5.
−5∣−3x+2∣=0
∣−3x+2∣=0
Rewriting the equation, the equation obtained is −3x+2=0.
Add 3x on both sides of −3x+2=0, and divide both sides by 3.
2=3x
2/3=x
Thus, the solution is x=2/3.
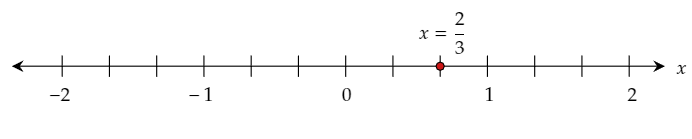
Graph the obtained solution on the given number
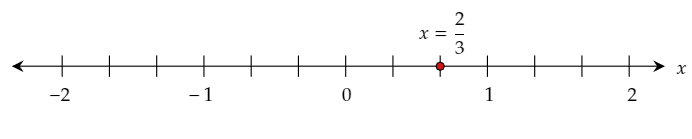
The required solution is x=2/3.
The solution can be represented on the given number line as:
Page 81 Exercise 12 Answer
It is given that the depth of the river bottom in feet is given by the absolute value function d(h)=1/5
∣h−240∣−48, where h is the horizontal distance from the left-hand shore in feet. Also, it is given that buoys are to be placed where the river bottom is 30 ft below the surface.
The question requires to determine the horizontal distance from the left-hand shore where the buoys should be placed.
To determine the horizontal distances, substitute the depth of the river bottom as −30
ft in the given absolute value function, isolate the absolute value on one side of the equation, rewrite the equation as two equations, and solve the equations for x
to find the solutions, and thus, the horizontal distances from the left-hand shore where the buoys should be placed.
The depth of the river bottom is 30 ft when d(h)=−30.
Substitute −30 for d(h) in d(h)=1/5∣h−240∣−48, add 48 on both sides, and multiply both sides by 5.
−30=1/5∣h−240∣−48
18=1/5∣h−240∣
90=∣h−240∣
Rewriting the equation, the two equations obtained are h−240=90 or h−240=−90.
Add 240 on both sides of h−240=90.
h=330 Add 240 on both sides of h−240=−90.
h=150
Thus, the buoys should be placed 150 feet and 330 feet away from the left-hand shore.
The buoys should be placed 150 feet and 330 feet away from the left-hand shore.
Page 84 Exercise 13 Answer
Subtract 2 from both sides of the equation −1/2∣3x−3∣+2=1, and multiply both sides by −2.
−1/2
∣3x−3∣=−1
∣3x−3∣=2
Rewriting the equation, the two equations obtained are 3x−3=−2 or 3x−3=2.
Add 3 on both sides of 3x−3=−2 and divide both sides by 3.
3x=1
x=1/3
Add 3 on both sides of 3x−3=2 and divide both sides by 3.
3x=5
x=5/3
Therefore, the two solutions are x=1/3 or x=5/3.Thus, the values of x satisfying the given equation are option (A) x=5/3and option (C) x=1/3.
The given equation is written as ∣3x−3∣=2 where the absolute value expression is isolated.
When x is equal to −5/3, the value of ∣3(−5/3)−3∣ is ∣−5−3∣=8 and not 2. Thus, option (B) is incorrect.
When x is equal to −1/3, the value of ∣3(−1/3)−3∣ is ∣−1−3∣=4 and not 2. Thus, option (D) is incorrect.
When x is equal to 3, the value of ∣3(3)−3∣ is ∣9−3∣=6 and not 2. Thus, option (E) is incorrect.
When x is equal to −3, the value of ∣3(−3)−3∣ is ∣−9−3∣=12 and not 2. Thus, option (F) is incorrect.
When x is equal to 1, the value of ∣3(1)−3∣ is ∣3−3∣=0 and not 2. Thus, option (G) is incorrect.
When x is equal to −1, the value of ∣3(−1)−3∣ is ∣−3−3∣=6 and not 2. Thus, option (H) is incorrect.
The values of x satisfying the given equation are option (A) x=5/3 and option (C) x=1/3.
Page 84 Exercise 14 Answer
The given equation is −3∣x−4∣−4=3. The incorrect solution for solving the given equation is given.The given solution involves the equation ∣x−4∣=−7/3.
The absolute value ∣x−4∣ cannot be equal to the negative number −7/3.
Therefore, the equation cannot be solved and has no solution.
Thus, the error in the solution is that the equation ∣x−4∣=−7/3 cannot be rewritten as the given disjunction of the two linear equations.
The correct answer is that the given equation cannot be solved and has no solution.
The error in the solution is that the equation ∣x−4∣=−7/3 is never true, and cannot be rewritten as the given disjunction of the two linear equations.
There is no correct solution because the given equation cannot be solved, and thus, has no solution.