Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations
Page 277 Exercise 1 Answer
Given: A list of expressions is written on the board.
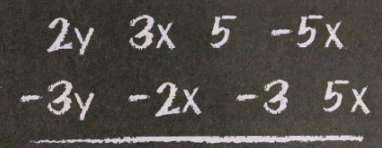
To Find: How can you make a list of fewer expressions that has the same combined value as those shown on the board? Write the expressions and explain your reasoning.
Like terms are terms whose variables and their exponents are the same.
To combine like terms, add or subtract the coefficients and keep the variables the same.
2y 3x 5 -5x
-3y -2x -3 5x
Combine the like terms from the given list:
2y − 3y = −y
3x − 5x − 2x + 5x = x
5 − 3 = 2
The new list is obtained by adding and subtracting the coefficients of the like terms, and it looks like: −y x 2
Page 277 Focus On Math Practices Answer
Given: Two expressions have a sum of 0.
To find: What must be true of the expressions?
Using the additive inverse property, every two expressions with opposite signs have a sum of 0.
The two expressions must have opposite signs to have a sum of 0.
Page 278 Essential Question Answer
Find: the properties of equality used to solve systems of linear equations.
We’ve now studied all four equality properties: subtraction, addition, division, and multiplication. For your convenience, we’ve compiled a list of all of them here. You can still have equality if you add, subtract, multiply, or divide the same amount from both sides of an equation.
When there is addition in an equation, the Subtraction Property of Equality is applied. It asserts that the same amount may be subtracted from both sides of the equation without altering the equality.
When there is a subtraction in an equation, the Addition Property of Equality is utilized. It asserts that the same amount may be added to both sides of the equation without affecting the equality.
When you have an equation containing a variable multiplied by a number, you may utilize the Division Property of Equality. It asserts that you can divide both sides of an equation by the same number (as long as that number is not equal to zero) and the equality remains unchanged.
When you have an equation with a variable divided by a number, you may apply the Multiplication Property of Equality. It says that you can multiply both sides of an equation by the same number without affecting the equation’s equality.
By removing a variable, you may use the properties of equality to solve systems of linear equations algebraically.
Elimination is an efficient method when:
Similar variable terms have the same or opposite coefficients, elimination is an effective technique.
One or both equations can be multiplied in such a way that similar variable terms have the same or opposite coefficients.
Page 278 Try It Answer
Given:
2r + 3s = 14
6r − 3s = 6
To Find the solutions of r and s.
The solution is s = 3.
Page 278 Convince Me Answer
Find a system of equations for a term to be eliminated by adding or subtracting.
To get an equation in one variable, use the elimination approach and either add or subtract the equations. When the coefficients of one variable are opposites, the equations are added to delete a variable; when the coefficients of one variable are equal, the equations are subtracted to eliminate a variable.
For example:
The solution of the linear system is (0,2).
Which means:
To remove a term by adding, the total of the term’s coefficients must equal zero.
To remove a term by subtracting, the difference between the term’s coefficients must equal zero.
To eliminate a term by adding, the sum of the coefficients of the term must equal 0.
To eliminate a term by subtracting, the difference of the coefficients of the term must equal 0.
Page 279 Try it Answer
Given:
3x − 5y = −9
x + 2y = 8
To find: Use elimination to solve the system of equations.
Solve using the elimination method
(x, y) = (2, 3)
Page 280 Exercise 1 Answer
Find: the properties of equality used to solve systems of linear equations.
We’ve now studied all four equality properties: subtraction, addition, division, and multiplication. For your convenience, we’ve compiled a list of all of them here. You can still have equality if you add, subtract, multiply, or divide the same amount from both sides of an equation.
When there is addition in an equation, the Subtraction Property of Equality is applied. It asserts that the same amount may be subtracted from both sides of the equation without altering the equality.
When there is a subtraction in an equation, the Addition Property of Equality is utilized. It asserts that the same amount may be added to both sides of the equation without affecting the equality.
When you have an equation containing a variable multiplied by a number, you may utilize the Division Property of Equality. It asserts that you can divide both sides of an equation by the same number (as long as that number is not equal to zero) and the equality remains unchanged.
When you have an equation with a variable divided by a number, you may apply the Multiplication Property of Equality. It says that you can multiply both sides of an equation by the same number without affecting the equation’s equality.
By removing a variable, you may use the properties of equality to solve systems of linear equations algebraically.
Elimination is an efficient method when:
Similar variable terms have the same or opposite coefficients, elimination is an effective technique.
One or both equations can be multiplied in such a way that similar variable terms have the same or opposite coefficients.
Page 280 Exercise 2 Answer
To find: How is solving a system of equations algebraically similar to solving the system by graphing? How is it different?
In both solving a system of equations and solving the system by graphing, the common goal is to find the solution to the system.
Say, for example, that we have a system of equations:
x+y=1 \\
2 x-y=2
\end{array}\right.\)
An example of algebraically solving the system follows.
The goal is to find ordered pairs that satisfy both equations.
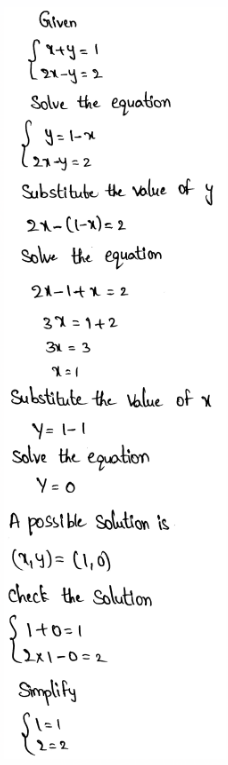
The ordered pair is a solution
(x, y) = (1,0)
When solving graphically, we graph the first and the second equation and search for points of intersection of the graphs.
The solution – intersection point is represented by the ordered pair of its coordinates.
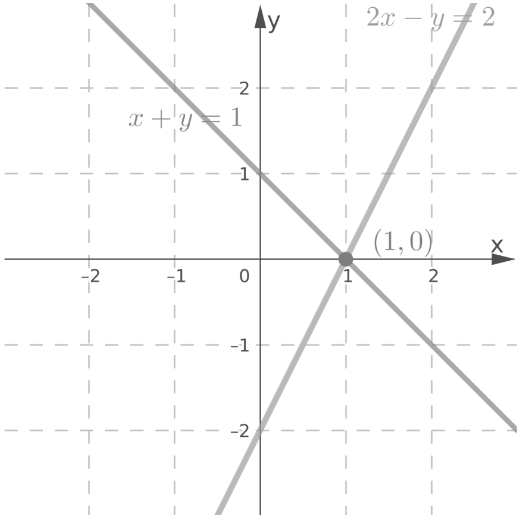
Both methods produce ordered pairs as solutions if they exist.
If there are no solutions, and impossible equation (such as1 = 0) will emerge in the algebraic method.
In the geometric method, no intersections will be noted when the system has no solutions.
The main difference is in precisely determining the solution.
When graphing, if the coordinates of the intersection are fractions or irrational numbers, the solution is approximated.
The algebraic methods, on the other hand, produce precise values.
In both solving a system of equations algebraically and by graphing, the common goal is to find the solution to the system.
The difference is in the precision of solutions. Algebraic solutions are precise, while the geometric may be approximate.
Page 280 Exercise 3 Answer
Given:
\(1 \frac{3}{4} x+y=2 \frac{3}{16}\) \(\frac{1}{4} x-y=-1 \frac{11}{16}\)To Find: Construct Arguments Consider the system of equations. Would you solve this system by substitution or by elimination? Explain.
\(\left\{\begin{array}{l}
1 \frac{3}{4} x+y=2 \frac{3}{16} \\
\frac{1}{4} x-y=-1 \frac{11}{16}
\end{array}\right.\)
Rewrite the system, using the identity Property of Multiplication:
\(\left\{\begin{array}{c}
1 \frac{3}{4} x+1 \cdot y=2 \frac{3}{16} \\
\frac{1}{4} x-1 \cdot y=-1 \frac{11}{16}
\end{array}\right.\)
Notice that the coefficient of y in the first equation, +1, is the inverse of the coefficient of y in the second equation, -1.
Therefore, by adding the 2 equations together, the term y would be cancelled.
The system can be solved through elimination because adding the 2 equations will remove the term y.
Page 280 Exercise 4 Answer
Given:
y − x = 28
y + x = 156
To Find: solve each system of equations by using elimination.
The ordered pair is a solution
(x, y) = (64, 92)
\(\left\{\begin{array}{l}y-x=28 \\
y+x=156
\end{array}\right.\)
Solve using the elimination method
(x, y) = (64, 92)
Page 280 Exercise 5 Answer
Given:
3c + 6d = 18
6c − 2d = 22
To find: solve each system of equations by using elimination.
The ordered pair is a solution
(c, d) = (4, 1)
\(\left\{\begin{array}{l}
3 c+6 d=18 \\
6 c-2 d=22
\end{array}\right.\)
Solve using the elimination method
(c, d) = (4, 1)
Page 281 Exercise 6 Answer
Given:
7x + 14y = 28
5x + 10y = 20
To Find: solve each system of equations by using elimination.
The statement is true,
Infinitely many solutions
\(\left\{\begin{array}{l}
7 x+14 y=28 \\
5 x+10 y=20
\end{array}\right.\)
Solve using the elimination method
Infinitely many solutions
Page 281 Exercise 7 Answer
Given:
2x − 2y = −4
2x + y = 11
To find: Leveled Practice Solve the system of equations using elimination.
The solution to the two equations is:
x = 3,y = 5
Page 281 Exercise 8 Answer
Given:
2y − 5x = −2
3y + 2x = 35
To Find: Solve the system of equations using elimination.
Check the solution
\(\left\{\begin{array}{l}2 \times 9-5 \times 4=-2 \\
3 \times 9+2 \times 4=35
\end{array}\right.\)
Simplify
\(\left\{\begin{array}{c}-2=-2 \\
35=35
\end{array}\right.\)
The ordered pair is a solution
(x, y) = (4, 9)
\(\left\{\begin{array}{l}2 y-5 x=-2 \\
3 y+2 x=35
\end{array}\right.\)
Solve using the elimination method
(x, y) = (4, 9)
Page 281 Exercise 9 Answer
Given: If you add Natalie’s age and Frankie’s age, the result is 44. If you add Frankie’s age to 3 times Natalie’s age, the result is 70.
To find: Write and solve a system of equations using elimination to find their ages.
Let x be the age of the first person and y the age of the second person.
The sum of ages of the first and the second person is 44, so it follows:
x + y = 44
Since the sum of 3 times the age of the first person and the age of the second person is 70, it follows:
3x + y = 70
A system of equations representing the situation is:
x + y = 44
3x + y = 70
Solve the system using elimination:
Check the solution
\(\left\{\begin{array}{l}13+31=44 \\
3 \times 13+31=70
\end{array}\right.\)
Simplify
\(\left\{\begin{array}{l}44=44 \\
70=70
\end{array}\right.\)
The ordered pair is a solution
(x, y) = (13, 31)
The system of equations is:
The system of equations is:
x + y = 44
3x + y = 70
The age of the first person is 13 and the age of the second person is 31.
The system of equations is:
x + y = 44
3x + y = 70
The age of the first person is 13 and the age of the second person is 31.
Page 281 Exercise 10 Answer
Given:
5x + 10y = 7
4x + 8y = 3
To Find: If possible, use elimination to solve the system of equations.
The statement is false
No solution
\(\left\{\begin{array}{l}
5 x+10 y=7 \\
4 x+8 y=3
\end{array}\right.\)
Solve using the elimination method
No solution
Page 282 Exercise 14 Answer
Given: Consider the system of equations.
x − 3.1y = 11.5
−x + 3.5y = −13.5
To Find: Solve the system by elimination.
Check the solution
\(\left\{\begin{array}{l}
-4-3.1 \times(-5)=11.5 \\
-(-4)+3.5 \times(-5)=-13.5
\end{array}\right.\)
Simplify
\(\left\{\begin{array}{l}
\frac{23}{2}=\frac{23}{2} \\
-\frac{27}{2}=-\frac{27}{2}
\end{array}\right.\)
The ordered pair is a solution
(x, y) = (-4, -5)
\(\left\{\begin{array}{l}
x-3.1 y=11.5 \\
-x+3.5 y=-13.5
\end{array}\right.\)
Solve using the elimination method
(x,y) = (−4,−5)
Given: Consider the system of equations.
x − 3.1y = 11.5
−x + 3.5y = −13.5
To Find: If you solved this equation by substitution instead, what would the solution be? Explain.
The system of equations is given by:
By substitution method, the solution to the system of equations is x = −4 and y = −5.
Page 282 Exercise 15 Answer
Given:
3x + 4y = 17
21x + 28y = 109
To Find: Higher Order Thinking Determine the number of solutions for this system of equations by inspection only. Explain.
Rewrite the first equation into the slope-intercept form:
Notice, the given equations have the same slope \(-\frac{3}{4}\) but different y intercepts, \(\frac{17}{4} \text { and } \frac{109}{28}\).
Therefore, the system of equations has no solution.
Since the equations, in slope-intercept form, have the same slope but different y-intercepts, the system of equations has no solution.
Page 282 Exercise 16 Answer
Given: Four times a number r plus half a number s equals twelve.
Twice the number r plus a quarter of the number s equals eight.
To Find: What are the two numbers?
Four times a number r plus half a number s equals twelve can be expressed as:
\(4 r+\frac{s}{2}=12\)
Twice the number r plus a quarter of the numbers equals eight can be expressed as:
\(2 r+\frac{s}{4}=8\)Solve the obtained equations:
\(\left\{\begin{array}{l}4 r+\frac{s}{2}=12 \\
2 r+\frac{s}{4}=8
\end{array}\right.\)
Multiply both sides
\(\left\{\begin{array}{l}8 r+s=24 \\
8 r+s=32
\end{array}\right.\)
Multiply both sides
\(\left\{\begin{array}{l}
8 r+s=24 \\
-8 r-s=-32
\end{array}\right.\)
Eliminate one variable by adding the equations
0 = -8
The statement is false
No solution
The system of equations has no solution.
The system of equations has no solution.
Page 282 Exercise 17 Answer
Given:
3m + 3n = 36
8m − 5n = 31
To find: Solve the system of equations.
Check the solution
\(\left\{\begin{array}{l}
3 \times\left(-\frac{29}{3}\right)+3 \times \frac{65}{3}=36 \\
8 \times\left(-\frac{29}{3}\right)+5 \times \frac{65}{3}=31
\end{array}\right.\)
Simplify
\(\left\{\begin{array}{l}
36=36 \\
31=31
\end{array}\right.\)
The ordered pair is a solution
\((\mathrm{m}, \mathrm{n})=\left(-\frac{29}{3}, \frac{65}{3}\right)\)
\(\left\{\begin{array}{l}
m=12-n \\
8 m+5 n=31
\end{array}\right.\)
Solve using the substitution method
\((\mathrm{m}, \mathrm{n})=\left(-\frac{29}{3}, \frac{65}{3}\right)\)