Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations
Page 269 Exercise 1 Answer
To determine the number of solutions of a system by looking at the equations?
The number of solutions of the equation is evident from the slope-intercept form of the equations.
When the equations have different slopes, the system has one solution.
When the equations have the same slopes but different y-intercepts, the system does not have a solution.
When the equations have the same slopes and y-intercepts, the system has infinitely many solutions.
The number of solutions of the system is evident from the slope-intercept form of the equations.
Depending on the slopes and y-intercepts of the equations, the system may have one, infinitely many, or no solutions.
Page 269 Exercise 2 Answer
Given:
2x − 9y = −5
4x − 6y = 2
To explain how many solutions does the system of equations has.
Rewrite the first equation in slope-intercept form:
2x − 9y = −5
Move the variable to the right,
−9y = −5 − 2x
Change the signs,
9y = 5 + 2x
Divide both sides by 9,
y = \(\frac{5}{9}+\frac{2}{9} x\)
Use the commutative property to reorder the terms,
y = \(\frac{2}{9} x+\frac{5}{9}\)
Rewrite the second equation in slope-intercept form:
4x − 6y = 2
Move the variable to the right,
−6y = 2 − 4x
Change the signs,
6y = −2 + 4x
Divide both sides by 6 and simplify,
y = \(-\frac{1}{3}+\frac{2}{3} x\)
Use the commutative property to reorder the terms,
y = \(\frac{2}{3} x-\frac{1}{3}\)
Now check the slopes of both the equation,
y = \(\frac{2}{9} x+\frac{5}{9}\)
y = \(\frac{2}{3} x-\frac{1}{3}\)
The equations of the linear system have different slopes this means that the system has one solution.
Therefore, the system has one solution.
Page 269 Exercise 3 Answer
Given:
y + 1 = 2x
y = \(\frac{1}{2} x+2\)
To find: Graph the system of equations and find the solution.
The first equation is written in slope-intercept form.
Calculate the value of y for x = 0:
y = −2x + 1,x = 0
Substitute x = 0,
y = −2 × 0 + 1
Calculate the product,
y = 0 + 1
y = 1
Using the same method, calculate the values of y for a few other values of x.
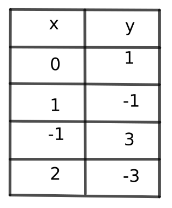
Draw the graph,
Plot the points on the graph.
Draw a line through the plotted points.
Using the same method, graph the line \(y = \frac{1}{2} x+2\).
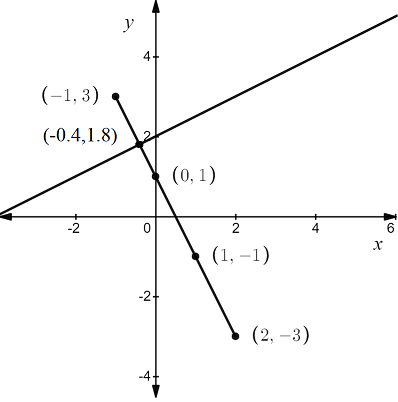
The lines intersect at the point (−0.4,1.8).
The point of intersection (−0.4,1.8) is the solution of the system and the graph is shown below,
Page 269 Exercise 5 Answer
Given: Finn bought 12 movie tickets. Student tickets cost $4, and adult tickets cost $8.Finn spent a total of $60.
To write and graph a system of equations to find the number of student and adult tickets Finn bought.
Let x be the number of the $4 items and y be the number of the $8 items.
Since the boy bought 12 items in total, the first equation of the system is:
x + y = 12
Solve the equation for y:
x + y = 12
Move the variable to the right,
y = 12 − x
Use the commutative property to reorder the terms,
y = −x + 12
y = -1.x + 12
From the slope-intercept form of a line, it follows:
m = -1, b = 12
Since the boy spent $60 total, the second equation of the system is:
4x + 8y = 60
Move the variable to the right
8y = 60 – 4x
Divide both sides by 8,
y = \(\frac{15}{2}-\frac{1}{2} x\)
Use the commutative property to reorder the terms,
y = \(-\frac{1}{2} x+\frac{15}{2}\)
From the slope-intercept form of a line, it follows:
m = \(-\frac{1}{2}, b=\frac{15}{2}\)
Therefore, the system representing the given situation is:
\(\left\{\begin{array}{l}y=-x+12 \\
y=-\frac{1}{2} x+\frac{15}{2}
\end{array}\right.\)
Draw the line y = -x + 122 using its slope and y-intercept.
y = -x + 12
Since the y-intercept of the line is 12, the line passes through the point (0, 12).
Plot the point (0, 122).
Since the slope of the line is m = \(\frac{-1}{1}\), move 1 unit down and 1 unit right starting from point (0, 12).
It follows that the line passes through point (1, 11) as well.
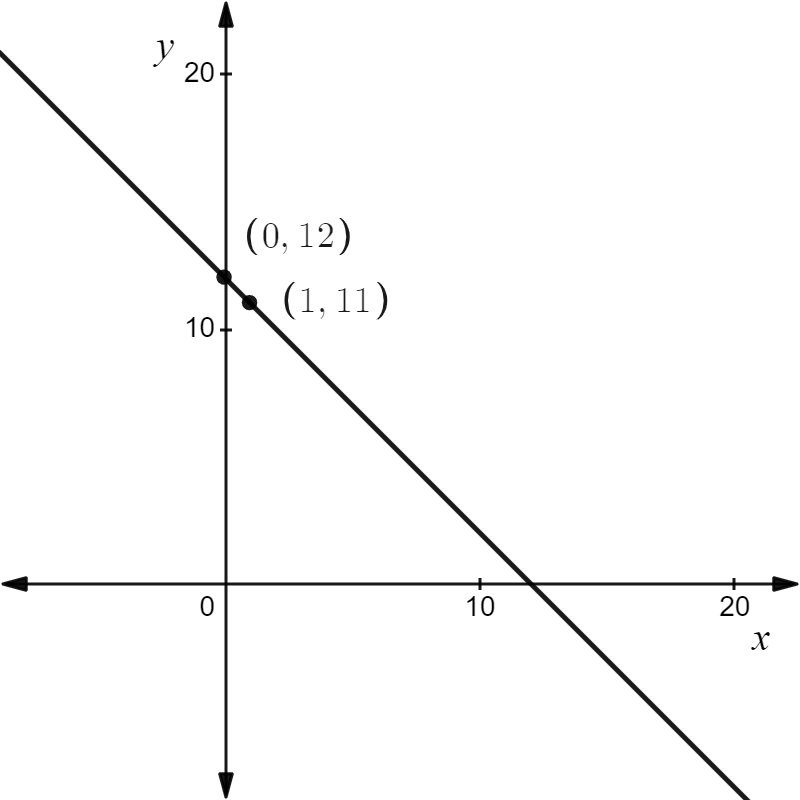
Draw the line y = \(-\frac{1}{2} x+\frac{15}{2}\) using its slope and y intercept.
y = \(-\frac{1}{2} x+\frac{15}{2}\)
Since the y-intercept of the line is \(\frac{15}{2}\), the line passes through point. \(\left(0, \frac{15}{2}\right)\)
The graph is shown below,
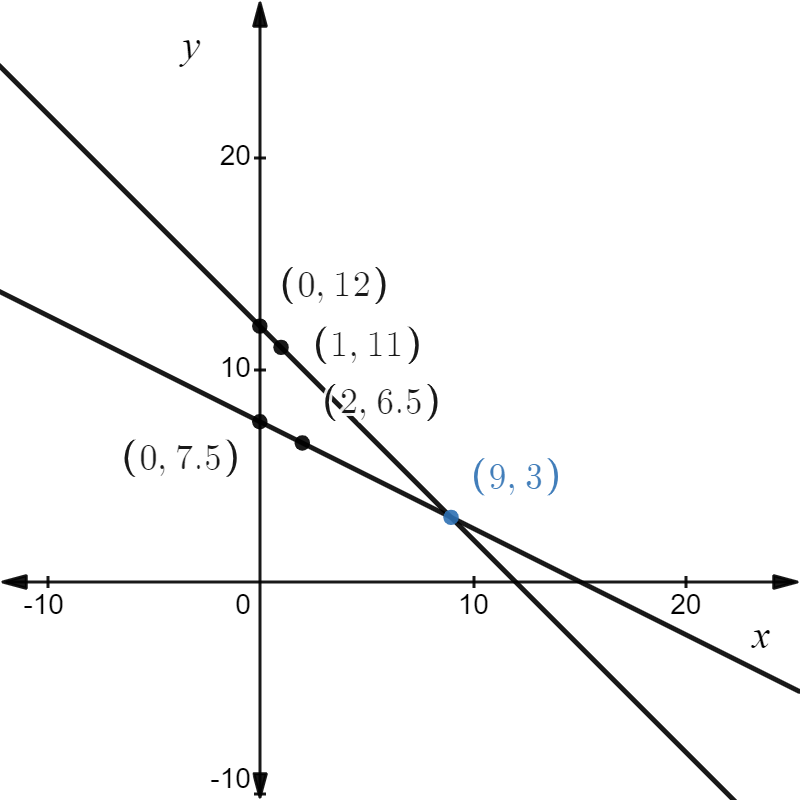
It follows that the lines intersect at point (9,3).
Since the solution to the system is (9,3), it follows that the boy bought 9 items for the price of $4 and 3 items for the price of $8.
The system representing the given situation is:
\(\left\{\begin{array}{l}
y=-x+12 \\
y=-\frac{1}{2} x+\frac{15}{2}
\end{array}\right.\)
The boy bought 9 items for the price of $4 and 3 items for the price of $8.
The graph is shown below,
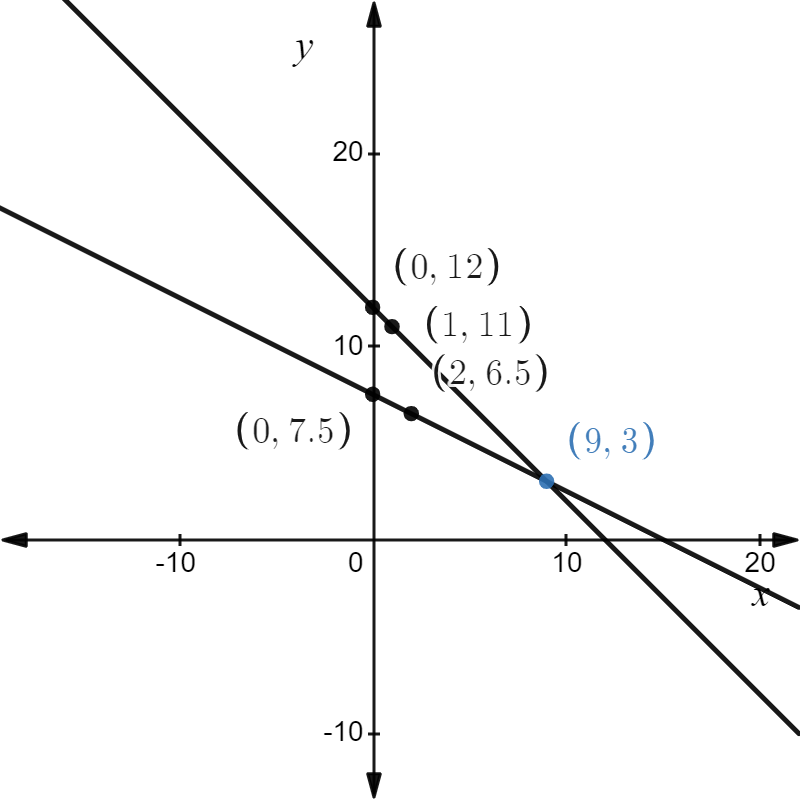
Page 269 Exercise 6 Answer
Given:
−x + 4y = 32
y = mx + 8
The find the value of m.
Rewrite the first equation in slope-intercept form:
−x + 4y = 32
Move the variable to the right,
4y = 32 + x
Divide both sides by 4,
y = \(8+\frac{1}{4} x\)
Notice the value m = \(\frac{1}{4}\) substituted to the second equation will give the system infinitely many solutions since both equations will be equal.
Check the obtained system of equations,
\(\left\{\begin{array}{l}
-x+4 y=32 \\
y=\frac{1}{4} x+8
\end{array}\right.\)
Simplify
\(\left\{\begin{array}{l}
-x+4 y=32 \\
-x+4 y=32
\end{array}\right.\)
Multiply both sides by -1
\(\left\{\begin{array}{c}
-x+4 y=32 \\
x-4 y=-32
\end{array}\right.\)
Eliminate one variable by adding the equations,
0 = 0
The statement is true and has infinitely many solutions.
The value of m is \(\frac{1}{4}\) and it gives infinitely many solutions.
Page 271 Focus On Math Practices Answer
Explain: Can you use the graph to determine the exact number of miles for which the cost of the taxi ride will be the same
There will be a point in the graph where both the lines intersect.
The point of intersection of the lines will give the exact miles for which the cost of both the rides will be the same.
The graph can be used to determine the exact miles for which the cost of both rides will be the same.
Page 272 Essential Question Answer
Systems of linear equations can be solved algebraically. When one of the equations can be easily solved for one of the variables, you can use substitution to solve the system efficiently.
Solve one of the equations for one of the variables. Then substitute the expression into the other equation and solve.
Solve for the other variable using either equation.
Example:
Solve the system −2y − x = −84.91 and 3x + 6y = 254.73 by using substitution.
STEP 1 Solve one of the equations for one variable.
−2y − x = −84.91
−x = −84.91 + 2y
= 84.91 − 2y
STEP 2 Substitute 84.91 − 2y for x in the other equation.
Then solve.
3(84.91−2y) + 6y = 254.73
254.73 − 6y + 6y = 254.73
254.73 = 254.73
The result is a true statement. This system has infinitely many solutions.
The substitution method is most useful for systems of 2 equations in 2 unknowns. The main idea here is that we solve one of the equations for one of the unknowns, and then substitute the result into the other equation.
The substitution method can be applied in four steps
Solve one of the equations for either x = or y =.
Substitute the solution from step 1 into the other equation.
Solve this new equation.
Solve for the second variable.
Page 272 Try It Answer
Given:
x + y = 50
2x + 5y = 160
To find: How many of each type of question was on the exam.
The number of tasks worth two points is represented by x and the number of tasks worth five points is represented by y.
The situation is represented by the following system of equations:
\(\left\{\begin{array}{l}
x+y=50 \\
2 x+5 y=160
\end{array}\right.\)
Solve the first equation for y:
x + y = 50
Move the variable to the right,
y = 50 − x
Use the commutative property to reorder the terms,
y = −x + 50
y = -x + 50
Reorder the terms of the equation:
y = 50 – x
\(\left\{\begin{array}{l}x+y=50 \\
2 x+5 y=160
\end{array}\right.\)
Substitute y = 50 − x into the second equation:
2x + 5⋅(50 − x) = 160
Use the Distributive Property to simplify the equation:
2x + 5⋅50 − 5⋅x = 160
Multiply the numbers:
2x + 250 − 5x = 160
Solve the equation for x:
2x + 250 − 5x = 160
Collect like terms
−3x + 250 = 160
Move the constant to the right
−3x = 160 − 250
−3x = −90
Divide both sides by −3
x = 30
There are 30 tasks worth two points.
x + y = 50
Substitute x = 30 into the first equation to obtain y:
30 + y = 50
y = 20
There are 20 tasks worth five points.
y = 50 – x
2x + 5.(50 – x) = 160
2x + 250 – 5x = 160
There are 30 tasks worth two points.
30 + y = 50
There are 20 tasks worth five points.
Page 272 Convince Me Answer
To find which equation to choose to solve for one of the variables.
When solving the equation for one of the variables, choose the simpler equation in the matter of coefficients of the terms.
Therefore, aim for the equation which has a coefficient of at least one term equal to 1.
Page 273 Try It Answer
Given:
\(y+\frac{1}{2} x=3\)
4y + 2x = -6
To find: Solve each system of equations.
\(y+\frac{1}{2} x=3\)
Move the expression to the right-hand side by adding its opposite to both sides
\(y+\frac{1}{2} x-\frac{1}{2} x=3-\frac{1}{2} x\)Since two opposites add up to zero, remove them from the expression
\(y = 3-\frac{1}{2} x\)
\(\left\{\begin{array}{l}
y=3-\frac{1}{2} x \\
4 y+2 x=-6
\end{array}\right.\)
Substitute the given value of y into the equation, 4y + 2x = -6
\(4\left(3-\frac{1}{2} x\right)+2 x=-6\) \(4\left(3-\frac{1}{2} x\right)+2 x=-6\)
Distribute 4 through the parentheses
12 − 2x + 2x = −6
Since two opposites add up to zero, remove them from the expression
12 = −6
The statement is false for any value of x
x ∈ ∅
Since the system has no solution for x, therefore system has no solutions.
Given:
y = \(\frac{1}{4} x-2\)
8y – 2x = -16
To find: Using substitution solve each system of equations.
\(\left\{\begin{array}{l}y=\frac{1}{4} x-2 \\
8 y-2 x=-16
\end{array}\right.\)
Substitute the given value of y into the equation 8y – 2x = -16
\(8\left(\frac{1}{4} x-2\right)-2 x=-16\)Distribute 8 through the parentheses
2x − 16 − 2x = −16
Cancel equal terms and eliminate the opposites.
0 = 0
x ∈ R
The statement is true since there are infinitely many solutions for x, the system has infinitely many solutions.
There are infinitely many solutions to the given system of equations.
Page 274 Exercise 1 Answer
Find: substitution, a useful method for solving systems of equations.
The substitution technique is a straightforward approach for solving linear equations algebraically and determining the variables’ solutions. It entails determining the value of the x-variable in terms of the y-variable and then substituting or replacing the value of the x-variable in the second equation, as the name implies.
Substitute to solve a problem of equations:
1. For each variable, solve one of the equations.
2. Step 1’s expression should be substituted into the other equation.
3. Solve the equation that results.
4. To determine the other variable, substitute the result from Step 3 into one of the original equations.
5.Make an ordered pair out of the answer.
Algebraically, systems of linear equations may be solved. When one of the equations is easily solved for one of the variables, substitution can be used to quickly solve the system.
STEP 1: For each variable, solve one of the equations. Then solve the other equation by substituting the expression.
STEP 2: Using either equation, solve for the other variable.
Page 274 Exercise 4 Answer
Given:
y = \(\frac{1}{2} x+4\)
x – y = 8
Find: solve the given equation.
Use substitution method to find the value of x and y.
Substitute the value of y = \(\frac{1}{2} x+4\) in x – y = 8,
\(x-\left(\frac{1}{2} x+4\right)=8\)
\(x-\frac{1}{2} x-4=8\)
\(\frac{2 x-x-8}{2}=8\)
Multiply both sides by 2,
\(\frac{2 x-x-8}{2} \times 2=8 \times 2\)
2x – x – 8 = 16
x – 8 = 16
x = 16 + 8
x = 24
The value of x = 24.
Now substitute the value of x = 24 in y = \(\frac{1}{2} x+4\),
y = \(\frac{1}{2} \times 24+4\)
y = 12 + 4
y = 16
The value of y = 16
The value of (x, y) = (24,16) by using substitution method.
Page 274 Exercise 5 Answer
Given:
3.25x − 1.5y = 1.25
13x − 6y = 10
Find: solve the given equation.
Find the value of x and then use the substitution method to solve the equation.
It means y has no solution. That is y ∈ ∅.
The given equation has no solution.
Page 274 Exercise 6 Answer
Given:
y − 0.8x = 0.5
5y − 2.5 = 4x
Find: solve the given equation.
Find the value of y and then use the substitution method to solve the equation.
x ∈ R
The value of x = x, x ∈ R.
By using the substitution method, the value of
(x, y) = (x,0.5 + 0.8y),x ∈ R.
Page 275 Exercise 7 Answer
Given:
p + r = 2,666
p = r + 276
Find: Pedro has ______ hits, and Rocky has _____ hits.
Use the substitution method.
Let p be the number of Pedro’s hits and r be the number of Ricky’s hits.
The two teammates have a combined hit total of 2666,
p + r = 2666
Pedro has 276 more hits than Ricky,
p = r + 276
Substitute the value of p = r + 276 in p + r = 2666,
(r + 276) + r = 2666
r + 276 + r = 2666
2r + 276 = 2666
2r = 2666 − 276
2r = 2390
Divide both sides by 2,
\(\frac{2 r}{2}=\frac{2390}{2}\)
r = 1195
So, Ricky hits r = 1195.
Substitute the value of r = 1195 in p + r = 2666,
p + 1195 = 2666.
Subtract 1195 on both sides,
p + 1195 − 1195 = 2666 − 1195
p = 1471
The number of Pedro’s hits p = 1471.
Pedro has 1471 hits, and Rocky has 1195 hits.
Page 275 Exercise 8 Answer
Given:
2y + 4.4x = −5
y = −2.2x + 4.5
Find: solution and
2y + 4.4x = −5
y = −2.2x + 4.5
2(−2.2x + ?) + 4.4x = −5
−4.4x + ? + 4.4x = −5
? ≠ −5
Use substitution method.
Substitute the value of y = −2.2x + 4.5 in 2y + 4.4x = −5,
2(−2.2x + 4.5) + 4.4x = −5
−4.4x + 9 + 4.4x = −5
9 ≠ −5
The given equation has no solution.
The statement is not true. There is no solution.
As,
2y + 4.4x = −5
y = −2.2x + 4.5
2(−2.2x + 4.5) + 4.4x = −5
−4.4x + 9 + 4.4x = −5
9 ≠ −5
Page 275 Exercise 9 Answer
Given:
x + 5y = 0
25y = −5x
Find:
x + 5y = 0
25y = −5x
x = □y
25y = −5(?)
25y = □y
The statement is true. There are Solutions.
Use substitution method.
Solve for x,
x + 5y = 0
x = −5y
Substitute the value of x = −5y in 25y = −5x,
25y = −5(−5y)
25y = 25y
Therefore, the statement is true. There are no solutions.
The statement is true. There are no solutions.
As,
x + 5y = 0
25y = −5x
x = −5y
25y = −5(−5y)
25y = 25y
Page 275 Exercise 10 Answer
Given:
481 people used the public swimming pool.
The daily prices are $1.25 for children and $2.25 for adults.
The receipts for admission totaled $865.25.
Find: number of children and adults swam at the public pool that day.
Use substitution method.
Let x be the number of children’s and y be the number of adults.
If one day 481 people used to swim, the combined number of children and adults on that day,
x + y = 481.
The ticket for children costs $1.25, and the ticket for adults costs $2.25, so the expression for total earnings on that day,
1.25x + 2.25y
The total earnings for the day were $865.25, so the expression must be equal to this amount,
1.25x + 2.25y = 865.25
Now solve for x,
x + y = 481
x = 481 − y
Substitute the value of x = 481 − y in 1.25x + 2.25y = 865.25,
1.25(481 − y) + 2.25y = 865.25
601.25 − 1.25y + 2.25y = 865.25
601.25 + 1y = 865.25
y = 865.25 − 601.25
y = 264
The number of adults y = 264.
Substitute the value of y = 264 in x = 481 − y,
x = 481 − 264
x = 217
The number of children x = 217.
The number of adults y = 264.
The number of children x = 217.
Page 275 Exercise 11 Answer
Given:
6x − 2y = −6
11 = y − 5x
And x = −9,y = −4
Find: the correct solution.
Use substitution method.
Solve for y,
11 = y − 5x
5x + 11 = y
Substitute the value of y = 5x + 11 in 6x − 2y = −6,
6x − 2(5x + 11) = −6
6x − 10x − 22 = −6
−4x − 22 = −6
−4x = −6 + 22
−4x = 16
Divide both sides by −4,
x = -4
The value of x = -4.
Substitute the value of x = −4 in y = 5x + 11,
y = 5(−4) + 11
y = −20 + 11
y = −9
The value of y = −9.
The correct solution of the given equation is(x, y) = (−4,−9).
Given:
6x − 2y = −6
11 = y − 5x
And x = −9,y = −4
Find: error Tim have made.
Use substitution method.
Solve for y in 6x − 2y = −6,
6x − 2y = −6
6x + 6 = 2y
Divide both sides by 2,
\(\frac{6 x+6}{2}=\frac{2 y}{2}\)
3x + 3 = y-2
The value of y = 3x + 3.
Substitute the value of y = 3x + 3 in 11 = y − 5x,
11 = 3x + 3 − 5x
11 − 3 = −2x
8 = −2x
Divide both sides by −2,
-4 = x-2
The value of x = -4.
Substitute the value of x = −4 in y = 3x + 3,
y = 3(−4) + 3
y = −12 + 3
y = −9
The value of y = −9.
The correct solution is (x,y) = (−4,−9).
Tim made an error by substituting the equation into the initial equation rather than into the other one.
The solution to the system is (x,y) = (−4,−9).
The student made an error by substituting the equation into the initial equation rather than into the other one.
Page 276 Exercise 14 Answer
Given:
The perimeter of a photo frame is 36 inches.
The length is 2 inches greater than the width.
Find: the dimensions of the frame.
Use the formula of perimeter and use substitution method.
According to the formula for polygon, the perimeter of the photo frame is the sum of its sides,
P = 2l + 2w
Substitute P = 36 and l = w + 2 in P = 2l + 2w,
36 = 2(w + 2) + 2w
36 = 2w + 4 + 2w
36 = 4w + 4
36 − 4 = 4w
32 = 4w
Divide both sides by 4,
\(\frac{32}{4}=\frac{4 w}{4}\)
8 = w
The length of the photo frame 8 inches.
Substitute the value of w = 8 in L = w + 2,
L = 8 + 2
L = 10
The width of the photo frame is 10 inches.
The dimensions of the frame are:
The length of the photo frame 8 inches.
The width of the photo frame is 10 inches.
Page 276 Exercise 15 Answer
Given:
The capacity of the auditorium is 500 people.
The members would like to false $2,050 every night to cover all expenses, by selling tickets.
Find: each type of ticket must have been sold for the members to raise exactly $2,050.
Use substitution method.
Let d be the number of adult and s be the number of students.
If one day 500 people used the facility, the combined number of adults and student on that day,
d + s = 500.
The ticket for adults costs $6.50, and the ticket for students costs $3.50, so the expression for total earnings on that day,
6.50d + 3.50s.
The total earnings for the day were $2050, so the expression must be equal to this amount,
6.50d + 3.50s = 2050.
Solve for d,
d + s = 500
d = 500 − s
Substitute the value of d = 500 − s in 6.5d + 3.5s = 2050,
6.5(500 − s) + 3.5s = 2050
3250 − 6.5s + 3.5s = 2050
3250 − 3s = 2050
3250 − 2050 = 3s
1200 = 3s
Divide both sides by 3,
s = 400
The number of students s = 400.
Substitute the value of s = 400 in d + s = 500,
d + 400 = 500
d = 500 − 400
d = 100
The number of adults d = 100.
To raise the fund of $2050, there should be 100 adults and 400 students.
Given:
At one performance, there were three times as many student tickets sold as adult tickets.
There were 480 tickets sold at that performance
Find: ticket sales fall below $2,050.
Use substitution method.
According to question s = 3d.
Since the total number of ticket sold is 480,
d + s = 480
Substitute s = 3d in d + s = 480,
d + 3d = 480
4d = 480
Divide both sides by 4,
d = 120
So, the number of adults are d = 120.
Substitute the value of d = 120 in s = 3d,
s = 3(120)
s = 360
So, the number of students are s = 360.
Total earning T from tickets,
T = s × 3.50 + d × 6.50.
Substitute the value of s = 360 and d = 120 in
T = s × 3.50 + d × 6.50,
T = s × 3.50 + d × 6.50
T = 360 × 3.50 + 120 × 6.50 = 2040
Total earning T from tickets are $2,040.
So, the goal is to fall short,
$2050 − $2040 = $10.
The goal to achieve total payment of $2050 is to fall short by $10.
Page 276 Exercise 16 Answer
Given:
y = 145 – 5x …(1)
0.1y + 0.5x = 14.5 …(2)
Find: the solution of the equation.
Try to compare both equations,
Rearrange the equation(2),
∴ 0.1y = 14.5 − 0.5x
∴y = 145 − 5x (multiply by10)
So here both lines are coincidental and they have infinite solutions.
Option A is correct.
Put x = 20 in eq.(1),
∴ y = 145 − 5(20)
∴ y = 145 − 100
∴ y = 45
means point (20,45) is solution.
Option B is correct.
Put x = 10 in eq.(1),
∴ y = 145 − 50
∴ y = 95
means point (10,95) is solution.
Option C is correct.
Here both lines are coincidental so they have infinite solutions.
So option D is incorrect.
Equations y = 145 − 5x and 0.1y + 0.5x = 14.5 have infinite solutions and (20,45) and (10,95) are also solutions.
Option A,B and C are correct options.