Envision Math Grade 8, Volume 1, Chapter 1 Real Number
Page 2 Question 1 Answer
A real number would be any number which can be discovered in the actual world. Numbers can be found all around us.
Natural numbers are being used to count objects.
Rational numbers are being used to portray fractions.
Irrational numbers are being used to calculate the square root of an amount.
Integers are used to measure temperature, among other things.
These various types of numbers combine form a gathering of real numbers.
Except complex numbers, everything come under real numbers.
It is denoted by R and it is the union of both rational and irrational numbers and it is represented by \(R=Q \cup \bar{Q}\)
Page 2 Question 2 Answer
A real number would be any number which can be discovered in the actual world. Numbers can be found all around us.
Natural numbers are being used to count objects.
Rational numbers are being used to portray fractions.
Irrational numbers are being used to calculate the square root of an amount.
Integers are used to measure temperature, among other things.
These various types of numbers combine to form a gathering of real numbers.
Real numbers are used in many places to solve problems. For example, it is used to portray fractions, determine square roots, measure temperature, and for counting things, etc.
Page 5 Exercise 1 Answer
We know that the addition of zeroes at the end of a decimal number doesn’t change its value.
A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.
Even though we add repeating zeroes, the number of decimals present in the given number is finite.
The given number terminates at this point. Thus, it is a terminating decimal.
A finite number of decimals can also be represented in the form of repeating zeroes at the end.
For example,
12.2750000 or 12.275
15.840000 or 15.84
These are some of the examples of terminating decimal which has repeating zeros in it.
A terminating decimal is a decimal that ends in repeating zeros.
Page 5 Exercise 2 Answer
We know that the addition of zeroes at the end of a decimal number doesn’t change its value.
But if the decimal gets repeated again and again, the loop goes endlessly and the digits repeat forever.
A number that has an infinite number of decimals in it is termed to be the repeating decimals.
A repeating decimal doesn’t terminate at any point. The decimal will be infinite.
For example,
15.57 or 15.575757….
\(19.75 \overline{4} \text { or } 19.754444444 \ldots\)These are some of the examples of repeating decimal which has repeating digits in it.
A repeating decimal is a decimal in which a digit or digits repeat endlessly.
Page 5 Exercise 4 Answer
We can write any number as a fraction.
A fraction can be used to describe the part of the things.
It is described as a part of a whole or a part of a set.
The division of any number is said to be the fraction.
For example, if we are going to eat half of the eight eggs we have, it is represented as,
\(\frac{1}{2} \times 8=4\)A fraction is a number that can be describe a part of a whole, a part of a set, a location on a number line, or a division of whole numbers.
Page 5 Exercise 7 Answer
Given decimal is 7.0001
We need to determine whether the given decimal is terminating or repeating.
The given number is 7.0001
It can also be written as 7.00010000000000000000…
Since they both represent the same.
This is because the addition of zeroes at the end of a decimal number doesn’t change its value.
A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.
Even though we add repeating zeroes, the number of decimals present in the given number is finite. i.e., .0001.
The given number terminates at this point. Thus, it is a terminating decimal.
The given number 7.0001 is a terminating decimal.
Page 5 Exercise 9 Answer
Given decimal is \(1.1 \overline{7} 8\)
We need to determine whether the given decimal is terminating or repeating.
The given number is \(1.1 \overline{7} 8\)
A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.
Even though we add repeating zeroes, the number of decimals present in the given number is finite.
If the number of decimals is infinite and the number gets repeated again and again, it is referred as repeating decimal.
The given number doesn’t terminate at any point as it has an infinite number of decimals.
The number 178 gets repeated again and again.
The given number can also be represented as 1.178178178…
Thus, it is a repeating decimal.
The given number \(1.1 \overline{7} 8\) is a repeating decimal.
Page 5 Exercise 10 Answer
Given decimal is −4.03479
We need to determine whether the given decimal is terminating or repeating.
The given number is −4.03479
A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.
Even though we add repeating zeroes, the number of decimals present in the given number is finite.
The given number terminates at this point as it has a finite number of decimals. Thus, it is a terminating decimal.
The given number -4.03479 is a terminating decimal.
Page 5 Exercise 11 Answer
We need to find the product of 2.2
Performing multiplication on the given numbers, we get,
2.2 = 2 x 2
= 4
Thus, the product will be 4.
The product of 2.2 = 4
Page 5 Exercise 12 Answer
We need to find the product of -5 . -5
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers, we get,
(−5)⋅(−5)=5×5
=25
Thus, the product will be 25.
The product of −5 ⋅ −5 = 25
Page 5 Exercise 13 Answer
We need to find the product of 7⋅7
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers, we get,
7 ⋅ 7 = 7 × 7
= 49
Thus, the product will be 49
The product of 7⋅7 = 49
Page 5 Exercise 14 Answer
We need to find the product of −6⋅(−6)⋅(−6)
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers, we get,
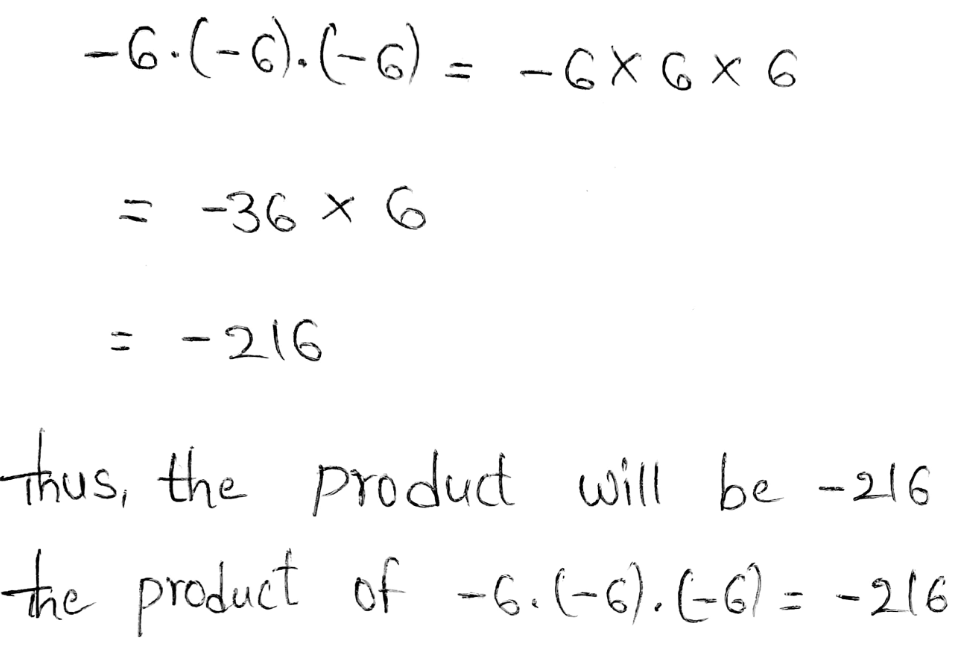
Thus, the product will be −216
The product of −6⋅(−6)⋅(−6) = −216
Page 5 Exercise 16 Answer
We need to find the product of −9⋅(−9)⋅(−9)
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers, we get,
The product of −9⋅(−9)⋅(−9) = −729
Page 5 Exercise 17 Answer
We need to simplify the given expression (4⋅10)+(5⋅100)
Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.
Adding a number to a certain time is simplified as the form of multiplication.
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers and adding the result, we get,
The simplification of the given number results in (4.10) + (5.100) = 540
Page 5 Exercise 19 Answer
We need to simplify the given expression (2.100)+(7.10)
Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.
Adding a number to a certain time is simplified as the form of multiplication.
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers and adding the result, we get,
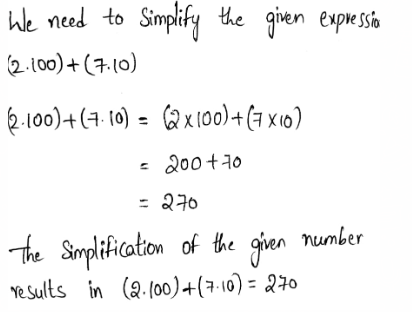
The simplification of the given number results in (2.100)+(7.10) = 270
Page 5 Exercise 20 Answer
We need to simplify the given expression (9⋅1000)+(4⋅10)
Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.
Adding a number to a certain time is simplified as the form of multiplication.
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers and adding the result, we get,
The simplification of the given number results in (9⋅1000)+(4⋅10)=9040
Page 5 Exercise 21 Answer
We need to simplify the given expression (3⋅1000)−(2⋅100)
Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.
Adding a number to a certain time is being simplified as the form of multiplication.
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers and subtracting the result, we get,
The simplification of the given number results (3.1000) – (2.100) = 2800
Page 5 Exercise 22 Answer
We need to simplify the given expression (2⋅10)+(7⋅100)
Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.
Adding a number to a certain time is being simplified as the form of multiplication.
In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.
The product of a negative and a positive number will result in a negative number.
Performing multiplication on the given numbers and adding the result, we get,
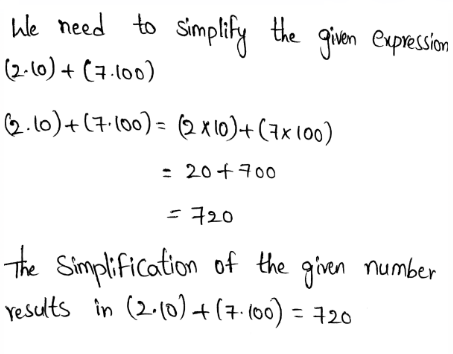
The simplification of the given number results in (2.10) + (7.100) = 720
Page 6 Exercise 1 Answer
We need to use the Graphic organizer to help you understand new vocabulary terms such as cube root, irrational number, a perfect cube, perfect square, scientific notation, and square root.
Cube root can be found by finding a number that when multiplied three times by itself gives the original number.
A square root can be found by finding a number that when multiplied two times by itself gives the original number.
If we multiply an integer three times by itself, it will result in a perfect cube.
If we multiply an integer two times by itself, it will result in a perfect square.
Expressing the biggest or the smallest number in decimal form is referred to the scientific notation.
A number that cannot be expressed as a fraction is said to be an irrational number.
Cube Root:
Definition – A number which when multiplied 3 times by itself gives the original number.
Example – \(\sqrt[3]{64}=4\)
Irrational number:
Definition – A number that cannot be expressed as a fraction but in decimal form.
Example – 0.24556766666…
Perfect cube:
Definition – The number obtained If we multiply an integer 3 times by itself.
Example – 3×3×3=27
Perfect square:
Definition – The number obtained If we multiply an integer 2 times by itself.
Example – 3×3=9
Scientific notation:
Definition – Expressing the biggest or the smallest number in decimal form.
Example – 1.543543543… = \(1.5 \overline{4} 3\)
Square Root:
Definition – A number which when multiplied 2 times by itself gives the original number.
Example – \(\sqrt[2]{16}=4\)
Page 7 Exercise 1 Answer
Given that, Jaylon has a wrench labeled 0.1875 inch and bolts labeled in fractions of an inch. We need to find which size bolt will fit best with the wrench.
The given bolt sizes are \(\frac{3}{8}, \frac{1}{8}, \frac{3}{16}, \frac{1}{4}\)inches.
Solving each fraction to find the equivalent size as that of the wrench given,
\(\frac{3}{8}=0.375\)
The bolt size which best fit the wrench is \(\frac{3}{16}\) inch bolt.
\(\frac{3}{16}\) inch size bolt will fit best with the wrench.
Page 7 Exercise 1 Answer
We need to explain how we can write these numbers in the same form.
The given wrench size is 0.1875 inch
This is of in decimal form.
Meanwhile, the given bolt \(\frac{3}{8}, \frac{1}{8}, \frac{3}{16}, \frac{1}{4}\)inches.
This is of fractional form.
We can easily convert the given fractions to decimals by dividing the fractions given.
It can be done as follows,
\(\frac{3}{8}=0.375\) \(\frac{1}{8}=0.125\) \(\frac{3}{16}=0.1875\) \(\frac{1}{4}=0.25\)We can write the given numbers in the same form by converting the fractions into decimals.
Page 7 Exercise 1 Answer
We need to explain why is it useful to write a rational number as a fraction or as a decimal.
A unique feature of a rational number is that it can be written in the form of a fraction.
Not every decimal is denoted to be the rational number.
Only repeating and the terminating decimal can come under the category of rational number.
It is useful to write it as a fraction or a decimal to make the computations easier.
It is useful to write a rational number as a fraction or as a decimal to help make the calculations easier.
Page 8 Exercise 1 Answer
Given that, in another baseball division, one team had a winning percentage of 0.444…..We need to determine the fraction of their games the team won.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each sides of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The winning percentage is converted to fractions as,
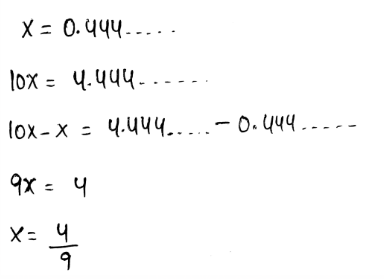
Page 9 Exercise 2 Answer
We need to write the repeating decimal 0.63333… as a fraction.
A repeating decimal can be written as a fraction by assuming the decimal as a variable..
After that, multiply each sides of it by the multiples of 10
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
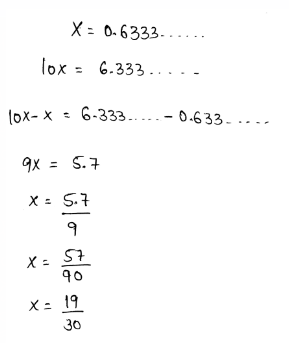
The repeating decimal 0.6333… is converted to fraction as \(\frac{19}{30}\)
Page 9 Exercise 3 Answer
We need to write the repeating decimal 4.1363636… as a fraction.
A repeating decimal can be written as a fraction by assuming the decimal as a variable..
After that, multiply each sides of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
The repeating decimal 4.1363636… is converted to fraction as \(\frac{455}{110}\)
Page 10 Exercise 2 Answer
We need to explain why we multiply by a power of 10 when writing a repeating decimal as a rational number.
A repeating decimal can be written as a fraction by assuming the decimal as a variable..
After that, multiply each sides of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
We can determine the power of ten to multiply by in the second step at the right is by calculating how many places after the decimal does the given numbers gets repeated.
Here, the given number gets repeated after one decimal place. Thus, the power of ten is one.
This step is done to convert the given repeating number to a fraction.
We can multiply a repeating decimal by a power of 10 when writing a repeating decimal as a rational number to convert it to a fractional number.
Page 10 Exercise 3 Answer
We need to explain how we could decide which power of 10 to multiply an equation when writing a decimal with repeating digits as a fraction.
A repeating decimal can be written as a fraction by assuming the decimal as a variable..
After that, multiply each sides of it by the multiples of 10.
Subtract both the expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
We can determine the power of ten to multiply by in the second step at the right is by calculating how many places after the decimal does the given numbers gets repeated.
Here, the given number gets repeated after one decimal place. Thus, the power of ten is one.
We can determine the power of ten to multiply an equation when writing a decimal with repeating digits as a fraction by determining the number of places after the decimal does the given number gets repeated.
Page 10 Exercise 4 Answer
Given that, a survey reported that \(63 . \overline{63}\)% of moviegoers prefer action films. This percent represents a repeating decimal. We need to write it as a fraction.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each sides of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
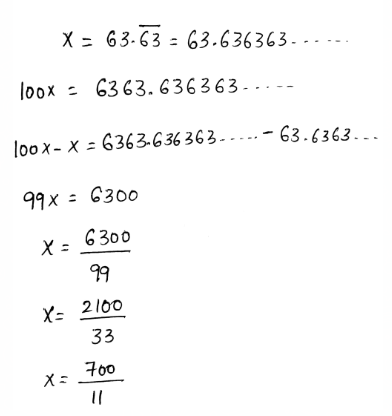
The given percent is written as a fraction as \(\frac{700}{11}\)
Page 10 Exercise 5 Answer
We need to write the given decimal 2.3181818… as a mixed number.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
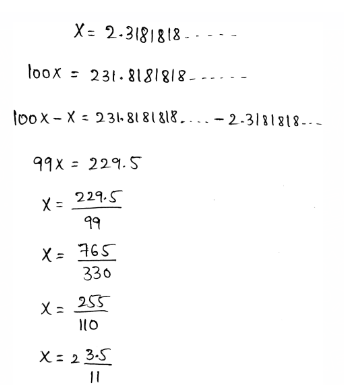
The mixed fraction of the given repeating decimal is \(x=2 \frac{3.5}{11}\)
Page 11 Exercise 10 Answer
Given that, Tomas asked 15 students whether summer break should be longer. He used his calculator to divide the number of students who said yes by the total number of students. His calculator showed the result as 0.9333….. . We need to write this number as a fraction.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
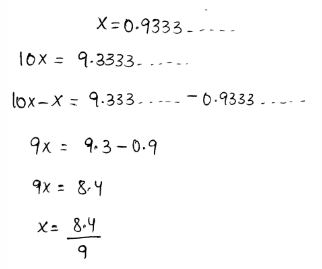
The given decimal 0.9333… is equal to \(x=\frac{8.4}{9}\)
Page 11 Exercise 12 Answer
We need to write the given decimal \(0 . \overline{8}\) as a fraction.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
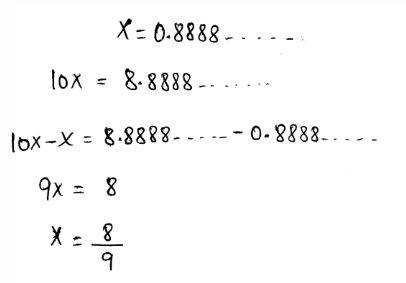
The given decimal is converted into a fraction as \(x=\frac{8}{9}\)
Page 12 Exercise 13 Answer
We need to write the given decimal \(1 . \overline{48}\) as a mixed number.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
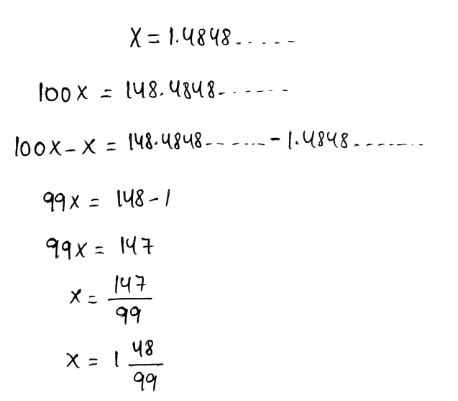
The given decimal is converted into a mixed number as \(x=1 \frac{48}{99}\)
Page 12 Exercise 14 Answer
We need to write the given decimal \(0 . \overline{6}\)
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
The given decimal is converted into a fraction as \(\frac{6}{9}\)
Page 12 Exercise 15 Answer
Given that a manufacturer determines that the cost of making a computer component is $2.161616. We need to write the cost as a fraction and as a mixed number.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
Subtract both expressions to write the repeating decimals as fractions.
The decimal is converted to fractions as,
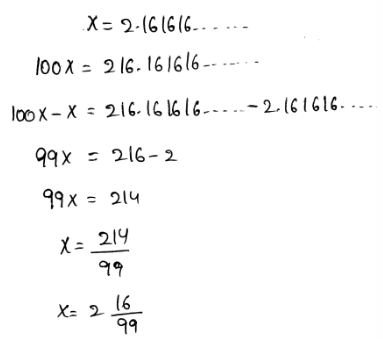
The given decimal is converted into a fraction as \(\frac{214}{99}\) and as a mixed number as \(2 \frac{16}{99}\)
Page 12 Exercise 16 Answer
We need to explain the need for the number of repeating digits we use while writing a repeating decimal as a fraction.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
The power of the number ten which we can use to convert the decimal to fraction can be obtained by looking into the number of repeating digits in a decimal.
If the number of repeating digits is two, then the power of ten multiplied with the decimal will also be two.
When writing a repeating decimal as a fraction, the number of repeating digits we use matters the most since it determines the power of ten which we multiply it with the decimal to make it as a fraction.
Page 12 Exercise 17 Answer
When writing a repeating decimal as a fraction, we need to explain why does the fraction always have only 9s or 9s and Os as digits in the denominator.
A repeating decimal can be written as a fraction by assuming the decimal as a variable.
After that, multiply each side of it by the multiples of 10.
The power of the number ten which we can use to convert the decimal to fraction can be obtained by looking into the number of repeating digits in a decimal.
If the number of repeating digits is two, then the power of ten multiplied with the decimal will also be two.
The subtraction of any number of the power of ten by one will result in a number 9 or the multiples of it.
This is why the denominator is always 9 or 9 and 0.
The number divided by 9s or 9s and 0s will result in repeating decimals. That is why when we convert that to a fraction, the denominator is always 9s or 9s and 0s.
Page 12 Exercise 18 Answer
We need to find the decimal which is equivalent to \(\frac{188}{11}\)
The given fraction is \(\frac{188}{11}\)
Converting the given fraction to a decimal by dividing the fraction, thus we get,
\(\frac{188}{11}=17.090909 \ldots\)= \(17 . \overline{09}\)
The decimal which is equivalent to \(\frac{188}{11} \text { is (A) } 17 . \overline{09}\)
Page 12 Exercise 19 Answer
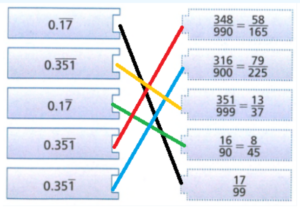
We need to draw lines to connect each repeating decimal on the left with an equivalent fraction on the right.
Solving each fraction one by one, we get,
\(\frac{58}{165}=0.351515 \ldots=0.35 \overline{1}\) \(\frac{79}{225}=0.351111 \ldots=0.35 \overline{1}\)\(\frac{13}{37}=0.351351 \ldots=0.3 \overline{5}\) 1
\(\frac{8}{45}=0.1777 \ldots=0.1 \overline{7}\) \(\frac{17}{99}=0.171717 \ldots=0 . \overline{17}\)