Envision Math Accelerated Grade 7 Volume 1 Chapter 3 Analyze And Use Proportional Relationships
Given:
Statement
To find/solve
Proportional relationships can be recognized by using the terms.
Terms are numbers compared in ratios.
Terms can be used to compare and solve the problem using this ratio.
Terms can be used to compare and solve the problem using this ratio.
Given:
Statement
To find/solve
If 2 values have a constant multiple (constant of proportionality ) and can be written as y = kx equation they are proportional (they have a proportional relationship).
Access to safe drinking water is measured by the percentage of the population having access to and using improved drinking water sources.
Improved drinking water sources should, but do not always, provide safe drinking water, and include piped household water connection, and public standpipes.

Question. Solve the given two ratios \(\frac{2 \text { dogs }}{3 \text { cats }}=\frac{2}{3}\) \(\frac{10 \text { dogs }}{15 \text { cats }}=\frac{10}{15}\)
Solve the given two ratios, and we get
\(\frac{2 \text { dogs }}{3 \text { cats }}=\frac{2}{3}\) \(\frac{10 \text { dogs }}{15 \text { cats }}=\frac{10}{15}\)=\(\frac{2}{3}\)
Here, we can see that both ratios result in the same answer.
Thus, the given ratios are equivalent to each other.
Thus, they are equivalent ratios.
\(\frac{2 \text { dogs }}{3 \text { cats }}\) and \(\frac{10 \text { dogs }}{15 \text { cats }}\) are an example of equivalent ratios.
The rate comes under the category of ratios.
But all ratios cannot be described as rates.
This is because the ratio deals with the same or different quantities.
While the rate deals with two different quantities.
For example, if we compare speed and distance together, the fraction is said to be the rate. Since the unit of both of them are different.
A rate is a type of ratio that has both terms expressed in different units.
A fraction is said to be the comparison of two quantities.
If we have a fraction in the fraction itself, it is then said to be a complex fraction.
A complex fraction has a fraction in the numerator, denominator, or in both of them.
For example: \(\frac{5}{\frac{12}{7}}\), \(\frac{\frac{8}{7}}{4}\) are some of the examples of the complex fractions.
A complex fraction has a fraction in its numerator, denominator, or both.
Question. Solving the equivalent ratio \(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{? \text { girls }}\)
We need to complete the given equivalent ratio \(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{? \text { girls }}\)
Solving the given equivalent ratio, we get
\(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{? \text { girls }}\) \(\frac{4}{7}=\frac{8}{x}\)x = \(8 \times \frac{7}{4}\)
x = 2 × 7
x = 14 girls
\(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{14 \text { girls }}\)Question. Solving the equivalent ratio \(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{? \text { tıres }}{1 \text { car }}\)
We need to complete the given equivalent ratio \(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{? \text { tıres }}{1 \text { car }}\)
Solving the given equivalent ratio, we get
\(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{? \text { tıres }}{1 \text { car }}\) \(\frac{16}{4}=\frac{x}{1}\)x = \(\frac{16}{4}\)
x = 4 tires
\(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{4 \text { tıres }}{1 \text { car }}\)Question. Solving the equivalent ratio \(\frac{8 \text { correct }}{10 \text { total }} = \frac{? \text { correct }}{50 \text { total }}\)
We need to complete the given equivalent ratio \(\frac{8 \text { correct }}{10 \text { total }} = \frac{? \text { correct }}{50 \text { total }}\)
Solving the given equivalent ratio, we get
\(\frac{8 \text { correct }}{10 \text { total }} = \frac{? \text { correct }}{50 \text { total }}\) \(\frac{8}{10}=\frac{x}{50}\)x = \(50 \times \frac{8}{10}\)
x = 5 × 8
x = 40 correct
\(\frac{8 \text { correct }}{10 \text { total }} = \frac{40\text { correct }}{50 \text { total }}\)Question. Solving the equivalent ratio \(\frac{16 \text { pearls }}{20 \text { opals }}=\frac{8 \text { pearls }}{? \text { opals }}\)
We need to complete the given equivalent ratio \(\frac{16 \text { pearls }}{20 \text { opals }}=\frac{8 \text { pearls }}{? \text { opals }}\)
Solving the given equivalent ratio, we get
\(\frac{16 \text { pearls }}{20 \text { opals }} = \frac{8 \text { pearls }}{? \text { opals }}\)
\(\frac{16}{20}=\frac{8}{x}\)
x = \(8 \times \frac{5}{4}\)
x = 2 × 5
x = 10 opals
\(\frac{16 \text { pearls }}{20 \text { opals }} = \frac{8 \text { pearls }}{10\text { opals }}\)Question. Solving the equivalent ratio \(\frac{7 \text { balls }}{9 \text { bats }}=\frac{? \text { balls }}{27 \text { bats }}\)
We need to complete the given equivalent ratio \(\frac{7 \text { balls }}{9 \text { bats }}=\frac{? \text { balls }}{27 \text { bats }}\)
Solving the given equivalent ratio, we get
\(\frac{7 \text { balls }}{9 \text { bats }} = \frac{? \text { balls }}{27 \text { bats }}\) \(\frac{7}{9}=\frac{x}{27}\)x = \(27 \times \frac{7}{9}\)
x = 3 × 7
x = 21 balls
\(\frac{7 \text { balls }}{9 \text { bats }} = \frac{21 \text { balls }}{27 \text { bats }}\)Question. Write the given situation as a rate. John travels 150 miles in 3 hours. Find the rate at which John travels.
We need to write the given situation as a rate. Here, John travels 150 miles in 3 hours.
Finding the rate at which John travels, we get
\(\frac{\text { Distance }}{\text { Number of hours }} = \frac{150 \text { miles }}{3 \text { hours }}\)= 50 miles per hour
John travels at the rate of 50 miles/hr
Question. Write the given situation as a rate. Here, Cameron ate 5 apples in 2 days. Find the rate at which Cameron eat.
We need to write the given situation as a rate. Here, Cameron ate 5 apples in 2 days.
Finding the rate at which Cameron eats, we get
\(\frac{\text { Number of apples }}{\text { Number of days }}=\frac{5}{2}\)= 2.5 apples per day
Cameron ate 2.5 apples per day.
Question. Write an equation that represents the pattern in the table. Find the rate of the given data.
We need to write an equation that represents the pattern in the table.
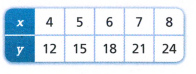
Finding the rate of the given data
\(\frac{y}{x}=\frac{12}{4}\) = 3
\(\frac{y}{x}=\frac{15}{5}\) = 3
\(\frac{y}{x}=\frac{18}{6}\) = 3
\(\frac{y}{x}=\frac{21}{7}\) = 3
\(\frac{y}{x}=\frac{24}{8}\) = 3
Therefore, the ratio is \(\frac{y}{x}=\frac{3}{1}\)
Thus, the equation of the pattern in the table will be
\(\frac{y}{x}=\frac{3}{1}\)y = 3x
The equation that represents the pattern in the table will be y = 3x
