Envision Math Accelerated Grade 7 Volume 1 Chapter 2 Real Numbers
Page 85 Exercise 2 Answer
The numbers given in decimal form can be written in fractional form.
The first step is to remove the decimal and divide the number by the power of ten.
Where the power of ten is decided by the number of digits after the decimal.
The second step is to write the fraction form in the simplest form.
The decimal form of number can be written in the fractional form by removing the decimal and then converting is to the simplest fractional form as mentioned above.
Page 85 Exercise 3 Answer
Rational numbers written in the form of fractions are precise.
The values of fractions are very accurate and the chances of error are very less.
So, rational numbers are preferred to be written in the form of fractions which can be converted into a decimal form or vice-versa.
It is useful to write a rational number as a fraction as it gives an accurate value.

Envision Math Accelerated Grade 7 Chapter 2 Exercise 2.1 Solutions
Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 86 Question 1 Answer
A repeating decimal is one in which the digits after the decimal get repeated.
It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equal to any variable.
Then, that equation is multiplied by 10,100,1000,..depending upon the number of repeating digits.
After solving the obtained equations, the variable comes out equal to a fraction.
The example is 0.444…
Let x= 0.444….…….(1)
Since,0.444…. has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 4.444…………(2)
Subtract equation (1) from (2)
10x−x = 4.444…−0.444…
9x = 4
x\(=\frac{4}{9}\)
A repeating decimal can be written as a fraction by a number of steps as shown above.
Page 86 Exercise 1 Answer
The winning percentage of a team is 0.444…
Let x = 0.444….…….(1)
Since, 0.444…. has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 4.444…………(2)
Subtract equation (1) from (2)
10x−x = 4.444…−0.444…
9x = 4
x\( = \frac{4}{9}\)
The team won \( = \frac{4}{9}\) of their games.
Page 87 Exercise 2 Answer
The given repeating decimal is 0.6333…
Let x = 0.6333….…….(1)
Since,0.6333…. has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 6.333…………(2)
Subtract equation (1) from (2)
10x − x = 6.333…−0.633…
9x= 5.7
x = \(\frac{5.7}{9}\)
x = \(\frac{57}{90}\)
x = \(\frac{19}{30}\)
0.6333…. can be written in the fractional form as\(\frac{19}{30}\).
Page 87 Exercise 3 Answer
The given repeating decimal is 4.1363636…
Let x = 4.1363636….…….(1)
Since, 4.1363636…. has two repeating unit
Multiply both sides of equation (1) by 100
100x = 413.6363… ………(2)
Subtract equation (1) from (2)
100x−x = 413.6363…−4.1363…
99x = 409.5
x = \(\frac{409.5}{99}\)
x = \(\frac{4095}{990}\)
x = \(\frac{455}{110}\)
x = \(\frac{91}{22}\)
4.1363636….can be written in the fractional form as \(\frac{91}{22}\)
Page 86 Exercise 1 Answer
A repeating decimal is the one in which the digits after the decimal get repeated.
It can be converted into a fraction by a method in which the given repeating decimals are put equal to any variable.
Then, that equation is multiplied by 10,100,1000,..depending upon the number of repeating digits.
After solving the obtained equations, the variable comes out equal to a fraction.
So, the power of ten can be known by the number of repeating digits present in the given repeating fraction.
By checking the number of repeating digits, we know by what power of ten we multiply in the second step.
Envision Math Grade 7 Real Numbers Exercise 2.1 Answers
Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 88 Exercise 1 Answer
A repeating decimal is the one in which the digits after the decimal get repeated.
It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equals to any variable.
Then, that equation is multiplied by 10,100,1000,.. depending upon the number of repeating digits.
After solving the obtained equations, the variable comes out equal to a fraction.
The example is 0.444…
Let x = 0.444….…….(1)
Since, 0.444…. has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 4.444…………(2)
Subtract equation (1) from (2)
10x−x = 4.444…−0.444…
9x = 4
x =\(\frac{4}{9}\)
A repeating decimal can be written as fraction by a number of steps as shown above.
Page 88 Exercise 2 Answer
A repeating decimal is the one in which the digits after the decimal get repeated.
It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equals to any variable.
Then, that equation is multiplied by 10,100,1000,.. depending upon the number of repeating digits.
After solving the obtained equations, the variable comes out equal to a fraction.
So, the power of ten can be known by the number of repeating digits present in the given repeating fraction.
We multiply by the power of ten to convert the irrational number to rational number.
In the second step, the given repeating decimal is multiplied by the power of ten to get a rational number.
Page 88 Exercise 3 Answer
A repeating decimal is the one in which the digits after the decimal get repeated.
It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equals to any variable.
Then, that equation is multiplied by 10,100,1000,.. depending upon the number of repeating digits.
After solving the obtained equations, the variable comes out equal to a fraction.
So, the power of ten can be known by the number of repeating digits present in the given repeating fraction.
By checking the number of repeating digits, we can know by what power of ten we have to multiply in the second step.
Page 88 Exercise 4 Answer
The given repeating decimal is \(63. \overline{63}\) =63.6363….
Let x = \(63. \overline{63}\)=63.6363…. …….(1)
Since, 63.6363…. has two repeating unit
Multiply both sides of equation (1) by 100
100x = 6363.6363…………(2)
Subtract equation (1) from (2)
100x−x = 6363.6363…−63.6363…
99x = 6300
x\(=\frac{6300}{99}\)
=\(\frac{700}{11}\)
\(63. \overline{63}\) can be represented in fractional form as\(\frac{700}{11}\)
Page 88 Exercise 5 Answer
The given repeating decimal is 0.16666…
Let x = 0.16666…. …….(1)
Since,0.16666…. has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 1.66666………(2)
Subtract equation (1) from (2)
10x−x = 1.66666…−0.16666…
9x = 1.5
x = \(\frac{1.5}{9}\)
x = \(\frac{15}{90}\)
x = \(\frac{1}{6}\)
0.16666… can be represented in fractional form as \(\frac{1}{6}\)
Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 88 Exercise 6 Answer
The given repeating decimal is 2.3181818…
Let x = 2.3181818….…….(1)
Since,2.3181818…. has two repeating unit
Multiply both sides of equation (1) by 100
100x = 231.8181818…………(2)
Subtract equation (1) from (2)
100x−x = 231.8181818…−2.3181818…
99x = 229.5
x = \(\frac{229.5}{99}\)
x = \(\frac{2295}{990}\)
x = \(2 \frac{35}{110}\)
2.3181818…..can be represented in mixed number form as \(2 \frac{35}{110}\).
Page 89 Exercise 7 Answer
The given repeating decimal is 0.2121…
Let x = 0.2121……….(1)
Since, 0.2121… has two repeating unit
Multiply both sides of equation (1) by 100
100x = 21.2121…………(2)
Subtract equation (1) from (2)
100x−x = 21.2121…−0.2121…
99x = 21
x = \(\frac{21}{99}\)
x = \(\frac{7}{33}\)
0.2121… is equals to \(\frac{7}{33}\)
Page 89 Exercise 8 Answer
The given repeating decimal is \(3. \overline{7}\)
=3.777…
Let x =\(3 . \overline{7}\) =3.777……….(1)
Since, \(3. \overline{7}\)=3.777… has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 37.777…………(2)
Subtract equation (1) from (2)
10x−x = 37.777…−3.777…
9x = 34
x = \(\frac{34}{9}\)
\(3. \overline{7}\) is equals to 34 \(\frac{34}{9}\).
Page 89 Exercise 10 Answer
The given repeating decimal is 0.93333…
Let x = 0.93333……….(1)
Since, 0.93333… has only one repeating unit
Multiply both sides of equation (1) by 10
10 x =9.33333… ………(2)
Subtract equation (1) from (2)
10x−x = 9.33333…−0.93333…
9x = 8.4
x= \(\frac{8.4}{9}\)
x=\(\frac{14}{15}\)
0.93333…..is equals to \(\frac{14}{15}\)
Total number of students in the class are 15.
In the previous part, it was calculated that the number of students who said yes was divided by the number of total students.
Comes out to be \(\frac{14}{15}\) as the given number was \(0.9 \overline{3}\).
Therefore, it can be seen that the numerator represents the number of students who said yes which is equals to 14.
14 students said that summer break should be longer.
Solutions For Envision Math Accelerated Grade 7 Chapter 2 Exercise 2.1
Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 89 Exercise 11 Answer
The given repeating decimal is \(0. \overline{87}\).
Let x= \(0. \overline{87}\) =0.8787……….(1)
Since 0.87 has two repeating unit
Multiply both sides of equation (a) by 100
100x=87.8787…………(2)
Subtract equation (1) from (2)
100x−x = 87.8787…−0.8787…
99x = 87
x = \(\frac{87}{99}\)
= \(\frac{29}{33}\)
\(0. \overline{87}\) is equals to \(\frac{29}{33}\).
Page 89 Exercise 12 Answer
The given repeating decimal is \(0. \overline{8}\).
Let x= \(0. \overline{8}\) =0.888… …….(1)
Since 0.8has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 8.888…………(2)
Subtract equation (1) from (2)
10x−x = 8.888…−0.888…
9x = 8
x\( =\frac{8}{9}\)
\(0. \overline{8}\) is equals to \(=\frac{8}{9}\)
Page 90 Exercise 13 Answer
The given repeating decimal is \(1. \overline{48}\)
Let x=\(1. \overline{48}\) = 1.484848… …….(1)
Since 1.48 has two repeating unit
Multiply both sides of equation (1) by 100
100x = 148.484848…………(2)
Subtract equation (1) from (2)
100x−x = 148.484848…−1.484848…
99x = 147
x= \(\frac{147}{99}\)
x= \(\frac{49}{3.3}\)
x= \(1 \frac{16}{33}\)
\(1. \overline{48}\) is equals to \(1 \frac{16}{33}\)
Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 90 Exercise 14 Answer
The given repeating decimal is \(0. \overline{6}\).
Let x = \(0. \overline{6}\) = 0.666……….(1)
Since 0.6 has only one repeating unit
Multiply both sides of equation (1) by 10
10x = 6.666… ………(2)
Subtract equation (1) from (2)
10x−x = 6.666…−0.666…
9x = 6
x\(=\frac{6}{9}\)
x=\(\frac{2}{3}\)
\(0. \overline{6}\) is equal to \(\frac{2}{3}\)
Page 90 Exercise 15 Answer
The given repeating decimal is 2.161616…
Let x = 2.161616……….(1)
Since, 2.161616…has two repeating unit
Multiply both sides of equation (1) by 100
100x = 2.161616…………(2)
Subtract equation (1) from (2)
100x−x = 216.161616…−2.161616…
99x = 214
x=\(\frac{214}{99}\)
2.161616…. is equals to \(\frac{214}{99}\)
Page 90 Exercise 16 Answer
When writing a repeating decimals as fractions, The number of repeating digits tells us that by what power of ten.
we have to multiple the given repeating fraction.
If there is one digit that is repeating, then we will multiply the equation made in the first step by 10.
If there are two digits that are repeating, then we will multiply the equation made in the first step by 100 and so on.
The number of repeating digits matters because it will help us to determine the power of ten by which we have to multiply.
Page 90 Exercise 17 Answer
While converting from repeating decimal to fraction, in the first step, the given decimal is put equals to that and then the equation.
Is multiplied by the power of ten and then subtracted one from that resulting equation so as to remove the repeating digits after decimals.
This is the reason that we get the series of 9s while converting repeating decimals to fractions.
The fractions always have 9s or 0s as digit in denominator while converting repeating decimals to fractions to remove the repeating digits.
Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 90 Exercise 18 Answer
The given fraction is \(\frac{188}{11}\)
Let x = \(17. \overline{09} .\)……….(1)
Since 17.09has two repeating unit
Multiply both sides of equation (1) by 100
100x = 1709.0909… ………(2)
Subtract equation (1) from (2)
100x−x = 1709.0909…−17.0909…
99x = 1692
x = \(\frac{1692}{99}\)
x = \(\frac{188}{11}\)
\(\frac{188}{11}\)is equalis to \(17 . \overline{09} .\)
Grade 7 Envision Math Exercise 2.1 Real Numbers Step-By-Step Solutions
Page 90 Exercise 19 Answer
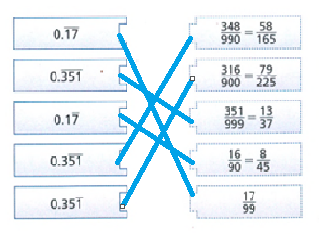
The given repeating decimal are \(0. \overline{17}, 0 . \overline{351}, 0 . \overline{17}, 0.3 \overline{51}, 0.35 \overline{1}\)
The repeating decimal \(0. \overline{17}\) is equivalent to \(\frac{17}{99}\)
The repeating decimal \(0. \overline{351}\) is equivalent to \(\frac{351}{999}\)=\(\frac{13}{37}\)
The repeating decimal \(0.1 \overline{7}\) is equivalent to \(\frac{16}{90}\)=\(\frac{8}{45}\)
The repeating decimal \( 0.3 \overline{51}\) is equivalent to \(\frac{348}{990}\)=\(\frac{58}{165}\)
The repeating decimal \( 0.35 \overline{1}\) is equivalent to \(\frac{316}{900}\)=\(\frac{79}{225}\)