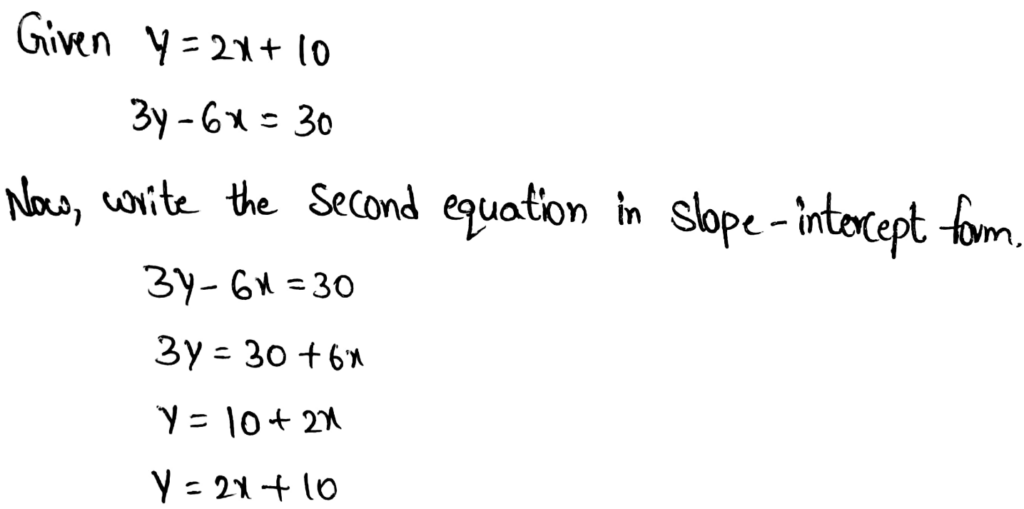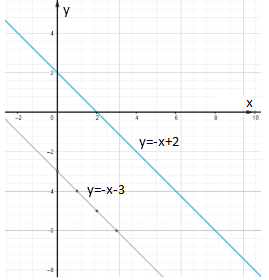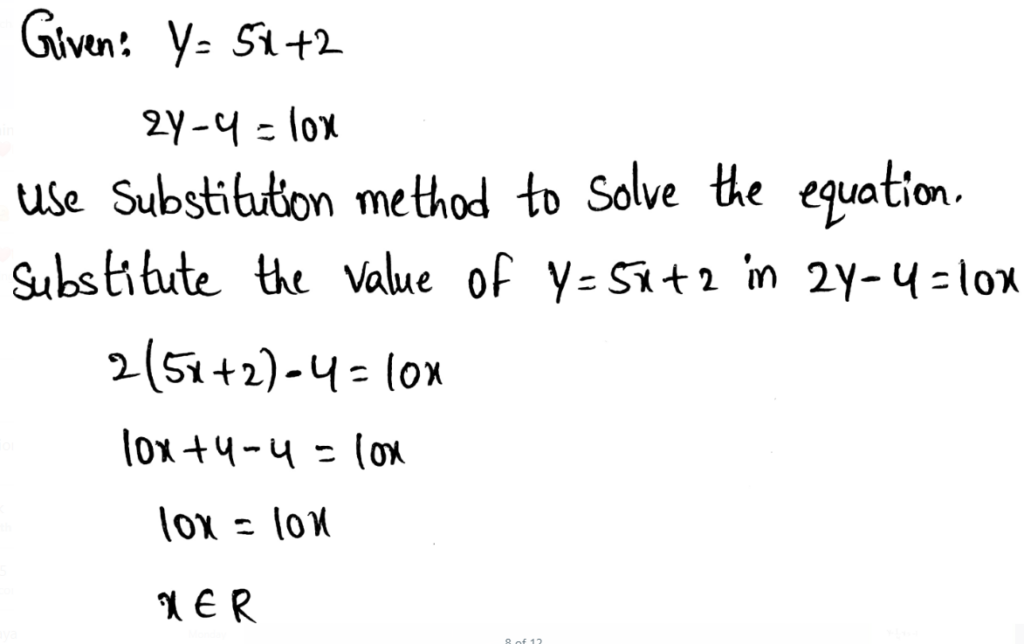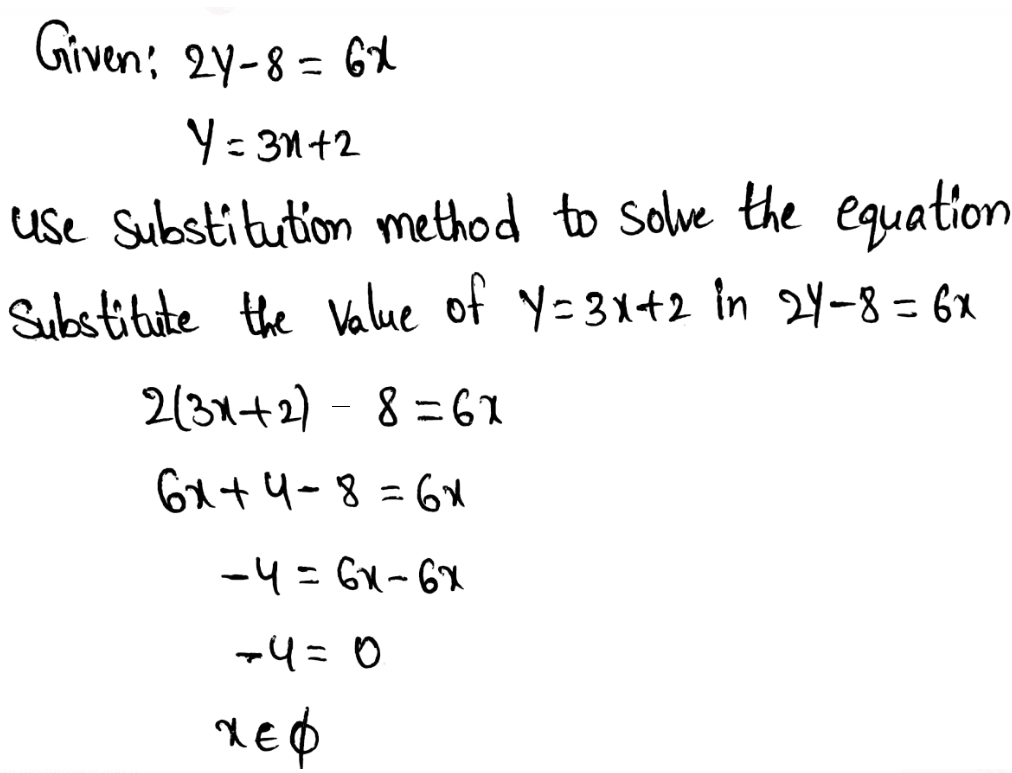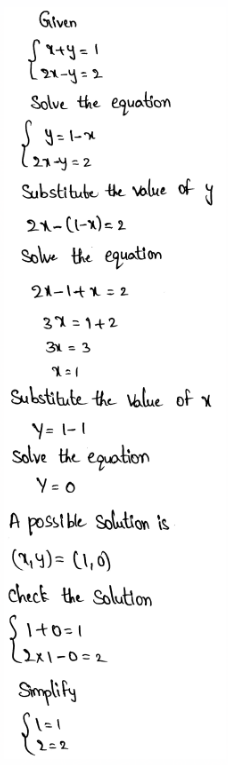Envision Math

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 315 Exercise 1 Answer

Given: Graph with two figure.

To find:

How can you map Figure A onto Figure B

To map Figure A onto Figure B, we have to do two transformations:

reflection across the y-axis

reflection across the x-axis

Notice that figures have the same shape and size, but orientation has changed. These are properties of the reflected figures.

Therefore, we can anticipate that there transformation will be reflection.

It is also important to say that is no matter what reflection was before.

Because the resulting picture, after the sequence of transformation, must be the same regardless of the order of transformation.

We can map Figure A onto Figure B using:

reflection across the y−axis.

Reflection across the x−axis.

Envision Math Grade 8 Volume 1 Chapter 6.5 Solutions

Page 315 Focus On Math Practices Answer

Given:

Graph for figure A and figure B

To find:

Is there another transformation or sequence of transformations that will map Figure A to figure B?

We can compose transformations by applying a sequence of two or more transformations.

And, if we look at the picture, we can see that we have to do more than one transformation to map Figure A to figure B.

To be precise, we have to:

– reflect the Figure A across the y-axis

– reflect the reflected figure across x-axis

It is important to emphasize that is no matter what transformation was before.

Because the resulting picture, after the sequence of transformation, must be the same

Yes, there is another transformation or sequence of transformations that will map Figure A to Figure B but the resulting picture, after the sequence of transformation, will be the same regardless of the order of transformations.

Page 316 Essential Question Answer

Given:

Graph for figure A and figure B

To find:

How can you use a sequence of transformations to map a preimage to its image?

We can compose transformations by applying a sequence of two or more transformations.

And, if we look at the picture, we can see that we have to do more than one transformation to map Figure A to Figure B.

To be precise, we have to:

reflect the Figure A across the y−axis

reflect the reflected figure across x−axis

It is important to emphasize that is no matter what transformation was before.

Because the resulting picture, after the sequence of transformation, must be the same regardless of the order of transformations.

The resulting picture, after the sequence of transformation, must be the same regardless of the order of transformations.

Congruence And Similarity Envision Math Exercise 6.5 Answers

Page 316 Convince Me Answer

Ava has decided to place the chairs directly across the couch.

She needs to do it by transformation.

We can see that Ava can compose these chairs across the couch by the method of transformation which is called linear transformation.

Finally, Ava can put the chairs across the couch by transformation.

Eva will use linear sequence for the transformation of chairs.

Page 317 Try It Answer

We had given two triangles ABC and A′′B′′C′′.

We need to find the transformation between them.

When two or more transformations are combined to form a new transformation, the result is called a sequence (or a composition) of transformations.

In a sequence of transformations, the first transformation produces an image upon which the second transformation is then performed.

The composition of transformation gives the mapping for the given triangle.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 318 Exercise 2 Answer

A preimage is rotated twice to its final position and opposite sign.

To compare the image and pre-image

If you follow is the rule :P(x, y) > 180° rotation

> P′(−x,−y). the negative signs don’t mean to make it negative but to change it to the opposite sign. If it’s positive it goes to negative. And if it’s negative is goes to positive. The rotated image would have the points: (1,2),(4,4),(3,7).

The signs don’t affect the position of the image.

Page 318 Exercise 3 Answer

Given:

A figure ABC, with vertices A(2,1),B(7,4) & C(2,7) is rotated clockwise about the origin, and then reflected across the y axis.

To: Describe another sequence that would result in the same image.

Step formulation: First perform the sequence of operation as given in question and then add another step to reconcile to the original image.

Perform the sequence of operation as given. First90∘

clockwise rotation about origin and then reflect about y
axis.

The sequence is shown below:

Now take the reflection of the last image about y = −x to reconsile to the original image. As shown in the below image:

Rotation about origin clockwise 90^∘ then reflection in y axis and finally the reflection about y = −x results in the same image.

Page 318 Exercise 4 Answer

Given:

To: Describe the transformation that maps the given figures.

Step formualtion: Take the reflection about the axis and then proceed.

First rotate WXYZ, 90^∘ anticlockwise about origin then translate 6 units down to map the figures. The sequence is shown below:

To map the images, WXYZ is rotated 90^∘ anticlockwise about origin and then translated 6 units downwards.

Page 318 Exercise 5 Answer

Given:

To: Describe the transformation that maps the given figures.

Step formualtion: Translate the figure 6 units down and then proceed.

To map the images, transform WXYZ 6 units down then reflection about y axis, then rotation about (−2,−4) in the clockwise direction for 90^∘ and then reflection about x = −2. The sequence is shown in the below figure:

To map the images, transform WXYZ 6 units down then reflection about y axis, then rotation about (−2,−4) in the clockwise direction for 90^∘ and then reflection about x = −2.

Envision Math Grade 8 Chapter 6.5 Explained

Page 318 Exercise 6 Answer

Given:

To find:

reflection of rectangle WXYZ

In order to find the reflection of the above we have to refer to the tip mentioned.

Draw a line y = 1

Since the point Z is one point above the line y = 1 the reflected point Z′ will be one point below the line y = 1

Using the same method, reflect points Y,X and W across the line y = 1 labeling them Y′X′ and W′

Translate each of the points Z′Y′X′ and W′ one unit right.

Label the translated points with Z′′,Y′′,X′′ and W′′

Connect the points to form a quadrilateral Z′′,Y′′,X′′ and W′′

The required image after a reflection across the line y = 1 and a translation 1 unit right is given.

Envision Math Grade 8 Topic 6.5 Congruence Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 319 Exercise 8 Answer

Given:

To find:

Location of translation of transformation of the given rectangle.

In order to find the location we have to follow the tip and plot the graph accordingly.

Draw the given rectangle on the graph.

Move all the points 3 units to the left and rename the rectangle as E′F′G′H′

Move all the points 3 units down.

The location of the quadrilateral E′F′G′H′ after two movement is shown

Rotate all the points 90^∘ about the origin

Therefore, the new location of E′F′G′H′ is shown

The new location of E′F′G′H′ is shown after 3 units left, 3 units right and 90^∘ rotation about the origin.

Solutions For Envision Math Grade 8 Exercise 6.5

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 319 Exercise 9 Answer

Given :

To describe a sequence of transformations that maps quadrilateral ABCD to quadrilateral HIJK.

First reflect the vertices of quadrilateral ABCD
then translate the vertices.

Reflect the vertices of quadrilateral ABCD along the x-axis

Then translate the vertices 6 units left and 1 unit upward to from quadrilateral HIJK

Thus, Reflection along the x-axis followed by the translation of 6 units left and 1 unit up maps the quadrilateral ABCD into the quadrilateral HIJK

Envision Math Grade 8 Chapter 6.5 Lesson Overview

Page 319 Exercise 10 Answer

Given:

To map △QRS to △Q′R′S′ with a reflection across the y-axis followed by a translation 6 units down.

Translate each of the points 6 units down then label the translated points.

The reflection line is x = 0.

Since the point R is two point left of the line x = 0, the reflected point R′ will be two point right of the line x = 0.

Using the same method, reflect points Q and S across the line x = 0 labeling them Q′,S′.

Translate each of the points Q′,R′,S′ six unit down.

Label the translated points with Q′,R′,S′ and connect them to form a triangle ΔQ′R′S′

Thus, the required image after a reflection across the line x = 0 and a translation 6 unit down is given.

Envision Math Grade 8 Volume 1 Chapter 6.5 Practice Problems

Page 319 Exercise 11 Answer

Given : A student says that he was rearranging furniture at home and he used a glide reflection to move a table with legs from one side of the room to the other.

To explain a glide reflection result in a functioning table

First draw the table image and point A.

Let the table be as shown and the point A represent the chair.

In glide reflection, the table is first translated as shown.

Then, the table is reflected along the line shown.

The resulting table after glide reflection is shown. it can be seen that it is a functioning table as the chair A is positioned correctly.

Thus, the resulting table after glide reflection is shown. it can be seen that it is a functioning table as the chair A is positioned correctly.

Envision Math 8th Grade Congruence And Similarity Topic 6.5 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 320 Exercise 13 Answer

Given :

To find which figure is the image of Figure A after a reflection across the x-axis and a translation 4 units right.

Reflect the figure A over the x-axis and translate the reflected figure.

Reflection of Figure A over the x-axis.

Translate the reflected figure 4 units to the right.

Therefore, the answer is Figure E.

Thus, the answer is letter D which is Figure E.

Given :

To find figure can be transformed into Figure G after a rotation 90^∘ about the origin, then a translation 13 units right and 4 units down.

First move the figure 4 units up and translate the figure then rotate 90^∘ about the origin.

In figure G, move the figure 4 units up.

Translate the figure 13 units to the left.

Rotate figure G′ through 90^∘ about the origin.

Then the 90^∘ rotated figure is similar to figure B.

Therefore, the answer is option A.

Thus, the correct answer is option A.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 309 Focus On Math Practices Answer

We can describe Maria’s change in position, when car returns to the position at which she began the ride, with rotation.

Because, a rotation is a transformation that turns a figure around a fixed point, called the center of rotation. And as we can see in the picture, each car turns around central part of the Ferris wheel.

If we want to come back to the start position, this means that we have to go through an entire drive, or an entire circle.

This transformation can be described by rotation for 360^∘.

This transformation can be described by rotation for 360^∘

Page 310 Essential Question Answer

Given:

The two dimensional figure.

To find:

How does a rotation affect the properties of a two-dimensional figure?

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Envision Math Grade 8 Volume 1 Chapter 6.4 Solutions

Page 310 Try It Answer

Given:

The architect continues to rotate the umbrella in a counter clockwise direction.

To find:

What is the angle of this rotation?

Rotation for 360^∘ (one complete circle around) means turning around until we point in the same direction again.

If we want to determined the measure of angle of rotation to the original position, we have to find the value r

that is true for the equation:

90^∘ + r = 360^∘

Notice that, rotation for 360^∘ (one complete circle around) means turning around until we point in the same direction again.

And in the equation we add 90^∘, because we do not rotate from the start position. The umbrella has been rotated already for 90^∘.

90^∘ + r = 360^∘

r = 270^∘

​Subtract from the both sides by 90^∘

Therefore, the angle of this rotation is 270^∘

Therefore, the angle of this rotation is 270^∘.

Congruence And Similarity Envision Math Exercise 6.4 Answers

Page 311 Try It Answer

Given:

The coordinates of the vertices of quadrilateral HIJK are H(1,4), I(3,2), J(−1,−4), and K(−3,−2)).

To find:

If quadrilateral is rotated 270^∘ about the origin, what are the vertices of the resulting image, quadrilateral H′I′J′K′

We use the concept that:

The rule for a rotation by 270^∘ about the origin is

(x, y) → (y,−x).

There are some rules for x – and y – coordinates of a point at rotation for 270^∘

In another words, when we rotate for 270^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x, y)→(y,−x)

Therefore, the vertices of quadrilateral H′I′J′K′ are:
​
H(1,4) → H′(4,−1)

I(3,2) → I′(2,−3)

J(−1,−4) → J′(−4,1)

K(−3,−2) → K′(−2,3)

The vertices of quadrilateral H′I′J′K′ are

H′(4,−1)

I′(2,−3)

J′(−4,1)

K′(−2,3)

Page 311 Try It Answer

Given:

A figure with two triangles.

To find:

The description of the rotation that maps ΔFGH to ΔF′G′H′

We find the number of degrees that figure rotates.

To describe the rotation that maps triangle FGH to triangle F′G′H′, we have to find the angle of rotation. In another words, we have to find the number of degrees that figure rotates.

The procedure is simple:

1. Draw rays from the origin through point G and point G′.(Notice that, we can choose any point of the figure, because all point are rotated for the same angle.)

2. Measure the angle formed by rays.

(Use a protractor to determine the number of degrees.)

Hence, a 180^∘ rotation about origin maps ΔFGH to ΔF′G′H′.

Envision Math Grade 8 Chapter 6.4 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.3 Page 312 Exercise 1 Answer

Given:

A rotation of two dimensional figure.

To find:

How does a rotation affect the properties of a two-dimensional figure?

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference ,after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Page 312 Exercise 2 Answer

Given:

If a preimage is rotated 360 degrees about the origin

To find:

How can you describe its image?

We use the fact that 360 degrees about the origin means turning around until you point in the same direction again.

So, when we rotated some figure 360^∘ about the origin, we actually put the figure on the same position. Like we did not even change it.

Therefore, the image will be the same as the preimage.

Therefore, the image will be the same as the preimage.

Page 312 Exercise 3 Answer

Given: AB is parallel to DC

To find:

How are sides A′B′ related to C′D′.

There are not change in shape, side lengths, angle measures and orientation between resulting image and the final original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Therefore, if side AB is parallel to side CD on the preimage, the side A′B′ and C′D′ will also be parallel.

Because side lengths and shape remain the same after rotation.

Therefore, if side AB is parallel to side CD on the preimage, the side A′B′ and C′D′ will also be parallel. Because side lengths and shape remain the same after rotation.

Page 312 Exercise 4 Answer

Given:

The coordinates of the vertices of rectangle ABCD are

A(3,−2), B(3,2), C(−3,2), and D(−3,−2).

To find:

The coordinates of the vertices A′B′C′D′.

when we rotate for 90^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before first coordinate:

There are some rules for x – and y – coordinates of a point at rotation for 90^∘. In another words, when we rotate for 90^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before first coordinate:

(x, y) → (−y, x)

Therefore, the vertices of rectangle A′B′C′D′ are:
​
A(3,−2)→A′(2,3)

B(3,2)→B′(−2,3)

C(−3,2)→C′(−2,−3)

D(−3,−2)→D′(2,−3)

The vertices of rectangle A′B′C′D′

A′(2,3)

B′(−2,3)

C′(−2,−3)

D′(2,−3)

Given:

The coordinates of the vertices of rectangle ABCD are A(3,−2), B(3,2), C(−3,2), and D(−3,−2).

To find:

The measures of angles of A′B′C′D′

As we already said, the rotation is a transformation that turns a figure around a fixed point, called the center of rotation. There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Therefore, the measures of the angles of A′B′C′D′ will be the same as the measures of the angles of A′B′C′D′.

To be precise, we know that figure A′B′C′D′ is also rectangle, because the rotation does not change the shape of figures.

So, as rectangle has four right angles, the measures of all angles will be 90^∘.

So, as rectangle has four right angles, the measures of all angles will be 90^∘.

Solutions For Envision Math Grade 8 Exercise 6.4

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.3 Page 312 Exercise 5 Answer

Given:

Graph with two triangles.

To find:

Counterclockwise rotation of ΔQRS.

We use the concept of rotation to solve the question.

To describe the rotation that maps triangle QRS to triangle Q′R′S′, we have to find the angle of rotation. In another words, we have to find the number of degrees that figure rotates.

The procedure is simple:

1. Draw rays from the origin through point Q and point Q′.(Notice that, we can choose any point of the figure, because all point are rotated for the same angle.)

2. Measure the angle formed by rays.

(Use a protractor to determine the number of degrees.)

Hence, 270^∘ rotation about origin maps QRS to Q′R′S′.

Hence, 270^∘ rotation about origin maps QRS to Q′R′S′.

Page 313 Exercise 6 Answer

Given:

Graph with two triangles.

To find:

The angle of rotation of the given maps about origin.

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

To describe the rotation that maps triangle PQR to triangle P′Q′R′, we have to find the angle of rotation. In another words, we have to find the number of degrees that figure rotates. The procedure is simple:

1. Draw rays from the origin through point Q and point Q′.(Notice that, we can choose any point of the figure because all point are rotated for the same angle.)

2. Measure the angle formed by rays.

(Use a protractor to determine the number of degrees.)

The angle of rotation about origin maps triangle PQR to triangle P′Q′R is 90^∘

The angle of rotation about origin maps triangle PQR to triangle P′Q′R is 90^∘.

Envision Math Grade 8 Volume 1 Chapter 6.4 Practice Problems

Page 313 Exercise 7 Answer

Given:

Graph with two triangles.

To find:

Is ΔXYZ rotation of ΔX′Y′Z′.

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

If triangle X′Y′Z′ is a rotation of triangle XYZ, each vertex of triangle X′Y′Z′

must be rotated around the origin for the same angle.

Therefore, we have to check angle measures for each corresponding pair of vertices.

To find out the angle measures, draw rays from the origin through each vertex of triangle XYZ and its corresponding vertex of triangle X′Y′Z′, then measure the angle formed by the rays.

Hence, yes X′Y′Z′ is rotation of XYZ.

Hence, yes X′Y′Z′ is rotation of XYZ.

Page 313 Exercise 8 Answer

Given:

ΔPQR is rotated 270^∘.

To find:

graph and label the coordinates.

We use the concept of rotation to find the graph.

To graph

The rotation for 270^∘ of triangle 270^∘ about origin we have to:

Draw the ray from the origin to vertex P.

Use a protractor to draw a 270^∘ angle in counterclockwise direction.

Plot vertex P′, the same distance from the origin as vertex.

We repeat the process to get it for other vertices.

There are some rules for x – and y – coordinates of a point at rotation for , the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

In another words, when we rotate for 270^∘ the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x,y)→(y,−x)

Therefore ,the vertices of triangle,P′Q′R′are:
​
P​(2,3) → P′(3,−2)

Q​(4,6) → Q′(6,−4)

R​(2,7) → R′(7,−2)

​But despite of that, we could also read the coordinates of vertices from the graph.

Therefore, the vertices of rectangle P′Q′R′ are:

P​(2,3) → P′(3,−2)

Q​(4,6) → Q′(6,−4)

R​(2,7) → R′(7,−2)

Page 313 Exercise 9 Answer

Given:

Graph with two triangles.

To find:

Is P′Q′R′ 270^∘ rotation of ΔPQR

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

If triangle P′Q′R′ is a 270^∘ rotation of triangle PQR, each vertex of triangle PQR must be rotated around the origin for 270^∘

Therefore, we have to check angle measures for each corresponding pair of vertices.

To find out the angle measures, draw rays from the origin through each vertex of triangle PQR and its corresponding vertex of triangle P′Q′R′, then measure the angle formed by the rays in the graph given below.

Therefore, we notice that we could also find out, if triangle P′Q′R′ is a 270^∘ rotation of triangle PQR, checking the relations between coordinates. Because, there are some rules for x – and y – coordinates of a point at rotation for 270^∘.

In another words, when we rotate for 270∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x,y) → (y,−x)

But that is not the case with these vertices:
​
P ​(3,3) → P′(−3,3)

Q (7,4) → Q′(−4,7)

R (3,5) → R′(−5,3)
​
So, we can conclude that triangle P′Q′R′ is not a 270^∘ rotation of triangle PQR.

So, we can conclude that triangle P′Q′R′ is not a 270^∘ rotation of triangle PQR

Envision Math 8th Grade Congruence And Similarity Topic 6.4 Key Concepts

Page 314 Exercise 10 Answer

To find: Why any rotation can be described by an angle between 20^∘ and 360^∘

Explanation:

Let’ start at any point of the coordinate system and slowly start to move around it. Once we have moved a quarter of the way around the circle, we will have a 90^∘ rotation. Then, when we keep moving, we will pass 180^∘ (or halfway) and later 270^∘ (or three quarters).

Once we reach the end of the circle, we will have passed a full 360^∘ around the circle. In another words, we will be right back where we started, at 0^∘.

It means turning around until you point in the same position again.

So, when we rotated some figure 360^∘ about the origin, we actually put the figure on the same position. Like we did not even change it.

Therefore, the rotation over 360^∘ we can observe like rotation that is reduced by 360^∘.

For example, a 420^∘ rotation will be:

420^∘ − 360^∘ = 60^∘ rotation

Because in the meantime, we will return to the starting position and from the starting position rotate for another 60^∘.

Once we have moved a quarter of the way around the circle, we will have a 90^∘ rotation. Then, when we keep moving, we will pass 180^∘ (or halfway) and later 270^∘ (or three quarters). Once we reach the end of the circle, we will have passed a full 360^∘ around the circle.

In another words, we will be right back where we started, at 0^∘ about the origin, we actually put the figure on the same position. Like we did not even change it. Hence, any rotation can be described by an angle between 0^∘ and 360^∘.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.3 Page 314 Exercise 11 Answer

Given:

A graph with a rectangle.

To find:

Rotated KLMN 270^∘ about origin.

Use the concepts of rotation to solve the question.

To graph

The rotation for 270^∘ of triangle PQR about origin we have to:

Draw the ray from the origin to vertex K.

Use a protractor to draw a 270^∘ angle in counterclockwise direction.

Plot vertex K′, the same distance from the origin as vertex K.

Repeat the procedure for other vertices.

We now join the vertices,

Therefore, the rotated rectangle is

Envision Math Grade 8 Topic 6.4 Similarity Practice

Page 314 Exercise 12 Answer

Given:

An architect is designing a new windmill with four sails. In her sketch, the sails’ center of rotation is the origin, (0,0), and the tip of one of the sails, point Q, has coordinates (2,−3). She wants to make another sketch that shows the windmill after the sails have rotated 270^∘ about their center of rotation

To find: What would be the coordinates of Q′?

We use the concept of rotation.

Let’s drawn first the windmill with four sails. We have information that point Q, the tip of one of the sails, has coordinates (2,−3).

And if we know what kind of form windmills generally have, we can draw the remaining sails.

All four sails are equal in size and intersect at a right angle.

Notice that we can draw these sails so that the default sail we rotated three times for 90^∘.

Therefore:

Draw the point Q and the ray from the origin to point Q.

(That will be the sketch of the given sail.)

Use a protractor to draw a 90^∘ angle in counterclockwise direction.

Plot point Q1 the tip of other sail, the same distance from the origin as point Q.

We repeat he process,

Now, we have to graph of the sails about origin, their center of rotation to make another sketch that shows the windmill after the rotation of the sails. and the ray. angle in counterclockwise direction. ‘the same distance from the origin as point

the rotation for 270^∘ In another words, we have to rotated each tip of the sails for 270^∘

So, let’s rotated the first one:

Draw the point Q and a ray from the origin to point Q

(That will be the sketch of the given sail.)

Use a protractor to draw a 270^∘ clockwise.

Plot point Q′ the same distance from origin as Q.

Notice that, the position of that sail, after rotation, is on the position of one of the existing sails before rotation.

This will be the case with other sails after rotation too.

Therefore, we can conclude that the sketch of the windmill will be the same as in the beginning (before rotation).

Only replacing each sail with some existing sail so that the angle between them is 270^∘

We still have to specify the coordinates of point – and – coordinates of a point at rotation for, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate: Q′

There are some rules for x and y

In another words, when we rotate for 270^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x,y) → (y,−x)

The coordinates will shift from

Q​(2,−3) → ​Q′(−3,−2)

Envision Math Grade 8 Chapter 6.4 Lesson Overview

Page 314 Exercise 13 Answer

Given:

Rotation about origin maps ΔTRI to ΔT′R′I′.

To find:

Which graph shows an angle you could measure to find the angle of rotation about the origin?

Use the concept of rotation to solve the question.

Looking at the all pictures we can immediately say that graph at B is not graph that show an angle of rotation about origin, because there are two rays from one vertex. Moreover, the one of the ray is not even through the origin.

Then, notice that image at C and D are rays between unmatched vertices. And we measure the angle between corresponding vertices to find out the angle of rotation.

The graph at A shows an angle we could measure to find the angle of rotation about origin.

Result

The graph at A shows an angle we could measure to find the angle of rotation about origin.

The graph at A shows an angle we could measure to find the angle of rotation about origin.

Given:

Rotation about origin maps ΔTRI to ΔT′R′I′

To find:

What is the angle of rotation about axis?

To find the angle of rotation about origin, we have to find the number of degrees that figure rotates.

We have already rays from the origin through point R and point R′.

So, use a protractor to determine the angle formed by rays.

Hence the angle of rotation is 180^∘

Since the angle of rotation is 180^∘.

Hence the rest of the options are incorrect.

Correct option is (B) 180^∘ 

Envision Math Accelerated Grade 7 Volume Chapter 1 Integers and Rational Numbers

Page 7  Exercise 1  Answer

Given:

The mission control uses “T minus” before lift-off.

After the rocket launch “T plus” is used while the rocket is in flight.

T represents the rocket launch.

Integer positive and negative is used to represent the situations

Finally, we concluded that the “T minus” and “T plus” as the rocket launch is used to represents the situations.

Page 7  Exercise 2  Answer

Given:

When preparing for a rocket launch, the mission control center uses the phrase

“T minus” before liftoff… T minus 3, T minus 2, T minus … After the rocket has launched

“T plus” is used while the rocket is in flight….. T plus $1,T plus 2, T plus 3…

To find:

What integers can you use to represent this situation?

Here both positive (Natural numbers) and negative (Additive inverse of Natural numbers).

Integers are represented because when the mission control center of rocket while preparing uses.

T minus (-) and when rocket is launched it is T plus (+) while the rocket is preparing in flight.

Therefore, according to the situation the integers used respectively.

Envision Math Accelerated Grade 7 Chapter 1 Exercise 1.1 Solutions

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 7  Exercise 3  Answer

Given:

When preparing for a rocket launch, the mission control center uses the phrase

“T minus” before liftoff…T minus 3, T minus 2, T minus 1… After the rocket has launched.

“T plus” is used while the rocket is in flight. …T plus 1, T plus 2, T plus 3…

To find:

How are “T minus 4” and “T plus 4” related?

T minus 4 and T plus 4 are related by an integer.

Whereas, minus 4 integers and its opposite plus 4 combine to form 0.

Here, minus 4 is the continuous of preparing to launch a rocket, and 4 is the continuous of the flying rocket.

Therefore, by this way “T minus 4” and “T plus 4” are related.

Page 8  Question  1  Answer

Any positive or negative number that does not contain decimal portions or fractions is called an integer.

All positive and negative whole numbers, as well as zero. The numbers used to count are positive integers.

The numbers are 1,2,3,4,5, and so on. They are the negative integers’ polar counterparts.

Their opposites, which are less than 0, are called negative integers. Zero is neither positive nor negative.

There is a negative integer for every positive integer, and these integers are known as opposites.

Finally, we concluded that the negative and positive representations of a number are combined in a pair of opposite integers.

Page 8  Exercise 1  Answer

To explain about how are the absolute values of integers are related

The absolute value of an integer equals the distance between it and 0, it will always be positive.

Subtracting a negative integer from its absolute value is the same as adding it.

A number’s absolute value is the distance between it and zero on a number line. The absolute value of a number n is represented by the symbol |n|.

On a number line, opposites are the same distance from 0 and are on opposing sides of 0.

Finally, we concluded that the absolute value is related to the distance from zero of a number.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 9  Exercise 2  Answer

Given:

The temperature was 75°

At noon, the temperature increased by 7°

By evening, the temperature decreased  by  7°

To find How did the temperature changed?

Explanation:

Temperature change = temperature increase- temperature decrease

So 7° −7°=0°

Finally, we concluded that the temperature change is 7° −7° =0°.

Page 9  Exercise 3  Answer

Given:
Shaniqua has $45 in her wallet. She spends $4 on snacks and $8 on a movie ticket

To find What integer represent the change in the amount of money in Shaniqua’s wallet?

And to find How much money does she have left?

Explanation:
What integer represent the change in the amount of money in Shaniqua’s wallet is  −$4−$8 =−$12

The money left in the wallet is  $45−$12  =  $33

Finally, we concluded that the integer represents in Shaniqua’s wallet is−$12 and the money left is$33

Grade 7 Envision Math Integers And Rational Numbers Exercise 1.1 Answers

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 10  Exercise 1  Answer

Given:

Opposites relate to integers because an integer’s opposite has to be the same number away from zero as the integer in question.

Example: 2,−5 are different from each other.

Two integers are opposites if their signs differ from each other in + and − signs. If the number doesn’t have the sign so the number is positive.

Page 10  Exercise 2  Answer

Given:

A helium atom has 2 protons and 2 electrons.

The helium atom has no charge, which means it has an oxidation number of  0.

Since the number of protons and electrons are equal.

The positive charge of the protons and the negative charge of electrons add up to zero.

Helium contains an equal number of positively charged particles and negatively charged particles. So, the helium atom has a zero charge.

Page 10  Exercise 3  Answer

Given:

We know the opposite of a number is called the additive inverse because the sum Of the two numbers is zero.

Add a positive number to a number by counting up from that number, and add a negative number to a.

An Integer plus its opposite sum to zero.

The opposite of a number is called the additive inverse because the two-number sum is zero. When two opposites are added together they equal to zero.

Page 10  Exercise 4  Answer

Given:

We need to use integers to represent Marcus’s location.

Let’s say the sea level is at zero.

As we assumed the surface of the ocean is at the zero.

So we need to add an integer in −18 equals to zero.

Thus the number is 18 which makes −18 equal to zero.

Hence, Marcus have to go 18 M to return to the surface.

Marcus have to go 18 M to return to the surface.

Page 10  Exercise 5  Answer

Given:

To analyze temperature for each day as follows. To measure the overall change in water temperature.

Water temperature on Sunday = 78° F

Water temperature on Monday changed by−3 degrees F

Water temperature on Tuesday changed by 3 degrees F

The total change of water temperature from Sunday to Tuesday is −3 + 3 = 0

Since overall temperature is zero, hence temperature on Sunday and on Tuesday is similar.

The water temperature on Tuesday is 78 degrees F.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 10  Exercise 6  Answer

Given :

To find Travis’s score

Lats assume travis’s score as x.

His score would have to be −5

​−3+3 = 0

1 + 4 = 5

5 + (−5) = 0
​
So the sum of all scores is zero.

If we sum those, we have :3−3 + 4 + 1 + x = 0

Then x = −5, Travis score is −5 points

Hence traves’s score is−5 points.

Page 11  Exercise 7  Answer

Given:

To find:  How much money he had before his purchase

The money he spent =$53

The money he left after spending money = $0

​= x−53 = 0

x = 0 + 53

x = 53
​
Therefore he had = $53

The final solution, Therefore he had $53.

Envision Math Accelerated Chapter 1 Exercise 1.1 Answer Key

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 11  Exercise 8  Answer

Given:

The given temperature was 8 degrees F.

It dropped to zero degrees F.

Therefore the change in temperature is−8 degrees F.

Hence the change in temperature is−8 degrees F.

Page 11  Exercise 9  Answer

Given:

Since an airplane descended 4000 feet before landing.

We have to determine the integer that represents the number of feet the airplane was above the ground before descent.

Since the distance above the ground is represented by the positive integer.

Therefore, the airplane was +4000 feet above the ground level.

Hence the airplane was +4000 feet above the ground level.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 11  Exercise 10  Answer

Given:

The above figure shows that the opposite of the integer represented by the point A is 7.

And the opposite of the integer represented by point B is− 8.

Therefore opposite of integers A and B is 7 and −8.

The final solution of an opposite integer is 7 and −8.

Given:

The opposite of the integer represented by the point A is 7.

And the opposite of the integer represented by point B is −8.

Therefore opposite of integers A and B is 7 and −8.

No, we don’t agree with Carolyn, because the opposite sides are different.

The final solution is above Solution I don’t agree with Carolyn because the opposite side is different.

Page 11  Exercise 11  Answer

Given:

The cost of 9 yards can be written as −9

It is given that the team has combined gain or loss of 0 yards

Let gain or lost x score in the next play

0−9 + x = 0

Now add both side by 9, and we get

x = 9

Finally, we concluded that the team must gain 9 yards.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 11  Exercise 12  Answer

Given:

The rise is at 12 meters

10  Drops at 6 meters

6  Starts at 1 meter

4  Above the ground level

0  Group level

−2 Drops = 4 meters

So the height of the car at end of the ride is

1−4+13−6=4

Finally, we concluded that the height of the car at the end of the ride is 4 meters.

Page 12  Exercise 13  Answer

Given:

According to the given title

​= −700 + 1400 − 1100

= 700 − 1100

= − 400
​
Finally, we concluded that the integer that represent base price of the car to the final price is -400.

Page 12  Exercise 14  Answer

Given:

|x| = 16, |y| = 16

To find when x and y are combined they equal 0

|x| = 16, |y| = 16

It can be written as

x = −16, y = 16

Or x = 16, y = −16

When x and y are combined
x + y = 0

Finally, we concluded that when x and y are combined they equal 0 i.e x + y = 0.

Page 12  Exercise 15  Answer

Given:

The situation represents −42

The opposite of the given situation varies according to the sign. So we get 42.

Finally, we concluded that a situation that can be represented by the opposite of −42 is 42.

Solutions For Envision Math Grade 7 Exercise 1.1 Integers And Rational Numbers

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers and Rational Numbers Exercise 1.1 Page 12  Exercise 16  Answer

Given:

Ann house is located at 0.

Ben lives 7 blocks from Ann.

Ben lives a number 7 on the number line and Carol lives 2 blocks from Ben.

The possible location for carl’s house is 7,3,−7−3.

Finally, we concluded that a situation that the possible location for carl house is 7,3,−7−3.

Page 12  Exercise 17  Answer

Given:

You walk down 9 flights of stairs.

You climb up 9 flights of stairs.

The temperature drops 9’F.

You spend $9 on a book.

You earn $9 from your job.

To Find:

Which of these situations can be represented with an integer that when combined.

With the opposite of -9 and makes 0? Select all that apply.

Situation-1: You climb up 9 flights of stairs, satisfied with an integer 9 that when combined with the opposite of -9 makes 0.

This is because when you climb up the stairs it means you are climbing up. So, it becomes positive in an integer that is +9.

Situation-2: You earn $9 from your job, satisfied with an integer 9 that when combined with the opposite of -9 makes 0.

This is because if you earn $9 from your job it means you are earning. So, it is positive in an integer that is +9.

Thus, these two situations apply that +9 combined with -9 makes 0.

Envision Math Volume 1 Chapter 1 Exercise 1.1 Grade 7 Guide

Page 12  Exercise 18  Answer

Given:

An airplane descends 80m.

An elevator ascends 80m.

The cost of a train ticket drops by $80.

You remove 80 songs from an MP3 player.

Suzy’s grandmother is 80 years old.

To find:
Which of these situations can be represented by the opposite of 80? Select all that apply.

Situation-1: An airplane descends 80m, satisfied with an integer -80 that when combined with the opposite of 80 makes 0.

This is because if an airplane descends it means that an airplane is landing down which in an integer is negative that is -80.

Situation-2: The cost of a train ticket drops by $80, satisfied with an integer -80 that when combined with the opposite of 80 makes 0.

This is because if the cost of a train drops it means the cost is dropping low which in an integer is negative that is -80.

Situation-3: You remove 80 songs from an MP3 player, and satisfy with an integer -80 that when combined with the opposite of 80 makes 0.

This is because if you remove 80 songs, the songs in MP3 reduces which in an integer is negative that is -80.

Thus, these two situations apply that +80 combined with -80 becomes 0.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 303 Exercise 1 Answer

Given:

To: How are the figures the same? How are they different?

The pencil worked as a axis of reflection along which the figure one is reflected to make the figure two. When the pencil is removed and the paper is folded along the line, the two figures will overlap each other.

The pencil worked as a axis of reflection along which the figure one is reflected to make the figure two. When the pencil is removed and the paper is folded along the line, the two figures will overlap each other

Envision Math Grade 8 Volume 1 Chapter 6.3 Solutions

Page 303 Exercise 2 Answer

Given:

To find: What do you notice about the size, shape, and direction of the two figures?

As the figure 2 is the reflection of figure 1 the shape and size must be same. Also it can be observed that both the figures are right-handed triangles. But the location of their vertices are different in both the quadrants. Hence, directions are different.

As the figure 2 is the reflection of figure 1 the shape and size must be same. But the directions are different.

Page 303 Focus On Math Practices Answer

Given: Dale draws a line in place of his pencil and folds the grid paper along the line.

To: How do the triangles align when the grid paper is folded? Explain.

The line in place of pencil is acting like a axis of reflection. So the distance of both the figures from the line will be equal. So when the paper is folded, the vertical line of the figures will overlap. The base of the figure will overlap. Since both the figures have same size so the third side will also overlap.

The vertical line of the figures will overlap. The base of the figure will overlap. Since both the figures have same size so the third side will also overlap.

Page 304 Essential Question Answer

Given: Two-dimentional figure.

To: How does a reflection affect the properties of a two-dimensional figure?

When reflection takes place about x axis, the x coordinate remains the same, but the y coordinate is transformed into its opposite sign.

When reflection takes place about y axis, the y coordinate remains the same, but the x coordinate is transformed into its opposite sign.

When reflection takes place about x axis, the x coordinate remains the same, but the y coordinate is transformed into its opposite sign.

When reflection takes place about y axis, the y coordinate remains the same, but the x coordinate is transformed into its opposite sign.

Page 304 Try It Answer

Given:

To: Draw the new location of the chair on the plan.

Step formulation: Take the mirror image of the chair and then draw the final image.

Take the reflection of the chair about the dotted line and then draw the final image.

The final image of chair is shown in the figure:

Page 304 Convince Me Answer

Given: Image is reflected.

To: How do the preimage and image compare after a reflection?

A reflection is a transformation that turns a figure into its mirror image by flipping it over a line. The line of reflection (or axis of reflection) is the line about which the figure is reflected over. If the reflecting point is on the line of reflection then the image is the same as the preimage. Also, the image is always congruent to its preimage i.e. have the same shape and size.

A reflection is a transformation that turns a figure into its mirror image by flipping it over a line. The line of reflection (or axis of reflection) is the line about which the figure is reflected over. If the reflecting point is on the line of reflection then the image is the same as the preimage. Also, the image is always congruent to its preimage i.e. have the same shape and size.

Page 305 Try It Answer

Given:
​
k = 2,6

L = 3,8

M = 5,4

N = 3,2
​
To find: The coordinates of point N′.

As the reflection is about the y axis, therefore, the y coordinate will remain the same and the x coordinate will change its sign.

i.e. N′= −3,2

The coordinates of N after reflection is −3,2.

Congruence And Similarity Envision Math Exercise 6.3 Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.2 Page 306 Exercise 4 Answer

Given:

A figure with two triangles.

To find:

Triangle X′Y′Z′ is a reflection of triangle XYZ.

From the picture we can see that vertices X and X′,Y and Y′,Z and Z′ are on the same distance from the line g,but on opposite sides.

Also, we can see that triangles have the same size and the same shape.

Therefore, triangle X′Y′Z′ is a reflection of triangle XYZ across the line g.

Triangle X′Y′Z′ is a reflection of triangle XYZ across the line g.

Page 306 Exercise 5 Answer

Given:

coordinate grid.

To find:

Describe the reflection of the figure EFGH.

We have to find the line of reflection over which a figure EFGH is reflected.

Notice that the line of reflection will be the line through the points that represent the half of lengths between the corresponding vertices.

In that case, we can say with certainty that each vertex of reflected figure will be on the same distance from the line of reflection.

Because the midpoint of the length divide length into two equal parts.

We first find the mid point of the length of vertices E and E′.

Let’s repeat the procedure for the corresponding vertices.

Now we draw all the points connecting the mid points to get the line of reflection.

Hence, EFG is reflected across y = 4.

Envision Math Grade 8 Chapter 6.3 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.2 Page 307 Exercise 7 Answer

Given:

The graph of a trapezoid.

To find:

Reflection of trapezoid ABCD across the y-axis.

Use the law of reflection to find solution of the question.

Let’s

reflect each vertex of trapeziod ABCD across the y-axis.

Before each reflection, we have to measure distance from each vertex to line of reflection, y-axis.

For example, vertex A is 2 units right from the y-axis. Therefore, vertex A′ must be 2 units left

from the line y-axis.

Then we repeat the procedure for other vertices,

Then joining the points we get,

Let’s identify first the points of the preimage:

A(2,8) B(6,8) C(8,3) D(2,3)

When we reflecting across the y-axis only x-values are opposite.

The y−values stay the same when we reflect a preimage the y-axis.

Because, during reflection across the y-axis and lines that are parallel with y-axis, we move only along the x-axis

Reflection acrossy−axis:(x,y)→(−x,y)

So, the points of the image:

A′(−2,8) B′(−6,8) C′(−8,3) D′(−2,3)

Plotted trapezoid is

A′(−2,8) B′(−6,8) C′(−8,3) D′(−2,3)

Page 307 Exercise 8 Answer

Given:

A figure with two triangles A′B′C′ and ABC

To find:

A′B′C′ and ABC are reflection across the line.

A reflection is a transformation that flips a figure across a line of reflection.

The preimage and image are the same distance from the line of reflection but on opposite sides So, figures have the same size and the same shape but different orientation after reflection.

If we look at the picture, we can see that corresponding vertices of triangles are not on the same distance from the line of reflection and that triangles are not opposite.

Therefore, the triangle A’B’C’ is not a reflection of triangle ABC.

The triangle A′B′C′ is not a reflection of triangle ABC.

Page 308 Exercise 11 Answer

Given:

Vertices of triangle ΔABC are A(−5,5),B(−2,3);C(−2,3)

To find:

The coordinate C′ when the triangle is reflected across y = −1.

When we reflect triangle ABC across the line y = −1,that means we are reflecting each vertex on the same distance from the line of reflection y = −1 on opposite side.

To find the coordinates of the vertex C′, first we have to measure the length between the vertex C and the line y = −1. Because, on the same distance from the line of reflection must be the corresponding vertex C′.

Notice that, when we reflect the figure across some line that is parallel to the x-axis

like y=−1,the x-values of all points of the figure will be the same

Because, we reflect the figure along y-axis. The y-values will changed.

If coordinates of vertex C are (−2,3) that implies that vertex C is 3 units up from y-axis. But we have to find the number of units to the line y = −1. So, we are looking for value of r that is true for equation:
​
3 − (−1) = r

r = 4
​
(Notice that when we move downwards. we subtract the values.)

The vertex C is 4 units up from the line of reflection. Therefore, the vertex C′ must be 4 units down from the line of reflection.

In another words, the second coordinate of point C′ will be:

−1 − 4 = −5

So, the coordinates of the vertex C′ are :​(−2,−5).

The coordinates of the vertex C′ are :​(−2,−5).

Solutions For Envision Math Grade 8 Exercise 6.3

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.2 Page 308 Exercise 12 Answer

Given:

A figure with two parallelogram.

To find:

What reflection of ABCD is A′B′C′D′.

To describe the reflection of a parallelogram ABCD, we have to find the line of reflection over which a parallelogram ABCD is reflected.

Notice that the line of reflection will be the

Line through the points that represent the half of lengths between the corresponding vertices.

In that case, we can say with certainty that each vertex of reflected figure will be on the same distance from the line of reflection.

Because the midpoint of the length divide length into two equal parts.

We find the midpoint of the length of vertices A and A′:

We repeat the process for rest of the vertices and then join the points to get the line of reflection.

Therefore, ABCD is reflected across the line y = 3.

Envision Math Grade 8 Volume 1 Chapter 6.3 Practice Problems

Page 308 Exercise 13 Answer

Given:

ΔJAR has vertices J(4,5);A(6,4);R(5,2)

To find:

Correct graph for ΔJAR across x = 1.

First notice that image of triangle at is not only reflected but also translate some units up from the original one. Therefore, the are not the same distance between the line of reflection and corresponding vertices.

Then, on the image C vertices are not reflect to the corresponding ones. Moreover, these two angles have not the same corresponding side lengths and angle measures.

Now we have two options: A or B.

Let’s look first at the image A. As we already said, reflected figures are the same distance from the line of reflection but on opposite sides.

If we look the number of units between vertex A and line, then between line and vertex A′, we can notice that these are not the same numbers. In another words, the vertices are not on the same distance from the line of reflection.

Let’s look first at the image B. As we already said, reflected figures are the same distance from the line of reflection but on opposite sides.

If we look the number of units between vertex B and line, then between line and vertex B′, we can notice that these are the same numbers. In another words, the vertices are on the same distance from the line of reflection. Hence B is the correct option.

Graph B is correct.

Given:

∠A = 90

To find:

m ∠ A

We use the corresponding angle measures remain the same by reflection.

The corresponding angle measures remain the same by reflection.

Therefore, true is:

m ∠ A = 90^∘ ⇒ ​m ∠ A′ = 90^∘

Therefore,

m ∠ A′ = 90^∘

Envision Math Accelerated Grade 7 Volume1 Chapter 1 Integers And Rational Numbers

Page 2  Question 1  Answer

Given:

There are four properties of operations in math.

These properties apply to addition, multiplication, and subtraction, but not to division and subtraction.

Because it shows several ways to reach the solution, the characteristics of operations can be utilized to solve problems with integers.

Finally, we concluded that there are different ways used to solve problems involving integers and rational numbers. 

Page 4  Exercise 1  Answer

Given:

We have to explore the habitability with low temperatures

The lowest record temperature in the world is −136° F(−92.21C) occurred in Antarctica.

Low temperatures also freeze water, rendering it unavailable as a liquid.

Life appears to be limited to a temperature range of minus 15 to 115 degrees Celsius. This is a liquid range.

Finally, we concluded that the low temperature of Life seems limited to a temperature.

Envision Math Accelerated Grade 7 Chapter 1 Integers And Rational Numbers Solutions

Page 5  Exercise 1  Answer

Given:

Correct answer: Commutative property is the correct answer.

Commutative property: The commutative qualities state that you can add or multiply two numbers in any order and get the same result. Assume that a and b are real numbers. wrong answer

Absolute value: It refers to a number’s distance from zero on the number line, without taking direction into account.

Distributive property: According to the distributive property, If p,q, and r are three rational numbers, then the connection between them is p(q+r)=(pq)+(pr)

Integer: Integer, positive or negative whole-valued number, or 0.

The integers are made up of the counting numbers 1,2,3 and….. as well as the subtraction procedure.

The consequence of subtracting a counting number from itself is zero.

Rational number: A rational number is one that has the form \(\frac{p}{q} \) where p and q are both integers and q is not zero.

The final answer is, The commutative property explains why  a × b = b × a and a + b = b + a

Page 5  Exercise 2  Answer

Given:

Correct answer: An integer is a correct answer

Integer:  Integer, positive or negative whole-valued number, or 0.

The integers are made up of the counting numbers 1,2,3 and….. as well as the subtraction procedure.

The consequence of subtracting a counting number from itself is zero.

On the number line, two opposed numbers have the same distance from zero but on opposite sides as −6 = 6 wrong answer.

Commutative property: The commutative qualities state that you can add or multiply two numbers in any order and get the same result. Assume that a and b are real numbers.

Absolute value: It refers to a number’s distance from zero on the number line, without taking direction into account.

Distributive property: According to the distributive property, If p,q, and r are three rational numbers, then the connection between them is p (q + r) = (pq) + (pr).

Associative property: The associative property of addition is a law that states that when we add, we can group the numbers in any order or combination

Rational number: A rational number is one that has the form \(\frac{p}{q}\), where p and q are both integers and q is not zero.

The final answer is The Integer of −6 = 6 because it is the unit from zero on the number line.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers And Rational Numbers Exercise Page 5  Exercise 3  Answer

Given:

Correct answer: An integer is a correct answer

Integer: Integer, positive or negative whole-valued number, or 0.

The integers are made up of the counting numbers 1,2,3 and….. as well as the subtraction procedure.

The consequence of subtracting a counting number from itself is zero

The number\(\frac{5}{3}\) is an integer. wrong answer.

Commutative property: The commutative qualities state that you can add or multiply two numbers in any order and get the same result. Assume that a and b are real numbers.

Absolute value: It refers to a number’s distance from zero on the number line, without taking direction into account.

Distributive property: According to the distributive property, If p,q, and r are three rational numbers, then the connection between them is p(q + r) = (pq) + (pr).

Associative property: The associative property of addition is a law that states that when we add, we can group the numbers in any order or combination

Rational number: A rational number is one that has the form \(\frac{p}{q} \) where p and q are both integers and q is not zero.

The final answer is The number \(\frac{5}{3}\) is an integer because it is 6 units from zero on the number line.

Page 5  Exercise 4  Answer

Given:

Correct answer: Integer is the correct answer

Integer: Integer, positive or negative whole-valued number, or 0.

The integers are made up of the counting numbers 1,2,3 and….. as well as the subtraction procedure.

The consequence of subtracting a counting number from itself is zero.

The set on natural numbers is made up of the counting numbers (1,2,3,4,5).

This sequence of numbers begins with 0 and continues indefinitely.

The new set of whole numbers is created when we add 0 to the set of natural numbers. (zero, one, two, three, four, five)

We’re dealing with integers if we also include a number on the other side.

Positive and negative whole numbers, including 0.

Are integers, however, they cannot be expressed as fractions or decimals. wrong answer

Commutative property: The commutative qualities state that you can add or multiply two numbers in any order and get the same result. Assume that a and b are real numbers.

Absolute value: It refers to a number’s distance from zero on the number line, without taking direction into account.

Distributive property: According to the distributive property, If p,q, and r are three rational numbers, then the connection between them is p(q + r)=(pq) + (pr).

Associative property: The associative property of addition is a law that states that when we add, we can group the numbers in any order or combination

Rational number: A rational number is one that has the form \(\frac{p}{q} \) where p and q are both integers and q is not z

The final answer is, The set integer consists of the counting number, their opposite, and zero.

Envision Math Grade 7 Chapter 1 Exercise Solutions Integers And Rational Numbers

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers And Rational Numbers Exercise Page 5  Exercise 5  Answer

Given:

Correct answer: Associative property is the correct answer

Associative property:  Because when we add, we can group the numbers in any order or combination that is (a+b)+c is equal to the sum of a + (b + c) wrong answer

Commutative property: The commutative qualities state that you can add or multiply two numbers in any order and get the same result. Assume that a and b are real numbers.

Absolute value: It refers to a number’s distance from zero on the number line, without taking direction into account.

Distributive property: According to the distributive property, If p,q, and r are three rational numbers, then the connection between them is p(q + r) = (pq) + (pr).

Integer: Integer, positive or negative whole-valued number, or 0.

The integers are made up of the counting numbers 1,2,3 and….. as well as the subtraction procedure.

The consequence of subtracting a counting number from itself is zero

Rational number: A rational number is one that has the form p q, where p and q are both integers and q is not zero.

The final answer is The sum of  (a + b) + c  is equal to the sum of a + (b + c) as explained by the associative property.

Page 5  Exercise 6  Answer

Given:

Correct answer: Distributive property is the correct answer

Distributive property: Distributive property states that the outcome of multiplying the sum of two or more addends by a number is the same as.

Multiplying each addend by the number separately and then putting the products together.

According to the distributive property n,y, and z are three rational numbers.

Then the connection between them is n × (y + z) can be written as  (n × y) + (n × z) wrong answer.

Commutative property: The commutative qualities state that you can add or multiply two numbers in any order and get the same result. Assume that a and b are real numbers.

Associative property: The associative property of addition is a law that states that when we add, we can group the numbers in any order or combination.

Absolute value: It refers to a number’s distance from zero on the number line, without taking direction into account.

Integer: Integer, positive or negative whole-valued number, or 0.

The integers are made up of the counting numbers 1,2,3….. as well as the subtraction procedure

The consequence of subtracting a counting number from itself is zero

Rational number: A rational number is one that has the form  \(\frac{p}{q} \), where p and q are both integers and q is not zero.

The final answer is If you evaluate n × (y + z) by writing it as (n × y) + (n × z) ,you have used the distributive property

Grade 7 Envision Math Accelerated Chapter 1 Answers

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers And Rational Numbers Exercise Page 5  Exercise 7  Answer

Given:

To add the given sum

First, we have to add the whole number

⇒ 2+6=8

Now combine the fraction

⇒ \(\frac{1}{3}+\frac{3}{5}\)=\(\frac{14}{15}\)

We get \(8 \frac{14}{15}\)

Finally, we concluded the solution is  \(8 \frac{14}{15}\).

Page 5  Exercise 8  Answer

Given:

To subtract the given sum.

First, we have to subtract the whole number

⇒ 9−4 = 5

Now combine the fraction

⇒ \(\frac{1}{10}-\frac{3}{4}\)=\(\frac{7}{20}\)

We get  \(4 \frac{7}{20}\)

Finally, we concluded the solution is \(4 \frac{7}{20}\)

Page 5  Exercise 9  Answer

Given:

19.86 + 7.091

To add the given sum

Add the decimals

​⇒ 19.860 + 7.091

19.860
​+7.091
−−−−
26.951
​

Finally, we concluded the solution is  26.951.

Page 5  Exercise 10  Answer

Given:

57 − 10.62

To add the given sum.

Subtract the decimals

57 − 10.62

57.00
10.62
–
−−−−
46.38
​

Finally, we concluded the solution is  46.38.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers And Rational Numbers Exercise Page 5  Exercise 11  Answer

Given:

4.08 × 29.7

To multiply the given decimal values

Multiply the numbers

⇒  ​4.08 × 29.7

= 121.176
​

Finally, we concluded the solution is 121.176

Page 5  Exercise 12  Answer

Given:

⇒ 15,183.3 ÷ 473

To divide the given decimal values.

Finally, we concluded the solution is 32.1.

Page 5  Exercise 13  Answer

Given:

To multiply the given fraction values.

To multiply

⇒ \(\frac{15}{16} \times 9 \frac{1}{5}\)

Factor the number 15

=\(\frac{5 \times 3 \times 46}{16 \times 5}\)

Cancel the factor
​
=\(\frac{69}{8}\)

Finally, we concluded the solution is  \(8 \frac{5}{8}\).

Envision Math Accelerated Volume 1 Chapter 1 Solutions Guide

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers And Rational Numbers Exercise Page 5  Exercise 14  Answer

Given:

To divide the given fraction values

Finally,  we concluded the solution is  \(\frac{172}{57}\)

​Page 5  Exercise 15  Answer

Given:

To find how much pepper will be added in each shake

\(1 \frac{7}{10}\)convert it into whole number we get \(\frac{17}{10}\)

To add  \(\frac{7}{8}\) in each shakers

Each will contain  \(\frac{1}{8}\)

\(\left(\frac{17}{10}\right)\left(\frac{1}{8}\right)\) = \(\frac{17}{80}\)

\(\frac{17}{80}\) kg  pepper will be added in each shakers.

Finally we concluded the solution is 17 \(\frac{17}{80}\) kg

Page 6  Exercise 2  Answer

To explain about fractions and decimals:

Fractions can be defined as the components of a whole and are represented as a numerical values.

A fraction is a chunk or sector of any quantity taken from a whole, the whole being any number.

When writing a number that is not a whole, decimals are utilized. Decimal numbers are numbers that fall in the middle of a range of whole numbers.

Divide the numerator by the denominator to convert a fraction to a decimal.

You can accomplish this with a calculator if necessary. As a result, we’ll have a decimal answer.

Finally, we concluded the A fraction describes the number of parts that make up a whole. The numerator and the denominator are used to express it.
A decimal is a fraction with a denominator of ten and can be expressed with a decimal point.

Page 6  Exercise 2  Answer

To explain about fractions and decimals:

Fractions can be defined as the components of a whole and are represented as numerical values.

A fraction is a chunk or sector of any quantity taken from a whole, the whole being any number.

When writing a number that is not a whole, decimals are utilized. Decimal numbers are numbers that fall in the middle of a range of whole numbers.

Divide the numerator by the denominator to convert a fraction to a decimal.

You can accomplish this with a calculator if necessary. As a result, we’ll have a decimal answer.

Finally, we concluded the A fraction describes the number of parts that make up a whole. The numerator and the denominator are used to express it.
A decimal is a fraction with a denominator of ten and can be expressed with a decimal point.

Page 6  Exercise 3  Answer

Given:

The number on the other side of the 0 number line and at the same distance from 0 is called the opposite of a number

It can be defined as an absolute value.

If two integers have the same absolute value but different signs, they are opposites.

Finally, we concluded the opposite of a number is the number on the other side of the 0 number line, and the same distance from 0 It can be defined as an absolute value.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers And Rational Numbers Exercise Page 6  Exercise 4  Answer

Given:

They might have either a positive or negative value. The value of a positive integer is larger than zero.

Negative integers are those that have a value that is less than zero.

There is no such thing as zero, which is neither positive nor negative.

The positive has the sign of(+), and the negative has the sign of (−).

Finally, we concluded that Positive numbers are any numbers greater than zero, and negative number are less than zero.

Page 6  Exercise 6  Answer

Given:

On a number line, we can arrange all of the whole numbers.

A number line is a horizontal line with evenly spaced points that correspond to the full numbers.

On the number line, two opposed numbers have the same distance from zero but on opposite sides.

Finally, we concluded that the opposite number was located on the same distance away from the zero of the number line.

Page 6 Exercise 7 Answer

Given:

Real-life integers are used to check financial status.

If there is a profit, we have positive numbers.

If there is a loss, we have negative numbers.

Fractions, integers, numbers with terminating decimals, and numbers with repeating decimals are considered to be rational numbers.

Except for complex and irrational numbers (π, root of imperfect numbers), all numbers are rational.

As a result, rational numbers are employed almost everywhere in real life, with a few exceptions.

Finally, we concluded that integers and rational numbers are used to have positive and negative numbers in real life.

Page 6  Exercise 8  Answer

Given:

Standard numbers, anything greater than zero, are described as ‘positive’ numbers.

We don’t put a plus sign (+) in front of them because we don’t need to since the general understanding is that numbers without a sign are positive.

‘Negative’ numbers are numbers that are less than zero. These are preceded by a negative symbol (−) to indicate that they are less than zero.

Integer values can also be calculated in real-life scenarios. For real-life scenarios, the integer value is either positive or negative.

Positive numbers represent kindness, happiness, togetherness, and well-being, whereas negative numbers represent boredom, melancholy, and low feelings, among other things.

Finally, we concluded that it is important of a positive or negative number is to calculate the difference.

Integers And Rational Numbers Envision Math Chapter 1 Grade 7 Explained

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 1 Integers And Rational Numbers Exercise Page 6  Exercise 9  Answer

Given:

The sign of the result when adding or subtracting positive and negative numbers is determined by whether the signs are similar or which number has a bigger value.

When both numbers have the same sign, adding positive and negative numbers is simple.

The difference between a positive number to a negative number is always positive.

Finally, we concluded that adding a positive number to a negative number has different of signs.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 297 Exercise 1 Answer

Label the vertices of the figures as ABCD and A′B′C′D′.

Check for the translation of each vertices.

Notice that there are equal translations and equal inclinations for each vertex.

Therefore, the figures have the same side lengths and same angle measures.

Equal translation and equal inclination of the vertices of the figure will result to the same side lengths and same angle measures of both figures.

Envision Math Grade 8 Volume 1 Chapter 6.1 Solutions

Page 297 Focus On Math Practices Answer

Given:

To find:

How to find that the method described shows the side lengths and angle measures equally.

In order to find whether the method described is correct or not we have to refer to the tip mentioned.

Notice that there are equal translations and equal inclinations for each vertices.

Therefore, the figures have the same lengths and same measures.

Hence, equal translation and inclination of vertices of the figure tell us that the method describes side length and angle measures as equal.

Page 298 Essential Question Answer

To find:

How does translation affect the properties of a two-dimensional figure?

In order to find how translation affects the two-dimensional figure, we have to refer to the tip and make a shape to verify it.

Draw the equilateral triangle;

Translate the triangle 3 units downwards from the initial position;

Translate again 2 units to the right from the previous position;

Notice that the shape and the dimensions of the translated triangle are the same as the original triangle;

The graph of the triangles is shown. The shape and the dimensions of the translated triangle are the same as the original triangle.

Congruence And Similarity Envision Math Exercise 6.1 Answers

Page 298 Try It Answer

Given:

Use the picture in the example for reference.

To find:

The new location of the table on the plan.

In order to find the new location of the table in the plan refer to the tip mentioned.

Take the arbitrary coordinates for the home such as forming a rectangle.

Using the picture in the example for reference, take arbitrary points forming a square for the fireplace such as

E(0,0),F(0,2),G(2,0) and H(2,2)

Plot the coordinates for the home and the fireplace.

In order to move the fireplace, translate the coordinates as per instructions.

Move the x−coordinate of the point F(0,2) by 6 unitsto the right to get (6,2)

Move the y−coordinate of the new point (6,2) by 3 units towards the downward direction parallel to the negative y−axis to get(6,−1)

Similarly, translate the other coordinates of the fireplace with the x−coordinate by 6 units to the right and y−coordinate by 3 units to the down.

Similarly, plot the coordinates for the original position of the windowO(3,5) and P(4,5) then translate the coordinates pointO(3,5) by 5 units to the right to get Q(8,5)​.

Similarly, translate the other points to get the coordinates of the new window Q(8,5) and (9,5)

The new location of the window is shown by translating the old coordinates of the position by 5 units to the right.

Page 298 Convince Me Answer

Given:

An equilateral triangle with side lengths 5 inches

To find:

The shape and dimensions of the translated figure.

In order to find how translation affects the two-dimensional figure, we have to refer to the tip and make a shape to verify it.

Draw the equilateral triangle;

Translate the triangle 3 units downwards from the initial position;

Translate again 2 units to the right from the previous position;

Notice that the shape and the dimensions of the translated triangle are the same as the original triangle;

The graph of the triangles is shown. The shape and the dimensions of the translated triangle are the same as the original triangle.

Envision Math Grade 8 Chapter 6.1 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 300 Exercise 2 Answer

Given:

A triangle with its translation.

To find:

How can the side lengths and angle measures for the two triangles be the same?

Recall that translation is a transformation that shifts a figure by space, but does not change the size, shape or orientation of the figure.

Therefore, both shapes are triangles of the same size and with congruent corresponding sides and angles.

Since translation moves the figure by the space and does not change its size, shape or orientation, both the initial triangle and its image are of the same size and with congruent corresponding sides and angles.

Page 300 Exercise 3 Answer

Given:

One vertex of a figure mapped to its image by translating the point 2 units left and 7 units down.

To find:

The rule that maps the other vertices of the figure to their images.

In order to find the rule that maps the vertices of the figure to their image use the tip mentioned.

Let (x, y) be a vertex of the original figure.

(x, y)

Translate the point 2 units left and 7 units down:

(x + (−2),y + (−7))

By using the signs in multiplication, it follows:

(x − 2,y − 7)

The rule that maps the vertices of the figure to their images is:

(x, y) → (x − 2,y − 7)

Page 300 Exercise 4 Answer

Given:

To find:

Correct figure which is translation of figure A

In order to find the correct figure which is translation of figure A use the tip mentioned.

The initial and the translated figure have the same size, shape and orientation.

Since figure C have a different orientation from figure A, it is not its image after a translation.

Since figure A and figure B have the same size, shape and orientation, assume that figure B is the image of figure A after a translation.

Vertices of figure B are obtained by translating the vertices of figure A 5 units upwards.

The figure B is the image of the figure A after a translation of 5 units upwards.

Page 300 Exercise 5 Answer

Given:

To find:

Graph the translation of Figure A 3 units right and 4 units up.

In order to graph the figure which is translation of figure A use the tip mentioned.

Plot figure A on the coordinate plane,

Translate all the vertices 3 units right

Translate all the vertices from the previous position 4 units up.

Join all the vertices of the figure translated 3 units right and 4 units up.

The graph of the translated figure is shown.

Page 300 Exercise 6 Answer

Given:

To find:

The translation needed to move the figure B to the same position as the image from the item 5.

In order to find the translation needed refer to the tip mentioned and then solve it accordingly.

From B to A the figure was translated 5 units downward.

From A to C the figure was reflected to the other side by multiplying −1 to the x values of figure A.

Figure B was translated 5 units downward then the x values were multiplied by −1 to obtain figure C.

Solutions For Envision Math Grade 8 Exercise 6.1

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 301 Exercise 7 Answer

Given:

The image of GRAM

To find:

Graph of G′R′A′M′ after a translation 11 units right and 2 units up

In order to plot the graph, we have to use the method of translation which is mentioned in the tip.

Translate each vertex 11 units right

Move from the previous position 2 units upward and label the new vertices G′,R′,A′ and M′

Connect the vertices G′,R′,A′ and M′, to make a G′R′A′M′

GRAM becomes G′R′A′M′ after translation

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 301 Exercise 9 Answer

Given:

To find:

Triangle whose image is translation of ΔDEF

In order to describe the translation, we need to refer to the tip mentioned.

The initial and the translated figure have the same size, shape, and orientation.

Since triangle △GHI and triangle △JKL have a different orientation from triangle △DEF,they are not its image after a translation.

Since triangle △DEF and triangle △MNO have the same size, shape and orientation, assume that triangle △MNO is the image of triangle △DEF after a translation.

The vertex N is obtained by translating the vertex E 10 units to the right.

The vertex M is obtained by translating the vertex D10 units to the right.

The vertex O is obtained by translating the vertex F 10 units right.

The triangle △MNO is the image of the triangle △DEF after a translation of 10 units right.

Page 301 Exercise 10 Answer

Given: The distance difference of both the figures is 3
unit left and 11 unit down.

To find: The similarities and differences between both the figure.

The similarity between both the figure is both are quadrilateral and on the same plane.

The difference between both the figure is if one lie in X-axis then the second one is in negative Y-axis.

The differences and similarities have been explained.

Envision Math Grade 8 Volume 1 Chapter 6.1 Practice Problems

Page 301 Exercise 11 Answer

The graph is given.

Have to graph this by shifting some points

The graph is plotted.

Page 301 Exercise 12 Answer

Given: Length of PQ.

To find: The length of P′Q′.

We will calculate the length by the properties of image formation.

The length of P′Q′ will be negative of the length of PQ.

So, the length of P′Q′ is −2.8

So, the length of P′Q′ is -2.8.

Given: The angle of R.

To find: The angle of R′.

We will calculate the angle by the properties of image formation.

The angle of R′ will be negative of the angle of R.

So, the angle of R′ will be 255 degree.

So, the angle of R′ will be 255 degree.

Envision Math 8th Grade Congruence And Similarity Topic 6.1 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 302 Exercise 13 Answer

The given figure is shown below:

To draw the image after the given translation

Translate vertex B and D ,120 units to the right.

Move the 2 vertices from the previous position 100 units upward to their final position B′ and D′ respectively.

Use a similar pair of translations to plot vertices A′ and C′ respectively.

Join the vertices A′,B′,C′ and D′ to get the translated shape.

The shape A′B′C′D′ is obtained after translating the given figure ABCD,120 units right and 100 units upwards.

Given:
Length of plot = 240 yards

Length of another plot = 120 yards

Width of plot = 100 yards

To: Find the combined area of the 2 plots in square yards. Step formulation: Find the individual area and then add them.

The combined area of both plots is 69600 yard².

Envision Math Grade 8 Chapter 6.1 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.1 Page 302 Exercise 14 Answer

Given: Image created by translation.

To: What is true about the preimage of a figure and its image created by a translation?

When the image is translated it moves with the same distance and direction from its preimage. Also the size and shape of the image is same as that of the image.

Correct options are:

1. Each point in the image moves the same distance and direction from the preimage.

3. The preimage and the image are the same size.

4. The preimage and the image are the same shape.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 295 Exercise 1 Answer

Given:

____ have a sum of 90^∘.

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are complementary when they add up to 90^∘.

Hence,

Complementary Angles have a sum of 90^∘.

Page 295 Exercise 2 Answer

Given:.

____ share the same ray.

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are adjacent angles when they share the same ray.

Hence,

Adjacent angles share the same ray.

Envision Math Grade 8 Chapter 6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 3 Answer

Given:.

____ are pairs of opposite angles made by intersecting lines.

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are vertical when they make pairs of opposite angles by intersecting lines.

Hence,

Vertical angles are pairs of opposite angles made by intersecting lines.

Page 295 Exercise 4 Answer

Given:.

____have a sum of 180^∘

To find:

Choose the best term to complete the sentence.

According to the tip mentioned above, we can conclude that angles are supplementary when they add up to make an angle of 180^∘.

Hence,

Supplementary angles have a sum of 180^∘.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 6 Answer

Given:

Two integers 6 and \(\frac{1}{2}\)

To find:

The multiplicative sum of the two integers.

In order to find the multiplication of the two integers, we have to multiply the first integer with the second integer.

Hence, 6 x \(\frac{1}{2}\) = 3.

Envision Math Grade 8 Congruence And Similarity Topic 6 Answers

Page 295 Exercise 8 Answer

Given:

To find:

Point W

In order to find the point W

we have to refer to the tip mentioned and follow the following steps.

Move up to the x−axis starting from the point W.

It follows that the x−coordinate of point W is −4

Move right to the y−axis from the point W​

It follows that the y−coordinate of point W is −3

The coordinates of point W are (−4,−3)

Hence, the coordinates of point W are (−4,−3)

Page 295 Exercise 9 Answer

Given:

To find:

Point X

In order to find the point X, we have to refer to the tip mentioned and follow the following steps.

Move downwards towards x−axis starting from the point X. Thus, the value of x−coordinate is −2

Move rightwards towards y−axis from the point X. Thus the value of y− coordinate is 2

Thus the coordinates of the point X(x,y) are (−2,2)

Hence, coordinates of the pointX(x,y) are (−2,2)

Envision Math Grade 8 Volume 1 Student Edition Solutions Guide

Page 295 Exercise 10 Answer

Given:

To find:

Point Y

In order to find the point Y, we have to refer to the tip mentioned and follow the following steps.\

Move downwards towards x−axis starting from the point Y. Thus, the value of x−coordinate is 3

Move leftwards towards y−axis from the point Y. Thus the value of y−coordinate is 5

The coordinates of the point Y are (3,5)

The coordinates of point Y are (3,5).

Solutions For Envision Math Grade 8 Topic 6

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 11 Answer

Given:

To find:

Point Z

In order to find the point Z, we have to refer to the tip mentioned and follow the following steps.

Move upwards towards x−axis starting from the pointZ. Thus, the value of x−coordinate is 2

Move rightwards towards y−axis from the point Z. Thus the value of y−coordinate is −3

Thus, coordinates of point Z are (2,−3)

Hence, the coordinates of point Z are (2,−3)

Grade 8 Envision Math Congruence And Similarity Questions

Page 295 Exercise 12 Answer

Given:

One angle from the pair of supplementary is 130^∘

The missing angle.

In order to find the missing angle we have to refer to the tip and subtract the angle given from 180^∘.

Calculation:

The sum of the supplementary angles = 180^∘

Angle given = 130^∘

If the angles are supplementary then their sum will be equal to 180^∘

Therefore,

Missing angle ​=180 − 130

=180 − 130

= 50^∘

Hence, the missing angle is equal to 50^∘.

Envision Math Topic 6 Congruence And Similarity Step-By-Step Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Topic 6 Page 295 Exercise 13 Answer

Given:.

One angle from the pair of supplementary is 139^∘

To find:

The missing angle.

In order to find the missing angle we have to refer to the tip and subtract the angle given from 180∘.

Calculation:

The sum of the supplementary angles =180^∘

Angle given = 139^∘

If the angles are supplementary then their sum will be equal to 180^∘

Therefore,
​
Missing angle

​= 180 − 139

= 41^∘

Hence, the missing angle is equal to 41^∘.

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 287 Essential Question Answer

Find: to solve a system of linear equation.

A system of linear equations is formed by two or more linear equations that use the same variables.

A linear system solution is the assignment of values to variables in such a way that all the equations are concurrently fulfilled.

Any ordered pair that makes all equations in the system true is a solution of a system of linear equations.

A system of linear equations is formed by two or more linear equations that use the same variable.

Take, for example, a system of linear equations:

The solution of the system is (2,1).

Any ordered pair that makes all equations in the system true simultaneously is a solution of a system of linear equations.

A system of linear equations is formed by two or more linear equations that use the same variables.

Envision Math Grade 8 Volume 1 Chapter 5 Review Exercise Solutions

Page 287 Use Vocabulary In Writing Answer

Find: Use vocabulary terms to find the number of solutions of two or more equations by using the slope and the y-intercept.

The lines will be parallel if the two linear equations have the same slope but distinct y-intercepts.

Because parallel lines never overlap, a system made up of two parallel lines has no solution.

If two linear equations have the same slope and y-intercept, they describe the same line.

There are an unlimited number of solutions since a line crosses itself everywhere.

In any other scenario when the slope varies, the system of equations will have a single solution.

There will be no solution for linear equations with the same slope but a different y-intercept.

There are an unlimited number of solutions to linear equations with the same slope and y-intercept.

In any other scenario, when the slope varies, the system of equations will have a single solution.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 288 Exercise 2 Answer

Given:
​
y = 2x + 10

3y − 6x = 30
​
Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

The equation y = 2x + 10 is written in slope-intercept form.

​
Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Page 288 Exercise 3 Answer

Given

2y = 18x + 72

Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

​
Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Analyze And Solve Systems Of Linear Equations Envision Math Review Exercise Answers

Page 288 Exercise 4 Answer

Given:

y – 2 = 4x

Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

Rewrite the first equation in slope-intercept form,
​

The equations of the linear system have different slopes.

Therefore, the system has no solution.

Since both equations are the not same, they don’t intersect at every point, so the system has no solutions.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 288 Exercise 5 Answer

Given:

Turkey costs $3 per pound at Store A and $4.50 per pound at Store B.

Ham costs $4 per pound at Store B and $6 per pound at Store B.

Michael spends $18 at Store A, and Ashley spends $27 at Store B.

Find: equations has one solution, no solution, or infinitely many solutions.

The relationship between the lines and the number of solutions are determined by the slopes and y-

Let x be the amount of the first kind of meat and y be the second kind of the meat.

Since the boy pays $18 in the first shop, the first equation of the system representing the situation,

3x + 4y = 18

Since the girl pays $27 in the second shop, the second equation of the system representing the situation,

4.5x + 6y = 27

The system of equations,

​
Since both equations are the same, they intersect at every point, so the system has infinitely many solutions.

Since the system has infinitely many solutions, it follows that there are infinitely many ways for them to buy the same amount of both kinds of meat.

Page 289 Exercise 1 Answer

Given:

y = \(\frac{1}{2} x+1\)

-2x + 4y = 4

Find: graph each system and find the solution.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

Write the second equation in slope-intercept form,

​
Using the same method, calculate the values of y for a few different values of x,

Plot the points (−4,−1),(−2,0),(0,1),(2,2) and (4,3) as shown in the below graph:

Each point on the line represents a solution in the above graph.

Since both lines overlap, the system has infinitely many solutions.

The system has infinitely many solutions.

The required graph is:

Envision Math Grade 8 Chapter 5 Review Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 289 Exercise 2 Answer

Given:
​
y = −x − 3

y + x = 2
​
Find: graph each system and find the solution.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

The first equation in the slope-intercept form,

y = −x − 3

Calculate the value of y for x = 0,
​
y = −x − 3

y = −0 − 3

y = −3
​
Using the same method, calculate the values of y for a few other values of x,

Plot the points (0,−3),(1,−4),(2,−5) and (3,−6) and joins the points as shown in the below graph:

The above graph show the slope intercept of y = −x − 3.

Write the second equation in slope-intercept form,
​
y + x = 2

y = 2 − x

y = −x + 2

Graph the line y + x = 2 as shown in the below graph:

The above graph show the slope intercept of y = −x − 3 and y = −x + 2.

Lines y = −x + 2 and y = −x − 3 are parallel, so the system has no solution.

The required graph:

Page 289 Exercise 3 Answer

Given:
​
2y = 6x + 4

y = −2x + 2
​
Find: graph each system and find the solution.

The relationship between the lines and the number of solutions are determined by the slopes and y-intercepts of the linear equations in a system.

To graph the first equation 2y = 6x + 4, find the intercepts of the graph of the equation,

2y = 6x + 4

Substitute x = 0 into the equation to find the y-intercept,
​
2y = 6⋅0 + 4

2y = 4

y = 2
​
Since the y-intercept is 2, the first point on the graph of the first equation is (0,2).

Now substitute the value of y = 0 in 2y = 6x + 4,

2(0) = 6x + 4

2(0) – 4 = 6x

-4 = 6x

Since the x-intercept \(-\frac{2}{3}\), the second point on the graph of the first equation is \(\left(-\frac{2}{3}, 0\right)\).

Plot the points (0, 2) and \left(-\frac{2}{3}, 0\right) on the graph as shown below:

To graph the second equation y = −2x + 2, find the intercepts of the graph of the equation,

y = −2x + 2

Substitute x = 0 into the equation to find the y-intercept,
​
y = −2⋅0 + 2

y = −0 + 2

y = 2
​
Since the y-intercept is 2, the first point on the graph of the second equation is (0,2).

Substitute y = 0 in the equation y = −2x + 2,
​
y = −2x + 2

0 = −2x + 2

2x = 2

x = 1
​
Since the x-intercept is 1, the second point on the graph of the second equation is (1,0).

Plot the points(1,0) and (0,2) on the graph as shown below:

The above graph show the slope intercept of y = −2x + 2.

The graph of 2y = 6x + 4 and y = −2x + 2 are shown below:

The above graph shows that the intersection point is (0,2).

Substitute x = 0 and y = 2 into the first equation 2y = 6x + 4,
​
2(2) = 6(0) + 4

4 = 0 + 4

4 = 4
​
It means that the statement is true.

Substitute x = 0 and y = 2 into the first equation y = −2x + 2,
​
y = −2x + 2
​
2 = −2(0) + 2

2 = 0 + 2

2 = 2
​
​It means that the statement is true.

Since both statements are true, the point (0,2) is the solution to the system.

The solution of the given system of equation is (0,2).

The required graph:

Solutions For Envision Math Grade 8 Review Exercise

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 290 Exercise 1 Answer

Given:
​

​−3y = −2x − 1

y = x − 1
​
Find: solve each system.

The solution of the given equation is (x, y) = (4, 3).

Page 290 Exercise 2 Answer

Given:
​
y = 5x + 2

2y − 4 = 10x
​
Find: solve each system.

​
It means the equation has infinite, many solutions.

The solution of the given equation has infinitely many solutions.

Envision Math Grade 8 Volume 1 Chapter 5 Review Practice Problems

Page 290 Exercise 3 Answer

Given:
​
2y − 8 = 6x

y = 3x + 2
​
Find: solve each system.

​
This means the equation has no solution.

There is no solution for the given system of equation. That is x ∈ ∅.

Envision Math 8th Grade Systems Of Equations Review Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 290 Exercise 4 Answer

Given:
​
2y − 2 = 4x

y = −x + 4
​
Find: solve each system.

The solution of the given equation is (x, y)=(1,3).

Page 290 Exercise 1 Answer

Given:
​
−2x + 2y = 2

4x − 4y = 4
​
Find: solve the equation.

There is no solution for the equation.

The statement is false for any value of x and y, so there is no solution. That is (x, y)∈ ∅.

Envision Math Grade 8 Chapter 5 Review Summary

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Review Exercise Page 290 Exercise 2 Answer

Given:
​
4x + 6y = 40

−2x + y = 4
​
Find: solve the equation.

The solution of the given equation is (x, y) = (1, 6).

Envision Math Grade 8 Topic 5 Review Problems And Solutions

Page 290 Exercise 3 Answer

Given:

A customer at a concession stand bought 2 boxes of popcorn and 3 drinks for $12.

Another customer bought 3 boxes of popcorn and 5 drinks for $19.

Find:

Box of popcorn cost? Drink cost?

Use the elimination method to solve the equation.

Let x be the number of box of popcorn and y the number of drinks.

Since the cost of 2 box of popcorn plus the cost of 3 drinks is $12,

2x + 3y = 12.

And since the cost of 3 box of popcorn plus the cost of 5 drinks is $19,3x + 5y = 19.

A system of equations representing the situation,

​
​The box of popcorn cost $3.

The drink cost $2.

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

Page 277 Exercise 1 Answer

Given: A list of expressions is written on the board.

To Find: How can you make a list of fewer expressions that has the same combined value as those shown on the board? Write the expressions and explain your reasoning.

Like terms are terms whose variables and their exponents are the same.

To combine like terms, add or subtract the coefficients and keep the variables the same.
​
2y  3x  5  -5x

-3y  -2x  -3  5x

Combine the like terms from the given list:
​
2y − 3y ​= −y

3x − 5x − 2x + 5x = x

5 − 3 = 2
​
The new list is obtained by adding and subtracting the coefficients of the like terms, and it looks like: ​−y  x  2

​

Page 277 Focus On Math Practices Answer

Given: Two expressions have a sum of 0.

To find: What must be true of the expressions?

Using the additive inverse property, every two expressions with opposite signs have a sum of 0.

The two expressions must have opposite signs to have a sum of 0.

Envision Math Grade 8 Volume 1 Chapter 5.4 Solutions

Page 278 Essential Question Answer

Find: the properties of equality used to solve systems of linear equations.

We’ve now studied all four equality properties: subtraction, addition, division, and multiplication. For your convenience, we’ve compiled a list of all of them here. You can still have equality if you add, subtract, multiply, or divide the same amount from both sides of an equation.

When there is addition in an equation, the Subtraction Property of Equality is applied. It asserts that the same amount may be subtracted from both sides of the equation without altering the equality.

When there is a subtraction in an equation, the Addition Property of Equality is utilized. It asserts that the same amount may be added to both sides of the equation without affecting the equality.

When you have an equation containing a variable multiplied by a number, you may utilize the Division Property of Equality. It asserts that you can divide both sides of an equation by the same number (as long as that number is not equal to zero) and the equality remains unchanged.

When you have an equation with a variable divided by a number, you may apply the Multiplication Property of Equality. It says that you can multiply both sides of an equation by the same number without affecting the equation’s equality.

By removing a variable, you may use the properties of equality to solve systems of linear equations algebraically.

Elimination is an efficient method when:

Similar variable terms have the same or opposite coefficients, elimination is an effective technique.

One or both equations can be multiplied in such a way that similar variable terms have the same or opposite coefficients.

Page 278 Try It Answer

Given: ​

​2r + 3s = 14

6r − 3s = 6
​
To Find the solutions of r and s.

​
The solution is s = 3.

Page 278 Convince Me Answer

Find a system of equations for a term to be eliminated by adding or subtracting.

To get an equation in one variable, use the elimination approach and either add or subtract the equations. When the coefficients of one variable are opposites, the equations are added to delete a variable; when the coefficients of one variable are equal, the equations are subtracted to eliminate a variable.

For example:
​
​
The solution of the linear system is (0,2).

Which means:

To remove a term by adding, the total of the term’s coefficients must equal zero.

To remove a term by subtracting, the difference between the term’s coefficients must equal zero.

To eliminate a term by adding, the sum of the coefficients of the term must equal 0.

To eliminate a term by subtracting, the difference of the coefficients of the term must equal 0.

Analyze And Solve Systems Of Linear Equations Envision Math Exercise 5.4 Answers

Page 279 Try it Answer

Given: ​

​3x − 5y = −9

x + 2y = 8
​
To find: Use elimination to solve the system of equations.

Solve using the elimination method

(x, y) = (2, 3)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 280 Exercise 1 Answer

Find: the properties of equality used to solve systems of linear equations.

We’ve now studied all four equality properties: subtraction, addition, division, and multiplication. For your convenience, we’ve compiled a list of all of them here. You can still have equality if you add, subtract, multiply, or divide the same amount from both sides of an equation.

When there is addition in an equation, the Subtraction Property of Equality is applied. It asserts that the same amount may be subtracted from both sides of the equation without altering the equality.

When there is a subtraction in an equation, the Addition Property of Equality is utilized. It asserts that the same amount may be added to both sides of the equation without affecting the equality.

When you have an equation containing a variable multiplied by a number, you may utilize the Division Property of Equality. It asserts that you can divide both sides of an equation by the same number (as long as that number is not equal to zero) and the equality remains unchanged.

When you have an equation with a variable divided by a number, you may apply the Multiplication Property of Equality. It says that you can multiply both sides of an equation by the same number without affecting the equation’s equality.

By removing a variable, you may use the properties of equality to solve systems of linear equations algebraically.

Elimination is an efficient method when:

Similar variable terms have the same or opposite coefficients, elimination is an effective technique.

One or both equations can be multiplied in such a way that similar variable terms have the same or opposite coefficients.

Envision Math Grade 8 Chapter 5.4 Explained

Page 280 Exercise 2 Answer

To find: How is solving a system of equations algebraically similar to solving the system by graphing? How is it different?

In both solving a system of equations and solving the system by graphing, the common goal is to find the solution to the system.
Say, for example, that we have a system of equations:

An example of algebraically solving the system follows.

The goal is to find ordered pairs that satisfy both equations.

The ordered pair is a solution

(x, y) = (1,0)

When solving graphically, we graph the first and the second equation and search for points of intersection of the graphs.

The solution – intersection point is represented by the ordered pair of its coordinates.

Both methods produce ordered pairs as solutions if they exist.

If there are no solutions, and impossible equation (such as1 = 0) will emerge in the algebraic method.

In the geometric method, no intersections will be noted when the system has no solutions.

The main difference is in precisely determining the solution.

When graphing, if the coordinates of the intersection are fractions or irrational numbers, the solution is approximated.

The algebraic methods, on the other hand, produce precise values.

In both solving a system of equations algebraically and by graphing, the common goal is to find the solution to the system.

The difference is in the precision of solutions. Algebraic solutions are precise, while the geometric may be approximate.

Solutions For Envision Math Grade 8 Exercise 5.4

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4Page 280 Exercise 3 Answer

Given:

To Find: Construct Arguments Consider the system of equations. Would you solve this system by substitution or by elimination? Explain.

Rewrite the system, using the identity Property of Multiplication:

Notice that the coefficient of y in the first equation, +1, is the inverse of the coefficient of y in the second equation, -1.

Therefore, by adding the 2 equations together, the term y would be cancelled.

The system can be solved through elimination because adding the 2 equations will remove the term y.

Page 280 Exercise 4 Answer

Given: ​

​y − x = 28

y + x = 156
​
To Find: solve each system of equations by using elimination.

The ordered pair is a solution

(x, y) = (64, 92)

Solve using the elimination method

(x, y) = (64, 92)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 280 Exercise 5 Answer

Given: ​

​3c + 6d = 18

6c − 2d = 22
​
To find: solve each system of equations by using elimination.

The ordered pair is a solution

(c, d) = (4, 1)

Solve using the elimination method

(c, d) = (4, 1)

Page 281 Exercise 6 Answer

Given: ​

7x + 14y = 28

5x + 10y = 20
​
To Find: solve each system of equations by using elimination.

The statement is true,

Infinitely many solutions

Solve using the elimination method

Infinitely many solutions

Envision Math Grade 8 Volume 1 Chapter 5.4 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 281 Exercise 7 Answer

Given: ​

​2x − 2y = −4
2x + y = 11
​
To find: Leveled Practice Solve the system of equations using elimination.

The solution to the two equations is:

x = 3,y = 5

Page 281 Exercise 8 Answer

Given: ​

​2y − 5x = −2

3y + 2x = 35
​
To Find: Solve the system of equations using elimination.

Check the solution

Simplify

The ordered pair is a solution

(x, y) = (4, 9)

Solve using the elimination method

(x, y) = (4, 9)

Page 281 Exercise 9 Answer

Given: If you add Natalie’s age and Frankie’s age, the result is 44. If you add Frankie’s age to 3 times Natalie’s age, the result is 70.

To find: Write and solve a system of equations using elimination to find their ages.

Let x be the age of the first person and y the age of the second person.

The sum of ages of the first and the second person is 44, so it follows:

x + y = 44

Since the sum of 3 times the age of the first person and the age of the second person is 70, it follows:

3x + y = 70

A system of equations representing the situation is:
​
x + y = 44

3x + y = 70

Solve the system using elimination:

Check the solution

Simplify

The ordered pair is a solution

(x, y) = (13, 31)

The system of equations is:

The system of equations is:
​
x + y = 44

3x + y = 70
​
The age of the first person is 13 and the age of the second person is 31.

The system of equations is:
​
x + y = 44

3x + y = 70
​
The age of the first person is 13 and the age of the second person is 31.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 281 Exercise 10 Answer

Given: ​

​5x + 10y = 7

4x + 8y = 3
​
To Find: If possible, use elimination to solve the system of equations.

The statement is false

No solution

Solve using the elimination method

No solution

Page 282 Exercise 14 Answer

Given: Consider the system of equations.
​
x − 3.1y = 11.5

−x + 3.5y = −13.5
​
To Find: Solve the system by elimination.

Check the solution

Simplify

The ordered pair is a solution

(x, y) = (-4, -5)

Solve using the elimination method

(x,y) = (−4,−5)

Given: Consider the system of equations.
​
x − 3.1y = 11.5

−x + 3.5y = −13.5
​
To Find: If you solved this equation by substitution instead, what would the solution be? Explain.

The system of equations is given by:

By substitution method, the solution to the system of equations is x = −4 and y = −5.

Envision Math 8th Grade Systems Of Equations Topic 5.4 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 282 Exercise 15 Answer

Given: ​

​3x + 4y = 17

21x + 28y = 109
​
To Find: Higher Order Thinking Determine the number of solutions for this system of equations by inspection only. Explain.

Rewrite the first equation into the slope-intercept form:

Notice, the given equations have the same slope \(-\frac{3}{4}\) but different y intercepts, \(\frac{17}{4} \text { and } \frac{109}{28}\).

Therefore, the system of equations has no solution.

Since the equations, in slope-intercept form, have the same slope but different y-intercepts, the system of equations has no solution.

Envision Math Grade 8 Topic 5.4 Elimination Method Solutions

Page 282 Exercise 16 Answer

Given: Four times a number r plus half a number s equals twelve.

Twice the number r plus a quarter of the number s equals eight.

To Find: What are the two numbers?

Four times a number r plus half a number s equals twelve can be expressed as:

Twice the number r plus a quarter of the numbers equals eight can be expressed as:

Solve the obtained equations:

Multiply both sides

Multiply both sides

Eliminate one variable by adding the equations

0 = -8

The statement is false

No solution

The system of equations has no solution.

The system of equations has no solution.

Envision Math Grade 8 Chapter 5.4 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.4 Page 282 Exercise 17 Answer

Given: ​

​3m + 3n = 36

8m − 5n = 31
​
To find: Solve the system of equations.

Check the solution

Simplify

The ordered pair is a solution

Solve using the substitution method

Envision Math Grade 8 Volume 1 Chapter 5 Analyze And Solve System Of Linear Equations

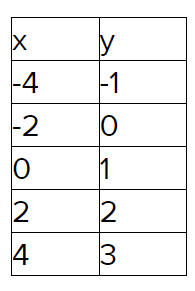
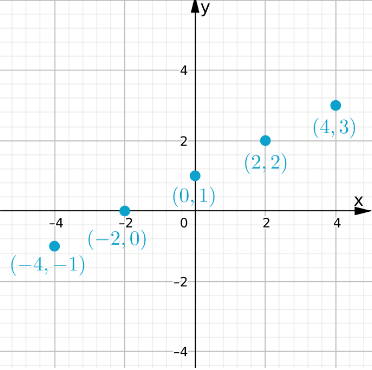
Page 269 Exercise 1 Answer

To determine the number of solutions of a system by looking at the equations?

The number of solutions of the equation is evident from the slope-intercept form of the equations.

When the equations have different slopes, the system has one solution.

When the equations have the same slopes but different y-intercepts, the system does not have a solution.

When the equations have the same slopes and y-intercepts, the system has infinitely many solutions.

The number of solutions of the system is evident from the slope-intercept form of the equations.

Depending on the slopes and y-intercepts of the equations, the system may have one, infinitely many, or no solutions.

Envision Math Grade 8 Volume 1 Chapter 5.3 Solutions

Page 269 Exercise 2 Answer

Given:
​
2x − 9y = −5

4x − 6y = 2
​
To explain how many solutions does the system of equations has.

Rewrite the first equation in slope-intercept form:

2x − 9y = −5

Move the variable to the right,

−9y = −5 − 2x

Change the signs,

9y = 5 + 2x

Divide both sides by 9,

y = \(\frac{5}{9}+\frac{2}{9} x\)

Use the commutative property to reorder the terms,

y = \(\frac{2}{9} x+\frac{5}{9}\)

Rewrite the second equation in slope-intercept form:

4x − 6y = 2

Move the variable to the right,

−6y = 2 − 4x

Change the signs,

6y = −2 + 4x

Divide both sides by 6 and simplify,

y = \(-\frac{1}{3}+\frac{2}{3} x\)

Use the commutative property to reorder the terms,

y = \(\frac{2}{3} x-\frac{1}{3}\)

Now check the slopes of both the equation,

y = \(\frac{2}{9} x+\frac{5}{9}\)

y = \(\frac{2}{3} x-\frac{1}{3}\)

The equations of the linear system have different slopes this means that the system has one solution.

Therefore, the system has one solution.

Analyze And Solve Systems Of Linear Equations Envision Math Exercise 5.3 Answers

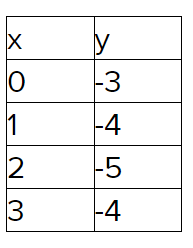
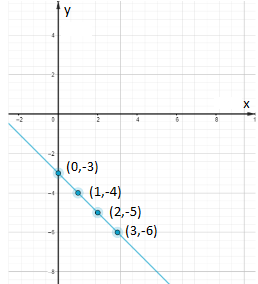
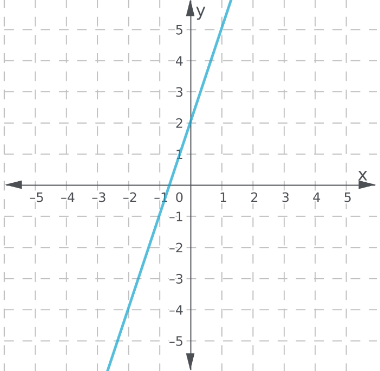
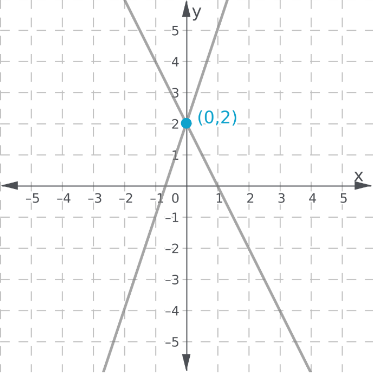
Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 269 Exercise 3 Answer

Given:

y + 1 = 2x

y = \(\frac{1}{2} x+2\)

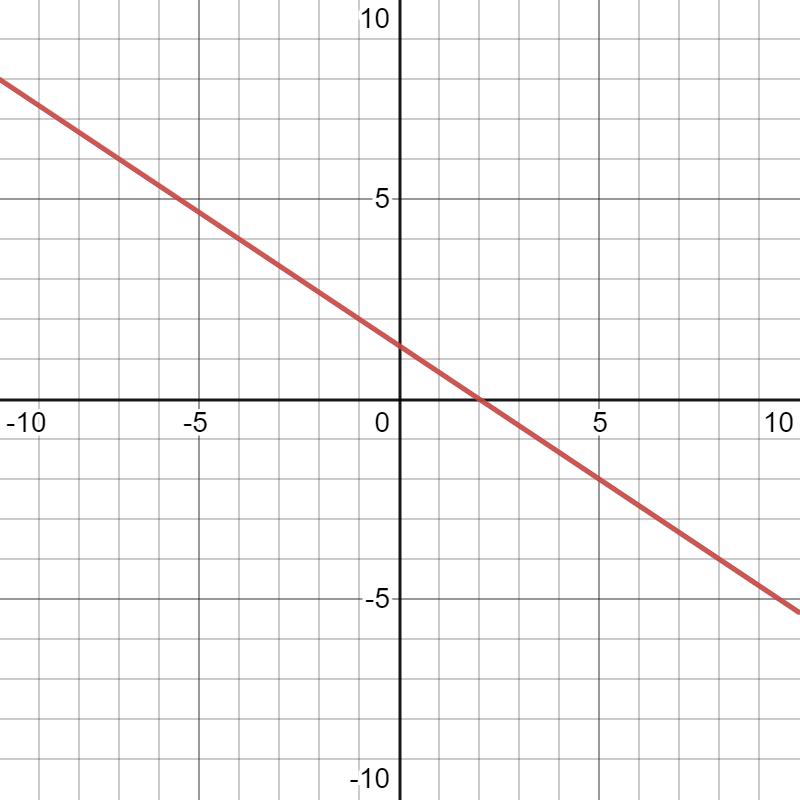
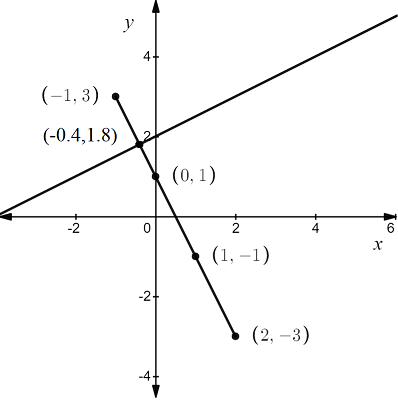
To find: Graph the system of equations and find the solution.

The first equation is written in slope-intercept form.

Calculate the value of y for x = 0:

y = −2x + 1,x = 0

Substitute x = 0,

y = −2 × 0 + 1

Calculate the product,

y = 0 + 1

y = 1

Using the same method, calculate the values of y for a few other values of x.

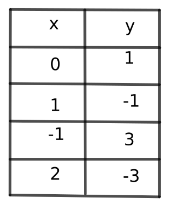
Draw the graph,

Plot the points on the graph.

Draw a line through the plotted points.

Using the same method, graph the line \(y = \frac{1}{2} x+2\).

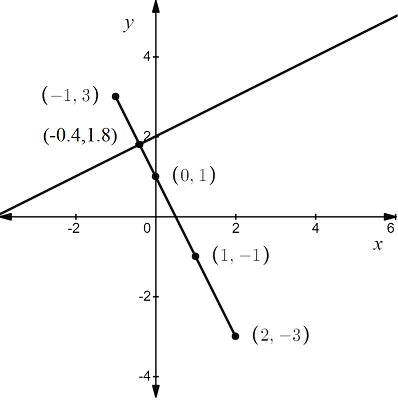
The lines intersect at the point (−0.4,1.8).

The point of intersection (−0.4,1.8) is the solution of the system and the graph is shown below,

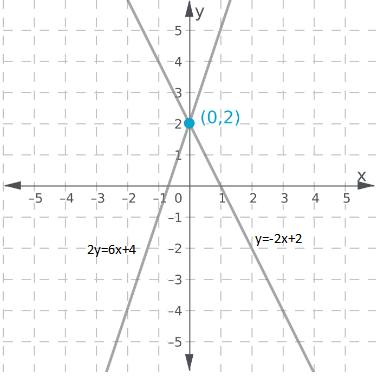
Page 269 Exercise 5 Answer

Given: Finn bought 12 movie tickets. Student tickets cost $4, and adult tickets cost $8.Finn spent a total of $60.

To write and graph a system of equations to find the number of student and adult tickets Finn bought.

Let x be the number of the $4 items and y be the number of the $8 items.

Since the boy bought 12 items in total, the first equation of the system is:

x + y = 12

Solve the equation for y:

x + y = 12

Move the variable to the right,

y = 12 − x

Use the commutative property to reorder the terms,

y = −x + 12

y = -1.x + 12

From the slope-intercept form of a line, it follows:

m = -1, b = 12

Since the boy spent $60 total, the second equation of the system is:

4x + 8y = 60

Move the variable to the right

8y = 60 – 4x

Divide both sides by 8,

y = \(\frac{15}{2}-\frac{1}{2} x\)

Use the commutative property to reorder the terms,

y = \(-\frac{1}{2} x+\frac{15}{2}\)

From the slope-intercept form of a line, it follows:

m = \(-\frac{1}{2}, b=\frac{15}{2}\)

Therefore, the system representing the given situation is:

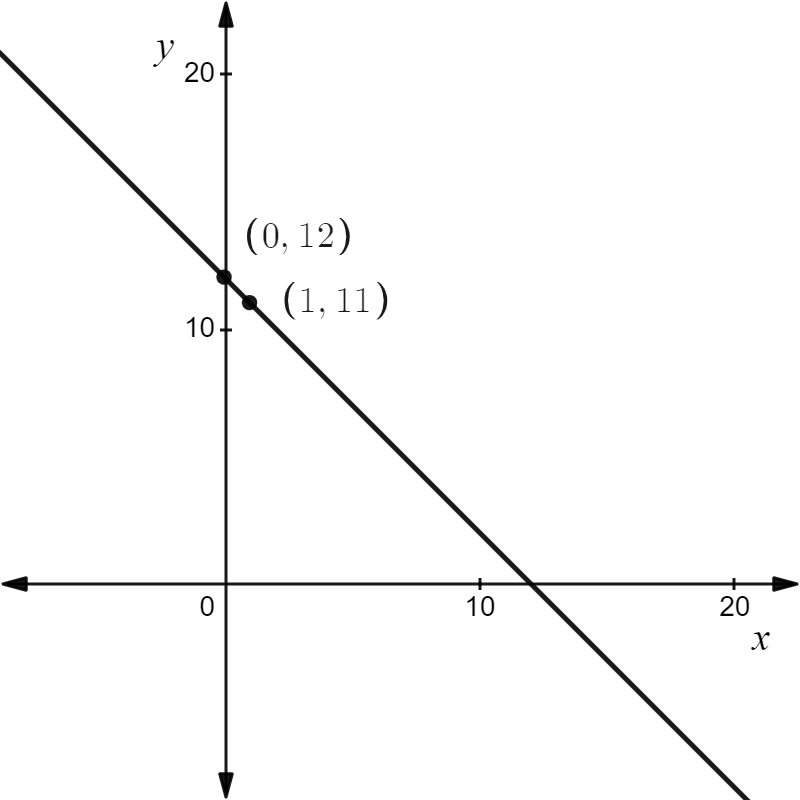
Draw the line y = -x + 122 using its slope and y-intercept.

y = -x + 12

Since the y-intercept of the line is 12, the line passes through the point (0, 12).

Plot the point (0, 122).

Since the slope of the line is m = \(\frac{-1}{1}\), move 1 unit down and 1 unit right starting from point (0, 12).

It follows that the line passes through point (1, 11) as well.

Draw the line y = \(-\frac{1}{2} x+\frac{15}{2}\) using its slope and y intercept.

y = \(-\frac{1}{2} x+\frac{15}{2}\)

Since the y-intercept of the line is \(\frac{15}{2}\), the line passes through point. \(\left(0, \frac{15}{2}\right)\)

The graph is shown below,

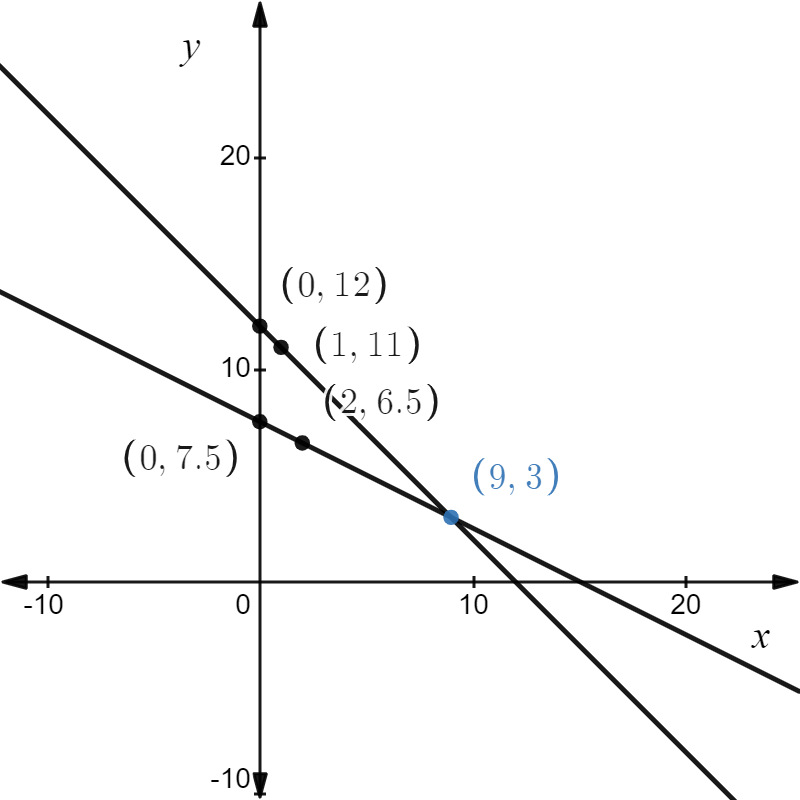
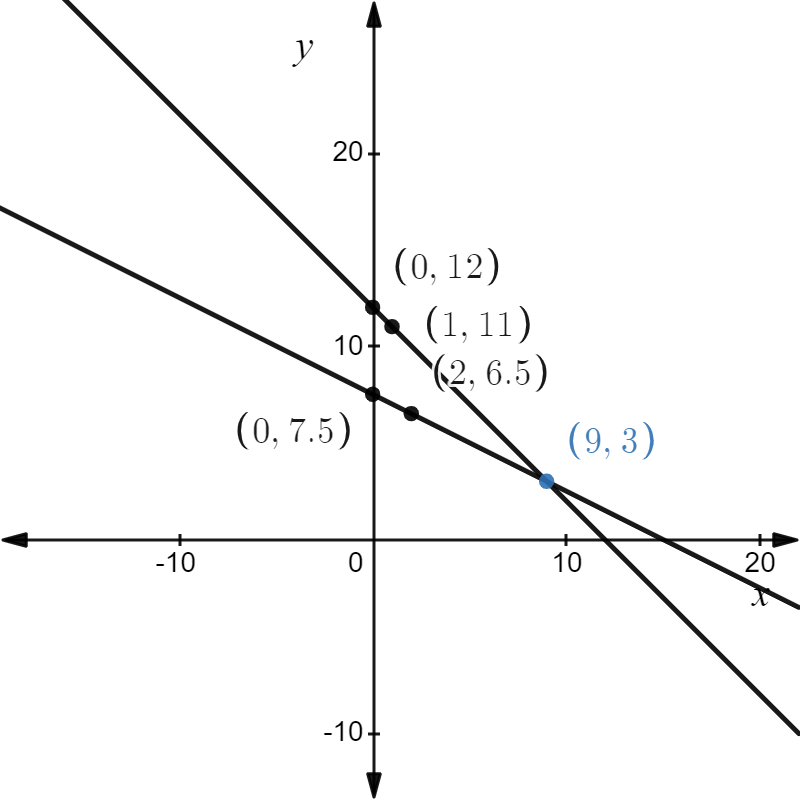
It follows that the lines intersect at point (9,3).

Since the solution to the system is (9,3), it follows that the boy bought 9 items for the price of $4 and 3 items for the price of $8.

The system representing the given situation is:

The boy bought 9 items for the price of $4 and 3 items for the price of $8.

The graph is shown below,

Page 269 Exercise 6 Answer

Given:

−x + 4y = 32

y = mx + 8

The find the value of m.

Rewrite the first equation in slope-intercept form:

−x + 4y = 32

Move the variable to the right,

4y = 32 + x

Divide both sides by 4,

y = \(8+\frac{1}{4} x\)

Notice the value m = \(\frac{1}{4}\) substituted to the second equation will give the system infinitely many solutions since both equations will be equal.

Check the obtained system of equations,

Simplify

Multiply both sides by -1

Eliminate one variable by adding the equations,

0 = 0

The statement is true and has infinitely many solutions.

The value of m is \(\frac{1}{4}\) and it gives infinitely many solutions.

Envision Math Grade 8 Chapter 5.3 Explained

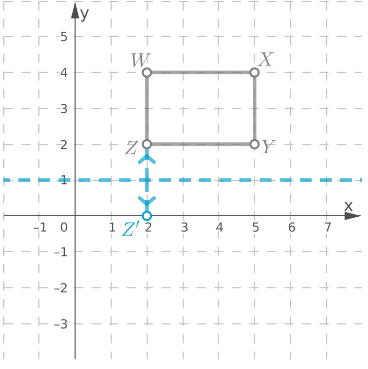
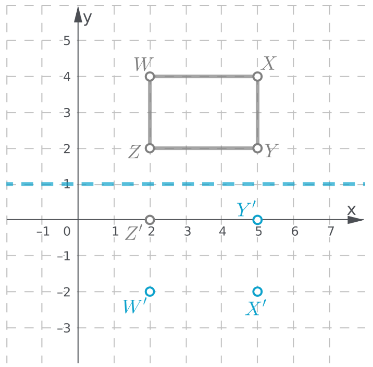
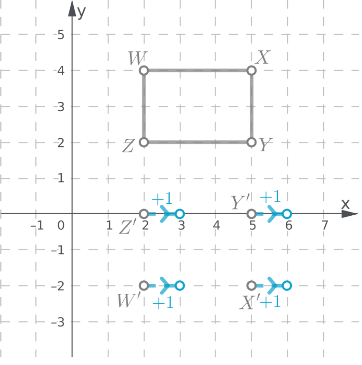
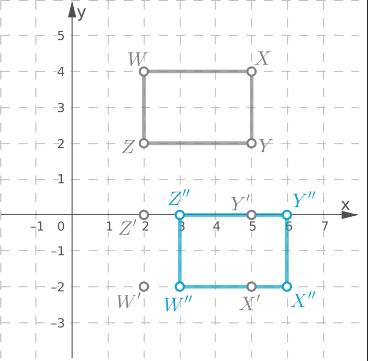
Page 271 Focus On Math Practices Answer

Explain: Can you use the graph to determine the exact number of miles for which the cost of the taxi ride will be the same

There will be a point in the graph where both the lines intersect.

The point of intersection of the lines will give the exact miles for which the cost of both the rides will be the same.

The graph can be used to determine the exact miles for which the cost of both rides will be the same.

Page 272 Essential Question Answer

Systems of linear equations can be solved algebraically. When one of the equations can be easily solved for one of the variables, you can use substitution to solve the system efficiently.

Solve one of the equations for one of the variables. Then substitute the expression into the other equation and solve.

Solve for the other variable using either equation.

Example:

Solve the system −2y − x = −84.91 and 3x + 6y = 254.73 by using substitution.

STEP 1 Solve one of the equations for one variable.
​
−2y − x = −84.91

−x = −84.91 + 2y

= 84.91 − 2y
​
STEP 2 Substitute 84.91 − 2y for x in the other equation.

Then solve.
​
3(84.91−2y) + 6y = 254.73

254.73 − 6y + 6y = 254.73

254.73 = 254.73
​
The result is a true statement. This system has infinitely many solutions.

The substitution method is most useful for systems of 2 equations in 2 unknowns. The main idea here is that we solve one of the equations for one of the unknowns, and then substitute the result into the other equation.

The substitution method can be applied in four steps

Solve one of the equations for either x = or y =.

Substitute the solution from step 1 into the other equation.

Solve this new equation.

Solve for the second variable.

Page 272 Try It Answer

Given:
​
x + y = 50

2x + 5y = 160
​
To find: How many of each type of question was on the exam.

The number of tasks worth two points is represented by x and the number of tasks worth five points is represented by y.

The situation is represented by the following system of equations:

Solve the first equation for y:

x + y = 50

Move the variable to the right,

y = 50 − x

Use the commutative property to reorder the terms,

y = −x + 50

y = -x + 50

Reorder the terms of the equation:

y = 50 – x

Substitute y = 50 − x into the second equation:

2x + 5⋅(50 − x) = 160

Use the Distributive Property to simplify the equation:

2x + 5⋅50 − 5⋅x = 160

Multiply the numbers:

2x + 250 − 5x = 160

Solve the equation for x:

2x + 250 − 5x = 160

Collect like terms

−3x + 250 = 160

Move the constant to the right

−3x = 160 − 250

−3x = −90

Divide both sides by −3

x = 30

There are 30 tasks worth two points.

x + y = 50

Substitute x = 30 into the first equation to obtain y:
​
30 + y = 50

y = 20
​
There are 20 tasks worth five points.

y = 50 – x

2x + 5.(50 – x) = 160

2x + 250 – 5x = 160

There are 30 tasks worth two points.

30 + y = 50

There are 20 tasks worth five points.

Page 272 Convince Me Answer

To find which equation to choose to solve for one of the variables.

When solving the equation for one of the variables, choose the simpler equation in the matter of coefficients of the terms.

Therefore, aim for the equation which has a coefficient of at least one term equal to 1.

Page 273 Try It Answer

Given:

4y + 2x = -6

To find: Solve each system of equations.

Move the expression to the right-hand side by adding its opposite to both sides

Since two opposites add up to zero, remove them from the expression

Substitute the given value of y into the equation, 4y + 2x = -6

Distribute 4 through the parentheses

12 − 2x + 2x = −6

Since two opposites add up to zero, remove them from the expression

12 = −6

The statement is false for any value of x

x ∈ ∅

Since the system has no solution for x, therefore system has no solutions.

Given:

y = \(\frac{1}{4} x-2\)

8y – 2x = -16

To find: Using substitution solve each system of equations.

Substitute the given value of y into the equation 8y – 2x = -16

Distribute 8 through the parentheses

2x − 16 − 2x = −16

Cancel equal terms and eliminate the opposites.

0 = 0

x ∈ R

The statement is true since there are infinitely many solutions for x, the system has infinitely many solutions.

There are infinitely many solutions to the given system of equations.

Solutions For Envision Math Grade 8 Exercise 5.3

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 274 Exercise 1 Answer

Find: substitution, a useful method for solving systems of equations.

The substitution technique is a straightforward approach for solving linear equations algebraically and determining the variables’ solutions. It entails determining the value of the x-variable in terms of the y-variable and then substituting or replacing the value of the x-variable in the second equation, as the name implies.

Substitute to solve a problem of equations:
1. For each variable, solve one of the equations.

2. Step 1’s expression should be substituted into the other equation.

3. Solve the equation that results.

4. To determine the other variable, substitute the result from Step 3 into one of the original equations.

5.Make an ordered pair out of the answer.

Algebraically, systems of linear equations may be solved. When one of the equations is easily solved for one of the variables, substitution can be used to quickly solve the system.

STEP 1: For each variable, solve one of the equations. Then solve the other equation by substituting the expression.

STEP 2: Using either equation, solve for the other variable.

Page 274 Exercise 4 Answer

Given:

y = \(\frac{1}{2} x+4\)

x – y = 8

Find: solve the given equation.

Use substitution method to find the value of x and y.

Substitute the value of y = \(\frac{1}{2} x+4\) in x – y = 8,

Multiply both sides by 2,

2x – x – 8 = 16

x – 8 = 16

x = 16 + 8

x = 24

The value of x = 24.

Now substitute the value of x = 24 in y = \(\frac{1}{2} x+4\),

y = \(\frac{1}{2} \times 24+4\)

y = 12 + 4

y = 16

The value of y = 16

The value of (x, y) = (24,16) by using substitution method.

Envision Math Grade 8 Volume 1 Chapter 5.3 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 274 Exercise 5 Answer

Given:
​
3.25x − 1.5y = 1.25

13x − 6y = 10
​
Find: solve the given equation.

Find the value of x and then use the substitution method to solve the equation.

It means y has no solution. That is y ∈ ∅.

The given equation has no solution.

Page 274 Exercise 6 Answer

Given:
​
y − 0.8x = 0.5

5y − 2.5 = 4x
​
Find: solve the given equation.

Find the value of y and then use the substitution method to solve the equation.

x ∈ R
​
The value of x = x, x ∈ R.

By using the substitution method, the value of

(x, y) = (x,0.5 + 0.8y),x ∈ R.

Page 275 Exercise 7 Answer

Given:
​
p + r = 2,666

p = r + 276
​
Find: Pedro has ______ hits, and Rocky has _____ hits.

Use the substitution method.

Let p be the number of Pedro’s hits and r be the number of Ricky’s hits.

The two teammates have a combined hit total of 2666,

p + r = 2666

Pedro has 276 more hits than Ricky,

p = r + 276

Substitute the value of p = r + 276 in p + r = 2666,
​
(r + 276) + r = 2666

r + 276 + r = 2666

2r + 276 = 2666

2r = 2666 − 276

2r = 2390
​
Divide both sides by 2,

r = 1195

So, Ricky hits r = 1195.

Substitute the value of r = 1195 in p + r = 2666,

p + 1195 = 2666.

Subtract 1195 on both sides,
​
p + 1195 − 1195 = 2666 − 1195

p = 1471
​
The number of Pedro’s hits p = 1471.

Pedro has 1471 hits, and Rocky has 1195 hits.

Page 275 Exercise 8 Answer

Given:
​
2y + 4.4x = −5

y = −2.2x + 4.5
​
Find: solution and ​

2y + 4.4x = −5

y = −2.2x + 4.5

2(−2.2x + ?) + 4.4x = −5

−4.4x + ? + 4.4x = −5

? ≠ −5
​
Use substitution method.

Substitute the value of y = −2.2x + 4.5 in 2y + 4.4x = −5,
​
2(−2.2x + 4.5) + 4.4x = −5

−4.4x + 9 + 4.4x = −5

9 ≠ −5
​
The given equation has no solution.

The statement is not true. There is no solution.

As,
​
2y + 4.4x = −5

y = −2.2x + 4.5

2(−2.2x + 4.5) + 4.4x = −5

−4.4x + 9 + 4.4x = −5

9 ≠ −5

​Envision Math 8th Grade Systems Of Equations Topic 5.3 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 275 Exercise 9 Answer

Given:
​
x + 5y = 0

25y = −5x
​
Find:
​
x + 5y = 0

25y = −5x

x = □y

25y = −5(?)

25y = □y
​
The statement is true. There are     Solutions.

Use substitution method.

Solve for x,
​
x + 5y = 0

x = −5y
​
Substitute the value of x = −5y in 25y = −5x,
​
25y = −5(−5y)

25y = 25y
​
Therefore, the statement is true. There are no solutions.

The statement is true. There are no solutions.

As,
​
x + 5y = 0

25y = −5x

x = −5y

25y = −5(−5y)

25y = 25y

​

Page 275 Exercise 10 Answer

Given:

481 people used the public swimming pool.

The daily prices are $1.25 for children and $2.25 for adults.

The receipts for admission totaled $865.25.

Find: number of children and adults swam at the public pool that day.

Use substitution method.

Let x be the number of children’s and y be the number of adults.

If one day 481 people used to swim, the combined number of children and adults on that day,

x + y = 481.

The ticket for children costs $1.25, and the ticket for adults costs $2.25, so the expression for total earnings on that day,

1.25x + 2.25y

The total earnings for the day were $865.25, so the expression must be equal to this amount,

1.25x + 2.25y = 865.25

Now solve for x,
​
x + y = 481

x = 481 − y

Substitute the value of x = 481 − y in 1.25x + 2.25y = 865.25,
​
1.25(481 − y) + 2.25y = 865.25

601.25 − 1.25y + 2.25y = 865.25

601.25 + 1y = 865.25

y = 865.25 − 601.25

y = 264
​
The number of adults y = 264.

Substitute the value of y = 264 in x = 481 − y,

x = 481 − 264

x = 217
​
The number of children x = 217.

The number of adults y = 264.

The number of children x = 217.

Envision Math Grade 8 Chapter 5.3 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 5 Analyze And Solve System Of Linear Equations Exercise 5.3 Page 275 Exercise 11 Answer

Given:
​
6x − 2y = −6

11 = y − 5x
​
And x = −9,y = −4

Find: the correct solution.

Use substitution method.

Solve for y,
​
11 = y − 5x

5x + 11 = y
​
Substitute the value of y = 5x + 11 in 6x − 2y = −6,
​
6x − 2(5x + 11) = −6

6x − 10x − 22 = −6

−4x − 22 = −6

−4x = −6 + 22

−4x = 16
​
Divide both sides by −4,

x = -4

The value of x = -4.

Substitute the value of x = −4 in y = 5x + 11,
​
y = 5(−4) + 11

y = −20 + 11

y = −9
​
The value of y = −9.

The correct solution of the given equation is(x, y) = (−4,−9).

Given:
​
6x − 2y = −6

11 = y − 5x
​
And x = −9,y = −4

Find: error Tim have made.

Use substitution method.

Solve for y in 6x − 2y = −6,
​
6x − 2y = −6

6x + 6 = 2y
​
Divide both sides by 2,

3x + 3 = y-2

The value of y = 3x + 3.

Substitute the value of y = 3x + 3 in 11 = y − 5x,
​
11 = 3x + 3 − 5x

11 − 3 = −2x

8 = −2x
​
Divide both sides by −2,

-4 = x-2

The value of x = -4.

Substitute the value of x = −4 in y = 3x + 3,
​
y = 3(−4) + 3

y = −12 + 3

y = −9
​
The value of y = −9.

The correct solution is (x,y) = (−4,−9).

Tim made an error by substituting the equation into the initial equation rather than into the other one.

The solution to the system is (x,y) = (−4,−9).

The student made an error by substituting the equation into the initial equation rather than into the other one.

Page 276 Exercise 14 Answer

Given:

The perimeter of a photo frame is 36 inches.

The length is 2 inches greater than the width.

Find: the dimensions of the frame.

Use the formula of perimeter and use substitution method.

According to the formula for polygon, the perimeter of the photo frame is the sum of its sides,

P = 2l + 2w

Substitute P = 36 and l = w + 2 in P = 2l + 2w,
​
36 = 2(w + 2) + 2w

36 = 2w + 4 + 2w

36 = 4w + 4

36 − 4 = 4w

32 = 4w
​
Divide both sides by 4,

8 = w

The length of the photo frame 8 inches.

Substitute the value of w = 8 in L = w + 2,
​
L = 8 + 2

L = 10
​
The width of the photo frame is 10 inches.

The dimensions of the frame are:

The length of the photo frame 8 inches.

The width of the photo frame is 10 inches.

Page 276 Exercise 15 Answer

Given:

The capacity of the auditorium is 500 people.

The members would like to false $2,050 every night to cover all expenses, by selling tickets.

Find: each type of ticket must have been sold for the members to raise exactly $2,050.

Use substitution method.

Let d be the number of adult and s be the number of students.

If one day 500 people used the facility, the combined number of adults and student on that day,

d + s = 500.

The ticket for adults costs $6.50, and the ticket for students costs $3.50, so the expression for total earnings on that day,

6.50d + 3.50s.

The total earnings for the day were $2050, so the expression must be equal to this amount,

6.50d + 3.50s = 2050.

Solve for d,
​
d + s = 500

d = 500 − s

Substitute the value of d = 500 − s in 6.5d + 3.5s = 2050,
​
6.5(500 − s) + 3.5s = 2050

3250 − 6.5s + 3.5s = 2050

3250 − 3s = 2050

3250 − 2050 = 3s

1200 = 3s
​
Divide both sides by 3,

s = 400

The number of students s = 400.

Substitute the value of s = 400 in d + s = 500,
​
d + 400 = 500

d = 500 − 400

d = 100
​
The number of adults d = 100.

To raise the fund of $2050, there should be 100 adults and 400 students.

Given:

At one performance, there were three times as many student tickets sold as adult tickets.

There were 480 tickets sold at that performance

Find: ticket sales fall below $2,050.

Use substitution method.

According to question s = 3d.

Since the total number of ticket sold is 480,

d + s = 480

Substitute s = 3d in d + s = 480,
​
d + 3d = 480

4d = 480
​
Divide both sides by 4,

d = 120

So, the number of adults are d = 120.

Substitute the value of d = 120 in s = 3d,
​
s = 3(120)

s = 360
​
So, the number of students are s = 360.

Total earning T from tickets,

T = s × 3.50 + d × 6.50.

Substitute the value of s = 360 and d = 120 in

T = s × 3.50 + d × 6.50,
​
T = s × 3.50 + d × 6.50

T = 360 × 3.50 + 120 × 6.50 = 2040
​
Total earning T from tickets are $2,040.

So, the goal is to fall short,

$2050 − $2040 = $10.

The goal to achieve total payment of $2050 is to fall short by $10.

Envision Math Grade 8 Topic 5.3 Substitution Method Solutions

Page 276 Exercise 16 Answer

Given:

y = 145 – 5x …(1)

0.1y + 0.5x = 14.5 …(2)

Find: the solution of the equation.

Try to compare both equations,

Rearrange the equation(2),

∴ 0.1y = 14.5 − 0.5x

∴y = 145 − 5x (multiply by10)

So here both lines are coincidental and they have infinite solutions.

Option A is correct.

Put x = 20 in eq.(1),

∴ y = 145 − 5(20)

∴ y = 145 − 100

∴ y = 45

means point (20,45) is solution.

Option B is correct.

Put x = 10 in eq.(1),

∴ y = 145 − 50

∴ y = 95

means point (10,95) is solution.

Option C is correct.

Here both lines are coincidental so they have infinite solutions.

So option D is incorrect.

Equations y = 145 − 5x and 0.1y + 0.5x = 14.5 have infinite solutions and (20,45) and (10,95) are also solutions.

Option A,B and C are correct options.