Envision Math

Envision Math Accelerated Grade 7 Volume 1 Chapter 4 Analyze And Solve Percent Problems

Question. Show proportional relationships between quantities and be used to solve problems.

We have to tell how can percents show proportional relationships between quantities and be used to solve problems.

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as a proportional relationship.

Percents can be expressed in terms of fraction or ratios.

In order to check whether they show a proportional relationship or not, we can test if their ratios are equivalent or not.

Also, we can graph the quantities and if it comes out as a straight line passing through the origin, then there will be a proportional relationship.

In certain problems when we have the values as same constant multiples, then we can use the concept of proportional relationship to solve the problem.

The knowledge and applications of ratio and proportions can be used to solve problems.

Equivalent ratio or graph of percents can show their proportional relationship.

Equivalent ratio or graph of percents can show their proportional relationship.

Given that, Activity trackers, also called fitness trackers, have become quite popular in recent years.

We need to check whether the data collected is actually helpful to the user.

You and your classmates will explore the types of data that an activity tracker collects, and how that data can help users reach their activity and fitness goals.

Activity trackers are nothing but an app or device which monitors your fitness-related metrics.

Some of the metrics it measures are heartbeats, calories, blood flow, and distance walking or running to enable the user to keep track of their fitness.

This will help people to achieve their fitness goals.

The data collected in those trackers are accurate and is helpful to the user.

The percentage difference will be less than 1% which indicates that the fitness trackers did a great job in tracking data.

Some of the metrics the fitness or activity trackers measure are heartbeats, calories, blood flow, and distance walking, or running to enable the user to keep track of their fitness.

Envision Math Accelerated Grade 7 Chapter 4 Percent Problems Solutions

Question. Comparison between two same or different quantities.

The ratio is nothing but the comparison between two same or different quantities.

A rate usually compares two different quantities.

The units of those quantities must be different.

Rates usually come under ratio. But all ratios cannot be expressed as the rate.

Ratios compare two same or different quantities.

A ratio that relates two quantities with different units of measure is a rate.

The ratio is nothing but the comparison between two same or different quantities.

A rate usually compares two different quantities.

The units of those quantities must be different. Rates usually come under ratio.

But all ratios cannot be expressed as the rate.

Ratios compare two same or different quantities.

When two equal ratios are expressed as a statement, then it is said to be in proportion.

For example:

\(\frac{8}{2}=\frac{36}{9}\)

These two are said to be in proportion since the ratios are equal.

A statement that two ratios are equal is called a proportion.

Question. Comparison between two same or different quantities.

The ratio is nothing but the comparison between two same or different quantities.

A rate usually compares two different quantities.

The units of those quantities must be different.

Rates usually come under ratio. But all ratios cannot be expressed as the rate.

Ratios compare two same or different quantities.

Here, the relationship “3 students out of 5 students” denotes that the units are the same.

This means that the given statement is a ratio, not a rate.

The relationship “3 students out of 5 students” is an example of a ratio.

Grade 7 Envision Math Accelerated Chapter 4 Percent Solutions Guide

Question. Write each number in two equivalent forms as a fraction, decimal, or percent number is 0.29.

We need to write each number in two equivalent forms as a fraction, decimal, or percent.

The given number is 0.29

The given number is 0.29

Writing the given decimal in its equivalent form, we get

​0.29 = \(\frac{29}{100}\)

Writing the given decimal in its equivalent form 0.29 \(=\frac{2.9}{10}\)

Question. Write each number in two equivalent forms as a fraction, decimal, or percent number is 35%.

We need to write each number in two equivalent forms as a fraction, decimal, or percent. The given number is 35 %

The given number is 35 %

Writing the given percent in its equivalent form, we get

​35 = \(\frac{35}{100}\)

=  \(\frac{7}{20}\)

Writing the given percent in its equivalent form, 35% = \(\frac{7}{20}\)

Question. Write each number in two equivalent forms as a fraction, decimal, or percent.

The given number is in the form of a fraction.

We need to write each number in two equivalent forms as a fraction, decimal, or percent.

The given number is \(\frac{2}{5}\)

The given number is \(\frac{2}{5}\)

Writing the given fraction in its equivalent form, we get

\(\frac{2}{5}\)  =  0.4

= \(\frac{40}{100}\)

Writing the given fraction in its equivalent form \(\frac{2}{5}\) = \(\frac{40}{100}\)

Envision Math Accelerated Volume 1 Chapter 4 Percent Problem Answers

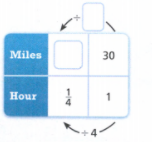
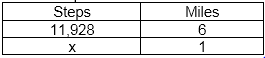
Question. Find the unknown number in the given proportion \(\frac{x \text { days }}{4 \text { years }}=\frac{365.25 \text { days }}{1 \text { year }}\)

We need to find the unknown number in the given proportion.

Solving the given proportion, we get

x = 4 × 365.25

x = 1461 days
​
Hence, The required answer is:

Question. find the unknow number in the given proportion \(\frac{33,264 \text { feet }}{x \text { miles }}=\frac{5280 \text { feet }}{1 \text { mile }}\)

We need to find the unknown number in the given proportion.

Solving the given proportion, we get

x \( = \frac{33264}{5280}\)

x =  6.3 miles

Hence the required answer is:

Envision Math 7th Grade Percent Problems Chapter 4 Solutions

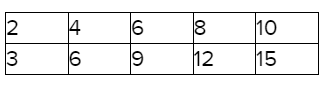
Question. A cooking magazine shows a photo of the main dish on the front cover of 5 out of the 12 issues it publishes each year. Write and solve a proportion to determine how many times a photo of the main dish will be on the front cover during the next 5 years.

Given that, A cooking magazine shows a photo of the main dish on the front cover of 5 out of the 12 issues it publishes each year.

We need to write and solve a proportion to determine how many times a photo of the main dish will be on the front cover during the next 5 years.

Given that,\(\frac{5}{12}\)

5 issues per 12 months. i.e., per year.

For five years, it will be

\(\frac{5}{12}\) \(=\frac{x}{12 \times 5}\)

\(\frac{5}{12}\)\(=\frac{x}{60}\)

x = 5 × 5

x = 25
​
Therefore, 25 out of the 60 issues.

25 times a photo of the main dish will be on the front cover during the next 5 years.

How To Solve Percent Problems Envision Math Grade 7 Chapter 4

Question. Complete the first and second columns of this table. While you work through the topic, return to complete the third column as learn the answers to  your questions from the second column.

We need to complete the first and second columns of this table.

While you work through the topic, return to complete the third column as learn the answers to your questions from the second column.

The percentage is also denoted as the ratio.

The ratio is nothing but the comparison between two same or different quantities.

The first term of the percent is often compared to the number 100.

For example, 35 % of shirts are sold denotes that out of 100 shirts, 35 has been sold out.

We can often denote the percent using the sign “%”.

What do I know about percents and how they are used?

A percent is a ratio in which the first term is compared to 100.

It is used for comparing two quantities.

What do I want to learn about how I will use percents in life?

I want to learn about how percents help us in our daily day-to-day life.

What I have learned about how percents are used?

I have learned that the percents are used to calculate the amount of one thing compared to the other.

Percents can be used to compare very small or very large quantities as a fraction of 100.

Envision Math Accelerated Grade 7 Volume 1 Chapter 3 Analyze And Use Proportional Relationships

Question. Allison and her classmates planted bean seeds at the same time as Yuki and her classmates in Tokyo did. Determine who should expect to have the taller plant at the end of the school year.

Given: 

Allison and her classmates planted bean seeds at the same time as Yuki and her classmates in Tokyo did.

Allison is video-chatting with Yuki about their class seedlings Assume that both plants will continue to grow at the same rate.

We need to determine who should expect to have the taller plant at the end of the school year.

The rate of growth of Allison Class’s bean seeds will be

=\(\frac{2.5}{5}\)

= 0.5 inches per day

Converting inches to the centimeter, we know that, 1 inch=2.54 centimeters

Thus, 0.5 inches = \(\frac{2.54}{2}\)

= 1.27 centimeter

The rate of growth of Yuki Class’s bean seeds will be,

=\(\frac{5.5}{4}\)

= 1.375 centimeters per day
​
Therefore, Yuki Class’s bean seeds grow taller per day.

Yuki’s class is expected to have the taller plant at the end of the school year.

Envision Math Accelerated Grade 7 Chapter 3 Exercise 3.2 Answer Key

Question. Explain how we can compare the growth rates of the seedlings.

We need to explain how we can compare the growth rates of the seedlings.

We need to determine the unit rate of each to determine which one will be tallest at the end of the year.

Since both plants will continue to grow at the same rate.

The rate of growth of Allison Class’s bean seeds will be 1.27 centimeters per day.

The rate of growth of Yuki Class’s bean seeds will be 1.375 centimeters per day.

Thus, the rate of growth or the unit rate determines the growth rates of both the seedlings.

This will help us to compare their growth.

The rate of growth or the unit rate helps us compare the growth rates of the seedlings.

Question. Explain what the students must have done before they can compare the heights of the plants.

We need to explain what the students must have done before they can compare the heights of the plants.

We need to determine the unit rate of each to determine which one will be tallest at the end of the year.

Since both plants will continue to grow at the same rate. The rate of growth of Allison Class’s bean seeds will be 1.27 centimeters per day.

The rate of growth of Yuki Class’s bean seeds will be 1.375 centimeters per day.

Thus, the rate of growth or the unit rate determines the growth rates of both the seedlings.

This will help us to compare their growth.

The students must have done finding out the rate of growth of both the seedlings before they can compare the heights of the plants.

Question. Sergio increases his target speed to 30 miles per hour. Determine how many more miles does Sergio need to ride in \(\frac{3}{4}\) hour to achieve this target speed.

Given:

Sergio increases his target speed to 30 miles per hour.

We need to determine how many more miles does Sergio need to ride in

\(\frac{3}{4}\)hour to achieve this target speed.

Forming an equation using the proportional relationship given, we get

\(\frac{30}{4}\)=x

x = 7.5

Therefore, Sergio rode ​7.5 miles in \(\frac{1}{4}\)hour.

Thus, Sergio needs to ride 30−7.5 = 22.5 miles in \(\frac{3}{4}\) hour to achieve this target speed.

Sergio must ride 7.5 miles in \(\frac{1}{4}\)hour to achieve this target speed, so he needs to ride an additional 22.5 miles per \(\frac{3}{4}\) hour.

Question. Bronwyn’s brother Daniel mows the lawn. He can mow 15,000 ft in \(\frac{3}{4}\) hour. Who mows the lawn in less time?

Given:

Every other weekend, Bronwyn’s brother Daniel mows the lawn. He can mow 15,000 ft in \(\frac{3}{4}\) hour.

To find/solve

Who mows the lawn in less time?

He mows more in less time, so he will finish faster than Bronwyn.

Envision Math Grade 7 Chapter 3 Proportional Relationships Exercise 3.2 Solutions

Question. Explain how does the unit rate describe Sergio’s cycling speed and how is the unit rate helpful in determining how much.

We need to explain how does the unit rate describe Sergio’s cycling speed and how is the unit rate helpful in determining how much.

Farther Sergio must cycle in a given amount of time each time he increases his target speed.

The unit rate helps in determining how many miles he travels per hour based on Sergio’s cycling speed.

The unit rate here is the rate of change in the number of miles every hour.

From the given information

\(\frac{30}{4}\)=x

x=7.5 miles

​This is for the target speed of 30 miles he needs to ride 7.5 miles in 15 minutes.

The unit rate describes Sergio’s cycling speed by determining the number of miles he can travel every hour. The unit rate is helpful in determining how much farther Sergio must cycle in a given amount of time each time he increases his target speed.

Question. Jacob mixes \(\frac{1}{3}\) cup of yellow paint for every \(\frac{1}{5}\) cup of blue paint to make green paint. How many cups of yellow paint are needed for 1 cup of  blue paint?

Given:

Jacob mixes \(\frac{1}{3}\) cup of yellow paint for every

\(\frac{1}{5}\) cup of blue paint to make green paint

To find/solve

How many cups of yellow paint are needed for 1 cup of blue paint?

First, we should find unit rate by dividing both by the denominator.

\(\frac{5}{3}\) Cups of yellow paint.

Question. Explain how is making a table of equivalent ratios to find the unit rate similar to finding the unit rate by calculating with fractions.

We need to explain how is making a table of equivalent ratios to find the unit rate similar to finding the unit rate by calculating with fractions.

For example, let the fraction be \(\frac{2}{3}\)

Making the table of equivalent ratios, we get.

Multiply both the numerator and the denominator by the same number, and we get

Therefore, the ratios \(\frac{2}{3}, \frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}\) are equivalent to each other.

The unit rate of the same by using the fractions are given as

​\(\frac{8}{12}\) =\(\frac{4}{6}\)

=\(\frac{2}{3}\)

We can easily see what the terms, with equivalent ratios are.

Both the unit rates and the equivalent ratios are the same.

Equivalent ratios will have the same value when simplified. Equivalent rates can be found similar to the equivalent ratios by performing the same multiplication or the division on both the numerator and the denominator.

Question. Brad buys two packages of mushrooms. Which mushrooms cost less per pound?

Given:

Brad buys two packages of mushrooms.

To find/solve

Which mushrooms cost less per pound?

First, we should find the unit rate by dividing both by the denominator. Cremini:

Chanterelle:

Chanterelle mushrooms cost less per pound.

Analyze And Use Proportional Relationships Grade 7 Exercise 3.2 Envision Math

Question. The recipe calls for \(1 \frac{1}{4}\) cups of flour and \(\frac{1}{2}\). How many cups of flour will Jed need if he uses 3 sticks of butter?

Given:

The recipe calls for \(1 \frac{1}{4}\)cups of flour and

To find/solve

How many cups of flour will Jed need if he uses 3 sticks of butter?

First we should find unit rate by dividing both by denominator.

Now we have to find equivalent ration that shows us how much flour is needed per 3 sticks of butter.

7.5 per 3

7.5 per 3 cups of flour will Jed need if he uses 3 sticks of butter.

Question. Find unit rate by dividing both by denominator Miles \(\frac{3}{5}\) and Hours \(\frac{1}{3}\)

Given:

Miles \(\frac{3}{5}\)

Hours \(\frac{1}{3}\)

To find/solve

First we should find unit rate by dividing both by denominator.

1.8 per 1.

Question. \(\frac{7 \mathrm{mi}}{\frac{1}{3} \mathrm{gal}}\) find unit rate by dividing both by denominator.

Given:

To find/solve.

First we should find unit rate by dividing both by denominator.

\(\frac{7 \mathrm{mi}}{\frac{1}{3} \mathrm{gal}}\)=\(\frac{21}{1}\)

Question. Find unit rate by dividing both by denominator \(\frac{\frac{3}{4}\text{ page }}{2 \text { minutes}}\)

Given:

\(\frac{\frac{3}{4} \text { page }}{2 \text { minutes }}\)

To find/solve

Page in 1 minute.

First we should find unit rate by dividing both by denominator.

\(\frac{3}{8}\) per 1

\(\frac{3}{8}\) per 1

Question. Hadley paddled a Canoe \(\frac{2}{4}\) mile in \(\frac{1}{4}\). How fast did Hadley paddle, in miles per hour?

Given:

Hadley paddled a Canoe\(\frac{2}{4}\) mile in \(\frac{1}{4}\)

To find/solve

How fast did Hadley paddle, in miles per hour?

First we should find unit rate by dividing both by denominator.

\(\frac{2}{4}\) per 1.

Hadley paddle, in miles per hour \(\frac{2}{4}\) per 1.

Question. A box of cereal states that there are 90 calories in a \(\frac{3}{4}\) cup serving. How many Calories are there in 4 cups of cereal?

Given:

A box of cereal states that there are 90 calories in a \(\frac{3}{4}\) cup serving

To find/solve

How many Calories are there in 4 cups of cereal?

First we should find unit rate by dividing both by denominator.

Now we just have to find equivalent ratio that will show the amount per 4.

480 per 4 Calories are there in 4 cups of cereal.

Question. A robot can complete 8 tasks in \(\frac{5}{6}\) hour. How long does it take the robot to complete one task?

Given:

A robot can complete 8 tasks in \(\frac{5}{6}\) hour

To find/solve

How long does it take the robot to complete one task?

We have to find the unit rate that will show us the ratio of fractions.

\(\frac{5}{48}\) per task

\(\frac{5}{48}\) per task take the robot to complete one task.

Given:

A robot can complete 8 tasks in \(\frac{5}{6}\) hour. Each task takes the same amount of time.

To find/solve

How many tasks can the robot complete in one hour?

We have to find unit rate that will show us the ratio of fraction.

\(\frac{48}{5}=9 \frac{3}{5} \text { per } 1\) tasks can the robot complete in one hour.

Envision Math Grade 7 Exercise 3.2 Solution Guide

Question. Find out which car can travel a greater distance on 1 gallon of gas.

Given:

You want to find out which car can travel a greater distance on 1 gallon of gas.

To find/solve

What is the gas mileage, in miles per gallon, for the blue car?

The ratio of miles per gallon

We have to divide both terms by the denominator term.

The gas mileage is \(\frac{71}{3}=23 \frac{2}{3} \text { per } 1\) in miles per gallon, for the blue car.

Given:

You want to find out which car can travel a greater distance on 1 gallon of gas.

To find/solve

What is the gas mileage, in miles per gallon, for the silver car?

The ratio of miles per gallon

We have to divide both terms by the denominator term.

34 per 1.

34 per 1 is the gas mileage, in miles per gallon, for the silver car.

Given:

You are running a fuel economy study. You want to find out which car can travel a greater distance on 1 gallon of gas.

To find/solve

Which car could travel the greater distance on 1 gallon of gas?

Blue car

Silver car

Silver car travel a greater distance on 1 gallon of gas.

Silver car travel a greater distance on 1 gallon of gas.

Question. \(\text { Henry incorrectly said the rate } \frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }}\) can be written as the unit rate \(\) pound per quart. Find the unit rate we have to divide both terms by the denominator.

Given:

\(\text { Henry incorrectly said the rate } \frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }}\) can be written as the unit rate \(\) pound per quart.

To find/solve

What is the correct unit rate?

To find unit rate we have to divide both terms by the denominator.

4 per 1 is the correct unit rate.

Given:

\(\text { Henry incorrectly said the rate } \frac{\frac{1}{5} \text { pound }}{\frac{1}{20} \text { quart }}\) can be written as the unit rate \(\) pound per quart.

To find/solve

What error did Henry likely make?

Ratios with fractions.

Convert the fractions so they have a common denominator, and multiply both fractions by the common denominator.

Simplify by dividing by the highest common factor.

He probably didn’t divide both terms by denominator.

He didn’t follow rules for finding unit rates.

He didn’t follow rules for finding unit rates.

Envision Math Accelerated Grade 7 Chapter 3 Exercise 3.2 Answers

Question. Ari walked \(2 \frac{3}{4}\) miles at a constant speed of \(2 \frac{1}{2}\)miles per hour. Beth walked \(1 \frac{3}{4}\)miles at a constant speed of \(1 \frac{1}{4}\) miles per hour. Cindy walked for 1 hour and 21 minutes at a constant speed of \(1 \frac{1}{8}\) miles per hour.

Given:

Ari walked \(2 \frac{3}{4}\) miles at a constant speed of \(2 \frac{1}{2}\)miles per hour. Beth walked \(1 \frac{3}{4}\)miles at a constant speed of \(1 \frac{1}{4}\) miles per hour. Cindy walked for 1 hour and 21 minutes at a constant speed of \(1 \frac{1}{8}\) miles per hour.

To find/solve

List the three people in order of the times they spent walking from least time to greatest time.

We should find unit rate of inches per feet.

Ari

Beth

Cindy

From this, we find out that

1.1 < 1.35 < 1.4

The three people in order of the times they spent walking from least time to greatest time is 1.1 < 1.35 < 1.4

Envision Math 7th Grade Exercise 3.2 Step-By-Step Solutions

Question. Fence A is \(1 \frac{4}{5}\) inches long on the blueprint and is to b\(1 \frac{1}{2}\). How long is Fence B on the blueprint/

Given:

Fence A is \(1 \frac{4}{5}\) inches long on the blueprint and is to b\(1 \frac{1}{2}\)

To find/solve

How long is Fence B on the blueprint?

We should find unit rate of inches per feet.

It shows us that there are 6/5 inches per feet. If the fence is long 5 feet we need to multiply

6 inches per 5 feet.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 339 Exercise 1 Answer

Given:

Two figures on a coordinate plane.

To find:

Are the two figures alike or different.

By looking at the figure, we can observe that the shapes of the two triangles are the same, and so are the orientations. The only difference is in the size.

In order to verify whether the two figures are truly similar, we have to find if a dilation maps ΔA′B′C′ to ΔABC.

From figure vertices of ΔABC are:

From figure vertices of ΔA′B′C′ are:

By comparing coordinates of the vertices of ΔABC and ΔA′B′C′ , we can check if the transformation is a dilation.

Comparing the x-coordinates of the vertices of ΔABC and ΔA′B′C′ :

= \(\frac{1}{2}\)

= \(\frac{1}{2}\)

= \(\frac{1}{2}\)

Similarly, comparing the y-coordinates of ΔABC and ΔA′B′C′ also gives us the scale factor \(\frac{1}{2}\) = 0.5.

Hence, we can conclude that ΔA′B′C′ is really a dilation of ΔABC.

The two triangles are alike in shape and orientation, but are different in size. We know this for sure, since ΔA′B′C′ was found to be the dilation of ΔABC.

Envision Math Grade 8 Volume 1 Chapter 6.7 Solutions

Page 339 Exercise 2 Answer

Given: look for relationships is ΔABC a preimage of ΔA′B′C′

To find:

How do we know that the above statement is true.

In order to find that whether the statement is true or not we have to verify it with the help of tip mentioned above.

We can observe that ΔABC and ΔA′B′C′ both have the same shape, same orientation and same angles as well. The only difference between the two triangles is the difference in size.

Hence, we can say that ΔA′B′C′ is a dilation of ΔABC, and therefore ΔABC.

Yes, ΔABC is the preimage of ΔA′B′C′, since ΔA′B′C′ looks like the dilated version of ΔABC.

Page 339 Focus On Math Practices Answer

Given:ΔABC & ΔA′B′C′

To: How can you use the coordinates of the vertices of the triangles to identify the transformation that maps the triangles.

We will multiply the coordinates of the ΔABC with a scale factor k to obtain the triangle  ΔA′B′C′. Now as the obtained triangle only differs by a scale factor of k in respect of given triangle hence it will have the same shape as that of ΔABC.

We will multiply the coordinates of the ΔABC with a scale factor k to obtain the triangle  ΔA′B′C′.Now as the obtained triangle only differs by a scale factor of k in respect of given triangle hence it will have the same shape as that of ΔABC.

Congruence And Similarity Envision Math Exercise 6.7 Answers

Page 340 Convince Me Answer

Given:

To: Convince what sequence of transformation makes the triangle similar.

Step formulation: Calculate the ratio of sides and then prove similarity

In last part we calculated the ratio of sides A′B′ to AB, ratio of A′C′ to AC and ratio of B′C′ to BC.

It is observed that the ratio of all three of the sides is equal to \(\frac{9}{4}\).

Hence on that basis it can be concluded that the triangles are similar.

As the ratio of sides are equal hence the triangles are similar.

Envision Math Grade 8 Chapter 6.7 Explained

Page 341 Try It Answer

Given:

To: Find the reflection of JKL about x = 1 followed by dilation of \(\frac{1}{2}\).

Step formulation: Find the reflection of each point and then find the dilation.

Reflection of point L about x = 1.

i.e. the coordinates(−2,1) will become(4,1).

Reflection of point J about x = 1. will become

i.e. the coordinates(−2,−4)will become(4,−4).

Reflection of point K about x = 1.

i.e. the coordinates (−4,0) will become (6,0).

The transformed image is shown below.

For the dilation, the scale factor is \(\frac{1}{2}\).

So, \(\left(L^{\prime}\right)^{\prime}=\frac{4+4}{2}, \frac{1+(-4)}{2}\)

= 4, -1.5

Similarly(K′)′= 5,2

The dilated figure is:

The dilated i.e. the last transformed image is:

Given:

To: Prove ΔJKL is similar to ΔPQR. Step formulation: Find the ratio of sides.

Two-dimensional figure are similar if we can map one figure to the other by a sequence of rotations, reflections, translation, and dilations.

So, we found the sequence of transformations that map the ΔJKL onto ΔPQR :

translation for 8 units right and 1 unit up

rotation about point L

dilation with scale factor 2 about point L

Therefore, we can conclude that ΔJKL is similar to ΔPQR.

ΔJKL ~ ΔPQR

As all the three ratio of the sides are equal hence ΔJKL is similar to ΔPQR.

Page 342 Exercise 2 Answer

Given: Angles and side lengths of similar figures.

To: How do the angle measures and side lengths compare in similar figures?

In similar figures the corresponding angles must be equal.

Also the ratio of all corresponding sides must be equal.

In similar figures the corresponding angles must be equal.

Also the ratio of all corresponding sides must be equal.

Solutions For Envision Math Grade 8 Exercise 6.7

Page 342 Exercise 5 Answer

Given:

To: Obtain the final image by performing the given operations.

Step formulation: Graph each of the given steps and then obtain the final image.

ΔABC is dilated by a factor of 2 with a center of dilation at point C, reflected across the x axis, and translated 3 units up is shown in the below figure.

The graph obtained by performing sequence of operations is:

Page 342 Exercise 6 Answer

Given:

To: Find is the ΔABC similar to ΔDEF.

Step formulation: First find the length of the sides of the triangle and the find the ratio of corresponding sides.

Calculate the lengths of the sides of ΔABC & ΔDEF.

AB = \(\sqrt{(-1-(-4))^2+(-2-(-2))^2}\)

AB = 3

Similarly we can calculate the lengths of all sides.

BC = \(\sqrt{5}\)

CA = \(\sqrt{2}\)

DE = \(3 \sqrt{2}\)

EF = \(\sqrt{34}\)

FD = 8

The ratio between the longest sides i.e. between AB & FD = \(\frac{3}{8}\)

Ratio between BC & EF = \(\frac{\sqrt{5}}{\sqrt{34}}\)

As we can observe that the ratio of the sides is not equal, hence the triangles are not similar.

As we can observe that the ratio of the sides is not equal, hence the triangles are not similar.

Envision Math Grade 8 Volume 1 Chapter 6.7 Practice Problems

Page 343 Exercise 7 Answer

Given:

To: Describe a sequence of transformations that maps RSTU to VXYZ.

Step formulation: By taking reflection, translation and dilation, map both the triangles.

Since the figure RSTU is on the right of y axis, so, first lets take the reflection about y axis.

Now translate the obtained figure to left to 3 units.

Now translate the obtained figure to down to 3 units.

The figure obtained is:

Now to map the images we need to do the dilation.

Coordinates of V = (−2,−1) and coordinates of R₁ = (−6,−3).

Therefore, in order to match the figure it has to be reduce by factor 3.

So, \(R_1^{\prime}=\left(\frac{-6}{3}, \frac{-3}{3}\right)\)

R₁‘ = (-2, -1)

So now the coordinates match. Similarly we can do for other vertices.

In order to map the images we did reflection about y axis then translation of 3 units to the left and down afterward the dilation of factor 3.

Envision Math 8th Grade Congruence And Similarity Topic 6.7 Key Concepts

Page 343 Exercise 8 Answer

Given:

To: Is the shown triangles similar?

Step formulation: Find the ratio of the corresponding sides and then compare.

Find the length of the sides.
​
MN = 6

NO = 6

PQ = 12

OQ = 9
​
Now find the ratio of side.

As the ratio of sides is not equal, hence the triangles are not similar.

As the ratio of sides is not equal, hence the triangles are not similar.

Page 343 Exercise 9 Answer

Given:

To: Find the dilated and rotated image.

Step formulation: First find the coordinates after dilation and then rotate the figure.

Coordinates after dilation are:
​
P → 2(2,2) = 4,4

Q → 2(4,2) = 8,4

R → 2(3,4) = 6,8
​
So the dilated image is:

Now rotate the figure about the origin to 180^∘.

Final figure obtained by dilating and rotating about origin:

Page 344 Exercise 12 Answer

Given:

To: Find two possible coordinates for missing point Y.

For each coordinate chosen, describe a sequence of transformations, including a dilation, that will map the triangles.

Step fromulation: First locate point Y and then find the transformations.

Since the triangles are similar therefore,

Put the known in the expression.

Simplifying and finding ZY.

ZY = 2

Hence point Y will be 2 units away from Z in the horizontal direction. It’s coordinates are(−4,2).

Now to map ΔJLK with ΔXYZ transformations have to be taken.

Since both are equidistant from origin, therefore, mirror about origin will occur first.

Now after mirror dilation of factor \(\frac{1}{2}\)

ΔJLK will map with ΔXYZ.

Also the other coordinate of Y is (−4,5).

Possible coordinates of Y are(−4,2),(−4,5). To map the triangles, ΔJKL has to be mirred first then dilated by \(\frac{1}{2}\)

Envision Math Grade 8 Chapter 6.7 Lesson Overview

Page 344 Exercise 13 Answer

Given:

To: Which of the given triangles could Rajesh use for the pennants?

The triangles ΔQRS and ΔXYZ are similar because both have the same included angle and are the isosceles triangles. Both are right-angled isosceles triangles.

Whereas, ΔJKL is isosceles but does not have the same included angle, i.e. it is not right-angled; and it has no pair in the given options so it is not the answer. Also ΔWVT is right-angled, but is not isosceles and has no pair in the given options so it is not the answer.

Rajesh can use triangles given in option(B) ΔQRS & ΔXYZ for the pennants.

Envision Math Grade 8 Topic 6.7 Transformations Practice

Page 344 Exercise 14 Answer

Given:

To: Match the given options with similar or not similar.

ΔTVW & ΔQRS are both right angled isosceles triangle. Hence these are similar.

ΔJKL is not isosceles and is also not similar to any of the given triangles.

ΔTVW & ΔQRS are the similar triangles.

ΔTVW & ΔJKL are not similar triangles.

ΔJKL & ΔQRS are not similar triangles.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 3 Analyze And Use Proportional Relationships

Question. Basketball contest, Elizabeth made 9 out of 25 free throw attempts. Alex made 8 out of 20 free throw attempts. Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex. Find out whether Janie’s reasoning is correct or not.

Given: In a basketball contest, Elizabeth made 9 out of 25 free throw attempts.

Alex made8 out of 20 free throw attempts. Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.

We need to find out whether Janie’s reasoning is correct or not.

Finding the rates of each of them:

For Elizabeth.

= 0.36

For Alex

= 0.4

The rate Alex is more. Therefore, Alex had a better free-throw record because she made more free throws than Elizabeth.

Janie’s reasoning is wrong.

Given: In a basketball contest, Elizabeth made 9 out of 25 free throw attempts.

Alex made8 out of 20 free throw attempts.

Janie said that Elizabeth had a better free-throw record because she made more free throws than Alex.

We need to decide who had the better free-throw record. Justify your reasoning using mathematical arguments.

Finding the rates of each of them:

For Elizabeth:

= 0.36

For Alex:

= 0.4

The rate of Alex is more. Therefore, Alex had a better free-throw record because she made more free throws than Elizabeth.

Alex had a better free-throw record because she made more free throws than Elizabeth.

Envision Math Accelerated Grade 7 Chapter 3 Exercise 3.1 Answer Key

Question. Explain which mathematical model we used to justify our reasoning.

We need to explain which mathematical model we used to justify our reasoning.

Also, explain if there are other models you could use to represent the situation.

Finding the rates of each of them.

The rate for Elizabeth is 0.36

The rate for Elizabeth is 0.4

The rate of Alex is more.

Therefore, Alex had a better free-throw record because she made more free throws than Elizabeth.

The mathematical model which I used here is finding the rates.

We could also use ratios and unit rates to determine the same.

The mathematical model which I used here is finding the rates. We could also use ratios and unit rates to determine the same.

Question. Explain how are ratios, rates, and unit rates used to solve problems.

We need to explain how are ratios, rates, and unit rates used to solve problems.

A rate is nothing but a measurement between two different quantities.

A ratio is a measurement between two same quantities.

A unit rate is a rate at which one quantity differs per unit of another quantity.

Examples are:

Rate –

Distance \(=\frac{\text { Speed }}{\text { Time }}\)

Here, speed and time are of different quantities. Ratio – \(\frac{x}{y}\)

Unit rate –

Distance \(=\frac{50 \text { miles }}{2 \text { hour }}\)

= 25 miles per hour

Here, 25 miles per hour is the unit rate.

The ratios, rates, and unit rates are used to solve problems in order to compare varying quantities by determining the number of units of one quantity per one unit of another quantity.

Question. Jennifer is a lifeguard at the same pool. She earns $137.25 for 15 hours of lifeguarding. Determine how much Jennifer earns per hour.

Given that, Jennifer is a lifeguard at the same pool. She earns $137.25 for 15 hours of lifeguarding.

We need to determine how much Jennifer earns per hour.

Finding the unit rate of Jennifer, we get

= 9.15 dollars per hour

Jennifer earns $9.15 per hour.

Question. A kitchen sink faucet streams 0.5 gallons of water in 10 seconds. A bathroom sink faucet streams 0.75 gallons of water in 18 seconds. Find which faucet will fill a 3-gallon container faster.

Given that, A kitchen sink faucet streams 0.5 gallons of water in 10 seconds.

A bathroom sink faucet streams 0.75 gallons of water in 18 seconds.

We need to find which faucet will fill a 3−gallon container faster.

The rate of kitchen sink faucet is:

​\(\frac{\text { Number of gallons of water }}{\text { Number of seconds }}=\frac{0.5}{10}\)

= 0.05 gallons of water per second.

The rate of bathroom sink faucet is:

​\(\frac{\text { Number of gallons of water }}{\text { Number of seconds }}=\frac{0.75}{18}\)

= 0.042 gallons of water per second
​
The rate of bathroom sink faucet is more. This means that the bathroom sink faucet fills faster.

The bathroom sink faucet will fill a 3−gallon container faster.

Envision Math Grade 7 Chapter 3 Proportional Relationships Worksheet Solutions

Question. Explain how are ratios, rates, and unit rates used to solve problems.

We need to explain how are ratios, rates, and unit rates used to solve problems.

A rate is nothing but a measurement between two different quantities.

A ratio is a measurement between two same quantities.

A unit rate is a rate at which one quantity differs per unit of another quantity.

Examples are:

Rate –

Distance \(=\frac{\text { Speed }}{\text { Time }}\)

Here, speed and time are of different quantities. Ratio – \(\frac{x}{y}\)

Unit rate –

Distance \(=\frac{50 \text { miles }}{2 \text { hour }}\)

=  25 miles per hour

Here, 25 miles per hour is the unit rate.

The ratios, rates, and unit rates are used to solve problems in order to compare varying quantities by determining the number of units of one quantity per one unit of another quantity.

Question. Dorian buys 2 pounds of almonds for $21.98 and 3 pounds of dried apricots for $26.25. Which is less expensive per pound? How much less expensive?

Given:

Dorian buys 2 pounds of almonds for $21.98 and 3 pounds of dried apricots for $26.25.

To find/solve:

Which is less expensive per pound? How much less expensive?

Almonds:

= \(\frac{21.98 \div 2}{2 \div 2}\)

= \(\frac{10.99}{1}\)

Apricots:

= \(\frac{26.25 \div 3}{3 \div 3}\)

= \(\frac{8.75}{1}\)

Now equivalent ratios we get,  10.99 – 8.75  =  2.24, Apricots for 2.24

Apricots for 2.24.

Question. Krystal is comparing two internet service plans. Plan 1 cost $34.99 per month. Plan 2 costs $134.97 every 3 months. Find the krystal plans to stay with one service plan for 1 year, which should she choose? How much will she save?

Given:

Krystal is comparing two internet service plans.

Plan 1 cost $34.99 per month. Plan 2 costs $134.97 every 3 months.

To find/solve:

If Krystal plans to stay with one service plan for 1 year, which should she choose? How much will she save?

Plan 1 :

= \(\frac{34.99 .12}{1.12}\)

= \(\frac{419.88}{12}\)

Plan 2 :

= \(\frac{134.97 \div 3}{3 \div 3}\)

= \(\frac{44.99}{1}\)

Now finding equivalent ratios. Plan 1 is cheaper for 539.88 – 419.88 = 120.

In plan 1 she will save.

Analyze And Use Proportional Relationships Grade 7 Envision Math

Question. Pam read 126 pages of her summer reading book in 3 hours. Zack read 180 pages of his summer reading book in 4 hours. Find they continue to read at the same speeds, will they both finish the 215 page book after 5 total hours of reading?

Given:

Pam read 126 pages of her summer reading book in 3 hours.

Zack read 180 pages of his summer reading book in 4 hours.

To find/solve:

If they continue to read at the same speeds, will they both finish the 215-page book after 5 total hours of reading?

Pam:

=\(\frac{126 \div 3}{3 \div 3}\)

Zack:

=\(\frac{180 \div 4}{4 \div 4}\)

She reads 42 pages per hour and he reads 45 pages per hour. Hence only Zack will finish.

Zack will finish.

Question. Megan walked 5 miles; her activity tracker had counted 9,780 steps. David’s activity tracker had counted 11,928 steps after he walked 6 miles. Find the steps for 1 mile.

Given:

Megan walked 5 miles; her activity tracker had counted 9,780 steps. David’s activity tracker had counted 11,928 steps after he walked 6 miles.

We know that:

Megan’s steps:

We find the steps for 1 mile:

Steps \(=\frac{9780}{5}\)

Steps = 1956

Megan takes 1956 steps per mile.

David’s steps:

We find the steps for 1 mile:

Steps \(=\frac{11928}{6}\)

Steps = 1988

David walks 1988 steps per mile.

Therefore David takes more steps to walk a mile.

1988−1956 = 32 more steps to walk a mile.

David takes more steps to walk 1 mile. David takes 32 more steps.

Question. A package of 5 pairs of insulated gloves costs $29.45. Find the price for 1 glove.

A package of 5 pairs of insulated gloves costs $29.45.

We know that:

We find the price for 1 glove:

Price \(=\frac{29.45}{5}\)

Price = 5.89

A single pair of gloves cost $ 5.89.

Question. Yellow packet white rice costs $6.30 for 18 ounces, Blue packet white rice costs $4.46 for 12 ounces and the green packet of white rice costs $2.59 for 7 ounces. Find the price for 1 ounce of the yellow packet of white rice.

Given:

Yellow packet white rice costs $6.30 for 18 ounces.

Blue packet white rice costs $4.56 for 12 ounces.

The green packet of white rice costs $2.59 for 7 ounces.

We know that:

We find the price for 1 ounce of the yellow packet of white rice:

Price \(=\frac{6.30}{18}\)

Price = 0.35

The price for 1 ounce of Yellow packet rice is $0.35.

We find the price for 1 ounce of the blue packet of white rice:

Price \(=\frac{4.56}{12}\)

Price = 0.38

The price for 1 ounce of Blue packet rice is $0.38.

We find the price for 1 ounce of the green packet of white rice:

Price \(=\frac{2.57}{7}\)

Price = 0.36

The price for 1 ounce of Green packet rice is $0.36.

The yellow package has the lowest cost per ounce of rice.

Question. The 5 panes cost $14.25. She breaks 2 more panes while repairing the damage. Find the cost for 1 pane of glass.

Given:

The 5 panes cost $14.25.

She breaks 2 more panes while repairing the damage.

We find the cost for 1 pane of glass:

Cost \( = \frac{14.25}{5}\)

Cost = 2.85

The cost for 1 pane of glass is $2.85.

We find the cost of 2 panes of glass:

Cost = 2.85 × 2

Cost = 5.7

The cost for 2 panes of glass is $5.70.

Question. The fare for 36 miles is $25.20. Find the cost per mile.

Given:

The fare for 36 miles is $25.20.

We first find the cost per mile:

Cost \(=\frac{25.20}{36}\)

Cost = 0.7

The cost per mile is 25.20.

Therefore, the required fare is

\(=\frac{25.20}{36}\)\(=\frac{x}{47}\)

x = 33.92

The fare for a 47-mile ride is $33.92

Therefore, the cost per mile is $0.7 and the fare for 47 miles is $33.92.

Envision Math Grade 7 Exercise 3.1 Solution Guide

Question. Company A has 12 tigers for $33.24. Company B has 6 tigers for $44.80 and Company C 15 tigers for $41.10. Find the cost per tiger for all the companies.

Given:

Company A: 12 tigers for $33.24.

Company B: 16 tigers for $44.80.

Company C: 15 tigers for $41.10.

We first find the cost per tiger for all the companies:

Company A

Cost = \(\frac{33.24}{12}\)

Cost = 2.77

The cost per tiger for Company A is $2.77.

Company B

Cost = \(\frac{44.80}{16}\)

Cost = 2.8

The cost per tiger for Company B is $2.80.

Company C

Cost = \(\frac{41.10}{15}\)

Cost = 2.74

The cost per tiger for Company C is $2.74.

Company C has the lowest cost per tiger.

Therefore, Company C has the lowest cost per tiger.

Given:

Company C  15 tigers for $41.10.

The cost per tiger for Company C is $2.74.

The students plan to sell the tigers for $5 each.

We know that the lowest cost per tiger is $2.74 for company C.

The students sell the mascots according to $5.

Therefore the profit that the students will make for each tiger they sell is:

profit  =  5−2.74

profit  =  2.26

Therefore, the students will obtain the profit of $2.26 for each tiger they sell.

Question. A contractor purchases 7 dozen pairs of padded work gloves for $103.32. He incorrectly calculates the unit price at $14.76 per pair. Find the cost of 1 unit pair of padded work gloves.

Given:

A contractor purchases 7 dozen pairs of padded work gloves for $103.32.

He incorrectly calculates the unit price at $14.76 per pair.

To find the cost of 1 unit pair of padded work gloves, we divide $103.32 by 84

Cost = \(\frac{103.32}{84}\)

Cost  =  1.23

Therefore, the cost of 1 unit pair of padded work gloves is $1.23.

Therefore, the unit price is $1.23.

Given:

A contractor purchases 7 dozen pairs of padded work gloves for $103.32.

He incorrectly calculates the unit price at $14.76 per pair.

To find the cost of 1 unit pair of padded work gloves, we divide $103.32 by 84

Cost = \(\frac{103.32}{84}\)

Cost = 1.23

Therefore, the cost of 1 unit pair of padded work gloves is $1.23.

He should have divided the total price by 84 since he bought 7 dozen pairs of gloves and 1 dozen equals to 12 units.

Therefore, the error the contractor was likely to make is total number of units. He should remember that there are 84 units and 7 dozen pair of gloves.

Question. A warehouse store sells 5.5-ounce cans of tuna in packages of 6 that cost $9.24. The store also sells 6.5 ounces cans of the same tuna in packages of 3 cans for $4.68. Find the cost of 1 ounce for each package.

Given:

A warehouse store sells 5.5-ounce cans of tuna in packages of 6 that cost $9.24.

The store also sells 6.5 ounces cans of the same tuna in packages of 3 cans for $4.68.

It also sells 3.5-ounce cans in packages of 4 cans for $4.48.

We find the cost of 1 ounce for each package:

Package 1: Cost = 9.24/(5.5 × 5) ​= 9.24/27.5 = 0.33​

Package 2: Cost = 4.68/(6.5 × 3) ​= 4.68/19.5 = 0.24​

Package 3: Cost = 4.48/(3.5 × 4)​ = 4.48/14 = 0.32​

We see that package 3 has the lowest cost per ounce of tuna that is $0.32.

Therefore, package 3 which cost $0.32 per ounce has the lowest cost per ounce of tuna.

Question. Irene’s car had 6 gallons of gas in its 15-gallon tank. Irene wants to fill it at least halfway. The gas costs $3.80 per gallon. Find the total gallon gas has filled.

Given:

Irene’s car had 6 gallons of gas in its 15-gallon tank.

Irene wants to fill it at least halfway. The gas costs $3.80 per gallon.

Irene’s car has a capacity of 15 gallons and it already has 6 gallons of gas filled.

Therefore the remaining capacity of the car’s tank is 9 gallons.

Irene wants to fill the tank at least halfway.

The half of the tank is 7.5 gallons.

We need 1.5 gallons to fill the tank halfway.

If Irene fill her tank it would cost her 9×3.80=34.20$

Therefore, Irene does not need more than 1.5 gallons of gas, and if Irene adds $3.80 and $7.60 worth

Envision Math Accelerated Grade 7 Chapter 3 Practice Answers

Envision Math Accelerated Grade 7 Volume 1  Chapter 3 Analyze And Use Proportional Relationships

Given:

Statement

To find/solve

Proportional relationships can be recognized by using the terms.

Terms are numbers compared in ratios.

Terms can be used to compare and solve the problem using this ratio.

Terms can be used to compare and solve the problem using this ratio.

Given:

Statement

To find/solve

If 2 values have a constant multiple (constant of proportionality ) and can be written as y = kx equation they are proportional (they have a proportional relationship).

Access to safe drinking water is measured by the percentage of the population having access to and using improved drinking water sources.

Improved drinking water sources should, but do not always, provide safe drinking water, and include piped household water connection, and public standpipes.

Question. Solve the given two ratios \(\frac{2 \text { dogs }}{3 \text { cats }}=\frac{2}{3}\) \(\frac{10 \text { dogs }}{15 \text { cats }}=\frac{10}{15}\)

Solve the given two ratios, and we get

=\(\frac{2}{3}\)

Here, we can see that both ratios result in the same answer.

Thus, the given ratios are equivalent to each other.

Thus, they are equivalent ratios.

\(\frac{2 \text { dogs }}{3 \text { cats }}\) and \(\frac{10 \text { dogs }}{15 \text { cats }}\) are an example of equivalent ratios.

The rate comes under the category of ratios.

But all ratios cannot be described as rates.

This is because the ratio deals with the same or different quantities.

While the rate deals with two different quantities.

For example, if we compare speed and distance together, the fraction is said to be the rate. Since the unit of both of them are different.

A rate is a type of ratio that has both terms expressed in different units.

A fraction is said to be the comparison of two quantities.

If we have a fraction in the fraction itself, it is then said to be a complex fraction.

A complex fraction has a fraction in the numerator, denominator, or in both of them.

For example: \(\frac{5}{\frac{12}{7}}\), \(\frac{\frac{8}{7}}{4}\) are some of the examples of the complex fractions.

A complex fraction has a fraction in its numerator, denominator, or both.

Question. Solving the equivalent ratio \(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{? \text { girls }}\)

We need to complete the given equivalent ratio \(\frac{4 \text { boys }}{7 \text { girls }} = \frac{8 \text { boys }}{? \text { girls }}\)

Solving the given equivalent ratio, we get

x = \(8 \times \frac{7}{4}\)

x = 2 × 7

x = 14 girls

Question. Solving the equivalent ratio \(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{? \text { tıres }}{1 \text { car }}\)

We need to complete the given equivalent ratio \(\frac{16 \text { tıres }}{4 \text { cars }} = \frac{? \text { tıres }}{1 \text { car }}\)

Solving the given equivalent ratio, we get

x  =  \(\frac{16}{4}\)

x  =  4 tires

Question. Solving the equivalent ratio \(\frac{8 \text { correct }}{10 \text { total }} = \frac{? \text { correct }}{50 \text { total }}\)

We need to complete the given equivalent ratio \(\frac{8 \text { correct }}{10 \text { total }} = \frac{? \text { correct }}{50 \text { total }}\)

Solving the given equivalent ratio, we get

x  =  \(50 \times \frac{8}{10}\)

x  =  5 × 8

x  =  40 correct

Question. Solving the equivalent ratio \(\frac{16 \text { pearls }}{20 \text { opals }}=\frac{8 \text { pearls }}{? \text { opals }}\)

We need to complete the given equivalent ratio \(\frac{16 \text { pearls }}{20 \text { opals }}=\frac{8 \text { pearls }}{? \text { opals }}\)

Solving the given equivalent ratio, we get

\(\frac{16 \text { pearls }}{20 \text { opals }} = \frac{8 \text { pearls }}{? \text { opals }}\)
​
\(\frac{16}{20}=\frac{8}{x}\)

x  =  \(8 \times \frac{5}{4}\)

x  =  2 × 5

x  = 10 opals

Question. Solving the equivalent ratio \(\frac{7 \text { balls }}{9 \text { bats }}=\frac{? \text { balls }}{27 \text { bats }}\)

We need to complete the given equivalent ratio \(\frac{7 \text { balls }}{9 \text { bats }}=\frac{? \text { balls }}{27 \text { bats }}\)

Solving the given equivalent ratio, we get

x  =  \(27 \times \frac{7}{9}\)

x  =  3 × 7

x  =  21 balls

Question. Write the given situation as a rate. John travels 150 miles in 3 hours. Find the rate at which John travels.

We need to write the given situation as a rate. Here, John travels 150 miles in 3 hours.

Finding the rate at which John travels, we get

= 50 miles per hour

John travels at the rate of 50 miles/hr

Question. Write the given situation as a rate. Here, Cameron ate 5 apples in 2 days. Find the rate at which Cameron eat.

We need to write the given situation as a rate. Here, Cameron ate 5 apples in 2 days.

Finding the rate at which Cameron eats, we get

= 2.5 apples per day

Cameron ate 2.5 apples per day.

Question. Write an equation that represents the pattern in the table. Find the rate of the given data.

We need to write an equation that represents the pattern in the table.

Finding the rate of the given data

\(\frac{y}{x}=\frac{12}{4}\) = 3

\(\frac{y}{x}=\frac{15}{5}\) = 3

\(\frac{y}{x}=\frac{18}{6}\) = 3

\(\frac{y}{x}=\frac{21}{7}\) = 3

\(\frac{y}{x}=\frac{24}{8}\) = 3

Therefore, the ratio is \(\frac{y}{x}=\frac{3}{1}\)

Thus, the equation of the pattern in the table will be

y = 3x

The equation that represents the pattern in the table will be  y = 3x

Envision Math Accelerated Grade 7 Volume 1 Chapter 2 Real Numbers

Question. Sofia wrote a decimal as a fraction. Nora said that her method and answer was incorrect but Sofia disagreed and says that this is the method she learned. Find the Nora or Sofia Correct.

Given:

Sofia wrote a decimal as a fraction

Nora said that her method and answer was incorrect

But Sofia disagrees and says that this is the method she learned.

To find Is Nora or Sofia correct.

The given Sofia answer is:

​0.1211211121112

x = 0.12

100(x) = 100(0.12)

100x = 12.12

​99x = 12

x = \(\frac{12}{99}\)

Nora says that her method and answer was incorrect. Actually, Sofia’s method and answer is incorrect as Nora said.

The correct method is:

​0.1211211121112

x = 0.12

100(x) = 100(0.12)

100 x = 12.12
​
Divide both sides by 100
​
\(\frac{100 x}{100}\)=\(\frac{12.12}{100}\)

x = 0.1212
​
Finally, we concluded that Sofia’s method and answer is incorrect.

To find Is what is another nonterminating decimal number that cannot be written as a fraction.

0.1211211121112

The given Sofia answer is in the rational fraction.

Any real number that cannot be written in fraction form is an irrational number.

These numbers include non-terminating, non-repeating decimals.

Finally, we concluded that irrational fractions is another nonterminating decimal number that cannot be written as a fraction.

Envision Math Accelerated Grade 7 Chapter 2 Exercise 2.2 Solutions

Question. Difference of rational and irrational numbers can be explained.

The difference of rational numbers and irrational numbers can be explained below

Finally, we concluded an irrational number is different from a rational number.

Question. Classify each number as a rational or irrational number.

Given:
​
​π = 3.565565556..

0.04053661 −17

0.76 3.275

To classify each number as a rational or irrational number

​π− Irrational number

0.04053661 − Rational number

0.76767676 −  Irrational number

3.565565556.. −  Rational number

−17  −  Rational number

3.275 − Irrational number

Finally, we classified each number as a rational or irrational number.

Question. Classify each number as a rational or irrational number and explain.

Given:

\(\begin{array}{llll}
\frac{2}{3} & \sqrt{25} & -0.7 \overline{5} & \sqrt{2}
\end{array} 7,548,123\)

To classify each number as a rational or irrational number and explain

Given:

\(\frac{2}{3}\) −  Is a rational number as it can be expressed in the form of  \(\frac{p}{q}\)

\(\sqrt{25}\)− The number is a perfect square so \(\sqrt{25}\)  = 5 is a rational number

\( −  0.7 \overline{5}\) −  Is an irrational number, the decimal expansion does not repeat or terminate

\(\sqrt{2}\) −  The number is not a perfect square so \(\sqrt{2}\) is an irrational number

7,548,123 − Is an irrational number because the expansion does not repeat or terminate

Finally, we explained and classified each number as a rational or irrational number.

Yes, Jen is correct

The number 4.567 as irrational because it does not repeat.

Finally, we concluded that Jen is correct and the number the number 4.567 as irrational because it does not repeat.

An irrational number differs from a rational number in the sense that it cannot be stated in the style of \(\frac{a}{b}\) , where a and b are both integers and b ≠ 0.

Furthermore, unlike a rational number, which might be recurring or terminating, an irrational number is non-repeating and non-terminating in decimals.

A square root of a not-perfect square is also shown by an irrational number.

Finally, we concluded that an irrational number is different from a rational number as.

The irrational number cannot be written in the form of \(\frac{a}{b}\)

Is non-repeating and non-terminating decimal.

It’s a square root of a not-perfect square.

It is not possible for a number to be both rational and irrational number.

This is because a rational number can be written in the form of \(\frac{p}{q}\) and rational number.

Cannot be written in the form of \(\frac{p}{q}\).

Finally, we concluded that a number cannot be both rational and irrational.

The given decimal is an Irrational number.

This is because the given decimal cannot be written in the form of \(\frac{a}{b}\)

Furthermore, the given decimal is a non-repeating and non-terminating decimal.

Finally, we concluded that the number 65.4349224…. is an irrational number.

Grade 7 Envision Math Exercise 2.2 Real Numbers Answers

Question. Find the number \(\sqrt{2500}\) rational or irrational? Explain.

Given:

Is the number \(\sqrt{2500}\) rational or irrational? Explain.

To find Is the number\(\sqrt{2500}\) rational or irrational? Explain.

The given square root is a rational number.

This is because the given number 2500 is a perfect square
​
​50 × 50  =  2500

⇒  \(\sqrt{2500}\)

= 50
​
The result of the square root is 50 which can be classified as an integer, Whole number, and natural number.

Finally, we concluded that the number \(\sqrt{2500}\) is a rational number.

Question. Classify each number as rational or irrational.

Given :

\(4. 2\overline{7} \) ,0.375,0.232342345…,\(\sqrt{62},-\frac{13}{1}\)

To Classify each number as rational or irrational.

An irrational number is different from a rational number in terms that the irrational number.

It cannot be written in the form of \(\frac{a}{b}\), Where a and b are both integers and b≠0.

A rational number is recurring or terminating, an irrational number is non-repeating and non-terminating in decimals.

A square root of a not-perfect square is also shown by an irrational number.

According to that, The table for the given numbers as rational and irrational numbers.

⇒ \(\begin{array}{|l|l|}
\hline \text { Rational } & \text { Irrational } \\
\hline 4.2 \overline{7} & 0.232342345 \ldots \\
\hline 0.375 & \sqrt{62} \\
\hline-\frac{13}{1} & \\
\hline
\end{array}\)

Finally, we concluded that The table for the given numbers as rational and irrational numbers.

⇒ \(\begin{array}{|l|l|}
\hline \text { Rational } & \text { Irrational } \\
\hline 4.2 \overline{7} & 0.232342345 \ldots \\
\hline 0.375 & \sqrt{62} \\
\hline-\frac{13}{1} & \\
\hline
\end{array}\)

Question. Find 5.787787778…. a rational number? Explain.

Given:

Is 5.787787778…. a rational number? Explain

To find Is 5.787787778….a rational number? Explain.

The given decimal 5.787787778…. is an Irrational number.

This is because the given decimal cannot be written in the form of \(\frac{a}{b}\).

Furthermore, the given decimal is a non-repeating and non-terminating decimal.

Finally, we concluded that 5.787787778…. …is an irrational number.

Envision Math Chapter 2 Exercise 2.2 Answer Key

Question. Find the number \(\sqrt{42}\) rational or irrational? Explain.

Given:

Is the number \(\sqrt{42}\) rational or irrational? Explain.

To find Is the number \(\sqrt{42}\) rational or irrational? Explain.

The given \(\sqrt{42}\) is an irrational number.

This is because the given number 42 is not a perfect square.

Therefore, the result of the given square root will be a non-terminating decimal.

Finally, we concluded that the number \(\sqrt{42}\) is irrational.

Question. Find which card shows irrational numbers. 

Given:

1. 10
2. \(\frac{6}{5}\)
3. π
4. \(\frac{11}{4}\)
5. 8.25635…
6. \(6. \overline{31}\)
7. -7

To find Which card shows irrational numbers?

From the given cards, the irrational numbers are π  and  8.25635…

These two cards are said to be irrational because they cannot be written in the form of \(\frac{a}{b}\) and are non-repeating and non-terminating decimals.

Finally, we concluded that C)π and D) 8.25635…. are the irrational numbers

Given:

⇒ \(7. \overline{27}, \frac{5}{9}, \sqrt{15}, \sqrt{196}\)

To Circle the irrational number in the list.

An irrational number is different from a rational number in terms that the irrational number cannot be written in the form of \(\frac{a}{b}\) , Where a and b are both integers and b ≠ 0.

A rational number is recurring or terminating, an irrational number is non-repeating and non-terminating in decimals.

A square root of a not-perfect square is also shown by an irrational number.

According to that, From the given list the irrational number is \(\sqrt{15}\) .

15 is not a perfect square.

Therefore, the result of the square root of 15 would be a non-terminating and non-repeating decimal.

Which is an irrational number.

Finally, we concluded that \(\sqrt{15}\) is the irrational number in the given list.

⇒ \(\sqrt{76+n}\) and.\(\sqrt{2 n+26}\)

Question. Find which numbers are rational.

Given:

5.737737773…,26, \(\sqrt{45}\) \(-\frac{3}{2}\) ,0,9

To find which numbers are rational.

Given:

5.737737773…,26, \(\sqrt{45}\) ,\(-\frac{3}{2}\) ,0,9 26, \(-\frac{3}{2}\) ,0,9.

These are rational numbers because a rational number can be written in the form of \(\frac{a}{b}\).

Finally we concluded 26,\(-\frac{3}{2}\) ,0,9 is rational numbers.

Solutions For Envision Math Grade 7 Exercise 2.2

Question. Find the which numbers are irrational.

Given:

5.737737773…,26, \(\sqrt{45}\) ,\(-\frac{3}{2}\) ,0,9

To find which numbers are irrational.

Given:

5.737737773…,26,\(\sqrt{45}\) ,\(-\frac{3}{2}\),0,9 5.737737773…, \(\sqrt{45}\).

These are irrational numbers because irrational numbers cannot be written in the form of \(\frac{p}{q}\).

Finally we concluded that 5.737737773…, \(\sqrt{45}\) are irrational numbers.

Deena says that 9.565565556… is a rational number, no it is wrong because 9.565565556… is an irrational number and it has a repeating value.

Finally, we concluded that Deena’s statement is wrong and 9.565565556… is an irrational number.

The given decimal form \(\frac{13}{3}\)   is a rational number because it can be expressed in the form of.

⇒ \(\frac{p}{q}\) and it is the fraction of two integers, where the numerator is 13 and the denominator is 3.

Finally, we concluded that the decimal form of \(\frac{13}{3}\) a rational number.

The given rational numbers are 2.888…  and  2.999…

The irrational number that is between the two rational numbers is 2.889888…  and  2.998999…

Finally, we concluded that the irrational number between two rational numbers is 2.889888… and 2.998999…

Question. Find the smallest value of n that will make each number rational given expression is \(\sqrt{76+n}\) and.\(\sqrt{2 n+26}\)

Given:

The given expression is \(\sqrt{76+n}\) and.\(\sqrt{2 n+26}\)

To find the smallest value of \[n\]that will make each number rational.

Given:

⇒ \(\sqrt{76+n}\) and .\(\sqrt{2 n+26}\)

Substitute n = 5 in the above equation
​
⇒ \(\sqrt{76+n}\)

⇒ \( = \sqrt{81}\)

⇒ \( = \frac{9}{\sqrt{2(5)+26}}\)

⇒ \( = \sqrt{36}\)

=6

Finally, we concluded the smallest value of n is n = 5.

Envision Math Grade 7 Volume 1 Chapter 2 Exercise 2.2 Guide

Question. Differentiate the rational and irrational \(\frac{8}{5}\),π,0,\( = \sqrt{1}\),4.46466…,−6,\(=\sqrt{2}\)

Given:

⇒ \(\frac{8}{5}\),π,0,\( = \sqrt{1}\),4.46466…,−6,\(=\sqrt{2}\)

To differentiate the rational and irrational

⇒ \(\begin{array}{|l|l|}
\hline \text { rational } & \text { irrational } \\
\hline \frac{8}{5} & \pi \\
\hline 0 & \sqrt{1} \\
\hline-6 & 4.46466 \ldots, \\
\hline & \sqrt{2} \\
\hline
\end{array}\)

Finally we concluded the rational are \(\frac{8}{5}\) ,0,6 and irrational are π,\(=\sqrt{1}\) ,4.46466 \(=\sqrt{2}\)

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 333 Exercise 1 Answer

Given: AB = 2, AC = 2, AD = 5 and AE = 5

To determine the similarity and difference between two triangles.

First, use the Pythagoras theorem, to find the longest side and find the ratio of the triangle.

The image of a dilation has the same shape, orientation and angle measures as the preimage.

But they have different side lengths.

Because, a dilation is a transformation that moves each point along the ray through the point, starting from a fixed center, and multiplies distance from the center by a common scale factor.

Therefore, there will be some difference in size of the figures after these transformation.

Hence, there will be some difference in size of the figures after these transformation.

Envision Math Grade 8 Volume 1 Chapter 6.6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 333 Exercise 2 Answer

A dilation will be reduction when the scale factor is between 0 and 1,because the image is smaller than the original figure.

When the image is larger than the original figure, in another words, when the scale factor is greater than 1 a dilation will be enlargement.

A dilation will be reduction when the scale factor is between 0 and 1 because the image is smaller than the original figure.

When the image is larger than the original figure, in another words, when the scale factor is greater than 1 a dilation will be enlargement.

A dilation will be reduction when the scale factor is between 0 and 1 because the image is smaller than the original figure.

When the image is larger than the original figure, in another words, when the scale factor is greater than 1 a dilation will be enlargement.

Page 334 Essential Question Answer

A dilation is a type of transformation that enlarges or reduces the size of a figure called the preimage.

A dilation is a type of transformation that create a new figure called the image, that has the same shape as the preimage but a different size than the preimage.

After dilation, the image has the same shape as the preimage, but the size of the image is a scaled version of the preimage.

Congruence And Similarity Envision Math Exercise 6.6 Answers

Page 335 Try It Answer

Given: A dilation marks the point L(3,6) to its image point L′(2,4). The preimage is given in the figure below:

To find: The dilation image L’M’N’, the scale factor and length of the side M′N′.

Since L (3,6) → L′ (2,4) it follow that the scale factor k is

K = \(\frac{4}{6}=\frac{2}{3}\)

The other two vertices of ΔLMN are M(3,3),N(6,3)

The image of the vertex M after the dilation with a scale factor K = \(\frac{2}{3}\) is

The image of the vertex N after the dilation with a scale factor K = \(\frac{2}{3}\) is

With these points, the dilation figure L′M′N′ can be constructed as follows:

Hence, the image of ΔLMN, the ΔL′M′N′ is shown above.

Now, to find the length of side M ′N′, Let x1 be the x-coordinate of point M′(2,2) and x2 be the x-coordinate of point N′(4,2)

Since the side M′N′ is parallel to x−axis, length of the side M′N′ equals

x₂ − x₁ = ∣4∣ − ∣2∣

x₂ − x₁ = ∣2∣

The dilation with a scale factor K = \(\frac{2}{3}\) is shown below and the length of the side M′N′ is 2 units.

Envision Math Grade 8 Chapter 6.6 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 336 Exercise 2 Answer

If the scale factor k is between 0and 1, a dilation is a reduction.

If the scale factor k is between is greater than 1,a dilation is an enlargement.

Hence Proved.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 336 Exercise 4 Answer

Given:

To find the scale factor of figure 3 with respect to figure 1.

We will calculate the base length of given figures.

The base length of the triangle in figure 1 is 1 unit.

The base length of the triangle in figure 3 is 4 unit.

Hence, the scale factor will be \(\frac{4}{1}\)

Evaluating the expression, it gives 4.

Hence, the scale factor is 4, which was derived by comparing the base lengths of the preimage and the image.

v

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 336 Exercise 5 Answer

To find: the coordinates of the image of Figure 2 after a dilation with center at the origin and a scale factor of 3.

We will find the vertices after the dilation by multiplying the scale factor with given vertices in figure 2.

Given:

Figure 2:

Let A,B,C be the vertices of the triangle in Figure 2. Point A is 2 units right and 2 units above the origin so its coordinates are (2,2).

Therefore, the vertices of the original image in Figure 2 are A(2,2),B(3,4),C(4,2).

To obtain the vertices of the image of triangle ΔABC after a dilation with a scale factor of 3,multiply the coordinates of points A, B and C by 3.

The image of point A after a dilation with a scale factor k = 3 is

A(2,2) → A′(3⋅2,3⋅2) → A′(6,6)

The image of point B after a dilation with a scale factor k = 3 is

B(3,4) → B′(3⋅3,3⋅4) → B′(9,12)

The image of point C after a dilation with a scale factor k = 3 is

C(4,2) → C′(3⋅4,3⋅2) → C′(12,6)

Therefore, the vertices of the image after dilation are A′(6,6), B′(9,12), C′(12,6)

Therefore, the vertices of the image after dilation are A′(6,6), B′(9,12), C′(12,6)

Page 337 Exercise 7 Answer

Given:

To find:

The coordinates of each point in the original figure.

D(−),(−)E(−),(−)F(−),(−)

Multiply each coordinate by _______

Find the coordinates of each point in the image:

D(−),(−)E(−),(−)F(−),(−)

Graph the image.

In order to obtain the vertices of the image of triangle after a dilation with a scale factor, we need to multiply the coordinates with that factor.

In the given graph;

Point D coincides with the origin, so the coordinates areD(0,0)

Point E is 2 units to the right of the origin, so the coordinates are E(2,0)

Point F is 2 units up from the origin, so the coordinates are F(0,2)

Therefore, the vertices of the initial triangle are;

D(0,0),E(2,0) and F(0,2))

To obtain the vertices of the image of the triangle ΔDEF after a dilation with a scale factor of 2, multiply the coordinates by 2.

The image of the point D after a dilation with the scale factor k = 2 is:

D(0,0) → D′(2⋅0,2⋅0) → D′(0,0)

The image of the point E after a dilation with the scale factor k = 2 is:

E(2,0) → E′(2⋅2,2⋅0) → E′(4,0)

The image of the point F after a dilation with the scale factor k = 2 is:

F(0,2) → F′(2⋅0,2⋅2) → F′(0,4)

Therefore, the vertices of the final triangle are D(0,0),E(4,0) and F(0,4).

Plot the points D′(0,0),E′(4,0) and F′(0,4):

The triangle D′E′F′ is shown:

The triangle D′E′F′ is shown.

The vertices of the initial triangle are D(0,0),E(2,0) and F(0,2)

Multiply the coordinates by 2 to obtain the vertices of the final triangle:

D(0,0),E(4,0) and F(0,4)

Envision Math Grade 8 Volume 1 Chapter 6.6 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 337 Exercise 8 Answer

Given:

To find:

The scale factor for the dilation

In order to find the scale factor, we need to compare the ratios of both dilations and then divide the number in fraction to obtain the scale factor.

The rectangle FGDE has sides with length of 5 and 6 units.

The rectangle F′G′D′E′ has sides with length of 15 and 18 units.

Therefore, the ratio of the side length in F′G′D′E′ to a corresponding side in FGDE s:

= \(\frac{3}{1}\)

Divide the numbers to get the scale factor: 3

The ratio of the side lengths is \(\frac{3}{1}\)

Therefore, the scale factor is 3

Envision Math 8th Grade Congruence And Similarity Topic 6.6 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 337 Exercise 10 Answer

Given:

In the figure small figure is dilation of large figure, origin is the center of dilation.

To find:

Whether the dilation is an enlargement or a reduction, and find the scale factor of the dilation.

In order to find the dilation is enlarge or reduce and to find the scale factor we have to refer to the tip mentioned.

The rectangle EFGH has the side length of 12 units.

The rectangle ABCD has a side length of 4 units.

Now the smaller figure, rectangle ABCD is the dilation of the larger rectangle EFGH. The larger figure is diluting in a smaller figure.

The Reduction is when a larger figure dilates into the smaller figure. Therefore, the dilation is a reduction.

The Scale factor is the ratio between the two same figures but different in sizes.

Scale Factor = Side length of \(\frac{A B C D}{E F G H}\)

Here, Side length of ABCD = 4 and EFGH = 12

Scale factor = \(\frac{4}{12}\)

Dividing the terms with 4.

Scale factor = \(\frac{1}{3}\)

The dilation is a reduction with the scale factor = \(\frac{1}{3}\)

Envision Math Grade 8 Chapter 6.6 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6Page 338 Exercise 13 Answer

Given:

Rectangle Q′U′A′D′ with its coordinates and Q′,U′,A′,D′, is the image of QUAD after a dilation with center, and scale factor is 6.

To find:

Coordinates of point D′.

In order to find the coordinates of D′ we have to first find the coordinates of D and then multiply it with the scale factor.

Plot the points Q(0,0),U(0,3),A(6,3) and D(6,0) to form the quadrilateral.

Since the center of dilation is (0,0), the coordinates of the points can be multiplied by the scale factor.

since, the scale factor is 6, it multiply all coordinates of all points by it:
​
Q(6⋅0,6⋅0) → Q′(0,0)

U(6⋅0,6⋅3) → U′(0,18)

A(6⋅6,6⋅3) → A′(36,18)

D(6⋅6,6⋅0) → D′(36,0)
​
Therefore the coordinates of the point D′ are (36,0)

Plot the points Q′(0,0), U′(0,18), A′(36,18), D′(36,0) to plot the dilated quadrilateral.

The coordinates of the point D′ are (36,0). The dilated quadrilateral Q′U′A′D′ is shown.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 325 Exercise 1 Answer

Notice that each block is 1 unit long and 1 unit wide so they are all congruent.

To fit the blue piece into the space provided, rotate it 180^∘ counter-clockwise.

Then, shift the blue piece 3 units to the left.

Lastly, shift the blue piece 4 units down.

The blue piece fitting on the provided space is shown in the figure.

Since each block is 1 unit long and 1 unit wide, it follows that they are all congruent. By rotating and shifting the position of the original blue piece, it can fit into the space as shown.

Page 325 Exercise 2 Answer

The piece should be rotated at 180^∘.

Then the piece should be translated 3 units right.

Then the piece should be translated 4 units down.

So, the knowledge of translation and rotation can be used to fit the piece in the space.

The piece should be rotated at 180∘, then translated 3 units right and then translated 4 units left.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 325 Essential Question Answer

The transformations that always produce congruent figures are TRANSLATIONS, REFLECTIONS, and ROTATIONS. These transformations are isometric, thus, the figures produced are always congruent to the original figures. The transformation that sometimes produce congruent figures is dilation.

Rotations, reflections, and translations are isometric.

That means that these transformations do not change the size of the figure. If the size and shape of the figure is not changed, then the figures are congruent.

A reflection followed by translation, a translation followed by rotation, and a rotation followed by reflection all preserve congruence.

A reflection followed by translation, a translation followed by rotation, and a rotation followed by reflection all preserve congruence.

Page 346 Exercise 3 Answer

If the sequence of translations, reflections and rotations maps one rug onto the other then the rugs are the same size and shape.

Ava uses translation followed by a rotation to map the living room rug onto the hearth rug.

Since the two rugs are the same size and the same shape, they are congruent figures

Page 326 Exercise 4 Answer

A sequence of translations, reflections, and rotations map one rug onto the other then the rugs are the same size and shape.

Congruent figures have the same size and shape. The two-dimensional figure is congruent ( ≃ ) if the second figure can be obtained from the first by a sequence of rotations, reflections, and translations.

Ava uses a translation followed by a rotation to map the living room rug onto the hearth rug.

Since the two rugs are the same size and the same shape, they are congruent figures.

The two rugs are the same size and the same shape, they are congruent figures.

Page 326 Try It Answer

Given:

To find: whether the orange and blue rectangles are congruent.

They are both rectangles, thus their corresponding angles are congruent. Their side length need to be checked, if they are congruent, if they do not they are not, by the definition of congruence. Their side lengths need to be checked, if they have the same side lengths they are congruent, if they do not they are not.

Hence, Their side lengths need to be checked, if they have the same side lengths they are congruent, if they do not they are not.

Page 326 Convience Me Answer

Given quadrilateral diagram in graph.

To find the quadrilateral PQRS is congruent to P′Q′R′S′

From the definition of Congruent Polygon,

Hence, the definition of Congruent Polygons

Page 327 Try It Answer

Given figures in a graph

To find the given figures are congruent or not.

Rotate each vertex of the first figure 90^∘

counterclockwise around the origin. Since the quadrilateral A′′B′′C′′D′′ maps onto the second figure, those figures are congruent.

Hence, the first rotated 90^∘ counterclockwise around the origin and then translated 13 units to the right maps onto the second figure, so those figures are congruent.

Page 328 Exercise 1 Answer

Given: Sequence of translations, reflections and rotations

To find: The sequence of translations, reflections, and rotations result in congruent figures

Rotations, reflections and translations are isometric. That means that these transformations do not change the size of the figure. If the size and shape of the figure is not changed, then the figures are congruent.

Hence, the size and shape of the figure is not changed, then the figures are congruent.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 328 Exercise 2 Answer

Given: Sequence of transformations have to include a translation, a reflection, and a rotation.

To find: The sequence of transformations have to include a translation, a reflection, and a rotation to result in congruent figures

A sequence of transformation does not have to include any of the given transformation to result in a congruent figure. An example of this is the following sequence.

A dilation with respect to a point and with a scale factor of 2,a dilation with respect to the same point and with a scale factor of \(\frac{1}{2}\).

Hence, the sequence of transformation does not have to include any of the given transformation to result in a congruent figure.

Page 328 Exercise 3 Answer

Given: A sequence of reflections, rotations, and translations.

To find: The preimage and image not only congruent, but identical in orientation.

There are multiple sequence with this property, one example would be the following sequence.

Reflection over a line, reflection over the same line.

Hence, Reflection over a line, reflection over the same line is an example of The preimage and image not only congruent, but identical in orientation.

Page 328 Exercise 4 Answer

Given: A rectangle with an area of 25 square centimeters is rotated and reflected in the coordinate plane.

To find: The area of the resulting image.

Rotations and reflections don’t change the measures, thus the area is still 25cm².

Hence, the area of the resulting image is 25cm².

Page 328 Exercise 5 Answer

Given:

To find: ΔABC≅ΔDEF

We will find the distance between two points and we have to find the given triangle is congruent or not.

Repeat the procedure to determine the length of the sides of both triangle
​

Therefore, corresponding sides of the triangle are congruent. ΔABC ≅ ΔDEF

Page 328 Exercise 6 Answer

Given:

To find ΔABC ≅ ΔGHI

We will find the distance of given triangle and find the given triangle is congruent or not.

For the two triangles to be congruent, the corresponding measures of both triangle must be same.

From figure ΔABC, the length of AC

The length of GI in triangle GHI is \(\sqrt{29}\).

Since the corresponding sides are not congruent, the two triangles are not congruent. ΔABC is not congruent to ΔGHI.

Hence, the corresponding sides are not congruent, the two triangles are not congruent.

Page 329 Exercise 7 Answer

As the shape only undergoes reflection and translation. Its shape and size can not change.

Thus, ΔQRS and ΔQ′R′S′ have the same size and shape.

Hence, ΔQRS and ΔQ′R′S′ have the same size and shape.

Page 329 Exercise 8 Answer

Given:

To find the ΔDEF and ΔD′E′F′ is congruent or not.

The length of all corresponding sides of both the triangles are equal therefore side-side-side congruence theorem.

ΔDEF Δ D′E′F′

Hence, the length of all corresponding sides of both the triangles are equal therefore side-side congruence theorem

ΔDEF Δ D′E′F′

Page 329 Exercise 9 Answer

Given: Quadrilateral ABCD and A′B′C′D′.

To find the ABCD is congruent to quadrilateral A′B′C′D′

Observe the quadrilateral ABCD

Reflect ABCD over y−axis translate it for 5 units downwards to draw A′B′C′D′. Since both transformation are isometries it follow that A′B′C′D′ is congruent to ABCD.

Hence, A′B′C′D′ is congruent to quadrilateral ABCD.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 329 Exercise 10 Answer

Given graph

To find the flags the same shape and size.

Construct an line x = 1.5

The flags are the same shape and size because the second flag can be formed by reflecting and translating the first flag.

Hence, the flags are the same shape and size because the second flag can be formed by reflecting and translating the first flag.

Page 330 Exercise 11 Answer

Given:

To find which two triangles are congruent.

We will compare the given triangles to find if they are congruent or not.

Plot the points

The ΔQRS with coordinates Q(4,7),R(2,2),S(7,2) ΔDEF with coordinates D(7,−5),E(2,−2),F(2,−7)

Next, translate ΔQ′R′S′ 9 units going down.

The final image of the ΔQRS is the ΔQ′R′S′ with coordinates Q”(7,−5), R'(2,−7) and S”(2,−2)

Since both have the same vertices ΔQ”R’S”≅ ΔDEF

Therefore, by using the rotation, translation and reflection the ΔQ”R’S” ≅ ΔDEF

Page Exercise 12 Answer

Given points L(7,9),M(9,5)

ΔLMN ≅ ΔXYZ

To find the given triangles are identical or not.

We will calculate the distance between two points LM and also XY and then we will find the given points are identical or not.

As we have already mentioned, congruent figures have the same shape and the same size.

If you look at the triangle LMN,you can notice that these triangle does not have the same size as triangleXYZ.

To be precise, the corresponding size length of triangle LMN are greater then of triangle XYZ.

Therefore, there is no sequence of transformations that maps triangle LMN onto triangle XYZ LMN

We can conclude that these two triangles are not congruent.

ΔLMN ≠​ ΔXYZ

Hence, We can conclude that these two triangles are not congruent.

ΔLMN ≠ ​ΔXYZ

Page 330 Exercise 13 Answer

Plot the points D(4,5),E(5,1),F(1,2)

Since the obtained triangle is correct, the initial triangle should have been reflected across the x−axis and translated 6 units left and 4 units up.

The student likely made the mistake of mapping ΔD′E′F′ onto ΔDEF instead of ΔDEF onto ΔD′E′F′.

Therefore, the students made a mistake by translating the triangle 6 units right, as a result of trying to map ΔD′E′F′ onto ΔDEF.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 330 Exercise 14 Answer

The triangle , a sequence of rotation maps ΔDEF onto ΔD′E′F′.

Given graph is rotation.

Option (B) is incorrect because the sequence of transformations maps ΔDEF onto ΔD′E′F′

Option(C) is incorrect because the sequence of translations maps ΔDEF onto ΔD′E′F′

Option(D) is incorrect because the sequence of reflections maps ΔDEF onto ΔD′E′F′

Hence, a sequence of rotations maps ΔDEF onto ΔD′E′F′.

Option(A) is correct.

The ΔDEF rotated 180∘ about the point (2,2) and then translated 1 unit to the left maps onto the ΔD′E′F′

ΔDEF ≅ ΔD′E′F′

Hence proved ΔDEF ≅ ΔD′E′F′, since ΔDEF can be mapped onto ΔD′E′F′ by rotating ΔDEF by 180° about point (2,2) and translating it to the left by 1 unit.

Page 331 Exercise 1 Answer

Rotation:

A rotation is a transformation that turns a figure about a fixed point called the center of rotation. An object and its rotation are the same shape and size, but the figures may be turned in different directions. Rotation may be clockwise or counterclockwise.

Reflection:

In geometry, a reflection is a type of rigid transformation in which the preimage is flipped across a line of reflection to create the image. Each point of the image is the same distance from the line as the preimage is, just on the opposite side of the line.

Translation:

Translation is used in geometry to describe a function that moves an object a certain distance. The object is not altered in any other way. It is not rotated, reflected, or resized. In a translation, every point of the object must be moved in the same direction and for the same distance.

Hence, the three transformations where the image and preimage have the same size and shape are rotation, reflection and translation.

Page 331 Exercise 2 Answer

Given:

To find: the coordinates of each point after quadrilateral RSTU is rotated 90^∘ about the origin.

We know that the coordinates of RSTU then we will rotated 90^∘ about the origin R′S′T′U′

Coordinates of RSTU:
​
R (1,−2)
S (2,−4)
T (4,−5)
U (3,−3)
​
Rotated 90^∘ about the origin:
​
R′(2,1)

S′(4,2)

T′(4,−5)

U′(3,3)

The coordinates of points R(1,−2), S(2,−4), T(4,−5), U(3−3) after a 90^∘ rotation about origin are
​
R′(2,1)

S′(4,2)

T′(5,4)

U′(3,3)

Page 331 Exercise 4 Answer

Given:

To find the coordinates of each point after quadrilateral MNPQ is reflected across the x−axis.

We know that the coordinates of MNPQ are reflected across the x−axis.

Find the coordinates of the quadrilateral MNPQ from the graph:

Reading from the graph, the vertices are

M(1,2), N(2,4), P(4,5), Q(3,3)

Change the signs of the y-coordinates of the vertices to get the reflected quadrilateral:

Reading from the graph, the coordinates of the reflected points are R(1,−2),S(2,−4),T(4,−5),U(3,−3)

Hence, the coordinates of the reflected quadrilateral RSTU are (1,−2),(3,−3),(4,−5),(2,−4).

Page 331 Exercise 5 Answer

Reflect the rotated figure M′N′P′Q′ across the y−axis.

Rotation 180^∘ about the origin, and then reflection across the y−axis.

Option D is correct.

Option(A) is incorrect because reflection across the x−axis, translation 4units down.

Option(B) is incorrect because reflection across the y−axis, translation 4 units down.

Option(C) is incorrect because the rotation 180∘ about the origin, and then reflection across x−axis.

Hence, the rotation 180^∘ about the origin, and then reflection across the y−axis.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 331 Exercise 6 Answer

Given:

To find the quadrilateral MNPQ congruent to quadrilateral RSTU.

We will find the congruent of given quadrilateral.

Rotate each vertex of the first figure 90°counterclockwise about the origin.

Now if we translate the quadrilateral P′N′M′Q′ 6 units down and 6 units to the right, it maps onto the second figure.

Hence, those figures are congruent.

The first figure rotated 90^∘ counterclockwise around the origin and then translated 6 units down and 6 units to the right maps onto the second figure , so those figures are congruent.

Envision Math Accelerated Grade 7 Volume 1 Chapter 2 Real Numbers

Page 85  Exercise 2  Answer

The numbers given in decimal form can be written in fractional form.

The first step is to remove the decimal and divide the number by the power of ten.

Where the power of ten is decided by the number of digits after the decimal.

The second step is to write the fraction form in the simplest form.

The decimal form of number can be written in the fractional form by removing the decimal and then converting is to the simplest fractional form as mentioned above.

Page 85  Exercise 3  Answer

Rational numbers written in the form of fractions are precise.

The values of fractions are very accurate and the chances of error are very less.

So, rational numbers are preferred to be written in the form of fractions which can be converted into a decimal form or vice-versa.

It is useful to write a rational number as a fraction as it gives an accurate value.

Envision Math Accelerated Grade 7 Chapter 2 Exercise 2.1 Solutions

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 86  Question 1  Answer

A repeating decimal is one in which the digits after the decimal get repeated.

It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equal to any variable.

Then, that equation is multiplied by 10,100,1000,..depending upon the number of repeating digits.

After solving the obtained equations, the variable comes out equal to a fraction.

The example is 0.444…

Let  x= 0.444….…….(1)

Since,0.444…. has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 4.444…………(2)

Subtract equation (1) from (2)

10x−x = 4.444…−0.444…

9x = 4

x\(=\frac{4}{9}\)

A repeating decimal can be written as a fraction by a number of steps as shown above.

Page 86  Exercise 1  Answer

The winning percentage of a team is  0.444…

Let  x = 0.444….…….(1)

Since, 0.444…. has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 4.444…………(2)

Subtract equation (1) from (2)

10x−x = 4.444…−0.444…

9x = 4

x\( = \frac{4}{9}\)

The team won \( = \frac{4}{9}\) of their games.

Page 87  Exercise 2  Answer

The given repeating decimal is  0.6333…

Let x = 0.6333….…….(1)

Since,0.6333…. has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 6.333…………(2)

Subtract equation (1) from (2)

10x − x = 6.333…−0.633…

9x= 5.7

x = \(\frac{5.7}{9}\)

x = \(\frac{57}{90}\)

x = \(\frac{19}{30}\)

0.6333…. can be written in the fractional form as\(\frac{19}{30}\).

Page 87 Exercise 3 Answer

The given repeating decimal is 4.1363636…

Let x = 4.1363636….…….(1)

Since, 4.1363636…. has two repeating unit

Multiply both sides of equation (1) by 100

100x = 413.6363… ………(2)

Subtract equation (1) from (2)

100x−x = 413.6363…−4.1363…

99x = 409.5

​x = \(\frac{409.5}{99}\)

​x = \(\frac{4095}{990}\)

​x = \(\frac{455}{110}\)

​x = \(\frac{91}{22}\)

4.1363636….can be written in the fractional form as \(\frac{91}{22}\)

Page 86  Exercise 1  Answer

A repeating decimal is the one in which the digits after the decimal get repeated.

It can be converted into a fraction by a method in which the given repeating decimals are put equal to any variable.

Then, that equation is multiplied by 10,100,1000,..depending upon the number of repeating digits.

After solving the obtained equations, the variable comes out equal to a fraction.

So, the power of ten can be known by the number of repeating digits present in the given repeating fraction.

By checking the number of repeating digits, we know by what power of ten we multiply in the second step.

Envision Math Grade 7 Real Numbers Exercise 2.1 Answers

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 88  Exercise 1  Answer

A repeating decimal is the one in which the digits after the decimal get repeated.

It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equals to any variable.

Then, that equation is multiplied by 10,100,1000,.. depending upon the number of repeating digits.

After solving the obtained equations, the variable comes out equal to a fraction.

The example is 0.444…

Let x = 0.444….…….(1)

Since, 0.444…. has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 4.444…………(2)

Subtract equation (1) from (2)

10x−x = 4.444…−0.444…

9x = 4

x =\(\frac{4}{9}\)

A repeating decimal can be written as fraction by a number of steps as shown above.

Page 88  Exercise 2  Answer

A repeating decimal is the one in which the digits after the decimal get repeated.

It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equals to any variable.

Then, that equation is multiplied by 10,100,1000,.. depending upon the number of repeating digits.

After solving the obtained equations, the variable comes out equal to a fraction.

So, the power of ten can be known by the number of repeating digits present in the given repeating fraction.

We multiply by the power of ten to convert the irrational number to rational number.

In the second step, the given repeating decimal is multiplied by the power of ten to get a rational number.

Page 88  Exercise 3  Answer

A repeating decimal is the one in which the digits after the decimal get repeated.

It can be converted into a fraction by a method in which firstly, the given repeating decimals is put equals to any variable.

Then, that equation is multiplied by 10,100,1000,.. depending upon the number of repeating digits.

After solving the obtained equations, the variable comes out equal to a fraction.

So, the power of ten can be known by the number of repeating digits present in the given repeating fraction.

By checking the number of repeating digits, we can know by what power of ten we have to multiply in the second step.

Page 88  Exercise 4  Answer

The given repeating decimal is \(63. \overline{63}\) =63.6363….

Let x = \(63. \overline{63}\)=63.6363…. …….(1)

Since, 63.6363…. has two repeating unit

Multiply both sides of equation (1) by 100

100x = 6363.6363…………(2)

Subtract equation (1) from (2)

100x−x = 6363.6363…−63.6363…

99x = 6300

x\(=\frac{6300}{99}\)

=\(\frac{700}{11}\)

\(63. \overline{63}\) can be represented in fractional form as\(\frac{700}{11}\)

Page 88 Exercise 5 Answer

The given repeating decimal is 0.16666…

Let x = 0.16666…. …….(1)

Since,0.16666…. has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 1.66666………(2)

Subtract equation (1) from (2)

10x−x = 1.66666…−0.16666…

9x = 1.5

x = \(\frac{1.5}{9}\)

x = \(\frac{15}{90}\)

x = \(\frac{1}{6}\)

0.16666… can be represented in fractional form as \(\frac{1}{6}\)

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 88  Exercise 6  Answer

The given repeating decimal is 2.3181818…

Let x = 2.3181818….…….(1)

Since,2.3181818…. has two repeating unit

Multiply both sides of equation (1) by 100

100x = 231.8181818…………(2)

Subtract equation (1) from (2)

100x−x = 231.8181818…−2.3181818…

99x = 229.5

x = \(\frac{229.5}{99}\)

x = \(\frac{2295}{990}\)

x = \(2 \frac{35}{110}\)

2.3181818…..can be represented in mixed number form as \(2 \frac{35}{110}\).

Page 89  Exercise 7  Answer

The given repeating decimal is 0.2121…

Let x = 0.2121……….(1)

Since, 0.2121… has two repeating unit

Multiply both sides of equation (1) by 100

100x = 21.2121…………(2)

Subtract equation (1) from (2)

100x−x = 21.2121…−0.2121…

99x = 21

x = \(\frac{21}{99}\)

x = \(\frac{7}{33}\)

0.2121… is equals to \(\frac{7}{33}\)

Page 89  Exercise 8  Answer

The given repeating decimal is \(3. \overline{7}\)

=3.777…

Let x =\(3 . \overline{7}\) =3.777……….(1)

Since, \(3. \overline{7}\)=3.777… has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 37.777…………(2)

Subtract equation (1) from (2)

10x−x = 37.777…−3.777…

9x = 34

x = \(\frac{34}{9}\)

\(3. \overline{7}\) is equals to 34 \(\frac{34}{9}\).

Page 89  Exercise 10  Answer

The given repeating decimal is 0.93333…

Let x = 0.93333……….(1)

Since, 0.93333… has only one repeating unit

Multiply both sides of equation (1) by 10

10 x  =9.33333… ………(2)

Subtract equation (1) from (2)

10x−x = 9.33333…−0.93333…

9x = 8.4

x= \(\frac{8.4}{9}\)

x=\(\frac{14}{15}\)

0.93333…..is equals to \(\frac{14}{15}\)

Total number of students in the class are 15.

In the previous part, it was calculated that the number of students who said yes was divided by the number of total students.

Comes out to be \(\frac{14}{15}\) as the given number was \(0.9 \overline{3}\).

Therefore, it can be seen that the numerator represents the number of students who said yes which is equals to 14.

14 students said that summer break should be longer.

Solutions For Envision Math Accelerated Grade 7 Chapter 2 Exercise 2.1

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 89  Exercise  11 Answer

The given repeating decimal is \(0. \overline{87}\).

Let x= \(0. \overline{87}\) =0.8787……….(1)

Since 0.87 has two repeating unit

Multiply both sides of equation (a) by 100

100x=87.8787…………(2)

Subtract equation (1) from (2)

100x−x = 87.8787…−0.8787…

99x  =  87

x = \(\frac{87}{99}\)

= \(\frac{29}{33}\)

\(0. \overline{87}\) is equals to \(\frac{29}{33}\).

Page 89 Exercise 12  Answer

The given repeating decimal is \(0. \overline{8}\).

Let x= \(0. \overline{8}\) =0.888… …….(1)

Since 0.8has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 8.888…………(2)

Subtract equation (1) from (2)

10x−x = 8.888…−0.888…

9x = 8

x\( =\frac{8}{9}\)

\(0. \overline{8}\) is equals to \(=\frac{8}{9}\)

Page 90  Exercise 13  Answer

The given repeating decimal is \(1. \overline{48}\)

Let x=\(1. \overline{48}\) = 1.484848… …….(1)

Since 1.48 has two repeating unit

Multiply both sides of equation (1) by 100

100x = 148.484848…………(2)

Subtract equation (1) from (2)

100x−x  = 148.484848…−1.484848…

99x = 147

x= \(\frac{147}{99}\)

x= \(\frac{49}{3.3}\)

x= \(1 \frac{16}{33}\)

\(1. \overline{48}\) is equals to \(1 \frac{16}{33}\)

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 90  Exercise 14  Answer

The given repeating decimal is \(0. \overline{6}\).

Let x = \(0. \overline{6}\) = 0.666……….(1)

Since 0.6 has only one repeating unit

Multiply both sides of equation (1) by 10

10x = 6.666… ………(2)

Subtract equation (1) from (2)

10x−x = 6.666…−0.666…

9x = 6

x\(=\frac{6}{9}\)

x=\(\frac{2}{3}\)

\(0. \overline{6}\) is equal to \(\frac{2}{3}\)

Page 90  Exercise 15  Answer

The given repeating decimal is 2.161616…

Let x = 2.161616……….(1)

Since, 2.161616…has two repeating unit

Multiply both sides of equation (1) by 100

100x = 2.161616…………(2)

Subtract equation (1) from (2)

100x−x = 216.161616…−2.161616…

99x = 214

x=\(\frac{214}{99}\)

2.161616…. is equals to \(\frac{214}{99}\)

Page 90   Exercise 16  Answer

When writing a repeating decimals as fractions, The number of repeating digits tells us that by what power of ten.

we have to multiple the given repeating fraction.

If there is one digit that is repeating, then we will multiply the equation made in the first step by 10.

If there are two digits that are repeating, then we will multiply the equation made in the first step by 100 and so on.

The number of repeating digits matters because it will help us to determine the power of ten by which we have to multiply.

Page 90  Exercise 17  Answer

While converting from repeating decimal to fraction, in the first step, the given decimal is put equals to that and then the equation.

Is multiplied by the power of ten and then subtracted one from that resulting equation so as to remove the repeating digits after decimals.

This is the reason that we get the series of 9s while converting repeating decimals to fractions.

The fractions always have 9s or 0s as digit in denominator while converting repeating decimals to fractions to remove the repeating digits.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers Exercise 2.1 Page 90  Exercise 18  Answer

The given fraction is \(\frac{188}{11}\)

Let x = \(17. \overline{09} .\)……….(1)

Since 17.09has two repeating unit

Multiply both sides of equation (1) by 100

100x = 1709.0909… ………(2)

Subtract equation (1) from (2)

100x−x = 1709.0909…−17.0909…

99x = 1692

x = \(\frac{1692}{99}\)

x = \(\frac{188}{11}\)

\(\frac{188}{11}\)is equalis to \(17 . \overline{09} .\)

Grade 7 Envision Math Exercise 2.1 Real Numbers Step-By-Step Solutions

Page 90 Exercise 19 Answer

The given repeating decimal are \(0. \overline{17}, 0 . \overline{351}, 0 . \overline{17}, 0.3 \overline{51}, 0.35 \overline{1}\)

The repeating decimal \(0. \overline{17}\) is equivalent to \(\frac{17}{99}\)

The repeating decimal \(0. \overline{351}\) is equivalent to \(\frac{351}{999}\)=\(\frac{13}{37}\)

The repeating decimal \(0.1 \overline{7}\) is equivalent to \(\frac{16}{90}\)=\(\frac{8}{45}\)

The repeating decimal \( 0.3 \overline{51}\) is equivalent to \(\frac{348}{990}\)=\(\frac{58}{165}\)

The repeating decimal \( 0.35 \overline{1}\) is equivalent to \(\frac{316}{900}\)=\(\frac{79}{225}\)

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 2 Real Numbers

Page 80  Question 1  Answer

Real numbers include rational and irrational numbers.
Real numbers help in measuring the quantities that vary continuously such as time, different from natural numbers.

Real numbers include rational and irrational numbers.
Real numbers help in measuring the quantities that vary continuously such as time, different from natural numbers.

Envision Math 2.0 Grade 7 Chapter 2 Real Numbers Solutions

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 82  Exercise 1  Answer

Natural resources like water, oil, and forests are in danger of someday being depleted.

They support the industry and economy of the country.

They are useful to man or could be useful under conceivable.

Technological, economic, or social circumstances or supplies drawn from the earth, supplies such as food, building and clothing materials, fertilizers, metals, water, and geothermal power.

They are divided into renewable and non-renewable resources.

Solar power, wind power, hydropower, and other renewable resources help us to reduce the dependency on non-renewable resources like oil and fossil fuels.

Thus, natural resources are essential for human life. We should protect natural resources from depletion.

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83  Exercise 1  Answer

• The decimal ending with repeating zeroes means it has an end.
• So, a terminating decimal is a decimal that ends in repeating zeros.

A terminating decimal is a decimal that ends in repeating zeros.

Page 83  Exercise 3  Answer

A counting number is any number like 1,2,3,…

The opposite is −1,−2,−3,…

These numbers are integers. So, the sentence is given by

An integer is either a counting number, the opposite of a counting number, or zero.

An integer is either a counting number, the opposite of a counting number, or zero.

Envision Math Grade 7 Real Numbers Practice Answers

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83  Exercise 4  Answer

• The given definition is of a function.
• So the statement becomes.
• A fraction is a number that can be used to describe a part of a whole, a part of a set, a location on a number line, or a division of whole numbers.

A fraction is a number that can be used to describe a part of a whole, a part of a set, a location on a number line, or a division of whole numbers.

Page 83 Exercise 5 Answer

The given number is 5.692.

Note that there are no dots after the last decimal digit  2, which means there are no digits after this.

So the given number is terminating decimal.

The given number 5.692 is a terminating decimal.

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83  Exercise 6  Answer

• The given number is −0.222222…
• Note that there are dots after the last decimal digit 2, which means there are infinite digits after this.
• So the given number is repeating decimal.

The given number −0.222222… is a repeating decimal.

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83 Exercise 7 Answer

The given number is 7.0001.

Note that there are no dots after the last decimal digit 1, which means there are no digits after this.

So the given number is terminating decimal.

The given number 7.0001 is a terminating decimal.

Page 83  Exercise 8  Answer

The given number is \(7.2 \overline{8}\).

Note that there is a bar on the last decimal digit 8, which means there are infinite digits after this.

So the given number is repeating decimal.

The given number \(7.2 \overline{8}\) is a repeating decimal.

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83 Exercise 9 Answer

The given number is \(1.\overline{178}\).

Note that there is a bar on the last decimal digits 178   which means there are infinite digits after this.

So, the given number is a repeating decimal.

The given number \(1.\overline{178}\) is a repeating decimal.

Page 83  Exercise 10  Answer

The given number is −4.03479.

Note that there are no dots after the last decimal digit 9, which means there are no digits after this.

So the given number is terminating decimal.

The given number −4.03479  is a terminating decimal.

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83 Exercise 11  Answer

The product to be found in
⇒ 2.2

Multiply the numbers
= 4

The product is given by 2.2 = 4.

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83  Exercise 12  Answer

The product to be found in
⇒  −5.(−5)

Multiply the numbers
= 25

The product is given by−5.(−5) = 25.

Page 83  Exercise 13  Answer

The product to be found in
⇒  7.7

Multiply the numbers
= 49

The product is given by 7.7 = 49.

Page 83  Exercise 14  Answer

The product to be found in
⇒  −6.(−6).(−6)

Multiply the first two numbers
= 36.(−6)

Multiply the numbers
= −216

The product is given by −6. (−6). (−6)=−216.

Page 83 Exercise 16 Answer

The product to be found in
⇒  −9.(−9).(−9)

Multiply the first two numbers
= 81.(−9)

Multiply the numbers
= −729

The product is given by −9. (−9).(−9)= −729.

Page 83 Exercise 18 Answer

The product to be found in
⇒  (2.100) + (7.10)

Find the products
= 200 + 70

Find the sum
= 270

The value is given by (2.100) + (7.10) = 270.

Page 83  Exercise 19  Answer

The product to be found in
⇒  (6.100)−(1.10)

Find the products
= 600−10

Find the sum
= 590

The value is given by(6.100)−(1.10)=590.

Real Numbers Solutions For Envision Math Grade 7 Volume 1

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83 Exercise 20 Answer

The product to be found in
⇒  (9.1,000) + (4.10)

Find the products
= 9000 + 40

Find the sum
= 9040

The value is given by(9.1,000) + (4.10)= 9040.

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 83  Exercise 21  Answer

The product to be found in
(3.1,000)−(2.100)

Find the products
= 3000−200

Find the sum
= 2800

The value is given by(3.1,000)−(2.100)= 2800.

Page 83  Exercise 22  Answer

The product to be found in
(2.10) + (7.100)

Find the products
= 20 + 700

Find the sum
= 720

The value is given by (2.10) + (7.100) = 720.

Envision Math 2.0 Chapter 2 Grade 7 Solution Guide

Envision Math 2.0: Grade 7 Volume 1 Chapter 2 Real Numbers Solutions Page 84  Exercise 1  Answer

Objective: To give definitions and examples to each term given in graphic organizer.

Definition of cube root: Given a number x, the cube root of x is the number a such that a³ = x

Example: The cube root of 27 is 3. Since 27 = 33.

Definition of irrational number: Irrational numbers have decimal expansions that neither terminate nor become periodic.

They are any real number that cannot be expressed as the quotient of two integers.

Example: √2,1.33333333…,e

Definition of the perfect cube: The perfect cube is an integer that is equal to some other integer raised to the third power.

If x is a perfect cube of y, then x = y³.

Example: Multiplying 5 three times, we get 125. Therefore,125 is a perfect cube.

Definition of perfect square: The perfect square is an integer that is equal to some other integer raised to the second power.

If x is a perfect square of y, then x = y².

Example: Multiplying 5 two times, we get 25. Therefore, 25 is a perfect square.

Definition of scientific notation: Scientific notation is a way of writing very large or very small numbers conveniently in decimal form.

Example: 0.00063 = 6.3 × 10⁻⁴

Definition of square root: Given a number x, the square root of x is the number a such that a² = x

Example: The square root of 121 is 11. Since 121=112.

Hence, we have given the definitions and examples to each term in a graphic organizer.