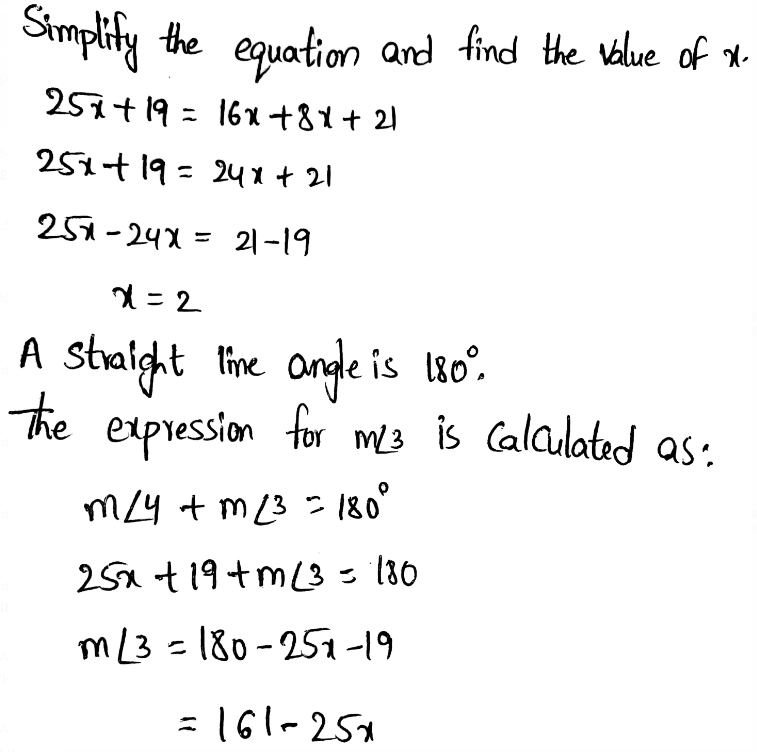Envision Math

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions

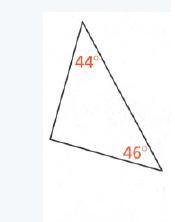
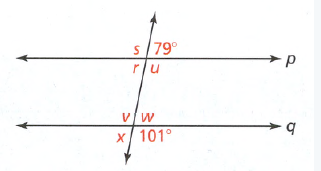
Question. Explain whether sorting the tiles with positive coefficients together and tiles with negative coefficients.

We need to explain whether sorting the tiles with positive coefficients together and tiles with negative coefficients.

Together help to simplify an expression that involves all the tiles.

The way of sorting the tiles with positive coefficients together and tiles with negative coefficients together will not help much.

Since we only add all the numbers alone and subtract the rest from them.

The main problem here exists with the numbers with variables.

We couldn’t able to do any arithmetic operations on them.

So, this won’t help much.

Sorting the tiles with positive coefficients together and tiles with negative coefficients together help to simplify an expression. That involves all the tiles wouldn’t help much.

Question. Explain how the properties of operations are used to simplify expressions.

We need to explain how the properties of operations are used to simplify expressions.

Simplification is the process of rewriting the given expression into its most compact form.

To simplify expressions, we can use the properties of operations such as distributive, commutative, and associative properties.

These properties will help in simplifying the terms by grouping them together.

Also, it combines like terms to get the simplified form.

The properties of operations are used to simplify expressions by grouping and combining the like terms together.

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.3 Answer Key

Question. Simplify the expression -6 – 6f + 7 – 3f – 9.

We need to simplify the expression − 6 − 6f + 7 − 3f − 9

The given expression is  −6−6f  +7 − 3f − 9

Simplifying it we get

​−6−6f + 7 − 3f − 9 = − 6f − 3f − 6 + 7 − 9

= −9f + 1 − 9

= − 9f − 8
​
The simplified expression is  −9f − 8

Simplification is the process of rewriting the given expression into its most compact form.

To simplify expressions, we can use the properties of operations such as distributive, commutative, and associative properties.

These properties will help in simplifying the terms by grouping them together.

Also, it combines like terms to get the simplified form.

We can sort the expressions into two groups.

One having the numbers alone.

The other having both the numbers and variables in it.

We can group each group separately and then do arithmetic operations to simplify it.

We will decide in what way to reorder the terms of an expression. When simplifying it is by looking at the variables and constants and grouping them separately to simplify it.

Question. Explain how the properties of operations are used to simplify expressions.

We need to explain how the properties of operations are used to simplify expressions.

Simplification is the process of rewriting the given expression into its most compact form.

To simplify expressions, we can use the properties of operations such as distributive, commutative, and associative properties.

These properties will help in simplifying the terms by grouping them together.

Also, it combines like terms to get the simplified form

The properties of operations are used to simplify expressions by grouping and combining the like terms together

Envision Math Grade 7 Chapter 5 Equivalent Expressions Exercise 5.3 Solutions

Question. Explain why constant terms expressed as different rational number types can be combined.

We need to explain why constant terms expressed as different rational number types can be combined.

The constant terms expressed as different rational number types can be combined because can be grouped together since they are all like terms.

The constant terms don’t have a variable in them.

So it can be grouped. It can be simplified, grouped, and combined no matter what since they are all like terms.

Constant terms expressed as different rational number types can be combined because they are all like terms.

Question. Explain how you know when an expression is in its simplest form.

We need to explain how you know when an expression is in its simplest form.

The expression is in its simplest form when it cannot be simplified further.

We cannot combine or group any further terms if they are simplified.

We cannot use any properties to simplify it further when they are simplified.

An expression is in its simplest form when we cannot group or combine them further.

Question. Simplify the expression -4b + (-9k) – 6 – 3b + 12.

We need to simplify the expression  −4b + ( −9k)−6 − 3b + 12.

The given expression is  −4b + (−9k) −6 −3b + 12

Simplifying it we get

​−4b + (−9k) − 6 − 3b + 12 = −4b − 9k − 6 − 3b + 12

= −4b − 3b − 9k − 6 + 12

= −7b − 9k + 6
​
The simplified expression is −7b − 9k + 6

Question. Simplify the expression -2 + 6.45z – 6 + (-3.25z).

We need to simplify the expression  −2 + 6.45z − 6 + ( −3.25z)

The given expression is  −2 + 6.45z − 6 + (−3.25z)

Simplifying it we get

​−2 + 6.45z − 6 + (−3.25z) =−2 − 6 + 6.45z − 3.25z

= −8 + 3.20z

=  3.2z − 8

The simplified expression is 3.2z − 8

Question. Simplify the expression -9 + (\(\frac{-1}{3}y\)) + 6-\(\frac{4}{3}y\).

We need to simplify the expression

− 9 + (\(\frac {-1}{3}y\)) + 6−\(\frac {4}{3}y\)

The given expression is − 9 + (\(\frac {-1}{3}y\)) + 6 −\(\frac {4}{3}y\)

Simplifying it, we get

− 9  +  (\(\frac{−1}{3}y\))+6−\(\frac{4}{3}y\)

= − 9 + 6 − \(\frac{1}{3}y\) − \(\frac{4}{3}y\)

= −3 + (\(\frac{ −y −4y}{3}\))

= −3 −\(\frac{5}{3}y\)

The simplified expression is − 3 −\(\frac {5}{3}y\)

Generate Equivalent Expressions Grade 7 Exercise 5.3 Envision Math

Question. Simplify the expression -2.8f + 0.9f – 12 – 4.

We need to simplify the expression − 2.8f + 0.9f − 12 − 4

The given expression is − 2.8f + 0.9f − 12 − 4

Simplifying it, we get

​− 2.8f + 0.9f − 12 − 4 = f(−2.8 + 0.9) − 16

= f( −1.9) −16

= −1.9f − 16
​
The simplified expression is −1.9f − 16

Question. Simplify the expression 3.2 – 5.1n – 3n + 5.

We need to simplify the expression  3.2 − 5.1n − 3n + 5

The given expression is  3.2 − 5.1n − 3n + 5

Simplifying it we get

​3.2 − 5.1n − 3n + 5

=  3.2 + 5 − 5.1n − 3n

=  8.2 − 8.1n
​
The simplified expression is  8.2 − 8.1n

Question. Simplify the given expression 2n + 5.5 – 0.9n – 8 + 4.5p.

We need to simplify the given expression.

The given expression is 2n + 5.5 − 0.9n − 8 + 4.5p

Combining the like terms together, we get

​2n + 5.5 − 0.9n − 8 + 4.5p

=  2n − 0.9n + 5.5 − 8 + 4.5p

=  n(2 − 0.9) − 2.5 + 4.5p

=  1.1n + 4.5p − 2.5

The simplified expression is 1.1n + 4.5p − 2.5

Question. Simplify the given expression 12 + (-4)\(-\frac{2}{5}j-\frac{4}{5}j\) + 5.

We need to simplify the given expression.

12 + (−4)\(−\frac{2}{5} j−\frac{4}{5} j\) + 5

Using the properties and combining the like terms together, we get

12 +  (−4)\(-\frac{2}{5} j-\frac{4}{5} j\) + 5

=   12− 4\(-\frac{2}{5} j−\frac{4}{5} j\) + 5

=   8 +  j(\(-\frac{2}{5} −\frac{4}{5} \)) + 5

=  13 +  j(\(\frac{−2−4}{5}\))

=  13 +  j\(\frac{−6}{5}\)

=  13− j\(\frac{6}{5}\)

The simplified expression is 13−\(\frac{6}{5} j\)

Envision Math Grade 7 Exercise 5.3 Solution Guide

Question. Simplify the given expression -5v + (-2) + 1 + (-2v) and to find which among the given expression is equal to it.

We need to simplify the given expression − 5v + ( −2) + 1 + (−2v) and to find which among the given expression is equal to it

Simplifying it, we get

​−5v + (−2) + 1 + ( −2v) = −5v − 2 + 1 − 2v

= −5v − 2v − 2 + 1

= −7v − 1

The given expression is equal to (C) −7v − 1

Question. Find which expression is equivalent to \(\frac{2}{3}x+(-3)+(-2)-\frac{1}{3}x\).

We need to find which expression is equivalent to \(\frac{2}{3}x+(-3)+(-2)-\frac{1}{3}x\)

Simplifying it, we get

\(\frac{2}{3}\)x +(−3)+(−2)−\(\frac{1}{3}\)x

= \(\frac{2}{3}\)x −3−2−\(\frac{1}{3}\)x

=  \(\frac{2}{3}\)x − \(\frac{1}{3}\)x −5

=  \(\frac{2x −x}{3}\) − 5

=  \(\frac{x}{3}\) − 5

=  (or)  \(\frac{1}{3}x\) − 5

The given expression is equivalent to  \(\frac{1}{3}x\) − 5

Question. The dimensions of a garden are shown. We need to write an expression to find the perimeter.

The dimensions of a garden are shown. We need to write an expression to find the perimeter.

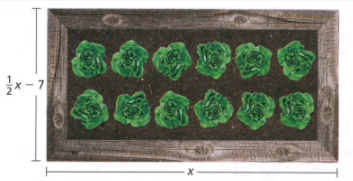
Add all the lengths to find the perimeter.

The perimeter of the rectangle is 2(l+w)

Here, substituting the given we get

2(1+w) = 2(\(\frac{1}{2}x\) −7+x)

=  2(\(\frac{1}{2}x\) +x−7)

= 2 (\(\frac{x+2x}{2}−7\))

=  2(\(\frac{3x}{2}\)−7)

=  3x−14

The expression to find the perimeter is 3x−14

Question. Simplify the given expression 8h + (-7.3d) – 14 + 5d – 3.2h

We need to simplify the given expression.

The given expression is  8h +(−7.3d) −14 + 5d − 3.2h

Combining the like terms together, we get

​8h + (−7.3d) − 14 + 5d − 3.2h

=  8h −7.3d −14 + 5d − 3.2h

=  8h − 3.2h − 7.3d + 5d − 14

=  4.8h − 2.3d − 14

The simplified expression is  4.8h − 2.3d − 14

Question. Simplify the given expression 4 – 2y + (-8y) + 6.2.

We need to simplify the given expression.

The given expression is  4 − 2y + (−8y) + 6.2

Combining the like terms together, we get

​4−2y + (−8y) + 6.2 = 4 − 2y − 8y + 6.2

=  4 − 10y + 6.2

=  4 + 6.2 − 10y

=  10.2 − 10y

The simplified expression is 10.2 − 10y

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.3 Answers

Question. Simplify the given expression \(\frac{4}{9}z-\frac{3}{9}z+5-\frac{5}{9}z-8\).

We need to simplify the given expression.

The given expression is \(\frac{4}{9} z-\frac{3}{9} z+5-\frac{5}{9} z-8\)

Combining the like terms together, we get

\(\frac{4}{9}z\)−\(\frac{3}{9}z\) + 5 −\(\frac{5}{9}z\) − 8

= \(\frac{4z−3z}{9}\)+5−\(\frac{5}{9}z\) − 8

= \(\frac{z}{9}\)−\(\frac{5z}{9}\) + 5 − 8

= \(\frac{−4}{9}z\) − 3 

The simplified expression is \(\frac{− 4z}{9} − 3\)

Question. Show that the given two expressions 11t – 4t is equivalent to 4t – 11t.

We need to explain whether  11t − 4t  is equivalent to  4t −11t.

We need to support our answer by evaluating the expression for t = 2.

The expression  11t − 4t  is not equivalent to  4t −11t.

Substitute t = 2 in both cases, we get

​11t −4t = 7t

=  7 × 2 = 14

4t−11t  = − 7t

= − 7 × 2 = −14

Thus, the value differs.

The given two expressions are not equivalent to each other.

Envision Math 7th Grade Exercise 5.3 Step-By-Step Solutions

Question. Observe the diagram the signs show the costs of different games at a math festival. Find how much would it cost n people to play Decimal Decisions and Ratio Rage.

Given that the signs show the costs of different games at a math festival.

We need to find how much would it cost n people to play Decimal Decisions and Ratio Rage.

The cost of playing Decimal decisions will be

12.70 − n + 9

The cost of Ratio Race will be

The total cost will be

12.70  −  n  + 9 +  \(\frac{n}{4}\)

=  12.7 −  n  + \(\frac{n}{4}\) + 9

= 12.7  + 9 + \(\frac{−4n+n}{4}\)

=  21.7 − \(\frac{3n}{4}\)

The cost to play Decimal Decisions-and Ratio Rage will be  21.7−\(\frac{3n}{4}\)

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions

They are different because in the first one, we have 2 diagrams and we have to find the right amount on each one and then add these amounts.

On the other hand in the second representation, we have 2 variables that we change and easily multiply by constants.

They are similar because they have the same end results and the same constants and coefficients.

Question. Use Commutative and distributive property for the equivalent expression 3x – 12

Given:

3x − 12

3x − 12

Use distributive property  a (b + c) = a×b +a×c

3x − 12 = 3(x − 4)

First equivalent expression is 3(x − 4)

Use commutative property a + b = b + a

3x − 12 = −12 + 3x

The second equivalent expression is  −12 + 3x.

Hence, the equivalent expressions are 3(x − 4) and −12 + 3x.

Question. Use commutative and distributive property for the equivalent expression \(-\frac{5}{4}x-\frac{3}{4}\)

Given:

Use commutative property a + b=b + a

\(-\frac{3}{4}-\frac{5}{4}\) x

First equivalent expression is \(-\frac{3}{4}-\frac{5}{4}\) x

Use distributive property a × (b + c) = a × b + a × c

\(\frac{1}{4}\) (−5x−3)

Second equivalent expression is \(\frac{1}{4}\) (−5x−3).

Hence, the equivalent expressions are \(-\frac{3}{4}-\frac{5}{4}\) x and \(\frac{1}{4}\)

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.2 Answer Key

Question. Use the distributive property to -5(x-2) equivalent expression.

Given:

−5(x−2)

− 5 (x − 2)

Use the distributive property to write an equivalent expression.

Distributive property  a × (b+c) = a × b + a × c

​−5(x−2)=−5× x − 5 × (−2)

=−5x + 10
​
Hence, we use the distributive property.

Equivalent expressions are expressions that have the same end value but are written differently.

Commutative property true only for multiplication and addition

Addition: ​ a + b = b + a

Multiplication:  a × b = b × a
​
Subtraction:  4−2 = 2−4

Division:   4 ÷ 2 = 2 ÷ 4

It can’t go with subtraction and division.

The commutative property is true only for multiplication and addition.

Question. Use the associative property when writing equivalent expressions for 2 reasons.

We can use the associative property when writing equivalent expressions for 2 reasons.

We can use it to get 2 values with the same variable in the bracket so we could add/multiply them.

Example:

\(\frac{1}{2} x+\left(\frac{1}{2} x+4\right) \)  Use associative property

x + 4

We can use it to get 2 values with variables in the bracket so we could extract the constant in front of these variables by using the distributive property.

\(\frac{1}{2} x+\left(\frac{1}{2} y+4\right) \)     Use associative property

\(\left(\frac{1}{2} x+\frac{1}{2} y\right)+4\)       Use distributive property

\(\frac{1}{2}\)(x+y)+4

So we can use it to easily add or extract values.

Question. Write an equivalent expression for the -3 + \(\frac{2}{3}\)\frac{1}{3}[/latex]y expression.

Given:

-3 + \(\frac{2}{3}\)y-4-\(\frac{1}{3}\)y

-3 + \(\frac{2}{3}\)y-4-\(\frac{1}{3}\)y

Use commutative property
​
​− 3 − 4 +\(\frac{2}{3}\)y-\(\frac{1}{3}\)y​

− 7 + \(\frac{1}{3}\)y

Hence, the equivalent expression is  −7 + \(\frac{1}{3}\)y

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.2 Answers

Question. Write an expression 3(x – 5) values of the expression for x ’s 1,2 and 3 find out x values.

Given:
​
​3(x − 5)

3x − 15

Put x = 1

​3(x−5) = 3(1 − 5)

= 3(−4)

= −12
​
​3x − 15 = 3(1) − 15

=  3−15

= −12

Put x = 2

​3(x − 5) = 3(2 − 5)

= 3(−3)

= −9

3x−15 = 3(2) − 15

= 6 − 15

= −9

Put x = 3

​3(x−5) = 3(3 − 5)

= 3( − 2)

= −6

3x−15 = 3(3) − 15

= 9 −15

= −6
​Given that we can see that they have the same values for some \(\backslash[x \mid]^{\prime} \)s so they are equivalent.

Property that makes them equivalent is distributive property.

The values of the expression for x ’s 1,2 and 3 are −12,−9, and −6. So they are equivalent.

Question. Write an equivalent expression for the 4x + \(\frac{1}{2}\) + 2x – 3 expression.

Given:

4x + \(\frac{1}{2}\)+2x-3

4x + \(\frac{1}{2}\)  + 2x-3

Use the commutative property

4x + 2x + \(\frac{1}{2}-3\)

6x + \(\frac{5}{2}\)

Hence, the equivalent expression is 6x+\(\frac{5}{2}\)

Envision Math Grade 7 Chapter 5 Equivalent Expressions Exercise 5.2 Solutions

Question. Write an equivalent expression for the -3(7 + 5g) expression.

We need to write an equivalent expression for the given expression

−3 (7 + 5g)

Using the distributive property, the expression becomes

​−3 (7 + 5g) = −3 × 7 + (−3) × 5g

= −21 − 15g

​The equivalent expression is −3(7 + 5g) = − 21 −15g

Question. Write an equivalent expression for the (x + 7) + 3y expression.

We need to write an equivalent expression for the given expression

(x + 7) + 3y

Using the associative property, the expression becomes

(x + 7) + 3y= x + (7 + 3y)

The equivalent expression is (x + 7) + 3y = x + (7 + 3y)

Question. Write an equivalent expression for the \(\frac{2}{9}-\frac{1}{5}\)x expression.

We need to write an equivalent expression for the given expression

\(\frac{2}{9}-\frac{1}{5}\)x

Using the distributive property extracting the common factors out, the expression becomes

\(\frac{2}{9}-\frac{1}{5}\)x  =  \(\frac{1}{5}\)(5×\(\frac{2}{9}\)-x)

=  \(\frac{1}{5}\)(\(\frac{10}{9}\) − x)

​=  \(\frac{1}{5}\) (1.1111……− x)

=  \(\frac{1}{5}\)(\(1 . \overline{1}-x\))

The equivalent expression is \(\frac{2}{9}\) – \(\frac{1}{5}\) x  = \(\frac{1}{5}\)(\(1 . \overline{1}-x\))

Question. Find the which expression is equivalent to t + 4 + 3 – 2t

We need to find which expression is equivalent to  t + 4 + 3 − 2t

The given expression is t + 4 + 3 − 2t

Simplifying it we get

​t + 4 +3−2t = t + 7−2t

=  t − 2t + 7

= −t + 7
​
−t + 7 expression is equivalent to  t + 4 + 3 − 2t

Question. The distance in feet that karina swims in a race is represented by 4d – 4, where d is the distance for each lap. Write an expression equivalent to 4d – 4.

Given that, the distance in feet that Karina swims in a race is represented by 4d − 4, where d is the distance for each lap.

We need to write an expression equivalent to  4d − 4

The given expression is 4d − 4

Using the distributive property, and extracting the common terms, we get

​4d − 4 = 4 × d − 4 × 1

= 4(d − 1)​
​
The equivalent expression is 4(d−1)

Envision Math Grade 7 Exercise 5.2 Solution Guide

Question. Use the associative property to write an expression equivalent to (w + 9) + 3

We need to use the Associative Property to write an expression equivalent to (w + 9) + 3

The given expression is  (w + 9) + 3

Using the associative property, we get

(w + 9) + 3 = w + (9 + 3)

The equivalent expression is (w + 9) + 3 = w + (9 + 3)

Question. Maria said the expression -4n + 3 + 9n – 4 is equivalent to 4n find the error Maria likely made.

Given that, Maria said the expression −4n + 3 + 9n − 4 is equivalent to 4n

We need to find the error Maria likely made.

The given expression is  −4n + 3 + 9n − 4a

Solving the expression, we get

​−4n + 3 + 9n − 4 = −4n + 9n + 3−4

= 5n − 1
​
The equivalent expression is 5n − 1. The possible error maria made is wrong addition and subtraction.

Maria added the wrong numbers which make her to do the error.

Question. Write an expression equivalent to x –  3y + 4.

We need to write an expression equivalent to x − 3y + 4.

Using the distributive property, and extracting the common terms, we get

​x − 3y + 4 = x−3(y−\(\frac{4}{3}\))

= x−3 (y−1.3333…)

= x − 3(\(y−1 . \overline{3}\))
​
The equivalent expression is =x−3(\(y−1 . \overline{3}\))

Question. The group chat shows the amount of money that each puts in to rent a car for a trip, four friends are combining their money. Use the commutative property to write two equivalent expressions.

Given that, To rent a car for a trip, four friends are combining their money.

The group chat shows the amount of money that each puts in.

One expression for their total amount of money is 189 plus p plus 224 plus q.

We need to use the Commutative Property to write two equivalent expressions.

The given expression is 189 + p + 224 + q

Using the commutative property to find the equivalent expression, we get

​189 + p + 224 + q = (189 + 224) + p + q

= 413 + p + q

​Another equivalent expression is

​189 + p + 224 + q = p + q +( 189 + 224)

= p + q + 413
​
The two equivalent expressions are  413 + p + q, p + q + 413

Given that, To rent a car for a trip, four friends are combining their money.

The group chat shows the amount of money that each puts in.

One expression for their total amount of money is 189 plus p plus 224 plus q.

If they need $500 to rent a car, we need to find at least two different pairs of numbers that p and q could be.

The given expression is 189 + p + 224 + q

The amount to rent a car will be $500

Thus, the expression becomes

​189 + p + 224 + q = 500

413 + p + q = 500

p + q = 500 − 413

p + q = 87

​So we need to find two values which added together to get 87 Therefore

​p = 40, q = 47

p = 20, q = 67

The two different pairs of numbers are p = 40, q = 47 and  p = 20, q = 67

Generate Equivalent Expressions Grade 7 Exercise 5.2 Envision Math

Question. Find the expressions is equivalent to \(\frac{3}{5}x + 3\).

We need to find which of the given expressions is equivalent to

Simplifying the given one by one, we get

​\(\frac{2}{5}x \) + 3 \(\frac{1}{5}x \)

= \(\frac{2}{5}x \) + \(\frac{16}{5}x \)

\(\frac{4}{5}x \)− \(\frac{1}{5}x \) + 3 = \(\frac{4x− 1x}{5} \) +3

= \(\frac{3}{5}x \) +3

\(\frac{2}{5}x \) + 3 \(\frac{3}{5}x \) − 1= \(\frac{2}{5}x \) +\(\frac{18}{5}x \) −1

= \(\frac{2x+ 18x}{5} \) −1 = 4x −1

1 + \(\frac{3}{5}\) x + 2  = \(\frac{3}{5}\) x+ 3

1 + \(\frac{x}{5}\)  +  2  = \(\frac{x}{5}\)  + 3

1 + \(\frac{2}{5}\)x  + 3  = \(\frac{2}{5}\)x + 4

The expressions that are equivalent to \(\frac{3}{4}\) x + 3 will be \(\frac{4}{5}\) x- \(\frac{1}{5}\) x + 3 and 1 +  \(\frac{3}{5}\) x + 2

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions

We have to sort the expressions given.

An expression is a mathematical phrase, which consists of variables and constants.

We can sort the given expression into two groups.

One group would contain the expressions which have brackets and the other group will have expressions without brackets.

The first group of expressions will be

​8p + 2p − 8

10p − 8

5p + 8 + 3p

10p + 4 + 2p + 2

3p + 4p + 6 + 5p

The second group of expressions will be
​
​8 (p + 1)

2 (5p − 4)

4 (2p + 2)

3 (4p + 2)

​
The expression are sorted into two groups, one with expressions having brackets and the other without brackets.

We have to sort the expressions given.

An expression is a mathematical phrase, which consists of variables and constants.

We can sort the given expression into two groups.

We can also group the expression with equivalent expressions in them.

In one group, we will put the expressions that can be made one from another by multiplying or extracting a number.

The first group of expressions will be

​10p − 8

2 (5p − 4) = 10

8p + 2p − 8 = 10p − 8

The second group of expressions will be
​
​5p + 8 + 3p = 8p + 8

8 (p + 1) = 8p + 8

4 (2p + 2) = 8p + 8

The third group of expressions will be
​
​3 (4p + 2) = 12p + 6

3p + 4p + 6 + 5p = 12p + 6

10p + 4 + 2p + 2 = 12p + 6
​
The expression can be grouped based on mutually equivalent expressions.

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.1 Answer Key

Question. How can algebraic expressions be used to represent and solve problems.

We have to tell that how can algebraic expressions be used to represent and solve problems.

The combination of variables and constants, in mathematics, is referred to as an expression.

The expression having algebraic terms are called as algebraic expressions.

These expressions are helpful in expressing the problems which consists of variables.

The variables are substituted with values given and then evaluated to obtain the solution or desired result.

The algebraic expressions represent the problems which can be evaluated by substituting values in the expression.

Question. How much it would cost to rent a scooter for 3 1/2 hours and watercraft for 1 ¾ hours.

We have to determine how much it would cost to rent a scooter for 3 1/2 hours and watercraft for 1 ¾ hours.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

The order of operation that will be followed is Brackets, multiplication or division, and addition or subtraction.

The expressions are
​
​s = \(3 \frac{1}{2}\)

= 3.5

w=\(1 \frac{3}{4}\)

= 1.75

We will evaluate as below:

​15.5s + 22.8w = x

15.5cot 3.5 + 22.8.1.75 = x

54.25 + 39.9 = x

x = 94.15
​
The renting of both these amounts of time will cost $94.15.

Question. Misumi used to determine her account balance after “w” week. She gets 3.5 dollars in a day and 8.74 per hour.

We have to give an expression for Misumi used to determine her account balance after “w” week.

She gets 3.5 dollars in a day and 8.74 per hour.

We consider “h” as the number of hours.

h = \(15\frac{1}{2}\)

The order of operation that will be followed is.

Brackets, multiplication or division, addition or subtraction.

We evaluate the expression as below:

​3.5 + 8.74⋅h = x

3.5 + 8.74.5.5 = x

3.5 + 48.07 = x

x = 51.57
​
She will receive the amount of $51.57 in that day.

Question. How should we determine which value to use for the constant and which value to use for the coefficient.

We have to tell that how should we determine which value to use for the constant and which value to use for the coefficient.

An expression is a mathematical phrase, which consists of variables and constants.

We determine the amount after w weeks as the below expression

217 + 25.5.w

In the given expression, w is the coefficient as the number of weeks can be changed.

And the constant amount is 25.5 which she always deposits.

Thus, in a problem, the factor whose value changes in different situations is considered as a variable, as its value varies.

While the value which remains the same is taken as constant.

The values which vary are considered as variables and the ones which are the same are determined as constants.

Envision Math Grade 7 Chapter 5 Equivalent Expressions Exercise 5.1 Solutions

Question. How can algebraic expressions be used to represent and solve problems.

We have to tell that how can algebraic expressions be used to represent and solve problems.

The combination of variables and constants, in mathematics, is referred to as an expression.

The expression having algebraic terms are called as algebraic expressions.

These expressions are helpful in expressing the problems which consist of variables.

The variables are substituted with values given and then evaluated to obtain the solution or desired result.

The algebraic expressions represent the problems which can be evaluated by substituting values in the expression.

Question. Explain how is a constant term different than a variable term for an expression that represents a real-world situation.

We need to explain how is a constant term different than a variable term for an expression that represents a real-world situation.

The constant term is nothing but a term that is constant i.e., the value doesn’t change no matter what.

The variable term is the one which is varying based on different values.

As the name suggests, it is a variable one.

For example, in the expression, 5x + 2 = 0

The term 2 is a constant since it doesn’t change no matter what.

The term x is a variable it changes based on the input.

The value of the constant doesn’t change while that of the variable changes based on its input.

Question. Explain why we can have different values when evaluating an algebraic expression.

We need to explain why we can have different values when evaluating an algebraic expression.

When evaluating an algebraic expression, we may have some different values.

But the end result is always the same. This is because we can choose which operation we can do first.

For example, both addition and subtraction are commutative.

If we do addition first, the values will be different.

Or if we do subtraction first, the values will be different.

But the end result obtained by the expression will be the same.

We can choose which operation we can choose first. This is why we can have different values when evaluating an algebraic expression.

Question. A tank containing 35 gallons of water is leaking at a rate of \(\frac{1}{4}\) gallon per minute. Write an expression to determine the number of gallons left in the tank after m minutes.

Given that, A tank containing 35 gallons of water is leaking at a rate of \(\frac{1}{4}\) gallon per minute.

We need to write an expression to determine the number of gallons left in the tank after m minutes.

Here, the rate is a variable since it varies every minute.

The amount of water is constant.

We need to find the number of gallons left after m minutes.

Thus, the expression becomes

35−\(\frac{1}{4}\) m

The number of gallons left in the tank after m minutes will be 35−\(\frac{1}{4}\) m

Question. Write an algebraic expression that Marshall can use to determine the total cost of buying a watermelon that weighs w pounds and some tomatoes that weigh t pounds. Find how much will it cost to buy a watermelon that weighs \(18\frac{1}{2}\) pounds and 5 pounds of tomatoes.

We need to write an algebraic expression that Marshall can use to determine the total cost of buying a watermelon that weighs w pounds and some tomatoes that weigh t pounds.

We need to find how much will it cost to buy a watermelon that weighs \(18 \frac{1}{2}\) pounds and 5 pounds of tomatoes.

The total of buying will be represented by the expression

0.68w + 3.25t

Given that, t = 5, w = \(18 \frac{1}{2}\)

Substituting this we get

​0.68w + 3.25t = 0.68 × \(18 \frac{1}{2}\)  + 3.25 × 5

=  0.68 × \( \frac{37}{2}\)  + 16.25

= 12.58 + 16.25

=  28.83

He have to pay $28.83 altogether.

Generate Equivalent Expressions Grade 7 Exercise 5.1 Envision Math

Question. Find the value of \(\frac{3}{8}\)x-4.5 when the value of x = 0.4.

The value of \( \frac{3}{8}\)x−4.5 when the value of x = 0.4

Substituting x = 0.4 in the given expression, we get

​\( \frac{3}{8}\)x − 4.5

=  \( \frac{3}{8}\) × 0.4−4.5

=  \( \frac{3}{2}\) × 0.1−4.5

=  0.15 − 4.5

=  −4.35

The value of ​\( \frac{3}{8}\)x − 4.5 = −4.35

Question. Find the value of 8.4n-3.2p when n = 2 and p = 4.

The value of  8.4n−3.2p when n = 2 and p = 4

Substituting the value of n = 2, p = 4 , we get

​8.4n − 3.2p = 8.4(2)−3.2(4)

= 16.8 − 12.8

= 4
​
The value of 8.4n−3.2p = 4

Question. Write an expression that represents the height of a tree that began at 6 feet and increases by 2 feet per year.

We need to write an expression that represents the height of a tree that began at 6 feet and increases by 2 feet per year.

Let y represent the number of years.

Here, the height of the tree initially is 6 feet.

The increase in height will be 2 feet per year.

Here, y represents the number of years.

Thus, the expression will be

6 + 2y

The expression that represents the height of a tree will be 6 + 2y

Question. Evaluate the expression for the value 3d-4 of the variable (s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is 3d−4

The value of d = 1.2

Substituting the value of the variable in the expression, we get

​3d−4 = 3(1.2) − 4

= 3.6 − 4

= −0.4

The value of 3d−4=−0.4

Question. Evaluate the expression for the value 0.5f – 2.3g of the variable(s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is  0.5f−2.3g

The value of f = 12, g = 2

Substituting the value of the variable in the expression, we get

​0.5f − 2.3g = 0.5(12) − 2.3(2)

= 6−4.6

= 1.4

The value of 0.5f − 2.3g = 1.4

Envision Math Grade 7 Exercise 5.1 Solution Guide

Question. Evaluate the given expression for the value \(\frac{2}{3}\) p+3 of the variable (s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is \( \frac{2}{3}\) p+3

The value p= \( \frac{3}{5}\)

Substituting the value of the variable in the expression, we get

= \(\frac{2}{5}+3\)

= \(\frac{2+15}{5}\)

= \(\frac{17}{5}\)

​The value of \( \frac{2}{3}\) p + 3 = \( \frac{17}{5}\) p + 3

Question. Evaluate the expression for the value 34 + \(\frac{4}{9}\)w of the variable(s).

We need to evaluate the given expression for the given value of the variable(s).

The given expression is 34 + \( \frac{4}{9}\)w

The value of w = − \( \frac{1}{2}\)

Substituting the value of the variable in the expression, we get

= \(34-\frac{2}{9}\)

= \(\frac{306-2}{9}\)

= \(\frac{304}{9}\)

= 33.78

The value of 34 + \( \frac{4}{9}\)w = 33.78

Question. Find the expression that can be used to determine the total cost of buying g pounds of granola for $3.25 per pound and f pounds of flour for $0.74 per pound.

We need to find the expression that can be used to determine the total cost of buying g pounds of granola for $3.25 per pound and f pounds of flour for $0.74 per pound.

The cost of buying granola is  3.25 × g

The cost of buying flour is  0.74 × f

Therefore, the total cost of buying both will be

3.25 × g + 0.74 × f = 3.25g + 0.74f

The expression that can be used to determine the total cost will be 3.25g + 0.74f

Question. Find the expression that can be used to determine the total weight of a box that by itself weighs 0.2 kilogram and contains p plaques that weigh 1.3 kilograms each.

We need to find the expression that can be used to determine the total weight of a box that by itself weighs 0.2 kilogram and contains p plaques that weigh 1.3 kilograms each.

The weight of the box will be 0.2kg

The number of plaques will be p

The weight of each plaques will be 1.3kg

Thus, the expression will be

Total weight of the box  = 0.2 +1.3p

The expression that can be used to determine the total weight of a box is (A) 1.3p + 0.2

Question. The expression -120 + 13m represents a submarine that began at a depth of 120 feet below sea level and ascended at a rate of 13 feet per minute. Find the depth of the submarine after 6 minutes.

Given that, the expression −120 + 13m represents a submarine that began at a depth of 120 feet below sea level and ascended at a rate of 13 feet per minute.

We need to find the depth of the submarine after 6 minutes.

Here, the given expression is −120 + 13m

Given that, m = 6

Substituting it, we get

​−120 + 13m =−120 + 13(6)

= −120 + 78

= −42
​
The depth of the submarine after 6 minutes will be −42

Question. The capacity is 3000 ft³ The expression to determine the amount of grain left. 

The capacity is  3000 ft³

The rate is \(\frac{3.5 f t^3}{s}\)

The expression to determine the amount of grain left will be

3000 − 3.5s

Here, s is the number of seconds.

The expression to determine the amount of grain left will be 3000 − 3.5s

Question. The expression 5 – 5x to have a negative value, we need to find what must be true about the value of x.

For the expression 5− 5x to have a negative value, we need to find what must be true about the value of x.

The given expression is  5− 5x

The value will be negative when the value of 5x is greater than the number 5.

If x is negative, thus x < 0  the expression becomes positive.

If x = 0 then the expression becomes positive.

If x = 1 then the expression becomes  5−5(1) = 5−5 = 0

If x > 1 then the expression becomes negative.

x >1 must be true about the value of x.

Envision Math Accelerated Grade 7 Chapter 5 Exercise 5.1 Answers

Question. The outside temperature was 73°F at 1 P.M and decreases at a rate of 1.5°F each hour. Find the expression that can be used to determine the temperature h hours after 1 P.M.

Given that, the outside temperature was 73 °F at 1 P.M and decreases at a rate of 1.5 °F each hour.

We need to find the expression that can be used to determine the temperature h hours after 1 P.M.

The rate is a variable that varies every hour.

The outside temperature initially was constant.

The temperature decreases thus we need to subtract the temperature from the outside temperature.

The expression that can be used to determine the temperature h hours after 1 P.M will be, 73 − 1.5h

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 5 Generate Equivalent Expressions

Question. How can properties of operations help to generate equivalent expressions that can be used in solving problems.

We have to tell that how can properties of operations help to generate equivalent expressions that can be used in solving problems.

We consider the below example:

On the expression  3 (2 + x), we apply the distributive property to get the equivalent expression as 6 + 3x.

Similarly, we can apply the distributive property on 24+18y to get the equivalent expression as  6 (4x + 3y).

Thus, the properties of operations help to generate equivalent expressions which are of help in solving problems.

The properties of operations help to generate equivalent expressions such as distributive property.

The exploration of activity trackers and the data to develop models based on individual fitness goals is as follows

Fitness tracker

It helps in motivating us.

To maintain a healthy diet.

To set our goals.

Its disadvantages are Lack of accuracy and expensive.

It helps in motivating us, To maintain a healthy diet, To set our goals, Its disadvantages are Lack of accuracy and expensive.

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate an expression it means that we substitute and replace some values.

• We are required to complete the given definition with an appropriate word.
• The combination of variables and constants, in mathematics, is referred to as an expression.
• When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.
• To substitute a value means to replace or exchange variables with the numbers given.
• Therefore, To evaluate a + 3  when a = 7, you can substitute 7 for ‘a’ in the expression.
• To evaluate a + 3 when a = 7, you can substitute 7 for ‘a’ in the expression.
• We are required to complete the given definition with an appropriate word.
• In mathematics, a function or a particular task performed to get some desired result on numbers is called as an operation.
• The digits or terms on which the operation is performed are called as operands.
• There are particular ways and rules to perform an operation.
• The set of rules which conveys that whether which term will go first in the problem is called as the order of operations.
• Therefore, The set of rules used to determine the order in which operations are performed is called the order of operations.
• The set of rules used to determine the order in which operations are performed is called the order of operations.

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate an expression it means that we substitute and replace some values in the place of variables.

We are required to complete the given definition with an appropriate word.

• The combination of variables and constants, in mathematics, is referred to as an expression.
• When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.
• The expression contains two or more terms which may be either variable or constant and are separated by arithmetic signs such as + (or)  −
• Therefore, Each part of an expression that is separated by a plus or minus sign is a term.
• Each part of an expression that is separated by a plus or minus sign is a term.
• We are required to complete the given definition with an appropriate word.
• The combination of variables and constants, in mathematics is referred to as an expression.
• When we multiply two or more terms, the result obtained is called as a product.
• The number of variables which are multiplied are called as factors.
• Therefore, When two numbers are multiplied to get a product, each number is called a factor.
• When two numbers are multiplied to get a product, each number is called a factor.

Envision Math Accelerated Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate the given expression which is 3(18-7) + 2.

We are required to evaluate the given expression which is  3(18−7) + 2.

The set of rules used to determine the order in which operations are performed is called the order of operations.

In order to evaluate the expression, we will have to follow the below order of operations.

Brackets, multiplication or division, addition or subtraction.

We will evaluate as below:

⇒ ​​3 . (18−7) + 2 = x

⇒ ​​ 3.11 + 2 = x

⇒ ​​ x = 33 + 2

⇒ ​​ x = 35
​
The result of the expression 3(18−7)+2 is obtained as 35.

Question. Evaluate the given expression which is (13 + 2) ÷ (9 – 4).

We are required to evaluate the given expression which is  (13 + 2) ÷ (9 − 4).

The set of rules used to determine the order in which operations are performed is called the order of operations.

In order to evaluate the expression, we will have to follow the below order of operations.

Brackets, multiplication or division, addition or subtraction

We will evaluate as below:

⇒ ​​ ​(13 + 2) ÷ (9 − 4) = x

⇒ ​​ 15 ÷ 5 = x

⇒  ​​ x = 3
​
The result of the expression  (13 + 2) ÷ (9 − 4)  is obtained as 3.

Envision Math Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate the given expression which is 24 ÷ 4.2 – 2.

We are required to evaluate the given expression which is  24 ÷ 4⋅2 − 2.

The set of rules used to determine the order in which operations are performed is called the order of operations.

In order to evaluate the expression, we will have to follow the below order of operations.

Brackets, multiplication or division, addition or subtraction

We will evaluate as below:

⇒ ​​  ​24 ÷ 4.2 − 2 = x

⇒ ​​ 6.2 −2 = x

⇒ ​​ 12 − 2 = x

⇒ ​​ x = 10
​
The result of the expression 24 ÷ 4⋅2 − 2 is obtained as 10.

Question. Evaluate the given expression which is ab by substituting the value of variables as a = -4 and b = 3.

We are required to evaluate the given expression which is ab by substituting the value of variables as a = − 4 and b = 3.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

To substitute a value means to replace or exchange variables with the numbers given.

We have

​a = −4

b = 3

We will evaluate as below:

​⇒   a⋅b

⇒  (−4)⋅(3)

⇒  −12
​
The result of the expression ab is obtained as -12.

Question. Evaluate the given expression which is 2a + 3b by substituting the value of variables as a = -4 and b = 3.

We are required to evaluate the given expression which is  2a+3b by substituting the value of variables as a = -4 and b = 3.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

To substitute a value means to replace or exchange variables with the numbers given.

The order of operation that will be followed is Brackets, multiplication or division, addition or subtraction

We have

​a = −4

b =3

We will evaluate as below:

​⇒  2a + 3b

⇒  2(−4)  + 3(3)

⇒  −8 + 9

⇒  1

The result of the expression 2a + 3b is obtained as 1.

Envision Math Grade 7 Volume 1 Chapter 5 Generate Equivalent Expressions Solutions

Question. Evaluate the given expression which is 2(a-b) by substituting the value of variables as a = -4 and b = 3.

We are required to evaluate the given expression which is  2(a−b) by substituting the value of variables as a = -4 and b = 3.

When we solve or evaluate an expression it means that we substitute and replace some values in the place of variables, to get the required result.

To substitute a value means to replace or exchange variables with the numbers given.

The order of operation that will be followed is. Brackets, multiplication or division, addition or subtraction.

We have

​a = −4

b = 3

We will evaluate as below:

​⇒   2(a−b)

⇒   2(−4−3)

⇒   2(−7)

⇒  −14

The result of  the expression 2(a−b) is obtained as -14.

Envision Math Accelerated Grade 7 Volume 1 Chapter 4 Analyze And Solve Percent Problems

Question. Jaime’s older brother and his three friends want to split the cost of lunch. They also want to leave a 15-20% tip. Determine how much should each person pay.

Given that, Jaime’s older brother and his three friends want to split the cost of lunch. They also want to leave a 15−20 % tip.

We need to determine how much should each person pay.

The total bill amount is $78

Finding the tip amount for each percentage given, we get:

\(\frac{15}{100} \times 78\) = 11.7

\(\frac{20}{100} \times 78\) = 1.56

Thus, the amount including the tip is somewhere between 78 + 11.7  =  89.7 and 78  + 15.6  =  93.6

Splitting the bill amount for each person, thus we get

\(\frac{89.7}{4} \) = 22.425

\(\frac{93.6}{4} \) = 23.4

Each person should pay somewhere in between $22.425 and $23.4

Envision Math Accelerated Grade 7 Chapter 4 Percent Problems Solutions

Question. Find which line on the receipt we have to use to calculate the tip.

We need to find which line on the receipt we have to use to calculate the tip.

The tip is usually calculated after the bill amount.

Here, the total bill amount is necessary to calculate the tip amount.

Therefore, from the given receipt

The last line i.e., the total will be used to calculate the tip.

We have to use the last line on the receipt to calculate the tip.

Conquer Percent Problems: Unleashing the Power of Envision Math Accelerated Grade 7, Chapter 4, Exercise 4.1

Question. Find the 0.08% of 720.

We need to find 0.08% of 720.

Finding the percentage, we get:

= \(\frac{8}{10000} \times 720\)

= \(\frac{8}{1000} \times 72\)

=  \(\frac{576}{1000}\)

=  0.576

The value is 0.576

We need to find 162.5% of 200.

Finding the percentage, we get:

= 162.5×2

= 325
​
The value is 325

We need to find 0.3% of 60.

Finding the percentage, we get:

= \(\frac{3}{1000} \times 60\)

= \(\frac{3}{100} \times 6\)

= \(\frac{18}{100}\)

= 0.18

The value will be 0.18

Analyze And Solve Percent Problems Exercise 4.1 Answers Grade 7

Question. Explain why 51% of a number is more than half of the number.

We need to explain why 51 % of a number is more than half of the number.

We know that half of the number means 50 % of the number.

Here, 51 % of the number means that it will be 1 % more than half.

For example, if the number is 200

Then the half of it will be

\(\frac{200}{2}\)  = 100

Thus, 51 % of the number will be

=  \(\frac{51}{100} \times 200\)

=51 × 2

=102
​
Thus, it will be more than half of the number.

51 % of a number is 1 % more than half of the number.

Question. How do the percents show the relationship between quantities.

We need to how do the percents show the relationship between quantities.

The percentage is also denoted as the ratio.

The ratio is nothing but the comparison between two same or different quantities.

The first term of the percent is often compared to the number 100.

For example, 35 % of shirts are sold denotes that out of 100 shirts, 35 has been sold out.

We can often denote the percent using the sign “%”.

A percent is a ratio in which the first term is compared to 100. It is used for comparing two quantities. Percents are used to calculate the amount of one thing compared to the other. Percents can be used to compare very small or very large quantities as a fraction of 100.

Question. Gene stated that finding 25% of a number is the same as dividing the number by \(\frac{1}{4}\). We need to determine whether Gene is correct or not.

Given that, Gene stated that finding 25 % of a number is the same as dividing the number by \(\frac{1}{4}\).

We need to determine whether Gene is correct or not.

25 % of a number is denoted by

\(\frac{25}{100}\)=\(\frac{1}{4}\)

Thus, when we divide the number by \(\frac{1}{4}\), it is the same as finding 25 % of the number.

For example, if the number is 200.

Thus, \(\frac{25}{100}\) × 200  = 25  ×  2  =  50

Also, \(\frac{200}{4}\) = 50

= 50

The result is the same.

Therefore, Gene is correct.

Envision Math Grade 7 Percent Problems Exercise 4.1 Solution Guide

Question. Find the percent of the 59% number of the 640.

We need to find the percent of the given number.

The given number is 59 % of the 640

Solving the given, we get:

\(\frac{59}{100}\)  ×  640

= \(\frac{59}{10}\)  ×  64

= \(\frac{3776}{10}\)

= 377.6

The answer is  377.6

We need to find the percent of the given number.

The given number is 0.20 % of the  3542

Solving the given, we get:

=  \(\frac{708.4}{100}\)

= 7.084

The answer is 7.084

We need to find the percent of the given number.

The given number is 195 % of the  568

Solving the given, we get:

\(\frac{195}{100}\) × 568

= \(\frac{110760}{100}\)

= 1107.6

The value is 1107.6

We need to find the percent of the given number.

The given number is 74 % of the 920

Solving the given, we get:

\(\frac{74}{100}\) × 920

=\(\frac{68080}{100}\)

= 680.8

The value is 680.8

Grade 7 Envision Math Accelerated Chapter 4 Answers

Question. Water is 2 parts hydrogen and 1 part oxygen  (H₂O). For one molecule of water, each atom has the atomic mass unit. Find what percent of the mass of a water molecule is hydrogen.

Given that, Water is 2 parts hydrogen and 1 part oxygen  (H₂O).

For one molecule of water, each atom has the atomic mass unit, u, shown.

We need to find what percent of the mass of a water molecule is hydrogen.

Finding the total mass, we get

16.00 + 1.01 + 1.01 = 18.02

We need to find what percent of the total mass is hydrogen.

\(\frac{x}{100}\) × 18.02  =  2.02

x  ×  18.02 = 2.02  × 100

x  ×  18.02  =  202

x  =  \(\frac{202}{18.02}\)

x  =  11.2

The percent is 11.2 %

% percent of the mass of a water molecule is hydrogen.

Question. A local little league has a total of 60 players, 80% of whom are right-handed. Find how many right-handed players are there.

Given that, a local Little League has a total of 60 players, 80 % of whom are right-handed.

We need to find how many right-handed players are there.

Let x be the number of right-handed people, thus we get, using equivalent ratios we get
​
\(\frac{x}{60}\)  ×  60

= \(\frac{80}{60}\)  ×  60

x  =  \(\frac{80 \times 60}{100}\)

x  =  \(\frac{4800}{100}\)

x  =  48
​
48 out of 60 players are right-handed.

Question. Sandra’s volleyball team has a total of 20 uniforms. Find how many uniforms are medium-sized.

Given that, Sandra’s volleyball team has a total of 20 uniforms.

20 % are medium-sized uniforms. We need to find how many uniforms are medium-sized.

Let x be the number of medium-sized uniforms, thus we get, using equivalent ratios we get

\(\frac{x}{20}\) × 20

=  \(\frac{20}{100}\) × 20

x  =  \(\frac{400}{100}\)

x  =  4

4 out of 20 uniforms are medium-sized.

Question. Meg is a veterinarian. In a given week, 50% of the 16 dogs she saw were Boxers. Steve is also a veterinarian. In the same week, 7 of the 35 dogs he saw this week were Boxers. Find which part Steve needs to find the part, the whole or the percent.

Given that, Meg is a veterinarian. In a given week, 50 % of the 16 dogs she saw were Boxers.

Steve is also a veterinarian. In the same week, 7 of the 35 dogs he saw this week were Boxers.

Each wants to record the part, the whole, and the percent.

We need to find which part Steve needs to find – the part, the whole, or the percent.

Finding the number of dogs Steve saw:

\(\frac{x}{100}\)  =  7

x  =  7  ×  \(\frac{100}{35}\)

x  =  \(\frac{700}{35}\)

x  =  \(\frac{100}{5}\)

x  =  20

Thus, 20 % of dogs Steve saw. Thus, he needs to find the percent.

Steve needs to find the percent.

Percent Problems Envision Math Chapter 4 Grade 7 Solutions

Question. The registration fee for a used car is 0.8% of the sale price of $5,700. Find the registration fee.

Given that, the registration fee for a used car is 0.8 % of the sale price of $5,700.

We need to determine the fee.

The registration fee is:

\(\frac{0.8}{100}\) × 5700

=  0.8  ×  57

=  45.6

The registration fee is $45.6

Question. The total cost of an item is the price plus the sales tax. Find the sales tax to complete the table.

Given that, the total cost of an item is the price plus the sales tax.

We need to find the sales tax to complete the table.

Then find the total cost of the item.

Finding the sales tax of the item, we get:

\(\frac{4}{100}\) × 40

=  \(\frac{160}{100}\)

=  1.6 dollars

The total price is calculated by adding selling price and sales tax.

Thus, we get

40 + 1.6 = 41.6 dollars

The sales tax is $1.6

The total price is $41.6

Question. Find whether 700% of 5 less than 10, greater than 10 but less than 100 or greater than 100.

We need to find whether 700 % of 5 less than 10, greater than 10 but less than 100 or greater than 100.

Solving the equation, we get:

\(\frac{700}{100}\) × 5

= 7  ×  5

=  35
Thus the value is greater than 10 but less than 100.

The value obtained is 35 which is greater than 10 but less than 100.

Question. A new health drink has 130% of the recommended daily allowance (RDA) for a certain vitamin. The RDA for this vitamin is 45 mg. Find how many milligrams of vitamins are in the drink.

Given that, A new health drink has 130 % of the recommended daily allowance (RDA) for a certain vitamin.

The RDA for this vitamin is 45 mg.

We need to find how many milligrams of vitamins are in the drink.

Finding the vitamin amount of a new health drink, we get:

\(\frac{130}{100}\)  ×  45

= \(\frac{13}{10}\)  ×  45

= \(\frac{13}{2}\)  ×  9

=  58.5

58.5 mg of vitamins are in the drink.

Question. Brad says that if a second number is 125% of the first number, then the first number must be 75% of the second number. Find whether he is correct or not.

Given that, Brad says that if a second number is 125 % of the first number, then the first number must be 75 % of the second number.

We need to find whether he is correct or not.

Finding the percentage of the second number

Here, y be the second number and x be the first number.

Thus, we get:

\(\frac{125}{100}\)  ×  x  =  y

x  =  y  ×  \(\frac{100}{125}\)

x  =  y  ×  \(\frac{4}{5}\)

x  =  y  × 0.8

0.8 is equal to 80 %

Thus, the first number must be 80 % of the second number. Hence, he is incorrect.

Question. Mark and Joe work as jewelers. Mark has an hourly wage of $24 and gets overtime for every hour he works over 40 hours. The overtime pay rate is 150% of the normal rate. Joe makes 5% commission on all jewelry he sells. Find who earns more money in a week if Mark works 60 hours and Joe sells $21,000 worth of jewelry.

Given that, Mark and Joe work as jewelers. Mark has an hourly wage of $24 and gets overtime for every hour he works over 40 hours.

The overtime pay rate is 150 % of the normal rate. Joe makes 5 % commission on all jewelry he sells.

We need to find who earns more money in a week if Mark works 60 hours and Joe sells $21,000 worth of jewelry.

For Mark:

Find his overtime pay rate, thus we get:

​x  =  \(\frac{150}{100}\)  ×  24

x  =  \(\frac{15}{5}\)  × 12

x  =  3 × 12

x  =  36

Finding the total pay rate, we get:

​20  ×  36  =  720

40  ×  24  =  960
​
Thus, the total is, 720  +  960  =  1680

Marks earns more money in a week.

Envision Math 7th Grade Exercise 4.1 Answer Key

Question. A forest covers 43,000 acres. A survey finds that 0.2% of the forest is old-growth trees. Find how many acres of old-growth trees.

Given that, A forest covers 43,000 acres.

A survey finds that 0.2 % of the forest is old-growth trees.

We need to find how many acres of old-growth trees are there.

Finding the acres of the forest which is old-growth trees, we get,

\(\frac{0.2}{100}\)  ×  43000

=  0.2  ×  430

=  2  ×  43

=  86

86 acres of old-growth trees are there.

Question. An Olympic-sized pool, which holds 660,000 gallons of water, is only 63% full. Find how many gallons of water are in the pool.

Given that, an Olympic-sized pool, which holds 660,000 gallons of water, is only 63 % full.

We need to find how many gallons of water are in the pool.

Finding the gallons of water are in the pool, we get

\(\frac{63}{100}\)  ×  660000

=  63  ×  6600

=  415800

415800 gallons of water is in the pool.

Envision Math Accelerated Grade 7 Volume Chapter 1 Integers and Rational Numbers

Question. Find the surfboard width between two surfboard models. Lindy’s board is \(23 \frac{1}{3}\) inches wide. Her board is between the 92 and 102 models.

Given:

To find the surfboard width between two surfboard models.

Lindy’s board is \(23 \frac{1}{3}\) inches wide. Her board is between the 92 and 102 models.

It is like this because

\(23 \frac{1}{3}\) < 24

And

\(23 \frac{1}{4}\) < \(24 \frac{1}{3}\)

The first one is obvious regarding to the second one \(\frac{1}{4}\)=0.25 < \(\frac{1}{3}\)=0.3333.

The first one is obvious regarding to the second one \(\frac{1}{4}\)=0.25 < \(\frac{1}{3}\)=0.3333.

Given:

Lindy’s surfboard wide = \(23 \frac{1}{3}\)

To find:

Between which two surfboards model is her custom surfboard’s width? How do you know?

Lindy’s surfboard wide which is also considered as a width of the surfboard with \(23 \frac{1}{3}\).

Though the thickness is not given we can never bother about it.

\(\frac{70}{3}\) is the width of the surfboard We changed the mixed fraction to a rational number because it is easy to understand.

Model 82 and Model 92 is the two surfboard models of Calvin, compared as wide which is approximately the width of Lindy’s surfboard.

Envision Math Accelerated Grade 7 Chapter 1 Exercise 1.2 solutions

Question. Find how Juanita write the fastball statistic in decimal form \(\frac{240}{384}\)=0.625.

Given:

To find how Juanita write the fastball statistic in decimal form

\(\frac{240}{384}\)=0.625

There were 384 pitches and out of that number 240 were fastballs

This is terminating decimal because after that number five comes infinite number of zeros, none other numbers will appear again.

The answer 0.625 is the decimal form of the fastball statistic

Question. Determine whether it is terminates or non terminates.

Given:

To determine whether it is terminates or non terminates.

1.\(\frac{100}{3}\)

\(\frac{100}{3}\)=\(33 . \overline{3}\)

It is repeating decimal numbers, there is infinite numbers after the decimal point

2. \(\frac{100}{5}\)

\(\frac{100}{5}\)= 20

This is actually an integer, there are only zeros after the decimal point

3.\(\frac{100}{6}\)=

\(\frac{100}{3}\)=\(33 . \overline{3}\)

It is repeating decimal numbers, there is infinite numbers after the decimal point

\(\frac{100}{3}\)=\(33 . \overline{3}\), \(\frac{100}{6}\)\(16 . \overline{6}\) Are repeating decimals. \(\frac{100}{5}\)= 20 Terminating decimals.

Question. Explain the given numbers –\(0.\overline{3}\), 3.1414414441444 are rational numbers or not.

Given:

To explain the given numbers −\(0.\overline{3}\), 3.1414414441444 are rational numbers or not.

First off, we need to know what a rational number is

A rational number is any number that can be made by dividing 2 integers.

For example:

1.5 would be a rational number because 1.5=3/2 (3 and 2 are both integers) With that being said, let’s begin.

First off, let’s start with −0.3, let’s ask ourselves, can we make this number by dividing 2 integers?

The answer is yes, we can, by doing we have the equivalent of −0.3, So now we know it’s a rational number.

As for the second one, it can’t be a rational number because it can’t be made by dividing to integers, so the answer is:

−0.3 Is a rational number, but 3.14144144414444 is not.

-0.3 is a rational number, but 3.14144144414444 is not.

Reasoning:

In mathematics, a rational number is a number that can be expressed as the quotient or fraction p/q of two integers. A numerator p and a non-zero denominator q.

Given:

Total pitches = 384

Fastball used times = 240

To find:

What decimal should Juanita use to update her report?

Times of fastball used divided by the total pitches

Therefore, Juanita should use the decimal 0.6205 to update her report.

Grade 7 Envision Math Exercise 1.2 Integers And Rational Numbers Answers

Question. Write how rational numbers written as decimals.

Given:

To write how rational numbers written as decimals

Rational numbers written as decimals

Any terminating or repeating decimal that can be written as a fraction using algebraic methods

An integer can be written as a fraction simply by giving it a denominator so any integer is a rational number.

Rational numbers become decimals after we divide the numerator with the denominator

Rational numbers become decimals after we divide numerators with denominators.

Question. Write how can you use division to find the decimal equivalent of a rational number.

Given:

To write how can you use division to find the decimal equivalent of a rational number.

How can you use division to find the decimal equivalent of a rational number

The decimal forms of rational numbers either end or repeat a pattern.

To convert fractions to decimals you just divide the top by the bottom divide the numerator by the denominator and if the division doesn’t come out evenly.

You can stop after a certain number of decimal places and round off.

The answer is the numerator divided by the denominator.

Question. Write the difference between a terminating decimal and a repeating decimal number.

Given:

To write the difference between a terminating decimal and a repeating decimal number.

Difference between a terminating decimal and a repeating decimal number.

Terminating decimal ends that means we know how many digits are after the decimal points.

On the other hand, repeating decimals has an infinite number of repeating digits after the decimal points.

The difference only is number of digits.

Question. Write the decimal equivalent of the rational number \(\frac{7}{20}\).

Given:

To write the decimal equivalent of the rational number \(\frac{7}{20}\).

\(\frac{7}{20}\), dividing both the number in two table.

\(\frac{7}{20}\)=\(\frac{3.5}{10}\)

= 0.35

The answer is 0.35.

Given:

To write the decimal equivalent of the rational number

\(\frac{-23}{20}\).

\(\frac{-23}{20}\), dividing both the number in two table.

\(\frac{-23}{20}\)=\(\frac{-1.15}{20}\)

= -1.15

The answer is -1.15.

Given:

To write the decimal equivalent of the rational number \(\frac{1}{18}\)

\(\frac{1}{18}\) dividing both the number in two table.

\(\frac{1}{18}\) =\(\frac{0.5}{9}\)

= 0.0555

\(0.0 \overline{5}\)  (Repeating)

The answer=\(0.0 \overline{5}\) (Repeating).

Given:

To write the decimal equivalent of the rational number\(\backslash\left[\frac{-60}{22} \backslash\right]\)

\(\frac{-60}{22}\), Dividing both the number in two tables

\(\frac{-60}{22}\) =\(\frac{-30}{11}\)

= -2.7272

\(2. \overline{72}\)  (Repeating)

The answer =\(2. \overline{72}\) (Repeating)

Question. A mile has 5280 feet there are 1000 feet left to pass, what part of a mile in decimal forms is left to pass? Find what part of a mile in decimal form, will you drive until you reach the exit?

Given: 

To find what part of a mile in decimal form, will you drive until you reach the exit?

A mile has 5280 feet there are1000 feet left to pass, what part of a mile in decimal form is left to pass?

=\(0. \overline{1893}\)

​The answer =\(0. \overline{1893}\) part of a mile in decimal form is left to pass.

Question. Write the decimal equivalent for each rational number \(\frac{2}{3}\).

Given:

To write the decimal equivalent for each rational number  \(\frac{2}{3}\)

Canceling the number using 3 table

\(\frac{2}{3}\)=\(0. \overline{6}\)

\(0. \overline{6}\) (Repeating)

The answer \( is 0. \overline{6}\) (Repeating )

Question. Write the decimal equivalent for each rational number \(\frac{3}{11}\).

Given:

To write the decimal equivalent for each rational number \(\frac{3}{11}\)

Canceling the number using 11 table

\(\frac{3}{11}\)=\(0. \overline{27}\)

\(0. \overline{27}\) (Repeating)

The answer \( is 0. \overline{27}\) (Repeating )

Question. Write the decimal equivalent for each rational number \(8 \frac{4}{9}\).

Given:

To write the decimal equivalent for each rational number \(8 \frac{4}{9}\)

Converting the mixed fraction into improper fraction

\(8 \frac{4}{9}\)=\(\frac{76}{9}\)

\(\frac{76}{9}\)=\(8. \overline{4}\) (Repeating)

The answer \(8 \frac{4}{9}\)= \(8. \overline{4}\) (Repeating)

Question. Write whether \(1.02 \overline{27}\) a rational number and also explain it.

Given:

To write whether \(1.02 \overline{27}\) a rational number and also explain it.

Yes, it is a rational number.

Explanation:

The given number is a rational number because it can also be written as fraction and it has also repeating digits.

The given number \(1.02 \overline{27}\) is a rational number.

Envision Math Chapter 1 Exercise 1.2 Answer Key

Question. Whether the fraction is terminating or not terminating \(\frac{1}{3}\).

Given:

To tell whether the fraction is terminating or not terminating.

Answer:

The given fraction is nonterminate

\(\frac{1}{3}\)=\(0. \overline{3}\)

Which means the \(\frac{1}{3}\) fraction has the repeating decimal.

The answer is given fraction \(\frac{1}{3}\) is repeating decimal.

Question. Whether the number -34 is a rational number or whole number or integer.

Given:

To tell whether the number −34 is a rational number or whole number or integer.

-34

Answer:

1. The given number −34 is not a whole number because it has a negative sign.

2. The given number can be considered as rational number because it has been written in a fractional form \(\frac{-34}{1}\).

3. The given number−34 is also a integer because the given number is a whole number with a negative sign.

The answer −34 is an integer, a rational number but not a whole number.

Question. Convert decimal to fraction \(2 \frac{5}{8}\).

Given:

To convert \(2 \frac{5}{8}\) into decimal.

To convert decimal to fraction

​\(2 \frac{5}{8}\)=\(\frac{21}{8}\)

2.625

Given:

To tell what was ariel’s likely error.

Ariel takes the value of \(\frac{5}{8}\) =0.58 it is the error of ariel

Explanation :

We are given that Ariel incorrectly the value of

\(2 \frac{5}{8}\)=2.58

We have to convert \(2 \frac{5}{8}\) into a decimal and we have to find the arials error

\(2 \frac{5}{8}\)=2+\(\frac{5}{8}\)

= 2  +  0.625

= 2.625

\(2 \frac{5}{8}\)=2.625 not 2.58

Ariel consider that value \( \frac{5}{8}\)

= 0.58

But actually the value is 0.625

Hence ariel takes value of 0.58 in place of0.625

Solution:

Ariel takes the value of \(\frac{5}{8}\) =0.58 it is the error of ariel.

Question. Find the value of a and b in a√b when you use division to find the decimal form. Find the decimal form we have to divide 3 by 11.

Given:

To find the value of a and b in a√b when you use division to find the decimal form.

To find the decimal form we have to divide 3 by 11

a√b

a=?

b=?

b is numerator = 3

a is denominator = 11

Solution: a = 11,b = 3

Given:

To find decimal form for \(\frac{3}{11}\)

To find the decimal form \(\frac{3}{11}\)

Canceling the terms with 11 table

=\(0. \overline{27}\).

Question. Find the decimal should the digital scale. Daniel wants to find \(3 \frac{1}{5}\) lb of ham.

Given:

To find what decimal should the digital scale.

Daniel wants to find \(3 \frac{1}{5}\) lb of ham

First, we have to change the mixed fraction to a normal fraction.

The scale shoulder read 3.2 lb

The scale should read 3.2 lb

Question. Find number of pounds of port she brought using a decimal \(18 \frac{8}{25}\) is a mixed fraction.

Given:

To find number of pounds of port she brought using a decimal.

\(18 \frac{8}{25}\) is a mixed fraction

In order to convert the mixed fraction to decimal form you need to divide the numerator by the denominator

\(\frac{8}{25}\) = 0.32

Next add the decimal\(\frac{8}{25}\) =0.32 to the whole number from the mixed fraction

18+0.32 = 18.32

This is how many pounds she bought .this decimal terminates.

The 18.32 number of pounds of pork she brought.

Question. Explain the given number 9.373 is a repeating decimal or not.

Given:

To explain the given number 9.373 is a repeating decimal.

9.373

It is not a repeating decimal

Reason:

There are no repeating digits,9.373 the number has only three digit after the decimal point.

It is a rational because rationals are all numbers that can be written as fractions.

The given number 9.373 is not a repeating decimal.

Question. Find how tall will the stack.

Given:

To find how tall will the stack be.

First box=\(3 \frac{3}{11}\)

Second box = 3.27

We have to convert the\(3 \frac{3}{11}\) into the normal form

\(3 \frac{3}{11}\) = 0.27

\(3 \frac{3}{11}\) = 3 + 0.27

3.27

If he stacks both the boxes

3.27 + 3.27 = 6.54

The stack height will be 6.54.

Solutions For Envision Math Accelerated Grade 7 Exercise 1.2

Question. Find the decimal should you watch for on the digital pressure gauge.

Given:

To find what the decimal should you watch for on the digital pressure gauge.

We should watch the dia0.1 on the pressure gauge

The air pressure in the tyre \(32 \frac{27}{200}\)

We need to convert the mixed fraction to decimal number

\(\frac{27}{200}\) = 0.135

\(32 \frac{27}{200}\) = 32 + 0.135

= 32.135

Thus the air pressure in the tyre = 32.135 pounds per square inch

Rounding to the nearest tenths we get 32.1 pounds per square inch

Solution:

The air pressure in the tyre =  32.135 pounds per square inch.

Question. Justify that the pizza should fit to the square box.

Given:

To justify that the pizza should fit to the square box.

Answer: The pizza fit in the box

Explanation:

The diameter of the pizza is D = \(10 \frac{1}{3}\)

The wide of the square box is b = 10.38

Wkt

For the pizza to fit inside the box, it must be fulfilled that

D ≤ b

We need to convert the decimal to a fraction

= \(\frac{519}{50}\)

Convert \(10 \frac{1}{3}\) into improper fraction

Multiply the diameter of the pizza by 50 both numerator and denominator

Multiply the wide of the  box 3 in both numerator and denominator

=\(\frac{1557}{150}\)

Therefore the pizza fit inside the box.

The pizza will fit inside the box.

Question. Convert the fraction to decimal choose the correct answer for \(117 \frac{151}{200}\).

Given:

To choose the correct answer for \(117 \frac{151}{200}\)

Answer:

Convert the fraction to decimal
​
\(\frac{151}{200}\) =0.755

\(117 \frac{151}{200}\) =117+0.755

117.055

117.055 is correct answer.

Envision Math Grade 7 Volume 1 Chapter 1 Exercise 1.2 Guide

Question. Convert the fraction to decimal  find the decimal equivalents for each fraction for \(\frac{-4}{5}, \frac{-5}{6}\).

Given:

To find the decimal equivalents for each fraction for \(\frac{-4}{5}, \frac{-5}{6}\)

To convert the fraction to decimal

\(\frac{-4}{5}\) = -0.8

\(\frac{-5}{6}\) = –\(0.8 \overline{3}\)

The decimal equivalent for \(\frac{-4}{5}\),\(\frac{-5}{6}\)

= −0.8,-\(0.8 \overline{3}\)

Given:

Which is a repeating decimal? which digit is repeating?

To find the repeating decimal.

\(\frac{-4}{5}\) = -0.8

\(\frac{-5}{6}\) = -0.8333……

-0.8333…… is the repeating decimal and the number 3 is repeating.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 359 Exercise 1 Answer

The figure of triangles which represent each flag is shown below.

The figure of triangles which represent each flag is:

We have to defined as, How are the side lengths of the triangles related?

The figure of triangles which represent each flag is shown below.

The figure of triangles which represent each flag is:

Given – The angles of both triangles are similar.

To do – How the measurements are related?

From the picture it is clearly visible that, the larger triangle have the same angle measure as the smaller triangle.

We can conclude from properties of triangles that angles are congruent.

The angles are congruent.

Page 359 Focus On Math Practices Answer

Given – Justin makes a third flag that has sides that are shorter than the sides of the small flag. Two of the angles for each flag measure the same.

To Find – prove that if the third angle of each flag have same measure.

By making the third flag which have sides smaller than the sides of small flag, the transformation method dilation is used.

By making the third flag which have sides smaller than the sides of small flag, the transformation method dilation is used.

From the properties of this transformation, it is known that corresponding angle measurement remains the same.

We can conclude that the third angle for each flag have same measurements.

Page 360 Try It Answer

Given – ∠Y = 92^∘,∠M = 92^∘,∠Z = 42^∘,∠L = 53^∘

To do – Find m ∠X, m ∠N

Step 1 of 4

For determining whether the given triangles are similar, we will use the Angle-Angle (AA) Criterion

The angles are similar if two angles of a triangle are congruent to the corresponding angles of another triangle.

Therefore, we have to find the missing angle measure first:

Sum of the measures of the interior angles of a triangle is 180^∘.

Step 2 of 4
​

​
Step 3 of 4

m ∠N:

Step 4 of 4

So, we get that two corresponding angles are not congruent:

∠X ≠ ∠L, ​∠Y ≅ ∠M,​ ∠Z ≠ ∠N

Using the Angle-Angle (AA) Criterion, we can conclude that triangle are not similar.

The answers are
​
46^∘

35^∘

​The triangles are not similar.

Page 361 Try It Answer

Given – Knowledge of transformations and parallel lines.

To do – Explain that why angle-angle criterion is true for all triangles.

Step 1 of 1

If QR ∥ YZ

Step 2 of 2

Then, ∠1 ≅ ∠5​ ∠2 ≅ ∠6

Because, these pair of angles are alternate interior angles.

Moreover, since ΔXYZ and ΔXRQ are isosceles triangles, the true is:

∠1 ≅ ∠2​ ∠5 ≅ ∠6

Therefore:

m∠1 = m∠2 = m∠5 = m∠6

Besides, m∠3 = m∠4, because that is the same angle.

So, using the Angle-Angle Criterion, we can conclude that the given triangles are similar.

ΔXYZ ∼ ΔXRQ

ΔXYZ ∼ ΔXRQ

Page 362 Exercise 1 Answer

To do – Using angle measures to determine whether two triangles are similar.

We will use Angle-Angle (AA) Criterion of triangles

Step 1 of 1

There are some rule called Angle-Angle (AA) Criterion.

This criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

Angle-Angle criterion measures will be used to determine whether two triangles are similar.

Page 362 Exercise 3 Answer

Given: Three pairs of triangles

Two right triangles

Two isosceles right triangles

Two equilateral triangles

To find: Which triangle pairs below are always similar

For this we will apply AA similarity criterion to check which pair is always similar

If we have two right angled triangles then definitely 1 pair of angles which is 900 is always same, but the other two angles can vary. Hence not all right triangles are similar, or two right

In isosceles right triangles, the three angles are always fixed. One angle will be a right angle with 90°measure, and the other two angles will always be 45° and 45°(since it is an isosceles triangle). Hence, any two isosceles right triangles will have the same angles, satisfying AA criterion; and thus will always be similar.

Measure of the angles of any equilateral triangle is fixed i.e. each angle is of 600. Hence any 2 equilateral triangles will follow the AA similarity criterion. Therefore two equilateral triangles are always similar.

Two equilateral triangles and two isosceles right triangles are always similar, whereas two right angled triangles are not always similar

Page 362 Exercise 4 Answer

Given: Two triangles in which first triangle has angles 44° and 46° and the second triangle has two angles 90° and 46°

To find: Whether the two triangles are similar or not

We will find all angles of the given triangles and check whether they follow the AA similarity criterion or not

In the given triangle the two angles are 44°
and 46°. Let the third angle be x.

Now, 44° + 46° + x = 180°(Angle sum property of triangle)
​
90° + x = 180°

x = 180° − 90° = 90°

​Hence the third angle of the triangle is 90°

Clearly the two triangles have two equal angles i.e. 46° and 90°

hence AA similarity criterion can be applied and therefore the two triangles are similar

The given two triangles are similar to each other

Page 362 Exercise 5 Answer

Given: Two triangles QLM and QRS with R lying on QL and S lying on QM.

∠QLM = ∠QRS = 90°

To find: Whether ΔQLM ∼ ΔQRS

We will try and apply AA similarity criterion to check the two triangles are similar or not.

In ΔQLM and ΔQRS

∠QLM = ∠QRS = 90° (Given)

∠Q = ∠Q (Common Angle)

Hence by AA similarity rule

ΔQLM ∼ ΔQRS

Hence ΔQLM ∼ ΔQRS

Page 362 Exercise 6 Answer

Given: Two triangles on same base two angles of one of the triangle are 560 and 760 and of the second triangle are 48° and 76°

To find:

Whether the two triangles are similar or not

Value of x

We will apple the property of The measure of the exterior angle of a triangle is equal to the sum of the remote interior angles.

Then we will check whether AA similarity criterion is applicable or not.

Let the third angle of the triangle with two angles 56° and 76° be y

Then, 56° + 76° + y = 180° (Sum of the three angles of a triangle is 180°)

y = 180 − 56 − 76 = 48°

Hence the three angles are 56°,76° and 48°

As both the triangles have two corresponding angles i.e. 48° and 76° equal hence by AA similarity rule we can say that the two triangles are similar to each other.

56° + 76° = 4x + 48° (The measure of the exterior angle of a triangle is equal to the sum of the remote interior angles.)

The two triangles are similar to each other the value of

x = 21°

Page 363 Exercise 7 Answer

Given: Two triangles ΔXYZ and ΔXTU with T and U lying on XY and XZ respectively.

The value of ∠X = 103°, ∠XUT = 48°, ∠XYZ = 46°

To find: Whether ΔXYZ ∼ ΔXTU or not

We will first find the value of ∠XTU and then compare the corresponding angles of the two triangles

In ΔXTU 103° + 48° + ∠XTU = 180° (Sum of all three angles of triangle is 180°)

∠XTU = 180 − 103 − 48 = 29°

In ΔXTU and ΔXYZ

Only one angle 103° matches hence the AA similarity criterion can not be applied.

hence the two triangles are not similar to each other

ΔXYZ is not similar to the ΔXTU

Page 363 Exercise 8 Answer

Given: ∠RST = (3x-9)^∘ and ∠NSP = (2x+10)^∘.

To find the value of x and the value of ∠RST and ∠NSP.

Use the definition of vertically opposite angles, and find the value of x.

Here, ∠RST = ∠NSP [By the definition of vertical opposite angle]

​
Now to check if the angles RTS and SPN are the same, substitute the value of x in each of the expressions.
​
∠RTS = x + 19°

=19 + 19

= 38°

∠SPN = 2x

= 2 × 19

= 38°
​
From this we can see that ∠RTS = ∠SPN

And previously, it was seen that ∠RST = ∠NSP

Hence, AA criterion is satisfied and the two triangles are similar.

For the value of x is 19°, the two triangles are similar, as it satisfies the AA criterion of similarity.

Page 363 Exercise 9 Answer

Given: ∠JIH = 43°, ∠JHI = 35° and ∠HFG = 97°

To determine whether △FGH ∼ △JIH.

First, find the value of m ∠J

By using the triangle angle sum theorem, it follows:
​
m ∠J + 43° + 35° = 180°

m ∠J = 180° − (43° – 35°)

= 102°

​By using the vertical angles theorem, it follows:

∠FHG ≅ ∠JHI

By using the definition of congruence, it follows:
​
m ∠FHG = m ∠JHI

m ∠JHI = 35°

​Solve for m ∠G

​m ∠G + 35∘ + 97∘ = 180°

m ∠G = 180° − (35° + 97°)

= 48°

​Since, all the angles of △FGH and △JIH are not congruent.

Therefore by the definition of similar triangles, it follows the △FGH and △JIH are not similar.

△FGH and △JIH are not similar because the corresponding angles are not congruent.

Page 363 Exercise 10 Answer

Given:

To find: Are the given triangles are similar.

Step formulation: First calculate the value of x and then use it to find other angles.

As vertical angles are equal therefore,

4x − 1 = 3x + 14

Take like terms on one side.
​
4x − 3x = 14 + 1

x = 15

Now find other angles.
​
∠T = x + 15

= 15 + 15

= 30°

​∠P = 2x

= 2 × 15

= 30°

​As two angles of the triangles are equal, hence, these are similar triangles.

Yes, the triangles are similar as they have two equal angles.

Page 363 Exercise 11 Answer

Given: Two triangles with angles.

To: Describe how to use angle relationships to decide whether any two triangles are similar.

If two angles of one triangle is equal to the two angles of another triangle, then the triangles are known as similar triangles.

This is how angle relationships can be used to check whether any two triangles are similar.

If two angles of one triangle are equal to the two angles of another triangle, then the triangles are known as similar triangles.

This is how angle relationships can be used to check whether any two triangles are similar.

Page 364 Exercise 12 Answer

Given:

To: Find whether the given triangles are similar?

Step formulation: Find the angles of both the triangles and then compare.

Sum of interior angles of triangle = 180°

​
Now, as both the triangles have the same angles, therefore, these are the similar triangles.

Yes, both the triangles have the same angles, therefore, these are the similar triangles.

Page 364 Exercise 13 Answer

Given:

To: Find which of the triangles are similar.

Step formulation: First find the angles of the triangles and then compare.

Calculate ∠Z.

​X + Y + Z = 180

104 + 45 + Z = 180

Z = 31°

​Similarly, ∠H = 45°

∠S = 104°

In ΔXYZ & ΔGHI: ∠Y = ∠H and ∠X = ∠G

Therefore,ΔXYZ ≅ ΔGHI

In ΔSQR & ΔGHI: ∠Q = ∠H and ∠G = ∠S

Therefore,ΔSQR ≅ ΔGHI

In ΔXYZ & ΔSQR: ∠Z = ∠R and ∠Y = ∠Q

Therefore,ΔXYZ ≅ ΔSQR

ΔXYZ ≅ ΔGHI

ΔSQR ≅ ΔGHI

ΔXYZ ≅ ΔSQR

Page 364 Exercise 14 Answer

Given:

To: Find whether the given triangles are similar?

Step formulation: First find the angles of the triangles and then compare.

Calculate ∠R.

​Q + S + R = 180

59 + 60 + R = 180

R = 61∘

​In the triangles ∠R = ∠H and ∠Q = ∠G

Therefore, triangles similar.

Yes, triangles are similar as they have equal angles.

Envision Math Accelerated Grade 7 Volume 1 Chapter 4 Analyze And Solve Percent Problems

Question. The florist uses purple and white flowers in the ratio of 3 purple flowers to 1 white flower.

Given:

The florist uses purple and white flowers in the ratio of 3 purple flowers to 1 white flower.

The florist uses purple and white flowers in a ratio of 3: 1.

That means there are 4 flowers in 1 arrangement.

He needs to make 30 identical arrangements.
​
​⇒  ​30⋅4 = 120

​⇒  30.3: 30.1
​
​⇒  90: 30

The florist will need 120 flowers for 30 identical arrangements. He will need 90 purple flowers and 30 white flowers.

The florist will need 120 flowers for 30 identical arrangements. He will need 90 purple flowers and 30 white flowers.

It is given that purple and white flowers are in the ratio of 3 purple flowers to 1 white flower.

That means that the purple flower will be related to the white flowers in a ratio of 3:1.

This means if there are 3 white flowers, we will require 9 purple flowers.

Purple will be 3 times the number of white flowers.

Purple flowers are 3 times the number of white flowers.

Envision Math Accelerated Grade 7 Chapter 4 Exercise 4.2 Answer Key

Question. The florist can only buy white flowers that have 3 white flowers and 2 red flowers.

Given:

The florist can only buy white flowers that have 3 white flowers and 2 red flowers.

He needs 90 out of 120 white flowers.

​⇒  90 ÷ 3 = 30

​⇒  30 ÷ 2 = 60
​
He has to buy 30 groups (2 red in every group).

The florist have to buy 60 red flowers, for 30 groups, 2 red flowers for every group.

Percent is the rate, number or amount in each hundred.

A fraction is a ratio or quantity which is not a whole number.

Fractions and percent can represent the same number just differently.

They are equivalent and that is a proportional relationship.

Percent and fractions can represent the same numbers (can be proportional).

Question. Camila makes 2 of her 5 shots attempted. Find the percent for Camila and then compare with Emily’s.

Given:

Camila makes 2 of her 5 shots attempted.

We find the percent for Camila and then compare with Emily’s.
​
\(\frac{2}{5}=\frac{p}{100}\)

0.4 = \(\frac{p}{100}\)

p = 40%

Camila made 40% of her shots. Camila’s percent of the shots made is less than Emily’s.

Camila made 40% of her shots. Camila’s percent of the shots made is less than Emily’s.

Question. Megan’s room is expanded so the width is 150% of 3 meters.

Given:

Megan’s room is expanded so the width is 150% of 3 meters.

We find the width of the room:
​
\( \frac{w}{3}\) = \( \frac{150}{100}\)

w = \(\frac{450}{100}\)

w = 450

The new width of the room is 4.5 meters.

​The new width of Megan’s room is 4.5 meters.

Given:

45% of iron per 8 mg.

We find the amount of iron needed each day:
​
\(\frac{8}{x}=\frac{45}{100}\)

​\(\frac{800}{45} \)

x = 17.8

Therefore, the amount of iron required each day is 17.8mg.

The amount of iron required each day is 17.8 mg.

Percent is the rate, number or amount in each hundred.

A fraction is a ratio or quantity which is not a whole number.

Fractions and percent can represent the same number just differently.

They are equivalent and that is proportional relationship.

Percent and fractions can represent the same numbers (can be proportional).

Given:

We know that  \(\frac{150}{100}\) is 150% and it is greater than 1 whole.

So \(\frac{75}{x}\) must be greater too.

That means that w must be less than 75.

Therefore, w must be less than 75.

Given:

We know that

x = \(\frac{17 \cdot 100}{68}\)

x = 25%

The percent proportion for the given bar diagram is 25%.

Therefore, the percent for the given bar diagram is 25%.

Envision Math Grade 7 Chapter 4 Percent Problems Exercise 4.2 Solutions

Question. Gia researches online that her car is worth $3,000. She hopes to sell it for 85% of that value, but she wants to get at least 70%. Find whether she get what she wanted or not.

Given that, Gia researches online that her car is worth $3,000.

She hopes to sell it for 85% of that value, but she wants to get at least 70%.

She ends up selling it for $1,800.

We need to find whether she get what she wanted or not.

Finding the 85 %, we get
​
\(\frac{85}{100}\)×3000

= 85 × 30

= 2550

Finding the 70 %, we get

\(\frac{70}{100}\)×3000

= 70 × 30

= 2100
​
But she got only $1800

She got less than what she wanted.

Question. The rabbit population in a certain area is 200% of last year’s population. There are 1100 rabbits this year. Find the number of rabbits there would be in the last year.

The rabbit population in a certain area is 200% of last year’s population.

There are 1100 rabbits this year.

We have to find the number of rabbits there would be in the last year.

The population of the rabbit is 200% in the last year.

While the number of rabbits in this year are 1100.

We will equate the number of rabbits to its percentage to calculate the number of rabbits in last year.

The calculation will be

w = 550

Therefore, the number of rabbits last year is 550.

There were 550 rabbits present last year.

Question. There is a company that makes hair-care products had 3000 people try a new shape. It is given that of the 3000 people, 9 had a mild allergic reaction. Find the percent of people who had a mild allergic reaction.

There is a company that makes hair-care products had 3000 people try a new shape.

It is given that of the 3000 people, 9 had a mild allergic reaction.

We have to find the percent of people who had a mild allergic reaction.

There are 3000 people who had hair care products.

Among those 3000 people, 9 of them had allergic reactions.

The ratio of people who had allergic reactions is \(\frac{9}{100}\).

To find the percent from the ratio, we evaluate as below:

p = 0.3

The percent of people who had a mild allergic reaction is 0.3.

Question. There is a survey given about who owned which type of car. Find the percent of people who were completely satisfied with the car.

There is a survey given about who owned which type of car.

We have to find the percent of people who were completely satisfied with the car.

A survey is given regarding people who owned different types of cars.

In the car satisfaction survey, 1100 people were completely satisfied with their car.

740 people were somewhat satisfied while 160 are not at all satisfied.

We have to find the percent of people who were completely satisfied.

The total number of people who were surveyed are

1100 + 740 + 160 = 2000

To find the percent, we evaluate as below:

p = 55

The percent of people who were completely satisfied with their type of car is 55%.

Analyze And Solve Percent Problems Grade 7 Exercise 4.2 Envision Math

Question. The Washington’s buy a studio apartment for $240000. They pay a down payment of $60000. Find that their down payment is what percent of the purchase price.

It is given that the Washington’s buy a studio apartment for $240000. They pay a down payment of $60000.

We have to find that their down payment is what percent of the purchase price.

The Washington’s buy a studio apartment for $240000.

They pay a down payment for the studio apartment is $60000.

We have to find that what percent of purchase price is of their down payment.

To find the percent, we evaluate as below:

p = 25

Their down payment is 25% percent of the purchase price.

It is given that the Washington’s buy a studio apartment for $240000. They pay a down payment of $60000.

We have to find that what percent of purchase price would be of a $12000 down payment.

The Washington’s buy a studio apartment for $240000.

They pay a down payment for the studio apartment is $60000.

We have to find that what percent of purchase price what percent of purchase price would be of a $12000 down payment.

To find the percent, we evaluate as below:

p = 5

The percent of the purchase price would a $12000 down payment be is 5%.

Question. A restaurant customer left $3.50 as a tip. The tax on  the meal was 7% and the tip was 20% of the cost including tax. Find that what information is not necessary to calculate the bill.

It is given that a restaurant customer left $3.50 as a tip.

The tax on the meal was 7% and the tip was 20% of the cost including tax.

The tip left by the customer at a restaurant is $3.50.

They percentage of tax on the meal was 7 % and of the tip it was 20% of the cost including the tax.

We have to find that what information is not necessary to calculate the bill.

For computing the bill, we do not need to include the tax.

The tax is not needed to compute the bill.

It is given that a restaurant customer left $3.50 as a tip.

The tax on the meal was 7% and the tip was 20% of the cost including tax.

The tip left by the customer at a restaurant is $3.50.

They percentage of tax on the meal was 7 % and of the tip it was 20% of the cost including the tax.

We have to find the amount of total bill.

For computing the bill, we will calculate as below:

x = 17.5

To get the total bill, we will also have to add the tip left by the customer.

17.5+3.5=21

The total bill of the customer in the restaurant is $21.

Question. Find the estimate for 380% of 60.

We have to find the estimate for 380% of 60.

The estimate for 380% of 60 will be evaluated as below:

x = 228

Therefore, the estimate is approximately 228.

The estimate for 380% of 60 will be 228.

Question. Marna thinks that about 35% of her mail is junk mail. She gets twice as much regular mail as junk mail. Verify whether the statement is correct or not.

Marna thinks that about 35% of her mail is junk mail.

She gets twice as much regular mail as junk mail.

We have to verify whether the statement is correct or not.

Marna gets twice as much regular mail as junk mail. So, the ratio of regular mail to junk mail is 2 is to 1.

Thus, if we consider the total mail as 100%, the ratio of both will be represented as

2:1=\(66.\overline{6}\) :\(33.\overline{3}\)

But, Marna thinks that she gets 35% mail as junk mail.

Which is not true, because actually, she gets \(33.\overline{3}\) of junk mail.

Therefore, she is not correct.

Marna’s statement is not correct because she gets around \(33.\overline{3}\) of junk mail and not 35%.

Question. Hypatia has read 13 chapters of a book. The book contains total 22 chapters. Find the percent of the chapters she has read.

It is given that Hypatia has read 13 chapters of a book.

The book contains total 22 chapters.

We have to find the percent of the chapters she has read.

The book has 22 chapters and Hypatia has read 13 of them.

The ratio of the chapters she has read will be \(\frac {13}{22}\).

So, the percent of chapters she has read will be

The percentage of the chapters Hypatia has read is\(59 . \overline{09}\)

Envision Math Grade 7 Exercise 4.2 Solution Guide

Question. A survey found that 27% of high school students and 94% of teachers and school employees drive to school. 

A survey found that 27% of high school students and 94% of teachers and school employees drive to school.

The ratio of students to employees is about 10 to 1.

Roger states that the number of students who drive to school is greater than the number of teachers and employees who drive to school.

We have to tell how Roger’s statement could be correct.

The information gained by the survey is that 27% of high school students and 94% of teachers and school employees drive to school.

The ratio of the students to employees is 10:1.

We express the ratio as 10:1 = 1000:100

We evaluate the percentages we get:

\(\frac{27}{100} \cdot 1000\) = 270

\(\frac{94}{100} \cdot 100\) = 94

Thus, if we count the teachers as employees then, Roger’s statement is right.

Roger’s statement is correct if we count the teachers as employees.

Question. Stefan sells Jin a bicycle for $114 and a helmet for $18. The total cost for Jin is 120% of what Stefan spent originally to buy the bike and helmet. How much did Stefan spend originally?

Given:

Stefan sells Jin a bicycle for $114 and a helmet for $18.

The total cost for Jin is 120% of what Stefan spent originally to buy the bike and helmet.

How much did Stefan spend originally?

To find/solve

How much money did he make by selling the bicycle and helmet to Jin?

? = 110

First, multiply both sides by the variable and then by the reciprocal.

110

He make 110 by selling the bicycle and helmet to Jin.

Question. This month you spent 140% of what you spent last month. Last month you spent $30. How much did you spend this month?

Given:

Last month you spent $30.

This month you spent 140% of what you spent last month.

Set up a proportion to model this situation.

To find/solve

How much did you spend this month?

? = 42

First, multiply both sides by the variable and then by the reciprocal.

42

The amount spends this month is 42.

Envision Math Accelerated Grade 7 Chapter 4 Exercise 4.2 Answers

Question. The owner of a small store buys coats for $50.00 each. She sells the coats for $90.00 each find percent of the purchase price is the selling price?

Given:

The owner of a small store buys coats for $50.00 each.

She sells the coats for $90.00 each

To find/solve

What percent of the purchase price is the selling price?

? = 180

First, multiply both sides by the variable and then by the reciprocal.

180

180 percent of the purchase price is the selling price.

Given:

The owner of a small store buys coats for $50.00 each.

The owner increases the sale price the same percent that you found in Part A when she buys jackets for $35 and sells them.

To find/solve

How many jackets must the owner buy for the total jacket sales to be at least $250?

? = 63

250 ÷ 63 = 3.97

3.97 ≈ 4

First, multiply both sides by the variable and then by the reciprocal.

4

4 jackets must the owner buy for the total jacket sales to be at least $250.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 353 Exercise 2 Answer

Given:-Two parallel lines and transversals lines

Find out:-Write the properties of parallel lines and transversals lines.

If we have two parallel lines and transversals lines then we use the properties:-

Alternate Interior angles are equal.

Alternate exterior angles are equal.

The Sum of angles made on the same sides of the transversals is 180^∘.

Corresponding angles are equal.

We use the four properties of parallel lines and transversals lines to solve the problems.

Envision Math Grade 8 Volume 1 Chapter 6.9 Solutions

Page 353 Focus On Math Practices Answer

Given: The measurements of the two angles are 65^∘.

To find m∠1 using assumption and explain the assumption reason.

It is given that the measurements of the two angles are 65^∘. Therefore, x is:

The assumption made to find m∠1 is to subtract the sum of the two given angle measures 65 degrees and 65 degrees from 180 degrees. It is reasonable because the given tiles are triangular and the sum of the angles in the triangle is 180 degrees.

Page 354 Try It Answer

Given:- ∠2 = 68^∘ and ∠3 = 40^∘

Find out:- ∠1 = ?

Use the angle sum property of a triangle.

Thus, the measure of unknown angle is 72^∘

The measure of unknown angle is 72^∘

Page 354 Convince Me Answer

Given:- angle measures of a triangle 23^∘,71^∘ and 96^∘

Explain:- these angle measures can be possible or not?

We use here angle sum property of a triangle, i.e. the sum of all interior angles is 180∘.

So,

23^∘ + 71^∘ + 96^∘ = 190^∘

This is not possible for a triangle.

A triangle could not have interior angle measures of 23^∘,71^∘ and 96^∘

Congruence And Similarity Envision Math Exercise 6.9 Answers

Page 354 Convince Me Answer

Given:- angle measures of a triangle 23^∘,71^∘ and 96^∘

Explain:- these angle measures can be possible or not?

We use here angle sum property of a triangle, i.e. the sum of all interior angles is 180∘.

So,

23^∘ + 71^∘ + 96^∘ = 190^∘

This is not possible for a triangle.

A triangle could not have interior angle measures of 23^∘,71^∘ and 96^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.9 Page 356 Exercise 2 Answer

Given:- ∠1 = 90^∘ and ∠2 = ∠3

Find out:- all the possible values of exterior angles.

Find the values of angles 2 and 3 using angle sum property, then find the measure for the exterior angles by using exterior angle property for a triangle.

The triangle can be represented as follows:

Given that ∠1 = 90^∘ and ∠2 = ∠3

Therefore, using angle sum property of the triangle,

∠1 + ∠2 + ∠3 = 180^∘

Now the exterior angles 4, 5 and 6 can be found using the exterior angle property:

∴ ∠6 = 45° + 45°, ∠5 = 90° + 45° and ∠4 = 90° + 45°

∠6 = 90°, ∠5 = 135° and ∠4 = 135°

These are all the possible exterior angles for this triangle.

All possible values of the exterior angle are ∠6 = 90∘, ∠5 = 135∘ and ∠4 = 135∘

Envision Math Grade 8 Chapter 6.9 Explained

Page 356 Exercise 3 Answer

Given:- two angles are 32^∘ and 87^∘ and one exterior angle is 93^∘

Find out:- all the interior angles and exterior angles of this triangle.

use the angle sum property of a triangle and exterior angle property.

By using the angle sum property of a triangle,
​
87^∘ + 32^∘ + ∠3 = 180^∘

∠3 = 180^∘ − 119^∘

∠3 = 61^∘

and ∠4 = 87^∘ + 32^∘ [exterior angle property of a triangle]

∠4 = 119^∘

and ∠6 = 87^∘ + 61^∘ [exterior angle property of a triangle]

∠6 = 148^∘

​Hence, the diagram of the triangle can be drawn as:

The remaining interior angle is 61^∘ and exterior angles are 119^∘ and 148^∘

The final diagram of the triangle is:

Page 356 Exercise 4 Answer

Given:- a ∥ b and some angles in the given diagram.

find out:- ∠1 and ∠2.

we use properties of parallel lines and transversals and linear pairs.

as
​
a ∥ b

∠2 = 37.3^∘  [alternate interior angles]

and ∠1 + 79.4^∘ + 37.3^∘ = 180^∘ [Co−interior angles]

∠1 = 180^∘ − 116.7^∘

∠1 = 63.3^∘

The angles are ∠1 = 63.3^∘ and ∠2 = 37.3^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.9 Page 356 Exercise 5 Answer

Given ∥ b and some angles in the given diagram.

find out:∠3 and ∠4 =?

we use properties of parallel lines and transversals and linear pairs.

The angles are ∠3 = 63.3^∘ and ∠4 = 142.7^∘

Envision Math Grade 8 Topic 6.9 Transformations And Congruence Practice

Page 356 Exercise 6 Answer

Given ΔABC, m ∠A = x^∘, m B = (2x)^∘, m ∠C = (6x+18)^∘

Find the measure of each angle.

Use the triangle angle sum theorem to find each angle.

The angle measures are: m ∠A = 18^∘, m ∠B = 36^∘, m ∠C = 126^∘

Envision Math Grade 8 Chapter 6.9 Lesson Overview

Page 357 Exercise 7 Answer

Given the figure of the triangle.

Use the exterior angle theorem to find the required answer.

Here in the figure, angle ∠1 is the exterior angle of the triangle.

m∠1 is equal to the sum of two remote interior angles.

According to the exterior angle theorem,
​
∠1 = 59^∘ + 56^∘

∠1 = 115^∘

∠1 is the exterior angle of the triangle.

m∠1 is equal to the sum of two remote interior angles.

m∠1 = 115^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.9 Page 357 Exercise 9 Answer

Given the figure.

Use the triangle angle sum theorem to find the required angle.

The required angle is m ∠C = 83.5^∘.

Solutions For Envision Math Grade 8 Exercise 6.9

Page 357 Exercise 10 Answer

Given the figure.

Use the exterior angle theorem to find the required answer.

Notice that, ∠4 is an exterior angle of the given triangle. Moreover, angle 1 and ∠2 are its remote interior angles. Therefore, we can use the fact that the measure of an exterior angle of a triangle is, equal to the sum of the measures of its remote interior angles and calculate the value of x.

Our friend got the wrong measure of ∠4 because

he probably think that m∠1, m∠2 and m∠4 have the sum of 180^∘

Therefore he got m∠4 = 51^∘, which is the measure of ∠3, the third interior angle of the given triangle.

do not have the sum of 180^∘

because, as we can see in the picture, not all three angles are interior.

The measure of the angle is ∠4 = 129^∘.

Envision Math Grade 8 Volume 1 Chapter 6.9 Practice Problems

Page 358 Exercise 12 Answer

Given the figure of the triangle.

Use the exterior angle theorem to find the required answer.

According to the exterior angle theorem,

m∠4 = m∠2 + m∠1

​
The value of m∠3 is calculated as:
​
m∠3 = 161 − 25 × 2

= 161 − 50

= 111^∘

The expression for m∠3 = 161 − 25x and the value of m∠3 = 111^∘

Page 358 Exercise 13 Answer

Given a figure of a triangle.

Use the triangle angle sum theorem to find the required angle.

The measure of the acute angle is x = 52.8^∘.

Page 358 Exercise 14 Answer

Given a figure of a triangle.

Use the exterior angle theorem to find the required angles.

Here in the figure, ∠A,∠B,∠C are interior angles. Angle ∠C is adjacent angle whereas ∠A,∠B are non-adjacent angles.

Therefore the remote interior angles for an exterior angle ∠F is ∠A and ∠B.

The two remote interior angles for an exterior angle ∠F is ∠A and ∠B.

Envision Math 8th Grade Congruence And Similarity Topic 6.9 Key Concepts

Page 358 Exercise 15 Answer

Given a figure of a triangle.

Use the exterior angle theorem to find the required angle.

​
The value of m∠3 = 7x + 10 = 7 × 20 + 10 = 150

The value of m∠3 = 150^∘.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 345 Exercise 1 Answer

Given: Two parallel lines.

To: Draw two parallel lines. Then draw a line that intersects both lines. Which angles have equal measures?

Step formulation: Draw the lines and then observe which angles are equal.

Two parallel lines with a transverse line is:

From the figure it can be observed as:
​
∠1 = ∠3 = ∠5 = ∠7

∠2 = ∠4 = ∠6 = ∠8

Equal angles formed when a transverse line cuts two parallel lines are:
​
∠1 = ∠3 = ∠5 = ∠7

∠2 = ∠4 = ∠6 = ∠8

Envision Math Grade 8 Volume 1 Chapter 6.8 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 345 Exercise 2 Answer

There are following properties and definitions should be satisfied to describe which angles have equal measures.

1. Alternate Interior Angles Theorem: When angles are formed inside of two parallel lines and intersect by traversal, are equal to their alternate pairs.

In the above figure, the interior angles:

∠A = ∠D, ∠B = ∠C

2. Alternate Exterior Angles Theorem: Two angles that lie on opposite sides of the transversal and are placed on two different lines, both either inside the two lines or outside, are called alternate angles.

In the above figure, the exterior angles are:

∠A = ∠D, ∠B = ∠C

3. Corresponding Angles Theorem: Corresponding angles are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line.

From the above figure, the corresponding angles are:

∠1 = ∠6, ∠2 = ∠9, ∠3 = ∠7, ∠4 = ∠8

4. Vertical Angles Congruence Theorem: The Vertical Angles are those angles when the opposite (vertical) angles of two intersecting lines are congruent.

From the above figure, the vertical angles are:

∠1 = ∠3,∠2 = ∠4

There are the following properties to describe which angles have equal measures.

1. Alternate Interior Angles Theorem

2. Alternate Exterior Angles Theorem

3. Corresponding Angles Theorem

4. Vertical Angles Congruence Theorem

Congruence And Similarity Envision Math Exercise 6.8 Answers

Page 345 Focus On Math Practices Answer

There are following properties and definitions should be satisfied to describe which angles have equal measures.

1. Alternate Interior Angles Theorem: When angles are formed inside of two parallel lines and intersect by traversal, are alternate pairs of angles are equal.

In the above figure, the interior angles:

∠A = ∠D,∠B = ∠C

2. Alternate Exterior Angles Theorem: Two angles that lie on opposite sides of the transversal and are placed on two different lines, both outside the two parallel lines are called alternate exterior angles. Alternate exterior angles are equal.

In the above figure, the exterior angles are:

∠A = ∠D,∠B = ∠C

3. Corresponding Angles Theorem: Corresponding angles are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line. Corresponding angles are equal.

From the above figure, the corresponding angles are:

∠1 = ∠6,∠2 = ∠8,∠3 = ∠7,∠4 = ∠8

4. Vertical Angles Congruence Theorem: The Vertical Angles are the opposite (vertical) angles of two intersecting lines. They are always congruent.

From the above figure, the vertical angles are:

∠1 = ∠3,∠2 = ∠4

There are the following properties to describe which angles have equal measures.

1. Alternate Interior Angles Theorem

2. Alternate Exterior Angles Theorem

3. Corresponding Angles Theorem

4. Vertical Angles Congruence Theorem

Envision Math Grade 8 Chapter 6.8 Explained

Page 346 Essential Question Answer

When two parallel lines and a third line that crosses them as in the figure shown below, the crossing line is called a transversal.

When a transversal intersects with two parallel lines, eight angles are produced.

The eight angles together form four pairs of corresponding angles.

The corresponding pairs are:

∠1 = ∠5,∠3 = ∠6,∠2 = ∠8,∠4 = ∠7

The alternate interior angles are formed inside of two parallel lines and intersect by traversal.

The alternate interior angles are:

∠3 = ∠8,∠4 = ∠5

Two angles that lie on opposite sides of the transversal and are placed on two different lines, both either inside the two lines or outside, are called alternate exterior angles.

The alternate exterior angles are:

∠1 = ∠7,∠2 = ∠6

All angles which are either exterior angles, interior angles, alternate angles, or corresponding angles are congruent.

When two parallel lines and a third line that crosses them, the crossing line is called a transversal.

All angles formed which are either exterior angles, interior angles, alternate angles, or corresponding angles, all of which are congruent.

Page 346 Try It Answer

The angles that are congruent to ∠8 are ∠4, ∠2, ∠6.

Because ∠8 and ∠4 are corresponding angles, angles that are on the same side of the transversal and the corresponding angles are congruent.

Therefore, ∠8 = ∠2 and ∠4 = ∠6 because these are alternate interior angles.

The angles that are supplementary to ∠8 are: ∠7,∠5,∠1,∠3

Those angles are the same side interior angles and those are:
​
m∠8 + m∠7 = 180

m∠8 + m∠5 = 180

m∠8 + m∠3 = 180

m∠8 + m∠1 = 180
​
These angles are supplementary.

The angles that are congruent to ∠8 are ∠4,∠2,∠6.

The angles that are supplementary to ∠8 are ∠7,∠5,∠1,∠3.

Page 346 Convince Me Answer

Given the figure in the question.

Explain why ∠4 and ∠5 are supplementary.

Use the definition of supplementary to find angles.

When two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are called supplementary angles.

If the sum of the measures of the two angles is 180∘, then the angles are supplementary.

In the given figure, ∠4 and ∠5 are the interior angles on the same side of the transversal. Therefore the sum of the measures of the two angles ∠4 and ∠5 is 180^∘ or ∠4 + ∠5 = 180^∘.

Therefore ∠4 and ∠5 are supplementary.

Angles ∠4 and ∠5 are the interior angles on the same side of the transversal. Therefore the sum of the measures of the two angles is supplementary.

Solutions For Envision Math Grade 8 Exercise 6.8

Page 347 Try It Answer

Given the figure is as follows:

Find the value of ∠2,∠7.

By the use of theorems which are given in the tip to find the value of required angles.

In the given figure, angles 99^∘ and ∠2 are the vertical angles.

Therefore, ∠2 = 99^∘

The measure of angles are

∠2 = 99^∘, ∠7 = 81^∘.

Page 347 Try It Answer

Given the figure in the question.

Find the value of x in the figure.

Use the definition of the corresponding angles theorem to find the value of x.

The value of x is 109^∘.

Page 348 Try It Answer

Given the figure.

Find the value of x if a ∥ b.

Use the alternate interior angle theorem to find the value of x.

According to the alternate interior angle theorem, the angles 86^∘ and (3x+17)^∘ are alternate interior angles and it follows that the angles must be congruent.

Therefore, 86 = (3x+17)^∘

Now the value of x is calculated as:
​
86 = 3x + 17

3x = 69

x = 23

The value of x is 23^∘ if a ∥ b in the given figure.

Given the figure.

Find the value of x.

Use the consecutive interior angle theorem to find the value of x.

According to the consecutive interior angle theorem, the angles of measures 100∘ and (7x – 4)^∘ are consecutive interior angles.

Therefore, 100 + (7x−4) = 180

Simplify the equation and find the value of x.

​
By the consecutive interior angle theorem, the value of x is 12.

Envision Math Grade 8 Volume 1 Chapter 6.8 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 349 Exercise 2 Answer

When two parallel lines and a third line crosses them as in the figure shown below, the crossing line is called a transversal.

When a transversal intersects with two parallel lines, eight angles are produced.

The eight angles together form four pairs of corresponding angles.

The corresponding pairs are:

∠1 = ∠5,∠3 = ∠6,∠2 = ∠8,∠4 = ∠7

The alternate interior angles are formed inside of two parallel lines and intersect by traversal.

The alternate interior angles are:

∠3 = ∠8,∠4 = ∠5

Two angles that lie on opposite sides of the transversal and are placed on two different lines, both either inside the two lines or outside, are called alternate exterior angles.

The alternate exterior angles are:

∠1 = ∠7,∠2 = ∠6

All angles which are either exterior angles, interior angles, alternate angles, or corresponding angles are congruent.

When two parallel lines and a third line that crosses them, the crossing line is called a transversal.

All angles formed which are either exterior angles, interior angles, alternative  angles, or corresponding angles all are congruent.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 349 Exercise 3 Answer

Given:

Two parallel lines are cut by a transversal.

To find:

number of angles made by the transversal and measure of those angles.

For finding number of angles and their measures we need to assume a transversal between two parallel lines anf then with the help of tip we have to find the measures of all angles.

When two parallel lines are cut by a transversal, 8 angles are formed as shown:

∠1 and ∠3are vertical angles, it follows:

∠1 ≅ ∠3

∠1,∠5 and ∠3,∠7 are corresponding angles.

and according to the corresponding angles theorem:

∠1 ≅ ∠5 ; ∠3 ≅ ∠7

Since, ∠1 ≅ ∠3, it can be concluded that:

∠1 ≅ ∠5 ≅ ∠3 ≅ ∠7

from the definition of congruent angles:

∠1 = ∠5 = ∠3 = ∠7

Similarly, it can be proved that:

∠2 = ∠4 = ∠6 = ∠8

When two parallel lines are cut by a transversal, 8 angles are formed.

There are two angle measures.

Envision Math 8th Grade Congruence And Similarity Topic 6.8 Key Concepts

Page 349 Exercise 4 Answer

Given: angle measures of some angles.

To find:

How to tell whether two lines are parallel with the help of angle measures.

Intersect them with a transversal, if the created corresponding angles are equal then they are parallel according to the corresponding angles theorem.

Intersect them with a transversal, if the created corresponding angles are equal then they are parallel according to the corresponding angles theorem.

Page 349 Exercise 6 Answer

Given:

m∠4 = 70

To find:

m ∠ 6

We need to refer to the tip for finding the above angle, alternate-interior angles property is also useful.

Since∠4 and ∠6 are alternate-Interior angles, it follows that:

m∠4 = m∠6

Substitute m∠4 = 70^∘ into the equation:

70^∘ = m∠6

Therefore, m∠6 = 70^∘.

The value of m∠6 = 70^∘.

Page 349 Exercise 8 Answer

Given:

To find:

Value of x

Use the corresponding angles property to find the value of x.

Notice that since a is parallel to b and t is their transversal line, the angles (2x+35)^∘ and 103^∘ are corresponding angles.

Thus, the two angles are congruent, and their measures are equal.

2x + 35 = 103

Solve the equation for x:

The value of x must be equal to 34^∘

Page 350 Exercise 9 Answer

Given:

To find:

value of u

In order to find the value of u we have to use the corresponding angle property.

Notice that u and 32^∘ are corresponding angles.

Using the corresponding angles theorem, it follows that:

u = 32

The value of u is 32^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 350 Exercise 10 Answer

Given:

To prove:

∠K and ∠B are corresponding angles.

In order to prove that the above angles are corresponding angles refer to the tip mentioned .

Although both ∠K and ∠B lie on the same side of the transversal, they do not have the same relative positions with respect to the parallel lines.

So they do not satisfy the second condition for the corresponding angles.

Therefore, ∠K and ∠B are not corresponding angles.

Hence, ∠K and ∠B are not corresponding angles.

Envision Math Grade 8 Chapter 6.8 Lesson Overview

Page 350 Exercise 11 Answer

Given:

A and B are parallel to each other.

∠6 = 155

To find: measure of ∠4

In order to find the value of the above, we have to use consecutive interior angle theorem.

Avenue C is the transversal to parallel avenue A and B

∠6 = 155

From the consecutive interior angle theorem, it follows:

∠6 + ∠4 = 180

Replace ∠6 = 155^∘:

155^∘ + ∠4 = 180^∘

Subtract 155∘ from both side:

155^∘ + ∠4 − 155^∘ = 180^∘ − 155^∘

Cancel 155∘ in left side of equation:

∠4 = 180^∘ − 155^∘

Calculate value of ∠4 :
​
180^∘ − 155^∘

= 25^∘

The measure of ∠4 is 25^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 350 Exercise 12 Answer

Given: measure of ∠6 = 53

To find: measure of ∠12

In order to find the value of the above, we have to use alternate interior angle theorem and supplementary angles theorem.

Observe that ∠6 and ∠11 are alternate interior angles, therefore:

m∠6 = m∠11

∠11 and ∠12 are supplementary angles, therefore:

m∠12 = 180 − m∠11

Substitute m∠11 = m∠6 into the equation:

m∠12 = 180 − m∠6

Substitute m∠6 = 53 into the equation:
​
m∠12 = 180 − 53

m∠12 = 127

The measure of m∠12 = 127^∘

Page 351 Exercise 14 Answer

Given:

To prove:

m ∥ n

In order to prove the above we can use alternate interior angles converse theorem.

Notice that the two angles of measure 74° are alternate interior angles.

Using the alternate interior angles converse, it follows that: m ∥ n

Using the alternate interior angles converse, it follows that:

m ∥ n

Page 351 Exercise 15 Answer

Given:

To find :

Value of x and each missing angle measure.

In order to find the value of x we can refer to alternate interior angles theorem and for the other angles, we can refer to the tip mentioned.

Line t intersects two parallel lines n and m, so it’s a transversal.

Angles ∠86° and (2x+25) are alternate interior angles.

From the alternate interior angles theorem, it follows:
​
2x + 25 = 86

2x = 61

x = 30.5

Angles (2x + 25) angle and ∠3 are same side interior angles.

By the same side interior angles theorem. since (2x+25) = 86 it follows:
​
m∠3 + 86 = 180

m∠3 = 94

Angles ∠3 and ∠1 are vertical angles.

Therefore, by the vertical angles congruence theorem:

m∠1 = m∠3

Substitute m∠3 = 94 into the equality:

m∠1 = 94

Angles ∠2 and 86 angles are vertical angles.

Therefore, by the vertical angles congruence theorem:

m∠2 = 86

Angles(2x + 25) and ∠6 are supplementary angles

Therefore, the sum of their measures is:
​
(2x+25) + m∠6 = 180

86 + m∠6 = 180

m∠6 = 94

Angles ∠4 and ∠6 are vertical angles.

Therefore, by the vertical angles congruence theorem:

m∠4 = m∠6

94 = m∠4

m∠4 = 94

Angles ∠4 and ∠5 are supplementary angles.

Therefore, the sum of their measures is:
​
m∠4 + m∠5 = 180

94 + m∠5 = 180

m∠5 = 86

The value of x = 30.5

The measures of other missing angles are as follows:
​
m∠1 = 94°,m∠2 = 86°

m∠3 = 94°,m∠4 = 94°

m∠5 = 86°,m∠6 = 94°

Page 351 Exercise 16 Answer

Given:

To find:

Value of x

if ​m∠1 = (63 − x)

m∠2 = (72 − 2x)
​
In order to find the above we have to refer the tip mentioned and use the theorems accordingly.

Since the labeled angles are corresponding angles, it follows that:

m∠1 = m∠2

Substitute ∠1 = 63 − x and ∠2 = 72 − 2x into the equation:

63 − x = 72 − 2x

Solve for the value of x:

​63 − x = 72 − 2x

x = 72 − 63

x = 9
​
Therefore, the value of x = 9

The value of x is 9

Given:

To find:

m∠1 and m∠2

In order to find the above we have to refer to the theorems mentioned in tip

Since line r and s are parallel, angles ∠1 and ∠2 are congruent according to the Corresponding Angle Theorem. It follows that:

∠1 ≅ ∠2

Since ∠1 and ∠2 are congruent angles, their measures are equal. It follows that:

m∠1 = m∠2

Substitute m∠1 = (63 – x)^∘ and m∠2 = (72 – 2x)^∘ into the equation:

(63 – x)^∘ = (72 – 2x)^∘

Solve for x:

​63 − x = 72 − 2x

x = 9
​
m∠1 = (63 – x)^∘

Substitute x = 9 into the equation:

m∠1 = (63 – 9)^∘

Subtract the numbers

m∠1 = 54^∘

m∠2 = (72 – 2x)^∘

Substitute x = 9 into the equation:
​
m∠2 = (72 – 2(9))^∘

m∠2 = (72 – 18)^∘

m∠2 = 54
​
Therefore, both angles have the same measurement since they are corresponding angles.

The measures of the angles are:

m∠1 = m∠2 = 54^∘

They are equal because they are corresponding angles.

Envision Math Grade 8 Topic 6.8 Transformations Practice

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 352 Exercise 17 Answer

Given:

To find:

∠b and ∠d

In order to find these angles we have to use supplementary angles theorem and also refer to the tip.

the Use the property of supplementary angles:
​
∠d + ∠136.9^∘ = 180^∘

∠d = 180^∘ − 136.9

∠d = 43.1
​
As m is parallel to n. so use property of alternate interior angles:

∠b = 60.7^∘

Hence, measurement of ∠b = 60.7^∘ and measurement of ∠d = 43.1^∘

Page 352 Exercise 18 Answer

Given:

To find:

Angles which are alternate interior angles.

In order to find the alternate interior angles refer to the tip mentioned.

The alternate interior angles are the angles formed when a transversal intersects two parallel lines, and lie on the inner side of the two parallel lines, on opposite sides of the transversal.

From this definition, we can easily identify the alternate interior angles by looking at the figure.

∠q and ∠t, ∠r and ∠k are alternate interior angles.

The alternate interior angles are ∠q and ∠t, ∠r and ∠k.

Page 352 Exercise 19 Answer

Given:

To find:

Value of w

To find the value of the above we have to use the theorem of supplementary angles.

Since the angles w and the angle of the measure of 101^∘ are adjacent angles that form a straight angle, they are supplementary angles and it follows:

w + 101 = 180

Solve the equation for w:
​
w + 101 = 180

w = 79

The value of w is 79

Given:

To find:

Mistake of Jacob.

in order to find the error in jacob’s calculation we have to use the theorems mentioned in tip.

The boy made a mistake by determining the angle of w, because from the Vertical Angles Congruence Theorem, the angle with measure of 101° is v.

Also, notice that w and 101^∘ form a linear pair.

Since w and 101^∘ are supplementary angles, therefore the value of w should be:

w = 180^∘ − 101^∘ = 79^∘

The boy might think that w is the vertical angle of the angle that measures 101^∘.

The boy might think that the angles that form linear pairs are equal.