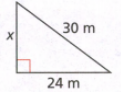
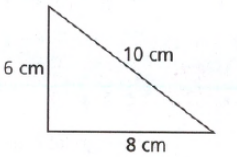
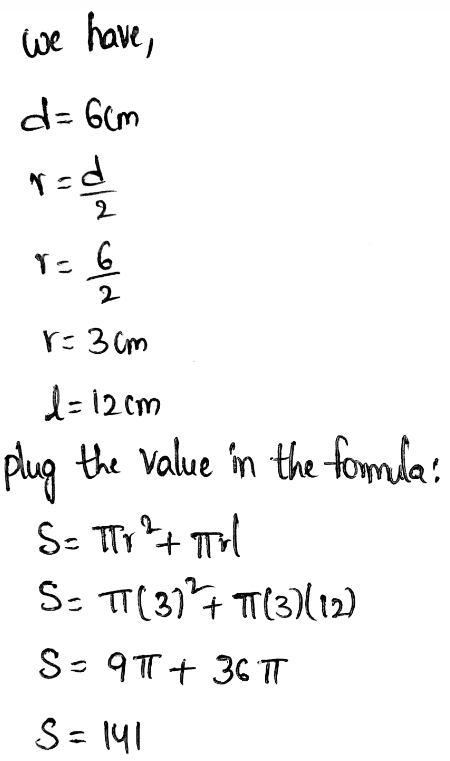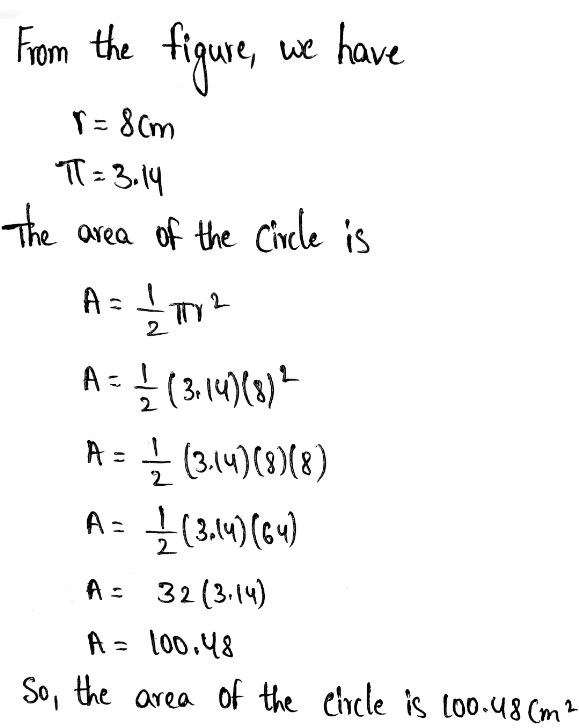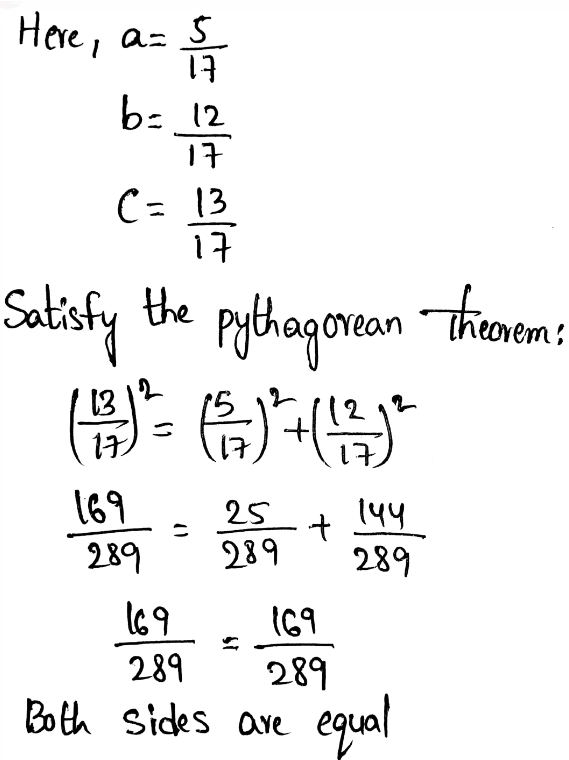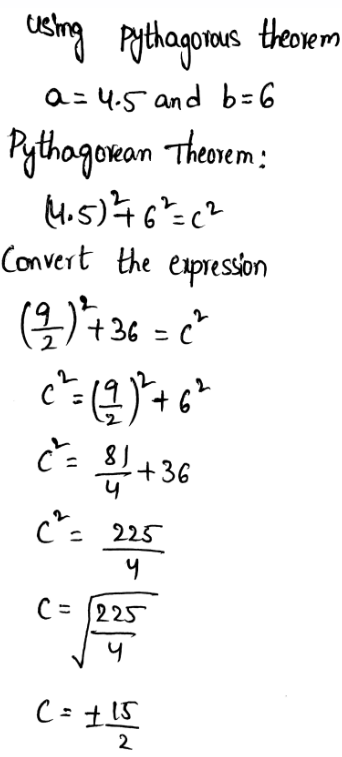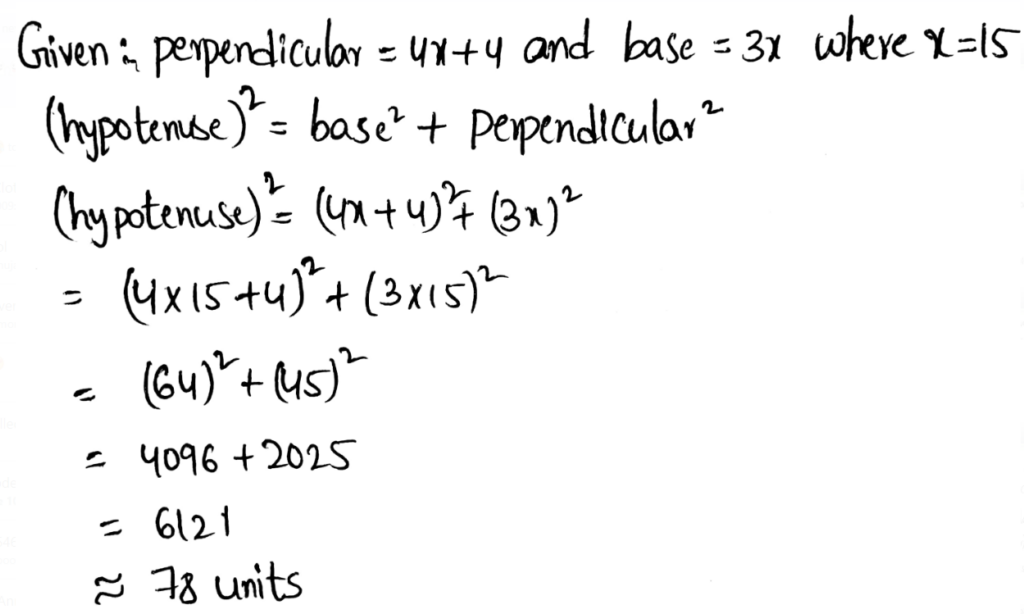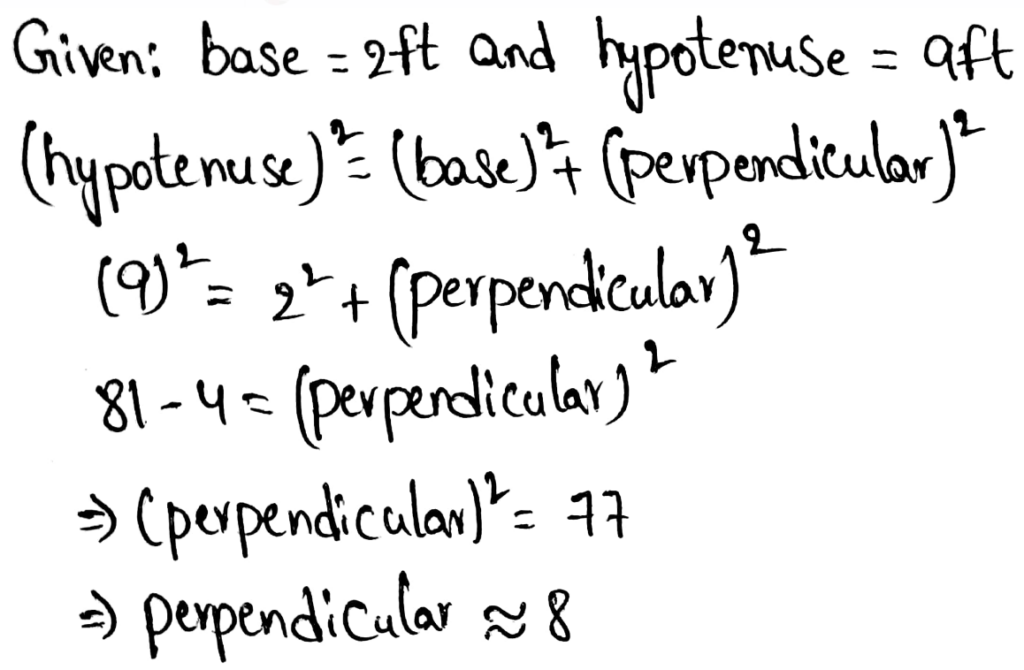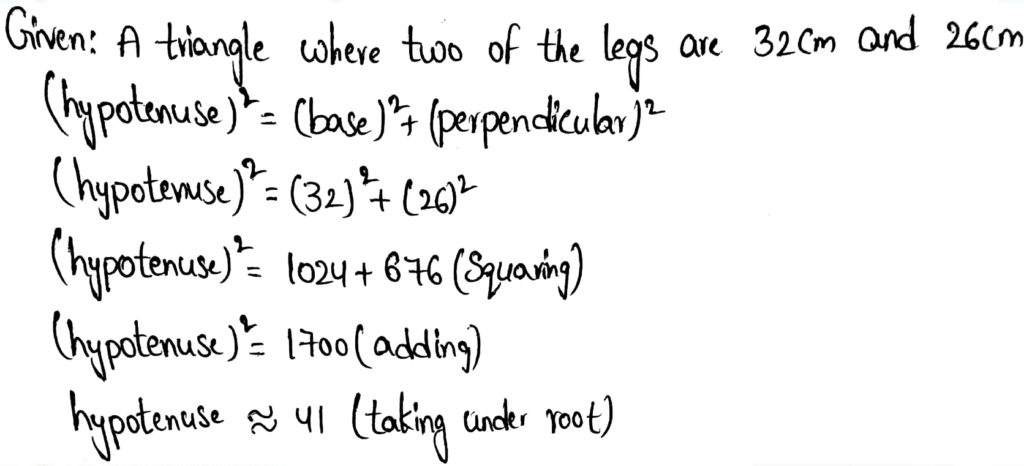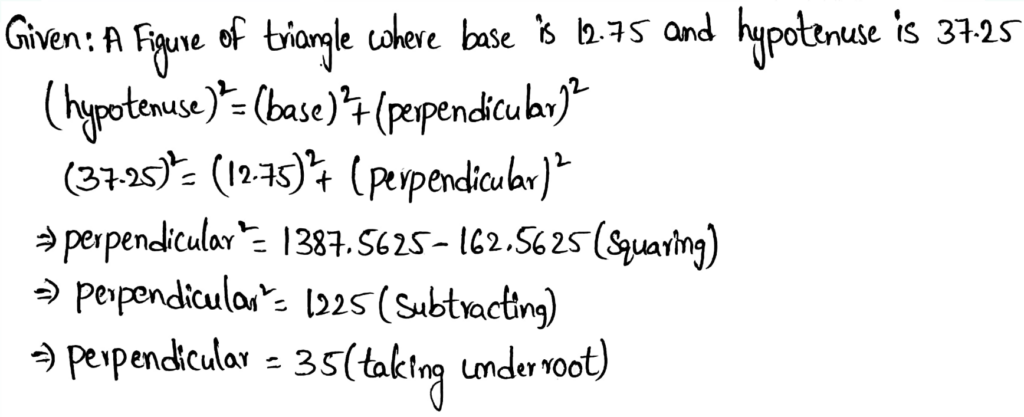Envision Math

Envision Math Grade 8 Volume 1 Chapter 8 Solve Problems Involving Surface Area And Volume

Page 417 Exercise 1 Answer

Given:

A tube-shaped container is shown below:

To find the figures from the tube:

First, look at the tube from the top and the bottom and then use the definition of circle and rectangle.

The top and the bottom shape of the container are represented by the circle of the radius r as shown

The tube is represented by the rectangle with one side equal to height h of the tube and the other side equal to the circumference of the circle of radius r.

So, the net of the tube-shaped container is shown below:

Hence, the net of a tube container is shown below:

Given:

Since the circular top and bottom fit perfectly on the ends of the container, the circumference of the circles must be equal to the length of the rectangle making up the tubular portion of the container.

Hence, the circumference of the circles must be equal to the length of the rectangle making up the tubular portion of the container.

Envision Math Grade 8 Chapter 8 Exercise 8.1 Solutions

Page 417 Focus On Math Practices Answer

A tube can be draw as

As we can see in the figure, that a tube have 2 circle and 1 rectangle with one side equal to the height h of the tube and the other side equal to the circumference of the circle of radius r.

So, we can conclude that if the circumference of the circles is equal to the length of the rectangle making up the tubular portion of the container then it will definitely represent a tube-shaped container.

Hence, if the circumference of the circles is equal to the length of the rectangle making up the tubular portion of the container then it will definitely represent a tube-shaped container.

Page 418 Try It

Given:

h = 9.5inches

r = 2.5 inches

To find the surface area:

Plug the values in S.A. = 2πr²+ 2πrh.

Hence, the curved surface area is S.A. = 60π square inches.

Envision Math Grade 8 Surface Area And Volume Exercise 8.1 Answers

Page 418 Convince Me Answer

The surface area of the cylinder when we have its height and the circumference of its base.

To find this, let’s take an example:

Find the area of the cylinder if the height of the cylinder is 7 meters and the circumference of its base is 14π.

To find the area of the cylinder:

First, find the radius of the cylinder and plug the values in S.A. = 2πr² + 2πrh.

​
Hence, we can find the area of the cylinder if you only know its height and the circumference of its base.

Page 419 Try It Answer

Given:

r = 7 feet

L = 9 feet

To find the surface area:

First, find the area of the circle and then the curved surface area of the cone and then add them.

Add the areas of the circular base and the curved to calculate the surface area of the cone:
​
A + L = 154 + 198

= 352

Hence, the surface area of the cone is 352 square feet.

Given:

d = 2.7 inches

To find the surface area:

First, find the radius using the formula d = \(\frac{r}{2}\) then plug the value of r in the surface formula.

Hence, the area of the sphere is 22.89 square inches.

Envision Math Grade 8 Volume 1 Student Edition Chapter 8 Exercise 8.1

Page 420 Exercise 3 Answer

Given:

C = 2π

To find the surface area of the cones:

First, find the value of r using the formula of the circumference of the circle.

​
Since 36π ≠ 56π, it follows that not all surface of any cone with base circumference 8π inches are equal.

Hence, the hypothesis of the boy is not correct.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 420 Exercise 4 Answer

Given:

To find the surface area:

First, find the radius of the cylinder using r = \(\frac{d}{2}\) and plug the values in the surface area formula.

Hence, the surface area of the cylinder is 69.1mm².

Page 420 Exercise 6 Answer

Given:

To find the surface area:

First, find the value of r using the diameter than the value in the surface area formula.

Hence, the area of the sphere is 4πcm².

Solutions For Envision Math Grade 8 Exercise 8.1

Page 421 Exercise 7 Answer

Given:

To find the surface area of the cylinder:

Plug the value of r and h in the surface area formula.

Page 421 Exercise 8 Answer

Given:

To find the surface area of the cone:

Plug the value r and l in the surface area formula.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 421 Exercise 9 Answer

Given:

To explain the error and find the correct surface area of the cylinder:

Use the formula S = 2πr² + 2πrh.

​
The surface area of the cylinder is about 498.8 square inches.

The calculated surface area of the girl is 76.9 square inches.

Hence, the girl miscalculates the surface area by using only the first term of the formula for the surface area of a cylinder:

S = 2πr² + 2πrh

S = 2πr²

Plug the values:
​
S = 2(3.14)(3.5)²

S ≈ 76.97

Hence, the correct surface area of the given cylinder is about 494.8 square inches and the girl miscalculates the surface area by using only the first term of the formula for the surface area of a cylinder.

Free Solutions For Envision Math Grade 8 Exercise 8.1

Page 421 Exercise 10 Answer

Given:

To find the correct surface area of the sphere:

Plug the values S = 4πr².

​
So, the surface area of the sphere is 84453.44yd².

Hence, the surface area of the sphere is 84453.44yd².

Envision Math Exercise 8.1 Step-By-Step Solutions Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 422 Exercise 11 Answer

Given:

To explain the error and find the correct surface area of the cylinder:

Use the formula S = 2πr² + 2πrh.

Hence, the surface area of the cylinder is 960.8in.².

Practice Problems For Envision Math Grade 8 Exercise 8.1

Page 422 Exercise 12 Answer

Given:

To find the number of bottles of paint:

Use the formula S = πr² + πrl.

First, draw 2D to understand the problem:

In the cone, the radius of the base is 4.1 and the slant height is l = 8.9.

So, she needs 12 bottles of paint.

Hence, she needs 12 bottles of paint.

Envision Math Grade 8 Chapter 8 Worksheet Solutions Exercise 8.1

Page 422 Exercise 13 Answer

Given:

To find the surface area:

Use the formula S = πr² + πrl.

Hence, the surface area of the cone is 141cm².

Given:

To find affection of the surface area of the cone:

Use the formula S = πr² + πrl.

Based on the part(a), the surface area of the cone (original) is 45π or approximately 141.37 square centimeters.

If the diameter and the slant height is cut in half, that will be

It is seen that the new surface area is \(\frac{1}{4}\)

times the original surface area S = 45π, that is

Hence, the diameter and the slant height of the cone is cut in half, the new surface area will become \(\frac{1}{4}\) times the original surface area.

Solve Problems Involving Surface Area And Volume Envision Math Solutions Exercise 8.1

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 8 Solve Problems Involving Surface Area And Volume Exercise 8.1 Page 422 Exercise 14 Answer

Given:

To find the surface area of the sphere:

Plug the value in the formula S = 4πr².

Hence, the surface area of the sphere is 1017.4 cm2.

Envision Math Grade 8 Student Edition Solutions Volume 1 Chapter 8 Solve Problems Involving Surface Area And Volume

Page 412 Exercise 1 Answer

A three dimensional object is in three dimensions having length, width and height.

Example: Cubes, prisms, pyramids, spheres, cones, and cylinders are all examples of three-dimensional objects.

Volume is the product of length, width and height.

Surface areas is the sum of products of length, width and height taken two at a time.

Volume of a prism = cross-sectional area × length.

The surface area of a 3D shape is the total area of all its faces.

Envision Math Grade 8 Volume 1 Chapter 8 Topic 8 Surface Area And Volume Solutions

Page 415 Exercise 1 Answer

The figure of circle is shown as

Here r is know as radius from center to circle which is constant throughout.

The radius is the distance from the center to the edge of a circle.

Envision Math Grade 8 Topic 8 Surface Area And Volume Answers

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 415 Exercise 2 Answer

The objects around you are three-dimensional.

A three dimensional object is in three dimensions having length, width and height.

Example: Cubes, prisms, pyramids, spheres, cones, and cylinders are all examples of three-dimensional objects.

Day to day life examples: cup, mobile phone, ball and bottle.

A shape that has length, width, and height is three dimensional.

Page 415 Exercise 3 Answer

A three dimensional object is in three dimensions having length, width and height.

Example: Cubes, prisms, pyramids, spheres, cones, and cylinders are all examples of three-dimensional objects.

Any side of a cube can be considered a base.

Any side of a cube can be considered a base.

Surface Area And Volume Solutions Grade 8 Envision Math Topic 8

Page 415 Exercise 5 Answer

Given:

The ________________ of a circle is a line segment that passes through its center and has endpoints on the circle.

The distance from one point on a circle through the center to another point on the circle.

It is also the longest distance across the circle.

The diameter of a circle is a line segment that passes through its center and has endpoints on the circle.

Hence, the diameter of a circle is a line segment that passes through its centre and has endpoints on the circle.

Envision Math Grade 8 Topic 8 Practice Problems For Surface Area And Volume

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 415 Exercise 7 Answer

Given:

9⋅3.14

To find the product:

Multiply 9 with 3.14.

We have,

9⋅3.14

Multiply the numbers:

= 28.26

It follows that the product is 28.26.

Hence, the product is 28.26.

Page 415 Exercise 8 Answer

Given:

4.2⋅10.5

To find the product:

Multiply 4.2 with 10.5.

We have,

4.2⋅10.5

Multiply the numbers:

= 44.10

It follows that the product is 44.10.

Hence, the product is 44.10.

Surface Area And Volume Solutions Grade 8 Envision Math Topic 8

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 415 Exercise 9 Answer

Given:

Hence, the area of the given circle is 100.48cm².

Envision Math Topic 8 Detailed Answers For Surface Area And Volume

Page 415 Exercise 10 Answer

Given:

To find the area of the circle:

First, find r using the diameter and then plug the value of r,π in the area of the circle formula.

So, the area of the circle is 56.52 cm²

Hence, the area of the given circle is 56.52cm².

How To Solve Surface Area And Volume Problems In Envision Math Grade 8

Page 415 Exercise 11 Answer

Given:

To find the missing value of x:

Use the Pythagorean Theorem and apply it to the given right triangle.

Hence, the missing value is x = 5in.

Envision Math 8th Grade Surface Area And Volume Topic 8 Solutions

Page 415 Exercise 12 Answer

Given:

To find the missing value of x:

Use the Pythagorean Theorem and apply it to the given right triangle.

​
Hence, the missing value is x = 18m.

Envision Math Grade 8 Volume 1 Chapter 7 Understand The Converse Of The Pythagorean Theorem

Page 387 Exercise 2 Answer

The Pythagorean equation states that if the lengths of any two sides are known the length of the third side can be calculated using

(hypotenuse)² = (base)² + (perpendicular)²

It relates the sides of a right triangle in a simple way.

So if the lengths of sides satisfies this, it is a right angled triangle.

If the sides satisfy

(hypotenuse)² = (base)² + (perpendicular)², then it is right angled triangle.

Page 387 Focus On Math Practices Answer

The Pythagorean equation states that if the lengths of any two sides are known the length of the third side can be calculated using

(hypotenuse)² = (base)² + (perpendicular)²

It relates the sides of a right triangle in a simple way.

So if the lengths of sides satisfies this, it is a right angled triangle.

Therefore, Kayla can use the straws that form a right triangle to make a triangle that is not a right triangle.

Kayla can use the straws that form a right triangle to make a triangle that is not a right triangle.

Envision Math Grade 8 Chapter 7 Solutions

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 388 Essential Question Answer

The Pythagorean equation states that if the lengths of any two sides are known the length of the third side can be calculated using

(hypotenuse)² = (base)² + (perpendicular)²

It relates the sides of a right triangle in a simple way.

So if the lengths of sides satisfies this, it is a right angled triangle.

If the sides satisfy (hypotenuse)² = (base)² + (perpendicular)²

then the triangle is right angled.

Page 388 Convince Me Answer

Given: Right angled triangle

To prove :Converse of the Pythagorean Theorem

We will write the converse of Pythagoras theorem and justify it.

The converse of the Pythagorean Theorem:

A triangle in which the sum of the square of the length of two sides is equal to the square of the length of the third side is a right triangle.

That means in a triangle ABC we have AC² = AB² + BC²

To prove: ∠B = 90°

Let us construct another triangle PQR as shown

By SSS congruency we have ΔABC ≅ ΔPQR

Using ‘corresponding sides of congruent parts are similar’ we get ∠B = 90°

Hence converse of Pythagoras theorem is proved.

Page 389 Try It Answer

Given: A triangle with sides 10,√205,√105 feet

To find: whether the triangle is right angled or not.

We will use the Pythagoras formula and verify it.

If the sides satisfy (hypotenuse)² = (base)² + (perpendicular)²

then the triangle is right angled.

By the converse of the Pythagorean Theorem:

​
​The formed triangle is a right angled.

Given lengths form right angled triangle.

Envision Math Grade 8 Converse Of The Pythagorean Theorem Answers

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 390 Exercise 1 Answer

If the triangle is a right triangle, the hypotenuse is its longest side.

Compare side lengths 10,√205,√105

Check if the lengths c = √205,

​
The triangle is a right triangle by the Converse of the Pythagorean Theorem.

Page 390 Exercise 3 Answer

The formula for the Pythagorean Theorem is: a² + b²= c²

The first component that can easily be substituted in the equation is the hypotenuse, which is the longest side of the right triangle. If the hypotenuse is already determined, the remaining values of the side lengths can be substituted in any of the remaining variables in the equation a,b.

Keep in mind that other variables can be used other than a,b, and c.

For example, a right triangle has side lengths of x = 4,

​y = 5

z = 3
​
So, we have

a² + b²= c²

Hence, the longest side of the triangle is to be substituted on the right side of the equation, while the remaining two side lengths are to be substituted on the left side of the equation.

Page 390 Exercise 4 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

​
Both sides are equal

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Page 390 Exercise 5 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is not the right triangle.

Hence, the given triangle is not the right angle triangle.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7

Page 390 Exercise 6 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is not the right triangle.

Hence, the given triangle is not the right-angle triangle.

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 391 Exercise 7 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is not the right triangle.

Hence, the given triangle is not the right angle triangle.

Page 391 Exercise 8 Answer

Given:

To determine the given triangle is a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Envision Math Exercise 7.1 Answers Grade 8

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 391 Exercise 9 Answer

Given:

Length of the triangle 5, 15, and √250.

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have.

​
Hence, the given triangle is the right angle triangle.

Page 391 Exercise 10 Answer

Given:

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Page 391 Exercise 11 Answer

Given:

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

So, the triangle is the right triangle.

Hence, the given triangle is the right angle triangle.

Page 391 Exercise 12 Answer

Given:

To determine the given sides form a right triangle or not.

Apply the converse of the Pythagorean Theorem and plug the values.

First, check for triangle 1.

So, the triangle is the right triangle.

Now, check for triangle 2.

So, the triangle is not the right triangle.

Now, check for triangle 3

So, the triangle is the right triangle.

Hence, the first and third triangles are right triangles.

Understand The Converse Of The Pythagorean Theorem Envision Math Grade 8 Solutions

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 392 Exercise 14 Answer

Given:

To find whether KM is the height of ΔJKL or not:

Apply the converse of the Pythagorean Theorem and plug the values.

To know if KM is the height of ΔJKL, it must be perpendicular to JL.

KM is perpendicular to JL, ΔKML must be a right triangle.

​
It follows that KM is not perpendicular to JL.

Hence, KM is not the height of ΔJKL using the concept of perpendicular lines and Pythagorean Theorem.

How To Solve Envision Math Grade 8 Converse Of The Pythagorean Theorem Problems

Page 392 Exercise 17 Answer

Given:

To find which of triangle represents right triangle:

Apply the converse of the Pythagorean Theorem and plug the values.

We have,

Here, a = 40

​b = 48

c = 52
​
Satisfy the Pythagorean Theorem:
​
52² = 48² + 40²

2704 ≠ 3904
​
Both sides are not equal.

Hence, it does not represent a right triangle.

We have,

Here, a = 25

​b = 60

c = 65
​
Satisfy the Pythagorean Theorem:
​
65² = 60² + 25²

4225 = 4225
​
Both sides are equal.

Hence, it represents a right triangle.

Hence, option(B) is correct.

Page 393 Exercise 2 Answer

Given:

ΔPQR has side lengths of 12.5 centimeters,30 centimeters, and 32.5 centimeters

To prove ΔPQR is a right triangle:

Hence, it represents a right triangle.

Hence, proved

Hence, we have proved that ΔPQR is a right triangle.

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 393 Exercise 4 Answer

Given:

To find: the unknown side length.

Using the Pythagoras equation:

c² = a² + b²

where c is hypotenuse of the right triangle whereas ‘a’ and ‘b’ are the other two legs.

Let c be the hypotenuse of the triangle and a and b be the length of the legs of the triangle.

Notice that the hypotenuse and one of the side of the right triangle is given:

The length of the second leg is 4√3

Free Envision Math Grade 8 Solutions For Exercise 7.1

Page 393 Exercise 5 Answer

Given: The lengths of the legs of a right triangle are 4.5 inches and 6 inches.

To find: the length of the hypotenuse

Using the Pythagoras equation:

c² = a² + b² where c is hypotenuse of the right triangle whereas ‘a’ and ′b’ are the other two legs.

Let a = 4.5 and b = 6 be the legs of a right triangle.

Substitute a = 4.5 and b = 6 to the

Since the length of the hypotenuse cannot be negative,

therefore, c = 7.5

The length of the hypotenuse is 7.5 inches.

Envision Math Grade 8 Pythagorean Theorem Chapter 7 Worksheet Solutions

Page 393 Exercise 6 Answer

Given: Sides of a triangle

To find: lengths which represent the sides of a right triangle.

Consider 5cm,10cm.15cm

a² + b² = c²

Substitute a = 5,b = 10 and c = 15 if the set of numbers is a pythagorean triple.

5² + 10² = 15²

L.H.S.= 25 + 100 = 125

R.H.S = 225

therefore, 125 ≠ 225

5cm,10cm.15cm does not represent the sides of a right triangle.

Consider 7 in., 14 in., 25 in.

a² + b² = c²

Substitute a = 7,b = 14 and c = 25 if the set of numbers is a pythagorean triple.

7² + 14² = 25²

L.H.S.= 49 + 196

= 245

R.H.S = 625

since 245 ≠ 625

7in.,14in.,25in. does not represent the sides of a right triangle.

Consider 13m,84m,85m

a² + b² = c²

Substitute a = 13,b = 84 and c = 85 if the set of numbers is a pythagorean triple.

13² + 84² = 85²

L.H.S = 169 + 7056

= 7225

R.H.S.= 7225

Since, L.H.S = R.H.S

Therefore, 13m,84m,85m represent the sides of a right triangle.

Consider 5ft,11ft,12ft

a² + b² = c²

Substitute a = 5,b = 11 and c = 12 if the set of numbers is a pythagorean triple.

5² + 11² = 12²

L.H.S = 25 + 121

= 146

R.H.S.= 144

Since, 146 ≠ 144

therefore, 5ft,11ft,12ft does not represent the sides of a right triangle.

Consider 6ft,9ft,√117ft

a² + b² = c²

Substitute a = 6,b = 9 and c = √117 if the set of numbers is a pythagorean triple.

6² + 9² = 117

L.H.S = 36 + 81

= 117

R.H.S = 117

Since, L.H.S = R.H.S

therefore,6ft,9ft,√117ft represent the sides of a right triangle.

Only 13m,84m,85m and 6ft,9ft,√117ft represent the sides of a right triangle.

Solutions For Envision Math Grade 8 Exercise 7.1

Envision Math Grade 8 Volume 1 Chapter 8 Surface Area And Volume Topic 8 Solutions Page 394 Exercise 1 Answer

Given:

To find: the height of the tree.

Using Pythagoras theorem, we will find the height of the tree.

The height of the tree is the sum of the lengths of the sides BC. and CD, it follows:

h = BC + CD

Notice that the figure is composed of two right triangles △ABC. and △ADC.

Therefore, the length of the sides BC and CD can be determined using the pythagorean Theorem;

a² + b² = c²

In the triangle △ABC, the side AB is the hypotenuse.

a² + b² = c²

Substitute a = BC, b = AC, and c = AB into the equation:

BC² + AC² = AB²

Substitute AC = 7 and AB = 9 into the equation:

Since the length cannot be negative, it follows:

BC ≈ 5.7

Similarly, using the pythagorean theorem, the length of the side CD in the △ADC is 24 .

h = BC + CD

Substitute BC ≈ 5.7 and CD = 24 into the equation:

h ≈ 5.7 + 24

h ≈ 29.7

Therefore, the height of the tree is about 29.7 feet.

Therefore, the height of the tree is about 29.7 feet.

Given:

To find: the height of the tree round to the nearest tenth.

Using pythagoras theorem, we will the height of the tree.

Triangle △BCD is a right triangle.

Substitute BC = 9 and CD = 7 into the Pythagorean Theorem formula, it follows:

Since side length is always positive, it follows:

DB = 4√2

Triangle △ACD is a right triangle.

Substitute AC = 25 and CD = 7 into the Pythagorean Theorem formula, it follows:

Since side length is always positive, it follows:

AD = 24

By using the Segment Addition Postulate, it follows:

AB = AD + DB

Substitute AD = 24 and DB = 4√2 into the equation:

AB = 24 + 4√2

The height of the tree is about 29.7ft.

Given: Javier moves backward so that his horizontal distance from the tree is 3 feet greater.

To find: the distance from his eyes to the top of the tree also be 3 feet greater

Use pythagorean theorem.

In △ABC, substitute a = 7,b = x and c = 25 in the Pythagorean theorem:

The person moves horizontally 3 feet away from tree to the point E

in △EBC. substitute a = 7+3,b = 24 and c = y in the Pythagorean theorem,

The length can not be negative, therefore the value of y is 26

When the person moves 3 feet horizontally, the distance from his eyes to the top of the tree increase by 1 feet.

This can be concluded by using Pythagorean theorem.

Given: the distance from his eyes to the top of the tree is only 20 feet

To find: Could Javier change his horizontal distance from the tree so that the distance from his eyes to the top of the tree is only 20 feet?

cosθ = \(\frac{\text { base }}{\text { hypotenuse }}\)

By the definition of cosine:

cosθ = \(\frac{7}{25}\)

When the person moves away from the tree θ decreases which increases value of cosθ

Increase in the value of cosθ decreases the distance from his eyes to top of tree.

cosθ = \(\frac{7}{25}\)

Notice that cosθ is inversely proportional to the distance from person’s eyes to top of tree.

Increase in the value of cosθ decreases the distance from his eyes to top of tree,

At some goint, the distance from his eyes to top of tree can become 20 feet

Envision Math Grade 8 Volume 1 Chapter 7 Understand The Converse Of The Pythagorean Theorem

Page 381 Focus On Math Practices Answer

We have already proved that the sum of the areas of two squares with sides a and b is the same with the area of a square with side c

We have proved this relationship with all right-angle triangles.

Instead of the actual length of the sides, we have used the symbols a, b, and c

while proving the relationship for Kelly’s triangle.

Hence, this relationship is true for any right-angle triangle. The only mandatory condition is a triangle to be a right angle triangle.

Yes, another right-angle triangle drawn by Kelly will also have the same relationship.

This relationship is true for any right-angle triangle.

Envision Math Grade 8 Chapter 7 Solutions

Page 382 Essential Question Answer

Let the right-angle triangle be ABC

The base of the triangle is a

The height of the triangle is b and hypotenuse side is c

According to the Pythagorean theorem, the sum of the square of the base and height is equal to the square of the hypotenuse side.

So, according to the Pythagorean theorem

a²+ b² = c²

According to the Pythagorean theorem, the sum of the square of two sides of a right-angle triangle is equal to the square of the hypotenuse side.
Hence, the relationship between the side lengths of the right angle triangle is given as a²+ b² = c²

Page 382 Try It Answer

Given: Sides of a right-angle triangle is 15cm, 25cm and 20cm

To find : The equation that describes the relationship between the sides of the right-angle triangle.

We will use the Pythagorean theorem to find the relationship between the length of the sides of the triangle.

Let, the base (a) of the right angle triangle be 15cm

Let the height(b)​ of the right angle triangle be 20cm

Let the hypotenuse side (c) by 25cm

According to the Pythagorean theorem, a²+ b² = c²

Substituting the value, we get,

15² + 20² = 25²

We will solve the equation 15² + 20² = 25², to prove whether the relationship is true.

225 + 400 = 625

Combining common terms, we get,

625 = 625

Hence, the relationship is true.

So, according to the Pythagorean theorem, 15² + 20² = 25²

The equation that describes the relationship between the length of the sides of right triangle is 15² + 20² = 25²

Envision Math Grade 8 Converse Of The Pythagorean Theorem Answers

Page 382 Convince Me Answer

The diagram is

In the above diagram, instead of the actual lengths of the side, symbols like a, b, and c is used.

Since the length of the sides is not given in actual numbers hence, this formula can be applied to any right-angle triangle.

The only mandatory condition is that triangle has to be the right triangle.

Hence, the Pythagorean theorem can be applied to the all right triangle.

The side opposite to the greatest angle is the longest side of the right-angle triangle.

The Pythagorean theorem is applied to all right triangles because the lengths of the sides are given in symbol rather than the actual lengths.

Page 383 Try It Answer

Given:

The hypotenuse = 32 meters.

One leg = 18 meters.

To find : The length of the other leg.

We will use the Pythagorean theorem to find the length of the other leg.

Since we are not given the length of which side is 18meters

We will consider a = 18meters and solve for b

The hypotenuse of the triangle is c = 32 meters

So, the length of the other leg is 10√7

The length of the another leg is 10√7

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 384 Exercise 1 Answer

Let the right-angle triangle be ABC

The base of the triangle is a

The height of the triangle is b and the hypotenuse side of the triangle is c

According to the Pythagorean theorem, the sum of the square of the base and height is equal to the square of the hypotenuse side.

So, according to the Pythagorean theorem a²+ b² = c²

According to the Pythagorean theorem, the sum of the square of two sides of a right-angle triangle is equal to the square of the hypotenuse side.

Hence, the relationship between the side lengths of the right angle triangle is given as a²+ b² = c²

Page 384 Exercise 2 Answer

The given diagram is

The diagram shows that the lengths of the legs are 4unit and 3 unit

While the length of the hypotenuse side is 5unit

we can see that the length of the hypotenuse is longer than other sides.

For any right triangle, the longest side is the hypotenuse side and the Pythagorean theorem is applied to only the right triangle.

Hence, the requested condition is that the square that would form the side of the hypotenuse would have the longest side.

Another condition is that each side of the triangle must be smaller than the sum of the other two sides.

If the side of the triangle are a, b, and c

Then a < b + c, b < a + c and c < a + b

No, any three squares cannot form the right triangle. The square forming the hypotenuse side would have the longest side and another condition is that each side of the triangle should be smaller than the sum of the other sides.

Page 384 Exercise 3 Answer

Given:

To find : Whether Xavier has given the correct length of the hypotenuse side.

In a right-angled triangle, 90-degree angle is the largest angle. The side opposite to the largest angle in a triangle is the longest side.

The triangle is

The length of the two legs are 21 units and 28 units

According to Xavier, the length of the hypotenuse is 18.5 units

But since the length of the other sides are 21 units and 28 units which is longer than Xavier’s hypotenuse side.

But since the length of the hypotenuse cannot be shorter than the other two sides, hence, the length given by Xavier is incorrect.

The length of the hypotenuse side should be longer than the other two sides. But the length of the hypotenuse side given by Xavier is less than the other two sides, hence, the length given by the hypotenuse side is an incorrect length.

Page 384 Exercise 4 Answer

Given: sides of a triangle is 4 and 5

To find: hypotenuse of triangle

We will put the given values in

Hypotenuse = \(\sqrt{\text { base }^2+\text { perpendicular }{ }^2}\)

Hypotenuse of the triangle is ≈6

Page 384 Exercise 5 Answer

Given: perpendicular = 8 and hypotenuse = 14

To find: base of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula

Base of the triangle is approximately 12 ft

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 384 Exercise 6 Answer

Given: perpendicular = 3.7mm and base = 7.5 mm

To find: hypotenuse of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula

Hypotenuse of the given triangle is approximately 8

Page 385 Exercise 9 Answer

Given: perpendicular = 4x + 4 and base = 3x where x = 15

To find: hypotenuse of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Hypotenuse of the given triangle is approximately 78 units.

Page 385 Exercise 10 Answer

Given: perpendicular=12.9cm and hypotenuse = 15.3 cm

To find: base of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Base of the given triangle is approximately a = ≈ 8 cm

Envision Math Exercise 7.1 Answers Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 385 Exercise 11 Answer

Given: perpendicular=10m and base = 24m

To find: hypotenuse of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Hypotenuse of the given triangle is approximately 26 m

Page 385 Exercise 12 Answer

Given: base = 2ft and hypotenuse = 9 ft

To find: perpendicular of the triangle

We will use the Pythagoras formula and find the dimension of side.

Putting all the given values in Pythagoras formula and solving as

Perpendicular of the given triangle is approximately 8

Envision Math Grade 8 Pythagorean Theorem Chapter 7 Worksheet Solutions

Page 386 Exercise 13 Answer

Given: A triangle where two of the legs are 32 cm and 26 cm

To find: Hypotenuse of triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

Length of hypotenuse of the given triangle is approximately 41 cm

Given: A triangle where two of the legs are 32 cm and 26 cm

To find: What mistake might the student have made?

We will write the dimension of hypotenuse calculated and match it with given one.

As per the calculation using

(hypotenuse)² = base² + perpendicular²

Hypotenuse is approximately 41 cm.

The mistake might be done in taking the values of legs incorrectly or in the formula.

Mistake might be in the formula taken or dimensions taken.

Page 386 Exercise 14 Answer

Given: A figure of triangle where base is 12.75 and hypotenuse is 37.25

To find: unknown side of the triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

Length of perpendicular of the triangle is 35

Understand The Converse Of The Pythagorean Theorem Envision Math Grade 8 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 7 Understand The Converse Of The Pythagorean Theorem Exercise 7.1 Page 386 Exercise 16 Answer

Given: A figure of triangle where two sides are 36 and 15 ft

To find: unknown side of the triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

​
Length of hypotenuse of the given triangle is 39 ft.

Solutions For Envision Math Grade 8 Exercise 7.1

Page 386 Exercise 17 Answer

Given: A figure of triangle where base is 11.25 cm and hypotenuse is 35.25 cm

To find: unknown side of the triangle

We will use the Pythagoras formula and find the dimension of the required side.

Putting all the given values in Pythagoras formula and solving as

Length of perpendicular of the given triangle is approximately33 cm.

Envision Math Grade 8 Volume 1 Chapter 7 Understand And Apply The Pythagorean

Page 372 Exercise 1 Answer

The Pythagorean Theorem is an equation that relates the side lengths of a right triangle, a²+ b² = c², where a and b are the legs of a right triangle and c is the hypotenuse.

Pythagoras theorem can be used to find any side of a right angled triangle when other two sides are known.

It can be used to know if a triangle is a right angled triangle or not.

Pythagorean Theorem can be used to solve problems

It can be used to find any side of a right angled triangle when other two sides are known.

Using it we can know whether a triangle is a right angled triangle or not.

Envision Math Grade 8 Volume 1 Chapter 7 Pythagorean Theorem Solutions

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 1 Answer

The square root of number y is a number x that satisfies the equation y = x ⋅ x.

The square root of a number is a factor that when multiplied by itself gives the number.

Page 375 Exercise 2 Answer

A line segment that connects two corners but does not form an edge.

We get a diagonal when we join any two corners (called “vertices”) that aren’t already connected by an edge.

A diagonal is a line segment that connects two vertices of a polygon and is not a side.

Envision Math Grade 8 Pythagorean Theorem Chapter 7 Answers

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 3 Answer

The total distance covered by the sides of a polygon is called its perimeter.

We can find the perimeter of any figure by adding all the sides of that figure.

The perimeter of a figure is the distance around it.

How To Solve Pythagorean Theorem Problems In Envision Math Grade 8

Page 375 Exercise 5 Answer

Given: 3² + 4²

To simplify the expression.

Find the squares of both the no. and add them.

On simplifying, we get 25.

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 6 Answer

Given: 2² + 5²

To simplify the expression.

Find the squares of both the no. and add them.

On simplifying, we get 29

Envision Math 8th Grade Chapter 7 Step-By-Step Pythagorean Theorem Solutions

Page 375 Exercise 7 Answer

Given: 10² − 8²

To simplify the expression.

Find the squares of both the no. and add them.

On simplifying, we get 36

Pythagorean Theorem Solutions Grade 8 Envision Math

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 8 Answer

Given: √81

To find: the square root.

Find the factors of the no.

√81 can be written as √9×9

Therefore,

√81 = √9²

Use formula √x² = x

We get

√81 = 9

The square root is 9

Envision Math Grade 8 Chapter 7 Pythagorean Theorem Exercises

Envision Math Grade 8 Pythagorean Theorem Solutions Page 375 Exercise 10 Answer

Given: √225

To find: the square root.

Find the factors of the no.

√225 can be written as √15×15

Therefore,

√225 = √15²

Use formula √x² = x

√225 = 15

The root is 15

Envision Math Grade 8 Chapter 7 Pythagorean Theorem Practice Problems

Page 375 Exercise 11 Answer

Given:

To determine: the distance between the two points.

Use the formula ∣x₂∣−∣x₁∣

The first point is (x₁,y₁)=(2,5)

The second point is (x₂,y₂)=(7,5)

The distance will be ∣x₂∣−∣x₁∣

= ∣7∣ − ∣2∣

= 2 units

The distance between the two points is 2 units.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 365 Essential Question Answer

Given: Two figures.

To: How can you show that two figures are either congruent or similar to one another?

In similar figures, the ratio of corresponding sides are equal. Also the included angles are equal.

In congruent figures, all the sides as well as the angles are equal.

In similar figures, the ratio of corresponding sides are equal. Also the included angles are equal.

In congruent figures, all the sides as well as the angles are equal.

Envision Math Grade 8 Volume 1 Chapter 6 Review Exercise Solutions

Page 365 Exercise 1 Answer

Given: Vocabulary words with their definition.

To: Complete each sentence by matching each vocabulary word to its definition.

Assume pairs of lines are parallel.

Alternate interior angles: Lie between pair of lines and on the opposite sides of the transversal.

Same side interior angles: Lie between pair of lines and on the same side of the transversal.

Corresponding angles: Lie on the same side of the transversal and in corresponding position.

An exterior angle of a triangle: Is formed by a side and an extension of an adjacent side of a triangle.

Remote interior angles of a triangle: Are two adjacent interior angles corresponding to each exterior angle of a triangle.

Alternate interior angles: Lie between pair of lines and on the opposite sides of the transversal.

Same side interior angles: Lie between pair of lines and on the same side of the transversal.

Corresponding angles: Lie on the sme side of the transversl and in corresponding position.

An exterior angle of a triangle: Is formed by a side and an extension of an adjacent side of a triangle.

Remote interior angles of a triangle: Are two adjacent interior angles corresponding to each exterior angle of a triangle.

Congruence And Similarity Envision Math Review Exercise Answers

Page 365 Use Vocabulary In Writing Answer

Given:

To: Prove that △ABC is congruent to △DEF

Step formulation: Find the lengths of the sides and then compare. and Use vocabulary terms from this Topic in your description.

In ΔABC, calculate the lengths of the sides by putting the coordinates in the above formula.

As all the three sides of both the triangles are equal, hence these are congruent triangles.

By comparing the lengths of the sides of both the triangles, these are found to be congruent.

Page 366 Exercise 1 Answer

Given:

To: Find the final image when there is a translation of 3 units to the left and then 2 units to up.

Step formulation: Perform the translation step by step as given in the question.

First move each coordinate of the figure to the left by 3 units.

There will be change only in x coordinate as the translation is in only x direction.

And then add 2 to the y coordinate as the change is along y direction.

New coordinates are:
​
(0.5−3,2+2) = (−2.5,4)

(3.5−3,2+2) = (0.5,4)

(−1−3,−3+2) = (−4,−1)

(5−3,−3+2) = (2,−1)

The final image formed is:

The final image when there is a translation of 3 units to the left and the 2 units to up is:

Page 366 Exercise 1 Answer

Given: A quadrilateral WXYZ is plotted on a graph with XY plane.

To find: The coordinates of the image of rectangle WXYZ after a reflection across the x−axis

We will plot the image of reflection of each point following the rule of reflection i.e. the reflected figures are at the same distance from the line of reflection but on opposite side.

A reflection is a transformation that flips a figure across a line of reflection. The preimage and image are the same distance from the line of reflection but on opposite sides.

So, figures have the same size and the same shape but different orientation after reflection.

Hence, figures have the same size and the same shape but different orientation after reflection.

Envision Math Grade 8 Chapter 6 Review Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Review Exercise Page 366 Exercise 2 Answer

Given: A quadrilateral WXYZ is plotted on a graph with XY plane.

To find: The coordinates of the image of rectangle WXYZ after a reflection across the y−axis

We will plot the image of reflection of each point following the rule of reflection i.e. the reflected figures are at the same distance from the line of reflection but on opposite side.

Graph the given quadrilateral WXYZ

Image of each vertex of WXYZ when line of reflection is y – axis.

Join the vertices of image to construct the polygon. Write the coordinates of each vertex of image

The coordinates of each vertex of image

Coordinates of image of W = (4,−2)

Coordinates of image of X = (2,−2)

Coordinates of image of Y = (2,−4)

Coordinates of image of Z = (4,−4)

Page 367 Part (b) Answer

Coordination Given: S (-4,-2), T(-2,-2), U(-2,-4), V(-4,-4)

Find : Coordinates of STUV after 270° rotation.

Rotate the image about the origin.

For 180° rotation around the origin, first, write down the location of the given points.

S (-4,-2)

T (-2,-2)

U (-2,-4)

V (-4,-4)

Signs will change for 270-degree rotation. Image STUV is in the 3rd quadrant after 270° rotation it will be in the 2nd quadrant.

All signs are negative after rotation some signs will change.

S’ (-2,4)

T’ (-2,2)

U’ (-4,2)

V’ (-4,4)

Coordinates of the image of quadrilateral STUV after a 270° rotation about the origin S’ (-2,4) T’ (-2,2) U’ (-4,2) V’ (-4,4).

Solutions For Envision Math Grade 8 Review Exercise

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Review Exercise Page 368 Exercise 1 Answer

Quadrilateral Given : Quadrilateral A location (1,1), (1,5), (4,4), (4,2). Quadrilateral B location (-3,-1), (-4,-1), (-5,-4), (-2,-4)

Prove : Quadrilateral A congruent to Quadrilateral B.

By observing both the Quadrilaterals, A’s longest side is 4 units but B’s longest side is 3 units.

Same, A’s smallest side is 2 units but B’s smallest unit is only 1.

As for the rule of congruence, All sides must be equal to each other.

Sides are not equal to each other than both Quadrilaterals are not congruent.

Since the quadrilaterals do not have equal corresponding sides they are not congruent.

Page 368 Exercise 2 Answer

Coordinates Given: Coordinates of parallelogram A (-4,1), B (0,1), C (1,-1),D (-3,-1).

Find : coordinates of parallelogram ABCD after dilation with the center.

We will dilate the image with center (0,0) and scale factor of \(\frac{1}{2}\).

For dilating the image we write all the Coordinates of parallelogram. A (-4,1), B (0,1), C (1,-1),D (-3,-1).

We will multiply all the Coordinates of the parallelogram with given scale factor \(\left(\frac{1}{2}\right)\).

Coordinates of image ABCD after dilation with center (0,0) and scale factor \(\frac{1}{2}\) are

Page 369 Exercise 1 Answer

Given: Coordinates of A (−4,1), B (−4,5)and C(−1,1)

To find: Whether the given two triangles are similar or not.

We will identify the coordinates of A’, B’ and C’ to check for dilation and thus be sure whether the two triangles are similar or not

The coordinates of the vertices of triangle ABC with line of reflection being Y – axis are as follows

Coordinates of A” = (4, 1)

Coordinates of B” = (4, 5)

Coordinates of C” = (1, 1)

Lets identify the coordinates of the three vertices of triangle

Coordinates of A’ = (8,2)

Coordinates of B’ = (8,10)

Coordinates of C’ = (2,2)

Whereas the Coordinates of A” = (4, 1)

B” = (4, 5)

C” = (1, 1)

On comparison of corresponding coordinates

A′′= (4,1) → A′ = (8,2)

B′′ = (4,5) → B′ = (8,10)

C′′= (1,1) → C′=(2,2)

Clearly there is an enlargement dilation with a scale factor of 2.

Hence definitely the triangle A’B’C’ is similar to the triangle ABC

As there is a dilation with scale factor 2 hence the two triangles are similar to each other

Envision Math Grade 8 Volume 1 Chapter 6 Review Practice Problems

Page 369 Exercise 2 Answer

Given: Two similar triangles ABC and A’B’C’

To find: Sequence of transformation

We will check for various types of transformation to get the sequence in which triangle ABC got transformed to A’B’C’

Triangles have opposite orientation hence first reflect triangle ABC with line of reflection Y – axis to get triangle A”B”C”

The side lengths and coordinates of A’, B’ and C’ are double as compared to the coordinates of A”, B” and C” hence there is a dilation factor of 2 with origin as center.

Hence the sequence of transformation includes reflection about the y-axis, and then dilation by a factor of 2 with origin as center.

Envision Math 8th Grade Congruence And Similarity Review Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Review Exercise Page 369 Exercise 1 Answer

Given: Two parallel lines a and b and a transversal

To find: Value of x

We will first find the measure of ∠4 using the property of vertically opposite angles and then we will use the property of corresponding angles to find x.

∠4 = 129° (Vertically opposite angles)

​
The value of x = 40°

Page 370 Exercise 1 Answer

Given: Two of the interior angles of the triangle = 48° and 102°

To find: Measure of the third missing angle

We will add the measure of the given two angles and then subtract from 180 to get the measure of the third angle

Sum of the given two interior angles = 48° + 102° = 150°

Let the missing third angle be x°

x° = 180° − 150°

(Sum of the interior angles of a triangle is 180°)

x° = 30°

The measure of the missing angle = 30°

Page 370 Exercise 2 Answer

Given: Exterior angle of the triangle is 115°. The two remote interior angles are 2x and 3x

To find: Value of x

As we know that the measure of exterior angle of a triangle is equal to the sum of the remote interior angles.

So we will equate 115° with the sum of 2x and 3x

Sum of the remote interior angles = 2x + 3x = 5x

Measure of exterior angle = Sum of the opposite interior angles

5x = 115°

x = \(\frac{115}{5}=23^0\)

The value of X is 23°

Envision Math Grade 8 Chapter 6 Review Summary And Examples

Page 370 Exercise 1 Answer

Given: ∠CXY = ∠CAB = 38°

To find: Whether ΔABC ≈ ΔXYC

There are some rule called Angle-Angle (AA) Criterion.

This criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

Hence, This criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

Envision Math Accelerated Grade 7 Volume 1 Student Edition Chapter 6 Solving Problems Using Equations And Inequalities

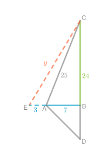
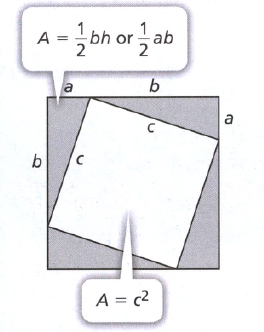
Question. Find out the relationship between the shapes.

Given: Three clues are given.

We have to find out the relationship between the shapes.

First, we will look for that shape which is common on both the left side and right side and then we will eliminate it and find out the relationship between the remaining shapes.

Let, C represents a circle, T represent a triangle and S represents a square.

Therefore, we get the following clues as

​4C  + 1T = 2S + 1T

3T + 2C = 2C + 1S

1S + 2C = 6T

​From the first clue we have

4C + 1T = 2S + 1T

4C + T−T = 2S + T − T (Subtracting T from both sides)

4C = 2S

\(\frac{4}{2}\)C=\(\frac{2}{2}\)S   (Dividing 2 from both sides)

S = 2C ———-(1)

From the second clue we have

3T+2C=2C+1S

3T + 2C − 2C = 2C + S − 2C     (Subtracting 2C from both sides)

S = 3T ———–(2)

From equation (1) and (2)

We have, S = 2C  and  S =   3T

Therefore, 2C = 3T———(3)

From equations (1), (2), and (3)

We get the relationship between the shapes

S=2C

S=3T

2C=3T

The relationship between the shapes are as follows: S = 2C, S = 3T, 2C = 3T

Envision Math Accelerated Grade 7 Chapter 6 Exercise 6.2 Answer Key

Question. Use properties of equality to solve the given equations

4C + 1T = 2S + 1T

3T + 2C = 2C + 1S

1S + 2C = 6T

We have to use properties of equality to reason about the equations.

Let, C represents a circle, T represent a triangle and S represents a square.

Therefore, we get the following clues as

​4C + 1T = 2S + 1T

3T + 2C = 2C + 1S

1S + 2C = 6T

​From the first clue we have

4C + 1T = 2S + 1T

4C + T − T = 2S + T−T             (Subtracting T from both sides)

4C = 2S

\(\frac{4}{2}\)C =  \(\frac{2}{2}\) S                      (Dividing 2 from both sides)

S = 2C ———-(1)

From the second clue we have

3T + 2C = 2C + 1S

3T + 2C − 2C = 2C + S − 2C     (Subtracting 2C from both sides)

S = 3T ———–(2)

From equation (1) and (2)

We have, S = 2C and S = 3T

Therefore, 2C = 3T——–(3)

From equations (1), (2), and (3)

We get the relationship between the shapes:

S = 2C

S = 3T

2C = 3T

We used the subtraction and division properties of equality to solve the given equations.

Envision Math Grade 7 Chapter 6 Solving Equations And Inequalities Exercise 6.2 Solutions

Question. A shape equation C represents a circle, T represent a triangle and S represents a square.

Given: A shape equation is given.

Relationship between shapes:

S = 2C

S = 3T

2C = 3T

We have to complete the equation only using triangles.

Let, C represents a circle, T represent a triangle and S represents a square.

Therefore, we get

4C + S = ?

From solving and discussing exercise 1 we have the following relationship between the shapes.

S = 2C

S = 3T

2C = 3T

Therefore, ​ 4C = 6T

S = 3T

​Hence, we get

4C + S = 6T + 3T = 9T

Therefore, the complete equation is 4C + S = 9T

The complete equation is 4C + S = 9T

Question. Write a two-step equation is similar to solving a one-step equation.

We have to explain how solving a two-step equation is similar to solving a one-step equation.

Solving a two-step equation is similar to solving a one-step equation because they both use properties of equality.

The properties of equality can be applied the same way when solving two-step equations as when solving one-step equations.

Both methods use properties of equality to determine the value of the variable or to make the equation balance.

Solving a two-step equation is similar to solving a one-step equation because they both use properties of equality.

Question. Andrew rents bowling shoes for $4 and he bowls 2 games. Find out the cost of each game.

Given:

Andrew rents bowling shoes for $4 and he bowls 2 games.

The total money he spent is $22

Given bar diagrams are:

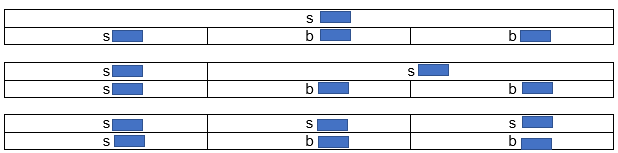
We have to complete the bar diagrams and find out the cost of each game.

The total money Andrew spent is $22

He rents the bowling shoes for $4 and played 2 games.

Therefore, we get the following bar diagrams:

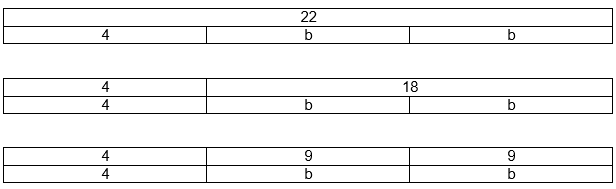
The total cost is $22

Therefore, 4 + 2b = 22

4 + 2b − 4 = 22− 4     (Subtracting 4 from both sides)

2b = 18

\(\frac{2}{2}\) = \(\frac{18}{2}\)   (Dividing 2 from both sides)

b = 9

Therefore, the cost of each game is $9.

The complete bar diagrams are:

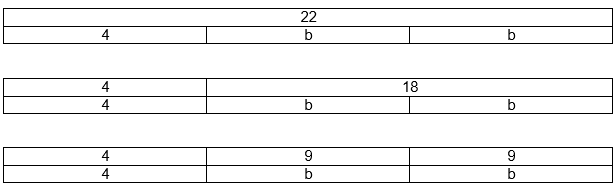
The cost of each game is $9.

Given:

Kristy ran 24 laps.

The total distance traveled by Kristy is 29.6 kilometers

She walked 0.2 km to the presentation table.

We have to determine the distance of each lap.

First, we will determine the total distance she traveled in 24 laps and then we will divide it by 24 to get the distance of each lap.

The total distance traveled by Kristy is 29.6 kilometers

She walked 0.2 km to the presentation table.

Therefore, total distance she covered in  24 laps = 29.6 − 0.2 = 29.4 km     (Subtraction)

Distance covered in 1 lap \(=\frac{29.4}{24}\)        (Division)

=1.225

Hence, the distance of each lap is 1.225 km

The two steps we used for solving the situation are subtraction and division.

The distance of each lap is 1.225 km. The two steps we used for solving the situation are subtraction and division.

Solving Problems Using Equations And Inequalities Grade 7 Exercise 6.2 Envision Math

Question. Solve the equation by using subtraction and division.

We have to explain what were the two steps we used to solve the equation.

The total cost is $22

Therefore, 4 + 2b = 22

4 + 2b−4 = 22 − 4       (Subtracting 4 from both sides)

2b = 18

\(\frac{2}{2}b\)=\(\frac{18}{2}\)              (Dividing 2 from both sides)

b = 9

Therefore, the cost of each game is $9.

We can see that the two steps we used to solve the equation are subtraction and division.

The two steps we used to solve the equation are subtraction and division.

Question. Write a two-step equation is similar to solving a one-step equation.

We have to explain how solving a two-step equation is similar to solving a one-step equation.

Solving a two-step equation is similar to solving a one-step equation because they both uses properties of equality.

The properties of equality can be applied the same way when solving two-step equations as when solving one-step equations.

Both methods use properties of equality to determine the value of the variable or to make the equation balance.

Two-step equations can be solved in two steps by using two different properties of equality.

Solving a two-step equation is similar to solving a one-step equation because they both use properties of equality.

Question. Use bar diagram for solve 4x – 3 = 13.

Given:

Bar diagram for 4x − 3 = 13 is given

we have to solve the bar diagram for x

4x−  3 = 13

4x − 3 + 3 = 13 + 3    (Adding 3 to both sides)

4x = 16

\(\frac{4x}{4}\)=\(\frac{16}{4}\) (Dividing 4 from both sides))

x = 4

The value of x is 4.

We used addition and division to determine the value of x from the bar diagram.

The value of x is 4.

Envision Math Grade 7 Exercise 6.2 Solution Guide

Question. Solve the equation 6p – 12 = 72 and said p = 14.

Given:

Clara solved a problem 6p − 12 = 72 and said p = 14.

We have to check whether Clara is correct or not.

First, we will substitute the value of p and calculate the left-hand side of the equation.

Given equation: 6p − 12 = 72 and p = 14

The left-hand side of the equation is 6p − 12

Substituting the value of p = 14 in 6p − 12 we get

6 (14) − 12      (Multiply)

=  84 − 12        (Subtract)

=  72

=   RHS

Since the left-hand side of the equation is equal to the right-hand side of the equation.

Therefore, the value of p is correct.

And hence, Clara is correct.

As the left-hand side of the equation is equal to the right-hand side of the equation. therefore, the value of p is correct. And hence, Clara is correct.

Question. Clyde is baking, and the recipe requires 1\(\frac{1}{3}\) cups of flour. Clyde has 2 cups of flour, but he is doubling the recipe to make twice as much. Find out how much more flour Clyde needs.

Given:  Clyde is baking, and the recipe requires  1\(\frac{1}{3}\)  cups of flour. Clyde has 2 cups of flour, but he is doubling the recipe to make twice as much.

We need to find out how much more flour Clyde needs.

Also, we need to write an equation to represent the problem.

Let c represent the amount of flour Clyde needs.

The number of cups required for the recipe is 1\(\frac{1}{3}\)

Clyde has two cups of flour.

He is doubling the recipe to make twice as much.

Here, c represents the amount of flour Clyde needs.

The equation that represents the problem will be

2 + c = 2 × 1\(\frac{1}{3}\)

The equation that represents the problem will be 2 + c = 2 × 1\(\frac{1}{3}\)

Given: Clyde is baking, and the recipe requires 1\(\frac{1}{3}\)cups of flour.

Clyde has 2 cups of flour, but he is doubling the recipe to make twice as much.

We need to find how much more flour does Clyde need. We need to solve the equation formed.

The equation formed will be 2 + c = 2 × 1\(\frac{1}{3}\)

Solving the given equation, we get

2 + c = \(\frac{8}{3}\)

c = \(\frac{8}{3}-2\)

c = \(\frac{8-6}{3}\)

c = \(\frac{2}{3}\)

\(\frac{2}{3}\) cups of flour Clyde needs to complete the recipe.

How To Solve Exercise 6.2 In Envision Math Grade 7

Question. Four times a number, n, added to 3 is 47. Write an equation that you can use to find the number.

Given: Four times a number, n, added to 3 is 47.

We need to write an equation that you can use to find the number.

Let the unknown number be n

The four times of the unknown number is added to three.

The result obtained is 47

The equation will be

4n + 3 = 47

The equation that we can use to find the number will be, 4n + 3 = 47

Given: Four times a number, n, added to 3 is 47.

We need to find the number represented by n

The equation formed from the given data is

4n + 3 = 47

Solving the equation, we get

​4n + 3 = 47

4n = 47 − 3

4n = 44

n  =  \(\frac{44}{4}\)

n = 11

The number represented by n is 11.

Envision Math 7th Grade Exercise 6.2 Step-By-Step Solutions

Question. Solve the equation 4x – 12 = 16.

We need to use the bar diagram to help you solve the equation  4x − 12 = 16.

The given equation is 4x − 12 = 16.

Solving the equation, we get

​4x − 12 = 16

4x = 16 + 12

4x = 28

x =  \(\frac{28}{4}\)

x = 7
​
Solving the given using the bar diagram, we get

​16 + 12 = 4x

28 = 4x

x = \(\frac{28}{4}\)

x = 7
​
The value of  x = 7

Question. Solve the given equation.

We need to complete the steps to solve the given equation.

We need to place the missing numbers in the given equation to solve it.

Thus, we get

\(\frac{1}{5}\)t+2−2 = 17−2

\(\frac{1}{5}\)t  = 15

5×\(\frac{1}{5}\)t = 5 × 15

t = 75

The value of  t = 75

Envision Math Accelerated Chapter 6 Exercise 6.2 Solving Equations And Inequalities

Question. Use the bar diagram to write an equation. Then solve for x.

We need to use the bar diagram to write an equation. Then solve for x.

The bar diagram given is

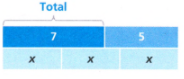
The equation formed from the bar diagram is

x + x + x = 7 + 5

Solving the given equation, we get

​x + x + x = 7 + 5

3x = 12

x = \(\frac{12}{3}\)

x = 4

The value of x = 4

Question. While shopping for clothes, Tracy spent $38 less than 3 times what Daniel spent. Find how much Daniel spent.

Given that, While shopping for clothes, Tracy spent $38 less than 3 times what Daniel spent.

We need to write and solve an equation to find how much Daniel spent.

Let x represent how much Daniel spent. Also, the amount Tracy spent is $10.

The equation represented by the given situation will be

3x − 38 = 10

Solving the given equation, we get

​3x − 38 = 10

3x = 10 + 38

3x = 48

x = \(\frac{48}{3}\)

x = 16

Daniel spent $16

Envision Math Accelerated Grade 7 Chapter 6 Exercise 6.2 Answers

Question. Solve the equation 0.5p – 3.45 = -1.2.

We need to solve the equation 0.5p − 3.45 = −1.2.

The given equation is 0.5p−3.45 = −1.2.

Solving the given we get

0.5p – 3.45 = -1.2.

0.5p = -1.2 + 3.45

0.5p = 2,25

p = \(\frac{2.25}{0.5}\)

p = \(\frac{22.5}{5}\)

p = 4.5

The value of p = 4.5

Question. Solve the equation \(\frac{n}{10}\) + 7 = 10

We need to solve the equation \(\frac{n}{10}\)+7 = 10

The given equation is n \(\frac{n}{10}\)+7 = 10

Solving the given we get

\(\frac{n}{10}\) + 7 = 10

\(\frac{n}{10}\) = 10− 7

\(\frac{n}{10}\) = 3

n = 3 × 10

n = 30

The value of n = 30

Question. A group of 4 friends went to the movies. In addition to their tickets, they bought a large bag of popcorn to share for $6.25.

Given:

A group of 4 friends went to the movies.

In addition to their tickets, they bought a large bag of popcorn to share for $6.25.

The total was $44.25

To find/solve

Write and solve an equation to find the cost of one movie ticket, m.

Use an equation to determine the cost of one ticket.

4m + 6.25 = 44.25

4m = 38

m = 9.50

The cost of one ticket is $9.50.

The equation is 4m + 6.25 = 44.25, The cost of one ticket is $9.50.

Given:

A group of 4 friends went to the movies.

In addition to their tickets, they bought a large bag of popcorn to share for $6.25.

The total was $44.25.

To find/solve

Draw a model to represent the equation.

4m + 6.25 = 44.25

4m = 38

m = 9.50

The bar diagram represents the equation

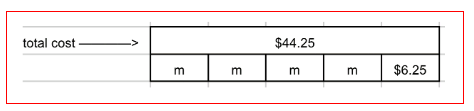
The bar diagram represents the equation

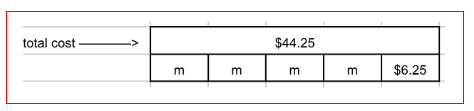
Given:

Oliver incorrectly solved the equation  2x + 4 = 10.

He says the solution is x = 7.

To find/solve

What is the correct solution?

The correct solution is

2x + 4 = 10

2x = 6

x = 3

The correct solution is x = 3.

Given:

Oliver incorrectly solved the equation 2x+4=10. He says the solution is x=7.

To find/solve

 What mistake might Oliver have made?

An expression is a finite combination of symbols that is well-formed according to rules that depend on the context.

Oliver did not use the inverse relationship of the equation.

He did not apply the properties of equality in order to balance the equation.

He added 4 on the right side of the equation instead of subtracting.

Oliver did not use the inverse relationship of the equation. He did not apply the properties of equality in order to balance the equation. He added 4 on the right side of the equation instead of subtracting.

Envision Math Grade 7 Chapter 6 Practice Problems Exercise 6.2

Question. What two properties of equality do you need to use to solve the equation?

An expression is a finite combination of symbols that is well-formed according to rules that depend on the context.

The two properties of equality that is needed to solve for the equation are the addition property of equality and the division property of equality.

Question. Find the solution of the equation 4.9x – 1.9 = 27.5

Given:

Use the equation 4.9x − 1.9 = 27.5

To find/solve

The solution is x =?

Determine the solution:
​
​4.9x −1.9 = 27.5

4.9x = 29.4

x = 29.4/4.9

x = 6

The solution is x = 6.

Question. At a party, the number of people who ate meatballs was 11 fewer than of the total number of people. Five people ate meatballs.

Given:

At a party, the number of people who ate meatballs was 11 fewer than of the total number of people.

Five people ate meatballs.

We form the equation as:

5=\(\frac{1}{3}\)x−11

Now we write a one-step equation that has the same solution:

\(\frac{1}{3}\)x = 16

Therefore, this is the required one-step equation that has the same solution.

Therefore, the required one-step equation with the same solution is \(\frac{1}{3}\)x=16

Envision Math Accelerated 7th Grade Exercise 6.2 Key

Question. In a week, Tracy earns $12.45 less than twice the amount Kalya earns. Tracy earns $102.45.

Given:

In a week, Tracy earns $12.45 less than twice the amount Kayla earns. Tracy earns $102.45.

We form the equation as:

102.45 = 2x − 12.45

Now we solve the equation

​2x = 102.45 + 12.45

2x = 114.9

x = \(\frac{114.9}{2}\)

x = 57.45

Therefore, Kayla earns $57.45.

Therefore, Kayla earns $57.45

Question. Solve the equation 2x + 4\(\frac{1}{5}\) = 9

Given: 2x+4\(\frac{1}{5}\) = 9

We solve the equation:

2x + 4\(\frac{1}{5}\) = 9

Now we use inverse operations and the subtraction property of equality to isolate the term with the variable.

​2x+ \(4 \frac{1}{5}-4\frac{1}{5}\)

= 9− 4\(\frac{1}{5}\)

2x = 4\(\frac{1}{5}\)

2x = \(\frac{41}{5}\)

Now we use inverse operations and the division property of equality to isolate the variable.

\(\frac{2x}{2}\) = \(\frac{41}{5}\).\(\frac{1}{2}\)

x = 4.1

Therefore, the required solution is x = 4.1

Envision Math Accelerated Grade 7 Volume 1 Chapter 6 Solving Problems Using Equations And Inequalities

Question. Six friends go white-water rafting. The total cost for the adventure is $683.88, including a $12 fee per person to rent flotation vests. Marcella says they can use the equation 6r + 12 = 683.88 to find the rafting cost, r, per person, Julia says they need to use the equation 6(r + 12) = 683.88.

Given:

Six friends go white-water rafting.

The total cost for the adventure is $683.88, including a $12 fee per person to rent flotation vests.

Marcella says they can use the equation 6r  + 12 = 683.88 to find the rafting cost, r, per person, Julia says they need to use the equation 6 (r + 12)  =  683.88

To find/solve

Question. Whose equation accurately represents the situation? Construct an argument to support your response.

The distributive property tells us how to solve expressions in the form of a (b  +  c).

The distributive property is sometimes called the distributive law of multiplication and division.

The equation given by Julia shows the correct representation of the situation.

In her equation she showed that the $12 fee for the flotation vests rental must be adequately distributed to the number of persons who will be using it.

Julia has an accurate representation of the equation.

Given:

Six friends go white-water rafting.

The total cost for the adventure is $683.88, including a $12 fee per person to rent flotation vests.

Marcella says they can use the equation 6r +12=683.88 to find the rafting cost, r, per person, Julia says they need to use the equation 6(r+12) = 683.88

To find/solve

Question. What error in thinking might explain the inaccurate equation?

In the first equation, it shows that the flotation vests rental is added to the rafting cost of all six friends.

Marcella may have thought that the $12 flotation vests fee is for all and not per person.

Marcella might be thinking that the flotation vest rental fee covers the whole group as one and not individually.

Question. How does the Distributive Property help you solve equations?

Solving equations using distributive property involves the quantities and variables found in the given situation.

It will enable to make difficult problems easier by breaking down the factor as a difference of two numbers which indicates the quantities stated in the problem.

Distributive property helps solve equations by multiplying the two terms in the parenthesis by the term outside the parenthesis.

Envision Math Accelerated Grade 7 Chapter 6 Exercise 6.3 Answer Key

Question. Can the equation 32x + 2.32 = 114.24 be used to find the original cost of each figurine in the problem above.

Given:

Can the equation 32x  +  2.32  =  114.24 be used to find the original cost of each figurine in the problem above.

To find/solve

Explain.

− \(\frac{1}{2}b\) +\( \frac{6}{2}\) = 5

− \(\frac{1}{2}b\) + 3 = 5

− \(\frac{1}{2}b\) − 3 + 3 = 5−3

− \(\frac{1}{2}b\) =2

− 2 (\(\frac{-1}{2}b\)) = (2) − 2

b = −4

0.4x − 0.18 = 9.2

0.4x = 9.2 + 0.18

x = 23.45

−4p = 848 = 44

-4p = 44−848

−4p = −804

P = 201

Solution

1)  B  =  −4

2)  X  =  23.45

3)  P  =  201

Question. How does the Distributive Property help you solve equations?

Given:

To find/solve

How does the Distributive Property help you solve equations?

Solving equations using distributive property involves the quantities and variables found in the given situation.

It will enable to make difficult problems easier by breaking down the factor as a difference of two numbers which indicates the quantities stated in the problem.

Distributive property helps solve equations by multiplying the two terms in the parenthesis by the term outside the parenthesis.

Question. How are the terms in parentheses affected when multiplied by a negative coefficient when the Distributive Property is applied?

Given

Statement

To find/solve

How are the terms in parentheses affected when multiplied by a negative coefficient when the Distributive Property is applied?

The terms inside the parenthesis are affected if a negative coefficient is multiplied using the distributive property.

If the terms inside the parenthesis are negative then the product will be positive and if the terms inside the parenthesis are positive the product will be negative.

The signs will be changed if the number outside has a negative coefficient.

Signs inside the parenthesis will be changed if the term outside has a negative coefficient.

Question. How can an area model help you set up an equation for a problem situation?

Given

Statement

To find/solve

How can an area model help you set up an equation for a problem situation?

Using an area model can easily visualize how to represent an equation for a given problem.

5 (x + 2) = 35

It can easily visualize the quantities involved in the problem.

Envision Math Grade 7 Chapter 6 Solving Equations And Inequalities Exercise 6.3 Solutions

Question. A family of 7 bought tickets to the circus. Each family member also bought a souvenir that cost $6. Total amount they spent was $147. How much did one ticket cost?

Given:

A family of 7 bought tickets to the circus.

Each family member also bought a souvenir that cost $6.

The total amount they spent was $147

To find/solve

How much did one ticket cost?

Determine the amount of one ticket

​7(x + 6) = 147

7x + 42 = 147

7x + 42 − 42 = 147 − 42

7x = 105

x = 15
​
One ticket costs $15.

Question. David says that the original price of the shorts was $41. Does his answer seem reasonable? Defend your answer by writing and solving an equation that represents the situation.

Given:

David says that the original price of the shorts was $41.

To find/solve

Does his answer seem reasonable? Defend your answer by writing and solving an equation that represents the situation.

David did not get the correct original price of the shorts and the price is not reasonable.

The correct equation that represents the situation is

​1/4 (x + 18) = 10.25

1/4x + 18/4 = 10.25

1/4x + 4.5 = 10.25

1/4x = 5.75

x = 23
​
The original price of the shorts is $23.

Solving Problems Using Equations And Inequalities Grade 7 Exercise 6.3 Envision Math

Question. Which of the following shows the correct use of the Distributive Property when solving \(\frac{1}{3}\)(33 – x) = 135.2 the equation.

We need to find which of the following shows the correct use of the Distributive Property when solving \(\frac{1}{3}\)(33-x) = 135.2

The given expression is \(\frac{1}{3}\)(33 − x)  =  135.2

Using the distributive property, the expression becomes

\(\frac{1}{3}\)(33 − x) = 135.2

\(\frac{1}{3}\)×33 − \(\frac{1}{3}\)x = 135.2

\(\frac{1}{3}\).33 −  \(\frac{1}{3}\).x = 135.2

The correct use of the given expression using the distributive property will be (D) 1

\(\frac{1}{3}\).33-\(\frac{1}{3}\).x = 135.2

Question. Use the Distributive Property to solve \(\frac{1}{8}\)(p + 24) = 9 equation.

We need to use the Distributive Property to solve the given equation.

The given equation is \(\frac{1}{8}\)(p + 24) = 9

The given expression is \(\frac{1}{8}\)(p+24) = 9

Using the distributive property, we get

\(\frac{1}{8}\)(p + 24) = 9

\(\frac{p}{8}\) + \(\frac{24}{8}\)= 9

\(\frac{p}{8}\)+3 = 9

\(\frac{p}{8}\) = 9−3

\(\frac{p}{8}\) = 6

p = 6 × 8

p = 48

The value of p=48

Question. Use the Distributive Property to solve the \(\frac{2}{3}(6a+9)\) = 20.4 equation.

We need to use the Distributive Property to solve the given equation.

The given equation is \(\frac{2}{3}(6a+9)\) = 20.4

The given expression is \(\frac{2}{3}(6a+9)\) = 20.4

Using the distributive property, we get

\(\frac{2}{3} {6a+9}\) = 20.4

\(\frac{2}{3}\) ×  6a + \(\frac{2}{3}\)×9 = 20.4

2 × 2a + 2 × 3 = 20.4

4a + 6 = 20.4

4a + 6 = 20.4

4a = 20.4 − 6

4a = 14.4

a = \(\frac{14.4}{4}\)

a = 3.6

The value of a = 3.6

Given:

If you apply the Distributive property first to solve the equation, what operation will you need to use last?

To find/solve

Using the distributive property.

6 \(\frac{d}{3}\) − 30 = 34

​2d−30 = 34

2d = 64

d = 32
​
When a distributive property is used as the first step to solve the equation, the last operation will be division.

Given:

If instead, you divide first to solve the equation, what operation would you need to use last?

To find/solve

Using the distributive property.

d = \(\frac{192}{6}\)

d = 32

When a distributive property is used as the first step to solve the equation, the last operation will be division.

Envision Math Grade 7 Exercise 6.3 Solution Guide

Question. A local charity receives \(\frac{1}{3}\) of funds raised during a craft fair and a bake sale. The total amount given to charity was $137.45. How much did the bake sale raise?

Given:

A local charity receives \(\frac{1}{3}\) of funds raised during a craft fair and a bake sale.

The total amount given to charity was $137.45.

To find/solve

How much did the bake sale raise?

Determine the amount raised by the bake sale.

x = 159.75

The amount raised by the bake sale is $159.75.

Question. Diagram shown for the equation is incorrect. Find the correct solution.

Given that, the solution shown for the equation is incorrect.

We need to find the correct solution.

The given equation is  − 3(6 − r) = 6

Solving the given using the distributive property, we get

-3(6-r) = 6

-18 + 3r = 6

-18 + 18 + 3r = 6 + 18

3r = 24

r = \(\frac{24}{3}\)

r = 8

The value of  r = 8 not  r = −8

The multiplication of two negative integers result in a positive product.

Given that, the solution shown for the equation is incorrect.

We need to find the error made.

The given equation is − 3(6 − r) = 6

Solving the given using the distributive property, we get

​− 3(6 − r) = 6

− 18 + 3r = 6

3r = 24

r = \(\frac{24}{3}\)

r = 8

The multiplication of two negative integers results in a positive product. The multiplication of two negative integers results in a positive product. Here, he has multiplied two negative integers and put the result as negative. This was likely the error he made.

Question. Vita wants to center a towel bar on her door that is \(27\frac{1}{2}\) inches wide. She determines that the distance from each end of the towel bar to the end of the door is 9 inches.

Given:

Vita wants to center a towel bar on her door that is \(27\frac{1}{2}\)inches wide.

She determines that the distance from each end of the towel bar to the end of the door is 9 inches.

Let x inches be the length of the towel bar.

The width of the door is 9 inches on each side of the towel bar.

So the width of the door is

9 + x + 9 = x + 18inches

It’s given that the width of the door is \(27\frac{1}{2}\)

∴ \(27\frac{1}{2}\) = 18 +x

Now we solve the equation:

\(27\frac{1}{2}\) = 18 + x

\(27\frac{1}{2}\) − 18 = 18 + x − 18 ( Subtract −18 on both sides)

x = 9\(\frac{1}{2}\)

x = 4.5

Therefore, the length of the towel bar is x = 4.5

Envision Math Accelerated Grade 7 Chapter 6 Exercise 6.3 Answers

Question. Apply the properties of equality to isolate the variable.

We need to explain how to isolate the variable in the equation \(\frac{-2}{3}n+7\) = 15

Apply the properties of equality to isolate the variable.

\(\frac{-2}{3}n+7\)− 7 = 15−7

\(\frac{-2}{3}n\) = 8

\(\frac{-3}{2}n\)×\(\frac{-2}{3}n\)

=  8 × \(\frac{-2}{3}n\)

n =− 12

Use the properties of equality to isolate the variable in the equation to get the solution of
​
n =−12

Use the properties of equality to isolate the variable in the equation to get the solution of n =−12.

Question. Find the equations which are equivalent to \(\frac{1}{2}\)(4+8x) = 17.

We need to find the equations which are equivalent to

\(\frac{1}{2}\)(4+8x) = 17

Determine the equation similar to the given

\(\frac{4}{2}\)  + \(\frac{8}{2}\)x = 17

2 + 4x = 17

4x = 15

x = \(\frac{15}{4}\)

​Determine the equation similar to the given
​
\(\frac{4+8 x}{2}\) = 17
​
2.(\(\frac{4+8 x}{2}\)) = 17.2

​4 + 8x = 34

8x = 30

x =  \(\frac{30}{8}\)

​The similar equations are 4 + 8x = 34 and 4x = 15.

Question. Clara has 9 pounds of apples. She needs 11/4 pounds to make one apple pie. If she sets aside 1.5 pounds of apples. How many apple pies clara makes.

Given:

Clara has 9 pounds of apples. She needs 11/4 pounds to make one apple pie. If she sets aside 1.5 pounds of apples.

The equation for the given situation is 1\(\frac{1}{4}\)p = 9-1.5

1\(\frac{1}{4}\)p = 9 −1.5

\(\frac{5}{4p}\) = 7.5

5p = 4(7.5)

5p = 30

p = 6

Clara can make 6 apple pies.

Question. Solve the given equation -4(1.75 + x) = 18

Given:

− 4 (1.75 + x) = 18

we have to solve the given equation.

First, we will apply distributive property and apply other properties of equality.

Given equation is − 4(1.75 + x) = 18

7 − 4x = 18                   (Distributive property)

− 7− 4x + 7 = 18 + 7   (Adding 7 to both sides)

−4x = 25

\(\frac{-4x}{-4}\)=\(\frac{25}{-4}\)                  (Dividing both sides by− 4)

x = −6.25

The value of x is  − 6.25

Envision Math 7th Grade Exercise 6.3 Step-By-Step Solutions

Question. A group of 4 friends travel in a train ticket cost for one person $6 and total amount they spent by 4 friends is $34 they buy a healthy snack bag find the value of healthy snack bag. write the equation which represents the total amount spent and then we will solve it.

Given:

Ticket cost for one person = $6

Cost of healthy snack bag = $b

The total amount spent by 4 friends is $34

We have to find the value of b.

First, we will write the equation which represents the total amount spent and then we will solve it.

Given:

Ticket cost for one person = $6

Cost of healthy snack bag = $b

The total amount spent by 4 friends is $34

Therefore,

Amount spent by one friend = 6 + b

Total amount spent by 4 friends = 4(6 + b) = 34

4 (6 + b) = 34

24 + 4b = 34                   (Distributive property)

24 + 4b −24 = 34 − 24  (Subtracting 24 from both sides)

4b = 10

\(\frac{4b}{4}\)=\(\frac{10}{4}\)                       (Dividing both sides by 4)

b = 2.5

Hence, the cost of a healthy snack bag is $2.50

Equation is 4(6 + b) = 34

The cost of a healthy snack bag is $2.50.

Envision Math Accelerated Grade 7 Volume 1 Chapter 6 Solving Problems Using Equations And Inequalities

Question. Explain how the expression 2m + 3 relates to the values in the table.

Given:

Golf balls in Marley’s collection are m

Golf balls in Tucker’s collection are 2m + 3

We have to explain how the expression 2m + 3 relates to the values in the table.

The expression 2m+3 showed the comparison of the number of golf balls in Marley’s and Trucker’s collections.

Golf balls in Marley’s collection are m

Golf balls in Tucker’s collection are 2m + 3

From the expression 2m + 3, it is clear that it represents how greater the number of golf balls in Tucker’s collection are compared to Marley’s collection.

The expression 2m + 3 showed the comparison of a number of golf balls in Marley’s and Tucker’s collections.

Envision Math Accelerated Grade 7 Chapter 6 Exercise 6.1 Answer Key

Question. The total price of the laptop is $335. The down payment $50 and Cole pays the rest of the money in 6 equal monthly payments. Write an equation that represents the relationship between the cost of the laptop and Cole’s payments.

Given:

The total price of the laptop is $335.

The down payment $50 and Cole pays the rest of the money in 6 equal monthly payments ‘p’.

We have to write an equation that represents the relationship between the cost of the laptop and Cole’s payments.

The total price of the laptop is $335.

The down payment is $50 and Cole pays the rest of the money in 6 equal monthly payments ‘p’.

Cost  = (50) + 6 ×  monthly payments

335 = (50) + 6 × p

335 = 50 + 6p

Therefore, 335 = 50 + 6p represents the relationship between the cost of the laptop and Cole’s payments.

335 = 50 + 6p represents the relationship between the cost of the laptop and Cole’s payments.

Question. The total money Claire spend is $9.49. There is 60% off on the hat and socks price is $5.49. Explain which equation represents correctly Claire’s shopping trip.

Given:

The total money Claire spend is $9.49

There is 60% off on the hat and socks price is $5.49.

The original price of hat is $x.

We have to explain which equation represents correctly Claire’s shopping trip.

First, we will calculate the price she paid for the hat and then add it to the price of the socks, this will give us the total price she paid.

The original price of hat is $x.

There is 60% off on the hat.

Therefore, Claire paid only 40% of the original price of the hat.

Hence, the price she paid for hat 40%x  = b 0.4x

She paid $5.49 for socks and in total, she paid $9.49.

Therefore,  Hat’s price added to the socks price will give us the total amount she spent.

Hence, 0.4x +  5.49 = 9.49

0.4x  +  5.49   = 9.49 represents Claire’s shopping trip.

Envision Math Grade 7 Chapter 6 Solving Equations And Inequalities Exercise 6.1 Solutions

Question.  Explained why both multiplication and addition are used in Cole’s payment.

Given:  335 = 50 + 6p

We have to explain why both multiplication and addition used in the equation.

Cole’s payment equation 335 = 50 + 6p I

In this equation, we used both multiplication and addition because:

We used multiplication to get the total monthly payment Cole paid in 6 months

Therefore, we get, 6 × p = 6p

To get the total cost, we have to add a down payment which is $50 to the monthly payments Cole made.

Therefore, we got the equation 335=50+6p by using both multiplication and addition.

Explained why both multiplication and addition are used in Cole’s payment equation, which is 335 = 50 + 6p

We need to check whether the equations \(\frac{1}{5}x\) + 2 = 6 and \(\frac{1}{5}\)(x+2) = 6 represent the same situation.

Simplifying the equations, we get

\(\frac{1}{5}x\) + 2 = 6

\(\frac{1}{5}x\)  = 6 – 2

\(\frac{x}{5}\) = 4

x = 20

The other one will be

\(\frac{1}{5}\)(x+2) =  6

x + 2 = 30

x = 28

Thus, both represent different situations.

Both equations represent different situations.

Question. If Cora has 36 apps, and Rita started some apps and Deleted 5 apps determine the apps Rita has.

Given:

Rita started “r” apps

Deleted 5 apps

Cora has twice of Rita

The equation that represents the number of apps

​2c = r − 5

c =  \(\frac{r-5}{2}\)

r − 5 = 2c

r − 5 + 5 = 2c + 5

r = 2c + 5

If Cora has 36 apps, determine the apps Rita has.

​r = 2c + 5

r = 2(36) + 5

r = 72 + 5

r = 77

r = 2c + 5 represents the number of apps each girl has.

Question. The search collected 19 stamps. Her collection is 6 less than 5 times the collection of Jessica how many stamps are in her collection of Jessica?

Given, Her collection is 6 less than 5 times the collection of Jessica.

The search collected 19 stamps. Her collection is 6 less than 5 times the collection of Jessica how many stamps are in her collection of Jessica?

The problem is about the stamp collection of Jessica.

The collection of Sarah is 6 less than 5 times the collection of Jessica.

Given:

11 hours this week

5 fewer

The equation that represents the number of hours for her babysitting

\(\frac{2}{3}\)h-5 = 11

The equation is \(\frac{2}{3}\)h-5 = 11

Question. The relationship between the weight of the crate and the number of oranges.

Given:

Total weight 24.5 pounds. One orange 0.38 lb

The equation that represents the relationship between the weight of the crate and the number of oranges is

24.5 = 15 + 0.38 × g

The equation is 24.5 = 15 + 0.38 × g.

Given:

37 guests

3 large table

7 late arriving table

The equation that represents the situation is

3n + 7 = 37

The equation is  3n + 7 = 37.

Given:

Each friend paid $12.75

Tip was $61

The equation that represents the situation is  4(12.75 + t) = 61.

The equation is  4(12.75 + t) = 61.

Solving Problems Using Equations And Inequalities Grade 7 Exercise 6.1 Envision Math

Question. Mia buys \(4 \frac{1}{5}\) pounds of plums. The total cost after using a coupon for 55 off her entire purchase was $3.23. Find the equation could represent the situation.

Given that, Mia buys \(4 \frac{1}{5}\) pounds of plums. The. total cost after using a coupon for 55 ¢ off her entire purchase was $3.23.

If c represents the cost of the plums in dollars per pound, we need to find what equation could represent the situation

The equation that represents the situation is  \(4 \frac{1}{5}\)  c−0.55 = 3.23.

The equation is  \(4 \frac{1}{5}\) c−0.55 = 3.23.

The situation could still be used even if the denominator is doubled.

Even if the denominator will be doubled, the situation could still be used as for making a larger field and making more buses to be used in the field trip.

The situation could still be used even if the denominator is doubled.

Question. Iguana costs $48. You already have $12 and plan to save $9 per week. We have to form an equation that represents the plan to afford the iguana.

Iguana costs $48. You already have $12 and plan to save $9 per week. We have to form an equation that represents the plan to afford the iguana.

Let w represent the number of weeks.

We form an equation:

12 + 9w = 48

This is the required equation.

Therefore, the required equation that represents the plan to afford the iguana is  12 + 9w = 48

Given:

Iguana costs $48. You already have $12 and you can buy the iguana after 6 weeks.

We have to form an equation that represents the amount that needs to be saved per week.

Let x represent the amount to be saved per week.

We form an equation:

12 + 6x = 48

This is the required equation.

Therefore, the required equation that represents the amount to save per week to buy the iguana is  12 + 6x = 48

Envision Math Accelerated Grade 7 Chapter 6 Exercise 6.1 Answers

Question. The life expectancy of a woman born in 1995 was 80.2 years. Find the equation for the life expectancy of a woman born in 2005.

The life expectancy of a woman born in 1995 was 80.2 years.

Between 1995 and 2005, the life expectancy increased by 0.4 years every 5 years.

We have to find the equation for the life expectancy of a woman born in 2005.

Let L represent the life expectancy of a woman born in 2005.

We are given that the life expectancy increased by 0.4 every 5 years.

Therefore, the life expectancy will increase by 0.8 in 2005.

We form equations:
​
​L − 0.4(2) = 80.2

L − 80.2 = 0.4(2)

20.2 + 0.4(2) = L
​
These are the required equations.

Therefore, the required equations that represent the life expectancy of a woman born in 2005 are, ​L − 0.4(2) = 80.2, L − 80.2 = 0.4(2), 20.2 + 0.4(2) = L

The equation that we formed for this particular problem is a linear equation.

The equations should be equivalent so that we get the same answer.

The equations can look different but should be rewritten as  L = 80.2 + 0.4(2)

No, the equations must be equivalent, they can look different but should be able to rewrite as L = 80.2 + 0.4(2)

Question. Solve the equation 5x – 13 = 12 and multiply x 5 times.

We are given the equation  5x−13 = 12

This equation shows that we have to multiply x 5 times.

Then deduct 13 from 5x, so that we will get the answer as 12.

We need an equation such that 5 times the value of x minus  13 is 12.

Given:

5x−13=12

We put the values 1, 2, 3, 4, and 5 for x in the equation:

For 1:

​5(1) − 13 = 12

5 − 13 = 12
​
−8 ≠ 12

For 2:

​5(2) − 13 = 12

10 − 13 = 12
​
−3 ≠ 12

For 3:

​5(3) − 13 = 12

15−13 = 12
​
2 ≠ 12

For 4:

​5(4) − 13 = 12

20 − 13 = 12
​
7 ≠ 12

For 5:

​5(5) − 13 = 12

25 − 13 = 12
​
12 = 12

Therefore, the solution of the given equation is 5.

Envision Math Grade 7 Exercise 6.1 Solution Guide

Question.  A garden contains 135 flowers each of which is either red or yellow. These are 3 beds of yellow flowers and 3 beds of red flowers. There are 30 yellow flowers in each yellow flower bed. Find out number of flowers in each red flower bed.

A garden contains 135 flowers each of which is either red or yellow. There are 3 beds of yellow flowers and 3 beds of red flowers.

There are 30 yellow flowers in each yellow flower bed.

Let

z − total number of flowers in the garden=135

y − number of flowers in each yellow flower bed=30

r − Number of flowers in each red flower bed.

We form the equation:

z = 3y + 3r

​∴ 135 = 3(30) + 3r

135 = 90 + 3r

3r = 135 − 90

3r = 45

r = \(\frac{45}{3}\)

r = 15

The number of flowers in each red flower bed is 15.

Therefore, the equation that represents the number of red and yellow flowers is  135  =  90 + 3r

A garden contains 135 flowers, each of which is either red or yellow.

There are 3 beds of yellow flowers and 3 beds of red flowers.

There are 30 yellow flowers each yellow flower bed.

To find/solve:

Write another real-world situation that your equation from Part A could represent.

An equation is a statement of equality between two expressions consisting of variables and numbers.

The equation that represents the number of red and yellow flowers is  3r + 90  = 135.

The equation that represents the number of red and yellow flowers is   3r + 90  = 135.

Envision Math Accelerated Grade 7 Volume 1 Chapter 6 Solving Problems Using Equations And Inequalities

Question. How can you solve real-world and mathematical problems with numerical and algebraic equations and inequalities?

Given

Statement

To find/solve

How can you solve real-world and mathematical problems with numerical and algebraic equations and inequalities?

The equation shows the relationship between variables and other quantities in a situation which involves different operations on numbers.

The left side of an equation must have the same value with the right side to make the equality true.

The variable will also indicate balance in the relationship of the equation.

The left side of an equation must have the same value with the right side to make the equality true.

The left side of an equation must have the same value with the right side to make the equality true.

We need to research the need for safe, clean water in developing countries.

Based on the research, we need to determine the type, size, and cost of a water filtration system needed to provide clean, safe water to a community.

Also, we have to develop a plan to raise money to purchase the needed filtration system.

Reverse osmosis systems are the most effective filters for drinking water.

Many of them feature seven or more filtration stages along with the osmosis process that makes them.

Effective at moving 99 percent of contaminants from water, including chemicals such as chlorine, heavy metals, pesticides, and herbicides.

Filtered water reduces corrosion and improves PH levels also extending the life of household fixtures.

It costs around $30 per square foot.

We can organize community parties to fetch donations for raising money for the purchase of the needed filtration system.

Reverse osmosis systems are the most effective filters for drinking water. It helps us in getting safe, clean water in developing countries.

A property of equality states that performing the same operation on both sides of an equation will keep the equation true.

Properties that state that performing the same operation on both sides of an equation will keep the equation true are called properties of equality.

The inverse relationship is involved in addition and subtraction because they can “undo” each other.

Addition and subtraction have a(n) inverse relationship because they can “undo” each other.

Like terms are terms that have same the variables and powers

Example:

5x+10x

Terms that have the same variable are called like terms.

Envision Math Accelerated Grade 7 Chapter 6 Exercise Key Answers

Question. Find the value of x to solve the given equation x + 9.8 = 1.2

We need to use properties to solve the given equation for x

The given equation is  x + 9.8 = 14.2

The given equation is   x + 9.8 = 14.2

Solving it, we get

​x + 9.8 = 14.2

x + 9.8 − 9.8 = 14.2 − 9.8

x = 4.4

The value of x=4.4

Question. Find the value of x solve the given equation 14x = 91.

We need to use properties to solve the given equation for x

The given equation is  14x = 91

The given equation is 14x = 91

Solving it, we get

14x = 91

\(\frac{14x}{14}\)=\(\frac{91}{14}\)

x = 13

The value of x = 13

Question. Find the value of x solve the given equation \(\frac{1}{3}x\)

We need to use properties to solve the given equation for x

The given equation is  \(\frac{1}{3}x\) = 24

The given equation is  \(\frac{1}{3}\)x = 24

Solving it, we get

\(\frac{1}{3}\)x = 24

3×\(\frac{1}{3}\)x = 3 × 24

x = 3 × 24

x = 72
​
The value of x = 72

Envision Math Grade 7 Chapter 6 Solving Equations And Inequalities Solutions

Question. Solve the expression and combine like terms \(\frac{1}{4}+\frac{1}{4}m-\frac{2}{3}k+\frac{5}{9}m\).

We need to combine like terms in the given expression.

The given expression is \(\frac{1}{4} k+\frac{1}{4} m-\frac{2}{3} k+\frac{5}{9} m\)

The given is, \(\frac{1}{4} k+\frac{1}{4} m-\frac{2}{3} k+\frac{5}{9} m\)

Combining the like terms, we get

=   \(\frac{1}{4} k−\frac{2}{3} k + \frac{1}{4} m+\frac{5}{9} m\)

=   k(\(\frac{1}{4}\)−\(\frac{2}{3}\)) + m( \(\frac{1}{4}\) + \(\frac{5}{9}\))

=  k(\(\frac{3−8}{12}\)) + m(\(\frac{9+20}{36}\))

=  k (\(\frac{−5}{12}\)) + m (\(\frac{29}{36}\))

=\(\frac{−5}{12}\) k + \(\frac{29}{36}\)m

The expression becomes  \(\frac{-5}{12} k+\frac{29}{36} m\)

Solving Problems Using Equations And Inequalities Grade 7 Envision Math

Question. Solve the expression and combine like terms -4b + 2w + (-4b) + 8w.

We need to combine like terms in the given expression.

The given expression is −4b + 2w + (−4b) + 8w

The given is, −4b + 2w + (−4b) + 8w

Combining the like terms, we get

​−4b + 2w + (−4b) + 8w

= −4b + 2w − 4b + 8w

=  b(−4−4) + w(2 + 8)

= −8b + 10w

The expression becomes −8b + 10w

Question. Solve the expression and combine like terms 6 – 5z + 8 – 4z + 1.

We need to combine like terms in the given expression.

The given expression is 6−5z + 8 − 4z + 1

The given is 6 − 5z + 8−4z + 1

Combining the like terms, we get

​6−5z + 8 − 4z + 1

=  6 + 8 + 1 − 5z − 4z

=  15 − z(5 + 4)

= 15 − 9z

The expression becomes 15 − 9z

Envision Math Grade 7 Chapter 6 Exercise Key Solutions

Question. A large box of golf balls has more than 12 balls. We need to describe how your inequality represents the situation.

We need to write an inequality that represents the situation

A large box of golf balls has more than 12 balls.

We need to describe how your inequality represents the situation.

Given that a large box of golf balls has more than 12 balls.

Let x be the number of golf balls in a large box.

If it is more than that, it is represented by the symbol <

Thus, the inequality equation will be

​12 < x

x > 12
​
The inequality that represents the situation x > 12

Envision Math Accelerated Grade 7 Chapter 6 Exercise Answers

Question. Write the similarities and differences between an equation and an inequality.

We have to write the similarities and differences between an equation and an inequality.

Similarities between an equation and an inequality:

Equation and inequality both use variables when writing and expressing.

Just like the equations, the solution to equality is a value that makes the inequality true.

Both expressions may have different solutions.

Differences:

An equation is a mathematical statement that shows the equal value of two expressions.

While an inequality is a mathematical statement that shows that an expression is lesser than or more than the other.

An equation has only one definite value of a variable while an inequality may have several values because of its range.

Both equations and inequalities show the relation between two expressions. The equation shows that the two expressions are equal while inequalities show that an expression is bigger or smaller than the other.