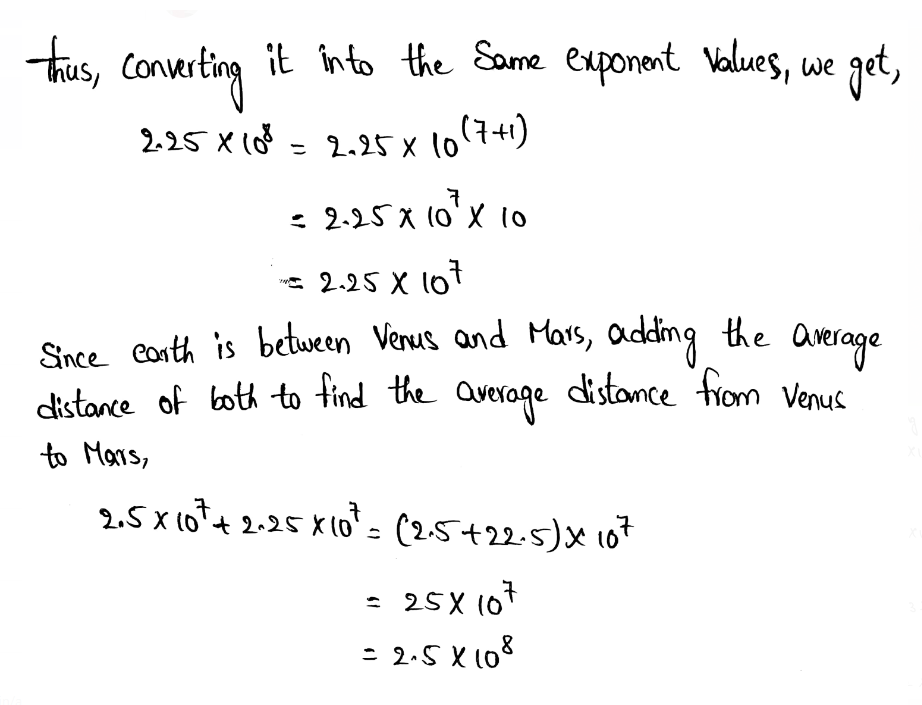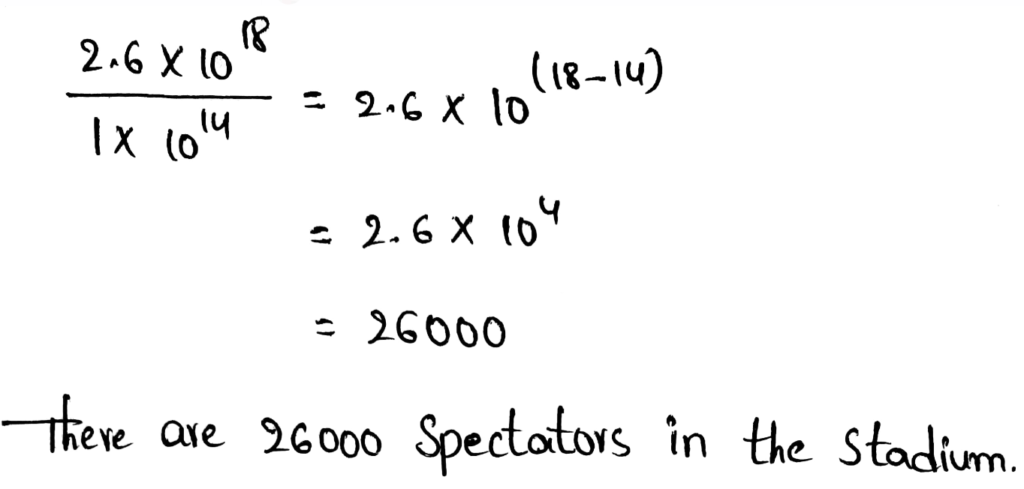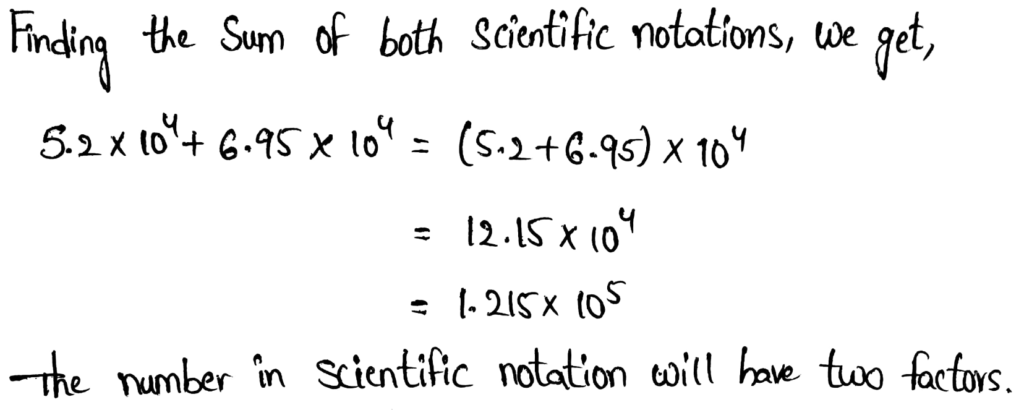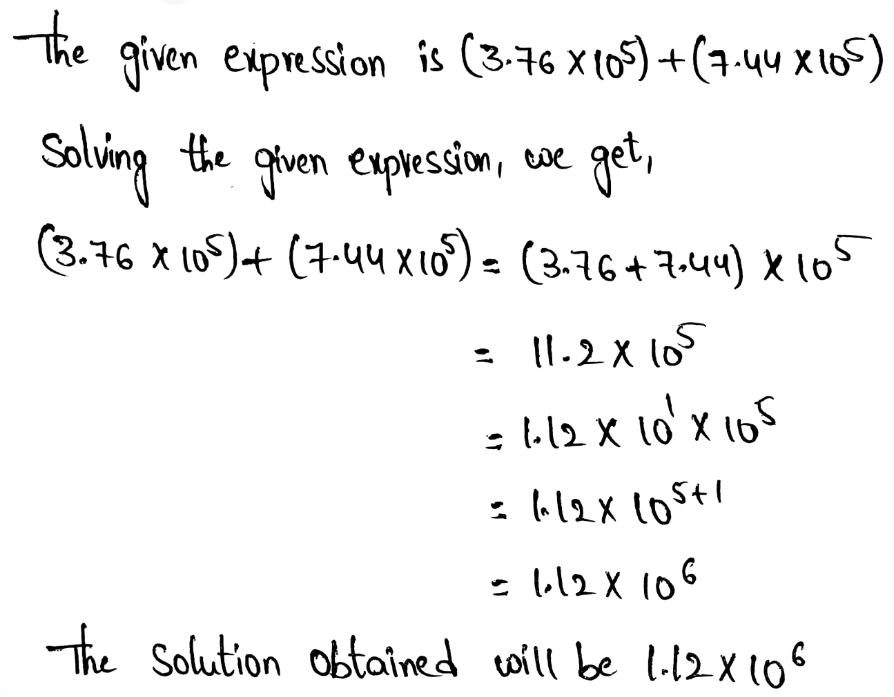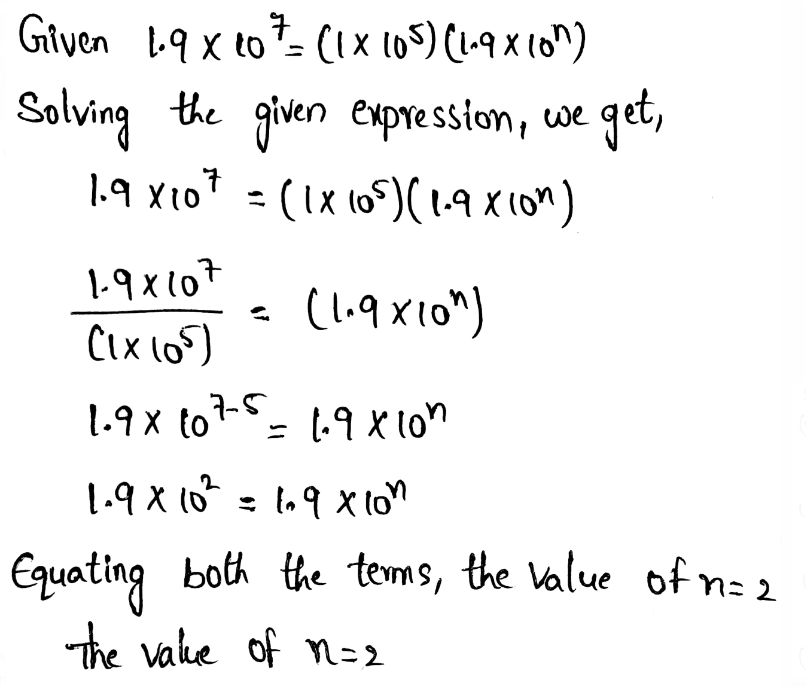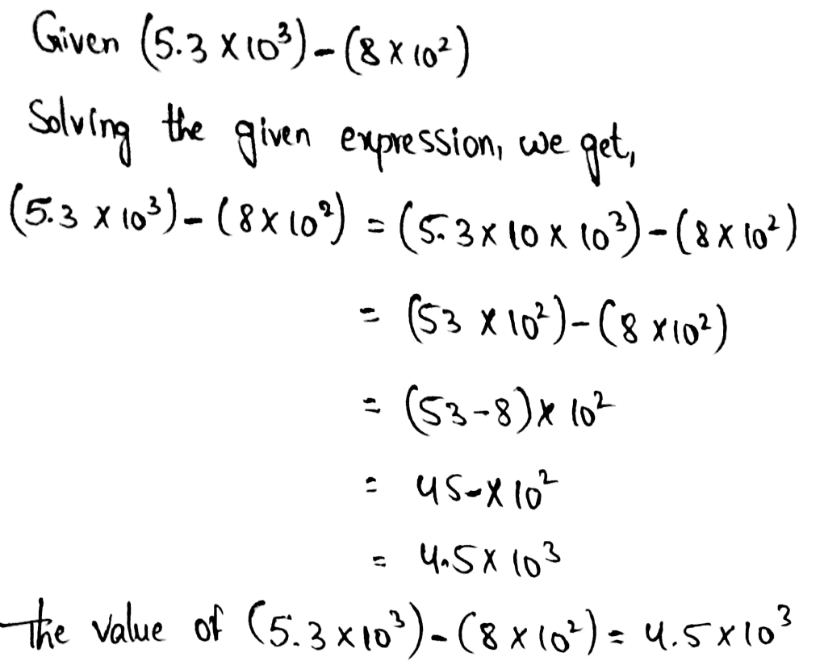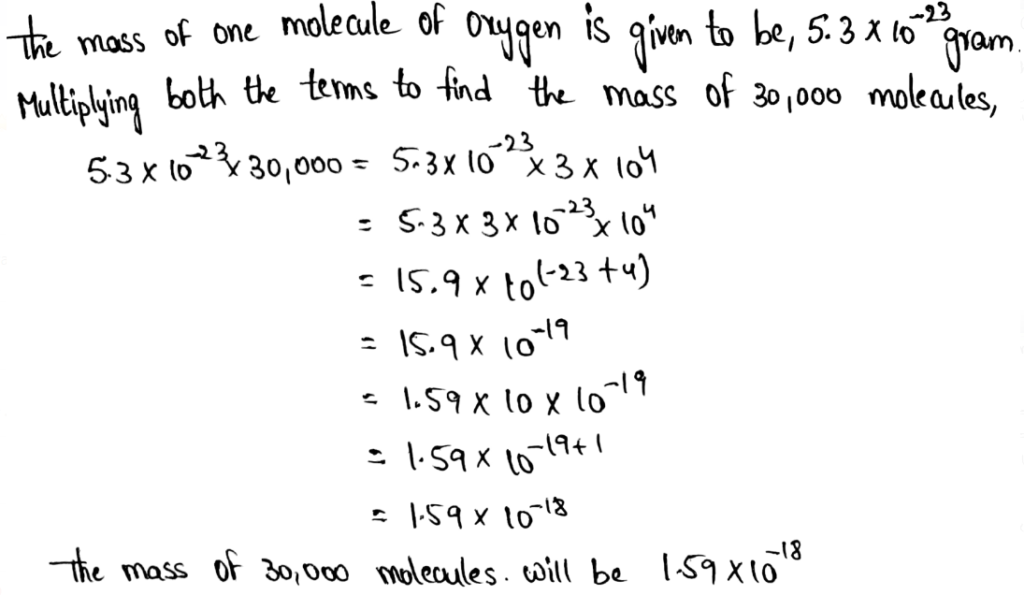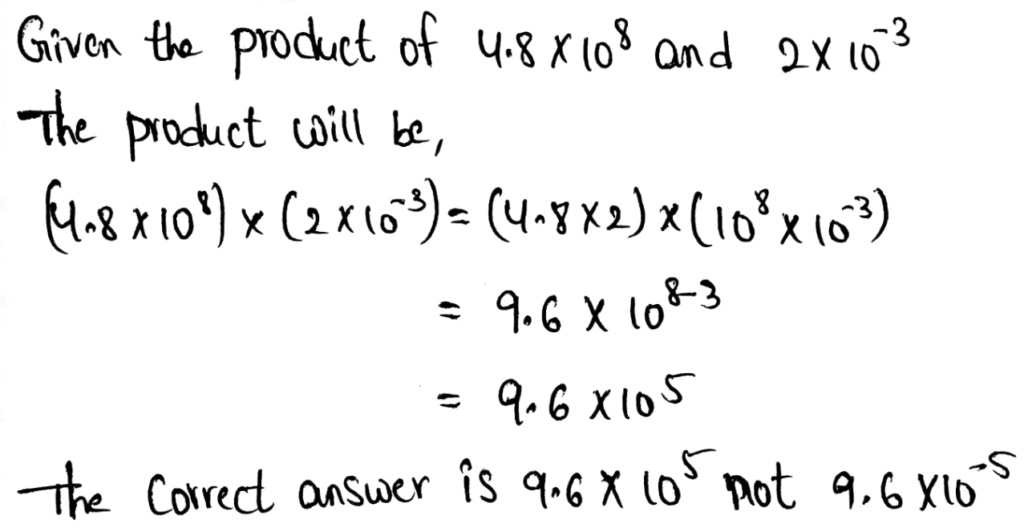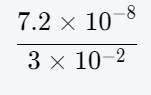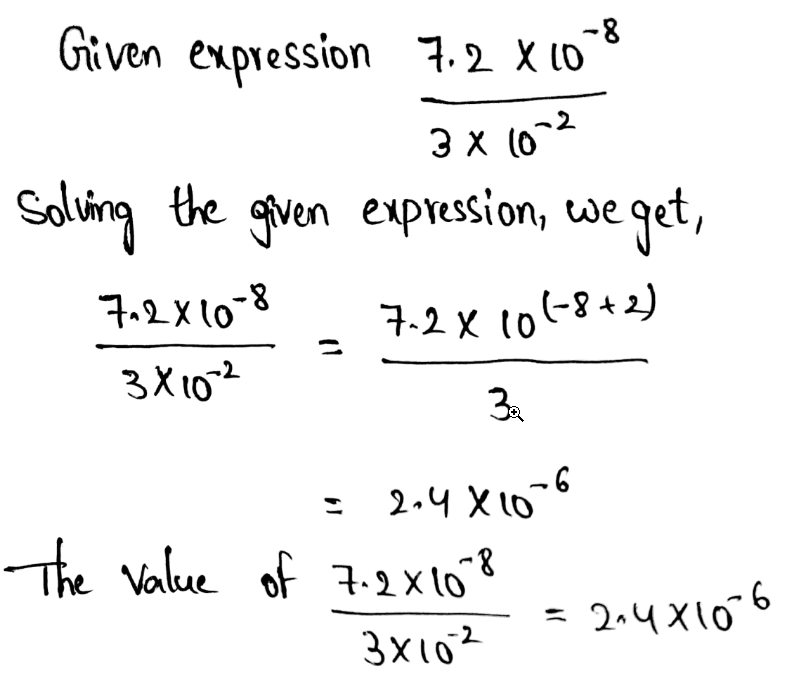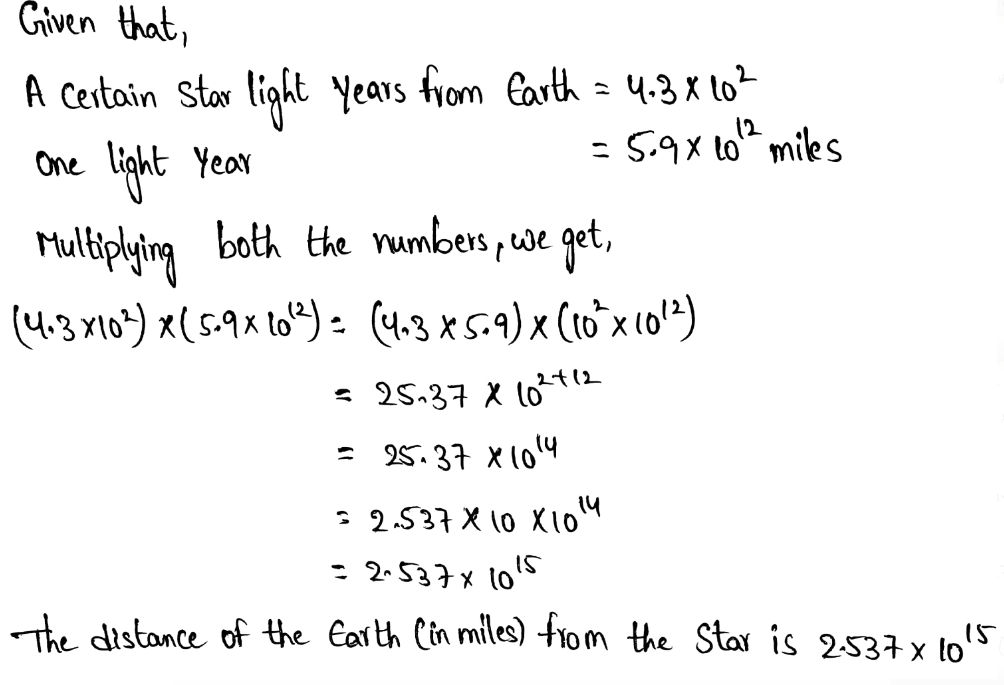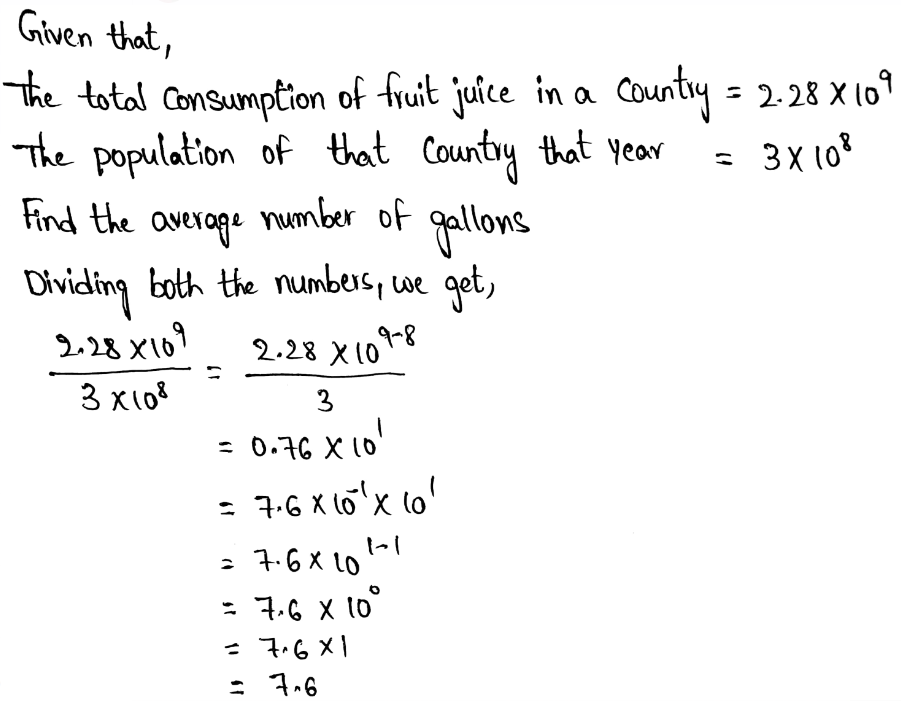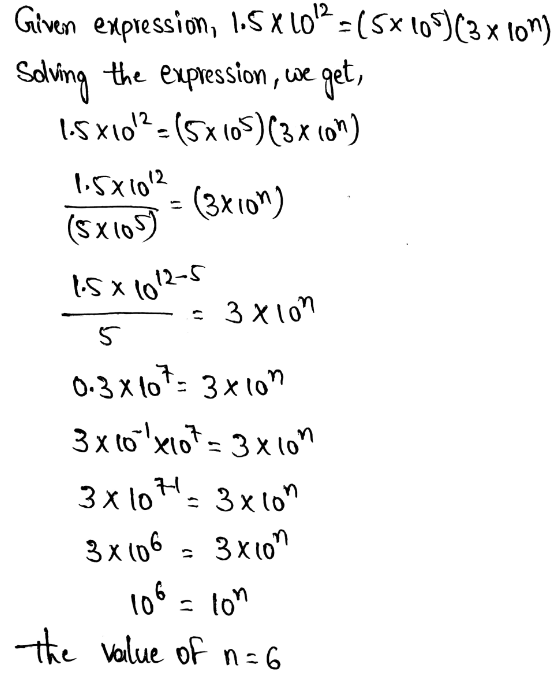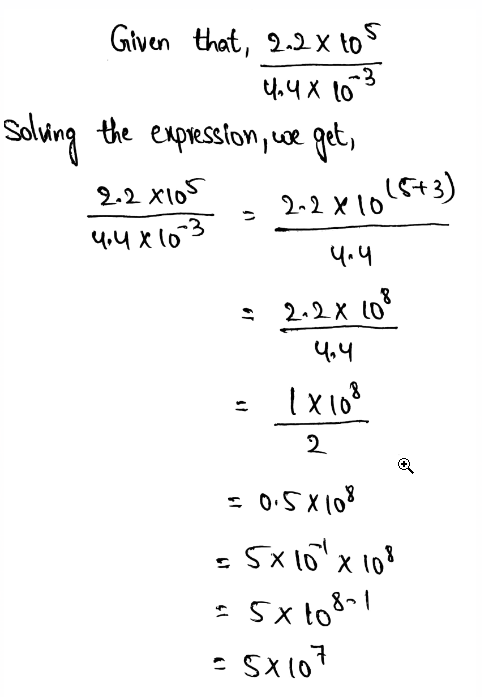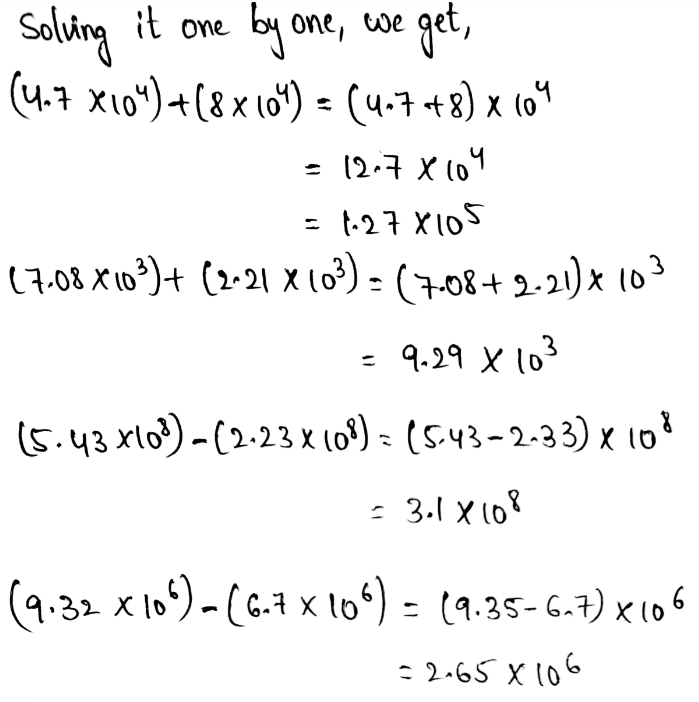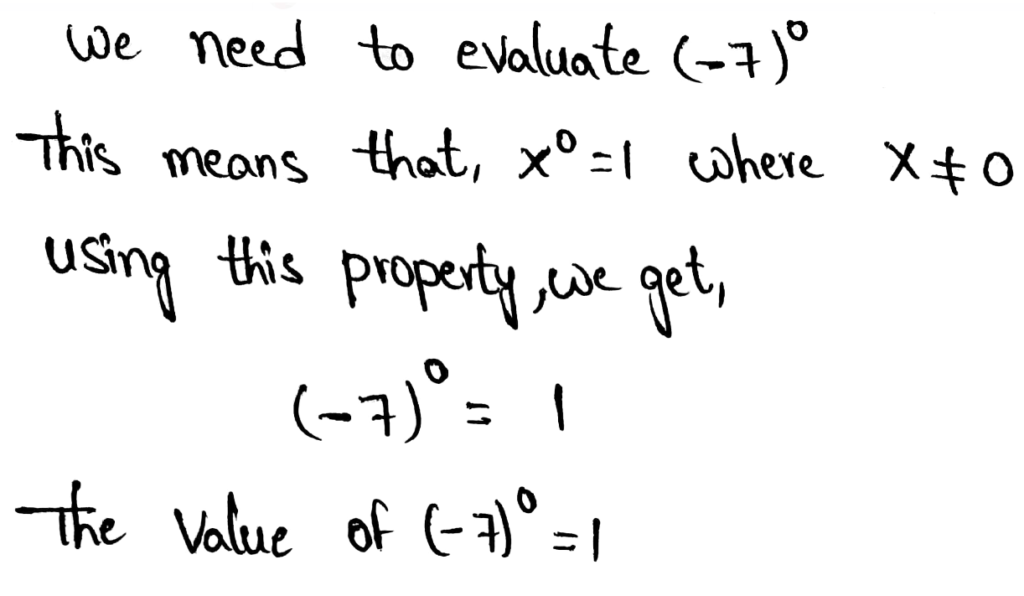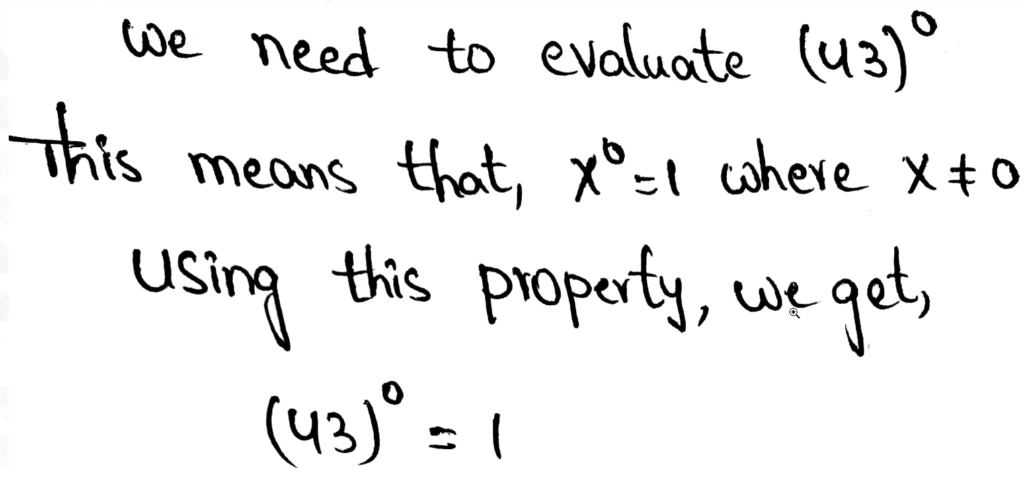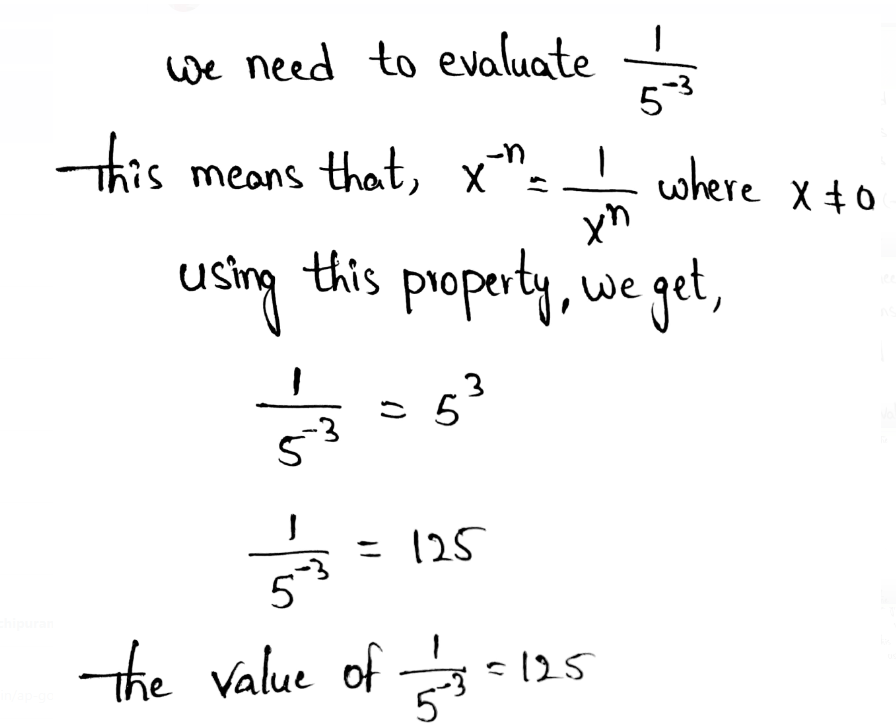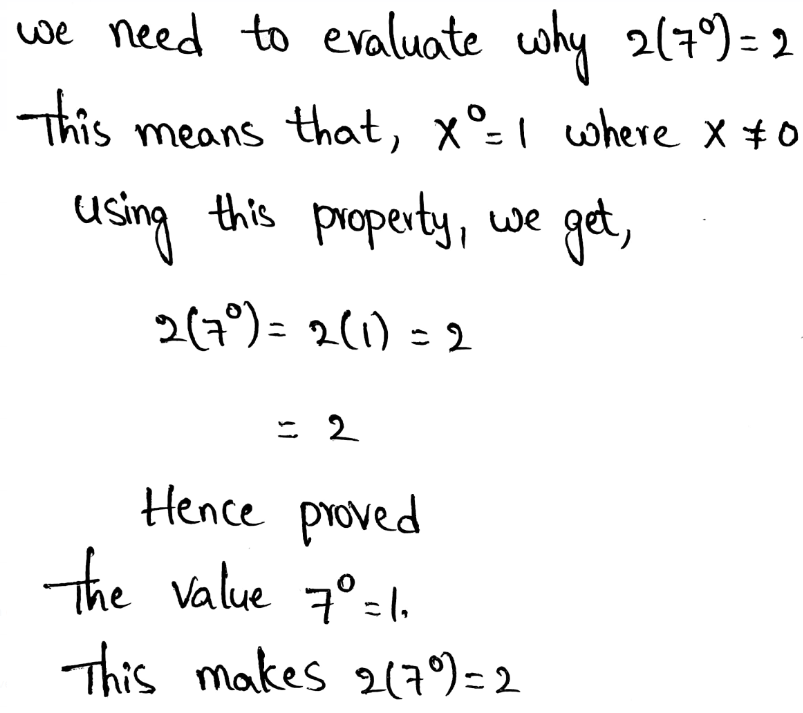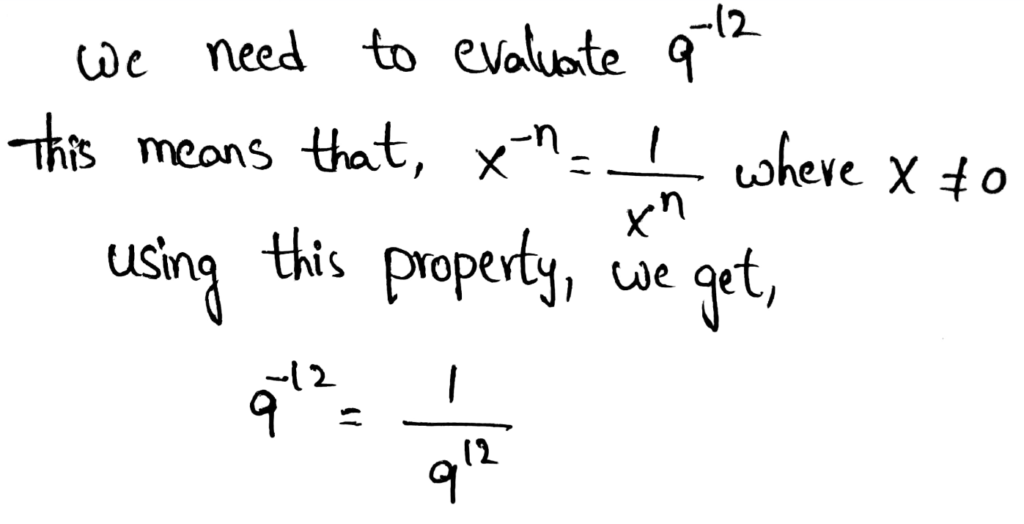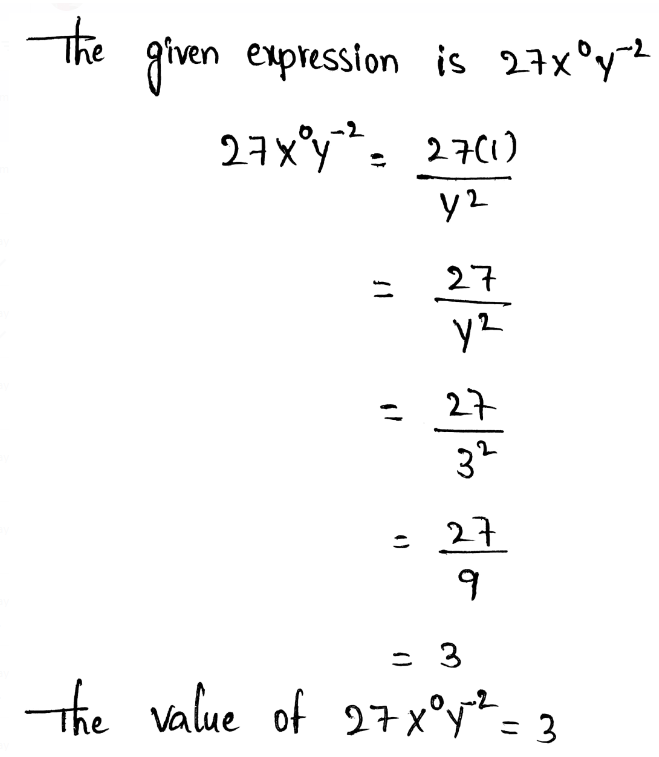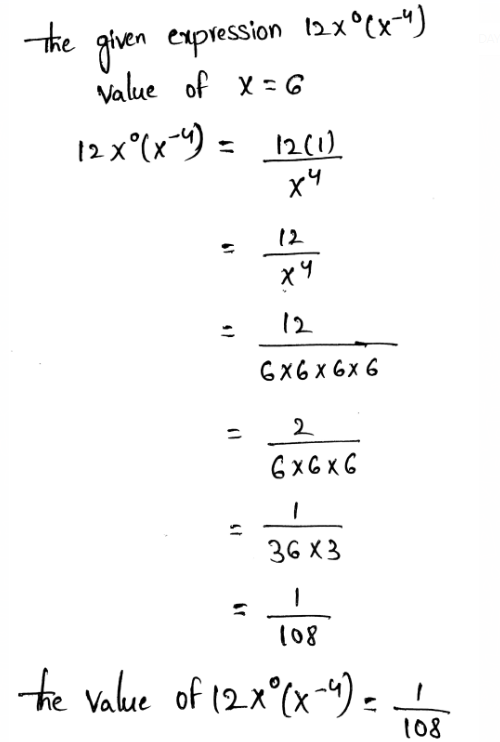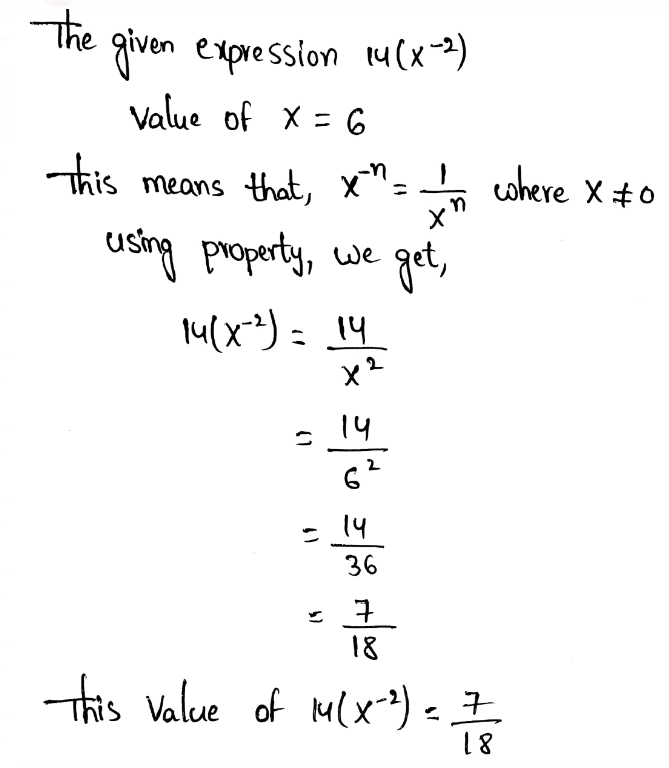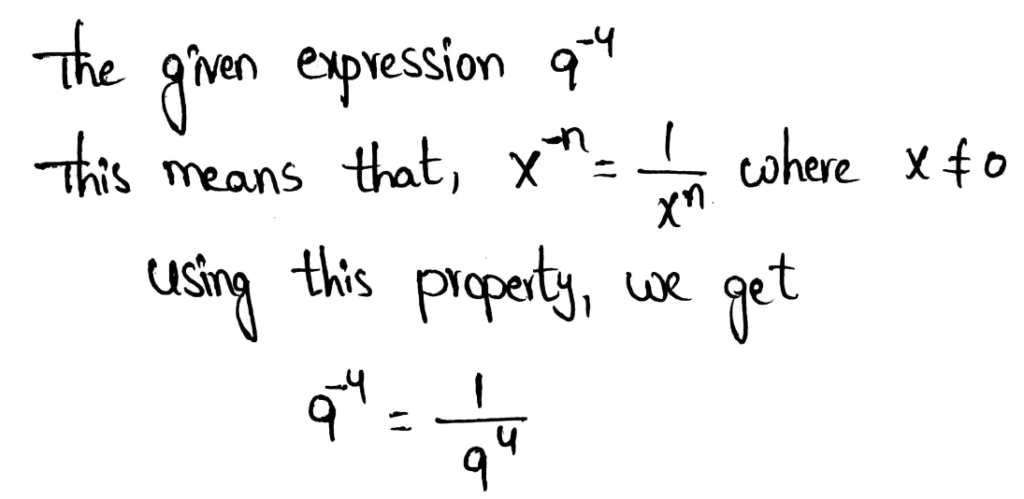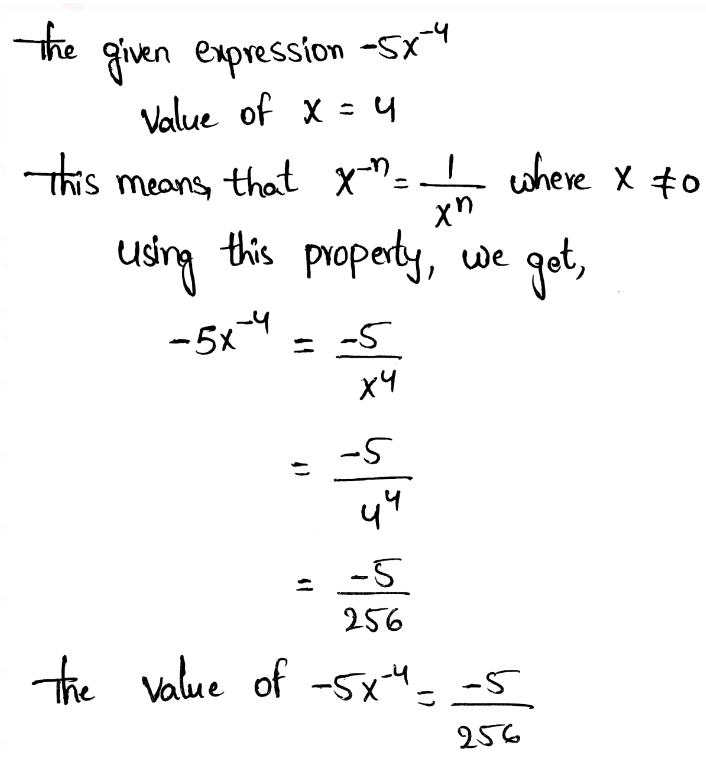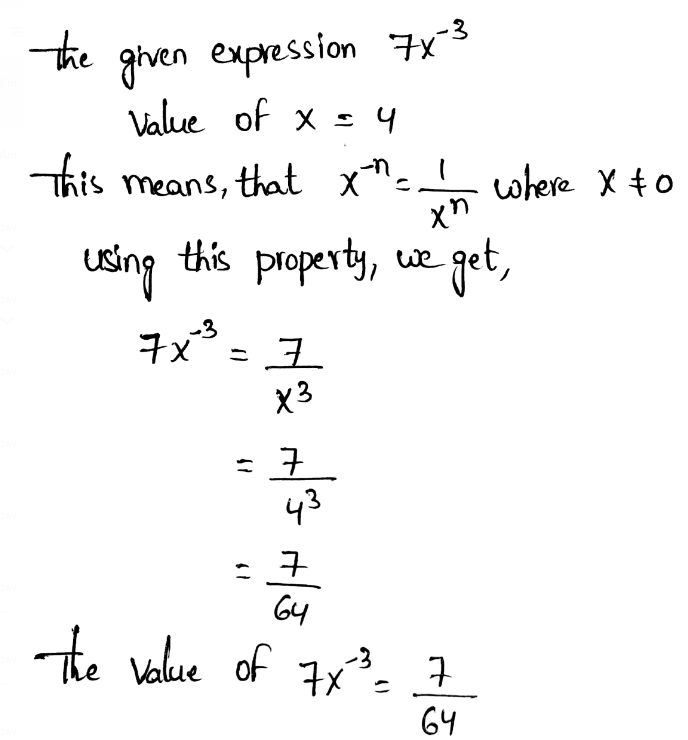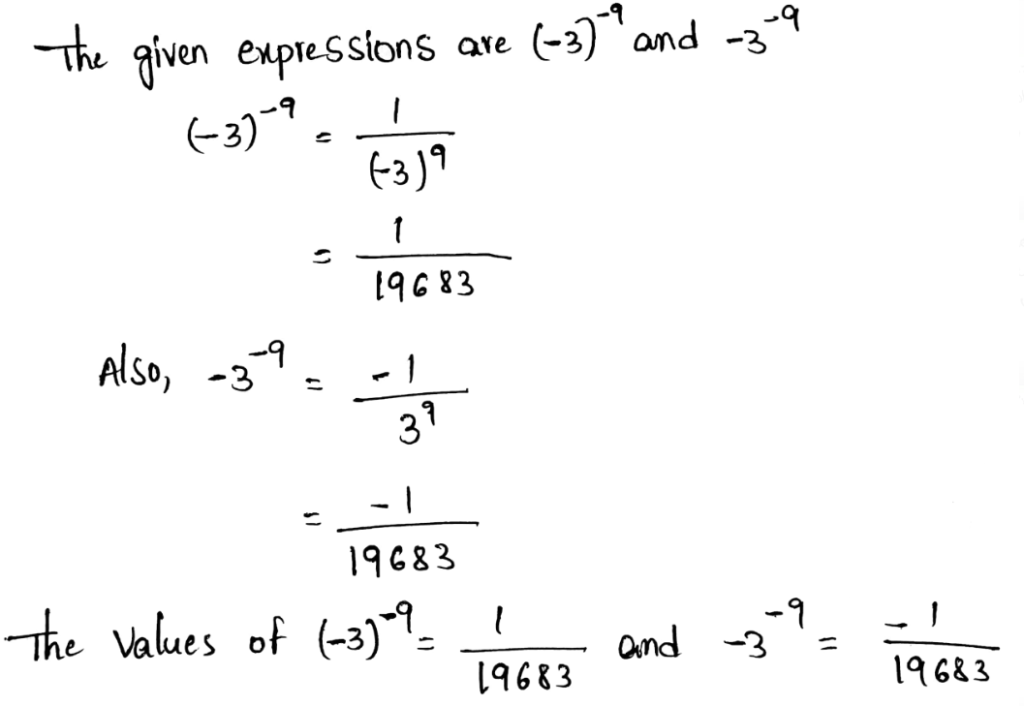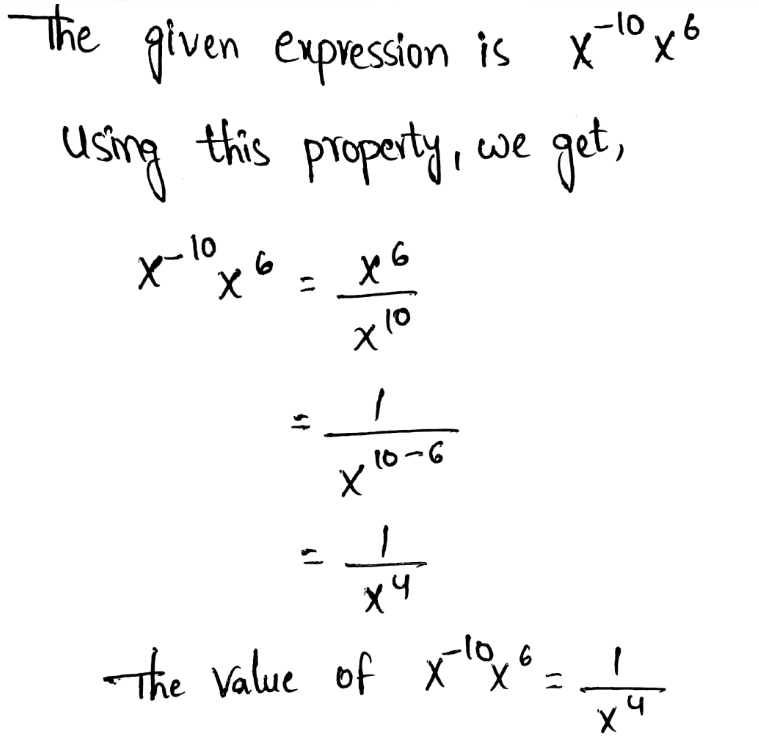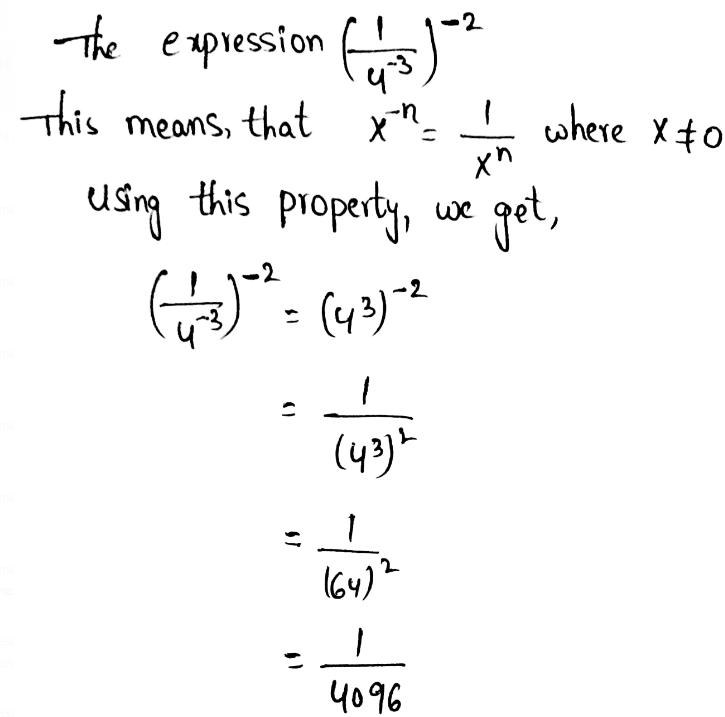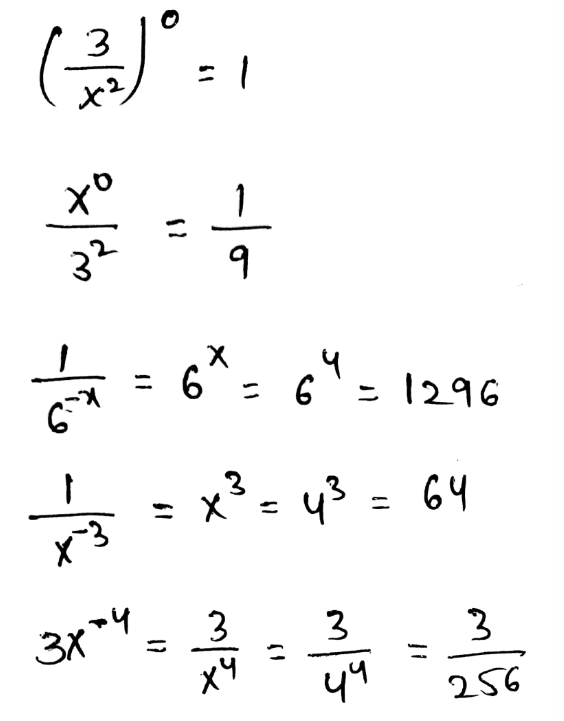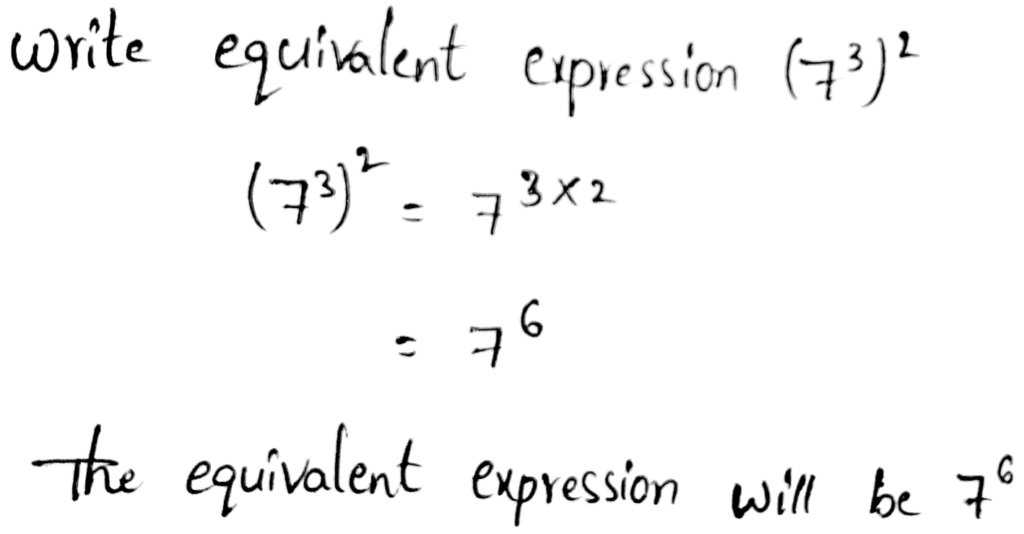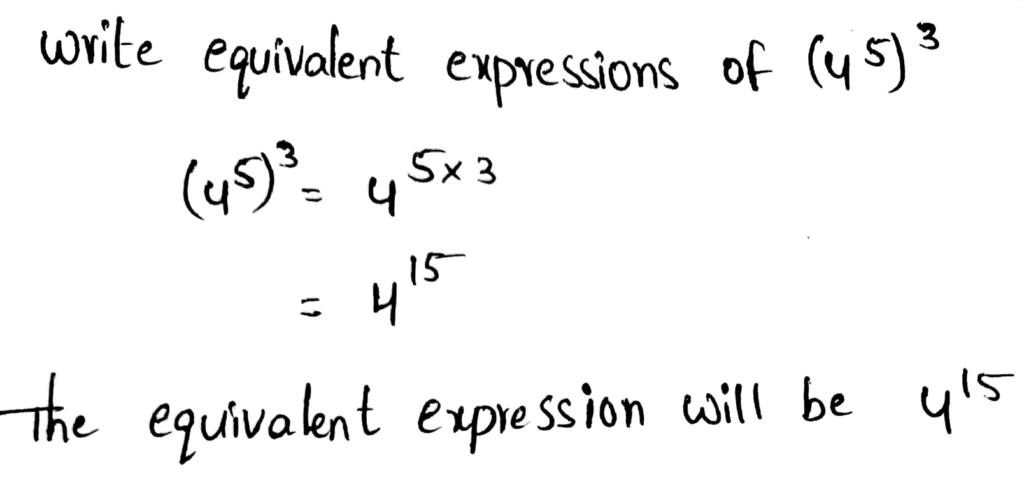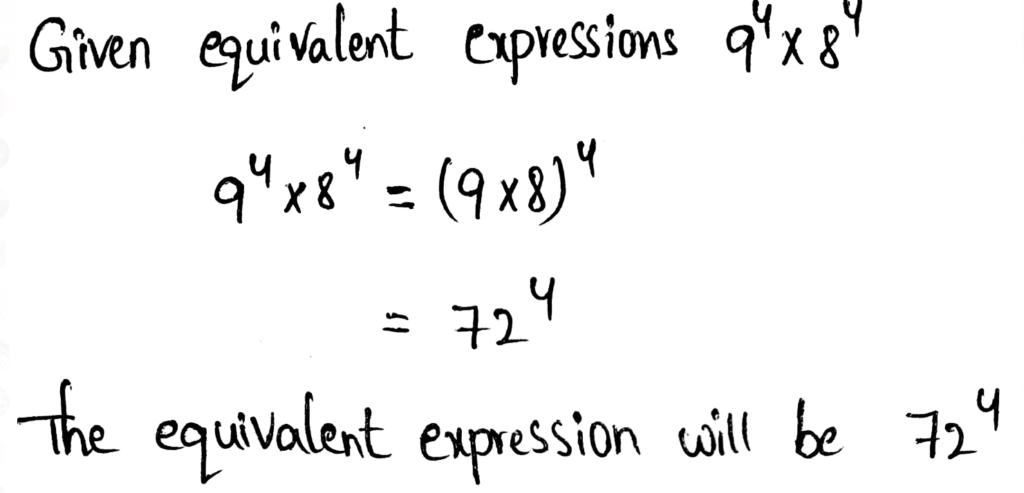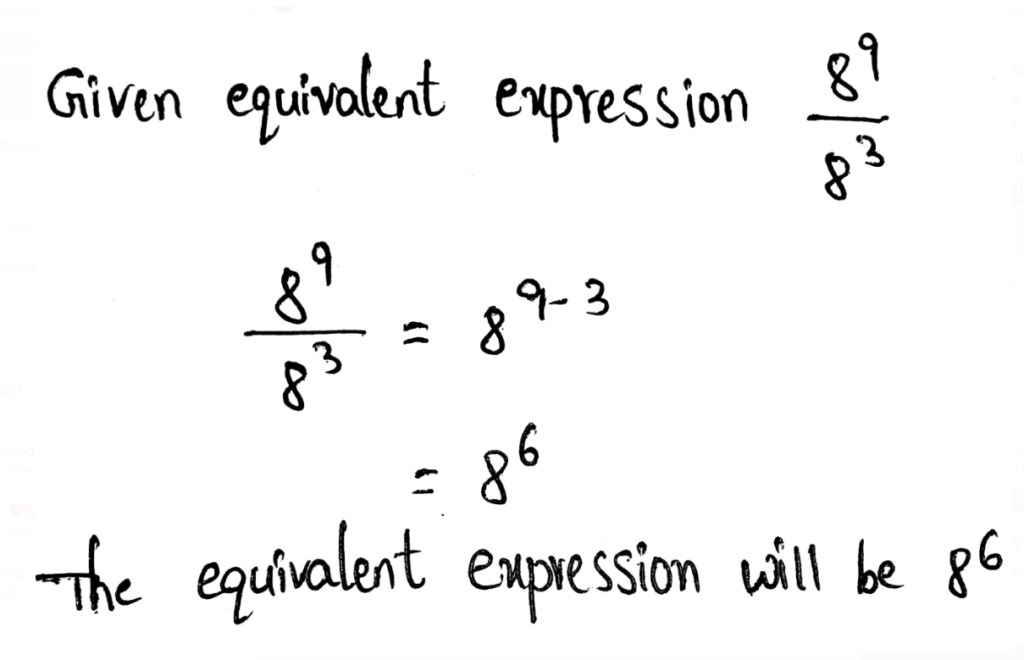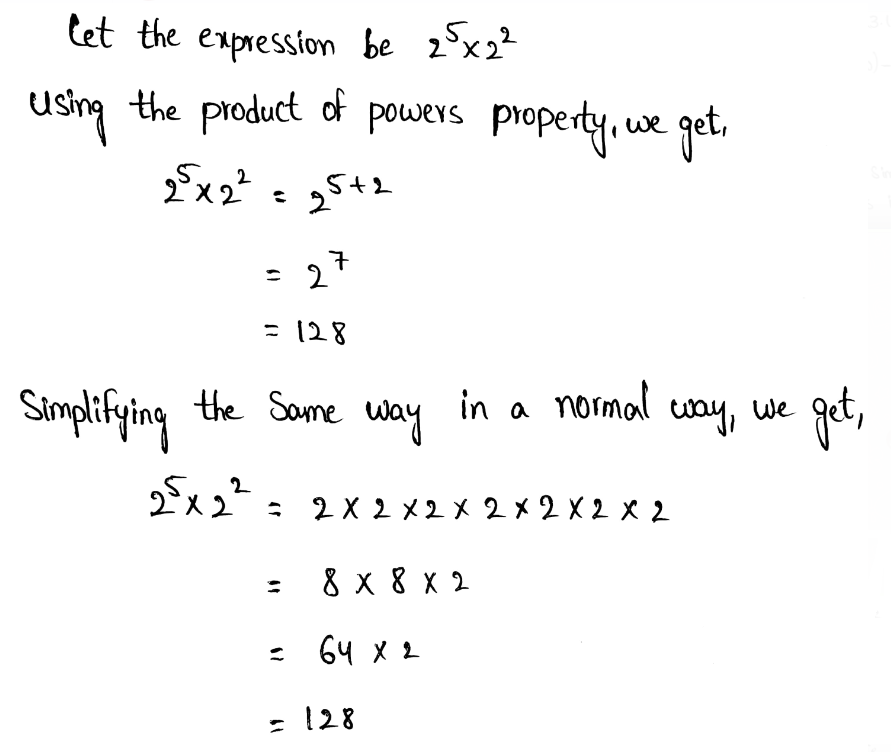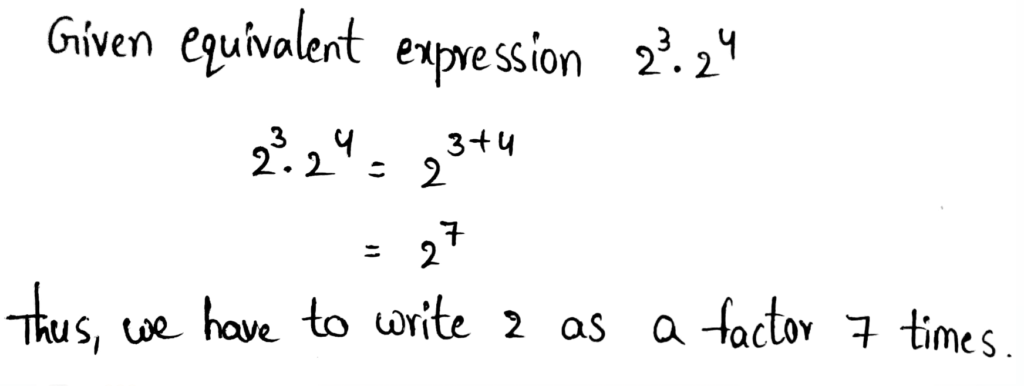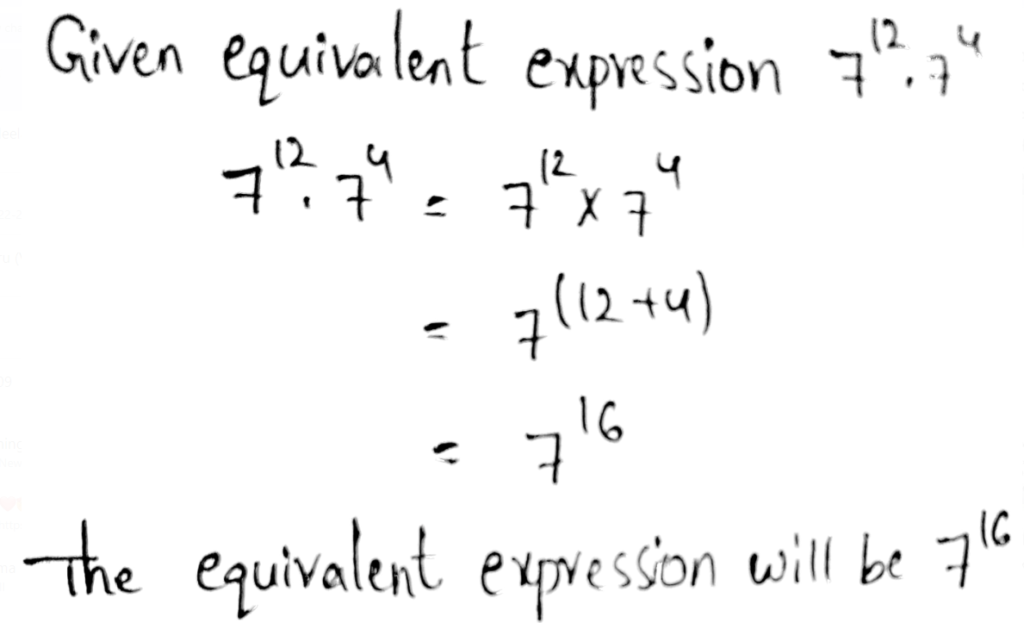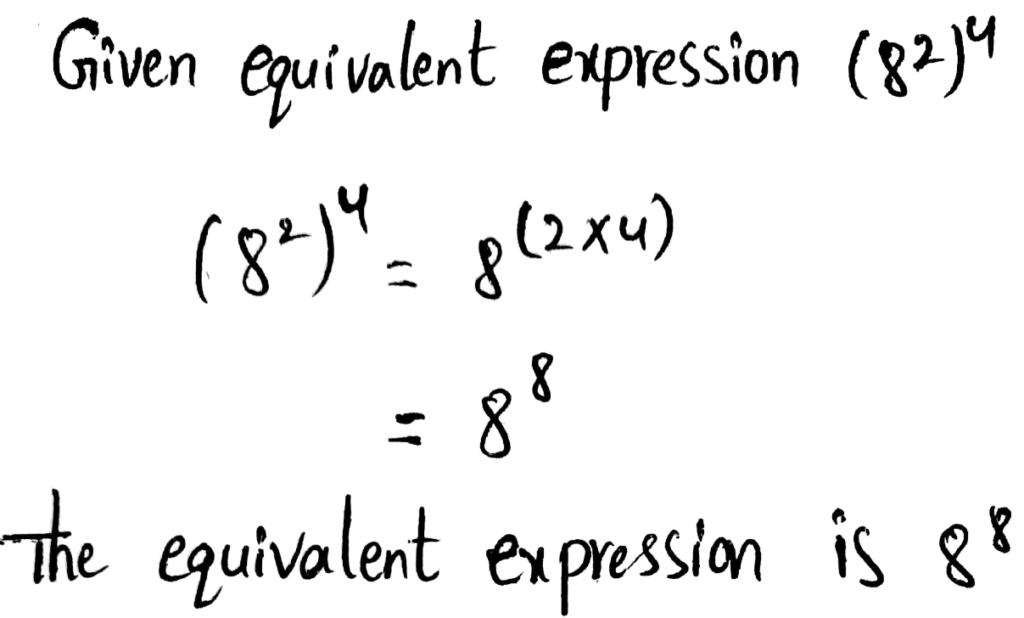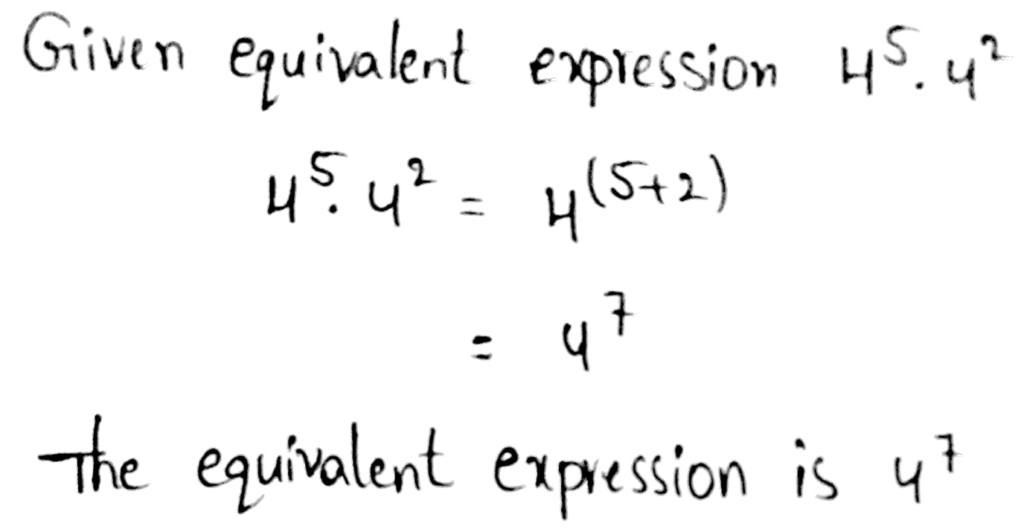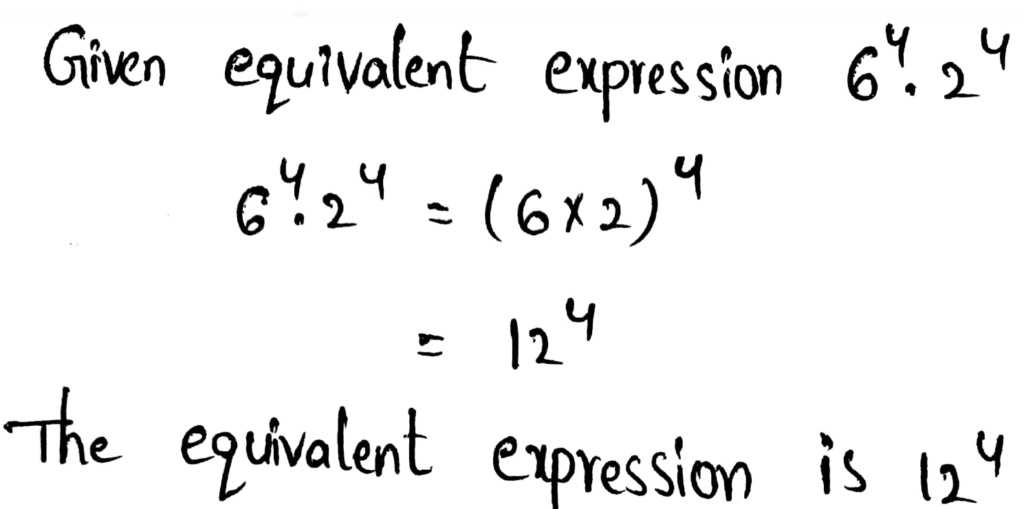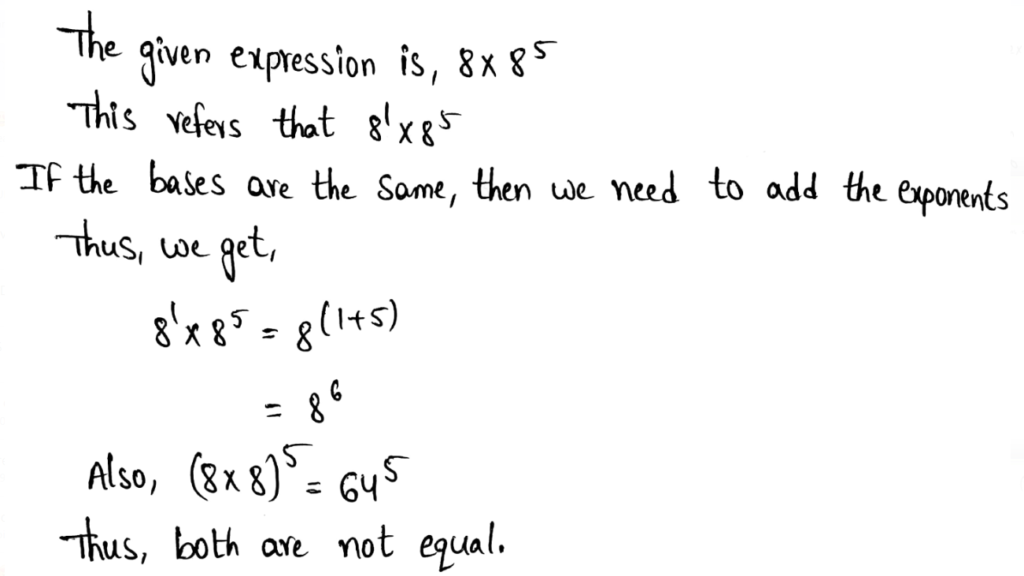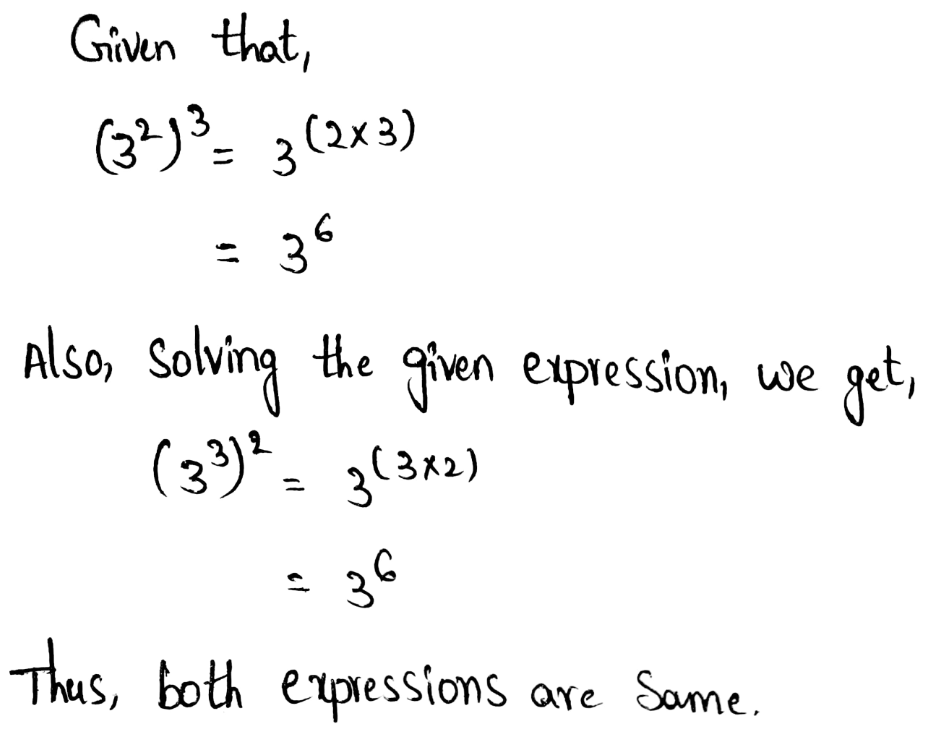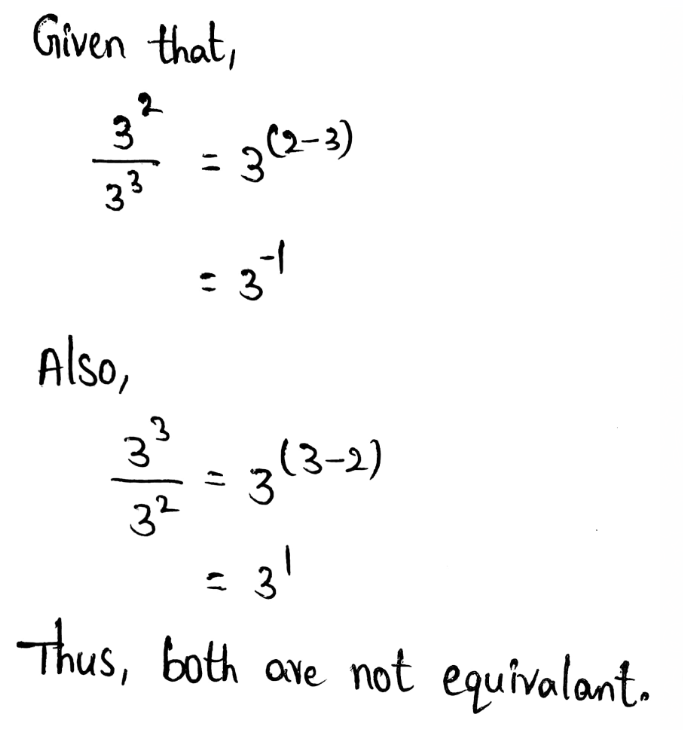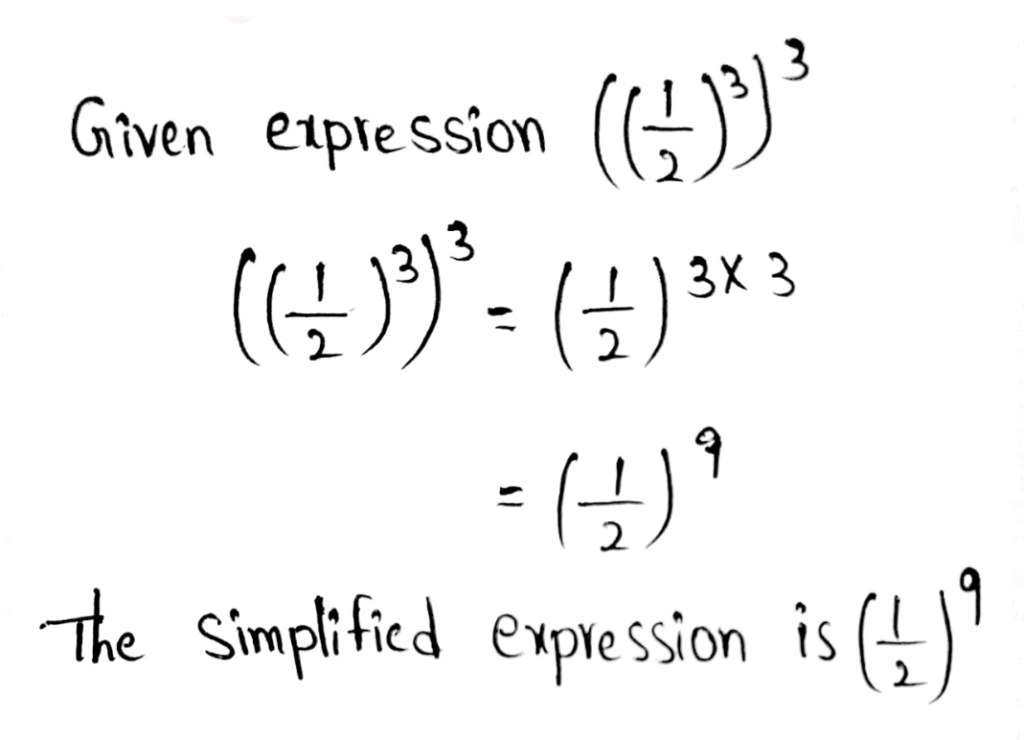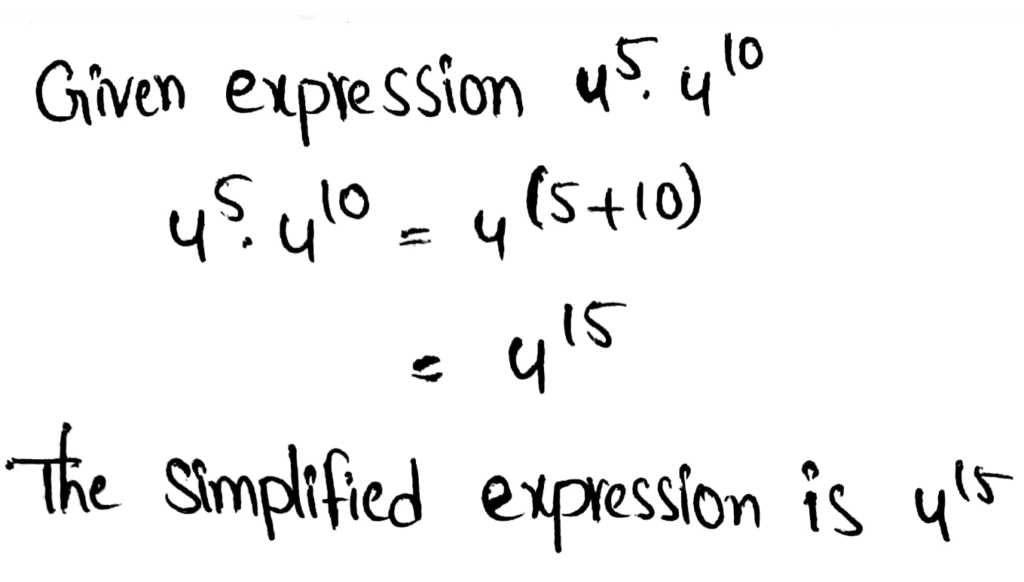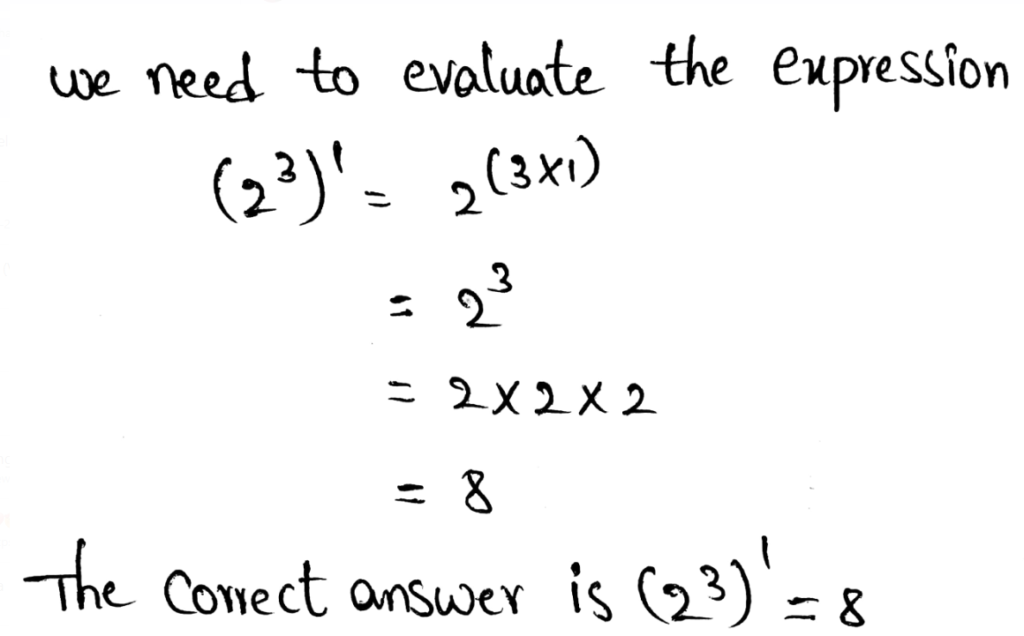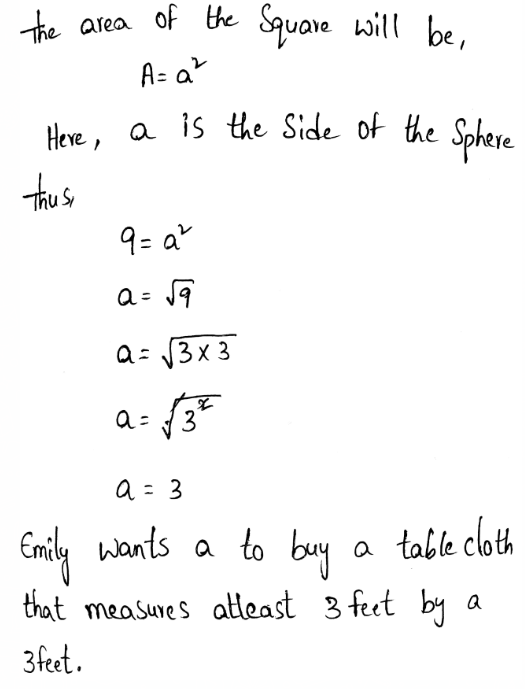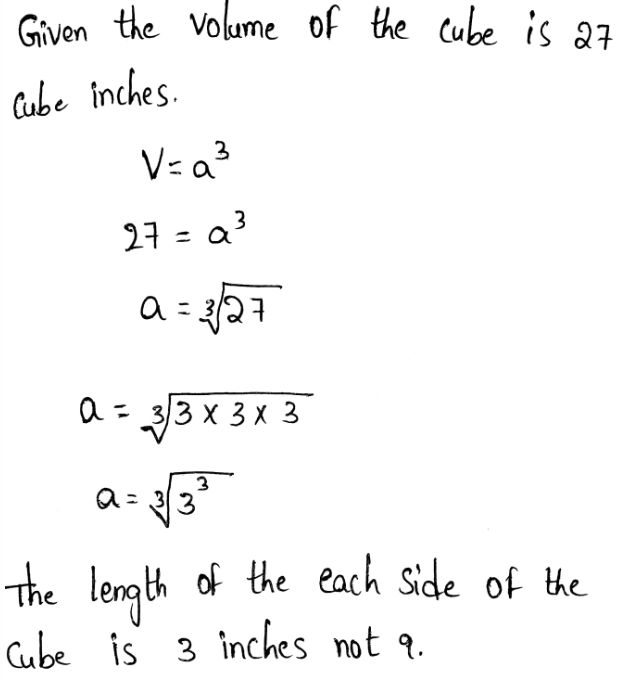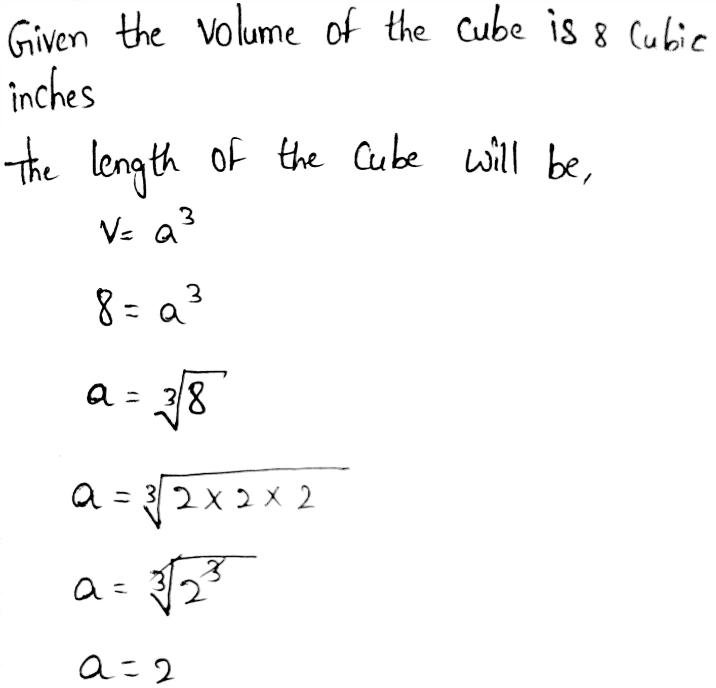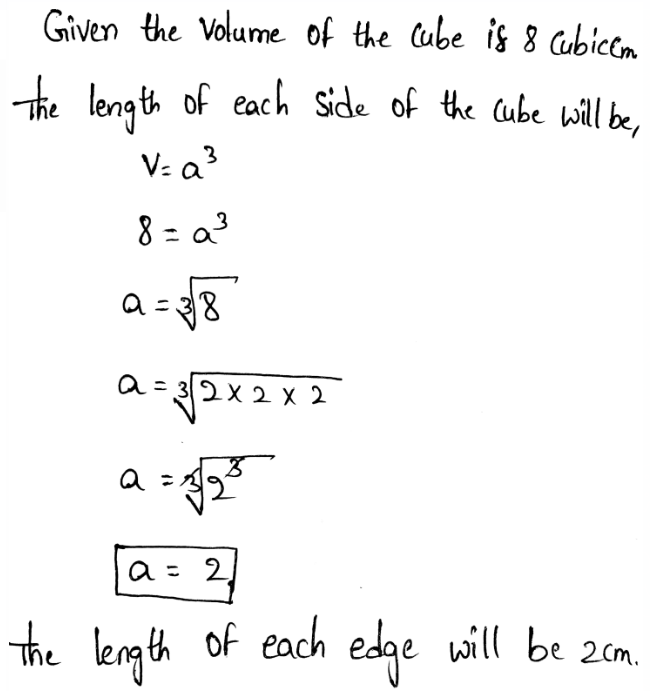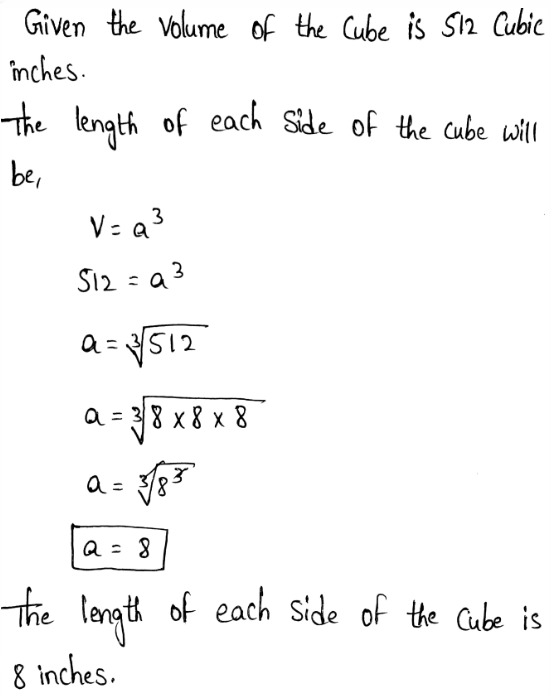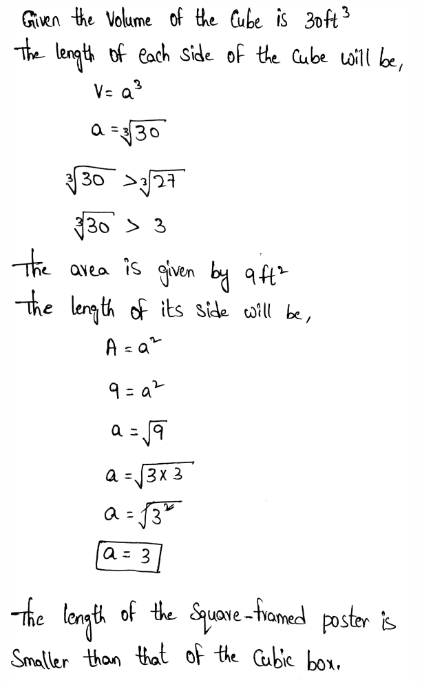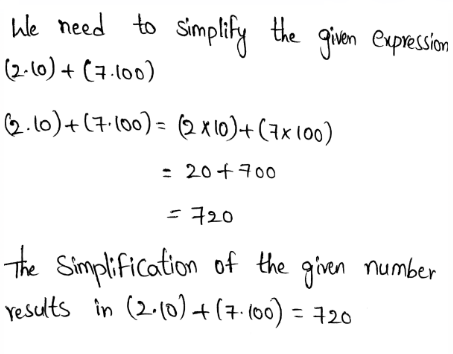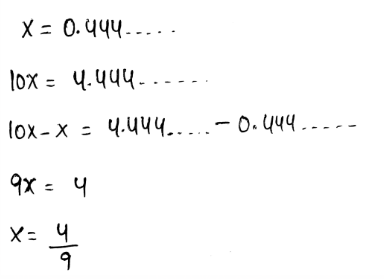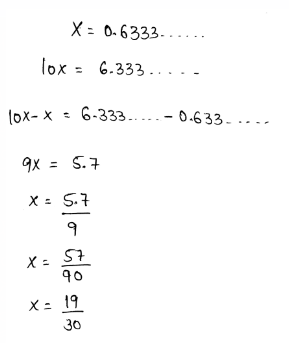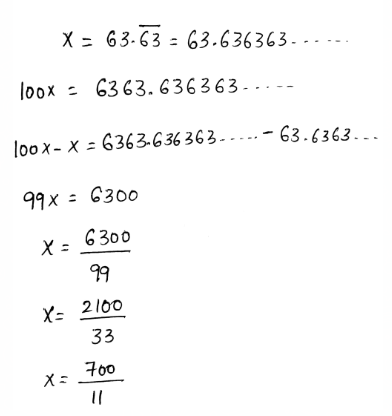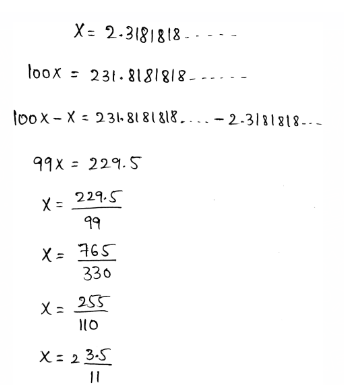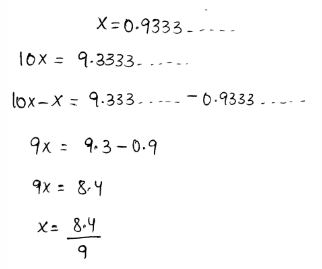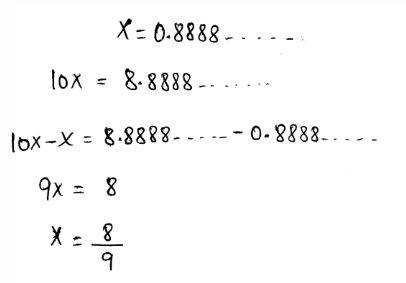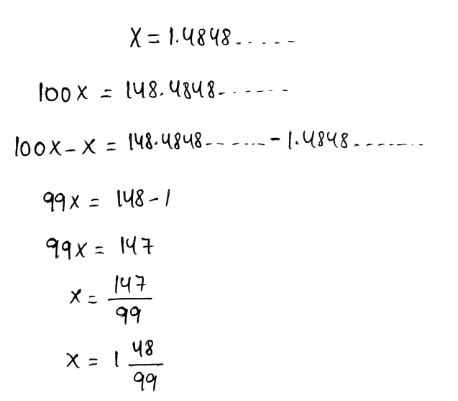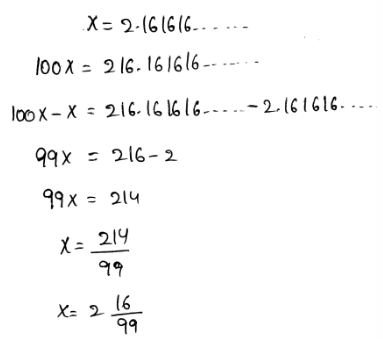Envision Math

Envision Math Grade 8 Volume 1 Chapter 1: Real Number

Page 73 Question 1 Answer

• A real number would be any number that can be discovered in the actual world. Numbers can be found all around us.
• Natural numbers are being used to count objects.
• Rational numbers are being used to portray fractions.
• Irrational numbers are being used to calculate the square root of an amount.
• Integers are used to measure temperature, among other things.
• These various types of numbers combine to form a gathering of real numbers.
• Except for complex numbers, everything comes under real numbers.
• It is denoted by R and it is the union of both rational and irrational numbers and it is represented by \(R=Q \cup \bar{Q}\)
• Real numbers are used in many places to solve problems. For example, it is used to portray fractions, determine square roots, measure temperature, and for counting things etc.

Envisionmath 2.0 Grade 8 Chapter 1 Real Number Solutions

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 73 Exercise 1 Answer

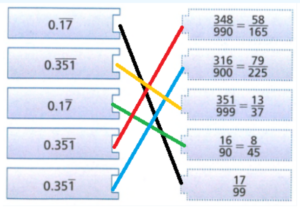
• We have to draw lines to connect each vocabulary word with its definition.
• Cube root is nothing but a number whose cube equals the original number.
• For example, The cube root of \(\sqrt[3]{64} \text { is } 4\).
• Square root is nothing but a number whose square equals the original number.
• Example – The square root of \(\sqrt{16} \text { is } 4\)
• A perfect cube is a number that is the result of multiplying the number three times by itself.
• Example – The cube of 5 is 125
• A perfect square is a number that is the result of multiplying the number two times by itself.
• Example – The square of 5 is 25
• Scientific is a way of expressing very big or very small numbers in compact form.
• Example – 3.5 ×10¹² which is equal to 3500000000000
• Power of powers property states that when we have an exponent which is raised to a power, then we need to multiply those by keeping the bases same.
• Example – (4²)³ = 4^{2 × 3} = 4⁶
• Power of products property states that when multiplying two powers with the same base, add the exponents by keeping the base same.
• Example – 2⁵⋅2¹⁰ = 2⁵⁺¹⁰ = 2¹⁵
• Product of powers property states that when multiplying two same exponents with the different bases, keep the exponents by multiplying the bases together.
• Example – 7² ⋅ 5² = (7 × 5)² = 35²

 

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 73 Exercise 1 Answer

We need to use vocabulary words to explain how to find the length of each side of a square garden with an area of 196 square inches.

The area of the square garden is given by 196 square inches.

The length cannot be negative.

Thus, the length of each side of a square garden is 14 inches.

The length of each side of a square garden is 14 inches.

Envisionmath 2.0 Grade 8 Topic 1 Essential Questions Review Answers

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 74 Exercise 2 Answer

• We need to write the given decimal \(0 . \overline{0} 4\) as a mixed number or fraction.
• A repeating decimal can be written as a fraction by assuming the decimal as a variable.
• After that, multiply each side of it by the multiples of 10
• Subtract both expressions to write the repeating decimals as fractions.
• The decimal is converted to fractions as,​
  ​
  The fraction of the given repeating decimal is \(x=\frac{4}{99}\)

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 74 Exercise 3 Answer

• We need to write the given decimal \(4 . \overline{45}\) as a mixed number or fraction.
• A repeating decimal can be written as a fraction by assuming the decimal as a variable.
• After that, multiply each side of it by the multiples of \(4 . \overline{45}\)
• Subtract both expressions to write the repeating decimals as fractions.
• The decimal is converted to a fraction as,

The mixed number of the given repeating decimal is \(x=4 \frac{45}{99}\)

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 74 Exercise 4 Answer

We need to write the given decimal 2.191919… as a mixed number or fraction.

• A repeating decimal can be written as a fraction by assuming the decimal as a variable.
• After that, multiply each side of it by the multiples of 10
• Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

The mixed number of the given repeating decimal is \(x=2 \frac{19}{99}\)

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 74 Exercise 1 Answer

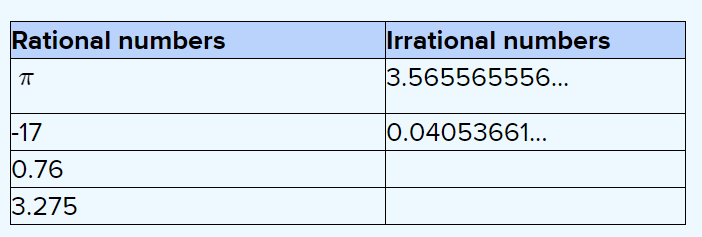
We need to determine which numbers are irrational from among the given.

• Irrational numbers cannot be represented as a fraction.
• Irrational numbers are non-terminating and non-repeating in nature.
• Only terminating and repeating decimals can be represented as a fraction.
• Rational numbers are terminating and repeating in nature.
• Only rational numbers can be represented as a fraction while irrational numbers cannot.

Thus, evaluating the given numbers one by one, we get,

\(\sqrt{36}=6\)

√23 = not a perfect square

\(-4.232323 \ldots=-4 . \overline{23}\)

0.151551555… = non-repeting

\(0 . \overline{35}=\text { repeating }\)

π = 3.14 = terminating

The irrational numbers are

(B) √23

(D) 0.151551555…

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 74 Exercise 2 Answer

We need to explain the number \(-0 . \overline{25}\) is rational or irrational.

• Irrational numbers cannot be represented as a fraction.
• Irrational numbers are non-terminating and non-repeating in nature.
• Only terminating and repeating decimals can be represented as a fraction.
• Rational numbers are terminating and repeating in nature.
• Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number \(-0 . \overline{25}\) is repeating in nature.

Hence, it is a rational number.

The given number \(-0 . \overline{25}\) is a rational number.

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 75 Exercise 1 Answer

We need to find between which two whole numbers does √89 lies.

• Finding where the given square root number lie in the number line, thus,
  ​
  √81 < √89 < √100

9 < √89 < 10
​
The given number lies between the whole numbers 9 and 10

√89 is between 9 and 10.

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 75 Exercise 2 Answer

We need to compare and order the following numbers. Locate each number on a number line.

• \(2 . \overline{3}, \sqrt{8}, 2.5,2 \frac{1}{4}\)
• The given numbers are \(2 . \overline{3}, \sqrt{8}, 2.5,2 \frac{1}{4}\)

Finding where the given square root number lie in the number line, thus,

√4 < √8 < √9

2 < √8 < 3

2.5 < √8 < 3
​
Since it is closer to 9 than 4

Also, \(2 \frac{1}{4}=\frac{9}{4}=2.25\)

Thus, the order becomes,

\(2 \frac{1}{4}<2 . \overline{3}<2.5<\sqrt{8}\)

The order of the given numbers is \(2 \frac{1}{4}<2 . \overline{3}<2.5<\sqrt{8}\)

Solutions For Envisionmath 2.0 Grade 8 Volume 1 Chapter 1

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 75 Exercise 1 Answer

We need to classify the number as a perfect square, a perfect cube, both, or neither. The given number is 27

For a number to be a perfect cube or a perfect square, the result of its cube root or its square root will be a whole number.

The given number is a perfect cube.

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 75 Exercise 3 Answer

We need to classify the number as a perfect square, a perfect cube, both, or neither. The given number is 64

For a number to be a perfect cube or a perfect square, the result of its cube root or its square root will be a whole number.

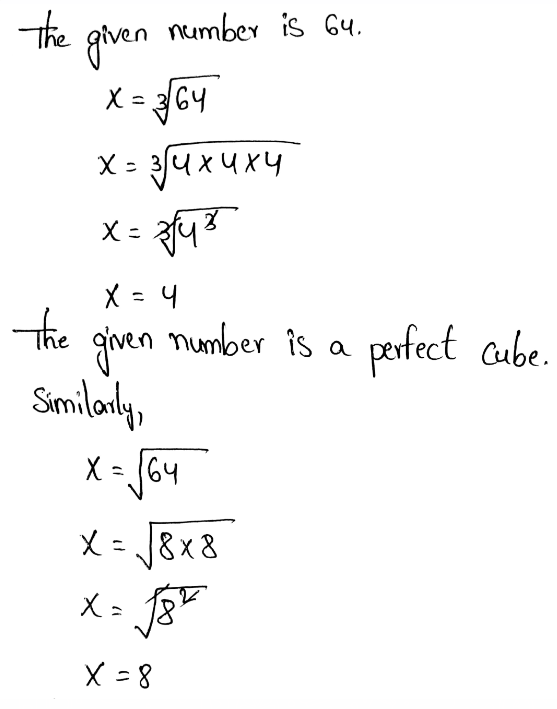
The given number is a perfect square.

The given number is both a perfect square and a perfect cube.

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 75 Exercise 4 Answer

We need to classify the number as a perfect square, a perfect cube, both, or neither. The given number is 24

For a number to be a perfect cube or a perfect square, the result of its cube root or its square root will be a whole number.

Thus, determining the given number, we get,

\(x=\sqrt[3]{24}\)

x = 2.88

The given number is not a perfect cube.

Similarly,

\(x=\sqrt{24}\)

x = 4.89

The given number is not a perfect square.

The given number is neither a perfect square and a perfect cube.

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 76 Exercise 2 Answer

We need to solve x² = 49

Solving the given expression, we get,

The value of x = +7 and x = −7

Envisionmath 2.0 Grade 8 Chapter 1 Real Number Step-By-Step Solutions

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 76 Exercise 3 Answer

We need to solve x³ = 25

Solving the given expression, we get,

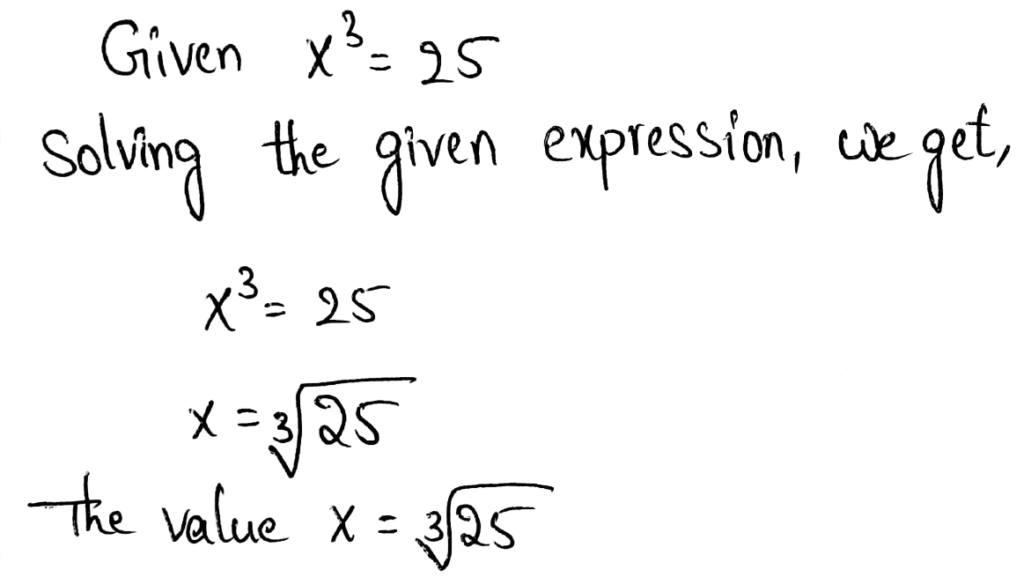
Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 76 Exercise 5 Answer

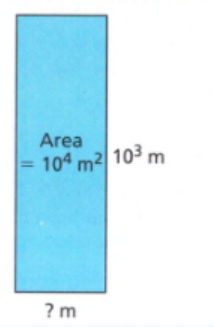
A container has a cube shape. It has a volume of 216 cubic inches. We need to find the dimensions of one face of the container.

The volume of a cube is given by, V = a³

where a is the dimension of one face of the container.

The dimensions of one face of the container is 6 inches.

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 76 Exercise 2 Answer

We need to use the properties of exponents to write an equivalent expression for a given expression (3⁶)⁻²

The power of powers property implies multiplying the powers to find the power of powers.

​
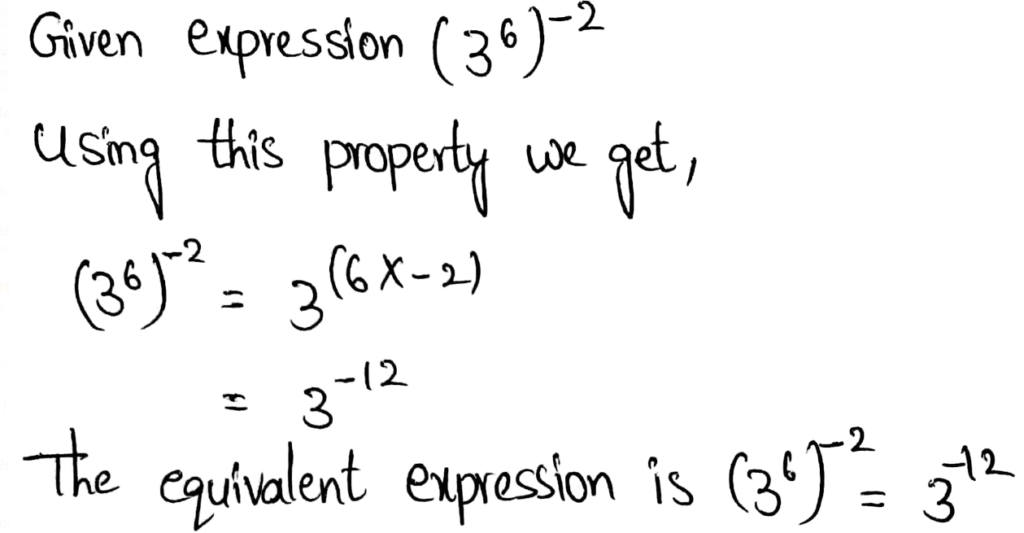
The equivalent expression is (3⁶)⁻² = 3⁻¹²

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 76 Exercise 3 Answer

We need to use the properties of exponents to write an equivalent expression for a given expression 7³ ⋅ 2³

The power of product property implies multiplying the bases when the exponents are the same.

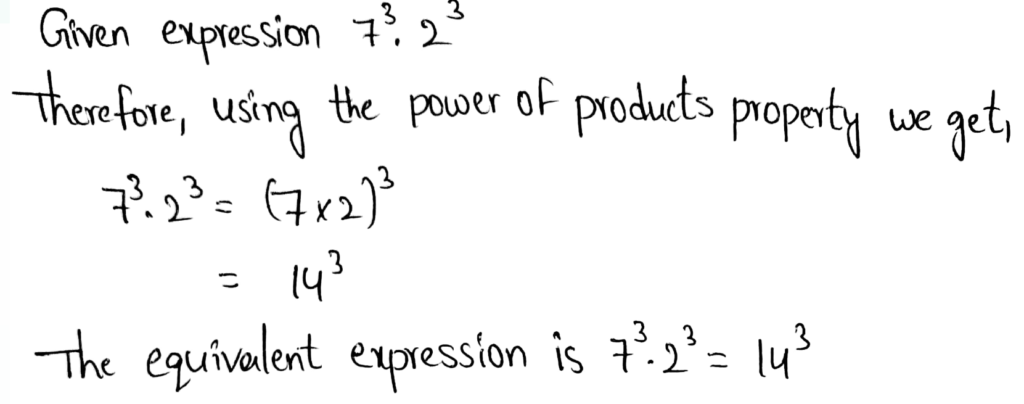
​The equivalent expression is 7³ ⋅ 2³ = 14³

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 77 Exercise 1 Answer

We need to rewrite the expression using a positive exponent.

The given expression is 9⁻⁴

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

Rewriting the expression using a positive exponent, we get, \(9^{-4}=\frac{1}{9^4}\)

Real Number Topic 1 Essential Questions Guide Envisionmath Grade 8

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 77 Exercise 3 Answer

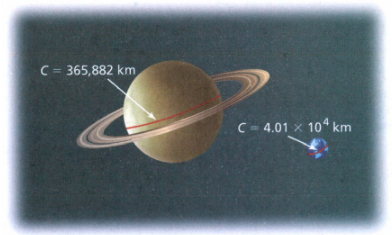
We need to evaluate the expression for x = 2 and y = 5

The given expression is −4x⁻² + 3y⁰

Given, −4x⁻² + 3y⁰

Evaluating this using the zero exponent’s property and the negative exponent’s property, we get,

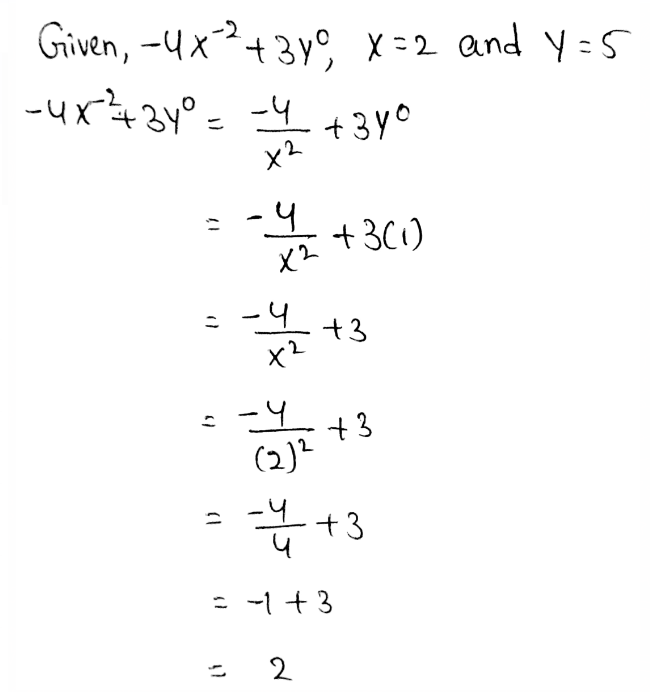
The value of −4x⁻² + 3y⁰

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 77 Exercise 4 Answer

We need to evaluate the expression for x = 2 and y = 5

The given expression is 2x⁰y⁻²

Given, 2x⁰y⁻²

Evaluating this using the zero exponent’s property and the negative exponent’s property, we get,

The value of \(2 x^0 y^{-2}=\frac{2}{25}\)

Envisionmath Grade 8 Volume 1 Chapter 1 Review Solutions

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 77 Exercise 1 Answer

Given that, In the year 2013 the population of California was about 38,332,521 people. We need to write the estimated population as a single digit times a power of 10.

Rounded to the greatest place value, we get,

38,332,521 = 40,000,000

There are 7 zeros in the rounded number.

Thus, the value will be,

40,000,000= 4 × 10⁷

The exponent is positive since the given number is greater than one.

The given value is written as a single digit times a power of ten, the estimate is 4 × 10⁷

 

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 77 Exercise 2 Answer

Given that the wavelength of green light is about 0.00000051 meter. We need to find the estimated wavelength as a single digit times a power of 10.

Rounded to the greatest place value, we get,

0.00000051 = 0.0000005

There are 7 zeros in the rounded number.

Thus, the value will be,

0.0000005 = 5 × 10^-7

The exponent is negative since the given number is less than one.

The given value is written as a single digit times a power of ten, the estimate is 5 × 10^-7

 

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 78 Exercise 1 Answer

We need to write 803,000,000 in scientific notation.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 803,000,000

The given number in scientific notation will be,

803,000,000 = 8.03 × 10⁸

The given number in scientific notation will be,803,000,000 = 8.03 × 10⁸

Envisionmath 2.0 Grade 8 Chapter 1 Real Number Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 78 Exercise 2 Answer

We need to write 0.0000000068 in scientific notation.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 0.0000000068

The given number in scientific notation will be,0.0000000068 = 6.8 × 10^-9

Negative exponents are used since the given number is very small.

The given number in scientific notation will be,0.0000000068 = 6.8 × 10^-9

 

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 78 Exercise 3 Answer

We need to write the answer to the given operation in scientific notation.

(4.1 × 10⁴) + (5.6 × 10⁶)

Performing the given addition, we get,

​
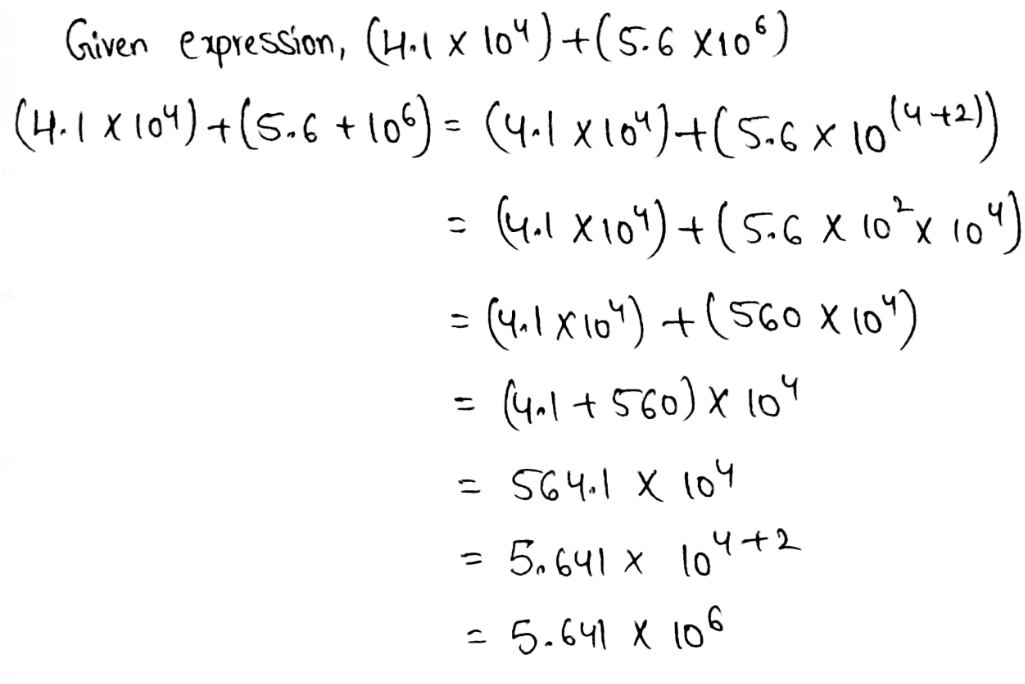
​The value of (4.1 × 10⁴) + (5.6 × 10⁶) in scientific notation is 5.641 × 10⁶

How To Solve Real Number Problems In Envisionmath Grade 8

Envision Math Grade 8 Volume 1 Student Edition Answers Chapter 1 Real Number Topic 1 Page 78 Exercise 4 Answer

Given that the population of Town A is 1.26 × 10⁵ people. The population of Town B is 2.8 × 10⁴ people. We need to know how many times greater is the population of Town A than the population of Town B.

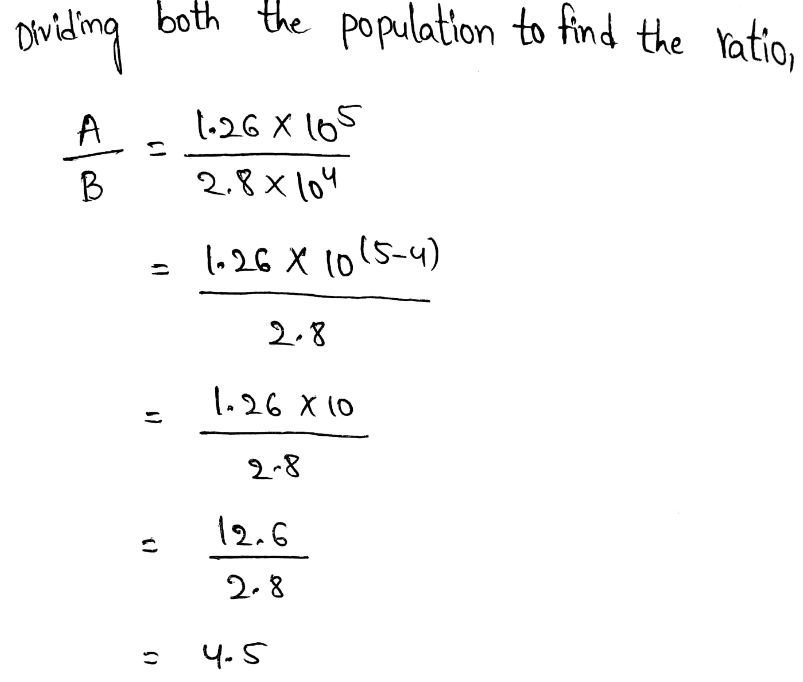
4.5 times greater is the population of Town A than the population of Town B.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10

Page 67 Question 1 Answer

Given that, the homecoming committee wants to fly an aerial banner over the football game. The banner is 1,280 inches long and 780 inches tall. We need to find the number of different ways can the area of the banner be expressed.

The given banner is a rectangle.

The area of the rectangle is given by the formula,

A = l × b

where l = length and b = breadth.

Thus, the area in standard form will be,

A = 1280 × 780 = 998,400

The area can also be represented in scientific notation will be,

A = 998,400 = 9.98 x 10⁵

The area of the banner is expressed in two different ways. In standard form as 998,400 and in scientific notation as 9.98 × 10⁵

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.10 Real Number Solutions

Page 68 Exercise 1 Answer

We need to determine what does the exponent tell you about the magnitude of the number.

Scientific notations make calculations easier by writing very large or very small numbers into their compact form.

For example, 0.0000005

This can be represented as 5 × 10^-7

In this way, we can rewrite large or small values into very compact forms using scientific notations.

The solutions in scientific notation are easiest to manipulate since it is easier to multiply values between one to ten and then using the exponent properties of power of 10 rather than multiplying the number in standard form with lots of zeroes in it.

Here, the exponent is negative this means that the magnitude is very small. If it was positive, then it denotes that the magnitude is large.

If the exponent is negative, then the magnitude of the number is very small.

If the exponent is positive, then the magnitude of the number is very large.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10 Page 68 Exercise 1 Answer

Given that, the planet Venus is on average 2.5 × 10⁷ kilometers from Earth. The planet Mars is on average 2.25 × 10⁸ kilometers from Earth. When Venus, Earth, and Mars are aligned, we need to find the average distance from Venus to Mars.

The planet Venus is on average 2.5 × 10⁷ kilometers from Earth.

The planet Mars is on average 2.25 × 10⁸ kilometers from Earth.

​The average distance from Venus to Mars is 2.5 × 10⁸ kilometers.

 

Page 69 Exercise 2 Answer

Given that, there are 1 × 10¹⁴ good bacteria in the human body. There are 2.6 × 10¹⁸ good bacteria among the spectators in a soccer stadium. We need to find the number of spectators are in the stadium. Also, we need to express our answers in scientific notation.

To find the number of spectators, divide the good bacteria among the spectators by the good bacteria in the human body, we get,

There are 26000 spectators in the stadium.

There are 26000 spectators in the stadium. The number in scientific notation will be 2.6 x 10⁴

 

Page 68 Exercise 1 Answer

In Example 1 and the Try It, we need to find why we moved the decimal point to get the final answer.

In Example 1, the answer obtained is 589.65 × 10²²

It was rewritten as 5.8965 × 10²⁴

In Try It, the answer obtained is 25 × 10⁷

It was rewritten as 2.5 × 10⁸

In both cases, we moved the decimal point to get the final answer.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Thus, to make it as a value between one and ten for easier calculation, we moved the decimal points.

The first factor in the scientific notation must be greater than or equal to one and less than 10.

This is why we have moved the decimal point to get the final answer.

Envision Math Grade 8 Student Edition Exercise 1.10 Real Numbers Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10 Page 70 Exercise 1 Answer

We need to explain how does using a scientific notation help when computing with very large or very small numbers.

Scientific notations make calculations easier by writing very large or very small numbers into their compact form.

For example, 0.00005

This can be represented as 5 × 10⁵

In this way, we can rewrite large or small values into very compact forms using scientific notations.

The solutions in scientific notation are easiest to manipulate since it is easier to multiply values between one to ten and then using the exponent properties of power of 10 rather than multiplying the number in standard form with lots of zeroes in it.

Scientific notation is a convenient way to write very large numbers or very small numbers. Also, the solutions in scientific notation are easiest to manipulate.

 

Page 70 Exercise 3 Answer

For the sum of (5.2 × 10⁴) and (6.95 × 10⁴) in scientific notation, we need to find why will the power of 10 be 10⁵

The first factor will have values between one and ten.

The second factor will be the power of ten.

Since the number obtained in the first factor is more than the number 10, we need to change the power of 10 to make the number less than 10.

The number obtained in the first factor is more than the number ten, that’s why we converted the power of 10 be 10⁵ to make the first factor in the scientific notation to be less than 10.

 

Page 70 Exercise 6 Answer

Given that, the mass of Mars is 6.42 × 10²³ kilograms. The mass of Mercury is 3.3 × 10²³ kilograms.

We need to find the combined mass of Mars and Mercury expressed in scientific notation.

Adding both the masses together, we get,
​
6.42 × 10²³ + 3.3 × 10²³ = (6.42+3.3) × 10²³

= 9.72 × 10²³

​The combined mass of Mars and Mercury is 9.72 × 10²³

Given that, the mass of Mars is 6.42 × 10²³ kilograms. The mass of Mercury is 3.3 × 10²³ kilograms.

We need to find the difference in the mass of the two planets expressed in scientific notation.

Subtracting both the masses together, we get,
​
6.42 × 10²³ − 3.3 × 10²³ = (6.42 − 3.3) × 10²³

= 3.12 × 10²³

​The difference in the mass of the two planets expressed in scientific notation is 3.12 × 10²³

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10 Page 71 Exercise 7 Answer

We need to perform the below operation and express our answer in scientific notation.

​The solution obtained will be 4.9×10^-11

 

Page 71 Exercise 8 Answer

We need to perform the below operation and express our answer in scientific notation.

The solution obtained will be 1.12×10⁶

 

Page 71 Exercise 9 Answer

We need to find the value of n in equation 1.9 × 10⁷ = (1 × 10⁵)(1.9 × 10ⁿ)

The value of n = 2

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10 Page 71 Exercise 10 Answer

We need to find the value of (5.3 × 10³) − (8 × 10²). Also, we need to express the answer in scientific notation.

Solving the given expression, we get,
​
The value of (5.3 × 10³) − (8 × 10²) = 4.5 × 10³

Real Number Solutions Grade 8 Exercise 1.10 Envision Math

Page 71 Exercise 11 Answer

We need to find the mass of 30,000 molecules. Also, we need to express the answer in scientific notation.

​
The mass of 30,000 molecules will be 1.59 × 10⁻¹⁸

 

Page 71 Exercise 12 Answer

Your friend says that the product of 4.8 × 10⁸ and 2 × 10^-3 is 9.6 × 10^-5

We need to find out whether the answer is correct or not.

Thus, it is wrong.

My friend’s calculation is incorrect.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10 Page 71 Exercise 13 Answer

We need to write the answer in scientific notation.

Solving the given expression, we get,

 

Page 71 Exercise 14 Answer

Given that, A certain star is 4.3 × 10² light years from Earth. One light year is about 5.9 × 10¹² miles. We need to find how far from Earth (in miles) is the star. We need to express our answer in scientific notation.

The distance of the Earth (in miles) from the star is 2.537 × 10¹⁵

 

 

Page 72 Exercise 15 Answer

Given that, the total consumption of fruit juice in a particular country in 2006 was about 2.28 × 10⁹ gallons. The population of that country that year was 3 × 10⁸

We need to find the average number of gallons consumed per person in the country in 2006.

The average number of gallons consumed per person in the country in 2006 is 7.6 gallons.

Envision Math Grade 8 Chapter 1 Exercise 1.10 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10 Page 72 Exercise 16 Answer

Given that, the greatest distance between the Sun and Jupiter is about 8.166 × 10⁸  kilometers. The greatest distance between the Sun and Saturn is1.515 × 10⁹ kilometers. We need to find the difference between these two distances.

The difference between these two distances is 6.984 × 10⁸

 

Page 72 Exercise 18 Answer

We need to find the value of n in equation 1.5 × 10¹² = (5 × 10⁵)(3 × 10ⁿ)

The value of n = 6 in the given expression.

We need to explain why the exponent on the left side of the equation is not equal to the sum of the exponents on the right side.

The given expression is,
​
1.5 × 10¹² = (5 × 10⁵)(3 × 10ⁿ)

1.5 × 10¹² = 15 × 10⁵⁺ⁿ

​If the number is larger than one, we need to add one into the exponent for each space we moved the decimal point.

Thus, we get,
​
1.5 × 10¹² = 1.5 × 10¹ × 10⁵⁺ⁿ

1.5 × 10¹² = 1.5 × 10⁵⁺ⁿ⁺¹

Hence, we can show in above step the exponent on the left side of the equation is not equal to the sum of the exponents on the right side.

 

Page 72 Exercise 19 Answer

The quotient of the decimal factor is less than one.

Thus, we need to subtract one from the exponent of ten for each space we move our decimal point to the right.

The value obtained is 5 × 107 The quotient of the decimal factor is less than one. Thus, we need to subtract one from the exponent of ten for each space we move our decimal point to the right.

Envision Math 8th Grade Exercise 1.10 Step-By-Step Real Number Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.10 Page 72 Exercise 20 Answer

We need to find which of the given equation(s) are true.

Solving it one by one, we get,
​

​The correct equations are

(A) (4.7 × 10⁴) + (8 × 10⁴)

(D) (9.35 × 10⁶) − (6.7 × 10⁶)

Envision Math Grade 8 Volume 1 Chapter 1 Real Numbers Topic 13 Mathematical Modeling Solutions

Page 63 Exercise 1 Answer

The video mentioned above shown some images that predict the pattern of the most hard-working organs in our body.

The reason is for knowing how each of them works and what does the pattern each of them follows.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “How many times heart beats I have per minute?”.

“How many times heart beats I have per minute?”.

This is the question that made up my mind after watching this video.

Envision Math 8th Grade Mathematical Modeling Topic 13 Solutions

Page 63 Exercise 2 Answer

The video mentioned above shown some images that predict the pattern of the most hard-working organs in our body.

The reason is for knowing how each of them works and what does the pattern each of them follows.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The main question that comes to my mind after watching this video is “How many times heartbeats I have per minute?”.

The main question that I will answer that I saw in the video is “How many times heartbeats I have per minute?”.

Page 63 Exercise 3 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “How many times heartbeats do I have per minute?”.

An answer that I was predicted to this main question is “78” heartbeats per minute.

An answer that I was predicted to this main question is “78” heartbeats per minute. I found this answer by keeping my right thumb over the wrist of the left hand and by calculating the number of beats I hear per minute.

Envision Math Grade 8 Volume 1 Chapter 1 Topic 13 Mathematical Modeling Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Topic 13 Act Mathematical Modeling

Page 63 Exercise 4 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.A number that I know which is too small to be the answer is 50since heartbeat below 60
results in death.

A number which is too large to be the answer is 110 since heartbeat above 110 will result in cardiac arrest.

On the number line below, we have written a number that is too small to be the answer. Also, we have written a number that is too large.

 

Page 63 Exercise 5 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too small to be the answer is 50 since heartbeat below 60 results in death.

A number which is too large to be the answer is 110
since heartbeat above 110 will result in cardiac arrest.

My heartbeat is 78 beats per minute.

Plotting my prediction on the same number line, I get,

 

Page 64 Exercise 8 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The following steps are used to refine my conjecture:

Take your pulses several times.

Recognize each one of the conjecture’s circumstances – The situations of a conjecture are the requirements that must be met already when we acknowledge the conjecture’s findings.

Create both examples and non-examples – Find items that meet the criteria and verify to see if they also fulfill the conjecture’s inference. Start by removing each situation one at a time and build non-examples that gratify the other circumstances but not the inference.

Seek out counterexamples – A counterexample meets all of the circumstances of a statement except the conclusion.

Try comparing yours with others.

From this way, I have found out that my heartbeats 78 times per minute.

Envision Math Grade 8 Topic 13 Real Numbers Modeling Answers

Page 64 Exercise 9 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude. I have found out that my heartbeats 78 times per minute.

The number of heartbeats per minute of an average healthy person is 72.

This is lesser than my prediction.

The answer to the Main Question is that the number of heartbeats per minute of an average healthy person is 72. It is less than my prediction.

 

Page 65 Exercise 10 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “How many times heartbeats do I have per minute?”.

An answer that I was predicted to this main question is “78” heartbeats per minute.

The answer that I saw in the video is “72” heartbeats per minute.

The answer that I saw in the video is “72” heartbeats per minute.

Envision Math Grade 8 Chapter 1 Topic 13 Solutions Guide

Page 65 Exercise 11 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “How many times heartbeats do I have per minute?”.

An answer that I was predicted to this main question is “78” heartbeats per minute.

The answer that I saw in the video is “72” heartbeats per minute.

My answer doesn’t match the answer in the video. This is because I may have done some serious physical activity before taking my pulse rate which makes it to be more than the normal rate.

My answer doesn’t match the answer in the video. This is because physical activity before taking my pulse rate increases my heartbeat.

 

Page 65 Exercise 12 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.
A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “How many times heartbeats do I have per minute?”.

An answer that I was predicted to this main question is “78” heartbeats per minute.

The answer that I saw in the video is “72” heartbeats per minute.

My answer doesn’t match the answer in the video. This is because I may have done some serious physical activity before taking my pulse rate which makes it to be more than the normal rate.

I am going to do some breathing exercises before taking my heartbeat to change my model.

Yes, I would change my model now that you know the answer.

Mathematical Modeling Solutions Grade 8 Envision Math Topic 13

Page 66 Exercise 14 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “How many times heartbeats do I have per minute?”.

An answer that I was predicted to this main question is “78” heartbeats per minute.

The answer that I saw in the video is “72” heartbeats per minute.

My answer doesn’t match the answer in the video. This is because I may have done some serious physical activity before taking my pulse rate which makes it to be more than the normal rate.

The pattern which I notice in my calculations is that the calculations differ based on the mental and physical condition I am in.

This helps me to know under which conditions my heartbeat increases or decreases.

The calculations differ based on the mental and physical condition I am in. This helps me to know under which conditions my heartbeat increases or decreases.

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions

Page 56 Exercise 17 Answer

We need to express 0.000000298 as a single digit times a power of ten rounded to the nearest ten millionth.

Rounded to the greatest place value, we get,

0.000000298=0.0000003

There are 7 zeros in the rounded number.

Thus, the value

3  x 10^-7

The value will be 3 x 10^-7

We need to explain how negative powers of 10 make small numbers easier to write and compare.

Negative powers of 10 are utilized in writing small quantities.

It will take up so much space to write very small quantities.

Here, the negative powers are used to move so many decimal spaces.

For example,

0.0000000000000004 can be written as 4 × 10^-16

This will save up so much space and enables easier calculation.

While writing small numbers, each negative power of 10 will be equal to one decimal place after the decimal point.

 

Page 57 Exercise 1 Answer

We need to explain what does the exponent in 10¹⁵ tell you about the value of the number.

The number given is 10¹⁵

The exponent here is 15

This means that the number of zeroes present in the number is 15

Thus, the number will be more than 1,000,000,000,000,000

This denotes that the value 10¹⁵ denotes quadrillions.

The exponent in 10¹⁵ tell us that the value of the number will be in quadrillions.

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.9 Real Number Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 57 Exercise 1 Answer

We need to explain how we can use the knowledge of powers of 10 to rewrite the number.

To rewrite any number into a power of 10, we need to use scientific notation.

In a scientific notation, it consists of two terms.

The first term will be of the number between one and ten. The second term will be the power of ten.

The exponent in the power of 10 denotes the number of zeroes present in the number.

If the exponent is negative, then it denotes the number of zeroes after the decimal point.

We can use the knowledge of powers of 10 to rewrite the number by placing the decimal after the first nonzero digit and by counting the number of digits after the decimal point.

Envision Math Exercise 1.9 Real Numbers Detailed Answers

Page 58 Exercise 1 Answer

Given that the height of Angel Falls, the tallest waterfall in the world, is 3,212 feet. We need to write this number in scientific notation.

The height of Angel falls is 3212ft

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

The number in scientific notation will be,

3212 = 3.212 x 10³

The number in scientific notation will be 3.212 x 10³

 

 

Page 59 Exercise 3 Answer

We need to write the numbers in standard form 9.225 × 10¹⁸

The given number in scientific notation is 9.225 × 10¹⁸

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

It can be written in standard form by counting the number of zeroes after the decimal point.

The number in standard form will be,

9.225 × 10¹⁸ = 9225000000000000000

The number in standard form will be, 9.225 × 10¹⁸ = 9225000000000000000

We need to write the numbers in standard form 6.3 × 10^-8

The given number in scientific notation is 6.3 × 10^-8

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

It can be written in standard form by counting the number of zeroes before the decimal point.

The number in standard form will be,

0.000000063

The number in standard form will be, 0.000000063

Envision Math Grade 8 Exercise 1.9 Real Numbers Answers

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 58 Exercise 1 Answer

We need to explain why very large numbers have positive exponents when written in scientific notation.

We will use a power of10 to estimate a quantity that is either too big or too small to count.

Quantities that are neither too big nor too small can easily be represented.

We have to count the number of zeroes to write it as a power of 10

The big numbers will have a positive exponent.

The small numbers will have a negative exponent.

The large numbers have positive exponents when written in scientific notation because the number is large and the number of zeroes is more.

 

Page 60 Exercise 1 Answer

Scientific notations make calculations easier by writing very large or very small numbers into their compact form.

For example, 0.00000000005

This can be represented as 5 × 10^-11

In this way, we can rewrite large or small values into very compact forms using scientific notations.

Scientific notation is a convenient way to write very large numbers or very small numbers.

 

Page 60 Exercise 2 Answer

Given that, Taylor states that 2,800,000 in scientific notation is 2.8 × 10⁻⁶ because the number has six places to the right of the 2. We need to find whether the
Taylor’s reasoning is correct or not.

Given that, Taylor states that 2,800,000 in scientific notation is 2.8 × 10⁻⁶

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, we have six places to the right of the 2.

Thus, the value will be, 2.8 × 10⁶

We will use negative exponent only when we have places to the left of the given number.

Taylor’s reasoning is wrong.

 

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 60 Exercise 4 Answer

We need to write the numbers in scientific form 586,400,000

The given number in standard form is 586,400,000

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

The number in scientific form will be,

586,400,000 = 5.8 x 10⁸

The number in the scientific form will be, 586,400,000=5.8 × 10⁸

 

Page 60 Exercise 7 Answer

We need to write the number displayed on the calculator screen in standard form. The number displayed is 7.6E12

The given number in scientific notation is 7.6E12=7.6 × 10¹²

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

It can be written in standard form by counting the number of zeroes after the decimal point.

The number in standard form will be,

7.6 x 10¹² = 760000000000000

The number in standard form will be, 7.6 x 10¹² = 7600000000000

Real Number Solutions Grade 8 Exercise 1.9 Envision Math

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 61 Exercise 8 Answer

Given that, the Sun is 1.5×108 kilometers from Earth. We need to write it as standard form.

The given number in scientific notation is 1.5 × 10⁸

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

It can be written in standard form by counting the number of zeroes after the decimal point.

The number in standard form will be,

1.5 x 108 = 150000000

The number in standard form will be, 1.5 x 10⁸ = 150000000

 

Page 61 Exercise 9 Answer

Brenna wants an easier way to write 0.0000000000000000587. We need to write this in scientific notation.

The given number in standard form is 0.0000000000000000587

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

The number in the scientific form will be,

0.0000000000000000587=5.87 × 10⁻¹⁷

The number in the scientific form will be, 0.0000000000000000587=5.87 × 10⁻¹⁷

Envision Math Grade 8 Real Number Practice Problems Exercise 1.9

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 61 Exercise 10 Answer

We need to check whether the number 23 × 10⁻⁸ is written in scientific notation or not.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 23 × 10⁻⁸

Thus, we are having two factors in this number.

Therefore, the given number is in scientific notation.

The given number 23 x 10⁻⁸ is in scientific notation.

 

Page 61 Exercise 12 Answer

Given that, Simone evaluates an expression using her calculator. The calculator display is shown on the right. We need to express the number 5.2E−11 in standard form.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 5.2E−11 that is 5.2E−11=5.2 × 10⁻¹¹

The given number in standard form will be,

5.2 × 10⁻¹¹ = 0.000000000052

The given number in standard form will be, 5.2 × 10⁻¹¹  = 0.000000000052

Envision Math Grade 8 Chapter 1 Exercise 1.9 Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 61 Exercise 13 Answer

We need to write the given number 0.00001038 in scientific notation.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 0.00001038

The given number in scientific notation will be,

0.00001038=1.038 × 10⁻⁵

The given number in scientific notation will be,0.00001038=1.038 × 10⁻⁵

 

Page 61 Exercise 15 Answer

Given that, Peter evaluates an expression using his calculator. The calculator display is shown at the right. We need to express the number 8.19E18 in standard form.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 8.19E18 = 8.19 × 10¹⁸

We need to count 18 decimal places to the right.

The given number in standard form will be,
8.19 x 10¹⁸ = 8190000000000000000

The given number in standard form will be, 8.19 × 10¹⁸ = 8190000000000000000

 

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 62 Exercise 16 Answer

We need to describe what we should do first to write 5.871 × 10^-7 in standard form.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 5.871×10^-7

We need to count 7 decimal places to the left.

The given number in standard form will be,

5.871 × 10^-7 = 0.0000005871

The given number in standard form will be, 5.871 × 10^-7 = 0.0000005871

The first step is to count 7 places to the left of the given decimal.

We need to express the number 5.871 × 10^-7 in standard form.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 5.871 × 10^-7

We need to count 7 decimal places to the left.

The given number in standard form will be,

5.817 x 10^-7 = 0.0000005871

The given number in standard form will be, 5.871 x 10^-7 = 0.0000005817

 

Page 62 Exercise 17 Answer

We need to express the given number 2.58×10^-2 in standard form.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 2.58 × 10^-2

We need to count 2 decimal places to the left.

The given number in standard form will be,

2.58 x 10^-2 = 0.0258

The given number in standard form will be, 2.58 × 10^-2 = 0.0258

Envision Math 8th Grade Exercise 1.9 Step-By-Step Real Number Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 62 Exercise 18 Answer

Given that, At a certain point, the Grand Canyon is approximately 1,600,000 centimeters across. We need to express this number in scientific notation.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 1,600,000

The given number in scientific notation will be,

1,600,000 = 1.6 x 10⁶

The given number in scientific notation will be,1,600,000 = 1.6 × 10⁶

 

Page 62 Exercise 20 Answer

We need to express the distance 4,300,000 meters using scientific notation in meters, and then in millimeters.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 4,300,000

The given number in scientific notation will be,

4,300,000=4.3×10⁶ meters.

The given number in scientific notation in millimeters will be,
​
4,300,000 = 4.3 × 10⁶

= 4.3 × 10⁶ × 10³ × 10^-3

= 4.3 × 10⁹ × 10^-3

= 4.3 × 109 millimeters
​
The given number in scientific notation will be 4.3 × 10⁶ meters or 4.3 × 10⁹ millimeters.

 

Page 62 Exercise 21 Answer

We need to find which of the given numbers is written in scientific notation.

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

The numbers in scientific notation are,

12 × 10⁶,6.89 × 10⁶

Here, 12 and 6.89 doesn’t consider as in scientific notation form since they both are not too big or too small numbers.

Among the given, the following numbers are written in scientific notation.

(A) 12 × 10⁶

(C) 6.89 × 10⁶

How To Solve Real Numbers Exercise 1.9 In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.9 Solutions Page 62 Exercise 22 Answer

Given that, Jeana’s calculator display shows the number to the right. We need to express this number in scientific notation.

The number shown in the calculator is 5.49E14

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 5.49E14

The given number in scientific notation will be,

5.49E14 = 5.49 × 10¹⁴

The given number in scientific notation will be, 5.49E14 = 5.49 × 1014

Given that, Jeana’s calculator display shows the number to the right. We need to express this number in standard form.

The number shown in the calculator is 5.49E14

The number in scientific notation will have two factors.

The first factor will have values between one and ten.

The second factor will be the power of ten.

Here, the given number is 5.49E14 = 5.49 ×10¹⁴

We need to count 14 places to the right of the decimal point.

The given number in standard form will be,

5.49 × 10¹⁴ = 549000000000000

The given number in standard form will be, 5.49 × 10¹⁴ = 549000000000000

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8

Page 51 Exercise 1 Answer

Given that, Keegan and Jeff did some research and found that there are approximately 7,492,000,000,000,000,000 grains of sand on Earth. Jeff says that it is about 7×10¹⁵ grains of sand. Keegan says that this is about 7×10¹⁸ grains of sand.

We need to find how might Jeff and Keegan have determined their estimates.

The amount of grains of sand is 7,492,000,000,000,000,000

Rewriting the given large quantity using a power of 10 for easy computations.

Here, Jeff considered only the zeroes of the obtained value.

This is why he estimated it about 7×10¹⁵

While Keegan considered both the zeroes and the nonzeroes after the number 7

This made him estimate the amount to be 7×10¹⁸

Jeff considered only the zeroes of the obtained value. Keegan considered both the zeroes and the nonzeroes after the number 7.

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.8 Real Number Solutions

Page 51 Exercise 2 Answer

Given that, Keegan and Jeff did some research and found that there are approximately 7,492,000,000,000,000,000 grains of sand on Earth. Jeff says that it is about 7×10¹⁵ grains of sand. Keegan says that this is about 7×10¹⁸ grains of sand.

We need to find whose estimate, Jeff’s or Keegan’s, is more logical.

The amount of grains of sand is 7,492,000,000,000,000,000

Rewriting the given large quantity using a power of 10 for easy computations.

Here, Jeff considered only the zeroes of the obtained value.

This is why he estimated it about 7×10¹⁵

While Keegan considered both the zeroes and the nonzeroes after the number 7.

This made him estimate the amount to be 7×10¹⁸

Keegan is more logical since the non-zero values are not after the decimal point so it needs to be considered as well.

Keegan is more logical.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 52 Exercise 1 Answer

We will use a power of 10 to estimate a quantity that is either too big or too small to count.

Quantities that are neither too big nor too small can easily be represented.

We have to count the number of zeroes to write it as a power of 10.

The big numbers will have a positive exponent.

The small numbers will have a negative exponent.

We can use a power of 10 to estimate a quantity when they are either too big or too small.

Envision Math Grade 8 Student Edition Exercise 1.8 Real Numbers Answers

Page 52 Exercise 1 Answer

Light travels 299,792,458 meters per second. Sound travels at 332 meters per second. We need to use power of 10 to compare the speed of light to the speed of sound.

Rounded to the greatest place value, we get,
​
299,792,458=300,000,000

322=300
​
There are 8 zeros in the rounded number 300,000,000

There are 2 zeros in the rounded number 300

The estimated speed of light is 3×10⁸ meters per second.

The estimated speed of sound is 1×10² meters per second.

3 × 10⁸ > 3 × 10², so the speed of light is faster than the speed of sound.

3 x 10⁸ > 3 x 10²

The speed of light is faster than the speed of sound.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 53 Exercise 2 Answer

Given that, there are approximately 1,020,000,000 cars in the world. The number of cars in the United States is approximately 239,800,000.

We need to compare the number of cars in the world to that in the United States.

Rounded to the greatest place value, we get,
​
1,020,000,000=1,000,000,000

239,800,000=200,000,000.
​
There are 9 zeros in the rounded number 1,000,000,000

There are 8 zeros in the rounded number 200,000,000

The cars in the world is 1×10⁹

The cars in US is 2×10⁸

Thus,

1 × 10⁹ > 2 × 10⁸

1 x 10⁹ > 2 x 10⁸

The number of cars in the world is more than that of the United States.

 

Page 52 Exercise 1 Answer

Given that, Country A has a population of 1,238,682,005 and Country B has a population of 1,106,487,394. We need to explain how we would compare these populations.

Rounded to the greatest place value, we get,

A = 1,238,682,005 = 1,200,000,000

There are 8 zeros in the rounded number

Similarly,

B = 1,106,487,394 = 1,100,000,000

There are 8 zeros in the rounded number

The population in country A will be 12 × 10⁸

The population in country B will be 11 × 10⁸

Thus, 12 × 10⁸ > 11 × 10⁸

12 × 10⁸ > 11 × 10⁸

Thus, country A’s population is more.

Real Number Solutions Grade 8 Exercise 1.8 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 54 Exercise 1 Answer

We will use a power of 10 to estimate a quantity that is either too big or too small to count.

Quantities that are neither too big nor too small can easily be represented.

We have to count the number of zeroes to write it as a power of 10

The big numbers will have a positive exponent.

The small numbers will have a negative exponent.

We can use a power of 10 to estimate a quantity when they are either too big or too small.

 

Page 54 Exercise 5 Answer

Given that, A scientist records the mass of a proton as 0.0000000000000000000000016726231 gram. We need to use a single digit times a power of 10 to estimate the mass.

Rounded to the greatest place value, we get,

0.0000000000000000000000016726231=00000000000000000000000020000000

There are 23 zeros in the rounded number.

Thus, the value will be,

2×10^-23

Since the value is less than one, the exponent is negative.

The mass of the proton is 2 x 10^-23

 

Page 54 Exercise 6 Answer

Given that, The tanks at the Georgia Aquarium hold approximately 8.4×10⁶ gallons of water. The tanks at the Audubon Aquarium of the Americas hold about 400,000 gallons of water. We need to use a single digit times a power of 10 to estimate how many times greater the amount of water is at the Georgia Aquarium.

Rounded to the greatest place value, we get,

400,000=400,000

There are 5 zeros in the rounded number.

​
Thus, it will be 21 times more.

21 times greater the amount of water is at the Georgia Aquarium.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 55 Exercise 7 Answer

Given that, a city has a population of 2,549,786 people. We need to estimate this population to the nearest million. Also, express our answer as the product of a single digit and a power of 10.

Rounded to the greatest place value, we get,

2,549,786=3,000,000

There are 6 zeros in the rounded number.

Thus, the value will be,

3 × 10⁶

The population is written as the product of a single digit and a power of ten, this number is 3 x 10⁶

 

Page 55 Exercise 8 Answer

We need to use a single digit times a power of 10to estimate the number 0.00002468

Rounded to the greatest place value, we get,

0.00002468=0.00002

There are 5 zeros in the rounded number.

Thus, the value will be,

0.00002 = 2 × 10^-5

The exponent is negative since the given number is less than one.

The given value is written as a single digit times a power of ten, the estimate is 2 x 10^-5

Envision Math Grade 8 Chapter 1 Exercise 1.8 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 55 Exercise 9 Answer

The approximate circumferences of Earth and Saturn are shown. We need to find how many times greater is the circumference of Saturn than the circumference of Earth.

The circumference of Saturn is C=365,882 km

Rounded to the greatest place value, we get, 400,000

There are 5 zeros in the rounded number.

The value will be 4×10⁵

​
Thus, the circumference of Saturn is ten times more than the circumference of Earth.

The circumference of Saturn is ten times more than the circumference of Earth.

 

Page 55 Exercise 10 Answer

We need to estimate 0.037854921 to the nearest hundredth. We need to express your answer as a single digit times a power of ten.

Rounded to the greatest place value, we get,

0.037854921=0.04

There are 2 zeros in the rounded number.

Thus, the value will be,

4 × 10^-2

The value will be 4 x 10^-2

Envision Math Exercise 1.8 Real Numbers Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 55 Exercise 11 Answer

We need to compare the numbers 6×10^-6 and 2×10^-8

We need to find which number has the greater value.

6 × 10^-6 has the greatest value.

Envision Math 8th Grade Exercise 1.8 Step-By-Step Real Number Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 55 Exercise 12 Answer

Given that, Taylor made $43,785 last year. We need to ue a single digit times a power of ten to express this value rounded to the nearest ten thousand.

Rounded to the greatest place value, we get,

43,785 = 40,000

There are 4 zeros in the rounded number.

Thus, the value will be,

40,000 = 4 × 10⁴

The value becomes 4 x 10⁴

 

Page 55 Exercise 13 Answer

The length of plant cell A is 8×10^-5 meter. The length of plant cell B is 0.000004 meter. We need to find how many times greater is plant cell A’s length than plant cell B’s length.

The length of plant cell B is 0.000004

20 times greatest is plant cell A’s length than plant B’s length.

Envision Math Grade 8 Exercise 1.8 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1Real Number Exercise 1.8 Page 56 Exercise 16 Answer

Given that, Earth is approximately 5×10⁹ years old. We need to find for which of the given ages could this be an approximation.

Rounded to the greatest place value, and converting them into the power of ten, we get,
​
4,762,100,000 = 5,000,000,000 = 5 × 10⁹

4,849,000,000 = 5,000,000,000 = 5 × 10⁹

48,000,000,000 = 50,000,000,000 = 5 × 10¹⁰

4.45 × 10⁹ = 4 × 10⁹

4.849999999 × 10⁹ = 5 × 10⁹

Earth is approximately 5×10⁹ years old. This approximation is true for,
​
4,762,100,000

4,849,000,000

4.849999999 × 10⁹

How To Solve Exercise 1.8 Real Numbers In Envision Math Grade 8

​
Page 56 Exercise 56 Answer

We need to express 0.000000298 as a single digit times a power of ten rounded to the nearest ten millionth.

Rounded to the greatest place value, we get,

0.000000298=0.0000003

There are 7 zeros in the rounded number.

Thus, the value will be,

3 × 10^-7

The value will be 3 x 10^-7

We need to explain how negative powers of 10 make small numbers easier to write and compare.

Negative powers of 10 are utilized in writing small quantities.

It will take up so much space to write very small quantities.

Here, the negative powers are used to move so many decimal spaces.

For example,

0.0000000000000004 can be written as 4 × 10^-16

This will save up so much space and enables easier calculation.

While writing small numbers, each negative power of 10 will be equal to one decimal place after the decimal point.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7

Page 45 Exercise 1 Answer

We need to determine whether the relationship shown for Set 1 is also true for Sets 2-5.

In the first set, the number of sit-ups they do is 64

In the next set, it will be 32 since it is half as many for each subsequent set.

For third set,16

The number of sit-ups is represented by the equivalent expression, 2⁷⁻ⁿ

where n is the number of sets.

This expression is used to determine the number of sit-ups they do in each set.

Using this expression, finding the number of sit-ups in

Set 1 – 2⁷⁻ⁿ = 2⁷⁻¹ = 2⁶ = 64

Set 2 – 2⁷⁻ⁿ = 2⁷⁻² = 2⁵ = 32

Set 3 – 2⁷⁻ⁿ = 2⁷⁻³ = 2⁴ = 16

Set 4 – 2⁷⁻ⁿ = 2⁷⁻⁴ = 2³ = 8

Set 5 – 2⁷⁻ⁿ = 2⁷⁻⁵ = 2² = 4

The relationship shown for Set 1 is also true for Sets 2-5.

Page 45 Exercise 1 Answer

Given that, Calvin and Mike do sit-ups when they work out. They start with 64 sit-ups for the first set and do half as many for each subsequent set.

We need to explain how could we determine the number of sit-up sets Calvin and Mike do.

In the first set, the number of sit-ups they do is 64

In the next set, it will be 32 since it is half as many for each subsequent set.

For third set,16

We know that, 64=2⁷

For each set, it is reduced as half.

The number of sit-ups is represented by the equivalent expression, 2⁷⁻ⁿ

where n is the number of sets.

This expression is used to determine the number of sit-ups they do in each set.

The expression is used to determine the number of sit-ups they do in each set is 2⁷⁻ⁿ

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.7 Real Number Solutions

Page 46 Question 1 Answer

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

This means that, x⁰ = 1 where x ≠ 0

Example, 15⁰ = 1

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

This means that, \(x^{-n}=\frac{1}{x^n}\) where x ≠ 0

Example, \(15^{-2}=\frac{1}{15^2}\)

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

 

Page 46 Exercise 1 Answer

We need to evaluate (−7)⁰

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

The value of (−7)⁰ = 1

We need to evaluate (43)⁰

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

We need to evaluate 1⁰

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

The value of 1⁰ = 1

We need to evaluate (0.5)⁰

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

The value of (0.5)⁰ = 1

Envision Math Grade 8 Student Edition Exercise 1.7 Real Numbers Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7 Page 47 Exercise 3 Answer

We need to evaluate \(\frac{1}{5^{-3}}\)

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

This means that, \(x^{-n}=\frac{1}{x^n} \text { where } x \neq 0\)

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

 

Page 46 Exercise 1 Answer

We need to evaluate why 2(7⁰) = 2

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

The value 7⁰ = 1. This makes 2(7⁰) = 2

 

Page 48 Exercise 1 Answer

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

This means that, x⁰ = 1 where x ≠ 0

Example, 17⁰ = 1

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

This means that, \(x^{-n}=\frac{1}{x^n} \text { where } x \neq 0\)

Example, \(5^{-2}=\frac{1}{5^2}\)

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

Real Number Solutions Grade 8 Exercise 1.7 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7 Page 48 Exercise 2 Answer

We need to describe what does the negative exponent mean in the expression 9⁻¹²

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

The negative exponent means that it can be written as a fraction with a positive exponent using the negative exponent property.

 

Page 48 Exercise 4 Answer

We need to simplify the expression 1999999⁰

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

 

Page 48 Exercise 6 Answer

We need to find the value of 27x⁰y⁻² when the value of x=4 and y=3

The given expression is 27x⁰y⁻²

Using the zero and negative exponents property, the expression will be,

The value of 27x⁰y⁻² = 3

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7 Page 49 Exercise 7 Answer

We need to complete the given table to find the value of a nonzero number raised to the power of 0.

The given table is,

By evaluating and completing the given table, we get,

4⁴ = 256

\(4^3=\frac{256}{4}=64\) \(4^2=\frac{64}{4}=16\) \(4^1=\frac{10}{4}=4\) \(4^0=\frac{4}{4}=1\)

The completed table is,

Envision Math 8th Grade Exercise 1.7 Step-By-Step Real Number Solutions 

Page 49 Exercise 8 Answer

We need to complete the given table to find the value of a nonzero number raised to the power of 0.

The given table is,

By evaluating and completing the given table, we get,
​
(−2)⁴ = −2 × −2 × −2 × −2 = 16

(−2)³ = −2 × −2 × −2 = −8

(−2)² = −2 × −2 = 4

(−2)¹ = −2

(−2)⁰ = 1
​
The completed table is,

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7 Page 49 Exercise 9 Answer

We need to simplify the given expression (−3.2)⁰

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

This means that, x⁰ = 1 where x ≠ 0

Using this property, we get,

(−3.2)⁰ = 1

The value of (−3.2)⁰ = 1

We need to write two expressions equivalent to the given expression (−3.2)⁰. Also, explain why the three expressions are equivalent.

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

Thus the value of the given expression is (−3.2)⁰ = 1

Therefore, the two expressions equivalent to the given expression is, 5⁰ and (−15)⁰

This is because according to zero exponent property, anything to the power of 0 will result in the number one.

The two expressions equivalent to the given expression is 5⁰ and (−15)⁰.

The three expressions are equivalent since according to zero exponent property, any number to the power of 0 will result in 1.

 

Part 49 Exercise 10 Answer

We need to simplify the expression 12x⁰(x⁻⁴) when the value of x = 6

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

Thus, using these properties, we get,

The value of \(12 x^0\left(x^{-4}\right)=\frac{1}{108}\)

We need to simplify the expression 14(x⁻²) when the value of x = 6

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

This means that, \(x^{-n}=\frac{1}{x^n} \text { where } x \neq 0\)

Using this property, we get,

This value of \(14\left(x^{-2}\right)=\frac{7}{18}\)

 

Page 49 Exercise 12 Answer

We need to compare the values using <, > or =

The gives value is \(\left(\frac{1}{4}\right)^0 ? 1\)

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

Using this property, we get,

\(\left(\frac{1}{4}\right)^0=1\)

Thus, the given value becomes, \(\left(\frac{1}{4}\right)^0=1\)

The given value becomes,\(\left(\frac{1}{4}\right)^0=1\)

How To Solve Exercise 1.7 Real Numbers In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7 Page 49 Exercise 13 Answer

We need to rewrite each expression using a positive exponent. The given expression is 9⁻⁴

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

Rewriting the expression using a positive exponent, we get,\(9^{-4}=\frac{1}{9^4}\)

 

Page 49 Exercise 14 Answer

We need to rewrite each expression using a positive exponent.

The given expression is \(\frac{1}{2^{-6}}\)

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

This means that, \(x^{-n}=\frac{1}{x^n} \text { where } x \neq 0\)

Using this property, we get,

\(\frac{1}{2^{-6}}=2^6\)

Rewriting the expression using a positive exponent, we get, \(\frac{1}{2^{-6}}=2^6\)

 

Page 49 Exercise 15 Answer

We need to evaluate 9y⁰ when y=3

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

This means that, x⁰ = 1 where x ≠ 0

Using this property, we get,

9y⁰ = 9(1)

= 9

The value of 9y⁰ = 9

Given: 9y⁰

We need to find whether the value of the given expression will vary depending on y

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

This means that, x⁰ = 1 where x ≠ 0

Using this property, we get,

9y⁰ = 9(1) = 9

The result obtained will not have any relation with the value of y

The value of the given expression does not vary depending on the value of y

 

Page 50 Exercise 16 Answer

We need to simplify the expression −5x⁻⁴ when x = 4

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

This means that, \(x^{-n}=\frac{1}{x^n} \text { where } x \neq 0\)

Using this property, we get,

We need to simplify the expression 7x⁻³ when x=4

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

This means that, \(x^{-n}=\frac{1}{x^n} \text { where } x \neq 0\)

Using this property, we get,

The value of \(7 x^{-3}=\frac{7}{64}\)

Envision Math Exercise 1.7 Real Numbers Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7 Page 50 Exercise 17 Answer

We need to evaluate the expression (−3)⁻⁸ and −3⁻⁸

The given expressions are (−3)⁻⁸ and −3⁻⁸

Evaluating using negative exponents property, we get,

The value of \((-3)^{-8}=\frac{1}{6561} \text { and }-3^{-8}=\frac{-1}{6561}\)

We need to evaluate are (−3)⁻⁹ and −3⁻⁹

The given expressions are (−3)⁻⁹ and −3⁻⁹

Evaluating using negative exponents property, we get,

The values of \((-3)^{-9}=\frac{-1}{19683} \text { and }-3^{-9}=\frac{-1}{19683}\)

 

Page 50 Exercise 19 Answer

We have to simplify the expression. We need to assume that x is nonzero. Our answer should have only positive exponents.

The expression is x⁻¹⁰x⁶

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

Using this property, we get,

The value of \(x^{-10} x^6=\frac{1}{x^4}\)

 

Page 50 Exercise 20 Answer

We need to find whether the value of the expression \(\left(\frac{1}{4^{-3}}\right)^{-2}\) is greater than 1, equal to 1, or less than 1.

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

Using this property, we get,

The value is less than 1.

The value of \(\left(\frac{1}{4^{-3}}\right)^{-2}=\frac{1}{4096}\) which is less than the number 1.

Given that, If the value of the expression is greater than 1, we need to show how you can change one sign to make the value less than 1. If the value is less than 1, we need to show how you can change one sign to make the value greater than 1 . If the value is equal to 1, we need to show how you can make one change to make the value not equal to 1.

The given expression is,\(\left(\frac{1}{4^{-3}}\right)^{-2}\)

It will be equal to the value \(\left(\frac{1}{4^{-3}}\right)^{-2}=\frac{1}{4096}\)

The value is less than the number 1.

In order to make the value greater than 1, change one of the signs of the expression as follows,

\(\left(\frac{1}{4^{-3}}\right)^2=\left(4^3\right)^2=64^2=4096\)

In this way, we can make it greater than one.

The sign was changed from \(\left(\frac{1}{4^{-3}}\right)^{-2} \text { to }\left(\frac{1}{4^{-3}}\right)^2\) to make it greater than one.

Envision Math Grade 8 Exercise 1.7 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.7 Page 50 Exercise 22 Answer

We need to find which expressions have values less than 1 when x = 4 from the given expressions.

The negative exponent property states that when the exponent is negative, we need to put the number as a denominator in a fraction by changing the exponent into positive.

The zero exponent property states that when the exponent is zero while the base is non-zero, then the result will be one.

Using these properties, solving the given, we get,

The values which are less than 1 are,

\(\frac{x^0}{3^2}\) \(3 x^{-4}\)

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number

Page 39 Exercise 1 Answer

Given that, One band’s streaming video concert to benefit a global charity costs $1.00 to view.The first day, the concert got 2,187 views. The second day, it got about three times as many views. On the third day, it got 3 times as many views as on the second day. If the trend continues, we need to determine how much money will the band raise on the day 7.

Using the prime factorization method, the money raised on the last day will be, \(2187 \times 3^7\)

Also, write the number 2187 in terms of prime factorization, we get,

The money will the band raise on the day 7 will be 3¹⁴

Page 39 Exercise 1 Answer

We need to use prime factorization to write an expression equivalent to the amount of money raised by the band on the last day of the week.

As we know that the money raised on day one is 2187, for each consecutive days the money is getting tripled.

Thus calculating the money raised for each day, we get,
​
2187 × 3 = 6561

6561 × 3 = 19683

19683 × 3 = 59049

59049 × 3 = 177147

177147 × 3 = 531441

531441 × 3 = 1594323
​
Thus, on the day 7,the money raised will be $1,594,323

The amount of money raised by the band on the last day of the week will be $1,594,323

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.6 Real Number Solutions

Page 40 Question 1 Answer

We can write equivalent expressions using the properties of integer exponents to simplify the expressions.

Also, we can combine the expressions using these properties.

We can distribute the exponents using these properties.

We can combine the exponents together if the bases are the same.

We can deduce the exponents if the bases are the same and if they are in the division.

In this way, the properties are helpful in simplifying the expressions.

The properties of integer exponents help you write equivalent expressions by combining, distributing and simplifying the powers and bases.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 40 Exercise 1 Answer

Given that, the local zoo welcomed a newborn African elephant that weighed 3⁴ It is expected that at adulthood, the newborn elephant will weigh approximately 3⁴ times as much as its birth weight. We need to find the expression that represents the expected adult weight of the newborn elephant.

The weight of the newborn will be 3⁴

The weight of the adult African elephant will be 3⁴ × 3⁴

We can combine the exponents together if the bases are the same using the properties of integer exponents.

Thus, the weight of the adult will be,

3⁴ x 3⁴ = 3⁴⁺⁴

= 3⁸

The weight of the adult African elephant will be 3⁸

 

Page 41 Exercise 2 Answer

Write equivalent expressions of (7³)² using the properties of exponents.

The power of powers property implies to multiply the powers to find the power of powers.

Therefore, using the power of powers property, we get,

Write equivalent expressions of (4⁵)³ using the properties of exponents.

The power of powers property implies multiplying the powers to find the power of powers.

Therefore, using the power of powers property, we get,

Write equivalent expressions of 9⁴×8⁴ using the properties of exponents.

The power of products property implies multiplying the bases when the exponents are same.

Therefore, using the power of products property, we get,

Write equivalent expressions of \(\frac{8^9}{8^3}\) using the properties of exponents.

The Quotient of powers property implies subtracting the powers when the bases are the same in a division.

 

Page 40 Exercise 1 Answer

We need to explain why the Product of Powers Property makes mathematical sense.

​
The properties of integer exponents help you write equivalent expressions by combining, distributing and simplifying the powers and bases.

Envision Math Grade 8 Student Edition Exercise 1.6 Real Numbers Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 42 Exercise 2 Answer

When we are writing an equivalent expression for 2³⋅2⁴, we need to find how many times would you write 2 as a factor.

The bases are the same, thus adding the powers together we get,

​
We have to write 2 as a factor 7 times.

 

Page 42 Exercise 5 Answer

We need to write an equivalent expression for 7¹²⋅7⁴

The bases are the same, thus adding the powers together we get,

​
​The equivalent expression is 7¹⁶

 

Page 42 Exercise 6 Answer

Write equivalent expressions of (8²)⁴ using the properties of exponents.

The power of powers property implies multiplying the powers to find the power of powers.

Therefore, using the power of powers property, we get,

The equivalent expression is 8⁸

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 42 Exercise 8 Answer

We need to write an equivalent expression for \(\frac{18^9}{18^4}\)

The bases are the same in the given fraction, thus subtracting the exponents we get,

The equivalent expression is 18⁵

 

Page 43 Exercise 16 Answer

We need to write an equivalent for the given expression \(\frac{3^{12}}{3^3}\)

If the bases are the same in a fraction, then we need to subtract the exponents together to get the result.

The equivalent expression is 3⁹

Real Number Solutions Grade 8 Exercise 1.6 Envision Math

Page 43 Exercise 17 Answer

We need to write an equivalent expression for the given expression 4⁵ . 4²

If the bases are the same, then we need to add the exponents together to get the result.

The equivalent expression is 4⁷

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 43 Exercise 18 Answer

We need to write an equivalent expression for the given expression 6⁴ . 2⁴

The power of products property implies multiplying the bases when the exponents are the same.

Therefore, using the power of products property, we get,

The equivalent expression is 12⁴

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 44 Exercise 20 Answer

We need to find whether the expression 8 x 8⁵ is equivalent to (8 x 8)⁵ or not.

The expression 8 x 8⁵ is not equivalent to (8 x 8)⁵

 

Page 44 Execise 21 Answer

We need to find whether the expression (3²)³ is equivalent to (3³)²

The power of powers property implies multiplying the powers to find the power of powers.

The expression (3²)³ is equivalent to (3³)²

Envision Math Grade 8 Chapter 1 Exercise 1.6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 44 Exercise 22 Answer

We need to find whether the expression \(\frac{3^2}{3^3}\) is equivalnet to \(\frac{3^3}{3^2}\) or not.

If the bases are the same in a fraction, then we need to subtract the exponents together to get the result.

Thus, we get,

The expression \(\frac{3^2}{3^3}\) is not equivalent to \(\frac{3^3}{3^2}\)

Envision Math 8th Grade Exercise 1.6 Step-By-Step Real Number Solutions

Page 44 Exercise 23 Answer

We need to find the width of the rectangle written as an exponential expression.

 

The width of the rectangle written as an exponential expression is w = 10¹m

Envision Math Exercise 1.6 Real Numbers Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 44 Exercise 24 Answer

We need to simplify the given expression \(\left(\left(\frac{1}{2}\right)^3\right)^3\)

The power of powers property implies multiplying the powers to find the power of powers.

The simplified expression is \(\left(\frac{1}{2}\right)^9\)

Envision Math Grade 8 Exercise 1.6 Practice Problems

Page 44 Exercise 25 Answer

we need to use a property of exponents to write (3b)⁵ as a product of powers.

This property states that, if the bases are the same, then we need to add the exponents together to get the result.

The given expression is (3b)⁵

Using the property we write it as,

(3b)⁵ = (3b)² x (3b)³

Writing the given expression as a product of powers, we get,

(3b)⁵ = (3b)² x (3b)³

 

Page 44 Exercise 26 Answer

We need to simplify the given expression 4⁵ . 4¹⁰

If the bases are the same, then we need to add the exponents together to get the result.

The simplified expression is 4¹⁵

How To Solve Exercise 1.6 Real Numbers In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.6 Real Number Page 44 Exercise 27 Answer

Given that, your teacher asks the class to evaluate the expression (2³)¹. Your classmate gives an incorrect answer of 16.

We need to evaluate the expression.

The power of powers property implies multiplying the powers to find the power of powers.

The correct answer is (2³)¹ = 8

Your teacher asks the class to evaluate the expression (2³)¹. Your classmate gives an incorrect answer of 16. We need to find which of the following error they made.

(A) Your classmate divided the exponents.

(B) Your classmate multiplied the exponents.

(c) Your classmate added the exponents.

(D) Your classmate subtracted the exponents.

The power of powers property implies multiplying the powers to find the power of powers.

Thus,

(2³)¹ = 2^3×1

= 2⁴ = 16

They liked added the exponents.

If they added the exponents, the result will be,

(2³)¹ = 2³⁺¹ = 2⁴ = 16

This will lead to the incorrect answer.

The likely error is that (c) Your classmate added the exponents.

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions

Page 25 Exercise 1 Answer

Given that, Matt and his dad are building a treehouse. They buy enough flooring material to cover an area of 36 square feet. We need to find all possible dimensions of the floor.

The given area is 36 square feet.

The factors of 36 will be,
​
36 = 3 × 3 × 2 × 2

36 = 9 × 4

36 = 18 × 2

36 = 3 × 12

36 = 6 × 6
​
Therefore, the possible dimensions are 9×4,6×6,3×12,18×2

The possible dimensions of the floor will be 9×4,6×6,3×12,18×2

 

Page 25 Exercise 2 Answer

We need to explain whether the different floor dimensions result in the same area.

The different floor dimensions obtained in the previous part is

9×4,6×6,3×12,18×2

All the floor dimensions result in the same area.

This is because the area of the square is A = s²

Here, the length of all the sides of the square is the same.

The area of the rectangle is A = l × b

Therefore, all the dimensions result in the same area.

Yes, the different floor dimensions result in the same area.

Page 26 Question 1 Answer

We need to explain how we could evaluate cube roots and square roots.

For finding the cube roots, find the number which when multiplied three times by itself gives the original number.

For example, if the number is 27

Then the cube root of this number is given by,
​

\(\sqrt[3]{27}=\sqrt[3]{3 \times 3 \times 3}\)

= 2
​
Thus, the cube root of the number 27 is 3.

For finding the square roots, find the number which when multiplied two times by itself gives the original number.

For example, if the number is 4.

Then the square root of this number is given by,
​

\(\sqrt[2]{4}=\sqrt[2]{2 \times 2}\)

= 2

Thus, the square root of the number 4 is 2.

Cube roots can be evaluated by finding the number which when multiplied three times by itself gives the original number.

Square roots can be evaluated by finding the number which when multiplied two times by itself gives the original number.

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.4 Real Number Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions Page 26 Exercise 1 Answer

We need to explain what we know about the length, width, and height of the birdhouse.

The birdhouse is cube-shaped.

Its area is given to be 216 cubic-inch.

We know that the volume of the cube will be,
​
V = s³

V=s×s×s
​
In a cube-shaped figure, all the lengths of the edges are equal.

This means that the length, width, and height of the birdhouse will be the same.

The length, width, and height of the birdhouse will be the same since the birdhouse is cube-shaped.

 

Page 26 Exercise 1 Answer

Given that, a cube-shaped art sculpture has a volume of 64 cubic feet. We need to find the length of each edge of the cube.

The volume of the cube is 64 cubic feet.

The volume formula will be,

V = a³

where a is the length of each edge of the cube.

Thus, substituting the given in the formula, we get,
​
64 = a³

\(a=\sqrt[3]{64}\) \(a=\sqrt[3]{4 \times 4 \times 4}\)

a = 4
​
The length of each edge of the cube is 4 feet.

 

Page 27 Exercise 2  Answer

We need to find the value of \(\sqrt[3]{27}\)

The given expression is \(\sqrt[3]{27}\)

Finding its cube root, we get,

\(\sqrt[3]{27}=\sqrt[3]{3 \times 3 \times 3}\)

= \(\sqrt[3]{3^3}\)

= 3

The value of \(\sqrt[3]{27}\) = 3

We need to find the value of √25

The given expression is √25

Finding its square root, we get,

\(\sqrt{25}=\sqrt{5 \times 5}\) \(\sqrt{25}=\sqrt{5^2}\)

= 5

The value of √25 = 5

We need to find the value of √81

The given expression is √81

Finding its square root, we get,

\(\sqrt{81}=\sqrt{9 \times 9}\) \(\sqrt{81}=\sqrt{9^2}\)

= 9

The value of √81 = 9

We need to find the value of \(\sqrt[3]{1}\)

The given expression is \(\sqrt[3]{1}\)

Finding its cube root, we get,

\(\sqrt[3]{1}=\sqrt[3]{1 \times 1 \times 1}\)

= \(\sqrt[3]{1^3}\)

= 1

The value of \(\sqrt[3]{1}\) = 1

Envision Math Grade 8 Exercise 1.4 Real Numbers Answers

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions Page 27 Exercise 3 Answer

Given that, Emily wants to buy a tablecloth to cover a square card table. She knows the tabletop has an area of 9 square feet. We need to find the minimum dimensions of the tablecloth Emily needs.

​

Emily wants to buy a tablecloth that measures at least 3 feet by 3 feet.

 

Page 26 Exercise 1 Answer

We need to find the cube root of 64

The given value is 64

Finding its cube root, we get,

\(\sqrt[3]{64}=\sqrt[3]{4 \times 4 \times 4}\)

=\(\sqrt[3]{4^3}\)

The cube root of 64 is 4.

Envision Math Grade 8 Real Number Practice Problems Exercise 1.4

Page 28 Exercise 1 Answer

We need to explain how we could evaluate cube roots and square roots.

For finding the cube roots, find the number which when multiplied three times by itself gives the original number.

For example, if the number is 27

Then the cube root of this number is given by,

\(\sqrt[3]{27}=\sqrt[3]{3 \times 3 \times 3}\)

= \(\sqrt[3]{3^3}\)

= 3

Thus, the cube root of the number 27 ia 3

For finding the square roots, find the number which when multiplied two times by itself gives the original number.

For example, if the number is 4

Then the square root of this number is given by,

\(\sqrt{4}=\sqrt{2 \times 2}\)

= \(\sqrt{2^2}\)

Thus, the square root of the number 4 is 2.

Cube roots can be evaluated by finding the number which when multiplied three times by itself gives the original number.

Square roots can be evaluated by finding the number which when multiplied two times by itself gives the original number.

 

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions Page 26 Exercise 1 Answer

We need to find the cube root of 64

The given value is 64

Finding its cube root, we get,

\(\sqrt[3]{64}=\sqrt[3]{4 \times 4 \times 4}\)

= \(\sqrt[3]{4^3}\)

= 4

The cube root of 64 is 4.

 

Page 28 Exercise 1 Answer

We need to explain how we could evaluate cube roots and square roots.

For finding the cube roots, find the number which when multiplied three times by itself gives the original number.

For example, if the number is 27

Then the cube root of this number is given by,

\(\sqrt[3]{27}=\sqrt[3]{3 \times 3 \times 3}\)

= \(\sqrt[3]{3^3}\)

= 3

Thus, the cube root of the number 27 is 3

For finding the square roots, find the number which when multiplied two times by itself gives the original number.

For example, if the number is 4

Then the square root of this number is given by,

\(\sqrt{4}=\sqrt{2 \times 2}\)

= \(\sqrt{2^2}\)

Thus, the square root of the number 4 is 2.

Cube roots can be evaluated by finding the number which when multiplied three times by itself gives the original number.

Square roots can be evaluated by finding the number which when multiplied two times by itself gives the original number.

 

Page 28 Exercise 3 Answer

Given that, a cube-shaped box has a volume of 27 cubic inches. Bethany says each side of the cube measures 9 inches because 9×3=27

We need to determine whether Bethany is correct.

 

Bethany’s statement is wrong.

Envision Math Exercise 1.4 Real Numbers Detailed Answers

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions Page 28 Exercise 4 Answer

Given that, a cube has a volume of 8 cubic inches. We need to find the length of each edge of the cube.

 

The length of each edge of the cube is 2 inches.

Page 28 Exercise 5 Answer

Given below is a model of the infield of a baseball stadium. We need to determine the length of each side of the infield.

The area of the infield (the square) is given by 81
square inches.

The length of its side will be,

A = a²

81 = a²

\(a=\sqrt{81}\) \(a=\sqrt{9 \times 9}\) \(a=\sqrt{9^2}\)

a = 9

The length of each side of the infield is 9 inches.

 

Page 28 Exercise 6 Answer

Given that, Julio cubes a number and then takes the cube root of the result. He ends up with 20. Find the number Julio started with.

If Julio cubes a particular number and then takes the cube root of the obtained result, he will end up with the same number.

For example, the number be 3

Taking the cube of it,

3 × 3 × 3 = 27

Taking the cube root of the result, we get,

 

\(\sqrt[3]{27}=\sqrt[3]{3 \times 3 \times 3}\)

 

= \(\sqrt[3]{3^3}\)

 

= 3

Thus, we obtained the same number at the end.

Therefore, the number julio started with will be 20.

The number Julio started with will be 20.

Real Number Solutions Grade 8 Exercise 1.4 Envision Math

Page 29 Exercise 7 Answer

We need to relate the volume of the cube to the length of each edge. The volume is given as V = 8cm³

 

The length of each edge will be 2cm.

How To Solve Real Numbers Exercise 1.4 In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions Page 29 Exercise 8 Answer

We need to relate the area of the square to the length of each edge. The area is given as A=16cm²

 

The length of each side of the square will be 4cm.

 

Page 29 Exercise 10 Answer

Given that the volume of a cube is 512 cubic inches. We need to find the length of each side of the cube.

 

The length of each side of the cube is 8 inches.

 

Page 29 Exercise 11 Answer

Given that, A square technology chip has an area of 25 square centimeters. We need to find the length of each side of the chip.

 

The length of each side of the chip is 5 cm.

Envision Math Grade 8 Chapter 1 Exercise 1.4 Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions Page 29 Exercise 12 Answer

We need to classify the number 200 as a perfect square, a perfect cube, both, or neither and also explain.

Finding its cube root,

\(\sqrt[3]{200}=5.8480\)

It is not a perfect cube.

Finding its square root, we get,

\(\sqrt{200}=14.1421\)

 

It is not a perfect square either.

 

The number 200 is neither a perfect square nor a perfect cube.

 

Page 29 Exercise 13 Answer

Given, A company is making building blocks. We need to determine the length of each side of the block.

The volume is given as V = 1ft³

 

The length of each side of the block is 1ft

 

Page 30 Exercise 16 Answer

Given that, Talia is packing a moving box. She has a square-framed poster with an area of 9 square feet. The cube-shaped box has a volume of 30 cubic feet. We need to find whether the poster lie flat in the box or not.

 

The length of the square-framed poster is smaller than that of the cubic box.

The poster lies flat in the box.

Envision Math 8th Grade Exercise 1.4 Step-By-Step Real Number Solutions

Envision Math Grade 8 Volume 1 Chapter 1 Real Number Exercise 1.4 Solutions Page 30 Exercise 17 Answer

We need to find which statements are true.

The statements are

49 is a perfect square.

9 is a perfect cube.

27 is a perfect cube.

14 is neither a perfect square nor a perfect cube.

1000 is both a perfect square and a perfect cube.

 

\(\sqrt{49}=\sqrt{7 \times 7}\)

= 7

Hence, 49 is a perfect square.

 

\(\sqrt[3]{9}=2.080\)

Hence, 9 is not a perfect cube.

 

\(\sqrt[3]{27}=\sqrt[3]{3 \times 3 \times 3}\)

 

= 3

Hence, 27 is a perfect cube.

\(\sqrt[3]{14}=2.410\) \(\sqrt{14}=3.7416\)

Hence, it is not a perfect square nor a perfect cube.

\(\sqrt[3]{1000}=\sqrt[3]{10 \times 10 \times 10}\)

 

= 10

 

\(\sqrt{1000}=31.62\)

The true statements are,

49 is a perfect square.

27 is a perfect cube.

14 is neither a perfect square nor a perfect cube.

 

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2

Envision Math Grade 8 Volume 1 Chapter 1 Exercise 1.2 Real Number Solutions

Page 13 Exercise 1 Answer

Given that, Sofia wrote a decimal as a fraction. Her classmate Nora says that her method and answer are not correct. Sofia disagrees and says that this is the method she learned.

We need to construct Arguments whether Nora or Sofia is correct or not.

The given decimal is 0.12112111211112…

Here, Sofia wrote this decimal as a fraction.

But it cannot be represented as a fraction since the given number is an irrational number.

Only terminating and repeating decimals can be represented as a fraction.

Here, the decimal is not terminating and it is not repeating. Thus, it cannot be represented as a fraction.

Nora’s Argument is correct. The given number cannot be represented as a fraction since it is an irrational number.

 

Page 13 Exercise 2 Answer

We need to write another nonterminating decimal number that can not be written as a fraction.

Only terminating and repeating decimals can be represented as a fraction.

If the decimal is not terminating and it is not repeating, it cannot be represented as a fraction.

Some of the examples of nonterminating decimal numbers that can not be written as fractions are,
​
0.15267389…

0.3512649…

0.125112511125…
​
Another nonterminating decimal number that can not be written as a fraction is 0.125112511125…

Page 13 Exercise 1 Answer

We need to find whether 0.12112111211112… is a rational number or not.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Here, the given number 0.12112111211112… is non-terminating and non-repeating in nature.

Hence, it is an irrational number.

The given decimal 0.12112111211112… is an irrational number.

Envision Math Grade 8 Student Edition Exercise 1.2 Real Numbers Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 14 Question 1 Answer

We need to explain how an irrational number is different from a rational number.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Terminating and repeating decimals are known as rational numbers while non-terminating and non-repeating decimals are known as irrational numbers.

Page 14 Exercise 1 Answer

We need to classify the below numbers as rational or irrational.

The numbers are

π

3.565565556…

0.04053661…

-17

0.76

3.275

Irrational numbers cannot be represented as a fraction. Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature. Only rational numbers can be represented as a fraction while irrational numbers cannot.

Rational numbers are:
​
π=3.14159

−17

0.76

3.275
​
Irrational numbers are:

3.565565556…

0.04053661…

 

Page 15 Exercise 2 Answer

We need to classify the below numbers as rational or irrational.
\(\frac{2}{3}\),√25,−0.75,√2,7,548,123

Irrational numbers cannot be represented as a fraction. Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature. Only rational numbers can be represented as a fraction while irrational numbers cannot.

Rational numbers are:

\(\frac{2}{3}\),√25,−0.75,7,548,123

Irrational number is: √2

Rational numbers: \(\frac{2}{3}\),√25,−0.75,7,548,123

Irrational numbers: √2

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 14 Exercise 1 Answer

Given that, Jen classifies the number 4.567 as irrational because it does not repeat. We need to construct arguments whether Jen is correct or not.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The number 4.567 is terminating in nature.

Hence, the given number is a rational number.

Jen’s argument is incorrect.

 

Page 16 Exercise 1 Answer

We need to describe the difference between the irrational number and a rational number.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Terminating and repeating decimals are known as rational numbers while non-terminating and non-repeating decimals are known as irrational numbers.

 

Page 16 Exercise 3 Answer

We need to explain whether a number could ever be both rational and irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

A number could never be both rational and irrational. It has to be one or the other.

Real Number Solutions Grade 8 Exercise 1.2 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 16 Exercise 4 Answer

We need to explain whether the number 65.4349224… is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number 65.4349224… is non-terminating and non-repeating in nature.

Hence, it is an irrational number.

The given number 65.4349224… is an irrational number.

 

Page 16 Exercise 5 Answer

We need to explain whether the number√2500 is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number √2500 = 50 is a perfect square number.

Hence, it is an rational number.

The given number √2500 is an rational number.

Envision Math Grade 8 Chapter 1 Exercise 1.2 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 16 Exercise 6 Answer

We need to classify each number as rational or irrational.
The numbers given are,
​
\(4.2 \overline{7}\)

0.375

0.232342345…

\(\sqrt{62}\) \(-\frac{13}{1}\)

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

Rational numbers are:

\(4.2 \overline{7}\)

0.375

\(-\frac{13}{1}\)

Irrational numbers are:

0.232342345…

\(\sqrt{62}\)

Rational numbers: \(4.2 \overline{7}, 0.375, \frac{-13}{1}\)

Irrational numbers: 0.232342345…, \(\sqrt{62}\)

 

Page 17 Exercise 7 Answer

We need to explain whether the number5.787787778… is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number 5.787787778… is non-terminating and non-repeating in nature.

Hence, it is an irrational number.

The given number 5.787787778… is an irrational number.

Envision Math 8th Grade Exercise 1.2 Step-By-Step Real Number Solution

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 17 Exercise 8 Answer

We need to explain whether the number √42 is rational or irrational.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The given number √42 is not the square root of a perfect square number.

Hence, it is an irrational number.

The given number √42 is an irrational number.

 

Page 17 Exercise 10 Answer

We need to circle the irrational number in the given list:

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.
​
\(7.2 \overline{7}=7.27777 \ldots\)

\(\frac{5}{9}\) \(\sqrt{196}=14\)

These are rational numbers since it is repeating and terminating in nature.

The number √15 is irrational since 15 is not a perfect square number.

The irrational number is circled below,

 

 

Page 17 Exercise 11 Part (a) Answer

The given numbers are 5.737737773…,26,√45 \(\frac{-3}{2}\),0,9

We need to find the rational numbers in it.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The rational numbers are 26,\(\frac{-3}{2}\),0,9

The rational numbers in the list will be 26,\(\frac{-3}{2}\),0,9

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 18 Exercise 14 Answer

We need to check whether the decimal form of \(\frac{13}{3}\) is a rational number or not.

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

The decimal form of the given number is,

\(\frac{13}{3}=4.33333 \ldots\)

The given number is non-terminating and repeating in nature.

Thus, the given number is rational.

The decimal form of \(\frac{13}{3}\) is rational.

How To Solve Exercise 1.2 Real Numbers In Envision Math Grade 8

Page 18 Exercise 18 Answer

We need to find the rational numbers among the following:

1. 1.111111…

2. 1.567…

3. 1.101101110…

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represented as a fraction while irrational numbers cannot.

1. 1.111111…

This number is rational since it is repeating in nature.

2. 1.567…

This number is irrational since it is non-repeating and non-terminating in nature.

3. 1.101101110…

This number is irrational since it is non-repeating and non-terminating in nature.

The correct option is (E) I only.

Only 1. 1.111111… is rational others are irrational.

Envision Math Grade 8 Exercise 1.2 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.2 Page 18 Exercise 19 Answer

We need to classify the given numbers as rational or irrational.

The numbers are

\(\frac{8}{5}, \pi, 0, \sqrt{1}, 4.46466 \ldots,-6, \sqrt{2}\)

The given numbers are \(\frac{8}{5}, \pi, 0, \sqrt{1}, 4.46466 \ldots,-6, \sqrt{2}\)

Irrational numbers cannot be represented as a fraction.

Irrational numbers are non-terminating and non-repeating in nature.

Only terminating and repeating decimals can be represented as a fraction.

Rational numbers are terminating and repeating in nature.

Only rational numbers can be represendted as a fraction while irrational numbers cannot.

\(\frac{8}{5}, \pi=\frac{22}{7}, 0, \sqrt{1},-6\) are rationa since it is terminating in nature.

4.46466…., √2 are irrational since it is nonterminating and the roots are not of the perfect squares.

 

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1

Page 2 Question 1 Answer

A real number would be any number which can be discovered in the actual world. Numbers can be found all around us.

Natural numbers are being used to count objects.

Rational numbers are being used to portray fractions.

Irrational numbers are being used to calculate the square root of an amount.

Integers are used to measure temperature, among other things.

These various types of numbers combine form a gathering of real numbers.

Except complex numbers, everything come under real numbers.

It is denoted by R and it is the union of both rational and irrational numbers and it is represented by \(R=Q \cup \bar{Q}\)

Page 2 Question 2 Answer

A real number would be any number which can be discovered in the actual world. Numbers can be found all around us.

Natural numbers are being used to count objects.

Rational numbers are being used to portray fractions.

Irrational numbers are being used to calculate the square root of an amount.

Integers are used to measure temperature, among other things.

These various types of numbers combine to form a gathering of real numbers.

Real numbers are used in many places to solve problems. For example, it is used to portray fractions, determine square roots, measure temperature, and for counting things, etc.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 1 Answer

We know that the addition of zeroes at the end of a decimal number doesn’t change its value.

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite.

The given number terminates at this point. Thus, it is a terminating decimal.

A finite number of decimals can also be represented in the form of repeating zeroes at the end.
For example,
​
12.2750000 or 12.275

15.840000 or 15.84
​
These are some of the examples of terminating decimal which has repeating zeros in it.

A terminating decimal is a decimal that ends in repeating zeros.

 

Page 5 Exercise 2 Answer

We know that the addition of zeroes at the end of a decimal number doesn’t change its value.

But if the decimal gets repeated again and again, the loop goes endlessly and the digits repeat forever.

A number that has an infinite number of decimals in it is termed to be the repeating decimals.

A repeating decimal doesn’t terminate at any point. The decimal will be infinite.

For example,

15.57 or 15.575757….

\(19.75 \overline{4} \text { or } 19.754444444 \ldots\)

These are some of the examples of repeating decimal which has repeating digits in it.

A repeating decimal is a decimal in which a digit or digits repeat endlessly.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 4 Answer

We can write any number as a fraction.

A fraction can be used to describe the part of the things.

It is described as a part of a whole or a part of a set.

The division of any number is said to be the fraction.

For example, if we are going to eat half of the eight eggs we have, it is represented as,

\(\frac{1}{2} \times 8=4\)

A fraction is a number that can be describe a part of a whole, a part of a set, a location on a number line, or a division of whole numbers.

 

Page 5 Exercise 7 Answer

Given decimal is 7.0001

We need to determine whether the given decimal is terminating or repeating.

The given number is 7.0001

It can also be written as 7.00010000000000000000…

Since they both represent the same.

This is because the addition of zeroes at the end of a decimal number doesn’t change its value.

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite. i.e., .0001.

The given number terminates at this point. Thus, it is a terminating decimal.

The given number 7.0001 is a terminating decimal.

 

Page 5 Exercise 9 Answer

Given decimal is \(1.1 \overline{7} 8\)

We need to determine whether the given decimal is terminating or repeating.

The given number is \(1.1 \overline{7} 8\)

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite.

If the number of decimals is infinite and the number gets repeated again and again, it is referred as repeating decimal.

The given number doesn’t terminate at any point as it has an infinite number of decimals.

The number 178 gets repeated again and again.

The given number can also be represented as 1.178178178…

Thus, it is a repeating decimal.

The given number \(1.1 \overline{7} 8\) is a repeating decimal.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 10 Answer

Given decimal is −4.03479

We need to determine whether the given decimal is terminating or repeating.

The given number is −4.03479

A number that has a finite number of decimals in it can also be represented by adding repeating zeroes at the end of it.

Even though we add repeating zeroes, the number of decimals present in the given number is finite.

The given number terminates at this point as it has a finite number of decimals. Thus, it is a terminating decimal.

The given number -4.03479 is a terminating decimal.

 

Page 5 Exercise 11 Answer

We need to find the product of 2.2

Performing multiplication on the given numbers, we get,

2.2 = 2 x 2
= 4

Thus, the product will be 4.

The product of 2.2 = 4

 

Page 5 Exercise 12 Answer

We need to find the product of -5 . -5

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​
(−5)⋅(−5)=5×5

=25
​
Thus, the product will be 25.

The product of −5 ⋅ −5 = 25

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 13 Answer

We need to find the product of 7⋅7

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​
7 ⋅ 7 = 7 × 7

= 49
​
Thus, the product will be 49

The product of 7⋅7 = 49

 

Page 5 Exercise 14 Answer

We need to find the product of −6⋅(−6)⋅(−6)

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​

​
Thus, the product will be −216

The product of −6⋅(−6)⋅(−6) = −216

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 16 Answer

We need to find the product of −9⋅(−9)⋅(−9)

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers, we get,
​
​
The product of −9⋅(−9)⋅(−9) = −729​

 

Page 5 Exercise 17 Answer

We need to simplify the given expression (4⋅10)+(5⋅100)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (4.10) + (5.100) = 540

 

Page 5 Exercise 19 Answer

We need to simplify the given expression (2.100)+(7.10)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (2.100)+(7.10) = 270

 

Page 5 Exercise 20 Answer

We need to simplify the given expression (9⋅1000)+(4⋅10)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (9⋅1000)+(4⋅10)=9040

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 5 Exercise 21 Answer

We need to simplify the given expression (3⋅1000)−(2⋅100)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is being simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and subtracting the result, we get,
​

​
The simplification of the given number results (3.1000) – (2.100) = 2800

 

Page 5 Exercise 22 Answer

We need to simplify the given expression (2⋅10)+(7⋅100)

Multiplication is one of the basic arithmetic operations. The result of which is termed to be the product.

Adding a number to a certain time is being simplified as the form of multiplication.

In multiplication, the product of two positive numbers or two negative numbers will result in a positive number.

The product of a negative and a positive number will result in a negative number.

Performing multiplication on the given numbers and adding the result, we get,
​
​
The simplification of the given number results in (2.10) + (7.100) = 720

 

Page 6 Exercise 1 Answer

We need to use the Graphic organizer to help you understand new vocabulary terms such as cube root, irrational number, a perfect cube, perfect square, scientific notation, and square root.

Cube root can be found by finding a number that when multiplied three times by itself gives the original number.

A square root can be found by finding a number that when multiplied two times by itself gives the original number.

If we multiply an integer three times by itself, it will result in a perfect cube.

If we multiply an integer two times by itself, it will result in a perfect square.

Expressing the biggest or the smallest number in decimal form is referred to the scientific notation.

A number that cannot be expressed as a fraction is said to be an irrational number.

 

Cube Root:

Definition – A number which when multiplied 3 times by itself gives the original number.

Example – \(\sqrt[3]{64}=4\)

Irrational number:

Definition – A number that cannot be expressed as a fraction but in decimal form.

Example – 0.24556766666…

Perfect cube:

Definition – The number obtained If we multiply an integer 3 times by itself.

Example – 3×3×3=27

Perfect square:

Definition – The number obtained If we multiply an integer 2 times by itself.

Example – 3×3=9

Scientific notation:

Definition – Expressing the biggest or the smallest number in decimal form.

Example – 1.543543543… = \(1.5 \overline{4} 3\)

Square Root:

Definition – A number which when multiplied 2 times by itself gives the original number.

Example – \(\sqrt[2]{16}=4\)

 

Page 7 Exercise 1 Answer

Given that, Jaylon has a wrench labeled 0.1875 inch and bolts labeled in fractions of an inch. We need to find which size bolt will fit best with the wrench.

The given bolt sizes are \(\frac{3}{8}, \frac{1}{8}, \frac{3}{16}, \frac{1}{4}\)inches.

Solving each fraction to find the equivalent size as that of the wrench given,
​
\(\frac{3}{8}=0.375\)

\(\frac{1}{8}=0.125\) \(\frac{3}{16}=0.1875\) \(\frac{1}{4}=0.25\)

The bolt size which best fit the wrench is \(\frac{3}{16}\) inch bolt.

\(\frac{3}{16}\) inch size bolt will fit best with the wrench.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 7 Exercise 1 Answer

We need to explain how we can write these numbers in the same form.

The given wrench size is 0.1875 inch

This is of in decimal form.

Meanwhile, the given bolt \(\frac{3}{8}, \frac{1}{8}, \frac{3}{16}, \frac{1}{4}\)inches.

This is of fractional form.

We can easily convert the given fractions to decimals by dividing the fractions given.

It can be done as follows,

\(\frac{3}{8}=0.375\) \(\frac{1}{8}=0.125\) \(\frac{3}{16}=0.1875\) \(\frac{1}{4}=0.25\)

We can write the given numbers in the same form by converting the fractions into decimals.

 

Page 7 Exercise 1 Answer

We need to explain why is it useful to write a rational number as a fraction or as a decimal.

A unique feature of a rational number is that it can be written in the form of a fraction.

Not every decimal is denoted to be the rational number.

Only repeating and the terminating decimal can come under the category of rational number.

It is useful to write it as a fraction or a decimal to make the computations easier.

It is useful to write a rational number as a fraction or as a decimal to help make the calculations easier.

 

Page 8 Exercise 1 Answer

Given that, in another baseball division, one team had a winning percentage of 0.444…..We need to determine the fraction of their games the team won.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The winning percentage is converted to fractions as,
​

 

Page 9 Exercise 2 Answer

We need to write the repeating decimal 0.63333… as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The repeating decimal 0.6333… is converted to fraction as \(\frac{19}{30}\)

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 9 Exercise 3 Answer

We need to write the repeating decimal 4.1363636… as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The repeating decimal 4.1363636… is converted to fraction as \(\frac{455}{110}\)

 

Page 10 Exercise 2 Answer

We need to explain why we multiply by a power of 10 when writing a repeating decimal as a rational number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
We can determine the power of ten to multiply by in the second step at the right is by calculating how many places after the decimal does the given numbers gets repeated.

Here, the given number gets repeated after one decimal place. Thus, the power of ten is one.

This step is done to convert the given repeating number to a fraction.

We can multiply a repeating decimal by a power of 10 when writing a repeating decimal as a rational number to convert it to a fractional number.

 

Page 10 Exercise 3 Answer

We need to explain how we could decide which power of 10 to multiply an equation when writing a decimal with repeating digits as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable..

After that, multiply each sides of it by the multiples of 10.

Subtract both the expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
We can determine the power of ten to multiply by in the second step at the right is by calculating how many places after the decimal does the given numbers gets repeated.

Here, the given number gets repeated after one decimal place. Thus, the power of ten is one.

We can determine the power of ten to multiply an equation when writing a decimal with repeating digits as a fraction by determining the number of places after the decimal does the given number gets repeated.

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 10 Exercise 4 Answer

Given that, a survey reported that \(63 . \overline{63}\)% of moviegoers prefer action films. This percent represents a repeating decimal. We need to write it as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each sides of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given percent is written as a fraction as \(\frac{700}{11}\)

 

Page 10 Exercise  5 Answer

We need to write the given decimal 2.3181818… as a mixed number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The mixed fraction of the given repeating decimal is \(x=2 \frac{3.5}{11}\)

 

Page 11 Exercise 10 Answer

Given that, Tomas asked 15 students whether summer break should be longer. He used his calculator to divide the number of students who said yes by the total number of students. His calculator showed the result as 0.9333….. . We need to write this number as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given decimal 0.9333… is equal to \(x=\frac{8.4}{9}\)

 

Page 11 Exercise 12 Answer

We need to write the given decimal \(0 . \overline{8}\) as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

The given decimal is converted into a fraction as \(x=\frac{8}{9}\)

 

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 12 Exercise 13 Answer

We need to write the given decimal \(1 . \overline{48}\) as a mixed number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given decimal is converted into a mixed number as \(x=1 \frac{48}{99}\)

 

Page 12 Exercise 14 Answer

We need to write the given decimal \(0 . \overline{6}\)

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,
​

The given decimal is converted into a fraction as \(\frac{6}{9}\)

 

Page 12 Exercise 15 Answer

Given that a manufacturer determines that the cost of making a computer component is $2.161616. We need to write the cost as a fraction and as a mixed number.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

Subtract both expressions to write the repeating decimals as fractions.

The decimal is converted to fractions as,

​
The given decimal is converted into a fraction as \(\frac{214}{99}\) and as a mixed number as \(2 \frac{16}{99}\)

 

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 1 Real Number Exercise 1.1 Page 12 Exercise 16 Answer

We need to explain the need for the number of repeating digits we use while writing a repeating decimal as a fraction.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

The power of the number ten which we can use to convert the decimal to fraction can be obtained by looking into the number of repeating digits in a decimal.

If the number of repeating digits is two, then the power of ten multiplied with the decimal will also be two.

When writing a repeating decimal as a fraction, the number of repeating digits we use matters the most since it determines the power of ten which we multiply it with the decimal to make it as a fraction.

 

Page 12 Exercise 17 Answer

When writing a repeating decimal as a fraction, we need to explain why does the fraction always have only 9s or 9s and Os as digits in the denominator.

A repeating decimal can be written as a fraction by assuming the decimal as a variable.

After that, multiply each side of it by the multiples of 10.

The power of the number ten which we can use to convert the decimal to fraction can be obtained by looking into the number of repeating digits in a decimal.

If the number of repeating digits is two, then the power of ten multiplied with the decimal will also be two.

The subtraction of any number of the power of ten by one will result in a number 9 or the multiples of it.

This is why the denominator is always 9 or 9 and 0.

The number divided by 9s or 9s and 0s will result in repeating decimals. That is why when we convert that to a fraction, the denominator is always 9s or 9s and 0s.

 

Page 12 Exercise 18 Answer

We need to find the decimal which is equivalent to \(\frac{188}{11}\)

The given fraction is \(\frac{188}{11}\)

Converting the given fraction to a decimal by dividing the fraction, thus we get,

\(\frac{188}{11}=17.090909 \ldots\)

= \(17 . \overline{09}\)

The decimal which is equivalent to \(\frac{188}{11} \text { is (A) } 17 . \overline{09}\)

 

Page 12 Exercise 19 Answer

We need to draw lines to connect each repeating decimal on the left with an equivalent fraction on the right.

Solving each fraction one by one, we get,

\(\frac{58}{165}=0.351515 \ldots=0.35 \overline{1}\) \(\frac{79}{225}=0.351111 \ldots=0.35 \overline{1}\)

\(\frac{13}{37}=0.351351 \ldots=0.3 \overline{5}\) 1

\(\frac{8}{45}=0.1777 \ldots=0.1 \overline{7}\) \(\frac{17}{99}=0.171717 \ldots=0 . \overline{17}\)