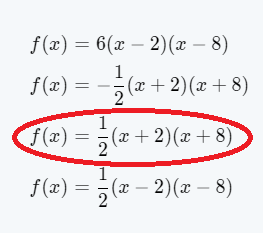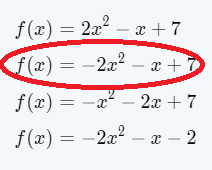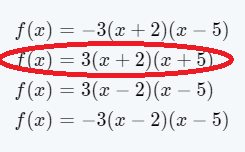Carnegie

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice

Page 287 Problem 1 Answer

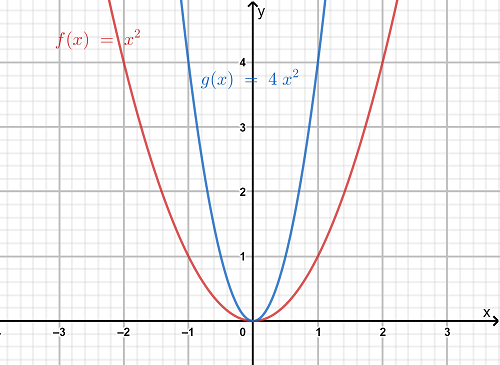
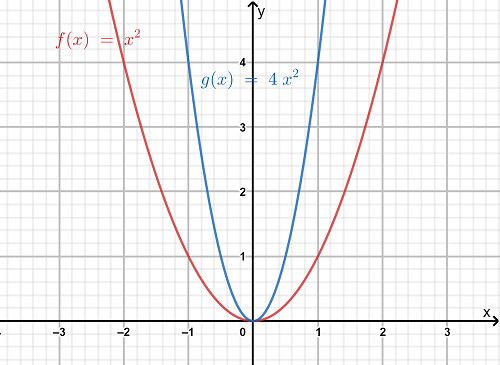
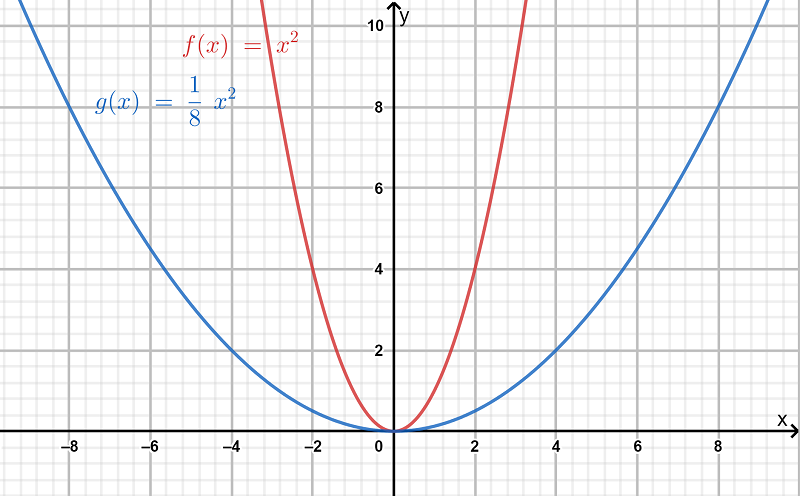
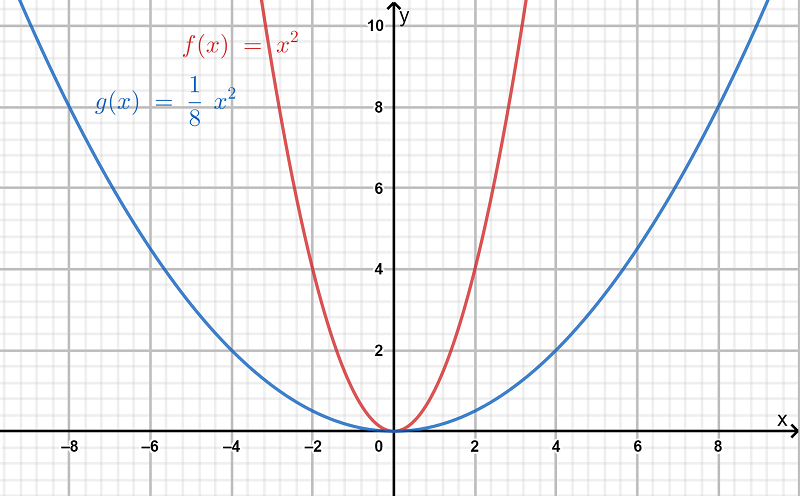
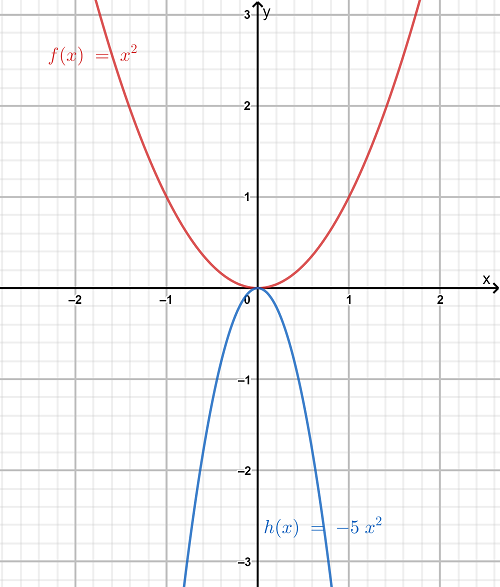
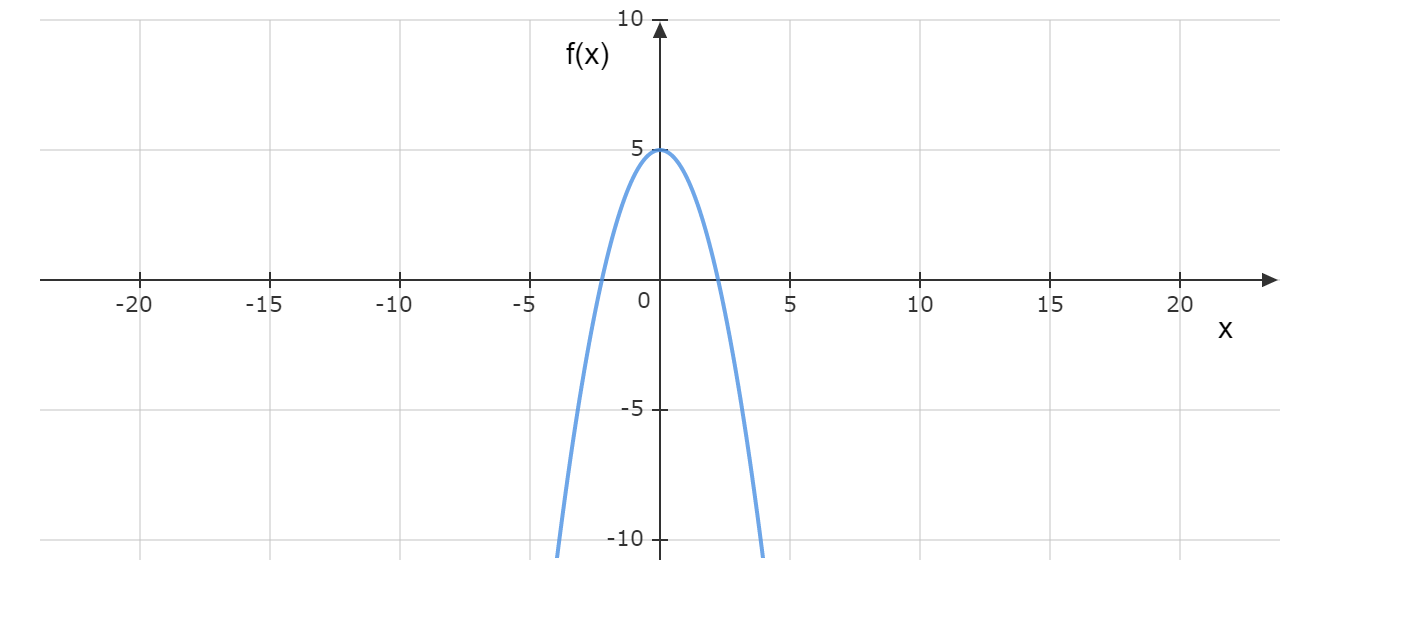
We have to explain the similarities and the difference between horizontal dilation, horizontal stretching, and horizontal compression of a quadratic function.

Given a quadratic function f(x)=ax²+bx+c,a≠0.Then we have the following transformations:

Horizontal dilation: When we replace the independent variable x in the equation of f by mx where m is a nonzero constant, it is called as horizontal dilation.

Depending upon the value of m,horizontal dilation has two classifications:

If m>1, then the graph of f(x) will be compressed horizontally by 1/m or we say the graph of f is compressed horizontally by a factor of 1/m.

This is called as horizontal compression.

If 0<m<1 , the graph of f(x) will be stretched horizontally by 1/m or we say the graph of f is stretched horizontally by a factor of 1/m.

This is called as horizontal stretching. Hence the similarity among the three is that they belong to the same category of transformation i.e the transformation occurs horizontally .

The difference between horizontal stretching and horizontal compression is that in the former case,the graph obtained after stretching is wider(in the horizontal direction) than the original graph of f(x) and in the latter case,the graph obtained after compression is narrower than the original graph of f(x).

The difference is illustrated below.

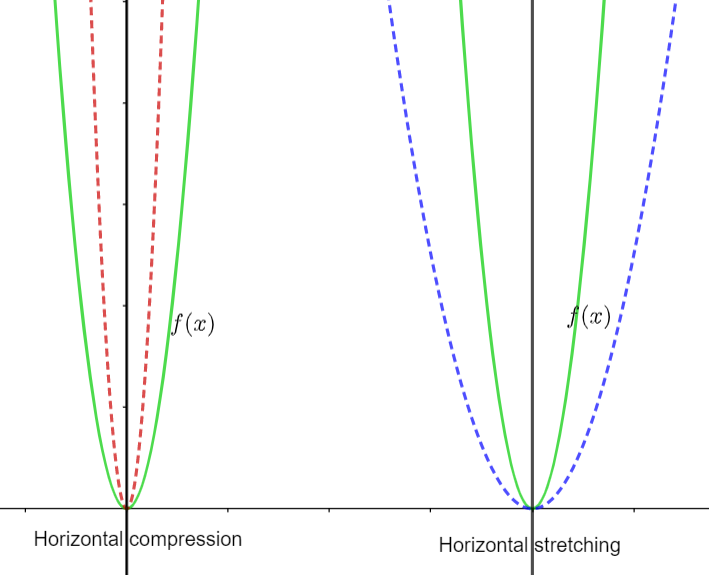
Hence we summarized the similarities and differences between horizontal dilation, horizontal stretching, and horizontal compression of a quadratic function.

Carnegie Learning Algebra II Chapter 2 Exercise 2.4 solutions

Page 287 Problem 2 Answer

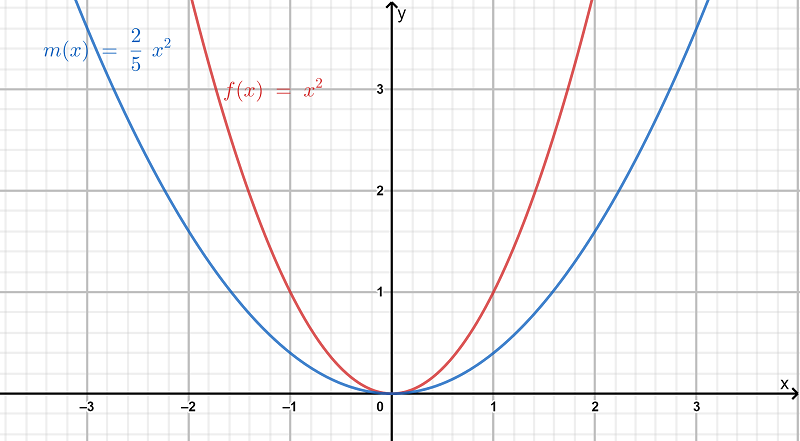
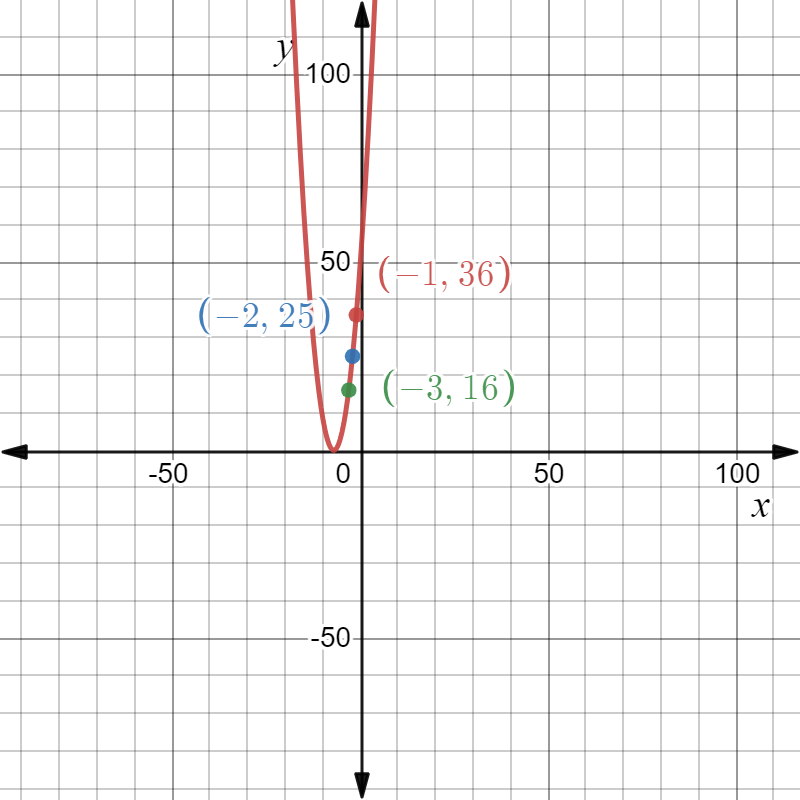
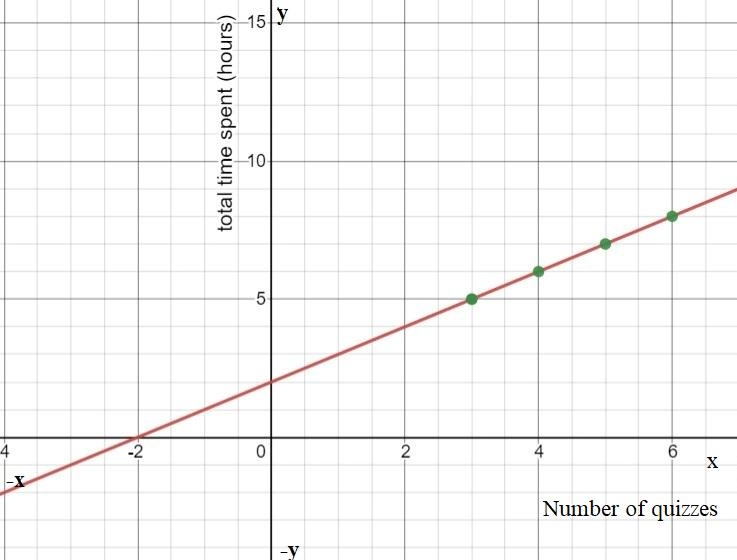
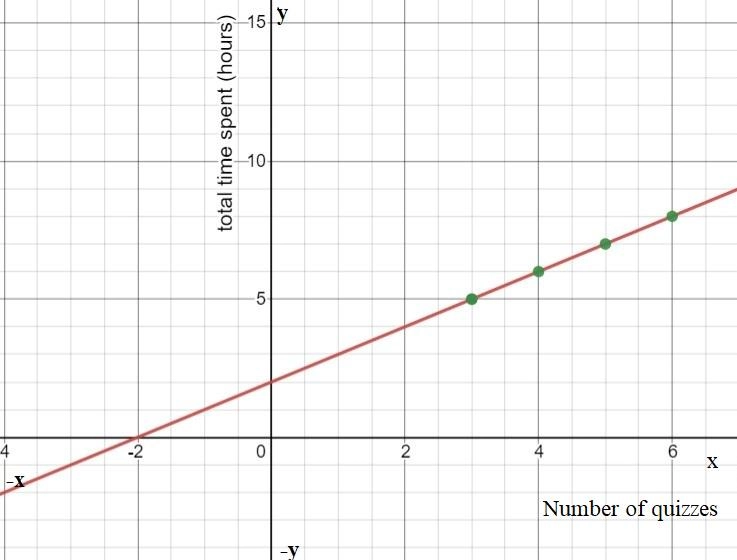
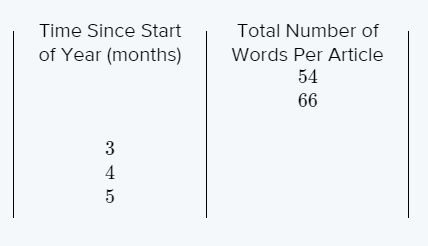
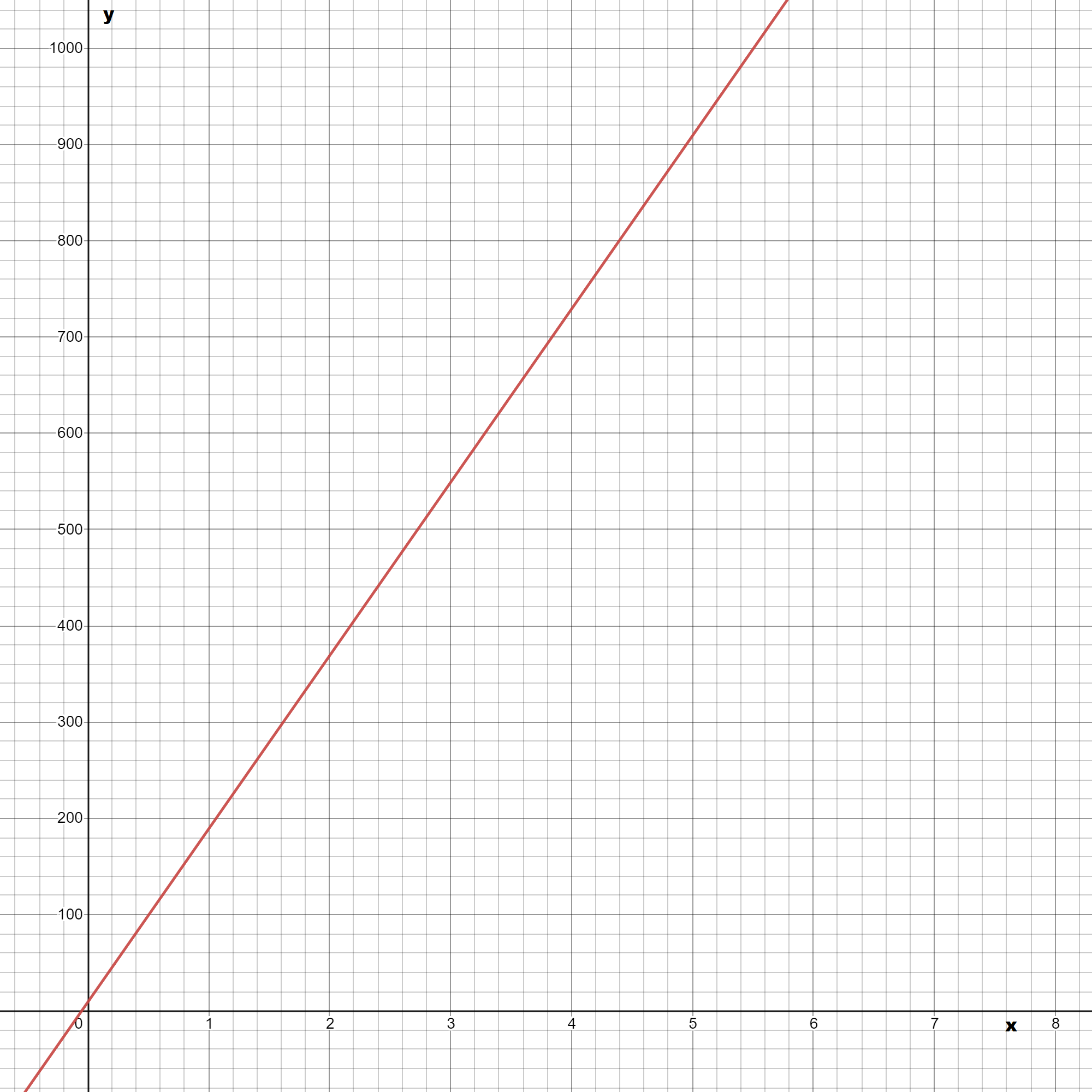
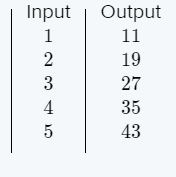
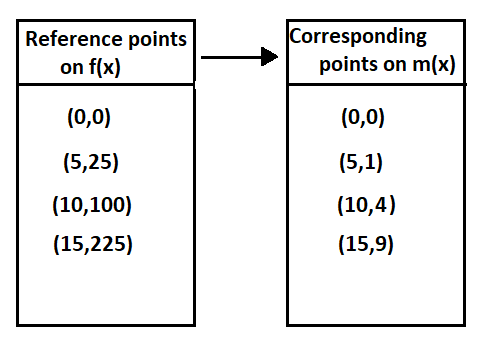
We are given that f(x)=x² and that m(x)=f(1/5x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as m(x)=f(1/5x)

=(x/5)²

=x²/25

Now we complete the table

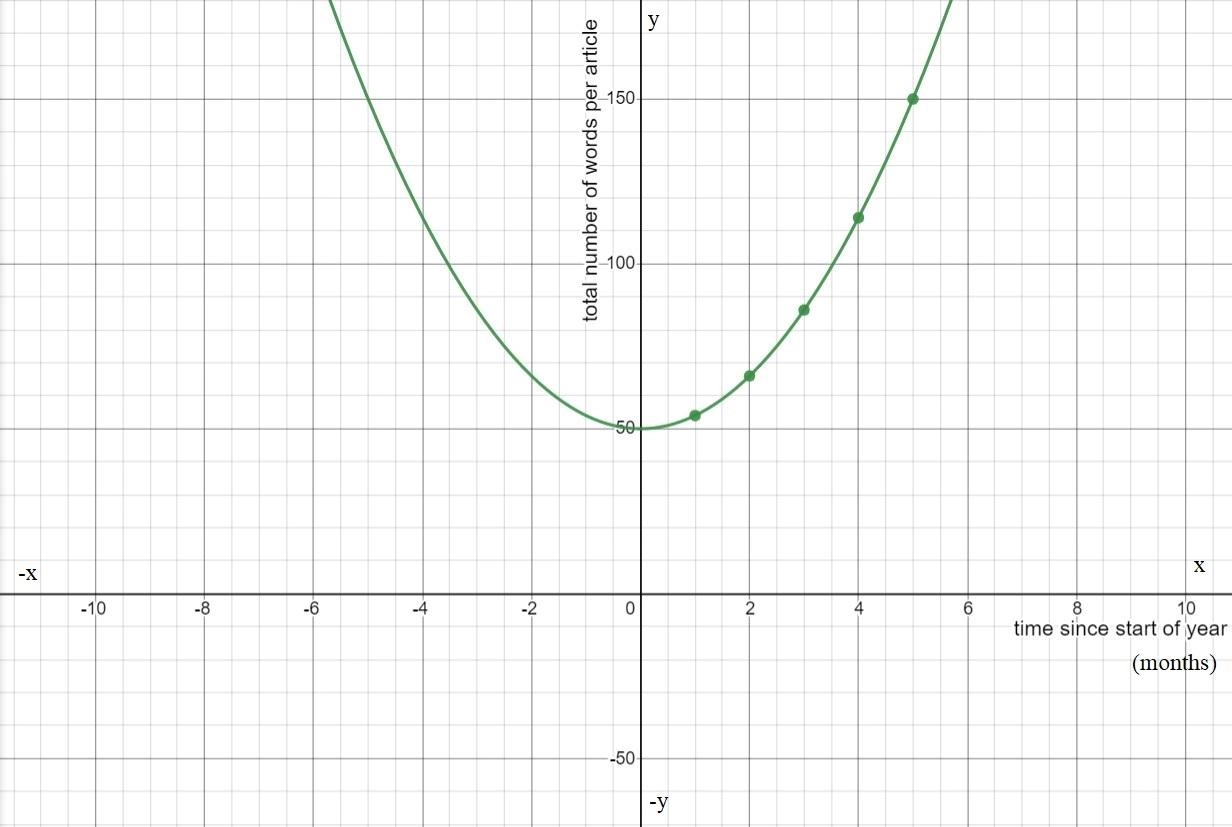
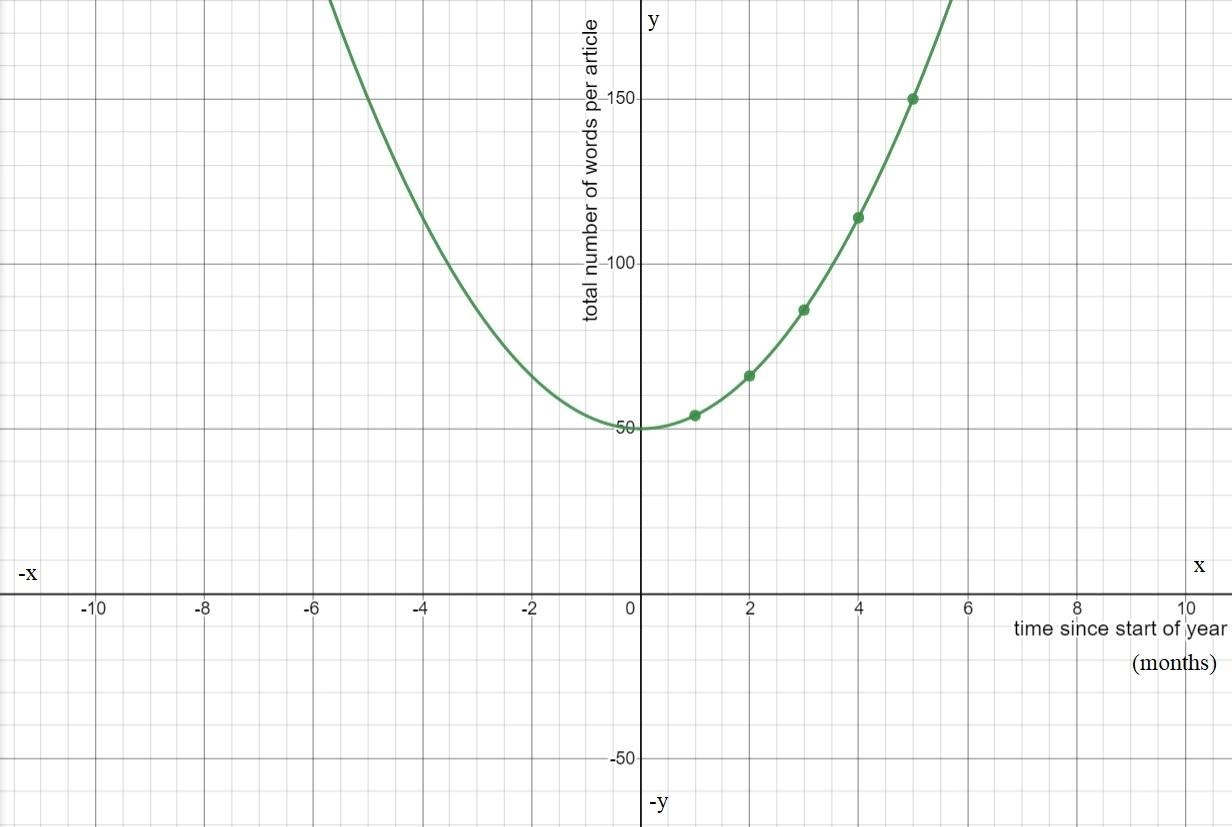
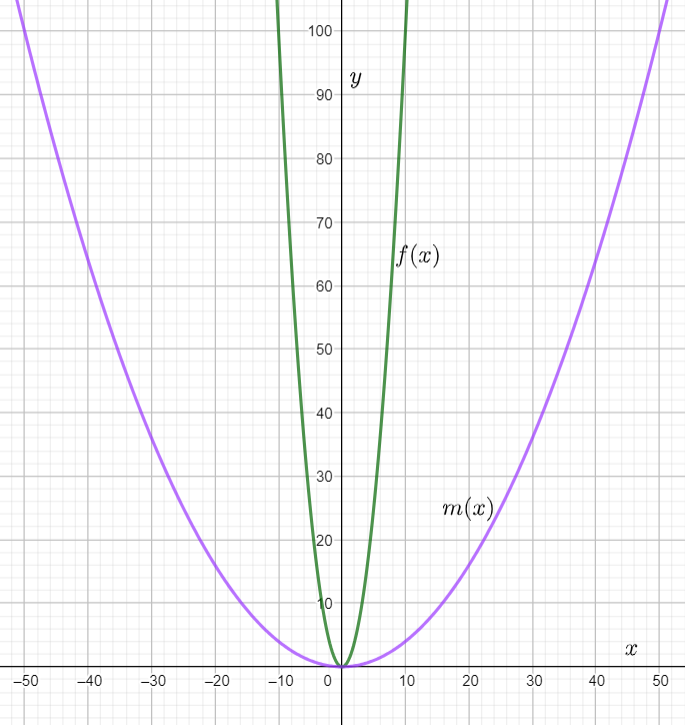
The graph of m(x) is  Plotting the graphs of f(x) and m(x) together we observe

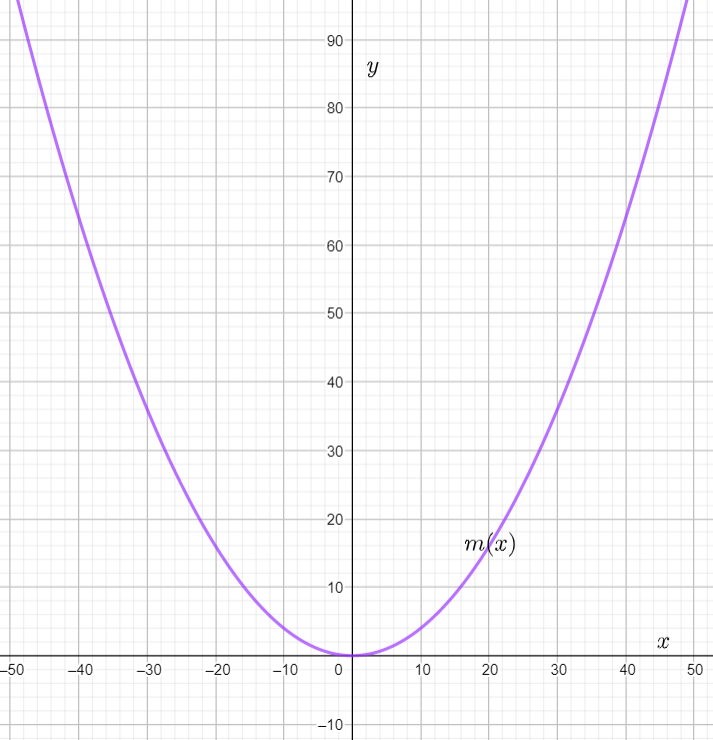
Hence the graph of m(x) looks the graph of f(x) stretched horizontally by a factor of 5.

Hence we completed the table of m(x) and found that m(x) is the horizontal stretch of f(x).

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 288 Problem 3 Answer

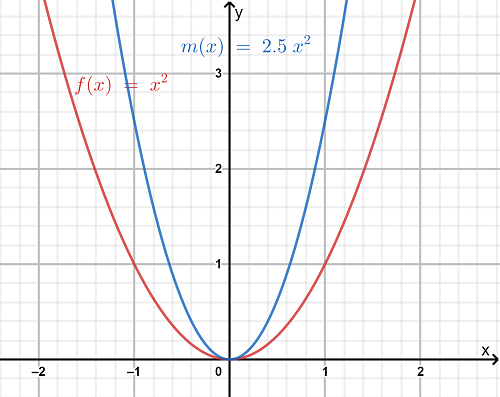
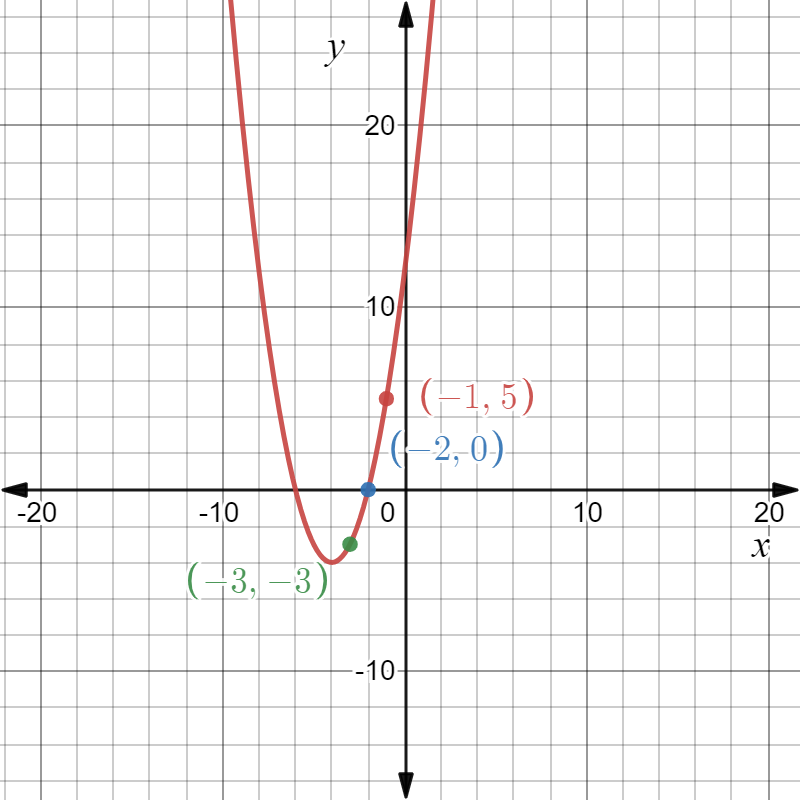
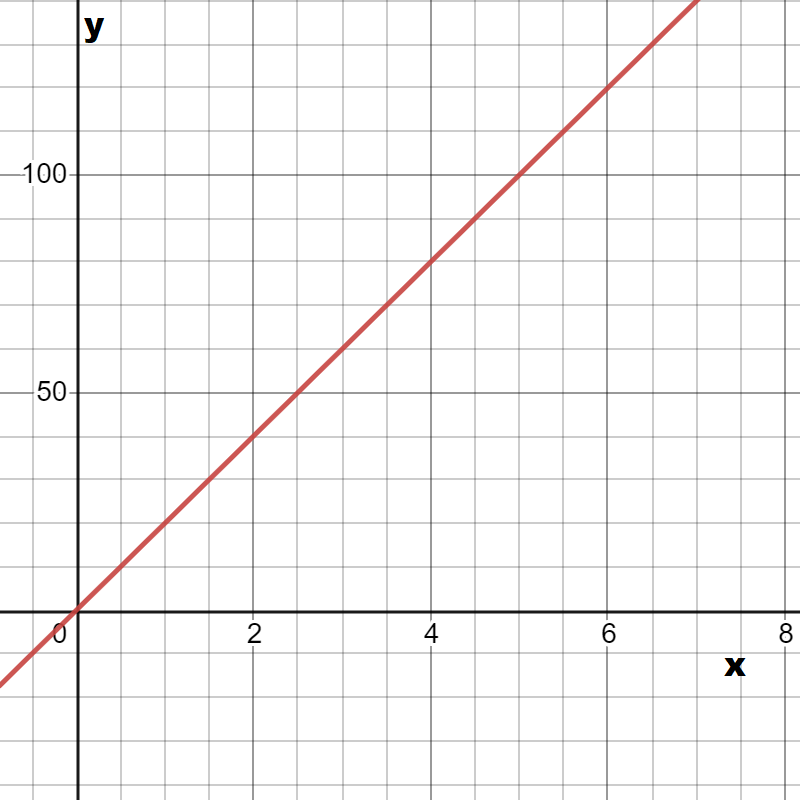
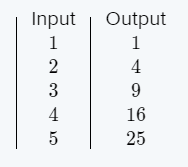
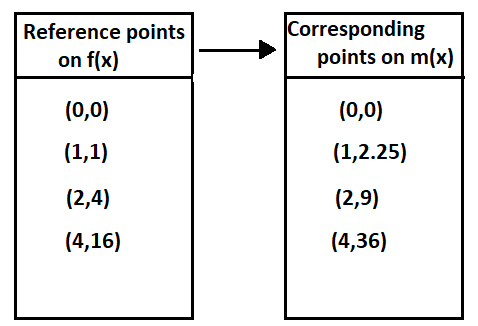
We are given that f(x)=x² and that m(x)=f(1.5x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(1.5x)

=(1.5x)²

=2.25x²

Now we complete the table

The graph of m(x) is

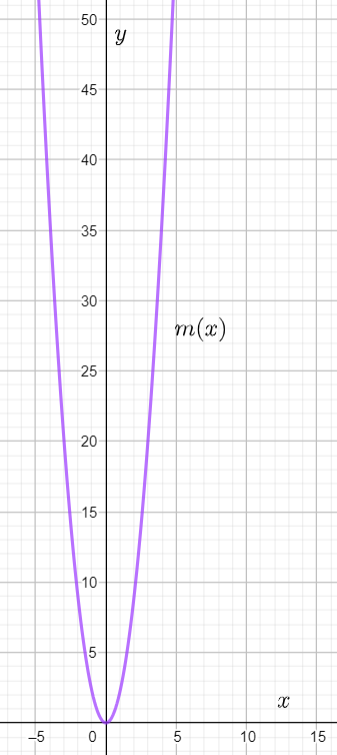
Plotting the graphs of f(x) and m(x) together we observe

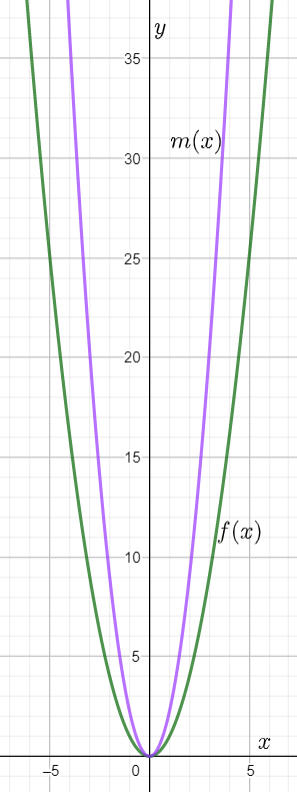
Hence the graph of m(x) looks like the graph of f(x) compressed horizontally by a factor of 1/1.5.

Since 1/1.5 =2/3, we can conclude m(x) is the horizontal compression of f(x) by a factor of 2/3.

Hence we completed the table of m(x) and found that m(x) is the horizontal compression of f(x).

Skills Practice Carnegie Learning Algebra II answers

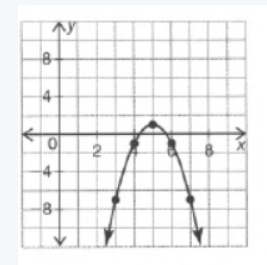
Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 288 Problem 4 Answer

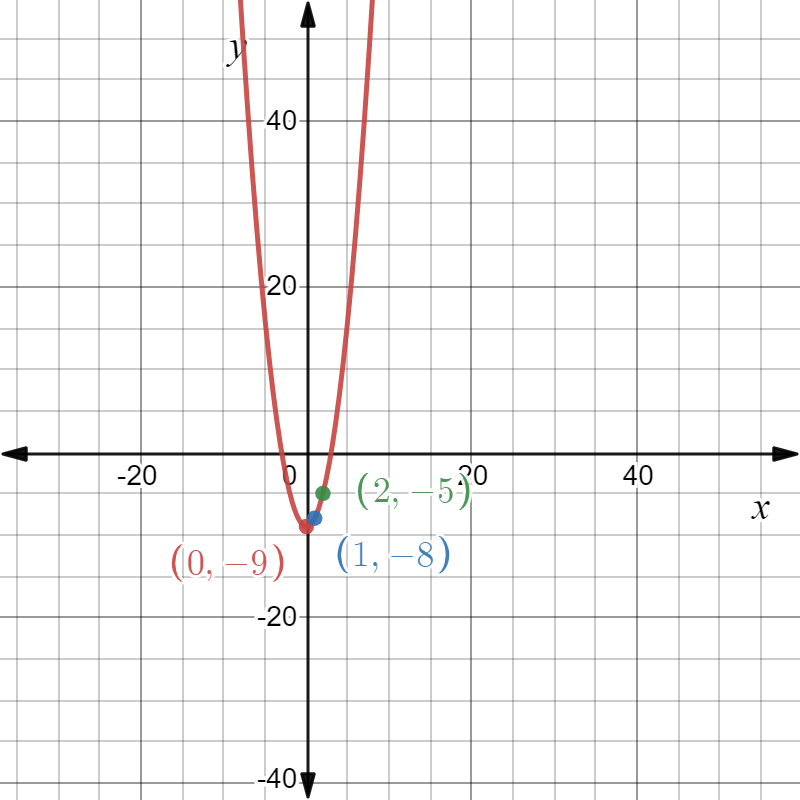
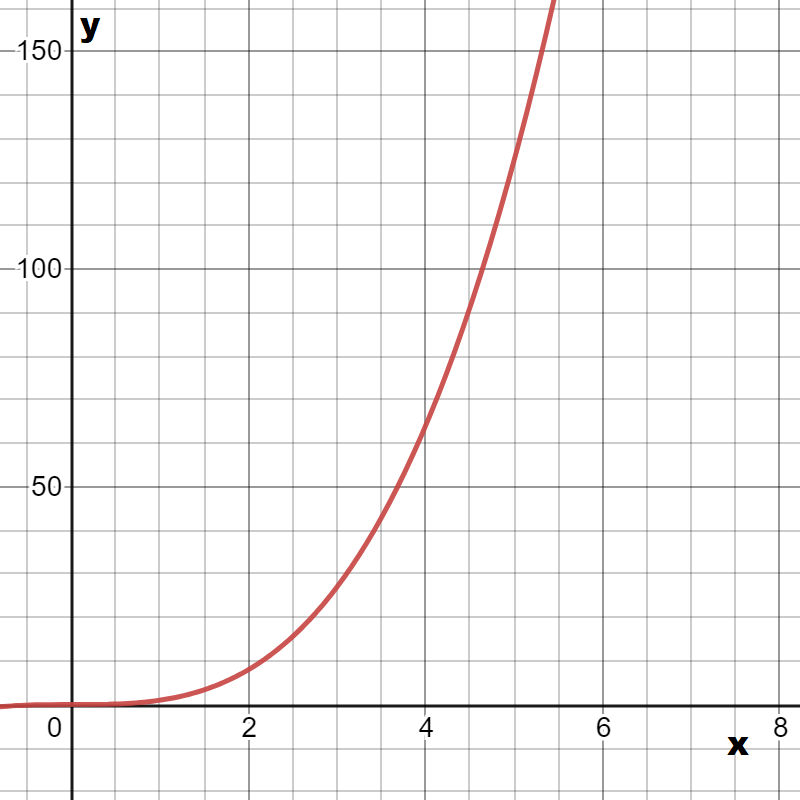
We are given that f(x)=x² and that m(x)=f(4x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compare to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(4x)

=(4x)²

=16x²

Now we complete the table

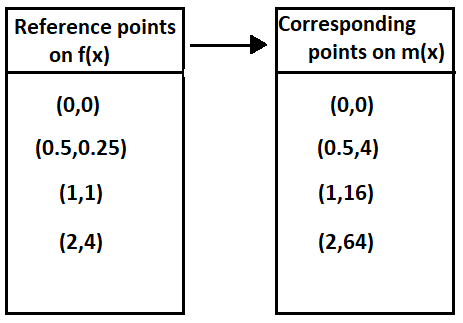
The graph of m(x) is

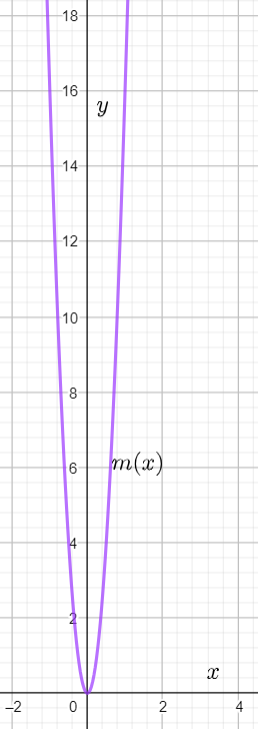
Plotting the graphs of f(x) and m(x) together we observe

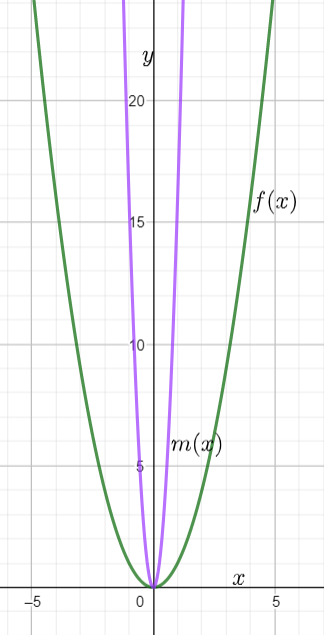
Hence the graph of m(x) looks like the graph of f(x) compressed horizontally by a factor of 1/4.

Since 1/4 =0.25, we can conclude that m(x) is the horizontal compression of f(x) by a factor of 0.25.

Hence we completed the table of m(x) and found that m(x) is the horizontal compression of f(x).

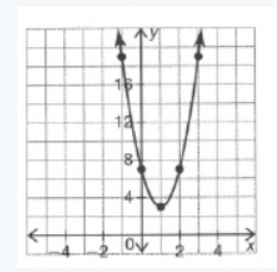
Page 288 Problem 5 Answer

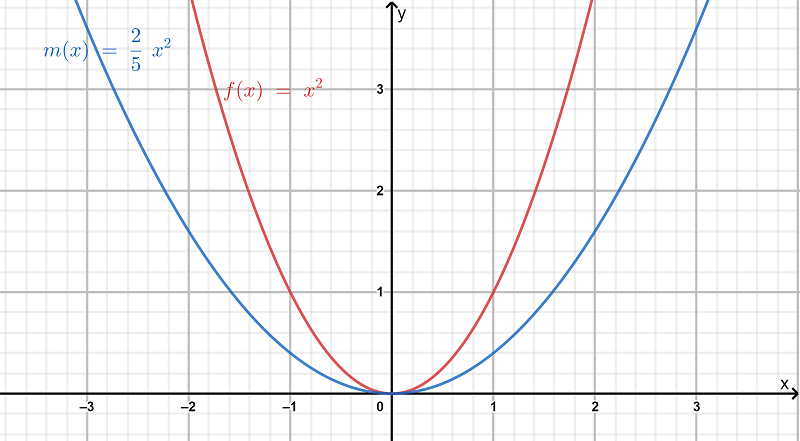
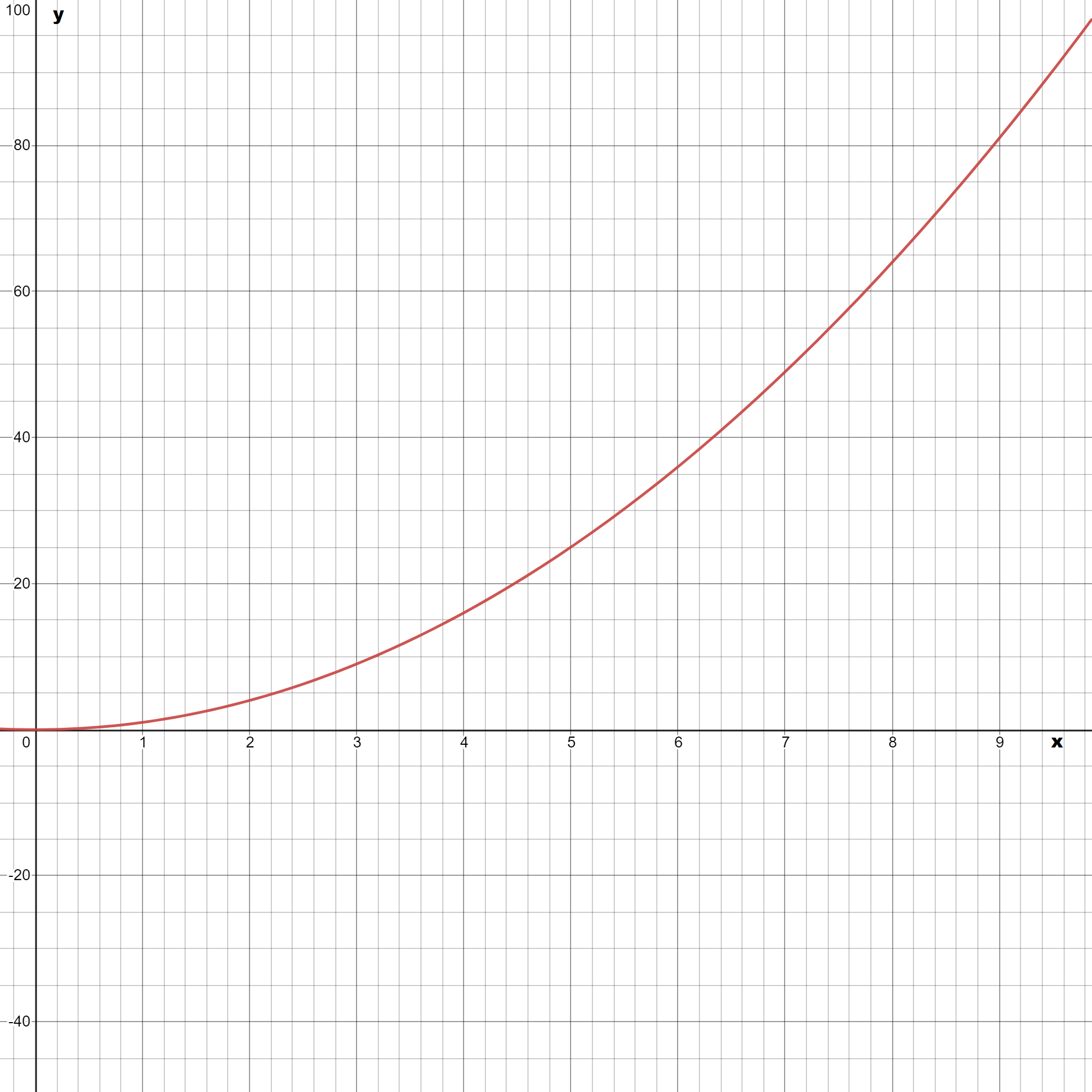
We are given that f(x)=x² and that m(x)=f(0.25x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compare to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(0.25x)

=(0.25x)²

=0.0625x²

Now we complete the table

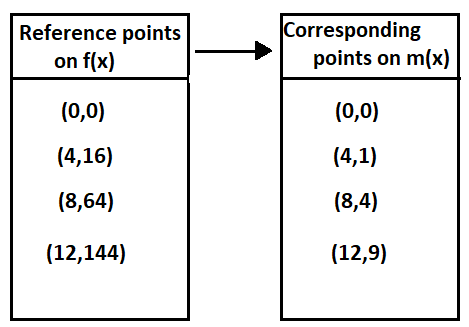
The graph of m(x) is

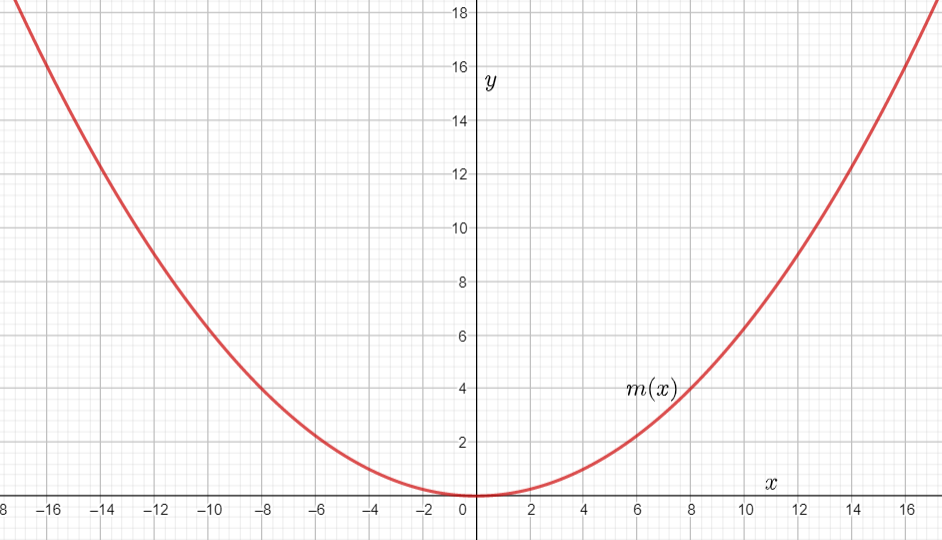
Plotting the graphs of f(x) and m(x) together we observe

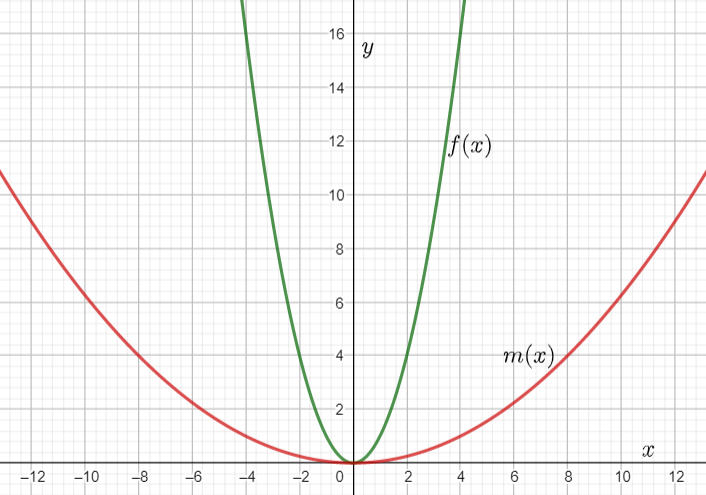
Hence the graph of m(x) looks like the graph of f(x) stretched horizontally by a factor of 1/0.25.

Since 1/0.25 =100/25 =4, we can conclude m(x) is the horizontal stretch of f(x) by a factor of 4.

Hence we completed the table of m(x) and found that m(x) is the horizontal stretch of f(x).

Carnegie Learning Algebra II practice questions Chapter 2

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 289 Problem 6 Answer

We are given that f(x)=x² and that m(x)=f(2/3x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(2/3x)

=(2/3x)²

=4/9x²

Now we complete the table

The graph of m(x) is

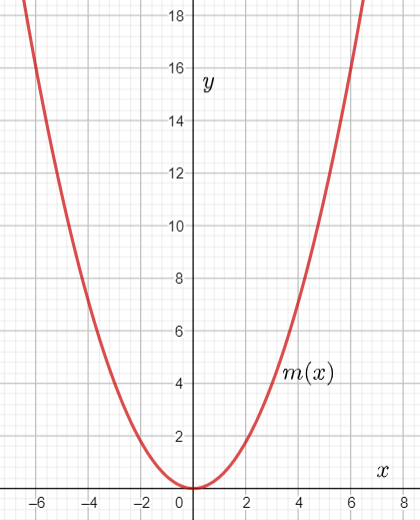
Plotting graphs of f(x) and m(x) together we observe

Hence the graph of m(x) looks like the graph of f(x) stretched horizontally by a factor of 1×2/3.

Since 1×2/3

=3/2

=1.5, we can conclude m(x) is the horizontal stretch of f(x) by a factor of 1.5.

Hence we completed the table of m(x) and found that m(x) is the horizontal stretch of f(x).

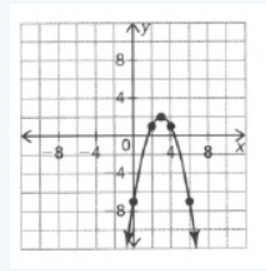
Page 289 Problem 7 Answer

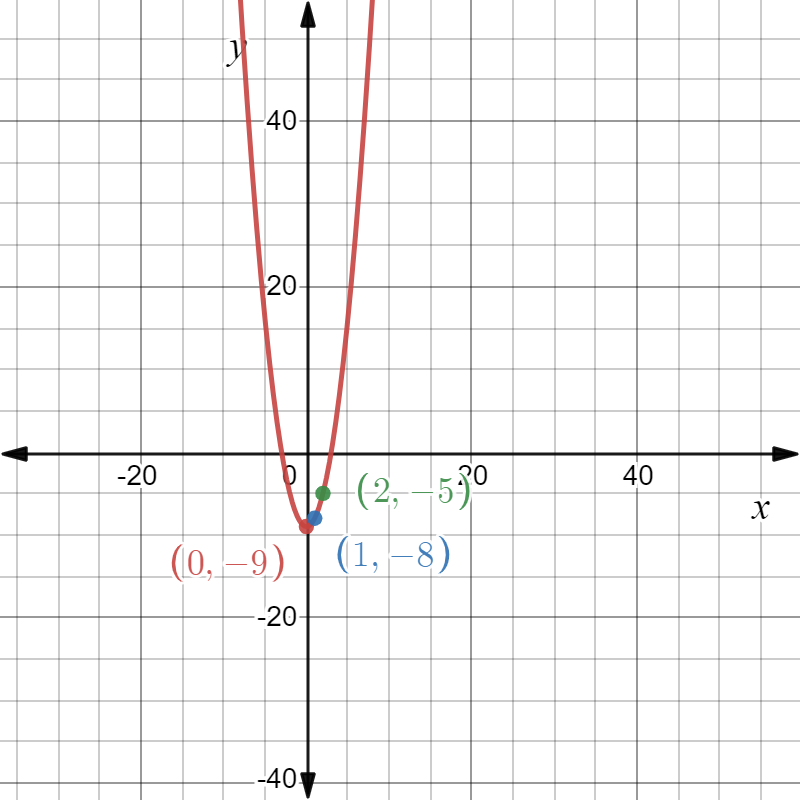
We are given that f(x)=x² and that m(x)=f(2x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(2x)

=(2x)²

=4x²

Now we complete the table

The graph of m(x) is

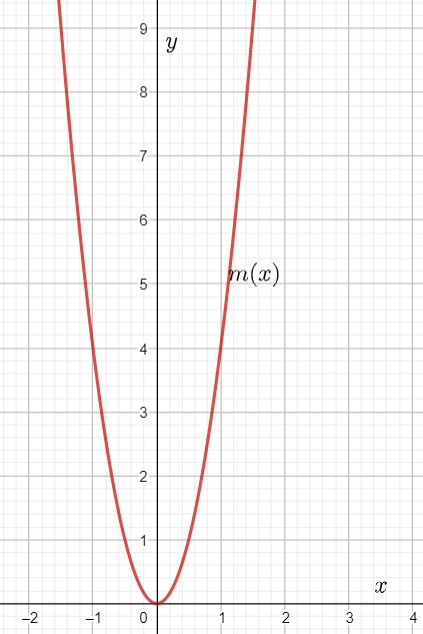
Plotting the graphs of m(x) and f(x) together we observe

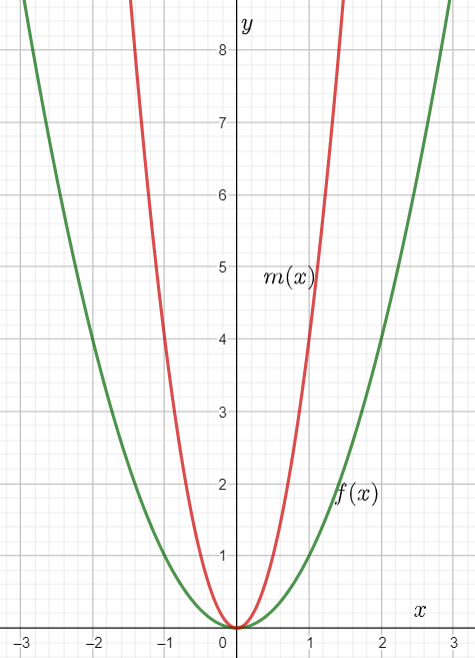
Hence the graph of m(x) looks like the graph of f(x) compressed horizontally by a factor of 1/2.

Since 1/2=0.5, we can conclude that m(x) is the horizontal compression of f(x) by a factor of 0.5.

Hence we completed the table of m(x) and found that m(x) is the horizontal compression of f(x).

Page 290 Problem 8 Answer

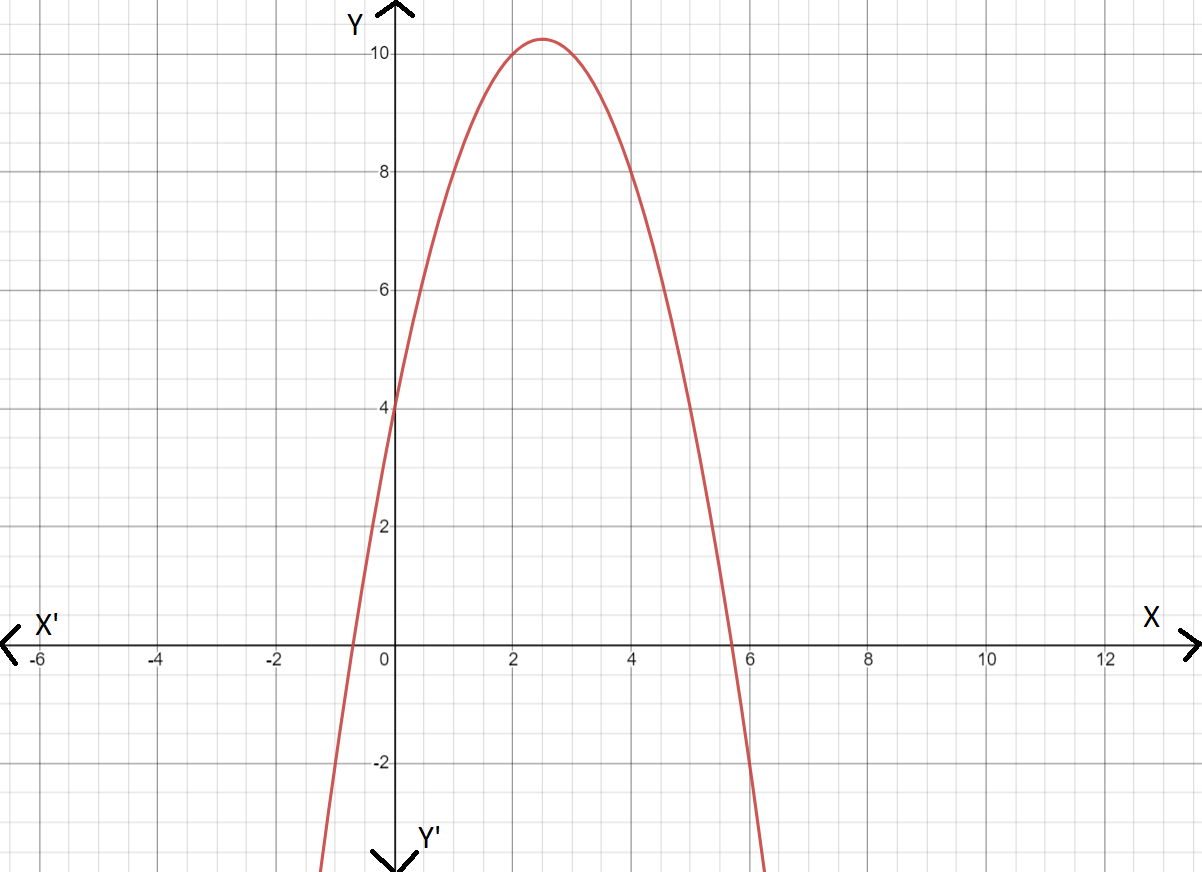
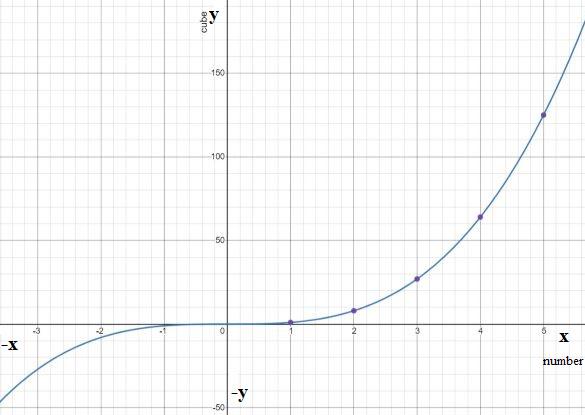
We are given the graph of f(x)

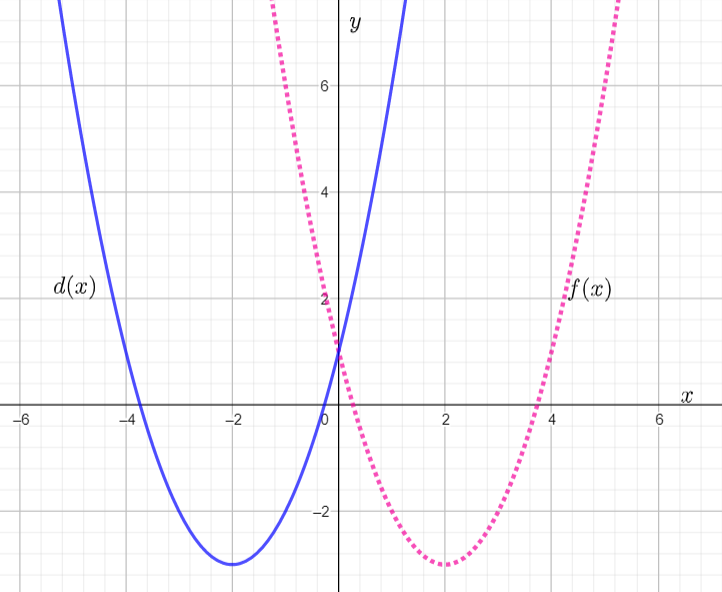
We have to sketch the graph of d(x)=f(−x).

The graph of the transformed function d(x) is the reflection of f(x) about the y−axis. Hence the graph of d(x) is

Hence we sketched the graph of d(x).

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 290 Problem 9 Answer

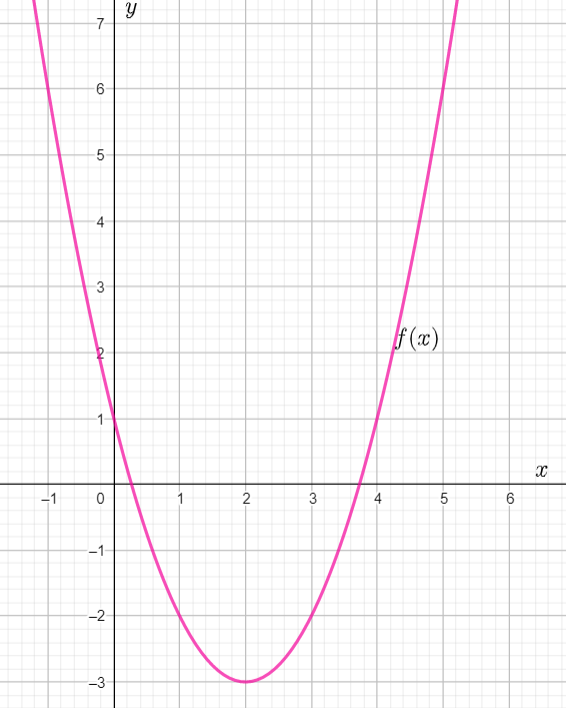
We are given the graph of f(x).

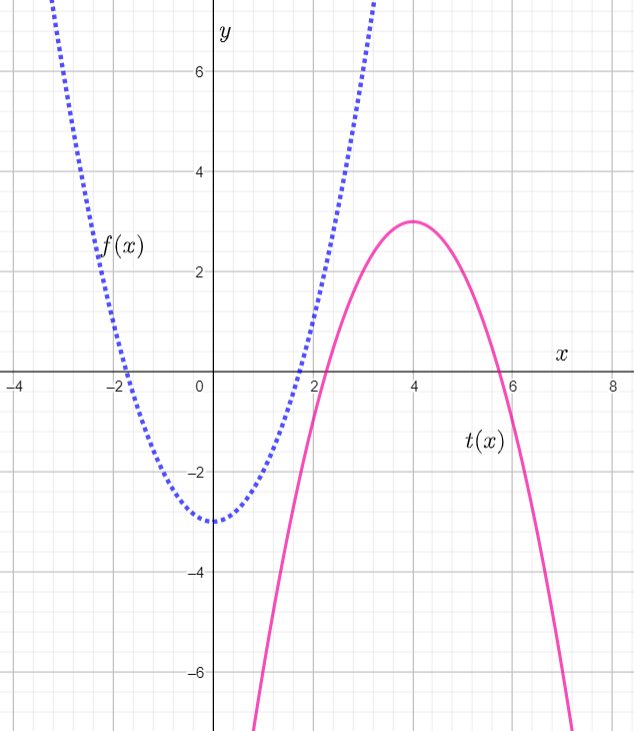
We have to sketch the graph of the transformed function t(x)=−f(x−4).

To obtain t(x) we first shift the graph of f(x) horizontally by constant 4. Since 4is positive, the graph shifts towards the right as shown below.

When the function f(x−4) is scaled by −1, the graph of f(x−4) reflects about the x−axis and we obtain the graph of t(x).

Hence we sketched the graph of t(x).

Page 290 Problem 10 Answer

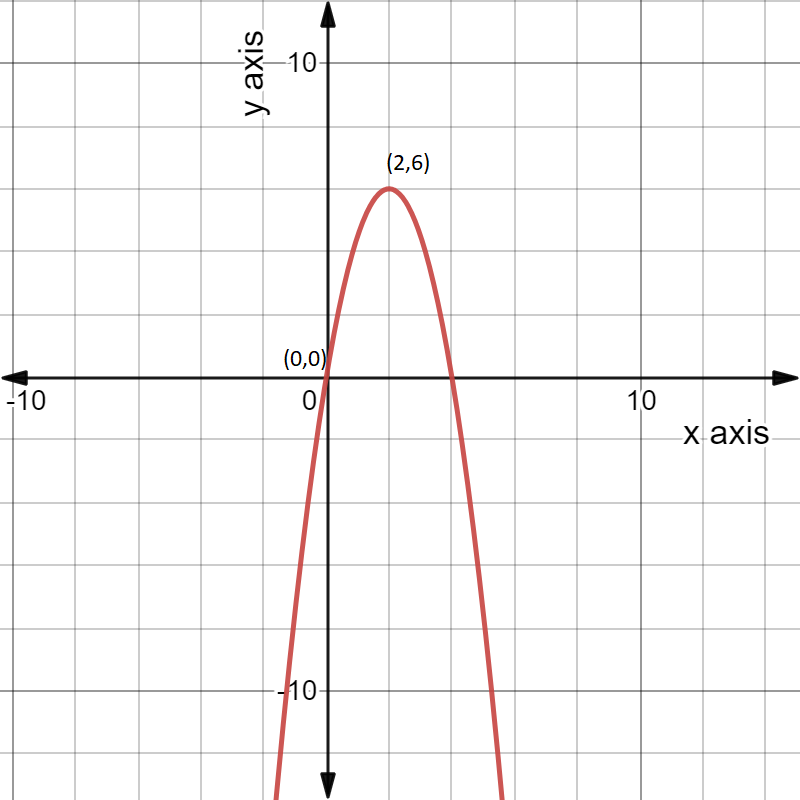
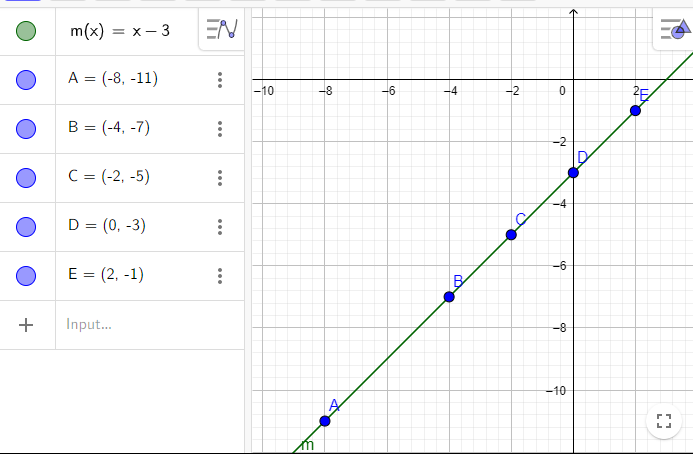
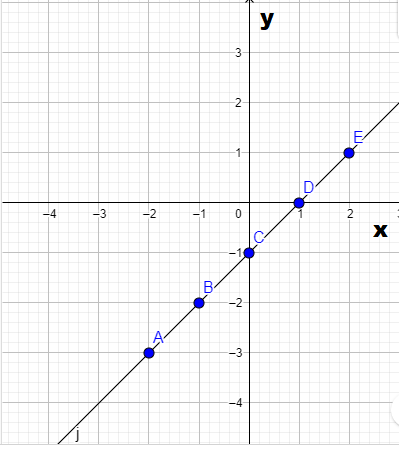
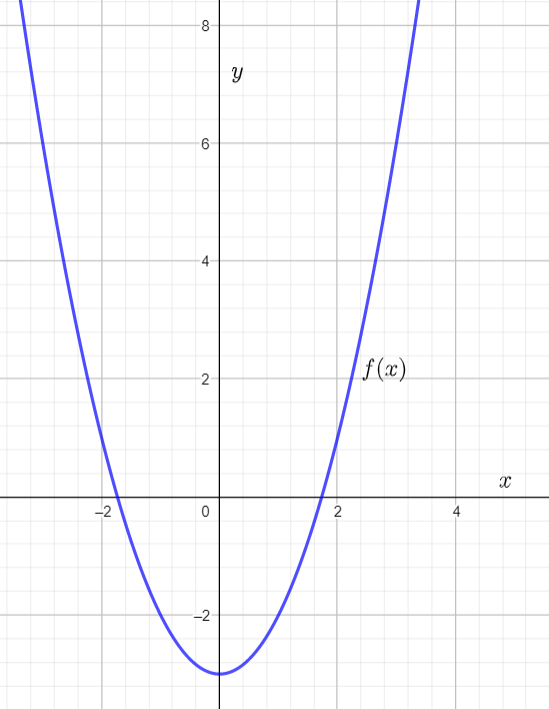
It is given the graph of the function f(x)

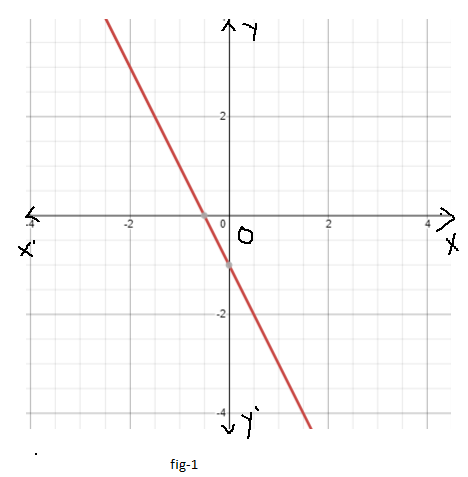
It is asked to sketch the graph of the function m(x)=−2f(x+3)+5.

To do this first find out the function f(x) by using the slope formula.

By using the function f(x) find the function m(x) and finally, sketch the function m(x).

From the given graph observe that the function f(x) passes through the point (0,0), and (1,1).

So the slope of the function will be 1−0/1−0 which is nothing but 1 .

So, the equation of the graph of the function f(x) will be f(x)=x+c.

Again the graph f(x) passes through the point (0,0).So, c=0.

So, the equation of the function f(x) will be f(x)=x.

Now find out the function m(x) by substituting x+3 instead of x in f(x).

m(x)=−2f(x+3)+5

m(x)=−2(x+3)+5

m(x)=−2x−6+5

m(x)=−2x−1

Now, sketch the graph of the function m(x)=−2x−1.

In the above graph X′OX and Y′ OY are considered as x−axis and y−axis respectively.

Hence the graph of the function m(x)=−2f(x+3)+5  is as follows:

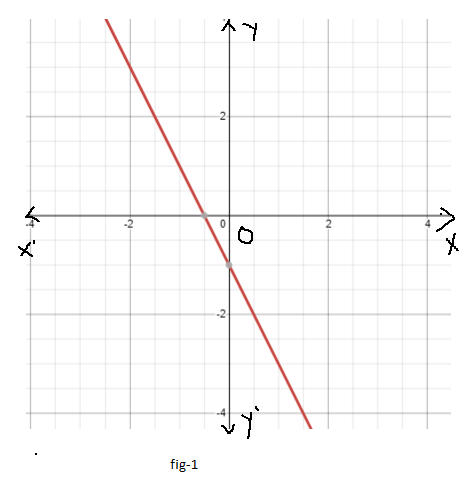
Chapter 2 Exercise 2.4 Carnegie Learning Algebra II key

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 290 Problem 11 Answer

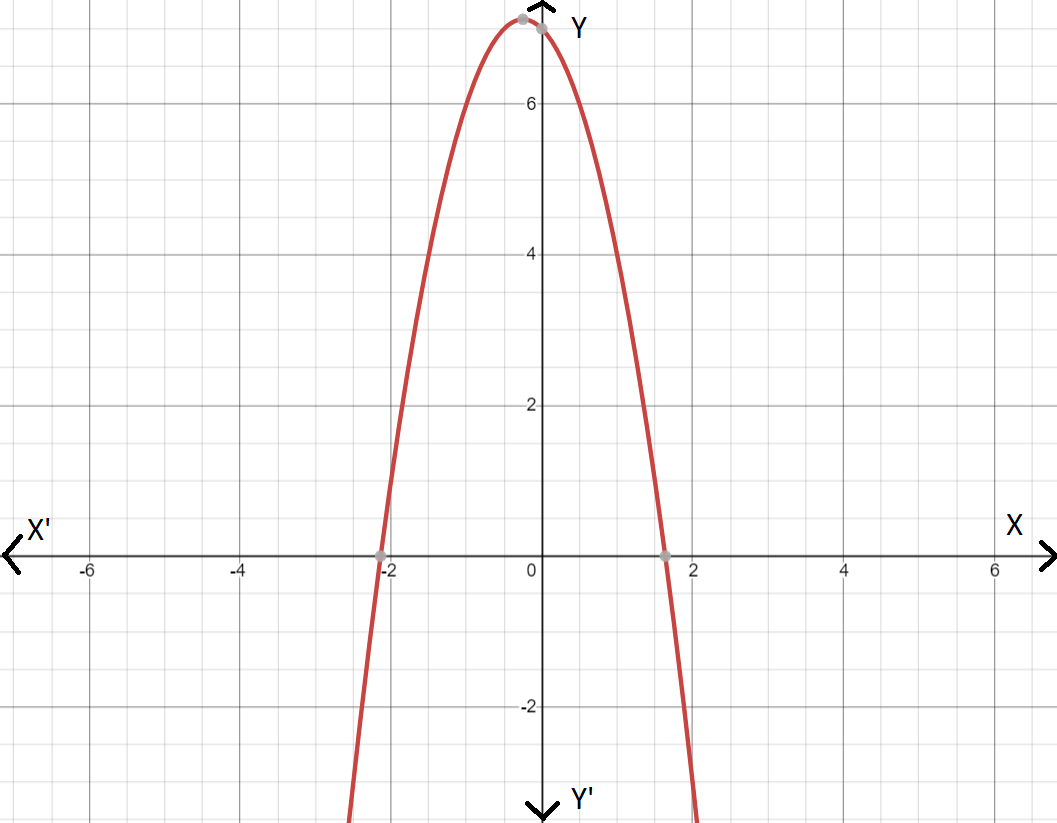
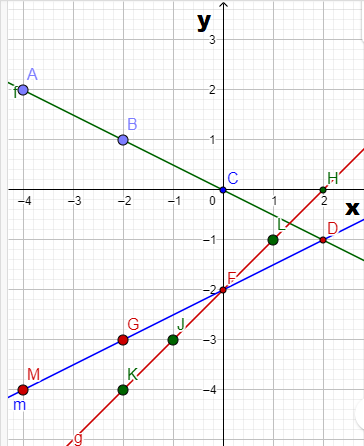
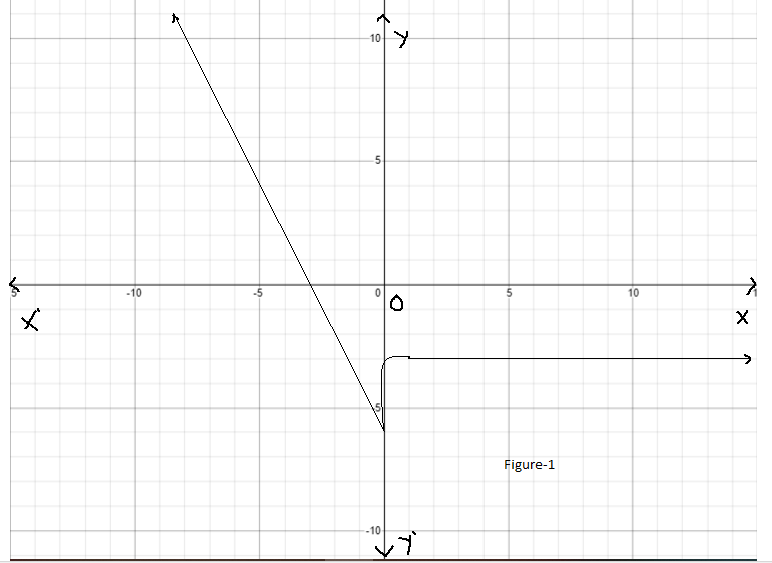
It is given a graph of a function. It is asked to find the graph of the function g(x)=f(−x+1)−4.

To find the graph of the function g(x) first, move down the graph of the function y=f(x) 4units.

Then take the reflection of the resulting graph with respect toy−axis .

Then shift the graph one unit to the left.

We have a graph of a function y=f(x).

Since we are interested to find the graph of the function g(x)=f(−x+1)−4, so first shift down the graph 4units.

Then the resultant graph will be as follows:

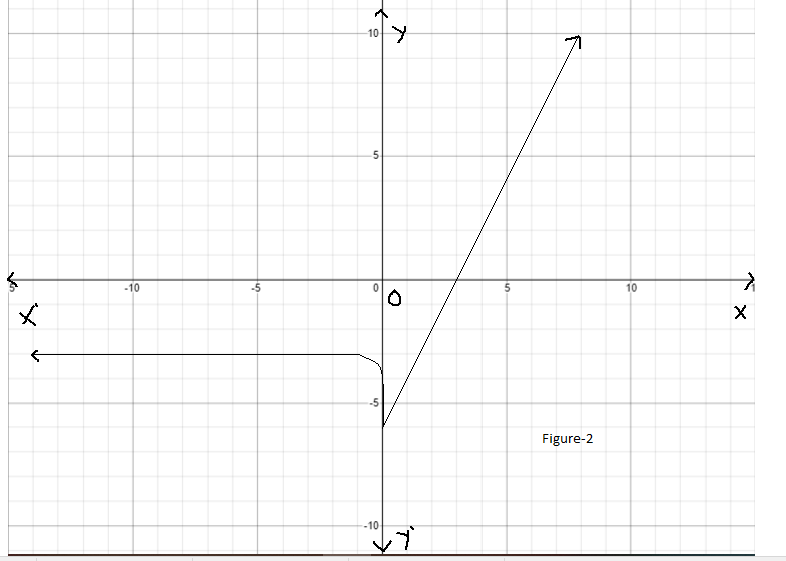
Now, take the reflection of the resultant graph with respect to the y−axis.

Then the resultant graph will be as follows:

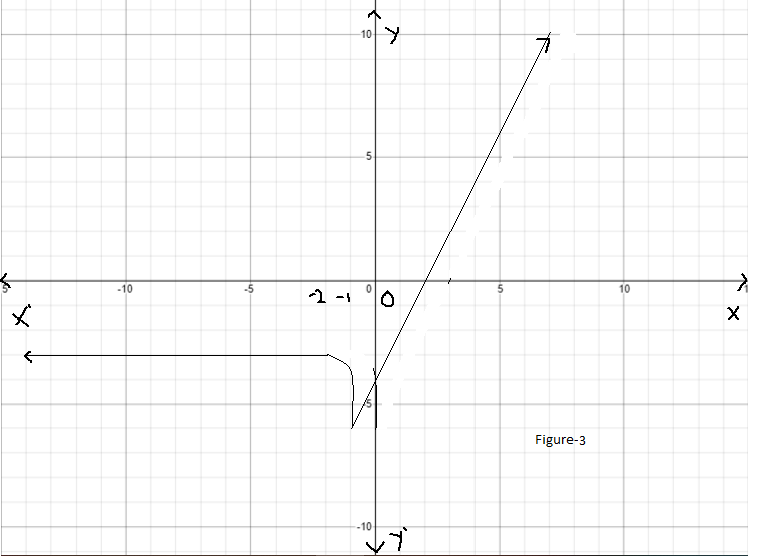
Finally shift the resultant graph one unit left to the present position:

Then the resultant graph will be:

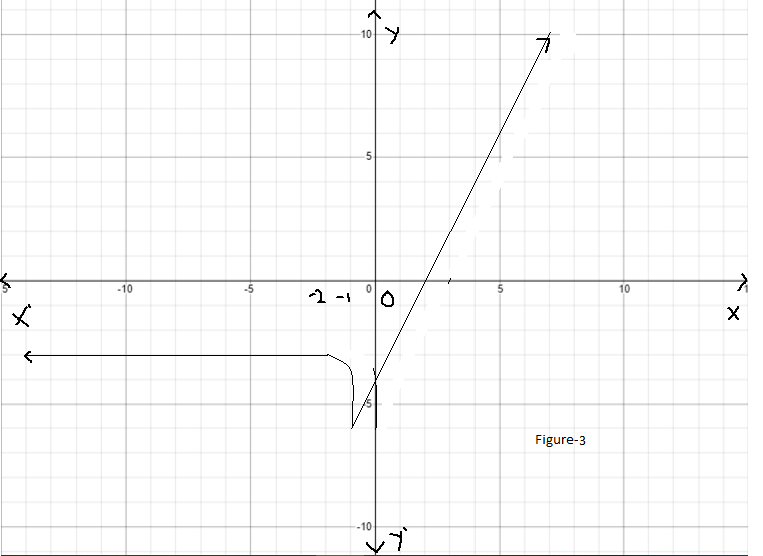
So, the graph of the function g(x)=f(−x+1)−4 will be as follows:

Hence, the graph of the function g(x)=f(−x+1)−4 is as follows:

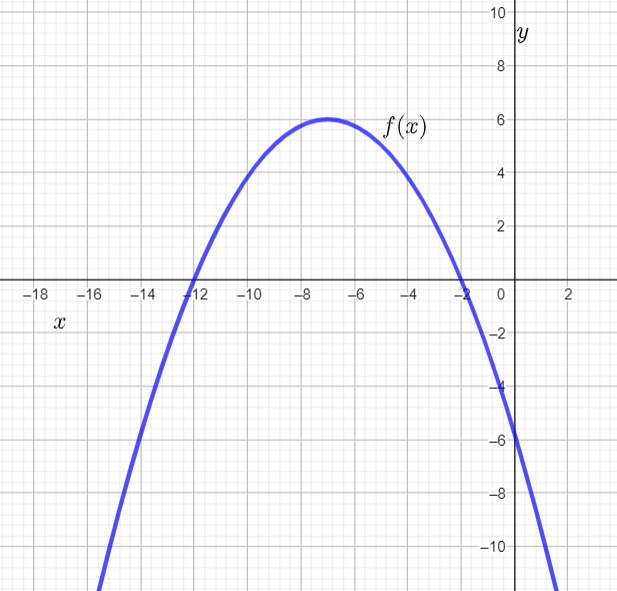
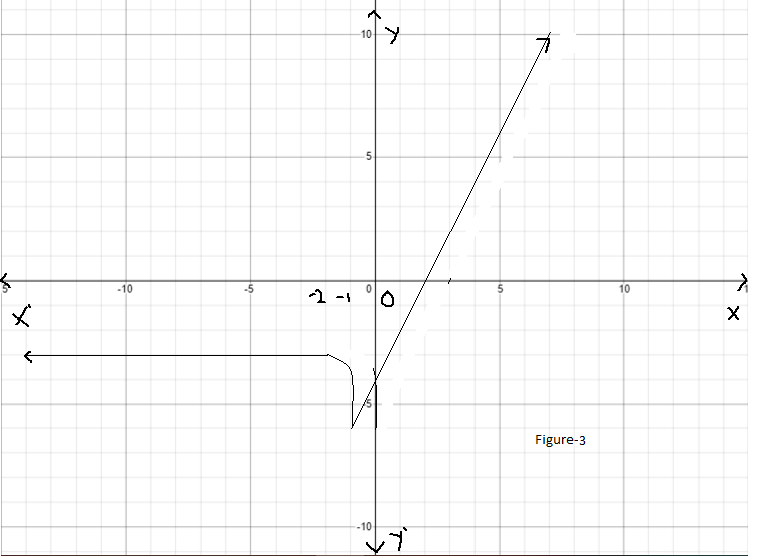
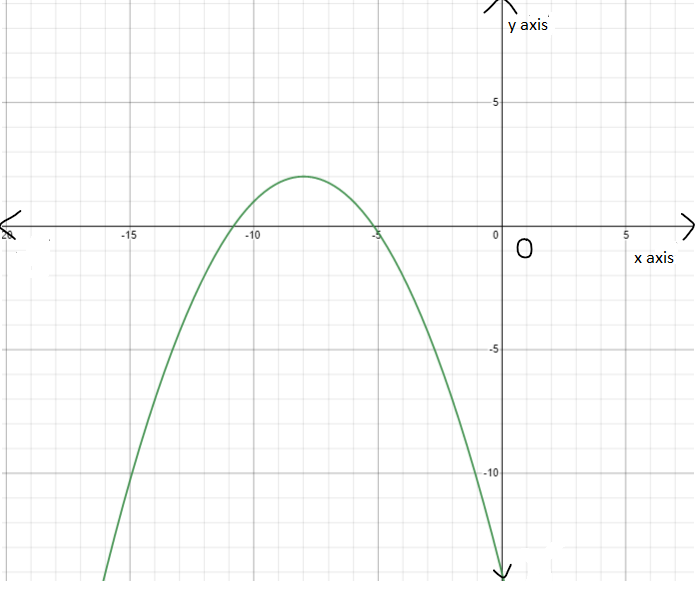
Page 291 Problem 12 Answer

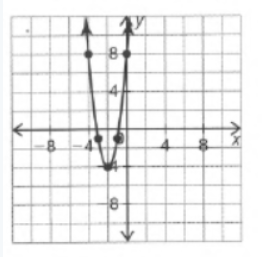
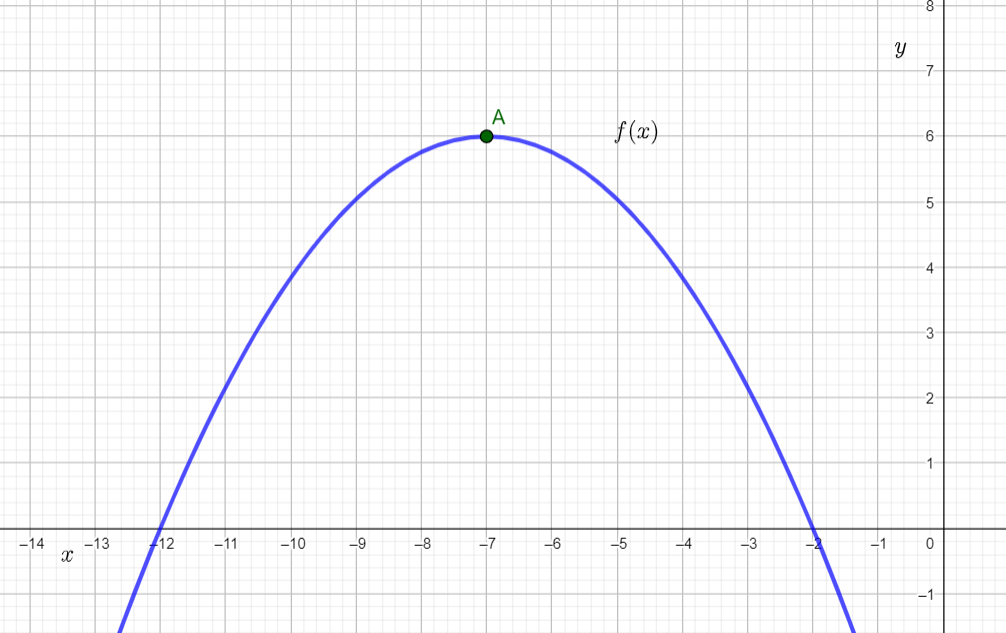
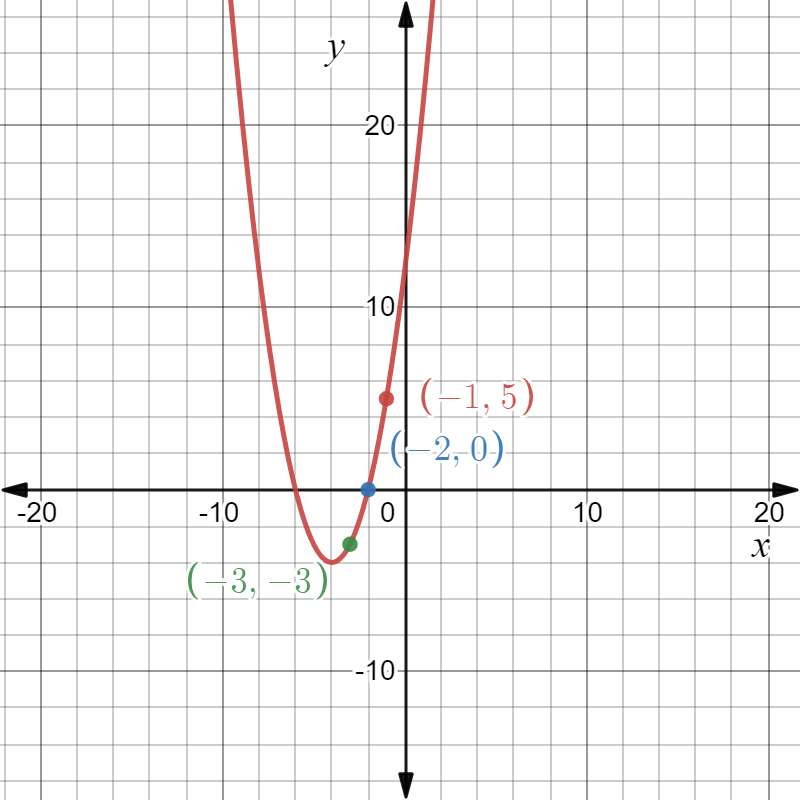
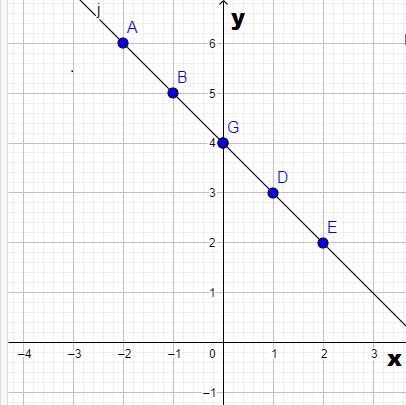
It is given a graph of a parabolic function y=f(x) whose vertex is at (−3,0) and the parabola passes through the point(−5,−4).

It is asked to find the graph of the transformed function r(x)=f(x/2+1)+2.

To find the transformed function first, find the explicit function of the parabola.

Then substitute x/2+1 instead of x and add 2.

Observe that in the given graph the parabola passes through the point (−5,4) and the vertex of the parabola is at (−3,0).

Now, we know that the general equation of the parabola having an axis parallel to negative y−axis is(x−α)²=−4ay .

So, the equation of the given parabola will be (x+3)²=−4ay.

Also, this parabola passes through the point (−5,−4).

So, (−5+3)²=−4a(−4)

So, a=4/16 and therefore a=1/4.

So, the equation of the parabola will be (x+3)²=−y.

So, f(x)=−(x+3)²

Now, to find the function r(x)=f(x/2+1)+2, substitute x/2+1 instead of x in the following way:

r(x)=f(x/2+1)+2

=−(x/2+1+3)²+2

=−(x/2+4)²+2

=−1/4(x+8)²+2

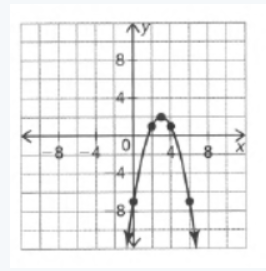
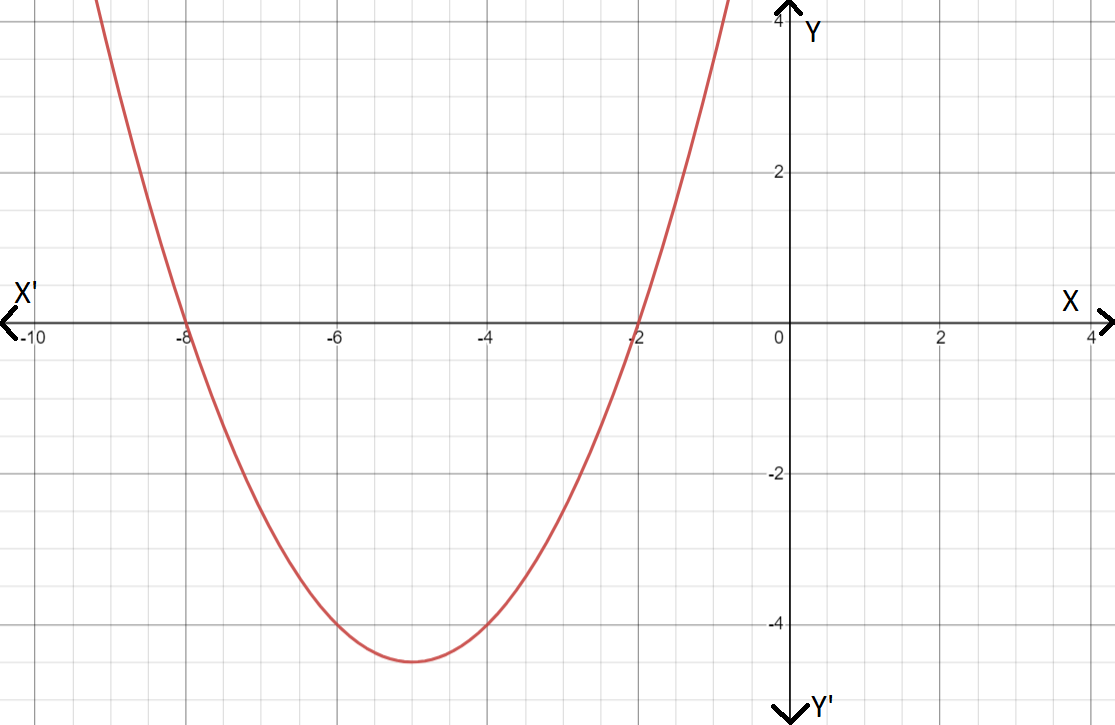
So, the graph of the transformed function r(x) is as follows:

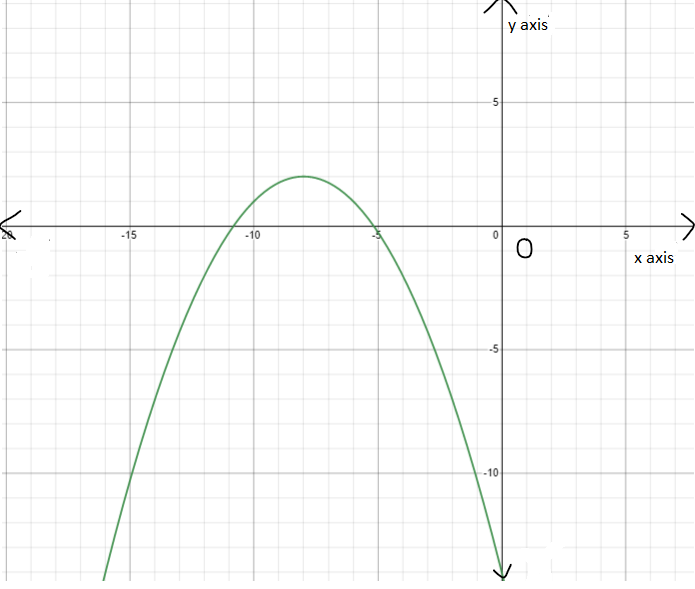
Hence, the graph of the transformed function r(x) is as follows:

How to solve Chapter 2 Exercise 2.4 Algebra II Carnegie Learning

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 291 Problem 13 Answer

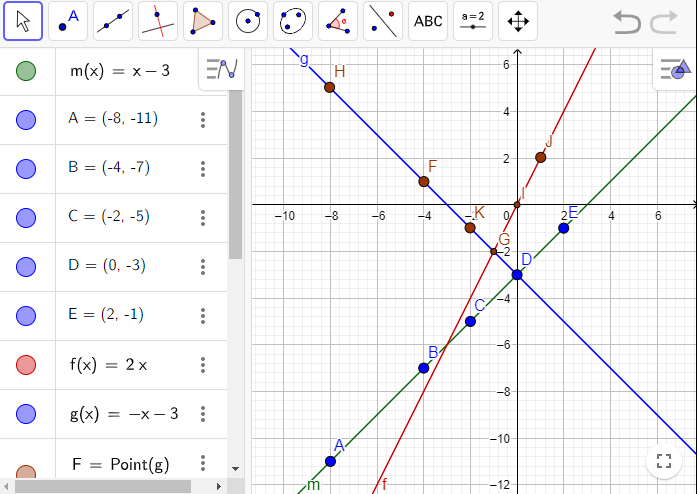
It is given a graph of a function f(x) and it is asked to find the graph of a function p(x)=−f(x+1)−3 .

First, find the coordinates of all the points.

Then shift down the graph 3 units. Next, shift the graph to left at 1 unit an f finally take a reflection about x axis.

We are interested to find the graph of p(x)=−f(x+1)−3.

First shift down the graph 3 units and then the resulting graph will be as follows:

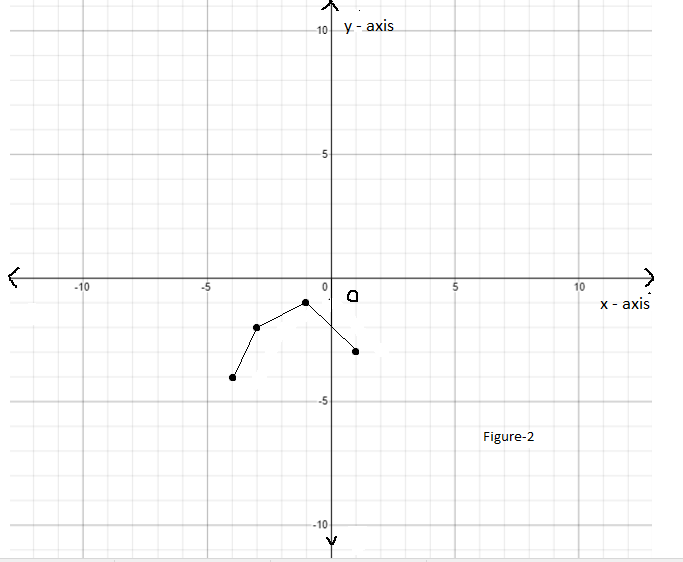
Next, shift the resulting graph to the left at 1 unit and then the resulting graph will be as follows:

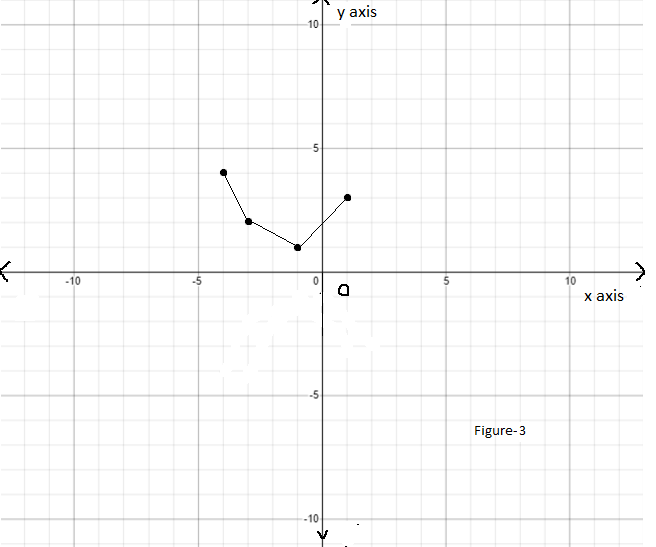
Finally, take the reflection of the resulting graph with respect to  x-axis

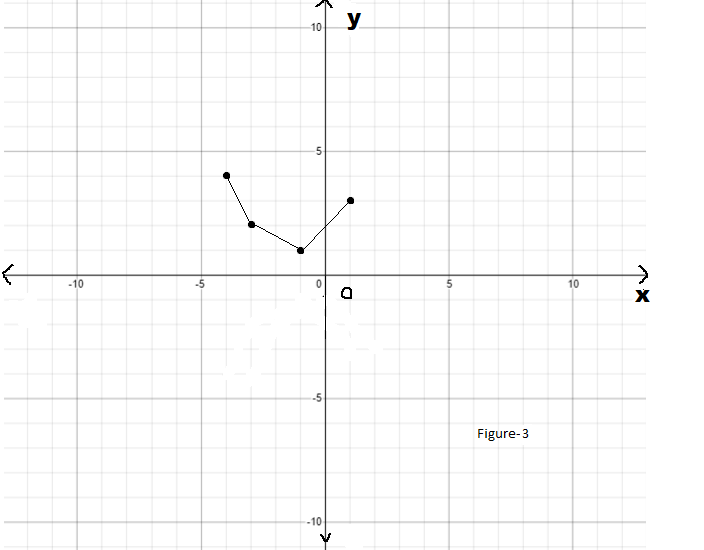
So, the graph of the function will be as follows:

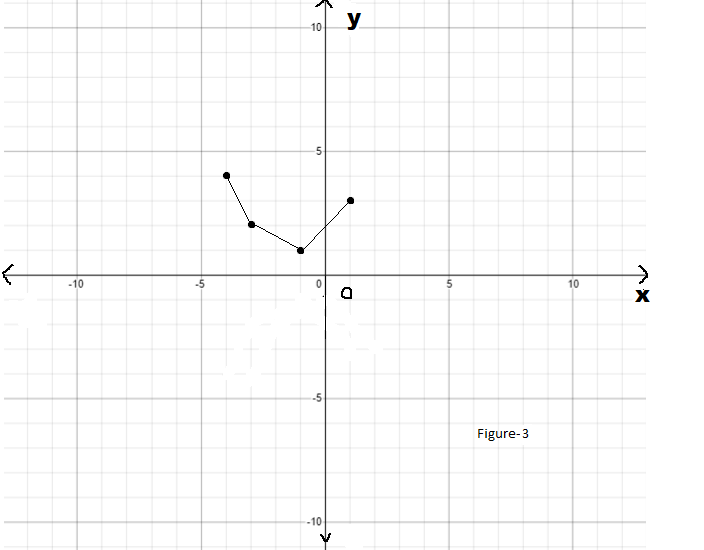
Hence, the required graph of the function p(x)=−f(x+1)−3 will be as follows:

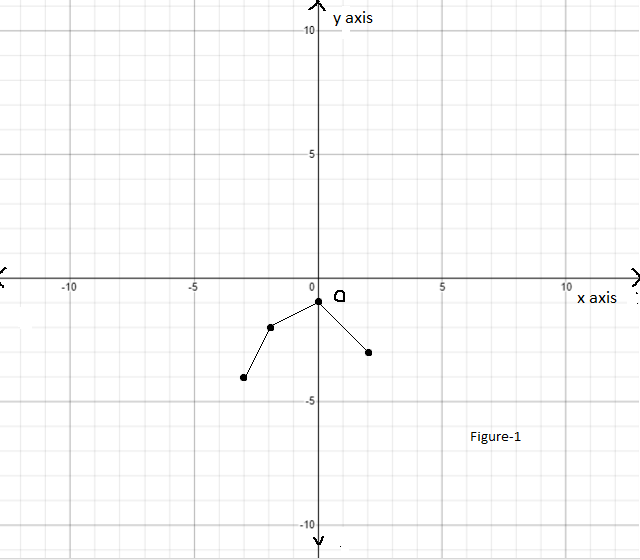
Page 291 Problem 14 Answer

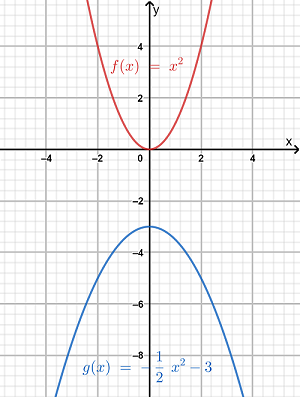
It is given two parabolas w(x) and v(x) and w(x) is transformed to v(x).

It is asked to find the equation of w(x) in terms of v(x).

To do this apply the transformation to the function v(x) to get the function w(x).

First, observe that the vertex of the parabola given by the function w(x) is (0,3) and the vertex of the parabola v(x) is (5,5).

So, first, move the parabola given by the function v(x) to the left side of 5 units. So, the resulting parabola is v(x+5).

Next, drag the resulting parabola vertically downward of 2 units. So the resulting parabola will be v(x+5)−2.

Now, invert the resulting parabola. So, the final equation of the parabola will be −(v(x+5)−2) and this is nothing but the parabola given by the function w(x).

So, w(x)=−(v(x+5)−2)

Hence the equation of the parabola given by the function w(x) in terms of v(x) is w(x)=−(v(x+5)−2)

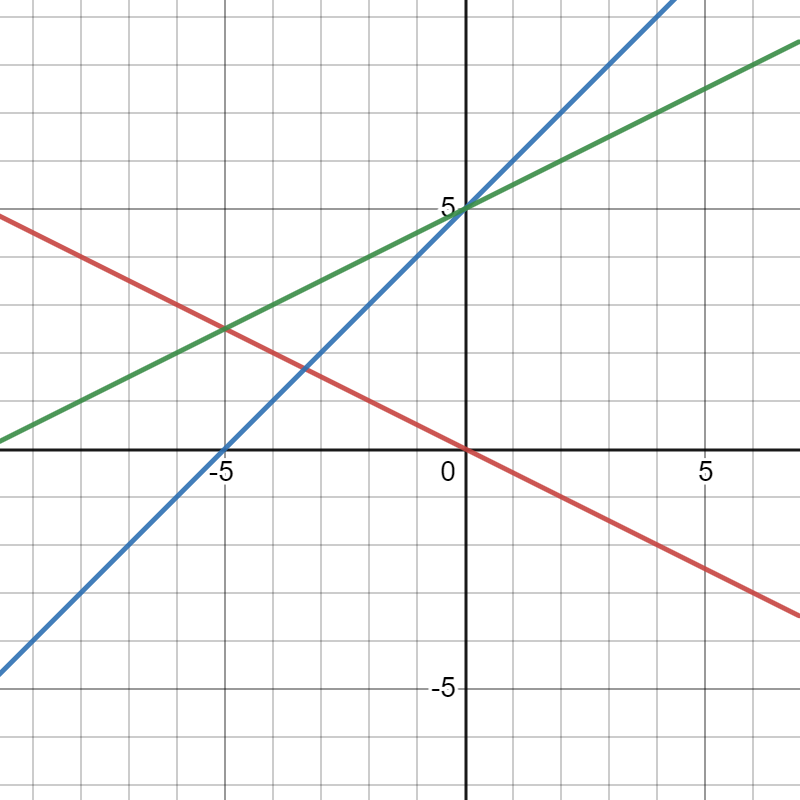
Page 292 Problem 15 Answer

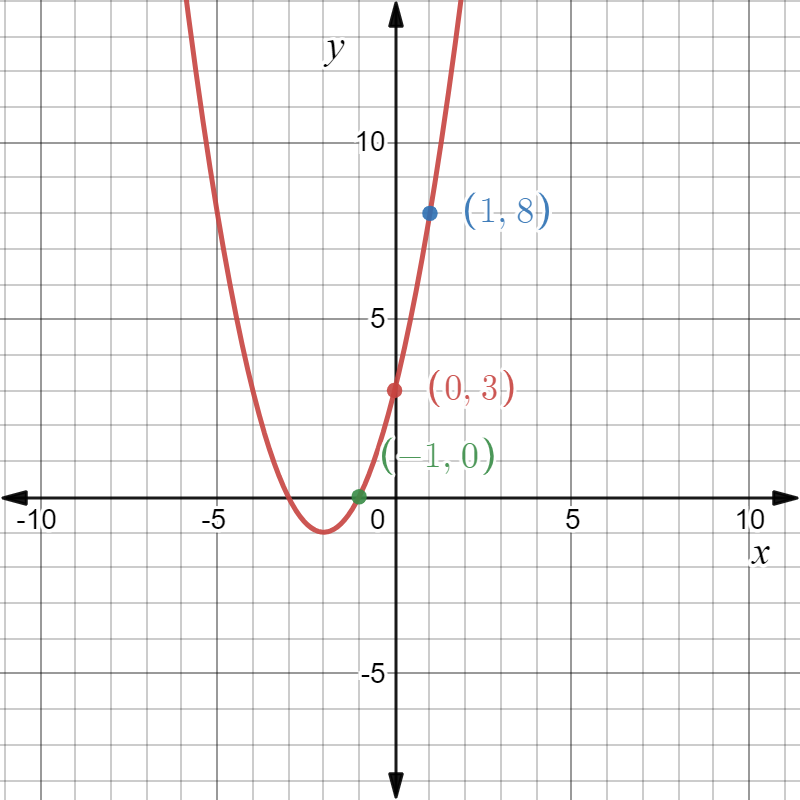
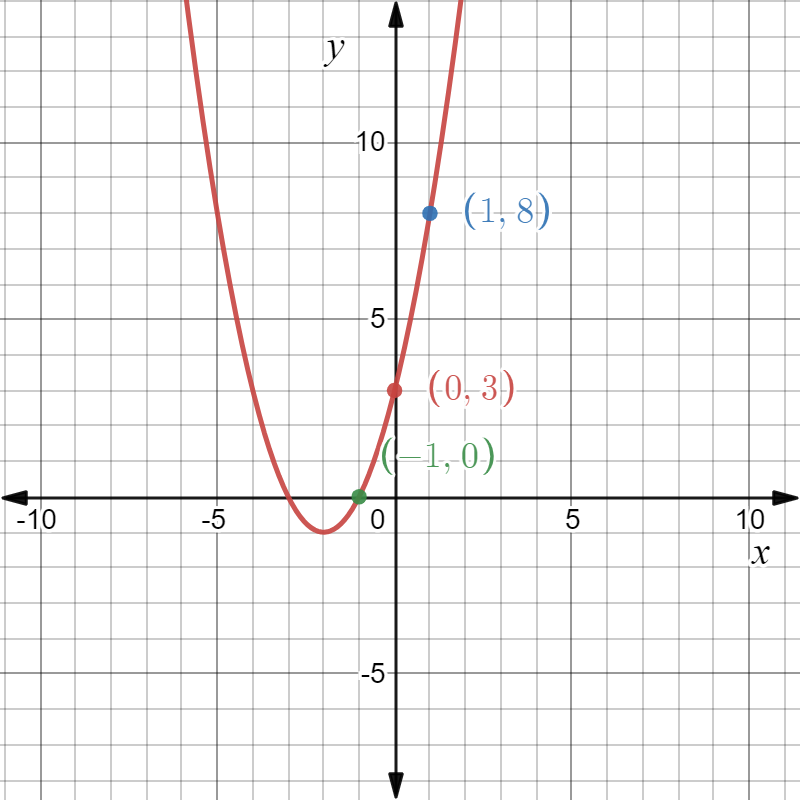
It is given the graph of the equation of the straight line y=x by w(x) and the graph of the equation y=−x+3 by v(x).

It is asked to write the function w(x) in terms of the function v(x).

To do this apply the transformations to the function v(x) to get the function w(x).

The function v(x) is the straight line passing through the origin.

Take the reflection of the function v(x) with respect to x−axis and then the resulting function will be −v(x).

Then move the resulting function upward at 3 units.

So, the resulting function will be −v(x)+3 and this function is nothing but the function w(x).

So, the function w(x) an be written as w(x)−v(x)+3.

Hence the function w(x) can be written in terms of the function v(x) as w(x)=−v(x)+3.

Algebra II Carnegie Learning skills practice solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 292 Problem 16 Answer

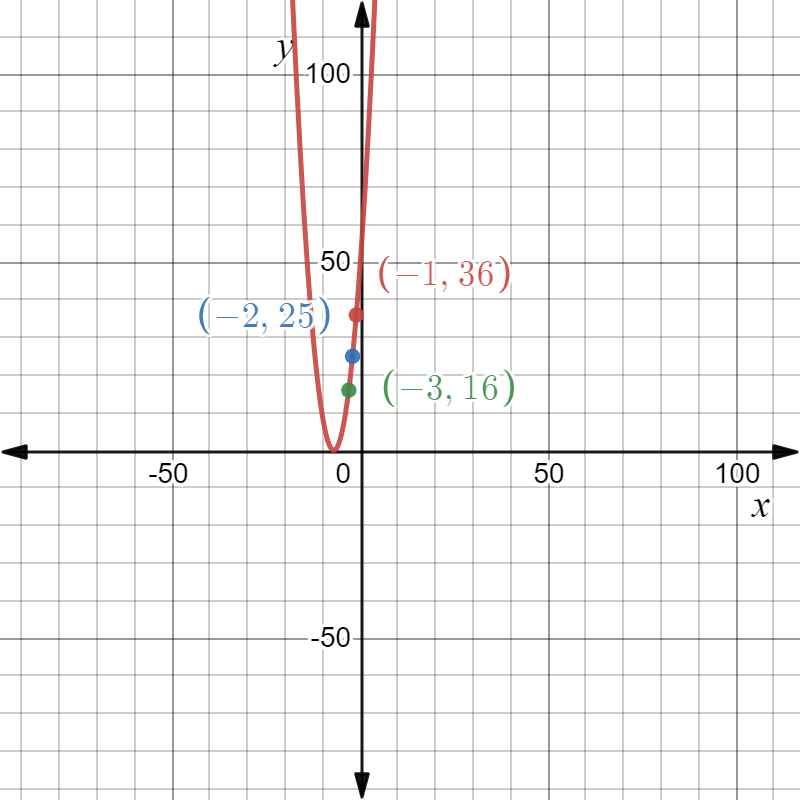
It is given a graph of the parabola whose axis is parallel to negative y−axis and vertex is at (−4,6) by the function v(x) and a parabola whose axis is  parallel to negative y−axis and vertex is at(4,−4)

by the function w(x).It is asked to find an equation of w(x) in terms of v(x).

To do this apply the transformation to the function v(x)  to get the function w(x).

First, move down the parabola given by the function v(x) by 10 units.

Then the resulting function will be v(x)−10.

Then move the resulting function at the right side 8 units.

Then the resulting function will be v(x−8)−10 and this is nothing but the function given by w(x)

Hence, the equation for w(x) in terms of v(x) is w(x)=v(x−8)−10.

Page 292 Problem 17 Answer

It is given the graphs of the two functions w(x) and v(x).

It is asked to write the equation for the function w(x) in terms of the function v(x).

To do this first, apply the transformation to the function v(x) and then get the function w(x).

First, move the function v(x) to the right side by 3units.

So, the resulting graph of the function will be v(x−8).

Now, take the reflection with respect to y−axis of the resulting graph of the function.

Then the resulting graph of the function will be v(−(x−8)) and this is nothing but the function w(x).

Hence, the equation of the function w(x) in terms of v(x) will be w(x)=v(−x+8).

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 283 Problem 1 Answer

We are given the parent quadratic function asf(x)=x² and its transformation asy=4x² and state if the transformation is a vertical stretch or vertical compression.

Then, we have to state if the graph includes a reflection or not.

We will graph each function on the same coordinate plane and then we can easily visualize the transformations taking place.

So, we have the graphs of the functions f and g as follows:

So, we observe from the graph that the function g is more steeper than the function f.

Hence, the transformation is a vertical compression of the graph off(x)=x².

Also, as both the graphs lie on the same side in the above graph, so there is no reflection included in the graph.

The graph of the functionsf(x)=x² andg(x)=4 x² is obtained as:

The transformation is a vertical compression and there is no reflection included in the graph.

Carnegie Learning Algebra II Chapter 2 Exercise 2.3 solutions

Page 283 Problem 2 Answer

We are given the parent quadratic function asf(x)=x² and its transformation as g(x)=1/8x² and state if the transformation is a vertical stretch or vertical compression.

Then, we have to state if the graph includes a reflection or not.

We will graph each function on the same coordinate plane and then we can easily visualize the transformations taking place.

So, we have the graph of the functions f and p as follows:

So, we observe from the graph that the function p is more wide than the function f.

Hence, the transformation is a vertical stretch of the graph off.

Also, from the given function, we have a=1/8.

So, the factor of stretch is 8.

Next, as both the graphs lie on the same side in the above graph, so there is no reflection included in the graph.

The graph of the functions f(x)=x² and g(x)=1/8 x² is obtained as follow

The transformation is a vertical stretch by a factor of 8 and there is no reflection included in the graph.

Page 284 Problem 3 Answer

We are given the parent quadratic function as f(x)=x² and its transformation as g(x)=−5x² and state if the transformation is a vertical stretch or vertical compression.

Then, we have to state if the graph includes a reflection or not.

We will graph each function on the same coordinate plane and then we can easily visualize the transformations taking place.

So, we have the graph of the given functions as follows:

So, we observe from the graph that the function h is more steeper than the functionf.

Hence, the transformation is a vertical compression of the graph off by a factor of 5 as a=5.

Also, as both the graphs lie on the opposite side in the above graph, so there is reflection included in the graph.

The graph of the functions f(x)=x² and g(x)=−5x² is obtained as follows:

The transformation is a vertical compression by a factor of 5 along with a reflection about x-axis.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 284 Problem 4 Answer

We are given the parent quadratic function as f(x)=x² and its transformation as m(x)=2.5x² and state if the transformation is a vertical stretch or vertical compression.

Then, we have to state if the graph includes a reflection or not.

We will graph each function on the same coordinate plane and then we can easily visualize the transformations taking place.

So, we have the graphs of the functions as follows:

So, we observe from the graph that the function m is more steeper than the function f.

Hence, the transformation is a vertical compression of the graph off by a factor of 2.5 as a=2.5.

Also, as both the graphs lie on the same side in the above graph, so there is no reflection included in the graph.

The graphs of the functionsf(x)=x² andm(x)=2.5x² is obtained as follows:

The transformation is a vertical compression by a factor of 2.5 and there is no reflection included in the graph.

Skills Practice Exercise 2.3 answers

Page 284 Problem 5 Answer

We are given the parent quadratic function asf(x)=x² and its transformation as d(x)=2/5x² and state if the transformation is a vertical stretch or vertical compression.

Then, we have to state if the graph includes a reflection or not.

We will graph each function on the same coordinate plane and then we can easily visualize the transformations taking place.

So, we have the graphs of both the functions as follows:

So, we observe from the graph that the function dis more wide than the function f.

Hence, the transformation is a vertical stretch of the graph off by a factor of 2/5 as a=2/5.

Also, as both the graphs lie on the same side in the above graph, so there is no reflection included in the graph.

The graphs of the functions f(x)=x² and d(x)=2/5x² is obtained as follows:

The transformation is a vertical stretch by a factor of 2/5 and there is no reflection included in the graph.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 284 Problem 6 Answer

We are given the parent quadratic function as f(x)=x² and its transformation as (x)=−1/2x³−3 and state if the transformation is a vertical stretch or vertical compression.

Then, we have to state if the graph includes a reflection or not.

We will graph each function on the same coordinate plane and then we can easily visualize the transformations taking place.

So, we have the graphs of the functions as follows:

So, we observe from the graph that the functiong is more wide than the functionf.

Hence, the transformation is a vertical stretch of the graph off by a factor of 1/2 as a=1/2.

Also, as both the graphs lie on the opposite side in the above graph, so there is reflection included in the graph.

The graph of the functionsf(x)=x² and g(x)=−1/2x²−3 is obtained as follows:

The transformation is a vertical stretch by a factor of 1/2 and there is no reflection included in the graph.

Page 285 Problem 7 Answer

Here, we are given the parent function as f(x)=x² and its transformation as g(x)=−4(f(x+3)).

We have to describe how the function g compares to f.

Then we have to use the coordinate notation to represent the transformation from f to g, according to the values of A,C and D So we will compare the given function g with the general transformation given as g(x)=A f(B(x−C))+D and determine the values of A,C and D.

So we have a function g as follows:

⇒g(x)=−4(f(x+3)).

Comparing with the general transformation function g(x)=A f(B(x−C))+D we get A=−4,B=1,C=−3 and D=0.

Hence, as per the value of A there will be a vertical compression by a factor of 2 along with a reflection of g as compared to the function f.

Again, as per the value of D there will be a vertical translation of 0 the unit below the function f.

Thus, the vertex will shift 0 unit below to the point given as (0,0).

The coordinate notation for the transformation from f(x) to g(x) is given as follows:(x,y)→(x,−4y+0).

The graph g(x) is a vertical compression by a factor of 2 followed by a reflection and then a vertical translation unit 0 above to (0,0).

The coordinate nation to represent the transformation fromf(x) to g(x)

is given  by (x,y)→(x,−4y+0).

Algebra II Chapter 2 Skills Practice solutions Exercise 2.3

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 285 Problem 8 Answer

Here we are given the parent function asf(x)=x² and its transformation as g(x)=1/3f(x−6)−3

We have to describe how the function g compares to f.

Then we have to use the coordinate notation to represent the transformation from f to g, according to the values of A, C and D

So, we will compare the given function g with the general transformation given as g(x)=Af(B(x−C))+D and determining the values of A, C and D.

So, we have a function g as follows:

⇒g=1/3 f(x−6)−3

Comparing with the general transformation function g(x)=Af(B(x−C)+D,

we get A=1/3,B=1,C=6 and D=−3

Hence, as per the value of A there will be a vertical compression by a factor of 1 along with a reflection of g as compared to the function f.

Again, as per the value of D there will be a vertical translation of−3 the unit below the function f.

Thus, the vertex will shift−3 unit below to the point given as (0,−3)

The coordinate notation for the transformation fromf(x) to g(x) is given as follows:(x,y)→(x,1/3y−3)

The graphg(x) is a vertical compression by a factor 1 followed by a reflection and then a vertical translation−3 unit above to(0,−3).

The coordinate nation represents the transformation fromf(x) to g(x)  is given  by (x,y)→(x,1/3y−3)

Page 285 Problem 9 Answer

Here we are given the parent function asf(x)=x² and its transformation as g(x)=−0.75 f(x+4)−2

We have to describe how the function g compares to f.

Then we have to use the coordinate notation to represent the transformation from f to g, according to the values of A, C and D.

So, we will compare the given function g with the general transformation given as g(x)=A f(B(x−C))+D and determining the values of A, C and D.

So we have a function g as follows:

⇒g(x)=0.75f(x+4)−2.

Comparing with the general transformation function g(x)=A f(B(x−C)+D,

we get A=0.75,B=1,C=−4and D=−2 .

Hence, as per the value of A there will be a vertical compression by a factor of 1 along with a reflection of g as compared to the function f.

Again, as per the value of D there will be a vertical translation of−2 the unit below the function f.

Thus, the vertex will shift−2 unit below to the point given as(0,−2).

The coordinate notation for the transformation from f(x) to g(x) is given as follows:(x,y)→(x,0.75y−2).

The graph g(x) is a vertical compression by a factor of 1 followed by a reflection and then a vertical translation−2 unit above to (0,−2).

The coordinate nation to represent the transformation from f(x) to g(x) is given  by (x,y)→(x,0.75y−2).

Page 285 Problem 10 Answer

Here, we are given the parent function asf(x)=x² and its transformation as g(x)=4/3f(x−1/3)+2/3

We have to describe how the function g compares to f.

Then we have to use the coordinate notation to represent the transformation from f to g, according to the values of A, C and D.

So, we will compare the given function g with the general transformation given as g(x)=A f(B(x−C))+Dand determining the values A,C and D

We have a function g as follows:

⇒g(x)=4/3f(x−1/3)+2/3.

Comparing with the general transformation function g(x)=A f(B(x−C)+D

we get A=4/3,B=1,C=1/3 and D=2/3.

Hence, as per the value of A there will be a vertical compression by a factor of 1along with a reflection of g as compared to the function f.

Again, as per the value of D there will be a vertical translation of 2/3 the unit below the function f.

Thus, the vertex will shift 2/3 unit below to the point given as (0,2/3).

The coordinate notation for the transformation from f(x) to g(x) is given as follows :(x,y)→(x,4/3y+2/3).

The graphg(x)  is a vertical compression by a factor of 1 followed by a reflection and then a vertical translation unit 2/3 above to (0,2/3).

The coordinate nation represents the transformation from f(x) to g(x)  is given by (x,y)→(x,4/3y+2/3).

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 286 Problem 11 Answer

The given graph in the question is

Here we have to find the respective equation of the graph.We will do so by using the straight-line formula which is y=mx+b.

Y is the y-value (distance along the y-axis, which is the vertical axis) and x is the x value (the distance along the x-axis, which is the horizontal axis).

So we can see that our boundary lines are at x=−4 and x=0.So we know that our function will look something like this (notice open and closed endpoints):

f(x)={ ……​ if x<−4

{ ……     if −4≤x<0

{ ……      if x≥0

We can pick two points (−4,0) and (−2,0) on the leftmost line to get the equation y=−4x.

We can see that the middle function is y=x²−4 and the rightmost function is just a horizontal line y=2.

So the piece wise function is :

f(x)={ −4x​   if x<−4

{ x²             if −4≤x<0

{ 0          if x≥0.

The function that represents the equation given in the question is f(x)=

{ −4x​         if x<−4

{ x²             if −4≤x<0

{ 0          if x≥0.

Page 286 Problem 12 Answer

The given graph in the question is

Here we have to find the respective equation of the graph We will do so by using the straight-line formula which is y=mx+b.

Y is the y-value (distance along the y-axis, which is the vertical axis) and x is the x value (the distance along the x-axis, which is the horizontal axis).

So we can see that our boundary lines are at x=2 and x=4.

So we know that our function will look something like this (notice open and closed endpoints):

f(x)={ ……​ if x<2

{ ……      if 2≤x<4

{ ……       if x≥4

We can pick two points (0,2) and (2,4) on the leftmost line to get the equation y=2x+4.

We can see that the middle function is y=x²+2 and the rightmost function is just the horizontal line y=2.

So the piecewise function is:

f(x)={ 2x+4 ​ if x<2

{ x²+2        if 2≤x<4

{ 4             if x≥4.

The function that represents the graph in the question is f(x)=

{ 2x+4 ​ if x<2

{ x²+2        if 2≤x<4

{ 4             if x≥4.

Carnegie Learning Skills Practice Exercise 2.3 explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 286 Problem 13 Answer

The given graph in the question is

Here we have to find the respective equation of the graph We will do so by using the straight-line formula which is y=mx+b.

Y is the y-value (distance along the y-axis, which is the vertical axis) and x is the x value (the distance along the x-axis, which is the horizontal axis).

So we can see that our boundary lines are at x=2 and x=4.So we know that our function will look something like this (notice open and closed endpoints):

f(x)= { …… ​ if x<2

{ ……       if 2≤x<4

{ ……       if x≥4

We can pick two points (0,2) and (2,4) on the leftmost line to get the equation y=2x+4.

We can see that the middle function is y=x²+2

and the rightmost function is just the horizontal line y=2.

So the piecewise function is:

f(x)= { 2x+4 ​ if x<2

{ x²+2      if 2≤x<4

{ 4            if x≥4.

The function that represents the graph in the question is f(x)=⎩

{ 2x+4 ​ if x<2

{ x²+2      if 2≤x<4

{ 4            if x≥4.

Page 286 Problem 14 Answer

The given graph in the question is

Here we have to find the respective equation of the graph

We will do so by using the straight-line formula which is y=mx+b.

Y is the y-value (distance along the y-axis, which is the vertical axis) and x is the x value (the distance along the x-axis, which is the horizontal axis).

So we see that our boundary lines are x=3 and x=−1.So we know that our function will look something like this(notice open closed endpoints):

f(x)= { …… ​ if x<−1

{ ……       if −1≤x<3

{ ……        if x≥3

we can pick two points (−1,1) and (0,2) on the leftmost line to get the equation y=−x+3

We can see that the middle function is y=x²−1 and the rightmost function is just the horizontal line y=2

So the piecewise function is:

f(x)= { −x+3​ if x<−1

{ x²−1       if −1≤x<3

{ 3             if x≥3

The function that represents the graph given in the question is f(x)=⎩

{ −x+3​ if x<−1

{ x²−1       if −1≤x<3

{ 3             if x≥3

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 286 Problem 15 Answer

The given graph in the question is

Here we have to find the respective equation of the graph

We will do so by using the straight-line formula which is y=mx+b.

Y is the y-value (distance along the y-axis, which is the vertical axis) and x is the x value (the distance along the x-axis, which is the horizontal axis).

So we can see that our boundary lines are at x=-8 and x=0. So we know that our function will look something like this(notice open and closed endpoints).

f(x)= { ……​ if x<4

{ ……      if 4≤x<6

{ ……      if x≥6

We can pick two points (0,4) and (2,6) on the leftmost line to get the equation y=4x+8.

We can see that the middle function is y=x²+4 and the rightmost function is just the horizontal line y=2

So the piece-wise function is

f(x)= { 4x+8         ​ if x<4

{ x²+4                 if 4≤x<6

{ 6                      if x≥6.

The function that represents the graph given in the question is f(x)=

{ 4x+8         ​ if x<4

{ x²+4                 if 4≤x<6

{ 6                      if x≥6.

Page 286 Problem 16 Answer

The given graph in the question is

Here we have to find the respective equation of the graph

We will do so by using the straight-line formula which is y=mx+b.

Y is the y value (distance along the y-axis, which is the vertical axis) and x is the x value (the distance along the x-axis, which is the horizontal axis).

So we can see that our boundary lines are at x=-8 and x=0. So we know that our function will look something like this(notice open and closed endpoints).

f(x)= { ……​ if x<−8

{ ……      if −8≤x<0

{ ……      if x≥0

We can pick two points (−8,−4)and(−6,0) on the leftmost line to get the equation y=−2x−4

We can see that the middle function is y=x²−2 and the rightmost function is just the horizontal line y=2.

So the piecewise function is

f(x)= { −8x−16  ​ if x<−8

{ x²−8             if −8≤x<0

{0                    if x≥0.

The function that represents the graph given in the question is f(x)=

{ −8x−16  ​ if x<−8

{ x²−8             if −8≤x<0

{0                    if x≥0.

Chapter 2 Exercise 2.3 Skills Practice guide

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.3 Skills Practice Page 286 Problem 17 Answer

We have to find the function which represents the given graph.

Note that the parabola opens downwards. Hence the general equation of this parabola is y=a(x−h)²+k.

Since the vertex of the parabola is (−7,6) [as marked in figure as A], we get its equation as

y=a(x+7)²+6

Now we have to find the value of a and for that we substitute the value of any point on the parabola to the equation above.

Note that (−2,0) is a point on the parabola and substituting this to the equation we get

0=a(−2+7)²+6

⇒a=−6/52

⇒a=−0.24

Hence the equation of the given graph is

y=−0.24(x+7)²+6

=−0.24(x²+14x+49)+6

=−0.24x²−3.36x−5.76

Thus the function which represents the given graph is y=−0.24x²−3.36x−5.76.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.2 Skills Practice

Page 277 Problem 1 Answer

Here it is asked to complete the sentence

” A(n)___________________is one of a set of key points that help identify the basic function “.

So here the answer is The reference point.

Therefore, the reference point is one of a set of key points that help identify the basic function.

Page 277 Problem 2 Answer

Here it is asked to complete the sentence

” The mapping, or movement, of all the points of a figure in a plane according to a common operation is called a(n)__________ “.

So here the answer is Transformation.

Therefore, the mapping, or movement, of all the points of a figure in a plane according to a common operation is called a transformation.

Carnegie Learning Algebra Ii Chapter 2 Exercise 2.2 Solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.2 Skills Practice Page 277 Problem 3 Answer

Here it is asked to complete the sentence

” The ______________ is the variable, term, or expression on which the function operates “.

So here the answer is The argument of a function.

Therefore, the argument of a function is the variable, term, or expression on which the function operates.

Page 277 Problem 4 Answer

Here it is asked to complete the sentence

” A(n)___________ is a type of transformation that shifts an entire figure or graph the same distance and direction.

So here the answer is Translation.

Therefore, a translation is a type of transformation that shifts an entire figure or graph the same distance and direction.

Page 278 Problem 5 Answer

Given that f(x)=x² and h(x)=(x+2)²−1

Here it is asked to complete the table and graph h(x).

First, we will complete the table.

When x=0 then

h(x)=(0+2)²−1=3

When x=1 then h(x)=(1+2)²−1 =8

When x=−1 then h(x)=(−1+2)²−1 =0

So the table is

The required graph of h(x) is as shown below,

Therefore, completed the table and the graph of the function is

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.2 Skills Practice Page 278 Problem 6 Answer

Given that f(x)=x² and h(x)=(x+7)²

Here it is asked to complete the table and graph h(x).

First, we will complete the table.

When x=−1 then h(x)=(−1+7)² =36

When x=−2 then h(x)=(−2+7)² =25

When x=−3 then h(x)=(−3+7)² =16

So the complete table is

The required graph of h(x) is

Therefore, completed the table and the graph of the function is

Skills Practice Exercise 2.2 Answers

Page 279 Problem 7 Answer

Given that f(x)=x² and h(x)=x²−9

Here it is asked to complete the table and graph h(x).

First, we will complete the table.

When x=0 then h(x)=0²−9 =−9

When x=1 then h(x)=1²−9 =−8

When x=2 then h(x)=2²−9 =−5

So the required table is

The required graph of h(x) is as shown below,

Therefore, completed the table and the graph of the function is

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.2 Skills Practice Page 280 Problem 8 Answer

Given that

f(x)=x² and h(x)=(x+4)²−4

Here it is asked to complete the table and graph h(x).

First, we will complete the table.

Whenx=−1 then h(x)=(−1+4)²−4 =5

When x=−2 then h(x)=(−2+4)²−4 =0

When x=−3 then h(x)=(−3+4)²−4 =−3

So the completed table is

The required graph of h(x) is as shown below,

Therefore, completed the table and the graph of the function is

Algebra Ii Chapter 2 Skills Practice Solutions Exercise 2.2

Page 280 Problem 9 Answer

Given g(x)=Af(B(x−C))+D Where f(x)=x²

Also Given g(x)=f(x+8)−9

To determine the value of C and D

To determine the vertex of the given function compares to the vertex of f(x)

Given g(x) = f(x + 8) − 9

Compare to given g(x) = Af(B(x − C)) + D we see that

C = −8 and D = −9

Given f(x) = x² so the vertex is (0, 0)

The vertex will be shifted from 8 units to the left and 9 units upward.

Hence the vertex for g(x) = f(x + 8) − 9 is (−8, −9)

Hence C=−9 and D=−9

The vertex for g(x)=f(x+8)−9 is (−8,−9)

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.2 Skills Practice Page 280 Problem 10 Answer

Given g(x)=A f(B(x−C))+D Where f(x)=x²

Also Given g(x)=f(x−5)−11

To determine the value of C and D

To determine the vertex of the given function compares to the vertex of f(x)

Given g(x) = f(x − 5) − 11

Compare to given g(x) = A f(B(x − C)) + D we see that

C = 5 and D = −11

Given f(x) = x² so the vertex is (0, 0)

The vertex will be shifted shifted from 5 units to the right and 11 units downward.

Hence the vertex for g(x) = f(x − 5) − 11 is (5, −11)

The vertex for g(x) = f(x − 5) − 11 is (5, −11)

Hence C = 5 and D = −11

Page 280 Problem 11 Answer

Given g(x)=A f(B(x−C))+D Where f(x)=x²

Also Given g(x)=f(x−6)+10

To determine the value of C and D

To determine the vertex of the given function compares to the vertex of f(x)

Given g(x) = f(x − 6) + 10

Compare to given g(x) = A f(B(x − C)) + D we see that

C = 6 and D = 10

Given f(x) = x² so the vertex is (0, 0)

The vertex will be shifted shifted from 6 units to the right and 10 units upward.

Hence the vertex for g(x) = f(x − 6) + 10 is (6, 10)

Hence C = 6 and D = 10

The vertex for g(x) = f(x − 6) + 10 is (6, 10)

Page 277 Problem 12 Answer

Given g(x) = A f(B(x − C)) + D Where f(x) = x²

Also Given g(x)=f(x+2)+3

To determine the value of C and D

To determine the vertex of the given function compares to the vertex of f(x)

Given g(x) = f(x + 2) + 3

Compare to given g(x) = A f(B(x − C)) + D we see that

C = −2 and D = 3

Given f(x) = x² so the vertex is (0, 0)

The vertex will be shifted shifted from 2 units to the left and 3 units upward.

Hence the vertex for g(x) = f(x + 2) + 3 is (−2, 3)

Hence C = −2 and D = 3

The vertex for g(x) = f(x + 2) + 3 is (−2, 3)

Page 281 Problem 13 Answer

Given g(x)=A f(B(x−C))+D Where f(x)=x²

Also Given g(x)=f(x+4)−2

To determine the value of C and D

To determine the vertex of the given function compares to the vertex of f(x)

Given g(x) = f(x + 4) − 2

Compare to given g(x) = A f(B(x − C)) + D we see that

C = −4 and D = −2

Given f(x) = x² so the vertex is (0, 0)

The vertex will be shifted shifted from 4 units to the left and 2 units downward.

Hence the vertex for g(x) = f(x + 4) − 2 is (−4, −2)

Hence C = −4 and D = −2

The vertex for g(x) = f(x + 4) − 2 is (−4, −2)

Carnegie Learning Skills Practice Exercise 2.2 Explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.2 Skills Practice Page 281 Problem 14 Answer

To write b(x) in terms of f(x) by refering the given graph

From the graph we see that f(x) = x² with vertex (0, 0)

Again grom the graph we see that the vertex of b(x) is (−5, −2)

Then b(x) = f(x + 5) − 2 by using g(x) = f((x − C)) + D Where f(x) = x , vertex of f(x) = (C, D)

Hence b(x) = f(x + 5) − 2 is the function in terms of f(x)

Page 281 Problem 15 Answer

To write c(x) in terms of f(x) by refering the given graph

From the graph we see that f(x) = x² with vertex (0, 0)

Again from the graph we see that the vertex of c(x) is (0, −6)

Then c(x) = f(x) − 6 by using g(x) = f((x − C)) + D Where f(x) = x , vertex of f(x) = (C, D)

Hence c(x) = f(x) − 6 is the function in terms of f(x)

Page 281 Problem 16 Answer

To write d(x) in terms of f(x) by refering the given graph

From the graph we see that f(x) = x² with vertex (0, 0)

Again from the graph we see that the vertex of d(x) is (4, 3)

Then d(x) = f(x − 4) + 3 by using g(x) = f((x − C)) + D Where f(x) = x , vertex of f(x) = (C, D)

Hence d(x) = f(x − 4) + 3 is the function in terms of f(x)

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.2 Skills Practice Page 281 Problem 17 Answer

To write d(x) in terms of b(x) by refering the given graph

From graph we see that b(x) = f(x + 5) − 2 with the vertex (−5, −2)

Again from the graph we see that the vertex of d(x) is (4, 3)

Then d(x) = b(x − 4) + 3 by using the result g(x) = f((x − C)) + D Where f(x) = x , vertex of f(x) = (C, D)

Hence d(x) = b(x − 4) + 3 is the function in terms of g(x)

Page 281 Problem 18 Answer

Here, we are given graphs of the parent quadratic functions along with its transformations.

We have to analyze the graph and write the function c(x) in terms of b(x).

So, we will first determine the coordinates of the vertices of both the graphs and using these, we will determine the translation taking place.

Then, we will be able to express c(x) in terms of b(x).

So, we observe that the vertex of function c(x) is at(−5,−2) and that of b(x) is at(−6,0).

So, there is a vertical translation by 4 units up followed by a horizontal translation by 5 units towards the right of the function c(x) as compared to b(x).

So, the function c(x) can be written in terms ofb(x) as⇒c(x)=b(x−5)−4.

Analyzing the graph, the function c(x) is written in terms of b(x) as follows:c(x)=b(x−5)−4.

Chapter 2 Exercise 2.2 Skills Practice Guide

Page 281 Problem 19 Answer

Here, we are given graphs of the parent quadratic functions along with its transformations.

We have to analyze the graph and write the function b(x) in terms of c(x).

So, we will first determine the coordinates of the vertices of both the graphs and using these, we will determine the translation taking place.

Then, we will be able to express b(x) in terms of c(x).

So, we observe that the vertex of function b(x) is at (5,−2) and that of c(x) is at (0,−6).

So, there is a vertical translation by 4 units below followed by a horizontal translation by 5 units of the function b(x) as compared to c(x).

So, the function b(x) can be written in terms of c(x) as⇒b(x)=c(x+5)+4

Analyzing the graph, the function b(x) is written in terms of c(x) as follows:b(x)=c(x+5)+4.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice

Page 269 Problem 1 Answer

Given- The standard form of a quadratic equation.

To find- An example for the standard form of a quadratic function and determine the x−intercepts, they−intercept, or the vertex of the graph, and the concavity of a parabola.

We can give an example of a quadratic equation in standard form, then describe the process to determine the x−intercept,y−intercept, the vertex, and the concavity of the parabola using the general quadratic equation in standard form.

The standard form of the quadratic function is of the form f(x)=ax²+bx+c, wherea,b,and c are real numbers with a≠0.

An example of a quadratic function in standard form isf(x)=3x²+6x−8

Here a=3

b=6

c=−8

To find the x−intercepts algebraically, we substitute y=0 in the equation and then solve for values of x.

In the same manner, to find for y−intercepts algebraically, we substitute x=0 in the equation and then solve for y.

To find the vertex of a quadratic equation,y=ax²+bx+c, we find the point{−b/2a,a(−b/2a)²+b(−b/2a)+x} by following these steps.

At first, we get the equation in the form y=ax²+bx+c.We calculate−b/2a.

This is the x−coordinate of the vertex.

To find they−coordinate of the vertex, we substitute x=−b/2a in the equation solve for y.

This is they−coordinate of the vertex.

Now, for determining the concavity of the function f(x)=ax²+bx+c, we will calculate its second derivative.

So,f(x)′′=2a

Thus, we have the concavity of the function f′′

(x)=2a, we can say that the sign off′′(x) directly depends on the sign of the coefficient a, as² is a positive number.

If a will be positive,2a will be positive, whereas if a will be negative,2a will be negative.

Therefore, we can say that a directly relates with the concavity of the function, as if a is positive,f′′(x) will be positive and the function will be concave up. If a is negative,f′′(x) will be negative and the function will be concave down.

Hence, for a quadratic function f(x)=ax²+bx+c,Ifa>0, thenf(x) is concave upward of the parabola,

Ifa<0,  thef(x) is concave downward of the parabola.

An example of a quadratic function in standard form is f(x)=3x²+6x−8

The x−intercept of the equation is the x−values when y=0.

They−intercept of the equation is they−values when x=0.

The vertex of the quadratic function f(x)=ax²+bx+c is the point{−b/2a,a(−b/2a)²+b(−b/2a)+c}

The concavity of parabola of the equation f(x)=ax²+bx+c is given by,

Ifa>0, the parabola is concave upward.

Ifa<0, the parabola is concave downward.

Carnegie Learning Algebra Ii Chapter 2 Exercise 2.1 Solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 269 Problem 2 Answer

Given- The factored form of a quadratic equation.

To find- An example for the factored form of a quadratic function and determine the x−intercepts, the y−intercept, or the vertex of the graph, and the concavity of a parabola.

We can give an example of a quadratic equation in standard form, then describe the process to determine the x−intercept, y−intercept, the vertex, and the concavity of the parabola using the general quadratic equation in factored form.

The factored form of the equation for a quadratic equation isy=a(x−r)(x−s) a product of three factors.

The values a,r,s are values that also determine the shape and position of the parabola.

An example of a quadratic function in factored form isy=2(x−5)(x−7)

Here,​a=2

r=5

s=7

To find the x−intercepts algebraically, we substitute y=0 in the equation and then solve for values of x.

In the same manner, to find for y−intercepts algebraically, we substitute y=0 in the equation and then solve for y.

To find vertex in factored form, we have to find the axis of symmetry and substitute the value of x and solve for y.

The axis of symmetry can be calculated given the formula,x=r+s/2, where r and s are zeroes of the equation.

Now, for determining the concavity of the function f(x)=a(x−r)(x−s) we will calculate its second derivative.

So,f′′(x)=2a

Thus, we have the concavity of the functionf′′ (x)=2a, we can say that the sign off′′(x)

directly depends on the sign of the coefficient a, as2 is a positive number.

If a will be positive,2a will be positive, whereas if a will be negative,2a will be negative.

Therefore, we can say that a directly relates to the concavity of the function, as if a is positive,f′′(x)

will be positive and the function will be concave up. If a is negative,f′′ (x) will be negative and the function will be concave down.

Hence, for a quadratic function f(x)=a(x−r)(x−s),

Ifa>0, then f(x) is concave upward of the parabola,

Ifa<0, then f(x) is concave downward of the parabola.

An example of a quadratic function in factored form isy=2(x−5)(x−7)

The x−intercept of the equation is the x−values when y=0.

They−intercept of the equation is they−values whenx=0.

To find vertex in factored form, we have to find the axis of symmetry and substitute the value of x=r+s/2 and solve for y.

The concavity of parabola of the equationf(x)=a(x−r)(x−s) is given by,

Ifa>0, the parabola is concave upward.

Ifa<0, the parabola is concave downward.

Page 269 Problem 3 Answer

Given- The vertex form of a quadratic equation.

To find- An example for the vertex form of a quadratic function and determine the x−intercepts, they−intercept, or the vertex of the graph, and the concavity of a parabola.

We can give an example of a quadratic equation in vertex form, then describe the process to determine the x−intercept, y−intercept, the vertex, and the concavity of the parabola using the general quadratic equation in factored form.

The vertex form of a quadratic equation isy=a(x−h)²+k

Here,y is the y−coordinate,x is the x−coordinate, and a is the constant that tells you whether the parabola is facing up (+a) or down(−a).

The coordinate(h,k) gives the vertex of the parabola.

An example of a quadratic function in factored form isy=5(x−6)²+8

Here,​a=5

h=6

k=8

They−intercept is the point at which the parabola crosses they−axis.

The x−intercepts are the points at which the parabola crosses the x−axis.

The x−intercept is the value of x at y=0.

They−intercept is the value of y at x=0.

The vertex of the equation is given by(h,k), which can be calculated by computi

Now, for determining the concavity of the function f(x)=a(x−h)²+k we will calculate its second derivative.

So,f′′(x)=2a

Thus, we have the concavity of the function f′′(x)=2a, we can say that the sign off′′(x) directly depends on the sign of the coefficient a,as² is a positive number.

If a will be positive,2a will be positive, where as if awill be negative,2a will be negative.

Therefore, we can say that a directly relates to the concavity of the function, as if a is positive,f′′(x)

will be positive and the function will be concave up.

If a is negative,f′′(x) will be negative and the function will be concave down.

Hence, for a quadratic function f(x)=a(x−h)²+k,

Ifa>0, then f(x) is concave upward of the parabola,

Ifa<0 An example of a quadratic function in factored form is y=5(x−6)²+8

The x−intercept of the equation is the x−values when y=0.

They−intercept of the equation is they−values when x=0.

The vertex of the equation is given by(h,k), which can be calculated by computing h=−b/2a, and then evaluating y ath to find k.

The concavity of parabola of the equationy=a(x−h)²+k is given by,

Ifa>0, the parabola is concave upward.

Ifa<0, the parabola is concave downward.

Skills Practice Exercise 2.1 Answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 269 Problem 4 Answer

Given- Concavity of a parabola of a quadratic function.

To find- To describe how to determine the concavity of a parabola.

We can determine the concavity of a parabola by calculating the second derivative of the quadratic function.

For a quadratic function f, we can determine the concavity by finding the second derivative.

The seconds derivative of the function is given by f′′=2a, where a is the coefficient of x².

So,f′′ is directly related to the sign of a.

When a will be positive,f′′=2a is positive.

When a will be negative,f′′=2a is negative.

In any quadratic function f, if the second derivative f′′ is positive, then the function is concave up.

And, If the second derivative f′′ is negative, then the function is concave down.

Concavity of a parabola shows that the parabola is concave up when it bends up, and concave down when it bends down.

It can be determined by calculating the second derivative of the quadratic function f.

So,f′′=2a, where a is the coefficient of x².

When a is positive,f′′=2a is positive and the parabola is concave up.

When a is negative,f′′ =2a is negative and the parabola is concave down.

Page 270 Problem 5 Answer

Given equations of four parabolas and a parabola plotted on the graph.

We need to match the parabola on the graph to its correct equation out of four equations given to us.

The given parabola on the graph : (Value of one smallest box on the x and y axes is 0.5 units)

Investigating each of the given equations:

f(x)=6(x−2)(x−8): If we choose any point between −2 and −8, say choose x=−4

Now 6(x−2)(x−4)=288>0 at x=−4.

But according to the graph y=−4 at x=−4. Hence this function does not match the graph.

f(x)=−1/2(x+2)(x+8) : If we choose the point x=−4

Now −1/2(x+2)(x+8)=6>0 at x=−4.

But according to the graph y=−4 at x=−4. Hence this function does not match the graph.

f(x)=1/2(x+2)(x+8): Now choose the point x=−4

Now 1/2(x+2)(x+8)=−4<0

at x=−4.

According to the graph also y=−4 at x=−4. Thus it satisfies this condition but it may or may not be true.

f(x)=1/2(x−2)(x−8): The value of f(x) at x=−2 is 20≠0

But according to the graph, at x=−2, the value of the graph is 0

Hence this function does not match the graph.

Thus the correct option is f(x)=1/2(x+2)(x+8).

Circling the function that matches the graph is:

Page 270 Problem 6 Answer

Given equations of four parabolas and a parabola plotted on the graph.

We need to match the parabola on the graph to its correct equation out of four equations given to us.

Investigating the given function equations:

f(x)=−2x²−x−2: This function cannot cannot match the given graph as at x=0, f(x)=−2

but according to the graph y=7 at x=0.

Hence this function does not match the graph. (Value of one smallest box along x and y axes is 0.5units)

f(x)=2x²−x+7: The value of f(x)=8 at x=1.

But according to the graph the value of y at x=1 is some value around 4.

Hence this function does not match the given graph.

f(x)=−x²−2x+7: The value of f(x)

at x=1/2  is 23/4. But according to the graph , y=6

at x=1/2

Hence this function does not match the graph.

f(x)=−2x²−x+7: The value of f(x)=6 which is the same as the value of y in the graph corresponding to x=1/2.

Since no other function matches the graph but this function matches some points corresponding to the graph, hence this function matches the graph.

Circling the equation of the parabola to the graph:

Algebra Ii Chapter 2 Skills Practice Solutions Exercise 2.1

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 270 Problem 7 Answer

Given equations of four parabolas and a parabola plotted on the graph.

We need to match the parabola on the graph to its correct equation out of four equations given to us.

From the graph it is clear that at x=4

we have y=2

In the function f(x)=4(x−2)²−2, the value of f(x)=14 at x=4. Hence this function does not match the graph.

f(x)=0.25(x−2)²+4: The value of f(x)=5 at x=4 and hence  this function does not match the graph .In the function −0.25(x+4)²+2, the value of f(x)=−2 at x=4.

Hence this function also does not match the graph .But for the function f(x)=0.25(x−4)²+2, the values of f(x) correspond to the y values in the graph for all values of x

Thus circling the correct equation :

Page 270 Problem 8 Answer

Given equations of four parabolas and a parabola plotted on the graph.

We need to match the parabola on the graph to its correct equation out of four equations given to us.

From the graph it is clear that y=0

at x=−2,x=−5

For the functions: f(x)=−3(x+2)(x−5),  the value of f(x)≠0 at x=−5

f(x)=3(x−2)(x−5), the value of f(x)≠0 at x=−2,x=−5

f(x)=−3(x−2)(x−5), the value of f(x)≠0 at x=−2,x=−5

But for the function f(x)=3(x+2)(x+5), the value of f(x) correspond to the y-value for all values of x.

Circling the equation that match with the graph given:

Page 271 Problem 9 Answer

Given equations of four parabolas and a parabola plotted on the graph.

We need to match the parabola on the graph to its correct equation out of four equations given to us.

The graph given:

In the graph we can see that x=0

we find y=4

Thus the functions f(x)=x²+5x−4 and f(x)=−x²+5x+10 , at the point x=0

gives the value f(x)=−4 and f(x)=10 respectively.

Hence these functions does not match the graph.

Now if we put f(x)=0 in the equation f(x)=x²+5x+4, we find the corresponding values of x, where the graph cuts the x-axis.

⇒x²+5x+4=0

⇒(x+4)(x+1)=0

⇒x=−4

x=−1

But in the graph the parabola cuts the x-axis at both positive and negative points. Hence this function does not match the graph.

Thus the only option that remains: f(x)=−x²+5x+4 is the function that matches the graph.

Encircling the correct option we get:

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 271 Problem 10 Answer

Given equations of four parabolas and a parabola plotted on the graph.

We need to match the parabola on the graph to its correct equation out of four equations given to us.

From the given graph we can see : y=0

at x=2

and y=2

at x=0

In the functions f(x)=1/2(x−2)²+2 and f(x)=1/2(x+2)² , when we put x=2, the value of f(x)≠0

Hence these functions does not match the graph.

In the function f(x)=−1/2(x−2)², the value of f(x)=−2 at x=0. Hence this also does not match the graph.

Hence the function f(x)=1/2(x−2)² is the equation that matches the graph.

Encircling the correct option we get:

Page 271 Problem 11 Answer

Given the y-intercept value and the axis of symmetry .

To determine the most efficient form of the quadratic function satisfying these conditions.

The axis of symmetry of the quadratic function y=ax²+bx+c is given by −b/2a

Given axis of symmetry = −3/8

According to the problem:

−3/8=−b/2a

⇒b=3/4a (Multiplying both sides by 2a)

Now as the point (0,3) satisfies the equation :

3=0+0+c

⇒c=3

Hence the most efficient form obtained: y=ax²+3/4ax+3

The quadratic function obtained is : y=ax²/+3/4ax+3

Page 271 Problem 12 Answer

Given three points that lies on the quadratic function.

To find the most efficient form of the quadratic function with this data.

Since the point (−1,12)

lies on the function, hence it satisfies the equation:

12=a−b+c…(1)

The point (5,12) lies on the function, hence it satisfies the equation:

12=25a+5b+c…(2)

The point (−2,−2) lies on the function, hence it satisfies the equation:

−2=4a−2b+c….(3)

Now doing the operation on equations 4×(1)−(3):

50=−2b+3c….(4)

Now doing the operation 25×(1)−(2):

288=24c−30b….(5)

Now doing the operation 8×(4)−(5):

400−288=30b−16b

⇒112=14b (Combining like terms)

⇒b=8 (Dividing both sides by 14)

Thus putting value of b in the equation (4)

we get: 50=−2(8)+3c

⇒50=−16+3c

⇒66=3c (Adding 16 on both sides)

⇒22=c (Dividing both sides by 3)

Now putting back the value of c and b in the equation (1)

we get: 12=a−8+22

⇒12=a+14 (Combining like terms)

⇒a=12−14 (Subtracting 14 from both sides)

⇒a=−2 (Combining like terms)

Hence the quadratic function looks like: y=−2x²+8x+22

The most efficient form of the quadratic function is y=−2x²+8x+22

Carnegie Learning Skills Practice Exercise 2.1 Explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 272 Problem 13 Answer

To convert factored form f(x) = (x+5)(x+7) into standard form.

f(x) = (x+5)(x+7)

f(x) = x²+5x−7x−35

f(x) = x²−2x−35.

Therefore, the standard form of quadratic equation is f(x) = x²−2x−35.

Page 272 Problem 14 Answer

To convert factored form f(x) = (x+2)(x+9) into standard form.

f(x) = (x+2)(x+9)

f(x) = x²+9x+2x+18.

f(x) = x²+11x+18.

Therefore, the standard form of quadratic equation is f(x) = x²+11x+18.

Page 272 Problem 15 Answer

To convert factored form f(x) = 2(x-4)(x+1) into standard form.

f(x) = 2(x-4)(x+1)

f(x) = 2(x²+x−4x−4).

f(x) = 2(x²−3x−4).

f(x) = 2x²−6x−8.

Therefore, the standard form of quadratic equation is f(x) = 2x²−6x−8.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 272 Exercise 1 Answer

To convert factored form f(x) = -3(x-1)(x-3) into standard form.

f(x) = -3(x-1)(x-3)

f(x) = -3(x²−3x−x+3)

f(x) = -3(x²−4x+3)

f(x) = -3x² +12x−9.

f(x) = 3x²−12x+9.

Therefore, the standard form of quadratic equation is f(x) =

Page 272 Exercise 2 Answer

To convert vertex form f(x) = 1/3 (x+3)(x+7) into standard form.

f(x) = 1/3(x+3)(x+7)

f(x) = 1/3(x²+7x+3x+21)

f(x) = 1/3(x²+10x+21)

f(x) = x²/3+10x/3+7

Therefore, the standard form of quadratic equation is f(x) =

Page 272 Exercise 3 Answer

To convert factored form f(x) = −5/8(x−6)(x+2). into standard form.

f(x) = −5/8(x−6)(x+2)

f(x) = −5/8(x²+2x−6x−12).

f(x) = −5/8(x²−4x−12)

f(x) = −5/8x²+5/2x+15/2

f(x) = 5/8x²−5/2x−15/2

Therefore, the standard form of quadratic equation is f(x) = 5/8x²−5/2/x−15/2

Page 272 Exercise 4 Answer

To convert vertex form f(x) = 3(x-4)² + 7. into standard form.

f(x) = 3(x−4)²+7

f(x) = 3(x²+16−8x)+7

Therefore, the standard form of quadratic equation is f(x) = 3x²−24x+55.

Chapter 2 Exercise 2.1 Skills Practice Guide

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 272 Exercise 5 Answer

To convert vertex form f(x) = −2(x+1)²−5.into standard form.

f(x) = −2(x²+1+2x)−5

f(x) = −2x²−2−4x−5

f(x) = −2x² −4x−7

f(x) = 2x²+4x+7.

Therefore, the standard form of quadratic equation is f(x) = 2x²+4x+7.

Page 272 Exercise 6 Answer

Given that the quadratic function is,

f(x)=2(x+7/2)²−3/2

The given function is in vertex form.

Now we have to convert the vertex form into the standard form.

Consider the given function

f(x)=2(x+7/2)²−3/2

=2(x²+49/4+2(x)(7/2))−3/2

=2x²+49/4(2)+14x−3/2

=2x²+49/2+14x−3/2

=2x²+14x+46/2

=2x²+14x+23

The standard form of the equation f(x)=2(x+7/2)²−3/2 is 2x²+14x+23.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 272 Exercise 7 Answer

Given that the quadratic function is,

f(x)=−(x−6)²+4

The given function is in vertex form.

Now we have to convert the vertex form into the standard form.

Consider the given function

f(x)=−(x−6)²+4

=−(x²+36−2(x)(6))+4

=−x²−36+12x+4

=−x²+12x−32

The standard form of the equation f(x)=−(x−6)²+4 is −x²+12x−32.

Page 272 Exercise 8 Answer

Given that the quadratic function is,

f(x)=−1/2(x−10)²−12

The given function is in vertex form.

Now we have to convert the vertex form into the standard form.

Consider the given function

f(x)=−1/2(x−10)²−12

=−1/2(x²+100−2(x)(10))−12

=−1/2x²−50+10x−12

=−1/2x²+10x−62

The standard form of the equation f(x)=−1/2(x−10)²−12 is −1/2 x²+10x−62.

Page 272 Exercise 9 Answer

Given that the quadratic function is,

f(x)=1/20(x+100)²+60

The given function is in vertex form.

Now we have to convert the vertex form into the standard form.

Consider the given function

f(x)=1/20(x+100)²+60

=1/20(x²+10000+2(x)(100))+60

=1/20x²+500+200x/20+60

=1/20x²+10x+560

The standard form of the equation f(x)=1/20(x+100)²+60 is 1/20x²+10x+560.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 273 Exercise 10 Answer

Given that Cory is training his dog, Cocoa, for an agility competition.

Cocoa must jump through a hoop in the middle of a course. The center of the hoop is 8 feet from the starting pole.

The dog runs from the starting pole for 5 feet, jumps through the hoop, and lands 4 feet from the hoop.

When Cocoa is 1 foot from landing, Cory measures that she is 3 feet off the ground.

Now we have to write the function to represent Cocoa’s height in terms of her distance from the starting pole.

We will set a Cartesian coordinate system with the origin at the starting pole.

The height of Cocos jump will be a quadratic function written in factored form

h(x)=a(x−x₁)(x−x₂),

where x₁ and x₂ are the roots of the quadratic equation.

For the roots we know x₁=5

x²=12 is the distance from the starting pole before and after the jump.

h(x)=a(x−5)(x−12)

Also, we know that 1 foot from landing Coco is 3 feet off the ground this means we have the following point of the graph (11,3) and if we replace these values in the above equation we get,

3=a(11−5)(11−12)

a(6)(−1)=3

a=−0.5

Thus the equation is : h(x)=−0.5(x−5)(x−12)

The function to represent Cocoa’s height in terms of her distance from the starting pole is h(x)=−0.5(x−5)(x−12).

Page 273 Exercise 11 Answer

Given that Sasha is training her dog, Bingo, to run across an arched ramp, which is in the shape of a parabola.

To help Bingo get across the ramp, Sasha places a treat on the ground where the arched ramp begins and one at the top of the ramp.

The treat at the top of the ramp is a horizontal distance of 2 feet from the first treat, and Bingo is 6 feet above the ground when he reaches the top of the ramp.

h=2

k=6

Now we have to write the function to represent Bingo’s height above the ground as he walks across the ramp in terms of his distance from the beginning of the ramp.

Now consider the general equation of the parabola,

f(x)=a(x−h)²+k

=a(x−2)²+6

Now at the point (0,0),

0=a(0−2)²+6

4a=−6

a=−6/4

a=−3/2

Therefore the function becomes,

f(x)=−3/2(x−2)²+6

The function to represent Bingo’s height above the ground as he walks across the ramp in terms of his distance from the beginning of the ramp is f(x)=−3/2(x−2)²+6.

How To Solve Skills Practice Exercise 2.1

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 274 Exercise 12 Answer

Given that Ella’s dog, Doug, is performing in a special tricks show.

Doug can fling a ball off his nose into a bucket 20 feet away.

Ella places the ball on Doug’s nose, which is 4 feet off the ground.

Doug flings the ball through the air into a bucket sitting on a 4-foot platform.

Halfway to the bucket, the ball is 10 feet in the air.

Here h=10

and k=10

Now we have to find the function to represent the height of the ball in terms of its distance from Doug.

Now consider the general equation of the parabola,

f(x)=a(x−h)²+k

=a(x−10)²+10

Now at the point (0,2),

2=a(0−10)²+10

2=100a+10

100a=−8

a=−8/100

a=−0.08

Therefore the function becomes,

f(x)=−0.08(x−10)²+10

The function to represent the height of the ball in terms of its distance from Doug is f(x)=−0.08(x−10)²+10.

Page 274 Exercise 13 Answer

Given that a spectator in the crowd throws a treat to one of the dogs in a competition.

The spectator throws the treat from the bleachers 19 feet above ground.

The treat amazingly flies 30 feet and just barely crosses over a hoop which is 7.5 feet tall.

The dog catches the treat 6 feet beyond the hoop when his mouth is 1 foot from the ground.

The equation is x²+7.5x+30.

Therefore, x²+7.5x+30.

Algebra Ii Chapter 2 Exercise 2.1 Answer Key

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.1 Skills Practice Page 275 Exercise 14 Answer

Given that Hector’s dog, Ginger, competes in a waterfowl jump.

She jumps from the edge of the water, catches a toy duck at a horizontal distance of 10 feet from the edge of the water and a height of 2 feet above the water, and lands in the water at a horizontal distance of 15 feet from the edge of the water.

Here x₁=0

and x₂=15

Now we have to find the function to represent the height of Ginger’s jump in terms of her horizontal distance.

Consider the general function of factored form

f(x)=a(x−x₁)(x−x₂)

=a(x−0)(x−15)

=ax(x−15)

At the point (10,2),

2=a10(10−15)

2=10a(−5)−50a=2

a=−2/50

a=−1/25

Now consider the figure,

Therefore the function becomes,

f(x)=−1/25x(x−15)

The function to represent the height of Ginger’s jump in terms of her horizontal distance is −1/25x(x−15).

Page 272 Exercise 15 Answer

Given that 7 feet high with a speed of 18 feet per second.

The aim is to find the equation.

Assume that x per second.

P=7+18x

Therefore, the expression is 7+18x.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice

Page 263 Problem 1 Answer

Fill in the blanks of the statements given

A ____________is a mathematical expression involving the sum of powers in one or more variables multiplied by coefficients.

A Polynomial equation is a mathematical expression involving the sum of powers in one or more variables multiplied by coefficients.

Page 263 Problem 2 Answer

Fill in the blanks of the statements given-

The ____________ of a polynomial is the greatest variable exponent in the expression.

The Degree of a polynomial is the greatest variable exponent in the expression.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice Page 263 Problem 3 Answer

Fill in the blanks of the statements given-

The _______________ states that if the product of two or more factors is equal to zero, then at least one factor must be equal to zero.

The Principle of Zero products states that if the product of two or more factors is equal to zero, then at least one factor must be equal to zero.

Page 264 Problem 4 Answer

m(x)=f(x)+g(x)

f(x)=−1/2x

g(x)=x+5

Predict the family function of m(x)

The family function of m(x) is,

h(x)=x

Hence the family function of m(x) is, h(x)=x the linear function

Graph-

Arnegie Learning Algebra Ii Chapter 1 Exercise 1.5 Solutions

Page 264 Problem 5 Answer

In the given graph of f(x) and g(x), note the points marked The x values from graph of f(x) and g(x) are (-4, -2, -1, 0, 1, 2, 4)

We know f(x) and g(x) expressionSubstitute the values of x from graph to find m(x)Draw a straight line through the points of m(x) to get graph of m(x).

The function m(x),​m(x)=f(x)+g(x)

f(x)=−1/2x

g(x)=x−2

x=(−4,−2,−1,0,1,2,4)

x=−4

m(x)=−1/2(−4)+(−4−2)

=4/2−6

=2−6

m(x)=−4

For x=−2

m(x)=−1/2(−2)+((−2)−2)

=1−4

m(x)=−3

For x=−1

m(x)=−1/2(−1)+((−1)−2)

=1/2−3

m(x)=−2.5

​The Function m(x) For x=0

m(x)=−1/2(0)+(0−2)

m(x)=−2

For x=1

m(x)=−1/2(1)+(1−2)

=−1/2−1

m(x)=−1.5

For x=2

m(x)=−1/2(2)+(2−2)

=−2/2

m(x)=−1

For x=4

m(x)=−1/2(4)+(4−2)

=−4/2+2

m(x)=0

The graph of m(x)

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice Page 265 Problem 6 Answer

In the given graph of f(x) and g(x), note the points marked The x values from graph of f(x) and g(x) are (-8, -4, -2, 0, 2)

We know f(x) and g(x) expression Substitute the values of x from graph to find m(x)Draw a straight line through the points of m(x) to get graph of m(x).

The function m(x)​m(x)=f(x)+g(x)

f(x)= 2x

g(x)=−x−3

m(x)=2x−x−3

m(x)=x−3

​The m(x) for x value -8 and -4​m(x)=x−3

for x=−8

m(x)=−8−3

m(x)=−11

for x=−4

m(x)=−4−3

m(x)=−7

​The m(x) for x values -2, 0 and 2​m(x)=x−3

for x=−2

m(x)=−2−3

m(x)=−5

for x=0

m(x)=0−3

m(x)=−3

for x=2

m(x)=2−3

m(x)=−1

​The graph of m(x) with points (-8,-11), (-4,-7), (-2,-5), (0,-3) and (2,-1)

The graph of m(x),f(x) and g(x)

Page 263 Problem 7 Answer

Find the value of k(x) and h(x) for given x values from given graph

To find j(x), Subtract h(x) from k(x)Complete the table by finding j(x) for each x givenMark the results in graph

The table of h(x) and j(x)

The complete table

The graph of j(x)

Skills Practice Exercise 1.5 Answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice Page 266 Problem 8 Answer

Find the value of k(x) and h(x) for given x values from given graph

To find j(x), Subtract h(x) from k(x)Complete the table by finding j(x) for each x givenMark the results in graph

The table for h(x) and k(x)

The complete table

The graph of j(x)

Page 266 Problem 9 Answer

Find the value of k(x) and h(x) for given x values from given graph

To find j(x), Subtract h(x) from k(x)Complete the table by finding j(x) for each x givenMark the results in graph

The table for h(x) and k(x)

The complete table

The graph of  j(x)

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice Page 267 Problem 10 Answer

Find the value of k(x) and h(x) for given x values from given graph

To find j(x), Subtract h(x) from k(x)Complete the table by finding j(x) for each x givenMark the results in graph

The table for h(x) and k(x)

The complete table

The graph of j(x)

Page 267 Problem 11 Answer

Find the value of k(x) and h(x) for given x values from given graph

To find j(x), Subtract h(x) from k(x)Complete the table by finding j(x) for each x givenMark the results in graph

The table for h(x),k(x) and j(x)

The complete table

The graph of j(x)

Algebra Ii Chapter 1 Skills Practice Solutions Exercise 1.5

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice Page 267 Problem 12 Answer

Find the value of k(x) and h(x) for given x values from given graph

To find j(x), Subtract h(x) from k(x)Mark the results in graph Complete the table after finding j(x) for each x given

The value of h(x) and k(x)

To find j(x)

The graph of j(x)

Page 268 Problem 13 Answer

Given- The three polynomial functions,h(x)=−3x+5

j(x)=−5x−7

k(x)=−8x−2

​To find- To show that h(x)+j(x) is equivalent to k(x).

We will first, add the functions h(x) and j(x), then compare the result with the function k(x) to show that they are equivalent.

The given functions are,

h(x)=−3x+5

j(x)=−5x−7

k(x)=−8x−2

Now,h(x)+j(x)=−3x+5+(−5x−7)

=−3x+5−5x−7

=−8x−2​

And,k(x)=−8x−2

We know that two polynomials are equivalent if they have equal coefficients of corresponding powers of the independent variable.

∴h(x)+j(x)=k(x)

So,h(x)+j(x) is equivalent to k(x).

On adding the functions h(x) and j(x), we get the value that is the same as the function k(x).

So, the function h(x)+j(x) is equivalent to k(x)

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice Page 268 Problem 14 Answer

Given- The three polynomial functions,h(x)=1/2x+9

j(x)=1/2x+6

k(x)=x+15​

To find- To show that h(x)+j(x) is equivalent to k(x).

We will first, add the functions h(x) and j(x), then compare the result with the function k(x) to show that they are equivalent.

The given functions are,

h(x)=1/2x+9

j(x)=1/2+6

k(x)=x+15​

Now,h(x)+j(x)=1/2

x+9+1/2

x+6

=1/2x+1/2x+9+6

=x+15

And,k(x)=x+15 We know that two polynomials are equivalent if they have equal coefficients of corresponding powers of the independent variable.

∴h(x)+j(x)=k(x)​

So,h(x)+j(x) is equivalent to k(x).

On adding the functions h(x) and j(x), we get the value that is the same as the function k(x).

So, the function h(x)+j(x) is equivalent to k(x)

Carnegie Learning Skills Practice Exercise 1.5 Explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.5 Skills Practice Page 268 Problem 15 Answer

Given- The three polynomial functions,h(x)=−12x−1

j(x)=−7x+11

k(x)=−19x+10​

To find- To show that h(x)+j(x) is equivalent to k(x).

We will first, add the functions h(x) and j(x), then compare the result with the function k(x) to show that they are equivalent.

The given functions are,

h(x)=−12x−1

j(x)=−7x+11

k(x)=−19x+10

Now,h(x)+j(x)=−12x−1+(−7x+11)=−12x−1−7x+11

=−19x+10

And,k(x)=−19x+10

We know that two polynomials are equivalent if they have equal coefficients of corresponding powers of the independent variable.

∴h(x)+j(x)=k(x)

So,h(x)+j(x) is equivalent to k(x).

On adding the function h(x) and j(x), we get the value that is the same as the function k(x).

So, the function h(x)+j(x) is equivalent to k(x).

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.4 Skills Practice

Page 257 Problem 1 Answer

Given the table.

The aim is to find the relation.

For 1 then 1.

For 2 then 2²=4.

For 3 then 3²=9.

For n then n².

Therefore, the sequence is n².

Page 257 Problem 2 Answer

Given:

To find: Complete each table, then graph the function.

Table

Required graph is

The graphical representation of Volume= (side length )³ is as shown below

Carnegie Learning Algebra Ii Chapter 1 Exercise 1.4 Solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.4 Skills Practice Page 258 Problem 3 Answer

Given:

To find: Complete each table, then graph the function.

Table

Required graph is

The graphical representation of the equation y=x−4

Page 258 Problem 4 Answer

Given:

To find: Complete each table, then graph the function

Table

Required graph is

The graphical representaion of the expression : Total time = time for quiz (3hr)+ time for project (2hr)

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.4 Skills Practice Page 258 Problem 5 Answer

y=2m²−5 is a quadratic equation which when plotted on a graph gives a parabolic curve.

Table

The graphical representation of the equation y=2m²−5 is as shown below

Page 259 Problem 6 Answer

Given:

To find: Complete each table, then graph the function.

Table:

Required graph is

The graphical representation of the equation y=4x²+50 is as shown below

Skills Practice Exercise 1.4 Answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.4 Skills Practice Page 260 Problem 7 Answer

Given the table.

The aim is to find the relation.

For 1 then 620.

For 2 then 620−40.

For 3 then 620−40−40.

The general formula is 620−40n.

Therefore, the n term is, 620−4n.

Page 260 Problem 8 Answer

Define the function and graph it. Analyse the pattern and predict the next term, of the following –

By observing the table, we can see that each term n is the 2n of the term,

e.g

f(1)=2¹

f(2)=2²=4

f(3)=2³=8

f(4)=2⁴=16

Therefore the next term in the sequence is, f(5)=2⁵=32

Final Answer The function is defined as

On the day, employees are sick.

Graph-

Page 261 Problem 9 Answer

Define a function and graph it to answer the question given.

Analyze the pattern and predict the 4th term-

By looking and analysing the sequence, we see that each term the number of passengers increases by 180

f(1)=180+9

f(2)=2⋅(180)+9=369

f(3)=3⋅(180)+9=549

f(5)=5⋅(180)+9=909

Thus the function may be defined as-f(x)=180x+9

The 4thterm is-f(4)=4⋅(180)+9=729

​The function may be defined as-f(x)=180x+9

The 4^th term is-729

Graph-

Algebra Ii Chapter 1 Skills Practice Solutions Exercise 1.4

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.4 Skills Practice Page 261 Problem 10 Answer

Define a function and graph it to answer the question given. Analyze the pattern and predict the 5th term-

Analyzing the pattern, we can see that the nth is the 20 times n, i.e

f(1)=20

f(2)=2⋅20=40

f(3)=3⋅20=60

f(4)=4⋅20=80

Thus the function is defined as-f(n)=20ⁿ

The 5^th term is-f(5)=20⋅5=100

The function is defined by-f(n)=20ⁿ

For 5 appetizers, Garry need 100 minutes to prepare.

Graph-

Page 262 Problem 11 Answer

Define a function and graph it to answer the question given. Analyze the pattern and predict the 5th term-

By analyzing the terms, we can see that each term is the cube of the given term, i.e

f(1)=1

f(2)=2³=8

f(3)=3³=27

f(4)=4³=64

The function may be defined as-f(x)=x³

The 5^th term may be given as,

f(5)=5³=125

The function is defined by-f(x)=x³

The volume of the box with side length5 feet is 125 cubic feet.

Graph-

Carnegie Learning Skills Practice Exercise 1.4 Explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.4 Skills Practice Page 262 Problem 12 Answer

Define a function and graph it to answer the question given. Analyze the pattern and predict the 5th

By looking and analyzing at the pattern, we can see that each term’s value is the square of the term i.e

f(1)=1

f(2)=2²=4

f(3)=3²=9

f(4)=4²=16

The function may be defined as f(x)=x²

Thus, the 5th term is, f(5)=5²=25

The function is defined as f(x)=x²

The area of the frame with side length of 5 inches is 25 square inches

Graph-

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice

Page 247 Problem 1 Answer

We have to define relation in our own words.

A relation is a subset of the Cartesian product. Or simply, a bunch of points (ordered pairs).

In other words, the relation between the two sets is defined as the collection of the ordered pair, in which the ordered pair is formed by the object from each set.

All functions are relations, but not all relations are functions.

Page 247 Problem 2 Answer

We have to define function in our own words.

A function is a relation which describes that there should be only one output for each input (or) we can say that a special kind of relation (a set of ordered pairs), which follows a rule i.e., every x-value should be associated with only one y-value is called a function.

A function is  an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).

Carnegie Learning Algebra Ii Chapter 1 Exercise 1.3 Solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 247 Problem 3 Answer

We have to define Function notation in our own words.

Function notation is the way a function is written.

It is meant to be a precise way of giving information about the function without a rather lengthy written explanation.

The most popular function notation is f(x) which is read as “f of x”.

Page 247 Problem 4 Answer

Given the table.

The aim is to find the expression.

For 1 then 11.

For 2 then 11+8.

For 3 then 11+8+8.

For n then 11+8(n−1).

Therefore, the expression is 11+8(n−1).

Page 248 Problem 5 Answer

Given:

To find: Determine whether the functions are equivalent.

From table, we write the equation as y=x².

From graph we see that points in table are on graph.

For example (1,1),(2,4),……are on the graph.

All the points in table are on graph

The function in table is equivalent to function in graph

Skills Practice Exercise 1.3 Answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 248 Problem 6 Answer

Given equation is y=x²−7x+1

We calculate y for x=0 and for x=2

We thus conclude that functions are equivalent

Substituting x=0 in given equation.

we get y=1

We can see that (0,1) is on graph also.

Also we substitute x=2 in given equation

we get y=−9

Also, (2,−9) is a point on graph

Function y=x²−7x+1 and function in graph are equivalent

Page 248 Problem 7 Answer

Given function is y=5(x−1)+4 We calculate y for x=0 We Finally conclude that functions aren’t equivalent

For x=0

we get y=−1 from given equation But (0,−1) is not there on straight line in graph (0,8) is there on graph.

Function y=5(x−1)+4 and function in graph are not equivalent

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 249 Problem 8 Answer

Given equation is f(x)=3(x+1)

i.e. y=3(x+1)

We calculate y for x=1 We finally conclude that functions aren’t equivalent

We substitute x=1 in given equation    we get y=6

(1,3) is there in table instead of (1,6)

i.e. (1,6) is not there in table

Function y=3(x+1) and function in table are not equivalent

Page 249 Problem 9 Answer

Given:  Alton is selling a few handmade toys at a community sale. After the first hour, Alton has earned $5.

After the second hour, he has earned $10 and after the third hour, he has earned $15

To find Function of graph.

Equation is y=5x from given data.

We can write three points (1,5),(2,10),(3,15) from given data

These three points are on straight line from graph

Function y=5x and function in graph are equivalent

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 251 Problem 10 Answer

Graph shows model for no. of pages printedBefore the policy was created, one student had already printed a 5-page paper.

He continues to print 4 pages per day.

No. of pages printed = 4 ×No. of days + 5

We model the number of pages the student prints.

No. of pages printed= 4×No. of days + 5

Page 252 Problem 11 Answer

We model the scenario as f(x)=−x²+5

Graph shows the model

Model is f(x)=−x²+5

Page 252 Problem 12 Answer

We are given a scenario ‘The cube of x plus 5’.The objective is to model the given scenario using a table, a graph and a function.

Given: The cube of x plus 5

The function of the given scenario is given as, f(x)=(x+5)³

Now, we find the function value using a table:

We find the function value for five values of x:

On graphing the value in the above table, we get

Hence, the function of the cube of x plus 5 is f(x)=(x+5)³

​which on graphing we get,

Algebra Ii Chapter 1 Skills Practice Solutions Exercise 1.3

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 253 Problem 13 Answer

We are given a problem that goes ‘Tommy is purchasing items from an online store.

The store charges $6 shipping and handling for each package.

‘The objective is to write an expression to represent the total shipping costs and find how much will Tommy pay in shipping and handling for 2 packages.

To do so, we find the function that models this scenario.

Given: Tommy is purchasing items from an online store. The store charges $6 shipping and handling for each package.

Then, the function that models this scenario isf(x)=6x which represents the total shipment cost.

For 2 packages, Tommy will pay:

f(2)=6×2

=$12

Hence, the expression that represents the total shipment cost is given by the function f(x)=6x and the cost for 2 packages is 12 dollars.

Page 253 Problem 14 Answer

We are given a problem that goes ‘A library has 45  books in their young adult science fiction collection.

During a collection drive, the library collects 9  new young adult science fiction books per day.

‘The objective is to find how many total young adult science fiction books will the library have after 1 week.

To do so, we find the function that models this scenario.

Given: A library has 45 books in their young adult science fiction collection.

During a collection drive, the library collects 9 new young adult science fiction books per day.

Then, the function that models this scenario is f(x)=9x where x represents the number of days.

After 1 week, the total young adult science fiction books will be:

f(7)=9×7

=63

Hence, the expression that represents the total young adult science fiction books at the library is given by the function f(x)=9x where x represents the number of days and there will be 63 young adult science fiction books at the library after 1 week.

Carnegie Learning Skills Practice Exercise 1.3 Explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 253 Problem 15 Answer

We are given a problem that goes ‘A group of friends is planning a trip to the movie theater.

The cost of one ticket for a movie is $8.50. The cost for each person to purchase snacks at the theater is $5.

‘The objective is to find how much will a group of 8 friends pay to purchase movie tickets and snacks at the theater.To do so, we find the function that models this scenario.

Given:  A group of friends is planning a trip to the movie theater.

The cost of one ticket for a movie is $8.50.

The cost for each person to purchase snacks at the theater is $5.

Since the cost of one ticket for a movie is $8.50 and the cost for each person to purchase snacks at the theater is $5, then total cost per person will be=8.50+5 =$13.5

Then, the function that models the scenario is f(x)=13.5x

where x represents the number of friends.

A group of 8 friends will then pay:

f(8)=13.5×8

=108

Hence, the expression that represents the total cost of tickets and snacks is given by the function f(x)=13.5x and a group of 8 friends will pay 108 dollars for the tickets and the snacks.

Page 254 Exercise 1 Answer

We are given a problem that goes ‘A bookstore advertises a book signing by calling each of the 12  members of their book club.

Each member of the book club calls two additional people.

The table lists the number of people who receive a call.’

The objective is to find how many people will receive a call in the 4th  round of calls.

To do so, we find the function that models this scenario.

Given: A bookstore advertises a book signing by calling each of the 12 members of their book club.

Each member of the book club calls two additional people.

Thus, the function that models this scenario is f(x)=12x where x represents the rounds of calls.

Then, number of people receiving a call in the 4^th round of calls is:

f(4)=12×4

=48

Hence, the expression that represents the number of people receiving calls in different rounds of calls is given by the function f(x)=12x where x represents the rounds of calls and the number of people receiving a call in the fourth round of calls are 48.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 254 Exercise 2 Answer

We are given a problem that goes ‘A photographer takes 46 photos per hour during a soccer game.

‘The objective is to find how many photos does the photographer take if the game lasts 3.5 hours.

To do so, we find the function that models this scenario.

Given: A photographer takes 46 photos per hour during a soccer game.

Thus, the function that models this scenario f(x)=46x where x represents the number of hours.

Then, the number of photos the photographers take if the game lasts 3.5 hours:

f(3.5)=46×3.5

=161

Hence, the expression that represents the number of photos taken by the photographers per hour during a soccer game is given by the function f(x)=46x where x represents the number of hours and the number of photos the photographers take if the game lasts 3.5 hours are 161.

Page 254 Exercise 3 Answer

We are given a problem that goes ‘ The high school choir hosts a concert for the community.

The members of the choir sell tickets for the concert. Each member of the choir sells 3 tickets.

Tickets are also sold at the door before the concert. A total of 125 tickets are sold at the door.

‘The objective is to find how many total tickets are sold if there are 18 members of the choir.

To do so, we find the function that models this scenario.

Given: The high school choir hosts a concert for the community.

The members of the choir sell tickets for the concert.

Each member of the choir sells 3 tickets.

Tickets are also sold at the door before the concert. A total of 125 tickets are sold at the door.

Thus, the function that models this scenario is f(x)=3x where x represents the number of members of the choir.

Then, if there are 18 members of the choir, the total number of tickets sold are:

f(18)=3×18

=54

Hence, the expression that represents the total number of tickets sold by the members of the choir is given by the function f(x)=3x where x represents the number of members of the choir.

The total number of tickets sold by the 18 members of the choir are 54.

Chapter 1 Exercise 1.3 Skills Practice Guide

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 255 Exercise 4 Answer

We are given two expressions 5x+3+3x²−2 and (5x+1)+3x².

The objective is to determine whether the given two expressions are equivalent or not.

To do so, we simplify both the expressions.

Given: 5x+3+3x²−2and (5x+1)+3x²

We simplify the first expression:

5x+3+3x²−2=3x²+5x+1

Rewriting the second expression, we get:

3x²+5x+1

We see that, the two expressions are equivalent.

Hence, the two expressions 5x+3+3x²−2 and (5x+1)+3x² are equivalent.

Page 255 Exercise 5 Answer

We are given two expressions 3x²+(x−2)(x+1)and (2x−2)(2x+1).

The objective is to determine whether the given two expressions are equivalent or not.

To do so, we simplify both the expressions.

Given: 3x²+(x−2)(x+1)…(1)and  (2x−2)(2x+1)…(2)

We first simply expression (1):

3x²+(x−2)(x+1)=3x²+x²+x−2x−2

=4x²−x−2

Now, we simplify expression (2):

(2x−2)(2x+1)=4x²+2x−4x−2

=4x²−2x−2

We see that, the two expressions are not equivalent.

Hence, the two expressions 3x²+(x−2)(x+1) and (2x−2)(2x+1) are not equivalent.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 255 Exercise 6 Answer

We are given two expressions (2x+1)²−2x(x−3) and 6x²+6x+2−(2x−1)².

The objective is to determine whether the given two expressions are equivalent or not.

To do so, we simplify both the expressions.

Given: (2x+1)²−2x(x−3)…(1)

6x²+6x+2−(2x−1)²…(2)

We first simplify expression (1):

(2x+1)²−2x(x−3)=4x²+1+4x−2x²+6x

=2x²+10x+1

Now, we simplify expression (2):

6x²+6x+2−(2x−1)²

=6x²+6x+2−(4x²+1−4x)

=6x²+6x+2−4x²−1+4x

=2x²+10x+1

We see that, the wo expressions are equivalent.

Hence, the two expressions (2x+1)²−2x(x−3) and 6x²+6x+2−(2x−1)² are equivalent.

How To Solve Skills Practice Exercise 1.3

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.3 Skills Practice Page 255 Exercise 7 Answer

Given: 7x²+1−(3x−1)(x+4) and 2x(x−3)+2x²−5x+5

To find: if L.H.S. and R.H.S. are equal, we need to expand and simplify both the equations and then compare them to prove that they are equivalent.

Expanding and simplifying L.H.S.

7x²+1−(3x−1)(x+4)

=7x²+1−(3x²+12x−x−4)

=7x²+1−3x²−12x+x+4

=4x²−11x+5

Expanding and simplifying R.H.S.

2x(x−3)+2x²−5x+5

=2x²−6x+2x²−5x+5

=4x²−11x+5

Comparing the simplified L.H.S and R.H.S.

L.H.S. = R.H.S.

Hence Proved

Yes, the equations (7x²+1)−(3x−1)(x+4) and 2x(x−3)+2x²−5x+5 are equivalent

Page 256 Exercise 8 Answer

Given: 8x(2x+1)+8x² and 8x(3x+1)

To find :if L.H.S. and R.H.S. are equivalent,

Expanding L.H.S.

8x(2x+1)+8x²=16x²+8x+8x²

=24x²+8x

Expanding R.H.S.

8x(3x+1)=24x²+8x

Comparing L.H.S. and R.H.S.

L.H.S.=R.H.S.

Hence proved

Yes, the equations 8x(2x+1)+8x² and 8x(3x+1) are equivalent

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice

Page 241 Problem 1 Answer

Given designs. The aim is to find the expression.

For design 1 there are 2 shaded parts.

For design 2 there are 3 shaded parts.

For design n there are n+1 shaded parts.

Therefore, the expression is n+1.

Page 241 Problem 2 Answer

Given the pattern.

The aim is to find the expression.

For first step is 3.

For second step is 3².

For nth step is 3n.

The expression is 3n.

Carnegie Learning Algebra Ii Chapter 1 Exercise 1.2 Solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice Page 241 Problem 3 Answer

Given: Charlie watches as a pattern develops. He starts with 3 guppy fish in his fish tank.

The next month, he finds 6 guppy fish in his tank. The following month, he finds 11 guppy fish in his fish tank.

To find: Write an expression to model the pattern of guppy fish in Charlie’s fish tank. Show your work.

The nth rule is quadratic ⇒ an²+bn+c, where    a+b+c=1term

3a – b = the first difference 2a = the constant difference between each two difference

∵ The first term is 3 ∴ a+b+c=3

∵ The first difference is 6−3=3

∴ 3a−b=3

∵ 6−3=3 and 11−6=5∵5−3=2

∴ The constant difference is 2

∴ 2a=2

⇒ divide both sides by 2

∴ a=1,

3a−b=3

∴ 3(1) – b = 3

∴ 3−b=3

⇒ subtract 3 from both sides

∴ b = 0

∵ a+b+c=3

∴ 1+0+c=3

∴ 1+c=3

⇒ subtract 1 from both sides

∴ c=2

∵ The nth rule is ⇒ an²

+bn+c , where n is the position of the number

∴ The nth rule =1n²+0n+2

∴ The nth rule = n²+2

Therefore, the expression of the pattern is n²+2.

Page 242 Problem 4 Answer

The download function (f(t),inkb) , expressed as a function of time (t, in minutes) is a quadratic function. Let f(t)=at²+bt+c, where a,b,c are arbitrary real numbers.

When t=1, we have f(t)=1 so that a+b+c=1.

When t=2, f(t)=7 so that 4a+2b+c=7.

When t=3,f(t)=17 so that 9a+3b+c=17.

When t=4, f(t)=31 so that 16a+4b+c=31.

The augmented matrix of the above linear system is A (say) =

To solve the above linear system, we have to reduce A to its RREf which is

This implies that a=2,b=0 and c=−1.

Thus, f(t)=2t²−1

The required table, duly filled up , is attached:

The scatter plot is,

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice Page 242 Problem 5 Answer

Given the table.

The aim is to find the x.

Using the table,

The nth terms is,

T_n=a+(n−1)d

T_n=9+(n−1)6

T_n=3+6n

​The nth number of books is,

x=(x−3−6n)−(6n−3)/3+6n.

Page 242 Problem 6 Answer

Given that the table.

The aim is to find y.

The nth term is,

T_n=3+n−1/2(2a+(n−1−1)d]

T_n=3+n−1/2(2(6)+(n−2)4)

T_n=3+(n−1)(6+2n−4)

T_n=3+2n²−2

T_n=2n²+1

​Therefore, y=2n²+1.is the required answer

Skills Practice Exercise 1.2 Answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice Page 243 Problem 7 Answer

Given the expression 6n+8,2(3n+4).

The aim is to show that 6n+8=2(3n+4).

By distributive law,

2(3n+4)=2(3n)+2(4)

2(3n+4)=6n+8

Therefore, 6n+8=2(3n+4).

Page 243 Problem 8 Answer

Given that n²+4n−n² and 4n.

The aim is to show that (n²+4n)−n²=4n.

Use the commutative law,

(n²+4n)−n²=n²+4n−n²

(n²+4n)−n²=n²−n²+4n

(n²+4n)−n²

=4n

Therefore, (n²+4n)−n²=4n.

Page 243 Problem 9 Answer

Given that 3x+5,2(x+3).

The aim is to find whether both are equivalent or not.

Use the distributive law,

2(x+3)=2(x)+2(3)

2(x+3)=2x+6

Which is not equal to 3x+5.

Therefore, both are not equivalent.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice Page 243 Problem 10 Answer

Given that 15−6x,15(1−6x).

The aim is to determine both are equivalent.

Use the distributive law,

15(1−6x)=15(1)−15(6x)

15(1−6x)=15−90x

Which is not equal to 15−6x.

Therefore, both are not equivalent.

Page 243 Problem 11 Answer

Given that (y+y+2+y)+3y and 6y+2.

The aim is to determine the equivalence relation.

Use the law,

(y+y+2+y)+3y=(2y+2+y)+3y

(y+y+2+y)+3y=(3y+2)+3y

(y+y+2+y)+3y=3y+3y+2

(y+y+2+y)+3y=6y+2

​Therefore, both are equivalent.

Algebra Ii Chapter 1 Skills Practice Solutions Exercise 1.2

Page 243 Problem 12 Answer

Given that 8y−3+10y,3(6y−1).

The aim is to determine the equation.

Use the distributive law,

3(6y−1)=3(6y)+3(−1)

3(6y−1)=18y−3

And, 8y−3+10y=8y+10y−3

9y−3+10y=18y−3

​Therefore, 3(6y−1)=8y−3+10y.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice Page 244 Problem 13 Answer

Given: A table lists the number of people who attended a museum (in thousands) over the course of several months.

We have to represent each pattern as an expression and as a graph. Then identify whether the pattern is linear, exponential, or quadratic.

The number of people who attended the museum is four times the number of months plus 7.

Hence, an expression to represent the pattern is 4x+7.

since the power of the variable x is 1.

The pattern is linear.

The graph is plotted as shown.

The expression is 4x+7. We can say from the graph that the expression is linear.

Page 244 Problem 14 Answer

Given: A local pet shelter is able to see many of their pets adopted. The table lists the number of pets that have been adopted over several weeks.

To find: We have to represent each pattern as an expression and as a graph. Then identify whether the pattern is linear, exponential, or quadratic.

Let n be the number of weeks.

Then we can write the expression as n²+7

The graph will be

This expression is quadratic.

There is a square in the equation, therefore it is quadratic.

Carnegie Learning Skills Practice Exercise 1.2 Explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice Page 245 Problem 15 Answer

Given: Emilio is looking at bunches of grapes at the market. He starts to notice a pattern in the number of grapes in each bunch.

To find: Write an expression for the number of grapes in each bunch.

Let n be the number of bunch.

The expression for the number of grapes in each bunch.

5 grapes=1²+5

14 grapes=2²+10

24 grapes=3²+15

36 grapes=4²+20

The general expression for the number of grapes in each bunch is n²+5n.

Page 245 Problem 16 Answer

Given: Nolan takes a photo of a parking lot every two hours. He counts the number of cars in each photo. The number of cars increases in each photo.

To find:  Write an expression for the number of cars in the parking lot.

Let n be number of two-hour intervals.

1 car,n=1→1^3→1

8 cars, n=2→2^3→8

27 cars, n=3→3³→27

64 cars, n=4→4³→64

Hence the general expression for the number of cars in the parking lot is n³.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.2 Skills Practice Page 246 Problem 17 Answer

Given: A store had a grand opening sale. During the sale, each person entering the store received a coupon for 10% off their entire purchase.

The table lists the number of people who received a coupon.

To find:We have to represent each pattern as an expression and as a graph. Then identify whether the pattern is linear, exponential, or quadratic.

Let n be the number of hours open.

Then we can write the expression as 3n².

The graph will be

Chapter 1 Exercise 1.2 Skills Practice Guide

This expression is quadratic.

There is a square in the expression, hence it is a quadratic expression.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.1 Skills Practice

Page 235 Problem 1 Answer

Here, first three patterns are given and we have to find next three patterns.

We can see in given first three patterns, there is an increment by 1 box in row as well as column.

So, we can find pattern 4,5 and 6 by increasing single box in row as well as column.

Therefore, the next three patterns are shown below :-

Carnegie Learning Algebra Ii Chapter 1 Exercise 1.1 Solutions

Page 235 Problem 2 Answer

Here, first three terms are given. Now, we have to find next three terms.

A box is increased by 1in middle column as well as one row line is also increased by 1in each pattern.

Therefore, in pattern4,5 and 6 one box in middle column and one row line is increased.

So, the next three patterns are shown below:-

Page 236 Problem 3 Answer

Here, first four terms are given. Now, we have to find next three terms

Here, we can see that in pattern1,2,3and 4 the number of boxes are 1,3,5 and 7.

From this it is clear that the number of boxes present in each pattern is increased by2.

Therefore, using this we can find next three terms pattern5,6and7.

The next three pattern are as below :-

Pattern5

Pattern6

Pattern7

Skills Practice Exercise 1.1 Answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.1 Skills Practice Page 238 Problem 4 Answer

To find: Here we need to find how many baby plants will she have started after 5

month Given : Here, Charlene has a flourishing spider plant, and she used to cuts three small pieces of the plant after that she separate each babies into its own pot with soil.

After a month she is able to cut three off each original babies. Approach : We will complete the table with the given information

She has a flourishing spider plant and from that she cuts three small pieces of plant so we will calculate accordingly  ,from the given information we can draw a table,

So, she will have 243 babies after 5 months.

Page 238 Problem 5 Answer

Given the relation.

The aim is to find the white squares.

Black Design-1 is 2

Black design-2 is 4

Black design 6 is 12.

The white part in the design are: 144−12=132

Therefore, there are 132  white boxes.

Algebra Ii Chapter 1 Skills Practice Solutions

Page 239 Problem 6 Answer

Given the table.

The aim is to find the round 6.

Using the sequence is 4n−1 for round n.

If n=6 then 45.

Therefore, the value is 45.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.1 Skills Practice Page 239 Problem 7 Answer

Given that: 6,13,27,55,……

To do: Find the next number in the given series.

Since,

The given series is

13−6=7=7……………………(1)

27−13=14=7×2…………………….(2)

55−27=28=14×2………………(3)

x−55=28×2………………….(4)

So,x=111

Therefore, the next number in the given series is, 111

Page 239 Problem 8 Answer

Given that: 3,5,9,17,…

To do: Find the next number in the given series.

Since,The given series is,5−3=2

9−5=4=2×2

17−9=8=4×2

x−17=8×2=16

x=33

Therefore, the next number in the given series is,33

Carnegie Learning Skills Practice Exercise 1.1 Explained

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.1 Skills Practice Page 240 Problem 9 Answer

Given that: 1,4,7,10,…

To do: Find the next number in the given series.

Since, The given series is,

4−1=3

7−4=3

10−7=3

x−10=3

x=13

Therefore, the next number in the given series is,13

Page 240 Problem 10 Answer

Given that: 1,5,9,13,…

To do: Find the next number in the given series.

Since,The given series is,

5−1=4

9−5=4

13−9=4

x−13=4

x=17

Therefore, the next number in the given series is, 17

How To Solve Skills Practice Exercise 1.1

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 1 Exercise 1.1 Skills Practice Page 240 Problem 11 Answer

Given that: 5, 8, 14, 26,…

To do: Find the next number in the given series.

Since,The given series is,8−5=3

14−8=3×2=6

26−14=6×2=12

x−26=12×2=24

So,x=54

Therefore, the next number in the given series is, 54