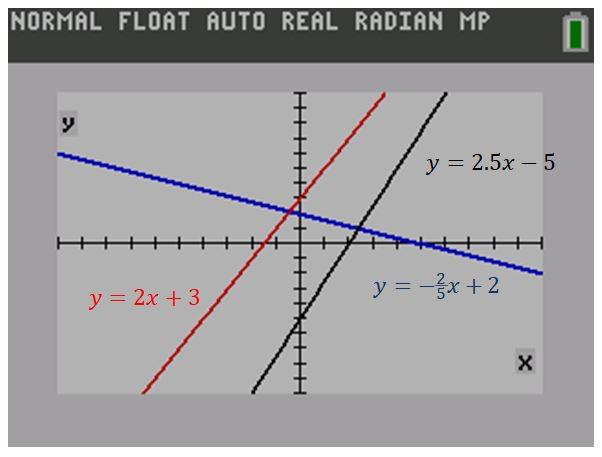
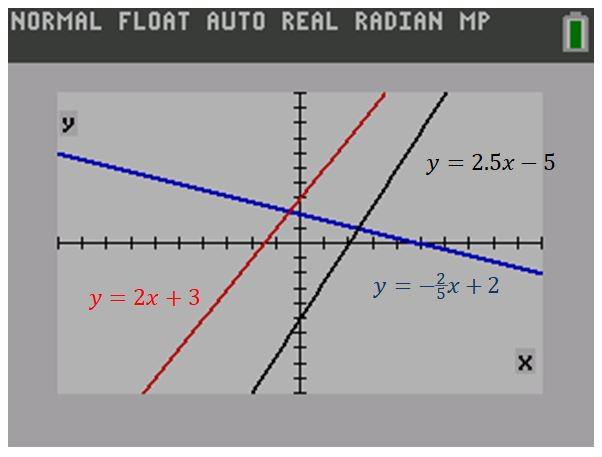
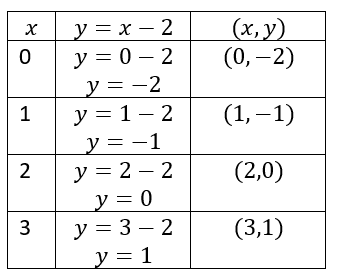Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

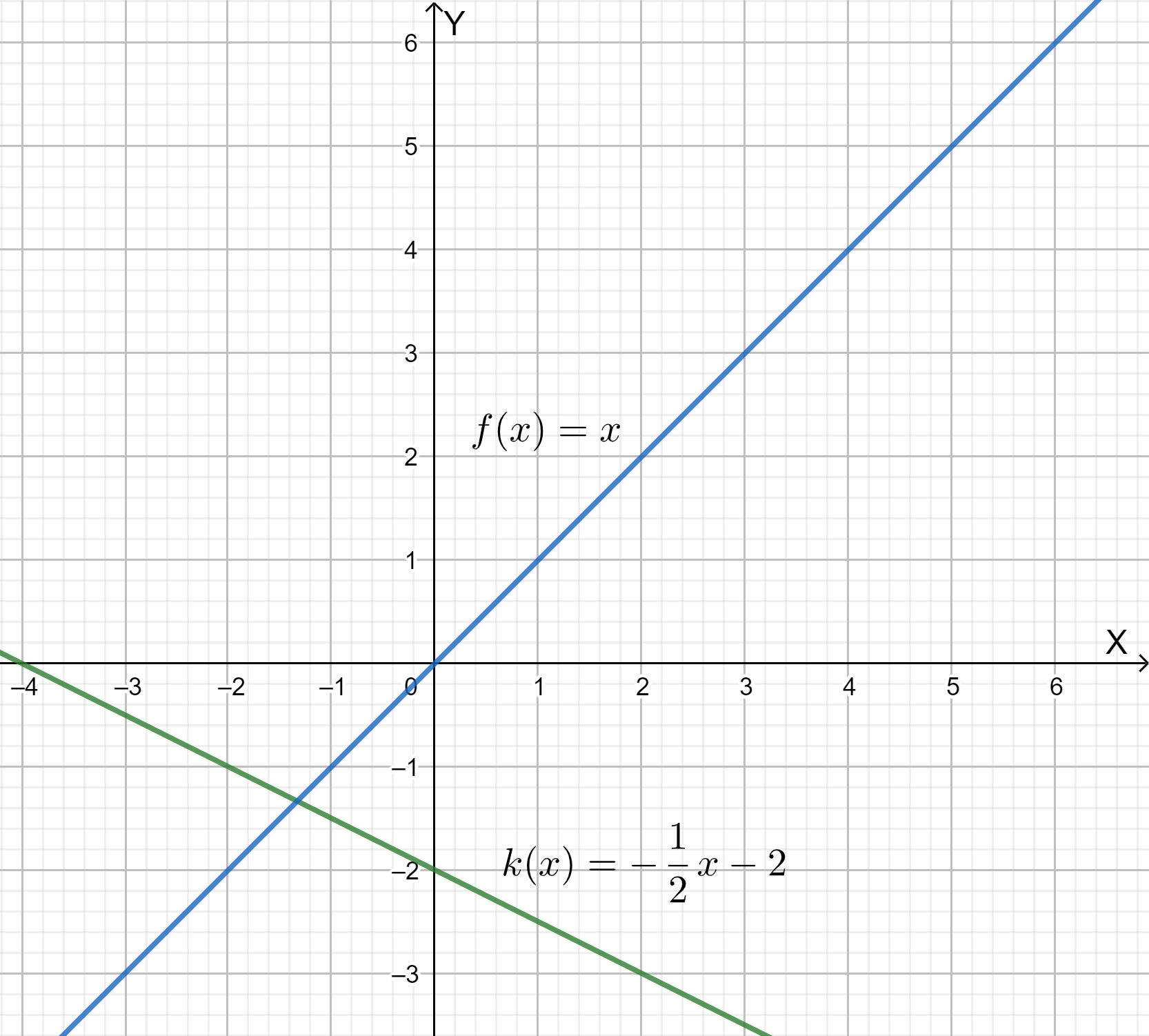
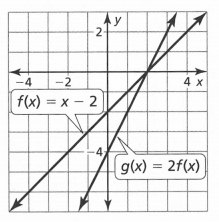
Page 137 Essential Question Answer

To solve a system of linear equations using substitution:

Isolate one of the two variables in one of the equations.
Substitute the expression that is equal to the isolated variable from ,into the other equation. This should result in a linear equation with only one variable.

Solve the linear equation for the remaining variable.
Use the solution of,  to calculate the value of the other variable in the system by using one of the original equations.

The substitution method is the algebraic method to solve simultaneous linear equations. The value of one variable from one equation is substituted in the other equation. In this way, a pair of the linear equation gets transformed into one linear equation with only one variable, which can then easily be solved.

Big Ideas Math Algebra 1 Chapter 5 Exercise 5.2 Solutions

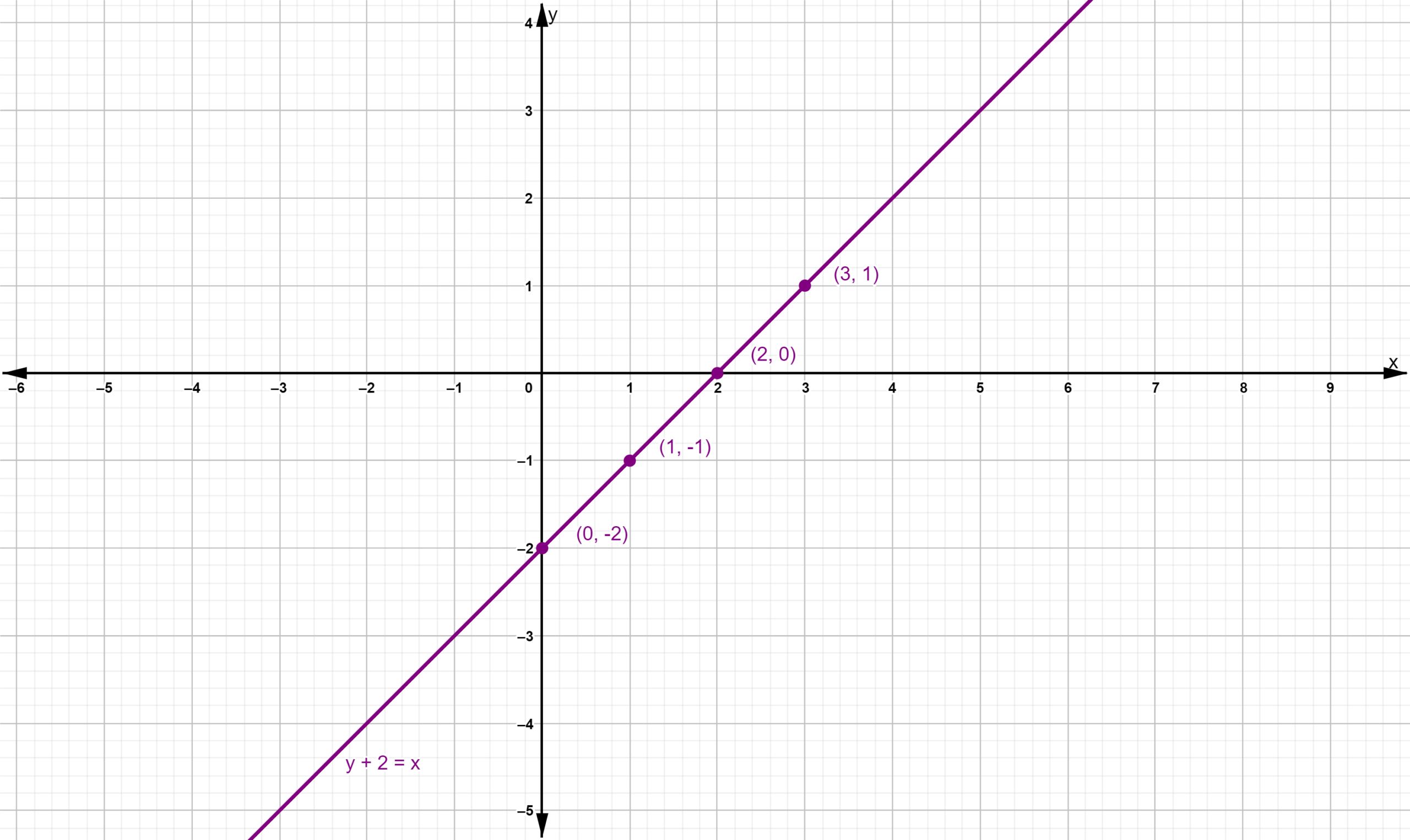
Page 137 Exercise 1 Answer

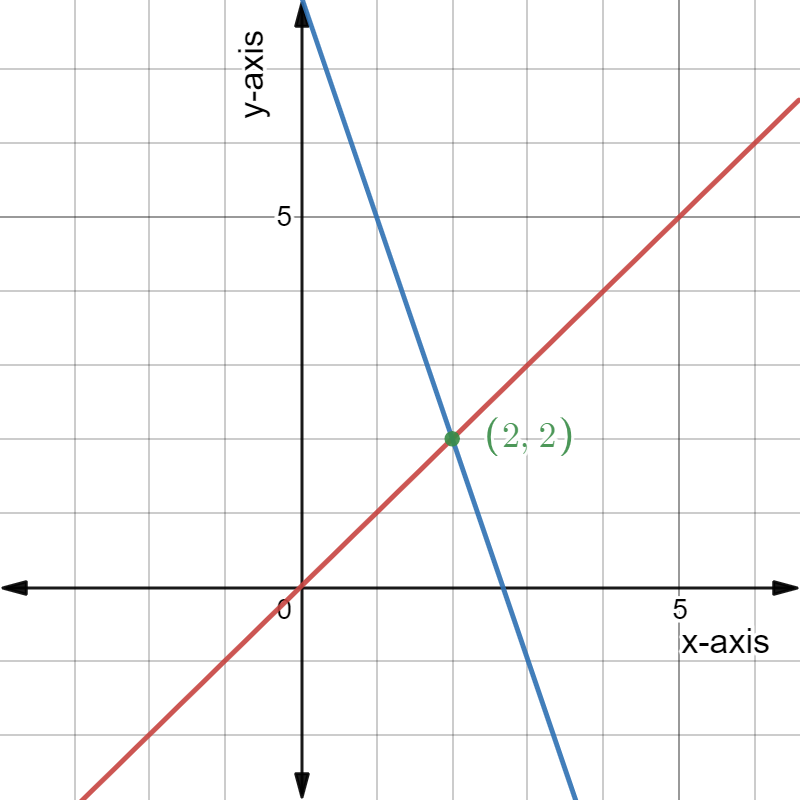
Given:  x + y =−7  &  −5x + y=5

To Solve: System of linear equations

To solve a system of equations using substitution:

Isolate one of the two variables in one of the equations.
Substitute the expression that is equal to the isolated variable from, into the other equation. This should result in a linear equation with only one variable.

Solve the linear equation for the remaining variable.
Use the solution of, to calculate the value of the other variable in the system by using one of the original equations.

We have the following system of linear equations:

x + y =−7  & −5x + y = 5

x + y =−7 ⇔  x =−y −7

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Putting value of x in the second equation:

−5x + y = 5  ⇔ −5(−y−7) + y=5

⇒ 6y + 35 = 5

⇒ 6y =−30

⇒ y =−5

∴x =−y−7 =−(−5)−7 =−2

We have the following system of linear equations:

x + y =−7  & −5x + y=5

x + y =−7 ⇔  y =−x−7

Putting value of y in the second equation:

−5x + y = 5 ⇔ −5x + (−x−7) = 5

⇒ −5x−x−7 = 5

⇒ −6x = 12

⇒ x =−2

∴y =−x−7 =−(−2)−7 =−5

The solution of the system of linear equations x + y =−7 & −5x + y=5 is (x,y)=(−2,−5).

The solution is same using both methods. I will prefer both methods to use for each system.

Given: x−6y = −11  &  3x + 2y =7

To Solve: System of linear equations

To solve a system of equations using substitution:

Isolate one of the two variables in one of the equations.
Substitute the expression that is equal to the isolated variable from,  into the other equation. This should result in a linear equation with only one variable.

Solve the linear equation for the remaining variable.
Use the solution of,  to calculate the value of the other variable in the system by using one of the original equations.

We have the following system of linear equations: 

x−6y = −11 &  3x + 2y

=7 x−6y =−11 ⇔ x = 6y−11

Putting value of x in the second equation:

3x + 2y= 7 ⇔ 3 (6y−11) + 2y = 7

⇒  20y−33 = 7

⇒  20y = 0

⇒  y = 2

∴x = 6y−11 = 6×2−11 = 1

We have the following system of linear equations:

x−6y = −11  &  3x + 2y = 7 x−6y

=−11 ⇔ y= \(\frac{x+11}{6}\)

Putting value of y in the second equation:

3x + 2y = 7 ⇔ 3x + 2 \(\frac{x+11}{6}\)=7

⇒ \(\frac{10 x}{3}+\frac{11}{3}\)=7

⇒ 10x +11=21

⇒ 10x=10

⇒ x=1

∴ \(\frac{x+11}{6}=\frac{1+11}{6}\)=2

The solution of the system of linear equations x−6y =−11 & 3x + 2y = 7 is (x,y)=(1,2).
The solution is same using both methods.I will prefer both methods to use for each system.

Given:  4x + y =−1 &  3x−5y =−18

To Solve: System of linear equations

To solve a system of equations using substitution:

Isolate one of the two variables in one of the equations.
Substitute the expression that is equal to the isolated variable from, into the other equation. This should result in a linear equation with only one variable.

Solve the linear equation for the remaining variable.
Use the solution of, to calculate the value of the other variable in the system by using one of the original equations.

We have the following system of linear equations:

4x+y=−1 & 3x−5y=−18

4x + y=−1⇔ x=\(\frac{-1-y}{4}\)

Putting value of x in the second equation:

3x−5y =−18 ⇔ 3(\(\frac{-1-y}{4}\))−5y=−18

⇒ \(-\frac{3}{4}-\frac{23 y}{4}\)=-18

⇒ −3−23y =−72

⇒ −23y =−69

⇒ y =3

∴x \(\frac{-1-y}{4}=\frac{-1-3}{4}\)=-1

=−1

We have the following system of linear equations:

4x + y =−1 & 3x−5y =−18

4x+y=−1 ⇔ y=−4x−1

Putting value of y in the second equation:

3x−5y=−18 ⇔ 3x−5(−4x−1)=−18

⇒ 3x + 20x + 5=−18

⇒ 23x =−23

⇒ x =−1

∴y =−4x−1 =−4(−1)−1 = 3

The solution of the system of linear equations 4x + y =−1  &  3x−5y =−18 is (x,y)=(−1,3).

The solution is same using both methods.I will prefer both methods to use for each system.

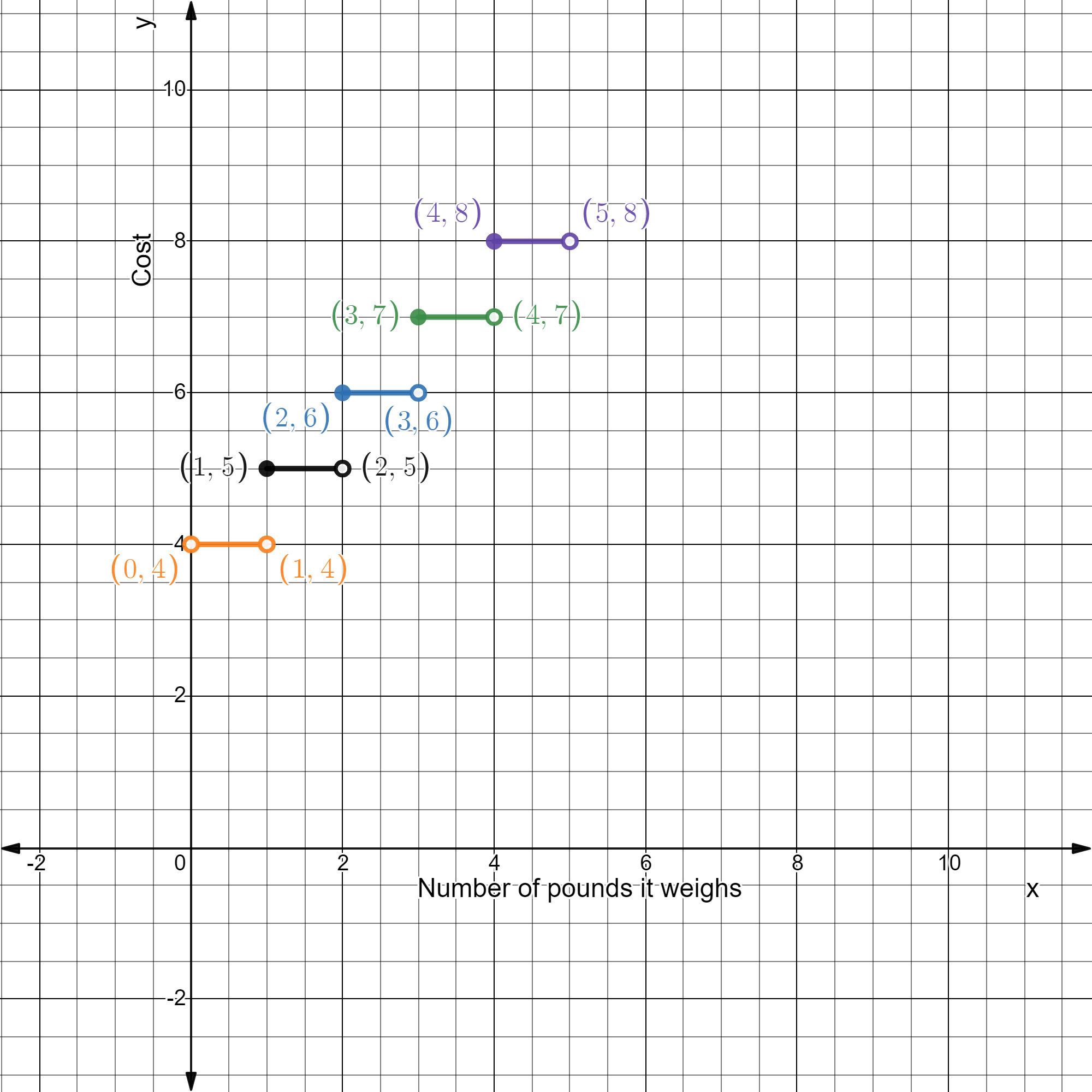
Page 138  Exercise 2   Answer

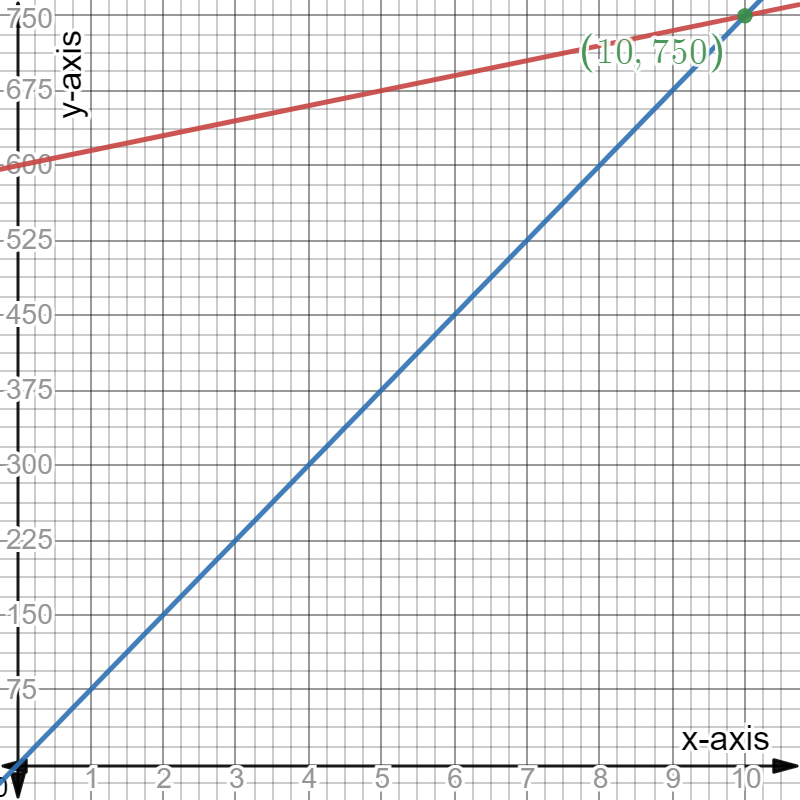
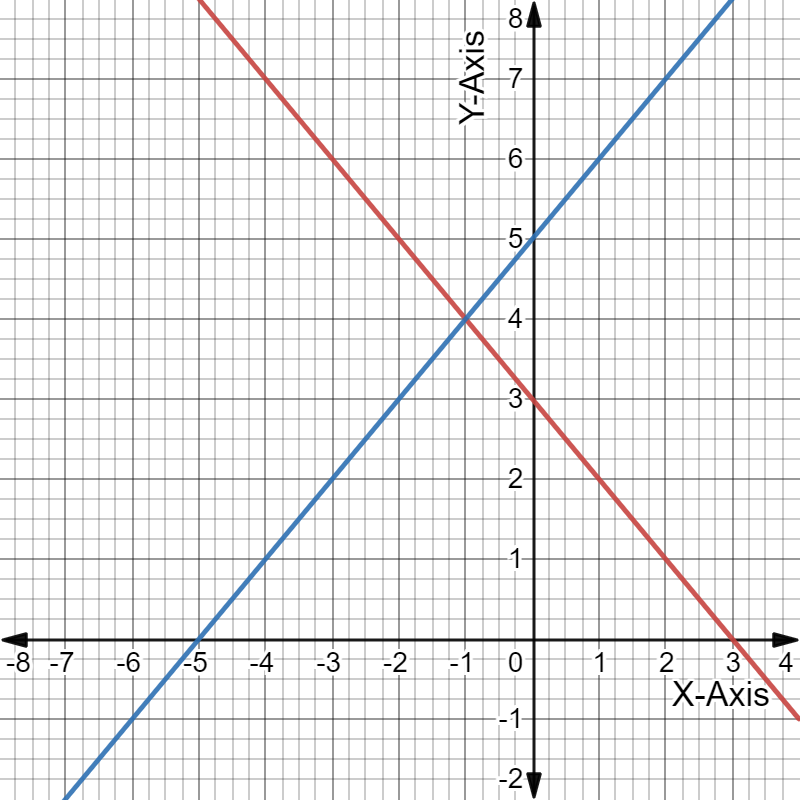
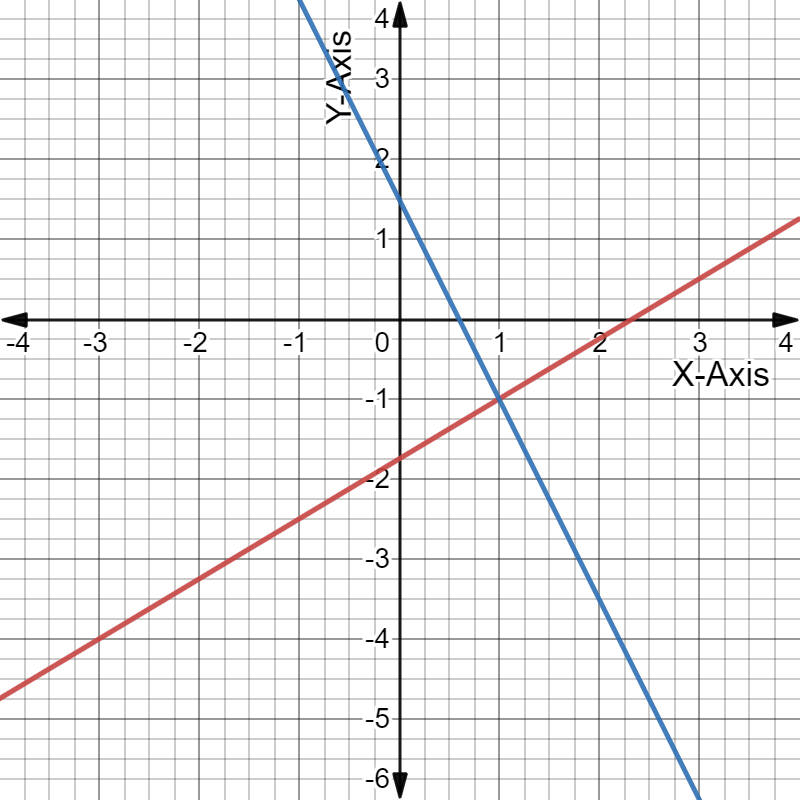
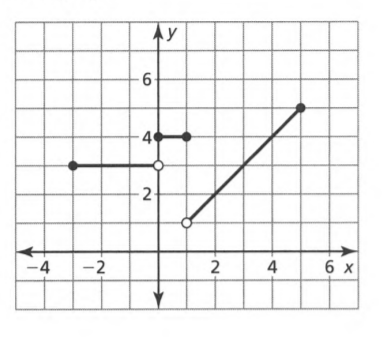
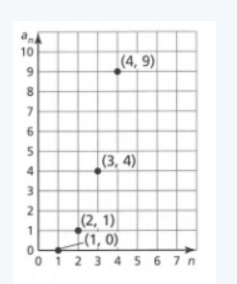
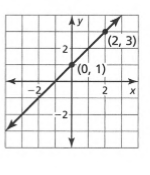
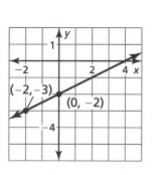
Given: The ordered pair generated at the right is (−2,−3).

To Write: A random ordered pair with integer coordinates.
A random ordered pair with integer coordinates is (−2,2).

The ordered pair generated at the right is (−2,−3).

A random ordered pair with integer coordinates is (−2,2).

Given: A random ordered pair with integer coordinates  (−2,2)

To Write: A system of linear equations that has your ordered pair as its solution. The equation will be of the form \(\frac{y-2}{x-(-2)}\)=n where n is any value.

The equation will be of the form \(\frac{y-2}{x+2}\)=n.

\(\frac{y-2}{x+2}\)=4 & \(\frac{y-2}{x+2}\)=3

⇒ y−2 = 4x + 8 & y−2 = 3x + 6

⇒ y−4x = 10 & y−3x = 8

A system of linear equations that has ordered pair (−2,2) as its solution are y−4x=10 and y−3x=8.

Given: A system of linear equations  y−4x = 10 and y−3x = 8

To Solve: System of linear equations

To solve a system of equations using substitution:

Isolate one of the two variables in one of the equations.

Substitute the expression that is equal to the isolated variable from Step 1 into the other equation. This should result in a linear equation with only one variable.

Solve the linear equation for the remaining variable.

Use the solution of Step 3 to calculate the value of the other variable in the system by using one of the original equations.

We have the following system of linear equations:

y−4x = 10 & y−3x = 8

y−4x = 10 ⇔  y = 10 + 4x

Putting value of y in the second equation:

y−3x = 8  ⇔ 10 + 4x−3x = 8

⇒ x = 8−10

⇒ x =−2

∴ y =10 + 4x=10 + 4(−2) = 10−8 = 2

The solution of the system of linear equations y−4x = 10 & y−3x = 8 is (x,y)=(−2,2).

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 138  Exercise 3  Answer

To solve a system of linear equations using substitution:

Isolate one of the two variables in one of the equations.

Substitute the expression that is equal to the isolated variable from point 1 into the other equation. This should result in a linear equation with only one variable.

Solve the linear equation for the remaining variable.

Use the solution of point 3 to calculate the value of the other variable in the system by using one of the original equations.

The Substitution method is the algebraic method to solve simultaneous linear equations. The value of one variable from one equation is substituted in the other equation. In this way, a pair of the linear equation gets transformed into one linear equation with only one variable, which can then easily be solved.

Solving Systems Of Equations Exercise 5.2 Answers

Page 140  Exercise 2  Answer

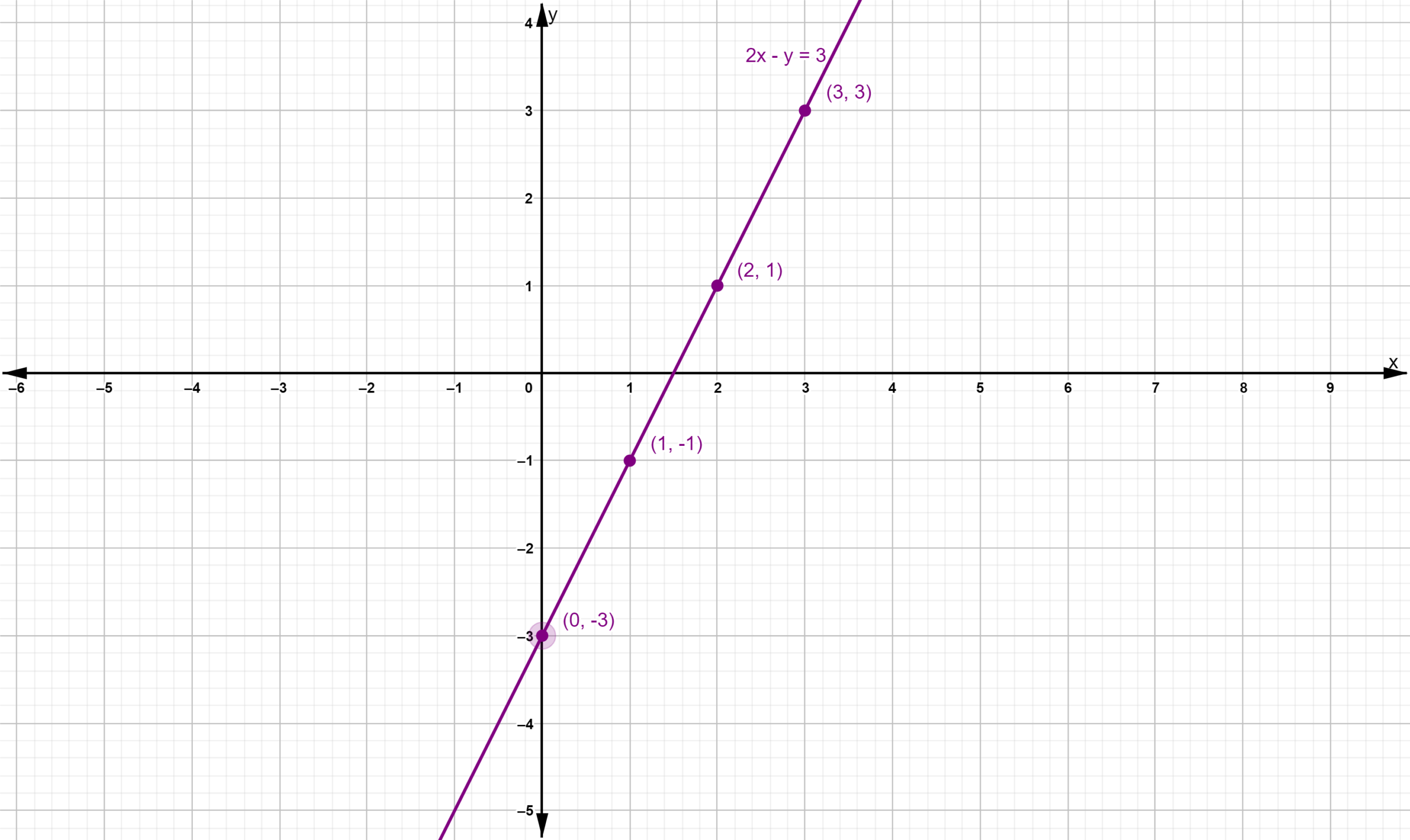
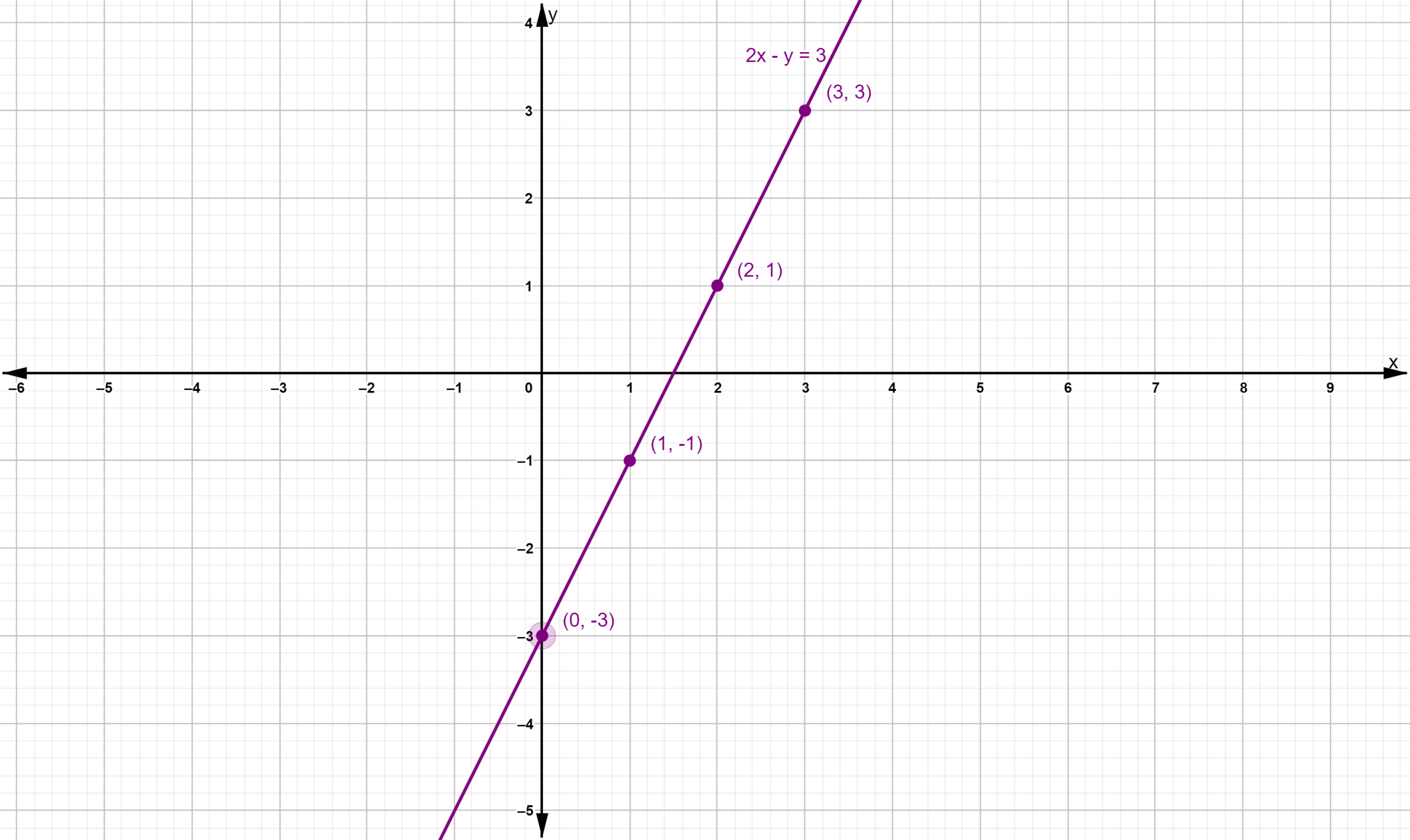
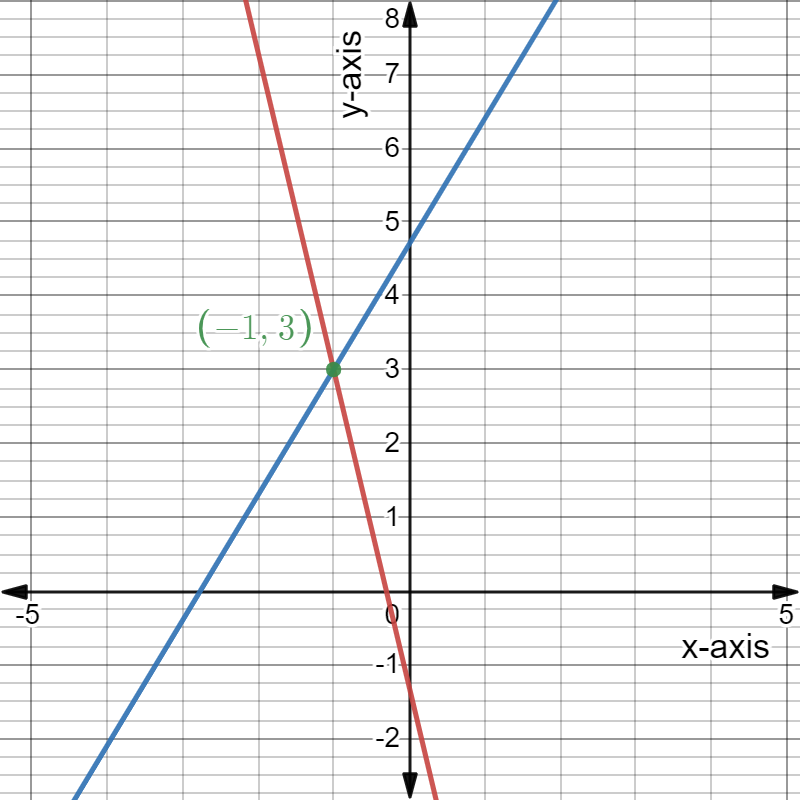
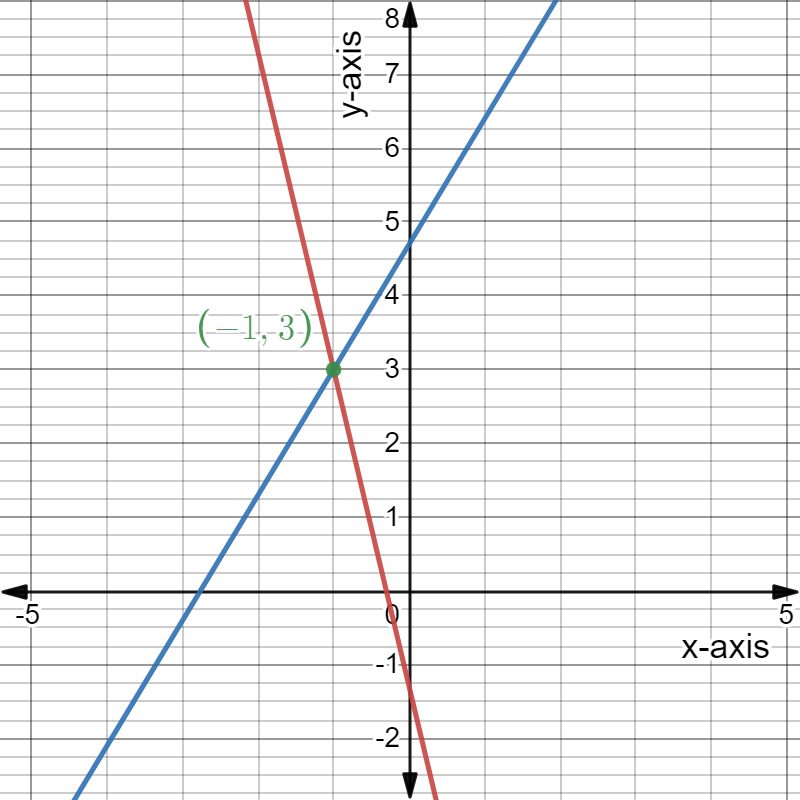
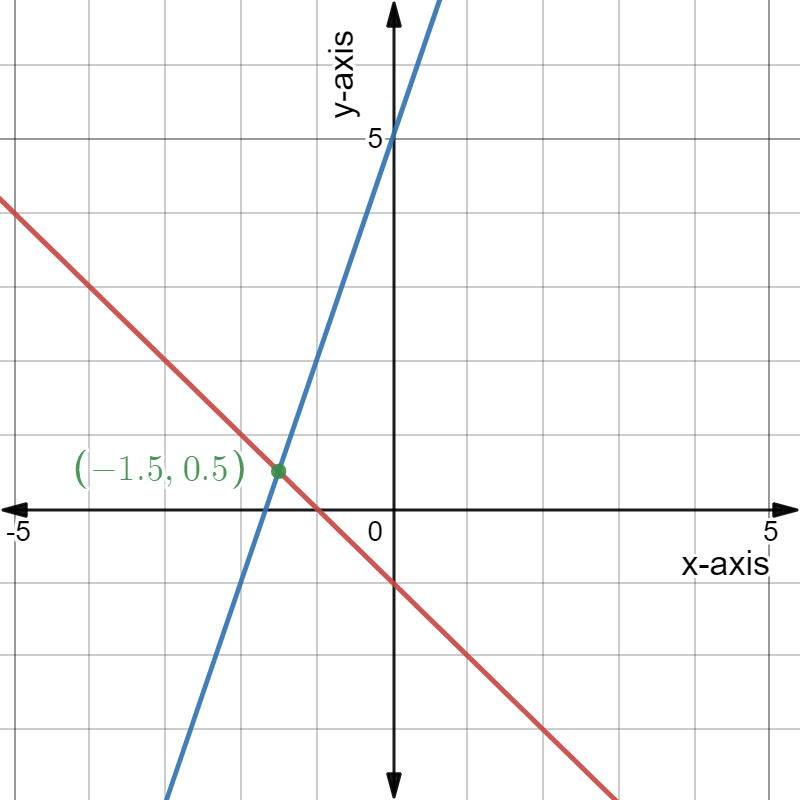
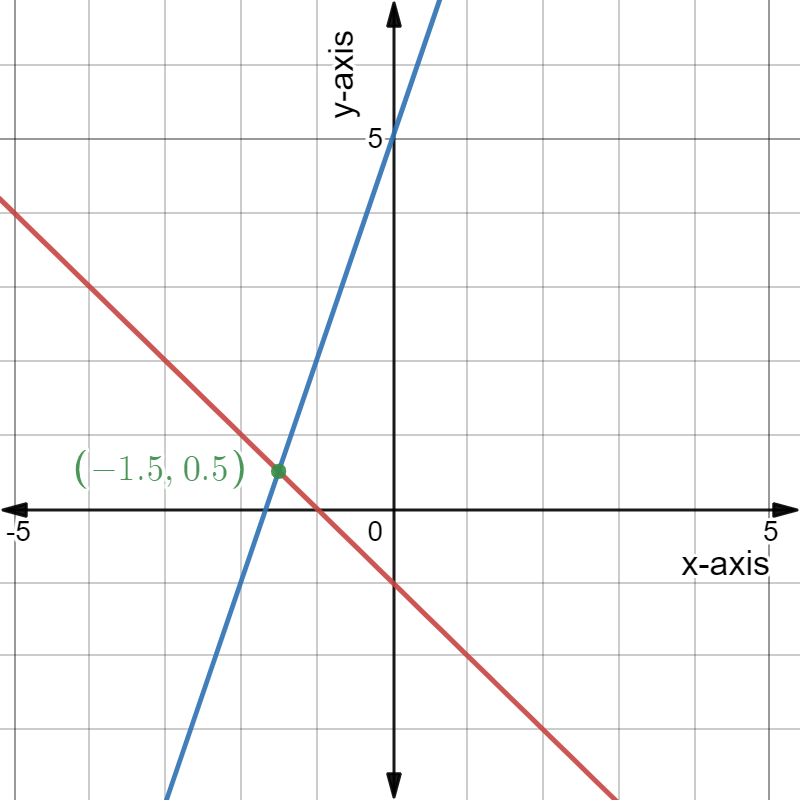
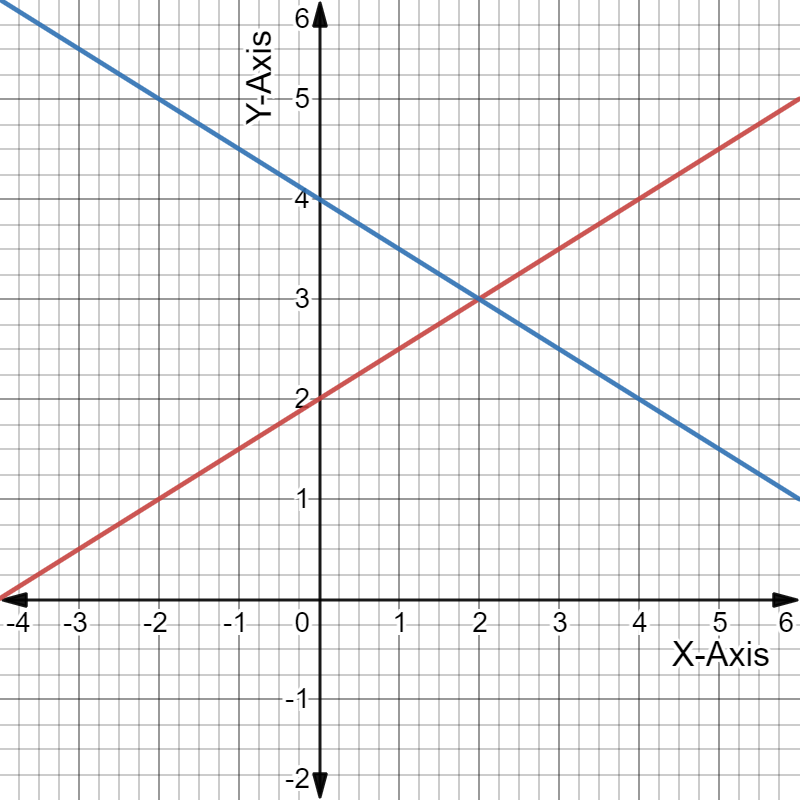
Given:  The System of linear equations is ​ 2x−y = 3, x = −2y −1
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of x, in terms of y.
We will put the second equation in first equation to find the value of y.

​2x−y = 3

⇒ 2×(−2y−1)−y = 3

⇒ −4y−2−y = 3

⇒ −5y=3 + 2

⇒ −5y = 5

⇒ y =−1

​
Now, put the value of y, in equation second to find out the value of x.

⇒ ​x =−2y−1

⇒ x =−2×−1−1

⇒ x =2−1

⇒ x =1

​
The solution of the system of linear equations  2x−y = 3,x =−2y−1 is x =1,y =−1.

Page 140  Exercise 3  Answer

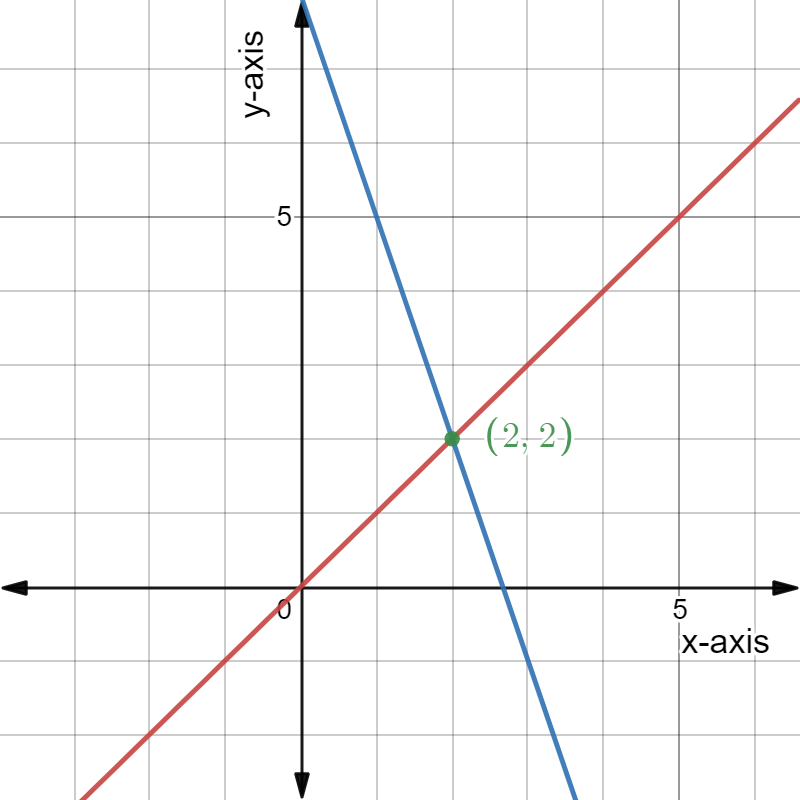
Given: The System of linear equations  is  ​x−3y =−1, x = y
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of x in terms of y. We will put the second equation in the first equation to find the value of y.

​⇒ x−3y =−1

⇒ y−3y =−1

⇒ −2y =−1

⇒ y\(=\frac{1}{2}\)

​

Now, put the value of y, in equation second to find out the value of x.

⇒ ​x = y

⇒ x\(=\frac{1}{2}\)

​
The solution of the system of linear equations   x−3y =−1, x =y is x\(=\frac{1}{2}\) ,y\(=\frac{1}{2}\).

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 140  Exercise 4  Answer

Given: The System of linear equations is ​x−2y =−3, y = x+1
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of y, in terms of x. We will put the second equation in first equation to find the value of x.

​x−2y =−3

⇒ x−2×(x+1) =−3

⇒ x−2x−2 =−3

⇒ −x =−3+2

⇒ x = 1
​

Now, put the value of x, in equation second to find the value of y.

⇒ ​y = x + 1

⇒ y = 1 + 1

⇒ y = 2

The solution of the system of linear equations   x−2y =−3,y = x+1 is x = 1,y = 2.

Page 140  Exercise 5  Answer

Given: The System of linear equations  is ​ 2x + y =3, x = 3y + 5
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of x, in terms of y. We will put the second equation in the first equation to find the value of y.

​2x + y =3

⇒ 2×(3y + 5) +y = 3

⇒ 6y+ 10 + y = 3

⇒ 7y = 3−10

⇒ 7y =−7

⇒ y =−1
​

Now, put the value of y, in equation second to find out the value of x.

​x = 3y + 5

⇒ x = 3×−1 + 5

⇒ x =−3 + 5

⇒ x = 2

​
The solution of the system of linear equations  2x + y = 3,x = 3y + 5 is x = 2,y =−1.

Big Ideas Math Student Journal Exercise 5.2 Explained

Page 140  Exercise 6   Answer

Given: The System of linear equations is

​3x + y=−5
y = 2x + 5

We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of y, in terms of x. We will put the second equation in first equation to find the value of x.

​3x + y =−5

⇒ 3x + 2x + 5 =−5

⇒ 5x =−5−5

⇒ 5x =−10

⇒x =−2

​
Now, put the value of x, in equation second to find the value of y.

⇒ ​y =2x + 5

⇒ y = 2×−2 + 5

⇒ y =−4 + 5

⇒ y = 1
​

The solution of the system of linear equations is x =−2,y = 1.

Page 140  Exercise 7  Answer

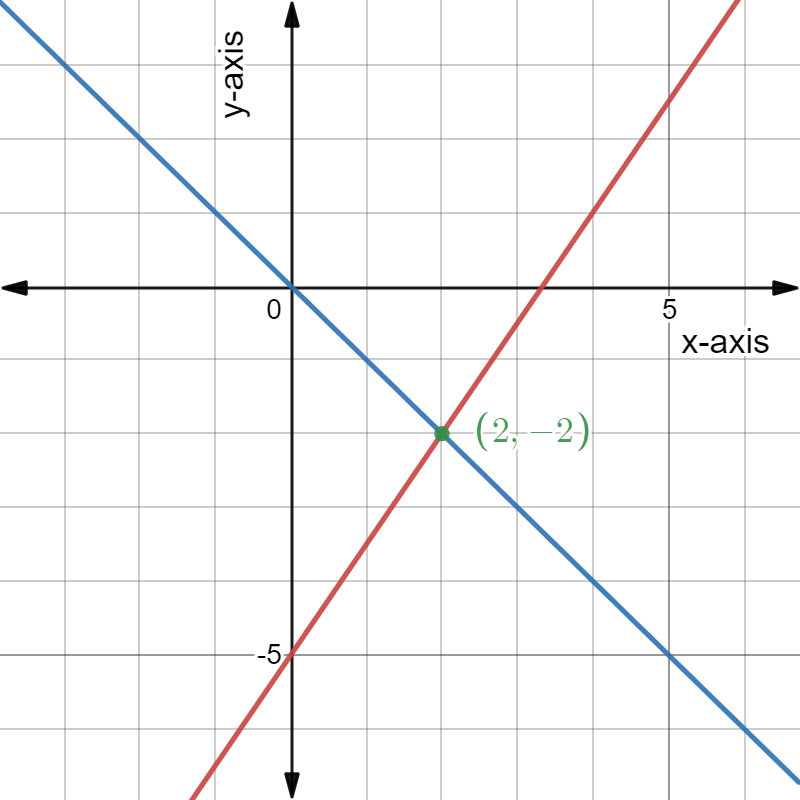
Given: The System of linear equations  is ​ y = 2x + 8 y =−2x
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of y, in terms of x. We will put the second equation in first equation to find the value of x.

​y = 2x + 8

⇒ −2x = 2x + 8

⇒ −2x−2x = 8

⇒ −4x = 8

⇒ x =−2
​

Now, put the value of x, in equation second to find the value of y.

​⇒ y =−2x

⇒ y =−2×−2

⇒ y =4

​
The solution of the system of linear equations y = 2x+8,y =−2x is x =−2,y =4.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 140  Exercise 8  Answer

Given:  The System of linear equations is    ​y\(=\frac{3}{4} x+1\)  , y\(=\frac{1}{4} x+3\)

​We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of y, in terms of x. We will put the second equation in first equation to find the value of x.

​y=\(\frac{3}{4} x+1\)

⇒ \(\frac{1}{4} x+3\)=\(\frac{3}{4} x+1\)

⇒ \(\frac{1}{4} x-\frac{3}{4} x\) =1-3

⇒ \(\frac{1-3}{4} x\) =-2

⇒ \(\frac{-2}{4} x=\) =-2

⇒ \(\frac{-x}{2}\) =-2

⇒ x = 4
​

Now, we put the value of x, in equation second to find the value of y.

⇒ ​y =\(\frac{1}{4} x+3\)

⇒ y = \(\frac{1}{4} \times 4\)+3

⇒ y = 1+3

⇒ y = 4
​

The solution of the system of linear equation y \(=\frac{3}{4} x+1\),\(=\frac{1}{4} x+3\) is x=4,y=4.

Page 140  Exercise 9  Answer

Given: The System of linear equations  is  2x−3y = 0, y = 4
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of y. We will put the second equation in first equation to find the value of x.

​2x−3y = 0

⇒ 2x−3×4 = 0

⇒ 2x = 12

⇒ x = 6

​
The solution of the system of linear equations is x = 6,y = 4.

Page 141  Exercise 11  Answer

Given: The  System of linear equations  is  \(=\frac{1}{2} x+1\), \(=\frac{-1}{2} x+9\)
​We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

In equation second, we already have the value of y, in terms of x. We will put the second equation in first equation to find the m value of x.

y\(=\frac{1}{2} x+1\)

⇒ \(\frac{-1}{2} x+9\)\(=\frac{-1}{2} x+1\)

⇒ \(\frac{-1}{2} x-\frac{1}{2} x=\)1-9

⇒ -x = -8

⇒ x = 8

Now, put the value of x, in equation second to find the value of y.

⇒ y = \(\frac{-1}{2} x+9\)

⇒ y = \(\frac{-1}{2} \times 8+9\)

⇒ y = -4+9

⇒ y = 5

The solution of the system of linear equation y\(y=\frac{1}{2} x+1\), y\(=\frac{-1}{2} x+9\) is x = 8,y = 5.

Chapter 5 Exercise 5.2 Solving Systems Practice

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 141  Exercise 13  Answer

Given:  System of linear equations  is ​7x−4y = 8, 5x−y = 2
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

From the second equation, we will find the value of y in terms of x.

⇒ ​5x−y = 2

⇒ y = 5x−2

We will put the above value of y, in first equation to find the value of x.

​7x−4y = 8

⇒ 7x−4×(5x−2) = 8

⇒ 7x−20x + 8=8

⇒ −13x=8−8

⇒ x=0
​

Now, we will put the value of x, in second equation to find the value of y.

⇒ ​y=5x−2

⇒ y=5×0−2

⇒ y=−2
​

The solution of the given system of linear equations   7x−4y = 8,5x−y = 2 is x = 0,y =−2.

Page 141  Exercise 14  Answer

Given: The System of linear equations  is ​y\(=\frac{3}{5} x-12\) ,\(=\frac{1}{3} x-8\)
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

From equation second, we already have the value of y, in terms of x. Now, we will put the second equation in the equation first to find the value of x.

y\(=\frac{3}{5} x-12\)

⇒ \(\frac{1}{3} x-8\)\(8=\frac{3}{5} x-12\)

⇒ \(\frac{1}{3} x-\frac{3}{5} x\) = 8-12

⇒ \(\frac{5 x-9 x}{15}\) = -4

⇒ -4x = -4 × 15

⇒ x = 15

From above step we will put the value of x, in equation second to find the value of y.

​⇒ y=\(\frac{1}{3} x-8\)

⇒ y\(=\frac{1}{3}\) ×15−8

⇒ y = 5−8

⇒ y =−3
​

The solution of the system of linear equations is x = 15,y = −3.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 141  Exercise 15  Answer

Given: The  System of linear equations is 3x−4y = −1, 5x + 2y = 7
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

From the second equation, we will find the value of y, in terms of x.

⇒​5x + 2y = 7

⇒ 2y = 7−5x

⇒ y\(=\frac{7-5 x}{2}\)

​Now, we will put the above equation in first equation to find the value of x.

​⇒ 3x−4y = −1

⇒ 3x−4\(\frac{7-5 x}{2}\)

⇒ 3x−2 × (7−5x) =−1

⇒ 3x−14 + 10 x = −1

⇒ 13x = 14−1

⇒ 13x = 13

⇒ x = 1
​

Now, put the value of x, in second equation to find the value of y.

⇒ ​y=\(\frac{7-5 x}{2}\)

⇒ y\(=\frac{7-5 \times 1}{2}\)

⇒ y\(=\frac{7-5}{2}\)

⇒ y\(=\frac{2}{2}\)
​
⇒ y = 1

The solution of the system of linear equations   3x−4y = −1, 5x + 2y =7 is x = 1,y = 1.

Page 141  Exercise 16  Answer

Given: The System of linear equations  is  ​y =−x  +3,x + 2y = 0
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

From the equation first, we already have the value of y, in terms of x. Now, we put the first equation in second equation to find the value of x.

⇒ ​x + 2y = 0

⇒ x  +2 × (−x+3) = 0

⇒ x−2x + 6 = 0

⇒ −x =−6

⇒ x = 6
​

Now, we put the above value of x, in the equation first to find the value of y.

​⇒ y =−x + 3

⇒ y =−6 + 3

⇒ y = −3

The solution of the system of linear equations y =−x + 3,x + 2y = 0 is x = 6,y =−3.

​Big Ideas Math Algebra 1 Exercise 5.2 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 141  Exercise 17  Answer

Given: The system of linear equations is y−5x =−2,−4x + y = 2
We need to solve the given equation to find the value of x and y.
We will solve the given system of linear equations using the substitution method.

We will find the value of y, from first equation in terms of x.

⇒ ​y−5x =−2

⇒ y = 5x−2

Now, we will put the above equation in second equation to find the value of x.

​⇒ −4x + y = 2

⇒ −4x + 5x−2 = 2

⇒ x = 2+2

⇒ x = 4
​

We will put the value of x, in first equation to find the value of y.

⇒ ​y = 5x−2

⇒ y = 5×4−2

⇒ y = 20−2

⇒ y = 18

The solution of the system of linear equations  y−5x = −2,−4x+y = 2, is x = 4,y = 18.

​
Page 141  Exercise 18  Answer

Given : ​4x−8y = 3, 8x + 4y = 1
​
To find the Solution of a system of linear equations using the substitution method.
Solve for x by adding 8y to both sides and divide it by 4.
Substitute the value of x in the second equation and solve for another variable.
Substitute value in one of the original equations and solve.

We have 4x−8y = 3 —- (1)

8x + 4y=1 ———-(2)

Solve equation (1) for x:

Add 8 y to both sides ⇒ 4x = 3 + 8y

Divided both sides by  4

⇒  x = \(\frac{3+8 y}{4}\)

⇒  x = \(\frac{3}{4}+\frac{8 y}{4}\)

⇒  x \(=\frac{3}{4}+2 y\)

Substitute value of x in equation (2):

​⇒  \(\rightarrow 8\left(\frac{3}{4}+2 y\right)+4 y\) = 1

⇒  \(\frac{3}{4} \cdot 8+2 y \cdot 8+4 y\)

⇒  3⋅2 + 16y + 4y = 1

⇒ 6 + 20y = 1

Subtract both sides by 6
⇒  20y = 1−5

⇒  20y =−5

Divide both sides by 20

⇒  y = \(-\frac{5}{20}\)

⇒ y  =\(-\frac{1}{4}\)

​

Substitute value of y in x\(=\frac{3}{4}+2 y\)

⇒ x\( = \frac{3}{4}+2\left(-\frac{1}{4}\right)\)

⇒ x\(\frac{3}{4}-\frac{2}{4}\)

⇒ x\( = \frac{1}{4}\)

Solution for given system of linear equation is x\(=\frac{1}{4}\) and y\(=\frac{-1}{4}\).

How To Solve Exercise 5.2 Big Ideas Math Chapter 5

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

Page 131  Exercise 1  Answer

Given: An equation y + 2 = x

To graph the equation
Identify the slope and y-intercept of the line and make a table of values to graph the given equation.

The given equation is y + 2 = x
Bring the equation in slope-intercept form.

Subtract 2 from both sides
y = x − 2

Comparing this equation with the slope-intercept form we get

The slope of the line is 1
The y-intercept of the line is−2

Make a table of values.

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Plot these points and graph the equation.

The graph of the equation y + 2 = x is

Page 131  Exercise 2  Answer

Given: An equation 2x − y = 3

To graph the equation
Identify the slope and y-intercept of the line and make a table of values to graph the given equation.

The given equation is  2x −y = 3
Bring the equation in slope-intercept form.

Subtract 3 from both sides
2x−3 = y
y = 2x−3

Comparing this equation with the slope-intercept form we get, The slope of the line is 2
The y-intercept of the line is−3

Make a table of values.

Plot these points and graph the equation.

The graph of the equation 2x−y = 3 is

Big Ideas Math Algebra 1 Chapter 5 Systems Of Equations Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations ExercisePage 131  Exercise 3  Answer

Given: An equation 5x +2y = 10

To graph the equation
Identify the slope and y-intercept of the line and make a table of values to graph the given equation.

The given equation is 5x + 2y = 10
Bring the equation in slope-intercept form.

Subtract 5x from both sides
2y=−5x + 10
Divide by 2
y=\(\frac{-5}{2} x\)+5

Comparing this equation with the slope-intercept form we get, The slope of the line is\(\frac{-5}{2} \), and the y-intercept of the line is 5

Make a table of values.

Plot these points and graph the equation.

The graph of the equation 5x+2y=10 is

Page 131 Exercise 4 Answer

Given: An equation y−3 = x

To graph the equation
Identify the slope and y-intercept of the line and make a table of values to graph the given

The given equation is  y−3=x
Bring the equation in slope-intercept form.

Add 3 on both sides
y=x+3
Comparing this equation with the slope-intercept form we get, The slope of the line is 1

Make a table of values.

Plot these points and graph the equation.

The graph of the equation y−3=x is

Solving Systems Of Linear Equations Chapter 5 Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 131 Exercise 5 Answer

Given: An equation 3x−y = −2

To graph the equation
Identify the slope and y-intercept of the line and make a table of values to graph the given equation.

The given equation is 3x−y = −2
Bring the equation in slope-intercept form.

Add 2 on both sides
3x + 2 = y
That is, y=3x + 2

Comparing this equation with the slope-intercept form we get, The slope of the line is 3
The y-intercept of the line is 2

Make a table of values.

Plot these points and graph the equation.

The graph of the equation 3x−y=−2 is

Page 131 Exercise 7 Answer

Given: An inequality  a−3>−2

To graph the solution.
Simplify the inequality so that the variable is on one side and then graph the solution keeping in mind that open circles are used for numbers that are less than or greater than and closed circles are used for numbers that are less than or equal to and greater than or equal to.

The given inequality is  a−3>−2
To simplify the inequality

Add 3 on both sides of the equation
a>−2 + 3
Simplify,  a>1

The number line is drawn with an open dot at 1 because the inequality used is greater than.

The graph of the solution of the inequality  a−3>−2 is

Page 131 Exercise 8 Answer

Given: An inequality −4≥−2c

To graph the solution.
Simplify the inequality so that the variable is on one side and then graph the solution keeping in mind that open circles are used for numbers that are less than or greater than and closed circles are used for numbers that are less than or equal to and greater than or equal to.

The given inequality is −4≥−2c
To simplify the inequality

Divide by 2 into both sides
\(\frac{-4}{2} \geq \frac{-2}{2} c\)

Simplify, −2≥−c
Multiplying by−1 reverses the sign of inequality.
2≤c
⇒  c≥2

The number line is drawn with a closed dot at 2 because the inequality used is greater than or equal to.

The graph of the solution of the inequality −4≥−2c is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 131 Exercise 9  Answer

Given: An inequality 2d−5<−3

To graph the solution.
Simplify the inequality so that the variable is on one side and then graph the solution keeping in mind that open circles are used for numbers that are less than or greater than and closed circles are used for numbers that are less than or equal to and greater than or equal to.

The given inequality is  2d−5<−3
To simplify the inequality

Add 5 on both sides
2d<−3 + 5
2d<2  (Divide by 2)
2d ÷ 2 < 2 ÷ 2
d<1

The number line is drawn with an open dot at 1 because the inequality used is less than.

The graph of the solution of the inequality 2d−5<−3 is

Big Ideas Math Student Journal Chapter 5 Solutions Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise Page 131 Exercise 10 Answer

Given: An inequality 8−3r≤5−2r

To graph the solution.
Simplify the inequality so that the variable is on one side and then graph the solution keeping in mind that open circles are used for numbers that are less than or greater than and closed circles are used for numbers that are less than or equal to and greater than or equal to.

The given inequality is 8−3r≤5−2r
To simplify the inequality

Add 3r on both sides
8≤5−2r + 3r
Subtract 5 from both sides
8−5≤r
Simplify
3≤r
That is, r≥3

The number line is drawn with a closed dot at 3 because the inequality used is greater than or equal to.

The graph of the solution of the inequality 8−3r≤5−2r is

Chapter 5 Solving Systems Of Equations Practice Problems

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

Page 132 Essential Question Answer

A linear equation is an algebraic equation where each term has an exponent of one and we know that there are linear equations in one variable and linear equations in two variables.

To solve a system of linear equations.

A System of Linear Equations is when we have two or more linear equations working together. A system of linear equations is a set of two linear equations with two variables.

For example, x + 2y = 1,3x + 4y = 10 mare both linear equations with two variables but when they are considered together, they form a system of linear equations.

A system of linear equations can be solved by substitution, elimination, and graphing. The substitution method is since each equation in the system has two variables, so one way to reduce the number of variables in an equation is to substitute an expression for a variable.

The elimination method is since each equation in the system has two variables, so one way to reduce the number of variables is to add or subtract the two equations in the system to eliminate, one of the variables.

Graph the first equation and the second equation on the same rectangular coordinate system and determine whether the lines intersect, are parallel, or are the same line to identify the solution to the system.

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

A system of linear equations can be solved by the substitution method where an equation is substituted in an expression for a variable, the elimination method where two equations are added or subtracted to eliminate one of the variables, and the graphing method which is solved by graphing the first and the second equation on the same rectangular coordinate system and determining whether the lines intersect.

Big Ideas Math Algebra 1 Chapter 5 Exercise 5.1 Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.1 Page 132  Exercise 1  Answer

Given: That your family opens a bed-and-breakfast and they spend $600 preparing a bedroom to rent and the cost to your family for food and utilities is $15 per night. Your family charges $75 per night to rent the bedroom.

To write an equation that represents the costs.

The family spends $600 to prepare the bedroom and for every night the cost for food and utilities is $15.
Let the number of nights be x.

So, the equation can be written as the cost for food and utility times the number of nights plus the cost spent to prepare the bedroom.
The equation that represents the costs is C=15x+600

Your family opens a bed-and-breakfast and they spend $600 preparing a bedroom to rent and the cost to your family for food and utilities is $15 per night so if they charge $75 per night to rent the bedroom then, an equation that represents the costs is C=15x + 600

Given: That your family opens a bed-and-breakfast and they spend $600 preparing a bedroom to rent and the cost to your family for food and utilities is $15 per night. Your family charges $75 per night to rent the bedroom.

To write an equation that represents the revenue (income).

The family spends $600 to prepare the bedroom and for every night the cost for food and utilities is $15.
And they charge $75 per night to rent the bedroom. Let the number of nights be denoted by x.

So, the income is the charge of rent for the bedroom per night.
The equation that represents the revenue or income isR=75x

Your family opens a bed-and-breakfast and they spend $600 preparing a bedroom to rent and the cost to your family for food and utilities is $15 per night so if they charge $75 per night to rent the bedroom then, an equation that represents the revenue or income is R=75x

Given: That your family opens a bed-and-breakfast and they spend $600 preparing a bedroom to rent and the cost to your family for food and utilities is $15 per night. Your family charges $75 per night to rent the bedroom.

If a set of two (or more) linear equations is called a system of linear equations then to, write the system of linear equations for this problem.
The family spends $600 to prepare the bedroom and for every night the cost for food and utilities is $15.

And they charge $75 per night to rent the bedroom. Let the number of nights be denoted by x.

The equation that represents the costs is the cost for food and utility times the number of nights plus the cost spent to prepare the bedroom which is represented by C=15x + 600.

The equation that represents the revenue or income is the charge of rent for the bedroom per night which is represented by R = 75x
So, a system of linear equations for this problem is​ C=15x + 600 R = 75x
​

Your family opens a bed-and-breakfast and they spend $600

preparing a bedroom to rent and the cost to your family for food and utilities is $15 per night so if they charge $75 per night to rent the bedroom then, the system of linear equations for this problem is ​C=15x + 600 R =75x
​

Page 132  Exercise 2  Answer

We are given a situation where a family is starting a bed and breakfast business.

We are asked to fill a given table.

The values to be filled are the cost incurred by the family while starting the business.
The cost incurred is 600 $ on preparing the bedroom to rent and 15$ is charged on the breakfast.

Also, the revenue generated by the said business.

The revenue generated is the amount charged from the customers that is 75 $.
We have to look for a break-even point as well.

Given: Cost incurred

15x + 600

Revenue generated

75x

where x is the number of days

Table:

The cost and revenue equation used to determine the number of nights the family in tabular form:
Table:

We are given a situation where a family is starting a bed and breakfast business.
We are asked to find the number of nights it will take to get the amount spent on preparing the bedroom back.

The values are the cost incurred by the family while starting the business.

The cost incurred is 600 $ on preparing the bedroom to rent and 15 $ is charged on the breakfast.

Also, the revenue generated by the said business.
The revenue generated is the amount that is charged to the customers that is 75 $.

We have to look for a break-even point.

Given: Cost incurred (equation)
15x + 600
Revenue generated (equation)
75x
where x is the number of days

Table: (from the above table )

From the table, we observe that on the tenth day, the cost incurred is the same as the revenue generated.
This is the break-even point.

Hence, the number of nights needed to get the investment back is 10.
The number of nights the family will take to get the amount spent on preparing the bedroom is 10.

We are given a situation where a family is starting a bed and breakfast business.
We are asked to mark points in a graph on the values of cost and revenue generated.

The values are the cost incurred by the family while starting the business.

The cost incurred is 600 $ on preparing the bedroom to rent and 15
$ is charged on the breakfast.

Also, the revenue generated by the said business.
The revenue generated is the amount charged from the customers that is 75 $.

Given: Cost incurred (equation)
15x + 600
Revenue generated (equation)
75x
where x is the number of days

Graph:

The cost and revenue equation generated when the family started a bed and breakfast business in graphical form is

We are given a situation where a family is starting a bed and breakfast business.
We are asked to find the point of intersection, and describe it and compare it with break-even point.

The values are the cost incurred by the family while starting the business.

The cost incurred is 600 $ on preparing the bedroom to rent and 15 $ is charged on the breakfast.

Also, the revenue generated by the said business.
The revenue generated is the amount charged from the customers that is 75$.

We have to look for a break-even point.

Given: Cost incurred (equation)
15x + 600
Revenue generated (equation)
75x
where x is the number of days

Graph:

The point of intersection is (10,750).
This is the value where the cost and revenue become equal. After this point, there is profit.

Comparison:

The point of intersection is the same as the break-even point i.e. (10,750).
They correspond to the same value, that is the solution for the given set of equations.
It is inferred that after this point profit margin begins. This point is where the two values become equal.

The cost and revenue equation used to determine the number of nights the family will take to get the amount spent on preparing the bedroom when represented graphically meets at a point (10,750).

Solving Systems Of Equations Exercise 5.1 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.1 Page 133  Exercise 4  Answer

Given: We are given an equation ​y=−4.3x−1.3 y=1.7x+4.7.

We are asked to solve it by either using a table or a graph.

We are also asked to explain our reasons for choosing any of the methods.

We have to check our results using a graphing calculator.

For the given equation we are using a graph.
We have to plot both the equations in the graph.

Their point of intersection is our required solution.
We are using a graph because it will give a clear, pictorial representation with exact values.

Equations(given): ​y=−4.3x−1.3 , y=1.7x + 4.7
​Graph:

Point of intersection: (−1,3). This is the required solution.

Test solution: (−1,3)

First equation :

y = −4.3x−1.3
3 = −4.3×(−1)−1.3
3 = 4.3−1.3
3 = 3
​
Second equation :

y = 1.7x+4.7
3 = 1.7×(−1)+4.7
3 = −1.7+4.7
3 = 3
​

The solution for the equation  ​y =−4.3x−1.3
y = 1.7x + 4.7 can be obtained using a graph as it gives the exact values.

The solution is (−1,3)as also checked by graphing calculator.

Given: We are given an equation ​y=x, y=−3x+8.
We are asked to solve it by either using a table or a graph.

We are also asked to explain our reasons for choosing any of the methods.
We have to check our results using a graphing calculator.

For the given equation we are using a graph.
We have to plot both the equations in the graph.

Their point of intersection is our required solution.
We are using a graph because will b give a clear, pictorial representation with exact values.

Equations(given): ​y = x ,y = −3x+8
Graph:

Point of intersection: (2,2). This is the required solution.

Test the solution: (2,2).

First equation :

​y=x
2=2
​
Second equation :

​y=−3x+8
2=−3×(2)+8
2=−6+8
2=2
The points are the correct solution.

The solution for the equation ​y = x, y =−3x + 8
Can be obtained using a graph as it gives the exact values.
The solution is (2,2) as also checked in graphing calculator.

Given: We are given an equation ​y = −x−1, y = 3x+5.
We are asked to solve it by either using a table or a graph.
We are also asked to explain our reasons for choosing any of the methods.
We have to check our results using a graphing calculator.

For the given equation we are using a graph.
We have to plot both the equations in the graph.
Their point of intersection is our required solution.
We are using a graph because will b give a clear, pictorial representation with exact values.

Equations(given): ​y =−x−1 , y = 3x + 5
Graph:

Point of intersection: (−1.5,0.5) The required set of values is the given solution.

Test solution: (−1.5,0.5)

First equation:

​y = −x−1
0.5 =−(−1.5)−1
0.5 = + 1.5−1
0.5 = 0.5
​
Second equation:

​y = 3x + 5
0.5 = 3×(−1.5)+5
0.5 = −4.5+5
0.5 = 0.5

The points are the correct solution.

The solution for the equation ​y = −x−1, y = 3x + 5

Can be obtained using a graph as it gives the exact values.
The solution is (−1.5,0.5)as also checked by graphing calculator.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.1 Page 135  Exercise 2  Answer

Given: We are given a set of linear equations ​x−y =−2, 2x + y = 5 along with an ordered pair (1,3).
We are asked to check whether the ordered pair is the solution for the system of linear equations.
In order to do so, we have to test the solution by putting the values of x and y in their respective positions in the linear equation.
We have to solve both equations with these values.
If the values are true, then the ordered pair is the solution for the given set.

Equations: ​x−y =−2, 2x + y = 5

Ordered pair: (1,3)

Test the solution:
Putting values of x and y as 1 and 3 respectively.

First Equation :

​x−y =−2
1−3 =−2
−2 =−2

Second equation:

​2x + y = 5
2×(1)+3 = 5
2 + 3 = 5
5=5

​The given ordered pair is the solution for the system of linear equations.

The equations ​x−y = −2, 2x + y=5 on testing for a solution using the ordered pair (1,3) stand true.

Page 135  Exercise 3  Answer

Given: We are given a set of linear equations ​y = x−2, y =−3x + 6 along with an ordered pair (2,0).
We are asked to check whether the ordered pair is the solution for the system of linear equations.

In order to do so, we have to test the solution by putting the values of x and y in their respective positions in the linear equation.
We have to solve both equations with these values.

If the values are true, then the ordered pair is the solution for the given set.

Equations: ​y = x−2, y =−3x + 6

​Ordered pair: (2,0)

Test the solution:
Putting values of x and y as 2 and 0 respectively.

First Equation :
​y = x−2
0 = 2−2
0=0
​
Second equation:
​y =−3x + 6
0 =−3×(2)+6
0 = −6+6
0 = 0

The given ordered pair is the solution for the system of linear equations.

The equations ​y =x−2, y =−3x + 6 on testing for a solution using the ordered pair (2,0) stand true.

Big Ideas Math Student Journal Exercise 5.1 Explained

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.1 Page 135  Exercise 4  Answer

Given: We are given a set of linear equations ​x−2y = 3, 2x−y = 0 along with an ordered pair (−1,−2).
We are asked to check whether the ordered pair is the solution for the system of linear equations.

In order to do so, we have to test the solution by putting the values of x and y in their respective positions in the linear equation.

We have to solve both equations with these values.

If the values are true, then the ordered pair is the solution for the given set.

Equations: ​x−2y = 3, 2x−y = 0​

Ordered pair: (−1,−2)

Test the solution:
Putting values of x and y as −1 and −2 respectively.

First Equation :

​x−2y = 3
−1−2×(−2) = 3
−1 + 4 = 3
3=3
​
Second equation:

​2x−y = 0
2×(−1)−(−2) = 0
−2 + 2 = 0
0 = 0

The given ordered pair is the solution for the system of linear equations.

The equations ​x−2y = 3, 2x−y = 0 on testing for a solution using the ordered pair (−1,−2) stands True.

Page 135  Exercise 5  Answer

Given: We are given a set of linear equations ​3x−2y =−12, 2x + 4y = 9 along with an ordered pair (−2,3).
We are asked to check whether the ordered pair is the solution for the system of linear equations.

In order to do so, we have to test the solution by putting the values of x and y in their respective positions in the linear equation.

We have to solve both equations with these values.

If the values are true, then the ordered pair is the solution for the given set.

Equations: ​3x−2y =−12,2x + 4y = 9

Ordered pair: (−2,3)

Test the solution:
Putting values of x and y as −2 and 3 respectively.

First Equation :

​3x−2y = −12
3×(−2)−2×(3) = −12
−6−6 =−12
−12 = −12
​
Second equation:
​2x + 4y = 9
2×(−2)+4×(3) = 9
−4 + 12 = 9
8 = 9

The given ordered pair is not the solution for the system of linear equations.

The equations ​3x−2y =−12, 2x + 4y = 9 o n testing for a solution using the ordered pair (−2,3) stand false.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.1 Page 135  Exercise 7  Answer

Given: We are given a set of equations ​3x−2y = 10, x + y = 0, and their graph.
We are asked to solve the equation using the graph.

In order to do so, we have to first find their point of intersection.
We need to get the coordinates of the point of intersection.

Using these values we have to solve the linear equation.
If these values satisfy, then the values are the solution for the set of linear equations.

Equations: ​3x−2y = 10, x + y = 0
​Graph:

Point of intersection: (2,−2).

Test the solution: (2,−2):
Putting values of x and y as 2 and −2 respectively.

First Equation :

​3x−2y = 10
3×(2)−2×(−2) = 10
6 + 4 = 10
10 = 10
​
Second equation:

​x + y = 0
2 + (−2) = 0
2−2  =0
0 = 0

The given ordered pair is the solution for the system of linear equations.

The solution for the equations ​3x−2y=10, x+y=0 using a graph is (2,−2).

Page 135  Exercise 8  Answer

Given: Graph of ​ x−2y = 5, 2x + y = −5

To Solve: The system of linear equations
Graph the first equation.

Graph the second equation on the same rectangular coordinate system.

Determine whether the lines intersect, are parallel, or are the same line.
Identify the solution to the system.

Graph of ​ x−2y = 5, 2x + y =−5:

From the graph, it can be clearly seen that the point of intersection is (−1,−3).

We will put the value of x and y in the given equation to check whether our answer is correct.
     x−2y=5              &         2x+y=−5

⇒ (−1)−2×(−3) = 5  &         ⇒ 2(−1)+(−3) =−5

⇒−1 + 6 = 5             &         ⇒ −2−3 =−5

⇒ 5 = 5                  &          ⇒ −5 =−5

The solution of the system of linear equations  x−2y =5, 2x + y =−5 is (x,y)=(−1,−3).

Page 135  Exercise  9 Answer

Given: Graph of ​x + 2y = 8, 3x−2y = 8

To Solve: The system of linear equations
Graph the first equation.

Graph the second equation on the same rectangular coordinate system.

Determine whether the lines intersect, are parallel, or are the same line.
Identify the solution to the system.

Graph of:​ x + 2y = 8, 3x−2y = 8

From the graph, it can be clearly seen that the point of intersection is (4,2).

We will put the value of x and y in the given equation to check whether our answer is correct.
x + 2y = 8          &   3x−2y = 8

⇒ 4 + 2×2 = 8   &    ⇒ 3×4−2×2 = 8

⇒ 4 + 4 = 8       &     ⇒ 12−4 = 8

⇒ 8 = 8           &    ⇒ 8 = 8

The solution of the system of linear equations ​x+2y = 8, 3x−2y = 8 ​is (x,y) = (4,2).

Chapter 5 Exercise 5.1 Solving Systems Practice

Page 136  Exercise 10  Answer

Given: ​ ​y=−x + 3 , y=x + 5
​

To Solve: The system of linear equations
Graph the first equation.

Graph the second equation on the same rectangular coordinate system.

Determine whether the lines intersect, are parallel, or are the same line.
Identify the solution to the system.

Graph of:​ y=−x + 3 : y=x + 5

​

From the graph, it can be clearly seen that the point of intersection is (−1,4).

The solution of the system of linear equations ​ y =−x + 3, y = x+  5 is (x,y) = (−1,4).

Page 136  Exercise  11 Answer

Given: y\(=\frac{1}{2} x+2\)

y\(=\frac{1}{2} x+4\)

To Solve: The system of linear equations

Graph the first equation.

Graph the second equation on the same rectangular coordinate system.
Determine whether the lines intersect, are parallel, or are the same line.

Identify the solution to the system.

Graph of ​:

​y\(=\frac{1}{2} x+2\)

y\(=\frac{1}{2} x+4\)

​From the graph, it can be clearly seen that the point of intersection is (2,3).

The solution of the system of linear equations

y\(=\frac{1}{2} x+2\)

y\(=\frac{1}{2} x+4\) is (x,y)=(2,3)

Page 136  Exercise 12  Answer

Given: ​3x−2y = 6, y = −3

​

To Solve: The system of linear equations

Graph the first equation.

Graph the second equation on the same rectangular coordinate system.
Determine whether the lines intersect, are parallel, or are the same line. Identify the solution to the system.

Graph of : ​3x−2y​ = 6 : y = −3

From the graph, it can be clearly seen that the point of intersection is (0,−3).
​

The solution of the system of linear equations ​3x−2y​ = 6, y =−3 is (x,y) = (0,−3).

Page 136  Exercise  13 Answer

Given: ​ y = 4x, y =−4x + 8

​

To Solve: The system of linear equations

Graph the first equation.
Graph the second equation on the same rectangular coordinate system.

Determine whether the lines intersect, are parallel, or are the same line.
Identify the solution to the system.

Graph of: ​ y = 4x: y =−4x + 8

​

From the graph, it can be clearly seen that the point of intersection is (1,4) .

The solution of the system of linear equations ​ y = 4x, y =−4x+8 is (x,y) = (1,4).

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.1 Page 136  Exercise 14  Answer

Given: y\(=\frac{1}{4} x+3\)

y\(=\frac{3}{4} x+5\)

To Solve: The system of linear equations
Graph the first equation.

Graph the second equation on the same rectangular coordinate system.
Determine whether the lines intersect, are parallel, or are the same line.

Identify the solution to the system.

Graph of y\(=\frac{1}{4} x+3\):\(=\frac{3}{4} x+5\)

From the graph, it can be clearly seen that the point of intersection is (−4,2).

The solution of the system of linear equations y\(=\frac{1}{4} x+3\),\(=\frac{3}{4} x+5\)
is (x,y)=(-4,2)

Big Ideas Math Algebra 1 Exercise 5.1 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.1 Page 136  Exercise 15  Answer

Given: ​ 3x−4y = 7, 5x + 2y = 3

​

To Solve: The system of linear equations
Graph the first equation.
Graph the second equation on the same rectangular coordinate system.
Determine whether the lines intersect, are parallel, or are the same line.
Identify the solution to the system.

Graph of: ​ 3x−4y = 7: 5x + 2y = 3

​

From the graph, it can be clearly seen that the point of intersection is (1,-1)

The solution of the system of linear equations ​ 3x−4y = 7, 5x + 2y = 3 is (x,y) = (1,−1).

Page 136  Exercise 16  Answer

Given: A test has twenty questions worth 100 points. The test consists of x true-false questions worth 4 points each and y multiple-choice questions worth 8 points each.

To Find: Number of each type of question on the test

In this question, we will apply the method given in the “Tip” section and solve accordingly.

Use the substitution method to solve the system of linear equations.

A test has twenty questions worth 100 points. The test consists of x true-false questions worth 4 points each and y multiple-choice questions worth 8 points each.

Let x= number of TF questions (4 points each) and y= number of MC questions (8 points each)
“Test has twenty questions” means x+y=20.
“100 points” means 4x+8y=100.

Substitution Method:
Solve for a variable using x=20−y

Substitute for x in another equation :

4(20−y) + 8y = 100
⇒ 80−4y  +8y = 100
⇒ 80 + 4y = 100
⇒ 4y = 20
⇒ y = 5
There are 5 multiple-choice questions.

Use any one of the two equations to find the value of x :

x + y = 20
⇒ x + 5 = 20
⇒ x = 15
There are 15 True-False questions.

A test has twenty questions worth 100 points. The test consists of x true-false questions worth 4 points each and y multiple-choice questions worth 8 points each.

There are 5 multiple-choice and 15 True-False questions.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions

Page 126  Essential Question  Answer

We have to take some steps to describe the function that is represented by more than one equation

Identify the intervals for which different rules apply.

Determine formulas that describe how to calculate an output from input in each interval.

Use braces and if-statements to write the function.

In this way, we can describe the function that is represented by more than one equation.

We have given an explanation of, How we can describe the function that is represented by more than one equation.

Big Ideas Math Algebra 1 Chapter 4 Exercise 4.7 Solutions

Page 127  Exercise 2  Answer

 Given: The given graph is

As we can see in the above graph
For the value of “x” is less than 0and greater than or equal to −3, the value of “y” is 0

For the range of value of x, −6≤x<−3, the value of “y” is −2

For the range of value of x , 0≤x<3, the value of “y” is 2

For the range of value of x, 3≤x<6, the value of “y” is 4.

Yes, the given graph represents y as a function of x.

Given: The given graph is

To find We have to find the value of the function for the given intervals.

\(f(x)=\left\{\begin{array}{c}, \text { if }-6 \leq x<3 \\, \text { if }-3 \leq x<0 \\, \text { if } 0 \leq x<3 \\, \text { if } 3 \leq x<6\end{array}\right.\)
​
Use the relation that we have got in from the above of this question.

From the above Equation, we can write the values of the function for the given interval

​

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.7 Page 127  Exercise 3  Answer

 Given: The given graph is

As we can see in the above graph, shows the modulus function.

A modulus function is a function that gives the absolute value of a number or variable.

It produces the magnitude of the number of variables.

It is also termed as an absolute value function.

So we can describe a function that is represented by more than one equation as

​f(x)=∣x∣

f(x)=x ,if x is positive ——–(1)

f(x)=−x, if xis negative ——–(2)

Page 127   Exercise 4  Answer

Given: The given graph is

As we can see in the above graph, shows the modulus function.
we can use two equations to describe the function represented by the graph, as\(f(x)=\left\{\begin{array}{r}x, \text { if } x>0 \\-x, \text { if } x<0\end{array}\right.\)
​
We can use two equations to describe the function represented by the graph, as
\(f(x)=\left\{\begin{array}{r}x, \text { if } x>0 \\-x, \text { if } x<0\end{array}\right.\)
​
​

Page 129 Exercise 2 Answer

Given: The given function is

\(f(x)= \begin{cases}3 x-1, & \text { if } x \leq 1 \\ 1-2 x, & \text { if } x>1\end{cases}\) and

To find We have to find the value of f(1).
Find the appropriate function for the required value of the function.
After finding the appropriate function, put the value of the domain of the required function in that function.

The domain of the required function is x=1.
We have to find the value of the function f(1), so the appropriate function is f(x)=3x−1,x≤1 because the value of “x” is one.
Now put x=1 in the above function, and we get

​f(x)=3x−1
f(1)=3(1)−1
f(1)=3−1
f(1)=2
​The value of the function is f(1)=2.

Writing Linear Functions Chapter 4 Exercise 4.7 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.7 Page 129  Exercise 3  Answer

Given: The given function is

\(f(x)= \begin{cases}3 x-1, & \text { if } x \leq 1 \\ 1-2 x, & \text { if } x>1\end{cases}\) and

To find We have to find the value of the function f(5).
Find the suitable function according to the domain of the required function.Then put the value of the domain in that function to get the answer.

The domain of the required function is x=5.
So the appropriate function is f(x)=1−2x,x>1 because the domain satisfies the condition of the equation.
We have to find the value of the function f(5).

Now put x=5 in the above function, we get

​f(x)=1−2x
f(5)=1−2(5)
f(5)=1−10
f(5)=−9

​The value of the function is f(5)=−9.

Page 129  Exercise 4  Answer

Given: The given functions are

\(f(x)= \begin{cases}3 x-1, & \text { if } x \leq 1 \\ 1-2 x, & \text { if } x>1\end{cases}\) and

To findWe have to find the value of the function f(−4).
Find the suitable function according to the domain value of the required function.
Then put the value of the domain in that function to get the answer.

The domain of the required function is x=−4.
So the appropriate function is f(x)=3x−1,ifx≤1, because the domain of the required function satisfies this function.

We have to find the value of the function f(−4).

Now put x=−4in the above function, and we get

​f(x)=3x−1
f(−4)=3(−4)−1
f(−4)=−12−1
f(−4)=−13

​The value of the function is f(−4)=−13.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.7 Page 129  Exercise 5  Answer

Given: The given functions are

\(f(x)= \begin{cases}3 x-1, & \text { if } x \leq 1 \\ 1-2 x, & \text { if } x>1\end{cases}\)nd

To findWe have to find the value of the function g(0).
Find the suitable function according to the domain value of the required function.
Then put the value of the domain in that function to get the answer.

The domain of the required function is x=0.
So the appropriate function is g(x)=2,if−3<x<1, because the domain of the required function satisfies this function.

Now we have to find the value of g(0).
The above function is a constant function, so we can say that for the given value, x=0, the value of the function remains the same. g(0)=2
The value of the function is g(0)=2.

Page 129  Exercise 6  Answer

Given: The given functions are

\(f(x)= \begin{cases}3 x-1, & \text { if } x \leq 1 \\ 1-2 x, & \text { if } x>1\end{cases}\) and

To find We have to find the value of the function g(−3).
Find the suitable function according to the domain value of the required function.
Then put the value of the domain in that function to get the answer.

The domain of the required function is x=−3.
So the appropriate function is g(x)=3x−1,ifx≤−3 because the domain of the required function satisfies this function.

Now we have to find the value of g(−3)
Now put x=−3 in the above function, and we get

​g(x)=3x−1
g(−3)=3(−3)−1
g(−3)=−9−1
g(−3)=−10

​The value of the function is g(−3)=−10.

Big Ideas Math Student Journal Exercise 4.7 Explained

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.7 Page 129  Exercise 7  Answer

Given: The given functions are

To find We have to find the value of the function g(1).
Find the suitable function according to the domain value of the required function.
Then put the value of the domain in that function to get the answer.

The domain of the required function is x=1.
So the appropriate function is g(x)=−3x because the domain of the required function satisfies this function.
Now put x=1in the above function, and we get

​g(x)=−3x
g(1)=−3(1)
g(1)=−3

​The value of the function is g(1)=−3.

Page 129  Exercise 9  Answer

Given: The given functions are

To findWe have to find the value of the function g(−5).
Find the suitable function according to the domain value of the required function.
Then put the value of the domain in that function to get the answer.

The domain of the required function is x=−5.
So the appropriate function is g(x)=3x−1 if x≤−3 because the domain of the required function satisfies this function.

Now put x=−5 in the above function, and we get

​g(x) = 3x−1
g(−5) = 3(−5)−1
g(−5) = −15−1
g(−5) = −16

​The value of the function is g(−5)=−16.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.7 Page 129 Exercise 11 Answer

Given: A function \(y=\left\{\begin{array}{l}4-x, \text { ifx }<2 \\x+3, \text { ifx } \geq 2\end{array}\right.\)

To graph the function and describe the domain and range.
Make a table of values and plot the points and sketch the graph from the graph, we can identify the domain which is the set of input values shown on the x-axis, and the range which is the set of output values shown on the y-axis.

The given piecewise function is \(y=\left\{\begin{array}{l}4-x, \text { ifx }<2 \\x+3, \text { ifx } \geq 2\end{array}\right.\)
​

For x<2, make a table of values usingy=4−x
Sincex<2, the point(2,2) is not considered and it is represented by an open dot.

For x≥2, make a table of values using y=x+3
Since x≥2, the point(2,5) is considered and it is represented by a closed dot.

Plot the points and sketch the graphs on the same coordinates axis.

From the graph, we see that the domain is the set of all real numbers, and the range is y>2

The graph of the function y={​4−x,ifx<2x+3,ifx≥2 is given below and the domain and range is described as a set of all real numbers andy≥0 respectively.

Page 130  Exercise 12  Answer

Given: A function\(y=\left\{\begin{array}{r}2 x, \imath f x<-2 \\2, i f-2 \leq x<2 \\-2 x, \text { ifx }>2\end{array}\right.\)

To graph the function and describe the domain and range.
Make a table of values and plot the points and sketch the graph from the graph, we can identify the domain which is the set of input values shown on the x-axis, and the range which is the set of output values shown on the y-axis.

The given piecewise function is \(y=\left\{\begin{array}{r}2 x, \imath f x<-2 \\2, \text { if }-2 \leq x<2 \\-2 x, \text { ifx } \geq 2\end{array}\right.\)

For x<−2, make a table of values using y=2x
Since x<−2, the point(−2,−4) is not considered and it is represented by an open dot.

For x≥2, make a table of values using y=−2x

Sincex≥2, the point(2,−4) is considered and it is represented by a closed dot.

The line y=2 is a horizontal line drawn between −2≤x<2
Plot the points and sketch the graphs on the same coordinates axis.

From the graph, we see that the domain is the set of all real numbers, and the range is y=2,y≤−4

The graph of the function \(y=\left\{\begin{array}{r}2 x, \text { if } x<-2 \\2, \text { if }-2 \leq x<2 \\-2 x, \text { ifx } \geq 2\end{array}\right.\) is given below and the domain and range are described as a set of all real numbers and y=2,y≤−4
respectively.

Page 130  Exercise 13  Answer

Given: A function y\(=\left\{\begin{array}{r}
-1, \imath f x \leq-1 \\
0, i f-1<x<2 \\
1, \text { ifx } \geq 2
\end{array}\right.\)

To graph the function and describe the domain and range.
Make a table of values and plot the points and sketch the graph from the graph, we can identify the domain which is the set of input values shown on the x-axis, and the range which is the set of output values shown on the y-axis.

The given piecewise function \(y=\left\{\begin{array}{r}
-1, \text { if } x \leq-1 \\
0, \text { if }-1<x<2 \\
1, \text { ifx } \geq 2
\end{array}\right.\)

The graph of y=−1 is a horizontal line.
The y-coordinate of all of the points on this line are−1
Since x≤−1, the point(−1,−1) is considered and it is represented by a closed dot.
The graph of y=0 is a horizontal line.
The y-coordinate of all of the points on this line are− 0
Since−1<x<2, the points(−1,0),(2,0) are not considered and it is represented by an open dot.

The graph of y=1 is a horizontal line.
The y-coordinate of all of the points on this line are −1
Sincex≥2, the point(2,1)is considered and it is represented by a closed dot.

Plot the points and sketch the graphs on the same coordinates axis.

From the graph, we see that the domain is the set of all real numbers and the range is y=−1,0,1

The graph of the function \(y=\left\{\begin{array}{r}
-1, \imath f x \leq-1 \\
0, \text { if }-1<x<2 \\
1, \text { ifx } \geq 2
\end{array}\right.\) is given below and the domain and range are described as a set of all real numbers andy=−1,0,1
respectively.

Chapter 4 Writing Linear Functions Exercise 4.7 Practice

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.7 Page 130  Exercise 14  Answer

Given: a graph

To write a piecewise function for the graph.
From the graph calculate the change in y coordinate with respect to the change in x coordinate of that line and using the general equation of a line the piecewise function for the given graph is written.

The given graph is

The two lines of this graph have values x<0,x≥0
For x<0, the run is−5, and rise is 7 for the graph so the slope of this line is\(\frac{-7}{5}\) and the line does not intersect the y-axis.

The general equation of a line is y=mx+b where m=slope,b= y-intercept.
The equation of this line is y=\(\frac{-7}{5}\)x+0

For all values of x<0, the function is y=\(\frac{-7}{5}\)x
For all values of x≥0,

The line is a horizontal line.
All the points in this line have the same y-coordinate 3
The equation of this line is y=3

The piecewise function for this graph is \(y=\left\{\begin{array}{c}
y=\frac{-7}{5} x, \text { if } x<0 \\
y=3, \text { ify }=x \geq 0
\end{array}\right.\)

The piecewise function for this graph is \(y=\left\{\begin{array}{c}
y=\frac{-7}{5} x, \text { if } x<0 \\
y=3, \text { ify }=x \geq 0
\end{array}\right.\)

Page 130 Exercise 15 Answer

Given: A graph

To write a piecewise function for the graph.
From the graph calculate the change in y coordinate with respect to the change in x coordinate of that line and using the general equation of a line the piecewise function for the given graph is written.

The given graph is

The three lines of this graph have values −3≤x<0 and 0≤x≤1 and 1<x≤5
For 1<x≤5, the rise and run is the same so the slope is 1 and the line does not intersect the y-axis.

The general equation of a line is y = mx+b where m = slope,b = y-intercept.
The equation of this line is y=x

For all values of −3≤x<0, the line is a horizontal line.
All the points in this line have the same y-coordinate 3
The equation of this line is y=3

For all values of 0≤x≤1, the line is a horizontal line.
All the points in this line have the same y-coordinate 4
The equation of this line is y=4

The piecewise function for this graph is\(y=\left\{\begin{array}{r}
3, i f-3 \leq x<0 \\
4, i f 0 \leq x \leq 1 \\
x, 1<x \leq 5
\end{array}\right.\)

​The piecewise function for this graph is \(y=\left\{\begin{array}{r}
3, i f-3 \leq x<0 \\
4, i f 0 \leq x \leq 1 \\
x, 1<x \leq 5
\end{array}\right.\)

Big Ideas Math Algebra 1 Exercise 4.7 Guide

Page 130  Exercise 16  Answer

Given a postal service charges $4 for shipping any package weighing up to but not including one pound and $1 for each additional pound or portion of a pound up to but not including five pounds.

To write and graph a step function that shows the relationship between the number of pounds a package weighs and the total cost for postage.

Using a table we organize the given information and write a step function based on this and then graph the function that shows the relationship between the number of pounds a package weighs and the total cost  for postage

It is given that a postal service charges $4 for shipping any package weighing up to but not including one pound.
It costs an additional $1 for each additional pound or portion of a pound up to but not including five pounds.
If the package weighs one or more than one pound then $1 is added for each additional pound.

The given information is organized in a table.

The above information can be written as a step function that shows the relationship between the number x of pounds a package weighs and the total cost y for postage as

The graph of this step function that shows the relationship between the number x of pounds a package weighs and the total cost y for postage is drawn.

A postal service charges $4 for shipping any package weighing up to but not including one pound and $1 for each additional pound or portion of a pound up to but not including five pounds then the step function is

And the graph is a step function that shows the relationship between the number x of pounds a package weighs and the total cost y for postage is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions

Page 121 Essential Question  Answer

Given: Patten is an arithmetic sequence

To find a Method to describe the pattern using an arithmetic sequence.
An arithmetic sequence is an ordered list of numbers in which the difference between each pair of consecutive terms, or numbers in the list, is the same.

To describe the pattern using an arithmetic sequence, take the difference of their consecutive term and you get these all differences are same.

Page 122  Exercise 2  Answer

Given: Pattern is an arithmetic sequence.

To find An example from real life to describe an arithmetic sequence.

Real-life example: In a passenger train, there are 125 passengers in the first carriage, 150 passengers in the second carriage and 175 passengers in the third carriage. If the total carriage in a train is 8, then find the number of passengers in 6th
carriage.

So, in this real-life problem, the number of passengers in the carriage is in arithmetic sequence because there is a common difference(d) between The number of passengers i.e.​d=150−125
d=25 and first term(a) is 125.

Real-life example: In a passenger train, there are 125 passengers in the first carriage, 150 passengers in the second carriage, and 175 passengers in the third carriage. If total carriage in a train is 8, then find the number of passengers in 6^thcarriage.

Big Ideas Math Algebra 1 Chapter 4 Exercise 4.6 Solutions

Page 122  Exercise 3  Answer

Given :

To find the Number of atoms in 23 molecules.

In order to find the solution, count the number of atoms till n=5
and make a sequence then find a₂₃.

Count the number of atoms in their respective number of molecules.
So, the sequence will be, 3,6,9,12,15,…….

Here, ​a₁=3
d=6−3
=3

For a₂₃, put n=23 in a_n=a₁+(n−1)d
a₂₃=a1+(23−1)d
a₂₃=3+22×3
a₂₃=69
​
There are 69 number of atoms in 23 molecules.

Page 124  Exercise 1  Answer

Given sequence: 1,8,15,22,…

To find the next three terms of the arithmetic sequence.
In order to find the solution, get the value of first term a1 and common difference d then use the formula
a_n=a₁+(n−1)d

As the given sequence is 1,8,15,22,…
And ​a₁=1
d=8−1
=7

For the next three terms, calculate a₅,a₆, and a₇.
For a₅, put n=5 in above formula
​a_n=a₁+(5−1)d
a₅=(1)+(4)⋅(7)
=1+28
=29
​
For a₆, put n=6
​a_n=a₁+(6−1)d
a₆=(1)+(5).(7)
=1+35
=36
​

For a₇,put n=7
​a_n=a₁+(7−1)d
a₇=(1)+(6).(7)
=1+42
=43
​
The next three terms of the arithmetic sequence will be 29,36,43.

Writing Linear Functions Chapter 4 Exercise 4.6 Answers

Page 124  Exercise 2  Answer

Given sequence: 20,14,8,2,…

To find the next three terms of the arithmetic sequence.
In order to find the solution, get the value of the first term a₁ and common differences then use the formula
a_n=a₁+(n−1)d

As the given sequence is 20,14,8,2,…
And ​a₁=20
d=14−20
=−6

For the next three terms, calculate a₅, a₆, and a₇.
For a₅, put n=5 in  above formula
​a_n​=a₁+(5−1)d
a₅=(20)+(4).(−6)
=20−24
=−4
​

For a₆ , put n=6 in above formula
​a_n​= a₁+(6−1)d
a₆= (20)+(5)⋅(−6)
= 20−30
= −10
​

For a₇, put n=7
​a_n​= a₁+(7−1)d
a₇= (20)+(6)⋅(−6)
= 20−36
=−16
So, the next three terms will be−4,−10,−16.

The next three terms of the arithmetic sequence will be −4,−10,−16.

Big Ideas Math Student Journal Exercise 4.6 Explained

Page 124  Exercise 3  Answer

Given sequence: 12,21,30,39,…

To find the next three terms of the arithmetic sequence.
In order to find the solution, get the value of the first term, a_1, and common difference,d then use the formula
a_n= a₁+(n−1)d

As the given sequence is 12,21,30,39,…
And ​a₁=12
d=21−12
​=9

For the next three terms, calculate a₅, a₆, and  a₇
For a₅, put n=5 in above formula
​a_n= a₁+ (5−1)d
a= (12)+ (4)⋅(9)
= 12 + 36
= 48
​

For a₇, put n=6
a_n= a₁ + (6−1)d
a₇= (12) + (5).(9)
= 12 + 45
= 57
​

For a₇, put n=7
a_n ​= a₁ + (7−1)d
a₇ = (12) + (6)⋅(9)
= 12 + 54
= 66
​
The next three terms of the arithmetic sequence will be 48,57,66.

Page 124   Exercise 4   Answer

Given sequence: 5,12,19,26,…

To find the Next three terms of the arithmetic sequence.
In order to find the solution, get the value of the first term,a_1, and common difference,d then use the formula
a_n=a₁+(n−1)d

As the given sequence is 5,12,19,26,…
And ​a₁=5
d=12−5
​=7

For the next three terms, calculate a₅, a₆, and a₇
For a₅, put n=5 in above formula
​a_n=a₁+(5−1)d
a₅=(5)+(4).(7)
=5+28
=33
​

For a₆, put n=6 in above formula
​a_n=a₁+(6−1)d
a₆=(5)+(5)⋅(7)
=5+35
=40
​

For a₇ , put n=7
a_n=a₁+(7−1)d
a₇=(5)+(6)⋅(7)
=5+42
=47

​So, the next three terms will be 33,40,47.
The next three terms of the arithmetic sequence will be 33,40,47.

Chapter 4 Writing Linear Functions Exercise 4.6 Practice

Page 124 Exercise 5 Answer

Given sequence: 3,7,11,15,…

To find the next three terms of the arithmetic sequence.
In order to find the solution, get the value of the first term, a_1, and common difference,d then use the formula
a_n=a₁+(n−1)d

As the given sequence is 3,7,11,15,…
And ​a₁=3
d=7−3
=4

For the next three terms, calculate a₅,a₆, and a₇.
For a5, putn=5 in above formula
​a_n​=a₁+(5−1)d
a₅=(3)+(4).(4)
=3+16
=19
​
For a₆, put n=6
​a_n=a₁+(6−1)d
a₆=(3)+(5)⋅(4)
=3+20
=23
​
For a₇, put n=7
a_n=a₁+(7−1)d
a₇=(3)+(6)⋅(4)
=3+24
=27

​So, the next three terms will be 19,23,27.
The next three terms of the arithmetic sequence will be 19,23,27.

Page 124 Exercise 6 Answer

Given sequence: 2,14,26,38,…

To find the next three terms of the arithmetic sequence.

In order to find the solution, get the value of the first term,a_1, and common difference,d then use the formula
a_n=a₁+(n−1)d

As the given sequence is2,14,26,38,…
And ​a₁=2
d=14−2
=12

For the next three terms, calculate a₅,a₆, and a₇
For a₅, putn=5 in above formula
​an​=a₁+(5−1)d
a₅=(2)+(4).(12)
=2+48
=50
​

For a₆, put n=6
​a_n=a1+(6−1)d
a₆=(2)+(5)⋅(12)
=2+60
=62
​
For a₇, put n=7
​a_n​=a1 +(7−1)d
a₇=(2)+(6)⋅(12)
=2+72
=74

​So, the next three terms will be 50,62,74.
The next three terms of the arithmetic sequence will be 50,62,74.

Page 124 Exercise 9 Answer

Given sequence is : \(\frac{15}{2}, \frac{13}{2}, \frac{11}{2}, \frac{9}{2}\),……

To find a Graph the given arithmetic sequence.
In order to find the solution, use the order of terms,n in x-axis and the value of terms in y-axis.

To make a graph, plot the points : \(\left(1, \frac{15}{2}\right)_t\left(2, \frac{13}{2}\right)_1\left(3, \frac{11}{2}\right)_{,}\left(4, \frac{9}{2}\right)\).

Here, the order of terms is in the x-axis, and the value of terms in the y-axis.The graph will be

Graph of a given arithmetic sequence

How To Solve Exercise 4.6 Big Ideas Math Chapter 4

Page 124  Exercise 10  Answer

Given sequence is 1,2.5,4,5.5,…

To find a Graph of the given arithmetic sequence.
In order to find the solution, use the order of terms,n in x -axis, and the value of terms in y-axis.

To make a graph, plot the points :(1,1),(2,2.5),(3,4),(4,5.5).
Here, the order of terms is on x-axis, and the value of terms on y-axis.

The graph will be

Graph of a given arithmetic sequence

Page 124 Exercise 12 Answer

Given sequence is: \(\frac{1}{4}, \frac{5}{4}, \frac{9}{4}, \frac{13}{4}\),…….

To find Graph the given arithmetic sequence.
In order to find the solution, use the order of terms,n in x- axis and the value of terms in y-axis.

To make graph , plot the points :\(\left(1, \frac{1}{4}\right)_1,\left(2, \frac{5}{4}\right)_{,}\left(3, \frac{9}{4}\right)_1\left(4, \frac{13}{4}\right)\).

Here, the Order of terms is in x-axis and the value of terms in y-axis. The Graph will be

Graph of given arithmetic sequence

Page 125 Exercise 13 Answer

Given: Graph is

To find whether the representation is an arithmetic progression or not.
First, read the graph and write the sequence then check whether the difference between any two consecutive terms is the same or not.

By observing the graph, the ordered pairs are such that the first coordinate is the position of the term and the second coordinate is the value of the term.
So, the sequence will be a₁ =0,a₂=1,a₃=4,a₄=9

Checking whether the sequence is arithmetic progression or not.
Calculating the difference of all consecutive terms.

​a₂−a₁
=1−0
=1

a₃−a₂
=4−1
=3

As the differences are not the same. So, the sequence is not an arithmetic progression.
The graph does not represent a_n arithmetic progression given by 0,1,4,9,…

Big Ideas Math Chapter 4 Exercise 4.6 Answer Key

Page 125 Exercise 14 Answer

Given: Graph is

To find whether the representation is an arithmetic progression or not.
First, read the graph and write the sequence then check whether the difference between any two consecutive terms is the same or not.

By observing the graph, the ordered pairs are such that the first coordinate is the position of the term and the second coordinate is the value of the term.
So, the sequence will be a₁=20, a₂=30, a₃=40, a₄=50

Checking whether the sequence is arithmetic progression or not.
Calculating the difference of all consecutive terms.
​a₂−a₁
=30−20
=10

a₃−a₂
=40−30
=10

a₄−a₃
=50−40
=10

As the differences are the same. So, the sequence is an arithmetic progression.
The graph represents a_n arithmetic progression given by 20,30,40,50,…

Page 125 Exercise 15 Answer

Given: Graph is

To find whether the representation is an arithmetic progression or not.
First, read the graph and write the sequence then check whether the difference between any two consecutive terms is the same or not.

By observing the graph, the ordered pairs are such that the first coordinate is the position of the term and the second coordinate is the value of the term.
So, the sequence will be a₁=21,​ a₂=18, a₃= 15,a₄=12

Checking whether the sequence is arithmetic progression or not.
Calculating the difference of all consecutive terms.
​a₂−a₁
=18−21
=−3

a₃−a₂
=15−18
=−3

a₄−a₃
=12−15
=−3
Hence, the sequence 21,18.15,12,…is an arithmetic progression.
The graph represents a_n arithmetic progression given by 21,18.15,12,…

Big Ideas Math Chapter 4 Writing Linear Functions Examples Exercise 4.6

Page 125 Exercise 16 Answer

Given sequence:−5.4,−6.6,−7.8,−9.0,…
To find the n^th term and a10

Substitute the values of the first term and common difference in the formula for n^th term and then substitute n=10i n the n^th term.

The given sequence is−5.4,−6.6,−7.8,−9.0,…
First-term a=−5.4
Common difference
​d=−6.6−(−5.4)​
=−6.6+5.4
=−1.2
​
The n^th term is ​a
=a+(n−1)d
=−5.4+(n−1)(−1.2)
=−5.4−1.2n+1.2
=−1.2n−4.2
​
Substitute n=10 in the n^th term, we get
​a₁₀=−1.2(10)−4.2
=−12−4.2
=−16.2
​
The equation for n^th  term of the sequence is−1.2n−4.2 and a10
=−16.2

Page 125 Exercise 17 Answer

 Given sequence: 43,38,33,28,…

To find the n^th term and a10
Substitute the values of the first term and common difference in the formula for n^th term and then substitute n=10 in the n^th term.

The given sequence is 43,38,33,28,…
First-term a=43
Common difference
​d=38−43
=−5

The n^th term is
​a_n=a+(n−1)d
=43+(n−1)(−5)
=43−5n+5
=−5n+48

​Substitute n=10 in the n^th term, we get
​a₁₀=−5(10)+48
=−50+48
=−2
​
The equation for n^th term of the sequence is−5n+48 and a₁₀
=−2

Page 125 Exercise 18 Answer

Given sequence: 6,10,14,18,…

To find the n^th term and a₁₀
Substitute the values of the first term and common difference in the formula for n^th term and then substitute n=10 in the n ^th term.

The given sequence is 6,10,14,18,…
First-term a=6
Common difference
​d=10−6
=4
​
The n^th term is
​an=a+(n−1)d
=6+(n−1)4
=6+4n−4
=4n+2
​
Substitute n=10 in the n^th term, we get
​a₁₀=4(10)+2
=42
​
The equation for the n^th term of the sequence is 4n+2 and a₁₀=42

Page 125 Exercise 19 Answer

Given sequence :−11,−9,−7,−5,…

To find the n^th term and a₁₀
Substitute the values of the first term and common difference in the formula for n^th term and then substitute n=10 in the n^th term.

The given sequence is−11,−9,−7,−5,…
First-term a=−11
Common difference
​d=−9−(−11)
=−9+11
=2

The n^th term is
​a_n=a+(n−1)d
=−11+(n−1)2
=−11+2n−2
=2n−13
​

Substitute n=10 in the n^th term, we get
​a₁₀=2(10)−13
=20−13
=7
​
The equation for n^th term of the sequence is 2n−13 and a₁₀=7

Page 125 Exercise 20 Answer

Given sequence:  34,37,40,43,…

To find the n^th term and a₁₀
Substitute the values of first term and common difference in the formula for n^th term and then substitute n=10 in the n^th term.

The given sequence is 34,37,40,43,…
First-term a=34
Common difference
​d=37−34
=3

The n^th term is
​a_n=a+(n−1)d
=34+(n−1)3
=34+3n−3
=3n+31
​
Substitute n=10 in the n^th term, we get
​a₁₀=3(10)+31
=61
​The equation for n^th term of the sequence is 3n+31 and a₁₀
=61

Solving Linear Functions In Exercise 4.6 Big Ideas Math

Page 125  Exercise 21  Answer

Given sequence is: \( \frac{9}{4}, \frac{7}{4}, \frac{5}{4}, \frac{3}{4}\)

To find the n^th term and a₁₀
Substitute the values of first term and common difference in the formula for n^th term and then substitute n=10 in the n^th term.

The given sequence is\( \frac{9}{4}, \frac{7}{4}, \frac{5}{4}, \frac{3}{4}\)

First-term a\(=\frac{9}{4}\)

Common difference
​d\(=\frac{7}{4}-\frac{9}{4}\)

The n^th  term is ​a_n=a+(n−1)d

\(=\frac{9}{4}\)+(n−1)\(\left(\frac{-2}{4}\right)\)

Substitute n=10 in the n^th term, we get

​a₁₀ \(=\frac{-10}{2}+\frac{11}{4}\)

​The equation for n^th  term of the sequence is \(\frac{-n}{2}+\frac{11}{4}\) and a₁₀=\(=\frac{-9}{4}\)

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions

Page 116 Essential Question Answer

Given: scatter plot.

To find Tell how can you analytically find a line of best fit for a scatter plot.

Firstly, we will pick any two points from the scatter plot, say (x₁,y₁),(x₂,y₂) such that the line of best-fit stays close to almost all the points. Then, we will substitute these points into the slope formula:m\(=\frac{y_2-y_1}{x_2-x_1}\).

The resultant value of m will be the slope of the line of best fit. Then, we will substitute the point (x₁,y₁)and the slope into the point-slope form of the equation of the line y−y₁=m(x−x₁).

Then, we will simplify the equation to get the form of slope-intercept form of the equation of the line y=mx+b, where, m is the slope and b is the y-intercept. The resultant equation will be the line of best fit for a scatter plot.

We can find the line of best fit for a scatter plot analytically using the slope formula and the point-slope form of the equation of the line and then, finally simplifying the equation to get the slope-intercept form of the equation of the line.

Big Ideas Math Algebra 1 Chapter 4 Writing Linear Functions Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions  Page 116  Exercise 1 Answer

Given:

The scatter plot shows the median ages of American women at their first marriage for selected years from 1960 through 2010.

The data from the scatter plot is shown in the table. Note that 0,5,10, and so on represent the number of years since 1960.

To find Tell what does the ordered pair (25,23.3) represent.

From the scatter plot, we can see that the x-coordinate represents the number of years since 1960.

Thus, 25 in the given ordered pair represents the year 1960+25=1985.

Also from the scatter plot, we can see that the y-coordinate represents the median ages of American women at their first marriage. Thus, 23.3 in the given ordered pair represents the median age of women in the year 1985 at their first marriage.

The ordered pair represents that the median age of American women at their first marriage for the year is 1985 is 23.3

Given:

The scatter plot shows the median ages of American women at their first marriage for selected years from 1960 through 2010.

The data from the scatter plot is shown in the table. Note that 0,5,10, and so on represent the number of years since 1960.

To find  Use the linear regression feature to find an equation of the line of best fit.

We will first input the given data in the table in our graphing calculator.

Then, we will use the linear regression feature of the graphing calculator.

Inputting the data from the given table into the graphing calculator, we get the following data

Now, using the linear regression feature in the graphing calculator, we get the line of best fit as y=0.13x+19.85

We have the equation of the line of best fit for the given data as y=0.13x+19.85 which is found using the linear regression feature in the graphing calculator.

Given:

A scatter plot has been.
It has been asked to find an equation of the line of best fit.
For this, a line is drawn and then its equation needs to be found out.

The scatter plot in the graph paper looks like

Now finding the slope of the line that best suits

m\(=\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{21-20}{3-1}\)

m\(=\frac{1}{2}\)

Now the line cuts the y-axis at(0,20)
The y−intercept must be 20 from the above graph
So, the line best suits are y\(=\frac{1}{2} x+20\)

And the graph looks like

The equation of the line that best suits the scatter plot is y\(=\frac{1}{2} x+20\) and its looks like

Writing Linear Functions Chapter 4 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Page 117 Exercise 2 Answer

To find a line that best suits the scatter plot is
To draw a line such that the number of points below that line and the number of points above the line must be almost equal.

A line best fits the scatter plot is the number of points above and below the line should be almost equal.

Page 119 Exercise 1 Answer

A table and an equation has been given.

It has been asked to find to determine whether the model is a good fit for the data in the table.

For this, the graph needs to be plotted using the graphing calculator and then the point from the table needs to be put and see it best suits the line of the equation or not.

Now plotting the equation y=−3x+2 using the graphing calculator

Now plotting all the points from the given table

The point best fit the line So it best fits the equation of the line

After analysis, it has been found that the given table is the best fit for the equation y=−3x+2 and it can be seen in the diagram below

Algebra 1 Student Journal Chapter 4 Writing Linear Functions Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Function Page 120 Exercise 2 Answer

A table and an equation has been given.

It has been asked to find to determine whether the model is a good fit for the data in the table.

For this, the graph needs to be plotted using the graphing calculator and then the point from the table need to be put and see it best suits the line of the equation or not.

Now plotting the equation y=−0.5x+1 using the graphing calculator

Now plotting all the points from the given table

The point above the line is only one and the rest all are below it. So this does not fit the equation.

After analysis, it has been found that the given table does not best fit the equation y=−0.5x+1 and it can be seen in the diagram below

Chapter 4 Writing Linear Functions Step-By-Step Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1

Page 96  Exercise 1  Answer

Given:

To find, find the slope and y-intercept

The slope of the line \(m=\frac{y_2-y_1}{x_2-x_1}\)

The slope-intercept form y=mx+b

Here​(x₁,y₁)=(2,3), (x₂,y₂)=(0,−1)
​
By substituting, we get

​m\(\frac{-1-3}{0-2}\)

=2
​

In the slope-intercept form, we substitute m=2 and take any point we get
​3=2(2)+b
3=4+b
b=3+4
b=−1
​
Substitute ​m=2 b=−1 in the slope-intercept form, and we get
y=2x−1

Using a graphing calculator, the graph of the equation y=2x−1 is

The graph passes through the given points(2,3) and(0,−1). So, the equation is correct.

For the given graph
The slope is m=2
The y-intercept is b=−1

The equation of each line in the slope-intercept form will be y=2x−1

Given:

To find, find the slope and y-intercept

The slope of the line m\(=\frac{y_2-y_1}{x_2-x_1}\)

The slope-intercept form y=mx+b

Here​(x₁,y₁)=(0,2) , (x₂,y₂)=(4,−2)
​
By substituting, we get

​m\(=\frac{-2-2}{4-0}\)

=−1
​

In the slope-intercept form, we substitute m=−1 and take any point we get
​2=−1(0)+b
b=2
​
Substitute​ m=−1 in the slope-intercept form, and we get
b=2
​y=(−1)x+2
y=−x+2
​

Using a graphing calculator, the graph of the equation y=−x+2 is

The graph passes through the given points(0,2) and(4,−2). So, the equation is correct.

For the given graph
The Slope​ m=−1
The y-Intercept b=2

The equation of each line in the slope-intercept form will be y=−x+2

Given:

To find, find the slope and y-Intercept

The slope of the line m\(m=\frac{y_2-y_1}{x_2-x_1}\)

The slope-intercept form y=mx+b

Here​(x₁,y₁)=(−3,3)(x₂,y₂)=(3,−1)
​
By substituting, we get

​m\(=\frac{-1-3}{3-(-3)}\)

In the slope-intercept form, we substitute m\(=\frac{-2}{3}\) and take any point we get

\(=\left(\frac{-2}{3}\right)(-3)+b\)
​
b=3−2

b=1
​
Substitute ​\(m=\frac{-2}{3}\) in the slope-intercept form, we get,

b=1

y\(=\frac{-2}{3} x\)+1

Using a graphing calculator, the graph of the equation y\(=\frac{-2}{3} x\)+1 is

The graph passes through the given points(−3,3) and(3,−1). So, the equation is correct.

For the given graph
The slope m\(=\frac{-2}{3}\)
The y-intercept b=1

The equation of each line in the slope-intercept form will be y\(=\frac{-2}{3} x+1\)

Given:

To find, find the slope and y-intercept
The slope of the line m \(=\frac{y_2-y_1}{x_2-x_1}\)
The slope-intercept form y=mx+b

Here​(x₁,y₁)=(4,0)(x₂,y₂)=(2,−1)
​
By substituting, we get

​m\(=\frac{-1-0}{2-4}\)

In the slope-intercept form, we substitute m\(=\frac{1}{2}\) and take any point we get

​0=\(4\left(\frac{1}{2}\right)+b\)

b+2=0

b=−2
​
Substitute​ m\(=\frac{1}{2}\) in the slope-intercept form, we get

b=−2
​
y\(=\frac{1}{2} x\)+(-2)

y\(=\frac{x}{2}-2\)

For the given graph

The slope m\(=\frac{1}{2}\)

The y-Intercept b=−2

The equation of each line in the slope-intercept form will be y\(=\frac{x}{2}-2\)

Big Ideas Math Algebra 1 Chapter 4 Exercise 4.1 Solution

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1 Page 97  Exercise 2  Answer

Given:

To find, the y-intercept of the line.
The y-intercept of the graph represents the point that crosses the y-axis.
In this graph, we can observe that the y-intercept is at y=20.

The y-intercept of the graph is y=20, this represents the initial cost of the smartphone plan.

Given:

To find, the slope of the line. Interpret the slope in the context.
The slope of the line m\(=\frac{y_2-y_1}{x_2-x_1}\)

Here we take two points from the graph
​(x₁,y₁)=(0,20)
(x₂,y₂)=(2000,80)
​
By substituting, we get

​m=\(\frac{80-20}{2000-0}\)

The slope of the line of the graph is m\(=\frac{3}{100}\), this represents the change in cost for a smartphone plan based on data usage.
​

Given:

To find, an equation that represents the cost as a function of data usage. The slope-intercept form y=mx+b

We get​ m\(=\frac{3}{100}\)
b=20
​By substituting, we get
y\(=\frac{3}{100}\)x+20
where x is the data usage.

The equation that represents the cost as a function of data usage will be y\(=\frac{3}{100}\)x+20

Writing Linear Functions Exercise 4.1 Big Ideas Math

Page 97  Exercise 3  Answer

​Given: The linear function

To find, the equation of the line
Here we solve it graphically.

For any graph of a linear function, we can determine the equation of the line by obtaining the slope and y-intercept.
Once those two values are identified, we can use the slope-intercept form of the function y=mx+b to write the equation of the line.

Let’s take the equation of the line y=−3x+7

We can write the equation of a line using the slope and the y-intercept For example the graph for the equation of the line y=−3x+7

Page 97   Exercise 4  Answer

Given:

To find, the equation of the line.

The slope of the line m\(=\frac{y_2-y_1}{x_2-x_1}\)

The slope-intercept form y=mx+b

We use two arbitrary points(x₁,y₁)=(6,9)(x₂,y₂)=(4,20)

​By substituting we get

​\(m=\frac{20-9}{4-6}\)

In the slope-intercept form, we substitute \(m=\frac{-11}{2}\)and take any point we get

​9\(=\left(\frac{-11}{2}\right)(6)+b\)

9=−33+b

b=33+9

b=42
​
Substitute​ m= \(\frac{-11}{2}\) in the slope-intercept form, we get

b=42
​
y=\(\frac{-11}{2}\)x+42

The graph for the equation y\(\frac{-11}{2} x+42\) will be

For the taken arbitrarily points,
The equation of the line y=\(\frac{-11}{2} x+42\)
The graph will be

Algebra 1 Student Journal Chapter 4 Exercise 4.1 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1 Page 99  Exercise 1  Answer

Given: ​Slope=0

y−Intercept=9

To find, the equation of the line
The slope-intercept form of the line is y=mx+b

Here Slope m=0
And y-Intercept b=9
By substituting, we get
​y=0(x)+9
y=9
​
The equation of the line for the given slope and y-intercept will be y=9.

Page 99  Exercise 2  Answer

Given: ​Slope=−1

y−Intercept=0
​
To find, the equation of the line
The slope-intercept form of the line y=mx+b

Here slope m=−1

The y-Intercept b=0

By substituting, we get

​y=(−1)x+b

y=−x
​

The equation of the line for the given slope and y-intercept will be y=−x

Page 99 Exercise 3  Answer

Given:​ Slope=2

y−Intercept=−3
​
To find, the equation of the line
The slope of the line y=mx+b

Here slope m=2

The y-intercept b=−3

By substituting, we get

​y=2x+(−3)

y=2x−3
​

The equation of the line for the given slope and y-intercept will be y=2x−3

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1 Page 99  Exercise 4  Answer

Given:​ Slope=−3

y−Intercept=7

To find, the equation of the line
The slope-intercept form of the line is y=mx+b

Here Slope m=−3

The y-Intercept b=7

By substituting, we get

y=−3x+7

The equation of the line for the given slope and y-intercept will be y=−3x+7

Page 99  Exercise 5  Answer

Given: ​Slope=4

y−Intercept=−2

To find, the equation of the line
The slope-intercept form of the line is y=mx+b

Here slope m=4
The y-intercept b=−2
By substituting, we get
​y=4x+(−2)
y=4x−2
​

The equation of the line for the given slope and y-intercept will be y=4x−2

Big Ideas Math Writing Linear Functions Exercise 4.1 Help

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1 Page 99  Exercise 6  Answer

Given:​ Slope\(=\frac{1}{3}\)

y−Intercept t=2

To find, the equation of the line
The slope of the line y=mx+b

Here slope m\(=\frac{1}{3}\)

The y-intercept b=2

By substituting, we get

​y=(\(\frac{1}{3}\))x+2

y\(=\frac{x}{3}+2\)
​

The equation of the line for the given slope and y-intercept will be y \(=\frac{x}{3}+2\)

Page 99  Exercise 7  Answer

Given: graph with two points (−1,3),(0,−1) on the line is

To write an equation of a line in slope-intercept form.

We’ll find the slope of the line using the formula of finding the slope of a line passing through two points m=\(\frac{y_2-y_1}{x_2-x_1}\)

Then we’ll write the equation in point-slope form using the formula y−y₁ =m(x−x₁) and simplify it to get a slope-intercept form.

The slope of line passing through the points (−1,3),(0,−1) is

​m\(=\frac{-1-3}{0-(-1)}\)

=−4
​

We have slope m=−4 and a point on the line (−1,3)

The equation of the line in point-slope form can be written as
​y−3=(−4)(x−(−1))
⇒ y−3=(−4)(x+1)
⇒ y−3=−4x−4
⇒ y=−4x−1
​
So, the slope-intercept form of a line is y=−4x−1 with
​m=−4
c=−1

fn-a
The equation of a line in slope-intercept form is y=−4x−1 with
​m=−4
c=−1

Page 99  Exercise 8  Answer

Given: graph with two points (2,4),(0,0) on the line

To write an equation of a line in slope-intercept form.

We’ll find the slope of the line using the formula of finding the slope of a line passing through two points m\(m=\frac{y_2-y_1}{x_2-x_1}\)

Then we’ll write the equation in point-slope form using the formula y−y₁
=m(x−x₁)and simplify it to get a slope-intercept form.

The slope of a line passing through the points (2,4),(0,0) can be found using the formula as-
​
m\(=\frac{0-4}{0-2}\)
​
\(=\frac{-4}{-2}\)

=2

We have m=2 and a point (2,4)
The equation of the line in point-slope form can be written as
​y−4=2(x−2)
⇒y−4=2x−4
⇒y=2x
​
So, the slope-intercept form of a line is y=2x n with
​m=2
c=0
​

The equation of a line in slope-intercept form is y=2x with
​m=2
c=0

Chapter 4 Exercise 4.1 Step-By-Step Solutions Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1 Page 99  Exercise 9  Answer

Given: graph with two points (2,3),(0,1) on the line

To write an equation of line in slope-intercept form.

We’ll find the slope of the line using the formula of finding slope of a line passing through two points m\(=\frac{y_2-y_1}{x_2-x_1}\)

Then we’ll write the equation in point-slope form using the formula y−y₁=m(x−x₁) and simplify it to get a slope-intercept form.

The slope of line passing through the points (2,3),(0,1) can be found using the formula as

​m\(=\frac{1-3}{0-2}\)

=1

We have, m=1 and a point (2,3)
The equation of the line in point-slope form can be written as
​y−3=1(x−2)
⇒y−3=x−2
⇒y=x+1
​
So, the slope-intercept form of line is y=x+1 with
​m=1
c=1

The equation of line in slope-intercept form is y=x+1 with
​m=1
c=1
​

​Page 99  Exercise 10  Answer

Given: graph with two points (0,5),(3,−4) on the line

To write an equation of a line in slope-intercept form.

We’ll find the slope of the line using the formula of finding the slope of a line passing through two points m\(=\frac{y_2-y_1}{x_2-x_1}\)

Then we’ll write the equation in point-slope form using the formula y−y₁
=m(x−x₁) and simplify it to get a slope-intercept form.

The slope of line passing through the points (0,5),(3,−4) can be found using the formula as

​m\(=\frac{-4-5}{3-0}\)

=−3
​

We have m=−3 and a point (0,5)
The equation of the line in point-slope form can be written as
​y−5=(−3)(x−0)
⇒y−5=−3x
⇒y=−3x+5

So, the slope-intercept form of a line is y=−3x+5 with
​m=−3
c=5
​

The equation of a line in slope-intercept form is y=−3x+5 with
​m=−3
c=5

​Exercise 4.1 Big Ideas Math Algebra 1 Guide 

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1Page 99  Exercise 11  Answer

Given: graph with two points (−2,−3),(0,−2) on the line is

To write an equation of a line in slope-intercept form.

We’ll find the slope of the line using the formula of finding the slope of a line passing through two points m\(m=\frac{y_2-y_1}{x_2-x_1}\)

Then we’ll write the equation in point-slope form using the formula y−y₁=m(x−x₁)
and simplify it to get a slope-intercept form.

The slope of a line passing through the points (−2,−3),(0,−2) can be found using the formula as

m\(=\frac{-2-(-3)}{0-(-2)}\)

We have, m\(=\frac{1}{2}\) and a point (−2,−3)

The equation of the line in point-slope form can be written as

​y−(−3)=\(\frac{1}{2}\)(x−(−2))

⇒y+3=\(\frac{1}{2}\)(x+2)

⇒y=\(\frac{1}{2}\)x+\(\frac{1}{2}\)(2)-3

⇒y=\(\frac{1}{2}\)x+1-3

⇒y=\(\frac{1}{2}\)-2

So, the slope-intercept form of a line is y=\(\frac{1}{2}\)-2 with ​m\(=\frac{1}{2}\)

c=−2
​

The equation of a line in slope-intercept form is y=\(\frac{1}{2}\)-2
with\(=\frac{1}{2}\)
c=−2
​

Page 99  Exercise 12  Answer

Given: graph with two points (0,3),(4,0) on the line

To write an equation of a line in slope-intercept form.

We’ll find the slope of the line using the formula of finding the slope of a line passing through two points m \(=\frac{y_2-y_1}{x_2-x_1}\).

Then we’ll write the equation in point-slope form using the formula y−y₁ =m(x−x₁) and simplify it to get a slope-intercept form.

The slope of a line passing through the points (0,3),(4,0) can be found using the formula as

​m\(=\frac{0-3}{4-0}\)

We have, m\(=\frac{-3}{4}\) and a point (0,3)
The equation of the line in point-slope form can be written as

​y−3\(=\left(\frac{-3}{4}\right)(x-0)\)

⇒ y−3=\(\frac{-3}{4} x\)

⇒ y\(=\frac{-3}{4} x+3\)

So, the slope-intercept form of a line is y=\(\frac{-3}{4} x+3\) with

​m\(=\frac{-3}{4}\)

c=3
​
The equation of a line in slope-intercept form is y=\(\frac{-3}{4} x+3\) with

​\(=\frac{-3}{4}[latex]

c=3

Page 100  Exercise 13  Answer

Given: Two points on the line (3,−1),(8,4)

To find equation of the line passing through the given two points.

Using the formula of equation of line passing through two points, we can find the required equation.

By using the formula of the equation of the line passing through two points,  y−y₁=[latex]\frac{y_2-y_1}{x_2-x_1}\)(x−x₁)

We can calculate the equation of a line passing through the points (3,−1),(8,4) as

​y−(−1)\(=\frac{4-(-1)}{8-3}\)(x−3)

⇒ y+1=\(\frac{5}{5}\) (x−3)

⇒ y+1=x−3

⇒ y−x+4=0
​
The equation of a line passing through the points (3,−1),(8,4) is y−x+4=0.

How To Solve Exercise 4.1 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1 Page 100  Exercise 14  Answer

Given: two points on the line (2,1),(3,5)

To find equation of the line passing through the given two points

Using the formula of equation of line passing through two points, we can find the required equation.

By using the formula of the equation of the line passing through two points- y−y₁\(=\frac{y_2-y_1}{x_2-x_1}\)(x−x₁) we can calculate the equation of the line passing through the points (2,1),(3,5) as

​y−1\(=\frac{5-1}{3-2}\)(x−2)

⇒ y−1=4(x−2)

⇒ y−1=4x−8

⇒ y−4x+7=0
​

The equation of line passing through the points (2,1), and (3,5) is y−4x+7=0

Page 100  Exercise 16  Answer

Given: two points on the line (−3,−2),(−4,−1)

To find equation of the line passing through the given two points.

Using the formula of equation of line passing through two points, we can find the required equation.

By using the formula of equation of the line passing through two points- y−y₁
\(=\frac{y_2-y_1}{x_2-x_1}\)(x−x₁) we can calculate the equation of line passing through the points (−3,−2),(−4,−1) as

​y−(−2)\(=\frac{-1-(-2)}{-4-(-3)}\)(x−(−3))

⇒ y+2\(=\frac{-1+2}{-4+3}\)(x+3)

⇒ y+2=\(\frac{1}{-1}\)(x+3)

⇒ y+2=−(x+3)

⇒ y+2=−x−3

⇒ y+x+5=0

The equation of the line passing through the points (−3,−2),(−4,−1) is y+x+5=0.
​

Page 100  Exercise 17  Answer

Given: Two coordinates are given​(8,0),(0,8)
​
Find, Equation of the line that passes through given coordinates. To find the equation of the line, first, find out the slope of the line using the formula ​m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\).

Then to find out the equation of the line using the slope-intercept form we will use the formula ​y=mx+c.

For Example, two points given are ​(7,5),(−9,5)
​
To find out the slope of the line we will substitute the values of the x,y coordinates in the formula ​mm\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

So m\(=\frac{5-5}{-9-7}\)

​\(=\frac{0}{-16}\)

=0
​

To find out the equation of the line we use the formula y=mx+c, substitute the value of mand one of the coordinates in the above formula, and get the value of c.

Then get the equation by substituting the value of m,c in the formula.

To calculate the slope we’ll use the formula, ​m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

​m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

​​\(=\frac{(8-0)}{(0-8)}\)

=−1
​
​Using the formula of slope-intercept, ​y=mx+c, along with the values of m and point (0,8)we calculate c as follows
​y=mx+c
8=(−1)×(0)+c
8=0+c
c=8
​
Substitute the value of m,c in the equation y=mx+c
​y=mx+c
y=(−1)×x+8
y=−x+8
​

The equation of the line that passes through the given points,(8,0),(0,8) is y=−x+8

Big Ideas Math Chapter 4 Exercise 4.1 Walkthrough

 Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1Page 100  Exercise 18  Answer

Two coordinates are provided(−1,7),(2,−5).

Find, the line’s equation that passes through the given coordinates.

To calculate the line’s equation, first determine the line’s slope using the formula.​m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

​
Then, using the slope-intercept form, we’ll use the formula to obtain the line’s equation y=mx+c.

For instance, consider the following two points:(4,7),(6,13) We’ll use the formula m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)to get the slope of the line by substituting the coordinate values x,y.

So,​m \(=\frac{13-7}{6-4}\)

​\(=\frac{6}{2}\)

=3
​

We apply the formula y=mx+c to determine the equation of the line,

Get the value of c by substituting the value of m and one of the coordinates in the given formula.

Substituting the value of m,c into the formula yields the equation.

To calculate the slope we’ll use the formula

​m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

​​m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

=−4
​

Using the formula of slope-intercept, ​y=mx+c, along with the values of m and point(−1,7) we calculate as follows
​y=mx+c
7=(−4)×(−1)+c
7=4+c
c=3
​

Substitute the value of m,c in the equationy=mx+c
​y=mx+c
y=(−4)×x+3
y=−4x+3
​

Equation of the line that passes through the given points(−1,7),(2,−5) , is y=−4x+3

Page 100  Exercise 20  Answer

Given: f(−5)=5,f(5)=15

Find a linear function with the values you’ve provided.

Using the function provided, find the coordinates.

To calculate the line’s equation, first determine the line’s slope using the formula.m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

Then, using the slope-intercept form, we’ll use the formula y=mx+c to obtain the line’s equation.

To find the coordinates, follow these steps:

The y-values are the value of f(x), thus we have the points.(−5,5),(5,15)

To calculate the formula we’ll use the formula,m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)
​
\(=\frac{(15-5)}{(5-(-5))}\)

=1
​

Using the formula of slope-intercept,y=mx+c , along with the values of m and point(5,15) , we calculate c as follows,
​y=mx+c
15=(1)×(5)+c
15=5+c
c=10
​

Substitute the value of m,c in the equation y=mx+c,
y=mx+c
y=(1)×x+10
y=x+10
​

Equation of the line that passes through the given points,(−5,5),(5,15) is y=x+10

Page 100  Exercise 22  Answer

Given: f(2)=6, f(7)=−4

Find, Linear function with the given values.

Find the coordinates using the Function given.

To find the equation of the line, first, find out the slope of the line using the formula m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\).

Then to find out the equation of the line using the slope-intercept form we will use the formula y=mx+c.

To find the coordinates:

The value of  f(x)
would be the y-values, hence we have the points(2,6),(7,−4)

To calculate the slope we’ll use the formula,m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

m=\(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

​\(=\frac{-10}{5}\)

=-2

Using the formula of slope-intercept, y=mx+c, along with the values of m and point(7,−4), we calculate c as follows,
​y=mx+c
−4=−2×7+c
−4=−14+c
c=10
​

Substitute the value of m,c in the equationy=mx+c,
​y=mx+c
y=−2×x+10
y=2x+10
​

Equation of the line that passes through the given points,(2,6),(7,−4) is y=2x+10

Algebra 1 Exercise 4.1 Explanation Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.1 Page 100  Exercise 23  Answer

Given: f(−2)=−2, f(4)=10

Find a linear function with the values you’ve provided.

Using the function provided, find the coordinates.

To calculate the line’s equation, first determine the line’s slope using the formula.m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

Then, using the slope-intercept form, we’ll use the formula y=mx+c to obtain the line’s equation.

To find the coordinates:

The y-values are the value of f(x), thus we have the points.(−2,−2),(4,10)

To calculate the formula we’ll use the formula,m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

=2
​

Using the formula of slope-intercept,y=mx+c, along with the values of m and point(4,10), we calculate c as follows
​y=mx+c
10=2×4+c
10=8+c
c=2
​

Substitute the value of m,c in the equation y=mx+c
​y=mx+c
y=2×x+2
y=2x+2
​

Equation of the line that passes through the given points, (−2,−2),(4,10)​ is y=2x+2.

Page 100  Exercise 24  Answer

Given: f(4)=0,f(2)=8

Find, Linear function with given values.

Find the coordinates using the function given.

To find the equation of the line, first, find out the slope of the line using the formula m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\).

Then to find out the equation of the line using the slope-intercept form we will use the formula y=mx+c.

To find the coordinates:

The value of f(x)
would be the y-values, hence we have the points (4,0),(2,8)

To calculate the slope we’ll use the formula,m \(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

m\(=\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)

=−4
​

Using the formula of slope-intercept,y=mx+c, along with the values of m and point(2,8), we calculate c as follows
​y=mx+c
8=−4×2+c
8=−8+c
c=16
​

Substitute the value of m,c in the equation y=mx+c,
​y=mx+c
y=−4×x+16
y=−4x+16
​

The equation of the line that passes through the given points, (4,0),(2,8) is y=−4x+16

Big Ideas Math Student Journal Exercise 4.1 Examples

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.6

Page 84 Essential Question  Answer

Given: The linear functions​ f(x)=x
g(x)=f(x)+c
h(x)=f(cx)
​
To find the comparison between the graphs of linear functions,

We will sketch the graph of the functions and then compare.

On graphing the functions, we will get

From the graph, we can see that f(x), and g(x) have different y-intercepts, and h(x), and f(x) have different slopes.
The slope of h(x) is c times the slope of f(x).
And the y−intercept of g(x) is c units more than f(x).

The linear function f(x)=x while comparing to the graphs of
g(x)=f(x)+c and
h(x)=f(cx), has different slopes and intercepts.

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Its graphical representation is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.6 Page 84  Exercise 2  Answer

Given: Two functions are ​f(x)=x
h(x)\(=\frac{1}{2} x\).

To find The graph of each function on the same coordinate axes.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and h(x)\(=\frac{1}{2} x\)

From the graph, it is clear that the lines f(x)=x and h(x)\(=\frac{1}{2} x\) intersect with each other. So, The lines have different slopes.

We can conclude the line equations f(x)=x and h(x) \(=\frac{1}{2} x\) intersect and have different slopes. Their graphical representation is

Given: Two functions are ​f(x)=x
h(x)=2x.
​
To find The graph of each function on the same coordinate axes.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and h(x)=2x is

From the graph, it is clear that the lines f(x)=x and h(x)=2x intersect with each other. So, The lines have different slopes.

We can conclude the line equations f(x)=x and h(x)=2x intersect and have different slopes. Their graphical representation is

Given: Two functions are​f(x)=x h(x)-\(=\frac{1}{2} x\).

To find The graph of each function on the same coordinate axes.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and h(x)-\(=\frac{1}{2} x\) is

From the graph, it is clear that the lines f(x)=x and h(x)-\(=\frac{1}{2} x\) intersect with each other. So, The lines have different slopes.

We can conclude the line equations f(x)=x and h(x)-\(=\frac{1}{2} x\) intersect and have different slopes. Their graphical representation is

Given: Two functions ​f(x)=x h(x)=−2x.
​
To find The graph of each function on the same coordinate axes.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and h(x)=−2x is

From the graph, it is clear that the lines f(x)=x and h(x)=−2x intersect with each other. So, The lines have different slopes.

We can conclude the line equations f(x)=x and h(x)=−2x intersect and have different slopes. Their graphical representation is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.6 Page 85  Exercise 3  Answer

Given: Two functions​ f(x)=x k(x)=2x−4
​
To find The graph of each function on the same coordinate axes and which matches the given graphs.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and k(x)=2x−4 is

From the graph, it is clear that the lines f(x)=x k(x)=2x−4 intersect with each other.

The graph of k(x)=2x−4. The graphical representation is

Given: Two functions​ f(x)=x k(x)=−2x+2.
​
To find The graph of each function on the same coordinate axes and which matches the given graphs in the options.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and k(x)=−2x+2 is

From the graph, it is clear that the lines f(x)=x and k(x)=−2x+2 intersect with each other.

The graph of k(x)=−2x+2. The graphical representation is

Given: Two functions are​ f(x)=x k(x)\(=\frac{1}{2} x+4\).

To find The graph of each function on the same coordinate axes and which matches the given graphs in the options.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and k(x)\(=\frac{1}{2} x+4\).

From the graph, it is clear that the lines f(x)=x and k(x)\(=\frac{1}{2} x+4\) intersect with each other.

The graph of k(x)\(=\frac{1}{2} x+4\) . The graphical representation is.

Given: Two functions are​ f(x)=x k(x)\(=\frac{-1}{2} x-2\).

To find The graph of each function on the same coordinate axes and which matches the given graphs in the options.
For finding the nature of the linear equations, let us draw the graphs.

The graphical representation of the functions f(x)=x and k(x)\(=\frac{-1}{2} x-2\) is.

From the graph, it is clear that the lines f(x)=x and k(x)=−2x+2 intersect with each other.

The graph of k(x)\(=\frac{-1}{2} x-2\) . The graphical representation is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.6 Page 85  Exercise 4  Answer

Given: linear function f(x)=x compare to the graphs of
​g(x)=f(x)+c
h(x)=f(C​x)
​
To find  how the graph of the linear function f(x)=x compares to the graphs of
g(x)=f(x)+c
h(x)=f(C​x) and
Use the given equations to draw the graphs.

Graphing the linear function f(x)=x.

Graphing g(x)=f(x)+c

And h(x)=f(cx)

As we can see in all three graphs the graphs results are the same. So, all three equations are having same results.

The linear function f(x)=x while comparing to the graphs of g(x)=f(x)+c and h(x)=f(cx)

The result we get after graphing is the same.

f(x)=x

g(x)=f(x)+c

h(x)=f(cx)

Page 89  Exercise 2  Answer

Given:

To find Describe the transformation from the graph of f to the graph of g.
Use the given data.

Given graph

The functions are f(x)=−x+1 and g(x)=f(x−2)

Put function f(x)=−x+1 in function g(x).

So we get g(x)=f(x−2)
=f(x)−f(2)…………..(1)
Put x=2 in f(x)=−x+1
f(2)=−2+1
=−1

Put value of f(x) and f(2) in equation (1) , we get
g(x)=−x+1−(−1)​
=−x+1+1
g(x)=−x+2

The graph g(x)=f(x−2) is the vertical translation of graph f(x).

Now, since the slopes are the same, the lines are parallel.

If I take f(x) and translate it up 2 units on the y-axis, I would have g(x) .

The Function g(x)=−x+2 is the transformation from the graph of f to the graph of g.

The Function g(x)=−x+2 is the transformation from the graph of f to the graph of g.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.6 Page 89  Exercise 3  Answer

Given:

To find Describe the transformation from the graph of f to the graph of g.
Use the given graph and given equations, to solve.

Given graph

The functions are f(x)=3x and g(x)=f(−x)

Put x=−x in function f(x)=3x , f(−x)=−3x

Put f(−x)=−3x in g(x)

g(x)=−3x

The graph g(x)=f(−x) is the horizontal translation of graph f(x).

Now, since the slopes are not the same, the lines are not-parallel they are crossing each other at point(0,0).

If I take f(x) and translate it Up to 2 units and down−2 units on the x-axis, I would have g(x).

The Function g(x)=−3x is the transformation from the graph of f to the graph of g.

The Function g(x)=−3x is the transformation from the graph of f to the graph of g.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.6 Page 89  Exercise 4  Answer

Given: The graphs of the functions as

The function is, ​g(x)\(=f\left(\frac{1}{2} x\right)\)

\(=\frac{1}{2} x-1\)
​
We first add the positive number one to the function f(x)=x−1 so the graph is vertically shifted upward by one unit which is the graph of y=x.

Now to this function, we multiply a positive term ​\(\frac{1}{2}\)<1 so that the current graph is compressed vertically by a factor of ​\(\frac{1}{2}\)<1 unit giving us the graph of \(y=\frac{x}{2}\). Add the negative number −1 to it so that the graph is vertically shifted downward by one unit giving us the graph of g(x)\(f\left(\frac{x}{2}\right)\)

The given graphs of the functions are as shown.

The function is ​g(x)=\(f\left(\frac{x}{2}\right)\)

\(=\frac{x}{2}-1\)
​

The graph of f(x)=x−1 is vertically shifted upward by one unit which is then compressed vertically by a factor of \(\frac{1}{2}\) and finally vertically shifted downward by one unit giving us the graph of g(x)=\(f\left(\frac{x}{2}\right)\)

Page 89  Exercise 5  Answer

Given:

To find Describe the transformation from the graph of f to the graph of g.
Use the given data.

Given graph

The functions are f(x)=x−2 and g(x)=2f(x)

Put f(x)=x−2 in g(x)

So we get, g(x)=2(x−2)
g(x)=2x−4

The graph g(x)=2f(x) is the horizontal translation of graph f(x).

Now, since the slopes are not the same, the lines are not parallel they are crossing each other at point (2,0) .

If I take f(x) and translate it up by-1 unit on the x-axis and down by−2 units on the y-axis, I would have g(x).

The Function g(x)=2x−4 is the transformation from the graph of f to the graph of g.

The function g(x)=2x−4 is the transformation from the graph of f to the graph of g.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.6 Page 89  Exercise 7  Answer

Given:f(x)=x and g(x)=3x−2

To find Sketch the graph of the equation.
Use the given data.

Given equations,f(x)=x and g(x)=3x−2 Sketching the graph of the above equations using ‘The DESMOS’ Graphing Calculator is

Black line is f(x)=x  , Purple line is g(x)=3x−2

Both the lines cross each other at points (1,1).

The graph g(x)=3x−2 is the vertical translation of graph f(x).

Now, since the slopes are not the same, the lines are not parallel to each other.

If I take f(x) and translate it up−2 and down−2 units on the y-axis, I would have f(x).

And the transformation in equation g(x)=3x−2.

putx=f(x) in the g(x) equation.

g(x)= 3 f(x)-2.

The transformation is g(x)=3f(x)−2 and graph of the equations f(x)=x and g(x)=3x−2 is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3

Page 106 Essential Question Answer

Given: Two lines

To find, whether the lines are parallel or perpendicular
We need to write the equations in the form, y=mx+c and find their slopes, if they are equal, then they are parallel, multiply the slopes, and if the value is −1, then they

Two lines are parallel if their slopes are equal and they are perpendicular if the product of their slopes is −1

Page 106 Exercise 1 Answer

Given: Three lines

To find, the lines which are parallel
We rewrite the equations in slope intercept form, graph the three lines and find the pair of lines that doesn’t intersect at any point

We have
Slope intercept form of 3x+4y=6 is y\(=\frac{-3}{4} x+\frac{3}{2}\)

Slope intercept form of 3x+4y=12 is y\(=\frac{-3}{4} x+3\)

Slope intercept form of 4x+3y=12 is y\(=\frac{-4}{3} x+4\)

From the graph
3x+4y=6 and 3x+4y=12 doesn’t intersect at any point, so they are parallel
4x+3y=12 intersect both lines, so it is not parallel with both lines

The lines 3x+4y=6 and 3x+4y=12 are parallel

Given: Three lines

To find, the lines that are parallel
We write the equations in slope intercept form, graph the three lines and find the set of lines that doesn’t intersect at any point

We have
Slope intercept form of 5x+2y=6 is y=\(\frac{-5}{2} x+3\)

Slope intercept form of 2x+y=3 is y=−2x+3

Slope intercept form of 2.5x+y=5 is y=−2.5x+5

The lines y\(=\frac{-5}{2} x+3\) (red line) and y=−2.5x+5 (blue line)doesn’t intersect at any point, so they are parallel

The parallel lines are 5x+2y=6​ and 2.5x+y=5

Big Ideas Math Algebra 1 Chapter 4 Exercise 4.3 Solution

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 107 Exercise 2 Answer

Given: Three lines

To find, the lines that are perpendicular
We rewrite the equations in slope-intercept form and map the equations, then find the lines that intersect at 90°

We have
Slope intercept form of 3x+4y=6 is y\(=\frac{-3}{4} x+\frac{3}{2}\)

Slope intercept form of 3x−4y=12 is y\(=\frac{3}{4} x-3\)

Slope intercept form of 4x−3y=12 is y\(\frac{4}{3} x-4\)

The lines 3x+4y=6 (red line) and 4x−3y=12 (green line) intersect at 90°

The lines intersecting at 90º are 3x+4y=6 and 4x−3y=12

Given: Three equations
2x+5y=10
−2x+y=3
2.5x−y=5.

​It is required to write each linear equation in slope-intercept form.

And then use a graphing calculator to graph the three equations in the same square viewing window.

And determine which two lines appear to be perpendicular. Then explain how do we tell which two lines are perpendicular.

To do this, use the graphing calculator TI −84 Plus to plot the graph of these equations.

Consider the given equations.
​2x+5y=10
−2x+y=3
2.5x−y=5.
​
Let’s write each linear equation in slope-intercept form.
​2x+5y=10
⇒ 5y=10−2x
⇒ 5y=−2x+10

∴y=\(-\frac{2}{5} x\)+2

​−2x+y=3

∴y=2x+3
​

And
​2.5x−y=5
⇒ −y=5−2.5x
⇒ y=−5+2.5x

∴y=2.5x−5.
​

Let’s graph these slope-intercept form equations by using the graphing calculator Tl−84 Plus. On calculator press Y=, and then enter the expression \(-\frac{2}{5} x\)+2, 2x+3 and 2.5 x-5 in
​Y₁=,
Y₂=,
Y₃=.

​

Now, to see its graph press GRAPH key on the calculator.

The first line y=\(-\frac{2}{5} x\)+2 and the third line y=2.5x−5 are perpendicular because they intersect at a right angle. And that the slope of the third line is 2.5\(=\frac{5}{2}\)

So, the slopes of the perpendicular lines are negative reciprocals.

The slope-intercept form of the given lines
​2x+5y=10
−2x+y=3, and
2.5x−y=5
​
Are
y\(=-\frac{2}{5} x\)+2
y=2x+3,and
y=2.5x−5 respectively.

And by using a graphing calculator the graph of three equations in the same square viewing window is given below.

The first line y=\(-\frac{2}{5} x+2\) and the third line y=2.5x−5 are perpendicular because they intersect at a right angle.

Page 107 Exercise 3 Answer

It is required to explain that how we can recognize lines that are parallel or perpendicular.

Before we think about how we can recognize when lines are parallel or perpendicular, let’s look at a graph with an example of each.

In this example, the red and black lines are parallel and the blue line is perpendicular to both of them.

Visually, we can see that lines are parallel because they will never intersect, they will continue on forever without ever crossing paths.
Algebraically, we can know that lines are parallel because they have the same slope.
​​y=2x−2
y=2x+1
​

Similarly, we can tell that lines are perpendicular when looking at them because when they intersect, it is at a perfect 90o angle.
Algebraically, we can know that lines are perpendicular because their slopes are negative reciprocals.
​y=2x−2
y=\(-\frac{1}{2} x+2\).

Parallel lines are in the same plane and are always the same distance apart.
Perpendicular lines are in the same plane and intersect at right angles.
Parallel lines have the same slope, perpendicular lines have negative reciprocal slopes.

Writing Linear Functions Exercise 4.3 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 107 Exercise 5 Answer

It is required to compare the slopes of the lines in Exercise 2.

And explain that how we can use slope to determine whether two lines are parallel.

There were two parts to Exercise 2, let’s look at these individually and then compare our results.

part-1. Consider the given three equations.
​3x+4y=6
3x−4y=12
4x−3y=12

And consider their slope-intercept form, from the Exercise 2.

​y=\(-\frac{3}{4} x+\frac{3}{2}\)

y=\(\frac{3}{4} x-3\)

y=\(\frac{4}{3} x-4\)

And consider the graph of them on the same coordinate plane.

We can see that the perpendicular lines are:
y=\(-\frac{3}{4} x+\frac{3}{2}\)

y=\(\frac{4}{3} x-4\)

The ones represented by the blue and black lines.

Part-2. Consider the given three equations.
​2x+5y=10
−2x+y=3
2.5x−y=5
​
And consider their slope-intercept form, from the Exercise 2.
​y\(=-\frac{2}{5} x+2\)
y=2x+3
y=2.5x−5

And consider the graph of them on the same coordinate plane.

We can see that the perpendicular lines are:

y\(=-\frac{2}{5} x+2\) and

y=2.5x−5

The ones represented by the blue and black lines.

In part-1. The perpendicular lines were:
​
\(=-\frac{3}{4} x+\frac{3}{2}\) and

y=\(\frac{4}{3} x-4\)

In part-2. The perpendicular lines were:
​
\(-\frac{2}{5} x+2\)

y=2.5x−5

​
The perpendicular lines in Exercise 2 have slopes that are reciprocals of each other and have opposite signs.

In part 1. Slope is \(-\frac{3}{4} \text { and } \frac{4}{3} \text {. }\)

In part 2. Slope is  \(-\frac{2}{5} \text { and } 2.5=\frac{5}{2} \text {. }\)

When two lines have slopes that are negative reciprocals, the lines will always be perpendicular.

The perpendicular lines in Exercise  2 have slopes that are reciprocals of each other and have opposite signs.

In part 1. Slope is  \(-\frac{3}{4} \text { and } \frac{4}{3} \text {. }\)

In part 2. Slope is  \(2.5=\frac{5}{2} \text {. }\)

When two lines have slopes that are negative reciprocals, the lines will always be perpendicular.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 109 Exercise 1 Answer

Given, a graph:

It is required to determine which of the lines are parallel.

To do this, calculate their slopes using the Slope Formula. And if their slopes are identical then lines are parallel.

Two lines are parallel if their slopes are identical.
Thus, we have to calculate their slopes using the Slope Formula.
m\(=\frac{y_2-y_1}{x_2-x_1}\)

Let’s identify the slope of each line.

Line a:

Substitute(x₁,y₁)=(−1,2) and (x₂ ,y₂)=(−2,−1)

Into the slope formula.
m\(=\frac{y_2-y_1}{x_2-x_1}\)

m=3
​

Line b:

Substitute (x₁,y₁)=(0,1)and (x₂,y₂)=(−1,−3)

Into the slope formula.
​m\(=\frac{y_2-y_1}{x_2-x_1}\)

m\(=\frac{-3-1}{-1-0}\)

m=\(\frac{-3-1}{-1-0}\)

m=4

​
Lines b and c have the same slope. So, they are parallel.
Lines b and c have the same slope. And they are parallel.

Algebra 1 Student Journal Chapter 4 Exercise 4.3 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 109 Exercise 2 Answer

Given, a graph :

It is required to determine which of the lines are parallel.

To do this, calculate their slopes using the Slope Formula. And if their slopes are identical then lines are parallel.

Two lines are parallel if their slopes are identical. Thus, we have to calculate their slopes using the Slope Formula.
m\(=\frac{y_2-y_1}{x_2-x_1}\)

Let’s identify the slope of each line.

Line a:

Substitute (x₁,y₁)=(−1,1) and (x₂,y₂)=(1,−3)

Into the slope formula.
​m\(=\frac{y_2-y_1}{x_2-x_1}\)

m\(=\frac{-3-1}{1-(-1)}\)

m=-2

​

Line b:

Substitute (x₁,y₁)=(0,1)and(x₂,y₂)=(1,−3/2)

Into the slope formula.
m\(\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{-3 / 2-1}{1-0}\)

m=\(\frac{-5}{2}\)

m=-\(\frac{5}{2}\)

And line c:

substitute (x₁,y₁)=(2,0)and (x₂,y₂)=(3,−2)

Into the slope formula.
m\(\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{-2-0}{3-2}\)

m=\(\frac{-2}{1}\)

m=-2

Lines a  and c have the same slope, they are parallel
Lines a  and c have the same slope. And they are parallel.

Page 109 Exercise 3 Answer

Given, Line a   passes through (−4,−1) and (2,2).

Line b  passes through (−5,−3) and (5,1).

Line c passes through (−2,−3) and (2,−1).

It is required to determine which of the lines are parallel. To do this, calculate their slopes using the Slope Formula. And if their slopes are identical then lines are parallel.

Two lines are parallel if their slopes are identical.
Thus, we have to calculate their slopes using the Slope Formula.
m\(=\frac{y_2-y_1}{x_2-x_1}\)

Let’s identify the slope of each line.

Line a:

Substitute (x₁,y₁ )=(−4,−1) and (x₂,y₂ )=(2,2)

Into the slope formula.
\(=\frac{y_2-y_1}{x_2-x_1}\)

m\(\frac{2-(-1)}{2-(-4)}\)

m\(=\frac{3}{6}\)

m\(=\frac{1}{2}\)

Line b:

Substitute (x₁ ,y₁ )=(−5,−3) and (x₂,y₂ )=(5,1)

Into the slope formula.
​m\(=\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{1-(-3)}{5-(-5)}\)

m=\(\)

m=\(\frac{2}{5}\)

And line c:
Substitute (x₁,y₁)=(−2,−3)and (x₂,y₂ )=(2,−1)

Into the slope formula.
​m\(=\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{-1-(-3)}{2-(-2)}\)

m\(=\frac{2}{4}\)

m\(=\frac{1}{2}\)

Lines a and c have the same slope. So, they are parallel.
​Lines a and c have the same slope. And they are parallel.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 109 Exercise 4 Answer

Given, Line a  passes through (−2,5) and (2,1
Line b  passes through (−4,3) and (3,4).

Line c passes through (−3,4) and (2,−6).

It is required to determine which of the lines are parallel.

To do this, calculate their slopes using the Slope Formula. And if their slopes are identical then lines are parallel.

Two lines are parallel if their slopes are identical.
Thus, we have to calculate their slopes using the Slope Formula.
m\(=\frac{y_2-y_1}{x_2-x_1}\)

Let’s identify the slope of each line.

Line a:
Substitute (x₁,y₁)=(−2,5)and (x₂,y₂)=(2,1)

Into the slope formula.
​m\(=\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{1-5}{2-(-2)}\)

m=\(\frac{-4}{4}\)

m=−1
​

Line b:
Substitute (x₁,y₁)=(−4,3)and (x₂,y₂)=(3,4)into the slope formula.
​m\(=\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{4-3}{3-(-4)}\)

m=\(\frac{1}{7}\)

And line c:

Substitute (x₁,y₁)=(−3,4)and (x₂,y₂)=(2,−6) into the slope formula.

​m\(=\frac{y_2-y_1}{x_2-x_1}\)

m= \(\frac{-6-4}{2-(-3)}\)

m=\(\frac{-10}{5}\)

m=−2
​

Because none of the lines have the same slope, none are parallel.
None of the lines have the same slope, so none of them are parallel.

Big Ideas Math Writing Linear Functions Exercise 4.3 Help

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 109 Exercise 5 Answer

Given:

Line a: 4x=−3y+9

Line b: 8y=−6x+16

Line c: 4y=−3x+9

It is required to determine which of the lines are parallel.
To do this, write them in the slope-intercept form of a line. Then identify the slope of the lines.
And if their slopes are identical then lines are parallel.

Two lines are parallel if their slopes are identical.
Let’s recall the slope-intercept form of a line.
y=mx+b
Here, we can identify the slope of the line as the value of m.

We will rewrite each equation in this form and find their slopes.
Line a: 4x=−3y+9
⇒​ ​4x=−3y+9
⇒ −3y+9=4x
⇒ −3y=4x−9

∴y=\(-\frac{4}{3} x\)+3

Line a has a slope of \(-\frac{4}{3} x\)[/latex].

Rewrite other equations in slope-intercept form and find their slopes.
Line b: 8y=−6x+16
​8y=−6x+16
⇒ y=\(\frac{-6 x+16}{8}\)

∴y\(=-\frac{3}{4} x+2\)
​
Line b has a slope of \(=-\frac{3}{4} \)

And line c: 4y=−3x+9
​⇒​ 4y=−3x+9
⇒ y=−3x+9

⇒ y \(\frac{-3 x+9}{4}\)
​
∴ y= \(-\frac{3}{4} x+\frac{9}{4}\)

Line c has a slope of \(-\frac{3}{4}\).

Because lines b and c have the same slope, they are parallel.
Lines b and c have the same slope, and they are parallel.

Page 109 Exercise 6 Answer

Given:

Line a: 5y−x=4

Line b: 5y=x+7

Linec: 5y−2x=5

It is required to determine which of the lines are parallel.
To do this, write them in the slope-intercept form of a line. Then identify the slope of the lines.
And if their slopes are identical then lines are parallel.

Two lines are parallel if their slopes are identical.
Let’s recall the slope-intercept form of a line.
y=mx+b
Here, we can identify the slope of the line as the value of m.

We will rewrite each equation in this form and find their slopes.
Line a: 5y−x=4
​⇒​ 5y−x=4
⇒ 5y=x+4

∴y=\(\frac{1}{5} x+\frac{4}{5}\)

Line a has a slope of \(\frac{1}{5}\).

Rewrite other equations in slope-intercept form and find their slopes.
Line b: 5y=x+7
⇒​ ​5y=x+7

∴y=\(\frac{1}{5} x+\frac{7}{5}\)

Line b has slope of \(\frac{1}{5}\).

And line c: 5y−2x=5
⇒​ 5y−2x=5
⇒​ 5y=2x+5

∴y=\(\frac{2}{5} x+1\)

Line c has slope of \(\frac{2}{5}\)

Because lines a and b have the same slope, they are parallel.
Lines a and  Line b have the same slope, and they are parallel.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 109 Exercise 7 Answer

Given, a line that passes through the (3,−1) and is parallel to the line y\(=\frac{1}{3} x-3\)

It is required to write the equation of a line parallel to the given equation that passes through the point (3,−1).

To do this, use the definition of parallel lines and slope-intercept form.

When lines are parallel, they have the same slope.
Consider the given line, which is written in slope-intercept form.
y\(=\frac{1}{3} x-3\)

And Slope-Intercept Form: y=mx+b

In the given equation we can see that the slope of the line is m\(=\frac{1}{3}\)

Therefore, all the lines that are parallel to the given one have a slope of \(=\frac{1}{3}\)

We can write a general equation in slope-intercept form for all lines parallel to the given equation.\(=\frac{1}{3} x+b\)

We are asked to write the equation of a line parallel to the given equation that passes through the point (3,−1).

By substituting this point into the above equation for x and y, we will be able to solve for the y−intercept b of the parallel line.

​y=\(\frac{1}{3} x+b\)

⇒−1\(=\frac{1}{3}(3)+b\)

⇒-1=1+b

∴b=−2
​

Now that we know that b=−2, we can write the equation of the line that is parallel to y\(=\frac{1}{3} x-3\) and passes through the point (3,−1).

y\(=\frac{1}{3} x-2\)

The equation of the line that is parallel to y\(=\frac{1}{3} x-3\) and passes through the point (3,−1) is

y\(=\frac{1}{3} x-2\).

Page 109 Exercise 8 Answer

Given: Point(1,−2) and, equation of a line y=−2x+1.

Hence, We have to find an equation of the line that passes through the given point and is parallel to the given line.

Firstly, We will find the slope of a given line by using the slope-intercept form that is,y=mx+c.

Then, We will use the point-slope form to get the equation of the line.

That is \(m=\frac{y-y_1}{x-x_1}\)

Where m is a slope of a line. x,y is the point.

From the given line equation that is,
y=−2x+1
On comparing with slope-intercept form y=mx+c
We get,m=−2=m₁
We know the two parallel lines have the same slope. That is,m₁ =m₂ =−2
Where, m₂ is the slope of a line whose point is(1,−2).

From the given point(1,−2).
And, slope m₂ =−2 from the above step
By using the point-slope formula we get

m=m₂=\(\frac{y-y_1}{x-x_1}\)

-2\(=\frac{y-(-2)}{x-1}\)

2x+y=0

An equation of the line that passes through the given point and is parallel to the given line is  2x+y=0.

Exercise 4.3 Big Ideas Math Algebra 1 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 110 Exercise 10 Answer

Given:

Hene, We have to determine which of the lines, if any, are parallel or perpendicular.

Firstly, We will observe the graph carefully.

We will find the slope of each line by using two point-slope formula that is
\(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

After that, we compare each line whether they are parallel,m₁ =m₂ or perpendicular,m₁ ×m₂=−1.

From the given graph

For line a: (−1,−2),(1,4).
By using the two-point slope formula\(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

Where,x₁ =−1,x₂ =1,y₁ =−2,y₂ =4.

On putting the values in the two-point slope formula we get,
\(\frac{4-(-2)}{1-(-1)}=\frac{y-(-2)}{x-(-1)}\)

y=3x+1

On putting the values in the two-point slope formula y=mx+c,
we get m=3.

For Line b: (−3,3),(3,1).
By using the two-point slope formula \(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

Where,x₁ =−3, x₂ =3, y₁ =3, y₂ =1.

On putting the values in the two-point slope formula we get,
\(\frac{1-3}{3-(-3)}=\frac{y-3}{x-(-3)}\)

y\(=\frac{-1}{3} x+2\)

On putting the values in the two-point slope formula y=mx+c,
We get m\(=\frac{-1}{3}\)

For Line c: (0,−1),(2,4).
By using the two-point slope formula \(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

Where,x₁ =0,x₂ =2,y₁ =−1,y₂ =4.

On putting the values in the two-point slope formula we get,
\(\frac{4-(-1)}{2-0}=\frac{y-(-1)}{x-0}\)

y\(=\frac{3}{2} x-1\)

On putting the values in the two-point slope formula y=mx+c,
We get y\(=\frac{3}{2}\).

Therefore, From the above steps and graph, we conclude that Line a is perpendicular to the line b.

The slope of the line a=3 and the slope of the line b \(=\frac{-1}{3}\).

As it satisfies the condition of the perpendicular lines that is m₁×m₂=−1,

\(3 \times \frac{-1}{3}\)=-1

−1=−1

Hence, the left-hand side is equal to the right-hand side.

The line a is perpendicular to the line b. As it satisfies the condition of the perpendicular lines.

Page 110 Exercise 12 Answer

Given:
Line a passes through(−2,−4),(−1,−1).

Line b passes through(−1,−4),(1,2).

Line c passes through(2,3),(4,2).

Hene, We have to determine which of the lines, if any, are parallel or perpendicular.

Firstly, We will find the slope of each line by using two point-slope formula that is\(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\).

After that, we compare each line whether they are parallel,m₁ =m_2, and perpendicular,m₁×m₂=−1.

Line a: From the points(−2,−4),(−1,−1) of
By using the two-point slope formula  \(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

Where,x₁=−2, x₂ =−1, y₁ =−4, y₂ =−1.

On putting the values in the two-point slope formula we get

y=3x+2

On comparing with the slope-intercept form y=mx+c
We get m=3.

 Line b: For points(−1,−4),(1,2) of
By using the two-point slope formula \(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

Where,x₁ =−1, x₂ =1, y₁ =−4, y₂ =2.

On putting the values in the two-point slope formula we get

y=3x−1

On comparing with the slope-intercept form y=mx+c,
We get m=3.

Line c: For points(2,3),(4,2) of
By using the two-point slope formula \(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)

Where,x₁ =2, x₂ =4, y₁ =3, y₂ =2.

On putting the values in the two-point slope formula we get

On comparing with the slope-intercept form y=mx+c
We get,m\(=\frac{-1}{2}\).

Therefore, From the above steps, we conclude that
Line a is parallel to the line b.
As the slope of the line a equal to the slope of the line b
That is m=3.

The line a is parallel to line b. And, the Slope of line a= slope of the line b=3.

Page 110 Exercise 13 Answer

Given:

Line a: y\(=\frac{3}{4} x+1\)

Line b: −3y=4x−3

Line c: 4y=−3x+9

Hene, We have to determine which of the lines, if any, are parallel or perpendicular.

Firstly, We will find the slope of each line, by comparing each line with the slope-intercept form y=mx+c.

After that, we compare each line whether they are parallel,m₁ =m_2, and perpendicular,m₁×m₂ =−1.

From the equation of the line a:

y=\(\frac{3}{4} x+1\)

On comparing with the slope-intercept form y=mx+c
We get,m\(=\frac{3}{4}\)

From the equation of the line b: −3y=4x−3

y\(=\frac{-4}{3} x+1\)

On comparing with the slope-intercept form
We get,m=-\(\frac{-4}{3}\)

From the equation of the line c: 4y=−3x+9

y\(=\frac{-3}{4} x+\frac{9}{4}\)

On comparing with the slope-intercept form
We get,m\(=\frac{-3}{4}\).

Therefore, From the above step, we conclude that Line a is perpendicular to the line b.

Slope of line a=\(\frac{3}{4}\) and line b=−\(\frac{4}{3}\)

As it satisfies the condition of the perpendicular lines that is m₁×m₂ =−1

\(\frac{3}{4} \times \frac{-4}{3}\)=-1

−1=−1

Hence, the left-hand side is equal to the right-hand side.

The linea is perpendicular to the line b. As it satisfies the condition of the perpendicular lines.

Big Ideas Math Chapter 4 Exercise 4.3 Walkthrough

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 110 Exercise 14 Answer

Given:

Line a: 5y−2x=1

Line b: y\(=\frac{5}{2} x-1\)

 Line c: y\(=\frac{2}{5} x+3\).

Hene, We have to determine which of the lines, if any, are parallel or perpendicular.

Firstly, We will find the slope of each line, by comparing each line with the slope-intercept form y=mx+c.

After that, we compare each line whether they are parallel,m₂  =m_2, and perpendicular,m₁×m₂ =−1.

From the equation of the line a: 5y−2x=1
y\(=\frac{2}{5} x+1\)

On comparing with the slope-intercept form y=mx+c
We get,m\(=\frac{2}{5}\)

From the equation of the line b: y\(=\frac{5}{2} x-1\)

On comparing with the slope-intercept form
We get,m=\(\frac{5}{2}\).

From the equation of the line c: y\(=\frac{2}{5} x+3\)

On comparing with the slope-intercept form
We get,m\(=\frac{2}{5}\)

Therefore, From the above step, we conclude that Line a
is parallel to the line c.

As the slope of lines a,c\(=\frac{2}{5}\)

Line a is parallel to the line c And, the slope of the line a= the slope of the line c\(=\frac{2}{5}\)

Page 110 Exercise 15 Answer

Given: Point(−2,2) and equation of the line y\(=\frac{2}{3} x+2\)

Hence, We have to find an equation of the line that passes through the given point and is perpendicular to the given line.

Firstly, We will find the slope of a given line by using the slope-intercept form that is,y=mx+c.

Then, We will use the point-slope formula to get the equation of the line.

That is,m\(=\frac{y-y_1}{x-x_1}\)

Where m is the slope of a line. x,y is a point.

From the given line equation that is\(y=\frac{2}{3} x+2\)

On comparing with slope-intercept form y=mx+c,
We get,m\(=\frac{2}{3}\)=m₁.

We know the two perpendicular lines have m₁ ×m₂=−1

Where,m₁=\(\frac{2}{3}\) from above.

Therefore,\(\frac{2}{3}\)×m₂=−1

m₂\(=\frac{-3}{2}\)

Where m₂ is the slope of a line whose point is(−2,2).

From the given point(−2,2).

And,slope,m₂=\(\frac{-3}{2}\) from the above step.
By using the point-slope formula we get

3x+2y=−2

An equation of the line that passes through the given point and is perpendicular to the given line 3x+2y=−2.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 4 Writing Linear Functions Exercise 4.3 Page 110 Exercise 16 Answer

Given: Point(3,1) and, equation os a line 2y=4x−3.

Hence, We have to find an equation of the line that passes through the given point and is perpendicular to the given line.

Firstly, We will find the slope of a given line by using the slope-intercept form that is,y=mx+c.

Then, We will use the point-slope formula to get the equation of the line.

That is,m\(=\frac{y-y_1}{x-x_1}\)

Where m is the slope of a line. x,y is a point.

From the given line equation that is,
​2y=4x−3
y=2x−\(\frac{3}{2}\)

On comparing with slope-intercept form y=mx+c
We get m=2=m₁.

We know the two perpendicular lines have m₁×m₂=−1

where m₁ =2 from above.

Therefore,2×m₂=−1

m₂\(=\frac{-1}{2}\)

Where m₂ is the slope of a line whose point is(3,1).

From the given point(3,1).
And,slope,m ₂\(\frac{-1}{2}\) from the above step.

By using the point-slope formula we get

m₂\(=\frac{y-y_1}{x-x_1}\)

x+2y=5

An equation of the line that passes through the given point and is perpendicular to the given line x+2y=5.

Big Ideas Math Student Journal Exercise 4.3 Examples

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.3

Page 6  Essential Question 9  Answer

To explain how do we use function notation to represent a function.

Using the method of function.

The notation y=f(x) defines a function named f. This is read as “y is a function of x.” The letter x represents the input value or independent variable.

The letter y, or f(x), represents the output value, or dependent variable.

The function notation represents a function that is y=f(x).

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

Page 69 Exercise 1 Answer

Given: Function is f(x)=2x−3 To graph the function in the graph

The given expression is f(x) = 2x-3 Now to graph the given expression

The graph that represents the expression f(x)=2x−3

The given expression is g(x)=x​+2 Now to graph the given expression

The solution for the given expression g(x)=x​+2 is

 So the question has no solution.

The given expression is h(x)=x²−1 Now to graph the equation

The solution for the given expression h(x)=x²−1 is

The given expression is j(x)=2x²−3 Now to graph the given expression

The solution for the given expression j(x)=2x²−3 is

Big Ideas Math Algebra 1 Chapter 3 Exercise 3.3 solution

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.3 Page 70 Exercise 2 Answer

Given: Function is f(x)=x+3
To graph the given function.
Using the method of function.

The given function is f(x)=x+3
Now substitute x=−1, we get,
f(−1)=−1+3
f(−1)=2
Then the point is(−1,2)

Now to draw a graph with the given function and mark the point(−1,2)

The solution for the given function f(x)=x+3 is

Given: Function is f(x)=x+3
To graph the given function.
Using the method of function.

The given function is f(x)=x+3
Now substitute x=0,
f(0)=0+3
f(0)=3
Then the point is(0,3)

To graph the function with the point (0,3)

The solution for the given function f(x)=x+3 is

Given: Function is
f(x)=x+3
To graph the given function.
Using the method of function.

The given function is f(x)=x+3
Now substitute x=1
f(1)=1+3
f(1)=4
Then the point is(1,4)

To draw a graph for the given function and with the point

The solution for the given function f(x)=x+3 is

Given: Function is f(x)=x+3
To graph the given function.
Using the method of function.

The given function is f(x)=x+3
Now substitute x=2 in the given function,
f(2)=2+3
f(2)=5
Then the point is(2,5)

To draw a graph for the given function and the point is(2,5)

The solution for the given function f(x)=x+3 is

Graphing linear functions Exercise 3.3 Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.3 Page 72 Exercise 1 Answer

Given: function is f(x)=x+4

To find its range.
Using the method of function.

The given function is f(x)=x+4
substitute x=4
f(4)=4+4
f(4)=8

To find the function of
f(0)=0+4
f(0)=4

substitute x=2
f(2)=2+4
f(2)=6

The solution for the function f(x)=x+4 is
f(4)=8
f(0)=4
f(2)=6

Page 72 Exercise 2 Answer

Given: A function of “x” is given to us.

To find  We have to find the function at x=−4,0,2
We will put the values of “x” in the given function and get the answer.

The given function is g(x)=5x
Putting the values of “x” in the given function, we get:
​x=−4
⇒ g(−4)=5×−4
⇒ g(−4)=−20
x=0
⇒ g((0)=0
x=2
⇒ g(2)=5×2
⇒ g(2)=10
​
The values of the function at x=−4,0,2 are−20,0,10

Page 72 Exercise 3 Answer

Given: A function of “x” is given to us.

To find We have to find the function at =−4,0,2
We will put the values of “x” in the given function and get the answer.

The given function is h(x)=7−2x
Putting the values of “x” in the given function, we get

​x=−4
⇒ h(−4)=7−2×−4
⇒ h(−4)=15

x=0
⇒ h(x)=7

x=2
⇒ h(2)=7−2×2
⇒ h(2)=3
​
The values of the function at x=−4,0,2 are 15,7,3

Algebra 1 Student Journal Chapter 3 Exercise 3.3 answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.3 Page 72 Exercise 4 Answer

Given: A function of “x” is given to us.

To find We have to find the function at x=−4,0,2
We will put the values of “x” in the given function and get the answer.

The given function is s(x)=12−0.25x
Putting the values of “x” in the given function, we get:
​x=−4
⇒ s(−4)=12−0.25×−4
⇒ s(−4)=13
s=0
⇒ s(0)=12
s=2
⇒ s(2)=12−0.25×2
⇒ s(2)=11.5
​

The values of the function at x=−4,0,2 are 13,12,11.5

Page 72 Exercise 5 Answer

Given: A function of “x” is given to us.

To find We have to find the function at =−4,0,2
We will put the values of “x” in the given function and get the answer.

The given function is ​t(x)=6+3x−2
t(x)=4+3x
​Putting the values of “x” in the given function, we get
​x=−4​
⇒ t(x)=4+3×−4
⇒ t(x)=−8
x=0
⇒ t(x)=4
x=2
⇒ t(x)=4+3×2
⇒ t(x)=10
​
The values of the function at x=−4,0,2 are −8,4,10

Page 72 Exercise 6 Answer

Given: A function of “x” is given to us.

To find  We have to find the function at x=−4,0,2
We will put the values of “x” in the given function and get the answer.

The given function is ​u(x)=−2−2x+7​
⇒u(x)=−2x+5
​Putting the values of “x” in the given function, we get
​x=−4
⇒ u(x)=−2×−4+5
⇒ u(x)=13
x=0
⇒ u(x)=5
x=2
⇒ u(x)=−2×2+5
⇒ u(x)=1
​
The values of the function at x=−4,0,2 are 13,5,1

Big Ideas Math linear functions Exercise 3.3 help

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.3 Page 72 Exercise 8 Answer

Given: A function of “x” is given to us. The value of the function is given at a certain “x”.

To find We have to find the value of x so that the function has the given value.

We will put the given value on the left-hand side of the given function and then solve the equation for “x”.

The given function is b(x)=−3x+1
Putting the given value b(x)=−20 in the above function and simplifying the equation for the value of “x”, we get
​−20=−3x+1
−21=−3x
x=7
​
The value of x so that the function has the given value is 7.

Page 72 Exercise 9 Answer

Given: A function of “x” is given to us. The value of the function is given at a certain “x”.

To find  We have to find the value of x so that the function has the given value.

We will put the given value on the left-hand side of the given function and then solve the equation for “x”.

The given function is r(x)=4x−3
Putting the given value r(x)=33 in the above function and simplifying the equation for the value of “x”, we get
​33=4x−3
36=4x
x=9
​
The value of x so that the function has the given value is 9.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.3 Page 72 Exercise 10 Answer

Given: A function of “x” is given to us. The value of the function is given at a certain “x”.

To find We have to find the value of x so that the function has the given value.

We will put the given value on the left-hand side of the given function and then solve the equation for “x”.

The given function is \(m(x)=\frac{-3}{5} x-4\)
Putting the given value m(x)=2 in the above function and simplifying the equation for the value of “x”, we get

​2\(=\frac{-3}{5} x-4\)

6\(=\frac{-3}{5} x\)

x=\(=\frac{-30}{3}\)

x=−10
​
The value of x so that the function has the given value is−10.

Page 72 Exercise 11 Answer

Given: A function of “x” is given to us. The value of the function is given at a certain “x”.

To find We have to find the value of x so that the function has the given value.

We will put the given value on the left-hand side of the given function and then solve the equation for “x”.

The given function is \(=\frac{5}{6} x-3\)
Putting the given valuew(x)=−18 in the above function and simplifying the equation for the value of “x”, we get

​−18\(=\frac{5}{6} x-3\)

−15\(=\frac{5}{6} x\)

x=\(-15 \times \frac{6}{5}\)

x=−3×6

x=−18
​
The value of x so that the function has the given value is−18.

Chapter 3 Exercise 3.3 step-by-step solutions Big Ideas Math

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 3 Graphing Linear Functions Exercise 3.3 Page 73 Exercise 13 Answer

Given: A linear function of “x” is given to us.

To find We have to complete the table and plot the points obtained on a graph.

We will put the values of “x” in the given function and get values of t(x)
then we will complete the table and plot the graph.

The given function is t(x)=1−2x.
Putting x=−4,−2,0, we get

​x=−4
t(−4)=1−2×−4
t(−4)=9

x=−2
t(−2)=1−2×−2
t(−2)=5

x=0
t(0)=1−2×0
t(0)=1
​
Putting the values x=2,4, we get

​x=2
t(2)=1−2×2
t(2)=−3

x=4
t(4)=1−2×4
t(4)=−7
​

The table that shows the value of the function at different values of x is given below

The graph of the linear function is given below

The table that shows the value of the function at different values of x is given below

The graph of the linear function is given below

Exercise 3.3 Big Ideas Math Algebra 1 guide