CA Foundation Maths Solutions For Chapter 7 Sets, Function & Relations

Sets, Function & Relations

Sets Introduction:

A set is a group of elements or objects that share at least one characteristic or property.
The objects within one set are similar in some respect.
Mathematically, a set can be defined as a group of well-defined objects that are similar in some respect. These objects are called the elements of the set.
For example, consider the set of vowels in the English alphabet. Let this set is represented by the letter V. This set contains 5 elements- a, e, i, o, u. this can also be written as:
V ≡ {a, e, i, o, u}
The following two conventions should be adhered to while denoting a set
1. A set must be denoted by a capital letter.
2. The elements of the set must be denoted in small letters.
A few examples of sets are given below:
A ≡ {1,2,3,4,5}
B≡ {a,b,c,d,e}
In the above examples, A and B are the names of the sets while 1,2,3,4,5, and a,b,c,d,e are the elements belonging to these sets respectively.
The symbol ∈ is used to denote that an element belongs to a particular set. Hence, to denote that 1 belongs to set A, write it as: 1 ε A
ε Is a Greek letter called epsilon.
In number systems, numbers can be classified in various ways as per their characteristics. The standard notations used to denote the commonly used sets of numbers are as shown below:

Read and Learn More CA Foundation Maths Solutions

N ≡ set of all natural numbers = {1,2,3,4,5 … )
W ≡ set ofall whole numbers= {0,1,2,3,4, … }
I ≡ set ofall Integers = {…..-3, -2, -1,0,1,2,3,…}
Q ≡ set ofall rational numbers
R ≡ set of all real numbers
P ≡ set ofall prime numbers
C ≡ set ofall complex numbers

Cardinality of Sets

Cardinality of a set refers to the total number of elements that are present in the set. For example, V= {a, e, i, o, u}
The cardinality of this set of vowels V is 5 as the total number of elements in the set is 5, This can be represented as: |V| = 5 or n(V) = 5

Classification of Sets based on Cardinality

Based on the concept of cardinality, sets can be classified into the following types:

Null Set/ Void Set/ Empty Set

Consider the set B≡ { )

This set has no elements. Hence, the cardinality of this set is zero.

This can be represented as:

|B| =0 or n (B) =0

Such a set is called a null set or a void set or an empty set. A null set can be represented as:

B≡ ∅

Infinite Set

Consider the set of natural numbers.

N= set of all natural numbers= {1, 2, 3, 4….}

This set does not have a final element. The number of elements n this set cannot be counted and is hence, infinite.

Such sets, where the cardinality of the set cannot be exactly determined, are called infinite sets. All the standard sets mentioned above are infinite sets.

Finite Set

Consider the set of the factors of a number, say 12. The factors of 12 are 1, 2, 3, 4, 6, and 12.

If this set is denoted by S, then S = {1,2,3,4,6,12}.

The cardinality of this set is 6. Since this set has a finite number of elements, it is known as a finite set. Hence, sets which have a finite number of elements are called finite sets.

Singleton Set /Singlet

A set which has one and only one element in it is called a singleton set or a singlet.

For example,

A≡ {a}
B≡ {0}

In the above cases, A and B are both singleton sets.

Note:

In the second example, B is not an empty set. It contains the element 0.

B would have been an empty set ifit did not contain any elements, i.e., B ≡ { }

Equivalent and Equal Sets

Equivalent sets

Two finite sets are said to be equivalent if their cardinality is the same, i.e., n(A) = n (B)

For example, if A ≡ {1,2,3,} and B ≡ {4,5,6}

Then, n {A} = n (B} = 3

Hence, A and B are equivalent sets.

Equal sets

Two sets are said to be equal if and only if they contain the same elements.

This implies that every elements of set B is present in set A and every element of set A is present in set B

For example, if A ≡ {a, b, c} and B ≡{c, b, a} then A and B are said to be equal sets.

Equality of sets is denoted as A = B. Note that the order in which the elements of the two equal sets are written is not important.

Two equal sets are always equivalent, but two equivalent sets may or may not be equivalent.

Representation of a Set

There are two ways of representing a set. They are,

Roster notation
Set Builder notation (or Rule Method)

Roster Notation

Consider the set of vowels:

V ≡ (a, e, i, o, u}

Here, each vowel is individually listed down in the set V.

This method in which each element of a set is specified within the set is called the Roster method.

Note:

To denote an infinite set (such as the set of natural numbers) using the Roster method, write the first few elements followed by ‘…’ to indicate continuation up to infinity.

N ≡ (1, 2,3 }

Set Builder Notation

In the set Builder notation, instead of writing down every single element of a set, the common property of the elements of the set is described.

For example, in the Roster notation the set of the first five natural numbers is written as follows:

D≡ {1,2,3,4,5}

Now, if one were to describe this set in words, the description would say, “set D is a set of all elements x such that x is a natural number and x lies between 1 and 5 (both inclusive)”.

This is written in set Builder notation as follows:

D≡ {x|x ∈ N and 1 ≤ x ≤ 5}

Note:

The symbol | is read as “such that”.

Consider another example,

V≡{a, e, i, o, u)

This can be written as “the set V is a set of elements x, such that x is a vowel from the English alphabet.”

This can be written in set Builder notation as: V≡ {x|x is a vowel from the English alphabet)

Hence, in general, if all the elements of a set A have a common property B, then the set can be expressed in the set builder form in the following way:

A≡{x|x has property B}

Examples:

1. Convert the following sets from the set Builder notation to the Roster notation: P= {y|y ∈ w and y < 3)

Solution:

Here, P is a set of all numbers y, such that y is a whole number less than 3. The whole numbers less than 3 are 0,1 and 2. Hence, set P can be written in Roster notation as: P ={0,1,2}

2. Convert the following sets from the set Builder notation to the Roster notation: M ={x|x²- 5x + 6 = 0}

Solution:

Here, M is a set of all such numbers x that satisfy x² -5x + 6 = 0. To find the values of x, solve this quadratic equation.

x² – 5x + 6 = 0

x²- 3x- 2x + 6 = 0

x(x- 3)- 2(x- 3) = 0

(x – 3)(x- 2) = 0

X=3 or x=2

Hence, the set M can be written in the Roster form as: M ≡ {2,3}

Subsets and Supersets

Consider the set ofall students in a particular college. Now, the set of first year students studying in the same college is a part of this bigger set of all students.

Such a set, which is entirely present in a bigger set, is called a subset of the bigger set.

The bigger set is called the superset of the smaller set. Each element of the subset is definitely an element of the superset as well.

However, every element of the superset need not be part of the subset.

A is said to be the superset of B.

Consider the following example:

A≡ {1,2,3,4,5,6} and B≡ {1,2,3,}

Note that every element of the set B is also an element of the set A.

Hence, B is a subset of A or B is contained in A. A is said to be the superset of B.

Note:

A Null set is a subset of every set. Eveiy set is a subset of itself.

Mathematically, a subset is defined as: A is a subset of B if and only if every element of A is an element of B.

This is denoted as follows:

A⊆ B

For example,

A ≡ {1,2}, B ≡ { 1,2}
A ≡ {1,2,3}, B ≡ {1,2,3,4} in both cases, A £ B

In the first example,

B is also a subset of A. Hence, A ⊆ B and B ⊆ A.

∴ Set B = set A

Hence, both the sets are equal. Hence, two equal sets are subsets of each other.

Such a subset is called an Improper subset. Subset A is an improper subset of B if A = B.

In the second example,

B is not a subset of A, which can be denoted by B ⊄ A.

Such a subset, where the superset also contains other elements, is called a proper subset.

Set A is said to be a proper subset of B if A ⊆ B but B ⊆ A.

A proper subset is denoted by the symbol ⊂. Thus, in the second example A⊂B.

Power Set

A Power set is the set of all subsets of a set. Consider a set A≡ {1,2,3}

Now, consider a set {1}. This set is a subset of A. similarly, {1, 2} is also a subset of A similarly, list down all the subsets of A. they would be:

{1}
{2}
{3}
{1,2}
{1,3}
{2,3}
{1,2,3} …(Every set is a subset of itself)
{ } …. (Null set is a subset of every set)

Total number of subsets = 8

Hence, a set of these subsets is called the power set of A.

P≡{{ 1 },{2},{3},{1,2},(1,3),(2,3),{1,2,3},{ } } If is the number of elements (cardinality) in a set is n, then the cardinality of the power set is given by 2ⁿ.

Universal Set

Consider a college, consisting of students from three streams- Arts (set A), Commerce (set C) and Science (set S). All these students together form the set of all the students in the entire
college. Such a set is called a Universal set (set U).

A universal set is a set containing all the elements under consideration. It is represented by the capital letter U.

3. The universal set for the set of all numbers is as follows:

U≡ {-∞…….. ∞}. It includes all natural numbers, integers, rational numbers, irrational numbers, and so on.

Complement of a Set

The concept of complement of a set logically flows from the concept of a universal set.

The complement of a set A, which is a subset of a universal set IJ, includes all the elements present in U which are not present in A. it is denoted by A’.

Suppose,

U ≡ (a,b,c,d,e,f,g,h,i) and

A ≡ {a,b,c,d,e},

Then A’, or complement of the set A ≡ {f,g,h,i}

Union and Intersection of Sets

Consider the following example.

In a room, there are 5 people a, b, c, d, e. Out of them, a, b and c are men while d and e are women. Also, a and e study science while b, c and d study commerce.

∴ The set of males is: M ≡ (a,b, c)

The set of females is: F≡ {d, e)

The set of science students is S ≡ (a, e)

The set of commerce students is C≡(b,c,d}

If the number of female students who have taken science is to be found, find the elements common to the set of females (F) and the set of Science students (S).

This is called an intersection of set F and set S and is denoted by F ∩ S.

Hence, in the above case, F ∩ S ≡ (e)

Thus, an intersection of two sets is formed by the elements that are common to both the sets.

Similarly, consider sets M and F. There is no common element between them,

Hence, M ∩ F =ø

Such sets which have no element in common are called disjoint sets.

Now, consider the females who have not taken science. Here, check the set F and remove all elements ofset S present In this set. This is called the difference between two sets.

F – S ≡ {d}

Thus, difference of set A and set 13 is defined as the elements present in A blit not present in B.

A – B ≡ { x| x ∈ A and x ∉ B}

Now, suppose one wants to represent a set containing “either males or commerce students or both”. This would imply taking all the elements from set M and set C together into one set. This is called the union of set M and set C and is denoted by M∪C.

Thus, M∪C ≡{a,b,c,d}

Thus, the elements common to both M and C are not counted twice. Thus, the elements belonging to the intersection set are subtracted from the union set.

Hence, M∪C = M+C – M ∩ C

Note:

Though b and c exist in both sets, they are written only once while writing the union. This is because no element is ever written twice while writing a set.

Venn Diagrams

Sets can also be represented using diagrams known as Venn diagrams.
This method of representing sets is especially useful when multiple sets are given.
The closed figure corresponding to a set is used to denote that only the elements within this
closed figure belong to this set.
Any element lying outside this figure does not belong to this set. Though sets can be represented in the form of circles, triangles, rectangles and so on, the most commonly used figure in Venn Diagrams is a circle.
Consider the following example.
Let U be the universal set containing all the whole numbers between (and not including) 0 and 11.

Hence, U ≡ (1,2,3,4,5,6,7,8,9,10}

Let P be the set containing all the prime numbers between 0 and 11 (not including the two).

Thus. P ≡ (2,3,5,7)

Let E be the set containing all the even numbers between 0 and 11.

Hence, E = (2,4,6,8,10)

Hence P U E ={2,3,4,5,6,7,8,10}

Also, P ∩ E = {2}

This can be represented using a Venn diagram in the following manner.

This can be represented using a Venn diagram in the following manner

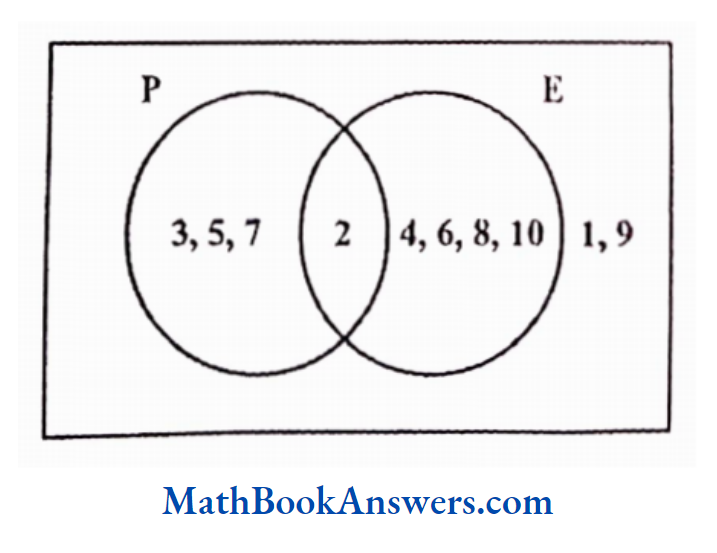
In the above diagram, the universal set is represented by the rectangle while all the other sets are represented by circles.

The common portion between the two sets P and E is the intersection of these two sets.

The universal set contains two numbers, 1 and 9, which do not belong to the set of prime or even numbers. Hence, they are written outside both the circles but within the universal set.

Now, consider the cardinality of these sets.

N(P) = 4, n(E) = 5 and n (PUE) = 8

Thus if we observe, n (PUE)≠ n(P)+n(E)

As explained earlier, the union set is obtained by adding the individual sets and subtracting the intersection set from the sum of individual sets.

Hence, n (P U E) = n (P) +n (E) – n [P ∩ E)

i.e., n (P U E) = 4 +5 -1 = 8

To generalize this, for any two sets A and B,

n (A U B) =n (A) +n(B) -n (A∩B)

Solved Examples

3. In a class of 100 students, 60 play foot balls, 40 play hockey while 10 do not play any sport. Find the number of students who play both hockey and football.

Solution:

N (U) = 100

Since 10 students do not play any game. Let F and H be the set of students playing football and hockey respectively,

n(FUH) = 100-10 =90

∴ n (F) =60

∴ n (H) = 40

The set of students who play both the games is n (F ∩ H)

∴ n(FUH) = n(F)+n(H)-n(F∩H)

∴ 90= 60+40-n (F ∩ H)

Hence, n (F ∩ H) = 100-90 = 10

∴10 students play both football and hockey.

Similarly, consider a universal set as shown below:

U≡ {1, 2, 3,4, 5, 6, 7,8, 9,15)

Let A be the set of all even numbers. Hence, A≡ {2,4,6,8}

Let B be the set ofal perfect squares. Hence, B ≡ {1,4,9}

Let C be the set ofall composite numbers. Hence, C ≡{4, 6, 8, 9, 15}

This can be represented using a Venn diagram as follows:

This can be represented using a Venn diagram as follows

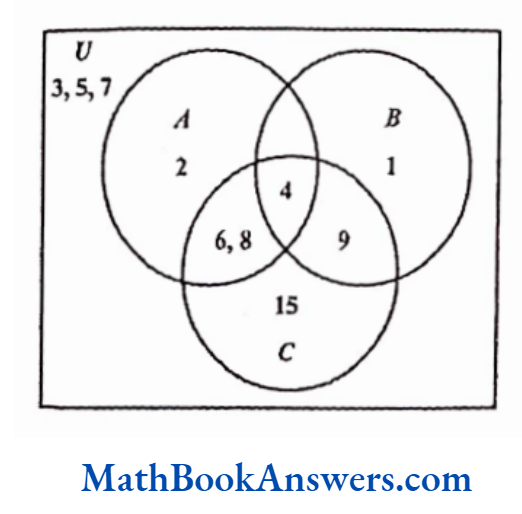
Such a Venn diagram is also known as a three-level diagram.

For a three-level diagram, the formula is

n (A U B U C) =n (A)+ n(B) +n(c)- n(A ∩ B) -n(A ∩ C) – n(B ∩ C)+ n (A ∩ B ∩ C)

So in this case,

n(AUBUC) = 4 + 3 + 5-1- 3- 2 +1 = 7

4. Mow many numbers lying in the range 5000 to 10000 are divisible by 7,11 or 137

Solution:

Let A, B and C be the set of numbers divisible by 7,1 1 and 1 3 respectively.

Lowest number in set A = 5005 and the highest number in A = 9996

∴ Number of Elements in A = \(\frac{9996-5005}{7}+1=714\)

Lowest number in set B = 5005 and the highest number in B = 9999

∴ Number of elements in B= 455

Lowest number in C= 5005 and the highest number in C= 9997

∴ Number of Elements in C = 385

Similarly,

Number of elements divisible by both 7 and 11=Number of elements in the set A ∩ B =65

Number of elements in the set A ∩ B =65

Number of elements in the set A ∩ C =55

Number of elements in the set B ∩ C =35

Number of elements in the set A ∩ B ∩ C = 5

∴Number of elements in the set A U B U C

n(A U B U C) = n(A) + n(B) + n(C)- n(A ∩ B)- n(A ∩ C)- n(B ∩ C) + n(A ∩ B ∩ C)

n(A U B U C) = 714+ 455+ 385 – 65 – 55- 35 +5 = 1404

5. Draw Venn diagrams for:

A – B – C
A ∩ B ∩ C’
A U B U C’

Solution:

1) A – B – C

A - B - C

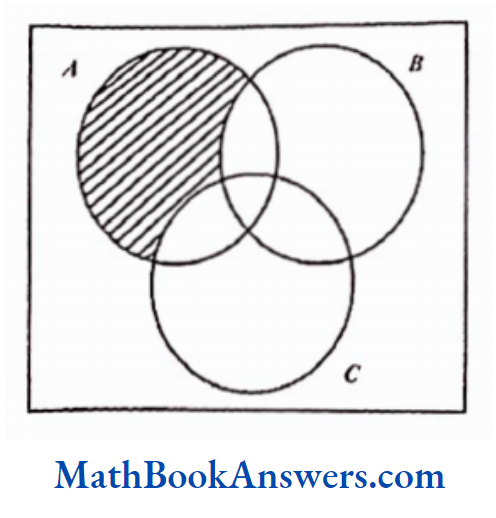
The shaded part comprises all the elements belonging to the set A – B – C

2) A ∩ B∩ C’

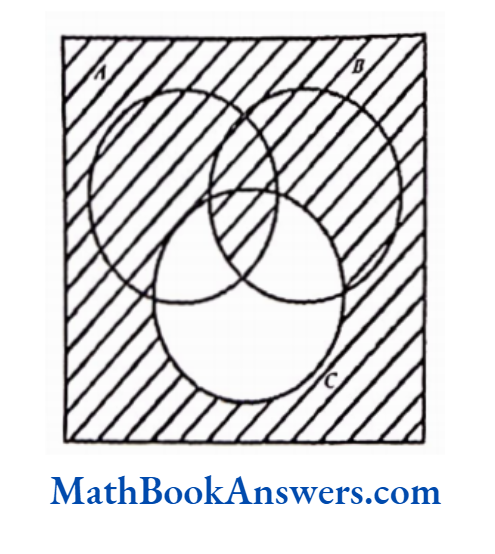
A n B n c'

3) A ∪ B ∪ C’

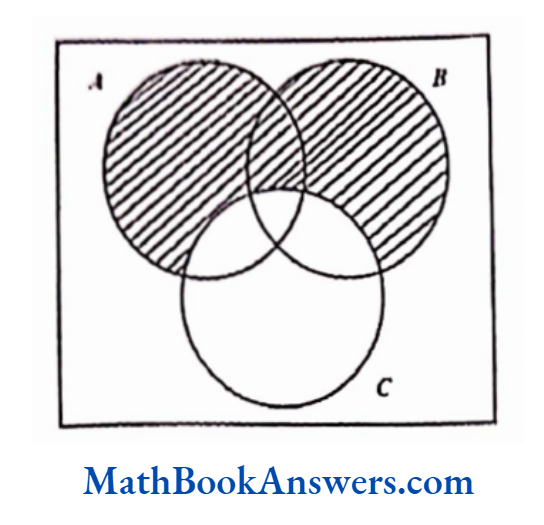
A u B u C

6. Express the following as Venn diagrams:

Every bull is an animal
Some bulls are in the stock market
No animal is a bull

Solution:

Let A = set of Animals, B = set ofbulls, C= set of things in the stock market

Every bull is an animal

Everybull is an animal

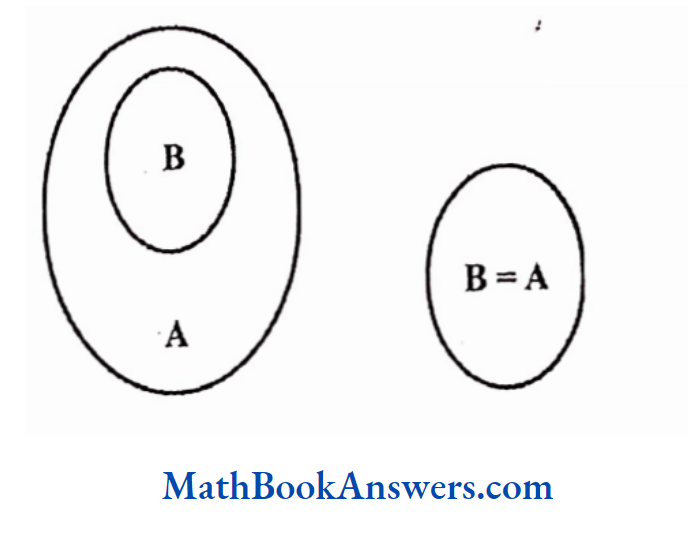
The first figure above is the general form of representing “Every bull is an animal”.

The second figure is true if and only if set B = set A i.e., every bull is an animal and vice versa. In the first figure, some animals may not be bulls.

Some bulls are in the stock market.

This can be represented in 3 different ways as shown

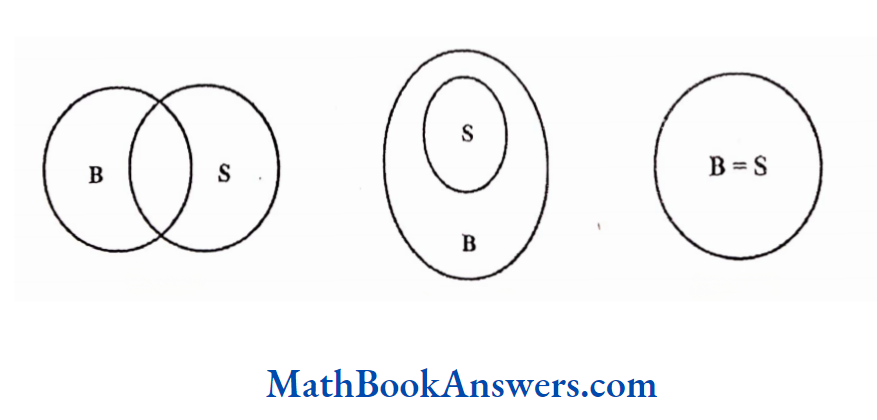
Some bulls are in the stock market

1: only some elements are common to set B and set S.

2: set S is a subset of set B i.e., all the things in the stock market are bulls. Hence, only some bulls will be things in the stock market.

3: set S = set B

No animal is a bull

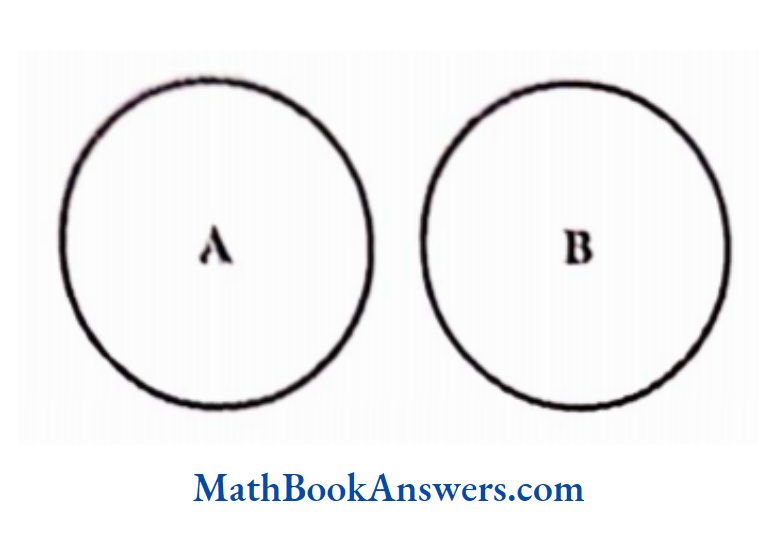
No animal is a bull

Here, A and B are disjoint sets.

7. Three of a popular actor’s films, A, B and C, were nominated for the best film award. 60 persons were asked which film deserved the award the most. 16 people thought only C deserved it. The number of people who thought that all the three films equally deserved the award was twice the number of people who thought that B and C deserved the award but A did not. The number of people who thought that B deserved the award was equal to twice the number ofpeople who thought all the three equally deserved it. The number of people who thought that A and B, but not C deserved the award was equal to the number ofpeople who thought that only A or A and C but not B deserved it. Find the maximum number ofpeople who thought that all the three films deserved the award?

Solution:

From the given data, we can draw the following Venn diagram.

From the given data, we can draw the following Venn diagram

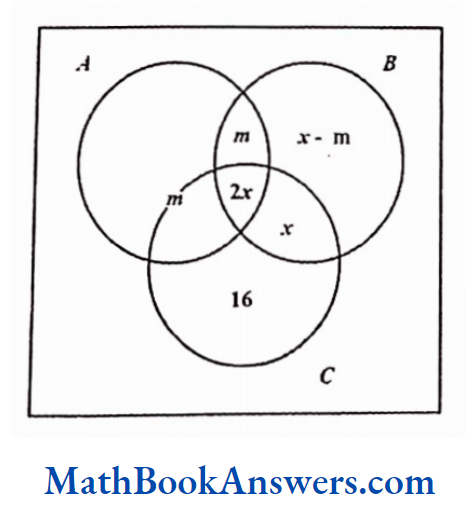
Here, x denotes the number of people who thought that all the three films deserved the award and m denotes the number of people who thought that oniy A or both A and C but not B deserved the award.

Hence, in the figure, m indicates the sum of the number of people who think that oniy A should get the award and the number of people who think that both A and but not B should get the award.

Thus,

2m+x -m +2x+x+16=60

∴ m+4x=44

∴ x is maximum when m = 0

∴ x = 11

∴2x = 22

The maximum no. of people who thought that all the three films deserved the award =22

Properties of Sots

Union of any sot with a null set is equal to the original set. A ∪ ø = A
Intersection ofany set with a null set is equal to a null set. A∩ ø = 0
The intersection of any set with its complement is a null set. A ∩A’ = 0
The union ofany set with its complement is the universal set. A U A = U
(A ∩ B)’ = A‘ U B’
(A ∪ B)’ = A’ ∩ B’
The last two properties are called De Morgan’s laws.
Associative Property
(A U B) U C = A U (B U C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Distributive Property
A U (B ∩ C) = (A U B) ∩ (A U C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Note:

For any two sets A and B,

n(A ∪ B) = n(A) +n(B)- n (A ∩ B)

For any three sets A, B and C, n(A U B U C) = n(A) + n{B) + n(C)- n(A ∩ B)- n(A ∩ C)-n(B ∩ c) + n(A ∩ B ∩ C)

Exercise – 1: Sets

Choose the most appropriate option or options (1) (2) (3) or (4).

1. The number of subsets of the set {2, 3, 5} is

3
8
6
none of these

Answer: (2)

No of subsets of a set with n elements = 2ⁿ

2. The number of subsets of a set containing n elements is

2ⁿ
2^-n
n
none of these

Answer: (1) 2ⁿ

No of subsets of a set with n elements = 2ⁿ

3. The null set is represented by

\(\{\Phi\}\)
{0}
ø
none of these

Answer: (3) ø

Null set = ∅

4. A = (2, 3, 5, 7), B { 4, 6, 8, 10} then A ∩ B can be written as

{ }
\(\{\Phi\}\)
(AUB)’
None of these

Answer: (1) { }

There is no element common to A & B

A ∩ B = { }

5. The set {x|0<x<5} represents the set when x may take integral values only

{0, 1, 2, 3, 4, 5}
{1,2, 3, 4}
{1, 2, 3, 4, 5}
none of these

Answer: (2){1, 2,3,4}

{x|0 < x < 5}

X can take 1, 2, 3, 4 but not 0, 5

6. The set {0, 2, 4, 6, 8, 10} can be written as

{2x | 0<x <5}
(x : 0<x<5}
{2x : 0≤x≤5}
none of these

Answer: (3} {2x : 0 ≤ x ≤ 5}

{0,2(1}, 2(2), 2(3), 2(4), 2(5)}

(2x : 0 ≤ x ≤ 5}

Using Q.7 to Q.10 If P = (1, 2, 3, 5, 7}, Q = (1, 3, 6, 10, 15},
Universal Set S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

7. The cardinal number of P ∩ Q is

3
2
0
none of these

Answer: (2)2

P ∩ Q = (1, 3} -> 2 elements

8. The cardinal number of P U Q is

10
9
8
none of these

Answer: (3) 8

Cardinal no ->n(P U Q}

n(PUQ} = n(P) + n (Q) – n (P ∩ Q}

=5+5-2=8

9. n (P’) is

10
5
6
none of these

Answer: (1) 10

n (P’}) = n (Universal set} – n (P)

= 15-5 = 10

10. n(Q’) is

4
10
4
none of these

Answer: (2)10

n (Q’) = n (Universal set} – n (P)

= 15-5 = 10

11. The set of cubes of the natural number is

a finite set
an infinite set
a null set
none of these

Answer: (2) an infinite set

-> required set = {1, 8, 27,…}

12.The set {2*|x is any positive rational number} is

an infinite set
a null set
a finite set
none of these

Answer: (1) an infinite set

-> required set = {2, 4, 8,…… }

13. {1- (-1)^x} for all integral x is the set

{0} 00
{2}
(0, 2}
none of these

Answer:(3) {0, 2}

-> {1 – (-1)^x} = 0 when x is even

{1 – (-1)^x}= 2 when x is odd

For x ∈ integral -> set is {0, 2}

14. E is a set of positive even number and 0 is a set of positive odd numbers, then E ∪ O is a

set of whole numbers
a set of rational number
N
none of these

Answer: (2) N

E U 0 = all natural no. -> N

15. If R is the set of positive rational number and E is the set of real numbers then

R⊆E
R⊂E
E⊂R
none of these

Answer: (2)R⊂ E

as all rational no belong to real no.

16. If N is the set ofnatural numbers and I is the set ofpositive integers, then

N=1
N⊂1
N⊆ 1
none of these

Answer: (1) N = 1

->N = {1,2, 3,…….}

I = {1, 2,3…… }

N = 1

17. If I is the set of isosceles triangles and E is the set of equilateral triangles, then

I⊂E
E⊂l
E =I
none of these

Answer: (2) E ⊂ 1

-> as all equilateral triangles are isosceles

But all isosceles are not equilateral

18. If R is the set of isosceles right angled triangles and I is set of isosceles triangles, then

R=1
R⊃I
R⊂l
none of these

Answer: (3)R⊂1

-> all right angle isosceles triangle are isosceles but all isosceles are not right-angled.

19. {n(n+1)/2: n is a positive integer} is

a finite set
an infinite set
is an empty set
none of these

Answer: (2) infinite set

{1,3,6……………….}

20. If A = {1, 2, 3, 5, 7}, and B = {x² : x∈A}

n(b) = n(A)
n(B) > n(A)
n(A)= n(B)
n(A)<n(B)

Answer: (3) n (A) = n (B)

A = {1,2, 3, 5, 7} n (A) = 5

B = (1,4, 9, 25, 49) n(B) = 5

N (A) = n (B)

21. AUA is equal to

A
E
ø
none of these

Answer: (1) A

A U A = A

22. A ∩ A is equal to

ø
A
E
none of these

Answer: (2)A

->A ∩ A = A

23. (AUB)’ is equal to

(A’nB)’
A’UB’
A’nB’
none of these

Answer: (3) A’ n B’

(A U B)’ = 1 – (A U B)

= 1 – (A U B)

(A U B)’ = . A’, n B’

24. (A∩B)’ is equal to

(A’ u B)’
A’ U B’
A’ ∩ B’
none of these

Answer: (2) A’ U B’

(A ∩ B)’ = A’ U B’

25. A∪ E is equal to (E is a superset of A)

A
E
ø
none of these

Answer: (2) E

26. A∩E is equal to (E is a superset of A)

A
E
ø
none of these

Answer: (1) A

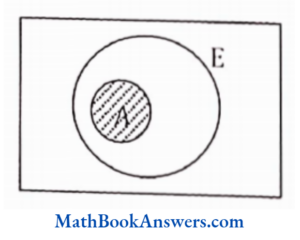
27. E∪E is equal to (E is a superset of A)

E
ø
2E
none of these

Answer: (1) E

28. A∩ E’ is equal to (E is a superset of A)

E
ø
A
none of these

Answer: (2) ø

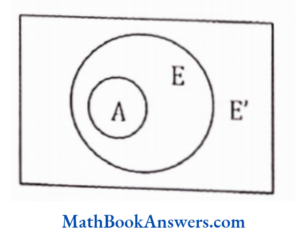
29. A ∩ ø is equal to (E is a superset of A)

A
E
ø
none of these

Answer: (3) ø

30. AUA’ is equal to (E is a superset of A)

E
ø
A
none of these

Answer: (3) E

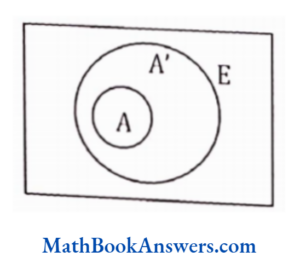30 th answer E = E

31. If K = { 1, 2, 3. 4, 5, 6, 7, 8, 9}, the subset of E satisfying 5 + x > 10 is

{5, 6, 7, 8, 9}
{6, 7,8, 9}
{7, 8, 9}
none of these

Answer: (2) {6, 7, 8, 9}

->E = 1 to 9

5 + x > 10

X > 5

x = 6, 7, 8, 9

32. If A Δ n = (A-B) U (B-A} and A = { 1. 2, 3, 4). B = {3,5,7} than A ΔB is

{1,2, 4, 5, 7}
{3}
{1,2, 3, 4, 5, 7}
none of these

Answer: (c) A Δ B = (A – B) U (B – A)

A = {1,2, 3, 4}

B = {3, 5,7}

A- B = {1, 2, 4}

B – A = (5, 7}

(A – B) U (B – A) = {1, 2, 4, 5, 7}

33. If A has 32 elements, B has 42 elements and A U B has 62 elements, the number of elements in A ∩ B is

12
74
io
none of these

Answer: (1) 12

n (A ∩ B) = n (A) + n (B) -n (A∩B)

62 = 32 + 42 – n (A ∩ B)

n (A ∩ B) = 74- 62 -> 12

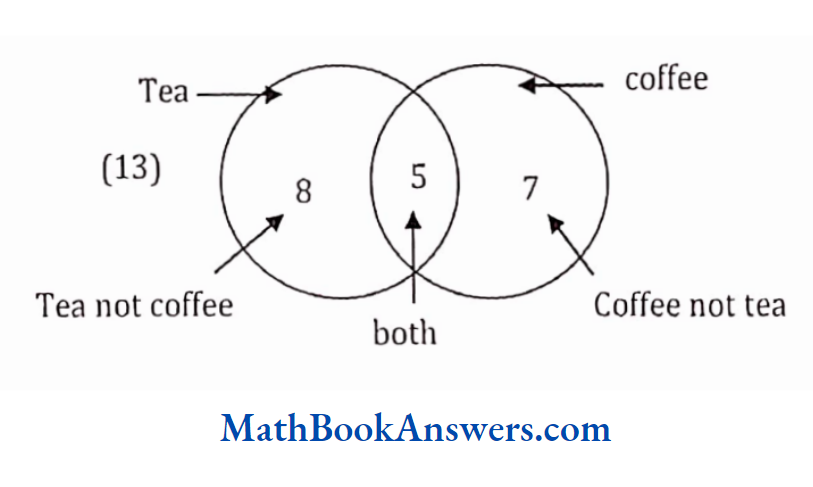
34. In a group of 20 children, 8 drink tea but not coffee and 13 like tea. The number of children drinking coffee but not tea is

6
7
1
none of these

Answer: (2) 7

35. The number of subsets of the sets {6, 8, 11} is

9
6
8
none of these

Answer: (3) 8 No. of subsects = 2ⁿ= 2³ = 8

36. The sets V = {x / x+2=0), R={x / x²+2x=0} and S = {x : x² + x- 2 = 0} are equal to one another if x is equal to

-2
2
1/2
none of these

Answer: (1) -2

If we go by choices

V = 0 = -2 + 2

R = 4 – 4 = 0

S=4-2-2=0

V = R = S for- 2

37. If the universal set E = {x |x is a positive integer <25}, A = {2, 6, 8, 14, 22}, B = {4, 8, 10, 14} then

(A n B}’=A’ U B’
(A n B]’= A’ n B’
(A’ n B)’= 0
none of these

Answer:(1) (A ∩ B)’ = A’ U B’

-> (A ∩ B) = {8, 14}

(A ∩ B)’ = {1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15 ………}

A’ = {1, 3,4,……24}

B’ = {1, 2, 3 ……….24} A’ U B’ = {1, 2, 3, 4, 5, 6, 7………. }

(A ∩ By = A’ U B’

38. If the set P has 3 elements, Q four and R two then the set P x Q x R contains

9 elements
20 elements
24 elements
none of these

Answer: P = 3 elements, Q = 4 elements R = 2 elements

n (P x Q x R) = 3 x 4 x 2 = 24 -> (3) 24

39. Given A = {2, 3}, B = {4, 5}, C = {5, 6} then A x (B∩C) is

{(2, 5), (3,5)}
{(5,2),(5,3)}
{(2, 3), (5, 5)}
none of these

Answer: A = {2,3} B = {4, 5}, C = {5, 6} A x (B ∩ C) B ∩ C = {5}

A x (B ∩ C) = {(2, 5), (3,5)}

(1) {(2,5), (3,5)}

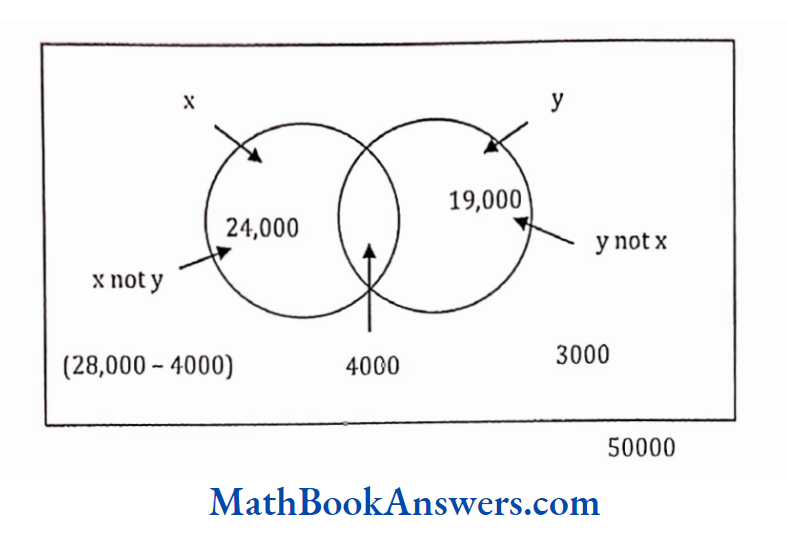
40. A town has a total population of 50,000. Out of it 28,000 read the newspaper X and 23,000 read Y while 4,000 read both the papers. The number of persons not reading X and Y both is

2,000
3,000
2,500
none of these

Answer: (2) 3000

Total Population 50000

41. If A = {1, 2, 3, 5, 7} and B = {1, 3, 6, 10, 15}. Cardinal number of A-B is

3
4
6
none of these

Answer: (1) 3

A – B = {2, 5, 7} ->3

42. At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. The number of women doctors attending the conference is

2
4
1
none of these

Answer: (3) 1

Total Indian attendees -> 29 + 23 = 52

Let M = 23 men w = 29 women D represent doctors

We are given

n (M U D) = 24

n (M) + n (D)- n (M ∩ D) = 24

23 + 4 – n (M ∩ D) = 24

n (M ∩ D) = 3

no. of male doctors = 3

Total doctors 4 & all Indian

no. of female doctors = 4-3 = 1

43. Let A = {a, b}. Set of subsets of A is called power set of A denoted by P(A}. Now n(P(A)) is

2
4
3
none of these

Answer: (2) 4

A = {a, b)

P (A) power set

n (P(a))

No. of subsets = 2² = n (Power set) = 4

44. Out or 2000 employees In an office 40% preferred Coffee (c), 54% liked (T), 64% used to smoke (S). Out of the total 28% used C and T, 32% used T and S and 30% preferred C and S, only 6% did none of these. The number having all the three Is

360
300
380
none of these

Answer: (1) 360

Coffee -> 48% = n (c) = 960

Tea -> 54% = n (T) = 1080

Smoke -> 64% = n(s) = 1280

n (c ∩ T) = 560 b (T ∩ S) = 640 n (C ∩ S) = 600

120 ->none

n(CUSUT) = 2000 -120 = 1880

1880 = n (c) + n (T) + n (s) – n(C∩T) – n (T∩S) – n (C ∩ S) + n (C ∩ S ∩ T)

1880 = 960 + 1080 + 1280 – 560 – 640 – 600 + n (C∩S∩T)

1880- 1520 = n (C∩S∩T) = 360

45. Following set notations represent: A⊂B; x ∉ A; A⊃B; {0}; A⊄ B

A is a proper subset of B; x is not an element of A; A contains B; singleton with an only element zero; A is not contained in B.
A is a proper subset of B; x is an element of A; A contains B; singleton with an only element zero; A is contained in B.
A is a proper subset of B; x is not an element of A; A does not contain B; contains elements other than zero; A is not contained in B.
None

Answer: (1)

A ⊂ B = A is proper subset of B
X ∉ A = x does not belong to A
A ⊃ B = A contains B
{0} = singleton with element 0
A ⊄ B = A is not contained in B

46. Represent the following sets in set notation: – Set of all alphabets in English language, set of all odd integers less than 25, set of all odd integers, set of positive integers x satisfying the equation x²+5x+7=0 :

A = {x:x is an alphabet in English}, 1 = (x:x is an odd integer>25},I = {2, 4, 6, 8 ….} I = {x: x²+5x+7=0}
A= {x:x is an alphabet in English},I = {x:x is an odd integer<25}, 1 = {1, 3, 5, 7 ….} I = {x: x²+5x+7=0}
A = {x:x is an alphabet in English},I = {x:x is an odd integer £ 25},I = (1, 3, 5, 7 ….} I = {x: x²+5x+7=0}
None

Answer: (2)

—> A = (x : x alphabet in english}

—>I = (x: x is odd integer < 25}

—>I = (x: x is set ofall odd int) = {1, 3.5,….. }

->I = {x: x² + 5x + 7 = 0}

47. Rewrite the following sets in a set builder form: – A = {a, e, i, o, u} B = {1, 2, 3, 4 ….} C is a set of integers between -15 and 15.

A = {x:x is a consonant}, B= {x:x is an irrational number}, C = {x:-15<x<15^ x is a fraction}
A = (x:x is a vowel}, B= {x:x is a natural number}, C = {x: -15³X³15^ x is a whole number}
A = {x:x is a vowel}, B = {x:x is a natural number}, C = {x: -15 <x<15^ X is a whole number}
None

Answer: (1)

A = {x: x is a vowel}

B = {1, 2, 3, 4,…..}->B={x| x is a natural no.}

C = {x: – 15 < x < 15 A x is a whole no}

48. If V = (0, 1, 2, …9}, X = {0, 2, 4, 6, 8}, Y = {3, 5, 7} and Z = {3 7} then YUZ, (VUY) ∩ X, (XUZ)UV are respectively: –

{3,5, 7},{0, 2,4,6, 8}, {0, 1, 2, …9}
{2,4, 6},{0, 2,4, 6, 8}, {0,1, 2, …9}
{2, 4, 6}, {0,1, 2, …9},{0, 2, 4, 6, 8}
None

Answer: (1) Go by choices

49. In question No. (48) (X U Y) ∩ Z and (ø ∪ V) nø are respectively: –

{0, 2, 4, 6, 8},ø
{3, 7}, ø
{3, 5, 7}, ø
None

Answer: (b) (3, 7},ø

-> (ø u V) ∩ ø -> ø

-> (x U y) n z -> x U y = (0, 2, 3,4,5, 6, 7, 8}

Z = (3, 7}

X U y ∩ Z = (3, 7}

50. What is the relationship between the following sets? A = {x:x is a letter in the word flower} B = {x:x is a letter in the word flow} C = {x:x is a letter in the word wolf} D = {x:x is a letter in the word follow}

B=C=D and all these are subsets of the set A
B=C≠D
B≠C≠D
None

Answer:(1) B = C = D ⊂ A

51. Comment on the correctness or otherwise or the following statements: –
(1) {a, b, c) = (c, b, a}
(2) {a,b,c,d)) ⊂ (a.c.d)
(3) {b} ∈ {{b}}
(4) {b} ⊂ ((b)) and
(5)ø ⊂{{b}}.

Only (4) is incorrect
(2) (3) are incorrect
(1) (2) are incorrect
All are incorrect

Answer: (1) only (4) is incorrect

->(b) ⊄ {{b}} as b is not an element of({b}}

-> ø ⊂ {{b}} as ø is not an element of {b}}

52. If A=(a, b, c). B=(a, b). C = (a, b, d}, D=(c, d) and E=(d) state which of the following statements are correct: –

(1)B⊂A
(2) D ≠ C
(3) C⊃E
(4) D ⊂ E
(5) D ⊂ B
(6) D = A
(7) B ⊄ C
(8) E⊂A
(9) E ⊄B
(10) a∈ A
(11) a⊂A
(12) (a) ∈ A
(13) (a) ⊂ A

(1) (2) (3) (9) (10) (13) only are correct
(2) (3) (4) (10) (12) (13) only are correct
(1) (2) (4) (9) (11) (13) only are correct
None

Answer: (1) is correct

53. Let A = (0), B = (0 1), C =ø, D = (0), E = (x|x is a human being 300 years old), F = (x|x ∈ A and x e B} state which of the following statements are true: –

(1) A ⊂ B
(2) B = F
(3) C ⊂D
(4) C= E
(5) A = F
(6) F = 1 and
(7) E = C = D

(1) (3) (4) and (5) only are true
(1) (2) (3) and (6) only are true
(1) (2) (3) and (4) are true
None

Answer: (1) is correct

54. If A = (0, 1} state which of the following statements are true: –

(1) (1) ⊂ A
(2) {1} ∈ A
(3) ø ∈ A
(4) 0 ∈ A
(5) 1 ⊂ A
(6) {0} ∈ A
(7) ø ⊂ A

(1) (4) and (7) only are true
(2) (3) and (6) only are true
(1) (4) and (6) only are true
None

Answer: (1) is correct

55. State whether the following sets are finite, infinite or empty: –

(1) X = (1, 2, 3,…..500)
(2) Y ={y: y=a²; a is an integer)
(3) A = (x:x is a positive integer multiple of 2)
(4) B = (x:x is an integer which is a perfect root of 26<x<35)

finite infinite infinite empty
infinite finite infinite empty
infinite infinite finite empty
None

Answer: (1) is correct

56. If A = {1, 2, 3, 4} B = {2, 3, 7, 9) and C = (1, 4, 7, 9} then

A ∩ B ≠ ø B ∩ C≠ ø A ∩ C≠ ø but A ∩ B ∩ C = ø
A ∩ B = ø B ∩ C = ø A ∩ C =ø A ∩B ∩C=ø
A ∩ B ≠ ø B ∩ C ≠ ø A ∩ C≠ ø A ∩ B ∩ C ≠ ø
None

Answer: (1) A ∩ B = (2, 3} B∩C = (7,9) A ∩ C = {1,4}

A∩B∩C=ø

57. If the universal set isX = (x:x ∈ N, 1≤ x ≤ 12} and A = (1, 9, 10), B = (3, 4, 6, 11, 12} and C = (2, 5, 6} are subsets of X then set A U (B ∩ C) is_.

{3, 4, 6, 12}
{1, 6, 9, 10}
{2, 5, 6,11}
None

Answer: (2) {1,6, 9, 10}

-> B ∩ C = {6}

A U (B ∩ C) = {1, 6, 9,10}

58. Identify the elements of P if set Q = (1, 2, 3} and P x Q = {(4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5,3), (6,1), (6,2), (6,3)}

{3, 4, 5}
{4, 5, 6}
{5, 6, 7}
None

Answer: (2) (4,5.6}

Set P will have the preimages of ordered

pairs of p x Q P= {4,5.6}

59. If A = (2, 3}, B = {4, 5), C = (5, 6} then A x (B U C) is

{(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
{(2,5), (3,5)}
{(2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (4, 6), (5, 5), (5, 6)}
None

Answer: (1)

B U C -> {4, 5, 6}

A x {B U C} = {(2, 4}, (2, 5), (2, 6), (3, 4), (3,5), (3,6)}

60. Complaints about works of canteen had been about Mess (M) Food (F) and Service (S). Total complaints 173 were received as follows :-n(M)=110,n(F)=55,n(S)=67,n(M∩F∩S’)=20,n(M∩S∩F’)=11 and n(F∩S∩M’)=16.Determine the complaints about all the three

6
53
35
None

Answer: (1) 6

n (M∩F∩S’) = 20

n (M∩S∩F’) = 11

n (F(∩S∩M’) = 16

-> n (M U FUS) = 173

173 = n (M) + n (F) + n(S) – n (M∩F) – n

(F∩S) – n (S∩M) + n (M∩S∩F)

173 = 110 + 55 + 67 – (20 + x) – (11 + x) – (16 +x) + x

59 = 20 + x+11+ x+16 + x-x

2x = 12 -> x = 6

61.Out of total 150 students 45 passed in Accounts 50 in Maths. 30 in Costing 30 in both Accounts and Maths. 32 in both Maths and Costing 35 in both Accounts and Costing. 25 students passed in all the three subjects. Find the number who passed at least in any one of the subjects.

63
53
73
None

Answer: (2) 53

n (A∩M) = 30

n (M∩C) = 32

n (A∩C) = 35

n (A∩M∩C) = 25

n (A∪M∪C) = 45 + 50 + 30-32-35 + 25

62. After qualifying out of 400 professionals, 112 joined industry, 120 started practice and 160 joined as paid assistants. There were 32, who were in both practice and service 40 in both practice and assistantship and 20 in both industry and assistantship. There were 12 who did all the three. Find how many could not get any of these.

88
244
122
None

Answer: (1) 88

n (Industry) 112 n (I n paid) = 20

n (practice) 120 n (Paid n practice) = 40

n (paid) 160

n (I U P U S)

= 112+ 120 + 160-20-40-32 + 12

= 32

no who are unemployed

= 400-312 = 88

63. On a survey of 100 boys it was found that 50 used white shirt 40 red and 30 blue. 20 were habituated in using both white and red shirts 15 both red and blue shirts and 10 blue and white shirts. Find the number ofboys using all the colours.

20
25
30
None

Answer: (2) 25

n (w) = 50 n (R) = 40 n (B) = 30

n (W ∩ R) = 20 n (R ∩ B) = 15

n (B ∩ w) = 10.

n (W ∪ R ∪ B) =n (w) + n (R) + n (B) – n (w ∩ R) – n (R ∩ B)- n (B ∩ w) + n (B ∩ R ∩ w)

100 = 50 + 40 + 30 – 20 – 15 – 10 + n (B ∩ R ∩ w)

n (B ∩ R ∩ w) = 25

64. Out of 60 students 25 failed in paper (1), 24 in paper (2), 32 in paper (3), 9 in paper (1) alone, 6 in paper (2) alone, 5 in papers (2) and (3) and 3 in papers (1) and (2). Find how many failed in all the three papers.

10
60
50
None

Answer: (1) 10

n (P1 ∩ P2’∩ P3’) = 9

n (P1∩P2∩P3’) = 6

n (P2∩P3∩P1′) = 5 n (P1∩ P2 ∩P3’) = 3

n (P2) = n (P2 alone) + n (P2 ∩ P3 ∩ P1’) + n (P1 ∩ P2 ∩ P2’) + n (P1 ∩ P2 ∩ P3)

24 = 6 + 5 + 3 + n (P1 ∩ P2 ∩ P3)-> 10

65. Out of 1000 students 658 failed in the aggregate, 166 in the aggregate and in group-] 434 in aggregate and in group-II, 372 in group-1, 590 in group-11 and 126 in both the groups. Find out how many failed in all the three.

Answer: (1) 106

1000 students,

658 failed in aggregate,

166 aggregate & G1,

434 in aggregate & G2,

372 in G1,

590 in G2,

126 in both G1 & G2

1000 = n (A) + n (G1) + n (G2) – n (G1 ∩ A) – n (G2 ∩A)- n (G1 ∩ G2) + n (G1 ∩ G2 ∩ A)

1000 = 658 + 372 + 590 – 166- 434 – 126 + n (G1 ∩ G2 ∩ A)

n (G1 ∩ G2 ∩ A) = 106

66. For any set A, (A’)’ is equal to

A’
A
none of these

Answer: (2) A

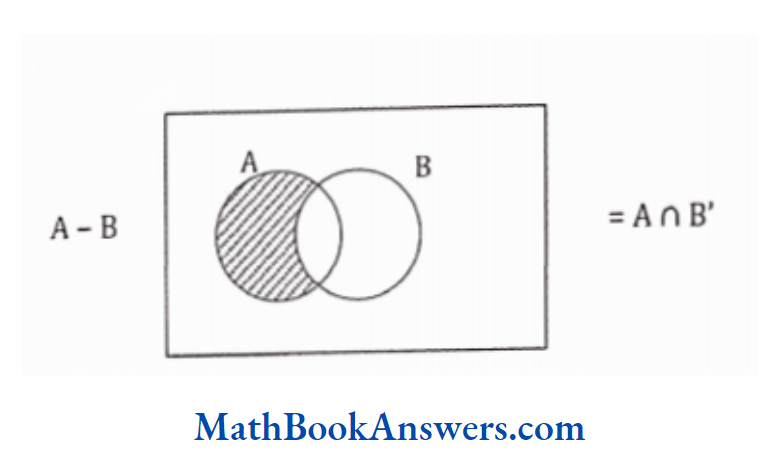
67. Let A and B be two sets in the same universal set. Then, A – B =

A ∩ B
A’∩ B
A ∩ B’
none of these

Answer: (3) A ∩ B’

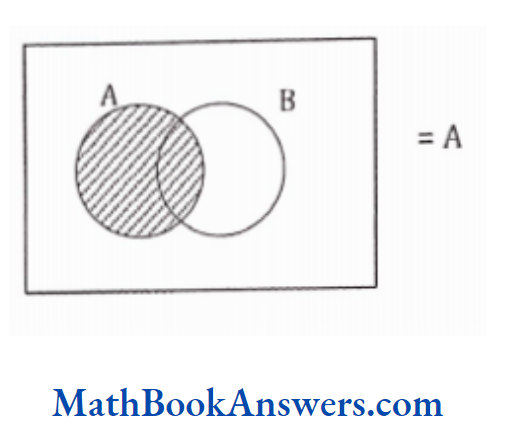
68. For any two sets A and B, A ∩ (A U B) =

A
B
D
none of these

Answer: (1) A

69. If A = {1, 3, 5, B} and B = {2, 4), then

4 6 A
{4} c A
B⊂A
none of these

Answer: (4) none of these

70. For any two sets A and B, (A – B) u (B – A) =

(A – B) ∪ A
(B – A) U B
(AUB)-(A∩ B)
(A U B) n (A ∩ B)

Answer: (3) (AUB)-(A∩ B)

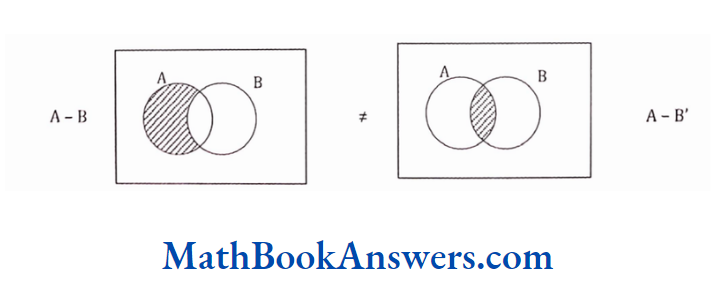
71. Which of the following statement is false:

A – B = A ∩ B’
A – B = A – (A ∩ B)
A – B = A – B’
A – B = (A U B) – B

Answer: (3) A – B = A – B’

72. For any three sets A, B and C

A ∩ (B – C) = (A ∩ B)- (A ∩ C)
A ∩ (B – C) = (A ∩ B) – C
A U (B – C) = (A U B) ∩ (A U C’)
All of these

Answer: (4) All of these

73. Let A = {x: x ∈R, x > 4} and B = {x ∈ R: x < 5}. Then, A n B =

[4, 5]
[4,5]
[4,5]
[4,5]

Answer: (2) (4.5)

i.e. all real no. between 4 & 5 excluding 4 &5

74. Let u be the universal set containing 700 elements. If A, B are sub-sets ofu such that n (A)- 200, n (B) = 300 and n (A ∩ B) = 100. Then, n (A’ ∩ B’) =

400
600
300
none of these

Answer: (3)

= universal – b (A U B)

= 700 – (n (A +n(B)-n(A ∩ B))

= 700 -(200 + 300 -100)

= 300

75. Let A and B be two sets such that n [A] = 16, n [B] = 14, n [A U B] = 25. Then, n [A ∩ B) is equal to

30
50
5
none of these

Answer: (3)

= n (A) + n (B) – n (A U B)

= 30-25

= 5

76. If A = {1, 2, 3, 4, 5}, then the number of proper subsets of A is

Answer: (3) no. of proper subsets

= 2ⁿ-1

= 32-1

= 31

77. In set-builder method the null set is represented by

{}
ø
{x:x≠x}
{x:x=x}

Answer: (3) (x:x≠x)

In set builder form

78. If A and B are two disjoint sets, then n (A U B) is equal to

n (A) + n (B)
n (A) + n (B)- n (A ∩ B)
n (A) + n (B) + n [A ∩ B]
n (A)∩ (B)

Answer: (a) n (A) + n (B)

We know n (A U B) = n (A) + n (B)

– n (A ∩ B)

n (A U B) = n (A) + n (B)

n (A ∩ B)00000 = 0 disjoint sets.

79. For two sets A U B = A iff

B⊆A
A⊆B
A ≠B
A = B

Answer: (1) B ⊆ A

A U B = A

Means A is superset of B

80. If A and B are two sets such that n (A) = 70, n (B) = 60, n (A U B) = 110, then n [A ∩ B) is equal to

Answer: (4) 20

n (A ∩) = n (A) + n (B) – n (A U B)

= 70 + 60-110

= 20

81. In a city 20% of the population travels by car, 50% travels by bus and 10% travels by both and bus. Then, persons travelling by car or bus is

Answer: (3) 60%

n (C U B) = n (C) + n (B) – n (C∩B)

= 20 + 50-10

= 60%

82. lf A∩B = B, then

A⊆ B
B⊆A
A = ø
B = ø

Answer: (2) B ⊆ A

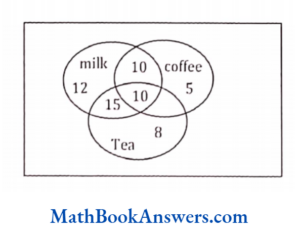
83. An investigator interviewed 100 students to determine their preference of three drinks: milk, coffee and tea. The investigator reported that 10 students take all three drinks milk, coffee and tea; 20 students take milk and coffee; 25 students take milk and tea; 20 students take coffee and tea; 12 students take milk only; 5 students take coffee only and 8 students take tea only. Then the number of students who did not take any of three drinks is

Answer: (4) 30

n (M∩C∩T) = 10

n (MUCUT)

= 12+5+10+10

= 70

do not drink

= 100-70 = 30

84. Two finite sets have m and n elements. The number of elements In the power set of first set Is 48 more than the total number of elements in power set of the second set. Then, the values, of m and n are:

Answer: (3) 6, 4

Let x be no of elements in second set’s power set n (P(S₂)) = x

N (P (S1)) = 48 + x

X = 2ⁿ

48+x=2^m

48 = 2^m – 2ⁿ

2ⁿ (2^m-n– 1) = 48

2ⁿ (2^m-n – 1) = 16 x 3

2ⁿ= 16

2^m-n-1= 3

2ⁿ = 16

2^m-n = 4

n=4

2^m/2ⁿ=4

2^m=64

m = 6

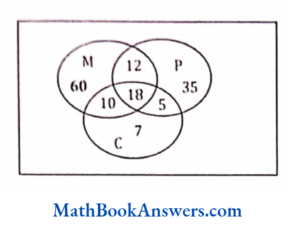
85. In a class of 175 students the following data shows the number of students opting one or more subjects. Mathematics 100; Physics 70; Chemistry 40; Mathematics and Physics 30; Mathematics and Chemistry 28; Physics and Chemistry 23; Mathematics, Physics and Chemistry 18. How many students have offered Mathematics alone?

Answer: (3)

86. For any two sets A and B, A ∩ (A U B)’ is equal to

A
B
ø
A ∩ B

Answer: (3) ø

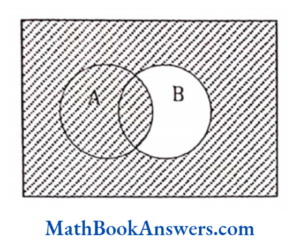
-> no interaction

87. Let F1 be the set of all parallelograms, F2 the set of all rectangles, F3 the set of all rhombuses, F4 the set ofall squares and F5 the set oftrapeziums in a plane. Then F1 may be equal to

F₂ ∩ F₃
F₃ ∩ F₄
F₂ U F₃
F₂ U F₃ U F₄U F₁

Answer: (4) F₂∪F₃∪F₄∪F₁

As all rectangle, square, rhombus are parallelograms only.

88. Out of 20 members in a family, 11 like to take tea and 14 like coffee. Assume that each one likes atleast one of the two drinks. Find how many like both coffee and tea:

Answer: (4)

Given that

n[T] = 11; n(C) = 14

and n(TUC) = 20

n(TUC) = n(T) + n(c) – n[T∪C]

= 11+14-20 = 5

(4) is correct

89. In a group of 70 people, 45 speak hindi, 33 speak English and 10 speak neither Hindi nor English. Find how many can speak both English as well as Hindi:

Answer: (3) n(H} = 45; n(E} = 33

n(H ∪ E}’ = 10 => n(H ∪ E) = 70-10 = 60

∴ (H∪E} = n(H) + n(E} – n(H ∪ E)

= 45 + 33-60 = 18

(3} is correct

90. In a survey of 300 companies, the number of companies using different media – newspapers (N), Radio (R) and Television (T) are as follows: n(N) = 200, n(R) = 100, n(T) = 40, n(N∩R] = 50, n(R∩T) = 20, n(N∩T) = 25 and n(N∩R∩T) = 5. Find the number of companies using none of these media:

20 companies
250 companies
30 companies
50 Companies

Answer: (2) n(N∪R∪T} = n(N} + n(R) + n(T) – n(N∩R] – n(N∩T} – n(R∩T} + n(N∩R∩T}

= 200 + 100 + 40-50-20-25 + 5

= 250

No. of companies using no media

= 300 – n(NURUT)

= 300-250 = 50

(4) is correct

91. In a town of 20,000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers, then the number of families which buy A only is

6600
6300
5600
600.

Answer: (1) Given

n(A) = 40% ; n(B) = 20% ; n(C) = 10%

n(A∩B) = 5%; n(B∩C) = 4%

n(C∩A) = 4%; n(A∩B∩C) = 2%

No. of families which buy only A

= n(A) – n(A∩B) – n(A∩C) + n(A∩B∩C) = 40-5-4+2 = 33%

= 20,000 x 33% = 6600

(1) is correct

92. Out of total 150 students, 45 passed in accounts, 30 in economics and 50 in maths, 30 in both accounts and maths, 32 in both maths and economics, 35 in both accounts and economics, 25 students passed in all the three subjects. Find the numbers who passed atleast in anyone of the subjects:

63
53
73
None.

Answer: (2) Total students = 150

n(A) = 45 ; n(E) = 30; n(M) = 50;

n(A∩M) = 30; n(M∩E) = 32

n(A∩M) = 35; n(M∩E∩M) = 25

∴ n (A∪E∪M) = 45 + 30 + 50 – 30 – 35 + 25 = 53

(2) is correct.

93. If A = {p,q,r,s}, B = {q,s,t), C = {m,q,n} find C – (A∩B)

{m,n}
{P<q}
{r,s}
{p,r}

Answer: (1)

⊂-(A ∩ B) ={m,q,n} – {p,q,r,s} ∩ {q,s,t}

= {m,q,n} – {q,s}

= { m;n }

(1) is correct.

94. If A = {X : X² – 3X + 2 = 0} B = {X:X²-4x + 12 = 0}, B-A =

{-6}
{1}
{1,2}
{2,-6}

Answer: x²- 3x + 2 = 0

Or x(x-2)-1(x-2)=0

Or (x-2) (x-1) = 0

x = 1;2

A = {1,2}

And x² + 4x – 12 = 0

Or x² + 6x – 2x – 12 = 0

Or x(x+6)-2(x+6)=0

Or (x+6) (x-2) = 0

x = -6 ; 2

B -A = {-6;2} -{1;2} ={-6}

A (1) is correct

95. For any two sets A and B, A∩(A’UB)=___________ where A’ represent the compliment of the set

A∩B
AUB
AUB
None of these

Answer: Tricks: Take an example and then decide the answer

Let U = {0,1,2,3,4,5}

A = {0,1,2,3}

B = {2,3,4,5}

A¹ = U – A = {4;5}

A¹ U B = {4,5} U{2,3,4,5}

= {2,3,4,5}

∴ A ∩ (A¹ U B}

= {0,1,2,3} ∩ {2,3,4,5}

∴ (1) is correct

2nd method = (A∩A’) U (A∩B} = { } U (A∩B} = A ∩ B

96. If A c B, then following is true

A ∩ B = B
A U B = B
A ∩ B = A
A ∩ B

Answer: (2)

97. There are 40 students, 30 of them passed in English, 25 of them passed in maths and 15 of them passed in both. Assuming that every student has passed atleast in one subject. How many students passed in English only but not in math’s.

Answer: (1) total students = 40

n(E) = 30; n(M) = 25

(E∩M)= 15

No. of stds. Passed in English only

n(E) – n(E∩M)

= 30-15 = 15

(1) is correct

98. If A = (1,2,3,4,5), B = (2,4) and C = (1,3,5) then (A -C) x B is

{(2,2),(2,4),(4,2),(4,4),(5,2),(5,4)}
{(1,2),(1,4),(3,2),(3,4),(5,2),(5,4)}
{(2,2),(4,2),(4,4),(4,5)}
{(2,2(,(2,4),(4,2),(4,4)}

Answer: (4) is correct

(A-C)xB = {2,4}x{2,4}=

{(2,2),(2,4),(4,2),(4,4)}

99. For any two sets A and B the set (AUB’)’ is equal to (where denotes compliment of the set)

B-A
A-B
A’-B’
B’-A’

Answer: (1) is correct

Tricks: Let U = {1,2,3,4,5}

A = {0,1,2,3}; B = {1,2,3}

B’ = U – B = {0,4,5}

A∪B’ = {0,1,2,4,5}

(AUB’)’ = U- (A U B’)= {3}

Then go by choices

For (1) B – A = {1,2,3} – {0,1,2} ={3}

(A∪B’)’ =U -(AUB’) = {3}

2 nd Method

(A∪B’)’

= A’D(B’)’

= A’ ∩ B

= B – A ∩ B

= B- A

100. The number of proper sub-set of the set {3,4,5,6,7} is

Answer: (2) No. of proper sub -sets = 2ⁿ– 1

= 2⁵-1 = 31

101. For a group of 200 person, 100 are interested in music, 70 in photography and 40 in swimming, furthermore 40 are interested in both music and photography, 30 in both music and swimming, 20 in photography and swimming and 10 in all the three. How many interested in photography but not in music and swimming?

Answer: (4) is correct

Let A = No. of persons interested in Music

B = No. of persons interested in photography

C = No. of persons interested in swimming

n(A) = 100; n(B) = 70; n(C) = 40;

n(A∩B) = 40; n(A∩C) = 30;

n(B∩C) = 20; n(A∩B∩C)= 10.

n(B∩A¹ ∩ C¹) = n(B) – n(B∩A) – n(B∩C)+n(A∩BnC)

= 70-40-20+10

= 20

102. Of the 200 candidates who were interviewed for a position at call center, 100 had a two wheeler, 70 had a credit card and 140 had a mobile phone 40 of them had both a two-wheeler and a credit card, 30 had both a credit card and mobile phone, 60 had both a two-wheeler and a mobile and 10 had all the three. How many candidates had none of them?

Answer: (3) is correct

Let n(A) = No. of candidates having two wheeler

n(B) = No. of candidates having credit cards

n(C) = No. of candidates having mobile phone.

Given

n(A) = 100; n(B) = 70; n(c) = 140

n(A∩B) = 40; n(B∩C)= 30; n(C∩A) = 60

n(A ∩ B ∩ C) = 10

n(A U B U C) = 100 + 70 + 140- 40-30-60 + 10 = 190

No. of candidates having none = 200 – 190= 10

103. In a class of 50 students 35 opted for Maths, 37 opted for commerce. The number of such student who opted for both maths and commerce is

Answer: (3) is correct

n(M) = No. of students opted for Maths = 35

n(C) = No. of students opted for commerce = 37

So; (MUC) = 50

n(M∩C) = 35 + 37- 50 = 22

104. A = (2,3), B=(4,5), C=(5,6) then Ax(B∩C)

[(5,2),(5,3)]
[(2.4),(5,3)]
[(2,5),(3,5)]
[(3,5),(2,6)]

Answer: (2)

B ∩ C = {4,5} ∩ {5,6} = {5}

= {(2,5);(3,5)}

105. In a class of 80 students, 35% play only cricket, 45% only tennis, how many play cricket?

Answer: Given n(C – T) = n(C) – n(C ∩ T) = 35%

n(T- C) = n(T) – n(C∩T) = 100

or; 35 + n(C∩T) + 45 + n(C∩T) – n(C∩T) = 100

or 80 + n(C∩T) = 100

n(C∩T) = 20%

n(C) = 35 + n(C∩T) = 35 + 20 = 55%

= 80 x 55% = 44

106. If set A = (x:x/2 ∈ z,0 ≤ 12}

B = {x: x is one digit prime number} and

C = {x:x/3 ∈ N, x ≤ 12} then A ∩ (B ∩ C) =

0
Set A
Set B
Set C

Answer: (1)

A = {2,4,6,8,10}

B = {2,3,5,7}

C = {3,6,9,12}

A ∩ (B ∩ C) = ø

No common element in all 3 sets.

107. Let A be the set of the squares ofnatural numbers and x ∈ A, y ∈ A. Then__________

x + y ∈ A
x- y ∈ A
x/y∈ A
xy ∈ A

Answer: (4) is correct

A = {x/x is the squares of natural Nos.} = {1,4,9,16,25……….. }

Tricks: then go by choices

Let x = 1: y = 4 ∈ A

x+y = 1 + 4 = 5 ∉ A.

x – y = 1 -4 = 3 ∉ A.

x/y=1/4 ∉ A.

But xy = 1 x 4 = 4 ∈ A.

(4) is correct.

108. The number of sub-sets formed from the letters of the word “ALLAHABAD”

128
16
32
None

Answer: (3) is correct

Let X = {Letters of word ALLHABAD)

= {A, L, H, B, D}

No. ofsub-sets = 2⁵ = 32

109. If f(x) =\( \frac{x-1}{x} \text { and } g(x)=\frac{1}{1-x} \)then fog(x) =

x-1
x
1-x
-x

Answer: \(\mathrm{fog}(\mathrm{x})=\mathrm{f}\{\mathrm{g}(\mathrm{x})\}=\frac{g(x)-1}{g(x)}\)

\(=\frac{\frac{1}{1-x}-1}{\frac{1}{1-x}}=\left(\frac{1-1+x}{1-x}\right) \times \frac{(1-x)}{1}\)

= x
Option (2) is correct

110. In a class of 35 students, 16 students play football and 24 students play cricket. Assume that each one play atleast one game, then number of students who play both the games is_______________

Answer: N (F ∩ C) =n (F) + n(C)- n(F U C)

= 16 + 24-35 = 5

Option (1) is correct.

111. If A = {ø,{ø}} then the Power Set of A is

{ø}, {0}
{ø,{ø},{ø}},A}
A
{A}, {ø}

Answer: (2)

A = {ø;{ø; }}

P(A) = {{}};{ø};{{ø}};{ø;{∅}}

= {ø;{ø};{{ø};A}}

112. If A = {x:x = 3ⁿ-2n – 1, where n∈ N}, B = {x:x = 4(n – 1}, where n∈N}. Then

A ⊂B
B⊂A
A = B
None

Answer: (1)

Putting n= 1,2,3……….; we Ret

A = {x/x = 3ⁿ – 2n – 1}

= {0 ; 4 ; 20 ; }

B = {x/x = 4(n – 1)}

= {0;4;8; 12; 16; 20;………}

Clearly ; A ⊂ B

113. The numbers of proper sub-sets of the set {3, 4, 5, 6, 7} is :

Answer: (2)

Formula

No. of proper sub-sets = 2ⁿ -1

= 2⁵-1 = 31

114. If A = {1, 2, 3, 4, 5, 6, 7} and B = {2, 4, 6, 8}. Cardinal number of A – B is:

Answer: A ∩ B = {1, 2, 3, 4, 5, 6, 7} n {2, 4,6,8}

= {2, 4, 6} => n (A ∩ B) = 3

n (A – B) = n(A) -n(A ∩ B)

=7-3=4

115. If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}; B = {1, 3, 4, 5, 7, 8}; C = {2, 6, 8} Then find (A – B) U C

{2, 6}
{2,6,8}
{2, 6, 8, 9}
None

Answer: (3)

A-B = A-(A ∩ B)

= {1,2, 3,4, 5, 6, 7, 8,9}

{1,3, 4, 5, 7, 8}

= {2,6,9}

(A – B) U C = {2 ; 6 ; 9} U {2 ; 6 ; 8}

{2 ; 6 ; 8 ; 9}

(3) is correct.

116. The no. of sub-set of the set (3, 4, 5} is:

Answer: (2)

No. of sub-sets = 2ⁿ = 2³ = 8

Function And Relation

Introduction

A Function is a rule that describes the dependence between two quantities and is generally denoted by f(x).

Take for e.g., f (x) = 2x+5

Let y= f(x)

In the above case, x is the input, y is the output and f(x) is the function that processes the input according to a certain rule to give the output.

The function f here multiplies the input value x by 2 and then adds 5 to it to give the corresponding value of the output y.

For this function, different values of x give different values of y. By plotting these points and joining them the following figure is obtained.

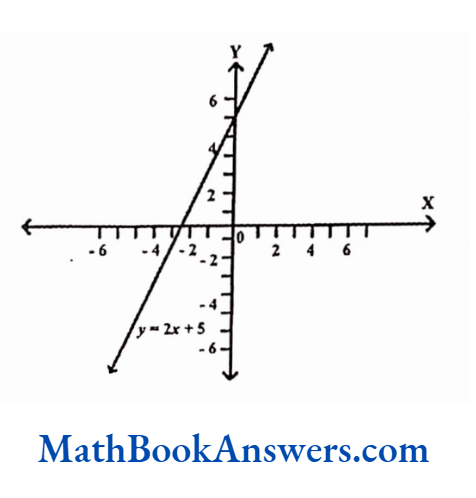
Function and Relation

Any function in general can be reprinted through the diagram given below.

Any function in general can be reprinted through the diagram given below

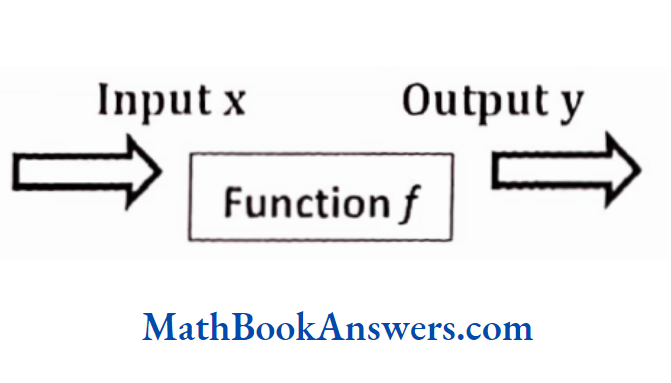
If x be the input and y the output fora function/, then the function is denoted as y = f(x).

This indicates that when input x is processed by a function /, the output obtained is y.

Thus, x is also called the independent variable, while y is called the dependent variable.

Therefore, a function can be considered to be a machine that transforms a given input into the corresponding output according to a certain rule defined by that function.

Some other examples of functions are

f(x) = x² + 3x-7

f(x) = cosx

f(x) = log ( |x| + 5)

A function can be represented using formulae, tables, graphs, algorithm, arrows etc.

The concepts of an ordered pair, Cartesian product and relation need to be understood to understand functions.

Cartesian Product

Consider two sets A and B

A ≡ {1,2,3}

B≡ {1.2,3.4}

The set of all ordered pairs of elements from A and elements from B, known as the Cartesian product, gives all the ways to possibly relate the elements of set A with those of set B.

The Cartesian product A x B is given by

Ax B ≡ {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4)(3,1), (3,2), (3,3), (3,4)}

Ax B ≡ {(a,b)| a ∈ A, b ∈ B}

Also,BxA = {(b, a) b∈ B, a ∈ A)

In a Cartesian product, the order in which a and b are written is important.

∴Ax B ≠ B x A

It is evident that the number of elements in the Cartesian product is the product of the number of elements in the two sets A and B.

Consider the following example.

Let set S= {I,II,III} represent three students and set M≡ {56,29,45}represent their scores out of 100 in maths in some order.

Then the different ways in which the students and marks can be related is represented by the Cartesian product Ax B.

∴ S x M≡ {(I,56), (I,29), (I,45), (II, 56), (II,29), (II, 45), (III, 56), (III, 29), (III, 45)}

Relations

Understand the concept of relation before moving on to functions.

Consider two sets P and Q.

P ≡ {1,2,3,4}

Q≡ {1,2,3,4,5,6,7,8,9,10}

Let R ≡ {(1,1), (2,4), (3,9)}

Observe that R ⊆ PxQ.

But elements of R have been chosen in a specific way i.e. (p, q) ∈ R only if q = p²

Thus R = {{p,q)| q = p², p ∈ P, q ∈ Q}

R is called a relation from P to Q and this is denoted by p R q or p~q

In general, any relation is a set of ordered pairs (p , q) ∈ PxQ Such that there exists some definite relationship R between p and q.

Note:

If R ≡ {{p,q)\q = p²,p∈P,q∈Q],it is not necessary that all elements of P and Q are a part of the relation.

Domain, Co- Domain and Range

The above relation R from p to Q can be expressed in the form of a diagram as follows:

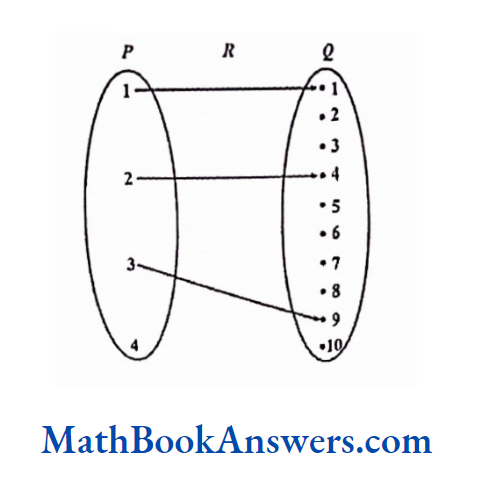
Domain, Co- Domain and Range

The direction of the arrow indicates the direction of the relation.

In the above figure the relation exists from set P to set Q and not vice versa.

The set of all first elements in the ordered pairs that belong to R is called the domain of R.

In this example, Domain ≡ {1,2,3}

Hence Domain ⊆ p.

The set of all second elements in the ordered pairs that belong to R is called the range of R.

In this example, Range = {1,4,9}.

Hence, Range ⊆ Q.

Q is called the co-domain of R. Thus, range ⊆ co-domain.

In other words, A function can be denoted as y= f{x}, where x is the independent variable and y is the dependent variable as discussed above.

Domain: The domain of a function is set of all the values that an independent variable can take i.e. values of “x” in this case.

Range: The range of a function is set of all the values which a dependent variable will take corresponding to the values taken by independent variables i.e. Values of “y” obtained corresponding to the value of x.

Types of Relations

Many-Many Relation

Consider the following relation.

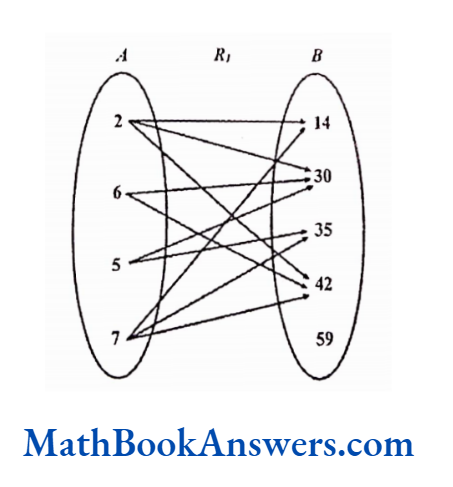
Many-Many Relation

A ≡ {2,6,5,7},B ≡ {14,30,35,42,59}

Relation R₁has ordered pairs (a,b)such that be is multiple of a

R₁ = {(2,14), (2,30), (2,42), (6,30), (6,42), (5,30), (5,35), (7,14), (7,35), (7,42)}

In this relation, more than one element in the domain has the relation with the same element in the range. Also, one element in the domain has the relation with more than one element in the range. Such a relation is called a many-many correspondence.

One-Many Relation

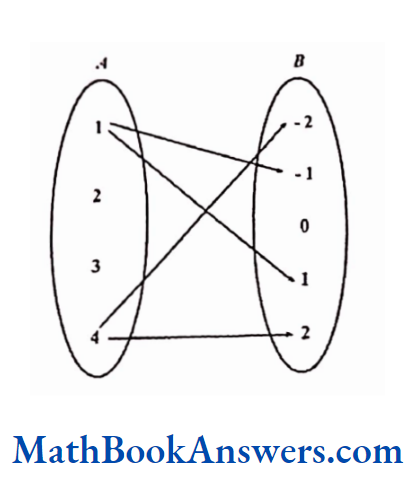
One-Many Relation

If A ≡ {1,2,3,4}, B ≡ {-2, -1,0,1,2}

Relation R₂has ordered pairss (a, b)such that b is the square root of a.

R₂ ≡ {(1,-1), (1,1), (4, -2), (4,2)}

In this relation, one element in the domain has the relation with more than one element in the range. Such a relation is called a one-many correspondence.

One-One Relation

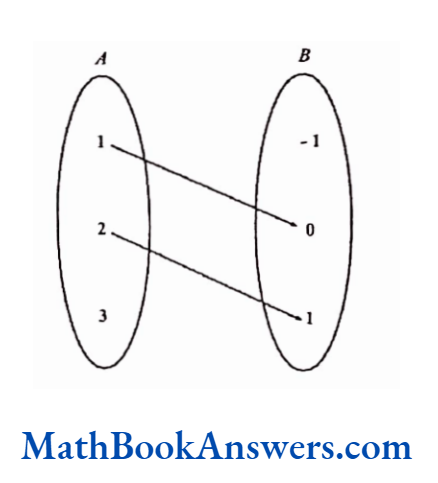
One-One Relation

If A≡ {1,2,3}, B ≡{-1,0,1}

If A ≡ {1,2,3), B ≡ {-1,0,1}

Relation R₃ has ordered pairs (a, b) such that b = (a- 1)

R₃ ≡ {(2,1), (2,1)}

In this relation, one element in the domain has the relation with exactly one element in the range. Such a relation is called a one – one correspondence.

Many-One Relation

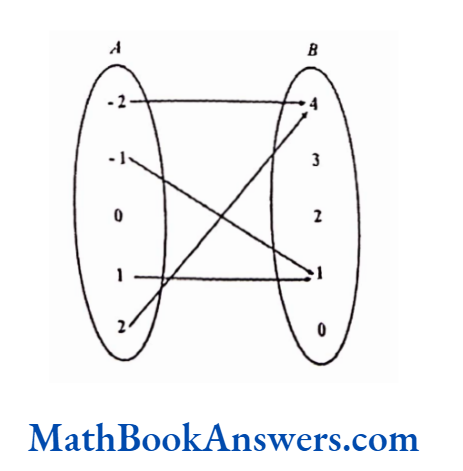
Many-One Relation

A≡ {-2,-1,0,1,2), B ≡ {0,1,2,3,4)

Relation R₄ has ordered pairs [a,b] such that b is the square of a

R₄ = {(-2,4), (-1,1), (1,1), (2.4)}

In this relation, more than one element in the domain has the relation with the same element in the range. Such a relation is called a many-one correspondence.

Equivalence Relation

Equivalence Relation

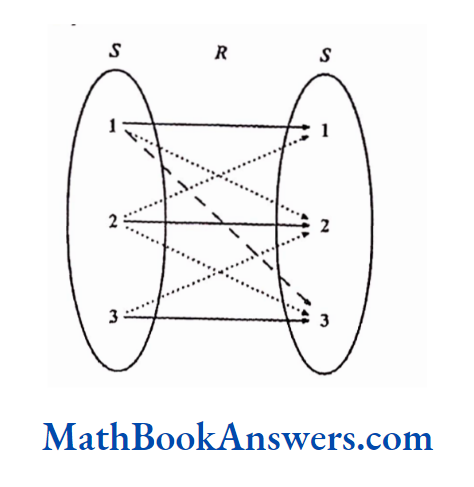
Let S be a set and R be a relation between S and itself.

R is called an equivalence relation on S if the relation R has the following three properties:

Reflexivity: Every element of S is related to itself

Symmetry: If an element s is related to t then t is related to s

Transitivity: If an element s is related to t and t is related to u, then s is related to u.

Consider the set S ≡ {1,2,3}

Now a relation R from S ~S is said to be an equivalence relation if:

S~S = {(1,1), (2,2), (3,3), (1,3), (3,1), (1,2), (2,1), (2,3), (3,2)}

Here the reflexivity relation exists as every element i.e., 1, 2, 3 is related to itself.

In addition, the symmetry relationship exists as every element is related to all other elements and vice versa i.e.,1 is related to 2 and 2 is related to 1.

Also, transitive relationship is satisfied since reflexive and symmetry relationships are satisfied i.e.,1 is related to 2,2 is related to 3 and simultaneously 1 is related to 3.

Congruence and equality are two common equivalence relations.

Functions

Any relation between sets A and B, is a function ifit satisfies the following conditions.

It should be a one- one or many -one relation.
Every element in A should be a part of the domain.

Thus, every function is a relation. However, not every relation need be a function.

Functions

Thus, if A and B are two sets and if there exists a relation so that each element of A is related with one and only one element of B, then a function from A to B exists.

Example 1:

Is the following relation a function?

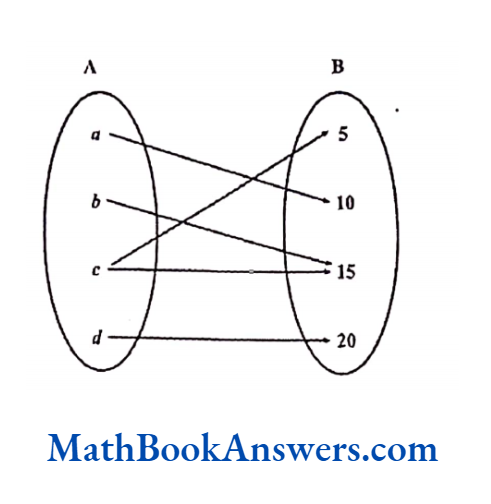
Example 1

Solution:

This relation is a many – many relations because c has a relation with 5 as well as 15. Also, b and c both have a relation with 15. Therefore, this is not a function.

Example 2:

Example 2

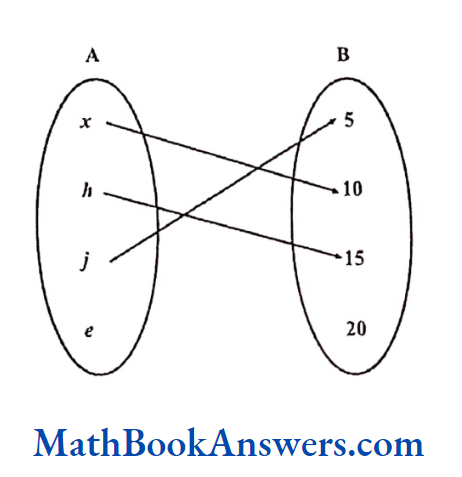
Find whether the relation shown above represents a function or not.

Solution:

This is a one- one relation. However, every element of A is not in the domain.

Hence, this is not a function.

Example 3:

Find the value of f(x) = \(\frac{x^6}{2 x-3}+\mathrm{x} \text { at } \mathrm{x}=\frac{3}{2} \text { and at } \mathrm{x}=1\)

Solution:

To find the value of a function at some value of the independent variable, substitute this value of the variable in the function.

\(\text { Put } \mathrm{x}=\frac{3}{2} \text { in } f(x)=\frac{x^6}{2 x-3}+x\)

Thus, \(f\left(\frac{3}{2}\right)=\left(\frac{1.5^6}{0}\right) \frac{3}{2}=\infty\) ,which is not defined.

Hence the function f(x)is not defined at x= 3/2

At x =1, \(f(1)=\frac{1^6}{2-3}+1=0\)

Types of Function

Into and on to Functions

A Function f : A → B is called a function from A onto B if the range of f = co-domain.

Thus, if every element of B has a pre-image in A, then f: A→B is a function from A onto B.

If there is at least one element of B that has no pre-image in A, then f : A → B is a function from A into B.

Thus functions can be of four kinds – one-one into, one-one onto, many-one into and manyone onto.

Example 4:

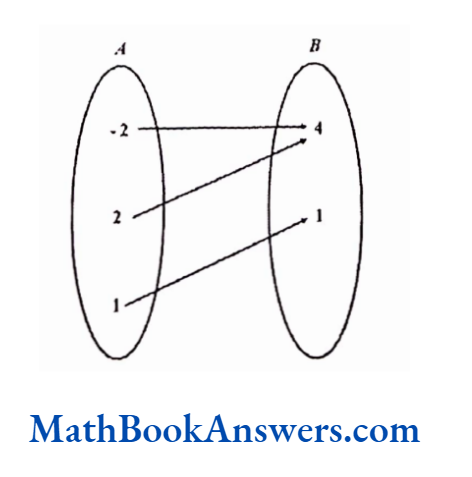
Is the given relation an onto function?

Find the co-domain and range for the function.

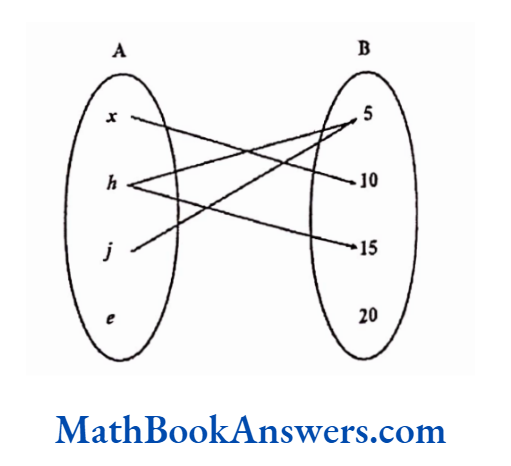
Example 4

Solution:

In this function,

Co-domain ≡ {5,10,15,20}

Range≡ {5,10,15}

This is not an onto function because the element 20 in B does not have a pre-image in A.

Injective, Surjective and Bijective Functions

An injective function, also called an injection is a one- one function.

Thus, a function f is an injective if and only if whenever f (x) = f (y),x = y

A many-one function is not an injection.

A subjective function, also called a surjection, is an onto function.

Thus a function f: X → Y is a surjective if and only if its range f{x} is equal to its co-domain Y.

A function f: X → Y is a bijective function or a bijection if for every y in Y, there is exactly one x in X such that f (x)=y.

Alternatively, f is bijective ifit is both one- one {injective} and onto {surjective}.

Even and Odd Functions

Even Functions

Let y=f (x) be a function such that x, y ∈ R.

If the values of f (x) and f(- x) are the same for all values of x in the domain, then the function is said to be an even function. For example, consider f(x) = x²

Here, f(1) = 1. also/(-1) = 1.

Similarly,f(-1) = -1² =1² = f (x)

Thus, f (x) is an even function. Other examples of even functions are cos x,|x|, x²ⁿ; n ∈ N

An even function of the form y=f(x) is symmetrical about they-axis. Similarly, an even function ofthe form x=f (y) is symmetrical about the x-axis.

The following graph shows the even function f (x) = x²- 3x² + 2

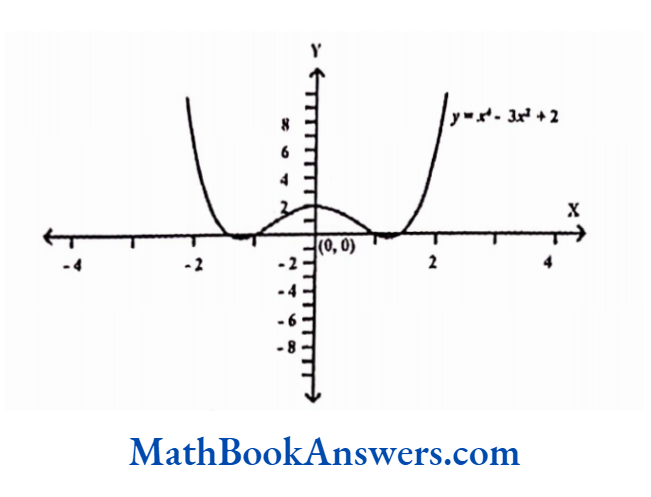
Even Functions

Thus, the graph of an even function appears the same on both sides of the y- axis. The left half of the plane appears as the mirror image of the right half of the plane.

Properties of Even Functions:

The sum, difference, product, or division of any two even functions is also an even function.

Odd Functions

Let y = f (x)be a function such that x, y ∈ R.

If f (x) = -f(-x) for all values of x in the domain, then the function is said to be an odd function.

Consider the function f(x) = x³

Here,f(1) = 1 while f(-1) = -1

Similarly, for any x, f(-x) = (-x)³ = -x³ = -f(x)

Thus f (-x) = -f (x) and f (x) = -f (-x)

Hence, this is an odd function.

Other examples of odd functions are sin x, tan x, x ²ⁿ⁺¹; n ∈ N

For odd functions the inverted left half of the graph looks like the mirror image of the right half of the graph.

In other words, an odd function is symmetrical about the origin.

The following graph shows the odd function f(x) = x³ + sin x

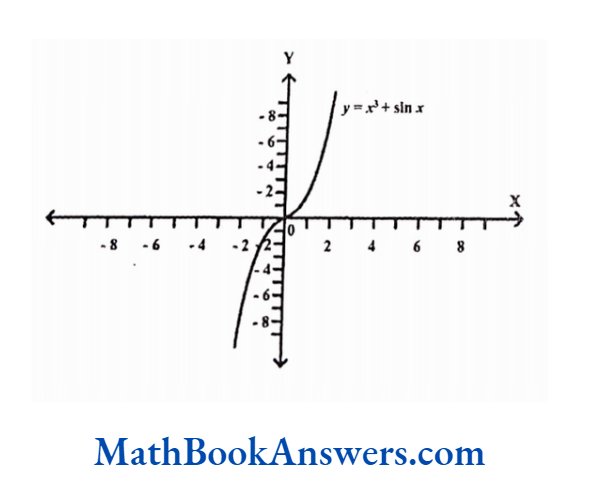
Odd Functions

Properties of Odd Functions:

The sum or difference of any two odd functions is an odd function.

Division or product of an even number of odd functions is an even function whereas that of an odd number of odd functions is an odd function. i.e„ odd function raised to
an even power is an even function whereas and odd function raised to an odd power is an odd function.

Neither Even nor Odd Functions

There are functions that satisfy the conditions neither of an even nor of an odd function. Such functions are said to be neither even nor odd functions.

For example: f (x) = x³ + 1

f(-x) = (-x)³ + 1 = -x³ + 1

∴ f (x) ≠ ± f(-x).

Thus, it is neither an even nor an odd function.

Note:

The only function that is both even and odd is the function defined by f (x) = 0 for all real x.

Every function can be expressed as a sum of an odd and an even function.

Even function x Odd function ≡ Odd function

Even function/odd function ≡ Odd function

Even function ± Odd function ≡ Neither even nor odd function

Composite Functions

Let two functions f and g be defined as f : A → B and g: B → C, such that f(x) = 2x + 1 and g (y) = y + 5

Then a function from A to C, g°f: A A → C, can be defined as

g° f (x) = g [ f (x)]

= f(x) + 5

= 2x + 1 + 5 = 2x + 6

If A = {1,3,5 }, then the function g° f (x)can be shown as follows:

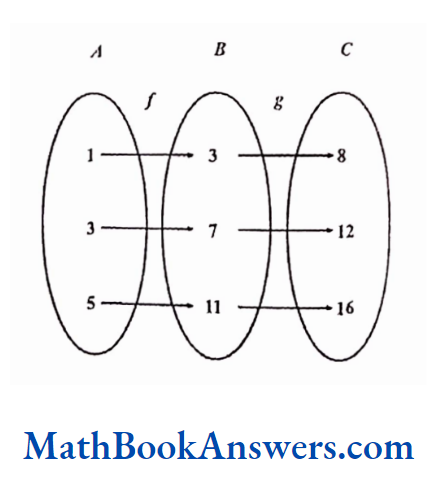
Composite function

Such a function is called a Composite function.

Example 5:

f(x) = x⁴

g(x) =√x,x > 0

Find g°f (2).

Solution:

g°f(x) = g(f(x))

f(2) = 2⁴ = 16

g(f(2)) = g(16)

g(f(2)) = g(16) = √16 = 4

Note that g°f(x) = g[f(x)] = f[x⁴]

= √x⁴

= x²

Example 6:

f(x) = 2x² – 5x + 9

g(x) = 3x + 7

Find f°g(x)and g°f(x). is fºg(x) = g°f(x)?

Solution:

f°g(x) = f[g(x)] = f(33x + 7)

Substitute g(x)for x in f (x).

f[g(x)] = 2(3x + 7)²- 5(3x + 7) + 9

= 2(9x² + 42x + 49)- 15x- 35 + 9

= 18x² + 69x + 72

g°f(x) = g[f(x)] = g(2x²- 5x + 9)

= 3(2x² – 5x + 9) + 7

= 6x² – 15x + 34

Thus ,f° g (x) ≠ g° f (x)

Piecewise Functions

A function, which has different definitions depending on the value of the independent variable, is a piecewise Function. Thus, the definition of function changes according to the domain.

For example:

y = x/2 for x ≤ 0,

= x for 0 < x < 2 and

= 2 for x ≥ 2

The modulus function is a piecewise function.

Example 7:

Find the value of f(2), f(-2)and f(0) for the function

f(x) = 2x + 3 for- ∞ ≤ x ≤ 0

= 2x- 3 for 0 < x ≤ ∞

Solution:

Here, two functions are defined for two different domains.

So, to find f(-2), use f(x) = 2x + 3

Thus, f(-2) =-1

However, for f(2) use the function f(x) = 2x- 3

Thus, f (2) = 2(2) -3 = 1

At x=0,we use f(x) = 2x + 3

∴ f(0) = 3

Inverse Functions

If f: A -> B Is a one one onto function, then for each x ∈ B, there exists one and only one y ∈ B such that f(x) = y

If one defines a relation from B to A such that for each £ B, there exists one and only one x ∈ A such that f(x) = y, then the relation is a function from B to A denoted by

f¹:B → A, and defined as f¹ (y) = x.

such a function is called an inverse function.

Consider the two functions given below:

f(x) = 2x + 3, where x ∈ I

g(x) =x-3/2 where x∈ I

For x = 3,

f(3) = 2(3) + 3 = 9

g(9) = (9-3)/2,= 3 = x

We can see that g(f(x)) = x for all x∈ l.

In such a case,g(x) is called the inverse of f(x). This is denoted by g (x) = f¹(x)

Note:

g(x) = f¹ {x) does not necessarily mean that f(x)) = g¹(x)

In the above example,

f(x) = 2x + 3 where x∈ I

g(x) = x-3/2, where x∈ I

Algebraically,f(g(x)) = 2(x- 3/2 + 3 = x)

But if x is even, say x=4, g(4) = 0.5 ∉ I

f(g(4)) is not defined as g(4) does not belong to the domain of f.

f(x) ≠ g^-1(x)

However, if the domains of f(x)and g(x)were x ∈ R, then the two functions would be inverses of each other.

Note that not all functions have an inverse.

Consider the function y = x², x ∈ I

The range of this function is y ∈ I, y≥ 0

For y = 1,x can be -1 or 1.

Thus, each value of y does not give a unique value of x.

If the inverse of the function y=x² was g(x), then g (1) would be both 1 and -1 which would make g(x) a one-many relation, which cannot be a function.

Condition for A Function to Have an Inverse:

The function should be a one-one relation. This ensures that the inverse relation is also one-one. If the function is many-one, the inverse relation is one- many and hence is not a function.

The co-domain of the original function becomes the domain of its inverse and vice-versa. Thus, the inverse relation will be a function if and only if the co-domain = range; of the function is a one-one onto function.

In other words, for a function to have an inverse it must be a bijection. Graphically a function y= f(x) has an inverse if no two points on the graph have the same y coordinate

Example 8:

Find out if the inverse of the following functions exists.
1. f(x) = x², where the domain and the co- domain are the set of integers;
2. f(x) = x- 3, where the domain and the co- domain are the set of integers.
3.f(x) = x², where the domain is {x|x ∈ R,x ≥ 0 }

Solution:

f(x) = X²

1. Here, we have f(-1) = f(1) = 1. Hence, this is a many-one relationship. Therefore, the inverse of this function does not exist.

2. f (x) = x- 3

Here, for each value of x, we have only one value of x-3.

Hence,it is a one- one relationship.

Also, f(x) = x- 3, so x = f(x) + 3

Thus, every value of f (x) corresponds to a unique integer value of x. So the function f(x) is an onto function.

Hence, this function is both one-one and onto. Hence, it has an inverse function.

f(x) =x²,{x|x∈R,x ≥ 0}

In this function, the domain is restricted to the set of positive real numbers and so is the co-domain.

The function is a one-one onto function.

∴ f(x)has an inverse.

Steps to Find the Inverse of a Function:

The inverse of a function can be found easily using three algebraic steps. However, this method should be used only after verifying that the inverse exists.

The steps are:

Write down the function in the form y = f(x).
Solve for x, Replace x with f^-1 (y)
Replace y with x to get the inverse function.

For example, consider/(x) = x- 3

Step 1: write down y = f(x).

Hence y = x- 3

Step 2: solve for x.

Thus, x- y + 3

Since y = /(x),x = f^-1{y)

Thus f^-1 (y) = y + 3

Step 3: Replace y by x in the above equation to get f^-1 (x) = x + 3

Thus, if we follow the four steps given above, we can find the inverse of any function.

Example 9:

Find the inverse function of:

1. \(f(x)=\frac{2 x+3}{7 x+5}\)

2. f(x)=e^x

Solution:

\(\text { 1) } f(x)=\frac{2 x+3}{7 x+5}\)

Step 1:

\(\mathrm{Y}=f(x)=\frac{2 x+3}{7 x+5}\)

Step 2:

y(7x + 5) = 2x + 3

7xy + 5y = 2x + 3

7xy- 2x = 3- 5y

x{7y- 2) = 3- 5y

\(x=\frac{3-5 y}{(7 y-2)}\)

Step 3:

Writing x as f^-1(y),

\(x=f^{-1}(y)=\frac{3-5 x}{(7 y-2)}\)

Step 4: Replacing y in the above equation by x,

\(f^{-1}(x)=\frac{3-5 x}{(7 x-2)}\)

2) f(x) = e^x

Step 1: y = f(x) = e^x

Step 2: y = e^x

Take log on both sides

log y = log e^x

log y = x log e [ log a^b = b log (a)]

∴ log y = x [log e = 1]

∴ x = log y

Step 3: x = f¹ (y) = log y

Step 4: Replacing y in the above equation by x,

f¹ (x) = log x

Some Standard Functions

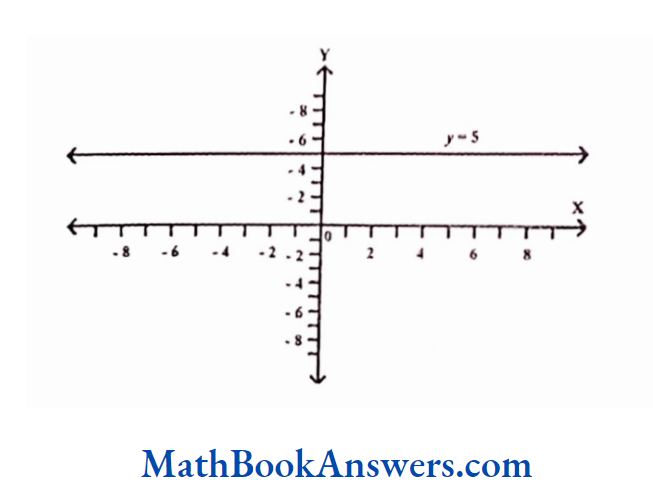
Constant Function

A Constant function is f(x) = c, where c ∈ R. The range of the function is {c} The graph of a constant function is as shown.

Constant Function

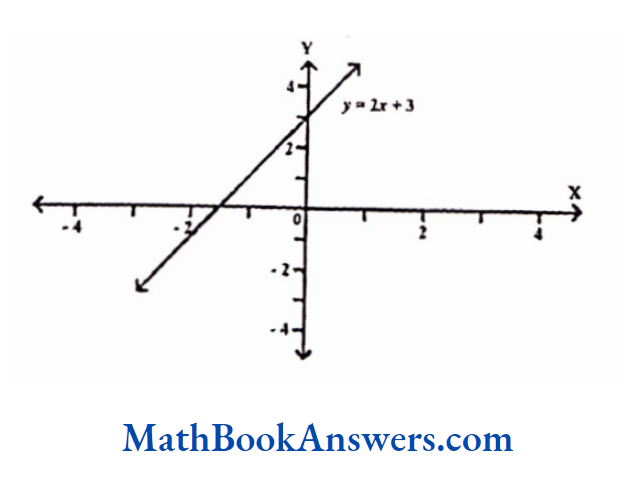
Linear Function

A linear function is of the form y = ax + b, where, a and b are real numbers. The graph of a linear function is a straight line. It intersects the x- axis at-b/a and it intersects the y-axis at be. The function y = x, passes through the origin.

Linear Function

Modulus Function

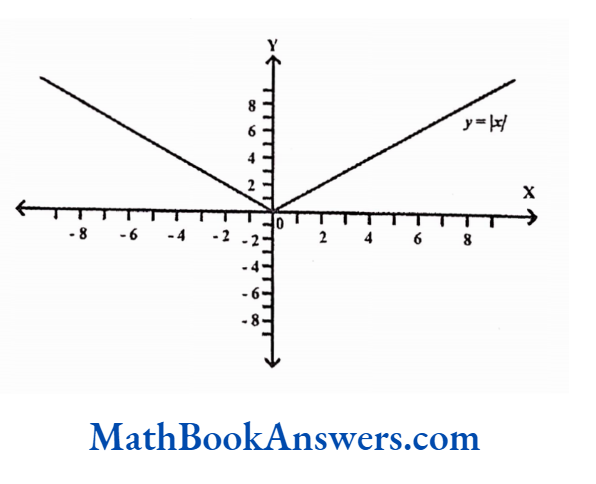
The modulus runction is used to find the positive value of an expression. It is also called the absolute value function. The function is denoted by

f(x) = |x|.

Thus.

f(x) = x if x ≥ 0

= -x if x < 0

The modulus function is an even function. Graphically it can be shown as,

The modulus function is an even function. Graphically it can be shown as

Exercise – 2: Relation

Choose the most appropriate option/options (1) (2) (3) or (4).

1. “Is smaller than” over the set of eggs in a box is

Transitive (T)
Symmetric (S)
Reflexive (R)
Equivalence (E)

Answer: (1) Transitive (T)

Let a be S₁ & b be in S₂: a < b

∴ (a, b) are a part of relation

Let c be in S₃: b < c

∴ a < b < c

-> a < c

(a, c) are part of relation not reflexive because it is smaller than not equal to & not symmetric as a < b but b < a then.

2. “Is equal to” over the set of all rational numbers is

[By using R = Reflexive; T = Transitive, S = Symmetric and E = Equivalence from Q. No. 2 to 8]

Answer: (4) Equivalence

a, a∈R->a = a

-> (a, a) ∈ R reflexive

a,b∈R->a=b

-> b = a -> (b, a) ∈ R symmetric

a,b∈R->a = b

b, c∈R->b = c

∴ a = c

∴ (a, c)∈ R

∴ transitive

∴ equivalence

3. “has the same father as”……over the set of children

R
S
T
All of these

Answer: (4) All of these

-> a has same father as himself reflexive

-> a & b have same father as b & a symmetric

-> a & b have same father & b & c have same father

Implies a & c have same father -> transitive

4. “is perpendicular to” over the set ofstraight lines in a given plane is

Answer: (2) S

a line cannot be perpendicular to itself

∴ not reflexive

a line perpendicular to another line

L₁ ⊥ L₂ -> L₂ ⊥ L_{1 ∴} symmetric

A line perpendicular to L₂ & L₂ ⊥ L₃

Implies L₁ || L₃

∴ not transitive

5. “is the reciprocal of’…… over the set of non-zero real numbers is

S
R
T
none of these

Answer: (1)S

a number is not a reciprocal of itself

∴ not reflexive

a number is reciprocal ofanother say

a =1/b -> b =1/a ∴ symmetric

let a, b e R & let b, c ∈ R

a=1/b b=1/c → 1/a=1/c->a=c

a,c ∉ R not transitive

6. {(x, y)/x ∈ x, y ∈ y, y = x } is

R
S
T
All of these

Answer: (4) All of these

7. {(x,y) / x + y = 2x where x and y are positive integers}, is

Answer: (4)E

{(x,y):y=2x-x}

->{(x,y):x = y}

It is reflexive, Transitive, symmetric

∴ equivalence

8. “Is the square of over n set of real numbers is

R
S
T
none of these

Answer: (4) none of these

[a, a] ∉ R as a² ∴ not reflexive

(a, b) ∈ R ≠>(b, a) ∈ R as a² = b ≠>b² = a

∴ not symmetric

(a, b) ∈ R ⇔ (b, c) ∈ R a² = b, b² = c => a⁴ =c not transitive

9. If A = {1,2,4}, B = {2,4,5} C = {2,5}, then (A-B) x (B – C) is

{(1,2),(1,5),(2,5}}
{(1,4}}
(1,4)
none of these

Answer: (2) {[1,4)}

A = {1, 2, 4}

B = {2, 4, 5}

C = {2, 5}

A- B = {1}

B – C = {4}

A – B x B – C

=>{(1,4)}

10. If R is a relation on the set A = { 1,2,3,4,5,6,7,8,9} given by x R y ⇔ y = 3x, then R =

{(3,1), (6,2), (8,2), (9,3)
{(3,1),(6,2),(9,3)
{(3,1), (2,6), (3,9)}
None of these.

Answer: (4) none of these

R – {(1, 3], (2,6),………….. (9,27)}

11. Let A = {1,2,3} B = {1,3,5}. If relation R from A to B is given by R = {(1,3),(2,5),(3,3) then R^-1 is

{(3,3),(3,1),(5,2)}
{(1,3),(2,5),(3,3)}
{ (1,3),(5,2)}
none of these

Answer: (1) {(3,3), (3, 1), (5,2)}

R = ((a,b) (a, c)}

R^-1 = {(b, a), (b, c)}

12. If A = {1,2,3}, B = {1,4,6,9} and R is relation from A to B defined by ‘x is greater than y. The range of R is

{1,4,6,9}
{4,6,9}
{ 1 }
none of these

Answer: (3) 1

R : {(x, y) : x > y, x ∈ A, y ∈ B)

Range => 1

As x ∈ A will be greater than only 1 from

y ∈ B

13. If R = {(x,y) : x,y ∈ Z, x² + y² ≤ 4} is a relation on Z, then domain of R is

{0,1,2}
{0.-1.-2}
{-2,-1,0,1,2}
none of these

Answer:(3) domain (-2,-1,0,1,2}

14. A relation R Is defined from (2,3,4,5) to {3,6,7,10} by: x R y ⇔ x is relatively prime to y. then, domain of R is

{2,3,5}
{3,5}
{2,3,4}
{2,3,4,5}.

Answer: (4) (2,3,4,5)

Domain of R : A→ B = A

15. Let R be a relation on N defined by x + 2y = 8. The domain of R is

{2,4,8}
{2,4,6,8}
{2,4,6}
{1,2,3,4}.

Answer: (3) {2.4,6)

For y to be a N no

X should be even < 8 & > 0

{2,4,6}

16. If the set A has p elements, B has q elements, then the number of elements in A x B is

p + q
p + q +1
pq
P2

Answer: (3)

n (A) = P n(B) = q (3) pq

n (AxB) = pq

17. Let R be a relation from a set A to a set B, then

R = A U B
R = A ∩ B
R⊆ AxB
R ⊆ B x A.

Answer: (3)R⊆AxB

All relations are a subset of the Cartesian product

18. R is a relation from a finite set A having m elements to a finite set B having n elements then the number of relations from A to B is

2^mn
2^mn-1
2mn
mⁿ

Answer: (1) 2^mn

If a relations is from A→ B

A has in elements B has n elements

Then no. of relations is 2^mn

19. If R is a relation on a finite set having n elements, then the number of relations on A is

2ⁿ
2^n²
n²
nⁿ.

Answer: (2) 2^n²

Relation → A → A

A has n elements no. of relations is

2^mn = 2^n²

20. \(\text { If } f(x)=\frac{2+x}{2-x} \text {, then } f^{-1}(x) \text { : }\)

\(\frac{2(x-1)}{x+1}\)
\(\frac{2(x+1)}{x-1}\)
\(\frac{x+1}{x-1}\)
\(\frac{x-1}{x+1}\)

Answer: (1)\( \mathrm{f}(\mathrm{x})=\frac{2+x}{2-x}=y(\text { let })\)

2 + x = 2y- xy
Or x + xy = 2y-2
Or x(1 + y) = 2 (y-1)

\(\text { Or } \mathrm{x}=\frac{2(y-1)}{1+y}\) \(f-1(x)=\frac{2(x+1)}{x-1}\)

(1) is correct

21. In the set N of all natural numbers the relation R defined by a R b “if and only if a divide b’, then the relation R is:

Partial order relation
Equivalence relation
Symmetric relation
None of these.

Answer: (1) it is transitive relation, i.e. partial order relation

22. On the set of lines, being perpendicular is a__________

Reflexive
Symmetric
Transitive
None of these

Answer: (2) is correct

It is symmetric relation because it x is perpendicular to y

Then y is also perpendicular to x

23. If A = {1,2,3} then the relation R = {{1,1},(2,3),(2,2),{3,3),(1,2)} on A is:

Reflexive
Symmetric
Transitive
Equivalence

Answer: (1) is correct

Reflexive relation.

x R x; (x;x)∈R

here, (1,1),(2,2),(3,3)∈ R

So; it is Reflexiv

24. The range of the reltation {(1,0)(2,0),(3,0)(4,0)(0,0) is

{1,2,3,4,0}
{0}
{1,2,3,4}
None

Answer: (2) is correct

Range = {0}

25. If a relation S = {1,2,3} then {(1,1),(2,2),(1,2),(2,1)} is symmetric and

Reflexive but not transitive
Reflexive as well as transitive
Transitive but not reflexive
Neither transitive nor reflexive

Answer: If S = {1,2,3} then

Then relation {{1,1); (1,2); (2,1)} is symmetric and transitive but not reflexive.

(3) is correct

26. If A = {1, 2} and B = {3,4}. Determine the number of relations from A and B:

Answer: (2)

No. of Relations = 2^n(AxB)

=2^(2×2) = 16.

27. A = {1,2, 3, 4 .. 10} a relation on A, R = {x,y):x + y = 10, x ∈ A, Y ∈ A, x ≥ Y} then domain of R^-1 is

{1,2, 3,4,5}
{0, 3, 5, 7, 9}
{1,2, 4, 5, 6, 7}
None

Answer: (1)

Given ; A = {1, 2, 3,…….; 10}

R = {x;y) / x + y= 10;X ∈A;Y ∈A;x≥y}

=> R = (5 ; 5) ; (6 ; 4) ; (7 ; 3) ; (8 : 2) ; (9 :1)

=> R^-1 = (5 ; 5) ; (4; 6) ; (3 ; 7) ; (2 ; 8) ; (1 ;9)

Domain of R^-1 = (5 ; 4; 3 ; 2 ;1)

Exercise – 3: Function

Choose the most appropriate option/options (1) (2) (3) or (4}.

1. If A = {x,y,z}, B = {p, q, r, s) which of the relation on A to B are function.

{n, p),(x,q), (y, r), (z, s}},
{(x, s}, (y, s), (z, s)}
{(y, p), (y, q), (y, r), (z, s),
{(x, p), (y, r), (z, s}}

Answer:(2) in a function, element from domain can have only one range in range and every element has a image

2. {(x, y)|x+y = 5} where x, y ∈ R is

not a function
a composite function
one-one mapping
none of these

Answer: (3) one-one mapping

3. {(x, y) | x = 4} where x, y ∈ R is a

not a function
function
one-one mapping
none of these

Answer: (1) not a function

as only one element has an image in the rang

4. {(x, y}, y=x²} where x, y ∈ R is

not a function
a function
inverse mapping
none of these

Answer: (2) a function

As every element in domain has only one image

5. {(x, y}|x<y} where x, y ∈ R is

not a function
one-one mapping
a function
none of these

Answer: (1) not a function

6. The domain of {(1, 7), (2, 6)} is

{1, 6}
{7, 6}
{1, 2}
{6,7}

Answer: {(1,7), (2, 6)}

Domain (3) {1, 2}

Set of first elements of a pair of a function

7. The range of {(3, 0), (2, 0), (1, 0), (0, 0}} is

{0,0}
{0}
{0, 0, 0, 0}
none of these

Answer: (2) {0}

Set of second elements of a pair of function

8. The domain and range of {{x,y} : y = x²} where x, y ∈ R is

(reals, natural numbers)
(reals, positive reals)
(reals, reals)
none of these

Answer: (2) (reals, positive reals)

Domain can take any real value & y = x² -> y will only take positive real no.

9. Let the domain of x be the set {1}. Which of the following functions are equal to 1

f(x) = x², g(x) = x
f(a) = x, g(x) = 1-x
f(x) = x² + x + 2, g(x) = (x+ l)²
none of these

Answer: (1) f(x) = x², g (x) = x

f1) = 1² = 1 & g(1) =1

∴ 1

10. If f(x) = 1/1-x, f(-1} is

0
1/2
0
none of these

Answer: (2) 1/2

\(f(x)=\frac{1}{1-x}\) \(f(-1)=\frac{1}{1-(-1)}=\frac{1}{2}\)

-> (2) 1/2

11. If g(x} = (x-1)/x, g(-1/2) is

Answer: (4) 3

\(g(x)=\frac{x-1}{x}\) \(g(-1 / 2)=\frac{-3 / 2}{-1 / 2} \rightarrow 3\)

12. If f(x} = 1/1-x and g(x) = (x-1}/x, than fog(x} is

x
1/x
-x
none of these

Answer: (1) x

\(f(x)=\frac{1}{1-x} g(x)=\frac{x-1}{x}\) \(f o g(x)=f(g(x))=\frac{1}{1-g(x)}\) \(=\frac{1}{1-\frac{(x-1)}{x}}\) \(=\frac{1(x)}{x-x+1} \rightarrow \frac{x}{1} \rightarrow \mathrm{X}\)

13. If f(x) = 1/1-x and g(x) = (x-1)/x, then gof(x) is

x-1
x
1/x
none of these

Answer: (2) x

\(f(x)=\frac{1}{1-x}\)

\(g(x)=\frac{(x-1)}{x}\) gof(x)

\(g(\mathrm{f}(\mathrm{x}))=\frac{f(x)-1}{f(x)}\) \(=\frac{\frac{1}{1-x}-1}{\frac{1}{1-x}}\) \(\rightarrow \frac{\frac{1-1+x}{1-x}}{\frac{1}{1-x}} \rightarrow \frac{x}{1} \rightarrow \mathrm{x}\)

14. The function f(x) = 2^x is

one-one mapping
one-many
many-one
none of these

Answer:(1) one-one mapping

15. The range of the function f(x) = log₁₀(1 + x) for the domain of real values of x when is 0≤ x ≤ 9 is

[0,1]
[0,1,2]
[0, -1]
none of these

Answer: (1) [0, 1]

16. The Inverse function f^-1 of f(x) = 2x is

1/2x
x/2
1/x
none of these

Answer: (2) x/2

f(x) = 2x

y = 2x->x =y/2

∴ Inverse -> f^-1 =x/2

17. If f(x)= x+3, g(x) = x², then fog(x) is

x² + 3
x² + x + 3
(x + 3)²
none of these

Answer: (1) x² + 3

Fog x = f(g(x)) = g(x) + 3 = x² + 3

18. If f(x) = x+3, g[x] = x², then f(x).g(x] is

(x + 3)²
x² + 3
x³ + 3x²
none of these

Answer:(3) x³ + 3x²

f(x).y(x) = (x + 3) (x²) = x³ + 3x²

19. The Inverse h^-1 when h(x) = log₁₀x is

log₁₀x
10x
log₁₀(1/x)
none of these

Answer: (2) 10x

h(x) = log₁₀ x

y = log₁₀x -> 10y = x

h^-1 = 10x

20. For the function h(x) = 10^1+x the domain of real values of x where 0 ≤ x ≤ 9, the range is

10 ≤ h(x) ≤ 10¹⁰
0 ≤ h(x) ≤ 10¹⁰
0<h(x)<10
none of these

Answer:(1) 10 ≤ h(x) ≤10¹⁰

h(x).10x+1, 0 ≤ x ≤ 9

at 0 smallest→ 10¹

At 9 biggest value→ 10¹⁰

10 ≤ h(x) ≤ 10¹⁰

21. Let A = (1,2,3), B = (2,3,4), then which of the following is a function from A to B?

{(1,2),(1,3),(2,3),(3,3)}
{(1,3), (2,4)}
{(1,3),(2,2), (3,3)}
{(1,2),(2,3),(3,2),(3,4)}.

Answer: (3) {(1,3), (2,2), (3,3)}

for a function every element in domain should have an image & not more than one

22. If f: Q —» Q is defined as f (x) = x², then f^-1 (9) is equal to

3
-3
{-3,3}
0

Answer:(3) {-3.3}

y = x²

x=y

f^-1(x)=y

f^-1=9

or -3->{-3,3}

23. Let f(x) = | x-1|. Then,

f(x²) = [f(x)]²
f(x+y) = f (x) f(y)
f(|x|) = |f(x)|
none of these

Answer: (4) none of these

24. If A = {1,2,3}, B = {x, y}, then the number of functions that can be defined from A into B is

12
8
3f(x)
-f(x)

Answer: (2) 8

25. Let A = {x ∈ R : x ≠ 0, – 4 ≤ x ≤ 4} and f: A —> R be defined by f(x) = |x|/x for x ∈ A. Then A is

{1,-1,}
{x:0≤x≤4}
{1}
{x:-4≤ x ≤ 0}

Answer: (1) {1,-1}

\(\frac{|x|}{x}=\left\{\begin{array}{cc}
1 & 4 \geq x>0 \\
-1 & -4 \leq x<0
\end{array}\right.\)

26. If f:R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x² + 7, then the values of x such that g (f(x)) = 8 are

1,2
-1,2
-1,-2
1,-2

Answer: (3) -1, -2

g(f(x)) = 8

f(x)² + 7 = 8

(2x + 3)² =1

2x + 3 = 1 or 2x + 3 = 1

2x = -2 X = -1

x = -2

27. Let R is the set of real numbers, such that the function f: R→ R and g : R → R are define by f(x) = x² + 3x + 1 and g(x) = 2x- 3. Find (fog):

4x² + 6x + 1
x² + 6x +1
4x²- 6x + 1
x² – 6x + 1.

Answer: (3) f(x) = x² + 3x + 1

g(x) = 2x – 3

fog = f{g(x)}

= f (2x – 3)

= (2x- 3)² + 3(2x – 3) +1

4x²- 2.2X.3 + 9 + 6x – 9 + 1

= 4x² – 6x + 1

(3) is correct

28. If R is the set ofreal numbers such that the function f: R →R is defined by f(x) = (x+1)², then find (fof)

(x+1)²+ 1
x²+1
{(x+1)²+1}²
None

Answer:(3) f(x) = (x + 1)²

fof=f{f(x)} = f{(x+1)²)

= { (X + 1)² + 1)²

(3) is correct

29. If f: R → R. f(x) = 2x + 7, then the inverse of f is:

f^-1 (x) = (x-7)/2
f^-1 (x) = (x + 7)/2
f^-1(x) = (x – 3)/2
None.

Answer: (1) Let y = f(x) = 2x+ 7

Or 2x = y-7

Or\(x=\frac{y-7}{2}\)

\(f^{-1}(x)=\frac{x-7}{2}\)

30. Let f: R → R be such that f(x) = 2^x, then f(x+y) equals:

f(x) + f(y)
f(x). f(y)
f(x) ÷ f(y)
None of these

Answer: (2) f(x) = 2X

f(x+y) = 2x+y = 2x2y = f(x).f(y)

(2) is correct

31. If A = {1,2,3,4,}; B = {2,4,6,8,} f(1) = 2, f(2) = 4, f{3) = 6 and f(4) = 8, and f: A->B then f^-1f: A->B then f-1 is:

{(2,1),(4.2),(6,3),(8,4)}
{(1,2),(2,4),(3,6),(4,8)}
{(1.4),(2,2),(3,6),(4,8)}
None of these

Answer:(1) f^-1 = {(2,1),(4,2),(6,3)1(8,4)}

(1) is correct

32. If f(x) = x² + x -1 and 4f(x) = f(2x) then find ‘x’

4/3
3/2
-3/4
None of these

Answer:(2) f(x) = x² + x-1

And 4f(x) = f(2x)

Or 4(x² + x- 1) = (2x)²+ 2x-1

Or 4x² + 4x – 4 = 4x² + 2x-1

Or4x-2x = 4-1

Or 2x = 3 x = 3/2

(2) is correct

33. X = {x,y,w,z} y ={1,2,3,4); H={(x,1);(y,2);(y,3);(z,4);(x,4)}

H is a function from x to y
H is not a function from x to y
H is a relation from y to x
None of these

Answer:(2) H is not a function from x to y because x has 2 images 1 & 4

(2) is correct

34. Given the function f(x) = (2x+3), then the value of f(2x) – 2f(x) + 3 will be:

Answer: (4) f(x) = 2x + 3

f(2x) – 2 f(x) + 3

= 2(2x) + 3 – 2(2x+3)+3

= 4x + 3 – 4x – 6 + 3 =0

(4) is correct

35. If f(x) = 2x + h then find f(x+h)-2f(x)

h-2x
2x-h
2x+h
None of these

Answer:(1) f(x) = 2x + h

f(x + h) – 2f(x)

= 2x + 2h + h – 4x – 2h

= h – 2x

(1) is correct

36. If F: A→ R a real valued function defined by f(x) =1/x then

R
R -{1}
R-{0}
R-N

Answer: (2)

f(x) =1/x is defined at all x ∈ R except x = 0

A = R – {0}

(3) is correct

37. If f: R — R, f(x) = x + 1, g: R → R g[x) = x² +1 then fog(-2) equals to

6
5
-2
None

Answer: (1) f(x) = x + 1

g(x) = x² + 1. => g(-2) = (-2)² +1 = 5

fog (-2) = f{g(-2)) = f(5)

=5+1=6

(1) is correct

38. If f(x-1) = x²- 4x + 8, then f(x+1) =

x² + 8
x² + 7
x² + 4
x² – 4x

Answer: (3) f(x-1)=x²-4x + 8

=(x-1-1)2-4 (x-1+1) + 8

f(x+1) = (x+ 1 + 1)² – 4(x+ 1 + 1)+8

= (x+2)²- 4(x+2) + 8

= x² + 4x + 4-4x-8 + 8

= x² + 4

(3) is correct

39. If A – {±2, +3}B = {1,4,9)ANS F = {(2,4),(-2,4),(3,9){-3,4)} Then F is defined as:

One to one function from A into B
One to one function from A onto B
Many to one function from A onto B
Many to one function from A into B.

Answer:(3)

(3) is correct

40. \(\text { If } f(x)=\frac{x}{\sqrt{1+x^2}} \text { and } g(x)=\frac{x}{\sqrt{1-x^2}} \text { find fog? }\)

x
1/x
\(\frac{x}{\sqrt{1+x^2}}\)
\(x \sqrt{1+x^2}\)

Answer:

(1) fog = f{g(x)}\(=f\left(\frac{x}{\sqrt{1-x^2}}\right)\)

\(=\frac{\frac{x}{\sqrt{1-x^2}}}{\sqrt{1+\frac{x^2}{1-x^2}}}\) \(=\frac{\frac{x}{\sqrt{1-x^2}}}{\sqrt{\frac{1-x^2+x^2}{1-x^2}}}\) \(=\frac{x}{\sqrt{1-x^2}} \times \frac{\sqrt{1-x^2}}{\sqrt{1}}=x\)

(1) is correct

41. E(x) = 3 +x, for -3 < x < 0 and 3 – 2x for 0<x<3, then value of f(2) will be

-1
1
3
5

Answer: (1) is correct

f(x) = 3 + 2x; when -3 < x < 0

= 3- 2x ; when 0 < x < 3

f(x=2) = 3- 2x² = -1

2 lies in 2nd condition

42. The range of the function f: N —> N; = (-1)^x-1 , is

{0,-1}
{1,-1}
{1,0}
{1,0,-1}

Answer: (2) is correct

f(x)-(-1)x-1

If x= odd no.

f(x) = odd no.

f(x) = 0; even N.

Range = {1 ; -1)

Domain = {Any real No.}

43. If f: R —> R is a function, defined by f(x) = 10x – 7, if g(x) = f^-1 {x), then the value of g(x) is
equal to

\(\frac{1}{10 x-7}\)
\(\frac{1}{10 x+7}\)
\(\frac{x+7}{10}\)
\(\frac{x-7}{10}\)

Answer: (3) is correct

Let y= f(x) = 10x-7

Or 10x = y + 7

\(x=\frac{y+7}{10}\) \(f-1(x)=\frac{x+7}{10}\) \(g(x)=\frac{x+7}{10}\)

44. If f(x) = x+2, g(x} = 7^x then go f(x} =

7^x.x+2.7^x
7^x+2
(7^x)+2
None

Answer: f(x) = x+2 ; g(x) = 7x

g,pf(x) = g{f(x)} = g(x+2) = 7^x+2

(2) is correct

45. If f(x)=\(\log \left(\frac{1+x}{1-x}\right) \text { then } f\left(\frac{2 x}{1+x^2}\right)\)

f(x)
2f(x)
3 f(x}
-f(x)

Answer: (2)

\(f\left(\frac{2 x}{1+x^2}\right)=\log \left(\frac{1+\frac{2 x}{1+2 x^2}}{1-\frac{2 x}{1+x^2}}\right)\) \(=\log \left(\frac{1+x^2+2 x}{1+x^2-2 x}\right)\) \(=\log \frac{(1+x)^2}{(1-x)^2}=\log \left(\frac{1+x}{1-x}\right)^2\) \(=2 \log \left(\frac{1+x}{1-x}\right)=2 f(x)\)

(2) is correct

46.\(\text { If } f(x)=\frac{x^2-25}{x-5} \text { then } f(5) \)

0
1
10
Undefined

Answer: (4) is correct

\(f(5)=\frac{x^2-25}{x-5}=\frac{5^2-25}{5-5}=\frac{0}{0}\)

Undefined

47. \(\mathrm{f}(\mathrm{x})=\left(a-x^n\right)^{\frac{1}{n}}\),a > 0 and n is positive integer then f [f(x)] =

x
a
x¹^/n
a ¹^/n

Answer: (1) is correct

\(\mathrm{f}\{\mathrm{f}(\mathrm{x})\}=\mathrm{f}\left\{\left(\mathrm{a}-\mathrm{x}^{\mathrm{n}}\right)^{1 / n}\right\}\) \(=\left[a-\left\{\left(a-x^n\right)^{\frac{1}{n}}\right\}^n\right]^{\frac{1}{n}}\) \(=\left[a-\left(a-x^n\right)\right]^{\frac{1}{n}}=\left[x^n\right]^{\frac{1}{n}}=x\)

48. If A = {1,2,3} and B = {4,6,7} then the relation R = {(2,4)(3,6)} is

A function
A function from A to B
Both {a} and (b}
Not a function

Answer: (4) is correct.

Note: -1 has no image

49. \(\text { If } f(x)=\frac{x}{x-1} \text {, then } \frac{f(x / y)}{f(y / x)}=\) ___________

x/y
y/x
-x/y
-y/x

Answer:

\(f(x)=\frac{x}{x-1}\) \(f(x / y)=\frac{x / y}{x / y-1}=\frac{x / y}{\frac{x-y}{y}}=\frac{x}{x-y}\) \(f(y / x)=\frac{y / x}{y / x-1}=\frac{y / x}{\frac{y-x}{x}}=\frac{y}{-(x-y)}\) \(\frac{f(x / y)}{f(y / x)}=\frac{\frac{x}{x-y}}{y}=-\frac{x}{y}\)

50. Let N be the set of all natural number; E be the set of all even natural numbers then the function f:N→ E defined as f{x) = 2x; V x ∈ N is:

One-one into
One-one onto
Many-one into
Many-one onto

Answer:(2) is correct

N = {1,2, 3,…;n}

E = {2,4, 6……;2n}

Clearly it is one-one onto mapping

51. Which of these is a function from A →B; A = {x,y,z}; B {a,b,c,d}

{(x,a)(x,b)(y,c)}
{(x,a}(x,b)(y,c)(z,d)}
{9x,a} (y,b) (z.d)}
{(a,x)(b,z)(c,y)}

Answer: (3)

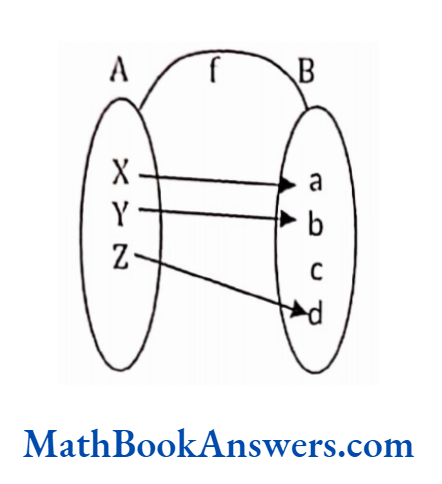
52. If (x) = 2x + 2, g(x) = x², fog(4) = ?

Answer: Fog (x) = f{g(x)}

= f(x²) = 2.x² + 2

Fog (4) = 2 x 4² + 2 = 34

(3) is correct

53. The domain (D) and range (R) of the function f(x) = 2-|x+1|is

D = Real numbers, R = (2,∞)
D= Integers, R= (0,2)
D = Integers, R = (-∞, ∞)
D = Real numbers, R = (-∞,2]

Answer: (4)

Lety = f(x) = 2-|x+1|

For any real values of x: f(x) is defined

Domain = D Real number

Minimum value of |x+1| is zero

Maximum value of range

=2-0=2

Range = – ∞ < y ≤ 2

= (-∞; 2]

54. If f (x) = 100 x then f^-1 (x) =

x/100
1/100x
1/100
None of these

Answer: (1) is correct

Let y = f (x) = 100x

\(X=\frac{y}{100} ; \text { So, } f^{-1}(x)=\frac{x}{100}\)

55. f: R —> R is defined by f (x) = 2^x then f is

One- one and onto
Many to one
One-one and into
One to many

Answer: (2) is correct

56.\(\text { If } f(x)=\frac{x-1}{x} \text { and } g(x)=\frac{1}{1-x} \text { then fog }(x)=\)

x-1
x
1-x
-x

Answer: fog(x) = f{g(x)}\(=\frac{g(x)-1}{g(x)}\)

\(=\frac{\frac{1}{1-x}-1}{\frac{1}{1-x}}=\left(\frac{1-1+x}{1-x}\right) \times \frac{(1-x)}{1}\)

= X

Option (2) is correct

57. \(\text { If } \mathrm{f}(\mathrm{x})=\frac{x+1}{x+2}=\text { then } \mathrm{f}\left[\mathrm{f}\left(\frac{1}{x}\right)\right]=\)____________

\(\frac{2 x+3}{3 x+5}\)
\(\frac{2 x+5}{3 x+2}\)
\(\frac{3 x+2}{5 x+3}\)
\(\frac{5 x+2}{2 x+3}\)

Answer: (1)

\(f\left(\frac{1}{x}\right)=\frac{1 / x+1}{1 / x+2}=\frac{1+x}{x} \times \frac{x}{1+2 x}\) \(=\frac{1+x}{1+2 x}\)

Now, \(\mathrm{f}\left[f\left(\frac{1}{x}\right)\right]=\mathrm{f}\left(\frac{1+x}{1+2 x}\right)\)

\(=\frac{\frac{1+x}{1+2 x}+1}{\frac{(1+x)}{1+2 x}+2}=\frac{\frac{3 x+2}{1+2 x}}{\frac{5 x+3}{1+2 x}}\) \(=\frac{3 x+2}{5 x+3} .\)

58. If f(x) = x² and g(x) = √x then

go f(3) = 3
go f(-3) = 9
go f(9) = 3
go f(-9) = 3

Answer:(1)

f(x) = x² ; g(x) = √x

go f(x) = g {f(x)}

√f(x) = √x²

= X

gof(3) = 3

(1) is correct.

Sets, Function & Relations

Function And Relation

Leave a Comment Cancel reply