CA Foundation Maths Solutions For Chapter 5 Permutations And Combinations

Permutations and Combinations Introduction

The concept of permutations and combinations is used to select or arrange some items out of a group according to certain predetermined conditions. This concept helps find the number of ways to arrange, select or reject these items.

The concepts of permutations and combinations derive from the principles of Factorials and the Fundamental principle of counting.

Factorial

The factorial of a natural number n, denoted by n! or |n_is the product of all-natural numbers from 1 up to n.

n! = 1 x 2 x 3 x … x (n- 1) x n

The factorials of the first few natural numbers are as given below.

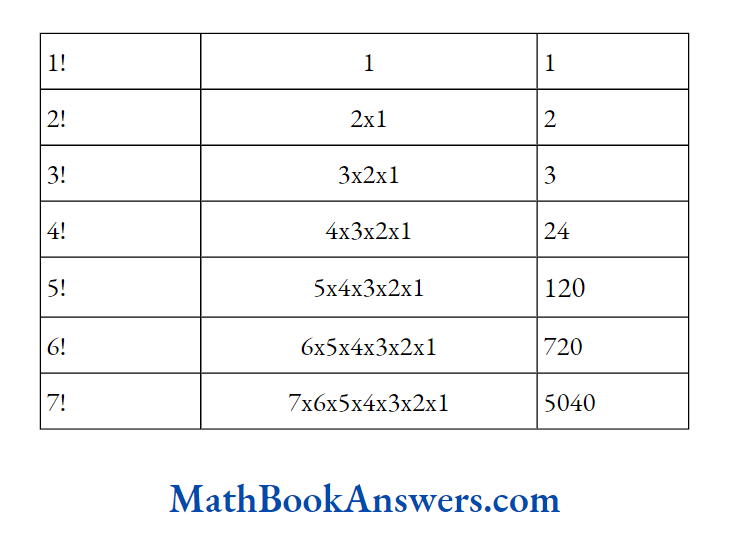
Remember:

n! = nx [(n- 1) x (n- 2) x (n- 3) x … x 1]
n! = n x (n- 1)!
n! = n x (n- 1) x (n- 2)!

Read and Learn More CA Foundation Maths Solutions

The factorial of 0 is defined to be one.

∴ 0! = 1

The factorial of negative numbers is not defined.

Permutations and Combinations

The task of selecting a number of objects from a given set of objects involves a number of choices the number of choices available depends on the purpose of selection.

If the order of selection is unimportant, the selection is called a combination, if the order of selection is important, the selection is called a permutation.

Consider the case ofselecting two out of three students A, B and C.

Case 1:

Suppose the task is to select two students out of A, B and C and rank them according to the marks they have scored. The different possibilities that exist are as follows:

Note that the selection (A, is different from the selection (B, A] here.

Total number of selections = 6

Here, the students are first selected and then arranged for a purpose. This kind of selection is called a permutation.

Case II:

Now suppose that the task is just to select two students out of three. In such a case, the order in which the students are selected is not important.

Hence, the possibilities in this case are (A, B), (B, C] and (A, C]

Note that (A, and (B, in the above case mean the same thing as both groups imply that students A and B have been selected.

Here, they do not need to be ranked.

total number of selections = 3

Here, the important thing is to just select the students and not to arrange them.

This kind of selection is called a combination.

Remember:

Permutations involve selection and then, arrangement of objects while combinations involve only selection of objects.

Example:

Suppose 4 people out of 7 are to be arranged for a photograph. This involves first selecting the 4 people and then arranging them. This is a permutation.

On the other hand, if 4 people out of 7 are to be chosen for a team, it just involves selecting the 4 people without any arrangement. This is a combination.

Solved Example:

Find out whether the following tasks involve permutations or combinations.

1. Arranging five girls on five chairs for a photograph
2. Forming a committee of five people from then boys and five girls.
3. Electing a captain and a vice -captain from a team of11.
4. Selecting a king or a queen from a pack of cards.

Solution:

1. Here, the girls need to be arranged such that there are five girls on five chairs. Since, it involves arranging the five girls; it is a case of permutations.
2. Here, just select five people out of ten boys and five girls. There is no arrangement involved. So, it is a case of combinations.
3. This task involvers selecting two people, and then arranging them in order, the first one being the captain and the second being the vice-captain. Hence, this is a case of permutations.
4. Here, just select two cards. In the previous task, a player selected was to be ‘made’ the captain or vice -captain. Here, just select a king or a queen out of the kings and queens in the pack of cards. Hence, this is a case of combinations.

To find the number of ways in which the permutations and combinations can be counted, first understand the fundamental principle of counting.

Fundamental Principle of Counting

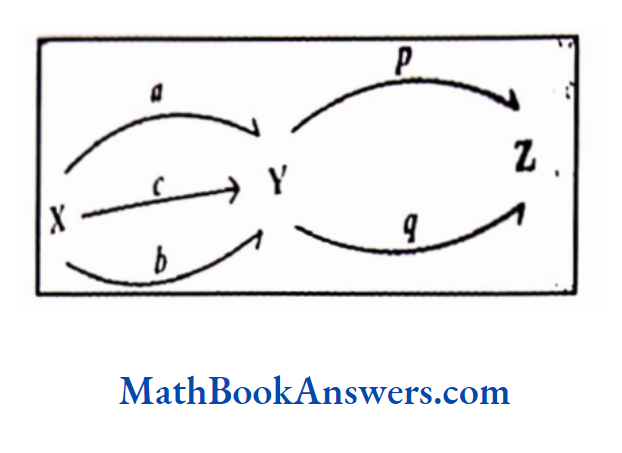
Suppose one needs to travel from X to Z via Y. There are three routes a, b, c, available to go from X to Y and two routes p, q available to go from Y to Z Ifone travels from X to Y taking the route a, then one can travel from Y to Z in two ways.

Thus, for every choice of route that one makes for travelling form X to Y, there are two ways to travel from Y to Z. As there are three routes to travel from X to Y, there are 2+2+2+=3x 2 ways to travel form X to z via Y.

The routes are (a,p),(a,q), b,p), (b,q),(c,p) and (c,q). If one considers travelling from X to Y as task 1, and travelling from Y to Z as another task 2, task 1 can be permed in 3 ways, task 2 can be performed in 2 ways, and task 1 and task 2 together can be performed in 3x 2 = 6 ways.

In general, the fundamental principle of counting says that, if we can accomplish one takes in xx ways, another task in x2 ways, and so on, until the n”‘ task which can be done in x„ ways
then all these tasks can be accomplished in X1×X2×X3× …xn ways.

Remember:

Consider two tasks; task 1 that can be done in m ways & task 2 that can be done in n ways.
Task 1 and task 2 can be done in m x n ways
Task 1 OR task 2 can be done in m + n ways.

Solved Examples:

1. Josephine likes to have passwords that have eight characters, the first four being different vowels and the last four being different numbers. How many different passwords can she have?

Solution:

The first four characters of Josephine’s password are to be chosen form the five vowels the first vowel can be chosen in 5 different ways. As all of them have to be different, the second
can be chosen only in 4 ways, the third in 3 ways and the last in 2 ways.

Similarly, the four numbers have to be different. Hence, the four numbers can be chosen form the 10 digits from  0 to 9 in 10, 9, 8 and 7 ways respectively.

Thus, the number of different passwords that Josephine can have.

= 5x4x3x2x 10 x9x8x7 = 604800

2. How many numbers greater than 5000 can be formed by arranging the digits 4, 5, 7, 9 using each digit only once?

Solution:

Since the number has to be greater than 5000, the first digit can be chosen in 3 ways only, I.e., it can be 5,7 or 9

Once this diÿit is chosen, the next, digit can be chosen in 3 ways, the next in 2 and the next in 1.

Thus, 3x3x2x1 = 18 such numbers can be formed.

Hence, 18 numbers greater than 5000 can be formed by arranging the digits 4,5,7, 9 using each digit only once.

3. How many numbers can be formed using the digits 4, 5, 7,9, if repetition ofdigits is allowed?

Solution:

In this case, there is no repetition of digits, also, there is no condition as to whether should be greater than or less than something, for each place one can choose any of the 4 digits

Thus, 4x4x4x4 = 256 such numbers can be formed.

Hence, 256 numbers can be formed using any of the digits 4, 5, 7, 9 if repetition of digits is allowed.

4. Four medical representatives Rl, R2, R3 and R4 are to visit one doctor each on Thursday. The doctors are Dl, D2, D3, and D4, Rl Will not visit only D1 and R2 will visit only D2 or D3. In how many ways can the visits be done such that no two representatives visit the same doctor?
Solution:

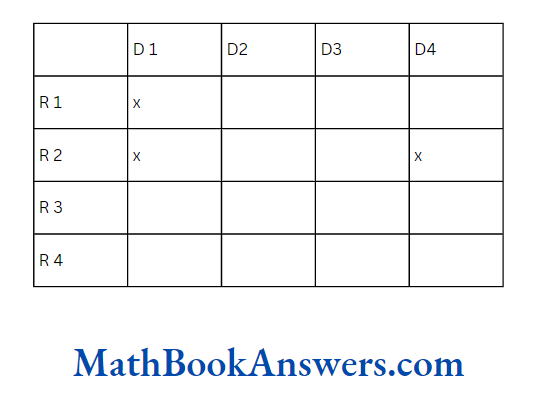
R2 can visit ldoctor (D2 or D3) in 2 ways. Then Rl is left with 2 choices (D2 /D3 or D4)

After this, R3 and R4 have 2 and 1 choices.

∴ the total number of ways in which the vistis can be done = 2x2x2x1= 8

5. Eight buildings in a residential complex are to be painted on their outsides in any one colour form among cream, blue, green, pink and white. The buildings are in a row. Two buildings can have the same colour but two adjacent buildings cannot. In how many ways can the buildings
be painted?

Solution:

The first building can be painted using any one of the five colours in 5 ways. The second building can be painted using any of the remaining four colours in 4 ways. The third building
can have any colour except the one with which the second building is painted.

Thus it can be painted in 4 ways. Thus, each building can be painted in 4 different ways using a colour except the one used to colour the previous building. Hence, the fourth, fifth, sixth, seventh and eighth buildings can be painted using 4 colours each.

Thus, the total number of ways in which the buildings can be painted = 5 x 4⁷

Permutations

If there are n objects ami one is supposed to arrange r (r < n) objects out of these, then the number of ways in which this can be done is written as nPr and is read as “the number of
permutations of n objects taken rata time”

The number of permutations is given as:

\({ }^3 P_2=\frac{n!}{(n-r)!}\)

The case where 2 out of 3 students were to be ranked can be written as \({ }^3 \mathrm{P}_2\).

\({ }^3 P_2=\frac{n!}{(3-2)!}=6\)

Remember:

If r= 0,

\({ }^n P_2=\frac{n!}{(n-0)!}=1\)

If r= 1,

\(n P_1=\frac{n!}{(n-1)!}=n\)

if r = n ,

\({ }^n \mathrm{P}_{\mathrm{n}}=\frac{n!}{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n!\)

if r = n-1,

\({ }_n P_{n-1}=\frac{n!}{(n-n+1)!}=\frac{n!}{1!}=\frac{n!}{1}=n!\)

Permutations with Repetitions

If one has to form words using the letters A, B and C, one can make 3P.j= 6 words i.e., ABC, ACB, BAC, BCA, CAB AND CBA.

But, if one has to from words using the letters A, B and A, then one can make only 3 different words- AAB, ABA and BAA.

Thus, repetition of letters reduces the number of words that can be formed.

Therefore, in case the n elements that are to be arranged among themselves have some repeated elements among them, the number of permutations is not equal to MP„ or not equal
to n!

If n objects are to be arranged among themselves and these contain p identical objects of one kind q identical objects of another kind, r identical objects of still another kind and so on, the total number of ways in which they can be arranged is given by \(\frac{n!}{p!q!r!\ldots}\)

Solved Examples:

1. How many words can be formed by arranging the letters of the word WEEDED?

Solution:

Total number of letters in the word WEEDED=6.

D occurs 2 times and E occurs 3 times.

Hence, the total number of words that can be formed by arranging these letters is:

\(\frac{6!}{2!\times 3!}=60\)

Thus 60 words can be formed by arranging the letters of the word WEEDED.

2. Akash has is DVDs out of which 3 are of a movie A, 5 are of a movie B and the rest are all different in how many ways can he arrange the DVDs on a shell?
Solution:

There are 15 objects out of which 3 are of one kind and 5 are ofanother kind.

The total number ofarrangements possible \(=\frac{15!}{3!\times 5!}\)

Circular Arrangements

The number of ways in which n objects can be arranged in a circle= (n-l)!

Explanation:

Consider four people A, B, C and D sitting on a circular table.

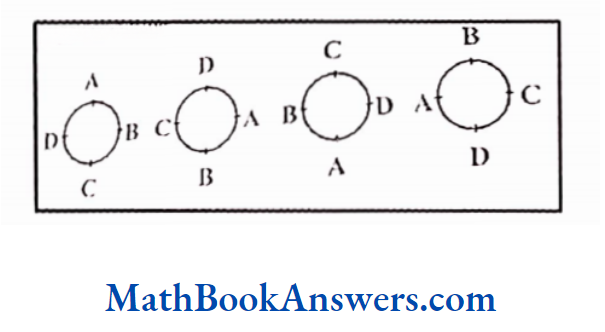
All the four arrangements shown above are one and the same as the beginning and end of a circle cannot be determined. However, had the four arrangements been linear, had the four arrangements been linear, they would be ABCD, DABC, CDAB and BCDA, which would be four different linear arrangements.

Thus, 4 linear arrangements. Would give rise to 1 circular arrangement.

But 4 people would give 4! Linear arrangements

4 people would give 4!/4 = 3! Circular arrangements.

Similarly, if there were n objects, n linear arrangements would give 1 circular arrangement.

n! Linear arrangements would give n! /n = (n-l)! Circular arrangements.

The number of ways in which n objects can be arranged in a circle = (n-l)!

Solved Examples:

1. In how many ways can 5 people be seated around a circular table?

Solution:

n objects can be arranged in a circle in (n-l)! Ways.

Similarly, 5 people can be seated around a circular table in (5-1)! = 4! =24 ways.

2. Seven girls and five boys are to be seated around a circular table such that two of the girls want to sit next to each other, in how many ways can they be seated?

Solution:

There are 12 people to be seated in a circle, as two girls want to sit next to each other; we consider them to be one entity.

Hence there are 11 people to be arranged in a circle, this can be done in 10! Ways

The two girls can be arranged among themselves in 2! Ways.

Thus the total number of ways in which the seven girls and five boys can be arranged = 10!x 2!

3. Five boys and five girls are to be arranged in a circle such that no two girls are next to each other, in how many ways can they be arranged?

Solution:

Since no two girls are to be next to each other, the boys and girls need to be arranged alternately.

Hence, the five boys can be arranged in a circle in 4! Ways.

There are five places in between the boys, in which the girls can be arranged in 5! Ways.

The total number of ways in which the five boys and five girls can be arranged= 4!x 5!

Note that once the boys are seated, the positions of the girls are relative to the positions of the boys and hence their arrangement is treated as a linear arrangement.

Some circulate arrangements are such that clockwise or anticlockwise arrangements are the same. A necklace is a typical example ofsuch a circular arrangement.

The number of arrangements of n objects in such a fashion is \(\frac{(n-1)!}{2}\)

4. In how many ways can 6 different beads be arranged to from a necklace?

Solution:

In a necklace, clokwise and anticlockwise arrangements are same.

n objects canbe arranged in a necklace in [ltex]1 / 2 \times(n-1)!\text { ways. }[/latex]

Thus, 6 beabs can form a necklace in \( 1 / 2 \times(6-1)!=\frac{5!}{2}=60 \text { ways. }\)

Combinations

If there are in objects and out of them (r < n) are to be selected, them the number of ways in which this can be done is ” C r and is read as “the number of combinations of objects taken r at a time”.
The number of combinations is given as:

\({ }^n C_r=\frac{n!}{(n-r)!r!}\)

If 2 students out of 3 are to be selected, it can be written as \({ }^3 C_2\)

\({ }^3 C_2=\frac{3!}{(3-2)!2!}=3\)

Thus, there, are 3 different ways in which 2 objects out of 3 can be selected. These 3 different possible cases are as given in case II.

Explanation:

Consider n objects out of which r are to be selected. Any combination of r objects out of these n objects can be arranged in \(r P_r\) ways, thus one combination of r objects gives r! Permutations.

As the number of combinations of n objects taken r at a time \({ }^n \mathrm{C}_{\mathrm{r}}\) these combinations in all give

\({ }^{\mathrm{n}} \mathrm{C}_r \times r \text { ! Permutations. }\)

This is nothing but the number of permutations of n objects taken r at a time.

\(\begin{aligned}
& { }^n \mathrm{P}_{\mathrm{r}}={ }^n \mathrm{C}_{\mathrm{r}} \times r! \\
& { }^n \mathrm{C}_{\mathrm{r}}=\frac{{ }^n \mathrm{Cr}}{r!}=\frac{n!}{(n-r)!r!}
\end{aligned}\)

Remember:

If r=0

\({ }^n C_0=\frac{n!}{(n-0)!\times 0!}=1\)

If r=1,

\({ }^n C_1=\frac{n!}{(n-1)!\times 1!}=n\)

If r=n,

\({ }^n C_n=\frac{n!}{(n-n)!\times n!}=1\)

If r =n-1

\({ }^n C_{n-1}=\frac{n!}{(n-n+1)!\times(n-1)!}=\frac{n!}{1!\times(n-1)!}=n\)

Some more useful rules involving Combinations

1. The number of ways in n which identical things can be divided in r groups when each person may get any number of things, including zero=\( (n+r-1) C_{(r-1)}\)

2. The number of ways in n which identical things can be divided in r groups when each person may get at least one thing = \({ }_{(n+r-1)} C_{(r-1)}\)

Solved Examples:

1. In how many ways can 24 chocolates be distributed among 4 children such that each one of them gets some or none?

Solution:

The number of distributions is \((21+1-1) C_{(4-1)}={ }^{27} C_3=2925\)

2. How many solution does the equation x + y +z= 10 have, if x, y, and z are natural numbers?

Solution:

Since x, y and z are all natural numbers; they cannot have a value 0. Hence, their value has to beadiest 1. Hence; this is similar to a problem of distributing 10 chocolates (each chocolate
corresponds to the number 1) among 3 people so that each person has at least one chocolate.

Thus, the number of solutions of this equation is given by \( { }^{10 \cdot 1} \mathrm{C}_{3 \cdot 1}={ }^9 \mathrm{C}_2=36\)

Remember:
The fundamental principle of counting says that, if we can accomplish one task in xx x x2 x x3 x ,…x„ ways.

If task 1 can be done in m ways and task 2 can be done in n ways then:

1. Task 1 and task 2 can be done in m xn ways.

2. Task 1 or task 2 can be done in m + n ways

The number of permutations of n objects taken rat a time is given by: \({ }^n P_r=\frac{n!}{(n-r)!}\)

If n objects are to be arranged among themselves and these contain p identical objects of one kind, q identical objects of another kind, r identical objects of still another kind and
so on, the total number of ways in which they can be arranged is given by \(\frac{n!}{p!q!r!_m}\)

The number of permutations of n different things taken r at a time when repetition is allowed = n x n x n x…..r times = nr

The number of ways in which n objects can be arranged in a circle when clockwise and anticlockwise arrangements are different = (n-l)l

The number of ways in which n objects can be arranged in a circle when clockwise and anticlockwise arrangements are same = (n-l)l / 2

Number ofselections of k consecutive things out of n things in a row =n-k+l

The number of combinations of n objects taken r at a time is given by

\({ }^n C_r=\frac{n!}{(n-r)!r!}\)

 

\(\begin{aligned}
& { }^n P_r={ }^n C_r x r! \\
& { }^n C_r={ }^n C_{n-r} \\
& \text { if }{ }^n C_x={ }^n C_y \text { then } x=y \text { or } x+y=n \\
& { }^n C_r={ }^{n \cdot 1} C_r+{ }^{n \cdot 1} C_{r-1}
\end{aligned}\)

the number of ways in which none or some elements from a set of n elements is

\({ }^n \mathrm{C}_{10}+{ }^n \mathrm{C}_1+\) \({ }^n C_2+\ldots .+{ }^n C_n=2 n\)

the number of ways in which n identical things can be divided in r groups when each person may get any number of things, including zero =\(n+r-1) C_{(r-1)}\)

the number of ways in which n identical things can be divided in r groups when each person may get at least one thing \(=11+r-1) C_{(r-1)}\)

Exercise – 1 Permutations

Choose the most appropriate option (1) (2) (3) or (4)

l. \({ }^4 P_3\) i is evaluated as

1. 43
2. 34
3. 24
4. None of these

Answer: (3) 24 \(\text { We know } \mathrm{nP}_{\mathrm{r}}=\frac{n!}{(n-r)!}\)

\({ }^4 P_3=\frac{4!}{(4-3)!}=\frac{4!}{1!}=24 \)

2.\({ }^4 P_4\) is equal to[/latex]

1. 1
2. 24
3. 0
4. none of these

Answer: (2) 24 \(\text { We know }{ }^n \mathrm{P}_{\mathrm{r}}=\frac{n!}{(n-r)!} \quad{ }^4 \mathrm{P}_4=\frac{4!}{0!}=\frac{4!}{1}=24\)

3. 7! is equal to

1. 5040
2. 4050
3. 5050
4. none of these

Answer: ( 5040 71 = 7x6x5x4x3x2x1 = 5040

4. 0! is a symbol equal to

1. 0
2. 1
3. Infinity
4. none of these

Answer: (1 01 = 1

5. In \(n P_{r^{\prime}}\) n is always

1. an integer
2. a fraction
3. a positive integer
4. none of these

Answer: Integer

6. In \(n P_{r^{\prime}}\) the restriction is

1. n > r
2. n ≥ r
3. n ≤ r
4. none of these

Answer: n ≥ r.

7. \(\text { In nP } P_r=n(n-1)(n-2) \ldots \ldots \ldots \ldots \ldots \ldots \ldots(n-r+1) \text {, }\) the number of factors is

1. n
2. r-1
3. n-r
4. r

Answer: r

8. \(n P_r\) can also written as

1. \(\frac{n!}{(n-r)!}\)
2. \(\frac{n!}{r!(n-r)!}\)
3. \(\frac{r!}{(n-r)!}\)
4. None of these

Answer: \(\text { ( } \frac{n!}{(n-r)!}\)

9.\(m+n P_2=56, m-n P_2=30 \text { then }\)

1. m =6, n = 2
2. m = 7, n= 1
3. m=4, n=4
4. none of these

Answer:

\(=\frac{(m+n)!}{(m+n-2)!}=56\)

= (m+n) (m+n-1) = 56

= m + n = 8

\(\frac{(m-n)!}{(m-n-2)!}=30\)

(m-n) (m-n-1) = 30

m – n = 6

10.\(\text { if } 5 \mathrm{P}_{\mathrm{r}}=60 \text {, }\) then the value of r is

1. 3
2. 2
3. 4
4. none of these

Answer: (1) 3 \(\frac{5!}{(5-r)!}=60\)

2 = (5 – r)! r = 3

11. \(\text { If } n_1+n_2 \mathbf{P}_2=132, n_1-n_2 \mathbf{P}_2=30\) then,

1. n 1 =6, n2=6
2. n1=10,n2=2
3. n1 = 9, n2 = 3
4. none of these

Answer: (3)

n₁=9  n₂=3

=(n₁+n₂)(n₁+n₂-1)=132

n₁+n₂=12

n₁=9

(n₁-n₂)(n₁-n₂-1)=30

n₁-n₂=6

n₂=3

12. The number of ways the letters of the word ‘COMPUTER’ can be rearranged is

1. 40,320
2. 40,319
3. 40,318
4. none of these

Answer:

40319

= Computer can be arranged in 8! Ways 8! = 40320

But we have to rearranged i.e., computer will not be counted 40320- 1 = 40319 ways.

13. The number of arrangements of the letters in the word ‘FAILURE’, so that vowels are always coming together is

1. 576
2. 575
3. 570
4. none of these

Answer: ( 576

= FAILURE = 7 letters

If vowels are clubbed as x

Total 4 letters FLR x

These can be arranged in 41 ways. Also, the vowels can arrange in 41 ways

No. of arrangement = 41 x 41= 576

14. 1 0 examination papers are arranged in such a way that the best and worst papers never come together. The number ofarrangements is

1. 9(8)!
2. 10!
3. 8(9)!
4. none of these

Answer: 89!

= Best fit worst paper be clubbed as 1 total papers =10-2 + 1 =9

9 Papers can be arranged in 91 ways

The 2 papers can be internally arranged in 2 ways No of arrangement’s = 2×91

When worst paper & best paper can be arranged

Now total arrangements = 101

Arrangement when both papers do not come together 10×91-2×91 = 9! [10-2)

= 101-2×9! = 9! x 8 = 89!

15. n articles are arranged in such a way that 2 particular articles never come together. The number of such arrangements is

1. (n-2) (n – 1]!
2. (n-1) (n-2)l
3. n!
4. none of these

Answer: ( (n – 2) (n-1)!

16. If 12 school teams are participating in a quiz contest, then the number of ways the first, second and third positions may be won is

1. 1,230
2. 1,320
3. 3,210
4. none of these

Answer:

(1320

= 12 school terms, 3 positions

Can be given & arranged in \({ }^{12} \mathrm{P}_3 \quad=\frac{12!}{9!}=12 \times 11 \times 10=1320\)

17. The sum of all 4-digit number containing the digits 2, 4, 6, 8, without repetitions is

1. 1,33,330
2. 1,22,220
3. 2,13,330
4. 1,33,320

Answer: 1,33,320.
= 4 digit number from 2,4,6,8

Without repetition can be made in 41 ways = 24 ways

24 numbers will be formed.
6 no. will end with 2
6 no. will end will 4
6 no. will end will 6
6 no. will end will 8

= 1,33,320

18. The number of 4-digit numbers greater than 5,000 can be formed out of the digits 3,4,5,6 and 7(No. digit is repeated]. The number ofsuch is

1. 72
2. 27
3. 70
4. none of these

Answer:  72

= 4 digit no. > 5000 first digit cannot be 3,4 it will be 5,6,7

3x4x3x2 =72

19. 4-digit numbers to be formed out of the figures 0, 1, 2, 3, 4 [no digit is repeated] then number of such numbers is

1. 120
2. 20
3. 96.
4. none of these

Answer: 96

= 4 digit number of 0,1,2,3,4          0 cannot occupy first digit’s place

4x4x3x2 = 96

20. The number of ways the letters of the word ‘TRIANGLE’ to be arranged so that the word ‘angle’ will be always present is

1. 20
2. 60
3. 24
4. 32

Answer: 24
Triangle has 0 letters.
If we chib angle as 1 No. of letters = 8- 5 + 1 = 4
4 letters can be arranged in 41 ways. There is no internal arrangement = 24 ways

21. If the letters word ‘DAUGHTER’ are to be arranged so that vowels occupy the odd places, then number of different words are

1. 2,880
2. 676
3. 625
4. 576

Answer: 2,880

= Daughter’s 5 consonants 3 vowels

Daughters has 4 odd places

3 vowels can occupy in 4P3 ways

First 5 consonants can be arranged in 51 ways

Total = 51 x4p3 = 2880 ways

22. The number of ways in which 7 girls form a ring is

1. 700
2. 710
3. 720
4. none of these

Answer: 720
= 7 girls form a ring = i.e. circular permutation

\(=\frac{1}{0}(n-1)!\quad=\frac{1}{0} \times 6!\quad=6 \times 5 \times 4 \times 3 \times 2=360 \times 2 \quad=720\)

23. The number of ways in which 7 boys sit in a round table so that two particular boys may sit together is

1. 240
2. 200
3. 120
4. none of these

Answer:

240
= Two come togethers <— club = total 7 – 2 + 1 = 6 boys to be arranged
= m 2 (6-1) ! = 240 ways

24. If 50 different jewels can be set to form a necklace then the number of ways is

1. 1/2×50!
2. 1/2×49!
3. 49!
4. none of these

Answer: \(\text { (} 1 / 249 \text { ! }\)

= so different vowels form a necklace in \(\frac{1}{2}(n-1)!\text { Ways }\)

\(\text { i.e. } \frac{1}{2}(50-1)!=\frac{1}{2} 49 \text { ! }\)

25. 3 ladies and 3 gents can be seated at a round table so that any two and only two of the ladies sit together. The number of ways is

1. 70
2. 27
3. 72
4. none of these

Answer: (72
= 3 ladies 3 gents
Constraint —> only 2 & only 2 sit together 2 ladies can let selected & arranged in \({ }^3 P_2\) ways

The remaining ladies out of 4 cannot Occupy places adjustment to the 2 only in 2 ways

The remaining 3 men can occupy places in 31 ways

\(\text { Total } \rightarrow{ }^3 \mathrm{P}_2 \times 31 \times 2=72 \text { ways. }\)

26. The number of ways in which the letters of the word ‘DOGMATIC’ can be arranged is

1. 40,319
2. 40,320
3. 40,321
4. none of these

Answer: 40,320
DOGMATIC 8 letters can be arranged in 8!

27. The number of arrangements of10 different things taken 4 at a time in which one particular thing always occurs is

1. 2015
2.  2016
3. 2014
4. none of these

Answer: 2016 \(=4 \times{ }^9 \mathrm{P}_3 \text { ways to arrange }=2016\)

28. The number of permutations of 10 different things taken 4 at a time in which one particular thing never occurs is

1. 3.020
2. 3,025
3. 3,024
4. none of these

Answer: 3024 \(={ }^9 \mathrm{P}_4=3024\)

29. Mr. X and Mr. Y enter into a railway compartment having six vacant seats. The number of ways in which they can occupy the seats is

1. 25
2. 31
3. 32
4. 30

Answer: (30. = Mr x can occupy & vacant seats in 6 ways
Mr Y will occupy remaining 5 seat in 5 ways. Total 30 ways

30. The number of numbers lying between 100 and 1000 can be formed with the digits 1, 2, 3, 4, 5, 6, 7 is

1. 210
2. 200
3. 110
4. none of these

Answer: 210

= 3 digit numbers > 100
From 1.2,3,4,5,6,7
first digit can be 1,2,3,4,5,6,7
Second digit can be repeated therefore ways
Similarly third digit with remaining 5 no. in 5 ways =7x6x5 = 210 ways

31. The number of numbers lying between 10 and 1000 can be formed with the digits 2,3,4,0,8,9 is

1. 124
2. 120
3. 125
4. none of these

Answer: 120

= two digit & three digit between 10 – 1000

0 can occupy first place The no. of ways = 6x5x4 = 120 ways

32. In a group of boys, the number of arrangements of 4 boys is 12 times the number of arrangements of 2 boys. The number of boys in the group is

1. 10
2. 8
3. 6
4. none of these

Answer: 6 \(\frac{(n)(n-1)(n-2)(n-3)}{n(n-1)}=12 \quad n=6 .\)

33. The total number of 9-digit numbers of different digits is

1. 10(9)!
2. 8(9)!
3. 9(9)!
4. none of these

Answer:  99!
= first digit cannot be 0. 9 ways

= total ways = 9x9x8x7x6x5x4x3x2xl = 99!

34. The number of ways in which 6 men can be arranged in a row so that the particular 3 men sit together, is

\((1) ${ }^4 P_4$
(2) ${ }^1 P_4 \times{ }^3 P_3$
(3) $(3)^2$\)
(none of these

Answer:\(\text { (}{ }^4 \mathrm{P}_4 \times{ }^3 \mathrm{P}_3\) = let 3 particulars men be 1

Total men 6 – 3 +1 = 4. They can sit in 41 ways

Internal arrangement among 3 particular Men can be made in 31 ways.

= Total = 41 x 31 ways

35. There are 5 speakers A, B, C, D and E. The number of ways in which A will speak always before B is

1. 24
2. 4 x 2
3. 5
4. none of these

Answer: (a] 24.
= S speakers

Total = 5 — 2 + 1 = 4 speakers They can speak in 41 ways.

Now there will be no internal arrangement i.e. A is before B-‘- 41 ways

36. There are 10 trains plying between Calcutta and Delhi. The number of ways in which a person can go from Calcutta to Delhi and return by a different train is

1. 99
2. 90
3. 80
4. none of these

Answer:  90.
= Let us say he takes an one train for going = 10 ways are possible

While coming he can take any train from the removing 9 trains in = 9 ways

Total = 10 x 9 = 90

37. The number of ways in which 8 sweats of different sizes can be distributed among 8 persons of different ages so that the largest sweat always goes to be younger assuming that each one of then gets a sweat is

1. 8
2. 5040
3. 5039
4. none of these

Answer: (5040
Sweats = 8 person (diffjv younger one gets largest rest 7 will get 7 sweats in 7! Ways

38. The number of arrangements in which the letters of the word ‘MONDAY’ be arranged so that the words thus formed begin with M and do not end with N is

1. 720
2. 120
3. 96
4. none of these

Answer:96.
= MONDAY 6 letters

Word should begin with M = 1 Way.

It cannot end with N, N can occupy any expect last position = 5 ways

Rest 4 letters can arrange in 4! Ways

1x1x2x3x4x4 =96 ways.

39. The total number of ways in which six V and four ’-’signs can be arranged in a line such that no two ’-’ signs occur together is

1. (7)!./ (3)!
2. (6)! x (7)!/(3)!
3. 35
4. none of these

Answer: 35 = Among 6 + here are 7 intervals

_+_+_+_+_+_+

No. of filling 7 gaps by 4’-‘signs

\(={ }^7 \mathrm{C}_4=35\)

40. The number of ways in which the letters of the word ‘MOBILE’ lie arranged so that consonants always occupy the odd places is

1. 36
2. 63
3. 30
4. none of these.

Answer: 36.

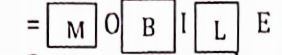
= M O B I L E = 3 consonants 3 vowels

3 consonants can be occupy places in \({ }^4 P_3 \text { ways }=31 \text { ways }\)

Vowels can occupy 3 places in \({ }^3 P_3 \text { ways }\)

= 3! = 6 total 3! x 3! = 36

41. 5 persons are sitting in a round table in such way that Tallest Person is always on the rightside of the shortest person; the number ofsuch arrangements is

1. 6
2. 8
3. 24
4. none of these

Answer: 6.

Let tallest, shortest come together

Total persons = 5- 2 + l = 4

4 People can arrange in (n-1] ways = 31 ways = 6 ways there is no internal arrangement 6 ways.

Exercise – 2 – Combinations

Choose the most appropriate option (1, 2, 3 or 4)

1. The value of \({ }^{12} \mathrm{C}_4+1{ }^{12} \mathrm{C}_3 \text { is }\)

1. 715
2. 710
3. 716
4. none of these

Answer:

715

\(\begin{aligned}
& \frac{12!}{4!8!}+\frac{12!}{3!9!} \\
& \frac{12 \times 11 \times 10 \times 9}{4 \times 3 \times 2 \times 1}+\frac{12 \times 11 \times 10}{3 \times 2 \times 1}
\end{aligned}\)

495+220=715

2. \(\text { If }{ }^n p_r=336 \text { and } n C_r=56 \text {, }\) , then n and r will be

1. (3.2)
2. (8, 3)
3. (7,4)
4. none of these

Answer:

(2) 8, 3)

\(\frac{{ }^n P_r}{{ }^n P_r}=\frac{336}{56}=\frac{\frac{n!}{(n-r)!}}{\frac{n!}{r!(n-r)!}}=6\)

r ! = 6 r = 3, n = 8

3. \(\text { If }{ }^{18} \mathrm{C}_{\mathrm{r}}={ }^{18} \mathrm{C}_{\mathrm{r}+2}\) the value of \({ }^r \mathrm{C}_5\) is

1. 55
2. 50
3. 56
4. none of these

Answer:

(3) 56

\({ }^{18} C_r={ }^{18} C_{r+2}\) \(=\frac{\frac{18!}{r!(18-r)!}}{\frac{18!}{(r+2)!(18-r-2)!}}=1\) \(=\frac{\frac{18!}{r!(18-r)(17-r)(16-r)!}}{\frac{18!}{(x+2)(r+1) r!(16-r)!}}=1\) \(=\frac{(r+2)(r+1)}{(18-r)(17-r)}=1\)

r² + 3r + 2 = 306 – 35 r + r2

38r= 304 = r = 8

\(8 C 5=\frac{8!}{5!3!}=\frac{8 \times 7 \times 6}{3 \times 2 \times 1}=56\)

4. \(\text { If }{ }^n C_{r-1}=56,{ }^n C_r=28 \text { and }{ }^n C_{r+1}=8 \text {, }\) then r is equal to

1. 8
2. 6
3. 5
4. none of these

Answer:

\(\frac{{ }^n C_r}{{ }^n C_{r+1}}=\frac{28}{8}=\frac{\frac{n!}{r!(n-r)!}}{\frac{n!}{(r+1)^{!}(n-r-1)!}}=\frac{7}{2}\) \(\frac{\frac{n!}{r!(n-r)(n-r-1)!}}{\frac{n!}{(r+1) r!(n-r-1)!}}=\frac{7}{2}\) \(\frac{r+1}{n-r}=\frac{7}{2} \quad=2 r+r=7 n-7 r\)

9 r- 7n + 2 = 0 (1)

\(\frac{{ }^n C_r-1}{{ }^n C_r}=\frac{56}{28}\) \(\frac{\frac{n!}{(r-1)!(n-r-1)!}}{\frac{n!}{r!(n-r)!}}=2 \frac{\frac{n!}{(r-1)!(n-r-1)(n-r)!}}{\frac{n!}{r(r-1)!(n-r)!}}=\) \(\frac{r}{n-r+1}=2=r=2 n-2 r+2\)

3r- 2n = 2 (2)

Multiply (2) by 3 = 9r- 6n = 6
Subtracting (2) from (1)

9r- 7n = -2

9r – 6n = 6

-n = – 8 = n = 8, r = 6

5. A person has 8 friends. The number of ways in which he may invite one or more of them to a dinner is.

1. 250
2. 255
3. 200
4. none of these

Answer: 255

= 8 friends, lie invites one or more

Total ways

\(={ }^8 \mathrm{C}_1+{ }^8 \mathrm{C}_2+{ }^8 \mathrm{C}_3+{ }^8 \mathrm{C}_4+{ }^8 \mathrm{C}_5+{ }^8 \mathrm{C}_6+{ }^8 \mathrm{C}_7+{ }^8 \mathrm{C}_8\)

= 8 + 28 + 56 + 70 + 56 + 28 + 8 +1

= 255

6. The number of ways in which a person can chose one or more of the four electrical appliances: T.V, Refrigerator, Washing Machine and a cooler is

1. 15
2. 25
3. 24
4. none of these

Answer:  15

\(={ }^4 \mathrm{C}_1+{ }^4 \mathrm{C}_2+{ }^4 \mathrm{C}_3+{ }^4 \mathrm{C}_4\)

He may select 1 or more in above way =4+6+4+1=15

7. \(\text { If }{ }^n C_{10}={ }^n C_{14} \text { then }{ }^{25} C_n \text { is }\)

1. 24
2. 25
3. 1
4. none of these

Answer: 25

n = 10 + 14 = 24

25C24 \(=\frac{25!}{24!1!}=25\)

8. Out of 7 gents and 4 ladies a committee of 5 is to be formed. The number of committees such that each committee includes at least one lady is

1. 400
2. 440
3. 441
4. none of these

Answer: 441

7 gents 4 ladies committee = 5 members

Committee includes atleast 1 lady

Different cases will be 1 lady, 2 ladies, 3 ladies or 4 ladies

When 1 ladies selected

\(\rightarrow{ }^1 \mathrm{C}_1 \times{ }^7 \mathrm{C}_4=4 \times 35=140\)

When 2 ladies selected

\(\rightarrow{ }^1 \mathrm{C}_2 \times{ }^7 \mathrm{C}_3=6 \times 35=210\)

When 3 ladies selected

\(\rightarrow{ }^1 \mathrm{C}_3 \times{ }^7 \mathrm{C}_2=4 \times 21=84\)

When 4 ladies selected

\(\rightarrow{ }^4 \mathrm{C}_4 \times{ }^7 \mathrm{C}_1=1 \times 7=7\)

Total when atleast 1 or more ladies
selected = 441

9. \(\text { If }{ }^{28} C_{2 r}:{ }^{2 \cdot 1} C_{2 r-1}=225: 11 \text {, }\) then the value of r is

1. 7
2. 5
3. 6
4. none of these

Answer: (1)7

\(\frac{{ }^{28} C_{2 r}}{{ }^{24} C_{2 r-4}}=\frac{\frac{28!}{(2 r)!(28-2 r)!}}{\frac{24!}{(2 r-4)!(28-2 r)!}}=\frac{225}{11}\) \(\frac{\frac{28!}{(2 r)!}}{\frac{24!}{(2 r-4)!}}=\frac{225}{11}\) \(=\frac{28 \times 27 \times 26 \times 25}{(2 r)(2 r-1)(2 r-2)(2 r-3)}=\frac{225}{11}\)

= 24024 = (2r) (2r – l)(2r – 2)(2r – 3)

= 14 x 13 x 12 x ll = 2r (2r – 1) (2r – 2) (2r- 3)

2r = 14 -> r = 7

10. The number of diagonals in a decagon is

1. 30
2. 35
3. 45
4. none of these

Answer: (b)35

A decagon has 10 points
diagonal will join 2 points
No of ways 2 points can be selected

\(={ }^{10 \prime} \mathrm{C}_2=45 \text { lines }\)

Total lines joining 2 points = 45 (-) lines making the sides of decagon (10)

Total diagonals 35

11. There are 12 points in a plane of which 5 are collinear. The number of triangles is

1. 200
2. 211
3. 210
4. none of these

Answer: (210
-» 12 points 5 collinear

For a triangle 3 non collinear points are required

Note: if are selected any 3 points from 5 collinear they will form a line & not a trianle

Total ways = 12C3-5C3

\(=\frac{12!}{3!9!}-\frac{5!}{3!2!}\)

= 220-10 = 210

12. The number of straight lines obtained by joining 16 points on a plane, no three of them being on the same line is

1. 120
2. 110
3. 210
4. none of these

Answer: 120

-» 16 points; no collinear points for a straight line 2 points are required Total ways of obtaining a straight line

\(={ }^{16} \mathrm{C}_2=\frac{16!}{2!14!}=\frac{16 \times 15}{2}=120\)

13. At an election there are 5 candidates and 3 members are to be elected. A voter is entitled to vote for any number of candidates not greater than the number to be elected. The number of ways a voter choose to vote is

1. 20
2. 22
3. 25
4. none of these

Answer: 25

election 5 candidates, 3 are elected when voter elects 1 candidate

\(\rightarrow{ }^5 \mathrm{C}_1=5\)

when voter elects 2 candidates

\(\rightarrow{ }^5 \mathrm{C}_2=10\)

when voter elects 3 candidates

\(\rightarrow{ }^5 \mathrm{C}_3=10\)

Total ways a voter chooses to votes = 25

14. Every two persons shakes hands with each other in a party anil the total number of handshakes is 66. The number of guests in the party is

1. 11
2. 12
3. 13
4. 14

Answer: 12
Total hand shake = 66
For a hand shake 2 hands are
selected

\(\begin{aligned}
& { }^n C_2=66 \\
& \frac{n!}{2!(n-2)!}=66 \quad \frac{n(n-1)(n-2)!}{(n-2)!}=132
\end{aligned}\)

n(n-l)= 132
n (n – 1) = 12 x 11 n = 12

15. The number of parallelograms that can be formed from a set of four parallel lines intersecting anotherset of three parallel lines is

1. 6
2. 18
3. 12
4. 9

Answer: 18
Set 1 = 4 parallel lines set 2 -* 3 parallel lines are intersecting for a parallelogram 2 lines from set 1 & 2 from set 2 need to be selected

Total ways = \( { }^4 \mathrm{C}_2 \times{ }^3 \mathrm{C}_2=6 \times 3=18\)

16. The number of ways in which 1 2 students can be equally divided into three groups is

1. 5775
2. 7575
3. 7755
4. none of these

Answer: 5775

Total ways of selecting

\(={ }^{12} C_4 \times{ }^8 C_4 \times 4 C 4\)

= 495 x 70 x 1 = 34650

So 3 groups are formed & order of selection is not important

So Total no. of ways \(=\frac{34650}{3!}=5775\)

17. 8 points are marked on the circumference of a circle. The number of chords obtained by joining these in pairs is

1. 25
2. 27
3. 28
4. none of these

Answer: 28

for a cords 2 points are required total ways = \({ }^8 \mathrm{C}_2\) = 28 ways

18. A committee of 3 ladies and 4 gents is to be formed out of 8 ladies and 7 gents. Mrs. X refuses to serve in a committee in which Mr. Y is a member. The number ofsuch committees is

1. 1530
2. 1500
3. 1520
4. 1540

Answer:  1540

Committee of 3L4G out of 8L&7G

Mrs x refuses to serve in which Mr y is member

Total committees that can be formed without taking constraint

\(={ }^8 \mathrm{C}_3 \times{ }^7 \mathrm{C}_4=56 \times 35=1960\)

Case: When x & y come together, no. of committees

2 ladies out of 7 & 3G out of 6 gents

\(={ }^7 \mathrm{C}_2 \times{ }^6 \mathrm{C}_3=21 \times 20=420\)

Therefore no. of committees when x y don’t come together

= 1960-420 = 1540

19. \(\text { If }{ }^{5000} \mathrm{C}_{92}={ }^{199} \mathrm{C}_{92}+{ }^{1{ }^{99} \mathrm{C}_91}\) then n is

1. 501
2. 500
3. 502
4. 499

Answer: (499

\({ }^{n+1} C_r={ }^n C_r+{ }^n C_{r-1}\)
n = 499, r = 92

\({ }^{500} \mathrm{C}_{92}={ }^{499} \mathrm{C}_{92}+\mathrm{n}^{\mathrm{n}} \mathrm{C}_{92-1} \quad \mathrm{n}=499\)

20. The Supreme Court lias given a 6 to 3 decision upholding a lower court; the number of ways it can give a majority decision reversing the lower court is

1. 256
2. 276
3. 245
4. 226

Answer:  256
6 to 3 decision -» upholding lower court

No. of judges = 9

To lower a decision, we need 50% T i.e. min 5 judges

No. of ways = \({ }^9 \mathrm{C}_9+{ }^9 \mathrm{C}_8+{ }^9 \mathrm{C}_7+{ }^9 \mathrm{C}_6+{ }^9 \mathrm{C}_5\)

= 1 + 9 + 36 + 84 + 126 = 256

21. Five bulbs of which three are defective are to be tried in two bulb points in a dark room. Number of trials the room shall be lighted is

1. 6
2. 8
3. 5
4. 7.

Answer: 7

5 bulbs. 3 defective

Total way of selecting

22. The ways ofselecting 4 letters from the word ‘EXAMINATION’ is

1. 136
2. 130
3. 125
4. none of these

Answer: 136

All letters distinct EXAMINATION

\(={ }^8 C_4 \text { ways }=70 \text { ways }\)

2 letters same, 2 distinct
\(\rightarrow{ }^3 \mathrm{C}_1 \times{ }^7 \mathrm{C}_2=63 \text { ways }\)

2 1etters alike & 2 letters alike
\(\rightarrow{ }^3 \mathrm{C}_2=3 \text { ways }\)

Total ways = 136 ways

23. \({ }^{51} \mathrm{C}_{31} \text { is equal to }\)

1. ⁵¹C₂₀
2. 2.⁵⁰C₂₀
3. 2.⁴⁵C₁₅
4. none of these

Answer: (1)

⁵¹C₂₀

—> ⁿC_r=ⁿCn-r

⁵¹C₃₁=⁵¹C_51-3

=⁵¹C₂₀

24. A candidate is required to answer 6 out of 12 questions which are divided into two groups containing 6 questions in each group. He is not permitted to attempt not more than four from any group. The number of choices are.

1. 750
2. 850
3. 800
4. none of these

Answer: (850

Total cases

1) 3 from G1 & 3 from G2

\(={ }^6 \mathrm{C}_3 \times{ }^6 \mathrm{C}_3=400\)

2) 2 from G1 & 4 from G2

\(={ }^6 \mathrm{C}_2 \times{ }^6 \mathrm{C}_4=225\)

3) 4 from G1 & 2 from G2

\(={ }^6 \mathrm{C}_4 \times{ }^6 \mathrm{C}_2=225\)

Total ways of choosing = 850

25. The results of 8 matches (Win, Loss or Draw) are to be predicted. The number of different forecasts containing exactly 6 correct results is

1. 316
2. 214
3. 112
4. none of these

Answer: 112
6 correct results can be predicted
\(\text { in }{ }^8 C_6 \text { ways }=\frac{56}{2} 28 \text { ways }\)

The remain 2 matches result are incorrect either it is lose or draw

Ml -> 2 ways M2 -» 2 ways Total 4 ways

Total ways of 6 correct exactly out of 8 matches =28×4=112

26. The number of 4 digit numbers formed with the digits 1, 1, 2, 2, 3, 4 is

1. 100
2. 101
3. 201
4. none of these

Answer: none of these

4 digit numbers 1,1,2,2,3,4

When nil (Hulls art’ different \(4 P_4\) ways – 4 ways = 24

When one digit repeated, remaining 2 different

\({ }^2 \mathrm{C}_1 \times{ }^3 \mathrm{C}_2 \times \frac{11}{2!} \text { (arrangement) }\) = 2 x 3 x 12 = 72

When double repetition occurs

\({ }^2 C_2 \times \frac{4!}{2!2!}=6 \text { ways }\)

Total = 102 ways

27. The number of ways a person can contribute to a fund out of 1 ten-rupee note, 1 five rupee note, 1 two-rupee and 1 one rupee note is

1. 15
2. 25
3. 10
4. none of these

Answer: 15

He can give any1 note in \({ }^4 \mathrm{C}_1\) ways = 4

He may contribute 2 notes in \({ }^4 \mathrm{C}_2\) = 6

He may contribute 3 noes in \({ }^4 \mathrm{C}_3\) = 4

He may contribute all four notes in \({ }^4 \mathrm{C}_4\) ways =1

Total ways = 15

28. The number of ways in which 9 things can be divided into twice groups containing 2,3, and 4 things respectively is

1. 1250
2. 1260
3. 1200
4. none of these

Answer: 1260

9 things into twice group of 2,3 & 4

\(\text { Total ways }={ }^9 \mathrm{C}_2 \times{ }^7 \mathrm{C}_3 \times{ }^4 \mathrm{C}_4\) = 1260

29. \({ }^n C_1+{ }^n C_2+{ }^n C_3+{ }^n C_1+\ldots . .+{ }^n C_n \text { equals }\)

1. 2n -1
2. 2n
3. 2n +1
4. none of these

Answer:

2n- 1

\({ }^n C_1+{ }^n C^2 \ldots \ldots \ldots \ldots \ldots{ }^n C_{n-1}+{ }^n C_n\) \(\text { we know }(1+x)^n={ }^n C_0 x^0+{ }^n C_1 x^1 \ldots \ldots \ldots\) \({ }^n C_n x^n\)

x = 1

\(\begin{aligned}
& (1+1)^n=1+{ }^n C_1+{ }^n C_2 \ldots \ldots \ldots{ }^n C_n \\
& 2^n-1={ }^n C_1+{ }^n C_2 \ldots \ldots{ }^n C_n
\end{aligned}\)

Exercise-3

(Mix Exercise – Perimilnllons & Combinations)

1. In how many ways can the letters of the word ’LEADER’ be arranged?

1. 72
2. 144
3. 360
4. 720
5. None of those

Answer: The word ‘LEADER’ contains 6 letters, namely 1 L, 2E, 1A, 1D) and IR.

Required number of ways =\(\frac{6!}{(1!)(2!)(1!)(1!))}=360\) .

2. In how many different ways ran the loiters of the word ‘RUMOUR’ ho nrmilled?

1. 80
2. 90
3. 30
4. 720
5. None of these

Answer: The word ‘RUMOUR’ contains 6 letters, namely 2R, 2U, 1M and 1U.

Required number of ways =\(\frac{6!}{(2!)(2!)(1!)(1!)}=180\)

3. How many words can he formed from the letters of the word ‘SIGNATURE’ so that the vowels always come together?

1. 720
2. 1440
3. 2880
4. 3600
5. 17280

Answer:

The word ‘SIGNATURE’ contains 9 different letters.

When the vowels IAUE are taken together, they can be supposed to form an entity, treated as one letter.

The, the letters to be arranged are SNGTR (IAUE)

These 6 letters can be arranged in \({ }^6 P_6=6!=720 \text { ways. }\)

The vowels in the group (IAUE) can be arranged amongst themselves in \({ }^4 P_4=4!=24 \text { ways. }\)

Required number of words = (720 * 24) = 17280.

4. In how many different ways can the letters of the word ‘OPTICAL’ he arranged so that the vowels always together?

1. 120
2. 720
3. 4320
4. 2160
5. None of these

Answer:

The word OPTICAL’ contains 7 different letters.

When the vowels OIA are always together, they can be supposed to form one letter.

Then, we have to arrange the letters PTCL (OIA).

Now, 5 letters can be arranged in 5 ! = 120 ways.

The vowels (OLA) can be arranged among themselves in 3 ! = 6 ways.

Required number of ways = (120 x 6) = 720.

5. In how many different ways can the letters of the word ’SOFTWARE’ he arranged in such a way that the vowels come together?

1. 120
2. 300
3. 1440
4. 13440
5. 720

Answer:

The word ‘SOFTWARE’ contains 8 different letters.

When the vowels OAE are always together, they can be supposed to form one letter.

Thus, we have to arrange the letters SFTWR (OAE).

Now, 5 letters can be arranged in 6 ! = 720 ways

The vowels (OAE) can be arranged among themselves in 3 ! = 6 ways.

Required number of ways = (720 x 6) = 4320.

6. In how many different ways can the letters of the word ‘LEADING’ he arranged in such a way that the vowels always come together?

1. 360
2. 480
3. 720
4. 5040
5. None of these

Answer: The word LEADING’ has 7 different letters.

When the vowels EAI are always together, they can be supposed to form one letter.

Then, we have to arrange the letters LDNG (EAD.

Now, 5 letters can be arranged in 5 ! = 120 ways.

The vowels (EAI) can be arranged among themselves in 3 ! = 6 ways.

Required number of ways = (120 x 6) = 720.

7. In how many different ways can the letters of the word ‘JUDGE’ be arranged in such a way that the vowels come together?

1. 48
2. 124
3. 160
4. None of these

Answer:

The word JUDGE’ has 5 different letters.

When the vowels UE are always together, they can be supposed to form one letter.

Then, we have to arrange the letters JDG (UE).

Now, 4 letters can be arranged in 4 ! = 24 ways.

The vowels (UE) can be arranged among themselves in 2 ! = 2 ways.

Required number of ways = (24 x 2) = 48.

8. In how many different ways can the letters of the word ‘AUCTION’ be arranged in such a way that the vowels always come together?

1. 30
2. 240
3. 144
4. 576
5. None of these

Answer: The word ‘AUCTION’ has 7 different letters.

When the vowels AUIO are always together, they can be supposed to form one letter.

Then, we have to arrange the letters CTN (AUIO).

Now, 4 letters can ho an.ingcd in 4 1 =ÿ 24 ways.

The vowols (AUIO) ran be nrmngi’d among themselves In 4 I = 24 ways,

Required number of ways (24 x 24} – 576.

9. In how many different ways can the letters of the ‘BANKING’ he arranged so that the vowels always come together?

1. 120
2. 240
3. 360
4. 540
5. 720

Answer: In The word ’HANKING’, wo Heat the two vowels Al as one letter. Thus, we have UNKNG (Al).

This has 6 letters of which N occurs 2 times and the rest are different.

Number of ways of arranging these letters =\(\frac{6!}{(2!)(1!)(1!)(1!)(1!)}=360\)

Now, 2 vowels Al can be arranged in 2 ! = 2 ways.

Required number of ways = (360 »2) = 720.

10. In how many different ways can the letters of the word ‘CORPORATION’ be arranged so that the vowels always come together?

1. 810
2. 1440
3. 2880
4. 50400
5. 5760

Answer:

In the word ’CORPORATION’, we treat the vowels OOAIO as one letter. Thus, we have CRPRTN (OOAIO).

This has 7 letters of which R occurs 2 times and the rest are different.

Number of ways of arranging these letters =

\(=\frac{7!}{2!}=2520 /\)

Now, 5 vowels in which O occurs 3 times and the rest are different, can be arranged in \(\frac{5!}{3!}\) = 20 ways.

Required number of ways = (2520 * 20) = 50400.

11. In how many different ways can the letters of the word ‘DETAIL’ be arranged in such a way that the vowels occupy only the odd positions?

1. 32
2. 48
3. 36
4. 60
5. 120

Answer: There are 6 letters in the given word, out of which there are 3 vowels and 3 consonants. Let us mark these positions as under: (1) (2) (3) (4) (5) (6)

Now, 3 vowels can be placed at any of the three places out of 4, marked 1, 3, 5.

Number of ways of arranging the vowels =

\({ }^3 P_3=3!=6 .\)

Also, the 3 consonants can be arranged at the remaining 3 positions.

Number of ways f these arrangements =

\({ }^3 P_3=3!=6 .\)

Total number of ways = (6 * 6) = 36.

12. In how many ways can a group of 5 men and 2 women be made out of a total of 7 men and 3 women?

1. 63
2. 90
3. 126
4. 45
5. 135

Answer:

Required number of ways = \(\left({ }^7 C_5 \times{ }^3 C_2\right)=\left({ }^7 C_2 \times{ }^3 C_1\right)=\left(\frac{7 \times 6}{2 \times 1} \times 3\right)=63\)

13. In how many ways a committee, consisting of 5 men and 6 women can be formed from 8 men and 10 women?

1. 266
2. 5040
3. 11760
4. 86400
5. None of these

Answer:

Required number of ways=

(⁸C₅x¹⁰C₆)= (8C₅x¹⁰C₄)= \(\left(\frac{8 \times 7 \times 6}{3 \times 2 \times 1} \times \frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1}\right)=11760 .\)

14. From a group of 7 men and 6 women, five persons are to be selected to form a committee so that at least 3 men are there on the committee. In how many ways car it do done?

1. 564
2. 645
3. 735
4. 756
5. None of these

Answer:

We may have (3 men and 2 women) or (4 men and 1 woman) or (5 men only)

Required number of ways = \(\left({ }^7 \mathrm{C}_3 \times{ }^6 \mathrm{C}_2\right)+\left({ }^7 \mathrm{C}_4 \times{ }^6 \mathrm{C}_1\right)+\left({ }^7 \mathrm{C}_5\right)\)

\(=\left(\frac{7 \times 6 \times 5}{3 \times 2 \times 1} \times \frac{6 \times 5}{2 \times 1}\right)+\left({ }^7 C_3 \times{ }^6 C_1\right)+\left({ }^7 C_2\right) \quad=525+\left(\frac{7 \times 6 \times 5}{3 \times 2 \times 1} \times 6\right)+\left(\frac{7 \times 6}{2 \times 1}\right)\)

= (525 + 210 + 21) = 756

15. In a group of 6 boys and 4 girls, four children are to be selected. In how many different ways can they be selected such that at least one boy should be there?

1. 159
2. 194
3. 205
4. 209
5. None of these

Answer: We may have (1 boy and 3 girls) or (2 boys and 2 girls) or (3 boys and 1 girl) or (4 boys).

Required number of ways =\(\left({ }^6 \mathrm{C}_1 \times{ }^4 \mathrm{C}_3\right)+\left({ }^6 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2\right)+\left({ }^6 \mathrm{C}_3 \times{ }^4 \mathrm{C}_1\right)+\left({ }^6 \mathrm{C}_4\right)\)

\(=\left({ }^6 \mathrm{C}_1 \times{ }^1 \mathrm{C}_1\right)+\left({ }^6 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2\right)+\left({ }^6 \mathrm{C}_3 \times{ }^1 \mathrm{C}_1\right)+\left({ }^6 \mathrm{C}_2\right)\) \(=(6 \times 4)+\left(\frac{6 \times 5}{2 \times 1} \times \frac{4 \times 3}{2 \times 1}\right)+\left(\frac{6 \times 5 \times 4}{3 \times 2 \times 1} \times 4\right)+\left(\frac{6 \times 5}{2 \times 1}\right)\)

= (24 + 90 + 80 + 15) = 209.

16. A box contains 2 white balls, 3 black balls and 4 red balls. In how many ways-can 3 balls be drawn from the box, if at least one black ball is to be included in the draw?

1. 32
2. 48
3. 64
4. 96
5. None of these

Answer:

We may have (1 black and 2 non-black) or (2 black and 1 non-black) or (3 black).

Required number of ways = \(\left({ }^3 \mathrm{C}_2 \times{ }^6 \mathrm{C}_2\right)+\left({ }^3 \mathrm{C}_2 \times{ }^6 \mathrm{C}_1\right)+\left({ }^3 \mathrm{C}_3\right)\)

\(=\left(3 \times \frac{6 \times 5}{2 \times 1}\right)+\left(\frac{3 \times 2}{2 \times 1} \times 6\right)+1\) =45 + 18 + 1 = 64

17. How many 3-digit numbers can be formed from the digits 2, 3, 5, 6, 7 and 9, which are divisible by 5 and none of the digits is repeated?

1. 5
2. 10
3. 15
4. 20

Answer:

Since each desired number Is divisible by 5, so we must have 5 at the unit place, So, there is 1 way of doing it.

Tens place can be filled by any of the remaining fi numbers.

So, there are S ways of filling the tens place.

The hundreds place can now be filled by any of the remaining 4 digits. So, there are 4 ways of filling it.

Required number of numbers = (1 × 5 × 4) = 20.

18. Evaluate:\(\frac{30!}{28!}\)

Answer: \(\text { We have, } \frac{30!}{28!}=\frac{30 \times 29 \times(28!)}{28!}=(30 \times 29)=870\)

19. Find the value of \(\text { (1) }{ }_{60} P_3 \text { (2) }{ }_4 P_4\)

Answer:

\(\text { (1) }{ }^{60} P_3=\frac{60!}{(60-3)!}=, \frac{60!}{57!}=\frac{60 \times 59 \times 58 \times(57!)}{57!}=(60 \times 59 \times 58)=205320 \text {. }\) \(\text { (b) }{ }^4 P_4=4 \text { ! }=(4 \times 3 \times 2 \times 1)=24 \text {. }\)

20. Find the value of

\((1) { }^{10} \mathrm{C}_3
(2) { }^{100} \mathrm{C}_{98}
(3) { }^{50} \mathrm{C}_{50}\)

Answer:

\(\text { (1) }{ }^{10} \mathrm{C}_3=\frac{10 \times 9 \times 8}{31}=\frac{10 \times 9 \times 8}{3 \times 2 \times 1}=120 \text {. }\) \(\text { (2) }{ }^{100} \mathrm{C}_{98}={ }^{100} \mathrm{C}_{(100-98)}={ }^{100} \mathrm{C}_2=\frac{100 \times 99}{2 \times 1}=4950 \text {. }\) \(\text { (3) }{ }^{50} C_{50}=1 .\left[{ }^n C_n=1\right]\)

21. How many words can be formed by using all letters of the word ‘BIHAR?

Answer: The word BIHAR contains 5 different letters.

Required number of words = 5P5 – 5! = (5x4x3x2xl) = 120.

22. How many words can be formed by using all the letters of the word ‘DAUGHTER’ so that the vowels always come together?

Answer:

Given word contains 8 different letters when the vowels AUE are always together, we may suppose them to form an entity, treated as one letter.

Then, the letters to be arranged are DGHTR (AUE).

These 6 letters to be arranged in 6Pfl = 6! = 720 ways.

The vowels in the group (AUE) may be arranged in 3! = 6 ways.

Required number of words = (720 x6) = 4320.

23. How many words can be formed from the letters of the word ‘EXTRA’ so that the vowels are never together?

Answer: The given word contains 5 different letters.

Taking the vowels EA together, we treat them as one letter.

Then, the letters to be arranged are XTR (EA)

These letters can be arranged in 4! = 24 ways.

The vowels EA maybe arranged amongst themselves in 2! =2 ways.

Number ofwords, each having vowels together = (24 x 2) = 48.

Total number ofwords formed by using all the letters of the given words = 5!= (5x4x3x2xl) = 120.

Number of words, each having vowels never together = (120 – 48) =72.

24. How many words can be formed from the letters of the word “DIRECTOR’ so that the vowels are always together?

Answer:

In the given word, we treat the vowels 1E0 as one letter

Thus, we have DRCTR (IEO).

This group has 6 letters of which R dccurs 2 times and others are different.

Number of ways of arranging these letters=\(\frac{6!}{2!}\) =360.

Now 3 vowels can be arranged among themselves in 3! = 6 ways.

Required number of ways = (360 x 6) = 2160.

25. In how many ways can a cricket eleven be chosen out of a batch of 15 players?

Answer:

Required number of ways = \({ }^{15} \mathrm{C}_{11}={ }^{15} \mathrm{C}_{(15.11)}={ }^{15} \mathrm{C}_4\)

\(=\frac{15 \times 14 \times 13 \times 12}{4 \times 3 \times 2 \times 1}=1365 \text {. }\)

26. In how many ways. A committee of 5 members can be selected from 6 men and 5 Ladies, consisting of 3 men and 2 ladies?

Answer:

(3 men out 6) and (2 ladies out of 5) are to be chosen.

Required number of ways =

\(\left({ }^6 \mathrm{C}_3 \times{ }^5 \mathrm{C}_2\right)=\left(\frac{6 \times 5 \times 4}{3 \times 2 \times 1} \times \frac{5 \times 4}{2 \times 1}\right)=200 .\)

27. The number of triangles that can be formed by choosing the vertices from a set of 12 points, seven of which lie on the same straight line, is:

1. 185
2. 175
3. 115
4. 105

Answer:

(1) No. of triangles =\(12 c_3-7 c_3\)

\(=\frac{12!}{3!9!}-\frac{7!}{314!}=220-35 \quad=185\)

28. A code word is to consists of two English alphabets followed by two distinct number from 1 to 9. How many such code words are there?

1. 6,15,800
2. 46,800
3. 7,19,500
4. 4,10,800

Answer:

(2) No. of code words = \(26 p_{p_2} \times{ }^9 \mathrm{P}_2\)

\(=\frac{26.25 \cdot 24!}{24!} \times \frac{9!}{7!}=650 \times 72=46,800\)

29. A boy has 3 library tickets and 8 books of his interest in the library. Of these 8, he does not want to borrow mathematics part-II unless mathematics part-I is also borrowed? In how many ways can he choose the three books to be borrowed?

1. 41
2. 51
3. 61
4. 71

Answer:

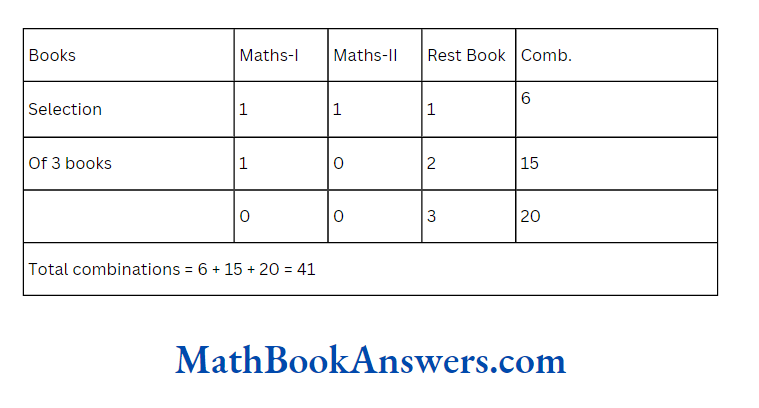
30. A supreme court bench consists of 5 judges. In how many ways, the bench can give a majority division?

1. 10
2. 5
3. 15
4. 16

Answer:

\(\text { (d) } \quad=5 c_3+5 c_4+5 c_5=10+5+1=16\)

31. Given: P (7,k) = 60 P (7, k- 3], Then:

1. k=9
2. k=8
3. k=5
4. k=0

Answer: (3]

P(7,K] = 60.p(7,k-3]

\(\frac{7!}{(7-k)!}=60 \times \frac{7!}{\mid 7-(k-3)!} \quad \text { or } \frac{1}{(7-k)!}=\frac{60 \times 1}{|7-(k-3)|!}\) \(\text { or } \frac{1}{(7-k)!}=\frac{60}{(10-k)(9-k)(8-k)(7-k)!}\)

Or(l0-k) (9-k) (8-k] = 60

(Make 3 factors of 60 so that their differences are 1.)

Comparing on both sides: we get

Or(10-k) (0-k) (8-k] = 5.4.3

10-k=5 Or k= 10-5 = 5 k = 5

32. The number of ways in which n books can be arranged on a shelfso that two particular books are not together is:

1. (n-2) x (n-l)l
2. (n-1) x (m+1)!
3. (n-2) x (n-l)l
4. (n-2) x (n+1)!

Answer:

Total no. of ways to arrange book as Qts. = n! – (n-2+l]!.2!

= n! – (n-2)! 2! n(n-l)! -2(n-l)! = (n-l)!. (n-2)!

33. In how many ways can the letters of the word FAILURE be arranged so that the consonants may occupy only old positions?

1. 576
2. 476
3. 376
4. 276

Answer: (1)

Consonants = F, L, R

Vowels = A, I, U, E

Total letters = 7

There will be 7 positions of letters

Odd positions are = 1,3,5,7

Even positions are = 2,4,6

From Questions,

No. of words = \(4 p_3 \cdot 4!=4!\times 4!\)

= 24 x 24 = 576

34. Five bulbs of which three are defective are to be tried in two lights-points in a dark-room. In how many trials the room shall be lighted?

1. 10
2. 7
3. 3
4. None of these

Answer: (2)

No. of bulbs = 5
Defective bulbs = 3
Non-defective bulbs = 2
No. of point in the room = 2

No. of ways to light the darkroom = \(3 c_1 \cdot 2 c_1+3 c_0 \cdot 2 c_2\)

= 3 x 2 + 1 x l = 6 + 1 = 7

35. In how many ways can a parly of 4 men and 4 women be seated at a circular table, so that no two women are adjacent?

1. 164
2. 174
3. 144
4. 154

Answer: (3)

No. of ways to sit 4 women = 4! = 24

Total ways to arrange = 6×24 = 144

36. \(\text { If }{ }^6 P_r=24{ }^6 C_r \text {, then find } r \text { : }\)

1. 4
2. 6
3. 2
4. 1

Answer: 1

\(6 p_r=24.6 c_r\) \(O r \frac{6!}{(6-r)!}=24 \cdot \frac{6!}{r!(6-r)!}\)

Or r!=24 or r!=4!

r = 4

37. Find the number of combinations of the letters of the word COLLEGE taken four together:

1. 18
2. 16
3. 20
4. 26

Answer: (1)

Letters are C, 0, L, L, E, E, G

Case i: 2 same & 2 same letters

= LIFE = Only 1 combination

Case II: LL and 2 out of C, 0, E, G \(=1 \times 4 c_2=6\)

EE and any 2 out of C, 0, L, G \(=1 \times 4 c_2=6\)

Case III: All different letters = Any 4 out of C, 0, L, E, G \(=5 c_4=5\)

Total no. of combinations = l+(6+6) +5 = 18

38. How many words can be formed with the letters of the word ‘ORIENTAL’ so that A and E always occupy odd places:

1. 540
2. 8640
3. 8460
4. 8450

Answer: (2)

As Qts. No. of words = \(4 p_2 \times 6!\) [because there are 4 Positions 1,3,5,7 for A & E)

\(=\frac{4!}{(4-2)} \times 720=12 \times 720=8640\)

39. \(\text { If }{ }^{1000} \mathrm{C}_{98}={ }_{999} \mathrm{C}_{97}+\mathrm{x}_{998} \text {, find } \mathrm{x} \text { : }\)

1. 999
2. 998
3. 997
4. 1000

Answer: (1) Tricks: go by choices

For (1) RHS = \(\left.{ }_{999} C_{97}+999 C_{98} ; \text { if } x=999\right)\)

\(=999{ }_{C_{97}}+999{ }_{C_{98}}=1000 c_{98}=L H S\)

40. How many number greater than a million can be formed with digits 4,5,5,0,4,5,3?

1. 260
2. 360
3. 280
4. 380

Answer: (2)

No. of Numbers \(=\frac{7!}{3!\cdot 2!}-1 \times \frac{6!}{3!.2!}\)

[Zero is fixed at 1st position with permutation 1]

=420-60 = 360

41. A building contractor needs three helpers and ten men apply. In how many ways can these selections take place?

1. 36
2. 15
3. 150
4. 120

Answer: (4)

Selection of 3 helpers out of10

\(10_{C_3}=\frac{10!}{3!(10-3)!}=\frac{10.9 .8 .7!}{3.2 \cdot 1.7!}=120\)

42. There are three blue balls, four red balls and five green balls. In how many ways can they be arranged in a row?

1. 26,720
2. 27,720
3. 27,820
4. 26,620

Answer: [2] No. ofarrangements = \(\frac{12!}{3!.4!5!}=27,720\)

43. If C(n,r): C(n, r+1) =1:2 and C(n, r+1) C(n, r + 2) = 2:3, determine the value of n and r:

1. (14,4)
2. (12,4)
3. (14,6)
4. None

Answer: (1)

Tricks: Go by choices

n = 14; r=4

44. Six seats of articled clerks are vacant in a ‘chartered accountant firm’ how many different batches of candidates can be chosen out of ten candidates?

1. 216
2. 210
3. 220
4. None

Answer: (2)

No. of selections = \({ }^{10} \mathrm{C}_6=\frac{10!}{6!4!}=210\)

45. Six person A, B, C, D, E and F are to be seated at circular table. In how many ways can this be done, if A must always have either B or C on his right and B must always have either C or D on his right?

1. 3
2. 6
3. 12
4. 18

Answer: (4)

B or C is right side of A

Arrangements are AB, AC,

C or Dis right side of B.

Their arrangement are BC or BD

Arrangement can be made as

Case I ABC, D,E,F can be arranged as [4-1]! = 6

Case II ABD C,E,F can be arranged as = [4-1]! = 6

Case III AC, BD, E,F can be arranged as = (4-1)! = 6

∴ total ways to arranged 6 persons = 6+6+6= 18

46. How many six-digit telephone numbers can be formed by using 10 distinct digits?

1. 106
2. 610
3. \({ }^{10} \mathrm{C}_6\)
4. \({ }_{10}^{10} \mathrm{P}_6\)

Answer: (4) Is correct

Total no. of (Units = 10 i.c. they are 0,1,2,3…………..;9

NO of six (I if,it distinct telephone no.

Being distinct dibits = \({ }^{10} P_6\)

47. In how many ways a committee of 6 members can be formed from a group of 7 boys and 4 girls having at least 2 girls in the committee.

1. 731
2. 137
3. 371
4. 351

Answer: 3

48. Number of ways of painting a face of a cube by 6 colours is

1. 36
2. 6
3. 24
4. 1

Answer: (2)

No. of faces of a cube = 6

No. of colours = 6

No, of ways to point 1 face =\({ }^6 \mathrm{C}_1=6\)

49. \(\text { If }{ }^{18} \mathrm{C}_{\mathrm{r}}={ }^{18} \mathrm{C}_{\mathrm{r}+2} \text { find the value of } \mathrm{r}_5 \text {. }\)

55
50
56
None of these

Answer:

\(\text { (3) If }{ }^{18} \mathrm{C}_{\mathrm{r}}={ }^{18} \mathrm{C}_{\mathrm{r}+2}\)

r+r+2 = 18

Or 2r= 16 r= 8

\({ }^r C_5={ }^8 C_5=56\)

50. 7. Books are to be arranged in such a way so that two particular books are always at first and last place. Final the number of arrangments.

1. 60
2. 120
3. 240
4. 480

Answer: (3)

Arrangement of 2 particular books = 2! = 2

i.e. either at lsl place or at last place

Arrangement of rest 5 books = 5! = 120

Total arrangements = 2×120 = 240

51. Find the number of arrangements in which the letters of the word ‘MONDAY’ be arranged so that the words thus formed begin with ‘M1 and do not end with ‘N’

1. 720
2. 120
3. 96
4. None

Answer: (3)

MONDAY

Total no. of words which begins with M = (6-1)! = 120

Total no. of words which begins M and ends With N

Total no. of words which begins with M but do not end with N

=1×4!x1 = 24

= 120-24 = 96

52. In how many ways can 17 billiard balls be arranged if 7 of them are black, 6 red and 4 white?

1. 4084080
2. 1
3. 8048040
4. None of these

Answer:

(1) Total no. of arrangements

\(=\frac{17!}{7!.6!\cdot 4!}=\frac{17.1615 .14 .13 .12 .11 .10 .9 .8 .7!}{7!.6!.4!}=4084080\)

=4084080

53. (n+1)! = 20(n-l)!, Find n

1. 6
2. 5
3. 4
4. 10

Answer: (3)

(n+1) I = 20(n-l)l Or (n+1) n.(n-l)! = 20(n-l)! Or (n+l).n = 5 x 4

n = 4

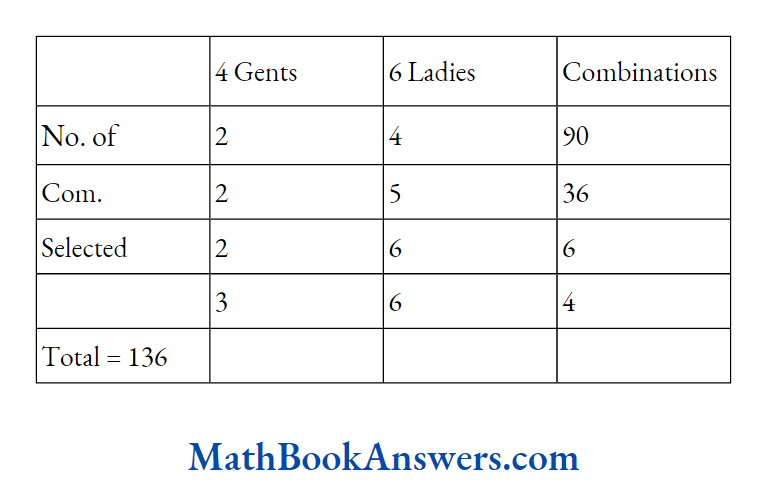
54. Out of 4 gents and 6 ladies, a committee is to be formed. Find the number of ways the committee can be formed such that it comprises of at least 2 gents and at least the number of ladies should be double of gents.

1. 94
2. 132
3. 136
4. 104

Answer:

55. In how many ways can the letters of ‘REGULATION’ be arranged so that the vowels come at odd places?

1. 14,400
2. 1,144
3. 1,44,252
4. None of these

Answer: (1)

REGULATION

Consonants = R,G,L,T,N

Vowels = E,U,A,l,0

Odd places are 1,3,5,7,9

Arrangement of vowels at these Places = ⁵P₅ = 5! = 120

Consonants will be arranged at remaining places = 5! = 120

Total No. ofarrangments = 120 x 120 = 14,400

56. Six points are on a circle. The number of quadrilaterals that can be formed are:

1. 30
2. 360
3. 15
4. None

Answer: (3)

No. of Quadrilaterals

⁶C₄ =\(\frac{6!}{4!2!}=\frac{6.5 .4!}{4!2!}=15\)

57. The number of ways of arranging 6 boy and 4 girls in a row so that all girls are together is:

1. 61.4!
2. 2(71.4!)
3. 7!.4!
4. 2.(6!.4!)

Answer: (3)

No of arrangement of 6 boys and 4 girls so that all 4 girls are together (6+1)1.41 =71.41 = 120960.

58. How many numbers not exceeding 1000 can be made from the digits 1,2,3,4,5,6,7,8,9 if repetition is not allowed

1. 364
2. 585
3. 728
4. 819

Answer: (2)

Given digits = 1,2,3,………9

Number less than 1000 will be of1 digit 2 digits and of 3 digits.

Total no. of numbers = \({ }^9 \mathrm{P}_1+{ }^9 \mathrm{P}_2+{ }^9 \mathrm{P}_3\)

= 9x9x8+9x8x7 = 585

59. A garden having 6 tall trees in a row. In how many ways 5 children stand, one in a gap between the trees in order to pose for a photograph?

1. 24
2. 120
3. 720
4. 30

Answer: (2)

1*2*3*4*5*6

Clearly there will be 5 positions for children = ⁵P₅ = 120

60. \({ }^{15} \mathrm{C}_3+{ }^{15} \mathrm{C}_3 \text { is equal to: }\)

1. \(16_{c_3}\)
2. \(30_{c_{16}}\)
3. \(15_{c_{16}}\)
4. \(15_{c_{15}}\)

Answer: (1)

\({ }^{15} \mathrm{C}_3+{ }^{15} \mathrm{C}_2={ }^{16} \mathrm{C}_3\)

61. How many ways a team of11 players can be made out of15 players if one particular player is not to be selected in the team.

1. 364
2. 728
3. 1,001
4. 1,234

Answer:

(1) No. of ways to make a 11 – member teams

\(={ }^{15-1} C_{11}={ }^1 C_{11}=\frac{14!}{11!3!}=364\)

62. Find the number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included.

39,000
37,600
39,600
36,000

Answer: (3)

No. of arrangement of 5 things =

\({ }^{12-1} C_{5-1} \cdot 5!={ }^{11} C_4 \cdot 5!\) \(=\frac{11!}{4!.7!} \times 120=330 \times 120=39600\)

63. In how many ways 3 Prizes out of 5 can be distributed amongst 3 brother equally?

1. 10
2. 45
3. 60
4. 120

Answer: (3)

No. of ways = \({ }^5 \mathrm{C}_1 \cdot{ }^4 \mathrm{C}_1 \cdot{ }^3 \mathrm{C}_1=5.4 .3=60\)

64. There are 12 question are to be answered to be Yes or No. how many ways can these be answered?

1. 1024
2. 2048
3. 4096
4. None

Answer: (3)

No. of ways = 2¹² = 4096

65. The letters the word VIOLENT are arranged so that the vowels occupy even place only. The number of permutations is

1. 144
2. 120
3. 24
4. 72

Answer: (1) Vowels = I, 0, E Consonants = V, L, N, T

No. of perms of vowels = ³P₃ = 3! = 6

Total no. of words = 4! x 3! = 24 x 6 = 144

66. \(\text { If } n P_4=20\left(n P_2\right)\) then the value of ‘n’ is___________

1. -2
2. 7
3. -2 and 7 both
4. None of these

Answer: (2) Note: n is always positive GO by choices

67. A man lias 3 sons and 6 schools within his roach, in how many ways, ho can send them to school, if no two of his sons aro to road in the some school?

1. \({ }_6 P_2\)
2. \({ }_6 P_3\)
3. 6³
4. 3⁶

Answer: (2)

No. of ways = ⁶P₃

68. How many permutations can be formed the letters of the word “DRAUGHT”, if both vowels may not be separated?

1. 720
2. 1,440
3. 140
4. 1,000

Answer: (2)

Total Perms. Of DRAUGHT = 61.2! = 720 x 2 = 1440.

69. \(\text { If }{ }^{13} \mathrm{C}_6+2{ }^{13} \mathrm{C}_5+{ }^{13} \mathrm{C}_4={ }^{15} \mathrm{C}_{\text {}} \text { then, } \mathrm{x}=\)

1. 6
2. 7
3. 8
4. 9

Answer:

\({ }^{13} \mathrm{C}_6+{ }^{13} \mathrm{C}_5+{ }^{13} \mathrm{C}_5+{ }^{13} \mathrm{C}_4={ }^{15} \mathrm{C}_{\mathrm{x}}\) \(\text { Or }{ }^{13} \mathrm{C}_6+{ }^{14} \mathrm{C}_5={ }^{15} \mathrm{C}_{\mathrm{x}}\) \(\text { Or }{ }^{15} \mathrm{C}_6+{ }^{14} \mathrm{C}_5={ }^{15} \mathrm{C}_{\mathrm{x}}\) \(\text { Or }{ }^{15} \mathrm{C}_6={ }^{15} \mathrm{C}_x\)

x=6

70. The total number ofshake hands in a group of10 persons to each other are.

1. 45
2. 54
3. 90
4. 10

Answer: (1)

Total no. of handshakes = ¹⁰C₂ = 45

71. A regular polygon has 44 diagonals then the No. of sides are

1. 8
2. 9
3. 10
4. 11

Answer: (4)No. of Diagonals in a polygon of “n” sides = ⁿC₂– n = 44

‘Tricks: Go by choices.

\(\text { For (a) }{ }^8 C_2-8=28-8 \neq 44\) \(\text { For (b) }{ }^9 \mathrm{C}_2-9=36-9 \neq 44\) \(\text { For }(\mathrm{c}){ }^{10} \mathrm{C}_2-10=45-10 \neq 44\) \(\text { (d) }{ }^{11} \mathrm{C}_2-11=55-11=44\)

(4) is correct

72. In how many ways to word “ARTICLE” can be arranged in a row so that vowels occupy even places?

1. 132
2. 144
3. 72
4. 160

Answer: (2)

In word ARTICLE

Vowels = A,I,E

Positions lor vowels = 2,4,6

Vowels can hr arranged In 3! = 6 ways

Rest letters can lie arranged in 4! = 24 ways

Total No. ofsuch arrangements = 6×24 = 144

73. How many different words can be formed with the letters of the word “LIBERTY”

1. 4050
2. 5040
3. 5400
4. 4500

Answer: (2)

LIBERTY

No. of words = 7! = 5040

74. In how ways can a family consist of 3 children have different birthday in a leap year.

1. 366x365x364
2. ³⁶⁶C₆
   
3. ³⁶⁵C₃
4. ³⁶⁶C₃-3

Answer:

(1) 1 Leap year = 366

No. of ways = \({ }^{366} \mathrm{C}_1 .{ }^{365} \mathrm{C}_1 .{ }^{36.1} \mathrm{C}_1\)

= 366x365x364

75. \(\text { If }{ }^{15} \mathrm{C}_{3 \mathrm{r}}={ }^{15} \mathrm{C}_{\mathrm{r}+3} \text { then } \mathrm{r}=\)

1. 2
2. 3
3. 4
4. 5

Answer:

\(

2r =3; so, r = 3/2(In fraction; so invalid)

0r3r+ r+ 3 = 15 0r 4r = 12; so, r=3

76. If 6 times the no. of permutations of n items taken 3 at a times is equal to 7 times the no. of permutations of (n-1) items taken 3 at a time then the value of n will be

1. 7
2. 9
3. 13
4. 21

Answer:

[latex]6 .{ }^n P_3=7 .(\mathrm{n}-1) \mathrm{P}_3 \text { (given) }\) \(\text { Or;6 } \frac{n!}{(n-3)!}=7 \cdot \frac{(n-1)!}{(n-1-3)!}\) \(\text { Or; } \frac{6 . n \cdot(n-1)!}{(n-3)(n-4)!}=\frac{7(n-1)!}{(n-4)!}\) \(\text { Or } \frac{6 n}{n-3}=7\)

Or 6n = 7n – 21 Or n = 21

77. \(\text { If }{ }^{1000} \mathrm{C}_{98}={ }^{999} \mathrm{C}_{97}+{ }^x \mathrm{C}_{98}\) then value of x will be

1. 999
2. 998
3. 997
4. None

Answer:

(1) Tricks: Go by choices

For (1) RHS = \({ }_{1000} \mathrm{C}_{97}+{ }^{999} \mathrm{C}_{901}\)

\(={ }^{999} \mathrm{C}_{97}+{ }_{999} \mathrm{C}_{98}\left[\mathrm{n}_{\mathrm{r}}={ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}-\mathrm{r}}\right]\) \(={ }^{1000} \mathrm{C}_{98} \text { (L.H.S) }\) \({ }^n C_r={ }^n C_{r-1}={ }^{n+1} C_r\)

78. \({ }^{{ }^G P_r}=360 \text { then find } r\)

1. 4
2. 5
3. 6
4. None

Answer: (1) Tricks: go by choices:

⁶P_r =360 LHS at r = 4 = ⁶P₄ = 6.5.4.3 = 360 R.H.S.

79. If 5 books of English 4 books of Tamil and 3 books of hindi are to be arranged in a single row so that books of same language come together

1. 1,80,630
2. 1,60,830
3. 1,03,680
4. 1,30,680

Answer: (3) Total no. of ways so that same language Books remain together

= 5 !. 4 !. 3 !. 3 !. = 120 x 24 x 6 x 6 = 1,03,680

80. 5 boys and 4 girls are to be seated in row. If the girls occupy even places then the no. of such arrangements

1. 288
2. 2808
3. 2008
4. 2880

Answer: (4)

Total no. ofstudents = 9

For girls’ position may be 2,4,6,8,

Total no. of arrangements of girls ⁴P₄ = 4! = 24

For boys = 5! 4! = 120×24 = 2880

81. A Person has 10 friends of which 6 of them are relatives, He wishes to Invite 5 persons so that 3 of them are relatives. In how many ways he can Invites?

1. 450
2. 600
3. 120
4. 810

Answer:

Friends = 10

Relatives = 6;

so, rest = 4 friends

Selection of 5 in which 3 are relatives = ⁶C₃. 4C₂ = 20×6 = 120 (c) is correct

82. A student has 3 books on computer, 3 books on economics, 5 on commerce. If these books are to be arranged subject wise then these can be placed on a sbelf in the_ number, of ways.

1. 25,290
2. 25,920
3. 4,230
4. 4,320

Answer: (1)

Total ways = 3!x3!x5!x3! = 6 x 6 x 120 x 6 = 25920

83. The number of 4-digit members that can be formed from seven digits 1,2,3,5,7,8,9 such that no digit being repeated in any number, which are greater than 3000 are

1. 120
2. 480
3. 600
4. 840

Answer: For detail see Quicker BMLRS

At 1st place 3,5,7,8,9 these 5 digit are suitable.

So, permutation of 1st place = 5

One of them will be used at that place.

Remaining 6 digits are suitable for next place.

Similarly doing as above, Total ways = 5.6,5.4 = 600

84. A question paper consists 10 questions, 6 in math and 4 in stats. Find out number of ways to solve question paper ifat least one question is to be attempted from each section.

1. 1024
2. 950
3. 945
4. 1022

Answer: (3)

No. of ways to attempt at least one from each (2⁶-1 ) 2⁴-1) = 945.

85. \({ }^{n P_r}=720 \text { and }{ }^n C_r=120 \text { find } r \text { ? }\)

1. 6
2. 4
3. 3
4. 2

Answer: (3)

ⁿP_r=ⁿC_r!=720

120. r! = 720 r!= 6 = 3! r= 3

86. There are 10 students in a class, including 3 girls. The number of ways to arrange them in a row, when any two’ girls out of them never come together

1. \(8_{p_3} \times 7!\)
2. \(3_{p_3} \times 7!\)
3. \(8_{p_3} \times 10!\)
4. None

Answer: (1)

Rost students = 7

Total no. of permutations of rest 7 stds. = 7!

Total no. of place for girls = 7 + 1 = 8. Total ways to arrange girls = ⁸P₃ .(7!)

87. In how many ways can a selection of 6 out of 4 teachers and 8 students be done so as to include at least two teachers?

1. 220
2. 672
3. 896
4. 968

Answer:

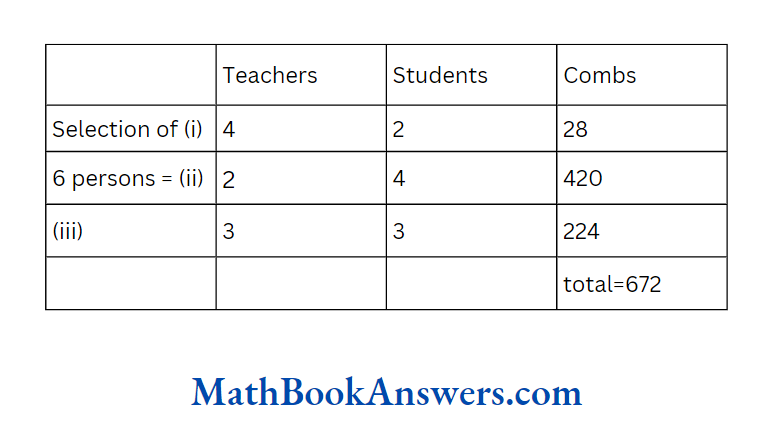
88. The maximum number of points of inter section of10 circles will be

1. 2
2. 20
3. 90
4. 90

Answer: (3)

To intersect 2 circles out of 10 are required

= \({ }^{10} \mathrm{C}_2\) x 2 = 45 x 2 = 90 Nos. of ways

(Each circle will cut at 2 points)

89. How many numbers between 1,000 and 1 0,000 can be formed with the digits 1, 2, 3, 4, 5, 6

1. 720
2. 360
3. 120
4. 60

Answer:

(2) is correct.

Total no. of numbers = \({ }^{(} p_4=6.5 .4 .3=360\)

90. \(\text { If }{ }^{n+1} C_{r+1}:{ }^n C_r:{ }^{n-1} C_{r-1}=8: 3: 1 \text {; }\) then find the value of n.

1. 14
2. 15
3. 16
4. 17

Answer: (2) is correct

Formula,\({ }^n C_r:{ }^{n-1} C_{r-1}=\frac{n}{r}=\frac{3}{1} ; \text { So, } n=3 r\)

\(\&{ }^{n+1} C_{r+1}:{ }^n C_r=\frac{n+1}{r+1}=\frac{8}{3} ;\)

So, 3n + 3 = 8r + 8

Or, 3 x 3r+ 3 = 8r + 8

Or, r= 8- 3 = 5. Hence, n = 3r = 3 x 5 = 15

91. In how many ways 4 members can occupy 9 vacant seats in a row

1. 3204
2. 3024
3. 49
4. 94

Answer: (2) is correct. Total ways =  ⁹P₄

= 9.8.7.6 = 3024

92. The number of arrangements that can be formed from the letters of the word ‘ALLAHABAD”

1. 7560
2. 3780
3. 30240
4. 15320

Answer:

\(\frac{9!}{(4!) \cdot(2!)}=\frac{9.8 \cdot 7 \cdot 6 \cdot 5(4!)}{(4!) \cdot 2 \cdot 1}=7560\)

Option (1) is correct

93. \(\text { If }{ }^{10} \mathrm{C}_3+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_5={ }^{11} \mathrm{C}_5\) then the value of n = _______

1. 10
2. 11
3. 12
4. 13

Answer:

\({ }^{10} \mathrm{C}_3+2 \cdot{ }^{10} \mathrm{C}_4+{ }^{10} \mathrm{C}_5={ }^{11} \mathrm{C}_5\) \(\text { Or; }{ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_1+{ }^{10} \mathrm{C}_1+{ }^{10} \mathrm{C}_5={ }^1 \mathrm{C}_5\) \(\text { Or; }{ }^{11} C_4+{ }^{11} C_5={ }^1 C_5\) \(\mathrm{Or} ;{ }^{12} \mathrm{C}_5={ }^n \mathrm{C}_5 \Rightarrow \mathrm{n}=12\)

Option (3) is correct

94. The number of parallelograms that can be formed by a set of 6 parallel lines intersected by the another set of 4 parallel lines is

1. 360
2. 90
3. 180
4. 45

Answer:

No. of parallelograms = \({ }^6 \mathrm{C}_2 \cdot{ }^4 \mathrm{C}_2\) =15X6 = 90 Option (2) is correct

95. \(^{12} C_3+2,^{12} C_1+{ }^{12} C_5={ }^{14} C_x\) The value of x

1. 3 or 5
2. 5 or 9
3. 7 or 1
4. 9 or 12

Answer:

\({ }^{12} \mathrm{C}_3+2{ }^{12} \mathrm{C}_4+{ }^{12} \mathrm{C}_5={ }^{14} \mathrm{C}_x\) \(\Rightarrow{ }^{12} C_3+{ }^{12} C_4+{ }^{12} C_4+{ }^{12} C_5={ }^{14} C_x\) \(\Rightarrow{ }^{13} \mathrm{C}_4+{ }^{13} \mathrm{C}_5={ }^{11} \mathrm{C}_x\) \(\Rightarrow{ }^{14} C_5={ }^{11} C_x \Rightarrow x=5\) \(\text { And }{ }^{14} C_5={ }^{14} C_{14 \cdot 5}={ }^{14} C_x \Rightarrow x=14-5=9\)

x = 5 or 9

96. The number of ways in which a man can invite one or more of his 7 friends to dinner is

1. 64
2. 128
3. 127
4. 63

Answer:  (3)

No. of ways to invite at least one friend = 2⁷ -1 = 128-1 = 127.

97. The number of words from the letters of the letters of the word BHARAT, in which B and H will never come together, is

1. 120
2. 360
3. 240
4. None

Answer: (3) Use Gap rule.

*A*R*A*T*

Total words = \( \frac{4!}{2!} \times 5 p_2=\frac{24}{2} \times 5 \times 4=240\)

98. The value of N in \(\frac{1}{7!}+\frac{1}{8!}=\frac{N}{9!} \operatorname{ls}\)

1. 81
2. 64
3. 78
4. 89

Answer: (1)

\(\frac{1}{7!}+\frac{1}{8!}=\frac{N}{9!}\) \(\mathrm{Or}^{\prime} ; \frac{1}{7!}+\frac{1}{8 \times 7!}=\frac{N}{9 \times 8 \times 7!}\) \(\operatorname{Or} ; \frac{1}{7!}\left(1+\frac{1}{8}=\right)=\frac{N}{9 \times 8 \times 7!}\) \(\Rightarrow \frac{9}{8}=\frac{N}{9 \times 8}\)

99. If \({ }^n P_r\)= 270 and \({ }^n C_r\)= 120 then r is

1. 4
2. 5
3. 3
4. 6

Answer: (3)

\({ }^n p_r={ }^n C_r, r!\)

Or; 720 = 120 (r!)

Or 6 = r! => r! = 3!

r = 3

100. A bag contains 4 red, 3 black and 2 white balls. In how many ways 3 balls can be drawn from this bag so that so that they include at least one black ball?

1. 46
2. 64
3. 86
4. None

Answer:

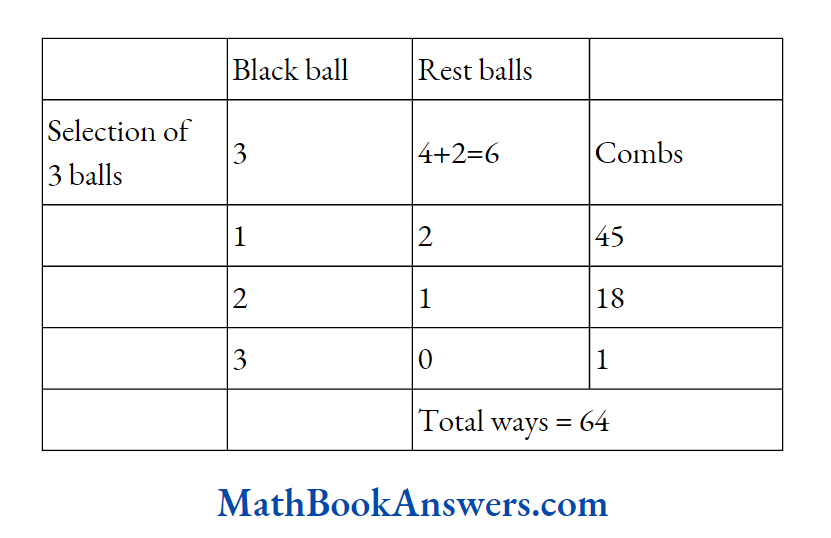
101. The letters of the words ‘CALCUTTA’ and ‘AMERICA’ are arranged in all possible ways. The ratio of the number of these arrangements is

1. 1:2
2. 2:1
3. 2:2
4. none of these

Answer: (2) 2:1

Words:

CALCUTTA

N0.of ways= \(\frac{8!}{2!2!2!}=5040\)

(C, A, T are repeated)

AMERICA

No. of ways = \( \frac{7!}{2!} \text { (A is repeated } \times 2 \text { ) } 2520\)

Ratio = 5040 : 2520 = 2:1

102. The number of different words that can be formed with 12 consonants and 5 vowels by taking 4 consonants and 3 vowels in each word is

1. \({ }^{12} \mathrm{C}_4 \times{ }^5 \mathrm{C}_3\)
2. \({ }^{17} \mathrm{C}_7\)
3. 4950 x 7!
4. none of these

Answer: (3) 4950x 7!

-» 12 consonants & 5 vowels

Selection of 4 consonants & 3 vowels = \({ }^{12} \mathrm{C}_1 \times{ }^5 \mathrm{C}_3\)

Also since words need to be formed arrangement is important

7 letters can arrange themselves in 7 ! ways

Total ways =

\({ }^{12} \mathrm{C}_4 \times{ }^5 \mathrm{C}_3 \times 7!=4950 \times 7!\text { ways }\)

103. Eight guests have to be seated 4 on each side of a long rectangular table.2 particular guests desire to sit on one side of the table and 3 on the other side. The number of ways in which the sitting arrangements can be made is

1. 1732
2. 1728
3. 1730
4. 1278.

Answer: (2) 1728

Total guests -> 8

If 2 are seated on one side & 3 on other remaining 3 have to be seated

No. of ways = \({ }^3 \mathrm{C}_2 \times{ }^1 \mathrm{C}_1=3 \text { ways }\)

Now the four on one side can arrange in 4 ! ways & other side also 4 ! ways

Total = 3×4!x4! = 1728

104. A question paper contains 6 questions, each having an alternative. The number of ways an examine can answer one or more questions is

1. 720
2. 728
3. 729
4. none of these

Answer: (2) 728

Any question can be solved in 3 ways

(1) 1st alternative (2) 2nd alternative (3) No answer

6 questions will have 36 ways = 729

But there will be one way which will have no answers to all question which is not required

729 – 1 = 728

105. The number of words that can be made by rearranging the letters of the word APURNA so that vowels and consonants appear alternate is

1. 18
2. 35
3. 36
4. none of these

Answer: (c) 36

A P U R N A 6 letter

3 vowels (A A U)

3 consonants (P R N)

The vowels can arrange in \(\frac{3!}{2!}\) ways = 3 ways (A is repeated)

The consonants can arrange in 3! ways = 6 ways

word can be arranged in 18 ways

We will have 2 cases

VCVCVC or CVCVC i.e., 2 ways Total = 36 ways

106. The number of arrangements of the letters of the word ‘COMMERCE’ is

1. 8
2. 8!/2!2!2!
3. 7 !
4. none of these

Answer: \(\text { (2) } \frac{8!}{2!2!2!}\)

COMMERCE, 8 letters (M-2, E=2, C=2)

Total arrangements = \(\frac{8!}{2!2!2!}\)

107. The number of ways in which 8 different beads be strung on a necklace is

1. 2500
2. 2520
3. 2250
4. none of these

Answer: (2) 2520

8 beads in a necklace

Formula for n beads in necklace is

\(\frac{1}{2}(n-1)!=\frac{1}{2}(8-1)!\quad=\frac{7!}{2}=2520\)

108. The number of different factors the number 75,600 has Is

1. 120
2. 121
3. 119
4. none of these

Answer: (1) 120

75600 no. of factors

-» 756 x 100 -» 756 (52) (22)

-»22. 33. 7. 52. 22-24. 33. 52.7

no. of factors (5+1) (4+1) (3+1) (2+1) = 120

109. (n-1) P_r+r ;(n-1) P_{(r-1)} is equal to

1. \({ }^n \mathrm{C}_r\)
2. \( n/(r n-r)\)
3. \({ }^n \mathrm{P}_r\)
4. none of these

Answer:

\({ }^n P_r\) \({ }^{n-1} P_r+r,(n-1) P_{(r-1)}={ }^n P_r\)

110. (2ⁿ)! can be written as

1. 2ⁿ {1.3.5…. (2n-l)}n
2. 2ⁿ n
3. {1.3.5…..(2n -1)}
4. none of these

Answer: (1) 2n (1. 3. 5…….(2n – 1) n !

(2n) ! = 2n (2n – 1)……… 3x2x1

= 2” (2n – 2)…….(2n-1)…3×1

= 2″ n ! . (1 . 3 . 5…….(2n – 1))