Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities
Page 38 Essential Question Answer
Solving inequalities is very similar to solving equations.
It just that when we divide we need to reverse the symbol on both sides of the equation by a negative number.
We can solve an inequality by using division just the way we solve an equation just we need to reverse the symbols of both the sides by a negative number.
Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions
Page 38 Exercise 1 Answer
To Find Complete the table. Decide which graph represents the solution of the inequality 6<3x
and write a solution of the inequality.
Evaluate the question to get the answer.
From the given we get,
6<3x
\(\frac{6}{3}<\frac{3 x}{3}\)
2<x
Now, the graph is

Now, using the graph we get the table as
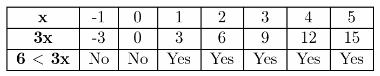
The graph that represents the solution of inequality 6<3x is


And the table is
Given: The inequalities are,2x<4, 3≥3x, 2x<8, 6≥3x
To Find Use a table to solve each inequality. Then write a rule that describes how to use division to solve the inequalities.
Evaluate the question to get the answer.
From the given, we get that
(i): 2x<4
x<2
(ii): 3≥3x
x≤1
(iii): 2x<8
x<4
(iv): 6≥3x
x≤2
Now, from the solution above we get the table as
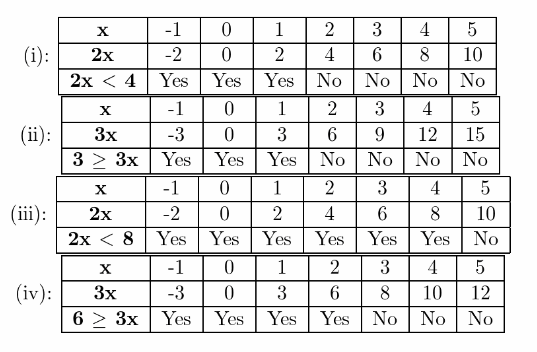
One of those rules is called the division property of inequality, and it basically says that if you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number.
The tables for solving the given inequalities are
One of those rules is called the division property of inequality, and it basically says that if you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number.
Big Ideas Math Algebra 1 Chapter 2 Exercise 2.3 Solution
Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.3 Page 39 Exercise 2 Answer
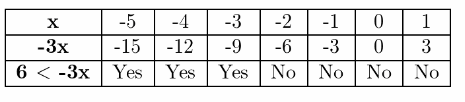
To Find Complete the table. Decide which graph represents the solution of the inequality 6<−3x
and write solutions for the inequalities.
Evaluate the question to get the answer.
From the given we get,
6<−3x
\(\frac{6}{-3}<\frac{-3 x}{-3}\)
−2>x
Now, plotting the solution we get

Now, using the result we complete the table as
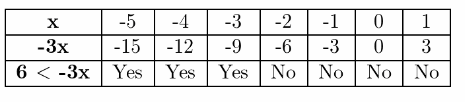
After solving 6<−3x we getx<−2 and the graph is

And the table is
Given: The inequalities are−2x<4,3≥−3x,−2x<8 & 6≥−3x
To Find Use a table to solve each inequality. Then write a rule that describes how to use division to solve the inequalities.
Evaluate the question to get the answer.
From the given we get
(i): −2x<4
x>−2
(ii): 3≥−3x
x≥−1
(iii): −2x<8
x>−4
(iv): 6≥−3x
x>−2
Using the result we get the table as
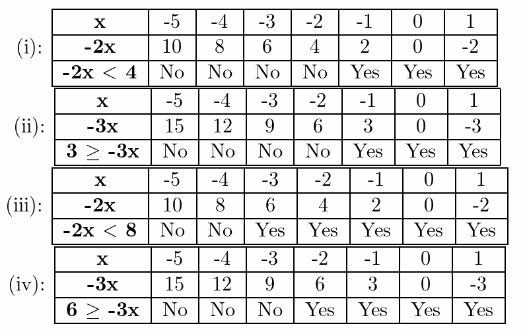
One rule is called the division property of inequality, and it basically says that if you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number. And change the sign of inequality if the number is negative.
The tables for solving the inequality are
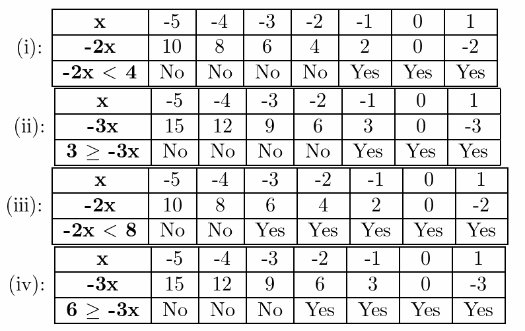
One rule is called the division property of inequality, and it basically says that if you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number. And change the sign of inequality if the number is negative.
Solving Linear Inequalities Exercise 2.3 Big Ideas Math
Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.3 Page 39 Exercise 3 Answer
Solving inequalities is very similar to solving equations.
But, when we multiply/divide by a negative number the sign changes direction >→< and vice versa.
Solving inequalities is very similar to solving equations but, when we multiply/divide by a negative number the sign changes direction>→< and vice versa
Page 39 Exercise 4 Answer
Given: The inequality is7x<−21
To Find Solve using the rule in Exercises (1) & (2)
Evaluate the question to get the answer.
Using the rule in Exercises (1) & (2)
in the given inequality we get
7x<−21
\(\frac{7 x}{7}<\frac{-21}{7}\)
x<−3
After solving the inequality 7x<−21 we get x<−3.
Given: The inequality is 12≤4x
To Find: Solve using the Exercise (1) & (2)
Evaluate the question to get the answer.
Using the rule in Exercises (1) & (2) we get
12≤4x
\(\frac{12}{4} \leq \frac{4 x}{4}\)
3≤x
After solving 12≤4x using Exercises (1) & (2) we get x≥3.
Given: The inequality is 10<−5x
To Find Solve using the Exercise (1) & (2)
Evaluate the question to get the answer.
Using the Exercises in (1) & (2) we get,
10<−5x
−2>x
After solving 10<−5x using the Exercise in (1) & (2) we get x<−2.
Given: The inequality is −3x≤0
To Find: Solve using the Exercise in (1) & (2)
Evaluate the question to get the answer.
Using the Exercises in (1) & (2) we get
−3x≤0
x≥0
After solving −3x≤0 using the Exercise in (1) & (2) we get x≥0.
Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.3 Page 41 Exercise 1 Answer
To Find Solve 16x<−30 and plot the graph.
Evaluate the question to get the answer.
From the given we get
6x<−30
\(\frac{6 x}{6}<\frac{-30}{6}\)
x<−5
Now, plotting the result we get

After solving 16x<−30 we get x<−5 and the required graph is

Page 41 Exercise 2 Answer
To Find Solve 48≤16f and graph the result.
Evaluate the question to get the answer.
From the given we get
48≤16f
3≤f.
Now, plotting the result we get the graph as

After solving 48≤16f we get f≥3 and the graph is

Algebra 1 Student Journal Chapter 2 Exercise 2.3 Answers
Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.3 Page 41 Exercise 3 Answer
To Find Solve\(\frac{-6}{7} \leq \frac{3}{7} f\) and graph the result.
Evaluate the question to get the answer.
From the given, we get that
\(\frac{-6}{7} \leq \frac{3}{7} f\)
−2≤f
Now, plotting the result we get the graph as

After solving\(\frac{-6}{7} \leq \frac{3}{7} f\) we get f≥−2 and the required graph is

Page 41 Exercise 4 Answer
To Find Solve −4m≥−16 and graph the result.
Evaluate the question to get the answer.
From the given we get
−4m≥−16
m≤4
Now, plotting the result we get

After solving −4m≥−16 we get m≤4 and the required graph is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.3 Page 41 Exercise 5 Answer
To Find Solve \(\frac{x}{-6}>\frac{1}{3}\) and graph the result.
Evaluate the question to get the answer.
From the given we get
\(\frac{x}{-6}>\frac{1}{3}\)
x<−2
Now, plotting the result we get the graph as

After solving \(\frac{x}{-6}>\frac{1}{3}\) and the required graph is

Page 42 Exercise 6 Answer
To Find Solve\(1 \leq-\frac{1}{4} y\) and graph the result.
Evaluate the question to get the answer.
From the given we get
\(1 \leq-\frac{1}{4} y\)
(1)(−4)≤\(-\frac{1}{4} y(-4)\)
−4≥y
Now, plotting the result we get the graph as

After solving 1≤−1\(1 \leq-\frac{1}{4} y\) we get y ≤−4 and the required graph is

Big Ideas Math Linear Inequalities Exercise 2.3 Help
Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 2 Solving Linear Inequalities Exercise 2.3 Page 42 Exercise 7 Answer
To Find Solve\(\frac{-2}{3}<-4 x\) and graph the result.
Evaluate the question to get the answer.
From the given we get
\(\frac{-2}{3}<-4 x\)
\(x<\frac{1}{6}\)
Now. plotting the result we get the graph as

After solving \(\frac{-2}{3}<-4 x\) we get \(x<\frac{1}{6}\) and the required graph is

Page 42 Exercise 8 Answer
To Find Solve\(\frac{-4}{5} x \geq-2\)and graph the result.
Evaluate the question to get the answer.
From the given we get
\(\frac{-4}{5} x \geq-2\)
\(x \leq \frac{5}{2}\)
Now, plotting the result we get the graph as

After solving\(\frac{-4}{5} x \geq-2\) we get \(x \leq \frac{5}{2}\) and the required graph is

Chapter 2 Exercise 2.3 Step-By-Step Solutions Big Ideas Math
