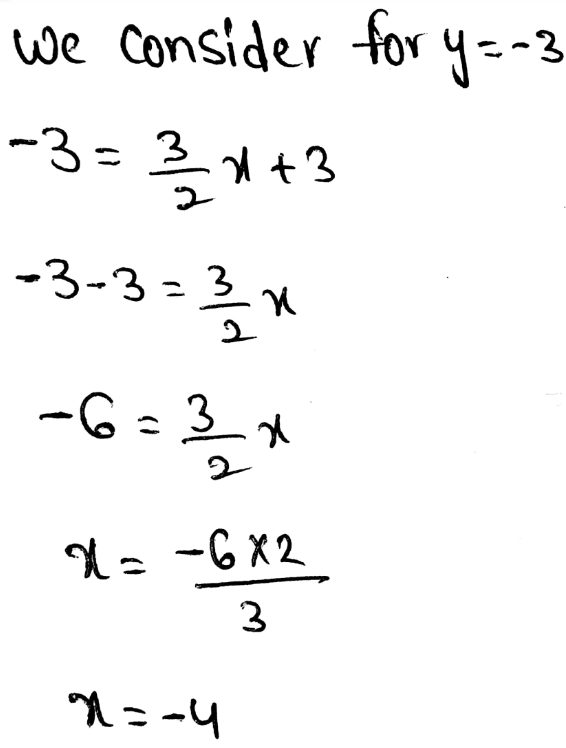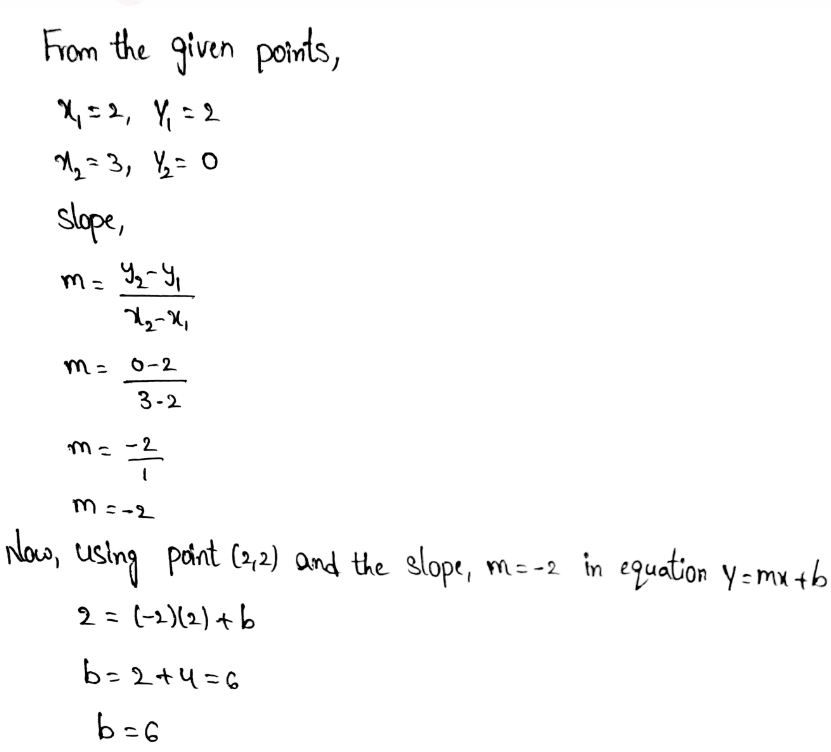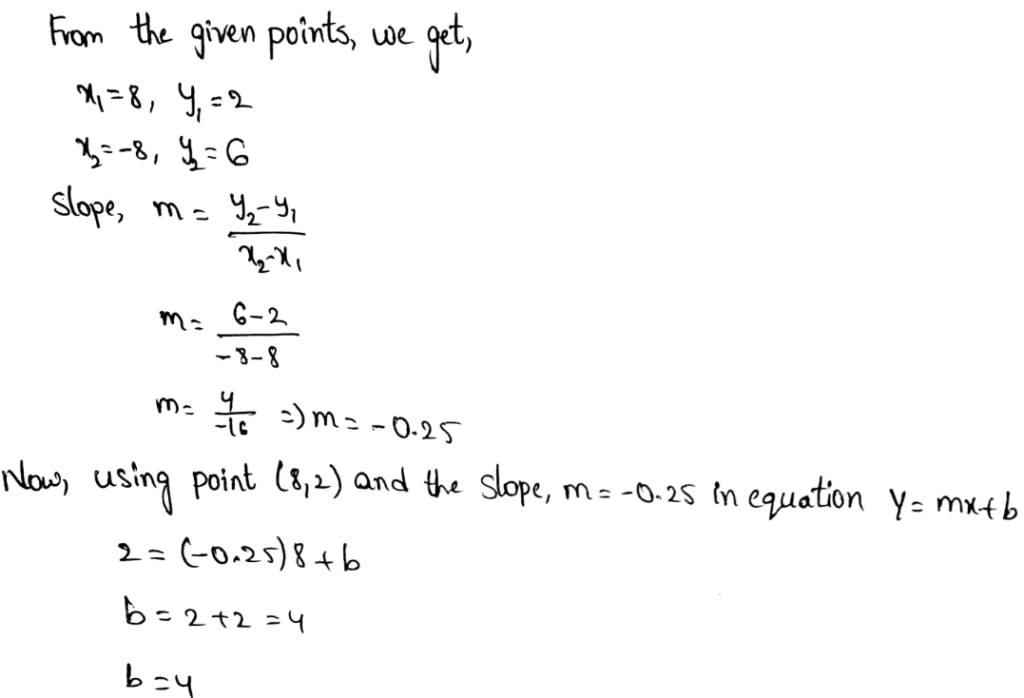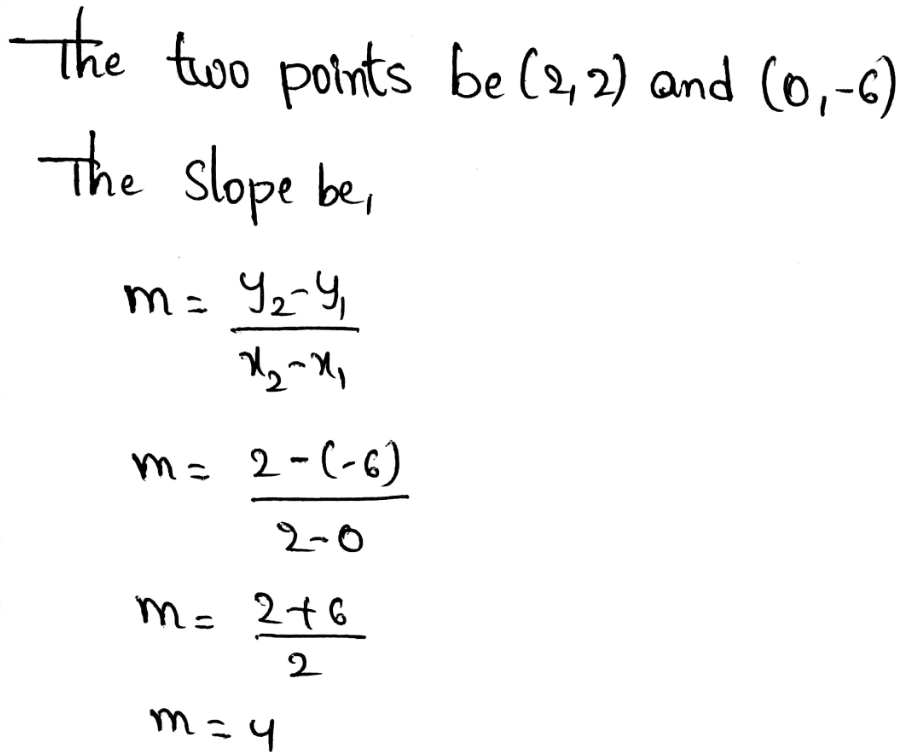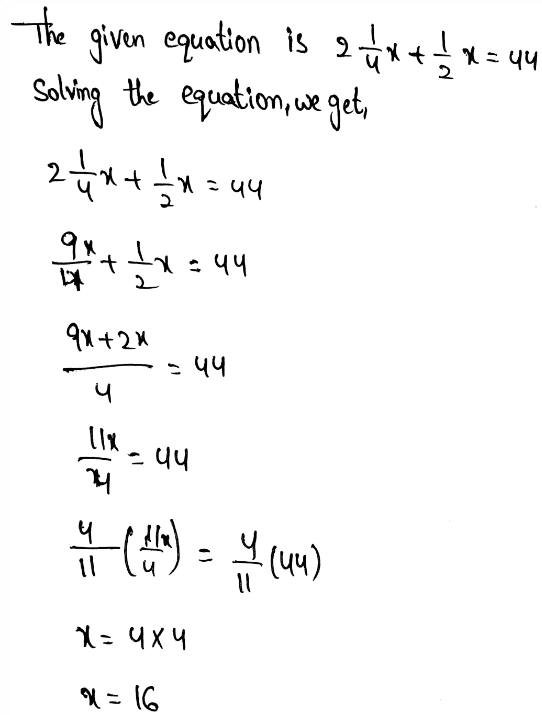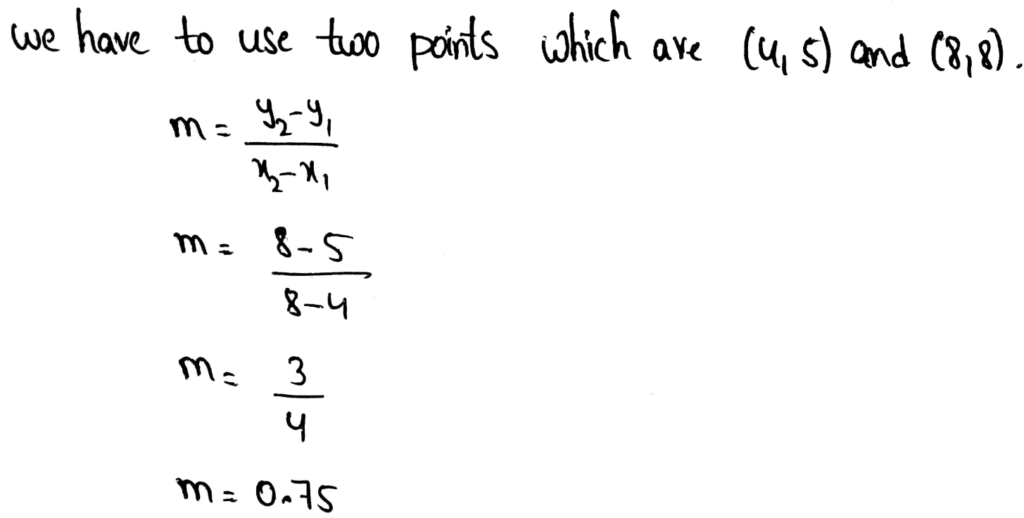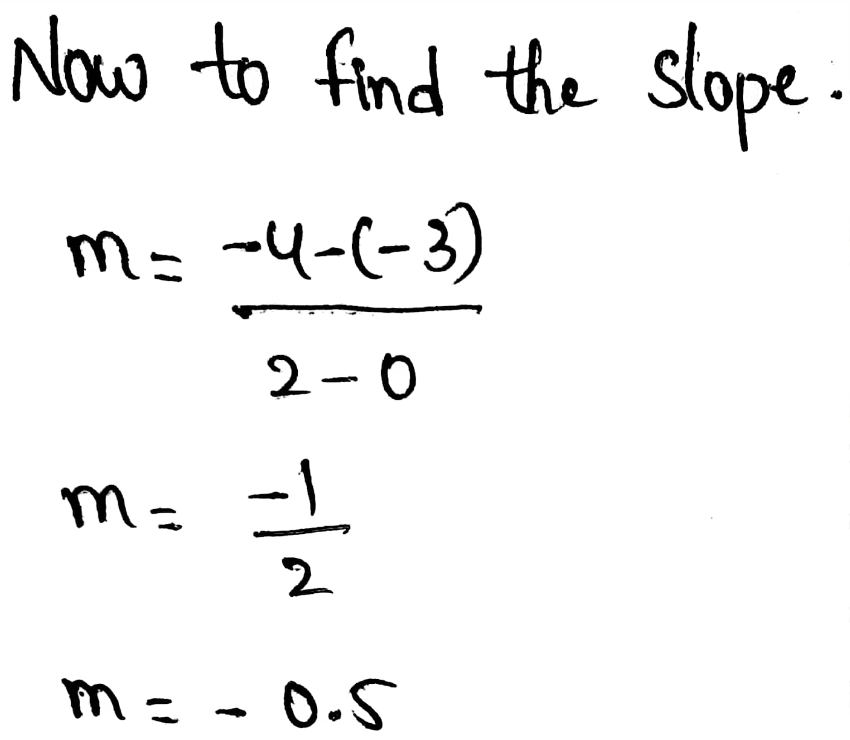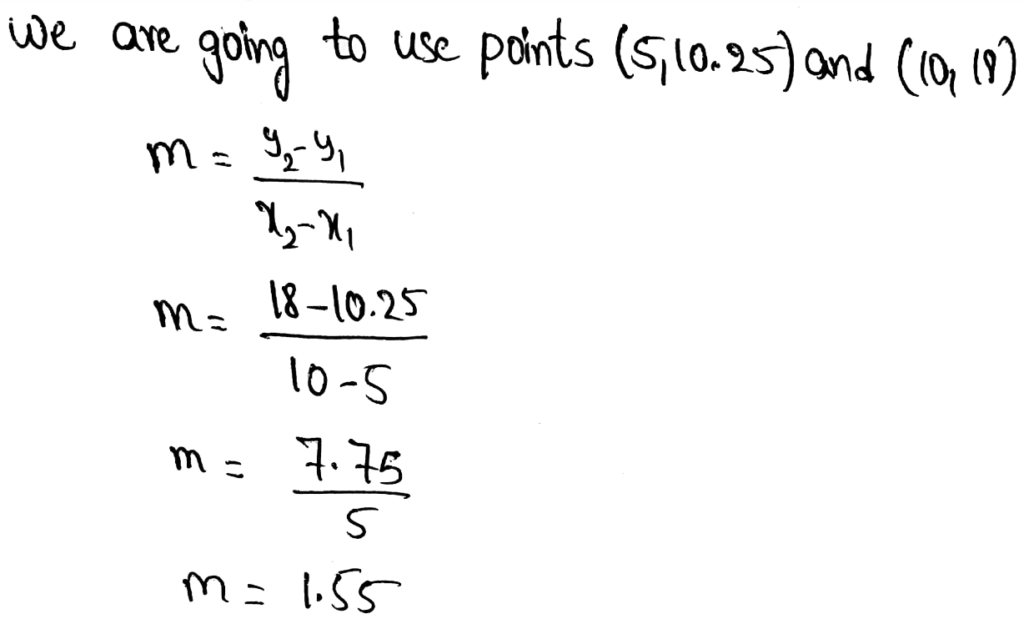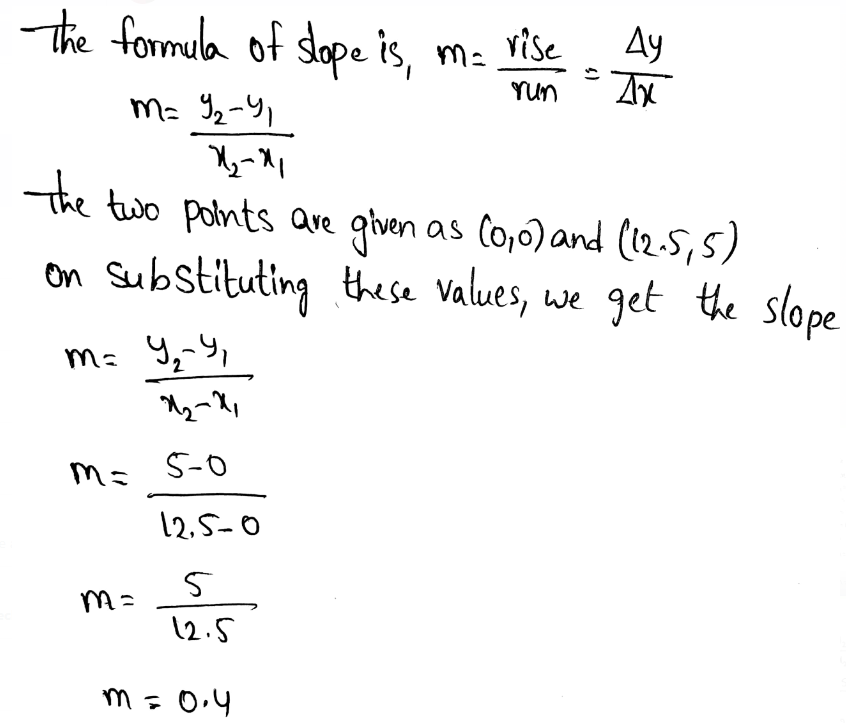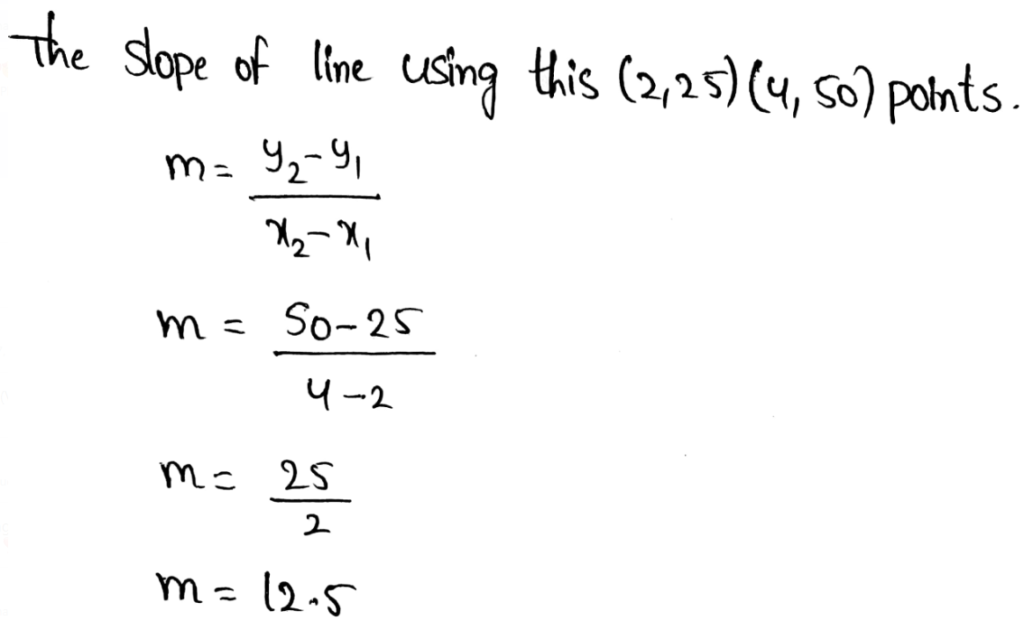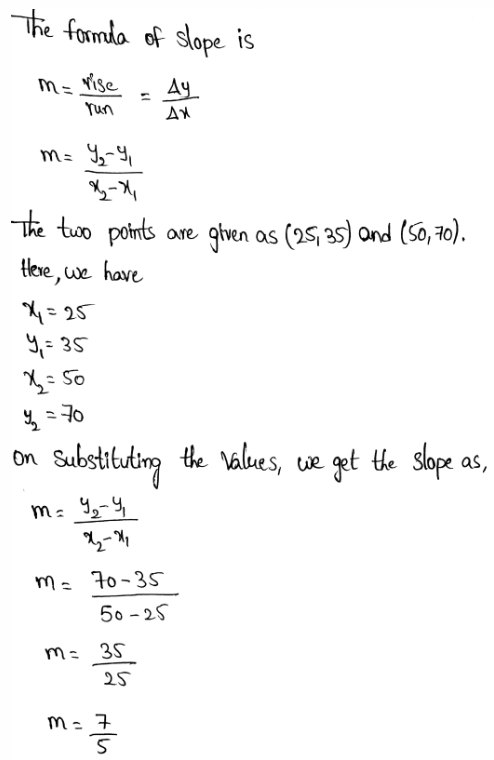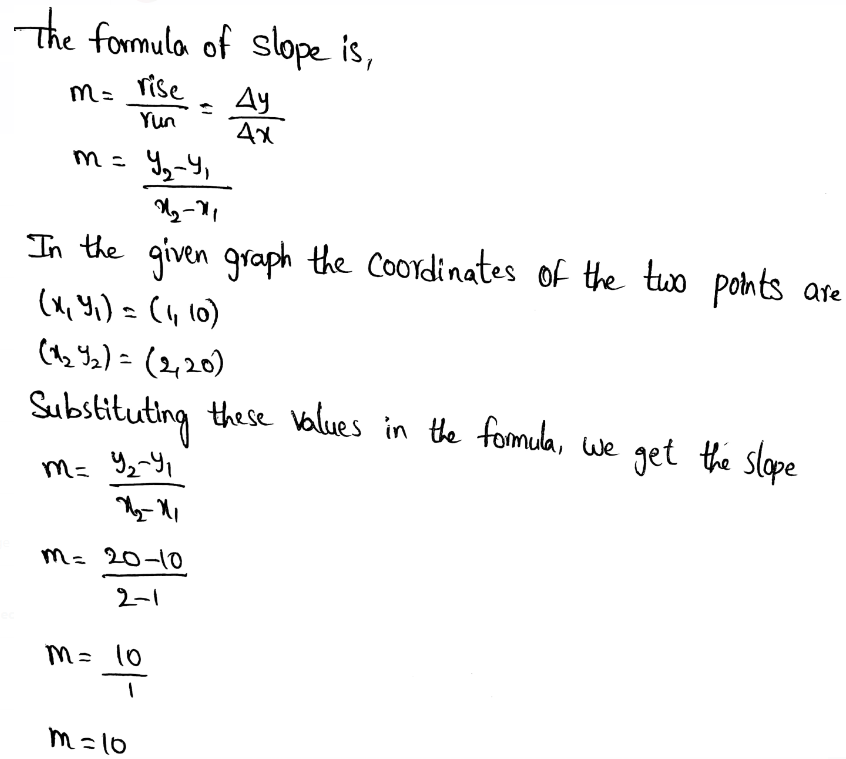Schindler

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3

Page 171 Exercise 1 Answer

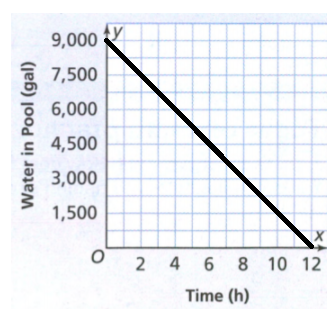
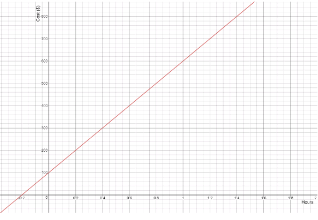
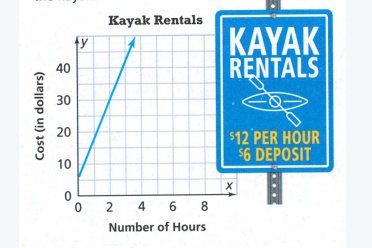
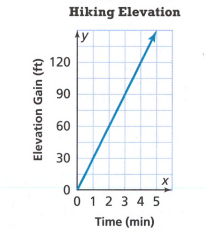
The Movies4You offer the deal that costs $10 for the first device and an additional $2 for each additional device, which means that they will for example charge $20 monthly for 6 devices.

The Family stream cots $12 a month for up to 4 devices which means that they are going to pay $12 if the number of devices is up to 4.

On the other hand, it means that if there are morthan 5 devices they are charging an additional $1 per device.

We make a table to see when each plan is the better deal:

Movies 4 you have a better deal when there is only one device connected.

Both of the services offer fixed costs per month for a number of devices.

They have a different fixed cost per month and different initial costs.

Movies 4 You has a better deal when there is only one device connected.

Envision Math Grade 8 Volume 1 Chapter 3 Exercise 3.3 Functions Solutions

Page 171 Exercise 1 Answer

We need to explain how we can represent the relationship between cost and number of devices.

The Movies 4 You offer the deal that costs $10 for the first device and an additional $2 for each additional device, which means that they will for example charge $20 monthly for 6 devices.

The Family stream costs $12 a month for up to 4 devices which means that they are going to pay $12 if the number of devices is up to 4.

On the other hand, it means that if there are more than 5 devices they are charging an additional $1 per device.

We make a table to see when each plan is the better deal:

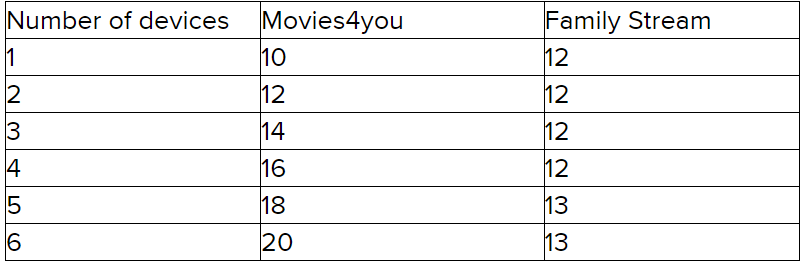
Movies 4 you have a better deal when there is only one device connected.

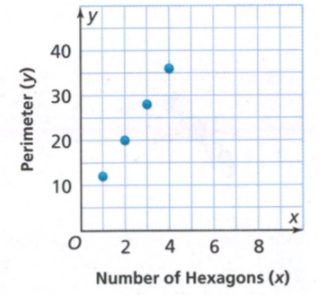
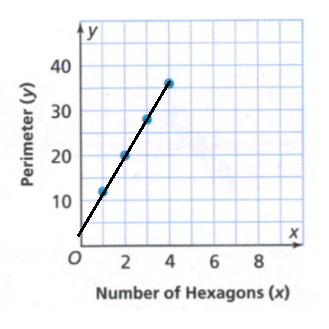
We can represent the relationship between cost and number of devices using a table. The table is as follows:

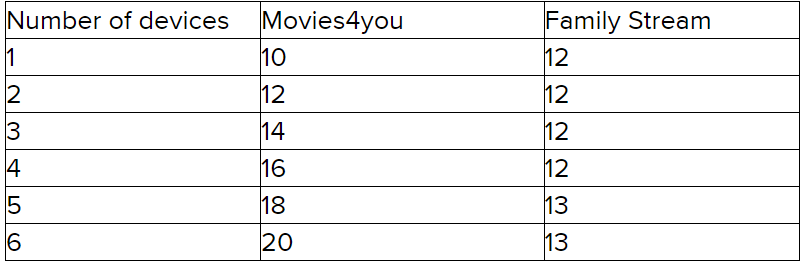
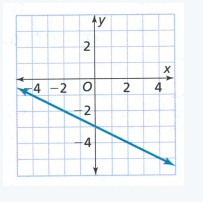
Page 171 Exercise 1 Answer

Movies 4 You is offering $10 for the first device and an additional $2 for each additional device. This means that our equation

would look like y = (x−1)⋅2 + 10 where x is the number of devices connected and y is the total cost.

For Family stream we have to pay $12 if we have up to 4 devices connected, and this would give the following equation y = 12 where x ≤ 4

Reason of that equation is that we have 5 or more devices connected it states that they charge an additional fee of $1 per device which change our equation y = (x−4)⋅1 + 12 to where x ≥ 5

For Movies 4 You the relationship is shown by the equation y = (x−1)⋅2 + 10 where x is the number of devices connected.

For Family stream the equation y = (x−4)⋅1 + 12 when x ≥ 5

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3 Page 172 Question 1 Answer

We can compare two different functions using the properties of functions.

We use the property of constant rate of change and the initial value which is the y-intercept to compare the two functions.

We can compare two functions by comparing their properties.

Page 172 Exercise 1 Answer

We need to determine what are the properties of functions that can be used to compare functions.

Some of the properties of functions are:

Linear functions: It is represented by f(x) = mx + b where m,b are real numbers.

Constant Function: It is represented by f(x) = b where b is a real number.

Identity Function: It is represented by f(x) = x where the input and the output are the same.

Square Function: It is represented by f(x) = x2 where the output is the square of the given input.

Cube Function: It is represented by f(x) = x3 where the output is the cube of the given input.

Square Root Function: It is represented by f(x) = √x where the output is the square root of the given input.

Reciprocal Function: It is represented by \(f(x)=\frac{1}{x}\) where the output is the inverse of the given input.

Absolute Value Function: It is represented by f(x)=∣x∣

Linear functions, Identity Function, Square Function, Cube Function, Square Root Function, Reciprocal Function, Absolute Value Function.

These are the properties of functions that can be used to compare functions.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3 Page 173 Exercise 2 Answer

Given :

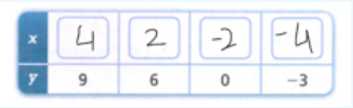
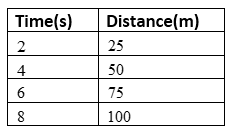
To be able to compare the two given functions, we have to put values for y in Function 2 and see the results that we get for x. we are going to calculate for the first 3 y values.

1 = 2x − 4

Add 4 to both sides of the equation

5 = 2x

Now we divide both sides by 2
​
x = 2.5

5.5 = 2x − 4
​
Add 4 to both sides of the equation

9.5 = 2x

Divide both sides with 2
​
x = 4.75

11.5 = 2x − 4
​
Add 4 to both sides of the equation

15.5 = 2x

Divide both sides of the equation with 2

7.75 = 2x

From this we can see that the Function 1 has greater rate of change and Function 2 has a greater initial value.

Therefore Function 1 has greater rate of change and Function 2 has a greater initial value.

Envision Math Grade 8 Exercise 3.3 Use Functions To Model Relationships

Page 172 Exercise 1 Answer

All linear equations produce straight lines when graphed.

But not all linear equations produce linear functions.

In order to be a linear function, a graph must be both linear and a function.

Linear equations help to compare linear functions by graphs.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3 Page 174 Exercise 1 Answer

We can compare two different functions using the properties of functions.

We use the property of constant rate of change and the initial value which is the y-intercept to compare the two functions.

We can compare two functions by comparing their properties.

Page 174 Exercise 4 Answer

Given :

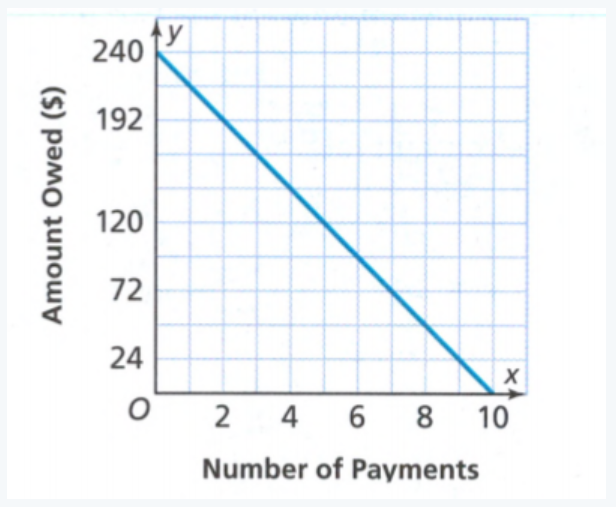
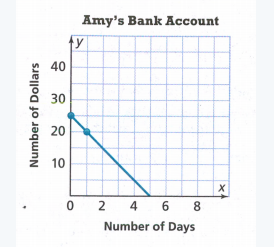
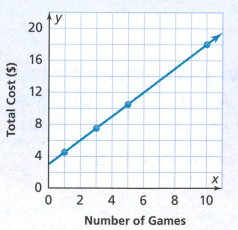
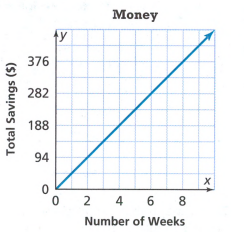
We find the constant rate of change and initial value for Samantha.

We see from the graph that the initial value is 240 and we can see that Samantha spent all this $240 on 10 payments.

We divide the amount of money with the number of payments, we get 4.

We can see she spends $24 per payment for the musical instrument.

In the task it states that Felipe pays $30 per payment.

Now we can see that she will spend $240 for the instrument and Felipe will spend $290.

Felipe’s instrument costs more.

Page 174 Exercise 5 Answer

Given :

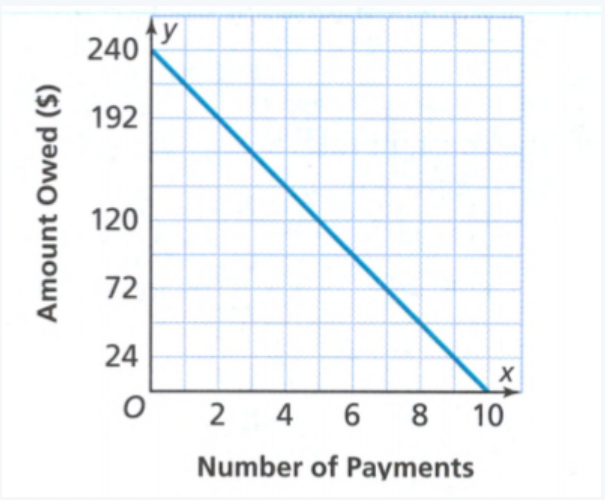
We need to divide the amount of money with the amount of pays to find how much Samantha pays.

∴ 240 ÷ 10 = 24

Since we already stated that Felipe pays $30 per month and Samantha pays $24 per month. This means that Felipe pays more each month.

Felipe pays more each month.

Envision Math Grade 8 Exercise 3.3 Solution Guide

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3 Page 175 Exercise 6 Answer

Given :

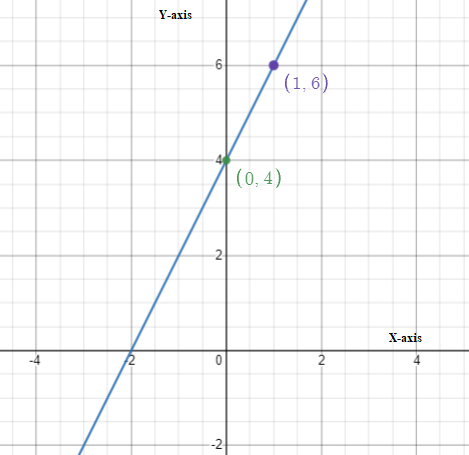
If we closely observe Function A, we see that the initial value of the function is 2. We also see that the rate at which the function is growing is 1, which means that the equation for the given function would be y = x + 2

Now we observe Function B. we see that the Function B starts from the origin.

If we observe the numbers in the table, we can see that y grows faster than x.

The function A has the same rate of change for x and y which is 1.

This means that Function B has the greater rate of change.

Therefore Function B has the greater rate of change.

How To Solve Exercise 3.3 Functions In Envision Math Grade 8

Page 175 Exercise 7 Answer

Given :

For initial value we have to find the ordered pair which has x = 0.Function A has the initial value of 4.

When we have a function written as an equation y = mx + b, we need to look at b and that is the initial value.

This means that Function B has the initial value of 3.

Function A has the greater value.

Function A has the greater initial value.

Functions And Modeling Relationships Grade 8 Exercise 3.3 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3 Page 175 Exercise 8 Answer

Given :

?

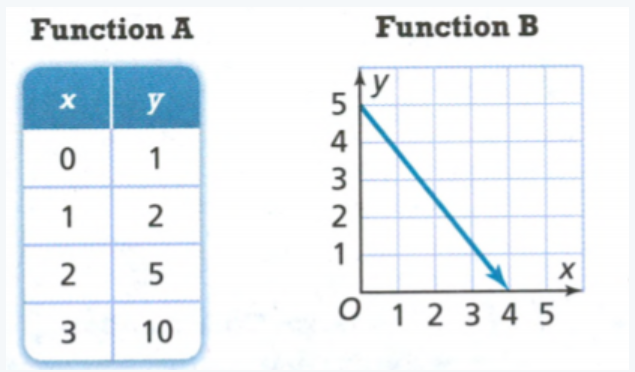
We observe Function A, we see that y changes is not always the same. This means that the given function is nonlinear.

If we observe the graph of Function B, we can see that it is a straight line which means that this function is linear.

Function A is nonlinear and Function B is linear.

Page 175 Exercise 10 Answer

Given :

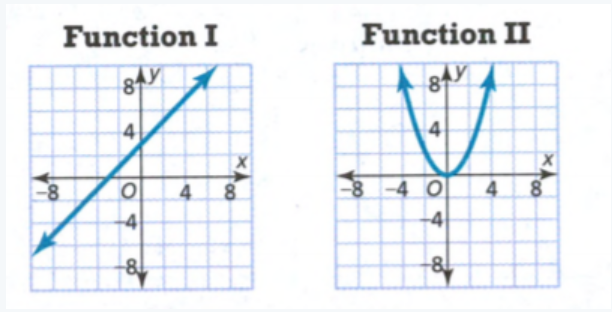
We observe that the graph of Function A is a straight line and therefore, it is linear.

The graph of Function B is a curve, therefore, it is nonlinear.

Function A is linear and Function B is nonlinear.

Envision Math Grade 8 Chapter 3 Exercise 3.3 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3 Page 175 Exercise 12 Answer

Given:

The function y = 4x + 3 describes Player A’s scores in a game of trivia.

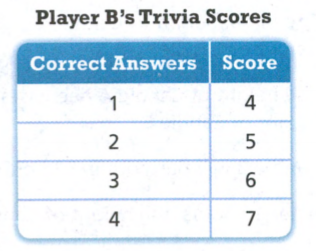
If we look at the given function, we observe that the initial value is 3 for Player A. The coefficient of x shows how much points he earns when the question is answered correctly, which is 4 per question answered correctly.

For Player B we can see that for every correct answer his score goes up by 1, which means that the points Player B gets when he answers questions correctly is 1. We subtract 1 form the first value of Score and that will be the initial value.

Player A earns 4 points per question answered correctly and Player B earns 1 point per question answered correctly.

Player A earns 4 points per question answered correctly and Player B earns 1 point per question answered correctly.

Page 176 Exercise 13 Answer

Given:

Athlete A can do 16 push-ups to start, and increase his total by 2 each day.

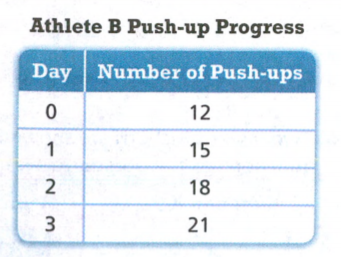
For Athlete A, the initial value is 16 push-ups that is already given, We look at the table for Athlete B, we see that on the first day, he was only able to do 12 push-ups.

Initial value in this situation tells us how many push-ups could each of them do before they started to train.

Therefore initial value in this situation tells us how many push-ups could each of them do before they started to train.

Envision Math 8th Grade Exercise 3.3 Step-By-Step Functions Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.3 Page 176 Exercise 14 Answer

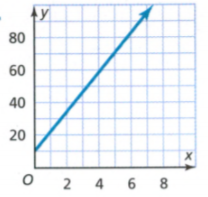
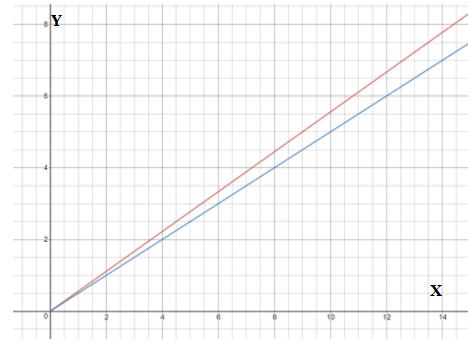
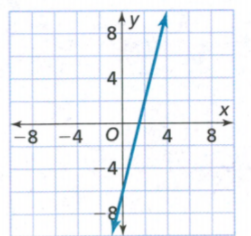
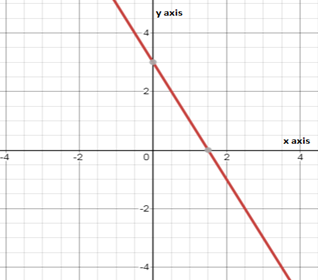
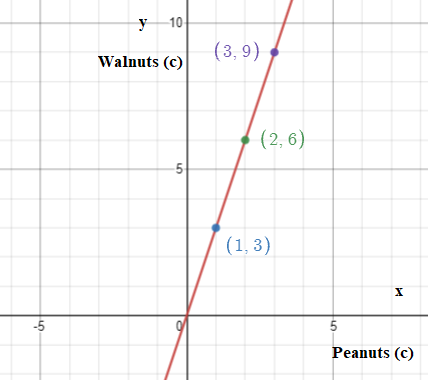
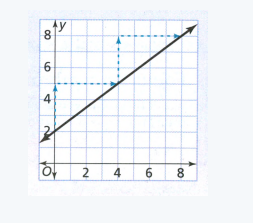
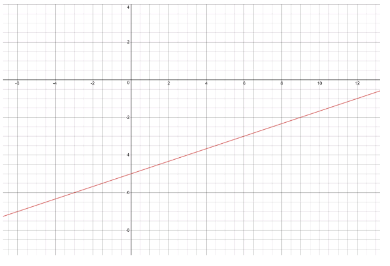
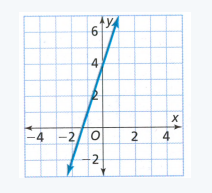
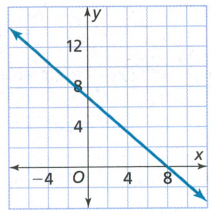
The equation y = 4x − 2 and the table and graph shown at the right describe three different linear functions. We need to find which function has the greatest rate of change and which has the least.

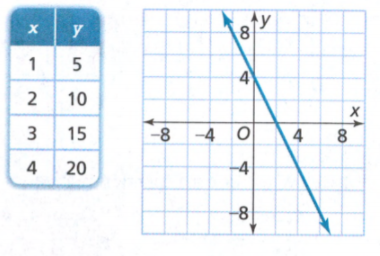
The given equation is y = 4x − 2

When,
​
x = 1 ⇒ y = 4 − 2 = 2

x = 2 ⇒ y = 8 − 2 = 6

x = 3 ⇒ y = 12 − 2 = 10

x = 4 ⇒ y = 16 − 2 = 14
​
The rate of change here is,

Rate of change = \(\frac{6-2}{2-1}\)

= \(\frac{4}{1}\)

= 4

Rate of change is more for the given table and very less for the given graph.

The given table function has the greatest rate of change and the given graph has the least.

Envision Math Grade 8 Solutions for Functions and Modeling Relationships – Exercise 3.1

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 159 Exercise 1 Answer

A relation is said to be a function if it relates one value of its domain to one value of its range.

Also, is one input has only one output, the relation is a function.

Jesse plan is to sell 50 tickets but it will not fulfill the requirement of $500 as different amount of tickets have different values.

In case of Alexis plan, the target will be achieved if each person sells the tickets of $50 .

Alexis plan would be recommended to fulfill the requirement.

Envision Math Grade 8 Volume 1 Chapter 3 Exercise 3.1 Functions Solutions

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 159 Exercise 1 Answer

• A relation is said to be a function if it relates one value of its domain to one value of its range.
• Also, is one input has only one output, the relation is a function.
• Jesse plan is to sell 50 tickets per head which will get them approximately $400 from each person.
• In case of Alexis plan, a person should sell the tickets of $50 and they will be able to collect $500 from 10 persons.
• Plans are different as they have different strategies to collect the amount whereas the similarity is that they have to collect equal amount, i.e. $500 .

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 160 Exercise 1 Answer

• A relation is said to be a function if it relates one value of its domain to one value of its range.
• Also, is one input has only one output, the relation is a function.
• Different weights of the boxes have different cost of shipping ,i.e. the cost of shipping has unique values.
• Yes. There is a relation between weight of the box and the cost to ship the box.

Envision Math Grade 8 Exercise 3.1 Model Relationships Functions

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 160 Exercise 1 Answer

The given points are (4,24),(5,35),(8,24),(2,20),(9,27)

Find: complete arrow diagram and explain

The completed arrow diagram is:

Each side length has one line connected to it. So, area is a function of side length.

The required arrow diagram is:

Yes. The area of the brochure is a function of the side length.

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 161 Exercise 3 Answer

A relation is said to be a function if it relates one value of its domain to one value of its range.

Also, is one input has only one output, the relation is a function.

Each cost of parking has different timings of parking by which it can be determined that for how much time the vehicle was parked according to the amount paid.

Heather is correct because this relation is a function.

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 160 Exercise 1 Answer

A relation is said to be a function if it relates one value of its domain to one value of its range.

Also, is one input has only one output, the relation is a function.

If there are two outputs of the input 24, then it is not a function.

The given relation is not a function because one input has two output.

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 162 Exercise 2 Answer

Given

Use different representation of a relation to determine whether the relation is a function?

We can use diagrams and tables to determine whether relation is function.

When we use diagrams than we simply have to look if there are multiple arrows connected to the same output.

When, we use tables again we simply have to look if the given inputs always give different outputs or the relation is a not function.

We use Diagram and table representations of a relation to determine whether the relation is a function.

Functions And Modeling Relationships Grade 8 Exercise 3.1 Envision Math

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 162 Exercise 3 Answer

Given

The relation is always a function and function is always a relation?

A relation does not always have to be a function, but a function is always a relation.

When we have some relation we can have multiple inputs give out different outputs, but the functions always give different outputs for every single inputs.

A relation does not always a function, but a function is always a relation.

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 162 Exercise 5 Answer

Given

Inputs are 3,4,1,5,2

Outputs are 4,6,2,8,5

Find the relation is function or not?

We can see from the table each of the inputs corresponds to exactly one output. This means that given relation is a function.

This relation is a function.

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 162 Exercise 6 Answer

Given

Inputs are 3,4,1,5,2,6

Outputs are 16,25,9,36,4,1

Find the relation is function or not?

We can see from the table each of the inputs corresponds to exactly one output. This means that given relation is a function.

There is 6 different x- coordinates with 6 different corresponding y- coordinates.

This relation is a function. Because for every input exactly one output.

Envision Math Grade 8 Chapter 3 Exercise 3.1 Solutions

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 163 Exercise 7 Answer

Given

Inputs are 1,2,3,4,5

Outputs are 19,23,23,29,31

Find the relation is function or not?

Here we are going to show how to make an arrow diagram.
​
1 → 19

2 → 23

3 → 23

4 → 29

5 → 31
​
Note that we put these values into a diagrams and in the right diagram with outputs we are going to have only 1 value 23.

Arrow diagram:
​
1 → 19

2 → 23

3 → 23

4 → 29

5 → 31
​
Given

Inputs are 1,2,3,4,5

Outputs are 19,23,23,29,31

Find the relation is function or not?

Here we are going to show how to make an arrow diagram.
​
1 → 19

2 → 23

3 → 23

4 → 29

5 → 31
​
A relation is an input if each input corresponds to only input.

The input 1 only corresponds to 19, 2 only corresponds to 23, 3 only corresponds to 23, 4 only corresponds to 29, 5 only corresponds to 31.

Therefore, the relation is a function. Each input corresponds to only one output.

Note that two inputs have the same output but this has no effect on whether it is a function. Repeating outputs do not determine if relation is a function, only repeating inputs determine if it is a function.

The relation is a function since each input corresponds to only one output.

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 163 Exercise 8 Answer

Given

Inputs are -2,-7,-3,3,-9,-6

Outputs are 2,1,9,4,5,8

Find the relation is function or not?

Given relation is a function because there is exactly one input corresponding to one output.

The relation is a function because there is exactly one input corresponding to one output.

Envision Math 8th Grade Exercise 3.1 Step-By-Step Functions Solutions

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 163 Exercise 10 Answer

Given

Inputs are 0,5,10,15,20,25

Outputs are 15,20,50,80,100,100

Find the relation is function or not?

Given relation is not a function because there is two different inputs corresponding to same output.

The input 20 and 25 corresponds to the same output 100.

The relation is not a function .

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 163 Exercise 11 Answer

Given

Inputs are 3,4,5,6,7,8

Outputs are 726,759,749,792,804,835

Find the relation is function or not?

Given relation is a function because there is exactly one inputs corresponding to exactly one output.

The relation is a function .

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 164 Exercise 13 Answer

Given

Inputs are 3,7,15,16

Outputs are 6,14,6,14

Find the relation is function or not?

Here we are going to show how to make an arrow diagram.
​
3 → 6

7 → 14

15 → 6

16 → 14
​
Note that we put these values into a diagrams and in the right diagram with outputs we are going to have only one value 14 and 6.

Arrow diagram of P:
​
3 → 6

7 → 14

15 → 6

16 → 14
​
Given

Inputs are 6,6,14,14

Outputs are 7,16,3,15

Find the relation is function or not?

Here we are going to show how to make an arrow diagram.
​
6 → 7

6 → 16

14 → 3

14 → 15
​
Note that we put these values into a diagrams and in the right diagram with outputs we are going to have only 1 value 6 and 14.

Arrow diagram:
​
6 → 7

6 → 16

14 → 3

14 → 15

Given

Inputs are 6,6,14,14

Outputs are 7,16,3,15

Find the relation is function or not?

6 → 7         3 → 6

6 → 16       7 → 14

14 → 3       15 → 6

14 → 15     16 → 14

Neither of these two relations are functions because for a relation to be a function, each input must correspond to exactly one output.

Neither of two given relations are functions.

How To Solve Exercise 3.1 Functions In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 164 Exercise 14 Answer

Given

Inputs are 1,6,12,18

Outputs are 2,12,24,36

Find the relation is function or not?

Here we are going to show how to make an arrow diagram.
​
1 → 2

6 → 12

12 → 24

18 → 36
​
If we look at the ordered pairs, than we can simply see that there is exactly one input of number 12 and on the diagram we can see that he drew 2 lines from the number 12 in inputs. This means that the mostly likely swapped x-coordinate with y-coordinate in one of the ordered pairs.

He most likely swapped x-coordinate with y-coordinate in one of the ordered pairs.

Envision Math Grade 8 Chapter 3 Exercise 3.1 Practice Problems

Envision Math Grade 8 Volume 1 Chapter 3 Functions Model Relationships Exercise 3.1 Solutions Page 164 Exercise 15 Answer

Given

Inputs are 49,61,10,76,23

Outputs are 13,36,27,52,52

Find the relation is function or not?

When we have to write ordered pairs from the diagram than we simply write the inputs which are in the left diagram as x-coordinate and the corresponding outputs as y-coordinate.

(49,13),(61,36),(10,27),(76,52),(23,52)

Given relation is a function because for it to be a function each input must correspond to exactly one output.

When we have to write ordered pairs from the diagram than we simply write the inputs which are in the left diagram as x-coordinate and the corresponding outputs as y-coordinate.

(49,13),(61,36),(10,27),(76,52),(23,52)

Given relation is a function.

Use Functions To Model Relationships – Envision Math Grade 8 Volume 1 Chapter 3

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 1 Answer

Slope of a line is the measure of the steepness and direction of a line.

Slope can be calculated by dividing the change in y by the change in x.

The formula of slope is:

The slope is the ratio of the vertical change to the horizontal change of a line.

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 2 Answer

A function can be given in the form of the equation representing slope-intercept form.

The form of equation which can be give is: y = mx + b

Where, m is the slope and b is the intercept.

The relation , y = mx + b is a proportional relationship between x and y if the intercept is equals to zero.

The relationship that can be modeled by the equation y = mx is a proportional relationship.

Envision Math Grade 8 Chapter 3 Use Functions To Model Relationships Solutions

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 3 Answer

A function can be given in the form of the equation representing slope-intercept form.

The form of equation which can be give is: y = mx + b

Where, m is the slope and b is the intercept.

The value of b gives y-intercept which is the point at which the line intersects the y-axis of the graph.

The y-value at which a line of a graph crosses the y-axis is called the y-intercept.

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 4 Answer

The function is a relation between the set of input to the set of output.

A function can be given in the form of the equation representing slope-intercept form.

The form of linear equation which can be give is: y = mx + b

Where, m is the slope and b is the intercept.

An equation written in the form y = mx + b is called the linear equation.

Envision Math Grade 8 Chapter 3 Answers

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 5 Answer

The given points are: (2,2) and (3,0)

We need to find the slope and the y−intercept of a line that passes through these points.

The slope of line through the points (2,2)and (3,0) = −2

y-intercept of line through the points (2,2) and (3,0) = 6

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 6 Answer

The given points are: (1,5) and (4,10)

We need to find the slope and y−intercept of a line that passes through these points.

Slope of line through the points (1,5) and (4,10) = 1.67

y-intercept of line through the points (1,5) and (4,10) = 3.33

Use Functions To Model Relationships Grade 8 Envision Math Solutions

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 7 Answer

The given points are: (8,2) and (−8,6)

We need to find the slope and y−intercept of a line that passes through these points.

Slope of line through the points (8,2) and (−8,6) = −0.25

y-intercept of line through the points (8,2) and (−8,6) = 4

How To Solve Functions To Model Relationships Envision Math Grade 8

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 8 Answer

Given that, Jenna’s mother is shopping for energy drinks in 12-ounce bottles for Jenna’s soccer team. Store A sells a case of 18bottles for $10. Store B sells a case of 12 bottles for $6. We need to find which store sells the drinks for less. Also, we need to use the given graph to compare the unit costs of the drinks.

Finding the unit rate of store A, we get,

Finding the unit rate of store B, we get,

Plotting the given proportional relationships in the given graph now, we get,

The line for the proportional relationship of store A is red in color.

The line for the proportional relationship of store B is blue in color.

Here, the line of store B is lower than A.

This means that store B sells the drinks in a lesser price.

Store B sells the drinks for less.

Envision Math 8th Grade Functions And Relationships Exercises

Envision Math Grade 8 Volume 1 Chapter 3 Page 157 Exercise 9 Answer

We need to write the equation for the graph of the line shown.

For finding the y-intercept, the value of x = 0

Analyzing the graph for which value of y, the value of x = 0

Thus, the y-intercept is −6

Find two points on the graph to find the slope of the line.

The equation of the slope-intercept form be,

y = mx + b

Here, m is the slope and b is the y-intercept.

Thus, we get,

y = 4x − 6

The equation for the graph of the line shown is y = 4x − 6

Envision Math Grade 8 Chapter 3 Solution Guide

Envision Math Grade 8 Volume 1 Chapter 3 Page 158 Exercise 1 Answer

We need to find whether the given table, arrow diagram, graph, ordered pairs, and the equation is a function or not.

TABLE:

In the given table, the same inputs are having two different outputs.

Here, the value x = 2 corresponds to both y = 6,8

Thus, it is not a function.

ORDERED PAIRS:

In the given ordered pairs, each input is having unique outputs.

Thus, the relation is a function.

EQUATION:

Graphing the given equation, y = 3x − 12, we get,

The obtained graph is a straight line. Thus, it is a function.

ARROW DIAGRAM:
In the given diagram, each input corresponds to only one output.

Thus, it is a function.

GRAPH:

In the given graph, the value x corresponds to two y values.

Thus, it is not a function.

The given arrow diagram ordered pairs, and the equation is a function.

The given table and the graph are NOT a function.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions

Page 147 Question 1 Answer

We need to explain how we can analyze connections between linear equations and use them to solve problems.

Equations that consist of degree one are said to be linear equations.

Linear equations will always result in a straight line when plotted on the graph.

The highest degree of the variables present in the linear equations must be one.

A linear equation must have a constant in it.

Linear equations can be solved by doing arithmetical operations on both sides of the equation. This will not affect the balance of the equation.

It can also be solved graphically.

Some of the examples of linear equations are,

5x + 2y = 3

15x – 5 = 0

We can analyze connections between linear equations by solving them arithmetically or by graphically, and we can also use them to solve real-life problems.

Envision Math Grade 8 Volume 1 Chapter 2 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 147 Exercise 3 Answer

The slope intercept form of a line is y = mx + b where them is the slope of the line and the b is the y−intercept of the line.

Example:

If we look at the graph of given line we can see the equation y = −2x + 3.

The slope of the given line is −2 and that means that our graph of the line will be decreasing. The y− intercept is 3 which tells us where the line will cross the y−axis.

The slope intercept form of a line is y = mx + b. The variable m in the equation stands for the slope. The variable bin the equation stands for the y−intercept.

Page 147 Exercise 1 Answer

Given that, Paddleboats rent for a fee of $25, plus an additional $12 per hour. We need to write the equation, in y = mx + b form, represents the cost to rent a paddleboat for x hours. Also, we have to explain how you write the equation. Use vocabulary words in your explanation.

The equation of the line is of the form y=mx+b

Here, b is a constant.

x is the number of hours while y is the cost to rent a paddleboat.

Given that, the initial investment is $25

The additional cost is $12 per hour.

Thus, the equation will be

y = 12x + 25

The equation is y = 12x + 25. Here, y is the cost to rent a paddleboat where x is the number of hours.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 148 Exercise 1 Answer

The given equation is 2x + 6x = 1000

We need to solve the given equation and find the value of x

​
The value of x = 125

Page 148 Exercise 2 Answer

The given equation is \(2 \frac{1}{4} x+\frac{1}{2} x=44\)

We need to solve the given equation and find the value of x

The value of x = 16

Envision Math Grade 8 Analyze And Solve Linear Equations Chapter 2 Answers

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 148 Exercise 3 Answer

The given equation is −2.3x − 4.2x = −66.3

We need to solve the given equation and find the value of x

​
The value of x = 10.2

Page 148 Exercise 4 Answer

Given that, Javier bought a microwave for $105. The cost was 30% off the original price. We need to find the price of the microwave before the sale.

Let x be the price of the microwave before the sale.

The price of the microwave before the sale is $150

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 148 Exercise 3 Answer

The given equation is 9x − 5x + 18 = 2x + 34

We need to solve the given equation and find the value of x

The value of x = 8

Analyze And Solve Linear Equations Solutions Grade 8 Envision Math

Page 149 Exercise 1 Answer

The given equation is 4(x+4) + 2x = 52

We need to solve the given equation and find the value of x

​
The value of x = 6

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 149 Exercise 2 Answer

The given equation is 8(2x+3x+2) = −4x + 148

We need to solve the given equation and find the value of x

​
The value of x = 3

Page 149 Exercise 3 Answer

Given that, Justin bought a calculator and a binder that were both 15% off the original price. The original price of the binder was $6.20. Justin spent a total of $107.27. We need to find the original price of the calculator.

The price of the binder at which Justin bought is,

= \(\frac{527}{100}\)

= 5.27

The total price spent by Justin is,

5.27 + x = 107.27

x = 102

This x be the discounted price of the calculator.

Therefore, the calculator’s original price will be,

The original price of the calculator is $120

Envision Math Grade 8 Chapter 2 Solutions For Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 149 Exercise 1 Answer

The given equation is x + 5.5 + 8 = 5x − 13.5 − 4x

We need to solve the given equation and find the value of x

​
The equation has no solutions.

The given equation doesn’t have any solutions.

Envision Math Grade 8 Chapter 2 Practice Problems Solutions

Page 149 Exercise 2 Answer

The given equation is \(4\left(\frac{1}{2} x+3\right)=3 x+12-x\)

We need to solve the given equation and find the value of x

The given equation doesn’t have any solutions.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 149 Exercise 4 Answer

Given that, the weight of Abe’s dog can be found using the expression 2(x+3), where x is the number of weeks. The weight of Karen’s dog can be found using the expression 3(x+1), where x is the number of weeks. We need to determine when will the dogs ever be the same weight.

Equating both the expressions, we get,
​
​
The dogs be the same weight after 3 weeks.

Page 150 Exercise 2 Answer

Given that, A 16-ounce bottle of water from Store A costs $1.28. The cost in dollars, y, of a bottle of water from Store B is represented by the equation y = 0.07x, where x is the number of ounces. We need to find the cost per ounce of water at each store. Also, find which store’s bottle of water costs less per ounce.

Cost of one ounce of water at store A,

= \(\frac{1.28}{16}\)= 0.08 dollars per ounce

Cost of one ounce of water at store B,

y = 0.07x

y = 0.07(1)

y = 0.07 dollars per ounce

Therefore, store B’s bottle of water costs less per ounce.

Store B’s bottle of water costs less per ounce.

How To Solve Linear Equations In Envision Math Grade 8 Chapter 2

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 151 Exercise 2 Answer

Given that, A mixture of nuts contains 1 cup of walnuts for every 3 cups of peanuts.

We need to graph the line.

The linear equation formed from the given data is

y = 3x

Graphing the given equation, we get,

The graph is,

Page 152 Exercise 1 Answer

We need to graph the line with the equation \(y=\frac{1}{2} x-1\)

Finding two points to draw the line,

Plot both the points (0, -1) and (2, 0) on the graph and connect them together with the line.

The graph will be,

The graph of the equation is,

Envision Math 8th Grade Step-By-Step Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Solutions Page 153 Exercise 1 Answer

Given that, each block below shows an equation and a possible solution. We need to shade a path from START to FINISH. Also, follow the equations that are solved correctly. You can only move up, down, right, or left.

Substituting each value in its corresponding equation, we get,
​
x = 2 ⇒ 2x + 3 = 7

2(2) + 3 = 7

4 + 3 = 7

7 = 7

TRUE
​
y = −1 ⇒ 9(−1)−1 = −10

−10 = −10

TRUE
​
t = 2 ⇒ 5(2) + 1 = 9

11 ≠ 9

FALSE
​
x = −1 ⇒ −11(−1) + 12 = 1

23 ≠ 1

FALSE
​
Repeat the same in the second row, we get,
​
p = −7 ⇒ 19−4(−7) = 9

19 + 28 = 9

47 ≠ 9

FALSE

j = 60 ⇒ 30−60 = 90

−30 ≠ 90

FALSE

m = 7 ⇒ 14 + 3(7) = 35

35 = 35

TRUE

h = 4 ⇒ 6(4)−1 = 25

23 ≠ 25

FALSE
​
Repeat the same in the third row, we get,
​
t = 5 ⇒ 20(5)−1 = 95

99 ≠ 95

FALSE

q = 3 ⇒ 20−3 = 17

17 = 17

TRUE

w = −1 ⇒ −4(−1) + 7 = 11

11 = 11

TRUE

a = 2 ⇒ −2 + 15 = 13

13 = 13

TRUE
​
Repeat the same in the fourth row, we get,
​
y = 4 ⇒ 7(4) + 4 = 32

32 = 32

TRUE

y = 6 ⇒ 23 = 1 + 4(6)

23 ≠ 25

FALSE

r = −9 ⇒ −9(−9)−4 = −85

77 ≠ −85

FALSE

x = −25 ⇒ 100 − 4(−25) = 0

200 ≠ 0

FALSE
​
Repeat the same in the fifth row, we get,
​
b = −4 ⇒ −6(−4) + 27 = 3

51 ≠ 3

FALSE

FALSE

x = −1 ⇒ 47−2(−1) = 45

49 ≠ 45

FALSE

k = 6 ⇒ −12 + 9(6) = 42

42 = 42

TRUE
​
The correct ones are marked as “T” while the incorrect ones are marked as “F”.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9

Page 141 Exercise 1 Answer

Given

statement

To find/solve

Construct an argument to defend Xiu’s statement.

A y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. These points satisfy x = 0.

Xiu stated correctly that they passed the one-mile mark couple of minutes ago because they did not start from the sea level, but were already 2,080 ft above the sea level.

The starting height was 2,080 ft, so Xiu is correct.

The starting height was 2,080 ft, so Xiu is correct.

A y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. These points satisfy x=0.

Jon knew that the Mountain Tram is moving at 800 vertical ft/min and multiplied that by the minutes that are needed to reach the 1 mile point. We know that

1 mile is equal to 5,280 ft.

Now we get,

800 × 6.5 = 5200

He was correct about that part but forgot that they started at 2,080 ft above the sea level.

He forgot that they started at 2,080 ft above the sea level.

He forgot that they started at 2,080 ft above the sea level.

Page 141 Exercise 1 Answer

We need to find whether there is a proportional relationship between x and y.

Also, check whether the equation y = mx represents the path of the tram or not.

We can partly use given equation y = mx because the tram starts moving from 2,080ft above the sea level and that must be added to the equation.

So now the new equation would look something like y = mx + b

We can use it but have to add the starting value to the equation.

Thus, there won’t be any proportional relationships that exists.

This is because the value of y depends on the value of both x and b

We can use the equation y = mx but we have to add the starting value to the equation. i.e., y= mx + b

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.9 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 142 Exercise 1 Answer

Given

To find/solve

Write a linear equation in slope-intercept form.

First, we have to look at the y-intercept to find out from which value has the graph started.

The y-intercept is 2

Secondly, we have to find the slope of the given line. To find the slope we are going to use two points on the graph that we can read which are (4,5) and (8,8).

Now the equation is y = 0.75x + 2.

Hence, the y-intercept is 2

and the slope is 0.75

The equation is y = 0.75x + 2.

Envision Math Grade 8 Chapter 2 Exercise 2.9 Solutions

Page 143 Exercise 2 Answer

Given

To find/solve

What is an equation for the line shown.

First, we have to find the y-intercept of the given line.

The y-intercept is 2.

Secondly, we have to find the slope of the given line. We have to use two points which are (4,0) and (0,2)

The equation is y = -0.5x + 2.

The equation is y = -0.5x + 2.

Given

To find/solve

Graph the line.

When we look at the equation of given line we can see that it has -5. This means that the y-intercept is -5.

The slope of given line is 1/3.

We have to find the y-intercept and the slope first, and simply graph the line after that.

We have to find the y-intercept and the slope first, and simply graph the line after that.

Envision Mathb8th Grade Exercise 2.9 Step-By-Step Linear Equation Solutions

Envision Math 8th Grade Exercise 2.9 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 144 Exercise 1 Answer

Given

Statement

To find/solve

Equation of a line.

A y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. These points satisfy x = 0.

The equation for a line of a non proportional relationship is y = mx + b

where m is the slope and b is the y-intercept.

The equation is y = mx + b

The equation is y = mx + b

Envision Math Grade 8 Exercise 2.9 Solution Guide

Page 144 Exercise 4 Answer

Given

To find/solve

Which student is correct.

A y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. These points satisfy x=0.

First we look at the graph to see what is the y-intercept.

The y- intercept is 5.

Now that we have found the intercept we can see that the line is decreasing which means that the slope is negative.

George is correct.

Hence, we found out that George is correct.

How To Solve Exercise 2.9 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 144 Exercise 5 Answer

Given

To find/solve

Draw a line to show the relationship between the number of hours the tent is rented, x, and the total cost of the tent,y

Since we know that the set-up fee is $100 then we know that this will be our y-intercept.

The cost per hour is additional $500. This is the slope of given equation. Now we can write whole equation.

y = 500x + 100

Now the graph is obtained by adding 100 to the variable then the graph of given equation will be translated 100 units up on the y-axis.

We have to find the equation of given line which is y = 500x + 100 and after that simply graph that line.

We have to find the equation of given line which is y = 500x + 100 and after that simply graph that line.

Given

To find/solve

What is the equation of the line in slope-intercept form?

To find the equation first we have to see the data that we are given in the task. Since it states that the cost of the tent is $500 per hour, that means that this will be our variable.

The set-up fee is in for every tent and it is a one-time pay per tent. This means that we have to add the $100 to the variable.

Now we know how our equation will look like

y = 500x + 100

The equation is y = 500x + 100.

The equation is y = 500x + 100.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 145 Exercise 6 Answer

Given

We need to find the y-intercept of the given equation y = 2x + 4. Also, find another point using the slope of the line and daw a line to connect the two points.

If we look at the equation we can see that we have added 4 to the variable and that means that the y-intercept will be 4. The point at which the line will cross y-axis is (0,4).

The slope is positive and that means that the graph will be increasing from left to right.

We will simply start at the y-intercept and move up to 2 points and then we will move 1 point to the right.

Draw a line through points (0,4) and (1,6). This is the line of the given equation.

Graph the given equation and draw a line to connect the obtained two points.

The y -intercept is 4, which means the line crosses the y -axis at the point (0,4)

The slope of the line is positive, so it goes increasing from left to right.Start at the y-intercept. Move up 2units, and then move right 1unit.

You are now at the point (1,6)

Graphing the given equation and plotting the points, we get,

Page 145 Exercise 7 Answer

Given

To find/solve

Write an equation.

We have to use two points from the graph that are visible and one of them will be the y-intercept (0,-3)

The other point we are going to use is (2,-4).

Now to find the slope.

The equation is y = -0.5x – 3

The equation is y = -0.5x – 3

Envision Math Exercise 2.9 Linear Equations Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 145 Exercise 8 Answer

Given

To find/solve

Write an equation.

We have to use two points from the graph that are visible and one of them will be the y-intercept (0,4)

The other point we are going to use is (-1,1).

Now to find the slope.

The equation is y = 3x + 4

The equation is y = 3x + 4

Page 145 Exercise 9 Answer

Given

To find/solve

Write an equation.

If we look at the kayak rentals in the task we can see that the cost per hour is $12, and that will be our variable.

As for the $6 deposit, that will happen only once every time someone rents a Kayak.

Now the equation is y = 12x + 6

The equation is y = 12x + 6.

Envision Math Grade 8 Exercise 2.9 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 145 Exercise 10 Answer

Given

To find/solve

Graph the equation y = 3x − 5.

In order to graph the given equation, we have to know the slope of the given equation, and they-intercept.

Since we know the y-intercept. We got the one point of the graph which is 0,−5.

Then if we need another equation to draw the graph when the y-coordinate is 0.

0 = 3x − 5

3x = 5

The graph becomes,

The two points are (0,−5)and (5/3,0).

The two points are(0,−5) and (5/3,0).

The graph is,

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 146 Exercise 11 Answer

Given

To find/solve

What is the correct equation.

Since we know that she had $25 in her bank account at start that means that the y-intercept is in point (0,25). Then the y-intercept is 25

Then she spends $5 every day this means the variable is subtracted by -5

Then the equation is y = −5x + 25.

Then the equation is y = −5x + 25.

Given

To find/solve

What mistake might Amy have made.

Amy has added only $5 to the variable and that would mean that she had $5 in her account on the start.

This means that she must have used the positive value of slope for the y-intercept as well.

She might have used the positive value of slope as y-intercept.

She might have used the positive value of slope as y-intercept.

Page 146 Exercise 12 Answer

Given

Graph

To find/solve

Write an equation for the line in slope intercept form.

From the graph we get the slope and y-intercept to write the equation.

The y-intercept is 12.25 and then means that we have to add that value to the variable.

To find the slope,

We know that each ticket cost $21, then it will be our slope.

The equation is y = 21x + 12.25

The equation is y = 21x + 12.25

Given

To find/solve

write an equation.

We can write the equation by reading the part where they show us the price of each ticket and the processing fee for each transaction.

As we can see the processing fee will be paid each transaction once and the price of each ticket will be $21, which means that we can order multiple that would give us the equation.

y = 21x + 12.25 which is the same as in the first part of the task.

We have the picture in the task which shows us the price of each ticket and the processing fee for each transaction.

We have the picture in the task which shows us the price of each ticket and the processing fee for each transaction and the equation is y = 21x + 12.25

Given

Graph

To find/solve

Is this graph a good representation of the situation.

Give graph would be a good representation of the situation if no one would buy more than 4 tickets.

Since the line of the graph is shown to the number of 4 tickets, we do not know from the graph how much will we have to pay for more than 4 tickets.

The graph is a good representation if we no one buys more than 4 tickets.

The graph is a good representation if we no one buys more than 4 tickets.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.9 Page 146 Exercise 13 Answer

Given

Graph the equation \(y=\frac{2}{5} x-1\)

To find/solve

What should you do first to graph the equation.

A y-intercept or vertical intercept is a point where the graph of a function or relation intersects they-axis of the coordinate system. These points satisfy x = 0.

When we have to graph some equation, then the first thing we want to do is to mark the y-intercept. This will show us where the graph of the line will begin.

Plot a point at the y-intercept.

Plot a point at the y-intercept.

Page 146 Exercise 14 Answer

Given

To find/solve

Write an equation for the line in slope-intercept form.

First, we want to find the y-intercept of the given line. As we can see from the graph the point of the y-intercept is (0,8).

This means that the y-intercept is 8.

Secondly, we want to find the slope of the given line. To do this we have to use two points from the graph that we can read. The first point is going to be the y-intercept and the second will be the x-intercept, which is (4,0).

The equation of the line is y = -2x + 8

The equation of the line is y = -2x + 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8

Page 135 Exercise 1 Answer

To find the age of horse in human years.

We find that by first dividing the horse age with 5 and after that multiplying the result by 2

10 * 2 = 20

The horse is 20 years old in human years.

So now we have to subtract 8 years from the years of the horse and we will get,

20 − 8 = 12

Hence, the horse was 12 human years old when Alex was born.

Page 135 Exercise 1 Answer

To find the age of cat in human years.

To find out how old is the cat in human years.

We have to divide the cat years with 8 and after that multiply the result with 2.

8 * 2 = 16

Hence, the cat is 16 human years old.

Page 136 Question 1 Answer

The y−intercept is the value of y−coordinate in point at which the line crosses the y−axis.

When the line crosses through the origin, the y−intercept is 0.

When the line crosses above the origin, the y−intercept is positive.

When the line crosses below the origin, the y−intercept is negative.

The y−intercept is the value of y−coordinate in point at which the line crosses the y−axis.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.8 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 136 Exercise 1 Answer

The given table is,

We need to find the pattern that we can see in the costs of different numbers of games given.

From the given table, the cost of one game is $4

The cost of three games is $8.

The difference between the cost and the number of games will be,
​
(3−1)games = (8−4)dollars

2games = 4dollars

1game = 2dollars
​
Thus, for the increase in one game, the cost increases by $2.

This can be represented by the equation,

(1+n)games = (4+2(n))dollars

Thus for 10 games, the cost will be,
​
(1+n)games = (4+2(n))dollars

(1+9)games = (4+2(9))dollars

10games = (4+18)dollars

10games = 22dollars
​
Thus, a certain pattern is observed.

The pattern which we observe in the costs of different numbers of games is that after every one game, there is $2 increase in the price.

Page 136 Exercise 1 Answer

We have to find the slope of the given line.

The cost of each game is 1.55

The y−intercept has to be read from the graph but it is not clear.

We are going to say that the y−intercept is 3.5.

Hence, the y−intercept is 3.5.

Page 137 Exercise 2 Answer

We can see that the y-intercept is 2 because the value of y-coordinate is 2 When the line crosses the y-axis.

We can see that the y-intercept is -0.5

y-intercept for the first graph is 2 and for the second graph is -0.5.

Envision Math Grade 8 Exercise 2.8 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 136 Exercise 1 Answer

We need to explain why does the y-intercept represent the cost to rent bowling shoes in these examples.

The y−intercept can be found when the value of x = 0

This means that the y−intercept is the value when there are no games.

That is, the number of games played is zero.

The y−intercept of the line is obtained to be $2.

This means that the cost to rent bowling shoes is $2.

At the y−intercept, the number of games played is zero. This is why the y−intercept represents the cost to rent bowling shoes.

Page 138 Exercise 1 Answer

The y−intercept is the value of y−coordinate in point at which the line crosses they−axis.

When the line crosses through the origin, the y−intercept is0

When the line crosses above the origin, the y−intercept is positive.

When the line crosses below the origin, the y−intercept is negative.

The y-intercept is the value of y-coordinate in point at which the line crosses the y−axis.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 138 Exercise 2 Answer

Since we know that the y−intercept is always 0 for the proportional relationships and the Bradyn’s graph passes through the origin which is point(0,0), that means that the both lines has y−intercept 0.

Hence, the both y−intercepts are 0.

Page 138 Exercise 3 Answer

When the line crosses above the origin, the y−intercept is positive.

When the line crosses below the origin, the y−intercept is negative.

When the line crosses above the origin, the y-intercept is positive.

When the line crosses below the origin, the y-intercept is negative.

Analyze And Solve Linear Equations Grade 8 Exercise 2.8 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 138 Exercise 5 Answer

The y−intercept on the given graph is 1.8

This means that the movie is 1.8 hours long.

Hence, the y−intercept on the given graph is 1.8.

Page 139 Exercise 6 Answer

The y−intercept is the point where the graph crosses the y−axis.

This means that we need to find the point which has x−coordinate is 0

The line crosses the y−axis at the point(0,7).

So, the y−intercept is 7.

Hence, the line crosses the y−axis at the point(0,7). So, the y−intercept is 7.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 139 Exercise 7 Answer

The y−intercept is the point where the graph crosses the y−axis.

This means that we need to find the point which has x−coordinate is 0

The line crosses the y−axis at the point (0,−4).

So, the y−intercept is −4.

Hence, the y−intercept is −4.

Page 139 Exercise 8 Answer

We can see from the graph the line passes through the origin.

This means that the graph passes through the point (0,0) and that means that the y-intercept is 0.

Hence, the y-intercept is 0.

Page 139 Exercise 9 Answer

We have to find the value of y−coordinate in the point at which the line crosses the y−axis.

We can see from the graph this point is(0,80). So,the y−intercept is 80

The height of the air balloon when it began to descent was 80 meters.

Hence, the height of the air balloon was 80 meters.

Envision Math Grade 8 Chapter 2 Exercise 2.8 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 139 Exercise 10 Answer

We can see from the graph the line crosses through the origin. So the y−intercept is 0.

When the y-intercept is for the given function it means that there was no gas in the canister.

Hence, the y−intercept is 0.

Page 140 Exercise 11 Answer

The y−intercept is the point where the graph crosses the y−axis.

This means that we need to find the point which has x−coordinate is 0

The line crosses the y−axis at the point(0,4).

So, the y−intercept is 4.

Hence, the y−intercept is 4.

The y−intercept tells us what the temperature was when it was sunrise.

The y−intercept tells us the temperature at sunrise.

Envision Math 8th Grade Exercise 2.8 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.8 Page 140 Exercise 12 Answer

Given

To find/solve

a. Explain your friend’s possible error.

A y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. These points satisfy x = 0.

On the given graph we can see that the y-intercept is -4. The student had switched the x-intercept and y-intercept.

The student has switched x and y intercepts.

The student has switched x and y intercepts.

To find/solve

Draw a line on the graph that does represent a y-intercept of 3.

On the given graph we can see the line that has y-intercept is 3.

Draw a line that crosses the y-axis at y = 3.

Draw a line that crosses the y-axis at y = 3.

How To Solve Exercise 2.8 Linear Equations In Envision Math Grade 8

Page 140 Exercise 13 Answer

Given

Graph

To find/solve

What is the y-intercept.

We simply have to look closely at each graph and find the point at which the line passes through the y-axis.

As we can see from the first graph the y-intercept is at point (0,-3) which means that the y-intercept of given graph is -3.

As for the second graph we can see that the point at which he line crosses the y-axis is (0,3). This means that the y-intercept for the second graph is 3.

The y-intercept of first graph is -3 and of the second graph is 3.

The y-intercept of first graph is -3 and of the second graph is 3.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7

Page 129 Exercise 1 Answer

It is given that A group of college students developed a solar-powered car and entered it in a race.

The car travels at a constant speed of 100 meters per 4 seconds.

We have to graphically represent the distance over time.

We know that the students have developed a solar powered car.

The speed of the car is constant which is 100 meters in 4 seconds.

We can graphically represent the same as below:

On x-axis we will mark the time, while distance on y-axis.

The given graph is the representation of distance over time.

It is given that A group of college students developed a solar-powered car and entered it in a race.

The car travels at a constant speed of 100 meters per 4 seconds.

We have to find the expression which can show the distance the car will travel over time.

We know that the students have developed a solar powered car.

The speed of the car is constant which is 100 meters in 4 seconds.

The expression for the same can be evaluated, but for which first we need to find the unit rate.

Thus, we divide the distance with time and get unit rate as

Therefore, the expression will be y = 25x.

The expression which can show the distance the car will travel over time will be y = 25x

It is given that A group of college students developed a solar-powered car and entered it in a race.

The car travels at a constant speed of 100 meters per 4 seconds.

We have to compare the representation and the expression of distance over time, and tell which shows clearly.

We know that the students have developed a solar powered car.

The speed of the car is constant which is 100 meters in 4 seconds.

The representation of the distance over time is

The expression for the same can be evaluated, but for which first we need to find the unit rate.

Thus, we divide the distance with time and get unit rate as

Therefore, the expression will be 25x.

On comparing the both, we can observe that the expression will provide much clear results ad compared to representation.

This is because representation would not be able to give clear result when the time period is longer.

On comparing the both, we can observe that the expression y = 25x will provide much clear results ad compared to representation.

This is because representation would not be able to give clear result when the time period is longer.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.7 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 130 Question 1 Answer

The table given shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.

We have to find the quantities to find the unit rate in order to compare the proportional relationship.

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as proportional relationship.

We are given the data regarding the relationship between the number of miles Manuel walks and the amount of money he will raise.

If we have to compare the proportional relationships, we will use the quantities Money Raised and the Miles Walked.

On doing so, we can find the amount of money earned for each mile which is unit rate.

The quantities that we should use to find the unit rate are Money Raised and the Miles Walked so that the proportional relationships can be compared.

Page 130 Exercise 1 Answer

We have to build a fence for which the length and cost is given.

We have to find the relation between the length of the fence and the cost.

We know that the students in Meg’s class are building a fence around the class garden.

For fencing and costing, the length of fence and the cost for each feet is to be known.

The length of fencing and cost both factors are related to each other.

This is because, to calculate the complete costing of the fencing work, we will have to multiply the total length of the fence suppose in feets and the cost required to build fence of 1 feet, which is its rate.

The length of fencing and cost both factors are related to each other as both are needed to find total costing.

Envision Math Grade 8 Exercise 2.7 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 130 Exercise 1 Answer

The graph of distance per gallon is given.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The equation for line involving slope is, y = mx.

Thus, the equation for the given line will be y = 20x.

The relationship given will tell us the amount of gasoline used for a certain distance.

The slope of the line is obtained as 20 and the equation for line is y = 20x.

Page 131 Exercise 2 Answer

The graph of a line is given.

We have to find the equation of the line.

The general equation of a line is y = mx, where m is the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

On substituting the value of slope in equation of line we get,

y = 0.4x

The equation of the line is obtained as y = 0.4x.

The graph of a line is given.

We have to find the equation of the line.

The general equation of a line is y = mx, where m is the slope of the line.

Here the equation given is y=−3x, so the slope is −3.

We consider the first point as (0,0).

For the second point, we take as x = 5 and then y = −3x = −3(5) = −15

So, the second point will be (5,−15)

Using, these two points we will draw the graph as below:

The graph of the line is obtained as

Analyze And Solve Linear Equations Grade 8 Exercise 2.7 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 130 Exercise 1 Answer

We need to explain how to do the equations y = mx and y = kx can be compared.

The equation y = mx represents that the relationship is proportional to each other.

That is the equation represents a linear equation.

Here, m is the slope of the line.

The equation y = kx is compared with y = mx

Thus, it denotes that,

k = m

This means that the slope of the line is k

This refers that the rate of change is k

When we compare both equations, the slope or the rate of change of the equation is m = k

Page 131 Exercise 1 Answer

We need to generalize the concept that the lines that slant upward from left to right have positive slopes. Lines that slant downward from left to right have negative slopes.

We know that when we plot linear equations, the graph will be of a straight line.

The straight line may go upwards or downwards depends upon the slope or its rate of change.

If the slope or the rate of change of the equation is negative, then the lines will slant downwards from left to right.

This will result in a negative slope.

If the slope or the rate of change of the equation is positive, then the lines will slant upwards from left to right.

This will result in a positive slope.

If the slope or the rate of change of the equation is negative, then the lines will slant downwards from left to right.

If the slope or the rate of change of the equation is positive, then the lines will slant upwards from left to right.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 132 Exercise 1 Answer

Any equation of proportional relationship looks like y = mx where “m” is the slope.

This means that the slope will show us how fast will the line increase or decrease and tells us the unit rate.

Any equation of proportional relationship looks like y = mx where “m” is the slope.

This means that the slope will show us how fast will the line increase or decrease and tells us the unit rate.

Page 132 Exercise 2 Answer

The graphs of lines that are in the form like y = mx always pass through the origin.

The graphs of lines that are in the form like y = mx always pass through the origin. They will only differ in the rate of increasing or decreasing of the line.

Page 132 Exercise 3 Answer

Given

To find the slope of the line using this (2,25)(4,50) points.

Hence, the equation is y = 12.5x

Page 132 Exercise 4 Answer

Given:

To find the slope and the constant of the proportionality we simply have to use two points that we can read from the graph.

The slope and the constant of proportionality are both 30.

Given:

To find the slope and the constant of the proportionality we simply have to use two points that we can read from the graph.

The graphs of the straight lines have equation that is equivalent to So, the equation is y = 30x

Therefore, the equation of the line is y = 30x

Envision Math Grade 8 Chapter 2 Exercise 2.7 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 132 Exercise 5 Answer

Given:

\(y=-\frac{1}{2} x\) To solve the graph equation

We are going to use two points that we can get from equation and through those two points we simply have to draw a straight line.

We are going to find the y when x = 0 and x = −2

y=\(-\frac{1}{2} * 0\)

y = 0

y=\(-\frac{1}{2} *-2\)

y = 1

The two points are (0,0) and (-2,1)

The graph of the line is

Page 133 Exercise 6 Answer

To find the equation of the line

We are going to use two points which are (4, 280) and (2, 140)

=\(\frac{140}{2}\)

= 70

The slope of the line is 70.

The equation of the line is y = 70x.

The heart’s resting heart rate is 70 beats each minute.

The heart’s resting heart rate is 70 beats each minute.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 133 Exercise 7 Answer

We can use two points from the graph which are (3, 0.75) and (4, 1)

=\(\frac{0.25}{1}\)

=\(\frac{1}{4}\)

The slope of the line is \(\frac{1}{4}\)

The equation of the given line is equivalent to y = mx

Hence, the equation of the line is y = \(\frac{1}{4}\)x.

Page 133 Exercise 8 Answer

Given

y = −x

Since we have minus sign before the x−that means that our line will be decreasing and the line that he drew is increasing.

He forgot to reflect given line across x−axis

The right graph is

No, the graph is wrong.

The correct graph is

Envision Math 8th Grade Exercise 2.7 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 133 Exercise 9 Answer

Given

We can use two points from the graph which are (2,24) and (4,48)

​
\(m=\frac{y_2-y_1}{x_2-x_1}\)

=\(\frac{24}{2}\)

= 12

The slope of the line is 12.

Given

If an equation is equivalent to y = mx then the equation represents a proportional relationship.

The graph of a proportional relationship always goes through the point(0,0) and it will always be a straight line

The graph of a proportional relationship always goes through the point(0,0) and it will always be a straight line.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 134 Exercise 10 Answer

Given

y = −5x

We are going to use the points which are x = 0 and x = −1

​y = −5x

y = −5(0) = 0

y = −5(−1) = 5
​
The two points are(0,0) and (−1,5).

To graph the line is

Page 134 Exercise 11 Answer

Given

We are going to use the points which are x = 0 and x = -5

= 0

= -3

The two points are (0,0) and (-5, -3).

To graph the line is

How To Solve Exercise 2.7 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.7 Page 134 Exercise 12 Answer

If they are giving out a 70% off the price of the ticket that simply means that we pay 30%of the original amount.

So the equation is y = 0.3x.

Hence, the equation of the given situation is y = 0.3x

Given

y = 0.3x From the part (a)

We are going to find will have x = 0 and x = 5.
​
y = 0.3x

y = 0.3(0)

= 0

y = 0.3(5)

= 1.5
​
The two points are (0,0) and (5,1.5).

Now as we know the line can only be in the quadrant I because the price of the ticket cannot be negative.

The price of the ticket cannot be negative

Envision Math Grade 8 Exercise 2.7 Practice Problems

Page 134 Exercise 13 Answer

Given

We can use two points from the graph which are (2,94) and (4,188)

The equation of the given line is equivalent to y = mx

The equation of the line is y = 47x.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6

Page 123 Exercise 1 Answer

We are given that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

We have to find that how much Rashida will earn refereeing soccer games in this fall.

We know that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

In order to calculate the money earned by Rashida by refereeing soccer games in this fall, we will first find the money she gets for 1 game, which will be evaluated when we divide the money earned by her by the number of games.

When she is the referee for 5 games,

Thus, Rashida earns $19.7 for refereeing one game.

In this fall she was the referee for 14 games, so she earns

14 × 19.7 = 275.8

Therefore, she earns $275.8 for 14 games.

Rashida will earn $275.8 for refereeing 14 soccer games this fall.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.6 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 123 Exercise 1 Answer

We are given that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

We have to find the relation between the number of games and her earnings.

We know that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

In order to calculate the money earned by Rashida by refereeing soccer games in this fall, we will first find the money she gets for 1 game, which will be evaluated when we divide the money earned by her by the number of games.

As Rashida gets her earnings from the game in which she is a referee, there is a relation between the number of games for which she works to her earnings.

Earning and number of games are related, as the earning can be calculated based on the rate and number of game in which she is a referee.

Envision Math Grade 8 Exercise 2.6 Analyze And Solve Linear Equations

Page 123 Exercise 1 Answer

We are given that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

We have to find the change in her earnings if she was paid on basis of per hour.

We know that Rashida earns money as a soccer referee for her town’s under- 10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.

She is paid on the basis of the number of games in which she is a referee.

In case, she is paid on the basis of hours she work, it is necessary to know that for how many hours does she work as a referee.

Also, the amount to be paid to be working for one hour is to be known.

Thus, on basis of hours, her earnings will be calculated where number of hours and pay per hour will be multiplied.

Rashida’s earnings will change if she was paid by hour and not by game, which completely depends on the number of hours she has worked.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 124 Question 1 Answer

We have to define the term slope.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Slope is the change in y divided by the change in x.

Page 124 Exercise 1 Answer

It is given that Jack graphs how far he plans to bike over a 3-day charity ride.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the line is obtained as 30.

Analyze And Solve Linear Equations Grade 8 Exercise 2.6 Envision Math

Page 125 Exercise 2 Answer

It is given that The graph shows the proportions of red and blue food coloring that Taylor mixes to make purple frosting.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope implies that to get the purple food colour, for every 5 blue drops we need to add 7 red drops.

The slope of the line is obtained as \(\frac{7}{5}\) which means that for every 5 blue drops we need to add 7 red drops.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 124 Exercise 1 Answer

It is given that Jack graphs how far he plans to bike over a 3-day charity ride.

We have to find the slope of the line.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

The constant of proportionality is the ratio of vertical distance to the horizontal distance.

The slope of a line is the same as the constant of proportionality.

There is no difference in them at all.

Unit Rate is the rate in which the second quantity is compared to the first quantity.

Whereas, the slope is the unit rate because in it, the second quantity or changes in y is compared to the first quantity which is change in x.

The slope of a line, unit rate and constant of proportionality all are the same.

Page 125 Exercise 1 Answer

We have to tell the relation among coordinates when the slope is negative.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Therefore, Slope is the change in y divided by the change in x.

When the slope is obtained as a negative value, there is decreasing or descending nature of quantities observed.

Negative slope simply means that the two variables are related negatively.

This means that when x increases, the value of y decreases and similarly, when x decreases, value of y increases.

Negative slope implies that the two variable or coordinates are negatively related to each other.

This means that when x increases, the value of y decreases and similarly, when x decreases, value of y increases.

Envision Math Grade 8 Chapter 2 Exercise 2.6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 126 Exercise 1 Answer

We have to define the term slope.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Slope is the change in y divided by the change in x.

Page 126 Exercise 2 Answer

We have to define slope and unit rate and find their relation.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

Unit Rate is the rate in which the second quantity is compared to the first quantity.

Whereas, the slope is the unit rate because in it, the second quantity or change in y is compared to the first quantity which is change in x.

The slope of a line and unit rate both are the same.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 126 Exercise 3 Answer

We have to define the term slope.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

The ratio of any two points located along a straight line is always constant.

As we know slope is nothing but the ratio.

Thus, the slope of a straight line among any two points is always constant or the same.

The slope of a straight line among any two points is always constant or the same, because the the ratio of any two points located along a straight line is always constant.

Page 126 Exercise 4 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the given line is obtained as 3.

Envision Math 8th Grade Exercise 2.6 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 126 Exercise 5 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

In the given problem situation, the dimensions of the model airplane as the ratio of centimetres to feet is given.

As the slope obtained is 5/3, it denotes that 5cm of dimension, will be equivalent to 3 feet of the dimension.

The slope obtained is 5/3, it denotes that 5 cm of dimension, will be equivalent to 3 feet of the dimension.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 127 Exercise 7 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the given line is obtained as 5.

Page 127 Exercise 8 Answer

We have to find the slope of the line passing through the given points (0,0) and (2,4).

The given graph tells us about the number of soda bottles which a machine makes over the given time.

In order to find, the number of bottles made in one minute, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The slope of the line that passes through the points (0,0) and (2,4) is obtained as 2.

How To Solve Exercise 2.6 Linear Equations In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 127 Exercise 9 Answer

We have to find the slope of the line passing through the given points (2.1,-4.2) and (2.5,-5).

The given graph tells us about the number of soda bottles which a machine makes over the given time.

In order to find, the number of bottles made in one minute, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The slope of the line that passes through the points (2.1,-4.2) and (2.5,-5) is obtained as -2.

Page 128 Exercise 11 Answer

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The slope of the given line is obtained as 10.

We have to find the slope of line on the given graph.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

In this problem situation, the slope obtained tells us that how many calories Natalia can burn in one minute.

The slope of the given line is obtained as 10, which tells us the amount of calories burned in one minute.

Envision Math Grade 8 Exercise 2.6 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 128 Exercise 12 Answer

We have to find the speed of the car from the graph given.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

We have to evaluate the speed of the car, for which we will consider the point (1,64) which is on the line.

As we know that if we divide the y-coordinate with the x-coordinate, we get the unit rate.

The speed of the car is obtained from the point as

The speed of the car is obtained as 64miles/hr

We have to identify the error that Anna made.

The given graph tells us about the speed of the car which is the ratio of distance given in miles to the time which is in hours.

Anna took Time on the x-axis and Distance over the y-axis, which is not appropriate and hence the error he made.

He must take Distance on the x-axis while Time on the y-axis.

Anna took Time on the x-axis and Distance over the y-axis, which is the error he made.

Page 128 Exercise 13 Answer

We have to find the slope of the line passing through the given points (0,0) and (2,4).

The given data tells us that the water level rises 11 centimetres every 5 minutes, which means the slope is 11/5.

In order to find the slope, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The value of y is obtained as 22.

Envision Math Exercise 2.6 Linear Equations Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 2 Analyze And Solve Linear Equations Exercise 2.6 Page 128 Exercise 14 Answer

We have to find the slope of the line passing through the given points (15,21) and (25,35).

In order to find the slope, we will have to divide the difference between the y coordinates to the difference in c-coordinates, which is nothing but slope.

The slope of the line that passes through the points (15,21) and (25,35) is obtained as 1.4.

We have to find the slope of the line passing through the given points (15,21) and (25,35).

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as proportional relationship.

We know that the line would definitely pass through the origin.

As the line in graph A does contradicts the statement, hence it is wrong.

The points we have are (15,21) and (25,35).

From the x and y coordinates of both the points, we can observe that the y-coordinate is greater than the x-coordinate.

This is seen in the graph B and not in graph C.

Thus, graph B is correct.

The graph B represents the given relationship between the two points.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5

Page 117 Exercise 1 Answer

Given

Meili going to pick the apple and between the apples.

Which orchard should mei li choose?

We simply going to solve each of given equation and find value for each.

20x =7.25

Divide both side of the equation by 20.

x ≈ 0.36

Price per lb for annie’s apple orchard is about $0.36

12x = 5

Divide both sides of the equation by 12

x ≈ 0.42

Now we can see that price per lb for franklin’s fruit orchard is about x ≈ 0.42

We simply compare values for first and second apple orchard to see which is cheaper.

0.36 < 0.42

Annie’s apple orchard is cheaper than franklin’s fruit orchard and that is why mei li should choose annie’s apple orchard.

She should pick annie’s apple orchard.

Envision Math Grade 8 Volume 1 Chapter 2 Exercise 2.5 Linear Equations Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 117 Exercise 1 Answer

We need to explain what information provided can be used to support the answer.

In Annie’s Apple Orchard, 20 lb costs $7.25

In Franklin’s fruit Orchard, 12 lb costs $5.00

The unit rate of each will be,

For Annie’s,

For Franklin’s,

Thus, Meili choose Franklin’s fruit Orchard since it costs less than Annie’s.

The information provided regarding the weight of the apple and its costs can be used to support my answer.

Page 117 Exercise 1 Answer

Given

Meili going to pick the apple and between the apples.

Which orchard should mei li choose?

We simply found out what is the price per one lb of apples. After we found that, we simply had to compare the results, the one that is cheaper is obviously the one she should pick.

We simply found out what is the price per one lb of apples. After we found that, we simply had to compare the results, the one that is cheaper is obviously the one she should pick.

Envision Math Grade 8 Exercise 2.5 Analyze And Solve Linear Equations

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 118 Question 1 Answer

Given

How can compare relationship proportional in different ways?

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.

For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.

For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Page 118 Exercise 1 Answer

Given

The equation is y = 2.5x

Who makes birds at a faster rate?

As we can see from the graph, Marlo makes 2 origami birds in 10 minutes, and we simply have to make an equation from this and calculate how much he needs to make 1 bird.

2y = 10x

Divide both side of the equation by 2.

y = 5x

This means that josh makes twice as many origami birds as Marlo makes.

Josh makes them faster.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 118 Exercise 1 Answer

Given

The equation is y = 2.5x

How do you lines compare.?

As we can see from the graph, marlo makes 2 origami birds in 10 minutes, and we simply have to make an equation from this and calculate how much he needs to make 1 bird.

This means that josh makes twice as many origami birds as marlo makes.

Josh makes them faster.

Analyze And Solve Linear Equations Grade 8 Exercise 2.5 Envision Math

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5

Page 120 Exercise 1 Answer

Given

How can compare relationship proportional in different ways?

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.

For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Proportional relationships can be represented by tables, graphs and equations.

We can find the unit rate for each relation and then compare them.
For all three representations, the unit rate is the value of the dependent variable when the independent variable is equal to 1.

Envision Math Grade 8 Chapter 2 Exercise 2.5 Practice Problems

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 120 Exercise 2 Answer

Given

Find the unit of rate or constant ?

We simply have to read from the graph for which ever of the values on the axis we need.

For example if the unit of hours is on the x-axis than we simply have to put that into the relation with the value that is on the y-axis.

We can find the unit rate or constant of proportionality for a relationship represented in a graph by:

Simply reading from the graph for which ever of the values on the axis we need.

For example if the unit of hours is on the x-axis than we simply have to put that into the relation with the value that is on the y-axis

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5

Page 120 Exercise 3 Answer

Given

Why can you use the constant of proportionality with any representation ?

We can use constant of proportionality with any representation because we can find the unit rate or the constant from the any data that we are given.

We can use constant of proportionality with any representation because we can find the unit rate or the constant from the any data that we are given.

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 120 Exercise 4 Answer

Given

The points are (0,0) and (4,24)

Who earn more per hour ?

We can simply graph both functions and see which of them makes more money

On the graph we can see function for Amanda and function for petra.

From the graph we can see that Amanda earns more money per hour

Amanda earns more money per hour.

How To Solve Exercise 2.5 Linear Equations In Envision Math Grade 8

Page 121 Exercise 6 Answer

Given

Find the unit of rate for Sam and bobby?

Who cycled faster?

First we have to find the unit rate for Sam.

Since we can see from the table that he can cycle at 20 miles in 2 hours we simply have to divided the number of miles with hours to find out how much he cycles in one hour.

20 ÷ 2 = 10

He can cycle at speed of 10mi/h

Now to find out the unit rate for bobby we are going to use points (2,18) and (4,36)

Again we simply have to divide miles with the hours to find out the unit rate for bobby.
​
18 ÷ 2 = 9

36 ÷ 4 = 9
​
We can see that bobby can cycle at speed of 9mi/h.

Sam can cycle faster.

Envision Math Grade 8 Chapter 2 Exercise 2.5 Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 121 Exercise 7 Answer

Given

y = 5x the equation y is amount of money and x is the selling pizza. Which pizzeria makes more money per pizza?

We are simply going to divide the number of pizzas sold for Leo’s pizza so we can simply compare the results.

The first point that we can see on the graph is (2,24) and we are going to use that point to find the unit rate for him.

24 ÷ 2 = 12

This means that Leo’s pizza makes money by the equation y = 12x

We can simply compare this result to the unit rate of Pauli’s pizzeria with the rate of Leo’s pizza.

15x > 12x

This means that Pauli’s pizzeria takes in more money per pizza.

Pauli’s pizzeria takes in more money per pizza.

Envision Math 8th Grade Exercise 2.5 Step-By-Step Linear Equation Solutions

Envision Math Grade 8 Volume 1 Chapter 2 Analyze And Solve Linear Equations Exercise 2.5 Page 122 Exercise 9 Answer

The table given shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.

We have to find the quantities to find the unit rate in order to compare the proportional relationship.

When there is a relationship between two variables, and the ratio of the two variables are equivalent, then it is known as proportional relationship.

We are given the data regarding the relationship between the number of miles Manuel walks and the amount of money he will raise

If we have to compare the proportional relationships, we will use the quantities Money Raised and the Miles Walked.

On doing so, we can find the amount of money earned for each mile which is unit rate.

The quantities that we should use to find the unit rate are Money Raised and the Miles Walked so that the proportional relationships can be compared.

The table given shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.

We have to compare the amount of money raised per mile by the three people.

In order to calculate the money raised per mile, we will have to divide the money raised by the miles walked by considering the values given from the table.

We will first calculate for Manuel as below:

Thus, Manuel gets the amount $15 for each mile walked.

It is already given that Petra earns $15 for every mile, which is the same as Manuel.

So, we can express amount earned by Petra and Manuel by y = 15x

The equation for the money raised by Beth is given as y = 20x

Now we compare the two equations,

15x < 20x

This concludes that Beth earns the maximum amount of money for per mile walked.

On comparing the money raised by the three people for every mile, Beth earns the most.