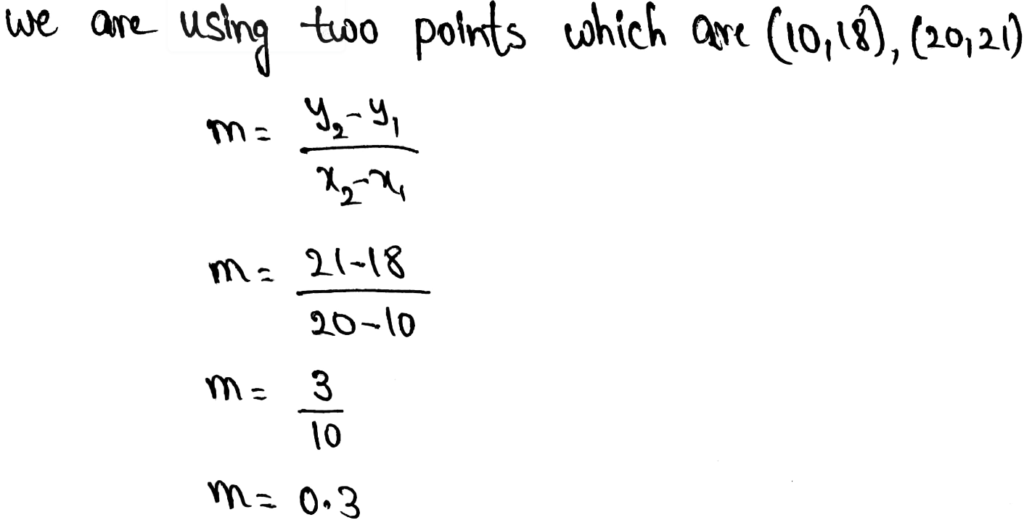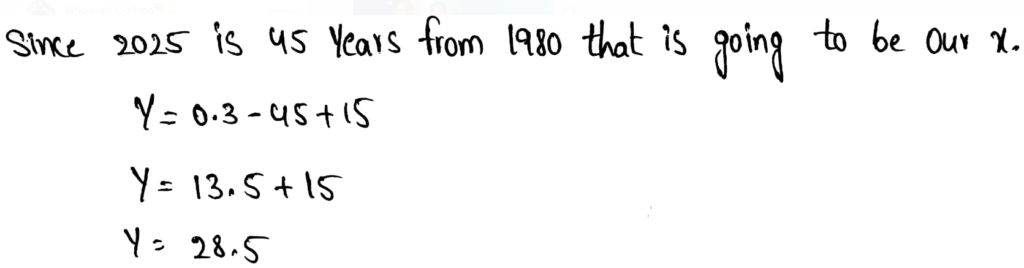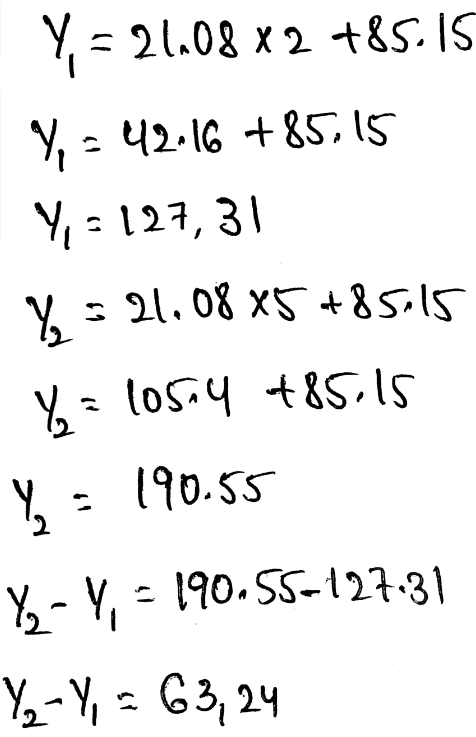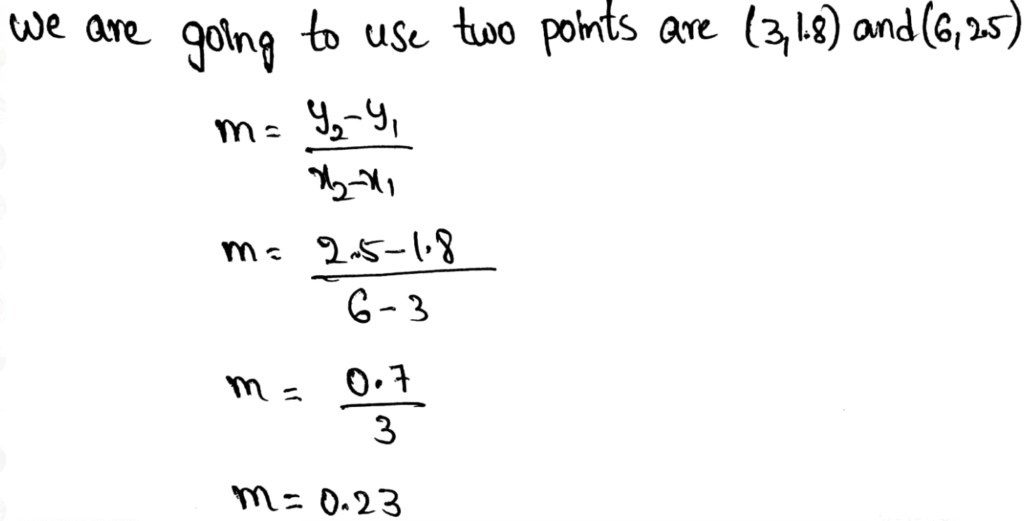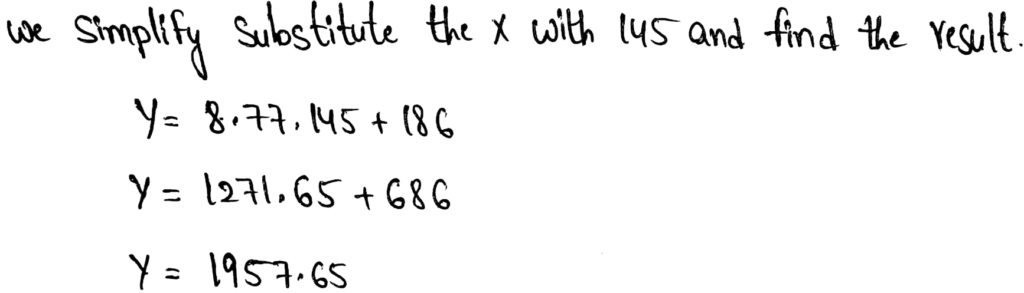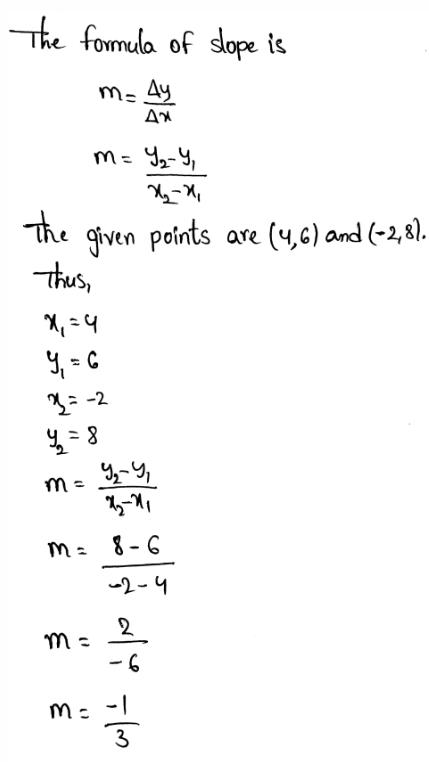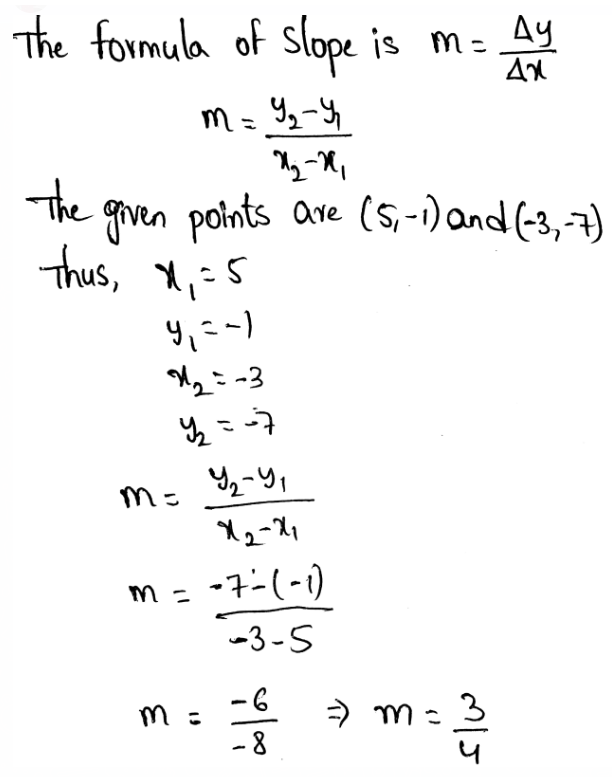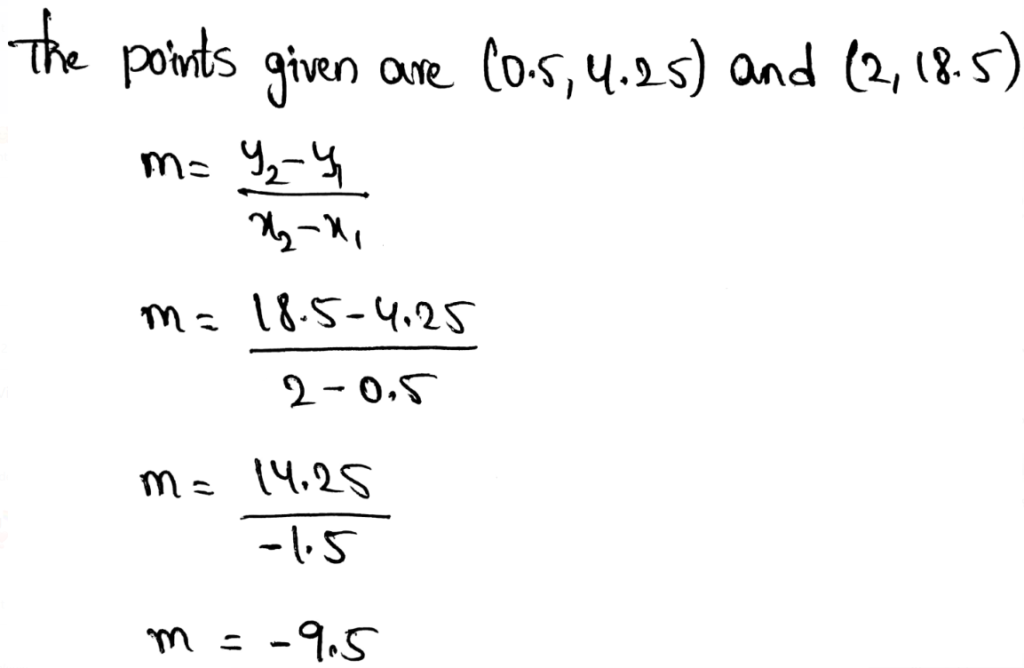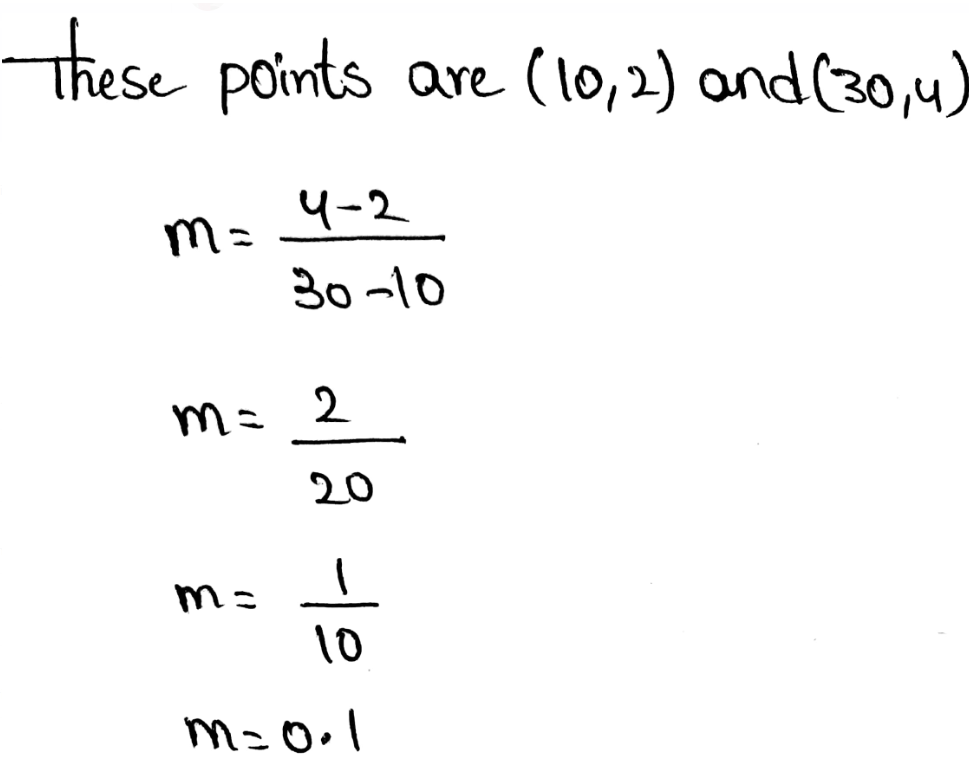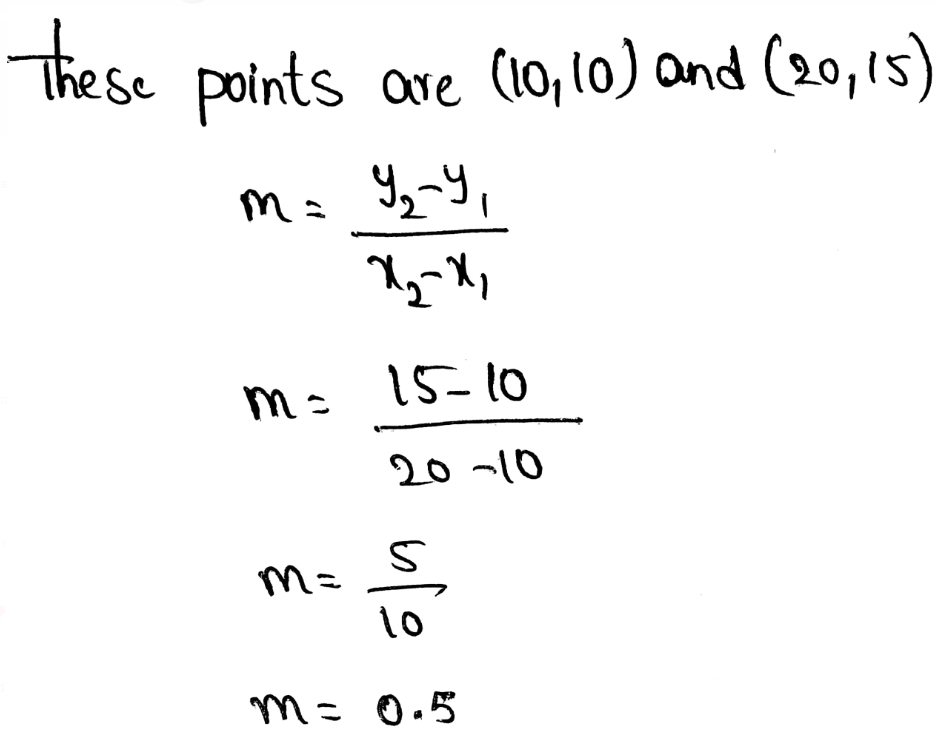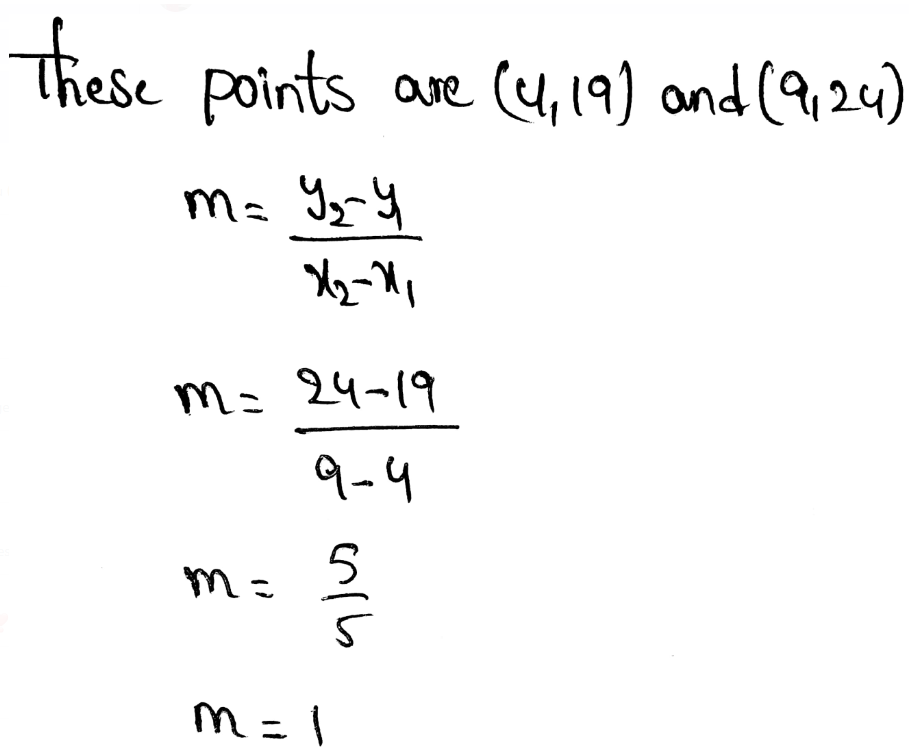Schindler

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1

Page 229 Exercise 6 Answer

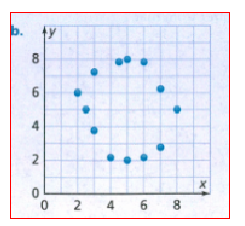
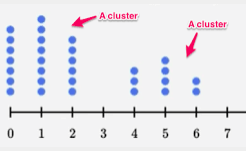
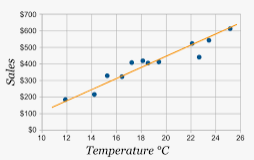
Given : a scatter plot

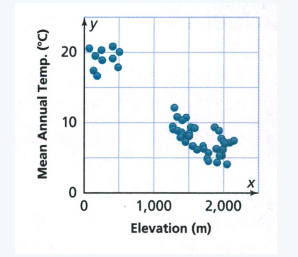
We have to check which statement are correct.

Given scatter plot

From the scatter plot it is clear that:

Majority of the elevations are in a cluster between 1,250 meters and 2,250 meters.

There is a gap in the data between 500 meters and 1,250 meters.

As the elevation increases the mean annual temperature decreases.

Therefore, first, second and fourth statements are correct.

First, second and fourth statements are correct

Envision Math Grade 8 Volume 1 Chapter 4 Solutions

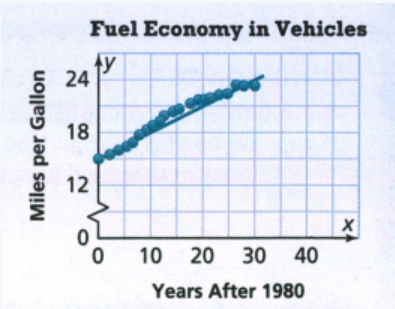
Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1Page 230 Exercise 1 Answer

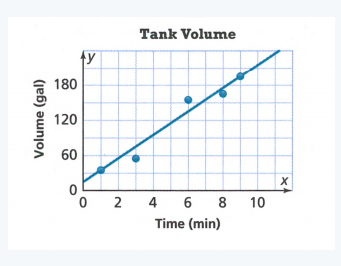
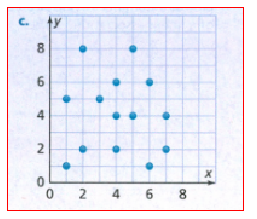
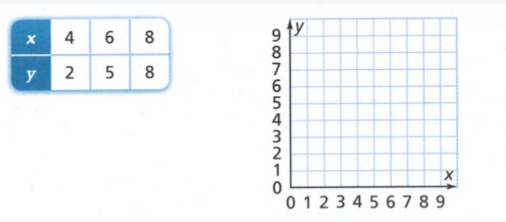
A table is given and we have to construct a scatter plot.

We will take ERA on x−axis and number of wins on y−axis and plot the graph from the data given in the table.

Given table:

Taking ERA on x−axis and number of wins on y−axis and plotting the graph.

We get the following scatter plot:

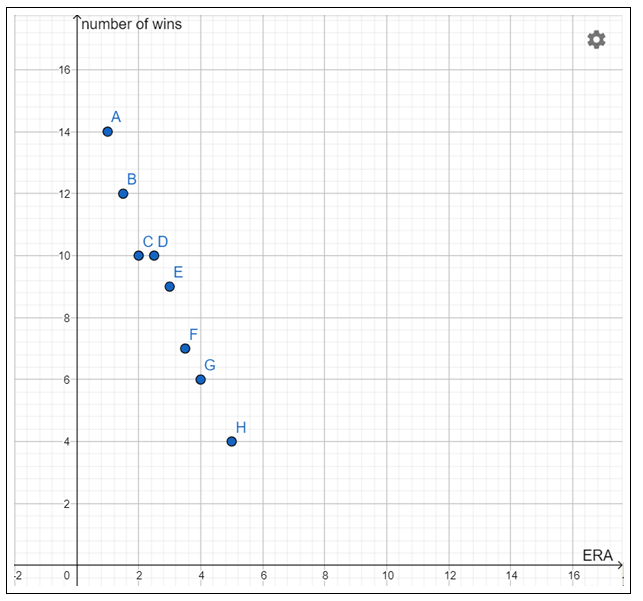
The scatter plot is :

Given: a table

We have to explain the relationship between ERA and number of wins.

From part 1(a) we have the following scatter plot

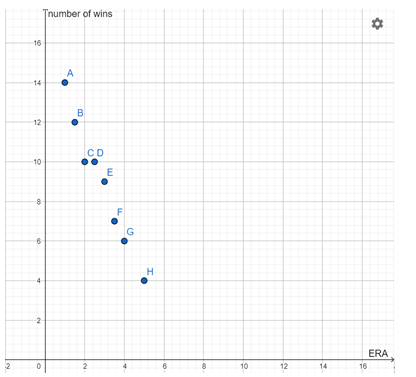
From the scatter plot it is clear as the points are closer to the trend line it is strong negative association.

We can conclude that as the ERA increases number of wins decreases.

It is strong negative association.

A table is given.

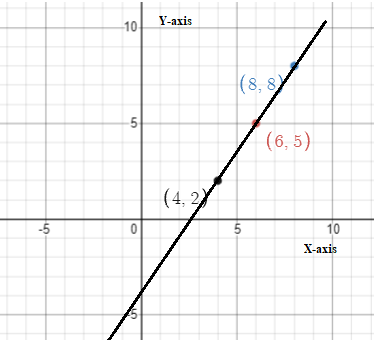
First, we will draw a trend line then we will find the slope and y-intercept using scatter plot.

Drawing trend line by placing a pencil in middle of the points on the scatter plot obtained in part 1(a).

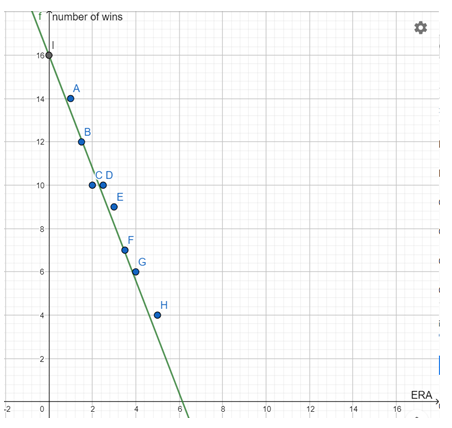
Taking points (1,14) and (2.5,10)

Slope = m=\(\frac{y_2-y_1}{x_2-x_1}=\frac{10-14}{2.5-1}=-2.6\)

Substituting values of slope and y-intercept in y=mx+c

We get the equation:

y = −2.6x + 16

Given ERA is 6, therefore, x = 6

Substituting x = 6 in y = −2.6x + 16

We get,

y = −2.6(6) + 16 = 0.4

Therefore, the number of wins of a pitcher with an ERA of 6 is 0.4.

Scatter plot with trend line:

The equation is y = −2.6x + 16

The number of wins of a pitcher with an ERA of 6 is 0.4

Investigate Bivariate Data Envision Math Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1Page 231 Exercise 1 Answer

Given: a table of poll results

We have to use the table and describe the poll result.

Given table

From the table it is clear that there are 43 people that are under 35 or are 35 years old and there are 57 people that are older than 35 years old.

Therefore, we can say that majority of the people are over 35 years old.

Majority of the people are over 35 years old.

Given: a table of poll results

We have to determine that what information the owner can get from the table.

Given table

From the table it is clear that:

Most of the people that are 35 or under 35 years old are there for snowboarding.

Most of the people that are older than 35 years are there for skiing

Therefore, we can say that most of the people that are under 35 or are 35 years old, they prefer snowboarding and the people that are older than 35 years, they prefer skiing.

Most of the people that are under 35 or are 35 years old, they prefer snowboarding and the people that are older than 35 years, they prefer skiing.

Given: a table of poll results

The majority of people that come to ski resort are over 35 years old, and they prefer skiing.

The rest of the people are 35 or under 35 years old and they prefer snowboarding over skiing.

Overall snowboarding is preferred over skiing.

The majority of people that come to ski resort are over 35 years old, and they prefer skiing.

The rest of the people are 35 or under 35 years old and they prefer snowboarding over skiing.

Overall snowboarding is preferred over skiing.

Envision Math Grade 8 Chapter 4.1 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 231 Exercise 1 Answer

Given table:

we have to use a different method to show the relationship between people’s age and the activity they prefer.

To display the data to show the relationship between people’s age and the activity they prefer we can use any other kind of diagram other than the table.

We can use any kind of diagram to show the relationship between people’s ages and which activity they prefer.

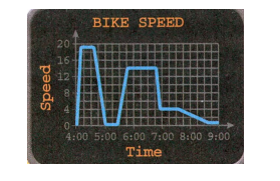
Page 232 Question 1 Answer

We have to explain how does a two-way frequency table show the relationships between sets of paired data.

Two-way frequency tables are a visual representation of the possible relationships between two sets of categorical data.

The categories are labeled at the top and the left side of the table, with the frequency (count) information appearing in the four (or more) interior cells of the table. The “totals” of each row appear at the right, and the “totals” of each column appear at the bottom.

For example: you conducted a survey at your school asking 100 people, whether they prefer digital or print textbooks.

Out of 100 people 42 students and 6 teachers like digital textbooks and 28 students and 24 teachers prefer print textbooks.

Here, teacher and students are one category (row category) and digital and print textbook are second type of category (column category).

Constructing two-way frequency table for this survey we get:

Explained how does a two-way frequency table show the relationships between sets of paired data.

Page 232 Exercise 1 Answer

Given table:

We have to complete the two-way frequency table by simply calculating the data missing in rows and columns.

Given table is :

The total of a row is represented on the right

Therefore, 32 − 19 = 13

13 is the value which will goes into top left corner.

The total of a column is represented at the bottom

Therefore, total YES votes are 13 + 28 = 41.

Total NO votes are 34

Therefore, 34 − 19 = 15

15 will go into middle of NO column.

Total votes of city B are 28 + 15 = 43

We know that total number of people are 75.

The complete two-way frequency table is:

The complete two-way frequency table is:

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 233 Exercise 2 Answer

Given: in total 100 students were asked.

Out of the 100 students, 19 girls rode in a car, 7 girls rode the bus, and 27 girls took the train.

Out of the boys, 12 took the train, 25 rode in a car and 10 rode the bus.

We have to construct a two-way frequency table.

We will simply write the given data in the table and we have to tell which mode of transportation is more preferred.

Given: out of the 100 students, 19 girls rode in a car, 7 girls rode the bus, and 27 girls took the train.

Out of the boys, 12 took the train, 25 rode in a car and 10 rode the bus.

Total students asked = 100

Constructing the two-way frequency table by writing the given data into the table.

From the table it is clear that most preferred transport (used) is car, out of 100 students that were asked 44 students go by car.

Two-way frequency table:

Most used mode of transportation is the car.

Page 232 Exercise 1 Answer

Given: two-way frequency table

We have to tell what pattern do we see from the table.

Given table:

From the table it is clear that most of the people have rain boots, out of 75 people 41 people have rain boots.

Most of the people own rain boots.

Solutions For Envision Math Grade 8 Bivariate Data

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Practice Page 234 Exercise 1 Answer

we have to explain how does a two-way frequency table show the relationship between sets of paired categorical data.

Two-way frequency tables are a visual representation of the possible relationships between two sets of categorical data.

The categories are labeled at the top and the left side of the table, with the frequency (count) information appearing in the four (or more) interior cells of the table. The “totals” of each row appear at the right, and the “totals” of each column appear at the bottom.

The two-way frequency table show the relationship between paired categorical data in the columns and rows.

The total the bottom right corner displays the total number of each cell in the table.

A two-way frequency table show the relationship between sets of paired categorical data.

In the columns and rows and the table makes easy to draw a conclusion and makes interpretation easy.

Page 234 Exercise 3 Answer

We have to explain how we can use the structure of a two-way frequency table to complete it.

First, we look for the column or row which have two values in it and to find the last value we use simple addition and subtraction to complete the table.

Let’s suppose we have a two-way frequency table with some data already in it.

We know that, the total of a row is displayed on the right and the total of a column is displayed on the bottom.

When we have two values in the row or column, we can find the last value by simple addition or subtraction, the total count is always equal to the sum of values in row or column.

The total count is always equal to the sum of values in row or column.

we can use addition or subtraction to find the last value when two values are already given in a row or column.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 234 Exercise 4 Answer

Given:

Total players are 60

We have to complete the table.

We can us addition or subtraction to complete the table, first we will look for that row or column which have two values in it.

Total number of players are 60.

Given table:

First, we will look for that row or column which have two values in it.

The total number of underclassmen students are 28

Therefore, 28 − 18 = 10

10 is the value that will come in the middle of first row.

The total number of the free throws are 31

Therefore, 31 − 18 = 13

13 is the value that will come in the middle of first column.

The total number of upperclassmen will be 13 + 19 = 32

Total number of 3-point shots are = 10 + 19 = 29

We know total players are 60.

Putting the calculated values in the table we get,

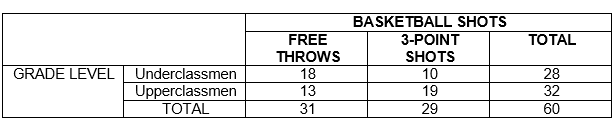
The complete two-way frequency table is:

Envision Math Grade 8 Chapter 4 Homework Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 234 Exercise 5 Answer

Given a table:

We have to explain whether the given statement is correct or not.

Given statement is false.

Given table is:

From the table it is clear that there are more high school students that wear contacts than middle school students that wear glasses

20 > 13

The given statement is incorrect.

Page 235 Exercise 8 Answer

Given:

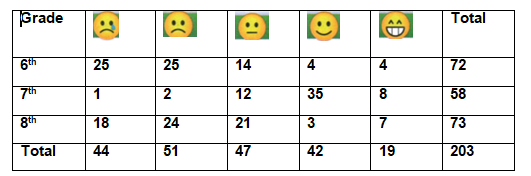
We are given the frequency table. We have to solve this frequency table to conclude the survey.

We consider the blank as x

Now,

The second column,
​
25 + 2 + 24 = x

∴ x = 51
​
The third column,
​
14 + x + 21 = 47

∴ x = 47 − 35

x = 12
​
Now, we consider the Total row,

We have:
​
44 + 51 + 47 + 42 + x = 203

∴ x = 203 − 184

x = 19
​
Now, we consider the fifth column:

We have:
​
4 + 8 + x = 19

∴ x = 19 − 12

x = 7
​
Now, we consider the third row:

We have:
​
x + 24 + 21 + 3 + 7 = 73

∴ x = 73 − 55

x = 18
​
Now, we consider the first column:

We have:
​
x + 1 + 18 = 44

∴ x = 44 − 19

x = 25
​
Now, we consider the first row:

We have:
​
25 + 25 + 14 + x + 4 = 72

∴ x = 72 − 68

x = 4
​
Now we consider the total column:

We have:
​
72 + x + 73 = 203

∴ x = 203 − 145

x = 58
​
Now, we consider the second row:

We have:
​
1 + 2 + 12 + x + 8 = 58

∴ x = 58 − 23

x = 35
​

Envision Math Grade 8 Chapter 4.1 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4.1 Page 235 Exercise 9 Answer

We are given the frequency table. Observe the given table to solve this question.

We observe the table.

The students studying for 1 to 2 hours are 147 in number.

The number of studying for 5 to 6 hours are 104

The statement states that more students study for 5 to 6 hours than for 1 to 2 hours.

This statement is False as the number of students studying for 5 to 6 hours is less than 1 to 2 hours.

The statement is false because the number of students studying for 1 to 2 hours is more than 5 to 6 hours.

Page 236 Exercise 10 Answer

Given:

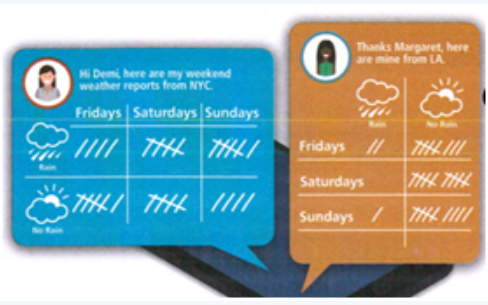
Construct a single, two-way frequency table to show the results.

We observe rain in NYC on Friday is 4, Saturday is 5, and Sunday is 6.

We observe that no rain in NYC on Friday is 6, Saturday is 5 and Sunday is 4.

We observe that rain in LA on Friday is 2, Saturday is 0 and Sunday is 1.

We observe that no rain in LA on Friday is 8, Saturday is 10, Sunday is 9.

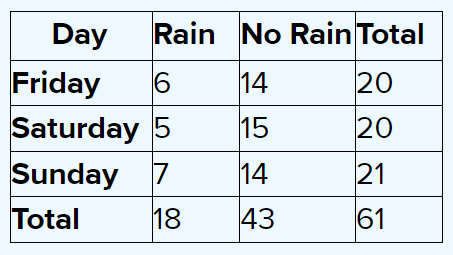
Given:

Through A.

We observe the frequency table from a.

We understand that the day that received the least rain in both LA and NYC is Saturday.

Saturday only has rain as 5.

Saturday saw the least rain in both NYC and LA with frequency as 5.

How To Solve Envision Math Grade 8 Topic 4.1

Page 236 Exercise 11 Answer

Given:

The total number of animals was 74.

There were 39 cats out of which 25 were male and 14 were female.

There were 35 dogs out of which 23 were male and 12 were female.

This is the required table.

Given:

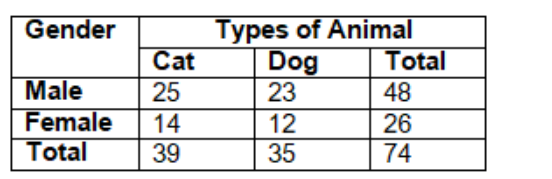
Through A.

We observe the frequency table from a.

We understand that the total number of males at the adoption centre is 48.

We also observe that the total number of females at the adoption centre is 26.

We observe that for males there a greater need for adoption at the centre.

Males have a greater need to be adopted at the adoption center because the number of males at the adoption center is greater than the females.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3

Page 223 Exercise 1 Answer

Given

Trend line passing through (25,100) and (80, 550).

To find/solve

Would this indicate that more or fewer calories were burned per minute? Explain.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

First we have to plot the second trend line. After we have plotted the new trend line, we can see that new trend line is below the current trend line which means that fewer calories were burned per minute. Also the new trend line is ascending slower.

This would indicate that fewer calories were burned per minute.

This would indicate that fewer calories were burned per minute.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.3 Bivariate Data Solutions

Page 224 Question 1 Answer

Given

Statement

To find/solve

Linear models help you to make a prediction.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 224 Exercise 1 Answer

Given

To find/solve

In 2025, the average fuel consumption is predicted to be about

First we are going to find the y-intercept. On the given graph the y-intercept is 15

Now we have to find the slope.

To find the slope we are going to use two points which are (10,18),(20,21)

Now that we know the equation of the trend line which is y = 0.3x − 15, we can simply find out the average fuel consumption in 2025.

The average fuel consumption in 2025 is predicted to be about 28.5 mpg.

The average fuel consumption in 2025 is predicted to be about 28.5 mpg.

Envision Math Grade 8 Exercise 4.3 Investigate Bivariate Data

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 225 Exercise 2 Answer

Given

ingredients needed to make 50,000 smoothies on a day when the high temperature is expected to reach 90∘F

To find/solve

Employees expect to have enough ingredients for the day’s smoothie sales.

To find out whether the Smoothie cafe is going to have enough ingredients we are simply going to use the equation from the last task.

The x that we are going to use is 90 because that is the temperature.
​

y = \(\frac{3}{5} .90+8\)

y = 54 + 8

y = 62
​
The expected number of smoothies to be sold on that day is about 62 thousands which mean that the cafe is not going to have enough ingredients.

The cafe is not going to have enough ingredients.

The cafe is not going to have enough ingredients.

Page 224 Exercise 1 Answer

Given- linear model

To find- Why can you use a linear model to predict the y value for a given x value.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

On linear model we can draw a trend line, which will show us how the result will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

On linear model we can draw a trend line, which will show us how the result will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

Investigating Bivariate Data Grade 8 Exercise 4.3 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 226 Exercise 1 Answer

Given- linear model

To find/solve- Linear models help you to make a prediction.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

On linear model we can draw a trend line, which will show us how the results will change in the future. We can read from the graph approximately the correct result.

Linear models can help us approximately find the value that we need with a trend line.

Page 226 Exercise 3 Answer

Given- linear model

To find- Prediction about any x-value.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

If we know the equation then we can find the prediction about any x-value.

If we do not know the equation for the given linear model that we simply first have to find that.

Yes, we can find the prediction about any x- value.

If we know the equation then we can find the prediction about any x-value.

If we do not know the equation for the given linear model that we simply first have to find that.

Yes, we can find the prediction about any x value.

Envision Math Grade 8 Chapter 4 Exercise 4.3 Solutions

Page 226 Exercise 4 Answer

Given

To find/solve

a. Using the slope, predict the difference in the amount spent on groceries between a family with five children and a family with two children.

We simply have to use two different x values which are 2 and 5. After that we simply have to subtract the value so we know the difference.
​
​
The difference is about $63,24.

The difference in amount spent on groceries between a family with five children and a family with two children is $63,24.

The difference is about $63,24.

The difference in amount spent on groceries between a family with five children and a family with two children is $63,24.

Given

To find/solve

b. How many children can you predict a family has if the amount spent on groceries per week in $169.47?

We are simply going to substitute the y, with 169.46 and calculate for x after that.

First we have to subtract 85.15 from both sides of the equation.
​
169.47 − 85.15 = 21.08x

84.32 = 21.08x
​
No we can simply divide both sides of the equation with 21.08

X = 4.

The family has 4 children.

The family has 4 children.

Envision Math 8th Grade Exercise 4.3 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 227 Exercise 6 Answer

Given

To find/solve

what the difference between the gas prices in 2013 and 2001 is

To find out what is the difference we simply have to find the equation for given graph.

First, we are going to find the slope.

To do so we are going to use two points from the trend line (3,18) and (6,25)

Secondly, we have to draw the line to the y-axis so we can find the y-intercept.

Now we can simply subtract the values

4.19 – 1.43 = 2.76

The difference between the gas prices in 2013 and 2001 is 2.76

The difference between the gas prices in 2013 and 2001 is 2.76.

How To Solve Exercise 4.3 Bivariate Data In Envision Math Grade 8

Page 228 Exercise 8 Answer

Given

To find/solve

what the hiker’s elevation will be after 145 minutes.

Finally we only have to round up the result to the nearest whole number.

y ≈ 1958

The biker’s elevation will be 1958ft after 145 minutes.

The biker’s elevation will be 1958ft after 145 minutes.

Page 228 Exercise 9 Answer

Given

To find/solve

How long it will take to fill the tank with 375 gallons of water.

If we look closely at the graph we can see that one point is (9,190) which the about the half way to the point at which we have 375 gallons.

Since we have a straight line, we can simply multiply give x-coordinate with 2 to get the time needed to fill the tank with 375 gallons of water.

9.2 = 18

18 hours is going to be needed for 375 gallons to be in the tank.

18 hours is going to be needed for 375 gallons to be in the tank.

Envision Math Grade 8 Exercise 4.3 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.3 Page 228 Exercise 11 Answer

Given: two points (0,453) and (10,359)

First, we will find the slope from the given points and find out the y-intercept.

Points from which trend line passes: (0,453) and (10,359)

From (0,453)it is clear that y-intercept is +453

Therefore, c = +453

Now, slope = \(\frac{y_2-y_1}{x_2-x_1}=\frac{359-453}{10-0}=-9.4\)

Therefore, m = -9.4

Now, substituting values of m and c in y = mx + c

We get, y = −9.4x + 453

Therefore, the trend line equation is y = −9.4x + 453

Option (D) is correct option.

The trend line equation is y = −9.4x + 453

Option (D) is correct option.

Envision Math Exercise 4.3 Bivariate Data Detailed Answers

Page 228 Exercise 12 Answer

Given: altitude = 415.4 feet

We will substitute the value y = 415.4 in y = -9.4x + 453 and solve it.

Given: altitude (y) = 415.4

Substituting value of y = 415.4 in y = −9.4x + 453

We get,
​
415.4 = −9.4x + 453

x = \(\frac{-37.6}{-9.4}=4\)

It will take 4 minutes to be at an altitude of 415.4 feet.

It will take 4 minutes.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2

Page 217 Exercise 1 Answer

It is given that Angus has a big test coming up.

We have to make a general statement about which option leads to a better result.

The data regarding Angus is given, where it is given that in different test at what time he sleeps and when he gets up.

On observing the given data, we can observe that in the test 6, Angus goes to bed at 9pm which is early and, in that test, he scores the highest marks and the best result.

Therefore, the better option which will lead to a better result is that he should go to bed early for the best results in the test.

The better option which will lead to a better result is that he should go to bed early for the best results in the test.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.2 Bivariate Data Solutions

Page 217 Exercise 1 Answer

We need to find the other factors should Angus take into consideration to make a decision.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

If we look closely at the test and their result, we can see that when he goes to bed early then Angus has the best results. The results differ by only a little but still the results are better when he goes to bed early.

The results are better when he goes to bed early.

The results are better when he goes to bed early.

Page 218 Question 1 Answer

We need to explain how we can describe the association of two data sets.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

We describe the relationship between the two sets of data with associations.

We can use the scatter plot for given relationship to determine whether there is strong, weak or no association.

We describe it with association.

We describe the relationship between the two sets of data with associations.

We can use the scatter plot for given relationship to determine whether there is strong, weak or no association.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2 Page 218 Exercise 1 Answer

To find – The relationship might there be between the two measurements

Correlation coefficient values can range between +1.00 to -1.00.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

The value of the correlation coefficient tells us about the strength and the nature of the relationship.

Correlation coefficient values can range between +1.00 to -1.00.

Statistical measures which show a relationship between two or more variable or two or more sets of data. For example, generally there is a high relationship or correlation between parent’s education and academic achievement.

Statistical measures which show a relationship between two or more variable or two or more sets of data. For example, generally there is a high relationship or correlation between parent’s education and academic achievement.

Envision Math Grade 8 Exercise 4.2 Investigate Bivariate Data

Page 218 Exercise 1 Answer

Given that, Georgia and her classmates also measure their foot length. Use a pencil to find the trend line. We need to sketch the trend line for the scatter plot.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Simply place the pencil on the scatter plot so it goes right through the middle of all point and then sketch line.

Place the pencil on the scatter plot so it goes right through the middle of all points and then sketch that line.

Place the pencil on the scatter plot so it goes right through the middle of all points and then sketch that line.

Page 219 Exercise 2 Answer

To find the association between the data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association.

Given graph has strong association.

To find the association between the data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association.

Given graph has weak association.

To find the association between the data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association.

Given graph has no association.

Investigating Bivariate Data Grade 8 Exercise 4.2 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2 Page 220 Exercise 1 Answer

We need to explain how we can describe the relationship between the two sets of data.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

The value of the correlation coefficient tells us about the strength and the nature of the relationship.

Correlation coefficient values can range between +1.00 to -1.00.

The relationship between the two sets of data is described using associations.

We can determine whether the two sets of data are having strong, weak, or have no associations between them.

Associations describe the relationship between the two sets of data.

Using a scatter plot, we can determine whether the given two sets of data is having strong, weak, or no association.

Page 220 Exercise 2 Answer

Given- a trend line

To find- How does a trend line describe the strength of the association?

If the points are close to the trend line then the association is strong

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil, than the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil, and do not have any pattern, than there is no association

We use the pencil to find the trend line. If the points are close to the trend line then the association is strong, if they are scattered around but not so close to the pencil, then the association is weak and if the points are scattered all around the graph, then there is no association.

We use the pencil to find the trend line. If the points are close to the trend line then the association is strong, if they are scattered around but not so close to the pencil, then the association is weak and if the points are scattered all around the graph, then there is no association.

Envision Math Grade 8 Chapter 4 Exercise 4.2 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2 Page 220 Exercise 5 Answer

To find- The association between the data.

The value of the correlation coefficient tells us about the strength and the nature of the relationship.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Place the pencil on the scatter plot so it goes right through the middle of all points.

If the points are all close to the pencil then the association is strong.

If the points are all scattered around and not close to the pencil, that the association is weak.

If the points are not close to the pencil and do not have any pattern then there is no association.

Given graph has no association.

Page 221 Exercise 6 Answer

Given

To find/solve
Best model of the data

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

If we look closely at the lines on the graph, then we can see that the line that we need is m.

All of the points are more close to line m than any other line.

Hence the best model is the line m.

All of the points are more close to line m than any other line.

Hence the best model is the line m.

Page 221 Exercise 8 Answer

To find- Positive or negative linear association.

A positive correlation is a relationship between two variables that move in tandem—that is, in the same direction.

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

Since we have the time working and the amount of money earned, then we know that the graph is going to be positive meaning that the more time working we have, the more money we are going to earn.

This is going to be a positive association.

This is going to be a positive association.

Envision Math 8th Grade Exercise 4.2 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.2Page 221 Exercise 9 Answer

Given

To find/solve

Relationship between the data .

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

As we can see on the graph the trend line is going to be descending which means that the association is going to be negative.

If we draw the trend line with pencil, then we can see the association is strong negative.

On the given graph we can see strong negative association.

If we draw the trend line with pencil, then we can see the association is strong negative.

On the given graph we can see strong negative association.

How To Solve Exercise 4.2 Bivariate Data In Envision Math Grade 8

Page 222 Exercise 13 Answer

Given- scatter plot showing a linear relationship.

To find- if a scatter plot shows a linear relationship

The Correlation coefficient is a statistical calculation that is used to examine the relationship between two sets of data.

The y-values change with respect to the x-values at a constant rate. This means that the points are going to be forming a line.

The y-values change with respect to the x-values at a constant rate.

The y-vales change with respect to thex-values at a constant rate. This means that the points are going to be forming a line.

The y-values change with respect to the x-values at a constant rate.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1

Page 211 Exercise 1 Answer

Based on the given data, we have to predict Luciana’s strategy.

The data regarding Luciana’s campaign is given.

From the data is observed that the maximum number of subscribers are gained when Luciana does around five to six social media posts in a day.

Thus, her strategy should simply be that she must do 5-6 social media posts every day. She should be careful and not do less than 5 social media posts on any day of the campaign in order to get the most number of subscribers.

Luciana’s strategy must be to do 5-6 social media posts each day in order to get most subscribers.

Envision Math Grade 8 Volume 1 Chapter 4 Exercise 4.1 Bivariate Data Solutions

Page 212 Exercise 2 Answer

Based on the given data, we have to tell the pattern between the time after posting and the number of new views.

The data regarding number of views on homepage is given.

From the data given, we can observe that when the time after posting the blog is more than 4 hours then the number of new views is decreased to two-digit numbers.

While when the time after posting is just 1-4 hours, then the new views are high and in three-digit numbers.

The pattern between the time after posting and the number of new views is than when time increases new views are decreased and when time is less, the number of new views is more.

Page 211 Exercise 1 Answer

Based on the given data, we have to tell the pattern between the time after posting and the number of new views.

The data regarding Luciana’s last social media campaign.

From the data given, we can observe that when she does around 1-4 social media posts in a day then she gets less number of new subscribers.

When she does 5-6 posts in a day, the highest numbers of subscribers are obtained.

But, when her posts are more than 6 in a day, again the number of subscribers decreases. This is the pattern observed from the data.

The pattern observed is that if there are 5-6 posts in a day new subscribers are increased, while if posts are less than 5 or more than 6 the number of subscribers are decreased.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 212 Exercise 1 Answer

We are required to find the coordinates of the point that represents the data in the fourth column.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

In the given data, age is in the x-coordinate while the number of entries is the y-coordinate.

In the fourth column, age is given as 13 years and the number of entries is 9.

Thus, the coordinate of that point will be (13,9).

The coordinates of the given point are (13,9).

Envision Math Exercise 4.1 Bivariate Data Detailed Answers

Page 213 Exercise 2 Answer

We have to describe the association between the two data sets.

Also we need to tell what the association suggests.

A scatter plot is a mathematical diagram which tells the relationship between paired data.

The scatter plot shows the relationship or association between the two sets of data.

There are three different types of association-

Positive association: The y-values increase as the x-values increase.

Negative association: The y-values decrease as the x-values increase.

No association: There is no consistent pattern between the x and y values.

From the graph given, we can observe that the association among the points scored and the minutes played is the positive associations.

This means that the y- values tend to increase when the x- values increase.

The association observed from the graph is positive association.

Envision Math Grade 8 Exercise 4.1 Investigate Bivariate Data

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 212 Exercise 1 Answer

We have to tell how the scale for both x and y axis will be chosen.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

In the given data, age is given as 10,11,12,13,14,15 years.

There is just a single value increment among the two values.

Age is marked on x-axis, so the scale on x-axis will be starting from 0 and will be increased by 1 unit only up to 15.

The number of entries is given as 8,8,9,9,10,10.

There is just a single value increment among the two values.

The number of entries is marked on y-axis, so the scale on x-axis will be starting from 0 and will be increased by 1 unit only up to 10.

The scale on x-axis is from 0 to 15 with increment of one unit only.

The scale on y-axis is from 0 to 10 with increment of one unit only.

Page 214 Exercise 1 Answer

We have to tell that how scatter plot shows the relationship between paired data.

Two sets of data are said to be paired if there exists a one-to-one relationship among them.

The relationship among the paired data is represented by a method of drawing scatter plot.

Scatter plot is a mathematical diagram on which points or coordinated of the data are plotted.

The scatter plot is used to tell the relationship among paired data by identifying the association among them.

The scatter plot shows the relationship or association between the two sets of data.

There are three different types of association-

Positive association: The y-values increase as the x-values increase.

Negative association: The y-values decrease as the x-values increase.

No association: There is no consistent pattern between the x and y values.

The relationship between paired data is observed based on the type of association which exists.

Investigating Bivariate Data Grade 8 Exercise 4.1 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 214 Exercise 2 Answer

We have to tell what scale must be used to construct the given scatter plot.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

On the x-axis, the hours of sleep will be marked. The scale will range from 0 to 9. This is because Marcy does not sleep more than 9 hours.

On the y-axis the points in the game will be marked. The scale for the same will be from 0 to 27 as the maximum points in a game is 27 only.

The scale on x-axis, will be from 0 to 9, on which the hours of sleep will be marked.

The scale on y-axis, will be from 0 to 27, on which the points in the game will be marked.

Envision Math Grade 8 Exercise 4.1 Solution Guide

Page 214 Exercise 3 Answer

We have to tell whether the statement given by Kylie is correct or not.

Kylie says that every scatter plot will have a cluster, gap and outlier.

We know that a scatter plot is a mathematical diagram.

The points on a scatter plot can be grouped or ungrouped. So, every scatter plot may not always be a cluster.

A gap on scatter plat is defined as the area where there are no data points.

This can only happen when the points are ungrouped and not always.

There may be an outlier in each scatter plot, but we can have a scatter plot which does not have a point away from rest all other points.

Thus, from all the above definitions, the statement made by Kylie is not correct.

Kylie says that every scatter plot will have a cluster, gap and outlier. This statement is wrong.

Envision Math Grade 8 Exercise 4.1 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 214 Exercise 5 Answer

We have to tell why clusters and outliers must be present in the scatter plot.

Germaine constructs a scatter plot to show how many people visit different theme parks in a month.

A group of points which are located closely around each other is called a cluster.

An outlier in each scatter plot, is the point which lies away from rest all other points.

In the given scatter plot, a cluster will obviously be present because we are aware that the people who tend to visit different theme parks for few months.

It is also possible that for some months, people do not want to visit a different theme park, so this will be an outlier in the graph.

In the given graph of scatter plot, clusters will be present because people may wish to visit different theme parks every month and outlier will be there are there are may be situation when they are not willing to visit a different theme park.

Envision Math Grade 8 Chapter 4 Exercise 4.1 Solutions

Page 215 Exercise 6 Answer

We have to complete the given scatter plot.

A scatter plot consists a coordinate plane which consists of two axis, one horizontal and the other vertical intersecting each other.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

In order to complete the scatter, we have to tell what points will be marked on the x and y-axis.

On the x-axis, the racing time in minutes will be marked.

On the y-axis, the laps will be marked.

The completed scatter plot will be

The scatter plot is completed as

Envision Math 8th Grade Exercise 4.1 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Exercise 4.1 Page 215 Exercise 8 Answer

We have to complete the scatter plot.

A Scatter plot is a mathematical diagram that represents the data.

We are given the data which shows the monthly attendance in thousands at museums in one country over a 12-month period.

The scatter plot will be completed on marking the data points as below:

The completed scatter plot is

The table shows the monthly attendance in thousands at museums in one country over a 12-month period.

We have to identify outliers in the scatter plot given

We are given the data which shows the monthly attendance in thousands at museums in one country over a 12-month period.

An outlier is a point, which is a single point away from all the other points plotted on the scatter plot.

On observing the scatter plot, the two outliers observed are the points (6,36) and (12,3).

The outliers identified are the points (6,36) and (12,3).

The table shows the monthly attendance in thousands at museums in one country over a 12-month period.

We have to identify the reason for existence of outlier.

We are given the data which shows the monthly attendance in thousands at museums in one country over a 12-month period.

An outlier is a point, which is a single point away from all the other points plotted on the scatter plot.

On observing the scatter plot, the two outliers observed are the points (6,36) and (12,3).

There was some discount on price of ticket to museum, which caused the first outlier which is (6,36).

In the month of December, some people do not visit museum because of holidays, so there is the second outlier (12,3).

The outliers are there because of discount on price and holidays in December.

How To Solve Exercise 4.1 Bivariate Data In Envision Math Grade 8

Page 216 Exercise 10 Answer

We have to check whether the given statements are true or not.

A scatter plot consists a coordinate plane which consists of two axis, one horizontal and the other vertical intersecting each other.

Ten athletes ran two races of the same length. The scatter plot shows their times.

The scatter plot is

On observing the scatter plot graph, the true statements which are:

Eight of the times for the second race were less than 17 seconds.

There were three athletes who had the same time in both races.

Thus, the false statements are

Nine of the times for the first race were at least 16 seconds.

There were seven athletes who were faster in the second race than in the first.

There were three athletes whose times in the two races differed by exactly 1 second.

The true statements are

Eight of the times for the second race were less than 17 seconds.

There were three athletes who had the same time in both races.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4

Page 206 Question 1 Answer

We have to tell the method to represent the relationship between paired data.

Using the same representation, predictions are to be made.

Two sets of data are said to be paired if there exists a one-to-one relationship among them.

The relationship among the paired data is represented by a method of drawing scatter plot.

Scatter plot is a mathematical diagram on which points or coordinated of the data are plotted.

The scatter plot has various uses, one of which is to make predictions regarding the data.

For which a best fit line is drawn and based on the location of points around the best fit, predictions are drawn whether the data is strong or not.

Scatter plot is used to represent the relationship between paired data and best fit line helps to make predictions in this method.

Envision Math Grade 8 Volume 1 Chapter 4 Topic 4 Bivariate Data Solutions

Page 209 Exercise 1 Answer

We are required to complete the given definition with appropriate word.

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is
​

​m = \(\frac{\Delta y}{\Delta x}\)

​
m = \(\frac{y_2-y_1}{x_2-x_1}\)

Therefore,

Slope is the change in y divided by the change in x.

Slope is the change in y divided by the change in x.

Envision Math Grade 8 Topic 4 Investigate Bivariate Data

Page 209 Exercise 2 Answer

We are required to complete the given definition with appropriate word.

In simple words, ratio is defined as the comparison of two quantities by dividing them.

A ratio of two quantities suppose p and q is represented p:q

Ratio is equivalent to fractions.

Therefore,

A relationship where for every x unit of one quantity there are y units of another quantity is a ratio.

A relationship where for every x unit of one quantity there are y units of another quantity is a ratio.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 3 Answer

We are required to complete the given definition with appropriate word.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

Therefore,

The x-axis is the horizontal line in a coordinate plane.

The x-axis is the horizontal line in a coordinate plane.

Page 209 Exercise 4 Answer

We are required to complete the given definition with appropriate word.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

The horizontal axis is called as the x-axis, while the vertical axis is termed as the y-axis.

The intersecting point of both the axis is origin.

Therefore,

The y-axis is the vertical line in a coordinate plane.

The y-axis is the vertical line in a coordinate plane.

Page 209 Exercise 5 Answer

We have to mark the given point (-2,4) on coordinate plane.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is y-coordinate.

In the given point (-2,4) the x-coordinate is -2 and the y-coordinate is 4.

We mark the point as below:

The point (-2,4) is labelled on coordinate plane as below:

Investigating Bivariate Data Grade 8 Topic 4 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 6 Answer

We have to mark the given point (0,3) on coordinate plane.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is y-coordinate.

In the given point (0,3) the x-coordinate is 0 and the y-coordinate is 3.

We mark the point as below:

The point (0,3) is labelled on coordinate plane as below:

Envision Math Grade 8 Chapter 4 Topic 4 Solutions

Page 209 Exercise 7 Answer

We have to mark the given point (3,-1) on coordinate plane.

A two-dimensional plane which consists of two axis, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is y-coordinate.

In the given point (3,-1) the x-coordinate is 3 and the y-coordinate is -1.

We mark the point as below:

The point (3,-1) is labelled on coordinate plane as below:

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 8 Answer

We have to mark the given point (−4,−3) on the coordinate plane.

A two-dimensional plane that consists of two axes, one horizontal and the other vertical intersecting each other is known as a coordinate plane.

Any point on the coordinate plane has two coordinates, one is the x-coordinate and the other is the y-coordinate.

If a point is expressed as an ordered pair, then the first digit will be the x-coordinate and the second is the y-coordinate.

In the given point (−4,−3) the x-coordinate is −4 and the y-coordinate is −3.

We mark the point as below:

The point −4,−3 is labeled on the coordinate plane as below:

Page 209 Exercise 9 Answer

We have to find slope among the given points (4,6) and (-2,8).

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

m = \(\frac{\Delta y}{\Delta x}\)

​
m = \(\frac{y_2-y_1}{x_2-x_1}\)

Slope is the change in y divided by the change in x.

Here we have the two points as (4,6) and (-2,8).

Slope between the pair of points (4,6) and (-2,8) is obtained as m = \(-\frac{1}{3}\)

Envision Math 8th Grade Topic 4 Step-By-Step Bivariate Data Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 4 Investigate Bivariate Data Topic 4 Page 209 Exercise 11 Answer

We have to find slope among the given points (5,-1) and (-3,-7).

Slope is defined as the ratio of the change in the y-coordinate to the change in x-coordinate.

It is represented by the letter m.

The formula of slope is

m = \(\frac{\Delta y}{\Delta x}\)

​
m = \(\frac{y_2-y_1}{x_2-x_1}\)

Slope is the change in y divided by the change in x.

Here we have the two points as (5,-1) and (-3,-7).

Slope between the pair of points (5,-1) and (-3,-7) is obtained as m = 3/4.

Page 209 Exercise 12 Answer

We have to express the fraction \(\frac{36}{60}\) as percent.

A per cent is a one part among 100 quantities.

In order to express the fraction as percent, first we divide and get the fraction as decimal.

Now, the percent is obtained by multiplying the decimal obtained with 100.

0.6 × 100 = 60

Thus, the fraction is expressed as 60%.

The fraction \(\frac{36}{60}\) is obtained as 60%.

How To Solve Bivariate Data In Topic 4 Envision Math Grade 8

Page 210 Exercise 1 Answer

The given vocabulary terms are,

Measurement data

Scatter plot

Cluster

Gap

Outlier

Trend line

Categorical data

Relative frequency table

We need to state their definitions and examples.

Measurement data

Definition – the type of data provided by figures

Examples – Length, Speed, height, distance.

Scatter plot

Definition – A mathematical diagram that displays values for correlated variables into a set of information using Cartesian coordinates.

Examples –

Cluster

Definition – A group of data that are very close to each other.

Examples –

Gap

Definition – The missed out points or information in a datasheet.

Examples –

Outlier

Definition -A value that seems to be separate or lies outside the given range.

Examples –

Trend line

Definition – A line drawn to show the direction in which the data prevails.

Example

Categorical data

Definition – A data that can be split down into groups.

Examples – Age, sex, etc.

Relative frequency table

Definition – The popularity or mode of data based on the samples obtained.

Examples – I ate 10 donuts out of 15: the frequency of eating is 10. the relative frequency of winning is \(\frac{10}{15}=\frac{2}{3} \times 100=66.6^{\%}\).

Measurement data – the type of data provided by figures.

Scatter plot – A mathematical diagram that displays values for correlated variables into a set of information using Cartesian coordinates.

Cluster – A group of data that are very close to each other.

Gap – The missed out points or information in a datasheet.

Outlier -A value that seems to be separate or lies outside the given range.

Trend line – A line drawn to show the direction in which the data prevails.

Categorical data – Data that can be split down into groups.

Relative frequency table – The popularity or mode of data based on the samples obtained.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3 Review Essential Question

Page 201 Question 1 Answer

We have to explain how we can use functions to model linear relationships.

To use functions to model linear relationships, we need to use linear functions.

The graph of those functions will be in the form of a straight line.

We can write the equation in the form of slope-intercept form such as y = mx + b

where m is the slope, b is the initial value of the dependent variable, x is the input and y is the output.

We can determine these values from the given values or from the given description of the relationship.

We need to construct a linear function to model linear relationships between any two quantities.

Envision Math Grade 8 Volume 1 Chapter 3 Topic 3 Review Essential Question

Page 201 Exercise 1 Answer

A function whose graph is not a straight line is a nonlinear function.

Nonlinear functions have a slope that varies between points.

A function whose graph is not a straight line is a nonlinear function.

Page 201 Exercise 2 Answer

m = \(\frac{y_2-y_1}{x_2-x_1}\)

Where m is the slope of the line

The slope of a line is also called a constant rate of change.

The slope of a line is also called a constant rate of change.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3 Review Essential Question Page 201 Exercise 3 Answer

A relation in which each input has exactly one output is a function.

A relation in which each input has exactly one output is a function.

Page 201 Exercise 4 Answer

The value of the output when the input is 0, or the y-intercept of the graph line is called a initial value.

It is the y-value of the point at which the line crosses the y-axis.

The value of the output when the input is 0, or the y-intercept of the graph line is called a initial value.

Envision Math Grade 8 Topic 3 Functions Review Essential Question

Page 201 Exercise 5 Answer

A period of time between two points of time or events is called an interval.

An open interval does not include its endpoints.

Open interval indicated with parenthesis. For example (0,2)

A closed interval include its endpoints.

A period of time between two points of time or events is called an interval.

Page 201 Exercise 1 Answer

Given

(0,−2),(2,6)

​
Therefore, the linear function in the slope-intercept form is y = 4x − 2

Page 202 Exercise 2 Answer

Given

{(−5,−3),(7,2),(3,8),(3,−8),(5,10)}

Since the input 3 corresponds to outputs of -8 and 8.

The relation is not a function. Because it has an input that corresponds to more than one output.

The relation is not a function since the input 3 corresponds to more than one output.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3 Review Essential Question Page 202 Exercise 1 Answer

If he buys one app each week that means that he spends $4.99
every week.

This means that on the right side of the equation we are going to have 4.99x

On the left side we are simply going to have y, which is the going to be the amount left on the card

We get this by adding to the right side and we have to subtract 4.99x

y = 100 − 4.99x

Hence, the equation is y = 100 − 4.99x

Essential Question Review For Functions Modeling Grade 8 Envision Math

Page 202 Exercise 2 Answer

Given:

The function is y = 100 − 4.99x

The initial value is going to be 100. After that each week he spends 4.99$

The required graph is:

Therefore the required graph is:

Envision Math Grade 8 Chapter 3 Topic 3 Solutions And Essential Question

Page 203 Exercise 1 Answer

For the function A we can see that the initial value is going to be 2.

For function B we do not see that and we must find the Initial value.

Since, we can see that the y is increasing by 2 for each increase of 1 in x that means that we get the initial value if we simply subtract 2 from the first value of y.

−1 − 2 = −3

The initial value of the function B is -3.

This means that function A has greater initial value.

Therefore the function A has greater initial value.

Page 203 Exercise 2 Answer

Given:

We can see the function A has -3x as variable which means that the rate of change is going to be -3.

For the function B we can see that the rate of change is 2 because for every change in x the y is greater by 2.

Function B has greater rate of change.

Therefore the function B has greater rate of change.

Envision Math 8th Grade Topic 3 Functions Essential Question

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3 Review Essential Question Page 203 Exercise 1 Answer

Given:

y-intercept is -0.5.

The points given are (0.5, 4.25) and (2, 18.5)

We first find the slope:

Now we write the equation of the line:

y = −9.5x − 0.5

Therefore the required equation of the line is y = −9.5x − 0.5

Page 203 Exercise 2 Answer

Given:

The initial value from the graph is 90.

We find the slope:

m = -10

Now we write the function:

y = −10x + 90

Therefore the required function is y = 10x + 90.

Page 204 Exercise 1 Answer

The graph of the function is a constant when the y-coordinate does not change when the x-coordinate does.

This means that the graph of the function is a constant in intervals 2, 4, 6.

Therefore the given graph is constant in the intervals 2, 4, 6.

Page 204 Exercise 2 Answer

The graph of the function is decreasing when the y-coordinates are decreasing as the x-coordinates are increasing.

The graph of the given function is decreasing in intervals 5, 7.

Therefore the given graph of the function is decreasing in intervals 5, 7.

How To Answer Essential Questions In Topic 3 Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3 Review Essential Question Page 204 Exercise 1 Answer

As we can see the graph is going to be a constant at first when there is maximum number of carrots. Then we are going to have a decrease until half the carrots are gone. In the last part there is simply a constant because the number of carrots is going to stay the same.

From the task we see that the graph of the function is first going to be a constant, after that it is going to decrease until half the carrots are left and in the end the graph is going to be constant.

Envision Math Grade 8 Topic 3 Review Practice Problems

Page 205 Exercise 1 Answer

We find the solution to the linear equation and then compare these solutions, choose the solution that is greater to find the letter of the row.

We consider:
​
3x + 8 − 8 = 12 − 8

3x = 4
​

x = \(\frac{4}{3}\)

5x − 4 + 4 = 5 + 4

5x = 9
​

x = \(\frac{9}{5}\)

As we can see \(\frac{4}{3}<\frac{9}{5}\) therefore the correct solution is N.

2n + 15 – 15 = 57 – 15

2n = 42

n = 21

3d – 7 + 7 = 53 + 7

3d = 60

d = 20

As we can see 21 > 20 therefore the correct solution is I.

We consider:
​
8x − 12 + 12 = 14 + 12

8x = 26
​

x = \(\frac{13}{4}\)

6p + 12 − 12 = 36 − 12

6p = 24
​
p = 4

As we can see \(\frac{13}{4}<4\) therefore the correct solution is C.

We consider:
​
54 − 14 = 8c + 14 − 14

8c = 40
​
c = 50

8m − 14 + 14 = 50 + 14

8m = 64
​
m = 8

As we can see 5 < 8 therefore the correct solution is E.

We consider:
​
12x + 16 − 16 = 100 − 16

12x = 84
​
x = 12

6z − 24 + 24 = 12 + 24

6z = 36
​
z = 6

As we can see 12 > 6 therefore the correct solution is B.

We consider:
​
59 + 81w − 59 = 68 − 59

81w = 9
​

w = \(\frac{1}{9}\)
​

​40r + 67 − 67 = 71 − 67

40r = 4
​

r = \(\frac{1}{10}\)

As we can see \(\frac{1}{9}>\frac{1}{10}\) therefore the correct solution is E.

We consider:
​
31g − 15 + 15 = 47 + 15

31g = 62
​
g = 2

99 − 22 = 22 + 35y − 22

77 = 35y
​

y = \(\frac{77}{35}\)

As we can see \(2<\frac{77}{35}\) therefore the correct solution is L.

We consider:
​
14r − 7 + 7 = 14 + 7

14r = 21
​

r = \(\frac{3}{2}\)

13 + 8 = 12t − 8 + 8

21 = 12t
​

t = \(\frac{21}{12}\)

As we can see \(\frac{3}{2}<\frac{21}{12}\) therefore the correct solution is T.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.6

Page 195 Exercise 1 Answer

We do not agree with jack’s statement because we can see that United States has not dropped a lot. The graph that represents the United States does not have a big decrease.

We do not agree with jack.

We do agree with Ashley’s statement because this means that china’s has had a huge increase.

As we can see on the graph the line that represents china had a huge increase.

We agree with Ashley’s statement.

Envision Math Grade 8 Volume 1 Chapter 3 Exercise 3.6 Functions Solutions

Page 195 Exercise 1 Answer

For Europe and United States we can see that their line on the graph is decreasing by a little bit.

This means that they have dropped the oil consumption over the given time.

They have dropped the oil consumption over the given time.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.6 Page 196 Question 1 Answer

If we sketch a graph of a function, than we can see the behavior of given function.

This way we do not have to read the data every time.

We can simply see the behavior on the sketch.

Page 196 Exercise 1 Answer

The input of given function is going to be the depth, because the water pressure is going to increase for each feet of the depth.

The output of given function is going to be the water pressure.

To sketch the given graph we can simply mark given points which are (10,19.1) and (14,20.9)

The depth is going to be the input and the water pressure is going to be the output of given function.

Page 196 Exercise 1 Answer

We need to explain how are the sketches of the two functions similar and different from each other.

The input of the given function is going to be the depth because the water pressure is going to increase for each foot of the depth.

The output of the given function is going to be the water pressure.

To sketch the given graph we can simply mark given points that are (10,19.1) and (14,20.9)

The unit rate is,

Therefore, the water pressure decreases with the increase in depth.

The decrease is not constant.

The sketch of the time and the oxygen level of the scuba diver is,

The decrease of the oxygen level in the tank is constant since she breathes at a constant rate.

The sketches of the two functions are similar in the way that these two functions are decreasing.

They are different because the decrease in the water pressure with respect to the depth is not constant while the decrease in the oxygen level in the tank is constant.

Envision Math Grade 8 Exercise 3.6 Use Functions To Model Relationships

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.6 Page 198 Exercise 1 Answer

We need to explain how does the sketch of a graph of a function help describe its behavior.

If we sketch a graph of a function, then we can see the behavior of the given function.

This way we do not have to read the data every time.

We can simply see the behavior on the sketch.

Page 198 Exercise 2 Answer

We need to describe how we know which variable goes with which axis when you graph.

When we need to determine which variable will go with which axis when we graph the output will always be the variable that will change depending on the input.

The input is always the variable that is changing independently.

Input is mostly going to be the time.

The output is the variables that change depending on the input which is mostly the time.

Envision Math Exercise 3.6 Functions Detailed Answers

Page 198 Exercise 4 Answer

Given that, a class plants a tree. We need to sketch the graph of the height of the tree over time.

Also, we need to identify the two variables.

To sketch the graph we have to identify the variables which are the height of the tree and the other variable is the time for how long was the tree planted.

The first variable is the height of the tree and second is the time.

Given that, A class plants a tree. We need to sketch the graph of the height of the tree over time.

Also, we have to describe the relationship between the two variables.

The height of the tree is going to be the output of a given function because it depends on the time which is going to be the input of the given function.

The height is the output and the time is the input.

When time increases by 1 year, the height of the tree increases by \(\frac{7}{3}\)feet.

Given that, A class plants a tree. We need to sketch the graph of the height of the tree over time.

Since now we know that the variables are going to be the height of the tree and the time, we can simply sketch the graph.

Keep in mind that the graph is going to start at 3 ft.

The graph is

Functions And Modeling Relationships Grade 8 Exercise 3.6 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.6 Page 198 Exercise 5 Answer

Given that, an airplane takes 15 minutes to reach its cruising altitude. The plane cruises at that altitude for 90 minutes, and then descend for 20 minutes before it lands. We need to sketch the graph of the height of the plane over time.

First we need to find the variables. Variables are the time and altitude.

We can see that it states the plane takes 15minutes to reach full altitude which means the function is going to be increasing.

If the plane is cruising that means that the plane is flying at the same altitude the same time which means that the function is going to be a constant during those 90 minutes.

In the last part when plane is descending the graph is also going to be descending.

In the first part the function is increasing, in the second it is a constant and in the last part the function is decreasing.

Page 199 Exercise 6 Answer

We need to determine what relationship between money (in dollars) and time (in months) does this graph shows. Also, we need to write a description of the given graph.

If we look at the graph we can see that the money is increasing from the start of January till the end of January. After that, we can a big drop in the money

If we look at the graph we can see that the money is increasing from the start of the January till the end of the January. After that we can a big drop in the money .

Envision Math Grade 8 Chapter 3 Exercise 3.6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.6 Page 199 Exercise 9 Answer

Given that, Melody starts at her house and rides her bike for 10 minutes to a friend’s house. She stays at her friend’s house for 60 minutes. We need to sketch a graph that represents this description.

From the question that we have in the task, we can see that the function is first going to increase and after that, it is going to be a constant because she will be at the same distance for 60 minutes.

After that, she goes back home and the graph is going to be decreasing

The graph is first going to increase than it is going to be constant and lastly it is going to decrease.

Page 199 Exercise 10 Answer

We need to find which among the below-given description best represents the graph shown.

(A) People are waiting for a train. A train comes and some people get on. The other people wait for the next train. As time goes by, people gradually leave the station.

(B) One train arrives and some people get off the train and wait in the station.

(C) People are waiting for a train. Everyone gets on the first train that comes.

(D) People are waiting for a train. A train comes and some people get on the train. The other people wait for the next train. Another train arrives and all of the remaining people get on.

We can see the given graph first we have a constant of people which means that the people are waiting for the train.

After that we can see that part of the people got on that train and there are fewer people now remaining at the station.

Now the second train arrives and the rest of the people leave the station.

Therefore, the correct answer is option D.

Envision Math 8th Grade Exercise 3.6 Step-By-Step Functions Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.6 Page 200 Exercise 12 Answer

The graph is going to rapidly increase at start, and after that is going to start to descend until a fan catches it.

Descend just has to lesser than the increase.

The graph is going to have a rapid increase at start and then it will start to decrease until it gets back to the ground.

How To Solve Exercise 3.6 Functions In Envision Math Grade 8

Page 200 Exercise 13 Answer

For the given variables we can make up a lot of descriptions.

Let’s say that the people are boarding a boat and there is a line in front of the boat. Each boat can carry only so many people, so there is going to be 2 boats that will pick up the people.

The first boat arrives after hour, and the second boat will arrive in 3 hours.

On the first boat only half the people boarded.

The rest of the people are waiting for the second boat.

After the second boat arrives the rest of the people board the boat.

There is some amount of people waiting to board a boat, after the first boat comes after an hour, half the people board the boat. The rest of the people wait for second boat which arrives two hours later and all of them board second boat.

Envision Math Grade 8 Chapter 3 Exercise 3.6 Practice Problems

Page 200 Exercise 14 Answer

The graph is going to have two constant parts and one decrease.

If at first they score same amount of runs in each of the first 4 innings than in this part the graph is a constant.

After that it will decrease to 0 and it will again be a constant

The graph is first going to have a constant. After that there will be a decrease to 0 and again the graph is going to become a constant.

The given graph would have more constant parts of the graph but there would also be an increase before each constant part and there is going to be a decrease after each constant.

There would be more constant parts which would have increase before them and the decrease after them.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5

Page 189 Exercise 1 Answer

Given

Martin went aunt’s house , he has two route one is down hill and another one is edge hill

Find the relationship of speed and time?

Each route will have corresponding time needed to travel.

The difference is that the route that goes up and down the hill does not have a constant speed and the route that goes around the edge of the hill will most probably have a constant speed.

Time to pass each route will be roughly the same.

Route that goes up and down that hill does not have a constant speed while the route that goes around the edge of the hill will have constant speed.

Envision Math Grade 8 Volume 1 Chapter 3 Exercise 3.5 Functions Solutions

Page 189 Exercise 1 Answer

Given

Martin went aunt’s house , he has two route one is down hill and another one is edge hill.

Find the relationship of speed and time?

For the route that goes up and down the hill martin will have to put in more effort into going up the hill and his speed will decreases but after he gets to the peak he will not have to put so much effort into it because he will be going downhill.

For the second route that goes around the edge of the hill, the speed on this route will be constant which means that he will be travelling at roughly the same speed the whole route.

The time needed for both routes should be roughly the same.

The time needed for each route is the same, the only difference will be that the route that goes up and down the hill will require more effort going up and no effort going down the hill, and the other route requires the same amount of effort through the whole route.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5 Page 190 Question 1 Answer

Given

Describe the two quantities ?

Since the air conditioner is on, the temperature in the room is falling at a constant speed up to the point at which the temperature in the room will be the same as the temperature of the air that the air conditioner is blowing.

The temperature is falling at a constant speed up to the point at which the temperature will be the same as the temperature of the air coming from the air conditioner.

Page 190 Exercise 1 Answer

Given

Find the relationship of speed and time?

Each route will have corresponding time needed to travel.

The difference is that the route that express train does not have a constant speed and the route that express train will most probably have a constant speed.

Time to pass each route will be roughly the same.

Route that goes up express train does not have a constant speed while the route that goes around the express train will have constant speed.

Envision Math Grade 8 Exercise 3.5 Use Functions To Model Relationships

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5 Page 190 Exercise 1 Answer

Given

Find the graph function changes the train speed increases?

As we can see from the graph, as the time passes the speed of the train is decreasing given function is linear.

The interval would best describe the process of train stopping.

At the time passes, the speed of the train is decreasing.

The function is linear.

Page 191 Exercise 3 Answer

Given

Write the graph scenario ?

The graph could represent a car trip somewhere, because first the distance is increasing at a constant speed which means someone is going somewhere.

The two constant intervals simply means that the car stopped, maybe for sightseeing.

Lastly, why this could be a car trip is because the function is decreasing in the interval 5 which means that we are coming back to the starting point.

The graph could be representing a car trip somewhere because we are going back to the starting point in the end.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5 Page 190 Exercise 1 Answer

Given

Whether the function increasing ?

From the slope of the linear function we know whether the function is increasing or decreasing because if the slope is positive value than the function will be increasing.

Positive slope of linear function means the function is increasing.

Page 192 Exercise 2 Answer

Given

Whether the function increasing or decreasing?

From the slope of the linear function we know whether the function is increasing or decreasing because if the slope is positive value than the function will be increasing but if the value is negative that the function is decreasing.

Positive slope of linear function means the function is increasing, and the negative slope of linear function means the function will be decreasing.

Functions And Modeling Relationships Grade 8 Exercise 3.5 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5Page 192 Exercise 3 Answer

Given

What kind the graph function is shown at same output or y-values , for each input value or, x-value?

If the output of some function is always the same that means that the graph of the function is going to be a constant.

The graph of the function is a constant.

Page 192 Exercise 5 Answer

Given

Which intervals increasing , decreasing and constant?

We simply have to read the graph to get the information that we need.

In the first interval the function is constant.

In the second interval the function is a decreasing.

In the third interval the function is increasing.

In the fourth interval the function is increasing.

In the fifth interval the function is constant.

In the sixth interval the function is decreasing.

1 → constant

2 → decreasing

3 → increasing

4 → increasing

5 → constant

6 → decreasing

Page 193 Exercise 6 Answer

Given

Which intervals increasing , decreasing and constant?

We simply have to read the graph to get the information that we need.

In the 1, 3 and 6 interval the function is increasing.

In the 4 interval the function is constant.

In the 2 and 5 interval the function is decreasing.

The function is increasing in intervals 1,3 and 6.

The function is decreasing in intervals 2 and 5.

The function is constant in interval 4 .

Envision Math Grade 8 Chapter 3 Exercise 3.5 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5 Page 193 Exercise 8 Answer

Given

Which intervals increasing , decreasing and constant?

We simply have to read the graph to get the information that we need.

In interval a) is increasing.

In interval b) is constant.

In interval c) is decreasing.

In interval d) is constant.

a) → increasing

b) → constant

c) → decreasing

d) → constant

Page 193 Exercise 9 Answer

Given

Which intervals increasing , decreasing and constant?

There are 3 intervals in which the function is increasing.

We can see on the given graph that there are 3 peaks.

The function is increasing up to the point until we got to the peak.

So this means that 3 interval in which the function is increasing are right before the peaks of the function.

The greatest increase is the first interval of the function before the first peak.

3 intervals in which the function is increasing which are right before the peeks of the function.

The first interval, where the function starts has the greatest increase.

Envision Math 8th Grade Exercise 3.5 Step-By-Step Functions Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5 Page 193 Exercise 10 Answer

Given

What is the constant interval represent?

The constant intervals on the given graph represent either the car travelling at constant speed or the car stopping because there is one constant interval which has no speed.

The constant intervals on the graph are showing the constant speed of the car, and the car stopping the interval where the car is not moving because there is no speed.

Page 194 Exercise 11 Answer

Given

How many intervals function is decreasing?

We simply have to need from the graph the information that we need

There are 3 intervals in which the function is decreasing.

3 intervals.

Given

How are the decreasing intervals alike?

Every decreasing interval lasts about the same amount of time.

The first and third intervals are roughly the same frequency as well.

The decreasing intervals last about the same amount of time

Second interval has the highest frequency while the first and the third have roughly the same frequency.

Second interval has higher frequency than the remaining two.

How To Solve Exercise 3.5 Functions In Envision Math Grade 8

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.5Page 194 Exercise 12 Answer

We can see that the function has intervals in which it is a constant which means the student is wrong.

There is one interval in which the speed is but it is still an interval in which the function is a constant.

Therefore, there are intervals in which the function is a constant.

The student forgot to include the interval in which the speed is 0.

This still counts as an interval of the function and in given interval the function is a constant.

The student forgot to include the interval in which the speed is 0.

Envision Math Grade 8 Chapter 3 Exercise 3.5 Practice Problems

Page 194 Exercise 14 Answer

We have to check all the graphs whether they fit the description.

It states that the graph is in interval 1 which means that the graph C is not the graph that we are looking for because the first interval in graph C is increasing.

In the second interval the function is increasing which means that graph B is not the graph that we are looking for because the second interval in the graph B is a constant.

In the third interval the function has to be a constant which both graphs A and D have.

In the last interval they should be decreasing which means that the only graph that is corresponding to the description in the graph D.

Hence, the right graph is graph D.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4

Page 183 Exercise 1 Answer

We need to determine the properties of the function.

We can use more different representations to help us determine the properties of functions, and those representations are the graphs and table data.

When we use graph we can see more easier whether the function is linear or not but it is more difficult to determine what is the initial value when we have bigger numbers.

The table data should show the initial value much more clearly but at the same time it is more difficult to determine whether the function is linear or not.

Graph help us to determine whether the function is linear easier, but the table data will show us the initial value more clearly.

Envision Math Grade 8 Volume 1 Chapter 3 Exercise 3.4 Functions Solutions

Page 184 Question 1 Answer

Given

How can you use a function to represent a linear relationship?

When we use an equation of a function that looks like y = mx + b,

The m represents the slope or the constant rate of change

The b is the y-intercept or the initial value

Now we know that a function that is in the form y = mx + b represents a linear relationship between x and y.

A function that is written in form y = mx + b represents a linear relationship between x and y.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 184 Exercise 1 Answer

Given

Height 8 inches

Triangle base is 15 inches

Show the graph of the function?

First we have to graph the new function. The new slope is going to be \(\frac{3}{5}=\frac{1}{5}\)

Since we know that there is no initial value than we know that the equation of the function is \(y=\frac{1}{5} x\).

For the last part we simply have to substitute the x with 110 and calculate from the equation.
​

​
\(y=\frac{1}{5} .110\)

y = 22

The height of the ramp is going to be 22 inches when the base length is 110 inches.

New slope \(\frac{1}{5}\)

New equation \(y=\frac{1}{5} x\)

The height of the ramp is going to be 22 inches when the base length is 110 inches

Page 185 Exercise 2 Answer

Given

After 2 weeks he feed to dog is \(8 \frac{1}{2}\)

After 5 weeks he feed to dog is \(21 \frac{1}{4}\)

Construct the function in the form of mx + c ?

We are simply going to subtract the amount he used after 3 weeks from the amount that her used after 5 weeks
​
d = 21.25 − 8.5

d = 12.75
​
Now we got the amount of food that he used in time period of 3 weeks.

Simply divide the result that we got with 3

d ÷ 3 = 12.75 ÷ 3 = 4.25.

Since we know the slope now, we need to find the initial value to be able to write the equation for the function.

To do this we can simply subtract 4.25 for every week that he fed the dogs from the value of food that he used after 2 weeks.

8.5 − 2.4.25 = 0

Now we know that the initial value is 0

Simply write equation

y = 4.25x

So, function is y = 4.25x

Envision Math Grade 8 Exercise 3.4 Use Functions To Model Relationships

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 185 Exercise 3 Answer

Given

Construct the function in the form of mx + b ?

If we would want to write the function for given graph than we simply have to find what is the slope of the given function, and the initial value of the function.

The initial value of the function is 1.

This means that printer needs 1 minute to warm-up before each printing.

Now to find the slope we can use 2 points that are already marked on the graph. These points are (10,2) and (30,4)

Now that we know the slope and the initial value we can simply write equation for given function

y = 0.1x + 1

y = 0.1x + 1

Page 184 Exercise 1 Answer

Given

Find the initial function of all function and proportional relationship?

The initial value of all linear functions that show a proportional relationship. Proportional relationships always start in the origin.

When we calculate y-intercept then we substitute x = 0. Which is same as initial values.

The initial value is same as y-intercept.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 186 Exercise 1 Answer

Given

How can you use a function to represent a linear relationship?

When we use an equation of a function that looks like y = mx + b,

The m represents the slope or the constant rate of change

The b is the y-intercept or the initial value

Now we know that a function that is in the form y = mx + b represents a linear relationship between x and y.

A function that is written in form y = mx + b represents a linear relationship between x and y.

Page 186 Exercise 3 Answer

Given

Find the initial function of all function and proportional relationship?

The initial value of all linear functions that show a proportional relationship is 0.

Proportional relationships always start in the origin.

The initial value is 0.

Functions And Modeling Relationships Grade 8 Exercise 3.4 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 186 Exercise 5 Answer

Given

Fill the missing data?

As we can see from the table both the x and y are increasing linearly. So we know that in the blank box in x row the missing number is 30 because the x is increasing by 10.

Same thing we can do for the y, we can see that y is increasing by 5. We simply need to add 5 to the third value in the y row and we get the last row.

20 + 5 = 25

The missing value of y is 25

The missing value of x is 30, and The missing value of y is 25.

Page 186 Exercise 6 Answer

Given

The data is 5

Find the equation form of y = mx + b ?

We can simply use two ordered pairs to find the equation that is described by the data in item 5.

We are going to be using points (10,10) and (20,15)

The way we find the slope is by the formula:

Now we can use the slope that we just calculated to find the initial value. We do this by calculating either one of the points.
​
10 = 0.5.10 + b

10 = 5 + b

10 − 5 = b

b = 5
​
Now we have everything we need to write the function for given line.

y = 0.5x + 5

So, equation of linear function is y = 0.5x + 5

Envision Math 8th Grade Exercise 3.4 Step-By-Step Functions Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 187 Exercise 7 Answer

Given

The points is (4,19) and (9,24)

Find the equation form of y = mx + b ?

We are going to be using points (4,19) and (9,24)

The way we find the slope is by the formula:
​

Now we can use the slope that we just calculated to find the initial value. We do this by calculating either one of the points.
​
19 = 4 + b

19 − 4 = b

b = 15
​
Now we have everything we need to write the function for given line.

y = x + 15

So, function is y = x + 15

Page 187 Exercise 8 Answer

Given

The line passing through (4.5,4.25) with y-intercept 2.5

Find the equation form of y = mx + b ?

We are going to be using points (4.5,4.25) with y-intercept 2.5

Since we know b in given task we can simply use the points through which the line passes and put the values into the equation to get the slope

−4.25 = 4.5m + 2.5

Subtract 2.5 from both sides of the equation
​
−4.25 − 2.5 = 4.5m

−6.75 = 4.5m
​
Now simply divide both sides of the equation with 4.5.

m = −1.5

The linear function we are looking for is y = −1.5x + 2.5

So, equation is y = -1.5x + 2.5

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 187 Exercise 9 Answer

Given
​
t = 0

at 8 Seconds

840 feet
​
Find the equation form of y = mx + b ?

We simply have to divide the distance that car has traveled with the time has passed which is 8 seconds.

840 ÷ 8 = 105

Now we know how much distance can the car pass in 1 seconds.

We can now simply write the equation because we know that the initial value is 0

d = 105t

Linear function is d = 105t

How To Solve Exercise 3.4 Functions In Envision Math Grade 8

Page 187 Exercise 10 Answer

Given
​
t = 0

after 56 minutes

8 inches
​
Find the equation form of y = mx + b?

In this task we must simply find how much time is needed for 1 inch of water to get into the bucket. We do this by dividing the amount of inches in the bucket.

56 ÷ 8 = 7

Now we know that it is needed 7 minutes for each inch that drips into the bucket.

Simply write the equation because we know that there is no initial value, in other words the initial value is 0.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 187 Exercise 11 Answer

Given

Find the equation form of y = mx + b ?

To find the linear function in the form of y = mx + b we needed to read two points from the graph and calculate the slope so we can find the initial value.

We are going to be using points (1,10) and (4,16)

The way we find the slope is by the formula:
​

Now we can use the slope that we just calculated to find the initial value. We do this by calculating either one of the points.
​
10 = 2 + b

10 − 2 = b

b = 8
​
Now we have everything we need to write the function for given line.

y = 2x + 8

y = 2x + 8

Page 187 Exercise 12 Answer

Given

Company charges $6.50

Flat fee $3.99

Find the equation form of y = mx + b ?

We can simply write the linear function from the data that we got in the task.

The sweatshirts are going to be our Variable x

And the shipping fee is going to be b

y = 6.5x + 3.99

y = 6.5x + 3.99

We need to describe how the linear function would change the shipping charge.

If the shipping charge would apply to each sweatshirt then we would have to change our linear function. If the shipping charge is applied to each sweatshirt than we would simply have to add 3.99 to the factor next to x, so that the shipping fee is applied to every single sweatshirt.

y = (6.5 + 3.99) × x

The linear function would change from y = 6.5x + 3.99 to y = (6.5 + 3.99)x

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 187 Exercise 13 Answer

Given:

1 poster + 6 comics for $12.75 and 1 poster + 13 comics for $19.75

We consider:

y as the total cost

x as the cost of comic books

m as the number of comic books.

b as the cost of posters.

We get two functions from the given data:

12.75 = 6m + 1

And

19.75 = 13m + 1

Subtracting both the equations we get:

7x = 7

x = 1

The cost of one comic book is $1.

Substituting the value of x in first equation we get:

b = 6.75

Therefore the required equation is:

y = m + 6.75

The required linear function is y = m + 6.75

Given:

The initial value of the package sold by another seller is $7.99.

We consider:

y as the total cost

x as the cost of comic books

m as the number of comic books

b as the cost of posters.

Since the shop sells poster with a comic book, initial value is the cost of one comic book plus one poster.

7.99 = x + b

We get:

x = 1

In a, the cost of one book plus poster = $1 + 6.75 = $7.75 which is lesser than $7.99.

Therefore, the seller B has the best deal.

In a, the cost of one book plus poster = $1 + 6.75 = $7.75 which is lesser than $7.99. Therefore, the seller B has the best deal.

Envision Math Grade 8 Chapter 3 Exercise 3.4 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 188 Exercise 15 Answer

Given:

To find the constant rate of change we simply have to use two points that we can read from the graph.

The constant rate of change is 25. This means that one cubic yard of mulch costs $25.

The constant rate of change is 25 and that means that one cubic yard of mulch costs per 25$.

Given that, the graph shows the relationship between the number of cubic yards of mulch ordered and the total cost of the mulch delivered.

We need to find the initial value. Also, we need to explain what it represents.

The given graph is,

The given graph is,

It is visible from the graph that the initial point on the graph is (0,50)

The initial value is nothing but the starting point of the graph.

Therefore, the initial value is found to be $50 for 0 mulch ordered.

Thus, this initial value represents the shipping fee incurs for each shipment done.

The initial value is $50. This initial value represents the shipping fee for each shipment.

Page 188 Exercise 17 Answer

Given that, some eighth-graders are making muffins for a fundraiser. They have already made 200 muffins and figure they can make 40 muffins in an hour.

We need to write a linear function in the form y = mx + b that represents the total number of muffins the students will make, y, and the number of additional hours spent making the muffins, x

Also, we need to find how many additional hours would the students spend to make 640 muffins.

The linear function is of the form y = mx + b

Here, b = 400 since they have already made those muffins.

Also, they can make 40 muffins in an hour.

Thus, the value of m = 40

Substituting this in the equation, we get,

y = 40x + 200

Finding the additional hours would the students spend to make 640 muffins, we get,
​
​
Thus, it took 11 more hours to make 640 muffins.

The linear equation will be y = 40x + 200

11 additional hours are needed to make 640 muffins.

Envision Math Exercise 3.4 Functions Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Exercise 3.4 Page 188 Exercise 17 Answer

Given:

Eight graders made 200 muffins. They can make 40 muffins per hour.

We consider:

Initial value as 200 muffins.

Let, x is the estimate, 40 muffins per hour.

Now we simply write linear function:

y = 40x + 200

Therefore the required linear function is y = 40x + 200

y = 40x + 200 From(A)

We consider:

Let y= 640

Putting this value in the linear function obtained from Part (A):
​
640 = 40x + 200

640 − 200 = 40x

40x = 440
​
x = 11

The students are going to need 11 additional hours if they want to make 640 muffins.

The students are going to need 11 additional hours if they want to make 640 muffins.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1

Page 177 Exercise 2 Answer

The relation shown in the arrow diagram is a function.

We can see that there are multiple arrows that go into 10 which is in the outputs on the right side.

When a relation is a function than all of the x-coordinates will have unique corresponding y-coordinate.

The given arrow diagram is a function.

Page 177 Exercise 4 Answer

Given :

We need to check whether the relation shown in the table is a function or not.

We plot the graph of the ordered pairs into the graph.

As we can see the relation is a function because the graph is a straight line.

According to the definition of the linear function, the graph of the function should always be a straight line.

Therefore, the given relation is a function by the definition of linear function.

Envision Math Grade 8 Volume 1 Chapter 3 Topic 3.1 Functions Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1 Page 178 Exercise 1 Answer

Given: three plans are proposed by Sarah, Gene and Paul.

y represents amount of money raised and x represents number of hours worked.

we have to show, whether each proposal is a linear function or not.

Sarah’s proposal: is a graph, the graph for Sarah’s proposal is a straight line, therefore, it represents a linear function.

Gene’s proposal is a table

from the table it is clear that,

for every 5 hours money raised changes by 35

therefore, rate of change \(\frac{35}{5}=7\) which makes it a linear function.

Paul’s proposal is: y = 10x + 7

which is in the form of linear equation y=mx+c

therefore, it is a linear function.

hence, all the three proposals are linear functions.

All three proposals are linear functions.

Given: three proposals are given for class fund raiser.

we need to find out the starting money which the class have in their account.

From the Paul’s equation y = 10x + 7

it is clear that the y-intercept is 7

i.e., when x = 0,y = 7

therefore, starting money = $7

from Sarah’s graph it is clear that starting money in the account is = $7 from

Gene’s table:

for every 5 hours there is $35 increase in money

therefore, rate of change is \(\frac{35}{5}=7\)

now to get the starting money subtract 5 multiply by rate from money raised in 5 hours

we get, 42 = 7(5) + c

c = 7

Therefore, it is clear that the starting money in the class account was = $7.

There was $7 in the class account.

Three fund raising proposals are given.

First, we will select a specific time and see how much money is earned at that time.

From Sarah’s graph the easiest point to read is 7 hours.

hence, we will check after 7 hours how much money each of the proposal would earn.

From Sarah’s proposal they would earn about $90 after 7 hours.

From Gene’s table, we can see that after 10 hours they would raise $77.

From Paul’s proposal we have the equation,

y = 10x + 7

substituting x = 7 we get,

y = 10(7) + 7 = 77

Therefore, after 7 hours they would raise $77 from Paul’s proposal.

Hence, we can say that Sarah’s proposal raises money at the fastest rate.

Sarah’s proposal raises money at the fastest rate.

Three fund raising proposals are given.

we have to recommend a proposal which will raise fastest.

we will recommend that proposal which raises the money at the fastest rate.

We would recommend Sarah’s proposal.

As Sarah’s proposal raises the money at the fastest rate.

Therefore, they would have to work for less hours in order to get $200.

We would choose Sarah’s proposal because it raises the money at the fastest rate.

Envision Math Grade 8 Topic 3.1 Use Functions To Model Relationships

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1 Page 179 Exercise 1 Answer

The video mentioned above shown some images that predict the amount of water we use every day.

The reason is for knowing the water wastage we do every day.

There is more percent of people who didn’t have enough water to drink. Hence, water conservation is necessary.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “How much water do I use while brushing my teeth?”.

“How much water do I use while brushing my teeth?”.

This is the question that made up my mind after watching this video.

Page 179 Exercise 2 Answer

The video mentioned above shown some images that predict the amount of water we use every day.

The reason is for knowing the water wastage we do every day.

There is more percent of people who didn’t have enough water to drink. Hence, water conservation is necessary.

You may frequently utilize visual cues to figure out what’s in the shot and what the remainder of the thing could appear like.

The first question that comes to my mind after watching this video is “How much water do I use while brushing my teeth?”.

The main question that I will answer that I saw in the video is “How much water do I use while brushing my teeth?”.

Page 179 Exercise 3 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The reason is for knowing the water wastage we do every day.

There is more percent of people who didn’t have enough water to drink. Hence, water conservation is necessary.

The first question that comes to my mind after watching this video is “How much water do I use while brushing my teeth?”.

An answer that I was predicted to this main question is four cups of water.

An answer that I was predicted to this main question is four cups of water I use while brushing my teeth. I found my answer by calculating the number of cups I use daily.

Functions And Modeling Relationships Grade 8 Topic 3.1 Envision Math

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1 Page 179 Exercise 5 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

A number that I know which is too small to be the answer is one cup since at least one cup of water is necessary to rinse our mouth after brushing.

A number that is too large to be the answer is 10 cups of water since we can even take a quick bath with those amount of water.

My prediction is that I use 4 cups of water every day while brushing.

Plotting my prediction on the same number line, I get,

Page 180 Exercise 7 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

To get the information I need regarding the amount of water usage, I can use a weighing machine for calculating mine and internet sources for calculating other’s usage.

This will determine the amount of water wastage I do each year.

A weighing scale can be used to get the information I need.

Envision Math Grade 8 Chapter 3 Topic 3.1 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1 Page 180 Exercise 9 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

The main question that comes to my mind after watching this video is “How much water do others use on average while brushing their teeth?”.

An answer to this main question is two cups of water.This is less than my prediction.

An answer to this main question is two cups of water. This is less than my prediction.

Envision Math 8th Grade Topic 3.1 Step-By-Step Functions Solutions

Page 181 Exercise 10 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The main question that comes to my mind after watching this video is “How much water do others use on average while brushing their teeth?”.

An answer to this main question is two cups of water.

An answer that I saw in the video is also the same.

The answer that I saw in the video is people on average use two cups of water while brushing their teeth.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1Page 181 Exercise 11 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “How much water do I use while brushing my teeth?”.

An answer that I was predicted to this main question is four cups of water.

An answer that I saw in the video is two cups of water.

This is because I use more cups of water to wash my teeth than others.

My answer doesn’t match the answer in the video. This is because I use more cups of water to wash my teeth than others.

Page 181 Exercise 12 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

The first question that comes to my mind after watching this video is “How much water do I use while brushing my teeth?”.

An answer that I was predicted to this main question is four cups of water.

An answer that I saw in the video is two cups of water.

This is because I use more cups of water to wash my teeth than others.

I have to change my model now that I know the answer. I have to use less amount of water to conserve water.

Yes, I would change my model now that I know the answer.

Envision Math Grade 8 Topic 3.1 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1 Page 182 Exercise 14 Answer

Informally, a conjecture is simply making judgments over something based on what you understand and monitor.

A conjecture is a declaration that is thought to be accurate based on data.

In general, a conjecture is your view or an informed guess over something you recognize.

You can’t indicate any of it; you simply observed a pattern and conclude.

The first question that comes to my mind after watching this video is “How much water do I use while brushing my teeth?”.

An answer that I was predicted to this main question is four cups of water.

I have used the units as the number of cups and the method I used is to calculate the number of cups of water I use to determine how much I use while brushing my teeth.

The calculations differ based on the amount of water. This helps me to know that when the amount of water increases the amount of water I conserve decreases.

Envision Math Topic 3.1 Functions Detailed Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 3 Use Functions To Model Relationships Topic 3.1 Page 182 Exercise 15 Answer

A conjecture is a result or statement in math that is thought to be valid based on basic evidence to back it up but for which no evidence or falsifiability has ever been produced.

A conjecture is nothing but a conclusion we made up where it doesn’t have any proof to make it false.

I use four cups of water every day to brush my teeth while on average he uses two cups every day.

Thus, he saves two cups of water every day.

Hence, in a year, he save 2 × 365 = 730 cups of water.

Therefore, \(\frac{730}{4}=\frac{365}{2}=182.5\) liters of water.

He saves 182.5 liters of water every day while brushing his teeth.