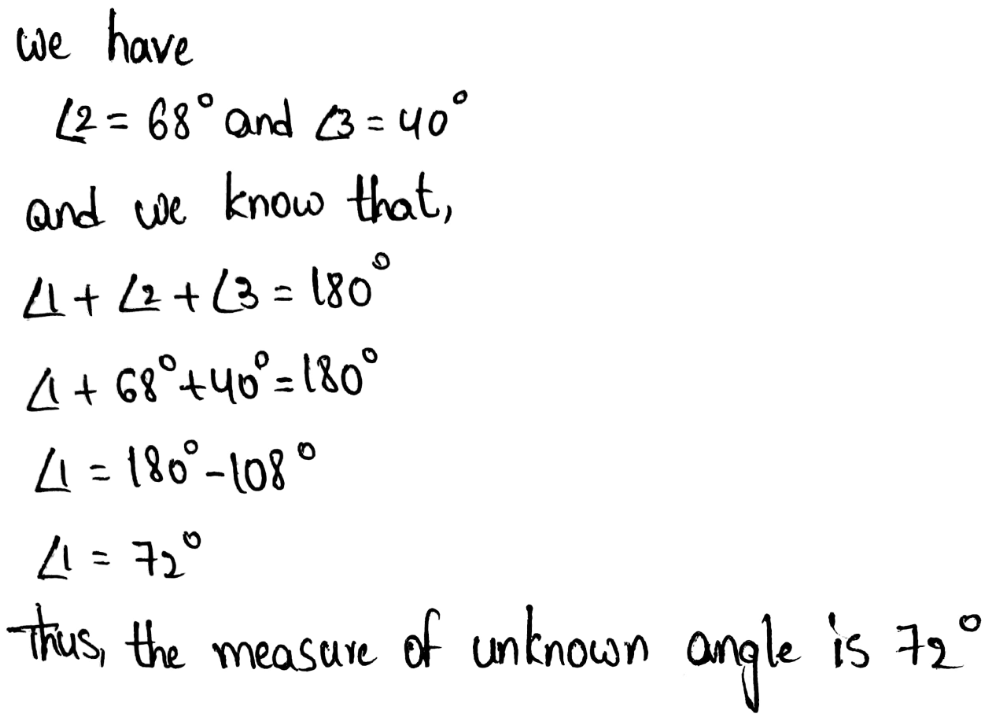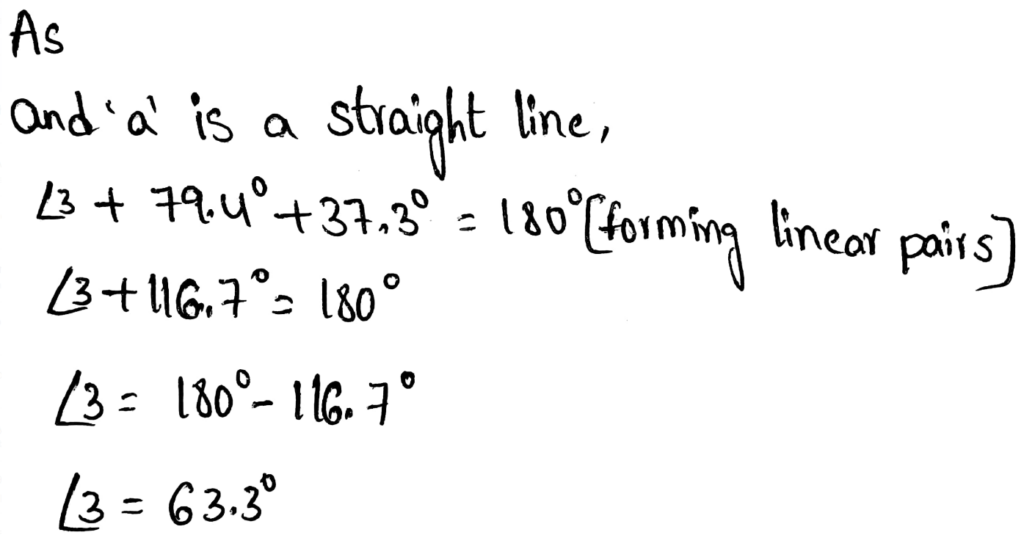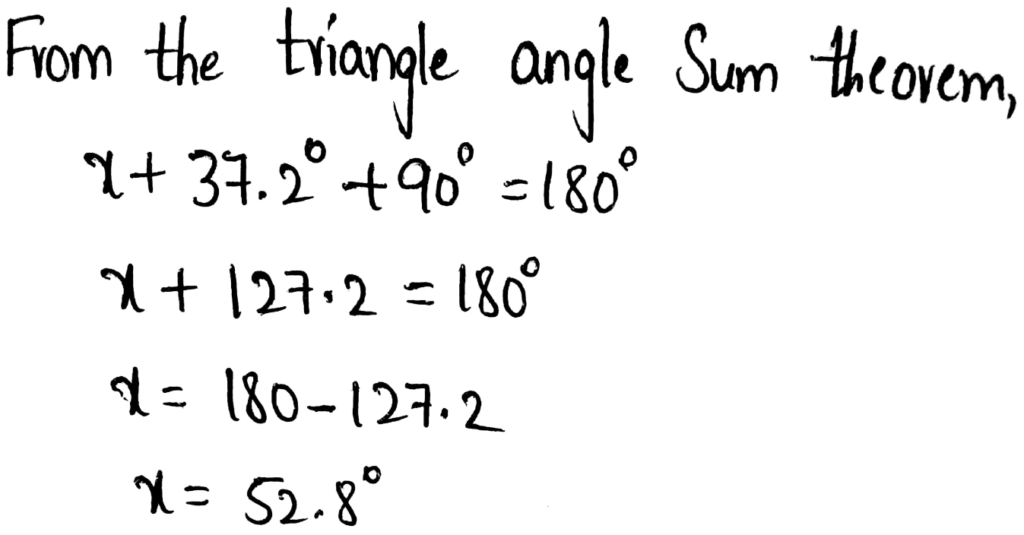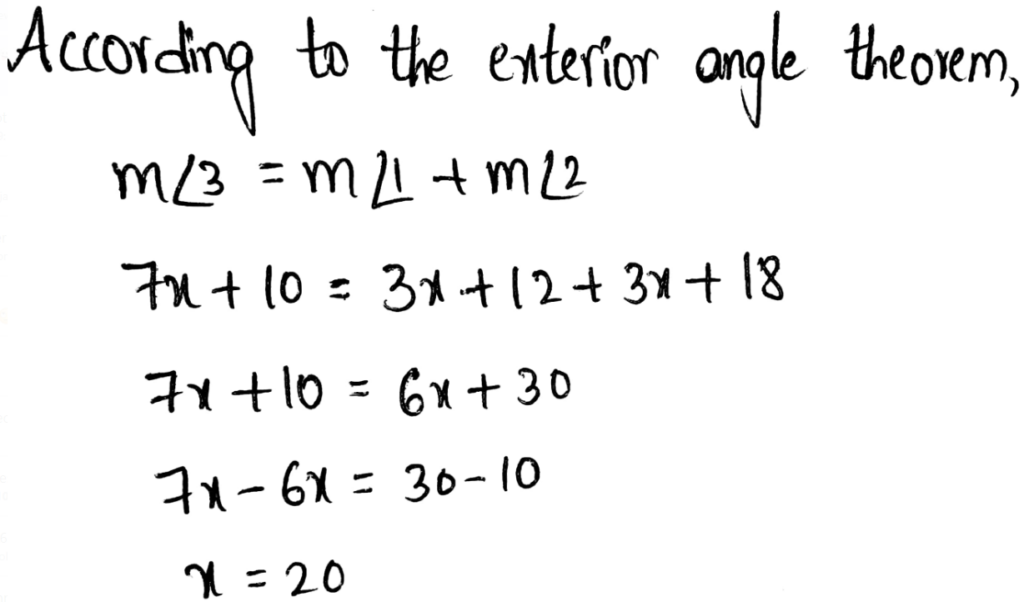Schindler

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

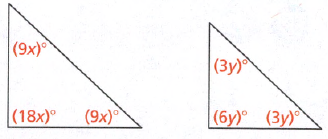
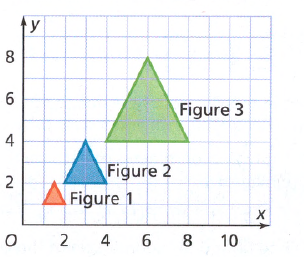
Page 365 Essential Question Answer

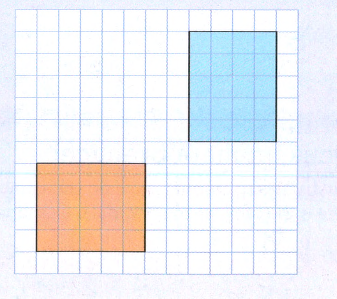
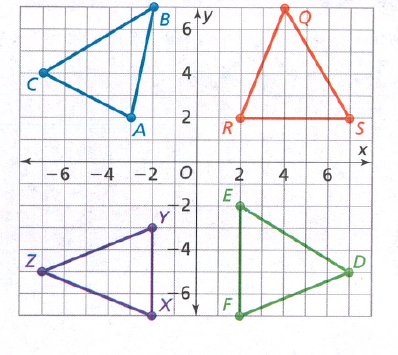
Given: Two figures.

To: How can you show that two figures are either congruent or similar to one another?

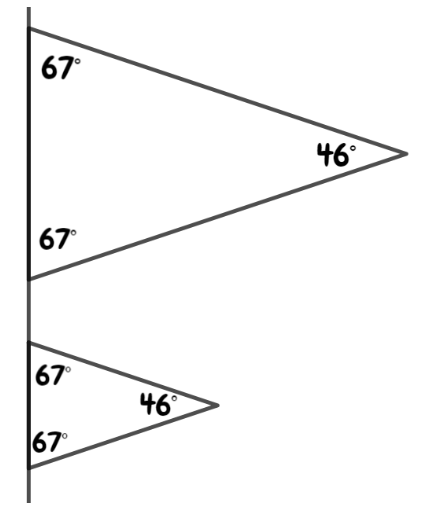
In similar figures, the ratio of corresponding sides are equal. Also the included angles are equal.

In congruent figures, all the sides as well as the angles are equal.

In similar figures, the ratio of corresponding sides are equal. Also the included angles are equal.

In congruent figures, all the sides as well as the angles are equal.

Envision Math Grade 8 Volume 1 Chapter 6 Review Exercise Solutions

Page 365 Exercise 1 Answer

Given: Vocabulary words with their definition.

To: Complete each sentence by matching each vocabulary word to its definition.

Assume pairs of lines are parallel.

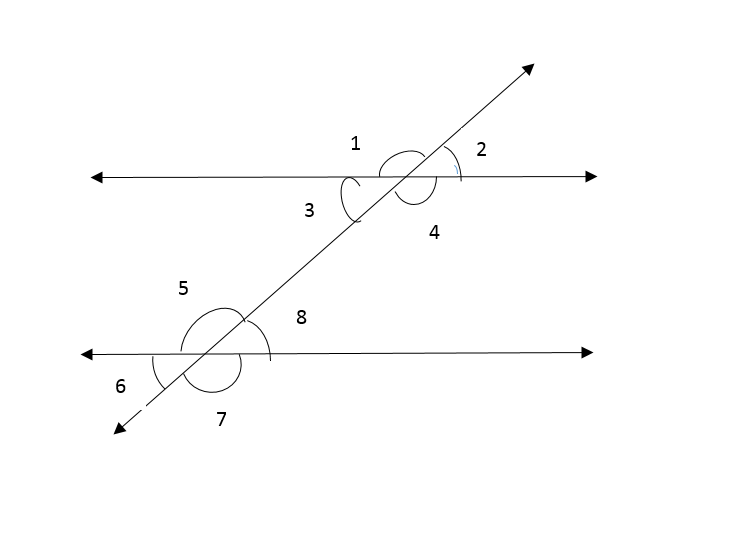
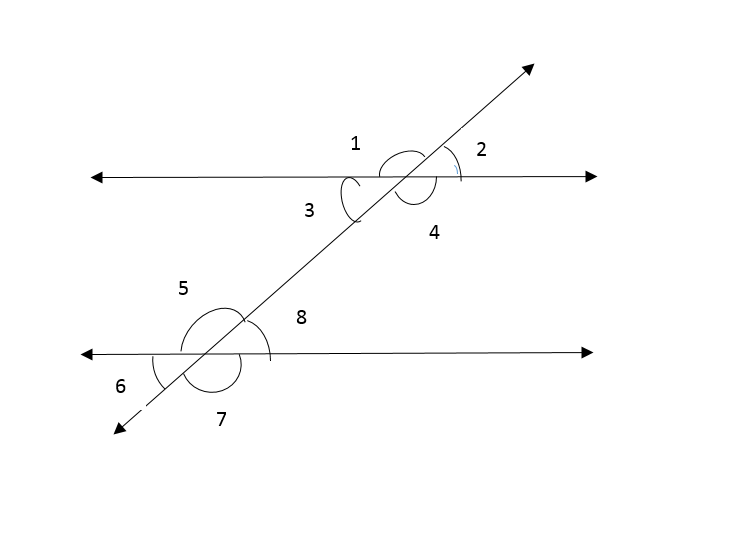
Alternate interior angles: Lie between pair of lines and on the opposite sides of the transversal.

Same side interior angles: Lie between pair of lines and on the same side of the transversal.

Corresponding angles: Lie on the same side of the transversal and in corresponding position.

An exterior angle of a triangle: Is formed by a side and an extension of an adjacent side of a triangle.

Remote interior angles of a triangle: Are two adjacent interior angles corresponding to each exterior angle of a triangle.

Alternate interior angles: Lie between pair of lines and on the opposite sides of the transversal.

Same side interior angles: Lie between pair of lines and on the same side of the transversal.

Corresponding angles: Lie on the sme side of the transversl and in corresponding position.

An exterior angle of a triangle: Is formed by a side and an extension of an adjacent side of a triangle.

Remote interior angles of a triangle: Are two adjacent interior angles corresponding to each exterior angle of a triangle.

Congruence And Similarity Envision Math Review Exercise Answers

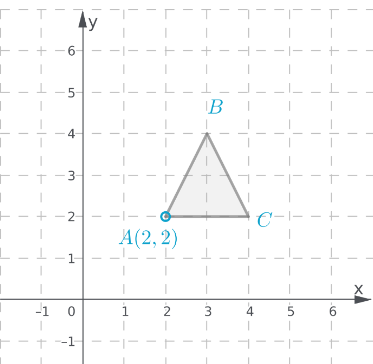
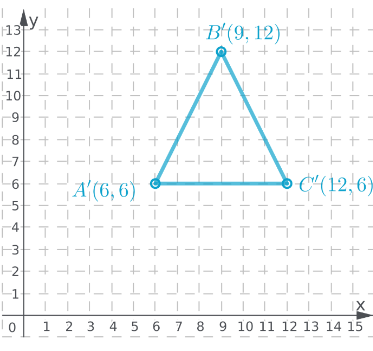
Page 365 Use Vocabulary In Writing Answer

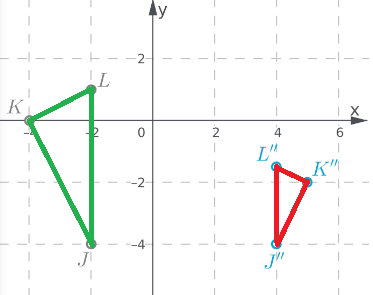
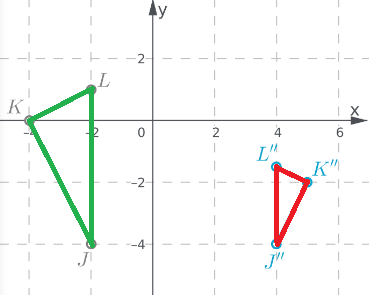
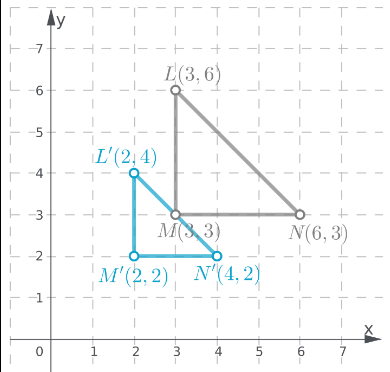
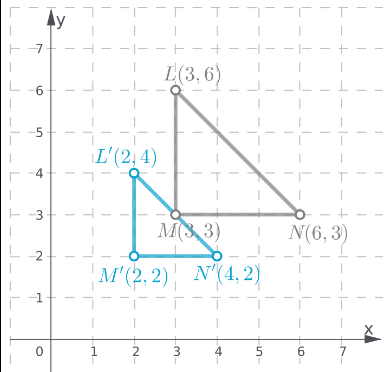
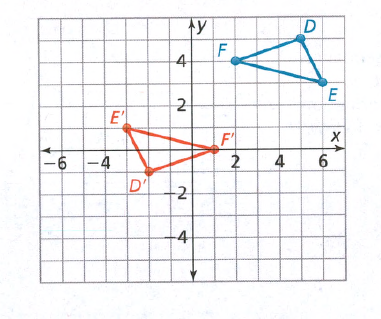
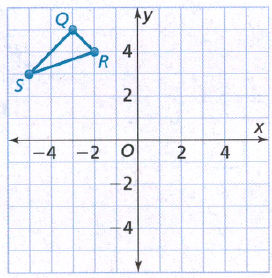
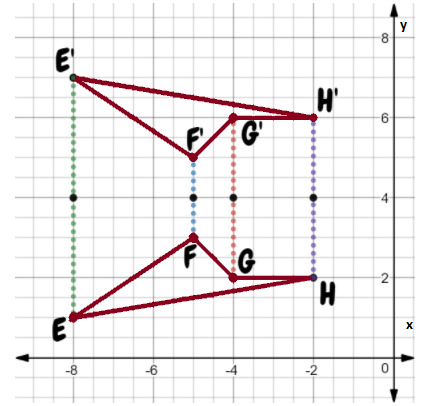
Given:

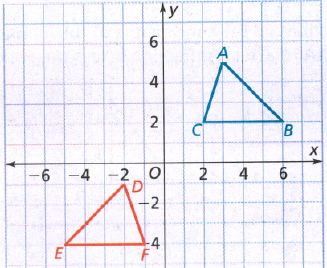
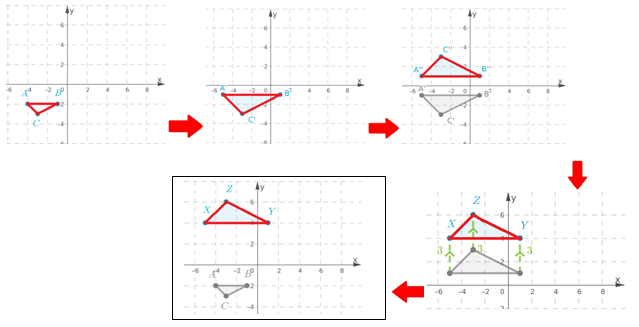
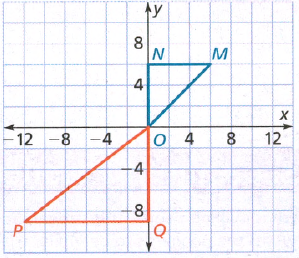
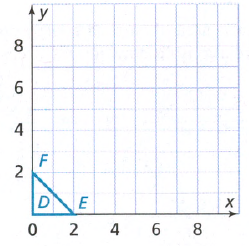
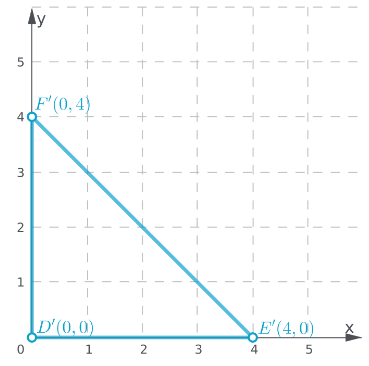
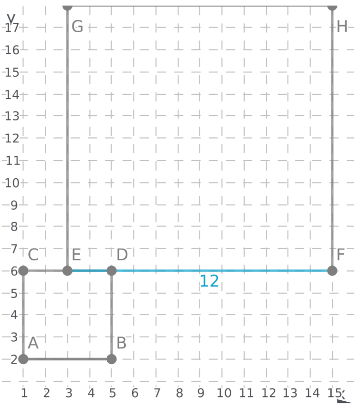
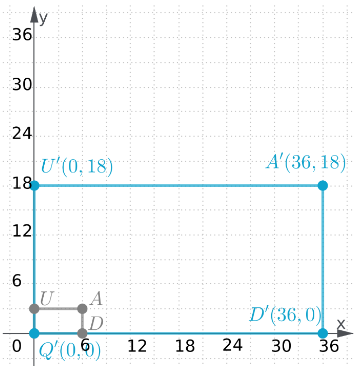
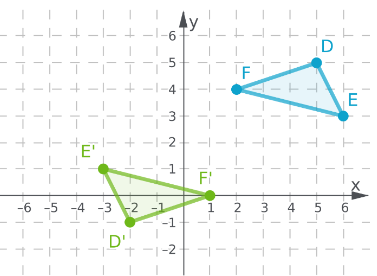
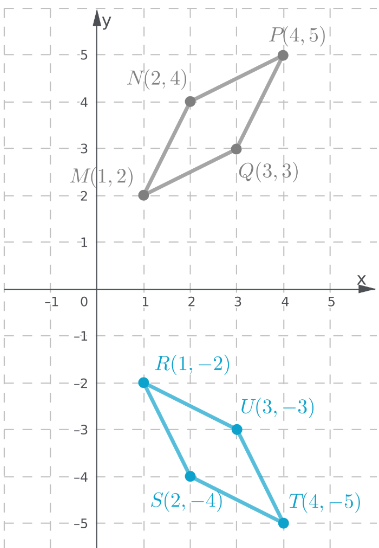
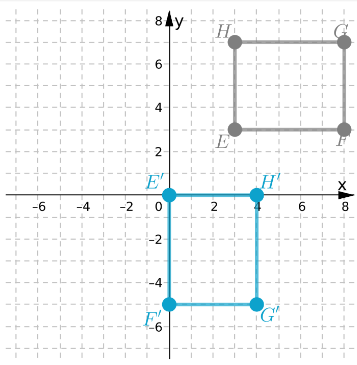
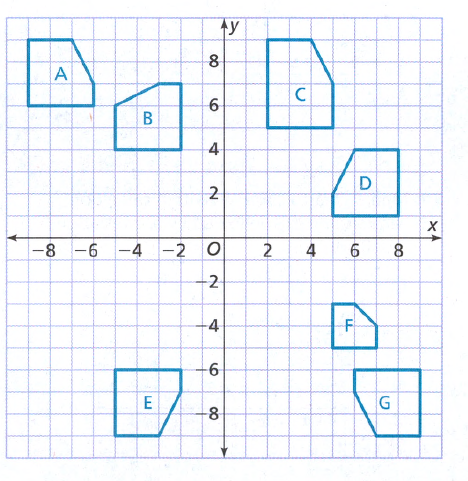
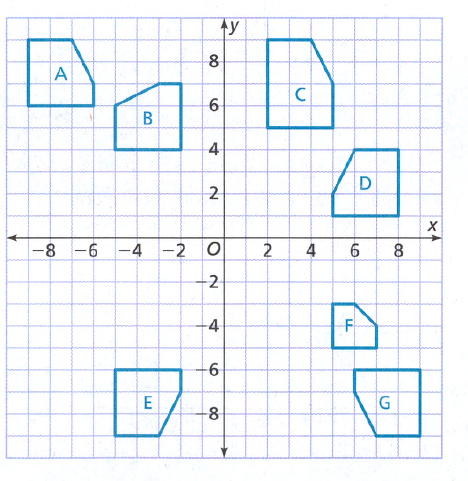
To: Prove that △ABC is congruent to △DEF

Step formulation: Find the lengths of the sides and then compare. and Use vocabulary terms from this Topic in your description.

In ΔABC, calculate the lengths of the sides by putting the coordinates in the above formula.

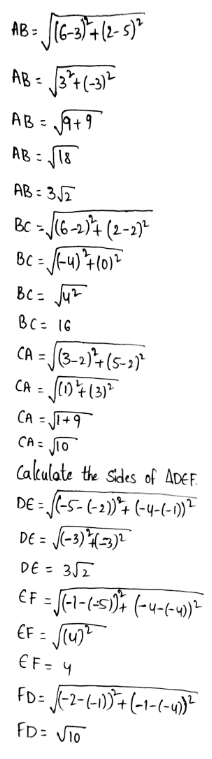
As all the three sides of both the triangles are equal, hence these are congruent triangles.

By comparing the lengths of the sides of both the triangles, these are found to be congruent.

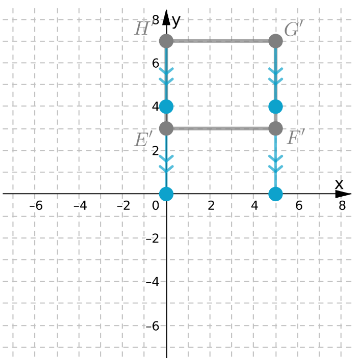
Page 366 Exercise 1 Answer

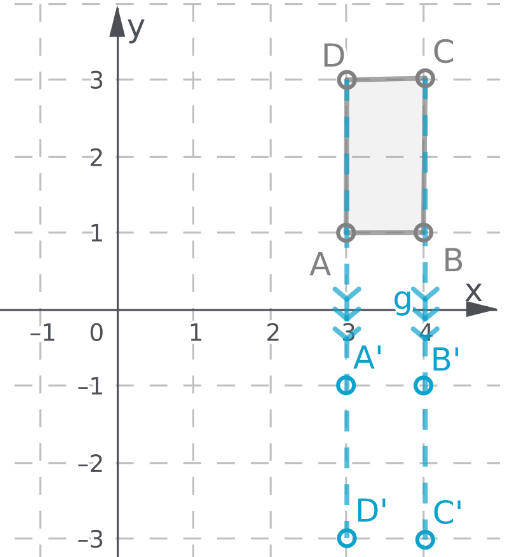
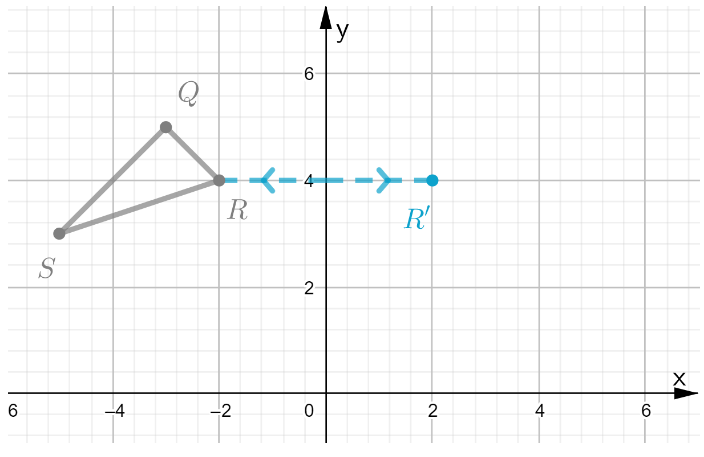
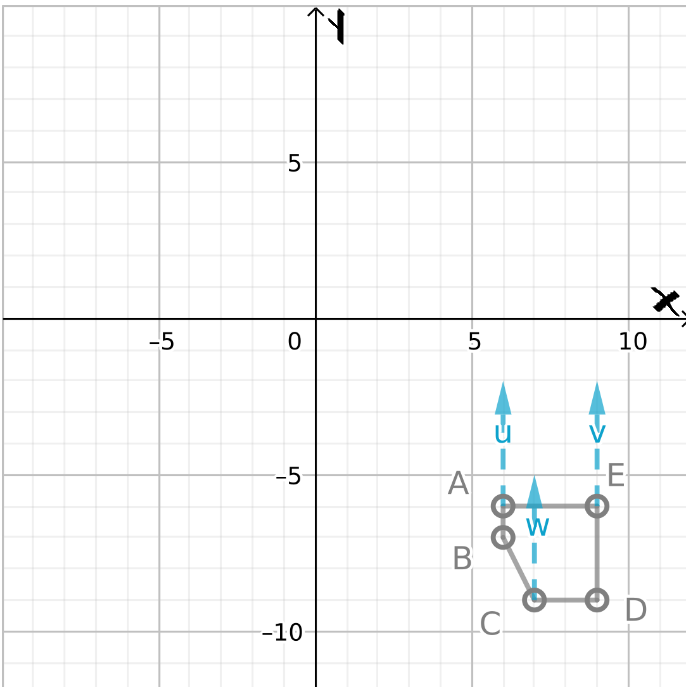
Given:

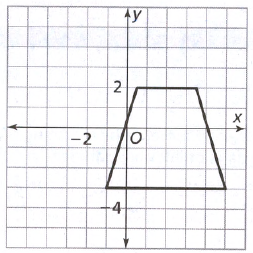
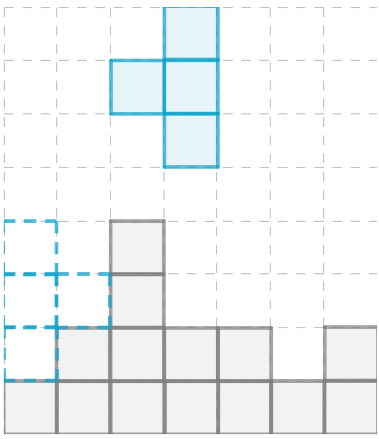
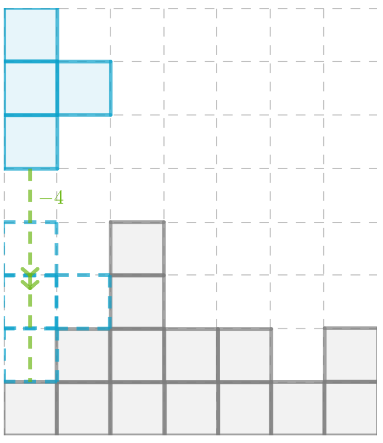
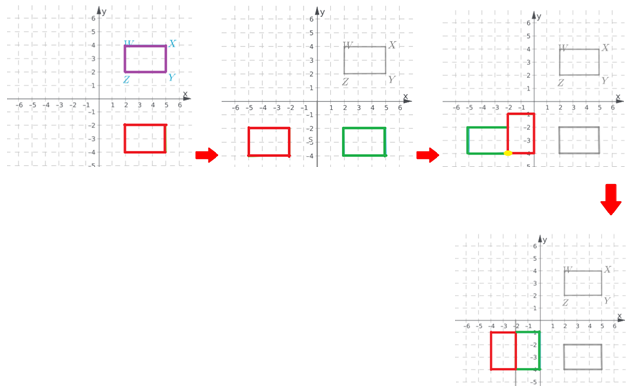
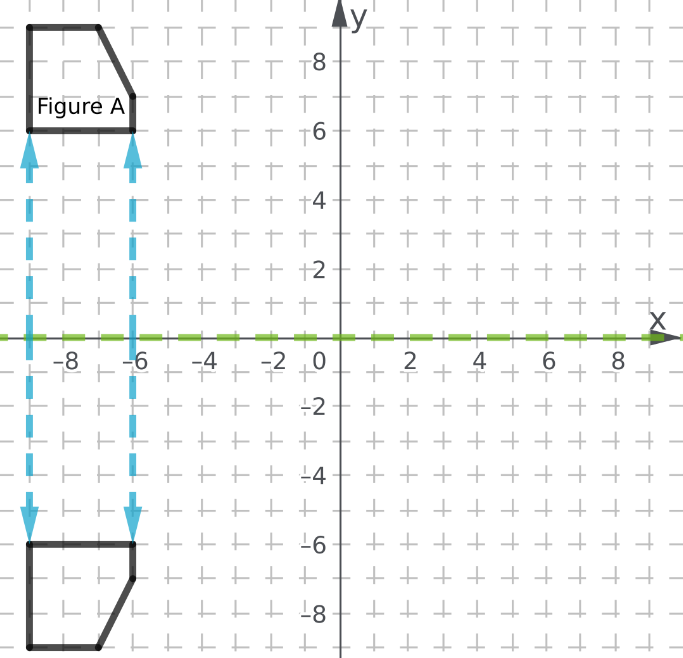
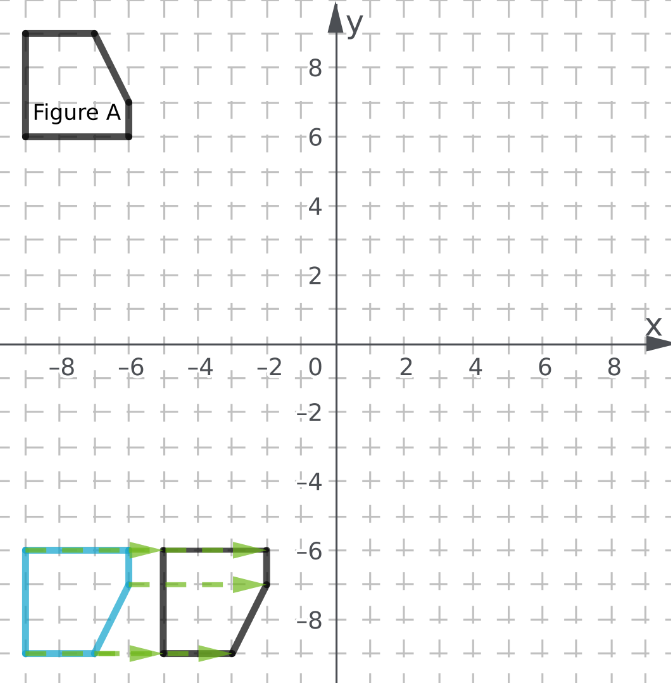
To: Find the final image when there is a translation of 3 units to the left and then 2 units to up.

Step formulation: Perform the translation step by step as given in the question.

First move each coordinate of the figure to the left by 3 units.

There will be change only in x coordinate as the translation is in only x direction.

And then add 2 to the y coordinate as the change is along y direction.

New coordinates are:
​
(0.5−3,2+2) = (−2.5,4)

(3.5−3,2+2) = (0.5,4)

(−1−3,−3+2) = (−4,−1)

(5−3,−3+2) = (2,−1)

The final image formed is:

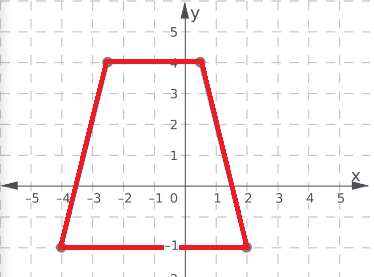
The final image when there is a translation of 3 units to the left and the 2 units to up is:

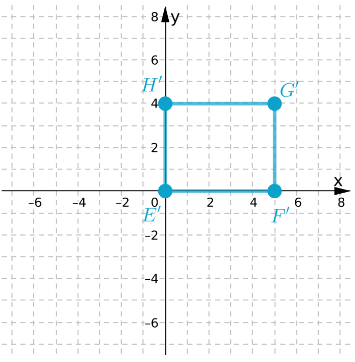
Page 366 Exercise 1 Answer

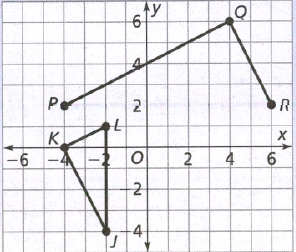
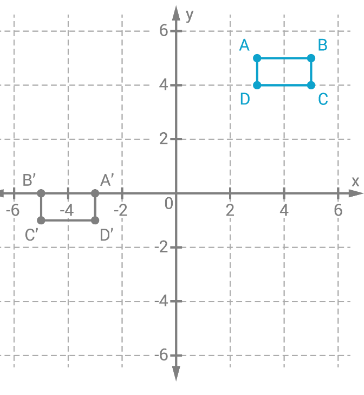
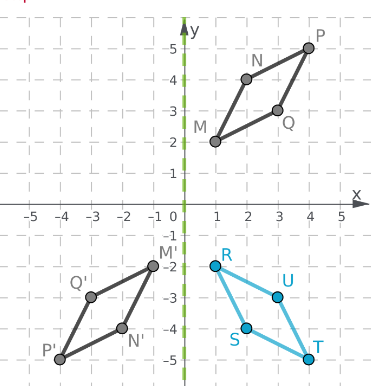
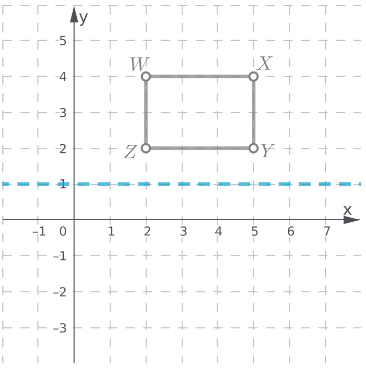
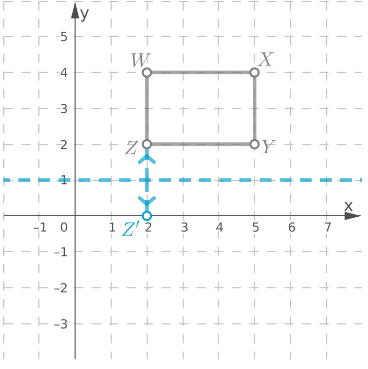
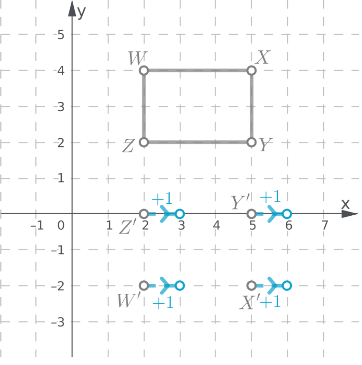
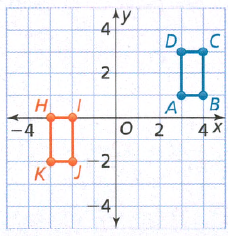
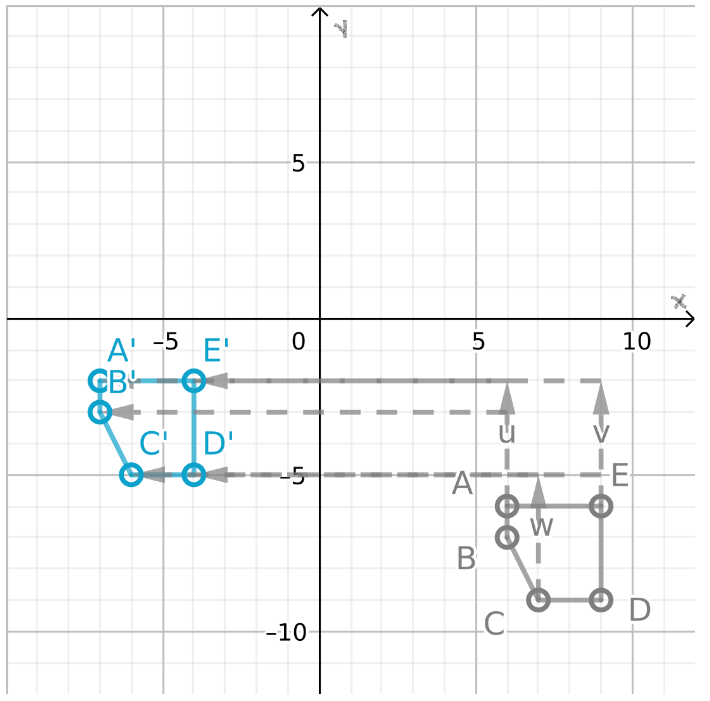
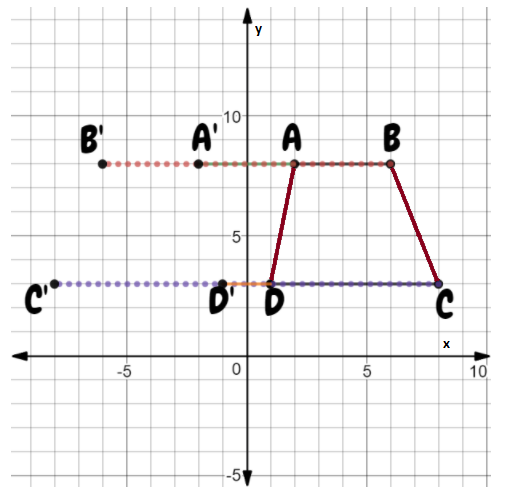
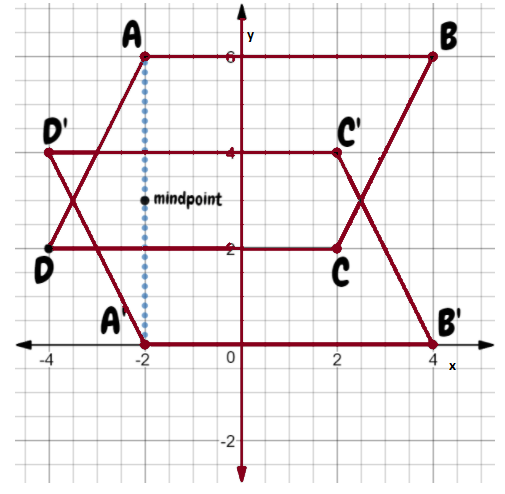
Given: A quadrilateral WXYZ is plotted on a graph with XY plane.

To find: The coordinates of the image of rectangle WXYZ after a reflection across the x−axis

We will plot the image of reflection of each point following the rule of reflection i.e. the reflected figures are at the same distance from the line of reflection but on opposite side.

A reflection is a transformation that flips a figure across a line of reflection. The preimage and image are the same distance from the line of reflection but on opposite sides.

So, figures have the same size and the same shape but different orientation after reflection.

Hence, figures have the same size and the same shape but different orientation after reflection.

Envision Math Grade 8 Chapter 6 Review Explained

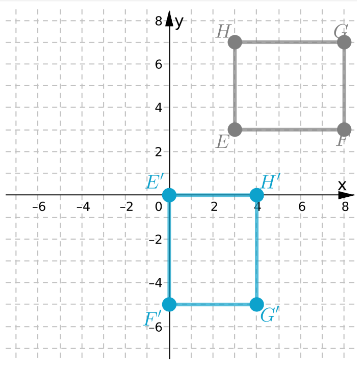
Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Review Exercise Page 366 Exercise 2 Answer

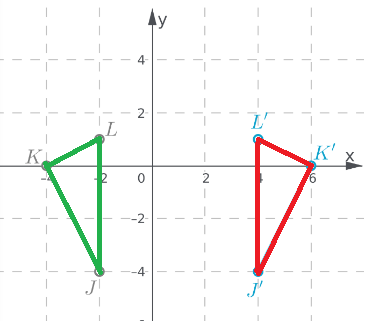
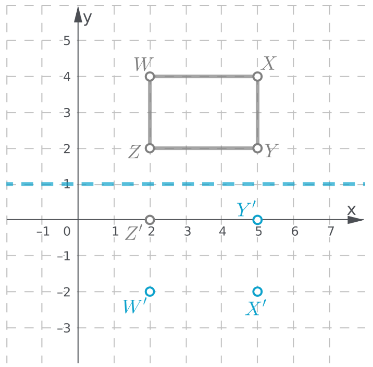
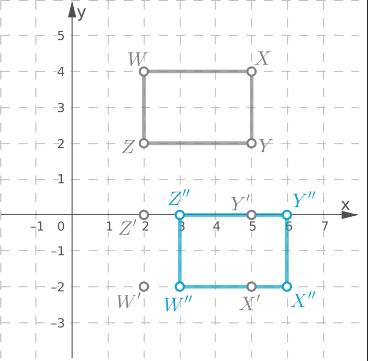
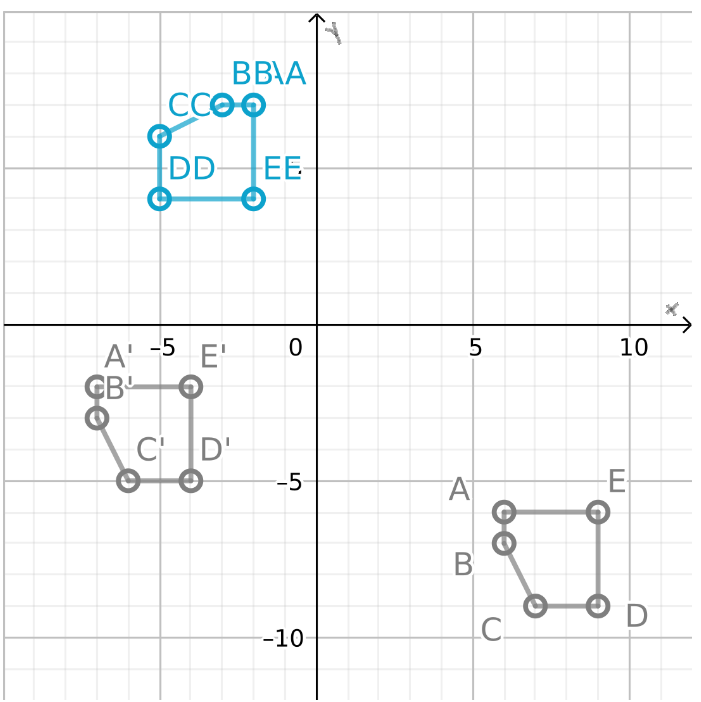
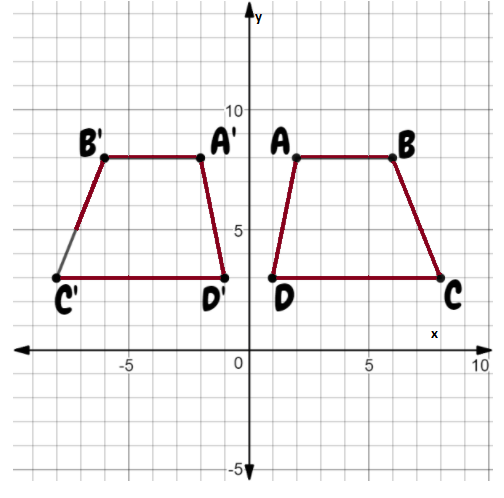
Given: A quadrilateral WXYZ is plotted on a graph with XY plane.

To find: The coordinates of the image of rectangle WXYZ after a reflection across the y−axis

We will plot the image of reflection of each point following the rule of reflection i.e. the reflected figures are at the same distance from the line of reflection but on opposite side.

Graph the given quadrilateral WXYZ

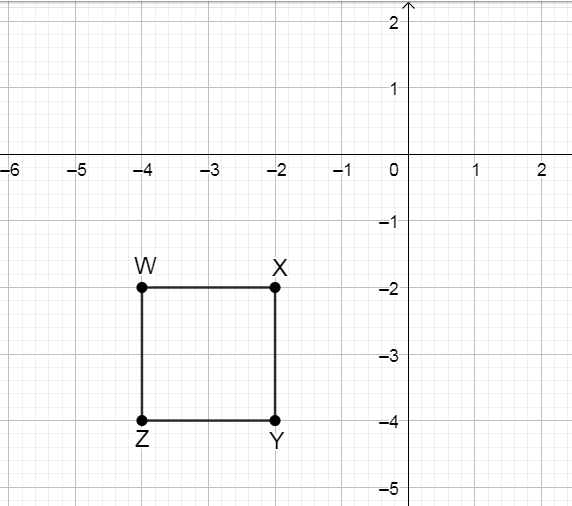
Image of each vertex of WXYZ when line of reflection is y – axis.

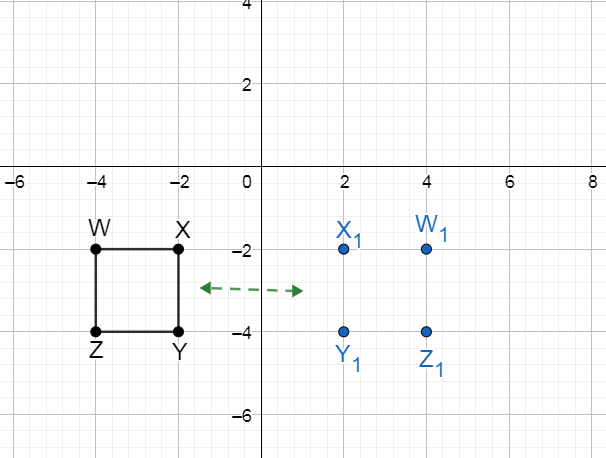
Join the vertices of image to construct the polygon. Write the coordinates of each vertex of image

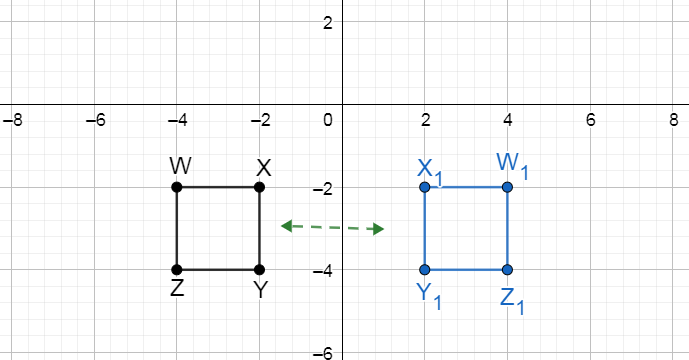
The coordinates of each vertex of image

Coordinates of image of W = (4,−2)

Coordinates of image of X = (2,−2)

Coordinates of image of Y = (2,−4)

Coordinates of image of Z = (4,−4)

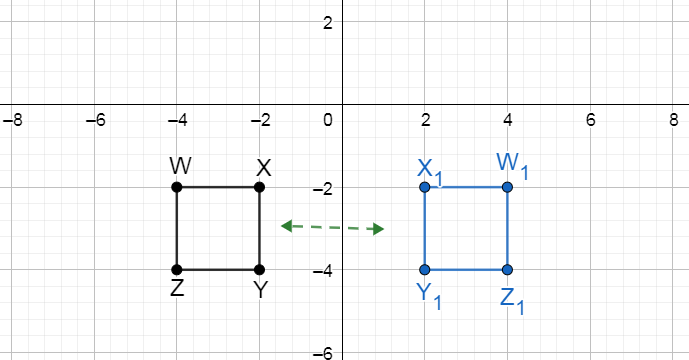
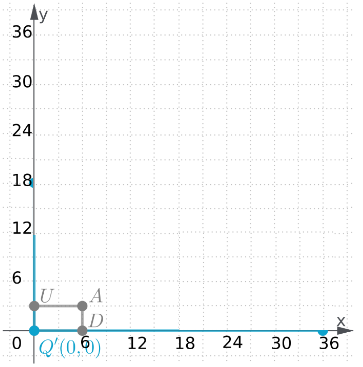
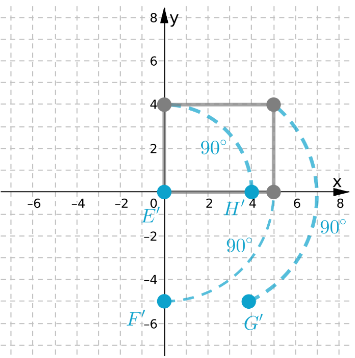
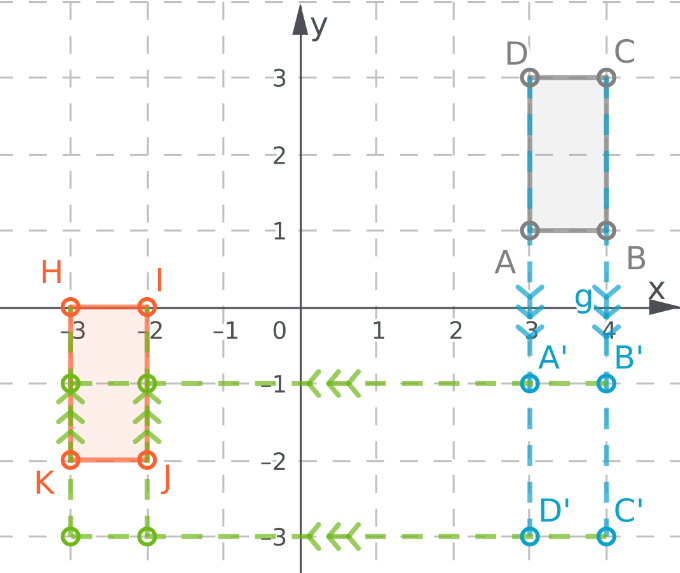
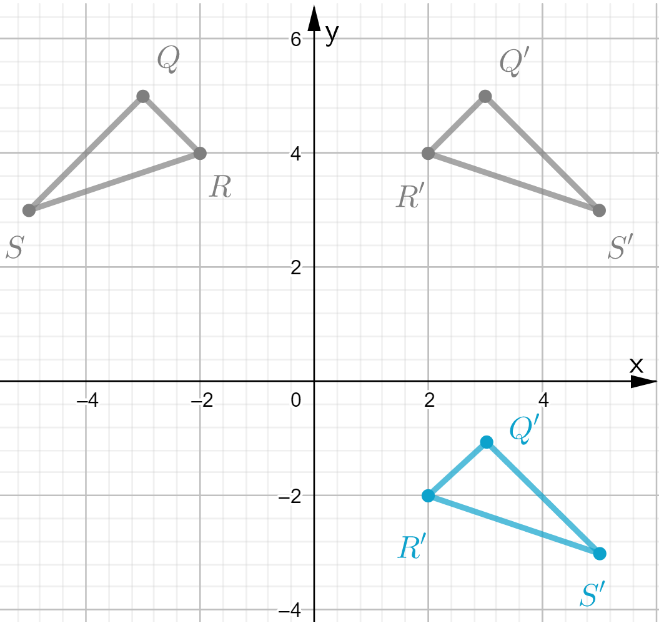
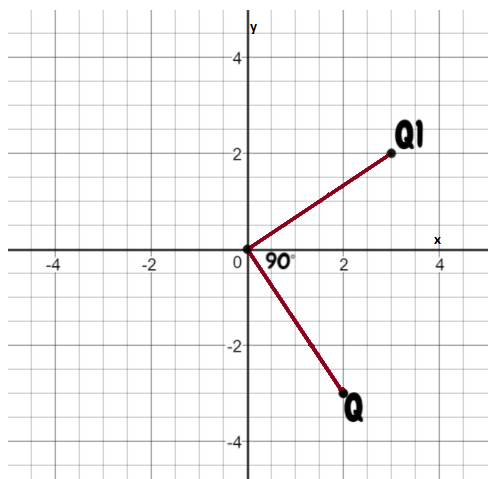
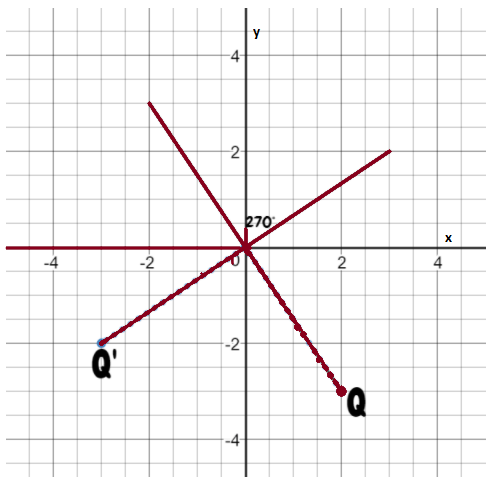
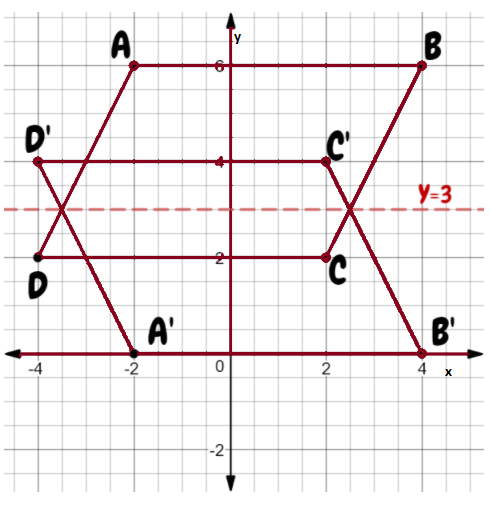
Page 367 Part (b) Answer

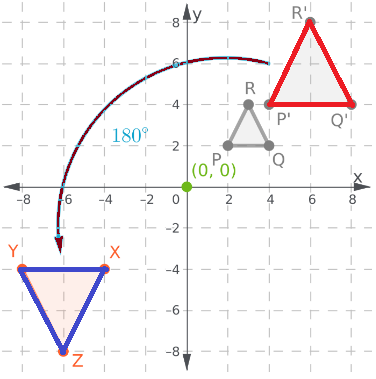
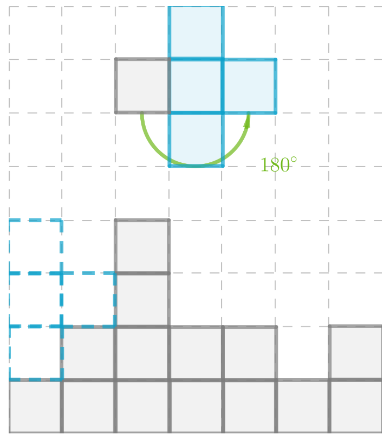
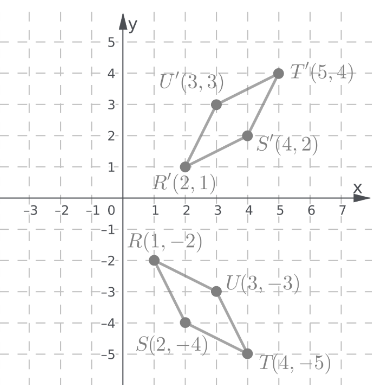
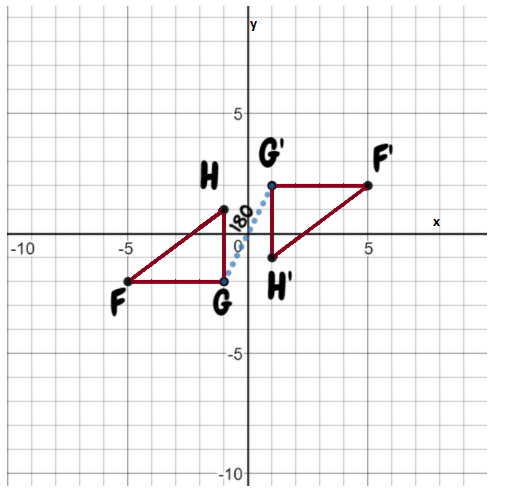
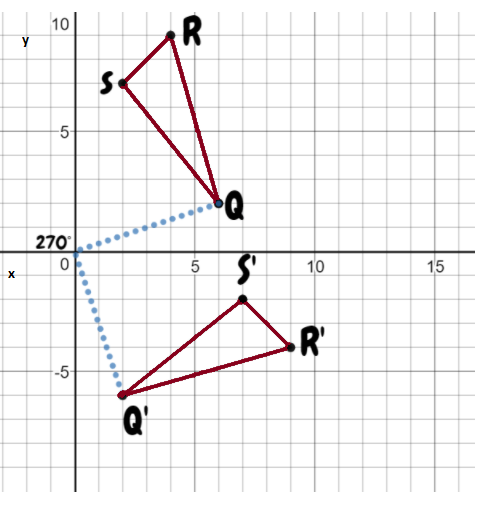
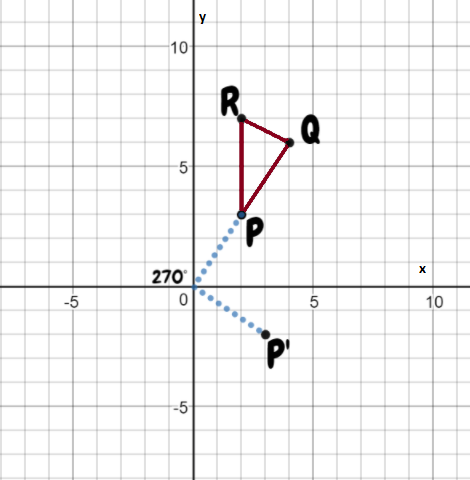
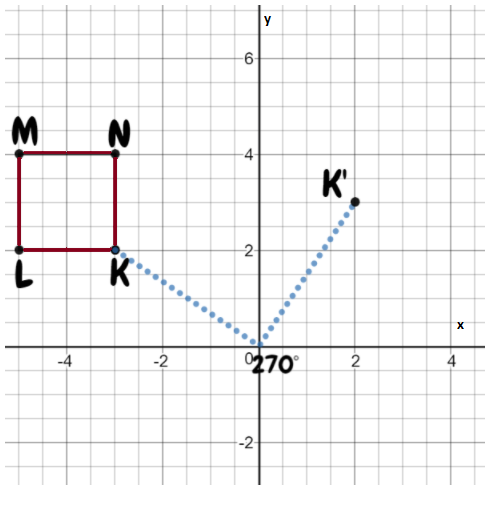
Coordination Given: S (-4,-2), T(-2,-2), U(-2,-4), V(-4,-4)

Find : Coordinates of STUV after 270° rotation.

Rotate the image about the origin.

For 180° rotation around the origin, first, write down the location of the given points.

S (-4,-2)

T (-2,-2)

U (-2,-4)

V (-4,-4)

Signs will change for 270-degree rotation. Image STUV is in the 3rd quadrant after 270° rotation it will be in the 2nd quadrant.

All signs are negative after rotation some signs will change.

S’ (-2,4)

T’ (-2,2)

U’ (-4,2)

V’ (-4,4)

Coordinates of the image of quadrilateral STUV after a 270° rotation about the origin S’ (-2,4) T’ (-2,2) U’ (-4,2) V’ (-4,4).

Solutions For Envision Math Grade 8 Review Exercise

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Review Exercise Page 368 Exercise 1 Answer

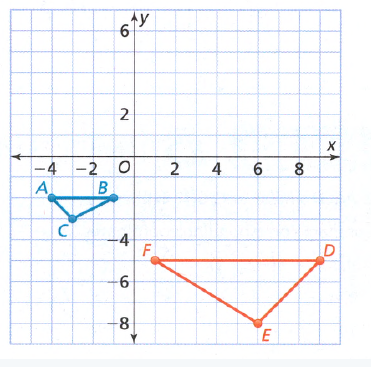
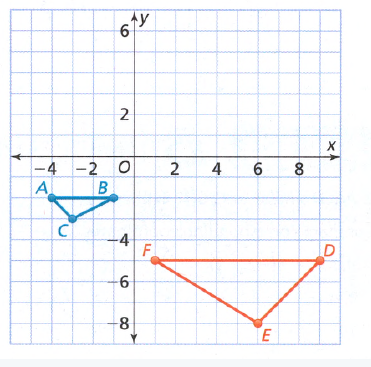
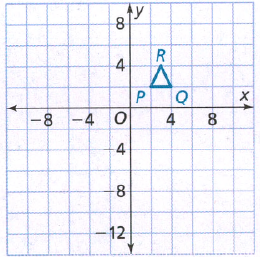
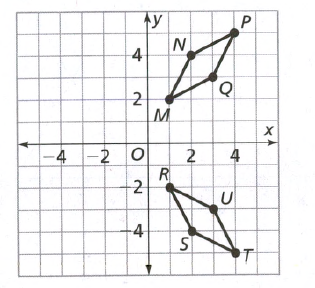
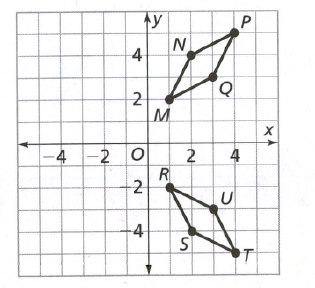
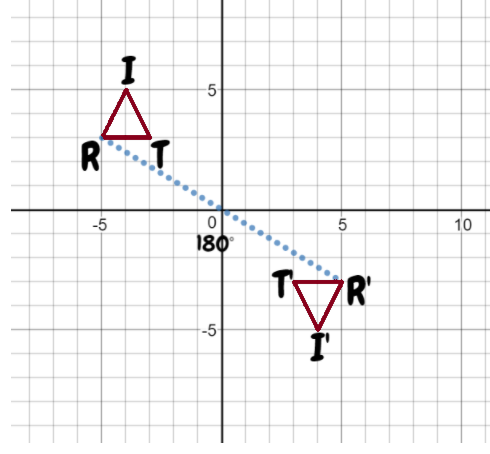
Quadrilateral Given : Quadrilateral A location (1,1), (1,5), (4,4), (4,2). Quadrilateral B location (-3,-1), (-4,-1), (-5,-4), (-2,-4)

Prove : Quadrilateral A congruent to Quadrilateral B.

By observing both the Quadrilaterals, A’s longest side is 4 units but B’s longest side is 3 units.

Same, A’s smallest side is 2 units but B’s smallest unit is only 1.

As for the rule of congruence, All sides must be equal to each other.

Sides are not equal to each other than both Quadrilaterals are not congruent.

Since the quadrilaterals do not have equal corresponding sides they are not congruent.

Page 368 Exercise 2 Answer

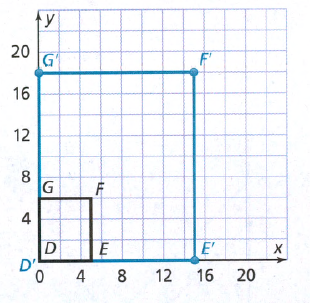
Coordinates Given: Coordinates of parallelogram A (-4,1), B (0,1), C (1,-1),D (-3,-1).

Find : coordinates of parallelogram ABCD after dilation with the center.

We will dilate the image with center (0,0) and scale factor of \(\frac{1}{2}\).

For dilating the image we write all the Coordinates of parallelogram. A (-4,1), B (0,1), C (1,-1),D (-3,-1).

We will multiply all the Coordinates of the parallelogram with given scale factor \(\left(\frac{1}{2}\right)\).

Coordinates of image ABCD after dilation with center (0,0) and scale factor \(\frac{1}{2}\) are

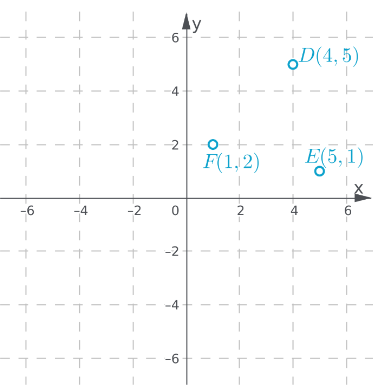
Page 369 Exercise 1 Answer

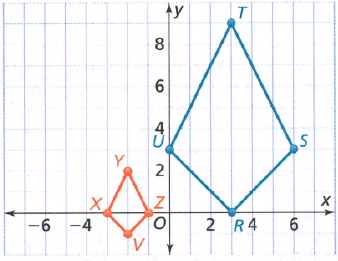
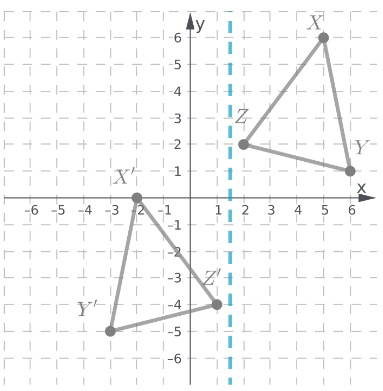
Given: Coordinates of A (−4,1), B (−4,5)and C(−1,1)

To find: Whether the given two triangles are similar or not.

We will identify the coordinates of A’, B’ and C’ to check for dilation and thus be sure whether the two triangles are similar or not

The coordinates of the vertices of triangle ABC with line of reflection being Y – axis are as follows

Coordinates of A” = (4, 1)

Coordinates of B” = (4, 5)

Coordinates of C” = (1, 1)

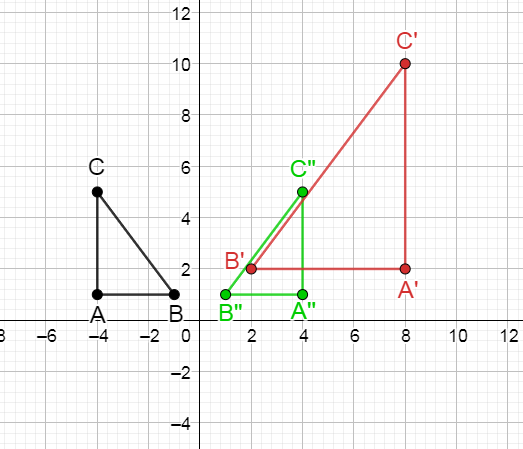
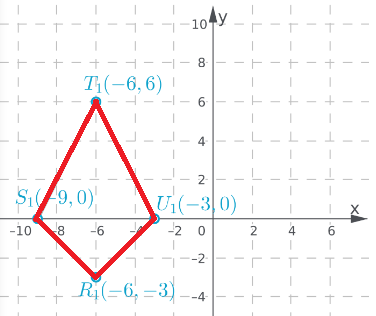
Lets identify the coordinates of the three vertices of triangle

Coordinates of A’ = (8,2)

Coordinates of B’ = (8,10)

Coordinates of C’ = (2,2)

Whereas the Coordinates of A” = (4, 1)

B” = (4, 5)

C” = (1, 1)

On comparison of corresponding coordinates

A′′= (4,1) → A′ = (8,2)

B′′ = (4,5) → B′ = (8,10)

C′′= (1,1) → C′=(2,2)

Clearly there is an enlargement dilation with a scale factor of 2.

Hence definitely the triangle A’B’C’ is similar to the triangle ABC

As there is a dilation with scale factor 2 hence the two triangles are similar to each other

Envision Math Grade 8 Volume 1 Chapter 6 Review Practice Problems

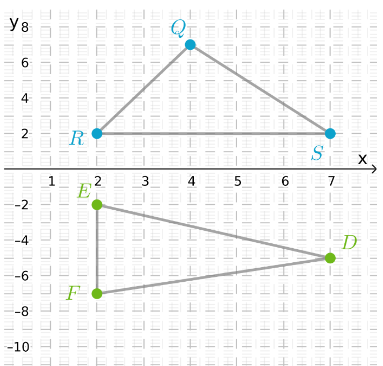
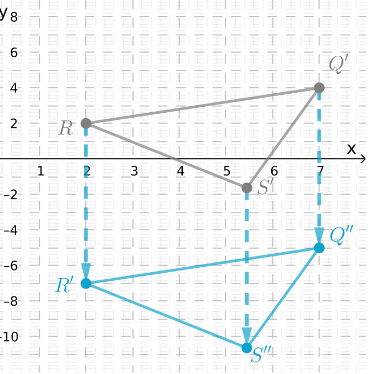
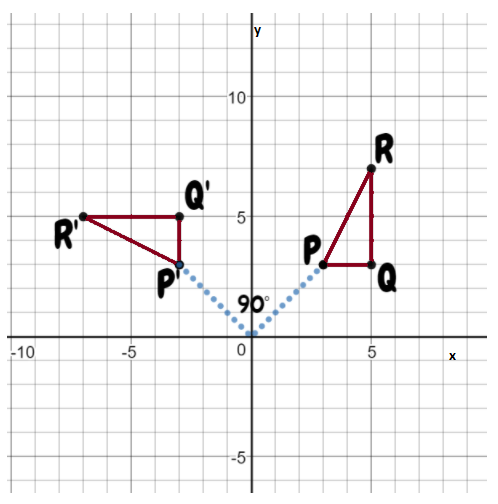
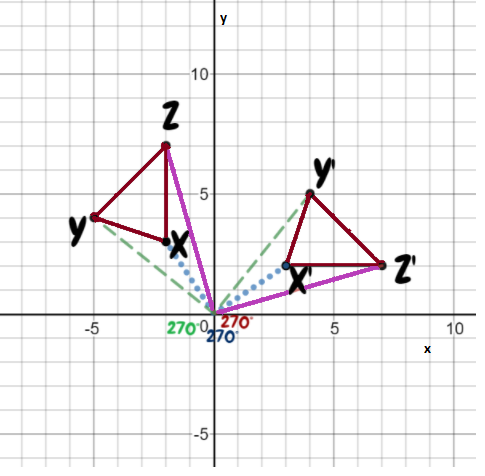
Page 369 Exercise 2 Answer

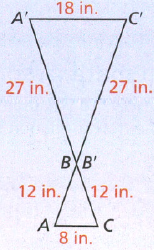
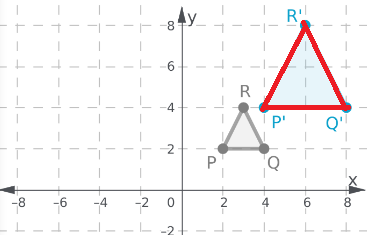
Given: Two similar triangles ABC and A’B’C’

To find: Sequence of transformation

We will check for various types of transformation to get the sequence in which triangle ABC got transformed to A’B’C’

Triangles have opposite orientation hence first reflect triangle ABC with line of reflection Y – axis to get triangle A”B”C”

The side lengths and coordinates of A’, B’ and C’ are double as compared to the coordinates of A”, B” and C” hence there is a dilation factor of 2 with origin as center.

Hence the sequence of transformation includes reflection about the y-axis, and then dilation by a factor of 2 with origin as center.

Envision Math 8th Grade Congruence And Similarity Review Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Review Exercise Page 369 Exercise 1 Answer

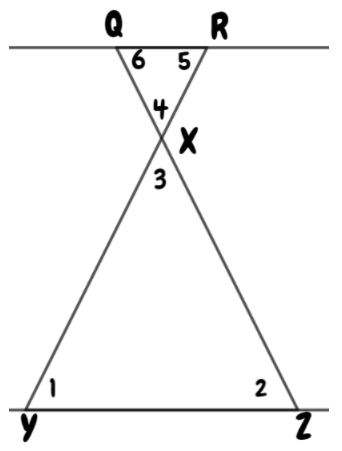
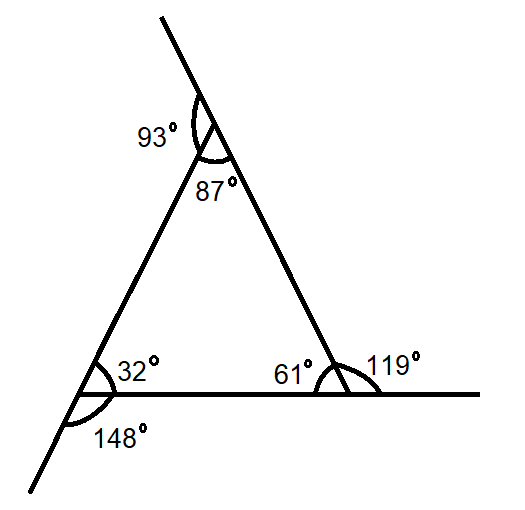
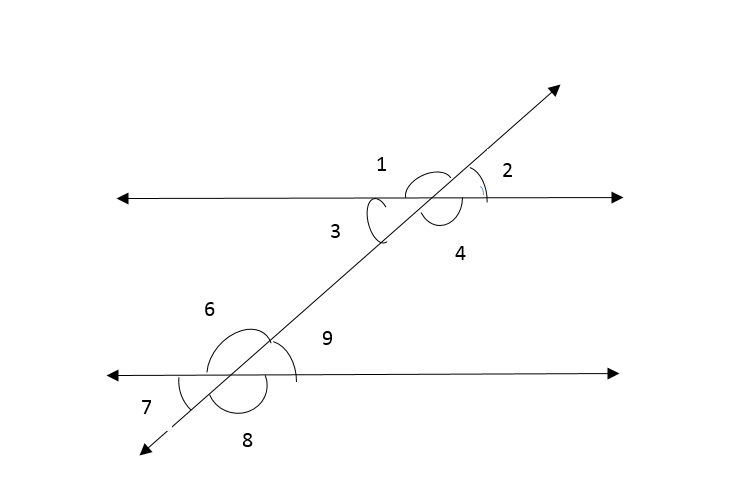
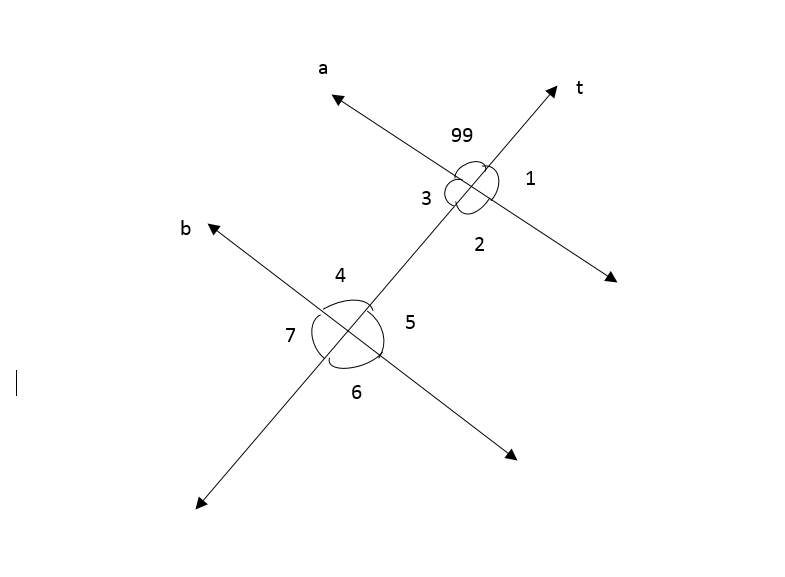
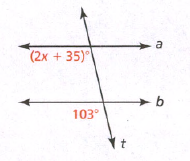
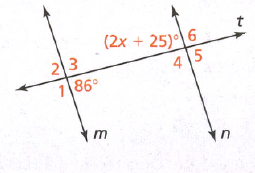
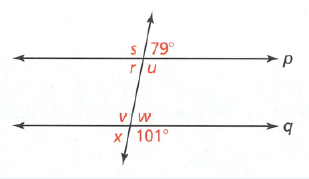
Given: Two parallel lines a and b and a transversal

To find: Value of x

We will first find the measure of ∠4 using the property of vertically opposite angles and then we will use the property of corresponding angles to find x.

∠4 = 129° (Vertically opposite angles)

​
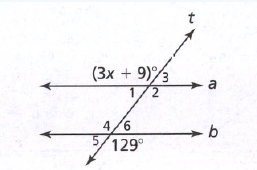
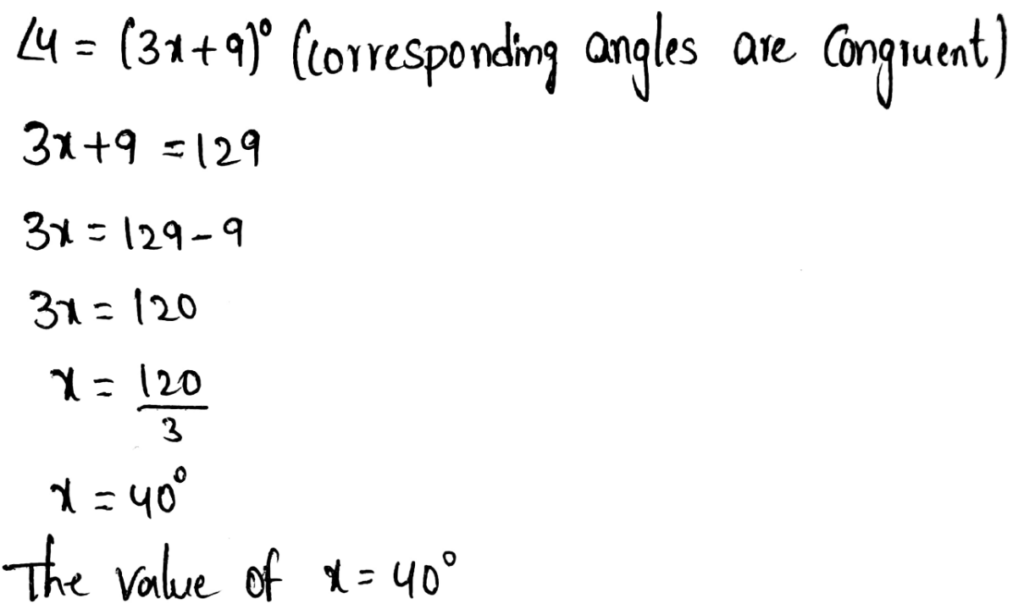
The value of x = 40°

Page 370 Exercise 1 Answer

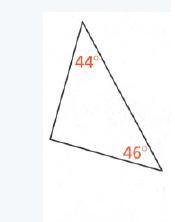
Given: Two of the interior angles of the triangle = 48° and 102°

To find: Measure of the third missing angle

We will add the measure of the given two angles and then subtract from 180 to get the measure of the third angle

Sum of the given two interior angles = 48° + 102° = 150°

Let the missing third angle be x°

x° = 180° − 150°

(Sum of the interior angles of a triangle is 180°)

x° = 30°

The measure of the missing angle = 30°

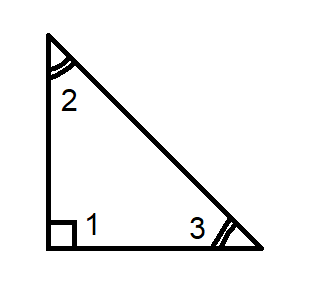
Page 370 Exercise 2 Answer

Given: Exterior angle of the triangle is 115°. The two remote interior angles are 2x and 3x

To find: Value of x

As we know that the measure of exterior angle of a triangle is equal to the sum of the remote interior angles.

So we will equate 115° with the sum of 2x and 3x

Sum of the remote interior angles = 2x + 3x = 5x

Measure of exterior angle = Sum of the opposite interior angles

5x = 115°

x = \(\frac{115}{5}=23^0\)

The value of X is 23°

Envision Math Grade 8 Chapter 6 Review Summary And Examples

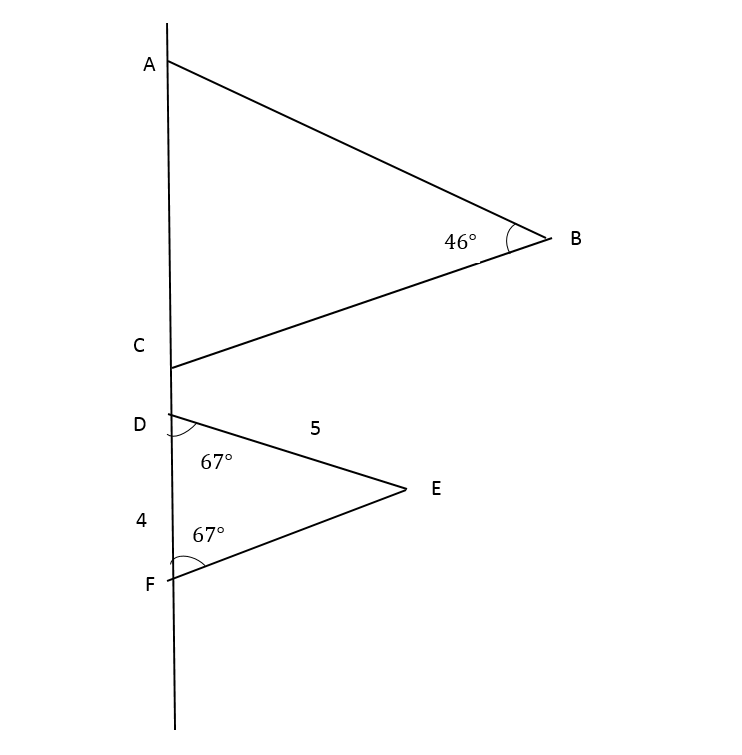
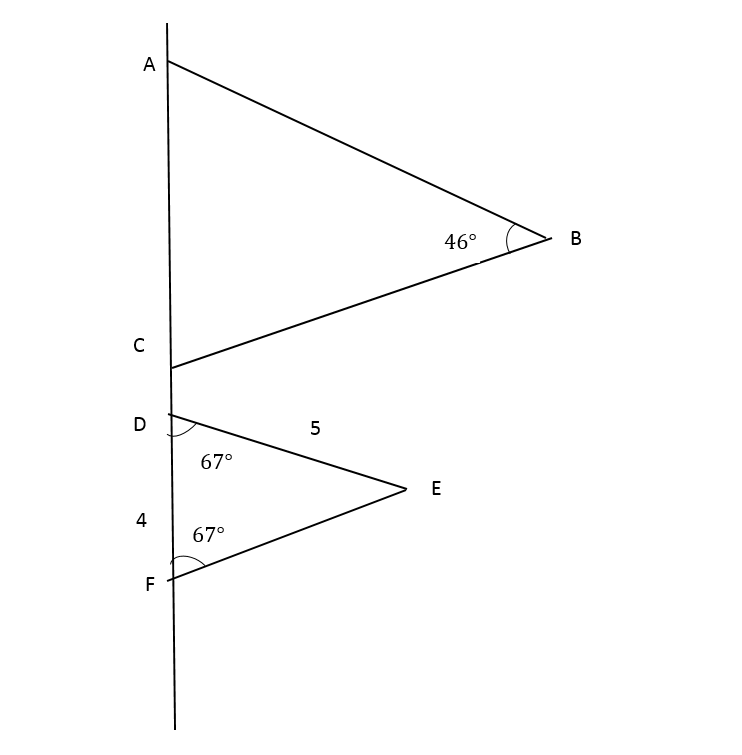
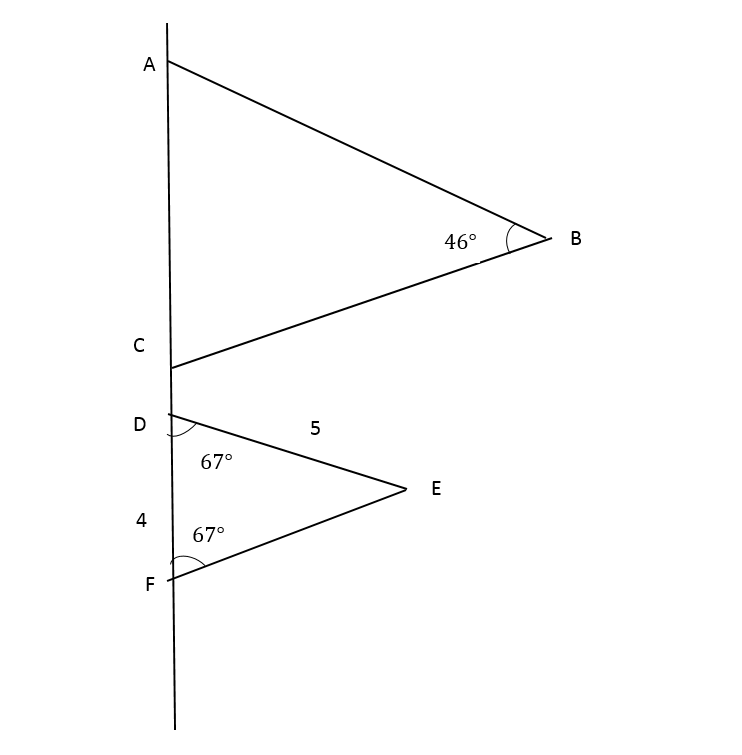
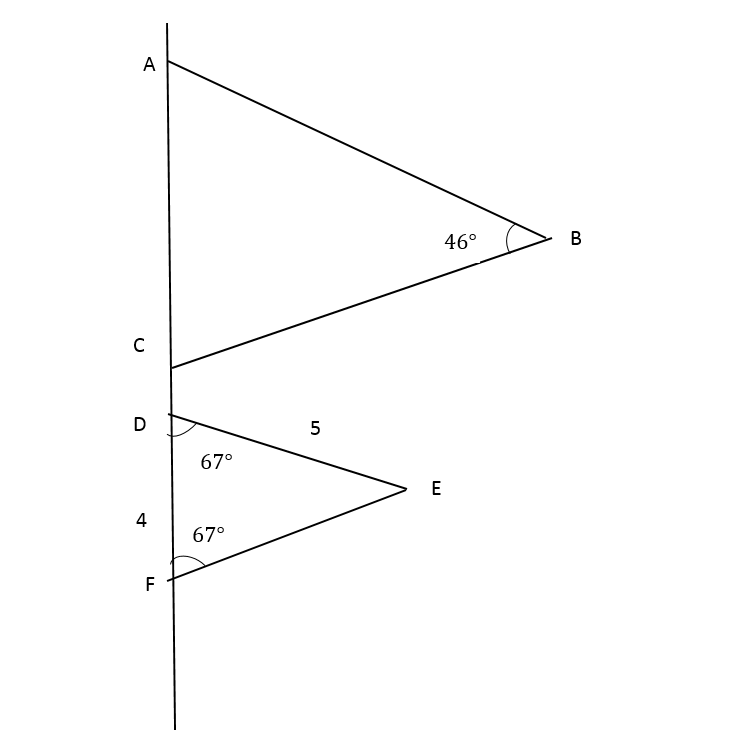
Page 370 Exercise 1 Answer

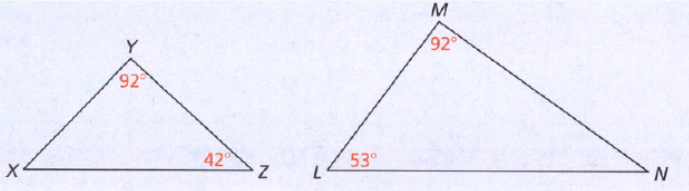
Given: ∠CXY = ∠CAB = 38°

To find: Whether ΔABC ≈ ΔXYC

There are some rule called Angle-Angle (AA) Criterion.

This criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

Hence, This criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 359 Exercise 1 Answer

The figure of triangles which represent each flag is shown below.

The figure of triangles which represent each flag is:

We have to defined as, How are the side lengths of the triangles related?

The figure of triangles which represent each flag is shown below.

The figure of triangles which represent each flag is:

Given – The angles of both triangles are similar.

To do – How the measurements are related?

From the picture it is clearly visible that, the larger triangle have the same angle measure as the smaller triangle.

We can conclude from properties of triangles that angles are congruent.

The angles are congruent.

Page 359 Focus On Math Practices Answer

Given – Justin makes a third flag that has sides that are shorter than the sides of the small flag. Two of the angles for each flag measure the same.

To Find – prove that if the third angle of each flag have same measure.

By making the third flag which have sides smaller than the sides of small flag, the transformation method dilation is used.

By making the third flag which have sides smaller than the sides of small flag, the transformation method dilation is used.

From the properties of this transformation, it is known that corresponding angle measurement remains the same.

We can conclude that the third angle for each flag have same measurements.

Page 360 Try It Answer

Given – ∠Y = 92^∘,∠M = 92^∘,∠Z = 42^∘,∠L = 53^∘

To do – Find m ∠X, m ∠N

Step 1 of 4

For determining whether the given triangles are similar, we will use the Angle-Angle (AA) Criterion

The angles are similar if two angles of a triangle are congruent to the corresponding angles of another triangle.

Therefore, we have to find the missing angle measure first:

Sum of the measures of the interior angles of a triangle is 180^∘.

Step 2 of 4
​

​
Step 3 of 4

m ∠N:

Step 4 of 4

So, we get that two corresponding angles are not congruent:

∠X ≠ ∠L, ​∠Y ≅ ∠M,​ ∠Z ≠ ∠N

Using the Angle-Angle (AA) Criterion, we can conclude that triangle are not similar.

The answers are
​
46^∘

35^∘

​The triangles are not similar.

Page 361 Try It Answer

Given – Knowledge of transformations and parallel lines.

To do – Explain that why angle-angle criterion is true for all triangles.

Step 1 of 1

If QR ∥ YZ

Step 2 of 2

Then, ∠1 ≅ ∠5​ ∠2 ≅ ∠6

Because, these pair of angles are alternate interior angles.

Moreover, since ΔXYZ and ΔXRQ are isosceles triangles, the true is:

∠1 ≅ ∠2​ ∠5 ≅ ∠6

Therefore:

m∠1 = m∠2 = m∠5 = m∠6

Besides, m∠3 = m∠4, because that is the same angle.

So, using the Angle-Angle Criterion, we can conclude that the given triangles are similar.

ΔXYZ ∼ ΔXRQ

ΔXYZ ∼ ΔXRQ

Page 362 Exercise 1 Answer

To do – Using angle measures to determine whether two triangles are similar.

We will use Angle-Angle (AA) Criterion of triangles

Step 1 of 1

There are some rule called Angle-Angle (AA) Criterion.

This criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

Angle-Angle criterion measures will be used to determine whether two triangles are similar.

Page 362 Exercise 3 Answer

Given: Three pairs of triangles

Two right triangles

Two isosceles right triangles

Two equilateral triangles

To find: Which triangle pairs below are always similar

For this we will apply AA similarity criterion to check which pair is always similar

If we have two right angled triangles then definitely 1 pair of angles which is 900 is always same, but the other two angles can vary. Hence not all right triangles are similar, or two right

In isosceles right triangles, the three angles are always fixed. One angle will be a right angle with 90°measure, and the other two angles will always be 45° and 45°(since it is an isosceles triangle). Hence, any two isosceles right triangles will have the same angles, satisfying AA criterion; and thus will always be similar.

Measure of the angles of any equilateral triangle is fixed i.e. each angle is of 600. Hence any 2 equilateral triangles will follow the AA similarity criterion. Therefore two equilateral triangles are always similar.

Two equilateral triangles and two isosceles right triangles are always similar, whereas two right angled triangles are not always similar

Page 362 Exercise 4 Answer

Given: Two triangles in which first triangle has angles 44° and 46° and the second triangle has two angles 90° and 46°

To find: Whether the two triangles are similar or not

We will find all angles of the given triangles and check whether they follow the AA similarity criterion or not

In the given triangle the two angles are 44°
and 46°. Let the third angle be x.

Now, 44° + 46° + x = 180°(Angle sum property of triangle)
​
90° + x = 180°

x = 180° − 90° = 90°

​Hence the third angle of the triangle is 90°

Clearly the two triangles have two equal angles i.e. 46° and 90°

hence AA similarity criterion can be applied and therefore the two triangles are similar

The given two triangles are similar to each other

Page 362 Exercise 5 Answer

Given: Two triangles QLM and QRS with R lying on QL and S lying on QM.

∠QLM = ∠QRS = 90°

To find: Whether ΔQLM ∼ ΔQRS

We will try and apply AA similarity criterion to check the two triangles are similar or not.

In ΔQLM and ΔQRS

∠QLM = ∠QRS = 90° (Given)

∠Q = ∠Q (Common Angle)

Hence by AA similarity rule

ΔQLM ∼ ΔQRS

Hence ΔQLM ∼ ΔQRS

Page 362 Exercise 6 Answer

Given: Two triangles on same base two angles of one of the triangle are 560 and 760 and of the second triangle are 48° and 76°

To find:

Whether the two triangles are similar or not

Value of x

We will apple the property of The measure of the exterior angle of a triangle is equal to the sum of the remote interior angles.

Then we will check whether AA similarity criterion is applicable or not.

Let the third angle of the triangle with two angles 56° and 76° be y

Then, 56° + 76° + y = 180° (Sum of the three angles of a triangle is 180°)

y = 180 − 56 − 76 = 48°

Hence the three angles are 56°,76° and 48°

As both the triangles have two corresponding angles i.e. 48° and 76° equal hence by AA similarity rule we can say that the two triangles are similar to each other.

56° + 76° = 4x + 48° (The measure of the exterior angle of a triangle is equal to the sum of the remote interior angles.)

The two triangles are similar to each other the value of

x = 21°

Page 363 Exercise 7 Answer

Given: Two triangles ΔXYZ and ΔXTU with T and U lying on XY and XZ respectively.

The value of ∠X = 103°, ∠XUT = 48°, ∠XYZ = 46°

To find: Whether ΔXYZ ∼ ΔXTU or not

We will first find the value of ∠XTU and then compare the corresponding angles of the two triangles

In ΔXTU 103° + 48° + ∠XTU = 180° (Sum of all three angles of triangle is 180°)

∠XTU = 180 − 103 − 48 = 29°

In ΔXTU and ΔXYZ

Only one angle 103° matches hence the AA similarity criterion can not be applied.

hence the two triangles are not similar to each other

ΔXYZ is not similar to the ΔXTU

Page 363 Exercise 8 Answer

Given: ∠RST = (3x-9)^∘ and ∠NSP = (2x+10)^∘.

To find the value of x and the value of ∠RST and ∠NSP.

Use the definition of vertically opposite angles, and find the value of x.

Here, ∠RST = ∠NSP [By the definition of vertical opposite angle]

​
Now to check if the angles RTS and SPN are the same, substitute the value of x in each of the expressions.
​
∠RTS = x + 19°

=19 + 19

= 38°

∠SPN = 2x

= 2 × 19

= 38°
​
From this we can see that ∠RTS = ∠SPN

And previously, it was seen that ∠RST = ∠NSP

Hence, AA criterion is satisfied and the two triangles are similar.

For the value of x is 19°, the two triangles are similar, as it satisfies the AA criterion of similarity.

Page 363 Exercise 9 Answer

Given: ∠JIH = 43°, ∠JHI = 35° and ∠HFG = 97°

To determine whether △FGH ∼ △JIH.

First, find the value of m ∠J

By using the triangle angle sum theorem, it follows:
​
m ∠J + 43° + 35° = 180°

m ∠J = 180° − (43° – 35°)

= 102°

​By using the vertical angles theorem, it follows:

∠FHG ≅ ∠JHI

By using the definition of congruence, it follows:
​
m ∠FHG = m ∠JHI

m ∠JHI = 35°

​Solve for m ∠G

​m ∠G + 35∘ + 97∘ = 180°

m ∠G = 180° − (35° + 97°)

= 48°

​Since, all the angles of △FGH and △JIH are not congruent.

Therefore by the definition of similar triangles, it follows the △FGH and △JIH are not similar.

△FGH and △JIH are not similar because the corresponding angles are not congruent.

Page 363 Exercise 10 Answer

Given:

To find: Are the given triangles are similar.

Step formulation: First calculate the value of x and then use it to find other angles.

As vertical angles are equal therefore,

4x − 1 = 3x + 14

Take like terms on one side.
​
4x − 3x = 14 + 1

x = 15

Now find other angles.
​
∠T = x + 15

= 15 + 15

= 30°

​∠P = 2x

= 2 × 15

= 30°

​As two angles of the triangles are equal, hence, these are similar triangles.

Yes, the triangles are similar as they have two equal angles.

Page 363 Exercise 11 Answer

Given: Two triangles with angles.

To: Describe how to use angle relationships to decide whether any two triangles are similar.

If two angles of one triangle is equal to the two angles of another triangle, then the triangles are known as similar triangles.

This is how angle relationships can be used to check whether any two triangles are similar.

If two angles of one triangle are equal to the two angles of another triangle, then the triangles are known as similar triangles.

This is how angle relationships can be used to check whether any two triangles are similar.

Page 364 Exercise 12 Answer

Given:

To: Find whether the given triangles are similar?

Step formulation: Find the angles of both the triangles and then compare.

Sum of interior angles of triangle = 180°

​
Now, as both the triangles have the same angles, therefore, these are the similar triangles.

Yes, both the triangles have the same angles, therefore, these are the similar triangles.

Page 364 Exercise 13 Answer

Given:

To: Find which of the triangles are similar.

Step formulation: First find the angles of the triangles and then compare.

Calculate ∠Z.

​X + Y + Z = 180

104 + 45 + Z = 180

Z = 31°

​Similarly, ∠H = 45°

∠S = 104°

In ΔXYZ & ΔGHI: ∠Y = ∠H and ∠X = ∠G

Therefore,ΔXYZ ≅ ΔGHI

In ΔSQR & ΔGHI: ∠Q = ∠H and ∠G = ∠S

Therefore,ΔSQR ≅ ΔGHI

In ΔXYZ & ΔSQR: ∠Z = ∠R and ∠Y = ∠Q

Therefore,ΔXYZ ≅ ΔSQR

ΔXYZ ≅ ΔGHI

ΔSQR ≅ ΔGHI

ΔXYZ ≅ ΔSQR

Page 364 Exercise 14 Answer

Given:

To: Find whether the given triangles are similar?

Step formulation: First find the angles of the triangles and then compare.

Calculate ∠R.

​Q + S + R = 180

59 + 60 + R = 180

R = 61∘

​In the triangles ∠R = ∠H and ∠Q = ∠G

Therefore, triangles similar.

Yes, triangles are similar as they have equal angles.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 353 Exercise 2 Answer

Given:-Two parallel lines and transversals lines

Find out:-Write the properties of parallel lines and transversals lines.

If we have two parallel lines and transversals lines then we use the properties:-

Alternate Interior angles are equal.

Alternate exterior angles are equal.

The Sum of angles made on the same sides of the transversals is 180^∘.

Corresponding angles are equal.

We use the four properties of parallel lines and transversals lines to solve the problems.

Envision Math Grade 8 Volume 1 Chapter 6.9 Solutions

Page 353 Focus On Math Practices Answer

Given: The measurements of the two angles are 65^∘.

To find m∠1 using assumption and explain the assumption reason.

It is given that the measurements of the two angles are 65^∘. Therefore, x is:

The assumption made to find m∠1 is to subtract the sum of the two given angle measures 65 degrees and 65 degrees from 180 degrees. It is reasonable because the given tiles are triangular and the sum of the angles in the triangle is 180 degrees.

Page 354 Try It Answer

Given:- ∠2 = 68^∘ and ∠3 = 40^∘

Find out:- ∠1 = ?

Use the angle sum property of a triangle.

Thus, the measure of unknown angle is 72^∘

The measure of unknown angle is 72^∘

Page 354 Convince Me Answer

Given:- angle measures of a triangle 23^∘,71^∘ and 96^∘

Explain:- these angle measures can be possible or not?

We use here angle sum property of a triangle, i.e. the sum of all interior angles is 180∘.

So,

23^∘ + 71^∘ + 96^∘ = 190^∘

This is not possible for a triangle.

A triangle could not have interior angle measures of 23^∘,71^∘ and 96^∘

Congruence And Similarity Envision Math Exercise 6.9 Answers

Page 354 Convince Me Answer

Given:- angle measures of a triangle 23^∘,71^∘ and 96^∘

Explain:- these angle measures can be possible or not?

We use here angle sum property of a triangle, i.e. the sum of all interior angles is 180∘.

So,

23^∘ + 71^∘ + 96^∘ = 190^∘

This is not possible for a triangle.

A triangle could not have interior angle measures of 23^∘,71^∘ and 96^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.9 Page 356 Exercise 2 Answer

Given:- ∠1 = 90^∘ and ∠2 = ∠3

Find out:- all the possible values of exterior angles.

Find the values of angles 2 and 3 using angle sum property, then find the measure for the exterior angles by using exterior angle property for a triangle.

The triangle can be represented as follows:

Given that ∠1 = 90^∘ and ∠2 = ∠3

Therefore, using angle sum property of the triangle,

∠1 + ∠2 + ∠3 = 180^∘

Now the exterior angles 4, 5 and 6 can be found using the exterior angle property:

∴ ∠6 = 45° + 45°, ∠5 = 90° + 45° and ∠4 = 90° + 45°

∠6 = 90°, ∠5 = 135° and ∠4 = 135°

These are all the possible exterior angles for this triangle.

All possible values of the exterior angle are ∠6 = 90∘, ∠5 = 135∘ and ∠4 = 135∘

Envision Math Grade 8 Chapter 6.9 Explained

Page 356 Exercise 3 Answer

Given:- two angles are 32^∘ and 87^∘ and one exterior angle is 93^∘

Find out:- all the interior angles and exterior angles of this triangle.

use the angle sum property of a triangle and exterior angle property.

By using the angle sum property of a triangle,
​
87^∘ + 32^∘ + ∠3 = 180^∘

∠3 = 180^∘ − 119^∘

∠3 = 61^∘

and ∠4 = 87^∘ + 32^∘ [exterior angle property of a triangle]

∠4 = 119^∘

and ∠6 = 87^∘ + 61^∘ [exterior angle property of a triangle]

∠6 = 148^∘

​Hence, the diagram of the triangle can be drawn as:

The remaining interior angle is 61^∘ and exterior angles are 119^∘ and 148^∘

The final diagram of the triangle is:

Page 356 Exercise 4 Answer

Given:- a ∥ b and some angles in the given diagram.

find out:- ∠1 and ∠2.

we use properties of parallel lines and transversals and linear pairs.

as
​
a ∥ b

∠2 = 37.3^∘  [alternate interior angles]

and ∠1 + 79.4^∘ + 37.3^∘ = 180^∘ [Co−interior angles]

∠1 = 180^∘ − 116.7^∘

∠1 = 63.3^∘

The angles are ∠1 = 63.3^∘ and ∠2 = 37.3^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.9 Page 356 Exercise 5 Answer

Given ∥ b and some angles in the given diagram.

find out:∠3 and ∠4 =?

we use properties of parallel lines and transversals and linear pairs.

The angles are ∠3 = 63.3^∘ and ∠4 = 142.7^∘

Envision Math Grade 8 Topic 6.9 Transformations And Congruence Practice

Page 356 Exercise 6 Answer

Given ΔABC, m ∠A = x^∘, m B = (2x)^∘, m ∠C = (6x+18)^∘

Find the measure of each angle.

Use the triangle angle sum theorem to find each angle.

The angle measures are: m ∠A = 18^∘, m ∠B = 36^∘, m ∠C = 126^∘

Envision Math Grade 8 Chapter 6.9 Lesson Overview

Page 357 Exercise 7 Answer

Given the figure of the triangle.

Use the exterior angle theorem to find the required answer.

Here in the figure, angle ∠1 is the exterior angle of the triangle.

m∠1 is equal to the sum of two remote interior angles.

According to the exterior angle theorem,
​
∠1 = 59^∘ + 56^∘

∠1 = 115^∘

∠1 is the exterior angle of the triangle.

m∠1 is equal to the sum of two remote interior angles.

m∠1 = 115^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.9 Page 357 Exercise 9 Answer

Given the figure.

Use the triangle angle sum theorem to find the required angle.

The required angle is m ∠C = 83.5^∘.

Solutions For Envision Math Grade 8 Exercise 6.9

Page 357 Exercise 10 Answer

Given the figure.

Use the exterior angle theorem to find the required answer.

Notice that, ∠4 is an exterior angle of the given triangle. Moreover, angle 1 and ∠2 are its remote interior angles. Therefore, we can use the fact that the measure of an exterior angle of a triangle is, equal to the sum of the measures of its remote interior angles and calculate the value of x.

Our friend got the wrong measure of ∠4 because

he probably think that m∠1, m∠2 and m∠4 have the sum of 180^∘

Therefore he got m∠4 = 51^∘, which is the measure of ∠3, the third interior angle of the given triangle.

do not have the sum of 180^∘

because, as we can see in the picture, not all three angles are interior.

The measure of the angle is ∠4 = 129^∘.

Envision Math Grade 8 Volume 1 Chapter 6.9 Practice Problems

Page 358 Exercise 12 Answer

Given the figure of the triangle.

Use the exterior angle theorem to find the required answer.

According to the exterior angle theorem,

m∠4 = m∠2 + m∠1

​
The value of m∠3 is calculated as:
​
m∠3 = 161 − 25 × 2

= 161 − 50

= 111^∘

The expression for m∠3 = 161 − 25x and the value of m∠3 = 111^∘

Page 358 Exercise 13 Answer

Given a figure of a triangle.

Use the triangle angle sum theorem to find the required angle.

The measure of the acute angle is x = 52.8^∘.

Page 358 Exercise 14 Answer

Given a figure of a triangle.

Use the exterior angle theorem to find the required angles.

Here in the figure, ∠A,∠B,∠C are interior angles. Angle ∠C is adjacent angle whereas ∠A,∠B are non-adjacent angles.

Therefore the remote interior angles for an exterior angle ∠F is ∠A and ∠B.

The two remote interior angles for an exterior angle ∠F is ∠A and ∠B.

Envision Math 8th Grade Congruence And Similarity Topic 6.9 Key Concepts

Page 358 Exercise 15 Answer

Given a figure of a triangle.

Use the exterior angle theorem to find the required angle.

​
The value of m∠3 = 7x + 10 = 7 × 20 + 10 = 150

The value of m∠3 = 150^∘.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 345 Exercise 1 Answer

Given: Two parallel lines.

To: Draw two parallel lines. Then draw a line that intersects both lines. Which angles have equal measures?

Step formulation: Draw the lines and then observe which angles are equal.

Two parallel lines with a transverse line is:

From the figure it can be observed as:
​
∠1 = ∠3 = ∠5 = ∠7

∠2 = ∠4 = ∠6 = ∠8

Equal angles formed when a transverse line cuts two parallel lines are:
​
∠1 = ∠3 = ∠5 = ∠7

∠2 = ∠4 = ∠6 = ∠8

Envision Math Grade 8 Volume 1 Chapter 6.8 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 345 Exercise 2 Answer

There are following properties and definitions should be satisfied to describe which angles have equal measures.

1. Alternate Interior Angles Theorem: When angles are formed inside of two parallel lines and intersect by traversal, are equal to their alternate pairs.

In the above figure, the interior angles:

∠A = ∠D, ∠B = ∠C

2. Alternate Exterior Angles Theorem: Two angles that lie on opposite sides of the transversal and are placed on two different lines, both either inside the two lines or outside, are called alternate angles.

In the above figure, the exterior angles are:

∠A = ∠D, ∠B = ∠C

3. Corresponding Angles Theorem: Corresponding angles are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line.

From the above figure, the corresponding angles are:

∠1 = ∠6, ∠2 = ∠9, ∠3 = ∠7, ∠4 = ∠8

4. Vertical Angles Congruence Theorem: The Vertical Angles are those angles when the opposite (vertical) angles of two intersecting lines are congruent.

From the above figure, the vertical angles are:

∠1 = ∠3,∠2 = ∠4

There are the following properties to describe which angles have equal measures.

1. Alternate Interior Angles Theorem

2. Alternate Exterior Angles Theorem

3. Corresponding Angles Theorem

4. Vertical Angles Congruence Theorem

Congruence And Similarity Envision Math Exercise 6.8 Answers

Page 345 Focus On Math Practices Answer

There are following properties and definitions should be satisfied to describe which angles have equal measures.

1. Alternate Interior Angles Theorem: When angles are formed inside of two parallel lines and intersect by traversal, are alternate pairs of angles are equal.

In the above figure, the interior angles:

∠A = ∠D,∠B = ∠C

2. Alternate Exterior Angles Theorem: Two angles that lie on opposite sides of the transversal and are placed on two different lines, both outside the two parallel lines are called alternate exterior angles. Alternate exterior angles are equal.

In the above figure, the exterior angles are:

∠A = ∠D,∠B = ∠C

3. Corresponding Angles Theorem: Corresponding angles are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line. Corresponding angles are equal.

From the above figure, the corresponding angles are:

∠1 = ∠6,∠2 = ∠8,∠3 = ∠7,∠4 = ∠8

4. Vertical Angles Congruence Theorem: The Vertical Angles are the opposite (vertical) angles of two intersecting lines. They are always congruent.

From the above figure, the vertical angles are:

∠1 = ∠3,∠2 = ∠4

There are the following properties to describe which angles have equal measures.

1. Alternate Interior Angles Theorem

2. Alternate Exterior Angles Theorem

3. Corresponding Angles Theorem

4. Vertical Angles Congruence Theorem

Envision Math Grade 8 Chapter 6.8 Explained

Page 346 Essential Question Answer

When two parallel lines and a third line that crosses them as in the figure shown below, the crossing line is called a transversal.

When a transversal intersects with two parallel lines, eight angles are produced.

The eight angles together form four pairs of corresponding angles.

The corresponding pairs are:

∠1 = ∠5,∠3 = ∠6,∠2 = ∠8,∠4 = ∠7

The alternate interior angles are formed inside of two parallel lines and intersect by traversal.

The alternate interior angles are:

∠3 = ∠8,∠4 = ∠5

Two angles that lie on opposite sides of the transversal and are placed on two different lines, both either inside the two lines or outside, are called alternate exterior angles.

The alternate exterior angles are:

∠1 = ∠7,∠2 = ∠6

All angles which are either exterior angles, interior angles, alternate angles, or corresponding angles are congruent.

When two parallel lines and a third line that crosses them, the crossing line is called a transversal.

All angles formed which are either exterior angles, interior angles, alternate angles, or corresponding angles, all of which are congruent.

Page 346 Try It Answer

The angles that are congruent to ∠8 are ∠4, ∠2, ∠6.

Because ∠8 and ∠4 are corresponding angles, angles that are on the same side of the transversal and the corresponding angles are congruent.

Therefore, ∠8 = ∠2 and ∠4 = ∠6 because these are alternate interior angles.

The angles that are supplementary to ∠8 are: ∠7,∠5,∠1,∠3

Those angles are the same side interior angles and those are:
​
m∠8 + m∠7 = 180

m∠8 + m∠5 = 180

m∠8 + m∠3 = 180

m∠8 + m∠1 = 180
​
These angles are supplementary.

The angles that are congruent to ∠8 are ∠4,∠2,∠6.

The angles that are supplementary to ∠8 are ∠7,∠5,∠1,∠3.

Page 346 Convince Me Answer

Given the figure in the question.

Explain why ∠4 and ∠5 are supplementary.

Use the definition of supplementary to find angles.

When two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are called supplementary angles.

If the sum of the measures of the two angles is 180∘, then the angles are supplementary.

In the given figure, ∠4 and ∠5 are the interior angles on the same side of the transversal. Therefore the sum of the measures of the two angles ∠4 and ∠5 is 180^∘ or ∠4 + ∠5 = 180^∘.

Therefore ∠4 and ∠5 are supplementary.

Angles ∠4 and ∠5 are the interior angles on the same side of the transversal. Therefore the sum of the measures of the two angles is supplementary.

Solutions For Envision Math Grade 8 Exercise 6.8

Page 347 Try It Answer

Given the figure is as follows:

Find the value of ∠2,∠7.

By the use of theorems which are given in the tip to find the value of required angles.

In the given figure, angles 99^∘ and ∠2 are the vertical angles.

Therefore, ∠2 = 99^∘

The measure of angles are

∠2 = 99^∘, ∠7 = 81^∘.

Page 347 Try It Answer

Given the figure in the question.

Find the value of x in the figure.

Use the definition of the corresponding angles theorem to find the value of x.

The value of x is 109^∘.

Page 348 Try It Answer

Given the figure.

Find the value of x if a ∥ b.

Use the alternate interior angle theorem to find the value of x.

According to the alternate interior angle theorem, the angles 86^∘ and (3x+17)^∘ are alternate interior angles and it follows that the angles must be congruent.

Therefore, 86 = (3x+17)^∘

Now the value of x is calculated as:
​
86 = 3x + 17

3x = 69

x = 23

The value of x is 23^∘ if a ∥ b in the given figure.

Given the figure.

Find the value of x.

Use the consecutive interior angle theorem to find the value of x.

According to the consecutive interior angle theorem, the angles of measures 100∘ and (7x – 4)^∘ are consecutive interior angles.

Therefore, 100 + (7x−4) = 180

Simplify the equation and find the value of x.

​
By the consecutive interior angle theorem, the value of x is 12.

Envision Math Grade 8 Volume 1 Chapter 6.8 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 349 Exercise 2 Answer

When two parallel lines and a third line crosses them as in the figure shown below, the crossing line is called a transversal.

When a transversal intersects with two parallel lines, eight angles are produced.

The eight angles together form four pairs of corresponding angles.

The corresponding pairs are:

∠1 = ∠5,∠3 = ∠6,∠2 = ∠8,∠4 = ∠7

The alternate interior angles are formed inside of two parallel lines and intersect by traversal.

The alternate interior angles are:

∠3 = ∠8,∠4 = ∠5

Two angles that lie on opposite sides of the transversal and are placed on two different lines, both either inside the two lines or outside, are called alternate exterior angles.

The alternate exterior angles are:

∠1 = ∠7,∠2 = ∠6

All angles which are either exterior angles, interior angles, alternate angles, or corresponding angles are congruent.

When two parallel lines and a third line that crosses them, the crossing line is called a transversal.

All angles formed which are either exterior angles, interior angles, alternative  angles, or corresponding angles all are congruent.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 349 Exercise 3 Answer

Given:

Two parallel lines are cut by a transversal.

To find:

number of angles made by the transversal and measure of those angles.

For finding number of angles and their measures we need to assume a transversal between two parallel lines anf then with the help of tip we have to find the measures of all angles.

When two parallel lines are cut by a transversal, 8 angles are formed as shown:

∠1 and ∠3are vertical angles, it follows:

∠1 ≅ ∠3

∠1,∠5 and ∠3,∠7 are corresponding angles.

and according to the corresponding angles theorem:

∠1 ≅ ∠5 ; ∠3 ≅ ∠7

Since, ∠1 ≅ ∠3, it can be concluded that:

∠1 ≅ ∠5 ≅ ∠3 ≅ ∠7

from the definition of congruent angles:

∠1 = ∠5 = ∠3 = ∠7

Similarly, it can be proved that:

∠2 = ∠4 = ∠6 = ∠8

When two parallel lines are cut by a transversal, 8 angles are formed.

There are two angle measures.

Envision Math 8th Grade Congruence And Similarity Topic 6.8 Key Concepts

Page 349 Exercise 4 Answer

Given: angle measures of some angles.

To find:

How to tell whether two lines are parallel with the help of angle measures.

Intersect them with a transversal, if the created corresponding angles are equal then they are parallel according to the corresponding angles theorem.

Intersect them with a transversal, if the created corresponding angles are equal then they are parallel according to the corresponding angles theorem.

Page 349 Exercise 6 Answer

Given:

m∠4 = 70

To find:

m ∠ 6

We need to refer to the tip for finding the above angle, alternate-interior angles property is also useful.

Since∠4 and ∠6 are alternate-Interior angles, it follows that:

m∠4 = m∠6

Substitute m∠4 = 70^∘ into the equation:

70^∘ = m∠6

Therefore, m∠6 = 70^∘.

The value of m∠6 = 70^∘.

Page 349 Exercise 8 Answer

Given:

To find:

Value of x

Use the corresponding angles property to find the value of x.

Notice that since a is parallel to b and t is their transversal line, the angles (2x+35)^∘ and 103^∘ are corresponding angles.

Thus, the two angles are congruent, and their measures are equal.

2x + 35 = 103

Solve the equation for x:

The value of x must be equal to 34^∘

Page 350 Exercise 9 Answer

Given:

To find:

value of u

In order to find the value of u we have to use the corresponding angle property.

Notice that u and 32^∘ are corresponding angles.

Using the corresponding angles theorem, it follows that:

u = 32

The value of u is 32^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 350 Exercise 10 Answer

Given:

To prove:

∠K and ∠B are corresponding angles.

In order to prove that the above angles are corresponding angles refer to the tip mentioned .

Although both ∠K and ∠B lie on the same side of the transversal, they do not have the same relative positions with respect to the parallel lines.

So they do not satisfy the second condition for the corresponding angles.

Therefore, ∠K and ∠B are not corresponding angles.

Hence, ∠K and ∠B are not corresponding angles.

Envision Math Grade 8 Chapter 6.8 Lesson Overview

Page 350 Exercise 11 Answer

Given:

A and B are parallel to each other.

∠6 = 155

To find: measure of ∠4

In order to find the value of the above, we have to use consecutive interior angle theorem.

Avenue C is the transversal to parallel avenue A and B

∠6 = 155

From the consecutive interior angle theorem, it follows:

∠6 + ∠4 = 180

Replace ∠6 = 155^∘:

155^∘ + ∠4 = 180^∘

Subtract 155∘ from both side:

155^∘ + ∠4 − 155^∘ = 180^∘ − 155^∘

Cancel 155∘ in left side of equation:

∠4 = 180^∘ − 155^∘

Calculate value of ∠4 :
​
180^∘ − 155^∘

= 25^∘

The measure of ∠4 is 25^∘

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 350 Exercise 12 Answer

Given: measure of ∠6 = 53

To find: measure of ∠12

In order to find the value of the above, we have to use alternate interior angle theorem and supplementary angles theorem.

Observe that ∠6 and ∠11 are alternate interior angles, therefore:

m∠6 = m∠11

∠11 and ∠12 are supplementary angles, therefore:

m∠12 = 180 − m∠11

Substitute m∠11 = m∠6 into the equation:

m∠12 = 180 − m∠6

Substitute m∠6 = 53 into the equation:
​
m∠12 = 180 − 53

m∠12 = 127

The measure of m∠12 = 127^∘

Page 351 Exercise 14 Answer

Given:

To prove:

m ∥ n

In order to prove the above we can use alternate interior angles converse theorem.

Notice that the two angles of measure 74° are alternate interior angles.

Using the alternate interior angles converse, it follows that: m ∥ n

Using the alternate interior angles converse, it follows that:

m ∥ n

Page 351 Exercise 15 Answer

Given:

To find :

Value of x and each missing angle measure.

In order to find the value of x we can refer to alternate interior angles theorem and for the other angles, we can refer to the tip mentioned.

Line t intersects two parallel lines n and m, so it’s a transversal.

Angles ∠86° and (2x+25) are alternate interior angles.

From the alternate interior angles theorem, it follows:
​
2x + 25 = 86

2x = 61

x = 30.5

Angles (2x + 25) angle and ∠3 are same side interior angles.

By the same side interior angles theorem. since (2x+25) = 86 it follows:
​
m∠3 + 86 = 180

m∠3 = 94

Angles ∠3 and ∠1 are vertical angles.

Therefore, by the vertical angles congruence theorem:

m∠1 = m∠3

Substitute m∠3 = 94 into the equality:

m∠1 = 94

Angles ∠2 and 86 angles are vertical angles.

Therefore, by the vertical angles congruence theorem:

m∠2 = 86

Angles(2x + 25) and ∠6 are supplementary angles

Therefore, the sum of their measures is:
​
(2x+25) + m∠6 = 180

86 + m∠6 = 180

m∠6 = 94

Angles ∠4 and ∠6 are vertical angles.

Therefore, by the vertical angles congruence theorem:

m∠4 = m∠6

94 = m∠4

m∠4 = 94

Angles ∠4 and ∠5 are supplementary angles.

Therefore, the sum of their measures is:
​
m∠4 + m∠5 = 180

94 + m∠5 = 180

m∠5 = 86

The value of x = 30.5

The measures of other missing angles are as follows:
​
m∠1 = 94°,m∠2 = 86°

m∠3 = 94°,m∠4 = 94°

m∠5 = 86°,m∠6 = 94°

Page 351 Exercise 16 Answer

Given:

To find:

Value of x

if ​m∠1 = (63 − x)

m∠2 = (72 − 2x)
​
In order to find the above we have to refer the tip mentioned and use the theorems accordingly.

Since the labeled angles are corresponding angles, it follows that:

m∠1 = m∠2

Substitute ∠1 = 63 − x and ∠2 = 72 − 2x into the equation:

63 − x = 72 − 2x

Solve for the value of x:

​63 − x = 72 − 2x

x = 72 − 63

x = 9
​
Therefore, the value of x = 9

The value of x is 9

Given:

To find:

m∠1 and m∠2

In order to find the above we have to refer to the theorems mentioned in tip

Since line r and s are parallel, angles ∠1 and ∠2 are congruent according to the Corresponding Angle Theorem. It follows that:

∠1 ≅ ∠2

Since ∠1 and ∠2 are congruent angles, their measures are equal. It follows that:

m∠1 = m∠2

Substitute m∠1 = (63 – x)^∘ and m∠2 = (72 – 2x)^∘ into the equation:

(63 – x)^∘ = (72 – 2x)^∘

Solve for x:

​63 − x = 72 − 2x

x = 9
​
m∠1 = (63 – x)^∘

Substitute x = 9 into the equation:

m∠1 = (63 – 9)^∘

Subtract the numbers

m∠1 = 54^∘

m∠2 = (72 – 2x)^∘

Substitute x = 9 into the equation:
​
m∠2 = (72 – 2(9))^∘

m∠2 = (72 – 18)^∘

m∠2 = 54
​
Therefore, both angles have the same measurement since they are corresponding angles.

The measures of the angles are:

m∠1 = m∠2 = 54^∘

They are equal because they are corresponding angles.

Envision Math Grade 8 Topic 6.8 Transformations Practice

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.8 Page 352 Exercise 17 Answer

Given:

To find:

∠b and ∠d

In order to find these angles we have to use supplementary angles theorem and also refer to the tip.

the Use the property of supplementary angles:
​
∠d + ∠136.9^∘ = 180^∘

∠d = 180^∘ − 136.9

∠d = 43.1
​
As m is parallel to n. so use property of alternate interior angles:

∠b = 60.7^∘

Hence, measurement of ∠b = 60.7^∘ and measurement of ∠d = 43.1^∘

Page 352 Exercise 18 Answer

Given:

To find:

Angles which are alternate interior angles.

In order to find the alternate interior angles refer to the tip mentioned.

The alternate interior angles are the angles formed when a transversal intersects two parallel lines, and lie on the inner side of the two parallel lines, on opposite sides of the transversal.

From this definition, we can easily identify the alternate interior angles by looking at the figure.

∠q and ∠t, ∠r and ∠k are alternate interior angles.

The alternate interior angles are ∠q and ∠t, ∠r and ∠k.

Page 352 Exercise 19 Answer

Given:

To find:

Value of w

To find the value of the above we have to use the theorem of supplementary angles.

Since the angles w and the angle of the measure of 101^∘ are adjacent angles that form a straight angle, they are supplementary angles and it follows:

w + 101 = 180

Solve the equation for w:
​
w + 101 = 180

w = 79

The value of w is 79

Given:

To find:

Mistake of Jacob.

in order to find the error in jacob’s calculation we have to use the theorems mentioned in tip.

The boy made a mistake by determining the angle of w, because from the Vertical Angles Congruence Theorem, the angle with measure of 101° is v.

Also, notice that w and 101^∘ form a linear pair.

Since w and 101^∘ are supplementary angles, therefore the value of w should be:

w = 180^∘ − 101^∘ = 79^∘

The boy might think that w is the vertical angle of the angle that measures 101^∘.

The boy might think that the angles that form linear pairs are equal.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 339 Exercise 1 Answer

Given:

Two figures on a coordinate plane.

To find:

Are the two figures alike or different.

By looking at the figure, we can observe that the shapes of the two triangles are the same, and so are the orientations. The only difference is in the size.

In order to verify whether the two figures are truly similar, we have to find if a dilation maps ΔA′B′C′ to ΔABC.

From figure vertices of ΔABC are:

From figure vertices of ΔA′B′C′ are:

By comparing coordinates of the vertices of ΔABC and ΔA′B′C′ , we can check if the transformation is a dilation.

Comparing the x-coordinates of the vertices of ΔABC and ΔA′B′C′ :

= \(\frac{1}{2}\)

= \(\frac{1}{2}\)

= \(\frac{1}{2}\)

Similarly, comparing the y-coordinates of ΔABC and ΔA′B′C′ also gives us the scale factor \(\frac{1}{2}\) = 0.5.

Hence, we can conclude that ΔA′B′C′ is really a dilation of ΔABC.

The two triangles are alike in shape and orientation, but are different in size. We know this for sure, since ΔA′B′C′ was found to be the dilation of ΔABC.

Envision Math Grade 8 Volume 1 Chapter 6.7 Solutions

Page 339 Exercise 2 Answer

Given: look for relationships is ΔABC a preimage of ΔA′B′C′

To find:

How do we know that the above statement is true.

In order to find that whether the statement is true or not we have to verify it with the help of tip mentioned above.

We can observe that ΔABC and ΔA′B′C′ both have the same shape, same orientation and same angles as well. The only difference between the two triangles is the difference in size.

Hence, we can say that ΔA′B′C′ is a dilation of ΔABC, and therefore ΔABC.

Yes, ΔABC is the preimage of ΔA′B′C′, since ΔA′B′C′ looks like the dilated version of ΔABC.

Page 339 Focus On Math Practices Answer

Given:ΔABC & ΔA′B′C′

To: How can you use the coordinates of the vertices of the triangles to identify the transformation that maps the triangles.

We will multiply the coordinates of the ΔABC with a scale factor k to obtain the triangle  ΔA′B′C′. Now as the obtained triangle only differs by a scale factor of k in respect of given triangle hence it will have the same shape as that of ΔABC.

We will multiply the coordinates of the ΔABC with a scale factor k to obtain the triangle  ΔA′B′C′.Now as the obtained triangle only differs by a scale factor of k in respect of given triangle hence it will have the same shape as that of ΔABC.

Congruence And Similarity Envision Math Exercise 6.7 Answers

Page 340 Convince Me Answer

Given:

To: Convince what sequence of transformation makes the triangle similar.

Step formulation: Calculate the ratio of sides and then prove similarity

In last part we calculated the ratio of sides A′B′ to AB, ratio of A′C′ to AC and ratio of B′C′ to BC.

It is observed that the ratio of all three of the sides is equal to \(\frac{9}{4}\).

Hence on that basis it can be concluded that the triangles are similar.

As the ratio of sides are equal hence the triangles are similar.

Envision Math Grade 8 Chapter 6.7 Explained

Page 341 Try It Answer

Given:

To: Find the reflection of JKL about x = 1 followed by dilation of \(\frac{1}{2}\).

Step formulation: Find the reflection of each point and then find the dilation.

Reflection of point L about x = 1.

i.e. the coordinates(−2,1) will become(4,1).

Reflection of point J about x = 1. will become

i.e. the coordinates(−2,−4)will become(4,−4).

Reflection of point K about x = 1.

i.e. the coordinates (−4,0) will become (6,0).

The transformed image is shown below.

For the dilation, the scale factor is \(\frac{1}{2}\).

So, \(\left(L^{\prime}\right)^{\prime}=\frac{4+4}{2}, \frac{1+(-4)}{2}\)

= 4, -1.5

Similarly(K′)′= 5,2

The dilated figure is:

The dilated i.e. the last transformed image is:

Given:

To: Prove ΔJKL is similar to ΔPQR. Step formulation: Find the ratio of sides.

Two-dimensional figure are similar if we can map one figure to the other by a sequence of rotations, reflections, translation, and dilations.

So, we found the sequence of transformations that map the ΔJKL onto ΔPQR :

translation for 8 units right and 1 unit up

rotation about point L

dilation with scale factor 2 about point L

Therefore, we can conclude that ΔJKL is similar to ΔPQR.

ΔJKL ~ ΔPQR

As all the three ratio of the sides are equal hence ΔJKL is similar to ΔPQR.

Page 342 Exercise 2 Answer

Given: Angles and side lengths of similar figures.

To: How do the angle measures and side lengths compare in similar figures?

In similar figures the corresponding angles must be equal.

Also the ratio of all corresponding sides must be equal.

In similar figures the corresponding angles must be equal.

Also the ratio of all corresponding sides must be equal.

Solutions For Envision Math Grade 8 Exercise 6.7

Page 342 Exercise 5 Answer

Given:

To: Obtain the final image by performing the given operations.

Step formulation: Graph each of the given steps and then obtain the final image.

ΔABC is dilated by a factor of 2 with a center of dilation at point C, reflected across the x axis, and translated 3 units up is shown in the below figure.

The graph obtained by performing sequence of operations is:

Page 342 Exercise 6 Answer

Given:

To: Find is the ΔABC similar to ΔDEF.

Step formulation: First find the length of the sides of the triangle and the find the ratio of corresponding sides.

Calculate the lengths of the sides of ΔABC & ΔDEF.

AB = \(\sqrt{(-1-(-4))^2+(-2-(-2))^2}\)

AB = 3

Similarly we can calculate the lengths of all sides.

BC = \(\sqrt{5}\)

CA = \(\sqrt{2}\)

DE = \(3 \sqrt{2}\)

EF = \(\sqrt{34}\)

FD = 8

The ratio between the longest sides i.e. between AB & FD = \(\frac{3}{8}\)

Ratio between BC & EF = \(\frac{\sqrt{5}}{\sqrt{34}}\)

As we can observe that the ratio of the sides is not equal, hence the triangles are not similar.

As we can observe that the ratio of the sides is not equal, hence the triangles are not similar.

Envision Math Grade 8 Volume 1 Chapter 6.7 Practice Problems

Page 343 Exercise 7 Answer

Given:

To: Describe a sequence of transformations that maps RSTU to VXYZ.

Step formulation: By taking reflection, translation and dilation, map both the triangles.

Since the figure RSTU is on the right of y axis, so, first lets take the reflection about y axis.

Now translate the obtained figure to left to 3 units.

Now translate the obtained figure to down to 3 units.

The figure obtained is:

Now to map the images we need to do the dilation.

Coordinates of V = (−2,−1) and coordinates of R₁ = (−6,−3).

Therefore, in order to match the figure it has to be reduce by factor 3.

So, \(R_1^{\prime}=\left(\frac{-6}{3}, \frac{-3}{3}\right)\)

R₁‘ = (-2, -1)

So now the coordinates match. Similarly we can do for other vertices.

In order to map the images we did reflection about y axis then translation of 3 units to the left and down afterward the dilation of factor 3.

Envision Math 8th Grade Congruence And Similarity Topic 6.7 Key Concepts

Page 343 Exercise 8 Answer

Given:

To: Is the shown triangles similar?

Step formulation: Find the ratio of the corresponding sides and then compare.

Find the length of the sides.
​
MN = 6

NO = 6

PQ = 12

OQ = 9
​
Now find the ratio of side.

As the ratio of sides is not equal, hence the triangles are not similar.

As the ratio of sides is not equal, hence the triangles are not similar.

Page 343 Exercise 9 Answer

Given:

To: Find the dilated and rotated image.

Step formulation: First find the coordinates after dilation and then rotate the figure.

Coordinates after dilation are:
​
P → 2(2,2) = 4,4

Q → 2(4,2) = 8,4

R → 2(3,4) = 6,8
​
So the dilated image is:

Now rotate the figure about the origin to 180^∘.

Final figure obtained by dilating and rotating about origin:

Page 344 Exercise 12 Answer

Given:

To: Find two possible coordinates for missing point Y.

For each coordinate chosen, describe a sequence of transformations, including a dilation, that will map the triangles.

Step fromulation: First locate point Y and then find the transformations.

Since the triangles are similar therefore,

Put the known in the expression.

Simplifying and finding ZY.

ZY = 2

Hence point Y will be 2 units away from Z in the horizontal direction. It’s coordinates are(−4,2).

Now to map ΔJLK with ΔXYZ transformations have to be taken.

Since both are equidistant from origin, therefore, mirror about origin will occur first.

Now after mirror dilation of factor \(\frac{1}{2}\)

ΔJLK will map with ΔXYZ.

Also the other coordinate of Y is (−4,5).

Possible coordinates of Y are(−4,2),(−4,5). To map the triangles, ΔJKL has to be mirred first then dilated by \(\frac{1}{2}\)

Envision Math Grade 8 Chapter 6.7 Lesson Overview

Page 344 Exercise 13 Answer

Given:

To: Which of the given triangles could Rajesh use for the pennants?

The triangles ΔQRS and ΔXYZ are similar because both have the same included angle and are the isosceles triangles. Both are right-angled isosceles triangles.

Whereas, ΔJKL is isosceles but does not have the same included angle, i.e. it is not right-angled; and it has no pair in the given options so it is not the answer. Also ΔWVT is right-angled, but is not isosceles and has no pair in the given options so it is not the answer.

Rajesh can use triangles given in option(B) ΔQRS & ΔXYZ for the pennants.

Envision Math Grade 8 Topic 6.7 Transformations Practice

Page 344 Exercise 14 Answer

Given:

To: Match the given options with similar or not similar.

ΔTVW & ΔQRS are both right angled isosceles triangle. Hence these are similar.

ΔJKL is not isosceles and is also not similar to any of the given triangles.

ΔTVW & ΔQRS are the similar triangles.

ΔTVW & ΔJKL are not similar triangles.

ΔJKL & ΔQRS are not similar triangles.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 333 Exercise 1 Answer

Given: AB = 2, AC = 2, AD = 5 and AE = 5

To determine the similarity and difference between two triangles.

First, use the Pythagoras theorem, to find the longest side and find the ratio of the triangle.

The image of a dilation has the same shape, orientation and angle measures as the preimage.

But they have different side lengths.

Because, a dilation is a transformation that moves each point along the ray through the point, starting from a fixed center, and multiplies distance from the center by a common scale factor.

Therefore, there will be some difference in size of the figures after these transformation.

Hence, there will be some difference in size of the figures after these transformation.

Envision Math Grade 8 Volume 1 Chapter 6.6 Solutions

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 333 Exercise 2 Answer

A dilation will be reduction when the scale factor is between 0 and 1,because the image is smaller than the original figure.

When the image is larger than the original figure, in another words, when the scale factor is greater than 1 a dilation will be enlargement.

A dilation will be reduction when the scale factor is between 0 and 1 because the image is smaller than the original figure.

When the image is larger than the original figure, in another words, when the scale factor is greater than 1 a dilation will be enlargement.

A dilation will be reduction when the scale factor is between 0 and 1 because the image is smaller than the original figure.

When the image is larger than the original figure, in another words, when the scale factor is greater than 1 a dilation will be enlargement.

Page 334 Essential Question Answer

A dilation is a type of transformation that enlarges or reduces the size of a figure called the preimage.

A dilation is a type of transformation that create a new figure called the image, that has the same shape as the preimage but a different size than the preimage.

After dilation, the image has the same shape as the preimage, but the size of the image is a scaled version of the preimage.

Congruence And Similarity Envision Math Exercise 6.6 Answers

Page 335 Try It Answer

Given: A dilation marks the point L(3,6) to its image point L′(2,4). The preimage is given in the figure below:

To find: The dilation image L’M’N’, the scale factor and length of the side M′N′.

Since L (3,6) → L′ (2,4) it follow that the scale factor k is

K = \(\frac{4}{6}=\frac{2}{3}\)

The other two vertices of ΔLMN are M(3,3),N(6,3)

The image of the vertex M after the dilation with a scale factor K = \(\frac{2}{3}\) is

The image of the vertex N after the dilation with a scale factor K = \(\frac{2}{3}\) is

With these points, the dilation figure L′M′N′ can be constructed as follows:

Hence, the image of ΔLMN, the ΔL′M′N′ is shown above.

Now, to find the length of side M ′N′, Let x1 be the x-coordinate of point M′(2,2) and x2 be the x-coordinate of point N′(4,2)

Since the side M′N′ is parallel to x−axis, length of the side M′N′ equals

x₂ − x₁ = ∣4∣ − ∣2∣

x₂ − x₁ = ∣2∣

The dilation with a scale factor K = \(\frac{2}{3}\) is shown below and the length of the side M′N′ is 2 units.

Envision Math Grade 8 Chapter 6.6 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 336 Exercise 2 Answer

If the scale factor k is between 0and 1, a dilation is a reduction.

If the scale factor k is between is greater than 1,a dilation is an enlargement.

Hence Proved.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 336 Exercise 4 Answer

Given:

To find the scale factor of figure 3 with respect to figure 1.

We will calculate the base length of given figures.

The base length of the triangle in figure 1 is 1 unit.

The base length of the triangle in figure 3 is 4 unit.

Hence, the scale factor will be \(\frac{4}{1}\)

Evaluating the expression, it gives 4.

Hence, the scale factor is 4, which was derived by comparing the base lengths of the preimage and the image.

v

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 336 Exercise 5 Answer

To find: the coordinates of the image of Figure 2 after a dilation with center at the origin and a scale factor of 3.

We will find the vertices after the dilation by multiplying the scale factor with given vertices in figure 2.

Given:

Figure 2:

Let A,B,C be the vertices of the triangle in Figure 2. Point A is 2 units right and 2 units above the origin so its coordinates are (2,2).

Therefore, the vertices of the original image in Figure 2 are A(2,2),B(3,4),C(4,2).

To obtain the vertices of the image of triangle ΔABC after a dilation with a scale factor of 3,multiply the coordinates of points A, B and C by 3.

The image of point A after a dilation with a scale factor k = 3 is

A(2,2) → A′(3⋅2,3⋅2) → A′(6,6)

The image of point B after a dilation with a scale factor k = 3 is

B(3,4) → B′(3⋅3,3⋅4) → B′(9,12)

The image of point C after a dilation with a scale factor k = 3 is

C(4,2) → C′(3⋅4,3⋅2) → C′(12,6)

Therefore, the vertices of the image after dilation are A′(6,6), B′(9,12), C′(12,6)

Therefore, the vertices of the image after dilation are A′(6,6), B′(9,12), C′(12,6)

Page 337 Exercise 7 Answer

Given:

To find:

The coordinates of each point in the original figure.

D(−),(−)E(−),(−)F(−),(−)

Multiply each coordinate by _______

Find the coordinates of each point in the image:

D(−),(−)E(−),(−)F(−),(−)

Graph the image.

In order to obtain the vertices of the image of triangle after a dilation with a scale factor, we need to multiply the coordinates with that factor.

In the given graph;

Point D coincides with the origin, so the coordinates areD(0,0)

Point E is 2 units to the right of the origin, so the coordinates are E(2,0)

Point F is 2 units up from the origin, so the coordinates are F(0,2)

Therefore, the vertices of the initial triangle are;

D(0,0),E(2,0) and F(0,2))

To obtain the vertices of the image of the triangle ΔDEF after a dilation with a scale factor of 2, multiply the coordinates by 2.

The image of the point D after a dilation with the scale factor k = 2 is:

D(0,0) → D′(2⋅0,2⋅0) → D′(0,0)

The image of the point E after a dilation with the scale factor k = 2 is:

E(2,0) → E′(2⋅2,2⋅0) → E′(4,0)

The image of the point F after a dilation with the scale factor k = 2 is:

F(0,2) → F′(2⋅0,2⋅2) → F′(0,4)

Therefore, the vertices of the final triangle are D(0,0),E(4,0) and F(0,4).

Plot the points D′(0,0),E′(4,0) and F′(0,4):

The triangle D′E′F′ is shown:

The triangle D′E′F′ is shown.

The vertices of the initial triangle are D(0,0),E(2,0) and F(0,2)

Multiply the coordinates by 2 to obtain the vertices of the final triangle:

D(0,0),E(4,0) and F(0,4)

Envision Math Grade 8 Volume 1 Chapter 6.6 Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 337 Exercise 8 Answer

Given:

To find:

The scale factor for the dilation

In order to find the scale factor, we need to compare the ratios of both dilations and then divide the number in fraction to obtain the scale factor.

The rectangle FGDE has sides with length of 5 and 6 units.

The rectangle F′G′D′E′ has sides with length of 15 and 18 units.

Therefore, the ratio of the side length in F′G′D′E′ to a corresponding side in FGDE s:

= \(\frac{3}{1}\)

Divide the numbers to get the scale factor: 3

The ratio of the side lengths is \(\frac{3}{1}\)

Therefore, the scale factor is 3

Envision Math 8th Grade Congruence And Similarity Topic 6.6 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6 Page 337 Exercise 10 Answer

Given:

In the figure small figure is dilation of large figure, origin is the center of dilation.

To find:

Whether the dilation is an enlargement or a reduction, and find the scale factor of the dilation.

In order to find the dilation is enlarge or reduce and to find the scale factor we have to refer to the tip mentioned.

The rectangle EFGH has the side length of 12 units.

The rectangle ABCD has a side length of 4 units.

Now the smaller figure, rectangle ABCD is the dilation of the larger rectangle EFGH. The larger figure is diluting in a smaller figure.

The Reduction is when a larger figure dilates into the smaller figure. Therefore, the dilation is a reduction.

The Scale factor is the ratio between the two same figures but different in sizes.

Scale Factor = Side length of \(\frac{A B C D}{E F G H}\)

Here, Side length of ABCD = 4 and EFGH = 12

Scale factor = \(\frac{4}{12}\)

Dividing the terms with 4.

Scale factor = \(\frac{1}{3}\)

The dilation is a reduction with the scale factor = \(\frac{1}{3}\)

Envision Math Grade 8 Chapter 6.6 Lesson Overview

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.6Page 338 Exercise 13 Answer

Given:

Rectangle Q′U′A′D′ with its coordinates and Q′,U′,A′,D′, is the image of QUAD after a dilation with center, and scale factor is 6.

To find:

Coordinates of point D′.

In order to find the coordinates of D′ we have to first find the coordinates of D and then multiply it with the scale factor.

Plot the points Q(0,0),U(0,3),A(6,3) and D(6,0) to form the quadrilateral.

Since the center of dilation is (0,0), the coordinates of the points can be multiplied by the scale factor.

since, the scale factor is 6, it multiply all coordinates of all points by it:
​
Q(6⋅0,6⋅0) → Q′(0,0)

U(6⋅0,6⋅3) → U′(0,18)

A(6⋅6,6⋅3) → A′(36,18)

D(6⋅6,6⋅0) → D′(36,0)
​
Therefore the coordinates of the point D′ are (36,0)

Plot the points Q′(0,0), U′(0,18), A′(36,18), D′(36,0) to plot the dilated quadrilateral.

The coordinates of the point D′ are (36,0). The dilated quadrilateral Q′U′A′D′ is shown.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 325 Exercise 1 Answer

Notice that each block is 1 unit long and 1 unit wide so they are all congruent.

To fit the blue piece into the space provided, rotate it 180^∘ counter-clockwise.

Then, shift the blue piece 3 units to the left.

Lastly, shift the blue piece 4 units down.

The blue piece fitting on the provided space is shown in the figure.

Since each block is 1 unit long and 1 unit wide, it follows that they are all congruent. By rotating and shifting the position of the original blue piece, it can fit into the space as shown.

Page 325 Exercise 2 Answer

The piece should be rotated at 180^∘.

Then the piece should be translated 3 units right.

Then the piece should be translated 4 units down.

So, the knowledge of translation and rotation can be used to fit the piece in the space.

The piece should be rotated at 180∘, then translated 3 units right and then translated 4 units left.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 325 Essential Question Answer

The transformations that always produce congruent figures are TRANSLATIONS, REFLECTIONS, and ROTATIONS. These transformations are isometric, thus, the figures produced are always congruent to the original figures. The transformation that sometimes produce congruent figures is dilation.

Rotations, reflections, and translations are isometric.

That means that these transformations do not change the size of the figure. If the size and shape of the figure is not changed, then the figures are congruent.

A reflection followed by translation, a translation followed by rotation, and a rotation followed by reflection all preserve congruence.

A reflection followed by translation, a translation followed by rotation, and a rotation followed by reflection all preserve congruence.

Page 346 Exercise 3 Answer

If the sequence of translations, reflections and rotations maps one rug onto the other then the rugs are the same size and shape.

Ava uses translation followed by a rotation to map the living room rug onto the hearth rug.

Since the two rugs are the same size and the same shape, they are congruent figures

Page 326 Exercise 4 Answer

A sequence of translations, reflections, and rotations map one rug onto the other then the rugs are the same size and shape.

Congruent figures have the same size and shape. The two-dimensional figure is congruent ( ≃ ) if the second figure can be obtained from the first by a sequence of rotations, reflections, and translations.

Ava uses a translation followed by a rotation to map the living room rug onto the hearth rug.

Since the two rugs are the same size and the same shape, they are congruent figures.

The two rugs are the same size and the same shape, they are congruent figures.

Page 326 Try It Answer

Given:

To find: whether the orange and blue rectangles are congruent.

They are both rectangles, thus their corresponding angles are congruent. Their side length need to be checked, if they are congruent, if they do not they are not, by the definition of congruence. Their side lengths need to be checked, if they have the same side lengths they are congruent, if they do not they are not.

Hence, Their side lengths need to be checked, if they have the same side lengths they are congruent, if they do not they are not.

Page 326 Convience Me Answer

Given quadrilateral diagram in graph.

To find the quadrilateral PQRS is congruent to P′Q′R′S′

From the definition of Congruent Polygon,

Hence, the definition of Congruent Polygons

Page 327 Try It Answer

Given figures in a graph

To find the given figures are congruent or not.

Rotate each vertex of the first figure 90^∘

counterclockwise around the origin. Since the quadrilateral A′′B′′C′′D′′ maps onto the second figure, those figures are congruent.

Hence, the first rotated 90^∘ counterclockwise around the origin and then translated 13 units to the right maps onto the second figure, so those figures are congruent.

Page 328 Exercise 1 Answer

Given: Sequence of translations, reflections and rotations

To find: The sequence of translations, reflections, and rotations result in congruent figures

Rotations, reflections and translations are isometric. That means that these transformations do not change the size of the figure. If the size and shape of the figure is not changed, then the figures are congruent.

Hence, the size and shape of the figure is not changed, then the figures are congruent.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 328 Exercise 2 Answer

Given: Sequence of transformations have to include a translation, a reflection, and a rotation.

To find: The sequence of transformations have to include a translation, a reflection, and a rotation to result in congruent figures

A sequence of transformation does not have to include any of the given transformation to result in a congruent figure. An example of this is the following sequence.

A dilation with respect to a point and with a scale factor of 2,a dilation with respect to the same point and with a scale factor of \(\frac{1}{2}\).

Hence, the sequence of transformation does not have to include any of the given transformation to result in a congruent figure.

Page 328 Exercise 3 Answer

Given: A sequence of reflections, rotations, and translations.

To find: The preimage and image not only congruent, but identical in orientation.

There are multiple sequence with this property, one example would be the following sequence.

Reflection over a line, reflection over the same line.

Hence, Reflection over a line, reflection over the same line is an example of The preimage and image not only congruent, but identical in orientation.

Page 328 Exercise 4 Answer

Given: A rectangle with an area of 25 square centimeters is rotated and reflected in the coordinate plane.

To find: The area of the resulting image.

Rotations and reflections don’t change the measures, thus the area is still 25cm².

Hence, the area of the resulting image is 25cm².

Page 328 Exercise 5 Answer

Given:

To find: ΔABC≅ΔDEF

We will find the distance between two points and we have to find the given triangle is congruent or not.

Repeat the procedure to determine the length of the sides of both triangle
​

Therefore, corresponding sides of the triangle are congruent. ΔABC ≅ ΔDEF

Page 328 Exercise 6 Answer

Given:

To find ΔABC ≅ ΔGHI

We will find the distance of given triangle and find the given triangle is congruent or not.

For the two triangles to be congruent, the corresponding measures of both triangle must be same.

From figure ΔABC, the length of AC

The length of GI in triangle GHI is \(\sqrt{29}\).

Since the corresponding sides are not congruent, the two triangles are not congruent. ΔABC is not congruent to ΔGHI.

Hence, the corresponding sides are not congruent, the two triangles are not congruent.

Page 329 Exercise 7 Answer

As the shape only undergoes reflection and translation. Its shape and size can not change.

Thus, ΔQRS and ΔQ′R′S′ have the same size and shape.

Hence, ΔQRS and ΔQ′R′S′ have the same size and shape.

Page 329 Exercise 8 Answer

Given:

To find the ΔDEF and ΔD′E′F′ is congruent or not.

The length of all corresponding sides of both the triangles are equal therefore side-side-side congruence theorem.

ΔDEF Δ D′E′F′

Hence, the length of all corresponding sides of both the triangles are equal therefore side-side congruence theorem

ΔDEF Δ D′E′F′

Page 329 Exercise 9 Answer

Given: Quadrilateral ABCD and A′B′C′D′.

To find the ABCD is congruent to quadrilateral A′B′C′D′

Observe the quadrilateral ABCD

Reflect ABCD over y−axis translate it for 5 units downwards to draw A′B′C′D′. Since both transformation are isometries it follow that A′B′C′D′ is congruent to ABCD.

Hence, A′B′C′D′ is congruent to quadrilateral ABCD.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 329 Exercise 10 Answer

Given graph

To find the flags the same shape and size.

Construct an line x = 1.5

The flags are the same shape and size because the second flag can be formed by reflecting and translating the first flag.

Hence, the flags are the same shape and size because the second flag can be formed by reflecting and translating the first flag.

Page 330 Exercise 11 Answer

Given:

To find which two triangles are congruent.

We will compare the given triangles to find if they are congruent or not.

Plot the points

The ΔQRS with coordinates Q(4,7),R(2,2),S(7,2) ΔDEF with coordinates D(7,−5),E(2,−2),F(2,−7)

Next, translate ΔQ′R′S′ 9 units going down.

The final image of the ΔQRS is the ΔQ′R′S′ with coordinates Q”(7,−5), R'(2,−7) and S”(2,−2)

Since both have the same vertices ΔQ”R’S”≅ ΔDEF

Therefore, by using the rotation, translation and reflection the ΔQ”R’S” ≅ ΔDEF

Page Exercise 12 Answer

Given points L(7,9),M(9,5)

ΔLMN ≅ ΔXYZ

To find the given triangles are identical or not.

We will calculate the distance between two points LM and also XY and then we will find the given points are identical or not.

As we have already mentioned, congruent figures have the same shape and the same size.

If you look at the triangle LMN,you can notice that these triangle does not have the same size as triangleXYZ.

To be precise, the corresponding size length of triangle LMN are greater then of triangle XYZ.

Therefore, there is no sequence of transformations that maps triangle LMN onto triangle XYZ LMN

We can conclude that these two triangles are not congruent.

ΔLMN ≠​ ΔXYZ

Hence, We can conclude that these two triangles are not congruent.

ΔLMN ≠ ​ΔXYZ

Page 330 Exercise 13 Answer

Plot the points D(4,5),E(5,1),F(1,2)

Since the obtained triangle is correct, the initial triangle should have been reflected across the x−axis and translated 6 units left and 4 units up.

The student likely made the mistake of mapping ΔD′E′F′ onto ΔDEF instead of ΔDEF onto ΔD′E′F′.

Therefore, the students made a mistake by translating the triangle 6 units right, as a result of trying to map ΔD′E′F′ onto ΔDEF.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 330 Exercise 14 Answer

The triangle , a sequence of rotation maps ΔDEF onto ΔD′E′F′.

Given graph is rotation.

Option (B) is incorrect because the sequence of transformations maps ΔDEF onto ΔD′E′F′

Option(C) is incorrect because the sequence of translations maps ΔDEF onto ΔD′E′F′

Option(D) is incorrect because the sequence of reflections maps ΔDEF onto ΔD′E′F′

Hence, a sequence of rotations maps ΔDEF onto ΔD′E′F′.

Option(A) is correct.

The ΔDEF rotated 180∘ about the point (2,2) and then translated 1 unit to the left maps onto the ΔD′E′F′

ΔDEF ≅ ΔD′E′F′

Hence proved ΔDEF ≅ ΔD′E′F′, since ΔDEF can be mapped onto ΔD′E′F′ by rotating ΔDEF by 180° about point (2,2) and translating it to the left by 1 unit.

Page 331 Exercise 1 Answer

Rotation:

A rotation is a transformation that turns a figure about a fixed point called the center of rotation. An object and its rotation are the same shape and size, but the figures may be turned in different directions. Rotation may be clockwise or counterclockwise.

Reflection:

In geometry, a reflection is a type of rigid transformation in which the preimage is flipped across a line of reflection to create the image. Each point of the image is the same distance from the line as the preimage is, just on the opposite side of the line.

Translation:

Translation is used in geometry to describe a function that moves an object a certain distance. The object is not altered in any other way. It is not rotated, reflected, or resized. In a translation, every point of the object must be moved in the same direction and for the same distance.

Hence, the three transformations where the image and preimage have the same size and shape are rotation, reflection and translation.

Page 331 Exercise 2 Answer

Given:

To find: the coordinates of each point after quadrilateral RSTU is rotated 90^∘ about the origin.

We know that the coordinates of RSTU then we will rotated 90^∘ about the origin R′S′T′U′

Coordinates of RSTU:
​
R (1,−2)
S (2,−4)
T (4,−5)
U (3,−3)
​
Rotated 90^∘ about the origin:
​
R′(2,1)

S′(4,2)

T′(4,−5)

U′(3,3)

The coordinates of points R(1,−2), S(2,−4), T(4,−5), U(3−3) after a 90^∘ rotation about origin are
​
R′(2,1)

S′(4,2)

T′(5,4)

U′(3,3)

Page 331 Exercise 4 Answer

Given:

To find the coordinates of each point after quadrilateral MNPQ is reflected across the x−axis.

We know that the coordinates of MNPQ are reflected across the x−axis.

Find the coordinates of the quadrilateral MNPQ from the graph:

Reading from the graph, the vertices are

M(1,2), N(2,4), P(4,5), Q(3,3)

Change the signs of the y-coordinates of the vertices to get the reflected quadrilateral:

Reading from the graph, the coordinates of the reflected points are R(1,−2),S(2,−4),T(4,−5),U(3,−3)

Hence, the coordinates of the reflected quadrilateral RSTU are (1,−2),(3,−3),(4,−5),(2,−4).

Page 331 Exercise 5 Answer

Reflect the rotated figure M′N′P′Q′ across the y−axis.

Rotation 180^∘ about the origin, and then reflection across the y−axis.

Option D is correct.

Option(A) is incorrect because reflection across the x−axis, translation 4units down.

Option(B) is incorrect because reflection across the y−axis, translation 4 units down.

Option(C) is incorrect because the rotation 180∘ about the origin, and then reflection across x−axis.

Hence, the rotation 180^∘ about the origin, and then reflection across the y−axis.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.5 Page 331 Exercise 6 Answer

Given:

To find the quadrilateral MNPQ congruent to quadrilateral RSTU.

We will find the congruent of given quadrilateral.

Rotate each vertex of the first figure 90°counterclockwise about the origin.

Now if we translate the quadrilateral P′N′M′Q′ 6 units down and 6 units to the right, it maps onto the second figure.

Hence, those figures are congruent.

The first figure rotated 90^∘ counterclockwise around the origin and then translated 6 units down and 6 units to the right maps onto the second figure , so those figures are congruent.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 315 Exercise 1 Answer

Given: Graph with two figure.

To find:

How can you map Figure A onto Figure B

To map Figure A onto Figure B, we have to do two transformations:

reflection across the y-axis

reflection across the x-axis

Notice that figures have the same shape and size, but orientation has changed. These are properties of the reflected figures.

Therefore, we can anticipate that there transformation will be reflection.

It is also important to say that is no matter what reflection was before.

Because the resulting picture, after the sequence of transformation, must be the same regardless of the order of transformation.

We can map Figure A onto Figure B using:

reflection across the y−axis.

Reflection across the x−axis.

Envision Math Grade 8 Volume 1 Chapter 6.5 Solutions

Page 315 Focus On Math Practices Answer

Given:

Graph for figure A and figure B

To find:

Is there another transformation or sequence of transformations that will map Figure A to figure B?

We can compose transformations by applying a sequence of two or more transformations.

And, if we look at the picture, we can see that we have to do more than one transformation to map Figure A to figure B.

To be precise, we have to:

– reflect the Figure A across the y-axis

– reflect the reflected figure across x-axis

It is important to emphasize that is no matter what transformation was before.

Because the resulting picture, after the sequence of transformation, must be the same

Yes, there is another transformation or sequence of transformations that will map Figure A to Figure B but the resulting picture, after the sequence of transformation, will be the same regardless of the order of transformations.

Page 316 Essential Question Answer

Given:

Graph for figure A and figure B

To find:

How can you use a sequence of transformations to map a preimage to its image?

We can compose transformations by applying a sequence of two or more transformations.

And, if we look at the picture, we can see that we have to do more than one transformation to map Figure A to Figure B.

To be precise, we have to:

reflect the Figure A across the y−axis

reflect the reflected figure across x−axis

It is important to emphasize that is no matter what transformation was before.

Because the resulting picture, after the sequence of transformation, must be the same regardless of the order of transformations.

The resulting picture, after the sequence of transformation, must be the same regardless of the order of transformations.

Congruence And Similarity Envision Math Exercise 6.5 Answers

Page 316 Convince Me Answer

Ava has decided to place the chairs directly across the couch.

She needs to do it by transformation.

We can see that Ava can compose these chairs across the couch by the method of transformation which is called linear transformation.

Finally, Ava can put the chairs across the couch by transformation.

Eva will use linear sequence for the transformation of chairs.

Page 317 Try It Answer

We had given two triangles ABC and A′′B′′C′′.

We need to find the transformation between them.

When two or more transformations are combined to form a new transformation, the result is called a sequence (or a composition) of transformations.

In a sequence of transformations, the first transformation produces an image upon which the second transformation is then performed.

The composition of transformation gives the mapping for the given triangle.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 318 Exercise 2 Answer

A preimage is rotated twice to its final position and opposite sign.

To compare the image and pre-image

If you follow is the rule :P(x, y) > 180° rotation

> P′(−x,−y). the negative signs don’t mean to make it negative but to change it to the opposite sign. If it’s positive it goes to negative. And if it’s negative is goes to positive. The rotated image would have the points: (1,2),(4,4),(3,7).

The signs don’t affect the position of the image.

Page 318 Exercise 3 Answer

Given:

A figure ABC, with vertices A(2,1),B(7,4) & C(2,7) is rotated clockwise about the origin, and then reflected across the y axis.

To: Describe another sequence that would result in the same image.

Step formulation: First perform the sequence of operation as given in question and then add another step to reconcile to the original image.

Perform the sequence of operation as given. First90∘

clockwise rotation about origin and then reflect about y
axis.

The sequence is shown below:

Now take the reflection of the last image about y = −x to reconsile to the original image. As shown in the below image:

Rotation about origin clockwise 90^∘ then reflection in y axis and finally the reflection about y = −x results in the same image.

Page 318 Exercise 4 Answer

Given:

To: Describe the transformation that maps the given figures.

Step formualtion: Take the reflection about the axis and then proceed.

First rotate WXYZ, 90^∘ anticlockwise about origin then translate 6 units down to map the figures. The sequence is shown below:

To map the images, WXYZ is rotated 90^∘ anticlockwise about origin and then translated 6 units downwards.

Page 318 Exercise 5 Answer

Given:

To: Describe the transformation that maps the given figures.

Step formualtion: Translate the figure 6 units down and then proceed.

To map the images, transform WXYZ 6 units down then reflection about y axis, then rotation about (−2,−4) in the clockwise direction for 90^∘ and then reflection about x = −2. The sequence is shown in the below figure:

To map the images, transform WXYZ 6 units down then reflection about y axis, then rotation about (−2,−4) in the clockwise direction for 90^∘ and then reflection about x = −2.

Envision Math Grade 8 Chapter 6.5 Explained

Page 318 Exercise 6 Answer

Given:

To find:

reflection of rectangle WXYZ

In order to find the reflection of the above we have to refer to the tip mentioned.

Draw a line y = 1

Since the point Z is one point above the line y = 1 the reflected point Z′ will be one point below the line y = 1

Using the same method, reflect points Y,X and W across the line y = 1 labeling them Y′X′ and W′

Translate each of the points Z′Y′X′ and W′ one unit right.

Label the translated points with Z′′,Y′′,X′′ and W′′

Connect the points to form a quadrilateral Z′′,Y′′,X′′ and W′′

The required image after a reflection across the line y = 1 and a translation 1 unit right is given.

Envision Math Grade 8 Topic 6.5 Congruence Practice Problems

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 319 Exercise 8 Answer

Given:

To find:

Location of translation of transformation of the given rectangle.

In order to find the location we have to follow the tip and plot the graph accordingly.

Draw the given rectangle on the graph.

Move all the points 3 units to the left and rename the rectangle as E′F′G′H′

Move all the points 3 units down.

The location of the quadrilateral E′F′G′H′ after two movement is shown

Rotate all the points 90^∘ about the origin

Therefore, the new location of E′F′G′H′ is shown

The new location of E′F′G′H′ is shown after 3 units left, 3 units right and 90^∘ rotation about the origin.

Solutions For Envision Math Grade 8 Exercise 6.5

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 319 Exercise 9 Answer

Given :

To describe a sequence of transformations that maps quadrilateral ABCD to quadrilateral HIJK.

First reflect the vertices of quadrilateral ABCD
then translate the vertices.

Reflect the vertices of quadrilateral ABCD along the x-axis

Then translate the vertices 6 units left and 1 unit upward to from quadrilateral HIJK

Thus, Reflection along the x-axis followed by the translation of 6 units left and 1 unit up maps the quadrilateral ABCD into the quadrilateral HIJK

Envision Math Grade 8 Chapter 6.5 Lesson Overview

Page 319 Exercise 10 Answer

Given:

To map △QRS to △Q′R′S′ with a reflection across the y-axis followed by a translation 6 units down.

Translate each of the points 6 units down then label the translated points.

The reflection line is x = 0.

Since the point R is two point left of the line x = 0, the reflected point R′ will be two point right of the line x = 0.

Using the same method, reflect points Q and S across the line x = 0 labeling them Q′,S′.

Translate each of the points Q′,R′,S′ six unit down.

Label the translated points with Q′,R′,S′ and connect them to form a triangle ΔQ′R′S′

Thus, the required image after a reflection across the line x = 0 and a translation 6 unit down is given.

Envision Math Grade 8 Volume 1 Chapter 6.5 Practice Problems

Page 319 Exercise 11 Answer

Given : A student says that he was rearranging furniture at home and he used a glide reflection to move a table with legs from one side of the room to the other.

To explain a glide reflection result in a functioning table

First draw the table image and point A.

Let the table be as shown and the point A represent the chair.

In glide reflection, the table is first translated as shown.

Then, the table is reflected along the line shown.

The resulting table after glide reflection is shown. it can be seen that it is a functioning table as the chair A is positioned correctly.

Thus, the resulting table after glide reflection is shown. it can be seen that it is a functioning table as the chair A is positioned correctly.

Envision Math 8th Grade Congruence And Similarity Topic 6.5 Key Concepts

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.4 Page 320 Exercise 13 Answer

Given :

To find which figure is the image of Figure A after a reflection across the x-axis and a translation 4 units right.

Reflect the figure A over the x-axis and translate the reflected figure.

Reflection of Figure A over the x-axis.

Translate the reflected figure 4 units to the right.

Therefore, the answer is Figure E.

Thus, the answer is letter D which is Figure E.

Given :

To find figure can be transformed into Figure G after a rotation 90^∘ about the origin, then a translation 13 units right and 4 units down.

First move the figure 4 units up and translate the figure then rotate 90^∘ about the origin.

In figure G, move the figure 4 units up.

Translate the figure 13 units to the left.

Rotate figure G′ through 90^∘ about the origin.

Then the 90^∘ rotated figure is similar to figure B.

Therefore, the answer is option A.

Thus, the correct answer is option A.

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 309 Focus On Math Practices Answer

We can describe Maria’s change in position, when car returns to the position at which she began the ride, with rotation.

Because, a rotation is a transformation that turns a figure around a fixed point, called the center of rotation. And as we can see in the picture, each car turns around central part of the Ferris wheel.

If we want to come back to the start position, this means that we have to go through an entire drive, or an entire circle.

This transformation can be described by rotation for 360^∘.

This transformation can be described by rotation for 360^∘

Page 310 Essential Question Answer

Given:

The two dimensional figure.

To find:

How does a rotation affect the properties of a two-dimensional figure?

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Envision Math Grade 8 Volume 1 Chapter 6.4 Solutions

Page 310 Try It Answer

Given:

The architect continues to rotate the umbrella in a counter clockwise direction.

To find:

What is the angle of this rotation?

Rotation for 360^∘ (one complete circle around) means turning around until we point in the same direction again.

If we want to determined the measure of angle of rotation to the original position, we have to find the value r

that is true for the equation:

90^∘ + r = 360^∘

Notice that, rotation for 360^∘ (one complete circle around) means turning around until we point in the same direction again.

And in the equation we add 90^∘, because we do not rotate from the start position. The umbrella has been rotated already for 90^∘.

90^∘ + r = 360^∘

r = 270^∘

​Subtract from the both sides by 90^∘

Therefore, the angle of this rotation is 270^∘

Therefore, the angle of this rotation is 270^∘.

Congruence And Similarity Envision Math Exercise 6.4 Answers

Page 311 Try It Answer

Given:

The coordinates of the vertices of quadrilateral HIJK are H(1,4), I(3,2), J(−1,−4), and K(−3,−2)).

To find:

If quadrilateral is rotated 270^∘ about the origin, what are the vertices of the resulting image, quadrilateral H′I′J′K′

We use the concept that:

The rule for a rotation by 270^∘ about the origin is

(x, y) → (y,−x).

There are some rules for x – and y – coordinates of a point at rotation for 270^∘

In another words, when we rotate for 270^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x, y)→(y,−x)

Therefore, the vertices of quadrilateral H′I′J′K′ are:
​
H(1,4) → H′(4,−1)

I(3,2) → I′(2,−3)

J(−1,−4) → J′(−4,1)

K(−3,−2) → K′(−2,3)

The vertices of quadrilateral H′I′J′K′ are

H′(4,−1)

I′(2,−3)

J′(−4,1)

K′(−2,3)

Page 311 Try It Answer

Given:

A figure with two triangles.

To find:

The description of the rotation that maps ΔFGH to ΔF′G′H′

We find the number of degrees that figure rotates.

To describe the rotation that maps triangle FGH to triangle F′G′H′, we have to find the angle of rotation. In another words, we have to find the number of degrees that figure rotates.

The procedure is simple:

1. Draw rays from the origin through point G and point G′.(Notice that, we can choose any point of the figure, because all point are rotated for the same angle.)

2. Measure the angle formed by rays.

(Use a protractor to determine the number of degrees.)

Hence, a 180^∘ rotation about origin maps ΔFGH to ΔF′G′H′.

Envision Math Grade 8 Chapter 6.4 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.3 Page 312 Exercise 1 Answer

Given:

A rotation of two dimensional figure.

To find:

How does a rotation affect the properties of a two-dimensional figure?

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference ,after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Page 312 Exercise 2 Answer

Given:

If a preimage is rotated 360 degrees about the origin

To find:

How can you describe its image?

We use the fact that 360 degrees about the origin means turning around until you point in the same direction again.

So, when we rotated some figure 360^∘ about the origin, we actually put the figure on the same position. Like we did not even change it.

Therefore, the image will be the same as the preimage.

Therefore, the image will be the same as the preimage.

Page 312 Exercise 3 Answer

Given: AB is parallel to DC

To find:

How are sides A′B′ related to C′D′.

There are not change in shape, side lengths, angle measures and orientation between resulting image and the final original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Therefore, if side AB is parallel to side CD on the preimage, the side A′B′ and C′D′ will also be parallel.

Because side lengths and shape remain the same after rotation.

Therefore, if side AB is parallel to side CD on the preimage, the side A′B′ and C′D′ will also be parallel. Because side lengths and shape remain the same after rotation.

Page 312 Exercise 4 Answer

Given:

The coordinates of the vertices of rectangle ABCD are

A(3,−2), B(3,2), C(−3,2), and D(−3,−2).

To find:

The coordinates of the vertices A′B′C′D′.

when we rotate for 90^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before first coordinate:

There are some rules for x – and y – coordinates of a point at rotation for 90^∘. In another words, when we rotate for 90^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before first coordinate:

(x, y) → (−y, x)

Therefore, the vertices of rectangle A′B′C′D′ are:
​
A(3,−2)→A′(2,3)

B(3,2)→B′(−2,3)

C(−3,2)→C′(−2,−3)

D(−3,−2)→D′(2,−3)

The vertices of rectangle A′B′C′D′

A′(2,3)

B′(−2,3)

C′(−2,−3)

D′(2,−3)

Given:

The coordinates of the vertices of rectangle ABCD are A(3,−2), B(3,2), C(−3,2), and D(−3,−2).

To find:

The measures of angles of A′B′C′D′

As we already said, the rotation is a transformation that turns a figure around a fixed point, called the center of rotation. There are not change in shape, side lengths, angle measures and orientation between resulting image and original figure by rotation.

The only difference, after rotation, is in x and y values in ordered pairs that represent the coordinates of vertices.

Therefore, the measures of the angles of A′B′C′D′ will be the same as the measures of the angles of A′B′C′D′.

To be precise, we know that figure A′B′C′D′ is also rectangle, because the rotation does not change the shape of figures.

So, as rectangle has four right angles, the measures of all angles will be 90^∘.

So, as rectangle has four right angles, the measures of all angles will be 90^∘.

Solutions For Envision Math Grade 8 Exercise 6.4

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.3 Page 312 Exercise 5 Answer

Given:

Graph with two triangles.

To find:

Counterclockwise rotation of ΔQRS.

We use the concept of rotation to solve the question.

To describe the rotation that maps triangle QRS to triangle Q′R′S′, we have to find the angle of rotation. In another words, we have to find the number of degrees that figure rotates.

The procedure is simple:

1. Draw rays from the origin through point Q and point Q′.(Notice that, we can choose any point of the figure, because all point are rotated for the same angle.)

2. Measure the angle formed by rays.

(Use a protractor to determine the number of degrees.)

Hence, 270^∘ rotation about origin maps QRS to Q′R′S′.

Hence, 270^∘ rotation about origin maps QRS to Q′R′S′.

Page 313 Exercise 6 Answer

Given:

Graph with two triangles.

To find:

The angle of rotation of the given maps about origin.

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

To describe the rotation that maps triangle PQR to triangle P′Q′R′, we have to find the angle of rotation. In another words, we have to find the number of degrees that figure rotates. The procedure is simple:

1. Draw rays from the origin through point Q and point Q′.(Notice that, we can choose any point of the figure because all point are rotated for the same angle.)

2. Measure the angle formed by rays.

(Use a protractor to determine the number of degrees.)

The angle of rotation about origin maps triangle PQR to triangle P′Q′R is 90^∘

The angle of rotation about origin maps triangle PQR to triangle P′Q′R is 90^∘.

Envision Math Grade 8 Volume 1 Chapter 6.4 Practice Problems

Page 313 Exercise 7 Answer

Given:

Graph with two triangles.

To find:

Is ΔXYZ rotation of ΔX′Y′Z′.

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

If triangle X′Y′Z′ is a rotation of triangle XYZ, each vertex of triangle X′Y′Z′

must be rotated around the origin for the same angle.

Therefore, we have to check angle measures for each corresponding pair of vertices.

To find out the angle measures, draw rays from the origin through each vertex of triangle XYZ and its corresponding vertex of triangle X′Y′Z′, then measure the angle formed by the rays.

Hence, yes X′Y′Z′ is rotation of XYZ.

Hence, yes X′Y′Z′ is rotation of XYZ.

Page 313 Exercise 8 Answer

Given:

ΔPQR is rotated 270^∘.

To find:

graph and label the coordinates.

We use the concept of rotation to find the graph.

To graph

The rotation for 270^∘ of triangle 270^∘ about origin we have to:

Draw the ray from the origin to vertex P.

Use a protractor to draw a 270^∘ angle in counterclockwise direction.

Plot vertex P′, the same distance from the origin as vertex.

We repeat the process to get it for other vertices.

There are some rules for x – and y – coordinates of a point at rotation for , the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

In another words, when we rotate for 270^∘ the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x,y)→(y,−x)

Therefore ,the vertices of triangle,P′Q′R′are:
​
P​(2,3) → P′(3,−2)

Q​(4,6) → Q′(6,−4)

R​(2,7) → R′(7,−2)

​But despite of that, we could also read the coordinates of vertices from the graph.

Therefore, the vertices of rectangle P′Q′R′ are:

P​(2,3) → P′(3,−2)

Q​(4,6) → Q′(6,−4)

R​(2,7) → R′(7,−2)

Page 313 Exercise 9 Answer

Given:

Graph with two triangles.

To find:

Is P′Q′R′ 270^∘ rotation of ΔPQR

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation.

If triangle P′Q′R′ is a 270^∘ rotation of triangle PQR, each vertex of triangle PQR must be rotated around the origin for 270^∘

Therefore, we have to check angle measures for each corresponding pair of vertices.

To find out the angle measures, draw rays from the origin through each vertex of triangle PQR and its corresponding vertex of triangle P′Q′R′, then measure the angle formed by the rays in the graph given below.

Therefore, we notice that we could also find out, if triangle P′Q′R′ is a 270^∘ rotation of triangle PQR, checking the relations between coordinates. Because, there are some rules for x – and y – coordinates of a point at rotation for 270^∘.

In another words, when we rotate for 270∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x,y) → (y,−x)

But that is not the case with these vertices:
​
P ​(3,3) → P′(−3,3)

Q (7,4) → Q′(−4,7)

R (3,5) → R′(−5,3)
​
So, we can conclude that triangle P′Q′R′ is not a 270^∘ rotation of triangle PQR.

So, we can conclude that triangle P′Q′R′ is not a 270^∘ rotation of triangle PQR

Envision Math 8th Grade Congruence And Similarity Topic 6.4 Key Concepts

Page 314 Exercise 10 Answer

To find: Why any rotation can be described by an angle between 20^∘ and 360^∘

Explanation:

Let’ start at any point of the coordinate system and slowly start to move around it. Once we have moved a quarter of the way around the circle, we will have a 90^∘ rotation. Then, when we keep moving, we will pass 180^∘ (or halfway) and later 270^∘ (or three quarters).

Once we reach the end of the circle, we will have passed a full 360^∘ around the circle. In another words, we will be right back where we started, at 0^∘.

It means turning around until you point in the same position again.

So, when we rotated some figure 360^∘ about the origin, we actually put the figure on the same position. Like we did not even change it.

Therefore, the rotation over 360^∘ we can observe like rotation that is reduced by 360^∘.

For example, a 420^∘ rotation will be:

420^∘ − 360^∘ = 60^∘ rotation

Because in the meantime, we will return to the starting position and from the starting position rotate for another 60^∘.

Once we have moved a quarter of the way around the circle, we will have a 90^∘ rotation. Then, when we keep moving, we will pass 180^∘ (or halfway) and later 270^∘ (or three quarters). Once we reach the end of the circle, we will have passed a full 360^∘ around the circle.

In another words, we will be right back where we started, at 0^∘ about the origin, we actually put the figure on the same position. Like we did not even change it. Hence, any rotation can be described by an angle between 0^∘ and 360^∘.

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.3 Page 314 Exercise 11 Answer

Given:

A graph with a rectangle.

To find:

Rotated KLMN 270^∘ about origin.

Use the concepts of rotation to solve the question.

To graph

The rotation for 270^∘ of triangle PQR about origin we have to:

Draw the ray from the origin to vertex K.

Use a protractor to draw a 270^∘ angle in counterclockwise direction.

Plot vertex K′, the same distance from the origin as vertex K.

Repeat the procedure for other vertices.

We now join the vertices,

Therefore, the rotated rectangle is

Envision Math Grade 8 Topic 6.4 Similarity Practice

Page 314 Exercise 12 Answer

Given:

An architect is designing a new windmill with four sails. In her sketch, the sails’ center of rotation is the origin, (0,0), and the tip of one of the sails, point Q, has coordinates (2,−3). She wants to make another sketch that shows the windmill after the sails have rotated 270^∘ about their center of rotation

To find: What would be the coordinates of Q′?

We use the concept of rotation.

Let’s drawn first the windmill with four sails. We have information that point Q, the tip of one of the sails, has coordinates (2,−3).

And if we know what kind of form windmills generally have, we can draw the remaining sails.

All four sails are equal in size and intersect at a right angle.

Notice that we can draw these sails so that the default sail we rotated three times for 90^∘.

Therefore:

Draw the point Q and the ray from the origin to point Q.

(That will be the sketch of the given sail.)

Use a protractor to draw a 90^∘ angle in counterclockwise direction.

Plot point Q1 the tip of other sail, the same distance from the origin as point Q.

We repeat he process,

Now, we have to graph of the sails about origin, their center of rotation to make another sketch that shows the windmill after the rotation of the sails. and the ray. angle in counterclockwise direction. ‘the same distance from the origin as point

the rotation for 270^∘ In another words, we have to rotated each tip of the sails for 270^∘

So, let’s rotated the first one:

Draw the point Q and a ray from the origin to point Q

(That will be the sketch of the given sail.)

Use a protractor to draw a 270^∘ clockwise.

Plot point Q′ the same distance from origin as Q.

Notice that, the position of that sail, after rotation, is on the position of one of the existing sails before rotation.

This will be the case with other sails after rotation too.

Therefore, we can conclude that the sketch of the windmill will be the same as in the beginning (before rotation).

Only replacing each sail with some existing sail so that the angle between them is 270^∘

We still have to specify the coordinates of point – and – coordinates of a point at rotation for, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate: Q′

There are some rules for x and y

In another words, when we rotate for 270^∘, the coordinates of the vertices of the resulting image are in reverse order and we have to put minus before second coordinate:

(x,y) → (y,−x)

The coordinates will shift from

Q​(2,−3) → ​Q′(−3,−2)

Envision Math Grade 8 Chapter 6.4 Lesson Overview

Page 314 Exercise 13 Answer

Given:

Rotation about origin maps ΔTRI to ΔT′R′I′.

To find:

Which graph shows an angle you could measure to find the angle of rotation about the origin?

Use the concept of rotation to solve the question.

Looking at the all pictures we can immediately say that graph at B is not graph that show an angle of rotation about origin, because there are two rays from one vertex. Moreover, the one of the ray is not even through the origin.

Then, notice that image at C and D are rays between unmatched vertices. And we measure the angle between corresponding vertices to find out the angle of rotation.

The graph at A shows an angle we could measure to find the angle of rotation about origin.

Result

The graph at A shows an angle we could measure to find the angle of rotation about origin.

The graph at A shows an angle we could measure to find the angle of rotation about origin.

Given:

Rotation about origin maps ΔTRI to ΔT′R′I′

To find:

What is the angle of rotation about axis?

To find the angle of rotation about origin, we have to find the number of degrees that figure rotates.

We have already rays from the origin through point R and point R′.

So, use a protractor to determine the angle formed by rays.

Hence the angle of rotation is 180^∘

Since the angle of rotation is 180^∘.

Hence the rest of the options are incorrect.

Correct option is (B) 180^∘ 

Envision Math Grade 8 Volume 1 Chapter 6 Congruence And Similarity

Page 303 Exercise 1 Answer

Given:

To: How are the figures the same? How are they different?

The pencil worked as a axis of reflection along which the figure one is reflected to make the figure two. When the pencil is removed and the paper is folded along the line, the two figures will overlap each other.

The pencil worked as a axis of reflection along which the figure one is reflected to make the figure two. When the pencil is removed and the paper is folded along the line, the two figures will overlap each other

Envision Math Grade 8 Volume 1 Chapter 6.3 Solutions

Page 303 Exercise 2 Answer

Given:

To find: What do you notice about the size, shape, and direction of the two figures?

As the figure 2 is the reflection of figure 1 the shape and size must be same. Also it can be observed that both the figures are right-handed triangles. But the location of their vertices are different in both the quadrants. Hence, directions are different.

As the figure 2 is the reflection of figure 1 the shape and size must be same. But the directions are different.

Page 303 Focus On Math Practices Answer

Given: Dale draws a line in place of his pencil and folds the grid paper along the line.

To: How do the triangles align when the grid paper is folded? Explain.

The line in place of pencil is acting like a axis of reflection. So the distance of both the figures from the line will be equal. So when the paper is folded, the vertical line of the figures will overlap. The base of the figure will overlap. Since both the figures have same size so the third side will also overlap.

The vertical line of the figures will overlap. The base of the figure will overlap. Since both the figures have same size so the third side will also overlap.

Page 304 Essential Question Answer

Given: Two-dimentional figure.

To: How does a reflection affect the properties of a two-dimensional figure?

When reflection takes place about x axis, the x coordinate remains the same, but the y coordinate is transformed into its opposite sign.

When reflection takes place about y axis, the y coordinate remains the same, but the x coordinate is transformed into its opposite sign.

When reflection takes place about x axis, the x coordinate remains the same, but the y coordinate is transformed into its opposite sign.

When reflection takes place about y axis, the y coordinate remains the same, but the x coordinate is transformed into its opposite sign.

Page 304 Try It Answer

Given:

To: Draw the new location of the chair on the plan.

Step formulation: Take the mirror image of the chair and then draw the final image.

Take the reflection of the chair about the dotted line and then draw the final image.

The final image of chair is shown in the figure:

Page 304 Convince Me Answer

Given: Image is reflected.

To: How do the preimage and image compare after a reflection?

A reflection is a transformation that turns a figure into its mirror image by flipping it over a line. The line of reflection (or axis of reflection) is the line about which the figure is reflected over. If the reflecting point is on the line of reflection then the image is the same as the preimage. Also, the image is always congruent to its preimage i.e. have the same shape and size.

A reflection is a transformation that turns a figure into its mirror image by flipping it over a line. The line of reflection (or axis of reflection) is the line about which the figure is reflected over. If the reflecting point is on the line of reflection then the image is the same as the preimage. Also, the image is always congruent to its preimage i.e. have the same shape and size.

Page 305 Try It Answer

Given:
​
k = 2,6

L = 3,8

M = 5,4

N = 3,2
​
To find: The coordinates of point N′.

As the reflection is about the y axis, therefore, the y coordinate will remain the same and the x coordinate will change its sign.

i.e. N′= −3,2

The coordinates of N after reflection is −3,2.

Congruence And Similarity Envision Math Exercise 6.3 Answers

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.2 Page 306 Exercise 4 Answer

Given:

A figure with two triangles.

To find:

Triangle X′Y′Z′ is a reflection of triangle XYZ.

From the picture we can see that vertices X and X′,Y and Y′,Z and Z′ are on the same distance from the line g,but on opposite sides.

Also, we can see that triangles have the same size and the same shape.

Therefore, triangle X′Y′Z′ is a reflection of triangle XYZ across the line g.

Triangle X′Y′Z′ is a reflection of triangle XYZ across the line g.

Page 306 Exercise 5 Answer

Given:

coordinate grid.

To find:

Describe the reflection of the figure EFGH.

We have to find the line of reflection over which a figure EFGH is reflected.

Notice that the line of reflection will be the line through the points that represent the half of lengths between the corresponding vertices.

In that case, we can say with certainty that each vertex of reflected figure will be on the same distance from the line of reflection.

Because the midpoint of the length divide length into two equal parts.

We first find the mid point of the length of vertices E and E′.

Let’s repeat the procedure for the corresponding vertices.

Now we draw all the points connecting the mid points to get the line of reflection.

Hence, EFG is reflected across y = 4.

Envision Math Grade 8 Chapter 6.3 Explained

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.2 Page 307 Exercise 7 Answer

Given:

The graph of a trapezoid.

To find:

Reflection of trapezoid ABCD across the y-axis.

Use the law of reflection to find solution of the question.

Let’s

reflect each vertex of trapeziod ABCD across the y-axis.

Before each reflection, we have to measure distance from each vertex to line of reflection, y-axis.

For example, vertex A is 2 units right from the y-axis. Therefore, vertex A′ must be 2 units left

from the line y-axis.

Then we repeat the procedure for other vertices,

Then joining the points we get,

Let’s identify first the points of the preimage:

A(2,8) B(6,8) C(8,3) D(2,3)

When we reflecting across the y-axis only x-values are opposite.

The y−values stay the same when we reflect a preimage the y-axis.

Because, during reflection across the y-axis and lines that are parallel with y-axis, we move only along the x-axis

Reflection acrossy−axis:(x,y)→(−x,y)

So, the points of the image:

A′(−2,8) B′(−6,8) C′(−8,3) D′(−2,3)

Plotted trapezoid is

A′(−2,8) B′(−6,8) C′(−8,3) D′(−2,3)

Page 307 Exercise 8 Answer

Given:

A figure with two triangles A′B′C′ and ABC

To find:

A′B′C′ and ABC are reflection across the line.

A reflection is a transformation that flips a figure across a line of reflection.

The preimage and image are the same distance from the line of reflection but on opposite sides So, figures have the same size and the same shape but different orientation after reflection.

If we look at the picture, we can see that corresponding vertices of triangles are not on the same distance from the line of reflection and that triangles are not opposite.

Therefore, the triangle A’B’C’ is not a reflection of triangle ABC.

The triangle A′B′C′ is not a reflection of triangle ABC.

Page 308 Exercise 11 Answer

Given:

Vertices of triangle ΔABC are A(−5,5),B(−2,3);C(−2,3)

To find:

The coordinate C′ when the triangle is reflected across y = −1.

When we reflect triangle ABC across the line y = −1,that means we are reflecting each vertex on the same distance from the line of reflection y = −1 on opposite side.

To find the coordinates of the vertex C′, first we have to measure the length between the vertex C and the line y = −1. Because, on the same distance from the line of reflection must be the corresponding vertex C′.

Notice that, when we reflect the figure across some line that is parallel to the x-axis

like y=−1,the x-values of all points of the figure will be the same

Because, we reflect the figure along y-axis. The y-values will changed.

If coordinates of vertex C are (−2,3) that implies that vertex C is 3 units up from y-axis. But we have to find the number of units to the line y = −1. So, we are looking for value of r that is true for equation:
​
3 − (−1) = r

r = 4
​
(Notice that when we move downwards. we subtract the values.)

The vertex C is 4 units up from the line of reflection. Therefore, the vertex C′ must be 4 units down from the line of reflection.

In another words, the second coordinate of point C′ will be:

−1 − 4 = −5

So, the coordinates of the vertex C′ are :​(−2,−5).

The coordinates of the vertex C′ are :​(−2,−5).

Solutions For Envision Math Grade 8 Exercise 6.3

Envision Math Grade 8 Volume 1 Student Edition Solutions Chapter 6 Congruence And Similarity Exercise 6.2 Page 308 Exercise 12 Answer

Given:

A figure with two parallelogram.

To find:

What reflection of ABCD is A′B′C′D′.

To describe the reflection of a parallelogram ABCD, we have to find the line of reflection over which a parallelogram ABCD is reflected.

Notice that the line of reflection will be the

Line through the points that represent the half of lengths between the corresponding vertices.

In that case, we can say with certainty that each vertex of reflected figure will be on the same distance from the line of reflection.

Because the midpoint of the length divide length into two equal parts.

We find the midpoint of the length of vertices A and A′:

We repeat the process for rest of the vertices and then join the points to get the line of reflection.

Therefore, ABCD is reflected across the line y = 3.

Envision Math Grade 8 Volume 1 Chapter 6.3 Practice Problems

Page 308 Exercise 13 Answer

Given:

ΔJAR has vertices J(4,5);A(6,4);R(5,2)

To find:

Correct graph for ΔJAR across x = 1.

First notice that image of triangle at is not only reflected but also translate some units up from the original one. Therefore, the are not the same distance between the line of reflection and corresponding vertices.

Then, on the image C vertices are not reflect to the corresponding ones. Moreover, these two angles have not the same corresponding side lengths and angle measures.

Now we have two options: A or B.

Let’s look first at the image A. As we already said, reflected figures are the same distance from the line of reflection but on opposite sides.

If we look the number of units between vertex A and line, then between line and vertex A′, we can notice that these are not the same numbers. In another words, the vertices are not on the same distance from the line of reflection.

Let’s look first at the image B. As we already said, reflected figures are the same distance from the line of reflection but on opposite sides.

If we look the number of units between vertex B and line, then between line and vertex B′, we can notice that these are the same numbers. In another words, the vertices are on the same distance from the line of reflection. Hence B is the correct option.

Graph B is correct.

Given:

∠A = 90

To find:

m ∠ A

We use the corresponding angle measures remain the same by reflection.

The corresponding angle measures remain the same by reflection.

Therefore, true is:

m ∠ A = 90^∘ ⇒ ​m ∠ A′ = 90^∘

Therefore,

m ∠ A′ = 90^∘