Marksparks

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

Page 157   Essential Question   Answer

In the above-given question, It is asked how one can graph a linear inequality in two variables.
Since a solution of a linear inequality in two variables is an ordered pair(x,y) for which the inequality is true.

The graph of a linear inequality in two variables shows all the solutions of the inequality in a coordinate plane.
We will give an example of inequality to prove the above.

Consider the inequality in two variables y ≥ −x − 5.
The graph of the inequality y ≥ −x − 5 is

Since y ≥ −x−5.

Put x = −2 and y = −2 in the above inequality, and we get

−2≥−(−2)−5

⇒ −2≥2−5

⇒ −2≥−3

Hence the inequality y ≥−x−5 is true for (−2,−2).
Therefore (−2,−2)  is the solution for the inequality y ≥−x−5.

1. Graph of the inequality y ≥ −x−5 

2. (-2,-2) is the solution of the inequality y ≥ −x−5.

Big Ideas Math Algebra 1 Chapter 5 Exercise 5.6 Solutions

Page 157  Exercise 1  Answer

In the above-given question, we were asked to write an equation represented by the dashed line in the given graph.

To solve the above we will use the Point slope form to write an equation of a line.
We calculate the slope of the dashed line given in the graph and consider one of the points on the line.

From the given graph, we have the points (3,0) and (0,−3) on the dashed line.
Therefore the slope of the dashed line is given by

m=\(\frac{-3-0}{0-3} \)

=1

Therefore the slope(m) of the dashed line is 1.

Since the slope of the dashed line is 1 and (0,−3) is one of the points on the dashed line.
Therefore the equation of the dashed line by the point-slope form is given by
y−y₁= m(x−x₁) ……(1)

Put  x₁ = 0, y₁ = −3 and m = 1 in the above equation, we get

y−(−3) = 1(x−0)

⇒ y+3 = x

⇒ y = x−3

Therefore y = x−3 is the equation of the dashed line.

An equation represented by the dashed line is y = x−3.

In the above-given question, the solutions of the inequality are represented by the shaded region below the dashed line y = x−3.

We were asked, to describe the solutions to the inequality represented by the shaded region.
We make use of the given graph to solve the above.

Since the line y = x−3 is represented by the dashed line.
Therefore the shaded region includes all points below the line y = x−3 but does not contain the points on the line y = x−3.

Hence the solutions of the inequality include points below the line y = x−3  and does not contain the points on the line y = x−3.

The solutions of an inequality represented by the shaded region include the points below the dashed line y=x−3 that does not contain the points on the line.

In the above-given question, we were asked to write an inequality that represents the above graph.
We make use of the given graph to solve this.

In the above graph, the solutions of the inequality are represented by the shaded region that is below the dashed line  y=x−3.

Since the solutions of the inequality include all the points below the dashed line and no points on the dashed line.

Hence the values of y are always less than  x−3.
Therefore we use strictly less than (<)  sign to represent the graph.
Therefore corresponding inequality that represents the graph is y<x−3.

The inequality represented by the graph is y< x−3.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.6 Page 157  Exercise 2  Answer

Given: Inequality y ≥ \(\frac{1}{4} x-3\).

We asked to enter the equation y\(=\frac{1}{4} x-3\) inside the graphing calculator.
To solve the above we simply enter the equation y=\(\frac{1}{4} x-3\) inside the calculator to get the desired result.

By entering the equation y=\(\frac{1}{4} x-3\) into the calculator, we get the graph of y=\(\frac{1}{4} x-3\)
Therefore the graph of y=\(\frac{1}{4} x-3\)after entering the corresponding equation inside the calculator is

Graph of the equation  y\(=\frac{1}{4} x-3\) after entering the equation y\(=\frac{1}{4} x-3\) inside the calculator is

Given:  The Inequality  y \(\geq \frac{1}{4} x-3\)

We asked to graph y \(\geq \frac{1}{4} x-3\).
Using a graphing calculator also to check the same by considering a point inside the region.
To solve the above we enter the equation y \(=\frac{1}{4} x-3\) inside the calculator then accordingly shade the region.

Enter the equation y=\(\frac{1}{4} x-3\) inside the graphing calculator. After entering the above equation we get the graph of y=\(\frac{1}{4} x-3\) is given by

Since inequality y \(\geq \frac{1}{4} x-3\) has the symbol≥.
Therefore the shaded region is above the graph of y=\(\frac{1}{4} x-3\)
Therefore the graph of y \(\geq \frac{1}{4} x-3\) is

Since  y\(\geq \frac{1}{4} x-3\)

Put(0,0) in the above inequality, and we get

⇒  \(\geq \frac{1}{4}(0)-3\)

⇒  0 ≥ 0−3

⇒  0 ≥−3

Hence the point(0,0) lies in the region y \(\geq \frac{1}{4}(0)-3\)
Therefore the point(0,0) is the solution of the inequality y\(\geq \frac{1}{4}(0)-3\)

1. Graph of y\(\geq \frac{1}{4}(0)-3\) by using a graphing calculator is

2. The inequality y\(\geq \frac{1}{4}(0)-3\) is true for(0,0).

Solving Systems Of Equations Exercise 5.6 Answers

Page 158  Exercise 3  Answer

Given: The Inequality y > x + 5.

We asked to graph the above inequality, and also to check the same using graphing calculator.
To solve the above we graph the equation y = x + 5 then accordingly shade the region.

Since the inequality y > x + 5 does not contain the equal to(=) sign.
Therefore we graph the equation y = x + 5 with a dashed line.
Therefore The graph of the equation y = x + 5 is given by

Since the inequality y>x+5 contains the strictly less then (>) sign.
Therefore the shaded region will be above the line y =x + 5 that does not contain the line.
Therefore the graph of the inequality  y > x + 5 is given by

Since y >  x + 5.

Put x = −1 and y = 1 in the above inequality, and we get

⇒ 1 >−1 + 5

⇒ 1 > 4

Hence(−1,1) does not satisfy the inequality y > x + 5.
Therefore(−1,1) is not a solution to the inequality y > x + 5.

1. Graph of y> x+5 is

2.Graph of y>x+5 using a graphing calculator is

3. (-1,1) is not a  solution  to the Inequality  y > x+5

Given: The  Inequality y≤\(\frac{-1}{2} x+1\)

We asked to graph the above inequality, and also to check the same using graphing calculator.
To solve the above we graph the equation y=\(\frac{-1}{2} x+1\) then accordingly shade the region.

We graph the linear equation y=\(\frac{-1}{2} x+1\)
with the continuous line, since the inequality contains the equal to(=) sign.
Therefore the graph of y=\(\frac{-1}{2} x+1\) is given by

Since the inequality y≤\(\frac{-1}{2} x+1\) contains the sign≤.
Therefore the shaded region will be below the line y=\(\frac{-1}{2} x+1\)
Therefore the graph of y ≤\(\frac{-1}{2} x+1\) is given by

Since y≤ \(\frac{-1}{2} x+1\)

Put x = −1 and y = −1 in the above inequality, and we get

−1≤ \(\frac{-1}{2}(-1)+1\)

⇒ −1≤ \(\frac{-1}{2}+1\)

⇒ −1≤\(\leq \frac{3}{2} \approx 1.5 \)

Hence the point(−1,−1) satisfy the inequality y≤\(\frac{-1}{2} x+1\)
Therefore(−1,−1) is the solution for the inequality y≤\(\frac{-1}{2} x+1\).

1. Graph of y=\(\frac{-1}{2} x+1\) is

2. Graph of y≤\(\frac{-1}{2} x+1\) using a graphing calculator is

3.The inequality y≤\(\frac{-1}{2} x+1\) is true for(−1,−1).

 Given: The inequality is y ≥−x−5

We have to graph this inequality.

For that, we have to draw a line y = −x−5 and shade the solution region which is above the line.
We can check this solution by using a random point.

We have y ≥−x−5
To graph this inequality
First, we have to draw a line y=−x−5 and shade the solution region which is above the line. i.e.

To check this solution Let us take a random point (0,0) So here,​ x = 0 y = 0 Therefore

​⇒  y ≥−x−5

​⇒  0≥−0−5

​⇒  0≥−5
​
Here,(0,0) is in the solution therefore, the solution is true.

The graph of the inequality y ≥−x−5 is

Big Ideas Math Student Journal Exercise 5.6 Explained

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.6 Page 158   Exercise 5  Answer

Let x is the number of books and y is the number of pencils.
A person has  $15 and wants to buy notebooks and pencils.

If the price of a notebook is  $2 and the price of a pencil is  $1.
Then the items of each type the person can buy are  2x + y ≤ 15.
An example of a real-life situation that can be modeled using a linear inequality in two variables is.

A person has $15 and wants to buy notebooks and pencils.
If the price of a notebook is $2 and the price of a pencil is $1.
Then the items of each type the person can buy are  2x + y ≤ 15.

Page 160  Exercise 2  Answer

Given: The given inequality is x−y ≥ 2  and the ordered pair is (5,3).

We have to find whether the ordered pair is a solution to the inequality.
For that, we have to check whether the given ordered pair satisfies the inequality.

We have the inequality x−y ≥ 2. The given ordered pair is(5,3)i.e.

⇒  ​​x−y​ ≥ 2

⇒ 5−3 ≥ 2

⇒ 2 ≥ 2

Here this solution is true.

The given ordered pair(5,3) is a solution to the inequality  x−y ≥ 2

Page 160   Exercise 3  Answer

 Given:  The inequality is​ x + 2y ≤ 4 and the ordered pair is (−1,2).

We have to find whether the ordered pair is a solution to the inequality.
For that, we have to check whether the given ordered pair satisfies the inequality.

We have the inequality​ x + 2y ≤ 4. The given ordered pair is (−1,2) i.e.

⇒ ​−1 + 2 × 2 ≤ 4

⇒ −1 + 4 ≤ 4

⇒ 3 ≤ 4
​
Here this solution is true.

The given ordered pair(−1,2) is a solution to the inequality x + 2y ≤ 4.

Page 160  Exercise 4  Answer

 Given:  The inequality is​ 5x + y < 7 and the ordered pair is (2,−2).

We have to find whether the ordered pair is a solution to the inequality.
For that, we have to check whether the given ordered pair satisfies the inequality.

We have the inequality​ 5x + y < 7. The given ordered pair is (2,−2) i.e.​​

⇒  5×2+(−2) < 7

⇒  10−2 < 7

⇒  8 < 7

Here this solution is not true.

The given ordered pair(2,−2) is not a solution to the inequality 5x + y < 7.

Page 160  Exercise 6  Answer

 Given:  The inequality is​  −x−2y ≥ 5 and the ordered pair is (−2,−3).

We have to find whether the ordered pair is a solution to the inequality.
For that, we have to check whether the given ordered pair satisfies the inequality.

We have the inequalit  y​−x−2y ≥ 5 .The given ordered pair is (−2,−3)i.e.​​

⇒  −x−2y ≥ 5
​
⇒  −(−2)−2(−3) ≥ 5

⇒  2−(−6) ≥ 5

⇒  2 + 6 ≥ 5

⇒  8 ≥ 5

​Here this solution is true.

The given ordered pair(−2,−3) is a solution to the inequality y−x−2y≥5.

Chapter 5 Exercise 5.6 Solving Systems Practice

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.6 Page 160  Exercise  7 Answer

 Given:  The inequality is y < 4.

We have to graph this inequality.
For that, we have to draw a line y = 4  and shade the solution region which is below the line.

We have y<4
To graph this inequality
First, we have to draw a line y=4 and shade the solution region which is below the line. i.e.

The graph of the inequality y<4 is

Page 160  Exercise 8  Answer

 Given: The inequality is y >−1.

We have to graph this inequality.
For that, we have to draw a line y = −1 and shade the solution region which is above the line.

We have y >−1
To graph this inequality
First, we have to draw a line y >−1
and shade the solution region which is above the line.

The graph of the inequality y >−1

Page 160  Exercise 9  Answer

 Given: The inequality is x >3.

We have to graph this inequality.
For that, we have to draw a line x=3 and shade the solution region which is greater than x=3.

We have x >3
To graph this inequality
First, we have to draw a line x = 3 and shade the solution region greater than x = 3. i.e.

The graph of the inequality x >3 is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.6 Page 160  Exercise 10  Answer

 Given: The inequality is x ≤−1.

We have to graph this inequality.
For that, we have to draw a line x =−1 and shade the solution region which is less than or equal to−1.

We have x ≤−1
To graph this inequality
First, we have to draw a line x =−1 and shade the solution region less than or equal to−1. i.e.

The graph of the inequality x = −1 is

Page 160  Exercise 11  Answer

 Given: The inequality is y <−2.

We have to graph this inequality.
For that, we have to draw a line y = −2 and shade the solution region which is below the line.

We have y <−2
To graph this inequality
First, we have to draw a line y <−2 and shade the solution region which is below the line. i.e.

The graph of the inequality y <−2 is

Page 160  Exercise 12  Answer

 Given: The inequality is x >−2.

We have to graph this inequality.
For that, we have to draw a line x = −2 and shade the solution region which is greater than−2.

We have x >−2
To graph this inequality
First, we have to draw a line x =−2 and shade the solution region greater than−2. i.e.

The graph of the inequality x >−2 is

Big Ideas Math Algebra 1 Exercise 5.6 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.6 Page 161  Exercise 13  Answer

 Given: The inequality is y< 3x + 1.

We have to graph this inequality.
For that, we have to draw a line y = 3x + 1 and shade the solution region which is below the line.

We have y < 3x + 1
To graph this inequality
First, we have to draw a line y = 3x + 1 and shade the solution region which is below the line. i.e.

The graph of the inequality y = 3x + 1 is

Page 161  Exercise 15  Answer

Given: x−y < 2

To find graph the inequality in a coordinate plane.
First, get y alone on one side, then consider the related equation obtained by changing the inequality.

Sign to an equality sign, then the graph of this equation is a line.
If the inequality is strict graph a dashed line and if the inequality is not strict graph a solid line.

The given inequality can be rewritten as

⇒  ​x−y < 2

⇒ ​ −y < 2 − x

⇒ ​ y > −2 + x
​
The related equation is y = −2 + x.

Since the inequality sign is strict, so draw a dashed line for the related equation.
Since the inequality sign is greater than, so shade the region above the boundary line.
So, the graph of the inequality x−y < 2 is

The graph of the inequality x−y < 2 in a coordinate plane is

Page 161  Exercise 16  Answer

Given: x + y ≥−3

To find  graph the inequality in a coordinate plane.
First, get y alone on one side, then consider the related equation obtained by changing the inequality.

Sign to an equality sign, then the graph of this equation is a line.
If the inequality is strict graph a dashed line and if the inequality is not strict graph a solid line.

The given inequality can be rewritten as

​⇒ ​ x + y ≥ −3

⇒ ​ y ≥ −3−x
​
The related equation is  y = −3−x.

Since the inequality sign is not strict, so draw a solid line for the related equation.
Since the inequality sign is greater than or equal to, so shade the region above the boundary line.
So, the graph of the inequality  x + y ≥−3 is

The graph of the inequality x + y ≥ −3 in a coordinate plane is

How To Solve Exercise 5.6 Big Ideas Math Chapter 5

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.6 Page 161  Exercise 17 Answer

Given: x + 2y < 4

To find a graph of the inequality in a coordinate plane.
First, get y alone on one side, then consider the related equation obtained by changing the inequality.

Sign to an equality sign, then the graph of this equation is a line.
If the inequality is strict graph a dashed line and if the inequality is not strict graph a solid line.

The given inequality can be rewritten as

⇒ ​ ​x + 2y < 4

⇒ ​ 2y < 4−x

⇒ ​ y<\(2-\frac{x}{2}\)

​The related equation is y=\(2-\frac{x}{2}\)

Since the inequality sign is strict, so draw a dashed line for the related equation.
Since the inequality sign is less than, so shade the region below the boundary line.
So, the graph of the inequality  x + 2y < 4 is

The graph of the inequality x + 2y < 4 in a coordinate plane is

Page 161  Exercise 18  Answer

Given: The linear function, −2x+3y>6.

Let’s assume it a linear equation, and Find the coordinates of the x, and y-axis intersecting points.
Plot them on the graph and draw a dotted line connecting those points.
Shade the area above that linear equation.

Let, the linear equation be −2x + 3y = 6.
Point of intersecting X – axis is (x,0)

⇒−2(x)+3(0)=6

⇒−2x=6

⇒x=−3

∴  The point of the intersecting X-axis is (-3,0)

Plot the points in graph

The graph of given inequality is

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.6 Page 161  Exercise 19  Answer

Given:  Profit on sale of each digital camera x is 100 and cell phone y is 50.

By selling digital cameras and cell phones store wants to make profit at least 300.
Find a linear equation and plot the linear equation on a graph.
Find any two points justifying the equation and interpret

Let, the number of digital cameras sold be x, cellphones sold be y.
Then, the linear inequality will be  100x + 50y ≥ 300.

Plot the inequality on graph
Identify any two points covered in the shaded area

At (1,4), i.e. one unit of digital camera and 4 units of cell phones sold profit will be

=100(1) + 50(4)

=300

At  (4,2),  i.e. 4 units of Digital cameras and 2 units of cell phones sold profit will be

=100(4) + 50(2)

=500(>300)

A linear inequality is 100x +50y ≥ 300. Graph of the above linear inequation is

Any point covered under the shaded area will solve the given inequation

Big Ideas Math Chapter 5 Exercise 5.6 Answer Key

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

Page 162  Essential Question  Answer

Let’s assume that inequality as a linear equation, and Find the coordinates of X−, Y− axis intersecting points.
Plot them on graph and draw a dotted(>,<)​ or a solid(≥,≤) line connecting those points.
Shade the area above that linear equation if the inequalities are >,≥ or below the linear equation if the inequalities are <,≤

A system of linear inequalities can be plotted on graph by using the mentioned process:

1. Let’s assume that inequality as a linear equation, and Find the coordinates of the  X, and Y  axis intersecting points.

2. Plot them on graph and draw a dotted  (>,<)  or a solid  (≥,≤)  line connecting those points.

3. Shade the area above that linear equations if the inequalities are  >,≥  or below the linear equation if the inequalities are  <,≤

Big Ideas Math Algebra 1 Chapter 5 Exercise 5.7 Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.7 Page 162  Exercise 1  Answer

Given: Linear function  2x + y ≤ 4

Let’s assume it a linear equation, and Find coordinates of X, Y− axis intersecting points.
Plot them on graph and draw a dotted line connecting those points.
Shade the area below that linear equation.

On  X− axis  (x,0)  coordinates are  (2,0)
On  Y− axis  (0,y)  coordinates are  (0,4)

Plot the coordinates on the graph

Graph and inequality  2x + y ≤ 4  matches each other, as the given graph and solved graph showing same picture

Given: Linear function,  2x−y ≤ 0

Let’s assume it a linear equation, and Find the coordinates of X, Y− axis intersecting points.
Plot them on graph and draw a solid line connecting those points.
Shade the area below that linear equation.

On X− the axis  (x,0)  coordinates are  (0,0).
Since line passes through the origin, let’s take another coordinate of x, i.e. (2,y).
Another coordinates are (2,4)

Plot coordinates on graph

Graph and inequality  2x−y ≤ 0  matches each other, as the given graph and solved graph showing the same picture

Solving Systems Of Equations Exercise 5.7 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.7 Page 162  Exercise 2  Answer

The given inequalities are:

⇒  2x + y ≤ 4

⇒  2x − y ≤ 0

Plot for the inequalities will be

Since both inequalities are  ≤  type, therefore, we shaded the reason left to the lines.

From the graph, the conclusion can be drawn that the point lies in the intersection of the shaded regions are the solutions of given linear inequalities.

The inequalities are:

⇒  2x + y ≤ 4

⇒  2x−y ≤ 0

The plot for the above inequalities is

Since both inequalities are less than equal to type. The red shaded region is a set of all points which satisfy the inequality one.
Similarly, the blue-shaded region is the set of all points which satisfy the 2nd inequality.

The intersection of two shaded regions is the set of all points which satisfy both the inequalities.
The unshaded region of the graph is a set of all points that satisfy none of the inequalities.

The region covered by intersection of two shaded regions. Will be the solution to linear inequalities The unshaded region of the graph is a set of all points that satisfy none of the inequalities. ​2x+y≤4,  2x−y≤0 Graph :

​

Page 163  Exercise 3  Answer

Given: How can you graph a system of linear inequalities?

Pick one point that is not on either line and decide whether these coordinates satisfy the inequality or not.
If they do, shade the half-plane containing that point.
If they don’t, shade the other half-plane.

Graph each of the inequalities in the system in a similar way.
The solution of the system of inequalities is the intersection region of all the solutions in the system.

Pick one point that is not on either line and decide whether these coordinates satisfy the inequality or not. If they do, shade the half-plane containing that point. If they don’t, shade the other half-plane. Graph each of the inequalities in the system in a similar way.
The solution of the system of inequalities is the intersection region of all the solutions in the system.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.7 Page 163  Exercise 4  Answer

Our aim is to find a region that represents, the solution of a system of linear inequalities when the graphing happens.

Let us consider an example of a system of linear inequalities.
⇒  ​y < 3

⇒  y > x−4

Following is graphing of the system.

In this graph, a region covered by both colors red and blue is the solution of the system.

When a graphing of a system of linear inequalities, then intersections of all shaded regions represent the solution of the system. This is where the solution of the system lies.

In this graph, a region covered by both colors red and blue is the solution of the system.

Page 163  Exercise 5  Answer

Given: That Do you think all systems of linear inequalities have a solution? Explain your reasoning.

The solution of a linear inequality is the ordered pair that is a solution to all inequalities in the system and the graph of the linear inequality is the graph of all solutions of the system.

Graph one line at the time in the same coordinate plane and shade the half-plane that satisfies the inequality.
The solution region which is the intersection of the half-planes is shown in a darker shade.
Usually, only the solution region is shaded which makes it easier to see which region is the solution region.

A system of linear inequalities can have none, one, or an infinite number of solutions; therefore, there are three.

Big Ideas Math Student Journal Exercise 5.7 Explained

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.7 Page 163  Exercise 6  Answer

Given that:

To prove: Use the graph’s shading to determine which way your inequality sign will face.
This works for single inequalities as well as systems of inequalities.
If you have more than one line on the graph, you’ll need to use these steps to write more than one inequality.

One of the lines has the equation y=3 As the solution is below it and the line is strong we can write the first inequality can write the first inequality y≤3 The other line has the equation x = 2. As shown in the graph

As the solution is at the left of it and the line is strong we can write the second inequality x ≤ 2  The system is \(\left\{\frac{y \leq 3}{x \leq 2}\right. \)

The equation of the given graph is: \(\left\{\frac{y \leq 3}{x \leq 2}\right. \)

Page 165  Exercise 1  Answer

Considered inequalities are

⇒ ​y > 2

⇒ y < x−2
​
Our aim is to check whether the point (0, 0) is the solution to the inequalities or not. Steps to be followed as:
1. Plot the inequalities.
2. Check that the point (0,0) is inside the feasible region or outside the feasible region.

If (0,0) is inside the feasible region, then it will be the solution to the given inequalities otherwise not a solution.

Following is the plot for the given inequalities:

It is clear that the point (0,0) lies outside of the feasible region, which indicates that the point (0, 0) is not the solution to the inequalities.

⇒ y > 2

⇒ y < x − 2

Chapter 5 Exercise 5.7 Solving Systems Practice

Page 165  Exercise 2  Answer

Provided linear inequalities provided are:

⇒ ​y < 3

⇒ y > x − 4
​

We have to check whether the point (−1,1) is solution to the inequalities or not. Steps to be followed:
1. Plot the given inequalities and the point in the graph.
2. Check whether the point lies inside the feasible region or not, if yes the point is the solution to those inequalities.

The following is graph corresponds to inequalities:

⇒ ​y < 3

⇒ y > x − 4

​

From the graph, it is clear that point (−1,1) lies in the feasible region

The point (−1,1) is the solution to the inequalities:

⇒ ​y < 3

⇒ y > x​ − 4

​

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.7 Page 165 Exercise 3 Answer

Given: The system of inequalities is

⇒ ​y ≥ x + 4

⇒ y ≤ 2x + 4

We need to check that the point (2,3) is the solution to the above system of inequalities. The sequence to solve the problem is:
1. Make a graph for the given inequalities and the given point.
2. Observe that the point is on the feasible region, if yes then it will be a solution, otherwise not a solution.

Le us draw the graph.

It is clear that point (2,3) does not lie on the feasible region(solution space).

Point (2,3) is not a solution to the system of linear inequalities:

⇒ ​y ≥ x + 4

⇒ y ≤2x + 4

​

Page 165  Exercise 4  Answer

Given: A system of linear inequalities is

⇒  ​y ≤−x + 4

⇒  y ≥ 5x −3.
​

We have to check that point (0,4) is a solution of the system or not. We have to follow the steps:
1. Plot a graph corresponding to linear inequalities and the point.
2. Check that the point lies in a feasible region, if yes, then it will be a solution, otherwise not a solution.

The graph for the above system of inequality is

Since point (0,4) lies on the feasible region, therefore it is a solution of the given system.

Point (0,4) is a solution of the system of inequalities:

​⇒ y ≤−x + 4

⇒ y ≥ 5x −3

​

Big Ideas Math Algebra 1 Exercise 5.7 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.7 Page 165  Exercise 6  Answer

The system of linear inequalities provided to us

​⇒ y < 3

⇒ x < 2.

​
We have to draw a graph corresponding to the system for that we have to go through the following steps:
1. Since the first inequality involves strictly less than type, so the dashed line will be drawn. It will be parallel to the x-axis at a distance of 3 units. A region must be shaded just above the line.

2. Similarly, for the first step, draw a dashed line parallel to the y-axis at a distance of two units. The region is covered left to the line.

Here is the graph corresponding to the system

Graph for the system of inequalities:

​⇒ y < 3

⇒ x < 2

will be graph:

Page 166   Exercise 7  Answer

Given: A system of linear inequalities is

⇒ ​y ≥ x−2

⇒ y <−x + 2.

​
We have to draw a graph corresponding to the system for that we have to go through the following steps:
1. Since the first inequality contains greater than equal to type inequality. So, we have to draw the line y=x−2 and shade the region above the line.

2. Since 2nd inequality consists of strictly less than type inequality. So, draw the dashed line y=−x+2 and shade the region below the line.

Following graph will be obtained:

Graph for the system of inequalities:

⇒ ​y ≥ x−2

⇒ y <−x + 2
​
will be graph:

Page 166 Exercise 8 Answer

The given system of linear inequalities is

⇒  ​2x + 3y < 6

⇒  y−1 ≥− 2x
​

We have to draw a graph corresponding to the system for that we have to go through the following steps:
1. Since the first inequality contains less than type inequality. So, we have to draw a dashed line for 2x+3y=6 and shade the region below the line.

2. Since 2nd inequality contains greater than equal to type inequality. So, draw the line y−1=−2x and shade the region above the line.

Here is the graph corresponding to the systems of given inequalities

Graph for the system of inequalities:

⇒ ​ 2x + 3y <6

⇒  y−1 ≥−2x
​
will be graph:

Page 166  Exercise 10  Answer

The given graph is

For the dashed line, there will be > inequality because the line is not connected and the red-shaded region is just above the dashed line.

For the non-breakable line there will be ≥ because the line is connected and the blue-shaded region is just below the line.

So, the linear inequality for the dashed line is y>1 and the connected line for the non-dashed is y≤3

y > 1 and y ≤ 3 are the linear inequality for the given graph:

How To Solve Exercise 5.7 Big Ideas Math Chapter 5

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.7 Page 165  Exercise 11  Answer

The graph is

Linear inequality for the given graph will be y−x ≥1 and x + y ≤ 1:

Page 166  Exercise 12  Answer

The graph provided to us is

We have to find the linear inequalities for the graph.
The general form of a line is given by y=mx+c, where m is the slope of the line and c is the intercept at the y-axis.

The slop of the line passing from the two points (x₁,x₂) and  (y₁,y₂)are given by  \(m=\frac{y_2-y_1}{x_2-x_1}\)

The following sequence must be followed to complete the solutions:

find the equations of the lines(blue and red).
Replace the= sign with suitable inequality signs <or>.

If the shaded region is below the line put <
If the shaded region is above the line put >.

A system of linear inequalities:

⇒ ​y + x < 1

⇒ y−x >−1

Represents the graph

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

Page 152  Exercise  1 Answer

Given: The equation  2x−1\(=\frac{-1}{2} x\)+4  is given.

To Find The linear equations are to be found by both sides of the equation.
Solution: The linear equation will be by putting the equations equal to some other variable.

The given equation is  2x−1\(=\frac{-1}{2} x\)+4  which has the variable x.
The left side of the equation which is made a linear equation is  y=2x−1

The right side of the equation, made a linear equation is  y\(=\frac{-1}{2} x\)+4
The linear equations on the left and right sides are​  y=2x−1 , y\(=\frac{-1}{2} x\)+4  respectivily .

Given: The equation given is 2x−1 \(=\frac{-1}{2} x\)+4

To Find The graphs are to be plotted of the linear equations with the intersection point of the graphs and finding that whether the x of the intersection point is the same as the solution of the given equation.
Solution: The graphs will be plotted, solved, and observed to answer the questions.

The linear equation y=2x−1 have the graph:

The linear equation of the right side is y\(=\frac{-1}{2} x\)+4 which is plotted as:

The graph plotted of the linear equations and the given equation is:

The graph shows that the point of intersection is(2,3), wherein the x of the intersection point is the same as the solution of the given equation, i.e.,2

The graph of the two linear equations are:

The intersection point is(2,3), and the x of the intersection point is the same as the solution of the given equation that is 2.

Given: The equation is given and the linear equations are plotted on the graph to solve that equation.

To Find The reason as to why the method of the graph is better is to be answered.
Solution: The graph will be observed to explain the reason that the graphical method is the better one.

The equation given is 2x−1\(=\frac{-1}{2} x\)+4
The equation is plotted on the graph which is easy to be observed and explained.
The intersection points are also easy to be plotted and observed.

The graphical methods work in this case as the linear equations are properly plotted on the graph and the intersection point and the solution of the equation both can be observed and answered easily as the points are clear in the graphs.

Big Ideas Math Algebra 1 Chapter 5 Exercise 5.5 Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.5 Page 153   Exercise 4   Answer

We have to compare algebraic method and the graphical method for solving a linear equation with variables on both sides.

The algebraic method has advantage to be more direct as it does not involve building a system of equations, drawing graphs, and checking if the graphical solution fits the original equation. Its disadvantages might be that it involves more computation.

The advantage of graphical method is that it involves less computation. Its disadvantage is that we have to perform graphing and check the results.

Algebraic method has more computation while graphical method has less computation but it involves drawing graph and checking result.

Page 155   Exercise 2   Answer

Given: 3x=x−4

Graph the system of linear equation.
Graph the equation and find the value of x for the solution.

It can be written as two equations as shown below.

​⇒y = 3x

⇒ y = x−4

​The graph for these two equations is sketched on the same coordinate plane and the point of intersection is determined.

The graph for the system is sketched using a graphing calculator as shown below.

The value of at the point of intersection is −2. Therefore, the solution to the given system is determined to be x = −2

Checking the solution x = −2 for the given system.

​3x = x−4

⇒ 3×−2 = −2−4

⇒ −6 = −6

The statement is true, therefore the solution is verified.

The solution to the system of equations 3x=x−4 is determined by graphing to be  x= −2. The graph is sketched below.

Solving Systems Of Equations Exercise 5.5 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.5 Page 155  Exercise 3  Answer

Given: 4x + 1 = −2x−5

Graph the system of linear equation.
Graph the equation and find the value of x for solution.

It can be written as two equations as shown below.

⇒ ​y = 4x + 1

⇒  y = −2x−5
​
The graph for these two equations is sketched on the same coordinate plane and the point of intersection is determined.

The graph for the system is sketched using a graphing calculator as shown below.

The value of at the point of intersection is −1. Therefore, the solution to the given system is determined to be x = −1.

Checking the solution x = −1 for the given system.
​4x + 1 = −2x−5

⇒ 4(−1)+1 = −2(−1)−5

⇒ −3 = 2−5

⇒ −3 =−3.

The statement is true, therefore the solution is verified.

The solution to the system of equations 4x + 1 = −2x−5 is determined by graphing to be x = −1. The graph is sketched below.

Page 155  Exercise 5  Answer

Given: −3x−5=6−3x

Graph the system of linear equation.
Graph the equation and find the value x of for solution.

It can be written as two equations as shown below.

⇒ ​y = −3x−5

⇒  y = 6−3x

​
The graph for these two equations is sketched on the same coordinate plane and the point of intersection is determined.

The graph for the system is sketched using a graphing calculator as shown below.

There is no point of intersection. Therefore, there is no solution to the given system.

The solution to the system of equations 3x-5=6-3x doesn’t exist. The graph is sketched below.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.5 Page 155 Exercise 6 Answer

Given: 7x−14 = −7(2−x)

Graph the system of linear equation.
Graph the equation and find the value of x for solution.

It can be written as two equations as shown below.

​⇒  y = 7x−14

​⇒  y = −14 + 7x
​

The graph for these two equations is sketched on the same coordinate plane and the point of intersection is determined.

The graph for the system is sketched using a graphing calculator as shown below.

The two lines coincide. Therefore, there are infinite number of solutions to the given system.

The solution to the system of equations 7x−14 = −7(2−x) are infinite in number. The graph is sketched below.

Big Ideas Math Student Journal Exercise 5.5 Explained

Page 156 Exercise 7 Answer

Given: |3x|=|2x + 10|

Graph the system of linear equation.
Graph the equation and find the value of x for solution.

It can be written as two equations as shown below.

​⇒  ​y = 3x

​⇒  y = 2x + 10
​
The graph for these two equations is sketched on the same coordinate plane and the point of intersection is determined.

The graph for the system is sketched using a graphing calculator as shown below.

The value of at the point of intersection is 10. Therefore, the solution to the given system is determined to be x=10.

Checking the solution x = 10 m for the given system.
​|3x| = |2x + 10|

⇒  |30| |3×10| = |2×10 + 10|

⇒  |30| = |20 + 10|

⇒  |30|=|30|

⇒ 30=30.

The statement is true, therefore the solution is verified.

The solution to the system of equations |3x| = |2x + 10|  is determined by graphing to be x = 10. The graph is sketched below.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.5 Page 156 Exercise 8 Answer

Given: The linear equation  ∣x−1∣ = ∣x + 3∣.

We asked to find the solution of the above linear equation by graphing.
To solve the above we will consider the system of equations and graph them.

Let y = ∣x−1| and y = |x + 3| be two linear equations.

Graph of y = |x−1| and y=|x+3| is given by

From the graph the point of intersection for the system​ y = ∣x−1|,  y = |x+3|  is(−1,2).

Since |x−1| = |x+3|

Here, the solution of the above equation is the x
value of the intersection point of the system​ y = |x−1|, y = |x+3| in the above graph.

Since(−1,2) is the point of intersection for the system ​y = |x−1|, y = |x+3|.
Therefore from the graph the value of x for the equation |x−1| = |x+3|  is −1.

Since |x−1|=|x + 3|.
Put x=−1 in the above equation, and we get

|−1−1|=|−1 + 3|

⇒ |−2|=|2|

⇒ 2=2

Since|−a|= an aϵℜ.

Hence the equation |x−1|=|x+3| is true for  x=−1.
Therefore −1 is the solution of the equation |x−1|=|x+3|.

-1 is the solution of the equation |x−1|=|x+3|:

Chapter 5 Exercise 5.5 Solving Systems Practice

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.5 Page 156 Exercise 9 Answer

Given: The linear equation  |x + 4| = |2−x|.
We asked to find the solution of the above linear equation by graphing. To solve the above we will consider the system of equations and graph them.

Let y = |x + 4| and y =|2−x| be two linear equations.

Graph of y = |x + 4| and y = |2−x| is given by

From the graph the point of intersection for the system ​y = |x + 4|, y = |2−x|  is(−1,3).

Since∣x+4∣=∣2−x∣.
Here, the solution of the above equation is the x value of the intersection point of the system​ y=∣x+4∣
y=∣2−x∣ in the above graph.

Since(−1,3) is the point of intersection for the system​ y=|x+4| ,y=∣2−x∣.
Therefore from the graph the value of x for the equation ∣x+4∣=∣2−x∣ is−1.

Since |x+4|=|2−x|

Put x=−1 in the above equation, and we get

|−1+4|=|2−(−1)|

⇒ |3| =|2+1|

⇒ |3| = |3|

⇒ 3 = 3

Hence the equation ∣x+4∣=∣2−x∣ is true for x = −1.
Therefore−1 is the solution for the equation |x+4|  = |2−x|.

-1 is the solution for the equation ∣x+4∣=∣2−x∣. And the graph is:

Big Ideas Math Algebra 1 Exercise 5.5 Guide

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

Page 147  Essential Question  Answer

Let’s consider a system of equations.
It is required to describe whether a system can have no solutions or infinitely many solutions.

Yes, a system of linear equations has no solution if the equations are inconsistent or the graph for the system has parallel lines.
A system has infinitely many solutions when it is consistent, and the graph for the system of equations coincides.

Yes, a system of linear equations can have no solution or infinitely many solutions.

Page 147  Exercise 2  Answer

Given: We are given the number of small and large beads in a necklace and a bracelet. We know the weight of the necklace and the bracelet.

To find We have to write a system of linear equations that represents the situation.
We will assume “x” is the weight (in grams) of a small bead and “y” is the weight (in grams) of a large bead.
Then we will multiply the number with their corresponding weight and get the equation.

Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

“x” is the weight (in grams) of a small bead and “y” is the weight (in grams) of a large bead
The equation that represents the weight of the necklace is:   40x + 6y = 10
The equation that represents the weight of the bracelet is:  20x + 3y = 5

The system of equations that represent the given scenario is

​⇒ 40x + 6y = 10

​⇒ 20x + 3y = 5

​

Given: We are given the number of small and large beads in a necklace and a bracelet. We know the weight of the necklace and the bracelet.

To find We have to graph the system in the coordinate plane and describe the two lines.
We will plot these graphs and check whether these lines are parallel or perpendicular or neither.

The system of equations is :

​⇒   40x + 6y = 10

​⇒   20x + 3y = 5

The plot of the system of equations is given below:

The plot of these two equations is coincident.
They can be represented by the same line as shown above in the graph.

The plot of the system of equations is

The two lines are coincidental.

Given: We are given the number of small and large beads in a necklace and a bracelet. We know the weight of the necklace and the bracelet.

To find We have to tell whether we can find the weight of each type of bead.
Now We calculate the weight of each bead by solving the system of equations.

We have made the system of equations in terms of the weight of each bead.
So when we solve them we can easily get to know the weight of each bead.

We can find the weight of each bead by solving the system of equations.
There are two equations and there are two variables in the equations. So, we can solve these equations for the values of “x” and “y”.

Big Ideas Math Algebra 1 Chapter 5 Exercise 5.4 Solutions

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 148  Exercise 3  Answer

Given: A system of linear equations.

To find We have to tell whether a system of linear equations can have no solution and infinitely many solutions.
A system of equations can have a unique solution, no solution, or infinitely many solutions.
We get to know about the solution of a system of equations by looking at the coefficient of variables and the constant part.

An example of a system of equations with no solution:

​⇒  ​ 2x + 3y = 10

​⇒   2x + 3y = 12
​
The coefficients of “x” and “y” are the same but the constants in both the equations are different. So, this system will have no solution.

An example of a system of equations with infinitely many solutions:

​​⇒   2x + 3y=6

​⇒   4x + 6y=12

The coefficients of “x” and “y” and the constant are proportional. So, they basically represent the same line on the graph. They have infinitely many solutions.

Yes, a linear system of equations has no solution or infinitely many solutions. The example of no solution is ​ 2x + 3y = 10, 2x + 3y = 12. The example of infinitely many solutions is​  2x + 3y = 6, 4x + 6y = 12.

Page 150  Exercise 2  Answer

Given: A system of equations is given to us. It is, y = 5x−1 y = −5x + 5
​
To findWe have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

​y = 5x−1——-(1)

y =−5x + 5——(2)

After adding them, we get

​⇒   ​2y = 5x−5x−1 + 5

​⇒   2y = 4

​⇒   y = 2
​

Putting y=2 in equation (1) we get

​​⇒   2 = 5x−1

​⇒   3 = 5x

​⇒   x\(=\frac{3}{5}\)

​The solution of the given system of equations y=5x−1,y=−5x+5 is x\(=\frac{3}{5}\) y=2.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 150  Exercise 3  Answer

Given: A system of equations is given to us. It is  2x−3y = 10, −2x + 3y = −10

​To find We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

​2x−3y = 10——-(1)

​−2x+3y = −10——(2)

​

After adding, Equation  (1) and  Equation (2), we get

​⇒   2x−2x−3y + 3y = 10−10

​⇒   0 = 0
​
This is true, so the given system of equations has infinitely many solutions.

The given system of equations 2x−3y = 10,−2x+3y = −10, has infinitely many solutions.

Page 150  Exercise 4  Answer

Given: A system of equations is given to us. It is   x + 3y = 6, −x−3y = 3
​
To find We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

x+3y = 6——(1)

−x−3y = 3—–(2)
​

After adding  Equation (1) and  Equation  (2), we get

​⇒  x−x + 3y−3y = 6 + 3

​⇒  0 = 9

This is not true, so the solution of the given system of equations does not exist.

The solution of the given system of equations x + 3y = 6,−x−3y = 3, does not exist.

Solving Systems Of Equations Exercise 5.4 Answers

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4Page 150  Exercise 5  Answer

Given: A system of equations is given to us. It is  6x + 6y = −3, −6x−6y = 3
​
To find We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

6x + 6y = −3——(1)

−6x−6y = 3——-(2)

After adding  Equation (1) and  Equation (2), we get

​⇒  ​6x−6x + 6y−6y = −3 + 3

​⇒  0 = 0
​
This is true, so the given system of equations has infinitely many solutions.

The given system of equations has infinitely many solutions.

Page 150  Exercise 6 Answer

Given: A system of equations is given to us. It is  2x−5y =−3, 3x + 5y = 8
​
To find: We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

​2x−5y=−3——(1)

3x+5y=8——–(2)

After adding  Equation (1) and Equation (2),  we get

​⇒  ​2x + 3x−5y + 5y =−3+8

​⇒  5x = 5

​⇒  x = 1
​

Putting x = 1 in  Equation (1)  we get

​​2x−5y=−3

⇒ 2×1−5y = −3

⇒  2 + 3 = 5y

⇒  5y = 5

⇒  y = 1
​

The solution of the given system of equations 2x−5y = −3, 3x + 5y = 8 is x = 1,y = 1.

Page 150  Exercise 7  Answer

Given: A system of equations is given to us. It is  2x+3y=1, −2x+3y=−7
​
To find We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

2x+3y=1——–(1)

−2x+3y=−7—–(2)

After adding Equation  (1) and  Equation (2) we get

​⇒  2x−2x + 3y + 3y = 1−7

⇒  6y = −6

⇒  y =−1

​

Putting y =−1 in equation  (1), we get

2x + 3y = 1

⇒  ​2x+3×−1 = 1

⇒ 2x−3 = 1

⇒  2x = 4

⇒  x = 2

​
The solution of the given system of equations  2x+3y = 1,−2x + 3y = −7 is x = 2,y =−1.

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 150   Exercise 8   Answer

 A system of equations is given to us. It is  4x + 3y = 17, −8x−6y = 34
​
To find We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.​4x+3y=17 −8x−6y=34
​

The given system of equations is:

​4x+3y=17——(1)

−8x−6y=34—–(2)

​
Multiplying the equation (1)  by 2, we get

⇒   ​8x + 6y = 34

⇒  −8x − 6y = 34

​
After adding equation (1) and equation (2), we get

​⇒  8x−8x + 6y−6y = 34 + 34

⇒  0 = 68

​
This is not true, so the solution of the given system of equations does not exist.

The solution of the given system of equations 4x + 3y = 17,−8x−6y = 34 does not exist.

Page 151  Exercise 10  Answer

Given: A system of equations is given to us. It is −2x + 5y = −21, 2x−5y = 21
​
To find: We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables

The given system of equations is:

⇒​ −2x + 5y = −21———(1)

⇒ 2x−5y = 21————-(2)
​

After adding them, we get

⇒ ​−2x + 2x + 5y−5y = −21 + 21

⇒ 0 = 0

​
This is true, so the given system of equations has infinitely many solutions.

The given system of equations −2x + 5y = −21,2x−5y = 21 has infinitely many solutions.

Page 151   Exercise 11   Answer

Given: A system of equations is given to us. It is  3x−8y = 3, 8x−3y = 8
​

To find We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

​3x−8y = 3———(1)

8x−3y = 8———(2)

After adding  equation (1) and equation  (2), we get

⇒ ​3x + 8x−8y−3y = 3 + 8

⇒  11x−11y = 11

⇒  x−y = 1

​
After subtracting equation (1) and equation  (2), we get

​⇒  3x−8x−8y + 3y = 3−8

⇒  −5x−5y = −5

⇒  x + y = 1
​

The system of equations is:

⇒   ​x−y = 1——–(3)

⇒   x + y = 1——–(4)
​

After adding equation (3) and equation  (4), we get

⇒​  x + x−y + y = 1 + 1

⇒  2x = 2

⇒  x = 1
​

Putting x=1 in equation  (1), we get

⇒  (3) ​1−y=1

⇒  0=y
​

The solution of the given system of equations 3x−8y = 3,8x−3y = 8 is x = 1,y = 0.

Big Ideas Math Student Journal Exercise 5.4 Explained

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 151  Exercise 12  Answer

Given: A system of equations is given to us. It is  18x + 12y = 24, 3x + 2y = 6
​
To find We have to solve the given system.
We will use the elimination or the substitution method and get the value of variables.

The given system of equations is:

​18x + 12y = 24——–(1)

3x + 2y=6———-(2)
​

Multiplying  the  equation (2)  by 6, we get

⇒​  18x + 12y = 24

⇒ 18x + 12y = 36
​

After subtracting equation (1) and equation (2), we get

​⇒ 18x−18x + 12y−12y = 24−36

⇒ 0 = −12
​
This is not true, so the solution of the given system of equations does not exist.

The solution of the given system of equations 18x+12y=24,3x+2y=6 does not exist.

Page 151  Exercise 14  Answer

Given: The given linear equations are:​−3x−5y=8, 6x+10y=−16.

To Find The given equations are to be solved with the respective variables.
Solution: The methods of substitution and elimination are two ways any linear equation can be solved.

The given equations are​:
−3x−5y = 8  6x + 10y =−16 ,with two variables  x & y.

This could be solved by the elimination method wherein equation −3x−5y = 8 will be multiplied by 2 to get solved.
This gives us the equation −6x−10y = 16, which is added to the equation 6x + 10y =−16, which cancels all the terms giving us no solution.

The graph below also shows that there exists no solution as the equations plotted shows the same line:

Solving the given equations −3x−5y = 8,6x + 10y = −16 we get that there exists no solution which is also proved by the graph below:

Page 151  Exercise 16  Answer

Given: The linear equations given are​ 5x + 7y = 7 7x + 5y = 5.

To Find The equations are to be solved with respect to the variables x & y.
Solution: This can be solved by the estimation method and the graph.

The given equations are :
​5x + 7y = 7 7x + 5y = 5  which are solved with respect to the variables  x & y​.

Multiplying the equation 5x + 7y =7 by 7 and  7x + 5y = 5 by 5 and subtracting them we get ​35x + 49y = 49, −35x−25y = −25.

By solving that we get the values of x & y as 0,1.

The graph below also shows the solution as

The equations 5x + 7y = 7,7x+5y = 5 solved gives the values x = 0 & y = 1 , which is shown in the graph below:

Chapter 5 Exercise 5.4 Solving Systems Practice

Page  151 Exercise 17  Answer

Given: The equation given is ​y=\(\frac{2}{3} x+7\), y=\(\frac{2}{3} x-5\).

To Find We need to find the values of x & y.
Solution: Solving these equations we get the values of variables shown by the graph.

The equations are rewritten as​ 3y−2x = 21 and 3y−2x =−15.
This is solved wherein we get no solution with respect to the variables.

The graph is shown below

The graph shows two parallel lines with no solution.

The solution of the​​y=\(\frac{2}{3} x+7\), y=\(\frac{2}{3} x-5\) equations are no solution also shown in the graph below:

Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations Exercise 5.4 Page 151  Exercise 18  Answer

Given: The equations given are​−3x+5y=15, 9x−15y=−45
​
To Find The equations are to be solved and the values of variables are to be found
Solution: The equations will be solved by the elimination method.

The equation −3x + 5y = 15 is multiplied by 3.

Simplifying them we get no solution as the variables are canceled.

The graph of the linear equations is:

And this shows that there exists no solution.

Solving the linear equations−3x + 5y = 15,9x−15y =−45 we get that there exists no solution which is given by the graph:

Big Ideas Math Algebra 1 Exercise 5.4 Guide

Page 151  Exercise 19 Answer

Given: Me and my friend have 15 & 25 as savings.

To FindThe linear equations for the problem are to be found, and the situation when I and my friend will have the same amount is to be found and explained.
Solution:  The linear equations will be made and solved.

The equation will be ​15 + 5x = y 25 + 5x = y.
Solving these we will get no solution, as the variables will be canceled.

The graph is shown as

This will show that there will be no situation wherein there will be the same amount.

The linear equations are​ 15 + 5x = y, 25 + 5x = y, which is plotted on the graph is shown as:

Which when solved gives no solution, and this shows that there will be any situation when there will be the same amount.

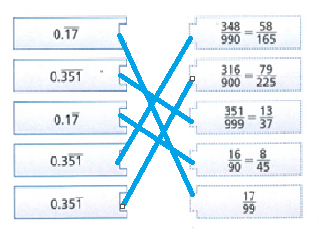
Big Ideas Math Algebra 1 Student Journal 1st Edition Chapter 5 Solving Systems Of Linear Equations

Page 142  Essential Question  Answer

We have to write how can we use the elimination method to solve a system of linear equations.

Multiply both the given equations by some suitable non-zero constants to make the coefficients of any one of the variables numerically equal.

Add or subtract one equation from the other in such a way that one variable gets eliminated.

We will get the value of one variable. Substitute value of the variable in the original equation to get value of another variable.

The elimination method is the best choice of use when the equations are in the standard form ax+by=c, and all the variables have coefficients other than 1.

Big Ideas Math Algebra 1 Chapter 5 Exercise 5.3 Solutions

Page 142  Exercise 1  Answer

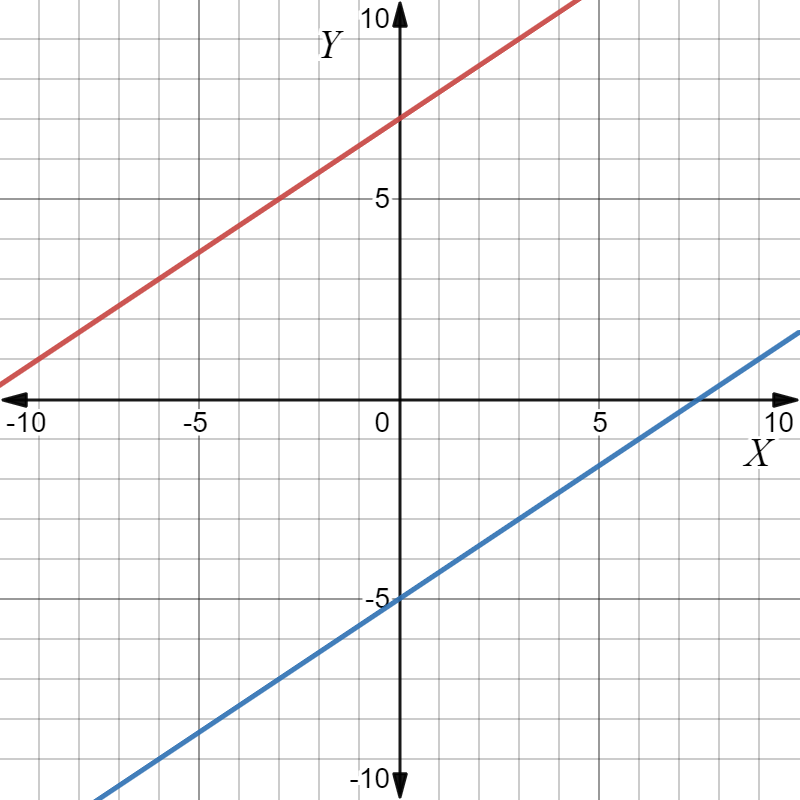
Given: The price for drink and sandwich you purchased is  $4.50 and your friend purchases a drink and five sandwiches for  $16.50.

To find Write a system of linear equations. Let x represent the price (in dollars) of one drink. Let y represent the price (in dollars) of one sandwich.

Write system of equations based on given conditions using the model number of drinks · price per drink + number of sandwiches · price per sandwiches = total price

Let x represent the price (in dollars) of one drink. Let y represent the price (in dollars) of one sandwich.

Given the situation is you purchased drink and sandwich for $4.50
Equation is x + y = 4.50

The second situation is your friend purchases a drink and five sandwiches for $16.50
Equation is x + 5y = 16.50

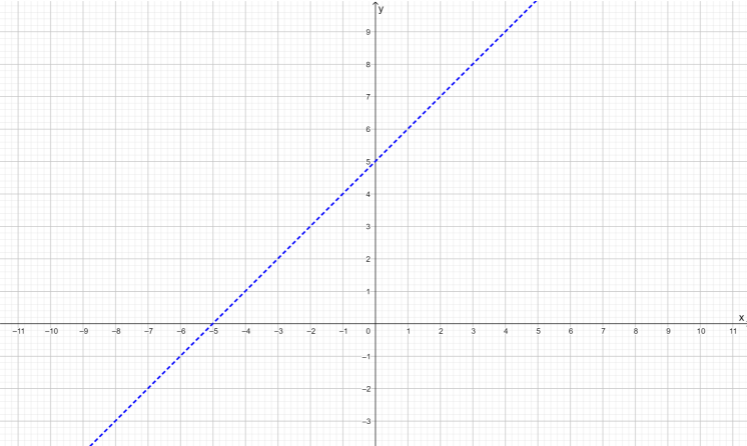
System of equations is ​x + y = 4.50 x + 5y = 16.50
​Read and Learn More Big Ideas Math Algebra 1 Student Journal 1st Edition Solutions

We have to subtract equation 1 from equation 2 and interpret the solution.
The system of linear equations is ​x + y = 4.50 x + 5y = 16.50

Subtract equation 1 from equation 2 we will get the value of y.
Substitute the value of yin in either of the equations to get the second variable.

We have:

x + y = 4.50 ——— (1)

x + 5y = 16.50 ——— (2)

Subtract (1) from (2)

​x + y−(x + 5y) = 4.50 −16.50

⇒   x + y−x−5y = −12

⇒  −4y = −12

Divide both sides by −4

⇒  y=3

We can substitute the value of y in equation (1) to find value of another variable.
​x + y = 4.50

⇒   x + 3 = 4.50

⇒   x = 4.50−3

⇒   x = 1.5

Subtracting equation 1 from equation 2 we get y = 3. We can use this result by substituting it in equation 1 to get value of another variable.
The solution of system of linear equations is x = 1.5,y = 3.

​

Page 142  Exercise 2  Answer

Given : System of linear equations are ​3x−y = 6 3x + y = 0
​
To find Solve system using two methods.
Solve by method 1 that is subtract equation 2 from equation 1
Substitute value we get after subtraction in either of the equations.

Solve by method 2 that is add two equations.
Substitute value we get after addition in either of the equation.

We have:

3x −y = 6 ——– (1)

3x + y = 0 ——–(2)

Method 1: Subtract Equation 2 from Equation 1

⇒   3x + y−(3x−y) =0−6

⇒   3x+ y−3x + y =−6

⇒   2y =−6

Divide both sides by 2

⇒ y=−3

Substitute value of y in equation (2)

​3x + y = 0

⇒  3x−3 = 0

⇒  3x = 3

Divide both sides by 3

⇒   x=1

Method 2: Add the two equations
​⇒  3x−y + 3x + y = 6+0

⇒  6x = 6

Divide both sides by  6

⇒  x = 1

Substitute x = 1  in equation (2)

​3x + y = 0

⇒   3(1) + y = 0

⇒  3 + y = 0

⇒  y = −3
​

The solution is same for both methods:
We get solutions as x = −1, and y = 3.
I would prefer method 2 as addition is more simpler than subtraction.

Given : System of linear equations are ​2x + y = 6, 2x−y =2
​
To find  The Solution of a system of linear equations using two methods.
Solve by method- 1 that is subtract equation-(2) from the equation- (1).

Substitute value we get after subtraction in either of the equations.
Solve by method- 2 that is add two equations.
Substitute value we get after addition in either of the equation.

We have :

2x + y = 6 ——–(1)

2x−y = 2———-(2)

Method 1: Subtract Equation 2 from Equation (1)

⇒​   2x−y−(2x + y) =2−6

⇒   2x−y−2x−y =−4

⇒  −2y =−4

⇒   y = 2

Substitute y = 2 in equation (2)

​2x−y = 2

⇒  2x−2 = 2

⇒  2x = 4

⇒  x = 2
​

Method 2: Add both equations

⇒   2x + y + (2x−y) = 6+2

⇒   4x = 8

⇒   x = 2

Substitute x=2 in equation  (2 )
​2x−y = 2

⇒   2(2)−y = 2

⇒   4−y = 2

⇒   4−2 = y

⇒    y = 2
​

Solution is same for both methods:
We get solutions as x = 2, and y = 2.
I would prefer method- 2 as addition is more simpler than subtraction.

Given : The system of linear equations are ​x−2y = −7, x + 2y = 5

To find the Solution of system of linear equations using two methods.
Solve by method 1 that is subtract equation-(2)  from the equation-(1).

Substitute value we get after subtraction in either of the equations.
Solve by method 2 that is add two equations.
Substitute value we get after addition in either of the equation.

We have:

x−2y = −7——-(1)

x + 2y = 5 ——-(2)

Method 1: Subtract Equation  (2) from  Equation (1)

⇒   x + 2y−(x−2y) = 5−(−7)

⇒   x + 2y−x + 2y = 5 + 7

⇒   4y = 12

⇒   y = 3

Substitute y=3 in equation (2)

​x + 2y = 5

⇒   x + 2(3) = 5

⇒   x + 6 = 5

⇒  x =−1
​

Method 2: Add both equations

⇒   x−2y + x + 2y =−7 + 5

⇒   2x = −2

⇒   x = −1

Substitute x=−1 in equation (2)

​x + 2y = 5

⇒  −1 + 2y = 5

⇒  2y = 6

⇒  y = 3
​

The solution is same for both methods:
We get solutions as x = −1, and y = 3.
I would prefer method as addition is more simpler than subtraction.

Solving Systems Of Equations Exercise 5.3 Answers

Page 143  Exercise 3  Answer

Given: The System of linear equation is ​2x + y = 7, x + 5y = 17
​
To find Can we eliminate a variable by adding or subtracting the equations as they are.
We cannot eliminate variable by adding or subtracting the equations as they are because the coefficient of x or y is not similar, so it cannot eliminate one variable.
To eliminate the variable we can either multiply equation 1 by 5 and subtract both equations or we can multiply equation 2 by 2 and subtract equations to get a solution.

We cannot eliminate variables by adding or subtracting the equations as they are.
We can either multiply equation 1 by  5  or we can multiply equation  2  by  2  to eliminate the variable.

Given: The system of linear equation is ​2x+y=7, x+5y=17
​
To find  Solution of equation
Multiply equation (1)  by 5.

Subtract equation we get after multiplying equation (1)  from equation  ( 2 ) to get value of variable.
Substitute value we get in either of equation.

We have:

2x  +  y = 7 ——-(1)

x +  5y = 17———–(2)

Multiply equation (1) by 5

⇒   10x + 5y = 35

Subtract equation we got after multiplying equation (1)  from equation  (2)

⇒  10x + 5y−(x + 5y) = 35−17

⇒  10x + 5y−x−5y = 18

⇒   9x = 18

Divide both sides by 9

⇒  x = 2

Substitute x=2 in  equation (1)

​2x + y = 7

⇒  2(2)+y =7

⇒  4 + y = 7

Subtract both sides by 4

⇒  y = 7−4

⇒  y = 3

By comparing with their partner, he also got same solution but he multiplied equation (2)   by 2.

Solution of system is x = 2,y = 3 Partner got same solution but he multiplied equation 2 by 2.

Page 143  Exercise 4  Answer

We have to write how can we use elimination method to solve a system of linear equations.

Multiply both the given equations by some suitable non-zero constants to make the coefficients of any one of the variables numerically equal.

Add or subtract one equation from the other in such a way that one variable gets eliminated.

We will get the value of one variable.

Substitute the value of the variable in the original equation to get the value of another variable.

The elimination method is the best choice of use when the equations are in the standard form and all the variables have coefficients other than one.

Page 143   Exercise 5   Answer

We have to write when we can add or subtract the equations in a system to solve the system, when do we multiply.

We can add or subtract the equations in a system when the coefficients of one variable are opposites we add the equations to eliminate a variable and when the coefficients of one variable are equal we subtract the equations to eliminate a variable.

For example: Consider the system of equation ​x + y = 2 x−y = 3, in this system coefficient of variables are opposite so, we add the equations.

If the coefficient of variables are not equal we will multiply the variable with a suitable number to make the coefficient equal. Consider a system of linear equations as ​x + 2y = 5 2x + y = 2, here coefficients are not equal so we will multiply either of the equations to make coefficients similar.

When the coefficients of one variable are opposites we add the equations to eliminate a variable and when the coefficients of one variable are equal we subtract the equations. If the coefficient of variables is not equal we will multiply variables with suitable numbers to make the coefficient equal.

Big Ideas Math Student Journal Exercise 5.3 Explained

Page 143  Exercise 6  Answer

The system of equations in  Exercise 3 is ​2x + y = 7, x + 5y = 17.

We multiply the equation by a constant because the coefficient of the variable is not the same.
We do multiplication to make coefficients similar so we can add or subtract the equation to eliminate variables.
If we solve the system without multiplying we have to use the substitution method to get a solution.

We multiply the equation by a constant because the coefficient of the variable is not the same. If we solve the system without multiplying we have to use the substitution method to get a solution.

Page 145  Exercise 1  Answer

Given : System of linear equations ​x + 3y = 17, −x + 2y = 8
​
To find the Solution of the system of linear equations by elimination.
Add both equations to eliminate variables.
Substitute the value of the variable in either of the equations and find another value.

We have:

x + 3y = 17 ———–(1)

−x + 2y = 8 ———–(2)

Add both equations

⇒   x + 3y + (−x + 2y) = 17 + 8

⇒   x + 3y−x + 2y  =25

⇒  5y = 25

Divide both sides by  5

⇒  y = 5

Substitute y=5 in equation (1)

​x + 3y = 17

⇒   x + 3(5) = 17

⇒   x + 15 = 17
​

Subtract both sides by 15

⇒   x = 17−15

⇒   x = 2
​
Solution of system of linear equations  x+3y = 17,−x+2y = 8, is x = 2,y = 5.

Page 145  Exercise 2  Answer

Given: The system of linear equations is  ​2x−y = 5 , 5x + y = 16
​

To find the Solution of the system of linear equations by elimination.
Add both equations to eliminate variables.
Substitute the value of the variable in either of the equations and find another value.

We have:

2x−y = 5———– (1)

5x + y = 16———(2)

Add both equations

⇒  2x−y + 5x + y=5 + 16

⇒  7x = 21

Divide both sides by 7

x \(=\frac{21}{7}\)
⇒ x = 3
​

Substitute  x = 3 in equation (2)

​5x + y = 16

⇒   5(3) + y = 16

⇒  15 + y = 16

Subtract both sides by 15

⇒  y  = 16−15

⇒  y = 1

​
Solution of system of linear equations is x = 3,y = 1.

Page 145  Exercise 3  Answer

Given: The system of linear equation is ​2x + 3y = 10, −2x−y = −2

To find the Solution of the system of linear equations by elimination.
Add both equations to eliminate variables.
Substitute the value of the variable in either of the equations and find another value.

We have:

2x + 3y = 10——-(1)

−2x−y = −2 ——( 2)

Add both equations

⇒   2x + 3y + (−2x−y) = 10 + (−2)

⇒   2x + 3y−2x−y = 10−2

⇒   2y = 8

​Divide both sides by  2

⇒   y\(=\frac{8}{2}\)

⇒  y=4
​

Substitute y=4 in equation   (1), and we get

2x + 3y=10

⇒  2x + 3(4)=10

⇒  2x + 12=10

​

Subtract both sides by  12

⇒  2x=−2

Divide both sides  by  2

⇒  x = −1

Solution of system of linear equation  2 x + 3y = 10,−2x−y = 2 is x = −1,y = 4.

Page 145  Exercise 4  Answer

Given : The system of linear equation is ​4x + 3y = 6, −x−3y = 3
​
To find the Solution of the system of linear equations by elimination.
Add both equations to eliminate variables.
Substitute the value of the variable in either of the equations and find another value.

We have:

4x + 3y = 6——-(1)

−x−3y = 3 ——–(2)

Add both equations

⇒   4x + 3y + (−x−3y) = 6 + 3

⇒  4x + 3y−x−3y = 9

⇒   3x = 9

​Divide both sides by 3
⇒  y = 3

Substitute y = 3 in  equation (2)

⇒ −x−3y = 3

⇒ −x−3(3) = 3

⇒ −x−9 = 3

​Add both sides by  9

​ ⇒  −x = 3 + 9

⇒ −x = 12

⇒   x = −12
​
Solution of the system of linear equations is x = −12,y = 3.

Chapter 5 Exercise 5.3 Solving Systems Practice

Page 145  Exercise 5  Answer

Given : The system of linear equation is ​5x + 2y =−28, −5x + 3y = 8
​
To find the Solution of the system of linear equations by elimination.
Add both equations to eliminate variables.
Substitute the value of the variable in either of the equations and find another value.

We have:

5x + 2y =−28 ——- (1)

−5x + 3y = 8———(2)

Add both equations

⇒  5x + 2y + (−5x+3y) =−28 + 8

⇒  5x + 2y−5x + 3y =−20

⇒  5y = −20

​Divide both sides by 5

⇒  y =−4

Substitute y=−4 in equation (2)

​−5x + 3y = 8

⇒ −5x + 3(−4) = 8

⇒ −5x−12 = 8

​

Add both sides by 12

⇒  −5x = 8 + 12

⇒  −5x = 20

Divide both sides by −5

⇒  x\(=\frac{-20}{5}\)

⇒  x=−4
​
Solution of the system of linear equation is x = −4, y =−4.

Page 145  Exercise 6  Answer

Given: The system of linear equation is  ​2x−5y = 8, 3x + 5y =−13
​
To find the Solution of the system of linear equations by elimination.
Add both equations to eliminate variables.
Substitute the value of the variable in either of the equations and find another value.

We have:

2x−5y = 8———(1)

3x + 5y =−13—–(2)

Add both equations

⇒ ​ 2x−5y + 3x + 5y = 8 + (−13)

⇒   5y = −5

​Divide both sides by 5

⇒  y =−1

Substitute y=−1 in equation (1)

2x−5y = 8

⇒  2x−5(−1) = 8

⇒  2x+5 = 8

​
Subtract both sides by  5

⇒  2x =  3

Divide both sides by  2

⇒  x\(=\frac{3}{2}\)

Solution of system of linear equation 2x−5y = 8, 3x + 5y =−13 is x\(=\frac{3}{2}\), y = −1.

Page 145 Exercise 7 Answer

Given : The system of linear equations ​2x + y =12, 3x−18 = y
​
To find the Solution of the system of linear equations by elimination.
Add both equations to eliminate variables.
Substitute the value of a variable in either of the equations and find another value.

We have:

2x + y=12——(1)

3x−18 = y
which can be written as 3x−y = 18 ——- (2)

Add both equations

⇒  2x + y + 3x−y =12 + 18

⇒  5x = 30

Divide both sides by 5

​⇒  x\(=\frac{30}{5}\)

⇒  x = 6
​

Substitute x = 6 in 3x−18 = y ,we get

​⇒   3(6)−18 = y

⇒  18−18 = y

⇒  y = 0
​
Solution of the system of linear equation is x = 6,y = 0.

Big Ideas Math Algebra 1 Exercise 5.3 Guide

Page 145  Exercise 8  Answer

Given: The system of equations is ​

4x + 3y = 14———(1)

2y = 6 + 4x———-(2)

We have to solve the system of linear equations by elimination.
Use the elimination method and eliminate one variable and then find the value of the other.
Also, check the solution.

Arrange  the   equation (2)   in a proper manner

​2y = 6 + 4x

⇒  −4x  +2y = 6

Thus, the revised system of equations is

⇒  ​4x + 3y = 14

⇒ −4x + 2y = 6

​

Adding these equations, we get.

⇒ 5y = 20

⇒ y = 4
​

Substitute the value of y in  equation  (2)

⇒​ −4x + 2y = 6

⇒  −4x + 2(4) = 6

⇒  −4x = 6−8

⇒  −4x = −2

⇒  x\(=\frac{1}{2}\)

Check the solution:

For equation 1:

​2y = 6 + 4x

2(4)=6+4(\(\frac{1}{2}\))

8=6+2

8=8
​

For equation 2:

​4x + 3y = 14

4(\(\frac{1}{2}\)) +3(4)=14

2 + 12 = 14

14= 14
​

Since the statement is true. Therefore, the solution is verified.

​
The solution of the system of linear equations ​ 4x + 3y = 14 ,2y = 6 + 4x is x\(=\frac{1}{2} \) , y=4.

Page 145  Exercise 9  Answer

Given: The system of equations is ​−4x = −2 + 4y, −4y = 1−4x.

We have to solve the system of linear equations by elimination.
Use the elimination method and eliminate one variable and then find the value of the other.
Also, check your solution.

Rearrange the equations

⇒ ​−4x−4y = −2

⇒  4x−4y = 1

Add both equations, and we get

⇒ -8y = -1

⇒ y=\(\frac{1}{8}\)

Substitute the value of y in equation one, and we get

​−4x−4y =−2

⇒ −4x−4(\(\frac{1}{8}\))=−2

⇒  − 4x-\(\frac{1}{2}\)=-2

⇒  −8x−1 = −4

⇒  −8x = −4+1

⇒  −8x = −3

⇒  x=\(\frac{3}{8}\)

​
Check the solution:

For equation 1:

​−4x =−2 + 4y

⇒  \(-4\left(\frac{3}{8}\right)\)=\(-2+4\left(\frac{1}{8}\right)\)

⇒  \(-\frac{3}{2}\)=\(-2+\frac{1}{2}\)

⇒  \(-\frac{3}{2}\)=\(\frac{-4+1}{2}\)

⇒  \(-\frac{3}{2}\)=\(-\frac{3}{2}\)

​

For equation 2:

​−4y =1 − 4x

⇒  \(-4\left(\frac{1}{8}\right)\)=1-\(-4\left(\frac{3}{8}\right)\)

⇒ ​ \(-\frac{-1}{2}\)=1-\(\frac{3}{2}\)

⇒  \(-\frac{-1}{2}\)=\(-\frac{-1}{2}\)

⇒  Thus the statement is true for both equations.

The solution of the system of linear equations ​−4x=−2+4y, −4y  = 1−4x is x=\(\frac{3}{8}\),y=\(\frac{1}{8}\).

Page 146  Exercise 10  Answer

Given: The given system of equations is  ​x + 2y = 20, 2x + y = 19.

We have to solve the system of linear equations by elimination.
Use the elimination method and eliminate one variable and then find the value of the other.
Also, check the solution.

The equations are given :​

​x + 2y = 20 ——–(1)

2x + y = 19———-(2)

Multiply the equation x + 2y = 20 one by  2

⇒  2x + 4y = 40.

Subtract  equation (1)  from  the  equation (2)

⇒ ​  2x + 4y = 40

⇒  −(2x + y = 19)

we get

​⇒  3y = 21

⇒  y = 7
​

Substitute the value of y in  the  equation (1)

​⇒  x + 2y = 20

⇒  x + 2(7) = 20

⇒   x +14 = 20

⇒   x = 20−14

⇒  x = 6.
​

Check the solution:

For equation 1:

​x + 2y = 20

⇒  6 + 2(7) = 20

⇒  6 + 14 = 20

⇒  20 = 20
​

For equation 2:

​2x + y = 19

⇒  2(6) + 7 = 19

⇒  12 + 7 = 19

⇒  19 = 19
​
Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations ​x + 2y = 20, 2x + y = 19 by elimination is ​x = 6 y = 7.

Page 146  Exercise 11   Answer

Given: The system of equations is ​ 3x−2y =−2, 4x−3y =−4.

We have to solve the system of linear equations by elimination.
Use the elimination method and eliminate one variable and then find the value of the other.
Also, check the solution.

The equations are given :​

3x−2y =−2——–(1)

4x−3y =−4———(2)

Multiply the equation 3x−2y =−2 by 3 and equation 4x−3y =−4 by 2 , we get

⇒  ​9x−6y = −6

⇒  8x−6y = −8

Subtracting the above equations gives

⇒  x = 2.

Substitute the value of x in  equation  (1)

​3x−2y = −2

⇒  3(2)−2y = −2

⇒  6−2y = −2

⇒ −2y = −8

⇒  y = 4
​

Check the solution:

For equation 1:

⇒ ​ 3x−2y =−2

⇒  3(2)−2(4) =−2

⇒  6−8 =−2

⇒ −2 =−2
​

For equation 2:

⇒  ​4x−3y =−4

⇒  4(2)−3(4) =−4

⇒  8−12 =−4

⇒ −4 =−4
​
Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations  ​3x−2y =−2, 4x−3y =−4 by elimination is ​x = 2, y = 4.

Page 146  Exercise 12  Answer

Given: The given system is

​9x + 4y = 11——-(1)

3x−10y = −2——-(2)

We have to solve the system of linear equations by elimination.
Use the elimination method and eliminate one variable and then find the value of the other.
Also, check the solution.

Multiply the second equation 3 x−10y =−2 by −3

⇒ −9x + 30y = 6

Now, add these two equations

⇒​  9x + 4y = 11

⇒ −9x + 30y =6

​We get

⇒ ​34y = 17

⇒ y\(\frac{1}{2}\)

​
Substitute the value of y in the equation (1)

​9x + 4y = 11

⇒  9x + 4(\(\frac{1}{2}\))=11

⇒  9x + 2=11

⇒  9x = 11−2

⇒  9x = 9

⇒  x =1.

Check the solution:

For equation 1:

3x−10y =−2

⇒  3(1)−10(\(\frac{1}{2}\))=−2

⇒  3−5 =−2

⇒  −2 =−2
​

For equation 2:

9x + 4y = 11

⇒  9(1)+4(\(\frac{1}{2}\))=11

⇒  9+2 = 11

⇒  11 = 11

​Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations  ​9x + 4y =11 , 3x−10y =−2 by elimination is ​x = 1, y=\(\frac{1}{2}\).

Page 146  Exercise 13  Answer

Given: The given system is  ​4x + 3y = 21, 5x + 2y = 21.

It is required to solve the system of linear equations by elimination.
Elimination method is used to eliminate one variable and solve the equation for the other, then substituting the known value, the other value is also evaluated.

The equations are given: ​

​4x + 3y = 21−−−(1)

5x + 2y  =21−−−(2)

​

Multiply the  equation (1)  by  2  and  equation (2)  by  3

⇒ ​ 8x + 6y = 42

⇒  15x + 6y = 63

​
Subtract them, and we get

⇒ ​−7x =−21

⇒  x = 3.

Substitute the value x of in  equation  (1)

​4x + 3y = 21

⇒  4(3) + 3y = 21

⇒  12 + 3y = 21

⇒  3y = 21−12

⇒  3y = 9

⇒  y = 3
​

Check the solution:

For equation 1:

​5x + 2y = 21

⇒  5(3) + 2(3) = 21

⇒  15 + 6 = 21

⇒  21 = 21
​

For equation 2:

​4x  +3y = 21

⇒  4(3) + 3(3) = 21

⇒  12 + 9 = 21

⇒  21 = 21
​
Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations ​ 4x + 3y = 21, 5x + 2y = 21 by elimination is ​x = 3, y = 3.

​How To Solve Exercise 5.3 Big Ideas Math Chapter 5 

Page 146   Exercise 14  Answer

Given: The given system is ​−3x−5y = −7, −4x−3y = −2.

It is required to solve the system of linear equations by elimination.
Elimination method is used to eliminate one variable and solve the equation for the other, then substituting the known value, the other value is also evaluated.

The equations are given ​:

−3x−5y=−7——(1)

−4x−3y=−2——(2)

Multiply the  equation (1) by 4  and  equation  (2)  by 3

⇒ ​−12x−20 y = −28

⇒ −12x−9y =−6

Subtract them, and we get

⇒ ​−11y = −22

⇒  y = 2
​

Substitute the value of y in  equation (1)

​−3x−5y =−7

⇒  −3x−5(2) =−7

⇒  −3x−10 =−7

⇒  −3x =−7 + 10

⇒  −3x = 3

⇒  x =−1
​

Check the solution:

For equation 1:

​⇒  −4x−3y = −2

⇒  −4(−1)−3(2) = −2

⇒  4−6 = −2

⇒  −2 = −2

​

For equation  2:
​
−3x−5y = −7

⇒  −3(−1)−5(2) = −7

⇒  3−10 =−7

⇒  −7 =−7
​

Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations ​ −3x−5y = −7, −4x−3y = −2 by elimination is ​x = −1, y = 2.

Page 146   Exercise 15   Answer

Given: The given system is​ 8x+4y=12, 7x+3y=10.

It is required to solve the system of linear equations by elimination.
Elimination method is used to eliminate one variable and solve the equation for the other, then substituting the known value, the other value is also evaluated.

The equations are given :​

8x+4y=12——(1)

7x+3y=10—–(2)

Multiply  the  equation (1)  by 3 and equation (2)  by 4

​⇒  24x + 12y=36

⇒  28x + 12y=40

Subtract them, and we get

​⇒  −4x =−4

⇒  x =1.

Substitute the value of x in equation (1)

​⇒  8x + 4y =12

⇒  8(1) + 4y =12

⇒  4y = 12−8

⇒  4y = 4

⇒  y = 1
​

Check the solution:

For equation 1:

7x + 3y = 10

⇒ 7(1) + 3(1) = 10

⇒  7 + 3 = 10
​

For equation 2:

8x + 4y = 12

⇒  8(1) + 4(1) = 12

⇒  8 + 4=12

⇒  12 = 12
​
Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations ​ 8x + 4y = 12, 7x + 3y = 10  ​by elimination is ​x = 1, y = 1.

​Big Ideas Math Chapter 5 Exercise 5.3 Answer Key

Page 146  Exercise 16  Answer

Given: The given system is  ​4x+3y=−7, −2x−5y=7.

It is required to solve the system of linear equations by elimination.
Elimination method is used to eliminate one variable and solve the equation for the other, then substituting the known value, the other value is also evaluated.

The equations are given: ​

​4x  +3y = −7—–(1)

−2x−5y = 7—–(2)

Multiply the  equation  (2) by 2

​4x + 3y = −7

⇒ −4x−10y = 14

​
Add them, and we get

​⇒ −7y = 7

⇒  y = −1
​

Substitute the value of y in  equation (1)

​4x + 3y =−7
⇒  4x + 3(−1) =−7

⇒  4x =−7+3

⇒  4x = −4

⇒  x = −1
​

Check the solution:

For equation 1:

​4x + 3y  =−7

⇒  4(−1) + 3(−1) =−7

⇒  −4−3 = −7

⇒  −7 = −7
​

For equation 2:

​−2x−5y = 7

⇒  −2(−1)−5(−1) = 7

⇒  2+5 = 7

⇒  7 = 7
​
Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations ​ 4x+3y = −7, −2x−5y = 7 ​by elimination is ​x =−1, y =−1.

Page 146 Exercise 17 Answer

Given: The given system is​ 8x−3y = −9, 5x + 4y = 12.

It is required to solve the system of linear equations by elimination.
Elimination method is used to eliminate one variable and solve the equation for the other, then substituting the known value, the other value is also evaluated.

The equations are given :​

8x−3y = −9——(1)

5x + 4y = 12——(2)

Multiply   the equation (1)  by 4 and  equation (2)   by 3

⇒ ​ 32x − 12y = −36

⇒  15x + 12y = 36

​
Add them, and we get

​⇒  47x = 0

⇒  x = 0
​

Substitute the value of x in  equation (1)

​8x−3y =−9

⇒  0−3y =−9

⇒  y = 3
​

Check the solution:

For equation 1:

​5x + 4y = 12

⇒  5(0) + 4(3) = 12

⇒  0 + 12 = 12

⇒  12 = 12
​

For equation  2:

​8x−3y =−9

⇒  8(0)−3(3) = −9

⇒  −9 =−9
​
Since the statement is true. Therefore, the solution is verified.

The solution of the system of linear equations ​ 8x−3y = −9,5x + 4y = 12 by elimination is ​x = 0 y = 3.

Page 146  Exercise 18  Answer

Given: The given system is ​−3x + 5y =−2, 2x−2y = 1.

It is required to solve the system of linear equations by elimination.
Elimination method is used to eliminate one variable and solve the equation for the other, then substituting the known value, the other value is also evaluated.

The equations are given: ​

−3x+5y=−2——–(1)

 2x−2y=1———–(2)

Multiply  the  equation (1) by 2  and  equation (2)  by 3

⇒ ​ −6x + 10y =−4

⇒  6x−6y = 3

Add them, and we get

​⇒  4y = −1

⇒  y = \(\frac{-1}{4}\).

Substitute the value y of in the equation

​−3x + 5y = −2

⇒  −3x + 5(\(\frac{-1}{4}\)) = −2

⇒  −12x−5 = −8

⇒  −12x = −8+5

⇒  −12x = −3

⇒   x = \(\frac{1}{4}\)

Check the solution:

For equation 1:

​2x−2y = 1

⇒  2(\(\frac{1}{4}\))−2(\(\frac{-1}{4}\))=1

⇒  \(\frac{1}{2}\)+\(\frac{1}{2}\)=1

⇒ \(\frac{2}{2}\) =1

⇒  1 = 1
​

For equation  2:

​−3x + 5y =−2

⇒  − 3(\(\frac{1}{4}\))+5(\(\frac{-1}{4}\))=−2

⇒  \(-\frac{3}{4}-\frac{5}{4}\)=−2

⇒  \(-\frac{8}{4}\)=−2

Since the statement is true. Therefore, the solution is verified.

​
The solution of the system of linear equations ​−3x+5y=−2, 2x−2y=1 ​by elimination is ​x=\(\frac{1}{4}\)  , y=−\(\frac{1}{4}\).

Page 146  Exercise 19  Answer

Given: The sum of two numbers is 22 and the difference is 6.

It is required to Find the two numbers.
Using the elimination method, the numbers can be evaluated.

Let the numbers be x and y.
The sum of the numbers is 22, therefore, an equation that represents the sum is

⇒  x + y = 22.

The difference of the numbers is 6, therefore an equation to represent the difference is

⇒  x−y = 6.

Therefore the system of equations is

⇒  ​x + y = 22

⇒  x−y = 6

Adding the two equations, we get

⇒  ​2x = 28

⇒  x = 14

Substitute the value of x in any of the equation

⇒  ​x−y = 6

⇒  14−y = 6

⇒  −y = 6−14

⇒  −y = −8

⇒  y = 8

The two numbers are 14 and 8.