Alekhya

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Quantities And Relationships

Page 38 Problem 1 Answer

Given increasing function and decreasing function To fill the table

Method used is increasing and decreasing function

We are given that

A function is described as increasing when the dependent variable increases as the independent variable increases.

If a function increases across the entire domain, then the function is called an increasing function.

A function is described as decreasing when the dependent variable decreases as the independent variable increases.

If a function decreases across the entire domain, then the function is called a decreasing function.

A graph is increasing if it rises from left to right, decreasing if it is falling from left to right, and constant if it is horizontal.

All the increasing and decreasing functions, constants are grouped in the table

Carnegie Learning Algebra I Chapter 1 Exercise 1.3 Solutions

Page 39 Problem 2 Answer

Given: Some of the functions are given

To determine the shape of its graph.

Method: Graphing calculator

The graph of the function f(x)=x is

So the graph off(x)=(1/2)x−5

The shape of its graph is

Page 39 Problem 3 Answer

Given functions To sort the graphs into two groups based on the equations representing the functions and record the function letter in the table.

Method used is  the concept of functions

The seven graphs from exercise 2 can be grouped as linear or exponential

A linear function is of the form y=mx+c

so the constant function are a linear function when m=0

An exponential function is of the formy=bx−k

The exponential function are then f(x)=(1/2)x−5

Where x is an integer (graph H)

f(x)=2x (graph K), and f(x)=(1/2)x (graph P)

The linear function aref(x)=x(graph G),f(x)=−2/3x+5(graph L)

f(x)=−x+3 where x is an integer (graph O), andf(x)=2

Wherex is an integer(graph U)

The table can be filled as

All the data s are arranged in the table

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.3 Quantities And Relationships Page 39 Problem 4 Answer

Given seven graphs and functions that are increasing functions, decreasing functions, or constant functions.

To find same about all the functions in each group Method used is the concept of function

All the in Group 1 are exponential functions

Also, all the functions in group 2 are linear functions

Functions in group 1 are exponential functions and group 2 are linear functions

Page 40 Problem 5 Answer

Given functions To identify which group represents linear and constant functions and which group represents exponential functions.

Method used is the concept of functions

All the functions in group 1 are exponential functions

Since they are of the form f(x)=ab x

All the functions in group 2 are linear functions

Since they are of the form f(x)=mx+b

All the functions in group 1 are exponential functions and in group 2 are linear functions

Quantities And Relationships Chapter 1 Exercise 1.3 Answers

Page 40 Problem 6 Answer

Given linear function f(x)=mx+b

To describe the m and b  values that produce a constant function. The method

used is the concept of functions

We are given the function f(x)=mx+b

f(x)=mx+b is the linear equation

The graph of the linear equation is a line.

The value of m tell us the steepness of the line that is the slope of the line b is the initial value

Whenx=0,f(x)=a(0)+b

That is, f(0)=b

So b is the initial value or y-intercept

The value of m steepness of the line and b is the initial value

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.3 Quantities And Relationships Page 40 Problem 7 Answer

Given different functions To sort the graphs and record the function letter in the appropriate column of the table shown

Method used is the concept of absolute minimum and absolute maximum value

GraphA has no absolute minimum or maximum since it doesn’t have a highest or lowest point

GraphB has an absolute maximum at(2,2) since that is the highest point in the graph.

GraphC has no absolute maximum or minimum since it doesn’t have a highest or lowest point

GraphD has an absolute minimum at(0,0) since that is the lowest point in the graph.

GraphF  has an absolute maximum at(0,4) since that is the highest point in the graph

GraphI has an absolute maximum at(0,0) since that is the highest point in the graph

Graph M has an absolute minimum at(0,0) since that is the lowest point in the graph

Graph Q has an absolute maximum at(2,4) since that is the highest point in the graph

Graph S does not have an absolute maximum or minimum since it doesn’t have a highest of lowest point

Graph T has an absolute minimum at(−4,−4) since that is the lowest point in the graph

Graph V has an absolute minimum at(3,−2) since that is the lowest point in the graph.

The table is then

All the data s are arranged in the table

Page 41 Problem 8 Answer

Given: Consider the graphs of functions that have an absolute minimum or an absolute maximum.

To sort the graphs into two groups based on the equations representing the functions and record the function letter in the table.

The method used: Functional method.

Group1 equations in the form of f(x)=a∣x+b∣+c,

Group 2 be the equations in the form of f(x)=ax²+bx+c,

f(x)=a∣x+b∣+c,

f(x)=∣x−3∣−2 (graphV),

f(x)=∣x∣ (graph D),

f(x)=−∣x∣ (graphI),

f(x)=−2∣x+2∣+4 (graphQ).

f(x)=ax²+bx+c,

f(x)=x²+8x+12 (graph T),

f(x)=x² (graph M),

f(x)=−3x²+4 (graph F),

f(x)=−1/2x²+2x (graphB).

The function letter is shown in the table.

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.3 Quantities And Relationships Page 41 Problem 9 Answer

Given: Consider the graphs of functions that have an absolute minimum or an absolute maximum.

To find what is the same about all the functions in each group?

Method used: Functional method.

To find the same about all the functions in each group;

The functions in Group1 is in the form off(x)=a∣x+b∣+c ,

The functions in Group 2 is of the form off(x)=ax²+bx+c.

The group1 and 2 in the form of

f(x)=a∣x+b∣+c,

f(x)=ax²+bx+c.

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.3 Quantities And Relationships Page 42 Problem 10 Answer

Given: which group represents quadratic functions and which group represents linear absolute value functions.

To identify which group represents quadratic functions and which group represents linear absolute value functions.

The method used: Functional method.

To identify which group represents;

Group 1 is in the form off(x)=a∣x+b∣+c ,

Group 1 are linear absolute value functions.

Group 2  is in the form of f(x)=ax²+bx+c

Group 2 is quadratic functions.

Group 2 represents quadratic functions and group1 represents linear absolute value functions.

Carnegie Learning Algebra I Quantities And Relationships Exercise 1.3 Solutions

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.3 Quantities And Relationships Page 43 Problem 11 Answer

Given: Enter the remaining functions into your graphing calculator.To determine the shapes of their graphs.Method used: Graphical method.

To determine the shapes of their graphs;

Graph

f(x)={ −2x+10,​−∞≤x<3

{ 4,                  3≤x<7

{ −2x+8,        7≤x≤+∞

Y1=(−2X+10)/(X<3)

Y2=(4)/((3≤X)(X<7))

Y3=(−2X+18)/(7≤X)

The shape of the graph is

Graph

f(x)= { −2,   x−2,

{ 1    ​−∞<x<0

{ 2          0≤x<+∞

Y1=(−2)/(X<0)

Y2=(1/2X−2)/(0≤X)

The shape of the given function is

Graph

f(x)= {1/2 x+4,     ​−∞≤x<2

{−3x+11,       2≤x<3

{  1/ 2x+1/2, 3≤x≤+∞

Y1=(1/2X+4)/(X<2)

Y2=(−3x+11)/((2≤X)(X<3))

Y3=(1/2X+1/2)/(3≤X)

The graph of the given function

The shape of the given functions are

Exercise 1.3 Quantities And Relationships Explained

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.3 Quantities And Relationships Page 45 Problem 12 Answer

Given: Glue your sorted graphs and functions to the appropriate function family Graphic Organizer on the pages that follow.

To write a description of the graphical behavior for each function family.

Method used: Functional method.

Linear Functions: GraphsG,L,O,U,

Increasing/Decreasing: increasing, decreasing, or constant,

Maximum/Minimum: none,

Curve/Line: Line.

Exponential Functions:

Graphs H,K,P,

Increasing/Decreasing: Only one,

Maximum /Minimum: None,

Curve/Line: Curve.

Quadratic Functions:

GraphsB,F,M,T,

Increasing/Decreasing: Both,

Maximum/Minimum: One,

Curve/Line: Curve.

Linear Absolute Value Functions:

Graphs D,I,Q,U,

Increasing/Decreasing: Both,

Maximum/Minimum: One,

Curve/Line: Two lines.

Linear Piecewise Functions:

Graphs A,C,S,

Increasing/Decreasing: Can be both,

Maximum/Minimum: None or one,

Curve/Line: Two or more lines.

The graphical behavior for each function family was explained.

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Quantities And Relationships

Page 24 Problem 1 Answer

Given: At 36,000 feet, the crew aboard the 747 airplane begins making preparations to land.

The plane descends at a rate of 1500 feet per minute until it lands.

To complete the table.

Using the method of Quantity function.

To complete the table.

Using the given function,

Thus, the expression is g(t)=36,000−1500t

Completed the table with the expression g(t)=36,000−1550t

Carnegie Learning Algebra I Chapter 1 Exercise 1.2 Solutions

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.2 Quantities And Relationships Page 25 Problem 2 Answer

Given: The airplane is at 36,000 feet

The plane descends at a rate of 1500 feet per minute until it lands.

To determine the unit of measure for each expression

Method: Mathematical reasoning

Independent Quantity and  Dependent Quantity

Considering the Quantity ,Time  and Height

0         36,000

2         33,000

4         30,000

6         27,000

12        18,000

20        6000

Expression 25000t/1 36,000

Write a function, g(t) to represent this problem situation.

g(t)=521500t

Think about the pattern you are used to calculate each dependent quantity value.

Using the table, I can only estimate the time. When plotting the points on my graph, I was able to approximate the intersection of the graphs of both functions.

When I used the function, I was able to determine an exact time when the plane would descend to 14,000 feet.

We can only estimate the time and we can able to determine an exact time when the plane would descend to 14,000 feet.

Page 25 Problem 3 Answer

Given: The plane descends at a rate of 1500 feet per minute until it lands.

To graph the g(t) on the coordinate plane.Using the method of the graph.

Graph which the coordinates

Graph of coordinates

Page 29 Problem 4 Answer

Given:

To Show why Ashley’s reasoning is correct.Using the method of Vertical line test.

To Show why Ashley’s reasoning is correct.

The vertical line test can be used to determine whether a graph represents a function.

Drawing any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value.

The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves.

Thus, the image is the same on both sides.

Shown that the image is same on both sides.

Page 29 Problem 5 Answer

Given: The graphs together all show vertical symmetry.

To identify other graphs that show vertical symmetry.

Using determination method.

The other graphs with vertical symmetry are graphs B,E,I,Q&U.

The other possible graphs with vertical symmetry are graphs B,E,I,Q&U.

Quantities And Relationships Chapter 1 Exercise 1.2 Answers

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.2 Quantities And RelationshipsPage 30 Problem 6 Answer

Given: Grouped these graphs together because each graph only goes through two quadrants.

To Explain why Duane’s reasoning is not correct.

Using the method of Graphical.

To Explain why Duane’s reasoning is not correct.

No, Duane’s reasoning is correct.

Because, every graph has four quadrant.

All the given four graph only goes through two quadrants.

Thus, Duane’s reasoning is correct.

Each of given graph goes through two quadrants.

So, Duane’s reasoning is correct.

Page 30 Problem 7 Answer

Given: Duane grouped the graphs together because each graph only goes through two quadrants.

To identify other graphs that only go through two quadrants.Using determination method.

The other graphs that go through only two quadrants are G,I,K,N,R&U.

The possible other graphs that go through only two quadrants are G,I,K,N,R&U.

Page 31 Problem 8 Answer

Given: Josephine grouped four graphs together, but did not provide any rationale.

To find What do you notice about the graphs Using determination method.

The graphs E,J,N&R can be together because none of them are functions.

They are not functions since they don’t pass the vertical line test.

The graphs E,J,N&R are not functions.

Page 31 Problem 9 Answer

Given: Josephine grouped the four graphs together, but did not provide any rationale.

To find What rationale could Josephine have providedUsing determination method.

For graphs E, the vertical line x=0 crosses the graph twice. For graph J&N, the vertical line x=2 crosses the graph twice.

For graph R, the vertical line x=2 so it will intersect infinitely many times with the vertical line x=2.

The rationale for  grouping these graph is then none  of the graphs pass the vertical line test so they are not functions.

The rationale for  grouping these graph is then none  of the graphs pass the vertical line test.

Carnegie Learning Algebra I Quantities And Relationships Exercise 1.2 Solutions

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.2 Quantities And Relationships Page 32 Problem 10 Answer

Given: A discrete graph is a graph of isolated points.

A continuous graph is a graph of points that are connected by a line or smooth curve on the graph.

Continuous graphs have no breaks.

To find that the graphs she grouped are functions

To Explain how you determined your conclusion.

Using  determination method

For graph E, the vertical line x=0 crosses the graph twice.

For graph J&N, the vertical line x=2 crosses the graph twice.

For graph R it is vertical line x=2 so it will intersect infinitely many times  with the vertical line x=2 .

None of the graphs pass the  vertical line test so they are not functions.

Judy grouped the four graphs together They are not functions since they don’t pass the vertical line test.

Page 32 Problem 11 Answer

Given: functions and non-functions.

Record your results by writing the letter of each graph in the appropriate column in the table shown.

Using determination method.

Only the graphs E,J,N&R fail the vertical line test. So, they are the only non-functions.

The remaining graphs are all functions.

The functions and non functions are shown.

Page 33 Problem 12 Answer

Given: the x-axis and the y -axis display values from −10  to 10 with an interval of 2 units.

To Label each function graph with the appropriate domain.

Using determination method.

The graph that are functions are graphs A, B,C,D,F,G,H,I,K,L,M,O,P,Q,S,T,U&V

The domain will be set of all real numbers if the graph is continuous and the set of integers if the graph is discrete.

Graphs A,B, C,D,G,H,I,L,M,P,Q,S,T,U&V are continuous so they have domains of the set of all real numbers.

Graph F,K,O&U are discrete so they have domains of the set of integers.

The graphs A,B,C,D,G,H,I,L,M,P,Q,S,T,U&V have domains of the set of all real numbers.

The graph F,K,O,U have domains of the set of integers.

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.2 Quantities And Relationships Page 33 Problem 13 Answer

Given: The relation is the mapping between a set of input values called the domain and a set of output values called the range.

To find: the mapping between the graphs

Method used : Algebraic relations

The Vertical Line Test is a visual strategy used to decide if a connection addressed as a chart is a capacity.

To apply the Vertical Line Test, think about the entirety of the upward lines that could be drawn on the chart of a connection.

In the event that any of the upward lines cross the chart of the connection at more than one point,then, at that point the connection isn’t a capacity

A discrete chart is a diagram of confined focuses.

A constant chart is a diagram of focuses that are associated by a line or smooth bend on the diagram. Consistent charts have no breaks.

The Vertical Line Test applies for both discrete and constant charts.

The graphs has been mapped and The Vertical Line Test applies for both discrete and constant charts.

Page 34 Problem 14 Answer

Given a graph of a function To explain what the function isMethod used vertical line test

Draw any graph that passes the vertical line test

Graph is plotted below

Since all the graphs that pass the vertical line test are functions

The graph passes through the vertical line test and so it is a function

Exercise 1.2 Quantities And Relationships Explained

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.2 Quantities And Relationships Page 34 Problem 15 Answer

Given a graph that is not a functionTo explain that it is not a functionMethod used is vertical line test

Draw any graph that do not passes the vertical line test

Plotted the graph below

Since all the graphs that fails the vertical line test are not functions

The graph does not passes the vertical line test so it is not a function.

Chapter 1 Exercise 1.2 Carnegie Learning Guide

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Quantities And Relationships

Page 4 Problem 1 Answer

Given: You may have purchased ice, gone grocery shopping, selected music, made food, or even cleaned in preparation.

To describe how you can determine which quantity is the independent quantity and which quantity is the dependent quantity in any problem situation.Using the method of the graph.

The dependent quantity is the quantity that charges when the other quantity changes and the independent quantity is the quantity that causes the dependent quantity to charge.

The dependent quantity is the quantity that charges when the other quantity changes and the independent quantity is the quantity that causes the dependent quantity to charge.

Carnegie Learning Algebra I Chapter 1 Exercise 1.1 Solutions

Page 5 Problem 2 Answer

Given: Scenario.To determine the independent and dependent quantities.Using the method of the graph.

Something’s Fishy:

In this scenario, the two quantities are time and gallons in the tank since the given rate is that the water drains from the tanks at a constant rate of 10 gallons per minute. The number of gallons left in the tank depends on how many minutes the tank has been draining.

Therefore: 

Independent quantity: time in minutes.

Dependent quantity: number of gallons remaining in the tank.

Smart Phone, but Is It a Smart Deal?

In this scenario, the two quantities are the number of weeks and the amount of interest you owe to your cousin.

As each week goes by, the amount of interest doubles so the amount of interest depends on the number of weeks.

Therefore:

Independent quantity: number of weeks.

Dependent quantity: the amount of interest in dollars.

Can’t Wait to Hit the Slopesl:

In this scenario, it is given that the ski lift is ascending up the mountain at a steady rate of 83 feet per minute.

The two quantities are then the height of the ski lift and the number of minutes that have passed.

The height of the ski lift depends on the number of minutes that have passed. Therefore:

Independent quantity: number of minutes.

Dependent quantity: height of the ski lift in feet.

It’s Magic:

In this scenario, the two quantities are the length of the remaining piece of rope and the total number of cuts.

The more times he cuts the rope, the short the remaining piece of rope gets so the length of the remaining piece of the rope depends on the total number of cuts.

Therefore:

Independent quantity: total number of cuts.

Dependent quantity: length of the remaining piece of rope in feet.

Baton Twirling:

In this scenario, the two quantities are the height of the baton and the amount of time since she needs the baton to be in the air for 2

seconds before she catches it when it comes back down. The height of the baton depends on the number of seconds that have passed.

Therefore:

Independent quantity: number of seconds.

Dependent quantity: height of the baton in feet.

Music Club:

In this scenario, it is given that Jermaine pays $1 per song.

This rate means the two quantities are the amount of money Jermaine has paid for songs and the number of songs he has purchases.

The amount of money he pays depends on the number of songs he purchases.

Therefore:

Independent quantity: number of songs.

Dependent quantity: total cost in dollars.

A Trip to School:

In this scenario, the two quantities are time in minutes and the distance she has traveled since her distance from home is changing.

The distance she is from home increases as the number of minutes increases so her distance depends on the number of minutes.

Therefore:

Independent quantity: time in minutes.

Dependent quantity: distance in miles.

Jelly Bean Challenge:

In this scenario, the two quantities are the number of jelly beans that each person guesses and how many jelly beans each person’s guess was off by since these are the two quantities that Mr. Wright is keeping track of.

A person’s guess determines how far off their guess is from the actual number of jelly beans so how far off their guess depends on how many jelly beans they guess.

Therefore:

Independent quantity: number of jelly beans a person guesses.

Dependent quantity: how many jelly beans the guess is off by.

Something’s Fishy: independent: time in minutes, dependent quantity: number of gallons remaining in the tank.

Smart Phone, but Is It a Smart Deal?: independent: number of weeks, dependent: amount of interest in dollars.

Can’t Wait to Hit the Slopesl: independent: number of minutes, dependent: height of the ski lift in feet.

It’s Magic: independent: total number of cuts, dependent: length of remaining piece of rope in feet.

Baton Twirling: independent: number of seconds, dependent: height of the baton in feet.

Music Club: independent: number of songs, dependent: total cost in dollars.

A Trip to School: independent: time in minutes, dependent: distance in miles.

Jelly Bean Challenge: independent: number of jelly beans a person guesses, dependent: how many jelly beans the guess is off by.

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.1 Quantities And Relationships Page 15 Problem 3 Answer

Given: A graph with the appropriate problem.

To find the similarities do you notice in the graphs? Using the method of the graph.

Graphs A and H have constant rates of change. Graphs A and B are only increasing. Graphs D and H are only decreasing.

Graphs C and F both have an increasing portion of the graph and a decreasing portion of the graph.

Graphs E and G are both increasing, constant, and then increasing again.

Graphs A and H have constant rates of change. Graphs A and B are only increasing.

Graphs D and H are only decreasing.

Graph C and F both have an increasing portion of the graph and a decreasing portion of the graph.

Graphs E and G are both increasing, constant, and then increasing again.

Quantities And Relationships Chapter 1 Exercise 1.1 Answers

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.1 Quantities And Relationships Page 15 Problem 4 Answer

Given: A graph with the appropriate problem situation.

To find what differences do you notice in the graphs Using the method of the graph.

Some graphs have constant rates of changes while others have variable rates of change.

Some graphs are either only increasing or decreasing while others have both increasing and decreasing portions.

Some graphs have constant rates of change while others have variable rates of change.

Page 15 Problem 5 Answer

Given: Independent and dependent quantities.

To find how did you label the independent and dependent quantities in each graph?Using the method of the graph.

For each graph, the independent quantity was labeled on the x axis and the dependent quantity was labeled on the y−axis.

For each graph, the independent quantity was labeled on the x axis and the dependent quantity was labeled on the y axis.

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.1 Quantities And Relationships Page 15 Problem 6 Answer

Given: Analyze each graph from left to right.To describe any graphical characteristics you notice.Using the method of the graph.

Graph A is only increasing and has a constant rate of change. It has an x – and y-intercept at (0,0). It has no negative y-values.

Graph B is only increasing and has a variable rate of change. It has a y-intercept at(0,1) and no x-intercept. It has only positive y-values.

Graph C is decreasing with a constant rate of change and then increasing with a constant rate of change.

It has both an x-intercept and y-intercept. It doesn’t have any negative y-values.

Graph D is only decreasing with a variable rate of change. It has a y -intercept at (0,20) and no x-intercept.

It has only positive y-values.

Graph E is increasing with a constant rate of change, then increasing at a greater constant rate of change, then constant with a rate of change of 0, and then increasing again at a constant rate of change.

It has an x – and y-intercept at (0,0). It doesn’t have any negative y-values.

Graph F is increasing at a variable rate of change and then decreasing at a variable rate of change.

It has a y-intercept at (0,6), no x-intercept, and a maximum at (1,22).

It only has y-values that are greater than or equal to 6.

Graph G is increasing at a constant rate of change, then constant with a rate of change of 0, and then increasing again at a constant rate of change.

It has an x – and y-intercept at (0,0). It doesn’t have any negative y−values.

Graph H is decreasing at a constant rate of change. It has a y intercept at (0,20).

If the graph continued for larger values of x, it would have an x-intercept at (20,0).

It doesn’t have any negative values of y.

Graph A: increasing with constant rate of change, x – and y intercept of (0,0), no negative y-values

Graph B: increasing with variable rate of change, no x-intercept, y intercept at (0,1), only positive y-values

Graph C: decreasing and then increasing with constant rates of changes, has an x-intercept and y−intercept, no negative y-values

Graph D: decreasing with variable rate of change, no x-intercept, y -intercept at(0,20), only positive y-values.

Graph E: increasing, constant, and then increasing with constant rates of changes, x – and y−intercept at (0,0), no negative y−values

Graph F: increasing and then decreasing with variable rates of changes, no x-intercept, y−intercept at (0,6), maximum at (1,22), only y-values greater than or equal to 6.

Graph G: increasing, constant, and then increasing with constant rates of changes, x- and y−intercept at(0,0). no negative y-values

Graph H: decreasing with constant rate of change, x-intercept at (20,0),y-intercept at (0,20), no negative y-values.

Page 16 Problem 7 Answer

Given:  Smart Phone, but Is It a Smart Deal? and Music Club.

To compare the graphs for each scenario given and describe any similarities and differences you notice.Using the method of the graph.

Smart Phone, but Is It a Smart Deal? (graph B) and Music Club (graph A) are both only increasing. Graph A is increasing at a constant rate.

Smartphone, but Is It a Smart Deal (graph B) and Music Club (graph A) are both only increasing. Graph A is increasing at a constant rate though while Graph B is increasing at a variable rate.

Carnegie Learning Algebra I Student Text Volume 1 3rd Edition Chapter 1 Exercise 1.1 Quantities And Relationships Page 16 Problem 8 Answer

Given:  Something’s Fishy and It’s MagicTo compare the graphs for each scenario given and describe any similarities and differences you notice.

Using the method of the graph.

Something’s Fishy (graph H)  and It’s Magic (graph D) are both only decreasing.

Graph D is decreasing at a variable rate while Graph H is decreasing at a constant rate.

Something’s Fishy (graph H)  and It’s Magic (graph D) are both only decreasing.

Graph D is decreasing at a variable rate while Graph H is decreasing at a constant rate.

Carnegie Learning Algebra I Quantities And Relationships Solutions

Page 16 Problem 9 Answer

Given: Baton Twirling and Jelly Bean ChallengeTo compare the graphs for each scenario given and describe any similarities and differences you notice.

Using the method of the graph.

Baton Twirling (graph C) and Jelly Bean Challenge (graph F) both have sections of increasing and decreasing.

Graph C decreasing and then increasing while Graph F increases and then decreases.

Graph C has constant rates of change while Graph F has variable rates of change.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Skills Practice

Page 363 Problem 1 Answer

To define the average rate of change in our own words

First, the rate of change can generally be expressed as a ratio between a change in one variable relative to a corresponding change in another.

The average rate of change:

The average rate of change can be simply defined as the average rate at which one quantity changes with respect to some other quantity

The average rate of change:

The average rate of change can be simply defined as the average rate at which one quantity changes with respect to some other quantity.

Page 363 Problem 2 Answer

Given: A graph that shows the number of vocabulary words a student can able to memorize based on the amount of time spent studying.

To find how many words does the student knows at the start of the study and we have to locate the position in the graph.

At the start, the student knows 0 vocabulary words and the event is represented by the y-intercept in the origin.

The blue-colored point is the point origin.

At the start, the student knows 0.75 vocabulary words and The blue color represents the origin.

Carnegie Learning Algebra Ii Chapter 4 Exercise 4.1 Solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Exercise 4.1 Skills Practice Page 364 Problem 3 Answer

Given: A graph that shows the number of vocabulary words a student can able to memorize based on the amount of time spent studying.

To find the relative minimum.

In the graph, It has two extrema which are located at x=0.333 and x=1.5

We know that the relative minimum is where the graph attains its lowest point on the domain of the function.

Here at x=0.333 the y-coordinate attains its minimum value.

The red colored point represent the relative minimum

The relative minimum is when for 0.33 hours the number of vocabulary words memorized is 9.25 (approximately 9 words).

Page 364 Problem 4 Answer

Given: A graph that shows the number of vocabulary words a student is able to memorize based on the amount of time spent studying.

To find: The minimum amount of time that a student studies before they begin to remember the vocabulary

From the graph, the student took about 0.75 hours before they began to remember the vocabulary.

It is because before 0.75 hours the number of vocabularies that the student memorized is negative which is not possible and negligible.

The number of vocabulary that the student memorized started to increase from 0.75 hours.

The red-colored point represents the estimated location on the graph

From the graph, the minimum amount of time the student studies before they begin to remember the vocabulary is 0.75 hours

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Exercise 4.1 Skills Practice Page 364 Problem 5 Answer

Given: A graph that shows the number of vocabulary words a student can able to memorize based on the amount of time spent studying.

To find how long the student has to study in order to remember 22 vocabulary words.

In the graph, They coordinate represents the number of hours spent studying and the x coordinate represents the number of vocabulary words memorized.

Here the y-coordinate of 22.5 is almost equal to the 22 vocabularies.

When they-coordinate is 22.5 the x coordinate has a value of 1.5 which implies that the student memorized the approximately 22 vocabularies in 1.5 hours.

Here the red colored point represents the location of the estimated point.

From the graph, we estimated that the student memorized approximately 22 vocabularies in 1.5 hours.

Page 364 Problem 6 Answer

Given: The graph has an x-intercept at (2,0)

To describe the activity of the student.

We need to verify the graph in order to find the activity of the student.

We know that, In the graph, the x-axis represents the number of hours spent studying and the y-axis represents the number of vocabulary words memorized.

Therefore the x-intercept (2,0) represent that the student memorized 0  vocabulary in 2 hours.

The student memorized 0 vocabulary (nothing) in 2 hours.

Page 364 Problem 7 Answer

Given: A graph that shows the number of vocabulary words a student is able to memorize based on the amount of time spent studying.

To describe whether the graph accurately shows the problem situation or not.

The graph so far showed the accurate details on how many hours the student took to memorize the vocabulary.

The situations given in the problem accurately match the x and y coordinates in the graph.

Yes, the graph accurately describes the problem situation.

Skills Practice Carnegie Learning Algebra Ii Exercise 4.1 Answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Exercise 4.1 Skills PracticePage 365 Problem 8 Answer

Given: (0,1.5)

To find: The average rate of change.

We need to substitute the given interval in the average rate of change formula.

are the x-coordinates of the given graph and f(a) and f(b) are the corresponding y-coordinates.

Substituting the given interval in the formula of the average rate of change.

A(x)=f(b)−f(a)/b−a

=f(1.5)−f(0)/1.5−0

=4.375−0/1.5−0

=4.375/1.5

≈2.92

The average rate of change for the given interval for each polynomial function is 2.92 (approximately).

Page 365 Problem 9 Answer

Given: (1,2)

To find: The average rate of change.

We need to substitute the given interval in the average rate of change formula.

are the x-coordinates of the given graph and f(a) and f(b) are the corresponding y-coordinates.

Substituting the given interval in the formula of the average rate of change.

A(x)=f(b)−f(a)/b−a

=f(2)−f(1)/2−1

=6−0/2−1

=6/1

A(x)=6

The average rate of change for the given interval for each polynomial function is6

Page 366 Problem 10 Answer

Given: (−2,0)​

To find: The average rate of change.

We need to substitute the given interval in the average rate of change formula.

(a,b)=(−2,0) are the x-coordinates of the given graph and f(a) And f(b) are the corresponding y-coordinates.

Substituting the given interval in the formula of the average rate of change.

A(x)=f(b)−f(a)/b−a

=f(0)−f(−2)/0−(−2)

=−6−4/0+2

=−10/2

A(x)=−5

The average rate of change for the given interval for each polynomial function is−5

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Exercise 4.1 Skills Practice Page 366 Problem 11 Answer

Given: (−3,−0.3)

We have determined the average rate of change for the given interval.

Here we will use the average rate of change formula to find the answer.

The average rate of change for the given interval (−3.−0.3):

The average rate of change=f(b)−f(a)/b−a

=f(−0.3)−f(−3)/−0.3−(−3)

=2.38−(−17.5)/−0.3+3

≈7.36

Hence the average rate of change for interval (−3,−0.3) is approximately equal to 7.36.

Page 367 Problem 12 Answer

Given: (−2,0.333)

We have determined the average rate of change for the given interval.

Here we will use the average rate of change formula to find the answer.

The average rate of change for the given interval (−2,0.333):

Average rate of change =f(b)−f(a)/b−a

=f(0.333)−f(−2)/0.333−(−2)

=1.85−(−4.5)/0.333+2

≈2.72

The interval is shown below

Hence the average rate of change for interval(−2,0.333) is approximately equal to 2.72.

The interval is shown below

How To Solve Chapter 4 Exercise 4.1 Algebra Ii Carnegie Learning

Page 367 Problem 13 Answer

Given: (2,3.5)

We have determined the average rate of change for the given interval.

Here we will use the average rate of change formula to find the answer.

The average rate of change for the given interval(2,3.5):

Average rate of change =f(b)−f(a)/b−a

=f(3.5)−f(2)/3.5−2

=−4.79−2.333/1.5

≈−4.74

Hence the average rate of change for interval (2,3.5) is approximately equal to.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Exercise 4.1 Skills PracticePage 368 Problem 14 Answer

Given: The graph models the profit a group of students earns running a tutoring business.

We have to find after how many weeks did it take the group to earn a profit and where is this information located on the graph.

Here we will use the graph to find the answer.

The given graph describes the Tutoring Business Profit.

The x−axis represents the number of weeks in business and y−axis represents the profit in dollars.

From the graph, the number of weeks after which the group earns a profit is at x=5 where x is the number of weeks.

And the point (5,0) where the information is located on the graph.

The location of the point (5,0) on the graph is shown below

Hence the group earns a profit after 5 weeks in business. The information is located at the  point (5,0).

Located the point (5,0) in the graph

Page 368 Problem 15 Answer

Given: The graph models the amount of money a company makes producing floral displays.

We have to find the what is the maximum number of floral displays that the company can create and continue to increase their profit and where is this information located on the graph.

Here we will use the graph to find the answer.

The given graph describes the Floral Business Profit.

The x−axis represents the number of floral displays made and y−axis represents the profit in dollars.

Find the point from where the x−coordinate and y−coordinate both are positive.

From the graph, we can see that at x=3 the company can create and increase their profit and the point which describes this information is (3,0)

Hence the maximum 3 number of floral displays that the company can create and continue to increase their profit and this point is located at (3,0).

The point (3,0) on the graph is

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Exercise 4.1 Skills Practice Page 369 Problem 16 Answer

Given: The graph models the number of gallons of water that are filtered at a filtration plant hourly.

We have to find how many gallons of water has the plant filtered after running for about 4.5 hours and where is this information located on the graph.

Here we will use the graph to find the answer.

The given graph describes the Gallons of water filtered. The x−axis represents time and y−axis represents the number of gallons filtered.

From the graph, we can see that after running for an 4.5 hours the amount of water filtered is approximately equal to 631 Gallons and the point which describes this relation is .The point is plotted in the graph

Hence  631 gallons of water have the plant filtered after running for about 4.5 hours. This information is located on the graph.

Located the point on the graph.

Carnegie Learning Algebra Ii Student Skills Practice Exercise 4.1 Explanations

Page 369 Problem 17 Answer

Given: The graph models the amount of profit Emilio earns from his own lawn-care business.

We have to find how much did Emilio initially invest to start his business and where is this information located on the graph.

The given graph describes the Lawn-Care Business Profit where x−axis represents the number of weeks in business and y−axis represents the profit.

From the graph, we can see that Emilio needs to invest 1 week to start his business and the which describe the information is (1,0).

Locate the point on the graph

Hence initially Emilio needs to invest 1 week to start his business and this information is located (1,0) on the graph.

Page 370 Problem 18 Answer

Given: The graph models the number of tricks that a dog can perform based on the number of hours it is trained.

We have to estimate how long it takes the dog to learn 8 tricks. and where is this information located on the graph

Here we will use the graph to find the answer.

The given graph describes the Dog tricks learned in time trained where x−axis represents the time spent training in hours and y−axis represents the number of tricks learned.

From the graph in 1 hour dog learned 8 tricks and the point which describes this information is (1,8).

Hence it takes 1 hour to the dog to learn 8 tricks and this information is located (1,8)on the graph.

Chapter 4 Carnegie Learning Algebra Ii Exercise 4.1 Worked Examples

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 4 Exercise 4.1 Skills Practice Page 370 Problem 19 Answer

Given: The graph models the number of electronic devices that are being used in a home during the hours of noon and4:00 pm.

We have to estimate the time when the greatest number of electronic devices are being used and where is this information located on the graph.

Here we will use the graph to find the answer.

The given graph describes the Electronic device usage where x−the axis represents the time since noon in hours and y−the axis represents the number of active electric devices.

From the graph, we can see that from 3 noon the maximum number of electronic devices are being used and the point which describes this information is (3,18).

Hence 3 pm is the time when the greatest number of electronic devices are being used and this information is located (3,18) on the graph.

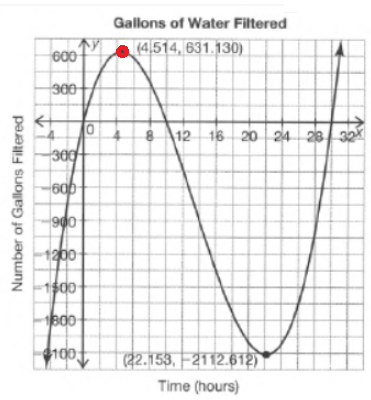
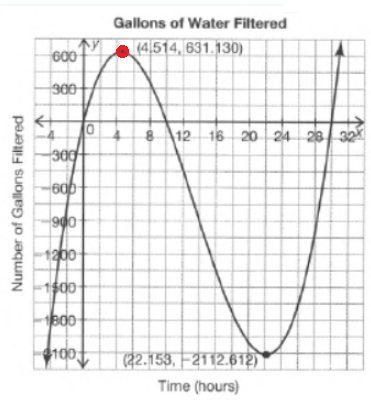
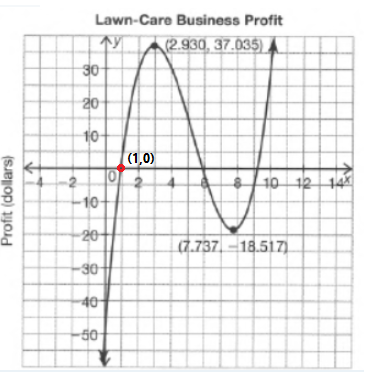
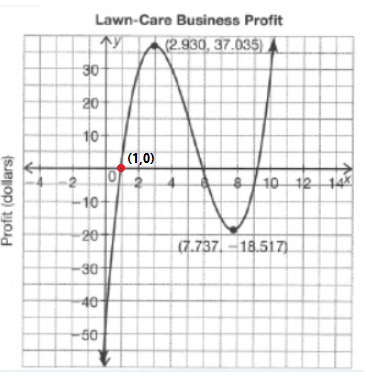
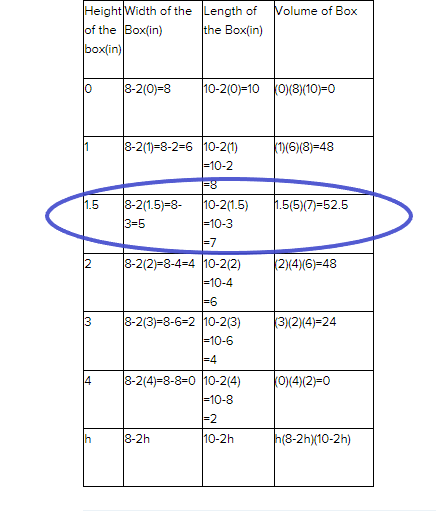
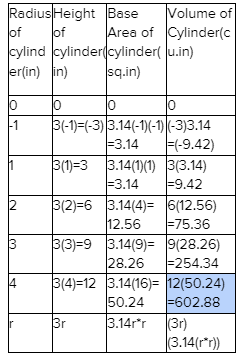
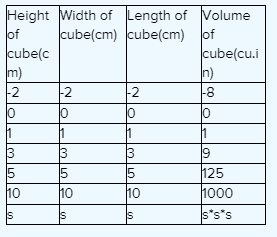
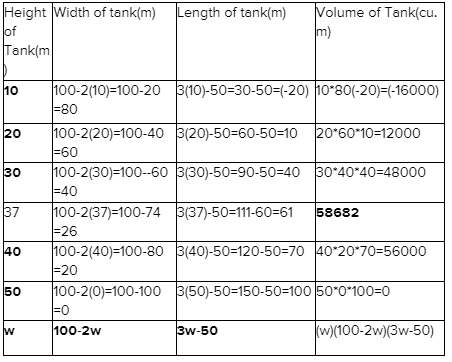
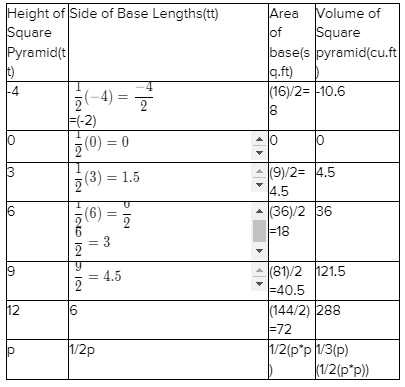
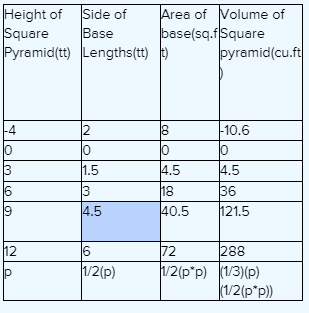
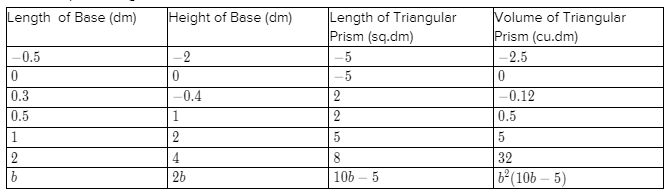
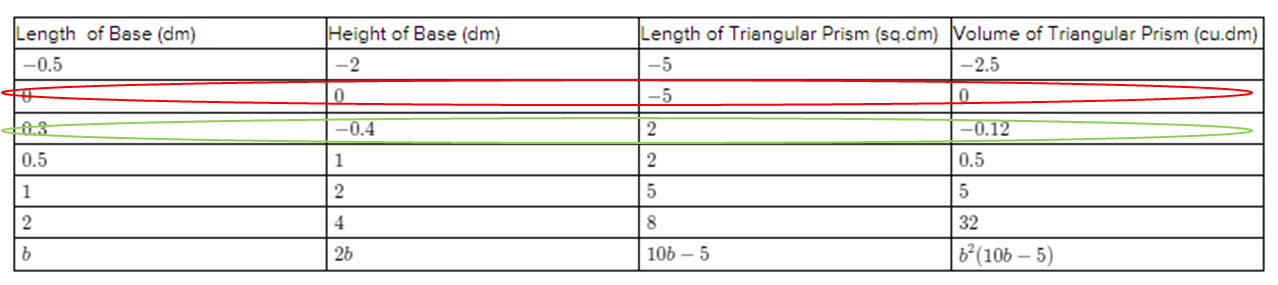
Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Skills Practice

Page 329 Problem 1 Answer

To give an example of the polynomial function, we need to write a function which has a variable with exponent.

The exponent should be positive and should be an integer.

We can choose any constant and can perform any operation like add, subtract, multiply or divide

We will first choose a variable from a to z.

Let us assume that we choose, x

Now let us assume that we choose the exponent to be 2

Our polynomial will look like x²

Let us assume we choose the constant to be 5 and operation to be add.

Our polynomial will look like x²+5

Example of polynomial function is x²+5.

Carnegie Learning II Chapter 3 Exercise 3.3 solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 329 Problem 2 Answer

To find a quartic function we will first write the variable with exponent as 4.

After this we can add other variable with exponents less than 4.

We can also perform any operation like add, subtract, divide or multiply with constants.

Let us select a variable x We have to use the exponent as 4

we get our function: x⁴

Now we can add more variable x with exponent value less than 4.

let’s choose 2 as exponent and operation as subtract we get,x⁴+x²

On adding a constant 6 we get,x⁴+x²+6

The example of quartic function is: x⁴+x²+6

Page 329 Problem 3 Answer

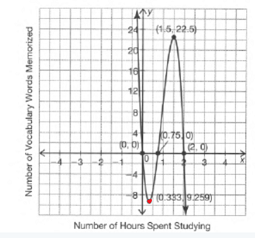
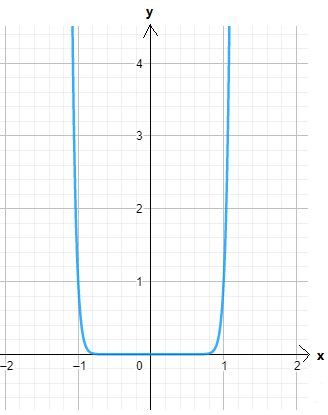
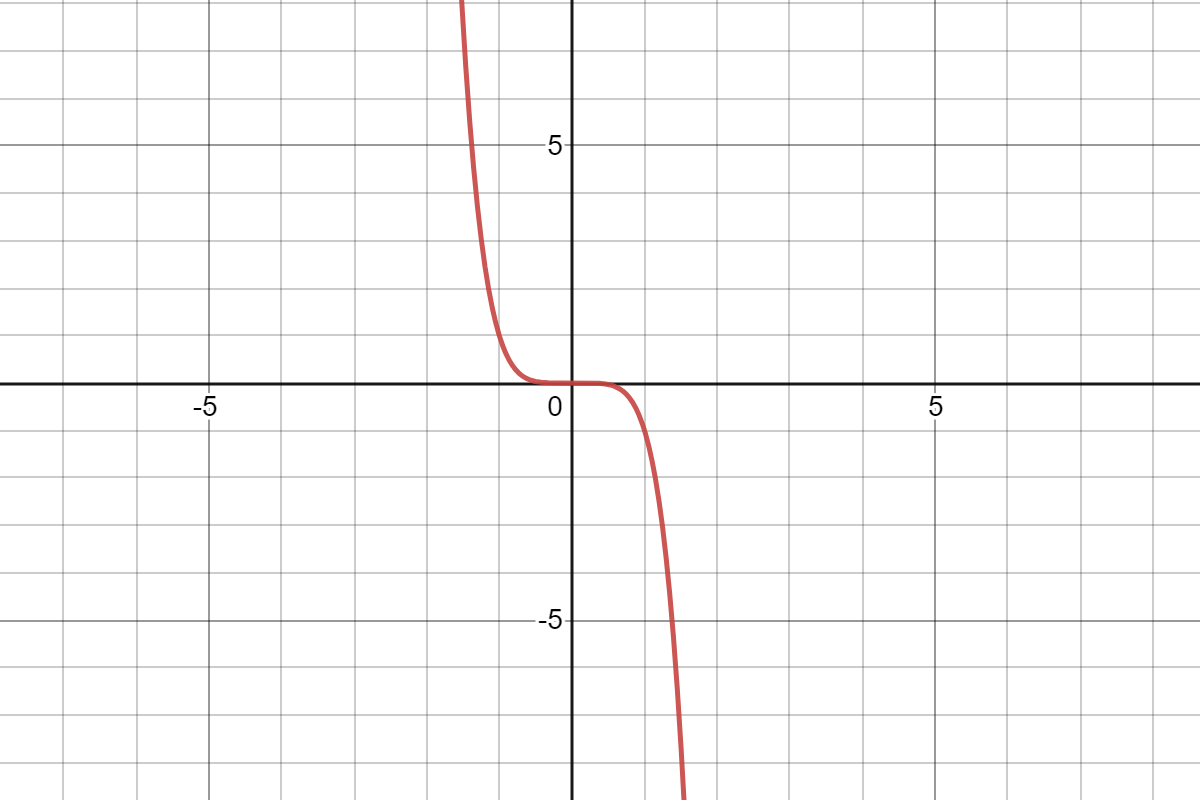
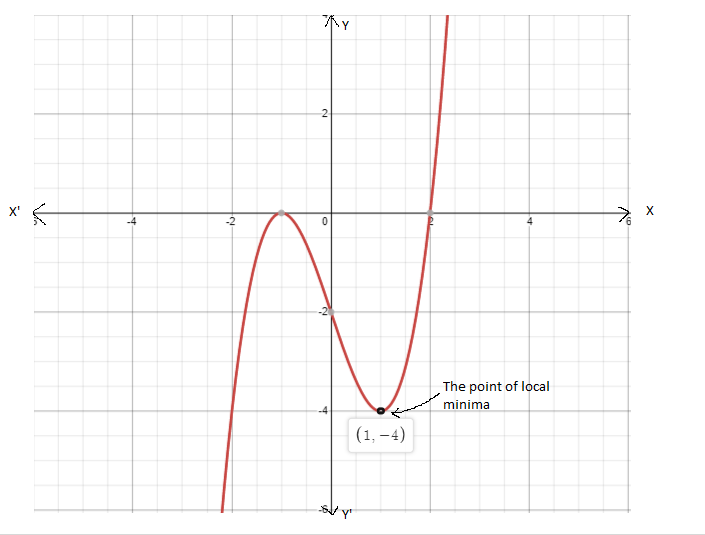
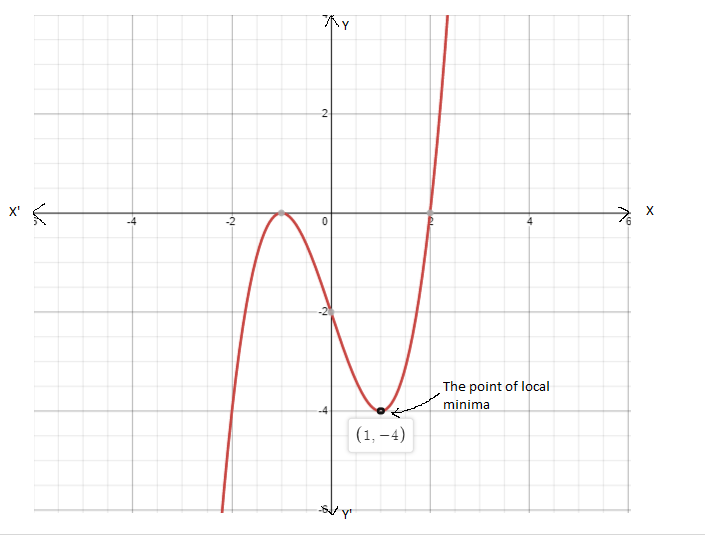
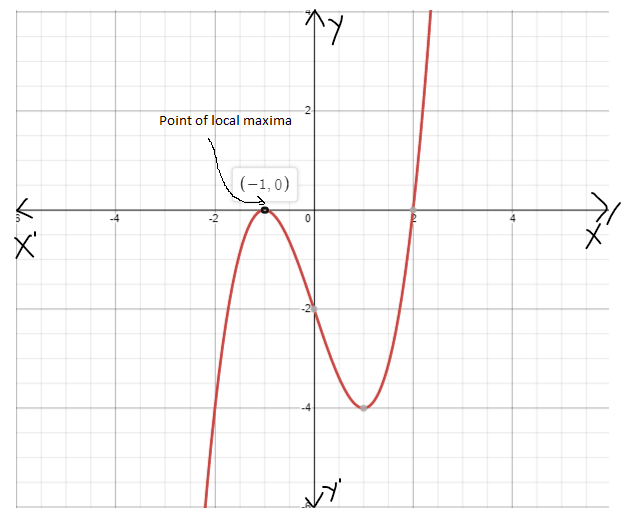
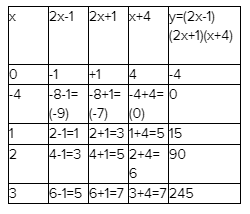
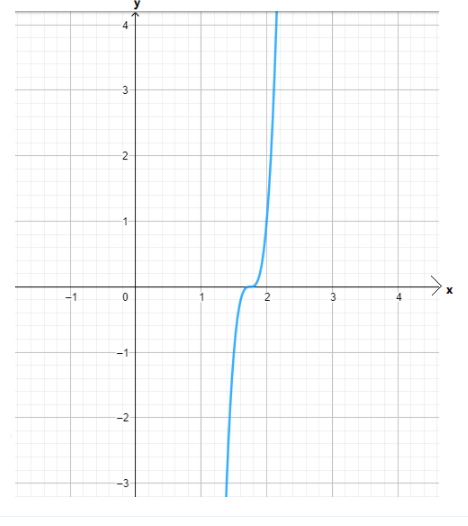
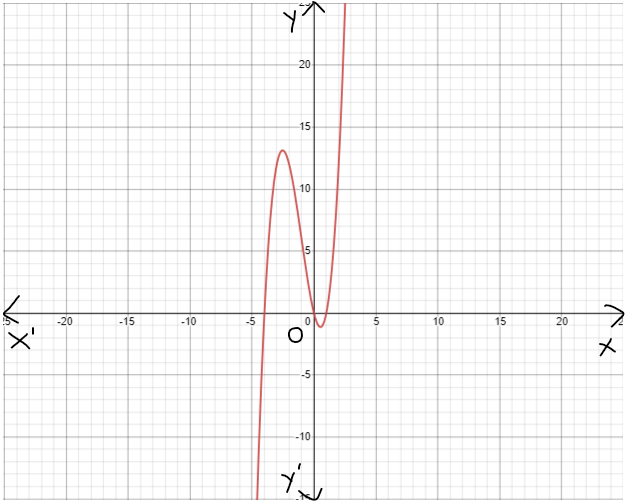
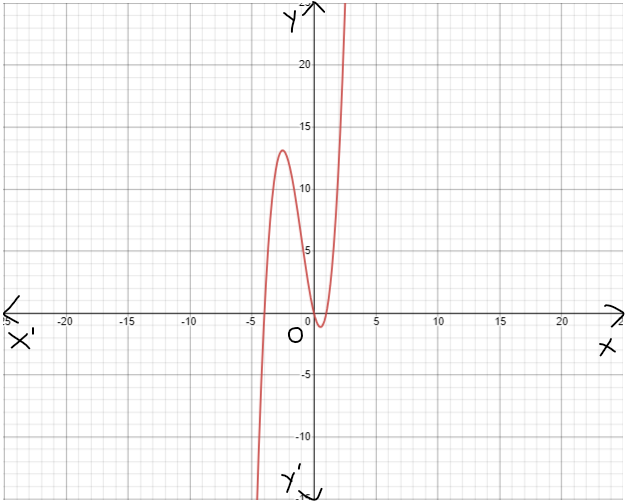
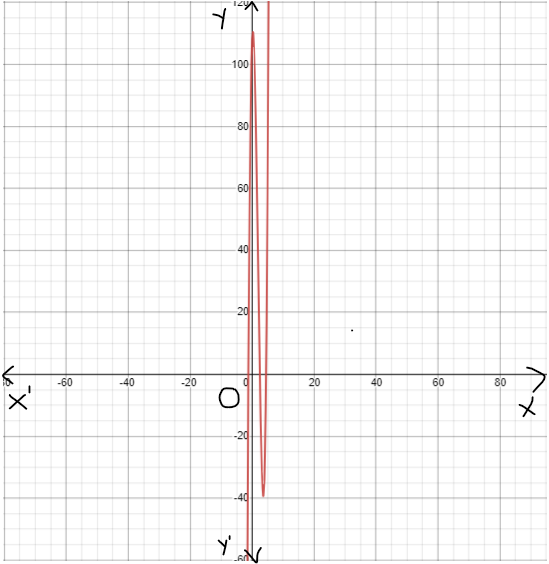
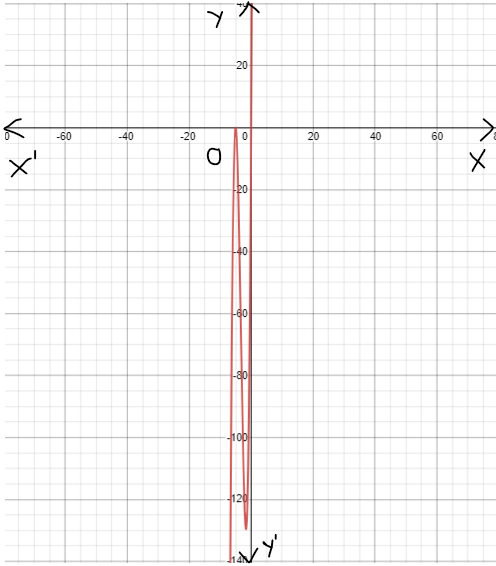
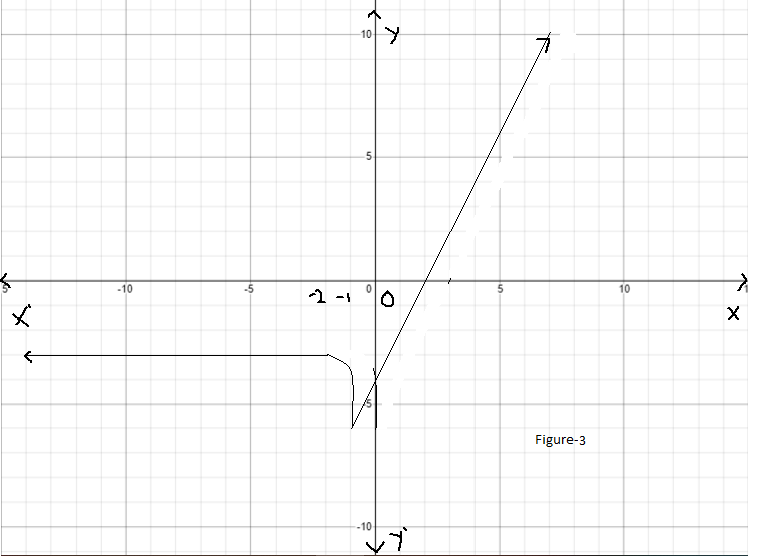
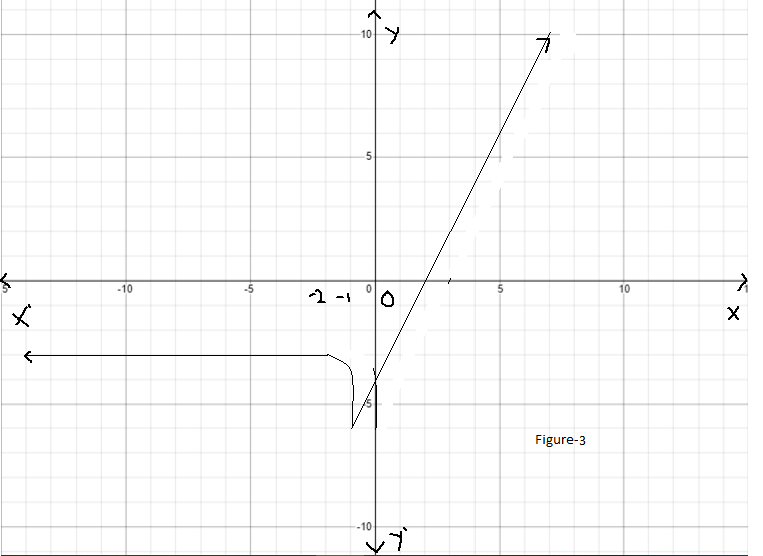
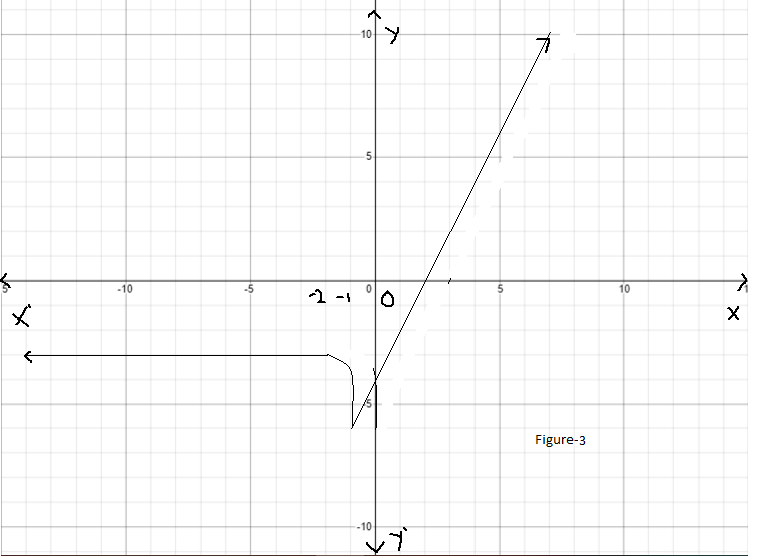
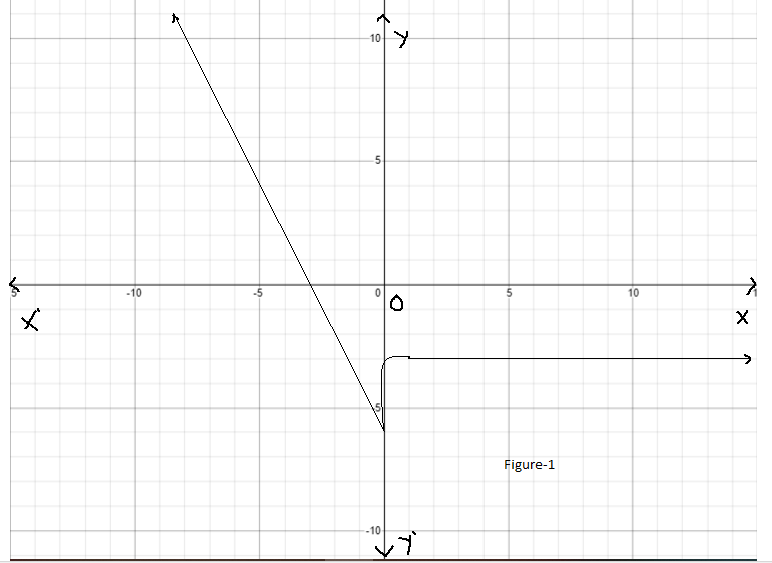
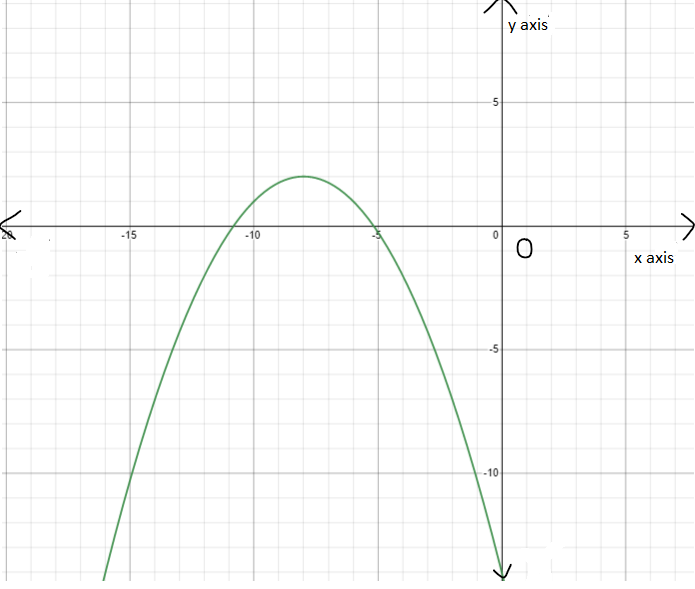
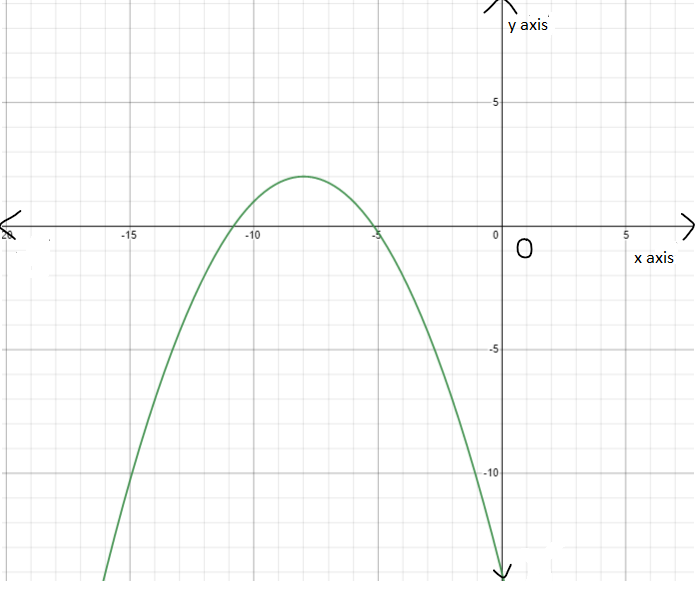
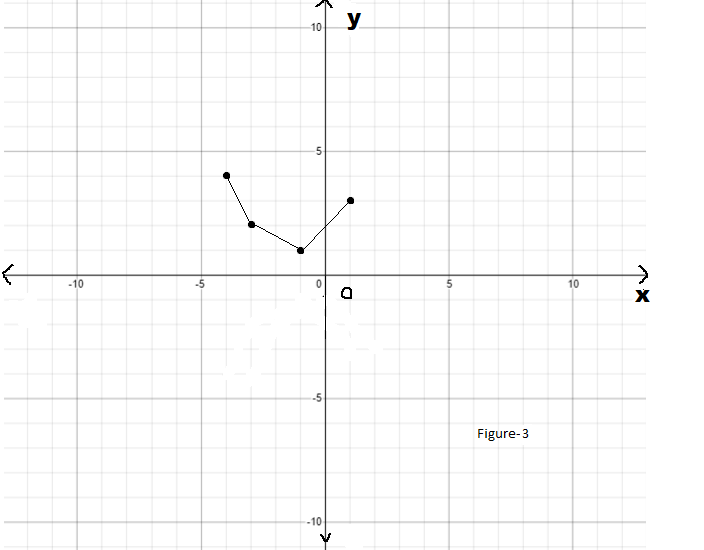
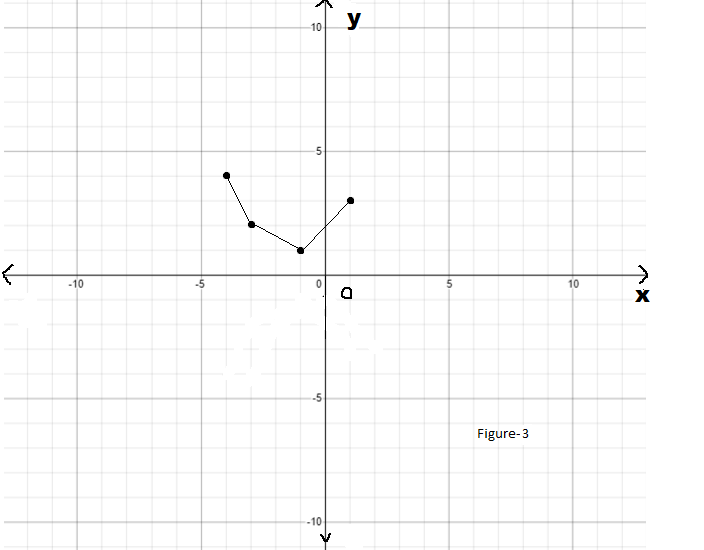
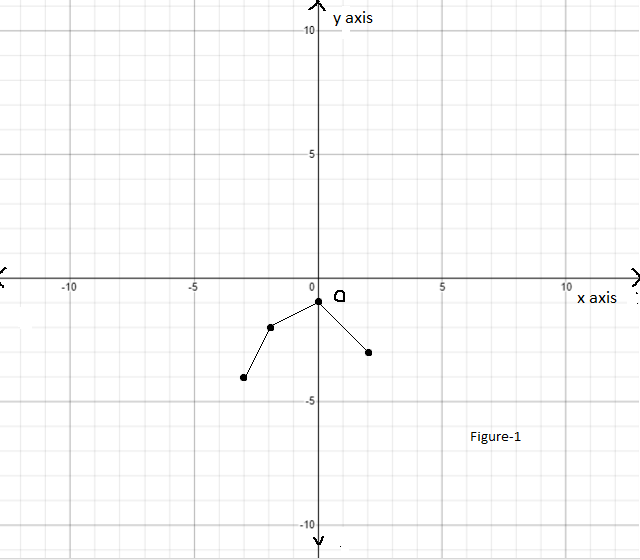
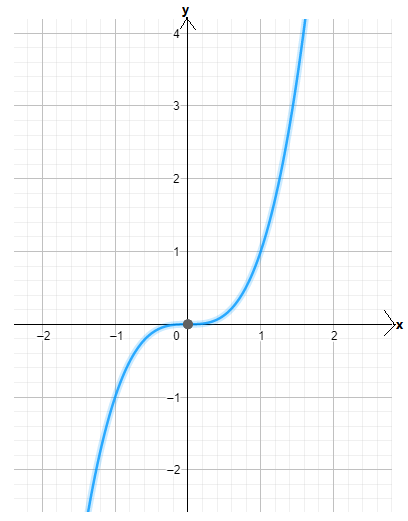
Given : The function c(x)=x³,h(x)=−3c(x)

and the reference points to plot the graph.

Our objective is to find whether the given function is even, odd, or neither.

Procedure:

Use the reference points to find the points of h(x).

Use the given points to create a table to plot the graph for each function.

Check whether the function satisfies the even function condition or odd function condition.

Finally, we came with a solution.

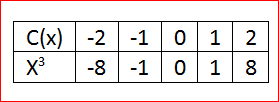
Let us find the values for c(x)=x³

for x=0, we have

⇒c(0)=0³

⇒c(0)=0

forx=1, we have

⇒c(1)=1³

⇒c(1)=1

for x=2, we have

⇒c(2)=2³

⇒c(2)=8

By this method we can have the table of values

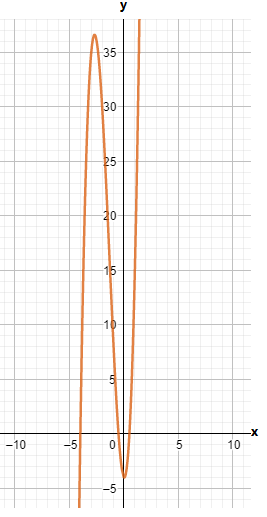
On creating the graph, we get

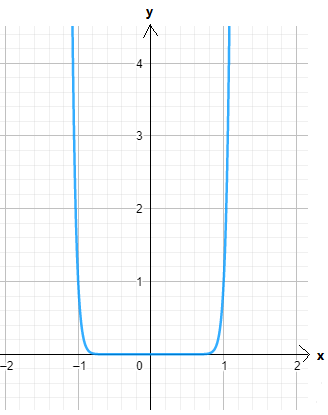
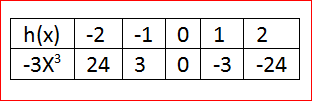
Let us find the values for

h(x)=−3c(x)

h(x)=−3x³

for x=0, we have

⇒h(0)=−3(0)³

⇒h(0)=0

for x=1, we have

⇒h(1)=−3(1)³

⇒h(1)=−3

for x=2, we have

⇒h(2)=−3(2)³

⇒h(2)=−2⁴

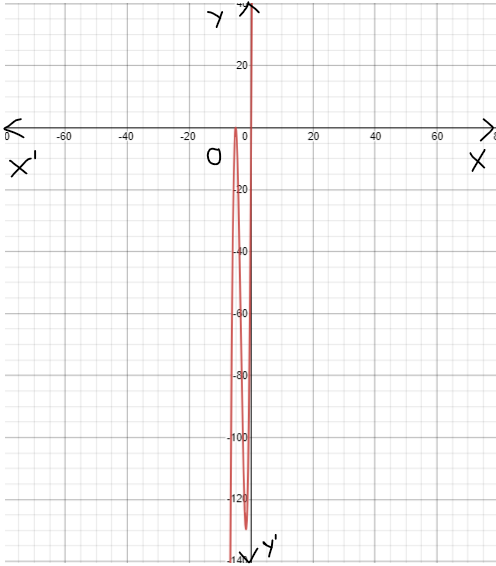
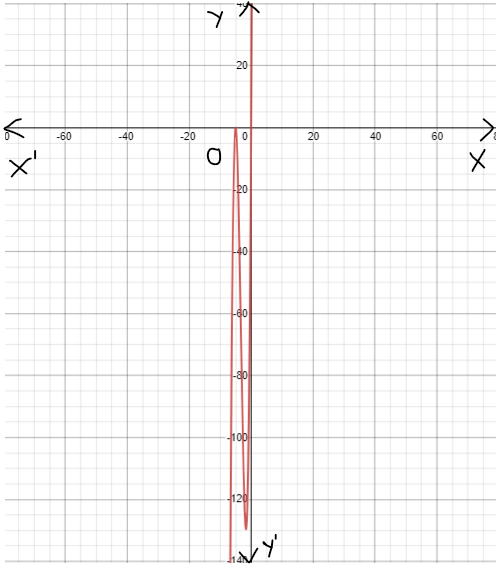
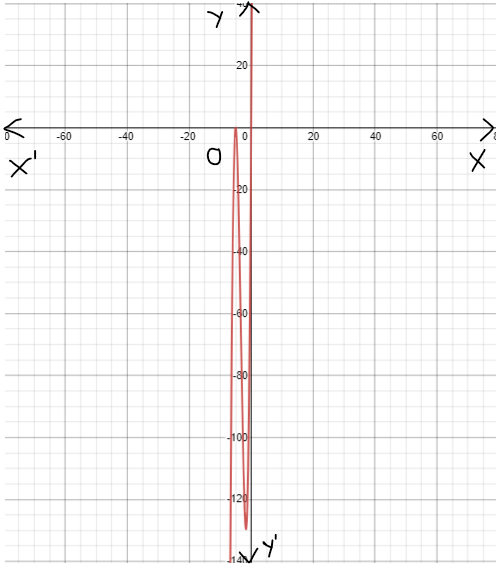
On creating the graph, we get

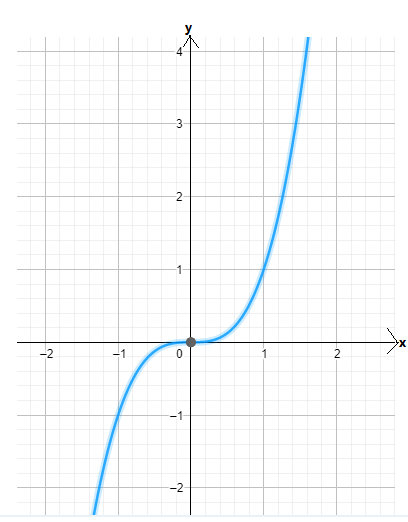
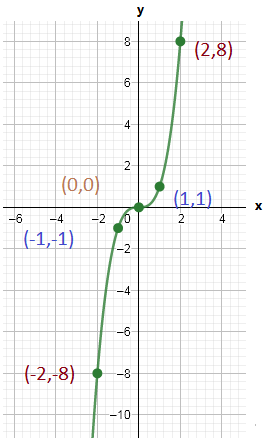
Since both the graphs have 180-degrees symmetry about the origin, both are odd functions.

And they satisfy the condition f(x)=−f(x)

c(x)=x³

c(−x)=−x³

⇒−x³

This function satisfies the odd function condition.

h(x)=−3x³

h(−x)=−3(−x³)

⇒3x³

This function also satisfies the odd function condition.

The graph of the functions c(x) and h(x)  is sketched below

Both the functions c(x) and h(x) are odd functions.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 330 Problem 4 Answer

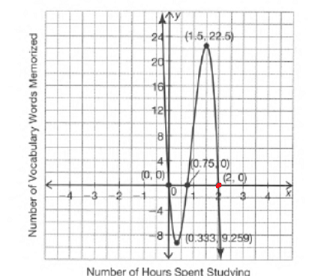
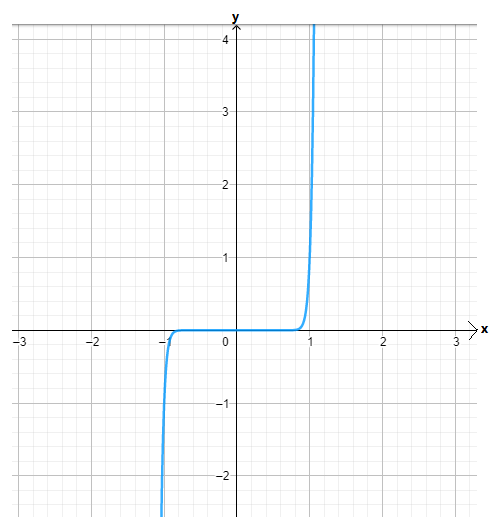
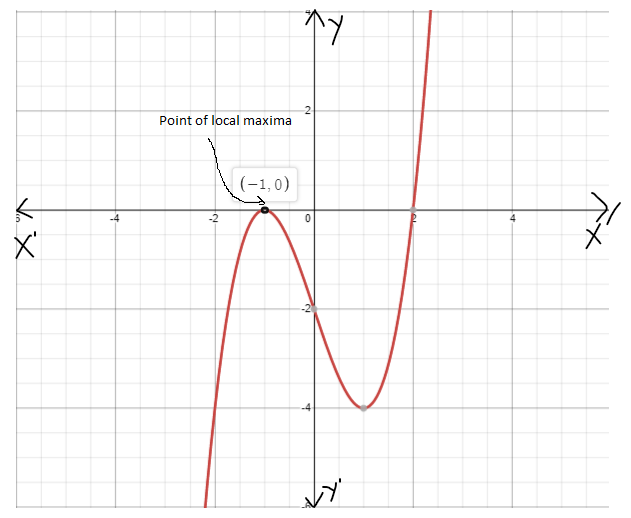
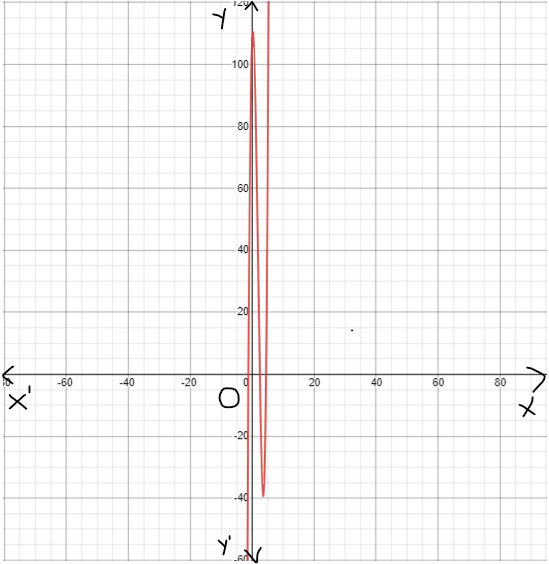
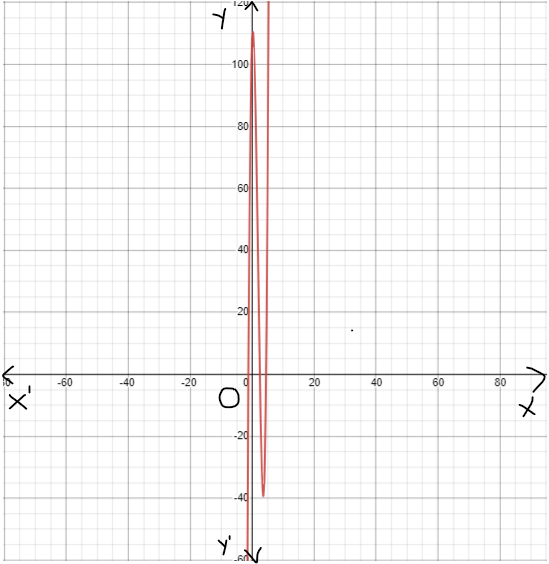
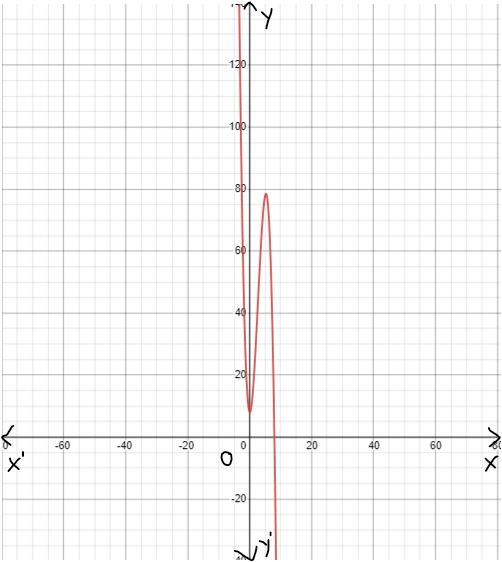
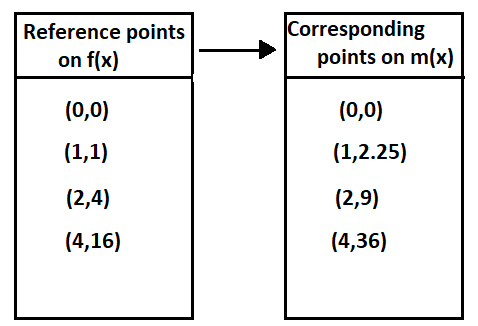
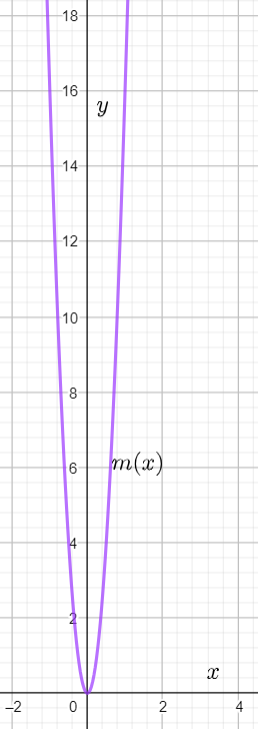
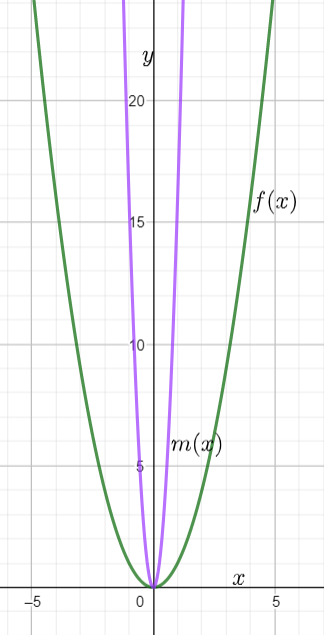
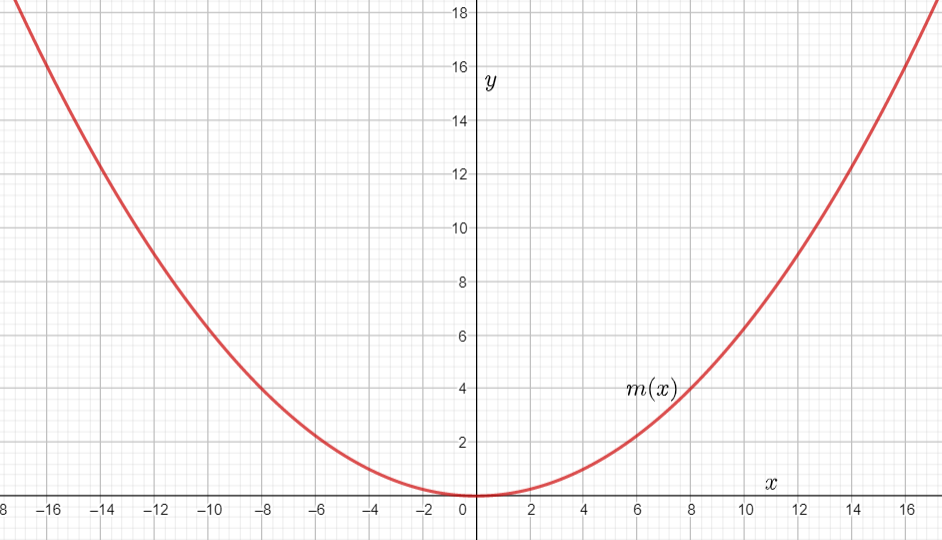
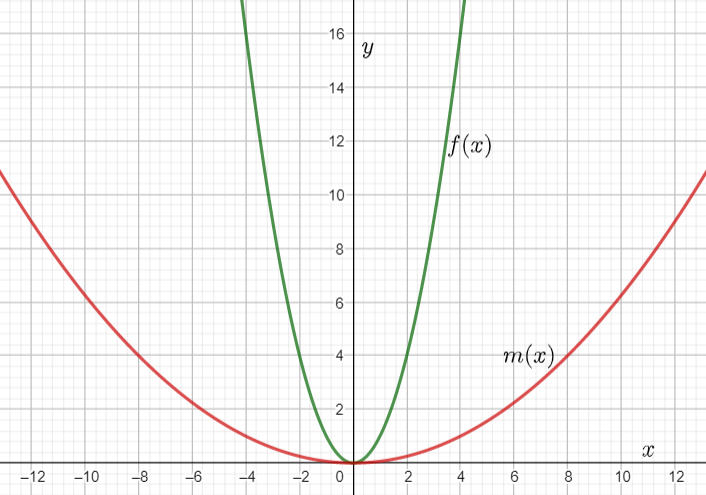
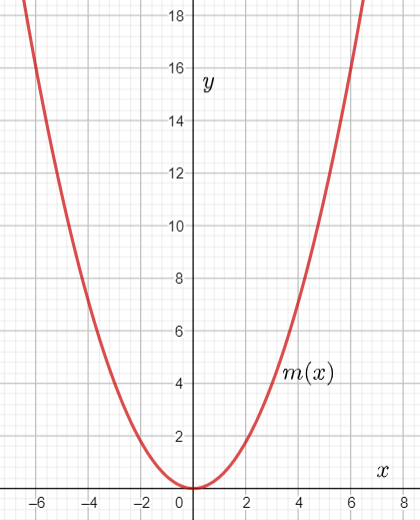
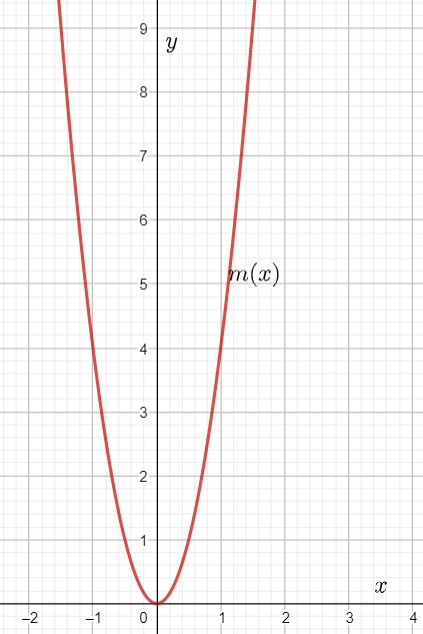
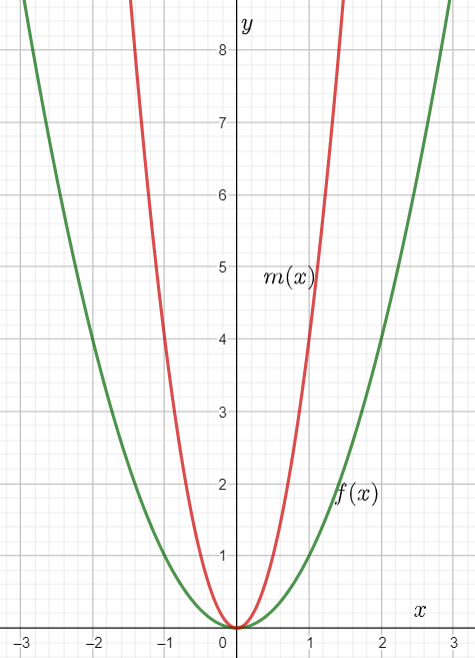
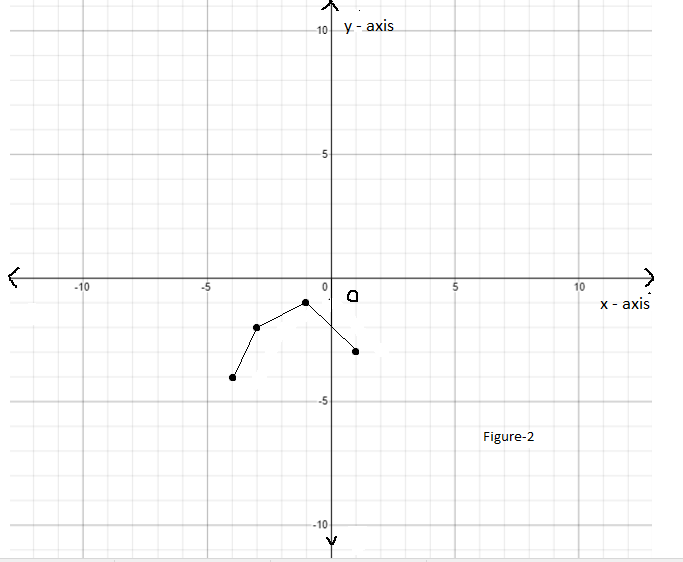
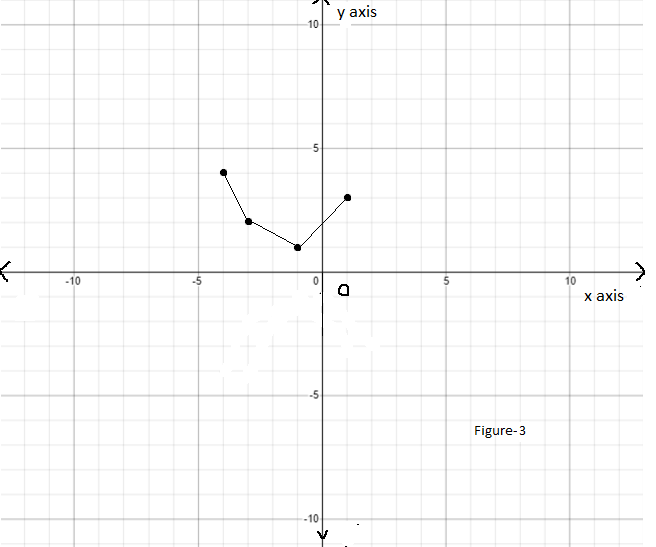
Given : The function m(x)=x⁴,n(x)=m(x)+4 and the points to plot the graph.

Our objective is to find whether the given function is even, odd, or neither.

Procedure:

Use the reference points to find the points of n(x).

Use the given points to create a table to plot the graph for each function.

Check whether the function satisfies the even function condition or odd function condition.

Finally, we came with a solution.

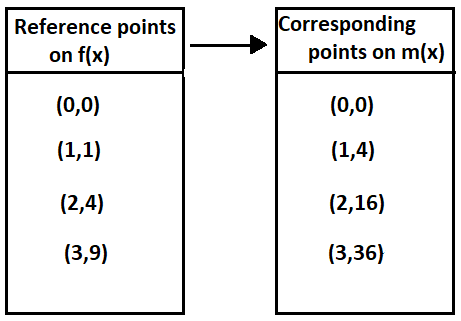
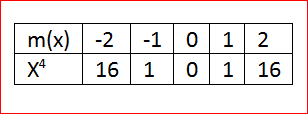
Let us create the table of values for m(x)=x4

Given the points,When x=0, we have

m(0)=0⁴

⇒0

When x=1, we have

m(1)=1⁴

⇒1

When x=2, we have

m(2)=2⁴

⇒16

By this method we can have the table of values

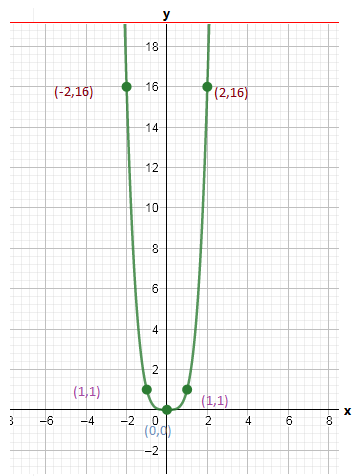
By using this table we can plot the graph as

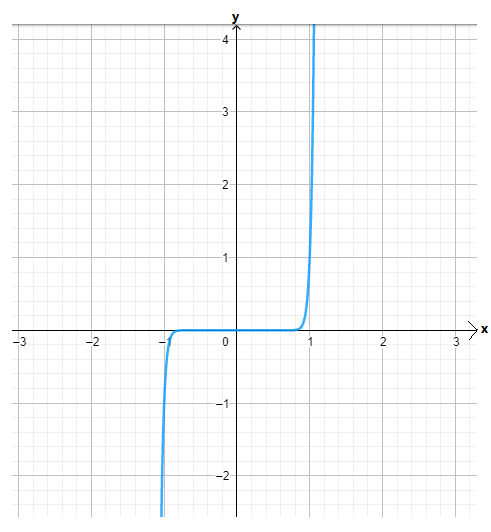
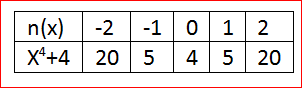
Let us create a table of values for

n(x)=m(x)+4

n(x)=x⁴+4

Whenx=0, we have

n(0)=0⁴+4

n(0)=4

When x=1, we have

n(1)=1⁴+4

n(1)=5

When x=2, we have

n(2)=2⁴+4

n(2)=20

By this method we can have the table of values

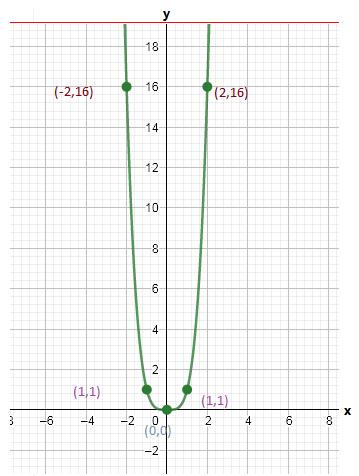
By using this points plot the graph as

Use the conditions in both the functions.

m(x)=x⁴

m(−x)=(−x)⁴

m(−x)=x⁴

This function satisfies the condition f(−x)=f(x)

so, the function m(x) is even.

n(x)=x⁴+4

n(−x)=(−x)⁴+4

n(−x)=x⁴+4

This function also satisfies the condition f(−x)=f(x)

so, the function n(x) is even.

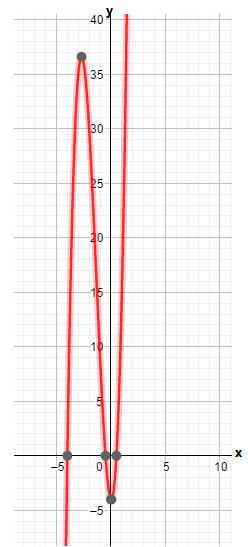
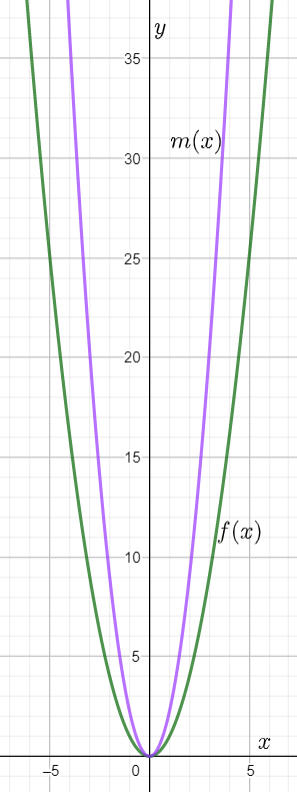
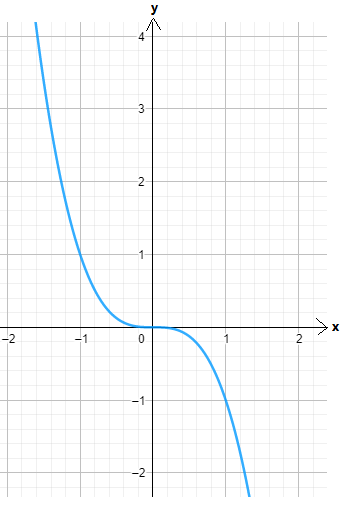
We have found that both the functions m(x) and n(x) are even because these functions satisfy the even function condition and they are symmetrical about the y−axis.

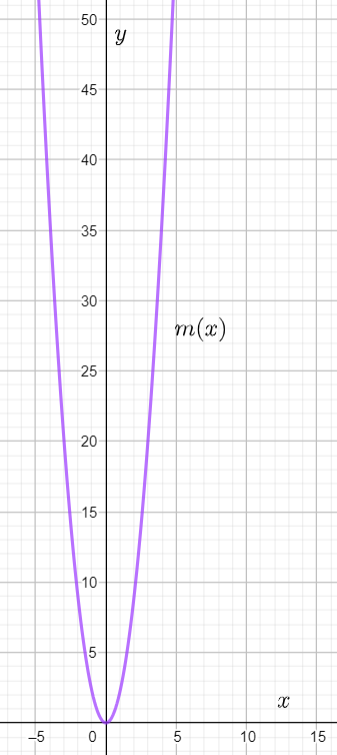
The graph of m(x)=x⁴ is

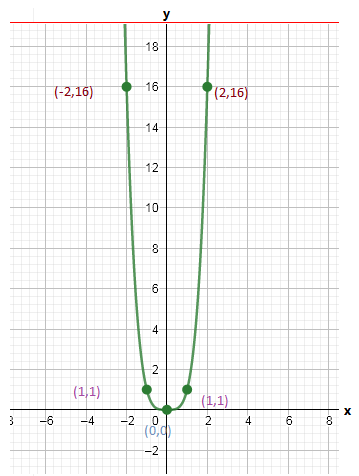
The graph of n(x)=m(x)+4 is

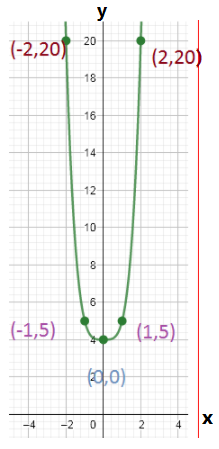
Skills Practice Carnegie Learning II Exercise 3.3 answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 330 Problem 5 Answer

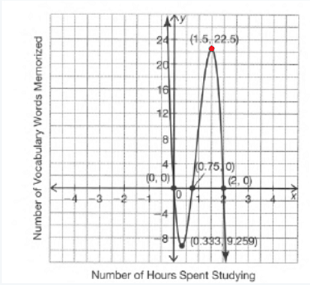
Given: The function c(x)=x³,g(x)=1/4 c(x) and the reference points to plot the graph.

Our objective is to find whether the given function is even, odd, or neither.

Procedure:

Use the reference points to find the points of g(x).

Use the given points to create a table to plot the graph for each function.

Check whether the function satisfies the even function condition or odd function condition.

Finally, we came with a solution.

Let us create the table of values forc(x)=x³

When x=0, we have

c(0)=0³

c(0)=0

When x=1, we have

c(1)=1³

c(1)=1

When x=2, we have

c(2)=2³

c(2)=8

By this way we can have the table of va

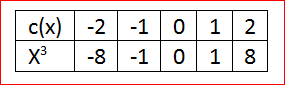
By using this table we can plot the graph as

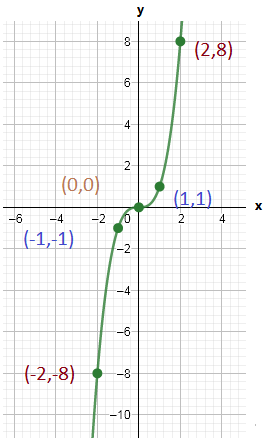
Let us create the table of values for

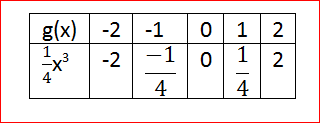
g(x)=1/4 c(x)

g(x)=1/4x³

When x=0, we have

g(0)=1/4(0)³

g(0)=1/4

Whenx=1, we have

g(1)=1/4(1)³

g(1)=1/4

Whenx=2, we have

g(2)=1/4(2)³

g(2)=2

By this way we can have the table of values

By using this table we can plot the graph as

Use the conditions in both the functions

c(x)=x³

c(−x)=(−x)³

c(−x)=−x³

This function satisfies the conditionf(−x)=−f(x)

so, the function c(x) is odd.

g(x)=1/4x³

g(−x)=1/4(−x)³

g(−x)=−1/4x³

This function satisfies the condition f(−x)=−f(x) so, the function g(x) is odd.

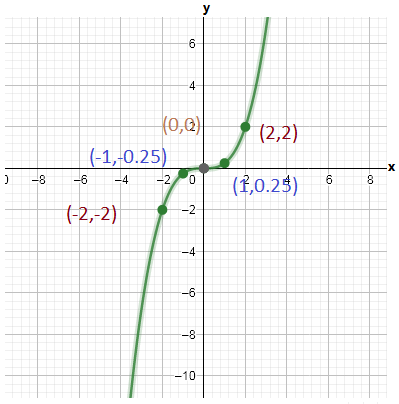
We have found that both the functions c(x) and g(x) are odd because these functions satisfy the odd function condition and they are symmetrical about the origin.

The graph of c(x)=x³ is

The graph of g(x)=1/4 c(x) is

Page 330 Problem 6 Answer

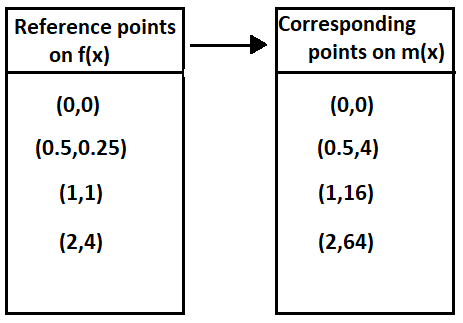
Given: The function m(x)=x⁴,p(x)=m(x−1) and the reference points to plot the graph.

Our objective is to find whether the given function is even, odd, or neither.

Procedure:

Use the reference points to find the points of p(x).

Use the given points to create a table to plot the graph for each function.

Check whether the function satisfies the even function condition or odd function condition.

Finally, we came with a solution.

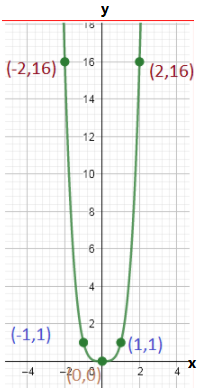
Let us create the table of values for m(x)=x⁴

When x=0,we have

m(0)=0⁴

m(0)=0

When x=1, we have

m(1)=1⁴

m(1)=1

By this way we can have the table of values

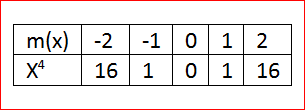
By using the table we can plot the graph as

Let us create the table of values for

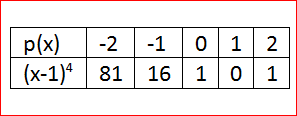
p(x)=m(x−1)

p(x)=(x−1)⁴

When x=0, we have

p(0)=(0−1)⁴

p(0)=1

Whenx=1, we have

p(1)=(1−1)⁴

p(1)=0

By this way we can have the table of values

By using the table we can plot the graph as

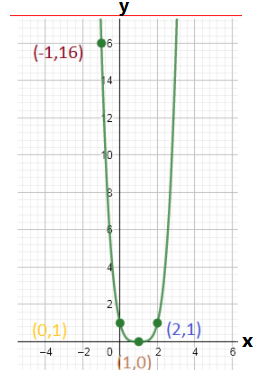
Use the condition in both the functions

m(x)=x⁴

m(−x)=(−x)⁴

m(−x)=x4

This function satisfies the condition f(−x)=f(x) so, the function is even.

p(x)=(x−1)⁴

p(−x)=(−x−1)⁴

This function does not satisfy both the conditions, hence this function is neither odd nor even.

We have found that the function m(x) is an even function and p(x) is neither odd nor even.

The graph of m(x)=x⁴ is

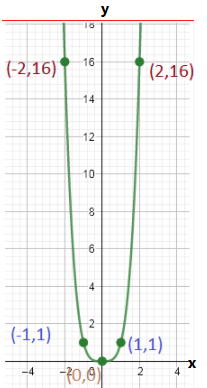
The graph of p(x)=m(x−1) is

Carnegie Learning II practice questions Chapter 3 Exercise 3.3

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 331 Problem 7 Answer

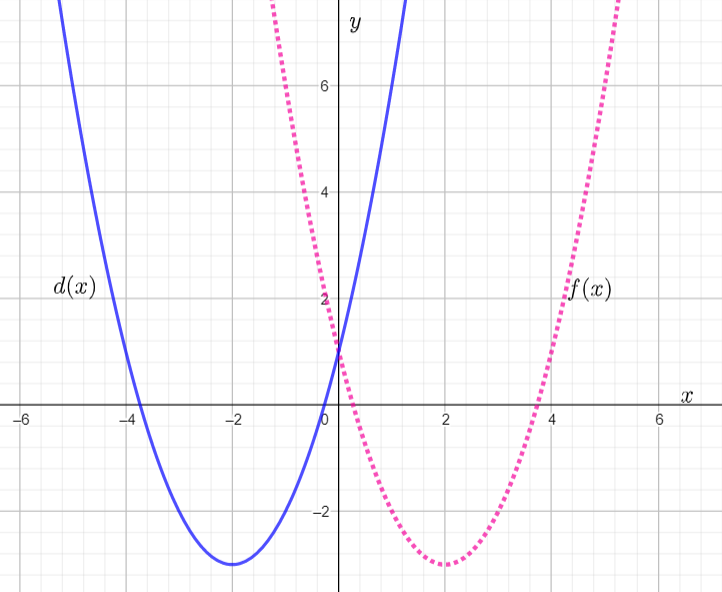
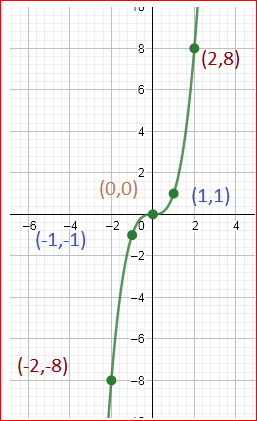
Given: The function c(x)=x³,d(x)=c(x)−3 and the reference points to plot the graph.

Our objective is to find whether the given function is even, odd, or neither.

Procedure:

Use the reference points to find the points of d(x).

Use the given points to create a table to plot the graph for each function.

Check whether the function satisfies the even function condition or odd function condition.

Finally, we came with a solution.

Let us create the table of values for c(x)=x³

Whenx=0, we have

c(0)=0³

c(0)=0

When x=1, we have

c(1)=1³

c(1)=1

By this way we can have the table of values

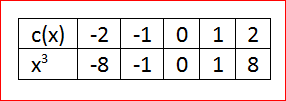
By using the table plot the graph as

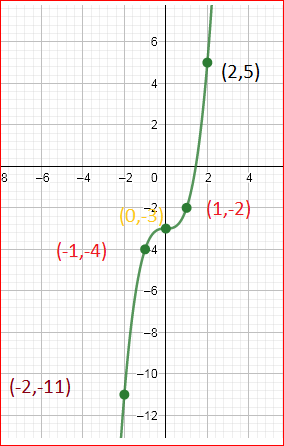
Let us create the table of values for

d(x)=c(x)−3

d(x)=x³−3

Whenx=0, we have

d(0)=0³−3

d(0)=−3

Whenx=1, we have

d(1)=1³−3

d(1)=−2

By this way we can have the table of val

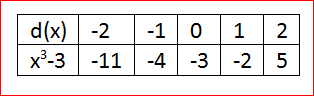
By using the table we can plot the graph as

Use the condition in both the functions

c(x)=x³

c(−x)=(−x)³

c(−x)=−x³

This function satisfy the conditionf(−x)=−f(x)

so, the function is odd.

d(x)=x³−3

d(−x)=(−x)³−3

d(−x)=−x³−3

This function does not satisfy both the conditions so, the function is neither even nor odd.

We have found that the function c(x) is an odd function because this satisfy the odd function condition and it is symmetrical about the origin and the function d(x) is neither even nor odd.

Page 331 Problem 8 Answer

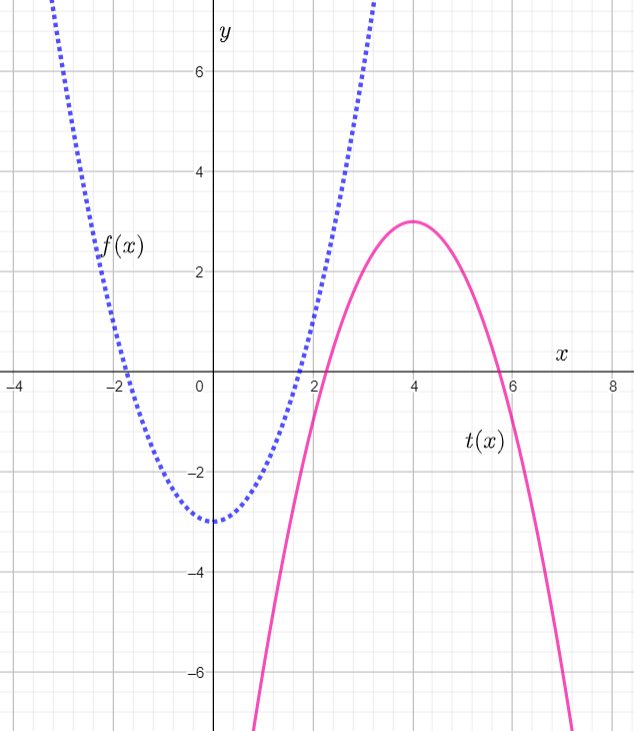
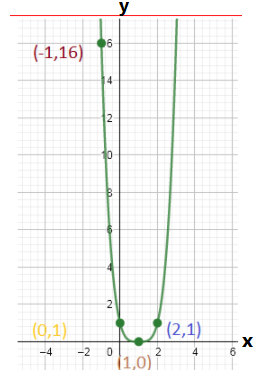
Given : The function m(x)=x⁴,t(x)=m(−2x) and the reference points to plot the graph.

Our objective is to find whether the given function is even, odd, or neither.

Procedure:

Use the reference points to find the points of.

Use the given points to create a table to plot the graph for each function.

Check whether the function satisfies the even function condition or odd function condition.

Finally, we came with a solution.

Let us create a table of values form(x)=x⁴

Whenx=0, we have

m(0)=0⁴

m(0)=0

By this way we can have the table of values as

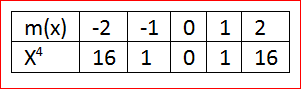
By using the table we can plot the

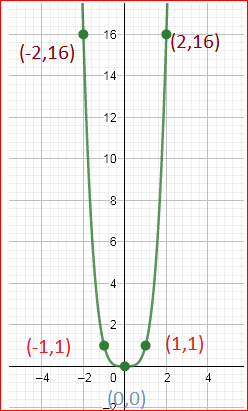
Let us create the table of values for

t(x)=m(−2x)

t(x)=(−2x)⁴

t(x)=16x⁴

When x=0, we have

t(0)=16(0)⁴

t(0)=0

By this way we can have the table of values as

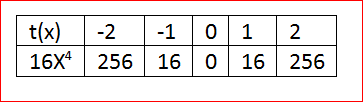
By using the table we can plot the graph as

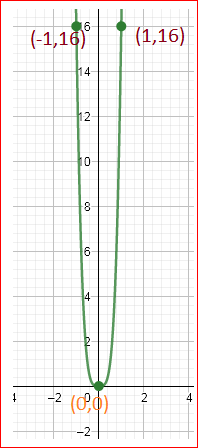
Use the condition in both the functions

m(x)=x⁴

m(−x)=(−x)⁴

m(−x)=x⁴

This function satisfy the condition f(−x)=f(x) hence this function is even.

t(x)=16x⁴

t(−x)=16(−x)⁴

t(−x)=16x⁴

This function satisfy the conditionf(−x)=f(x) hence this function is even.

We have found that both the functions are even because they satisfy the even function condition and they are symmetrical to y−axis.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 332 Problem 9 Answer

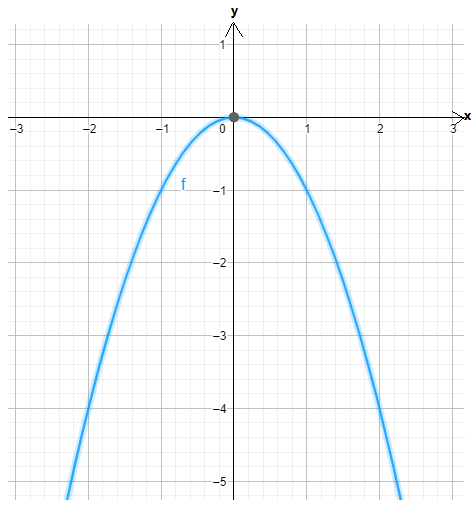
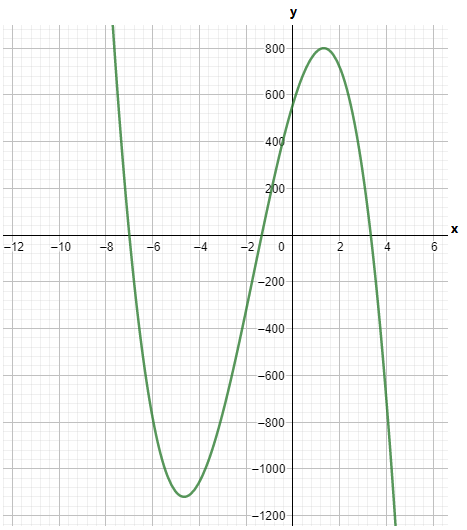
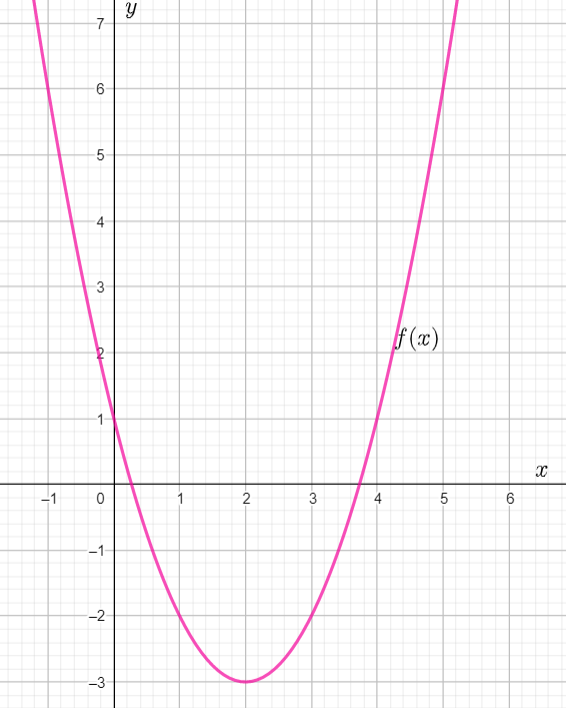
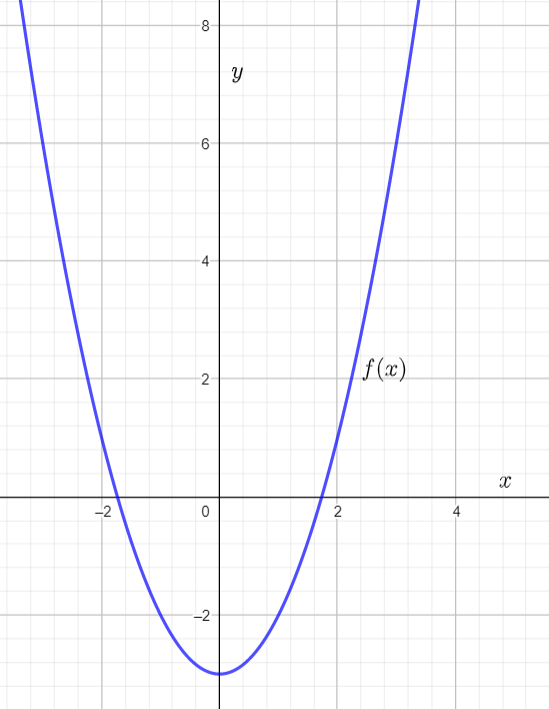
It is given the graphs of the functions g(x) and f(x). It is asked to write the function g(x) in terms of f(x).

First, observe that the function g(x) is obtained by reflecting the function f(x) about they−axis followed by a translation in the upward direction by 2 units.

Now, if the function is reflected along the y axis then the resulting function will be y=−f(x).

Now, take a translation of 2units in the upward direction.

Then the resulting function will be y=−f(x)+2.

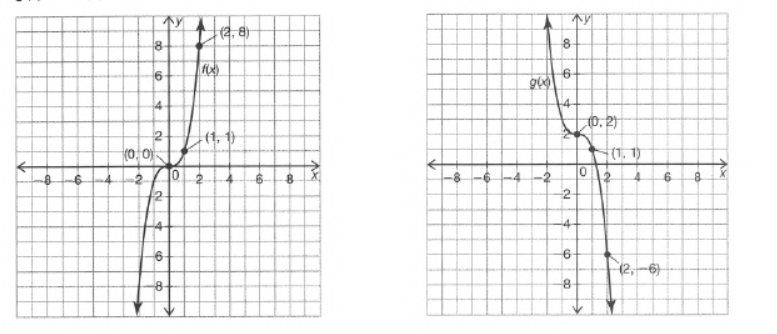
So, to write the function g(x) in the term of the function f(x) will be g(x)=−f(x)+2.

If the function g(x) is written by the function f(x) then that will be g(x)=−f(x)+2.

Page 332 Problem 10 Answer

It is given the graphs of the function f(x) and g(x). It is asked to find the graph of the function g(x) in terms of f(x).

First, observe that to obtain the graph of the function g(x),f(x) is shifted 3 units at the right.

So, to obtain the function of g(x) add 3 units with the function f(x).

So, g(x)=f(x)+3.

The function g(x) can be written in terms of f(x) as g(x)=f(x)+3.

Page 333 Problem 11 Answer

It is given the graphs of the function f(x) and g(x). It is asked to write the function g(x) in terms of f(x) .

First, observe that the function is inverted with respect axis to obtain the function.

Now, if is inverted with respect to axis then the resultant function will be.

Now, the resultant function is shifted unit in the negative direction of axis.

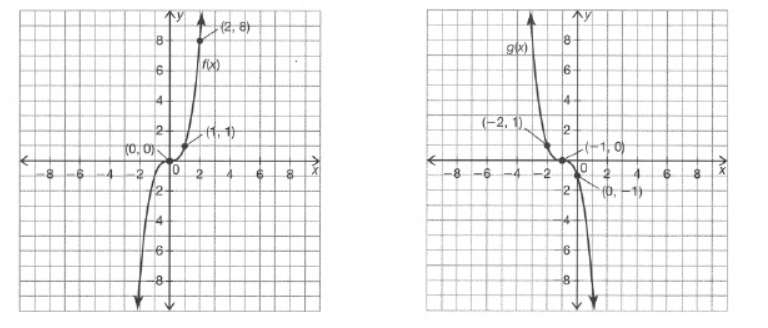
So, the resultant function will be.

So, the function for will be.

The graph of the function g(x) can be represented by the function f(x) as g(x)=−f(x+1).

Chapter 3 Exercise 3.3 Carnegie Learning II key

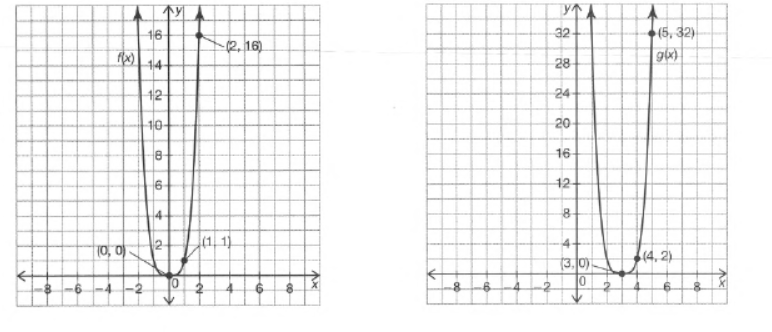
Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 333 Problem 12 Answer

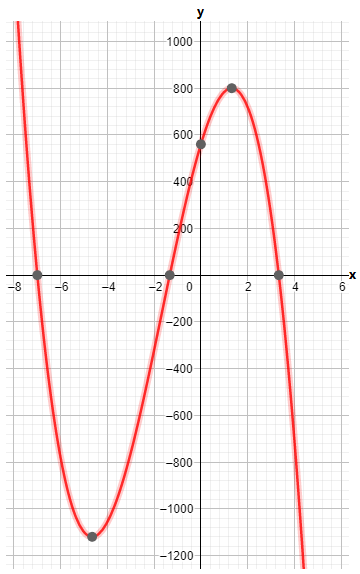
It is given the graph of the functions f(x) and g(x). It is asked to write the function g(x) in terms of f(x).

First, observe that the function g(x) is obtained by shifting and inverting the function f(x).

Now, consider that the function is shifted a units and magnified by b units.

So, the resulting function g(x) will be g(x)=bf(x+a).

Now, from the graph of the function f(x) we have

f(0)=0, f(2)=1⁶.

From the given graph of g(x), we have g(0)=−8, g(−2)=0 and g(−1)=−1/2.

The function of g(x) is g(x)=bf(x+a) ……. (1)

Substitutex=−2in (1).

g(−2)=bf(−2+a)

0=bf(−2+a)

Now, observe thatb≠0 otherwise, an absurd situation will arise.

So, f(a−2)=0

f(a−2)=f(0)

a−2=0

a=2

So, g(x)=f(x+2) …… (2)

Now, substitute x=0 in (2).

g(0)=bf(2)

−8=b16

b=−8/16

b=−1/2

So, the function g(x) will be g(x)=−1/2 f(x+2).

The function g(x) can be written in the term of the function f(x) as g(x)=−1/2f(x+2).

Page 334 Problem 13 Answer

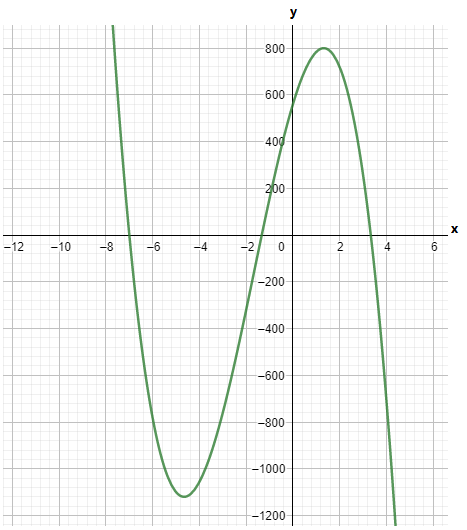
It is given the graph of the functions f(x) and g(x).

It is asked to write the function g(x) in terms of f(x).

First, observe that the function g(x) is obtained by shifting up along the yaxis followed by a magnification.

Consider that the function f(x) is shifted up along y axis at a unit a and the function f(x) is magnified at a unit b

Consider that the function of g(x) in terms of f(x) is as follows:

g(x)=f(x−1)+3

An equation for g(x) in terms of f(x)  is g(x)=f(x−1)+3.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 334 Problem 14 Answer

It is given the graph of the functions f(x) and g(x). It is asked to express the function g(x) in terms of f(x).

First, observe that the function g(x) is obtained by magnifying the function f(x) followed by the translation.

Consider that to obtain the function g(x)  the function f(x) is magnified by b units and translated by a units.

Then the function g(x) will be g(x)=bf(x)+a.

Now, observing the graph of a function f(x)

we get f(0)=−10, f(1)=−9, f(2)=5⁴.

Consider, the function g(x)=bf(x)+a …… (1)

Substitute x=0 in equation (1).

g(0)=bf(0)+a

−24=b(−10)+a

a−10b=−24…… (2)

Substitute x=1 in the equation (1).

g(1)=bf(1)+a

−22=b(−9)+a

a−9b=−22……(3)

Solve the equation(2) and(3) .

10b−9b=24−22

b=2

Now, substitute the value of b=2 in equation (3).

a=−22+9×(2)

a=−4

So, the function g(x) will be g(x)=2f(x)−4.

The function g(x) can be expressed by the function f(x) as g(x)=2f(x)−4.

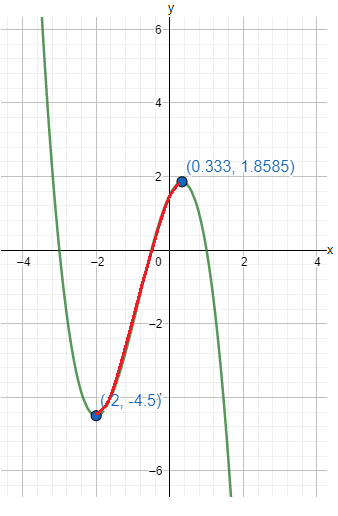
Page 335 Problem 15 Answer

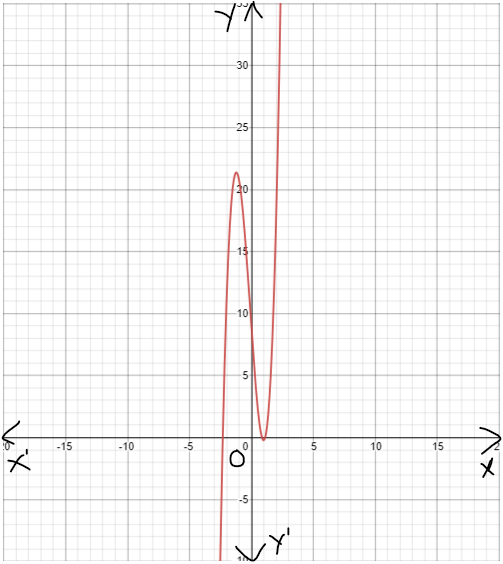
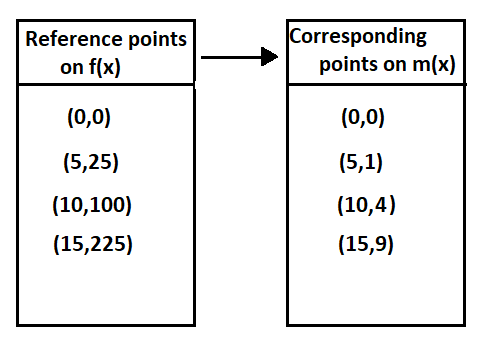
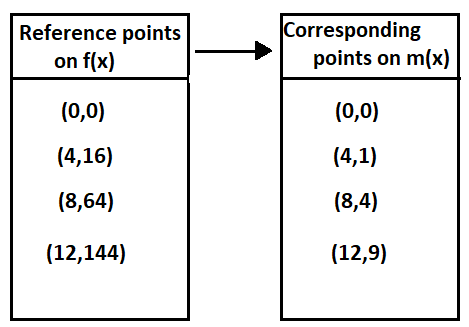
Given:  The functions

p(x)=x⁴

m(x)=−p(0.5x)+2

Our objective is to find the specific equation form(x)

Procedure:

Explain the transformed function using the form in the tip.

Find the value of p(0.5x). Now, find the specific equation of m(x).

The given function is p(x)=x⁴ and the transformed function ism(x)=−p(0.5x)+2

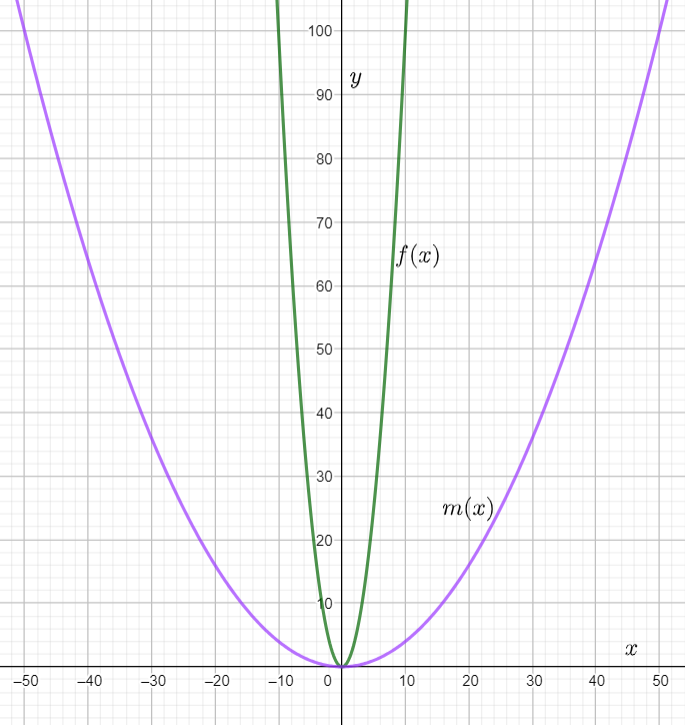
The graph of both the functions is

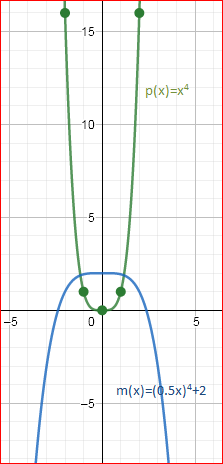
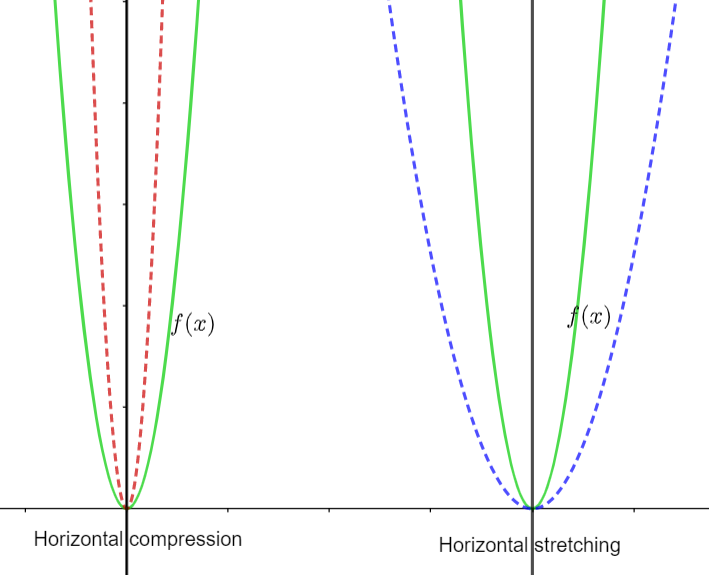
From the above graph we can conclude that the graph is horizontally stretched by a factor 2, translated two units up and reflected about the line y=2

The reflection of a function causes the graph to appear as a mirror image of the original function. That is f(−x) is a reflection of f(x) across the y−axis.

Finding the equation of m(x)

p(x)=x⁴

p(0.5x)=p(0.5x)⁴

p(0.5x)=0.0625x⁴

m(x)=−p(0.5x)+2

m(x)=−0.0625x⁴+2

We have found the specific equation of m(x) as−0.0625x⁴+2.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 335 Problem 16 Answer

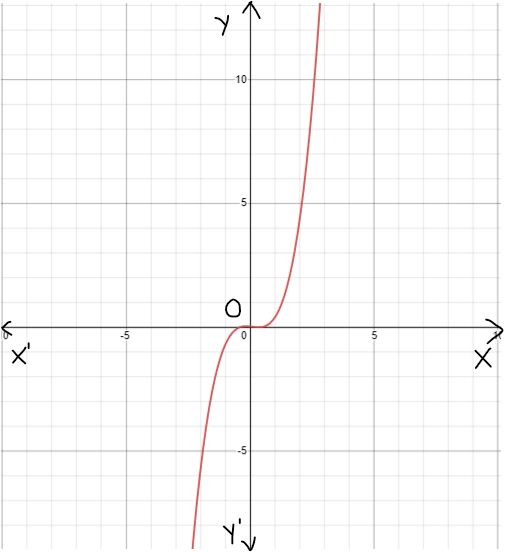
Given: The functions

p(x)=x³

m(x)=4p(x−3)−5

Our objective is to find the specific equation of m(x).

Procedure:

Explain the transformed function using the form in the tip.

Find the value of 4p(x−3). Now, find the specific equation of m(x).

The given function is p(x)=x³ and the transformed function is m(x)=4p(x−3)−5

The graph of both the functions is

From the above graph we can conclude that the graph is vertically shifted downwards by 5 units, the graph is vertically stretched by a factor of 4 units and the graph is horizontally shifted to the right by 3 units.

Finding the equation of m(x)

p(x)=x³

4p(x−3)=4p(x−3)³

m(x)=4p(x−3)−5

m(x)=4(x−3)³−5

We have found the specific equation of m(x) as 4(x−3)³−5.

Page 335 Problem 17 Answer

Given : The functions

p(x)=x⁵

m(x)=0.5p(−x)+4

Our objective is to find the specific equation of m(x)

Procedure:

Explain the transformed function using the form in the tip.Find the value of p(−x).Now, find the specific equation of m(x).

The given function is p(x)=x⁵ and the transformed function ism(x)=0.5p(−x)+4

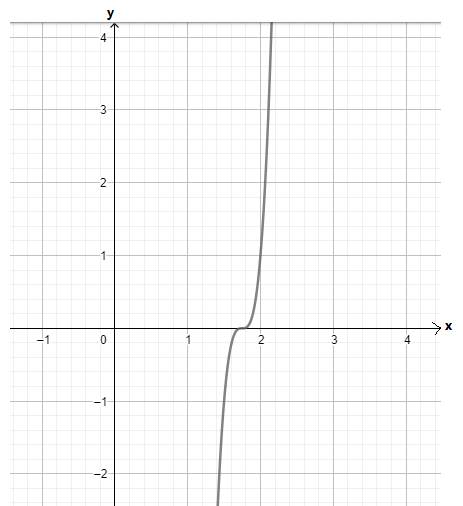
The graph of both the functions is

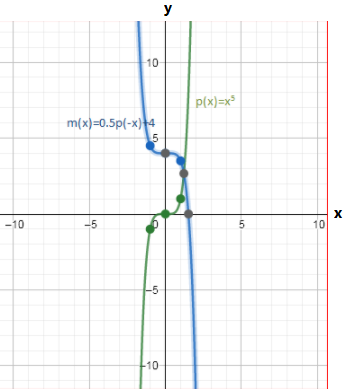
From the above graph we can conclude that the graph is vertically shifted upwards by 4 units and the graph is vertically stretched by the factor of 0.5 units.

Finding the equation of m(x)

p(x)=x⁵

p(−x)=(−x)⁵

m(x)=0.5p(−x)+4

m(x)=−0.5x⁵+4

We have found the specific equation of m(x) as−0.5x⁵+4.

The graph of p(x)=x⁵ and m(x)=0.5p(−x)+4 is shown below

How to solve Chapter 3 Exercise 3.3 II Carnegie Learning

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 336 Problem 18 Answer

Given: The functions

p(x)=x³

m(x)=−p(x+5)

Our objective is to find the specific equation ofm(x)

Procedure:

Explain the transformed function using the form in the tip.Find the value of−p(x+5).Now, find the specific equation of m(x).

The given function is p(x)=x³ and the transformed function ism(x)=−p(x+5)

The graph of both the functions are

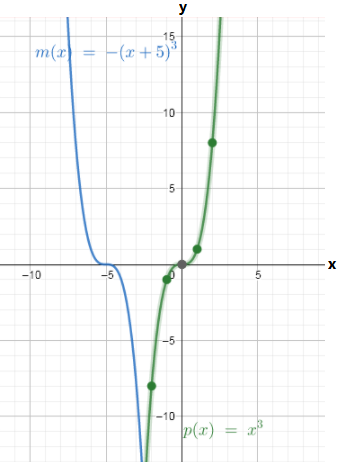
From the above graph we conclude that the graph is reflected about the line and the graph is horizontally shifted to the left by 5 units.

p(x)=x³

p(x+5)=(x+5)³

m(x)=−p(x+5)

m(x)=−(x+5)³

We have found the specific equation of m(x) as−(x+5)³.

The graph of p(x)=x³ and m(x)=−p(x+5) is shown below

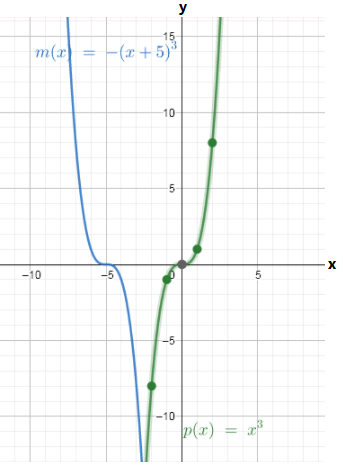
Page 336 Problem 19 Answer

Given: The functions

p(x)=x⁴

m(x)=2p(−x−2)

Our objective is to find the specific equation of m(x)

Procedure:

Explain the transformed function using the form in the tip.Find the value of p(−x−2).Now, find the specific equation of m(x).

The given function is p(x)=x⁴ and the transformed function ism(x)=2p(−x−2)

The graph of both the functions are

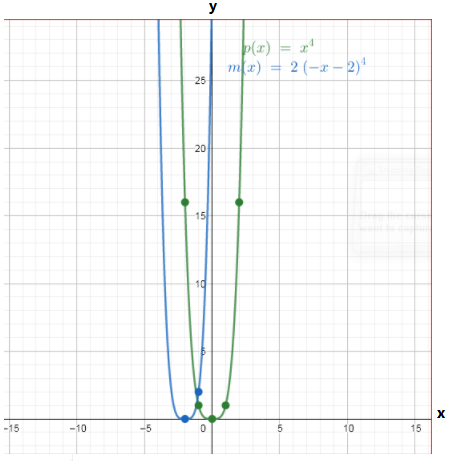
From the above graph we can conclude that is vertically stretched by a factor of 2 units and the graph is horizontally shifted to the right by the factor of 2 units

p(x)=x⁴

p(−x−2)=(−x−2)⁴

m(x)=2p(−x−2)

m(x)=2(−x−2)⁴

We have found the specific equation of m(x) as 2(−x−2)⁴.

The graph of p(x)=x⁴ and m(x)=2p(−x−2) is shown below

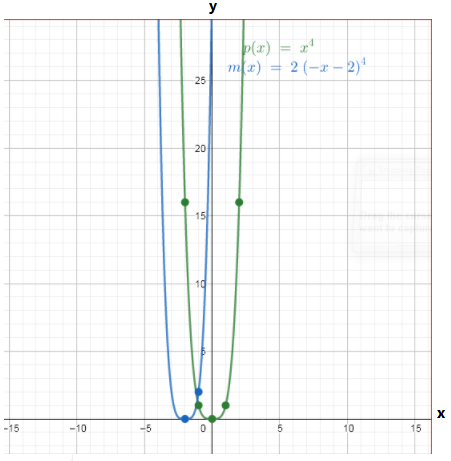
Page 336 Problem 20 Answer

Given: The functions

p(x)=x⁵

m(x)=p(x+4)−1

Our objective is to find the specific equation of m(x)

Procedure:

Explain the transformed function using the form in the tip.

Find the value of p(x+4). Now, find the specific equation of m(x).

The given function is p(x)=x⁵ and the transformed function ism(x)=p(x+4)−1

The graph of both the functions are

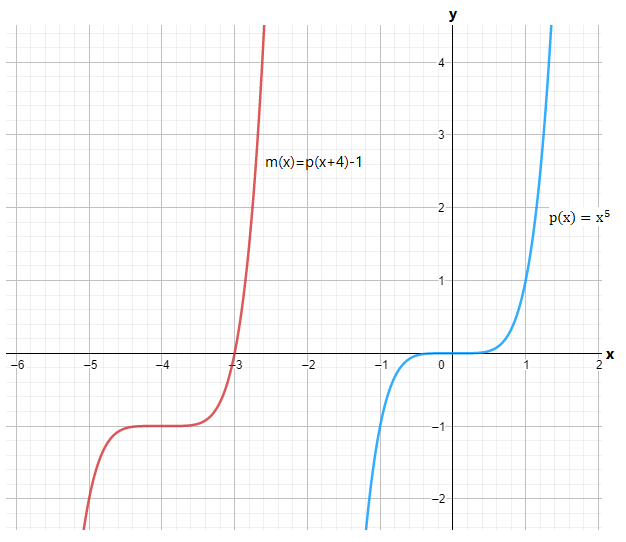
From the above graph we can conclude that the graph is horizontally shifted to the left by 4 units and the graph is vertically shifted downwards by 1 unit.

p(x)=x⁵

p(x+4)=(x+4)⁵

m(x)=p(x+4)−1

m(x)=(x+4)⁵−1

We have found that the specific equation of m(x) as(x+4) is ⁵−1.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 337 Problem 21 Answer

Given :

The functions

f(x)=x

g(x)=x²

h(x)=x³

j(x)=x⁴

k(x)=x⁵

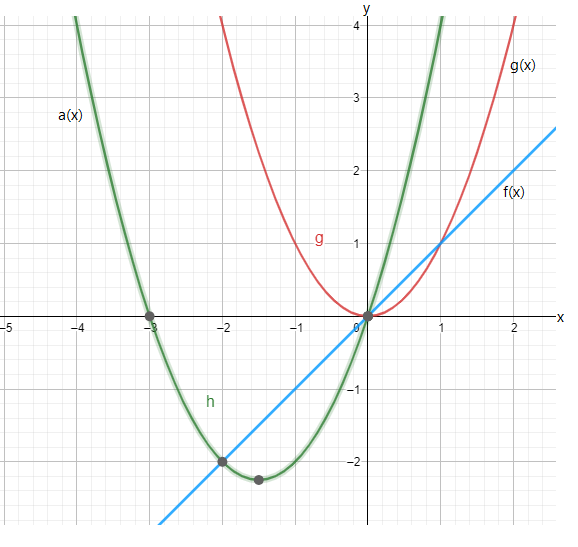
Our objective is to find the specific equation of a(x)=g(x)+3f(x)

Procedure:

Create the table with the values given in the function a(x).

Sub the values in the function a(x).

Plot the graph using the table values.

From the given equationa(x)=g(x)+3f(x)

Create the table values using the function g(x) and f(x)

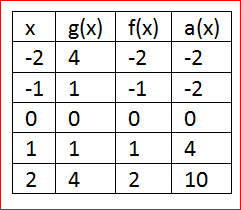
Sub the values of the function g(x) and f(x) in a(x)

a(x)=g(x)+3f(x)

a(x)=x²+3x

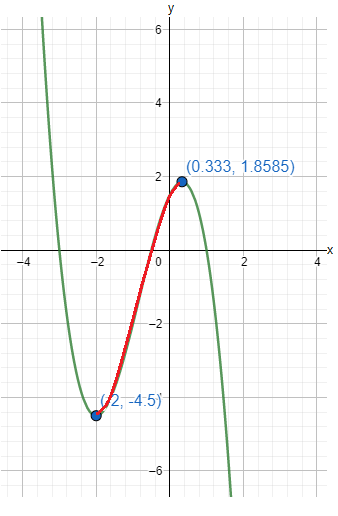
The graph which shows the given functions as follows

We have found the specific equation fora(x)=x²+3x.

The graph is shown below

Page 337 Problem 22 Answer

Given:  The functions

f(x)=x

g(x)=x²

h(x)=x³

j(x)=x⁴

k(x)=x⁵

Our objective is to find the specific equation of a(x)=0.5j(x)−g(x)

Procedure:

Create the table with the values given in the function a(x).

Sub the values in the function a(x).

Plot the graph using the table values.

From the given equation a(x)=0.5j(x)−g(x)

Create the table values using the function j(x) and g(x)

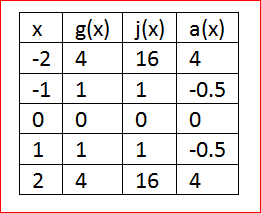
Sub the values of the function j(x) and g(x) ina(x)

a(x)=0.5j(x)−g(x)

a(x)=0.5x⁴−x²

The graph which shows the given functions as follows

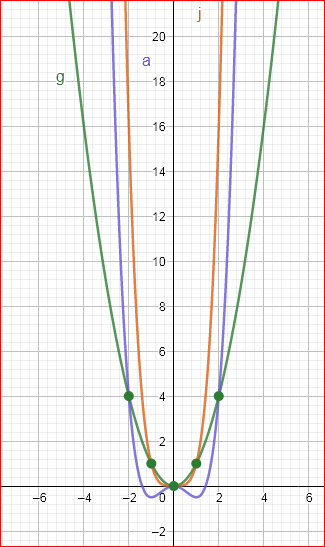
We have found the specific equation fora(x)=0.5x⁴−x².

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 338 Problem 23 Answer

Given : The functions

f(x)=x

g(x)=x²

h(x)=x³

j(x)=x⁴

k(x)=x⁵

Our objective is to find the specific equation a(x)=k(x)+2j(x)−h(x)

Procedure:

Create the table with the values given in the function a(x).

Sub the values in the function a(x).

Plot the graph using the table values.

From the given equation a(x)=k(x)+2j(x)−h(x)

Create the table values using the function k(x),j(x) and h(x)

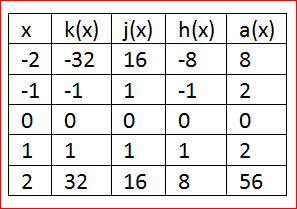
Sub the values of the function k(x),j(x) and h(x) in a(x)

a(x)=k(x)+2j(x)−h(x)

a(x)=x⁵+2x⁴−x³

The graph which shows the given functions as follows

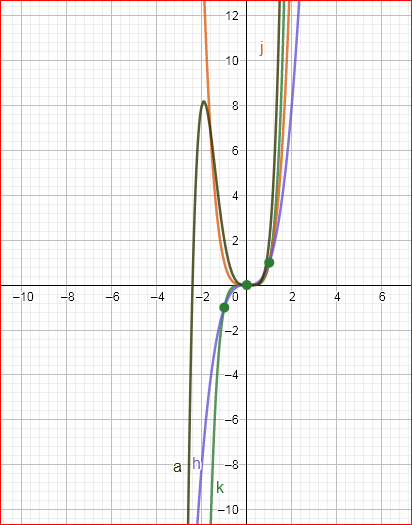
We have found the specific equation fora(x)=x⁵+2x⁴−x³.

Page 338 Problem 24 Answer

Given: The functions

f(x)=x

g(x)=x²

h(x)=x³

j(x)=x⁴

k(x)=x⁵

Our objective is to find the specific equation a(x)=−h(x)+5g(x)+4

Procedure:

Create the table with the values given in the function a(x).

Sub the values in the function a(x).

Plot the graph using the table values.

From the given equation a(x)=−h(x)+5g(x)+4

Create the table values using the function h(x) and g(x)

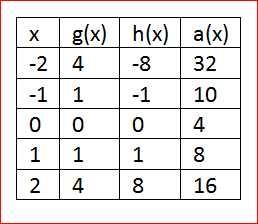
Sub the values of the function g(x) and h(x) in a(x)

a(x)=−h(x)+5g(x)+4

a(x)=−x³+5x²+4

The graph which shows the given functions as follows

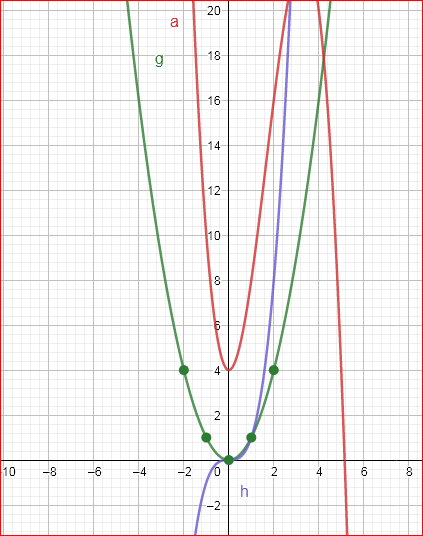
We have found the specific equation fora(x)=−x³+5x²+4.

Carnegie Learning II answer key Chapter 3 Exercise 3.3

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.3 Skills Practice Page 339 Problem 25 Answer

Given :

The functions

f(x)=x

g(x)=x²

h(x)=x³

j(x)=x⁴

k(x)=x⁵

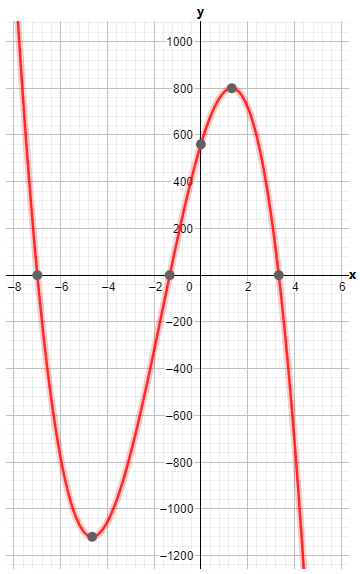
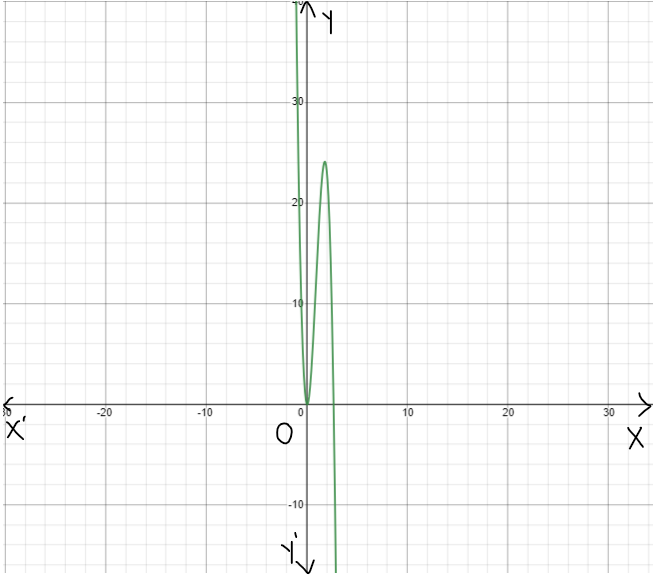
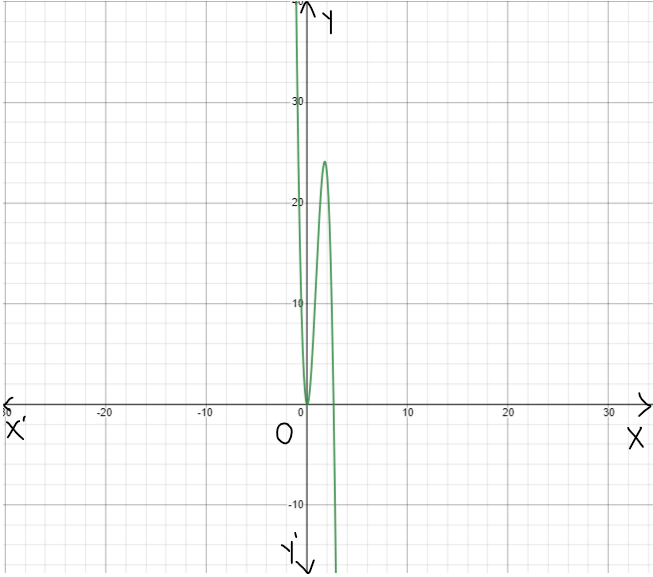
Our objective is to find the specific equation of a(x)=j(x)−0.5h(x)−6g(x)+f(x)

Procedure:

Create the table with the values given in the function a(x).

Sub the values in the function a(x). Plot the graph using the table values.

From the given equationa(x)=j(x)−0.5h(x)−6g(x)+f(x)

Create the table values using the function j(x),h(x),g(x) and f(x)

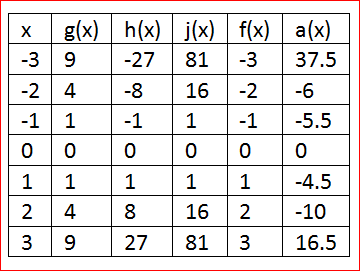
Sub the values of the function j(x),h(x),g(x) and f(x) in a(x)

a(x)=j(x)−0.5h(x)−6g(x)+f(x)

a(x)=x⁴−0.5x³−6x²+x

The graph which shows the given functions as follows

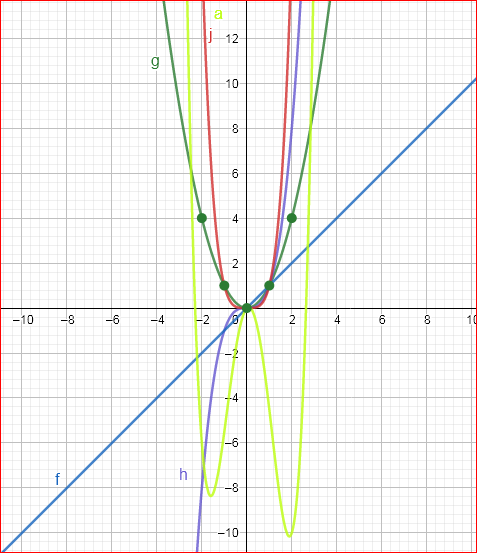
We have found the specific equation fora(x)=x⁴−0.5x³−6x²+x.

Page 339 Problem 26 Answer

Given:

The functions

f(x)=x

g(x)=x²

h(x)=x³

j(x)=x⁴

k(x)=x⁵

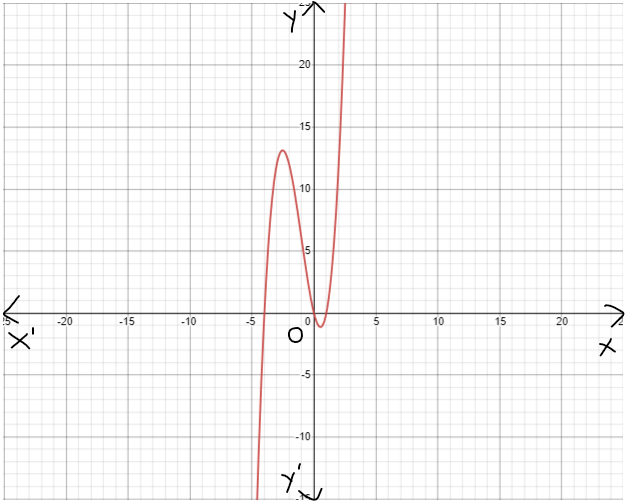
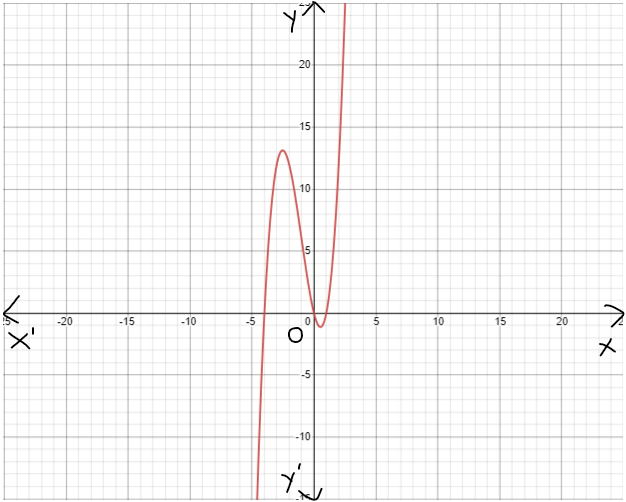
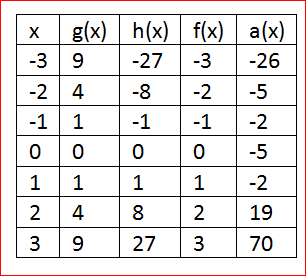
Our objective is to find the specific equation of a(x)=2h(x)+3g(x)−2f(x)−5

Procedure:

Create the table with the values given in the function a(x).Sub the values in the function a(x).

Plot the graph using the table values.

From the given equation a(x)=2h(x)+3g(x)−2f(x)−5

Create the table values using the functions h(x),g(x) and f(x)

Sub the values of the function h(x),g(x) and f(x) in a(x)

a(x)=2h(x)+3g(x)−2f(x)−5

a(x)=2x³+3x²−2x−5

The graph which shows the given functions as follows

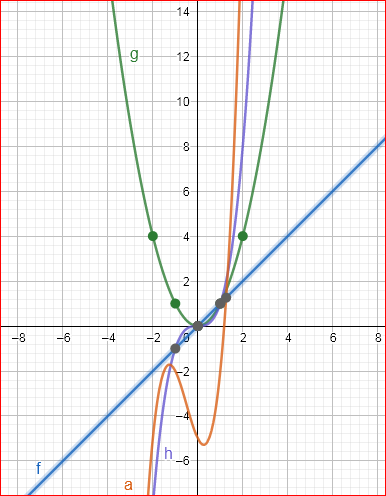
We have found the specific equation fora(x)=2x³+3x²−2x−5.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Skills Practice

Page 323 Problem 1 Answer

It is given a graph of a function that is divided into two identical parts by a line. It is asked to identify the type of the function.

If a line divides a function then there will be two parts of the function. Now, if the two parts are identical then the function will be an even function.

So, the correct option will be even function.

Power Function is of type f(x)=axb

and if a line divides the function into two parts then those two parts are not identical.

So, the power function is an incorrect option.

A function is said to be odd if for all x, f(−x)=−f(x)

and for this function also there is no line that divides the function into two identical parts.

So, the odd function is also an incorrect option.

If a function is divided by a line into two identical parts then the function may not be symmetrical about a line or a point and also may not have end behaviour.

So, end behaviour, symmetric about a point and line are the incorrect options.

If a line divides a function into two identical parts then the function is an even function.

Carnegie Learning Algebra II Chapter 3 Exercise 3.2 solutions

Page 323 Problem 2 Answer

Given: A statement to fill up with various options.

To find: Correct choice of option.

The correct choice of option in this case will be ‘odd function’ as the given case relates to the nature of odd function.

Hence, the ‘odd function’ the word to be substituted in blank space.

Page 323 Problem 3 Answer

Given: A statement to fill up with various options.

To find: Correct choice of option.

The correct choice of option in this case will be ‘symmetric about a point’ as the suitable option relating to central point was this.

Hence, the ‘symmetric about a point’ the word to be substituted in blank space.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills Practice Page 323 Problem 4 Answer

Given: A statement to fill up with various options.

To find: Correct choice of option.

The correct choice of option in this case will be ‘even function’ as the given case relates to the nature of even function.

Hence, the ‘even function’ the word to be substituted in blank space.

Page 323 Problem 5 Answer

Given: A statement to fill up with various options. function of form P(x)=axn

To find: Correct choice of option.

The correct choice of option in this case will be ‘power function’ as the given function in the statement represents the general from of power function.

Hence, the ‘even function’ the word to be substituted in blank space.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills PracticePage 324 Problem 6 Answer

Given: A function f(x)=x⁴

To find: Sketch its graph and describe end behaviour.

Sketch graph of the given function f(x)=x⁴ is

Using the graph for the given function we can state that the nature of end behaviour will be as

For x→∞ then,f(x)→∞

Similarly for x→−∞ then,f(x)→∞

Both sides the function is going to positive infinity as the given function is even function.

The graph for the given function is sketched below and the function is an even function with end behavior approaching infinity.

Page 324 Problem 7 Answer

Given: A function f(x)=x³

To find: Sketch its graph and describe end behaviour.

Graph of the given function f(x)=x³ is

Using the graph for the given function we can state that the nature of end behaviour will be as

For x→∞ thenf(x)→∞

And x→−∞ thenf(x)→−∞

This function is due to odd function nature of the graph.

Hence, the graph for the given function was sketched  below and the function is an odd function with end behavior approaching to positive and negative infinity for the respective values of x.

Skills Practice Carnegie Learning Algebra II Exercise 3.2 answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills Practice Page 324 Problem 8 Answer

Given: A function f(x)=x²⁰

To find: Sketch its graph and describe end behaviour.

Graph of the given function is,

Using the graph for the given function we can state that the nature of end behaviour will be as

For x→∞ thenf(x)→∞

Similarly for x→−∞ thenf(x)→∞

Both sides the function is going to positive infinity as the given function is even function.

The graph for the given function is sketched below and the function is an even function with end behavior approaching infinity.

Page 324 Problem 9 Answer

Given: A function f(x)=x²⁵

To find: Sketch its graph and describe end behaviour.

Graph of the given function is,

Using the graph for the given function we can state that the nature of end behaviour will be as

For x→∞ thenf(x)→∞ and x→−∞ thenf(x)→−∞

This function is odd function due to its nature of the graph.

Hence, the graph for the given function is sketched below and the function is an odd function with end behavior approaching to positive and negative infinity for the respective values of x.

Carnegie Learning Algebra II practice questions Chapter 3 Exercise 3.2

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills Practice Page 324 Problem 10 Answer

Given: A function f(x)=−x5

To find: Sketch its graph and describe end behaviour.

Graph of the given function is,

Using the graph for the given function we can state that the nature of end behaviour will be as

For x→∞ thenf(x)→−∞ and x→−∞ thenf(x)→∞

This function is odd function due to its nature of the graph.

Hence, the graph for the given function was sketched and the function is odd function with end behaviour approaching to positive and negative infinity for opposite value of x.

Page 324 Problem 11 Answer

Given: A function f(x)=−x²

To find: Sketch its graph and describe end behaviour.

Graph of the given function is,

Using the graph for the given function we can state that the nature of end behaviour will be as

For x→∞ thenf(x)→−∞

Similarly for x→−∞ thenf(x)→−∞

Both sides the function is going to negative infinity as the given function is even function.

The graph for the given function is sketched below and the function is an even function with end behavior approaching negative infinity.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills Practice Page 325 Problem 12 Answer

Given: A graph of some function.To find: Nature of the graph as odd, even or none.

The given graph function is represnting behaviour of approaching positive infinity for value of largex to be positive, while its again to positive infinity for the negative large value of x.

Also the function is symmetrical to the y-axis.

So, all these points lead to the conclusion that the given function is even function.

Hence, the given function is odd function as it is symmetrical to y-axis.

Page 325 Problem 13 Answer

Given: A graph of some function.To find: Nature of the graph as odd, even or none.

The given graph function is represnting behaviour of approaching positive infinity for value of largex

to be positive, while its negative infinity for the large negative value of x.

But, the function is neither symmetric to y-axis nor to the origin point.

So, all the reasonings lead to the conclusion that the given function is neither odd nor even function

Hence, the given function is neither odd nor even function.

How to solve Chapter 3 Exercise 3.2 Algebra II Carnegie Learning

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills Practice Page 325 Problem 14 Answer

Given: A graph of some function.To find: Nature of the graph as odd, even or none.

The given graph function is represnting behaviour of approaching negative infinity for value of largex

to be positive, while its again to negative infinity for the negative large value of x.

But, the function is neither symmetric to y-axis nor to the origin point.

So, all the reasonings lead to the conclusion that the given function is neither odd nor even function.

Hence, the given function is neither odd nor even function.

Page 325 Problem 15 Answer

Given: A graph of some function.To find: Nature of the graph as odd, even or none.

The given graph function is represnting behaviour of approaching positive infinity for value of large x to be positive, while its again to positive infinity for the negative large value of x.Also the function is symmetrical to the y-axis.

So, all these points lead to the conclusion that the given function is even function.

Hence, the given function is odd function as it is symmetrical to y-axis.

Page 326 Problem 16 Answer

Given: Function f(x)=x³−4x+3.To find: Nature of the function as odd, even or none.

Replacing the valuex=−x

f(−x)=(−x)³−4x+3

f(−x)=−x³+4x+3

Also finding the value of−f(x)

−f(x)=−(x³−4x+3)

−f(x)=−x³+4x−3

So, we can say that f(−x)≠−f(x)

The given function is neither odd nor even function.

Hence, solving for the given condition algebraically, we conclude that the given function is neither odd nor even function.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills Practice Page 326 Problem 17 Answer

Given: Function f(x)=5x²+13.

To find: Nature of the function as odd, even or none.

Replacing the valuex=−x

f(−x)=5(−x)²+13

f(−x)=5x²+13

So, we can say that f(−x)=f(x)

The given function is an even function.

Hence, solving for the given condition algebraically, we conclude that the given function is an even function.

Page 327 Problem 18 Answer

Given: Function.f(x)=3x⁵−x

To find: Nature of the function as odd, even or none.

Replacing the valuex=−x

f(−x)=3(−x)⁵−(−x)

f(−x)=−3x⁵+x

Also finding the value of−f(x)

−f(x)=−(3x⁵−x)

−f(x)=−3x⁵+x

So, we can say that f(−x)=−f(x)

The given function is an odd function

Hence, solving for the given condition algebraically, we conclude that the given function is an odd function.

Carnegie Learning Algebra II Student Skills Practice Exercise 3.2 explanations

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.2 Skills PracticePage 327 Problem 19 Answer

Given :f(x) =−2x⁷+5x³+x

We will put x in f(x) as −x

If we get the answer as f(x) then it is an even function, if we get -f(x) then it is an odd function.

Otherwise, it is neither even nor odd.

Let us substitute−x in f(x), we get

f(-x) = −2(−x)⁷+5(−x)³+(−x)

f(-x)=−2(−1)⁷x⁷+5(−1)³x³+(−1)x

f(-x)=−2(−1)x⁷+5(−1)x³+(−1)x

f(-x)=2x⁷−5x³−x taking (−1) common we get

f(-x)=−(−2x⁷+5x³+x)

f(-x) = -f(x)

Function f(x) = −2x⁷+5x³+x is an odd function.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Skills Practice

Page 317 Problem 1 Answer

It is asked to provide an example for relative minima. Also, it is asked to graph a function that has relative minima.

Consider a function f(x)=x³−3x−2 .

Differentiate this function with respect to x.

f′(x)=3x²−3 and f′′(x)=6x.

For relative maxima and minima f′(x)=0.

3x²−3=0

x²−1=0

x²=1

x=±1

So, when x=1 then f′′(x)=6>0.

So, the point x=1 is a local minimum.

The graph of the function f(x)=x³−3x−2 is as follows:

In the above graph, the local minimum is the point x=1.

The graph of the function f(x)=x³−3x−2 is as follows:

In the above graph x=1 is a point of local minimum.

Carnegie Learning Algebra II Chapter 3 Exercise 3.1 solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.1 Skills Practice Page 317 Problem 2 Answer

It is asked to provide an example for relative minima. Also, it is asked to graph a function that has relative minima.

Consider the function f(x)=x³−3x−2

Now, differentiate the function two times with respect to x.

f′(x)=3x²−3 and f′′(x)=6x

Now, for local maxima f′(x)=0.

3x²−3=0

x²−1=0

x²=1

x=±1

Now, for x=−1, f′′(x)=−6<0.

So, the point x=−1 is a local maximum.

The graph of the function f(x)=x³−3x−2 is as follows:

In the above graph the point x=−1 is a point of local maxima.

The graph of the function f(x)=x³−3x−2 is as follows:

In the above graph x=−1 is a point of local maxima.

Page 317 Problem 3 Answer

In the above graph x=−1 is a point of local maxima.

Consider a function f(x)=x³+5x²+6x−7.

Observe that the highest power of x is 3.

So, the degree of the polynomial function is 3 .

So, this is a cubic function.

The graph of the function f(x)=x³+5×2+6x−7is as follows:

The above graph is drawn by taking X′OX as x−axis and Y′OY as y−axis.

The function f(x)=x³+5x²+6x−7 is a cubic function and the graph of his function is as follows:

Page 317 Problem 4 Answer

It is asked to provide an example of a function that has roots with multiplicity or repeated roots.

Also, it is asked to give the graph of the function of the repeated roots.

Multiplicity means the number of repetitions of a root of an equation.

Consider a function f(x)=x(x−4)²(x−2)³.

To find the roots of the polynomial f(x) set f(x)=0.

x(x−4)²(x−2)³=0

This gives either x=0 or (x−4)²=0 or (x−2)³=0.

Now, when (x−4)²=0, then the function f(x) has a root x=4 of multiplicity 2.

Now, when (x−2)³=0, then the function f(x) has a root x=2 of multiplicity 3.

Also, the function f(x) has a root x=0 of multiplicity 1.

The graph of the function f(x)=x(x−4)²(x−2)³ is as follows:

The above graph is drawn by taking X′ OX as x−axis and Y′OY as the y−axis.

The function f(x)=x(x−4)²(x−2)³ has the roots x=4 of multiplicity 2 and the root x=2 of multiplicity 3

Skills Practice Carnegie Learning Algebra II Exercise 3.1 answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.1 Skills Practice Page 317 Problem 5 Answer

Given is a table with Length width, height and volume.

Expressions given are formula to find the corresponding value of Length, Width and VolumeUse the expressions and find the value to complete the table And then circle the Relative maximum or minimum value A relative maximum point is a point where the function changes direction from increasing to decreasing.

Similarly, a relative minimum point is a point where the function changes direction from decreasing to increasing.

The table of Length, Width, Height and Volume of box:

The complete table

Page 318 Problem 6 Answer

Given is a Table with Radius ,height, Base Area and Volume of the cylinder.

To complete the Table, Find height, base area and volume of cylinder Use the formula given and find for each radius given in table And then Circle the Relative Maximum or minimum value

The Table of Radius, Height, Base Area and Volume of the cylinder:

The Expression for Volume of Cylinder:(3r)(3.14r²)

The Complete table and Relative minimum

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.1 Skills Practice Page 318 Problem 7 Answer

Given is a height of cube in which height, length and width is sameTo complete the table, find volume of the cube which is product of Length, width and height.

Then find Relative maximum or minimum and circle that value.

The table of Length, height, Width and volume of the cube:

The Expression for volume of cube is s 3

The Complete table

Page 318 Problem 8 Answer

Given is a table with Length width, height and volume.

Expressions given are formula to find the corresponding value of Length and WidthUse the expressions and find the value to complete the table And then circle the Relative maximum or minimum value A relative maximum point is a point where the function changes direction from increasing to decreasing.

Similarly, a relative minimum point is a point where the function changes direction from decreasing to increasing.

The table of Length, width, height and volume of Tank:

Height of Tank(m)

Width of tank(m)

Length of tank(m)

Volume of

The Expression for Volume of Tank:V=w(100−2w)(3w−50)

The Relative maximum is at volume 58682

The complete table

Page 319 Problem 9 Answer

Given is the Height of Square Pyramid, using given expressions find Side of base length for each height value

Then Use expression given for Area of base to find for each height given

To find volume of Square Pyramid, use the formulaThen Circle the relative Maximum or minimum value.

The Table of Height, Side of base length, Area of base and Volume of Square Pyramid:

Height of Square Pyramid(tt)

Side

The Complete table

Page 319 Problem 10 Answer

The given table is

To do: Complete the given table.

The formula of volume of a triangular prism is

V=1/2×b×h×l

Where, b is the base, h is the height and l is the length of the triangular prism.

For the prism having length of the base, b=−0.5

Let, h=−2

And, l=−5

V=1/2×(−0.5)×(−2)×(−5)

V=−2.5 cu.dm

For the prism having the length of base, b=0

Let h=0

And, l=−5

Volume, V=1/2×0×0×(−5)

V=0 cu.dm

For the prism having the length of the base, b=0.3

Let, h=−0.4

And, l=2

Volume, V=1/2×0.3×(−0.4)×2

V=−0.12 cu.dm

For the prism having length of the base, b=0.5

Let, h=1

And, l=2

Volume, V=1/2×0.5×1×2

V=0.5 cu.dm

For the volume of the triangular prism, V=5cu.dm

Let, b=1

And, h=2

Now, by using the formula of volume of a triangular prism,

5=1/2×1×2×l

⇒l=5

For the prism having the height of the base, h=4

And, the length of the base, b=2

Let, l=8

V=1/2×2×4×8

V=32cudm

For the prism having the length of the base, b and length of the triangular prism, l=10 b−5.

Let, h=2b

V=1/2×b×2b×(10b−5)

V=b²(10b−5)

Now, complete the given table

Now, circle the relative maximum and relative minimum in the above table

The completed table with circles of relative minimum and maximum is shown below.

Page 320 Problem 11 Answer

Given is a three factors 2x−1 ,2x+1 and x+4 Multiply the three factors to find product

Then Assume random value for x and draw the graph for given factorsAnd then use same random value of x and draw the graph

The Product:

(2x−1)(2x+1)(x+4)=(2x(2x)+2x(1)−1(2x)−1(1))(x+4)

(2x−1)(2x+1)(x+4)=(4x²+2x−2x−1)(x+4)

(2x−1)(2x+1)(x+4)=(4x²−1)(x+4)

(2x−1)(2x+1)(x+4)=(4x²(x)+4x²

(4)−1(x)−1(4))

(2x−1)(2x+1)(x+4)=4x³+16x²−x−4

The Table for graph of factors

The Graph of three factors

The Graph of Final Expression is

The product of three factors(2x−1)(2x+1)(x+4) are4x³+16x²−x−4.And The graph of two expressions are same so they are Equivalent.

Carnegie Learning Algebra II practice questions Chapter 3 Exercise 3.1

Page 320 Problem 12 Answer

Given is a three factors 4x−7 Multiply the three factors to find product

Then Assume random value for x to find y and draw the graph for given factors And then use same random value of x and draw the graph he product:

(4x−7)(4x−7)(4x−7)=(4x(4x)+4x(−7)−7(4x)−7(−7))(4x−7)

(4x−7)(4x−7)(4x−7)=(16x²−28x−28x+49)(4x−7)

(4x−7)(4x−7)(4x−7)=(16x²−56x+49)(4x−7)

(4x−7)(4x−7)(4x−7)=16x²

(4x)−56x(4x)+49(4x)+16x²(−7)−56x(−7)+49(−7)

(4x−7)(4x−7)(4x−7)=64x³−224x²+196x−112x²+392x−343

(4x−7)(4x−7)(4x−7)=64x³−336x²+588x−343

The table for final Expression

The Table of three factors

To draw a graph, Mark the points from tablesThe graph for three factors

The graph of the final expression

The product of three factors(4x−7)³ are 64x³−336x²+588x−343.

The graph of two expressions are same so they are Equivalent and it is shown below

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.1 Skills Practice Page 320 Problem 13 Answer

It is given the three factors10−3x ,7+x and 8+6x

It is asked to multiply the three factors to find their product.

Also, it is asked to find the graph to verify whether the product is right or wrong.

The given linear factors are (10−3x), (7+x) and (8+6x).

Consider the factors in the following fashion.

(10−3x)(7+x)(8+6x)

When the factors are in this fashion then the graph of the function is as follows:

Now, multiply the linear factors as follows:

(10−3x)(7+x)(8+6x)

={10(7+x)−3x(7+x)}(8+6x)

={70+10x−21x−3x²}(8+6x)

={70−11x−3x²}(8+6x)

=70(8+6x)−11x(8+6x)−3x²(8+6x)

=560+420x−88x−66x²−24x²−18x³

=560+332x−90x²−18x³

Now, the graph of the product function will be as follows:

The product of  three linear factors (10−3x)(7+x)(8+6x) is 560+332x−90x²−18x³.

The two graphs it verifies that the two graphs are the same. So, the linear product is equivalent.

Page 321 Problem 14 Answer

It is given the linear factors (x/2),(2x/3),(x/4−1).

It is asked to find the product of the linear factors.

Also, it is asked to verify by drawing the graph whether the product and the linear factors are equivalent or not.

The given linear factors are (x/2),(2x/3),(x/4−1).

Write the linear factors in the following fashion:

f(x)=(x/2)(2x/3)(x/4−1)

Then the graph of the function f(x)=(x/2)(2x/3)(x/4−1) is as follows:

Now, multiply the given linear factors as follows:

f(x)=(x/2)(2x/3)(x/4−1)

=2x²/6(x/4−1)

=2x³/24−2x²/6

=x³/12−x²/3

Now, the graph of the function f(x)=x³/12−x²/3 is as follows:

The graph of the function f(x)=(x/2)(2x/3)(x/4−1) is as follows:

The graph of the function f(x)=x³/12−x²3 is as follows:

The above two graphs show that that the product of the linear factors is equivalent to the expression x³/12−x²/3.

Chapter 3 Exercise 3.1 Carnegie Learning Algebra II key

Page 321 Problem 15 Answer

It is given the linear factors 0.25x,(12x−1),(8−3x). It is asked to find the product of the linear factors.

Also, it is asked to verify by drawing the graph whether the product and the linear factors are equivalent or not.

The given linear factors are 0.25x,(12x−1),(8−3x).

Write the linear factor in the following fashion: f(x)=0.25x(12x−1)(8−3x).

The graph of the function f(x) is as follows:

Now, product the linear factors as follows:

f(x)=0.25x(12x−1)(8−3x)

=0.25x{12x(8−3x)−(8−3x)}

=0.25x(96x−36x²−8+3x)

=0.25x(99x−36x²−8)

=24.75x²−9x³−2x

Now, the graph of the function f(x)=24.75x²−9x³−2x is as follows:

The graph of the function f(x)=0.25x(12x−1)(8−3x) is as follows:

Also the graph of the function f(x)=24.75x²−9x³−2x is as follows:

So, the above two graphs, it verifies that 0.25x(12x−1)(8−3x)=24.75x²−9x³−2x.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.1 Skills Practice Page 321 Problem 16 Answer

It is given the algebraic expression x(x²+3x−4). It is asked to find the product of the linear factor x

with the quadratic factor(x²+3x−4). Also, it is asked to verify by the graph whether the expression x(x²+3x−4) is equivalent to the product.

The given linear factor is x and the quadratic factor is (x²+3x−4).

Now, write the product of these in the following fashion:

x(x²+3x−4)

Now, the graph of the expression x(x²+3x−4) is as follows:

Now, multiply the expression f(x)=x(x²+3x−4) as follows:

f(x)=x(x²+3x−4)

=x³+3x²−4x

Now, the graph of the function f(x)=x³+3x²−4x is as follows:

The graph of the expression f(x)=x(x²+3x−4)

The graph of the expression f(x)=x³+3x²−4x is as follows:

The above two graphs verify that the expression x(x²+3x−4) is equivalent to x³+3x²−4x.

Page 321 Problem 17 Answer

It is given the linear factor (2x−9) and the quadratic factor (4x²−5x−12).

It is asked to find the product of the linear and quadratic factors.

Also, it is asked to verify by the graph that expression  (2x−9)(4x²−5x−12) is equivalent to resultant expression.

Consider that f(x)=(2x−9)(4x²−5x−12).

Now, the graph of the function f(x)=(2x−9)(4x²−5x−12) is as follows:

Now, find the product f(x)=(2x−9)(4x²−5x−12).

f(x)=(2x−9)(4x²−5x−12)

=2x(4x²−5x−12)−9(4x²−5x−12)

[By using the Distributive Property]

=8x³−10x²−24x−36x²+45x+108

=8x³−46x²+21x+108

Now, the graph of the expression f(x)=8x³−46x²+21x+108 is as follows:

The graph of the expression f(x)=(2x−9)(4x²−5x−12) is as follows:

The graph of the function f(x)=8x³−46x²+21x+108 is as follows:

The above two graphs verify that (2x−9)(4x²−5x−12)=8x³−46x²+21x+108.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.1 Skills Practice Page 322 Problem 18 Answer

It is given linear factor 7x and a quadratic factor (x+5)².

It is asked to find the product of the linear and quadratic factors.

Also, it is asked to explain whether the expression 7x(x+5)² is equivalent to the resultant expression after multiplication.

Consider that f(x)=7x(x+5)².

Now, the graph of the function f(x)=7x(x+5)² is as follows

Now, find the product of the expression f(x)=7x(x+5)².

f(x)=7x(x+5)²

=7x(x²+10x+25)

=7x³+70x²+175x

[By using the Distributive Property]

Now, the graph of the expression f(x)=7x³+70x²+175x is as follows:

The graph of the function f(x)=7x(x+5)² is as follows:

The graph of the expression f(x)=7x³+70x²+175x

The above two graphs verify that 7x(x+5)²=7x³+70x²+175x.

How to solve Chapter 3 Exercise 3.1 Algebra II Carnegie Learning

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 3 Exercise 3.1 Skills Practice Page 322 Problem 19 Answer

It is given the quadratic factor (x²+1) and linear factor (8−x).

It is asked to find the product of the quadratic factor and linear factor.

Also, it is asked to verify by the graph that the expression(x²+1)(8−x) is equivalent to the resultant expression of the product.

Consider the expression f(x)=(x²+1)(8−x).

The graph of the function f(x)=(x²+1)(8−x) is as follows:

Now, find the product of the factors of the function f(x)=(x²+1)(8−x).

f(x)=(x²+1)(8−x)

=x²(8−x)+(8−x)

=8x²−x³+8−x

Now, the graph of the function f(x)=8x²−x³+8−x is as follows:

The graph of the function f(x)=(x²+1)(8−x)  is as follows:

The graph of the function f(x)=8x²−x³+8−x  is as follows:

The above two graphs verify that (x²+1)(8−x)=8x²−x³+8−x.

Page 322 Problem 20 Answer

It is given the quadratic factor (−2.3+1.1x+0.9x²) and the linear factor (4.5x−3.8).

It is asked to find the product of the linear and quadratic factors.

Also, it is asked to verify by the graph that the expression (−2.3+1.1x+0.9x²)(4.5x−3.8) is equivalent to the resultant expression after multiplication.

Consider that f(x)=(−2.3+1.1x+0.9x²)(4.5x−3.8).

Now, the graph of the function f(x)=(−2.3+1.1x+0.9x²)(4.5x−3.8) is as follows:

Now, multiply the function f(x)=(−2.3+1.1x+0.9x²)(4.5x−3.8).

f(x)=(−2.3+1.1x+0.9x²)(4.5x−3.8)

=(−2.3+1.1x+0.9x²)(4.5x)−(−2.3+1.1x+0.9x²)3.8

=−10.35x+4.95x²+4.05x³+8.74−4.18x−3.42x²

=4.05x³+1.53x²−14.53x+8.74

Now, the graph of the function f(x)=4.05x³+1.53x²−14.53x+8.74 is as follows:

The graph of the function f(x)=(−2.3+1.1x+0.9x²)(4.5x−3.8) is as follows:

The graph of the function f(x)=4.05x³+1.53x²−14.53x+8.74 is as follows:

The above two graphs verify that (−2.3+1.1x+0.9x²)(4.5x−3.8)=4.05x³+1.53x²−14.53x+8.74.

Chapter 3 Carnegie Learning Algebra II Exercise 3.1 worked examples

Page 322 Problem 21 Answer

It is given the quadratic factor (−3/4x²+1/8) and the linear factor (1/4−7x/8).

It is asked to find the multiplication of the linear and quadratic factors.

Also, it is asked to verify by the graph that the expression (−3/4x²+1/8)(1/4−7x/8) is equivalent to the resultant product.

Consider the function f(x)=(−3/4x²+1/8)(1/4−7x/8) .

Now, the graph of the function f(x)=(−3/4x²+1/8)(1/4−7x/8 is as follows:

Now, multiply the factors in the function f(x)=(−3/4x²+1/8)(1/4−7x/8).

f(x)=(−3/4x²+1/8)(1/4−7x/8)

=−3/4x²(1/4−7x/8)+1/8(1/4−7x/8)

=−3/16x²+21x³/32+1/32−7x/64

Now, the graph of the function f(x)=−3/16x²+21x³/32+1/32−7x/64 is as follows:

The graph of the function f(x)=(−3/4x²+1/8)(1/4−7x/8) is as follows:

The graph of the function f(x)=−3/16x²+21x³/32+1/32−7x/64 is as follows:

The above two graphs verify that (−3/4x²+1/8)(1/4−7x/8)=−3/16x²+21x³/32+1/32−7x/64.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice

Page 303 Problem 1 Answer

Given: The number i

i=√−1

⇒ A number such that its square equals−1

Option E: A number such that its square equals−1

Page 303 Problem 2 Answer

Given: Imaginary number

Applying the above-given definition,

A number of the form bi Where b is not equal to 0

Option H: A number of the form bi where b is not equal to 0

Page 303 Problem 3 Answer

We need to match the definition of the pure imaginary number with the several available options.

Among the several available options, the correct option for the pure imaginary number is H.

That is, a pure imaginary number is a number of the form bi where b is not equal to 0.

Therefore, the correct option for the pure imaginary number is H.

Page 303 Problem 4 Answer

We need to match the definition of the complex numbers with the several available options.

Among the several available options, the correct option for the definition of a complex number is F.

That is, a complex number is a number in the form a+ib where a and b are real numbers.

Therefore, the correct option for the definition of a complex number is F.

Carnegie Learning Algebra II Chapter 2 Exercise 2.6 solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 303 Problem 5 Answer

We need to match the definition of the real part of a complex number with the several available options.

Among the several available options, the correct option for the real part of a complex number is B.

That is, the real part of a complex number is the term a of a number written in the form a+bi.

Therefore, the correct option for the real part of a complex number is B.

Page 303 Problem 6 Answer

We need to match the definition of the immaginary part of a complex number with the several available options.

Among the several available options, the correct option for the immaginary part of a complex number is I.

That is, the immaginary part of a complex number is a term bi of a number written in the form a+bi.

Therefore, the correct option for the immaginary part of a complex number is I.

Page 303 Problem 7 Answer

We need to match the definition of the complex conjugate with the several available options.

Among the several available options, the correct option for the complex conjugate is D.

That is, the complex conjugate is a pair of numbers of the form a+bi and a−bi.

Therefore, the correct option for the complex conjugate is D.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 303 Problem 8 Answer

We need to match the definition of the monomial with the several available options.

Among the several available options, the correct option for the monomial is J.

That is, monomial is a polynomial with one term.

Therefore, the correct option for the monomial is J.

Page 303 Problem 9 Answer

We need to match the definition of the binomial with the several available options.

Among the several available options, the correct option for the binomial is C.

That is, binomial is a polynomial with two terms.

Therefore, the correct option for the binomial is C.

Page 303 Problem 10 Answer

We need to match the definition of the trinomial with the several available options.

Among the several available options, the correct option for the trinomial is G.

That is, a trinomial is a polynomial with three terms.

Therefore, the correct option for the trinomial is G.

Skills Practice Carnegie Learning Algebra II Exercise 2.6 answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 304 Problem 11 Answer

We need to find the value of i48.

We know that i²=−1.

So, i⁴⁸=(i²)²⁴

i⁴⁸=(−1)²⁴

i^{48}=1

Therefore, the value of i48 is 1.

Page 304 Problem 12 Answer

Given imaginary number is i⁵⁵.

To Do: Calculate the power.

i⁵⁵=(i⁴)¹³⋅i³

=(1)¹³⋅(−i)

∵i⁴=1 and i³=−i

=(1)⋅(−i)

=−i

The power of i⁵⁵=−i.

Page 303 Problem 13 Answer

Given imaginary number is i1000.

To Do: Calculate the power.

i¹⁰⁰⁰=(i⁴)²⁵⁰

=(1)²⁵⁰

∵i⁴=1

=1

The power of i¹⁰⁰⁰=1.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 304 Problem 14 Answer

Given imaginary number is i⁻²².

To Do:  Calculate the power.

i⁻²²=(i⁻²)¹¹

=(−1)¹¹

∵i⁻²=−1

=−1

The power of i⁻²²=−1.

Page 304 Problem 15 Answer

Given imaginary number is i−7.

To Do:  Calculate the power.

i−7=(i⁻²)³⋅(i)⁻¹

=(−1)³⋅(−i)

∵i⁻²=−1 and i⁻¹=−i

=(−1)⋅(−i)

=i

The power of i⁻⁷=i.

Page 305 Problem 16 Answer

Given number is √−72

To Do: Convert the number using imaginary number i.

√−72 =√36⋅2⋅(−1)

=6√2i

∵√36 =6 and √−1=i

√−72=6√2i

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 305 Problem 17 Answer

Given number is 38−√−200+√121

To Do: Convert the number using imaginary number i.

38−√−200+√121

=38−√100⋅2⋅(−1)+√121

=38−10√2⋅(−1)+11

∵√100 =10 and √121

=11 and √−1

=i

=49−10√2/i

The required expression for38−√−200+√121

=49−10√2/i

Page 305 Problem 18 Answer

Given number is √−45+21

To Do: Convert the number using imaginary number i.

√−45 + 21 = √9 ⋅ 5 ⋅ (−1) + 21

= 3√5i + 21 ∵ √−1 = i and √9 = 3

The required expression for √−45 + 21 = 3√5i + 21

Carnegie Learning Algebra II practice questions Chapter 2 Exercise 2.6

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 305 Problem 19 Answer

Given number is √−48−12/4

To Do: Convert the number using imaginary number i.

√−48 − 12/4

√16 ⋅ 3 ⋅ (−1) − 12/4

=4√3i − 12/4

∵ √−1 = i and √16 = 4

=4(√3i − 3)/4

= √3i − 3

√−48 − 12/4 = √3i − 3

Page 305 Problem 20 Answer

Given number is 1+√4−√−15/3

To Do: Convert the number using imaginary number i.

=3−√15/i³

∵√−1=i

=1−√5/3i

The required expression for 1+√4−√−15/3

=1−√5/3i

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 305 Problem 21 Answer

Given : −√−28+√21/3−√12/6

We have to rewrite the above expression using “i”.

−√−28 + − = − + − √21/3√12/6 √4 × 7 × (−1) √21/3√4 × 3/6

= −(√4 × √7 × √−1) + − √21/3√4 × √3/6

= −(2 × √7 × i) + − √21/3/2 × √3/2 × 3           [∵ i = √−1 ]

= −2√7i + − √21/3√3/3

= −2√7i +(√21 − √3)/3

The required expression for −√−28 + − = −2 i + √21/3√12/6 √7(√21 − √3)/3

Page 305 Problem 22 Answer

Given : √−75+√80/10

We have to rewrite the above expression using “i

“.√−75 + √80/10

√25 × 3 × (−1) + √16 × 5/10=

=(√25×√3×√−1)+(√16×√5)/10

=(5×√3×i)+(4×√5)/10   [∵ i=√−1 ]

=5×√3×i¹⁰+4×√5/10

=5×√3×I/5×2+2×2×√5/5×2

=√3×i²+2×√5/5

=√3i/2+2√5/5

The required expression for√−75+√80/10=√3i/2+2√5/5

Page 306 Problem 23 Answer

Given : (2+5i)−(7−9i)​

We have to simplify the above expression.

(2+5i)−(7−9i)=2+5i−7+9i

=(2−7)+(5i+9i)

=−5+14i

The required expression for(2+5i)−(7−9i)=−5+14i

Chapter 2 Exercise 2.6 Carnegie Learning Algebra II key

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 306 Problem 24 Answer

Given : −6+8i−1−11i+13

We have to simplify the above expression.

−6 + 8i − 1 − 11i + 13 = (−6 − 1 + 13) + (8i − 11i)

=6+(−3i)

=6−3i

The required expression for −6+8i−1−11i+13=6−3i

Page 306 Problem 25 Answer

Given : −(4i−1+3i)+(6i−10+17)

We have to simplify the above expression.

−(4i − 1 + 3i) + (6i − 10 + 17) = −4i + 1 − 3i + 6i − 10 + 17

= (1 − 10 + 17) + (−4i − 3i + 6i)

= 8 + (−i)

= 8 − i

−(4i − 1 + 3i) + (6i − 10 + 17) = 8 − i

Page 306 Problem 26 Answer

Given : 22i+13−(7i+3+12i)+16i−25

We have to simplify the above expression.

22i+13−(7i+3+12i)+16i−25=22i+13−7i−3−12i+16i−25

=(13−3−25)+(22i−7i−12i+16i)

=−15+19i

22i+13−(7i+3+12i)+16i−25 =−15+19i

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 306 Problem 27 Answer

Given :  9+3i(7−2i)

We have to simplify the above expression.

9+3i(7−2i)=9+(3i×7)−(3i×2i)

=9+21i−6i²

=9+21i−6(−1)       [∵ i=√−1⇒i²=−1 ]

=9+21i+6

=(9+6)+21i

=15+21i

9+3i(7−2i)= =15+21i

Page 306 Problem 28 Answer

Given :  (4−5i)(8+i)

We have to simplify the above expression.

(4−5i)(8+i)=4(8+i)−5i(8+i)

=(4×8+4×i)−(5i×8+5i×i)

=(32+4i)−(40i+5i²)

=32+4i−40i−5i²

=32+4i−40i−5(−1)  [∵ i=√−1⇒i²=−1 ]

=32+4i−40i+5

=(32+5)+(4i−40i)

=37−36i

The required expression for(4−5i)(8+i)=37−36i

How to solve Chapter 2 Exercise 2.6 Algebra II Carnegie Learning

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 306 Problem 29 Answer

Given :  −0.5(14i−6)−4i(0.75−3i)

We have to simplify the above expression.

−0.5(14i−6)−4i(0.75−3i)=−(0.5×14i−0.5×6)−(4i×0.75−4i×3i)

=−(7i−3)−(3i−12i²)

=−7i+3−3i+12i²

=−7i+3−3i+12(−1) [∵ i=√−1⇒i²=−1 ]

=−7i+3−3i−12

=(3−12)+(−7i−3i)

=−9−10i

The required expression for−0.5(14i−6)−4i(0.75−3i)=−9−10i

Page 306 Problem 30 Answer

Given :  (1/2i−3/4)(1/8−3/4i)

We have to simplify the above expression.

(1/2i−3/4)(1/8−3/4i)=1/2i(1/8−3/4i)−3/4

(1/8−3/4i) =(1/2i×1/8−1/2i×3/4i)−(3/4×1/8−3/4×3/4i)

=(1/16i−3/8i²)−(3/32−9/16i)

=1/16i−3/8i²−3/32+9/16i

=1/16i−3/8(−1)−3/32+9/16i [∵ i=√−1⇒i²=−1 ]

=1/16i+3/8−3/32+9/16i

=(3/8−3/32)+(1/16i+9/16i)

=(3×4−3/32)+(1/16+9/16)i

=(12−3/32)+(1+9/16)i

=9/32+10/16i

=9/32+5/8i

(1/2i−3/4)(1/8−3/4i)=9/32+5/8i

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 307 Exercise 1 Answer

To find the product of(3+i)(3−i)

We have to multiply (3+i)(3−i)

First, open the brackets.

⇒(3+i)(3−i)

⇒3(3−i)+i(3−i)

⇒9−3i+3i−i²

⇒9−i²

⇒9−(−1)

⇒9+1

⇒10

The product of (3+i)(3−i)=10

Page 307 Exercise 2 Answer

To find the product of(4i−5)(4i+5)

We have to multiply (4i−5)(4i+5)

First, open the brackets.

⇒(4i−5)(4i+5)

⇒4i(4i+5)−5(4i+5)

⇒16i²+20i−20i−25

⇒16i²−25

⇒16(−1)−25

⇒−16−25

⇒−41

The product of (4i−5)(4i+5)=−41

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 307 Exercise 3 Answer

To find the product of(1/3+3i)(1/3−3i)

We have to multiply (1/3+3i)(1/3−3i)

First, open the brackets.

⇒(1/3+3i)(1/3−3i)

⇒1/3(1/3−3i)+3i(1/3−3i)

⇒1/9−i+i−9i²

⇒1/9−9i²

⇒1/9−9(−1)

⇒1/9+9

⇒82/9

The product of (1/3+3i)(1/3−3i)=82/9

Page 307 Exercise 4 Answer

To find the product of(0.1+0.6i)(0.1−0.6i)

First, open the brackets.

⇒(0.1+0.6i)(0.1−0.6i)

⇒0.1(0.1−0.6i)+0.6i(0.1−0.6i)

⇒0.01−0.06i+0.06i−0.36i²

⇒0.01−0.36i²

⇒0.01−0.36(−1)

⇒0.01+0.36

⇒0.37

The product of (0.1+0.6i)(0.1−0.6i)=0.37

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 307 Exercise 5 Answer

To identify the expression 4xi+7x as monomial, binomial or trinomial

The expression is 4xi+7x

This can be rewritten as ⇒(7+4i)x

There is only one x term. It is a monomial

The expression 4xi+7x is a monomial

Page 307 Exercise 6 Answer

To identify the expression−3x+5−8xi+1 as monomial, binomial or trinomial

The expression is −3x+5−8xi+1

⇒−3x+5−8xi+1

⇒6+(−3−8i)x

⇒6−(3+8i)x

There are two terms 6 and (3+8i)x. So this is a binomial.

The expression−3x+5−8xi+1 is a binomial

Page 307 Exercise 7 Answer

To identify the expression 6x²i+3x² as monomial, binomial or trinomial

The expression is 6x²i+3x²

⇒6x²i+3x²

⇒(6i+3)x²

There is only one term. So this is a monomial.

The expression 6x²i+3x² is a monomial

Page 307 Exercise 8 Answer

To identify the expression 8i−x³+7x²i as monomial, binomial or trinomial

The expression is 8i−x³+7x²i

⇒8i−x³+7x²i

⇒−x³+7ix²+8i

There are three terms x³,7ix² and 8i. So this is a trinomial

The expression 8i−x³+7x²iis a trinomial

Algebra II Carnegie Learning skills practice Exercise 2.6 solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 308 Exercise 9 Answer

Given: The expression is xi−x+i+2−4i.

To identify that the expression is monomial, binomial, or trinomial.

The expression can be written as: xi−x+i+2−4i=x(i−1)+2−3i

Since there is only one term so the expression is monomial.

The expression xi−x+i+2−4i is monomial.

Page 308 Exercise 10 Answer

Given: The expression is−3x³i−x²+6x³+9i−1.

To identify that the expression is monomial, binomial, or trinomial.

The expression can be written as:−3x³i−x²+6x³+9i−1=3x³(2−i)−x²+9i−1

SInce here the highest term is 3 so the expression is trinomial.

The expression−3x³i−x²+6x³+9i−1 is monomial.

Page 308 Exercise 11 Answer

Given: The expression is (x−6i)².

Simplify the expression.

Simplify the expression

(x−6i)²=x²+(6i)²−2x(6i)

(x−6i)²=x²+36i²−12xi

(x−6i)²=x²−12xi−36

The simplified expression is(x−6i)²

=x²−12xi−36.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 308 Exercise 12 Answer

Given: The expression is(2+5xi)(7−xi).

Simplify the expression.

Simplify the expression

(2+5xi)(7−xi)=2(7−xi)+5xi(7−xi)

(2+5xi)(7−xi)=14−2xi+35xi−5x²i²

(2+5xi)(7−xi)=14+33xi+5x²

The simplified expression is(2+5xi)(7−xi)=14+33xi+5x².

Page 308 Exercise 13 Answer

Given: The expression is 3xi−4yi.

Simplify the expression.

Simplification of the expression by taking i common,

3xi−4yi=i(3x−4y)

The simplified expression is 3xi−4yi=i(3x−4y).

Page 308 Exercise 14 Answer

Given: The expression is(2xi−9)(3x+5i).

Simplify the expression.

Simplify the expression

(2xi−9)(3x+5i)=2xi(3x+5i)−9(3x+5i)

(2xi−9)(3x+5i)=6x²i+5xi²−27x−45i

(2xi−9)(3x+5i)=i(6x²−45)−32x

The simplified expression is(2xi−9)(3x+5i)=i(6x²−45)−32x.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 309 Exercise 15 Answer

Given: The expression is(x+4i)(x−4i)(x+4i).

Simplify the expression.

Simplify the expression (x+4i)(x−4i)(x+4i)=(x+4i)(x²−16i²)

⇒(x+4i)(x−4i)(x+4i)=(x+4i)(x²+16)

⇒(x+4i)(x−4i)(x+4i)=x³+16x+4x²i+64i

The simplified expression is(x+4i)(x−4i)(x+4i)=x³+16x+4x²i+64i.

Page 309 Exercise 16 Answer

Given: The expression is(3i−2xi)(3i−2xi)+(2i−3xi)(2i−3xi).

Simplify the expression.

Simplify the expression

(3i−2xi)(3i−2xi)+(2i−3xi)(2i−3xi)=(3i−2xi)²+(2i−3xi)²

(3i−2xi)(3i−2xi)+(2i−3xi)(2i−3xi)=(9i²+4x²i²−12xi²)+(4i²+9x²i²−12xi²)

(3i−2xi)(3i−2xi)+(2i−3xi)(2i−3xi)=(−9−4x²+12x)+(−4−9x²+12x)

(3i−2xi)(3i−2xi)+(2i−3xi)(2i−3xi)=24x−13x²−13

​The simplified expression is(3i−2xi)(3i−2xi)+(2i−3xi)(2i−3xi)=24x−13x²−13.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 309 Exercise 17 Answer

Given: The complex number is 7+2i.

To find the conjugate of the complex number.

Find the conjugate of the complex number

The conjugate of a complex number can be found by changing the sign or the operator of the imaginary number.

So, the conjugate will be 7−2i.

The conjugate of the complex number is 7−2i.

Page 309 Exercise 18 Answer

Given: The complex number is 3+5i.

To find the conjugate of the complex number.

Find the conjugate of the complex number

The conjugate of a complex number can be found by changing the sign or the operator of the imaginary number.

So, the conjugate will be3−5i.

The conjugate of the complex number is 3−5i.

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 309 Exercise 19 Answ

Given : The Complex Number z=8i

To Find: The conjugate of the complex number  zˉ

Given the complex number z=8i———————— (1)

We know that z=a+ib

Here,

a= Real part

b = Imaginary part

From (1) we know that a=0 and b=8i

We also know that the conjugate of z is zˉ

=a−ib—————(2)

Hence to find the conjugate of the complex number sub a and b in (2)

Conjugate of the Complex Number ​zˉ

=a−ib

=0−i8

zˉ=−8i​

We found that the conjugate of 8i is −8i

Page 309 Exercise 20 Answer

Given: The complex number z= −7i

To Find: The conjugate of the complex number zˉ

We know that z=a+ib

Here a= Real part and b= Imaginary part

From the given data z=−7i

We get a=0 and b=−7i

Hence to find the conjugate of the complex number zˉ

=a−ib—————–(1)

Sub the values of a and b in (1) zˉ

=a−ib

=0−(−7i)zˉ

=7i

We have found the conjugate of the complex number −7i is 7i

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 309 Exercise 21 Answer

Given: The complex number z=2−11i

To Find: The conjugate of the complex number zˉ

We know z=a+ib

Here a= Real part and b= Imaginary part

Given the complex number z=2−11i

Here a=2 and b=−11i

To find the conjugate of the complex number zˉ

=a−ib——————-(1)

Sub the values of a and b in (1) zˉ

=a−ib zˉ

=2−(−11i)zˉ

=2+11i

​We have found the conjugate of the complex number 2−11i is 2+11i

Page 309 Exercise 22 Answer

Given: The complex number z=−13−6i

To Find: The conjugate of the complex number zˉ

We know that z=a+ib

Here a= Real part and b= Imaginary part

From the given data z=−13−6i

We get a=−13 and b=−6i

To find the conjugate of the complex number zˉ

=a−ib——————(1)

Sub the values of a and b in (1)zˉ

=a−ibzˉ

=−13−(−6i)zˉ

=−13+6i

​We have found the conjugate of the complex number −13−6i is −13+6i

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 309 Exercise 23 Answer

Given: The complex number z=−21+4i

To Find: The conjugate of the complex number zˉ

We know that z=a+ib

Here a= Real part and b= Imaginary part

From the given data z=−21+4i

We get a=−21 and b=4i

To find the conjugate of the complex number zˉ

=a−ib—————-(1)

Sub the values of a and b in (1) zˉ

=a−ib zˉ

=−21−(4i)zˉ

=−21−4i

​We have found the conjugate of the complex number −21+4i is −21−4i

Page 310 Exercise 24 Answer

Given: The complex number z=3+4i/5+6i

To Calculate: Each quotient

From the given data z=3+4i/5+6i

we can get

a=3

b=4

c=5

d=6​

We know the formula a+ib/c+id={ac+bd/c²+d²}+i{bc−ad/c²+d²}

sub the values in this formula ={(3)(5)+(4)(6)/52+62}+i{(4)(5)−(3)(6)/52+62}

=15+24/61+i{20−18/61}

=39/61+i ²/61

Hence the solution for the given complex number is 39/61+i²/61

Page 310 Exercise 25 Answer

Given: The complex number z=8+7i/2+i

To Calculate: Each quotient

From the given data z=8+7i/2+i

we get

a=8

b=7

c=2

d=1​

We know the formula a+ib/c+id={ac+bd/c²+d²}+i{bc−ad/c²+d²}

sub the above found values in the formula =(8)(2)+(7)(1)/22+12+i{(7)(2)−(8)(1)/22+12}

=16+7/5+i14−8/5

=23/5+i6/5

Hence the solution for the given complex number is 23/5+i6/5

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 310 Exercise 26 Answer

Given: The complex number z=−1+5i/1−4i

To Calculate: Each quotient

From the given data z=−1+5i/1−4i

we get

a=−1

b=5

c=1

d=−4​

We know the formula a+I b/c+id

=ac+bd/c²+d²+i{bc−ad/c²+d²}

sub the above found values in the formula =(−1)(1)+(5)(−4)/12+(−4)²+i{(5)(1)−(−1)(−4)/12+(−4)²}

=−1−20/17+i5−4/17

=−21/17+i{1/17}​

Hence the solution for the given complex number is −21/17+i{1/17}

Page 307 Exercise 27 Answer

We are given: 6−3i/2−i

We are required to calculate the quotient.

We will multiply the numerator and denominator by the complex conjugate of the denominator and simplify the equation.

Given: 6−3i/2−i

The complex conjugate of the denominator is 2+i.

Multiplying and dividing this, we get

6−3i/2−i×2+I/2+i

=(6−3i)(2+i)/22−i²

=12−6i+6i−3i²/2−(−1)

=12−3(−1)/2+1

=12+3/3

=15/3

=5

The quotient of 6−3i/2−i is 5

Carnegie Learning Algebra II Student Skills Practice Exercise 2.6 explanations

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.6 Skills Practice Page 310 Exercise 28 Answer

We are given: 4−2i/−1+2i

We are required to calculate the quotient.

We will multiply the numerator and denominator by the complex conjugate of the denominator and simplify the equation.

Given: 4−2i/−1+2i

The complex conjugate of the denominator is: −1−2i.

Multiplying and dividing this, we get

4−2i/−1+2i×−1−2i/−1−2i

=(4−2i)(−1−2i)/(−1)²−(2i)²

=−4+2i−8i+4i²/1−2i²

=−4−6i−4/1+2

=−8−6i/3

The quotient of 4−2i/−1+2i is −8−6i/3.

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions

Page 294 Problem 1 Answer

The objective is to determine the equation for the quadratic function using the given graph.

We are given: The two x−intercepts (−7,0) ,(5,0) and one point (−4,−9)

Given: The two x−intercepts (−7,0),(5,0), and one point (−4,−9)

To obtain the values of a,b, and c, we will substitute the given points in the equation of the standard form, y=ax²+bx+c…(1).

Using the point(−7,0), we substitute x=−7 and y=0 into equation (1) and we will obtain an equation containing variables a,b,c,

we get,

0=a(−7)²+b(−7)+c

49a−7b+c=0…(2)

Using the point (5,0), we substitute x=5 and y=0 into equation (1) and we will obtain an equation containing variables a,b,c,we get,

0=a(5)²+b(5)+c

25a+5b+c=0…(3)

Using the point (−4,−9), we substitute x=−4 and y=−9 into equation (1) and we will obtain an equation containing variables a,b,c, we get,

−9=a(−4)²+b(−4)+c

16a−4b+c=−9…(4)

​In order to obtain the values of the variables a,b,c, we will solve the obtained equations simultaneously.

Solving (2) and (3) simultaneously, we get,

49a−  7b+  c=0
25a+  5b+  c=0
(-)     (-)     (-)
________________
24a−12b=0

b=2a​

Solving (3) and (4),

9a+9b=9

b=1−a

Comparing both,

3a=1

a=1/3

Then, b=2/3.

And, c=7(2/3)−49(1/3)=14−49/3=−35/3

Therefore, a=1/3,b=2/3,c=−35/3.

Carnegie Learning Algebra Ii Chapter 2 Exercise 2.5 Solutions

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 294 Problem 2 Answer

The objective is to determine the equation of the parabola in the vertex form using the given graph.

We are given: Vertex (−4,3) and y− intercept (0,11)

Given: Vertex (−4,3) and the y−intercept (0,11)

In order to obtain the distance from the axis of symmetry, we will substitute all the given values in the equation y=a(x−h)²+k, we get,

y=a(x+4)²+3

11=a(0+4)²+3

11=16a+3

16a=8

a=0.5

​The equation in the vertex form is,

y=a(x−h)²+k

y=1/2(x+4)²+3

The equation is, y=1/2(x+4)²+3

Hence, the equation for the quadratic function using the given data is y=1/2(x+4)²+3.

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 295 Problem 3 Answer

Given the points (2,0),(0,−12).

The aim is to find the equation.

The slope is, y=−12−0/0−2

=12/2

=6.

The equation is,

y+12=6(x)

y=6x−12

​Therefore, the equation is y=6x−12.

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 295 Problem 4 Answer

The objective is to determine the equation of the parabola in the vertex form using the given graph.

We are given: Vertex (−6,−1) and Point

Given: Vertex (−6,−1) and Point (−3,35)

To obtain the distance from the axis of symmetry, we will substitute all the given values in the equation y=a(x−h)²+k,

we get,

y=a(x+6)²−1

35=a(−3+6)²−1

35+1=9a

9a=36

a=4

The equation in the vertex form is,

y=a(x−h)²+k

y=4(x+6)²−1

The equation is, y=4(x+6)²−1

Hence, the equation for the quadratic function using the given data is y=4(x+6)²−1.

Exercise 2.5 Chapter 2 Carnegie Learning Answers

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 296 Problem 5 Answer

The objective is to determine the equation for the quadratic function using the given data.

We are given: the three points which lie on the parabola are (5,−56),(1,−4),(−10,−26)

Given: Three points as (5,−56),(1,−4),(−10,−26)

We will obtain three sets of equations when we substitute the given points in the standard form of the parabola equations, we get,

For Point (5,−56):−56=25a+5b+c…(1)

For Point (1,−4):−4=a+b+c…(2)

For Point (−10,−26):−26=100a−10b+c…(3)

To evaluate the values of the missing variable, we will solve any two equations simultaneously

Adding (2) and (3), solving simultaneously, we get,

First, we will multiply (2) by 10

10a+10b+10c=−40

100a−10b+c=−26
___________________
110a+11c=−66…(4)
___________________

Subtracting (1)  and (2), solving simultaneously, we get,

First, we will multiply (2) by 5

25a+ 5b+  c=   −56

5a+  5b+  5c=  −20

(-)     (-)       (-)      (+)
_________________

20a+4c=−36…(5)
_________________

Subtracting (4) and (5), solving simultaneously, we get,

First, we will multiply (4) by 4 and (5) by 11

440a+  44c=  −264

220a+  44c=  −396

(-)        (-)           (+)
_________________
220a=132⇒a=0.6
_________________

Now, we will substitute a=0.6 in (5), we get,

20(0.6)+4c=−36

4c=−36−12

c=−12

Now, on substituting a=0.6,c=−12 in (2),

we get,

0.6+b−12=−4

b=7.4

​The equation in the standard form on substituting all the values is,

y=ax²+bx+c

y=0.6x²+7.4x−12

​Hence,  the equation for the quadratic function using the given data is y=0.6x²+7.4x−12.

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 296 Problem 6 Answer

The objective is to determine the equation for the quadratic function using the given data.

We are given: the three points which lie on the parabola are (−8,8),(−4,6),(4,38)

Given: Three points as (−8,8),(−4,6),(4,38)

We will obtain three sets of equations when we substitute the given points in the standard form of the parabola equations, we get,

For Point (−8,8):8=64a−8b+c…(1)

For Point (−4,6):6=16a−4b+c…(2)

For Point (4,38):38=16a+4b+c…(3)

To evaluate the values of the missing variable, we will solve any two equations simultaneously

Adding (2) and (3), solving simultaneously, we get,

16a−4b+c=6

16a+4b+c=38
_______________
32a+2c=44…(4)
______________

Adding (1) and (3), solving simultaneously, we get,

First, we multiply (3) by 2

64a−8b+c=8

32a+8b+2c=76
_______________
96a+3c=84…(5)
________________

Subtracting (4) and (5), solving simultaneously, we get,

First, we will multiply (4) by 3 and  (5) by 2

96a+  6c=  132

192a+  6c=  168
(-)       (-)         (-)
________________________
−96a=−36⇒a=0.375
________________________

Now, we will substitute a=0.375 in (4), we get,

32(0.375)+2c=44

2c=44−12

2c=32

c=16

Now, on substituting a=0.375,c=12 in (2), we get,

16(0.375)−4b+12=6

4b=12

b=3

The equation in the standard form on substituting all the values is,

y=ax²+bx+c

y=0.375x²+3x+12

​Hence,  the equation for the quadratic function using the given data is y=0.375x²+3x+12.

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 296 Problem 7 Answer

The objective is to determine the equation for the quadratic function using the given data.

We are given: the three points which lie on the parabola are (−2,3),(2,−9),(5,−60)

Given: Three points as (−2,3),(2,−9),(5,−60)

We will obtain three sets of equations when we substitute the given points in the standard form of the parabola equations, we get,

For Point (−2,3):3=4a−2b+c…(1)

For Point (2,−9):−9=4a+2b+c…(2)

For Point (5,−60):−60=25a+5b+c…(3)

To evaluate the values of the missing variable, we will solve any two equations simultaneously

Adding (1) and (2), solving simultaneously, we get,

4a−2b+c=3

4a+2b+c=−9
______________
8a+2c=−6…(4)
______________

Subtracting (2) and (3), solving simultaneously, we get,

First, we will multiply (2) by 5 and (3) by 2

20a+  10b+  5c=  45

50a+  10b+  2c=  −120

(-)        (-)       (-)       (+)
___________________________
−30a+3c=165…(5)
____________________________

Subtracting (4) and (5), solving simultaneously, we get,

First, we multiply (4) by 3 and (5) by 2.

24a+6c=−18

−60a+6c=330

(+)        (-)         (-)
___________________________
84a=−348⇒a=−29/7
___________________________

Now substitute a=−29/7 in (4),

we get,8(−29/7)+2c=−6

2c=27.14285

c=13.57142

Now, substitute a=4.142857,c=13.57142 in (2),

we get,

4(4.142857)+2b+13.57142=−9

b=13.571424

​The equation in the standard form on substituting all the values is, y=ax²+bx+c

y=4.142857x²+13.571424x+13.57142

​Hence,  the equation for the quadratic function using the given data is y=4.142857x²+13.571424x+13.57142.

Algebra Ii Chapter 2 Exercise 2.5 Detailed Solutions

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 298 Problem 8 Answer

Given: (−2,−2),(1,−5),(2,−18)

To find: The system of equations

A quadratic equation through given points.

Put these points in f(x)=ax²+bx+c

We will get three equations in a,b,c. Solve it by the substitution method.

For (−2,−2): 4a−2b+c=−2…(1)

For (1,−5): a+b+c=−5…(2)

For (2,−18): 4a+2b+c=−18…(3)

a=−2+2b−c/4 From 1…(5)

6b+3c−2/4=−5 From 2…(4)

4⋅−2+2b−c/4+2b+c=−18 From 3

4b−2=−18

b=−4

Putting in(4),3c−26/4=−5

c=2

a=−2+2(−4)−2/4 From 5

a=−3

⇒a=−3,​c=2,​b=−4

The required quadratic equation: −3x²−4x+2

The quadratic equation: −3x²−4x+2

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 300 Problem 9 Answer

Given: (−1,2),(4,27),(−3,20)

To find: The system of equations

A quadratic equation through given points.

Put these points in f(x)=ax²+bx+c

We will get three equations in a,b,c. Solve it by the substitution method.

For (−1,2): a−b+c=2…(1)

For (4,27): 16a+4b+c=27…(2)

For (−3,20): 9a−3b+c=20…(3)

Substitute​a=2+b−c…(4)

20b−15c+32=27 From 2&4

b=3c−1/4…(5)

6b−8c+18=20 From 3&4

6⋅3c−1/4−8c+18=20 From 5

−7c−3/2+18=20

c=−1

b=3(−1)−1/4 From 5

a=2−1−(−1) From 4

a=2

⇒a=2,​c=−1,​b=−1

The required quadratic equation: 2x²−x−1

The quadratic equation: 2x²−x−1

Carnegie Learning Chapter 2 Exercise 2.5 Explained

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 301 Problem 10 Answer

Given: (5,−6),(−2,8),(3,4)

To find: The system of equations

A quadratic equation through given points.

Put these points in f(x)=ax²+bx+c

We will get three equations in a,b,c. Solve it by the substitution method.

For (5,−6): 25a+5b+c=−6…(1)

For (−2,8):

4a−2b+c=8…(2)

For (3,4):

9a+3b+c=4…(3)

Substitute​a=−6−5b−c/25 From 1…(4)

4⋅−6−5b−c/25−2b+c=8 From 2&4

−70b+21c−24/25=8

b=−−3c+32/10…(5)

30b+16c−54/25=4 From 3&4

30(−−3c+32/10)+16c−54/25

=4 From 5

c−6=4

c=10

b=−−3⋅10+32/10 From 5

b=−1/5

a=−6−5(−1/5)−10/25 From 4

a=−3/5

⇒a=−3/5,​c=10,​b=−1/5

The required quadratic equation: −3/5x²−1/5x+10

The quadratic equation: −3/5x²−1/5x+10

Carnegie Learning Algebra II – 1st Edition Chapter 2 Exercise 2.5 Solutions Page 302 Problem 11 Answer

Given: (1,17),(−1,−9),(2,105)

To find: The system of equations

A quadratic equation through given points.

Put these points in f(x)=ax²+bx+c

We will get three equations in a,b,c. Solve it by the substitution method.

For (1,17): a+b+c=17…(1)

For (−1,−9): a−b+c=−9…(2)

For (2,105): 4a+2b+c=105…(3)

a=17−b−c For 1…(4)

17−b−c−b+c=−9 From 2&4

−2b+17=−9

b=13

4(17−b−c)+2b+c=105

−2b−3c+68=105

−2⋅13−3c+68=105 Substitute​b=13

−3c+42=105

c=−21

a=17−13−(−21) From 4

a=25

⇒a=25,​c=−21,​b=13

The required quadratic equation: 25x²+13x−21

The quadratic equation: 25x²+13x−21

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice

Page 287 Problem 1 Answer

We have to explain the similarities and the difference between horizontal dilation, horizontal stretching, and horizontal compression of a quadratic function.

Given a quadratic function f(x)=ax²+bx+c,a≠0.Then we have the following transformations:

Horizontal dilation: When we replace the independent variable x in the equation of f by mx where m is a nonzero constant, it is called as horizontal dilation.

Depending upon the value of m,horizontal dilation has two classifications:

If m>1, then the graph of f(x) will be compressed horizontally by 1/m or we say the graph of f is compressed horizontally by a factor of 1/m.

This is called as horizontal compression.

If 0<m<1 , the graph of f(x) will be stretched horizontally by 1/m or we say the graph of f is stretched horizontally by a factor of 1/m.

This is called as horizontal stretching. Hence the similarity among the three is that they belong to the same category of transformation i.e the transformation occurs horizontally .

The difference between horizontal stretching and horizontal compression is that in the former case,the graph obtained after stretching is wider(in the horizontal direction) than the original graph of f(x) and in the latter case,the graph obtained after compression is narrower than the original graph of f(x).

The difference is illustrated below.

Hence we summarized the similarities and differences between horizontal dilation, horizontal stretching, and horizontal compression of a quadratic function.

Carnegie Learning Algebra II Chapter 2 Exercise 2.4 solutions

Page 287 Problem 2 Answer

We are given that f(x)=x² and that m(x)=f(1/5x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as m(x)=f(1/5x)

=(x/5)²

=x²/25

Now we complete the table

The graph of m(x) is  Plotting the graphs of f(x) and m(x) together we observe

Hence the graph of m(x) looks the graph of f(x) stretched horizontally by a factor of 5.

Hence we completed the table of m(x) and found that m(x) is the horizontal stretch of f(x).

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 288 Problem 3 Answer

We are given that f(x)=x² and that m(x)=f(1.5x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(1.5x)

=(1.5x)²

=2.25x²

Now we complete the table

The graph of m(x) is

Plotting the graphs of f(x) and m(x) together we observe

Hence the graph of m(x) looks like the graph of f(x) compressed horizontally by a factor of 1/1.5.

Since 1/1.5 =2/3, we can conclude m(x) is the horizontal compression of f(x) by a factor of 2/3.

Hence we completed the table of m(x) and found that m(x) is the horizontal compression of f(x).

Skills Practice Carnegie Learning Algebra II answers

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 288 Problem 4 Answer

We are given that f(x)=x² and that m(x)=f(4x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compare to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(4x)

=(4x)²

=16x²

Now we complete the table

The graph of m(x) is

Plotting the graphs of f(x) and m(x) together we observe

Hence the graph of m(x) looks like the graph of f(x) compressed horizontally by a factor of 1/4.

Since 1/4 =0.25, we can conclude that m(x) is the horizontal compression of f(x) by a factor of 0.25.

Hence we completed the table of m(x) and found that m(x) is the horizontal compression of f(x).

Page 288 Problem 5 Answer

We are given that f(x)=x² and that m(x)=f(0.25x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compare to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(0.25x)

=(0.25x)²

=0.0625x²

Now we complete the table

The graph of m(x) is

Plotting the graphs of f(x) and m(x) together we observe

Hence the graph of m(x) looks like the graph of f(x) stretched horizontally by a factor of 1/0.25.

Since 1/0.25 =100/25 =4, we can conclude m(x) is the horizontal stretch of f(x) by a factor of 4.

Hence we completed the table of m(x) and found that m(x) is the horizontal stretch of f(x).

Carnegie Learning Algebra II practice questions Chapter 2

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 289 Problem 6 Answer

We are given that f(x)=x² and that m(x)=f(2/3x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(2/3x)

=(2/3x)²

=4/9x²

Now we complete the table

The graph of m(x) is

Plotting graphs of f(x) and m(x) together we observe

Hence the graph of m(x) looks like the graph of f(x) stretched horizontally by a factor of 1×2/3.

Since 1×2/3

=3/2

=1.5, we can conclude m(x) is the horizontal stretch of f(x) by a factor of 1.5.

Hence we completed the table of m(x) and found that m(x) is the horizontal stretch of f(x).

Page 289 Problem 7 Answer

We are given that f(x)=x² and that m(x)=f(2x).

We are asked to complete the table and draw the graph of m(x).

We also have to describe how the graph of m(x) compares to the graph of f(x).

Since f(x)=x²

we have m(x) as

m(x)=f(2x)

=(2x)²

=4x²

Now we complete the table

The graph of m(x) is

Plotting the graphs of m(x) and f(x) together we observe

Hence the graph of m(x) looks like the graph of f(x) compressed horizontally by a factor of 1/2.

Since 1/2=0.5, we can conclude that m(x) is the horizontal compression of f(x) by a factor of 0.5.

Hence we completed the table of m(x) and found that m(x) is the horizontal compression of f(x).

Page 290 Problem 8 Answer

We are given the graph of f(x)

We have to sketch the graph of d(x)=f(−x).

The graph of the transformed function d(x) is the reflection of f(x) about the y−axis. Hence the graph of d(x) is

Hence we sketched the graph of d(x).

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 290 Problem 9 Answer

We are given the graph of f(x).

We have to sketch the graph of the transformed function t(x)=−f(x−4).

To obtain t(x) we first shift the graph of f(x) horizontally by constant 4. Since 4is positive, the graph shifts towards the right as shown below.

When the function f(x−4) is scaled by −1, the graph of f(x−4) reflects about the x−axis and we obtain the graph of t(x).

Hence we sketched the graph of t(x).

Page 290 Problem 10 Answer

It is given the graph of the function f(x)

It is asked to sketch the graph of the function m(x)=−2f(x+3)+5.

To do this first find out the function f(x) by using the slope formula.

By using the function f(x) find the function m(x) and finally, sketch the function m(x).

From the given graph observe that the function f(x) passes through the point (0,0), and (1,1).

So the slope of the function will be 1−0/1−0 which is nothing but 1 .

So, the equation of the graph of the function f(x) will be f(x)=x+c.

Again the graph f(x) passes through the point (0,0).So, c=0.

So, the equation of the function f(x) will be f(x)=x.

Now find out the function m(x) by substituting x+3 instead of x in f(x).

m(x)=−2f(x+3)+5

m(x)=−2(x+3)+5

m(x)=−2x−6+5

m(x)=−2x−1

Now, sketch the graph of the function m(x)=−2x−1.

In the above graph X′OX and Y′ OY are considered as x−axis and y−axis respectively.

Hence the graph of the function m(x)=−2f(x+3)+5  is as follows:

Chapter 2 Exercise 2.4 Carnegie Learning Algebra II key

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 290 Problem 11 Answer

It is given a graph of a function. It is asked to find the graph of the function g(x)=f(−x+1)−4.

To find the graph of the function g(x) first, move down the graph of the function y=f(x) 4units.

Then take the reflection of the resulting graph with respect toy−axis .

Then shift the graph one unit to the left.

We have a graph of a function y=f(x).

Since we are interested to find the graph of the function g(x)=f(−x+1)−4, so first shift down the graph 4units.

Then the resultant graph will be as follows:

Now, take the reflection of the resultant graph with respect to the y−axis.

Then the resultant graph will be as follows:

Finally shift the resultant graph one unit left to the present position:

Then the resultant graph will be:

So, the graph of the function g(x)=f(−x+1)−4 will be as follows:

Hence, the graph of the function g(x)=f(−x+1)−4 is as follows:

Page 291 Problem 12 Answer

It is given a graph of a parabolic function y=f(x) whose vertex is at (−3,0) and the parabola passes through the point(−5,−4).

It is asked to find the graph of the transformed function r(x)=f(x/2+1)+2.

To find the transformed function first, find the explicit function of the parabola.

Then substitute x/2+1 instead of x and add 2.

Observe that in the given graph the parabola passes through the point (−5,4) and the vertex of the parabola is at (−3,0).

Now, we know that the general equation of the parabola having an axis parallel to negative y−axis is(x−α)²=−4ay .

So, the equation of the given parabola will be (x+3)²=−4ay.

Also, this parabola passes through the point (−5,−4).

So, (−5+3)²=−4a(−4)

So, a=4/16 and therefore a=1/4.

So, the equation of the parabola will be (x+3)²=−y.

So, f(x)=−(x+3)²

Now, to find the function r(x)=f(x/2+1)+2, substitute x/2+1 instead of x in the following way:

r(x)=f(x/2+1)+2

=−(x/2+1+3)²+2

=−(x/2+4)²+2

=−1/4(x+8)²+2

So, the graph of the transformed function r(x) is as follows:

Hence, the graph of the transformed function r(x) is as follows:

How to solve Chapter 2 Exercise 2.4 Algebra II Carnegie Learning

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 291 Problem 13 Answer

It is given a graph of a function f(x) and it is asked to find the graph of a function p(x)=−f(x+1)−3 .

First, find the coordinates of all the points.

Then shift down the graph 3 units. Next, shift the graph to left at 1 unit an f finally take a reflection about x axis.

We are interested to find the graph of p(x)=−f(x+1)−3.

First shift down the graph 3 units and then the resulting graph will be as follows:

Next, shift the resulting graph to the left at 1 unit and then the resulting graph will be as follows:

Finally, take the reflection of the resulting graph with respect to  x-axis

So, the graph of the function will be as follows:

Hence, the required graph of the function p(x)=−f(x+1)−3 will be as follows:

Page 291 Problem 14 Answer

It is given two parabolas w(x) and v(x) and w(x) is transformed to v(x).

It is asked to find the equation of w(x) in terms of v(x).

To do this apply the transformation to the function v(x) to get the function w(x).

First, observe that the vertex of the parabola given by the function w(x) is (0,3) and the vertex of the parabola v(x) is (5,5).

So, first, move the parabola given by the function v(x) to the left side of 5 units. So, the resulting parabola is v(x+5).

Next, drag the resulting parabola vertically downward of 2 units. So the resulting parabola will be v(x+5)−2.

Now, invert the resulting parabola. So, the final equation of the parabola will be −(v(x+5)−2) and this is nothing but the parabola given by the function w(x).

So, w(x)=−(v(x+5)−2)

Hence the equation of the parabola given by the function w(x) in terms of v(x) is w(x)=−(v(x+5)−2)

Page 292 Problem 15 Answer

It is given the graph of the equation of the straight line y=x by w(x) and the graph of the equation y=−x+3 by v(x).

It is asked to write the function w(x) in terms of the function v(x).

To do this apply the transformations to the function v(x) to get the function w(x).

The function v(x) is the straight line passing through the origin.

Take the reflection of the function v(x) with respect to x−axis and then the resulting function will be −v(x).

Then move the resulting function upward at 3 units.

So, the resulting function will be −v(x)+3 and this function is nothing but the function w(x).

So, the function w(x) an be written as w(x)−v(x)+3.

Hence the function w(x) can be written in terms of the function v(x) as w(x)=−v(x)+3.

Algebra II Carnegie Learning skills practice solutions

Carnegie Learning Algebra II Student Skills Practice 1st Edition Chapter 2 Exercise 2.4 Skills Practice Page 292 Problem 16 Answer

It is given a graph of the parabola whose axis is parallel to negative y−axis and vertex is at (−4,6) by the function v(x) and a parabola whose axis is  parallel to negative y−axis and vertex is at(4,−4)

by the function w(x).It is asked to find an equation of w(x) in terms of v(x).

To do this apply the transformation to the function v(x)  to get the function w(x).

First, move down the parabola given by the function v(x) by 10 units.

Then the resulting function will be v(x)−10.

Then move the resulting function at the right side 8 units.

Then the resulting function will be v(x−8)−10 and this is nothing but the function given by w(x)

Hence, the equation for w(x) in terms of v(x) is w(x)=v(x−8)−10.

Page 292 Problem 17 Answer

It is given the graphs of the two functions w(x) and v(x).

It is asked to write the equation for the function w(x) in terms of the function v(x).

To do this first, apply the transformation to the function v(x) and then get the function w(x).

First, move the function v(x) to the right side by 3units.

So, the resulting graph of the function will be v(x−8).

Now, take the reflection with respect to y−axis of the resulting graph of the function.

Then the resulting graph of the function will be v(−(x−8)) and this is nothing but the function w(x).

Hence, the equation of the function w(x) in terms of v(x) will be w(x)=v(−x+8).