Alekhya

Financial Algebra 1st Edition Chapter 4 Consumer Credit Page 188 Problem 1 Answer

The given data is, ​P=18000

T=8yrs

R=4.3%

How much will she pay in interest

The interest is calculated as,

I=PTR/100

=18000×8×4⋅3/100

=$6192

Therefore, the solution is calculated as, $6192.

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit ​Page 189 Problem 2 Answer

Considering the previous example’s values.

Calculate the impact an increase in the monthly payment of $50 has on the length of the loan.

The loan length is calculated as,

⇒ \(=\frac{\ln \left(\frac{M}{P}\right)-\ln \left(\left(\frac{M}{p}-\frac{r}{12}\right)\right)}{12 \ln \left(1+\frac{\gamma}{12}\right)}\)

Additional amount = $50

Initial = $300

⇒ \(t=\frac{\ln \left(\frac{350}{25000}\right)-\ln \left(\frac{350}{25000}-\frac{5.9}{100^* 12}\right)}{12 \ln \left(1+\frac{5.9}{12 * 100}\right)}\)

⇒ \(=\frac{-4.2687-(-4.7013)}{0.05885}\)

= 7.35

= 7 years

Therefore, the solution is calculated as, 7 years.

Cengage Financial Algebra Chapter 4.3 Consumer Credit Guide

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 190 Problem 3 Answer

Considering the previous example’s values.

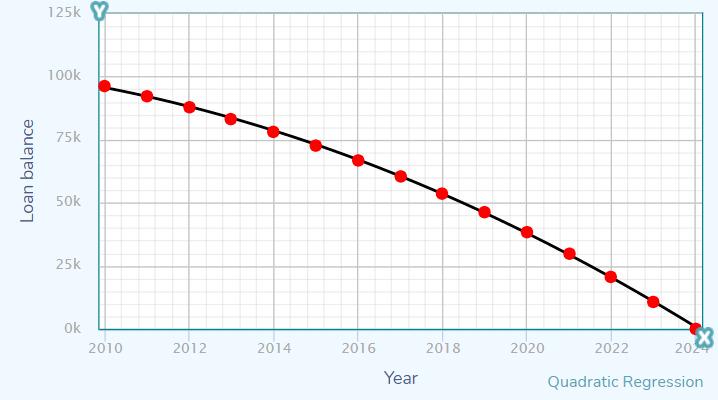
Compare the computed loan balances when x=2

The linear equation is, y=−6777,539x+13726080,

The quadratic equation is, y=−1007797000+1006140x−251,0951x²,

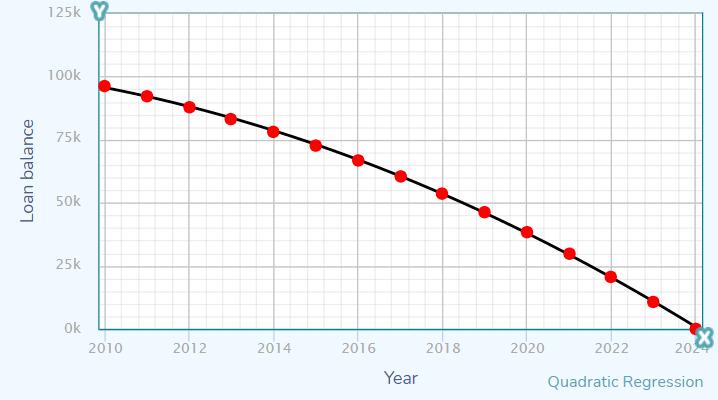
The cubic equation is, y=50082020000,00001−74983100x+37423,4x²−6,22616x³

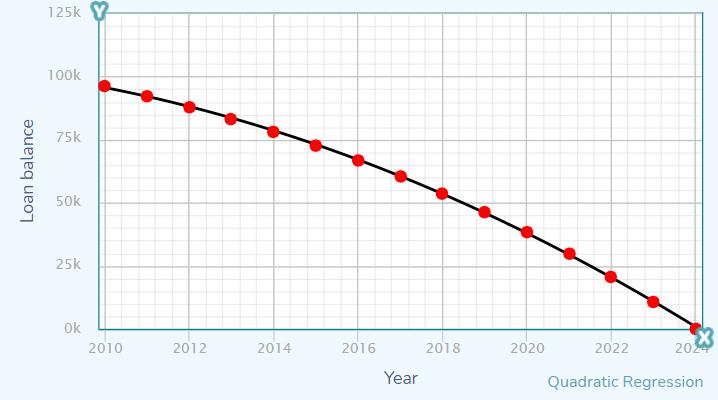
Therefore, the solution is calculated for the equations and proved using the graphs.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 4 Answer

Find how might the quote apply to what you have learned

The quote implies that the loan and debts are considered as, which worries because this makes sure that the payment of the loan occurs every month on time and thus needs to make sure that enough money is set aside each month to pay for the loan.

But if the loans are failed to pay off, it is possible to lose everything.

Therefore, the payments of the loans have to be paid on time every month, to avoid worries.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 5 Answer

The given data is,​P=32000

r=6.1 %

t=10 yrs

​Calculate the total interest.

Hence the monthly payment formula is,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{32,000\left(\frac{0.061}{12}\right)\left(1+\frac{0.061}{12}\right)^{12 \times 10}}{\left(1+\frac{0.061}{12}\right)^{12 \times 10}-1}\)

⇒ \(\Rightarrow M=\$ 356.87\)

The total paid is the product of the monthly payment as,

$356.87×12×10=$42,824.40

$42,824.40−$32,000=$10,824.40

​Therefore, the solution is calculated as, $10824.4.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 6 Answer

The given data is, ​P=15000

t=4 yrs

r=5.5 %​

Calculate how much will the person pay in interest over the life of the loan.

Hence the monthly payment formula is,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{15,000\left(\frac{0.055}{12}\right)\left(1+\frac{0.055}{12}\right)^{12 \times 4}}{\left(1+\frac{0.055}{12}\right)^{12 \times 4}-1}\)

⇒ \(M=\$ 348.85\)

The total paid is the product of the monthly payment as,

$348.85×12×4=$16,744.80

$16,744.80−$15,000=$1,744.80

​Therefore, the solution is calculated as, $1744.8.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 7 Answer

The given data is, ​P=7000

t=8 yrs

r=8.6 %

​Calculate which loan will have the lower interest Over its lifetime.

Hence the monthly payment formula is,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{7,000\left(\frac{0.086}{12}\right)\left(1+\frac{0.086}{12}\right)^{12 \times 8}}{\left(1+\frac{0.086}{12}\right)^{12 \times 8}-1}\)

⇒ \(M=\$ 101.10\)

The total paid is the product of the monthly payment and the number of payments,

$101.10×12×8=$9,705.60

$9,705.60−$7,000=$2,705.60

Hence the monthly payment formula is,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{7,000\left(\frac{0.10}{12}\right)\left(1+\frac{0.10}{12}\right)^{12 \times 5}}{\left(1+\frac{0.10}{12}\right)^{12 \times 5}-1}\)

⇒ \(M=\$ 148.73\)

The total paid is the product of the monthly payment and the number of payments,

$148.73×12×5=$8,923.80

$8,923.80−$7,000=$1,923.80

Therefore, the solution is considered as first national bank.

Solutions For Exercise 4.3 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 8 Answer

The given data is, ​P=$25000

r=7.7 %

t=2 to 10 yrs

Find the monthly payment formula for this loan situation.

Let t represent the number of years from 2 to 10 inclusive.

Hence the monthly payment formula is,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{25,000\left(\frac{0.077}{12}\right)\left(1+\frac{0.077}{12}\right)^{12 \times t}}{\left(1+\frac{0.077}{12}\right)^{12 \times t}-1}\)

⇒ \(M=\frac{160.417 \times 1.00642^{12 \times t}}{1.00642^{12 \times t}-1}\)

Therefore, the solution is calculated as, M=160.417×1.0064212×t/1.0064212×t−1

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 9 Answer

The given data is,​P=$25000

r=7.7%

t=2 to 10 yrs ​

Find the total interest formula for this loan situation.

Let t represent the number of years from 2 to 10 inclusive.

⇒ \(M=\frac{160.417 \times 1.00642^{12 \times t}}{1.00642^{12 \times t}-1}\)

⇒ \(\frac{160.417 \times 1.00642^{12 \times t}}{1.00642^{12 \times t}-1} \times 12 \times t\)

⇒ \(\frac{160.417 \times 1.00642^{12 \times t}}{1.00642^{12 \times t}-1} \times 12 \times t-25,000\)

Therefore, the solution is 160.417×1.0064212×t/1.0064212×t−1×12×t−25,000

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 10 Answer

The given data is,​P=$25000

r=7.7%

t=2 to 10yrs

Construct a graph

The graph is drawn as,

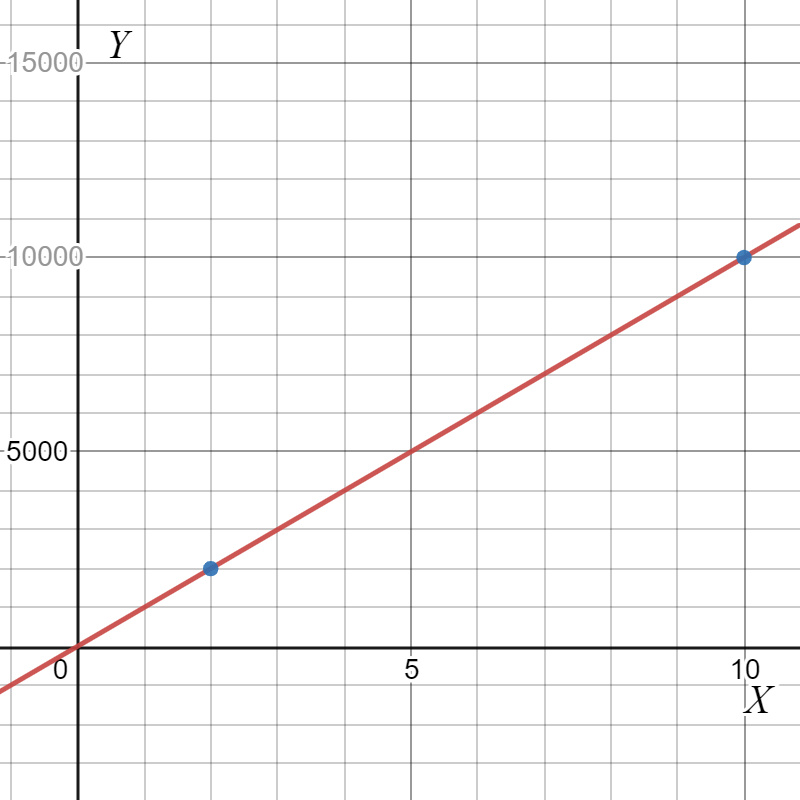
Therefore, the graph is drawn as, x is horizontal and y is vertical axis.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 11 Answer

The given data is, P=$25000

r=7.7 %

t=2 to10 yrs

​Use your graph to estimate the interest for a 6×1/2-year loan.

After plotting the graph, if t is an amount of 6 and a half, then the interest is about $6900.

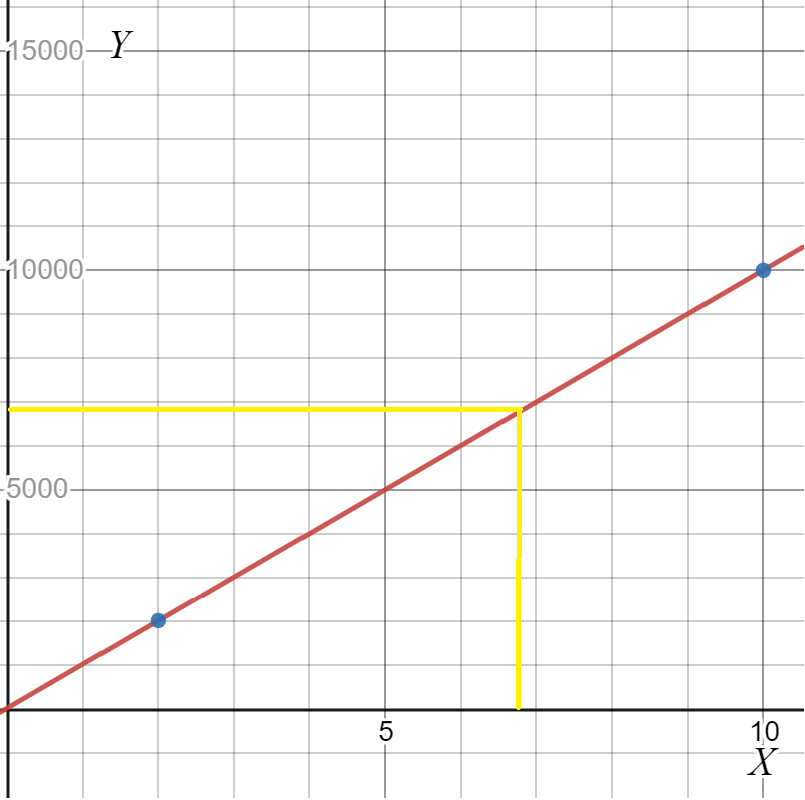
Therefore, the graph was plotted and the solution was $6900.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 12 Answer

The given data is, ​P=$20000

r=7.1 %

t=1/10 yr​

Find the length of the loan.

Substituting the values,ln500

20000−(ln(500/20000−0.071/12))/12ln(1+0.071/12)

t=3.8 years

​Therefore, the solution is calculated as nearly 3.8 years.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 13 Answer

The given data is, ​M=$350

p=14,000

r=6.8

​Calculate the number of years.

⇒ \(t=\frac{\ln \left(\frac{M}{p}\right)-\ln \left(\frac{M}{p}-\frac{r}{12}\right)}{12 \ln \left(1+\frac{r}{12}\right)}\)

⇒ \(=\frac{\ln \left(\frac{350}{14000}\right)-\ln \left(\frac{350}{14000}-\frac{0.068}{12}\right)}{12 \ln \left(1+\frac{0.068}{12}\right)}\)

⇒ \(≈3.8 years\)

Therefore, decreasing the monthly payments by $50, increased the length of the loan by 0.5 years.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 191 Problem 14 Answer

The given data is,​P=$22000

t=15 years

r=4.85 %

​Calculate how much will he pay the bank in interest over the life of the loan.

The monthly payment formula is,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{22,000\left(\frac{0.0485}{12}\right)\left(1+\frac{0.0485}{12}\right)^{12 \times 15}}{\left(1+\frac{0.0485}{12}\right)^{12 \times 15}-1}\)

M= $172.26

The total paid is the product of the monthly payment,

⇒ \(\$ 172.26 \times 12 \times 15=\$ 31,006.80\)

⇒ \(\$ 31,006.80-\$ 22,000=\$ 9,006.80\)

≈$9000.

Therefore, the solution is calculated as, $9000.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 1 Answer

Considering the table for the given yearly payment schedule. Calculate the loan amount.

Therefore, the value under the loan balance in the payment schedule is calculated as, $10000.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 2 Answer

Considering the table for the given yearly payment schedule. Calculate the length of the loan.

Therefore, the last value under the year column is 10 years.

Chapter 4 Exercise 4.3 Consumer Credit Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 3 Answer

Considering the table for the given yearly payment schedule. Calculate the monthly payment.

The principal is considered as, 1455.93.

Dividing it by 12 to get the monthly pay,

1455.93/12≈121.33

Therefore, the solution is 121.33.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 4 Answer

Considering the table for the given yearly payment schedule. Calculate the total interest paid.

Therefore, the total interest is calculated as, $4559.31, added from the entries under interest paid.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 5 Answer

Considering the table for the given yearly payment schedule. Construct a scatterplot using the data points (year, loan balance).

The graph was plotted as shown,

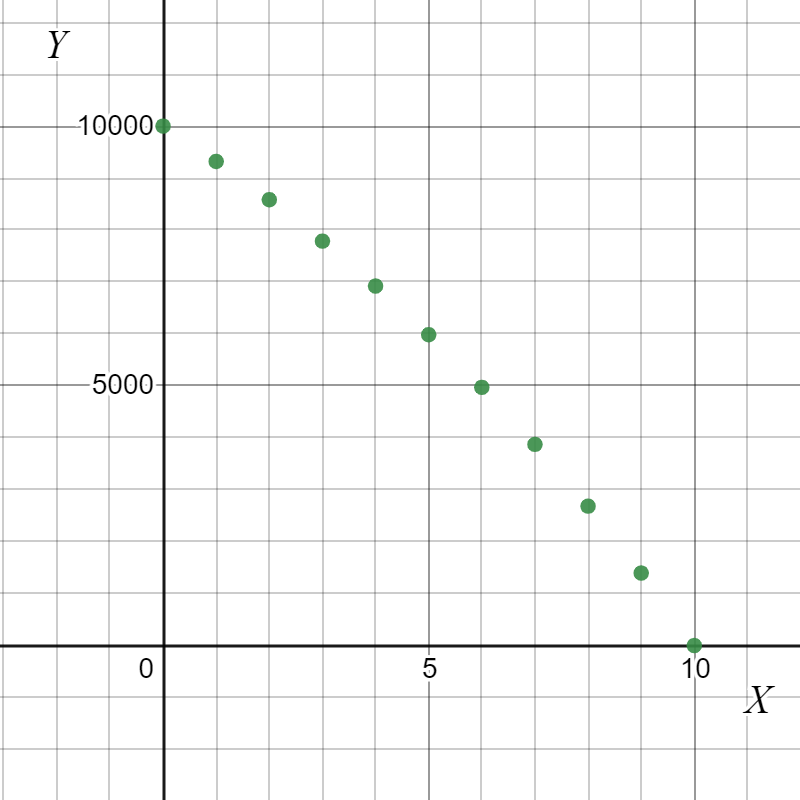
Therefore, the given graph was plotted as,

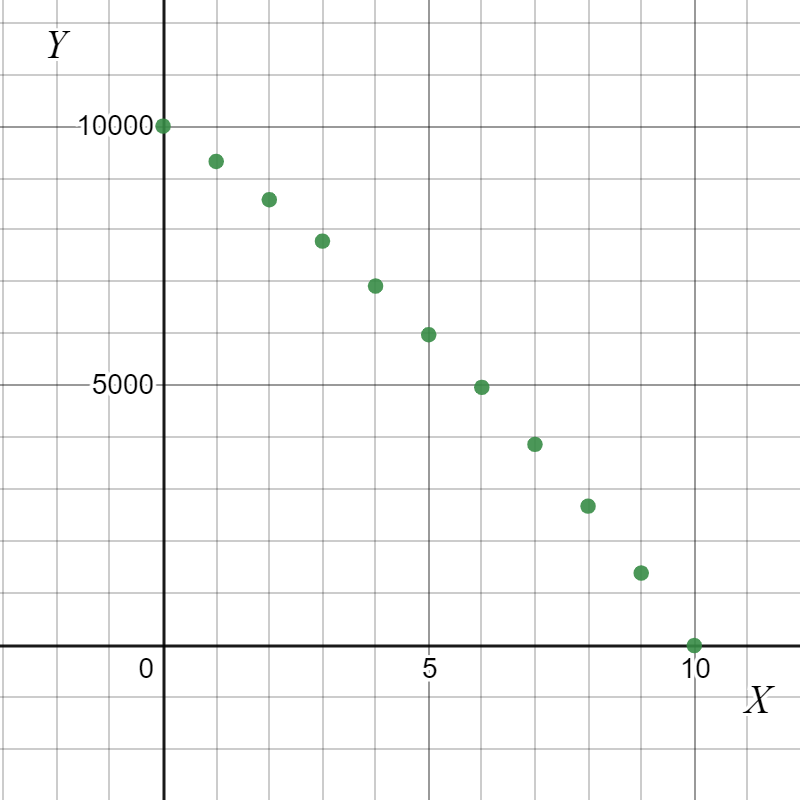
Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 6 Answer

Given a yearly payment schedule

To do: Write a linear regression

Determining the regression using STAT> CALC>4:LinReg(ax+b)L1,L2 then we get the following

​y=ax+b

a≈−992.49

b≈10554.14

Substituting in the equation y=ax+b

we get y=−992.49x+10554.14

Therefore, the linear regression equation is y=−992.49x+10554.14

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 7 Answer

Given a yearly payment schedule

To do: Write a quadratic regression

Determining the regression using STAT> CALC>5:QuadReg L1,L2 then we get the result as follows

y=ax²+bx+c

a≈−39.35

b≈−599.01

c≈9963.93

Substituting in the form of the quadratic equation we get

y=−39.35x²−599.01x+9963.93

Therefore, the quadratic regression equation is y=−39.35x²−599.01x+9963.93

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 8 Answer

Given a yearly payment schedule

To do: Write a cubic regression

Determining the regression equation using STAT>CALC>6: CubicReg L1,L2 then we get the results as

​y=ax³+bx²+cx+d

a≈−1.04

b≈−23.71

c≈−658.64

d≈−10001.46

substituting in the equation we get

y=−1.04x³−23.71x²−658.64x+10001.46

Therefore, the cubic regression equation is y=−1.04x³−23.71x²−658.64x+10001.46

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 9 Answer

Given a payment schedule

To do: Find the loan amount

The first number given in the column of the loan balance is 35,000.00 $ then the loan amount will be this

Therefore, the loan amount is 35,000.00 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 10 Answer

Given the payment schedule

To do: Find the length of the loan

The starting year is 2009 and the ending year is 2027 the difference between them is 18

so, the length of the loan is 18 years

Therefore, the length of the loan is 18 years

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 11 Answer

Given a payment schedule

To do: Find the approximate monthly payment

The summation of principal paid and interest paid for the value of 4065.23 then

4065.23/12≈338.77

so, the monthly payment will be 338.77 $

Therefore, the monthly payment is 338.77 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 12 Answer

Given a payment schedule

To do: Find the total interest paid

Summation of all the year’s interests we get​=3291.90+3215.15+3130.78+3038.04+2936.10+2824.03+2700.85+2565.44+2416.59+2252.96+2073.10+1875.39+1658.05+1419.14+1156.53+867.84+550.51+201.69

=$38,174.09

​Therefore, the total interest paid 38,174.09 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 13 Answer

Given a payment schedule

To do: Construct a scatter plot

The graph of the year-to-load balance is as

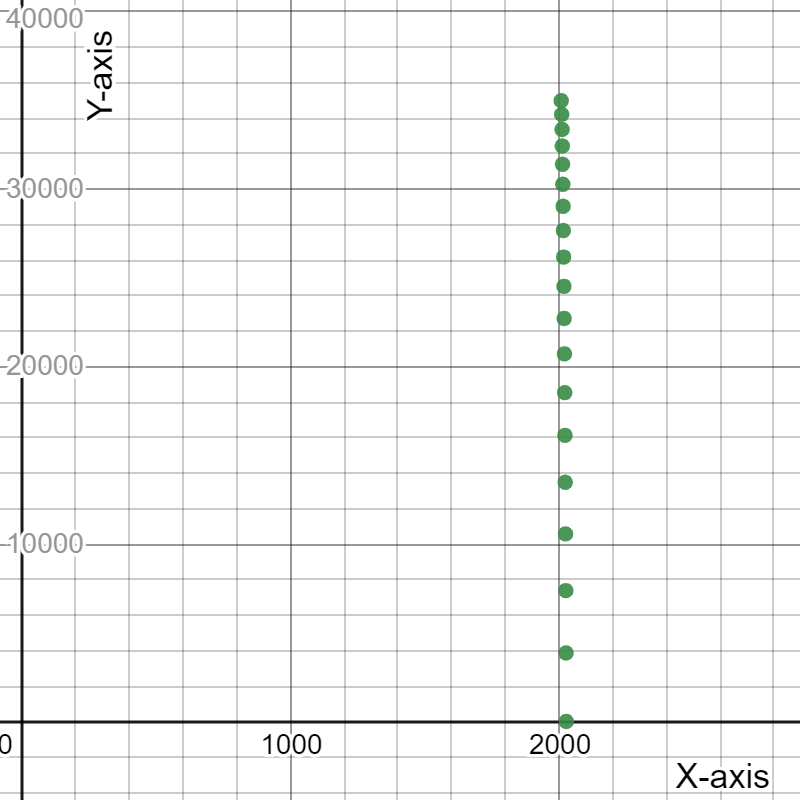
Therefore, the scatter plot is as

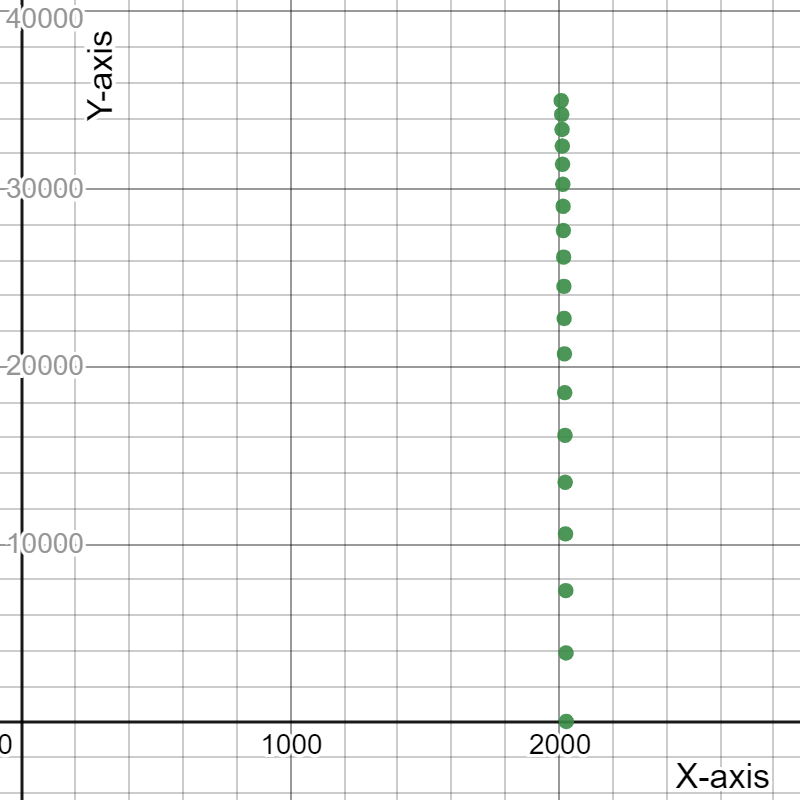
Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 14 Answer

Given a payment schedule

To do: Find the linear regression

Determining the regression using STAT> CALC>4: Lin Reg(ax+b) L1,L2 then we get the result as

y=ax+b

a≈−1870.62

b≈3796896.07

Substituting in the line equation we get y=−1870.62x+3796896.07

Therefore, the linear regression is y=−1870.62x+3796896.07

Cengage Financial Algebra Consumer Credit Exercise 4.3 Solutions

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 15 Answer

Given a  payment schedule

To do: Write a quadratic regression

Determining the regression using STAT> CALC>5: QuadRegL1,L2 using these we get

​y=ax²+bx+c

a≈−76.07

b≈−305369.01

c≈306434730.37

Substituting the values in the quadratic equation we get

y=−76.07x²−305369.01x+306434730.37

Therefore, the quadratic regression is y=−76.07x²−305369.01x+306434730.37

How To Solve Cengage Financial Algebra Chapter 4.3 Consumer Credit

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.3 Consumer Credit Page 192 Exercise 16 Answer

Given a payment schedule

To do: Write a cubic regression

Determining the regression using STAT> CALC>6: CubicReg L1, L2 and the results using this are

y=ax³+bx²+cx+d

a≈−2.81

b≈16936.85

c≈−34,006,808.68

d≈2.2760898E10≈22,760,898,000​

substituting the values in the general equation we get

y=−2.81×3+16936.85x²−34,006,808.68x+22,760,898,000

Therefore, the cubic regression equation is y=−2.81×3+16936.85x²−34,006,808.68x+22,760,898,000

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 183 Problem 1 Answer

We are given: p=$41,000

r=0.065

t=5 .

We have to find the monthly payment.

We will be using the formula of monthly payment :

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

We will substitute the given values in the formula

⇒ \(M=\frac{41000\left(\frac{0.065}{12}\right)\left(1+\frac{0.065}{12}\right)^{12(5)}}{\left(1+\frac{0.065}{12}\right)^{12(5)}-1}\)

⇒ \(M=\frac{41000(0.0054166666666667)(1+0.00541666666666667)^{60}}{(1+0.00541666666666667)^{60}-1}\)

⇒ \(M=\frac{222.0833333333333(1.0054166666666667)^{60}}{(1+0.0054166666666667)^{60}-1}\)

⇒ \(M=\frac{222.0833333333333(1.38281732421)}{0.38281732421}\)

⇒ \(M=\frac{307.1006807516375}{0.38281732421}\)

⇒ \(M=802.2120769622562\)

The monthly payment is $802.2120769622562, we can round off the answer to the nearest cent.

Therefore, we get $802.21

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 184 Problem 2 Answer

We are given: Borrowed money=x dollars

Monthly payment=y dollars

Number of years=3

Number of months=36.

We have to express the finance charge algebraically.

Firstly, we will find the total of monthly payments.

The total of monthly payments is given by: 36×y=36y dollars.

Now, we will find the finance charge.

Total amount of monthly payments−Borrowed amount

Finance charge=36y−x dollars.

We can express the finance charge algebraically as 36y−x dollars.

Cengage Financial Algebra Chapter 4.2 Consumer Credit Guide

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 184 Problem 3 Answer

We are given: p=$1000

r=0.075

t=1 .

We have to find the monthly payment.

We will be using the formula of monthly payment :

We will substitute the given values in the formula

⇒ \(M=\frac{1000\left(\frac{0.075}{12}\right)\left(1+\frac{0.075}{12}\right)^{12(1)}}{\left(1+\frac{0.075}{12}\right)^{12(1)}-1}\)

⇒ \(M=\frac{1000(0.00625)(1+0.00625)^{12(1)}}{\left(1+\frac{0.075}{12}\right)^{12(1)}-1}\)

⇒ \(M=\frac{1000(0.00625)(1.00625)^{12}}{\left(1+\frac{0.075}{12}\right)^{12}-1}\)

⇒ \(M=\frac{(6.25)(1.07763259886)}{(1.07763259886)^{12}-1}\)

⇒ \(M=\frac{(6.25)(1.07763259886)}{(1.07763259886)-1}\)

⇒ \( M=\frac{6.735203742875}{0.07763259886}\)

⇒ \(M=86.75741689214363 \)

The monthly payment is$86.75741689214363.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 4 Answer

We are given that :

Monthly payments are made for a five-year loan and a two-year loan.

We have to find how many more monthly payments are made for a five-year loan than for a two-year loan.

Number of monthly payments is the product of 12 months and number of years.

Several monthly payments for a five-year loan is given by: 12×5=60.

Number of monthly payments for a five-year loan is given by:12×2=24.

Now, we will subtract the number of monthly payments for a two-year loan from the number of monthly payments for a five-year loan.

60−24=36 .

36 more monthly payments are made for a five-year loan than for a two-year loan.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 5 Answer

We are given: an A2x1/2 loan.

We have to find the number of monthly payments that must be made for a 2×1/2-year loan.

Number of monthly payments is the product of 12 months and number of years.

Number of monthly payments for a 2 x1/2 loan is given by :

​2×1/2×12=5

2×1/2

2×1/2×12=2.5×12

2×1/2×12=60 .

​60 monthly payments must be made for a 2×1/2-year loan.

Number of monthly payments for a2x1/2the loan is given by :

​2×1/2×12=5

2×1/2

2×1/2×12=2.5×12

2×1/2×12=60 .

​60 monthly payments must be made for a 2×1/2-year loan.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 6 Answer

We are given: p=$7000

r=0.0975

t=1.

We have to find the monthly payment for a one-year loan

We will be using the formula of monthly payment.

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1} .\)

We will substitute the given values in the formula

⇒ \(M=\frac{7000\left(\frac{0.0975}{12}\right)\left(1+\frac{0.0975}{12}\right)^{12(1)}}{\left(1+\frac{0.0975}{12}\right)^{12(1)}-1}\)

⇒ \(M=\frac{7000(0.008125)(1+0.008125)^{12}}{(1+0.008125)^{12}-1}\)

⇒ \(M=\frac{56.875(1.10197721973)}{1.10197721973-1}\)

⇒ \(M=\frac{62.67495437214375}{0.10197721973}\)

M = 614.5975987390625.

The monthly payment for a one-year loan is $614.5975987390625, we can round off the answer to the nearest cent.

Therefore we get $614.60.

Solutions For Exercise 4.2 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit  Page 185 Problem 7 Answer

The given data is, ​p=7,000,

r=0.0975,

t=3

Calculate the monthly payment for a three-year loan.

Substituting the given data as

⇒ \(M=\frac{7000\left(\frac{0.0975}{12}\right)\left(1+\frac{0.0975}{12}\right)^{12(3)}}{\left(1+\frac{0.0975}{12}\right)^{12(3)}-1}\)

⇒ \(M=\frac{7000\left(\frac{0.0975}{12}\right)\left(1+\frac{0.0975}{12}\right)^{36}}{\left(1+\frac{0.0975}{12}\right)^{36}-1}\)

Using the calculator, \(\frac{7000(0.0975 / 12)(1+0.0975 / 12) 36}{(1+0.0975 / 12)^{36}-1}=225.05\)

Therefore, the solution was calculated as, $225.05

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 8 Answer

The given data is, ​p=7,000,

r=0.0975,

t=3

​Calculate the monthly payment for a five-year loan.

Substituting the given data as

⇒ \(M=\frac{7000\left(\frac{0.0975}{12}\right)\left(1+\frac{0.0975}{12}\right)^{12(5)}}{\left(1+\frac{0.0975}{12}\right)^{12(5)}-1}\)

⇒ \(M=\frac{7000\left(\frac{0.0975}{12}\right)\left(1+\frac{0.0975}{12}\right)^{60}}{\left(1+\frac{0.0975}{12}\right)^{60}-1}\)

Using the calculator, \(\frac{7000(0.0975 / 12)(1+0.0975 / 12)^{60}}{(1+0.0975 / 12)^{60}-1}=147.87\)

Therefore, the solution was calculated as, $147.87.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 9 Answer

The given data is, ​​p=10,000,

r=0.0725,

t=3

​Calculate the monthly payment.

Substituting the given data as

⇒ \(M=\frac{10000\left(\frac{0.0725}{12}\right)\left(1+\frac{0.0725}{12}\right)^{12(3)}}{\left(1+\frac{0.0725}{12}\right)^{12(3)}-1}\)

⇒ \(M=\frac{10000\left(\frac{0.0725}{12}\right)\left(1+\frac{0.0725}{12}\right)^{36}}{\left(1+\frac{0.0725}{12}\right)^{36}-1}\)

Using the calculator \(\frac{10000(0.0725 / 12)(1+0.0725 / 12)^{36}}{(1+0.0725 / 12)^{36}-1}=309.92\)

Therefore, the solution was calculated as, $309.92.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 10 Answer

The given data is, ​​p=10,000,

r=0.0725

t=3

​Calculate the total amount of the monthly payments.

Considering the previous question as the Monthly payment is 309.92, The total of monthly payments as,309.92×36=11157.12.

Therefore, the solution is calculated as, 309.92.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 11 Answer

The given data is, ​ p​=10,000

r=0.0725

t=3

Calculate the finance charge.

Considering the previous question as,

The total of monthly payments is, $11,157.12, Subtracting principal from a total of monthly payments,

​​11,157.12−10,000=1,157.12.

Therefore, the solution is calculated as, $1157.12.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 12 Answer

The given data is,​​p=6,000,

r=0.1,

t=4

​Calculate the monthly payment.

Substituting the values as

⇒ \(M=\frac{6000\left(\frac{0.1}{12}\right)\left(1+\frac{0.1}{12}\right)^{12(4)}}{\left(1+\frac{0.1}{12}\right)^{12(4)}-1}\)

⇒ \(M=\frac{6000\left(\frac{0.1}{12}\right)\left(1+\frac{0.1}{12}\right)^{48}}{\left(1+\frac{0.1}{12}\right)^{48}-1}\)

Using the calculator, \(\frac{6000(0.1 / 12)(1+0.1 / 12)^{48}}{(1+0.1 / 12)^{48}-1}=152.18\)

​Therefore, the solution is calculated as, $152.18.

Chapter 4 Exercise 4.2 Consumer Credit Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 13 Answer

The given data is,​​p=6,000,

r=0.1

t=4

​Find the total amount of the monthly payments.

Considering the previous question, the Monthly payment is 152.18.

The total of monthly payments is 152.18×48=7,304.64.

Therefore, the solution is calculated as, $7304.64

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 14 Answer

The given data is,​​p=6,000,

r=0.1

t=4

​Calculate the finance charge.

Considering the previous question, The total of monthly payments is, 7304.64, Subtracting principal from the total of monthly payments,

7,304.64−6,000=1,304.64

Therefore, the solution is calculated as, 1304.64.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Problem 15 Answer

The given data is,​R=$3000

N=$1200

v=35 %

​Calculate the maximum amount that could be borrowed from Broadway.

This shows that the collateral for a loan is, 3000+1200=4200 USD

Since the borrower’s value is 35 %, 4200×0.35=1470 USD.

Therefore, the solution is calculated as 1470 USD.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Exercise 1 Answer

The given data is,​​p=8,700,

r=0.0931,

t=3.5

​Calculate the monthly payment for this loan.

Substituting the values in the formula, Using the calculator,

⇒ \(M=\frac{8700\left(\frac{0.0931}{12}\right)\left(1+\frac{0.0931}{12}\right)^{12(3.5)}}{\left(1+\frac{0.0931}{12}\right)^{12(3.5)}-1}\)

⇒ \(M=\frac{8700\left(\frac{0.0931}{12}\right)\left(1+\frac{0.0931}{12}\right)^{42}}{\left(1+\frac{0.0931}{12}\right)^{42}-1}\)

​(8700(0.0931/12)(1+0.0931/12)∧42)/((1+0.0931/12)∧42−1)​

Therefore, the solution is calculated as, $243.52.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 185 Exercise 2 Answer

The given data is, ​p=7500

r=6.875 %

Calculate how many monthly payments the person makes.

The monthly payments are calculated as, Multiply 6 by 12.

1 year =12 months.

So 6 years 6×12=72 months.

Therefore, the solution is calculated as 72 months.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 3 Answer

The given data is, ​P=15320

r=10.29 %

Calculate the finance charge for this loan to the nearest dollar.

Substituting the value is substituted as,​

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{15,320\left(\frac{0.1029}{12}\right)\left(1+\frac{0.1029}{12}\right)^{12 \times 2}}{\left(1+\frac{0.1029}{12}\right)^{12 \times 2}-1}\)

⇒ \(\$ 708.99 \times 12 \times 2=\$ 17,015.76\)

⇒ \(\$ 17,015.76-\$ 15,320=\$ 1,695.76\)

Therefore, the solution is calculated as, $1695.76.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 4 Answer

The given data is that the credit union will lend the person $8000 for three years at 8.25 % APR.

The same loan at her savings bank has an APR of 10.5 %.

Calculate how much would the given person would save in finance charges if joined the credit union.

Using the monthly payment formula,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{8,000\left(\frac{0.0825}{12}\right)\left(1+\frac{0.0825}{12}\right)^{12 \times 3}}{\left(1+\frac{0.0825}{12}\right)^{12 \times 3}-1}\)

⇒ \(M=\$ 251.61\)

⇒ \(\$ 251.61 \times 12 \times 3=\$ 9,057.96\)

⇒ \(\$ 9,057.96-\$ 8,000=\$ 1,057.96\)

Also calculating the values as,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{8,000\left(\frac{0.105}{12}\right)\left(1+\frac{0.105}{12}\right)^{12 \times 3}}{\left(1+\frac{0.105}{12}\right)^{12 \times 3}-1}\)

⇒ \(M=\$ 260.02\)

⇒ \(\$ 260.02 \times 12 \times 3=\$ 9,360.72\)

⇒ \(\$ 9,360.72-\$ 8,000=\$ 1,360.72\)

⇒ \(\$ 1,360.72-\$ 1,057.96=\$ 302.76\)

Therefore, the solution is calculated as, $302.76.

Cengage Financial Algebra Consumer Credit Exercise 4.2 Solutions

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 5 Answer

The given data is, ​P=$5000

d=$800

n=$202.5

​Calculate the interest on this installment agreement.

The paid is the product of the monthly payments as,

​$202.50×12×2+$800=$5,660

$5,660−$5,000=$660

​Therefore, the solution is calculated as, $660.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 6 Answer

The given data is, ​P=$5000

d=$800

n=$202.5

​Calculate the monthly payment for this loan using the table.

The monthly payment formula is as,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{5,000\left(\frac{0.13}{12}\right)\left(1+\frac{0.13}{12}\right)^{12 \times 2}}{\left(1+\frac{0.13}{12}\right)^{12 \times 2}-1} \)

⇒ \(M=\$ 237.71\)

Therefore, the solution is calculated as, $237.71.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 7 Answer

The given data is, ​P=$5000

d=$800

n=$202.5

​Calculate the interest the finance company charges.

The product of the monthly payments is,

$237.71×12×2=$5,705.04

$5,705.04−$5,000=$705.04

​Therefore, the solution was calculated as, $705.04.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 8 Answer

The given data is, ​P=$5000

d=$800

n=$202.5

​Calculate whether Rob uses the installment plan or borrows the money from the finance company.

Since Rob has to pay less interest, the installment plan is a better choice.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 9 Answer

The given data is, P=$8400

r=7 %

t=2 yrs

Explain what was incorrectly entered.

Since Lee missed the parentheses in the calculator, hence can’t differentiate between numerator and denominator.

Hence the BODMAS rule is applied as,

​(8400(.07/12)(1+0.07/12)∧24)/((1+0.07/12)∧24−1).

Therefore, the solution is calculated as 376.089.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 10 Answer

The given data is,p=430,000,

r=0.08,

t=30​

Compute the monthly payment.

Substituting the value in the formula,

⇒ \(M=\frac{430,000\left(\frac{0.08}{12}\right)\left(1+\frac{0.08}{12}\right)^{12(30)}}{\left(1+\frac{0.08}{12}\right)^{12(30)}-1}\)

⇒ \(M=\frac{430,000\left(\frac{0.08}{12}\right)\left(1+\frac{0.08}{12}\right)^{360}}{\left(1+\frac{0.08}{12}\right)^{360}-1}\)

Therefore, the solution is calculated as, $3155.19.

How To Solve Cengage Financial Algebra Chapter 4.2 Consumer Credit

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 11 Answer

The given data is, ​p=430,000,

r=0.08,

t=30​

Find the total of all of the monthly payments for the 30 years.

Considering the values from the previous question, The monthly payment is 3155.19

Multiple monthly payments by the month are,

3155.19×30×12=3155.19×360

=1,135,868.40

​Therefore, the total amount of monthly payments is $1135868.4

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 12 Answer

The given data is, P=430000

r=8 %

t=30 yrs

​Calculate the finance charge.

Considering the previous question as the Total of monthly payments is, $1135868.4, Subtracting principal from total monthly payments,

1,135,868.40−430,000=705,868.40

Therefore, the solution is calculated as a finance charge, $705868.4

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 13 Answer

The given data is, P=430000

r=8%

t=30yrs​

Prove which is greater, the interest or the original cost of the home.

Considering the values from the previous questions,

Hence, the interest or Finance charge is $705868.4, Compare the interest ($705868.4)

with original cost ($430000).

Therefore, the interest is more than the original cost of the home.

Step-By-Step Solutions For Chapter 4.2 Consumer Credit Exercise

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.2 Consumer Credit Page 186 Exercise 14 Answer

The given table is considered. Write the spreadsheet formula to compute cell D₂

Write the spreadsheet formula to compute cell E₂.

The cell should contain the time in month for the data in the second row as,

Time in months=D₂

The years of the second row are given in the cell,

Time in years=C₂

Time in months

D₂= Time in years ×12

=C₂×12

The formula for the monthly payment is,

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(M=\frac{p\left(\frac{r}{12}\right)\left(1+\frac{r}{12}\right)^{12 t}}{\left(1+\frac{r}{12}\right)^{12 t}-1}\)

⇒ \(E 2=\frac{A 2\left(\frac{B 2}{12}\right)\left(1+\frac{B 2}{12}\right)^{12 \times C 2}}{\left(1+\frac{B 2}{12}\right)^{12 \times C 2}-1}\)

⇒ \(E 2=(A 2 *(B 2 / 12) *(1+B 2 / 12) \hat{0}(12 * C 2)) /((1+B 2 / 12) \hat{0}(12 * C 2)-1)\)

Therefore, the solution is calculated as D₂=C₂⋅1₂ and E₂=(A₂x(B₂/1₂)∗(1+B₂/12)0

(12∗C₂))/((1+B₂/12)0

(12x C₂)−1).