Alekhya

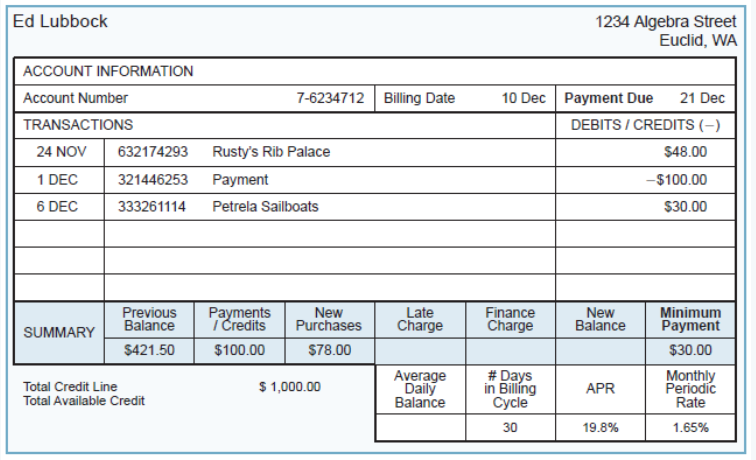
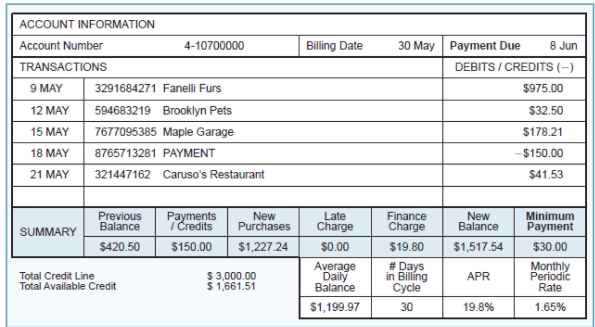
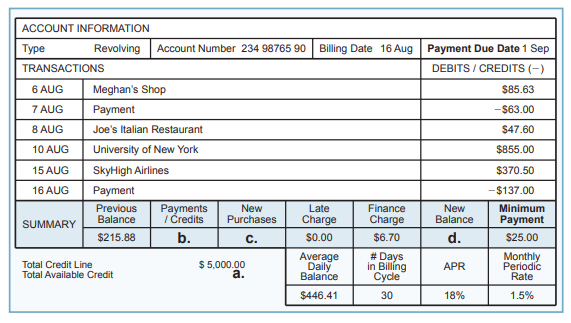
Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership

Page 253 Problem 1 Answer

Given; the exponential depreciation equation

To find: How might a better-fitting exponential depreciation equation look when superimposed over the same scatterplot?

The exponential depreciation function can be determined using exponential regression calculated by hand, by computer software, or by a graphing calculator.

When you use the statistics feature on a graphing calculator, the data is entered into two lists as shown.

The independent variable is the age of the car and the dependent variable is the car value.

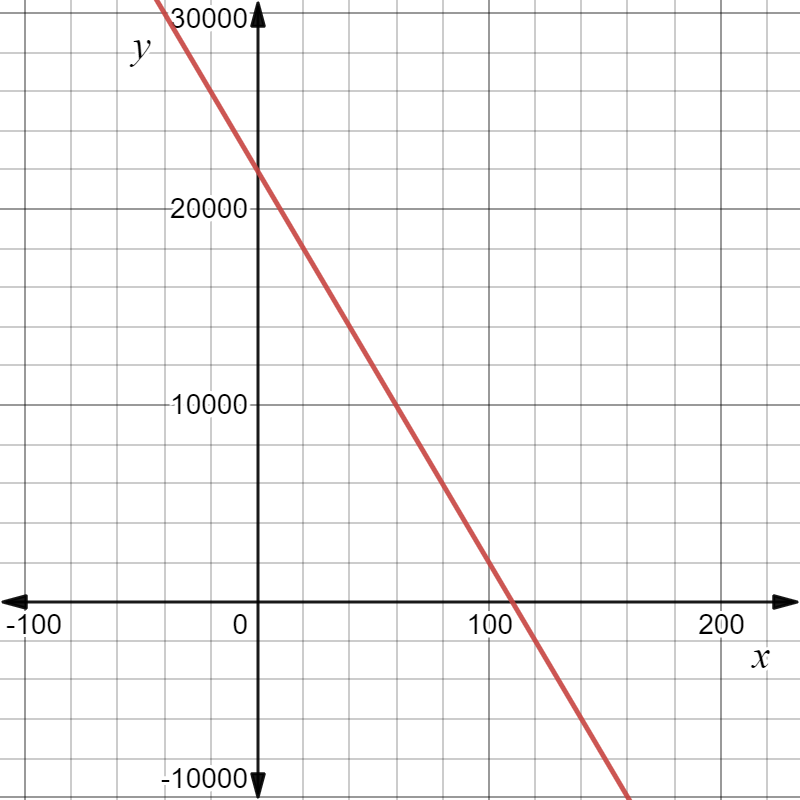
Using the formaty=a×bx,where a=25,921.87 and b=0.92,the exponential depreciation function is y=25,921.87×0.92x.

The graph of this function, superimposed over the scatterplot, appears to be a good fit.

An exponential decay curve fits the following equation: y=e−t/τ.

The graph of the function looks like this

The results become clearer if we take the natural log of both sides:

Hence we conclude that An exponential decay curve fits the following equation: y=e−t/τ.

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

The results become clearer if we take the natural log of both sides:

Cengage Financial Algebra Chapter 5.6 Automobile Ownership Guide

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 254 Problem 2 Answer

Given ; y=a⋆b∧

x,a=32,567.98722,b=0.875378566.

To find: Determine the depreciation percentage.

The exponential decay function was introduced as

y=A(1−r)^x.

The graphing calculator uses the format y=a⋅bx.

a=32,567.98722,

b=0.875378566

​y=32,567.98722×.87

=28506.75

The depreciation percentage.WILL BE 28.50 %

Hence the depreciation percentage will be given by 28.50 %

Page 255 Problem 3 Answer

Given; A car originally sells for D dollars.

After A years, the value of the car has dropped exponentially to P dollars.

To find: Write an algebraic expression for the exponential depreciation rate expressed as a decimal.

The exponential depreciation equation is of the form y=P(1−r)x with D the original value, P

the depreciation rate per period and A the number of periods.

y=D(1−P%)A

y=D(1−P%)A

Hence an algebraic expression for the exponential depreciation rate expressed as a decimal. y=D(1−P%)A

Solutions For Exercise 5.6 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 256 Problem 4 Answer

Given; value of the car is 22,022. and we have half the purchase so we will divide by 2/11011

A car originally sold for 26,600.a rate of5.5 per year.

To find; How old would the car be had it been purchased at half its value

The length of time, x,

can be determined using the following formula.

x=ln(y/A)

ln(1−r)

Because y equals the value of the car after x years, y = 24,000. The new car price, A, is22,022.

The variable r represents the depreciation rate expressed as a decimal. Therefore, r=0.55

x=ln(22,022/24,000)

ln(1−0.55)

≈0.107

Hence the car was 1 year old approxx , At the time of the purchase, the car was about 0.1077 years old.

Page 257 Problem 5 Answer

Given: I once bought an old car back after I sold it because I missed it so much and I had forgotten that it never ran . . .

I just wanted it back. I could only remember what was good about it. – Connie Chung, Television News Commentator

We have to find that how might the quote apply to what you have learned

Over time, a person could attach an increasing sentimental value to a car and thus the car is then worth more than just some monetary value.

Due to the sentimental value, it might then be difficult to sell a car, because even though the car might not be worth much money, the car might be worth much sentimentally.

We get, Somebody could attach sentimental values to a car

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 257 Problem 6 Answer

Given: Seamus bought a car that originally sold for $40,000. It exponentially depreciates at a rate of 7.75% per year.

We have to write the exponential depreciation equation for this car.

The exponential depreciation equation is of the form y=P(1−r)x with P the original, r the depreciation rate per period and x the number of periods.

y=40,000(1−0.0775){x}

We get,y=40,000(1−0.0775){x}

Page 257 Problem 7 Answer

Given: Shannon’s new car sold for $28,000. Her online research indicates that the car will depreciate exponentially at a rate of 51/4% per year.

We have to write the exponential depreciation formula for Shannon’s car.

The exponential depreciation equation is of the form y=P(1−r)x with P the original value, r the depreciation rate per period and x the number of periods.

r=51/4%=5.25%=0.0525

y=28,000(1−0.0525){x}

We get, y=28,000(1−0.0525)x

Chapter 5 Exercise 5.6 Automobile Ownership Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 257 Problem 8 Answer

Given: Chris purchased a used car for $19,700. The car depreciates exponentially by 10% per year.

We have to find that how much will the car be worth after 6 years?

The exponential depreciation equation is of the form y=P(1−r)x with P the original value, r the depreciation rate per period and x the number of periods.

y=19,700(1−0.10){x}

Replace x with 6

y=19,700(1−0.10)6

=$10,469.39

We get, $10,469.39

Page 257 Problem 9 Answer

Given: y=a⋆bx,a=20,952.11, and b=0.785.

To find: What is the rate of depreciation for this car? How much is this car worth after 6 years, 78 months, and w months?

Exponential depreciation equation: y=P(1−r)x with P as original value, r as depreciation rate and x is the period.

1−b=1−0.785=0.215=21.5%

y=20,952.11×0.7856

=4,902.82

y=20,952.11×0.78578/12

=4,343.91

y=20,952.11×0.785w

Hence, rate of depreciation for this car, car’s worth are respectively:  21.4

%, 4902.82, 4343.91and 20,952.11×0.785w

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 257 Problem 10 Answer

Given: y=a⋆bx,a=18,547.23, and b=0.8625.

To find: What is the rate of depreciation for this car? How much is this car worth after 6 years, 78 months, and w months?

Exponential depreciation equation: y=P(1−r)x

with P as original value, r as depreciation rate and x is the period.

1−b=1−0.8625=0.1375=13.75%

y=18,547.23×0.86256

=7,635.43

y=18,547.23×0.862578/12

=7,091.09

y=18,547.23×0.8625w/12

Hence, the required results are: 13.75%,$7,635.43,$7,091.09,18,547.23×0.8625w/12

Page 257 Problem 11 Answer

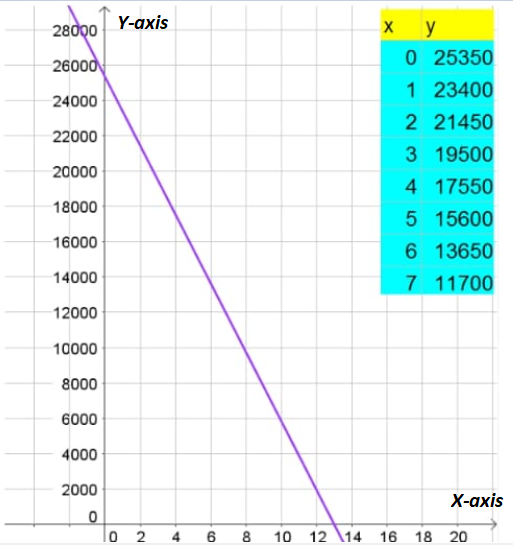
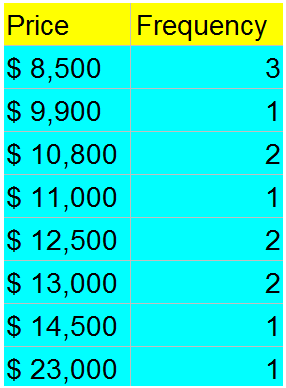
Given: The historical prices of a car are recorded for 17 years as shown.

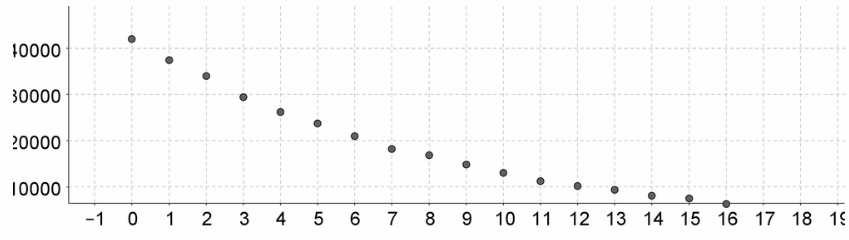
To find: Construct a scatterplot for the data.

Age is on horizontal axis and value in Dollars on vertical axis:

Hence, the scatter

Page 257 Problem 12 Answer

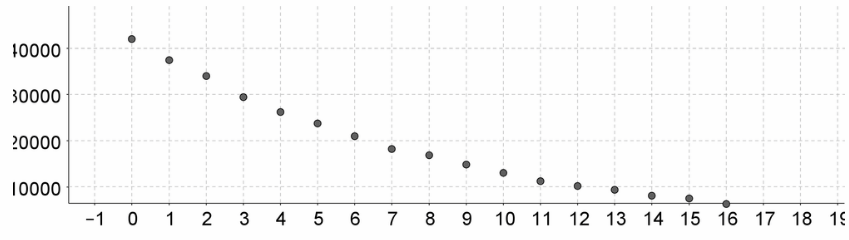
Given: The historical prices of a car are recorded for 17 years as shown.

To find: Determine the exponential depreciation formula that models this data. Round to the nearest hundredth.

Enter the year in list L1 and values in list L2 using the command STAT>1:Edit

Next, we can determine the exponential depreciation using STAT>CALC>0:L1 L2

The calculator then returns:

y=a×bx

a=42,228.36

b=0.89

y=42,228.36×0.89x

​Hence, exponential depreciation formula that models this data y=42,228.36×0.89x.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 257 Problem 13 Answer

Given: The historical prices of a car are recorded for 17 years as shown.

To find: Determine the depreciation rate.

Since, we have the equation ​y=a×bx

y=42,228.36×0.89x

And the exponential depreciation equation: y=P(1−r)x

Which implies,  1−r=0.89

r=11

​Hence, the depreciation rate is 11%.

Page 258 Problem 14 Answer

Chaz bought a two-year-old car. He paid D dollars. This make and model depreciates at a rate of E percent per year.

Need to write an expression for the original selling price of the car when it was new.

As the exponential depreciation equation is of the form y=P(1−r)x ,where P is the original value,r is the depression rate per period expressed as a decimal and x is the number of periods. We have, y=D

,r=E/100,x=2, Putting the values in the formula gives us:

D=P(1−E/100)2

Further, solving for P gives us:

P=D(1−E/100)2

=D(1−0.01E)2

An expression for the original selling price of the car when it was new is D

(1−E/100)2.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 258 Problem 15 Answer

Given a car that originally sells for$30,000 when new but exponentially depreciates after 5 years to $18,700.

Need to tell what is the exponential depreciation rate, expressed as a percent to the nearest tenth of a percent.

As the exponential depreciation equation is of the form y=P(1−r)x,where is the original value,r is the depression rate per period expressed as a decimal and x is the number of periods. We have,P=30,000

,y=18,700,x=5, Putting the values in the formula gives us:

18,700=30,000(1−r)5

⇒0.06233=(1−r)5

⇒0.9098=1−r​

Further solving for r gives us:r=1−0.9098

=0.0902​

In percentage r=9.02%P

The exponential depreciation rate, expressed as a percent to the nearest tenth of a percent is 9 .02%

Page 258 Problem 16 Answer

Given a car that originally sells for $52,000 when new but exponentially depreciates to$45,000 after 32 months.

What is the exponential depreciation rate, expressed as a percent to the nearest tenth of a percent.

As the exponential depreciation equation is of the form y=P(1−r)x, where P is the original value,r is the depression rate per period expressed as a decimal and x is the number of periods.

We have, P=52,000,y=45,000,x=32/12

When r is the depression rate per year. Putting all the values in the formula gives us:

45,000=52,000(1−r)32/12

⇒0.8654=(1−r)32/12

⇒0.947=1−r

Further solving for r gives us:​r=1−0.947

=0.053

In percentage r=5.3%

The exponential depreciation rate per year, expressed as a percent to the nearest tenth of a percent is5.3%.

Cengage Financial Algebra Automobile Ownership Exercise 5.6 Solutions

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 258 Problem 17 Answer

Given a new car sells for$27,300. It exponentially depreciates at a rate of 6.1% to $22,100.

Need to tell how long did it take for the car to depreciate to this amount and round your answer to the nearest tenth of a year.

As the exponential depreciation equation is of the form y=P(1−r)x, where P is the original value, r is the depression rate per period expressed as a decimal and x is the number of periods.

Using this find the required result.

We have,P=27,300,

y=22,100,

r=0.061,

Putting all the values in the formula gives us:

22,100=27,300(1−0.061)x

⇒0.8095=0.939x

Taking natural logarithm both the sides gives us:

ln0.8095=ln0.939x

Further solving for x

gives us:x=ln0.8095

ln 0.939

=3.4

Rounding your answer to the nearest tenth of a year, it take3.4 years for the car to depreciate to this amount.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 258 Problem 18 Answer

Given Amber bought a used car valued at $16,000. When this car was new, it was sold for$28,000.

If the car depreciates exponentially at a rate of 9% per year, then approximately how old is the car.

As the exponential depreciation equation is of the form y=P(1−r)x, where P is the original value,r is the depression rate per period expressed as a decimal and x is the number of periods.

Using the given formula, find the required result.

We have,P=28,000,

y=16,000,

r=0.09

Then, putting the values in the formula gives us:

16,000=28,000(1−0.09)x

⇒0.5714=0.91x​

Taking natural logarithm both the sides gives us:

ln0.5714=ln0.91x

⇒ln0.5714=xln0.91

Solving for x gives us:

x=ln0.5714

ln0.91

=5.9​

If the car depreciates exponentially at a rate of 9%per year, then the car is approximately 5.9 years old.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.6 Automobile Ownership Page 258 Problem 19 Answer

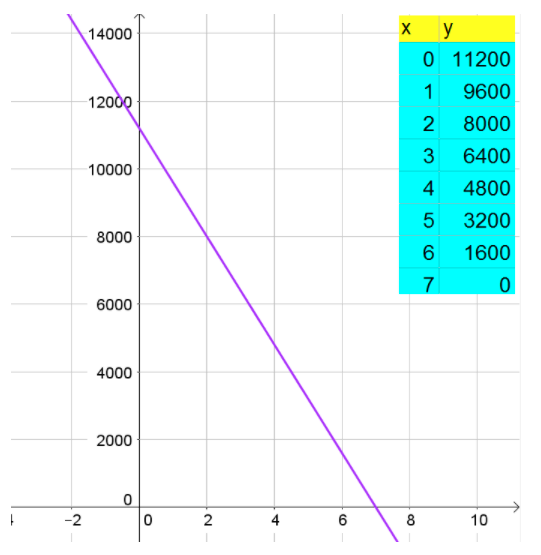
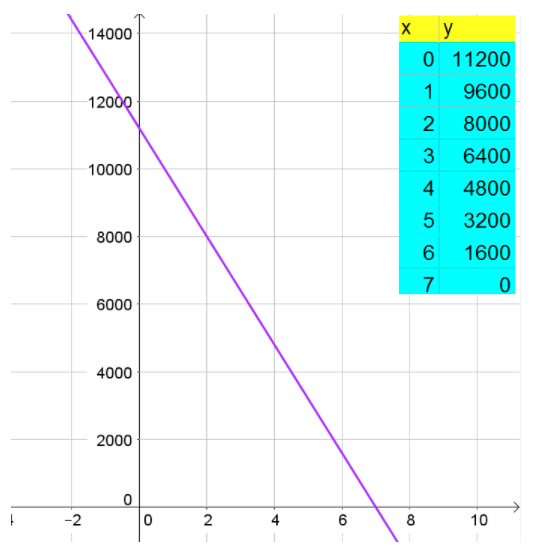
Given a car originally sold for$25,900. It depreciates exponentially at a rate of 8.2% per year.

Nina put$10,000 down and pays $550 per month to pay off the balance.

Need to tell after how many years will her car value equal the amount she paid for the car to that point and what will that value be.

As the exponential depreciation equation is of the form y=A(1−r)x, where A is the original value of the car,r is the depression rate per period expressed as a decimal and x is the number of periods and y is the value of the car after x years.

Using this formula, find the required result.

We have,A=25,900,

r=0.082,

In one year,y=10,000+550(12x),

Putting the values in the formula gives us:

10,000+550(12x)=25,900(1−0.082)x

⇒10,000+6,600x=25,900(0.918)x

Solving for x using a calculator gives us x=1.83804.

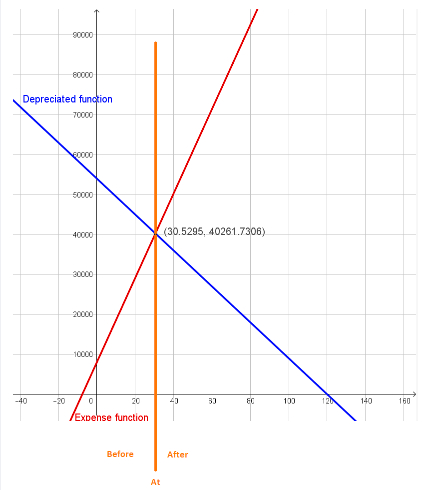
Substitute the valus of x in y,

Then,y=$10,000+$550(12×1.83804)

=$22,131.11​

Rounding the value gives usy=$22,131.

After 1.83804 years her car value equal the amount she paid for the car to that point and the value will be$22,131 (rounded).

How To Solve Cengage Financial Algebra Chapter 5.6 Automobile Ownership

Page 258 Problem 20 Answer

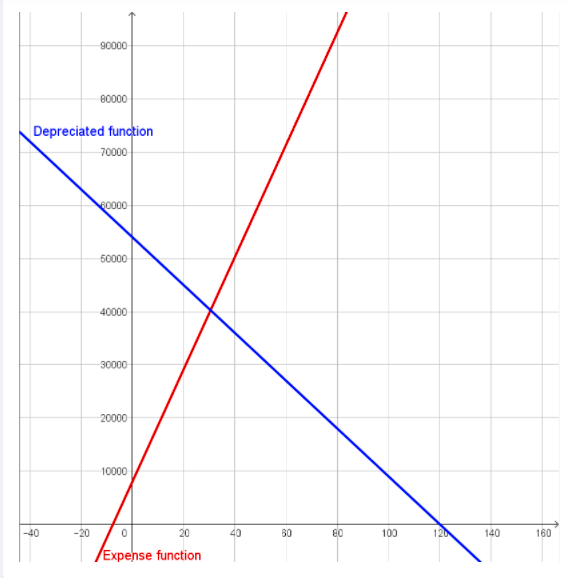
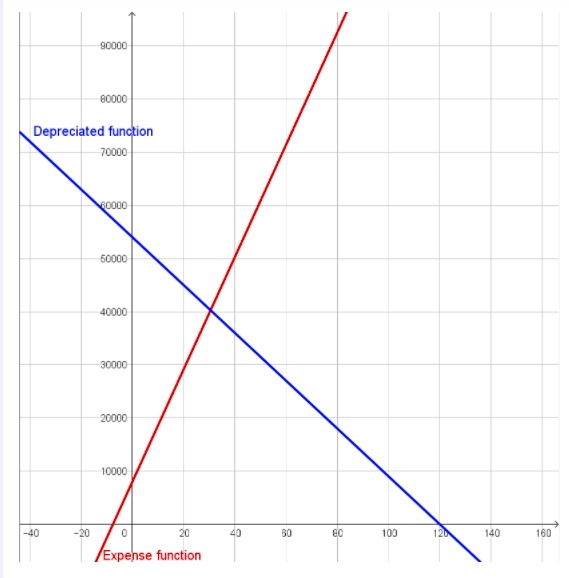
Given Jazmine’s car originally sold for $46,000.It depreciates exponentially at a rate of 10.3%per year.

Jazmine put$12,000 down and pays $800 per month to pay off the balance.

Need to tell after how many years will her car value equal the amount she paid to date for the car and what will that value be.

The exponential depreciation equation is of the form y=A(1−r)x, where A is the original value,r is the depression rate per period expressed as a decimal and x is the number of periods and y is the value of the car after x years.

Using this find the required result

We have,A=46,000,

r=0.103,

In one year,y=12,000​+800(12x),

Putting the values in the formula gives us:

12,000+800(12x)=46,600(1−0.103)x

⇒12,000+9,600x=46,600(1−0.103)x

Solving for x

using a calculator gives us x=2.46372.

Substitute the value of x in y:

Then,y=$12,000+$800(12×2.46372)

=$35,651.71

≈$35,652​

After 2.46372 years her car value equal the amount she paid for the car to that point and the value will be $35,652 (rounded).

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership

Page 246 Problem 1 Answer

Given: A car sells for D dollars and totally depreciates after T years.

Here we will define the intercepts of the straight line depreciation equation.

Let x represent the time in years. The minimum x−value is 0 years, the purchase year of the car.

Because the car totally depreciates after T years, the maximum x−value will be T.

In a straight line depreciation equation, the intercepts are (0, maximum car value) and (maximum lifespan, 0 )

Let y represent the value of the car at any time during its lifetime.

The minimum y−value is zero dollars and the maximum y−value is the pur− chase price of D dollars.

Knowing this information, you can identify the intercepts as (0,D) and (T,0).

The intercepts are  (0,D) and (T,0).

Cengage Financial Algebra Chapter 5.5 Automobile Ownership Guide

Page 246 Problem 2 Answer

Given: A car is purchased for D dollars and totally depreciates after T years.

Here By using this given data we will find the slope of the depreciation line.

Two points determine a line, so you only need two points to determine the slope of a line.

Let the coordinates of the y−intercept be the first point.

That is, (x₁,y₁)=(0,D). Let the coordinates of the x−intercept be the second point. That is, (x₂,y₂)=(T,0).

Using the slope ration we get y₂−y₁/x₂−x₁

Put all the values 0−D/T−0=−D/T

The slope of the depreciation line is −D/T

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 247 Problem 3 Answer

Given: A  car that was purchased for $22,000 and totally depreciates after 11 years.

Here by using this data we will plot the graph of the depreciation line.

The general form for the equation of a straight line is

y=mx+b

Where in represents the slape of the line and b represents the y−intercept.

The two intercepts of the given line are (0,22,000) and (11,0)

Thus the slope is  0−22,000/11−0=−2000

And the Y-intercept is 22,000

Thus equation of line is written as y=−2,000x+22,000

Graph is

The equation of line is y=−2,000x+22,000 and the graph is

Page 248 Problem 4 Answer

Given: A car sells for $18,495 dollars and straight line depreciates to zero after 9 years.

Here by using this data we will find the equation of the line.

The intercepts are (0,18,495) and (9,0).

Thus slope is  y₂−y₁/x₂−x₁

=0−18,495/9−0

=−18,495/9

=−2,055

The y-intercept of the line is 18,495

Thus the equation of line is  y=−2,055x+18,495

Because x represents years, it is necessary to convert W months into years by dividing by 12.

Thus the value of car after W months is  y=−2,300(W/12)+27,600

The value of the car is =−2,300(W/12)+27,600

Solutions For Exercise 5.5 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 248 Problem 5 Answer

Given : Value of car is D dollars

The straight line depreciation equation for a car is y=−4,000x+D

Here we will find the value of x with respect to the value of the car after the car’s value decreased by 25%.

The original value of the car is y intercept of the equation.

We must determine the actual value of the car after it has dropped by 25%. This can be done

As we can find 25% of the original value of the car and then subtract that amount from the original value

0.25×D=0.25D

D−0.25D=0.75D

The value is 0.75D

We are trying to determine a length of time. Solve the depreciation equation for x.

Y/0.75D/0.25D

0.25D/4000

=−4,000x+D

=−4,000x+D

=4,000x

=x

The length of the time is represented as 0.25D/4000=x

Page 249 Problem 6 Answer

Given;The expense function be altered so that it refl ects a more accurate amount spent over time

To find ; What effect might that have on the graphs?

Let x represent time in months and y represent dollars.

Celine’s expense function is the sum of her monthly payments over this time period and her initial down payment.

Expense function y=560x+4,000

The time, x, is in months rather than years. Express Celine’s depreciation function in terms of months as well.

Celine’s car totally depreciates after 10 years, or 120 months.

To determine her monthly depreciation amount, divide the original car value by 120.

33,600/120

=280

Celine’s car depreciates 280 per month. To calculate the slope of the depreciation equation, use the intercepts (0,33,600) and 120,0.

Slope0−33,600/120−0

=−33,600/120

=−280

Depreciation function y=−280x+33,600

Using a graphing calculator, the coordinates of the intersection point, rounded to the nearest hundredth, are 35.24,23,733.33.

This means that after a little more than 35 months, both your expenses and the car’s value are the same In the region before the intersection point, the expenses are lower than the value of the car.

The region after the intersection point indicates a period of time that the value of the car is less than what you have invested in it.

Hence we conclude that after a little more than 35 months, both your expenses and the car’s value are the same.

In the region before the intersection point, the expenses are lower than the value of the car.

The region after the intersection point indicates a period of time that the value of the car is less than what you have invested in it.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Problem 7 Answer

We have to find how might those words apply to what we have learned.

We will explain it by two statement which are stated below.

Computers have improved over the years in their tech while becoming more affordable for the masses.

Cars too have improved but the cost for a car has increased over the years.

Therefore, Unlike computers and other tech which has improved over the years and dropped in expenses (becoming more accessible to the public), cars have improved but simultaneously increased in cost.

Page 250 Problem 8 Answer

Given : Delia purchased a new car for $25,350. This make and model straight line depreciates to zero after 13 years.

We have to identify the coordinates of the x – and y -intercepts for the depreciation equation.

We will find it.

Here,x is the number of years and y is the price.

Now,The x intercept has y zero.

The model depreciates to 0 after 13 years, which implies that when x=13

⇒y=0

i.e. (13,0)

Now,The y-intercept has x zero.

At time x=0, Delia purchases the car and thus the price is $25,350.

i.e. (0,25350)

Therefore, the coordinates of the x – and y -intercepts for the depreciation equation is(13,0),(0,25350)

Page 250 Problem 9 Answer

Given: Delia purchased a new car for $25,350.

This make and model straight line depreciates to zero after 13 years.

We have to find the slope of the depreciation equation.

We will use above formula.

Here,We have, x – and y-intercept is (13,0),(0,25350)​

So,y₂−y₁/x₂−x₁

=25350−0/0−13

=−1,950

​Therefore,−1,950 is the slope of the depreciation equation.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Problem 10 Answer

Given: Delia purchased a new car for $25,350. This make and model straight line depreciates to zero after 13 years.

We have to write the straight-line depreciation equation that models this situation.

We will use above information.

Here,

We have,

m=−1,950

b=25350​

So,y=mx+b

y=−1950x+25350

​Therefore,

y=−1950x+25350

Page 250 Problem 11 Answer

Given: Delia purchased a new car for $25,350. This make and model straight line depreciates to zero after 13 years.

We have to draw the graph of the straight line depreciation equation.

We will put different values of x to get the values of y and then draw a graph.

Here,We have ,y=−1950x+25350

We will put different values of x to get the values of y in the above equation.

So, the graph is :

Therefore,           

Given : Vince purchased a used car for $11,200. This make and model used car straight line depreciates to zero after 7 years.

We have to identify the coordinates of the x-and y-intercepts for the depreciation equation.

We will find it.

Here,x is the number of years and y is the price.

Now,The x -intercept has y zero.

After 7 years, the price is depreciated to 0 .This implies that when ​x=7

⇒y=0​

i.e.  (0,11200)

Noe, The y-intercept has x zero.

When x=0, Vince purchase the car and then the price was$11,200.

i.e. (7,0)

Therefore,  the coordinates of the x – and y -intercepts for the depreciation equation is(0,11200),(7,0)

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Problem 13 Answer

Given : Vince purchased a used car for$11,200. This make and model used car straight line depreciates to zero after 7 years.

We have to find the slope of the depreciation equation.

We will use above formula.

Here,We have,  x- and y-intercept is (7,0),(0,11200)​

So, y₂−y₁/x₂−x₁

=11200−0/0−7

=−1,600

​Therefore, The slope of the depreciation equation is−1,600

Page 250 Problem 14 Answer

Given: Vince purchased a used car for $11,200. This make and model used car straight line depreciates to zero after 7 years.

We have to write the straight line depreciation equation that models this situation.

We will use above information.

Here,We have,m=11200

y=−1600

So, y=mx+b

y=−1,600x+11,200

​Therefore,

y=−1,600x+11,200

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Problem 15 Answer

Given: Vince purchased a used car for $11,200. This make and model used car straight line depreciates to zero after 7 years.

We have to Draw the graph of the straight line depreciation equation.

So,

We get,

Page 250 Problem 16 Answer

Given: Examine the straight line depreciation graph for a car.

To find: At what price was the car purchased?

The price at purchase is the price at time 0 and is thus the y-intercept (intersection of the graph with the y axis).

28000

The price of the car at purchase is at time 0 and as per the graph it is 28000.

Chapter 5 Exercise 5.5 Automobile Ownership Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Problem 17 Answer

Given: Examine the straight line depreciation graph for a car.

To find: After how many years does the car totally depreciate?

The car totally depreciates if the value becomes zero and thus at the x-intercept (intersection of the graph with the x-axis).

So, in 10 years does the car totally depreciate

So, in 10 years does the car totally depreciate

Page 250 Problem 18 Answer

Given: Examine the straight line depreciation graph for a car.

We have to Write the equation of the straight line depreciation graph shown.

x − and y−intercept found in previous exercises (0,28000) and (10,0)

The slope can be determined with y₂−y₁/x₂−x₁

y₂−y₁/x₂−x₁

=0−28000/10−0

=−2,800

The equation of the straight line depreciation is y=mx+b with m the slope and b the y-intercept

y=−2,800x+28,000

We get,

y=−2,800x+28,000

Given: The straight line depreciation equation for a luxury car is y=−3,400x+85,000

To find: What is the original price of the car?

The price at purchase is the price at time 0 and is thus the y-intercept (x is zero).

y=−3,400×0+85,000=85,000

We get,

y=−3,400×0+85,000=85,000

Page 250 Problem 19 Answer

Given: The straight line depreciation equation for a luxury car is y=−3,400x+85,000

To find: How much value does the car lose p

The yearly depreciation is given by the slope (number in front of the x in the straight line depreciation equation) $3,400

The slope of the graph gives the yearly depreciation. So as per the equation, it is $3,400.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Problem 20 Answer

Given: The straight-line depreciation equation for a luxury car is y=−3,400x+85,000

To find: How many years will it take for the car to totally depreciate?

The car totally depreciates if the value becomes zero and thus at the x-intercept ( y is zero).

0=−3,400x+85,000

Add 3,400x to both sides of the equation

3,400x=85,000

Divide both sides of the equation by 3400

x=25

25 years

It will take 25 years for the car to totally depreciate.

Page 250 Exercise 1 Answer

Given: The straight line depreciation equation for a motorcycle is y=−2,150x+17,200

To find: What is the original price of the motorcycle?

The price at purchase is the price at time 0 and is thus the y-intercept ( x is zero).

u=−2.150×0+17.200=17.200

We get,

u=−2.150×0+17.200=17.200

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Exercise 2 Answer

The straight-line depreciation equation for a motorcycle is y=−2,150x+17,200

To find: How much value does the motorcycle lose per year.

The yearly depreciation is given by the slope (number in front of the x in the straight line depreciation equation) $2,150

The motorcycle loses its value by$2,150 per year.

Page 250 Exercise 3 Answer

Given: The straight line depreciation equation for a motorcycle is y=−2,150x+17,200

To find: How many years will it take for the motorcycle to totally depreciate.

The car totally depreciates if the value becomes zero and thus at the x-intercept (y is zero).

0=−2,150x+17,200​

Add 2,150x to both sides of the equation

2,150x=17,200

Divide both sides of the equation by 2,150

x=8

It would take8 years for the motorcycle to totally depreciate.

Page 250 Exercise 4 Answer

Given: The straight line depreciation equation for a car is y=−2,750x+22,000

To find: What is the car worth after 5 years?

Replace x with 5 in the straight line depreciation equation.

y=−2,750×5+22,000

=8,250

​We get,y=8250

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 250 Exercise 5 Answer

Given: The straight line depreciation equation for a car is y=−2,750x+22,000

To find: What is the car worth after 8 years

Replace x with 8 in the straight line depreciation equation.

y=−2,750×8+22,000=0

The worth of the car after 8 years is $0.

Page 250 Exercise 6 Answer

Given: The straight line depreciation equation for a car is y=−2,750x+22,000

Suppose that A represents a length of time in years when the car still has value.

We have to Write an algebraic expression to represent the value of the car after A yea

Replace x with A in the straight line depreciation equation.

y=−2,750A+22,000

We get,y=−2,750A+22,000

Page 251 Exercise 7 Answer

Given: The straight line depreciation equation for a car is y=−2,750x+22,000

To find: What is the car worth after 5 years?

Replace x with 5 in the straight line depreciation equation.

y=−2,750×5+22,000

=8,250

​We get,y=8250

Cengage Financial Algebra Automobile Ownership Exercise 5.5 Solutions

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 251 Exercise 8 Answer

Given: The straight line depreciation equation for a car is y=−2,750x+22,000

To find: What is the car worth after 8

Replace x with 8 in the straight line depreciation equation.

y=−2,750×8+22,000=0

The worth of the car after 8 years is $0.

Page 251 Exercise 9 Answer

Given: The straight line depreciation equation for a car is y=−2,750x+22,000 Suppose that A represents a length of time in years when the car still has value.

We have to Write an algebraic expression to represent the value of the car after A years.

Replace x with A in the straight line depreciation equation.

y=−2,750A+22,000

We get,

y=−2,750A+22,000

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 251 Exercise 10 Answer

Given: The graph of a straight line depreciation equation is shown.

We have to Use the graph to approximate the value of the car after 4 years.

Find the vertical line with 4 years at the bottom and determine the intersection between the vertical line and the blue line.

Determine the horizontal line that also goes through this point and read the value of this line on the y-axis.

$12,800

As per the graph, the approximate value of the car after 4 years is $12,800.

Page 251 Exercise 11 Answer

Given: The graph of a straight line depreciation equation is shown.

we have to Use the graph to approximate the value of the car after 5 years.

Find the vertical line with 5 years at the bottom and determine the intersection between the vertical line and the blue line.

Determine the horizontal line that also goes through this point and read the value of this line on the y-axis.

So, we get $9,600

We get, $9,600

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile OwnershipPage 251 Exercise 12 Answer

Given: The graph of a straight line depreciation equation

We have to Use the graph to approximate when the car will be worth half its original value.

The original value is the value at the intersection of the blue graph and the y-axis.

$25,600 Half of the original value is then the original value divided by 2

$25,600÷2=$12,800

Determine the horizontal line at the value $12,800, find its intersection with the blue line.

Find the vertical line that also goes through this intersection and determine the number of years of this vertical line.

4 years

We get,4 years

Page 251 Exercise 13 Answer

Given: A car is originally worth $34,450. It takes 13 years for this car to totally depreciate.

We have to write the straight line depreciation equation for this situation.

x – and y-intercept

(0,34450)and(13,0)

The slope can be determined with y₂−y₁/x₂−x₁

y₂−y_{1 /}x₂−x₁

=0−34450/13−0

=−2,650

The equation of the straight line depreciation is y=mx+b with m the slope and b the y-intercept

y=−2,650x+34,450

We get,

y=−2,650x+34,450

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 251 Exercise 14 Answer

Given: A car is originally worth $34,450. It takes 13 years for this car to totally depreciate.

We have to find that how long will it take for the car to be worth half its value

Equation found in previous exercise

y=−2,650x+34,450

Half of its value is the original value divided by 2.

34,450/2

=−2,650x+34,450

Subtract 34,450 from both sides of the equation−17,225=−2,650x

Divide both sides of the equation by −2,650/6.5=x

It will take 6.5 years for the car to be half its value.

Page 251 Exercise 15 Answer

Given: A car is originally worth $34,450. It takes 13 years for this car to totally depreciate.

We have to find that how long will it take for the car to be worth Round your answer to the nearest tenth of a year.$10,000?

Equation found in previous exercise

y=−2,650x+34,450

The value is$10,000

10,000=−2,650x+34,450

Subtract 34,450 from both sides of the equation−24,450=−2,650x

Divide both sides of the equation by −2,650/9.2=x

It will take 9.2 years for the car to be worth it.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 251 Exercise 16 Answer

Given: The original price of a car is entered into spreadsheet cell A1 and the length of time it takes to totally depreciate is entered into cell B1.

We have to write the spreadsheet formula that calculates the amount that the car depreciates each year.

x-and y-intercept (0,A1) and (B1,0)

The slope can be determined with y₂−y₁/x₂−x₁

y₂−y₁/x₂−x₁

=0−A1/B1−0

=−A1/B1

We get,−A1/B1

Page 251 Exercise 17 Answer

Given: The original price of a car is entered into spreadsheet cell Al and the length of time it takes to totally depreciate is entered into cell B1.

The spreadsheet user is instructed to enter a length of time in years that is within the car’s lifetime in cell C1.

We have to write the spreadsheet formula that will calculate the car’s value after that period of time.

The equation of the straight line depreciation is y=mx+b with m the slope and b the y-intercept

y=−A1/B1

x+A1

Replace x with C1

y=−A1/B1×C1+A1

We get,−A1/B1×C1+A1

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 251 Exercise 18 Answer

Given: Winnie purchased a new car for $54,000. She has determined that it straight line depreciates to zero over 10 years.

When she purchased the car, she made an $8,000 down payment and financed the rest with a 4-year loan at 4.875%.

You can use the monthly payment formula from the last chapter to determine the monthly payment to the nearest cent.

We have to Create an expense and depreciation function.

Expense function:

Purchase price=$54,000

Down payment= $8,000

r= Interest rate =4.875%=0.04875

t= Number of years =4

The principal (amount loaned) is the purchase price decreased by the down payment:

p= Principal

= Purchase price − Down payment

=$54,000−$8,000

=$46,000​

Suppose the first determine the monthly payment using the monthly payment loan formula:

M=p(r/12)(1+r/12)12t

(1+r/12)12t−1

=46000(0.04875/12)(1+0.04875/12)12×4

(1+0.04875/12)12×4−1

≈1,056.74

Suppose x represent the number of months and let y represent the total expense.

The total expense is the total of the monthly payments and the down payment, while the total of the monthly payments is the product of the number of months and the monthly payment.

y= Total expense = Total monthly payments + Down payment = Number of months × Monthly payment+ Down payment

​=x×1,056.74+8,000

=1,056.74x+8,000

​Depreciation function

Let x represent the number of months and let y represent the value of the car.

General depreciation function:

y=ax+b

with a the slope and b the y-intercept.

When x=0, the value of the car is $54,000 (purchase price).

This then implies that (0,54000) needs to be a point on the depreciation function and thus they-intercept is $54,000.

b=y-intercept =54,000

After 10 years (or 10×12=120 months), the car has depreciated to 0 and thus (120,0) needs to be a point on the depreciation function as well.

We can then calculate the slope using y₂−y₁/x₂−x₁ with (x₁,y₁)=(0,54000) and (x₂,y₂)=(120,0).

a=y₂−y₁/x₂−x₁

=0−54000/120−0

=−54000/120

=−450

We finally determine the depreciation function by replacing a by −450 and replacing b by 54,000 in the general depreciation function:

y=ax+b=−450x+54,000

Expense function: y = 1, 056.74x + 8, 000

Depreciation function: y = −450x + 54, 000

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 251 Exercise 19 Answer

Given: Winnie purchased a new car for $54,000. She has determined that it straight line depreciates to zero over 10 years.

When she purchased the car, she made an $8,000 down payment and financed the rest with a 4-year loan at 4.875%.

You can use the monthly payment formula from the last chapter to determine the monthly payment to the nearest cent.

We have to draw the Graph these functions on the same axes.

Expense function

Purchase price =$54,000

Down payment=$8,000

r= Interest rate =4.875%=0.04875

t= Number of years =4

The principal (amount loaned) is the purchase price decreased by the down payment:

p= Principal

= Purchase price − Down payment

=$54,000−$8,000

=$46,000

​Let us first determine the monthly payment using the monthly payment loan formula:

M=p(r/12)(1+r/12)12t

(1+r/12)12t−1

=46000(0.04875/12)(1+0.04875/12)12×4

(1+0.04875/12)12×4−1

≈1,056.74​

Let x represent the number of months and let y represent the total expense.

The total expense is the total of the monthly payments and the down payment, while the total of the monthly payments is the product of the number of months and the monthly payment.

y= Total expense = Total monthly payments + Down payment = Number of months × Monthly payment + Down payment

​=x×1,056.74+8,000

=1,056.74x+8,000​

Depreciation function

Suppose x represent the number of months and let y represent the value of the car.

General depreciation function:

y=ax+b with a the slope and b the y-intercept.

When x=0, the value of the car is $54,000 (purchase price). This then implies that (0,54000) needs to be a point on the depreciation function and thus the y-intercept is $54,000.

b=y−intercept =54,000

After 10 years (or 10×12=120 months), the car has depreciated to 0 and thus (120,0) needs to be a point on the depreciation function as well.

We can then calculate the slope using y₂−y₁/x₂−x₁ with (x₁,y₁)=(0,54000) and (x₂,y₂)=(120,0).

a=y₂−y₁/x₂−x₁

=0−54000/120−0

=−54000/120

=−450

We finally determine the depreciation function by replacing a by −450 and replacing b

by 54,000 in the general depreciation function:

y=ax+b=−450x+54,000

So, the graph is

We get,

Step-By-Step Solutions For Chapter 5.5 Automobile Ownership Exercise

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.5 Automobile Ownership Page 251 Exercise 20 Answer

Given: Winnie purchased a new car for $54,000. She has determined that it straight line depreciates to zero over 10 years.

When she purchased the car, she made an $8,000 down payment and financed the rest with a 4-year loan at 4.875%.

You can use the monthly payment formula from the last chapter to determine the monthly payment to the nearest cent.

We have to Interpret the region before, at, and after the intersection point in light of the context of this situation.

Expense function

Purchase price =$54,000

Down payment =$8,000

r= Interest rate =4.875%=0.04875

t= Number of years =4

The principal (amount loaned) is the purchase price decreased by the down payment:

p= Principal

= Purchase price − Down payment

=$54,000−$8,000

=$46,000

Let us first determine the monthly payment using the monthly payment loan formula:

M=P(T/12)(1+r/12)12t

(1+r/12)12t−1

=46000(0.04875/12)(1+0.04875/12)12×4

(1+0.04875/12)12×4−1

≈1,056.74

Let x represent the number of months and let y represent the total expense.

The total expense is the total of the monthly payments and the down payment, while the total of the monthly payments is the product of the number of months and the monthly payment

y= Total expense =Total monthly payments + Down payment = Number of months × Monthly payment + Down payment​

=x×1,056.74+8,000

=1,056.74x+8,000​

Depreciation function

Let x represent the number of months and let y represent the value of the car.

General depreciation function: y=ax+b with a the slope and b the y-intercept.

When x=0, the value of the car is$54,000 (purchase price). This then implies that (0,54000) needs to be a point on the depreciation function and thus they-intercept is $54,000.

b=y-intercept =54,000

After 10 years (or 10×12=120 months), the car has depreciated to 0 and thus (120,0) needs to be a point on the depreciation function as well.

We can then calculate the slope using y₁−y₁/x₂−x₁ with (x₁,y₁)=(0,54000) and (x₂,y₂)=(120,0).

a=y₂−y₁/x₂−x₁

=0−54000/120−0

=−54000/120

=−450

We finally determine the depreciation function by replacing a by −450 and replacing b by 54,000 in the general depreciation function:

y=ax+b=−450x+54,000

Graph is:

Before Intersection

Before the intersection, we note that the depreciation function is above the expenses function, which means that the value of the car exceeds the expenses made

At Intersection Let us first determine the intersection, which is the value of x for which the expense function and the depreciation function are equal :

1,056.74x+8,000=−450x+54,000

Subtract 8,000 from each side:

1,056.74x=−450x+46,000

Add 450x to each side:

1,506.74x=46,000

Divide each side by 1,506.74 :

x=46,000

1,506.74

≈30.5

Thus the intersection occurs at x=30.5. Let us determine the corresponding expense/depreciation by evaluating the expense function at 30.5 (which should be roughly the same as the depreciation function evaluate at 30.5):

y=1,056.74(30.5)+8,000≈40,261.73

This then implies that the intersection has x=30.5 and y=40,261.73, which means that: after 30.5 months, the depreciation and the expenses are both equal to$40,261.73.

After intersection

After the intersection, we note that the depreciation function is below the expenses func

Before intersection: The value of the car exceeds the expenses made.

At intersection: After30.5 months, the depreciation and the expenses are both equal to $40,261.73.

After intersection: The expenses made exceed the value of the car.

Financial Algebra 1st Edition Chapter 5 Automobile Ownership

Page 239 Problem 1 Answer

Given: Annual premium is x dollars and surcharge on each semiannual payment is y dollars.

To find: The amount of his semiannual payment algebraically.

For doing so, we will refer to the fact that the amount of his semiannual payment is the sum of the annual premium and surcharge.

Dividing the annual premium by 2:x/2.

Adding the y-dollar surcharge:x/2+y.

Each of the two semiannual payments is x/2+y.

Each of the two semiannual payments is x/2+y.

Page 240 Problem 2 Answer

Given:Cost of fixing pole, bicycle, the car is x, y, w dollars respectively.

To find: The amount that can be claimed under Keith’s property damage liability insurance.

Total damage can be claimed.

Sum of the damages is x+y+w.

The amount that can be claimed under Keith’s property damage liability insurance is x+y+w.

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Page 240 Problem 3 Answer

Given: x dollars is deductible on comprehensive insurance. y dollars is the amount of damage.

To find: The cost that the insurance company pays.

The deductible amount is deducted from the total damage. So, the company pays y−x.

The company pays y−x.

Page 241 Problem 4 Answer

Given:50/100 BI liability insurance and$10,000 PIP insurance.

Owner hurts28 children each of whom needs$10,000 medical care.

To find: The amount the insurance company pays in total for these medical claims.

The owner has a maximum limit of$50,000 per person and a total limit of $100,000.

The owner needs28×$10,000=$280,000 for total medical expenses which is greater than the total limit of the insurance.

So, the company pays$100,000 and the rest is to be paid by the owner.

The amount the insurance company pays in total for these medical claims is$100,000.

Cengage Financial Algebra Chapter 5.4 Automobile Ownership Guide

Page 242 Problem 5 Answer

Given: We have learned the topics.To find: The quote in the context of what you learned.

The use of a car frequently leads to problems between parents and their children, which is why you should not lend your automobile to them.

Furthermore, adolescent drivers have the greatest accident rate, thus your children are more likely to be involved in an accident than other (older) persons.

The use of a car frequently causes friction between parents and their children, which is why you should never give your automobile to them.

Page 242 Problem 6 Answer

Given: Rachel has$25,000 worth of property damage insurance.

She causes$32,000 worth of damage to a sports car in an accident.

To find The damages that the insurance company have to pay.

When the amount of damage exceeds the insurance company’s coverage, the insurance company will pay the maximum amount of coverage.

So, the company pays$25,000.

The company pays$25,000.

Page 242 Problem 7 Answer

Given: The insurance company pays the maximum coverage of$25,000.

To find: The amount Rachel has to pay.

Here, the amount of damage exceeds the amount covered by the insurance company.

So, the owner pays the remaining claims of$32,000−$25,000=$7,000.

Rachel pays$7,000.

Page 242 Problem 8 Answer

Given: Ronald Kivetsky bought a new car and received these price quotes from his insurance company.

To find The annual premium.

The annual premium is the total of the insurance company’s quotes.

The annual premium is the total of the insurance company’s quotes.

So, the annual premium is $234+$266+$190+$11+$344+$410+$12=$1467.

The annual premium is$1467.

Page 242 Problem 9 Answer

Given: Annual premium is$1467.

To find: The semiannual premium.

For doing so, we will use the formula semiannual premium=  annual premium/2.

We know that semiannual premium=  annual premium/2

⇒$1,467÷2=$733.50.

The semiannual premium is$733.50.

Page 242 Problem 10 Answer

Given: Semiannual premium is$733.50.

To find: How much less would Ronald’s semiannual payments be if he dropped the optional collision insurance.

The owner pays the rest of the amount after the company pays.

The annual premium without collision insurance is $234+$266+$190+$11+$344+$12=$1057.

We know that​ semiannual premium = annual premium /2

$1,057÷2=$528.50.

The difference is$733.50−$528.50=$205

Ronald pays$205 less.

Page 242 Problem 11 Answer

Given : The annual premium is $924

We have to find  the amounts of the three payments.

We will use some simple rule of percentage.

Here,The first payment is 40% of the annual premium.

So, 40%×$924=0.40×$924

=$369.60​​

The second and third payment is 30% of the annual premium.

So, 30%×$924=0.30×$924

=$277.20​

​Therefore,The three payments are: $369.60,$277.20,$277.20

Solutions For Exercise 5.4 Financial Algebra 1st Edition

Page 242 Problem 12 Answer

Given : Each person can collect up to$50,000

We have to find how much money must the insurance company pay out for these three people.

We will find it.

Here, The cost of a person that is beneath $50,000 are completely covered, that over $73,000

are covered up to $50,000.

So, $23,000+$500+$50,000=$73,500

Therefore,$73,500,  the insurance company pay out for these three people.

Page 242 Problem 13 Answer

Given: Leslie submits a claim to her insurance company.

We have to find how much must Leslie pay for the repair.

We will find it.

Here, Leslie must pay the deductible which is $500​

Therefore,$500 amount must Leslie pay for the repair.

Page 243 Problem 14 Answer

Given: Felix Madison has $10,000 worth of property damage insurance and a $1,000 deductible collision insurance policy.

He had a tire blowout while driving and crashed into a $1,400 fire hydrant.

The crash caused $1,600 in damages to his car.

We have to find which insurance covers the damage to the fire hydrant.

Here, The damage to the fire hydrant falls under the property damage insurance.

Therefore, Property damage insurance.

Page 243 Problem 15 Answer

Given:Felix Madison has $10,000 worth of property damage insurance and a $1,000 deductible collision insurance policy.

He had a tire blowout while driving and crashed into a $1,400 fire hydrant.

The crash caused $1,600 in damages to his car.

We have to find how much will the insurance company pay for the fire hydrant.

Here,As the damages to the fire hydrant is less than the total coverage, the insurance company pays the total damages.

So, $1,400​

Therefore,$1,400​amount will the insurance company pay for the fire hydrant.

Page 243 Problem 16 Answer

Given: Felix Madison has $10,000 worth of property damage insurance and a $1,000 deductible collision insurance policy.

He had a tire blowout while driving and crashed into a $1,400 fire hydrant.

The crash caused $1,600 in damages to his car.

We have to find which insurance covers the damage to the car.

Here,The damage to our own car is covered by the collision insurance policy.

Therefore,Collision insurance policy.

Page 243 Problem 17 Answer

Given : Felix Madison has$10,000 worth of property damage insurance and a$1,000 deductible collision insurance policy.

He had a tire blowout while driving and crashed into a $1,400

fire hydrant. The crash caused $1,600 in damages to his car.

We have to find how much will the insurance company pay for the damage to the car.

We will use above information.

Here, The insurance company pays the difference between the total damages to the car and the deductible.

So,$1,600−$1,000=$600

Therefore,$600 amount  will the insurance company pay for the damage to the car

Page 243 Problem 18 Answer

Given: Eric must pay his p dollar annual insurance premium by himself.

We have to express how much he must save each month to pay this premium algebraically.

We will use above information.

Here,The amount he must save each month is the annual premium divided by the number of months in a year.

So, the amount is p/12

Therefore, he must save each month to pay this premium algebraically is p/12

Page 243 Problem 19 Answer

Given: Epic’s company raises his insurance 15% We have to express how much he must save each month to pay this premium algebraically.

We will use above information.

Here,The annual premium is increased by 15% of the premium i.e. p+15%×p=115%×p​

Hence, the amount he must save each month is, 115%×p/12

Therefore, he must save each month to meet this new premium algebraically is115%×p/12

Page 243 Problem 20 Answer

Given: Mollie has 100/300/50 liability insurance and $50,000 PIP insurance.

We have to find what insurance will cover this, and how much will the company pay?.

We will use above information.

Here, In the given case, the pole and the minivan are public and private property, thus the damage will be covered by property damage.

Then is covered by the liability insurance.

Now,The total cost of the damage is the sum of the cost of the pole($7,000) and the cost of the damage to the minivan ($6,700).

i.e.Total cost

= Cost pole + Cost damage minivan

=$7,000+$6,700

=$13,700​

So,The insured has a 100/300/50 liability insurance, where the last number 50

represents the insurance coverage of property damage and thus the insurance coverage is $50,000.

As the total cost of $13,700 is less than the insurance coverage of $50,000, the insurance company will pay the total cost of $13,700.

Therefore,Liability insurance (property damage) Company pays $13,700

Page 243 Problem 21 Answer

Given: The minivan’s driver sues for $4,000,000

We have to find what insurance will cover this, and how much will the company pay?.

We will use above information.

Here,As we know that the type of insurance that covers this is Bodily Injury insurance.

This type of insurance applies because the conditions are met: People are hurt and sues you for your negligence.

Now,The insurance company will pay the maximum of Kaylee’s insurance of$100,000

The first two numbers in 100/300/50 represent $100,000/$300,000 BI insurance.

The first number is the maximum amount the insurance company will pay to any one person.

Hence, the insurance company will pay the minivan’s driver $100,000

Therefore,Bodily Injury insurance,$100,000

Page 243 Problem 22 Answer

Given : The minivan’s driver (from part b) had medical bills totaling $60,000 from his hospital trip and physical therapy after the accident.

We have to find what insurance will cover this, and how much will the company pay.

We will use above information.

Here,As we know that the type of insurance that covers this is Personal Injury Protection insurance or PIP insurance.

This type of insurance applies because this insurance covers medical payments without regard to who is at fault.

Now,$50,000 PIP insurance means the insurance company will pay a limit of $50,000 per person, per accident.

Hence, The insurance company will pay the maximum amount of Kaylee’s insurance of $50,000

Therefore,

PIP insurance, $50,000

Page 243 Problem 23 Answer

Given : The three passengers in Mollie’s car are hurt and each requires $12,000 worth of medical attention.

We have to find what insurance will cover this, and how much will the company pay.

We will use above information.

Here, As we know that the type of insurance that covers this is Personal Injury Protection insurance or PIP insurance.

This type of insurance applies because this insurance covers medical payments without regard to who is at fault.

Now,$50,000 PIP insurance means the insurance company will pay a limit of $50,000 per person, per accident.

As there is no individual person who claims for more than $50,000

Hence, the insurance company will pay the entire amount of the medical expenses of $12,000×3=$36,000

Therefore,PIP insurance, $36,000

Page 243 Exercise 1 Answer

Given: The insurance company offers her a 35% discount for her annual premium.

We have to express algebraically the amount she must save each month to pay the new, lower premium.

We will use above information.

Here,The new premium is the previous premium decreased by 35% of the premium

i.e.  x−35%×x=65%×x

Now,The amount she must save each month is then the new premium divided by the number of months in a year.

Hence,65%×x/12 Therefore, the amount she must save each month to pay the new, lower premium is 65%×x/12

Page 244 Exercise 2 Answer

Given: The annual premium would have been x dollars to insure the car, but they are entitled to a 10

percent discount since they have other cars with the company.

We have to express their annual premium after the discount algebraically.

We will use some simple percentage rule.

Here,The new premium is the previous premium decreased by 10% of the premium.

i.e. x−10%×x=90%×x

Therefore,90%×x,their annual premium after the discount is expressed algebraically.

Chapter 5 Exercise 5.4 Automobile Ownership Walkthrough Cengage

Page 244 Exercise 3 Answer

Given: The Schuster family have to pay a y-dollar surcharge for this arrangement,

We have to express their quarterly payment algebraically.

We will use above information.

Here, We have, The annual premium is 90%×x

Now. the  quarterly payment is : ​

90%×x/4+y

⇒22.5%×x+y​

Therefore,The quarterly payment is,22.5%×x+y

Page 244 Exercise 4 Answer

Given: Marc currently pays x dollars per year for auto insurance

We have to express his annual premium for next year algebraically if he completes the course.

We will use above information.

Here,The new premium is the previous premium increased by 15% of the premium and decreased by the d dollars for completing the course.

So, x+15%×x−d=115%×x−d

Therefore,115%×x−d, his annual premium for next year is expressed algebraically

Page 244 Exercise 5 Answer

Given:  The insurance company will lower his rate by d dollars.

We have to express his semiannual premium for next year algebraically if he does not complete the course.

We will use above information.

Here, The new premium is the previous premium increased by 15% of the premium.

i.e.  x+15%×x=115%×x

Now, The semiannual premium is 115%×x/2

=57.5%×x​

Therefore, The semiannual premium is 57.5%×x​

Cengage Financial Algebra Automobile Ownership Exercise 5.4 Solutions

Page 244 Exercise 6 Answer

Given: A  stem-and-leaf plot which gives the number of juniors who took a driver education course at Guy Patterson High School over the last two decades.

We have to construct a box-and-whisker plot based on the data.

We will use above information.

Here,Firstly we have to order the data values from smallest to largest:41,42,43,45,45,46,51,51,58,58,58,59,60,60,60,61,62,65,71,71

So, the minimum (smallest data value) is 4.

Now, The median is the middle value of the sorted data set.

As there are 20 data values, the median is the average of the 10th and 11th data values : M=Q2

=58+58/2

=116/2

=58​

The first quartile is the median of the data values below the median (or at 25% of the data).

As there are 10 data values below the median, the first quartile is the average of the 5th and 6th data value :Q1=45+46/2

=91/2

=45.5​

The third quartile is the median of the data values above the median (or at 75%of the data).

As there are 10 data values above the median, the third quartile is the average of the 15th and 16th data value :Q3 =60+61/2

=121/2

=60.5

So, the maximum (largest data value) is 71

Now, The first quartile is at 25% of the sorted data list, the median at 50% and the third quartile at 75%.

So, the Box plot of the given data is,

Therefore,

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership

Page 232 Problem 1 Answer   

Given ; ​ ​$540 ​$550 ​$550 ​$550 ​$550  $600 ​$600 ​$600 ​$675 ​$700 ​$700 ​$700 ​$990 ​$990 ​$990 ​$990 ​$990 ​$1,000 ​$1,200 ​$1,200 ​$1,200

​To find; Use the frequency distribution to find the number of car stereos selling for less than 800.

Jerry can set up a frequency distribution. A frequency distribution is a table that gives each price and the frequency—the number of stereos that are advertised at each price.

Jerry adds the numbers in the frequency column to find the total frequency—the total number of pieces of data in his data set.

He wants to make sure he did not accidentally leave out a price.

Because there are  prices in the set, and the sum of the frequencies is19 when the stereos selling for less than 800 Jerry concludes his frequency distribution is correct

Hence the number of car stereos selling for less than 800 is 19 so frequency will be 19

Page 233 Problem 2 Answer   

Given ; He is not interested in any of the car steroes priced below $ 650 because they are in poor condition

To find : Find the mean of the data set that remains after those prices are removed.

Jerry creates another column in his table for the product of the fi rst two column entries.

The sum of the entries in the third column, 4540  is used to find the mean.

This is the same sum you would find if you added the original 8 prices.

Divide by 8  to find the mean, and round to the nearest cent 4540/8

=$567.5

The mean of the prices is $567.5

Hence the mean price of the stereos is $567.5

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra Chapter 5.3 Automobile Ownership Guide

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 233 Problem 3 Answer   

Given; Rod was doing Internet research on the number of gasoline price changes per year in gas stations in his county.

To find: Find the range and the upper and lower quartiles for the stem-and-leaf plot.

A stem-and-leaf plot displays data differently than a frequency table.

To read the stem-and-leaf plot, look at the fi rst row. In this plot, the numbers to the left of the vertical line represent the tens place digit, and are the stems.

The numbers to the right of the vertical line represent the digits in the ones place, in ascending order, and are the leaves.

The first row represents these numbers.

11,11,12,13,17,19

The second row represents these numbers.

20,23,26,26

The last row represents the number 72.

Here we see that lower quartile will be 23 and upper quartiles will be 55

Hence we conclude that the lower quartile will be 23 and upper quartiles will be 55

Page 234 Problem 4 Answer   

Given ;

To find: what percent of the gas stations had 55 or fewer price changes?

The box part of the diagram helps you fi nd the interquartile range, because it displays Q1 and  Q3.

Q3−Q1=55−23=32

The interquartile range is 32. That means 50 of all the gas prices are within this range.

Hence we conclude that 50 % percent of the gas stations had 55 or fewer price changes

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 235 Problem 5 Answer

Given ;

To find: Examine the modified boxplot. Is 400 an outlier.

Quartiles are shown on the boxplot, so you can fi nd the interquartile range.

The interquartile range is

IQR=Q3−Q1=w−x

Q1−1.5(IQR)=x−1.5(w−x)

There are no lower outliers.

The boundary for upper outliers is Q3+1.5(IQR)=w+1.5(w−x)

There is at least one upper outlier, the high price of 600. From this boxplot, you cannot tell if there are any others, because the boxplot does not give all the original data.

Boxplots are drawn to scale, so the long whisker on the right means that there could be more than one outlier.

Hence we conclude that 400 is not a outliner

Page 236 Problem 6 Answer   

The Objective is to Interpret the quote in the context of what you learned

In order to create a theory, you need something to base your theory on (else it will be completely unfounded).

The basis for the theory is then data, as we can use data to show/indicate that some theory could be true.

If you do not base your theory on data, then it is possible that your theory is completely wrong and thus you then made a capital mistake.

Hence, If you do not base your theory on data, then it is possible that your theory is completely wrong and thus you then made a capital mistake.

Solutions For Exercise 5.3 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Problem 7 Answer

Given that the frequency table

To find median By finding the middle value

The data set contains 33 prices, the median will be the 17^th data value.

Add the first number of frequencies until obtain 17:

1+4+3+1+7+1=17

hence, The 17^th number in the dataset is 750

The median of the dataset is 750

Page 236 Problem 8 Answer   

Given that the frequency table

To find mode By finding the most appear number

From the given dataset, 700 appears most i.e 7 times

So, The mode is 700

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Problem 9 Answer

Given that the frequency table

To find the range by using the basic calculation

From the given dataset:

Highest value: 1200

lowest value: 540

Range​=1200−540=660​

Therefore, Range=660

Page 236 Problem 10 Answer

Given that Martina found the mean of the data from Example 1 by adding the prices in the first column and dividing by the number of prices she added

To find why Martina got incorrect answer

By using mean definition

She didn’t consider that how many times that the price occur.

She have to first calculate sum of the multiplication of the price and the frequency of that price and then divide this sum with the number of prices

Page 236 Problem 11 Answer  

Given that the prices of the Chevrolet HHR retro trucks

To find frequency table for the given dataset

By using the frequency values

The frequency table is

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Problem 12 Answer

Given that the prices of the Chevrolet HHR retro trucks

To find mean for the given dataset

By using the basic calculation

Mean =8500+8500+8500+9900+10800+10800+11000+12500+12500+13000+13000+14500+23000/13

=156500/13

=12038.46≈12038

​Mean for the given dataset is 12038

Page 236 Problem 13 Answer   

Given that the prices of the Chevrolet HHR retro trucks

To find median for the given dataset By using the basic calculation

The given dataset contains 13 values. So, 7thvalue is the middle value

The 7^th value in the given dataset is 11000

The median value is $11000

Page 236 Problem 14 Answer

Given that the prices of the Chevrolet HHR retro trucks

To find mode for the given dataset

By using the basic calculation

From the given dataset, 8500 appears most number of times

So the mode is $8500

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Problem 15 Answer

Given that the prices of the Chevrolet HHR retro trucks

To find range for the given dataset By using the basic calculation

From the given dataset:

Lowest value: 8500

highest value: 23000

Range​=23000−8500

=$ 14500​

Therefore, the range is$ 14500.

Page 236 Problem 16 Answer   

Given that the prices of the Chevrolet HHR retro trucks

To find the four quartiles for the given dataset

By using the basic calculation

From 6(b), median=11000

First quartile is the middle number from smallest number to the median

Q1=8500+9900/2

=9200​

Second quartile is the median value

Q2=11000

Third quartile is the middle value from median to the highest number

Q3=13000+13000/2

=13000

Fourth quartile is the highest value

Q4=23000

The four quartiles are 9200, 11000, 13000, 23000

Page 236 Problem 17 Answer   

Given that the prices of the Chevrolet HHR retro trucks

To find the interquartile range for the given dataset

By using the basic calculation

From 6(f)

First quartile =9200

Third quartile=13000

Interquartile range=third quartile−first quartile

=13000−9200

=$ 3800

The interquartile range is $3800

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Problem 18 Answer

Given that the prices of the Chevrolet HHR retro trucks

To find the boundary for upper outliers for the given dataset

By using the basic calculation

From 6(f), Third quartile Q3

=13000

From 6(g), Interquartile range IQR=3800

The boundary for the upper outliers=Q3+1.5IQR

=13000+1.5⋅3800

=$18700

​The boundary for the upper outliers is $18700

Page 236 Problem 19 Answer   

Given that the prices of the Chevrolet HHR retro trucks

To find the boundary for lower outliers for the given dataset

By using the basic calculation

From 6(f), The first quartileQ1

=9200

From 6(g), The interquartile range IQR=3800

The boundary for lower outliers​=Q1−1.5IQR

=9200−1.5⋅3800

=3500

​The boundary for lower outliers $3500

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Problem 20 Answer

Given that the prices of the chervrolet HHR retro trucks

To find number of outliers for the given dataset

By using the basic calculation

From 6(h), The upper outlier is $18700

From 6(i), The lower outlier is $3500

From the given dataset $23000 is above the upper outlier. All remaining values are between the lower and upper outlier.

So, There is only one outlier

Page 236 Problem 21 Answer   

Given that the prices of the Chevrolet HHR retro trucks

To draw a modified box-and-whisker plot for the given dataset

By using the basic calculation

The box-and-whisker plot for the given data is

Page 236 Exercise 1 Answer   

Given that the dataset of 33 values

To draw a modified box-and-whisker plot for the given dataset

By using the given data

The data in ascending order is

540,550,550,550,550,600,600,600,675,700,700,700,700,700,700,700,750,775,775,800,870,900,900,990,990,990,990,990,990,1000,1200,1200,1200

The five number summery is  minimum, first quartile, median, third quartile, maximum values

Minimum value is 540

Median is the middle value in that sorted data.

Median=750

First quartile is the median of the data below the median value

Q1=675+600/2

=637.5

Third quartile is the median of the data above the median value

Q3=990+990/2

=990

maximum value is 1200

The box-and-whisker plot is

The box-and-whisker plot for the given data is

Chapter 5 Exercise 5.3 Automobile Ownership Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Exercise 2 Answer

Given that the dataset of 33 values

To find that how can we determine if it would be appropriate to create a modified boxplot for this data

By using the given data

If the given dataset contains the outliers, then we can create a modified boxplot for the given data.

But for this problem, there are no outliers(From 7(a))

Page 236 Exercise 3 Answer

Given that the dataset of 33 values

To find outliers By using the given data

The data in ascending order is

540,550,550,550,550,600,600,600,675,700,700,700,700,700,700,700,750,775,775,800,870,900,900,990,990,990,990,990,990,1000,1200,1200,1200

From 7(a)

The first quartile Q1

=637.5

The third quartile Q3

=990

The interquartile range is IQR=Q3−Q1

=990−637.5

=352.5

​The upper outlier is Q3+1.5IQR=990+1.5⋅352.5

=1518.75

​The lower outlier is Q1−1.5IQR=637.5−1.5⋅352.5

=108.75

​All the values from the dataset are in between the lower and upper outlier.

So, there are no outliers for the given distribution of data

There are no outliers for the given distribution

Page 237 Exercise 4 Answer  

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find number of students polled

By using the count

By counting the number of values on the right side, We get 27 students were polled

Page 237 Exercise 5 Answer

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find the mean to the nearest cent By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

Mean=17+41+41+42+49+47+53+53+53+53+53+61+63+64+66+67+68+69+71+73+75+75+77+82+82+83+84/27

=1662/27

=61.56

≈62​

The mean of the given dataset is 62

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 237 Exercise 6 Answer

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find the median.

By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,83,84

The data in ascending order are

17,41,41,42,47,49,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

There are 27 values in the data. So, 14th value is the middle value

The median is 64

The median of the given dataset is 64

Page 237 Exercise 7 Answer   

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find the mode By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

The mode is the number that occur most

In the given dataset  53 occur 5 times

The mode is 53

The mode for the given dataset is 53

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 237 Exercise 8 Answer

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find the range By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

Range is the difference between the highest and lowest values of the data

Highest value: 84

Lowest value: 17

Range=84−17=67

​The range for the given dataset is 67

Page 236 Exercise 9 Answer   

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find the four quartiles.

By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

From 10(c), The median is 64

First quartile is the middle number from smallest number to the median

Q1=53

Second quartile is the median value

Q2=64

Third quartile is the middle value from median to the highest number

Q3=75

Fourth quartile is the highest value

Q4=84

The four quartiles for the given dataset are 53, 64, 75, 84

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 237 Exercise 10 Answer

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find percent of the students spent $ 53 or more on gas

By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

From the data, Total number of students=27

Number of students spent $53 or more on gas=21

percentage of students spent $53 or more on gas​=21/27∗100

=77.78

​The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

From the data,

Total number of students=27

Number of students spent $53 or more on gas=21

percentage of students spent $53or more on gas​=21/27∗100

=77.78

Page 237 Exercise 11 Answer   

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find the interquartile range

By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

From 10(f),

Q1=53

Q3=75

The interquartile range​=Q3−Q1

=75−53

=$ 22​

The interquartile range is $22

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 237 Exercise 12 Answer

Given that the stem-and-leaf plot of the cold spring high school students poll data

To find the percent of the students spent from $ 53 to $ 75 on gas

By using the count

The values from the stem-and-leaf plot are

17,41,41,42,49,47,53,53,53,53,53,61,63,64,66,67,68,69,71,73,75,75,77,82,82,83,84

From the data,

Total number of students=27

Number of students spent from 53 to 75 on gas =16 percent of the students spent from $ 53 to $ 75 on gas​=16/27∗100

=59.26​

59.26% students spent from $53 to $75 on gas

Page 237 Exercise 13 Answer   

Given: In earlier parts, the first and third quartiles were​

Q1=$53

Q3=$75

IQR=$22.

To find: The boundary for the lower outliners.The lower outliners have aQ{1}−1.5 IQRboundary.

Q − 1.5 . 1 IQR = $53 − 1.5 × $22

= $20

The boundary for the lower outliners is $20.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 237 Exercise 14 Answer

Given: In earlier parts, the first and third quartiles were​

Q1=$53

Q3=$75

IQR=$22.

To find The boundary for the upper outliners.The upper outliners have aQ{3}+1.5IQR boundary.

Q3 + 1.5IQR = $75 + 1.5 × $22

= $108

The boundary for the upper outliners is $108.

Page 237 Exercise 15 Answer   

Given: Outliner’s boundaries are$20,$108.

To find The number of outliners. The items in the dataset that are lower than$108

or higher than$20

are known as outliners. So, our one any only outliner is$17.

We have only one outliner.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 236 Exercise 16 Answer

Given: Stem-and-leaf plot of data is provided.

To do: Draw a modified boxplot.

For doing so, we will refer to the fact that the boxplot’s whiskers are at their smallest and largest values (not including the outliers).

The boxplot’s whiskers are at their smallest and largest values (not including the outliers). The box has a vertical line at the median and starts at the first quartile and finishes at the third quartile.

The first quartile accounts for25% of the sorted data list, the median for50%, and the third quartile for75%.

An outlier is denoted by the letter “X”.

The modified boxplot is

Page 237 Exercise 17 Answer   

Given: Stem-and-leaf plot of data is provided.

To find The total frequency.

Count how many leaves there are in the plot. i.e. the number of entries on the right side of the vertical line. So, the total frequency is 18.

The total frequency is 18.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.3 Automobile Ownership Page 237 Exercise 18 Answer

Given: Stem-and-leaf plot of data is provided.To find: The number of people with monthly payments between$210 and $219.

There is no element behind21 in the stem-and-leaf plot, indicating that there are no elements between$210 and $219.

Zero. None of the people had monthly payments between$210 and $219.

Cengage Financial Algebra Automobile Ownership Exercise 5.3 Solutions

Page 237 Exercise 19 Answer   

Given: Stem-and-leaf plot of data is provided.

To find The mode monthly payment.

A value that appears the most in a data collection is known as the mode.226 occurs three times in this example, and no other element appears as frequently.

The mode monthly payment is 226.

Page 237 Exercise 20 Answer  

Given: A stem-and-leaf plot of data is provided.

To find The median monthly payment.

The median is the sorted dataset’s middle element.

The median is the sorted dataset’s middle element.

Because there are18 items in the collection, the median is the average of the ninth and tenth elements.

$187+$192/2

=$189.50.

The median monthly payment is$189.50.

Page 237 Exercise 21 Answer   

Given: Frequency table of a data set is provided.

To find The mean of the given data.

For doing so, we will usemean=price×frequency/total frequency

We know thatmean=price×frequency/total frequency

So, Mean =xy+5w+64+18v/9+y+v

Therefore, Mean =xy+5w+64+18v/9+y+v.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership

Page 225 Problem 1 Answer

Given; Maxine compiled a list of these car prices: 7,500,6,500,5,750,4,900,6,250, and 4,200.

To find; Find the mean of the prices.

Maxine should start by finding the mean or arithmetic average of the five prices. The mean is often called the average.

mean=7,500+6,500+5,750,+4,900+6,250+4,200/6

=35100/6

=5850

​Hence the mean price of the car is 5850

Page 226 Problem 2 Answer

Given: price of the car 1,200,1,650,1,500,2,000,1,400,1,850,and1,600.

To find: Find the mean and median of the following prices for a used car extended warranty:

here we will first find the mean of the price

1,200+1,650+1,500+2,000+1,400+1,850+1,600./7

=11200/7

=1600

​Hence the mean is found to be 1600

Now in next step we will arrange the given price in ascending order to get the median

1200 −1450−1500−1600−1650−1850−2000

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

from here we can see that the middel of the term is 1600

so it is given meadian 1600

Here we acknowledge that both mean and meadian are 1600 so the given data is skewed

Cengage Financial Algebra Chapter 5.2 Automobile Ownership Guide

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 226 Problem 3 Answer

Given ;

To find ; Find the median

Put the numbers in ascending order. Then, pair the numbers.

Since there is an even number of scores, there is no number left alone in the middle.

Circle the last two numbers that were paired.

find the mean of the two innermost circled numbers. 9600+10200/2

=19800/2

=9900

​Hence the median of the price of the car is found to be 9900

Page 226 Problem 4 Answer

Given ; 6,700,, 5,800 , 9,100,8,650,7,700,and7,800.

To find: Find the range of the used car prices

The range of a data set is a measure that shows dispersion (how spread out the data are).

The range is the difference between the greatest and least numbers in the data.

The greatest price is 9100 and the least is 5800.

The range is the difference between these two prices.

9100−5800=3300

Therefore, the range is  3300

Hence the range of the car price is foudn to be 3300

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 227 Problem 5 Answer

Given; the quartiles for the tire pressures of cars at an auto clinic.

15,17,21,25,31,32,32,32,34

To find ; What percent of the numbers in a data set are aboveQ3

The numbers are in ascending order.

Q1 is the fi rst quartile or lower quartile, and 25 % of the numbers in the data set are at or below Q1.

Q2is the second quartile. Half the numbers are below Q2, and half are above, so Q2 is equal to the median.

Q3 is the third quartile, or upper quartile, and 75 % of the numbers are at or below Q3.

Q4 is the maximum value in the data set because 100 % of the numbers are at or below that number.

first find Q2.

Because Q2 equals the median,Q2=31.

For Q1, find the median of the numbers below the median, which are 15,17,21,and25.

The median of these numbers is Q1=19.

17+21/2

=19

For Q3, find the median of the numbers in the data set that are above the median, which are 32,32,32,34. The two middle numbers are 32,

so Q3=32

Now The quartile values are

Q1=19,Q2=31, Q3=32 ,Q4=34. and from the given data we can see that above 32 is only one data that is 34

15,17,21,25,31,32,32,32,34

so the percentage will be 25 %

Hence we have found the percent of the numbers in a data set are above Q3 is 25 %

Solutions For Exercise 5.2 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 228 Problem 6 Answer

Given ; $6,700,$5,800,$9,100,$8,650,$7,700, and $7,800.

To find; Find the interquartile range for the data is the fi rst quartile or lower quartile, and 25 % of the numbers in the data set are at or below Q1.

Q2 is the second quartile. Half the numbers are below Q2,and half are above, so Q2 is equal to the median.

Q3 is the third quartile, or upper quartile, and75 % of the numbers are at or below Q3.

Q4 is the maximum value in the data set because 100 % of the numbers are at or below that number.

$6,700,$5,800,$9,100,$8,650,$7,700, and $7,800.

Arrange in ascending order 5800 , 6700 , 7700 , 7800 , 8650 ,9100 ,

7,700+7,800/2

=7,750

Q2=7750

Q1=5800+6700/2

=6250

​Now Q3

=8650+9100/2

=8875

​The difference Q3−Q1 is the interquartile range (IQR).

The interquartile range gives the range of the middle 50 % of the numbers.

A small interquartile range means that the middle 50 %  of the numbers are clustered together.

A large interquartile range means that the middle50 % of the numbers are more spread out.

To find the interquartile range, subtract. The interquartile range is ​Q3−Q1

=8875−6250

=2625

​Hence we have found the interquartile range of the data is  Q3−Q1=2625

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 22 Problem 7 Answer

Given; The store that charged 545 for a tire had a sale and lowered its price to399.

To find: Is the new price an upper outlier?

The interquartile range is used to identify outliers.Outliers may occur on the lower or upper end of the data set.

The numbers are in ascending order. 45,88,109,129,146,189,202,218,and 399(due to sale )

The median, Q2,is146

Q1=88+109/2

=98.5​

Q3=202+218/2

=210

Use Q1−1.5(IQR) to compute the boundary for lower outliers

IQR=210−98.5=111.5

Any number below −68.75 is an outlier. There are no lower outliers.

98.5−1.5(111.5)=−68.75

Use Q3+1.5(IQR) to compute the boundary for upper outliers.

210+1.5(111.5)=377.25

Any number above 377.25 is an upper outlier, so399 is an upper outlier.

Hence we found that 399 is teh upper outlier and we alsofoudn that the new number ie, 399 is also a upper outlier

Page 228 Problem 8 Answer

Given ; 15,17,21,25,31,32,32,32,34

To find: Find the mode of the tire pressures

The mode is the most-occurring item and is often used with non-numerical variables, such as the winning  tire pressure from the given data we can see that the most ofteen occuring data is 32

so the mode of the given data is 32

Hence the mode of the given data15,17,21,25,31,32,32,32,34 is 32

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Problem 9 Answer

In the above question the have asked to answer

Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.

Answer:- Reading and writing is currently a necessity to be able to participate in the current community.

However, Statistics will become equally important in the near future, because we come across data and Statistics on a daily basis (which will most likely become even worse in the near future) and thus we will require basic Statistical thinking to be able to understand this information.

In the near future, Statistical thinking will become equally important to reading and writing.

Page 229 Problem 10 Answer

Given 7,12,1,7,6,5,11

We need to find mean, median, mode, and range

Given 7,12,1,7,6,5,11

Mean:- Add all the values and divide by 7.

7+12+1+7+6+5+11/7

=49/7

=7​

Median Arrange the values in ascending or descending order and identify the middle value.

1,5,6,7,7,11,12

Median=7.

Mode:- Mode is the value that appears more no. of times than any other value in the list. In this case only the value 7 appears twice.

mode = 7

Range:-​ The range is the difference between the greatest and least numbers in the data.

Range =12−1

=11​

Therefore the mean median mode and range are 7,7,7 and 11 respectively.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Problem 11 Answer

Given 85,105,95,90,115

We need to find mean, median, mode, and range

Given 85,105,95,90,115

Mean:-​ Add all the values and divide by

85+105+95+90+115/5

=490/5

=98

​Median:- Arrange the values in ascending or descending order and identify the middle value.

85,90,95,105,115

Median=95

Mode:-Mode is the value that appears more no. of times than any other value in the list. In this case no value appears more than once. So there is no mode.

Range:-​The range is the difference between the greatest and least numbers in the data.

Range =115−85​

=30

Therefore the mean median mode and range are 98, 95, no mode and 11 respectively

Page 229 Problem 12 Answer

Given 10,14,16,16,8,9,11,12,3

We need to find mean, median, mode, and range

Given 10,14,16,16,8,9,11,12,3

Mean Add all the values and divide by 9.

10+14+16+16+8+9+11+12+3/9

=99/9

=11​

Median Arrange the values in ascending or descending order and identify the middle value.

3,8,9,10,11,12,14,16,16

Median=11

Mode:- Mode is the value that appears more no. of times than any other value in the list. In this case only the value 16 appears twice.

Range:-​ The range is the difference between the greatest and least numbers in the data.

Range =16−3

​=13

Therefore the mean median mode and range are 11, 11, 16 and 13 respectively

Chapter 5 Exercise 5.2 Automobile Ownership Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Problem 13 Answer

Given 10, 8, 7, 5, 9, 10, 7

We need to find mean, median, mode, and range

Given

Mean:- Add all the values and divide by 7

10 + 8 + 7 + 5 + 9 + 10 + 7/7=56/7

= 8

Median:- Arrange the values in ascending or descending order and identify the middle value.

Mode:- Mode is the value that appears more no. of times than any other value in the list. In this case both appear twice.

10.8.7.5.9, 10.7

5, 7, 7, 8, 9, 10, 10

median = 8

7 and 10

Range:- The range is the difference between the greatest and least numbers in the data.

Range = 10 − 5

= 5

Therefore the mean median mode and range are 8, 8, 7and10, and 5 respectively.

 Page 225 Problem 14 Answer

Given 45,50,40,35,75

We need to find mean, median, mode, and range

Given 45,50,40,35,75

Mean:- Add all the values and divide by 5

45+50+40+35+75/7

=245/5

=49

Median Arrange the values in ascending or descending order and identify the middle value.

35,40,45,50,75

Median=45

Mode:- Mode is the value that appears more no. of times than any other value in the list. In this case no value appears more than once. So there is no mode.

Range:- The range is the difference between the greatest and least numbers in the data.

Range =75−35​

=40

Therefore the mean median mode and range are 49, 45, no mode and 40 respectively

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Problem 15 Answer

Given 15,11,11,16,16,9

We need to find mean, median, mode, and range

Given:-15,11,11,16,16,9

Mean:- Add all the values and divide by 6

15+11+11+16+16+9/6

=78/6

=13

Median:- Arrange the values in ascending or descending order and identify the middle value.

9,11,11,15,16,16

median = 13

Mode:- Mode is the value that appears more no. of times than any other value in the list. In this case both 11and16 appear twice.

This data set is bi-modal.

Range:- The range is the difference between the greatest and least numbers in the data.

Range =16−9

=7

Therefore the mean median mode and range are 13, 13, 11and16, and 7 respectively

Page 229 Problem 16 Answer

Given data:- $24,600,$19,000,$33,000,$15,000,$20,000

We need to find mean.

Given data values: $24, 600, $19, 000, $33, 000, $15, 000, $20, 000

We note that there are 5 data values.

The mean is the sum of all values divided by the number of values:

xˉ = =∑ⁿ  x_i/n
           _i=1

=24600 + 19000 + 33000 + 15000 + 20000/5

=111600/5 ≈ 22320

Thus the mean price is $22, 320

Therefore the mean price is $22, 320.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Problem 17 Answer

In the above question they have given $110,$145,$130,$160,$400

We need to find mean.

Given data values:

$110, $145, $130, $160, $400

We note that there are 5 data values.

The mean is the sum of all values divided by the number of values:

xˉ =∑ⁿ  x_i/n
        _i=1

=110 + 145 + 130 + 160 + 400/5

=945/5

= 189

Thus the mean price is $189.

Therefore the mean price is $189.

Page 229 Problem 18 Answer

In the above question they have given

$110,$145,$130,$160,$400

We need to find median.

Given data values:

$110, $145, $130, $160, $400

Order the data values from smallest to largest:

$110, $130, $145, $160, $400

The median is the middle value of the sorted data set Since there are 5 data values, the median is the third data value in the sorted data set:

M = $145

Thus the median price is $145.

Therefore the median price is $145.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Problem 19 Answer

Given data is $110,$145,$130,$160,$400

We need to find data outliner.​

$400 is extremely different from others′ salary.

Other values are between 100 and 200 .

​Therefore Stephanie′s salary is an outlier in the data set

Page 229 Problem 20 Answer

Given $110,$145,$130,$160,$400

We need to find number do you think is better representative of the data, the mean or the median

In part (c), we concluded that there was an outlier present among the salaries.

The mean is strongly influenced by the outlier, because it takes the sum of all data values (including the outlier) before dividing by the number of outliers.

However, the median is not influenced by the outlier as it is just the middle value of the sorted data set and thus the median is better representative as it is not influenced by the outlier.

I think the median is not influenced by the outlier.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Problem 21 Answer

Given $110,$145,$130,$160,$400

We need to given a explanation for part d

In part (c), we concluded that there was an outlier present among the salaries.

The mean is strongly influenced by the outlier, because it takes the sum of all data values (including the outlier) before dividing by the number of outliers.

However, the median is not influenced by the outlier as it is just the middle value of the sorted data set and thus the median is better representative as it is not influenced by the outlier.

Median is not influenced by the outlier, while the mean is strongly influenced by the outlier.

Page 229 Exercise 1 Answer

In the above question they have given $59.00,$71.00,$50.00

We need to find mean.

Given data values: $59.00, $71.00, $50.00

We note that there are 3 data values.

The mean is the sum of all values divided by the number of values:

xˉ =∑ⁿ  x_i/n
       _i=1

=59.00 + 71.00 + 50.00/3

=180.00/3

= 60.00

Thus the mean price is $60.00.

Therefore the mean price is $60.00.

Cengage Financial Algebra Automobile Ownership Exercise 5.2 Solutions

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Exercise 2 Answer

In the above question they have given $59.00, $71.00, $50.00

We need find total cost .

Given data values: $59.00, $71.00, $50.00

The total cost of all three ads is the sum of the cost of each ad.

Total cost = Sum of cost of each ad

= 59.00 + 71.00 + 50.00

= 180.00

Thus the total cost of running all three ads would then be $180.00.

Therefore the total cost of running all three ads would then be $180.00.

Page 229 Exercise 3 Answer

Given: Lake Success Shop saver$59.00

Glen Head Buyer $71.00

Floral Park Money saver$50.00

To Find: The objective is to Find :

If each of the three newspapers used the mean price as their ad price, what would it cost Rosanne to run ads in all three papers

We will use the value of mean Which is find in a part.

Given data values are:

Now, from part(a):

The value of mean is 60.

Now, If she had to pay mean price to each ad then also it would cost$180.

Total Price = Mean price ×3

​=60×3

=$180​

Hence, the cost Rosanne to run ads in all three papers is $180

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Exercise 4 Answer

Given: Lake Success Shop saver$59.00

Glen Head Buyer$71.00

Floral Park Money saver$50.00

To Find: The objective is to find the range of these ad prices.

We will use the definition of Range

Given data values are:

$59.00,$71.00.$50.00

Now, The range is the difference between the greatest and least numbers in the data.

So, Range=71−50

=$21

​Hence, the range of the given ad prices is $21

Page 229 Exercise 5 Answer

Given: We are given Dan’s grade91,82,90,89

To Find: The objective is to find the grade does he need on his final exam to have a 90 average.

We will use the definition of mean.

We have Dan’s Grade.

91,82,90,89

Now, Firstly we let the missing grade be x

So, we note that there are Five data values.

91,82,90,89,x

Now, by the definition of mean. The mean is the sum of all values divided by the number of values:

xˉ=∑ⁿ  x_i/n
       _i=1

=91+82+90+89+x/5

=352+x/5

Now, we want mean to be 90

So, 352+x/5

=90

Now, we multiply each side by 5

So, we get:352+x=450

Finally subtract 352 from each side we get:x=98

Hence, 98 grade Dan’s  need on his final exam to have a 90 average.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 229 Exercise 6 Answer

Given: We are given:Elliot Savings from an entire year=$6,000

To Find: The objective is to find savings per week if he plans to work the entire year with only two weeks off.

We will use the formula: Savings per week = Savings per year

Number of (work) weeks

Now, we have

Elliot Savings from an entire year=$6,000

Now, As we know that there are52 weeks in a year and since we take 2 weeks off, there are 52−2=50 weeks that we plan to work.

Now, The amount we need to save each week is then the total savings from an entire year divided by the number of weeks.

So, we use the Formula Savings per week

= Savings per year/ Number of (work) weeks

=$6,000/50

=$120

​Hence,  Elliot should plan to save$120 each week if he plans to work the entire year with only two weeks off.

Page 230 Exercise 7 Answer

Given: We are given the mean of five numbers is 16.

Four numbers are 13,20,11 and 21

To Find: The objective is to find the fifth number.

We will use the definition and formula of mean.

We have the four numbers.

13,20,11 and 21

Now, Firstly we let the missing fifth number be x

So, we note that there are Five data values.

13,20,11,21,x

Now, by the definition of mean.

The mean is the sum of all values divided by the number of values:

xˉ=∑ⁿ  x_i/n
       _i=1

=13+20+11+21+x/5

=65+x/5

Now, we want mean to be16:

65+x/5

=16

Now, we multiply each side by5

so, we get:

65+x=80

Finally subtract 65

from each side, so we get:x=15

Therefore, the fifth number is 15

Hence, the fifth number is15

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 230 Exercise 8 Answer

Given: We are given: The quartiles of a data set are:Q1=50,

Q2=72,

Q3=110, and Q4=140

​To Find: The objective is to Find the interquartile range.

We will use the definition of  interquartile range.

We have,

The quartiles of a data set are:

Q1=50 ,Q2=72,Q3=110, and Q4=140

By using the definition of interquartile range:

The interquartile range is the difference between the first quartileQ1 and the third quartileQ3:

IQR=Q3−Q1

=110−50

=60​

Hence,  the interquartile range is IQR=60

Page 230 Exercise 9 Answer

Given: We are given $450,$100,$180,$600,$300,$350,$300, and $400.

To Find: The objective is to Find the four quartiles.

We will use the Definitions.

We have the dataset.

$450,$100,$180,$600,$300,$350,$300, and $400.

Now, Firstly we sort the Dataset:

$100,$180,$300,$300,$350,$400,$450,$600

The first quartile is then the average between the second and third element in the sorted dataset

Q1=$180+$300/2

=$240

The second quartile is the median and is the average of the two middle elements in the sorted dataset.

Q2=$300+$350/2

=$325

The third quartile is the average between the sixth and seventh element in the sorted dataset.

Q3=$400+$450/2

=$425

The forth quartile is the last element in the sorted dataset.

Q4=$600

Hence,  the four quartiles are $240,$325,$425,$600

How To Solve Cengage Financial Algebra Chapter 5.2 Automobile Ownership

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 230 Exercise 10 Answer

Given: We are given $450,$100,$180,$600,$300,$350,$300, and $400

To Find: The objective is to  Find the interquartile range.

We will use the definition of Interquartile range.

We have the data values.

$450,$100,$180,$600,$300,$350,$300, and $400

The first quartile is then the average between the second and third element in the sorted dataset

Q1=$180+$300/2

=$240

​The third quartile is the average between the sixth and seventh element in the sorted dataset.

Q3=$400+$450/2

=$425

​Now, using the definition of  Interquartile range.

The interquartile range is the difference between the third and the first quartile.

IQR=Q3−Q1

IQR=$425−$240

IQR=$185

​Hence, the interquartile range for the given data set is$185

Page 230 Exercise 11 Answer

Given: We are given $450,$100,$180,$600,$300,$350,$300, and $400

To Find: The objective is to Find the boundary for the lower outliers. Are there any lower outliersWe will use the definitions.

We have the data values:

$450,$100,$180,$600,$300,$350,$300, and $400 from part (a) and (b) we have:

Q1=$240

Q3=$425

IQR=$185

Now, The boundary for lower outliers is Q1−1.5IQR

∴Q1−1.5IQR=$240−1.5×$185

Q1−1.5IQR=−$37.50​

There appear to be no lower outliers, because there are no prices below −$37.50

So, there are no lower outliners.

Hence,  the boundary for the lower outliers is −$37.50,  and there are no lower outliers

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 230 Exercise 12 Answer

Given: We are given $450,$100,$180,$600,$300,$350,$300, and $400

To Find: The objective is to Find the boundary for the upper outliers. Are there any upper outliers.We will use the definitions.

We have the data values:

$450,$100,$180,$600,$300,$350,$300, and $400

From part (a) and (b) we have:

Q1=$240

Q3=$425

IQR=$185

Now, The boundary for upper outliers is Q3+1.5IQR

Q3+1.5IQR=$425+1.5×$185

=$702.50​

There appear to be no upper outliers, because there are no prices that are above $702.50

So, there are no upper outliners

Hence,  the boundary for the upper outliers is $702.50,  and there are no upper outliers

Page 230 Exercise 13 Answer

Given: We are given the mean of five different numbers which is 50

To Find: The objective is to Create a list of five different numbers whose mean is50

We will use the definition and formula of mean.

Now, An example of such a list is 30,40,50,60,70.

Now, we use the definition of mean.

The mean is then the sum of all elements divided by the number of elements:

30+40+50+60+70/5

=250/5

=50

​Hence, the list of five different numbers whose mean is 50 are: 30,40,50,60,70

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 230 Exercise 14 Answer

Given: We are given the median of six different numbers which is 10

To Find: The objective is to Create a list of six different numbers whose median is 10

We will use the definition of median.

Now, An example of such a list is 2,4,9,11,13,15

By using the definition of median

The median is then the average between the two middle elements of the sorted dataset (the given dataset is already sorted):

9+11/2

=20/2

=10

Hence, the list of six different numbers whose median is 10 is:

2,4,9,11,13,15

Page 230 Exercise 15 Answer

Given: We are given the mean and median of five numbers 12

To Find:  The objective is to Create a list of five numbers whose mean and median are both12

We will use the definition of mean and median

Now, An example of such a list is 8,10,12,14,16

As we know that  the mean is the sum of all elements divided by the number of elements 8+10+12+14+16/5=12

And the median is the middle element in the sorted dataset (the given dataset has already been sorted).

Hence, The list of five numbers whose mean and median are both 12 is:8,10,12,14,16

Practice Problems For Automobile Ownership Exercise 5.2 Cengage

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.2 Automobile Ownership Page 230 Exercise 16 Answer

To Find: The objective is to Create a list of numbers whose mean, median, and mode are all 10

We will use the definitions

Let the list of numbers only contain 10:10,10,10,10,10 then the mean, median and mode are all 10.

Hence, The list of numbers whose mean, median, and mode are all 10 is:  Let the list of numbers only contain10:10,10,10,10,10

Page 230 Exercise 17 Answer

To Find: The objective is to  Create a list of numbers with two upper outliers and one lower outlier.We will use the definitions.

Now, an example of such dataset is: 0,10,10,10,10,10,10,10,10,10,20,20

because its quartiles are all  10,  thus the IQR is 0  and the boundary for the upper/lower outliers is then also 10.

Hence, The list of numbers with two upper outliers and one lower outlier is: 0,10,10,10,10,10,10,10,10,10,20,20

Page 230 Exercise 18 Answer

To Define: The objective is to  Explain why you cannot find the range of a data set if you are given the four quartiles.We will use the definitions.

This can be explained as: Because you cannot determine the lower boundary of the data based on only the quartiles and you need the lower boundary because the range is the difference between the upper and lower boundary of values.

Hence, Because you cannot determine the lower boundary of the data based on only the quartiles and you need the lower boundary, because the range is the difference between the upper and lower boundary of values.

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership

Page 219 Problem 1 Answer

Given that  sales tax rate in Mary Ann′s state is 4%.

Also given the price of the car is x dollars.

We have to find the total cost of the car with sales tax algebraically.

As we know that the sales tax is the product of the price of the item with the sales tax rate,

So we have it as Sales tax= Price of item × Sales tax rate

=x×4/100

Sales tax=0.04x dollars

​Hence we have the Sales tax algebraically as 0.04x dollars

Cengage Financial Algebra Chapter 5.1 Automobile Ownership Guide

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 219 Problem 2 Answer

Given that Ramon plans to sell his car and places an ad with x lines.

The news paper charges y dollars for the first g lines and p dollars per extra line to run the ad for a week.

Also given that x>g

We have that The news paper charges y dollars for the first g lines and p dollars per extra line to run the ad for a week.

As we have given that x>g

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Now we have the extra numbers that are extra chargable is x−g

So that we have the cost of running the ad for a week as ​gy+(x−g)p

cost of running the ad for a week=gy+xp−gp dollars.

​Hence we have the cost of running the ad for a week as gy+xp−gp dollars.

Page 220 Problem 3 Answer

Given that Smithtown News charges $38 for a classified ed ad that is 4 or fewer lines long.

Each line above four lines costs an additional $6.25.

We can express the piece wise function

Now let us assume that c(x) represent the cost.

Now let us consider the number of lines of the ad as x

Now we have the piece wise function as

c(x)={​38                        when x≤4

{  38+6.25(x−4)        when x>4

​Hence we have the piecewise function as

c(x)={​38                ​ when x≤4

{  38+6.25(x−4)     when x>4

​Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 221 Problem 4 Answer

We are given : The piece-wise function :

p(w)={​60                    ​ when w≤5

{  60+8(w−5)              when w>5

We have to: Translate the function into words.

Answer: Translating we get: The classified ad charges $60 for the first 5−lines and $60+8(w−5) for each additional line w

Translating we get: The classified ad charges $60 for the first 5−lines and $60+8(w−5) for each additional line w

Page 221 Problem 5 Answer

We have to : Find the cusp of the graph of the piece-wise function :

c(x)={​42.50               ​ when x≤5

{   42.50+7(x−5)      when x>5

​The cost function changes from c(x)=38 to c(x)=38+6.25(x-4) when x becomes laeger than 4

x-coordinates cusp=4

y-coordinates cusp=c(4)=38

The coordinates of the cusp are:(4,38)

Solutions For Exercise 5.1 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 222 Problem 6 Answer

We have to find :

How much does a six-line ad cost.

Cost 4 additional lines = Number of additional lines × Cost per additional line

= 4 × 7

= $28

Total cost = Cost first 2 lines + Cost 4 additional line

= $19.50 + $28

= $47.50

Total cost = $47.50

Page 222 Problem 7 Answer

We have to find :

How much would a four-line ad with a photo cost.

Total cost = Cost first 3 lines + Cost 1 additional line + Cost Photo

= $45 + $8.50 + $40

= $93.50

The total cost of a four-line ad with a photo cost : $93.50

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 222 Problem 8 Answer

We are given that : Cost first 4 lines : g dollars

Cost per additional line : d dollars

We have to : Write an expression for the cost of a7 line advertisement.

We have find the cost of the 7−line ad, thus we are placing 7−4=3 additional lines beside the basic 4−line ad

Cost 3 additional lines = Number of additional lines × Cost per additional line

= 3 × d

= 3d

Total cost = Cost first 4 lines + Cost 3 additional line

= g + 3d

The cost of a 7 line advertisement : g + 3d

Page 222 Problem 9 Answer

We have to :

Express the cost of an x−line ad algebraically.

Cost x − m additional lines = Number of additional lines × Cost per additional line

= (x − m) × d

= d(x − m) dollars

Total cost = Cost first m lines + Cost x − m additional line

= g + d(x − m) dollars

Total cost = g + d(x − m) dollars.

Chapter 5 Exercise 5.1 Automobile Ownership Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 222 Problem 10 Answer

We have to find : How much does Samantha need to pay for these extra charges, not including the price of the car.

State tax = State tax rate × Purchase price

= 4% × $4, 200

= 0.04 × $4, 200

= $168

Total extra charges = State tax + Charge license plates + Charge state safety and emissions inseption

= $168 + $47 + $35

= $250

Total extra charges = $250

Page 222 Problem 11 Answer

We have to find : What would the new price be if Ralph reduced it according to the suggestion.

Discount = Discount rate × Selling price

= 5% × $18, 500

= 0.05 × $18, 500

= $925

New selling price = Selling price − Discount

= $18, 500 − $925

= $17, 575

New selling price : $17,575

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 222 Problem 12 Answer

We are given,

Cost first 200 characters: $46

Cost per additional character: $0.15

We have to,express the cost c(x) of an ad as a piece wise function.

Let us assume : x = number of characters in ad

c(x) = cost of ad

Cost x − 200 additional characters = Number of additional characters × Cost per additional character

= (x − 200) × 0.15

= 0.15(x − 200)

c(x) = Total cost = Cost first 200 characters + Cost x − 200 additional characters

= 46 + 0.15(x − 200) if x > 200

c(x) = {46                     if x ≤ 200

{46 + 0.15(x − 200)     if x > 200

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 222 Problem 13 Answer

We have to, Graph the function :

c(x)={​46              if x≤200

46+0.15(x−200)  if x>200

​Sketching the graph we get :

The required graph :

Page 222 Problem 14 Answer

We have to: Find the coordinates of the cusp in the graph.

We can see that : the cost function changes from c(x) = 46 to c(x) = 46 + 0.15(x − 200) when x becomes larger than 200

So we have : The x−coordinate of the cusp is at x = 200

y−coordinates cusp = c(x) = 46

The coordinates of the cusp are : (46, 200)

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 222 Problem 15 Answer

We have to find : How much would the magazine charge to print a2x1/2−inch ad

The amount to be paid for the 2×1/2 inch ad :

21/2 × 67 = $167.50

The amount to be paid for the 2×1/2 inch ad :

$167.50

Page 223 Problem 16 Answer

We have to : Find if the newspaper charges$48 for the first three lines and $5

for each extra line, how much will this ad cost.

Cost 2 additional lines = Number of additional lines × Cost per additional line

= 2 × 5

= $10

Total cost = Cost first 3 lines + Cost 2 additional line

= $48 + $10

= $58

Total cost = $58

Cengage Financial Algebra Automobile Ownership Exercise 5.1 Solutions

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 223 Problem 17 Answer

We have to find : If Ruth buys the car for 8% less than the advertised price, how much does she pay

We are given that :

Selling price = $52, 900

Discount rate = 8% = 0.08

Discount = Discount rate × Selling price

= 8% × $52, 900

= 0.08 × $52, 900

= $4, 232

New selling price= Selling price − Discount

= $52, 900 − $4, 232

= $48, 668

New selling price = $48, 668

Page 223 Problem 18 Answer

We have to : How much sales tax must be paid.

Discount = Discount rate × Selling price

= 8% × $52, 900

= 0.08 × $52, 900

= $4, 232

New selling price = Selling price − Discount

= $52, 900 − $4, 232

= $48, 668

Sales tax = Sales tax rate × New selling price

= 6% × $48, 668

= 0.06 × $48, 668

= $2, 920.08

Sales tax = $2, 920.08

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 223 Problem 19 Answer

We are given that : Advertised price=$12,000

Selling price=$11,200

Commission rate=4%=0.04

We have to find : How much must be paid for the ad.

Commission = Commission rate × Advertised price

= 4% × $12, 000

= 0.04 × $12, 000

= $480

Commission = $480

Page 223 Exercise 1 Answer

We are given the Piecewise function :

c(x)={​38                     when x≤4

{  38+6.25(x−4)        when x>4

​We have to find the cost of a three-line ad.

Answer: We know that, cost is 38 if no. of lines is less than or equal to 4

Therefore,cost of a 3−line ad =38 cost of a 3−line ad =38

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 223 Exercise 2 Answer

We are given the Piece wise function :

c(x)={​38                       ​ when x≤4

{  38+6.25(x−4)            when x>4

​We have to find the difference in cost between a one-line ad and a four-line ad.

We know that, the cost is 38 is the number of lines is less than or equal to 4.

Therefore, there is no difference in cost between a one-line ad and a four-line ad.

There is no difference in cost between a one-line ad and a four-line ad.

Page 223 Exercise 3 Answer

We are given the Piece wise function :

c(x)={​38                    when x≤4

{  38+6.25(x−4)   when x>4

​We have to: Find the cost of a seven-line ad.

Cost of a 7−line ad :

c(7) = 38 + 6.25(7 − 4)

= 38 + 6.25(3)

= 56.75

Cost of a 7−line ad = 56.75

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 223 Exercise 4 Answer

We are given the Piecewise function :

c(x) = {  38                           when x ≤ 4

{ 38 + 6.25(x − 4)     when x > 4

We have to: Graph this function on your graphing calculator

Sketching the graph we get :

Sketching the graph we get

Page 223 Exercise 5 Answer

We are given the Piecewise function :

c(x) = {  38                       when x ≤ 4

{ 38 + 6.25(x − 4)  when x > 4

We have to: Find the coordinates of the cusp from the graph.

The cost function changes from c(x) = 38 to c(x) = 38 + 6.25(x − 4) when x become larger than 4

x−coordinates cusp = 4

y−coordinates cusp = c(4) = 38

The coordinates of the cusp are : (4, 38)

How To Solve Cengage Financial Algebra Chapter 5.1 Automobile Ownership

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 223 Exercise 6 Answer

We are given that: The piecewise function describes a newspaper’s classified ad rates :

y={​21.50               ​ when x≤3

{    21.50+5(x−3)         when x>3

​We have to: Translate the function into words.

Answer : Translating we get :

A newspaper charges $21.50 for the first 3−lines and $5 for each additional line

Translating we get :

A newspaper charges $21.50 for the first 3−lines and $5 for each additional line

Page 223 Exercise 7 Answer

Given

y={ 21.50           ​ when x≤3

{ 21.50+5(x−3)    when x>3

If the function is graphed,

we need to find the coordinates of the cusp.

Given:

c(x) = { 21.50                 if x ≤ 3

{ 21.50 + 5(x − 3)  if x > 3

The cusp is the point in the graph where the two straight lines meet,where each straight line will represent one ”piece” of the piecewise function.

The x−coordinate of the cusp is at x = 3,because the cost function changes from c(x) = 21.50 to c(x) = 21.50 + 5(x − 3) when x becomes larger than 3 x−coordinates cusp = 3

The y−coordinates of the cusp is then the cost function evaluated at x34 : y−coordinates cusp = c(3) = 21.50

Thus the coordinates of the cusp are then (3, 21.50)

Thus the coordinates of the cusp are then (3, 21.50)

Step-By-Step Solutions For Chapter 5.1 Automobile Ownership Exercise

Cengage Financial Algebra 1st Edition Chapter 5 Exercise 5.1 Automobile Ownership Page 223 Exercise 8 Answer

In the above question they have given

​Charge: $15

Cost first 5 lines: $2.5 per line

Cost per additional line: $8

​We need find  If x is the number of lines in the ad, write a piecewise function for the cost of the ad, c(x)

Let x represent the number of lines in the ad and let c(x) represent the cost of the ad.

When x ≤ 5, then the cost is $2.5 per line for each of the first 5 lines (thus you need to pay for 5 lines even if you use less than 5 lines and $8 per additional line

The cost of the lines is then the product of the price per line and the number of lines x :

Cost x lines = Number of lines × Cost per line ad additional line beside the basic5 ad line

= 5 × 2.5

= 12.5 if x ≤ 5

The total cost is then the sum of the charge and the cost of the x lines:

c(x) = Total cost x lines

= Charge + Cost per line

= 15 + 12.5

= 27.5 if x ≤

When x > 5, then the costs is $2.5 per line for the first 5 lines and $8 per additional line.

The cost of the first 5 lines is 1

Cost 5 lines = Number of lines × Cost per line 2.5 perline.

= 5 × 2.5

We are interested in placing a

= 12.5

x−line ad, thus we are placing x−5

Cost x − 5 additional tines = Number of additional lines × Cost per ad additionall ines beside the basic5 − line ad.

= (x − 5) × 8

= 8(x − 5)

x−line ad then includes the charge, the cost of the first 3 lines and the cost of the additional x−3

c(x) = Total cost lines.

= Charge + Cost first 3 tines + Cost x − 3 additional line

= 15 + 12.5 + 8(x − 5) Combining this in for

= 27.5 + 8(x − 5) if x > 3

c(x) = {27.5                             if x ≤ 5

{27.5 + 8(x − 5)            if x > 5

piecewise function for the cost of the ad, c(x) is

{27.5   if                            x ≤ 5

{27.5 + 8(x − 5)                if x > 5

Financial Algebra 1st Edition Chapter 4 Consumer Credit

Page 211 Problem 1 Answer

Given; six laws regulate consumer credit in the United States.

To find; Find when each act was signed into law.

What problem was the act trying to help solve?

What are the major provisions of each act?

Prepare a poster displaying your findings.

we have given laws

Equal Credit Opportunity Act

Electronic Funds Transfer Act

Fair Credit Reporting Act

Fair Credit Billing Act

Fair Debt Collection Practices Act

Truth-in-Lending Act

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

The Equal Credit Opportunity Act was signed on October 28,1974.

The act was trying to solve discrimination against applicants by a creditor.

The act made it unlawful to discriminate on the basis of race, color, religion, sex, national origin, etc.

The Electornic Funds Transfer Act was signed on November 10,1978.

The act established the rights, liabilities and responsibilities of everybody involved in electronic funds transfers.

Thus the act was trying to solve the lack of law with regards to electronic funds transfers.

The Fair Credit Reporting Act was signed on October 26, 1970.

The act was trying to solve the lack of accuracy, fairness and privacy of consumer information.

The Fair Credit Billing Act was signed in1974.

The act was trying to protect consumers from unfair billing practices and to create a set guideline in dealing with billing errors of credit/charge card accounts.

The Fair Debt Collection Practices Act was signed on September 20,1977.

The act was trying to eliminate abusive practices involving consumer debts and promoting fair debt collection.

Moreover, the act also provided people with a right to dispute the debt information.

The Truth-in-Lending Act was signed on May 29,1968.

The act was trying to eliminate the lack of informaton given to consumers and to provide a standardized manner to calculate costs associated with the debt.

Hence we have discuss about the laws , signed date and problem

Equal Credit Opportunity Act

Electronic Funds Transfer Act

Fair Credit Reporting Act

Fair Credit Billing Act

Fair Debt Collection Practices Act

Truth-in-Lending Act

Cengage Financial Algebra Chapter 4 Assessment Consumer Credit Guide

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 211 Problem 2 Answer

Given; Here we have given that we have to Visit two lending institutions in your area

To find; Find the APR, monthly payment, and finance charge for a $15,000, three-year loan at the two lenders.

]”financer”, which compares different lending institutions and some other useful information about loans at those lending institutions including the monthly payment,

the APR and the total cost (finance charge).

For example, Sofi will lend 15,000

for an estimated Annual Periodic rate of 5.49% to 12.99%.

It’s monthly payback would be $452.87, while the total finance charge (total cost) would be $1,303.35.

Since there are 36 months in 3 years, the total monthly payback would be 36×$452.87=$16,303.32 (product of number of months and the monthly payment).

Another lending institution dabur will lend $15,000 for an estimated Annual Periodic rate of 4.99% to 29.99%.

Its monthly payback would be $455.25,while the total finance charge (total cost) would be $1,388.86.

Since there are 36 months in 3 years, the total monthly payback would be 36×$455.25=$16,389

(product of number of months and the monthly payment).

Hence we conclude that there are 36 months in 3 years, the total monthly payback would be36×$455.25=$16,389 product of number of months and the monthly payment).

Page 212 Problem 3 Answer

Given; information on the FICO score.

To find: What is the range of possible scores?

How can each score be interpreted?

What contributes to the FICO score? Summarize the information you find from the websites.

Prepare your information in a report.

The FICO score ranges from 300 to 850.

A FICO score is a credit score, which takes into account the payment history, the amount of debts, the types of credit used, the length of credit history and new credit accounts.

The FICO score determines how worthy a possible borrower is of being given a loan.

A FICO score of 800+is considered to be exceptional.

A FICO score of 740 to 799 is considered to be very good.

A FICO score of 670 to 739 is considered to be good.

A FICO score of 580 to 669 is considered to be below average.

A FICO score of 579 or less is considered to be poor.

People with a FICO score below 620 might have trouble finding loans at a favorable rate.

You we can improve your FICO score by paying your bills on time, keeping a low balance on credit cards and paying off debts.

Hence we cocnlude that the Range from 300 to 850

The FICO score determines how worthy a possible borrower is of being given a loan.

The payment history, the amount of debts, the types of credit used, the length of credit history and new credit accounts all contribute to the FICO scores.

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 212 Problem 4 Answer

Given ; There are three major credit reporting agencies in the United States.

they are named Equifax, Experian, and TransUnion.

They keep records of your credit activity and provide your potential creditors with information on your financial habits.

To find ; Summarize the information you obtain in a report.

Equifax gives out credit scores of consumers, where the credit scores are based on information of over 800 million consumers and more than 88 million businesses.

Equifax is based in Atlanta and was founded in 1899. The company was founded by Cator and Guy Woolford.

The company proves credit and demographic data to business and sells credit monitoring to consumers along with fraud-prevention services.

The company had a revenue of approximately3.362

billion U.S. dollars in 2017 , while it had a net income of 587.3 million dollars in 2017.

The company also had approximately 10,300 employees in 2017.

Experian gives out credit scores of consumers, where the credit scores are based on information of over 1 billion people and over 25 million businesses.

Experian is based in Dublin, Ireland (although it also operates in the UK, the US, Brazil and 33 other countries).

The company was founded in 1996 and its current CEO is Brian Cassin.

The company proves credit services, but also sells analytic decisions and marketing assistance to businesses.

The company had a revenue of approximately 4.335 billion U.S. dollars in 2017, while it has a net income of 0.865 billion dollars in 2017.

The company also had approximately 15,587 employees in 2017.

TransUnion gives out credit scores of consumers, where the credit scores are based on information of over 1 billion people and over 65,000 businesses.

TransUnion is based in Chicago, Illinois. The company was founded in 1968 and its current CEO is James M. Peck.

The company proves credit services, but also sells credit and fraud-protection products.

The company had a revenue of approximately 1.93 billion U.S. dollars in 2017, while it has a net income of 120.6 billion dollars in 2016.

The company also had approximately 4,700 employees in2016.

Hence we have given teh information about the theree major credit reporting agencies

Equifax was found in 1899 and is based in Atlanta.

Experian was founded in1996 and is based in Dublin, Ireland.

TransUnion was founded in1968 and is based in Chicago, Illinois.

Solutions For Chapter 4 Assessment In Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 212 Problem 5 Answer

Given; finance charges for a  31000 new-car loan over a five-year period.

Prepare your information on a poster.

To find: Find the APR, monthly payment, and finance charges

Here we will use a site called “financer”, which compares different lending institutions and some other useful information about loans at those lending institutions including the monthly payment, the APR and the total cost (finance charge).

For example, freedomplus will lend $30,000 for an estimated Annual Periodic rate of 4.99% to 29.99%.

Its monthly payback would be $572.90, while the total finance charge (total cost) would be $4,373.97.

However, if you decide to lend $35,000, then the monthly payback becomes$668.38 and the finance charge (total cost) becomes $5,102.97

Another lending institution personalloands will lend $30,000 for an estimated Annual Periodic rate of 5.99%to 29.99%.

It’s monthly payback would be $579.84, while the total finance charge (total cost) would be $4,790.67.

However, if you decide to lend $35,000, then the monthly payback becomes $676.49 and the finance charge (total cost) becomes$5,589.12.

Hence we conclude that  the monthly payback becomes $676.49 and the finance charge (total cost) becomes $5,589.12.

Page 212 Problem 6 Answer

Given; When the bank representative comes to speak, act as moderator for the discussion. Keep a log of the questions and which student asked them

To find: Write a thank you letter to the bank representative after the session.

Here are some of the the question which we can ask from the representative the local bank representative about loans and credit cards:

How much money can you borrow? Minimum? Maximum?

What are the conditions to be able to get a loan?

What costs should you expect to pay on a loan?

What are the possible terms on a loan?

What will happen when you fail to make multiple payments on a loan?

How old do you have to be to qualify for a credit card?

What costs should you expect to pay on a credit card?

What will happen when you fail to make multiple payments on a credit card? etc.

Hence we have high lighted Some possible questions that you could ask the local bank representative about loans and credit cards:

How much money can you borrow? Minimum? Maximum?

What are the conditions to be able to get a loan?

What costs should you expect to pay on a loan?

What are the possible terms of a loan?

What will happen when you fail to make multiple payments on a loan?

How old do you have to be to qualify for a credit card?

What costs should you expect to pay on a credit card?

What will happen when you fail to make multiple payments on a credit card? etc.

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 212 Problem 7 Answer

Given:  Interview your parents or relatives about their use of loans and credit cards.

To find; Find what they consider wise spending habits, and what they have learned about credit.

If they agree to let you see their last credit card statement, show them how to check entries in the statement, including the average daily balance and the finance charge.

Here are Some possible questions that you could ask your family members about loans and credit cards:

How much money did you borrow? How much did you still need to pay off?

What did you borrow money for?

What were the conditions to be able to get a loan?

What costs should you expect to pay on a loan?

How long till the loan is paid off?

When should you get a loan? What is a good reason to get a loan?

What costs should you expect to pay on a credit card?

Which purchases should you use a credit card for?

How regularly should you make payments to a credit card?

Should you pay off your debts on a credit card as soon as possible? etc.

Hence we have given examples of Some possible questions that you could ask your family members about loans and credit cards:

How much money did you borrow? How much did you still need to pay off?

What did you borrow money for?

What were the conditions to be able to get a loan?

What costs should you expect to pay on a loan?

How long till the loan is paid off?

When should you get a loan? What is a good reason to get a loan?

What costs should you expect to pay on a credit card?

Which purchases should you use a credit card for?

How regularly should you make payments to a credit card?

Should you pay off your debts on a credit card as soon as possible? etc.

Page 212 Problem 8 Answer

Given; Go to the store and interview a customer service representative

To find; Find out if any local store has an installment plan. Get the monthly payment and finance charge for a specific item in the store, purchased under the installment plan.

Prepare a report for the class.

An installment plan is a sum of money that needs to be paid in small amounts over a fixed period.

More precisely, the installment plan is then a type of loan.

The length of an installment plan can vary from a few months to 30 years, while a mortgage is a type of installment loan.

For example, Apple offers an installment loan on the purchase of an iPhone. The loan is a 24-month loan at a 0% annual periodic rate (APR).

The monthly payments will then be the total purchase price divided by 24, as we do not have to pay any finance charge at an APR of 0% and thus the finance charge is $0

Hence we conclude that The monthly payments will then be the total purchase price divided by 24, as we do not have to pay any finance charge at an APR of 0% and thus the finance charge is

Chapter 4 Consumer Credit Assessment Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 212 Problem 9 Answer

Given; lists the terms and conditions of major credit cards.

To find; Research two different cards by going to the provider’s links. Compare and contrast the advantages and disadvantages of each.

There are different website which compares different types of credit cards.

For example, I compared low rate credit cards, when you expect to spend about $2,000 per month.

A possible credit card is the low rate credit card of ANZ, which requires an annual fee of$58 and has an annual interest rate of 12.49%.

You will also have to pay 0% interest for the first 15 months when transferring the money to a different credit card account and 21.74% interest afterwards.

Another possible credit card is the low-rate credit card of ANZ, which requires an annual fee of$0

(no annual fee) and has an annual interest rate of 11.8%.

You will also have to pay 11.80% interest when transferring the money to a different credit card account.

Hence we have compared and contrasted some of the points of credit card and some of the advantages and disadvantages

Page 213 Problem 10 Answer

Given;  The circumference of the earth is approximately 24,901 miles at the equator measure of typical credit card measures 54mm by 85mm.

To find; How many credit cards (end to end) would it take to circle the earth?

we have measure of credit card 54mm by 85mm.

we know the circumference of a circle is C=2πr

here we will take ​r=85/2

=42.5

​Now 24901=42.5

=585.90

​Hence there will be 586 credit card will be required

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 213 Problem 11 Answer

Given that the circumference of the earth is approximately 24,901 miles at the equator measure of typical credit card measures 54mm by 85mm.

To find; How many credit cards (end to end) would it take to circle the earth?

we have a measure of credit card54mm by 85mm.

here we will take  r=85/2

we know the circumference of a circle is C=2πrnow 24901=42.5

=585.90

Hence there will be 586 credit cards will be required

Page 213 Problem 12 Answer

Given; The typical credit card measures 54 mm by 85mm.

To find: How many times would 1 billion credit cards circle the earth at the equator?

we have given a measure of credit card 54mmby85mm.

One billion is equal to 1,000,000,000

1,000,000,000/85

=11764705

​Hence we conclude that that11764705 times would 1 billion credit cards circle the earth at the equator

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 213 Problem 13 Answer

Given; Shania bought a $1,455 drum set on the installment plan.

The installment agreement included a 15 % down payment and 18 monthly payments of 80.75  each.

To find; How much is the down payment

Purchase price: $1,455

Down payment rate=15\%

Monthly payment= $80.78

Number of months =18

The down payment is the product of the down payment rate and the purchase price:

Down payment =Down payment rate × Purchase Price

=15%×$1,455

=0.15×$1,455

=$218.25​

Hence the monthly down payment is found to be =$218.25

Cengage Financial Algebra Consumer Credit Assessment Solutions

Page 213 Problem 14 Answer

Given: Shania bought a 1455 drum set on the installment plan.

The installment agreement included a 15% down payment and 18 monthly payments of 80.78 % each

To find; What is the total amount of the monthly payments?

Purchase price: $1,455

Down payment rate=15%

Monthly payment= $80.78

Number of months=18

The total amount of the monthly payments is the product of the number of months and the monthly payment:

Total amount of the monthly payments =Number of months × Monthly payment

​=18×$80.78

=$1,454.04​

Hence  the total amount of the monthly payments will be =$1.454.04

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 213 Problem 15 Answer

Given; Shania bought a $ 1455 drum set on the installment plan.

The installment agreement included a 15 % down payment and 18 monthly payments of 80.75 each.

To find: How much will Shania pay for the drum set on the installment plan

Purchase price:$1,455

Down payment rate=15\%

Monthly payment= $80.78

Number of months=18

The down payment is the product of the down payment rate and the purchase price:

Down payment = Down payment rate $\times$ Purchase Price​

=15%×$1,455

=0.15×$1,455

=$218.25

The total amount of the monthly payments is the product of the number of months and the monthly payment:

Total amount of the monthly payments = Number of months × Monthly payment

​=18×$80.78

=$1,454.04

The total cost is the sum of the total amount of the monthly payments and the down payment:

Total cost = Total amount of the monthly payments+ Down payment

=$1,454.04+$218.25

=$1,672.29​

Hence The amount of money will Shania pay for the drum set on the installment plan is =$1,672.29

Page 213 Problem 16 Answer

Given: Shania bought a 1455 drum set on the installment plan.

The installment agreement included a  15 % down payment and 18 monthly payments of 80.78 each.

To find: What is the finance charge

we have given :

Down payment rate=15%

Monthly payment= $80.78

Number of months=18

Down payment = Down payment rate Purchase Price

​=15%×$1,455

=0.15×$1,455

=$218.25

The total amount of the monthly payments is the product of the number of months and the monthly payment:

Total amount of the monthly payments = Number of months Monthly payment

​=18×$80.78

=$1,454.04

Total cost = Total amount of the monthly payments +Down payment

​=$1,454.04+$218.25

=$1,672.29

​Finance Charge = Total cost − Purchase price

=$1,672.29−$1,455

=$217.29

​Hence the finance charge for Shania will be $217.29

Cengage Financial Algebra Chapter 4 Consumer Credit Concepts Explained

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 213 Problem 17 Answer

Given; that Carly took a $7,000, three-year loan with an APR of 8.15%

To find; What is the monthly payment?

We have P= 7,000

r= 0.0815

And t= 3

⇒ \(M=\frac{7000\left(\frac{0.0815}{12}\right)\left(1+\frac{0.0815}{12}\right)^{12(3)}}{\left(1+\frac{0.0815}{12}\right)^{12(3)}-1}\)

⇒ \(M=\frac{7000\left(\frac{0.0815}{12}\right)\left(1+\frac{0.0815}{12}\right)^{36}}{\left(1+\frac{0.0815}{12}\right)^{36}-1}\)

⇒ \(\left(7000(0.0815 / 12)(1+0.0815 / 12)^{\wedge} 36\right) /\left((1+0.0815 / 12)^{\wedge} 36-1\right)\)

Hence the monthly payment will be $219.84

Page 213 Problem 18 Answer

Given; that Carly took a $7,000,three-year loan with an APR of 8.15%

To find; What is the total amount of the monthly payments?

We have P= 7,000

r= 0.0815

And t= 3

⇒ \(M=\frac{7000\left(\frac{0.0815}{12}\right)\left(1+\frac{0.0815}{12}\right)^{12(3)}}{\left(1+\frac{0.0815}{12}\right)^{12(3)}-1}\)

⇒ \(M=\frac{7000\left(\frac{0.0815}{12}\right)\left(1+\frac{0.0815}{12}\right)^{36}}{\left(1+\frac{0.0815}{12}\right)^{36}-1}\)

⇒ \(\left(7000(0.0815 / 12)(1+0.0815 / 12)^{\wedge} 36\right) /\left((1+0.0815 / 12)^{\wedge} 36-1\right)\)

Now the total monthly payment will be ​

219.84×36=7,914.24

​hence the total monthly payment will be $7,914.24

Practice Problems For Consumer Credit Assessment Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 213 Problem 19 Answer

Given; Carly took a  $7,000, three-year loan with an APR of 8.15%.

To find; What is the finance charge?

We have P= 7,000

r= 0.0815

And t= 3

⇒ \(M=\frac{7000\left(\frac{0.0815}{12}\right)\left(1+\frac{0.0815}{12}\right)^{12(3)}}{\left(1+\frac{0.0815}{12}\right)^{12(3)}-1}\)

⇒ \(M=\frac{7000\left(\frac{0.0815}{12}\right)\left(1+\frac{0.0815}{12}\right)^{36}}{\left(1+\frac{0.0815}{12}\right)^{36}-1}\)

⇒ \(\left(7000(0.0815 / 12)(1+0.0815 / 12)^{\wedge} 36\right) /\left((1+0.0815 / 12)^{\wedge} 36-1\right)\)

(7000(0.0815/12)(1+0.0815/12)^36)/((1+0.0815/12)^36−1)

Now the total monthly payment will be 219.84×36=7,914.24

Now the finance charge will be 7,914.24−7,000=914.24

Hence the finance charge for Carly will be $914.24

Page 213 Problem 20 Answer

Given; that Sarah is taking out a $24,400 four-year new-car loan with an APR of 6.88%

To find out what is the finance charge for this loan? Round to the nearest hundred dollars.

We have p =24,400

r= 0.0688

t = 4

⇒ \(M=\frac{24400\left(\frac{0.0688}{12}\right)\left(1+\frac{0.0688}{12}\right)^{12(4)}}{\left(1+\frac{0.0688}{12}\right)^{12(4)}-1}\)

⇒ \(M=\frac{24400\left(\frac{0.0688}{12}\right)\left(1+\frac{0.0688}{12}\right)^{48}}{\left(1+\frac{0.0688}{12}\right)^{48}-1}\)

⇒ \(\frac{24400(0.0688 / 12)(1+0.0688 / 12)^{48}}{(1+0.0688 / 12)^{48}-}\)

Now the monthly payment of $582.93

Now the total  monthly payment is 582.93×48=27,980.64

finance charge 27,980.64−24,400=3,580.64

Hence the finance charge will be =$3,600

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 214 Exercise 1 Answer

Given;  The policy of the Black Oyster Pawnshop is to lend up to the value of a borrower’s collateral.

Pete wants to use a  $2,000 guitar and a $900 camera as collateral for a loan

To find;  What is the maximum amount that he could borrow from Black Oyster?

The collateral is a $2,000 guitar and a $900

camera: Total collateral =$2,000+$900

=$2,900

The amount that Pete can borrow is 30% of the total collateral

The amount that can be borrowed =30%×Total collateral

=0.30×$2,900

=$870

Hence the maximum amount that he could borrow from Black Oyster would be $870

Page 214 Exercise 2 Answer

Given: Juan purchased a tool set for $t on the installment plan.

He made a 15 % down payment and agreed to pay $m per month for the next  y years

To find: Express the finance charge algebraically.

Purchase price: t dollars

Down payment rate =15%

Monthly payment=mdollars

Number of months =y years =12y months

Down payment = Down payment rate×Purchase Price

​=15%×t

=0.15×t

=0.15t

The total amount of the monthly payments is the product of the number of months and the monthly payment:

The total amount of the monthly payments= Number of months × Monthly payment

​=12y×m

=12my

The total cost is the sum of the total amount of the monthly payments and the down payment:

The finance charge is then the total cost decreased by the purchase price:

Finance Charge = Total cost − Purchase price

=(12my+0.15t)−t

=12my+0.15t−1y

=12my+(0.15−1)t

=12my−0.85t

​Hence the finance charge algebraically will be shown as 12my−0.85t

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 214 Exercise 3 Answer

Given; that the finance charge on Lauren’s credit card bill last month was $13.50.

Her APR is 18 %

To find; What was her average daily balance?

APR=18%

Finance charge =$13.50

The APR is the annual periodic rate.

The monthly periodic rate is then the annual periodic rate divided by 12,

Monthly periodic rate = APR / Number of months in a year

=18%/12

=1.5%

​The finance charge is the product of the average daily balance and the monthly percentage rate:

Finance charge = Monthly percentage rate × Average daily balance Divide each side by the monthly percentage rate

Average daily balance = Finance charge / Monthly percentage rate

=$13.50/1.5%

=$13.50/0.015

$900.00

​Hence her average daily balance will be $900.00

Page 214 Exercise 4 Answer

Given; a loan with an APR of 19.5 %

To find;  What is the monthly period rate

we have APR=19.5%

The APR is the annual periodic rate.

The monthly periodic rate is then the annual periodic rate divided by 12,

Monthly periodic rate= APR / Number of months in a year

=19.5%/12

=1.625%

​Hence the monthly period rate will be 1.625%

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 214 Exercise 5 Answer

Given; that Harold borrowed  $ 8,000 for five years at an APR of 6.75 %

To find out: What is Harold’s monthly payment?

We have

p= 8,000

r= 0.0675

t= 5

⇒ \(M=\frac{8000\left(\frac{0.0675}{12}\right)\left(1+\frac{0.0675}{12}\right)^{12(5)}}{\left(1+\frac{0.0675}{12}\right)^{12(5)}-1}\)

⇒ \(M=\frac{8000\left(\frac{0.0675}{12}\right)\left(1+\frac{0.0675}{12}\right)^{60}}{\left(1+\frac{0.0675}{12}\right)^{60}-1}\)

⇒\(\left(8000(0.0675 / 12)(1+0.0675 / 12)^{\wedge} 60\right) /\left((1+0.0675 / 12)^{\wedge} 60-1\right)\)

Hence the monthly payment for Harold will be  Monthly payment =$157.47

Page 214 Exercise 6 Answer

Given; that Harold borrowed $8,000 for five years at an APR of .6.75 %

To find; What is the total amount that Harold paid in monthly payments for the loan

we have

p=8,000,

r=0.0675

t=5

⇒ \(M=\frac{8000\left(\frac{0.0675}{12}\right)\left(1+\frac{0.0675}{12}\right)^{12(5)}}{\left(1+\frac{0.0675}{12}\right)^{12(5)}-1}\)

⇒ \(M=\frac{8000\left(\frac{0.0675}{12}\right)\left(1+\frac{0.0675}{12}\right)^{60}}{\left(1+\frac{0.0675}{12}\right)^{60}-1}\)

(8000(0.0675/12)(1+0.0675/12)^60)/((1+0.0675/12)^60−1)

⇒ Monthly payment =$157.47 now the total monthly payment is 157.47×60=9,448.20 =$9,448.20​

Hence the total amount that Harold paid in monthly payments for the loan was $9,448.20

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 214 Exercise 7 Answer

Given that the amount borrowed is $8000

From the above question we have got the total monthly payment as $9,448.20

We have to find the amount Harold will pay in finance charges.

Given that the amount borrowed is $8000

Now we have the  finance charges can be found by subtracting the amount borrowed from the total amount of monthly charges which is

Finance charge = Total of the monthly payments − Amount borrowed

=$9,448.20−$8,000

=$1,448.20​

Hence we have got the amount of finance charges that will be paid by Harold as $1,448.20

Page 215 Exercise 8 Answer

Given that  Ciana wants to take out a $7,500 loan with a 5.3% APR.

She can afford to pay $128 per month for loan payments.

We have found the length of her loan.

Now we have the loan formulas as \(t=\frac{\ln \frac{M}{p}-\ln \left(\frac{M}{p}-\frac{r}{12}\right)}{12 \ln \left(1+\frac{r}{12}\right)}\)

On substituting the values given we have \(t=\frac{\ln \frac{128}{7,500}-\ln \left(\frac{128}{7,500}-\frac{0.053}{12}\right)}{12 \ln \left(1+\frac{0.053}{12}\right)}\)

= 5.66

≈5.7

So we have the length of the loan as 5.7 years.

Hence the length of the loan is 5.7 years.

tep-By-Step Guide To Consumer Credit Assessment Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 215 Exercise 9 Answer

Given that Ciana wants to take out a $7,500 loan with a 5.3% APR.

She can afford to pay $128 per month for loan payments.

We have to find the  increase of $20 to the monthly payment have do to the length of her loan

⇒ \( t=\frac{\ln \frac{148}{7,500}-\ln \left(\frac{148}{7,500}-\frac{0.053}{12}\right)}{12 \ln \left(1+\frac{0.053}{12}\right)}\)

=4.79

≈ 4.8

Now We have the loan length from the previous problem is 5.7 years.

Now we have the new length of the loan for the new monthly payment of $148 is

Now we can find the increase in the monthly payment as the difference between the old and the new loan length is

5.7−4.8=0.9 years

On the increase of the monthly amount by $20 the length of the loan will decrease by 0.9 years

Hence we can say that On an increase of monthly amount by $20 the length of the loan will decrease by 0.9 years

Page 215 Exercise 10 Answer

We have to find what is the total of all of the purchases made this billing cycle

The total of all the payments will be given in the credit card statement under the SUMMARY section underneath the New Purchases;

According to the given credit card statement we have

Total new purchases =$2,057.55

Hence we have the total new purchase from the given credit card statement is $2,057.55

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 215 Exercise 11 Answer

We have to find the amount of total payments.

The total of all the payments will be given in the credit card statement under the SUMMARY section underneath the Payments/Credits;

According to the given credit card statement we have

Amount of total payments =$1,340.00

Hence we have the Amount of total payments from the given credit card statement is $1,340.00

Page 214 Exercise 12 Answer

We have to find the sum of the daily balances.

Now we have the balances along with the length from the given credit card statement as

1 day at $978.00

8 days at $978.00+$676.00=$1,654

4 days at $1,654+721.80=$2,375.80

8 days at $2,375.80+$93.15=$2,468.95

3 days at $2,468.95−$1,340.00=$1,128.95

3 days at$1,128.95+$115.75=$1,244.70

3 days at$1,244.70+$450.95=$1,695.65

As we know the sum of the daily balances is the product of the number of days with the current balance so we have it as

1×$978.00+8×$1,654+4×$2,375.80+8×$2,468.95+3×$1,128.95+3×$1,244.70+3×$1,695.65

=$55,672.70

​So we have the sum of balances as $55,672.70

Hence we have the sum of balances as $55,672.70

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 215 Exercise 13 Answer

We have to find the average daily balance of the given credit card statement.

Now from the previous question we have got the sum of daily balances as $55,672.70

And we have the n number of days as 30 As we know the formula for the average balance is the sum of daily balances divided by the number of days so we have it as

$55,672.70/30

≈$1,855.76

So we have the average daily balance as $1,855.76

Hence we have the average daily balance for the given credit card statement as $1,855.76

Page 215 Exercise 14 Answer

We have to find the monthly periodic rate

We can find the monthly periodic rate at the bottom right corner under the section Monthly Periodic Rate of the credit card statement;

Here we have it as Monthly Periodic Rate =1.65%

Hence we have the  Monthly Periodic Rate as 1.65%

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 215 Exercise 15 Answer

We have to find the Finance Charge.

We already found the value of the Average daily amounts in one of the previous problems and we have it as $1,855.76

Also, we know the Monthly Percent Rate as 1.65%

Now we have the finance charge as nothing but the product of the average daily balances with the Monthly Periodic Rate which is

​$1,831.84×1.65%

=$1,855.76×0.0165

≈$30.62

​So we have the Finance Charge as $30.62

Hence we have got the Finance Charge according to the Credit card statement as $30.62

Page 215 Exercise 16 Answer

We have to find the NEW BALANCE.

From the previous problems we have ​ New Purchases =$2,057.65

Total payments =$1,340.00

Finance charge $30.62

​We could find the Previous balance in the credit card statement underneath the summary statement and we have it as Previous balance =$978.00

similarly, the last charge can be found in the summary section of the credit card statement which is

Late charge =$0.00

Now we have the new balance the previous balance increased by the new purchase, late charge and finance charge and decreased by the payments and it is

$978.00+$2,057.55−$1,340.00+$0.00+$30.62=$1,726.17

So we have the new balance as $1,726.17

Hence we have the NEW BALANCE as $1,726.17

Cengage Financial Algebra 1st Edition Chapter 4 Assessment Consumer Credit Page 215 Exercise 17 Answer

We have to find the value of AVAILABLE CREDIT.

From the privious problem, we have a new balance of $1,726.17

We can find the total credit line at the left side bottom of the credit card statement and here we have it as

Total credit line =$3,000.00

Now we have the available credit is the difference between the total credit line and the new balance that is $3,000.00−$1,726.17=$1,273.83

So we have the available credit as $1,273.83

Hence we have the AVAILABLE CREDIT from the given credit card statement as $1,273.83

Financial Algebra 1st Edition Chapter 4 Consumer Credit

Page 208 Problem 1 Answer

We will determine whether there a better time during the billing cycle when Elena could have made her payment so that the average daily balance would have been less.

The closer the payment is made to the beginning of the billing cycle, the lower the average daily balance will be.

The closer the payment is made to the beginning of the billing cycle, the lower the average daily balance will be.

Page 208 Problem 2 Answer

We will determine when might Elena have made her purchases during the billing cycle in order to decrease her finance charge.

The later in the billing cycle purchases are made, the lower the average daily balance, which results in a lower finance charge.

The later in the billing cycle purchases are made, the lower the average daily balance, which results in a lower finance charge.

Page 209 Problem 3Answer

Given – The best way to deal with credit card debt is to educate yourself.We will determine how might the quote apply to what we have learned.

The quote implies that you need to be cautious when dealing with a credit card,because when you use a credit card,

then you will create debts and you should always be cautious when entering into any debt agreement.

The caution is due to the fact that you need to be sure that you can pay back these debts, because else you could lose everything you own.

The quote implies that you need to be cautious when dealing with a credit card.

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra Chapter 4.6 Consumer Credit Guide

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.6 Consumer Credit Page 209 Problem 4 Answer

Given – Ralph just received his June FlashCard bill. He did not pay his May bill in full, so his June bill shows a previous balance and a finance charge.

The average daily balance is$470, and the monthly periodic rate is1.5%.

We will determine what should Ralph’s finance charge be.

The finance charge is the product of the average daily balance and the monthly periodic rate.

Hence,​$470×1.5%=$470×0.015

=$7.05

​Ralph’s finance charge is$7.05.

Page 209 Problem 5 Answer

Given – Lauren did not pay her January FlashCard bill in full, so her February bill has a finance charge added on.

The average daily balance is$510.44, and the monthly periodic rate is2.5%.

We will find Lauren’s finance charge on her February statement.

The finance charge is the product of the average daily balance and the monthly periodic rate.

Hence,​$510.44×2.5%=$510.44×0.025

=$12.76

​Lauren’s finance charge on her February statement is$12.76.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.6 Consumer Credit Page 209 Problem 6 Answer

Given – Jennifer did not pay her FlashCard bill in full in September. Her October bill showed a finance charge, and she wants to see whether or not it is correct.

The average daily balance is$970.50, and the APR is28.2%.

We will find the finance charge for her October statement.

The finance charge is the product of the average daily balance and the monthly periodic rate.

The monthly periodic rate is the APR divided by the number of months in a year.

​$970.50×28.2%/12

=$970.50×0.0235

=$22.81​

The finance charge for her October statement is$22.81.

Page 209 Problem 7 Answer

Daniyar paid his April FlashCard with an amount equal to the new purchases shown on his bill.

His May bill shows an average daily balance of$270.31 and a monthly periodic rate of1.95%.

We will find the finance charge on Daniyar’s May statement.

The finance charge is the product of the average daily balance and the monthly periodic rate.

​$270.31×1.95%=$270.31×0.0195

=$5.27

​The finance charge on Daniyar’s May statement is$5.27.

Solutions For Exercise 4.6 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.6 Consumer Credit Page 209 Problem 8 Answer

Given;  He made no additional payments or purchases before he received his next bill.

The monthly periodic rate on this account is 2.015 %

To find; What expression represents the finance charge on ∣ his June statement?

we know that The finance charge is the product of the balance and the monthly periodic rate.

​z×2.015%=z×0.02015

​Hence we conclude that the expression represents the finance charge on  his June statement z×2.015%=z×0.02015

Page 210 Problem 9 Answer

Given: Ed Lubbock’s FlashCard bill is below. There are entries missing.

To find : What is Ed’s average daily balance?

Here we will Determine the balances and the amount of time this balance is accurate.

If a payment was made, then you need to decrease the previous balance by this amount.

If a purchase was made, then you need to increase the previous balance by the amount of the purchase.

Note that the 4 transactions are given underneath TRANSACTIONS and their amounts are given under DEBITS/CREDITS(-).

Note that the dates are given along with the transactions, which allows you determine how long each balance remained constant.

13 days at 421.5 (previous balance) 7 days at 421.50+48.00=469.50

5 days at 469.50−100.00=369.50

5 days at 369.50+30.00=399.50

The average daily balance is the sum of the daily balances divided by the number of days.

13×421.50+7×469.50+5×369.50+5×399.50/30

=420.37

Hence we conclude that  the average daily balance is 420.37

Chapter 4 Exercise 4.6 Consumer Credit Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.6 Consumer Credit Page 208 Problem 10 Answer

Given; Ed Lubbock’s FlashCard bill is below. There are entries missing.

To find; What is Ed’s finance charge?

The average daily balance found 420.37

we know that The finance charge is the product of  daily balance and the monthly periodic rate.

​​420.37×1.65%=420.37×0.0165

​=6.94

​Hence we conclude that the finance charge is foudn to be 6.94

Page 208 Problem 11 Answer

Given: Ed Lubbock’s FlashCard bill is below. There are entries missing.

To find: What is Ed’s new balance?

The average daily balance found 420.37

we know that The finance charge is the product of daily balance and the monthly periodic rate.

420.37×1.65%=420.37×0.0165

=6.94

The new balance is the previous balance decreased by the payments/credits and increased by the new purchases/finance charge.

Finance charge found in part:6.94

421.50−100.00+78.00+6.94

=406.44

​Hence we concllude that the  new balance is foudn to be 406.44

How To Solve Cengage Financial Algebra Chapter 4.6 Consumer Credit

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.6 Consumer Credit Page 208 Problem 12 Answer

Given; Ed Lubbock’s FlashCard bill is below. There are entries missing.

To find; What is Ed’s available credit?

The average daily balance found 420.37 we know that The finance charge is the product of daily balance and the monthly periodic rate.

420.37×1.65%=420.37×0.0165

=6.94

The new balance is the previous balance decreased by the payments/credits and increased by the new purchases/finance charge.

Finance charge found in part:

6.94421.50−100.00+78.00+6.94

=406.44

The total available credit is the total credit line decreased by the new balance.

1,000.00−406.44=593.56

Hence we conclude that the total avalable credit 593.56

Cengage Financial Algebra Consumer Credit Exercise 4.6 Solutions

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.6 Consumer Credit Page 208 Problem 13 Answer

Given; Ed Lubbock’s FlashCard bill is below. There are entries missing.

To find; If the  30 charge to Petrela Sailboats had been posted on ,12/9 would the finance charge be higher or lower for this billing cycle? Explain

Answer: Hence we conclude that  the finance charge for this billing cycle will be Lower because the later charge decreases the average daily balance.

Hence we conclude that  the finance charge for this billing cycle will be Lower because the later charge decreases the average daily balance.

Financial Algebra 1st Edition Chapter 4 Consumer Credit

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 202 Problem 1 Answer

Given a spreadsheet

To do: Write the spreadsheet formula to compute the new balance in cell F2

The given spreadsheet is empty there is no entry in any cell

so, we can use zero amount in the calculation.

The formula to compute the new balance we use

A₂−B₂+C₂+D₂+₂=F₂

Therefore,the formula to find the new balance F2 is A2−B2+C2+D2+E2

Cengage Financial Algebra Chapter 4.5 Consumer Credit Guide

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 203 Problem 2 Answer

Given Rhonda balance

To do: Write an algebraic expression that represents her current available credit

Given that there is a previous balance of 567.91 $ and on-time credit card payment is also the same for the last month, there is no balance then the expression will be the subtraction from credit line from purchases then we get x−y as the expression

Therefore,

The algebraic expression that represents her current available credit x−y

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 203 Problem 3 Answer

Given a summary statement

To do: Find the error in the summary

From the given summary the new balance will be  850−560=290 $ and 290+300+3+4.78=597.78 $ but given as 504.78 $ this is the mistake in the summary

Therefore, the error in the summary is in the cell of new balance given as 504.78 $ but the actual new balance should be 597.78 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 4 Answer

Given quote is Credit card companies pay college students generously to stand outside dining halls, dorms, and academic buildings and encourage their fellow students to apply for credits cards.– Louise Slaughter, American Congresswoman

To do: Write how might the quote apply to what you have learned

From the given quote we understand that the credit card companies will pay for college students which will generate curiosity among them and apply for credit cards as the students will be more interested to listen to their peers

This will be an example for advertising especially for college students

Therefore, the given quote is applied for advertising for college students

Solutions For Exercise 4.5 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 202 Problem 5 Answer

Given the flashcard statement

To do: Find the sum of all purchases made

In the given table we sum of all purchases are given under new purchases i.e.,1,227.24 $

Therefore, the sum of all purchases is 1,227.24 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 6 Answer

Given –

The Flash Card : We will determine when is the payment for this statement due.

The data at which the payment for this statement is due is given in the top right corner of the Flash Card Statement.

Payment Due =8Jun

The payment for this statement is due till 8 June.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 7 Answer

Given –

We will find the minimum amount that can be paid.

From the image, the minimum amount that can be paid=$30.

Minimum amount that can be paid=$30.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 8 Answer

Given –

We will find the number of days which are in the billing cycle.

The number of days in the billing cycle is given at the bottom of the FlashCard statement underneath “* Days in Billing Cycle”

Number of Days in Billing Cycle=30

The number of Days in Billing Cycle are 30.

Chapter 4 Exercise 4.5 Consumer Credit Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 9 Answer

Given –

We will determine the previous balance.

We will see the first entry in the summary.

Hence, the previous balance=$420.50

The previous balance is=$420.50

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 10 Answer

Given – Rebecca has a credit line of $6,500 on her credit card. She had a previous balance of $398.54 and made a $250 payment.

The total of her purchases is$1,257.89.

We will find Rebecca’s available credit.

Available credit= Credit line – previous balance−total amount of purchases made+payment

Available credit =6500−398.54−1257.89+250

Available credit =$5,093.57

The available credit is$5,093.57.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 11 Answer

Given -The APR on Leslie’s credit card is currently 21.6%.

We will find the monthly periodic rate.

Given: APR=21.6%

=0.216

​The APR is the annual periodic rate.

The monthly periodic rate is the annual periodic rate divided by 12 , because there are12 months in a year.

Monthly periodic rate= APR/Number of months in a year

=21.6%/12

=1.8%

Cengage Financial Algebra Consumer Credit Exercise 4.5 Solutions

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 204 Problem 12 Answer

Given – Sheldon’s monthly periodic rate is 1.95%.

We will determine the APR.

Given: Monthly periodic rate=1.95%

The APR is the annual periodic rate.

The annual periodic rate is the monthly periodic rate multiplied by 12, because there are 12months in a year.

APR=Monthly periodic rate×Number of months in a year

​=1.95%×12

=23.4%

The ARN is 23.4%.

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 13 Answer

Given –

The credit card summary :

We need to express the sum of the cycle’s daily balances algebraically.

We note that the sum of the cycle’s daily balances=Average daily balance×No. of days in billing cycle

Hence, Sum of the cycle′s daily balances = WX

We conclude that : Sum of the cycle′s daily balances = WX

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 14 Answer

Given –

The credit card summary :

We need to express the monthly periodic rate as an equivalent decimal without the% symbol.

Given: APR=Y%

The APR is the annual periodic rate.

The monthly periodic rate is the annual periodic rate divided by 12, because there are 12 months in a year.

Monthly periodic rate= APR/Number of months in a year

=Y%/12

=Y/100/12

=Y/12×100

=Y/1200

Monthly periodic rate =Y/1200

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 15 Answer

Given – The credit card summary :

We need to express the monthly periodic rate as an equivalent decimal without the % symbol.

Given: APR=Y%

The APR is the annual periodic rate.

The monthly periodic rate is the annual periodic rate divided by 12, because there are 12 months in a year.

Monthly periodic rate = APR/ Number of months in a year

=Y%/12

=Y/100/12

=Y/12×100

=Y/1200

Monthly periodic rate =Y/1200

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 16 Answer

Given –

We will find the amounts a,b,c, and d.

The previous balance is given in the SUMMARY of the FlashCard statement underneath “Previous balance”.

Previous balance=$215.88

The finance charge is given in the SUMMARY of the FlashCard statement underneath “Finance charge”.

Finance charge=$6.70

The total credit line is given in the bottom left corner of the FlashCard statement next to “Total Credit Line”.

Total credit line=$5,000.00

The amounts of the transactions (debits and credits) are given in the column “DEBITS/CREDITS” (where the debits are the positive amounts and the credits are the negative amounts).

The new balance is then the previous balance increased by the debits, decreased by the credits and increased by the finance charge.

New balance =Previous balance +Debits−Credits+Finance charge

=215.88+(85.63+47.60+855.00+370.50)−(63.00+137.00)+6.70

=215.88+1358.73−200.00+6.70

=1381.81

​The total available credit is the total credit line decreased by the new balance:

Total available credit=Total credit line−New balance​

=5000−1381.81

=3618.19

​The payments/credits are the negative amounts in the column “DEBITS/CREDITS” of the FlashCard summary.

First payment: $63.00

Second payment:$137.00

The summary should contain the sum of all payments/credits underneath “Payments/Credits”.

Payments/Credits=First payment+ Second payment​

=63.00+137.00

=200.00

​The new purchases are the positive amounts in the column “DEBITS/CREDITS” of the FlashCard summary.

First purchase:$85.63

Second purchase:$47.60

Third purchase: $855.00

Fourth purchase: $370.50

The summary should contain the sum of all purchases underneath “New Purchases”.

New Purchases= First purchase+Second purchase+Third purchase+ Fourth purchase

​=85.63+47.60+855.00+370.50

=1358.73

​The previous balance is given in the SUMMARY of the FlashCard statement underneath “Previous balance”.

Previous balance=$215.88

The finance charge is given in the SUMMARY of the FlashCard statement underneath “Finance charge”.

Finance charge=$6.70

The total credit line is given in the bottom left corner of the FlashCard statement next to “Total Credit Line”.

Total credit line=$5,000.00

The amounts of the transactions (debits and credits) are given in the column “DEBITS/CREDITS” (where the debits are the positive amounts and the credits are the negative amounts).

The new balance is then the previous balance increased by the debits, decreased by the credits and increased by the finance charge.

New balance= Previous balance + Debits − Credits + Finance charge

=215.88+(85.63+47.60+855.00+370.50)−(63.00+137.00)+6.70

=215.88+1358.73−200.00+6.70

=1381.81

​We obtain :

a=3618.19

b=200.00

c=1358.73

d=1381.81

​Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 17 Answer

Given –

We need to check the new balance entry on the monthly statement below by using the first five entries.

If the new balance is incorrect, we will write the correct amount.

The previous balance is given in the SUMMARY of the FlashCard statement underneath “Previous balance”.

Previous balance=$424.41

The total payments is given in the SUMMARY of the FlashCard statement underneath “Payments/Credits”.

Total payments=$104.41

The total of the new purchses is given in the SUMMARY of the FlashCard statement underneath “New Purchases”.

New Purchases=$103.38

The late charge is given in the SUMMARY of the FlashCard statement underneath “Late charge”.

Late charge=$23.00

The finance charge is given in the SUMMARY of the FlashCard statement underneath “Finance charge”.

Finance charge=$7.77

The amounts of the transactions (debits and credits) are given in the column “DEBITS/CREDITS” (where the debits are the positive amounts and the credits are the negative amounts).

The new balance is then the previous balance increased by the new purchases, decreased by the total payments and increased by the finance charge.

New balance=Previous balance+New purchases−Total payments+Late charge+Finance charge

​=424.41+103.38−104.41+23.00+7.77

=454.15

We then note that the new balance is $454.15 as claimed by the summary of the credit card statement.

The new balance is $454.15 as claimed by the summary of the credit card statement.

How To Solve Cengage Financial Algebra Chapter 4.5 Consumer Credit

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 18 Answer

Given –

A credit card statement is modeled using the following spreadsheet. Entries are made in columns A–F.

We will write the formula to calculate the available credit in cell G₂.

The previous balance is given underneath “Previous balance”, which is thus cell A₂.

Previous balance=A₂

The total payments are given underneath “Payments/Credits”, which is thus cell B2.

Total payments=B₂

The total of the new purchases is given underneath “New Purchases”, which is thus cell C₂.

New Purchases=C₂

The late charge is given underneath “Late charge”, which is thus cell D2.

Late charge=D₂

The finance charge is given underneath “Finance charge”, which is thus cell E₂.

Finance charge=E₂

The credit line is given underneath “Credit line”, which is thus cell F₂.

Credit line=F₂

The available credit needs to be given underneath “Available Credit”, which is thus ce llG₂

Available credit=G2

The new balance is then the previous balance increased by the new purchases, decreased by the total payments and increased by the finance charge

New balance = Previous balance − Total payments + New purchases + Late charge + Finance charge

=A₂−B₂+C₂+D₂+E₂

​The available credit is then the credit line decreased by the new balance:

Available= Credit line−New balance

G₂ G₂=F₂−(A₂−B₂+C₂+D₂+E2)

=F₂−A₂+B₂−C₂−D₂−E₂

​We conclude that :

G₂=F₂−A₂+B₂−C₂−D₂−E₂

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 19 Answer

Given –

We need to determine the amount

The previous balance is given in the SUMMARY of the FlashCard statement underneath “Previous balance”.

Previous balance=$939.81

The total payments is given in the SUMMARY of the FlashCard statement underneath “Payments/Credits”. Let us name the total payments ASAP.

Total payments=x

The total of the new purchases is given in the SUMMARY of the FlashCard statement underneath “New Purchases”.

New Purchases=$125.25

The late charge is given in the SUMMARY of the FlashCard statement underneath “Late charge”.

Late charge=$3.00

The finance charge is given in the SUMMARY of the FlashCard statement underneath “Finance charge”.

Finance charge=$15.38

The New Balance is given in the SUMMARY of the FlashCard statement underneath “new balance”.

New balance=$833.44

The new balance is then the previous balance increased by the new purchases, decreased by the total payments and increased by the finance charge.

New balance=Previous balance+New purchases−Total payments+ Late charge+Finance charge

833.44+x/x

x=939.81+125.25−x+3.00+15.38

=1083.44−x

=1083.44

=1083.44−833.44

=250

​We then note that the total payment is$250.

The amount of the payment made on this credit card is$250.

Step-By-Step Solutions For Chapter 4.5 Consumer Credit Exercise

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.5 Consumer Credit Page 205 Problem 20 Answer

Given – The previous balance after the last billing cycle is represented by A, recent purchases by B, payments by C, finance charge by D, and late charge by E.

We need to express the relationship among the variables that must be true for the new balance to be zero.

Given: Previous balance =A

Total payments =C

New Purchases =B

Late charge=E

Finance charge=D

New balance=0

The new balance is then the previous balance increased by the new purchases, decreased by the total payments, and increased by the finance charge.

New balance=Previous balance+New purchases−Total payments+ Late charge+ Finance charge

0=A+B−C+E+D

C=A+B+D+E

Thus we then note that the equation is0=A+B−C+E+D needs to be true when the balance is zero, or equivalently C=A+B+D+E

The relationship among the variables is: C=A+B+D+E

Financial Algebra 1st Edition Chapter 4 Consumer Credit Page 195 Problem 1 Answer

Given about Carrie’s card

To do: Find how much is Carrie responsible for paying

Under the act of truth lending, there is a maximum liability of 50 $

so, Carrie is responsible for paying 50 $

Therefore, Carrie is responsible for paying 50 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 196 Problem 2 Answer

Given about the paul last month payments

To do: Find the average daily balance

From the given data we have x dollars for 6 days means 6x

y dollars for 12 days means 12y

w dollars for q days means qw

d dollars for 2 days means 2d then the average will be 6x+12y+qw+2d/q+20

Therefore,the average daily balance is 6x+12y+qw+2d/q+20

Read and Learn  More Cengage Financial Algebra 1st Edition Answers

Cengage Financial Algebra Chapter 4.4 Consumer Credit Guide

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 196 Problem 3 Answer

Given about steve finance

To do: Express his finance charge

From the given data APR is p % so, p/12 and here average daily balance is d $

Then the finance charge will be (p/100/12)d

Therefore, the finance charge is (p/100/12)d

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 4 Answer

Given that Life was a lot simpler when what we honored was father and mother rather than all major credit cards. – Robert Orben, American Comedy Writer

To do: Interpret the quote

In the given quote we have horned by parents i.e., mother and father which means that while using credit cards we should have enough money in the cards as stores won’t honor your cards and the credit card makes easy for life

Therefore, the quote says that While using credit cards we should have enough money in the cards as stores won’t honor your cards and the credit card makes easy for life

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 5 Answer

Given that Janine’s credit card was stolen, and the thief charged a $44 meal using it before she reported it stolen

To do: Find how much of this is Janine responsible for paying

Given that the card was stolen and before it was charged $44 as we know that the maximum liability will be $50 then Janine have to pay the entire amount i.e.,44 $

Therefore, Janine has to pay  $44

Solutions For Exercise 4.4 Financial Algebra 1st Edition

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 6 Answer

Given that Dan’s credit card was lost on a vacation. He immediately reported it missing.

The person who found it days later used it and charged $x worth of merchandise on the card, where x> $200

To do: Find how much of the  $x is Dan responsible for paying

From the given question we get to know that Dan reported as soon it was lost i.e. before used so that he is responsible for paying $0

Therefore, Dan is responsible to pay  $0

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 7 Answer

Given that Felix was given a card with an APR of 12 %

To do: Find his monthly percentage

Given APR=12 % and we know that there are 12 months in a year then we get monthly percentage rate​=12/12

=1 %

​Therefore, His monthly percentage rate is 1 %

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 8 Answer

Given that Oscar was given a card with an APR of 15 %

To do: Find his monthly payment

Given that APR=15 % and we know that number of months in a year are 12

Then Monthly percentage rate​=15/12

=1.25 %

​Therefore, the monthly percentage rate is 1.25 %

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 9 Answer

Given the credits of Felix and oscar

To do: Find how much more would Oscar pay than Felix

Solving for Felix From part a we know that the monthly percentage rate is 1 % then Finance charge​=1 %×800 $

=8 $

​Solving for Oscar From part b we know that the monthly percentage rate is 1.25 % then Finance charge​=1.25 %× $800

=10 $ ​the difference between them is 2 $

Therefore, Oscar has to pay 2 $ more than Felix

Chapter 4 Exercise 4.4 Consumer Credit Walkthrough Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 10 Answer

Given all the finance charges per days

To do: Find the average daily balance

The sum of the daily balances is ​
9(778.12)=7003.08

8(1876)=15008

4(2112.50)=8450

10(1544.31)=15443.1 ​is 45904.18 $ and the total number of days given is 9+8+4+10=31

Now the average daily balance will be 45904.18/31

=1480.78 $

Therefore, the average daily balance is 1480.78 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 11 Answer

Given the finance charges with respect to the days

To do: Find the finance charge

From part a we know that the average daily balance is 1,480.78 $

Now we have to find monthly percentage rate given APR=19.2 $

Monthly percentage rate ​= APR/ Number of months in a year

=19.2/12

=1.6 % then finance charge​=1.6×1,480.78

=23.69 $​

Therefore,The finance charge=23.69 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 12 Answer

Given the set of daily balances

To do: Find the average  daily balance

The sum of daily balances =number of days at balance×balance

so we get​

​=x×y+r×q+w×d+m×p

=xy+rq+wd+mp and number of billing days will be x+r+w+m

Then the average daily balance will be =xy+rq+wd+mp/x+r+w+m

Therefore, the average daily balance=xy+rq+wd+mp/x+r+w+m

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 13 Answer

Given Suzanne’s average daily balance and finance charge

To do: Find the monthly percentage rate

Given average daily balance=x

finance charge=y then monthly percentage rate=y/x

Therefore,The monthly percentage rate=y/x

Cengage Financial Algebra Consumer Credit Exercise 4.4 Solutions

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 14 Answer

Given the data on Suzzanne’s income

To do: Find APR From the previous part, we know that the monthly percentage rate=y/x and

we know that the annual percentage will consider 12 months multiplying with it we get12y/x which is the APR

Therefore,the APR=12y/x

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 15 Answer

Given Jared’s income details

To do: Find the monthly percentage rate

From the given data we know that the average daily basis is 560 $ the finance charge is 8.12 $

Then monthly percentage rate= finance charge/average daily basis

on substituting  we get

=8.12/560

=1.45 %

​Therefore, the monthly percentage rate is 1.45 %

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 197 Problem 16 Answer

Given Jared’s income details

To do: Find the APR

The annual percentage income is the multiplication of the monthly percentage rate and the number of months in a year

we know that the monthly percentage rate=1.45 % and we also know that there are 12

months in a year then

APR=1.45 %×12

=17.4 %

​Therefore, APR=17.4 %

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 198 Problem 17 Answer

Given Helene’s credit details

To do: Find her daily balance if she puts the down payment on the credit card today

Given that Today’s balance=712.0 $

down payment=5,000 $ then the daily balance will be712.0+5,000=5,712.0 $

Therefore,the daily balance is 5,712.0 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 198 Problem 18 Answer

Given Helene’s credit details

To do: Find her average daily balance

We know that daily balance is 5,712.04 $ for 30 days it will be 5,712.04 $×30 then average daily balance=30×5,712.04 $/30

=5,712.04 $

​Therefore,the average daily balance is 5,712.04 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 198 Problem 19 Answer

Given Helene’s credit details

To do: Find the finance charge

We know that the daily balance is 5,712.04 $ and given APR=16.8 %

with this monthly rate will be 0.618/12

now finance charge​=5,712.04×0.618/12

=79.97 $

Therefore,

Finance charge=79.97 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 198 Problem 20 Answer

Given Helene’s credit card details

To do: Find her average daily balance

Given that for 29 days we have  $712.04 and for a day we have  $5712.04 then average daily balance is 29×$712.04+1×$5,712.04/30

=$878.71

Therefore,the average daily balance is  $878.71

How To Solve Cengage Financial Algebra Chapter 4.4 Consumer Credit

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer CreditPage 198 Problem 21 Answer

Given Helene’s credit card details

To do: Find the finance charge

We know that the average daily balance= $878.71 and APR=0.168/12 then

the finance charge will be $878.71×0.168/12

=$12.30

Therefore,the finance charge is  $12.30

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 198 Problem 22 Answer

Given Helene’s credit card details

To do: Find how much can she save in finance charges

We have  the finance charge for the billing period is  $79.97 and the finance charge for the average daily balance is  $12.30

we get $79.97−$12.30=$67.67

Therefore, She saves  $67.67 finance charge

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 23 Answer

Given the debit card register

To do: Find the missing values

The previous balance decreased by the payment amount will be the new balance

Following this we get

a.m−x

b.m−x−z

c.m−x−z−y

d.m−x−z−y−v

e.m−x−z−y−v+r

f.m−x−z−y−v+r−g

​Therefore, the missing values are m−x,m−x−z,m−x−z−y,m−x−z−y−v,m−x−z−y−v+r,m−x−z−y−v+r−g

Step-By-Step Solutions For Chapter 4.4 Consumer Credit Exercise

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 24 Answer

Given that Jill’s credit card was stolen. The thief charged a900 $ kayak on the card before she reported it stolen

To do: Find how much of the thief’s purchase is Jill re

The maximum liability will be  $50 for which she is responsible

Therefore,Jill is responsible for 50 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 25 Answer

Given that Jill’s average daily balance would have been 1,240 $ without the thief’s purchase

To do; Find the sum of her daily balances

The product of the number of days and average daily balance will give the daily balances then we get

30×$1,240=$37,200

Therefore, The sum of her daily balances is 37,200 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 26 Answer

Given that Jill’s credit card was stolen. The thief charged a 900 $ kayak on the card before she reported it stolen

To do: Find the sum of Jill’s daily balances

From the data, we get that before thief purchase we have 1,240 $ after thief purchase is 2,140 $ then the sum of Jill’s balances is

20×$1,240+10×$2,140=$46,200

Therefore,the sum of Jill’s balances is=46,200 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 27 Answer

Given that Jill’s credit card was stolen. The thief charged a900 $ kayak on the card before she reported it stolen

To do: Find the average daily balance

Using the balance which we have previously increased by the thief’s purchase is the average daily balance we get

20×$1,240+10×$2,140=$46,200 when divided by the number of days we get

$46,200/30

=$1,540

Therefore, the average daily basis is 1,540 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 28 Answer

Given Kristin’s credit details

To do: Find the finance charge

Firstly we have x×12%/12=x×1% and after the arrival of x we get x×13.2%/12

=x×1.1% the difference between these two will be x×1.1%−x×1%=x×0.1%

=0.001x

​Therefore, the  increase in this month’s finance charge is 0.001x

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 29 Answer

Given data of credit card bill

To do: Find the total amount of overchange

The product of overcharge per credit card with the number of months is the total amount of debtors then we get

6×1,000,000×12×5=$360,000,000

Therefore,the total amount of overchange is =$360,000,000

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 30 Answer

Given daily balances of Naoko

To do: FCengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit ind the finance charge

Tha Naoko will not need to pay finance charges for next month then the September bill will be 0 $

Therefore,the finance charge for September month is 0 $

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 31 Answer

Given the daily balances of Naoko

To do: Explain why the credit card company need to calculate his average daily balance

Naoko’s September bill is 0 $ which means we don’t have to pay any finance charges then the average daily balance is not needed

Therefore,there is no need to calculate average daily balance

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 32 Answer

Given Naoko’s daily balances

To do: Find average daily balance

Firstly the sum of daily balances is ​

=2×99.78+15×315.64+11×515.64+2×580.32

=11,766.84​ and the number of billing days will be 2+15+11+2=30

Now the average daily balance is =11,766.84/30

≈392.23

​Therefore, the average daily balance is 392.23 $

Practice Problems For Consumer Credit Exercise 4.4 Cengage

Cengage Financial Algebra 1st Edition Chapter 4 Exercise 4.4 Consumer Credit Page 199 Problem 33 Answer

Given: Naoko daily balances

To do: Find the mistake of average daily balance

We have to calculate as all the number of daily balances with 4 then we get

=99.78+315.64+515.64+580.32/4

=1,511.38/4

≈377.85

now we got the correct answer

Therefore, the mistake he made is by summing all the balances and not dividing with 4