Chapter 3 Numeric And Algebraic Expressions
Section 3.1: Understand And Represent Exponents
Page 117 Exercise 1 Answer
Folding the sheet in half gives 2 sections.
Folding the sheet in half a second time then gives 4 sections.
Folding in half for the third time gives 8 sections.
Folding in half for the fourth time gives 16 sections.
Folding in half for the fifth time gives 32 sections.
Note that 2 × 2 = 4, 4 × 2 = 8, 8 × 2 = 16, and 16 × 2 = 32. The number of sections then doubled each time we folded it.
Result
2, 4, 8, 16, and then 32 sections
The number of sections doubled each time we folded it.
Read And Learn More: enVisionmath 2.0 Grade 6 Volume 1 Solutions
Page 117 Exercise 1 Answer
From the Solve & Discuss It! exercise, we know after the 5th fold there are 32 sections and that the number of sections doubles each time we fold the paper.
For the 6th fold, there will then be
32 × 2 = 64 sections.
For the 7th fold, there will be
64 × 2 = 128 sections.
Result
6th fold: 64 sections
7th fold: 128 sections
Page 118 Exercise 1 Answer
2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 29 = 512
After 3 hours there are 512 bacteria cells.
Since after 3 hours there are 29 bacteria cells, which can be written as 23 × 3. That means that after one hour there are 23 bacteria cells. Thus, after two hours there are 26 bacteria cells.
Result
29 = 512
Page 119 Exercise 2 Answer
The base is \(\frac{1}{2}\). The exponent is 3. We need to rewrite the power as repeated multiplication and then evaluate.
\(\left(\frac{1}{3}\right)^3=\frac{1}{3} \times \frac{1}{3} \times \frac{1}{3}=\frac{1 \times 1 \times 1}{3 \times 3 \times 3}=\frac{1}{27}\)Result
\(\frac{1}{27}\)
Page 119 Exercise 3 Answer
The evaluation for Rafael’s expression:
1.8 × 104 = 1.8 × 10,000 = 18,000.
Result
18,000
Page 120 Exercise 1 Answer
A power consists of a base and an exponent. Powers can be evaluated using repeated multiplication, just as repeated multiplication can be represented using exponents.
For example,
74 = 7 × 7 × 7 × 7 = 2401.
Result
A power consists of a base and an exponent. Powers can be evaluated using repeated multiplication, just as repeated multiplication can be represented using exponents.
Page 120 Exercise 2 Answer
n the expression 45, 4 is used five times as a factor.
Written as repeated multiplication 45 = 4 × 4 × 4 × 4 × 4.
Result
4 is used five times as a factor.
45 = 4 × 4 × 4 × 4 × 4
Page 120 Exercise 3 Answer
One to any power always equals one,
since 1n = 1 × 1 × … × 1 (n times).
Thus, 1 to any power equals 18.
Result
1 to any power equals 18.
Page 120 Exercise 4 Answer
Any nonzero number to a power of 0 equals 1 so 100 = 1:
2.5 × 100 = 2.5 × 1 = 2.5
Result
2.5
Page 120 Exercise 5 Answer
For \(\left(\frac{1}{2}\right)^3\), the base is \(\frac{1}{2}\), the number which we multiply three times by itself, since three is the exponent.
\(\left(\frac{1}{2}\right)^3\) can be written as repeated multiplicaton as \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\)
Result
\(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\)
Page 120 Exercise 6 Answer
To write 81 as a repeated multiplication of 3s one must multiply 3 with itself four times.
3 ⋅ 3 = 9
3 ⋅ 3 ⋅ 3 = 27
3 ⋅ 3 ⋅ 3 ⋅ 3 = 81
Thus, 81 can be written as 3 ⋅ 3 ⋅ 3 ⋅ 3 or as 34
Result
81 = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 34
Page 120 Exercise 7 Answer
To write 125 as a repeated multiplication of 5s one must multiply 5 three times.
5 ⋅ 5 = 25
5 ⋅ 5 ⋅ 5 = 25 ⋅ 5 = 125
Thus, 125 can be written as 5 ⋅ 5 ⋅ 5, or as 53.
Result
125 = 5 ⋅ 5 ⋅ 5 = 53
Page 120 Exercise 8 Answer
The expression 0.75 × 0.75 × 0.75 × 0.75 × 0.75 can be written as a power with an exponent of 5 since 0.75 is used as a factor 5 times.
0.75 × 0.75 × 0.75 × 0.75 × 0.75 = 0.755
Result
0.755
Page 120 Exercise 9 Answer
The expression \(\frac{3}{8}\) x \(\frac{3}{8}\) x \(\frac{3}{8}\) can be written as a power with an 3 since \(\frac{3}{8}\) is used as a factor 3 times.
\(\frac{3}{8} \times \frac{3}{8} \times \frac{3}{8}=\left(\frac{3}{8}\right)^3\)Result
\(\left(\frac{3}{8}\right)^3\)Page 120 Exercise 10 Answer
To evaluate \(\left(\frac{1}{6}\right)^2\), we can rewrite the expression as repeated multiplication and then multiply. Since the base is \(\frac{1}{6}\) and the exponent is 2, we will use \(\frac{1}{6}\) as a factor two times:
\(\left(\frac{1}{6}\right)^2=\frac{1}{6} \times \frac{1}{6}=\frac{1 \times 1}{6 \times 6}=\frac{1}{36}\)Result
\(\frac{1}{36}\)Page 120 Exercise 11 Answer
Any nonzero number to the power of zero equals one.
450 = 1
Result
1
Page 120 Exercise 12 Answer
To evaluate 0.15, we can rewrite the expression as repeated multiplication and then multiply. Since the base is 0.1 and the exponent is 5, we will use 0.1 as a factor five times:
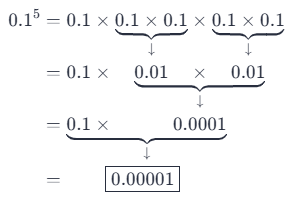
Result
0.00001
0.15 = 0.1 ⋅ 0.1 ⋅ 0.1 ⋅ 0.1 ⋅ 0.1 = 0.00001
Result
0.00001
Page 120 Exercise 13 Answer
To evaluate 73 , we can rewrite the expression as repeated multiplication and then multiply. Since the base is 7 and the exponent is 3, we will use 7 as a factor three times:
73 = 7 × 7 × 7 = 49 × 7 = 343
Result
343
73 = 7 ⋅ 7 ⋅ 7 = 49 ⋅ 7 = 343
Result
343
Page 120 Exercise 14 Answer
4.5 ⋅ 104 = 4.5 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 4.5 ⋅ 10000 = 45000
Result
45000
Page 120 Exercise 15 Answer
0.6 ⋅ 106 = 0.6 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 0.6 ⋅ 1000000 = 600000
Result
600000
Page 120 Exercise 16 Answer
Any nonzero number to the power of zero equals one, thus 100 = 1.
3.4 ⋅ 100 = 3.4 ⋅ 1 = 3.4
Result
3.4
Page 121 Exercise 17 Answer
Repeated multiplication can be written as a power where the exponent is the number of times the base is used as a factor.
For 9 × 9 × 9 × 9, the base of 9 is used as a factor 4 times. The exponent for the expression is then 4.
Result
4
Page 121 Exercise 18 Answer
The expression is 1.29 so the exponent is 9.
Result
9
Page 121 Exercise 19 Answer
Repeated multiplication can be written as a power where the exponent is the number of times the base is used as a factor.
For \(\frac{1}{6} \times \frac{1}{6} \times \frac{1}{6}\), the base of \(\frac{1}{6}\) is used as a factor 3 times. The exponent for the expression is then 3.
Result
3
Page 121 Exercise 20 Answer
Any number raised to the power of one equals the number itself, hence there is no need to write the exponent. In cases such as this, where the exponent is not written it is one.
7 = 71
Result
1
Page 121 Exercise 21 Answer
The expression 83 can be written as 8 × 8 × 8, which is then equal to 64 × 8 which gives us 512.
Result
8 × 8 × 8 = 512
Page 121 Exercise 22 Answer
To evaluate \(\left(\frac{1}{5}\right)^4\), we can rewrite the expression as repeated multiplication and then multiply. Since the base is \(\frac{1}{5}\) and the exponent is 4, we will use \(\frac{1}{5}\) as a factor four times:
\(\left(\frac{1}{5}\right)^4=\frac{1}{5} \times \frac{1}{5} \times \frac{1}{5} \times \frac{1}{5}=\frac{1 \times 1 \times 1 \times 1}{5 \times 5 \times 5 \times 5}=\frac{1}{25 \times 25}=\frac{1}{625}\)Result
\(\left(\frac{1}{5}\right)^4=\frac{1}{5} \times \frac{1}{5} \times \frac{1}{5} \times \frac{1}{5}=\frac{1}{625}\)Page 121 Exercise 23 Answer
To evaluate 0.62, we can rewrite the expression as repeated multiplication and then multiply. Since the base is 0.6 and the exponent is 2, we will use 0.6 as a factor two times:
0.62 = 0.6 × 0.6 = 0.36
Result
0.36
Page 121 Exercise 24 Answer
To evaluate \(\left(\frac{1}{4}\right)^2\), we can rewrite the expression as repeated multiplication and then multiply. Since the base is \(\frac{1}{4}\) and the exponent is 2, we will use \(\frac{1}{4}\) as a factor two times:
\(\left(\frac{1}{4}\right)^2=\frac{1}{4} \times \frac{1}{4}=\frac{1 \times 1}{4 \times 4}=\frac{1}{16}\)Result
\(\frac{1}{16}\)Page 121 Exercise 25 Answer
Any nonzero number to the power of zero equals one. Thus, 580 = 1.
Result
1
Page 121 Exercise 26 Answer
To evaluate 6.2 × 103, we can rewrite the expression 103 as repeated multiplication and then multiply. Since the base is 10 and the exponent is 3, we will use 10 as a factor three times:
6.2 × 103 = 6.2 × 10 × 10 × 10 = 6.2 × 1000 = 6200
Result
6200
6.2 ⋅ 103 = 6.2 ⋅ 1000 = 6200
Result
6200
Page 121 Exercise 27 Answer
A company rents two storage unites which are both cube-shaped. The volume of a cube is given by the formula V = s3, where s is the side length.
The first unit is 8 ft tall, since it is cube shaped all of its sides are 8 ft. The volume of the first unit is V1 = 83 = 512 ft. The second unit is 6.5 ft tall, since it is also cube shaped all of its sides are 6.5 ft, and the volume is
6.53 = 274.625 ft.
The difference in the volume of the two storage units is
512 − 274.625 = 237.375.
A common mistake may be to first find the difference between the lengths of sides and then raise that to the power of three. For example, (8−6.5)3 = 1.53 = 3.375, which is obviously not equal to 237.375.
Result
237.375 ft
Page 121 Exercise 28 Answer
Jia is tiling a floor with side length 12 feet and she wants the tiles to be squares with side length 2 feet. How many tiles does Jia need to cover the entire floor?
The area of the floor which needs to be covered is A1 = 122 = 144 feet. One square tile with side length 2 feet covers the area of A2 = 22 = 4. To cover all 144 feet of the floor Jia needs 144 ÷ 4 = 36 tiles.
Result
Jia needs 36 tiles to cover the entire floor.
Page 121 Exercise 29 Answer
A marine biologist studies the population of seals in a research area. He found out that there is 3.27 × 102 seals in the area, which is exactly 327 seals since:
3.27 × 102 = 3.27 × 10 × 10 = 3.27 × 100 = 327
Result
There is 327 seals in the research area.
Page 121 Exercise 29 Answer
A marine biologist studies the population of seals in a research area. He found out that there is 3.27 × 102 seals in the area, which is exactly 327 seals since:
3.27 × 102 = 3.27 × 10 × 10 = 3.27 × 100 = 327
Result
There is 327 seals in the research area.
Page 122 Exercise 30 Answer
Zach invested $50 and tripled his money in two years, which means after two years he has $50 × 3 = $150.
Kayla also invested $50 and after two years the amount was equal to 503 dollars, so Kayla had 503 = 50 × 50 × 50 = 2500 × 50 = $175,000.
Result
After two years, Kayla had more money.
Page 122 Exercise 31 Answer
Malik read that the land area of Alaska is about 5.7 ⋅ 105 square miles, which is equal to 570000 square miles.
5.7 ⋅ 105 = 5.7 ⋅ 100000 = 570000
Result
The land area of Alaska is about 570000 square miles.
Page 122 Exercise 32 Answer
Any nonzero number to the power of zero equals one, thus 100 = 1 and 1 × 1.00 = 1 × 1 = 1.
One to any power gives one because raising a number to the power of n means multiplying that number n times with itself, and 1 ⋅ 1 = 1. Thus, 14 = 1.
All three expressions are equal to 1, thus 100 = 14 = 1 × 1.00.
Result
All three expressions are equal to 1.
Page 122 Exercise 33 Answer
If 0.33 = n, what is n?
0.33 = 0.3 ⋅ 0.3 ⋅ 0.3 = 0.09 ⋅ 0.3 = 0.027 ⟹ n = 0.027
Result
n = 0.027
Page 122 Exercise 34 Answer
The same digits are used for the expressions 25 and 52, however in the expression 25 two is the base and five is the exponent and in the expression 52 five is the base and two is the exponent.
Values of expressions which contain exponents can be compared without calculating their actual value if either bases or exponents are the same, for example: 23 is less than 26, and 53 is less than 63 , Since neither is the case for 25 and 52 , they have different bases and different exponents, we must first calculate their vales and then compare them.
25 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32
52 = 5 ⋅ 5 = 25
Now, we can see that 25 is greater than 52.
Result
25 is greater than 52 since 25 = 32 and 52 = 25.
Page 122 Exercise 35 Answer
Kristen rewrote the expression 80,000 × 25 using exponents as (8 × 103) × 52. We need to determine if she was right.
80,000 × 25
80,000 can be written as 8 ⋅ 10,000, which can further be written using exponents as 8 × 104. Kristen has the wrong exponent for the power of 10 and she didn’t notice that 8 can also be written as 8 = 23.
25 can be written as 52.
So, the correct answer is:
(23 × 104) × 52.
Result
The correct response is (23 × 104) × 52.
Page 122 Exercise 36 Answer
Rewriting 1,000,000 as repeated multiplication gives:
1,000,000 = 10 × 100,000
= 10 × 10 × 10,000
= 10 × 10 × 10 × 1,000
= 10 × 10 × 10 × 10 × 100
= 10 × 10 × 10 × 10 × 10 × 10
Since 1,000,000 can be rewritten as repeated multiplication where 10 is used as a factor 6 times, then it can be written as a power where the base is 10 and the exponent is 6.
Result
Since 1,000,000 = 10 × 10 × 10 × 10 × 10 × 10, the expression can be written as a power where the base is 10 and the exponent is 6.
Page 122 Exercise 37 Answer
Isabella saved 2 nickles today and she doubles the number of nickles she saves each day. The number of nickels she has saved each day is then:
First day: 2
Second day: 2 ⋅ 2 = 4
Third day: 2 ⋅ 2 ⋅ 2 = 2 ⋅ 4 = 8
Forth day: 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 ⋅ 8 = 16
Fifth day: 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 ⋅ 16 = 32
Sixth day: 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 ⋅ 32 = 64
Seventh day: 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 ⋅ 64 = 128
Eighth day: 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 ⋅ 128 = 256
Ninth day: 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 ⋅ 256 = 512
Result
It will take Isabella nine days to save more than 500 nickles.
Page 122 Exercise 38 Answer
We are given the four expressions 210, 5 × 5 × 5 × 5, 45, and 4 × 4 × 4 × 4 × 4 and need to determine which one is NOT equal to 1,024.
Note that 1,024 is an even number so it must have even factors. The expression 5 × 5 × 5 × 5 does not have even factors since 5 is an odd number. This means that 5 × 5 × 5 × 5 ≠ 1,024. Therefore, B. 5 × 5 × 5 × 5 is not equal to 1,024.
We can verify our answer by showing the other three expressions are equal.
45 has a base of 4 and an exponent of 5 so it can be written as repeated multiplication where the base of 4 is used as a factor 5 times. Therefore, 45 = 4 × 4 × 4 × 4 × 4.
210 has a base of 2 and an exponent of 10 so it can be written as repeated multiplication where the base of 2 is used as a factor 10 times. Therefore, 210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2. Multiplying each pair of 2s then gives 210 = 4 × 4 × 4 × 4 × 4.
The other three expressions are all equal to each other so they must all equal 1,024.
Result
B. 5 × 5 × 5 × 5
Which expression is NOT equal to 1024?
We know that the expression A 210 is equal to 1024. Expressions C and D are equal, 45 = 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4.
Futher more, expressions C and D are equal to expression A, thus equal to 1024.
\(4^5=\left(2^2\right)^5=2^{10}=1024\) \(4 \cdot 4 \cdot 4 \cdot 4 \cdot 4=4^5=\left(2^2\right)^5=2^{10}=1024\)Expression B 5 ⋅ 5 ⋅ 5 ⋅ 5 is equal to 54 which is equal to 625, and not equal to 1024.
The answer to the question which expression is not equal to 1024 is expression B 5 ⋅ 5 ⋅ 5 ⋅ 5.
Result
Expression B 5 ⋅ 5 ⋅ 5 ⋅ 5 is not equal to 1024.
Page 122 Exercise 39 Answer
Which expression is equal to \(\frac{1}{36}\)?
Expression A:
\(\frac{1}{3} \cdot \frac{1}{6}=\frac{1}{3 \cdot 6}=\frac{1}{18}\)Expression B:
\(\frac{1}{4} \cdot\left(\frac{1}{3}\right)^3=\frac{1}{4} \cdot \frac{1^3}{3^3}=\frac{1}{4} \cdot \frac{1}{27}=\frac{1}{4 \cdot 27}=\frac{1}{108}\)Expression C:
\(\left(\frac{1}{2}\right)^2 \cdot\left(\frac{1}{3}\right)^2=\frac{1^2}{2^2} \cdot \frac{1^2}{3^2}=\frac{1}{4} \cdot \frac{1}{9}=\frac{1}{4 \cdot 9}=\frac{1}{36}\)Expression D:
\(\frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3}=\frac{1}{2} \cdot\left(\frac{1}{3}\right)^3=\frac{1}{2} \cdot \frac{1^3}{3^3}=\frac{1}{2} \cdot \frac{1}{3^3}=\frac{1}{2} \cdot \frac{1}{27}=\frac{1}{2 \cdot 27}=\frac{1}{54}\)Result
The expression C is equal to \(\frac{1}{36}\).
